Prerpints.org logo
Preprint
Article

Development of a Model for Detecting the State of Instability of the Mechanical Part of a Synchronous Electric Drive System Operating with a Dynamic Load Using an Artificial Neural Network

Altmetrics

Downloads

100

Views

35

Comments

0

Submitted:

26 October 2023

Posted:

27 October 2023

You are already at the latest version

Alerts
Abstract
Keywords: Аrtificial neural network, electric drive system, database, stability, training algorithm, technological mechanisms.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

1.1. The subject of the study, the state of the issue

The automation of modern technological equipment is accompanied by the use of a large number of electromechanical systems, with the help of which the tasks of improving the quality of products and the efficiency of technological equipment are solved [1,2,3,4,5,6,7]. In many cases, dozens of electric drives are used to control technological processes that are connected by control, power, and load circuits.
An electric drive is a controlled electromechanical system that provides an energy basis for technological processes used in various industries. The mechanical energy generated by this system is transferred to the actuating body of the technological mechanism and controls its movement in accordance with the prescribed law.
Electric drive systems are widely used in the production of metallic and non-metallic materials, aerospace engineering, energy, manufacturing, processing of various goods, transport systems, medicine, and household appliances. The widespread use of electric drive systems is owing to the following circumstances [8,9,10]:
  • the possibility of producing electric motors with a wide range of power and speed,
  • the possibility of ensuring high efficiency,
  • high operational reliability and no environmental pollution,
  • ample opportunities for creating an intelligent control system.
Despite the circumstances noted, the electric drive, which is a complex multichain system with feedback and a large number of adjustable parameters, creates special difficulties in improving the efficiency of automated control systems. Many electric drive systems operate under the influence of arbitrarily varying loads. The use of traditional methods to control these systems is not always advisable or effective. The main way to improve the control system is to improve the static and dynamic characteristics of the electric drive. The indicators of the quality and accuracy of an automated control system (ACS) are determined by the ability of the system to return to a steady state after the disappearance of the external influence and completion of the transition process. Therefore, there is a need to consider the proposed new approaches and methods of control of electric drive systems with various technological mechanisms and electric motors, as well as the purpose of the study as a result of their analysis.

1.2. Analysis of the references on the problem

There have been many studies on electric drive systems and their control. This section analyzes studies that consider approaches to intelligent control and issues of ensuring the stability of the system.
Studies have shown that in certain operating modes, the characteristics of the electric motor can have a significant impact on the mechanical parts of the system [11,12,13,14,15]. Mechanical vibrations affect the behavior and properties of the electrical power part of the electric drive. Although the electromagnetic torque of the motor has a controlling effect on the mechanical part of the electric drive, the dynamics of the electric drive system must be considered as a combined elastic electromechanical system.
Although elastic vibrations do not affect the duration of transients, they do not reduce the performance of the system, but increase the transfer load, which contributes to the rapid wear of the working equipment of the system. Therefore, the study and regulation of the mechanical part of the electric drive system are of practical interest in matters of control.
The authors of the paper [16] proposed a method that provides high accuracy and reliability for the control of an electromechanical system. They can be used to control various motors, pumps, valves, and other types of machines. This study used a control device that was placed in the feedback circuit of the mechanical part of the system and allowed the restoration of the output speed without directly measuring it.
In the proposed scheme for controlling the system of a wind generator and capacitor energy storage system, a damping controller was used [17]. This made it possible to suppress the strong mechanical vibrations on the turbine shaft and tower, leaving the frequency unchanged. The proposed control scheme makes it possible ensures efficient frequency regulation of the power system without violating the structural integrity of the mechanical part of the system [17].
A system of dynamic modeling of an elastic mechanical part for servicing a synchronous motor with permanent magnets and bidirectional converters is known, which provides a high control efficiency [18]. The speed tracking controller implemented in it has better performance than the traditional PI control algorithm, which proves the efficiency of the developed method [18]. In another study, a controller for the dynamic behavior of a control system was proposed. The implementation of the proposed method is based on the calculation of a complex transfer function and tangents of the Nichols geometric angle, which provides stability margins [19]. A simple torque-limiting design is proposed to ensure the smooth operation of the speed controller of the electric drive system [20].
It was found in [21] that considering the counter-electromotive force leads to an increase in the damping properties of the electric drive system and feedback gain coefficients. A method for selecting these coefficients is proposed based on their comparison with the coefficients obtained in an electromechanical system without considering the counter-electromotive force and an approximate assessment of its effect on the nature of the transients.
In [22], an intelligent approach based on machine training was proposed for the stable operation of an electric-drive control system. In particular, the backward stepwise method and Lyapunov method are used for design, and the sensors controlled by machine training are optimized and improved. An adaptive constraint method was adopted to design the sensor-observation training. The proposed method is expected to be applied in a multimachine system operating under conditions of power shortages and power outages.
Of particular interest is the analysis of the stability of electromechanical systems used in innovative technologies [23]. The authors of this work substantiated that ensuring the stability of mechanical and electrical transmission systems should be considered as part of the application of innovative technology.
In [24], the issues of developing a simulation model for the stability control of a multi-stage electric drive system were considered. The simulation results and experiments show that the developed control algorithm has better command tracking ability, noise immunity, and servo performance than a traditional PID controller. At the same time, compared with the traditional mathematical model, the proposed model is closer to real working conditions. It can better consider nonlinear factors in the power system and provide a solution to the control mismatch problem.
In [25], using the Lagrange-Maxwell and Lyapunov equations, the influence of fluctuations in the amplitude of the torque of an electric motor on the vibration stability of the system was considered.
A model was developed by determining the transfer functions of the drive links to study the stability of the system [26]. This model can be used to evaluate the primary factors affecting the stable operation of a system.
In several studies using various methods, the stability conditions of an electric drive motor of one type or another are considered [27,28,29].
There are known studies in which the behavior of changes in the characteristics of an electric machine is considered to analyze the stability of the power system and assess the stability margin [30,31,32]. In [31], using a system of differential equations characterizing the operation of a synchronous machine and its excitation system, it was possible to analyze the static stability of the power system, stability margin, and degree of oscillations. Installation of a mode controller was proposed. In different parametric planes, the boundary areas of stability were obtained, and the parameters that had the greatest influence on stability were identified [32]. The obtained results and the software can be used in the design and development of new electric drive systems.
The analysis shows that there are studies of scientific and technical interest aimed at improving the ACS of electric drive systems. Some of the proposed approaches are aimed at controlling the vibrations occurring in the elastic contours of the electric drive system and preventing harmful effects using various regulators. The results obtained in this direction are important for ensuring the operating mode of the electric drive system and preventing emergencies. However, in these works, information about the stability state of the electric drive system is not coordinated with the operation of the regulator. Meanwhile, ignoring stability conditions during transient processes can lead to incomplete use of the regulator’s capabilities.
Another group of works under consideration offers models, algorithms, and methods for determining the stability state of an electric machine or other circuits that are part of an electric drive system. The results obtained relate to special cases and, in addition, there are no solutions that consider stability conditions. Our observations show that there is a significant need to improve the effectiveness of ACS sustainability. This is due to:
  • insufficient integration of control systems, methods and means of ensuring stability,
  • lack of high productivity and accurate methods and means of determining the stability of the system,
  • incomplete application of intelligent solutions for detecting and classifying system stability.
Considering that the availability of accurate information about the stability of the system is of paramount importance for the improvement of the ACS by electric drive, as well as considering the possibilities of increasing the efficiency by taking into account the conditions of stability, the purpose of this work and the tasks that need to be solved for its implementation were formed.
The aim of this study is to develop a model for detecting the state of instability of the mechanical part of an electric drive system using an artificial neural network, which will provide high performance and the possibility of coordinated work with the regulator in the control system.
The remainder of this paper is organized as follows. The first section presents the status of the issue under consideration. The most interesting studies related to electric drive systems and their controls were analyzed. The necessity and purpose of using a new approach to detect system instability is substantiated. Section 2 presents the main tasks that need to be solved to detect the state of instability of the system as well as comments on their test objects. Section 3 presents an algorithm for building a database and assessing the degree of influence of input data. The indicators characterizing the performance of the model for various training algorithms, number of layers characterizing the network architecture, number of neurons in the hidden layer, and activation functions used were analyzed. An algorithm for applying an unstable state detection model to an electric drive system was proposed. Comments and recommendations regarding the results of this study are provided in Section 4.

2. Materials and Methods

2.1. Statement of the problem and justification of the methodology

Artificial have been used with great success in control systems [33,34,35]. Neural networks are powerful tools for creating control systems. This is due to a number of unique properties, namely, [36]:
  • ability to learn from experience and generalized data,
  • the ability to adapt to changes in the properties of the control object,
  • ability to avoid errors when programming and evaluating a controlled object.
Considering the above and the applicability of artificial neural network controllers in control systems [37], in this study, a model of artificial neural networks was used to classify stability.
To determine the state of stability of the system using a neural network, the following main tasks were solved:
  • creating a database,
  • assessment of the impact of database input data on the classification of the stability state,
  • comparative analysis of neural networks trained using different methods,
  • selection and analysis of neural network architecture,
  • proposed a model for detecting the state of stability in the control system.
The methodology for solving these problems and the reasons for their application are discussed in a specific example. In particular, a synchronous electric drive system, widely used in the ore crushing process, was considered as an example. This is because the system operates under harsh conditions owing to the random nature of the load change, which has a significant impact on the performance of its mechanical part. Separate connections and parts of the mechanical part of the electric drive system operating with a variable load may wear out and deform; consequently, the system may become unstable. Considering the above, this study considered the stability of the mechanical part of an electric drive system.

3. Results

3.1. Creating a database

A database must be created to train the neural network. To create a database, a differential equation describing the dynamic phenomena of an electric drive system with dynamic loads and discrete masses is used [38].
{ J 1 d ω 1 d t + c ( φ 1 − φ 2 ) = ( β + M N θ p ) ( ω o − ω 1 ) , J 2 d ω 2 d t − c ( φ 1 − φ 2 ) = M o + m 1 ω 2 − m 2 ( ω 2 ) 3 .
The following designations were used:
φ 1 ' ' = d ω 1 d t ,   φ 2 ' ' = d ω 2 d t ,   φ 1 ' = ω 1 ,   φ 2 ' = ω 2 ,
where J 1 , J 2 are the moments of inertia of the rotor of the motor and the mechanism, respectively; M o is the initial torque of the resistance of the mechanism; c is the rigidity of the connection between the mechanism and the motor; φ 1 is the angular displacement of the motor shaft; φ 2 is the movement of the mechanism reduced to the motor shaft; ω 1 is the electric rotation speed of the rotor; ω 0 is the synchronous motor speed; ω 2 is the angular velocity of the actuating link of the mechanism; θ is the motor internal angle; M N is the electromagnetic torque of the synchronous motor rotor; M o is the initial value of the torque of the mechanism; β is the rigidity of the synchronous motor characteristics; s k is the critical slip of the motor; m 1 , m 2 are the coefficients describing the nature of the change in the resistance torque of the mechanism.
The details for determining the stability condition from the system of equations (1) are presented in [38]. The system of equations (1) was modified and solved, leading to the following characteristic equation [38]:
λ 3 + A 1 λ 2 + A 2 λ + A 3 = 0 ,
where
A 1 = a + b − 3 D Ω 4 2 ,   A 2 = a ( b − 3 D Ω 4 2 ) + c 1 + c 2 ,   A 3 = c 1 ( b − 3 D Ω 4 2 ) + c 2 a .
One of the roots of characteristic equation (2) is equal to zero λ 1 = 0 , which means that the system is not asymptotically stable. In order for the system to be stable, it is necessary that all other real parts of the roots λ 2 , λ 3 , λ 4 of the characteristic equation be negative, i.e., Re ( λ k ) < 0 . According to the Vishnegradsky criterion, it is necessary and sufficient to ensure the following conditions:
A 1 > 0 ,     A 2 > 0 ,     A 1 A 2 > A 3 .
As a result, the following stability conditions were obtained
a + x > 0 ,     a x + c 1 + c 2 > 0 ,     c 1 x + c 2 a > 0 ,     a x ( a + x ) + c 1 a + c 2 x > 0 ,
h 1 − ( a − x ) c 1 c 2 x c 1 + a c 2 h 2 + c 1 + c 2 a c 2 + x c 1 h 3 = 0 ,
where
x = b − 3 D Ω 4 2 ,   h 1 = c 2 Ω 3 + c 1 Ω 4 c 1 + c 2 ,   h 2 = Ω 4 − Ω 3 c 1 + c 2 , h 3 = 1 c 1 + c 2 ( − a c 2 Ω 3 − b c 1 Ω 4 + c 2 E + c 1 F + c 1 D Ω 4 3 ) .
The following designations were used:
β J 1 = a , m 1 J 2 = b ,   c J 1 = c 1 ,   c J 2 = c 2 ,   m 2 J 2 = D ,   M o J 2 = F ,   ( β + M N ) ω o J 1 = E .
The solution was implemented under the following initial conditions:
( φ 1 ( 0 ) φ 2 ( 0 ) ω 1 ( 0 ) ω 2 ( 0 ) ) = ( φ 1 ( 0 ) φ 2 ( 0 ) Z 1 ( 0 ) Z 2 ( 0 ) ) = ( Ω 1 Ω 2 Ω 3 Ω 4 ) .
Condition (4) was obtained for the initial value of ω 2 . Condition (5) is obtained at the initial value, that is, ω 1 .
The details of the database generation algorithm are described below.
The input data of the system were generated using the principle of randomness. Then, stability conditions (4) were checked for various values of the input parameters, and condition (5) was checked only when they were satisfied. The obtained results were registered in the database.
A database containing more than two million data points was created, consisting of 10 input features and one response.
To increase the efficiency of the database, the influence of the input data on stability conditions was evaluated.
The degree of importance of the influence of the input data on the output signal was evaluated using an ANOVA algorithm [39]. In this case, the input data are estimated by digits from 0 to infinity, and the higher the score, the more this factor will affect the performance of the system.
As shown in Table 1, the resistance torque and angular velocity of rotation created by the mechanism as well as the angular displacement of the motor shaft play an important role.
The influence of the coefficients ( m 1 , m 2 ) on the resistance torque of the mechanism, angular velocities of the electric motor, and mechanism of the output signal of the system were investigated (Figure 1 and Figure 2).
The obtained results prove that the stability state of the system is strongly related to the resistance torque of the mechanism. For the system to be in a stable state, it is necessary that the value of coefficient exceeds coefficient m 2 by ten times (Figure 1). It was established that after a certain level of angular velocity of the mechanism, the system operates in a stable mode.

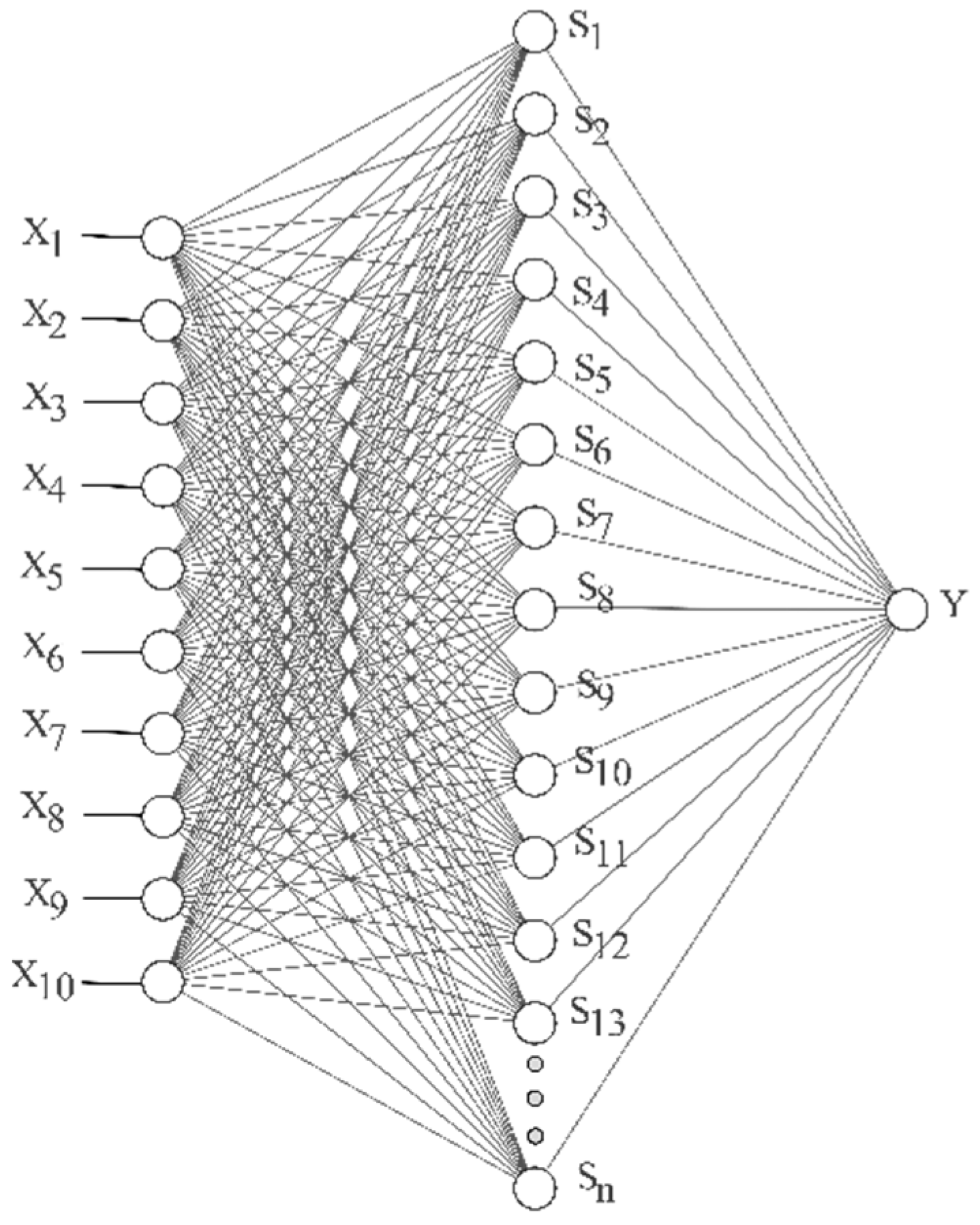
3.2. Building a neural network

There are no clear rules for choosing the neural network architecture and training method, and the algorithm for selecting the activation function is unknown. Therefore, it is necessary to study the architecture of the network and the possibility of selecting a training method for the task under consideration. The successful choice of network structure, activation function, and training algorithm will improve the accuracy and performance of the artificial neural network.
First, it involves the use of various teaching methods. The neural networks trained using different methods were compared. To ensure comparability of the results, training was performed for a network with homogeneous parameters.
To solve this problem, the simplest structure of the neural network was considered:10 input neurons, one hidden layer, and one output neuron (Figure 3).
The results were tested using the example of a two-mass synchronous electric drive system. The test data are presented in Table 2.
The research was carried out using the TensorFlow and Keras packages [40], using various algorithms for optimizing network training. The following algorithms were used: Adam, RMSProp, Stochastic Gradient Descent (SGD), AdaDelta and Nadam. A total of 1,008,422 data elements were used, 30% of which were used for the network validation.
In the hidden layer, the neuron activation function was chosen by ReLU, and in the output layer by sigmoid [41].
The training rate was assumed to be 0.1, and only for SGD - 0.3. At a given training rate, the errors in detecting the system instability and accuracy for various training algorithms were estimated (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8).
The results are shown in Table 3.
The results show that the AdaDelta optimization algorithm is unsuitable for use because unacceptably poor results are obtained, whereas the other algorithms show acceptable results (Figure 4, Figure 5, Figure 6 and Figure 7) and can be used to assess the state of stability.
A change in the number of neurons in the hidden layer does not lead to any significant changes in the case of the Adam, RMSProp, and Nadam algorithms, or in the case of SGD. Changing the number of neurons has a significant impact on the AdaDelta algorithm (Figure 8), but because this algorithm provides results with low accuracy, it is unsuitable for use in this case.
Subsequently, the network architecture is considered. The network was observed using the following data.
  • Number of hidden layers: 1.
  • Number of neurons in hidden layer: 5, 10 and 20.
  • Activation function in hidden layer: ReLU.
  • Activation function in the output layer: Softmax.
  • The data classification algorithm is disabled.
After training the network, the accuracy of the network was only 50%, and when using new input data that were not used in training the network, the accuracy of the network further decreased to 48.8% (Table 4). To improve the results, an attempt was made to increase the number of neurons in the hidden layer, increasing it first to 10 and then to 20, but the results show that this approach is not as effective because almost the same results were obtained. This is because, in the example under consideration, the input data values were unevenly distributed. Some data values exceeded the numerical values of the others by 100 times. A Data Standardization algorithm [42] was used to select an efficient network architecture. Among the well-known algorithms for data standardization, a high-performance Z-score algorithm was selected [43]. Using this method:
  x i n e w = x i − x ¯ i σ ,   i = 1 , 2 , … , k
where k is the number of parameters to be standardized, x ¯ i is the average value of the i - th parameter, and σ is the standard deviation of the i - th parameter.
The performance of neural networks with different numbers and activation functions in the hidden layer was studied using the Data Standardization algorithm (Table 4).
The results show that the number of neurons in the hidden layer does not have a significant impact on the accuracy of the network. The use of input data standardization algorithms has a significant impact on network performance.
Various algorithms have been successfully used for classification problems. Taking into account the fact that obtaining information about the stability of the system relates to classification tasks, we considered the Decision Tree, Linear Discriminant Analysis, Logistic Regression, Naïve Bayes and Ensemble algorithms [44,45,46].
One of the algorithms successfully used in classification problems is the Decision Tree algorithm, which is based on rules and does not require any assumptions. Its advantage is its high degree of interpretability.
The Linear Discriminant Analysis algorithm is not only a dimensionality reduction tool but also an effective classification method. Despite its simplicity, this algorithm can produce acceptable and interpretable classification results and requires little time for training and testing.
Logistic Regression is a parametric method with high reliability. The problem in this case is that a certain set of assumptions is required for the algorithm to operate correctly.
The Naïve Bayes algorithm can perform a large number of probabilistic calculations in a short period. It can process a large amount of data.
The Ensemble algorithm was based on a combination of predictions obtained using a set of different models. Training is performed with a stochastic training algorithm, which means that different weights can be found with each training, which can lead to different predictions.
The characteristic data obtained from the Decision Tree, Linear Discriminant Analysis, Logistic Regression, Naïve Bayes and Ensemble algorithms are shown in Table 5.
The evaluation of the neural networks considered by us, which showed the best results in terms of accuracy, is shown in Figure 9 and in terms of training time in Figure 10.
The results obtained show that the best indicator was recorded by the neural network models with the structure shown in Figure 3. Among them, “Model 4”, “Model 5”, “Model 6” and “Model 8” were identified with an accuracy of 98.1% and higher. Among the classification models, the highest accuracy is provided by models using the “Logistic Regression” algorithm with an accuracy of 96.2%. Simultaneously, the training time of Model 4 was much shorter (168 s) than the other best indicators. When analyzing the results obtained, the advantage of the neural network model over the classification model was noted. In addition, it is noted that to improve the control system of electric drives operating with a dynamic load, it is most appropriate to use a model with one hidden layer, five neurons, and a model architecture with a ReLU activation function in this layer.

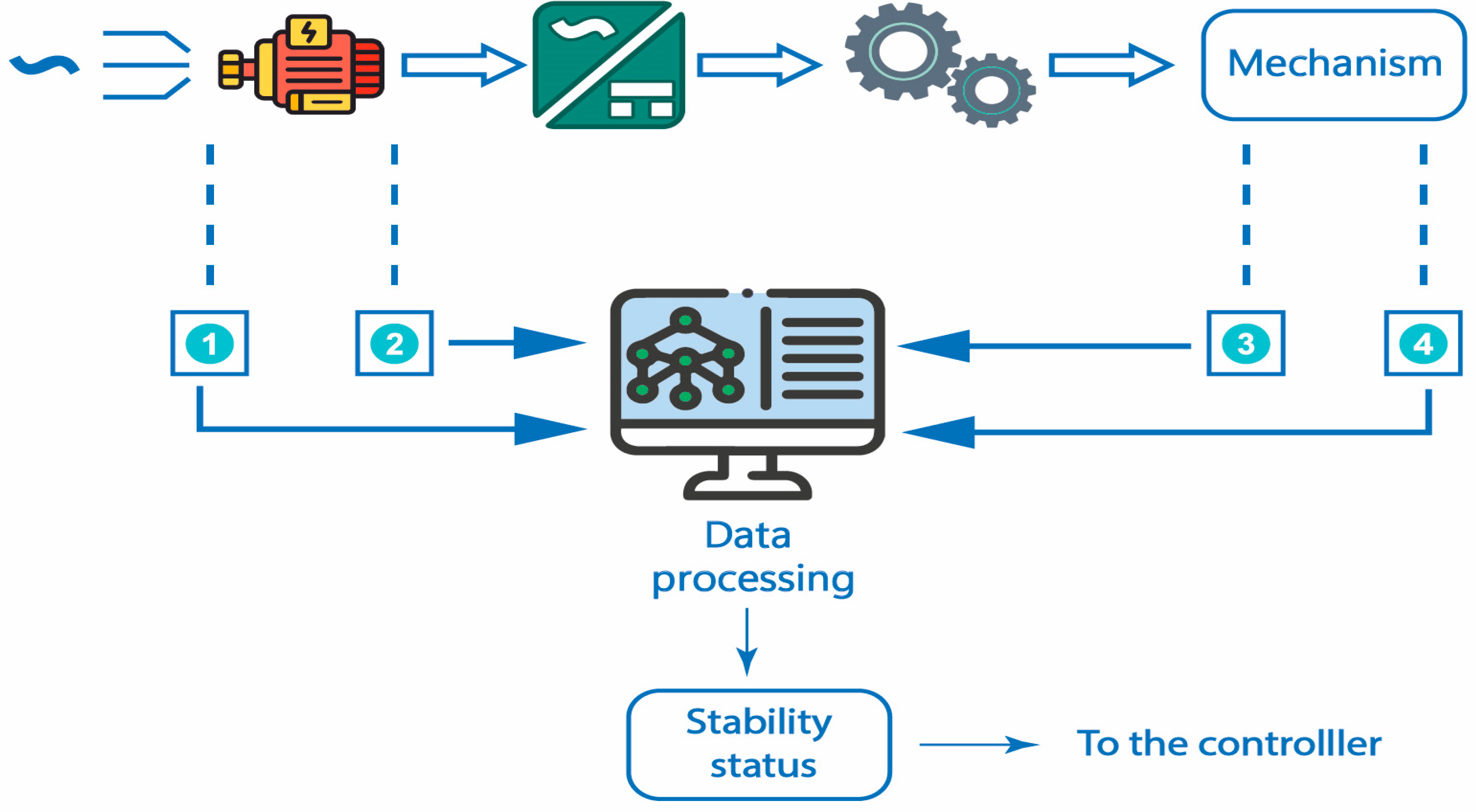
3.3. Algorithm for applying the instability state detection model in the automatic control system of the electric drive system

Advances in technology present new requirements and challenges for electric-drive control systems. These solutions could be implemented by improving the system. Using the capabilities of the instability state detection model can provide a significant development for an electric drive control system operating under a randomly varying load. Electric drive systems operating with dynamic loads may accidentally be in an unstable mode during operation, and as a result, the efficiency of the system decreases or fails. Therefore, unstable operating modes must be avoided. The implementation of the latter can be ensured by introducing an unstable mode detection system into the electric-drive control system. The analysis of the development of a model for detecting the state of instability based on an artificial neural network provides reason to assert the expediency of its application in control systems. In modern ACS, neurocontrollers have begun to be used, and can be successfully adapted to our proposed model for detecting the state of instability. Figure 11 shows a block diagram of the possibility of using the instability-detection model in the ACS of the electric drive.
The block diagram consists of:
  • Drive-motor power converter
  • Strain gauges of the mechanical transmission link, technological mechanism, and electric motor torque (1)
  • Motor rotation speed sensor (2)
  • Mechanism rotation speed sensor (3)
  • Strain gauge of resistance torque of mechanism (4)
  • Units of data processing and stability status signaling.
The corresponding signals from the strain gauges of the electric motor and mechanism torques, as well as the rotation speed sensors, were transmitted to the data processing unit with a given frequency. The received signals are processed in accordance with the neural model to detect the instability state of the system and signal its stability. Information about the status of the electric drive system is transmitted to the controller, which implements its regulatory function in accordance with the situation.
Transients of a synchronous electric drive system with a changing load were considered in the following cases: 1) without a stability state detection model and 2) coordinated operation of the stability state detection model with a regulator (Figure 12). The results of the study show that the coordinated work of the regulator with a neural network model that considers the state of stability leads to an improvement in the quality of the dynamic indicators of the system.

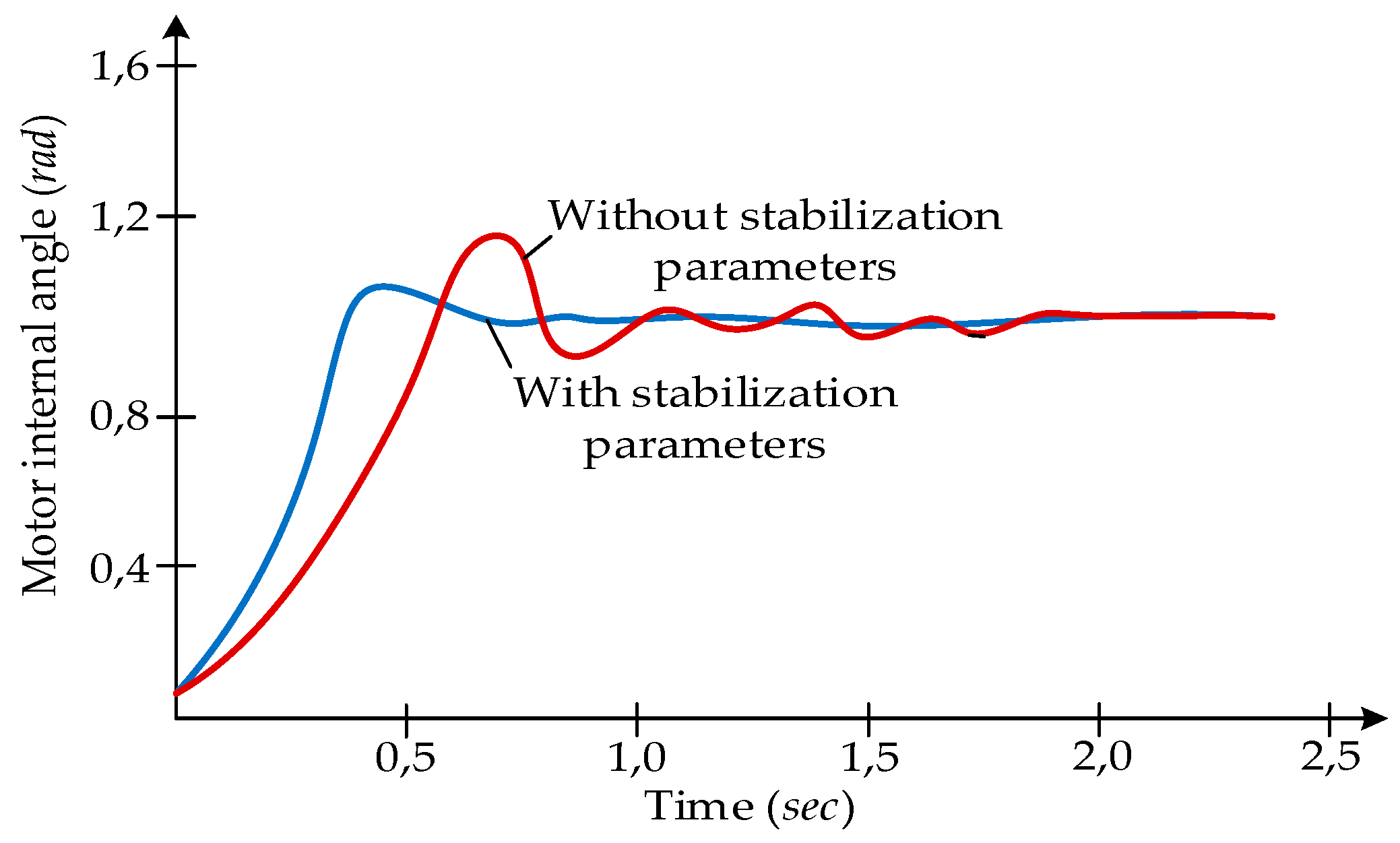
4. Discussion

This study considers the features of the application of an electric drive system operating with a dynamic load, and the research carried out in recent years in the direction of developing their ACS. The hypotheses presented in well-known studies were analyzed and evaluated, and appropriate comments on their applications were provided. It follows from the analysis of the works that they mostly touched upon approaches aimed at eliminating undesirable consequences caused by the vibrations of elastic links through the use of various regulators. To solve the problems of detecting unstable states, in the considered works only the stability issues of the individual nodes of the system are considered. However, the analysis shows that the information obtained for the state of system stability in individual works is not sufficiently adapted to the operation of the control system. The priority task for various industries is to improve the operating modes of the electric drive control system, which can be achieved by detecting emerging instability and adapting this information to the operation of the controller. Considering the comprehensive research in this work, an artificial neural network model for detecting instability in an electric drive system was developed and proposed for further use, which can be successfully adapted into an automated control system.
A Python programming environment was used to conduct experiments. The data with the greatest impact on stability were determined by evaluating the importance levels of the signals collected to create the database. This allowed us to obtain an objective idea of the main causes of the unstable state of an electric drive system.
From the practical evaluation of the results obtained, it follows:
1. A model built to detect the unstable state of the mechanical part of a synchronous electric drive system can provide high accuracy when standardizing its input data. Testing a neural network model with observable structured data and a training algorithm shows that the accuracy of training increases by 1.9 times, and the training time decreases by 2.6 times with standardized input data. The results obtained allow us to assert the expediency of the standardization of input signals for the development of neural network models of electromechanical systems.
2. Among the various algorithms for training a neural network model for detecting the unstable state of the mechanical part of an electric drive system. In particular, the Nadam algorithm ensures 99.7 accuracy of training and validation accuracy. The worst indicator was recorded by the AdaDelta algorithm with an accuracy of 45.25%.
3. To detect the instability of the electric drive system, models created on the basis of an artificial neural network, with the right choice of architecture, are preferable to models based on known classification algorithms.
4. The influence of the number of neurons in the hidden layer of the network on the accuracy of training was insignificant, whereas it had a significant impact on the duration. Tests show that if five neurons of the hidden layer of the network with homogeneous parameters are replaced by 10, the accuracy of the model increases by 0.1%, and the operation speed decrease by 1.47 times.
A new hypothesis for the development of an intelligent model for detecting the unstable state of the mechanical part of an electric drive system was proposed. This allows the creation of a model capable of detecting the unstable state of the system with high accuracy in a short period of time. By adapting it to the automatic control system of an electric drive, high control efficiency can be ensured. In addition, the presented algorithm can be used to develop high-performance models of electromechanical systems with different technical and economic requirements, or to modify existing models.
An analysis of the results shows that a neural network model built to detect instability can be installed in real controllers. This will allow the adaptation of the instability detection model to the ACS without additional difficulties and improve system performance. The presented analysis provides grounds to conclude that the results obtained have a wide range of applications; in particular, they can be used to develop intelligent control systems that ensure the high reliability and high performance of various electrical drive systems.

5. Conclusion

This study demonstrates the effectiveness of using information coordinated with the regulator obtained from the model of detecting the state of instability in the automatic control system of the electric drive. The architecture of the artificial neural network and the choice of the training method used in the model of detecting instability of the mechanical part of an electric drive system are substantiated. The results obtained can become the basis for solving problems of control, research, and monitoring of the electric drive systems for various purposes.
The study results show:
  • advantage of an instability state detection model built based on an artificial neural network over classification models,
  • significant influence of the number of neurons in the hidden layer on the duration of network training,
  • the potentialities of the electric drive control system increase with the coordinated operation of the instability detection model and the regulator.

Author Contributions

Conceptualization, M.B., V.H.; methodology, resources, validation, M.B. and V.H; software, V.H.; formal analysis, M.B.; investigation, M.B.; data curation, M.B., V.H.; writing—original draft preparation, writing—review and editing, M.B., V.H.; visualization, M.B.; supervision, project administration, funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this article are available on request of the corresponding author.

Acknowledgments

This work was supported by the Science Committee of RA, in the frames of the research project № 21T-2B195.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kuhn, A.M.; May, M. C.; Liu, Yu.; Kuhnle, A.; Tekouo, W.; Lanza, G. Towards Narrowing the Reality Gap in Electromechanical Systems: Error Modeling in Virtual Commissioning. Production Engineering 2022, 17, 535–545. [Google Scholar] [CrossRef]
  2. Baghdasaryan, M.; Ulikyan, A.; Arakelyan, A. Application of an Artificial Neural Network for Detecting, Classifying, and Making Decisions about Asymmetric Short Circuits in a Synchronous Generator. Energies 2023, 16, 2703. [Google Scholar]
  3. Xu, L.; Tang, Y. H.; Pu, W.; Han, Y. Hybrid Electromechanical-Electromagnetic Simulation to SVC Controller Based on ADPSS Platform. Journal of Energy in Southern Africa 2014, 26, 112–122. [Google Scholar] [CrossRef]
  4. Chaban, A.; Lis, M.; Szafraniec, A.; Levoniuk, V. Mathematical Modelling of Transient Processes in a Three Phase Electric Power System for a Single Phase Short-Circuit. Energies 2022, 15, 1126. [Google Scholar] [CrossRef]
  5. Baghdasaryan, M.; Davtyan, D. Energy Saving in the Ore Beneficiation Technological Process by the Optimization of Reac-Tive Power Produced by the Synchronous Motors. International Review of Electrical Engineering 2021, 16, 377–384. [Google Scholar]
  6. Tang, Y.; Wan, L.; Hou, J. Full Electromagnetic Transient Simulation for Large Power Systems. Global Energy Interconnection 2019, 2, 29–36. [Google Scholar] [CrossRef]
  7. Pacheco-Paez, J.C.; Chimal-Eguía, J.C.; Páez-Hernández, R.; Ladino-Luna, D. Global Stability of the Curzon-Ahlborn Engine with a Working Substance That Satisfies the van Der Waals Equation of State. Entropy 2022, 24, 1655. [Google Scholar] [CrossRef]
  8. Silaghi, H.; Gamcova, M.; Silaghi, A.; Spoială, V.; Silaghi, A.; Spoială, D. Intelligent Control of Electrical Drive System Used for Electric Vehicles. Scientific Bulletin of the Electrical Engineering Faculty 2018, 1(38), 5–10. [Google Scholar] [CrossRef]
  9. Tergemes, K.T.; Amangaliyev, Y.Z.; Karassayeva, A.R. Perspective Directions of the Development of Electric Transports’ Electric Drive. 2019 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 01-04 October 2019, IEEE. USA, 2019. [CrossRef]
  10. Semenov, A.S.; Egorov, A.N.; Khubieva, V.M. Assessment of Energy Efficiency of Electric Drives of Technological Units at Mining Enterprises by Mathematical Modeling Method – ICIEAM 2019: 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25-29 March 2019, IEEE. New York, USA, 2019. [CrossRef]
  11. Wach, P. Dynamics of Electromechanical Systems. In Dynamics and Control of Electrical Drives, Springer, Berlin, Heidelberg, 2011, Pp. 9–107. [CrossRef]
  12. Baghdasaryan, M.K. Methods for Investigating the Operation Modes of the Electrical Drive Motor Used in the Mineral Raw Material Grinding Process. In Methods of Research and Optimization of the Mineral Raw Material Grinding Proces, NOVA Science Publishers, New York, USA, 2019, Pp. 165–179.
  13. Nana, B.; Yamgoué, S. B.; Woafo, P. Dynamics of an Autonomous Electromechanical Pendulum-like System with Experimentation. Chaos, Solitons & Fractals 2021, 152. [CrossRef]
  14. Zhang, X.; Tao, T.; Jiang, G.; Mei, X.; Zou, C. A Refined Dynamic Model of Harmonic Drive and Its Dynamic Response Analysis. Shock and Vibration 2020, 1–12. [Google Scholar] [CrossRef]
  15. Yang, J.; Feng, Z.; Gao, H.; Wang, T.; Xu, K. Multibody Dynamics Analysis of a Silent Chain Drive Timing System. Journal of Mechanical Science and Technology 2023, 37, 1653–1664. [Google Scholar] [CrossRef]
  16. Korneev, A.P.; Niu, Y.; Mansoor, M.S.G.; Jabbar, Z.S.; Tawfeq, J. F.; Radhi, A.D. Design and Implementation of a Distributed Parameter Electromechanical System Control System for Automation and Optimization. Jurnal Pengabdian Dan Pemberdayaan Masyarakat Indonesia 2023, 3, 28–34. [Google Scholar]
  17. Yan, W.; Wang, X.; Gao, W.; Gevorgian, V. Electro-Mechanical Modeling of Wind Turbine and Energy Storage Systems with Enhanced Inertial Response. Journal of Modern Power Systems and Clean Energy 2020, 8, 820–830. [Google Scholar] [CrossRef]
  18. Yu, Y.; Mi, Z. Dynamic Modeling and Control of Electromechanical Coupling for Mechanical Elastic Energy Storage System. Hindawi Publishing Corporation Journal of Applied Mathematics 2013. [CrossRef]
  19. Oustaloup, A.; Pommier, V.; Lanusse, P. Design of a Fractional Control Using Performance Contours. Application to an Electromechanical System. Fractional Calculus and Applied Analysis 2023, 6, 1–24. [Google Scholar]
  20. Popenda, A.; Szafraniec, A.; Chaban, A. Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation. Energies 2021, 14, 7882. [Google Scholar] [CrossRef]
  21. Iov, I.A.; Kuznetsov, N.K.; Dolgih, E.S. Development and Research of Motion Control Algorithms of Elastic Electromechanical Systems Taking into Account the Damping Properties of the Electric Drive. International Conference on Automatics and Energy (ICAE 2021) Vladivostok, Russia, 7-8 October 2021; Journal of Physics: Conference Series, 2096. [CrossRef]
  22. Yu, L.; Su, L.; Qin, F.; Wang, L. Application of Multi-Machine Power System Supervised Machine-Learning in Error Correction of Electromechanical Sensors. Energy Reports 2022, 8, 1381–1391. [Google Scholar] [CrossRef]
  23. Ma, Y. Realization and Application of Stability Condition of Electromechanical Transmission System. Academic Journal of Science and Technology 2022, 2, 65–67. [Google Scholar] [CrossRef]
  24. Wu, S.; Zhou, Y.; Zhang, J.; Ma, S.; Lian, Y. Research on Stability Control Method of Electro-Mechanical Actuator under the Influence of Lateral Force. Electronics 2022, 11, 1237. [Google Scholar] [CrossRef]
  25. Ju, J.; Liu, Y.; Zhang, C. Stability Analysis of Electromechanical Coupling Torsional Vibration for Wheel-Side Direct-Driven Transmission System under Transmission Clearance and Motor Excitation. World Electric Vehicle Journal 2022, 13, 46. [Google Scholar] [CrossRef]
  26. Sobieraj, S.; Sieklucki, G.; Gromba, J. Relative Stability of Electrical into Mechanical Conversion with BLDC Motor-Cascade Control. Energies 2021, 14, 704. [Google Scholar] [CrossRef]
  27. Moreno-Chuquen, R.; Florez-Cediel, O. Online Dynamic Assessment of System Stability in Power Systems Using the Unscented Kalman Filter. International Review of Electrical Engineering 2019, 14, 465–472. [Google Scholar] [CrossRef]
  28. Kim, D.; Lee, Y.; Oh, S.; Park, Y.; Choi, J.; Park, D. Aerodynamic Analysis and Static Stability Analysis of Manned/Unmanned Distributed Propulsion Aircrafts Using Actuator Methods. Journal of Wind Engineering and Industrial Aerodynamics 2021, 214, 104648. [Google Scholar] [CrossRef]
  29. Hoogreef, M.F.M.; Soikkeli, J.S.E. Flight Dynamics and Control Assessment for Differential Thrust Aircraft in Engine Inoperative Conditions Including Aero-Propulsive Effects. CEAS Aeronautical Journal 2022, 739–762. [Google Scholar] [CrossRef]
  30. Tian, D.; He, C. H. A Fractal Micro-Electromechanical System and Its Pull-in Stability. Journal of Low Frequency Noise, Vibration and Active Control 2021, 40, 1380–1386. [Google Scholar] [CrossRef]
  31. Konoval, V.; Prytula, R.; Skrypnyk, O. Static Stability Analysis of Power Systems. Poznan University of Technology Academic Journals, Electrical Engineering 2015, 82, 12–19. [Google Scholar]
  32. Strebulyaev, S.N. Investigation of the Stability of the Electric Drive System. Bulletin of the Nizhny Novgorod University 2014, 4, 343–349. [Google Scholar]
  33. Kaminski, M.; Tarczewski, T. Neural Network Applications in Electrical Drives—Trends in Control, Estimation, Diagnostics, and Construction. Energies 2023, 16, 4441. [Google Scholar] [CrossRef]
  34. Mahfouz, H.; Kassem, R.; Sayed, K. Artificial Neural Networks Applied on Induction Motor Drive for an Electric Vehicle Propulsion System. Electrical Engineering 2022, 104, 1769–1780. [Google Scholar]
  35. Şimşir, M.; Bayır, R.; Uyaroğlu, Y. Real-Time Monitoring and Fault Diagnosis of a Low Power Hub Motor Using Feedforward Neural Network. Computational Intelligence and Neuroscience 2016, 13, 1–13. [Google Scholar] [CrossRef]
  36. Rios, J.D.; Alanis, Al.Y.; Arana-Daniel, N.; Lopez-Franco, C. Neural Block Control. In Neural Networks Modeling and Control, Edgar N. Sanchez. 2020, Pp 32–83.
  37. Dewes, R.S.; Karaa, T. Design and Simulation of a PID Neural Network Controller for PMDC Motor Speed and Position Control. European Journal of Science and Technology 2022, 44, 46–50. [Google Scholar]
  38. Baghdasaryan, M.K.; Babayan, A.H.; Avetisyan, A.G.; Hovhannisyan, V.D. Developing a Mathematical Model to Reveal and Evaluate the Conditions of Stability of the System “Electric Drive Synchronous Motor-Mechanism”. Proceedings National Polytechnic University of Armenia, Electrical Engineering, Energetics 2023, 1, 38–49. [Google Scholar]
  39. Tripathy, G.; Sharaff, A. AEGA: Enhanced Feature Selection Based on ANOVA and Extended Genetic Algorithm for Online Customer Review Analysis. The Journal of Supercomputing 2023, 79, 13180–13209. [Google Scholar] [CrossRef] [PubMed]
  40. Haghighata, E.; Juanes, R. SciANN: A Keras/TensorFlow Wrapper for Scientific Computations and Physics-Informed Deep Learning Using Artificial Neural Networks. Computer Methods in Applied Mechanics and Engineering 2021, 373. [Google Scholar] [CrossRef]
  41. Rodríguez, A.I.; Buitrago, X.D. How to Choose an Activation Function for Deep Learning. Tekhnê 2022, 19, 23–32. [Google Scholar]
  42. Shanker, M.; Hu, M.Y.; Hung, M.S. Effect of Data Standardization on Neural Network Training. Omega 1996, 24, 385–397. [Google Scholar] [CrossRef]
  43. Mohamad, B.; Usman, D. Standardization and Its Effects on K-Means Clustering Algorithm. Research Journal of Applied Sciences, Engineering and Technology 2013, 6, 3299–3303. [Google Scholar] [CrossRef]
  44. Njoku, O. C. Decision Trees and Their Application for Classification and Regression Problems. M.S. Thesis, Missouri State University, USA, 2019. [Google Scholar]
  45. Faouzi, J.; Colliot, O. Classic Machine Learning Algorithms. In Machine Learning for Brain Disorder, Springer, 2023, pp. 1–60.
  46. Shah, T.N.; Khan, M. Z.; Ali, M.; Khan, B.; Muhammad, H. Critical Analysis of Six Frequently Used Classification Algorithms. University of Swabi Journal 2018, 2, 36–40. [Google Scholar]
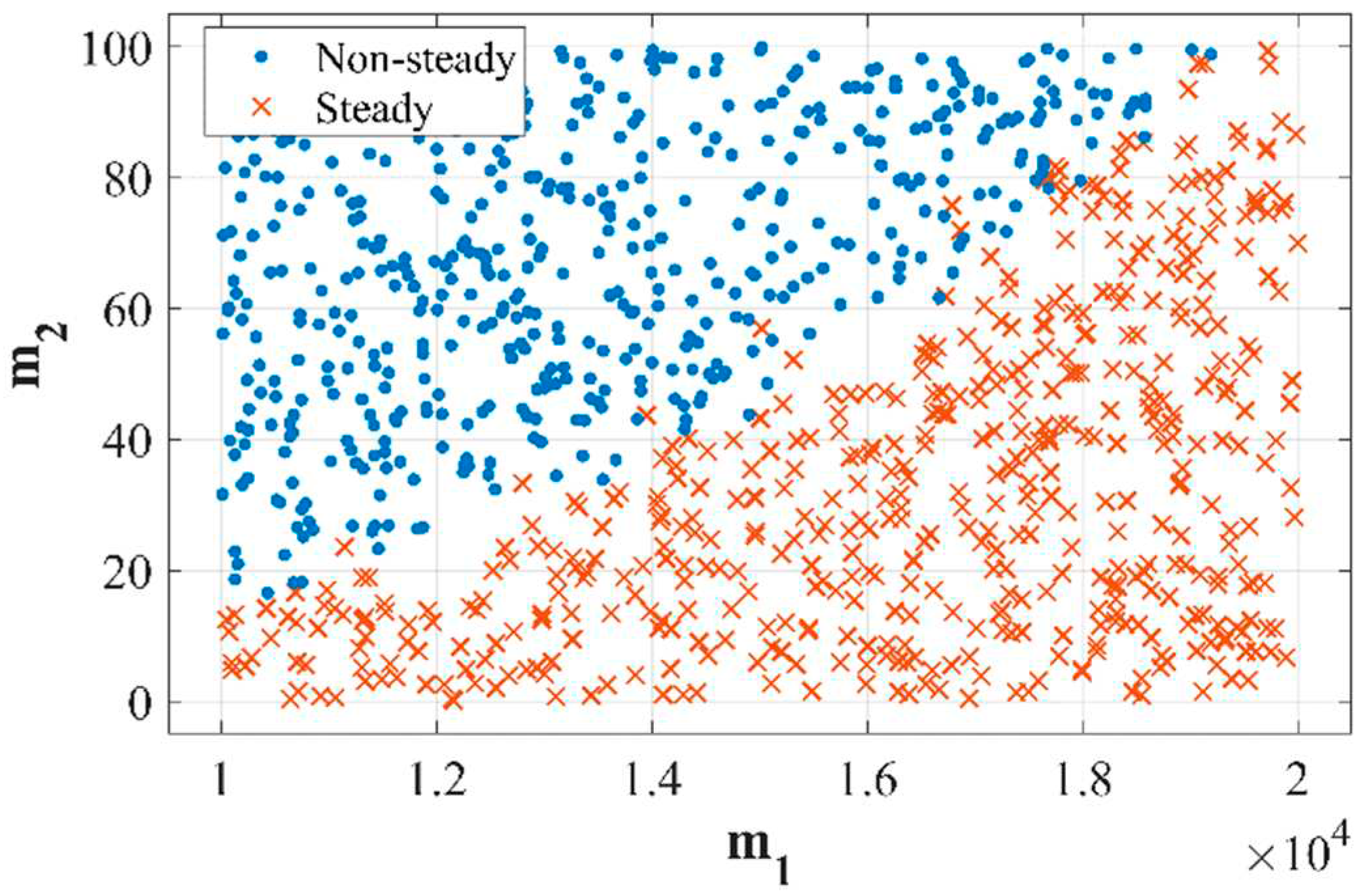
Preprints 88817 g001
Figure 1. Influence of the coefficients m1 and m2 characterizing resistance torque of the mechanism on the stability of the system.
Figure 1. Influence of the coefficients m1 and m2 characterizing resistance torque of the mechanism on the stability of the system.
Preprints 88817 g001
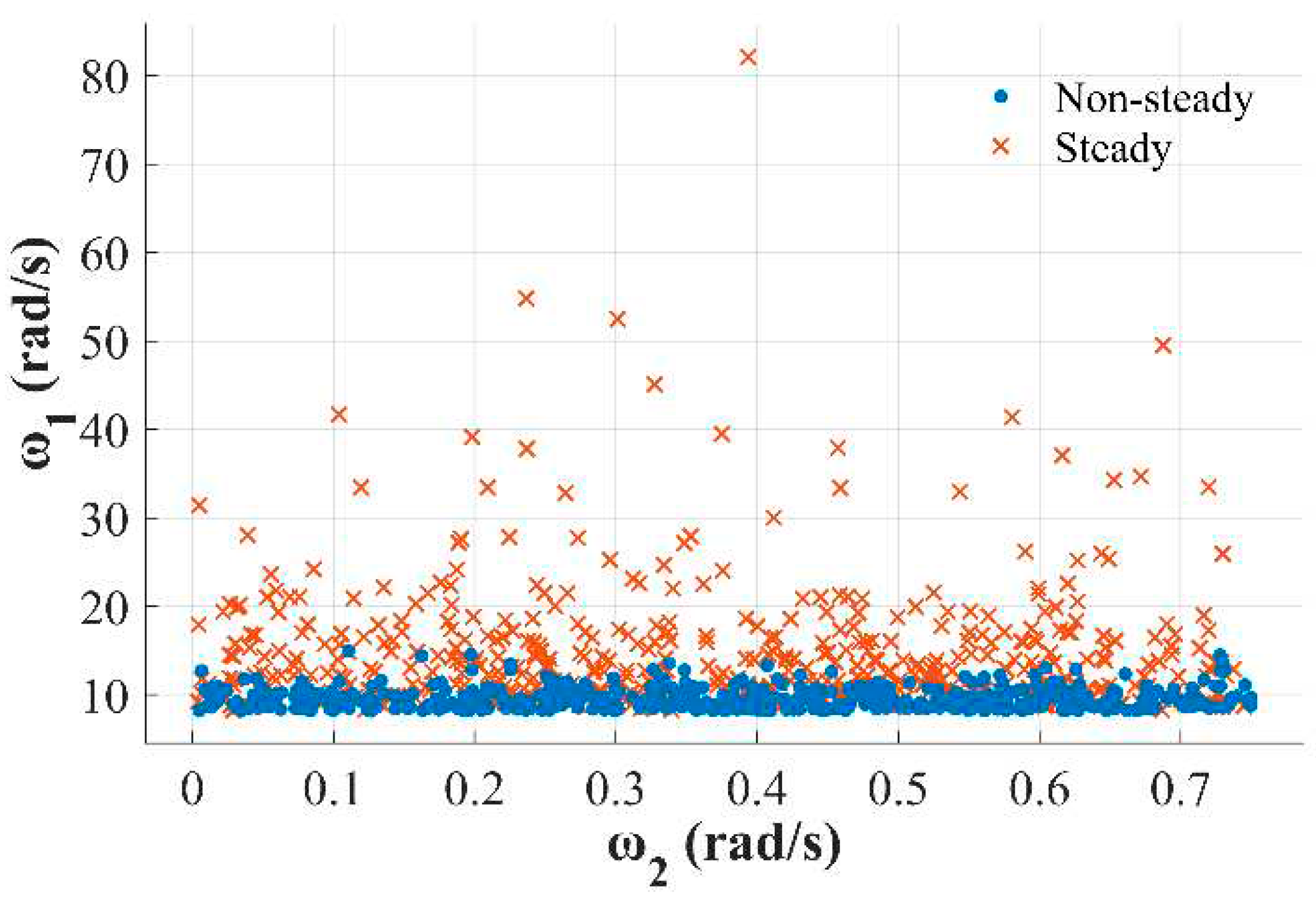
Preprints 88817 g002
Figure 2. Influence of the displacement angles of the electric motor and mechanism on the stability of the system.
Figure 2. Influence of the displacement angles of the electric motor and mechanism on the stability of the system.
Preprints 88817 g002
Preprints 88817 g003
Figure 3. The structure of the studied neural network.
Figure 3. The structure of the studied neural network.
Preprints 88817 g003
Preprints 88817 g004
Figure 4. Dependance of training losses on the number of iterations.
Figure 4. Dependance of training losses on the number of iterations.
Preprints 88817 g004
Preprints 88817 g005
Figure 5. Dependence of training accuracy on the number of iterations.
Figure 5. Dependence of training accuracy on the number of iterations.
Preprints 88817 g005
Preprints 88817 g006
Figure 6. Dependence of validation losses on the number of iterations.
Figure 6. Dependence of validation losses on the number of iterations.
Preprints 88817 g006
Preprints 88817 g007
Figure 7. The dependence of the accuracy of the validation on the number of iterations.
Figure 7. The dependence of the accuracy of the validation on the number of iterations.
Preprints 88817 g007
Preprints 88817 g008
Figure 8. The dependence of the accuracy of the validation on the number of neurons in the hidden layer.
Figure 8. The dependence of the accuracy of the validation on the number of neurons in the hidden layer.
Preprints 88817 g008
Preprints 88817 g009
Figure 9. Degrees of accuracy of networks with different architectures.
Figure 9. Degrees of accuracy of networks with different architectures.
Preprints 88817 g009
Preprints 88817 g010
Figure 10. Training time for networks with different architectures.
Figure 10. Training time for networks with different architectures.
Preprints 88817 g010
Preprints 88817 g011
Figure 11. A block diagram of the use of the instability detection model in ACS.
Figure 11. A block diagram of the use of the instability detection model in ACS.
Preprints 88817 g011
Preprints 88817 g012
Figure 12. Change in the internal angle of a synchronous electric motor of an electric drive in the transient process with and without taking into account the stability state.
Figure 12. Change in the internal angle of a synchronous electric motor of an electric drive in the transient process with and without taking into account the stability state.
Preprints 88817 g012
Table 2. List Of Parameters Used For The Experiment.
Table 2. List Of Parameters Used For The Experiment.
Variable parameters Range of values Variable parameters Range of values
J 1 600-14000 kg.m 2 φ 1 ' 1-30 rad/s
J 2 520-1000 kg.m 2 φ 1 ' ' 0-0.65 pad/s2
M o 890-865 kg.m φ 2 0-1.5 rad
c 2500-2550000 kg.m/rad φ 2 ' 1-28 rad/s
φ 1 0-2.5 rad φ 2 ' ' 0-0.5 pad/s2
Fixed parameters M N = 2400 k g . m ,   s k = 0.25 ,   ω o = 25 r a d / s
Table 3. Results Of Teaching Methods.
Table 3. Results Of Teaching Methods.
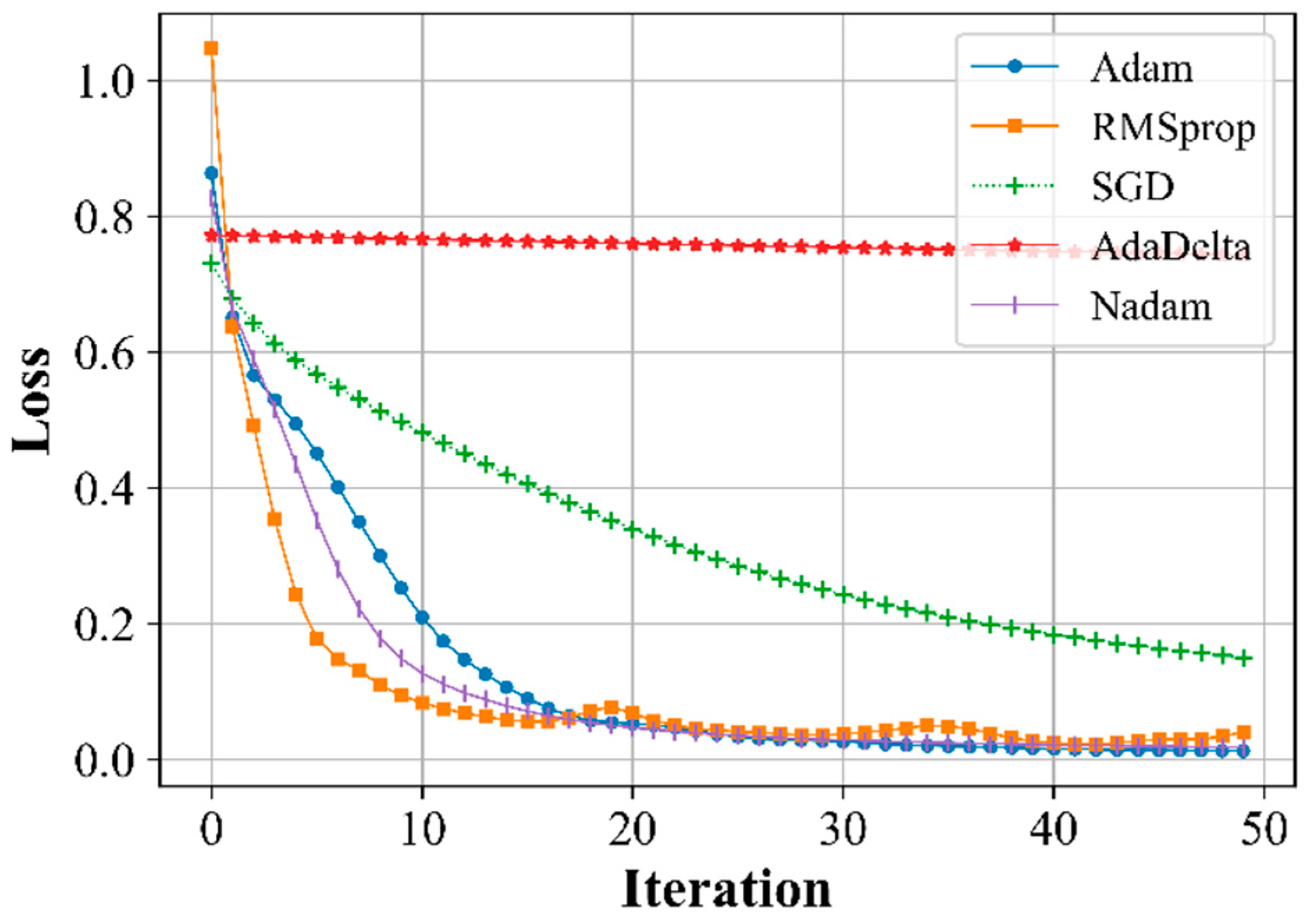
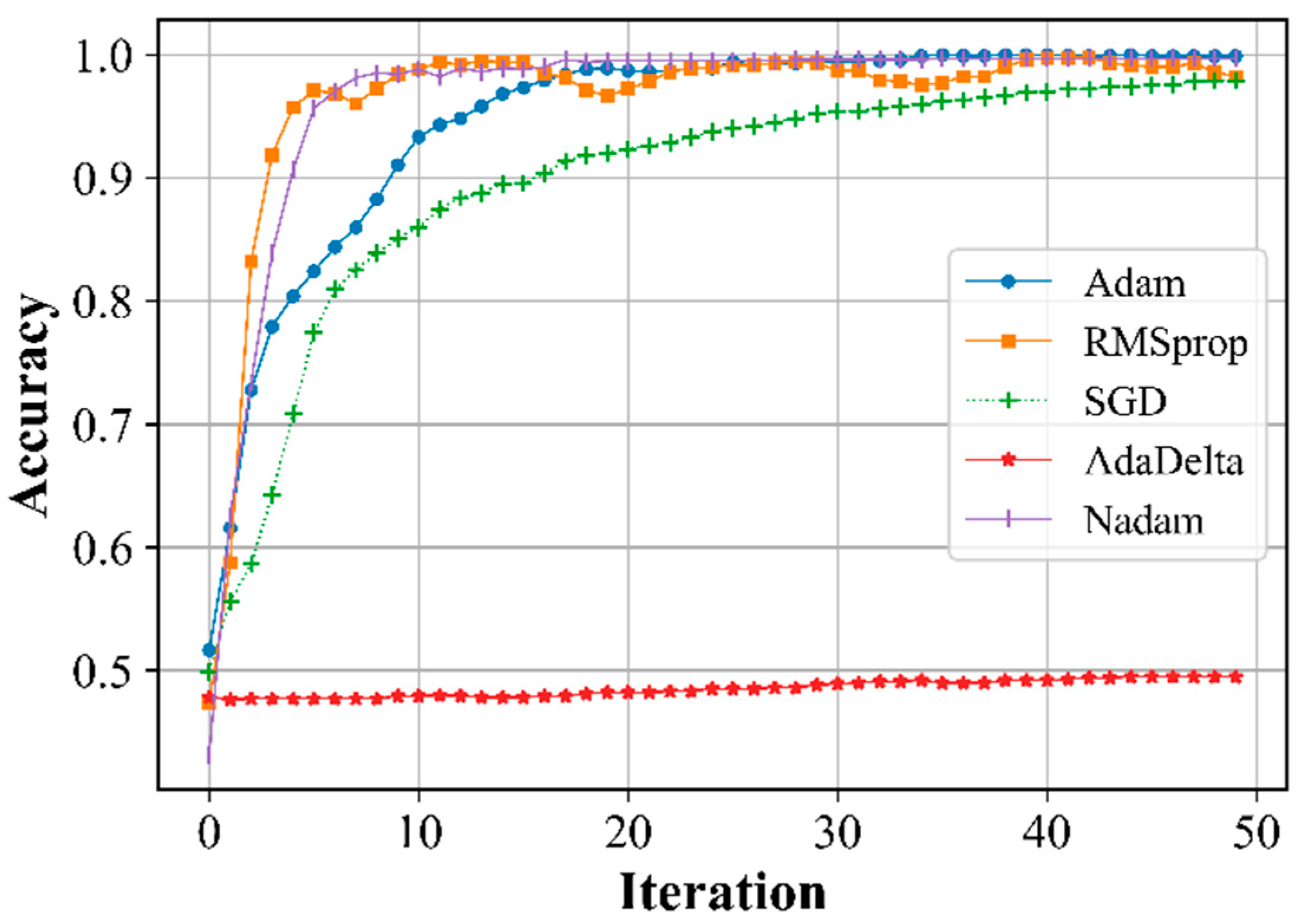
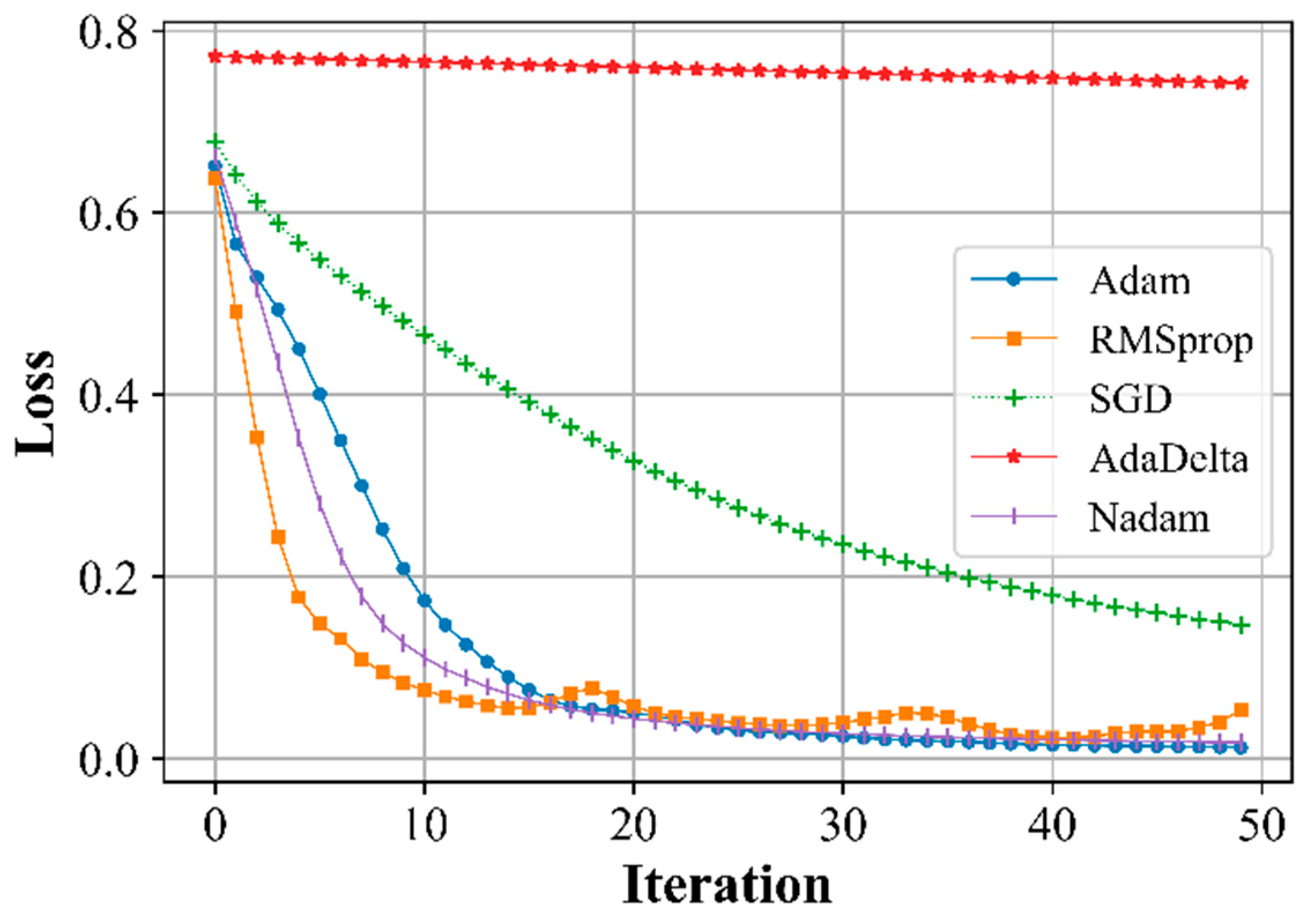
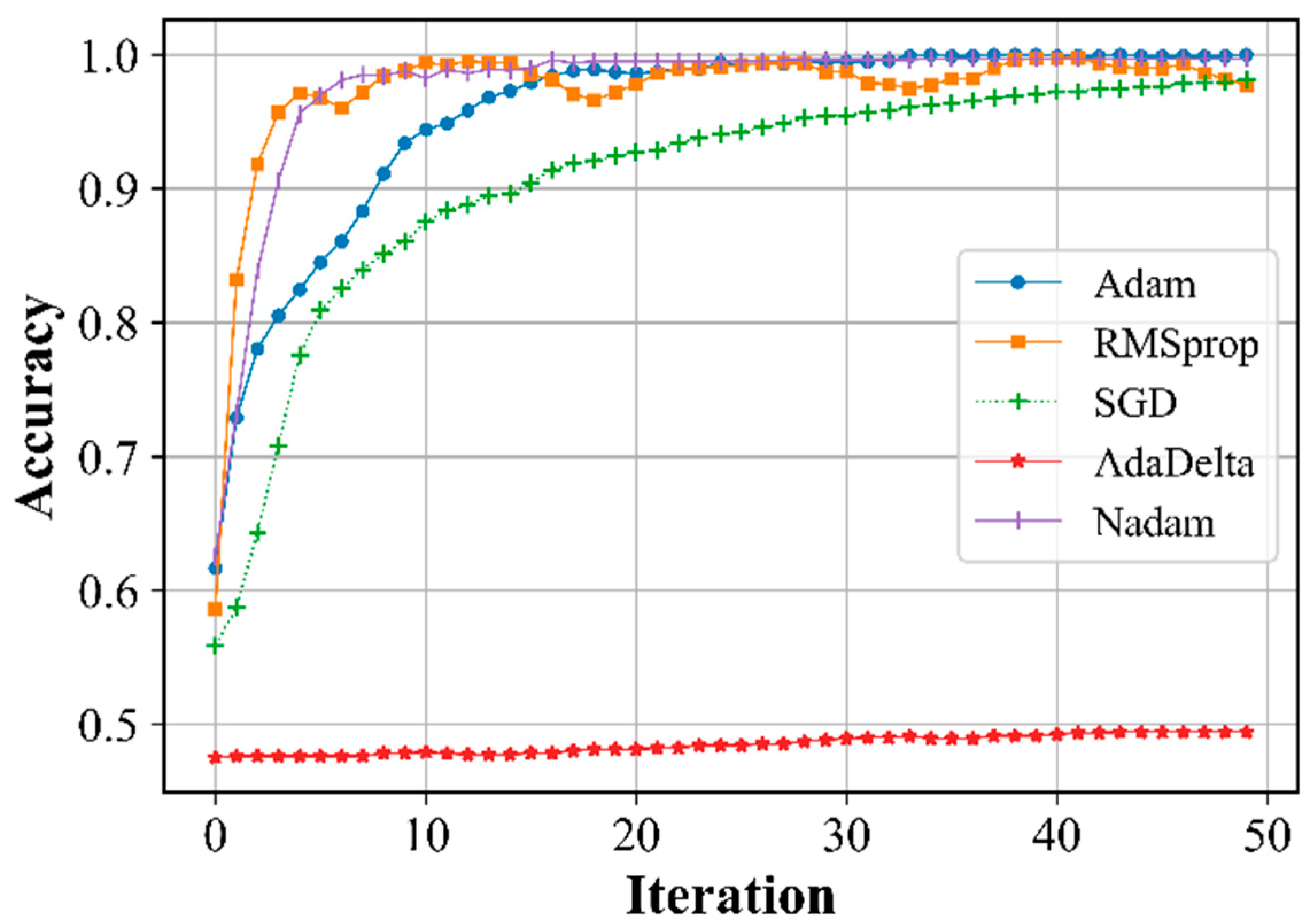
Training method Training Loss Training Accuracy Validation loss Validation accuracy
Adam 0.0156 0.999 0.0153 0.999
RMSprop 0.0356 0.9862 0. 0373 0.9831
SGD 0. 1337 0. 9791 0.1313 0. 9783
AdaDelta 0. 8833 0.4525 0. 8830 0.4511
Nadam 0. 0136 0. 9970 0. 0131 0. 9971
Table 4. Performance Results For Neural Networks With Different Structures.
Table 4. Performance Results For Neural Networks With Different Structures.
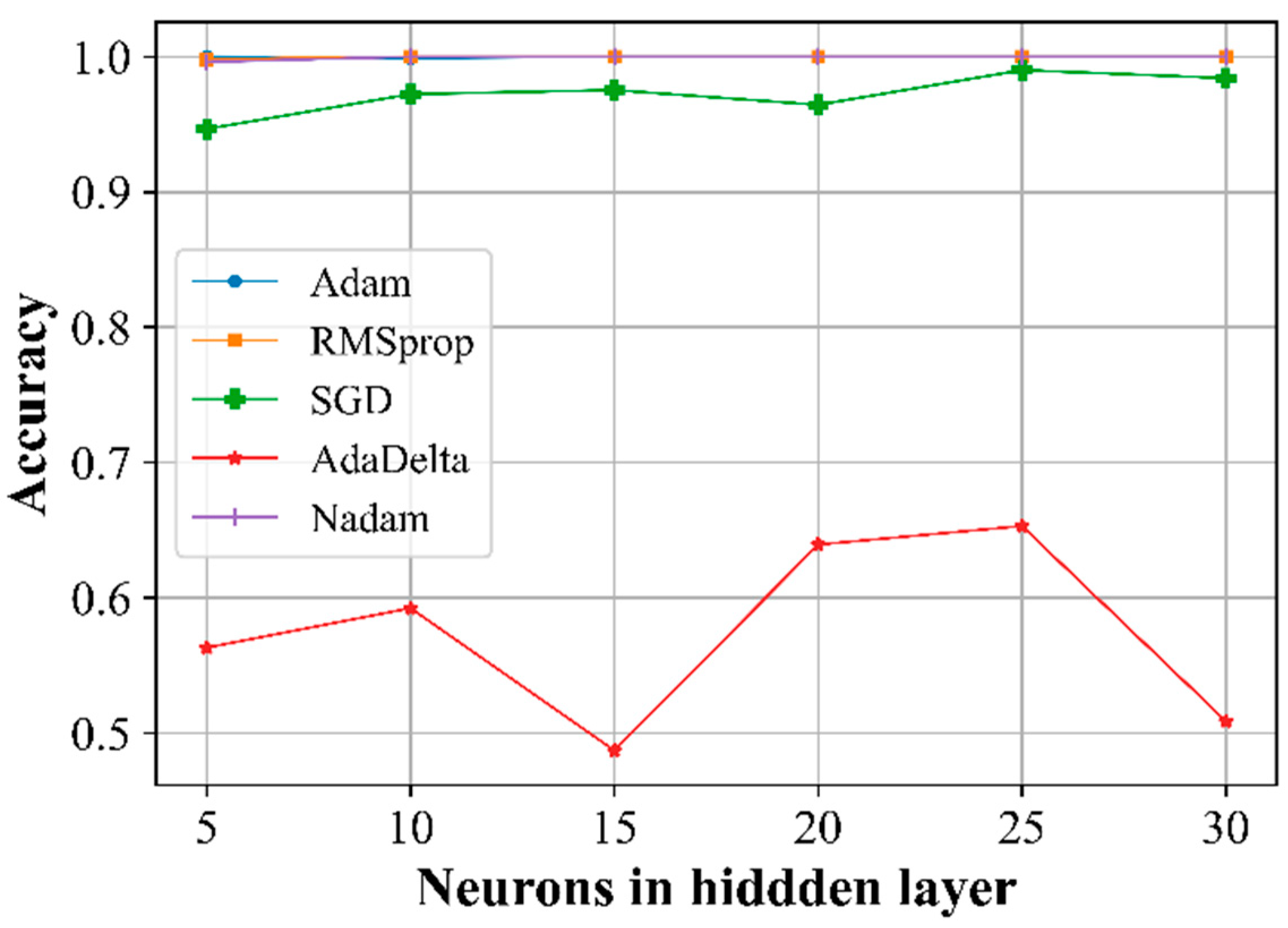
Neuron structure Number of neurons in the hidden layer Activation function in the hidden layer Data classification Duration of training
(s)		 Accuracy
(%)
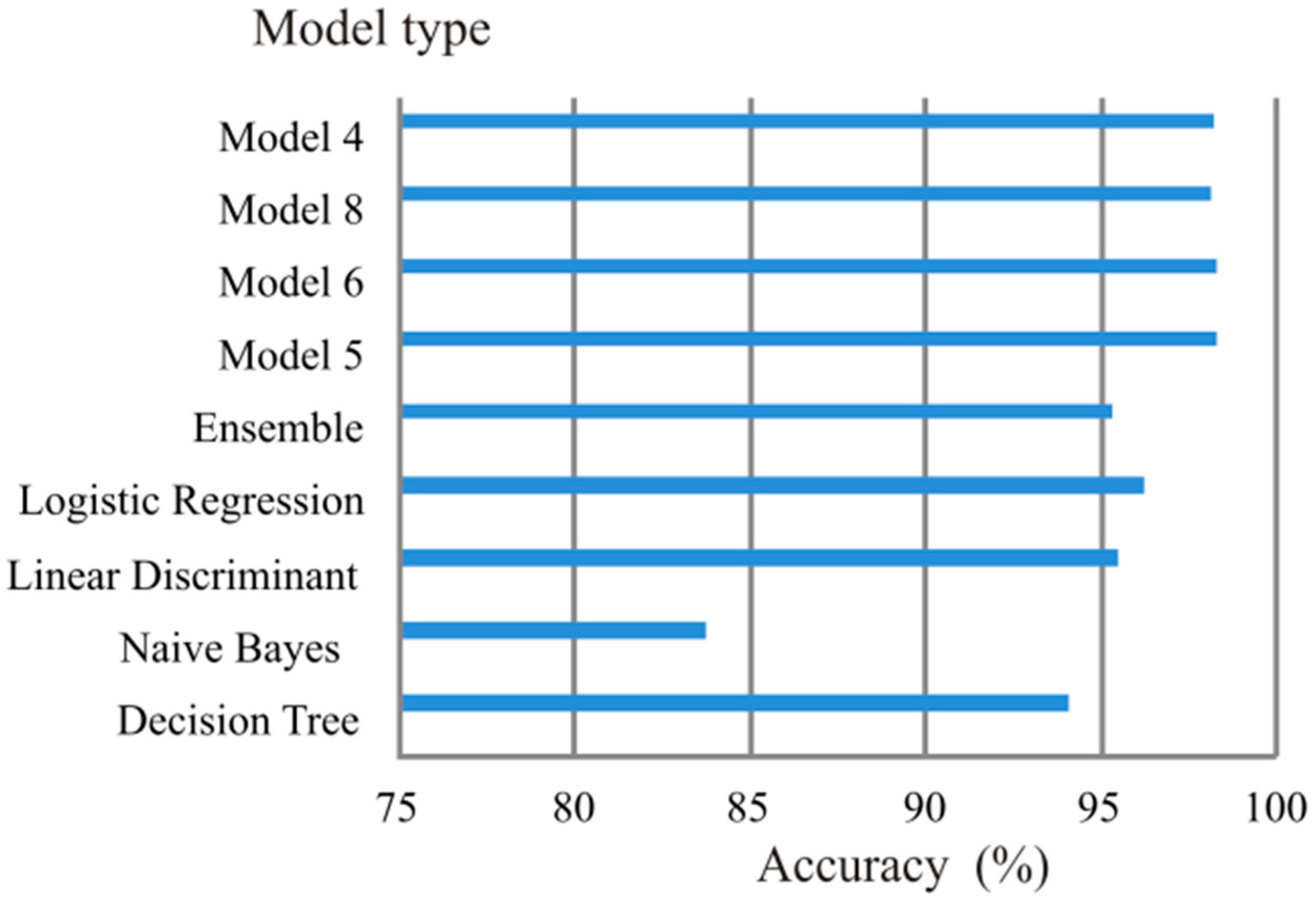
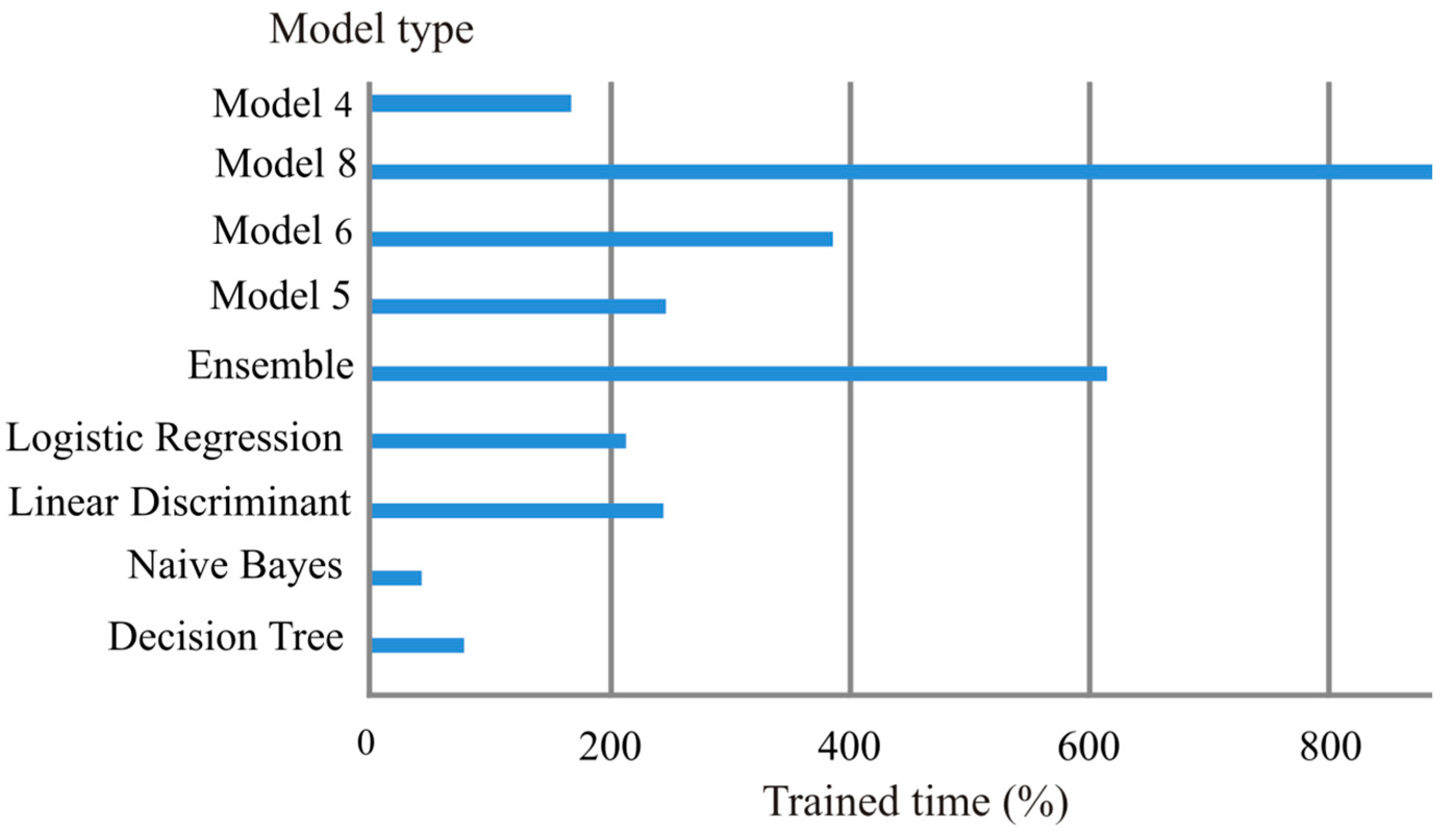
Model 1 5 ReLU - 557 48.8
Model 2 10 ReLU - 652 51.1
Model 3 20 ReLU - 712 48.9
Model 4 5 ReLU + 168 98.2
Model 5 10 ReLU + 248 98.3
Model 6 20 ReLU + 388 98.1
Model 7 5 Sigmoid + 748 97.8
Model 8 10 Sigmoid + 882 98.3
Model 9 20 Sigmoid + 906 98.2
Table 5. Performance Results Of The Well-Known Neural Network Algorithms.
Table 5. Performance Results Of The Well-Known Neural Network Algorithms.
Classification methods Characteristic parameters
Duration of training (s) Accuracy (%)
Decision Tree 80 94.1
Linear Discriminant 215 95.5
Logistic Regression 246 96.2
Naïve Bayes 45 82.7
Ensemble 615 95.3
Table 1. Numerical Results Of Data Impact Assessment.
Table 1. Numerical Results Of Data Impact Assessment.
Features Degree of data impact Features Degree of data impact
ω 2 ∞ M o 677
φ 1 ∞ c 474
m 1 ∞ ω 1 39.79
m 2 ∞ φ 2 6.37
J 1 ∞ J 2 444
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated