Submitted:
27 October 2023
Posted:
27 October 2023
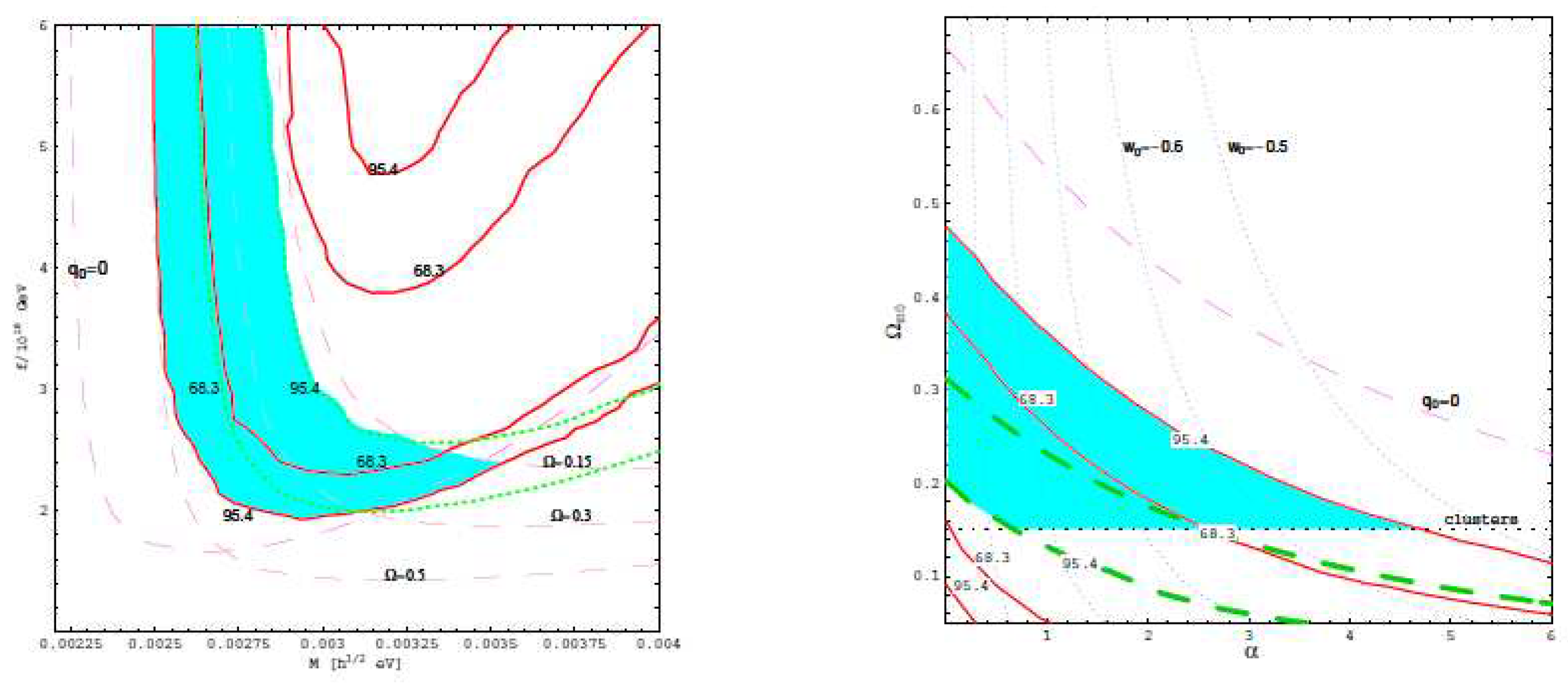
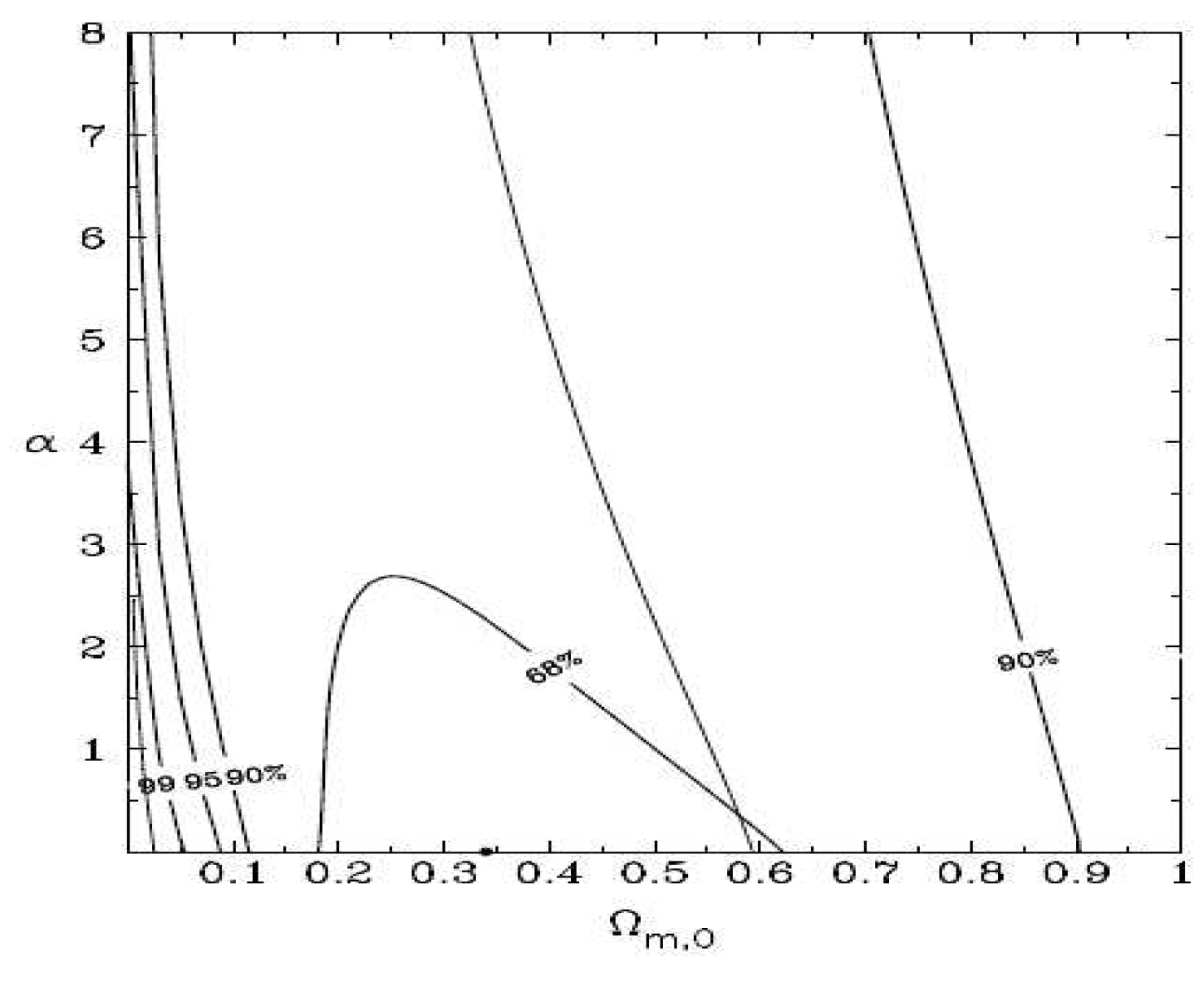
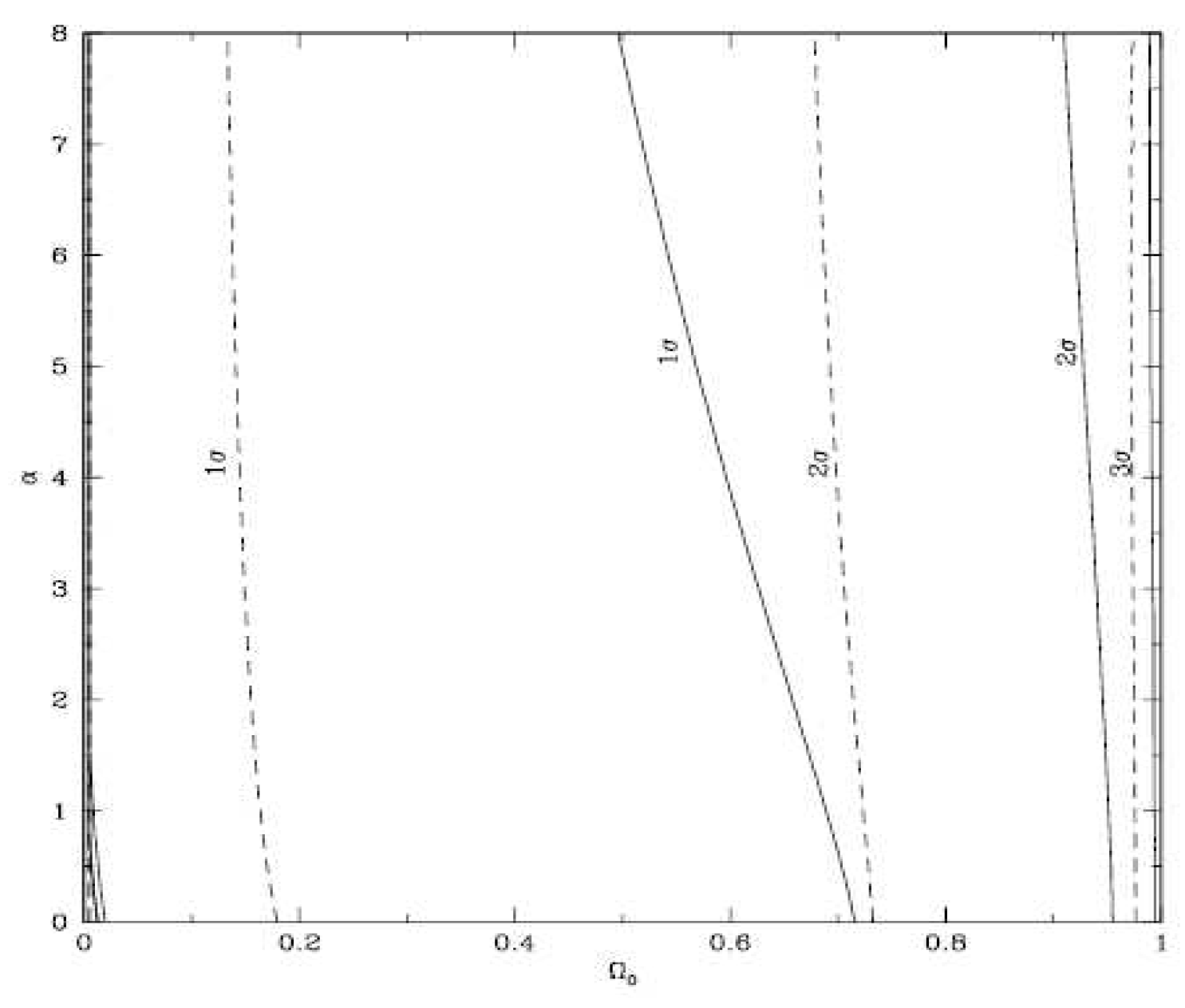
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Cosmological Dark Energy Models
2.1. CDM Model
2.2. Dynamical Dark Energy Scalar Field CDM Models
- (i)
- The EoS parameter – For quintessence fields, , while for phantom fields, .
- (ii)
- The sign of the kinetic term – For quintessence fields, the kinetic term in the Lagrangian has a positive sign, while it is negative for phantom fields.
- (iii)
- The dynamics of the scalar field – The quintessence field rolls gradually to the minimum of its potential, while the phantom field rolls to the maximum of its potential.
- (iv)
- Temporal evolution of dark energy – For quintessence fields, the dark energy density remains almost unchanging with time, while it increases for phantom fields.
- (v)
- Forecasting the future of the universe – The quintessence models predict either an eternal expansion of the universe, or a repeated collapse, depending on the spatial curvature of the universe. On the other hand, the phantom models predict the destruction of any gravitationally-related structures in the universe. Depending on the asymptotic behavior of the Hubble parameter , the future scenarios of the universe are divided into: a big rip for which for a finite future time ; a little rip for which at an infinite future time , and a pseudo rip for which for an infinite future time .
2.2.1. Quintessence Scalar Field
- a)
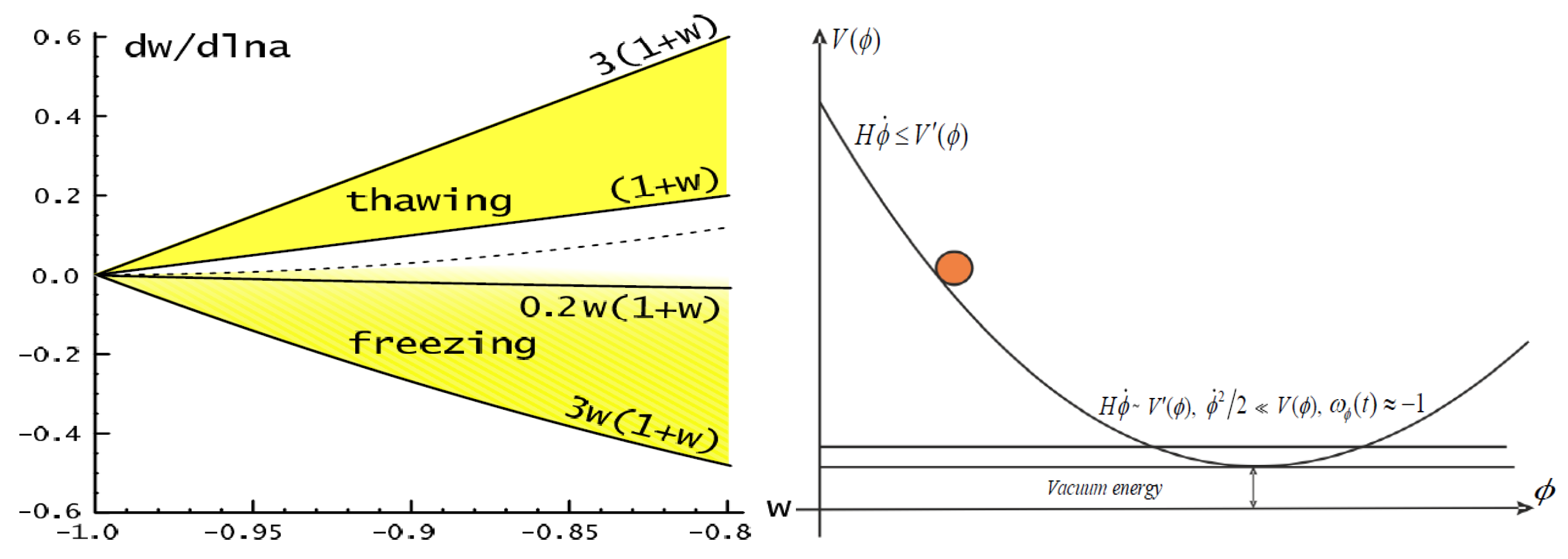
- In the thawing models, the scalar field is too suppressed by the retarding effect of the Hubble expansion, represented by the term in Equation (10), until recently. This results in a much slower evolution of the scalar field compared to the Hubble expansion, and the thawing scalar field manifests itself as the vacuum energy, with the EoS parameter . The Hubble expansion rate decreases with time, and after it falls below , the scalar field begins to roll to the minimum of its potential. The value of the EoS parameter for the scalar field thus increases over time and becomes .
- b)
- In the freezing models, the scalar field is always suppressed (it is damped), i.e., . Freezing scalar field models have so-called tracking solutions. According to tracking solutions, the quintessence component tracks the background EoS parameter (radiation in the radiation-dominated epoch and matter in the matter-dominated epoch) and eventually only recently grows to dominate the energy density in the universe. This leads to the accelerated expansion of the universe at late times, since the scalar field has a negative effective pressure. The tracker behavior allows the quintessence model to be insensitive to initial conditions. But this requires fine tuning of the potential energy, since .
2.2.2. Phantom Scalar Field
2.3. Parameterized Dark Energy Models
2.3.1. wCDM Parameterization
2.3.2. XCDM Models
2.4. Quintessential Inflation Models
2.5. Interacting Dark Energy Models
2.5.1. Coupling of the First Type
2.5.2. Coupling of the Second Type
3. Constraints From Observational Data
3.1. Type Ia Supernovae
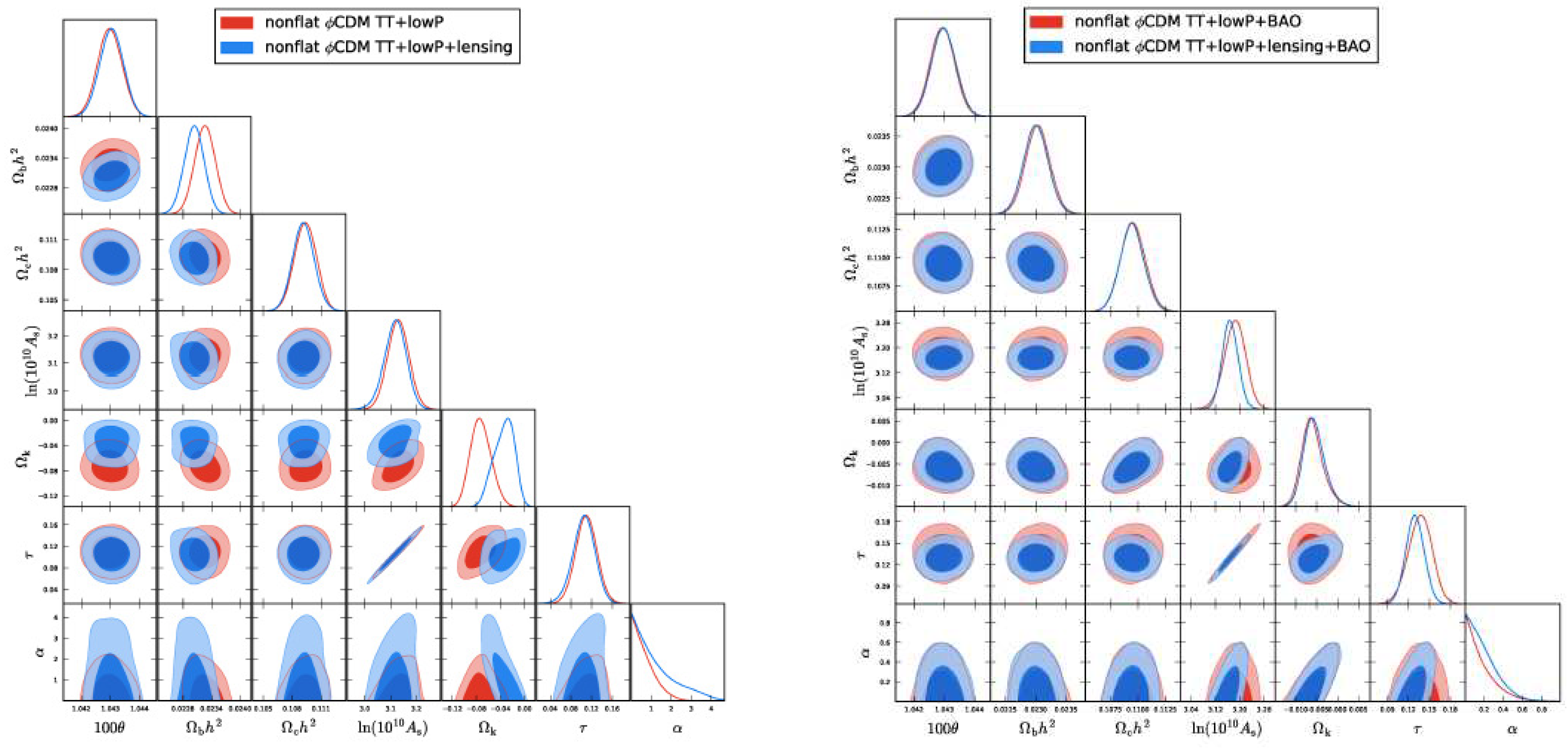
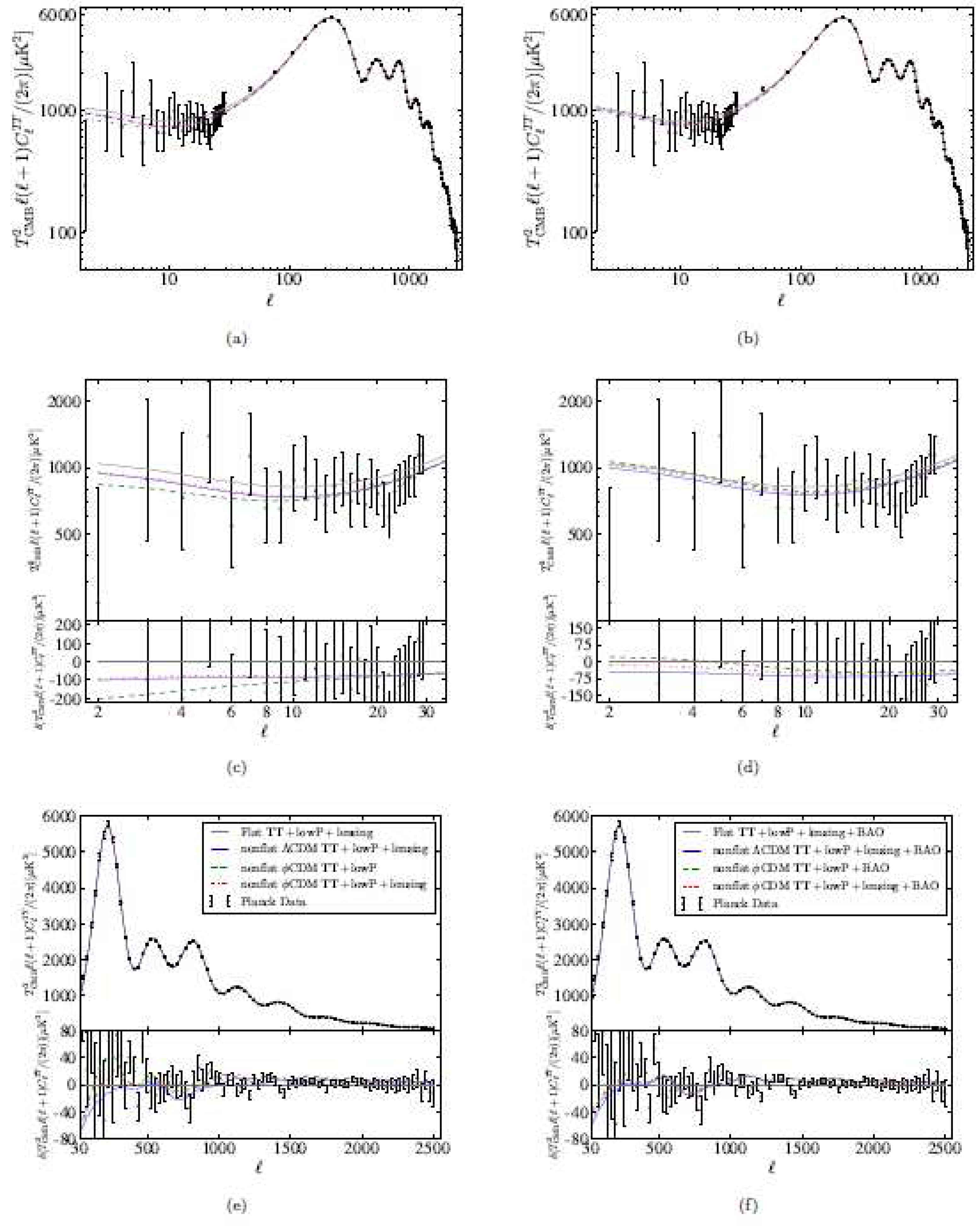
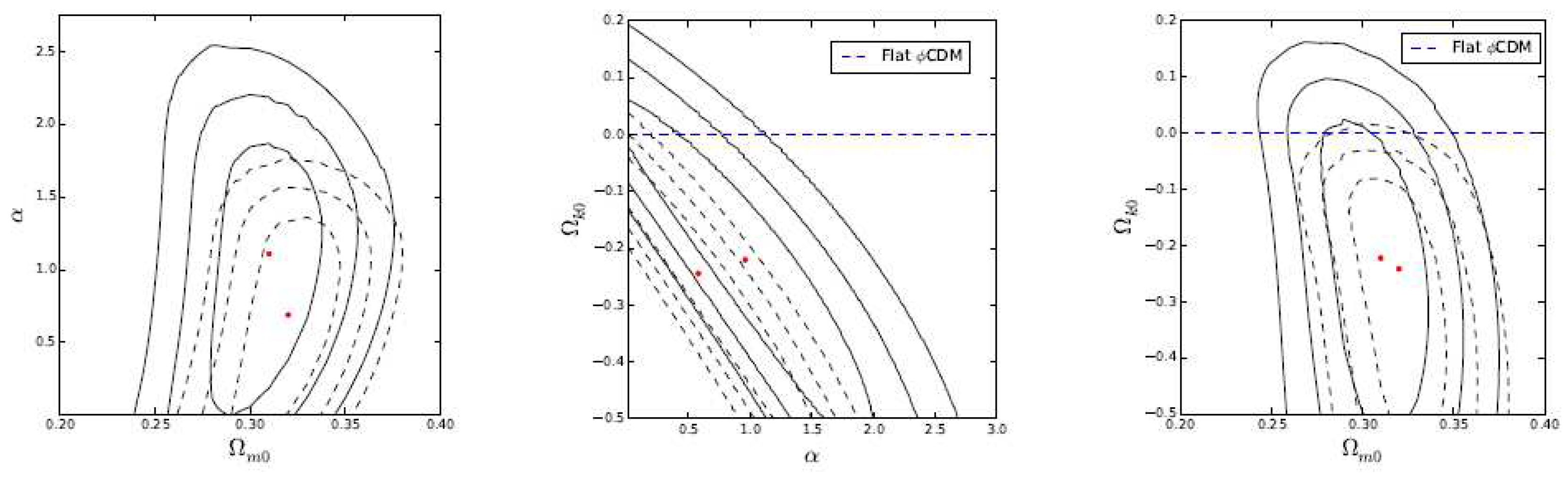
3.2. Cosmic Microwave Background Radiation Data
3.3. Large Scale Structure Growth Rate Data
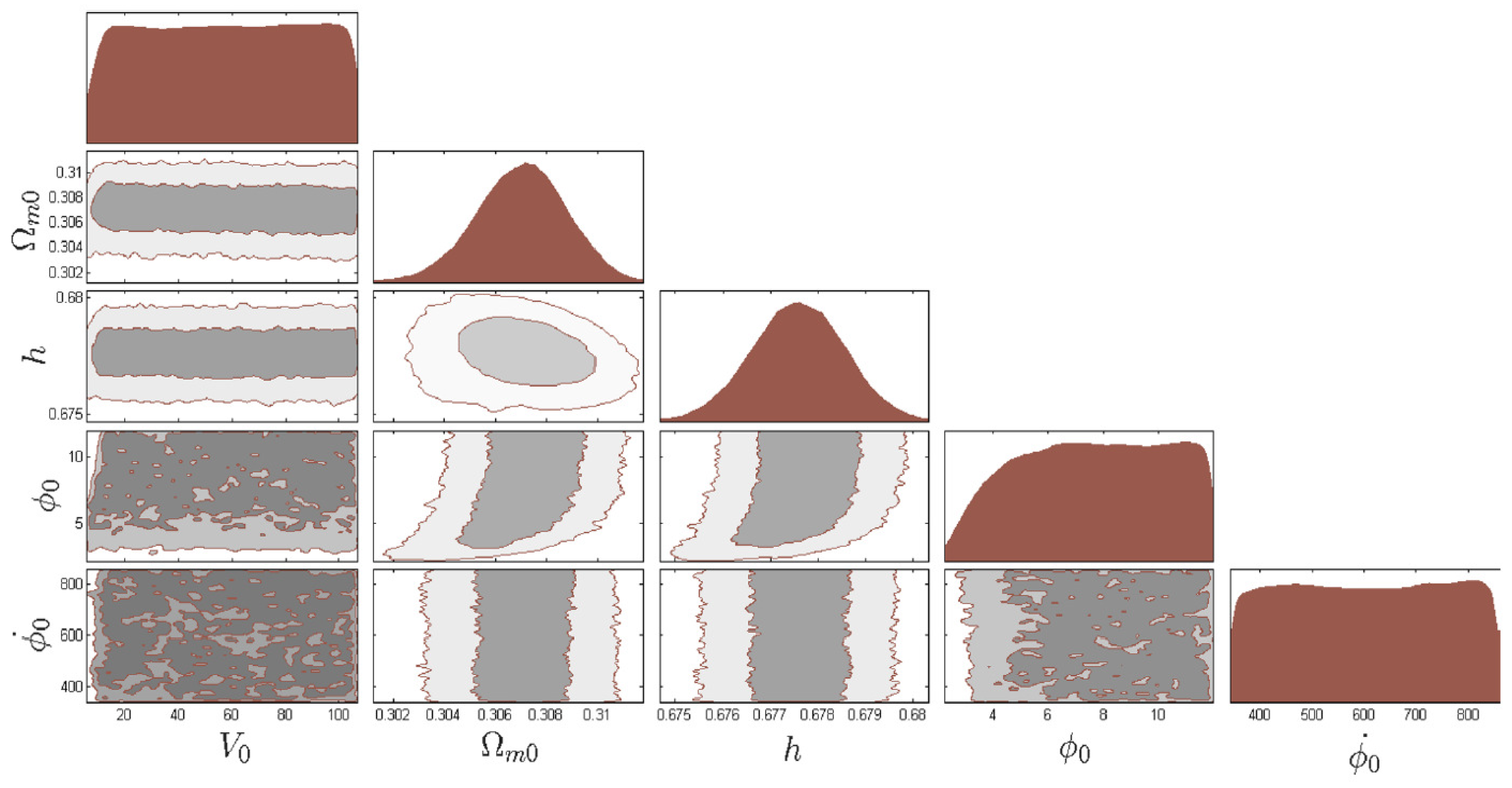
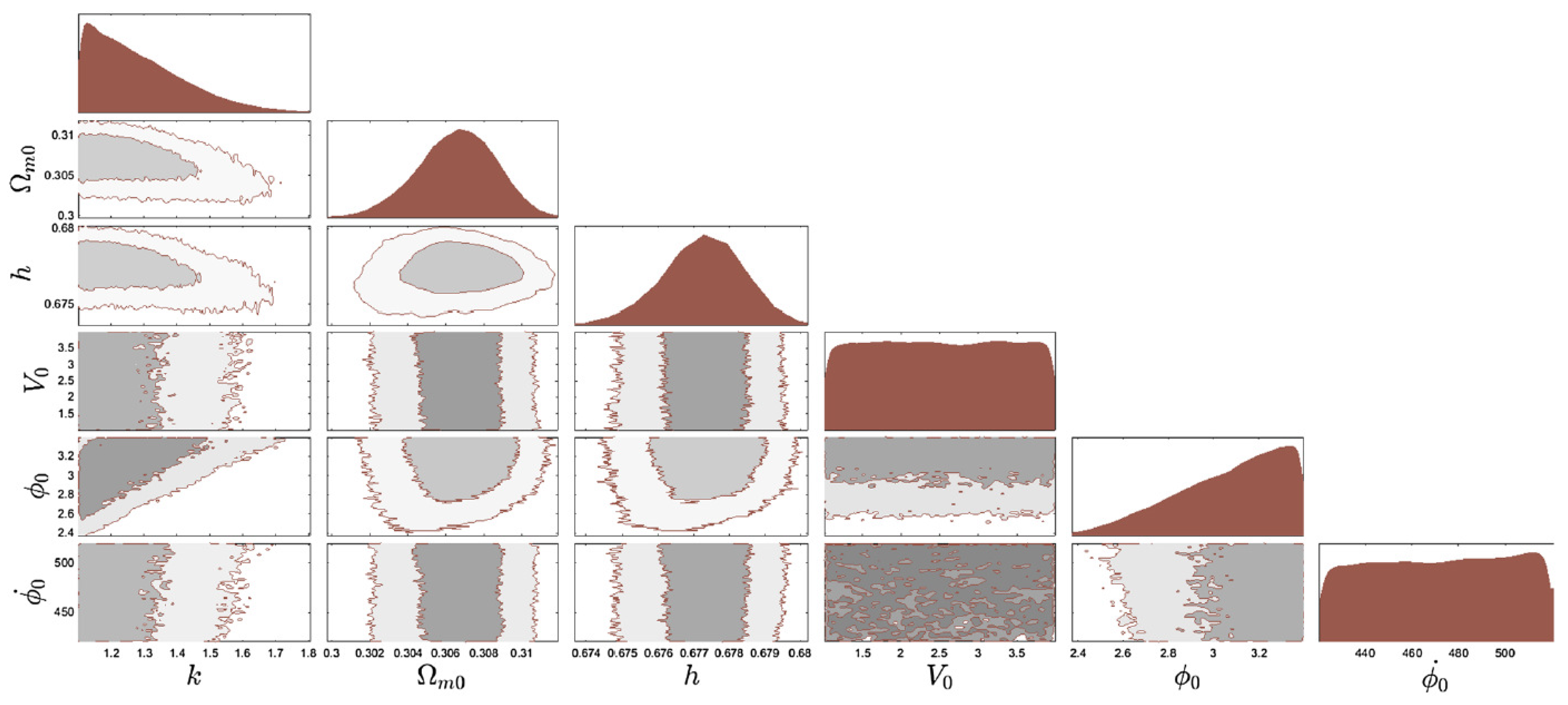
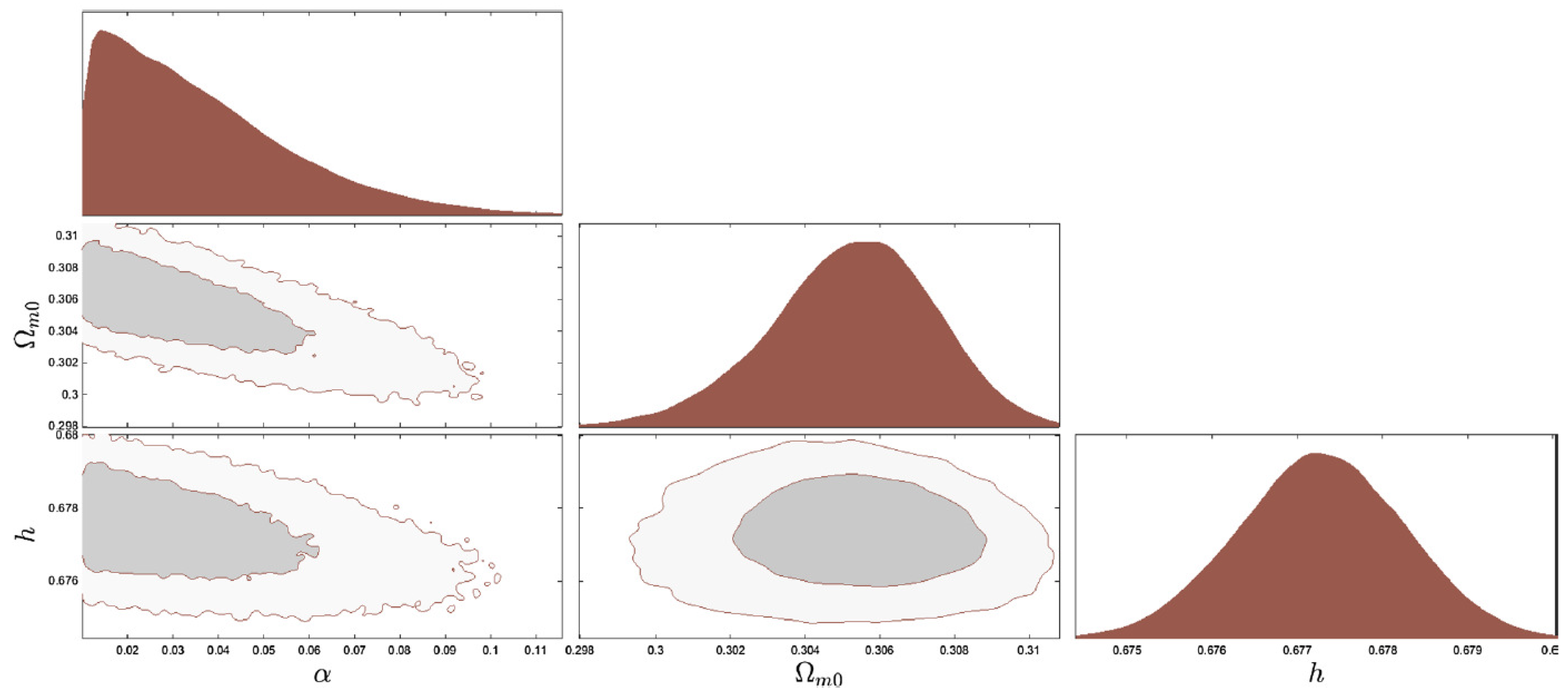
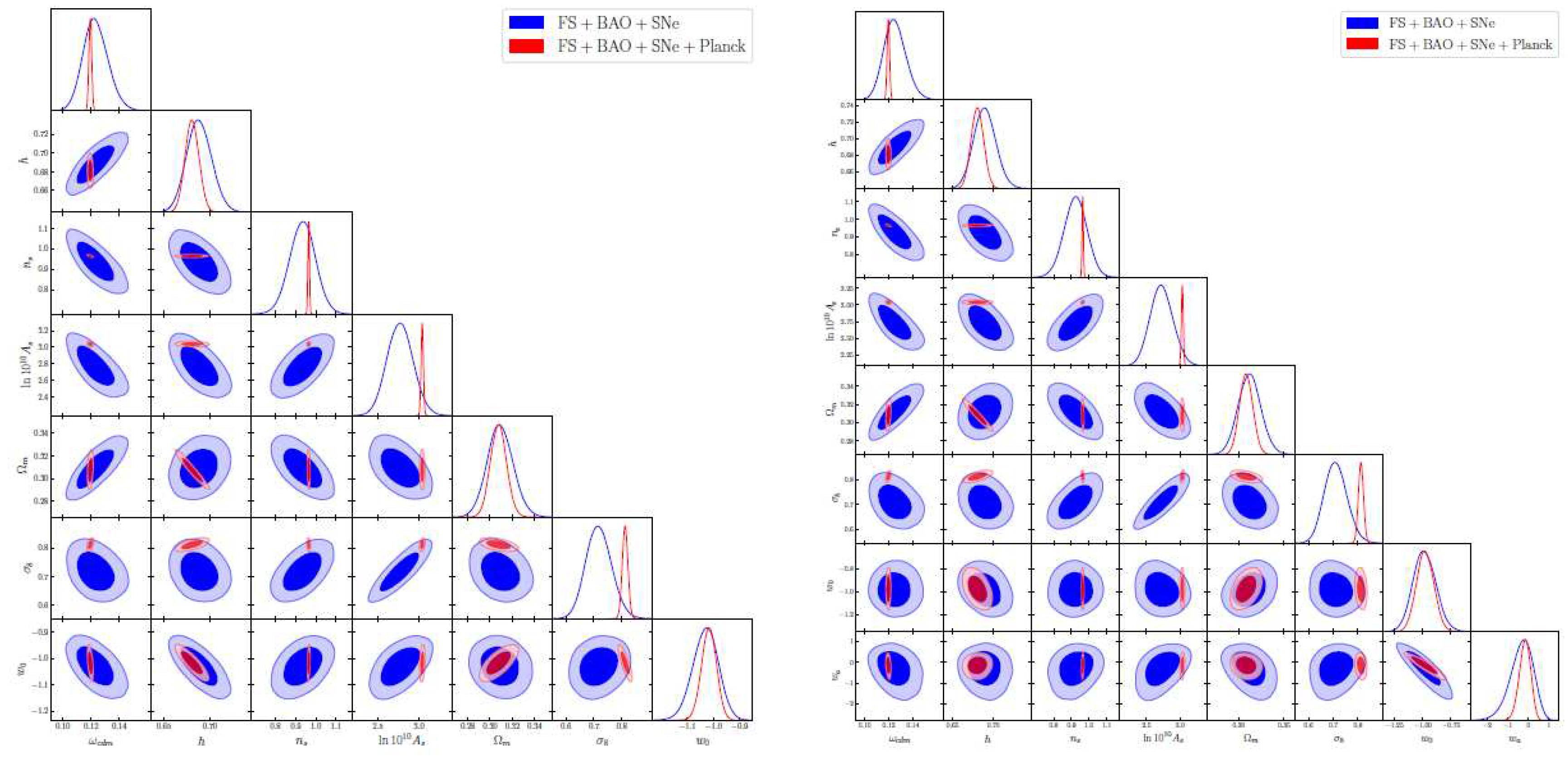
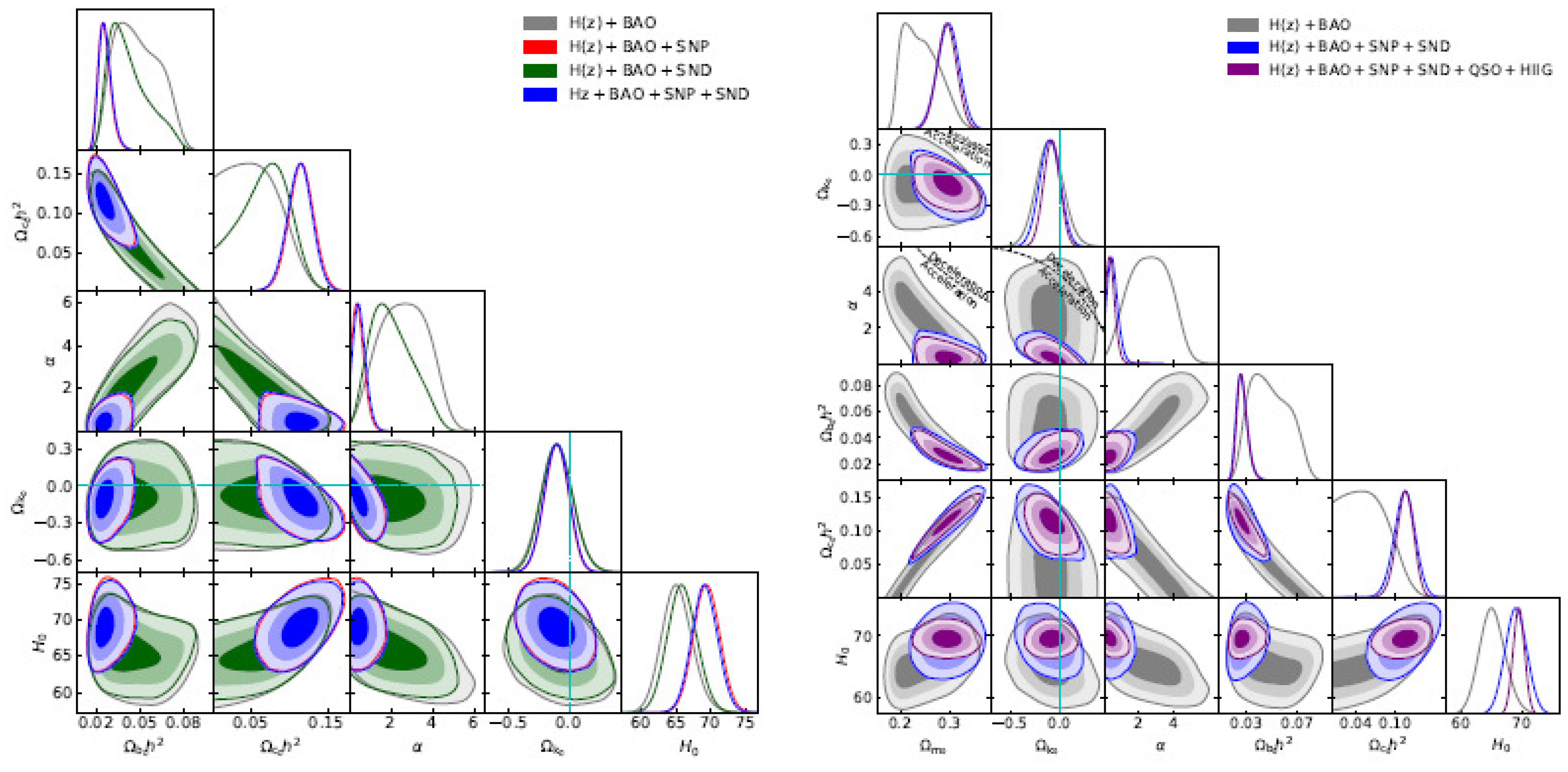
3.4. Baryon Acoustic Oscillations Data
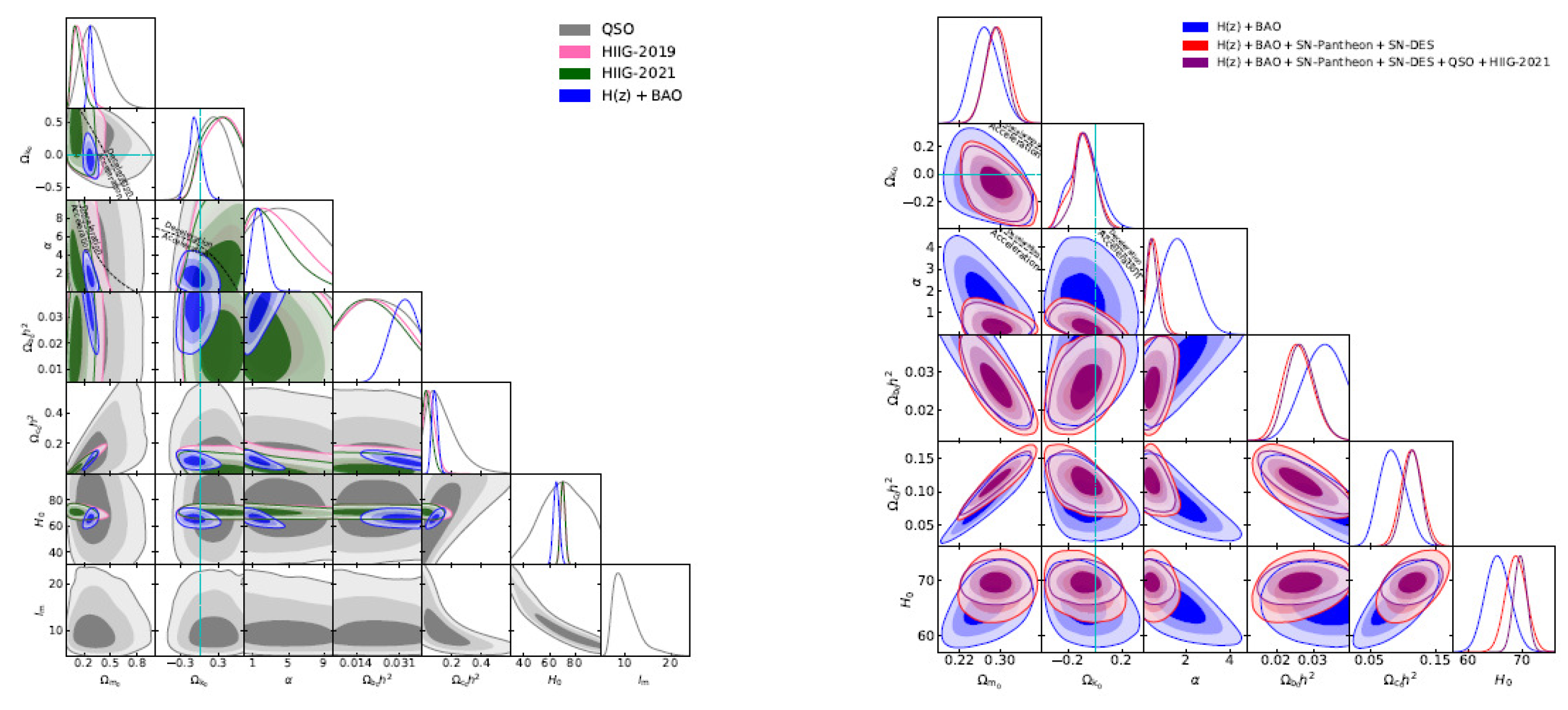
3.5. Hubble Parameter Data
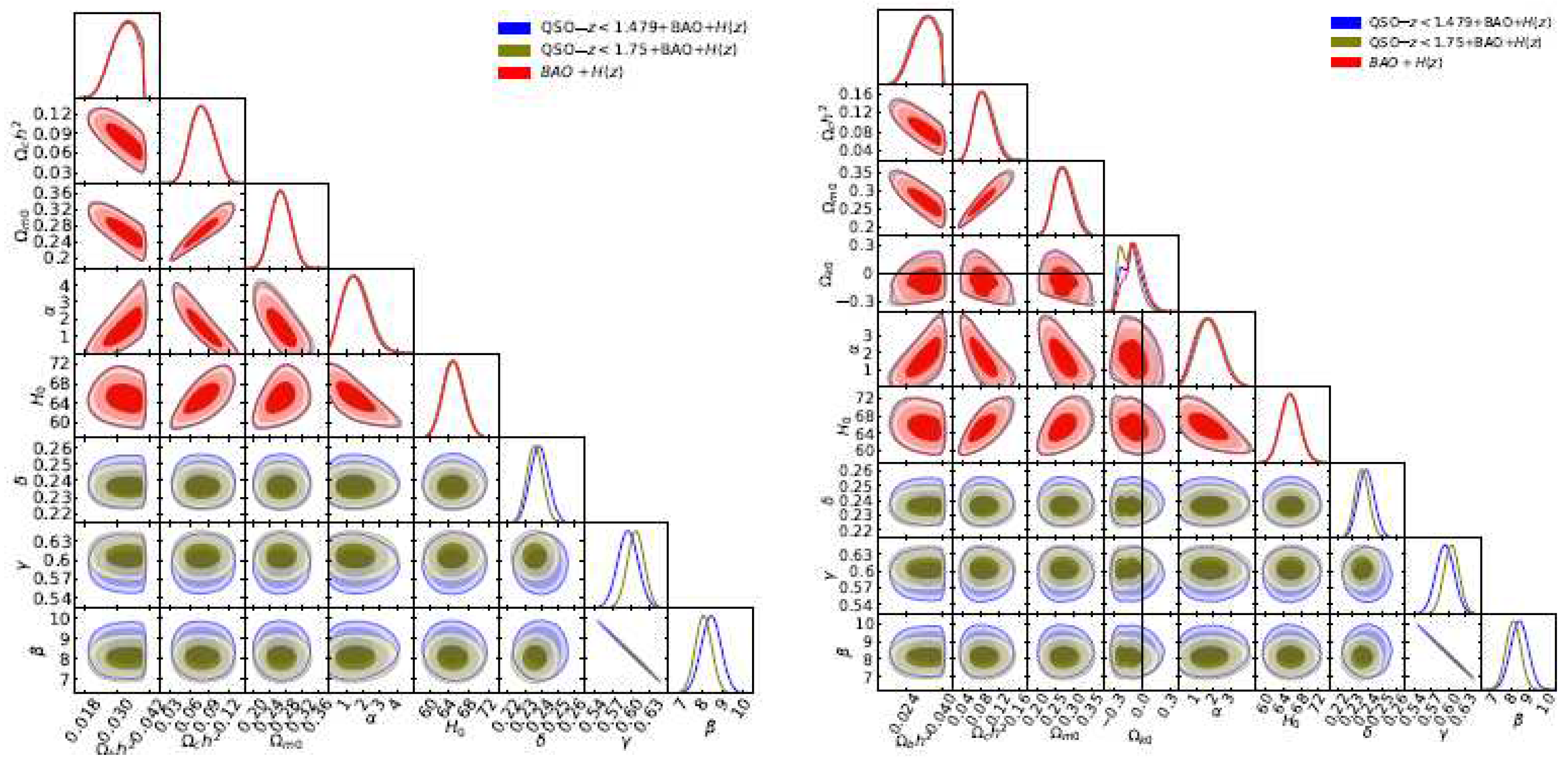
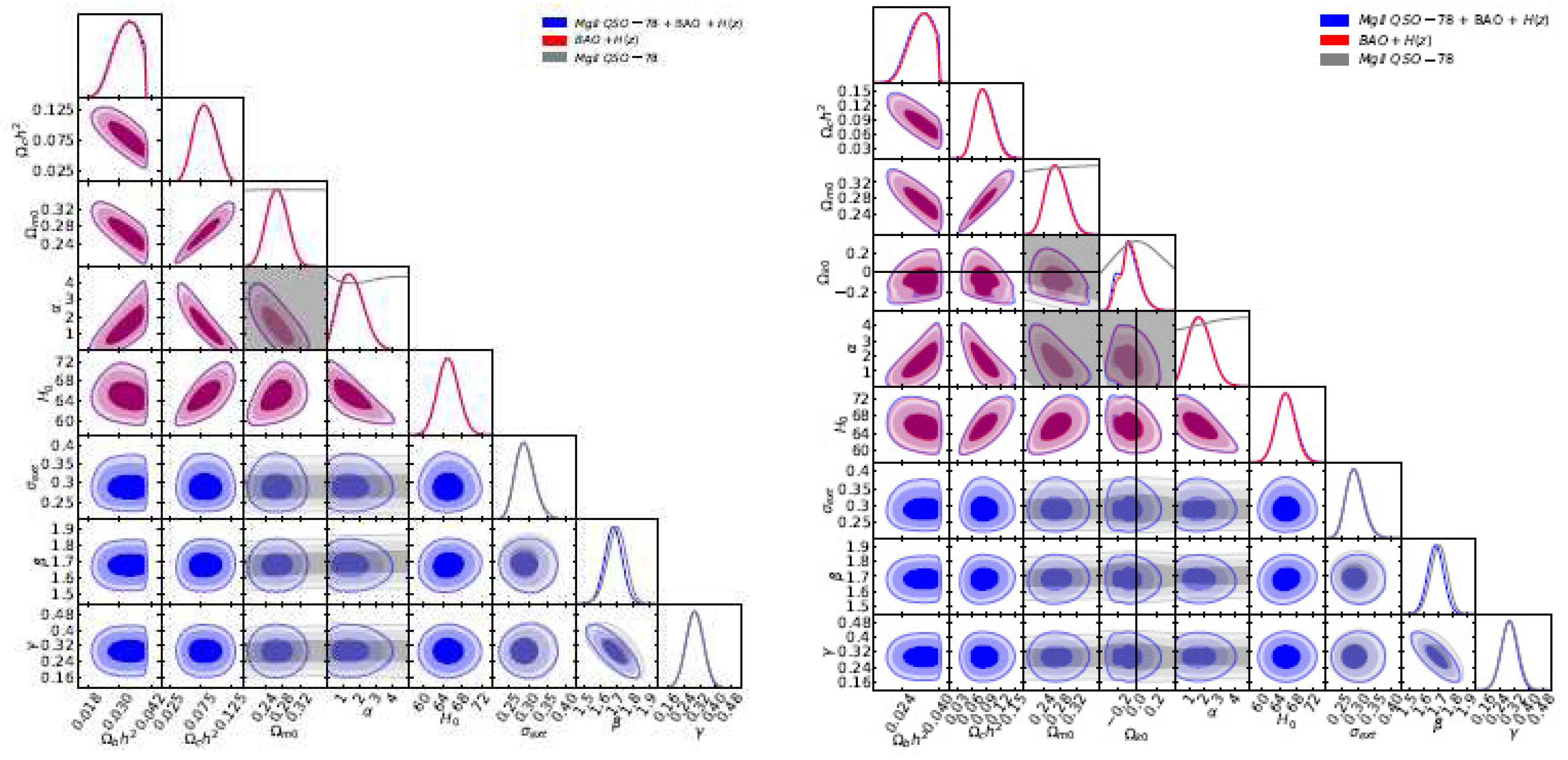
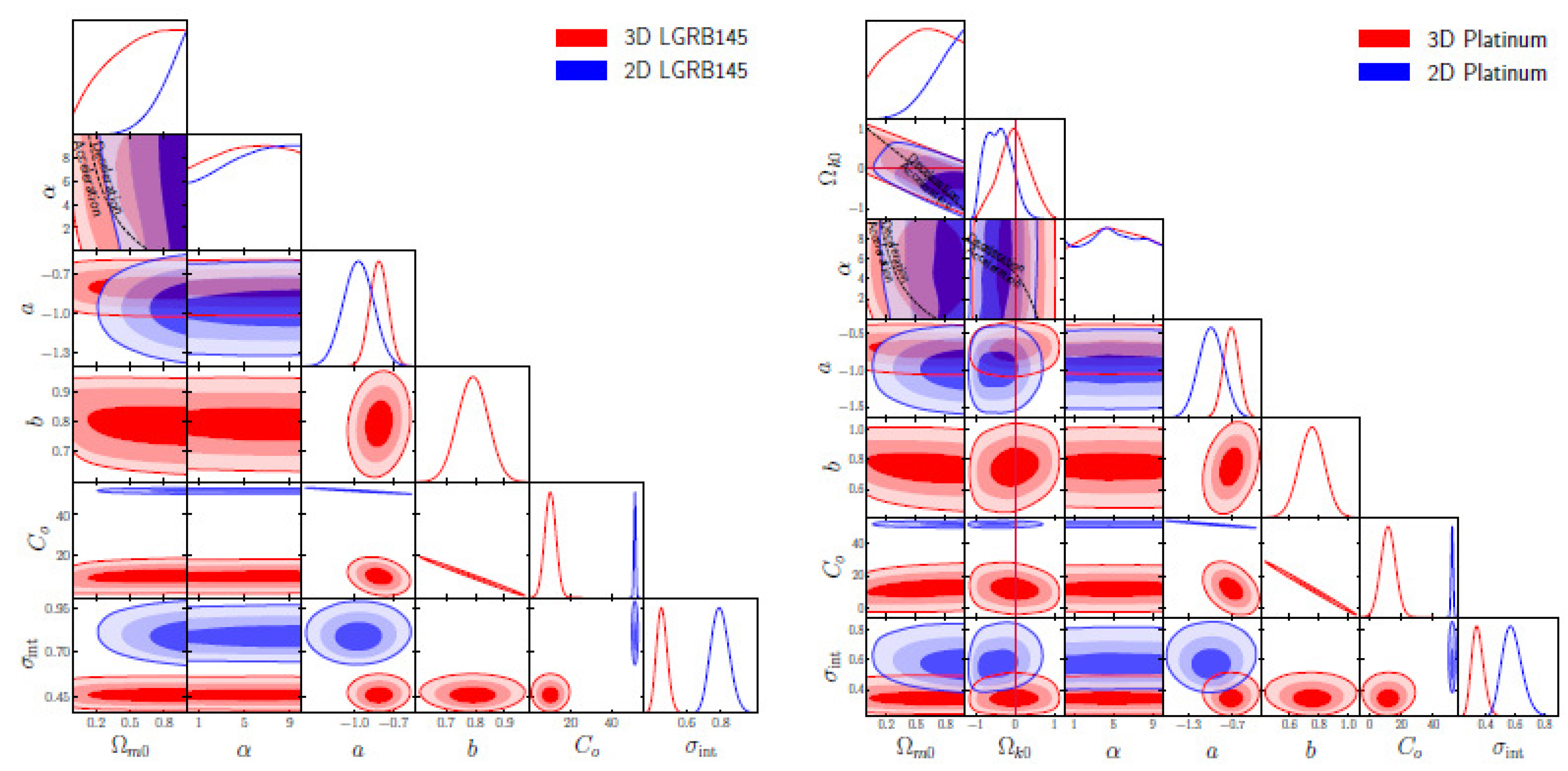
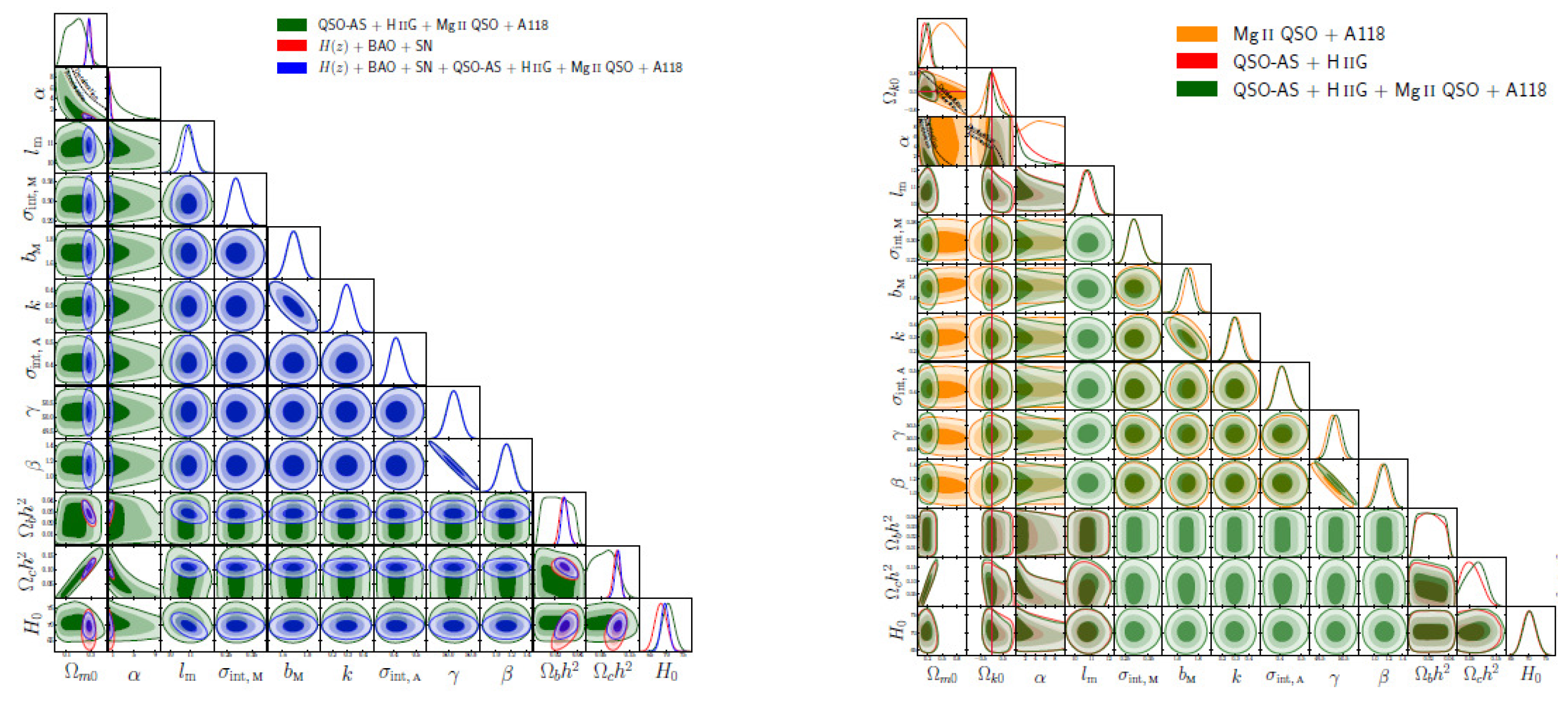
3.6. Quasar Angular Size Data
3.7. Gamma Ray Burst Distances Data
3.8. Starburst Galaxy Data
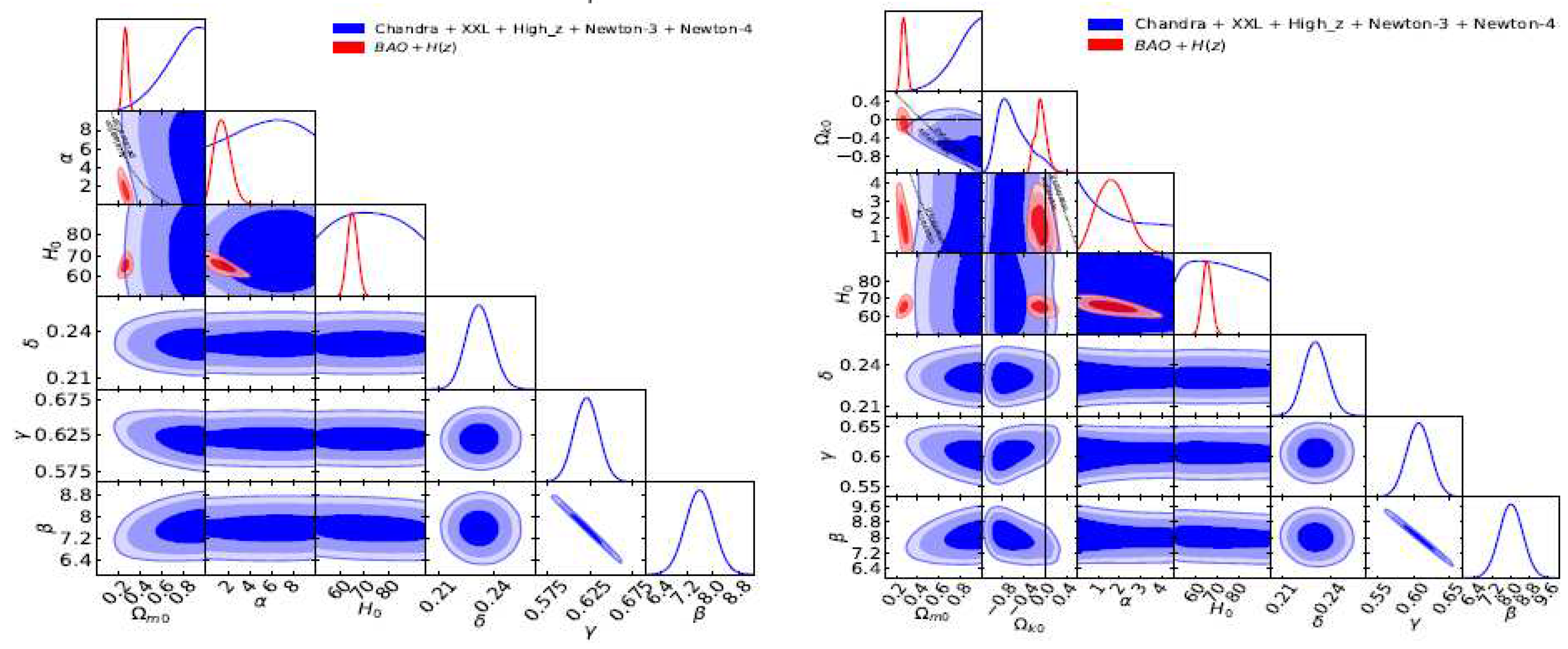
3.9. X-Ray Gas Mass Fraction of Clusters Data
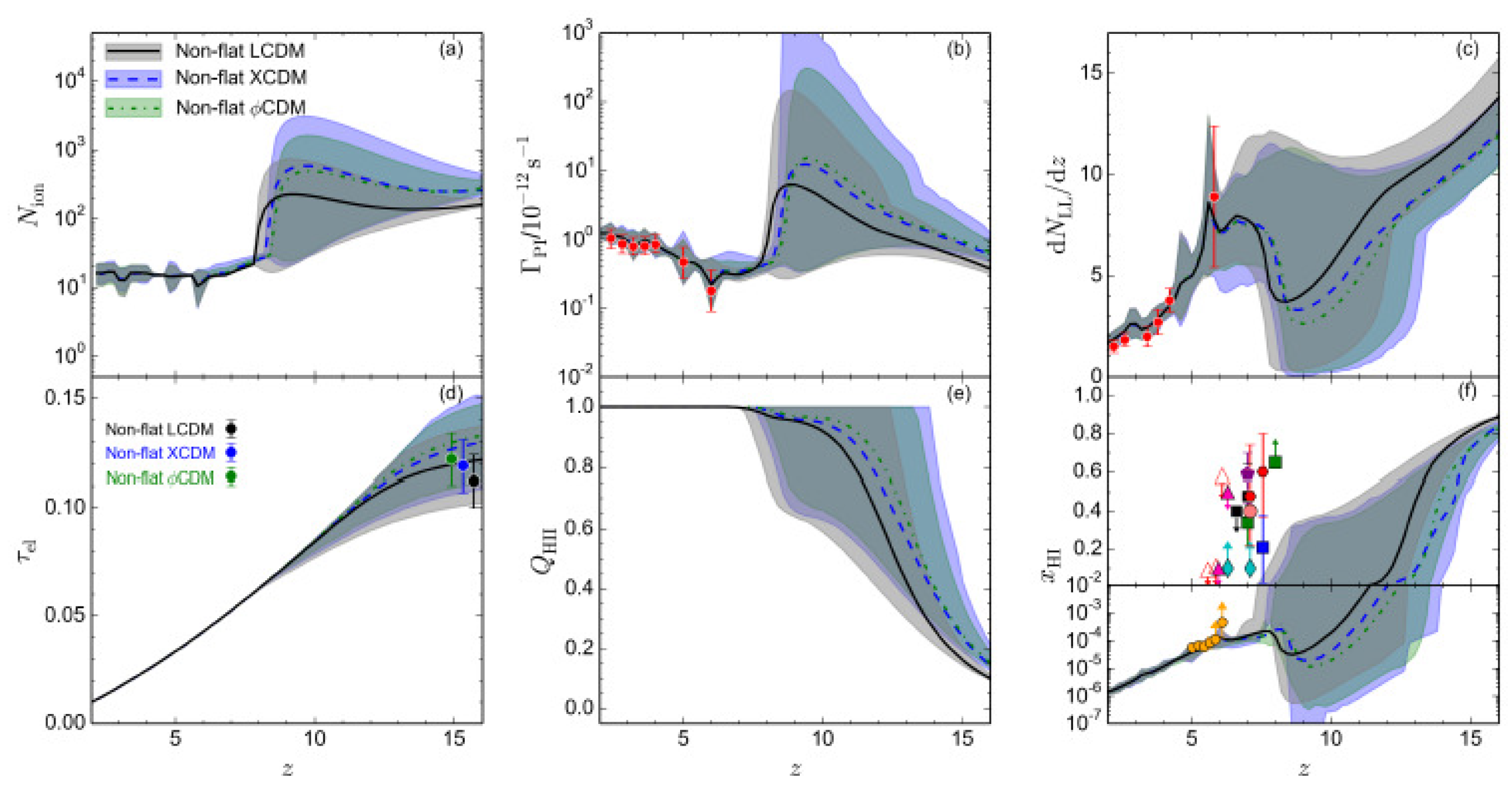
3.10. Reionization Data
3.11. Gravitational Lensing Data
3.12. Compact Radio Sources Data
4. Discussion and Conclusions
Acknowledgments
References
- A. G. Riess, A. V. Filippenko, P. Challis, A. Clocchiatti, A. Diercks, P. M. Garnavich, R. L. Gilliland, C. J. Hogan, S. Jha, R. P. Kirshner, et al., Astron. J. 116, 1009 (1998).
- S. Perlmutter, G. Aldering, G. Goldhaber, R. A. Knop, P. Nugent, P. G. Castro, S. Deustua, S. Fabbro, A. Goobar, D. E. Groom, et al., Astrophys. J 517, 565 (1999).
- A. G. Riess, L.-G. Strolger, S. Casertano, H. C. Ferguson, B. Mobasher, B. Gold, P. J. Challis, A. V. Filippenko, S. Jha, W. Li, et al., Astrophys. J 659, 98 (2007).
- G. F. Smoot, C. L. Bennett, A. Kogut, E. Wright, J. Aymon, N. Boggess, E. Cheng, G. De Amici, S. Gulkis, M. Hauser, et al., Astrophys. J 396, L1 (1992).
- C. L. Bennett, A. Banday, K. M. Gorski, G. Hinshaw, P. Jackson, P. Keegstra, A. Kogut, G. F. Smoot, D. T. Wilkinson, and E. L. Wright, Astrophys. J. Lett. 464, L1 (1996).
- D. N. Spergel, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, et al., The Astrophysical Journal Supplement Series 148, 175 (2003).
- D. N. Spergel, R. Bean, O. Doré, M. R. Nolta, C. L. Bennett, J. Dunkley, G. Hinshaw, N. Jarosik, E. Komatsu, L. Page, et al., Astrophys. J. Suppl. 170, 377 (2007).
- G. Hinshaw, J. L. Weiland, R. S. Hill, N. Odegard, D. Larson, C. L. Bennett, J. Dunkley, B. Gold, M. R. Greason, N. Jarosik, et al., Astrophys. J. Suppl. 180, 225 (2009).
- M. R. Nolta, J. Dunkley, R. S. Hill, G. Hinshaw, E. Komatsu, D. Larson, L. Page, D. N. Spergel, C. L. Bennett, B. Gold, et al., Astrophys. J. Suppl. 1, 296 (2009).
- E. Komatsu, K. M. Smith, J. Dunkley, C. L. Bennett, B. Gold, G. Hinshaw, N. Jarosik, D. Larson, M. R. Nolta, L. Page, et al., Astrophys. J. Suppl. 192, 18 (2011).
- Planck Collaboration, P. A. R. Ade, N. Aghanim, C. Armitage-Caplan, M. Arnaud, M. Ashdown, F. Atrio-Barandela, J. Aumont, C. Baccigalupi, A. J. Banday, et al., Astron. Astrophys. 571, A16 (2014).
- Planck Collaboration, P. A. R. Ade, N. Aghanim, M. Arnaud, M. Ashdown, J. Aumont, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, et al., Astron. Astrophys. 594, A13 (2016).
- Planck Collaboration, N. Aghanim, Y. Akrami, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A. J. Banday, R. B. Barreiro, N. Bartolo, et al., Astron. Astrophys. 641, A6 (2020).
- SDSS, http://www.sdss.org/ (2000).
- S. Dodelson, V. K. Narayanan, M. Tegmark, R. Scranton, T. Budavári, A. Connolly, I. Csabai, D. Eisenstein, J. A. Frieman, J. E. Gunn, et al., Astrophys. J 572, 140 (2002).
- 2dFGRS, http://www.mso.anu.edu.au/2dFGRS/ (2002).
- W. J. Percival, S. Cole, D. J. Eisenstein, R. C. Nichol, J. A. Peacock, A. C. Pope, and A. S. Szalay, Mon. Not. Roy. Astron. Soc. 381, 1053 (2007).
- DES, https://www.darkenergysurvey.org/ (2013).
- J. Kwan, C. Sánchez, J. Clampitt, J. Blazek, M. Crocce, B. Jain, J. Zuntz, A. Amara, M. R. Becker, G. M. Bernstein, et al., Mon. Not. Roy. Astron. Soc. 464, 4045 (2017).
- D. J. Eisenstein, I. Zehavi, D. W. Hogg, R. Scoccimarro, M. R. Blanton, R. C. Nichol, R. Scranton, H.-J. Seo, M. Tegmark, Z. Zheng, et al., Astrophys. J 633, 560 (2005).
- C. Blake, E. A. Kazin, F. Beutler, T. M. Davis, D. Parkinson, S. Brough, M. Colless, C. Contreras, W. Couch, S. Croom, et al., Mon. Not. Roy. Astron. Soc. 418, 1707 (2011).
- F. Beutler, C. Blake, M. Colless, D. H. Jones, L. Staveley-Smith, L. Campbell, Q. Parker, W. Saunders, and F. Watson, Mon. Not. Roy. Astron. Soc. 416, 3017 (2011).
- L. Anderson, É. Aubourg, S. Bailey, F. Beutler, V. Bhardwaj, M. Blanton, A. S. Bolton, J. Brinkmann, J. R. Brownstein, A. Burden, et al., Mon. Not. Roy. Astron. Soc. 441, 24 (2014).
- A. J. Ross, L. Samushia, C. Howlett, W. J. Percival, A. Burden, and M. Manera, Mon. Not. Roy. Astron. Soc. 449, 835 (2015).
- S. Alam, M. Ata, S. Bailey, F. Beutler, D. Bizyaev, J. A. Blazek, A. S. Bolton, J. R. Brownstein, A. Burden, C.-H. Chuang, et al., Mon. Not. Roy. Astron. Soc. 470, 2617 (2017).
- M. Ata, F. Baumgarten, J. Bautista, F. Beutler, D. Bizyaev, M. R. Blanton, J. A. Blazek, A. S. Bolton, J. Brinkmann, J. R. Brownstein, et al., Mon. Not. Roy. Astron. Soc. 473, 4773 (2018).
- HST, https://www.stsci.edu/hst (1990).
- D. Stern, R. Jimenez, L. Verde, M. Kamionkowski, and S. A. Stanford, JCAP 02, 008 (2010).
- A. G. Riess, L. Macri, S. Casertano, H. Lampeitl, H. C. Ferguson, A. V. Filippenko, S. W. Jha, W. Li, and R. Chornock, Astrophys. J 730, 119 (2011).
- M. Moresco, L. Verde, L. Pozzetti, R. Jimenez, and A. Cimatti, JCAP 07, 053 (2012).
- C. Zhang, H. Zhang, S. Yuan, S. Liu, T.-J. Zhang, and Y.-C. Sun, Research in Astronomy and Astrophysics 14 (2014).
- T. Delubac, J. E. Bautista, N. G. Busca, J. Rich, D. Kirkby, S. Bailey, A. Font-Ribera, A. Slosar, K.-G. Lee, M. M. Pieri, et al., Astron. Astrophys. 574, A59 (2015).
- M. Moresco, Mon. Not. Roy. Astron. Soc. 450, L16 (2015).
- M. Moresco, L. Pozzetti, A. Cimatti, R. Jimenez, C. Maraston, L. Verde, D. Thomas, A. Citro, R. Tojeiro, and D. Wilkinson, JCAP 05, 014 (2016).
- A. L. Ratsimbazafy, S. I. Loubser, S. M. Crawford, C. M. Cress, B. A. Bassett, R. C. Nichol, and P. Väisänen, Mon. Not. Roy. Astron. Soc. 467, 3239 (2017).
- P. J. E. Peebles and B. Ratra, Rev. Mod. Phys. 75, 559 (2003).
- E. J. Copeland, M. Sami, and S. Tsujikawa, Int. J. Mod. Phys. D15, 1753 (2006).
- J. Frieman, M. Turner, and D. Huterer, Ann. Rev. Astron. Astrophys. 46, 385 (2008).
- R. R. Caldwell and M. Kamionkowski, Ann. Rev. Nucl. Part. Sci. 59, 397 (2009).
- S. Tsujikawa, Lect. Notes Phys. 800, 99 (2010).
- S. Tsujikawa, arXiv:1004.1493 (2010).
- D. H. Weinberg, M. J. Mortonson, D. J. Eisenstein, C. Hirata, A. G. Riess, and E. Rozo, Phys. Rept. 530, 87 (2013).
- J. Yoo and Y. Watanabe, Int. J. Mod. Phys. D21, 1230002 (2012).
- V. C. Rubin, N. Thonnard, and W. K. Ford, Jr., Astrophys. J. 238, 471 (1980).
- V. A. Rubakov, Proceedings, 2011 European School of High-Energy Physics ESHEP 2011): Cheile Gradistei, Romania, September 7-20, 2011 pp. 151–195 (2014).
- M. Tristram, A. J. Banday, M. Douspis, X. Garrido, K. M. Górski, S. Henrot-Versillé, S. Ilić, R. Keskitalo, G. Lagache, C. R. Lawrence, et al., arXiv:2309.10034 (2023).
- A. Silvestri and M. Trodden, Rept. Prog. Phys. 72, 096901 (2009).
- M. Lopez-Corredoira, arXiv:2307.10606 (2023).
- P. J. E. Peebles, Principles of physical cosmology (Univ. Pr., Princeton, USA, 1994).
- S. Weinberg, Cosmology (Oxford Univ. Pr., Oxford, UK, 2008).
- S. Dodelson and F. Schmidt, Modern cosmology (Academic Press is an imprint of Elsevier, London, UK, 2021).
- D. Baumann, Cosmology (Cambridge University Press, 2022).
- D. Huterer, A Course in Cosmology (Cambridge University Press, 2023).
- S. M. Carroll, W. H. Press, and E. L. Turner, Annu. Rev. Astro. Astrophys. 30, 499 (1992).
- S. M. Carroll, Living Rev. Rel. 4, 1 (2001).
- E. J. Copeland, M. Sami, and S. Tsujikawa, Int. J. Mod. Phys. D15, 1753 (2006).
- J. Martin, Comptes Rendus Physique 13, 566 (2012).
- A. Padilla, arXiv:1502.05296 (2015).
- N. Deruelle and J.-P. Uzan, Relativity in Modern Physics, Oxford Graduate Texts (Oxford University Press, 2018).
- S. Weinberg, Rev. Mod. Phys. 61, 1 (1989).
- S. Weinberg, Sources and detection of dark matter and dark energy in the universe. Proceedings, 4th International Symposium, DM 2000, Marina del Rey, USA, February 23-25, 2000 pp. 18–26 (2000).
- T. Padmanabhan, Phys. Rept. 380, 235 (2003).
- E. Di Valentino, Universe 8, 399 (2022).
- E. Abdalla, G. F. Abellán, A. Aboubrahim, A. Agnello, Ö. Akarsu, Y. Akrami, G. Alestas, D. Aloni, L. Amendola, L. A. Anchordoqui, et al., Journal of High Energy Astrophysics 34, 49 (2022).
- P. J. E. Peebles, Annals Phys. 447, 169159 (2022).
- E. Di Valentino, O. Mena, S. Pan, L. Visinelli, W. Yang, A. Melchiorri, D. F. Mota, A. G. Riess, and J. Silk, Class. Quant. Grav. 38, 153001 (2021).
- A. Bernui, E. Di Valentino, W. Giarè, S. Kumar, and R. C. Nunes, Phys. Rev. D 107, 103531 (2023).
- F. Niedermann and M. S. Sloth, arXiv:2307.03481 (2023).
- H. B. Benaoum, L. Á. García, and L. Castañeda, arXiv:2307.05917 (2023).
- G. A. Hoerning, R. G. Landim, L. O. Ponte, R. P. Rolim, F. B. Abdalla, and E. Abdalla, arXiv:2308.05807 (2023).
- J.-J. Wei and F. Melia, Astrophys. J 955, 101 (2023).
- T. L. Smith and V. Poulin, arXiv:2309.03265 (2023).
- E. M. Teixeira, R. Daniel, N. Frusciante, and C. van de Bruck, arXiv:2309.06544 (2023).
- M. Raveri, arXiv:2309.06795 (2023).
- T. Kodama, T. Shinohara, and T. Takahashi, arXiv:2309.11272 (2023).
- S. Aiola, E. Calabrese, L. Maurin, S. Naess, B. L. Schmitt, M. H. Abitbol, G. E. Addison, P. A. R. Ade, D. Alonso, M. Amiri, et al., JCAP 2020, 047 (2020).
- A. G. Riess, L. M. Macri, S. L. Hoffmann, D. Scolnic, S. Casertano, A. V. Filippenko, B. E. Tucker, M. J. Reid, D. O. Jones, J. M. Silverman, et al., Astrophys. J 826, 56 (2016).
- V. Bonvin, F. Courbin, S. H. Suyu, P. J. Marshall, C. E. Rusu, D. Sluse, M. Tewes, K. C. Wong, T. Collett, C. D. Fassnacht, et al., Mon. Not. Roy. Astron. Soc. 465, 4914 (2017).
- A. G. Riess, S. A. Rodney, D. M. Scolnic, D. L. Shafer, L.-G. Strolger, H. C. Ferguson, M. Postman, O. Graur, D. Maoz, S. W. Jha, et al., Astrophys. J 853, 126 (2018).
- S. Birrer, T. Treu, C. E. Rusu, V. Bonvin, C. D. Fassnacht, J. H. H. Chan, A. Agnello, A. J. Shajib, G. C. F. Chen, M. Auger, et al., Mon. Not. Roy. Astron. Soc. 484, 4726 (2019).
- A. G. Riess, S. Casertano, W. Yuan, L. M. Macri, and D. Scolnic, Astrophys. J. 876, 85 (2019).
- A. G. Riess, S. Casertano, W. Yuan, J. B. Bowers, L. Macri, J. C. Zinn, and D. Scolnic, Astrophys. J. Lett. 908, L6 (2021).
- S. Joudaki, C. Blake, C. Heymans, A. Choi, J. Harnois-Deraps, H. Hildebrandt, B. Joachimi, A. Johnson, A. Mead, D. Parkinson, et al., Mon. Not. Roy. Astron. Soc. 465, 2033 (2017).
- T. M. C. Abbott, M. Aguena, A. Alarcon, S. Allam, O. Alves, A. Amon, F. Andrade-Oliveira, J. Annis, S. Avila, D. Bacon, et al., Phys. Rev. D 105, 023520 (2022).
- O. H. E. Philcox and M. M. Ivanov, Phys. Rev. D 105, 043517 (2022).
- Planck Collaboration, N. Aghanim, Y. Akrami, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A. J. Banday, R. B. Barreiro, N. Bartolo, et al., Astron. Astrophys. 641, A5 (2020).
- E. Di Valentino, A. Melchiorri, and J. Silk, Nature Astron. 4, 196 (2019).
- E. Di Valentino, A. Melchiorri, O. Mena, S. Pan, and W. Yang, Mon. Not. Roy. Astron. Soc. 502, L23 (2021).
- E. Di Valentino, Universe 8, 399 (2022).
- B. Ratra and P. J. E. Peebles, Phys. Rev. D37, 3406 (1988).
- B. Ratra and P. J. E. Peebles, Astrophys. J. 325, L17 (1988).
- C. Wetterich, Nucl. Phys. B302, 645 (1988).
- P. Brax and J. Martin, arXiv:astro-ph/0210533 (2002).
- E. V. Linder, Gen. Rel. Grav. 40, 329 (2008).
- Y.-F. Cai, E. N. Saridakis, M. R. Setare, and J.-Q. Xia, Phys. Rept. 493, 1 (2010).
- L. Amendola and S. Tsujikawa, Dark Energy (Cambridge University Press, 2015).
- S. Bahamonde, C. G. Böhmer, S. Carloni, E. J. Copeland, W. Fang, and N. Tamanini, Phys. Rept. 775-777, 1 (2018).
- D. Piras and L. Lombriser, arXiv:2310.10717 (2023).
- P. H. Frampton, K. J. Ludwick, and R. J. Scherrer, Phys. Rev. D84, 063003 (2011).
- R. R. Caldwell and E. V. Linder, Phys. Rev. Lett. 95, 141301 (2005).
- C. Schimd, I. Tereno, J.-P. Uzan, Y. Mellier, L. van Waerbeke, E. Semboloni, H. Hoekstra, L. Fu, and A. Riazuelo, Astron. Astrophys. 463, 405 (2007).
- R. R. Caldwell, Phys. Lett. B545, 23 (2002).
- E. Elizalde, S. Nojiri, and S. D. Odintsov, Phys. Rev. D70, 043539 (2004).
- R. J. Scherrer and A. A. Sen, Phys. Rev. D78, 067303 (2008).
- S. Dutta and R. J. Scherrer, Phys. Lett. B676, 12 (2009).
- P. H. Frampton, K. J. Ludwick, and R. J. Scherrer, Phys. Rev. D85, 083001 (2012).
- K. J. Ludwick, Mod. Phys. Lett. A32, 1730025 (2017).
- L. A. Escamilla, W. Giarè, E. Di Valentino, R. C. Nunes, and S. Vagnozzi, arXiv:2307.14802 (2023).
- P. J. Steinhardt, L.-M. Wang, and I. Zlatev, Phys. Rev. D59, 123504 (1999).
- T. Chiba, A. De Felice, and S. Tsujikawa, Phys. Rev. D87, 083505 (2013).
- N. A. Lima, A. R. Liddle, M. Sahlén, and D. Parkinson, Phys. Rev. D 93, 063506 (2016).
- I. Zlatev, L.-M. Wang, and P. J. Steinhardt, Phys. Rev. Lett. 82, 896 (1999).
- E. V. Linder, Phys. Rev. D91, 063006 (2015).
- S. Bag, S. S. Mishra, and V. Sahni, JCAP 08, 009 (2018).
- A. A. Starobinsky, Phys. Lett. B 91, 99 (1980).
- A. H. Guth, Phys. Rev. D 23, 347 (1981).
- V. F. Mukhanov and G. V. Chibisov, JETP Lett. 33, 532 (1981).
- A. A. Starobinsky, Phys. Lett. B 117, 175 (1982).
- A. D. Linde, Phys. Lett. B 108, 389 (1982).
- A. D. Linde, Phys. Lett. B 129, 177 (1983).
- F. Lucchin, S. Matarrese, and M. D. Pollock, Phys. Lett. B 167, 163 (1986).
- F. Lucchin and S. Matarrese, Phys. Rev. D32, 1316 (1985).
- F. Lucchin and S. Matarrese, Phys. Lett. B 164, 282 (1985).
- S. Dodelson, Modern cosmology (Academic Press. ISBN, Amsterdam, 2003).
- D. S. Gorbunov and V. A. Rubakov, Introduction to the theory of the early universe: Cosmological perturbations and inflationary theory (World Scientific, Hackensack, USA, 2011).
- V. Mukhanov, Physical foundations of cosmology (Cambridge University Press, 2005).
- L. Senatore, in Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings (2017).
- P. J. E. Peebles and A. Vilenkin, Phys. Rev. D 59, 063505 (1999).
- J. Rubio and C. Wetterich, Phys. Rev. D 96, 063509 (2017).
- B. Ratra, Phys. Rev. D96, 103534 (2017).
- C.-Q. Geng, C.-C. Lee, M. Sami, E. N. Saridakis, and A. A. Starobinsky, JCAP 06, 011 (2017).
- Y. Akrami, R. Kallosh, A. Linde, and V. Vardanyan, JCAP 06, 041 (2018).
- K. Dimopoulos and C. Owen, JCAP 06, 027 (2017).
- C. Wetterich, Astron. Astrophys. 301, 321 (1995).
- L. Amendola, Mon. Not. Roy. Astron. Soc. 312, 521 (2000).
- L. Amendola, Phys. Rev. D62, 043511 (2000).
- W. Zimdahl and D. Pavon, Phys. Lett. B521, 133 (2001).
- X. Liu, S. Tsujikawa, and K. Ichiki, arXiv:2309.13946 (2023).
- R. C. Nunes and E. Di Valentino, 104, 063529 (2021).
- Y. Zhai, W. Giarè, C. van de Bruck, E. Di Valentino, O. Mena, and R. C. Nunes, JCAP 07, 032 (2023).
- S. Pan and W. Yang, arXiv:2310.07260 (2023).
- O. Farooq, F. R. Madiyar, S. Crandall, and B. Ratra, Astrophys. J. 835, 26 (2017).
- J. Ryan, Y. Chen, and B. Ratra, Mon. Not. Roy. Astron. Soc. 488, 3844 (2019).
- S. Mitra, C.-G. Park, T. R. Choudhury, and B. Ratra, Mon. Not. Roy. Astron. Soc. 487, 5118 (2019).
- N. Khadka and B. Ratra, Mon. Not. Roy. Astron. Soc. 497, 263 (2020).
- N. Khadka and B. Ratra, Mon. Not. Roy. Astron. Soc. 492, 4456 (2020).
- N. Khadka and B. Ratra, Mon. Not. Roy. Astron. Soc. 502, 6140 (2021).
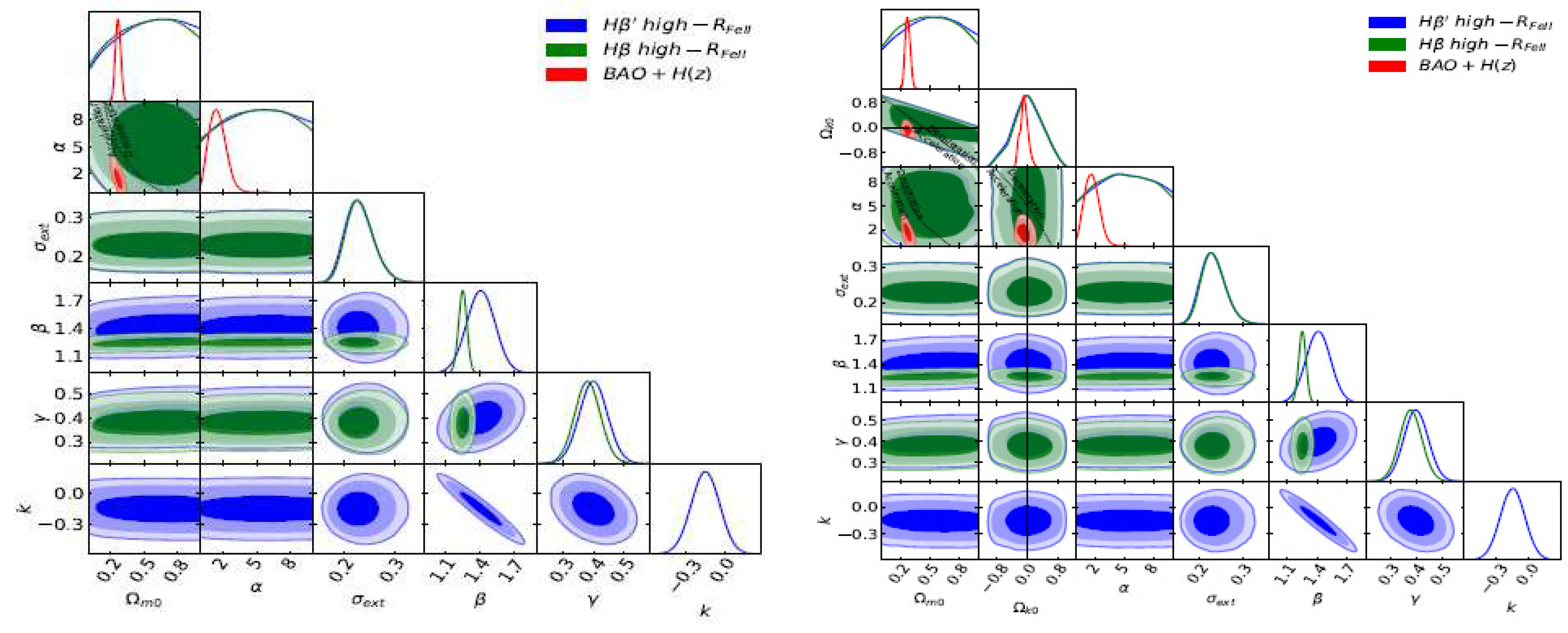
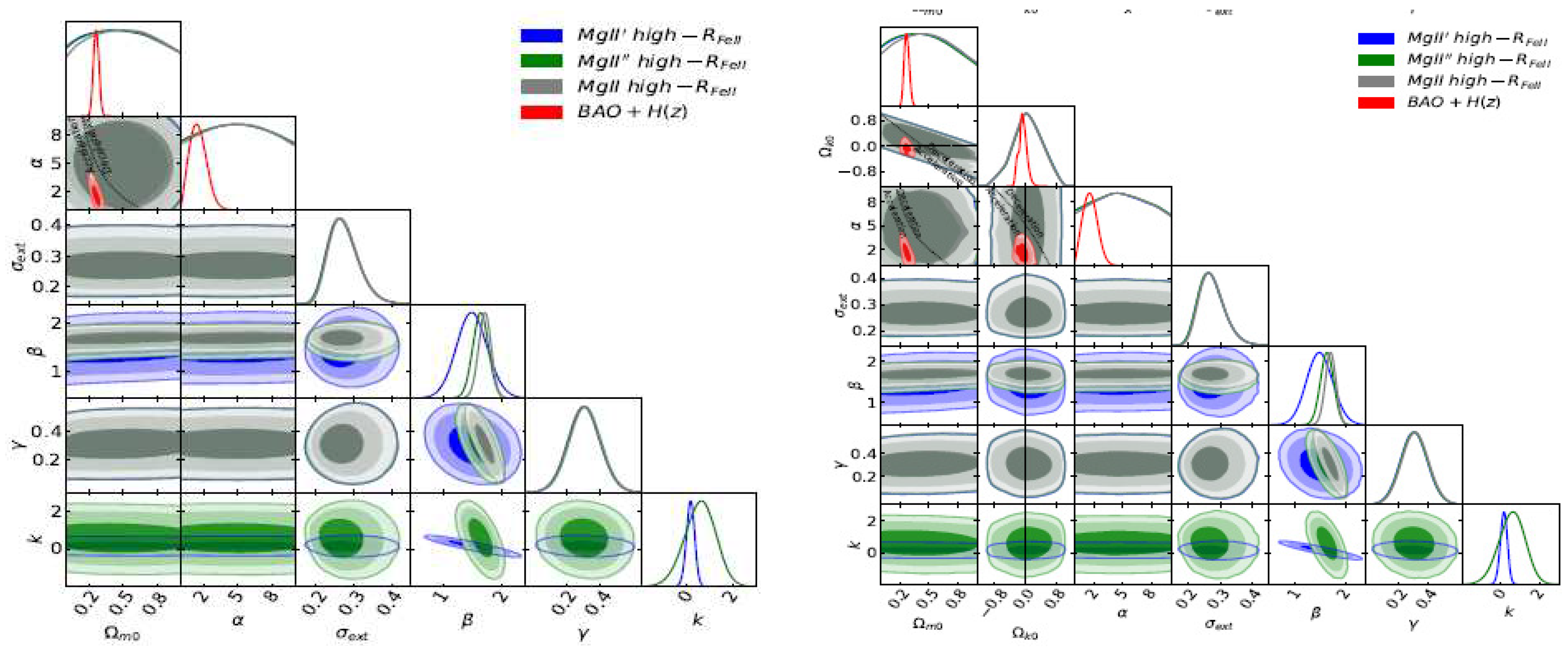
- N. Khadka, Z. Yu, M. Zajaček, M. L. Martinez-Aldama, B. Czerny, and B. Ratra, Mon. Not. Roy. Astron. Soc. 508, 4722 (2021).
- N. Khadka and B. Ratra, Mon. Not. Roy. Astron. Soc. 510, 2753 (2022).
- N. Khadka, M. L. Martínez-Aldama, M. Zajaček, B. Czerny, and B. Ratra, Mon. Not. Roy. Astron. Soc. 513, 1985 (2022).
- S. Cao, J. Ryan, and B. Ratra, Mon. Not. Roy. Astron. Soc. 504, 300 (2021).
- S. Cao, N. Khadka, and B. Ratra, Mon. Not. Roy. Astron. Soc. 510, 2928 (2022).
- S. Cao, M. Zajaček, S. Panda, M. L. Martínez-Aldama, B. Czerny, and B. Ratra, Mon. Not. Roy. Astron. Soc. 516, 1721 (2022).
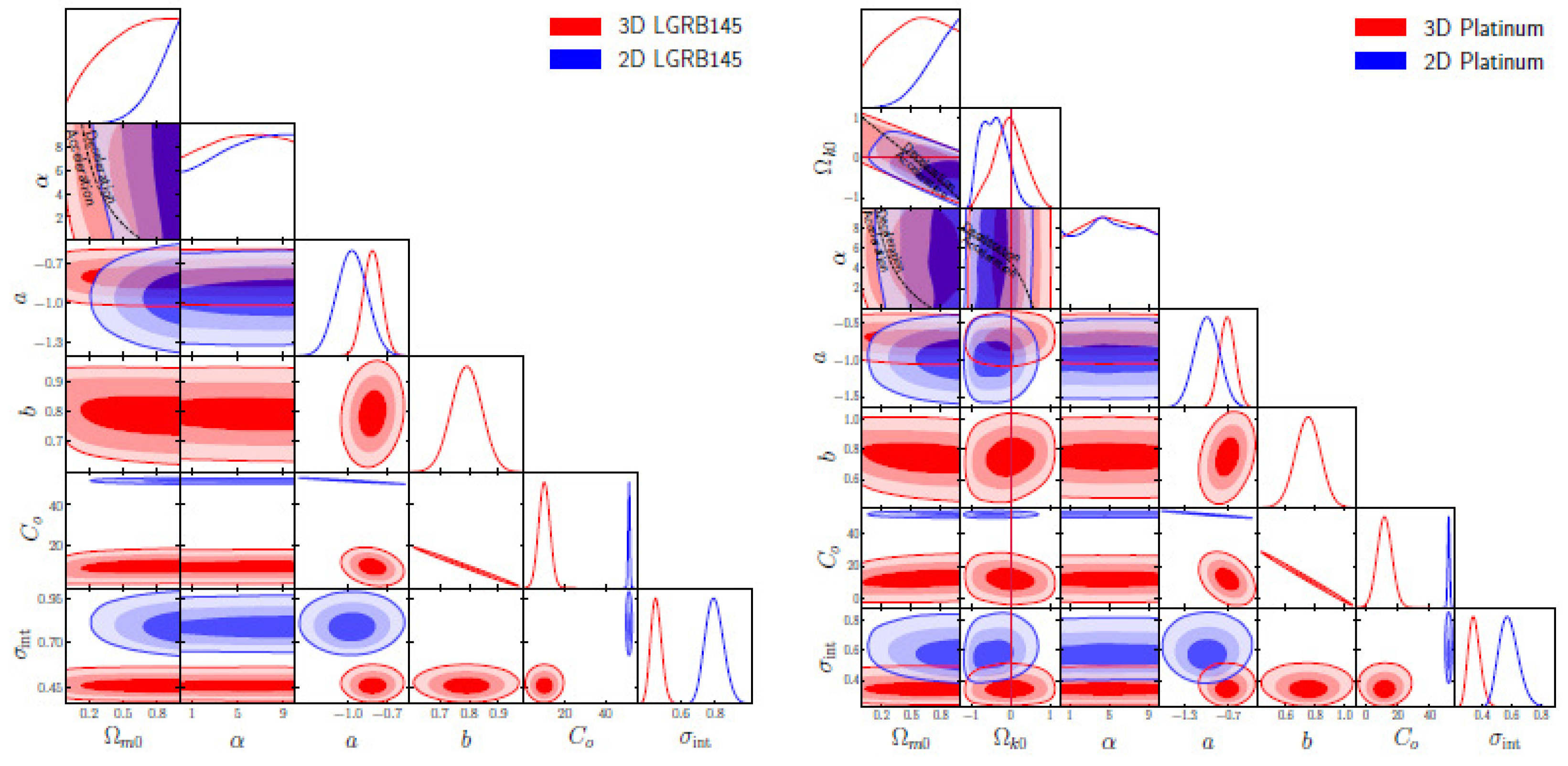
- S. Cao, M. Dainotti, and B. Ratra, Mon. Not. Roy. Astron. Soc. 512, 439 (2022).
- S. Cao, M. Dainotti, and B. Ratra, Mon. Not. Roy. Astron. Soc. 516, 1386 (2022).
- S. Cao and B. Ratra, Mon. Not. Roy. Astron. Soc. 513, 5686 (2022).
- S. Gariazzo, E. Di Valentino, O. Mena, and R. C. Nunes, Phys. Rev. D 106, 023530 (2022).
- W. Yang, S. Pan, O. Mena, and E. Di Valentino (2022), 2209.14816.
- D. N. Spergel, Science 347, 1100 (2015).
- M. S. Madhavacheril, F. J. Qu, B. D. Sherwin, N. MacCrann, Y. Li, I. Abril-Cabezas, P. A. R. Ade, S. Aiola, T. Alford, M. Amiri, et al., arXiv:2304.05203 (2023).
- D. Brout, D. Scolnic, B. Popovic, A. G. Riess, A. Carr, J. Zuntz, R. Kessler, T. M. Davis, S. Hinton, D. Jones, et al., Astrophys. J 938, 110 (2022).
- A. G. Riess, L.-G. Strolger, J. Tonry, S. Casertano, H. C. Ferguson, B. Mobasher, P. Challis, A. V. Filippenko, S. Jha, W. Li, et al., Astrophys. J 607, 665 (2004).
- D. M. Scolnic, D. O. Jones, A. Rest, Y. C. Pan, R. Chornock, R. J. Foley, M. E. Huber, R. Kessler, G. Narayan, A. G. Riess, et al., Astrophys. J 859, 101 (2018).
- M. Fierz and W. Pauli, Proc. Roy. Soc. Lond. A173, 211 (1939).
- J. Polchinski, String theory. Vol. 1: An introduction to the bosonic string, Cambridge Monographs on Mathematical Physics (Cambridge University Press, 2007).
- N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali, Phys. Lett. B429, 263 (1998).
- G. R. Dvali, G. Gabadadze, and M. Porrati, Phys. Lett. B485, 208 (2000).
- A. Yu. Kamenshchik, U. Moschella, and V. Pasquier, Phys. Lett. B511, 265 (2001).
- S. Capozziello, S. Carloni, and A. Troisi, Recent Res. Dev. Astron. Astrophys. 1 (2003).
- R. J. Scherrer, Phys. Rev. Lett. 93, 011301 (2004).
- A. Nicolis, R. Rattazzi, and E. Trincherini, Phys. Rev. D79, 064036 (2009).
- M. Shifman, Int. J. Mod. Phys. A25, 199 (2010).
- J. Khoury and M. Wyman, Phys. Rev. D80, 064023 (2009).
- S. Wang, Y. Wang, and M. Li, Phys. Rept. 696, 1 (2017).
- R. R. Caldwell, M. Kamionkowski, and N. N. Weinberg, Phys. Rev. Lett. 91, 071301 (2003).
- P. G. Ferreira and M. Joyce, Phys. Rev. D58, 023503 (1998).
- P. Brax and J. Martin, Phys. Lett. B 468, 40 (1999).
- V. Sahni and L.-M. Wang, Phys. Rev. D62, 103517 (2000).
- T. Barreiro, E. J. Copeland, and N. J. Nunes, Phys. Rev. D61, 127301 (2000).
- A. Albrecht and C. Skordis, Phys. Rev. Lett. 84, 2076 (2000).
- L. A. Urena-Lopez and T. Matos, Phys. Rev. D62, 081302 (2000).
- H.-Y. Chang and R. J. Scherrer, arXiv:1608.03291 (2016).
- J. A. Frieman, C. T. Hill, A. Stebbins, and I. Waga, Phys. Rev. Lett. 75, 2077 (1995).
- V. Barger, Y. Gao, and D. Marfatia, Phys. Lett. B648, 127 (2007).
- M. Chevallier and D. Polarski, Int. J. Mod. Phys. D10, 213 (2001).
- E. V. Linder, Phys. Rev. Lett. 90, 091301 (2003).
- B. Ratra, Phys. Rev. D 40, 3939 (1989).
- B. Ratra, Phys. Rev. D 31, 1931 (1985).
- D. Bettoni and J. Rubio, Galaxies 10, 22 (2022).
- B. Ratra and P. J. E. Peebles, Phys. Rev. D52, 1837 (1995).
- G. Y. Chitov, T. August, A. Natarajan, and T. Kahniashvili, Phys. Rev. D 83, 045033 (2011).
- S. Mandal, G. Y. Chitov, O. Avsajanishvili, B. Singha, and T. Kahniashvili, JCAP 05, 018 (2021).
- S. Podariu and B. Ratra, Astrophys. J. 532, 109 (2000).
- P. Caresia, S. Matarrese, and L. Moscardini, Astrophys. J. 605, 21 (2004).
- P. Binetruy, Phys. Rev. D 60, 063502 (1999).
- F. Perrotta, C. Baccigalupi, and S. Matarrese, Phys. Rev. D 61, 023507 (1999).
- C. Baccigalupi, S. Matarrese, and F. Perrotta, Phys. Rev. D 62, 123510 (2000).
- J. L. Tonry, B. P. Schmidt, B. Barris, P. Candia, P. Challis, A. Clocchiatti, A. L. Coil, A. V. Filippenko, P. Garnavich, C. Hogan, et al., Astrophys. J 594, 1 (2003).
- G. Aldering, C. W. Akerlof, R. Amanullah, P. Astier, E. Barrelet, C. Bebek, L. Bergstrom, J. Bercovitz, G. M. Bernstein, M. Bester, et al., in Future Research Direction and Visions for Astronomy, edited by A. M. Dressler (2002), vol. 4835 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, pp. 146–157.
- M. Doran, K. Karwan, and C. Wetterich, JCAP 11, 007 (2005).
- D. N. Spergel, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, et al., Astrophys. J. Suppl. 148, 175 (2003).
- A. C. S. Readhead, B. S. Mason, C. R. Contaldi, T. J. Pearson, J. R. Bond, S. T. Myers, S. Padin, J. L. Sievers, J. K. Cartwright, M. C. Shepherd, et al., Astrophys. J 609, 498 (2004).
- R. Rebolo, R. A. Battye, P. Carreira, K. Cleary, R. D. Davies, R. J. Davis, C. Dickinson, R. Genova-Santos, K. Grainge, C. M. Gutiérrez, et al., Mon. Not. Roy. Astron. Soc. 353, 747 (2004).
- M. Tegmark, M. A. Strauss, M. R. Blanton, K. Abazajian, S. Dodelson, H. Sandvik, X. Wang, D. H. Weinberg, I. Zehavi, N. A. Bahcall, et al., Phys. Rev. D 69, 103501 (2004).
- W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, J. Kennicutt, Robert C., H. C. Ford, J. A. Graham, et al., Astrophys. J 553, 47 (2001).
- A. Fuzfa and J. M. Alimi, AIP Conf. Proc. 861, 858 (2006).
- P. Astier, J. Guy, N. Regnault, R. Pain, E. Aubourg, D. Balam, S. Basa, R. G. Carlberg, S. Fabbro, D. Fouchez, et al., Astron. Astrophys. 447, 31 (2006).
- A. Pavlov, S. Westmoreland, K. Saaidi, and B. Ratra, 88, 123513 (2013).
- O. Farooq, D. Mania, and B. Ratra, Astrophys. Space Sci. 357, 11 (2015).
- N. Suzuki, D. Rubin, C. Lidman, G. Aldering, R. Amanullah, K. Barbary, L. F. Barrientos, J. Botyanszki, M. Brodwin, N. Connolly, et al., Astrophys. J 746, 85 (2012).
- J. Simon, L. Verde, and R. Jimenez, 71, 123001 (2005).
- E. Gaztanaga, A. Cabre, and L. Hui, Mon. Not. Roy. Astron. Soc. 399, 1663 (2009).
- W. J. Percival, B. A. Reid, D. J. Eisenstein, N. A. Bahcall, T. Budavari, J. A. Frieman, M. Fukugita, J. E. Gunn, Ž. Ivezić, G. R. Knapp, et al., Mon. Not. Roy. Astron. Soc. 401, 2148 (2010).
- O. Farooq, S. Crandall, and B. Ratra, Phys. Lett. B 726, 72 (2013).
- M. Blomqvist, H. du Mas des Bourboux, N. G. Busca, V. de Sainte Agathe, J. Rich, C. Balland, J. E. Bautista, K. Dawson, A. Font-Ribera, J. Guy, et al., Astron. Astrophys 629, A86 (2019).
- A. Halder and M. Pandey, Mon. Not. Roy. Astron. Soc. 508, 3446 (2021).
- R. J. Cooke, M. Pettini, and C. C. Steidel, The Astrophysical Journal 855, 102 (2018).
- D. Camarena and V. Marra, Monthly Notices of the Royal Astronomical Society 504, 5164 (2021).
- M. Doran, M. J. Lilley, J. Schwindt, and C. Wetterich, Astrophys. J. 559, 501 (2001).
- P. de Bernardis, P. A. R. Ade, J. J. Bock, J. R. Bond, J. Borrill, A. Boscaleri, K. Coble, B. P. Crill, G. de Gasperis, G. de Troia, et al. (Boomerang), in Cosmology and Particle Physics (2001), vol. 555 of American Institute of Physics Conference Series, pp. 85–94.
- S. Hanany, P. Ade, A. Balbi, J. Bock, J. Borrill, A. Boscaleri, P. de Bernardis, P. G. Ferreira, V. V. Hristov, A. H. Jaffe, et al., Astrophys. J. Lett 545, L5 (2000).
- A. Hebecker and C. Wetterich, Phys. Lett. B 497, 281 (2001).
- R. R. Caldwell, M. Doran, C. M. Mueller, G. Schafer, and C. Wetterich, Astrophys. J. Lett. 591, L75 (2003).
- G. Hinshaw, D. N. Spergel, L. Verde, R. S. Hill, S. S. Meyer, C. Barnes, C. L. Bennett, M. Halpern, N. Jarosik, A. Kogut, et al., Astrophys. J. Suppl. 148, 135 (2003).
- A. Kogut, D. N. Spergel, C. Barnes, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, M. Limon, S. S. Meyer, L. Page, et al., Astrophys. J. Suppl. 148, 161 (2003).
- T. J. Pearson, B. S. Mason, A. C. S. Readhead, M. C. Shepherd, J. L. Sievers, P. S. Udomprasert, J. K. Cartwright, A. J. Farmer, S. Padin, S. T. Myers, et al., Astrophys. J 591, 556 (2003).
- B. S. Mason, T. J. Pearson, A. C. S. Readhead, M. C. Shepherd, J. Sievers, P. S. Udomprasert, J. K. Cartwright, A. J. Farmer, S. Padin, S. T. Myers, et al., Astrophys. J 591, 540 (2003).
- C. L. Kuo, P. A. R. Ade, J. J. Bock, C. Cantalupo, M. D. Daub, J. Goldstein, W. L. Holzapfel, A. E. Lange, M. Lueker, M. Newcomb, et al., Astrophys. J 600, 32 (2004).
- W. J. Percival, C. M. Baugh, J. Bland-Hawthorn, T. Bridges, R. Cannon, S. Cole, M. Colless, C. Collins, W. Couch, G. Dalton, et al., Mon. Not. Roy. Astron. Soc. 327, 1297 (2001).
- J. A. Peacock, S. Cole, P. Norberg, C. M. Baugh, J. Bland-Hawthorn, T. Bridges, R. D. Cannon, M. Colless, C. Collins, W. Couch, et al., Nature 410, 169 (2001).
- L. Verde, A. F. Heavens, W. J. Percival, S. Matarrese, C. M. Baugh, J. Bland-Hawthorn, T. Bridges, R. Cannon, S. Cole, M. Colless, et al., Mon. Not. Roy. Astron. Soc. 335, 432 (2002).
- N. Y. Gnedin and A. J. S. Hamilton, Mon. Not. Roy. Astron. Soc. 334, 107 (2002).
- R. A. C. Croft, D. H. Weinberg, M. Bolte, S. Burles, L. Hernquist, N. Katz, D. Kirkman, and D. Tytler, Astrophys. J. 581, 20 (2002).
- V. Pettorino, C. Baccigalupi, and G. Mangano, JCAP 01, 014 (2005).
- P. Mukherjee, A. J. Banday, A. Riazuelo, K. M. Gorski, and B. Ratra, Astrophys. J. 598, 767 (2003).
- P. Brax, J. Martin, and A. Riazuelo, 6th Workshop on Non-Perturbative Quantum Chromodynamics pp. 315–325 (2002).
- K. M. Gorski, B. Ratra, R. Stompor, N. Sugiyama, and A. J. Banday, Astrophys. J. Suppl. 114, 1 (1998).
- L. Samushia and B. Ratra, Astrophys. J. Lett. 680, L1 (2008).
- S. W. Allen, D. A. Rapetti, R. W. Schmidt, H. Ebeling, G. Morris, and A. C. Fabian, Mon. Not. Roy. Astron. Soc. 383, 879 (2008).
- J. R. Gott, III, M. S. Vogeley, S. Podariu, and B. Ratra, Astrophys. J. 549, 1 (2001).
- G. Chen, J. R. Gott, III, and B. Ratra, Publ. Astron. Soc. Pac. 115, 1269 (2003).
- B. Fields and S. Sarkar, J. Phys. G. 33, 220 (2006).
- Y. Chen, B. Ratra, M. Biesiada, S. Li, and Z.-H. Zhu, Astrophys. J. 829, 61 (2016).
- Planck Collaboration, R. Adam, P. A. R. Ade, N. Aghanim, M. I. R. Alves, M. Arnaud, M. Ashdown, J. Aumont, C. Baccigalupi, A. J. Banday, et al., Astron. Astrophys. 594, A10 (2016).
- M. Betoule, R. Kessler, J. Guy, J. Mosher, D. Hardin, R. Biswas, P. Astier, P. El-Hage, M. Konig, S. Kuhlmann, et al., Astron.Astrophys. 568, A22 (2014).
- C.-G. Park and B. Ratra, Astrophys. J. 868, 83 (2018).
- Planck Collaboration, N. Aghanim, Y. Akrami, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A. J. Banday, R. B. Barreiro, N. Bartolo, et al., Astron. Astrophys. 607, A95 (2017).
- A. Font-Ribera, P. McDonald, N. Mostek, B. A. Reid, H.-J. Seo, and A. Slosar, JCAP 1405, 023 (2014).
- J. Ooba, B. Ratra, and N. Sugiyama, Astrophys. Space Sci. 364, 176 (2019).
- D. Blas, J. Lesgourgues, and T. Tram, JCAP 2011, 034 (2011).
- B. Audren, J. Lesgourgues, K. Benabed, and S. Prunet, JCAP 2013, 001 (2013).
- C.-G. Park and B. Ratra, Astrophys. Space Sci. 364, 134 (2019).
- J. W. Henning, J. T. Sayre, C. L. Reichardt, P. A. R. Ade, A. J. Anderson, J. E. Austermann, J. A. Beall, A. N. Bender, B. A. Benson, L. E. Bleem, et al., Astrophys. J 852, 97 (2018).
- C.-G. Park and B. Ratra, Phys. Rev. D 101, 083508 (2020).
- A. Pavlov, L. Samushia, and B. Ratra, Astrophys. J. 760, 19 (2012).
- A. Orsi, C. Baugh, C. Lacey, A. Cimatti, Y. Wang, and G. Zamorani, Mon. Not. Roy. Astron. Soc. 405, 1006 (2010).
- J. E. Geach, A. Cimatti, W. Percival, Y. Wang, L. Guzzo, G. Zamorani, P. Rosati, L. Pozzetti, A. Orsi, C. M. Baugh, et al., Mon. Not. Roy. Astron. Soc. 402, 1330 (2010).
- W. J. Percival and B. M. Schaefer, Mon. Not. Roy. Astron. Soc. 385, 78 (2008).
- L. Guzzo, M. Pierleoni, B. Meneux, E. Branchini, O. Le Fèvre, C. Marinoni, B. Garilli, J. Blaizot, G. De Lucia, A. Pollo, et al., Nature 451, 541 (2008).
- C. Blake, T. Davis, G. B. Poole, D. Parkinson, S. Brough, M. Colless, C. Contreras, W. Couch, S. Croom, M. J. Drinkwater, et al., Mon. Not. Roy. Astron. Soc. 415, 2892 (2011).
- C. Blake, S. Brough, M. Colless, C. Contreras, W. Couch, S. Croom, T. Davis, M. J. Drinkwater, K. Forster, D. Gilbank, et al., Mon. Not. Roy. Astron. Soc 415, 2876 (2011).
- B. A. Reid, L. Samushia, M. White, W. J. Percival, M. Manera, N. Padmanabhan, A. J. Ross, A. G. Sánchez, S. Bailey, D. Bizyaev, et al., Mon. Not. Roy. Astron. Soc. 426, 2719 (2012).
- L. Anderson, E. Aubourg, S. Bailey, D. Bizyaev, M. Blanton, A. S. Bolton, J. Brinkmann, J. R. Brownstein, A. Burden, A. J. Cuesta, et al., Mon. Not. Roy. Astron. Soc. 427, 3435 (2012).
- A. Pavlov, O. Farooq, and B. Ratra, Phys. Rev. D 90, 023006 (2014).
- L. Samushia, W. J. Percival, and A. Raccanelli, Mon. Not. Roy. Astron. Soc. 420, 2102 (2012).
- O. Avsajanishvili, N. A. Arkhipova, L. Samushia, and T. Kahniashvili, Eur. Phys. J. C74, 3127 (2014).
- G. Gupta, S. Sen, and A. A. Sen, JCAP 1204, 028 (2012).
- R. Giostri, M. Vargas dos Santos, I. Waga, R. R. R. Reis, M. O. Calvão, and B. L. Lago, JCAP 3, 027 (2012).
- O. Avsajanishvili, Y. Huang, L. Samushia, and T. Kahniashvili, Eur. Phys. J. C78, 773 (2018).
- J. Sola Peracaula, A. Gomez-Valent, and J. de Cruz Pérez, Phys. Dark Univ. 25, 100311 (2019).
- H. Gil-Marín, W. J. Percival, L. Verde, J. R. Brownstein, C.-H. Chuang, F.-S. Kitaura, S. A. Rodríguez-Torres, and M. D. Olmstead, Mon. Not. Roy. Astron. Soc. 465, 1757 (2017).
- H. Gil-Marín, J. Guy, P. Zarrouk, E. Burtin, C.-H. Chuang, W. J. Percival, A. J. Ross, R. Ruggeri, R. Tojerio, G.-B. Zhao, et al., Mon. Not. Roy. Astron. Soc. 477, 1604 (2018).
- F. G. Mohammad, D. Bianchi, W. J. Percival, S. de la Torre, L. Guzzo, B. R. Granett, E. Branchini, M. Bolzonella, B. Garilli, M. Scodeggio, et al., Astron. Astrophys. 619, A17 (2018).
- H. Hildebrandt, M. Viola, C. Heymans, S. Joudaki, K. Kuijken, C. Blake, T. Erben, B. Joachimi, D. Klaes, L. Miller, et al., Mon. Not. Roy. Astron. Soc. 465, 1454 (2017).
- C.-G. Park and B. Ratra, Astrophys. Space Sci. 364, 82 (2019).
- L. Samushia and B. Ratra, Astrophys. J. 703, 1904 (2009).
- L. Samushia, A. Dev, D. Jain, and B. Ratra, Phys. Lett. B 693, 509 (2010).
- S. Capozziello, V. F. Cardone, M. Funaro, and S. Andreon, Phys. Rev. D 70, 123501 (2004).
- J. Ooba, B. Ratra, and N. Sugiyama, Astrophys. J. 866, 68 (2018).
- J. Ryan, S. Doshi, and B. Ratra, Mon. Not. Roy. Astron. Soc. 480, 759 (2018).
- A. Chudaykin, M. M. Ivanov, and M. Simonović, Phys. Rev. D 103, 043525 (2021).
- R. C. Nunes, S. K. Yadav, J. F. Jesus, and A. Bernui, Monthly Notices of the Royal Astronomical Society 497, 2133 (2020).
- E. de Carvalho, A. Bernui, F. Avila, C. P. Novaes, and J. P. Nogueira-Cavalcante, Astron. Astrophys. 649, A20 (2021).
- L. Samushia and B. Ratra, Astrophys. J. Lett. 650, L5 (2006).
- G. Chen and B. Ratra, Astrophys. J. Lett. 612, L1 (2004).
- K. M. Wilson, G. Chen, and B. Ratra, Mod. Phys. Lett. A 21, 2197 (2006).
- G. Chen and B. Ratra, Publ. Astron. Soc. Pac. 123, 1127 (2011).
- O. Farooq, D. Mania, and B. Ratra, Astrophys. J. 764, 138 (2013).
- O. Farooq and B. Ratra, Phys. Lett. B 723, 1 (2013).
- N. G. Busca, T. Delubac, J. Rich, S. Bailey, A. Font-Ribera, D. Kirkby, J. M. Le Goff, M. M. Pieri, A. Slosar, É. Aubourg, et al., Astronomy & Astrophysics 552, A96 (2013).
- O. Farooq and B. Ratra, Astrophys. J. Lett. 766, L7 (2013).
- Y. Chen, S. Kumar, and B. Ratra, Astrophys. J. 835, 86 (2017).
- C.-H. Chuang and Y. Wang, Mon. Not. Roy. Astron. Soc. 435, 255 (2013).
- S. Cao, M. Biesiada, J. Jackson, X. Zheng, Y. Zhao, and Z.-H. Zhu, JCAP 02, 012 (2017).
- S. Cao, X. Zheng, M. Biesiada, J. Qi, Y. Chen, and Z.-H. Zhu, Astron. Astrophys. 606, A15 (2017).
- S. Cao, J. Ryan, and B. Ratra, Mon. Not. Roy. Astron. Soc. 497, 3191 (2020).
- R. Chávez, R. Terlevich, E. Terlevich, F. Bresolin, J. Melnick, M. Plionis, and S. Basilakos, Mon. Not. Roy. Astron. Soc. 442, 3565 (2014).
- R. Chávez, M. Plionis, S. Basilakos, R. Terlevich, E. Terlevich, J. Melnick, F. Bresolin, and A. L. González-Morán, Mon. Not. Roy. Astron. Soc. 462, 2431 (2016).
- G. Risaliti and E. Lusso, Astrophys. J. 815, 33 (2015).
- G. Risaliti and E. Lusso, Nature Astron. 3, 272 (2019).
- S. Cao, J. Ryan, N. Khadka, and B. Ratra, Mon. Not. Roy. Astron. Soc. 501, 1520 (2021).
- J. S. Wang, F. Y. Wang, K. S. Cheng, and Z. G. Dai, Astron. Astrophys. 585, A68 (2016).
- F. F. Dirirsa, S. Razzaque, F. Piron, M. Arimoto, M. Axelsson, D. Kocevski, F. Longo, M. Ohno, and S. Zhu, Astrophys. J. 887, 13 (2019).
- A. L. González-Morán, R. Chávez, R. Terlevich, E. Terlevich, F. Bresolin, D. Fernández-Arenas, M. Plionis, S. Basilakos, J. Melnick, and E. Telles, Mon. Not. Roy. Astron. Soc. 487, 4669 (2019).
- E. Lusso, G. Risaliti, E. Nardini, G. Bargiacchi, M. Benetti, S. Bisogni, S. Capozziello, F. Civano, L. Eggleston, M. Elvis, et al., Astron. Astrophys. 642, A150 (2020).
- T. M. C. Abbott, S. Allam, P. Andersen, C. Angus, J. Asorey, A. Avelino, S. Avila, B. A. Bassett, K. Bechtol, G. M. Bernstein, et al., Astrophys. J. 872, L30 (2019).
- D. Brout, D. Scolnic, R. Kessler, C. B. D’Andrea, T. M. Davis, R. R. Gupta, S. R. Hinton, A. G. Kim, J. Lasker, C. Lidman, et al., Astrophys. J 874, 150 (2019).
- Y. Homayouni, J. R. Trump, C. J. Grier, K. Horne, Y. Shen, W. N. Brandt, K. S. Dawson, G. F. Alvarez, P. J. Green, P. B. Hall, et al., Astrophys. J 901, 55 (2020).
- Z. Yu, P. Martini, A. Penton, T. M. Davis, U. Malik, C. Lidman, B. E. Tucker, R. Sharp, C. S. Kochanek, B. M. Peterson, et al., Mon. Not. Roy. Astron. Soc. 507, 3771 (2021).
- M. L. Martínez-Aldama, B. Czerny, D. Kawka, V. Karas, S. Panda, M. Zajaček, and P. T. Życki, Astrophys. J 883, 170 (2019).
- N. Khadka, M. Zajaček, S. Panda, M. L. Martínez-Aldama, and B. Ratra, Mon. Not. Roy. Astron. Soc. 515, 3729 (2022).
- M. L. Martínez-Aldama, M. Zajaček, B. Czerny, and S. Panda, Astrophys. J 903, 86 (2020).
- M. Zajaček, B. Czerny, M. L. Martinez-Aldama, M. Rałowski, A. Olejak, R. Przyłuski, S. Panda, K. Hryniewicz, M. Śniegowska, M.-H. Naddaf, et al., Astrophys. J 912, 10 (2021).
- L. Samushia and B. Ratra, Astrophys. J. 714, 1347 (2010).
- M. Kowalski, D. Rubin, G. Aldering, R. J. Agostinho, A. Amadon, R. Amanullah, C. Balland, K. Barbary, G. Blanc, P. J. Challis, et al., Astrophys. J 686, 749 (2008).
- B. E. Schaefer, Astrophys. J. 660, 16 (2007).
- Y. Wang, Phys. Rev. D 78, 123532 (2008).
- N. Khadka and B. Ratra, Mon. Not. Roy. Astron. Soc. 499, 391 (2020).
- L. Amati, F. Frontera, M. Tavani, J. J. M. in’t Zand, A. Antonelli, E. Costa, M. Feroci, C. Guidorzi, J. Heise, N. Masetti, et al., Astron. Astrophys. 390, 81 (2002).
- N. Khadka, O. Luongo, M. Muccino, and B. Ratra, JCAP 09, 042 (2021).
- E. E. Fenimore and E. Ramirez-Ruiz, arXiv:astro-ph/0004176 (2017).
- J. P. Hu, F. Y. Wang, and Z. G. Dai, Mon. Not. Roy. Astron. Soc. 507, 730 (2021).
- F. Y. Wang, J. P. Hu, G. Q. Zhang, and Z. G. Dai, Astrophys. J. 924, 97 (2022).
- M. G. Dainotti, V. F. Cardone, and S. Capozziello, Mon. Not. Roy. Astron. Soc. 391, 79 (2008).
- M. G. Dainotti, R. Willingale, S. Capozziello, V. Fabrizio Cardone, and M. Ostrowski, Astrophys. J. 722, L215 (2010).
- M. G. Dainotti, V. F. Cardone, S. Capozziello, M. Ostrowski, and R. Willingale, Astrophys. J. 730, 135 (2011).
- M. G. Dainotti, A. Lenart, G. Sarracino, S. Nagataki, S. Capozziello, and N. Fraija, Astrophys. J. 904, 97 (2020).
- M. G. Dainotti, S. Nagataki, K. Maeda, S. Postnikov, and E. Pian, Astron. Astrophys. 600, A98 (2017).
- M. G. Dainotti, A. L. Lenart, N. Fraija, S. Nagataki, D. C. Warren, B. De Simone, G. Srinivasaragavan, and A. Mata, Publ. Astron. Soc. Jap. 73, 970 (2021).
- M. G. Dainotti, N. Omodei, G. P. Srinivasaragavan, G. Vianello, R. Willingale, P. O’Brien, S. Nagataki, V. Petrosian, Z. Nuygen, X. Hernandez, et al., Astrophys. J. Suppl. 255, 13 (2021).
- D. Mania and B. Ratra, Phys. Lett. B 715, 9 (2012).
- E. R. Siegel, R. Guzman, J. P. Gallego, M. Orduna Lopez, and P. Rodriguez Hidalgo, Mon. Not. Roy. Astron. Soc. 356, 1117 (2005).
- S. Cao, J. Ryan, and B. Ratra, Mon. Not. Roy. Astron. Soc. 509, 4745 (2022).
- A. L. González-Morán, R. Chávez, E. Terlevich, R. Terlevich, D. Fernández-Arenas, F. Bresolin, M. Plionis, J. Melnick, S. Basilakos, and E. Telles, Mon. Not. Roy. Astron. Soc. 505, 1441 (2021).
- A. G. Riess, S. Casertano, W. Yuan, J. B. Bowers, L. Macri, J. C. Zinn, and D. Scolnic, Astrophys. J. 908, L6 (2021).
- S. W. Allen, R. W. Schmidt, H. Ebeling, A. C. Fabian, and L. van Speybroeck, Mon. Not. Roy. Astron. Soc. 353, 457 (2004).
- I. Waga and J. A. Frieman, Phys. Rev. D 62, 043521 (2000).
- G. Chen and B. Ratra, Astrophys. J. 582, 586 (2003).
- S. Podariu, R. A. Daly, M. P. Mory, and B. Ratra, Astrophys. J. 584, 577 (2003).
- K.-H. Chae, G. Chen, B. Ratra, and D.-W. Lee, Astrophys. J. Lett. 607, L71 (2004).
- L. Campanelli, G. L. Fogli, T. Kahniashvili, A. Marrone, and B. Ratra, Eur. Phys. J. C 72, 2218 (2012).
- Y. Chen and B. Ratra, Astron. Astrophys. 543, A104 (2012).
- M. Bonamente, M. K. Joy, S. J. La Roque, J. E. Carlstrom, E. D. Reese, and K. S. Dawson, Astrophys. J. 647, 25 (2006).
- J. S. B. Wyithe and J. S. Bolton, Mon. Not. Roy. Astron. Soc. 412, 1926 (2011).
- G. D. Becker and J. S. Bolton, Mon. Not. Roy. Astron. Soc. 436, 1023 (2013).
- A. Songaila and L. L. Cowie, Astrophys. J. 721, 1448 (2010).
- J. X. Prochaska, J. M. O’Meara, and G. Worseck, Astrophys. J 718, 392 (2010).
- D. Maoz, J. N. Bahcall, D. P. Schneider, N. A. Bahcall, S. Djorgovski, R. Doxsey, A. Gould, S. Kirhakos, G. Meylan, and B. Yanny, Astrophys. J. 409, 28 (1993).
- E. E. Falco, in 31st Liege International Astrophysical Colloquium: Gravitational Lenses in the Universe (1993).
- D. Crampton, C. L. Morbey, O. Le Fevre, F. Hammer, L. Tresse, S. J. Lilly, and D. J. Schade, astro-ph/9410041 (1994).
- C. S. Kochanek, E. E. Falco, and R. Schild, Astrophys. J. 452, 109 (1995).
- A. O. Jaunsen, M. Jablonski, B. R. Pettersen, and R. Stabell, Astron. Astrophys. 300, 323 (1995).
- A. G. Riess, W. H. Press, and R. P. Kirshner, Astrophys. J. 473, 88 (1996).
- P. M. Garnavich, S. Jha, P. Challis, A. Clocchiatti, A. Diercks, A. V. Filippenko, R. L. Gilliland, C. J. Hogan, R. P. Kirshner, B. Leibundgut, et al., Astrophys. J 509, 74 (1998).
- S. T. Myers, N. J. Jackson, I. W. A. Browne, A. G. de Bruyn, T. J. Pearson, A. C. S. Readhead, P. N. Wilkinson, A. D. Biggs, R. D. Blandford, C. D. Fassnacht, et al., Mon. Not. Roy. Astron. Soc. 341, 1 (2003).
- I. W. A. Browne, P. N. Wilkinson, N. J. F. Jackson, S. T. Myers, C. D. Fassnacht, L. V. E. Koopmans, D. R. Marlow, M. Norbury, D. Rusin, C. M. Sykes, et al., Mon. Not. Roy. Astron. Soc. 341, 13 (2003).
- L. I. Gurvits, K. I. Kellermann, and S. Frey, Astron. Astrophys. 342, 378 (1999).
- J. L. Atteia, B. Cordier, and J. Wei, International Journal of Modern Physics D 31, 2230008 (2022).
- L. Amati, P. T. O’Brien, D. Götz, E. Bozzo, A. Santangelo, N. Tanvir, F. Frontera, S. Mereghetti, J. P. Osborne, A. Blain, et al., Experimental Astronomy 52, 183 (2021).
| 1 | For the latter model, the first Friedmann’s equation and Klein-Gordon scalar field equation for these models are defined, respectively as
|
| 2 | Here, is the current age of the universe, given by
|
| 3 | This model is described by a Lagrangian of the form . |
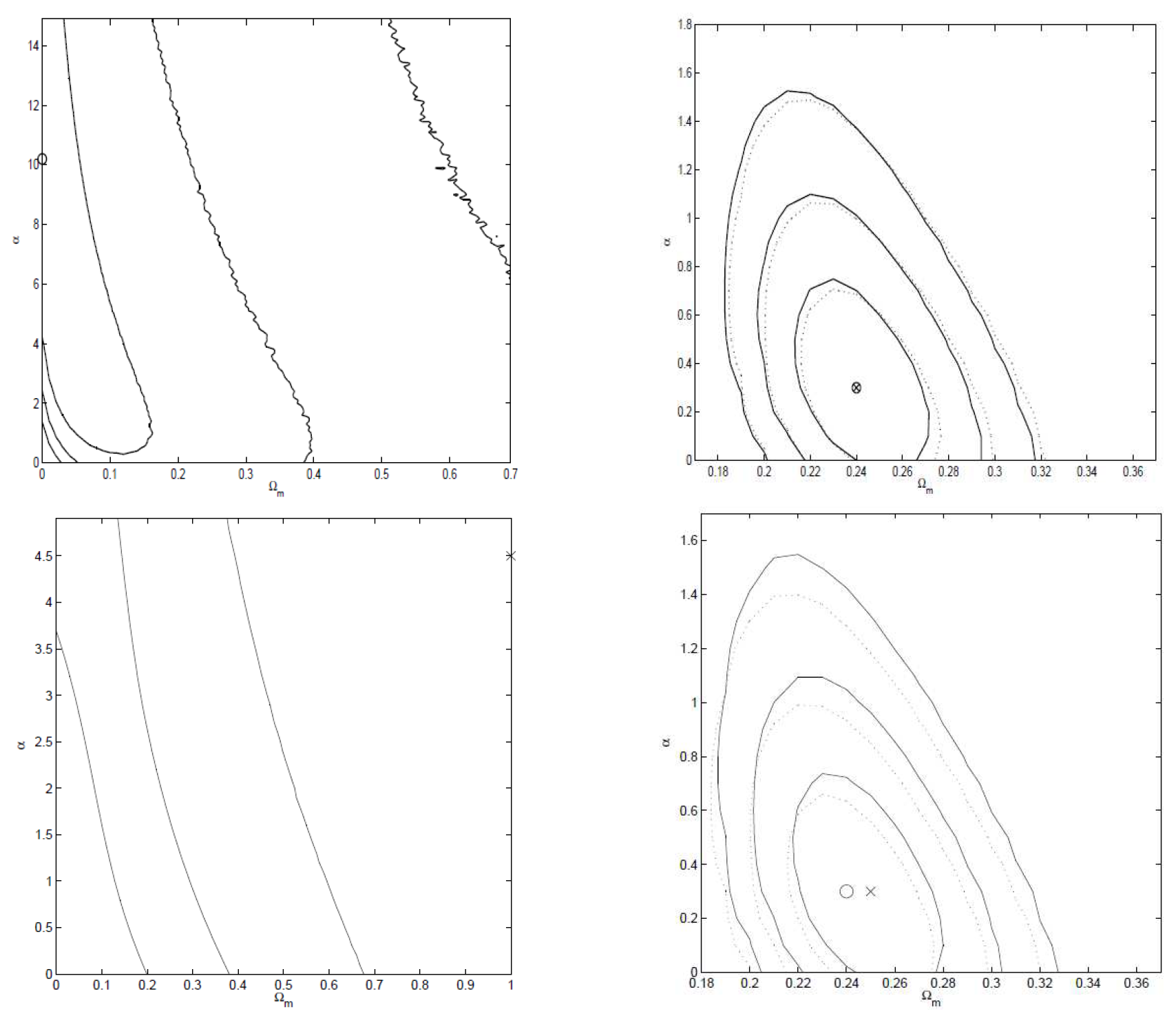
| 4 | The observational constraints on a projection of the Integrated Sachs-Wolfe (ISW) effect on the CMB temperature anisotropy was obtained for a fixed value of the Jordan-Brans-Dicke (JBD) parameter at present epoch , the latter being defined as
|
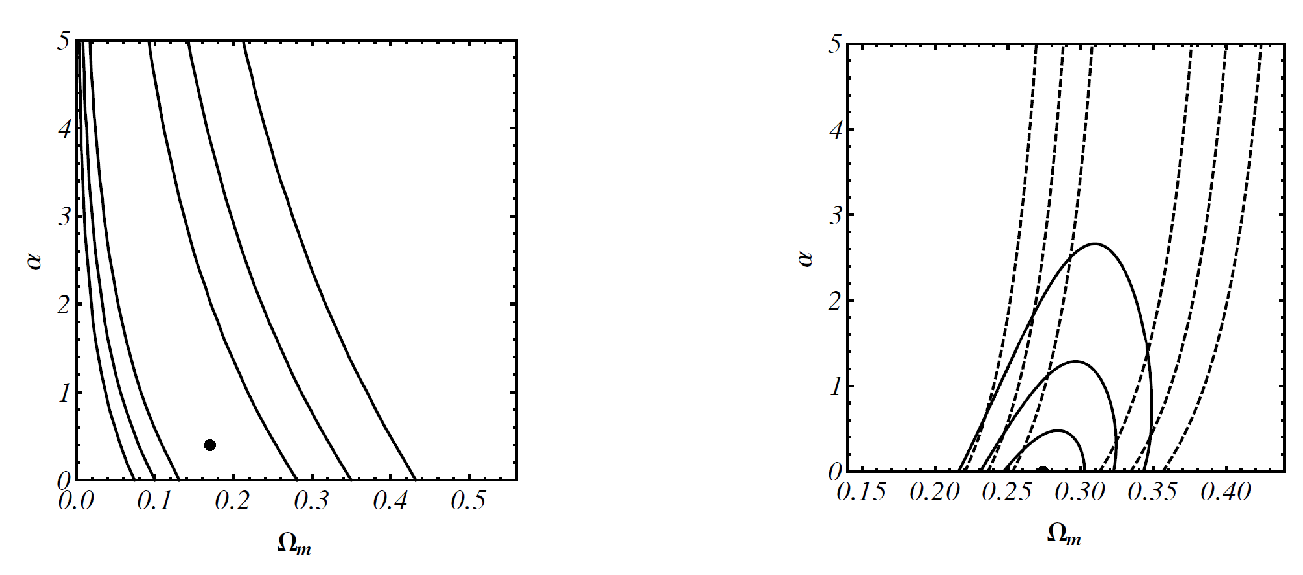
| 5 | This is done by fixing at present epoch the amplitude of the initial energy density fluctuations generated in the early inflation epoch for this model, and comparing model predictions of the large angular scale spatial anisotropy in the CMB radiation with observational data. The authors computed model predictions as a function of the model parameter , as well as other cosmological parameters, following Brax et al. [236], and then determined the normalization amplitude by comparing these predictions with COBE-DMR CMB temperature anisotropy measurements of Bennett [5] and Gorski et al. [237] |
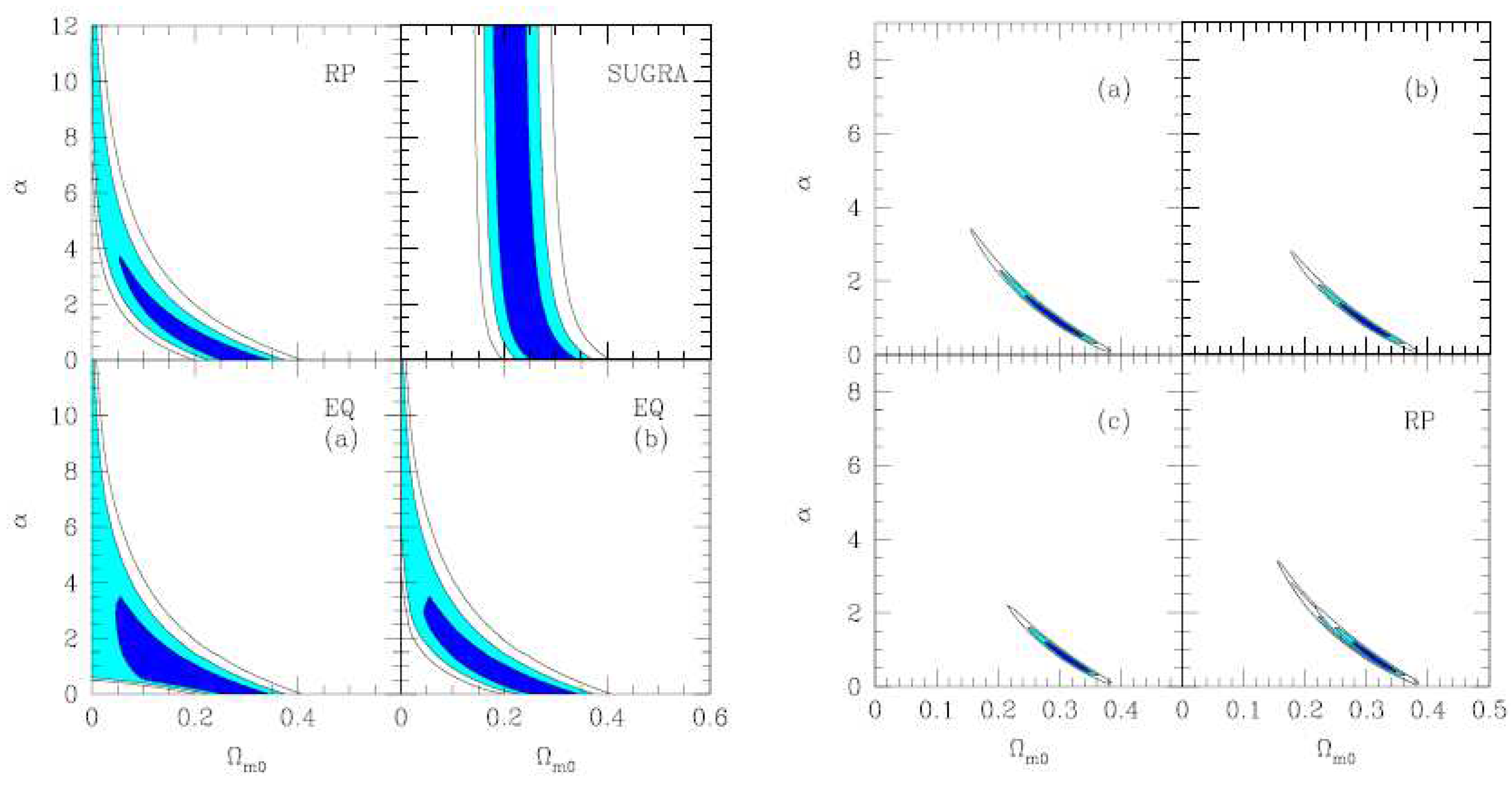
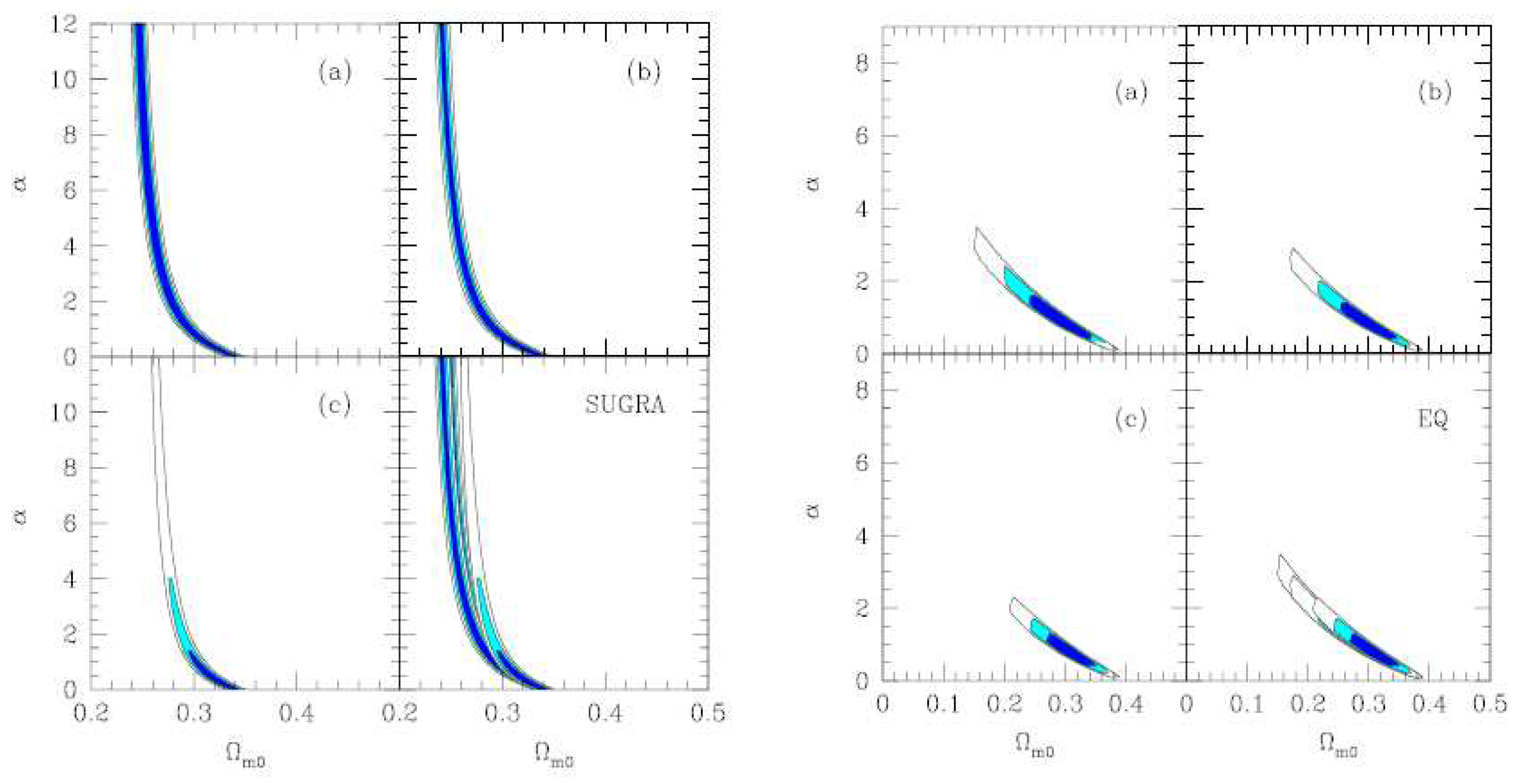
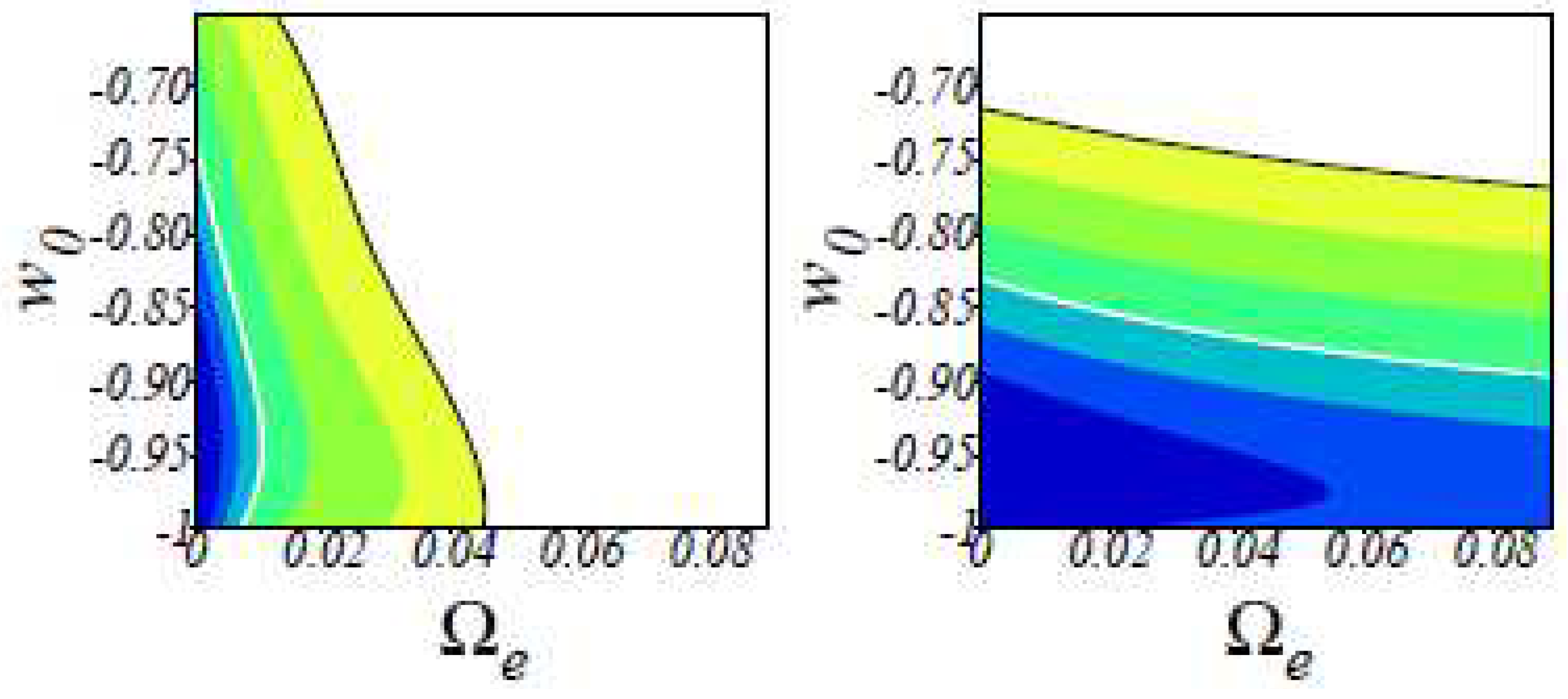
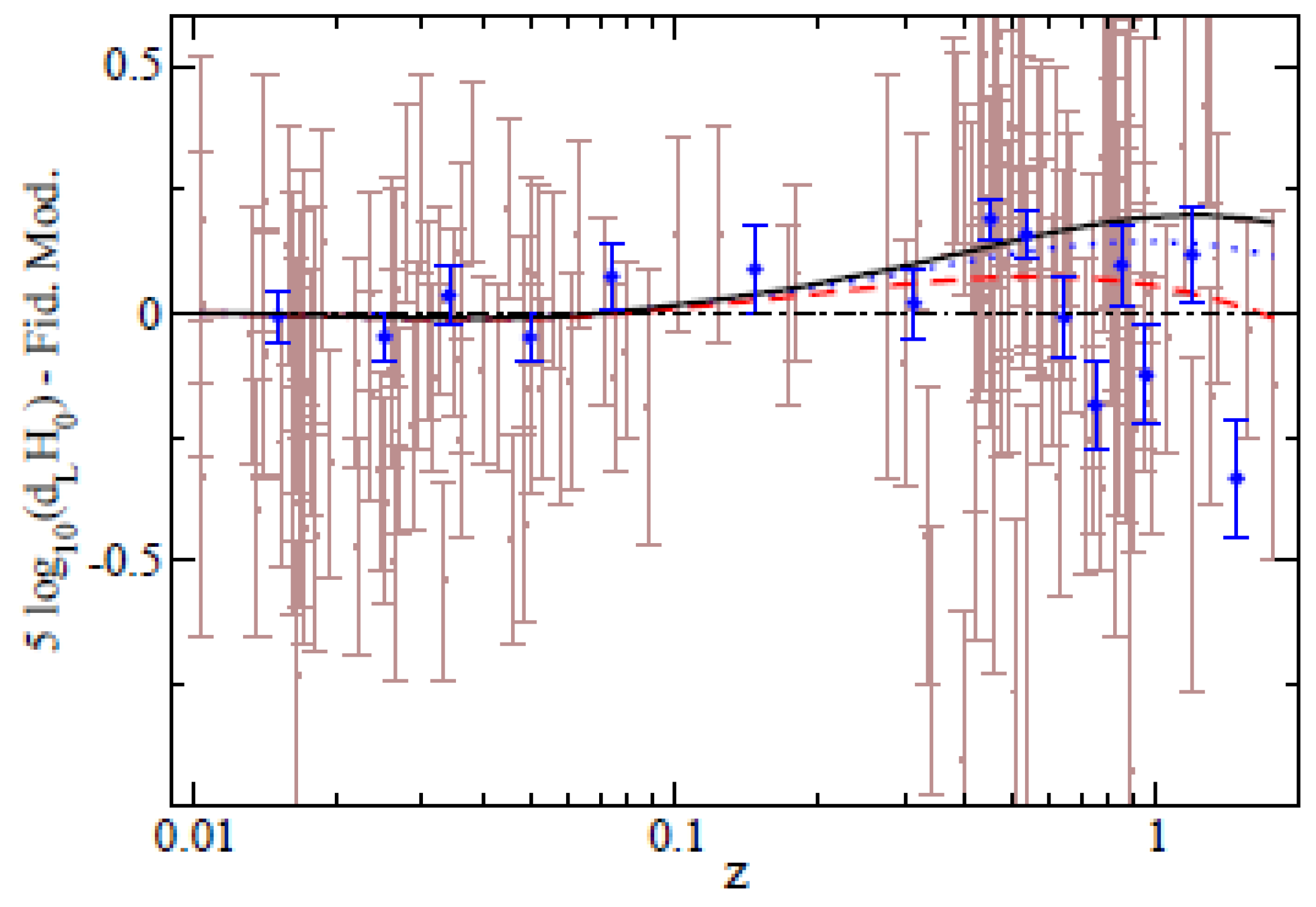
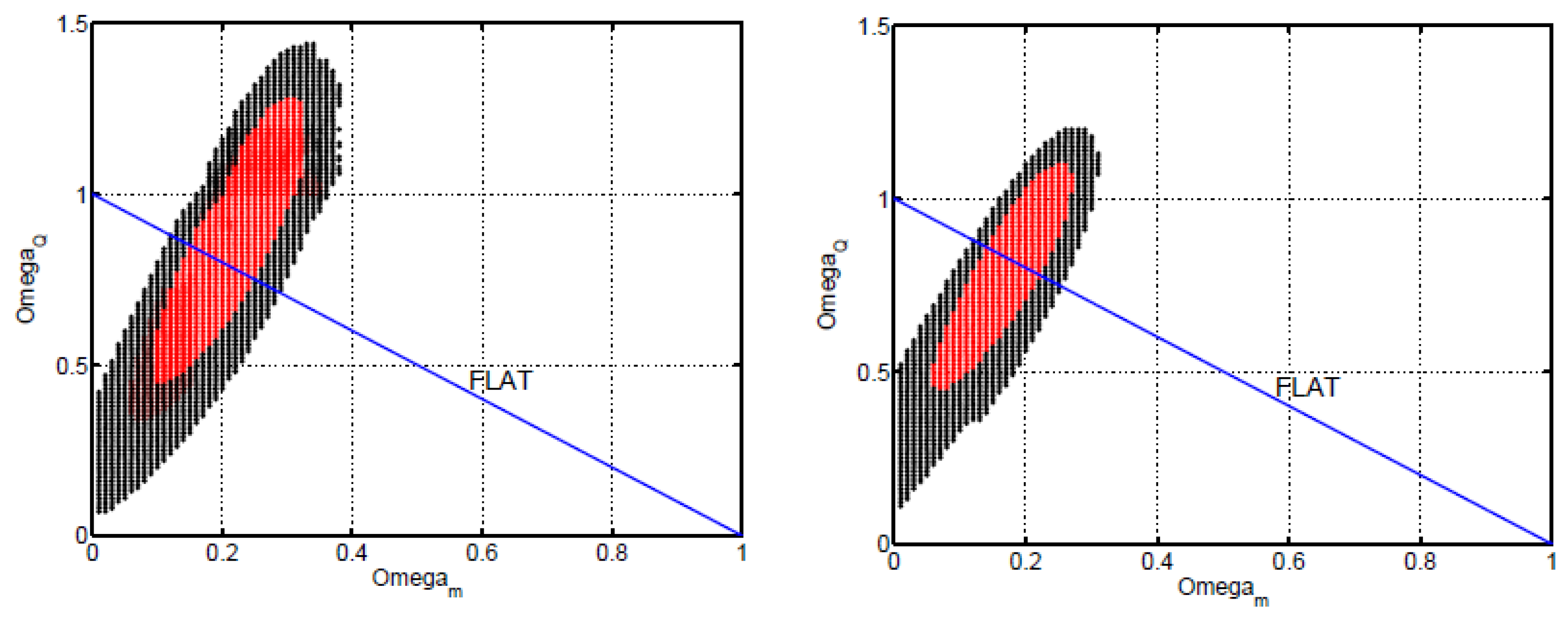
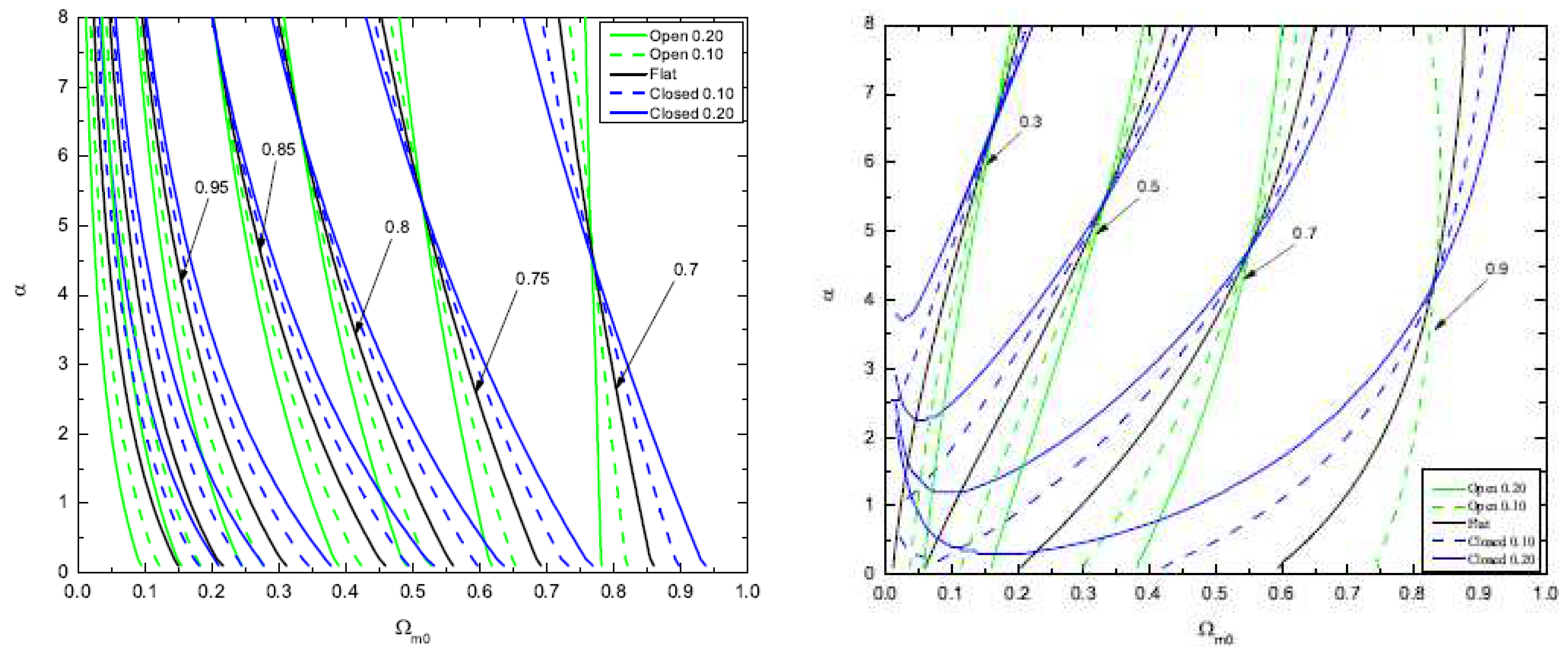

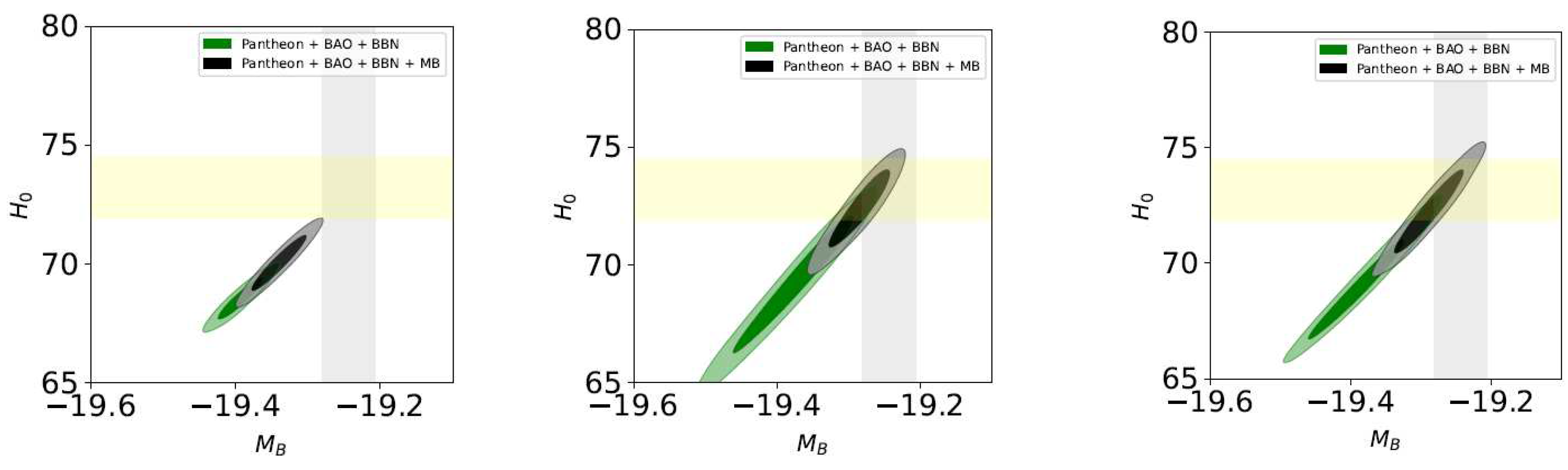
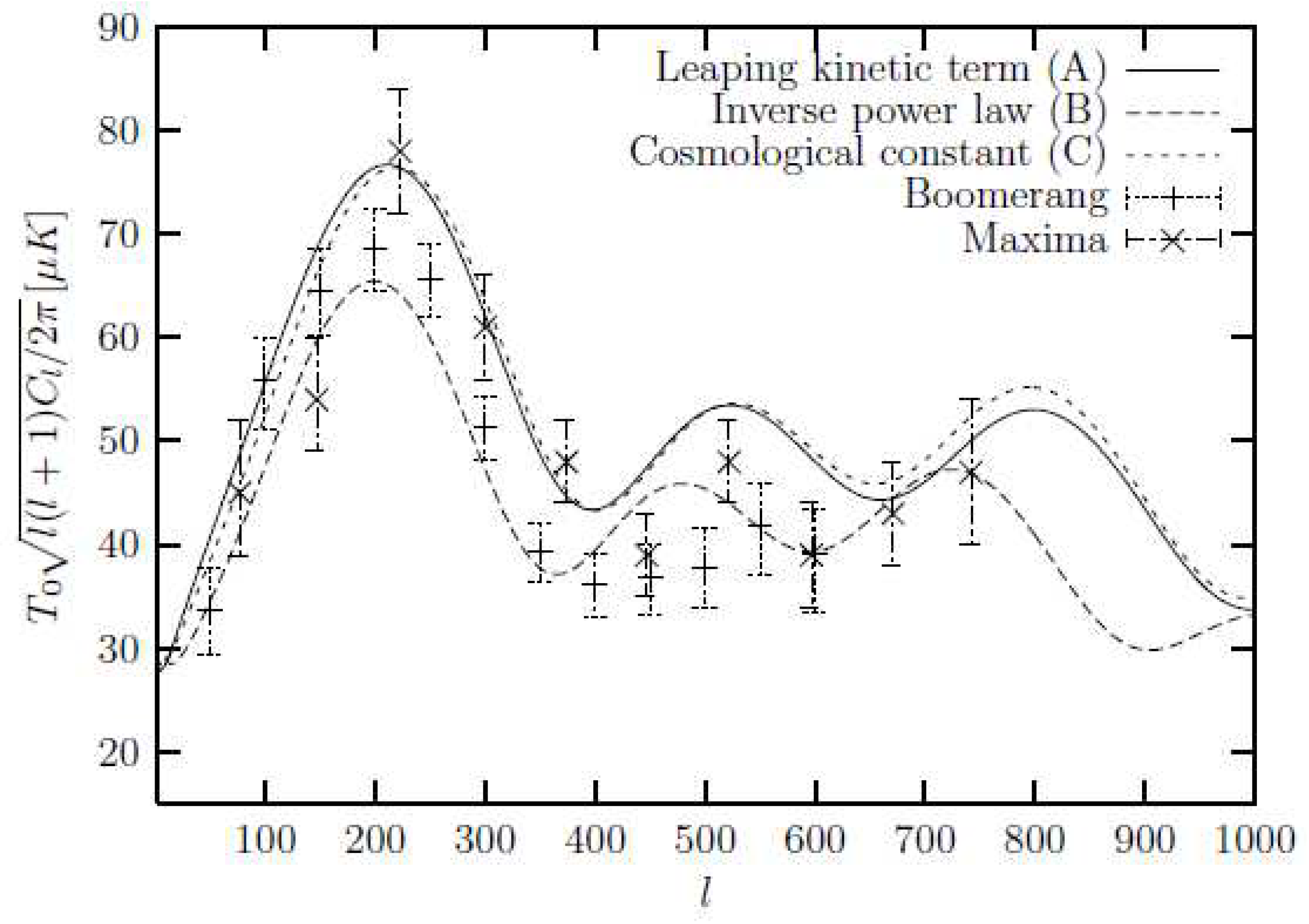

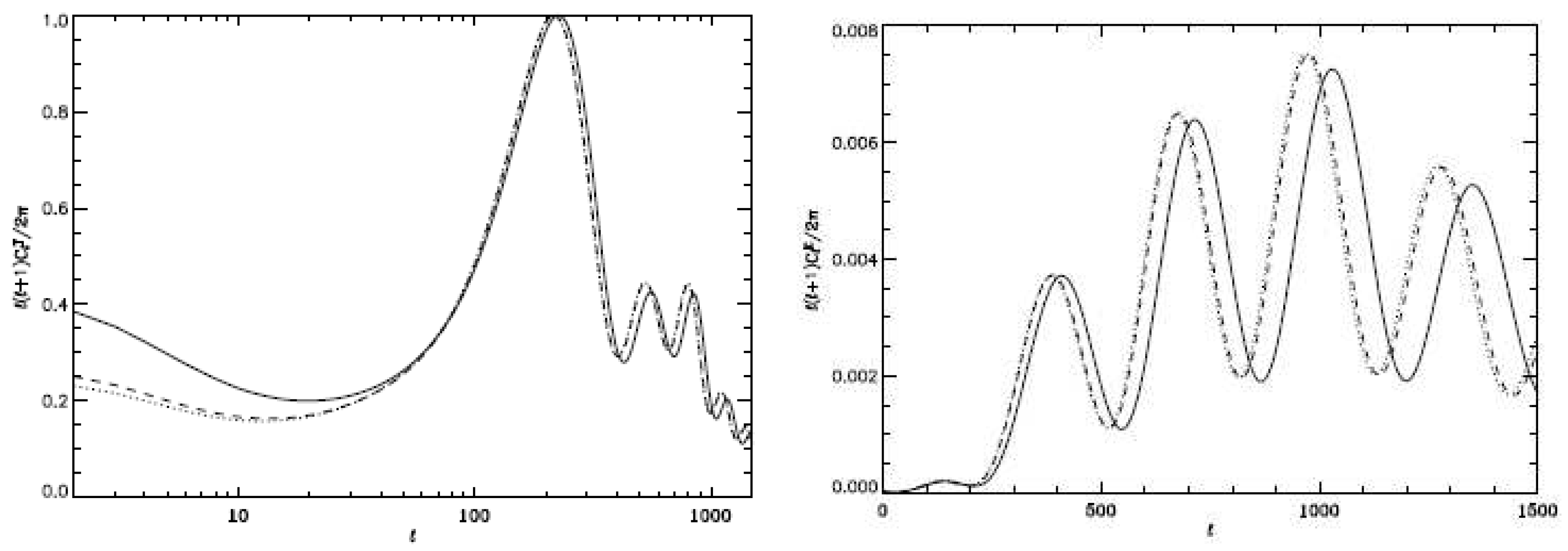
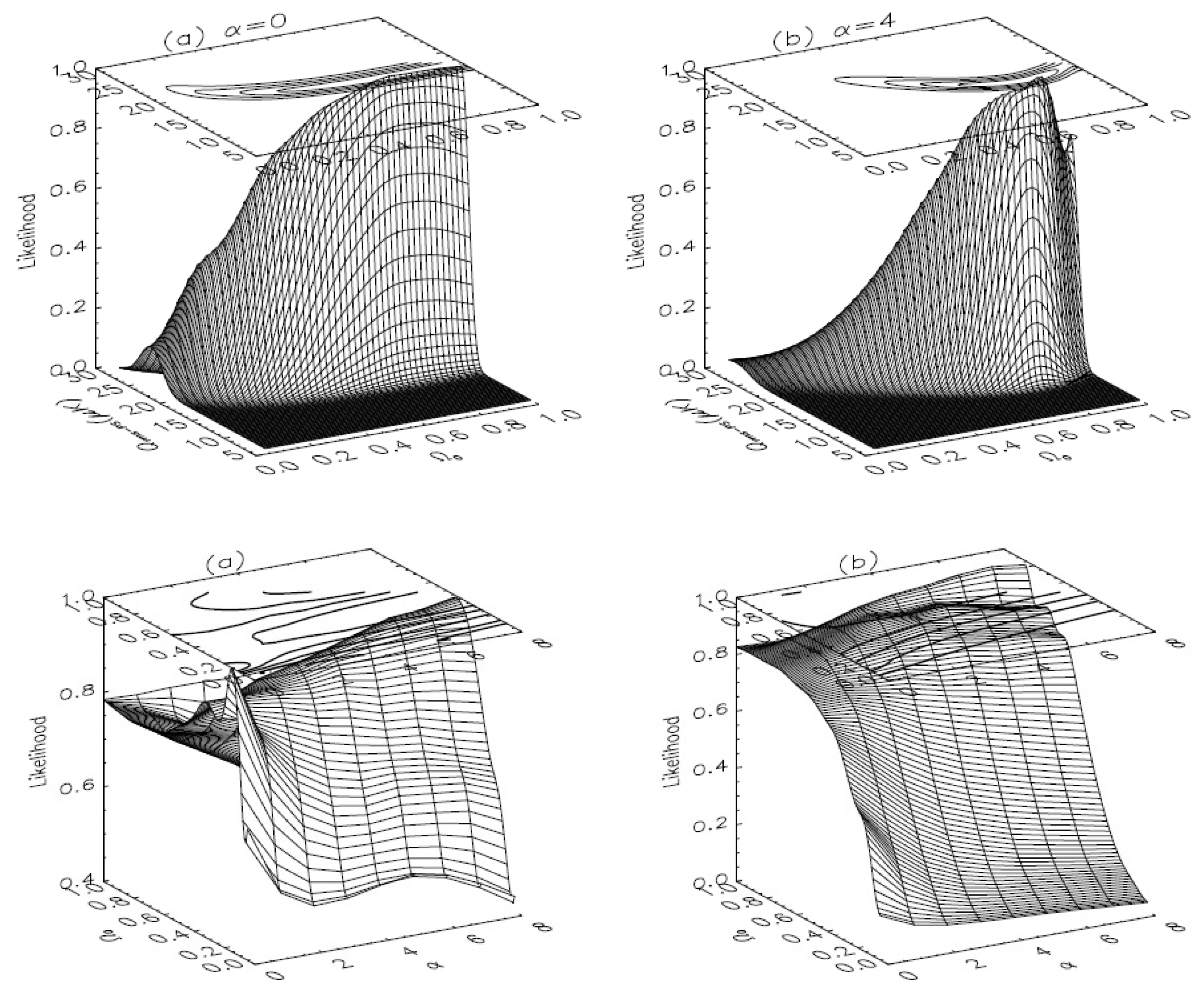
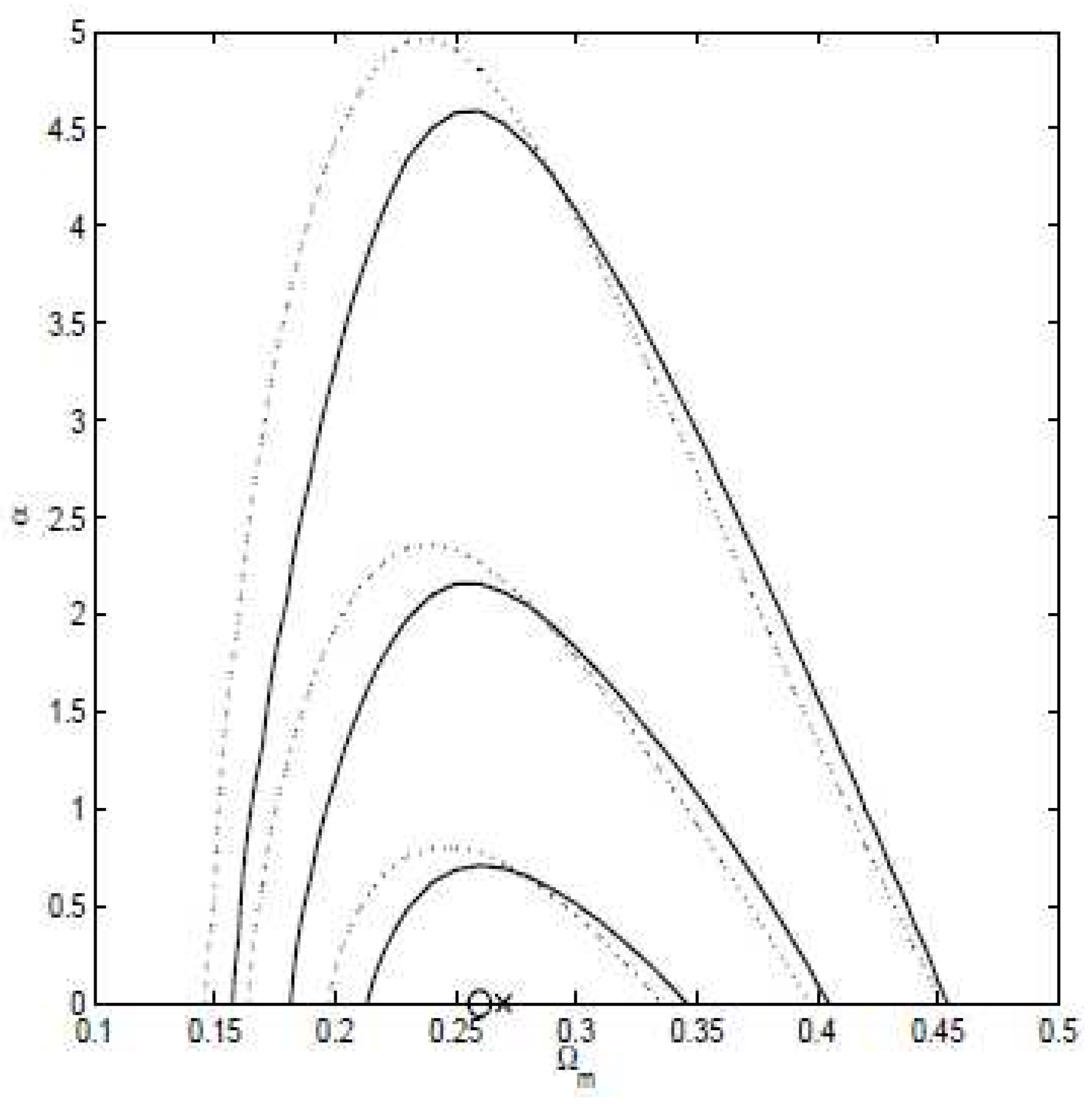
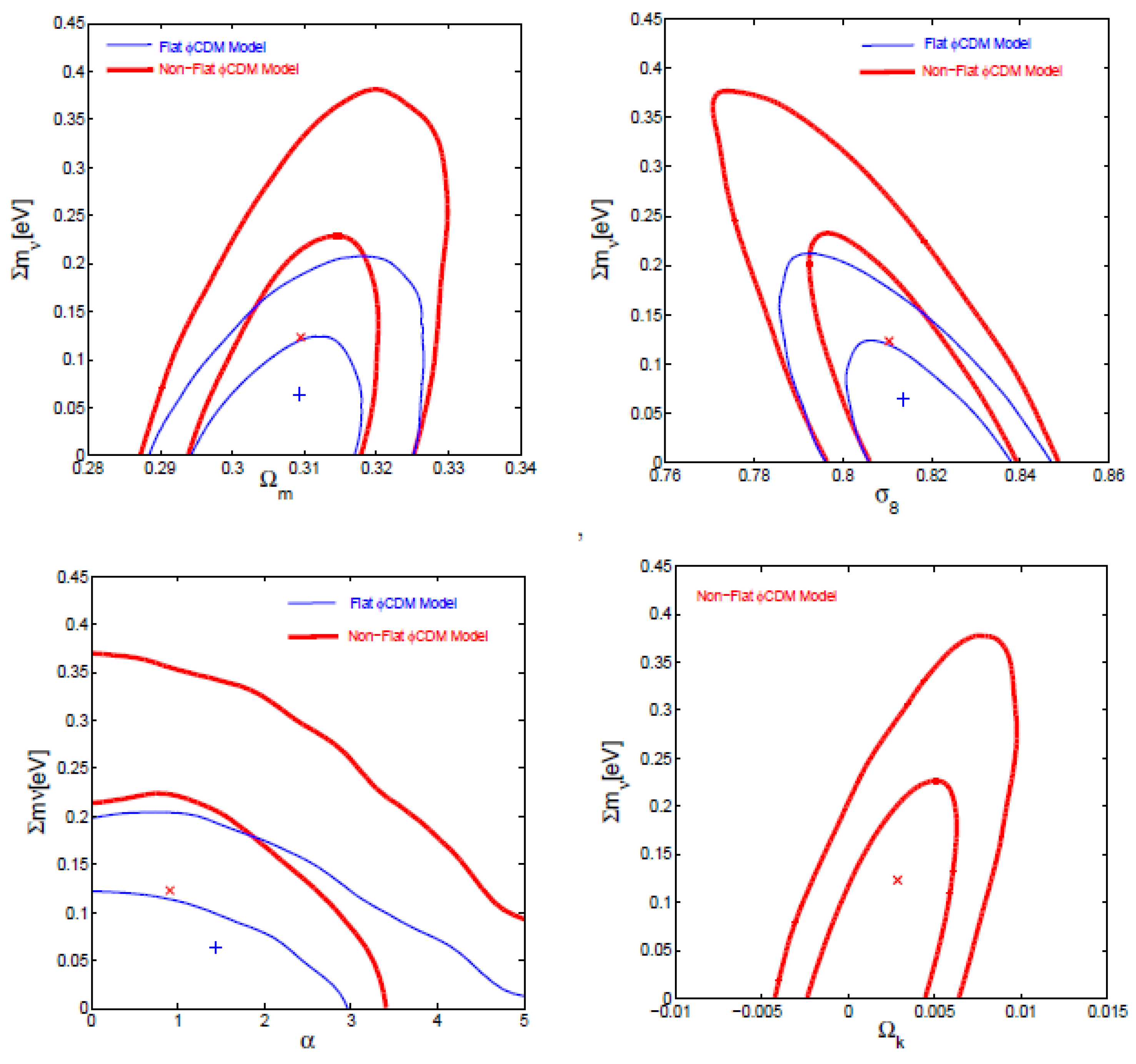
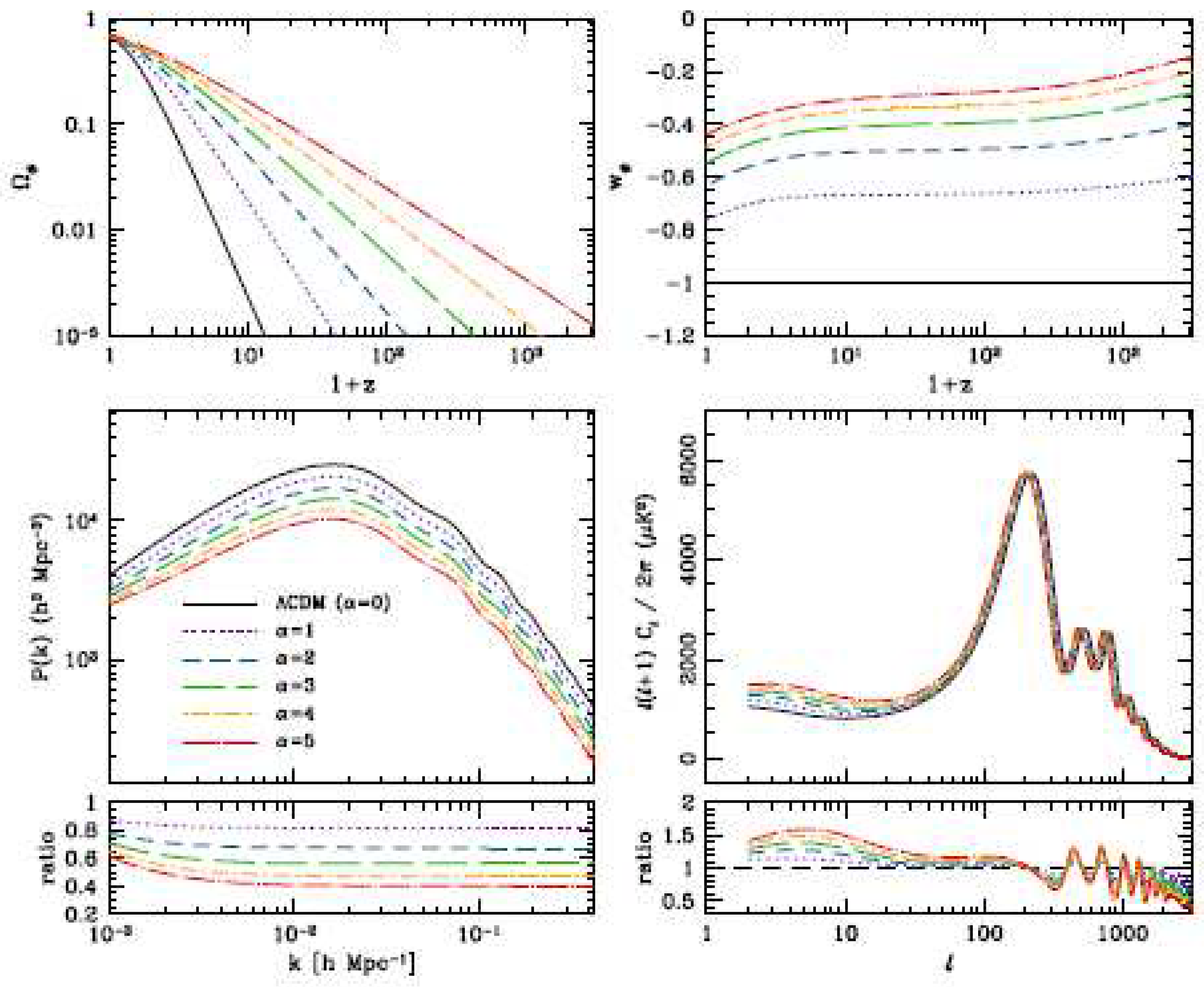
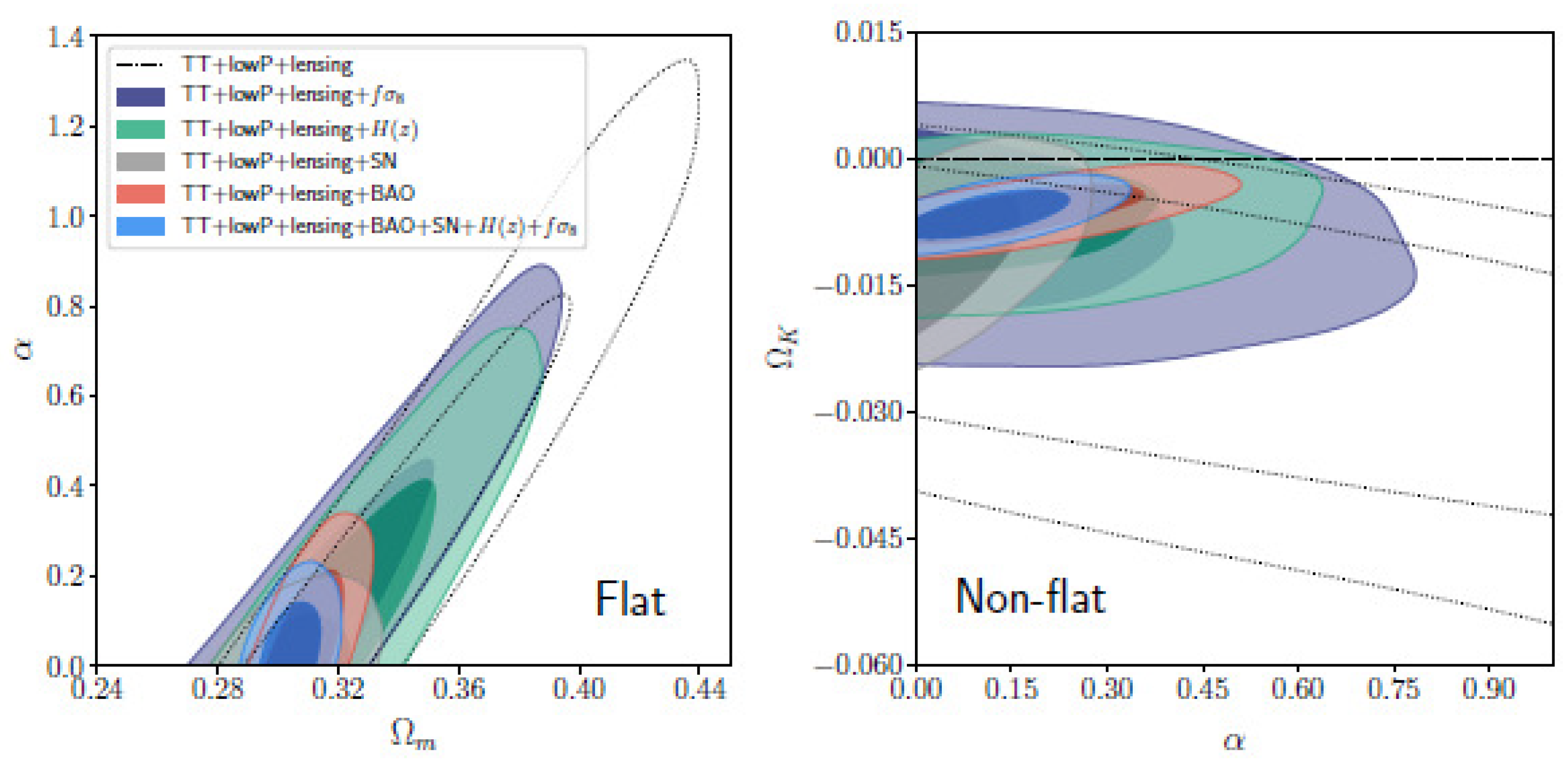
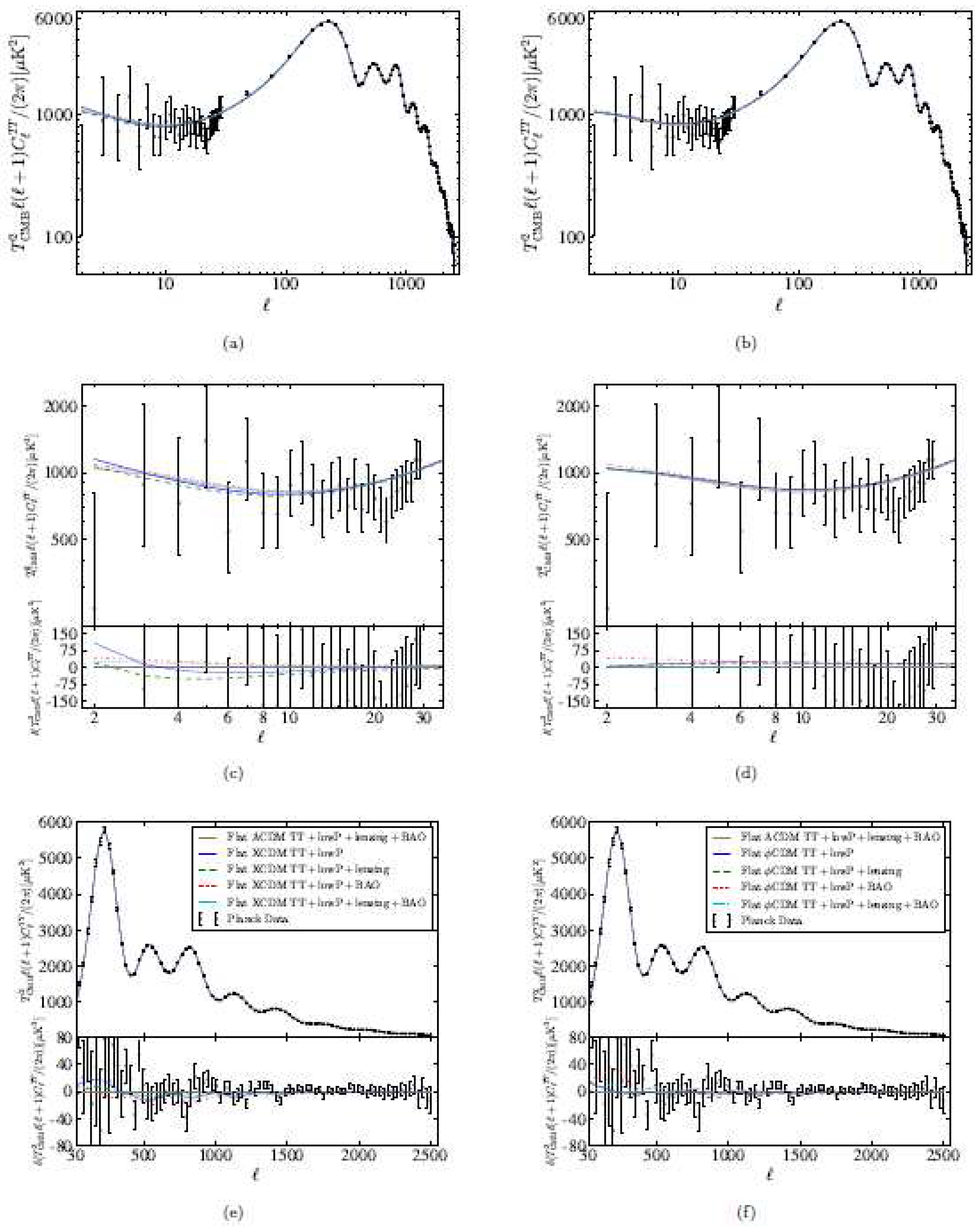
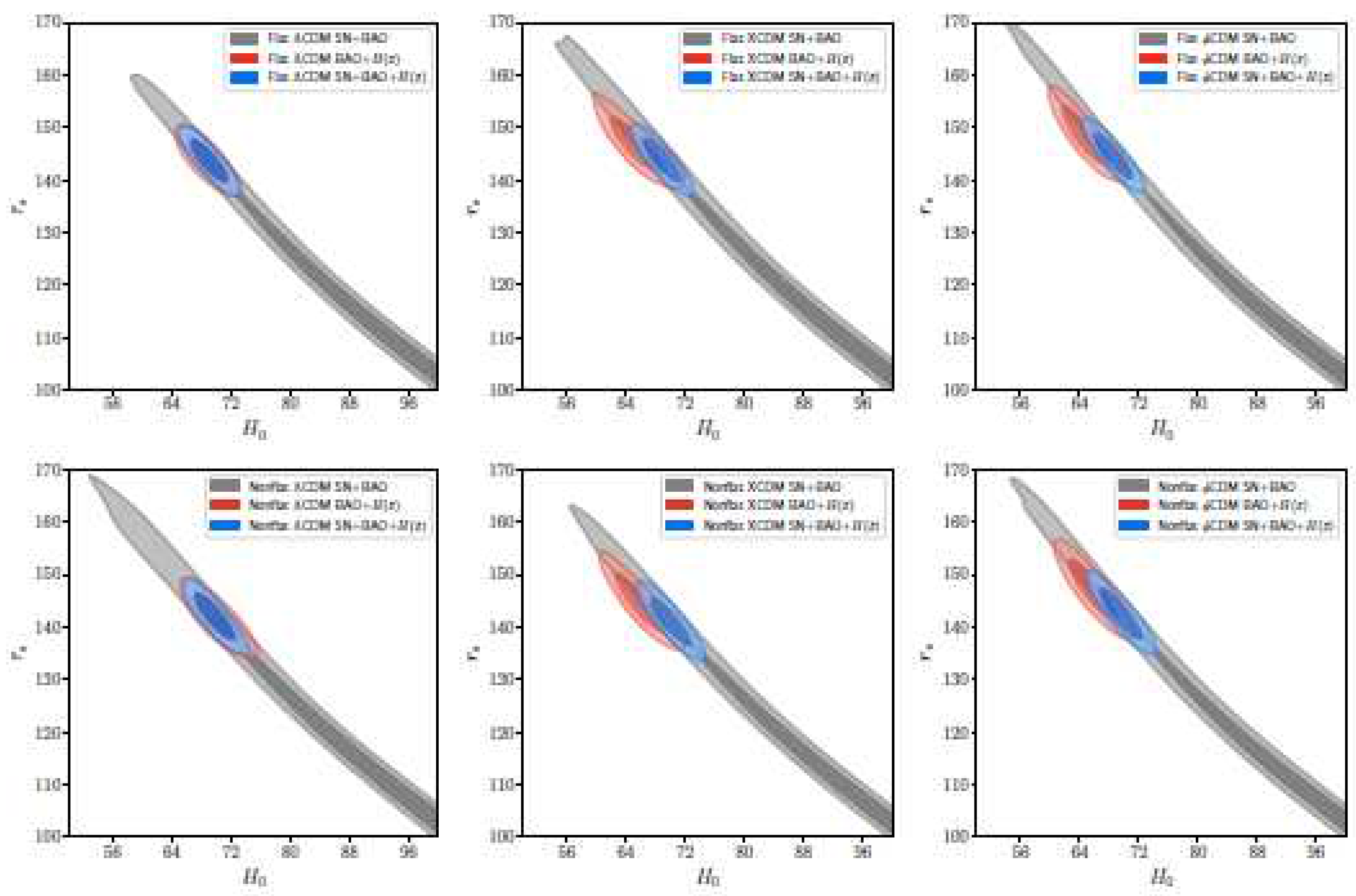
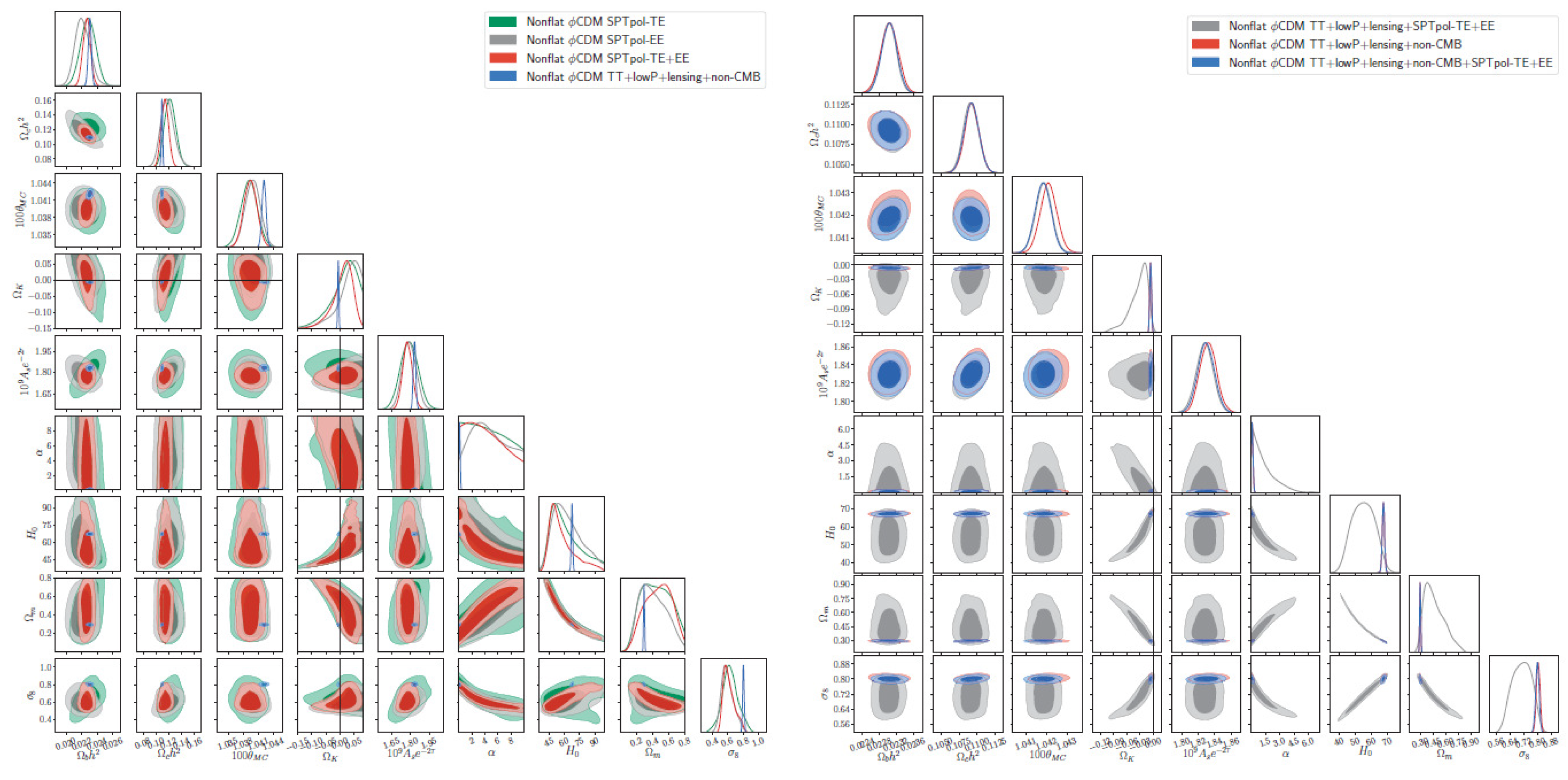
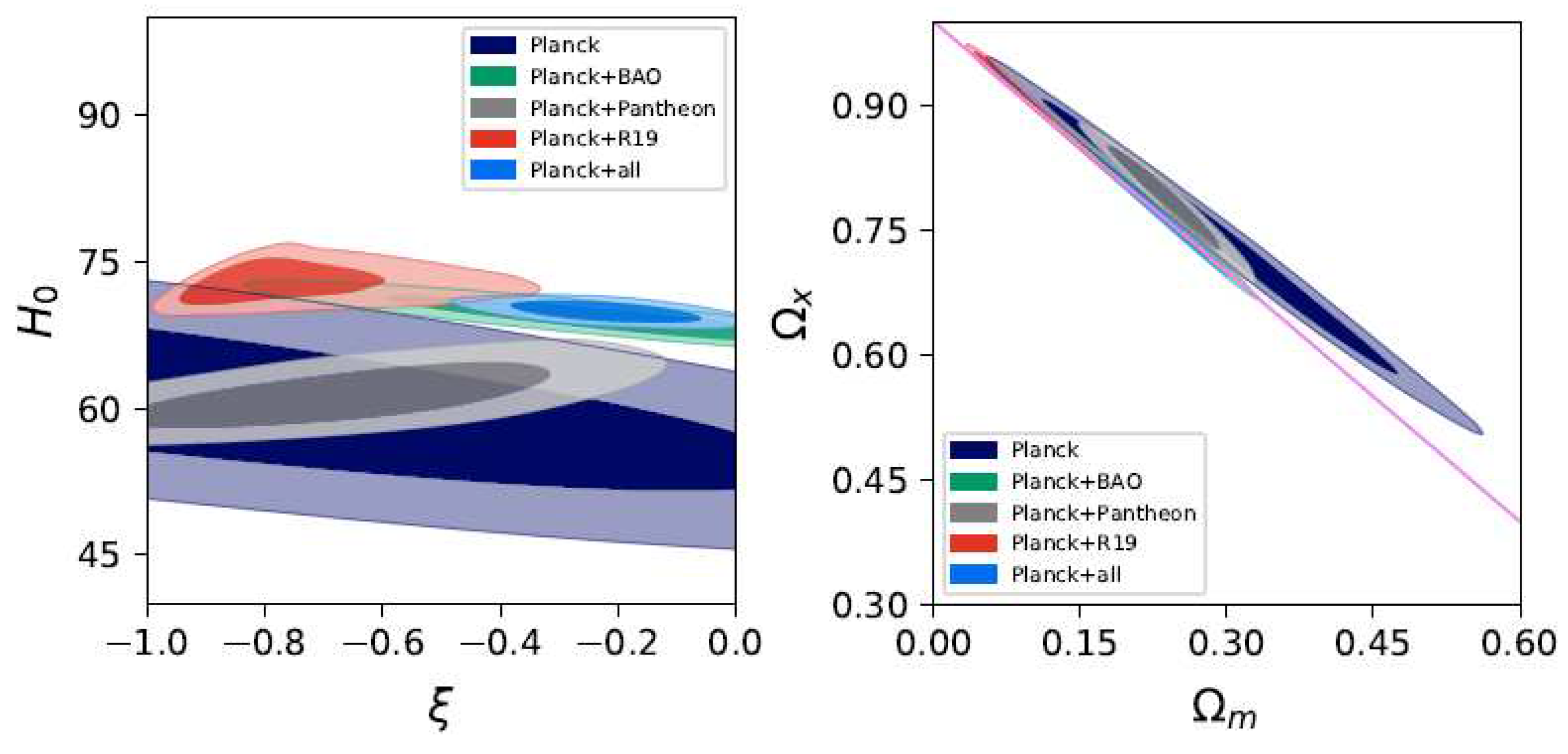
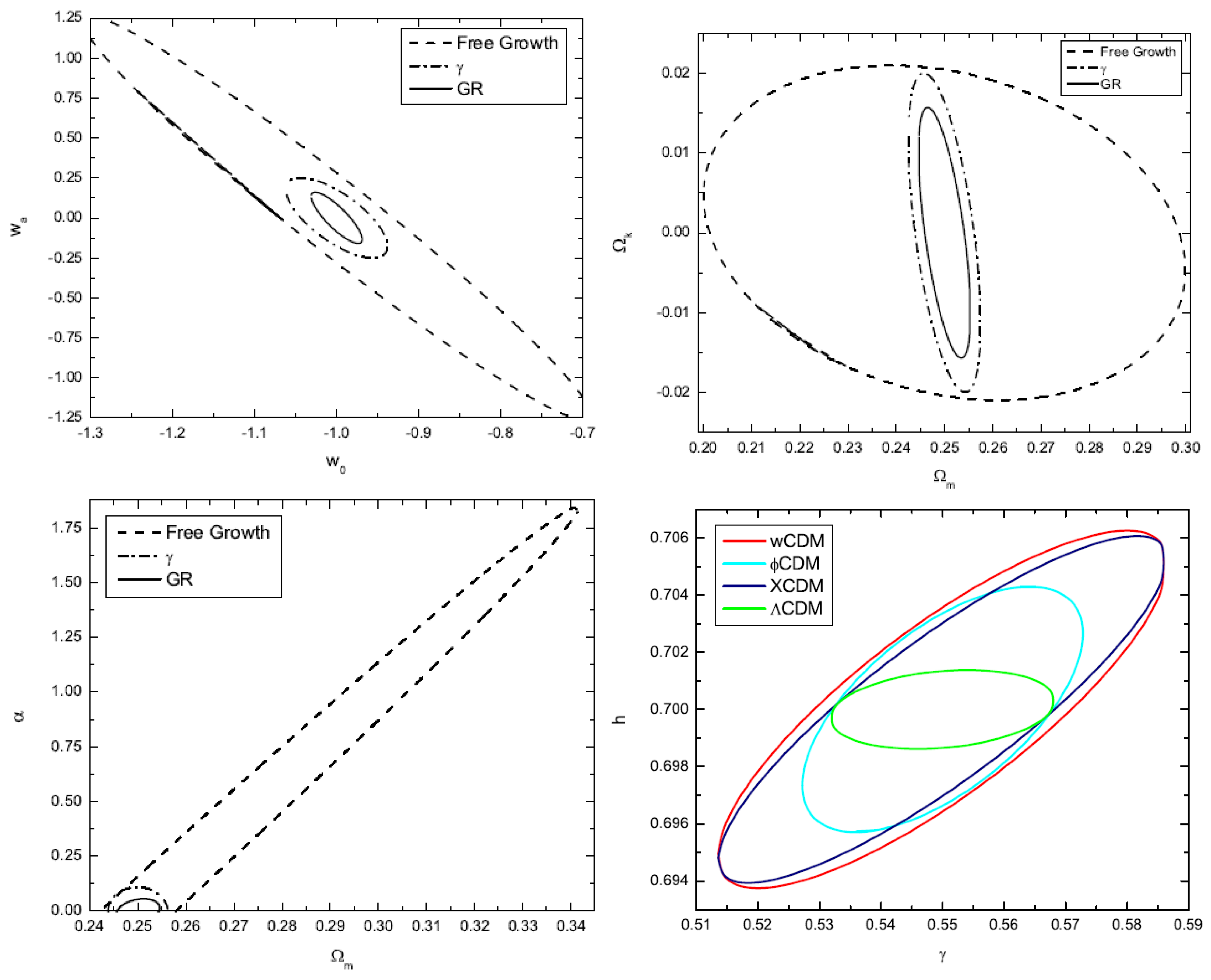
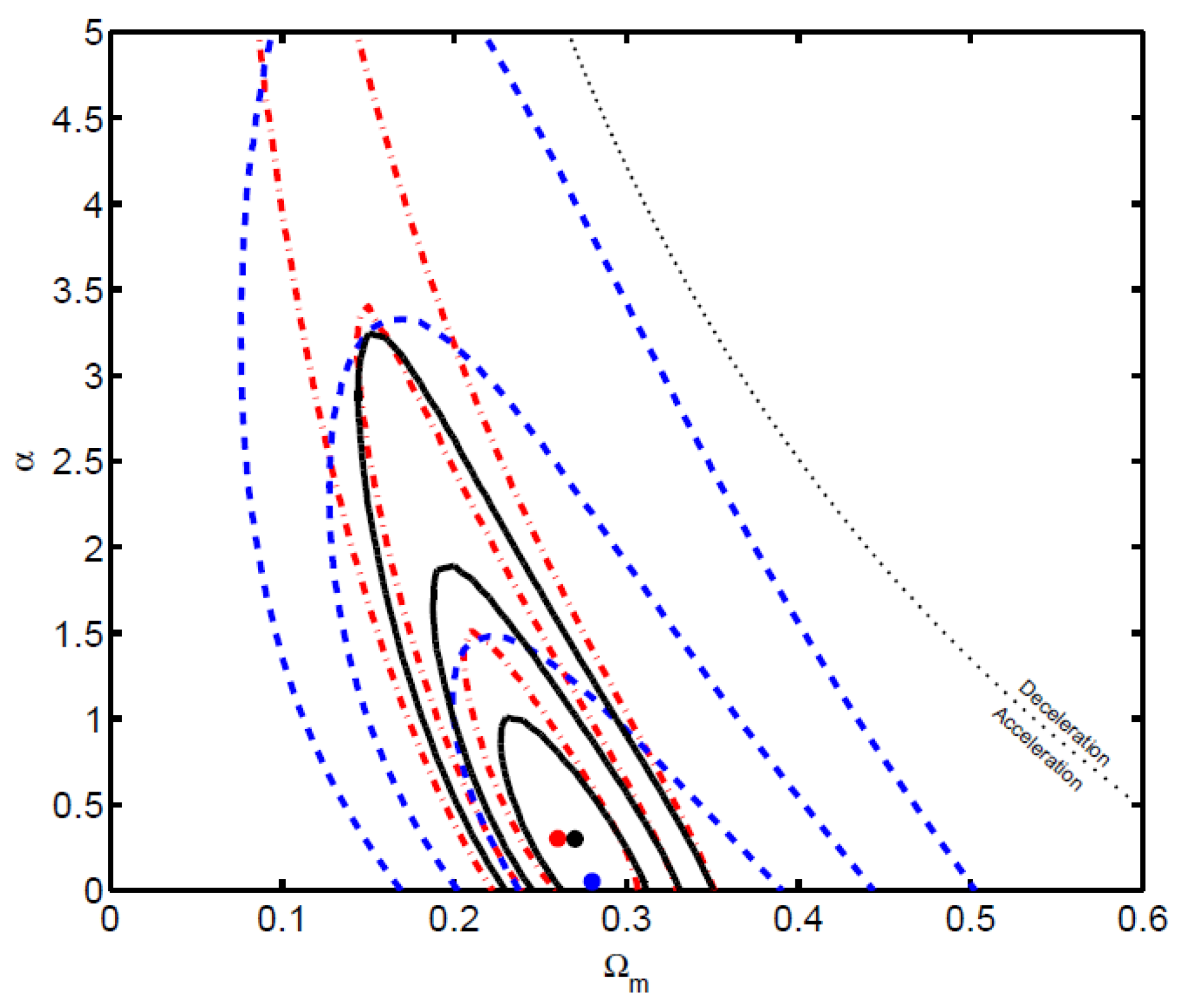
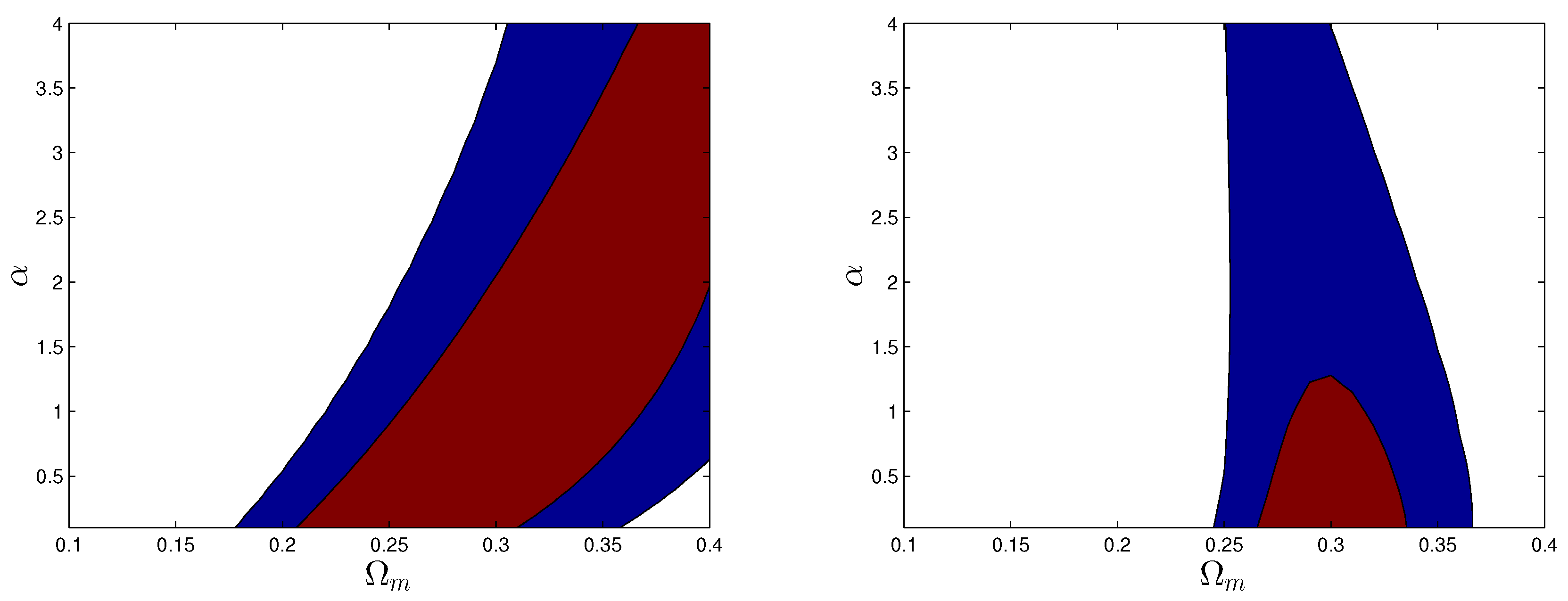
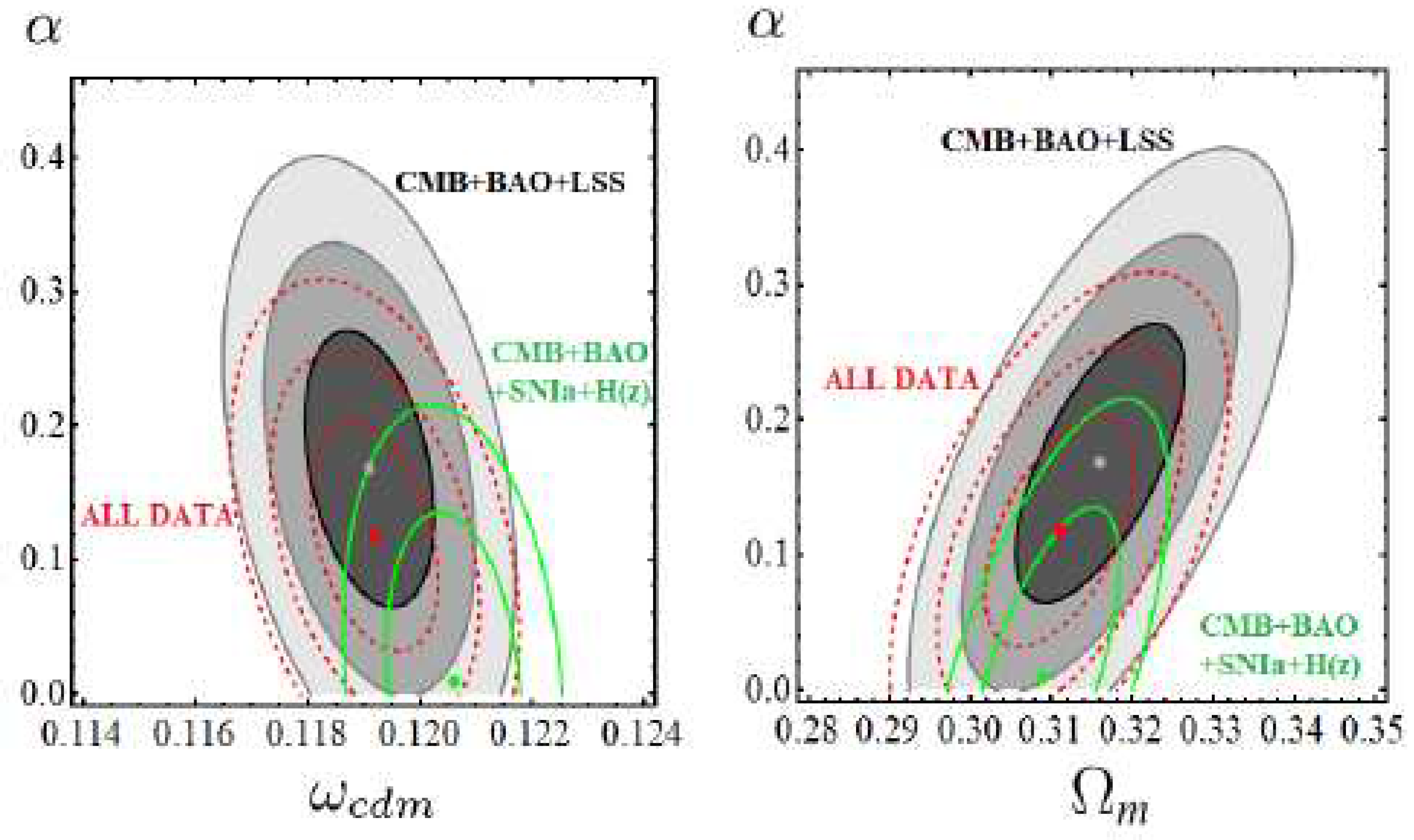
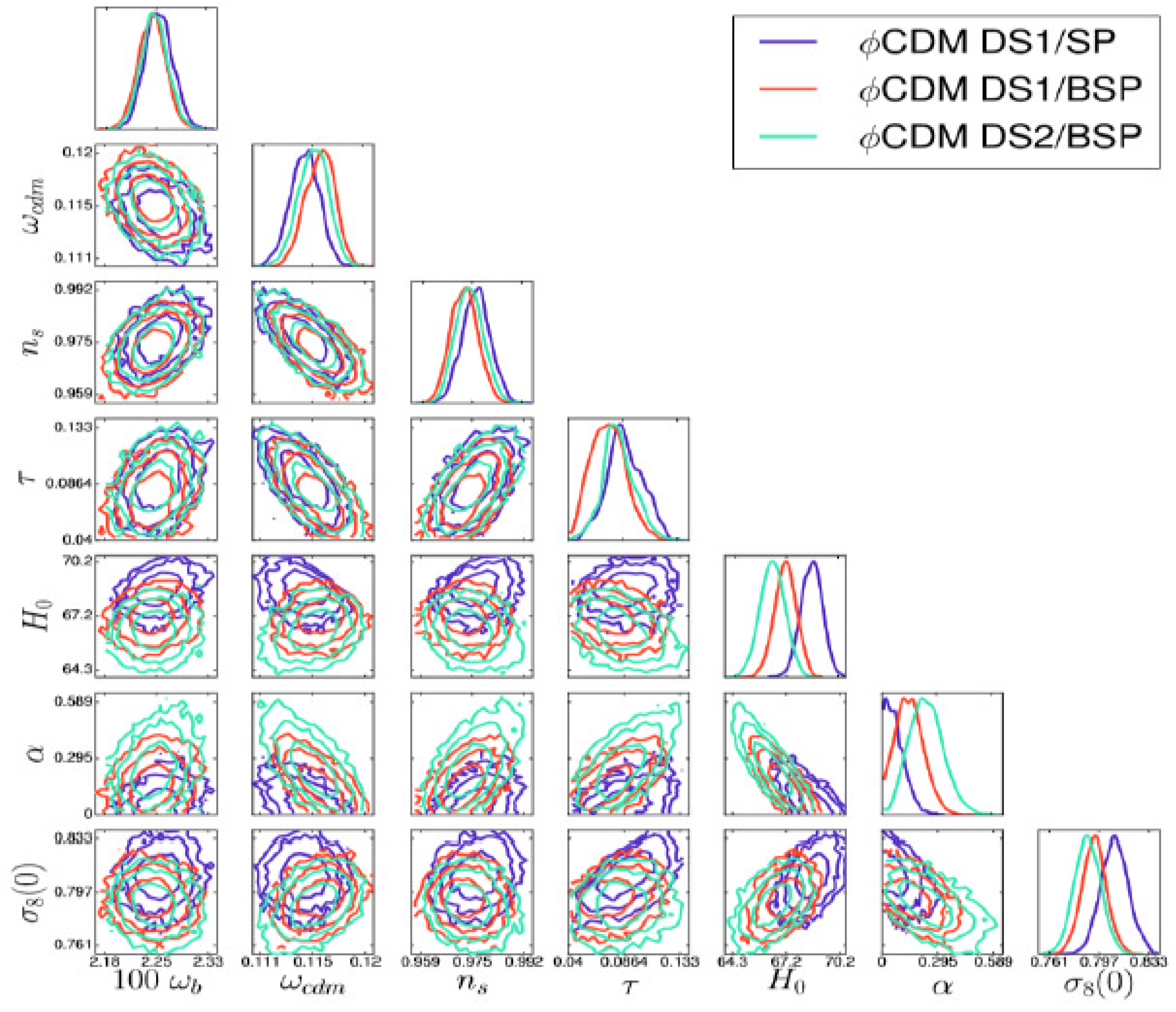
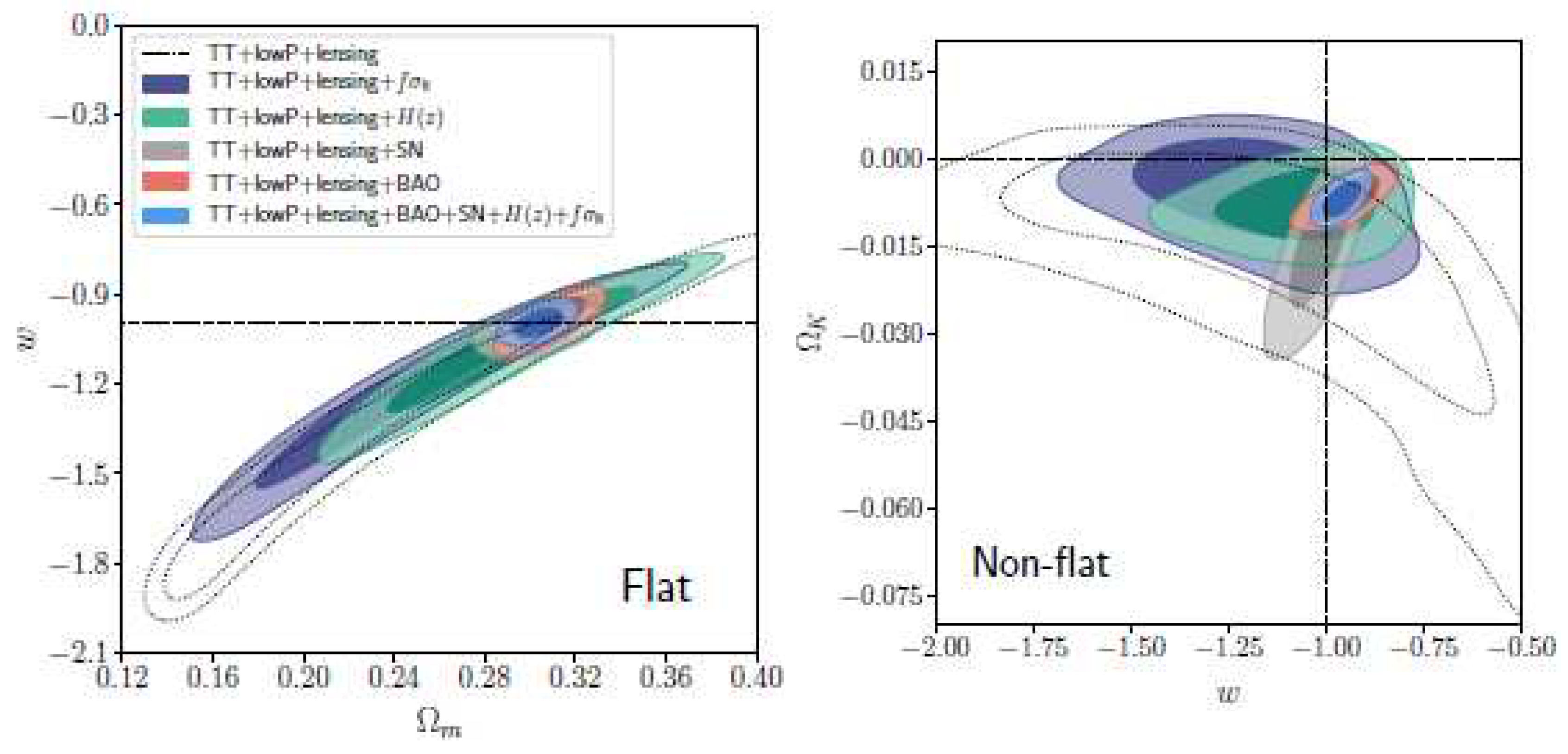
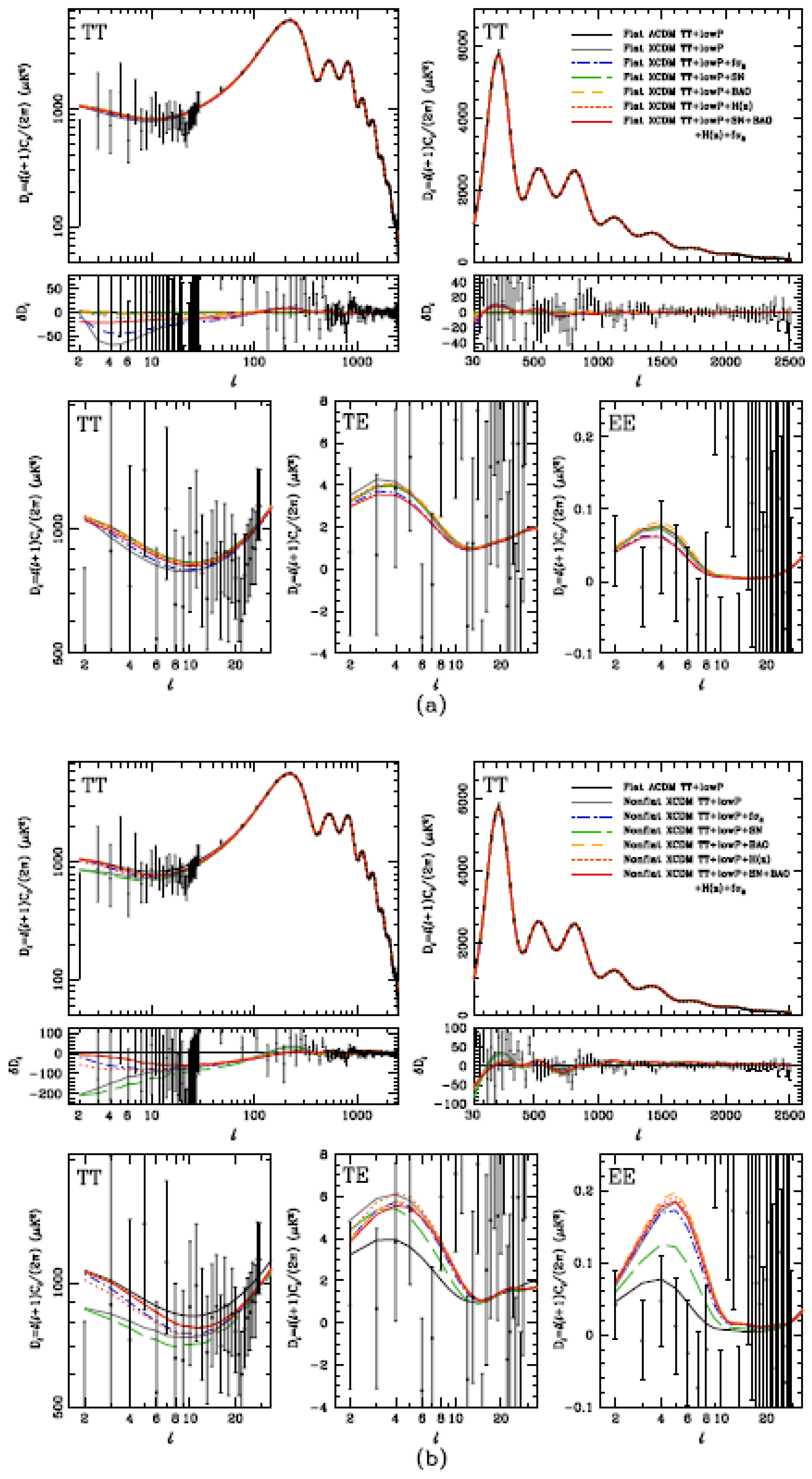
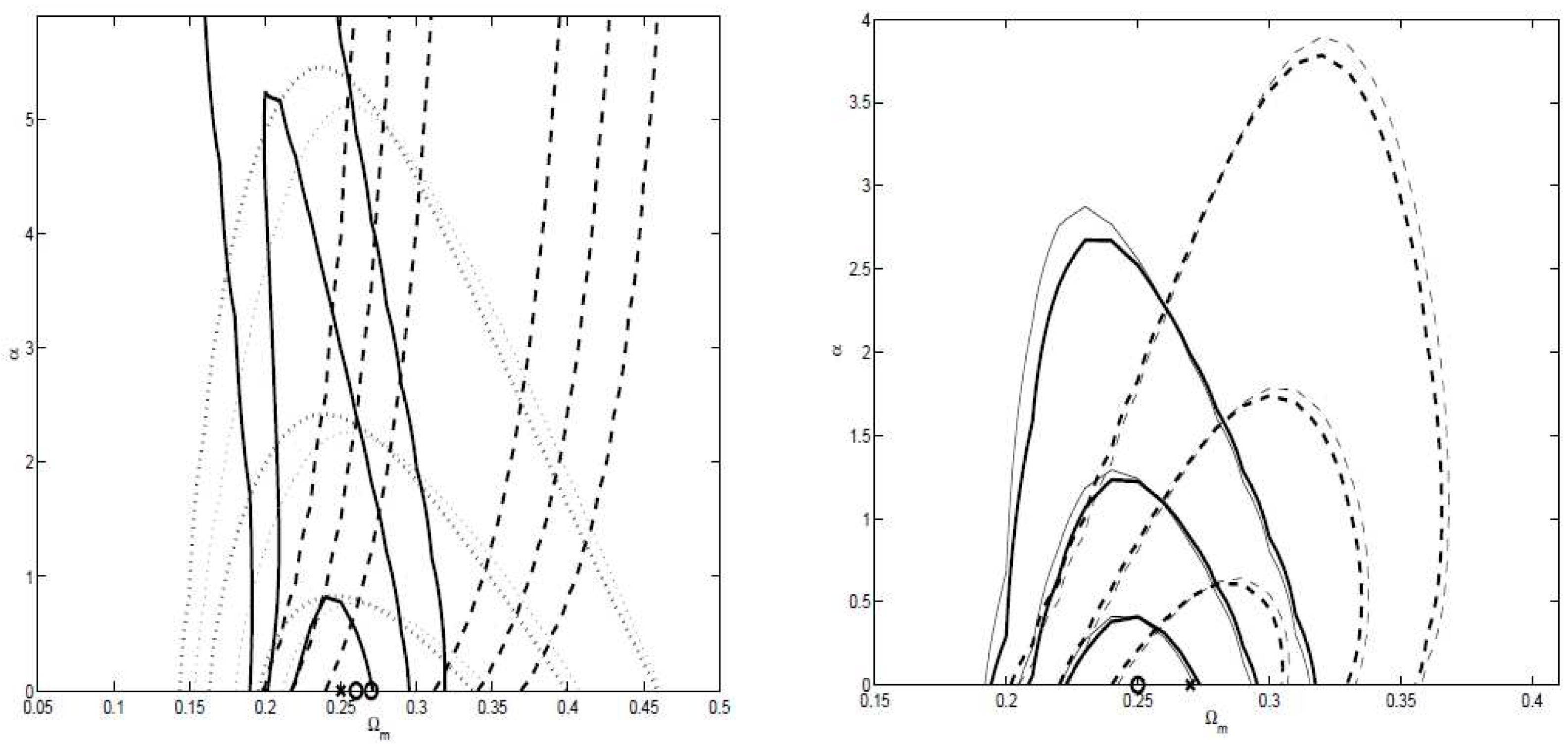
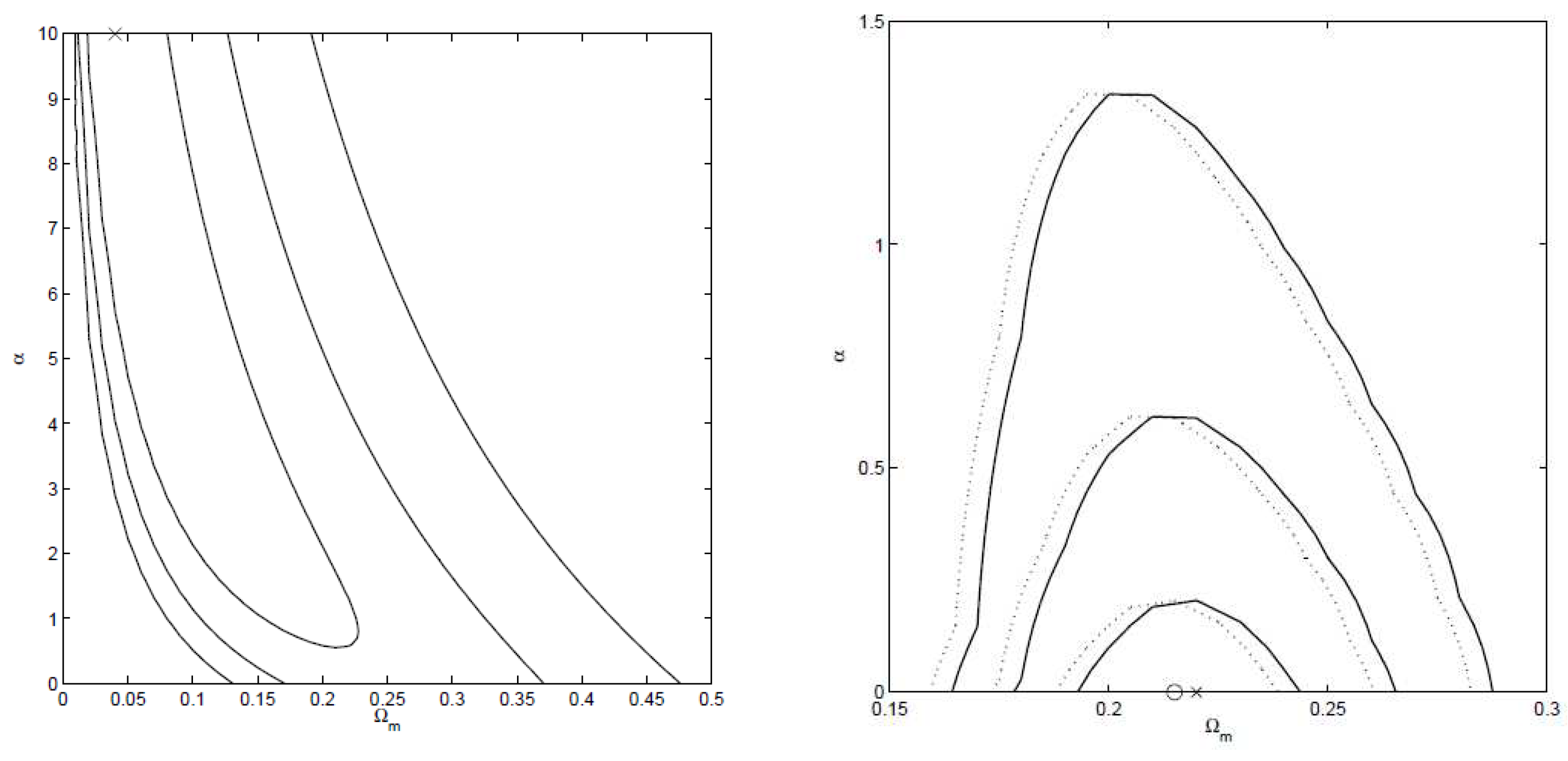
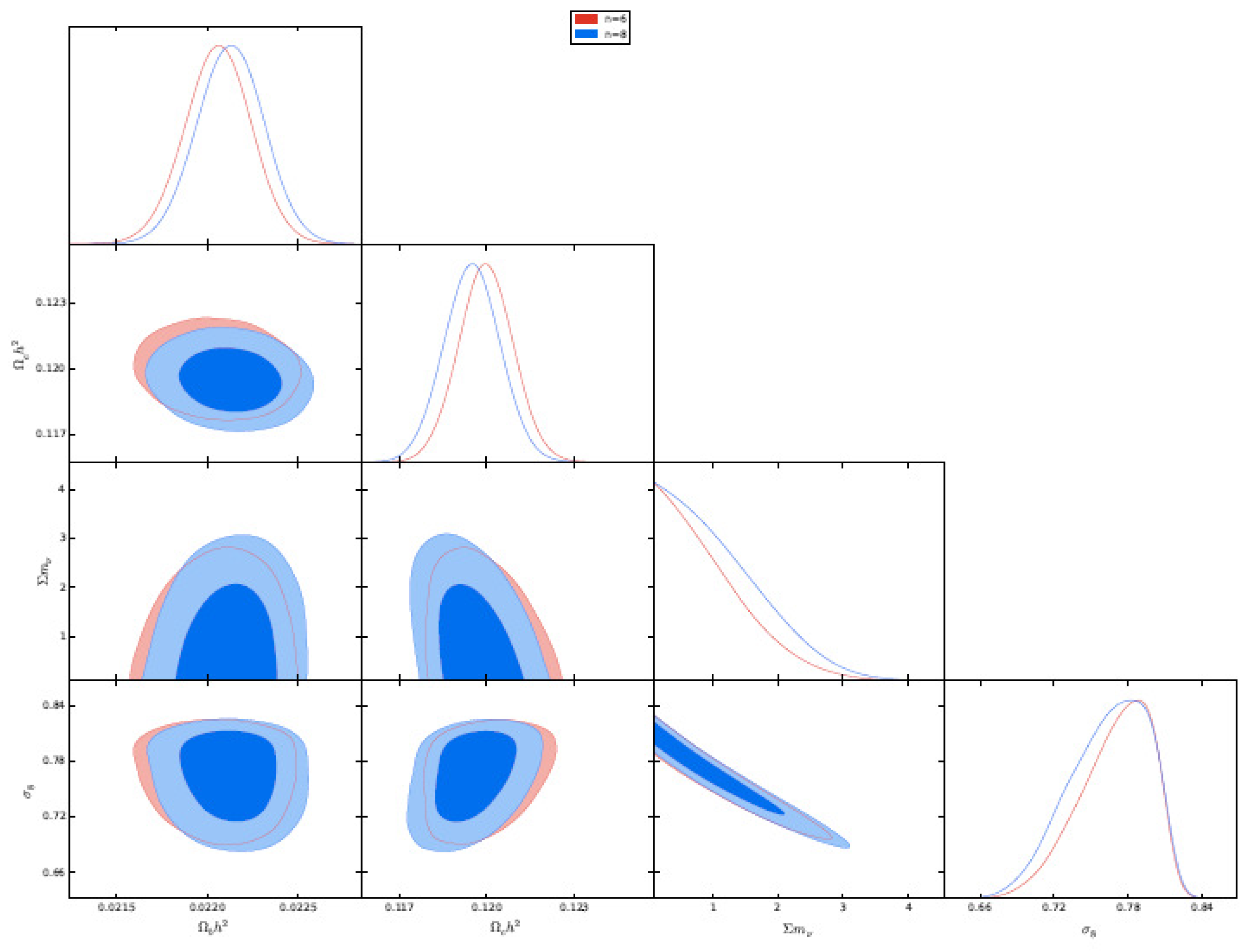
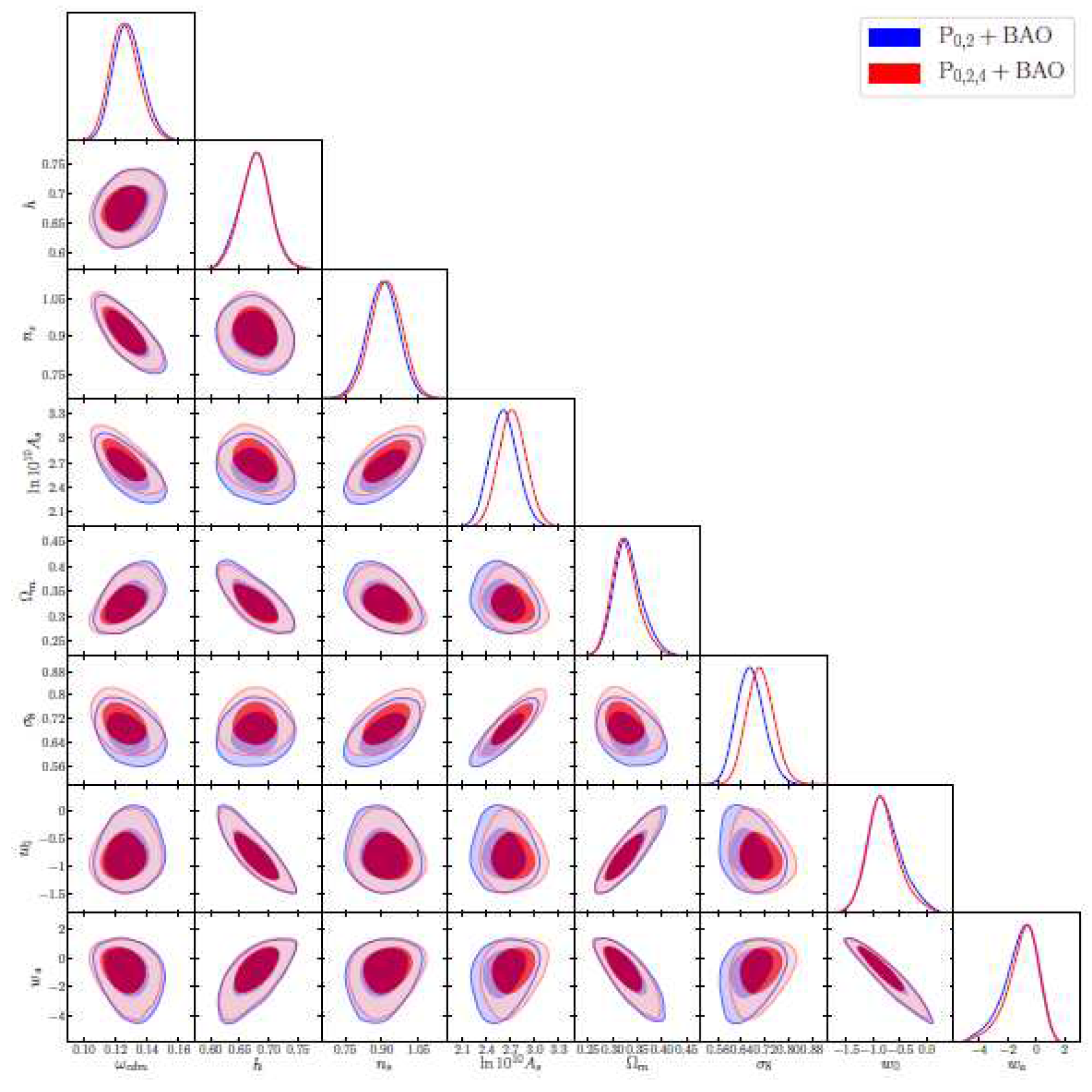
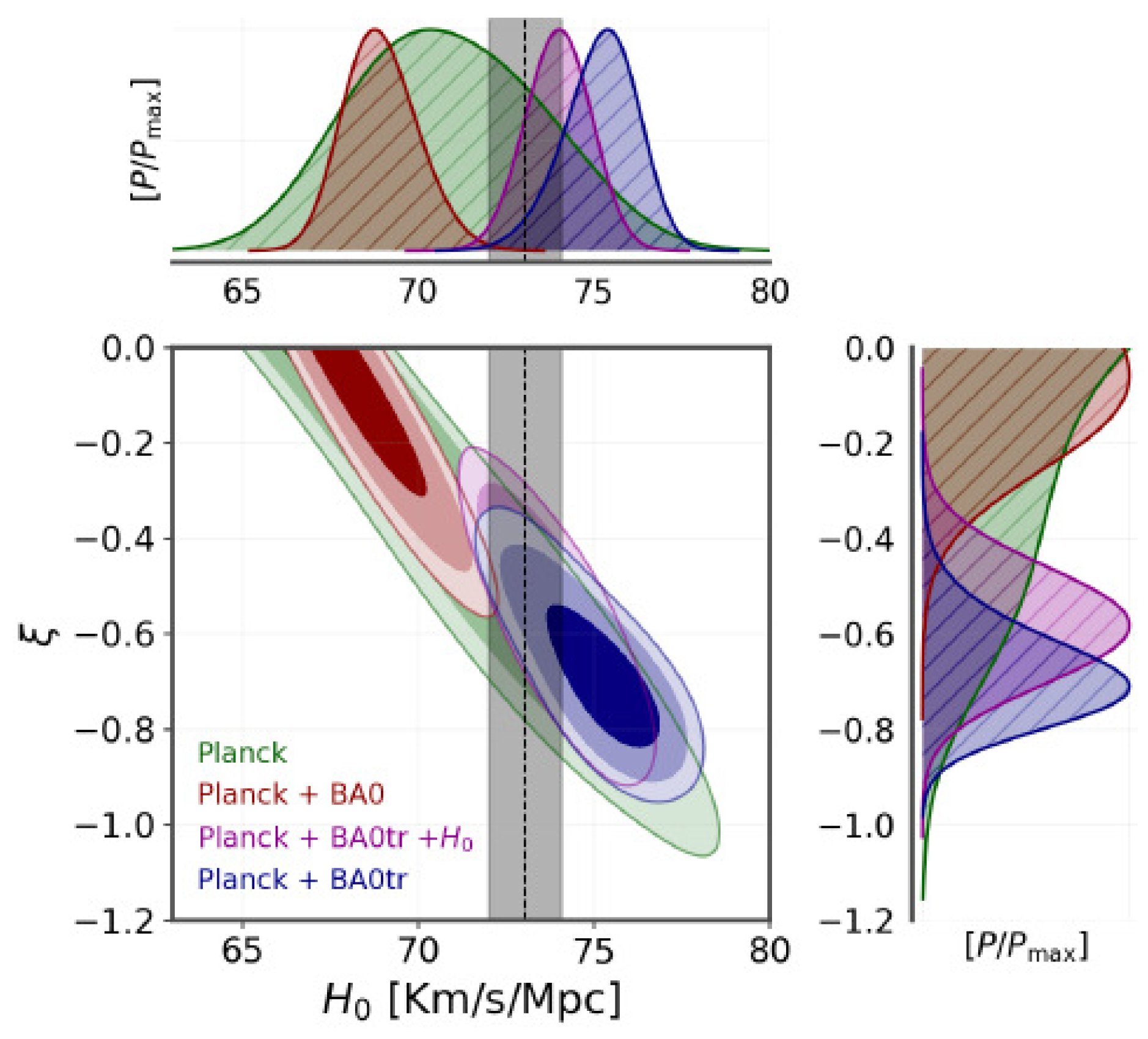
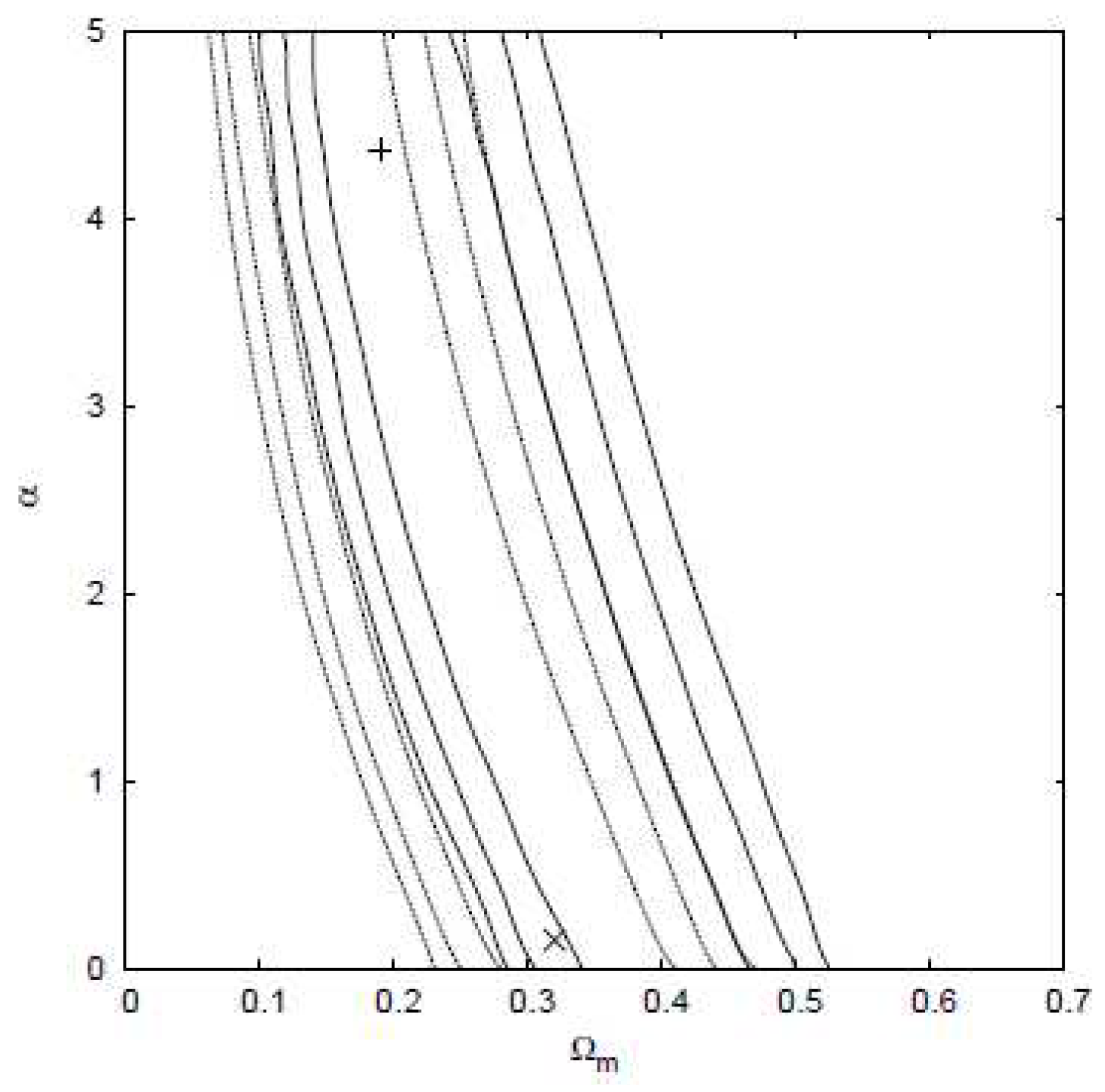
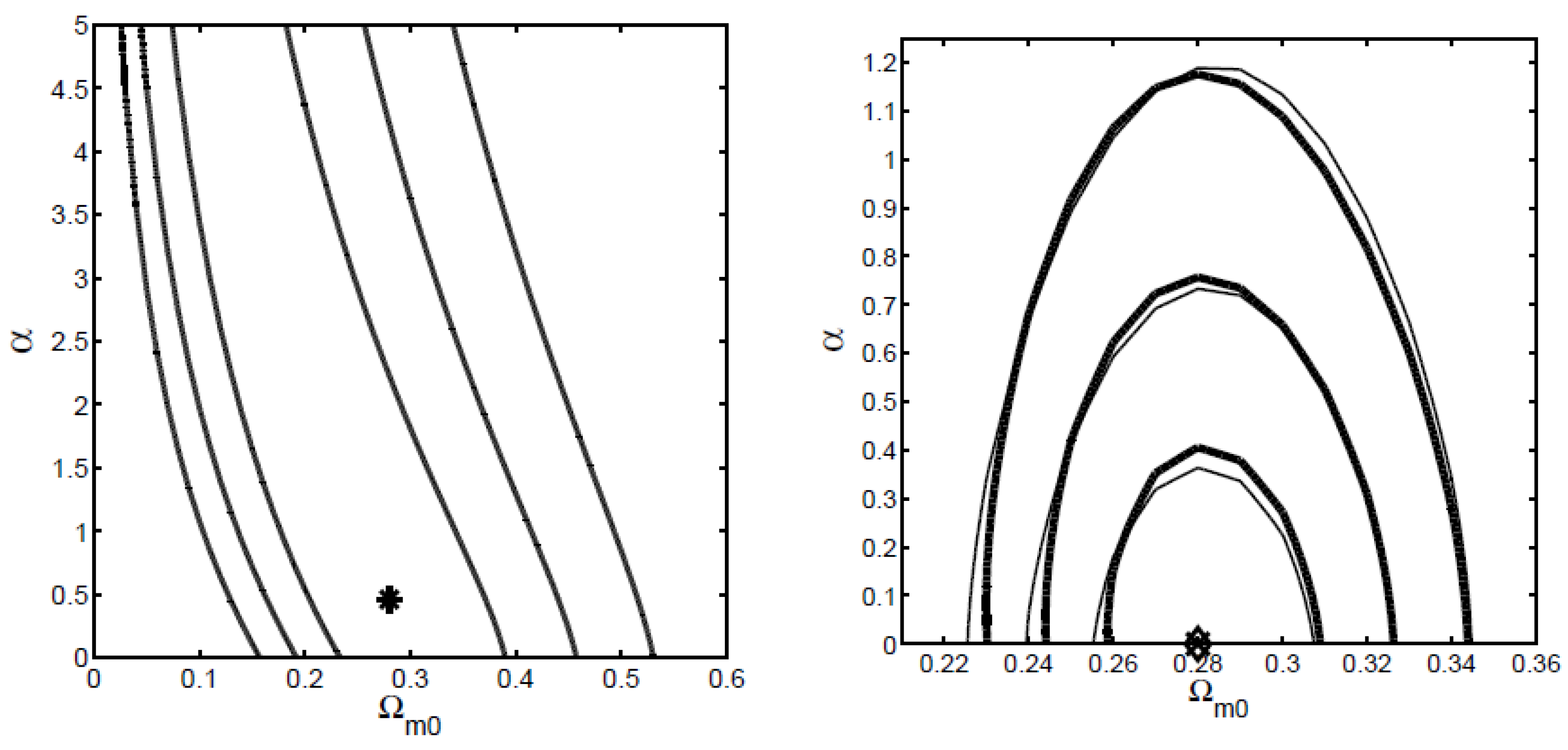
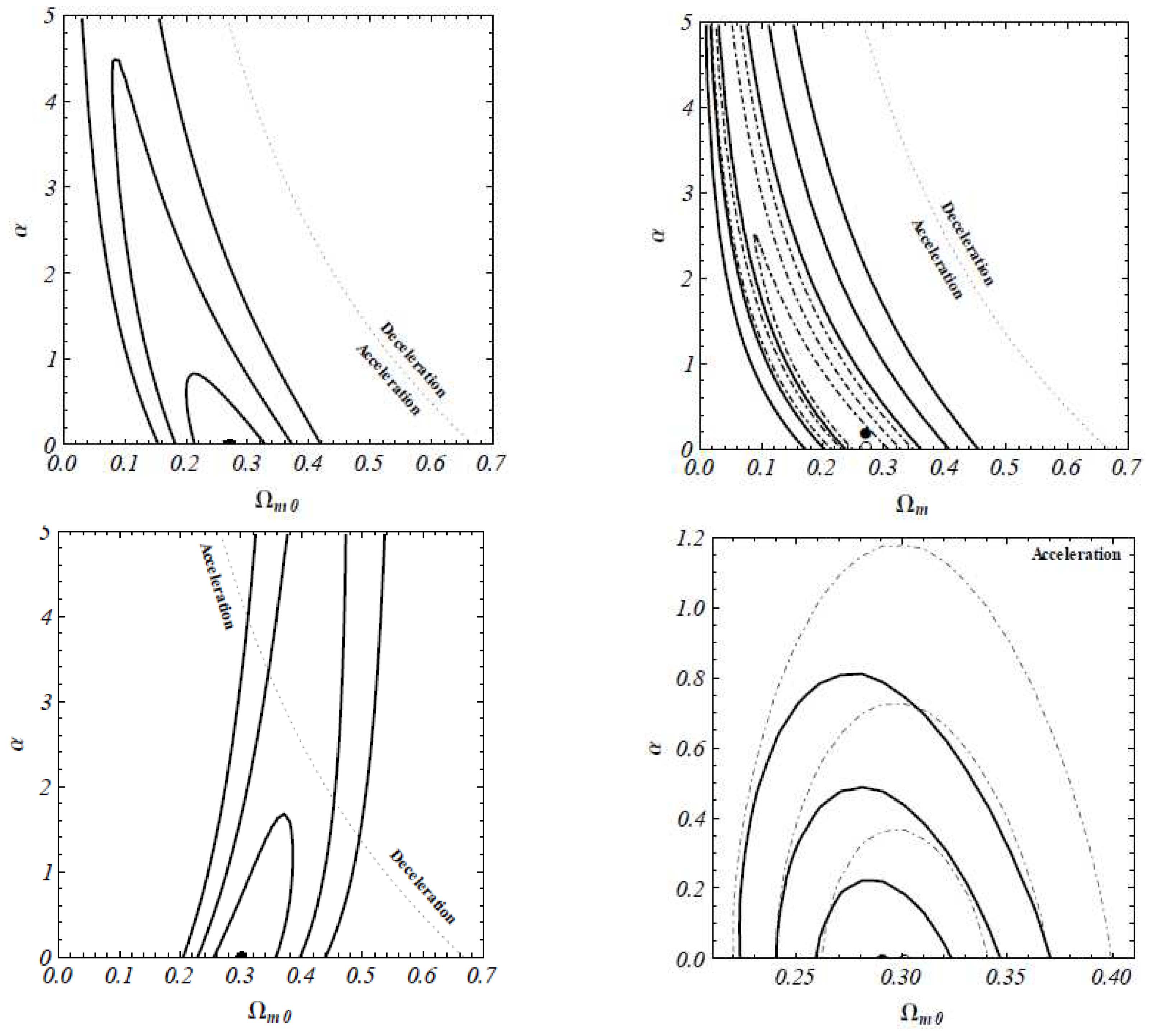
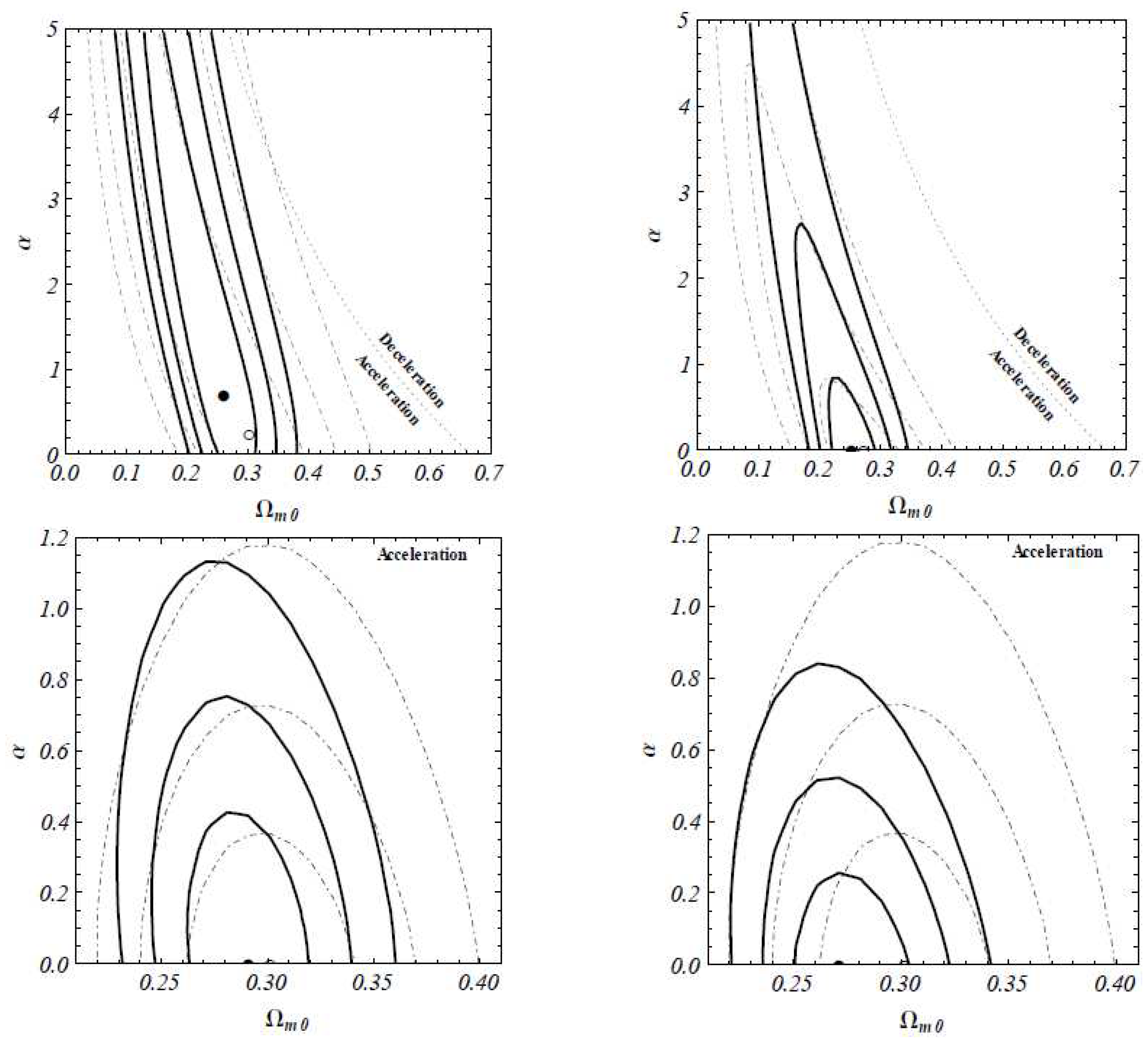
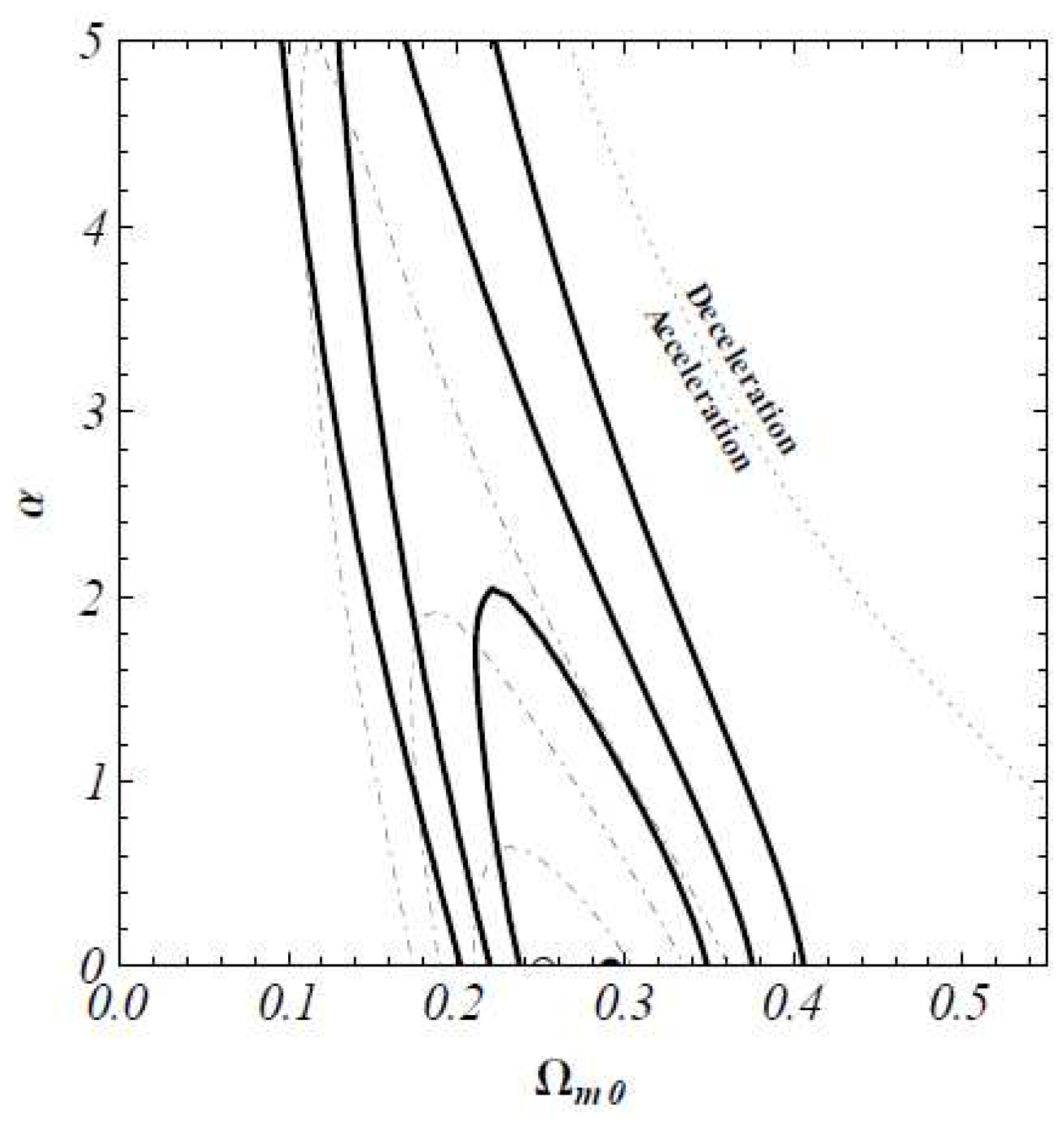
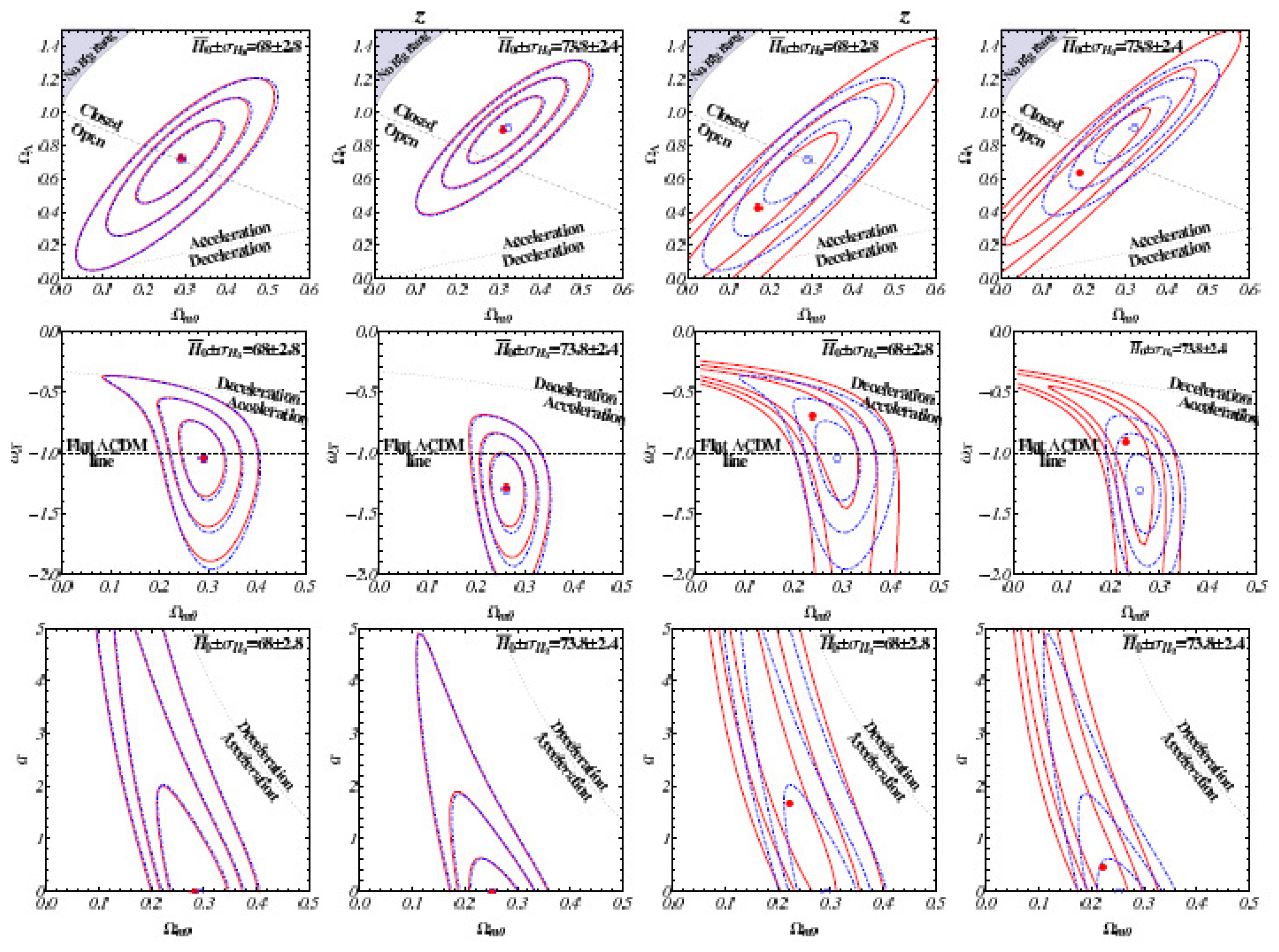
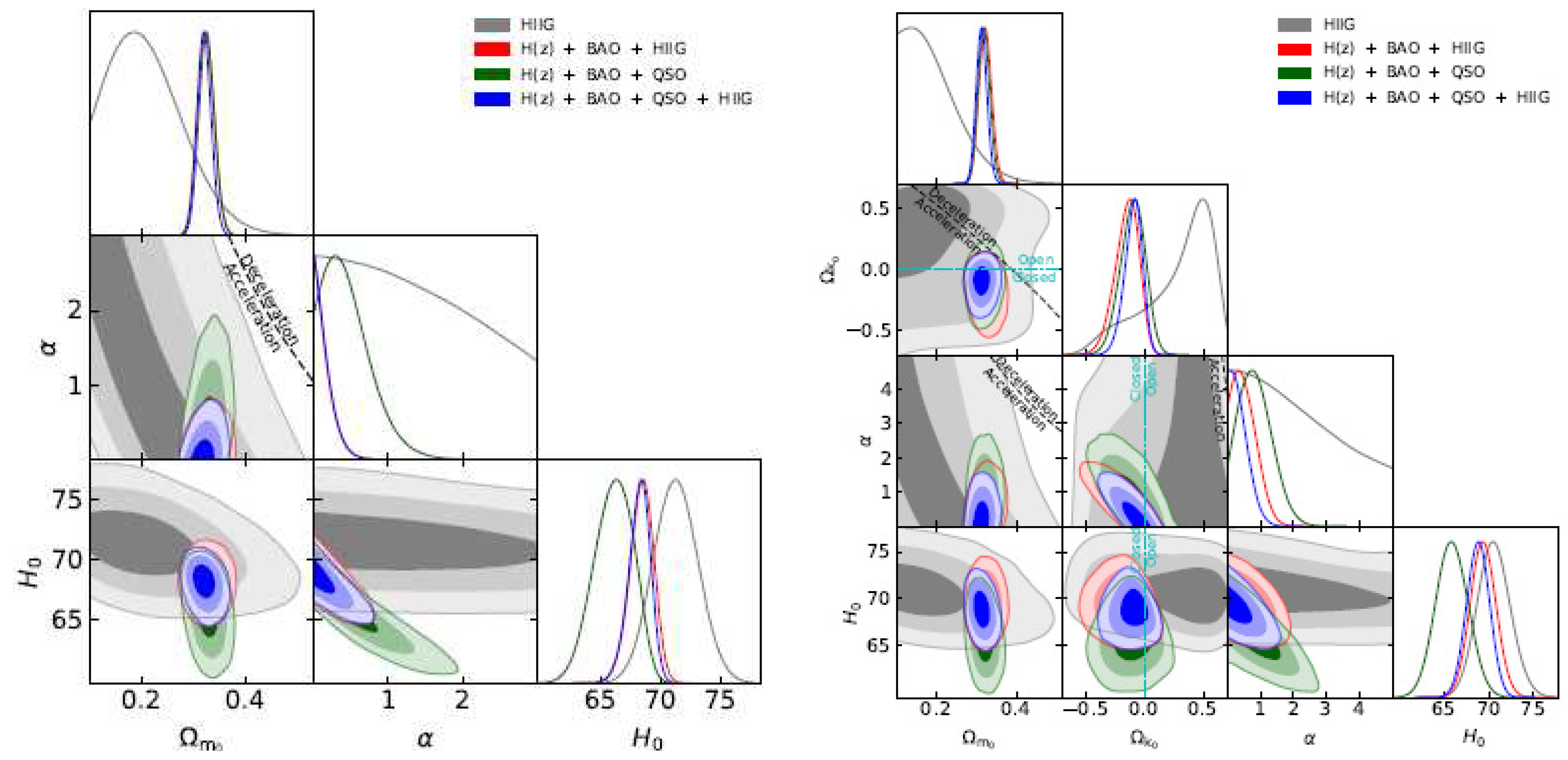
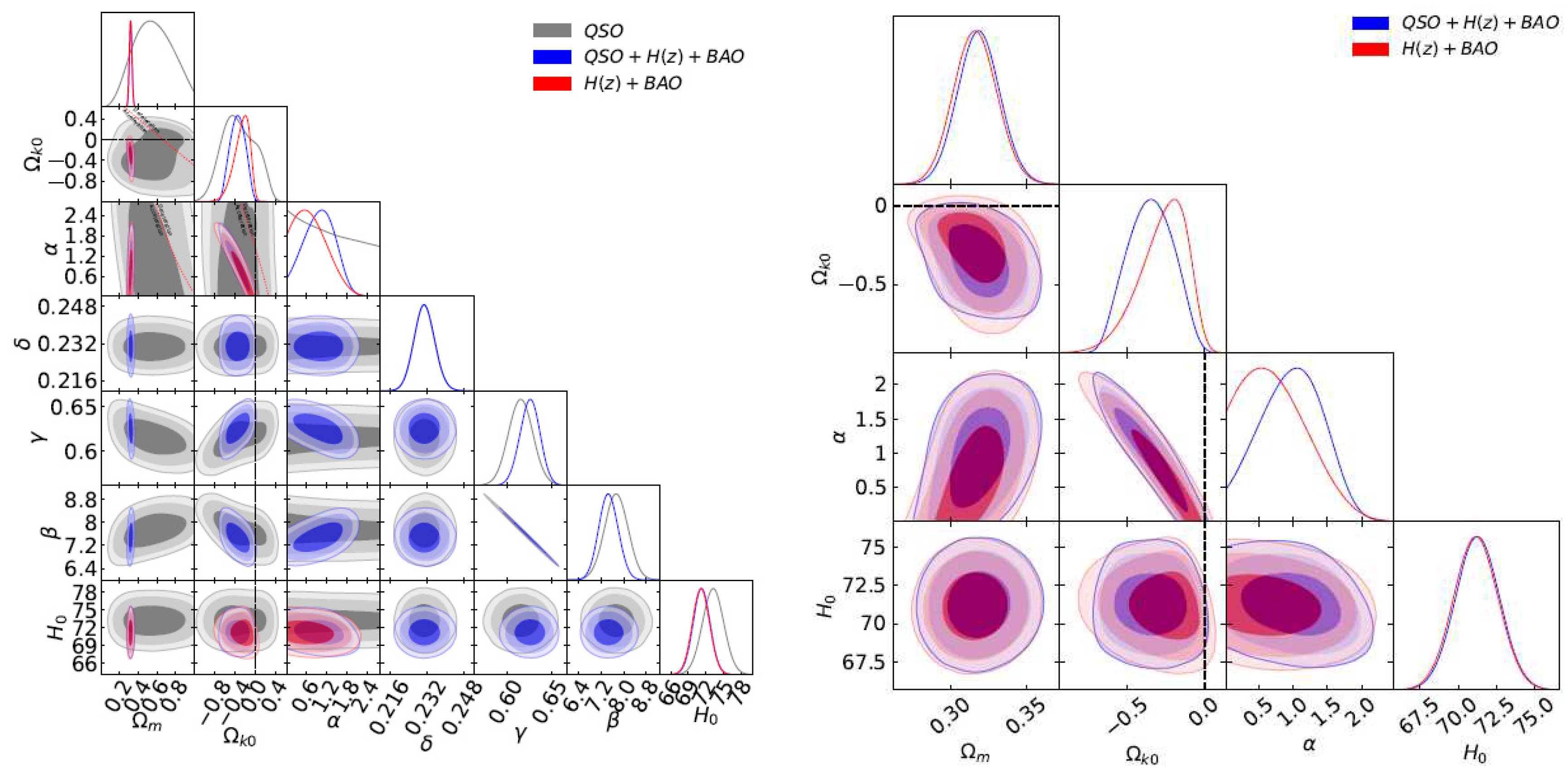
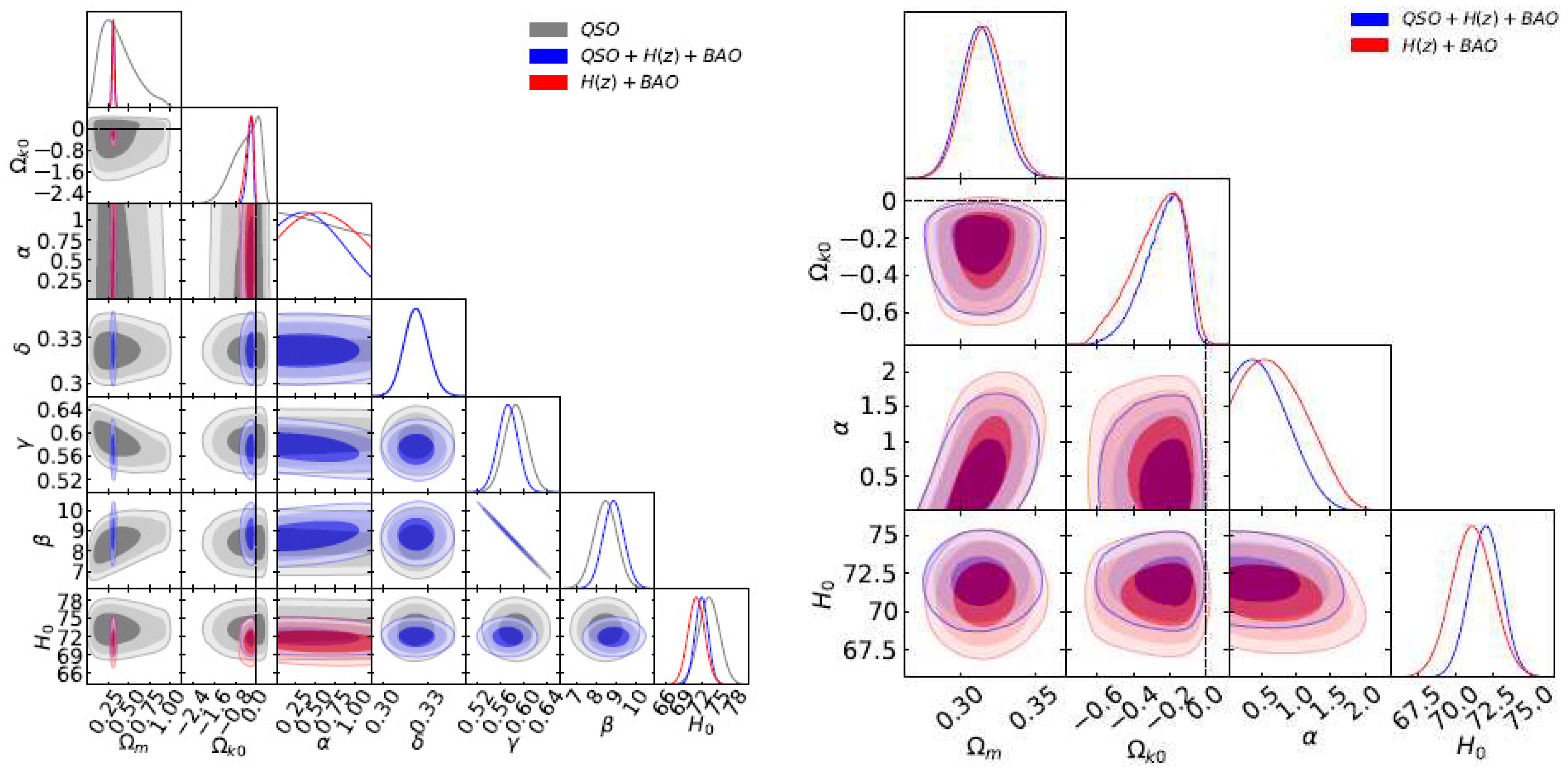
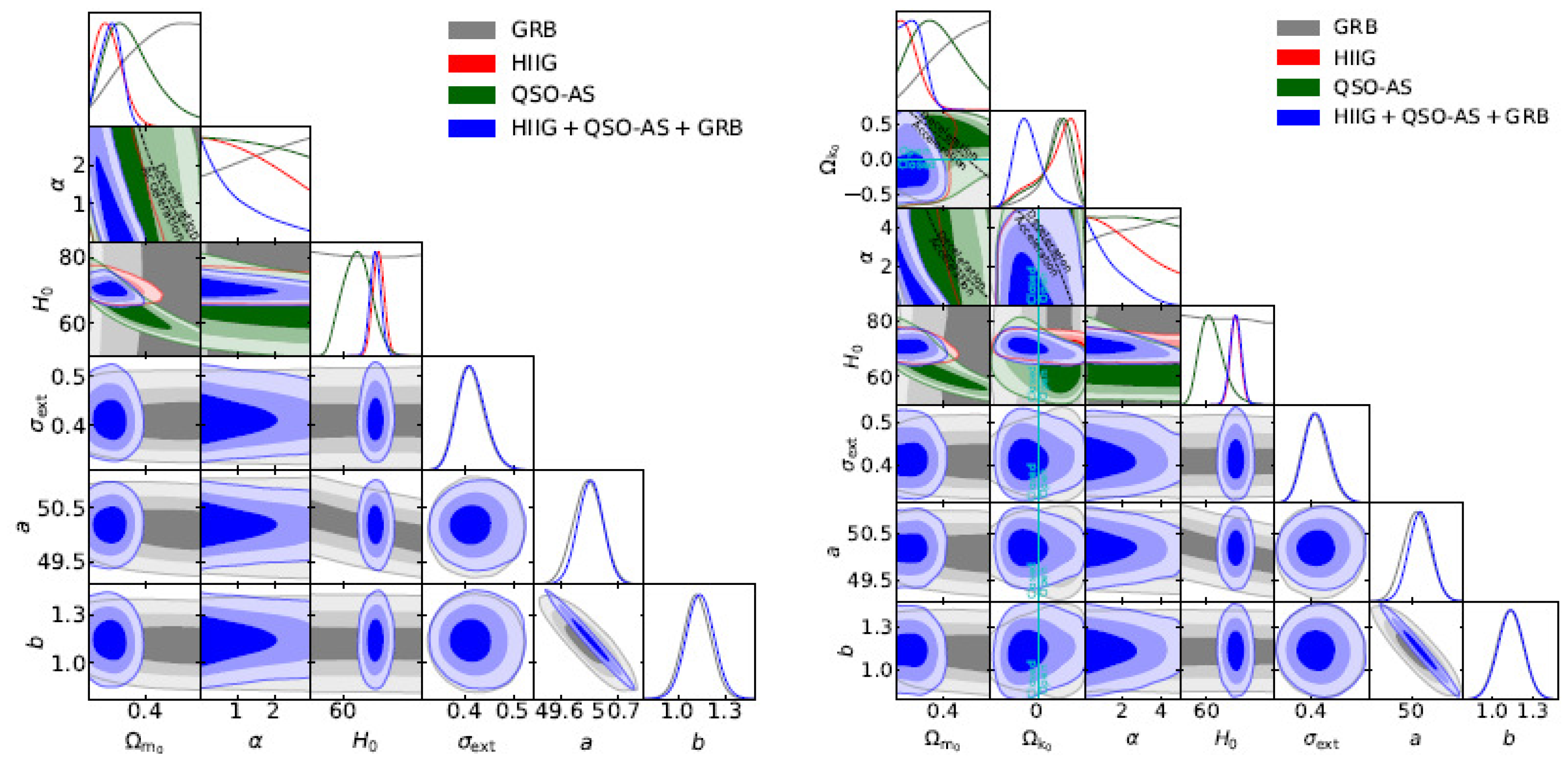
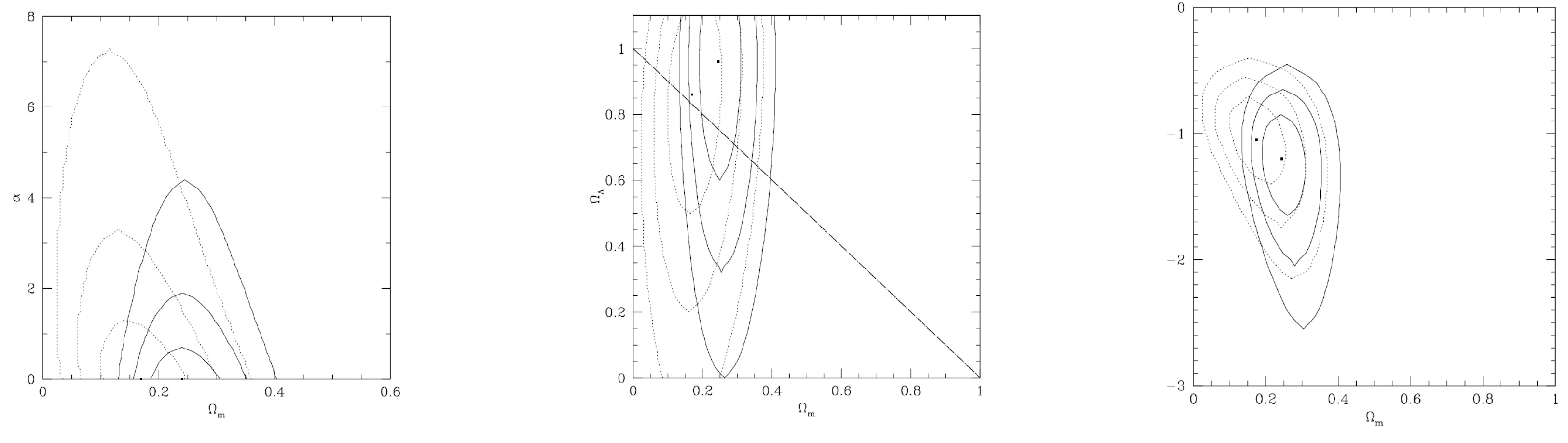
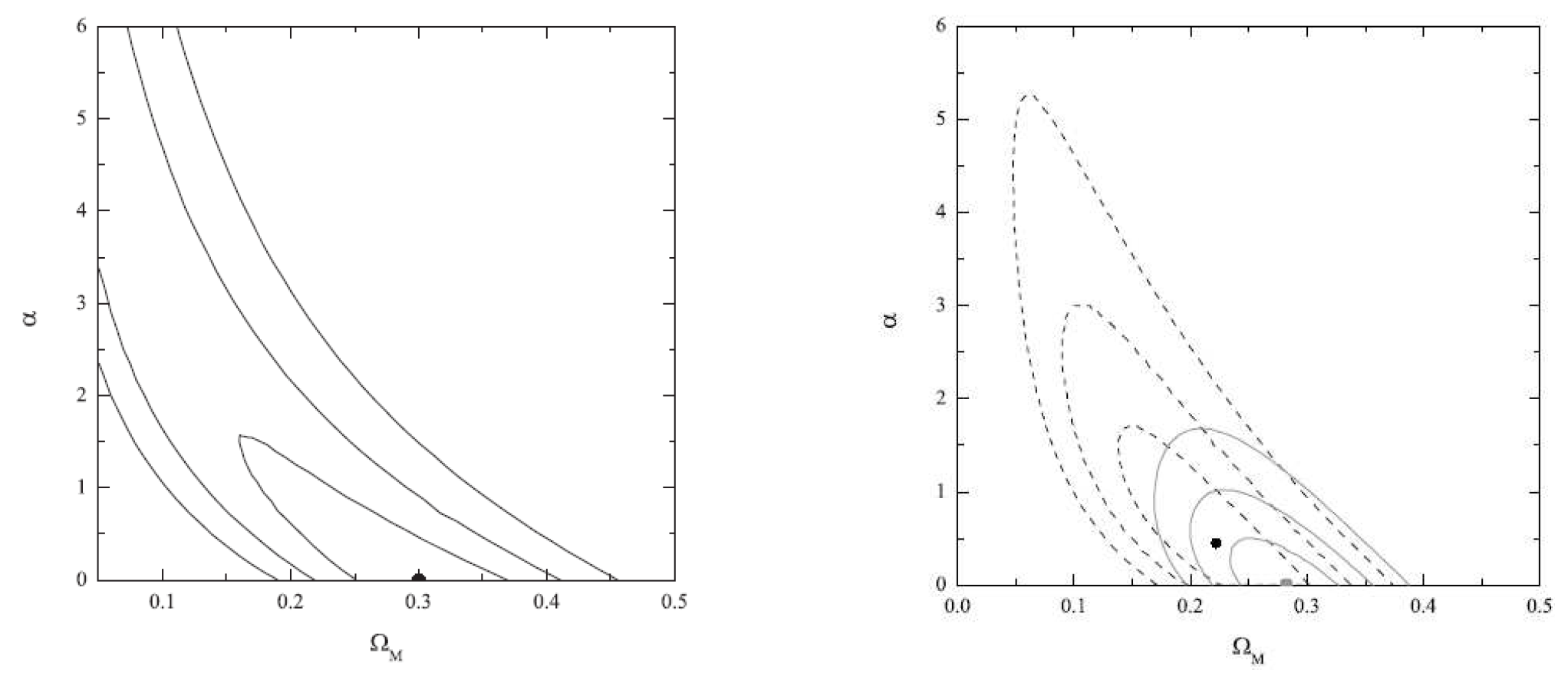
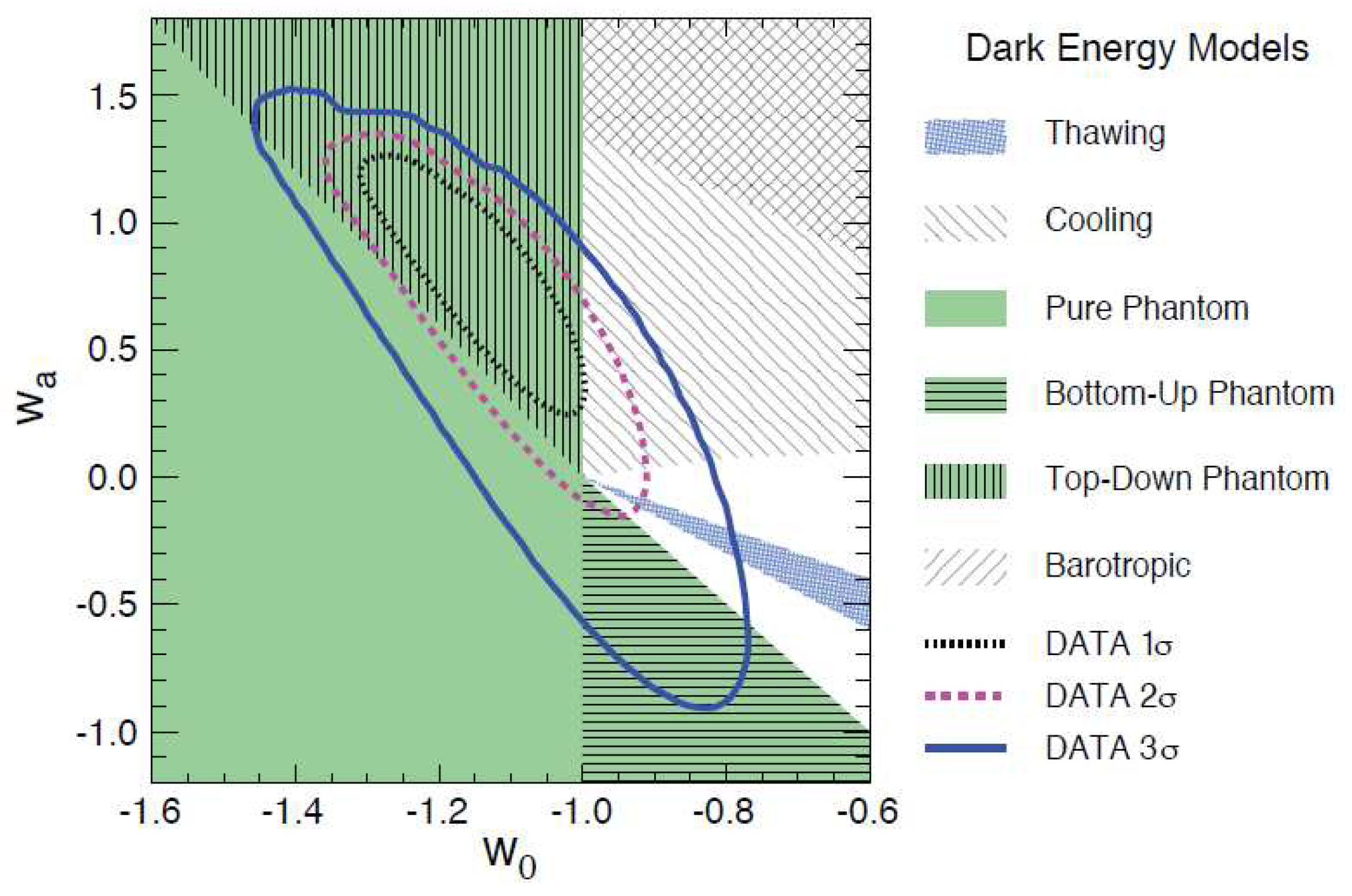
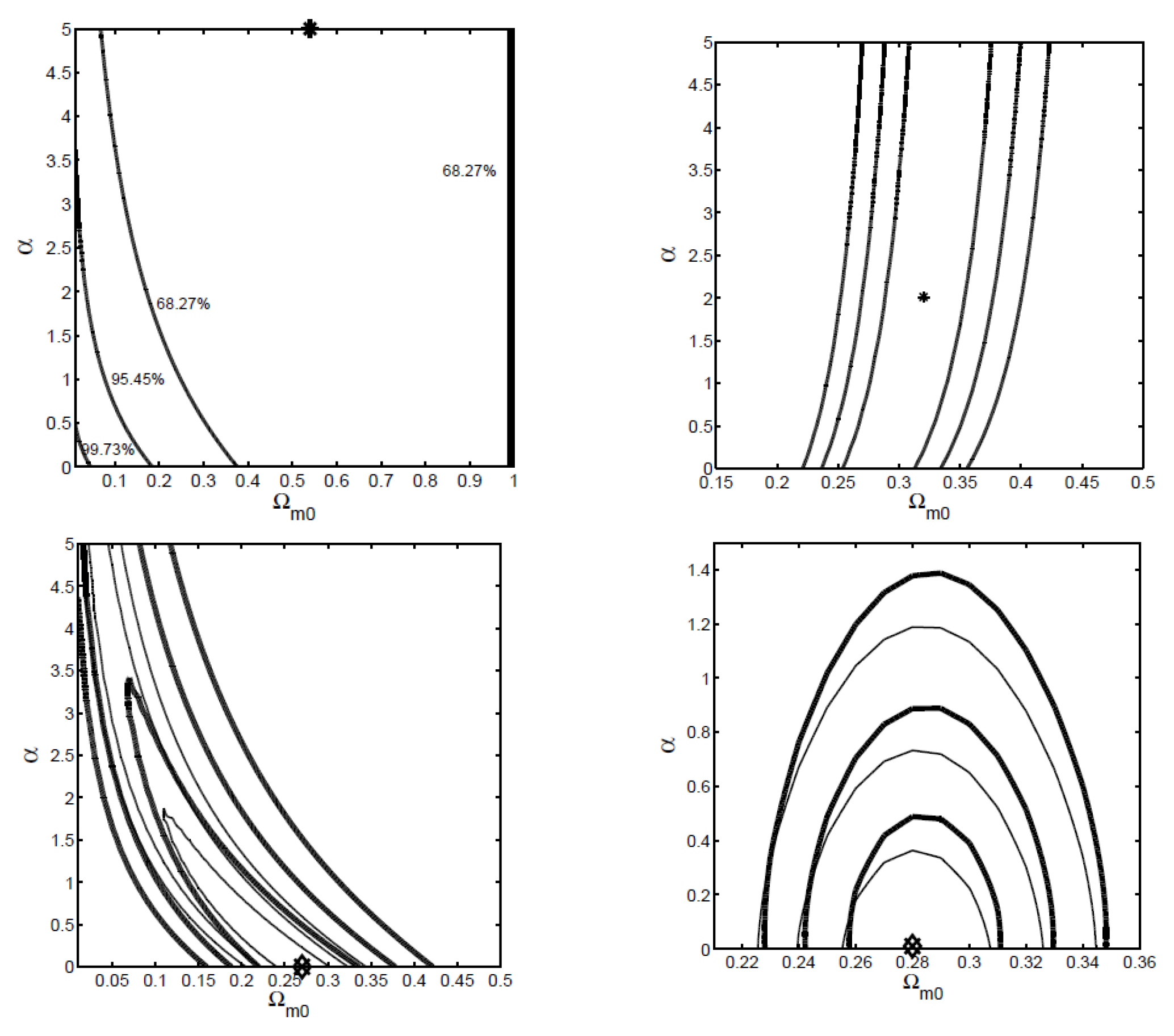
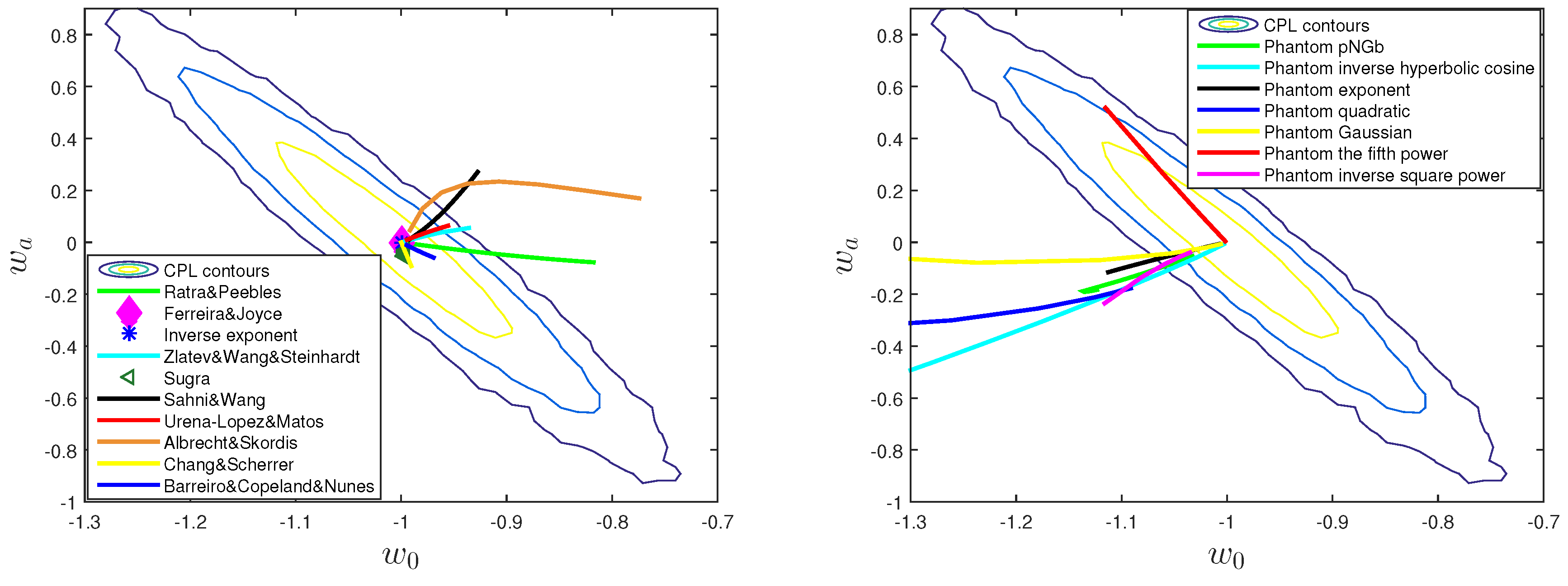
| Name | Form | Reference | ||
|---|---|---|---|---|
| Ratra-Peebles | ; | Ratra & Peebles [91] | ||
| () | ||||
| Exponential | ; | Wetterich [92], Ratra & Peebles [90], | ||
| () | Lucchin & Matarrese [122], Ferreira & Joyce [176] | |||
| Zlatev-Wang-Steinhardt | Zlatev et al. [112] | |||
| Sugra | ; | Brax & Martin [177] | ||
| () | ||||
| Sahni-Wang | ; | Sahni & Wang [178] | ||
| (, ) | ||||
| Barreiro-Copeland-Nunes | ; | Barreiro et al. [179] | ||
| (, ) | ||||
| Albrecht-Skordis | ; | Albrecht & Skordis [180] | ||
| (A, , ) | ||||
| Urẽna-López-Matos | ; | Urena-Lopez & Matos [181] | ||
| (, ) | ||||
| Inverse exponent potential | Caldwell & Linder [100] | |||
| Chang-Scherrer | ; | Chang & Scherrer (2016) [182] | ||
| () | ||||
| Name | Form | Reference | ||
|---|---|---|---|---|
| Fifth power | Scherrer & Sen [104] | |||
| Inverse square power | Scherrer & Sen [104] | |||
| Exponent | ; () | Scherrer & Sen [104] | ||
| Quadratic | Dutta & Scherrer [105] | |||
| Gaussian | ; () | Dutta & Scherrer [105] | ||
| Pseudo-Nambu-Goldstone boson (pNGb) | ; () | Frieman et al. [183] | ||
| Inverse hyperbolic cosine | ; () | Dutta & Scherrer [105] | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





