Correction of Spacecraft Magnetic Field Noise: Initial KMAG Observation in the Solar Wind

Preprint

Article

Correction of Spacecraft Magnetic Field Noise: Initial KMAG Observation in the Solar Wind

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 October 2023

Posted:

31 October 2023

You are already at the latest version

Alerts

Abstract

The Korean Pathfinder Lunar Orbiter (KPLO)-MAGnetometer (KMAG) consists of three triaxial fluxgate sensors (MAG1, MAG2, and MAG3) to measure the magnetic field around the Moon. The three sensors are mounted in the order of MAG3, MAG2, and MAG1 inside a 1.2 m long boom away from the satellite body. Before it arrived on the Moon, we compared the magnetic field measurements taken by DSCOVR and KPLO in the solar wind to verify the measurement performance of the KMAG instrument. We found that there were artificial disturbances in the KMAG measurement data, such as step-like and spike-like disturbances, which were produced by the spacecraft body. To remove spacecraft-generated disturbances, we applied a multi-sensor method, employing the gradiometer technique and principal component analysis and using KMAG magnetic field data and confirmed the successful elimination of spacecraft-generated disturbances. This indicates that the multi-sensor method is able to clean the magnetic field data measured onboard the KPLO.

Keywords:

Subject: Environmental and Earth Sciences - Space and Planetary Science

1. Introduction

The Korean Pathfinder Lunar Orbiter (KPLO)-MAGnetometer (KMAG) instrument was designed to measure the intrinsic lunar magnetic field and the global response of the Moon to magnetic fields originating from the Sun and Earth using three triaxial magnetometers mounted on a 1.2 m long boom. In magnetic field observations during of space exploration missions, it has been well known that a satellite’s power, propulsion subsystem, and onboard instruments generate their own magnetic fields, producing magnetic interference.

The spacecraft magnetic interference field is a major noise source, which is displayed on a magnetometer instrument during payload observation. Thus, it is difficult to perform accurate in situ measurement of intrinsic magnetic fields in space [1,2,3]. To avoid the magnetic disturbance produced by spacecraft on previous lunar missions, the boom on the Lunar Prospector and Kaguya is 2.5 m [4] and 12 m [5,6] long, respectively. Another way to minimize the spacecraft-generated fields is to clean up the spacecraft magnetically. This magnetic cleaning procedure is complex, and there are many constraints involved in carrying out the design and manufacture of the other onboard instruments [7]. Even if the magnetic cleaning process is applied during the development stage, it is not easy to remove this noise. Therefore, the magnetic field instrument usually uses a specific configuration wherein the magnetometer is installed on a long boom.

When a short magnetometer boom was used in previous missions, a multi-sensor method, employing the gradiometer technique and principal component analysis, was applied to the magnetic field analysis to separate the spacecraft-generated magnetic fields. The first study of the gradiometer technique involved fitting a dipole to a spacecraft-generated field, as proposed by Ness et al. [2]. This technique was successfully applied to magnetic field data from Mercury obtained by the Mariner 10 satellite (5.8 m) [8]. Neubauer et al. [3] suggested that using multiple (three or more) magnetometers is more accurate than double magnetometers to correct a spacecraft-generated field. Pope et al. [9] successfully identified the magnetic interference generated from the Venus Express and eliminated the satellite interference in the time domain by applying the gradiometer technique. The gradiometer technique has been applied to remove magnetic interference during many space missions [10,11]. Recently, Constantinescu et al. [12] used the maximum variance analysis and gradiometer technique to reduce spacecraft-generated magnetic field disturbances from magnetic field measurements observed at the geosynchronous GK2A satellite [13].

In the case of the KMAG instrument, the boom length is 1.2 m due to the KPLO design constraints; therefore, the KMAG had three magnetometers installed to find a noise source using multi-sensor techniques. The KMAG magnetic field measurements in the solar wind were compared with the DSCOVR magnetometer observation dataset to verify the stability and reliability of KMAG data. The KMAG data was found to be very stable and had good reliability. However, we confirmed that an unwanted spacecraft interference field existed in the observation data, as we expected. To identify a spacecraft-generated magnetic field, we used the dataset of three magnetometers installed inside the boom and a magnetoresistance sensor inside the spacecraft body [14]. In general, a spacecraft-generated magnetic field is reduced according to the distance from the center of the spacecraft, and the dependence on distance is also confirmed under the condition of multiple magnetic sources inside the spacecraft, as suggested by Park et al. [15].

In this study, we clearly identified the spacecraft-generated magnetic field from KPLO and applied a multi-sensor method, employing the gradiometer technique and principal component analysis and using KMAG magnetic field data. Spacecraft-induced magnetic fields in the solar wind were successfully eliminated by using a multi-sensor method.

The remainder of the paper is organized as follows: Section 2 describes the instrumental information of the KPLO satellite and the KMAG sensor. Section 3 outlines the proposed principal component gradiometer technique and modification of the dataset. Section 4 describes how the proposed method eliminates spacecraft-generated disturbances in KMAG data, and Section 5 concludes the study.

2. Instrumentation: KMAG

The KPLO-MAGnetometer (KMAG) is one of six scientific payload instruments on the Korean Pathfinder Lunar Orbiter satellite mission. The scientific objective is to investigate lunar magnetic anomalies and electromagnetic properties within the Earth’s magnetosphere and interplanetary magnetic field. The technical objective is to investigate the space operation of a multi-sensing technique and fluxgate sensor. The KMAG system has two magnetometers, MAG and anisotropic magnetoresistive (AMR) sensors, within the fluxgate magnetometer control electronics (FCE) units.

The MAG consists of three triaxial fluxgate magnetometers inside a 1.2 m boom using a carbon-fiber-reinforced plastic tube. Figure 1 illustrates the placement of the three magnetometers: MAG1 is positioned at the tip of the KMAG boom, and MAG2 and MAG3 are installed closer to the spacecraft body. Their distance from the spacecraft body is 1.20, 0.95, and 0.58 m, respectively. Each sensor has a measurement range of ±1000 nT, with less than 0.2 nT resolution at a sampling rate of 10 Hz. The magnetic noise level remains lower than 50 pT/Hz^0.5 at 1 Hz. In the ground calibration process, the orthogonality and linearity of each magnetometer are confirmed, ensuring that errors are below 0.9° and 0.05, respectively. The KMAG boom is deployed at an angle of 135° from the top floor of the spacecraft. The sensor coordinate system for each magnetometer is structured so that the Z-axis aligns with the direction from the boom tip to the spacecraft body. The X-axis is placed counterclockwise, perpendicular to the Z-axis, and the Y-axis completes a right-handed orthogonal set.

The FCE unit controls the overall KMAG system, including command, data handling, and communication with the spacecraft. This unit consists primarily of the analog board (AB), digital board (DB), onboard computer (OBC), and low-voltage power supply (LVPS). Notably, the OBC contains a low-resolution AMR sensor, a Honeywell HMC1053, which measures unusually large magnetic field signals from the spacecraft body. The original purpose of the AMR sensor was ground test assistance. However, the AMR sensor now contributes to eliminating the magnetic interference associated with spacecraft operations. The AMR sensor operates within a measured range of ±60 μT, with a resolution of 100 nT at a sampling rate of 10 Hz. However, as the AMR sensor is susceptible to temperature variations, it is necessary to monitor the temperature in order to calibrate the magnetic field data accurately. For this study, the data of the AMR sensor was transformed to match the coordinate system of the MAG sensors. Table 1 summarizes the specifications for each magnetometer integrated into the KMAG.

3. Clearance Technique for Spacecraft-Generated Magnetic Disturbances

During space missions, the operation of electronic devices inside the spacecraft can generate magnetic fields that interfere with the measurement of the ambient magnetic field. Although ground calibration can be conducted to remove the magnetic interference from the spacecraft, unexpected disturbances can remain for the operating period of the spacecraft after launch. These spacecraft-generated disturbances pose a significant challenge for accurate magnetic field measurements and necessitate the implementation of proper mitigation strategies. Therefore, to obtain reliable magnetic field measurements, it is imperative to monitor the spacecraft’s operational phase and implement in-orbit clearance procedures to address the disturbance signals.

3.1. Elimination of Artificial Disturbance

In general, the magnetic field measured by the magnetometer is described by the integration of the ambient magnetic field B(t), the spacecraft-generated magnetic field bⁱ(t), and the constantly specific disturbance at the micro-time scale, called the sensor offset, Zⁱ(t). The summation of magnetic fields measured by sensor i is expressed as

B^{i} = B (t) + \sum_{q = 1}^{N} b_{q}^{i} (t) + Z^{i} (t)

(1)

where the index q indicates the number of sources for the spacecraft-generated disturbance to N. The sensor offset is a constant value for each sensor in Equation (1). The first and second terms on the right-hand side can be considered as the dipole field. The dipole field characterized by magnetic moment M is

B_{d i p o l e} = \frac{μ_{0}}{4 π} [\frac{3 \overset{⇀}{r} (\overset{⇀}{r} \cdot M)}{{| r |}^{5}} - \frac{M}{{| r |}^{3}}]

(2)

where

μ_{0}

is the magnetic permeability of free space and

\overset{⇀}{r}

is the position vector between the measuring point and the magnetic moment. Considering the negligible difference in position vectors between the magnetic moment of the ambient field B(t) for each magnetometer, it is assumed that the simultaneously observed ambient field is identical for all sensors. However, in the presence of interference, denoted as b(t), the position vectors for each sensor exhibit significant differences compared to the ambient field scenario. As a result, subtracting the measurements from two sensors positioned at distinct locations eliminates the ambient field term B(t) from Equation (1), while retaining the terms associated with interference b(t) and the sensor offset Z(t):

Δ B^{i j} (t) = B^{i} (t) - B^{j} (t) = \sum_{q = 1}^{N} b_{q}^{i j} (t) + Δ Z^{i j} (t)

(3)

Under the assumption that the offset term Z(t) does not vary rapidly for instantaneous time, it can be ignored. Consequently, the difference in measurements between the two sensors can be simplified as solely the disparity in interference measured by the sensors. Although the position of the artificially disturbed source should be defined to eliminate interference, it is impossible to track all accurate positions of the source. However, during magnetically in-orbit correction performed on previous space missions, the measured disturbance depended on the distance of the sensor position from the source, without considering the number and position of the source [2,15]. Therefore, if the interference measured by each sensor shows a dependence on the distance of the sensor from the spacecraft when the spacecraft is maneuvering, the artificial disturbance can be efficiently removed by using the variances between the two sensors. From these assumptions, multiple disturbed sources can be considered a single disturbed source. Equations (1) and (3) are used to reduce to the form of a single disturbed source:

B^{i} = B (t) + b^{i} (t) + Z^{i} (t)

(4)

Δ B^{i j} (t) = Δ b^{i j} (t) - Δ Z^{i j} (t)

(5)

In addition, when the spacecraft temporarily maneuvers, the transient variation of the variance in the measurement, which is affected by the artificial disturbance, is much greater than the variation of the ambient field at that time. This variance could be used to determine the degree of significant AC disturbance for each direction. Using variance analysis, it is possible to define the maximum variance direction corresponding to the artificial disturbance at the sensor position and isolate it [16,17]. The maximum-variance direction of the measurement represents a more robust component of the disturbance than other regular and random disturbances. We applied principal component analysis (PCA) to define the direction of maximum variance, called the variance principal system (VPS).

The interference removal process can be outlined as follows: (1) Restrict the interference period associated with spacecraft maneuvering. (2) Determine the rotation matrix of Bⁱ(t) and ΔB^ij(t) at the sensor coordinates, emphasizing the component with the maximum variance. (3) Correct the interference of only Bⁱ(t) on the maximum variance direction by utilizing the variance.

With the VPS, by using the measurement from sensor j, the relation-corrected sensor i measurement can be written as

B_{L}^{1, i} = R_{1 k}^{i} B^{0, i} - α^{0, i j} R_{1 k}^{i j} Δ B^{0, i j}

(6)

B_{M}^{1, i} = R_{2 k}^{i} B^{0, i}

(7)

B_{N}^{1, i} = R_{3 k}^{i} B^{0, i}

(8)

where R is the rotation matrix from the coordinates in the sensor system toward the variance principal system as the LMN coordinates; in this coordinate system, the L, M, and N axes parallel the maximum, intermediate, and minimum variance directions, respectively. The subscript nk of R indicates that row k of R is the projection of n along the axes defined by the L, M, and N directions. The superscript 0 in Equations (6)-(8) indicates the uncorrected measurement in the VPS system, and the superscript 1 means the first-order correction.

α^{0, i j}

is the scaling factor. Assuming the disturbance difference between Bⁱ(t) and ΔB^ij(t) is due to the sensor position, the relationship between Bⁱ(t) and ΔB^ij(t) is proportional and is reflected in the scaling factor. Therefore, to eliminate the disturbance signal in Bⁱ(t) by using their proportionality, the

α^{0, i j}

factor is considered as the ratio of the variance of measurements:

α^{0, i j} = \pm \sqrt{\frac{V a r ({(B^{0, i})}_{L})}{V a r ({(Δ B^{0, i j})}_{L})}}

(9)

Since the orientation for the maximum variance is uncertain in Equation (9), the ± sign indicates that the positive direction on the L-axis is arbitrary. After performing this process, the orientation is determined by selecting the minimized correlation coefficient between the corrected measurement and the difference. Hence, Equations (6)-(8) can be simplified for the sensor’s coordinate system with the correction matrix A, including the scaling factor and rotation matrix:

A^{0, i j} = - α^{0, i j} {({(R^{i})}^{- 1})}_{k x} {(R^{0, i j})}_{x l}

(10)

B^{1, i} = B^{0, i} + A^{0, i j} Δ B^{0, i j}

(11)

Briefly, with regard to this method, only the measurement corresponding to the maximum variance direction is corrected by using the scaling factor, based on the assumption that the artificial disturbance transiently causes the largest variance.

3.2. Mitigation of Amplified High-Frequency Noise

In the magnetic disturbance correction process, there is an instance where the difference between Bⁱ and B^j becomes small. For example, in cases where MAG1 needs to be calibrated with MAG3 data instead of MR data, the difference ΔB^0,ij between the MAG1 and MAG3 data in Equations (9) and (11) is relatively more minor than when using MR data. Since the small ΔB^0,ij leads to an increasing scaling factor A^0,ij in Equation (10), an artificial high-frequency noise shown with broad variance is included in the corrected result. To prevent interference from the amplified high-frequency noise affecting the outcome, the mitigation process uses uncorrected and corrected values over only the direction of maximum variance before applying the rotation matrix rⁱ. Our strategy is to select a time interval that is not affected by disturbances generated by the spacecraft for mitigated correction. Then, we calculate and average the variance for an arbitrary time window over both values. By using the averaged variance values, we compute the ratio as follows:

r^{i} = \sqrt{\frac{V a r (R_{1 k}^{i} B^{0, i})}{V a r ({(B^{1, i})}_{L})}}, ({(B^{0, i})}_{L} = R_{1 k}^{i} B^{0, i})

(12)

B_{L, a f t e r}^{1, i} = r^{i} \times B_{L, b e f o r e}^{1, i}

(13)

Finally, the high-frequency noise is mitigated by multiplying the ratio by the corrected value only in the maximum variance direction, as in Equation (13).

4. Results

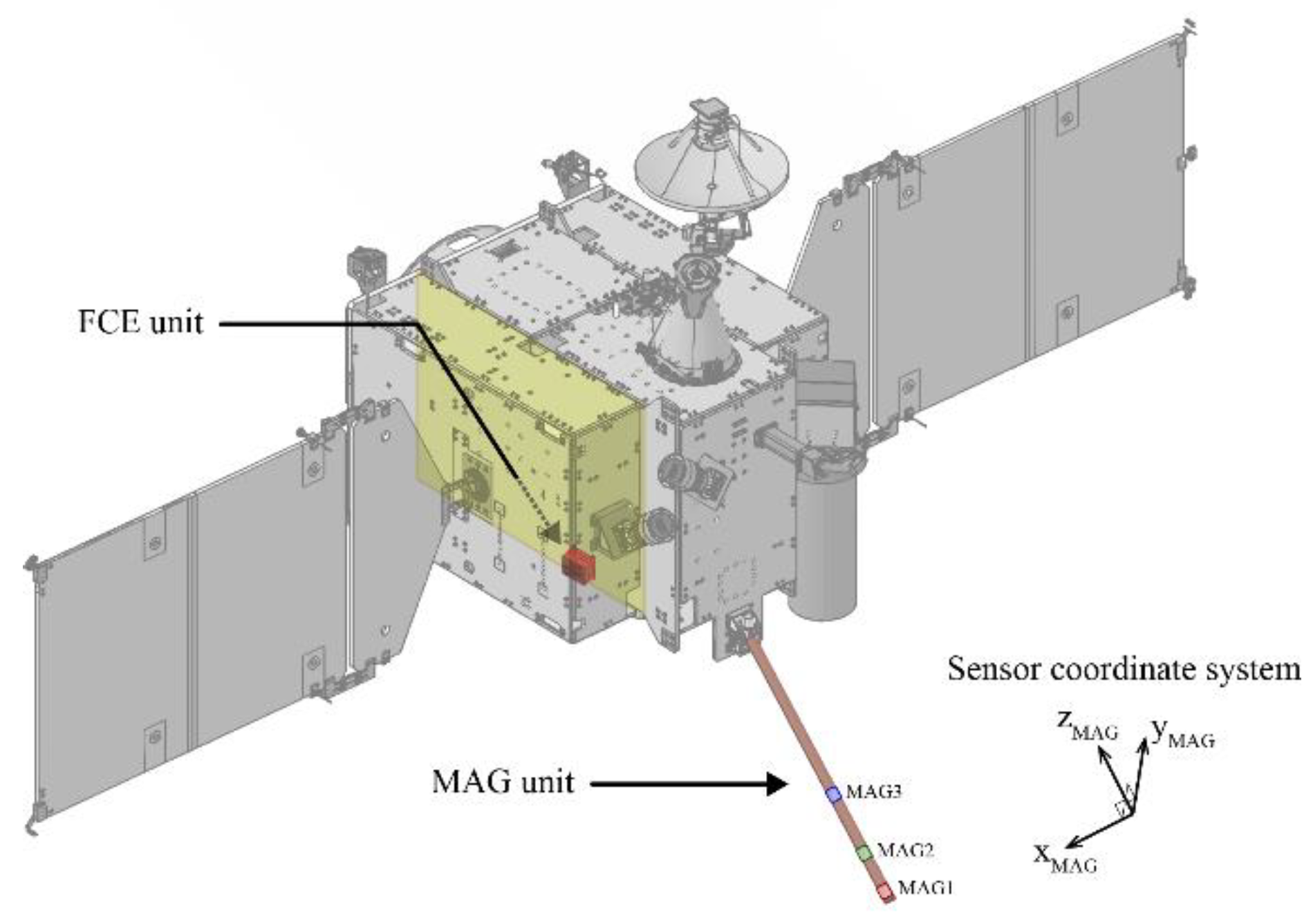
Before the lunar orbit insertion, the KMAG team conducted a calibration procedure to account for the disturbances generated by the spacecraft maneuvering and calculated the daily zero-offset value for the dataset. Two days after deploying the KMAG boom, an unexpected disturbance appeared in the KMAG observation data from the spacecraft maneuvering. Since the zero-offset calculation uses the method that minimizes the variance of the field magnitude, the measured magnetic field containing disturbances made the result of the zero-offset calculation inaccurate. This section outlines a case concerning the clearance results and process associated with a spacecraft-generated disturbance on 6 August 2022 at a position just outside the Earth’s bow shock.

4.1. Comparison of DSCOVR FGM and KMAG

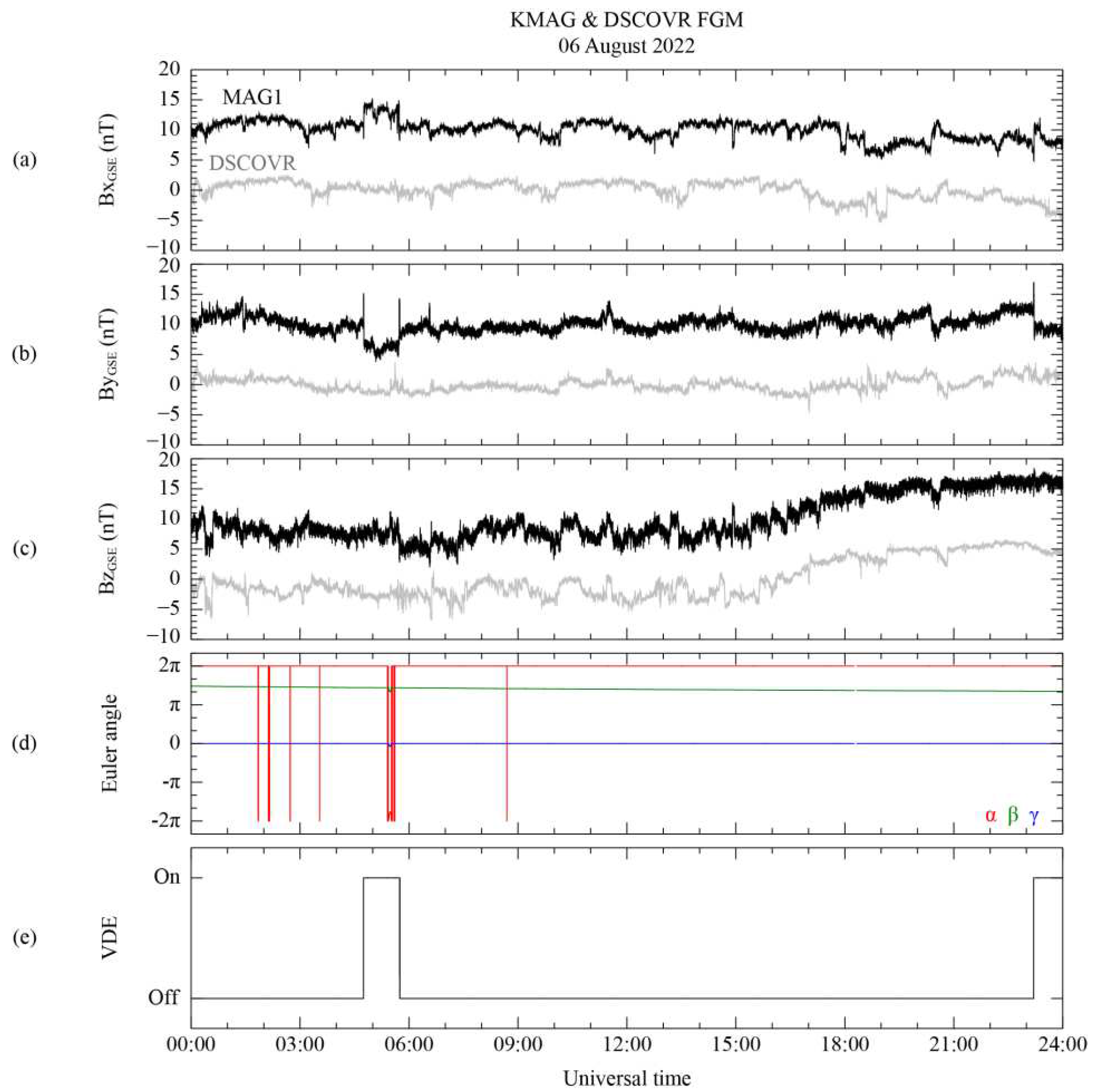
Figure 2 displays the time series of the magnetic field measured by the KPLO-MAG1 and DSCOVR-FGM using the GSE coordinate system and the operational information of the KPLO satellite related to the attitude and interior electronics on 6 August 2022. All components of the magnetic field data from MAG1 are displayed in Figure 2a–c by adding 10 nT after subtracting the daily-averaged value to compare with DSCOVR FGM measurements. Note that the daily averaged value from MAG1 does not represent its daily zero offset value. Additionally, we confirmed that there were no dynamic solar wind events during the same period. 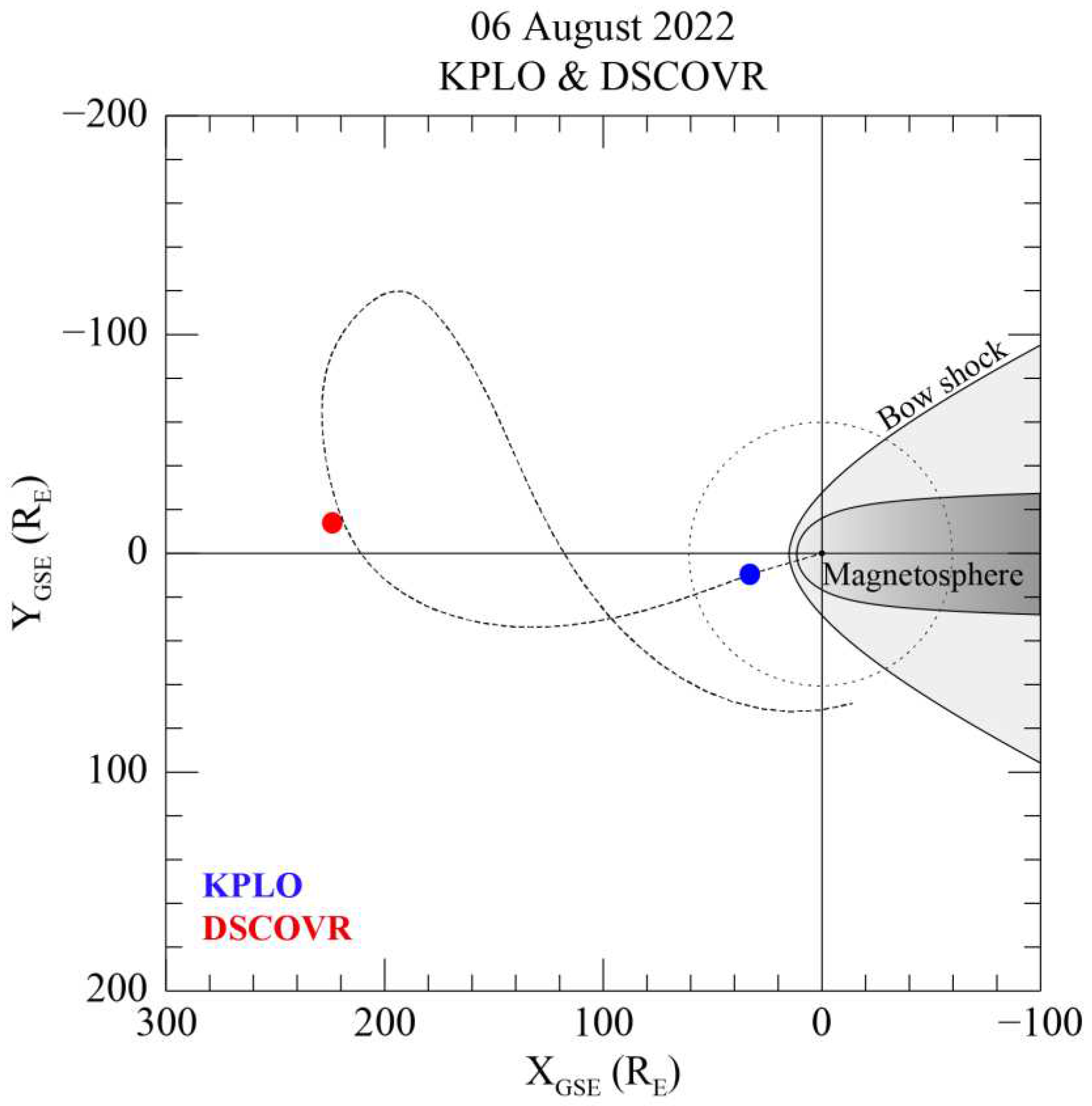As shown in Figure 3, the DSCOVR satellite is positioned at the L₁ point (223.9 R_E, −14.9 R_E, −24.4 R_E) in the geocentric solar ecliptic (GSE) coordinate system, while the KPLO is located just outside the Earth’s bow shock (32.9 R_E, 8.7 R_E, −8.2 R_E), with R_E referring to the Earth’s radius. According to Richardson and Paularena [18], if the difference in distance of both satellites in the GSE Y-Z plane is less than 50 R_E in the interplanetary medium, it is possible to measure the same solar magnetic field. Therefore, since the distance between the DSCOVER and KPLO satellites is approximately 16 R_E on the Y-Z plane, the KMAG can observe a similar magnetic field to that measured by the DSCOVR FGM. Nevertheless, the difference of ~191 R_E between the two satellites along the X_GSE direction causes a 40 min delay in solar wind propagation. The calculations for this time delay were applied to the KMAG measurements in Figure 2.

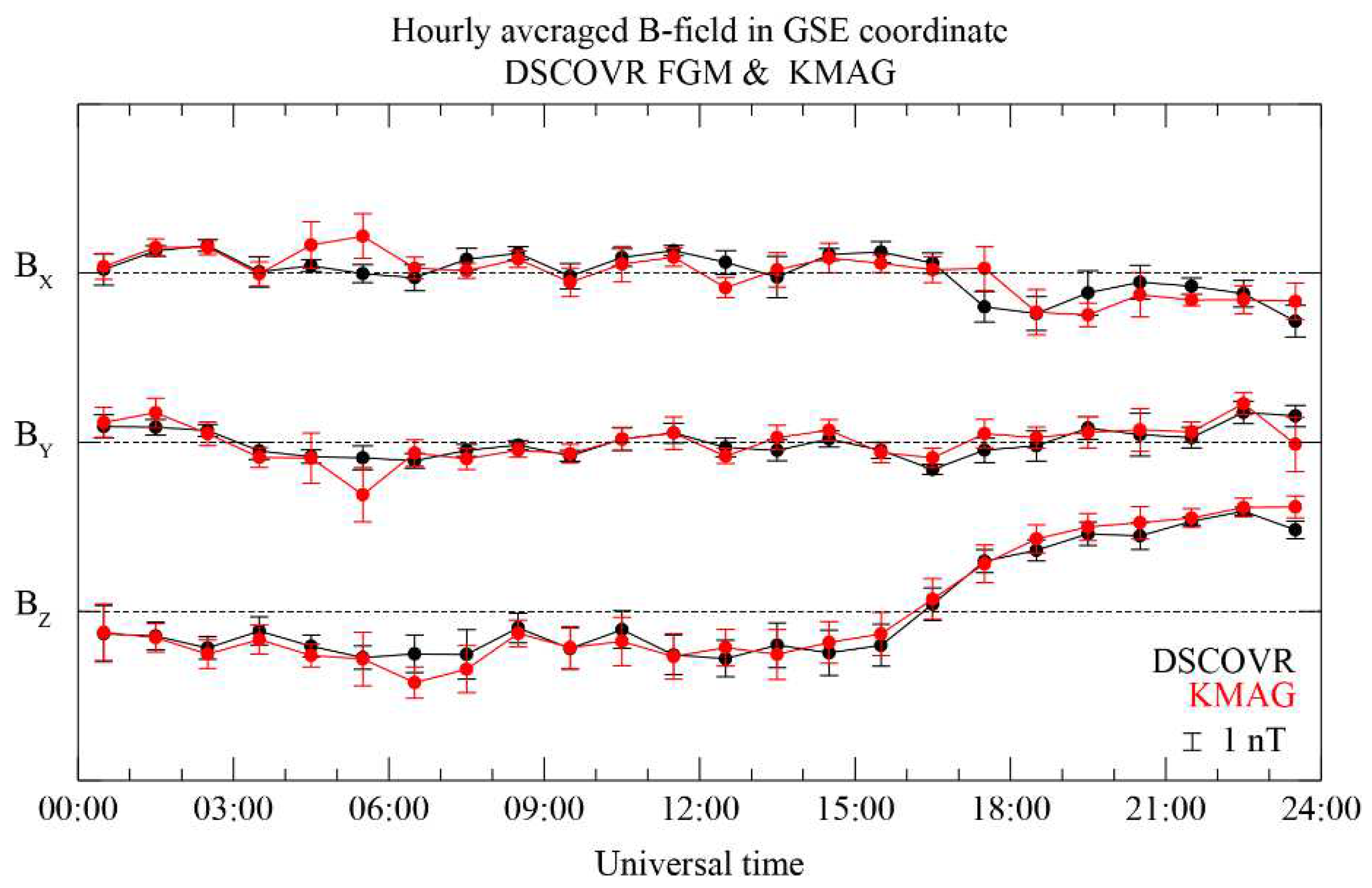
To evaluate the consistency of magnetic measurements from each position within the interplanetary region, we conducted a comparison of hourly averaged magnetic fields, as illustrated in Figure 4. Given the absence of significant IMF magnetic field variations within a 1 hour window during quiet solar wind conditions, we calculated the standard deviation based on 1 h boxcar averaged data without temporal overlaps. The relationship between measurements shows notably high correlation coefficients of 0.77, 0.86, and 0.98 in the B_X, B_Y, and B_Z components, respectively, except for a 2 h interval starting from 04:00 UT. In addition, the background magnetic field, as measured by the DSCOVR FGM, exhibits a standard deviation of less than 1 nT throughout the entire observation period. MAG1 measurements show a comparable standard deviation of less than 1 nT over the same duration. However, there are instances of abrupt and substantial variations in the averaged magnitude and standard deviation, particularly for the B_X and B_Y components in the MAG1 measurement. These variations increase up to four times compared to the DSCOVR FGM measurements during the time intervals of 04:44 to 05:44 UT and 23:11 to 24:00 UT, which can be characterized as unknown disturbed periods.

This result suggests two perspectives. Firstly, the consistency of the observations between DSCOVR FGM and KMAG shows that KMAG is a reliable tool for magnetic field measurements. Secondly, considering that DSCOVR FGM can accurately observe the background magnetic field, the difference in measurement between the two satellites for the unknown disturbed period implies that the KMAG measurement may have originated from other magnetic sources.

Thus, for the results in Figure 2a–c, it is considered that KMAG measured the magnetic fields related to different magnetic sources about the background field during the unknown disturbed period. To find the disturbed magnetic source, we conducted a survey of the satellite’s attitude data. Figure 2d confirms that the satellite’s Euler angle with all directions suddenly varied for about 12 min from 05:24 to 05:36 UT. Variations in the spacecraft’s Euler angles indicate changes in its attitude, such as spinning or flipping, which is strongly linked to the disturbed magnetic field. When the spacecraft's attitude changes, the operation of electronic equipment within its body is typically expected. However, this finding is inadequate to explain the measurement taken before 05:24 UT. To find the disturbance source, an additional investigation was conducted to determine the relationship between spacecraft-generated disturbance and spacecraft maneuvering using the monitoring data of the valve drive electronics (VDE), as depicted in Figure 2e.

The identification of VDE activation indicates that the circuit inside the spacecraft is carrying an electrical current relevant to the operation of the thrusters, as indicated by as turned-on or -off signals depending on whether electronic devices are activated or not. The VDE switching signal clearly coincides with the time of abrupt variations in KMAG observation data, or the unknown disturbance period. For example, the occurrence of the VDE switching-on signal for 1 h from 04:44 UT accurately coincides with abrupt variations in KMAG measurements. Consequently, these abrupt variations in the measurements, as depicted in Figure 2a–c, indicate that the measurement includes artificial disturbances generated by the spacecraft.

4.2. Elimination of Artificial Disturbance

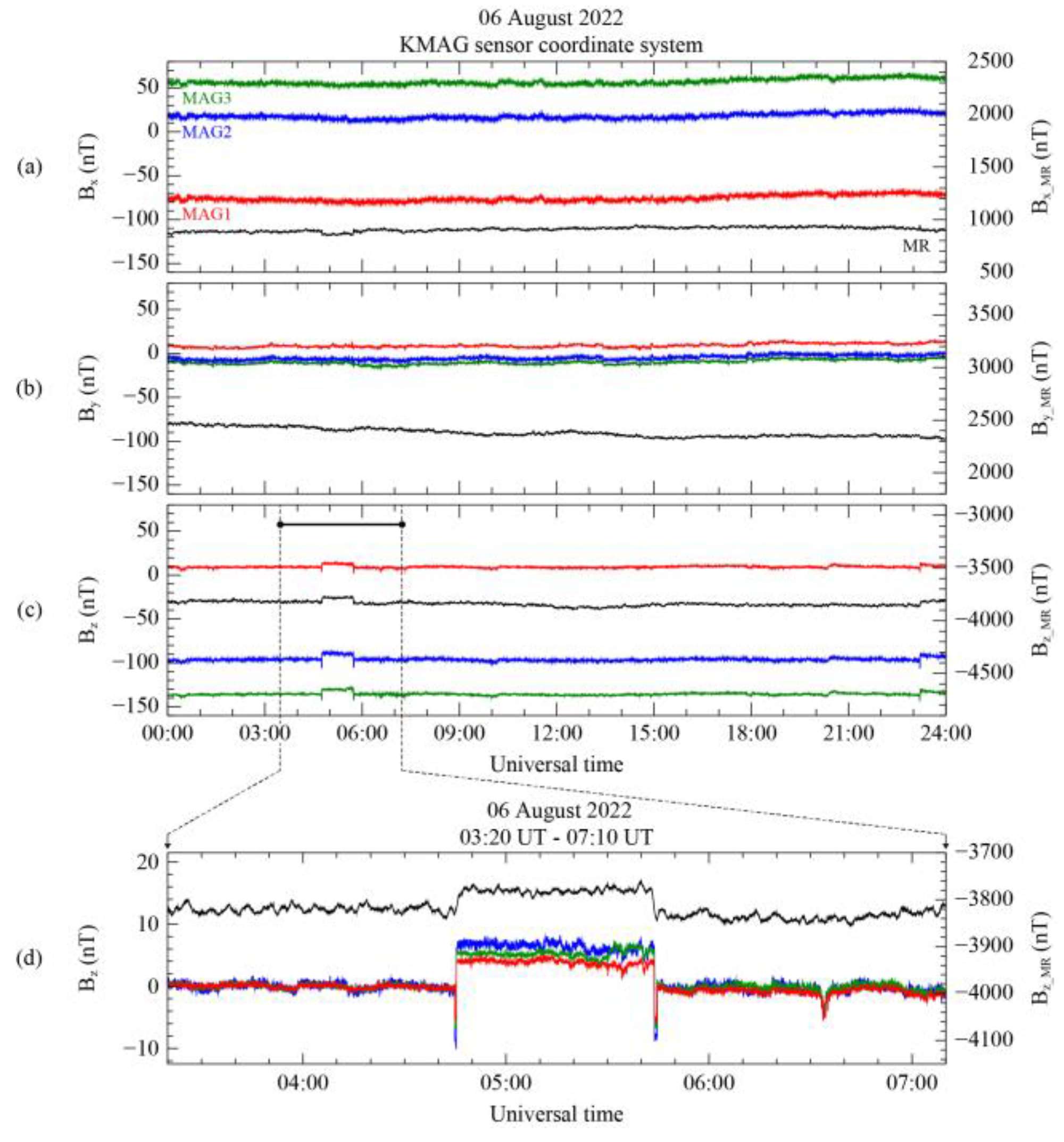
Figure 5 shows the measurements from MAG1, MAG2, MAG3, and MR sensors on 6 August 2022 in the sensor reference coordinate system. Note that since the zero offset calculation was not yet applied to each sensor’s data, the magnetic field observation in Figure 5 does not represent a realistic value for the background. The MAG and MR measurements are expressed on the left and right axes, respectively, in units of nT. In Figure 5a, the abrupt changes in the B_X component from all MAG sensors are not shown from 04:44 to 05:44 UT. However, there is a decrease of approximately 40 nT in the measured B_X in MR. As shown in Figure 5b, although the B_Y from the MR sensor gradually decreases over time by about 100 nT, the MAG and MR sensor measurements show no evidence of the artificial disturbance toward the Y-direction. The B_Z components from the MAG and MR sensors in Figure 5c simultaneously show a step-like shape disturbance from 04:44 to 05:44 UT.

The magnitude of this disturbance increased suddenly compared to the period before the disturbance, by ~4.5 nT for MAG1, ~6.1 nT for MAG2, ~7.0 nT for MAG3, and ~60.0 nT for MR. These varying disturbance magnitudes are dependent on the distance of each sensor from the center of the spacecraft. The relationship between disturbance magnitude and sensor position obviously indicates the presence of an additional magnetic source within the spacecraft body. By analyzing the readings of the MR sensor, which detected a disturbance in the B_X and B_Z components, it can be deduced that the magnetic disturbance was caused by a source with a magnetic moment aligned parallel to the B_Y component. Hence, the detection of magnetic disturbances with all sensors exhibiting distance-dependent variations in the same directional components again strongly supports that these disturbances originated from within the satellite’s interior. Figure 5d shows a zoomed-in view of the 230 min interval of the BZ component of the magnetic field measurement for all KMAG sensors, indicated by the black bar in Figure 5c. Note that the measurements from all MAG sensors were adjusted by subtracting the daily average, except for the MR measurement. Spike-like disturbances are observed just before and after the step-like disturbance in the measurements obtained from all MAG sensors. The spike-like disturbances have a shorter interval of ~2 min compared to the step-like disturbances. However, since the MR sensor measurement was averaged in the preprocessing, the spike-like disturbance is not presented in the MR sensor measurement. For this reason, MR sensor measurement is useful for the removal of step-like disturbance only.

Therefore, our strategy is to preferentially eliminate the step-like disturbance from the data of each MAG by using MR measurements, and then remove the spike disturbance using only MAG data. The time interval over the disturbance elimination is selected from 04:30 UT to 06:00 UT to isolate the targeted step-like disturbance. Using the gradiometer technique mentioned in Section 3.1, we determined the direction for the maximum variance to find the scaling factor and the rotation matrix. To compare the most evident difference from the magnetic source inside the spacecraft body, we used the data from the inboard sensor and the outmost sensor of the spacecraft, MR and MAG1.

As shown in Figure 6, the step-like disturbance was extracted in the difference ΔB^0,ij between the MAG1 and MR sensors for each component in the VPS coordinate system using the PCA method. Specifically, Figure 6a–c shows these components, which were rotated to align with the directions of maximum, intermediate, and minimum variance. These components correspond to the LMN coordinate components explained in Section 3.1. In Figure 6a, the step-like disturbance is also extracted for the selected time interval and the second disturbance after 23:00 UT. The extraction of both step-like disturbances to the maximum variance components at the same time implies that both disturbances can be eliminated in the first-order correction process simultaneously. 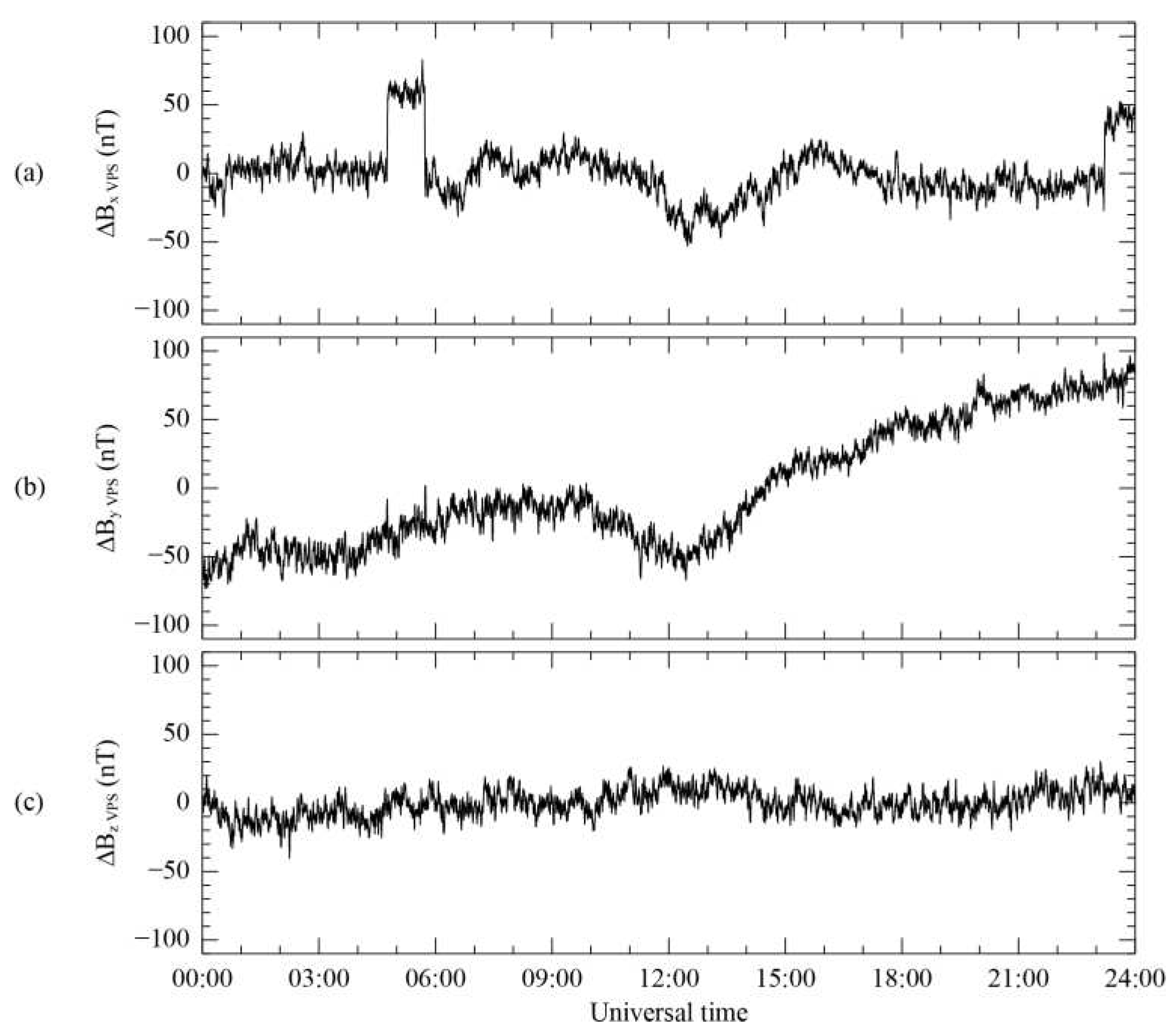Figure 6b shows the largest change of ΔB_Y, by ~140 nT across all time periods, while Figure 6a shows that ΔB_X changes by ~90 nT over the entire period of the data. However, it is important to note that the variance direction is determined based on the difference values of ΔB_X ~65 nT, ΔB_Y ~40 nT, and ΔB_Z ~20 nT for the isolated time interval. In other words, the rotation matrix used to transform to the VPS coordinates only reflects these difference values in the isolated time range. Figure 6c shows the minimum variation in the same interval, representing the minimum variance direction. Since the MR measurement initially includes high-frequency noise, the result obtained by subtracting both sensor measurements reflects this noise in all components, as demonstrated in Figure 6a–c. However, in the first-order correction process, the high-frequency noise can be ignored due to the significantly more significant variance of the step-like disturbance.

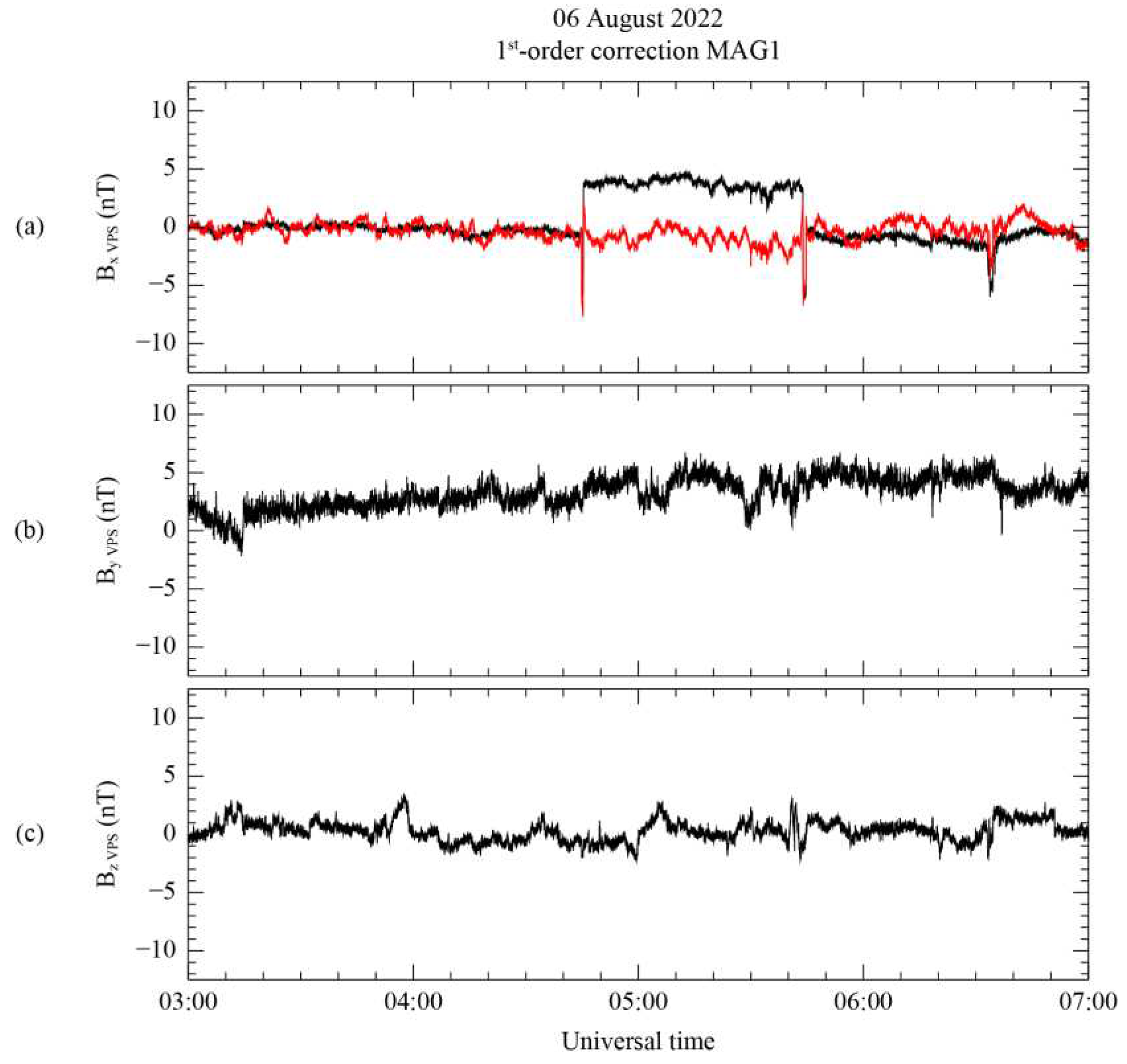
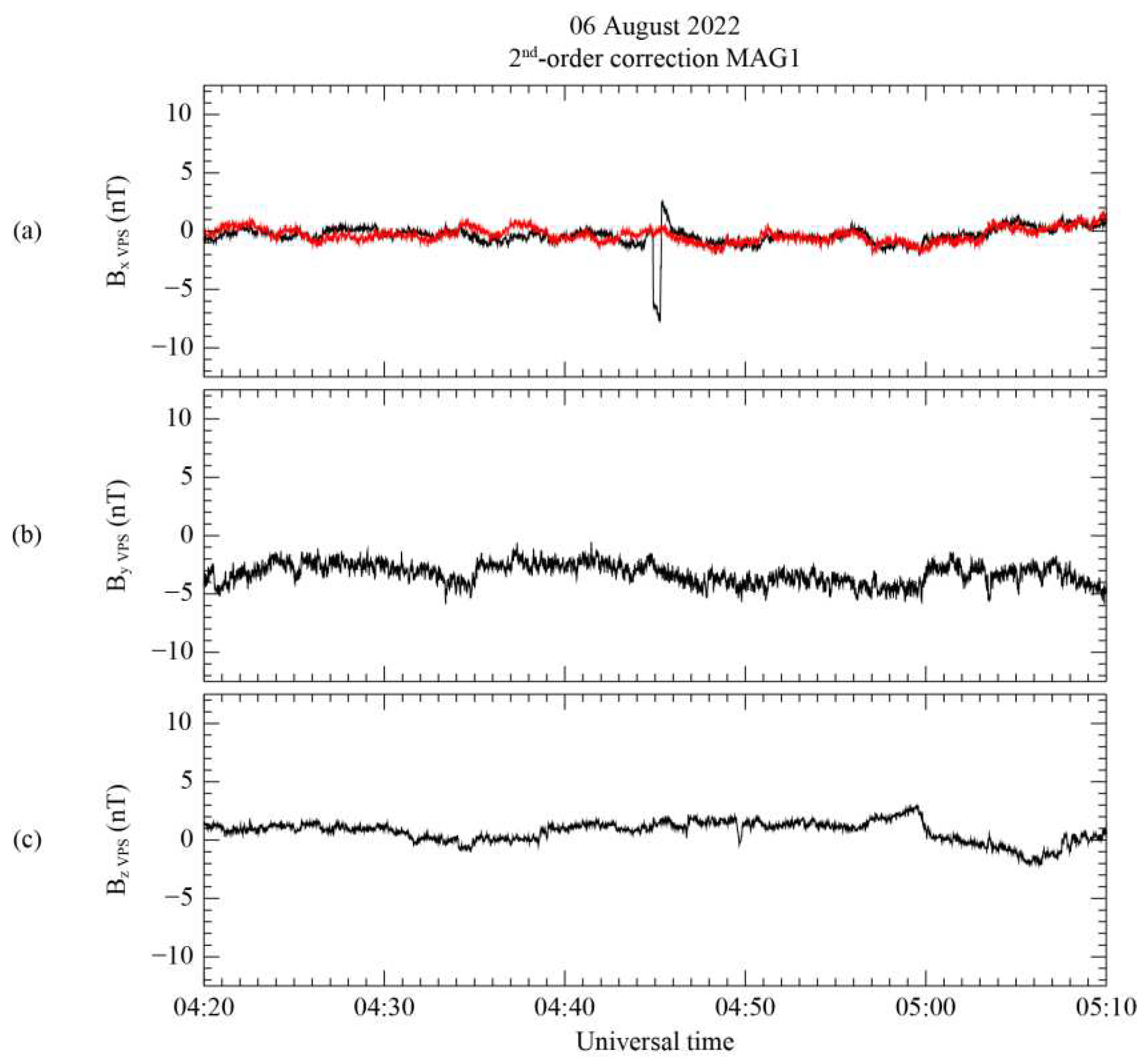
The initial measurement and the first-order corrected results are shown in on the initial VPS coordinate system in Figure 7 as black and red lines, respectively, with the mean value subtracted. In Figure 7a, the targeted step-like disturbance occurring between 04:45 and 05:44 UT is successfully eliminated in the maximum-variance direction, while the spike-like disturbance still persists. Additionally, the initial MR measurement introduces high-frequency noise in the first-order corrected result, which is subsequently mitigated following the method outlined in Section 3.2. Despite the correction process, the corrected result after 05:44 UT differs from the uncorrected measurement. According to Constantinescu et al. [12], this discrepancy arises because spacecraft-generated disturbances continue to affect magnetic field measurements even after the maneuver has concluded. In accordance with Equations (6)-(8), it is important to note that the intermediate and minimum variance direction components in Figure 7b and 7c do not influence this correction step.

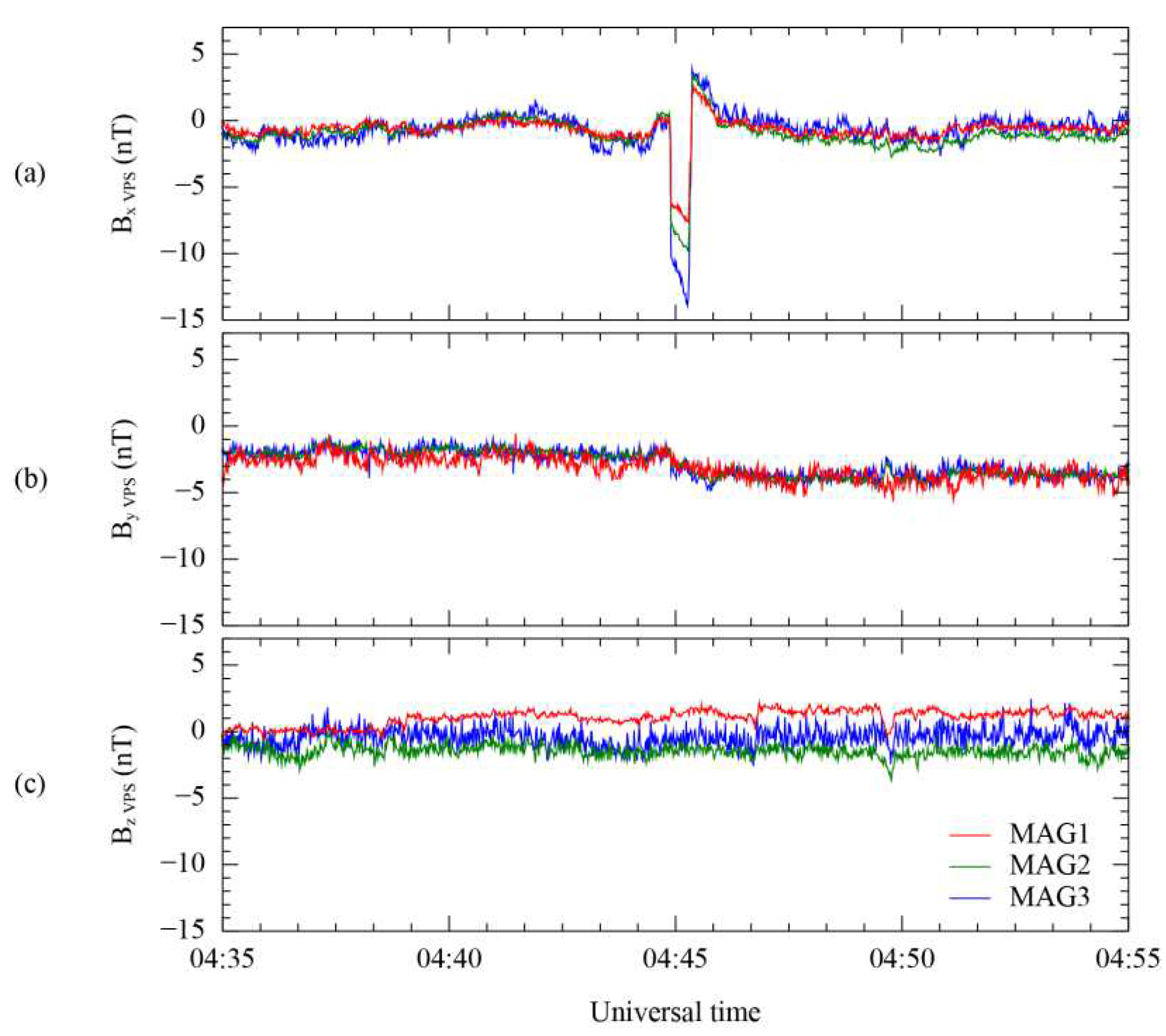
Figure 8 shows a spike-like disturbance still present in the first-order corrected results of measurements from the three MAG sensors. We selected an isolated time range of 6 min from 04:42 to 04:48 UT to decouple the spike-like disturbances after the first-order correction. The disturbance in this period, shown in Figure 8, corresponds to the spike just before the step-like disturbance. The spike-like disturbance in the Bx components on the VPS coordinates is extracted from the first-order corrected results of the three MAG sensors using the calculated rotation matrix, as depicted in Figure 8a. The minimum peak magnitude of each disturbance on the Bx component is −7.5 nT for MAG1, −9.8 nT for MAG2, and −13.8 nT for MAG3. Similar to the case of the step-like disturbance, this result also indicates that the magnitude of these disturbances is well sorted for the differences in distance between magnetometers. On the other hand, other components in Figure 8b,c show only high-frequency noise initially included in the measurement. The high-frequency noise tends to have a larger amplitude in the MAG3 measurement than MAG1 and MAG2. This tendency for noise is also shown in Figure 8a. Therefore, we can expect that the different amplitudes of high-frequency noise affect the results after the second-order correction according to Equations (6)-(8) when we use only MAG sensors to conduct the second-order correction.

In the second-order correction, the initially corrected results are adjusted by the maximum variance direction to extract the spike-like disturbance. Since the MR sensor cannot measure spike-like disturbances, the measurement from the MAG3 sensor is used to eliminate the disturbance. The MAG3 sensor is located farthest from the MAG1 sensor. The second-order correction result of the MAG1 measurement over the remaining spike-like disturbance is plotted in Figure 9. In the VPS coordinate system for the first-order correction result, the first-order and second-order correction results are depicted as black and red lines, respectively, using the same format as Figure 7. As in the case of Figure 7, the second-order correction is conducted only for the component in the maximum variance direction. In addition, although there are two spike-like disturbances just before and after the step-like disturbance, we perform the correction for the preferentially observed spike-like disturbance in time as a target. In Figure 9a, the second-order correction process eliminates the targeted spike-like disturbance from 04:44 to 04:47 UT from the maximum variance direction. Mitigation of the generated high-frequency noise after the second-order correction was also conducted.

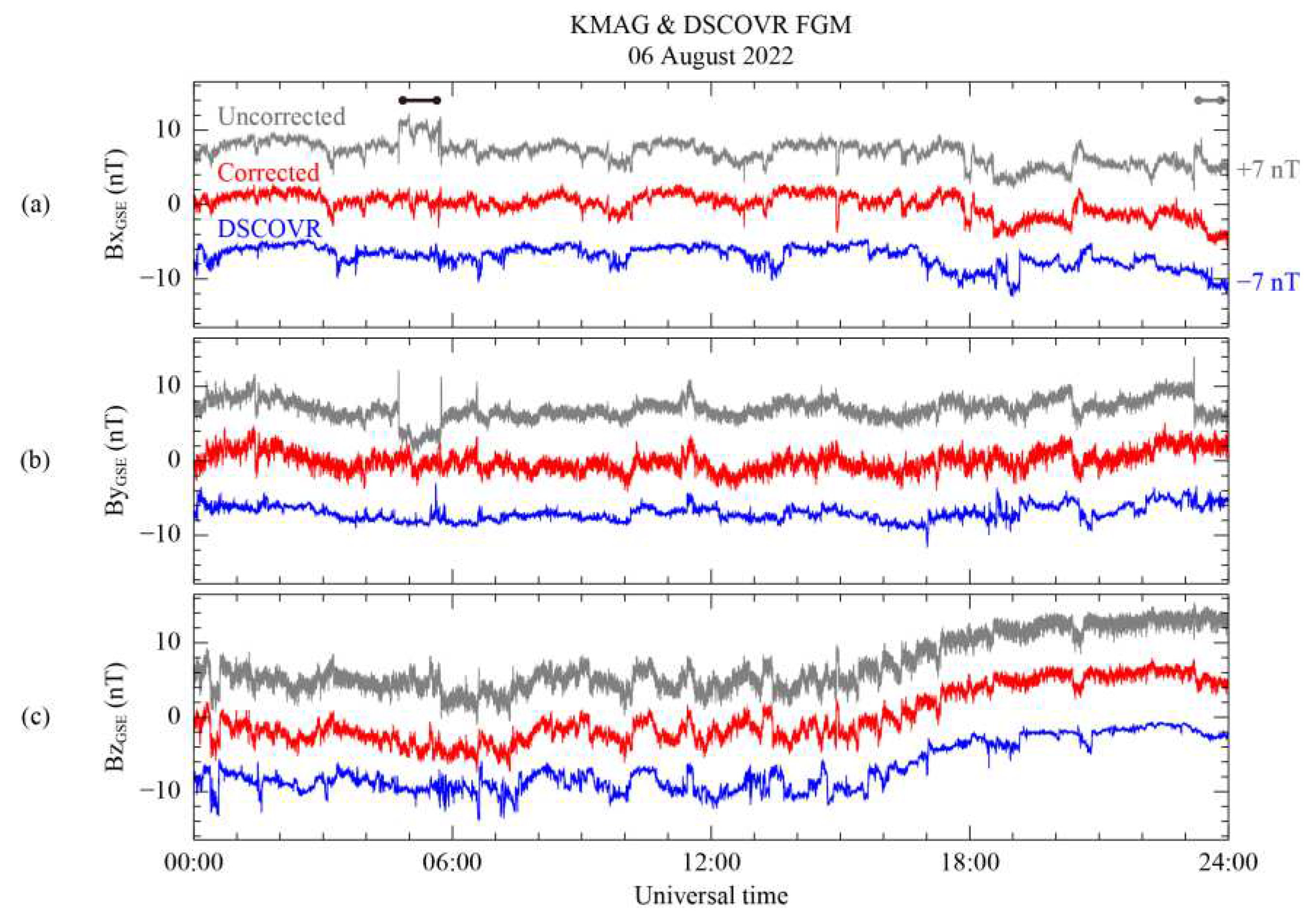
Figure 10 shows the DSCOVR FGM measurement and the corrected MAG1 measurement in the GSE coordinate system. Both measurements are subtracted from their daily average. To compare the two measurements, the DSCORVR magnetic field data was time-shifted by 40 min over the KMAG observation. The time shift was determined by identifying peaks in the magnetic field data collected by two spacecraft over 4 h starting at 10:00 UT. On the Bx and By components in Figure 10a and 10b, indicated by a black bar, the step-like disturbance from 04:44 to 05:44 UT for raw measurements (gray) is successfully eliminated in the corrected data (red). Although the scaling matrix A^0,ij in Equation (10) is applied over all time ranges, only the disturbance is clearly removed. In addition, another step-like disturbance exists from 23:20 UT, indicated by a gray bar. This disturbance is removed after the correction process. Considering the switching-on signal on the VDE and the magnetic field components B_Y and B_Z related to the disturbance in Figure 2, it can be seen that the two disturbances under the black and gray bars share the same generating source. For this reason, even if the scaling matrix is only calculated for the time range indicated by the black bar, the matrix can eliminate disturbance for the time range of the gray bar at the same time. As a result, Figure 10 shows good agreement between DSCOVR and KMAG observations.

5. Summary and Conclusions

We described the data correction method for the KMAG magnetometer to remove magnetic disturbances coming from the spacecraft. It is crucial to remove any disturbances to accurately determine changes in the background magnetic field, which is necessary to calculate the zero offset or identify magnetic events on the Moon. Therefore, the disturbances have to be eliminated during the initial data-processing phase before the zero-offset calculation. Based on our observations, we confirmed that the disturbance generated by the spacecraft is related to its maneuvering, as indicated by the Euler angle and VDE data. When the KMAG’s three sensors, MAG1, MAG2, and MAG3, are sensing spacecraft-generated disturbances, the magnitude of changes in the disturbances depends on how far away the sensor is from the spacecraft body. The spacecraft-generated disturbance that occurred on 6 August 2022 consisted of two types of disturbances, step-like and spike-like. The final correction result shows that the use of the maximum-variance gradiometer technique is reasonable to eliminate disturbances originating from spacecraft operations. By assuming that the disturbance has a greater variance than the variation of the background field, principal component analysis can be used to arrange the magnetic disturbance in the direction with the maximum variance. We set the isolated time range for each type of disturbance and addressed them sequentially. The time range for applying the technique to address spacecraft disturbance can vary depending on the duration of the maneuvering period. This applies not only to the current event but also to future events. In the correction process, modified data from the MR sensor is used to remove the step-like disturbance that shows the most significant difference. Since the modified MR data no longer exhibit a spike-like shape disturbance, using the first-order corrected data of MAG1 and MAG3, which are located farthest from each other, eliminates the spike-like disturbance within the 2 min time range.

Consequently, it is a useful method for eliminating noise, as we confirmed that the corrected results of the KMAG data are in alignment with the DSCOVR magnetic field data. In the future, the KMAG team is scheduled to perform data processing using the reduction technique to address disturbances generated by the spacecraft during the lunar orbit phase of the KPLO satellite.

Author Contributions

Conceptualization, J.L., H.J. and K.K.; Funding acquisition, H.J. and Y.C.; Investigation, J.L., H.J. and K.K.; Methodology, H.J. and K.K.; Resource, H.P., W.J. and E.K.; Software, J.L. and K.K.; Validation, J.L., H.J., K.K., H.P., W.J. and Y.J.; Visualization, J.L; Writing—original draft, J.L.; Writing—review & editing, H.J. and K.K.

Funding

The current research was supported by the Space Challenge Program funded by the Korea government, NRF-2022M1A3B8076421. This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government, NRF-2021M1A3A4A06098620.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ness, N.F. Magnetometers for space research. Space Sci. Rev. 1970, 11, 459–554. [Google Scholar] [CrossRef]
Ness, N.F.; Behannon, K.W.; Lepping, R.P.; Schatten, K.H. Use of two magnetometers for magnetic field measurements on a spacecraft. J. Geophys. Res. 1971, 76, 3564–3573. [Google Scholar] [CrossRef]
Neubauer, F.M. Optimization of multimagnetometer systems on a spacecraft. Journal of Geophysical Research 1975, 80, 3235–3240. [Google Scholar] [CrossRef]
Binder, A.B. Lunar prospector: overview. Science 1998, 281, 1475–1476. [Google Scholar] [CrossRef] [PubMed]
Kato, M.; Sasaki, S.; Takizawa, Y. Kaguya Project Team The Kaguya mission overview. Space Sci. Rev. 2010, 154, 3–19. [Google Scholar] [CrossRef]
Matsushima, M.; Tsunakawa, H.; Iijima, Y.; Nakazawa, S.; Matsuoka, A.; Ikegami, S.; Ishikawa, T.; Shibuya, H.; Shimizu, H.; Takahashi, F. Magnetic cleanliness program under control of electromagnetic compatibility for the SELENE (Kaguya) spacecraft. Space Sci. Rev. 2010, 154, 253–264. [Google Scholar] [CrossRef]
Narvaez, P. The magnetostatic cleanliness program for the Cassini spacecraft. The Cassini-Huygens Mission: Orbiter In Situ Investigations 2004, Volume 2, 385-394.
Ness, N.F.; Behannon, K.W.; Lepping, R.P.; Whang, Y.C.; Schatten, K.H. Magnetic field observations near Mercury: Preliminary results from Mariner 10. Science 1974, 185, 151–160. [Google Scholar] [CrossRef] [PubMed]
Pope, S.A.; Zhang, T.L.; Balikhin, M.A.; Delva, M.; Hvizdos, L.; Kudela, K.; Dimmock, A.P. In In Exploring planetary magnetic environments using magnetically unclean spacecraft: a systems approach to VEX MAG data analysis; Annales Geophysicae; Copernicus Publications Göttingen, Germany: 2011; Vol. 29, pp 639-647.
Kellock, S.; Austin, P.; Balogh, A.; Gerlach, B.; Marquedant, R.; Musmann, G.; Smith, E.; Southwood, D.; Szalai, S. In In Cassini dual technique magnetometer instrument (MAG); Cassini/Huygens: A Mission to the Saturnian Systems; SPIE: 1996; Vol. 2803, pp 141-152.
Olsen, N.; Clausen, L.T.; Sabaka, T.J.; Brauer, P.; Merayo, J.M.; Jørgensen, J.L.; Léger, J.; Nielsen, O.V.; Primdahl, F.; Risbo, T. Calibration of the Ørsted vector magnetometer. Earth Planets Space 2003, 55, 11–18. [Google Scholar] [CrossRef]
Constantinescu, O.D.; Auster, H.; Delva, M.; Hillenmaier, O.; Magnes, W.; Plaschke, F. Maximum-variance gradiometer technique for removal of spacecraft-generated disturbances from magnetic field data. Geosci. Instrum. Methods Data Syst. 2020, 9, 451–469. [Google Scholar] [CrossRef]
Song, Y.; Lee, D.; Bae, J.; Kim, Y.; Choi, S. Flight dynamics and navigation for planetary missions in Korea: past efforts, recent status, and future preparations. J. Astron. Space Sci. 2018, 35, 119–131. [Google Scholar] [CrossRef]
Lee, H.; Jin, H.; Jeong, B.; Lee, S.; Lee, S.; Baek, S.; Shin, J.; Lee, J.; Park, H.; Kim, K. KMAG: KPLO magnetometer payload. Publ. Astron. Soc. Pac. 2021, 133, 034506. [Google Scholar] [CrossRef]
Park, H.H.; Jin, H.; Kim, T.Y.; Kim, K.H.; Lee, H.J.; Shin, J.H.; Jang, Y.H.; Jo, W.H. Analysis of the KPLO magnetic cleanliness for the KMAG instrument. Adv. Space Res. 2022, 69, 1198–1204. [Google Scholar] [CrossRef]
Sonnerup, B.U.; Scheible, M. Minimum and maximum variance analysis. Anal. Methods Multi-Spacecr. Data 1998, 1, 185–220. [Google Scholar]
Song, P.; Russell, C.T. Time series data analyses in space physics. Space Sci. Rev. 1999, 87, 387–463. [Google Scholar] [CrossRef]
Richardson, J.D.; Paularena, K.I. Plasma and magnetic field correlations in the solar wind. J. Geophys. Res. Space Phys. 2001, 106, 239–251. [Google Scholar] [CrossRef]

Figure 1. Overview of KMAG instrument on KPLO satellite, consisting of FCE unit (red box), located inside spacecraft body, and MAG boom (orange), deployed externally. Within the boom are three magnetometers: MAG1 (red), MAG2 (green), and MAG3 (blue).

Figure 2. KMAG and DSCOVR FGM observations in geocentric solar ecliptic coordinate system on 6 August 2022 with KPLO satellite maneuvering information. (a–c) Magnetic field components B_X, B_Y, and B_Z, respectively, from KMAG (black line) and DSCOVR (gray line). Each component is subtracted by its mean value. DSCOVR measurements are time-shifted by 40 min. (d,e) Euler angle for each component (a: red; b: blue; c: green) and valve drive electronics information for KPLO satellite, respectively.

Figure 3. Positions of KPLO (blue) and DSCOVR (red) spacecraft, projected onto ecliptic plane in GSE coordinates.

Figure 4. Temporal variation in hourly averaged magnetic field subtracting daily mean value to support Figure 2. Black and red lines correspond to DSCOVR FGM and MAG1 sensor measurements, respectively; horizontal line represents 0 nT in each component.

Figure 5. KMAG observations on 6 August 2022 in sensor frame coordinates. (a–c) B_X, B_Y, and B_Z components of magnetic field, respectively, observed from MAG1 (red), MAG2 (green), MAG3 (blue), and MR (black). (d) Expanded view in time range from 03:20 to 07:10 UT displays B_Z component from all sensors.

Figure 6. Difference ΔB^0,ij between MR and MAG1 before correction in corresponding VPS coordinate system of ΔB0ij. Components B_X (a), B_Y (b), and B_Z (c) are aligned with the directions of maximum, intermediate, and minimum variance, respectively. Mean values are subtracted from all components. Corresponding average for each component is subtracted from all components.

Figure 7. Uncorrected (black) and first-order corrected (red) measurements from MAG1 on VPS coordinates. Components B_X (a), B_Y (b), and B_Z (c) are oriented along the directions of maximum, intermediate, and minimum variance in that order. Corresponding average for each component is subtracted from all components.

Figure 8. First-order corrected results of MAG1 (red), MAG2 (green), and MAG3 (blue) by using MR on each VPS coordinate system. Components B_X (a), B_Y (b), and B_Z (c) are oriented in the direction of maximum, intermediate, and minimum variance. Average for each component is subtracted from all components.

Figure 9. First-order corrected (black) and second-order corrected (red) measurements from MAG1 on VPS coordinates. Components B_X (a), B_Y (b), and B_Z (c) are aligned with the directions of maximum, intermediate, and minimum variance, respectively. Corresponding average for each component is subtracted from all components.

Figure 10. Comparison between final corrected MAG1 and DSCOVR FGM measurements for 6 August 2022 in GSE coordinate system. (a–c) Magnetic field components B_X, B_Y, and B_Z, respectively. Corrected MAG1 measurements (red) are shown with initial uncorrected measurements (gray). Blue lines represent measurements from DSCOVR FGM.

Table 1. Requirement specifications of KMAG magnetometer.

Parameter	Performance
Magnetometer type	Fluxgate (racetrack)
Measurable range	±1000 nT
Resolution	<0.2 nT at 10 Hz sampling rate
Mass	3.5 kg
Power	Input: +28 V (unregulated +24–32.8 V) Consumption: 4.6 watt
Operating temperature	KMAG Assy.: −55–70 °C FCE: −20–50 °C
Noise level	<50 pT Hz^−1/2 at 1 Hz
Axis alignment	<1°

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Correction of Spacecraft Magnetic Field Noise: Initial KMAG Observation in the Solar Wind

Abstract

1. Introduction

2. Instrumentation: KMAG

3. Clearance Technique for Spacecraft-Generated Magnetic Disturbances

3.1. Elimination of Artificial Disturbance

3.2. Mitigation of Amplified High-Frequency Noise

4. Results

4.1. Comparison of DSCOVR FGM and KMAG

4.2. Elimination of Artificial Disturbance

5. Summary and Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe