Prerpints.org logo
Preprint
Article

Phase Transition and Point Defects in the Ferroelectric Molecular Perovskite (MDABCO)(NH4)I3

Altmetrics

Downloads

126

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 October 2023

Posted:

31 October 2023

You are already at the latest version

Alerts
Abstract
We measured the anelastic, dielectric and structural properties of the metal-free molecular perovskite (ABX$_{3}$) (MDABCO)(NH$_{4}$)I$_{3}$, which has already been demonstrated to become ferroelectric below $T_{\text{C}}=$ 448~K. Both the dielectric permittivity measured in air on discs pressed from powder and the complex Young's modulus measured on resonating bars in vacuum show that the material starts deteriorating with loss of mass just above $T_{\text{C}}$, introducing defects and markedly lowering $T_{\text{C}}$. The elastic modulus softens of 50\% when heating through the initial $T_{\mathrm{C}}$, contrary to usual ferroelectrics, which are stiffer in the paraelectric phase. This suggests improper ferroelectricity, where the primary order parameter of the transition is not the electric polarization, but the orientational order of the MDABCO molecules. The degraded material presents thermally activated relaxation peaks in the elastic energy loss, whose intensities increase together with the decrease of ~$T_{\mathrm{C}}$. The peaks are much broader than pure Debye, due to the general loss of crystallinity, also apparent from X-ray diffraction, but their relaxation times have parameters typical of point defects. It is argued that the major defects should be of the Schottky type, mainly due to the loss of (MDABCO)$^{2+} $ and I$^{-}$, leaving charge neutrality, and possibly also (NH$_{4}$)$^{+}$ vacancies. The focus is on an anelastic relaxation process peaked around 200~K at $\sim 1$~kHz, whose relaxation time follows the Arrhenius law with $\tau $$_{0}$~$\sim $\ $10^{-13}$\ s and $E\simeq 0.4$~eV. This peak is attributed to I vacancies (V$_{\text{X}}$) hopping around MDABCO vacancies (V$_{\text{A}}$) and its intensity presents a peculiar dependence on temperature and content of defects. The phenomenology is thoroughly discussed in terms of lattice disorder introduced by defects and of partition of V$_{\text{X}}$ among sites that are far from and close to the cation vacancies. A method is proposed for calculating the relative concentrations of V$_{\text{X}}$, that are untrapped, paired with V$_{\text{A}}$ or forming V$_{\text{X}}$--V$_{\text{A}}$--V$_{\text{X}}$ complexes.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

New organic and hybrid metal-organic ferroelectrics are being synthesized in the last years, and are filling the gap between the polymer and the oxide ferroelectrics in terms of piezoelectric properties, at least in one case even superior to those of PbZr 1 − x Tix O 3 (PZT) [1], and with advantages in terms of simplicity and cost effectiveness of preparation and flexibility of use. In fact, these materials can be prepared with purely chemical methods and deposited as films on surfaces of any shape. One major drawback is their limited thermal resistance, due to the weaker bonds and the volatility of the organic molecules at moderate temperatures.
The present record of piezoelectric response among metal-organics belongs to the hexagonal perovskite ( TMFM ) x ( TMCM ) 1 − x CdCl 3 with d 33 = 1500 pC/N [1]. Yet, in principle, a cubic paraelectric phase is the most favourable for obtaining large piezoelectric responses below T C , thanks to the reduced anisotropy, that allows for more orientations of the spontaneous polarization, as in the well known perovskite oxides BaTi O 3 , PbZr 1 − x Tix O 3 , etc.. The first cubic perovskite of this type is the metal-free (MDABCO)( NH 4 ) I 3 [2], composed of corner-sharing I 6 octahedra with NH 4 in the centre and MDABCO molecules in the interstices among the octahedra. The MDABCO 2 + cation is obtained from the roughly spherical DABCO = N 2 ( C 2 H 4 )3 by attaching a methyl ( CH 3 ) group to one N in order to induce an electric dipole moment. Ferroelectricity, with a Curie temperature of 448 K, is due to the alignment of the dipole moments of these cations along a 111 direction and their concomitant displacement along the same direction [3,4]. The piezoelectric constant of (MDABCO)( NH 4 ) I 3 is d 33 = 14 pC/N, enhanced to 63 pC/N upon substitution of the methyl with an amino group in MDABCO [5].
This molecular ferroelectric has also been studied with computational methods. It has been found with density functional theory calculations, that the spontaneous polarization arising from the alignment of the dipole moment of MDABCO 2 + along the 111 axes is much amplified by a displacement of MDABCO 2 + ions along the same axis [3,4]. Phase-field simulations have also been performed, in order to derive a phase diagram and piezoelectric and dielectric properties as a function of strain, useful for enhancing such properties in thin films through epitaxial strain [6].
Further characterisation of (MDABCO)( NH 4 ) I 3 regards its thermoelectric properties [7,8] and the static mechanical properties evaluated by nanoindentation and high-pressure [9,10]. It has also been demonstrated that this material can be prepared by mechanosynthesis [11], and the effects of various substitutions have been studied [5,12].
We present anelastic and dielectric spectroscopy measurements of (MDABCO)( NH 4 ) I 3 on samples of pressed powder, bringing information on the process of thermal decomposition occurring already close to T C . The defects formed in this manner produce peaks in the elastic energy loss versus temperature, which are analyzed in terms of mobility of iodine vacancies and their trapping by cation vacancies.

2. Results

2.1. Anelastic spectra

Figure 1 presents the normalized Young’s modulus E / E 0 and elastic energy loss Q − 1 = E ″ / E ′ curves of bars B1–B3 during heating and cooling cycles in high vacuum. All curves are obtained exciting the fundamental flexural resonance with an initial frequency at room temperature of 0.8 − 1.0 kHz. The curves are normalized dividing by the initial modulus E 0 , which was 11 GPa for B1, 6.6 GPa for B2 and 7.4 GPa for B3. The variability of the initial Young’s modulus may be attributed to non-homogeneous density along the bars, evident from the non uniform color just after extracting them from the press.
During the initial heating (curves 1, 4 and 9), all the E T curves start softening almost linearly, as usual in normal solids, where the same anharmonicities responsible for thermal expansion also cause softening [13]. The slight relative stiffening above ∼ 380 K seems an extrinsic effect, possibly the loss of the solvent of the Ag paint of the electrode in the centre of the sample. In fact, the samples are measured immediately after applying the Ag electrode (see Methods). The samples remain then stable, as demonstrated by the perfectly reproducible thermal cycles on B2, where 400 K were not exceeded (curves 2 and 3). Heating through T C = 446 ± 3 K causes a steep drop of E, observed with perfect reproducibility on the three samples (curves 3, 4 and 9). Sample B1 broke immediately after passing this temperature, which coincides with T C ≃ 448 K reported for single crystals [2], while the other samples did not, but where evidently deteriorated by heat. In fact, heating of sample B3 was immediately stopped after the negative step in E (curve 4), and during the subsequent cooling T C was depressed to 389 K. The anelastic spectrum was now reproducible during heating and cooling except for a thermal hysteresis of 20 K of the depressed T C (curves 5–8).
If heating was extended beyond the initial T C (curve 9), further softening occurred, that was not recovered during cooling (curve 10). Reaching 500 K resulted in ∼ 50 % unrecoverable softening and a depression of T C down to 307 K. The decrease of T C and E are evidently due thermal decomposition beyond ∼ 450 K, presumably through Schottky defects, like loss of (MDABCO) I 2 , with formation of vacancies of MDABCO and iodine. These defects depress T C and weaken the lattice.
The elastic energy loss Q − 1 in the initial state is relatively low below room temperature and soon rises above 0.01 at higher T (B2). After heating above T C , in addition to the permanent softening and lowering of T C , at least three new peaks appear in the Q − 1 curves, labelled P1–P3. Their intensities are correlated with the maximum temperature reached, the magnitude of the permanent softening and the decrease of T C , proving that they are due to the defects introduced by the partial thermal decomposition. Indeed, Figure 2 shows that these peaks, including the rising background in the virgin state, are shifted to higher T when measured at higher frequency, meaning that they are all thermally activated. The steps at T C = 389 K in sample B3 and T C = 307 K in sample B1 are the low-temperature tail of the relaxation of domain walls, which disappears in the high-temperature phase. Peaks P1 (only partially visible) and P2 are stable and can be measured reproducibly during cooling and heating. Instead, the Q − 1 T curve above 300 K changed after four days in vacuum; in place of the single P3 peak, there were two, one much smaller at slightly lower temperature and one of about the same intensity of P3, but broader and shifted at higher temperature of 50 K (not shown).

2.2. Dielectric spectra

Figure 3 presents the real part and dielectric losses of disc D1 measured in air. The dielectric measurements on these samples of pressed powder were affected by the presence of intense Maxwell-Wagner relaxations from free charges, possibly of intergrain origin, and by poor adhesion of the Ag electrodes to the sample surface. The latter caused small jumps in ε ′ , as in Figure 5 at 470 K. For this reason, rather than the Curie-Weiss peak in ε ′ observed in single crystals at T C ≃ 448 K [2], here an anomaly appears at T C in the free charge relaxation (heating curves in Figure 3). Correspondingly, the dielectric losses are very high. As also found in the anelastic experiments, heating at 1.3 K/min up to 490 K in air causes partial thermal decomposition and depresses T C down to 310 K. This effect is fully consistent with that observed in the anelastic measurement up to 500 K in high vacuum, resulting in T C = 308 K, and suggests that there is not much difference in loss of material above T C in air or vacuum (see also Figure 9 later on).
Preprints 89111 g003
Figure 3. Dielectric permittivity measured in air on disc D1 at three frequencies during heating (thin lines) and subsequent cooling (thick lines). The partial thermal decomposition at the highest temperatures caused a decrease of T C .
Figure 3. Dielectric permittivity measured in air on disc D1 at three frequencies during heating (thin lines) and subsequent cooling (thick lines). The partial thermal decomposition at the highest temperatures caused a decrease of T C .
Preprints 89111 g003
The left panel of Figure 4 presents ε ′ of D1 measured at 1 MHz during various thermal cycles. Only a decrease is observed during the first cooling from a temperature lower than T C . Curves 2 and 3 correspond to those at 1 MHz in Figure 3. In curve 4 (perhaps lower than curve 3 because of a partial detachment of the electrode) cooling is extended to lower temperature, so that it is more evident that the small step at the original T C becomes sharper and spiked and is followed by dielectric stiffening, parallel to the elastic stiffening ( ε ′ must be compared with the compliance 1 / E ).
Preprints 89111 g004
Figure 4. Dielectric permittivity measured at 1 MHz during heating (thin lines) and cooling (thick lines) on disc D1 and a piece of bar B3. Curves 2 and 3 correspond to those at 1 MHz in Figure 3.
Figure 4. Dielectric permittivity measured at 1 MHz during heating (thin lines) and cooling (thick lines) on disc D1 and a piece of bar B3. Curves 2 and 3 correspond to those at 1 MHz in Figure 3.
Preprints 89111 g004
The analogy between the dielectric and elastic susceptibilities is more evident in the right panel, where it is shown ε ′ of a piece of bar B3 measured on heating and cooling, after the anelastic measurements 5–8 of Figure 1. Here the spike is absent and there is only a decrease of ε ′ from the high- to the low-temperature phase, at the same temperatures of the elastic steps, whose temperatures are indicated by vertical lines.
Preprints 89111 g005
Figure 5. Dielectric permittivity of sample D1 during cooling, after having reached 490 K.
Figure 5. Dielectric permittivity of sample D1 during cooling, after having reached 490 K.
Preprints 89111 g005
The losses below room temperature are initially featureless and decrease to < 0.001 at 100 K, similarly to the anelastic losses. In order to check for counterparts of the anelastic peaks P1 and P2, Figure 5 presents the dielectric spectrum of disc D1 after having reached 490 K. The transition has been depressed to 305 K, indicating that the sample is in a state similar to that of bar B1 in Figure 2. The thermally activated maximum around 200 K in tan δ seems compatible with P2, but the steep background makes any quantitative comparison or analysis difficult.

2.3. XRD and TGA

Figure 6 presents the X-ray diffractograms of the as-prepared powder of (MDABCO)( NH 4 ) I 3 and of bars B1–B3 after the anelastic measurements of Figure 1. There is a perfect correlation between the degradation of the spectra, in the sequence powder, B2, B3, B1, and the lattice disorder resulting from thermal decomposition at increasing maximum temperatures.
Figure 7 presents the normalized TGA curves measured heating the powder in a Al2O3 crucible at 2 K/min and 5 K/min in N2. Two steps are observed, a first with onset around 390 K should be the loss of water, while a second with onset around 435 K may be due to the loss of cations and anions, with formation of Schottky defects.

2.4. AFM and PFM

In order to verify the existence of piezoelectric response, a film of (MDABCO)( NH 4 ) I 3 was deposited from solution on an ITO/glass substrate for being analyzed by AFM and PFM (Figure 8). The deposition parameters were not sufficiently optimized, because the optical images from AFM ( ∼ 480   μ m × 360   μ m) show that the surfaces are inhomogeneous. Some zones have valleys, others have a rough appearance. Both types of zones show variation in thickness of micrometers, as estimated by refocusing the optical image. The topographical AFM images show the presence of some agglomerations of grains, partially embedded in a glassy matrix. The grains have dimensions of up to 1 μ m.
The PFM images were obtained applying an AC voltage of about 5 V, due to the large thickness of the films. Some grains have piezoelectric response, demonstrated by the contrast in the images of PFM amplitude and PFM phase in correspondence with some grains.

3. Discussion

3.1. Thermal decomposition

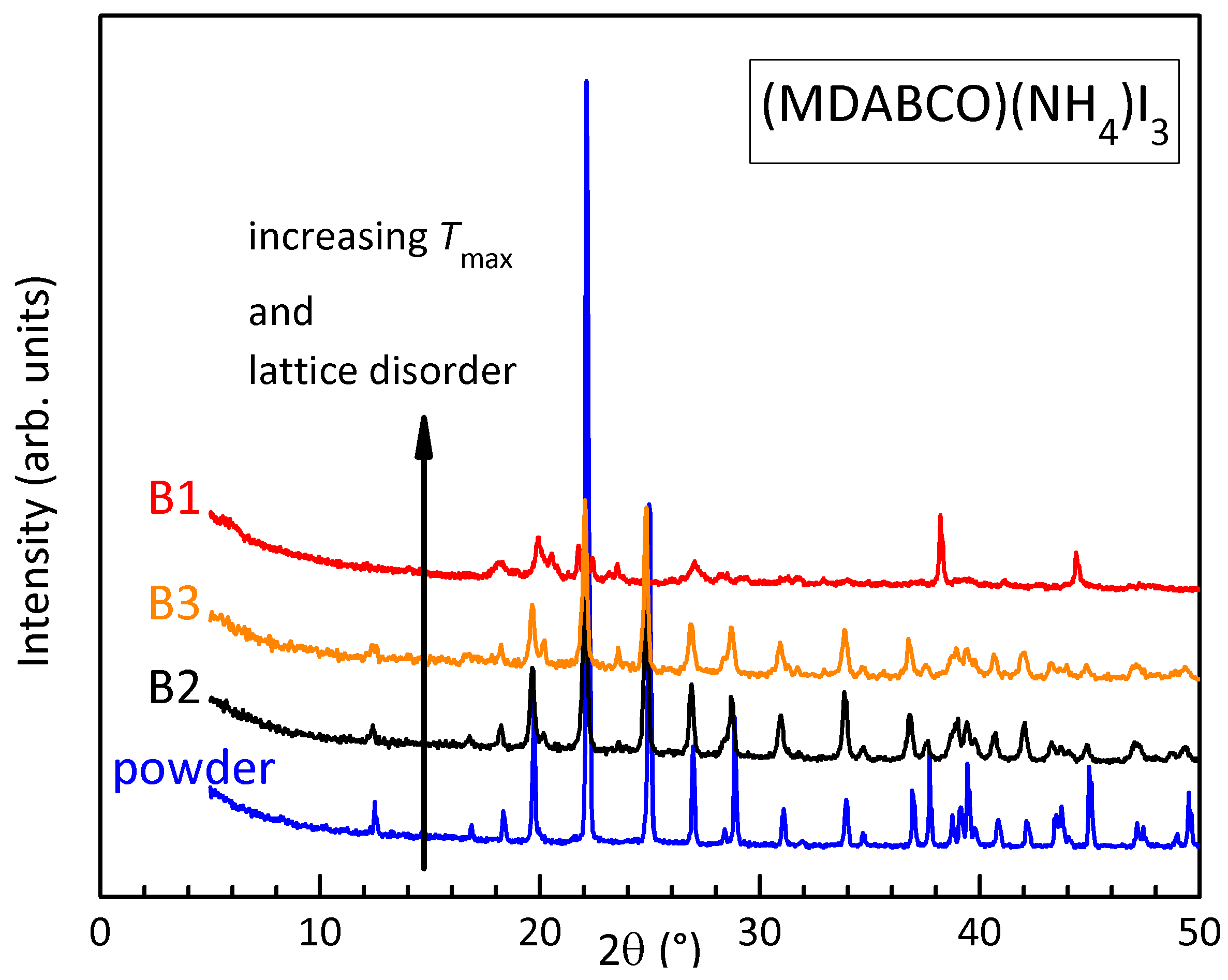
From these measurements one deduces that polycrystalline (MDABCO)( NH 4 ) I 3 suffers thermal decomposition in vacuum already just above 445 K, as demonstrated by the lowering of T C , the appearance of intense thermally activated processes in the anelastic and dielectric spectra and the degradation of the XRD spectra.
Figure 9 show the lowering of T C as a function of T max , the maximum temperature reached during the anelastic measurement in high vacuum or dielectric measurements in air. The points at the top correspond to the initial state and are obtained setting T max = T C . Both sets of data follow a same line, so that there is no visible effect of the atmosphere on the process of thermal degradation. Single crystals have a reduced exposed surface with respect to polycrystals and should follow a higher curve. In fact. the crosses are the reported T C during heating and cooling of single crystals measured with DSC and SHG [2], where T max is set to the upper values of the abscissas in the respective figures (hence it might be higher). Considering that in our polycrystals the thermal hysteresis of reduced T C does not exceed 20 K (curves 5–8 of Figure 1), it seems likely that the hysteresis of > 50 K reported in the single crystals is rather due to the fact that during cooling the samples were degraded.
Preprints 89111 g009
Figure 9. Transition temperature T C after having reached T max in air or high vacuum..
Figure 9. Transition temperature T C after having reached T max in air or high vacuum..
Preprints 89111 g009
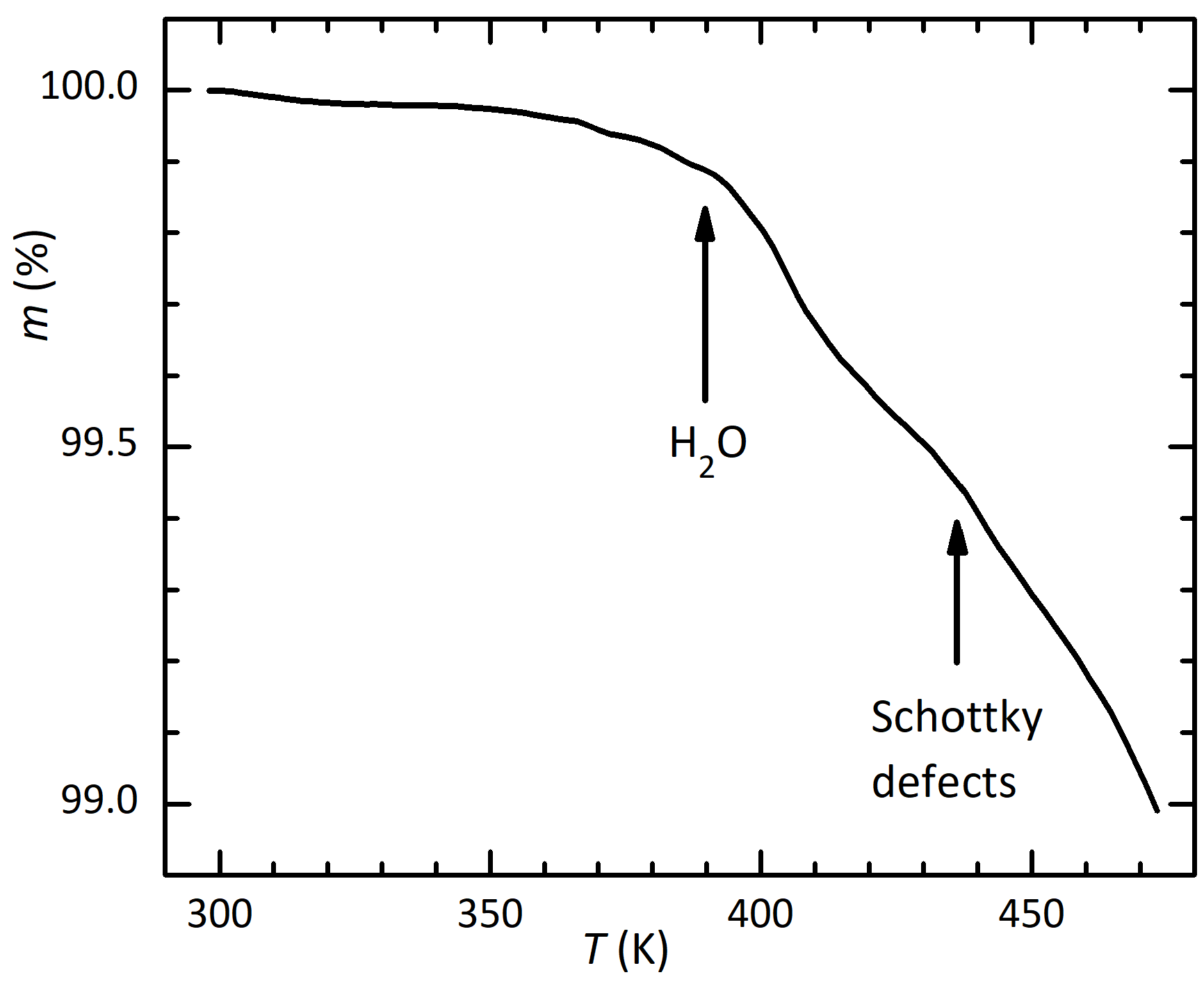
Further evidences of mass loss above 440 K in < 10 − 5 mbar are a marked rise of pressure above that temperature during continuous pumping, in the anelastic measurements, and a yellow/brown coloration of the quartz tube enclosing the sample holder. This is typical of the deposition of iodate compounds.
The major mechanism of degradation of perovskites ABX 3 at high temperature is the formation of Schottky defects, namely pairs or complexes of anion X and cation A or B vacancies in order to leave unchanged the neutral total charge according to the formal valence of the ions. These vacancies can then migrate into the bulk, with the combined effects of depressing the temperatures of the structural transitions, softening the lattice and producing anelastic and dielectric relaxation, if the vacancies or their complexes have electric or elastic dipoles. Both effects are very strong in the present measurements.

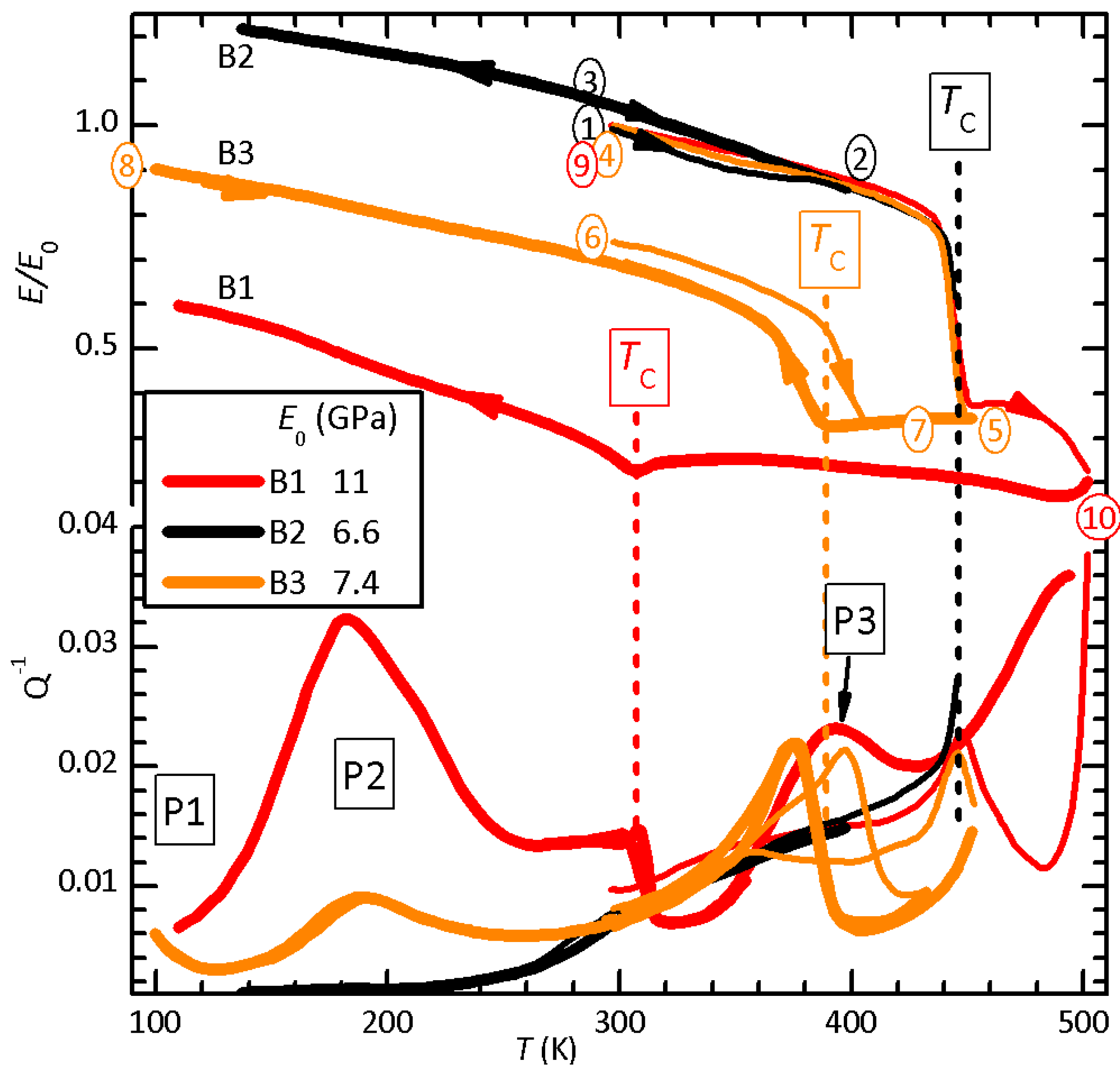
3.2. Elastic and dielectric anomalies at T C

The elastic anomaly in normal ferroelectrics is a steplike softening below T C [14] of piezoelectric origin [15], opposite to what observed in the present case, where all three samples soften above T C . The explanation of this behaviour comes from the fact that, even though the material is ferroelectric below T C , the transition is mainly due to the loss of the free rotation of the molecular cation MDABCO 2 + . From this point of view, the step in the modulus is nothing other than the softening from the coupling between strain and the molecular rotation mode, which is frozen below T C . The transition is then similar to the other order-disorder transitions of the molecular orientations in the metal-organic perovskites NH 4 -Zn(HCOO)3[16] and TMCM-MnCl3 [17,18], also improper ferroelectric, and to the tetragonal-to-orthorhombic transitions in MAPb I 3 [19] and FAPb I 3 [20]. As discussed in those previous cases, part of the stiffening in the low-temperature phase can be due to the formation of stronger H bonds of the ordered molecules with the surrounding halide octahedra.
The above observations are corroborated by the fact that, when T C is lowered, the dielectric anomaly becomes more evident (opposite with respect to the anelastic one, see Figure 3, Figure 5) but it is not a Curie-Weiss peak, whose slope at low temperature should be higher than at high temperature. This fact, together with the softening rather than stiffening when passing to the paraelectric phase, demonstrates that the transition is not Curie-Weiss with the polarization as order parameter, but it is driven by something else, and the appearance of the electric polarization is a side effect.

3.3. Grain boundary relaxation

The mechanical loss Q − 1 of as-pressed (MDABCO)( NH 4 ) I 3 is relatively low but starts increasing considerably above room temperature (B1 in Figure 1), is thermally activated (Figure 2) and is repeatable up to 400 K. This rise of dissipation above room temperature should be due to grain boundary (GB) sliding. Grain boundary relaxation is usually considered relevant at temperatures higher than half the melting temperature [21], and causes a very broad peak in the mechanical losses [22]. Our material starts decomposing already slightly above 400 K and therefore peak P4 may be due to GB sliding. Indeed, organic polycrystals are used as model systems to study the anelasticity from GB sliding in rocks at room temperature rather than at ≫ 1000 K, since the respective melting temperatures pass from thousands to hundreds of kelvin [23].
The GB peak results from a very broad distribution of relaxation times, due to the distribution of sizes of the grains and of the degrees of coherency of their boundaries. In Al2O3 and MgO it has been found that the low-temperature components of the GB peak disappear with annealing, interpreted as due to an increase of the degree of GB coherency with grain growth [22]. The same process may occur in our organic polycrystal: exceeding T C would not only cause loss of material, but also anneal the GB structure formed during pressing at room temperature, so explaining why in Figure 1  Q − 1 above room temperature in sample B3 is lower than in unannealed B2.

3.4. Point defects relaxations

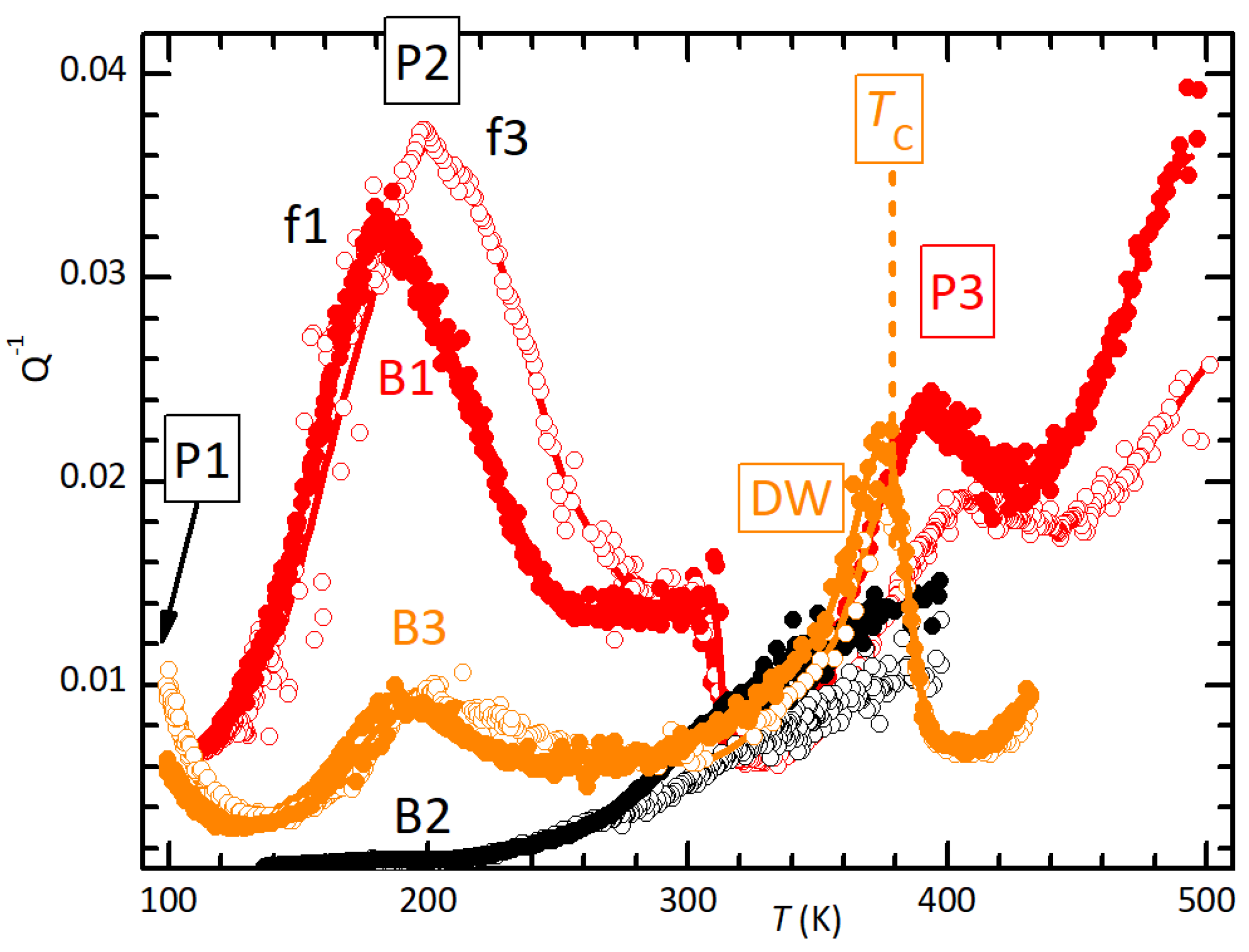
At least three thermally activated peaks, P1–P3, appear when T C is depressed by partial decomposition, and they must be due to newly created defects.
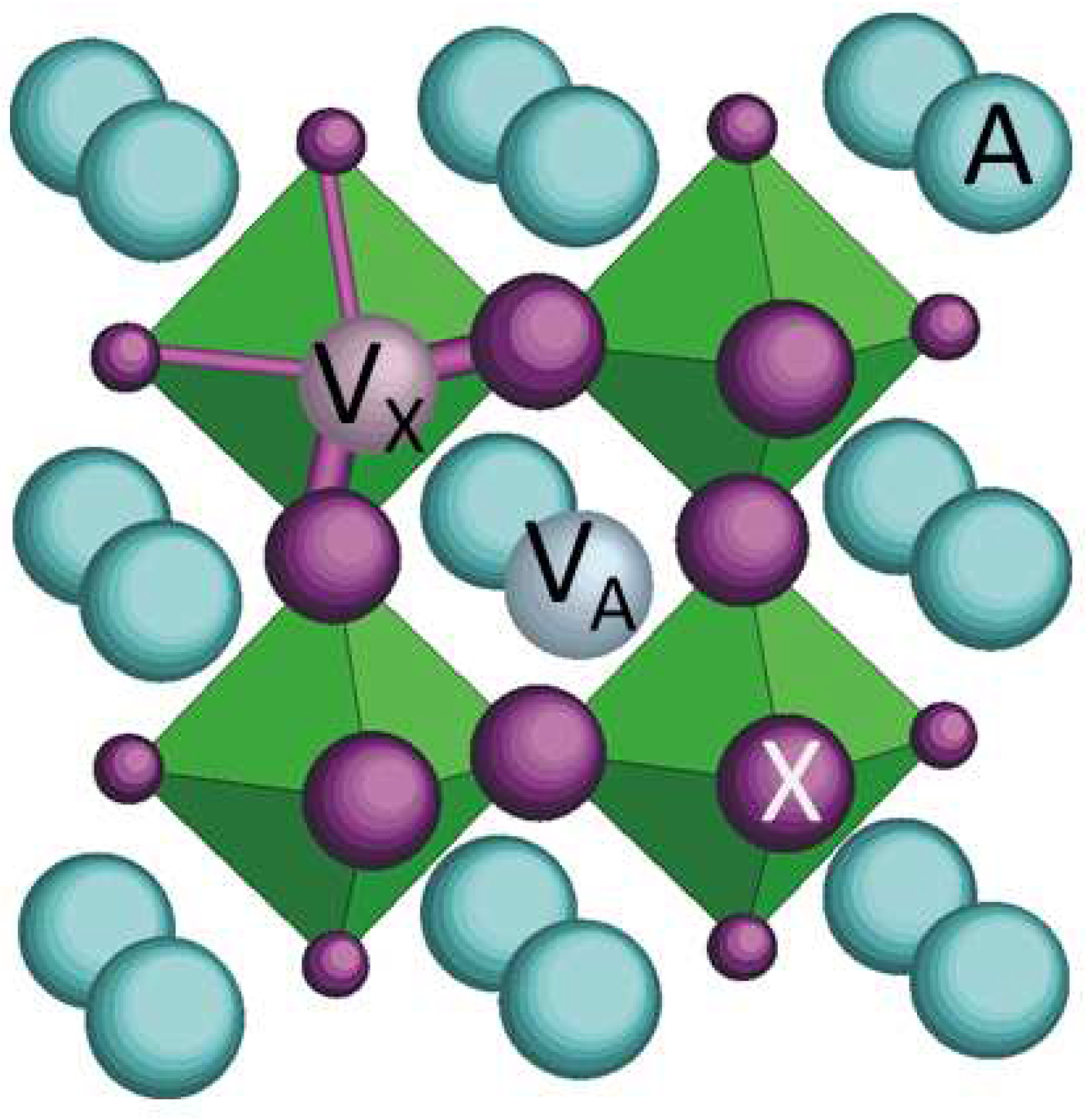
In defective perovskites ABX 3 (Figure 10) the most abundant and mobile defects causing anelastic relaxation are the X vacancies ( V X ). When a V X jumps to a nearest neighbour X position along an edge of a BX6 octahedron, the direction of its two nearest neighbour B atoms, at the centres of the octahedra, rotates of 90 ∘ and therefore also the local anisotropic strain (elastic dipole) rotates. The elastic energies of these three types of elastic dipoles change upon application of a uniaxial stress and therefore induce changes of their average populations. This results in a relaxation of the macroscopic strain due the elastic dipoles with a kinetics determined by their mean hopping time; this is called anelastic relaxation [24]. If a periodic stress with angular frequency ω is applied, the continuous readjustment of these populations causes an additional retarded anelastic strain, and therefore an increment of the elastic compliance S = 1 / E given by Δ S = Δ / 1 + ι ω τ , where the relaxation time generally follows the Arrhenius law
τ = τ 0 exp E / T
with 10 − 15 s < τ 0 < 10 − 12 s for point defects, and the relaxation strength is
Δ ∝ n Δ λ 2 k B T ,
where n is the defect population and Δ λ the change of elastic dipole after the jump/reorientation of the defect. Each process contributes to the losses as a Debye relaxation [24,25]
Q − 1 = S ″ S ′ = Δ ω τ 1 + ω τ 2 ,
peaked at the temperature such that ω τ T ≃ 1 . Notice that isolated V X do not have an electric dipole and therefore do not cause dielectric relaxation, while pairs of cation and anion vacancies have both elastic and electric dipoles.
Even though peaks P1-P3 are considerably broader than Debye relaxations, they are clearly due to well defined defects with quite different activation barriers E. It would be tempting to make parallels with the anelastic relaxation spectra of other defective perovskites, like O deficient SrTi O 3 − δ [26] and partially decomposed (TMCM)MnCl3 [18], but the present situation is different. Oxide perovskites are quite stable compounds and may loose only O atoms at high temperature in reducing atmosphere. The charge compensation in SrTi O 3 − δ from the loss of O2− anions can be achieved by the reduction of 2 δ Ti4+ cations to Ti3+. The resulting defects are V O and small polarons and the anelastic spectra of SrTi O 3 − δ and BaTi O 3 − δ show peaks due to their hopping, with clearly distinct peaks for vacancies that are isolated and paired [26,27].
In these halide perovskites heated close to the decomposition temperature it is unlikely that only anion vacancies are formed, since the organic cation is volatile and the prevalent mechanism of decomposition is expected to be the formation of Schottky defects, namely neutral pairs or complexes of cation and anion vacancies. In (TMCM)MnCl3 it was assumed that an equal concentration of TMCM+ and Cl− was formed [18] for two reasons: i) A = TMCM is organic and more volatile than inorganic B = Mn; ii) vacancies on the B-site of perovskites are rare, though they may be created under particular circumstances [28,29,30]. A reason for the tendency to loose A rather than B ions is that the BX6 octahedra are clearly the stable backbone of the lattice, because the B-X bonds are shorter than the A–X ones and therefore stronger, especially when they involve larger charge (B4+ and A2+ or B2+ and A+). That the B–X bonds are much stronger than the A–X ones is demonstrated by the common tilting transitions of the octahedra upon cooling [31]. In fact, during cooling, the weaker and more anharmonic A–X sublattice contracts more than the rigid network of BX6 octahedra, and the octahedra, unable to compress, rigidly tilt [32]. In the present case both the conditions of smaller volatility of B and stronger B–X bonds are impaired: not only both cations are organic, but B2+ has larger charge than A+. It is therefore possible that in (MDABCO)( NH 4 ) I 3 the loss through Schottky defects of NH 4 + with one I − is not negligible with respect to the loss of MDABCO 2 + with two I − . Yet, only jumps of V X are expected to occur over barriers E < 0.5 eV, small enough to cause anelastic relaxation below room temperature. In fact, the jumps of V A and V B are 2 times longer than the octahedron edge and must occur with the participation of another V X or cation vacancy of the other type. As a consequence, vacancies V X are far more mobile than V A / B , and this is true not only in perovskite oxides but also in the metal-organic halide perovskites for photovoltaic applications [33].
Peaks P1–P3 should therefore be attributed to different types of jumps of the I − vacancies V X + among quasistatic MDABCO 2 + vacancies V A 2 − and possibly NH 4 + vacancies V B − . The major mobile defects that should be considered are V X + that are: i) isolated, ii) paired with V A 2 − and iii) paired with V B − ; iv) form neutral V A 2 − − 2 V X + complexes. Pairs of V X + , as in perovskite oxides, are unlikely to form in presence of cation vacancies, that provide stronger binding energies of electrostatic nature.
We are not aware of studies of the mobility of V X in presence of cation vacancies in perovskites, but we assume that the jumps within the sites nearest neighbour to the cation vacancies are faster than those in the unperturbed lattice, because the missing cation certainly lowers the hopping barrier. It is less obvious to establish which cation vacancy provides the easiest environment for V X hopping, whether the octahedron centred on V B or the cuboctahedron centred on V A . We assume that V B lowers more than V A the hopping barrier for V X , because of the shorter B–X bond. The influence of V B should therefore be more sensible than V A .
Based on the above considerations, as a first guess we assume that P1 is due to jumps of V X around V B , or equivalently to the reorientation of V B – V X pairs, and P2 to V A – V X pairs. The possible V X – V A – V X complex, presumably with V X on opposite sides of V A , requires a two-step reorientation, and the stronger lattice relaxation around an in-line V X – V A – V X complex suggests a higher barrier, due the unfavourable intermediate state.
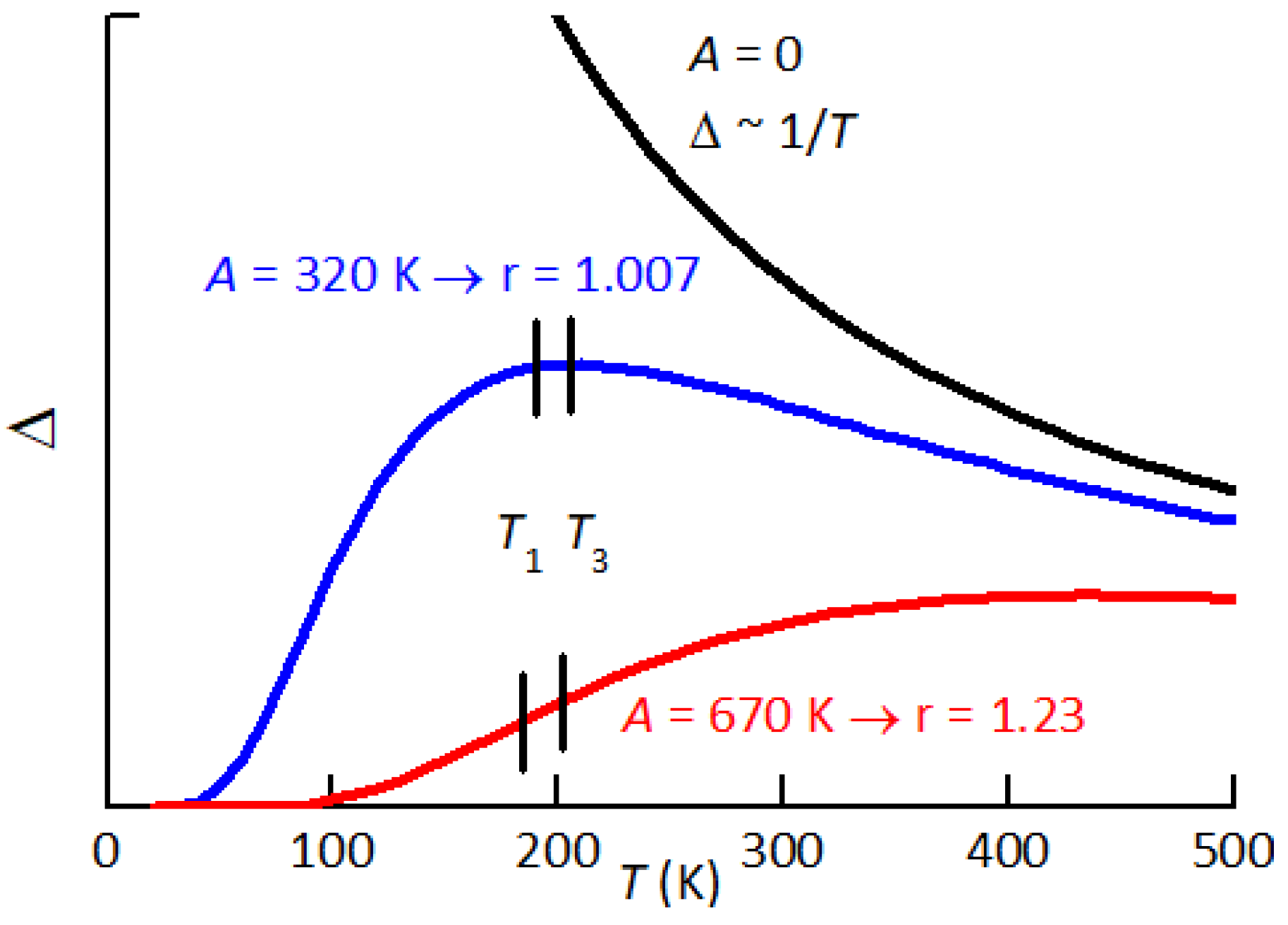
Finally, one should consider the plethora of jumps between non-equivalent sites, e.g. between 1st and 2nd neighbours to a cation vacancy. These jumps would contribute both to the broadening of the major relaxation peaks and to the background. In fat, if one considers the relaxation between states differing in energy of A, then the relaxation strength is reduced by the factor [34]
Δ → Δ / cosh 2 A / 2 k B T ,
which below k B T ∼ A transforms the 1 / T divergence of Δ into an exponential decrease to 0 (Figure 11).
Therefore, jumps between strongly inequivalent positions, like those for forming and separating a defect pair, produce relaxation processes distinct from those cited above, and with a much depressed intensity. This type of relaxation between inequivalent states is hardly distinguishable in SrTi O 3 − δ with δ ≲ 0.01 , where a small but distinct peak can be attributed to the partial dissociation of pairs of V O [26].
We should also take into account the temperature dependence of the relaxation strengths Eq. (2), which are proportional to n T / T , where n is the relative concentration of the defect. This fact should help distinguishing the population of isolated vacancies from those of the defect complexes, since the first rises with temperature while the others decrease, due to the thermal dissociation.
The considerable width of the peaks with respect to single Debye relaxations is justified by the presumably high concentration of defects and by the softness of the lattice, that result in large local deviations of the bond lengths and angles from the ideal lattice.

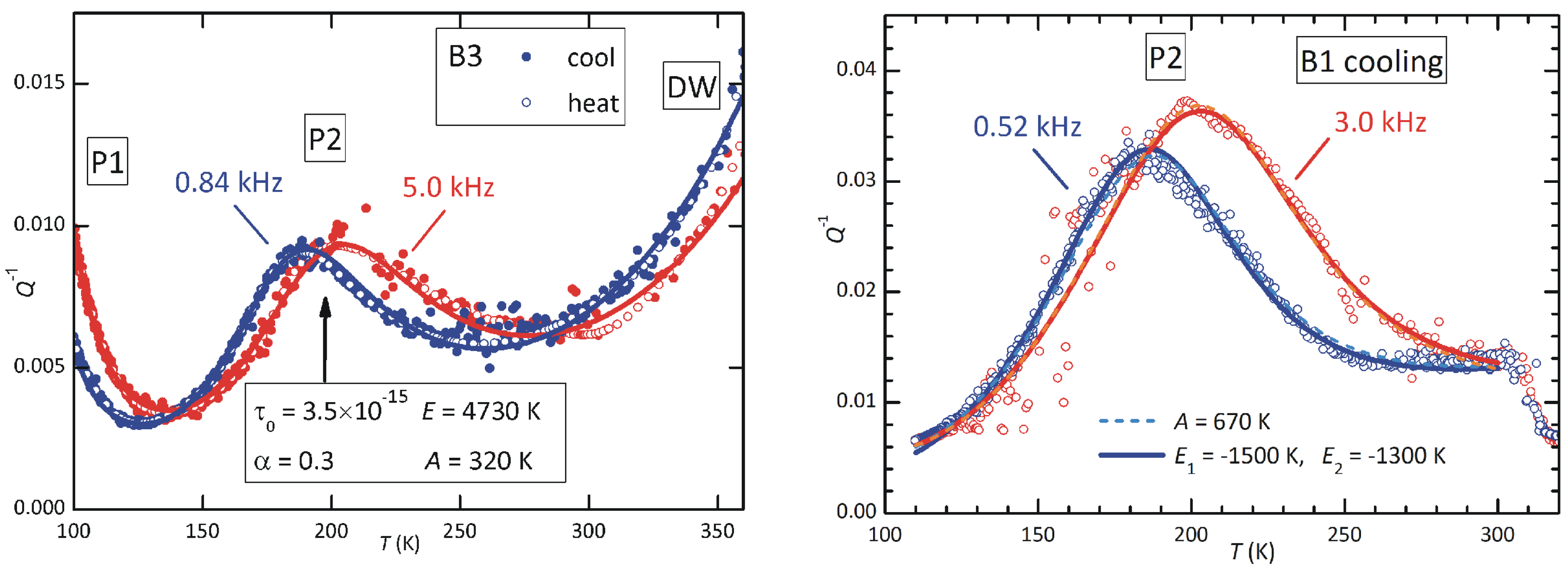
3.5. Two possible scenarios for P2

The attention will be focused on peak P2, because it is clearly observable in both samples annealed at high temperature and is stable, while peak P3 is observable only at the highest content of defects and is not stable; of P1 only the high-temperature tail could be seen. A feature of P2 is the change of the temperature dependence of its intensity when passing from low- to high-defect concentration. The peak is maximum at T 1 and T 3 when measured at the low and high frequencies f 1 and f 3 . If we define the ratio of the intensities at these temperature
r = Δ T 3 / Δ T 1
then at low defect content (sample B3) it is r ≃ 1 , while at high content of defects (sample B1) it is r ≃ 1.2 . The rise of r at rising defect concentration is large and can be explained by two concomitant mechanisms: i) increase of the lattice disorder and therefore of the average asymmetry A in Eq. (4); ii) increase with temperature of the population of the defects producing P2. We will discuss the two possibilities separately, although they can be concomitant, in the hypothesis that P2 is due to the reorientation of V A – V X pairs and possibly also V X – V A – V X complexes.
We first assume that the population of such defects depends little on temperature in the range where P2 is observed and therefore only a change of A in Eq. (4) occurs. Figure 11 shows how the 1 / T dependence of the relaxation strength Δ is depressed by increasing the average asymmetry A between relaxing states. The two values A = 320 and 670 K are those of the fits of P2 at low and high defect concentrations, yielding r = 1.007 and 1.23 respectively. The fits are obtained with the expressions
Q − 1 = Δ 0 T cosh 2 A / 2 T 1 ω τ α + ω τ − β τ = τ 0 exp E / T cosh A / 2 T
which are a generalization of Eq. (3) to include asymmetric broadening with α , β ≤ 1 and energy asymmetry A. The factor in the expression of the relaxation time is due to the fact that τ − 1 = ν 12 + ν 21 between states 1, 2 with energies ± A / 2 separated by a barrier E 1 , 2 = E ∓ A / 2 . In this formula the energies are expressed in kelvin, actually being E / k B and A / k B , because in this manner their influence on the fitting curves is more transparent.
The fit of sample B3 includes the two adjacent peaks, P1 and that attributed to domain wall relaxation, plus a linear background. The parameters of interest of P2 are in the first column of Table 1:
Table 1. Parameters used in the fits of Figure 12.
Table 1. Parameters used in the fits of Figure 12.
sample: B3 B1 B1
A (K) 320 670 0
B 1 (K) – – 1500
B 2 (K) – – 1300
τ 0 (s) 3.5 × 10 − 15 1.2 × 10 − 13 3.4 × 10 − 12
E (K) 4730 4500 3600
α 0.3 0.1 0.15
β 0.3 0.6 0.6
The relaxation time extrapolated to infinite temperature, τ 0 , is typical of point defects, and the activation energy E / k B = 4730 K corresponds to 0.41 eV. This would be the barrier for the local motion of an iodine vacancy around a MDABCO vacancy. The effective activation energy for the long range diffusion of I would be larger, because it would include the higher barrier for escaping from V A and, as discussed above, the activation energy for hopping in the unperturbed lattice might be higher than around a cation vacancy. The peak is much broader than a single time relaxation, since α = β are definitely < 1 , and this justifies an average asymmetry A that is 6–7% of the activation energy.
The parameters of peak P1 cannot be reliably determined, but we mention that its relaxation time has τ 0 ≃ 10 − 14 s and E ≃ 0.15 eV. This values are again typical of point defects, but it is unlikely that an iodine vacancy can diffuse so fast in the unperturbed lattice, and we suggest that this is the barrier for hopping around a NH 4 vacancy. In addition, at such low temperature all the V X are trapped, as will be shown later.
The right panel of Figure 12 shows a similar fit of P2 at high content of defects (sample B1). The parameters corresponding to the continuous lines are in the second column of Table I: the average site energy disorder, A, is doubled, which is reasonable, and the peak shape is much more asymmetric, with very different broadening parameters α and β . With such broad shape, there is not much sensitivity to changes of the pair of parameters τ 0 and E, and it is possible to fit with 10 − 14 s < τ 0 < 10 − 12 s accordingly varying E within 3800 K – 4800 K. A similar remark holds for the previous fit.
While this pair of fits is compatible with the hypothesis that P2 is due to the hopping of V X around V A , the presence of various types of defects, confirmed by the presence of peak P1, calls for an analysis of the defect populations as a function of temperature.

3.6. Calculation of the populations of defects

In order to calculate the populations of the various types of defects, based on their respective energies and geometries, we will adapt the calculation of the mean occupation numbers n i from the grand partition function [35]
Z = ∏ i = 1 N 1 + e β μ − E i
where, for each site i with energy E i , 1 is the statistical weight for being unoccupied and the second term for being occupied; β = 1 / k B T and μ is the chemical potential, or Fermi energy in this case. The mean occupation numbers with a total of M occupied states are calculated as
M = 1 β ∂ ln Z ∂ μ = ∑ i = 1 N e β μ − E i 1 + e β μ − E i = ∑ i = 1 N n i .
By grouping different types of sites and assigning different site energies, it is possible to obtain the occupations n i of coexisting defects configurations and calculating them by numerically solving the above implicit equation for μ [34,36].
In the present case n i = 1 represents a V X vacancy in site Xi and n i = 0 a regular Xi site. For simplicity, let us consider the case that only V A 2 − + 2 V X + Schottky defects are formed. Then, there are c X = δ iodine vacancies V X + and c A = δ / 2 MDABCO vacancies V A 2 − per mole. The V A are assumed to be static and isolated, so that each of them has m = 12 X nearest neighbour (nn) sites. In Z we can group together the c 0 = 3 − m c A normal sites with energy E 0 = 0 and those nn to a same V A with binding energy E k =   B < 0 so that, for N unit cells,
Z = ∏ i = 1 N c 0 1 + e β μ ∏ k = 1 N c A 1 + e β μ − B m = z 0 N c 0 z A N c A .
At this point it is possible to introduce arbitrary conditions on the type of V A – V X complexes, by expanding and manipulating the sub-partition function z A of each set of m sites nn to a V A . From the polynomial expansion of z A we retain only the terms with up to two V X
z A = 1 + m e β μ − B 1 + m 2 e 2 β μ − B 2
setting B 1 < 0 as the energy of a V A – V X complex and B 2 < 0 as that of a V X – V A – V X complex. In addition, we suppose that the latter can only have V X on opposite sides of V A , so that there are only m / 2 such configurations. In this manner, Eq. (8) becomes
c X = 1 β N ∂ ln Z ∂ μ = 1 β ∂ ∂ μ c 0 ln 1 + e β μ + c A ln 1 + m e β μ − B 1 + m 2 e 2 β μ − B 2 = = c 0 e β μ 1 + e β μ + c A m e β μ − B 1 + m e 2 β μ − B 2 1 + m e β μ − B 1 + m 2 e 2 β μ − B 2
with
c X = δ c A = δ / 2 c 0 = 3 − m c A = 3 − m δ / 2
where, setting
y = e β μ w 1 = e − β B 1 > 1 w 2 = e − β B 2 > 1 ,
we recognize the occupation numbers of isolated V X and V A – V X and V X – V A – V X complexes as
n 0 = 3 − m 2 δ y 1 + y n 1 = δ 2 m y w 1 1 + m y w 1 + m 2 y 2 w 2 2 n 2 = δ 2 m y 2 w 2 2 1 + m y w 1 + m 2 y 2 w 2 2
The chemical potential in y is determined by the condition
δ = n 0 + n 1 + n 2 .
This is a 3rd degree polynomial equation in y , which is best solved numerically. Notice that, without the V X – V A – V X complexes ( w 2 = 0 ), the equation is of 2nd degree and n 0 and n 1 have a simple closed form. The inclusion of additional defects, for example V B – V X pairs, can be done easily in the same manner, but, with only two measurements of P2, it is not worth introducing new parameters. It is also not worth including the numerical solution of Eq. (10) in the non-linear fitting procedure of the anelastic spectra, and therefore we simply identify a combination of binding energies B 1 and B 2 and reasonable values of δ , that roughly reproduce the observed temperature dependences of P2.
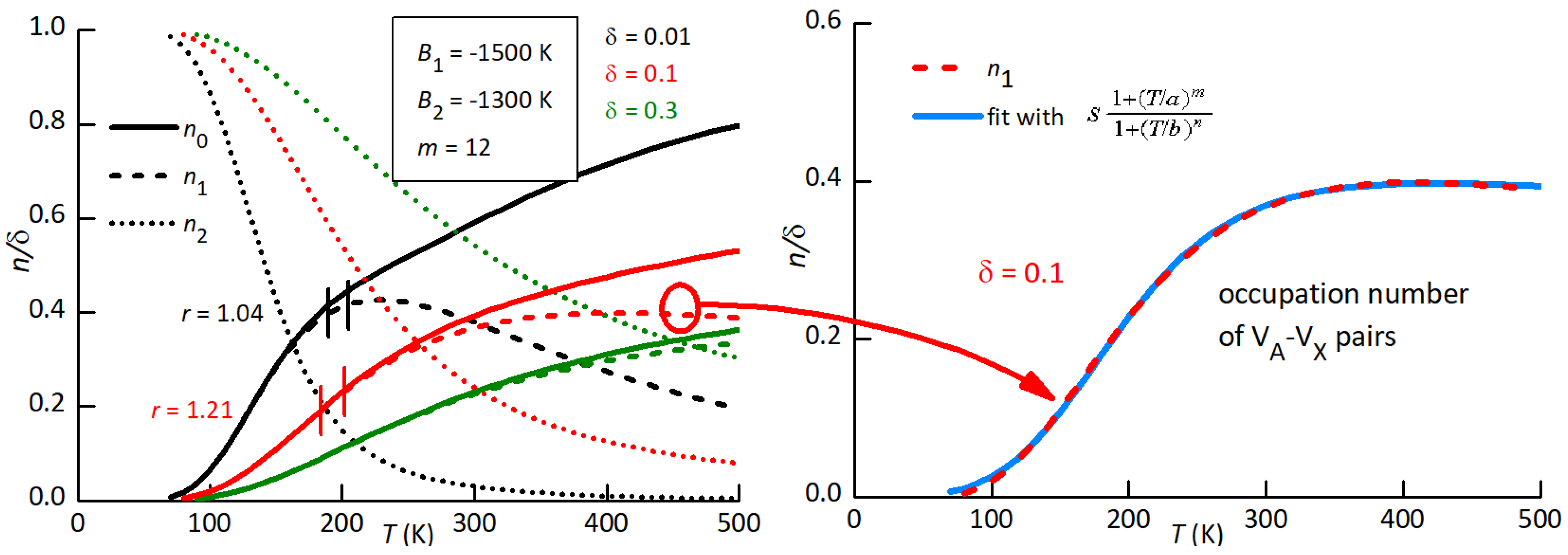
Figure 13 shows the occupation numbers calculated with B 1 = − 1500 K, B 2 = − 1300 K at three defect concentrations δ . In the low-T limit all V X are trapped and therefore n 2 = 1 , but above 100 K they start to detrap, each time forming a V A – V X pair and an isolated V X , so that n 1 ≃ n 0 . Finally, at T > B 1 , B 2 there is equal probability of occupying all sites, and the populations depend only on total number of trap and free sites. In the intermediate region, n 1 has a maximum, that shifts to higher T with increasing δ , and can therefore account for the behaviour of P2. In fact, passing from δ = 0.01 to 0.1 the ratio r of the intensities of P2, Eq. (5), passes from 1.04 to 1.21, compatible with Figure 12.
Therefore, we fitted again P2 at high defect concentration using Eq. (3) with A = 0 and Δ 0 ∝ n 1 T , δ = 0.1 . In practice, we fitted the intermediate n 1 T curve in Figure 13 with a rational expression (blue line in the right panel of Figure 13), that we introduced in the final fitting expression for Q − 1 T
The dashed lines in Figure 12 are obtained in this manner with the following parameters: τ 0 = 3.4 × 10 − 12 s, E = 3610 K (0.31 eV), α = 0.15 , β = 0.6 , and the resulting fit practically coincides with the previous one with constant Δ 0 and A > 0 . This suggests that it is possible to equally well fit peak P2 assuming intermediate situations with slightly different values of the binding energies to the cation vacancies and A > 0 .
We have therefore shown that peak P2 can be explained in terms of reorientation of V A – V X pairs, corresponding to the local hopping of an iodine vacancy around a MDABCO vacancy, with an activation energy E = 0.35 ± 0.05 eV. The change in the temperature dependence of the P2 intensity, passing from low to high defect concentrations, can be explained both in terms of increasing lattice disorder (site energy asymmetry A) and with the presence of at least another type of V X trapping ( V X – V A – V X complexes), that compete with the V A – V X pairs. The introduction of V B – V X pairs, possibly giving rise to peak P1, could only improve the description of the anelastic spectra, but the present data, at only two defects concentrations and limited in the low temperature range, do not justify fittings with so many parameters.

4. Materials and Methods

4.1. Powders

(MDABCO)( NH 4 ) I 3 has been synthesized as reported in [9], and in detail:
1.27 g (5 mmol) of MDABCOI (synthesized according to [37]) and 0.74 g of NH 4 I (5 mmol) were dissolved in 7.5 ml of H2O, 2.5 ml HI (57%) and 1 ml of H3P O 3 . The reaction mixture became opalescent, and H2O was added dropwise until it turned transparent again. It was kept in an ice-bath for one hour and then at room temperature for several hours, during which a microcrystalline solid precipitated. It was isolated by removing the supernatant with a pipette, and dried at 50 °C in air on filter paper.

4.2. TGA

Thermogravimetric analysis was performed with a TGA/DSC2 apparatus (Mettler Toledo), in a temperature range from 298 to 473K at scan rate of 5 K/min and 2 K/min under nitrogen.

4.3. Bulk samples

The bulk samples were obtained by pressing the powder into rectangular dies with dimensions 40 × 6 mm2 and circular with 13 mm diameter, for few minutes, obtaining bars and discs with thicknesses of 0.6–0.9 mm with densities 2.09-2.01. The applied pressures were 0.29 GPa for bars B1 and B2, 0.37 GPa for B3, 0.75 GPa for disc D1. The average density of the bars was 2.05 ± 0.04 g/cm3, but, due to the difficulty of distributing uniformly the powder on the bottom of the die, it was inhomogeneous along their length. This was evident from the non uniform color along their length and may explain the large differences of the initial values of E in the three tested bars.

4.4. Anelastic spectroscopy

The bars were suspended and on thin thermocouple wires, fixed with drops of Ag paint. An electrode was placed close to the centre of the bar for electrostatically exciting their flexural resonance modes at frequency f, as described in Ref. [38]. The capacitance between sample and electrode is inserted in a circuit resonating at ∼ 13 MHz, whose frequency is modulated by the sample vibration at 2 f . The demodulated and rectified signal is detected with a lock-in amplifier locked at 2 f . The Young’s modulus is obtained from the resonating frequency of the first mode as [24]
E = ρ f 1 l 2 1.028 t 2
where l, t, ρ are the sample’s length, thickness and density, which usually vary much less than E with temperature. Then, the temperature dependence of the Young’s modulus is deduced from E / E 0 = ( f / f 0 ) 2 , where the reference f 0 and E 0 are the resonance frequency and modulus, chosen as the starting values at the first measuring cycle. The elastic energy loss coefficient, Q − 1 = E ″ / E ′ , was measured from the width of the resonance peak or the decay of free oscillations.

4.5. Dielectric spectroscopy

The dielectric permittivity ε = ε ′ + i ε ″ was measured with a HP4284A LCR meter with a four wire probe during heating and cooling at 1.5–2 K/min in a modified Linkam HFS600E-PB4 stage. The cell is not perfectly air-tight, so that during cooling the external humidity may penetrate and condense, with subsequent liquefaction and extrinsic dielectric anomalies during heating above 270 K, as in curve 2 of Figure 4.

4.6. Films

Films of (MDABCO)( NH 4 ) I 3 on 1 × 1 cm2 ITO/glass substrates were prepared by drop-casting a 10 times diluted solution of precursors prepared as described in Sect. 4.1. Two drops were deposited on the substrate placed over a hot-plate at 80 °C, and after the resulting layer was dried, two more were added.

4.7. AFM, PFM

Surface morphology imaging was carried out with a commercial AFM (XE100, Park Systems, Suwon, Republic of Korea) in noncontact mode, using ACTA tips (Applied NanoStructures, Mountain View, CA, USA). The PFM tests were performed on the same microscope, using Pt coated tips (NSC36Pt, Mikromasch - Innovative Solutions Bulgaria, Sofia, Bulgaria) to apply the local electric field and to record material’s mechanical response. The out-of-plane piezoelectric response of the material was demodulated using an external lock-in amplifier (SR830, Stanford Research Systems, Sunnyvale, CA, USA).

5. Conclusions

We measured the complex Young’s modulus and dielectric permittivity of the ferroelectric organic perovskite (MDABCO)( NH 4 ) I 3 in polycrystalline form. The samples of pressed powder were measured during temperature cycles with increasing maximum temperature below and above the transition temperature T C in air and vacuum. Thermal decomposition starts already at T C , as indicated by the decreased T C during cooling and the subsequent cycles, and by the concomitant appearance of intense anelastic and dielectric relaxation processes.
The observations are explained in terms of the formation of Schottky defects at high temperature, namely loss of neutral complexes of anions X and cations A and B in perovskite ABX 3 , with the respective vacancies migrating into the bulk. The anelastic spectra are interpreted in terms of hopping of iodine vacancies V X partially trapped by cation vacancies, V A and V B , which are much less mobile. In particular, the two peaks of elastic energy loss starting from the lowest temperature are interpreted in terms of reorientation of V B – V X and V A – V X pairs. Of the first peak only the high-temperature tail is observed, but the second is fitted taking into account the lattice disorder and the temperature dependence of the various populations of defects: isolated V X , V A – V X pairs and V X – V A – V X complexes. These populations are calculated with a simple method based on the Fermi-Dirac statistics.

Author Contributions

Conceptualization, Francesco Cordero; Data curation, Floriana Craciun, Patrizia Imperatori and Gloria Zanotti; Formal analysis, Francesco Cordero and Maria Dinescu; Investigation, Francesco Cordero, Floriana Craciun, Patrizia Imperatori, Venanzio Raglione, Gloria Zanotti, Antoniu Moldovan and Maria Dinescu; Methodology, Francesco Cordero, Floriana Craciun, Patrizia Imperatori and Gloria Zanotti; Writing - original draft, Francesco Cordero; Writing - review and editing, Floriana Craciun, Gloria Zanotti and Maria Dinescu.

Acknowledgments

The authors acknowledge the technical assistance of M.P. Latino (CNR-ISM) for the realization of the anelastic and dielectric experiments and of Laura Lilla (CNR-ISB) for performing the TGA/DSC measurements.

References

  1. Liao, W.Q.; Zhao, D.; Tang, Y.Y.; Zhang, Y.; Li, P.F.; Shi, P.P.; Chen, X.G.; You, Y.M.; Xiong, R.G. A molecular perovskite solid solution with piezoelectricity stronger than lead zirconate titanate. Science 2019, 363, 1206. [Google Scholar] [CrossRef]
  2. Ye, H.Y.; Tang, Y.Y.; Li, P.F.; Liao, W.Q.; Gao, J.X.; Hua, X.N.; Cai, H.; Shi, P.P.; You, Y.M.; Xiong, R.G. Metal-free three-dimensional perovskite ferroelectrics. Science 2018, 361, 151. [Google Scholar] [CrossRef]
  3. Wang, H.; Liu, H.; Zhang, Z.; Liu, Z.; Lv, Z.; Li, T.; Ju, W.; Li, H.; Cai, X.; Han, H. Large piezoelectric response in a family of metal-free perovskite ferroelectric compounds from fi rst-principles calculations. npj Comp. Mater. 2019, 5, 17. [Google Scholar] [CrossRef]
  4. Allen, D.W.; Bristowe, N.C.; Goodwin, A.L.; Yeung, H.H.M. Mechanisms for collective inversion-symmetry breaking in dabconium perovskite ferroelectrics. J. Mater. Chem. C 2021, 9, 2706. [Google Scholar] [CrossRef]
  5. Zhang, H.; Xu, Z.K.; Wang, Z.X.; Yu, H.; Lv, H.P.; Li, P.F.; Liao, W.Q.; Xiong, R.G. Large Piezoelectric Response in a Metal-Free Three-Dimensional Perovskite Ferroelectric. J. Am. Chem. Soc. 2023, 16, 4892. [Google Scholar] [CrossRef]
  6. Li, C.; Zhou, L.; Guo, X.; Huang, Y.; Zhang, H.; Dong, S.; Wu, Y.; Hong, Z. Phase diagrams, dielectric, and piezoelectric properties of metal-free perovskite thin films: Phase-field simulations. J. Mater. Res. 2023, 38, 664. [Google Scholar] [CrossRef]
  7. Wang, J.J.; Fortino, D.; Wang, B.; Zhao, X.; Chen, L.Q. Extraordinarily Large Electrocaloric Strength of Metal-Free Perovskites. Adv. Mater. 2020, 32, 1906224. [Google Scholar] [CrossRef]
  8. Gao, R.; Shi, X.; Wang, J.; Zhang, G.; Huang, H. Designed Giant Room-Temperature Electrocaloric Effects in Metal-Free Organic Perovskite [MDABCO](NH4)I3 by Phase-Field Simulations. Adv. Funct. Mater. 2021, 2021, 2104393. [Google Scholar] [CrossRef]
  9. Ehrenreich, M.G.; Zeng, Z.; Burger, S.; Warren, M.R.; Gaultois, M.W.; Tan, J.C.; Kieslich, G. Mechanical properties of the ferroelectric metal-free perovskite [MDABCO](NH4)I3. Chem. Comm. 2019, 55, 3911. [Google Scholar] [CrossRef]
  10. An, L.C.; Li, K.; Li, Z.G.; Zhu, S.; Li, Q.; Zhang, Z.Z.; Ji, L.J.; Li, W.; Bu, X.H. Engineering Elastic Properties of Isostructural Molecular Perovskite Ferroelectrics via B-Site Substitution. Small 2021, 17, 2006021. [Google Scholar] [CrossRef]
  11. Lyu, F.; Chen, Z.; Shi, R.; Yu, J.; Lin, B.L. Solid phase synthesis of metal-free perovskite crystalline materials. J. Solid State Chem. 2021, 304, 122548. [Google Scholar] [CrossRef]
  12. Gale, S.D.; Lloyd, H.; Male, L.; Warren, M.R.; Saunders, L.K.; Anderson, P.A.; Yeung, H.H.M. Materials discovery and phase behaviour limits in MDABCO perovskites 2023.
  13. Ledbetter, H. Relationship between bulk-modulus temperature dependece and thermal expansivity. phys. stat. sol. (b) 1994, 181, 81. [Google Scholar] [CrossRef]
  14. Strukov, B.A.; Levanyuk, A.P. Ferroelectric Phenomena in Crystals; Springer: Heidelberg, 1998. [Google Scholar]
  15. Cordero, F.; Craciun, F.; Trequattrini, F.; Galassi, C. Piezoelectric softening in ferroelectrics: ferroelectric versus antiferroelectric PbZr1-xTixO3. Phys. Rev. B 2016, 93, 174111. [Google Scholar] [CrossRef]
  16. Zhang, Z.; Li, W.; Carpenter, M.A.; Howard, C.J.; Cheetham, A.K. Elastic properties and acoustic dissipation associated with a disorder-order ferroelectric transition in a metal-organic framework. CrystEngComm 2015, 17, 370. [Google Scholar] [CrossRef]
  17. You, Y.M.; Liao, W.Q.; Zhao, D.; Ye, H.Y.; Zhang, Y.; Zhou, Q.; Niu, X.; Wang, J.; Li, P.F.; Fu, D.W.; Wang, Z.; Gao, S.; Yang, K.; Liu, J.M.; Li, J.; Yan, Y.; Xiong, R.G. An organic-inorganic perovskite ferroelectric with large piezoelectric response. Science 2017, 357, 306. [Google Scholar] [CrossRef]
  18. Cordero, F.; Craciun, F.; Trequattrini, F.; Ionita, S.; Lincu, D.; Mitran, R.A.; Fruth, V.; Brajnicov, S.; Moldovan, A.; Dinescu, M. Phase Transition and Dynamics of Defects in the Molecular Piezoelectric TMCM-MnCl3 and the Effect of Partial Substitutions of Mn. Crystals 2023, 13, 409. [Google Scholar] [CrossRef]
  19. Cordero, F.; Craciun, F.; Trequattrini, F.; Imperatori, P.; Paoletti, A.M.; Pennesi, G. Competition between Polar and Antiferrodistortive Modes and Correlated Dynamics of the Methylammonium Molecules in MAPbI3. J. Phys. Chem. Lett. 2018, 9, 4401. [Google Scholar] [CrossRef]
  20. Cordero, F.; Trequattrini, F.; Craciun, F.; Paoletti, A.M.; Pennesi, G.; Zanotti, G. Cation reorientation and octahedral tilting in the metal-organic perovskites MAPI and FAPI. J. Alloys Compd. 2021, 867, 158210. [Google Scholar] [CrossRef]
  21. Benoit, W. High-temperature relaxations. Mater. Sci. Engin. A 2004, 370, 12. [Google Scholar] [CrossRef]
  22. Pezzotti, G. Internal friction of polycrystalline ceramic oxides. Phys. Rev. B 1999, 60, 4018. [Google Scholar] [CrossRef]
  23. McCarthy, C.; Takei, Y. Anelasticity and viscosity of partially molten rock analogue: Toward seismic detection of small quantities of melt. Geophys. Res. Lett. 2011, 38, L18306. [Google Scholar] [CrossRef]
  24. Nowick, A.S.; Berry, B.S. Anelastic Relaxation in Crystalline Solids; Academic Press: New York, 1972. [Google Scholar]
  25. Schaller, R.; Fantozzi, G.; Gremaud, G. (Eds.) Mechanical Spectroscopy Q-1 2001: with Applications to Materials Science; Trans Tech Publications: Totton, UK, 2001. [Google Scholar]
  26. Cordero, F. Hopping and clustering of oxygen vacancies in SrTiO3 by anelastic relaxation. Phys. Rev. B 2007, 76, 172106. [Google Scholar] [CrossRef]
  27. Cordero, F.; Trequattrini, F.; Quiroga, D.A.B.; Jr., P.S.S. Hopping and clustering of oxygen vacancies in BaTiO3-δ and the influence of the off-centred Ti atoms. J. Alloys Compd. 2021, 874, 159753. [Google Scholar] [CrossRef]
  28. Wang, L.; Sakka, Y.; Shao, Y.; Botton, G.A.; Kolodiazhnyi, T. Coexistence of A- and B-Site Vacancy Compensation in La-Doped Sr1-xBaxTiO3. J. Am. Ceram. Soc. 2010, 93, 2903. [Google Scholar] [CrossRef]
  29. Boström, H.L.B.; Bruckmoser, J.; Goodwin, A.L. Ordered B-Site Vacancies in an ABX3 Formate Perovskite. J. Am. Chem. Soc. 2019, 141, 17978. [Google Scholar] [CrossRef] [PubMed]
  30. Vandewalle, L.; Konstantinovic, M.J.; Depover, T.; Verbeken, K. The Potential of the Internal Friction Technique toEvaluate the Role of Vacancies and Dislocations in theHydrogen Embrittlement of Steels. steel research int. 2021. [Google Scholar] [CrossRef]
  31. Glazer, A.M. The classification of tilted octahedra in perovskites. Acta Cryst. B 1972, 28, 3384. [Google Scholar] [CrossRef]
  32. Cordero, F.; Trequattrini, F.; Deganello, F.; Parola, V.L.; Roncari, E.; Sanson, A. Effect of doping and oxygen vacancies on the octahedral tilt transitions in the BaCeO3 perovskite. Phys. Rev. B 2010, 82, 104102. [Google Scholar] [CrossRef]
  33. Senocrate, A.; Moudrakovski, I.; Kim, G.Y.; Yang, T.Y.; Gregori, G.; Grätzel, M.; Maier, J. The Nature of Ion Conduction in Methylammonium Lead Iodide: A Multimethod Approach. Angew. Chem. 2017, 26, 7863. [Google Scholar] [CrossRef]
  34. Cordero, F. Anelastic (dielectric) relaxation of point defects at any concentration, with blocking effects and formation of complexes. Phys. Rev. B 1993, 47, 7674. [Google Scholar] [CrossRef]
  35. Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon Press: London, 1969. [Google Scholar]
  36. Cannelli, G.; Cantelli, R.; Cordero, F. Statistical model for the trapping of interstitials by substitutional (interstitial) atoms in solids. Phys. Rev. B 1985, 32, 3573. [Google Scholar] [CrossRef] [PubMed]
  37. Kurutos, A.; Orehovec, I.; Saftic, D.; Horvat, L.; Crnolatac, I.; Piantanida, I.; Deligeorgiev, T. Cell penetrating, mitochondria targeting multiply charged DABCO-cyanine dyes. Dyes and Pigments 2018, 158, 517. [Google Scholar] [CrossRef]
  38. Cordero, F.; Bella, L.D.; Corvasce, F.; Latino, P.M.; Morbidini, A. An insert for anelastic spectroscopy measurements from 80 K to 1100 K. Meas. Sci. Technol. 2009, 20, 015702. [Google Scholar] [CrossRef]
Preprints 89111 g001
Figure 1. Normalized Young’s moduli E / E 0 and Q − 1 curves measured on samples B1-B3 during cooling (thick) and heating (thin) in high vacuum, exciting the fundamental flexural resonance, initially at 0.8 − 1.0 kHz. Only splines through the experimental data are shown.
Figure 1. Normalized Young’s moduli E / E 0 and Q − 1 curves measured on samples B1-B3 during cooling (thick) and heating (thin) in high vacuum, exciting the fundamental flexural resonance, initially at 0.8 − 1.0 kHz. Only splines through the experimental data are shown.
Preprints 89111 g001
Preprints 89111 g002
Figure 2. Anelastic spectra of samples B1-B3 measured exciting the 1st (filled symbols) and 3rd (open symbols) flexural resonances at 1.1 and 5.9 kHz (B1), 0.81 and 4.9 kHz (B2) and 0.93 and 5.4 kHz (B3). All measurements are during cooling and B3 both cooling and heating.
Figure 2. Anelastic spectra of samples B1-B3 measured exciting the 1st (filled symbols) and 3rd (open symbols) flexural resonances at 1.1 and 5.9 kHz (B1), 0.81 and 4.9 kHz (B2) and 0.93 and 5.4 kHz (B3). All measurements are during cooling and B3 both cooling and heating.
Preprints 89111 g002
Preprints 89111 g006
Figure 6. XRD diffractograms of the powder of (MDABCO)( NH 4 ) I 3 and of samples B1–B3 after the measurements in Figure 1.
Figure 6. XRD diffractograms of the powder of (MDABCO)( NH 4 ) I 3 and of samples B1–B3 after the measurements in Figure 1.
Preprints 89111 g006
Preprints 89111 g007
Figure 7. TGA of the powder of (MDABCO)( NH 4 ) I 3 at 5 K/min.
Figure 7. TGA of the powder of (MDABCO)( NH 4 ) I 3 at 5 K/min.
Preprints 89111 g007
Preprints 89111 g008
Figure 8. AFM, PFM amplitude and PFM phase of a (MDABCO)( NH 4 ) I 3 film deposited on ITO.
Figure 8. AFM, PFM amplitude and PFM phase of a (MDABCO)( NH 4 ) I 3 film deposited on ITO.
Preprints 89111 g008
Preprints 89111 g010
Figure 10. Section of the ABX 3 perovskite lattice passing through a pair of A and X vacancies. The B atoms/molecules are at the centers of the octahedra. The X sites nearest neighbour to V A are drawn with a larger size than the others.
Figure 10. Section of the ABX 3 perovskite lattice passing through a pair of A and X vacancies. The B atoms/molecules are at the centers of the octahedra. The X sites nearest neighbour to V A are drawn with a larger size than the others.
Preprints 89111 g010
Preprints 89111 g011
Figure 11. Temperature dependence of the relaxation strength between states differing in energy of A. The two curves with A = 250 K and 550 K would explain the observed behaviour of peak P2 at low and high defect oncentrations.
Figure 11. Temperature dependence of the relaxation strength between states differing in energy of A. The two curves with A = 250 K and 550 K would explain the observed behaviour of peak P2 at low and high defect oncentrations.
Preprints 89111 g011
Preprints 89111 g012
Figure 12. Fits of the anelastic spectra at low (left panel, sample B3) and high (right panel, sample B1) concentrations of defects. The fitting formulas and parameters are indicated in the text. The two fits of P1, dashed and continuous lines, are nearly coincident.
Figure 12. Fits of the anelastic spectra at low (left panel, sample B3) and high (right panel, sample B1) concentrations of defects. The fitting formulas and parameters are indicated in the text. The two fits of P1, dashed and continuous lines, are nearly coincident.
Preprints 89111 g012
Preprints 89111 g013
Figure 13. Populations n 0 of isolated V X , n 1 of V A – V X pairs, n 2 of V X – V A – V X complexes with the indicated parameters values. The dashed lines in the right panel are fits of the n 1 curves at δ = 0.01 and 0.1 with the indicated rational expression.
Figure 13. Populations n 0 of isolated V X , n 1 of V A – V X pairs, n 2 of V X – V A – V X complexes with the indicated parameters values. The dashed lines in the right panel are fits of the n 1 curves at δ = 0.01 and 0.1 with the indicated rational expression.
Preprints 89111 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated