Prerpints.org logo
Preprint
Article

Learning Adaptive Quantization Parameter for Consistent Quality Oriented Video Coding

Altmetrics

Downloads

101

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 October 2023

Posted:

31 October 2023

You are already at the latest version

Alerts
Abstract
In industry 4.0 era, video applications such as surveillance visual systems, video conferencing, or video broadcasting have been playing a vital role. In these applications, for manipulating and tracking objects in decoded video, the quality of decoded video should be consistent because it largely affects to the performance of the machine analysis. To cope with this problem, we propose a novel perceptual video coding (PVC) solution in which a full reference quality metric named Video Multimethod Assessment Fusion (VMAF) is employed together with a deep convolutional neural network (CNN) to obtain the consistent quality while still achieving the high compression performance. First of all, to achieve the consistent quality requirement, we propose a CNN model with an expected VMAF as input to adaptively adjust the quantization parameters (QP) for each coding block. Afterwards, to increase the compression performance, a Lagrange coefficient of Rate-Distortion optimization (RDO) mechanism is adaptively computed under Rate-QP and Quality-QP models. Experimental results show that the proposed PVC has achieved two targets simultaneously: the quality of video sequence is kept consistently with an expected quality level and the bit rate saving of the proposed method is higher than traditional video coding standards and relevant benchmark, notably with around 10% bitrate saving in average.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the growth of data in video services on telecommunications networks, ensuring the quality of experience (QoE) for viewers is one of the urgent requirements. QoE is generally defined as the level of satisfaction or dissatisfaction of users when using a certain service or application [1]. To achieve user satisfaction, image quality stability is one of the most important criteria. In [2], an experiment indicated that the Mean Opinion Score (MOS) is decreased significantly when the quality changing frequency is increased. The reason is that the quality changing between frames in a video sequence typically causes the annoying experience to human visual perception (see Figure 1). Therefore, keeping the video quality consistent is a necessary process to improve QoE in video coding.
Along with the quality of human perceptual vision, consistent quality of video signal also needs for increasing efficiency of the visual sensor networks. Because the visual sensor network not only allows user to observe image, but also provides input images to learning machine systems for analysis purpose. In these systems, the quality of video directly affects the analysis performance. As shown in [3,4], the accuracy of object detection algorithms are directly proportional to the quality of video. Thus, the keeping stability of quality video at high level is beneficial for learning machine systems. Several methods have been proposed to improve the stability of video quality in a rate control algorithm. In [5], a method is proposed to provide the smooth quantization under CBR (constant bitrate) encoding by introducing a low filtering mechanism to smooth the quantization parameters produced from the traditional rate control algorithm. In [6], a sequential rate control algorithm was proposed for real-time video coding. However, in [5,6] methods used mean squared error (MSE) to measure visual quality although this metric does not reflect exactly the human perceptual quality. Thus, in [7], a new visual quality metric (VQM) is proposed. However, the proposed metric also uses MSE beside the motion information content in computing VQM. To address the causes of quality fluctuation in RDO, in [8], the Lagrange multiplier λ is adjusted according to the video content in the RDO process in order to ensure that reconstructed video always achieves the stable quality level. In particularly, the Lagrangian multiplier and quantization parameter (QP) for each frame are computed so that the difference of quality between the predicted frame and the correspondingly decoded frame is minimized. With the goal of achieving a constant quality level among frames, method in [9] uses the probability density function of the transform coefficients to estimate the depth of the coding tree. From there, the quality of the coding blocks is adjusted to ensure a stable quality level. In [10], the content-adapted quality-distortion model for the H.264 encoding standard is used to estimate the distortion between the original frame and the decoded frame. Based on the estimated distortion value, the QP parameter for each frame is found to achieve the desired quality level.
Another issue related to the visual quality of video signal is the quality assessment metric. In general, conventional objective quality assessment metrics are preferable in practical applications since they offer a specific computational formula and may be easily implemented in the encoder. Peak Signal to Noise Ratio (PSNR) and Mean Square Error (MSE) are the two most commonly used objective measures, respectively. In [11], a PSNR based method is proposed to control the constant quality of reconstructed video sequence. In this method, to keep the video quality is constant in terms of PSNR, the QP of each frame is adjusted according to the average PSNR of the previous frames. If the average PSNR is less than the PSNR target, the QP of the current frame is reduced and vice-versa. However, it has been demonstrated that PSNR or MSE only have a weak relationship with the human visual system (HVS). Therefore, Netflix created a metric called VMAF, which uses a machine-learning model that is trained on user feedback, to reflect the viewer’s viewpoint [12]. By using Support Vector Machine (SVM) regression, this metric is created by combining several fundamental metrics such as VIF [13], Detail Loss Metric - DLM [14], and Motion. In practical, the industry usually uses the VMAF metric extensively because its superior accuracy compared to traditional metrics [15,16,17].
Because of its benefits, VMAF is proposed to replace conventional metrics in some literatures such as [18,19]. In these methods, the relationship between sum of squared difference (SSD) and VMAF is built. Consequently, Lagrange multiplier in RDO function is computed based on VMAF instead of MSE. Also using perceptual visual to improve RDO, methods proposed in [20,21] used neural network to predict QP value. In particularly, authors in [20] proposed a perceptual adaptive quantization based on a VGG - 16 model on high efficiency video coding (HEVC) for bitrate reduction while maintaining subjective visual quality. In [21], the proposed method used CNN model to predict the visibility threshold for each image patch and then estimate QP value based on this visibility threshold. However, in these mentioned methods, the proposed methods only focus on improving Rate-Distortion (RD) performance of encoder while the stability of video quality at frame-level is not considered. To overcome the drawbacks of the previous methods, we proposed a VMAF-based method to predict QP by using CNN model in article [22]. However, this method is applied for intra-mode encoding and for low resolution video sequences only. To develop a method which can be applied for variety of video resolutions in both intra-mode and inter-mode, in this paper, we proposed: (1) An estimation for the rate-quantization parameter and distortion-quantization parameter functions based on VMAF metric instead of PSNR. (2) An CNN-based algorithm to estimate QP value at block-level in order to achieve a target quality for overall frame.
The rest of the paper is organized as follows. In section 2, the background works on RDO modeling and perceptual RDO for quality consistency are introduced. Then, the framework of the proposed system is illustrated in section 3. Experimental parameters and simulation results are presented in section 4. Finally, section 5 concludes the contributions of this work.

2. Background Works

In this section, we review the original RDO modeling adopted in video coding standards such as H.264/AVC or HEVC and the perceptual RDO models for video quality consistency.

2.1. RDO Modeling

Initially introduced in H.264/AVC standard [23], RDO model brings a significant RD performance improvement compared to the predecessor video codecs [24]. RDO model helps encoder to select an optimal mode among a large number of coding options. The target of RDO is to minimize the distortion for a given rate R c by appropriately selecting the coding parameters, namely
m i n { D } s u b j e c t t o R ≤ R c
where R and D are rate and distortion computed for a coding unit which may be a macroblock, a frame, or even a group of frames. To solve the above problem, Lagrange multiplier solution is used. Then, the problem (1) is converted to the following form:
m i n { J } w h e r e J = D + λ × R
where J is a Lagrange cost function and λ is the Lagrange multiplier. When RD curve is convex, and both and are differentiable everywhere, the function J is minimum when its derivative equals to zero, i.e.,
d J d R = d D d R + λ = 0
In [22], the rate distortion model is represented by:
R D = a × l o g 2 b D
where a and b are constant. The distortion QP model is represented by:
D = Q P 2 3
where Q P is quantization parameter. Putting (4) and (5) into (3), λ can be derived as:
λ = − d D d R = c × Q P 2
where c is set to 0 . 136 in H.264/AVC standard.
Standard video encoders usually use objective distortion metrics such as PSNR or MSE to build distortion model although these metrics do not work well as human visual distortion metrics. In [25,26], the structural similarity index (SSIM) [27] is used to establish an adaptive Lagrange multiplier in RDO. Based on the observation between QP and SSIM value, a distortion model is derived as:
D S S I M = 10 − 4 × e Q P + 11 . 804 6 . 8625
The Lagrange multiplier is computed in [23] as:
λ = 2 . 39 × e Q P + 11 . 804 6 . 8625
and in [24] as:
λ = 10 − 7 × 4 . 04 σ s d − 11 . 50 × e Q P + 11 . 804 6 . 8625
in which σ s d is the standard deviation of transformed residuals for one frame.
Because VMAF is considered as a perceptual distortion metric better than PSNR and SSIM, [28] proposed a method using VMAF to replace objective metrics in RDO. In particular, VMAF is estimated as a function of some visual factors including brightness adaptability, texture complexity, contrast masking and timing masking. After that, R-D cost function is computed based on the estimated VMAF. In [29], CNN is used to estimate the perceptual distortion in terms of VMAF score between original and reconstructed frame. However, VMAF does not have a computational formula, these methods established an approximate relationship between VMAF and SSE in RDO function [19,26,29]. To avoid computing VMAF via another objective score, in our method, a CNN model is used to replace RDO function. To train CNN, distortion of frame is assessed in terms of VMAF score and Lagrange multiplier is recomputed according to the new R-D model.

2.2. Perceptual RDO for Video Quality Consistency

To maintain consistency in video coding, some previous methods are proposed to minimize the variance of distortion between frames. Due to the scene changes in consecutive frames, QP values are estimated at frame level or MB level to control the distortion of each frame. However, intervening in the RDO process to recompute the QP value may affect the performance of the encoder. Specifically, the target of RDO is to estimate the QP that satisfies the optimal point of rate and distortion. Meanwhile, to keep consistency in video quality may require a different QP value to the QP value in RDO. Therefore, the problem here is to find an optimized QP value to achieve the two goals simultaneously: optimizing rate and distortion while achieving the expected quality for output video. In [10], to control quality at frame level, a Distortion-Quality model is proposed to assign a suitable QP value to each frame. In particular, before coding k t h frame, SSE value of the frame is estimated. Based on the proposed model, encoder selects a suitable Q P k ∗ value in a set of considered QP values to minimum the difference between the distortion and SSE as the following:
QP k ∗ = arg min QP k ∈ Q D T − D p ( QP k )
where Q is a set of considered QP values, D T is corresponding target of k t h frame and D p ( QP k ) is the frame-level predicted distortion by using QP k .
Similar to [10], algorithm in [8] also tries to minimize the difference between the estimated reconstruction quality and target reconstruction quality. However, beside the estimating quantization step size, this method fine tune λ in RDO for better quality consistency.
A common feature of the above methods is that they try find QP values at the frame level. However, assigning a fixed QP value to the entire frame will cause waste bitrate in coding process. In a frame, macroblocks (MBs) with different contents may require different amount of coded bit. In addition, in video quality assessment, some MBs in a frame may less important than some the others. Thus, MBs in a frame requires different QP values to increase coding performance. In our proposed method, the CNN model is used to estimate QP value for each MB in a frame. Besides, RDO is integrated into the proposed CNN model to achieve the two goals simultaneously as above stated: improving performance of video coding while achieve the expected quality of reconstructed video sequence.

3. Proposed Method

This section describes a method learning adaptive quantization parameter estimation (LAQP) in which a CNN model is used to predict QP for MBs in a video coding frame to achieve an expected VMAF score. First, it presents the overall architecture of the proposed perceptual video coding framework. Afterwards, it describes the method to propose distortion-quantization (D-Q) model and rate-quantization (R-Q) model for RDO process. Finally, the process of training CNN model to predict QP is described.

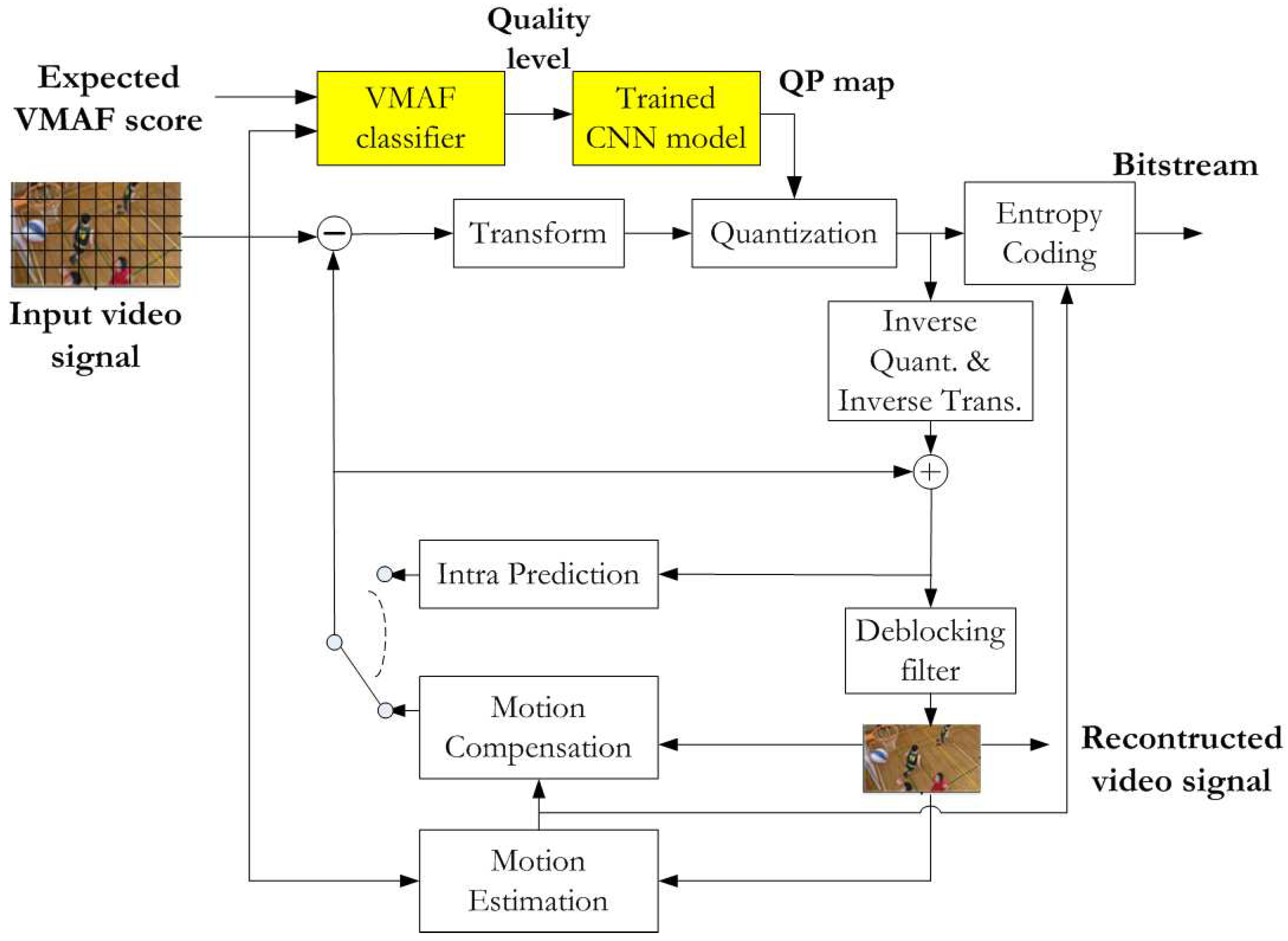
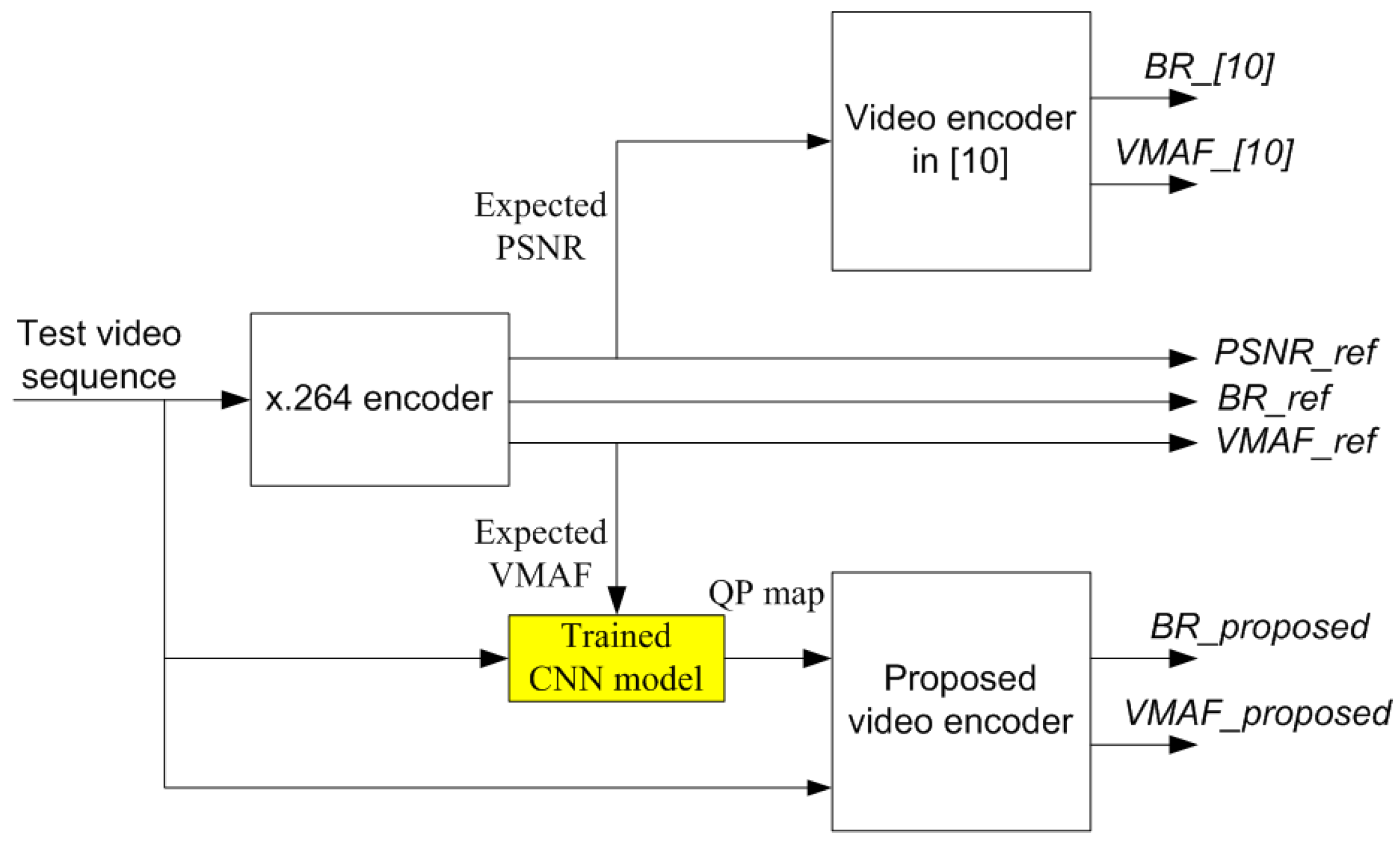
3.1. Overall Coding Framework

Figure 2 illustrates the overall encoding framework of the proposed PVC. Initially, the current frame of video sequence is split into macroblocks with the size of 16×16. Each macroblock is fetched into trained CNN model along with an expected quality level of frame to estimate a QP value for that macroblock. In this method, the quality level is used at frame level. The reason is that VMAF metric is not suitable for small size such as macroblock. In addition, in a frame, contribution of macroblocks to quality of the whole frame are not uniform because the contents of macroblocks are different. Therefore, with a quality level of the whole frame, the QP values of macroblocks are different.
As mentioned above, the goal of our work is to propose an algorithm to estimate QP values for macroblocks in a frame to control quality of video consistent with an expected VMAF score which is corresponding a specific quality level. In this work, there are 9 quality levels representing for VMAF score from 55 to 100. After predicting QP values for all macroblocks, a QP map (as shown in Figure 3) including all these QP values is used to encode the current frame. The output of encoder is a reconstructed frame with quality level corresponding to the expected VMAF score.

3.2. VMAF-based RDO Modelling

To train a CNN model to replace RDO process in estimating QP values for macroblocks, a VMAF-based RDO model is proposed to generate training dataset. In previous perceptual-based video coding methods, D-Q and R-Q models are developed to determine an optimal QP value at frame or macroblock level. However, it is difficult to integrate an objective metric into RDO because there is not exists a specific formula for objective metric. Therefore, to build the perceptual-based RDO function, some researches proposed an objective function which is approximate of subjective metrics. Then, D-Q and R-Q models are derived via this approximate function [19,26,29]. In this work, to propose a perceptual-based RDO function, D-Q and R-Q models are built based on VMAF metric. In particular, based on hypothesis that the distortion is inversely proportional to the quality, the distortion D of the frame is simply computed as the following equation:
D = 1 V M A F
To derive the function of R and D in terms of QP, 10 video sequences with length of 50 frames are encoded. After encoding, we obtain the fitting curve describing the distortion function and the rate function in terms of QP. Figure 4 shows the fitting curve of function R and D for “City” video sequence. The blue dots are the actual data, the red line is the estimation function that fits to the actual data. As shown in the figure, the fitting curves of R-Q and D-Q function are third-degree polynomials with R-squared values are 0.96 and 0.90, respectively. For the other sequences, the fitting curves are also third-degree polynomials with R-squared are shown in Table 1. The average of R-squared of 10 R-Q and D-Q fitting curves are 0.93 and 0.91, respectively. Based on R-D and D-Q fitting curves of 10 video sequences, two general R-Q and D-Q functions for all video sequences are established in which parameters of polynomial are average values of parameters of 10 fitting curves. In particularly, for I frame, the R-Q and D-Q functions are established as below:
R V M A F _ I = − 1 , 49 . Q P 3 + 185 , 3 . Q P 2 − 7716 . Q P
D V M A F _ I = 3 . 10 − 4 . Q P 3 − 3 . 10 − 2 . Q P 2 + 0 , 82 . Q P
Based on (9) and (10), the new Lagrange multiplier is computed as the following:
λ V M A F _ I = 9 . 10 − 4 . Q P 2 − 6 . 10 − 2 . Q P + 0 , 82 − 4 , 47 . Q P 2 + 370 , 6 . Q P − 7716
Similarly, for P frame, R-Q function, D-Q function and Lagrange multiplier are computed as below:
R V M A F _ P = 0 , 1 . Q P 3 − 9 , 55 . Q P 2 + 268 , 44 . Q P
D V M A F _ P = 5 , 85 . Q P 3 − 3 . 10 − 3 . Q P 2 + 0 . 03 . Q P
λ V M A F _ P = 17 , 55 . Q P 2 − 6 . 10 − 3 . Q P + 0 , 03 0 , 3 . Q P 2 − 19 , 1 . Q P + 288 , 44
For B frame:
R V M A F _ B = − 0 , 22 . Q P 3 + 26 , 08 . Q P 2 − 1039 . Q P
D V M A F _ B = 7 , 57 . Q P 3 − 6 , 10 − 3 . Q P 2 + 0 , 19 . Q P
λ V M A F _ B = 22 , 71 . Q P 3 − 12 , 10 − 3 . Q P 2 + 0 , 19 . Q P − 0 , 66 . Q P 3 + 52 , 16 . Q P 2 − 1039 . Q P
Based on above D-Q and R-Q functions, the minimum Lagrange cost function in (2) is computed to select optimal QP values for macroblocks. However, in this proposed method, instead of using RDO process, CNN is used to predict QP values. Therefore, RDO process is used offline to generate dataset for training CNN. The dataset generation and architecture of CNN model is described in following section.

3.3. CNN Model for QP map Prediction

To achieve an expected VMAF score for the whole coding frame, a CNN model is proposed to predict the optimal QP value for each MB. The input of CNN model includes a MB accompany to the expected VMAF score of the current frame. The output of CNN model is the optimal QP value for that MB. To train the proposed CNN model, a dataset includes MBs labeled QP values corresponding to quality levels is built. The dataset generation is described as following.

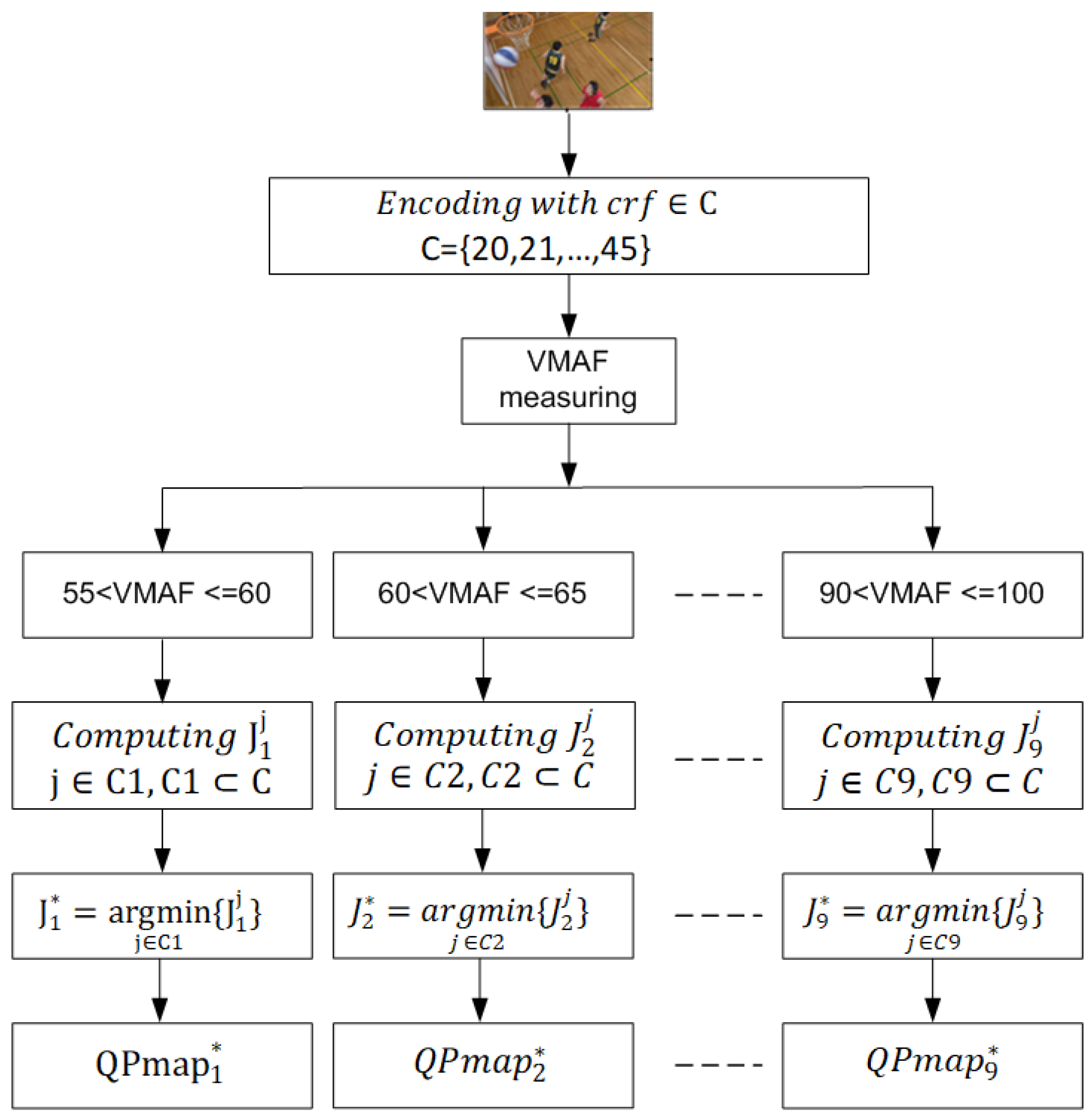
3.3.1. Dataset Collecting and Labelling

The flow chart in Figure 5 describes the process generating labels Q P m a p ∗ including QP values of each MB in a frame corresponding to each quality level. In the first step, a frame is encoded with different values of constant rate factor (crf) from 20 to 45. After encoding and decoding, the quality of reconstructed frame is measured in VMAF metric and classified according to the quality level. Because the similarity of consecutive VMAF scores, six consecutive VMAF scores are grouped into a quality level. To generate a dataset for training model, 15 video sequences with resolutions 352x280, 1280x720 are encoded. Each video sequence includes 50 frames with the configuration of group of pictures (GOP) is IBBBPPBBBPP. After measuring quality of reconstructed frames, we observe that the range of VMAF values is from 55 to 100. Therefore, VMAF scores are grouped into 9 groups as described in Figure 5. Assumed that there are n values of VMAF in the quality level i t h as following:
V M A F i = V M A F i 1 , V M A F i 2 , . . . , V M A F i n
In the second step, the Lagrange cost function J i j value corresponding to crf j t h in the quality level i t h is computed by following equation:
J i j = D V M A F j + λ V M A F j . R V M A F j
where j ∈ 20 , 21 . . . , 45 and D V M A F j , λ V M A F j , R V M A F j are computed as shown in Eq. (12) – Eq. (19) depending on the type of frame I, P or B. In the third step, a minimum J i ∗ at quality level i t h is selected as following:
J i ∗ = m i n j = 1 , n ¯ J i j
Finally, Q P m a p i ∗ corresponding to crf j t h at the quality level i t h is considered as the optimal QP map for the current frame to achieve quality level i t h . QP values in this Q P m a p i ∗ are used as the label for MBs in the current frame.

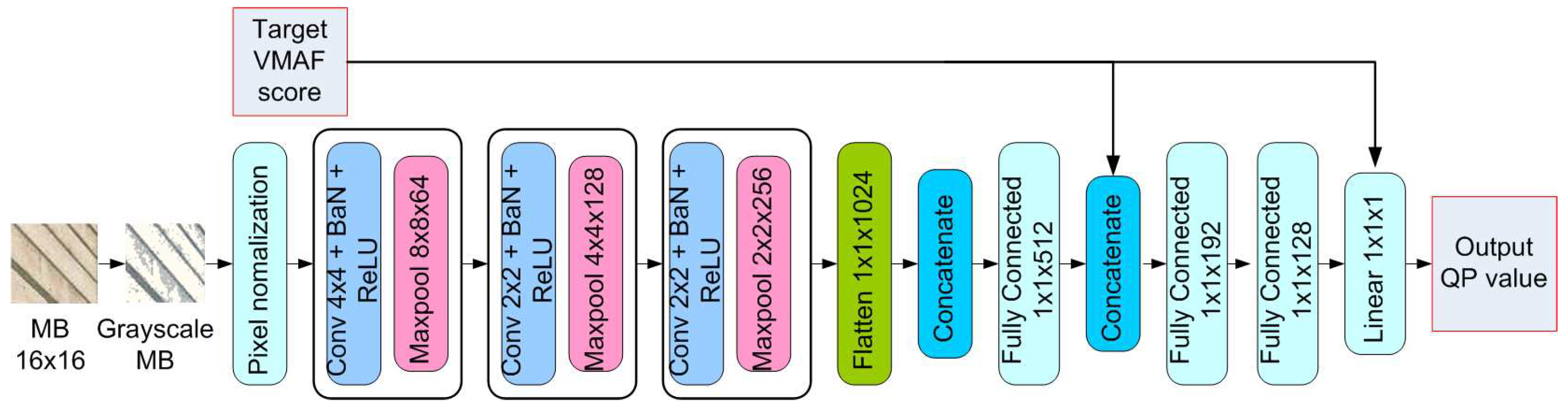
3.3.2. Training CNN model

To predict QP map for a frame with an expected VMAF score, the CNN model structure is proposed as in Figure 6. In this study, to extract features of macroblocks, the proposed CNN architecture is inspired from VGG-16 model [30]. However, in this case, the input of the proposed model is a small size macroblock instead of a large size image as in VGG-16. Therefore, we reduced the number of layers of VGG-16. After testing various CNN models with different numbers of convolution layers, the model with highest accuracy is selected with the following architecture:
  • Preprocessing layers: The pixels of input MB 16 × 16 are preprocessed by converting into grayscale and then normalized to values between 0 and 1.
  • Convolutional layers: The data through the preprocessing layers will be convolutionalized with 4 × 4 kernels at the first convolutional layer to extract the low-level features and 2 × 2 kernels for higher lever features. In addition, the batch normalization layer is used to normalize the feature map to stabilize the learning process and reduce the number of training epochs. After the convolutional layers, the pooling layer is added to reduce the size of each feature map. Besides, the dropout layer is used to drop features randomly with probabilities 20%.
  • Fully connected layers: The feature maps from the convolutional layers are concatenated together and then flattened into a column vector. And then, the column vectors are passed through three fully connected layers which compile the features extracted by previous layers to form the final output as QP value. Because the target VMAF score is a requirement for output reconstructed video, a target VMAF score is supplemented as an external feature in the feature vectors for fully connected layers.
In the proposed model, Mean Absolute Error (MAE) is used to measure the accuracy. MAE is computed as the following equation:
M A E = 1 n ∑ j = 1 n | y j − y ^ j |
where y ^ j is the predicted QP value, y j is the ground truth QP value of each MB j t h , n is number of MB. After training with 100 epochs, the MAE of the proposed model is 1 . 26 .

4. Performance Evaluation

4.1. Test Methodology

In the test methodology, the proposed method is compared with standard video codec x.264 [23] and a relevant method proposed in [10] in terms of BD-VMAF and BD-Rate [31]. Here, the practical x.264 video coding reference software was selected due to its low complexity and popular used in general. It should be noted that the proposed method can be integrated into x.265 [32] or vvc [33] in the future works.
The BD-VMAF metric is used to evaluate the effectiveness of the proposed algorithm in controlling the quality level while BD-Rate reflects performance of the proposed method in saving the bitrate when compared with the other methods. Six popular video sequences with resolutions of 352×280 and 1280×720 are used and encoded with 4 crf values 29, 32, 35 and 37.
The overall testing process is shown in Figure 7. In the first step, the video test sequence is encoded in a video codec standard, i.e., x.264. Assuming that, in this step, quality of reconstructed video sequence measured in VMAF metric and in PSNR metric is VMAF_ref and PSNR_ref, respectively. The bitrate of encoding process is BR_ref bps. In the second step, the video test sequence is fetched into CNN model accompanied by VMAF_ref to predict QP map. In this case, VMAF_ref is used as the expected VMAF score for CNN model. Then, the predicted QP map is applied to video encoder to encode frames of video test sequence. Assuming that the quality score of reconstructed video sequence in the second step is VMAF_proposed and bitrate is BR_proposed. Similarly, the video test sequence accompanies PSNR_ref is fetched into video encoder using method [10]. In this case, the PSNR_ref is considered as expected quality level for encoder. The quality score of reconstructed video sequence is VMAF_[10] and bitrate is BR_[10]. Finally, the parameters including VMAF score and bitrate of three reconstructed video sequences are compared to evaluate the effectiveness of the methods.

4.2. RD Performance Evaluation

The BD-Rate and BD-VMAF comparison between methods are shown in Table 2. As shown in results, compared to x.264 codec reference and the method content adaptive distortion – quantization (CADQ) proposed in [10], the proposed method can save bitrate up to 3.36% and 10.03%, respectively. Meanwhile, the VMAF score of the proposed method gains 1.59% and 2.16% although the RD performance of the proposed method is lower than x.264 in case of “Container” sequence. It means that the proposed method can achieve quality level almost the same as the expected quality level while the bitrate saving is guaranteed. In overall, by using the CNN model, the proposed method estimated an optimal QP value for encoding macroblock to obtain two targets simultaneously: achieving a target quality level for the reconstructed frames and increasing RD performance.

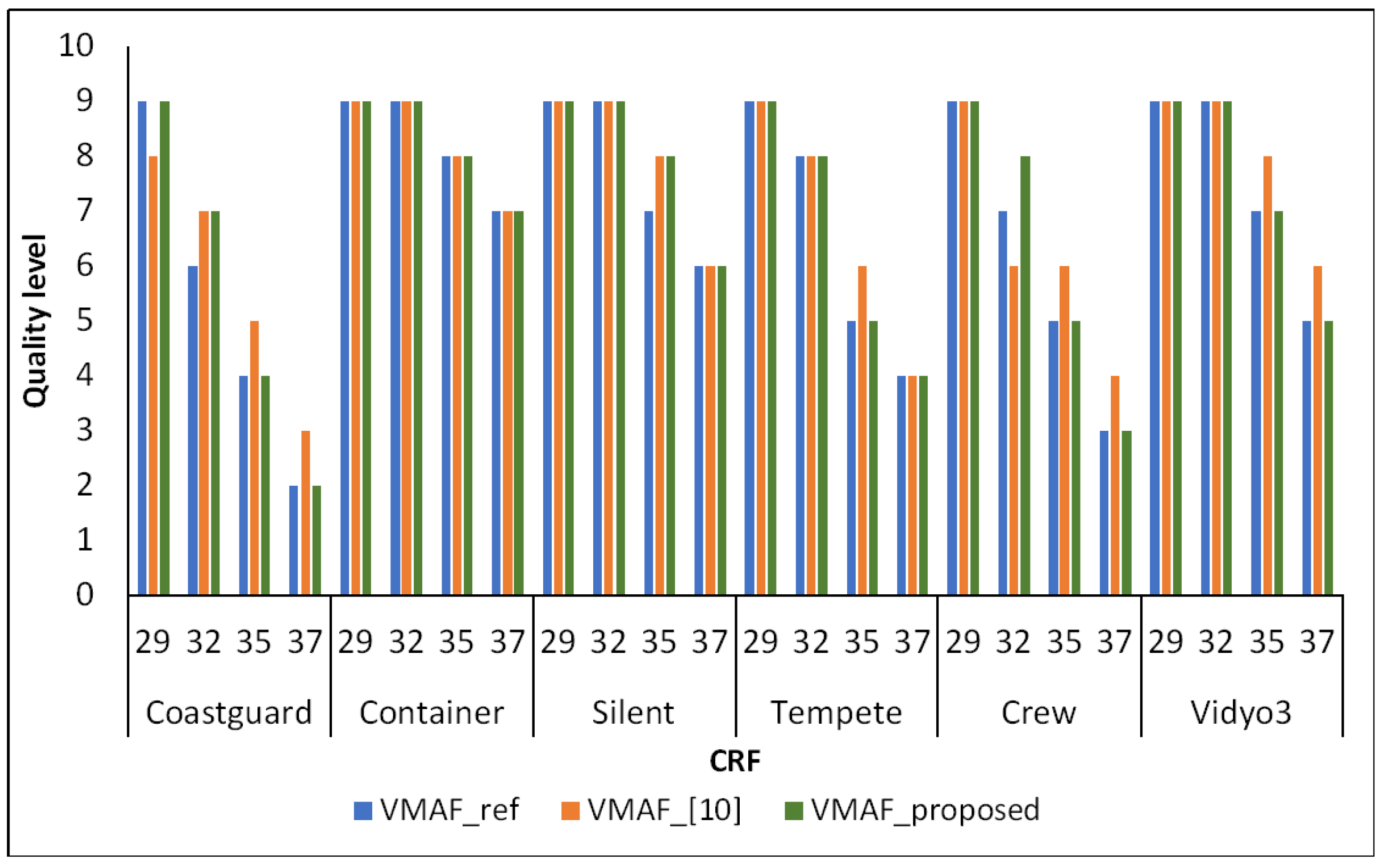
4.3. Expected Quality Level Assessment

The quality levels of 24 reconstructed sequences (6 video sequences x 4 cases of crf) in three methods are shown in Figure 8 in which the quality level of x.264 codec is considered as the expected quality level for the other two methods. As shown in the figure, quality of reconstructed video in the proposed method is different to the expected level just in three cases of "Coastguard", "Crew" with crf 32 and "Silent" with crf 35. Meanwhile, in method [10], the output quality level is different to the expected quality in cases of "Coastguard", "Crew" with crf 32, "Silent", "Tempete", "Crew", "Vydio3" with crf 35 and "Coastugard", "Crew", "Vydio3" with crf 37. It means that with predict QP value, the proposed method can achieve expected quality better than method in [10].

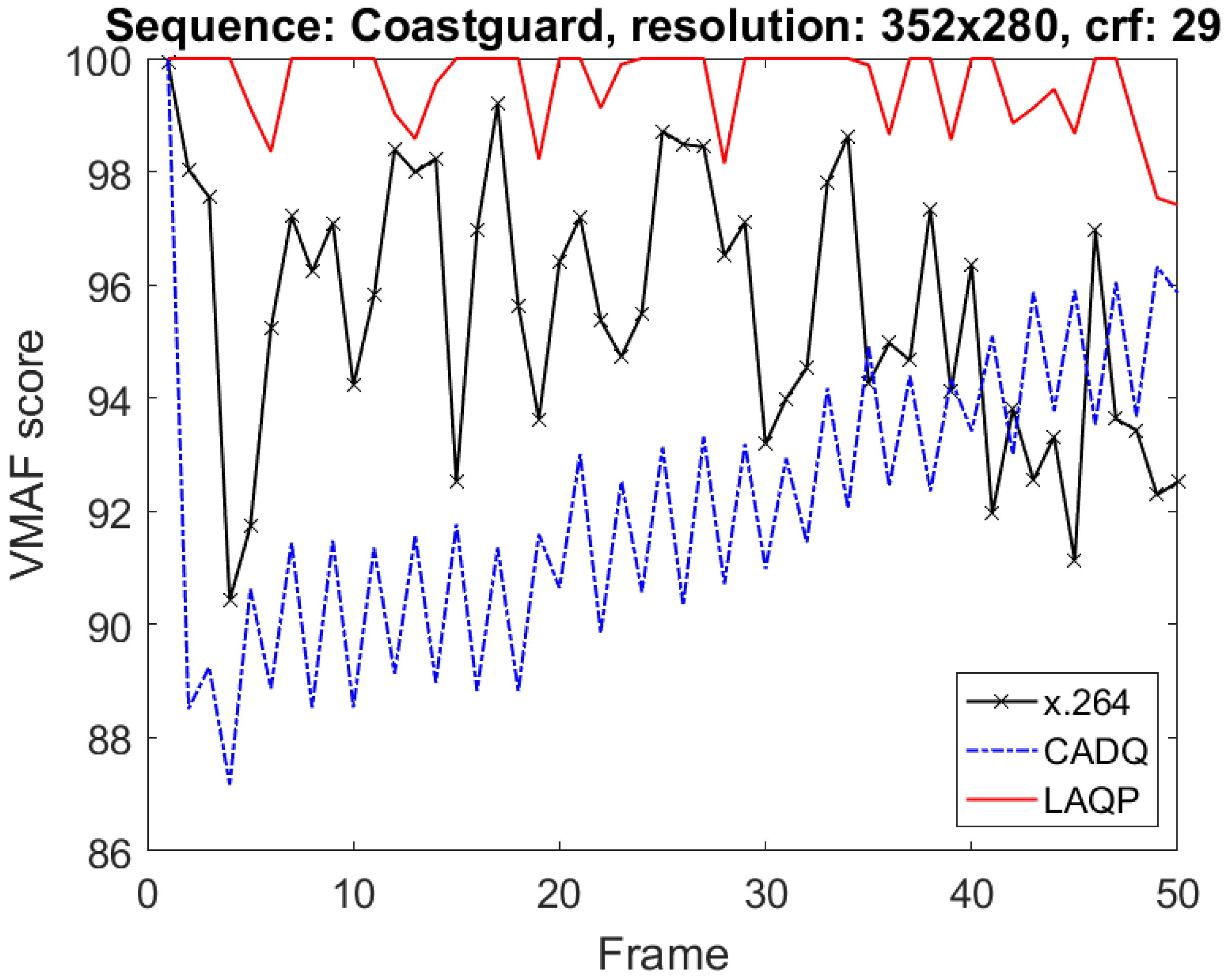
4.4. Quality Consistency Evaluation

Besides achieving the expected quality, the smoothness of quality between frames in a sequence is also considered. The smoothness is computed by variance of VMAF score of frames in a video sequence. Table 3 shows the quality variance of 6 output video sequences in x.264 codec, the method in [10] and the proposed method while Figure 9 describes the quality curves of "Coastguard" sequence in three methods. As shown results, the average quality variance in x.264 is 8.19 while the method [10] and the proposed method is 6.07 and 4.02, respectively. Especially, in cases of crf 29, 32, the average variance of "Silent" sequence in the proposed method is 0. It means that the proposed CNN-based method not only achieves the expected quality but also achieves the quality consistency better than the other methods.

5. Conclusions

In this paper, a CNN-based method is proposed to estimate QP value for video coding to achieve an expected quality level in terms of VMAF score. The inputs of CNN model inlcude a macroblock of the current frame accompany with an expected VMAF score for that frame at the output of decoder side. The output of CNN model is an estimated QP value for that macroblock.
The experimental results show that with a target quality level, the proposed method can save the bitrate up to 5.82% and improve the quality up to 4.28% when compared to the conventional x.264 codec. In addition, the proposed method also save bitrate up to 27.65% and gain the quality up to 4.11% when compared with the relevant method in [10]. Besides improvement of RD performance, the proposed method also achieves smoothness higher than the other methods in terms of quality variance.

Author Contributions

Funding acquisition, T.V.H.; Conceptualization, T.V.H. and X.H.V.; Methodology, T.V.H. and X.H.V.; Project administration, T.V.H.; Software, M.D.N. and S.N.Q; Validation, H.P.C and T.S.; Visualization, H.P.C and T.S; Writing—original draft, M.D.N and S.N.Q; Writing—review and editing, T.V.H. and X.H.V.. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by Research Collaboration Project between PTIT and Naver Corp. for under grant number 01-PTIT-NAVER-2022.

Data Availability Statement

The data is available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kjell Brunnström, Sergio Ariel Beker, Katrien de Moor, Ann Dooms, Sebastian Egger, et al., “Qualinet white paper on definitions of quality of experience,“ 2013. hal-00977812.
  2. T. Hossfeld, M. Seufert, C. Sieber, and T. Zinner, “Assessing effect sizes of influence factors towards a QoE model for HTTP adaptive streaming,” 2014 6th Int. Work. Qual. Multimed. Exp. QoMEX 2014, pp. 111–116, 2014. [CrossRef]
  3. X. Chen, J. N. Hwang, D. Meng, K. H. Lee, R. L. De Queiroz, and F. M. Yeh, “A quality-of-content-based joint source and channel coding for human detections in a mobile surveillance cloud,” IEEE Trans. Circuits Syst. Video Technol., vol. 27, no. 1, pp. 19–31, 2017. [CrossRef]
  4. S. Milani, R. Bernardini and R. Rinaldo, "A saliency-based rate control for people detection in video," 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 2013, pp. 2016-2020. [CrossRef]
  5. Z. He, W. Zeng, and C. W. Chen, “Low-pass filtering of rate-distortion functions for quality smoothing in real-time video communication,” IEEE Trans. Circuits Syst. Video Technol., vol. 15, no. 8, pp. 973–981, 2005. [CrossRef]
  6. B. Xie and W. Zeng, “A sequence-based rate control framework for consistent quality real-time video,” IEEE Trans. Circuits Syst. Video Technol., vol. 16, no. 1, pp. 56–71, 2006. [CrossRef]
  7. L. Xu, S. Li, K. N. Ngan, and L. Ma, “Consistent visual quality control in video coding,” IEEE Trans. Circuits Syst. Video Technol., vol. 23, no. 6, pp. 975–989, 2013. [CrossRef]
  8. Q. Cai, Z. Chen, D. O. Wu, and B. Huang, “Real-time constant objective quality video coding strategy in high efficiency video coding,” IEEE Trans. Circuits Syst. Video Technol., vol. 30, no. 7, pp. 2215–2228, 2020. [CrossRef]
  9. C. W. Seo, J. H. Moon, and J. K. Han, “Rate control for consistent objective quality in high efficiency video coding,” IEEE Trans. Image Process., vol. 22, no. 6, pp. 2442–2454, 2013. [CrossRef]
  10. H. Avc, I. Applications, C.-Y. Wu, and P. Su, “A content-adaptive distortion – quantization model,” IEEE Trans. Circuits Syst., vol. 24, no. 1, pp. 113–126, 2014, [Online]. Available: http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=6562767.
  11. F. De Vito and J. C. De Martin, “PSNR control for GOP-level constant quality in H.264 video coding,” Proc. Fifth IEEE Int. Symp. Signal Process. Inf. Technol., vol. 2005, pp. 612–617, 2005. [CrossRef]
  12. Z. Li, A. Aaron, A. Katsavounidis, Ioannis Moorthy, and M. Manohara, “Toward A Practical Perceptual Video Quality Metric,” Netflix Blog, 2016. http://techblog.netflix.com/2016/06/toward-practical-perceptual-video.html.
  13. H. R. Sheikh and A. C. Bovik, “Image information and visual quality,” IEEE Trans. Image Process., vol. 15, no. 2, pp. 430–444, 2006. [CrossRef]
  14. S. Li, F. Zhang, L. Ma, and K. N. Ngan, “Image quality assessment by separately evaluating detail losses and additive impairments,” IEEE Trans. Multimed., vol. 13, no. 5, pp. 935–949, 2011. [CrossRef]
  15. R. Rassool, “VMAF reproducibility: validating a perceptual practical video quality metric,” IEEE Int. Symp. Broadband Multimed. Syst. Broadcast. BMSB, 2017. [CrossRef]
  16. C. Lee, S. Woo, S. Baek, J. Han, J. Chae, and J. Rim, “Comparison of objective quality models for adaptive bit-streaming services,” 2017 8th Int. Conf. Information, Intell. Syst. Appl. IISA 2017, vol. 2018-Janua, pp. 1–4, 2018. [CrossRef]
  17. N. Barman, S. Schmidt, S. Zadtootaghaj, M. G. Martini, and S. Möller, “An evaluation of video ality assessment metrics for passive gaming video streaming,” Proc. 23th ACM Work. Pack. Video, PV 2018, pp. 7–12, 2018. [CrossRef]
  18. S. Deng, J. Han, and Y. Xu, “VMAF based rate-distortion optimization for video coding,” IEEE 22nd Int. Work. Multimed. Signal Process. MMSP 2020, 2020. [CrossRef]
  19. Z. Luo, C. Zhu, Y. Huang, R. Xie, L. Song, and C. C. J. Kuo, “VMAF oriented perceptual coding based on piecewise metric coupling,” IEEE Trans. Image Process., vol. 30, pp. 5109–5121, 2021. [CrossRef]
  20. I. Marzuki and D. Sim, “Perceptual adaptive quantization parameter selection using deep convolutional features for HEVC encoder,” IEEE Access, vol. 8, pp. 37052–37065, 2020. [CrossRef]
  21. M. M. Alam, T. D. Nguyen, M. T. Hagan, and D. M. Chandler, “A perceptual quantization strategy for HEVC based on a convolutional neural network trained on natural images,” Appl. Digit. Image Process. XXXVIII, vol. 9599, p. 959918, 2015. [CrossRef]
  22. T. H. Vu, H. P. Cong, T. Sisouvong, X. HoangVan, S. NguyenQuang and M. DoNgoc, "VMAF based quantization parameter prediction model for low resolution video coding," 2022 International Conference on Advanced Technologies for Communications (ATC), Ha Noi, Vietnam, 2022, pp. 364-368. [CrossRef]
  23. T. Wiegand, G. Sullivan, and A. Luthra, “Draft ITU-T recommendation and final draft international standard of joint video specification (ITU-T Rec. H.264ISO/IEC 14 496-10 AVC),” vol. 2002, pp. 7–14, 2003.
  24. G. J. Sullivan and T. Wiegand, “Rate-distortion optimization for: Video compression,” IEEE Signal Process. Mag., vol. 15, no. 6, pp. 74–90, 1998. [CrossRef]
  25. C. L. Yang, R. K. Leung, L. M. Po, and Z. Y. Mai, “An SSIM-optimal H.264/AVC inter frame encoder,” Proc. - 2009 IEEE Int. Conf. Intell. Comput. Intell. Syst. ICIS 2009, vol. 4, pp. 291–295, 2009. [CrossRef]
  26. X. Wang, L. Su, Q. Huang and C. Liu, "Visual perception based Lagrangian rate distortion optimization for video coding," 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 2011, pp. 1653-1656. [CrossRef]
  27. Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. Image Process., vol. 13, no. 4, pp. 600–612, Apr. 2004. [CrossRef]
  28. X. Tong, C. Zhu, R. Xie, J. Xiong, and L. Song, “A VMAF directed perceptual rate distortion optimization for video coding,” IEEE Int. Symp. Broadband Multimed. Syst. Broadcast. BMSB, vol. 2020-Octob, pp. 3–7, 2020. [CrossRef]
  29. C. Zhu, Y. Huang, R. Xie, and L. Song, “HEVC VMAF-oriented perceptual rate distortion optimization using CNN,” 2021 Pict. Coding Symp. PCS 2021 - Proc., 2021. [CrossRef]
  30. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” 2014, arXiv:1409.1556. [Online]. Available: http://arxiv.org/abs/1409.1556.
  31. G. Bjontegaard, “Calculation of average PSNR differences between RD-curves,” ITU-T VCEG-M33, 2011.
  32. https://x265.readthedocs.io/en/master/.
  33. Versatile Video Coding, Standard ISO/IEC 23090-3, ISO/IEC JTC 1, Jul. 2020.
Preprints 89098 g001
Figure 1. Example of video with inconsistent quality, (a-d): Foreman video frame number x – y; (e-h): Difference with the original images.
Figure 1. Example of video with inconsistent quality, (a-d): Foreman video frame number x – y; (e-h): Difference with the original images.
Preprints 89098 g001
Preprints 89098 g002
Figure 2. Framework of the proposed method.
Figure 2. Framework of the proposed method.
Preprints 89098 g002
Preprints 89098 g003
Figure 3. A sample of QP map.
Figure 3. A sample of QP map.
Preprints 89098 g003
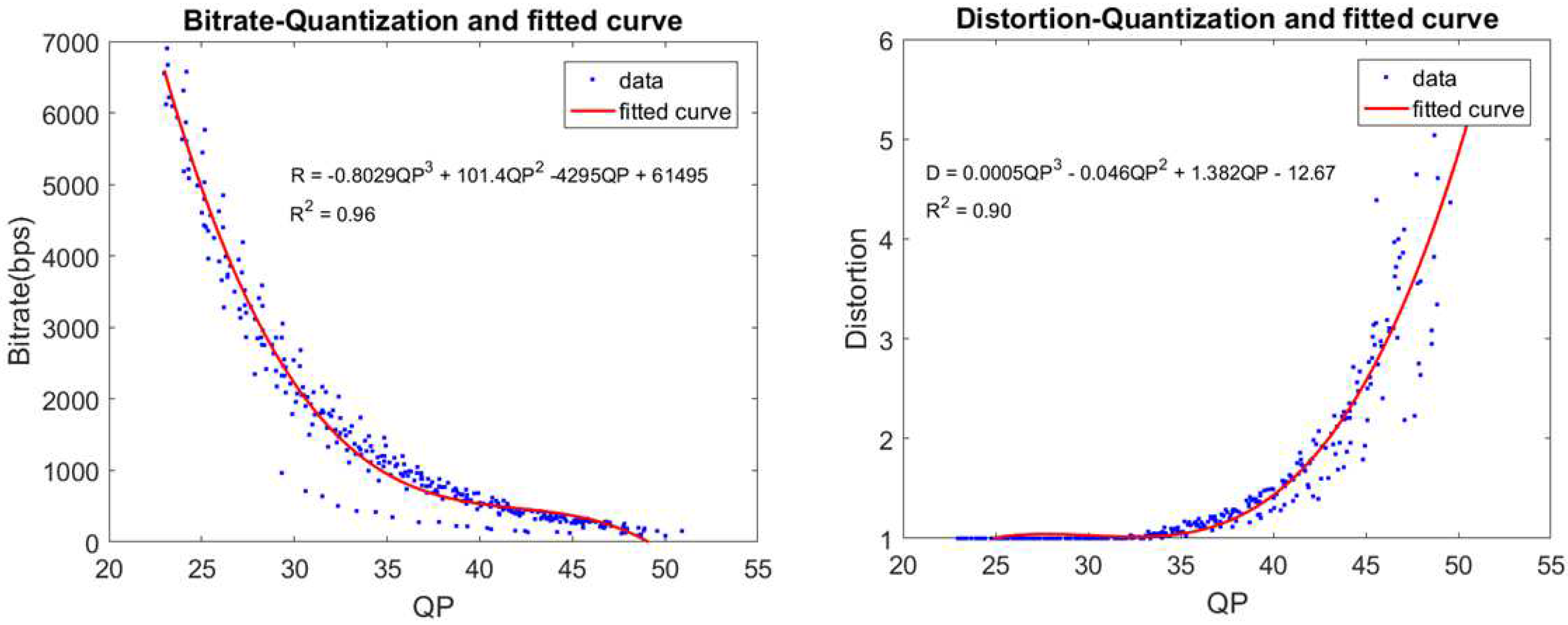
Preprints 89098 g004
Figure 4. The fitting curve of "City" sequence for rate and distortion function.
Figure 4. The fitting curve of "City" sequence for rate and distortion function.
Preprints 89098 g004
Preprints 89098 g005
Figure 5. Steps in dataset generation process.
Figure 5. Steps in dataset generation process.
Preprints 89098 g005
Preprints 89098 g006
Figure 6. Architecture of the proposed CNN model.
Figure 6. Architecture of the proposed CNN model.
Preprints 89098 g006
Preprints 89098 g007
Figure 7. Architecture of test methodology for the proposed method.
Figure 7. Architecture of test methodology for the proposed method.
Preprints 89098 g007
Preprints 89098 g008
Figure 8. Comparison of quality level between methods
Figure 8. Comparison of quality level between methods
Preprints 89098 g008
Preprints 89098 g009
Figure 9. Comparison of quality level between methods
Figure 9. Comparison of quality level between methods
Preprints 89098 g009
Table 1. The R-squared of functions R ( Q P ) and D ( Q P ) for "City" sequence.
Table 1. The R-squared of functions R ( Q P ) and D ( Q P ) for "City" sequence.
Video sequences R-squared of R ( Q P ) R-squared of D ( Q P )
Hall 0.95 0.93
City 0.96 0.90
Foreman 0.90 0.90
Crew 0.84 0.94
Four-people 0.92 0.94
Ice 0.94 0.91
Kris 0.89 0.91
Mobile 0.99 0.88
Soccer 0.91 0.97
Waterfall 0.98 0.83
Average 0.93 0.91
Table 2. BD-Rate and BD-VMAF comparison between methods.
Table 2. BD-Rate and BD-VMAF comparison between methods.
Video
sequence		 crf x.264 codec CADQ [10] Our LAQP LAQP
vs. x.264		 LAQP
vs. CADQ
BR_
ref 		VMAF_
ref 		BR_
[10] 		VMAF_
[10] 		BR_
Proposed 		VMAF_
Proposed 		BD-
Rate 		BD-
VMAF 		BD-
Rate 		BD-
VMAF
Coastguard
352x288		 29 339.26 96 469.73 92 524.46 100 -2.15 0.53 -16.21 3.55
32 241.02 84 280.23 85 275.41 90
35 110.28 73 153.42 76 130.91 75
37 75.22 65 102.87 69 80.09 64
Container
352x288		 29 99.51 100 142.14 100 98.56 100 1.28 0.72 -27.65 4.11
32 63.21 99 81.15 96 63.6 99
35 43.56 93 50.5 92 44.85 95
37 34.9 87 39.19 87 35.52 89
Silent
352x288		 29 131.84 100 143.89 100 107.64 100 -4.08 4.28 -1.60 2.20
32 91.84 98 94.58 98 85.24 100
35 63.91 88 60.5 91 61.45 93
37 50.22 80 46.85 84 45.23 85
Tempete
352x288		 29 283.87 98 382.01 98 306.59 100 -4.74 0.89 -7.88 1.57
32 187.94 91 217.23 92 217.2 95
35 126.62 80 123.33 80 118.57 79
37 98.92 72 88.69 72 83.34 71
Crew
1280x720		 29 502.26 97 518.7 98 537.59 97 -4.64 1.44 -3.37 1.09
32 348.33 88 313.61 95 376.43 91
35 245.98 77 254.21 81 249.18 80
37 194.04 67 195.07 71 185.69 69
Vidyo3
1280x720		 29 512.69 100 499.98 100 495.39 100 -5.82 1.65 -3.51 0.41
32 362.5 97 398.7 99 372.61 98
35 255.7 88 253.45 90 241.93 90
37 201.24 80 204.13 80 205.69 80
Average -3.36 1.59 -10.03 2.16
Table 3. Quality variance comparison between methods.
Table 3. Quality variance comparison between methods.
Video sequence crf x.264 CADQ LAQP
Coastguard 29 5.57 6.68 0.59
32 4.98 6.18 4.83
35 5.41 5.34 5.10
37 4.24 5.81 4.51
Container 29 0.08 0.15 0.11
32 2.83 0.47 1.11
35 4.49 0.88 1.41
37 5.05 0.99 0.89
Silent 29 0.11 0.74 0.00
32 4.94 1.09 0.00
35 12.94 1.59 1.34
37 13.10 2.30 2.12
Tempete 29 2.94 1.58 0.3
32 6.93 3.57 1.59
35 5.84 4.71 3.67
37 6.22 5.43 3.09
Crew 29 10.15 15.67 10.60
32 20.53 18.73 12.04
35 26.30 23.73 15.32
37 37.39 26.90 18.89
Vidyo3 29 1.24 1.53 1.19
32 2.99 2.92 2.44
35 7.23 5.21 2.49
37 5.12 3.56 2.76
Average 8.19 6.07 4.02
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated