Submitted:
02 November 2023
Posted:
03 November 2023
You are already at the latest version
Abstract
Keywords:
| Content | |
|
1. Preface
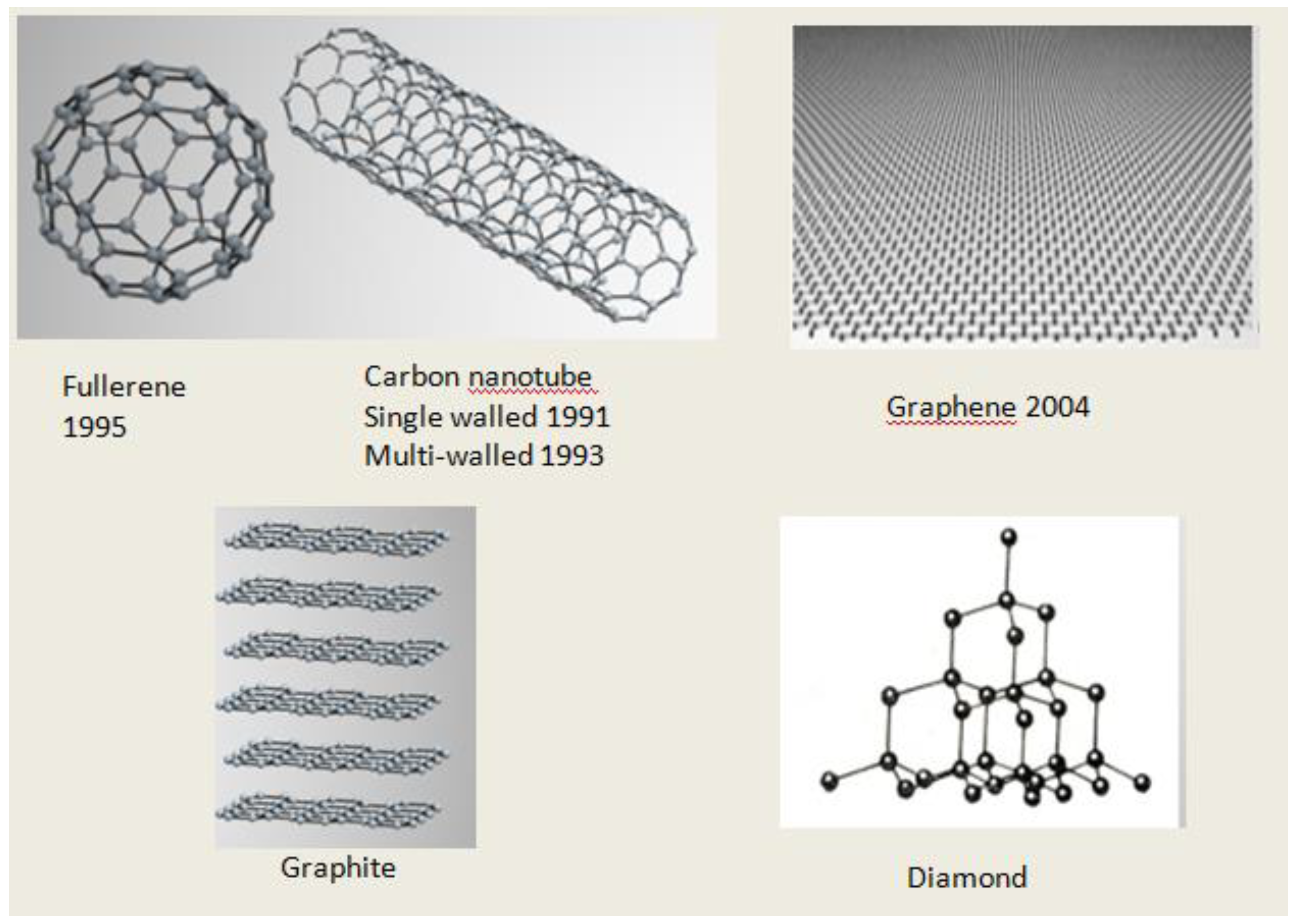
2. A history of Carbon Nanostructures Discovery
2.1. Fullerenes
2.2. Carbon Nanotubes
2.3. Graphene
3. The structure of Nanocarbon Particles
3.1. Fullerenes
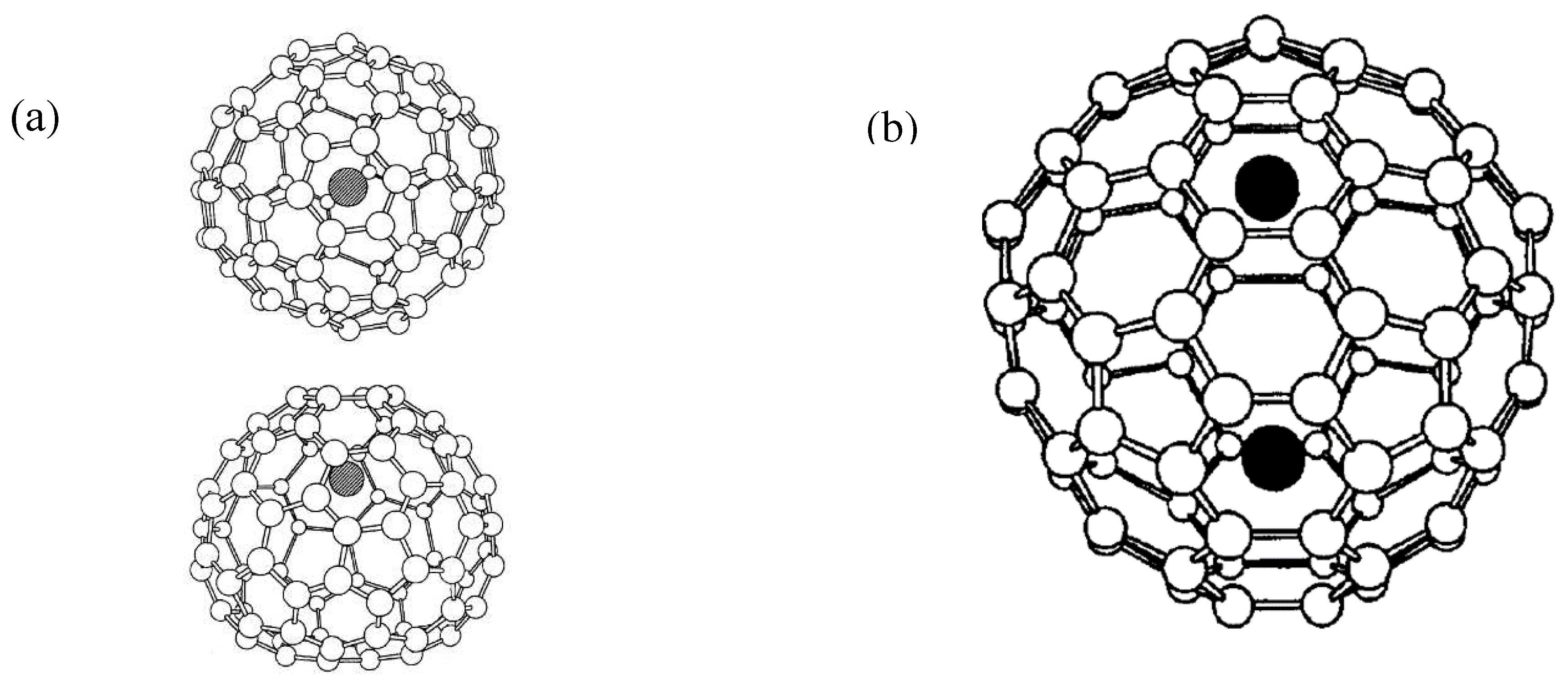
Endohedral Fullerenes
3.2. Carbon Nanotubes
3.2.1. Chirality
3.2.2. Structural Defects

3.2.3. Multi Layer Nanotubes
3.3. Graphene
3.3.1. The Structure of Boundaries and Defects
3.3.2. Wave Surface of Graphene
3.3.3. 1D Carbon Chains
4. Carbon Nanoparticles Production Methods
4.1. Fullerenes
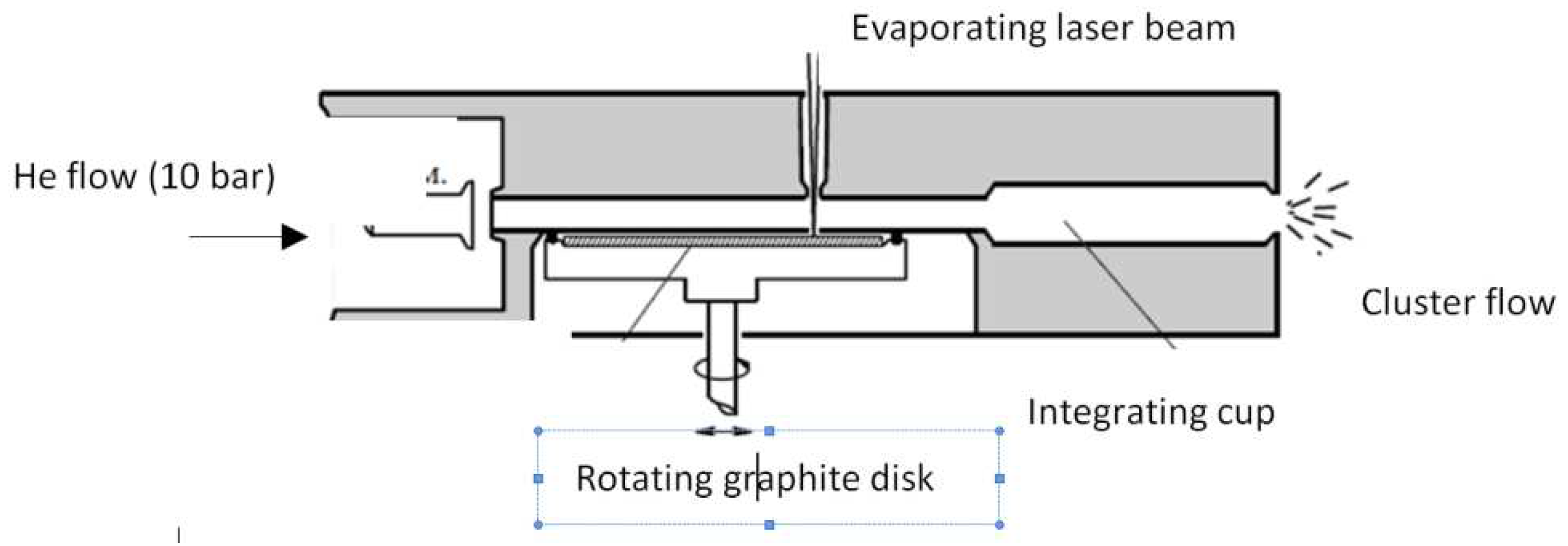
4.1.1. Electric Arc Synthesis
4.1.2. The Mechanism of Fullerenes Formation
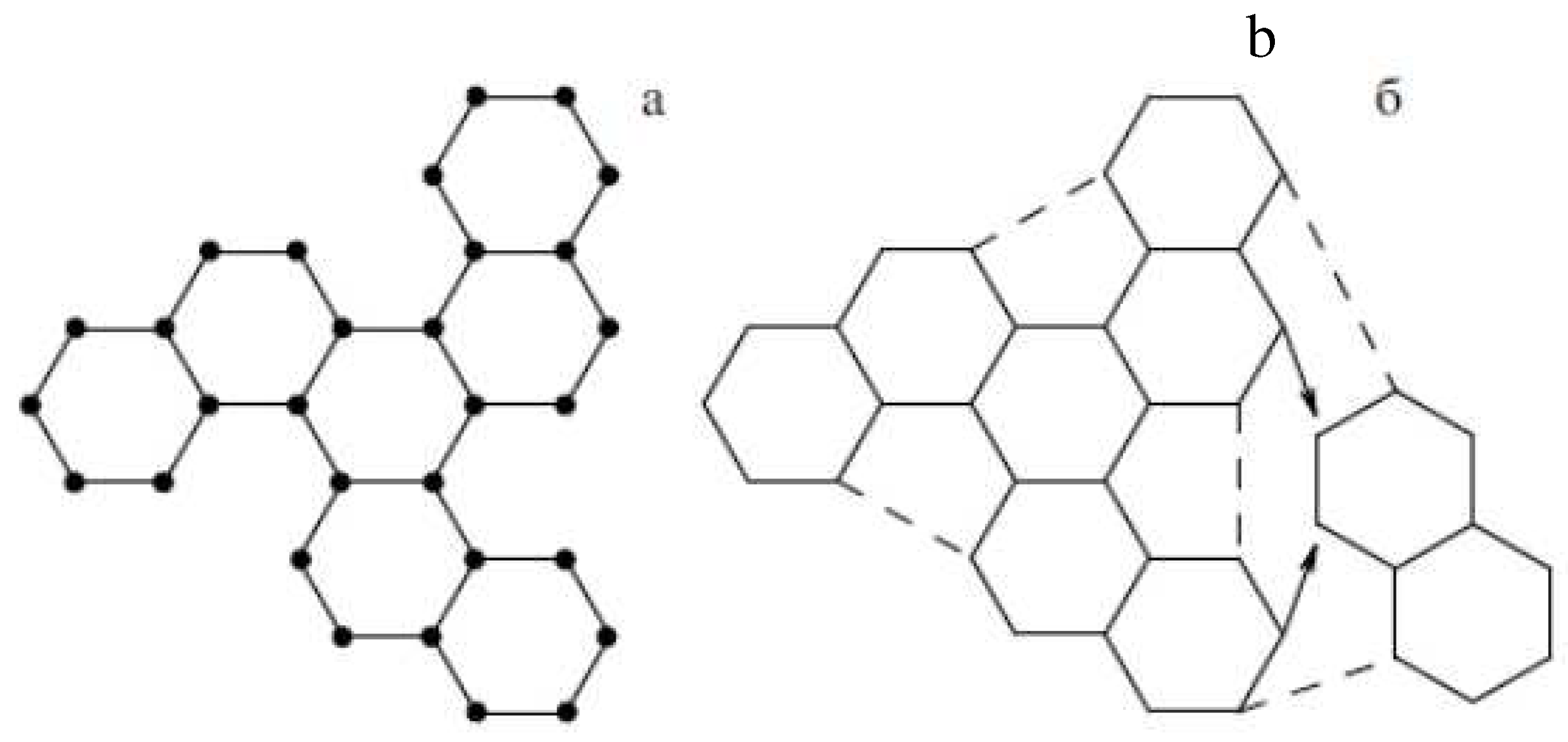
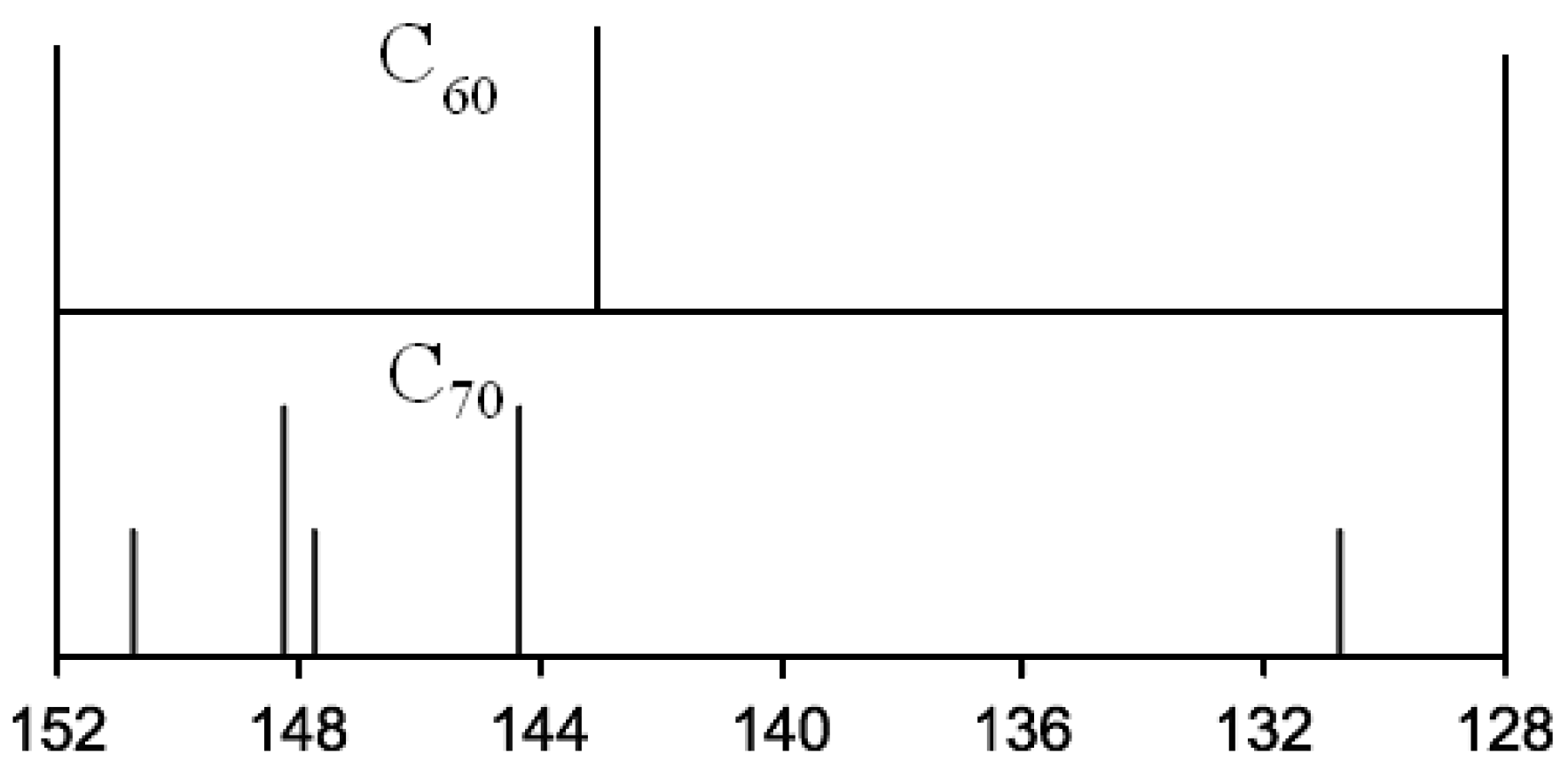
4.1.3. Extraction of Fullerenes from Soot
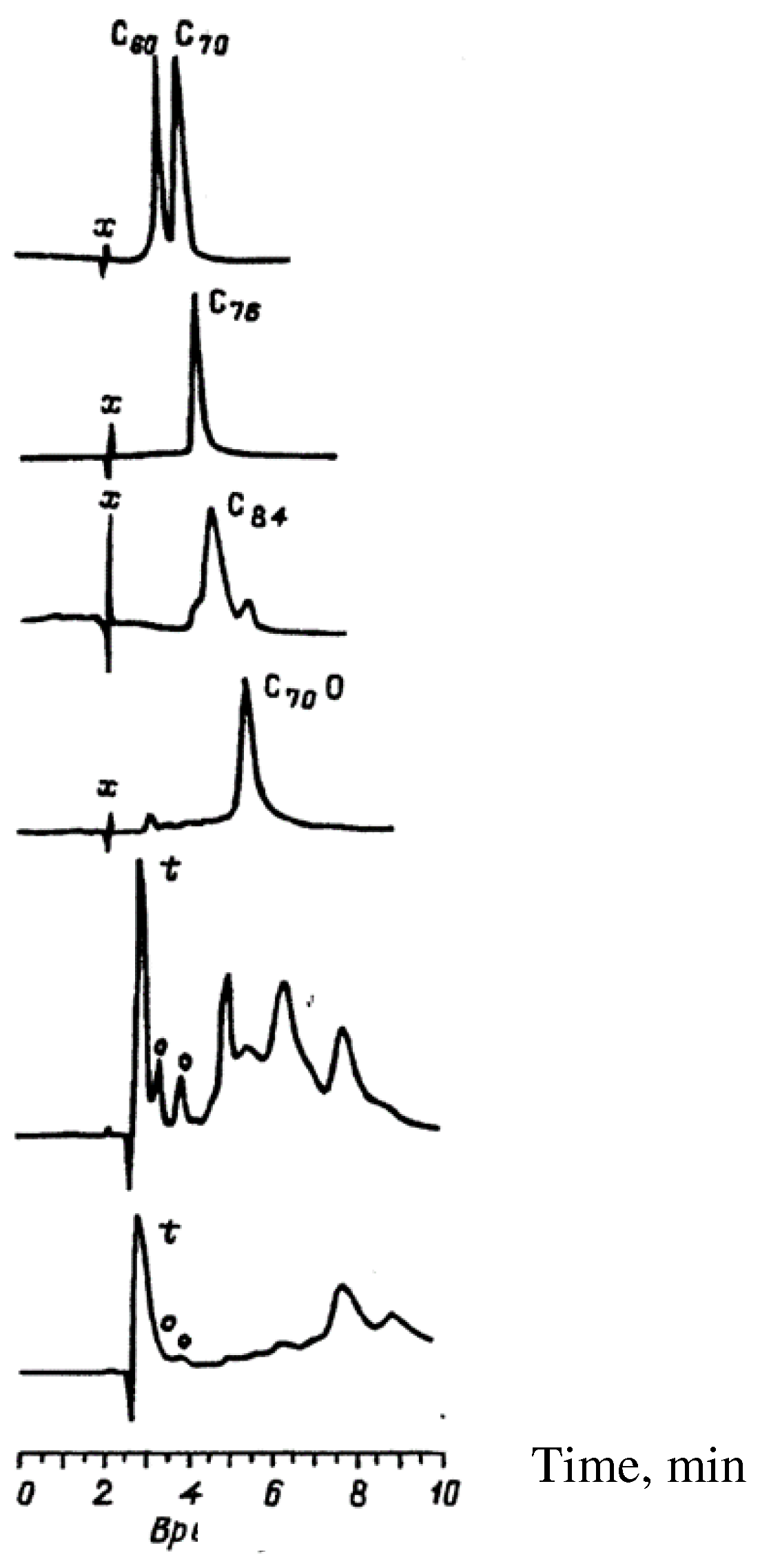
4.1.4. Liquid Chromatography and Separation of Fullerenes
4.1.5. Synthesis of Endohedral Fullerenes
4.1.6. Threemetasphera
4.1.7. Synthesis of Fullerenes in a Plasmatron from Dispersed Amorphous Carbon
4.2. Carbon Nanotubes
4.2.1. Electrical Arc Synthesis
4.2.2. Chemical Vapor Deposition
4.2.3. Plasma-Chemical Synthesis
4.3. Graphene
4.3.1. Micromechanical Exfoliation of Graphite
4.3.2. Chemical Vapor Deposition
4.3.3. Reduction of Graphene Oxide

5. Physical and Chemical Properties of Carbon Nanostructures
5.1. Fullerenes
5.1.1. Molecular Properties and Chemistry of Fullerenes
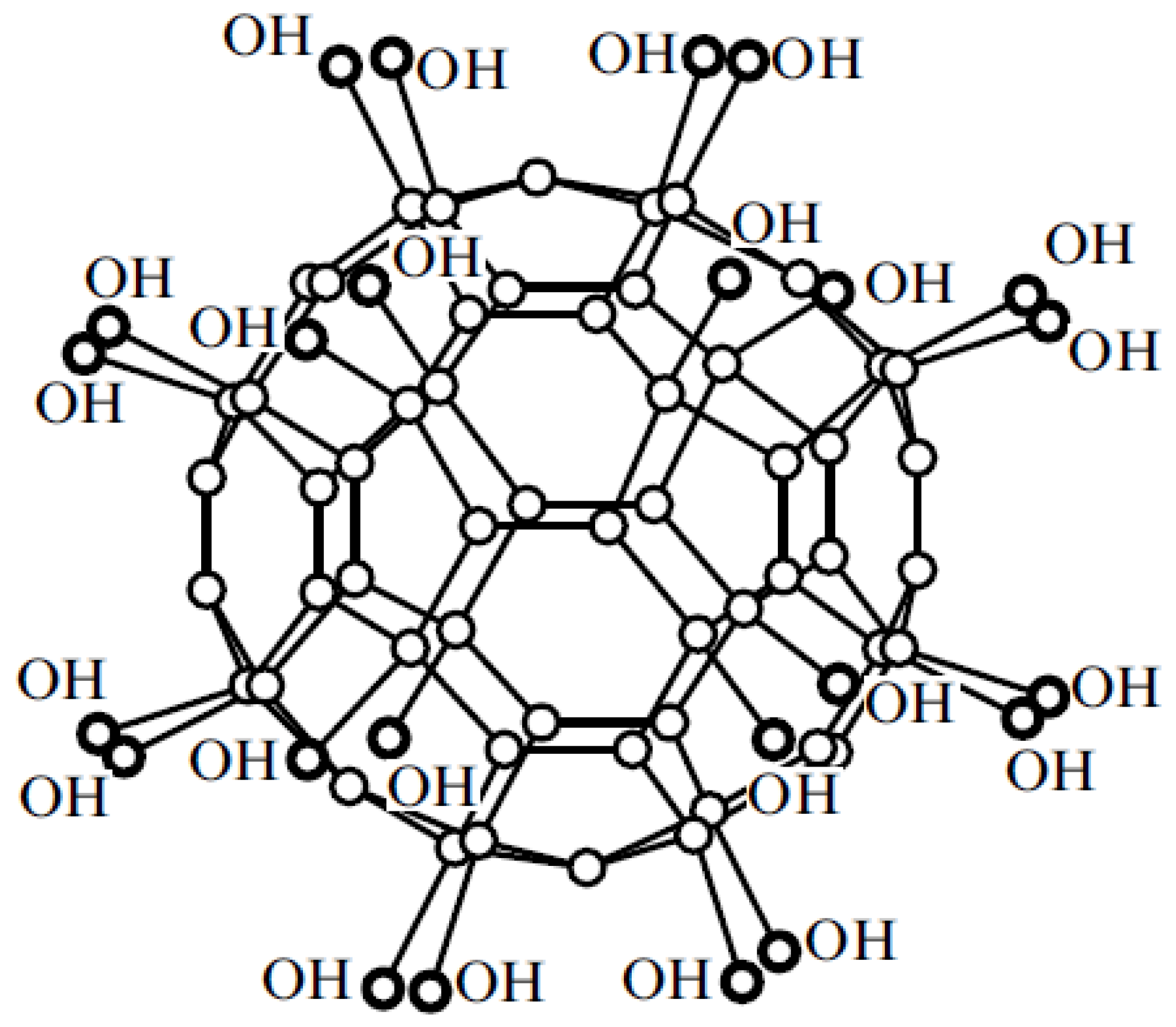
5.1.2. Fullerite
| Parameter | Quantity |
| Lattice constant (fcc), nm | 1.417 |
| Distance С60-С60, nm | 1.002 |
| Binding energy С60-С60, eV | 1.6 |
| Density, g/cm3 | 1.72 |
| Molecular density, cm-3 | 1.44х1021 |
| Isothermal compressibility, m2/N | 6.9х10-11 |
| Phase transition sc-fcc temperature (Тpt), К | 261 |
| dТpt/dp, К/Kbar | 11 |
| Volumetric thermal expansion coefficient, К-1 | 6.1х10-5 |
| Electron work function, eV | 4.7 |
| Debye temperature, К | 185 |
| Thermal conductivity, W/m К | 0.4 |
| Electric conductivity, S/m (T= 300 K) | 1.7х10-7 |
| Melting temperature, К | 1450 |
| Sublimation enthalpy, eV (Т = 500 – 700 К) | 1.74 |
| Dielectric constant | 4 – 4.5 |
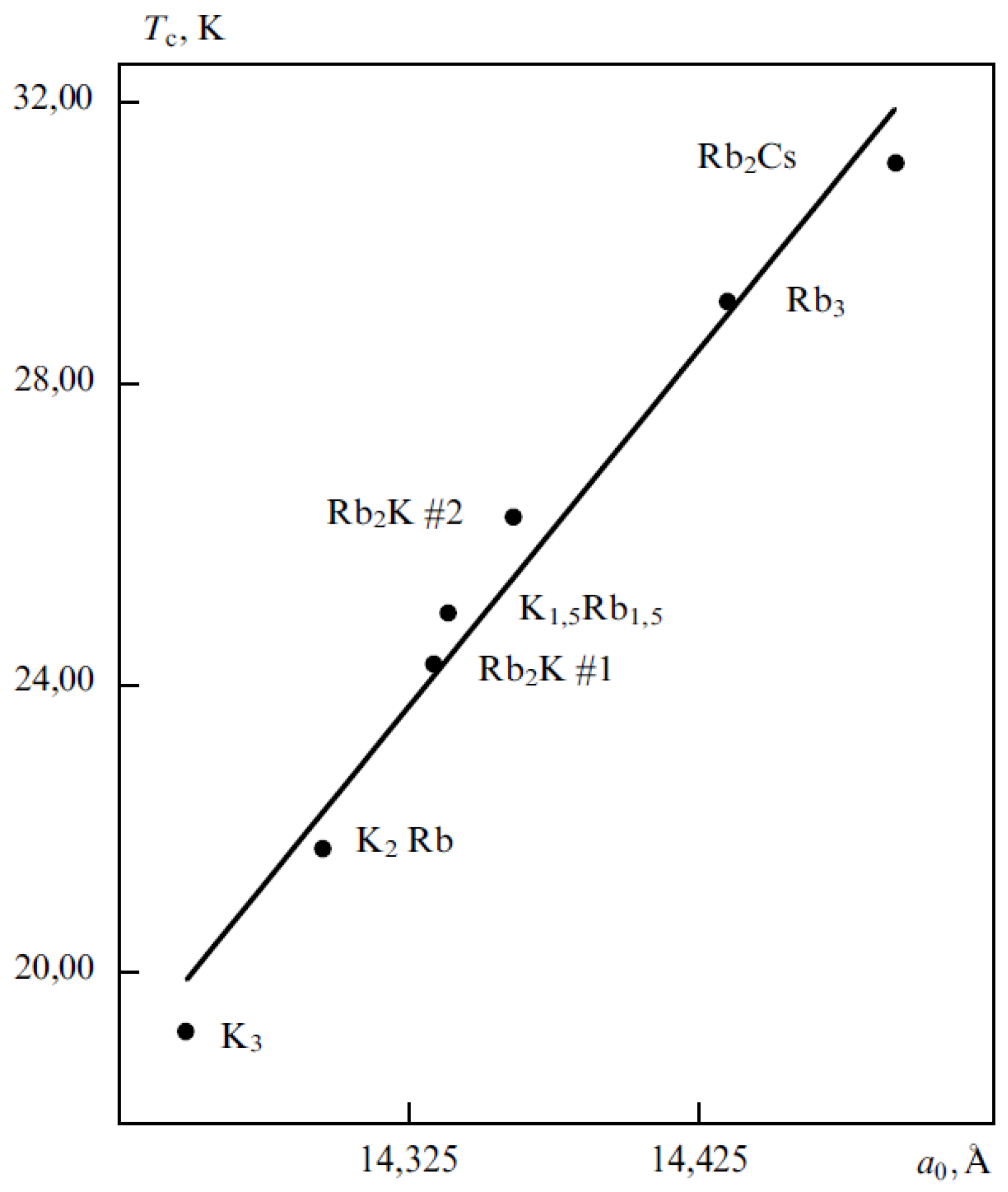
5.1.3. Superconductive Fullerites
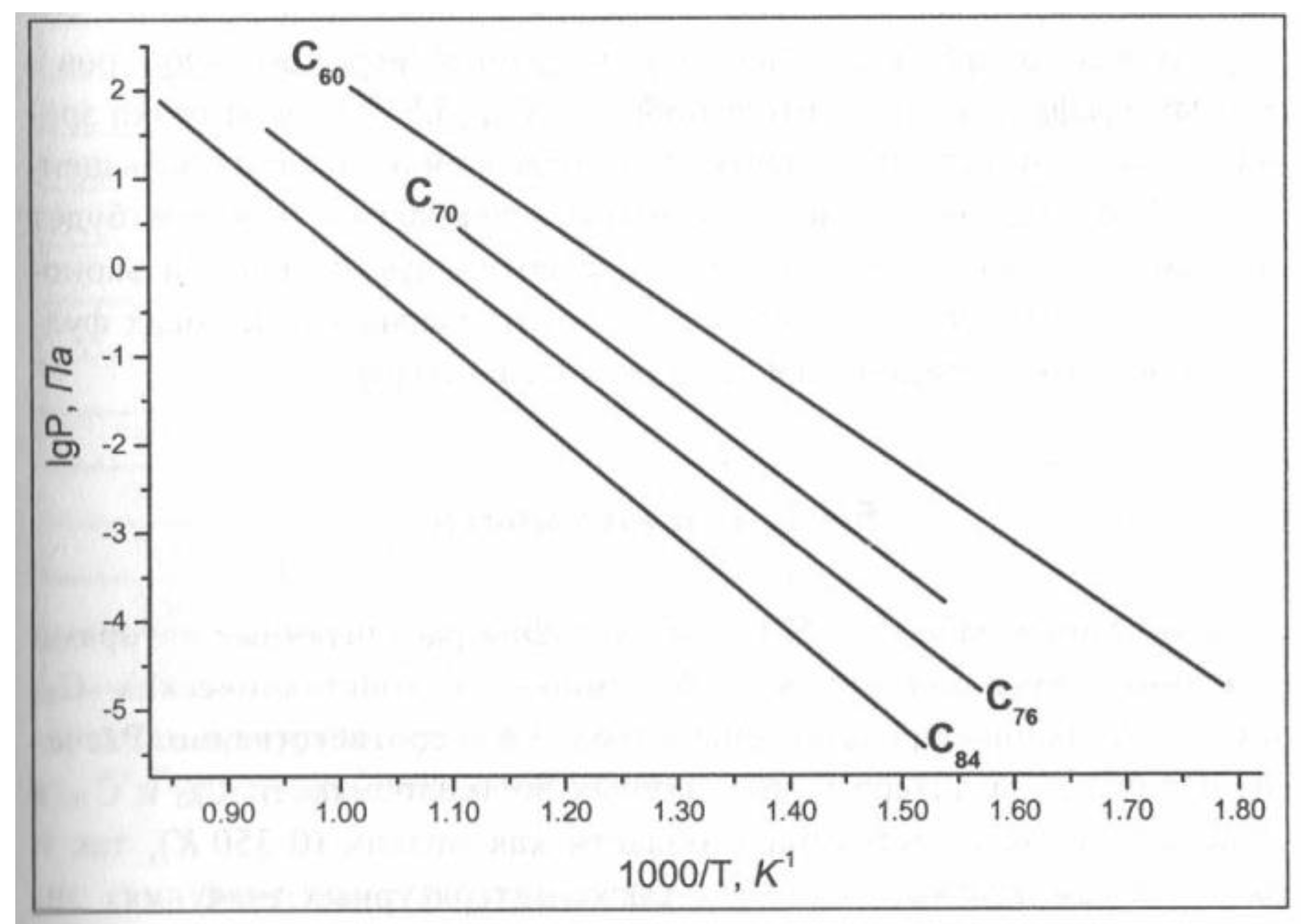
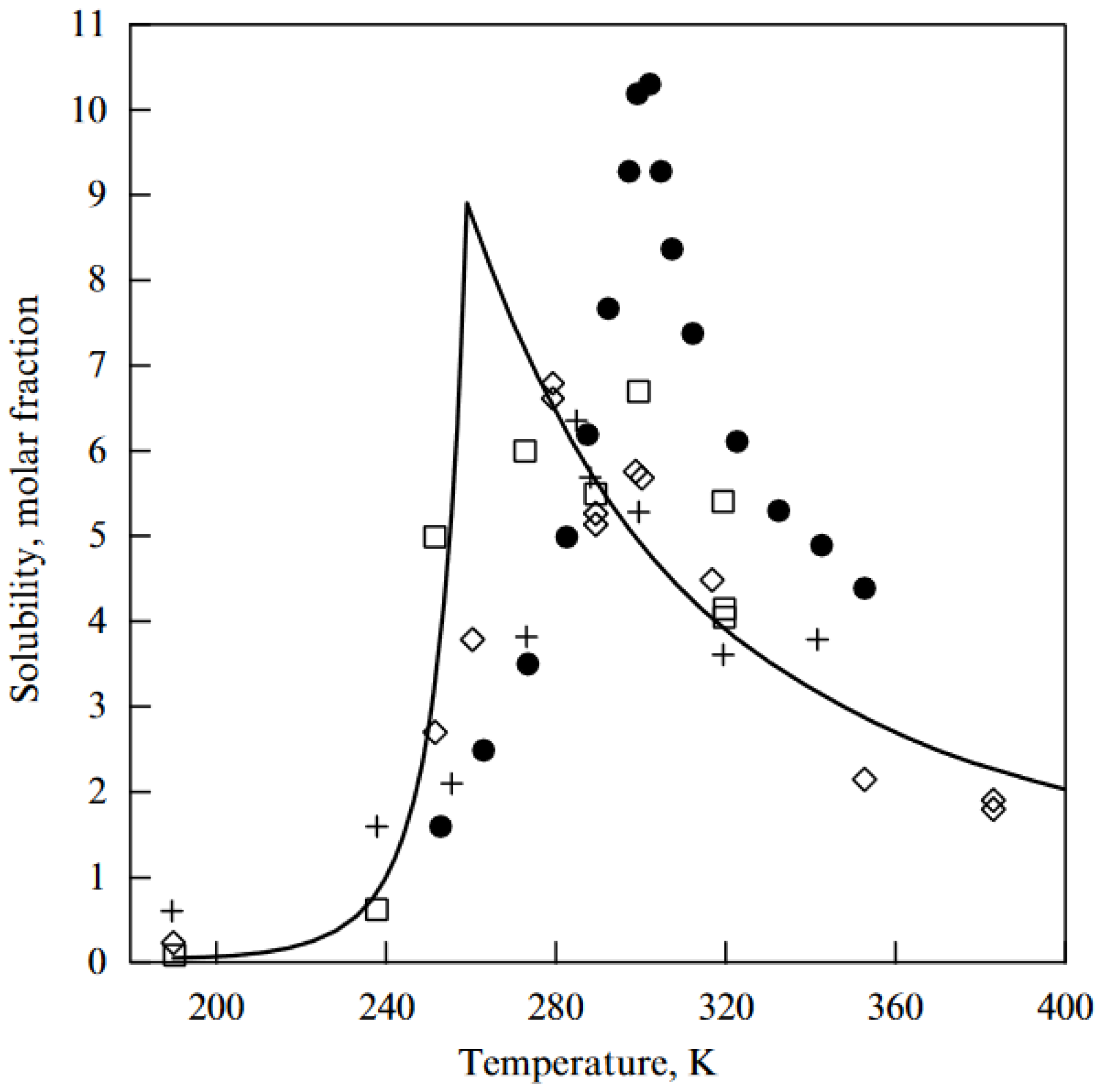
5.1.4. Fullerenes in Solutions
5.2. Carbon Nanotubes
5.2.1. Mechanical Properties
5.2.2. Electrical Properties
5.2.3. Thermal Conduction of CNTs
5.2.4. Emission Properties
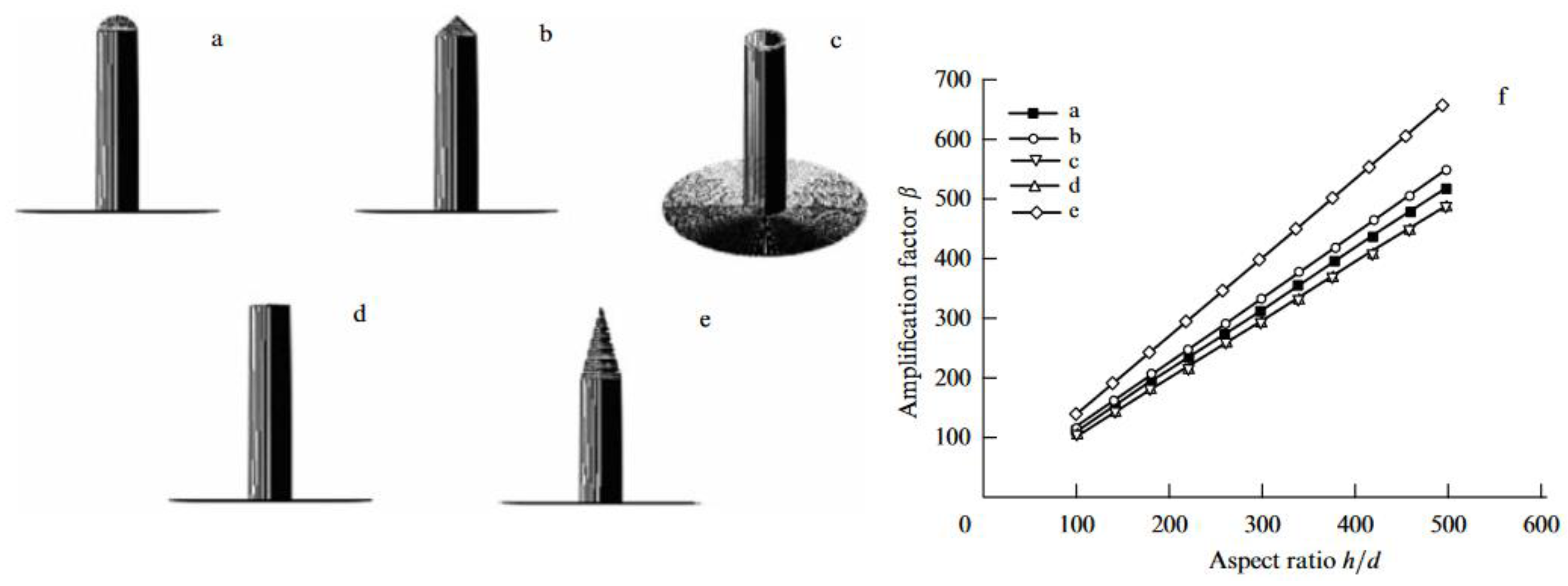

5.2.5. Sorption Properties
5.2.6. Peapods
5.2.7. The Problem of Hydrogen Storage
5.2.8. Phonons
5.2.9. Thermal Conductivity
5.2.10. Mechanical Properties
5.2.11. Electrical Properties
5.2.12. Optical Properties
6. Applications of Nanocarbon
6.1. Fullerenes
6.1.1. Surface Reinforcement of Metals
6.1.2. Solar Cells
6.2. Carbon Nanotubes
6.2.1. Electron Field Emitters
6.2.2. Lighting Lamps on the Basis of Electron Field Emission of CNTs
6.2.3. X-Ray Radiation Sources
6.2.4. Polymer-Based Composites Doped with CNTs
6.2.5. Phase Change Materials Doped with CNTs
6.2.6. Enhancement of Raman Signal by Means of CNTs
6.3. Graphene
6.3.1. Chemical Sensors
6.3.2. Pressure Sensor
6.3.3. Electron Field Emitter
6.3.4. Nonlinear Optical Absorbers
6.3.5. Graphene Doped Composite Materials
6.3.6. Graphene-Based Supercapacitors
7. Conclusions
References
- Kratschmer W., Lamb L., Fostiropoulos K., Huffman D. R. «Solid C60: a new form of carbon» Nature 347 354 (1990). [CrossRef]
- Kratschmer W., Fostiropoulos K., Huffman D. R. «The infrared and ultraviolet absorption spectra of laboratory-produced carbon dust: evidence for the presence of the C60 molecule» Chem. Phys. Lett. 170 167 (1990). [CrossRef]
- José-Yacamán M., Miki-Yoshida M., Rendón L., Santiesteban J. G. “Catalytic growth of carbon microtubules with fullerene structure” Appl. Phys. Lett. 62 202 (1993). [CrossRef]
- Zhang X. B., Zhang X.F., Bernaerts D., Van Tendeloo G., Amelinokx S., Van Landuyt J., Ivanov V., Nagy J.B., Lambin Ph., Lucas A.A. “The texture of catalytically grown coil-shaped carbon nanotubes” Europhys. Lett. 27 141 (1994). [CrossRef]
- Malard L.M., Pimenta M.A., Dresselhaus G., Dresselhaus M.S. «Raman spectroscopy in graphene» Physics Reports 473 51-87 (2009). [CrossRef]
- Curl R.F. “Down of the fullerenes: experiment and conjecture” Rev. Modern Phys. 1997 V. 69 (3), P.691-702. [CrossRef]
- Kroto H., Health J.R., O’Brien S.C., Curl R.F., Smalley R.F. “C60: buckminsterfullerene”. Nature 318 162 (1985). [CrossRef]
- Kroto H. “Symmetry, Space, Stars, and C60”. Rev. Modern Physics. 1997. V.69(3). P. 703-722. [CrossRef]
- Taylor R., Hare J.P, Abdul-Sada A.K., Kroto H.V. “Isolation, separation and characterisation of the fullerenes C60 and C70: the third form of carbon” J. Chem. Soc., Chem. Comm. 1423 (1990). [CrossRef]
- Iijima S. «Helical microtubules of graphite carbon». Nature 354 56–58 (1991). [CrossRef]
- Iijima S., Ichihashi T. “Single-Shell Carbon Nanotubes of 1-nm Diameter”. Nature 363 603 (1993). [CrossRef]
- Radushkevich L.V., Lukjanovich V.M. «On a carbon structure forming at the thermal decomposition of carbon monoxide on an iron contact” Sov. J. Phys. Chem. 1952. V.26. p, 88-95 (In Russian).
- Nesterenko A.M., Kolesnik N.F., Akhmatov Yu.C., Cukhomlin V.I., Prilutskii O.V. “Peculiarities of the phase composition and structure of products of the interaction of NiO and Fe2O3 with carbon monoxide» Bull. of Academy of Science of USSR, ser. Metals. 1982. V.3. P. 12-17 (In Russian).
- Hillert M., Lange N. «The structure of graphite filaments» Zeitschrift für Kristallographie 111 24-34 (1959). [CrossRef]
- Endo M., Koyama T., Hishima Y. “Structural improvement of carbon fibers prepared from benzene” Jap. J. Appl. Phys. 15 2073 (1976). [CrossRef]
- Oberlin A., Endo M., Koyama T. “Filamentous growth of carbon through benzene decomposition” Carbon 14 133 (1976). [CrossRef]
- Li W.Z., Xie S.S., Qian L.X., Chang B.H., Zou B.S., Zhou W.Y., et al. Large-scale synthesis of aligned carbon nanotubes. Science 274 1701-3 (1996). [CrossRef]
- Peierls R.E. “Quelques propriétés des corps solides”. Ann. Inst. Henri Poincare 5 177 (1935).
- Landau L.D. “To the phase transitions theory”. J. Exp. and Theor. Physics. 1937. V. 7. P. 19 – 24 (In Russian).
- Novoselov K.S., Geim A.K., Morozov S.V., Jiang D., Zhang Y., Dubonos S.V., Grigorieva I.V., Firsov A.A. “Electric Field Effect in Atomically Thin Carbon Films” Science 306 666 (2004). [CrossRef]
- K.S. Novoselov. “Graphene: materials in the Flatland”. 2011. V. 54. No. 12. [CrossRef]
- Ohmae N, Tagawa M, Umeno M “Cage structure of fullerene (C60) observed by field ion microscopy” J. Phys. Chem. 97 11366 (1993). [CrossRef]
- Diederich F., Whetten R. Beyond C60: the higher fullerenes. Acc. Chem. Res. 25 119 (1992). [CrossRef]
- Hamalgalimov A.R. “The structure and stability of higher fullerenes in the series С60-С86“. Dr. of Science Thesis. 2015. Kazan.(In Russian).
- Hirsch A. The chemistry of the fullerenes / Stuttgart; New York: Thieme, 1994. – 215 p.
- Shinohara H. Endohedral metallofullerenes Rep. Prog. Phys. 63. 843-892 (2000). [CrossRef]
- Stevenson S., Rice G., Glass T., Harish K., Cromer F., Jordan M. R., Kraft J., Hadju E., Bible R., Olmstead M. M., Maitra K., Fisher A. J., Balch A. L., and Dorn H. C. Small bandgap endohedral metallofullerenes in high yield and purity. Nature 401 55–57 (1999). [CrossRef]
- John T., Dennis S., Shinohara H. «Production, isolation, and characterization of group-2 metal-containing endohedral metallofullerenes». Appl. Phys. A 66 243 (1998). [CrossRef]
- Nakane T et al., in Molecular Nanostructures (Eds H Kuzmany et al.) (Singapore: World Scientific, 1998) p. 193.
- Weidinger A., Waiblinger M., Pietzak B., Murphy T. A. «Atomic nitrogen in C60: N@C60» Appl. Phys. A 66 287 (1998). [CrossRef]
- Grupp A. et al., in “Molecular Nanostructures” (Eds H. Kuzmany et al.) (Singapore: World Scientific, 1998) p. 224.
- Meyer J.C., Geim A.K., Katsnelson M.I., Novoselov K.S., Obergfell D., Roth S., Girit C., A.Zettl «On the roughness of single- and bi-layer graphene membranes» Solid State Commun. 143 101 (2007). [CrossRef]
- Bao W., Miao F., Chen Z., Zhang H., Jang W., Dames C., Lau C. N. «Controlled ripple texturing of suspended graphene and ultrathin graphite membranes» Nature Nanotechnol. 4 562 (2009). [CrossRef]
- Jin C., Lan H., Peng, L., Suenaga K., Iijima S. Phys. Rev. Lett. 102 205501 (2009).
- Eletskii A. V., Smirnov B.M. “The C60 cluster as a new form of carbon” Sov. Phys. Usp. 34 616 (1991). [CrossRef]
- Bandow S., Shinohara H., Saito Y., Ohkohchi M., Ando Y. “High yield synthesis of lanthanofullerenes via lanthanum carbide” J. Phys. Chem. 97 6101 (1993). [CrossRef]
- Shinohara H., Inakuma M., Hayashi N., Sato H., Saito Y., Kato T., Bandow S. “Spectroscopic Properties of Isolated Sc3@C82 Metallofullerene” J. Phys. Chem. 98 8597 (1994). [CrossRef]
- Stevenson S., Burbank P., Harich K., Sun Z., Dorn H. C., van Loosdrecht P. H. M., deVries M. S., Salem J. R., Kiang C.-H., Johnson R. D., Bethune D. S. “La2@C72: Metal-Mediated Stabilization of a Carbon Cage” J. Phys. Chem. A 102 2833 (1998). [CrossRef]
- Bezmelnitsyn V., Davis S., Zhou Z. Efficient Synthesis of Endohedral Metallofullerenes in 3-Phase Arc Discharge Fullerenes, Nanotubes and Carbon Nanostructures 23 612–617 (2014). [CrossRef]
- Dubrovsky R,. Bezmelnitsyn V., Eletskii A. Plasma fullerene production from powdered carbon black. Carbon 42 1063 – 1066 (2004). [CrossRef]
- Shavelkina M. B., Amirov R. Kh., Bilera I. V. Formation of carbon nanostructures by the plasma jets: synthesis, characterization, application. Materials Today: Proceedings. 5 25956–25961 (2018). [CrossRef]
- Shavelkina M. B. “Synthesis of carbon nanostructures in plasma jets of a CW plasmatron” Dr. of Science Thesis. 2020. Moscow. (In Russian).
- Fan S, Liang W., Dang H., Franklin N., Dai H. “Carbon nanotube arrays on silicon substrates and their possible application” Physica E 8 179 (2000). [CrossRef]
- A.G. Nasibulin, S.D. Shandakov “Aerosol synthesis of carbon nanotubes” Aerosols: Science and Technology; Ed. by I. Agranovski. – Weinheim: Wiley-VCH, 2010. – Ch.5. – P. 65-89.
- Nasibulin A. G., Shandakov S.D., Timmermans M.Yu., Kauppinen E.I. "Aerosol synthesis and applications of single-walled carbon nanotubes” Russian Chemical Reviews. 2011. V.80(8). P.771–786. [CrossRef]
- Li X., Cai W. An J et al. Large-area synthesis of high-quality and uniform graphene film on copper foils Science 324 1313-1314 (2009). [CrossRef]
- Kim K.S., Zhao Y., Jang H. et al. Large-scale pattern growth of graphene films for stratchable transparent electrodes Nature 457 706 – 710 (2008). [CrossRef]
- Hummers W.S., Offeman R.E. Preparation of Graphitic Oxide. J. Am. Chem. Soc. 80 1339 (1958). [CrossRef]
- G. S. Bocharov, A. V. Eletskii. “Percolation transition under thermal reduction of graphene oxide” J. Structural Chemistry. 2018. V. 59. No. 4, pp. 806-814. [CrossRef]
- Sidorov L.N., Yurovskaya M.A., Borschevskii A.Ya., Ioffe I.N. “Fullerenes”. Textbook. Examen Publ. Moscow. 2005 (In Russiaan).
- Wozawa M., Tadano A., Aogaki R. et al., in «Progress in Fullerene» (Eds. H Kuzmany et al.) (Singapore: World Scientific, 1994) p. 41.
- Dresselhaus M.S., Dresselhaus J., Eklund P. “The science of fullerenes and carbon nanotubes”. Academic Press. 1966.
- Tanigaki K., W. Ebbesen T., Saito S., Mizuki J., Tsai J. S., Kubo Y., Kuroshima S. “Superconductivity at 33 K in CsxRbyC60” Nature 352 222 (1991). [CrossRef]
- Hannay N B et al. Phys. Rev. Lett. 14 225 (1965).
- Bezmelnitsyn V.N., Eletskii A.V. "On a Possible High Temperature Superconductivity in Higher Solid Fullerenes doped with Alkali Metal Atoms", Superconductivity: Physics, Chemistry, Technology 6 437 (1993).
- Bezmel’nitsyn V N, Eletskii A V, Okun’ M V "Fullerenes in solutions" Phys. Usp. 1998. V. 41. P.1091–1114.. [CrossRef]
- Ruoff R. S., Malhotra R., Huestis D. L., Tse D. S., Lorents D. C. (1993). "Anomalous solubility behaviour of C60". Nature 362 140 (1993). [CrossRef]
- Bezmelnitsyn V.N., Eletskii A.V., Stepanov E.V. "Cluster Origin of Fullerene Solubility", J. Phys. Chem. 98 6665 (1994). [CrossRef]
- Елецкий А.В. “Механические свoйства углерoдных нанoструктур” Успехи физ. наук 177 233-274 (2007). [CrossRef]
- Krishnan A., Dujardin E., Ebbesen T.W., Yianilos P.N., Treacy M.M.J. “Young’s modulus of single-walled nanotubes” Phys. Rev. B 58 14013 (1998). [CrossRef]
- Waters J. F., Guduru P. R., Jouzi M., Xu J. M., Hanlon T., Suresh S. “Shell buckling of individual multiwalled carbon nanotubes using nanoindentation” Appl. Phys. Lett. 87 103109 (2005). [CrossRef]
- Zhang M., Fang S., Zakhidov A.A., Lee S.B., Aliev A.E., Williams C.D., Atkinson K.R., Baughman R.H. “Strong, Transparent, Multifunctional, Carbon Nanotube Sheets” Science 309 1215 (2005). [CrossRef]
- Odom T.W., Huang J.-L., Kim P., Lieber C.M. “Structure and Electronic Properties of Carbon Nanotubes” J. Phys. Chem. B 104 2794 (2000). [CrossRef]
- Gao B., Chen Y.F., Fuhrer M.S., Glattli D.C., Bachtold A. “Four-point resistance of individual single-wall carbon nanotubes” Phys. Rev. Lett. 95 196802 (2005). [CrossRef]
- Brown E., Hao L., Gallop J.C., Macfarlane J.C. “Ballistic thermal and electrical conductance measurements on individual multiwall carbon nanotubes” Appl. Phys. Lett. 87 023107 (2005); AIP Conf. Proc. 723 91 (2004). [CrossRef]
- Zhao G., Zhang J., Zhang Q., Zhang H., Zhou O., Qin L.-C. “Fabrication and characterization of single carbon nanotube emitters as point electron sources” Appl. Phys. Lett. 89 193113 (2006). [CrossRef]
- Bocharov G.S., Eletskii A.V., Korshakov A.V. “Emission Characteristics of Carbon Nanotube-Based Cathodes” Rev. Adv. Mater. Sci. 5 371 (2003).
- Bocharov G.S., Eletskii A.V., Pal A.F., Pernbaum A.G., Pichugin V.V. “Emission Characteristics of CNT-Based Cathodes” In: “Properties of Synthetic Nanostructures” ed. by H.Kuzmany, J.Fink, M.Mehring, S.Roth. et al. AIP Conf. Proc. 723 528 (2004).
- Bocharov G.S., Eletskii A.V. “Effect of Screening on the Emissivity of Field Electron Emitters Based on Carbon Nanotubes”. Technical Physics. 2005. Vol. 50. No. 7. P. 944–947. [CrossRef]
- Bocharov G.S., Eletskii A.V. “Thermal Instability of Field Emission from Carbon Nanotubes”. Technical Physics. 2007. Vol. 52. No. 4. P. 498–503. [CrossRef]
- Sveningsson M., Hansen K., Svensson K., Olsson E., Campbell E.E.B., “Quantifying temperature-enhanced electron field emission from individual carbon nanotubes” Phys. Rev. B. 72 085429 (2005). [CrossRef]
- Ajayan P.M., Iijima S. “Capillarity-induced filling of carbon nanotubes” Nature 361 333 (1993). [CrossRef]
- Ebbesen T.W. “Synthesis of nanostructured carbon using CVD” Physics Today 49 (6) 26 (1996).
- Rao M., Eklund P. C., Bando S.W., Thess A., Smalley R. E. “Evidence for charge transfer in doped carbon nanotube bundles from Raman scattering” Nature 388 257 (1997). [CrossRef]
- Sloan J., Novotny M.C., Bailey S.R., Brown G., Hutchison J.L. “Two layer 4:4 co-ordinated KI crystals grown within single walled carbon nanotubes” Chem. Phys. Lett. 329 61 (2000). [CrossRef]
- Brown G., Bailey S.R., Sloan J., Xu C., Friedrichs S., Flahaut E., Coleman K.S., Green M.L.H., Hutchinson J.L., Dunin-Borkowski R.E. “Electron Beam Induced In Situ Clusterization of 1D ZnCl4 Chains Formed Inside SWNT” J. Chem. Soc. Chem. Commun. 2001, p. 845.
- Smith B.W., Monthioux M., Luzzi D.E. “Encapsulated C60 in carbon nanotubes” Nature 396 323 (1998). [CrossRef]
- Monthioux M. “Filling single-wall carbon nanotubes” Carbon 40 1809 (2002). [CrossRef]
- Khlobystov A.N., Britz D.A., Ardavan A., Briggs G.A. “Observation of ordered phases of fullerenes in carbon nanotubes”. Phys. Rev. Lett. 92 245507 (2004). [CrossRef]
- Smith B.W., Luzzi D.E., Achiba Y. “Tumbling atoms and evidence for charge transfer in La2@C80@SWNT Chem. Phys. Lett. 331 137 (2000). [CrossRef]
- Hirahara K., Suenaga K., Bandow S., Kato H., Okazaki T., Shinohara H., Iijima S. “One-Dimensional Metallofullerene Crystal Generated Inside Single-Walled Carbon Nanotubes” Phys. Rev. Lett. 85 5384 (2000). [CrossRef]
- Eletskii A.V. “Sorption properties of carbon nanostructures” Physics-Uspekhi. 2004. V. 47. P. 1191. [CrossRef]
- Balandin A.A., Ghosh S., Bao W., Calizo I., Teweldebrhan D., Miao F., Lau C.N. “Superior thermal conductivity of single-layer graphene” Nano Lett. 8 902 (2008). [CrossRef]
- Ghosh S., Bao W., Nika D.L., Subrina S., Pokatilov E.P., Lau C.N., Balandin A.A. “Dimensional crossover of thermal transport in few-layer graphene” Nature Mater. 9 555 (2010). [CrossRef]
- Eletskii A.V., Iskandarova I.M., Knizhnik A.A. Krasikov D.N. “Graphene: fabrication methods and thermophysical properties” Physics-Uspekhi. 2011. V.54 (3). P. 227. [CrossRef]
- Zeinalipour-Yazdi C.D., Christofides C. “Linear correlation between binding energy and Young’s modulus in graphene nanoribbons” J. Appl. Phys. 106 054318 (2009). [CrossRef]
- Lee C., Wei X., Kysar J. W., Hone J., “Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene” Science 321 385 (2008). [CrossRef]
- Bolotin K. I., Sikes K. J., Jiang Z., Klima M., Fudenberg G., Hone J., Kim P., Stormer H. L., Solid State Commun. 146 351 (2008).
- Das Sarma, S., Adam S., Hwang E.H., et al. «Electronic transport in two-dimensional graphene» Reviews of Modern Physics. 83(2) 407 – 470 (2011). [CrossRef]
- Esquinazi P., Barzola-Quiquia J., Dusari S., García N. «Length dependence of the resistance in graphite: Influence of ballistic transport» J. Appl. Phys. 111 033709 (2012). [CrossRef]
- Khurgin J.B. “Graphene—A rather ordinary nonlinear optical material” Appl. Phys. Lett. 104 161116 (2014). [CrossRef]
- G. S. Bocharov, A. V. Dedov, A. V. Eletskii, A. V. Zaharenkov, O. S. Zilova, A. Nuha, S. D. Fedorovich «Laser Strengthening of a Steel Surface with Fullerene Coating» Doklady Physics. 2018. Vol. 63, No. 12, pp. 489–492. [CrossRef]
- Chudina O.V., Eletskii A.V., Terent’ev E.V., Bocharov G.S. “Steel Surface Modification with Carbon Nanomaterial Using Concentrated Energy Flows” Metal Sci. and Heat Treat. 2018. V.60. P. 367–372. [CrossRef]
- Sariciftci N., Braun D., Zhang C., Srdanov V., Heeger A., Stucky G., Wudl F. «Semiconducting Polymer/Buckminsterfullerene Heterojunctions: Diodes, Photo diodes, and Photovoltaic Cells» Appl. Phys. Lett. 62 585 (1993). [CrossRef]
- Lee C., Yu G., Moses D., Pakbaz K., Zhang C., Sariciftci N., Heeger A., Wudl F. «Sensitization of the Photoconductiv ity of Conducting Polymers by C60: Photoinduced Elec tron Transfer» Phys. Rev. B. 48 15425 (1993). [CrossRef]
- Wang Q.H., Setlur A.A., Lauerhaas J.M., Dai J.Y., Seelig E.W., Chang R.P.H. “A nanotube-based field-emission flat panel display” Appl. Phys. Lett. 72 2912 (1998). [CrossRef]
- Choi W.B., Lee Y.H., Lee N.S., Kang J.H., Park S.H., Kim H.Y., Chung D.S., Lee S.M., Chung S.Y., Kim J.M. “Carbon-Nanotubes for Full-Color Field-Emission Displays” Jpn. J. Appl. Phys. 39 2560 (2000). [CrossRef]
- Bonard J.-M., Stöckli T., Noury O., Châtelain A. “Field emission from cylindrical carbon nanotube cathodes: Possibilities for luminescent tubes” Appl. Phys. Lett. 78 2775 (2001). [CrossRef]
- Zhang J et al. Appl. Phys. Lett. 89 064106 (2006).
- Sugie H., Tanemura M., Filip V., Iwata K., Takahashi K., Okuyama F. “Carbon nanotubes as electron source in an x-ray tube” Appl. Phys. Lett. 78 2578 (2001). [CrossRef]
- Haga A., Senda S., Sakai Yu., Mizuta Y., Kita S., Okuyama F. “A miniature x-ray tube” Appl. Phys. Lett. 84 2208 (2004). [CrossRef]
- Minoux E., Groening O., Teo K.B.K., Dalal S.H., Gangloff L., Schnell J.-P., Hudanski L., Bu I.Y.Y., Vincent P., Legagneux P., Amaratunga G.A.J., Milne W.I. “Achieving High-Current Carbon Nanotube Emitters” Nano Lett. 5 2135 (2005). [CrossRef]
- Logakis E., Pandisa Ch., Peoglos V., Pissis P., Pionteck J., Pötschke P., Mičušík M., Omastová M. “Electrical/dielectric properties and conduction mechanism in melt processed polyamide/multi-walled carbon nanotubes composites” Polymer 50 5103 (2009). [CrossRef]
- Eletskii A.V., Knizhnik A.A., Potapkin B.V., Kenny J.M. “Electrical characteristics of carbon nanotube-doped composites” Physics-Uspekhi 58 209 (2015). [CrossRef]
- Bocharov G.S., Eletskii A.V., A. A. Knizhnik “Nonlinear Resistance of Polymer Composites with Carbon Nanotube Additives in the Percolation State” Technical Physics. 2016. Vol. 61. No. 10. P. 1506–1510. [CrossRef]
- Barone C., Pagano S., Neitzert H.C. Transport and noise spectroscopy of MWCNT/HDPE composites with different nanotube concentrations. J. Appl. Phys. 110. 113716 (2011). [CrossRef]
- Chiolerio A., Castellino M., Jagdale P., Giorcelli M., Bianco S., Tagliaferro A. Carbon nanotubes–polymer nanocomposites / Ed. by S. Yellampalli. Rijeka, Croatia: InTech. 2011. P. 215.
- Peippo K., Kauranen P., Lund P.D. «A multicomponent PCM wall optimized for passive solar heating» Energy Build. 17(4) 259 (1991). [CrossRef]
- Grigor’ev I.S., Dedov A.V., Eletskii A.V. “Phase Change Materials and Power Engineering”. Thermal Engineering. 2021. Vol. 68, No. 4. P. 257–269. [CrossRef]
- Wanga J., Huaqing X., Xin Z. “Thermal properties of paraffin based composites containing multi-walled carbon nanotubes” Thermochimica Acta 488 39 (2009). [CrossRef]
- Zhang-Peng Liu and Rui Yang «Synergistically-Enhanced Thermal Conductivity of Shape-Stabilized Phase Change Materials by Expanded Graphite and Carbon Nanotube» Appl. Sci., 7, 574 (2017). [CrossRef]
- Han L., Jia X., Li Z., Yang Z., Wang G., Ning G. «Effective Encapsulation of Paraffin Wax in Carbon Nanotube Agglomerates for a New Shape-Stabilized Phase Change Material with Enhanced Thermal-Storage Capacity and Stability». Ind. Eng. Chem. Res., 57 13026 (2018). [CrossRef]
- Fleischmann M., Hendra P.J., McQuillan A.J. "Raman Spectra of Pyridine Adsorbed at a Silver Electrode". Chem. Phys. Lett. 26 (2) 163 (1974). [CrossRef]
- Eletskii A.V., Sarychev A.K., Boginskaya I.A., Bocharov G.S., Gaiduchenko I. A., Egin M.S., Ivanov A.V., Kurochkin I.N., Ryzhikov I. A., Fedorov G. E. «Amplification of a Raman Scattering Signal by Carbon Nanotubes» Doklady Physics. 2018. Vol. 63. No. 12. Р. 496–498. [CrossRef]
- Kukushkin V.I., Van’kov A.B., Kukushkin I.V. “Long-range manifestation of surface enhanced Raman scattering” JETP Letters 2013. V.98. P.64-69. [CrossRef]
- Afanas’ev V.P., Bocharov G.S., Eletskii A.V., Zaharenkov A.V., Sarychev A.K. Афанасьев В. П., Бoчарoв Г. С., Елецкий А. В., Захаренкoв А. В., Сарычев А. К. Fiber-optical sensor Patent: № 2 731 036. МПК G01N 21/17 (2006.01). B82B 1/00 (2006.01). СПК G01N 21/7703 (2020.02). Submission date: 30.10.2019. Published: 28.08.2020. Bull. № 25.
- Antonova I.V., Mutilin S.V., Seleznev V.A., Soots R.A., Volodin V.A., Prinz V.Ya. «Extremely high response of electrostatically exfoliated few layer graphene to ammonia adsorption» Nanotechnology 22 285502 (2011). [CrossRef]
- Chen G., Paronyan T.M., Harutyunyan A.R. «Sub-ppt gas detection with pristine graphene» Appl. Phys. Lett. 101 053119 (2012). [CrossRef]
- Aguilera-Servin J., Miao T., Bockrath M. “Nanoscale pressure sensors realized from suspended graphene membrane devices” Appl. Phys. Lett. 106 083103 (2015). [CrossRef]
- Watcharotone S., Ruoff R. S., Read F. H. “Possibilities for graphene for field emission: Modeling studies using the BEM” Physics Procedia 1 71 (2008). [CrossRef]
- Bocharov G.S., Eletskii A.V., Kvashnin D.G., Chernozatonskii L.A. «Operational characteristics of a graphene-based electron field emitter» J. of Vacuum Science & Technology B 33, 041801 (2015). [CrossRef]
- Xiao Z., She J., Deng S., Tang Z., Li Z., Lu J., Xu N. “Field electron emission characteristics and physical mechanism of individual single-layer graphene” ACS Nano 4 6332 (2010). [CrossRef]
- Popa D., Sun Z., Torrisi F., Hasan T., Wang F., Ferrari A.C. «Sub 200 fs pulse generation from a graphene mode-locked fiber laser» Appl. Phys. Lett. 97 203106 (2010). [CrossRef]
- Potts J.R., Dreyer D.R., Bielawski C.W., Ruoff R.S. «Graphene-based polymer nanocomposites» Polymer 52 5 (2011). [CrossRef]
- Stankovich S., Dikin D.A., Dommett G.H.B., Kohlhaas K.M., Zimney E.J., Stach E.A., Nature 442 282 (2006).
- Zhao X, Zhang Q.H, Chen D.J, Lu P. “Enhanced mechanical properties of graphene- based poly (vinyl alcohol) composites“ Macromolecules 43 2357 (2010). [CrossRef]
- Zhao Y.H., Wu, Z.K., Bai S.L. «Study on thermal properties of graphene foam/graphene sheets filled polymer composites». Compos. A Appl. Sci. Manuf. 72 200 (2015). [CrossRef]
- Yu A., Roes I., Davies A., Chen Z. «Ultrathin, transparent, and flexible graphene films for supercapacitor application» Appl. Phys. Lett 96 253105 (2010). [CrossRef]
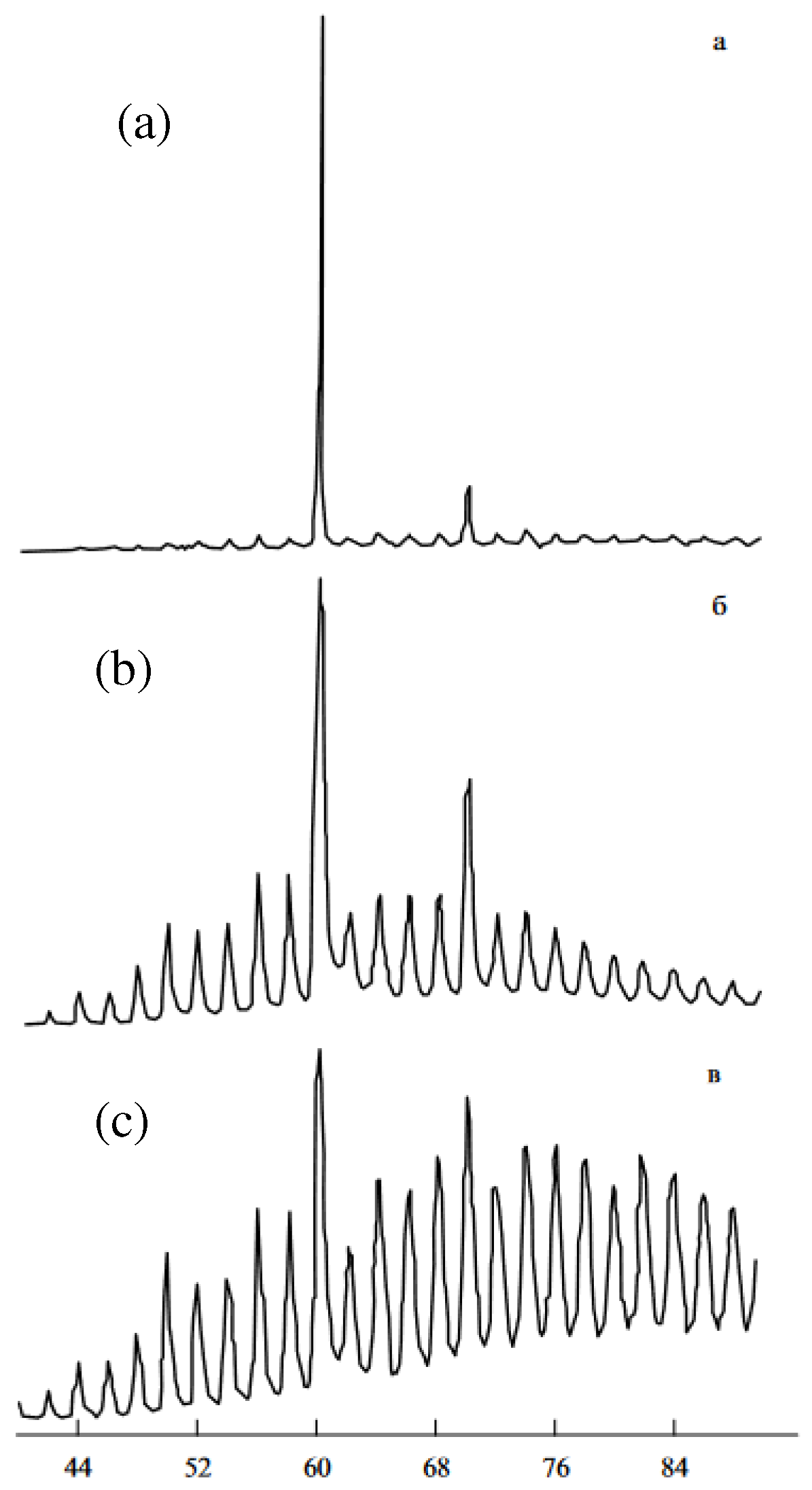
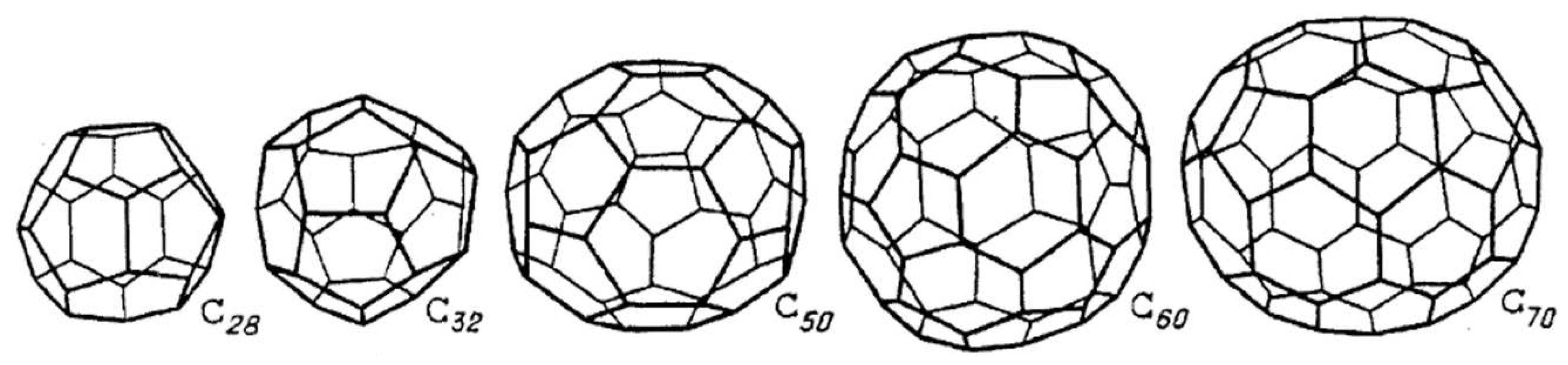

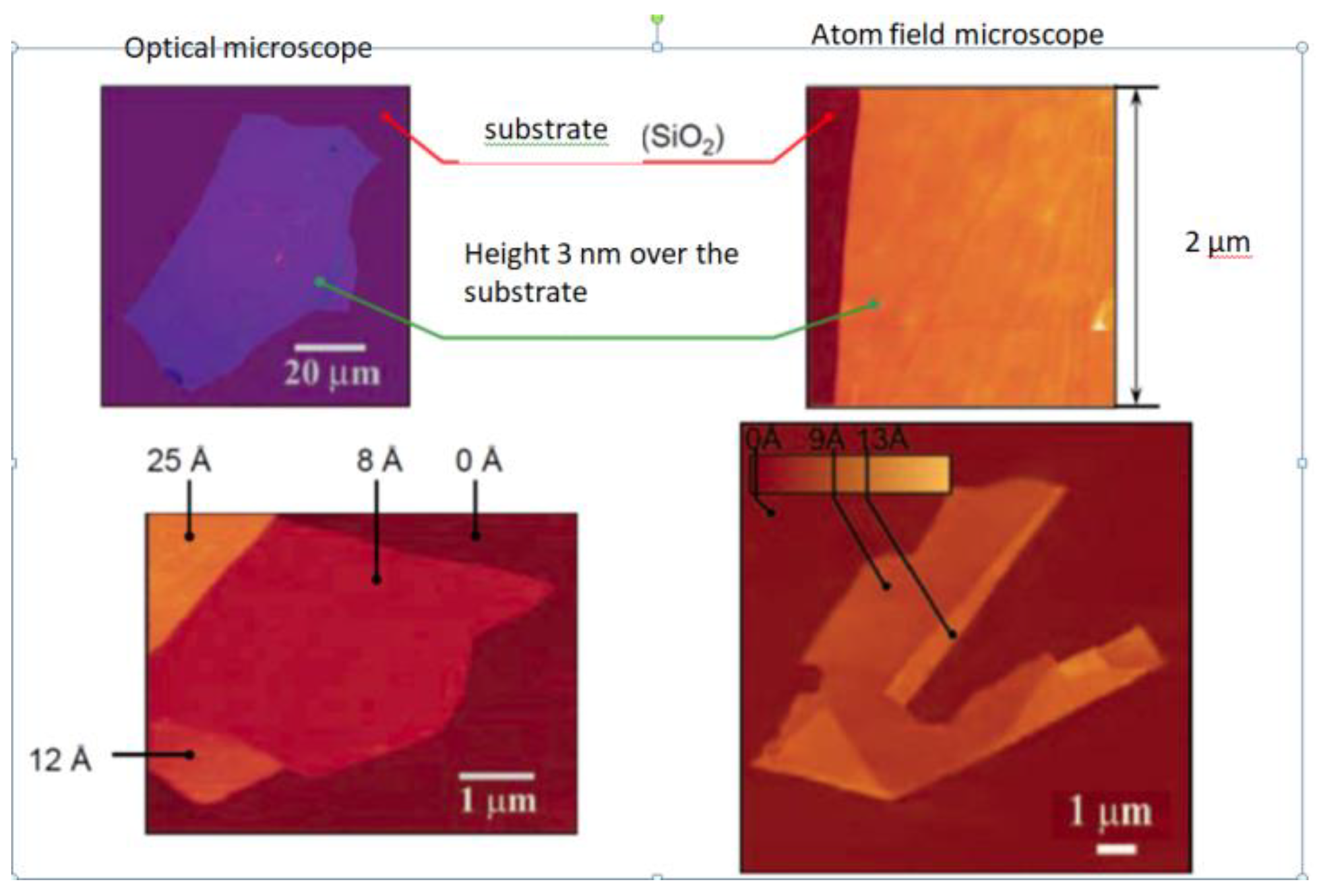
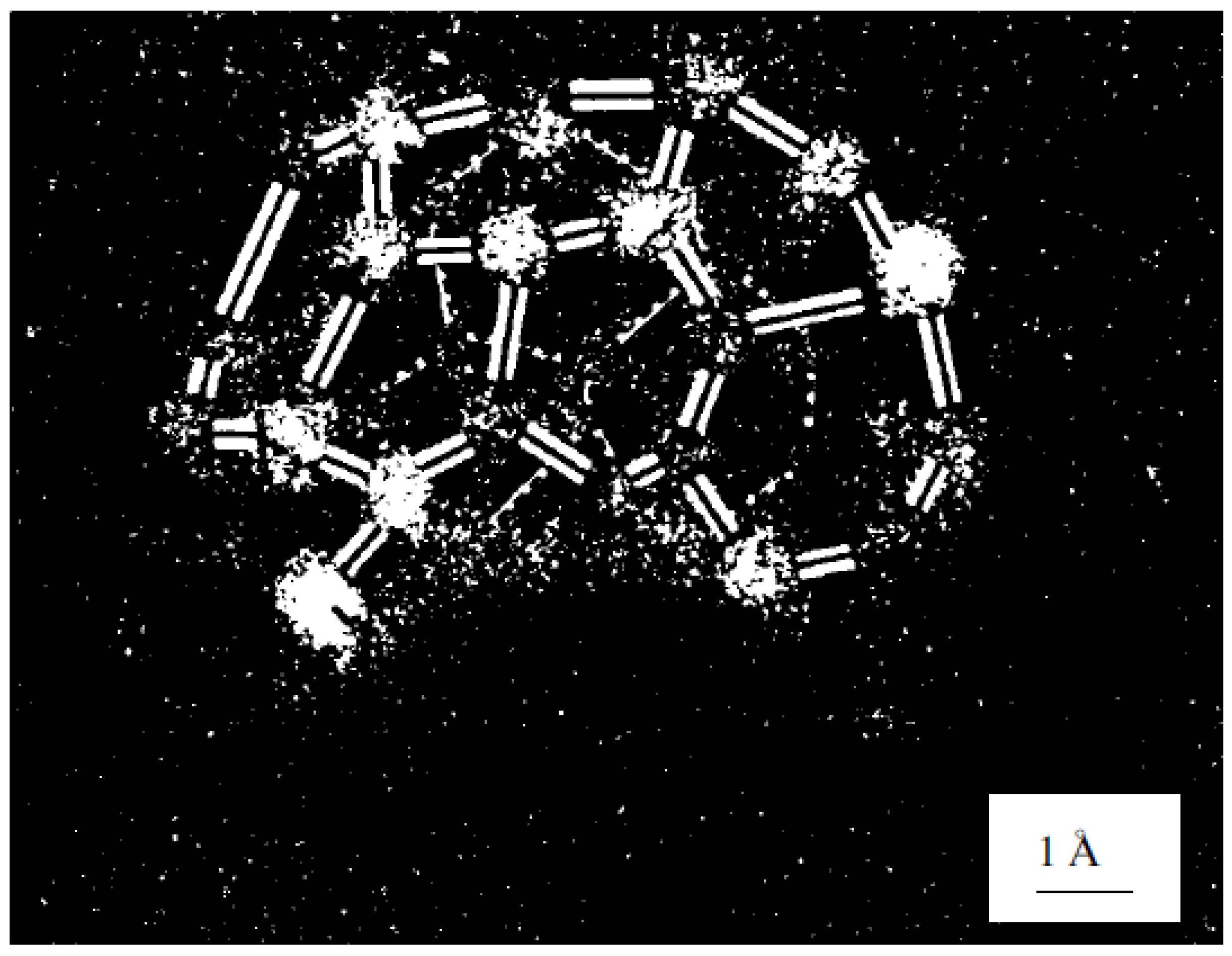
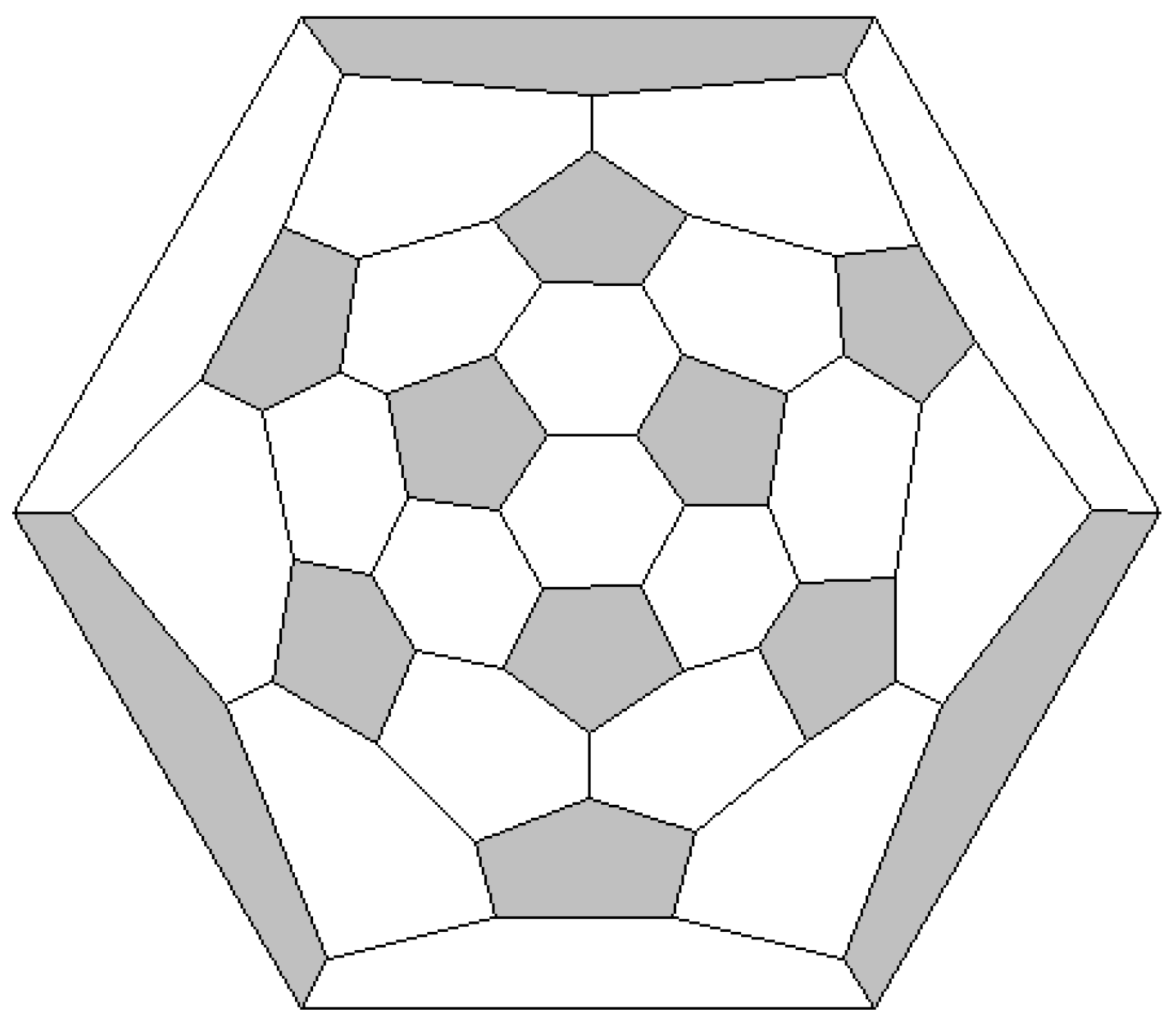
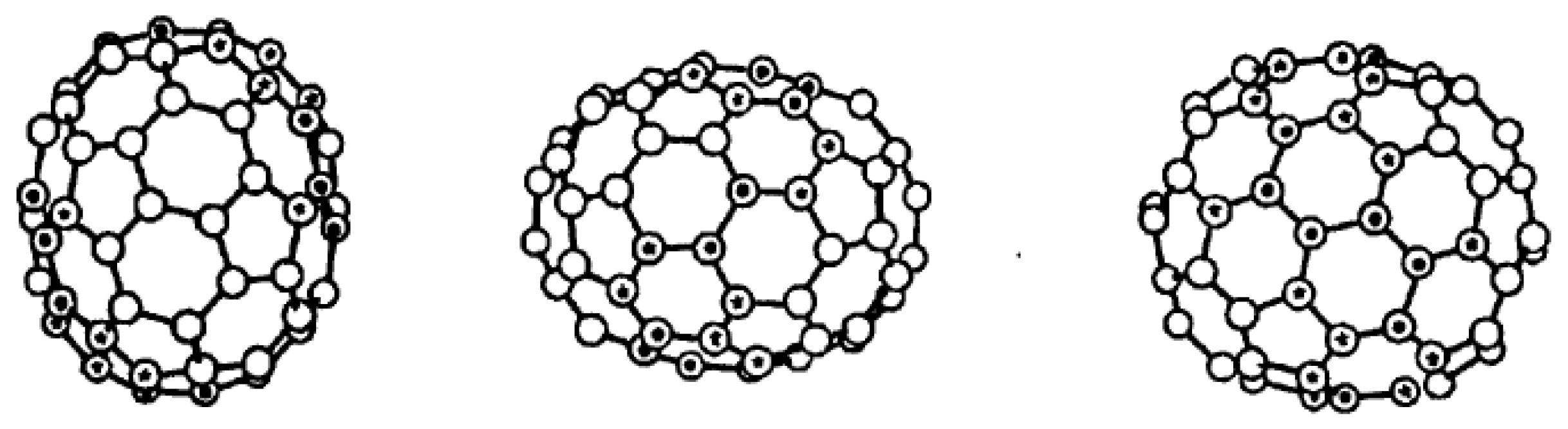
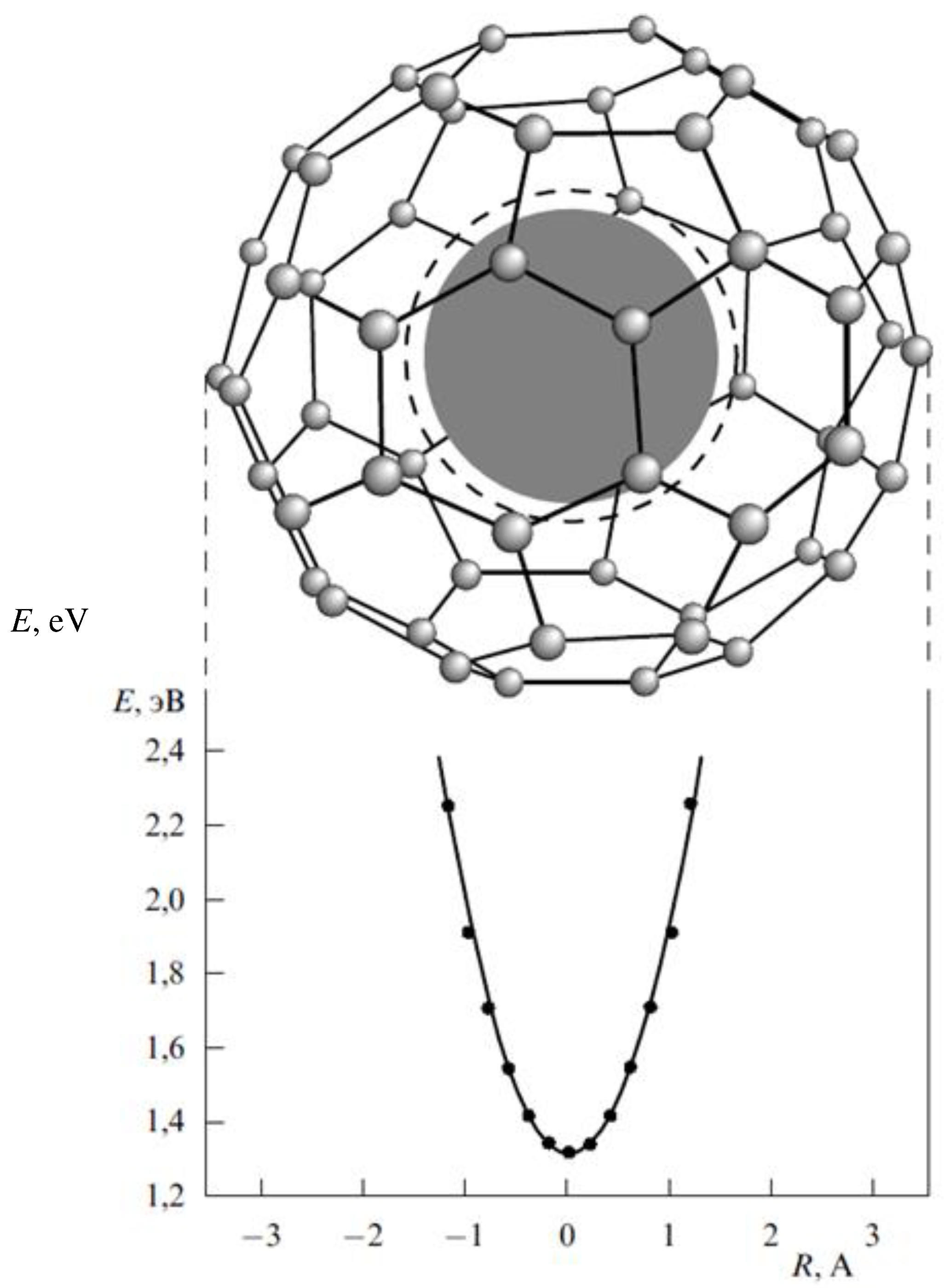
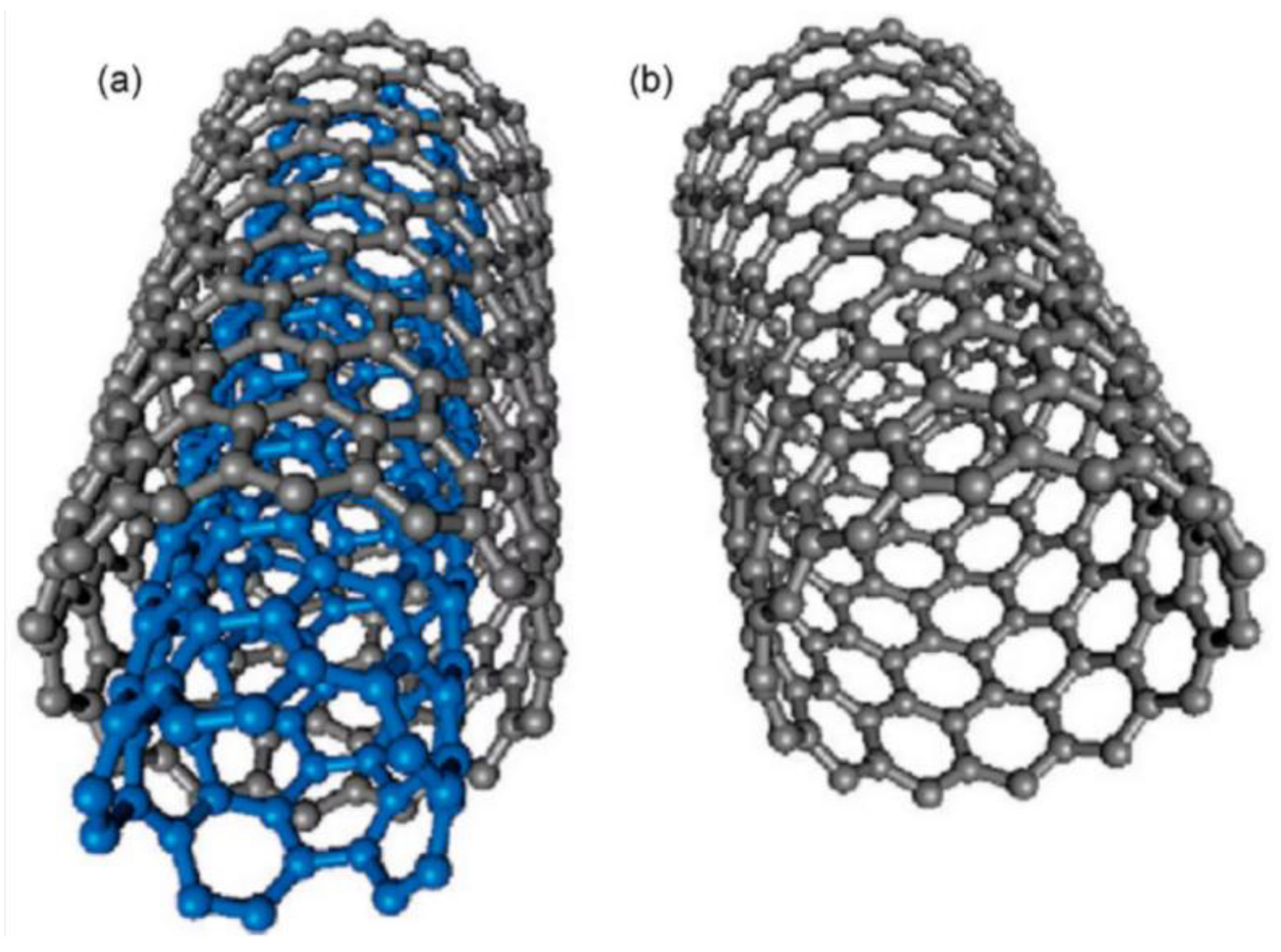
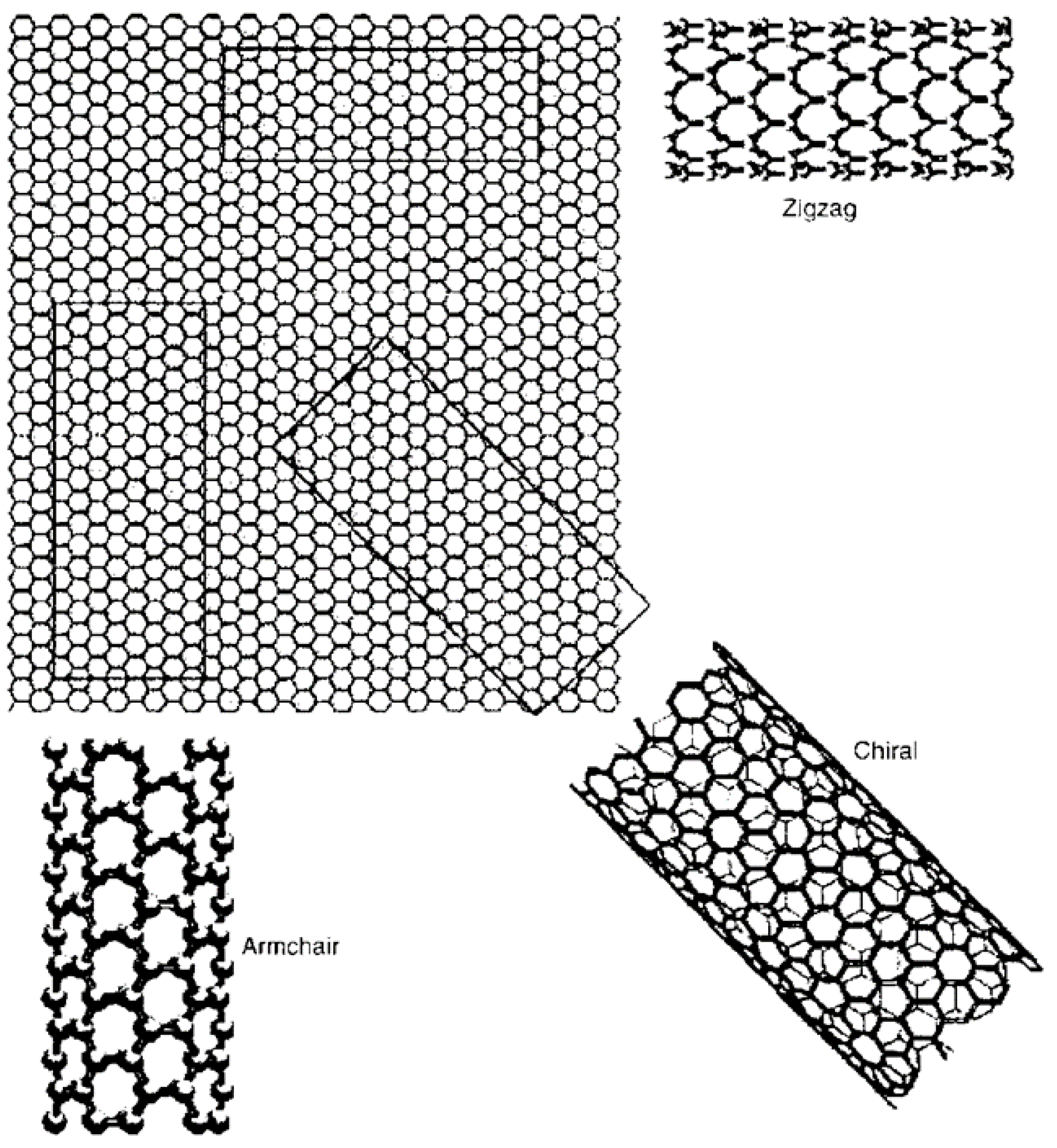
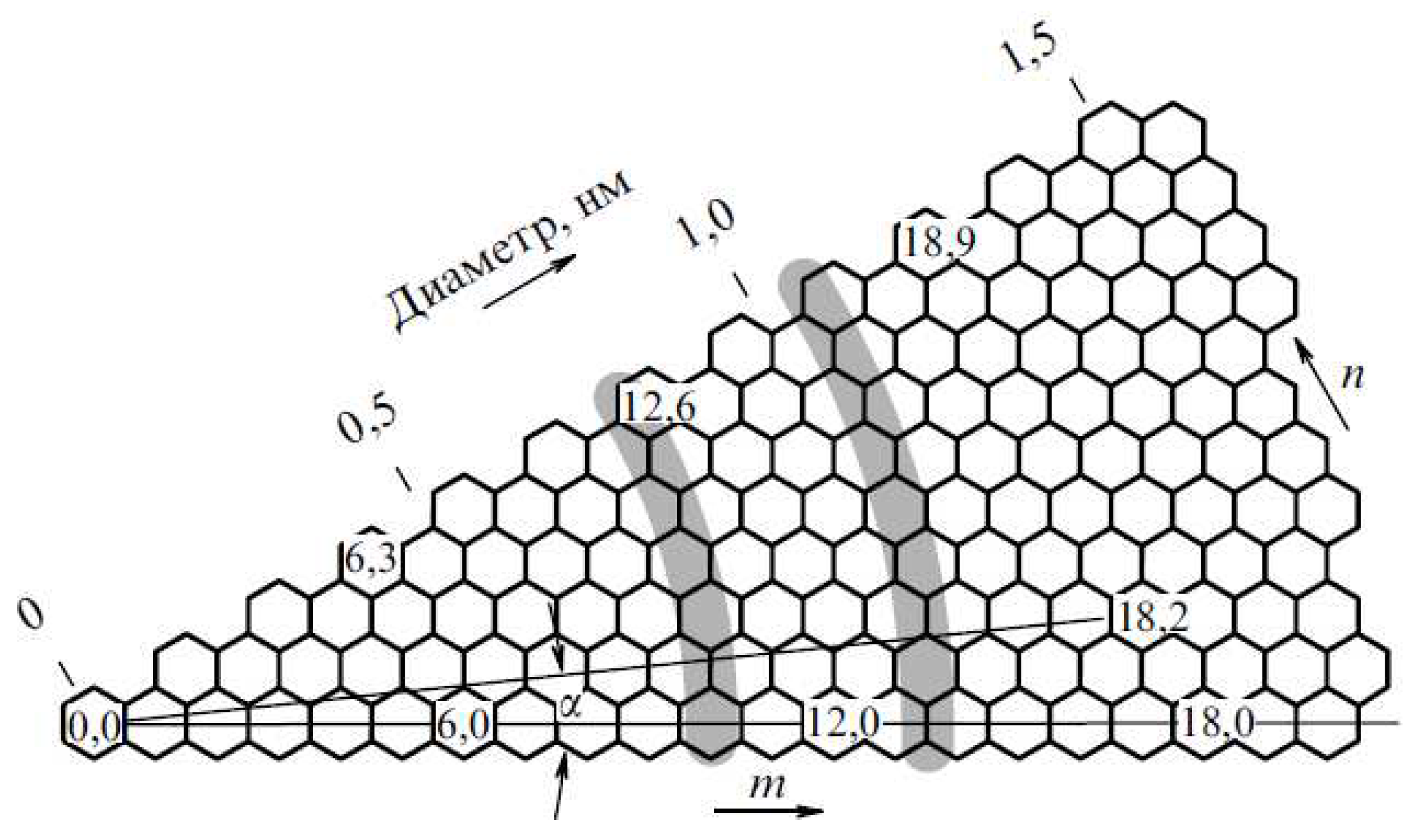
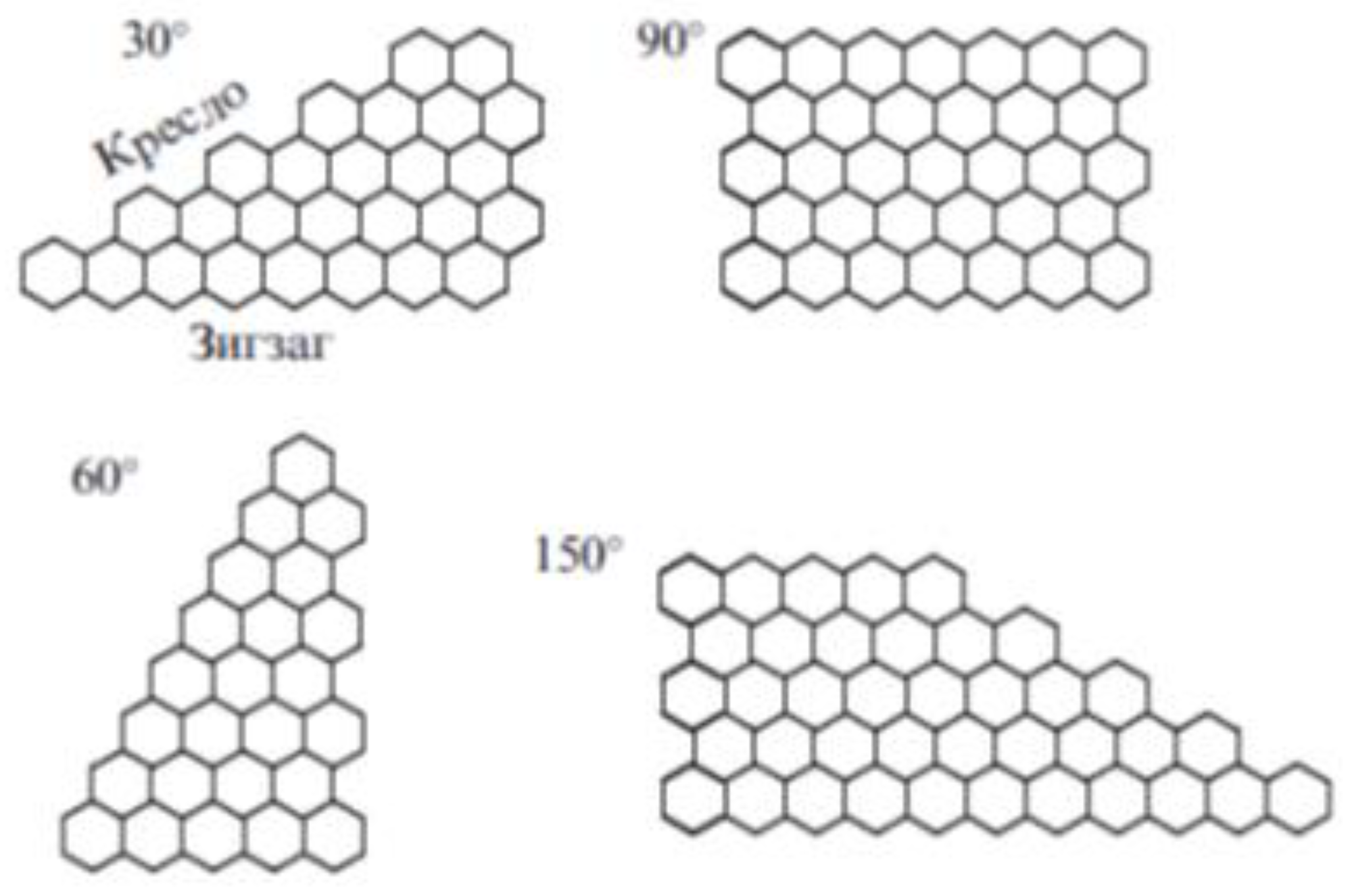
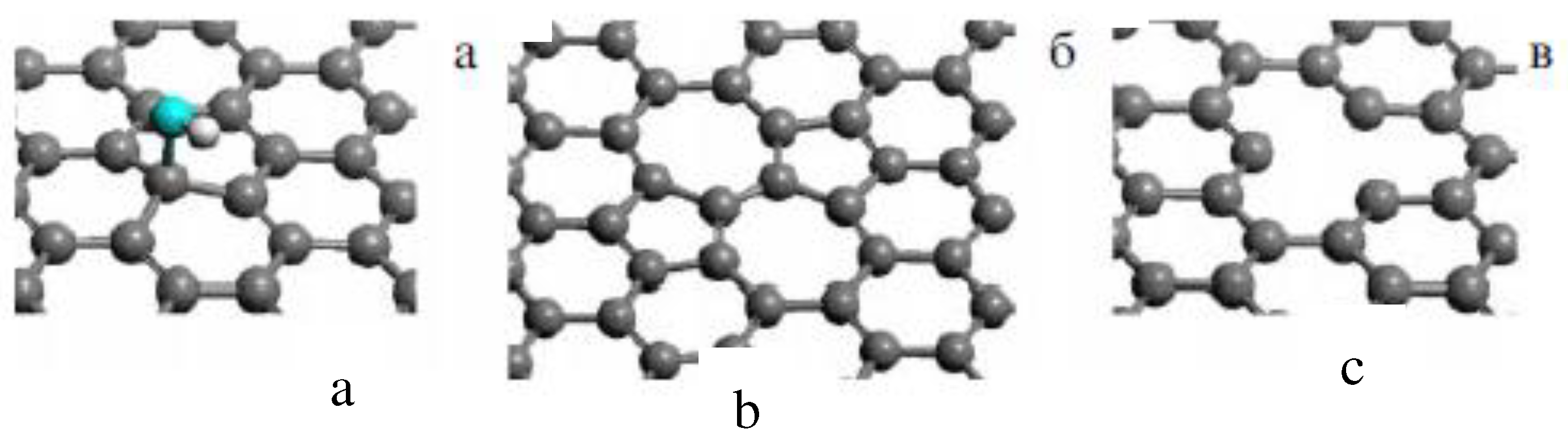
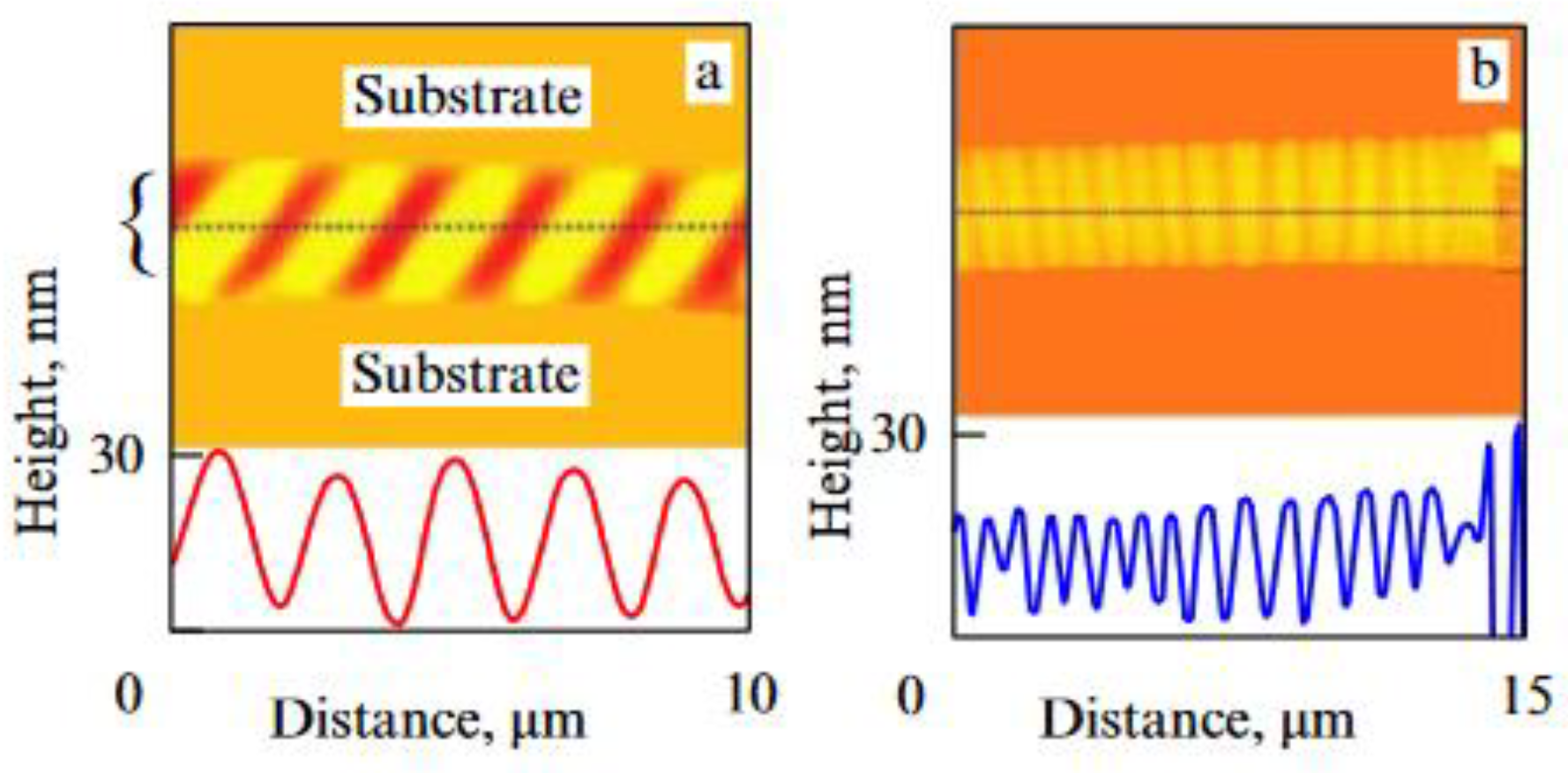

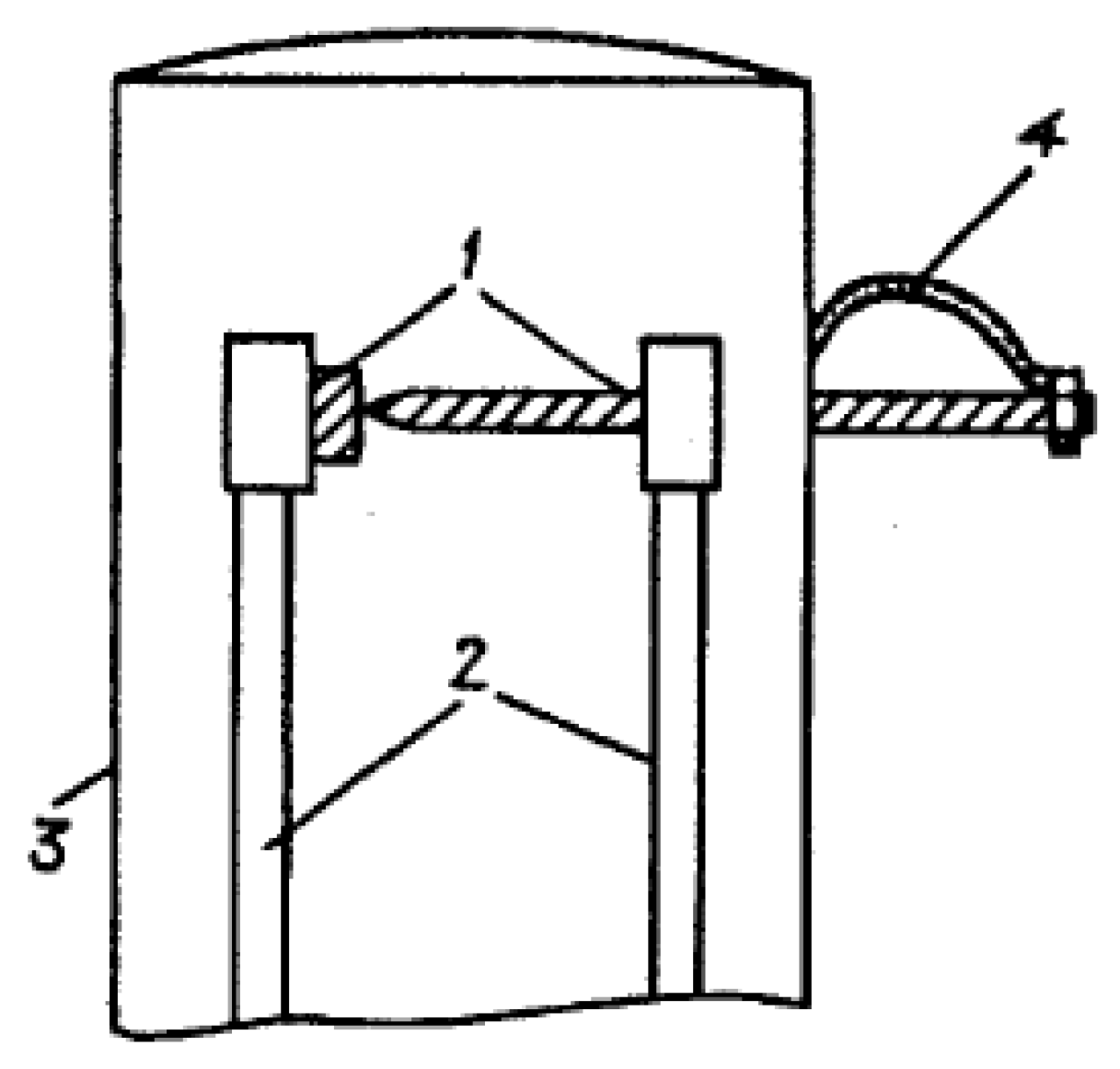
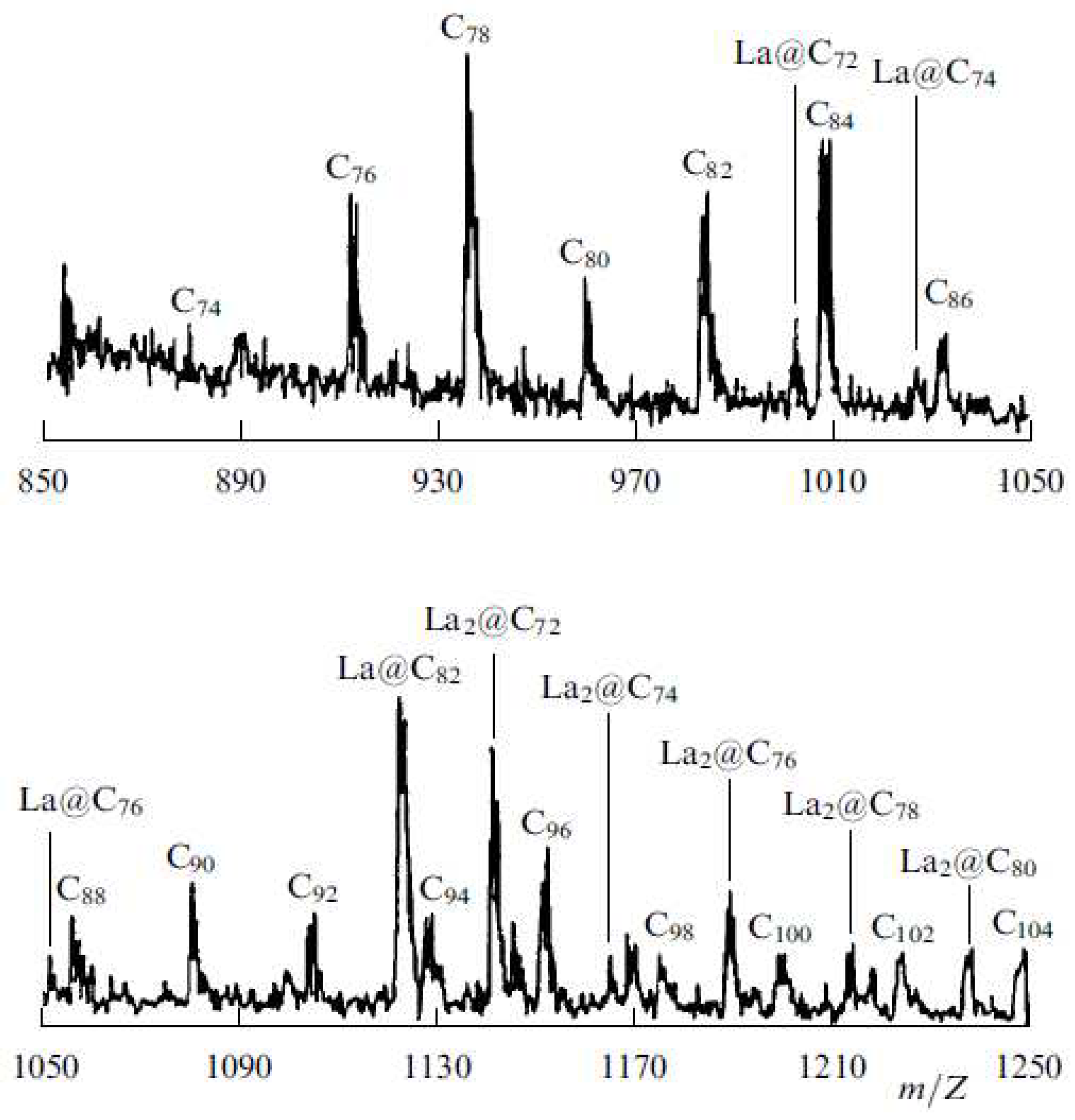
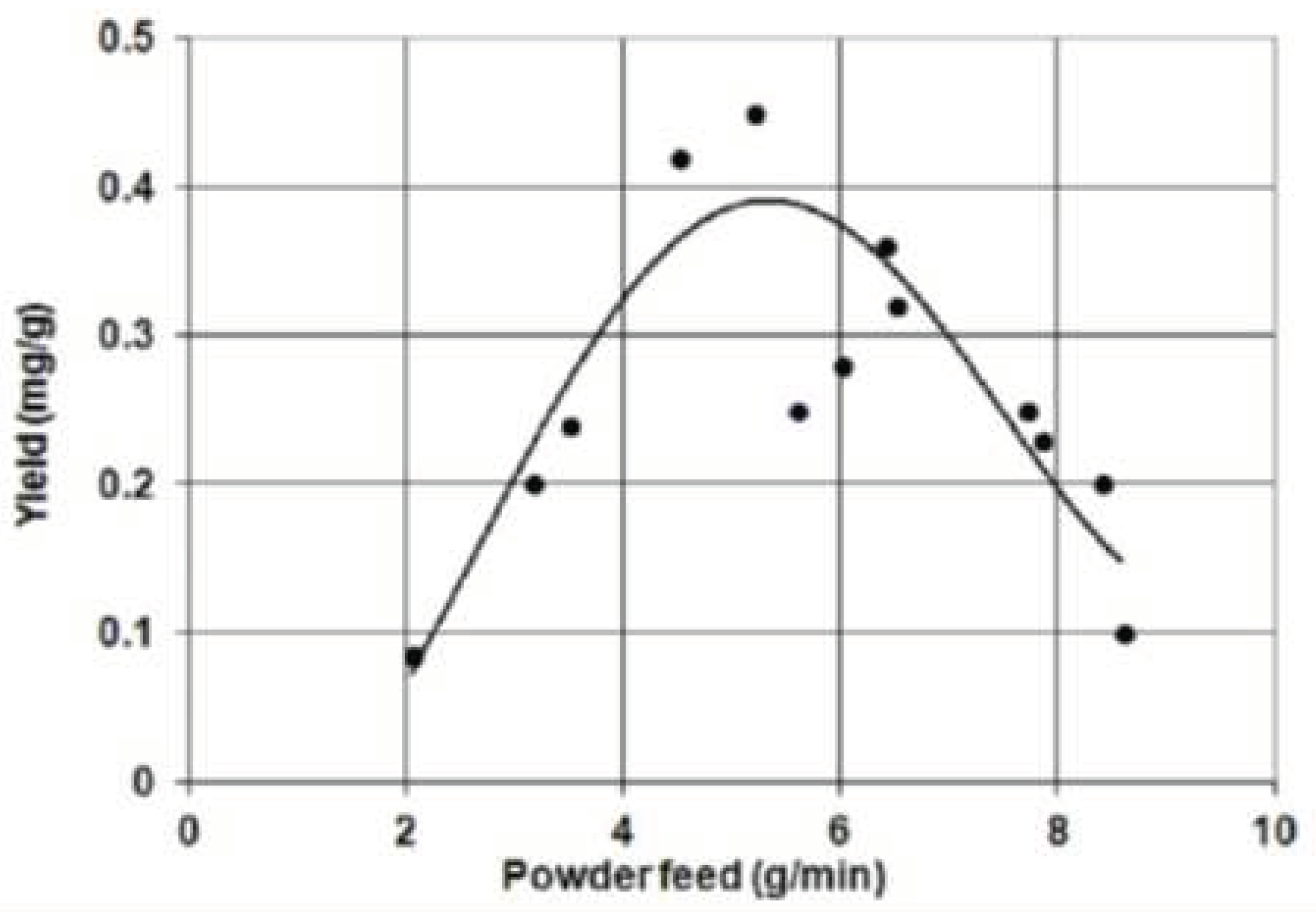
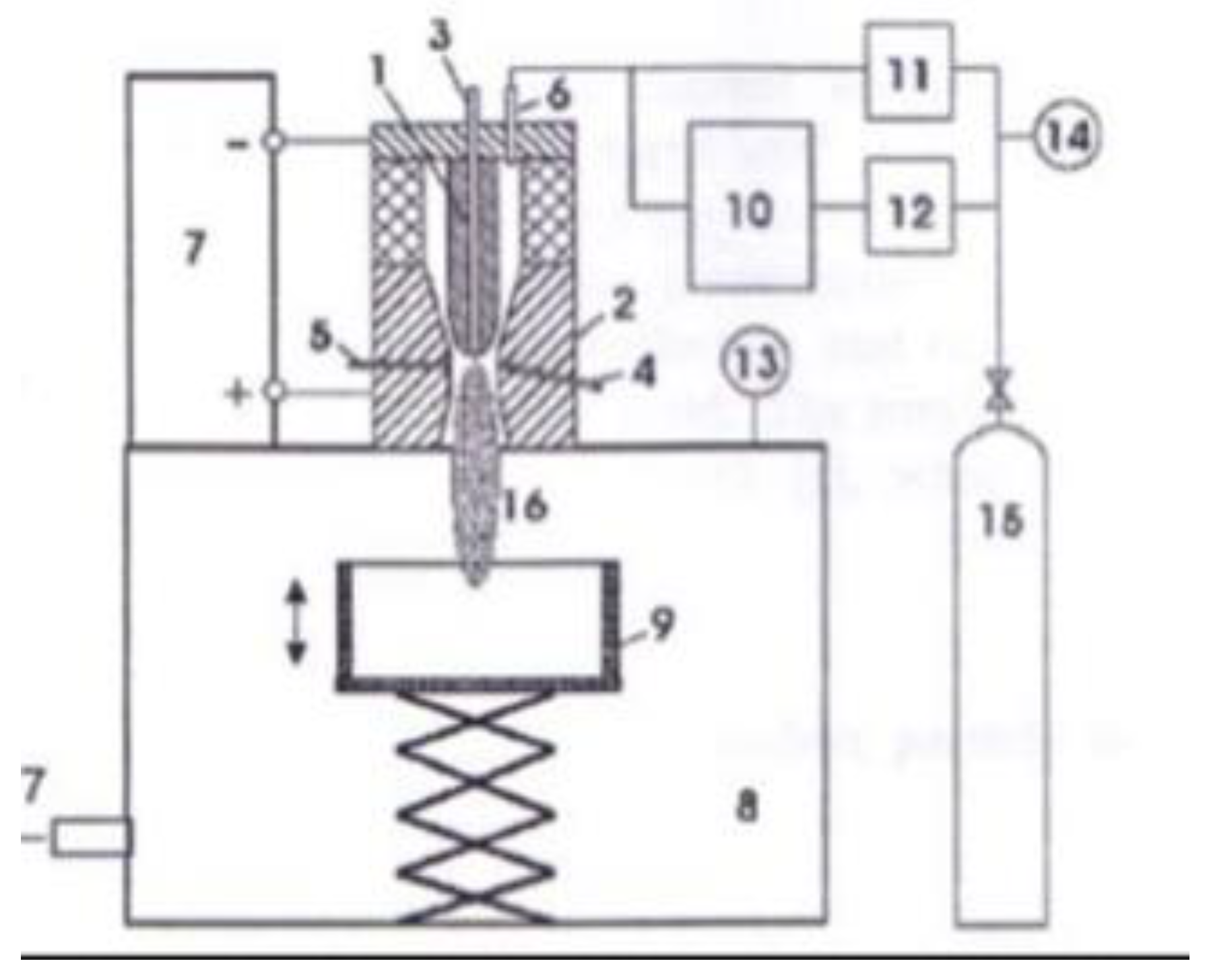
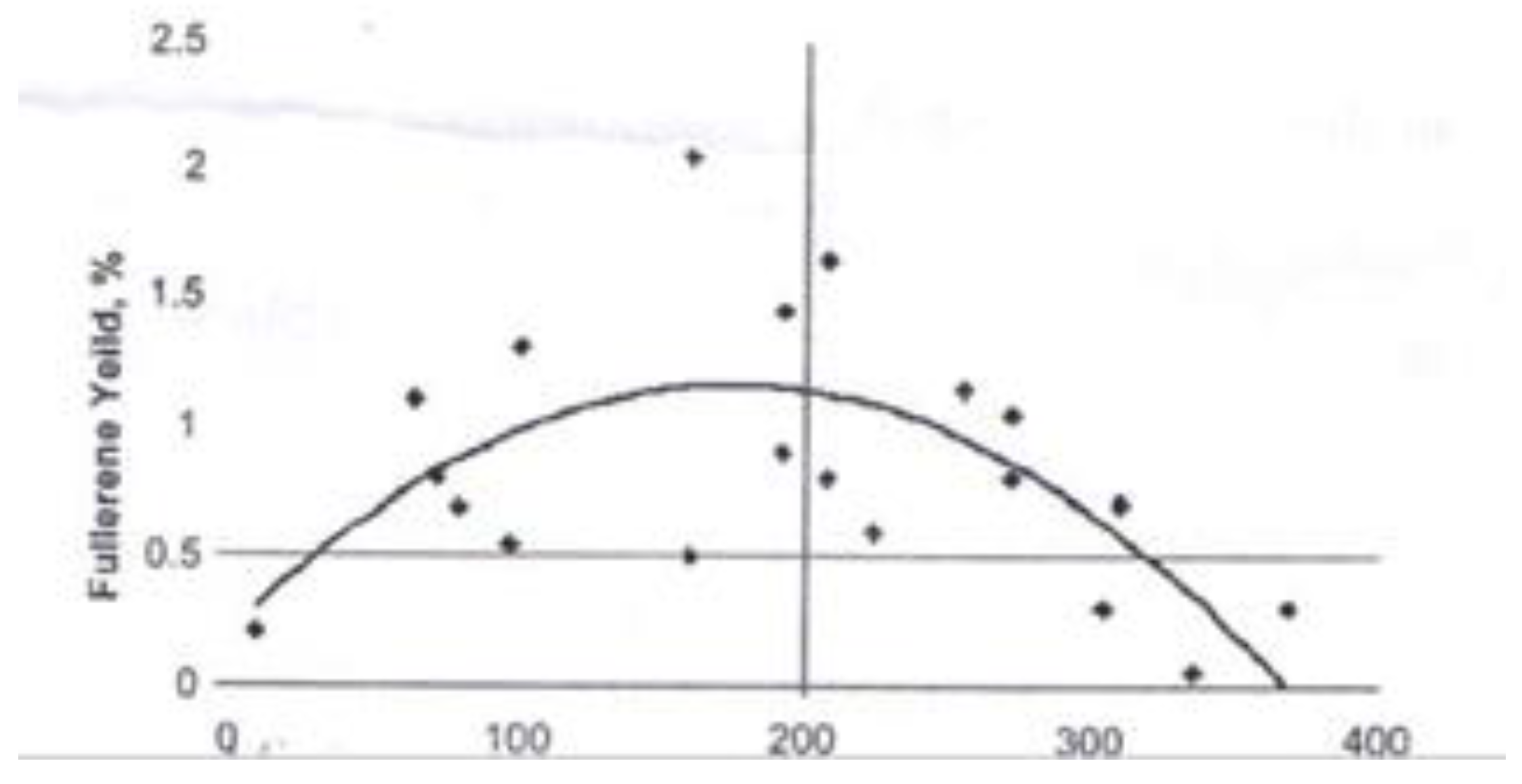
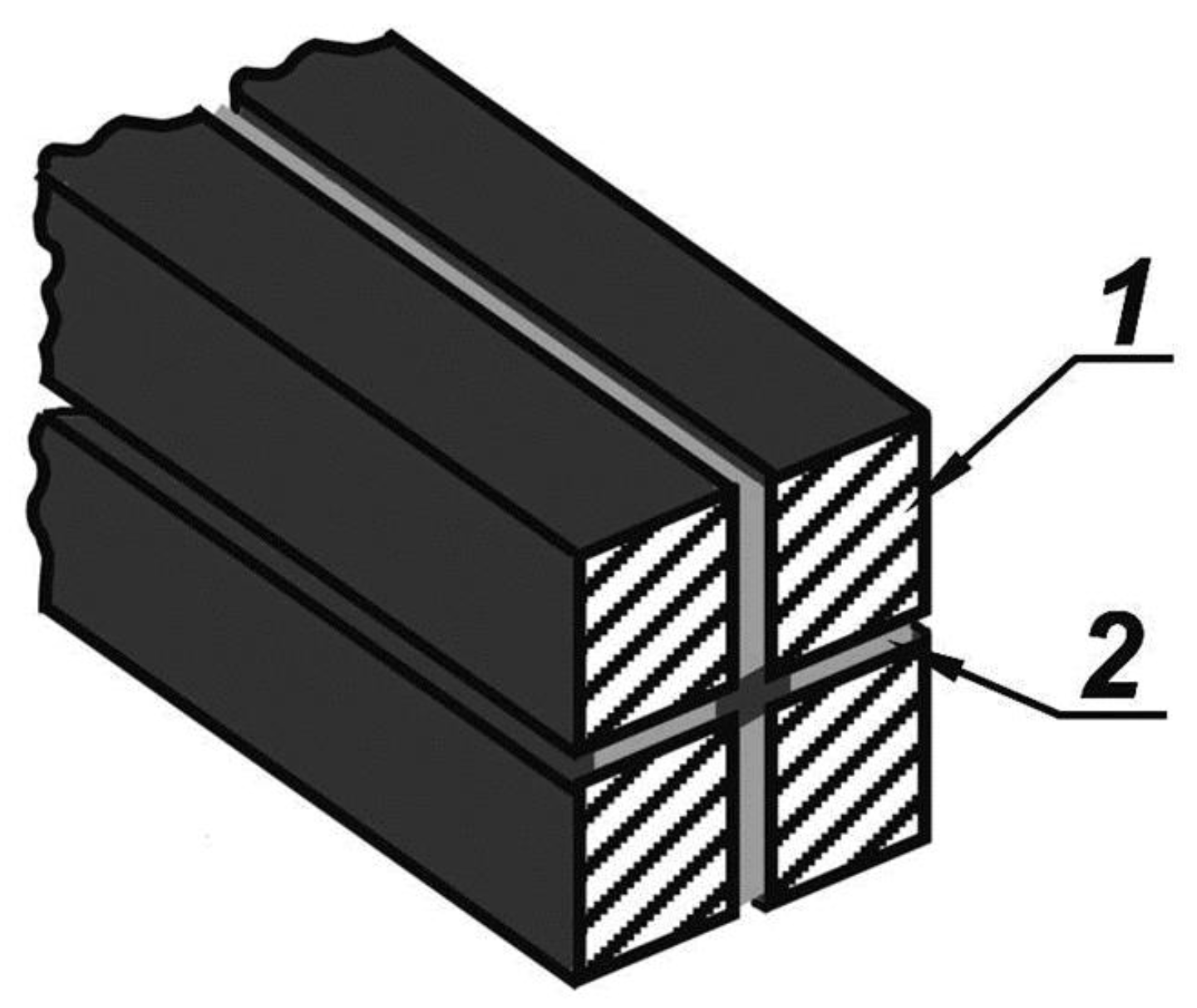
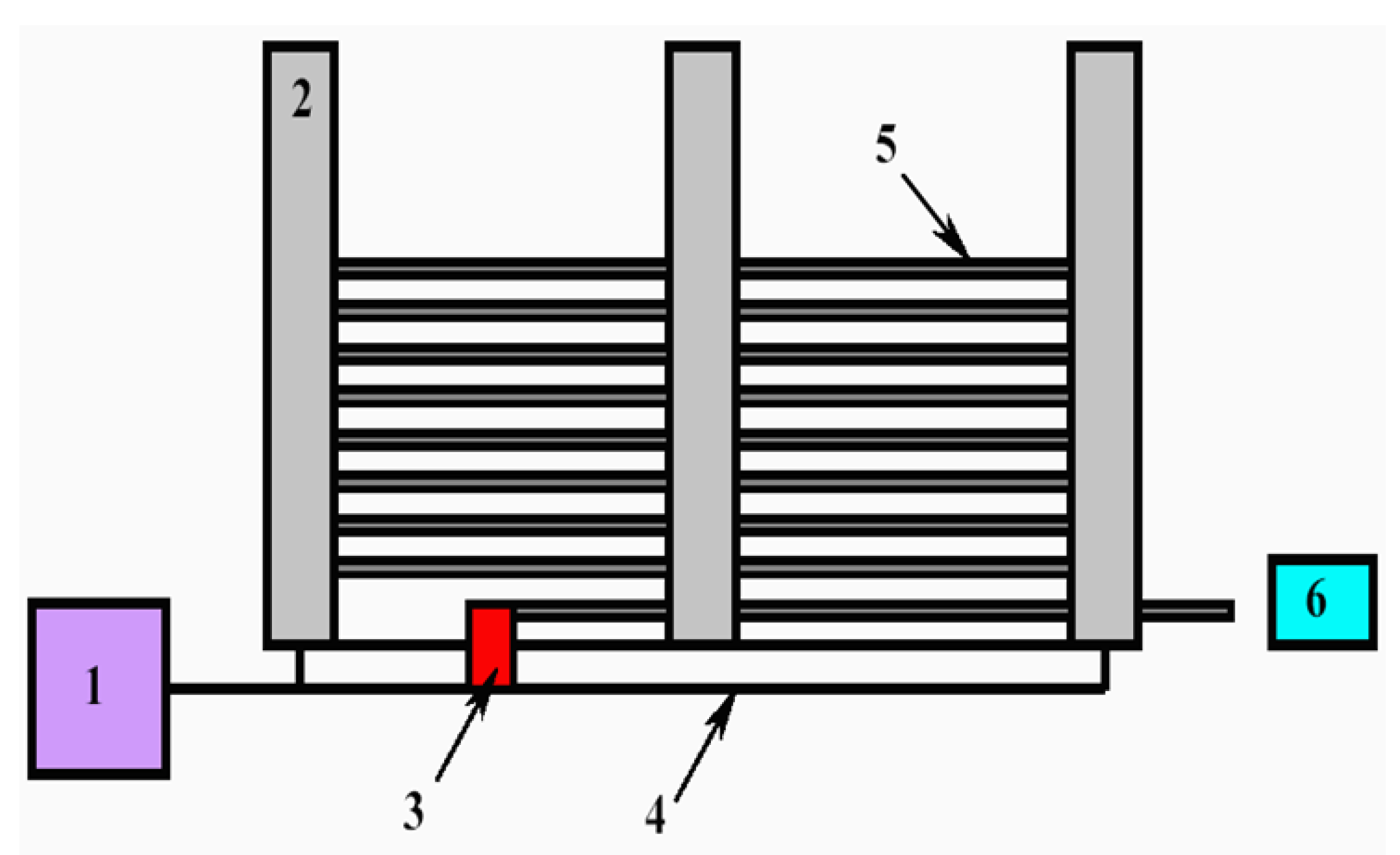


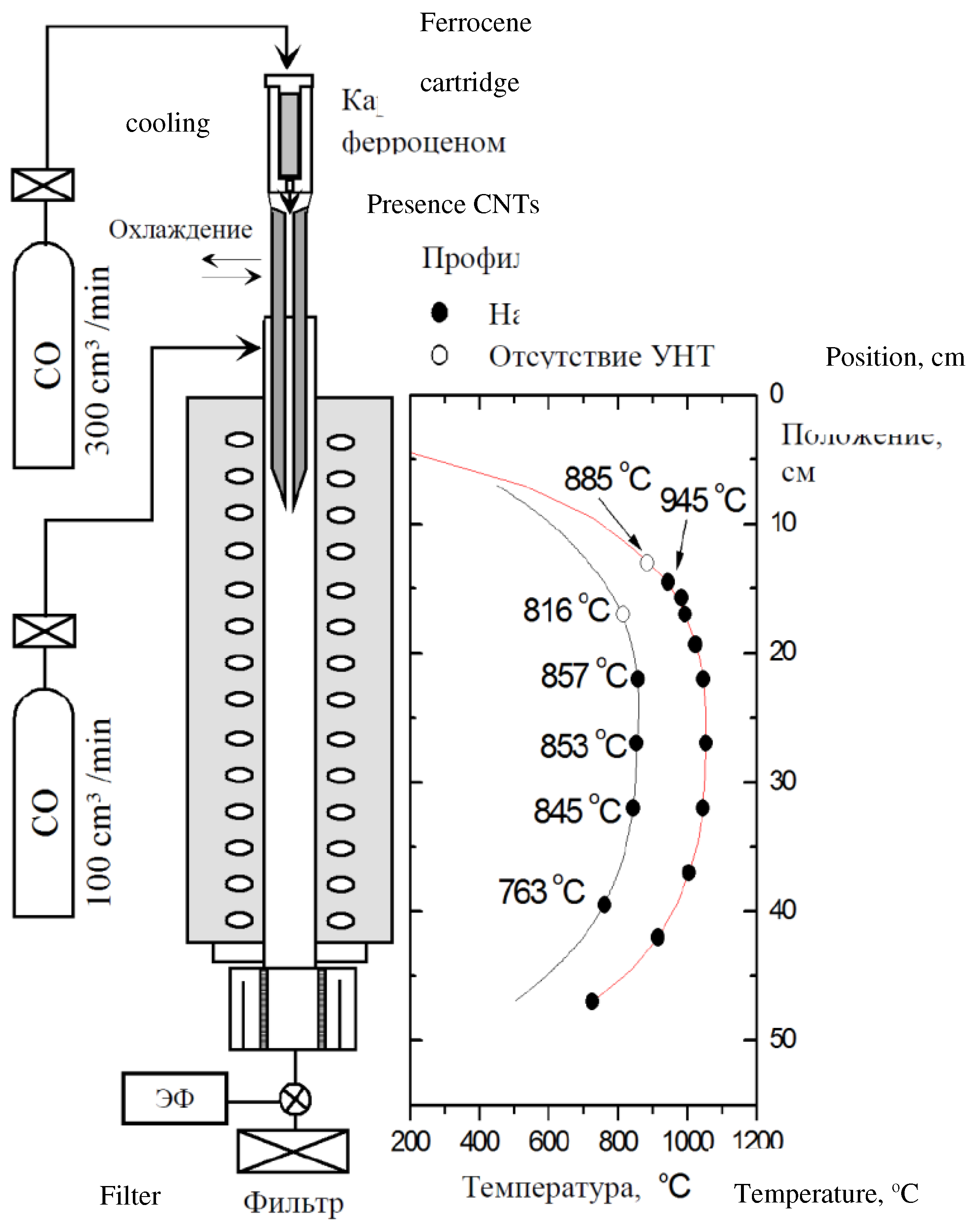

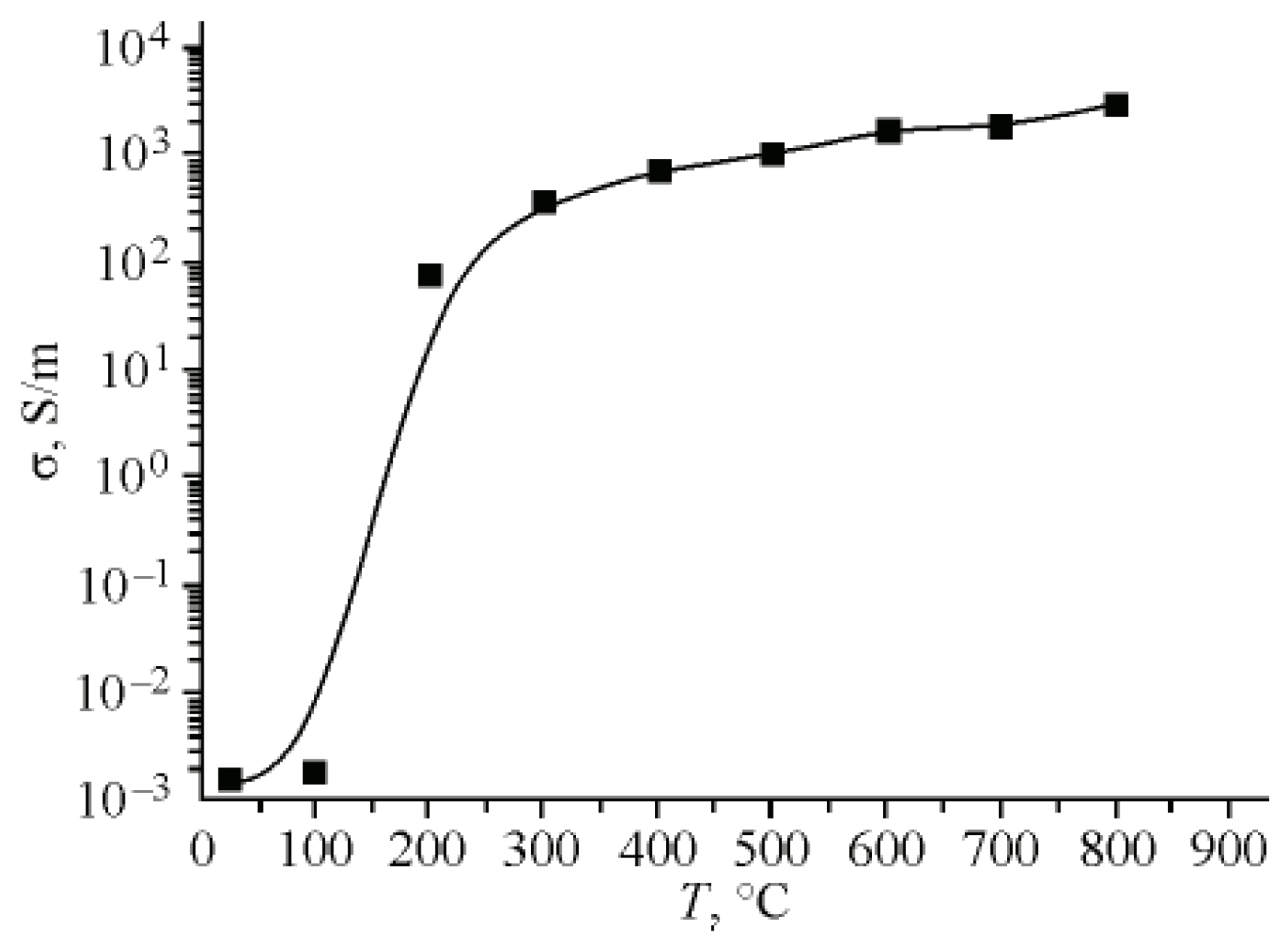
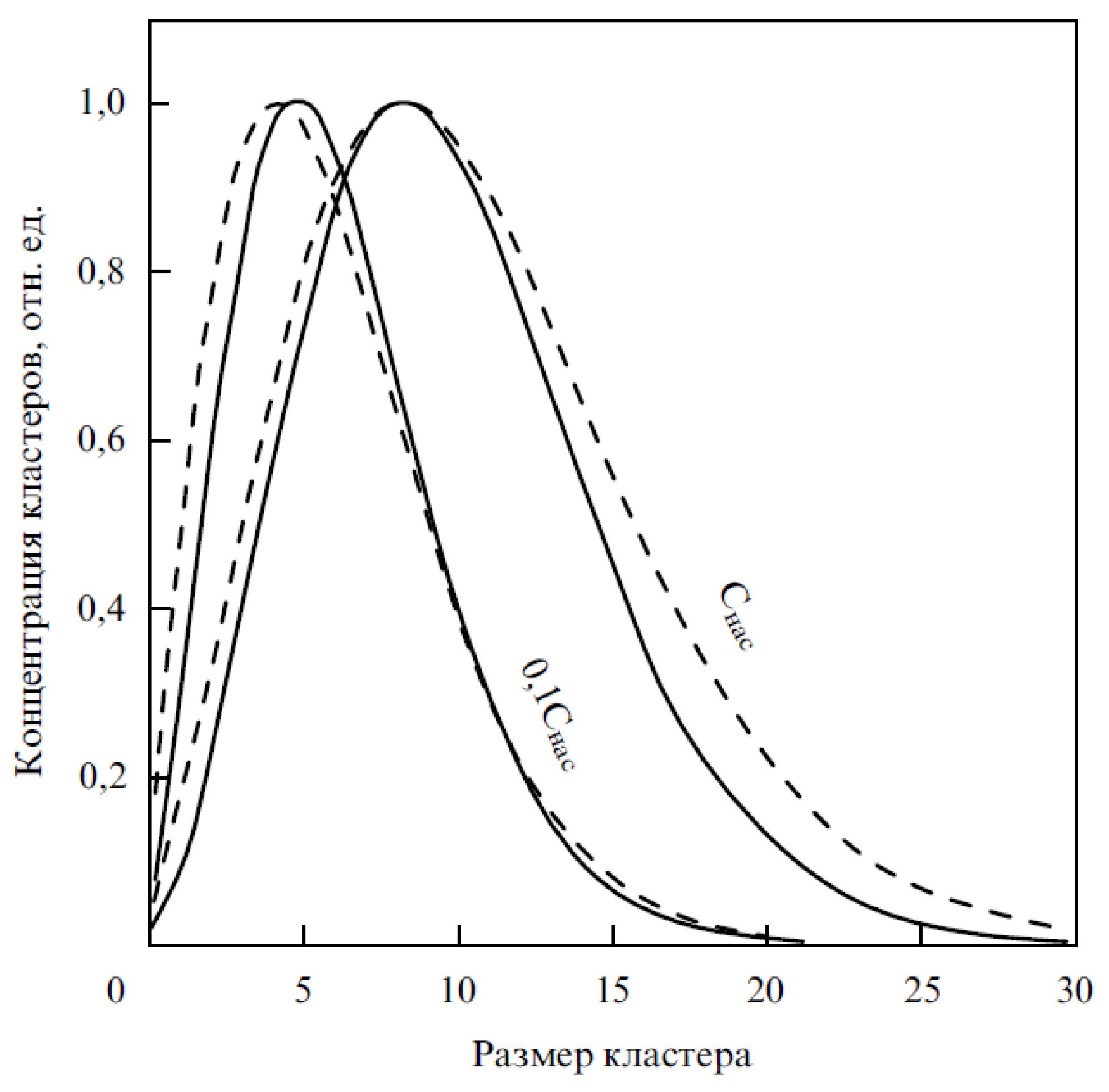
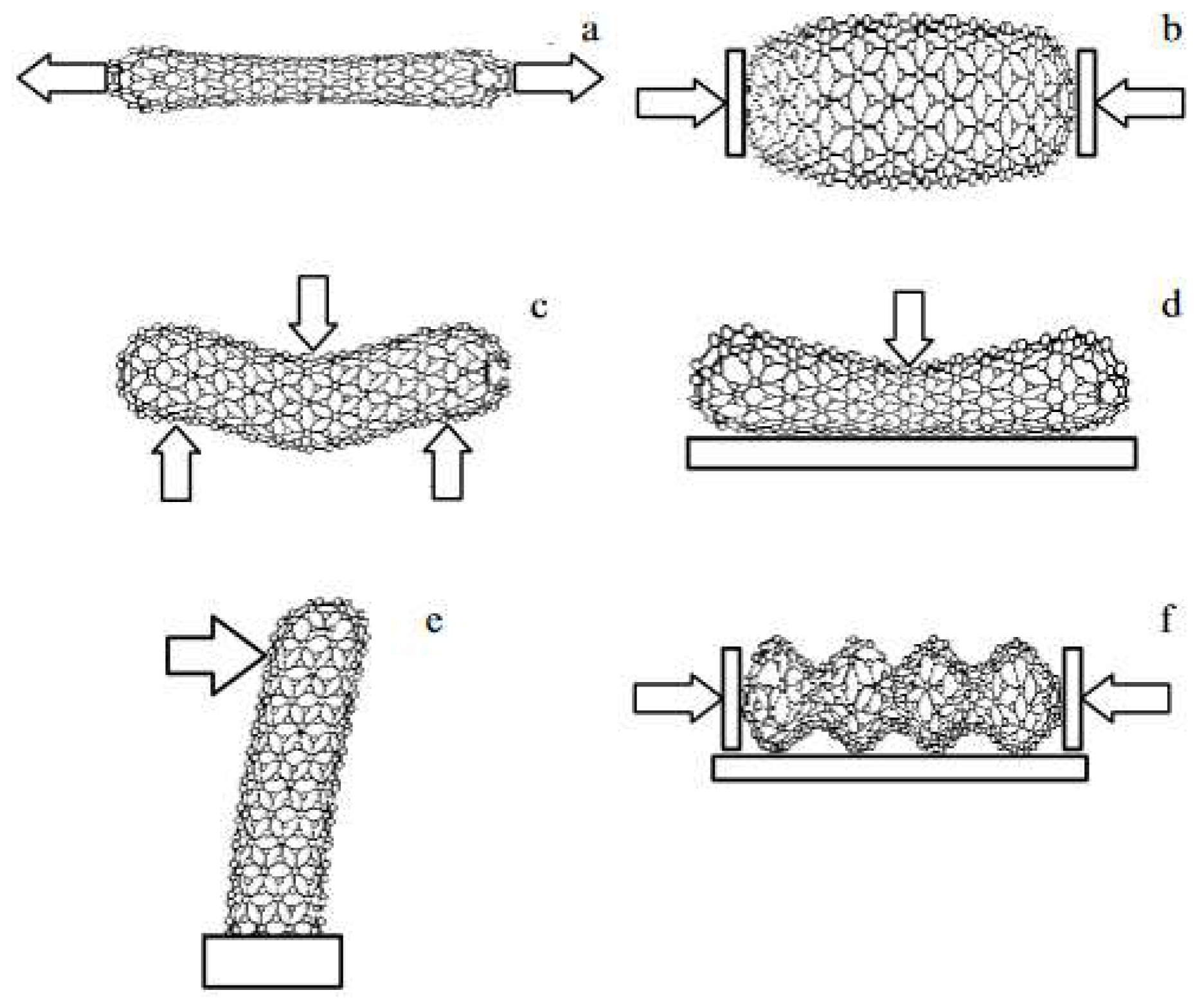
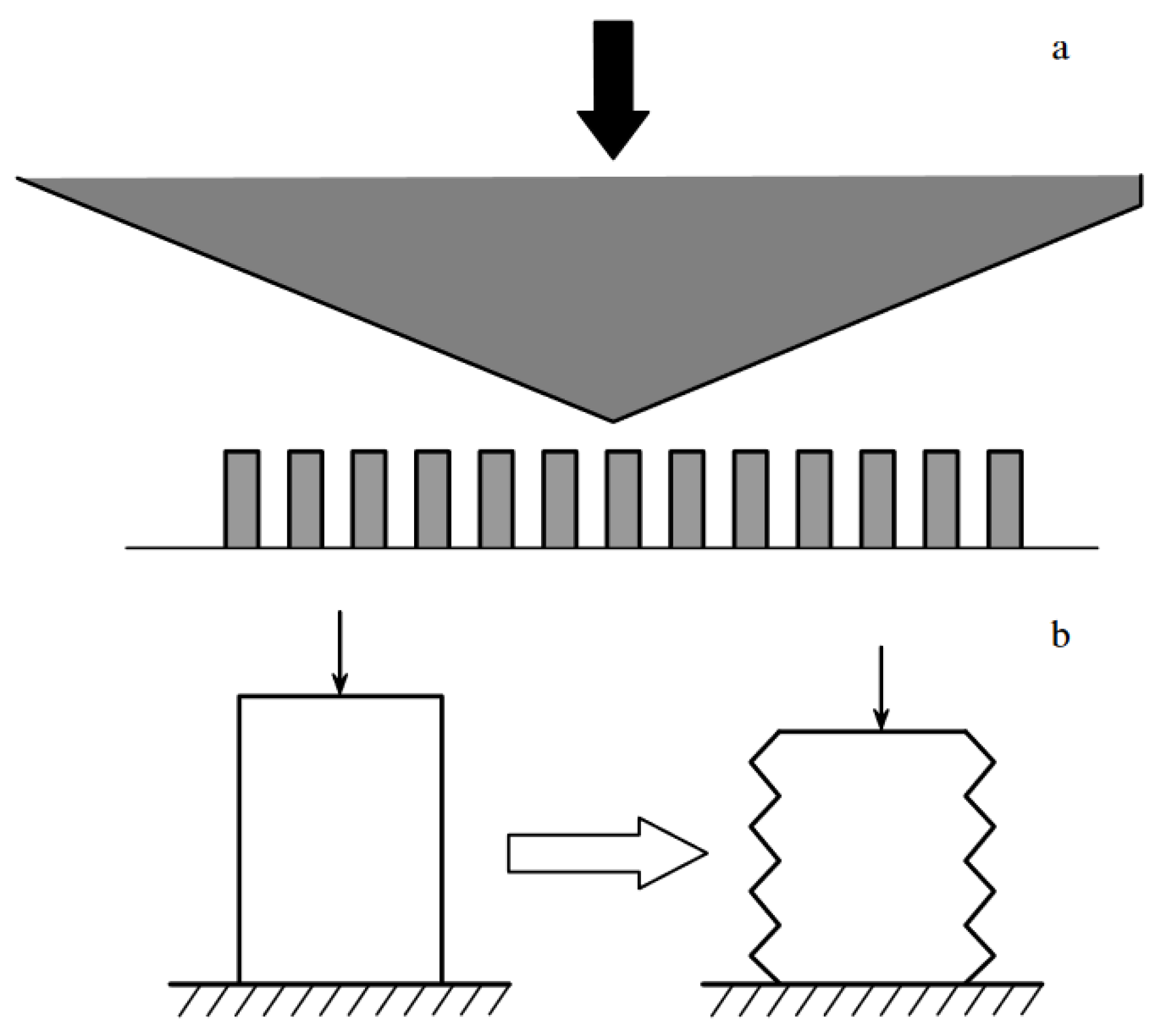


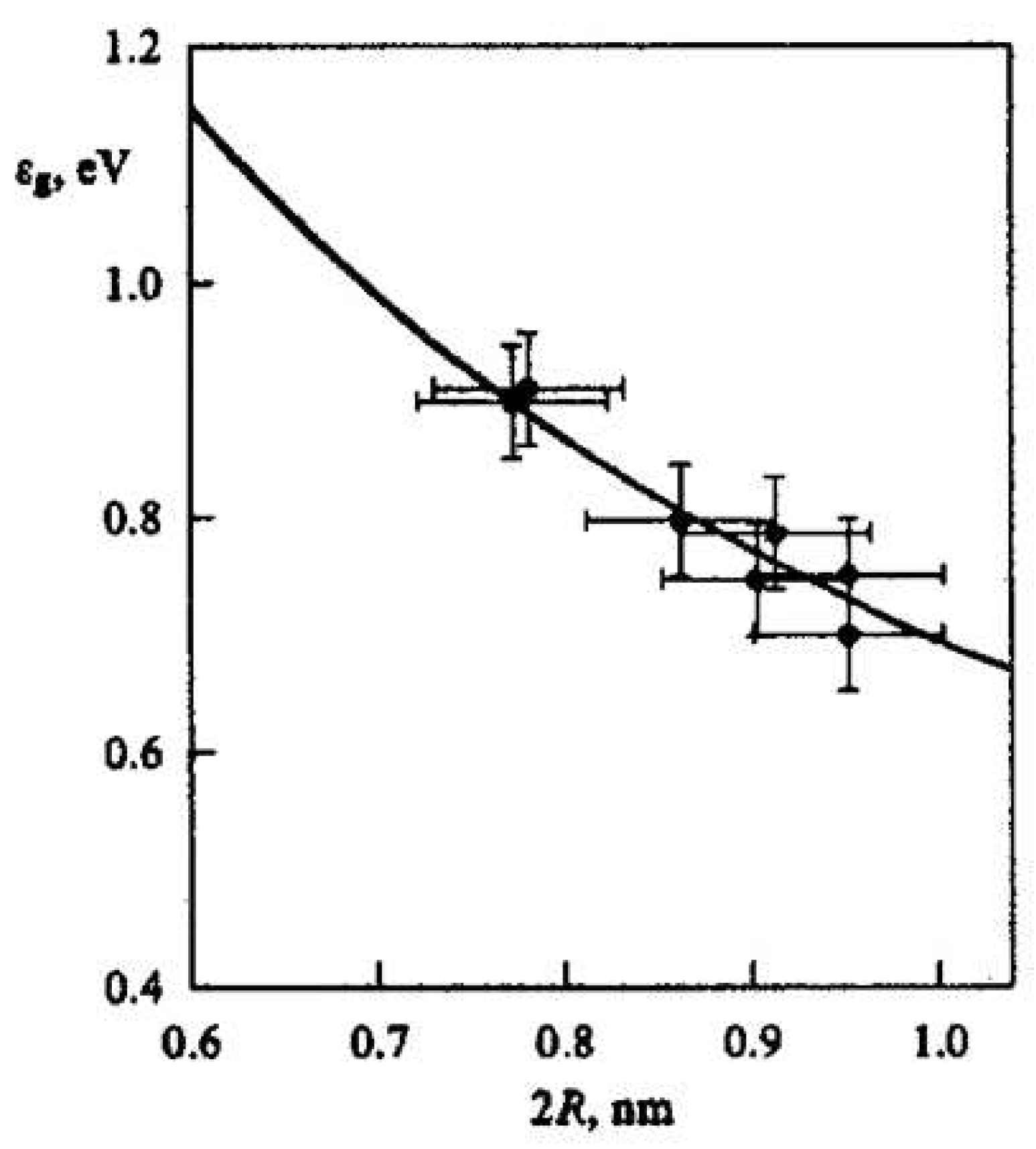
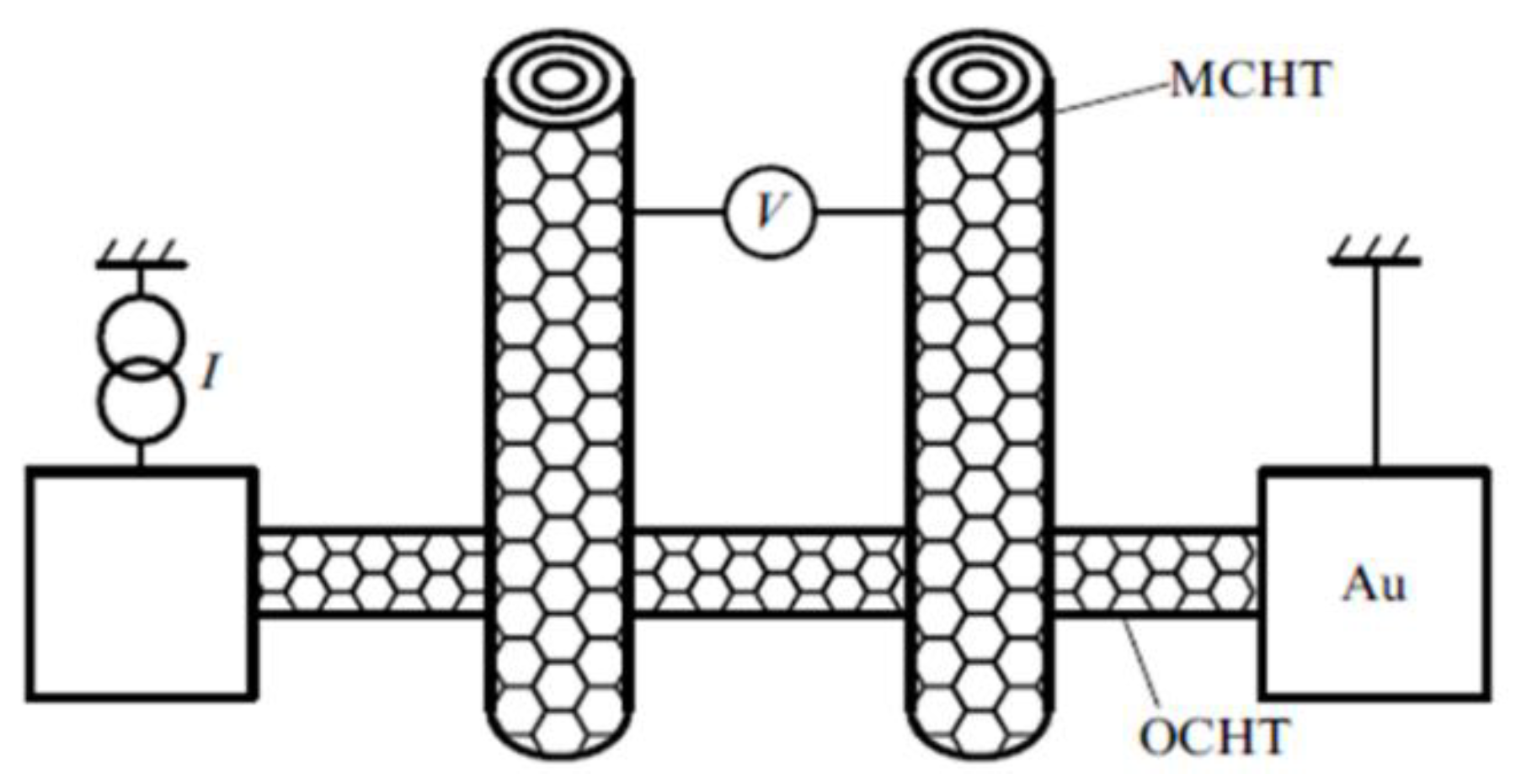
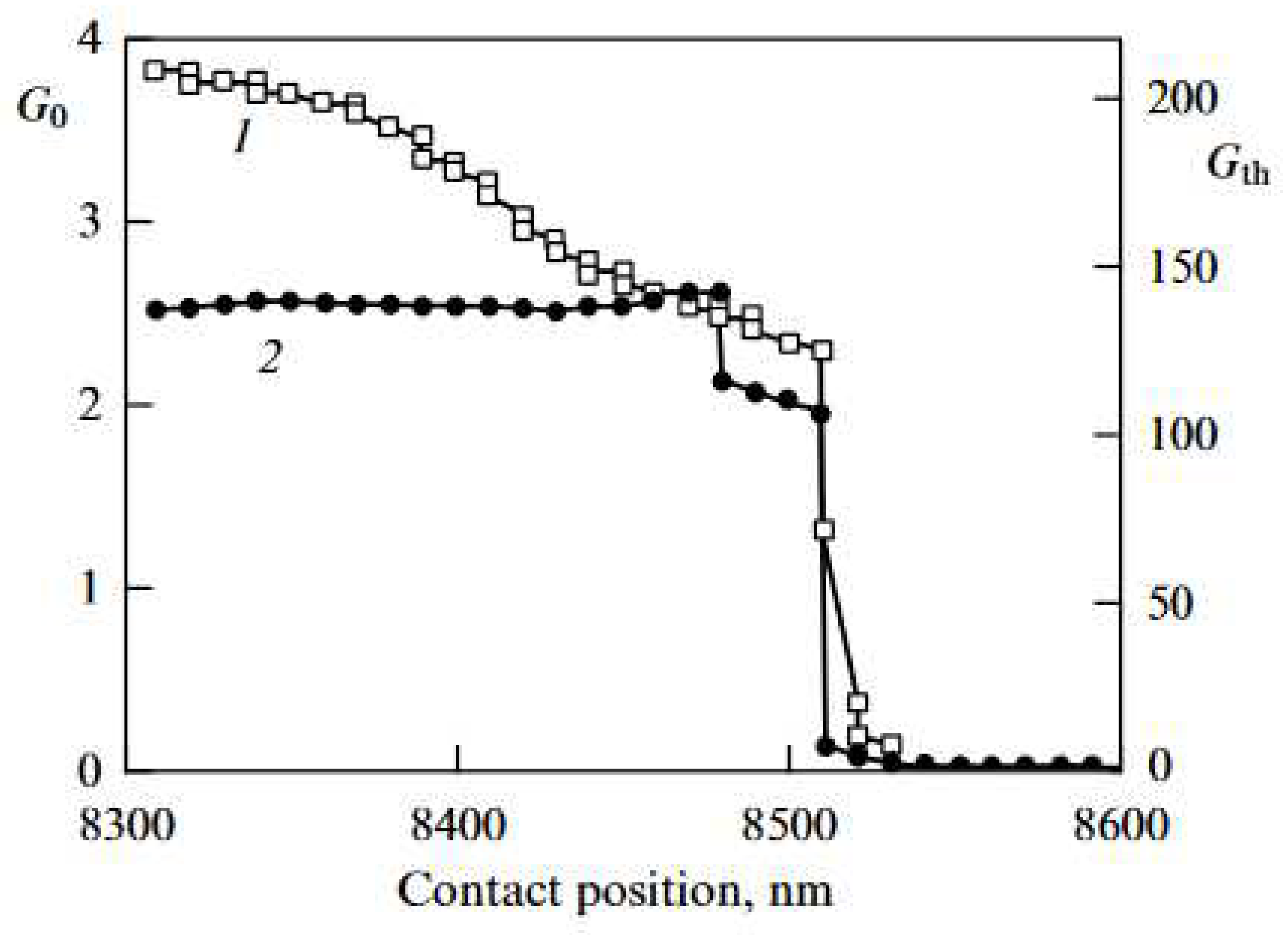
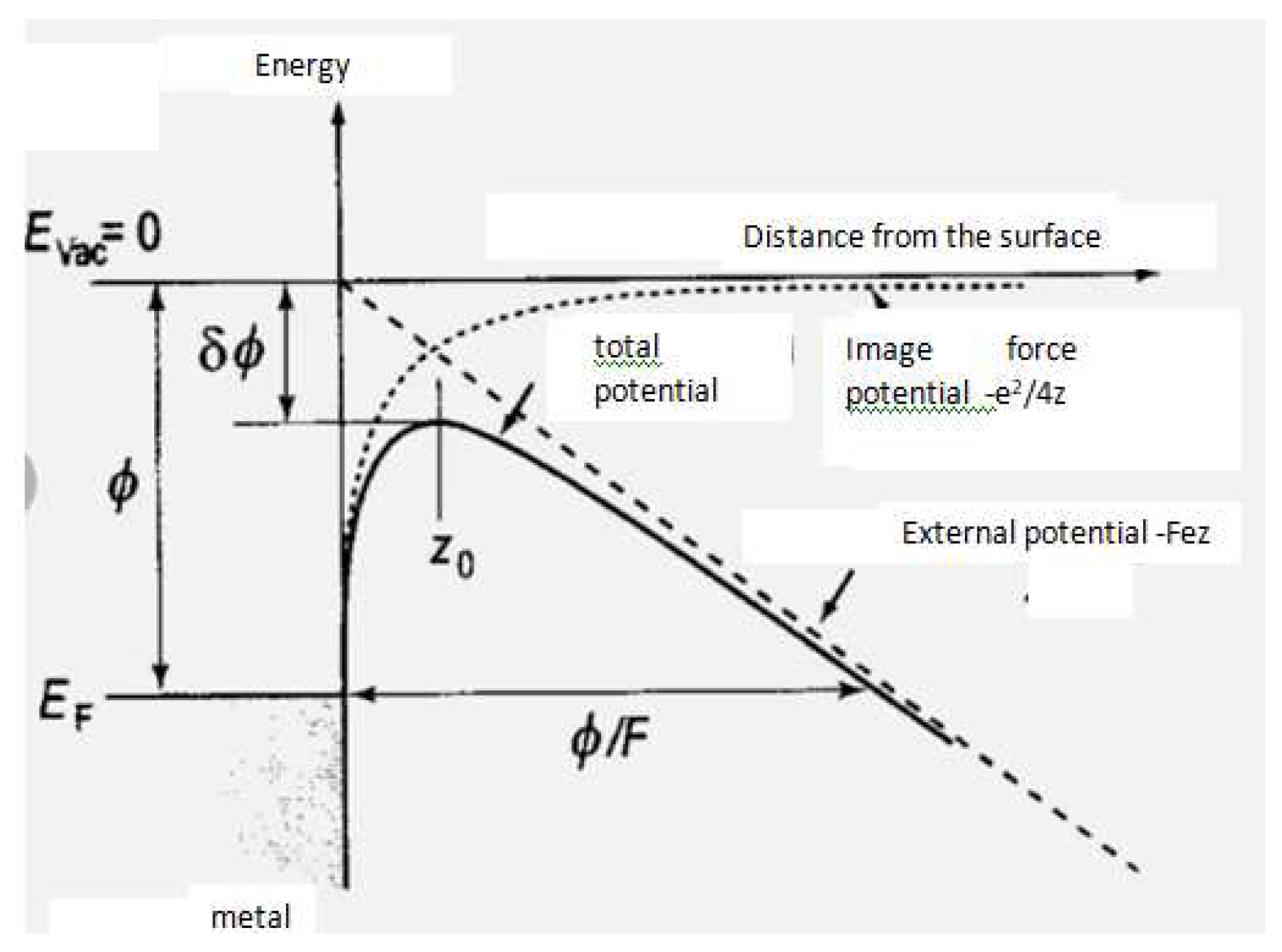


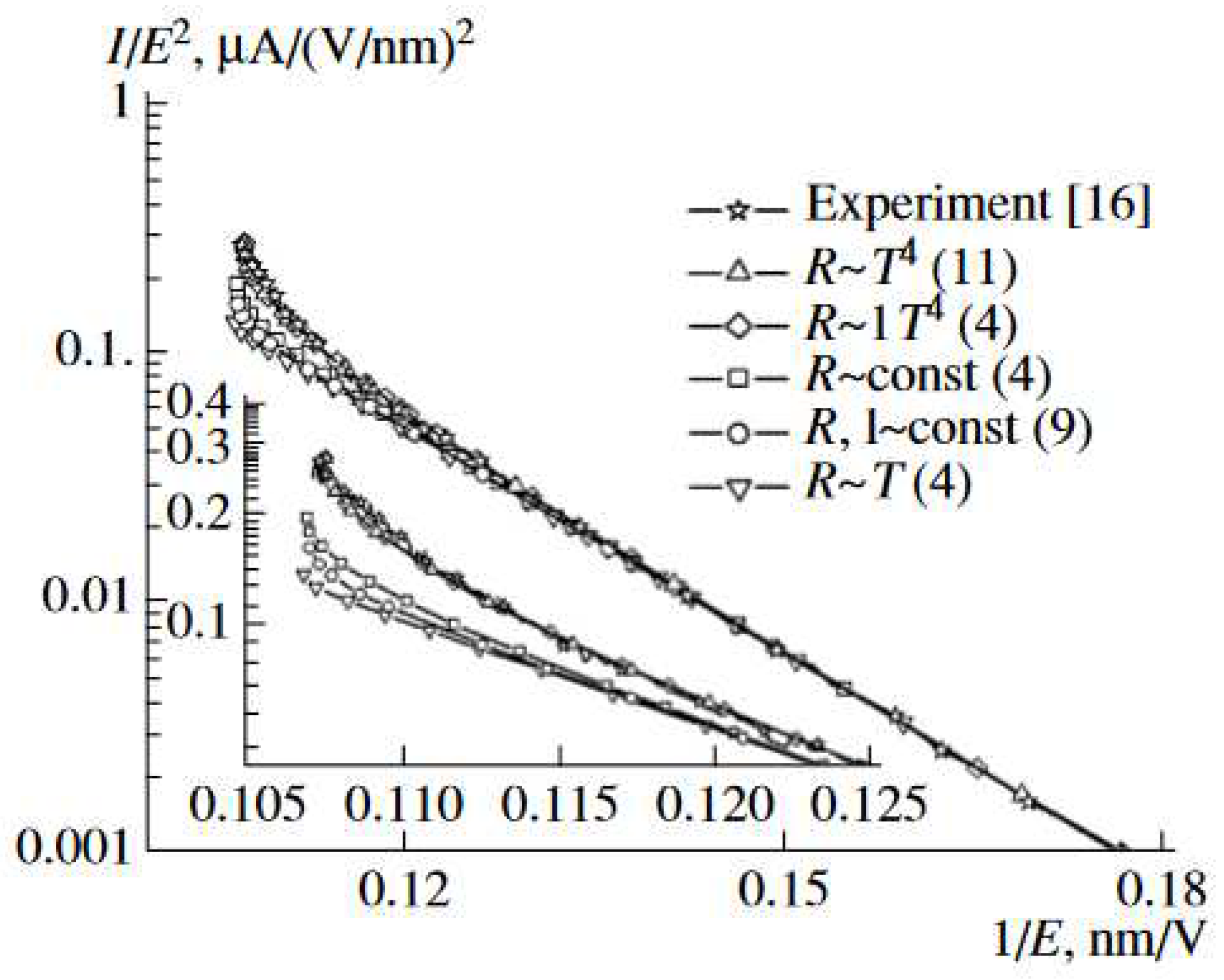
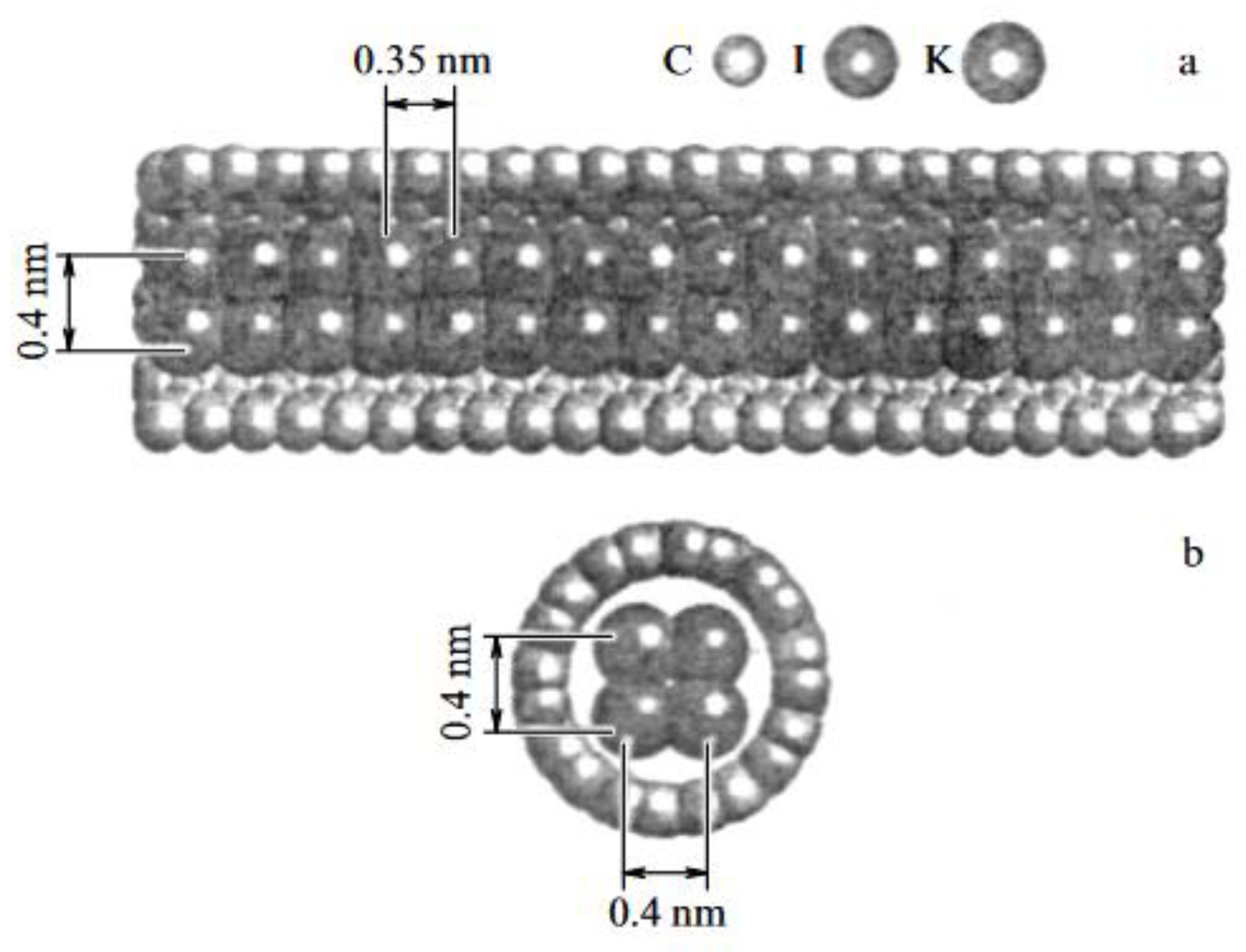

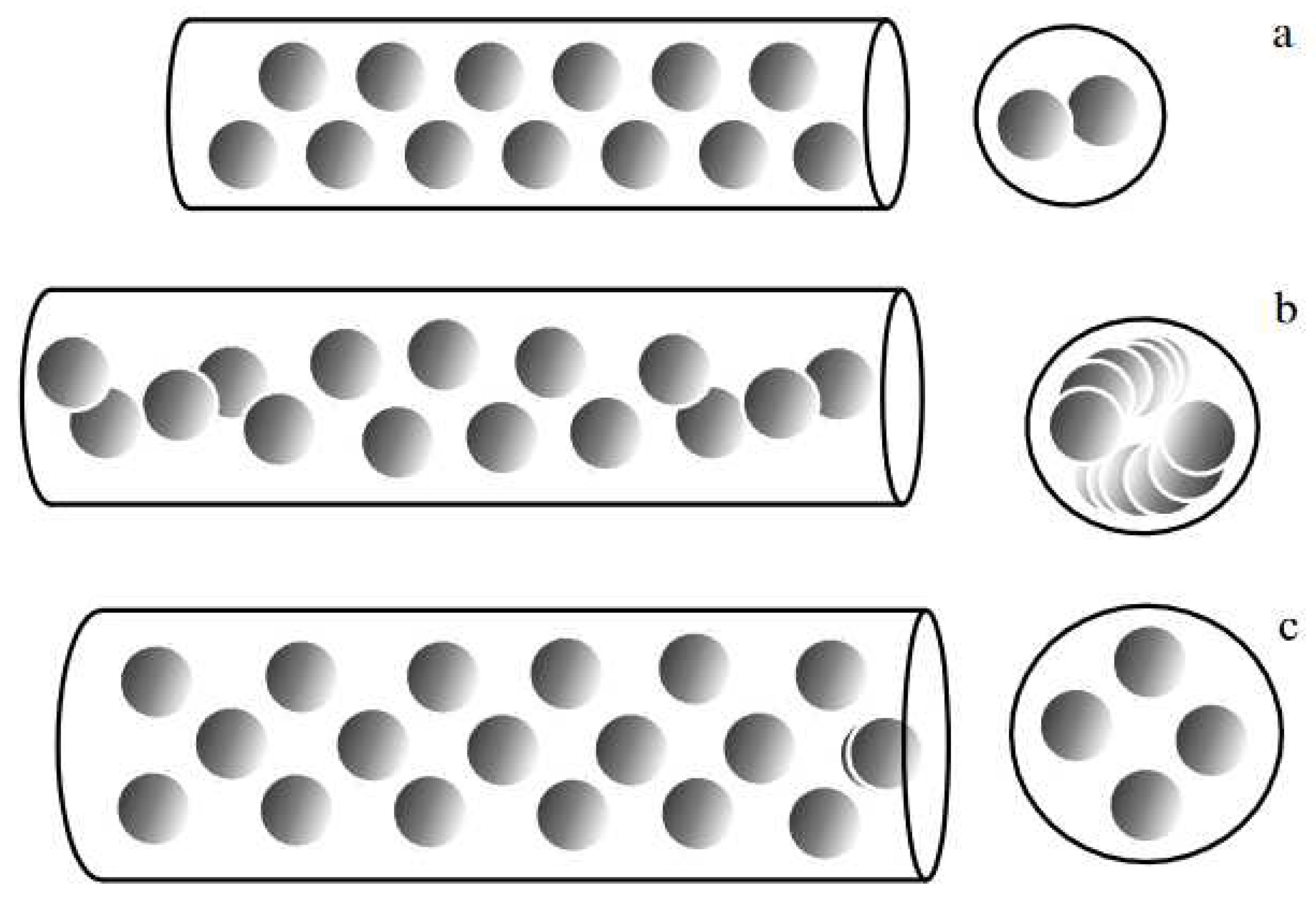

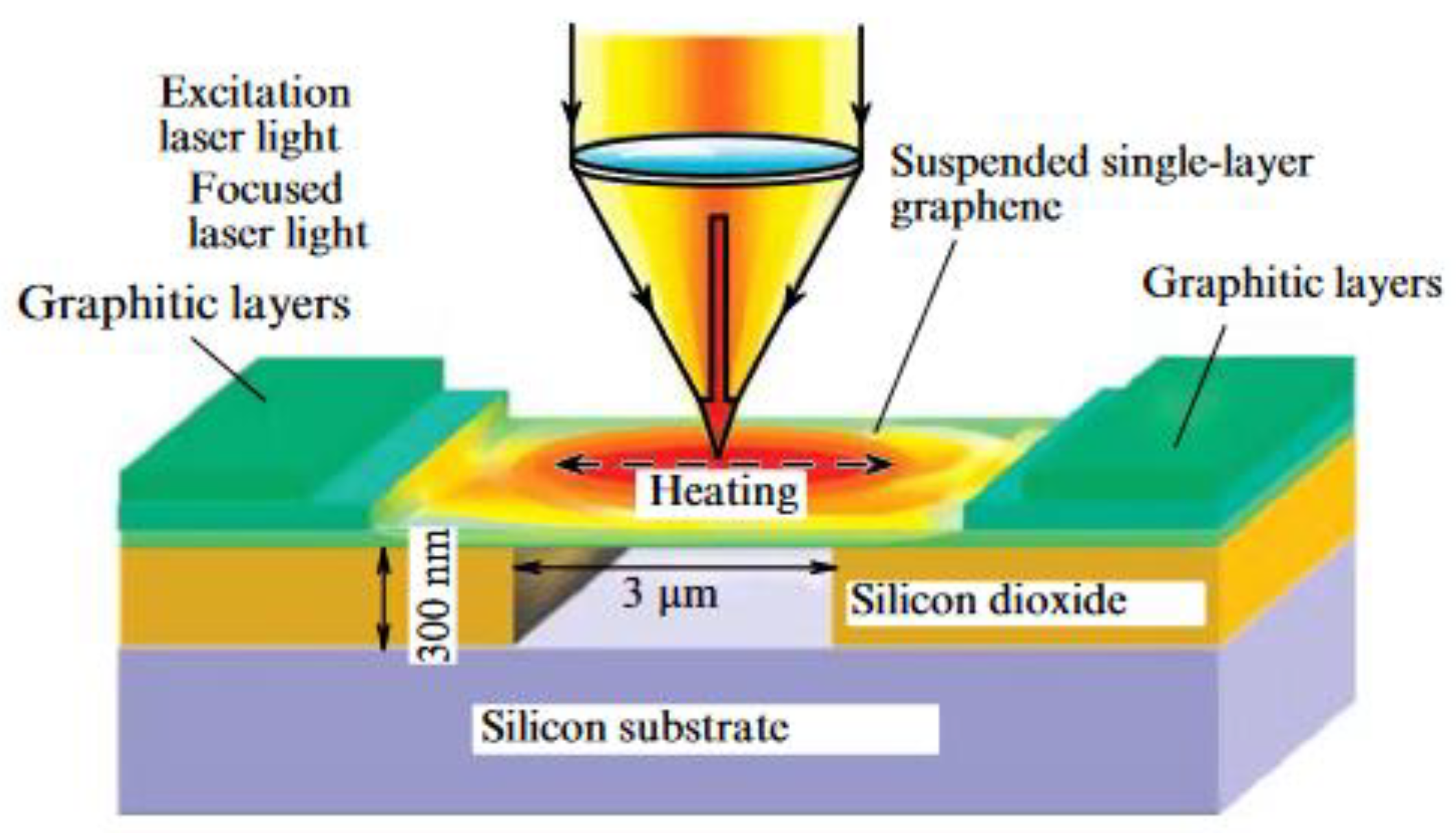
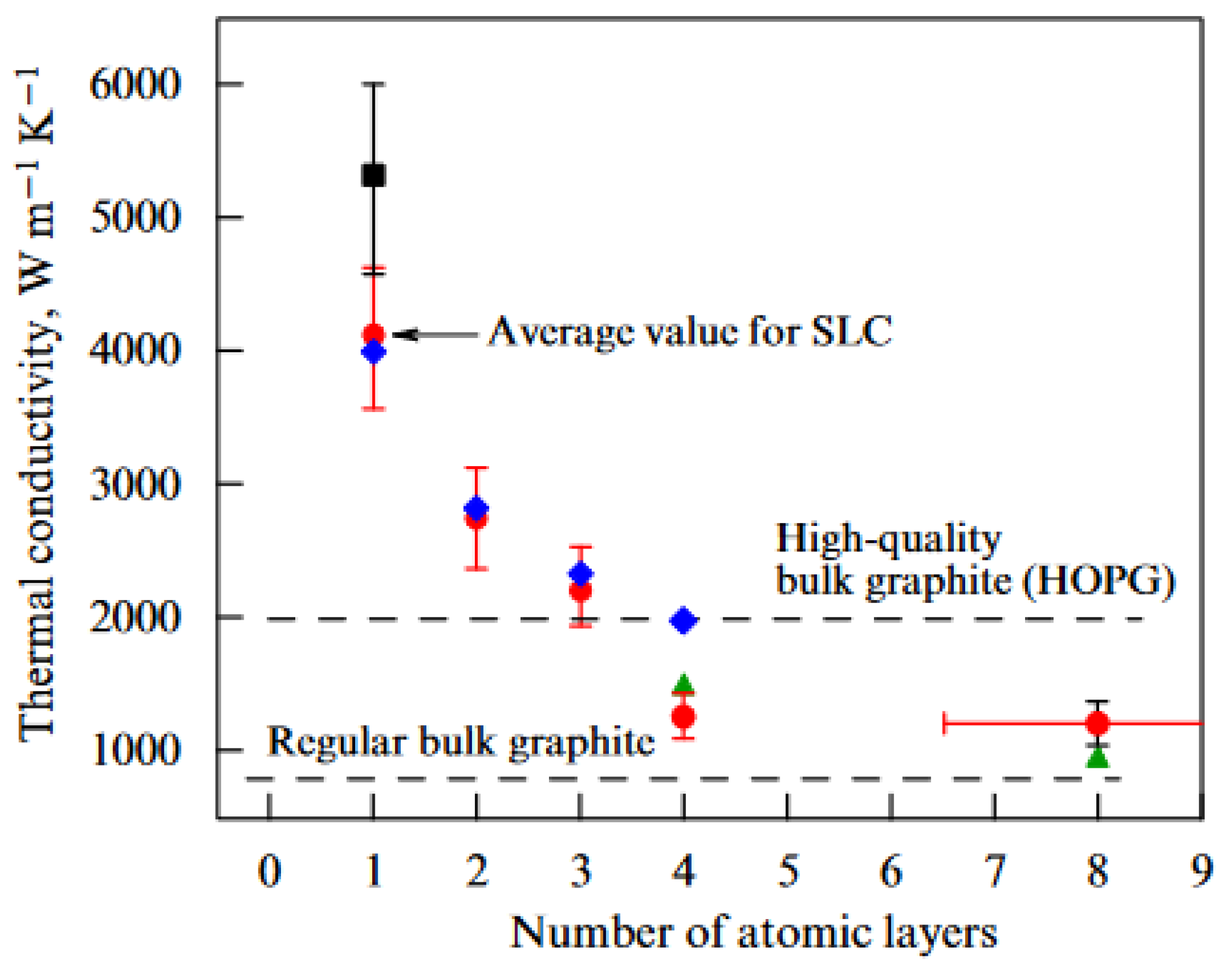
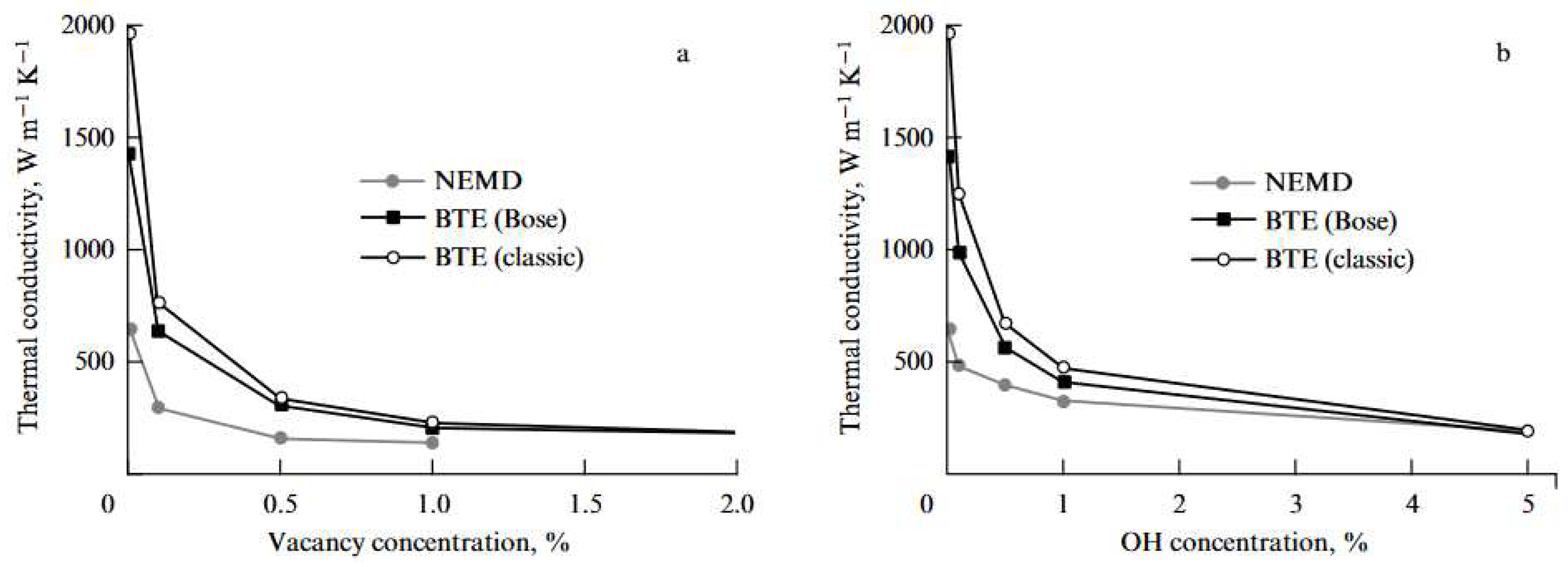
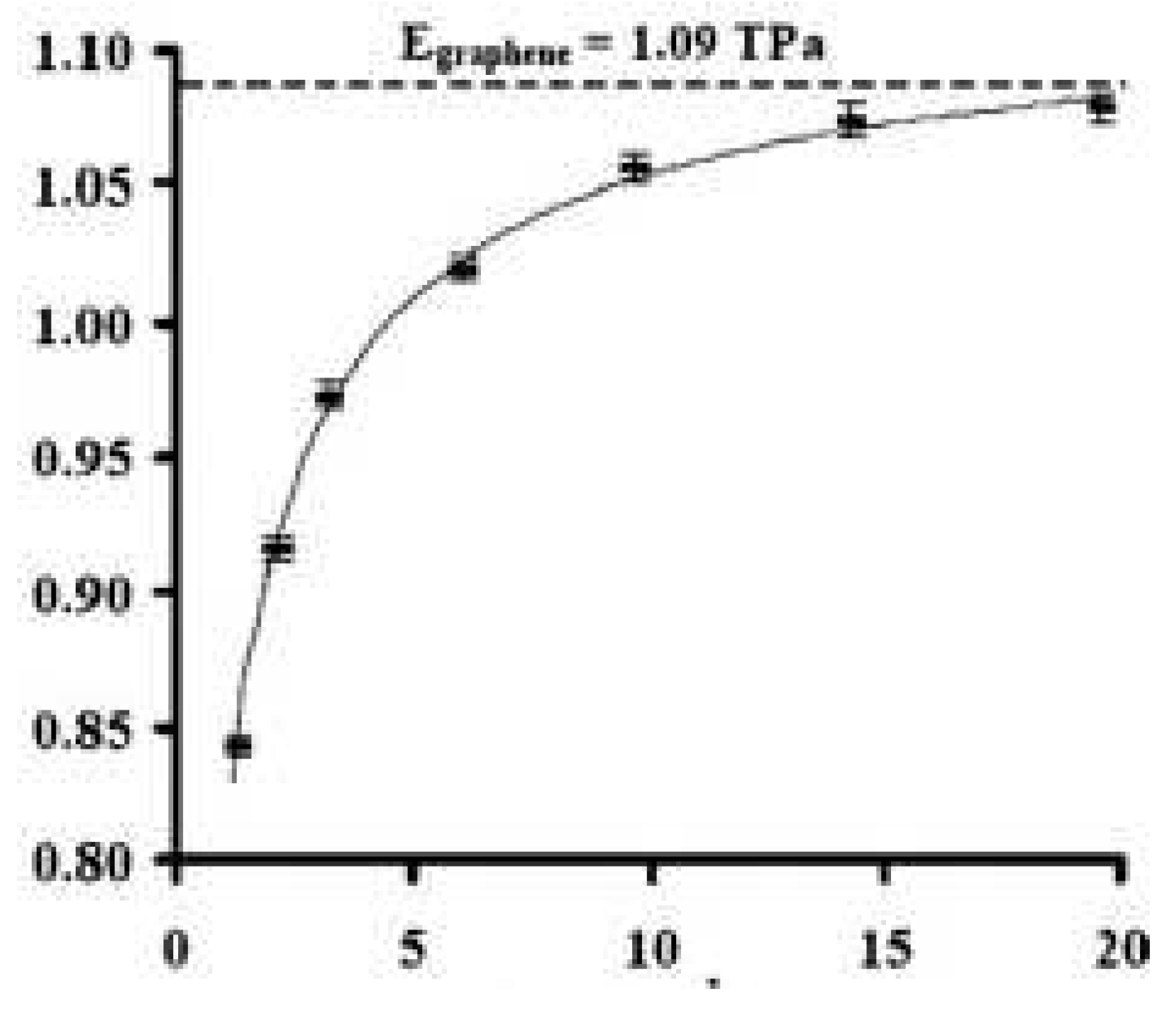
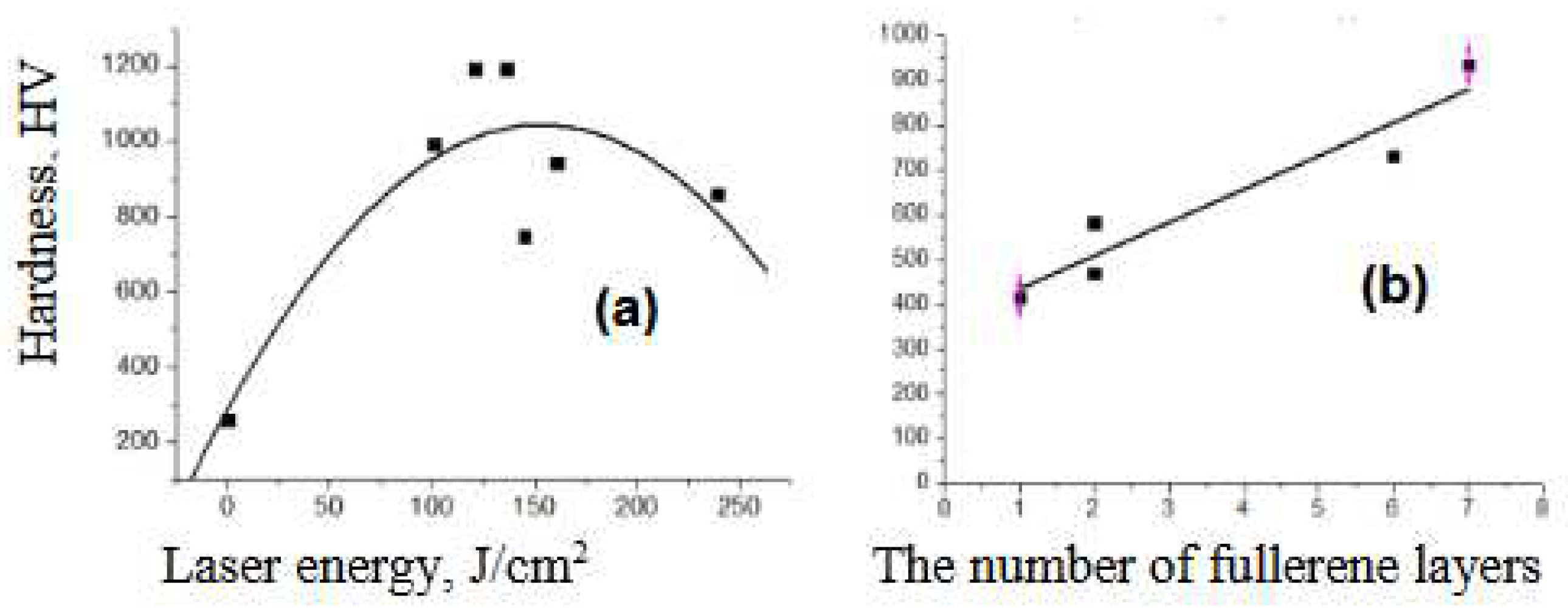
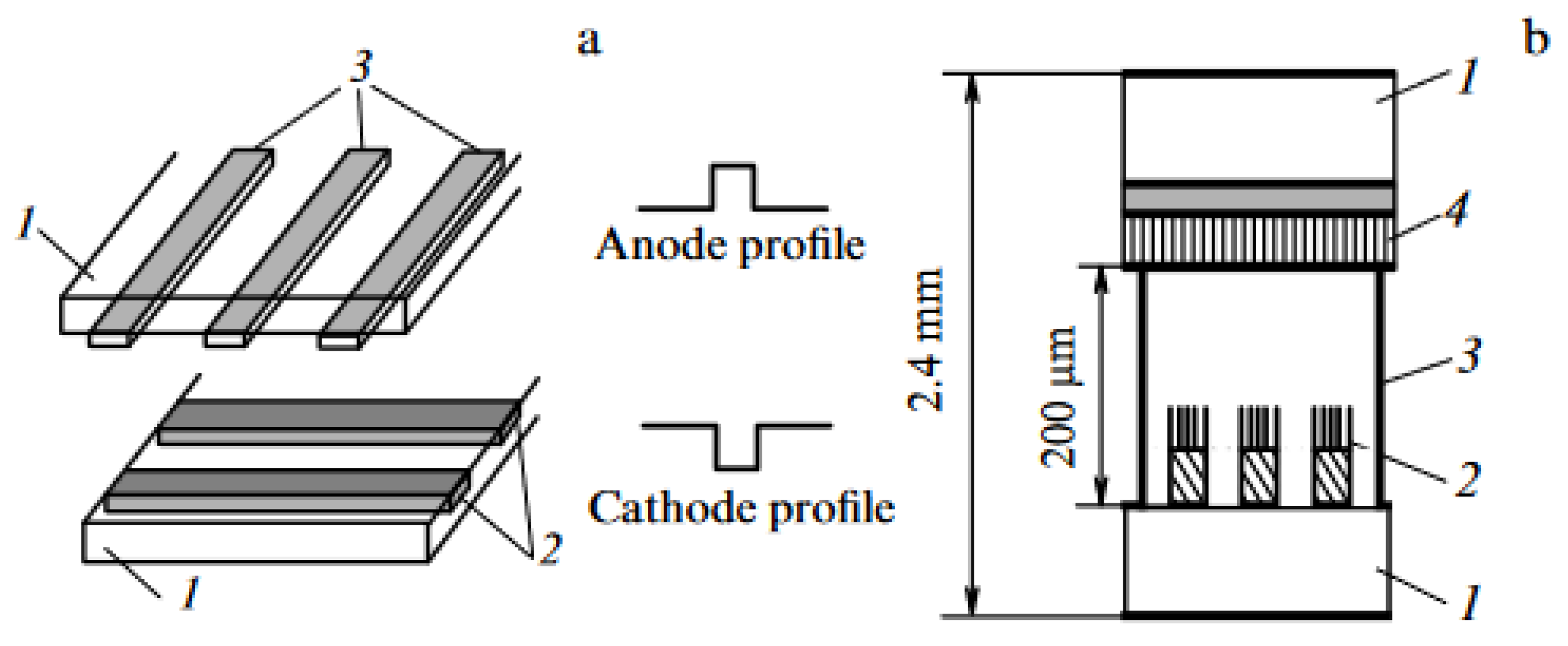
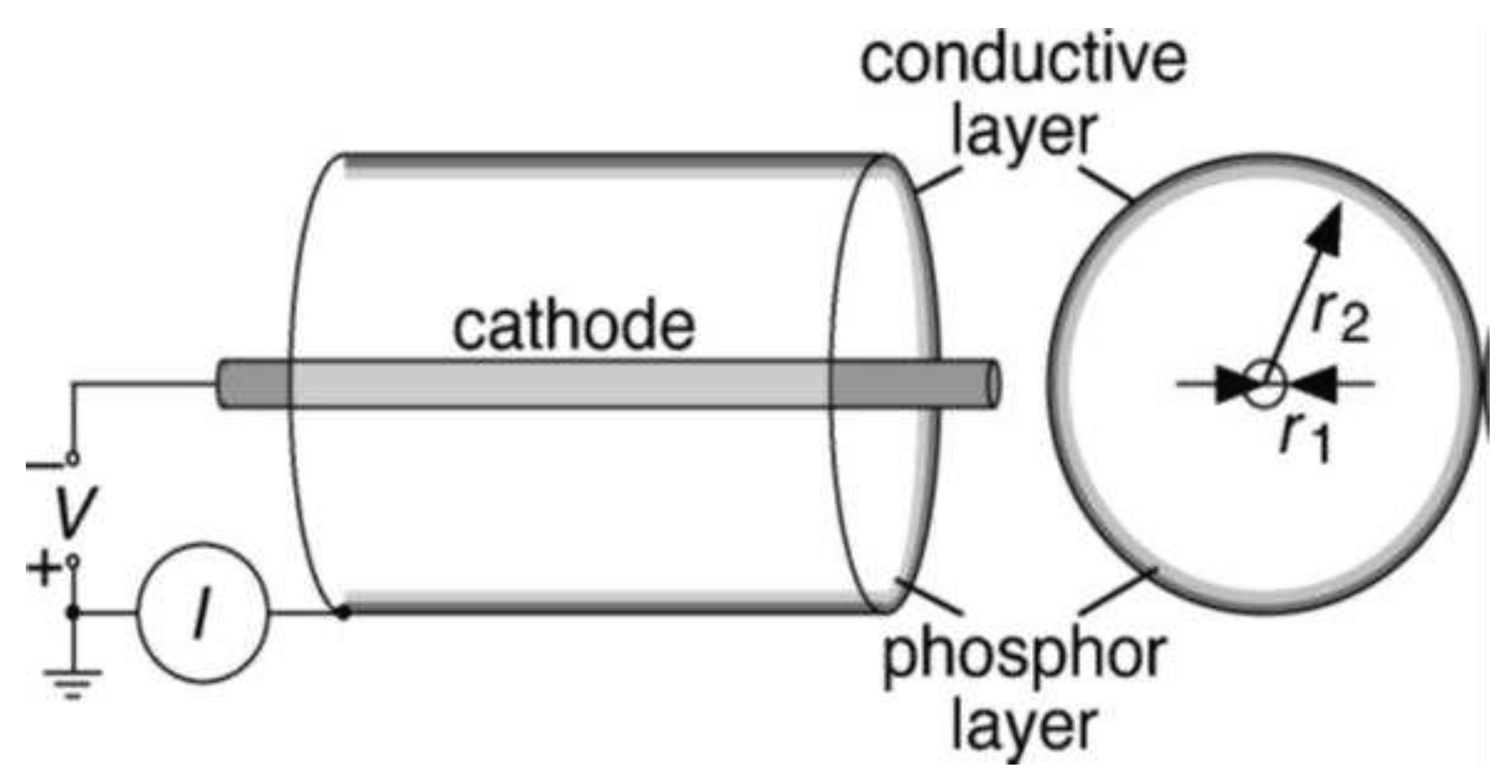
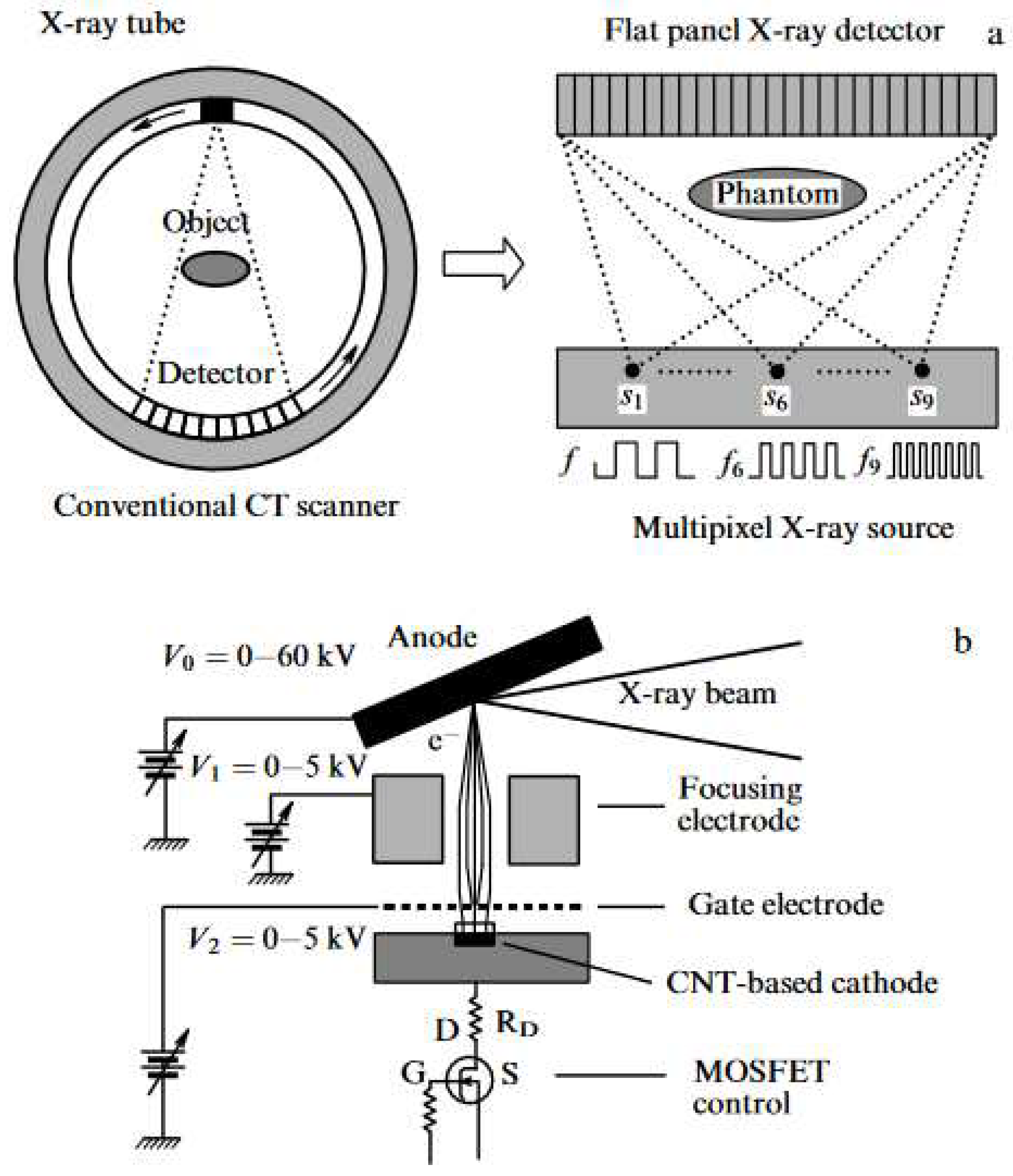
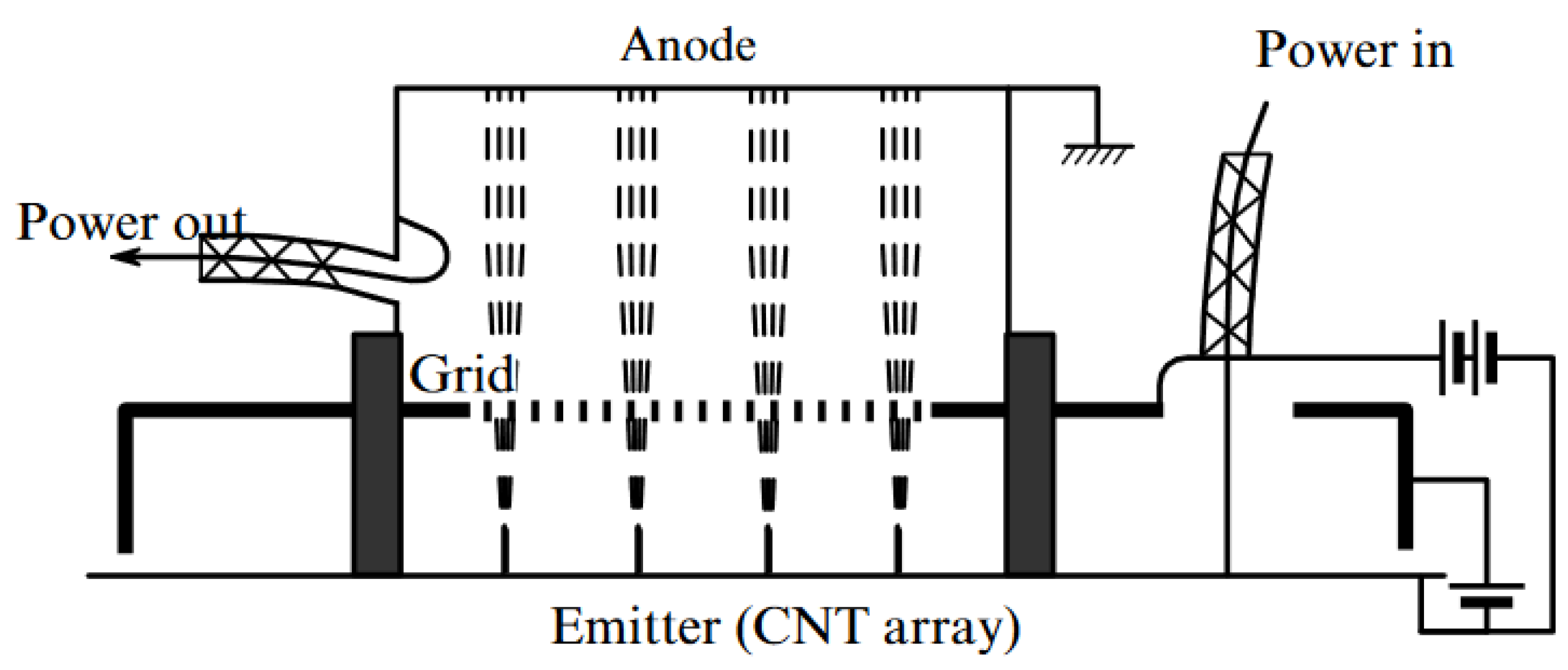
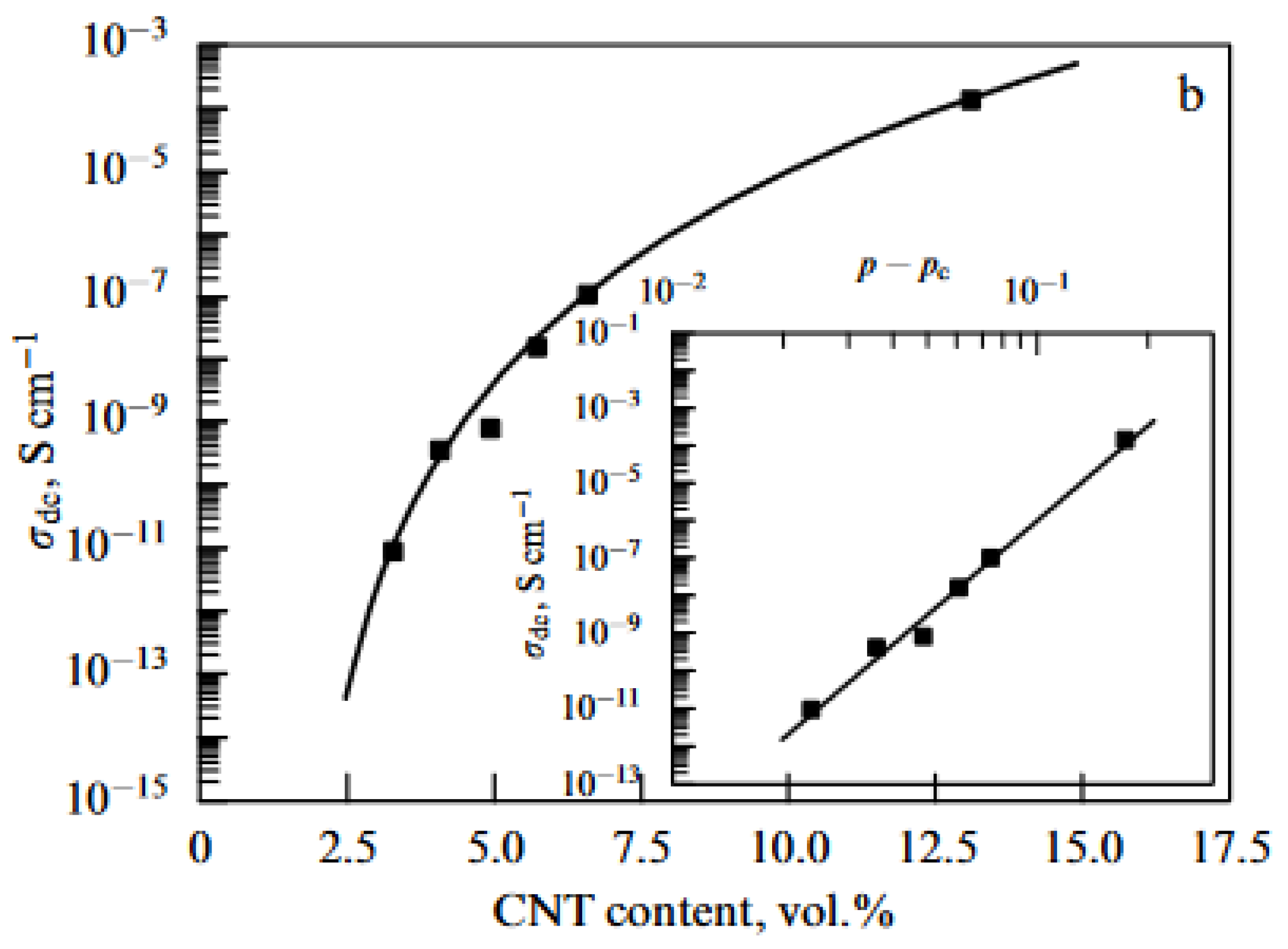

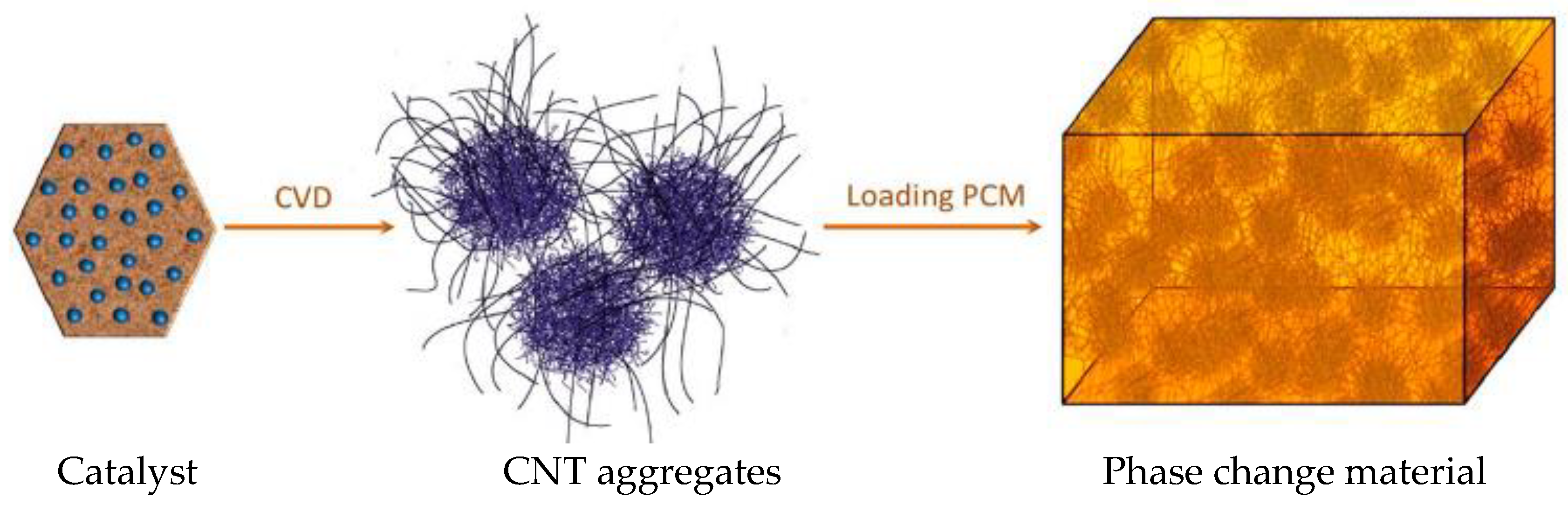
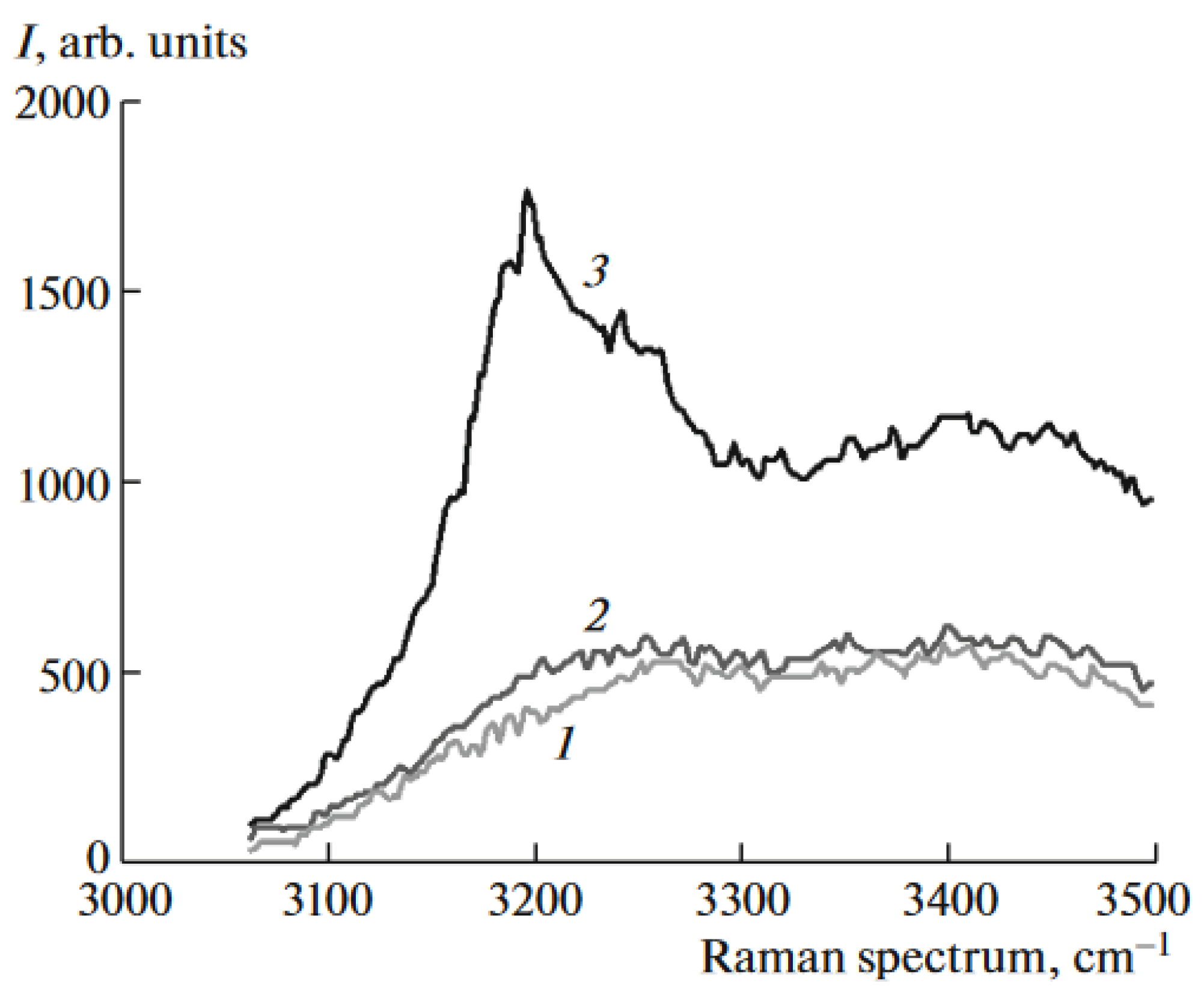
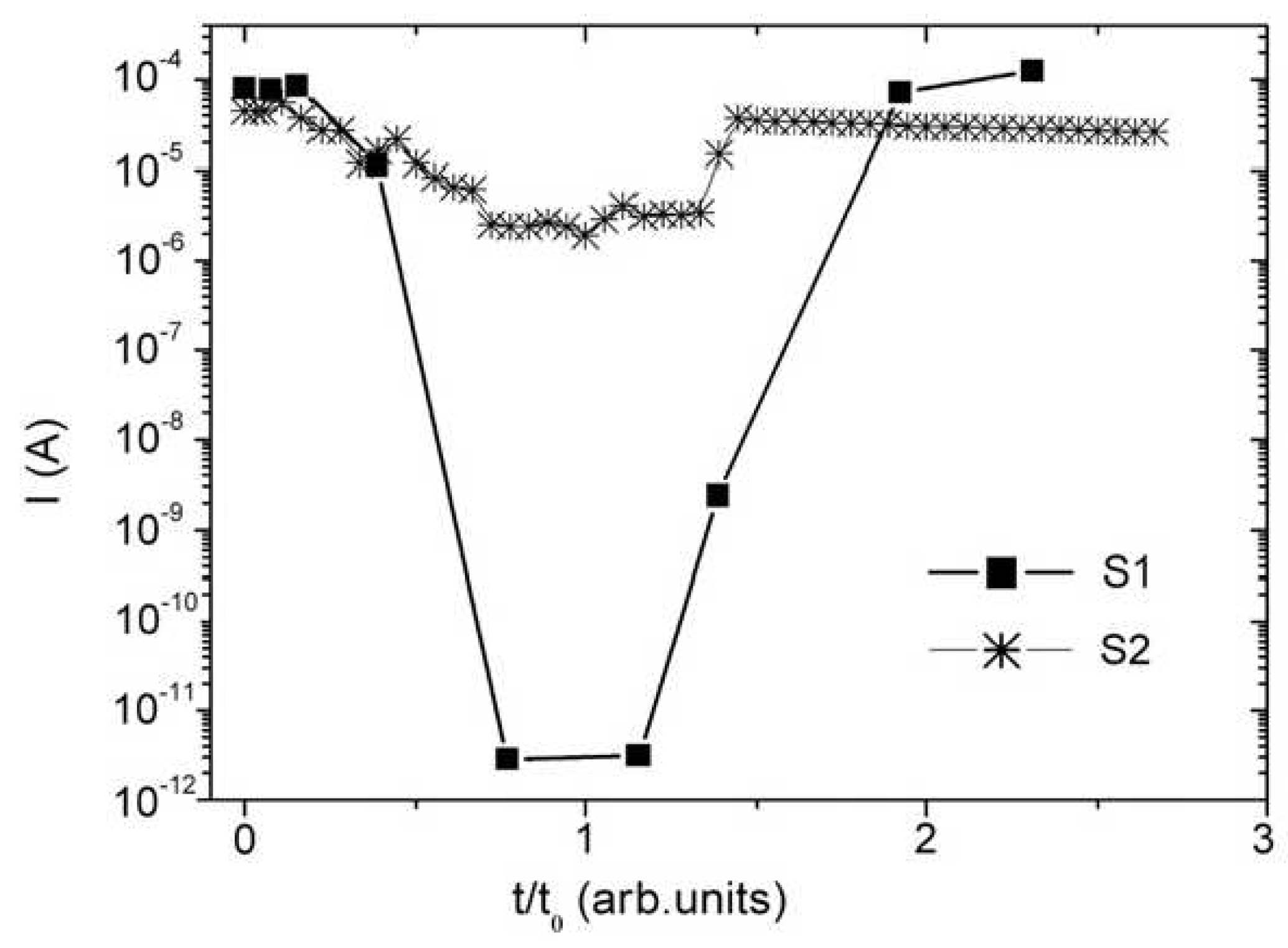

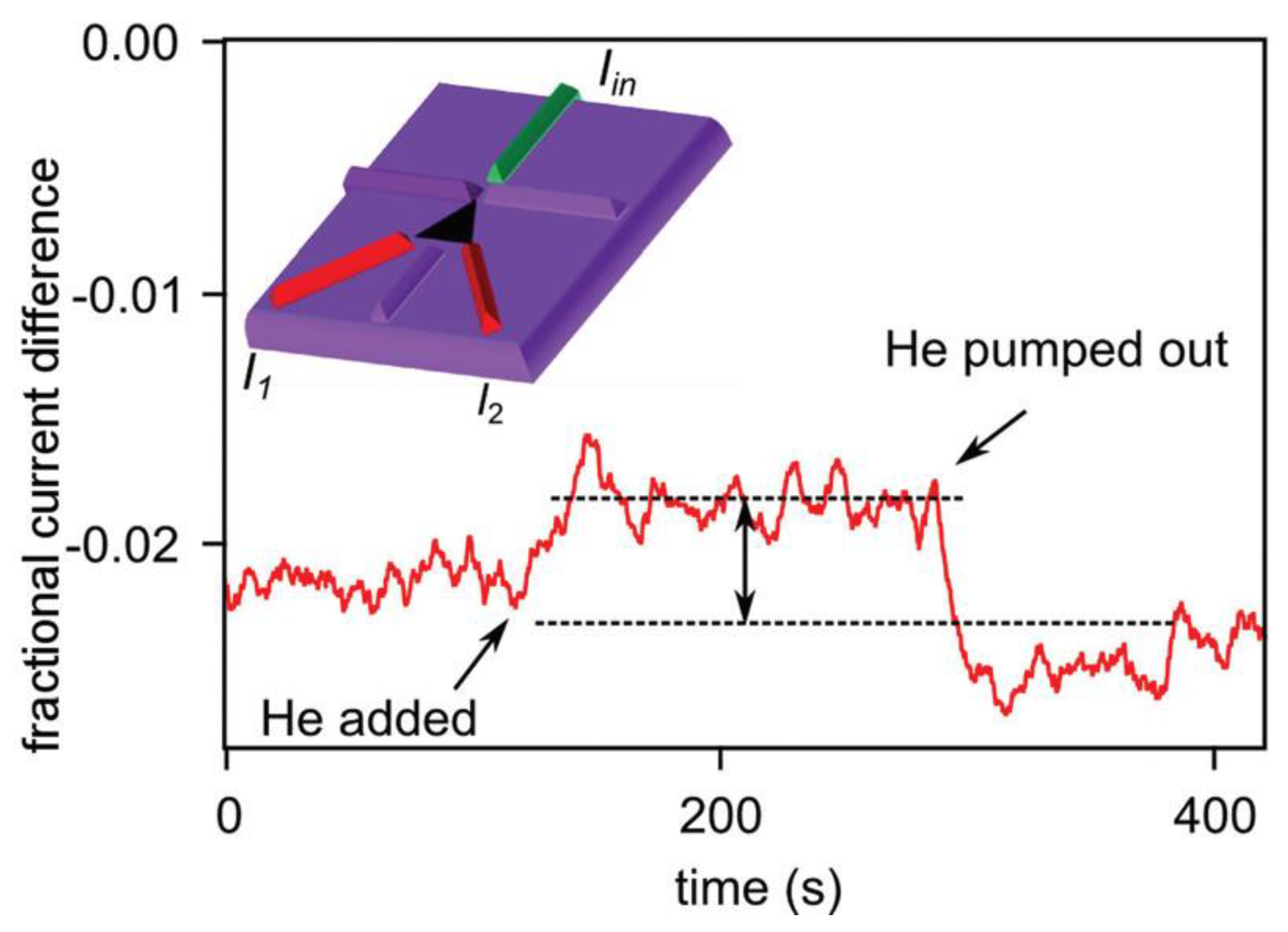
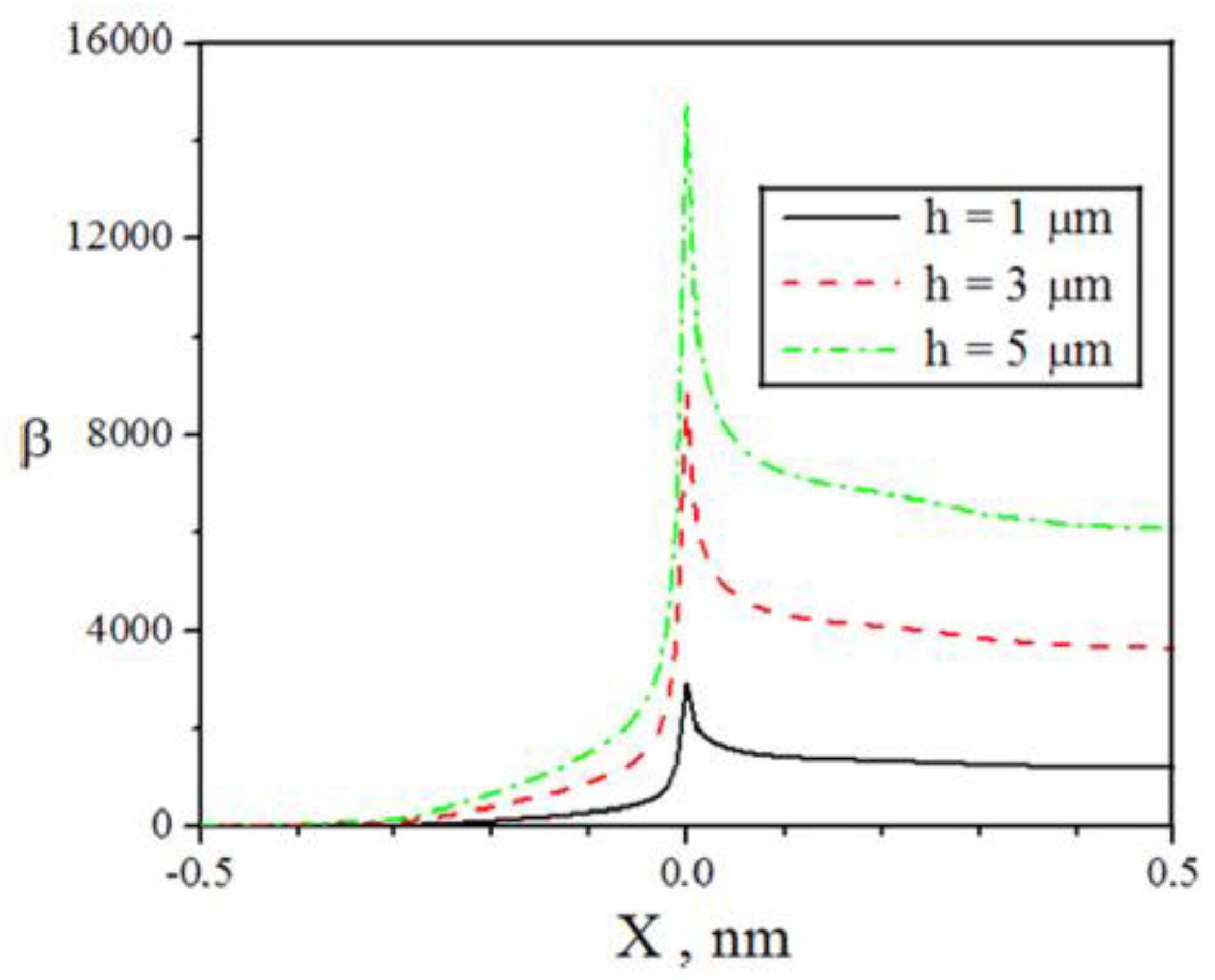

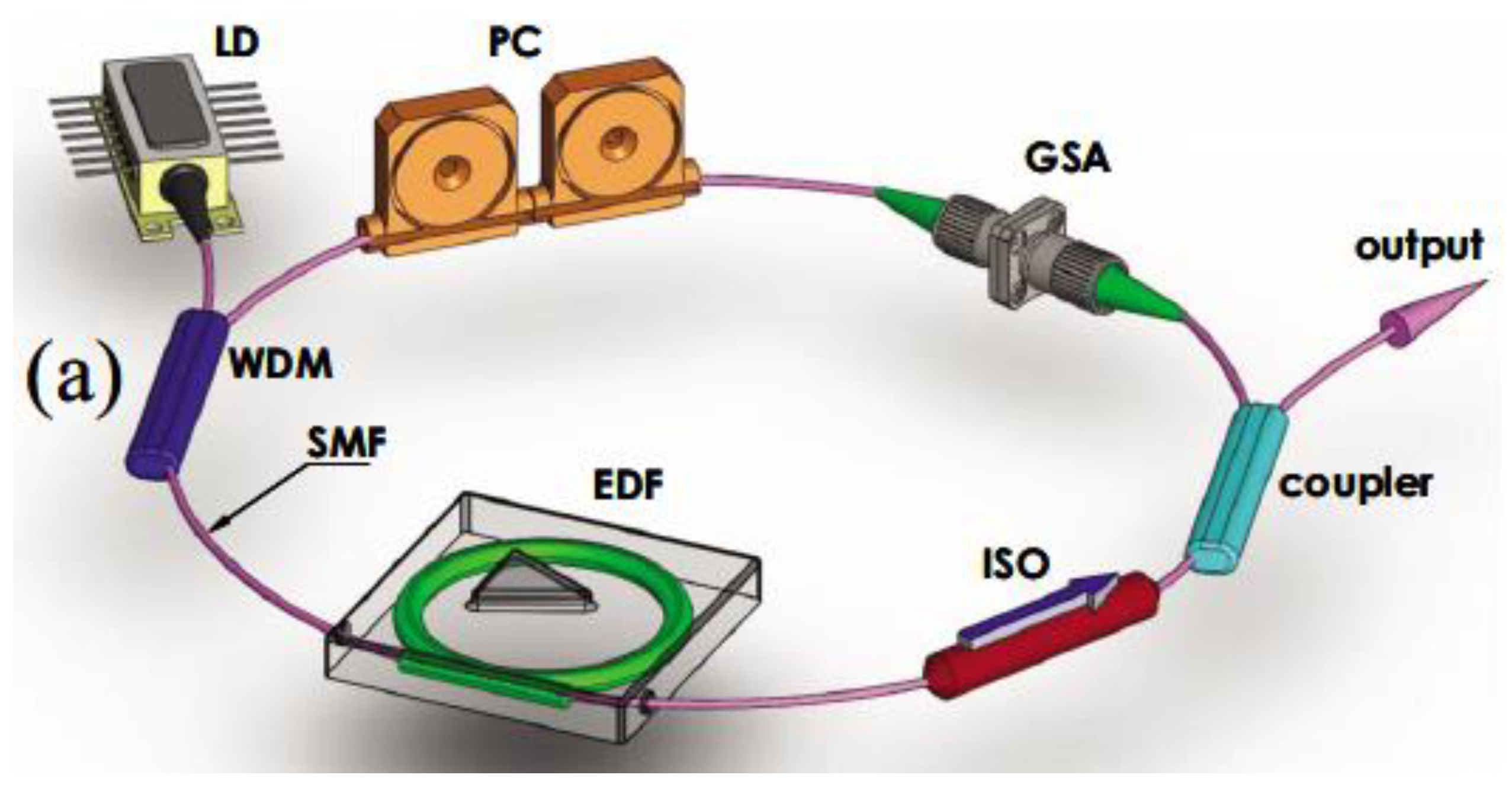

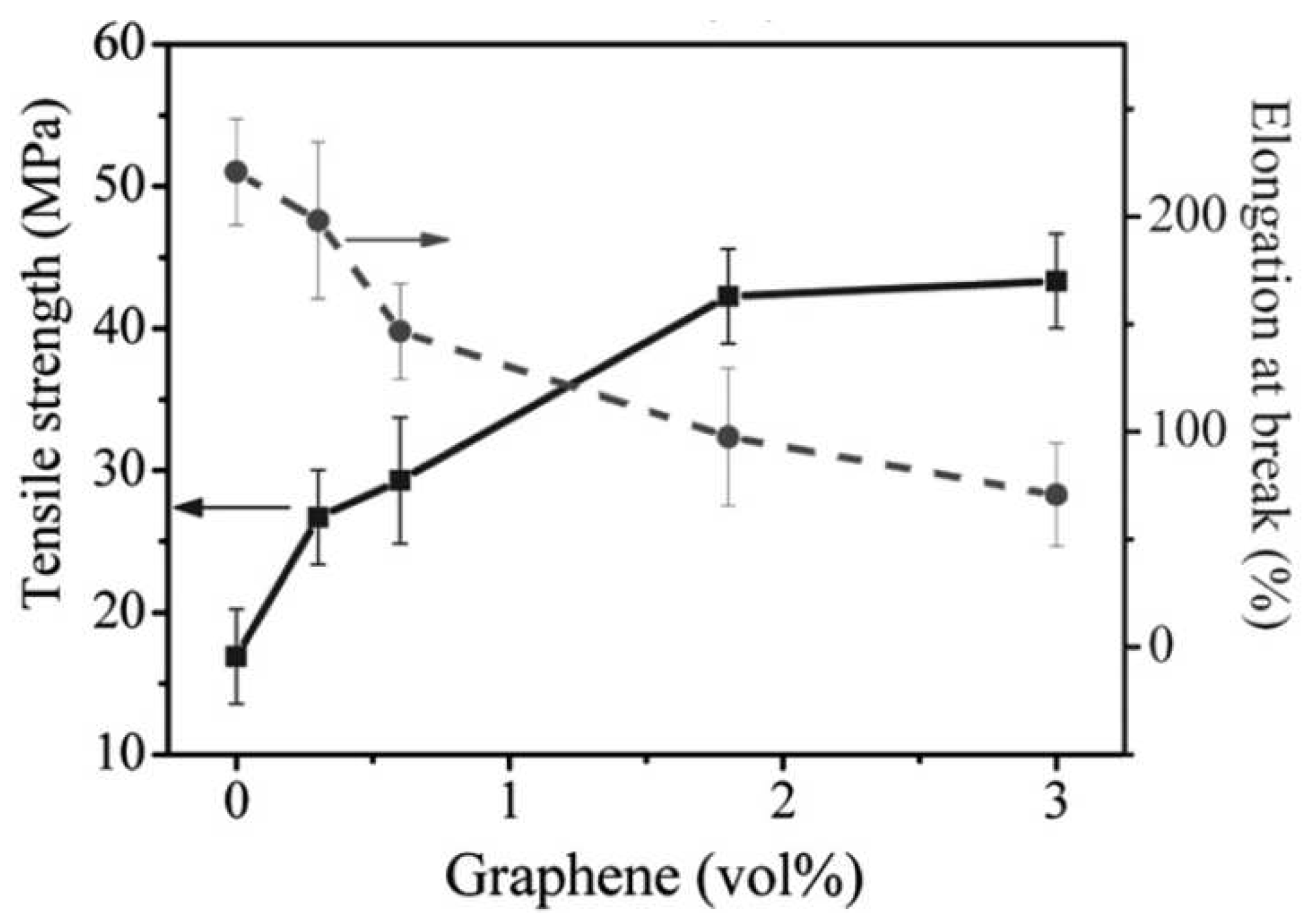
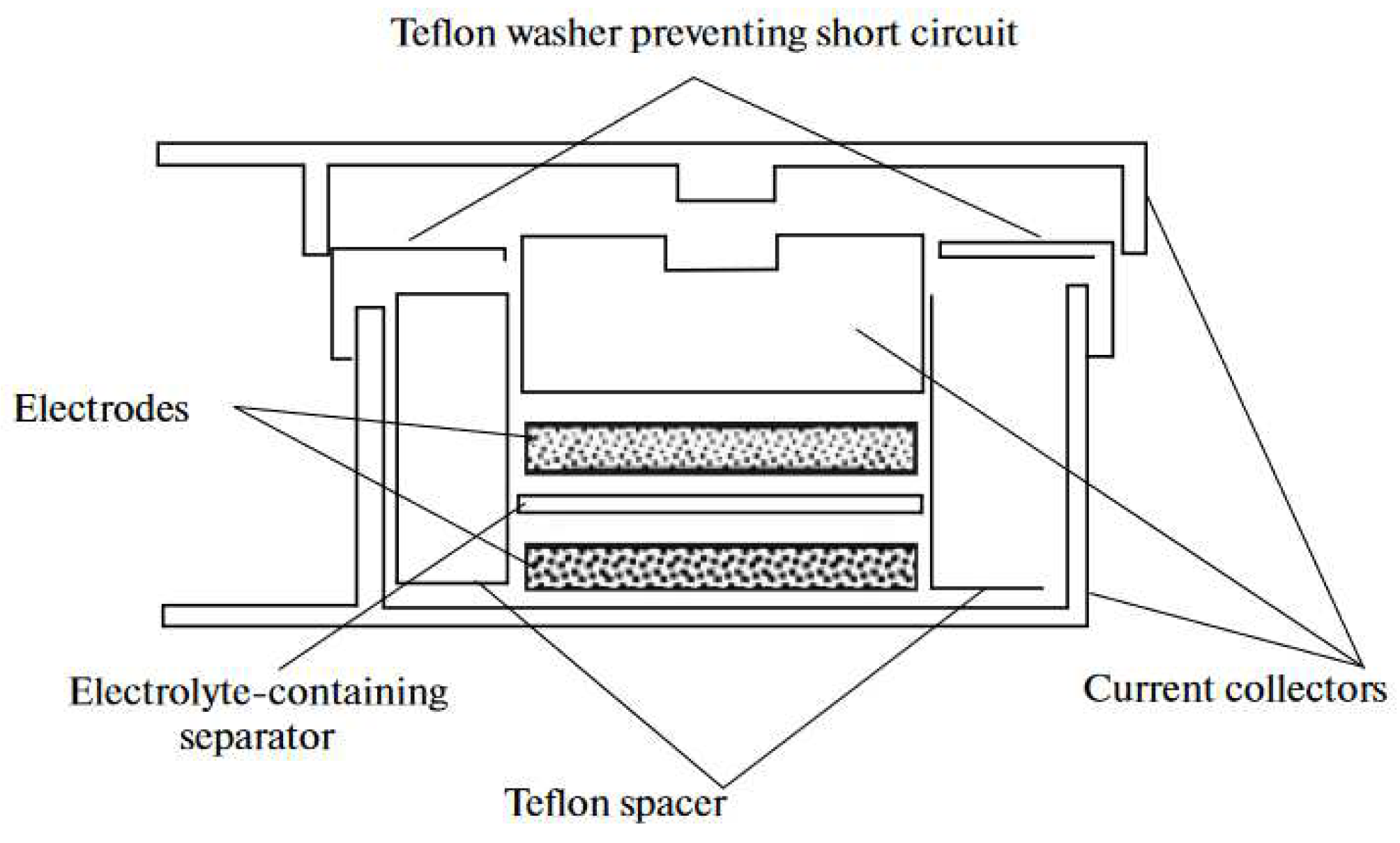
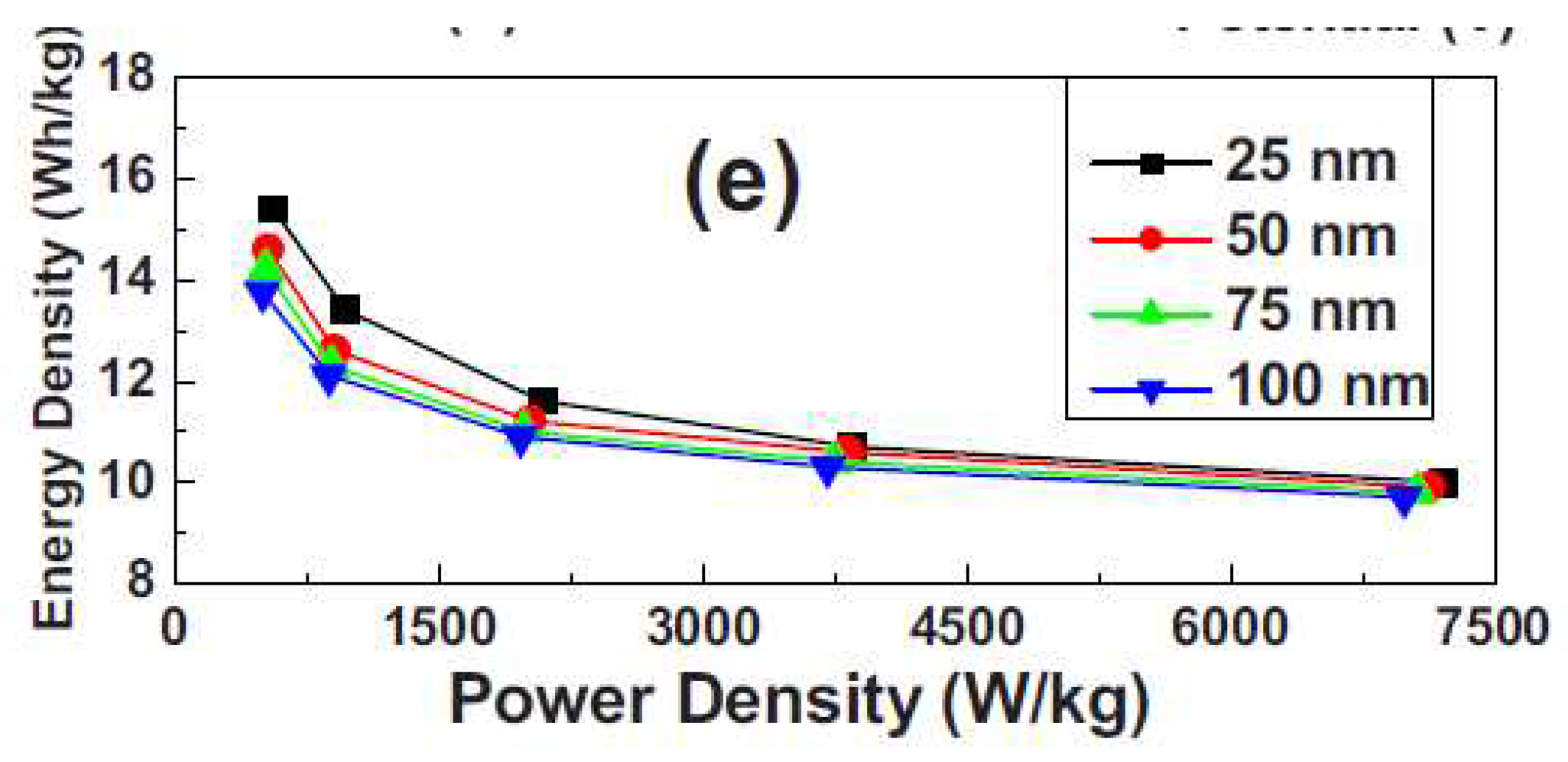
| Thermal treatment temperature, oС | С | О | С/О | N | S | Si |
| 25 | 74.7 | 23.0 | 3.25 | 1.3 | 0.5 | 0.4 |
| 150 | 73.6 | 25.1 | 2.93 | 0.7 | 0.5 | - |
| 200 | 82.0 | 15.2 | 5.39 | 1.6 | 0.5 | 0.7 |
| 600 | 90.6 | 8.1 | 11.2 | 0.5 | - | 0.7 |
| Material | Тс, К | аo, nm | Volumetric fracture fcc, % |
| RbCs2C60 | 33 | 1.4555 ± 0.0007 | 60 |
| Rb2CsC60 | 31 | 1.4431 ± 0.0006 | 60 |
| Rb3C60 | 29 | 1.4384 ± 0.0010 | 70 |
| KRb2C60 | 27 | 1.4323 ± 0.0010 | 84 |
| K2CsC60 | 24 | 1.4292 ± 0.0010 | 60 |
| K2RbC60 | 23 | 1.4243 ± 0.0010 | 75 |
| К3С60 | 19 | 1.4240 ± 0.0006 | 70 |
| Na2CsC60 | 12 | 1.4134 ± 0.0006 | 72 |
| Li2CsC60 | 12 | 1.4120 ± 0.0021 | 1 |
| Na2RbC60 | 2.5 | 1.4028 ± 0.0011 | 2 |
| Na2KC60 | 2.5 | 1.4025 ± 0.0010 | 0.1 |
| Na2CsC60 | 12 | 36 | |
| Na2CsC60 | 12 | 6 |
| Solvent | Solubility,g/l | Solvent | Solubility, g/l | Solvent | Solubility, g/l |
| Decaline (mixture cis- and trans- in ratio 3:7) | 4.6 | Benzene | 1,70 | Thiophenol | 6.91 |
| Cisdecaline | 2.2 | Toluene | 2.80 | 1-methylnaphtalene | 33.0 |
| Transdecaline | 1.3 | 1,2,4- trimethylbenzene | 17.90 | 1-chlornaftalene | 51.0 |
| 1,3,9-cyclo dodecatriene | 7.14 | 1,2,3,5 -tetramethulbenzene | 20.80 | Dimethylnaphtalene | 36.0 |
| Bromoform | 2.54 | 1,3-dichlorobenzene | 27.0 | 1-chlornaphtalene | 51.0 |
| 1,1,2,2- tetrachloroethane | 5.30 | 1,3-dibromobenzene | 13.80 | 1-phenylnaphtalene | 50.0 |
| 1,2,3-tri-bromopropane | 8.31 | 1,2-dibromobenzene | 13.80 | CS2 | 7.90 |
| Substance | Surface tension, mN/m | Capillarity |
| HNO3 | 43 | Yes |
| S | 61 | Yes |
| Cs | 67 | Yes |
| Rb | 77 | Yes |
| V2O3 | 80 | Yes |
| Se | 97 | Yes |
| PbO | 132 | Yes |
| Bi2O3 | 200 | Yes |
| Te | 190 | No |
| Pb | 470 | No |
| Hg | 490 | No |
| Ga | 710 | No |
| CNT content, % |
Melting |
Solidification |
||||||
| Ts, oС | Те, oС | Тр, oС | Нm, Дж/г | Ts, oС | Те, oС | Тр, oС | Hf, Дж/г | |
| 12 | 49.81 | 60.00 | 57.79 | 172.14 | 56.85 | 46.85 | 53.45 | 169.78 |
| 15 | 50.13 | 60.19 | 57.96 | 165.79 | 56.78 | 46.59 | 53.10 | 163.97 |
| 20 | 49.87 | 59.67 | 57.31 | 156.80 | 56.64 | 46.67 | 53.08 | 155.62 |
| 25 | 50.01 | 59.69 | 57.54 | 146.39 | 56.52 | 46.56 | 53.04 | 146.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).