Prerpints.org logo
Preprint
Article

Timber-Based Strategies for Seismic Collapse Prevention and Energy Performance Improvement in Masonry Buildings

Altmetrics

Downloads

105

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts
Abstract
This study investigates the effectiveness of a range of timber-based solutions for seismic and energy retrofitting of existing masonry buildings. These solutions are designed not only to prevent structural collapse during earthquakes but also to create integrated interventions that enhance thermo-physical performance and reduce emissions in existing buildings. Various case scenarios were considered and both mechanical and energetic behavior post-intervention were evaluated. Timber-engineered products serve as foundational components for the retrofit approach, encompassing one-dimensional vertical elements (strong-backs) and various types of panels (cross-laminated timber panels, laminated veneer lumber panels, and oriented strand board panels). The analyzed retrofit techniques share a common principle, involving the attachment of these timber-based elements to the building's wall surfaces through mechanical point-to-point connections. The proposed solutions integrate strong-backs and timber panels with membranes and insulation layers, yielding cohesive and highly effective interventions. Finite element modeling was employed to analyze the mechanical and thermal responses of the retrofitted walls. A comprehensive comparative analysis of various techniques was conducted to determine the most effective solution for each specific scenario.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In recent decades, Europe's construction sector has undergone a profound transformation, shifting its focus from the construction of new buildings to the enhancement of existing building stock. With many buildings nearing the end of their design lifespan, the need to address energy inefficiencies and structural vulnerabilities has become increasingly evident. Retrofitting initiatives have gained prominence, offering a crucial means to not only enhance the overall performance of existing structures but also to fortify sustainability and resilience within the built environment [1,2].
Seismic safety holds paramount importance, especially in regions across Europe prone to earthquakes. The seismic vulnerability of existing masonry structures has emerged as a pressing concern, with profound implications for human safety, infrastructure resilience, and cultural heritage preservation. Many masonry buildings, constructed before modern seismic design standards, exhibit inherent vulnerabilities that pose risks during seismic events. Those vulnerabilities become particularly evident in regions prone to seismic activity, where ground motions can lead to extensive damage, economic losses, and, tragically, the loss of lives [3,4,5]. Moreover, these events threaten cultural heritage, placing historical masonry buildings at risk, necessitating careful consideration of retrofitting and preservation strategies.
Simultaneously, thermal comfort and energy-saving measures are mandated by European legislation [6]. These requirements significantly impact occupant well-being, construction costs, and environmental sustainability. Existing buildings, particularly historical ones, contribute substantially to Europe's energy consumption and carbon emissions. Improving their performance can dramatically mitigate environmental effects and operational costs and enhance the decarbonization (reduction of CO2 emissions) of the building sector to reach the goal of Net Zero Emissions (NZE) by 2050 [7]. Additionally, rising energy prices increase the risk of energy poverty. Refurbishment of these highly inefficient buildings could therefore help to tackle this problem and improve the lives of their inhabitants.
When designing a retrofit intervention, structural, energetic, and architectural aspects must be considered simultaneously to obtain a cost-optimal renovation. The present study investigates the effectiveness of timber-based coating retrofit solutions aimed at reducing the seismic vulnerability of existing unreinforced masonry (URM) structures while improving the energy performance. The mechanical retrofit is provided by timber products fixed to the masonry wall using dry fasteners spreading along the walls surface which guarantee fast execution and reversibility of the intervention. Insulation layers and membranes were added to improve the hygro-thermal performance and the durability of the system.
Timber-based retrofit solutions for existing masonry buildings have emerged as a promising and innovative approach to address the seismic vulnerability of these historical structures while preserving their cultural heritage offering a compelling alternative to conventional retrofitting techniques [8]. In recent decades, timber has reemerged as a sustainable and versatile material, garnering attention for its potential. Timber's inherent properties, including high strength-to-weight ratio, flexibility, and renewable nature, make it an ideal choice for retrofitting interventions that seek to fortify existing masonry buildings against seismic forces.
Various authors in the literature have examined the mechanical performance of diverse timber-based retrofit solutions. Research contributions include a preliminary numerical analysis by Giongo et al. [9], which involved masonry walls subjected to in-plane loading following their retrofitting with timber panels. Meanwhile, the properties of timber-to-masonry wall connections have been experimentally investigated by Riccadonna et al. [10] and Rizzi et al. [11], considering dry and adhesive connections, respectively. Additionally, Giongo et al. [12] conducted full-scale onsite testing of masonry walls retrofitted with cross-laminated timber (CLT) panels, measuring 6 cm in thickness and fixed using the dry fasteners previously examined by Riccadonna et al. [10]. Further insights into the effectiveness of this CLT-based coating have been provided by Cassol et al. [13,14], by means of parametric simulations considering the behavior of the retrofit applied on masonry piers, walls with openings and buildings. Further insight on the experimental and numerical behavior of masonry walls retrofitted with timber panels has been provided also by Borri et al. [15], Pozza et al. [16], Lucchini et al. [17], Iuorio et al. [18] and Sustersic and Dujic [19].
In parallel, the behavior of masonry walls retrofitted with timber strong-backs (vertical timber elements) to improve the wall out-of-plane response has been tested by Giaretton et al. [20], Dizhur et al. [21] and Cassol et al. [22]. Damiani et al.[23], Guerrini et al. [24] and Miglietta et al. [25] tested the effectiveness on the in-plane behavior of a strengthening strategy that sees vertical timber strong-backs supplemented with horizontal timber blocking elements to create a frame that is then sheathed by oriented timber-based sheets (OSB panels). The experimental campaigns included in-plane quasi-static cyclic tests performed on masonry piers and shake-table tests performed on full-scale building prototypes, tested in bare and retrofitted conditions, respectively.
Further numerical simulations were performed by Busselli et al. [26] and Cassol et al. [27] to evaluate both the seismic and the thermo-physical properties of various aforementioned timber-based retrofit solutions, with the aim of designing integrated retrofit interventions. In this context, an alternative solution named Nested Building Approach was studied by Valluzzi et al. [28]. The analyzed solution consisted of removing the building internal elements and inserting a new inner structure realized with CLT panels coupled with insulation and finishing layers. Also in this case both the improvement of the seismic and hygrothermal performances were numerically investigated.

2. Retrofit solutions

The retrofit solutions studied herein consist of connecting timber-based products (panels and strong-backs) to the surface of the walls of a building using mechanical point-to-point connections, with the aim of improving the in-plane and the out-of-plane capacity of the URM walls. Insulation layers, membranes and finishing layers were added to guarantee the durability of the timber elements and to improve the thermophysical performance of the retrofits. Four solutions were analyzed with the structural retrofit provided by cross laminated timber (CLT) panels, laminated veneer lumber (LVL) panels, or by two different combinations of timber strong-backs and oriented strand boards (OSB) panels. Two configurations of the non-structural layers were designed for each solution, acknowledging that the intervention could be applied to either the internal or external side of the masonry walls, see Figure 1. The selected thicknesses of the timber panels were compatible with those used the in-situ campaigns performed by [10,11,12], while the timber strong-back cross-sections were selected based on the experimental campaigns reported in [20,21,22].
For the internal solutions, expanded rigid polyurethane foam (PIR) panels were employed for the insulation; a vapor barrier was applied close to the inner finishing layer (plasterboard sheets) and a breathable and waterproof membrane was installed on the masonry wall surface to avoid imbibition of the timber elements. For the external installations, PIR panels, covered on both sides by saturated fiberglass facers, were used to create an External Thermal Insulation Composite System (ETICS). A breathable, waterproof and reflective membrane was applied to the outer surface of the timber elements to hinder the passage of sunrays while a waterproof membrane was installed between the masonry wall and the timber elements, similarly to what done for the internal solutions. A maximum value of 125 mm was assumed as limit for the retrofit thickness in the case of internal application, with the aim of limiting the reduction of internal volume due to the intervention. The thickness of the insultation layers of the external solutions was calculated analytically based on the maximum thermal transmittance (U=0.28 W m-2 K-1) allowed by the Italian regulation [29] for existing buildings, considering the climatic zone E. The effectiveness of the integrated retrofit interventions was evaluated considering the improvement of both mechanical and energy performance.

3. Seismic analyses

3.1. Numerical model

The numerical models were realized using the finite element software Abaqus/Standard [30]. A simplified micro modelling approach was adopted for simulating the masonry wall. In this approach, the size of the masonry units (i.e., bricks) is expanded to incorporate the mortar joints. The expanded masonry units are modelled as continuum elements and the interaction between such elements is reproduced by selecting proper interface properties. The expanded masonry units (EMU) were modelled with an equivalent, homogeneous and isotropic material. The EMU elastic modulus EEMU was determined considering the elastic modulus and the thickness of the bricks (Eb and hb) and the mortar joints (Em, hm), as indicated in Equation 1. The EMU nonlinear behavior was described by the Concrete Damage Plasticity (CDP) constitutive model. Such model was developed by Lubiner et al. [31] and was further elaborated by Lee and Fenves [32] and it allows simulating the post cracked behavior of quasi brittle materials such as masonry. The tensile and the compressive behaviors of the EMU under axial loading were implemented using bilinear and parabolic stress-strain relations, respectively. The EMU compressive strength fc,EMU was calculated as indicated in Eurocode 6 [33] (see Equation 2), while the EMU tensile strength ft,EMU was defined as equal to the brick tensile strength ft,b. The fracture energy values governing the post cracked behavior of the EMU were calculated as recommended by Lourenço and João [34].
E E M U = ( h b + h m ) · E b · E m h b · E m + h m · E b
f c , E M U = 0.45 · f c , b 0.7 · f c , m 0.3
The horizontal mortar joints (i.e., bed joints) and the vertical mortar joints (i.e., head joints) are characterized by different properties and, consequently, their contribution was accounted for by adopting different approaches. The interfaces simulating the head joints were provided with a hard-contact interaction property which allows for compression stress transfer only. The head joints were assumed to be cracked (e.g., due to shrinkage), which meant that both the cohesive and the friction contributions from these interfaces were neglected. The modelling approach adopted for the bed joints can simulate both the tensile and the shear-cracking failure modes. Contact properties: traction separation, cohesive and tangential friction, were used to model the joint interfaces. The uncoupled stiffness coefficients for the normal direction (kn) and tangential directions (ks and kt) were determined considering the mortar and brick elastic moduli and dimensions, as indicated in Equations 3 and 4. The quadratic traction stress criterion [30] was used to define damage initiation, see Equation 5, where the Macauly brackets indicate that in the normal direction only the tensile stresses were considered. The maximum normal strength (tn,max) and shear strengths (ts,max and tt,max) were assumed to be equal to the tensile strength (fm,t) and the cohesion (c) of the masonry joints. The post cracked behavior was defined assuming a linear damage evolution based on the energy dissipated during the crack propagation. The tensile and shear fracture energy values were calculated as recommended by Lourenço and João [34]. The mixed mode damage evolution was modelled according to the Benzeggagh-Kenane (BK) law, which is suitable for representing the damage evolution when the shear behavior is the same along the two reference directions of the shear plane, assuming a BK exponent equal to 2. The viscosity coefficient for the damage stabilization was assumed equal to 0.02. In the tangential direction, a further contribution due to friction was considered. The friction coefficient was assumed equal to 30° and a limit to the maximum value of the shear stress fv,lim was fixed (fv,lim = 0.065 fc,b [35]).
k n = E b · E m h m · ( E b − E m )
k s = k t = G b · G m h m · ( G b − G m )
t n t n , m a x 2 + t s t s , m a x 2 + t t t t , m a x 2 = 1
Timber was modelled as an orthotropic material where inelastic phenomena, such as compression crushing at the panel’s toe, were simulated using a plastic constitutive model. The CLT panels were modelled as three-layers solids, while the LVL panels and the OSB sheets were simulated using equivalent orthotropic materials. The point-to-point connections between the timber elements and the masonry wall, the anchoring connections and the timber-to-timber connections were modelled using one-dimensional wire elements. The properties of such elements were calibrated on the outcomes of different experimental campaigns, while the wire extremities were fixed to the timber and the masonry using coupling constraints with adequate influence radii. A regular mesh pattern with eight nodes three dimensional elements (C3D8R) was used. The selected mesh size (30 mm) is the maximum size that allowed describing the behavior of the EMU with adequate accuracy (for the validation process, please refer to section 3.2). The horizontal and the vertical loads were applied as uniform pressures, and the geometric nonlinearities were considered. Quasi-static analyses were performed to improve the convergence and to reduce the computational cost of the simulations.

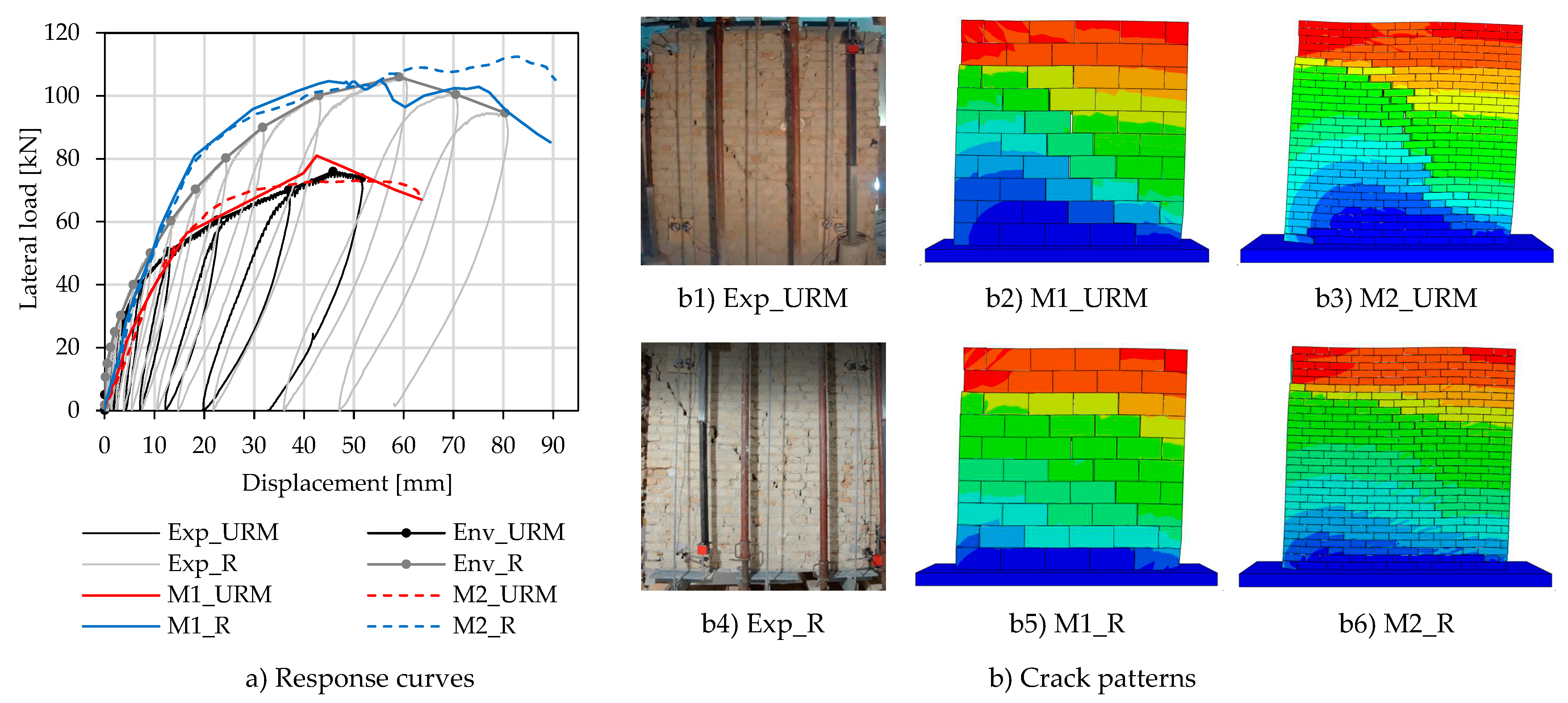
3.2. Model validation

The models reproducing the unreinforced masonry (URM) condition and the retrofitted condition with the retrofit provided by the application of a CLT panel were validated on the results from in-situ full-scale semi-cyclic shear-compression testing of triple-leaf clay brick masonry walls performed by Giongo et al. [12]. Such walls were characterized by a composite failure mode with an initial phase of rocking followed by diagonal shear failure. The application of the retrofit produced an increase of 41% in the load-bearing capacity, while the initial stiffness of the wall appeared not to be modified. Figure 2 presents the comparison between the experimental and numerical results. Two numerical models were used: a simplified model (M1), which was realized adopting equivalent masonry units six times the size of a brick to reduce the computational effort of the simulations, and a detailed model (M2) implemented considering the actual brick pattern and size. It can be observed that the numerical outcomes are consistent with the experimental data in terms of failure mechanism, initial stiffness and load capacity.

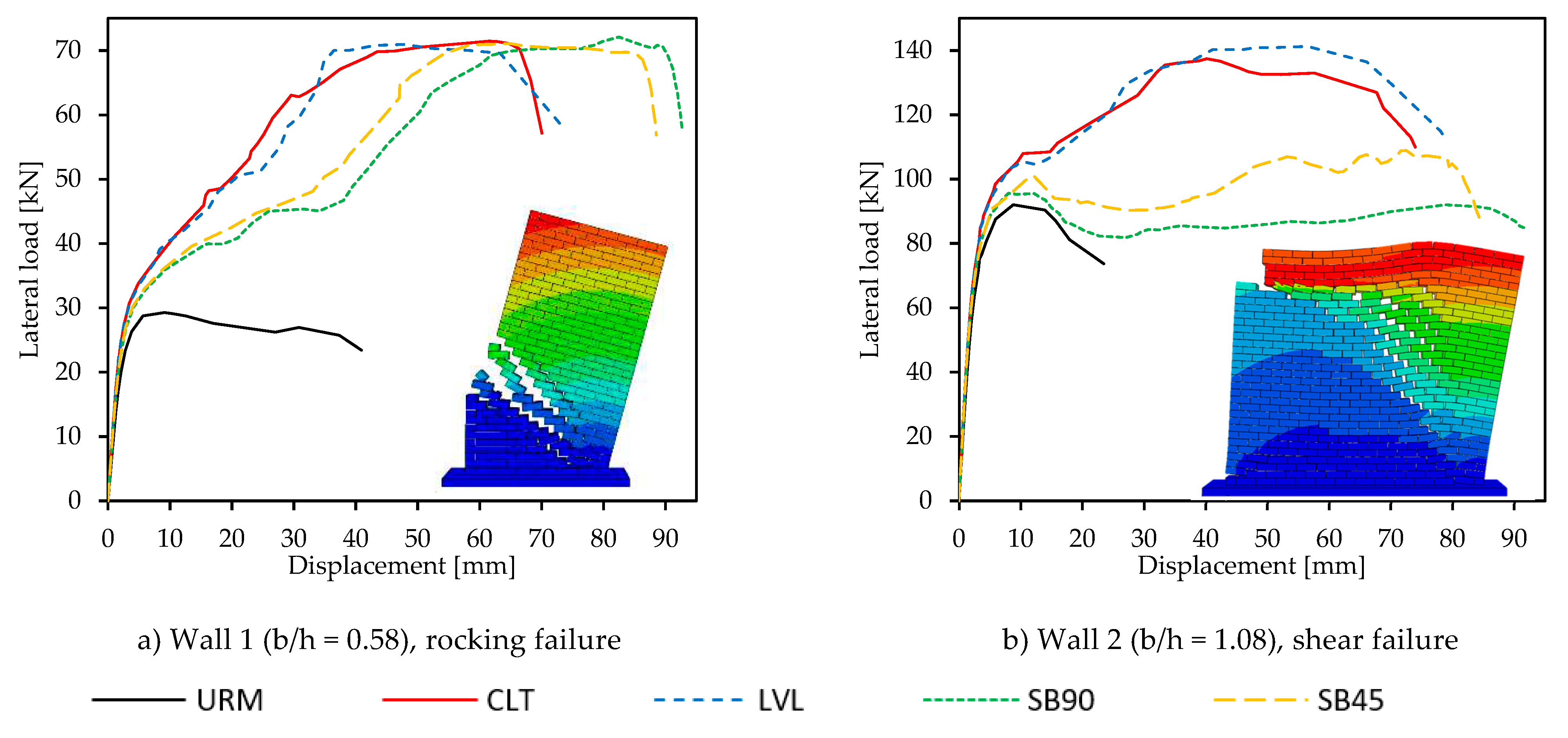
3.3. Results

The effectiveness of the proposed retrofit solution was further investigated using the modelling approaches described in the previous sections. The timber retrofits were applied to two double-leaf clay brick masonry walls characterized by different aspect ratios (i.e., b/h 0.58 and 1.08) and failure modes (i.e., rocking and shear). Such walls were 3000 mm high and 250 mm thick; the bricks’ dimensions were 240 x 120 x 75 mm, and the bed joints were 15 mm thick. The overburden was applied as a uniform pressure of 0.1 MPa, a conservative value representing the vertical load typically encountered in a three-story URM building. The horizontal load was applied to the side of the masonry walls at an average height from the base of 2565 mm, targeting the blocks within the third, fourth and fifth rows from the top. The adopted masonry properties are shown in Table 1. The retrofit was provided by a single timber panel as long as the wall for the slender wall (wall 1) and by three side-by-side panels for the stocky and longer wall (wall 2). The panel-to-panel side connection for the solutions where CLT and LVL panels were used was realized by inserting fully threaded timber screws at an angle of 45° to the joint line (8 mm diameter screws spaced at 200 mm). The layout of the masonry-to-timber connections was the same for all the investigated retrofit configurations matching that of the experimental campaign reported in [12] (≈ 4 fasteners/m2, horizontal spacing = 500 mm, vertical spacing = 540 mm). The timber strong-backs and the horizontal timber “blocking” elements were fixed to the masonry wall by adopting the same fastener spacing used for the solutions with the timber panels. The OSB sheets were connected to the timber frames with nailed connections (fastener spacing = 100 mm) and, if multiple OSB sheets were used, the sheet-to-sheet joints were realized in correspondence with the strong-back location. Tensile anchors (i.e., hold-downs) were fixed next to the wall’s corner, while a single shear anchor (angle bracket) for each timber panel was used. The timber properties were determined assuming a timber grade C24 for the boards of the CLT panels [36] and a timber grade C18 for the strong-backs [36]. The properties of the equivalent materials used to simulate the LVL panels and OSB sheets were defined as indicated in [37] (LVL-X) and [38] (OSB 3). The timber-to-masonry connection properties were calibrated on the experimental outcomes reported in [10], the properties of the anchors were defined based on the experimental results reported in [39], the timber panel-to-panel side connections were modelled as recommended by [40], and the OSB panels-to-timber connections were implemented considering the experimental results reported in [41].
Figure 3 shows the lateral load-displacement curves of the retrofitted masonry walls. All the analyzed retrofit solutions increased considerably the load bearing and displacement capacities of the masonry walls. The ultimate displacement of the walls was evaluated as the displacement corresponding to a strength degradation of 20% of the maximum lateral capacity [42]. In the case of rocking behavior (wall 1), the failure of the retrofitted walls occurred when the ultimate strength of the tensile anchors was reached and, consequently, the four analyzed solutions provided the same load bearing capacity (71 kN, with an increase of 145%). The stiffness of the retrofit is responsible for the displacement required to engage the maximum load-bearing capacity and the displacement capacity of the solutions. The response of the timber panel retrofit solutions (CLT and LVL) was very similar due to the comparable stiffness of the timber panels. Such solutions reached the maximum load-bearing capacity at a drift of 1.15%, while the increase in displacement capacities was 70% (at a drift of 2.25%). Expectedly, the solutions with the strong-backs and the OSB sheets (SB90 and SB45) proved more deformable than the panel solutions due to the reduced stiffness of the retrofit. The maximum load-bearing capacity was engaged at a drift of 1.83% (SB45) and 2.14% (SB90), while the increase in the displacement capacity was 115% (SB45) and 133% (SB90). In the case of shear behavior (wall 2), the failure of the walls retrofitted with timber panels (CLT and LVL) was determined by the capacity of the timber-to-masonry connections being exceeded. The CLT and LVL solutions allowed an increase in the load-bearing capacity of 52% and in the displacement capacity of 226% (drift = 2.50%). The SB45 and SB90 solutions were less effective than the timber panel ones due to the reduced stiffness of the timber retrofit and the limited strength of the OSB panel-to-strong-back nailed connections. The solutions with the strong-backs and the OSB sheets, when applied to squat masonry walls (wall 2), improved only the displacement capacity with increases of 265% (SB45) and 300% (SB90), and drift values of 2.80% (SB45) and 3.07% (SB90). SB45 appeared to be slightly more effective than SB90 due to the bigger inertia modulus of the SB45 strong-backs in the direction parallel to the wall.

4. Energy performance analyses

A numerical model of the analyzed components was developed in COMSOL Multiphysics® [43] to assess the thermal performance of the retrofit solutions both in winter and summer seasons. At first, a steady-state heat transfer model was created for the different configurations. This allowed the calculation of solutions’ thermal transmittances considering the structure's minor thermal bridges. Then, a time-dependent heat transfer model was created to simulate a typical temperature pattern occurring during the summer season. This analysis allows for the evaluation of the periodic thermal properties often used in regulatory requirements. Finally, the response factors [45,46,47,48,49,50,51] of the retrofit solutions were simulated in order to obtain the thermal response in terms of specific heat flux on the internal side after the application of a triangular temperature excitation. Response factors underlie the calculation methods used by many building energy simulation software (e.g., EnergyPlus™ [52], TRNSYS [53]). Thus, an experimental assessment of such factors could result in a more accurate simulation of real walls’ behavior. Moreover, recent experimental techniques [54] show how the exploitation of triangular pulses applied on one side of a wall can be adopted in the assessment of the U-value of the wall, both under controlled conditions and in-situ, by significantly reducing the test time. Preliminary results show good agreement between U-values obtained with the pulse method and the U-value calculated with the standard stationary procedure suggested by the [55,56].

4.1. Numerical model

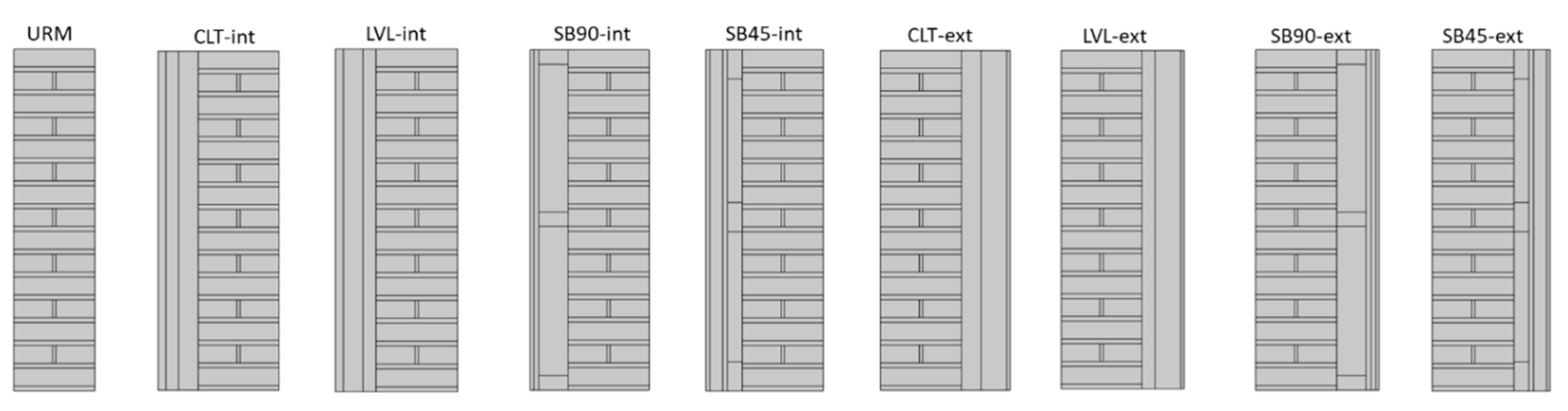
4.1.1. Geometry and materials

At first, the bi-dimensional geometry of the masonry wall and of the 8 retrofit solutions was first created in order to build the model in COMSOL Multiphysics®. Figure 4 shows the different geometric models of the 9 configurations that were modelled, obtained by replicating the retrofit stratigraphy seen in Figure 4. To each closed element, a material was associated. Thermophysical properties of the adopted materials are the ones reported in Table 2.

4.1.2. Model description

The governing heat transfer mechanisms consisted of (i) heat conduction across the wall and (ii) heat convection on the surfaces. The Newton-Robin boundary condition on the two vertical surfaces was set by defining the heat transfer coefficient and the air’s temperatures (see Equation 6.
q 0 = h ⋅ ( T A I R − T s )
where q0 [W m-2] is the boundary convective heat flux, h [W m-2 K-1] is the heat transfer coefficient and TAIR [°C] is the air’s temperature and Ts [°C] is the temperature of the wall surface. For the internal side, the heat transfer coefficient was set equal to hint =7.69 W m-2 K-1, while for the external side hext was set equal to 25 W m-2 K-1, according to the Standard EN ISO 6946:2018 [44]. Conversely, the two horizontal surfaces were set as adiabatic. The air’s temperature was defined according to the study being performed, either stationary or periodic, as described in the following sections.

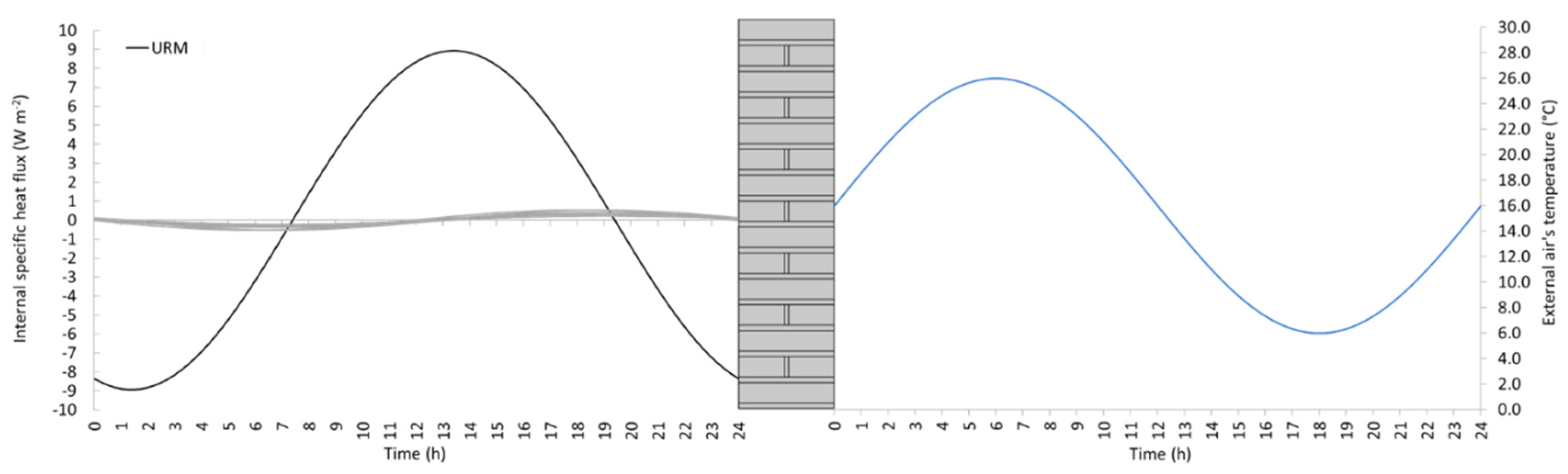
4.1.3. Steady-state regime

A stationary analysis was run to determine the thermal transmittance of the different retrofit solutions. As a matter of fact, constant airs’ temperatures at the internal and external sides were set, namely TAIR,i = 20 °C and TAIR,e = 0 °C, with a thermal gradient of 20 K. The steady-state study was run considering a relative tolerance of the solver equal to 0.001.
Starting from numerical results, it was possible to calculate the thermal transmittance. At first, the thermal resistance of the wall Rwall [m2 K W-1] was determined according to Equation 7, and then the thermal transmittance U of each retrofit solution, expressed in W m-2 K-1, was assessed through Equation 8.
R w a l l = T s i − T s e q ˙
U = 1 R s i + R w a l l + R s e
where Tsi [°C] and Tse [°C] are the internal and external surface temperatures calculated as line average on each surface, respectively. q ˙ [W m-2] is the specific heat flux obtained as line average on each one of the vertical surfaces.

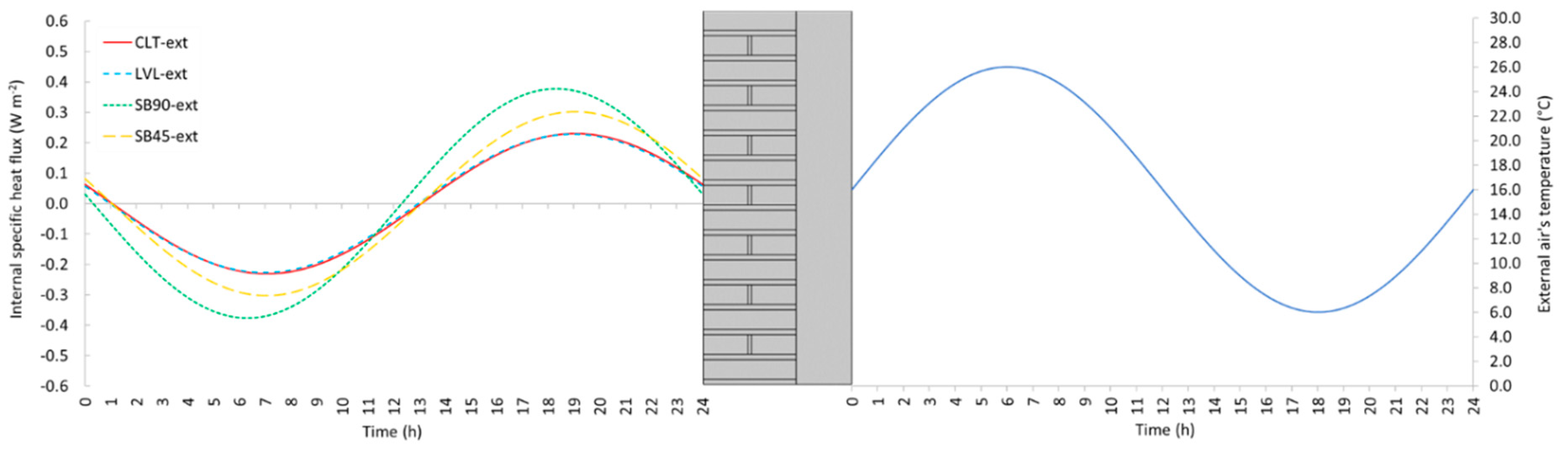
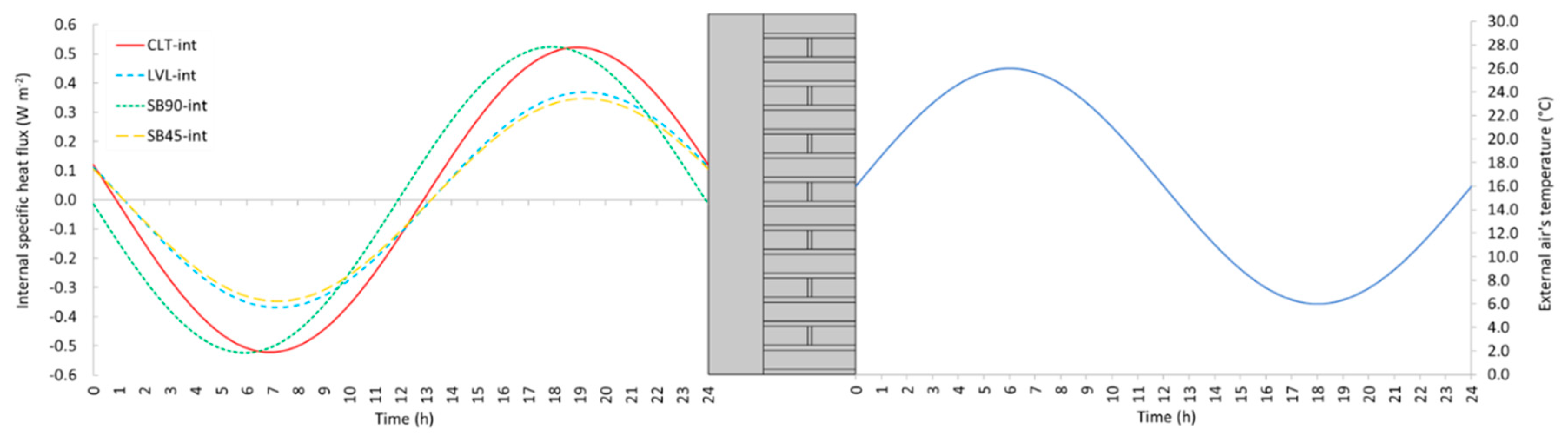
4.1.4. Periodic regime

A dynamic periodic study is required to analyze the summer performance. The selected regime was a periodic one, in which the internal air’s temperature was set constant equal to TAIR,i = 16 °C, while the external one TAIR,e was forced to follow a sinusoidal function with 10 K of semi-amplitude, 16 °C of average temperature and a period of 24 h (Equation 9).
T A I R , e = 16   ° C + 10 ⋅ sin ⁡ 2   π ⋅ τ T
where τ [s] is the time expressed in [s] and T is the 24 h-period of the solicitation. The initial condition in the solid domain was taken equal to the wall’s average temperature, that was 16 °C. In this way, the transient period of the simulation was reduced.
The relative and absolute tolerances of the time-dependent solver were stricter than the stationary study and were set equal to 10-4 and 10-5, respectively. Those values were necessary in order to obtain accurate results in the time-dependent study. Simulations were run for a period of 10 days with 1 min time-step, and the Runge-Kutta method was chosen as the resolution method, which is extremely suitable for oscillatory problems.
Periodic thermal parameters were calculated starting from the numerical results, in terms of temperatures and specific heat fluxes, analyzing them in a 24 h period in the stabilized regime, thus, after the transient time. The periodic thermal transmittance Yie [W m-2 K-1] was calculated by taking the ratio of the semi-amplitude of the specific heat flux function over the semi-amplitude of the external air’s temperature function, both considered in the same period of 1 day. The decrement factor f [–] was calculated by taking the periodic thermal transmittance Yie and dividing it by the U-value. The phase shift Δτie, expressed in hours, was determined as the difference between the moments at which the maximum values of the specific heat flux and of the external air’s temperature occur.

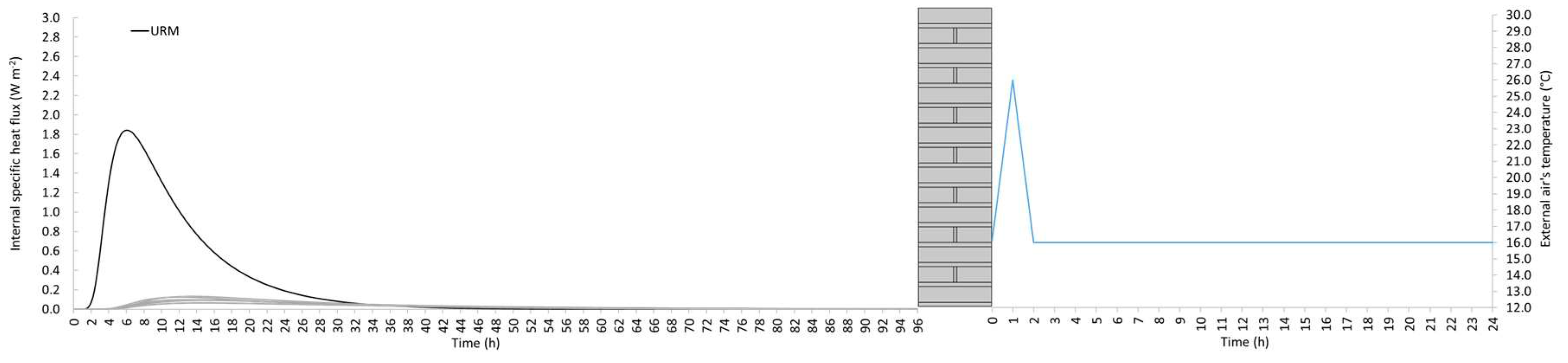
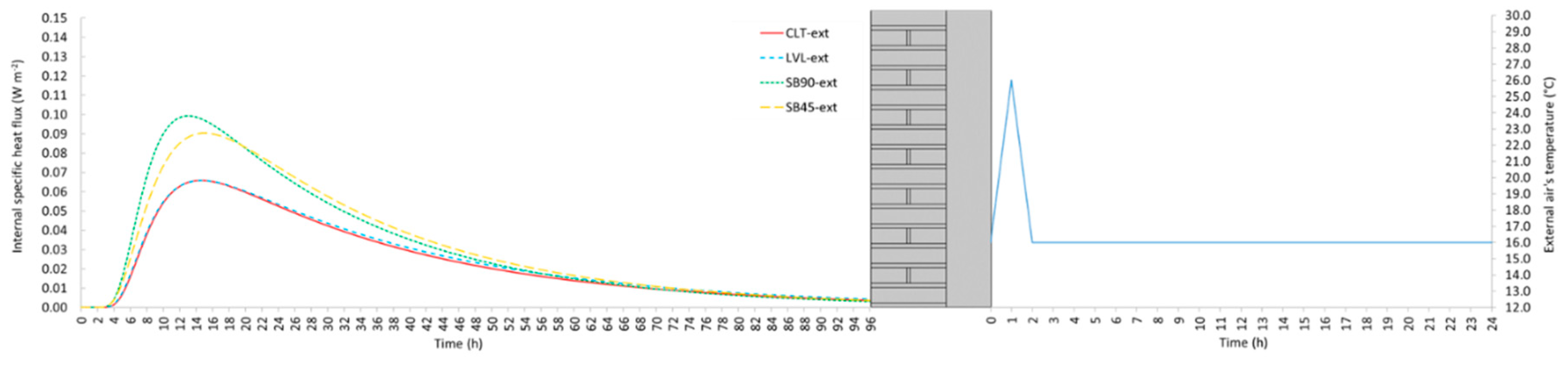
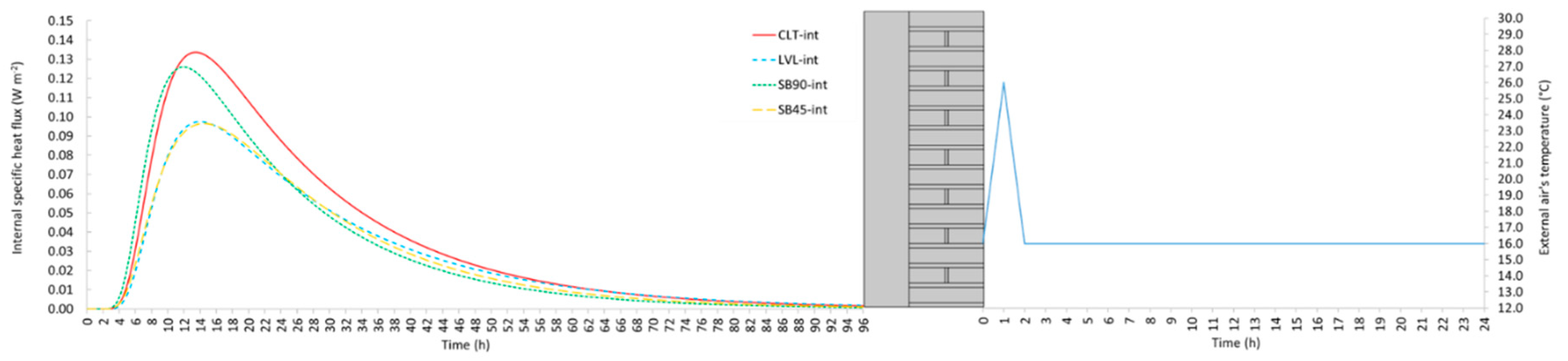
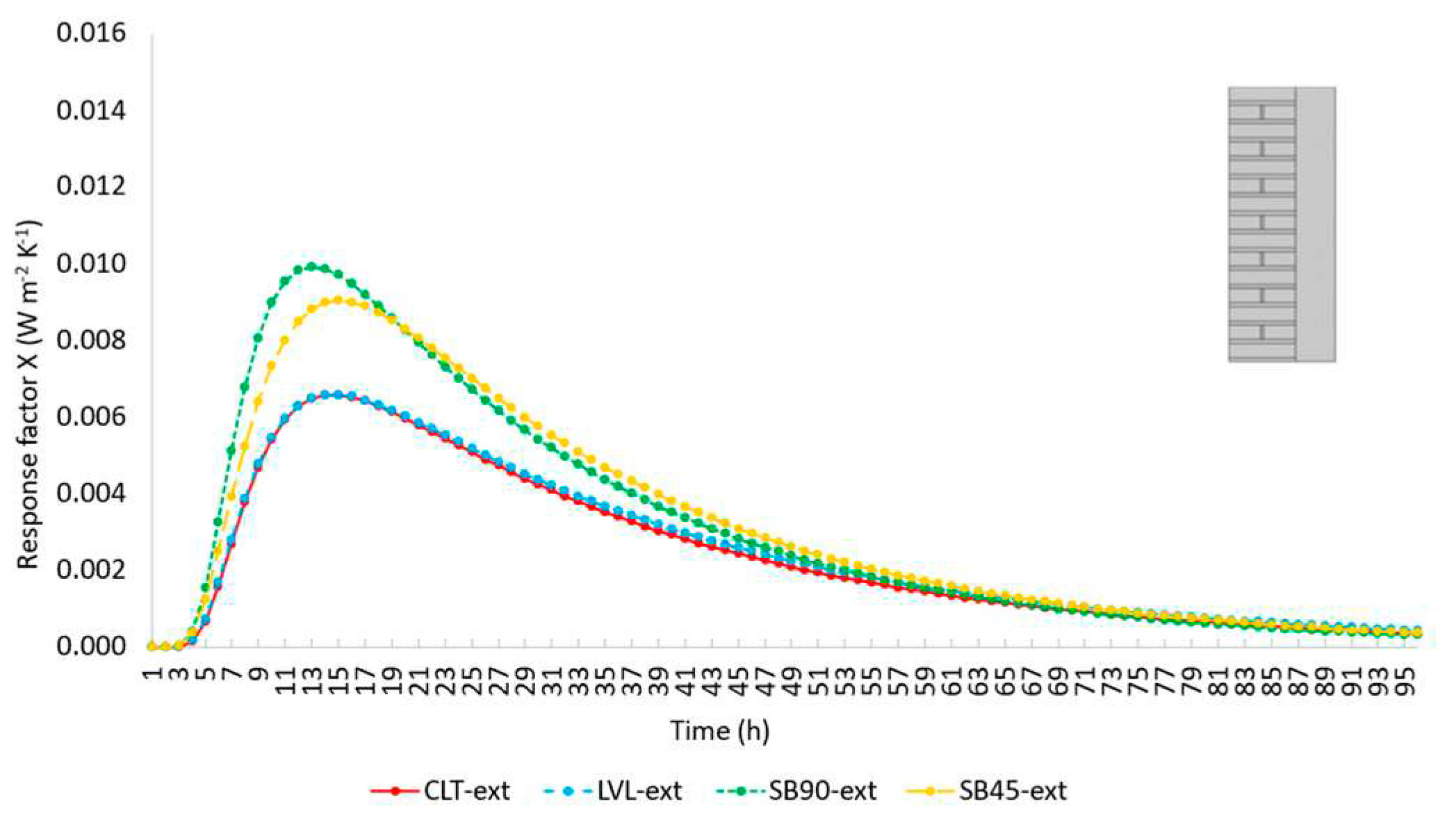
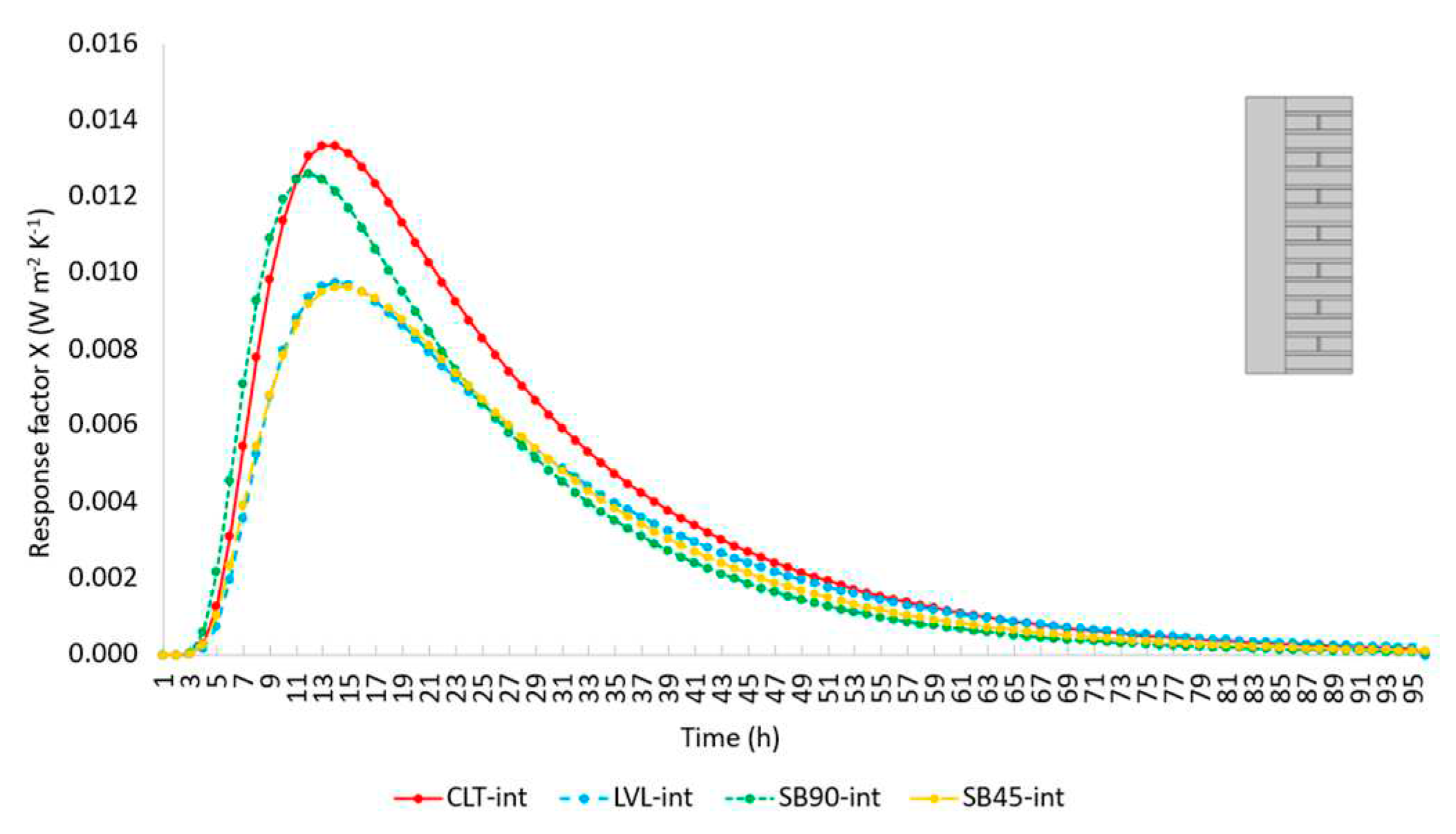
4.1.5. Dynamic regime

Among dynamic studies, it is also possible to analyze the thermal behavior of the retrofit solutions by applying a temperature impulse on the external side and investigating the response in time in terms of internal heat flux. This is known as response factor [45,46,47,48,49,50,51]. In particular, the external air’s temperature was forced to follow a triangular function, as shown in Equation 10, while the internal air’s temperature was kept equal to 16 °C. The initial condition was set equal to 16 °C in the whole solid domain.
T A I R , E = 16 + 10 ⋅ t ,   0 < t ≤ 1   h   T A I R , E = 26 − 10 ⋅ t − 1 ,   1 < t ≤ 2   h   T A I R , E = 16 ,   2 < t ≤ 96   h
Notwithstanding the theory [45,46,47,48,49,50,51] defines response factors as responses to a unitary temperature solicitation of 1 K, the simulation was run by setting the temperature increment to 10 K. Indeed, a unit change in temperature would produce heat fluxes that are not graphically appreciable, especially for the retrofit solutions. Heat fluxes were then divided by 10 K with the aim of obtaining a unitary response X (W m-2 K-1), and values were reported for each hour over a period of 4 days (as seen in Equation 11). This range of time is also the simulation time selected for the analysis, and it was obtained by considering the analyzed component that had shown the longest thermal response in order not to neglect significant terms in the series.
X j = q s , ¡ ˙ Δ T
where j is the time-index (with j = 1, 2, …, N), q s , ¡ ˙ is the specific heat flux on the internal side (W m-2 K-1) and ΔT [K] is the temperature magnitude equal to 10 K. The response factor series starts from 1, which is the moment at which the peak of the temperature excitation occurs.

4.1.6. Mesh selection

To numerically solve the heat transfer problem, it was necessary to discretize the domain into non-overlapping triangles. However, to assess the effect that different discretization levels of the geometry have on the results, a sensitivity analysis of the mesh was performed for each retrofit configuration. By running the stationary study and changing the user-defined mesh from normal (i.e., maximum size = 7.04 cm, minimum size = 0.03 cm) to extremely fine (i.e., maximum size = 1.05 cm, minimum size = 0.002 cm), changes in the results were analyzed. Table 3 shows the percentage differences of the specific heat flux across the different configurations obtained as the difference in the result considering successive meshes. It can be noticed that the mesh does not have any influence on the simulation results. Only the two timber-frame retrofits (internal and external) showed a slight difference between meshes, which can be explained by the non-planar geometry in correspondence with the strong-back. Nevertheless, differences are negligible (-0.02% to -0.01%). For this reason, domains were discretized with a normal mesh with the advantage of reducing the computational time.

4.2. Results and discussion

Results of the complete energetic analysis, both in terms of thermal transmittance and in terms of periodic thermal parameters of the different retrofit solutions and the URM wall are shown in Table 4.
The heat flow by heat transmission across opaque components is known to be one of the main shares of the total thermal load of a building. The quantity of energy transferred between internal and external environments depends on both the component type and the temperature differential. In winter design scenarios, this heat flow is assessed under steady-state conditions, where temperature remains constant over time. Thus, the thermal parameter associated with the winter thermal performance is the thermal transmittance. According to Table 4, it can be noticed that all the retrofit solutions, both internal and external, show improvements in the thermal insulation with respect to the URM wall (with U-value equal to 2.072 W m-2 K-1). On average, all U-values are lower than the initial case, and in the specific, best winter performances were obtained for the CLT-ext and the LVL-ext, which resulted being very effective with values equal to 0.244 and 0.257 W m-2 K-1, respectively. It can be noticed that for the CLT and LVL structural layers, passing from internal to external insulation, the U-value decreases and this is explained by the greater total thickness, despite the higher value of thermal conductivity adopted in the external configuration (i.e., 0.026-0.028 W m-2 K-1 for the PIR ETICS). On the contrary, in the timber-frame structure, both SB90 and SB45, an increase in U-value is noticed by placing the insulation layer on the external side instead of the internal one. This is because on average thermal transmittances of external timber-frame solutions have a less thermal resistant insulation layer. By comparing analytical U-values than the numerical ones, it can be noticed that CLT and LVL retrofit solutions do not significantly change (errors lower than 0.05%), while a relevant difference was obtained for timber-frame solutions. As a matter of fact, U-values increase by 30% to 40% for the SB90 (internal and external) and by 17% to 21% for the SB45 retrofit solutions (internal and external) when considering numerical U-values, instead of analytical ones. This increase is due to the thermal bridges caused by the strong-backs. Almost all solutions exceed the U-value prescribed by the Standard when taking into account thermal bridge effects, except for the SB45-int, CLT-ext and LVL-ext.
When it comes to cooling periods, external climatic conditions, such as air temperature, can undergo remarkable changes, differently from those assumed in winter seasons. For this reason, the thermal behavior of opaque components must be evaluated under non-stationary conditions. Following the results of Table 4, it can be seen that the retrofit solutions exhibit a significantly better performance than the URM. In fact, Figure 5 shows the specific heat flux on the internal side for the URM wall (in black) and the other retrofit solutions (in grey) as a function of the time. On the right, it is reported the external solicitation in terms of air temperature. It is evident that both attenuation and phase shift are enhanced. The goal of the retrofit solution, from the energetic point of view, is to obtain lower values of periodic thermal transmittance, as well as of the decrement factor, while, in terms of phase shift, the higher the value, the better the solution.
On average, installing the insulation layer on the external side is more effective in attenuating and shifting the heat flux. The best performance was obtained for the CLT-ext and the LVL-ext. The massive presence of either cross-lam or laminated veneer lumber gives to the configuration a lower thermal diffusivity than the timber-frame solutions. This can be noticed also in Figure 6, which represents the internal specific heat flux (W m-2) as a function of the time for the external retrofit solutions. On the right side, the external air temperature function expressed in °C is reported over a period of 24 h. As regards the timber-frame solutions, the SB45 configuration attenuates more the heat flux than the SB90 one. Despite the slightly lower total thickness of the SB45 (i.e., 36 cm vs. 38 cm), the two 4 cm insulation layers installed with a layer of OSB in the middle can dump and shift greatly the external solicitation than a single 9 cm layer of PIR ETICS.
On the other hand, when the insulation layer is applied on the internal side of the masonry wall, a different behavior is noticed. The most effective solutions become the LVL-int and the SB45-int, as seen in Figure 7. The only difference between the two is in terms of attenuation, while the phase shift is comparable.
Smaller performance enhancements were obtained for the SB90-int solutions, where the highest oscillation in terms of internal heat flux and the lowest phase shift was noticed (11.9 h). The presence of 90 mm of PIR insulation, which is characterized by higher thermal diffusivity than bulk layers like either CLT or LVL, leads to higher values of periodic thermal transmittance (Yie) and decrement factor (f), and lower phase shift (Δτie).
By considering all the retrofit solutions, it can be stated that the most effective solutions in terms of energy retrofit (both in winter and summer seasons) are the CLT-ext and the LVL-ext with external insulation. The external configuration can be convenient during a retrofit, especially because it does not affect the indoor space of the building. While, if restrictions on the external façade are present, it is suggested to adopt either the LVL-int or the SB45-int retrofit solutions in order to enhance the thermal performance. Both configurations show higher attenuation and longest phase shift among internal retrofit solutions.
Figure 8, Figure 9 and Figure 10 summarize the results in terms of specific heat flux after the impulsive temperature excitation. Figure 8 represents all the heat fluxes comprising the behavior of the URM wall. Figure 9 and Figure 10 give instead the heat fluxes obtained on the internal side, separately for external and internal retrofit solutions, respectively. Results on the left side are displayed for a period of 96 h, while the temperature profile spans just 24 h, for the sake of clarity. The temperature was maintained constant at 16 °C after the temperature impulse until the end of the simulation. Figure 11 and Figure 12 represent the response factor on the non-excited side on the wall after the application of a unitary temperature excitation on the opposite side, obtained by dividing the internal specific heat flux by the magnitude of the temperature excitation (i.e., 10 K) and then, by sampling the data series every hour.
In order to verify the accuracy of simulation results related to the dynamic regime, a summation of the response factor series over the time was performed for each analyzed component and the result was compared to the U-value obtained from the stationary simulation [50], as seen in Equation 12.
∑ j = 0 j = 96   h X j = U
According to the response factor theory [50], and since the response factor is defined as a time-series, it is infinite, thus, the summation must be performed for an infinite period. However, after some time, values become extremely small and they no long influence significantly the summation. In this study, the sum was conducted for a period of 96 h (i.e., simulation period). As a result of this study, negligible differences (about < 5%) with respect to the steady-state thermal transmittance were found, as visible in Table 5. Larger differences are registered for the external retrofit solutions than the internal ones (i.e., -5.29% for the LVL-ext and -0.29% for the CLT-int). This is explained by the longer thermal response obtained in retrofit solutions with external insulation rather than internal. However, these values are far below the uncertainty of the thermal transmittance measurements (approximately 10%), thus, the analysis is considered correct. The assessment of the U-value through the response factor theory instead of performing a stationary simulation is a promising technique that can be replicated experimentally, as well, especially for the internal retrofit solutions (where errors are almost negligible). By slightly increasing the test time the experimental procedure could be extended also to more massive walls like the external retrofit solutions.

5. Conclusions

The retrofit solutions studied herein were designed and analyzed considering both structural and energetic aspects, with the aim of realizing integrated interventions characterized by low impact and fast execution. The outcomes obtained for the various techniques were compared to individuate the best performing solution for any given scenario. The following conclusions were drawn:
  • The timber panel retrofits (i.e., CLT and LVL panels) proved to be more effective than the solutions with the timber frame and the OSB sheathing (i.e., SB90 and SB45) in improving the in-plane mechanical behavior of double-leaf masonry walls. Increases in lateral load-carrying capacity of 145% and 52% and in displacement capacities of 70% and 226% were obtained for the timber panel retrofits in the cases of rocking and shear failure modes, respectively.
  • In the case of rocking behavior, the solutions with the timber frame and the OSB sheathing exhibited the same load carrying capacity as the panel-based retrofits (as the wall capacity was limited by the strength of the tension anchors at the base) even though the maximum capacity was engaged at larger drift values (>1.80%), exceeding the limits typically adopted for masonry structures. In the case of shear failure, the solutions SB45 and SB90 produced a considerable increase only in the wall displacement capacity (increases > 265%).
  • The energy performance of the masonry walls was noticeably improved by the application of the retrofit solutions. Reductions in the thermal transmittance (U) up to 87% and of the periodic thermal transmittance (Yie) up to 97% were noticed.
  • The most effective solutions in terms of energy retrofit (both in winter and summer seasons) are the external solutions CLT-ext and the LVL-ext. However, if the retrofit is applied on the internal side, it is suggested to adopt either the LVL-int or the SB45-int solutions. As expected, the thickness of the insulation layer plays a major role in determining the effectiveness of the solutions. Consequently, if a limitation to the total thickness of the intervention is considered (i.e., for the internal solutions), the possibility of inserting the insulation layers between the timber elements allows larger improvements in the wall thermophysical properties.
  • The assessment of the U-value by adopting the response factor theory (i.e., by applying a triangular temperature profile of air’s temperature) instead of performing a stationary simulation seems being a promising technique also in the experimental field, where stationary tests are usually extremely time consuming. Deviations with respect to the stationary U-value are negligible for less massive walls, such as the internal retrofit solutions, while are more significant in the case of external retrofit because of the longer response time. However, these deviations remain below the threshold of measurement uncertainty.
  • The retrofit solution with the LVL panels appeared to be the best performing, improving both the mechanical and the thermophysical properties of the URM walls considerably. However, all the analyzed solutions can be considered quite promising and worthy of further study.

Author Contributions

Conceptualization, D.C., M.D., A.P., I.G.; methodology, D.C., M.D., A.P., I.G.; software, D.C., M.D.; validation, D.C., M.D.; data curation, D.C., M.D.; writing—original draft preparation, D.C., M.D.; writing—review and editing, A.P., I.G.; supervision, A.P., I.G.; funding acquisition, I.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The research work was carried out within the framework of the 2022-2024 ReLUIS-DPC network (Italian University Network of Seismic Engineering Laboratories and Italian Civil Protection Agency).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Gkatzogias, K.; Crowley, H.; Veljkovic, A.; Pohoryles, D.A.; Norl´en, H.; Tsionis, G.; Bournas, D.A. REEBUILD: integrated techniques for the seismic strengthening and energy efficiency of existing buildings – prioritising EU regions for building renovation: seismic risk, EUR 31149, Publications Office of the European Union, Luxembourg, in: Energy Efficiency, Socioeconomic Vulnerability, 2022. ISBN 978-92-76-55022-8, doi:10.2760/263803, JRC128988.
  2. European Commission. Energy Performance of Buildings. Text, July 31, Energy - European Commission, 2014, https://ec.europa.eu/energy/en/topics/ energy-efficiency/energy-performance-of-buildings/overview.
  3. Ricci, P.; De Luca, F.; Verderame, G.M: 6th April 2009 L’Aquila earthquake, Italy: reinforced concrete building performance, Bull. Earthq. Eng. 9 (1) (2011) 285–305.
  4. Indirli, M.; Kouris, L.A.S.; Formisano, A.; Borg, R.P.; Mazzolani, F.M. Seismic damage assessment of unreinforced masonry structures after the Abruzzo 2009 earthquake: the case study of the historical centers of L’Aquila and castelvecchio subequo, January 1, Int. J. Architect. Herit. 7 (5) (2013) 536–578, https:// doi.org/10.1080/15583058.2011.654050.
  5. Bournas, D.A.; Negro, P.; Taucer, F.F. Performance of industrial buildings during the Emilia earthquakes in Northern Italy and recommendations for their strengthening. Bull. Earthq. Eng. 12 (5) (2014) 2383–2404, . [CrossRef]
  6. European Commission, The European green Deal - Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions, European Commission, Brussels, November 12, 2019.
  7. International Energy Agency (IEA) Net Zero by 2050 - A Roadmap for the Global Energy Sector. 2021, 224.
  8. Iovane, G.; Sandoli, A.; Marranzini, D.; Landolfo, R.; Prota, A.; Faggiano, B. Timber based systems for the seismic and energetic retrofit of existing structures. In Proceedings of the XIX ANIDIS Conference, Seismic Engineering in Italy, 2023, Procedia Structural Integrity 44 1870–1876.
  9. Giongo, I.; Schiro, G.; Piazza, M. On the Use of Timber-Based Panels for the Seismic Retrofit of Masonry Structures. In Proceedings of the 3rd International Conference on PROTECTION OF HISTORICAL CONSTRUCTIONS; Lisbon, Portugal, July 12 2017.
  10. Riccadonna, D.; Giongo, I.; Schiro, G.; Rizzi, E.; Parisi, M.A. Experimental Shear Testing of Timber-Masonry Dry Connections for the Seismic Retrofit of Unreinforced Masonry Shear Walls. Construction and Building Materials 2019, 211, 52–72, doi:10.1016/j.conbuildmat.2019.03.145.
  11. Rizzi, E.; Giongo, I.; Riccadonna, D.; Piazza, M. Testing of irregular stone masonry strengthened with cross-laminated timber. In Proceedings of the 4th International Conference on Protection of Historical Constructions; Athens, Greece, 2021.
  12. Giongo, I.; Rizzi, E.; Riccadonna, D.; Piazza, M. On-Site Testing of Masonry Shear Walls Strengthened with Timber Panels. Proceedings of the Institution of Civil Engineers - Structures and Buildings 2021, 174, 389–402, doi:10.1680/jstbu.19.00179.
  13. Cassol, D.; Giongo, I.; Piazza, M. Numerical Study on Seismic Retrofit of URM Walls Using Timber Panels. In Proceedings of the 8 th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering; Athens, Greece, June 27 2021.
  14. Cassol, D.; Nagliati, E.; Giongo, I. Seismic retrofit of a URM building with timber-based coating: a numeric study. In Proceedings of the SAHC 2032 - 13th International Conference on Structural Analysis of Historical Constructions, Kyoto Japan, 12-15 September 2023.
  15. Borri, A.; Sisti, R.; Corradi, M. Combined Reinforcement of Rubble Stone Walls with CLT Panels and Steel Cords. Structures and Buildings 2021.
  16. Pozza, L.; Marchi, L.; Trutalli, D.; Scotta, R. In-Plane Strengthening of Masonry Buildings with Timber Panels. Proceedings of the Institution of Civil Engineers - Structures and Buildings 2021, 174, 345–358, doi:10.1680/jstbu.19.00121.
  17. Lucchini, A.; Mazzucchelli, E.; Mangialardo, S.; Persello, M. Façadism and CLT Technology: An Innovative System for Masonry Construction Refurbishment. In Proceedings of the 4th IAHS World Congress on Housing—Sustainable Housing Construction; Funchal, Portugal, December 16 2014.
  18. Iuorio, O.; Dauda, J.A. Retrofitting Masonry Walls against Out-Of-Plane Loading with Timber Based Panels. Applied Sciences 2021, 11, 5443, doi:10.3390/app11125443.
  19. Sustersic, I.; Dujic, B. Seismic Strengthening of Existing Buildings with Cross Laminated Timber Panels. World 2012, 15, 19.
  20. Giaretton, M.; Ingham, J.; Dizhur, D. Timber Strong-Backs as Cost-Effective Seismic Retrofit Method for URM Buildings. In Proceedings of the NZSEE Conference; Wellington, New Zealand, April 27 2017.
  21. Dizhur, D.Y.; Giaretton, M.; Giongo, I.; Ingham, J.M. Seismic Retrofit of Masonry Walls Using Timber Strong-Backs. SESOC Journal 2017, 30, 30–44.
  22. Cassol, D.; Giongo, I.; Ingham, J.; Dizhur, D. Seismic Out-of-Plane Retrofit of URM Walls Using Timber Strong-Backs. Construction and Building Materials 2021, 269, 121237, doi:10.1016/j.conbuildmat.2020.121237.
  23. Damiani, N.; Miglietta, M.; Guerrini, G.; and Graziotti, F. An innovative timber system for the seismic retrofit of unreinforced brick masonry buildings. In Brick and Block Masonry-From Historical to Sustainable Masonry, 2020 pp. 508-516.
  24. Guerrini, G.; Damiani, N.; Miglietta, M.; Graziotti, F. Cyclic Response of Masonry Piers Retrofitted with Timber Frames and Boards. Proceedings of the Institution of Civil Engineers - Structures and Buildings 2021, 174, 372–388, doi:10.1680/jstbu.19.00134.
  25. Miglietta, M.; Damiani, N.; Guerrini, G.; and Graziotti, F. Full-scale shake-table tests on two unreinforced masonry cavity-wall buildings: Effect of an innovative timber retrofit. Bulletin of Earthquake Engineering, 2021 19(6), 2561-2596.
  26. Busselli, M.; Cassol, D.; Prada, A.; Giongo, I. Timber Based Integrated Techniques to Improve Energy Efficiency and Seismic Behaviour of Existing Masonry Buildings. Sustainability 2021, 13, 10379. [CrossRef]
  27. Cassol, D.; Busselli, M.; Prada, A.; Giongo, I. Timber-based integrated solutions for the seismic retrofit of URM walls. In Proceedings of CEES 2021 - International Conference on Construction, Energy, Environment and Sustainability, Coimbra Portugal, 12-15 October 2021.
  28. Valluzzi, M.R.; Saler, E.; Vignato, A.; Salvalaggio, M.; Croatto, G.; Dorigatti, G.; Turrini, U. Nested Buildings: An Innovative Strategy for the Integrated Seismic and Energy Retrofit of Existing Masonry Buildings with CLT Panels. Sustainability 2021, 13, 1188, doi:10.3390/su13031188.
  29. Applicazione delle metodologie di calcolo delle prestazioni energetiche e definizione delle prescrizioni e dei requisiti minimi degli edifici, Appendice B: requisiti specifici per gli edifici esistenti soggetti a riqualificazione energetica, Decreto interministeriale 26 giugno, Italia 2015.
  30. ABAQUS Computer Software and User’s Manual; Simulia; Dassault Systèmes: Providence, RI 02919, USA;
  31. Lubliner, J.; Oliver, S.; Oñate, E. A Plastic-Damage Model for Concrete. International Journal of Solid and Structures 1989, 25, 299–326.
  32. Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures.
  33. EN 1996-1-1:2013, Eurocode 6 – Design of masonry structures – Part 1-1: General rules for reinforced and unreinforced masonry structures, European Committee for Standardization: Brussels Belgium, 2013.
  34. Lourenço, P.B.; João, M.P. Seismic Retrofitting Project: Recommendations for Advanced Modeling of Historic Earthen Sites; Los Angeles: Getty Conservation Institute: Guimarães, Portugal: TecMinho–University of Minho, 2018;
  35. Ministero delle Infrastrutture e dei Trasporti DECRETO 17 Gennaio 2018 Aggiornamento delle. In Norme Tecniche per le Costruzioni; Ministero delle Infrastrutture e dei Trasporti: Rome, Italy, 2018.
  36. UNI EN 338, Structural Timber – Strength Classes; European Committee for Standardization: Brussels, Belgium, 2016;
  37. UNI EN 14279:2009, Laminated Veneer Lumber (LVL) - Definitions, Classification and Specifications; European Committee for Standardization: Brussels, Belgium, 2009;
  38. 38. UNI EN 300, 2006, Oriented Strain Boards (OSB) – Definitions, classification and specifications, European Committee for Standardization, Brussels, 2006.
  39. M. Piazza, T. Sartori, ‘Caratterizzazione Meccanica Attraverso Prove Monotone e Cicliche Dei Principali Dispositivi Di Connessione Utilizzati Negli Edifici Multipiano in Legno’, ReLUIS 2015-PR4_Allegato_01-UR_UNITN, 2015.
  40. A. Hossain, I. Danzig, T. Tannert, Cross-Laminated Timber Shear Connections with Double-Angled Self-Tapping Screw Assemblies. J. Struct. Eng. 2016, 142, 04016099, doi:10.1061/(ASCE)ST.1943-541X.0001572.
  41. T. Sartori and R. Tomasi, ‘Experimental investigation on sheathing-to-frame connections in wood shear walls’, Engineering Structures 56 2197-2205, 2013.
  42. Morandi, P.; Albanesi, L.; Magenes, G. In-plane test campaign on different load-bearing URM typologies with thin shell and web clay units. Proceedings of the 16th International Brick and Block Masonry Conference, Padova, Italy, 2016.
  43. COMSOL Multiphysics® v. 6.1. www.comsol.com. COMSOL AB, Stockholm, Sweden.
  44. EN ISO 6946:2018, Building Components and Building Elements - Thermal Resistance and Thermal Transmittance - Calculation Methods; European Committee for Standardization: Brussels, Belgium, 2018.
  45. Mitalas, G. and Stephenson, D.G. Room thermal response factors, ASHRAE Trans.73 (1) (1967) 1–10.
  46. Stephenson D.G. and Mitalas, G.P. Cooling load calculations by the thermal response factor method, ASHRAE Trans., 73 1967.
  47. G.P. Mitalas and D.G. Stephenson, Calculation of heat flows through walls and roofs, ASHRAE Trans., 74 (1968) 182-188.
  48. Li, X.Q.; Chen, Y.; Spitler, J.D.; Fisher, D. Applicability of calculation methods for conduction transfer function of building constructions. Int. J. Therm. Sci., 48 (7) (2009), pp. 1441-1451, https://doi:10.1016/j.ijthermalsci.2008.11.006.
  49. Bettanini, E.; Brunello, P. F. Lezioni di impianti tecnici. CLEUP Editore, 1990, vol.2.
  50. Davies, M. G. 2004. Building Heat Transfer. WILEY.
  51. Hittle, D. Response Factors and Conduction Transfer Functions, 1992. www.web.mit.edu.
  52. U.S. Department of Energy’s (DOE) Building Technologies Office (BTO), and managed by the National Renewable Energy Laboratory (NREL). Energyplus. California, USA 1996. https://energyplus.net/.
  53. University of Wisconsin--Madison. Solar Energy Laboratory. TRNSYS, a Transient Simulation Program. Madison, Wis. :The Laboratory, 1975. https://www.trnsys.com/.
  54. Rasooli, A.; Itard, L.; Ferreira, C.I. A response factor-based method for the rapid in-situ determination of wall’s thermal resistance in existing buildings, Energy Build., 119 (Supplement C) (2016), pp. 51-61. [CrossRef]
  55. European Standards, ENI SO 8990, Thermal insulation – Determination of steady-state thermal transmission properties – Calibrated and guarded hot box, 1996.
  56. EN 1934: Ente nazionale italiano di unificazione UNI 2000. UNI EN 1934. Thermal performance of buildings - Determination of thermal resistance by hot box method using heat flow meter – Masonry.
Preprints 89859 g001
Figure 1. Timber-based retrofit solutions.
Figure 1. Timber-based retrofit solutions.
Preprints 89859 g001
Preprints 89859 g002
Figure 2. Validation of the unreinforced (URM) and retrofitted (R) masonry wall models by means of a comparison between the envelope (Env) of the experimental curves (Exp) [12] and the results of the simplified (M1) and detailed (M2) models.
Figure 2. Validation of the unreinforced (URM) and retrofitted (R) masonry wall models by means of a comparison between the envelope (Env) of the experimental curves (Exp) [12] and the results of the simplified (M1) and detailed (M2) models.
Preprints 89859 g002
Preprints 89859 g003
Figure 3. Lateral load - Displacement curves of the retrofitted walls.
Figure 3. Lateral load - Displacement curves of the retrofitted walls.
Preprints 89859 g003
Preprints 89859 g004
Figure 4. Walls’ configurations modelled in COMSOL environment®.
Figure 4. Walls’ configurations modelled in COMSOL environment®.
Preprints 89859 g004
Preprints 89859 g005
Figure 5. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the URM wall (in black) and for the other retrofit solutions (in grey). On the right, the external air temperature function is expressed in °C as a function of the time.
Figure 5. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the URM wall (in black) and for the other retrofit solutions (in grey). On the right, the external air temperature function is expressed in °C as a function of the time.
Preprints 89859 g005
Preprints 89859 g006
Figure 6. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the retrofit solutions with external thermal insulation. On the right, the external air temperature function is expressed in °C as a function of the time.
Figure 6. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the retrofit solutions with external thermal insulation. On the right, the external air temperature function is expressed in °C as a function of the time.
Preprints 89859 g006
Preprints 89859 g007
Figure 7. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the retrofit solutions with internal thermal insulation. On the right, the external air temperature function is expressed in °C as a function of the time.
Figure 7. Stabilized periodic regime: Internal specific heat flux (W m-2) trend in the 24 h period for the retrofit solutions with internal thermal insulation. On the right, the external air temperature function is expressed in °C as a function of the time.
Preprints 89859 g007
Preprints 89859 g008
Figure 8. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the URM wall (in black) and for the other retrofit solutions (in grey). On the right, the external air temperature function is expressed in °C as a function of the time (over a 24 h period).
Figure 8. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the URM wall (in black) and for the other retrofit solutions (in grey). On the right, the external air temperature function is expressed in °C as a function of the time (over a 24 h period).
Preprints 89859 g008
Preprints 89859 g009
Figure 9. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the retrofit solutions with external thermal insulation. On the right, the external air’s temperature function is expressed in °C as a function of the time (over a 24 h period).
Figure 9. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the retrofit solutions with external thermal insulation. On the right, the external air’s temperature function is expressed in °C as a function of the time (over a 24 h period).
Preprints 89859 g009
Preprints 89859 g010
Figure 10. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the retrofit solutions with internal thermal insulation. On the right, the external air’s temperature function is expressed in °C as a function of the time (over a 24 h period).
Figure 10. Dynamic regime: Internal specific heat flux (W m-2) trend in the 96 h period for the retrofit solutions with internal thermal insulation. On the right, the external air’s temperature function is expressed in °C as a function of the time (over a 24 h period).
Preprints 89859 g010
Preprints 89859 g011
Figure 11. Dynamic regime: Response factor on the non-excited side (W m-2 K-1) reported in the 96 h period every hour for retrofit solutions with external thermal insulation.
Figure 11. Dynamic regime: Response factor on the non-excited side (W m-2 K-1) reported in the 96 h period every hour for retrofit solutions with external thermal insulation.
Preprints 89859 g011
Preprints 89859 g012
Figure 12. Dynamic regime: Response factor on the non-excited side (W m-2 K-1) reported in the 96 h period every hour for retrofit solutions with internal thermal insulation.
Figure 12. Dynamic regime: Response factor on the non-excited side (W m-2 K-1) reported in the 96 h period every hour for retrofit solutions with internal thermal insulation.
Preprints 89859 g012
Table 1. Masonry properties.
Table 1. Masonry properties.
Material E [MPa] G [MPa] fc [MPa] ft [MPa] c [MPa]
Clay bricks 3000 1200 20.00 2.00 -
Mortar 300 120 1.30 0.05 0.15
Table 2. Thermophysical properties of the materials.
Table 2. Thermophysical properties of the materials.
Materials Thickness [mm] ρ [kg/m3] 1 λ [W/(mK)] 2 cp [J/(kgK)] 3
Clay brick masonry 250 1800 0.800 840
CLT panel 60 420 0.120 1600
LVL panel 40 530 0.130 2720
OSB panel 15 650 0.130 1700
PIR 40 – 60 - 90 36 0.022 1453
PIR (ETICS application) 40 - 80 - 90 35 0.028 - 0.026 1464
Plaster 12 1000 0.250 2000
Fibre-cement board 15 950 0.300 1000
Skim-coating 10 950 0.310 950
Plasterboard 12-24 1800 0.900 910
Vapour barrier 0.02 500 0.390 1700
Breathable membrane 0.03 250 0.300 1800
Breathable and
reflective membrane		 0.05 300 0.300 1800
1 Density. 2 Conductivity. 3 Mass specific heat at constant pressure.
Table 3. Percentage variation of the steady-state specific heat flux as a function of the mesh size and of the retrofit solution (beyond the URM wall).
Table 3. Percentage variation of the steady-state specific heat flux as a function of the mesh size and of the retrofit solution (beyond the URM wall).
Configuration Mesh size
Normal Fine Finer Extra Fine Extremely Fine
URM - 0.00% 0.00% 0.00% 0.00%
INTERNAL
RETROFIT 		CLT - 0.00% 0.00% 0.00% 0.00%
LVL - 0.00% 0.00% 0.00% 0.00%
SB90 - 0.00% 0.00% -0.01% -0.02%
SB45 - 0.00% 0.00% -0.01% -0.02%
EXTERNAL
RETROFIT 		CLT - 0.00% 0.00% 0.00% 0.00%
LVL - 0.00% 0.00% 0.00% 0.00%
SB90 - 0.00% 0.00% 0.00% -0.01%
SB45 - 0.00% 0.00% 0.00% -0.01%
Table 4. Results of the energetic analysis.
Table 4. Results of the energetic analysis.
Configuration Stationary Periodic
U (W m-2 K-1) Yie (W m-2 K-1) f (-) Δ τ i e (h)
URM 2.072 0.894 0.432 7.4
INTERNAL RETROFIT CLT 0.354 0.052 0.148 12.9
LVL 0.282 0.037 0.131 13.2
SB90 0.297 0.052 0.176 11.9
SB45 0.270 0.035 0.129 13.2
EXTERNAL RETROFIT CLT 0.244 0.023 0.094 13.0
LVL 0.257 0.023 0.089 12.9
SB90 0.316 0.038 0.119 12.3
SB45 0.319 0.030 0.095 13.0
Table 5. The sum of the 96 terms of the response factor series for each analyzed component and their percentage differences with respect to the stationary U-value.
Table 5. The sum of the 96 terms of the response factor series for each analyzed component and their percentage differences with respect to the stationary U-value.
Configurations Response factor
∑ 96   h X j   (W m-2 K-1) Error (%)
URM 2.072 0.02%
INTERNAL
RETROFIT 		CLT 0.351 -0.29%
LVL 0.279 -1.25%
SB90 0.296 -0.35%
SB45 0.268 -0.77%
EXTERNAL
RETROFIT 		CLT 0.235 -4.02%
LVL 0.244 -5.27%
SB90 0.309 -2.18%
SB45 0.310 -2.95%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated