Prerpints.org logo
Preprint
Article

Prediction of the Onset and Offset of the Rainy Season in Senegal Using Kohonen Self-Organizing Maps

Altmetrics

Downloads

156

Views

71

Comments

0

Submitted:

06 November 2023

Posted:

08 November 2023

You are already at the latest version

Alerts
Abstract
This study investigates the spatio-temporal variability of the onset, offset, and Length of the rainy season in Senegal over the 1981-2018 period. The onset, offset dates, and length of the rainy season are crucial parameters for agricultural planning in West Africa, which exhibits high interannual and spatial variability in rainfall. The objective is to detect and spatially classify these phenological parameters across Senegal using different approaches. Daily precipitation data from the Climate Hazards group InfraRed Precipitation with Stations (CHIRPS) dataset over the study period and ERA5 reanalysis were used. The method of was applied to detect the onset, offset dates, and length of the rainy season. The Kohonen algorithm was then used to spatially classify these parameters on topological maps. A hierarchical ascendant classification was also performed to reduce the number of classes obtained. Finally, a composite analysis of moisture transport before the onset and end of the 1984 and 2007 seasons was conducted with ERA5 data. The results show a meridional gradient of the start of the season, progressively later from southeast to northwest, while the end follows a north-south gradient. The duration of the rainy season ranges from 45 days in northern Senegal to 150 days in the south. The maximum number of dry days also decreases from north to south. The Kohonen self-organizing maps allow spatial prediction of the onset, end date, and duration of the rainy season across Senegal. The dynamics analysis reveals that early onset years are associated with stronger and earlier northward moisture transport over West Africa, underscoring the role of this parameter in triggering the rainy season. These promising results can provide an early warning to policymakers and farmers on the start and end dates of the season in each area of Senegal.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Precipitation is a vital element for tropical regions and a crucial socio-economic factor for developing countries. In West Africa, where the economy is mainly based on rainfed agriculture, the choice of cultivated species, as well as the optimal periods for carrying out agricultural work, depend closely on the level of interannual variability in rainfall and intra-seasonal characteristics of precipitation, such as the length of the rainy season, the frequency of heavy rainfall events, or the existence of prolonged dry spells within the rainy season. This interannual variability in rainfall can lead to irregularity in the start and end of the rainy season, making it difficult for farmers to optimize the planting period for seeds and adapt to the duration of the growing season. A delay of one or two weeks in the arrival of the rains can be enough to dash hopes for a normal harvest, while a "false start" for planting, followed by prolonged dry periods (more than two weeks) can be critical for seed germination and plant growth. In most tropical regions, the start and end dates of the rains are important parameters for the agricultural calendar. More precise knowledge of the variability of the started date , ended date, and length of the rainy season is therefore essential for many agricultural activities and for planning optimal food yields. However, accurately detecting these events is a complex task due to the spatiotemporal variability of precipitation. Classical methods for detecting the start of the rainy season are generally based on pre-established precipitation thresholds ([1];[2,3]), which are often regional or local, and do not account for the spatiotemporal variability of precipitation. Since the 1970s, studies on the onset of the rainy season in West Africa have proposed three main approaches. These approaches strongly depend on the spatial and temporal scales of the meteorological processes considered. Thus, at the climatological scale (the regional scale whose spatial extension is of the order of 2,500 to 10,000 km), the onset corresponds to the seasonal migration of the monsoon system from the Guinean latitudes ( 5°N) to the Sahelian latitudes ( 10-15°N). According to ([4,5]), this onset of the rainy season can be estimated from zonal indices based either on deep convection from the Satelite Outgoing Longwave Radiation (OLR), or from rain gauge rainfall data. Depending on the activity, the onset date can change. From the hydrologist’s point of view, i.e. at the meso-scale, whose spatial extension is of the order of 10 to 1,000 km,the definition is based on the occurrence of the first organized convective system generating rainfall over the Sahelian belt ([6]); From the agronomist’s point of view, i.e. at the local scale, whose spatial extension is between 1 and 10 km. The definition of onset is based on the first useful rains recorded at the station or plot scale. Modern approaches based on using the [1] method and Kohonen’s self-organizing maps (SOM) offer a promising alternative to these classical methods. [7,8] used these SOMs to characterize synoptic-scale meteorological events over Senegal and measure their impact on the structure and modulation of the daily rainfall seasonal cycle. Indeed, in addition to detecting, they make it possible to accurately predict these rainy season events using sophisticated algorithms that can learn from historical and spatial data. The objective of this paper is therefore to detect and classify the onset and offset dates of the rainy season, the length of the season and rainfall breaks in West Africa and Senegal in particular, using a Machine Learning based approach. Section 2 describes the datasets and methodology used for this study. We will then analyze the results in section 3 and discuss them in the same section. Finally, we will present the conclusion of this study in section 4.

2. Materials and Methods

2.1. Materials

Precipitation data from the Climate Hazards group InfraRed Precipitation with Stations (CHIRPS) are used with a spatial resolution of 0.05° x 0.05° in longitude and latitude ([9]) to calculate the onset and end dates of the rainy season. These data are provided by USGS (United States Geological Survey) to FEWSNET (Famine Early Warning Systems Network)and used by the Regional AGRHYMET Center (Agronomy, Hydrology, Meteorology). CHIRPS is a dataset that combines ground observation data and satellite observations to produce daily and monthly rainfall estimates across the globe from 1981 to present. CHIRPS data are freely available and provided in Network Common Data Form (NetCDF) format. CHIRPS has been validated using various precipitation observation data, and results indicate good performance for drought monitoring ([10,11]) which is why we chose it as the reference observation dataset. To detect atmospheric conditions associated with these events, the fifth generation of ERA5 atmospheric reanalyses from ECMWF covering the global climate from 1940 to present is used. ERA5 is produced by the Copernicus Climate Change Service (C3S) of ECMWF. The data cover the Earth on a 25 km horizontal resolution. ERA5 includes uncertainty information for all variables at reduced spatial and temporal resolutions.

2.2. Methods

2.2.1. Determining the onset and offset of the rainy season

In this work, we used the method of [2] to determine the onset, offset dates, and length of the rainy season over the 1981-2018 period. The onset date of the season is defined from the first of May as the first day of a wet 4-day sequence accumulating at least 20 mm of rain, and not followed by a dry spell of more than 10 consecutive days in the 20 days following the onset. Thus, the agronomic cessation date (offset) of the rainy season is determined as the last day (+1) of a wet sequence of 4 consecutive days receiving at least 20 mm without being preceded by a dry spell of more than 10 consecutive days in the 20 days preceding it. The cumulative rainfall threshold of 20 mm was adopted following experimental studies conducted by ICRISAT (International Crops Research Institute for the Semi-Arid Tropics) on millet cultivation in Niger ([1,12]). This amount of rainfall appears to correspond to the water requirements for crop survival. The length of the rainy season is calculated by taking the difference between the onset and cessation dates of the rainy season, as defined above.

2.2.2. Self-Organizing Maps Method

Self-organizing maps (SOMs) are part of the family of neural methods for "unsupervised learning". That is, in a first approach, these methods are used for descriptive purposes. The data to be analyzed consists of observations whose structure we seek to understand. For these methods, there is no specific goal to be achieved, nor any known answer in advance [13]. The purpose of these maps is to represent multidimensional observations on a low dimensional space (usually 1D or 2D) which is commonly called the topological map. In these methods, each class is represented by a neuron which is characterized by a so-called reference vector. The map consists of a set of interconnected neurons through an undirected graph structure. The map grid summarizes the information contained in the multivariate dataset. The grid of neurons presents a topological order, which means that neighboring regions close on the SOM map represent a similar situation, while dissimilar regions are mapped further apart. The reference vectors are determined by a learning process ([13]), by minimizing a nonlinear cost function. We have found that self-organizing maps can be used for all kinds of purposes, especially in climate research ([14]), although they were originally used in statistical research. The SOM map is well suited to the problem we are solving. It has a higher discriminating power to separate the different classes than the empirical orthogonal functions (EOF) ([15]) or the K-Means algorithm ([16]) because of the topological constraint between the different classes. In addition, SOM is able to handle the nonlinear aspects of the phenomenon we are analyzing, unlike EOF, which mainly deals with the linear aspects of the phenomenon ([17]). More details on SOM and its advantages over other clustering methods like k-means can be found in the literature (e.g. [16,18,19,20]). For instance, [17] compared the feature extraction performances of SOM and EOF techniques using artificial data representative of known patterns. It was shown that SOM could extract the patterns from a linear progressive sinusoidal wave like EOF does, even with noise added. Thus, SOM applications are becoming increasingly useful in geosciences as it has been shown to be an effective feature extraction technique that has many advantages over conventional data analysis methods ([17]). Regarding rainfall variability, SOM has already been used ([7,8]). SOM has many tunable parameters. [20] analyzed the impact of the choice of these parameters through a sensitivity study on artificial data representative of known patterns. We used the famous SOFT toolbox developed at the Laboratory of Computer and Information Science, Helsinki University of Technology (Copyright (C) 2000-2005 by Esa Alhoniemi, Johan Himberg, Juha Parhankangas and Juha Vesanto). The SOM map architectures were determined using the default settings of the Kohonen package, i.e. batch learning (which is the fastest learning algorithm, [21]); linear initialization; hexagonal lattice map structure (which is the most popular neighborhood and gives a smoother map); map sheet shape and Gaussian neighborhood function; default sizes for the maps.

2.2.3. Hierarchical Ascendant Classification

After obtaining the SOM topological map, it is possible to apply a hierarchical ascendant classification (HAC) algorithm under neighborhood constraint on the matrix composed of the reference vectors to reduce this large number of cells to a limited number of classes containing the map cells. HAC is a classification method belonging to the family of hierarchical methods. It is an iterative classification method. The principle consists of a set of partitions P of N elements into increasingly fine classes obtained by successive groupings of parts. It is a method which in this study makes it possible to calculate a hierarchy of partitions from the topological map. Each partition makes it possible to group the neurons of the map in a different way. The different partitions of the hierarchy are determined iteratively, starting with the finest partition which is composed of all the neurons in the map. The hierarchical classification uses this initial partition and proceeds with successive groupings by merging at each iteration two neuron sub-sets. The choice of the two sub-sets which will merge at a given step is made using a similarity measure defined between two sub-sets. We choose, among all the pairs of sub-sets which constitute the partition at this stage, the two most similar neuron sub-sets, in the sense of the chosen distance measure. These successive groupings produce a binary tree of classification called a dendrogram, whose root corresponds to the class grouping all the individuals. This dendrogram represents a hierarchy of partitions. We can then choose a partition by truncating the tree at a given level. In this work, the interannual variability, the spatial distribution of the onset, end dates and duration of the season in Senegal were studied over the 1981-2018 period. We then performed a composite analysis of atmospheric parameters to study the atmospheric and/or oceanic conditions associated with these events (onset and offset).

3. Results and Discussion

3.1. Spatial variability of onset and cessation of the rainy season in Senegal

The rainy season in West Africa corresponds to the period when the main agricultural activities take place. In Senegal, as in other Sahelian countries, rainy season is highly variable temporarely and spatially . This spatio-temporal variability makes the selection of seed varieties and crop types difficult to plan. Figure 1 below illustrates this spatio-temporal fluctuation in the onset dates of the rainy season in Senegal. 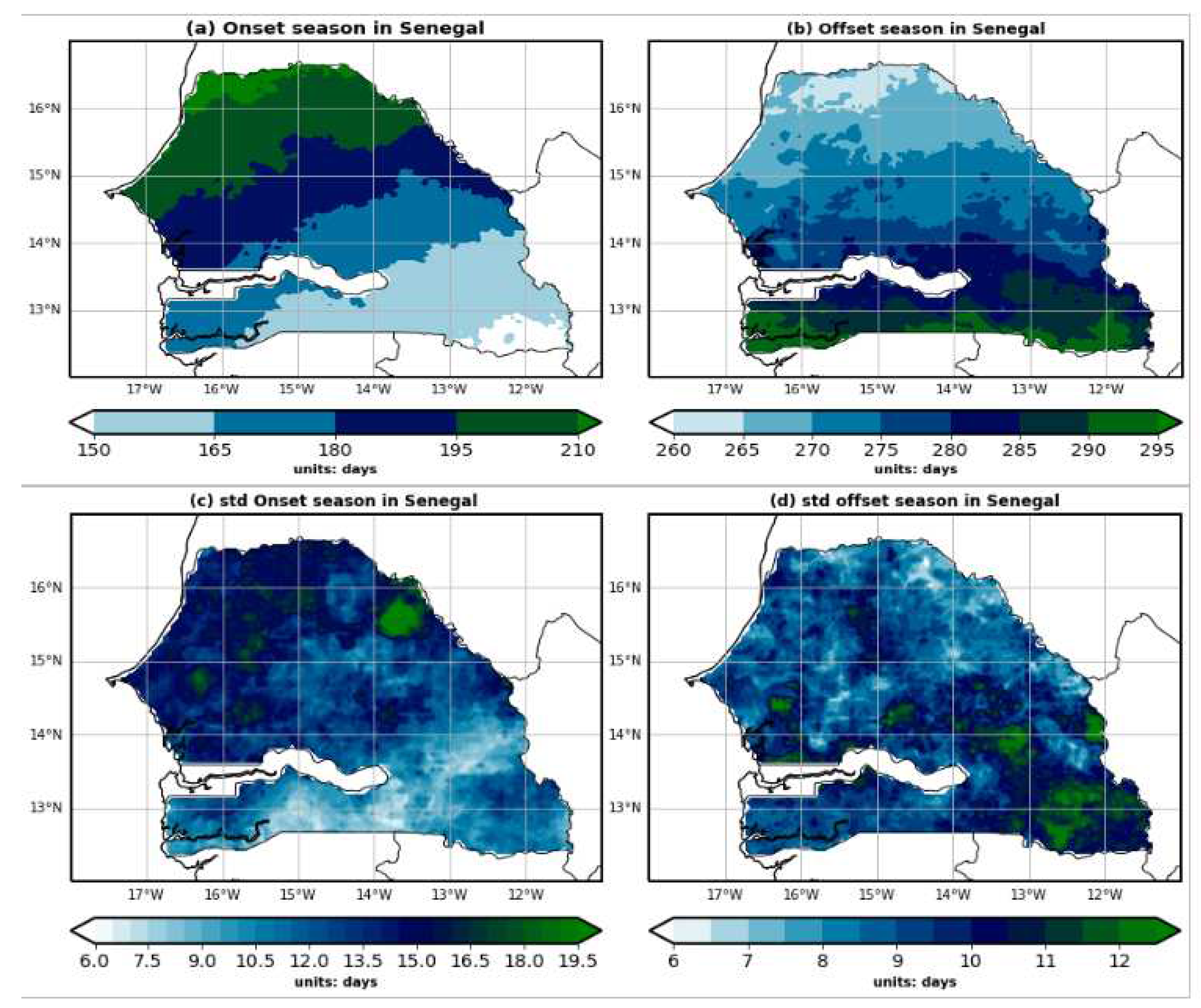Figure 1a and 1b show the meridional gradients (from south to north) of the start and end of the rainy season in Senegal. The start and end of the rainy season exhibit a dual gradient in Senegal: a gradient oriented from southeast to northwest for the start of the season, and a gradient from south to north for the season end date. However, this gradient translates into increasingly late start dates going from southeast to northwest, and increasingly late end dates going from north to south. Indeed, the rainfall withdrawal begins first in the northern part of Senegal around September 17 to 27, then progressively from September 28 to October 7 towards the center, between latitudes 14° and 15° N. Thus, the end of the season is defined in a relatively symmetrical way with respect to the beginning, underlining the contradiction between the sudden onset of the monsoon and its gradual withdrawal. All this justifies that the latitudinal gradient of the start and end of the season, from south to north or from north to south, is consistent with the zonal structure of rainfall, associated with the seasonal progression of the Intertropical Convergence Zone (ITCZ). These results therefore correspond to the same latitudinal distribution of the West African summer monsoon, which is linked to a shift of the ITCZ from a quasi-stationary position at 5°N in May-June to another quasi-stationary position at 10°N in July-August ([22]). This north-south gradient of start and end dates of the season is in perfect agreement with the results of [2], who demonstrated that the spatial configurations of rainfall accumulation and intensity, as well as the onset, cessation dates and length of the season describe a clear gradient oriented from south to north. In addition, their studies confirmed the dual (south to north and southeast to northwest) gradient in Senegal. However, this meridional distribution of the beginning and end of the season is accompanied by a variability in the standard deviation (Figure 3c, d), where the variation is between 6 and 19 days for the onset of the season and between 6 and 12 days for the offset of the season. The average onset date of the rainy season in Senegal is June 29, with a standard deviation of 6 days, meaning the season can start up to 6 days before or after the expected date. Similarly, the average end date of the season is October 4, with a standard deviation of about 5 days. These results corroborate the studies of [23], who showed that in 80% of cases, the rainy season starts at the earliest during the second half of June and ends at the latest during the first half of October.

3.2. Spatial variability of the length of the rainy season (LRS) in Senegal

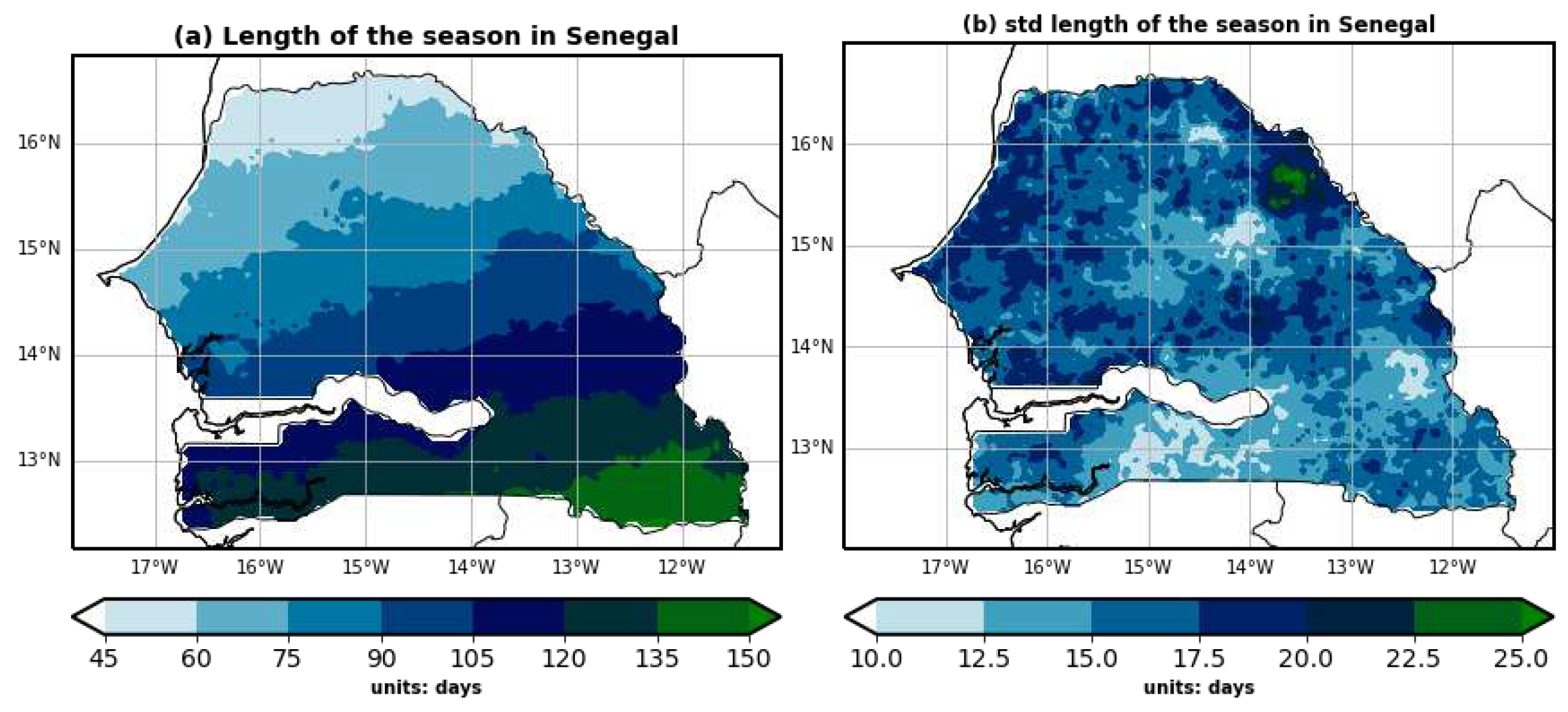
The duration of the rainy season varies from year to year and from place to place. This duration is calculated by taking the difference between the onset and cessation dates of the rainy season, as defined above. The spatial distribution of this duration in Senegal shows a north-south gradient, with a decrease in the duration of the season going from south to north (Figure 2). This figure indicates that the duration of the rainy season in Senegal varies from 45 to 150 days (Figure 2a), with a standard deviation ranging between approximately 10 and 25 days (Figure 2b). Thus, the longer duration of the rainy season in southern and central Senegal indicates a higher probability of rainy days in this region, as well as significant rainfall accumulations. In addition, the extension of the rainy season in the south of the country can be attributed to an earlier onset and a later end compared to the north of the country. This difference in the duration of the rainy season between the north and south of the country can sometimes reach 105 days, which is in perfect agreement with the results of [24].
The spatial variability in the length of the rainy season can have several implications. For example, the season length can impact water availability and agriculture in different regions of the country. A longer rainy season in southern and central Senegal suggests a higher probability of rainy days in this part of the country, as well as higher seasonal rainfall accumulations. This can be beneficial for agriculture and water supply, as greater precipitation can aid crop growth and recharge water resources. In addition, the extension of the rainy season in the south of the country, with an earlier onset and later end compared to the north of the country, can also present challenges. For example, a longer rainy season may increase the risk of flooding in some regions. Additionally, the variability in the rainy season can affect agricultural planning and planting schedules, as farmers must account for these variations to optimize yields. Therefore, this duration of the rainy season is of considerable interest for planning agricultural activities. Indeed, in order to minimize the risks associated with late starts and early ends to the rainy season, Senegalese farmers can adjust their farming activities to occur between the second half of July and the first half of October. However, it should be noted that the shortening of the rainy season is exacerbated by the dry spells that frequently occur during the rainy season ([1,25,26]).
After identifying spatial variations in the start, end, and duration of the rainy season, we then established, for each region of Senegal, the expected period for the start and end of the rainy season.

3.3. Prediction of the onset and offset in Senegal by Kohonen maps

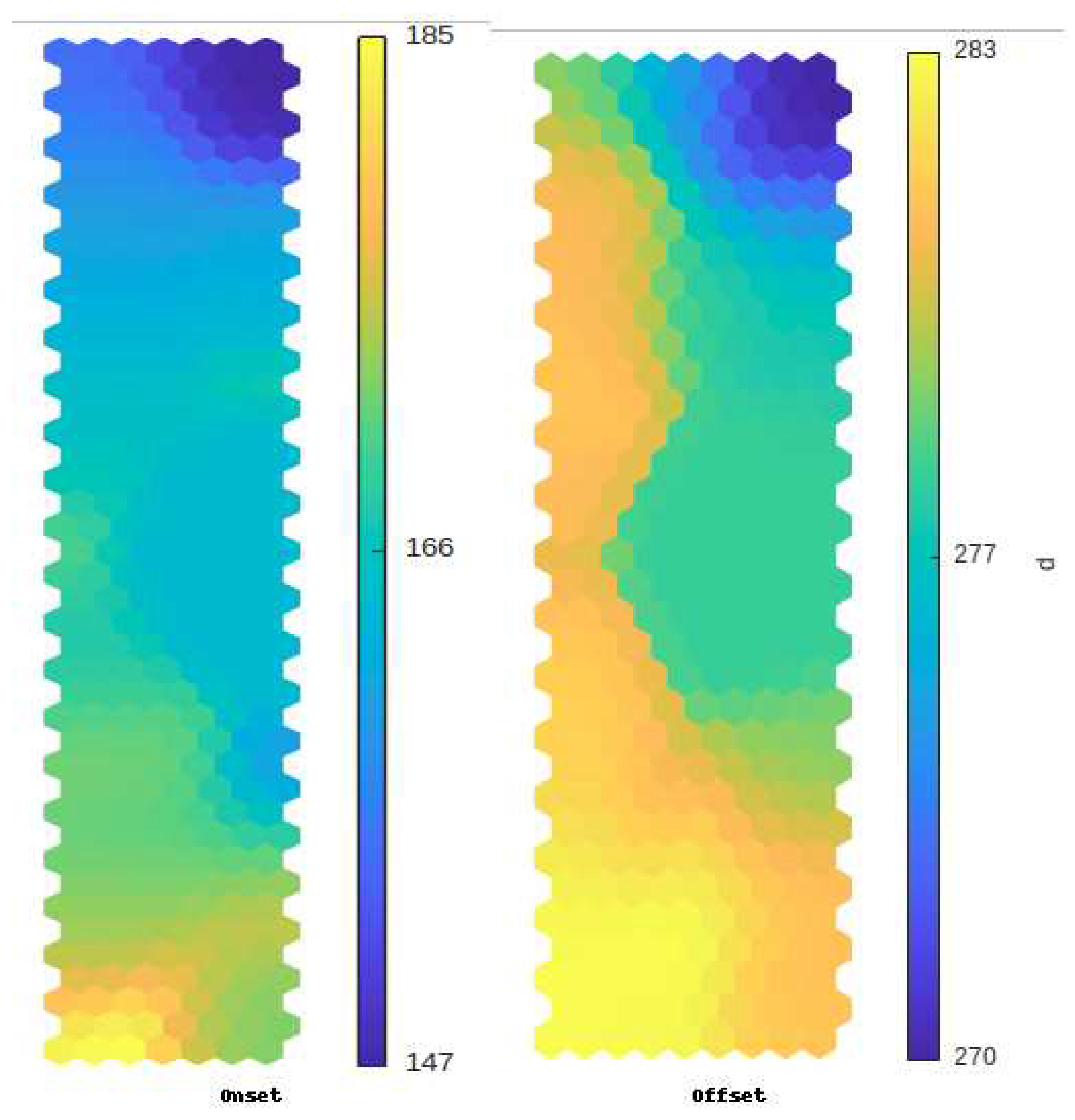
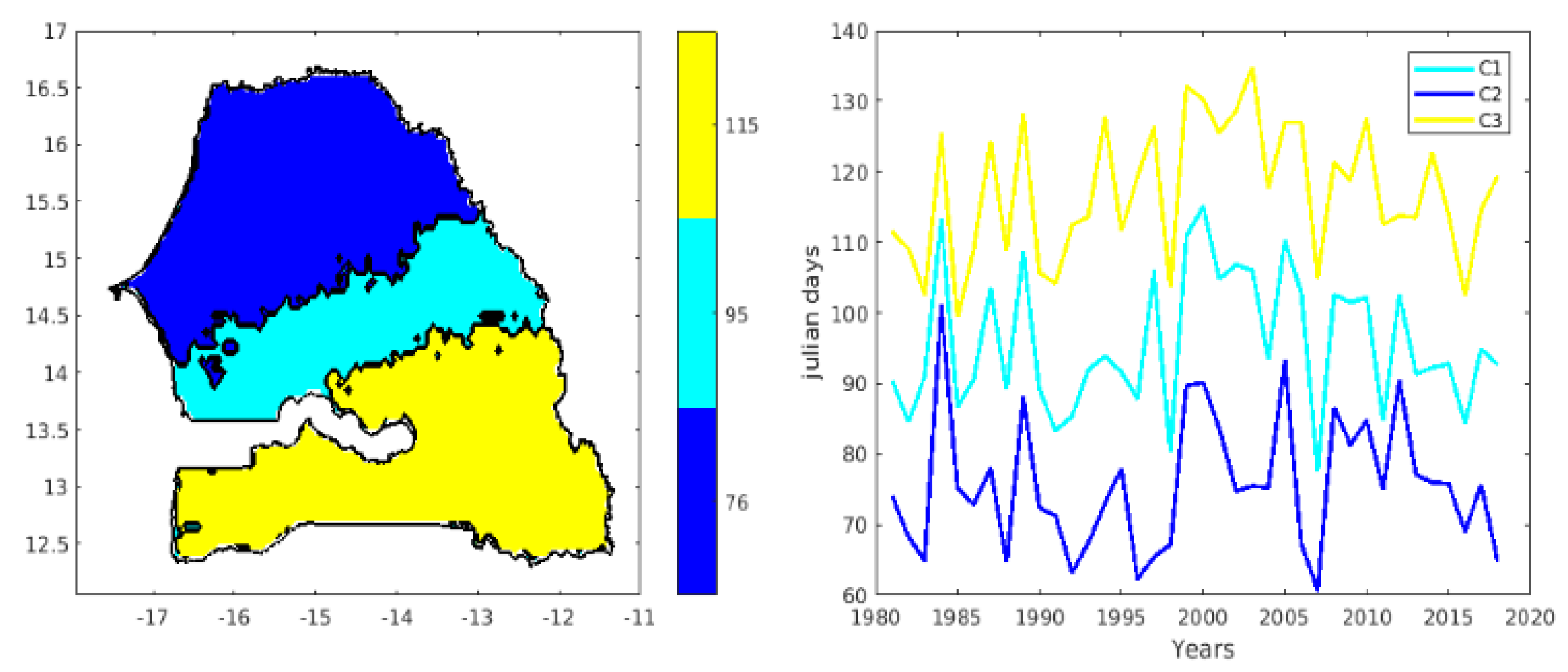
To classify the onset and cessation phases of rain in Senegal, we used CHIRPS precipitation data. We extracted the Senegalese area, with longitude coordinates (-18, -11) and latitude coordinates (11, 17) and a spatial resolution of 0.05° x 0.05°. We obtained annual average maps from 1981 to 2018, for a total of 38 years. Each year is made up of 14,000 pixels, or (100 * 140). To form the training dataset, we formed a dataset of 14,000 observations (pixels) and 38 variables (years). The Kohonen algorithm was applied to the database described above. Several SOM applications were carried out by varying the initialization parameters. The best map in terms of vector quantization was retained, and we finally obtained a map of 43 × 7, or 301 neurons for the Onset, and a map of 33 x 9, for a total of 297 neurons for the Offset. We then projected the pixels of the year 1984 onto the obtained Onset and Offset maps. 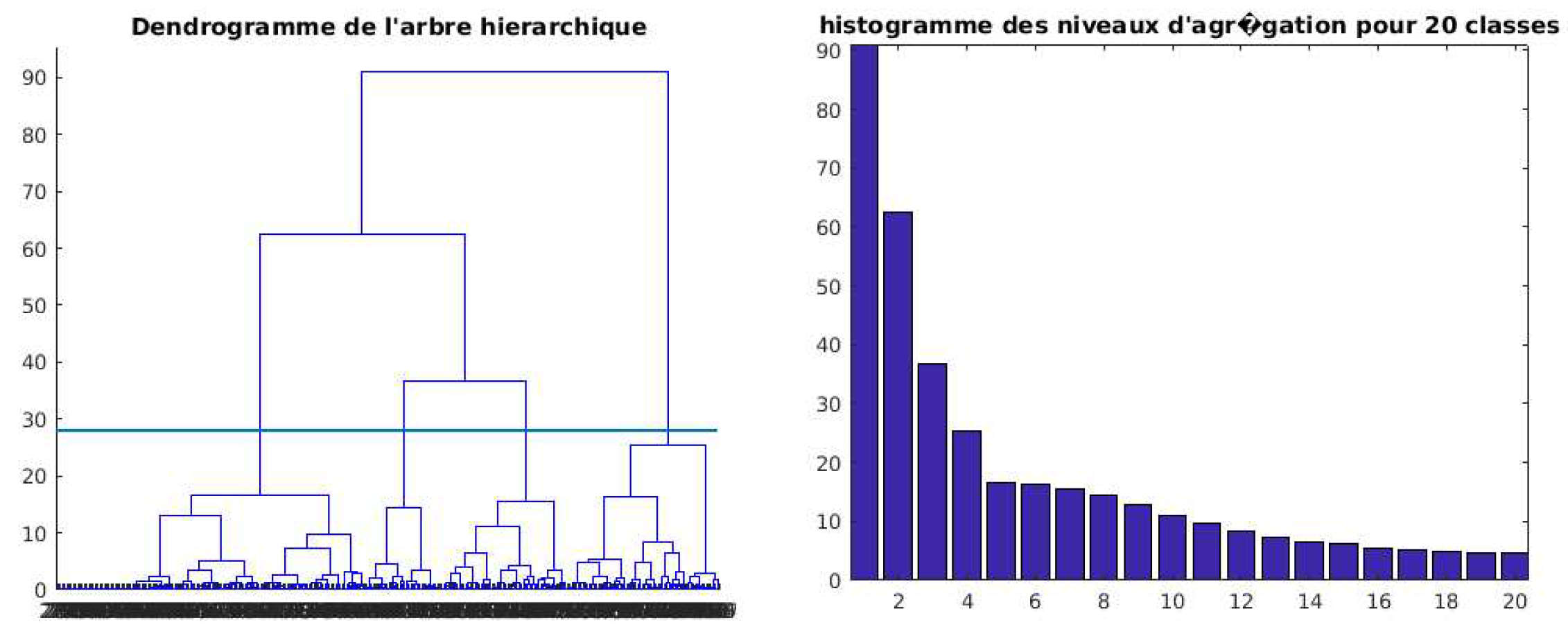The two figures show a good organization of the topology of the observations (pixels) on the map (Figure 3). We note that the two maps are well organized, with the weak values at the top right of the map and the strong values at the bottom of the map. Given the large number of neurons in each map (301 neurons for the Onset and 297 neurons for the Offset), we grouped them into a smaller number of classes by applying a hierarchical agglomerative clustering (HAC) with the Ward criterion as the aggregation criterion for the neurons of the self-organizing map. Figure. 4 shows the dendrogram and histogram of the aggregation levels of the neurons in the Onset neuron map. Based on this figure, we chose 4 classes. The same work was done with the Offset map (Figure not shown) and we also retained 4 classes for the latter.
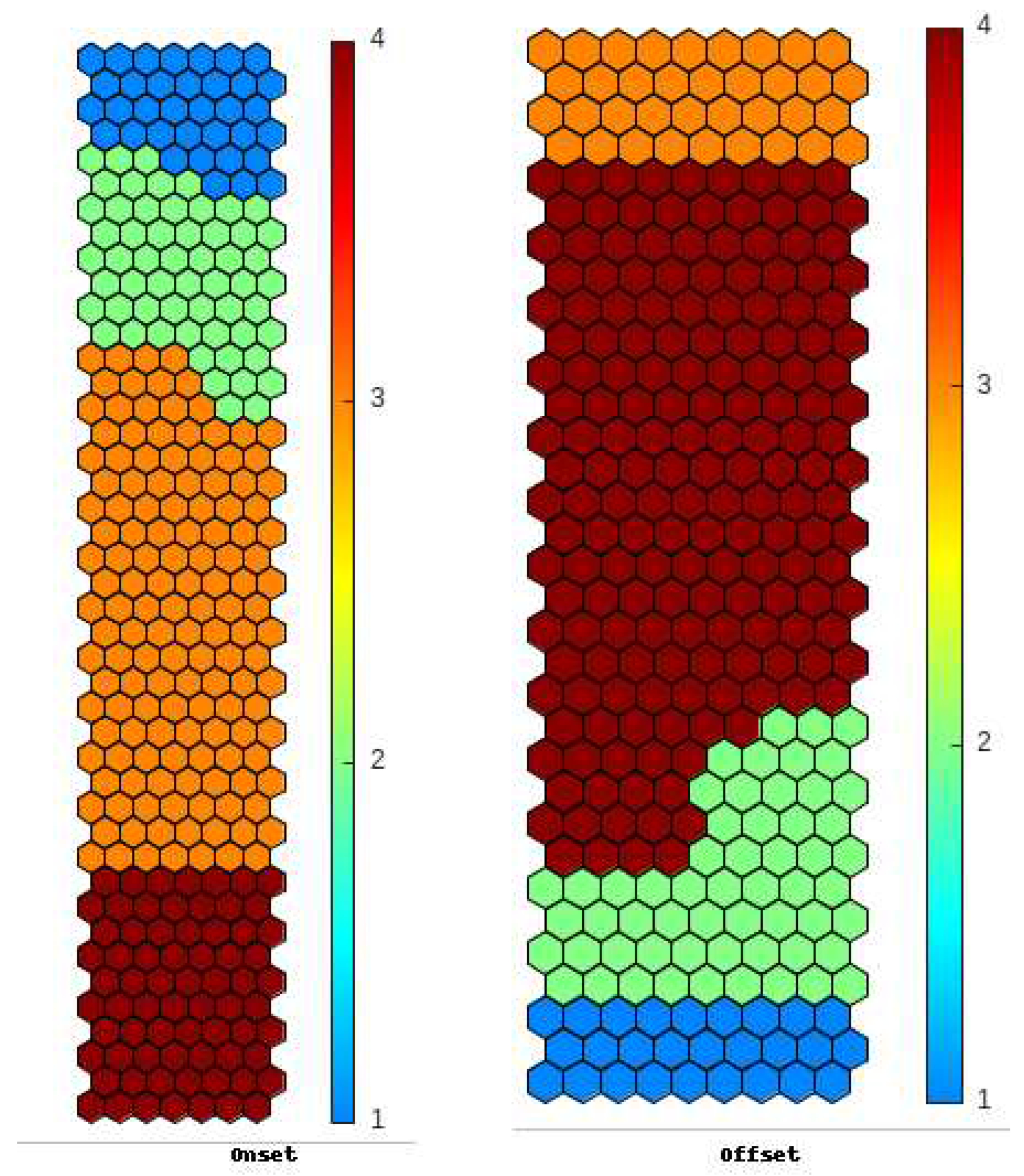
Figure 5: Representation of the 4 classes on the self-organizing map for onset (left) and offset (right). The color bar represents the class numbers. We note that for onset, class 3 corresponds to the neurons in the middle of the map, while class 4 corresponds to the neurons at the bottom of the map. However, for offset, the representation is different. We note that classes 1 and 2 correspond to the neurons at the bottom of the map, but the neurons at the top of the map correspond to class 3.
Preprints 89781 g003
Figure 3. Projection of the pixels of the years 1984 onto the self-organizing maps of the Onset and Offset.
Figure 3. Projection of the pixels of the years 1984 onto the self-organizing maps of the Onset and Offset.
Preprints 89781 g003
Preprints 89781 g004
Figure 4. Dendrogram (left) and histogram (right) of aggregation levels for 20 classes obtained from the hierarchical classification of neurons.
Figure 4. Dendrogram (left) and histogram (right) of aggregation levels for 20 classes obtained from the hierarchical classification of neurons.
Preprints 89781 g004
Preprints 89781 g005
Figure 5. Classification of neurons on the topological map: for onset (left) and for offset (right).
Figure 5. Classification of neurons on the topological map: for onset (left) and for offset (right).
Preprints 89781 g005
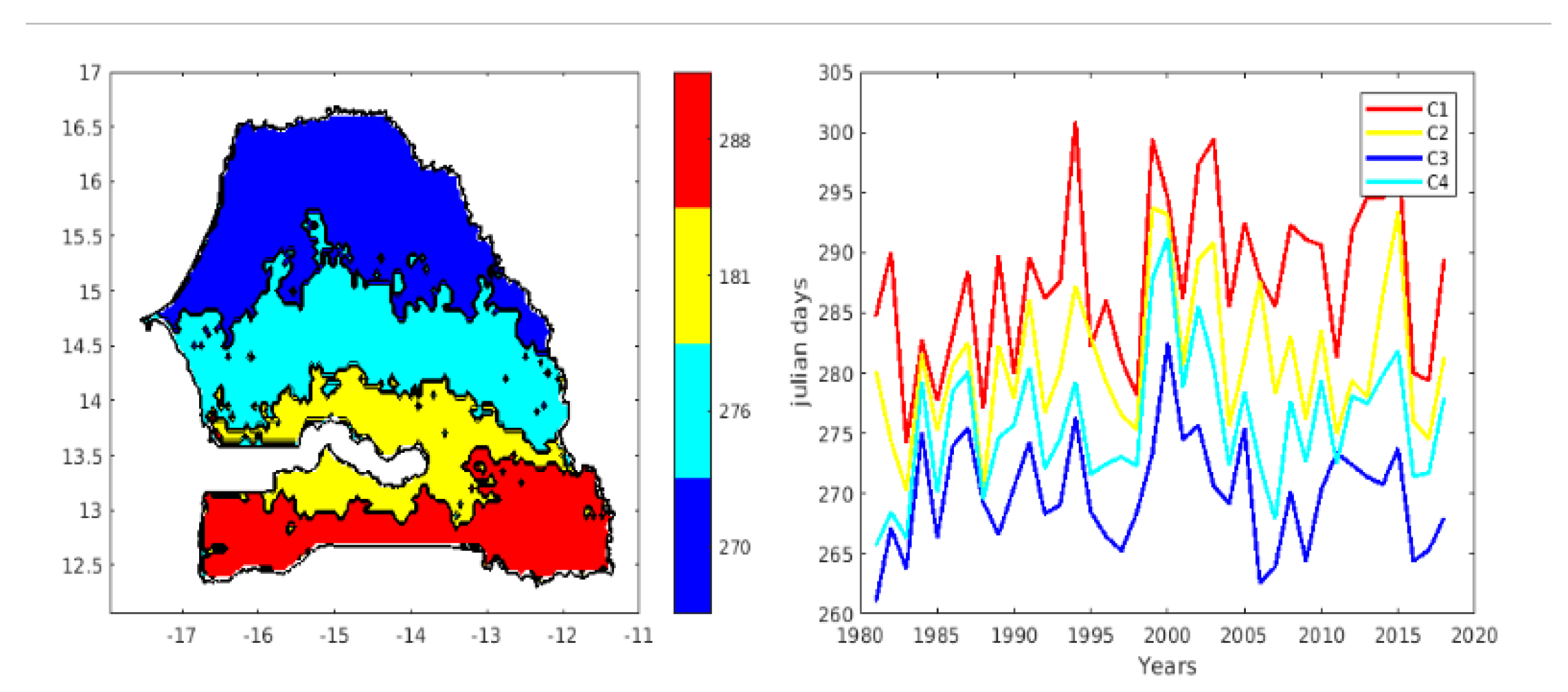
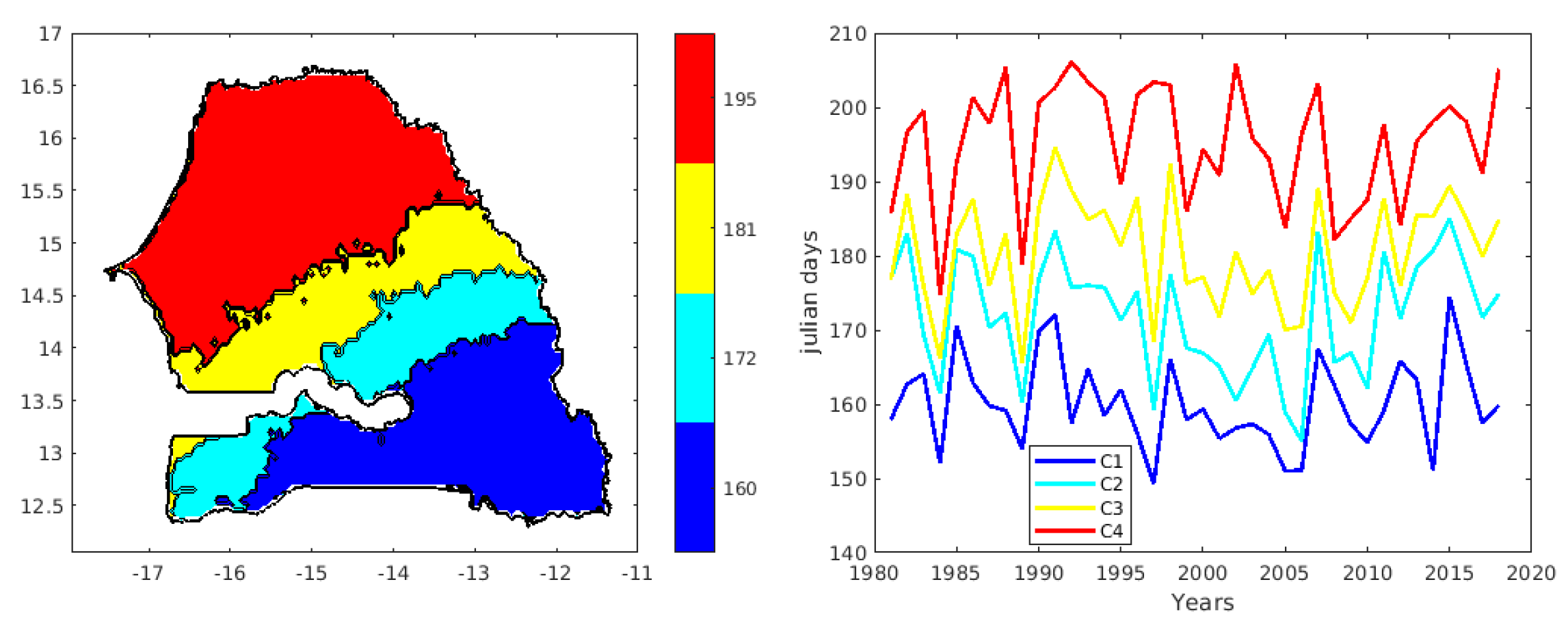
After classifying the neurons into different classes, we projected the data from each class onto the geographical map of Senegal. The left map in Figure 6 shows the spatial distribution of the different onset phases of the season, averaged over the period 1981-2018. We observe a clear meridional gradient in the onset of the season, with later starts in the north of the country and earlier starts in the south. These results indicate that the start date of the season is aro, (255, 255, 255)und June 9 (day 160) in the southeastern regions of Senegal (blue on the map), extending to latitude 13°N in the eastern part of the country. Moving from the southeast towards the center of Senegal, the start dates of the season are expected around June 19 (day 172). In the north-central part of Senegal (yellow on the map), the start dates of the season are expected around June 27 (day 181). The northwestern part of Senegal (red on the map) is characterized by a start date of the season around July 11 (day 195). Examining the interannual variability averaged over each class over the period 1981-2018 (see Fig. 6 on the right), we observed start dates for the rainy season that were sometimes early (1984, 1997, 2005, and 2014) and sometimes late (1989, 1991, 2007, and 2015). An interannual irregularity in the start dates is observed across the different classes, as well as between the clusters. This difference between the clusters is due to the spatial variability of the seasonalities between the south and north of Senegal. In other words, this variability in the start can be explained by the climatic differences between these two zones (the south has a sub-Guinean climate and the north has a Sahelian climate). As with the spatial variability, we find that the interannual variability of the start of the season follows the south-north gradient. However, a weak south-north gradient is observed in some years, such as 1984 and 2007.
Figure 7 (right) shows the interannual variability of the end date of each class for the four classes obtained in Senegal. We note a weak meridional gradient in the end date of the season between the years 1984 to 1994 approximately and a strong meridional gradient between 1995 to 2018. Similarly to the start date, the cessation date also shows years with low variations between the north and south (for example 1984, 1985, 1986, etc.). Interannual variability within each class in Senegal over the period 1981-2018 (see Figure. 6 on the right) shows long seasons (class 3) and short seasons (class 2). An interannual irregularity in the lengths of seasons is observed across the different classes, as well as within each class (Figure 8). We observe years with low variability in the length of the season (1984, 1989, 2007) and years with high variability in the length (1988, 1991, 2002, etc.). Years such as (2001, 2003, and even 2010) are marked by long rainy seasons and others such as (2007, 1994, 1992, etc.) are marked by short lengths of season (Figure 8). This section is not mandatory, but can be added to the manuscript if the discussion is unusually long or complex.
Preprints 89781 g007
Figure 7. Prediction of the offset dates of the rainy Season in Senegal using Kohonen Neural Networks (Spatial End Classification on the left, and the time series of classes on the right).
Figure 7. Prediction of the offset dates of the rainy Season in Senegal using Kohonen Neural Networks (Spatial End Classification on the left, and the time series of classes on the right).
Preprints 89781 g007
Preprints 89781 g008
Figure 8. Spatial and temporal classification of the length of the rainy season in Senegal (1981-2018)
Figure 8. Spatial and temporal classification of the length of the rainy season in Senegal (1981-2018)
Preprints 89781 g008
Similar to the spatio-temporal variability of the start date, the spatio-temporal variability of the cessation dates and durations of the rainy season in Senegal can also be explained by the climatic differences between the south, which has a sub-Guinean climate, and the north, which has a Sahelian climate. After having classified the spatio-temporal variability of the start, end, and duration dates of the season, it is now interesting to analyze the intra-seasonal indices that can modulate these starts and ends (late and/or early) of the rainy season in Senegal.

3.4. Dynamic analysis

To better characterize the onset and cessation of the rainy season, the behavior of certain atmospheric parameters was analyzed for the years 1984 and 2007, particular years marked respectively by an early start and a late start on almost all of Senegalese territory. This analysis focused on a period of several weeks, or four weeks, preceding the dates of the start and end of the rainy season during these years. The transport of moisture plays a primary role in determining the characteristics of precipitation in West Africa, including Senegal, as shown by several studies ([27,28]). These complex meteorological phenomena are indeed influenced by atmospheric circulations, jet streams, air masses and ocean-atmosphere interactions ([22,29,30]). 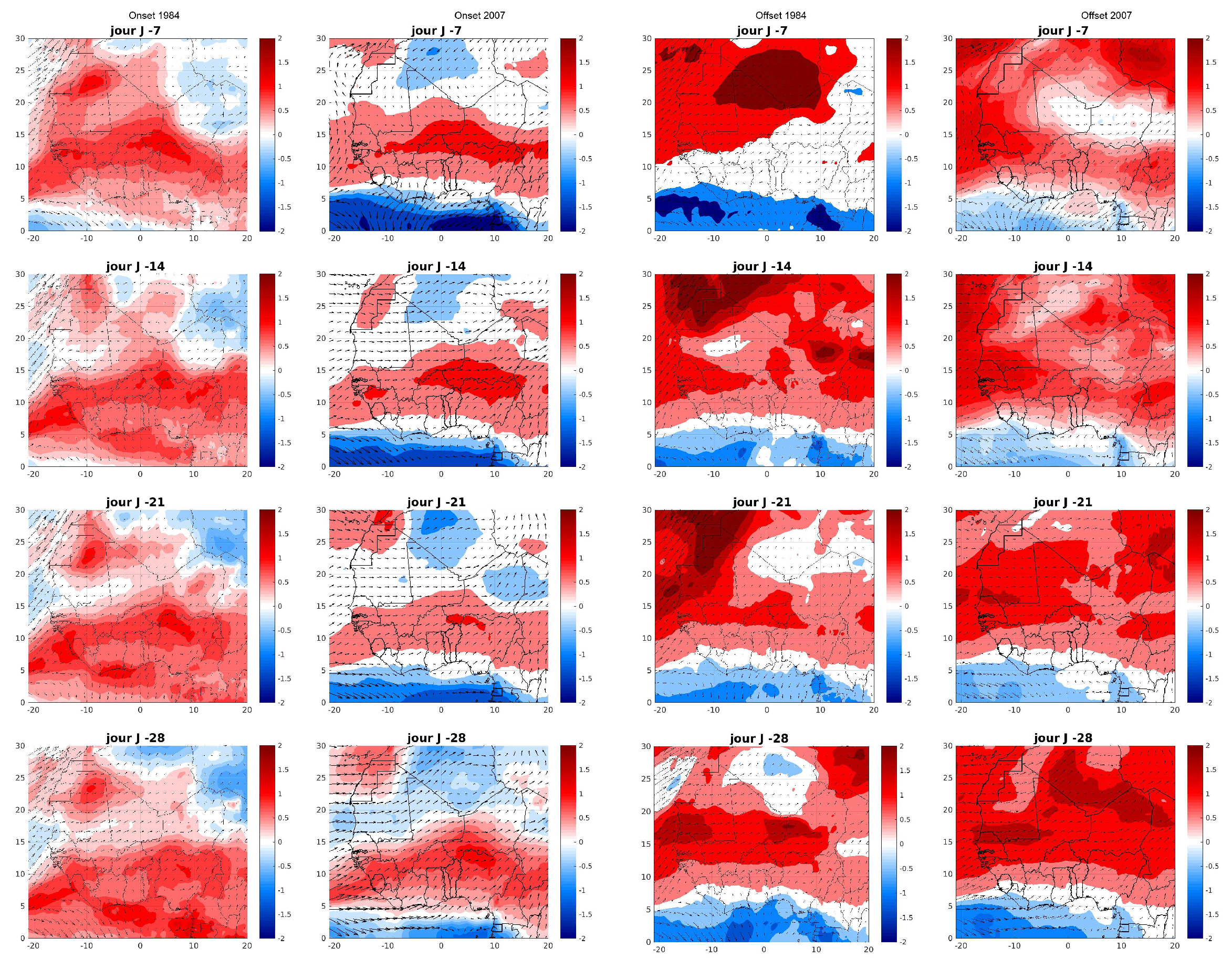Figure 9 thus represents the weekly average of the surface-850 hPa integrated moisture transport, materialized by streamlines, and of the the surface-850 hPa integrated specific humidity over the same deph, represented by a color code during one, two, three and four weeks preceding the start and end dates of the rainy season in Senegal. It is found that the moisture transport that precedes the start of the rainy seasons (1984 and 2007) is oriented from the oceanic zones to the continental lands, and is crucial to start the rainy season. The moist winds carry water vapor from the ocean to the land, and when these moist air masses come into contact with the drier and warmer air above the land, condensation occurs, causing the formation of clouds and precipitation. Figure 9 shows the integrated and specific humidity transport over West Africa during two rainy seasons, one early in 1994 and the other late in 2007. The two left columns show the humidity transport during the start of the rainy season, while the two right columns show the humidity transport during the cessation of the rainy season. The humidity transport is represented by streamlines, and the anomalies of the integrated specific humidity are shown by a color code. It is observed that the moisture transport preceding the onset of the rainy seasons (1994 and 2007) is oriented from the oceanic zones to the continental lands, and is crucial to initiate the rainy season. Moist winds carry water vapor from the ocean to the land, and when these moist air masses come into contact with the drier and warmer air above the land, condensation occurs, causing the formation of clouds and precipitation.
Preprints 89781 g009
Figure 9. Composite analysis of moisture transport and integrated specific humidity anomalies between 1000 and 850 hPa during weeks before the onset and offset of the rainy seasons of 1984 and 2007
Figure 9. Composite analysis of moisture transport and integrated specific humidity anomalies between 1000 and 850 hPa during weeks before the onset and offset of the rainy seasons of 1984 and 2007
Preprints 89781 g009
The two rainy seasons (1984 and 2007) are characterized by moisture fluxe from the Atlantic Ocean. However, there are significant differences between the two seasons. The moisture transport calculated for 1984 (a year with an early start of the rainy season) follows a southwest trajectory at latitudes above 5°N during the various forecast periods. A strong concentration of moisture is noted above the Atlantic Ocean, and a strong penetration of moisture into the continent. This configuration may be due to a high pressure system over the Atlantic and low pressure over the continent, which facilitated the transport of moisture to the continent ([31,32,33]). In contrast, for 2007 (a year with a late start of the rainy season), the moisture transport adopts a west direction at latitudes above 5°N during the different lead times except for the 7-day lead time, where it adopts a south direction over the ocean. At latitudes below 5°N, the moisture transport is eastward over the ocean. The specific humidity anomalies for 1984 decrease from south to north. In other words, the moisture is stronger in the south and tends to decrease as it advances towards the northeast of the continent. We also note for 2007 that the Sahelian band to the ocean is much more humid than the south of West Africa and the Sahara in all lead times. In addition, it is noticed that the progression of moisture towards the continent and the north decreases with the delay. In other words, the moisture transport moves northward the closer we get to the start date of the season. However, the moisture transport has advanced much further northward in West Africa at the early start of the year 1984 compared to the year 2007, where there is a late start. Similarly, moisture transport plays a role in determining the end of the rainy season ([22,33]). As seasons change and air masses shift, moisture transport can diminish, leading to decreased rainfall. Factors like the retreat of monsoon systems and the shift of jet streams influence the amount of moisture available for precipitation. In Figure. 9, for the season end dates, the meridional gradient of specific humidity is still observed according to the different lead times. The two rainy seasons ended in a somewhat similar fashion, with high moisture concentrations over the continent’s North and low moisture concentrations in the South. It is observed that the high concentrations are pushed back northward over the continent as the end of the season approaches. The results seem to show that years with stronger moisture transport (e.g. 1984) can lead to earlier onsets of the rainy season and more abundant rainfall. Conversely, when moisture transport is weakened, the rainy season may be delayed (e.g. 2007) or precipitation may be less abundant.

4. Conclusions

This study has demonstrated a spatio-temporal variability in the dates of the onset, offset, and duration of the rainy season in Senegal from 1981 to 2018. These findings provide useful information for the planning of agricultural activities. The onset of the rainy season is later from the south-east to the north-west of Senegal, with a meridional gradient. This variability is due to atmospheric dynamics, which are influenced by the position of monsoon systems and jet streams.
The cessation of the rainy season also follows a north-south gradient, with a longer duration in the south than in the north. This variability is also due to atmospheric dynamics, which are influenced by the evolution of monsoon systems and jet streams. The length of the rainy season varies between the north and south of Senegal, from 45 to 150 days. This variability is due to the combination of the meridional gradient of the onset and end of the rainy season.
Self-organizing maps derived from the Kohonen algorithm can be used to classify the spatio-temporal distribution of the onset, end, and duration of the rainy season in Senegal. These maps are based on historical data from the rainy season.
In addition, the analysis of atmospheric dynamics shows that moisture transport plays a major role in the onset of the rainy season. Years with stronger moisture transport (e.g., 1984) can lead to earlier rainy season onsets and more abundant precipitation. Conversely, when moisture transport is weakened, the rainy season can be delayed (e.g., 2007) or precipitation can be less abundant. These results confirm the relevance of machine learning methods for intra-seasonal forecasting. There are promising opportunities to develop decision-support tools for agricultural development actors. Further studies will be needed to refine these approaches and assess their potential benefits.
Further work could deepen the analysis of links with the main climate variability modes on interannual and intraseasonal timescales. For example, the ENSO phenomenon (El Niño Southern Oscillation) modulates atmospheric dynamics and deep convection over West Africa. El Niño events are associated with rainfall deficits while La Niña favors rainfall surpluses. The influence of ENSO on the onset and offset of the rainy season in Senegal could be quantified. Similarly, the Madden-Julian Oscillation (MJO) corresponds to intraseasonal variability of convection in the tropics. As MJO modulates convective activity, it could affect the onset and cessation dates of the rainy season. Finally, equatorial Kelvin waves, propagating east to west, are known to interact with monsoon dynamics. Their role in triggering early season rainfall deserves further investigation. Analyzing the links between these tropical phenomena and the rainy season in Senegal, using statistical and machine learning methods, would improve intraseasonal forecasts and better understand scale interactions. Probabilistic forecasts could be developed from climate model outputs.

Data Availability Statement

Not applicable

Acknowledgments

This research is a part of a PhD study conducted in the Laboratoire Physique de l’Atmosphère et de l’Océan-Siméon Fongang (LPAO-SF)/ESP/UCAD

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ITCZ Intertropical Convergence Zone
CHIRPS Climate Hazards group InfraRed Precipitation with Stations
OLR Outgoing Longwave Radiation
LRS length of the rainy season
SOMs Self-organizing maps
HAC hierarchical agglomerative clustering
MJO Madden-Julian Oscillation
ENSO El Niño Southern Oscillation

References

  1. Sivakumar, M.V.K. Empirical analysis of dry spells for agricultural applications in West Africa. Journal of Climate, 1992, 5(5), 532–539. [CrossRef]
  2. Marteau R., Sultan B., Moron V., Baron C., Traore S. B. et Alhassane A. Démarrage de la saison des pluies et date de semis du mil dans le sud-ouest du Niger. Actes du XXIIIème colloque de l’Association Internationale de Climatologie, Risques et changement climatique, Rennes, France, 2010, 379–-384.
  3. Liebmann, B., Bladé, I., Kiladis, G.N., Carvalho, L.M., B. Senay, G.,Allured, D., Leroux, S. and Funk, C. Seasonality of African precipitation from 1996 to 2009.,Journal of Climate, 2012, 25(12), 4304–-4322. [CrossRef]
  4. Sultan, B., and S. Janicot, 2000: Abrupt shift of the ITCZ over West Africa and intra-seasonal variability. Geophys. Res. Lett., 2000, 27, 3353–3356. [CrossRef]
  5. Fontaine, Bernard, et al. (2009) "West African monsoon onset: earlier onset, but slower progression." Geophysical Research Letters, 2009, 36(18).
  6. Balme, M., S. Galle, and T. Lebel, 2005: Démarrage de la saison des pluies au Sahel: Variabilité aux échelles hydrologique et agronomique, analysée à partir des données EPSAT-Niger.Secheresse, 2005, 16, 15–22.
  7. Guèye, A.K., Janicot, S., Niang, A. Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part I: synoptic time scale.Clim Dyn, 2011, 36, 1–18. [CrossRef]
  8. GUÈYE, A. K., JANICOT, Serge, NIANG, Awa, et al. Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part II: Interannual time scale. Climate dynamics, 2012, vol. 39, p. 2251-2272. [CrossRef]
  9. Funk, C.C., Peterson, P.J., Landsfeld, M.F., Pedreros, D.H., Verdin, J.P., Rowland, D., Romero, B.E., Husak, G.J., Michaelsen, J.C., and Verdin, A.P., (2014): A quasi -global precipitation time series for drought monitoring:U.S. Geological Survey Data Series, 832, 4 p.,. [CrossRef]
  10. Badr, H. S., Dezfuli, A. K., Zaitchik, B. F., and Peters-Lidard, C. D. (2016). Regionalizing Africa: patterns of precipitation variability in observations and global climate models. Journal of Climate, 29(24), 9027-9043. [CrossRef]
  11. Herold, N., Behrangi, A., and Alexander, L. V. (2017). Large uncertainties in observed daily precipitation extremes over land. Journal of Geophysical Research: Atmospheres, 122(2), 668-681. [CrossRef]
  12. Davy, E. G., Mattei, F., Solomon, S. I., 1976 : An evaluation of climate and water resources for development of agriculture in the Sudano-Sahelian zone of West Africa,Special environmental Report N° 9, world Meteorological Organisation, WMO-No.459, Geneva..
  13. Kohonen, T., 2001. Self-Organizing Maps: Third, Extended Edition. Springer Series in Information Sciences,Springer-Verlag, vol. 30,Berlin, Germany, ISBN 978-3-540-67921-9.
  14. Richardson, A., Risien, C., Shillington, F., 2007.Using self organizong maps to identifiy patterns in satellite imagery.Prog. Oceanogr. 59 (2–3), 223–239.. [CrossRef]
  15. Lorenz, E.N., 1956. Empirical orthogonal functions and statistical weather prediction, Stat. Forecasting Proj. Rep., Tech. Rep. 1, 1–49, Dep. of Meteorol., MIT, Cambridge.
  16. Badran, F., Yacoub, M., Thiria, S., 2005. chap. In: Dreyfus, G. (eds.), Self-organizing Maps and Unsupervised Classification, Springer, Neural Networks, Berlin Heidelberg, pp. 379–442. [CrossRef]
  17. Liu, Y., Weisberg, R.H., Mooers, N.K., 2006. Performance evaluation of the self-organizing map for future extraction. J. Geophys. Res. 111,C05018. [CrossRef]
  18. Bação, F., Lobo V., and Painho M., (2005) :Self-organizing Maps as Substitutes for K-Means Clustering V.S. Sunderam et al. (Eds.): ICCS 2005, LNCS 3516, pp. 476 – 483, 2005. Springer-Verlag Berlin Heidelberg 2005.
  19. Kiang, M.Y., Kumar, A., 2001. An evaluation of self-organizing map networks as a robust alternative to factor analysis in data mining applications.Inf. Syst. Res. 12 (2), 177–194. [CrossRef]
  20. Liu, Y., Weisberg, R.H., 2005. Patterns of ocean current variability on the West Florida Shelf using the self-organizing map. J. Geophys. Res.110, C06003. [CrossRef]
  21. Vesanto, J., Himberg, J., Alhoniemi, E., Parhankangas, J., 2000. SOM toolbox for Matlab 5, report. Helsinki University of Technology,Helsinki, Finland.
  22. Sultan, B., and S. Janicot,2003: The West African monsoon dynamics. Part II: The pre-onset and the onset of the summer monsoon. J. Climate, 16, 3407–3427.
  23. Sané T., Diop M., Sagna P., (2008) : Étude de la qualité de la saison pluvieuse en Haute Casamance (Sud Sénégal).Sécheresse;, 19 (1): 23-8.
  24. Touré, A.K.; Fall, C.M.N.;Diakhaté, M.; Wane, D.;Rodríguez-Fonseca, B.; Ndiaye, O.;Diop, M.; Gaye, A.T.: Predictability of Intra-Seasonal Descriptors of RainySeason over Senegal Using Global SST Patterns.Atmosphere 2022, , 13,1437. [CrossRef]
  25. Panthou, G., Vischel, T., Lebel, T., Blanchet, J., Quantin, G., and Ali, A. (2014): Extreme rainfall in West Africa: A regional modeling.Water Resources Research, , 50(8), 7236-7252. [CrossRef]
  26. Salack, S., Giannini, A., Diakhaté, M., Gaye, A. T., and Muller, B. (2014): Oceanic influence on the sub-seasonal to interannual timing and frequency of extreme dry spells over the West African Sahel.Climate Dynamics, 42(1), 189-201. [CrossRef]
  27. ENGEL , T., F INK , A., K NIPPERTZ , P., P ANTE ( NÉ G LÄSER ), G. and B LIEFERNICHT , J. (2017). West African monsoon water cycle: 2. Extreme Precipitation in the West African Cities of Dakar and Ouagadougou: Atmospheric Dynamics and Implications for Flood Risk Assessments.J. Hydrometeorol., 115(D19).
  28. Mouhammed Fall, Abdou Lahat Dieng, Saïdou Moustapha Sall, Youssouph Sane, and Moussa Diakhaté,: “Synoptic Analysis of Extreme Rainfall Event in West Africa: the Case of Linguère.”American Journal of Environmental Protection, vol. 8, no. 1 (2020):1-9. [CrossRef]
  29. Meynadier, R., Bock, O., Guichard, F., Boone, A., Roucou, P., and Redelsperger, J. L. (2010): West African monsoon water cycle: 2. Assessment of numerical weather prediction water budgets.Journal of Geophysical Research: Atmospheres, 115(D19). [CrossRef]
  30. Thorncroft, C. D., Nguyen, H., Zhang, C., and Peyrille, P. (2011). Annual cycle of the West African monsoon: regional circulations and associated water vapour transport.Quarterly Journal of the Royal Meteorological Society,, 137(654), 129-147. [CrossRef]
  31. Messager, C., Gallée, H., and Brasseur, O. (2010). Precipitation sensitivity to regional SST in a regional climate simulation during the West African monsoon for two dry years. Climate dynamics, 36(1), 623-640. [CrossRef]
  32. Pu, B., and Cook, K. H. (2010). Dynamics of the West African westerly jet. Journal of Climate, 23(23), 6263-6276. [CrossRef]
  33. Janicot, S., Caniaux, G., Chauvin, F., de Coëtlogon, G., Fontaine, B., Hall, N., Thorncroft, C. (2011). Intraseasonal variability of the West African monsoon. Atmospheric Science Letters, 12(1), 58-66. [CrossRef]
Preprints 89781 g001
Figure 1. Spatial Distribution of the Onset and End of the Rainy Season (top) and Rainfall Anomalies (bottom) in Senegal.
Figure 1. Spatial Distribution of the Onset and End of the Rainy Season (top) and Rainfall Anomalies (bottom) in Senegal.
Preprints 89781 g001
Preprints 89781 g002
Figure 2. Spatial Distribution of the Length of the Rainy Season (a) and its Standard Deviation (b) in Senegal.
Figure 2. Spatial Distribution of the Length of the Rainy Season (a) and its Standard Deviation (b) in Senegal.
Preprints 89781 g002
Preprints 89781 g006
Figure 6. Prediction of the onset dates of the rainy season in Senegal using Kohonen neural networks (Spatial onset classification on the left, and time series of classes on the right).
Figure 6. Prediction of the onset dates of the rainy season in Senegal using Kohonen neural networks (Spatial onset classification on the left, and time series of classes on the right).
Preprints 89781 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated