Prerpints.org logo
Preprint
Article

Evaluation and Modelling of the Coastal Geomorphological Changes of Deception Island Since 1970 Eruption and Its Involvement in Research Activity

Altmetrics

Downloads

109

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts
Abstract
Deception Island is an active volcano with a submerged caldera open to the sea, giving it a horseshoe-shaped structure. Several post-caldera-collapsed volcanic events, as well as hydrodynamics within this natural bay, have modified its inner coastline, shaping new tephra deposits and altering the landscape. A hydrodynamic model is presented to predict accretion and erosion trends on the coast, which impact the mobility of researchers and tourists, whether on foot or by boat. Historical orthophoto images and spatiotemporal differences in digital elevation and bathymetric models have been used for validation purposes. The model reveals that the south-facing coast is more susceptible to erosion, while the east-west-facing coast experiences sedimentation. However, a visual study of the coastline has indicated erosion ratios in cliff areas in sedimentary zones. This is likely due to the erosive effect caused by ice floe fragments accumulating in these areas due to wave action. Only a portion of the significant total loss of surface material is received within the bay, including its own erosion, and accumulates on the bay's floor. This is partially due to the volume being composed of snow, and there is also a transfer of material to the exterior to balance the figures.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Deception Island is a horseshoe-shaped active volcano in the Bransfield Strait with an inner bay named Port Foster (Figure 1). This large natural harbour has been a focus of human activity in the South Shetland Islands since the early nineteenth century. The island was visited by a succession of sealing and whaling vessels, culminating in the establishment of a Norwegian whaling station from 1911 to 1931 [1]. Four scientific stations were established from 1944, but two of which were destroyed during the last 1967-1970 volcanic eruptions (Chilean station in Pendulum Cave and British station in Whalers Bay). The two current active scientific bases are the Argentinian Base “Decepción” installed in 1948 and the Spanish Antarctic “Base Gabriel de Castilla” in 1989, see Figure 1b. Since then, to protect its landscape and ecosystems, some areas have been declared as Antarctic Specially Protected Area (ASPA) under the Antarctic Treaty System [2].
Antarctica is a region devoid of government jurisdiction, and the mapping of Deception Island is typically undertaken by interested nations or commissioned by scientific organizations such as the Scientific Committee on Antarctic Research (SCAR). Over the years, various cartographic representations of the island have been created, utilizing different scales, geodetic systems, and projections. This multiplicity of cartographic sources has made it challenging to assess the island's significant temporal changes in both its terrestrial and underwater features [4,5].
Throughout its history, Deception Island has experienced geomorphological transformations, often coinciding with volcanic eruptions in 1842, 1912, 1917, 1967, 1969, and 1970 [6,7,8,9,10]. The period from 1967 to 1970, in particular, brought about substantial alterations to the island's landscape and shoreline, primarily in the northern sector. It gave rise to new volcanic structures such as cinder cones (depicted in Figure 2a1) and maar and tuff cones, primarily because of phreatomagmatic eruptions [6,8,11,12,13]. The large amount of new unconsolidated pyroclastic material has been displaced by snow and glaciers melting through streams and hydrodynamic transport within Port Foster from then [4]. This ongoing process has resulted in visible annual alterations to the coastline. Several instances of dynamic sediment erosion along the coast and localized cliff erosion are noteworthy. These include the creation of openings at Port Forster, such as those at Kroner Lake (depicted in Figures 2b1 and 2b2) and Hidden Lake. The latter event involved the breach of a wall measuring 2 meters in width and 2 meters in height, as seen in Figures 2c1 and 2c2, which occurred in 2006. Additionally, there has been a notable and consistent annual sedimentation, resulting in the infilling at the base of craters formed during the 1970 eruption, as evident in Figure 2a2. A previous study evaluated in these craters some sedimentation ratios of up to 1 m / year in the period 1992–2006 [14]. A new 2020 satellite image offers a clear view of this filling of some of them (mainly numbers 1,4,5 and 6 following Figure 2a2). Further descriptions of the remaining craters can be found in [15]. Furthermore, a significant retreat of more than 200 metres has been identified at the front of Black Glacier, as highlighted in Figures 2d1 and 2d2.
Likewise, because of the prolonged human interest, there have been studies of many bathymetric surveys of Port Foster, the submerged caldera of Deception Island. The first known dating from 1829 and with a remarkably constant rate of uplift averaged over 160 years following Cooper et al. [5]. In that paper was evaluated, with surveys of 1948 and 1993 (covering the last eruption period), that the bay has sedimentation ratios of up to 5 cm / yr. This value is comparable to sedimentary rates in other caldera lakes, such as Crater Lake (Oregon, USA), although without recent eruptions [16]. Roobol [17] assessed that the shallow bay was further silted by laharic debris up to 4 m from the Pond Glacier moraines in the last erupted period. Furthermore, the water dynamics of Port Foster have also received some attention [18,19,20,21,22].
The coast is the most common walking route used by researchers to collect field data and visitors. Between 1956 and 1968 this shoreline had first an increase of 2 km, mainly because of a small central islet, and secondly, a reduction of 1.4 km essentially due to the inclusion of this islet during the 1969 eruption [4]. Since those years, annually, the mobility routes from the two active Antarctic bases have had to adapt to new and unexpected conditions. This can influence the footpaths, the evacuation routes (see Figure 1b), or the transfers of people by inflatable boats, so future coastal geomorphology is important for the security reasons. In addition to this, although Antarctica is considered an active part in the sea level rise [23] by contributions from glacier ice mass loss and icesheets, its uninhabited coastline is not considered in global studies [24,25], and therefore of relevance. Starting this study from the geomorphological situation of the island from the last eruption of 1970, its objective focusses on the identification and quantification of historical changes in the inland watershed, coastline, and bay seabed using several resources (elevation and bathymetric data, new historical orthophotos [26], satellite images, and geomorphological information) and its contract with a numerical DELFT3D model [27] in the inner coastline. This computational model is widely used to simulate the main physical processes that are relevant in coastal environments, such as embayments and estuaries [28,29,30,31]. It is based on the hydrostatic flow assumption and solves the short-wave averaged 3D shallow-water equations. Considering the geomorphological trends of accretion and erosion in this study, possible short-term implications that could affect human mobility in the interior of the island will be identified for future research campaigns.

2. Data Input and Pre-Processing

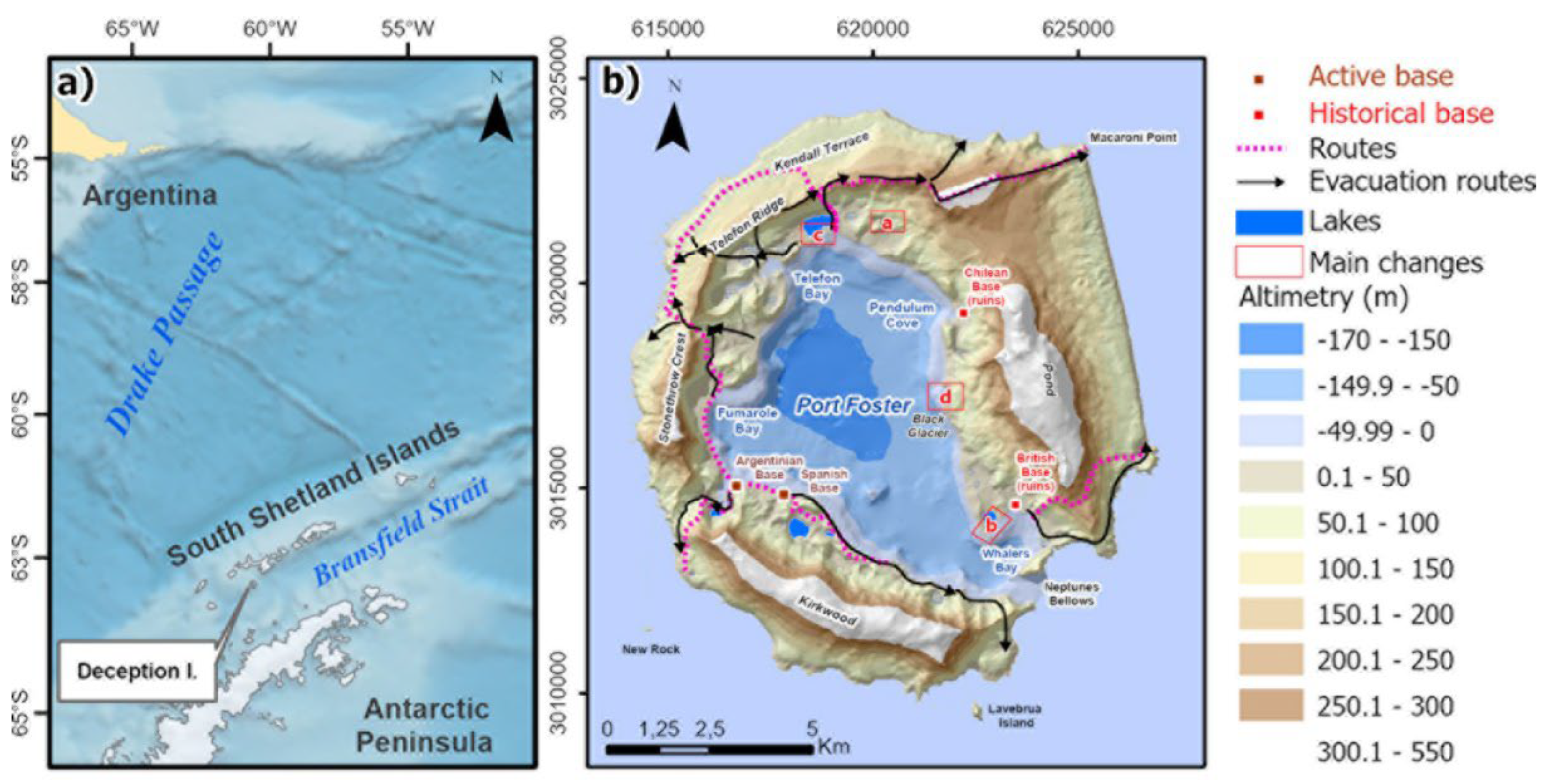
2.1. Satellite Images, Coastlines, and Other Geospatial Information

The Spanish Army Geographical Service (SGE), now the Army Geographical Centre (CGE), developed a topographic map of the island on the scale of 1: 25 000 with 10 m contour/bathymetric levels and linked to a geological and Geomorphological map [32]. An initial version was produced in 1984 from a 1968 flight, improved with topographic field work and some 1986 aerial photogrammetric frames in 1994 [33], and finally, a new updated version in digital format, based on a Quickbird satellite image (QB) and a digital elevation model from previous data for the orthorectification process, in 2006 [34]. Although in this new map a georeferenced error was detected and fixed, the lack of enough Ground Control Points (GCPs) on the outer coast and in high elevations maintained some positioning errors in the east of the island. This discrepancy has been verified with almost 100 control points from subdecimeter differential GPS relative to a geodetic network called REGID (in Spanish, REd Geodesica Isla Decepción) [35,36].
This QB image was taken on 2003-january-21, with a spatial resolution of about 0.6 m in panchromatic and acquired already orthorectified with an unknown digital elevation model. With the new Reference Elevation Model of Antarctica (REMA) [37], a 2 m resolution Digital Elevation Model (DEM) and 52 GCPs, a new orthorectification of this 2003 QB image was produced. It was processed by ENVI 5.0 software with Rational Polynomial Coefficient following the same methodology applied to a new Kompsat-3 satellite image (K3), acquired in 2020-February-09, with a resolution of 0.7 m resolution in panchromatic [26]. In addition, a new orthophoto from a 1968 photogrammetric flight [26], a few partial clouded Sentinel 2 images (8 from 2016 and one free cloud but full snow cover in 2022) from the European Spatial Agency (ESA), and some Google Earth images (6 images from 1985) were analysed. Sentinel 2 and Google Earth images were used to identify the most important sedimentary plumes from alluvial fans and evaluate a hydrological discharge (see Table 1). The weather conditions of the area make it difficult to take images without clouds, and for this reason, the imagery repository is not very wide.
The vector information base of the study was primarily from the SIMAC database, a scientific geodatabase created in 2006 [3] as well as new digitalization from other sources. The new information objective was on the changes of the inner coast of the island (data identified as Coastlines) mostly from the 1968 [26], 1970, 2003 and 2020 [26] orthophotos and satellite images. The delineation of the coastline for the mentioned years was performed to accurately represent the alterations in the contour of Port Foster Bay, extending to regions where substantial morphodynamic changes of the coast were observed. In areas with low cliffs that exhibit a short beach during low tide, the delineation was adjusted to align with the cliff, as it constitutes the primary eroded feature (notably, the southern part of the island, running along the coast between the Spanish and Argentinean bases, as depicted in Figure 1b). Another aspect of spatial data acquisition was the digitization of sedimentary plumes, a result of visual analysis of the image catalogue.
All cartographic information analysed in this study can be consulted in Table 1 planimetric errors are linked to scale or spatial resolution.

2.2. Digital Elevation Models

Regarding DEMs, although SIMAC includes a 1956 Triangulated Irregular Network (TIN), a DEM derived from 50 m contour lines of the 1959 British Directorate of Overseas Surveys (DOS) map [39], the transform projection and coastline showed important differences with the DEM derived by a 10 m level contour TIN of 1968-1986 CGE cartography. The Torrecillas et al. study [4] contrasts both DEMs without clear conclusions except the affected area by the last volcanic process. The new orthophotos of the flights of 1957 and 1968 required DEM computation, so they are a new source of altimetric information for this study [26]. The most recent DEMs are all from satellite acquisition, highlighting the aforementioned REMA [37]. REMA was produced from several individual stereoscopic DEMs attained from pairs of submeter resolution satellite imagery acquired from 2009 to 2021, and vertically registered to satellite altimetry measurements, with submeter absolute uncertainties and relative uncertainties of decimetres. The REMA height in water areas, such as Port Foster, offers values of around 20m, a value like the mean undulation geoid following [40], indicating that no geoid correction has been applied in this area, so a mean value of 20 m was subtracted. Although 61 ESA Sentinel 1 scenes were processed between 2014 and 2022 using DinSAR methodology to obtain DEMs [41], the results were not successful.
All the DEM input data used in this study could be consulted in Table 2 and transformed into WGS84 UTM 20S (EPSG 32720). As a global altimetric error, we considered 1.5 times the spatial resolution. This value is slightly higher than the 1/3 of level contours equidistant for DEM derived from TIN and higher than the GCPs altimetric error in new DEM derived from orthophotos or REMA specifications.

2.3. Digital Bathymetry Models

As a collapse caldera with a flat bottom and steep walls, the bathymetry of the inner bay is an important part of Deception Island. In fact, this bay can almost be considered as a lake with an important reception of the tephra after eruptive processes [42,43]. In addition to this, the presence of submerged volcanoes such as the Stanley Patch volcano, the largest volcanic cone located in the southern sector of the bay [44], and the narrow entrance to Port Foster (Neptune´s Bellows, see Figure 1b) require precise bathymetry for navigation purposes.
The oldest Digital Bathymetry Model (DBM) of this study was elaborated and compilated by some Spanish public institutions such as SGE/CGE, the Instituto Hidrográfico de la Marina (IHM) and the Instituto Español de Oceanografia (IEO) between 1988 and 1991 with an orthometric height from a local tide gauge reference and a submeter Differencial GPS [32]. It was included in the CGE maps with 10 m bathymetric contours, the same as level contours and according with the scale map. New Spanish bathymetry data was measured in two different campaigns in 2012 [18] and 2016 obtained a xyz file with an altimetric error of 0.5 m and 5 m for planimetry following the metadata information.
From the Marine Geosciences Data system (MGDS), seven subsets were downloaded having as descriptor ‘Sea depth (uncorrected, calc. sw sound vel.1500 m/s) metres’. These subsets are from the Laurence M. Gould expedition (LMG prefix) between 2000 and 2009 and the points located in Port Foster were selected and joined into one GIS file (see Figure A1). Anomalous depth measurements produced by false return were identified using GIS tools (Spatial outlier detection) and deleted. Also, the 2006 itinerary around Walers Bay was not considered due to a flashing anomalous value in the temporal track. The final set contained 17256 points (11289 only in 2000) and a mean grid was calculated using 50 m cells, the same resolution in [45] used with some of these files in the same zone. This grid date was associated with 2005, as the mean year, and the mean standard deviation was 1.87 m with a s = 2.2 m. These values were not corrected for tidal effects, of which the maximum amplitude is 2.025 m [19,20] like the mean standard deviation. A similar value of 2 m was assumed for overlapping outer beams in [45]. In terms of positioning error, a positional uncertainty of 5 m can be considered as the previous data being highly probable the use of GPS Differential. The navigation paths thought that the narrow Neptune Bellows suggested that this value is also appropriate.
All input bathymetric data could be consulted in Table 3.

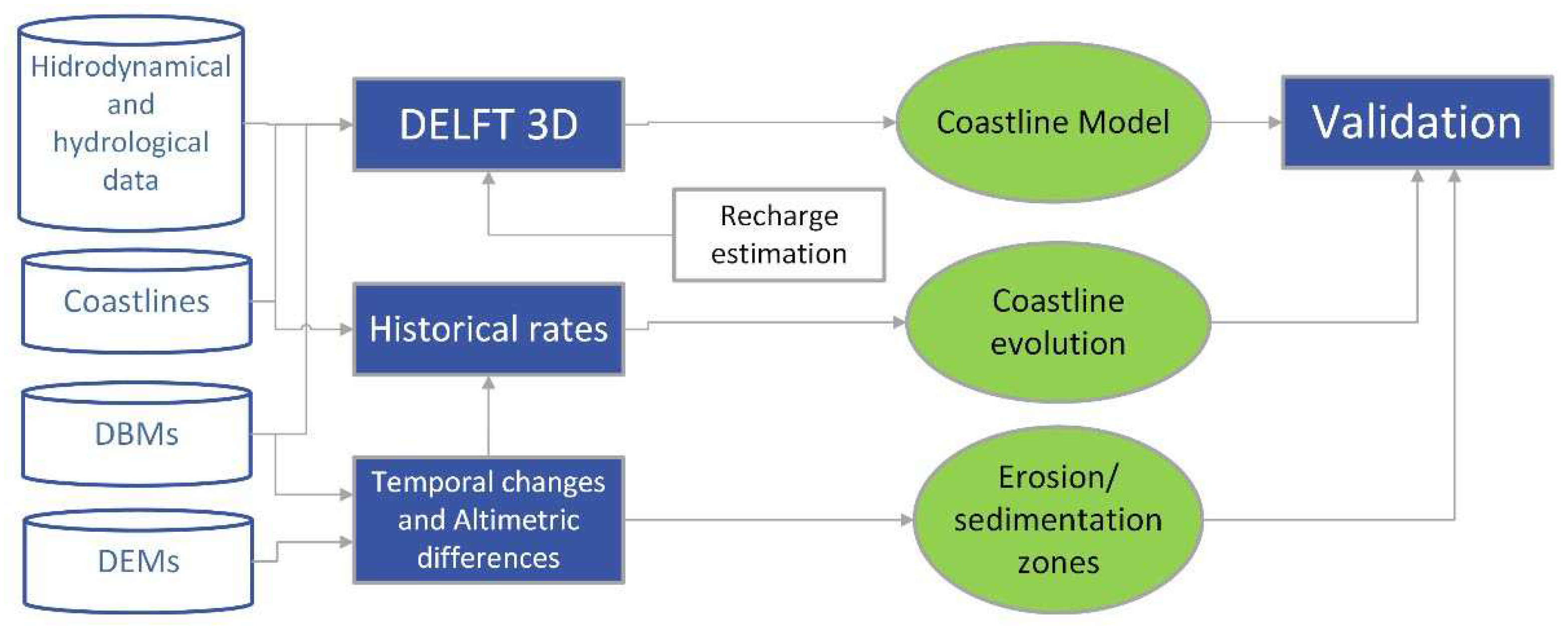
3. Methodology

The methodology employed in this study is described in Figure 3. It encompassed three primary processes: one concerning the establishment of a coastal numerical model, and two GIS studies dedicated to identifying and quantifying historical geomorphological changes (DEMs and DBMs alterations), as well as tracking coastline evolution for model evaluation.

3.1. Numerical Model

The model used in this study was DELFT3D, developed by WL|Delft Hydraulics, and it has been implemented with a 2D (depth averaged) configuration. This model solves the shallow water equations with Boussinesq and hydrostatic approximations [27]. The continuity equation assumes incompressible flow and is defined as:
∂ u ∂ x + ∂ v ∂ y = Q
where u and v are the components of the velocities in the x and y directions, respectively, and Q indicates the mass transport per unit area.
Furthermore, the momentum equations are described by:
D u D t = 1 ρ 0 P x + F x + M x + f v
and
D v D t = 1 ρ 0 P y + F y + M y + f u
where t is the time, ρ 0 is the reference density of the water, f is the Coriolis parameter, P x and P y represent the pressure gradients in x and y directions, respectively (including barotropic and baroclinic terms), F x and F y are the horizontal Reynolds tensor in both directions and finally, M x and M y represent the contributions due to external sources, such as the wind action on the free surface or the wave action on the water column.
The model also incorporates morphodynamical evolution equations, which calculate the total transport as the sum of bed and suspended load transports. These transport rates are obtained using the depth-integrated advection-diffusion equation [52] for different sediment fractions, which can be cohesive or non-cohesive and are defined based on their densities and sizes. The calculation of bed shear stress uses the roughness predictor of [31]. The level of the bed is updated during each time step of the flow calculation, considering the exchange with suspended sediment transport and the gradient of bed load transport.

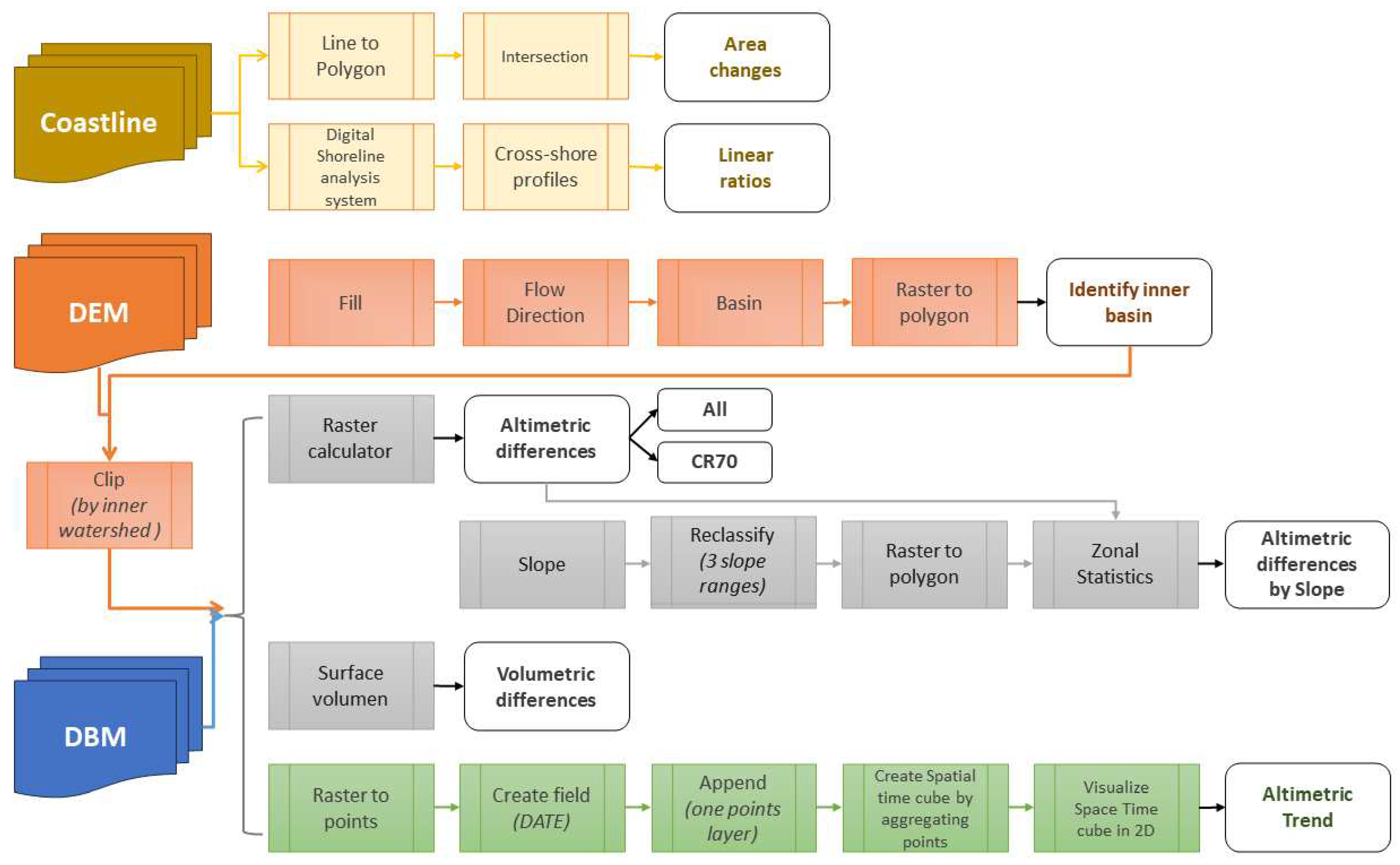
3.2. Coastline Evolution

Digitising changes in the inner coastline over time involved the analysis of orthophotos of 1968, 2003, and 2020 and the inclusion of a partial 1970 coastline from [38] within the QGIS environment [53]. The methodology used was also implemented in GIS through two different approaches: (i) assessment of area changes and (ii) linear ratios (see Figure 4).
In the first step, conducted in QGIS, the linear coastline shapefiles were converted into polygons to delineate the intersection areas between the current shoreline (2020) and the preceding shorelines (1968, 1970, and 2003). These polygons facilitated the identification of regions where erosion or sedimentation had taken place within the inner bay over time, allowing for a comparison with the results derived from the DELFT 3D model. The sediment plumes observed in the orthophotos were an important aid in accurately delineating the coastlines (see Figure 11d). A sediment plume refers to the visible cloud of suspended sediment particles in the water, carried by currents and tides. By distinguishing the sediment plume from the actual coastline for each year, digitized coastlines can more accurately represent the true shoreline and capture changes that have occurred over time. This approach often focused the analysis on slope alterations and retreats in specific areas of the island, such as the Spanish and Argentinian bases. This ensures that the visual comparison of shoreline changes, as derived from the generated shapefiles, corresponds with the transformations occurring within the inner bay of Deception Island.
In addition, DSAS software has been used to evaluate dynamic rates derived by comparing coastlines from 1970, 2003, and 2020 in a second step. This software is an ArcGIS extension [54] and a powerful tool specifically designed for the analysis and monitoring of coastlines using geospatial data [55,56]. Specifically, this application has been used in this study to visualise and assessment of changes in the position over time and the identification of vulnerable areas. Coastline retreat/accretion ratios have been obtained at specific locations, excluding areas that have shown minimal changes in their position after the first step. For the calculation of these, DSAS uses cross-shore profiles, and the ratios were obtained by dividing the maximum calculated value of the coastline displacement within each of the analysed profiles by the time (in years) between the evaluated coastlines.

3.3. DEMs and DBMs Temporal Changes

The DEM and DBM datasets in ESRI GRID format were the input data in this section. The temporal changes methodology carried out with GIS tools in the ArcGIS Pro environment [54]. Both datasets followed the same procedures for change evaluation, except the determination of inner watershed was executed only for the DEM dataset. The GIS methodology is shown in Figure 4 and consists of four subprocesses: (i) Altimetric differences with a study case in CR70, (ii) altimetric differences by range slope, (iii) volumetric differences, and (iv) a Space Time Pattern study. As a previous step, the delimitation of the DEM study was defined using the determination of the inner watershed limit. Altimetric differences are used to identify areas of gain and loss in the temporal range. Slope classification is intended to assess the influence of positional error on these differences. Volumetric difference calculations allow for the isolation of positional errors from elevations, elucidating the overall trend within the inner basin. This trend will be spatially delineated by the statistical analysis of temporal studies. These studies will help us to understand the surface dynamics and their potential influence on, as well as material contribution to, the bay.
The Altimetric differences by range slope needed the Altimetric differences as input data. These differences use an arithmetic operation between two times. The three slope ranges were divided to adapt them at the island of morphology in land and water with breaks at 2º and 9º. They clearly grouped the most interesting study areas and potential erosion/accretion zones (eg beaches, abrupt relief, cliff, or caldera rims). The zonal statistics used a polygon layer of these slopes.
The volumetric differences established discrete altimetric levels for their evaluation at -150, -100, 0, 100, 200, 300 and 400 m. These datasets do not have a specific capture date so that, for CGE DEM, 1986 was used as collected date corresponding with the DEM information for the most surface. REMA was assigned 2015 as the middle year like 2014 for the IHM DBM. In addition to this, the DEMs retained their original spatial resolution (2 or 2.7 m), while in the case of BDM, two new resampled raster files with a resolution were utilised (DBM IHM 50 m and DBM CGE 50m). Annual ratios per unit of 3D area were computed to provide comparable values.
The space-time analysis highlights the trends with statistical significance over time. Three were carried out, one with DEM and two in DBM dataset:
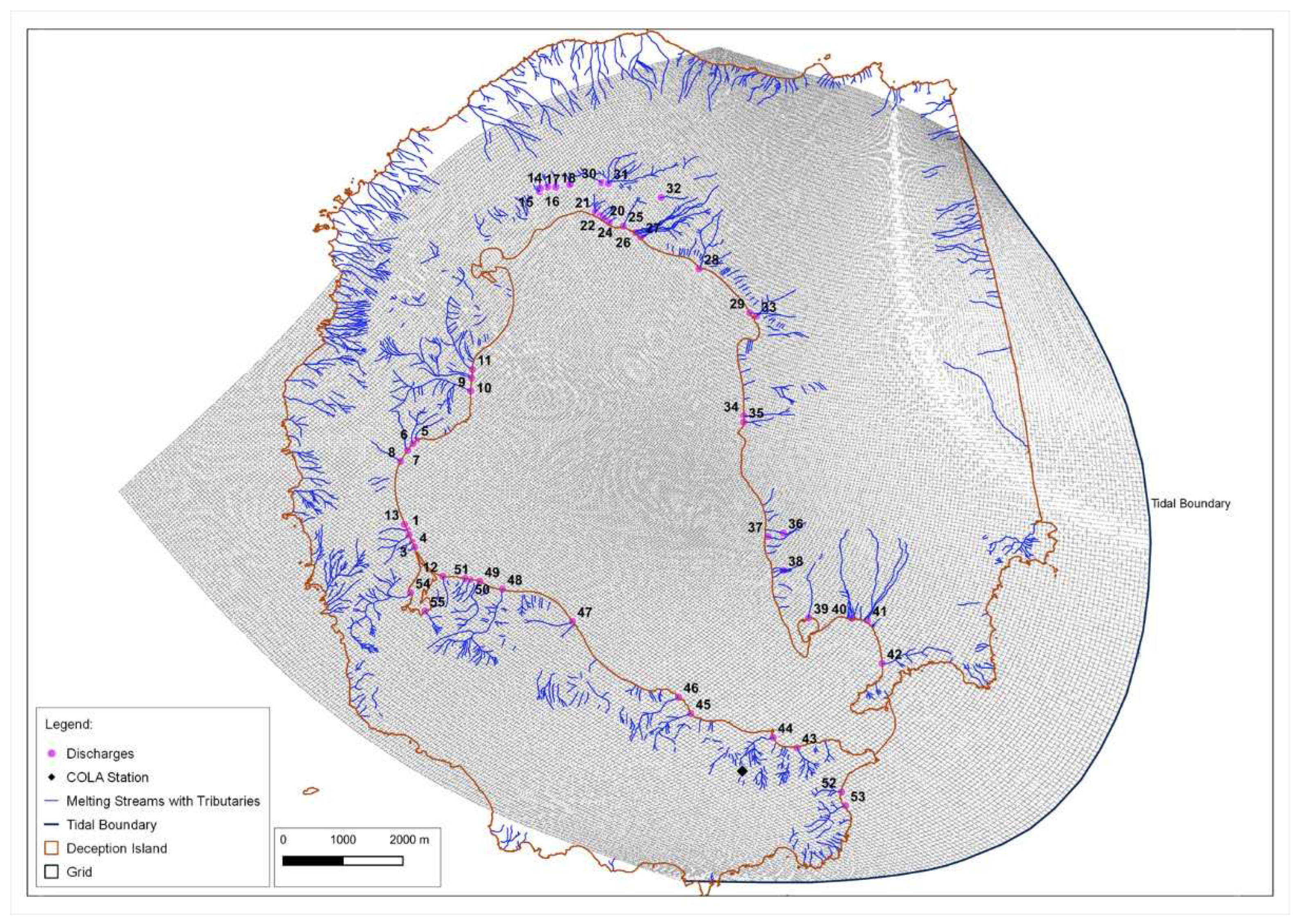
  • The DEM space-time analysis started in 1956 (including the last volcanic event) and used a 1-year time step to cover DOS DEM (1956) and its own 1957 DEM. It used a 50 m resample DEM using a cubic technique to decrease the planimetric and altimetric errors. The space-time cube has aggregated 73073 points into 46368 fishnet grid locations covered by 64 years.
  • The DBM dataset included two data structures by aggregating points into space-time bins (i) only MGDS data (2000-11-19 to 2009-03-29) in a 1-month study, with 17256 points into 1560 fishnet grid locations and 200 m of spatial resolution to increase the existence of several points in the same cell and (ii) using the original resolution of DBM CGE, DBM IHM and External DBM South Shetlands in a unique point layer and including the MGDS mean layer in the same format (see Table 3). This last study used a 1-year study, 200m of spatial resolution, 10032219 points in 2601 fishnet grid locations over 28 years.
Lastly, regarding the error margins in these calculations, altimetric differences will be influenced by positional and altimetric errors and the propagation of both into the arithmetic operation. The superficial and volumetric error was simplified to the error associated with the determination of the 1 hm3 box.

4. Results

4.1. Numerical Model

4.1.1. Model Setup

The model domain was defined as a computational curvilinear grid (Figure 5), with a total of 731 x 731 cells and a maximum resolution of 15 x 10 m2 within Deception Island. The initial condition of the simulation was the value obtained with field measurements during surveys carried out in 2012 (for more details, see [19]), avoiding cold start, the inner bay bathymetry used in the model was the DBM CGE (Table 3). On the other hand, the outer open-sea bathymetry, representing the areas beyond the coastline, was the External DBM South Shetlands (Table 3). The 2003 coastline data (Table 1) are used to accurately depict the coastline in the model and ensure consistency with the conditions observed in 2003.
As field-measured data on actual river flows resulting from snow melt were not available, river flows based on the length of the different main waterways and the number of tributaries for each of these watercourses from their source to the discharge point indicated (see Figure 5). Since there is no known single experimental formula to estimate the flow derived from snowmelt, we developed our own formula to categorise the rivers according to the criteria described (i.e., length of the main rivers and tributaries), allowing us to estimate their flow and place it in the range of 10-100 l/s. The formula used to determine the flow rate in the rivers is as follows:
0.01   l s ∗   E n t i t y   + 0.01   l s ∗   n o .   o f   t r i b u t a r i e s 2
In this formula, the entity is a value between 1 and 5, depending on the total length of the main rivers up to the discharge point. The number of tributaries varies in each river, considering tributaries with a minimum appreciable length. The lowest assigned flow was 10 l/s and 95 l/s as the maximum.
To calculate the flow resulting from snowmelt, the following formula was used:
Q t h a w   =   Q m e a s u r e d   ⋅   1000   b a s i n   a r e a   h a
River discharges were modelled to occur during three months of the year (January, February and March) to simulate the actual situation of snowmelt on the island, which is frozen during the rest of the year. This allows the mobilisation of all sediments deposited during these three months within the inner bay, leading to erosion or sedimentation of the inner coast. Table B.1 in the Appendix section shows the modelled characteristics for each discharge in terms of river flow.
The boundary conditions (Tidal Boundary in Figure 5) of the free surface are given by the nine principal astronomical components [57] as are: M2, K1, O1, S2, P1, Q1, K2, N2, and MF, obtained from data observed during field surveys [19,20,58]. Wind and atmospheric pressure conditions with each 1-hour interval were obtained from a meteorological station during the same tide level survey [20,58], and were introduced with a constant value for the entire grid.
Like previous studies [27,59,60,61,62], the morphodynamic module was found to be very sensitive to the mean diameter of the sediment. According to data provided by field surveys developed in the area [14], a single sediment was defined, with characteristics like silt due to its prevalence in 85% of the island. In agreement with a previous work [63], the suspended bed load and suspended sediment transport factors were defined as 1 and 0.5, respectively. Considering the numerical constraints of the model (Courant number), the time step was defined as 0.1 min. In addition, a spatially uniform time-varying wind field has been defined throughout the spatial domain with hourly data from AEMET.

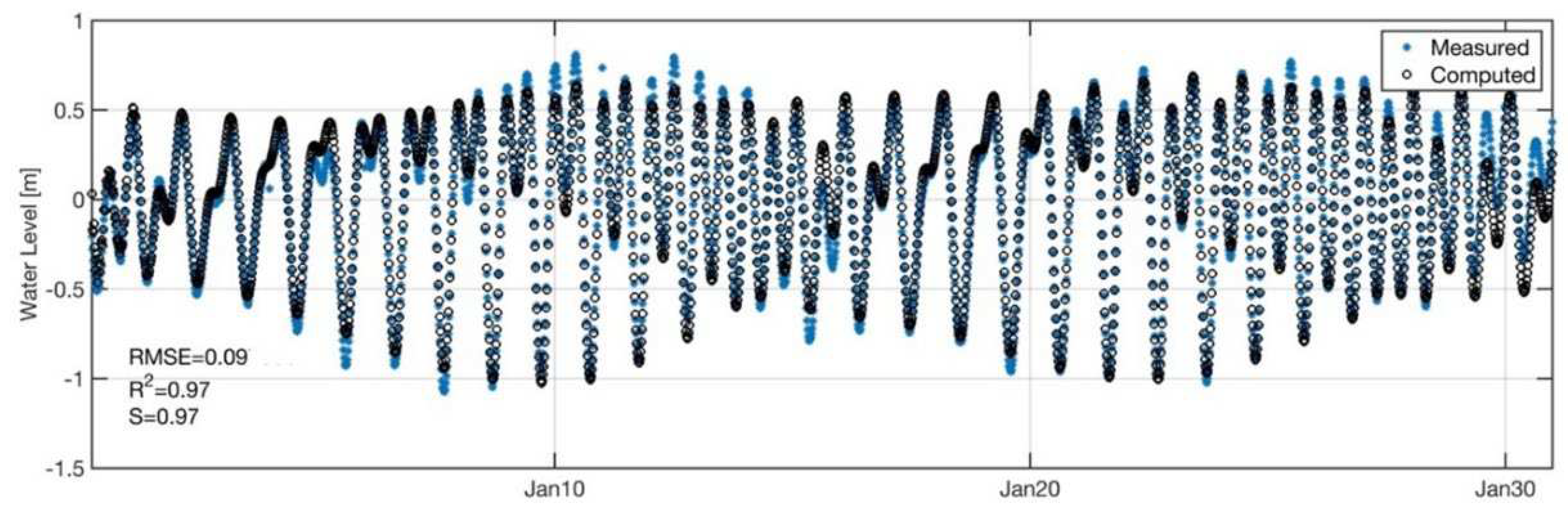
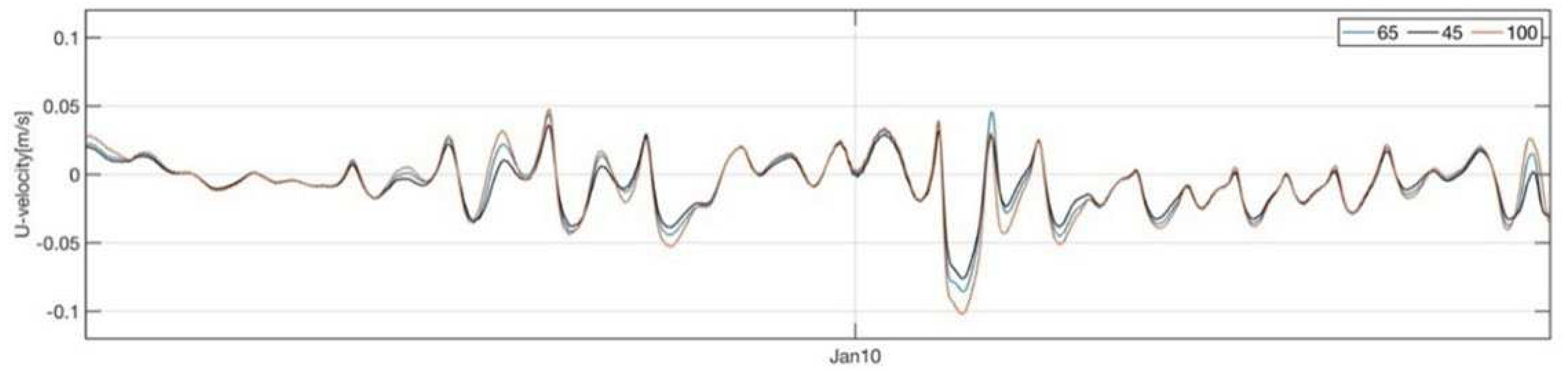
4.1.2. Model Calibration

The model was calibrated for the water level variable and for the harmonic components of the velocity (M2 and K1), both amplitude and phase. The water level data was obtained from the field survey conducted in 2012 (COLA Station in Figure 5) and the data for the harmonic velocity components were compared with the results of previous studies [20,58]. The full month of January 2012 was selected as the calibration date because it was a month where there was no lack of data and with average meteorological conditions. The results are shown in Figure 6, where it is observed that the agreement is excellent for the water level, obtaining values of R2  ≈ 0.98 and the Skill coefficient ≈ 0.97.
For the case of velocities, the results shown in Table 4 have been obtained. The phases values are correctly represented with a correlation coefficient (R2) of 0.9, however, the amplitudes are not correctly represented with those obtained in previous studies [58], varying by one order of magnitude. Therefore, it was decided to test different values of Chèzy (45, 65, 100) to perform a sensitivity study. Figure 7 shows how by changing the Chèzy coefficient the values do not vary more than 30% in the peaks and in the rest follow a trend with a maximum variation of 3%. If the values of the amplitudes of the M2 and K1 components are calculated, the values are very close to each other, varying by 4%. Therefore, it is thought that the results obtained with the numerical model are correct and although it is not possible to give a final value of the sedimentation rate, it will be possible to define sedimentation patterns by determining the accretion and erosion zones.
Once the model has been calibrated, a full year (2012 January-2013 January) has been simulated with the same forcings described in the previous section. The results are shown in Figure 8. The bathymetry and coastline used at the beginning of the simulation are based on data from 2003. This means that regardless of the specific date chosen for the simulation, the initial conditions for the bathymetry and coastline will remain consistent and reflect the characteristics observed in 2003.

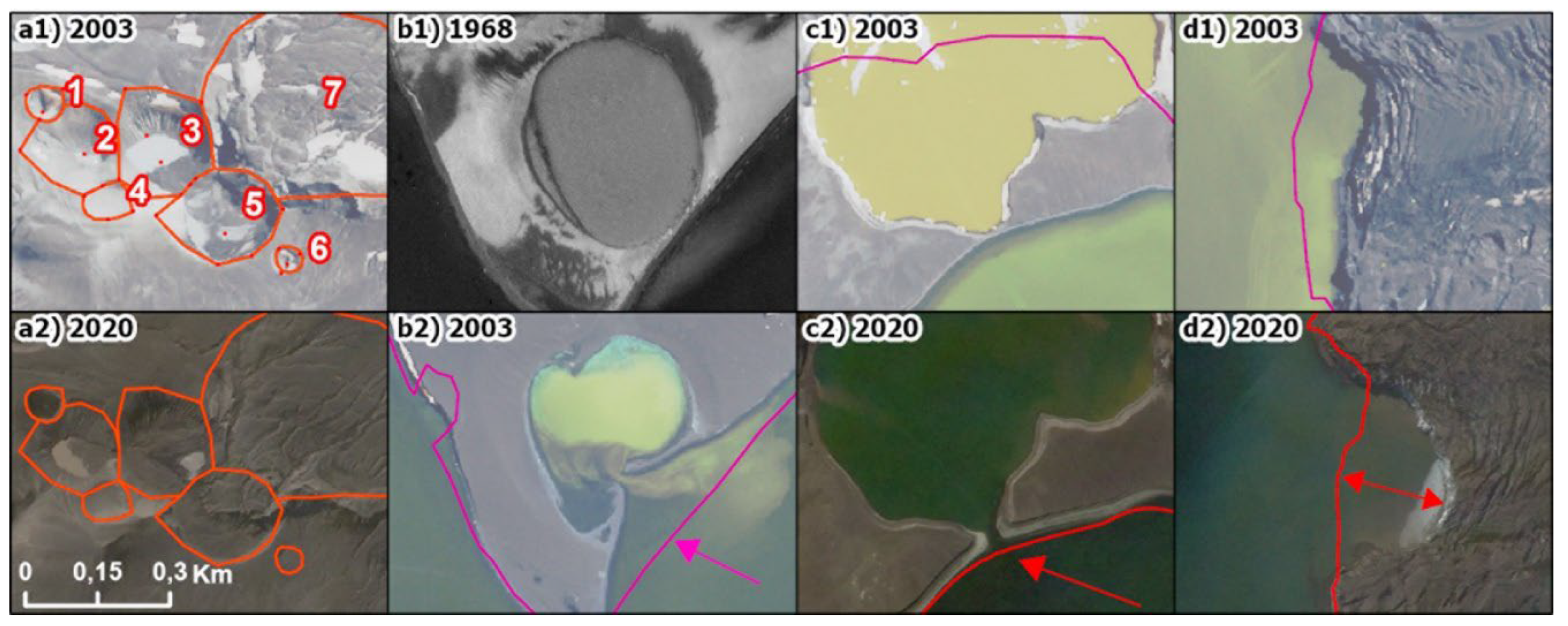
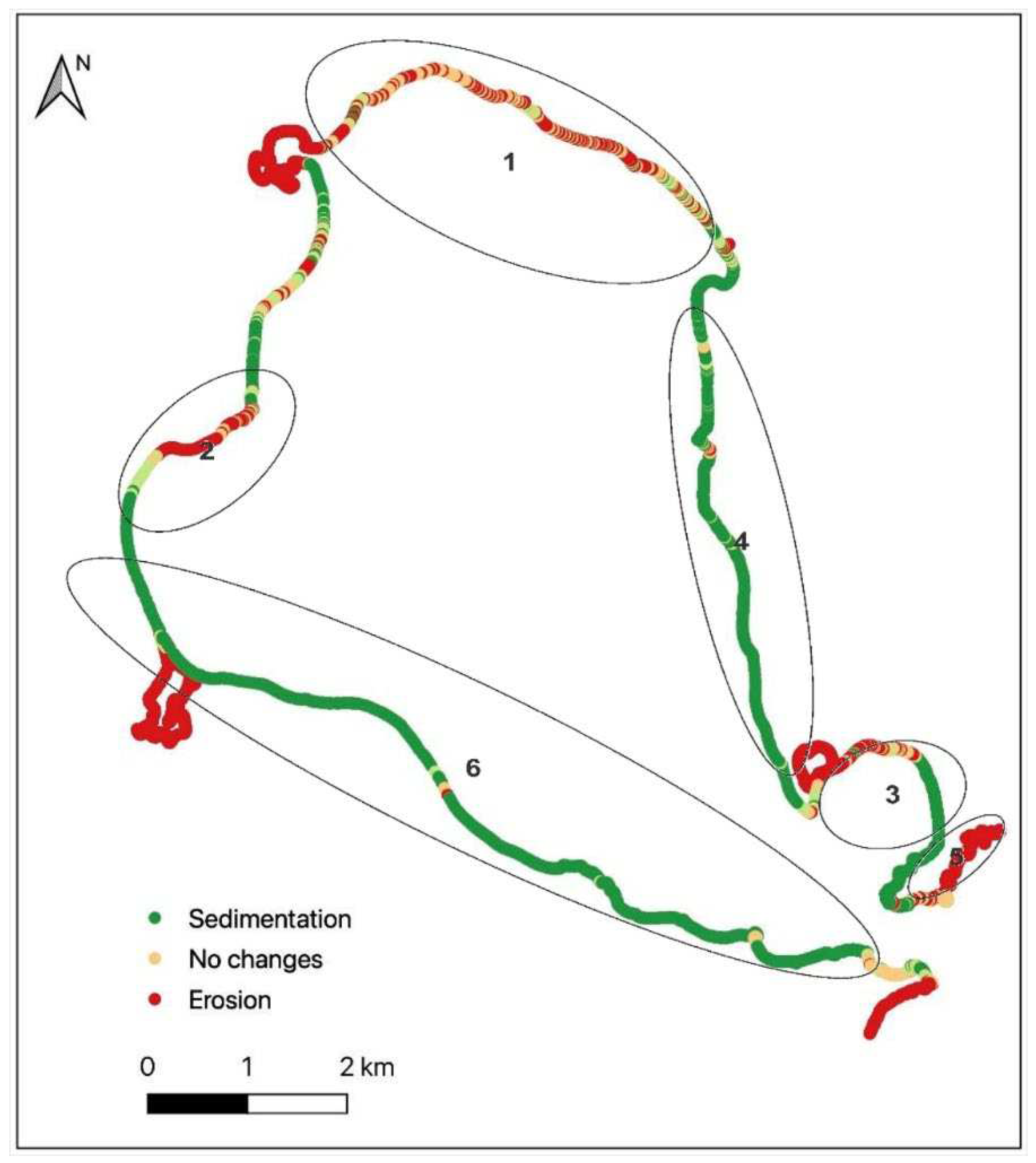
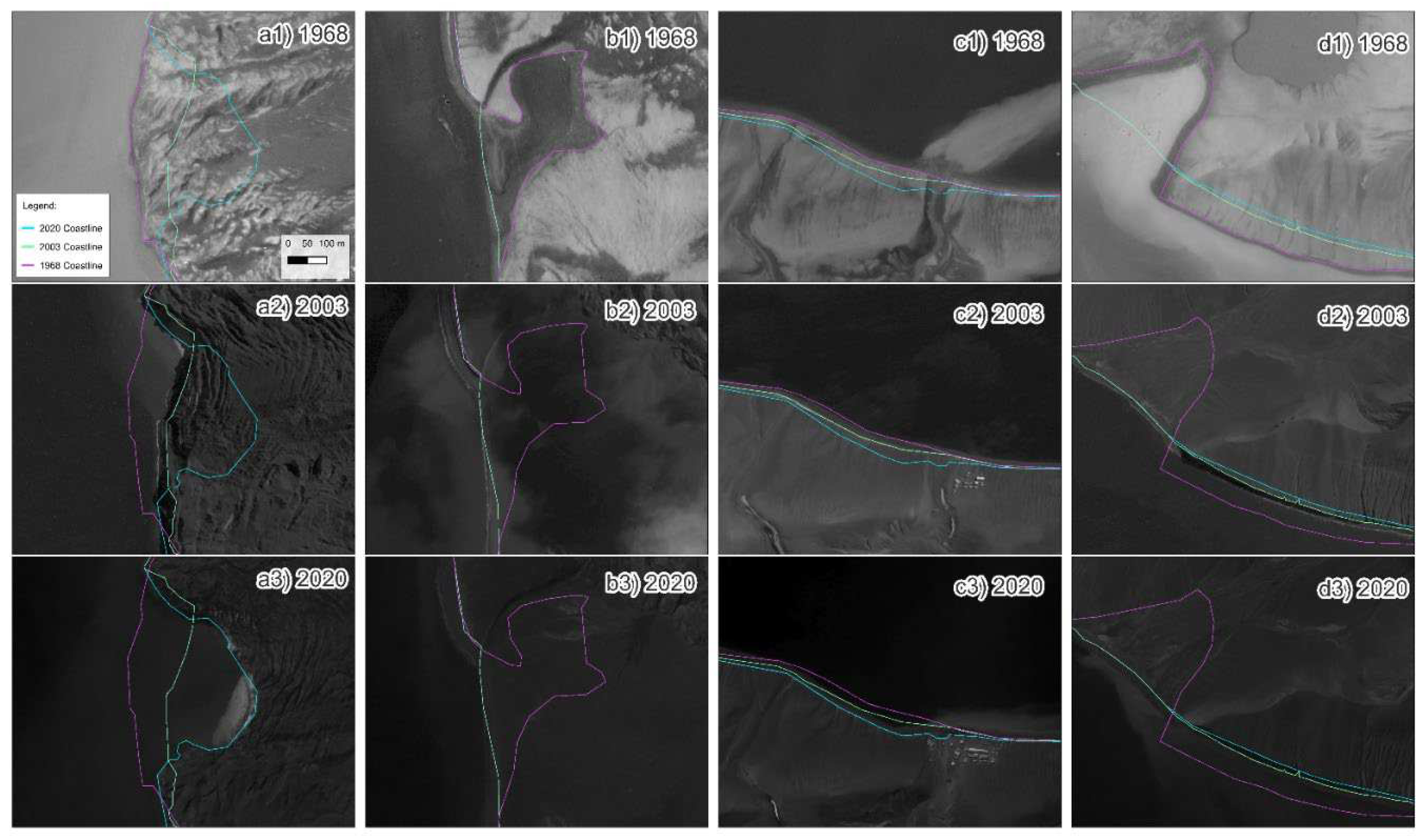
4.2. Coastline Evolution

Following the methodology described in Section 3.2, Figure 9 illustrates differences for two distinct time intervals: 1970-2003 (Figure 9a) and 2003-2020 (Figure 9b). These figures represent coastal erosion and/or lake opening (in blue) and coastal sedimentation/accretion (in red) identified through visual changes. During the first period under study, there was an increase in the water area of 0.772 km2, primarily due to erosion and inclusion of Kroner Lake (Figure 8 zone 3), while it decreased by 0.229 km2 due to sedimentation along the shoreline. Between 2003 and 2020, the interior water area of the bay expanded by 0.480 km2, which encompassed the opening of Hidden Lake (zone 1) and glacier retreat (zone 4) and decreased by 0.048 km2 due to sediment movement. The annual ratios for the increase in bay area remained similar at 0.023 km2 / yr and 0.028 km2 / yr in both periods, while the land area decreased from 0.007 km2 / yr in the first period to 0.002 km2 / yr in the second period. The profiles analyzed using DSAS software were superimposed, with color-coding indicating the intensity of the annual coastline evolution ratio in corresponding areas. It should be noted that the opening or addition of the crater lakes is not represented in this visualisation.
According to the results obtained, the coastal dynamics decrease over the years, with more intensity observed following the completion of the last dated eruptions. During this studied period, a significant sediment influx reached the island, leading to considerable changes along its coastline. Between 1970 and 2003, there was a higher level of interaction around the entire Port Foster area, with more evenly distributed sedimentation and erosion. Generally, the sedimentary process was concentrated in the eastern part of the island, while erosion was predominant in the northern and western regions (6-9 m / yr), with a slight retreat in the southern coast (0.3-2 m / yr).
Figure 10 collects some zooms of the most notable gain-loss observed after performing the visual analysis of the coastlines. It shows the main erosion and sedimentation that occurs in the western part of the island, specifically in the Black Glacier by retreat (Figure 10a) and its southern region (Figure 10b). Additionally, it shows the erosion of the slope in front of the Spanish base (Figure 10c) and part of the erosion in the northern area of Port Foster Bay (Figure 10d). In the second analysis interval, between 2003 and 2020, a reduction in the intensity of coastal modifications was observed in Port Foster. However, there is a clear dominance of erosion around its bay. Particularly, notable erosion is evident in the northern and northwest parts of the island (0.3-2 m / yr), as well as in the south, where the Spanish and Argentinean bases are located. It is essential to highlight the significant retreat experienced by the Black Glacier, which increased its annual retreat to 14 m in the 2003-2020 interval compared to the 7 m / yr it experienced between 1970 and 2003, representing a 100% increase in its annual retreat.
Regarding sedimentation, areas located at the ends of the Black Glacier saw a coastline advance of approximately 150-200 m in the south and 50-100 m in the north between 1970 and 2003. This progress was halted in the second period analysed. Other areas that were less prominent in terms of coastline advance during the first interval experienced inverse changes in the second period, even showing a retreat in their values.
The linear values quantify their error in the need to have 2 pixels to identify an object. Using the 1m resolution that encompasses all the orthophotos, the average error for each linear measurement, two points, is set at 2.8 m. The error in linear ratios will correspond to the linear error derived from the definition of its profile line divided by the square root of the years of the studied period. Establishing the margin of error in surface determination will be simplified to the error in determining the 1 ha of its bounding box coordinates, following the Law of variation transmission [64], the surface error will be assessed at 28 m² / ha. All the provided figures have been given in decimal units above the unit of error in this section and in subsequent sections.

4.3. DEM Evolution

4.3.1. Inner Watershed

Following the methodology of Figure 4, after the determination of the new inner watershed from REMA, temporal altimetric variations were calculated and are depicted in Figure 11, spanning over six decades from 1957. The upper panels illustrate the evolution over successive time intervals, whereas the lower ones delineate these temporal segments from the two new DEMs (1957 DEM and 1968 DEM) to the most recent one (REMA). Notice the prevalence of green areas in Figure 11a,b, particularly around the sites of the most recent volcanic eruptions (zones 1 and 2), contrasted by the loss in red in zone 2, signifying lahar-induced changes. In particular, the areas covered by ice (inside the white line) exhibit the most significant and dynamic differences. These aspects are more pronounced in Figure 11c, 11d and 11e. Snowy areas are complicated surfaces to position altimetrically in the photogrammetric process, as commented on the CGE map [33], lack control points, and are highly susceptible to thawing periods, which could also make these findings possible. The error of these differences is established following the quadratic composition of their sum [64], evaluating each individual surface at 4 m based on rounding its worst positional error value (2.7 m) to about 5.6 m, while excluding values ± 5 m in the representation.
The temporal trend study is shown in Figure 12a and only shows three uptrend zones, one related to the last events of the 1969 eruption [12] in zone 1, and two gain zones (2 and 3). Zone 2 is on the shoreline and was commented on in the previous section, but zone 3 corresponds to two lakes so that area is not taken into consideration. The global trend statistic is -0,097 with a trend p-value of 0,922. There is no statistically significant increase or decrease in the other zones over time.
These differences were classified using slope ranges, see Table 5, suitable for defining the different geomorphology of the Port Foster (Figure 12a) and as a control of influence of the positional error. Statistical evaluation is present in this table where general negative values are present in all differences studies except for 1968-1957. Flat areas exhibit the smallest standard deviation values, as expected, compared to steep terrain. Except for the 1968-1956 period, the new DEMs, which have been created using the same control points, exhibit similar positional errors and include 1968 eruption. The rest is according with the increase of slope and height variation due to this positional error. It is also noted that the largest temporal differences in relation to REMA show material gains in flat areas, while losses occur in steep areas.
The volumetric values, temporal evolution, and annual ratios for the unit of 3D area between the digital models are shown in Table 6. The volume was determined by moving the reference plane 100 m upward in each DEM. Table 6 includes the difference with respect to the same plane defined in the previous temporal model (Dif. Vol. column) and a temporal and spatial ratio value based on the provided area 3D. Except for the period that includes the most recent eruption (1968 DEM and CGE DEM) with a gain of 0.19 km3, the remaining DEMs show losses. The negative ratios in the last three DEMs have been reduced from -0.50 to -0.23 hm3, and higher loss values are detected at elevations exceeding 300 m, associated with snow and therefore represent volume losses not related to the terrain itself. Ice melt activity is significant on the island and generates extensive sediment plumes, as delineated in Figure 12c from satellite images. The volumetric error for each 1 hm3 is estimated at 0.03 hm3 and for annual ratios this error must be divided by the square root of the years of the study period following [64].

4.3.2. CR70

In 2006, 27 points were measured with subdecimeter differential GPS to define the dimensional characteristics of the 1970 craters (see Figure 2a). These new craters were evaluated in [14] and some infill rates of up to 1.5m / yr were calculated on the floor. Now, these measurements have been compared with REMA using ellipsoidal height (thereby eliminating the uncertainty in the value of the geoid undulation), and their results are shown in Figure 12d and Table B.2. The floors present increased heights (colours yellow and green) in coherence with the visual analysis of the 2020 satellite image and REMA hillshade in the background. In contrast, the inferred rims of the craters have loss probably due to the less planimetric/altimetric precision of REMA DEM compared to GPS or an erosion effect on the crater wall. The absence of a specific date for DEM values (2009-2021) makes it impossible to establish an exact rate. However, the altimetric gain is approximately 9 m in crater number 6 (Figure 2a1), which is fully filled according to the 2020 image. Craters 2 and 3 have gained 6 m and 2 m, respectively, with a noticeable rise at the floor due to the active displacement of material uphill from the Mount Goddard alluvial fans. Unfortunately, the 52 GCP used in the orthophotos could not be used to validate the altimetric changes in the terrain because they were located on the rooftops of the stations' buildings or on rocks. The error in these altimetric differences is assessed based on the error derived from REMA at 1 m, as the GPS derivatives were established at 4 mm [14].

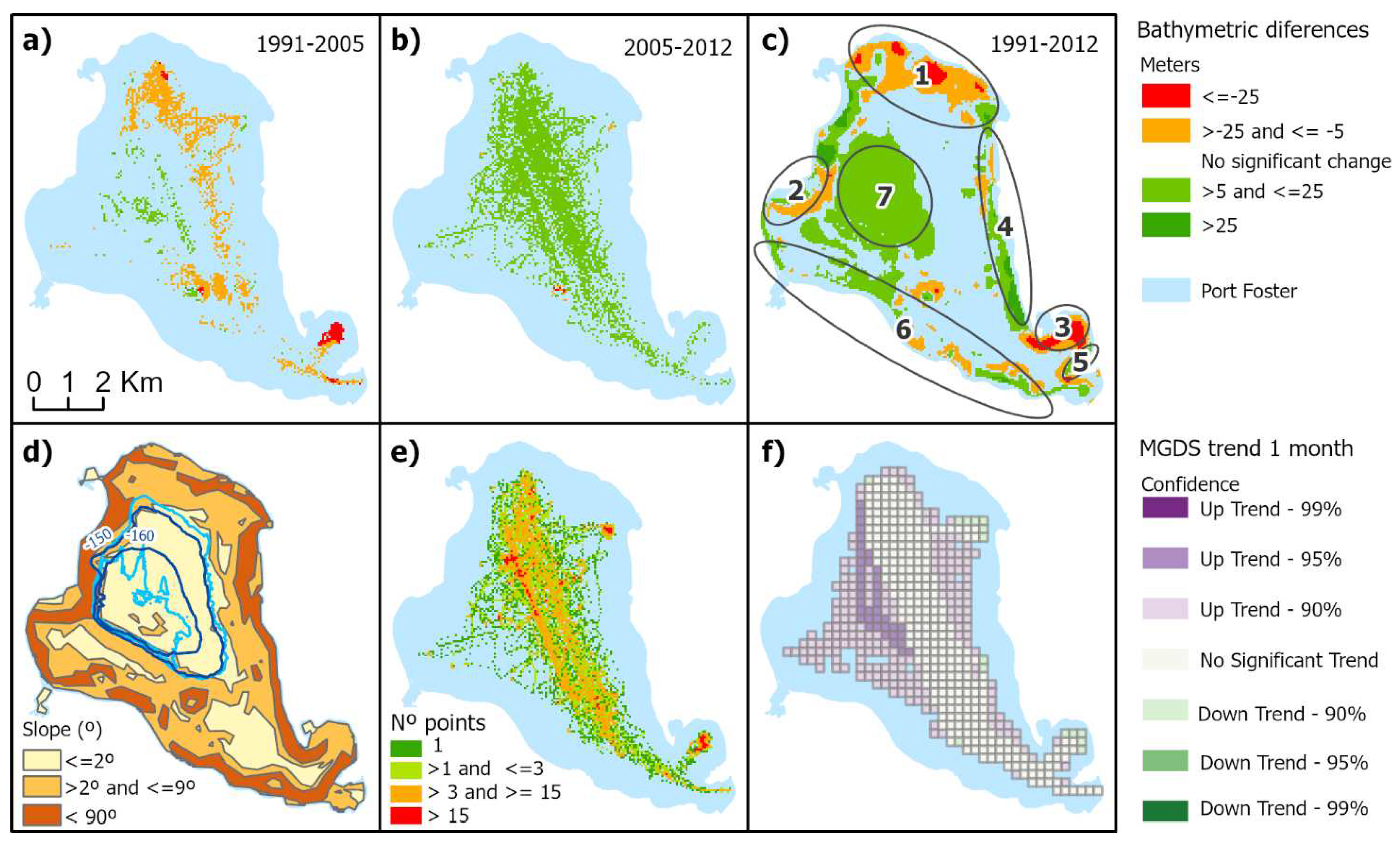
4.4. DBM Evolution

The DBM range differences are shown in Figure 13 and cover more than 50 years. The error associated with these differences will be taken from an average value of 3 m, which, through variance transmission, provides a threshold of 4.3 m, disregarding it in graphical representation, and to match its representation to that of the DEM in Figure 11, not significant changes was defined in ±5m.
Following the first line of images in this figure (Figure 13a, b, and c), surprisingly high values of altimetric differences were found again. The most extensive area with an increase in height (Figure 13c, zone 7) is the bottom isobath of 150 m, where the sea bottom is almost featureless and flat below this depth (see Figure 13d). Losses are mainly concentrated in zones 1 and 3, which are closer to the shoreline.
These differences were classified using slope ranges that were suitable to define the different geomorphologies of the bay and to evaluate the influence of positional error (Figure 13d and Table 6). The altimetric reference seems better in the case of MDGS and IHM bathymetries with a standard deviation of 3.4 m and a global sedimentation (mean gain of 5.8 m and high value of 6.2 m in flat areas). The global study from 1991 to 2012 has a clear positional error compensating in the ranges following Table 6. In this way, the mean difference in medium and high slope decreases with increasing slope, while the standard deviation increases too. As in the DEM study, high values are associated with steep terrain (dark brown in Figure 13d).
Volume has been determined by shifting the reference plane 50 m downward in each DBM and is displayed in Table 6. In this case, the volume corresponds to the water, not the land; therefore, the reference is 'BELOW’. The overall volume of the bay has increased, but from the bathymetric elevation of 150 m onwards, it increases, indicating clear bottom sedimentation. The volumetric error for each 1 hm3 is estimated at 0.03 hm3 following [64].
Lastly, the space-time trend analysis using MGDS data (Figure 13e displays a heat map with the number of measurements) exhibits statistical significance only in specific areas, as illustrated in Figure 13f. These significant areas are found primarily in shallower, flat seabed, and correlate with sedimentary regions, as seen in Figure 13c. Unfortunately, the second study, which encompassed all bathymetric points, did not produce zones that displayed statistical significance over time. Evidently, the data's precision (exceeding 1 m) and certain height uncertainties have influenced the results of this second spatio-temporal analysis.

5. Discussion

Figure 8 shows the coastal variations between the start and end of a simulation year. Since currents have not been precisely calibrated, erosion and sedimentation rates may not be very accurate. However, trends and patterns of gain and loss patterns can be examined and corroborated using historical studies. This model illustrates that erosion along this coastline is particularly notable in areas with a southern orientation, such as zones 1, 2, 3, and 5. Sedimentary action tends to be concentrated along coasts oriented to the east (west shoreline) west (east shoreline), and northeast (south shoreline).
The study of the evolution of the bay's coastline reveals erosion values greater than sedimentation. In detail, erosion is concentrated in a large part of the bay and its zonal comparison with the changes detected along its coast over time shows some similarities in Figure 9: (i) There is significant erosion in the north (zone 1) since the last eruption, especially up to 2003, when there was significant erosion due to the transport of materials deposited after the eruption; (ii) Also, between 2003 and 2020 there is a notable change, which is the opening of Hidden Lake (Figure 2c) due to this erosive effect (zone 1); (iii) Zone 2 does experience coastal retreat, but it occurred prior to 2003; (iv) A similar effect is observed in Kroner lake (Figure 2b) in zone 3; (v) Between Zone 1 and 2, the model reveals an erosive initiation that is also detected in the historical study.
The discrepancies are located: (i) In the south of the island (zone 6), where the historical represents the erosion produced on the slope in front of the Argentinean and Spanish bases (Figure 10c) and a sedimentary area in the model; (ii) The same inconsistency is found in the middle of Zone 4, where glacier retreat is identified in the historical study (Figure 10a), but it is a sedimentary area in the model. This (ii) case is likely not due to the bay dynamics and may be linked to global warming. In the (i) case, the slope erosion is believed to result from the impact of the sea ice fragments left by the bay's melting and accumulating in this area against the weak volcanic material. In this regard, the area is confirmed to be sedimentary based due to its current dynamics. The numerical model presents a limitation in accurately evaluating erosion caused by snowfall on the slopes, particularly when the surface of slopes is elevated relative to the coastal shoreline. The annual snow melting process can lead to slope erosion as the melted snow water flows over them and transports sediment, gradually washing away the exposed surfaces. Since the numerical model may not incorporate detailed representations of snowmelt erosion processes, it may not fully capture the erosion observed in the field. Snowmelt erosion is influenced by various factors such as slope gradient, surface characteristics, and snowmelt patterns, which are challenging to simulate accurately in a numerical model.
Another observation of the erosion detected by the model within various lakes (eg, Kroner Lake in Figure 2b) and inland intrusions (northwest of zone 6) may be influenced by multiple factors. In addition to the influence of tides and simulated sea-level variations in the model, these areas have river discharge points where the flow resulting from snowmelt is transported. This creates zones where there is interaction between sediment deposition and its collection by the tides, which then transport it to other areas of the bay. As a result, part of the sediment tends to accumulate at the lakes’ exits. These areas require a more refined modelling approach, but fortunately, they are not decisive in this study.
Regarding sedimentation, there are several similarities between the model and the coastline study. It is worth highlighting some cases: (i) The eastern part of the island, particularly around the Black Glacier, exhibits significant areas of sediment deposition, noticeable until 2003; (ii) A substantial accumulation of sediment in the southeastern part, following the termination of the Black Glacier (zone 4, see Figure 9b and Figure 10b). The entrance to the bay also presents areas of both sedimentation and erosion that were not considered.
It should be noted that when analysing the evolution of the coastline from images, the presence of shadows can pose a challenge, even when using high-contrast images. Shadows can obscure and distort the coastline, making it difficult to accurately define its boundaries. It is important to consider the impact of shadows when interpreting and analysing coastline changes, as they can affect the accuracy of the results. Additional techniques, such as image enhancement and careful manual interpretation, have been employed to mitigate the effects of shadows and improve the precision of coastline delineation.
The study of changes derived from the DEM, in many cases, the altimetric differences are quite large and highly localised in snow-covered areas, probably influenced by the lack of control points in those regions, the precision of the value and the slope of the area. However, as shown in Table 5, these differences often cause erosion rates losses, in sloped areas (except for the 1968-1957 period) despite having an overall negative value (1968-1957; SIMAC-1968; REMA-1957; and REMA-1968). This DEM study only has a few reliable values along the coast, finding some consistencies with the model in terms of sedimentation (south of zone 4) and erosion in zones 1 and 2.
The contrast between Figure 8 and DBM analysis shows a coherence between the most eroded coastline and the most nearby seabed in Zones 1, 2 and 3 in Figure 13. In addition to this, the sedimentation areas are also similar, with a notable infilling occurring between the 1970 eruption and the year 2003 in the southern part of the Black Glacier. The most extensive area with an increase in height (Figure 13c, zone 7) is the bottom isobath of 150 m, where the sea bottom is almost featureless and flat below this depth (see Figure 13d). This area was studied by Cooper et al. [5] with shallowing rates of up to 0.3 m / yr from 1829. Table 6 from the bathymetric elevation of 150 m onwards, it increases, indicating clear bottom sedimentation.
According to Table 6, the DEM loss volume is significantly greater than sedimentation in the bay. Adjusting the reference plane, the study reveals that the highest loss ratios occur in the upper areas that are permanently covered in snow. Consequently, it can be understood that most volumetric loss is due to snow. Furthermore, the positive evaluation of the inner watershed in the period 1957-1968, with part of the last eruptive process, is 0.19 km3, the volume of erupted ash valued between 0.12 km3 [65] and 0.20 km3 [12], and more recently 0.10 km3 [4] is a possible figure. In addition to this, the area of the temporal sedimentation plumes drawn in Figure 12c shows a continuous and high active discharge of tephra according to zones 4 and 6 in the model. The material loss ratios have been decreasing since the last eruptive process. Although they remain relatively high, the evaluation and filling of most of the study case in CR70, see Figure 12b, due to the active displacement of material uphill from the Mount Goddard alluvial fans, is a sample of this activity and the possibility of high sedimentation rates in certain areas. Volumetric changes in DBM indicate the loss of material from the steep walls of the caldera, some of which will accumulate on the sea floor. However, there must be a transfer to the outer part of the bay to balance the losses and gains.
Following data analysis, we compared these results with other studies on bay dynamics: (i) Flexas et al. [18] found that temperature gradients across Neptune's Bellows, driven by the Bransfield current, cause water to accumulate toward the northeast entrance of Port Foster. They proposed that counterclockwise propagating internal tides create shadow areas on the bay's eastern side, aligning with our model results in Figure 8. (ii) In a study by Berrocoso et al. [21] , they explored the connection between the distribution of water temperature in Port Foster Bay and the island's seismic and volcanic activity of the island. They suggested a link between increased seawater temperature and the resumption of volcanic hydrothermal activity. Their water circulation model over tides, with cold water entering the bay and mixing with warmer water, corresponds to our erosion patterns in the northern part of the island. (iii) Figueiredo developed a hydrodynamic model [21]. His simulation showed limited particle exchange between the bay and its surroundings over one month, contradicting our observations of significant material displacement and sediment accumulation in the eastern area. The discrepancy may be due to the short simulation period in this study of only one month as the study period, making it difficult to draw significant conclusions from it. In summary, these comparisons indicate that our findings align with some previous studies but differ from others, suggesting the complexity and variability of Deception Island's coastal dynamics.
After this discussion, it can be concluded that the model simulates reality well and can serve as a future tool to know the depositional trend of the study area. Therefore, if this model is maintained over time, the evacuation routes (Figure 1b) along the inner coast and the accessibility to active scientific bases will not be affected except for the recession due to erosion identified on the slopes in front of the two bases, which could impede access as the altimetric difference between the beach and the terrain increases.

6. Conclusions

This study includes a numerical hydrodynamic model to evaluate future trends on the inner coast of Deception Island. Its bay is the main area for researchers and tourists to develop their activity by walking or by boat. The high morphological dynamism of the island allows for significant changes in the coastline within a few years, so future modifications could affect evacuation routes due to volcanic hazards or disable certain walking routes, so its modelling and evaluation of future evolution is important. Also, this area is complicated in terms of climate, where the long period of ice cover leaves the summer season only as a geomorphology study window. The numbers of cloudy days are predominant and limit the collection of clean satellite images as well. In this way, only a few historical satellite images and aerial frames are available. Cartographic data are another remarkable problem. The inexistence of a continuous updated of data in this government-free zone makes it necessary to mix various historical sources and find methodologies to adequately compare them with precision. Fortunately, in recent years, the cartographic projection, geodetic systems, and geoid height models have been better defined.
The proposed hydrodynamic model included the FLOW module with the sediment transport equation. The model has been forced to have boundary conditions at the water level boundary conditions corresponding to 10 tidal constituents obtained in previous studies. Excellent agreement was obtained for the tidal levels. In the absence of real measured data, a sensitivity study of the currents was carried out to make an estimate. It was found that by varying the Chèzy coefficient, the change in currents was not significant (3%), so the currents could be considered valid. The sediment transport pattern in the interior of the bay can only be induced by currents and wind, so these forcings would be sufficient to determine the trends of accretion / erosion.
The results obtained from the DELFT3D model for shoreline erosion/accretion changes during a whole year follow the same trend as those obtained from difference bathymetric surveys during the years 1991-2012. Therefore, the reliability of the results is high. The main bathymetric changes in the closer coastal areas and sedimentary plumes from melting activity are according to the model as well. While the overall volume of the island has been decreasing over time, this reduction is much greater than that observed in the bay because it is linked to ice loss in areas above 300m in elevation. It was challenging to discriminate areas with accumulated snow because many of them are covered with ash and blend in with the ground. However, some coastal erosion areas have been detected, consistent with the model dynamics and bathymetric changes (zones 1 and 2), as well as sedimentary areas (zones 4 and 6).
The erosion of this coastline is sensible on the border with the south orientation, where the walking path could be affected. If this model is maintained over time, the evacuation routes along the inner coast and the accessibility to active scientific bases will not be affected. However, the study of the visual evolution of the coastline reveals a discrepancy in front of scientific bases, where it identifies substantial erosion on the slope facing the beach. This dynamic could indeed impact the accessibility of the bases. The evolution of the coastline has determined erosional ratios up to 2 m / yr in slopes/cliff. Also, in less than 15 years, four craters from the last event are nearly visible infill with values up to 9 m. A considerable portion of the overall loss of surface material is received within the bay, including its own erosion from the submerged caldera's lateral walls, and accumulates at the bay's bottom. However, there is a substantial outward transfer of material to balance the figures. These observations highlight the dynamic nature of the coastline and the impact of various factors on the erosion and sedimentation processes on the inner coast.
Although the model was focused primarily on other factors such as tidal currents and morphodynamical processes, it could improve including changes in air pressure and wind at more points on the island to introduce both spatial and temporal variation, as well as an extensive field survey with different locations of tides and currents to calibrate and validate the model more accurately. Also, this study uses historical data with metres uncertainty and some field data. Although resampling techniques were applied and slope ranges were defined, altimetric/bathymetric differences showed high values and spatial-temporal trends did not offer statistical significance in all temporal studies. These altimetric differences joined to bathymetric modification found required the acquisition of new precise DEM, maybe with unmanned aerial vehicle (UAV) flight, a new bathymetry and snowmelt runoff measurements to improve and validate these results.
Finally, though it was not the study's objective, it is essential to highlight the significant retreat experienced by the only glacier of the island, which increased its annual retreat to 14 m in the 2003-2020 interval compared to the 7 m / yr it experienced between 1970 and 2003, representing a 100% increase in its annual retreat. This loss aligns with the DEM volumetric loss detected primarily in the high-altitude area and linked to snow mass loss.

Author Contributions

Conceptualization, C.T. and C.Z. methodology, C.T., C.Z., J.d.l.F. and GP.; validation, C.T. and B.J.-a.; formal analysis, C.T., C.Z. and J.d.l.F.; writing—original draft preparation, C.T., C.Z. and J.d.l.F.; writing—review and editing, C.T., C.Z., J.d.l.F., B.J.-a. and G.P.; visualization, C.T., C.Z., J.d.l.F. and G.P.; supervision, C.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Spanish Ministry of Economy, Industry and Competitiveness project: “Seguimiento y vigilancia de procesos geodinámicos activos mediante deformación geodésica GNSS en diferentes escenarios (Antártida, Golfo de Cádiz y Latinoamérica)” (CTM2017-84210-R) and Portuguese Science and Technology Foundation through the Portuguese Polar Program under the PERMANTAR projects (PROPOLAR/FCT) and THAWIMPACT/2022.06628.PTDC.

Data Availability Statement

SIMAC information can be applied by email to the corresponding author.

Acknowledgments

Special thanks to Spanish “Instituto Hidrográfico de la Marina” and promoters of global projects as the Marine Geoscience Data System (MGDS) or Antarctic projects as Reference Elevation Model of Antarctica (REMA).

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Appendix A

Preprints 89833 g0a1
Figure A1. MGDS point data from the Laurence M. Gould expedition.
Figure A1. MGDS point data from the Laurence M. Gould expedition.
Preprints 89833 g0a1

Appendix B

Table B1. Characteristics of river discharges.
Table B1. Characteristics of river discharges.
Id Flow (m3/s) Tributaires Location Entity
1 0.02 0 Argentine Base 2
2 0.04 2 Argentine Base 3
3 0.025 1 Argentine Base 2
4 0.01 0 Argentine Base 1
5 0.02 0 West 2
6 0.045 3 West 3
7 0.03 0 West 3
8 0.02 0 West 2
9 0.085 9 West 4
10 0.09 10 West 4
11 0.08 8 West 4
12 0.02 0 Argentine Base 2
13 0.02 0 West 2
14 0.03 2 Lake 2
15 0.01 0 Lake 1
16 0.01 0 Lake 1
17 0.01 0 Lake 1
18 0.02 0 Lake 2
19 0.03 2 Lake 2
20 0.01 0 Lake 1
21 0.035 3 Lake 2
22 0.01 0 Lake 1
23 0.02 0 Lake 2
24 0.01 0 Lake 1
25 0.04 2 Lake 3
26 0.075 5 North 5
27 0.075 5 North 5
28 0.055 3 North-East 4
29 0.055 5 North-East 3
30 0.03 2 Crater_70 2
31 0.065 3 Crater_70 5
32 0.01 0 Crater_70 1
33 0.03 2 North-West 2
34 0.03 2 Black glacier 2
35 0.025 1 Black glacier 2
36 0.01 0 West 1
37 0.01 0 West 1
38 0.025 3 South-West 1
39 0.02 0 Entry 2
40 0.07 6 Entry 4
41 0.055 3 Entry 4
42 0.035 3 Entry 2
43 0.055 5 Entry 3
44 0.05 4 Entry 3
45 0.065 5 Entry 4
46 0.065 5 Entry 4
47 0.01 0 Spanish Base 1
48 0.08 6 Argentine Base 5
49 0.04 2 Argentine Base 3
50 0.015 1 Argentine Base 1
51 0.015 1 Argentine Base 1
52 0.04 2 Entry 3
53 0.06 4 Entry 4
54 0.095 9 Argentine Base 5
55 0.05 4 Argentine Base 3
Table B2. Ellipsoidal height differences between field work and REMA.
Table B2. Ellipsoidal height differences between field work and REMA.
Nº point 2006 h(m) REMA h (m) Differences
1 52,2 50,1 -2,0
2 61,1 59,6 -1,5
3 57,7 56,4 -1,3
4 43,2 52,1 8,9
5 80,1 86,4 6,3
6 62,9 56,1 -6,8
7 59,8 54,4 -5,4
8 90,3 83,8 -6,5
9 98,1 87,9 -10,2
10 94,1 86,7 -7,5
11 69,8 65,7 -4,1
12 50,4 50,1 -0,3
13 65,4 61,1 -4,3
14 77,5 74,9 -2,6
15 64,5 62,5 -2,0
16 57,3 64,4 7,1
17 81,3 79,8 -1,5
18 93,7 90,4 -3,4
19 98,4 95,5 -2,9
20 34,2 40,3 6,1
21 108,9 105,0 -3,9
22 45,1 46,9 1,9
23 45,1 45,0 -0,1
24 48,9 54,0 5,2
25 48,0 47,2 -0,7
26 46,7 44,6 -2,1
27 46,6 46,3 -0,3

References

  1. Dibbern, J.S. Fur Seals, Whales and Tourists: A Commercial History of Deception Island, Antarctica. Polar Record 2010, 46, 210–221. [Google Scholar] [CrossRef]
  2. Secretariat of the Antarctic Treaty Compilation of Key Documents of the Antarctic Treaty System; 2nd ed.; Secretariat of the Antarctic Treaty: Bueno Aires, 2014; ISBN 978- 987-1515-76-9.
  3. Torrecillas, C.; Berrocoso, M. The Multidisciplinary Scientific Information Support System ( SIMAC ) for Deception Island. Antarctica 2006, 397–402. [Google Scholar] [CrossRef]
  4. Torrecillas, C.; Berrocoso, M.; Pérez-López, R.; Torrecillas, M.D. Determination of Volumetric Variations and Coastal Changes Due to Historical Volcanic Eruptions Using Historical Maps and Remote-Sensing at Deception Island (West-Antarctica). Geomorphology 2012, 136, 6–14. [Google Scholar] [CrossRef]
  5. Cooper, A.P.R.; Smellie, J.L.; Maylin, J. Evidence for Shallowing and Uplift from Bathymetric Records of Deception Island, Antarctica. Antarct Sci 1998, 10, 455–461. [Google Scholar] [CrossRef]
  6. Smellie, J.L. Lithostratigraphy and Volcanic Evolution of Deception Island, South Shetland Islands. Antarct Sci 2001, 13, 188–209. [Google Scholar] [CrossRef]
  7. Clapperton, C.M. The Volcanic Eruption At Deception Island, December 1967. British Antarctic Survey Bulletin 1969, 83–90. [Google Scholar]
  8. Smellie, J.L. The 1969 Subglacial Eruption on Deception Island (Antarctica): Events and Processes during an Eruption beneath a Thin Glacier and Implications for Volcanic Hazards; 2002. E. [CrossRef]
  9. Aristarain, A.J.; Delmas, R.J. Ice Record of a Large Eruption of Deception Island Volcano (Antarctica) in the XVIIth Century. Journal of Volcanology and Geothermal Research 1998, 80, 17–25. [Google Scholar] [CrossRef]
  10. Birkenmajer, K. Lichenometric Dating of a Mid-19th Century Lava Eruption on Deception Island (West Antarctica). Bulletin - Polish Academy of Sciences: Earth Sciences 1991, 39, 467–475. [Google Scholar]
  11. Roobol, M.J. A Model for the Eruptive Mechanism of Deception Island from 1820 to 1970. British Antarctic Survey Bulletin 1980, 49, 137–156. [Google Scholar]
  12. Baker, P.E.; Roobol, M.J. a; Davies, S.M.; McReath, I.; Harvey, M.R. The Geology of the South Shetland Islands: V. Volcanic Evolution of Deception Island. British Antarctic Survey Scientific Reports 1975, 78, 79 pp. [Google Scholar]
  13. Ortiz, R.; Vila, J.; Garcia, A.; Camacho, A.G.; Diez, J.L.; Aparicio, A.; Soto, R.; Viramonte, J.G.; Risso, C.; Petrinovic, I.; et al. Geophysical Features of Deception Island. In Recent Progress in Antarctic Earth Science; Yoshida, Y., Ed.; Terrapub: Japan, 1992; pp. 443–448. [Google Scholar]
  14. Berrocoso, M.; Torrecillas, C.; Jigena, B.; Fernández-Ros, A. Determination of Geomorphological and Volumetric Variations in the 1970 Land Volcanic Craters Area (Deception Island, Antarctica) from 1968 Using Historical and Current Maps, Remote Sensing and GNSS. Antarct Sci 2012, 24, 367–376. [Google Scholar] [CrossRef]
  15. Pedrazzi, D.; Kereszturi, G.; Lobo, A.; Geyer, A.; Calle, J. Geomorphology of the Post-Caldera Monogenetic Volcanoes at Deception Island, Antarctica — Implications for Landform Recognition and Volcanic Hazard Assessment. Journal of Volcanology and Geothermal Research 2020, 402. [Google Scholar] [CrossRef]
  16. Hans Nelson, C.; Bacon, C.R.; Robinson, S.W.; Adam, D.P.; Platt Bradbury, J.; Barber, J.H.; Schwartz, D.; Vagenas, G. The Volcanic, Sedimentologic, and Paleolimnologic History of the Crater Lake Caldera Floor, Oregon: Evidence for Small Caldera Evolution. Geol Soc Am Bull 1994, 106, 684–704. [Google Scholar] [CrossRef]
  17. Roobol, M.J. Historic Vulcanic Activity at Deception Island.Pdf. British Antarctic Survey Bulletin 1973, 23–30. [Google Scholar]
  18. Flexas, M.M.; Arias, M.R.; Ojeda, M.A. Hydrography and Dynamics of Port Foster, Deception Island, Antarctica. Antarct Sci 2017, 29. [Google Scholar] [CrossRef]
  19. Jigena Antelo, B.; Vidal, J.; Berrocoso, M. Determination of the Tide Constituents at Livingston and Deception Islands (South Shetland Islands, Antarctica), Using Annual Time Series. Dyna (Medellin) 2015, 82, 209–218. [Google Scholar] [CrossRef]
  20. Jigena, B.; Vidal, J.; Berrocoso, M. Determination of the Mean Sea Level at Deception and Livingston Islands, Antarctica. Antarct Sci 2014, 27, 101–102. [Google Scholar] [CrossRef]
  21. Berrocoso, M.; Prates, G.; Fernández-Ros, A.; Peci, L.M.; de Gil, A.; Rosado, B.; Páez, R.; Jigena, B. Caldera Unrest Detected with Seawater Temperature Anomalies at Deception Island, Antarctic Peninsula. Bull Volcanol 2018, 80. [Google Scholar] [CrossRef]
  22. Martins Figueiredo, D.; José Pinto dos Santos, A.; Duarte Mateus, M. Hydrodynamic Modelling of Port Foster (Deception Island, Antarctica) Implementation of a Two-Dimensional Tidal Model and an Approach on the Three-Dimensional Model as Well as Generation of Internal Waves Engenharia Do Ambiente, 2015.
  23. Jigena-Antelo, B.; Estrada-Ludeña, C.; Howden, S.; Rey, W.; Paz-Acosta, J.; Lopez-García, P.; Salazar-Rodriguez, E.; Endrina, N.; Muñoz-Pérez, J.J. Evidence of Sea Level Rise at the Peruvian Coast (1942–2019). Science of The Total Environment 2023, 859, 160082. [Google Scholar] [CrossRef] [PubMed]
  24. Almar, R.; Ranasinghe, R.; Bergsma, E.W.J.; Diaz, H.; Melet, A.; Papa, F.; Vousdoukas, M.; Athanasiou, P.; Dada, O.; Almeida, L.P.; et al. A Global Analysis of Extreme Coastal Water Levels with Implications for Potential Coastal Overtopping. Nature Communications 2021 12:1 2021, 12, 1–9. [Google Scholar] [CrossRef]
  25. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global Probabilistic Projections of Extreme Sea Levels Show Intensification of Coastal Flood Hazard. Nature Communications 2018 9:1 2018, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
  26. Prates, G.; Torrecillas, C.; Berrocoso, M.; Goyanes, G.; Vieira, G. Deception Island 1967-1970 Volcano Eruptions from Historical Aerial Frames and Satellite Imagery (Antarctic Peninsula). Remote Sensing 2023, Vol. 15, Page 2052 2023, 15, 2052. [Google Scholar] [CrossRef]
  27. Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and Validation of a Three-Dimensional Morphological Model. Coastal Engineering 2004, 51, 883–915. [Google Scholar] [CrossRef]
  28. Iglesias, G.; Sánchez, M.; Carballo, R.; Fernández, H. The TSE Index – A New Tool for Selecting Tidal Stream Sites in Depth-Limited Regions. Renew Energy 2012, 48, 350–357. [Google Scholar] [CrossRef]
  29. Hansen, J.E.; Elias, E.; List, J.H.; Erikson, L.H.; Barnard, P.L. Tidally Influenced Alongshore Circulation at an Inlet-Adjacent Shoreline. Cont Shelf Res 2013, 56, 26–38. [Google Scholar] [CrossRef]
  30. Ruggiero, P.; Walstra, D.J.R.; Gelfenbaum, G.; van Ormondt, M. Seasonal-Scale Nearshore Morphological Evolution: Field Observations and Numerical Modeling. Coastal Engineering 2009, 56, 1153–1172. [Google Scholar] [CrossRef]
  31. Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. Journal of Hydraulic Engineering 2007, 133, 649–667. [Google Scholar] [CrossRef]
  32. Smellie, J.L.; López-Martínez, J.; Headland, R.K.; Hernández-Cifuentes, F.; Maestro, A.; Millar, I.L.; Rey, J.; Serrano, E.; Somoza, L.; Thomson, J.W. Geology and Geomorphology of Deception Island; López-Martínez, J., Smellie, J.L., Thomson, J.W., Thomson, M.R.A., Eds.; British Antarctic Survey: Cambridge, 2002.
  33. Servicio Geográfico del Ejercito. Universidad Autónoma de Madrid Deception Island Map 1:25.000. Spanish Antarctic Cartography; Madrid, Spain, 1994.
  34. Centro Geográfico del Ejército español, C.G.E. New Topographic Map of Deception Island 1:25000; Madrid (Spain), 2006.
  35. Rosado, B.; Fernández-Ros, A.; Berrocoso, M.; Prates, G.; Gárate, J.; deGil, A.; Geyer, A. Volcano-Tectonic Dynamics of Deception Island (Antarctica): 27 years of GPS Observations (1991–2018). Journal of Volcanology and Geothermal Research 2019, 381. [Google Scholar] [CrossRef]
  36. Berrocoso, M.; Fernández-Ros, A.; Torrecillas, C.; Enríquez de Salamanca, J.M.; Ramírez, M.E.; Pérez-Peña, A.; González, M.J.; Páez, R.; Jiménez, Y.; García-García, A.; et al. Geodetic Research on Deception Island. In Antarctica; Springer-Verlag: Berlin/Heidelberg, 2006; pp. 391–396. [Google Scholar]
  37. Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef]
  38. Brecher, H.H. Institute of Polar Studies Photogrammetric Maps of a Volcanic Eruption Area, Deception Island, Antarctica; 1975.
  39. Directorate of Overseas Survey (D.O.S.) Deception Island Map 1:25.000; 1959.
  40. Jigena, B.; Berrocoso, M.; Torrecillas, C.; Vidal, J.; Barbero, I.; Fernandez-Ros, A. Determination of an Experimental Geoid at Deception Island, South Shetland Islands, Antarctica. Antarct Sci 2016, 28, 1–16. [Google Scholar] [CrossRef]
  41. Braun, A. Retrieval of Digital Elevation Models from Sentinel-1 Radar Data - Open Applications, Techniques, and Limitations. Open Geosciences 2021, 13, 532–569. [Google Scholar] [CrossRef]
  42. Somoza, L.; Martı́nez-Frı́as, J.; Smellie, J.L.L.; Rey, J.; Maestro, A.; Martínez-Frías, J.; Smellie, J.L.L.; Rey, J.; Maestro, A.; Martínez-Frías, J.; et al. Evidence for Hydrothermal Venting and Sediment Volcanism Discharged after Recent Short-Lived Volcanic Eruptions at Deception Island, Bransfield Strait, Antarctica. Mar Geol 2004, 203, 119–140. [Google Scholar] [CrossRef]
  43. Rey, J.; Maestro, A.; Somoza, L.;; Smellie, J.L. Submarine Morphology and Seismic Stratigraphy of Port Foster. In Geology and geomorphology of Deception Island; López-Martínez, J.; S.J.L.; T.J.W.; T.M.R.A., Ed.; British Antarctic Survey: Cambridge, 2002; pp. 40–46.
  44. Hopfenblatt, J.; Geyer, A.; Aulinas, M.; Álvarez-Valero, A.M.; Gisbert, G.; Kereszturi, G.; Ercilla, G.; Gómez-Ballesteros, M.; Márquez, A.; García-Castellanos, D.; et al. Formation of Stanley Patch Volcanic Cone: New Insights into the Evolution of Deception Island Caldera (Antarctica). Journal of Volcanology and Geothermal Research 2021, 415, 107249. [Google Scholar] [CrossRef]
  45. Barclay, A.H.; Wilcock, W.S.D.; Ibanez, J.M.; Ibáñez, J.M. Bathymetric Constraints on the Tectonic and Volcanic Evolution of Deception Island Volcano, South Shetland Islands. Antarct Sci 2009, 21, 153–167. [Google Scholar] [CrossRef]
  46. Smith, K.L. Underway Hydrographic, Weather and Ship-State Data (JGOFS) from Laurence M. Gould Expedition LMG0010 (2000). Interdisciplinary Earth Data Alliance (IEDA); 2014.
  47. Smith, C. Underway Hydrographic, Weather and Ship-State Data (JGOFS) from Laurence M. Gould Expedition LMG0102 (2001). Interdisciplinary Earth Data Alliance (IEDA); 2012.
  48. Blanchette, R. Underway Hydrographic, Weather and Ship-State Data (JGOFS) from Laurence M. Gould Expedition LMG0704 (2007). Interdisciplinary Earth Data Alliance (IEDA) 2010.
  49. Leger, D. Underway Hydrographic, Weather and Ship-State Data (JGOFS) from Laurence M. Gould Expedition LMG0712 (2007). Interdisciplinary Earth Data Alliance (IEDA) 2009.
  50. Blanchette, R. Underway Hydrographic, Weather and Ship-State Data (JGOFS) from Laurence M. Gould Expedition LMG0903 (2009). Interdisciplinary Earth Data Alliance (IEDA) 2011.
  51. Fremand, A.C. A Bathymetric Compilation of the South Shetland Islands, 1991-2017 - British Antarctic Survey; 2019.
  52. Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas. 1993. [Google Scholar]
  53. QGIS.org QGIS Geographic Information System. Open Source Geospatial Foundation Project.
  54. Environmental Systems Research Institute, Inc., 2010. R.C. ArcGIS Pro. Version 3.1. Available online: www.arcgis.com (accessed on 28 September 2023).
  55. Tanguy, R.; Whalen, D.; Prates, G.; Vieira, G. Shoreline Change Rates and Land to Sea Sediment and Soil Organic Carbon Transfer in Eastern Parry Peninsula from 1965 to 2020 (Amundsen Gulf, Canada). Arct Sci 2023. [Google Scholar] [CrossRef]
  56. Molina, R.; Anfuso, G.; Manno, G.; Prieto, F.J.G. The Mediterranean Coast of Andalusia (Spain): Medium-Term Evolution and Impacts of Coastal Structures. Sustainability (Switzerland) 2019, 11. [Google Scholar] [CrossRef]
  57. Lenn, Y.-D.; Chereskin, T.K.; Glatts, R.C. Seasonal to Tidal Variability in Currents, Stratification and Acoustic Backscatter in an Antarctic Ecosystem at Deception Island. Deep Sea Research Part II: Topical Studies in Oceanography 2003, 50, 1665–1683. [Google Scholar] [CrossRef]
  58. Vidal, J.; Berrocoso, M.; Jigena, B. Hydrodynamic Modeling of Port Foster, Deception Island (Antarctica). Nonlinear and Complex Dynamics 2011, 193–203. [Google Scholar] [CrossRef]
  59. Eelkema, M.; Wang, Z.B.; Stive, M.J.F. Impact of Back-Barrier Dams on the Development of the Ebb-Tidal Delta of the Eastern Scheldt. J Coast Res 2012, 285, 1591–1605. [Google Scholar] [CrossRef]
  60. Dissanayake, P.; Wurpts, A. Modelling an Anthropogenic Effect of a Tidal Basin Evolution Applying Tidal and Wave Boundary Forcings: Ley Bay, East Frisian Wadden Sea. Coastal Engineering 2013, 82, 9–24. [Google Scholar] [CrossRef]
  61. Luijendijk, A.P.; Ranasinghe, R.; de Schipper, M.A.; Huisman, B.A.; Swinkels, C.M.; Walstra, D.J.R.; Stive, M.J.F. The Initial Morphological Response of the Sand Engine: A Process-Based Modelling Study. Coastal Engineering 2017, 119, 1–14. [Google Scholar] [CrossRef]
  62. Zarzuelo, C.; López-Ruiz, A.; Ortega-Sánchez, M. Evaluating the Impact of Dredging Strategies at Tidal Inlets: Performance Assessment. Science of The Total Environment 2019, 658, 1069–1084. [Google Scholar] [CrossRef] [PubMed]
  63. Nienhuis, J.H.; Ashton, A.D.; Nardin, W.; Fagherazzi, S.; Giosan, L. Alongshore Sediment Bypassing as a Control on River Mouth Morphodynamics. J Geophys Res Earth Surf 2016, 121, 664–683. [Google Scholar] [CrossRef]
  64. Ghilani, C.D.; Wolf, P. Elementary Surveying, Global Edition; Pearson Education Limited, 2016; ISBN 9781292060675.
  65. Roobol, M.J. The Volcanic Hazard at Deception Island, South Shetland Islands. British Antarctic Survey Bulletin 1982, 51, 237–245. [Google Scholar]
Preprints 89833 g001
Figure 1. Deception island: (a) Map situation using the General Bathymetric Chart of the Oceans (GEBCO) Web Map Service in EPSG 3395; (b)Altimetric and Bathymetric digital models with hillshade, lakes, historical and active scientific bases, walks and evacuation routes from [3], and changes of the main inner zones represented in geodetic and projection system EPSG 32720 (as all figures in this paper from here).
Figure 1. Deception island: (a) Map situation using the General Bathymetric Chart of the Oceans (GEBCO) Web Map Service in EPSG 3395; (b)Altimetric and Bathymetric digital models with hillshade, lakes, historical and active scientific bases, walks and evacuation routes from [3], and changes of the main inner zones represented in geodetic and projection system EPSG 32720 (as all figures in this paper from here).
Preprints 89833 g001
Preprints 89833 g002
Figure 2. Overlap of the 1968 (purple line) and 2003 (red line) coastline in some 1968-2003-2020 visual geomorphological changes in Deception Island: (a) Infill of the 1970 eruption craters, mainly 1, 4, 5 and 6 with the inferred 1970 rim in orange; (b) Coastal erosion near Kroner Lake and opening to Port Foster (using a new 1968 orthophoto in b1); (c) Coastal erosion near Hidden Lake and its opening to Port Foster and (d) Black Glacier retreat acceleration. Zone letters are linked to red squares in Figure 1b and all images have the same scale.
Figure 2. Overlap of the 1968 (purple line) and 2003 (red line) coastline in some 1968-2003-2020 visual geomorphological changes in Deception Island: (a) Infill of the 1970 eruption craters, mainly 1, 4, 5 and 6 with the inferred 1970 rim in orange; (b) Coastal erosion near Kroner Lake and opening to Port Foster (using a new 1968 orthophoto in b1); (c) Coastal erosion near Hidden Lake and its opening to Port Foster and (d) Black Glacier retreat acceleration. Zone letters are linked to red squares in Figure 1b and all images have the same scale.
Preprints 89833 g002
Preprints 89833 g003
Figure 3. Methodology.
Figure 3. Methodology.
Preprints 89833 g003
Preprints 89833 g004
Figure 4. GIS methodology.
Figure 4. GIS methodology.
Preprints 89833 g004
Preprints 89833 g005
Figure 5. Mesh composition with COLA station (black diamond), tidal boundary, and melting streams with their tributaries and discharge points.
Figure 5. Mesh composition with COLA station (black diamond), tidal boundary, and melting streams with their tributaries and discharge points.
Preprints 89833 g005
Preprints 89833 g006
Figure 6. Calibration for COLA station. Blue circles correspond to the measured tide level data, and the white fill circles to the computed tide level data.
Figure 6. Calibration for COLA station. Blue circles correspond to the measured tide level data, and the white fill circles to the computed tide level data.
Preprints 89833 g006
Preprints 89833 g007
Figure 7. Results of the sensitivity study on the currents, changing the Chèzy coefficient at 45, 60, and 100.
Figure 7. Results of the sensitivity study on the currents, changing the Chèzy coefficient at 45, 60, and 100.
Preprints 89833 g007
Preprints 89833 g008
Figure 8. Sedimentation (green) and erosion (red) coastline patterns after a one-year simulation with the DELFT 3D numerical model and definition of study zones.
Figure 8. Sedimentation (green) and erosion (red) coastline patterns after a one-year simulation with the DELFT 3D numerical model and definition of study zones.
Preprints 89833 g008
Preprints 89833 g009
Figure 9. Overlap of the annual coastline regression on the gain-loss areas using opposite colours for a better contrast: (a) 1970-2003 and (b) 2003-2020.
Figure 9. Overlap of the annual coastline regression on the gain-loss areas using opposite colours for a better contrast: (a) 1970-2003 and (b) 2003-2020.
Preprints 89833 g009
Preprints 89833 g010
Figure 10. Some 1968 (purple line)-2003 (light green line)-2020 (blue line) visual coastline changes in Deception: column (a) the Black Glacier retreat; column (b) Sedimentation to the south of the Black Glacier; (c) Erosion of the existing slope in front of the Spanish base, and (d) Erosion in Pendulum Cove.
Figure 10. Some 1968 (purple line)-2003 (light green line)-2020 (blue line) visual coastline changes in Deception: column (a) the Black Glacier retreat; column (b) Sedimentation to the south of the Black Glacier; (c) Erosion of the existing slope in front of the Spanish base, and (d) Erosion in Pendulum Cove.
Preprints 89833 g010
Preprints 89833 g011
Figure 11. Temporal differences of DEMs over REMA hillshade and permanent snow (white line): (a) 1957-1968, (b) 1968-SIMAC, (c) SIMAC-REMA, (d) 1957-REMA, and (e) 1968-REMA.
Figure 11. Temporal differences of DEMs over REMA hillshade and permanent snow (white line): (a) 1957-1968, (b) 1968-SIMAC, (c) SIMAC-REMA, (d) 1957-REMA, and (e) 1968-REMA.
Preprints 89833 g011
Preprints 89833 g012
Figure 12. (a) Altimetric trend 1956-2020 (mainly red square) and inner watersheds; (b) slope ranges from CGE DEM; (c) satellite plume areas (own source) and some geomorphological elements from [32] and (d) altimetric differences in GNSS points between SIMAC-REMA over REMA hillshade.
Figure 12. (a) Altimetric trend 1956-2020 (mainly red square) and inner watersheds; (b) slope ranges from CGE DEM; (c) satellite plume areas (own source) and some geomorphological elements from [32] and (d) altimetric differences in GNSS points between SIMAC-REMA over REMA hillshade.
Preprints 89833 g012
Preprints 89833 g013
Figure 13. Port Foster temporal bathymetric study: (a) bathymetric differences between 1991-2005: (b) 2005-2012; (c) 1991-2012; (d) Slope areas in degrees with bathymetry contour -160 and -150m from 1991 (dark blue) and 2012 (light blue); (e) Heat maps of nº points in 50m cells from MDGS data and (f) trend of this MDGS data along its period.
Figure 13. Port Foster temporal bathymetric study: (a) bathymetric differences between 1991-2005: (b) 2005-2012; (c) 1991-2012; (d) Slope areas in degrees with bathymetry contour -160 and -150m from 1991 (dark blue) and 2012 (light blue); (e) Heat maps of nº points in 50m cells from MDGS data and (f) trend of this MDGS data along its period.
Preprints 89833 g013
Table 1. Orthophotos, satellite images, coastlines and cartographic information.
Table 1. Orthophotos, satellite images, coastlines and cartographic information.
Denomination Digital Source Description/
Spatial Resolution or Scale		 Date
1968 orthophoto Own from [26] Orthophoto from
FIDASE flight / 0.8 m		 1968
New QB1 Own from [3] QuickBird Satellite image/ 0.6 m 2003-jan-20
K31 Own from [26] KOMPSAT-32 Satellite image/ 0.7 m 2020-feb-09
Sentinel images ESA Sentinel 2 Satellite
Images/ 10 m		 2017-mar-30, 2019-feb-23,
2019-dec-30, 2020-feb-08,
2020-dec-27,2021-jan-13,
2021-jan-06, 2021-feb-02,
2022-mar-29 (snow cover)
Google Earth Images Google Earth Satellite images /
several resolutions		 2002-jan-15, 2005-oct-20 (snow cover), 2013-dec-29.
Sediment plumes Own from all satellite images Visual delineation of sediment plumes 2002-2022
Level contours SIMAC from CGE map Line / 1:25 000 1970 and 2003
Melting Streams SIMAC from CGE map Line / 1:25 000 1970 and 2003
Coastline 1968 Own from [26] Line / 1:25 000 1968
Coastline 1970 SIMAC from [38] Line / 1:25 000 1970
Coastline 2003 SIMAC from new QB Line / 1:25 000 2003
Coastline 2020 Own from [26] Line / 1:25 000 2020
Geomorphological map SIMAC from [32] Group layers /
1:25 000		 2002
1 Generation of a new True-Ortho with REMA. 2 Includes material ©KARI 2020, Distribution (SI Imaging Services, Republic of Korea), all rights reserved.
Table 2. Digital Elevation Models (DEM).
Table 2. Digital Elevation Models (DEM).
Denomination Digital Source Format Used/
Spatial Resolution		 Date
DOS DEM SIMAC from [39] ESRI Grid/ 20 m 1956
1957 DEM Own from [26] Tiff file/ 2.7 m 1957
1968 DEM Own from [26] Tiff file/ 2.7 m 1968
CGE DEM SIMAC from CGE map ESRI Grid/ 2 m 1968 and 1986
REMA REMA [37] Two Tiff files (45_04_2_2_2m_v2.0 and 45_05_2_1_2m_v2.0)/ 2 m 2009-20211
1 Ellipsoidal Height.
Table 3. Digital Bathymetry Models (DBM).
Table 3. Digital Bathymetry Models (DBM).
Denomination Digital Source Format Used/Spatial Resolution or Distance Between Points Date
DBM CGE Adapted from CGE/IHM/IEO [32] ESRI Grid/ 2 m 1988-91
Bathymetry LMG0010 MGDS [46] Ten Dat files/ points in line each < 120 m 2000
Bathymetry LMG0102 MGDS [47] One Dat file/ points in line each < 120 m 2001
Bathymetry LMG0704 MGDS [48] Two Dat files/ points in line each < 120 m 2007
Bathymetry LMG0712 MGDS [49] One Dat file/ points in line each < 120 m 2007
Bathymetry LMG0903 MGDS [50] Four Dat files/ points in line each < 120 m 2009
DBM MGDS mean Interpolated from previous MGDS Esri Grid / 50 m 20051
DBM IHM IHM [18] Esri Grid / 10 m 2012 (central bay)
2016 (some coastal zones)
External DBM South Shetlands British Antarctic Survey
[51]		 A Ascii file/ 100 m 1991-2017
1 Considered as mean time.
Table 4. Results of the amplitude (u) and phase (φ) results of the measured and computed current data of the harmonic components M2 and K1.
Table 4. Results of the amplitude (u) and phase (φ) results of the measured and computed current data of the harmonic components M2 and K1.
u [m/s] φ [º]
Measured Computed Measured Computed
M2 0.13 0.013 33 34
K1 0.09 0.009 173 180
Table 5. Statistical data from inner watershed DEM differences.
Table 5. Statistical data from inner watershed DEM differences.
Type Difference Area Min/Max Mean (m) Std dev (m)
DEM REMA-SIMAC All -84 / 74 -2,3 8,1
Flat (<=2º) -1.2 3.7
Medium slope (<=9º) -3.4 7.1
High slope (>9º) -6 13.1
1968-1957 All -78 / 86 4 8.9
Flat (<=2º) 1.4 8.4
Medium slope (<=9º) 3.6 9.4
High slope (>9º) 4.5 8.6
SIMAC-1968 All -78 / 62 -0.5 13
Flat 3.4 7.1
Medium slope 0.2 10.9
High slope -0.7 13.8
REMA-SIMAC All -84 / 74 -6.9 12.2
Flat -2.6 4.2
Medium slope -5.5 7.8
High slope -7.9 13.9
REMA-1957 All -88 / 65 -3.4 12
Flat 2.2 8.3
Medium slope -1.6 12
High slope -4.1 12.2
REMA-1968 All -94 / 56 -7.5 12.4
Flat 0.8 8.2
Medium slope -5.3 12.2
High slope -8.7 12.4
DBM SIMAC-
MDGS mean		 All -51 / 34 -3.4 7.5
Flat (<=2º) -1.5 4.3
Medium slope (<=9º) -7.5 9.9
High slope (>9º) -12.5 15.7
MDGS mean-
IHM mean		 All -51 / 34 5.8 3.4
Flat 6.2 2.4
Medium slope 5.3 3.6
High slope 0.5 10.3
SIMAC-
IHM mean		 All -50 / 76 1.5 10.8
Flat 4.6 4.3
Medium slope -0.5 10.1
High slope -0.04 17.1
Table 6. Volumetric study.
Table 6. Volumetric study.
Type Dataset Plane (m) Reference Area 3D (km2) Vol. Land/
Water
(km3)		 Dif. Vol. (km3) Ratio
(hm3 / yr)
DEM REMA 0 ABOVE 48,06 5,94 -0,32 -0,23
100 ABOVE 23,93 2,77 -0,23 -0,33
200 ABOVE 12,33 1,15 -0,13 -0,37
300 ABOVE 5,27 0,37 -0,06 -0,36
400 ABOVE 1,48 0,07 -0,02 -0,50
CGE DEM 0 ABOVE 48,02 6,26 -0,03 -0,03
100 ABOVE 24,31 3,00 -0,10 -0,23
200 ABOVE 13,25 1,28 -0,09 -0,40
300 ABOVE 5,71 0,42 -0,06 -0,60
400 ABOVE 1,75 0,09 -0,03 -0,89
1968 DEM 0 ABOVE 47,42 6,28 0,19 0,36
100 ABOVE 25,50 3,10 0,13 0,46
200 ABOVE 14,19 1,37 0,09 0,55
300 ABOVE 6,46 0,48 0,06 0,78
400 ABOVE 2,12 0,12 0,03 1,38
1957 DEM 0 ABOVE 47,17 6,10 NA
100 ABOVE 24,33 2,97 NA
200 ABOVE 13,51 1,29 NA
300 ABOVE 6,06 0,43 NA
400 ABOVE 1,84 0,09 NA
DBM DBM IHM1 0 BELOW 38,53 3,90 0,09 0,0966
-100 BELOW 22,72 0,83 0,02 0,0004
-150 BELOW 9,32 0,07 -0,02 -0,0010
DBM CGE1 0 BELOW 37,76 3,81 NA
-100 BELOW 20,81 0,81 NA
-150 BELOW 8,60 0,09 NA
1 Resampled to 50 m.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated