Effects of Gofio on the Rheological Properties of Aloe Vera Juice

Preprint

Article

Effects of Gofio on the Rheological Properties of Aloe Vera Juice

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Francisco José Rubio-Hernández^*

,Julia Rubio-Merino,Elvira García-López

Francisco José Rubio-Hernández^*

,Julia Rubio-Merino,Elvira García-López

This version is not peer-reviewed

Submitted:

07 November 2023

Posted:

08 November 2023

You are already at the latest version

Alerts

Abstract

Considering nutritional qualities of gofio (Gf) and aloe vera juice (AVJ), their combination is indicated as an easy and fast source of ingest of basic bio elements. As the texture of the final product must be accepted by customers, the influence of Gf concentration on the rheological behavior of Gf/AVJ suspensions was determined. Shear thinning index of AVJ maintains unaltered despite the presence of Gf particles, although the viscosity value increases as expected. Linear viscoelastic studies on Gf/AVJ confirmed this is a viscoelastic liquid that changes from chewy to creamy texture with Gf concentration increase.

Keywords:

Subject: Chemistry and Materials Science - Food Chemistry

1. Introduction

Aloe vera juice (AVJ) is obtained by crushing and centrifugation of the leaf pulp of the plant aloe vera (L.) Burm. F. It has been included as food product due to its beneficial content in vitamins, minerals, amino acids, enzymes, sugars, and bioactive compounds [1,2]. The list of aloe vera species is large, although the most widely used in nutritional applications is Aloe Barbadensis Miller [3]. The use of aloe vera juice in food applications requires a comprehensive insight on its rheological behavior because the high content of insoluble polymer particles affects its storage, processing, and ingesting [4]. This kind of studies is specifically indicated considering the variety of non-Newtonian behaviors observed in AVJ, referred to shear dependent viscosity [5] and viscoelastic properties [4].

Gofio Canario [6] is a variety of flour made from toasted cereals (corn, wheat, spelled or oats) mainly used in Canary Islands. It is a highly nutritious food, being the basis of the diet of Canary Islands inhabitants even before Spanish colonization. It contains proteins, carbohydrates, fibers, vitamins B1, B2, B3, C, and different trace elements [7].

Considering nutritional qualities of gofio (Gf) and AVJ, their combination supplies an easy and fast source of ingest of basic bio elements. As the texture of the final product must be accepted by customers, the aim of this study is to determine the influence of Gf concentration on the rheological behavior of Gf/AVJ suspensions.

2. Materials and Methods

Canary Gf, AVJ, and citric acid (CA) were used for the preparation of Gf/AVJ suspensions. Canary Gf is a mixture of corn, wheat, and oats fabricated in La Gomera (Canary Islands, Spain). AVJ was the supernatant resulting from crushing and centrifugation of aloe vera pulp, which was extracted from leaves of 3-years old aloe vera plants. This age is considered the minimum value to ensure AVJ contains enough amounts of polysaccharides and flavonoids to optimum nutritionally [8]. Finally, citric acid (

99.5 %

purity) was purchased to Panreac Química S.A. (Spain) and used as received. The addition of CA is justified by the necessity to avoid oxidation and degeneration of AVJ [9]. Despite these precautions, samples were rejected two days later of their preparation to avoid misinterpretations of the results due to possible physical-chemical variations.

Gf/AVJ suspensions were prepared as follows. Aloe vera gel was carefully extracted from an adult leaf and vigorously crushed with a stirrer RZR1 (Heidolph Instruments, Germany) at

800 r p m

for

10 m i n

, using a PR30 pitched-blade impeller. After that, it was centrifugated in a centrifuge (ALC Model4218, U.S.A.) at maximum velocity

(6000 r p m)

and the supernatant was extracted. Then,

0.1 %

respect to supernatant weight was calculated and this amount of CA was added to obtain the AVJ. Power law relationship between the viscosity value measured at

100 1 / s

and the concentration of AVJ [10] was used to estimate AVJ concentration used in this study. The estimated value was

1.11 ° B x at 25 ℃

. After that, different amounts of Gf were added to the AVJ and mixed with the same stirrer at

75 r p m

until homogenization

(\geq 15 m i n)

. The pH of the pastes increased from

3.6

4.4

when the amount of Gf increased. The density of Gf/AVJ suspensions was determined weighting

1 m L

of each suspension. These results are summarized in Table 1.

Electron microscopy of canary Gf (SEM image) shows rounded particles (Figure 1) with high polydispersity, this last probably due to Gf used in this research is a mix of three different cereals. It is well known that starch resulting from different cereals conforms to different shape and size [11]. The average particle size

(11.6 μ m)

and polydispersity

(1.6 μ m)

of Gf particles were obtained processing SEM images with a MATLAB tool (MathWorks^®). The polydispersity index was calculated from the standard deviation of the initial distribution in units of

1 / 2 (σ_{M} + σ_{m})

, being

σ_{M}

and

σ_{m}

the maximum and minimum particle size, respectively [12]. The density of Gf

(489 k g / m^{3})

was estimated as being the average of the density of the three cereals taken from the bibliography.

Rheological measurements were performed with a stress-controlled rheometer Gemini 150 (Malvern Instruments Ltd., U.K.). This device is equipped with a Peltier module for the temperature control. Each experiment was conducted on fresh samples. The temperature was fixed to

25.00 \pm 0.05 ℃

. A double-gap geometry was used to record rheometric data. One remarkable characteristic of the double-gap geometry when is compared to concentric cylinders is the reduced inertia of the rotor, being especially useful for oscillatory shear measurements.

Rheological tests were preceded by a pre-shear phase to erase random or hazardous initial sample state due to stresses the sample could experiment when is placed into rheometric geometry. The pre-shear consisted in the application of a constant shear rate

(10 s^{- 1})

during

30 s

. This time of shear was enough in all cases to achieve steady state

(\frac{Δ τ}{τ} \leq 1 % for 10 s)

. After that, samples rested for 60 s allowing structural rebuild. Then, the rheological test was subsequently applied to the sample. The rheological tests were carried out in triplicate.

Two rheological tests were used to describe textural properties of Gf/AVJ suspensions. First, steady viscous flow was characterized with the steady flow curve protocol. It consisted in the growing application of a shear rate ramp from

0.1 s^{- 1}

200 s^{- 1}

logarithmically distribute to achieve more specific information on suspensions near the rest state. The behavior far the rest state can be properly characterized knowing the response of suspensions at a small number of increasing shear rates. Each shear rate was applied until a steady response was recorded. The condition to ensure that the steady response was achieved is the same as indicated before

(\frac{Δ τ}{τ} \leq 1 % for 10 s)

. Second, the linear viscoelastic response of the at-rest microstructure developed by Gf/AVJ suspensions was characterized using small amplitude oscillatory shear (SAOS) analysis. This rheological test consists in the application of a frequency sweep maintaining constant the strain amplitude in the linear viscoelastic regime. Elastic and viscous components as a function of the experiment duration were quantified recording storage and dissipation modulus, respectively, and plotting vs the angular frequency of the oscillatory shear.

3. Results and Discussion

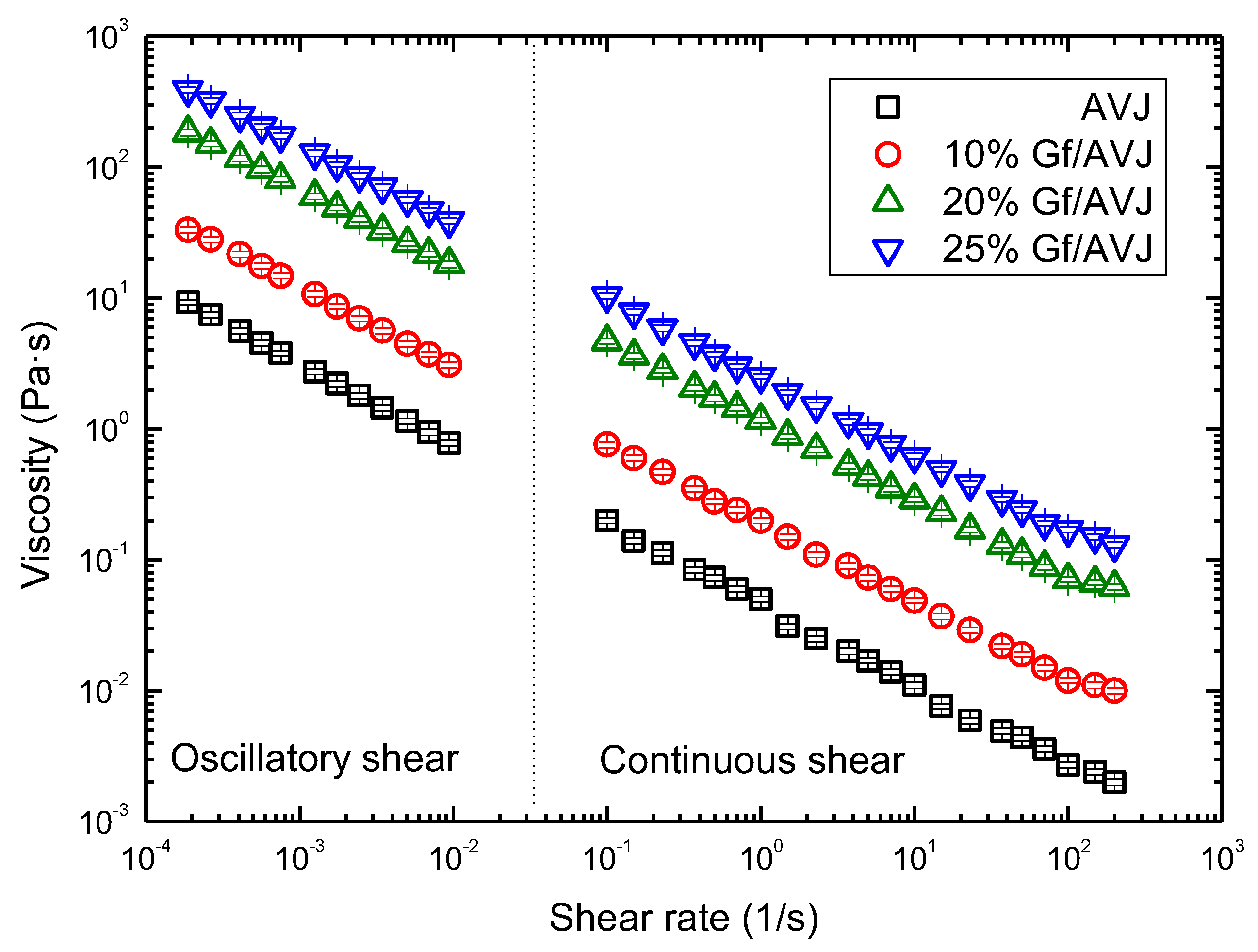
3.1. Steady Viscous Behavior

Steady viscosity curves of Gf/AVJ suspensions showed that the viscosity increased with the increase of Gf amount (Figure 2). On the other hand, the viscosity of each Gf/AVJ suspension decreased with shear rate indicating (non-Newtonian) shear-thinning behavior. The decrease in viscosity of AVJ (black square symbols) has been previously reported [10], and is due to breaking of structural units due to hydrodynamic forces generated during shear [13]. This is a typical non-Newtonian behavior also found in fruit-based products [14,15,16].

The dependence of the viscosity

(η)

with shear rate

(\dot{γ})

was fitted with the power law model (Ostwald-de Waele),

η = K {\dot{γ}}^{n - 1}

(1)

In Equation (1)

K

and

n

are consistency and flow indexes, respectively. As can be seen, good correlation between experimental and predicted values was found for the liquid phase (AVJ) and Gf/AVJ suspensions (Table 1). It is worthy to note that the “strange” units of the consistency index

(P a \cdot s^{n})

can become a handicap for the comparison of the value of this magnitude taken by different materials. Fortunately, in this specific case,

n

-values coincide

(~ 0.40)

for all the suspensions and, therefore, we can affirm that the consistency of Gf/AVJ suspensions increases with Gf content. In addition, the abrupt shear-thinning behavior characterized by a relatively small

n

-value is not affected by Gf concentration. Consequently, the shear-thinning behavior of Gf/AVJ suspensions should be justified by the shear-thinning behavior shown by the carrier liquid (AVJ). In other words, Gf/AVJ suspensions are non-Newtonian systems resulting from the dispersion of a solid phase (Gf) in a non-Newtonian carrier liquid (AVJ). Therefore, the fact that

n

-value was independent on Gf content allow us to conclude that the shear-thinning behavior of the liquid phase (AVJ) is the main cause of the shear-thinning behavior observed in Gf/AVJ suspensions. AVJ is a dispersion of high molecular weight insoluble polysaccharides entangled at rest. Increasing shear disentangles polysaccharide molecules and tend to align them along the flow direction. Consequently, the flow field distortion is less at high shear and the viscosity is lower.

The presence of Gf particles gives place to an additional flow field distortion (higher viscosity) at each shear rate value. The ability of Gf particles and aggregates to distort the flow field can be quantified with the intrinsic viscosity

([η])

of the suspensions [17]. Krieger-Dougherty equation [18] relates the viscosity of the suspension with the volume fraction

(ϕ)

occupied by the solid phase,

η = η_{ℓ} {(\frac{1}{1 - \frac{ϕ}{ϕ_{m}}})}^{[η] ϕ_{m}}

(2)

In Equation (2)

η_{ℓ}

is the viscosity of AVJ and

ϕ_{m}

is the maximum packing fraction achieved by Gf particles dispersed in Gf/AVJ suspensions. Although Krieger-Dougherty equation was formulated assuming Newtonian behavior of the suspension, its utility for the estimation of the flow field distortion in non-Newtonian suspensions has shown also valid [19]. Experimental relative viscosity values corresponding to four different shear rate values

(0.1, 1, 10, 100 s^{- 1})

against Gf volume fraction overlapped within the experimental error, indicating that the shape and size of Gf aggregates are not significantly affected by the shear rate. To confirm this result, Krieger-Dougherty equation was fitted to these experimental data. The resulting values of the parameters of Krieger-Dougherty equation confirmed that the intrinsic viscosity practically does not vary when the shear rate increases

(15.9 t o 17.1)

. This means that the shape and size of Gf aggregates is not affected by the mechanical action due to shear. In addition, the maximum packing fraction was the same independently the shear rate value

(0.25)

. In conclusion, the shear-thinning behavior observed in Gf/AVJ suspensions is mainly due to the shear thinning behavior shown by AVJ solvent.

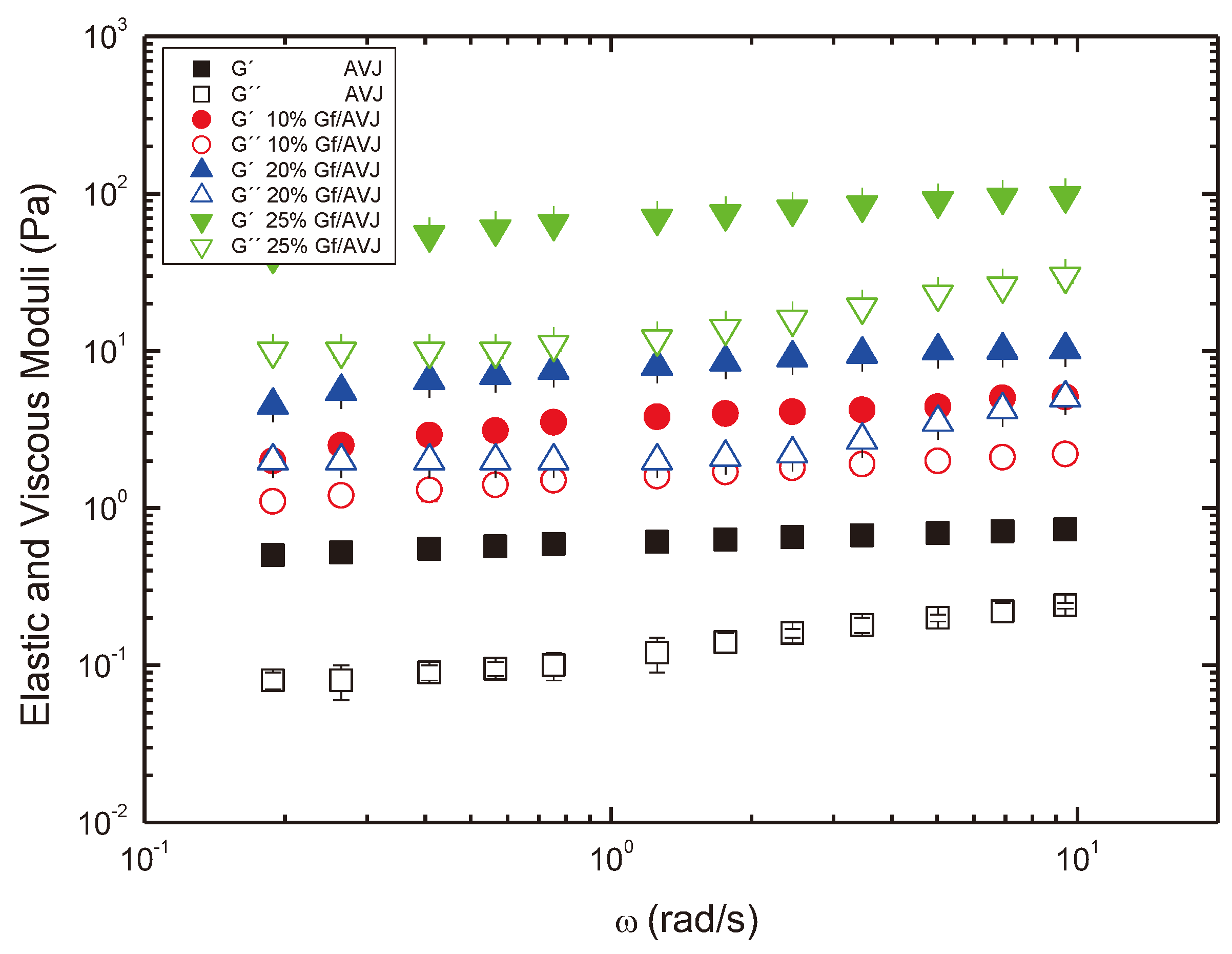
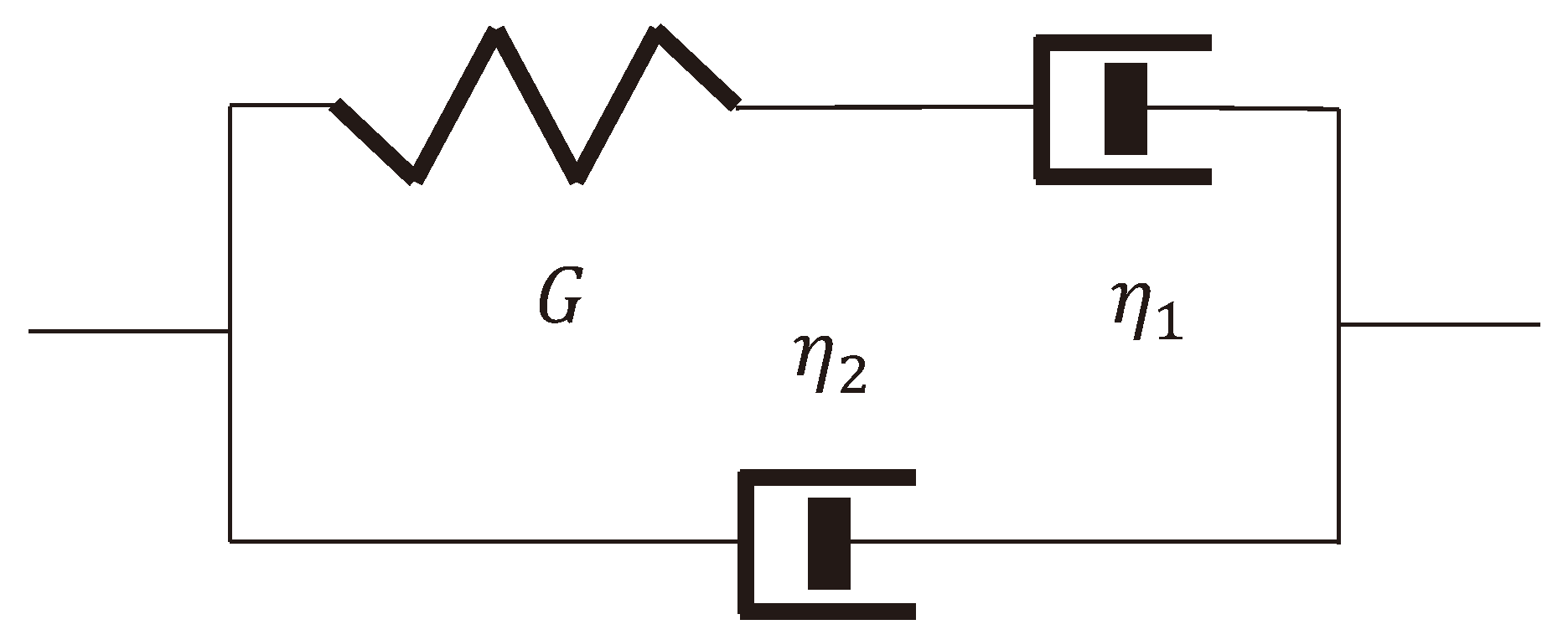
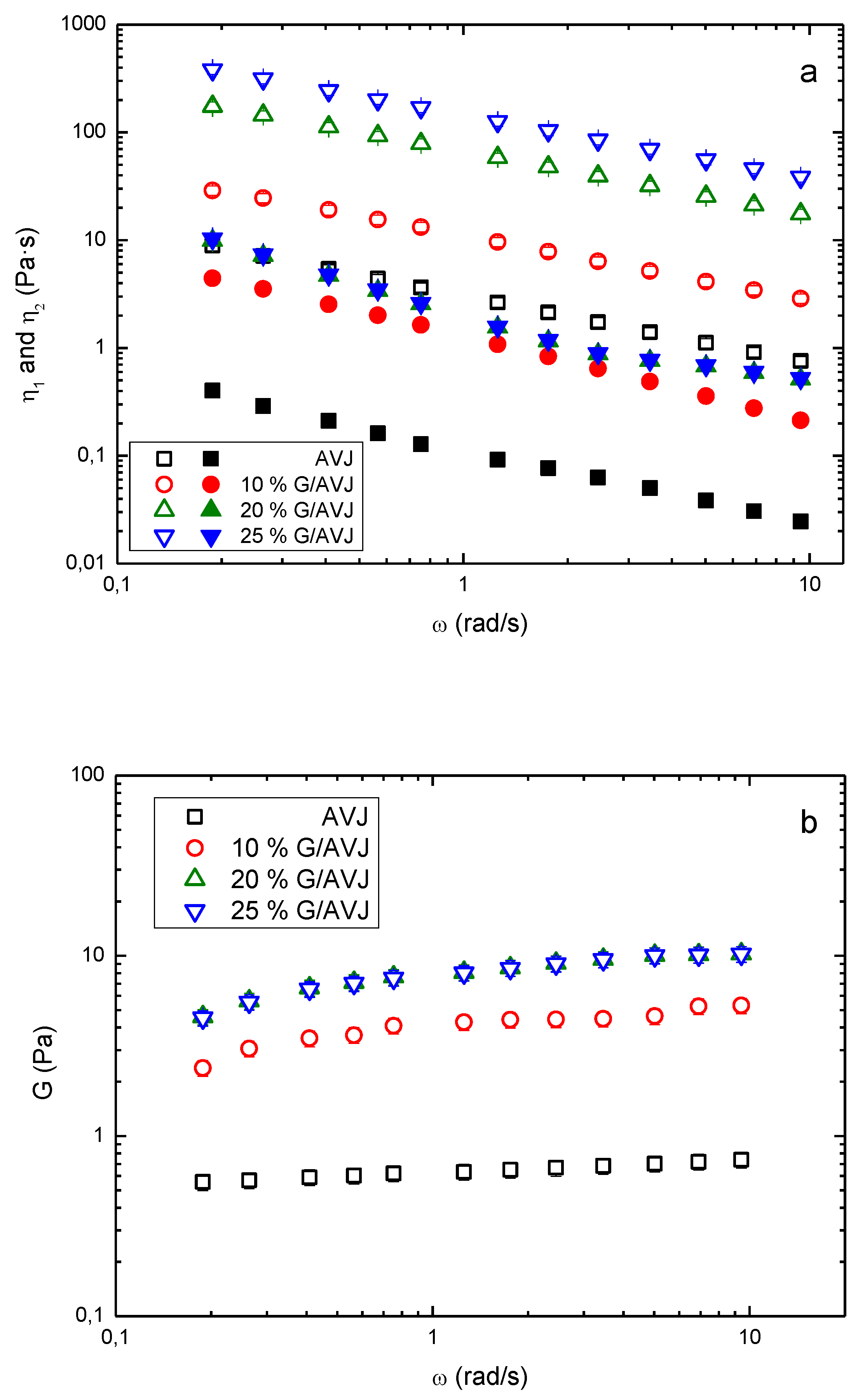
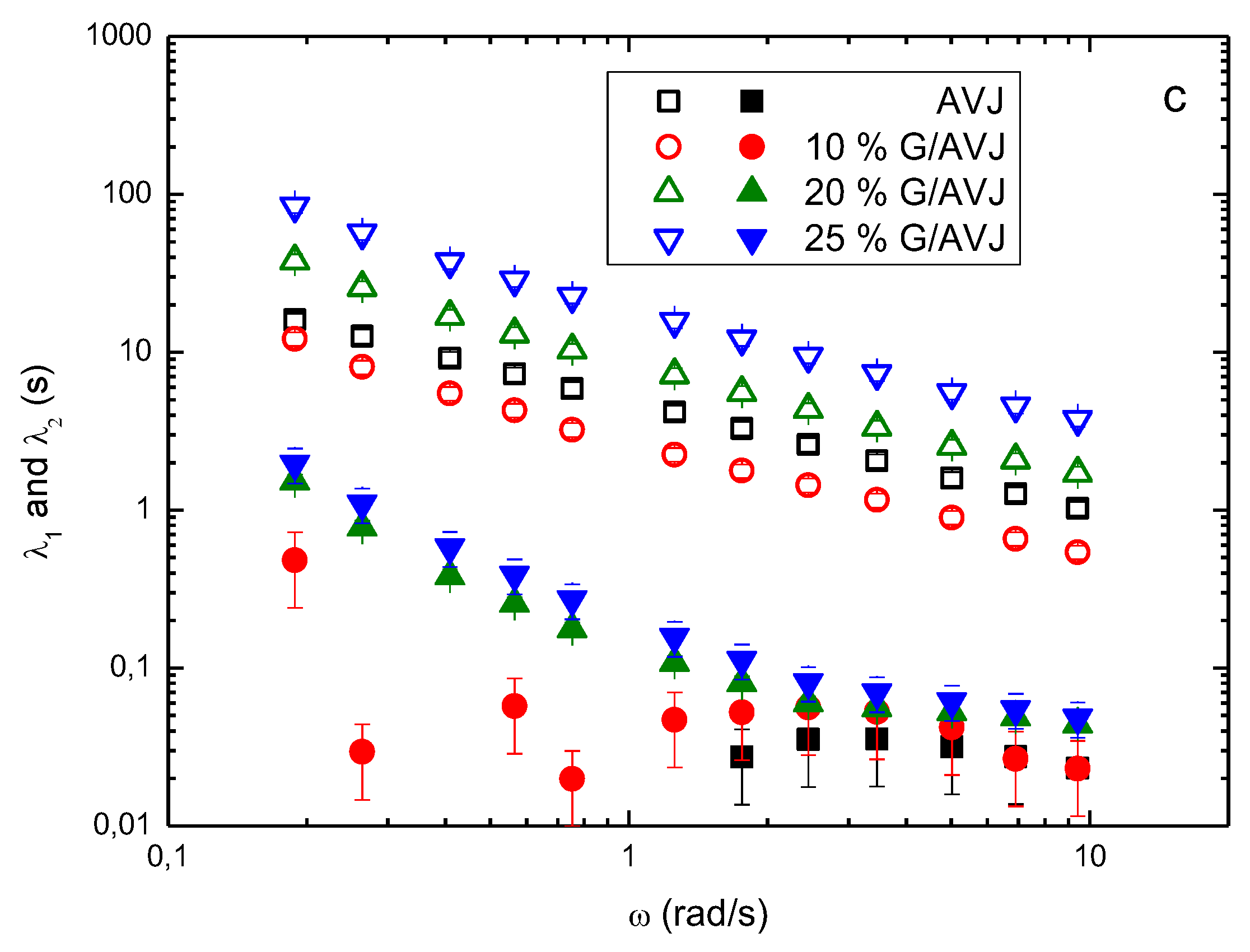
3.2. Viscoelastic Behavior

The viscoelastic flow of G/AVJ suspensions was characterized using Small Amplitude Oscillatory Shear (SAOSstrain) tests. With this rheological technique the linear viscoelastic response of the microstructure-at-rest developed by the suspensions is analyzed. The importance of this study is justified by the fact that help to determine the stability of the storage suspension against sedimentation. With this rheological study, the variation of the deformation

(γ)

imposed to the suspension is sinusoidal,

γ (t) = γ_{o} s i n ω t

(3)

Therefore, firstly an amplitude

(γ_{o})

sweep is applied to the sample maintaining constant the angular frequency

(ω)

of the oscillation. The aim of this first part of the SAOSstrain test is to determine the maximum

γ_{o}

-value delimiting the linear viscoelastic (LVE) behavior of the suspension.

The LVE response of suspensions to the sinusoidal deformation is an out of phase sinusoidal shear stress

(τ)

τ (t) = τ_{o} s i n (ω t + δ) = (τ_{o} c o s δ) s i n ω t + (τ_{o} s i n δ) c o s ω t

(4)

In Equation (4)

τ_{o}

is the stress amplitude and

δ

is the phase difference between input (deformation) and output (stress) signals. From Equation (4) two viscoelastic moduli are defined,

G ´ (ω) = \frac{τ_{o}}{γ_{o}} c o s δ

(5)

G ´ ´ (ω) = \frac{τ_{o}}{γ_{o}} s i n δ

(6)

G ´

is the elastic or storage modulus and

G ´ ´

is the viscous or loss modulus. The accomplishment of LVE behavior condition implies that both moduli must be independent on

γ_{o}

. Results corresponding to amplitude of deformation sweep tests showed that the viscoelastic moduli do not depend on

γ_{o}

(LVE behavior) when the amplitude of the oscillatory shear is lower than

0.01

After the LVE region was detected, the behavior of Gf/AVJ suspensions at short and long experimental times was tested varying the frequency of the SAOSstrain maintaining constant the amplitude into the LVE regime. This second rheological test is named frequency sweep. More concretely, to be sure that responses of Gf/AVJ suspensions to frequency sweep rheological tests were recorded in the LVE region, an amplitude

γ_{o} = 0.001

was maintained constant during oscillatory shear. Results of frequency sweeps in the LVE regime obtained with Gf/AVJ suspensions are shown in Figure 3. As can be seen, Gf/AVJ is a viscoelastic gel in all cases [20]. This qualification results from the fact that booth moduli are practically independent on the frequency. This is an indication of the existence of a relatively strong microstructure, which gives the suspensions a gel appearance. This gel-microstructure is mainly built by polymeric molecules dispersed in the AVJ. We arrive to this conclusion because

G ´

and

G ´ ´

dependence with angular frequency is qualitatively similar for AVJ solvent and Gf/AVJ suspensions. Certainly, the value of both moduli increases with Gf concentration, which is an indication of some additional effect due to the increase of solid phase.

For the analysis of

G ´ (ω)

and

G ´ ´ (ω)

experimental data Jeffreys model (Figure 4) will be used. Jeffreys mechanical analog is the simplest equivalent encompassing the entire spectrum of mechanical behaviors [21]. Therefore, it is indicated for the analysis of the general LVE response of non-Newtonian fluids.

The constitutive equation that corresponds to the mechanical analog shown in Figure 4 is,

τ + \frac{η_{1}}{G} \dot{τ} = (η_{1} + η_{2}) \dot{γ} + η_{1} \frac{η_{2}}{G} \ddot{γ}

(7)

In Equation (7)

η = η_{1} + η_{2}

is the steady-state shear viscosity and

G

is the elastic modulus. With the definitions

λ_{1} = \frac{η_{1}}{G}

and

λ_{2} = \frac{η_{1} η_{2}}{η G}

for relaxation and retardation times, respectively, Equation (7) can be re-written as,

τ + λ_{1} \dot{τ} = η \dot{γ} + η λ_{2} \ddot{γ}

(8)

Jeffreys material functions can be expressed in terms of the experimentally accessible magnitudes

G ´

and

G ´ ´

, enhancing its utility for the physical interpretation of the LVE behavior of Gf/AVJ suspensions. Substituting Eqs. (3-6) in Equation (8), the following relationships are obtained,

λ_{1} = \frac{η}{G ´} - \frac{G ´ ´}{G ´ ω}

(9)

λ_{2} = \frac{G ´ ´}{G ´ ω} - \frac{G ´^{2} + G ´ ´^{2}}{G ´ η ω^{2}}

(10)

η_{2} = \frac{G ´ ´}{ω} - \frac{G ´^{2}}{η ω^{2} - G ´ ´ ω}

(11)

η_{1} = η - \frac{G ´ ´}{ω} + \frac{G ´^{2}}{η ω^{2} - G ´ ´ ω}

(12)

G = G ´ [1 + \frac{G ´^{2}}{{(η ω - G ´ ´)}^{2}}]

(13)

To obtain the function

η (ω)

, the experimental dependence of the steady-state viscosity with shear rate given by Equation (1) was re-written using the relationship

{\dot{γ}}_{o} = γ_{o} ω

with

γ_{o} = 0.001

η (ω) = K {(γ_{o} ω)}^{n - 1}

(14)

Therefore, the dependence of Jeffreys-based material functions

(η_{1}, η_{2}, G)

and characteristic times

(λ_{1}, λ_{2})

with angular frequency can be finally obtained. The results are shown in Figures 5a–c.

As can be seen,

η_{1}

is highly dependent on frequency and Gf content. More specifically, decreases with frequency and increases with Gf content. Although as in the ideal Jeffreys model

η_{2}

represents the viscosity of the completely unstructured material, i.e., theoretically it should be independent of the frequency, we can see that it decreases with frequency. However, it is worthy to note that

η_{1} ≫ η_{2}

by some orders of magnitude. Results from Figure 5a correspond to very low shear rate range after using the relationship

{\dot{γ}}_{o} = γ_{o} ω

. Specifically, the shear rate interval

[10^{- 4} - 10^{- 2} s^{- 1}]

is accessible with the use of oscillatory rheological tests. Therefore, these results can be combined with results obtained in the shear rate range

[10^{- 1} - 10^{2} s^{- 1}]

using continuous rheological tests to obtain information on the viscosity dependence with the shear rate in a much wider range. As can be seen in Figure 2, the results obtained using both methods are consistent.

The shear modulus

G

increases only very slightly with frequency (Figure 5b). This means that Gf/AVJ suspensions stiffness only a little bit when the experimental time decreases. It is worthy to note that this material function raised a saturation value when Gf concentration was

20 % w / w

, i.e., the microstructure achieved the stiffer state with this Gf concentration.

The relaxation time

λ_{1}

and the retardation time

λ_{2}

decrease with frequency (Figure 5c). As the retardation time

λ_{2}

is much lower than the relaxation time

λ_{1}

, liquid-like behavior is dominant in the full frequency range. On the other hand,

λ_{1}

increases with Gf content suggesting liquid-like behavior due to higher presence of Gf particles in the suspension. In other words, the presence of higher Gf content in the suspension gives place to higher dissipation of energy (viscous effect, liquid-like behavior). Note that, from data shown in Figure 3 the relative increase of the viscous modulus

G ´ ´

is higher than the relative increase of the elastic modulus

G ´

when the amount of Gf in suspensions increases. Therefore, it is apparent that the elastic behavior of AVJ solvent due to entanglement of polysaccharide molecules is diminished by the presence of Gf particles probably due to breaking of links, reducing the extent and stiffness of the network formed by polysaccharide molecules. From a sensorial point of view, this means that increasing the addition of Gf to AVJ changes the texture of the suspension from chewy to creamy.

4. Conclusions

Considering that the texture of food products must be accepted by customers, the influence of Gf concentration on the rheological behavior of Gf/AVJ suspensions was studied.

Rheological measurements were performed with a stress-controlled rheometer with a double-gap geometry to record rheometric data. In this way, the inertia of the rotor was reduced, which is especially useful for oscillatory shear (viscoelastic) measurements.

Steady flow curves showed abrupt shear-thinning behavior of Gf/AVJ suspensions independently of the Gf content. Therefore, the shear-thinning behavior of Gf/AVJ suspensions is justified by the shear-thinning behavior of the carrier liquid (AVJ). The presence of Gf particles gives place to an additional flow field distortion increasing the viscosity at each shear rate value. The ability of Gf particles and aggregates to distort the flow field was quantified determining the intrinsic viscosity

([η])

of the suspensions at several shear rates using Krieger-Dougherty equation. Results indicated that the shape and size of Gf aggregates is not affected by the mechanical action due to shear. Therefore, it was confirmed that the shear-thinning behavior observed in Gf/AVJ suspensions is mainly due to the shear thinning behavior shown by AVJ solvent.

Small amplitude oscillatory shear (SAOS) was applied to Gf/AVJ suspensions to characterize the microstructure-at-rest. Gel appearance of the suspensions was confirmed measuring the dependence of linear viscoelastic moduli with the experimental time using frequency sweep tests. Jeffreys mechanical model was used for the analysis of the LVE response of Gf/AVJ suspensions. It was obtained that liquid-like behavior is dominant in the full frequency range despite gel appearance of suspensions. In addition, increasing Gf content enhances the liquid-like behavior of suspensions or diminishes the elastic response, i.e., from a sensorial point of view, increasing presence of Gf changes the texture of suspensions from chewy to creamy.

Author Contributions

Conceptualization, F.J.R.H.; methodology J.R.M. and E.L.G.; data curation, J.R.M. and E.L.G.; writing—original draft preparation, F.J.R.H.; writing—review and editing, F.J.R.H., J.R.M., and E.L.G.; supervision, F.J.R.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The figures and tables used to support the findings of this study are included in the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Hes, M.; Dziedzic, K.; Górecka, D.; JedrusekGolinska, A.; Gujska, E. Aloe vera (L.) Webb.: Natural Sources of Antioxidants-A Review. Plant Foods Hum. Nutr. 2019, 74, 255–265. [Google Scholar] [CrossRef] [PubMed]
Chhikara, N.; Kaur, A.; Mann, S.; Garg, M.K.; Sofi, S.A.; Panghal, A. Bioactive compounds, associated health benefits and safety considerations of Moringa oleifera L.: an updated review. Nutr. Food Sci. 2020, 51, 255–277. [Google Scholar] [CrossRef]
Domínguez-Fernández, R.N.; Arzate-Vázquez, I.; Chanona-Pérez, J.J.; Welti-Chanes, J.S.; Alvarado-González, J.S.; Calderón-Domínguez, G.; Garibay-Febles, V.; Gutiérrez-López, G.F. Aloe vera gel: structure, chemical composition, processing, biological activity, and importance in pharmaceutical and food industry. Rev. Mex. Ing. Quim. 2012, 11, 23–43. [Google Scholar]
Sonowane, S.K.; Gokhale, J.S.; Mulla, M.Z.; Kandu, V.R.; Patil, S. A comprehensive overview of functional and rheological properties of aloe vera and its applications in foods. J. Food Sci. Technol. 2021, 58, 1217–1226. [Google Scholar] [CrossRef] [PubMed]
Matabura, V.V.; Rweyemamu, L.M.P. Effects of Xanthan gum on rheological properties of Aloe-vera-Moringa leaf juice blends. Tanzan. J. Sci. 2021, 47, 583–596. [Google Scholar] [CrossRef]
Diario Oficial de la Unión Europea (DOUE). Reglamento de Ejecución (U.E.) nº 128/2014.
Caballero-Mesa, J.M. Estudio toxicológico, higiénico-sanitario y nutricional del gofio canario. PhD Thesis, Universidad de La Laguna, Canary Island, Spain, 2010. [Google Scholar]
Hu, Y.; Xu, J.; Hu, Q. Evaluation of antioxidant potential of aloe vera (aloe vera barbadensis Miller) extracts. J. Agric. Food Chem. 2003, 51, 7788–7791. [Google Scholar] [CrossRef] [PubMed]
He, Q.; Liu, C.; Kojo, E.; Tian, Z. Quality and safety assurance in the processing of aloe vera gel juice. Food Control 2005, 16, 95–104. [Google Scholar] [CrossRef]
Hulle, N.R.S.; Patruni, K.; Rao, P.S. Rheological properties of aloe vera (aloe barbadensis Miller) juice concentrates. J. Food Process Eng. 2014, 37, 375–386. [Google Scholar] [CrossRef]
Prieto-Méndez, J.; Rubio-Hinojosa, C.U.; Román-Gutiérrez, A.D.; Méndez-Marzo, M.A.; González-Ramírez, A.; Prieto-García, F. Degradación física del almidón de cebada (hordeum sativun Jess). Correlación entre la gelatinización y el tamaño de gránulos. Multiciencias 2009, 9, 115–125. [Google Scholar]
Masoero, E.; Delgado, E.; Pellenq, R.M.; Ulm, F.J.; Yip, S. Nanostructure and nanomechanics of cement: Polydisperse colloidal packing. Phys. Rev. Lett. 2012, 109, 155503. [Google Scholar] [CrossRef] [PubMed]
Rao, M.A. Rheology of fluid and semisolid foods. Principles and applications; Springer: New York, U.S.A., 2007. [Google Scholar]
Dak, M.; Verma, R.C.; Sharma, G.P. Flow characteristics of juice of “Totapuri” mangoes. J. Food Eng. 2006, 76, 557–561. [Google Scholar] [CrossRef]
Sesmero, R.; Mitchell, J.; Mercado, J.; Quesada, M. Rheological characterization of juices obtained from transgenic pectate lyase-silenced strawberry fruits. Food Chem. 2009, 116, 426–432. [Google Scholar] [CrossRef]
Rubio-Merino, J.; Rubio-Hernández, F.J. Activation energy for the viscoelastic flow: Analysis of the microstructure-at-rest of (water- and milk-based) fruit beverages. Food Chem. 2019, 293, 486–490. [Google Scholar] [CrossRef] [PubMed]
Rubio-Hernández, F.J.; Ayúcar-Rubio, M.F.; Velázquez-Navarro, J.F.; Galindo-Rosales, F.J. Intrinsic viscosity of SiO₂, Al₂O₃, and TiO₂ aqueous suspensions. J. Colloid Interface Sci. 2006, 298, 967–972. [Google Scholar] [CrossRef] [PubMed]
Krieger, I.M.; Dougherty, T.J. Concentration dependence of the viscosity of suspensions. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
Gómez-Merino, A.I.; Rubio-Hernández, F.J.; Velázquez-Navarro, J.F.; Aguiar, J.; Jiménez-Agredano, C. Study of the aggregation state of anatase-water nanofluids using rheological and DLS methods. Ceram. Int. 2014, 40, 14045–14050. [Google Scholar] [CrossRef]
Sánchez, A. Colloidal gels of fumed silica: microstructure, surface interactions, and temperature effects. PhD Thesis, North Carolina State University, U.S.A., 2006. [Google Scholar]
Leite, R.T.; de Souza-Mendes, P.R.; Thompson, R.L. A simple method to analyze materials under quasilinear large amplitude oscillatory shear flow (QL-LAOS). J. Rheol. 2019, 63, 305–317. [Google Scholar] [CrossRef]

Figure 1. SEM image of Canary Gf (corn, wheat, and oats mixture). The average particle size was

11.6 μ m

with a polydispersity index of

1.6 μ m

Figure 1. SEM image of Canary Gf (corn, wheat, and oats mixture). The average particle size was

11.6 μ m

with a polydispersity index of

1.6 μ m

Figure 2. Viscosity vs. shear rate. Note the consistence of the results obtained using continuous and oscillatory shear tests.

Figure 3. Frequency sweeps in the LVE region.

γ_{o} = 0.001

. Gf/AVJ is a stronger viscoelastic gel when the Gf amount increases in the Gf/AVJ suspension.

Figure 3. Frequency sweeps in the LVE region.

γ_{o} = 0.001

. Gf/AVJ is a stronger viscoelastic gel when the Gf amount increases in the Gf/AVJ suspension.

Figure 4. The Jeffreys mechanical analog.

Figure 5. Jeffreys material functions of Gf/AVJ suspensions vs. angular frequency: a)

η_{1}

open symbols,

η_{2}

full symbols; b)

G

; and c)

λ_{1}

open symbols,

λ_{2}

full symbols. See text for interpretation.

Figure 5. Jeffreys material functions of Gf/AVJ suspensions vs. angular frequency: a)

η_{1}

open symbols,

η_{2}

full symbols; b)

G

; and c)

λ_{1}

open symbols,

λ_{2}

full symbols. See text for interpretation.

Table 1. Composition and properties of Gf/AVJ suspensions. Density and pH slightly increased with the amount of Gf. Viscosity vs. shear rate experimental data was fitted with a power law. The consistency of the suspension increases with the amount of Gf.

$Gf (% w / w)$	$p H$	$Density (k g / m^{3})$	$K$ $(P a \cdot s^{n})$	$n (-)$	$R^{2}$
0	$3.6 \pm 0.1$	$262 \pm 1$	$0.045 \pm 0.001$	$0.39 \pm 0.01$	$0.9897$
5	$3.6 \pm 0.1$	$273 \pm 1$	$0.072 \pm 0.001$	$0.38 \pm 0.01$	$0.9988$
10	$3.8 \pm 0.1$	$285 \pm 1$	$0.191 \pm 0.003$	$0.41 \pm 0.01$	$0.9954$
15	$4.0 \pm 0.1$	$296 \pm 1$	$0.443 \pm 0.005$	$0.41 \pm 0.01$	$0.9965$
20	$4.2 \pm 0.1$	$307 \pm 1$	$1.15 \pm 0.02$	$0.41 \pm 0.01$	$0.9938$
25	$4.4 \pm 0.1$	$319 \pm 1$	$2.48 \pm 0.04$	$0.41 \pm 0.01$	$0.9944$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Effects of Gofio on the Rheological Properties of Aloe Vera Juice

Abstract

1. Introduction

2. Materials and Methods

3. Results and Discussion

3.1. Steady Viscous Behavior

3.2. Viscoelastic Behavior

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe