Superelsatic SMA Honeycomb Damper for Seismic Protection of Bridges

Despite the fact that SMA restrainers exhibit a superelastic strain capacity of 7%, this capacity appears inadequate for isolated bridges due to the typically greater than 20cm relative dis-placements between girders during intense seismic events. In order to perform such a stroke, a SMA restrainer of greater than 3 metres in length might be required. In order to reduce the length of restrainers, a novel honeycomb damper constructed from superelastic shape memory alloy (SMA) is proposed. The proposed device, denoted as the superelastic SMA honeycomb damper (SHD), is comprised of steel plates to prevent the SMA plane from collapsing and superelastic SMA honeycomb to provide self-centering capability. By incorporating the large strain capacity of SMA and the geometrically nonlinear deformation of honeycomb structures, SHD has been developed to satisfy the requirements of bridge restrainers with large strokes. It is capable of functioning as a restrainer and energy dissipation device when subjected to dynamic tension and compression loads. The SHD was initially investigated from a theoretical perspective. Following this, a mul-ti-cell SHD specimen was manufactured. The specimen underwent axial tensile and compressive experiments in order to examine the mechanical properties of SHDs. Finally, experimental results were investigated through numerical simulation analyses of the SHDs using a three-dimensional high-fidelity finite element model. Additionally, a method for enhancing SHD was proposed. The findings indicate that SHD is capable of exhibiting superior self-centering capability and sta-ble hysteretic responses when subjected to earthquakes.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Numerous seismic incidents have provided evidence that bridges with simple supports are susceptible to unseating failure as a result of excessive displacements between the piers and girders^1-4. In addition to unseating failure, the intractable problem of dynamic impact between load-bearing members of bridges during intense earthquakes poses a threat to the structural integrity of the bridges and consequently compromises their resistance to seismic events^{1, 4}.

In order to address these challenges, steel-based restrainers were employed to restrict the movement of two adjacent spans⁵. However, the displacement capacity of these rigid restrainers is relatively low. As a consequence, the bridge's substructure may be subjected to a substantial instantaneous load and subsequently collapse during a strong or near-fault earthquake.

To enhance the seismic resistance performance of steel-based restrainers, Javanmardi et al.⁶ developed a hexagonal honeycomb steel damper (HHSD) which is composed of steel plates with multiple cellular and two anchors that distribute the load. An assessment of the device's performance under quasi-static cyclic conditions indicates that the proposed HHSD possesses a remarkable capacity for energy dissipation and a wide range of ductility. There are also proposals for shape memory alloy (SMA) restrainers that can withstand significant displacement and function as energy dissipation devices^{5, 7-19}. Re-strainers can demonstrate high fatigue resistance, energy consumption, anti-corrosion, and self-centering abilities with the use of SMA material^20-24. Therefore, SMAs are regarded as the optimal material for bridge restrainers. They are capable of reshaping to their initial configuration following a 7% strain deformation, and their characteristic flag-shaped hysteretic behaviour allows them to dissipate input energy when loaded^25-29.

Cellular structures have gained considerable interest in engineering applications due to the distinctive energy absorption properties and high stiffness-to-mass ratios that they offer in comparison to metallic restrainers^30-32. An in-plane deformation behaviour and buckling mechanism analysis were conducted by Michailidis et al.30 on a Ni-Ti SMA structure with narrow walls. It was observed that the honeycomb structure retains its capacity for self-recovery even after undergoing substantial deformation, provided that the strain of the SMA material remains below 7% (ultimate recoverable strain of SMA material) ³⁰. This affords the honeycomb structure a notable advantage in that it can withstand a maximum macro strain of 41.7%.

In this paper, a self-centering SMA honeycomb damper (SHD) is proposed. The material utilises the geometrical nonlinearity of honeycomb structures and the superelastic nature of SMA materials. Its overall strain is much bigger than local strain^{6, 33, 34}.

In the introduction, the configuration and operational mechanism of SHD are described. A specimen of SHD is subsequently fabricated and evaluated. Discussion follows of the results. Experimental results are then used to validate a three-dimensional finite element model of the specimen. Furthermore, the impact of wall thickness on the properties of SHD is examined through the implementation of parametric analyses. Additionally, a method to improve the deformation capacity of SHDs is suggested at last.

2. Superelsatic SMA honeycomb damper

2.1. Design principle and configuration

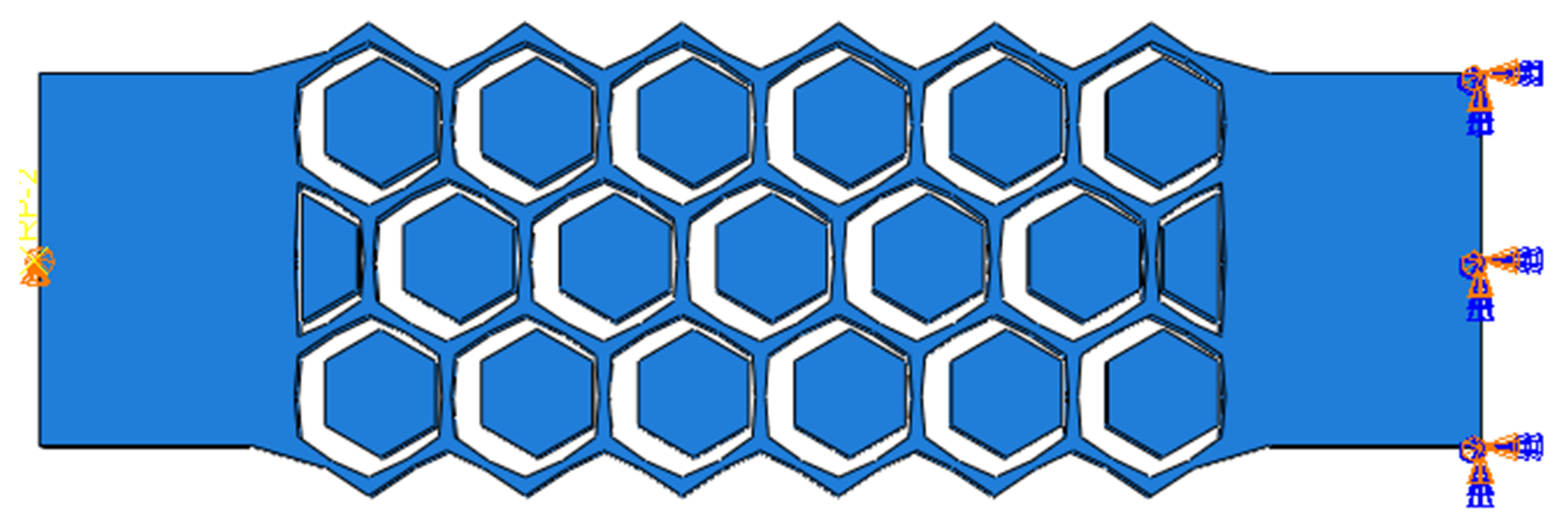
The honeycomb, as depicted in Figure 1, possesses a hexagonal configuration. Due to its thin walls and porous interiors, it exhibits a substantial capacity for deformation when stretched or compressed transversely due to its geometric nonlinearity. Motivated by this phenomenon, we proposed a superelstic SMA honeycomb damper in an attention to enhance the deformation of superelastic SMA restrainers through their geometrical nonlinearity.

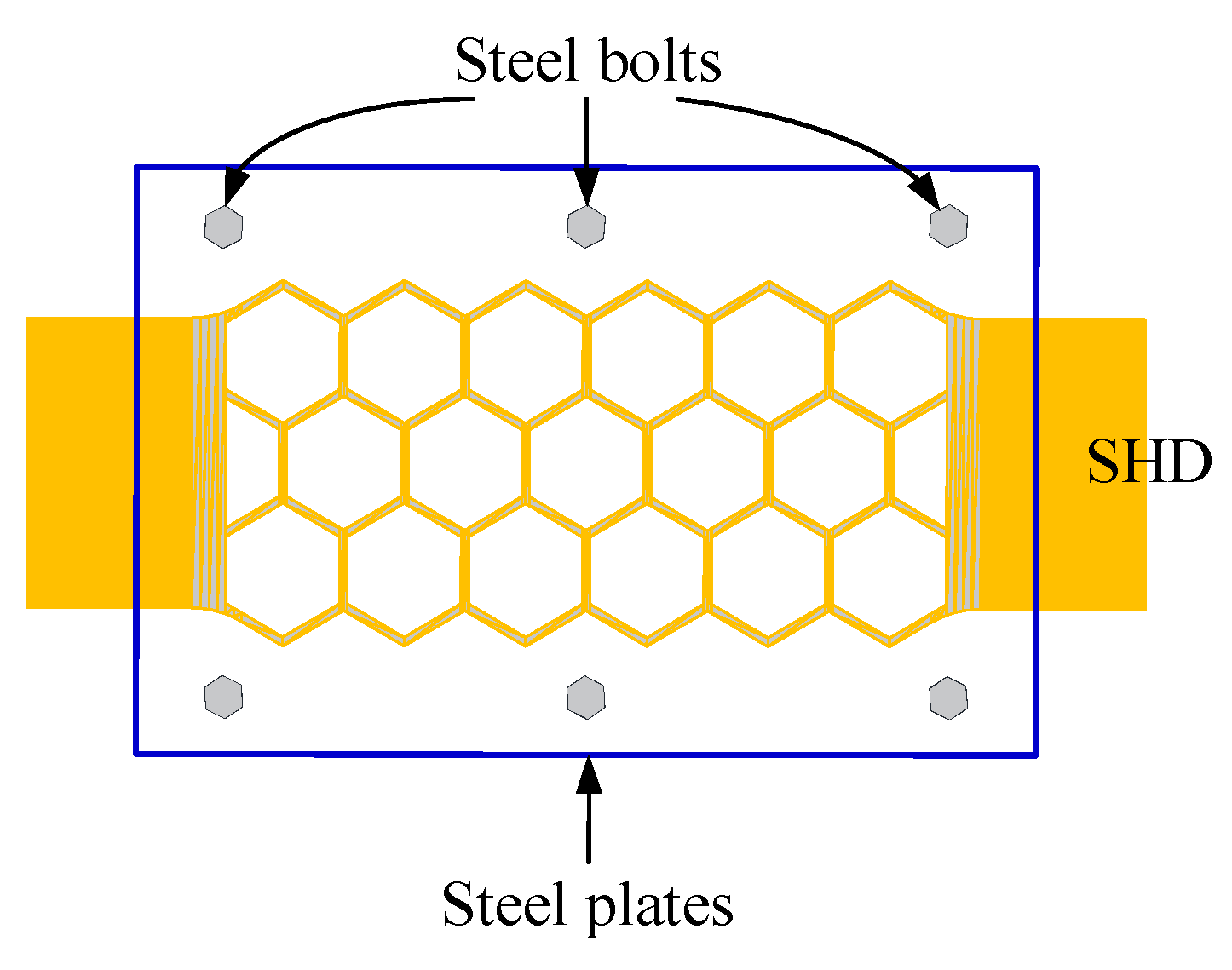
Figure 2 illustrates the Superelsatic SMA honeycomb damper (SHD) that was proposed. It is comprised of two steel plates that encase the superelastic SMA honeycomb plate, which provides energy dissipation and self-centering capabilities. When the restrainer is compressed, the out-of-plane deformation of the SHD will be restricted by the steel plates.

2.2. Working mechanism

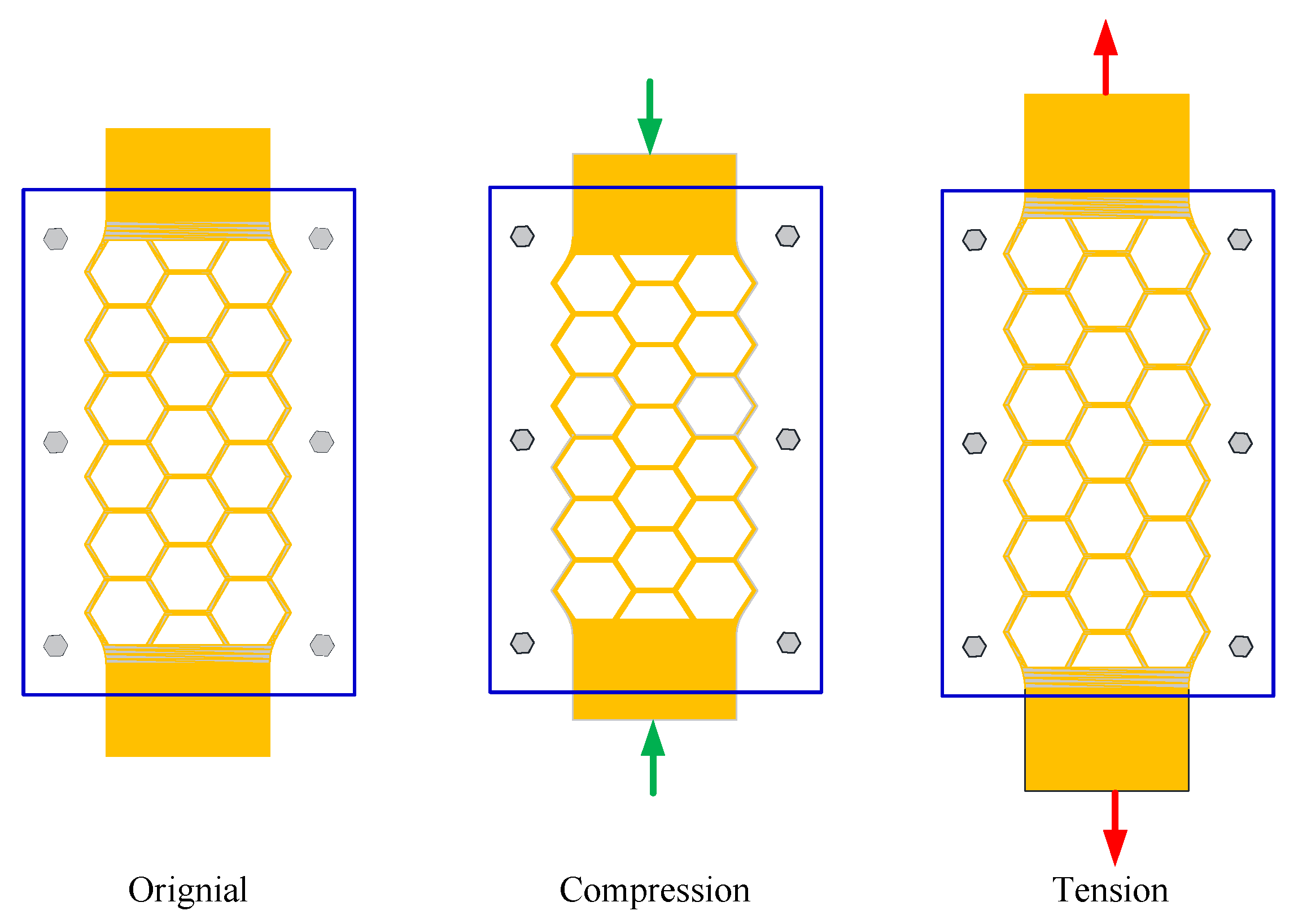
The working mechanism of SHD is depicted in Figure 3. Compression of the superelastic SMA honeycomb plate results in the compression of its geometrical shape, as well as the development of compressive strain in the SMA materials. The geometrical nonlinearity of superelastic SMA plates increases their capacity for deformation. An impending macro strain on the damper in excess of 7% is reasonable. The geometrical shape of the superelastic SMA honeycomb plate undergoes stretching under tension, accompanied by the development of tensile strain in the SMA materials. The geometrical nonlinearity of superelastic SMA plates further amplifies their deformation capacity. Incorporating the superlastic characteristic of SMA materials enables the damper to restore its initial configuration upon removal of the load.

2.3. Theoretical analysis of a singular hexagonal cell

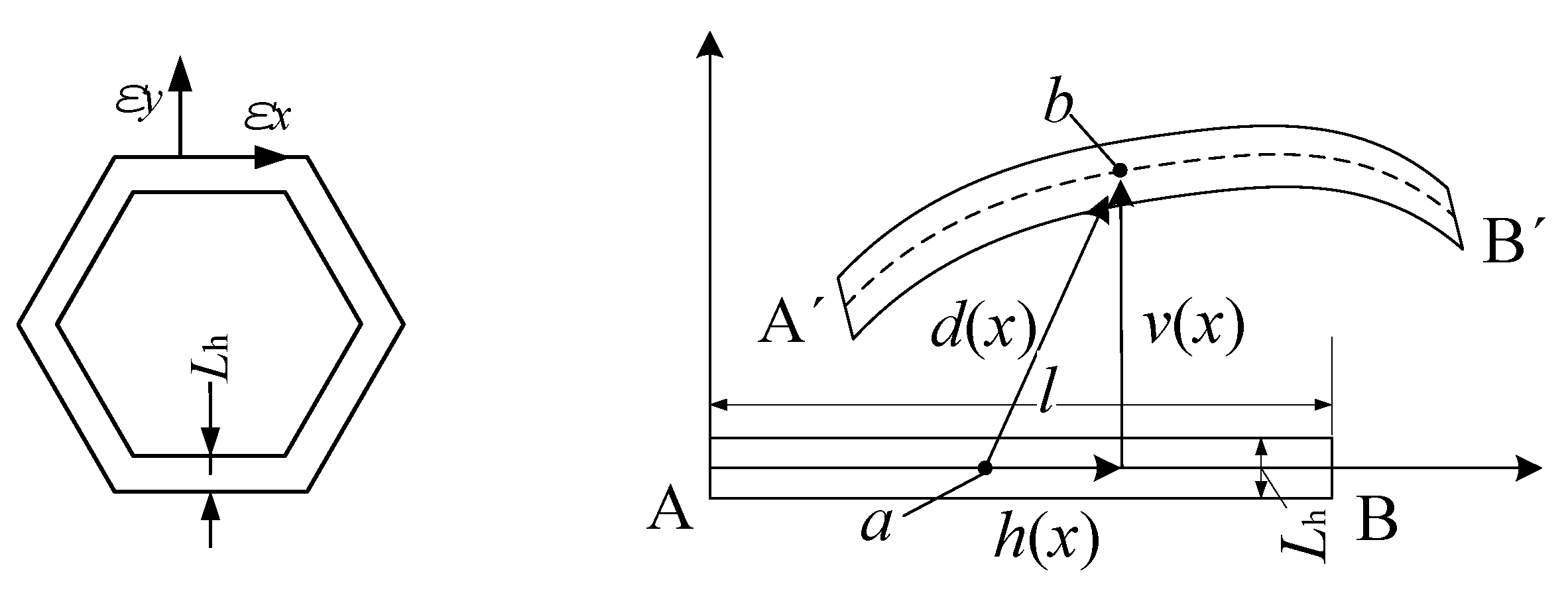
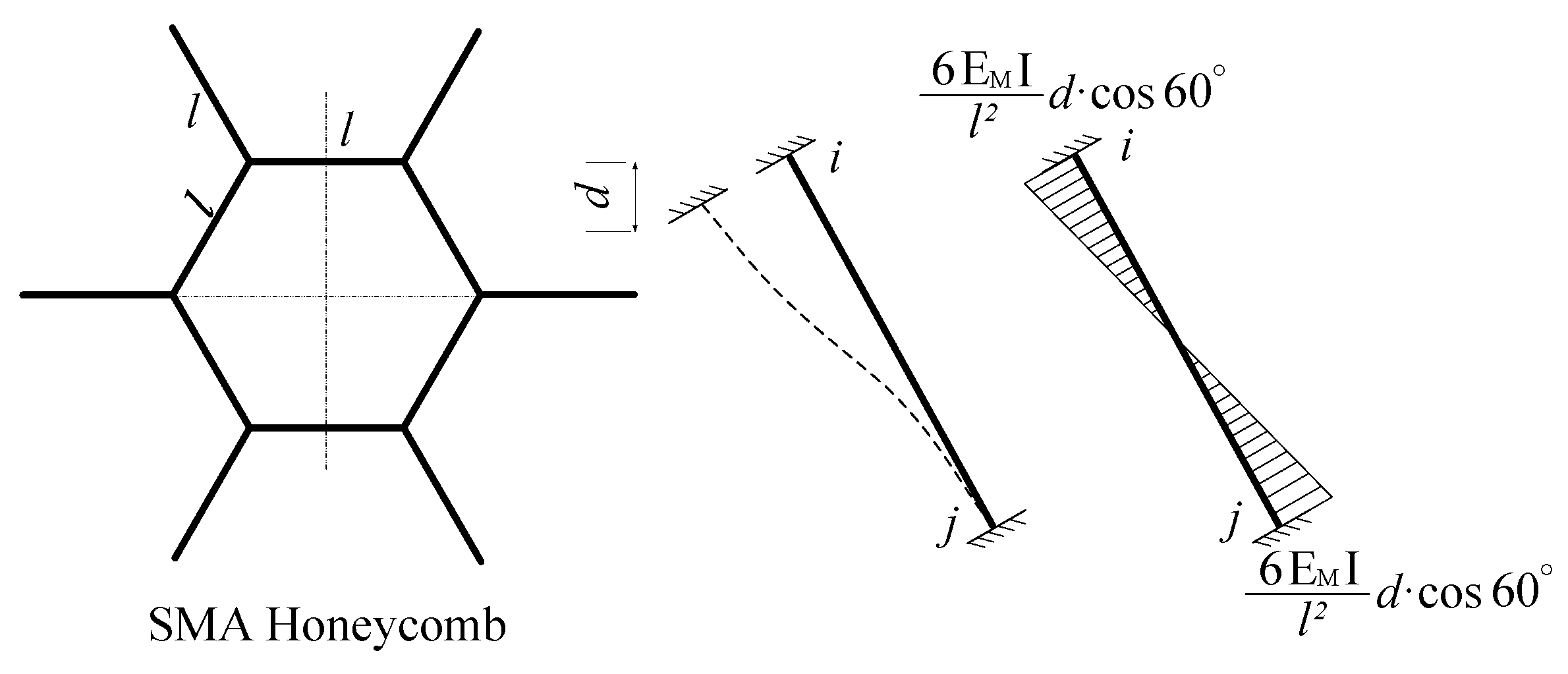
Figure 4 illustrates a regular hexagonal cell that originates from a honeycomb structure. The figure illustrates that the cell wall has a length of l and a thickness of L_h. The cell undergoes a reshaping process through bending when subjected to an in-plane load (specifically, along the y-axis in this study). As a result, each cell wall can be regarded as a nonlinear beam capable of withstanding significant displacements and rotations³⁰.

According to the local coordinate system depicted in Figure 4, the honeycomb beam is simplified as a straight beam with a thickness of L_h and a length of l. The beam will bend and move when the honeycomb is loaded (point a to point b). v(x) and h(x) are used to express the displacement vector of the points along the longitudinal and transverse directions. The Euler Bernoulli beam theory postulates that the cross section of small strain beam stays perpendicular to the central axis both before and after deformation. In other words, when the beam experiences warping and transverse shear deformation, the transverse strain can be disregarded, and the plane stays flat and perpendicular to the central axis after deformation. According to the above assumption, the axial strain of any point with initial local coordinate (x, y) is given by:

ε (x, y) = γ (x) + y k (x)

(1)

where γ(x) is the axial strain function of each point on the central axis and k is the bending curvature. The dis-placement vector components in the vertical and horizontal directions can be expressed by v(x) and h(x) as:

γ = \sqrt{{(1 + \frac{d h}{d x})}^{2} + {(\frac{d v}{d x})}^{2}} - 1

(2)

k = \frac{[\frac{d v}{d x} \frac{d^{2} h}{d x^{2}} - (1 + \frac{d h}{d x}) \frac{d^{2} v}{d x^{2}}]}{[{(1 + \frac{d h}{d x})}^{2} + {(\frac{d v}{d x})}^{2}]}

(3)

The internal virtual work contribution of each node in the weak form of the equilibrium equation can be written as:

δ W_{l}^{I} = \int_{0}^{1} (N δ e + M δ k) d x

(4)

N \equiv \int_{- L_{h} / 2}^{L_{h} / 2} σ d y

(5)

M \equiv \int_{L_{h} / 2}^{L_{h} / 2} σ y d y

(6)

where N(x) and M(x) are the combined axial forces and bending moments on the honeycomb wall, respectively, and σ is the axial stress on the honeycomb wall. Corresponding to the Euler-Lagrange equations of equations (1), (2) and (3), the consistency between them and the equilibrium equation has been proved in detail in literature [30].

3. Experimental test

3.1. Specimen

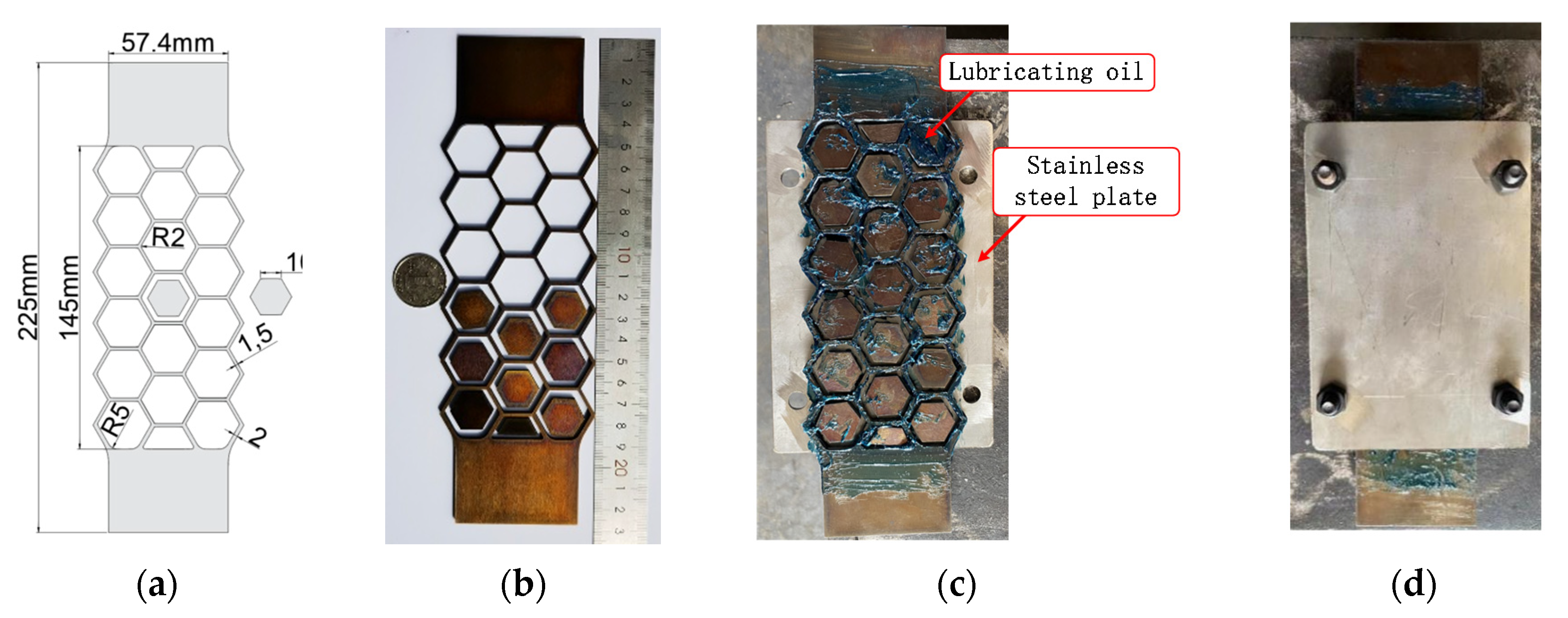
A prototype of the SMA honeycomb damper is conceptualised and produced, as illustrated in Figure 5a, on the basis of the parameter analyses of SHD. Graded wall thickness of the honeycomb structure was implemented in order to avert premature fracture of SMA materials. Subsequent layers had respective wall thicknesses of 1.5mm and 2mm for the initial and subsequent layers. SMA hexagonal core plates were inserted into each cell with spaces left for SHD deformation in order to prevent the structure from entirely buckling.

The specimen consists of a series of internal hexagonal blocks, a shape memory alloy (SMA) honeycomb plate, and two stainless steel plates. The damper is equipped with internally installed solid hexagonal blocks that function as displacement limiting devices.

Initially, a nitinol shape memory alloy (SMA) plate measuring 225mm in length and 75mm in width underwent a heat treatment process at a temperature of 400 °C for a duration of 30 minutes. In this manner, the plate would exhibit an excellent superelastic characteristic³⁵. Subsequently, the SMA honeycomb and SMA hexagonal core plates were precisely cut from the original plate using a molybdenum wire. Following that, the hexagonal core plates of the Shape Memory Alloy (SMA) were affixed within the SMA honeycomb structure, ensuring that any spaces or voids were adequately filled with lubricating oil. Finally, the SMA honeycomb and core plates were enveloped by a pair of stainless steel plates, securely fastened together using steel bolts.

3.2. Test setup and loading procedure

A MTS servo hydraulic system was utilised to apply cyclic tensile and compressive loading processes axially on the specimen, as depicted in Figure 6.

The specimen was affixed using the upper and lower clamping arms of the MTS servo hydraulic system. Subsequently, a pseudo-static displacement load procedure was performed at a strain rate of 0.00025/s via the upper clamping arm. The displacement loading procedure commences with an amplitude of 2mm, increasing by 2mm at each stage of loading until the specimen fractures. A single cycle loading was carried out for every amplitude of displacement.

3.3. Experimental results

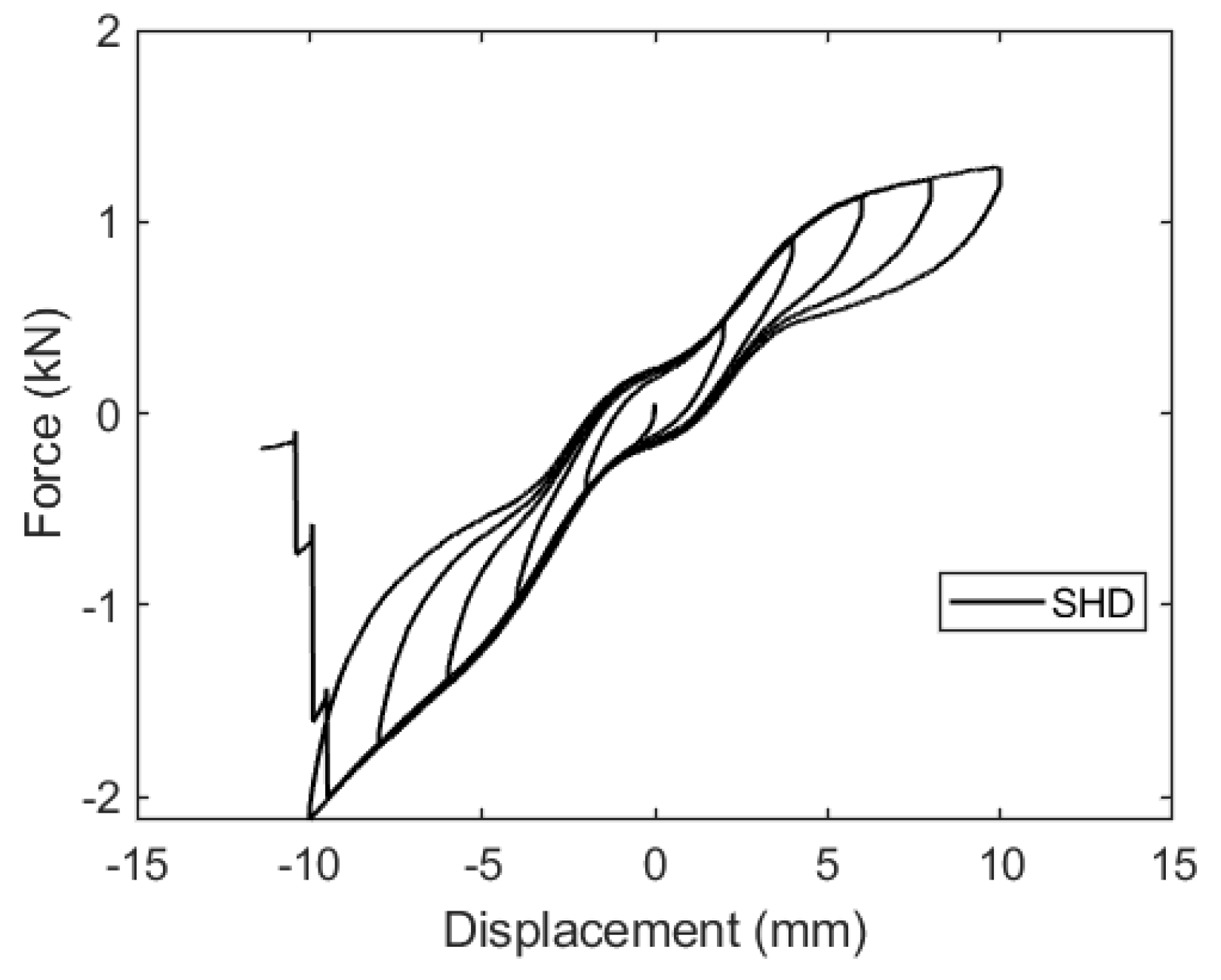
Figure 7 illustrates the force-displacement relationship of the specimen, revealing responses in the form of a stable flag-shape. This suggests that SHD exhibit a consistent hysteretic performance and a remarkable ability to self-center. The specimen exhibits a macroscopic fracture strain of 6.9%, marginally exceeding the fracture strain observed in superelastic SMA plates or bars. It should be noted that there exists a discrepancy between the observed fracture strain in the experiment and the expected fracture strain, with the latter being 10% or greater.

The fracture parts are situated at the outermost part of the honeycomb cell's sharp edge and one of its interior connecting nodes (see Figure 8). Based on the observed fracture morphology of the specimen, it can be inferred that the failure occurred due to a notable stress concentration at the sharp edge during the tensioning or compressing processes. Shape memory alloys (SMA) exhibit a pattern of metal fatigue and the formation of microcracks following cyclic tension and compression. Moreover, microcracks tend to develop fast during the loading process, which ultimately results in the fracture of the specimen.

4. Numerical simulation of SHD

4.1. Finite element model

A three-dimensional finite element (FE) model of the SHD was created using the Abaqus 2021 software package, as depicted in Figure 9³⁶. The interaction between steel plates and shape memory alloy (SMA) honeycomb was modelled as a hard contact condition, with a friction coefficient of 0.3. In order to maintain consistency with the experimental condition, the lower surface of the SHD model was fixed, while a displacement loading procedure was applied to a reference point that was connected to the upper surface of the model. The particular properties of the SMA material are defined based on the reference [10].

4.2. Experimental and simulated results

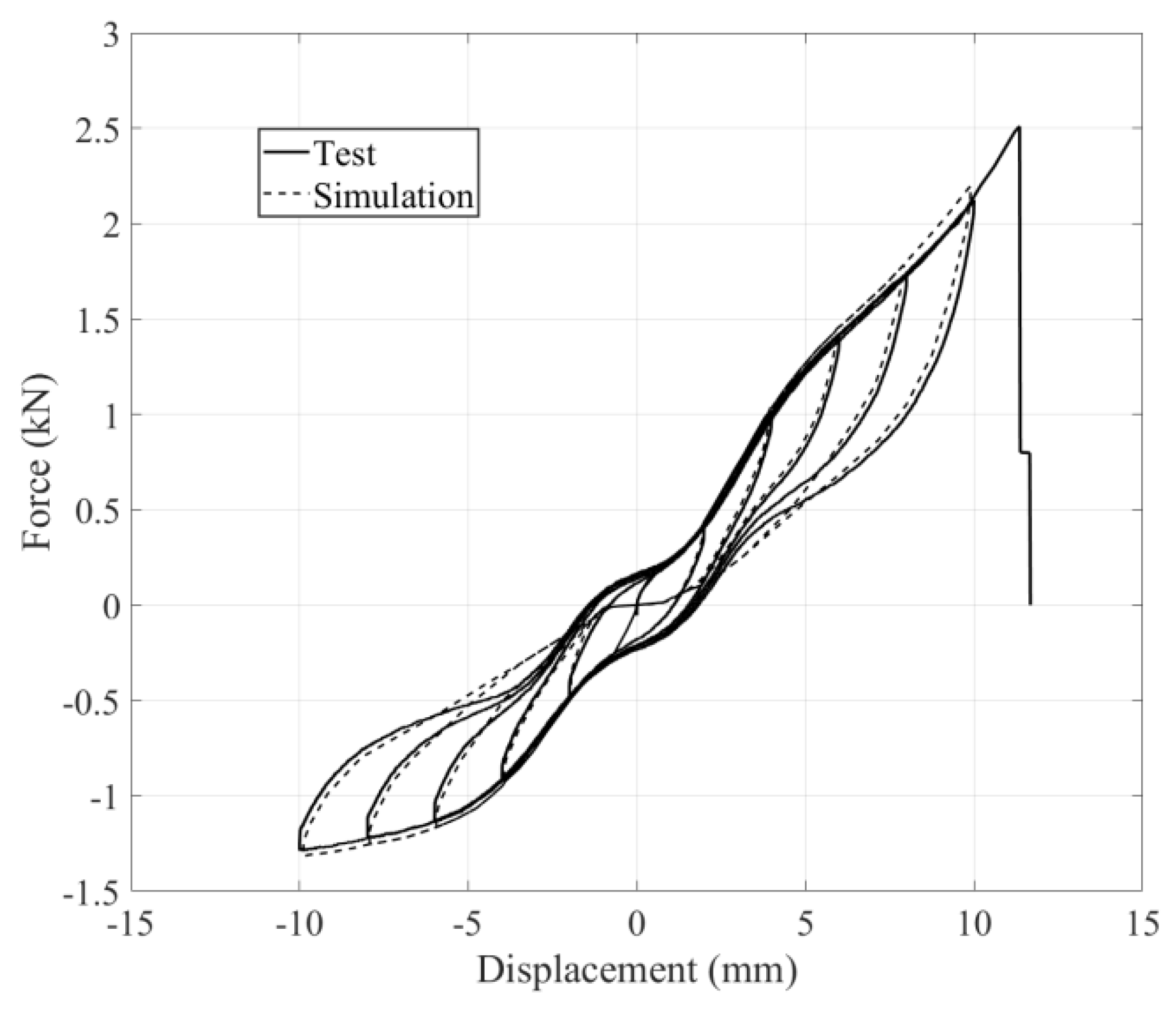
In Figure 10, a comparison is made between the hysteresis responses of the SHD obtained from experimental data and those obtained from simulation. The simulated replies demonstrate a strong capacity for accurately predicting experimental results.

Figure 11 depicts the strain distribution of the honeycomb plate at a displacement of 12mm upon fracture. The localization of maximal strain in the specimen is evident at the corners, precisely where the fracture occurred, as illustrated in Figure 8. The largest strain observed is 10.62%, which is significantly greater in magnitude compared to the fracture strain of 7%. Consequently, the specimen experienced fracture at this particular juncture.

5. Improvement of SHD

The investigation revealed that the specimen experienced fracture at a macroscopic strain of 6.9%, a value that is notably lower than the supposed design target. The occurrence of fracture in the honeycomb structure can be attributed to the presence of localised stress concentration at its corner. Consequently, it is necessary to enhance the layout of SHDs in order to achieve the anticipated design objective of achieving a long stroke.

5.1. Optimization of SHD

The SMA honeycomb structure can be represented in a simplified manner as a beam with fixed ends, as illustrated in Figure 12. The graphic also illustrates the distribution of bending moment for this particular beam configuration.

In the study conducted by Aydogdu et al.[29], it was found that beams with varying cross-sectional heights along the length direction exhibit a more uniform strain distribution and a notable reduction in stress concentration. This effect is particularly observed in beams that possess in-plane rotation angles and relative displacement at both ends. The stress distribution along the walls of a shape memory alloy (SMA) honeycomb structure will exhibit uniformity when the wall thickness corresponds to the distribution of bending moments.

Therefore, the thickness of both ends of a non-horizontal cell wall can be estimated as follows:

b = \sqrt[3]{\frac{12 M_{p}}{t \cdot ω E_{M}}}

(1)

where b is the minimum wall thickness at the beam's end, Mp is the bending moment at the beam's end, and t is the thickness of the honeycomb plate, indicating the beam's bending curvature.

ω

is calculated as:

ω = \frac{M_{p}}{E_{M} \cdot I}

(2)

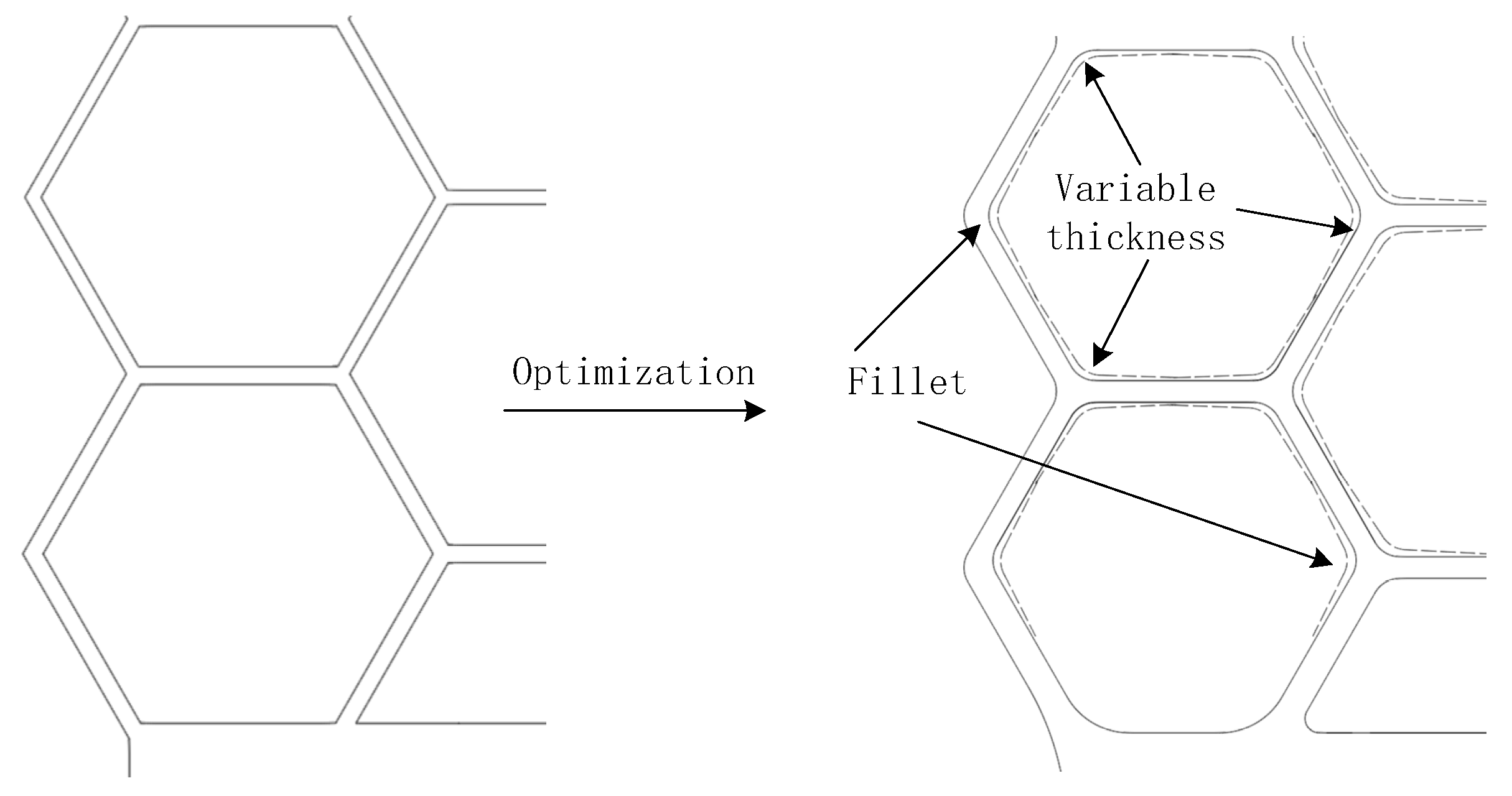
The wall thickness in the middle of the cell wall is calculated using the initial λ. Figure 13 demonstrates the optimization of SMA honeycomb with variable wall thickness.

5.2. Validation of optimization

A numerical model of the SHD system was developed using an optimisation approach. The strain distribution of this model was then compared to that of the original model in order to assess the efficacy of the optimisation scheme. The minimum thickness of the nonhorizontal cell wall ends was computed as:

b_{1} = \sqrt[3]{\frac{12 M_{p 1}}{t \cdot ω_{1} E_{M}}} = \sqrt[3]{\frac{12 \times 6 \times 1.40625 \times 1 0^{- 12} \times 0.0019 \times 0.5}{0.1 \times 0.3867 \times 0.0225}} = 0.002531 m

(3)

Figure 14 shows the optimized numerical model of SHD. R represents the radius of the chamfer angle (unit: mm).

The fracture strain strain distribution of the optimised model is depicted in Figure 15. After optimisation, there has been a significant reduction in the tension concentration within the specimen. The fracture strain of the optimised model is 6.59% at 15% overall strain, which is significantly less than the SMA strain at fracture for the unoptimized specimen model. It suggests that by employing a fillet and variable wall thickness scheme, fatigue fractures in SMA honeycomb can be effectively delayed, thereby preventing the premature failure of SHD.

6. Conclusions

In the paper, an innovative SMA honeycomb damper (SHD) is proposed. A prototype of the suggested damper was constructed, subjected to experimental testing, and subsequently analysed through numerical investigation. The primary findings indicate:

1. The SHD integrates the geometrically nonlinear characteristic of honeycomb structures with superelastic shape memory alloy (SMA) materials. Consequently, it possesses the ability to provide a substantial deformation within a restricted length.

2. The SHD exhibits exceptional self-centering capacity and stable hysteretic responses. The incorporation of this technique in the seismic design of structures has the potential to significantly improve their resilience.

3. The stress concentration present at the sharp edges of shape memory alloy (SMA) honeycomb structures can be effectively mitigated by adjusting the thickness of the non-horizontal cell wall. This enables SHD to exhibit a comparatively larger stroke in comparison to analogous SMA-based devices. SHD has the capability to provide more than 15% of the overall recoverable global strain, whereas the local strain remains below the maximum recoverable strain of SMA material.

Acknowledgments

The project was financially supported by the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (Grant 2019D19), National Natural Science Foundation of China (Grants 52178124, 51978183, 52108445); Natural Science Foundation of Guangdong Province (Grant 2022A1515011250).

References

Chen, X.; Xiong, J. Seismic resilient design with base isolation device using friction pendulum bearing and viscous damper. Soil Dyn. Earthquake Eng. 2022, 153, 107073. [Google Scholar] [CrossRef]
Xiang, N.; Alam, M.S.; Li, J. Yielding Steel Dampers as Restraining Devices to Control Seismic Sliding of Laminated Rubber Bearings for Highway Bridges: Analytical and Experimental Study. J. Bridge Eng. 2019, 24(11), 04019103. [Google Scholar] [CrossRef]
Pang, Y.; He, W.; Zhong, J. Risk-based design and optimization of shape memory alloy restrained sliding bearings for highway bridges under near-fault ground motions. Engineering Structures 2021, 241, 112421. [Google Scholar] [CrossRef]
Cao, S.; Ozbulut, O.E.; Dang, X.; Tan, P. Experimental and numerical investigations on adaptive stiffness double friction pendulum systems for seismic protection of bridges. Soil Dynamics and Earthquake Engineering 2024, 176, 108302. [Google Scholar] [CrossRef]
Alam, M.S.; Bhuiyan, M.R.; Billah, A.M. Seismic fragility assessment of SMA-bar restrained multi-span continuous highway bridge isolated by different laminated rubber bearings in medium to strong seismic risk zones. Bulletin of Earthquake Engineering 2012, 10, 1885–1909. [Google Scholar] [CrossRef]
Javanmardi, A.; Ghaedi, K.; Ibrahim, Z.; Huang, F.; Xu, P. Development of a new hexagonal honeycomb steel damper. Archives of Civil and Mechanical Engineering 2020, 20, 1–19. [Google Scholar] [CrossRef]
Hedayati Dezfuli, F.; Alam, M.S. Smart lead rubber bearings equipped with ferrous shape memory alloy wires for seismically isolating highway bridges. Journal of Earthquake Engineering 2018, 22(6), 1042–1067. [Google Scholar] [CrossRef]
Ozbulut, O.E.; Hurlebaus, S. Seismic assessment of bridge structures isolated by a shape memory alloy/rubber-based isolation system. Smart Mater. Struct. 2010, 20(1), 015003. [Google Scholar] [CrossRef]
Shrestha, B.; He, L.-X.; Hao, H.; Bi, K.; Ren, W.-X. Experimental study on relative displacement responses of bridge frames subjected to spatially varying ground motion and its mitigation using superelastic SMA restrainers. Soil Dynamics and Earthquake Engineering 2018, 109, 76–88. [Google Scholar] [CrossRef]
Zheng, Y.; Dong, Y. Performance-based assessment of bridges with steel-SMA reinforced piers in a life-cycle context by numerical approach. Bulletin of Earthquake Engineering 2019, 17, 1667–1688. [Google Scholar] [CrossRef]
Zheng, Y.; Dong, Y.; Li, Y. Resilience and life-cycle performance of smart bridges with shape memory alloy (SMA)-cable-based bearings. Constr. Build. Mater. 2018, 158, 389–400. [Google Scholar] [CrossRef]
Cao, S.; Ozbulut, O.E. Long-stroke shape memory alloy restrainers for seismic protection of bridges. Smart Mater. Struct. 2020, 29, 115005. [Google Scholar] [CrossRef]
Li, S.; Hedayati Dezfuli, F.; Wang, J.-q.; Shahria Alam, M. Seismic vulnerability and loss assessment of an isolated simply-supported highway bridge retrofitted with optimized superelastic shape memory alloy cable restrainers. Bulletin of Earthquake Engineering 2020, 18(7), 3285–3316. [Google Scholar] [CrossRef]
Shrestha, B.; He, L.; Hao, H.; Bi, K.; Ren, W. Experimental study on relative displacement responses of bridge frames subjected to spatially varying ground motion and its mitigation using superelastic SMA restrainers. Soil Dyn. Earthquake Eng. 2018, 109, 76–88. [Google Scholar] [CrossRef]
Cardone, D.; Sofia, S. Numerical and Experimental Studies on the Seismic Retrofit of Simply Supported Bridges Using Superelastic Restrainers. Advanced Materials Research 2012, 446-449, 3291–3294. [Google Scholar] [CrossRef]
Guo, A.; Zhao, Q.; Li, H. Experimental study of a highway bridge with shape memory alloy restrainers focusing on the mitigation of unseating and pounding. Earthquake Eng. Eng. Vibr. 2012, 11(2), 195–204. [Google Scholar] [CrossRef]
Fang, C.; Zheng, Y.; Chen, J.; Yam, M.C.; Wang, W. Superelastic NiTi SMA cables: Thermal-mechanical behavior, hysteretic modelling and seismic application. Eng. Struct. 2019, 183, 533–549. [Google Scholar] [CrossRef]
Qiu, C.; Fang, C.; Liang, D.; Du, X.; Yam, M.C. Behavior and application of self-centering dampers equipped with buckling-restrained SMA bars. Smart Mater. Struct. 2020, 29(3), 035009. [Google Scholar] [CrossRef]
Fang, C.; Qiu, C.X.; Wang, W.; Alam, M.S. Self-Centering Structures Against Earthquakes: A Critical Review. JOURNAL OF EARTHQUAKE ENGINEERING 2023. [Google Scholar] [CrossRef]
Ge, J.; Saiidi, M.S.; Varela, S. Computational studies on the seismic response of the State Route 99 bridge in Seattle with SMA/ECC plastic hinges. Frontiers of Structural and Civil Engineering 2019, 13, 149–164. [Google Scholar] [CrossRef]
Wang, J.; Li, S.; Dezfuli, F.H.; Alam, M.S. Sensitivity analysis and multi-criteria optimization of SMA cable restrainers for longitudinal seismic protection of isolated simply supported highway bridges. Eng. Struct. 2019, 189, 509–522. [Google Scholar] [CrossRef]
Zheng, W.-Z.; Wang, H.; Li, J.; Shen, H.-J. Parametric study of SMA-based friction pendulum system for response control of bridges under near-fault ground motions. Journal of Earthquake Engineering 2021, 25(8), 1494–1512. [Google Scholar] [CrossRef]
Deng, J.D.; Hu, F.L.; Ozbulut, O.E.; Cao, S.S. Verification of multi-level SMA/lead rubber bearing isolation system for seismic protection of bridges. Soil Dynamics and Earthquake Engineering 2022, 161. [Google Scholar] [CrossRef]
Zheng, W.; Tan, P.; Li, J.; Wang, H.; Tan, J.; Sun, Z. Sliding-LRB incorporating superelastic SMA for seismic protection of bridges under near-fault earthquakes: A comparative study. Soil Dynamics and Earthquake Engineering 2022, 155, 107161. [Google Scholar] [CrossRef]
Vaiana, N.; Capuano, R.; Rosati, L. Evaluation of path-dependent work and internal energy change for hysteretic mechanical systems. Mechanical Systems and Signal Processing 2023, 186. [Google Scholar] [CrossRef]
Deng, J.; Hu, F.; Ozbulut, O.E.; Cao, S. Verification of multi-level SMA/lead rubber bearing isolation system for seismic protection of bridges. Soil Dynamics and Earthquake Engineering 2022, 161, 107380. [Google Scholar] [CrossRef]
Cao, S.; Ozbulut, O.E.; Wu, S.; Sun, Z.; Deng, J. Multi-level SMA/lead rubber bearing isolation system for seismic protection of bridges. Smart Mater. Struct. 2020, 29, 055045. [Google Scholar] [CrossRef]
Zheng, W.; Wang, H.; Li, J.; Shen, H. Performance evaluation of bridges isolated with SMA-based friction pendulum system at low temperatures. Soil Dyn. Earthquake Eng. 2019, 125, 105734. [Google Scholar] [CrossRef]
Li, S.; Wang, J.; Alam, M.S. Seismic performance assessment of a multispan continuous isolated highway bridge with superelastic shape memory alloy reinforced piers and restraining devices. Earthq Eng Struct Dyn 2021, 50(2), 673–691. [Google Scholar] [CrossRef]
Michailidis, P.A.; Triantafyllidis, N.; Shaw, J.A.; Grummon, D.S. Superelasticity and Stability of a Shape Memory Alloy Hexagonal Honeycomb under In-plane Compression. International Journal of Solids & Structures 2009, 46 (13), 2724–2738. [Google Scholar] [CrossRef]
Galehdari, S.; Khodarahmi, H. Design and analysis of a graded honeycomb shock absorber for a helicopter seat during a crash condition. International journal of crashworthiness 2016, 21(3), 231–241. [Google Scholar] [CrossRef]
Lee, M.; Lee, J.; Kim, J. Seismic Retrofit of Structures Using Steel Honeycomb Dampers. International Journal of Steel Structures 2017, 17(1), 215–229. [Google Scholar] [CrossRef]
Yang, T.; Li, T.; Tobber, L.; Pan, X. Experimental and numerical study of honeycomb structural fuses. Engineering Structures 2020, 204, 109814. [Google Scholar] [CrossRef]
Zhakatayev, A.; Kappassov, Z. Analytical modeling and design of negative stiffness honeycombs. Smart Materials and Structures 2020, 29 (4), 045024 (13pp). [Google Scholar] [CrossRef]
Wang, W.; Fang, C.; Liu, J. Large size superelastic SMA bars: heat treatment strategy, mechanical property and seismic application. Smart Mater. Struct. 2016, 25(7), 075001. [Google Scholar] [CrossRef]
Systemes, D. ABAQUS 2017 Documentation. English. Version Version 2018, 6. [Google Scholar]

Figure 1. A honeycomb.

Figure 2. Superelsatic SMA honeycomb damper.

Figure 3. Superelsatic SMA honeycomb damper.

Figure 4. Honeycomb beam in local coordinate system.

Figure 5. The specimen: (a) dimensions of the SMA honeycomb, (b) installment of the SMA honeycomb, (c) lubricating oil applied, and (d) installment of the two stainless steel plates.

Figure 6. The test setup.

Figure 7. Experimental response of the specimen.

Figure 8. Fracture of the specimen.

Figure 9. Finite element model of SHD.

Figure 10. Experimental response of the specimen.

Figure 11. The simulated strain distribution of the specimen at a displacement of 12mm.

Figure 12. Bending moment distribution of nonhorizontal cell wall.

Figure 13. Optimization of SMA honeycomb.

Figure 14. Optimized numerical model of SHD.

Figure 15. Strain distribution of the optimized SHD numerical model.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer