Prerpints.org logo
Preprint
Review

Vehicle Relocation in One-Way Carsharing: A Review

Altmetrics

Downloads

142

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 November 2023

Posted:

09 November 2023

You are already at the latest version

Alerts
Abstract
Carsharing has become increasingly popular in recent years as a sustainable transportation solution, offering individuals access to shared vehicles on a short-term basis. One-way carsharing, in particular, presents unique challenges due to its flexible nature, allowing users to pick up and drop off vehicles at different locations within a designated service area. This flexibility increases the service ridership but comes at the expense of vehicle imbalance among the stations, as some stations may have excess vehicles while other stations have vehicle shortages. Therefore, carsharing companies need to decide on strategies to ensure a balanced distribution of vehicles among the stations. This is essential as unbalanced vehicle distribution can lead to the unavailability of vehicles when needed or, conversely, result in an increased number of unnecessary rebalancing trips, thereby exacerbating traffic congestion and environmental pollution. Such issues can potentially undermine the overall contribution of carsharing to urban sustainability. To this end, this paper reviews the vehicle imbalance problem that arises in this field and the solution algorithms that solve them.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

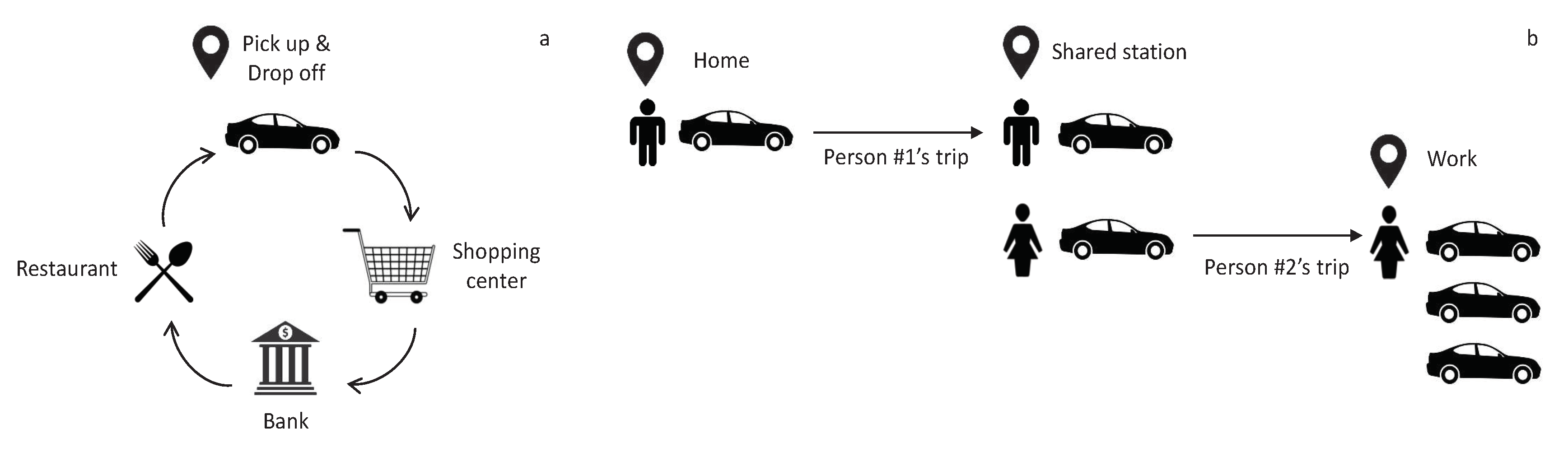
1. Introduction

Carsharing services (CSS) have gained more attention and interest from both industry and academia. Numerous car rental agencies started to provide one-way CSS in addition to conventional rental services. Global Market Trends estimated that the CSS market size exceeded 2 billion USD in 2020, and the annual growth rate is expected to grow over 24% by 2026.
Carsharing is an attractive mobility option due to its various advantages. Carsharing is a cost-effective mobility option as users only pay for the time and distance they use, eliminating expenses associated with vehicle ownership like insurance and maintenance [179]. Refraining from owning a car would require individuals to limit their travels to essential trips, resulting in a reduction in the overall number of vehicles on the roads, leading to lower carbon emissions and congestion [181]. It was shown by [3] that carsharing can decrease C O 2 emissions between 3% and 18%. Moreover, it can complement public transit systems, providing first- and last-mile connectivity and therefore promoting sustainable urban mobility [158,180,181].
There are two types under which carsharing operates: one-way and two-way. The latter mandates users pick up and return the car to the same location. In contrast, the former offers a more flexible and convenient option as commuters can pick up and return the vehicle from different stations. Figure 1 shows the key difference in operating two-way and one-way carsharing. However, the flexibility associated with operating one-way CSS is associated with an operational challenge of vehicle balancing among the network’s stations, as some stations may have excess vehicles while others may have a shortage of vehicles throughout the day. Vehicle unavailability at certain stations can cause demand losses and poor service levels. Therefore, operating a one-way station-based carsharing faces a huge operational challenge of vehicle balancing. Two commonly used strategies were explored to achieve system balance in practice and literature: demand management and vehicle relocation strategies.
Demand management, on the one hand, can be done either by trip selection or by trip’s dynamic pricing. The former allows the carsharing operator to choose profitable trips from a total demand, i.e., the operator doesn’t necessarily need to fulfill all the commuting requests [70]. Dynamic pricing imposes high rental rates for trips that increase imbalances and lower fares for trips that improve the system’s balance, as the work of [115]. However, commuters’ acceptance of discounted trips to balance the system is not guaranteed. Vehicle relocation strategies, on the other hand, mandate vehicle movement between stations to achieve vehicle balance, and it can be user-based (UB) or operator-based (OB) relocation.
UB relocation is usually done by customer incentivization, where commuters are incentivized to change the pickup or delivery station or the vehicle access time. By doing this, the customer may choose a less favorable location to reduce the balancing problem. Carsharing operators yet need to find the optimal destination for a commuter to drop off the vehicle, the optimal incentive value, and the prediction of the commuter’s willingness to accept the incentivized trip [170]. [177] showed that substantial profit can be realized when commuters are incentivized to be more flexible in their choice of pickup and delivery locations.
OB relocation, on the other hand, necessitates the operator to relocate the vehicles, which has been studied by [90,138]. Operators either utilize a part-time staff [143] or full-time staff [142,178] to perform the vehicle relocations. A trade-off between the staff and fleet sizes is among the key tactical decisions to be made by the operator. For example, hiring a relatively large fleet and distributing them among stations would lower the need for vehicle relocation and, therefore, the number of relocation staff hired. Several operational decisions should be made when operating an OB relocation, such as staff and vehicle routing and scheduling to ensure vehicle availability.
As described above, trip pricing to control the demand does not guarantee system balance. Moreover, UB relocation is usually for short-distance relocations as it causes the users to alter their origin or destination slightly. Therefore, it cannot guarantee a balanced system, even if all commuters accept the incentives for vehicle relocations. Therefore, carsharing operators must accompany pricing strategies or UB relocations with OB relocations to guarantee system balance. Therefore, we focus on this study on the OB vehicle relocation formulations.
This paper aims to review the operational research issues arising in operating station-based one-way carsharing and the proposed solution approaches to address them. The aim is to provide scholars and carsharing operators with an overview of how to relocate vehicles effectively to ensure vehicle availability and, therefore, increase carsharing ridership over private car ownership [2] from one hand. On the other hand, finding optimal routes and optimal vehicle assignment to relocation staff can decrease the total miles driven and, hence, lower the emissions generated. The works of [167] and [96] inspire this research. [167] have surveyed the operational research issues in shared mobility in general. The authors have successively reviewed the strategic, tactical, and operational decisions from the operations research point of view and reviewed methods that solve these problems. [96] have addressed the service operation issues of one-way carsharing systems from various aspects and scopes. However, this is still an active field, and several research dimensions have emerged since that date.
We review the vehicle rebalancing problem that arises in operating one-way carsharing. Although this is an operational problem, there exists a connection between these challenges and strategic as well as tactical considerations. Therefore, we review studies that address strategic, tactical, and operational aspects, particularly those related to optimizing the OB relocation of vehicles. We systematically review vehicle rebalancing, resource dimensioning and allocation, trip pricing, and station decisions. For each topic, we present an overview of the problem and describe selected solution approaches that we think are important. We further extend the review to include how the three-level decisions can impact the commuters’ travel behavior and acceptance of the carsharing service. In other words, we review studies that simultaneously considered the operator’s decisions and the commuters’ convenience when planning the operation on one-way CSS.

2. Vehicle rebalancing

OB vehicle relocation can be either predictive or non-predictive [56]. Predictive rebalancing is when the operator utilizes the historical trip transactions or complete vehicle reservation information to plan the relocation proactively. Non-predictive relocations, or immediate relocation, refers to the immediate fulfillment of the relocation demand [33].
The predictive rebalancing approach is performed in two steps: relocation needs determination and relocation plan execution as in the work of [56]. In the former, the operator estimates the commuter’s vehicle pickup and drop off at the network’s stations, then vehicle inventory at these stations is estimated, and finally, relocation needs are computed. In the latter, the network flow model is optimized where the operator first determines the upper and lower vehicle threshold at stations. Then, an optimal relocation plan is performed so that the difference between the estimated inventory level and the thresholds is minimized.
[172] also studied predictive relocation, where the authors used the Markovian model to approximate the stations’ future states, and then the rebalancing strategy is optimized accordingly. We are unaware of the existence of another optimization-based proactive relocation modeling. Non-predictive relocation can be either static or dynamic [56,167].
Static rebalancing refers to the case where vehicles’ movement is only performed by relocation staff while no commuters’ demands take place during the relocation. This is commonly observed when performing overnight relocation with no commuter vehicle demand. This type of relocation is relatively easier to solve due to lower uncertainty. While overnight relocation helps redistribute vehicles after a day’s use, it may not effectively address fluctuations in demand and usage patterns that occur throughout the day. Overnight relocation was studied by [143]. An integer programming model to solve the overnight vehicle rebalancing problem was proposed. The authors considered temporary workers to be hired to redistribute vehicles. The model aims to minimize the total rebalancing costs while fulfilling the commuters’ demands by developing relocators’ employment plans and schedules. Workers were allowed to move only using the shared vehicles that could be shared with other temporary workers. To minimize movement costs, return restriction constraints were incorporated into the model, ensuring that the last movement of each relocator would be back to their original location. This way, participating relocators would not be required to bear the cost of participating in the relocations operation. The authors proposed an iterative optimization approach to solve large-scale relocation problems. It was shown that using a time-based salary reduces about 49% working hours and about 34% of relocation costs.
Similar to [143] work, [168] considered vehicle movement only by relocation staff. The authors presented a stochastic, mixed-integer program (MIP) to create the least cost vehicle relocation plan while the stations’ demand is satisfied with a probability of at least p. The model assesses each station’s short-term planning period, the fleet size, and available parking spaces. If there is a shortage of vehicles, then vehicle movement is needed from a neighbor station. If the parking space at a station exceeds a threshold, then a vehicle movement to a neighbor station is done to satisfy the demand with a certain probability. Two distinct algorithms were introduced for efficiently solving stochastic programs in which randomness affects only the constraints’ right-hand side. These algorithms are based on the concept of p-efficient points.
More formally, each station i is characterized by a capacity C i and initial vehicles number V i . Moreover, there is a demand for vehicles and for parking spaces donated by a random variables of known distributions ζ i v and ζ i s , respectively. The demand must be fulfilled with probability of at least p. The relocation costs between stations i and j is donated by a i j , and there is an additional penalty costs for each relocated vehicle γ . A binary decision variables x i j indicates whether a vehicle is relocated from i to j. An integer decision variable y i j presents the number of vehicles relocated from i to j. The mathematical model is formulated as the following:
min ∑ i , j ∈ N   ( a i j x i j + δ y i j )
s . t . P r V i + ∑ j = 1 n ( y j i − y i j ) + ζ i s ≥ ζ i v , i ∈ N C i − V i + ∑ j = 1 n ( y i j − y j i ) + ζ i s ≥ ζ i v , i ∈ N ≥ p
∑ j ∈ N y i j ≤ V i ∀ i ∈ N
∑ j ∈ N y j i ≤ C i − V i ∀ i ∈ N
y i j ≤ M x i j ∀ i , j ∈ N
y i j ≥ 0 and integer , x i j ∈ { 0 , 1 } ∀ i , j ∈ N
The objective (1) is to minimize the relocation costs. Constraints (2) ensure that the demand (for both the vehicles and parking spaces) is satisfied with at least a probability p. Constraints (3) ensure that the total number of relocated vehicles out of a station can’t exceed its initial inventory V i . While Constraints (4) ensure that the number of relocated vehicles to a station i can’t exceed its capacity. Constraints (5) are proposed to link x and y.
The authors conducted a thorough computational experiments using actual data obtained from the Singapore carsharing system. The system consisted of 14 stations, a combined capacity of 202 spaces, and a fleet of 94 vehicles. They conducted simulation studies and found that the suggested solution strategies were effective and reliable. Furthermore, they analyzed the trade-offs between relocation costs and the service level provided. The authors assumed unrealistic assumption of relocation staff availability for relocation operations. Modeling the relocators’ routes and schedules is vital in ensuring vehicle availability and system profitability.
Another stream of research formulated the static relocation problem as a set of relocation pickup and delivery requests, i.e., requests to move a vehicle out of a station to prevent it from running out of parking lots and requests to deliver vehicles to a station to prevent it from running out of vehicles, respectively. We review two research works on this topic.
Determining the set of pickup and delivery requests of shared vehicles and finding the optimal relocators’ routes to serve these requests to maximize the operator’s profit was solved by [129]. The authors formulated a set-packing model to solve the problem and developed a branch-and-cut-and-price algorithm. Specifically, the developed algorithm is a branch-and-bound algorithm in which a column generation method is first applied in the branch-and-bound branch, followed by the linearization of the problem using a relaxation method.
The authors determined only the routes of the relocation staff to serve the pickup and delivery requests separately. [171], on the other hand, optimally found the routes and schedules of the relocation staff to maximize the number of served requests by considering pickup and delivery pairs. The authors proved the efficiency of their model in terms of running time and solution quality compared with treating the pickup and delivery requests separately. The authors considered staff route familiarity, which is measured as the ratio of time reduction of a familiar staff’s relocation time to the unfamiliar staff’s relocation time. For example, higher road familiarity leads to a lower relocation time and distance, especially in complex road conditions where the unfamiliar staff will find it difficult to reach the destination even with the powerful navigation function of Google Maps.
Dynamic vehicle relocations refer to the case that commuters’ can also move the shared vehicles during the OB relocations. [109] proposed two formulations for operating and non-operating hours. The former model optimizes the operator’s profit by solving an exact model for relocation operations that determines, at the beginning of the day and for each vehicle, the optimal initial location. The overnight relocation model can achieve this initial vehicle distribution. The authors formulated the problem as a time-space network and defined the following arcs:
-
A c : donates customer request on arc a = ( i t , j t ′ ) , each time a commuter request is transversed by this arc, there is a negative variation of vehicle energy, i.e. c a < 0 , and a positive profit, i.e. p a > 0 .
-
A w : waiting arc for either vehicles or relocation staff at a station i, a = ( i t , i t ′ ) . Each waiting arc is associated with a positive energy variation, c a > 0 , and a zero profit, i.e. p a = 0
-
A r : vehicle relocation arc by at least one relocator, a = ( i t , j t ′ ) . Each relocation arc is associated with a negative energy variation, i.e. c a < 0 , and a negative profit, i.e. p a < 0 .
-
A t : transfer arc a = ( i t , j t ′ ) , represents the relocator’s movement when they don’t move by vehicle or wait at a station. Each transfer arc is correlated with a zero energy consumption, c a = 0 , and a zero generated profit, p a = 0 .
Where the authors defined two sets of binary decision variables, related to the vehicle x a h , a ∈ A r ∪ A w ∪ A c and relocators y a q , a ∈ A r ∪ A w ∪ A t taking value 1 when vehicle and relocator travel on arc a = ( i t , j t ′ ) respectively. Moreover, the authors defined decision variables related to the vehicle battery charge, z t h donating the vehicle h charge at time t.
max ∑ h ∈ H   ∑ a ∈ A c ∪ A r   p a x a h
∑ h ∈ H x a h ⩽ d a a ∈ A c
∑ h ∈ H ∑ a = ( i t , i t + 1 ) ∈ A w x a h ≤ C i i ∈ S , 0 ≤ t < T m a x
∑ h ∈ H ∑ a ∈ ( δ + ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) x a h ≤ C i i ∈ S
∑ i ∈ S ∑ a ∈ ( δ + ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) x a h = 1 h ∈ H
∑ a ∈ ( δ + ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) x a h = ∑ a ( δ − ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) x a h h ∈ H , i ∈ S , 1 < t < T m a x
∑ i ∈ S ∑ a ∈ ( δ + ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) y a q = 1 q ∈ Q
∑ a ∈ ( δ + ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) y a q = ∑ a ( δ − ( i 0 ) ) ∩ ( A c ∪ A w ∪ A r ) y a q h ∈ H , i ∈ S , 1 < t < T m a x
( x , y ) ∈ B 1 < t < T m a x
∑ h ∈ H x a h ⩽ ∑ q ∈ Q y a q a ∈ A r
∑ q ∈ Q y a q ⩽ B ∑ h ∈ H x a h a ∈ A   r
x a h ∈ { 0 , 1 } h ∈ H , a ∈ A c ∪ A w ∪ A r
y a q ∈ { 0 , 1 } q ∈ Q , a ∈ A r ∪ A t ∪ A w
The objective (7) is to maximize the profit, which is a function of the revenue associated with the fulfilled customers’ requests minus the vehicle relocation costs. Constraints (8) guarantee that the customer demand is not exceeded. Stations’ capacity constraints at any time t > 0 and at instant t = 0 are guaranteed in Constraints (9) and (10), respectively. Constraints (11) ensure the vehicle’s departure from one station at the beginning of time 0, while the flow conservation at the network nodes is in Constraints (12). Same conditions for the relocators are ensured in Constraints (13) and (14). Constraints (15) impose the feasibility of the assigned trips regarding the battery charge. Matching vehicles and relocators on the relocation arcs are imposed in Constraints (16) and (17). Constraints (16) ensure that the number of vehicles traveling on a relocation arc a ∈ Ar is not greater than the number of relocation staff, and Constraints (17) impose a limitation on the number of relocators who can travel on a vehicle.
The above formulation describes the relocation for the operating hours by determining the optimal initial location for each vehicle on the network. To meet the optimal initial locations of the vehicles, the authors extended the model to the staff’s operations during non-operating hours. Additional variable R i that presents the number of requested vehicles at station i at the start of the next planning period. The system configuration at the end of the day determines the initial vehicle position and initial battery charge o h , z h 0 . The same network is operated but with the removal of the commuter requests during non-operating hours. Therefore, the overnight model for vehicle relocation is as follows:
max Z
s . t . Z ≤ z h T m a x ∀ h ∈ H
∑ α ∈ ( δ + ( o h ) ) ∩ ( A w ∪ A r ) x a h = 1 ∀ h ∈ H
∑ α ∈ ( δ − ( i T m a x ) ) ∩ ( A w ∪ A r ) x a h = R i ∀ h ∈ H , i ∈ S
The objective (20) is to maximize the charge level for all vehicles at the end of the day, which is defined in (21). Constraints (22) ensure the vehicle’s departure from its initial location, while Constraints (23) ensure the required vehicle distribution.
Finding the optimal solution for the presented model is impractical. Therefore, the authors proposed two model-based heuristics for addressing the relocation problem in the context of large-scale instances during operational hours. First, the authors proposed the removal or reduction of the relocation density. This method ensures that the problem remains feasible as the relocators can still move in the waiting arcs. The impact of relocation arc reduction on the optimal solution obtained depends on the number of relocation arcs removed. Another approach proposed is the rolling horizon approach, where the authors split the planning period into ρ sub-periods, and the rebalancing arcs associated with the following period after the first sub-period are disabled. The resultant model is then optimally solved, with the initial period’s value being set, and this process is repeated for the subsequent sub-periods.
The two models for the daily relocation and the overnight staff schedules give the readers a comprehensive optimization tool for managing shared vehicles with battery constraints.

3. Resource dimensioning and allocation

Most of the previously mentioned problems assumed that vehicles could be relocated between stations regardless of staff’s availability to perform the relocation tasks. Resource dimensioning refers to the problem of determining the ideal number of vehicles and relocation staff to be hired in a working day to fulfill the relocation demand. Resource allocation refers to determining the optimal allocation of the resources at the network’s stations and the staff’s assignments to various relocation tasks. Determining the optimal number and allocation of resources is crucial in determining the profitability of the carsharing system. We review five papers related to this topic, each distinctively formulated the problem.
[94] was the first to incorporate the staff balancing in modeling vehicle relocation in carsharing. The authors proposed a three-phase decision support system that combines optimization, trend analysis, and simulation to identify parameters that yield near-optimal results for vehicle relocation operations. Staff rebalancing was considered at the optimization phase of the three-phase approach. The relocators’ movements were modelled by binary decision variables indicating relocator’s activities at each time t, whether a relocator relocates a vehicle between two stations, being rebalanced between stations, waiting at a station, or maintaining a vehicle at a station. Although the model details the relocators’ activities, it becomes computationally challenging for large-scale problems. Moreover, the authors haven’t considered the optimal staff and vehicle level to minimize the overall costs.
Considering the spatial and temporal user’s flexibility regarding vehicle pickup and drop off on the system profitability and vehicle utilization was also studied by [142]. [157] proposed a dynamic decision support system to maximize the carsharing profit by solving the vehicle relocation problem. The authors optimized the relocation operations and determined the ideal fleet size. An interesting feature of their model is the testing the impact of increasing the reservation time, which is the interval between vehicle request and pickup, on the optimal number of the fleet size. It was shown that increasing the reservation time from 0 to 30 minutes can result in a substantial reduction of approximately 86% in the fleet size. However, the authors did not consider staff balancing and availability in their model.
Later, [140] solved the vehicle relocation and staff balancing problem while optimizing the staff and fleet sizes to minimize the overall relocation costs. The authors formulated the problem using two integrated multi-traveling salesman formulations; one presents the vehicle relocation, and the other presents the staff balancing. The following questions regarding the vehicle relocation and staff balancing were answered by solving the model: (1) given a set of user reservations, what should be the ideal fleet and staff size to fulfill all these requests? (2) how should the vehicles be relocated between the stations? (3) what should be the relocator’s assignment to different relocation tasks? Since the model can’t solve instances of 40 users within an acceptable time, the authors proposed a decomposition-based heuristic that divides the relocation model into a master problem (MP) and a subproblem (SP). The MP focuses on solving vehicle relocation problems without considering staff rebalancing. On the other hand, the SP utilizes the relocation solutions obtained from the MP to address the staff rebalancing problem. After each MP and the SP iteration execution, a set of additional constraints called “Relocation Restrictions” are identified and incorporated into the MP for subsequent iterations. The results indicate that fleet size is more sensitive to demand than staff size. Additionally, there is an inverse relationship between staff size and vehicle cost. The main drawback of this formulation is that it assumes an optimized resource allocation at the beginning of the planning period. Moreover, the model focused on fulfilling the commuter’s request without measuring the waiting times for order fulfillment, which is a key service for users’ choice of shared mobility [75].
It is noteworthy to mention that the authors of [109] mentioned in Section 2 have considered the staff balancing when deploying the relocation plan. Similar to their work, the authors in [147] formulated the vehicle relocation problem and staff balancing using a time-space network. However, the authors included determining the optimal vehicle and staff sizes and allocations to satisfy user demands with the minimum overall costs. The model was formulated as a multi-vehicle routing problem with complex coupling constraints, which proved difficult to address using existing solvers. Therefore, the authors devised a tailored solution approach based on Lagrangian relaxation embedded with forward dynamic programming and branch-and-bound. This custom approach allowed for a more efficient and precise resolution of the model.

4. Trip pricing

The previously mentioned studies rely entirely on relocation staff to achieve system balance by considering a fixed rental rate between stations throughout the day. Though never proven, the theory is that carsharing systems could yield higher profits by managing the demand through pricing. In other words, significantly low rental prices will attract more commuters to the service and, therefore, increase the operator’s revenue. However, it may not necessarily increase the profit as it may increase the relocation expenses due to the increased decentralization of vehicles throughout the network.
[81] optimizes the vehicle fleet size and trip pricing while considering the vehicle relocation and staff assignment to maximize the overall profit. Based on [138] work, in which the authors optimized the vehicle relocations between stations, [115] introduced new decision variables to account for price variations between pairs of zones and periods of the day. More formally, considering a predefined set of carsharing stations at which the set of origin-destination demand is known in advance, the problem aims to find newly optimized prices between station groups throughout a typical working day such that the profit is maximized while fulfilling the demand. A summary of research works that studied the operational and tactical decisions are summarized in Table 1.

5. Carsharing stations related decisions

Vehicle availability is a crucial factor in the success of carsharing systems. However, it is vital that users be able to access the service within an acceptable walking distance. Mainly, the number of stations that can be operated is constrained by the availability of budget and land space. Many researchers have studied station-related decisions regarding the number of stations to be installed, their locations, and their size. Station size can refer to the number of car parking spaces allocated or the number of chargers installed. This section presents a series of papers that explicitly consider station-related decisions and vehicle relocation.
The station location and vehicle relocation problem was solved by [70]. More formally, the authors proposed mixed-integer linear programming (MILP) under three trip selection schemes to optimally determine the station location for a given carsharing demand to maximize the operator’s profit. This was the first work that considered the trip selection, which gives the operator more flexibility in managing the supply-demand imbalance issue. The authors showed the importance of the trip selection strategy (i.e., selecting profitable trips out of total demand) in determining carsharing profitability. They showed that fulfilling all commuters’ requests would be unprofitable even under high-pricing trips as it mandates the operator to deploy more vehicles. The authors, however, only considered the overnight relocation while neglecting the staff balancing, as the main focus of the study was on the depot location selection.
[174] addressed the station location selection, optimal fleet size, and vehicle balancing problem to minimize the overall costs associated with these decisions under stochastic demand. To solve a large-scale problem, the authors proposed a continuum approximation model under stochastic and dynamic trip demands. The location problem is NP-hard, making the problem hard to solve; therefore, the authors proposed a continuum approximation approach to overcome the modeling challenges. This work may not be under mathematical modeling.
[164] jointly optimized the charging station location, fleet size, allocation, and relocation operations. An accelerating solution based on Lagrangian relaxation was proposed to deal with the complexity of the problem. The authors have neglected the difference in the energy demand for different trips and assumed the operation of a homogeneous fleet. This is an important distinction, as rental fare and energy consumption for a two-seat vehicle should be less than a four-seat vehicle. After performing a series of sensitivity analyses, it was found that the total number of vehicles deployed is dominated by demand, and the number of charging stations is not very sensitive to penalty and relocation costs. However, the scale of the problem is still challenging.
[92] proposed a mixed-integer non-linear program (MINLP) to optimize the fleet size, station capacity, and vehicle relocation by considering a time-varying state of charge of vehicles. In the previously mentioned studies, the authors assumed that the vehicle could be available for rental if fully charged, reducing vehicle utilization. Moreover, tracking the vehicle charge state causes a huge computational burden. The authors proposed a hybrid heuristic method to handle the computation burden.
The model is split into two subproblems: One focuses on determining the strategic decisions of fleet sizing and number of parking spaces, which is referred to as station capacity. The second one deals with the operational-level decisions regarding vehicle rebalancing. It is crucial to optimize both levels jointly. More explicitly, at the strategic level, the model calculates the upper and lower bounds for the fleet size. These bounds are determined by assuming that electric vehicles (EVs) are fully charged before departure or by disregarding the constraints related to the battery capacity, respectively. Once the fleet size and station capacity are known, a set of small-scale linear programs is created to determine how to relocate vehicles effectively to meet travel demand within a rolling time frame. The model utilizes a shadow price algorithm and a golden section line search method to optimize station capacity and fleet size, aiming to maximize the overall profit. Results indicate that allocating only a few vehicles or providing limited parking spaces for high demand will result in numerous unfulfilled requests. Conversely, an excessive allocation of vehicles and parking spaces might result in the system being underutilized. It should be noted that the authors haven’t optimized the stations’ locations and numbers.
[72] also presented a MINLP; however, the authors aim to optimize the station capacity location along with vehicle relocation to maximize the daily profit. The authors established a correlation between the location variables and the likelihood of a user’s travel choice. To address this, they have developed a specialized gradient algorithm.
Similarly, [175] presented a two-stage stochastic program aimed at optimizing carsharing profitability. The number of parking spaces and vehicle and staff sizes are determined in stage one; stage two assesses the profitability of the stage one decisions and determines the vehicle relocation and vehicle assignment in response to various demand realizations. To address the complexities arising from the interactions among variables across these two stages, the authors introduced a novel concept termed service reliability (SR). The SR-based modeling approach separates the long-term strategic planning and the short-term operational decisions into two distinct problems. These problems are connected through SR. In other words, the first-stage decisions are optimized for a specific SR. Then, in the second stage, operational decisions are made considering the actual stochastic demand to maximize overall profit and mitigate the negative impacts of fluctuating and uncertain demand. It was shown that the SR-based two-stage model has the potential to assist one-way carsharing service providers in achieving higher profitability.
An interesting approach involves integrating optimization and simulation modeling to explore the integration of strategic planning and operational decisions. In [165] work, the authors optimized the allocation of the parking space and how vehicles should be distributed initially to specific zones while considering the relocation activities to minimize the overall expenses. The operational planning problem incorporates demand uncertainty. The model is formulated as the following:
min C i ∑ i ∈ N   x i + w ∗ v + R ( x , v ) + Q ( x , v )
s . t . g ( x , v ) ≤ α
x i ≥ v i , ∀ i ∈ N
∑ i = 1 N v i = v
x i , v i ∈ Z +
Where C i , is the cost of renting a parking space in zone i; x is a vector with a dimension that presents the number of zones, and its value presents the number of parking spaces at each zone. w is the vehicle’s daily depreciation costs; v presents the system’s total number of vehicles; while v i presents the number of vehicles initially placed in zone i. Vehicle balancing costs are presented by R ( x , v ) , Q ( x , v ) presents the additional parking costs incurred when a commuter doesn’t find an available parking space; g ( x , v ) is the commuter loss rate due to vehicle unavailability at the time of rental; α is the maximum customer rate loss that can be tolerated.
The objective (24) is to minimize the overall costs, which include the parking rental costs, vehicle depreciation costs, and relocation costs. Constraint (25) is the main constraint not to exceed a demand loss rate α . While Constraints (26),(27), and (28) defines the search space.
To facilitate the computation, the model is relaxed by incorporating the violation of Constraint (25) in the objective function as a penalty costs μ . The updated objective function is shown in (29).
min f ( x , v ) = C i ∑ i ∈ N   x i + w ∗ v + R ( x , v ) + Q ( x , v ) + μ ∗ ( g ( x , v ) − α ) 2
Due to the computational complexity of solving the relocation operation, which must respond to real-time demand changes, a discrete event simulator is adopted. In other words, a discrete event simulator is created to approximate the values f ( x , v ) , R ( x , v ) , Q ( x , v ) , g ( x , v ) for a given x and y as shown in (30), (31),(32),(33), respectively.
More formally, for a given decision variables, parameters, and the number of simulations, k, the simulator generates the necessary set of sample points that encompass the rebalancing costs, r k , additional parking costs, q k , and the number of customers loss rate, g k for each demand scenario. γ i j is the rebalancing costs from zone i to j, r i j is the number of rebalanced vehicles from zone i to j, p i is the parking costs at zone i, s i t is the number of vehicles at zone i at time t, d i j t is the vehicle pickup demand between zone i to j at time t.
f ( x , v ) ∼ C i ∑ i ∈ N   x i + w ∗ v + R ^ ( x , v ) + Q ^ ( x , v ) + μ ∗ ( g ^ ( x , v ) − α ) 2
R ^ ( x , v ) = ∑ r k K , r k = ∑ t ∈ T ∑ j ∈ N , i ≠ j   ∑ i ∈ N   γ i j ∗ r i j t
Q ^ ( x , v ) = ∑ q k K , q k = ∑ t ∈ T ∑ i ∈ N p i ∗ m a x ( s i t − x i , 0 )
g ^ ( x , v ) = ∑ g k K , g k = ∑ t ∈ T ∑ i ∈ N m a x ( ∑ j ∈ N , ≠ i d i j t − s i t , 0 ) ∑ t ∈ T ∑ j ∈ N , ≠ i ∑ i ∈ N d i j t
The simulator calculates the rebalancing decisions between zones by applying an integer programming model at the start of every hour. The objective is to minimize the rebalancing costs (34), while guaranteeing that each zone can meet the specific loss rate for the following hour. The model is formulated as the following:
min ∑ j ∈ N , ≠ i   ∑ i ∈ N   r i j t γ i j
L i t ≤ s i t − ∑ j ∈ N , ≠ i   r i j t + ∑ j ∈ N , ≠ i   r j i t ≤ U i t
∑ j ∈ N , ≠ i   r i j t ≤ s i t
r ∈ Z +
To explicitly consider the stochastic nature of the demand, the model calculates the lower ( L i t ) and upper bound ( U i t ) of vehicle stock at each zone to meet the required service rate on vehicle pickups and returns, respectively. This is guaranteed in Constraints (35). The lower limit of the vehicle stocks is assumed when there are only vehicle returns, i.e., no commuter is requesting a vehicle pickup for the next hour. The upper limit of vehicle stocks is assumed to be the station’s capacity. Constraints (36) ensure that the number of relocated vehicles out of a station is not greater than the number of existing vehicles. Constraints (37) specifies the domain of the decision variables.
The performance of various system configurations is assessed. The results demonstrate that the optimal solutions when no rebalancing operations are considered to lead to a significantly higher number of parking spaces to be rented and more vehicles to be purchased, which doesn’t improve the demand loss rate. Moreover, rebalancing is highly needed in the case of high demand fluctuations and high demand imbalance.
Recently,[156] proposed a holistic, collaborative mathematical formulation that encloses the three decision levels. The authors optimized the strategic planning decisions involving the number, location, and parking capacities of stations. They also optimized the tactical planning decisions related to fleet size and initial vehicle distribution while considering all-day vehicle relocation and dynamic trip selection at the operational level. The trip selection decision mandates the operator to choose profitable and balanced trips, enhancing the self-balance ability.
Their model suggests that operators are advised to prioritize medium-long distance travel within a travel time range of 30-60 minutes during periods of low demand. In high-demand and limited-source scenarios, the selection of balanced trips is recommended. Another important finding is that relocation cases yield higher profits compared to self-balanced cases, indicating that vehicle relocation has a significant impact on earnings and meeting demand while costs remain relatively unaffected. Consequently, vehicle relocation is crucial for maximizing profits and accommodating demand. This study is unique in providing a comprehensive formulation encompassing strategic, tactical, and operational decisions, as well as offering flexibility in trip selection.
Table 2 summarizes the research works that studied the tactical and operational decisions while considering the vehicle balancing decisions. It is noteworthy to mention that, for the sake of completeness, we have added references that are not reviewed in the text.

6. Operators decisions and commuters demand

Considering the overall benefits of both the operator and the users while designing and operating CSS have been studied. This is particularly important when considering that the system is subsidized with a public fund, which enables the decision-makers to evaluate a trade-off between the operator’s profit and commuters’ service level. In this section, we review three research works related to this topic. [75,102] built a bi-level program to find the optimal configuration of a carsharing system by considering the commuters’ reaction to this configuration. The scope of the carsharing decisions is different in each work. To maximize the operator’s profit, [102] optimized the fleet size, pricing, and vehicle relocation in the upper level while minimizing the corresponding users’ commuting costs in the lower level. We review the [75] more thoughtfully.
The bi-level program involves the optimization of variables in one model, known as the lower level, based on the optimal solutions of another optimization model. The upper level encompasses the main objective function along with additional constraints. The problem considered in [75] is to maximize the operator’s rental revenue by determining station location, size, and vehicle inventories subject to budget constraints in the upper level. And in the lower level, the user’s travel and waiting times are minimized.
More formally, the operator’s decision variables are x i , y i , and z i , where x i is a binary decision variable indicates whether a station should be opened in location i, y i is an integer variable to indicate the capacity of station i, and z i is the number of vehicles located initially at station i. There is a cost associated with each decision. The costs are related to station setup costs c s , additional parking space costs c p , and the cost of deploying a shared vehicle c v . The operator aims to find the optimal network configurations ( x , y , z ) , donated by x , subject to budget constraints C to maximize the revenue of the shared flows throughout the network. However, the operator does not determine the shared flows.
From the commuters’ perspective, the problem is finding the network’s flows to maximize their utility. For a given origin-destination (O-D) pair, indexed by k in the following, the commuters aim to minimize the traveling and waiting times. The demand from node i to the destination of index k is donated by D i k . Two continuous decision variable decisions are made by the commuters, v i j k and w i k . v i j k indicates a flow from node i to j for demand pair k. While w i k presents the total waiting time at node i for a demand pair k. Therefore, the decisions made by the commuters at the lower level are ( v , w ) donated by v .
To present the operator’s operational decisions, the authors defined a to present the checkout replacement ratio. For example, if a=1, there exists enough capacity to handle vehicles’ checkouts and returns, while if a ≥ 1, returns may exceed the capacity. M is a very large number.
The bi-level network can be formulated as follows:
m a x x , y , z ∑ k   ∑ ( i , j ) ∈ A s   r i j v i j k
s . t . ∑ i ∈ V s   c s x i + c p y i + c v z i ≤ C
M x i ≥ y i i ∈ V s
z i ≤ y i i ∈ V s
y i ≤ y u b i ∈ V s
x i ∈ { 0 , 1 }
y i , z i ∈ Z + n
lower level
m i n w , v ∑ k   ∑ ( i , j ) ∈ A   c i j v i j k + ∑ i ∈ V w i k
s . t . ∑ j : ( i , j ) ∈ A   v i j k − ∑ j : ( i , j ) ∈ A   v j i k = D i k i ∈ V , k ∈ K ( α i k )
v i j k ≤ f i j w i k ( i , j ) ∈ A ∖ A ̲ , k ∈ K ( β i j k )
M x i ≥ ∑ k   v i j k ( i , j ) ∈ A s ( γ i j k )
M x j ≥ ∑ k   v i j k ( i , j ) ∈ A s ( δ i j k )
∑ k   ∑ j , ( i , j ) ∈ A s   v i j k ≤ z i i ∈ V s ( ζ i )
∑ k   ∑ j , ( i , j ) ∈ A s   v i j k ≤ α ( y i − z i ) i ∈ V s ( η i )
w i k ≥ 0 i ∈ V , k ∈ K ( λ i k )
v i j k ≥ 0 ( i , j ) ∈ A , k ∈ K ( μ i j k )
The carsharing operator aims to maximize the rental revenue of the shared vehicles’ fulfilled requests. However, as indicated earlier, this is a commuters’ decision in response to the network configurations. The main constraints were considered in the upper-level decisions.
  • Budget constraints in (39).
  • Parking slots availability only on opened stations in Constraints (40)
  • Number of vehicles assigned to a station doesn’t exceed its capacity in Constraints (41)
  • Limiting the number of opened stations in Constraints (42)
Commuters react to the network’s settings ( x , y , z ) in the lower level to minimize the travel and waiting times (45). The main constraints considered regarding the shared flow are as follows:
  • Flow conservation for each node in Constraints (46).
  • Relating the travel and waiting times for frequency-based links in Constraints (47).
  • Flows are only between opened stations in Constraints (48) and (49)
  • Capacity constrains for the shared stations in Constraints (50) and (51)
In a concise notations, the bi-level program is written in the following form:
max x ∈ X F ( v ) s . t . G ( x , v ) ≤ 0 min v ∈ V f ( v ) s . t . g ( x , v ) ≤ 0
Where upper and lower decision vectors are given by x = ( x , y , z ) and v = ( w , v ) , respectively. While upper and lower-level objective functions are given by F ( v ) and f ( v ) , respectively. G ( x , v ) and g ( x , v ) are the upper and lower constraint sets, respectively. For a given feasible region of a network settings x , the commuters’ feasible region Ω ( x ) is defined as the following:
Ω ( x ) = { v ∣ g ( x , v ) ≤ 0 , v ∈ V }
The commuters’ reaction set Ψ ( x ) is defined as the following:
Ψ ( x ) = { v ∣ v = arg m i n v f ( v ) ; v ∈ Ω ( x ) }
The set which the operator optimizes the system settings for the given commuters’ choice from the reaction set is defined by the inducible region (IR) as follows:
IR = { ( x , v ) ∣ G ( x , v ) ≤ 0 , x ∈ X , y ∈ Ψ ( x ) }
Karush–Kuhn–Tucker (KKT) approach for solving bi-level problems was applied in [75] and [102] works. The method involves substituting the lower-level program with the KKT conditions. This would transform the bi-level model into a mathematical model featuring equilibrium constraints if the lower-level program is convex and satisfies the linear constraint qualifications [176]. This resulting program is a large MIP that existing solvers can solve. However, solving a network with more than 40 nodes within a reasonable time was hard. This formulation is considered optimistic as the model favors the user’s benefits over the operator’s.
Interesting research that simultaneously considered the operator’s and commuter’s benefits in a multi-objective MILP is done by [90]. The authors used the weighted sum approach to combine the operator and commuters’ benefits into one scalar objective function. This approach allows for an efficient frontier generation that allows the decision-makers to explore the trade-offs between the operator’s profits and the user’s benefits.
From the operator’s perspective, the problem involves determining the strategic, tactical, and operational decisions. In particular, the operator aims to optimally find the location of sharing stations, their capacities, and fleet sizes while considering the dynamic relocation and the charging requirements to maximize their revenue. From the commuter’s perspective, the problem aims to maximize the user’s benefits of the monetary value of the utility gained for each fulfilled trip from origin to destination.
To cope with real-world problem size, the authors proposed an aggregate model to reduce the number of relocation variables by adopting the concept of a virtual hub. Instead of relocating between any two stations, the proposed virtual hub concept assumes that the relocated vehicles are accumulated at a virtual hub and then relocated to the stations. Sensitivity analysis based on real data from France was demonstrated. The authors varied the demand levels, the accessibility distance to the shared station, and the subsidy levels provided and observed the number of vehicles used, rentals served, relocations performed, and the utilization of vehicles and how those dimensions impact the net user’s and operator’s benefits. For an average of 150 trips in various scenarios, the runs were terminated when either reaching a 2% optimality gap or a 9-hour run.

7. Future research direction

In this section, we shed light on various practical considerations that have received no or little attention in the literature.
Most of the cited works have assumed the deployment of standard vehicle options, often in the form of sedans or compact cars. However, expanding the fleet to include heterogeneous vehicles of varying sizes and capacities can better accommodate the diverse needs of commuters and provide them with more tailored transportation options at various rental rates and energy consumption. For example, by providing SUVs for family outings or electric vehicles for environmentally conscious users, CSS can effectively enrich commuters’ overall experience.
Another practical concern that has not received enough attention is the deployment of fast and slow charging stations when operating electric vehicle-sharing systems. Most of the referenced research studies have overlooked the distinction between slow and fast charging methods when optimizing the operational dynamics of electric vehicle-sharing systems. The distinction between fast and slow charging deployment plays a significant role in the operational and tactical decisions made. On one hand, deploying fast charging can significantly reduce the charging time. This will help in better management of fleet operations by minimizing vehicle downtime. On the other hand, traditional or slow charging often necessitates larger fleet sizes to account for the time vehicles spend unavailable during charging. Addressing this aspect of operational design can significantly enhance the feasibility and appeal of electric vehicle-based carsharing, fostering its sustained growth and acceptance among users.
From another perspective, research efforts should study the factors influencing commuter choice within a shared mobility system in more detail. Investigating the trade-offs commuters consider while commuting with a shared vehicle, such as cost, convenience, travel distance, and personal preferences, can help optimize carsharing systems’ design and operation. This ultimately can improve the system’s efficiency and user satisfaction.
The operation of carsharing in a multimodal transportation system and how it impacts urban mobility in urban settings should also be studied in more detail. Urban planners can improve mobility through synchronized services through collaboration with other mobility providers such as public transport. Therefore, a wider range of commuters can be considered.

8. Conclusion and future work

To conclude, we reviewed the main operational research problems that arise in the design and operation of one-way carsharing systems. We reviewed the models and the solutions approaches to solve them. Although this area has been theoretically covered in [96] work, our aim is to review the main operational research issues that arise in this field.
We further extend the review to include the research studies that consider the impact of the operator’s decisions on the commuter’s mobility experience.
Lastly, we shed light on some practical considerations overlooked in the literature that may interest researchers.

Author Contributions

Conceptualization, Fayez Eliyan, A.; methodology, Fayez Eliyan, A.; resources, Fayez Eliyan, A.; writing—original draft preparation, Fayez Eliyan, A.; writing—review and editing, Fayez Eliyan, A. and L.Kerbache.; supervision, L.Kerbache.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

We would like to thank Dr. Roberto Baldacci for his valuable comments and guidance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shams Esfandabadi, Z.; Diana, M.; Zanetti, M. Carsharing services in sustainable urban transport: An inclusive science map of the field. Journal Of Cleaner Production. 2022, 357, 131981. [Google Scholar] [CrossRef]
  2. Chen, X.; Cheng, J.; Ye, J.; Jin, Y.; Li, X.; Zhang, F. Locating Station of One-Way Carsharing Based on Spatial Demand Characteristics. Journal Of Advanced Transportation. 2018, 2018, 5493632. [Google Scholar] [CrossRef]
  3. Amatuni, L.; Ottelin, J.; Steubing, B.; Mogollón, J. Does car sharing reduce greenhouse gas emissions? Assessing the modal shift and lifetime shift rebound effects from a life cycle perspective. Journal Of Cleaner Production. 2020, 266, 121869. [Google Scholar] [CrossRef]
  4. Fortunato, S. Community detection in graphs. Phys. Rep.-Rev. Sec. Phys. Lett.. 2010, 486, 75–174. [Google Scholar] [CrossRef]
  5. Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E. 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
  6. Vehlow, C.; Reinhardt, T.; Weiskopf, D. Visualizing Fuzzy Overlapping Communities in Networks. IEEE Trans. Vis. Comput. Graph.. 2013, 19, 2486–2495. [Google Scholar] [CrossRef] [PubMed]
  7. Šubelj, L.; Bajec, M. Robust network community detection using balanced propagation. Eur. Phys. J. B.. 2011, 81, 353–362. [Google Scholar] [CrossRef]
  8. Clauset, A. , Newman, M. & Moore, C. Finding community structure in very large networks. Phys. Rev. E. 2004, 70, 066111. [Google Scholar] [CrossRef]
  9. Blondel, V.; Guillaume, J.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech.-Theory Exp.. 2008, 2008, P10008. [Google Scholar] [CrossRef]
  10. Šubelj, L.; Bajec, M. Unfolding communities in large complex networks: Combining defensive and offensive label propagation for core extraction. Phys. Rev. E.. 2011, 83, 036103. [Google Scholar] [CrossRef]
  11. Li, J.; Wang, X.; Eustace, J. Detecting overlapping communities by seed community in weighted complex networks. Physica A. 2013, 392, 6125–6134. [Google Scholar] [CrossRef]
  12. Fabio, D.; Fabio, D.; Carlo, P. Profiling core-periphery network structure by random walkers. Sci. Rep. 2013, 3, 1467. [Google Scholar]
  13. Nepusz, T.; Petróczi, A.; Négyessy, L.; Bazsó, F. Fuzzy communities and the concept of bridgeness in complex networks. Phys. Rev. E.. 2008, 77, 016107. [Google Scholar] [CrossRef]
  14. Fabricio, B.; Liang, Z. Fuzzy community structure detection by particle competition and cooperation. Soft Comput. 2013, 17, 659–673. [Google Scholar] [CrossRef]
  15. Wang, W.; Liu, D.; Liu, X.; Pan, L. Fuzzy overlapping community detection based on local random walk and multidimensional scaling. Physica A. 2013, 392, 6578–6586. [Google Scholar] [CrossRef]
  16. Zhang, Y.; Yeung, D. Overlapping Community Detection via Bounded Nonnegative Matrix Tri-Factorization. In Proc. ACM SIGKDD Conf. 2012, 606–614. [Google Scholar]
  17. Havens, T.; Bezdek, J.; Leckie, Palaniswami, M. A Soft Modularity Function For Detecting Fuzzy Communities in Social Networks. IEEE Trans. Fuzzy Syst.. 2013, 21, 1170–1175. [Google Scholar] [CrossRef]
  18. Newman, M. Network data. (http://www-personal.umich.edu/ mejn/netdata/,2013).
  19. Šubelj, L.; Bajec, M. Ubiquitousness of link-density and link-pattern communities in real-world networks. Eur. Phys. J. B.. 2012, 85, 1–11. [Google Scholar] [CrossRef]
  20. Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E.. 2008, 78, 046110. [Google Scholar] [CrossRef]
  21. Liu, W.; Pellegrini, M.; Wang, X. Detecting Communities Based on Network Topology. Sci. Rep.. 2014, 4, 5739. [Google Scholar] [CrossRef]
  22. Danon, L.; Diaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech.-Theory Exp. 2005; P09008. [Google Scholar]
  23. Gregory, S. Fuzzy overlapping communities in networks. J. Stat. Mech.-Theory Exp. 2011; P02017. [Google Scholar]
  24. Lancichinetti, A.; Fortunato, S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys. Rev. E.. 2009, 80, 016118. [Google Scholar] [CrossRef]
  25. Hullermeier, E.; Rifqi, M. A Fuzzy Variant of the Rand Index for Comparing Clustering Structures. In Proc. IFSA/EUSFLAT Conf. 2009; 1294–1298. [Google Scholar]
  26. Takiddin, A. An Artificial Intelligence Tool to Detect and Classify Skin Cancer. (College of Science,2020).
  27. Linares, M.; Zakaria, A.; Nizran, P. Skin Cancer. Primary Care: Clinics In Office Practice. 2015, 42, 645–659. [Google Scholar] [CrossRef] [PubMed]
  28. Liu-Smith, F.; Jia, J.; Zheng, Y. UV-Induced Molecular Signaling Differences in Melanoma and Non-melanoma Skin Cancer. Ultraviolet Light In Human Health, Diseases And Environment. 2017, 27–40.
  29. Raghavan, U.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev E.. 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed]
  30. Lou, H.; Li, S.; Zhao, Y. Detecting community structure using label propagation with weighted coherent neighborhood propinquity. Physica A.. 2013, 392, 3095–3105. [Google Scholar] [CrossRef]
  31. Sobolevsky, S.; Campari, R. General optimization technique for high-quality community detection in complex networks. Phys. Rev. E.. 2014, 90, 012811. [Google Scholar] [CrossRef]
  32. Fortunato, S.; Barthelemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. U. S. A.. 2007, 104, 36–41. [Google Scholar] [CrossRef]
  33. Barth, M. & Todd, M. Simulation model performance analysis of a multiple station shared vehicle system. Transportation Research Part C: Emerging Technologies. 1999, 7, 237–259. [Google Scholar] [CrossRef]
  34. Wang, X.; Li, J. Detecting communities by the core-vertex and intimate degree in complex networks. Physica A.. 2013, 392, 2555–2563. [Google Scholar] [CrossRef]
  35. Chen, Q.; Wu, T.; Fang, M. Detecting local community structure in complex networks based on local degree central nodes. Physica A.. 2013, 392, 529–537. [Google Scholar] [CrossRef]
  36. Zhang, S.; Wang, R.; Zhang, X. Identification of overlapping community structure in complex networks using fuzzy c-means clustering. Physica A.. 2007, 374, 483–490. [Google Scholar] [CrossRef]
  37. Sun, P.; Gao, L.; Han, S. Identification of overlapping and non-overlapping community structure by fuzzy clustering in complex networks. Inf. Sci.. 2011, 181, 1060–1071. [Google Scholar] [CrossRef]
  38. Psorakis, I.; Roberts, S.; Ebden, M.; Sheldon, B. Overlapping community detection using Bayesian non-negative matrix factorization. Phys. Rev. E.. 2011, 83, 066114. [Google Scholar] [CrossRef] [PubMed]
  39. Liu, J. Fuzzy modularity and fuzzy community structure in networks. Eur. Phys. J. B.. 2010, 77, 547–557. [Google Scholar] [CrossRef]
  40. Stiglic, M.; Agatz, N.; Savelsbergh, M.; Gradisar, M. Enhancing urban mobility: Integrating ride-sharing and public transit. Computers & Operations Research. 2018, 90, 12–21. [Google Scholar] [CrossRef]
  41. Meng, L.; Somenahalli, S.; Berry, S. Policy implementation of multi-modal (shared) mobility: review of a supply-demand value proposition canvas. Transport Reviews. 2020, 40, 670–684. [Google Scholar] [CrossRef]
  42. Velaga, N.; Rotstein, N.; Oren, N.; Nelson, J.; Norman, T.; Wright, S. Development of an integrated flexible transport systems platform for rural areas using argumentation theory. Research In Transportation Business & ManagementResearch In Transportation Business 2012, 3, 62–70. [Google Scholar] [CrossRef]
  43. Shaheen, S.; Chan, N. Mobility and the Sharing Economy: Potential to Facilitate the First- and Last-Mile Public Transit Connections. Built Environment. 2016, 42, 573–588. [Google Scholar] [CrossRef]
  44. Chen, P.; Nie, Y. Analysis of an idealized system of demand adaptive paired-line hybrid transit. Transportation Research Part B: Methodological. 2017, 102, 38–54. [Google Scholar] [CrossRef]
  45. Shen, C.; Quadrifoglio, L. Evaluation of Zoning Design with Transfers for Paratransit Services. Transportation Research Record Journal Of The Transportation Research Board. 2012, 2277, 82–89. [Google Scholar] [CrossRef]
  46. Lee, A.; Savelsbergh, M. An extended demand responsive connector. EURO Journal On Transportation And Logistics. 2014, 6, 1–26. [Google Scholar] [CrossRef]
  47. Savelsbergh, M. & Sol, M. The General Pickup and Delivery Problem. Transportation Science. 1995, 29, 17–29. [Google Scholar]
  48. Liu, L.; Sun, L.; Chen, Y.; Ma, X. Optimizing fleet size and scheduling of feeder transit services considering the influence of bike-sharing systems. Journal Of Cleaner Production. 2019, 236, 117550. [Google Scholar] [CrossRef]
  49. Lee, A.; Savelsbergh, M. An extended demand responsive connector. EURO Journal On Transportation And Logistics. 2017, 6, 25–50. [Google Scholar] [CrossRef]
  50. Basciftci, B.; Hentenryck, P. Capturing Travel Mode Adoption in Designing On-demand Multimodal Transit Systems. (2021).
  51. Dalmeijer, K.; Hentenryck, P. Transfer-Expanded Graphs for On-Demand Multimodal Transit Systems. (2019).
  52. Li, X.; Quadrifoglio, L. Feeder transit services: Choosing between fixed and demand responsive policy. Transportation Research Part C: Emerging Technologies. 2010, 18, 770–780. [Google Scholar] [CrossRef]
  53. Narayan, J.; Cats, O.; Van Oort, N.; Hoogendoorn, S. Integrated route choice and assignment model for fixed and flexible public transport systems. Transportation Research Part C: Emerging Technologies. 2020, 115, 102631. [Google Scholar] [CrossRef]
  54. Posada, M.; Andersson, H.; Häll, C. The integrated dial-a-ride problem with timetabled fixed route service. Public Transport. 2017, 9. [Google Scholar] [CrossRef]
  55. Quadrifoglio, L.; Li, X. A methodology to derive the critical demand density for designing and operating feeder transit services. Transportation Research Part B: Methodological. 2009, 43, 922–935. [Google Scholar] [CrossRef]
  56. Wang, L.; Liu, Q.; Ma, W. Optimization of dynamic relocation operations for one-way electric carsharing systems. Transportation Research Part C: Emerging Technologies. 2019, 101, 55–69. [Google Scholar] [CrossRef]
  57. Yan, X.; Zhao, X.; Han, Y.; Hentenryck, P.; Dillahunt, T. Mobility-on-demand versus fixed-route transit systems: An evaluation of traveler preferences in low-income communities. Transportation Research Part A: Policy And Practice. 2021, 148, 481–495. [Google Scholar] [CrossRef]
  58. Liang, X.; Almeida, Correia, G. ; Van Arem, B. Optimizing the service area and trip selection of an electric automated taxi system used for the last mile of train trips. Transportation Research Part E: Logistics And Transportation Review. 2016, 93, 115–129. [Google Scholar] [CrossRef]
  59. Pinto, H.; Hyl,; M. ; Mahmassani, H.; Verbas, I. Joint design of multimodal transit networks and shared autonomous mobility fleets. Transportation Research Part C: Emerging Technologies. 2020, 113, 2–20. [Google Scholar] [CrossRef]
  60. Shen, Y.; Zhang, H.; Zhao, J. Integrating shared autonomous vehicle in public transportation system: A supply-side simulation of the first-mile service in Singapore. Transportation Research Part A: Policy And Practice. 2018, 113, 125–136. [Google Scholar] [CrossRef]
  61. Dai, Z.; Liu, X.; Chen, X.; Ma, X. Joint optimization of scheduling and capacity for mixed traffic with autonomous and human-driven buses: A dynamic programming approach. Transportation Research Part C: Emerging Technologies. 2020, 114, 598–619. [Google Scholar] [CrossRef]
  62. Abe, R. Preferences of urban rail users for first- and last-mile autonomous vehicles: Price and service elasticities of demand in a multimodal environment. Transportation Research Part C: Emerging Technologies. 2021, 126, 103105. [Google Scholar] [CrossRef]
  63. Fafoutellis, P.; Mantouka, E. Major Limitations and Concerns Regarding the Integration of Autonomous Vehicles in Urban Transportation Systems: Proceedings of 4th Conference on Sustainable Urban Mobility (CSUM2018), 24 - 25 May, Skiathos Island, Greece. (2019,1).
  64. Pakusch, C.; Stevens, G.; Boden, A.; Bossauer, P. Unintended Effects of Autonomous Driving: A Study on Mobility Preferences in the Future. Sustainability. 2018, 10, 2404. [Google Scholar] [CrossRef]
  65. Talamini, G.; Pires, Ferreira, D. An informal transportation as a feeder of the rapid transit system. Spatial analysis of the e-bike taxi service in Shenzhen, China. Transportation Research Interdisciplinary Perspectives. 2019, 1, 100002. [Google Scholar] [CrossRef]
  66. Jia, J.; Zhang, H.; Shi, B. Exploring Bike-Sharing Behavior Affected by Public Transportation Disruption: Case of Washington, DC, Metro Shutdown. Journal Of Transportation Engineering, Part A: Systems. 2021, 147, 04020163. [Google Scholar] [CrossRef]
  67. Eren, E.; Uz, V. A review on bike-sharing: The factors affecting bike-sharing demand. Sustainable Cities And Society. 2020, 54, 101882. [Google Scholar] [CrossRef]
  68. Zhou, F.; Zheng, Z.; Whitehead, J.; Perrons, R.; Washington, S.; Page, L. Examining the impact of car-sharing on private vehicle ownership. Transportation Research Part A: Policy And Practice. 2020, 138, 322–341. [Google Scholar] [CrossRef]
  69. Br, stätter, G. ; Kahr, M.; Leitner, M. Determining optimal locations for charging stations of electric car-sharing systems under stochastic demand. Transportation Research Part B: Methodological. 2017, 104, 17–35. [Google Scholar] [CrossRef]
  70. Almeida Correia, G.; Antunes, A. Optimization approach to depot location and trip selection in one-way carsharing systems. Transportation Research Part E: Logistics And Transportation Review. 2012, 48, 233–247. [Google Scholar] [CrossRef]
  71. Fassi, A.; Awasthi, A.; Viviani, M. Evaluation of carsharing network’s growth strategies through discrete event simulation. Expert Systems With Applications. 2012, 39, 6692–6705. [Google Scholar] [CrossRef]
  72. Huang, K.; Almeida Correia, G.; An, K. Solving the station-based one-way carsharing network planning problem with relocations and non-linear demand. Transportation Research Part C: Emerging Technologies. 2018, 90, 1–17. [Google Scholar] [CrossRef]
  73. Kumar, V.; Bierlaire, M. Optimizing Locations for a Vehicle Sharing System. (2012). 2012.
  74. Lin, M.; Huang, C.; Xu, Z. MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustainable Cities And Society. 2020, 53, 101873. [Google Scholar] [CrossRef]
  75. Nair, R.; Miller-Hooks, E. Equilibrium network design of shared-vehicle systems. European Journal Of Operational Research. 2014, 235, 47–61. [Google Scholar] [CrossRef]
  76. Seign, R.; Schüßler, M.; Bogenberger, K. Enabling sustainable transportation: The model-based determination of business/operating areas of free-floating carsharing systems. Research In Transportation Economics. 2015, 51, 104–114. [Google Scholar] [CrossRef]
  77. Cepolina, E.; Farina, A. A new shared vehicle system for urban areas. Transportation Research Part C: Emerging Technologies. 2012, 21, 230–243. [Google Scholar] [CrossRef]
  78. George, D.; Xia, C. Fleet-sizing and service availability for a vehicle rental system via closed queueing networks. European Journal Of Operational Research. 2011, 211, 198–207. [Google Scholar] [CrossRef]
  79. Lokhandwala, M.; Cai, H. Siting charging stations for electric vehicle adoption in shared autonomous fleets. Transportation Research Part D: Transport And Environment. 2020, 80. [Google Scholar] [CrossRef]
  80. Sun, X.; Tang, W.; Chen, J.; Zhang, J. Optimal investment strategy of a free-floating sharing platform. Transportation Research Part E: Logistics And Transportation Review. 2020, 138. [Google Scholar] [CrossRef]
  81. Xu, M.; Meng, Q.; Liu, Z. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment. Transportation Research Part B: Methodological. 2018, 111, 60–82. [Google Scholar] [CrossRef]
  82. Xu, M.; Meng, Q. Fleet sizing for one-way electric carsharing services considering dynamic vehicle relocation and nonlinear charging profile. Transportation Research Part B: Methodological. 2019, 128, 23–49. [Google Scholar] [CrossRef]
  83. Bruglieri, M.; Colorni, A.; Luè, A. The Vehicle Relocation Problem for the One-way Electric Vehicle Sharing: An Application to the Milan Case. Procedia - Social And Behavioral Sciences. 2014, 111, 18–27. [Google Scholar] [CrossRef]
  84. Huwer, U. Public transport and car-sharing - benefits and effectsof combined services. Transport Policy. 2004, 11, 77–87. [Google Scholar] [CrossRef]
  85. Sachan, A.; Mathew, T. Integrated Multimodal Transit Route Network Design with Feeder Systems. Transportation Research Procedia. 2020, 48, 756–763. [Google Scholar] [CrossRef]
  86. Shaheen, S.; Chan, N. Mobility and the Sharing Economy: Potential to Overcome First-and Last-Mile Public Transit Connections. (UC Berkeley: Transportation Sustainability Research Center. 2016. [Google Scholar]
  87. Tabassum, S.; Tanaka, S.; Nakamura, F.; Ryo, A. Feeder Network Design for Mass Transit System in Developing Countries (Case study of Lahore, Pakistan). Transportation Research Procedia. 2017, 25, 3129–3146. [Google Scholar] [CrossRef]
  88. Wang, H.; Cheu, R.; Lee, D. Dynamic relocating vehicle resources using a microscopic traffic simulation model for carsharing services. 3rd International Joint Conference On Computational Sciences And Optimization, CSO 2010: Theoretical Development And Engineering Practice. 2010, 1, 108–111. [Google Scholar]
  89. Mahéo, A.; Kilby, P.; Hentenryck, P. Benders Decomposition for the Design of a Hub and Shuttle Public Transit System. Transp. Sci.. 2019, 53, 77–88. [Google Scholar] [CrossRef]
  90. Boyacı, B.; Zografos, K.; Geroliminis, N. An optimization framework for the development of efficient one-way car-sharing systems. European Journal Of Operational Research. 2015, 240, 718–733. [Google Scholar] [CrossRef]
  91. Huang, K.; An, K.; Rich, J.; Ma, W. Vehicle relocation in one-way station-based electric carsharing systems: A comparative study of operator-based and user-based methods. Transportation Research Part E: Logistics And Transportation Review. 2020, 142, 102081. [Google Scholar] [CrossRef]
  92. Huang, K.; An, K.; Almeida Correia, G. Planning station capacity and fleet size of one-way electric carsharing systems with continuous state of charge functions. European Journal Of Operational Research. 2020, 287, 1075–1091. [Google Scholar] [CrossRef]
  93. Çalık, H.; Fortz, B. A Benders decomposition method for locating stations in a one-way electric car sharing system under demand uncertainty. Transportation Research Part B: Methodological. 2019, 125, 121–150. [Google Scholar] [CrossRef]
  94. Kek, A.; Cheu, R.; Meng, Q.; Fung, C. A decision support system for vehicle relocation operations in carsharing systems. Transportation Research Part E: Logistics And Transportation Review. 2009, 45, 149–158. [Google Scholar] [CrossRef]
  95. Zhang, S.; Zhao, X.; Li, X.; Yu, H. Heterogeneous fleet management for one-way electric carsharing system with optional orders, vehicle relocation and on-demand recharging. Computers & Operations Research. 2022, 145, 105868. [Google Scholar] [CrossRef]
  96. Illgen, S.; Höck, M. Literature review of the vehicle relocation problem in one-way car sharing networks. Transportation Research Part B: Methodological. 2019, 120, 193–204. [Google Scholar] [CrossRef]
  97. Alfian, G.; Rhee, J.; Yoon, B. A simulation tool for prioritizing product-service system (PSS) models in a carsharing service. Computers & Industrial Engineering. 2014, 70, 59–73. [Google Scholar] [CrossRef]
  98. Hu, L.; Liu, Y. Joint design of parking capacities and fleet size for one-way station-based carsharing systems with road congestion constraints. Transportation Research Part B: Methodological. 2016, 93, 268–299. [Google Scholar] [CrossRef]
  99. Pantuso, G. Exact solutions to a carsharing pricing and relocation problem under uncertainty. Computers And Operations Research. 2022, 144. [Google Scholar] [CrossRef]
  100. Li, H.; Hu, L.; Jiang, Y. Dynamic pricing, vehicle relocation and staff rebalancing for station-based one-way electric carsharing systems considering nonlinear charging profile. Transportation Letters. 2022. [Google Scholar] [CrossRef]
  101. Huang, K.; An, K.; Almeida, Correia, G. ; Rich, J.; Ma, W. An innovative approach to solve the carsharing demand-supply imbalance problem under demand uncertainty. Transportation Research Part C: Emerging Technologies. 2021, 132, 103369. [Google Scholar] [CrossRef]
  102. Lu, R.; Almeida, Correia, G. ; Zhao, X.; Liang, X.; Lv, Y. Performance of one-way carsharing systems under combined strategy of pricing and relocations. Transportmetrica B: Transport Dynamics. 2021, 9, 134–152. [Google Scholar] [CrossRef]
  103. Cocca, M.; Giordano, D.; Mellia, M.; Vassio, L. Free floating electric car sharing design: Data driven optimisation. Pervasive And Mobile Computing. 2019, 55, 59–75. [Google Scholar] [CrossRef]
  104. Roni, M.; Yi, Z.; Smart, J. Optimal charging management and infrastructure planning for free-floating shared electric vehicles. Transportation Research Part D: Transport And Environment. 2019, 76, 155–175. [Google Scholar] [CrossRef]
  105. Folkestad, C.; Hansen, N.; Fagerholt, K.; Andersson, H.; Pantuso, G. Optimal charging and repositioning of electric vehicles in a free-floating carsharing system. Computers & Operations Research. 2020, 113, 104771. [Google Scholar] [CrossRef]
  106. Xu, M.; Wu, T.; Tan, Z. Electric vehicle fleet size for carsharing services considering on-demand charging strategy and battery degradation. Transportation Research Part C: Emerging Technologies. 2021, 127, 103146. [Google Scholar] [CrossRef]
  107. Wu, Y.; Chen, M.; Wang, X. Incentivized self-rebalancing fleet in electric vehicle sharing. IISE Transactions. 2022, 54, 173–185. [Google Scholar] [CrossRef]
  108. Prencipe, L.; Theresia, van Essen, J. ; Caggiani, L.; Ottomanelli, M.; Homem de Almeida Correia, G. A mathematical programming model for optimal fleet management of electric car-sharing systems with Vehicle-to-Grid operations. Journal Of Cleaner Production. 2022, 368, 133147. [Google Scholar] [CrossRef]
  109. Gambella, C.; Malaguti, E.; Masini, F.; Vigo, D. Optimizing relocation operations in electric car-sharing. Omega. 2018, 81, 234–245. [Google Scholar] [CrossRef]
  110. Cai, L.; Wang, X.; Luo, Z.; Liang, Y. A hybrid adaptive large neighborhood search and tabu search algorithm for the electric vehicle relocation problem. Computers & Industrial Engineering. 2022, 167, 108005. [Google Scholar] [CrossRef]
  111. Chang, X.; Wu, J.; Almeida, Correia, G. ; Sun, H.; Feng, Z. A cooperative strategy for optimizing vehicle relocations and staff movements in cities where several carsharing companies operate simultaneously. Transportation Research Part E: Logistics And Transportation Review. 2022, 161, 102711. [Google Scholar] [CrossRef]
  112. Lai, M.; Hu, Q.; Liu, Y.; Lang, Z. A rolling-horizon decision framework for integrating relocation and user flexibility in one-way electric carsharing systems. Transportation Research Part C: Emerging Technologies. 2022, 144, 103867. [Google Scholar] [CrossRef]
  113. Yang, S.; Wu, J.; Sun, H.; Qu, Y.; Wang, D. Integrated optimization of pricing and relocation in the competitive carsharing market: A multi-leader-follower game model. Transportation Research Part C: Emerging Technologies. 2022, 138, 103613. [Google Scholar] [CrossRef]
  114. Schiffer, M.; Hiermann, G.; Rüdel, F.; Walther, G. A polynomial-time algorithm for user-based relocation in free-floating car sharing systems. Transportation Research Part B: Methodological. 2021, 143, 65–85. [Google Scholar] [CrossRef]
  115. Jorge, D.; Molnar, G.; De Almeida, Correia, G. Trip pricing of one-way station-based carsharing networks with zone and time of day price variations. Transportation Research Part B: Methodological. 2015, 81, 461–482. [Google Scholar] [CrossRef]
  116. Shan, A.; Hoang, N.; An, K.; Vu, H. A framework for railway transit network design with first-mile shared autonomous vehicles. Transportation Research Part C: Emerging Technologies. 2021, 130, 103223. [Google Scholar] [CrossRef]
  117. Lau, S.; Susilawati, S. Shared autonomous vehicles implementation for the first and last-mile services. Transportation Research Interdisciplinary Perspectives. 2021, 11, 100440. [Google Scholar] [CrossRef]
  118. Stokkink, P.; Geroliminis, N. Predictive user-based relocation through incentives in one-way car-sharing systems. Transportation Research Part B: Methodological. 2021, 149, 230–249. [Google Scholar] [CrossRef]
  119. Abbasi, S.; Ko, J.; Kim, J. Carsharing travel distance and its associated factors: A case study of Seoul, South Korea. Journal Of Cleaner Production. 2022, 362, 132380. [Google Scholar] [CrossRef]
  120. Safdar, M.; Jamal, A.; Al-Ahmadi, H.; Rahman, M.; Almoshaogeh, M. Analysis of the Influential Factors towards Adoption of Car-Sharing: A Case Study of a Megacity in a Developing Country. Sustainability. 2022, 14. [Google Scholar] [CrossRef]
  121. Wang, Y.; Mi, X. A Comparative Study on Demand Forecast of Car Sharing Users Based on ARIMA and LSTM. 2020 5th International Conference On Electromechanical Control Technology And Transportation (ICECTT). pp. 565-574 (2020).
  122. Cocca, M.; Teixeira, D.; Vassio, L.; Mellia, M.; Almeida, J.; Silva, A. On Car-Sharing Usage Prediction with Open Socio-Demographic Data. Electronics. 2020, 9. [Google Scholar] [CrossRef]
  123. Brahimi, N.; Zhang, H.; Dai, L.; Zhang, J. Modelling on Car-Sharing Serial Prediction Based on Machine Learning and Deep Learning. Complexity. 2022, 2022, 1–20. [Google Scholar] [CrossRef]
  124. Rožanec, J.; Kažič, B.; Škrjanc, M.; Fortuna, B.; Mladenić, D. Automotive OEM Demand Forecasting: A Comparative Study of Forecasting Algorithms and Strategies. Applied Sciences. 2021, 11. [Google Scholar] [CrossRef]
  125. Yu, D.; Li, Z.; Zhong, Q.; Yi, A.; Chen, W. Demand Management of Station-Based Car Sharing System Based on Deep Learning Forecasting. Journal Of Advanced Transportation. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
  126. Yoon, T.; Cherry, C.; Ryerson, M.; Bell, J. Carsharing demand estimation and fleet simulation with EV adoption. Journal Of Cleaner Production. 2019, 206, 1051–1058. [Google Scholar] [CrossRef]
  127. Maybury, L.; Corcoran, P.; Cipcigan, L. Mathematical modelling of electric vehicle adoption: A systematic literature review. Transportation Research Part D: Transport And Environment 2022, 107, 103278. [Google Scholar] [CrossRef]
  128. Weikl, S.; Bogenberger, K. A practice-ready relocation model for free-floating carsharing systems with electric vehicles – Mesoscopic approach and field trial results. Transportation Research Part C: Emerging Technologies 2015, 206–223. [Google Scholar] [CrossRef]
  129. Qin, H.; Su, E.; Wang, Y.; Li, J. Branch-and-price-and-cut for the electric vehicle relocation problem in one-way carsharing systems. Omega. 2022, 109, 102609. [Google Scholar] [CrossRef]
  130. Bogyrbayeva, A.; Jang, S.; Shah, A.; Jang, Y.; Kwon, C. A Reinforcement Learning Approach for Rebalancing Electric Vehicle Sharing Systems. IEEE Transactions On Intelligent Transportation Systems. 2021, 1–11. [Google Scholar] [CrossRef]
  131. Pezzella, F.; Pisacane, O. A two-phase optimization method for a multiobjective vehicle relocation problem in electric carsharing systems. Journal Of Combinatorial Optimization. 2018, 36. [Google Scholar] [CrossRef]
  132. Liu, Y.; Xie, J.; Chen, N. Stochastic one-way carsharing systems with dynamic relocation incentives through preference learning. Transportation Research Part E: Logistics And Transportation Review. 2022, 166, 102884. [Google Scholar] [CrossRef]
  133. Bitencourt, L.; Dias, B.; Soares, T.; Borba, B.; Quirós-Tortós, J. e-Carsharing siting and sizing DLMP-based under demand uncertainty. Applied Energy. 2023, 330, 120347. [Google Scholar] [CrossRef]
  134. Hayashi, N.; Sakurama, K. Communication-aware distributed rebalancing for cooperative car-sharing service. IET Control Theory & Applications 2022. [Google Scholar] [CrossRef]
  135. Lin, D.; Kuo, J. The vehicle deployment and relocation problem for electric vehicle sharing systems considering demand and parking space stochasticity. Transportation Research Part E: Logistics And Transportation Review. 2021, 156, 102514. [Google Scholar] [CrossRef]
  136. Wang, D.; Liao, F. Incentivized user-based relocation strategies for moderating supply–demand dynamics in one-way car-sharing services. Transportation Research Part E: Logistics And Transportation Review. 2023, 171, 103017. [Google Scholar] [CrossRef]
  137. Ait-Ouahmed, A.; Josselin, D.; Zhou, F. Relocation optimization of electric cars in one-way car-sharing systems: modeling, exact solving and heuristics algorithms. International Journal Of Geographical Information Science. 2018, 32, 367–398. [Google Scholar] [CrossRef]
  138. Jorge, D.; Correia, G.; Barnhart, C. Comparing Optimal Relocation Operations With Simulated Relocation Policies in One-Way Carsharing Systems. IEEE Transactions On Intelligent Transportation Systems. 2014, 15, 1667–1675. [Google Scholar] [CrossRef]
  139. Wang, N.; Jia, S.; Liu, Q. A user-based relocation model for one-way electric carsharing system based on micro demand prediction and multi-objective optimization. Journal Of Cleaner Production. 2021, 296, 126485. [Google Scholar] [CrossRef]
  140. Nourinejad, M.; Zhu, S.; Bahrami, S.; Roorda, M. Vehicle relocation and staff rebalancing in one-way carsharing systems. Transportation Research Part E: Logistics And Transportation Review. 2015, 81, 98–113. [Google Scholar] [CrossRef]
  141. Lee, J.; Park, G. Planning of Relocation Staff Operations in Electric Vehicle Sharing Systems. Intelligent Information And Database Systems. 2013, 256–265. [Google Scholar] [CrossRef]
  142. Boyacı, B.; Zografos, K.; Geroliminis, N. An integrated optimization-simulation framework for vehicle and personnel relocations of electric carsharing systems with reservations. Transportation Research Part B: Methodological. 2017, 95, 214–237. [Google Scholar] [CrossRef]
  143. Yang, J.; Hu, L.; Jiang, Y. An overnight relocation problem for one-way carsharing systems considering employment planning, return restrictions, and ride sharing of temporary workers. Transportation Research Part E: Logistics And Transportation Review. 2022, 168, 102950. [Google Scholar] [CrossRef]
  144. Bekli, S.; Boyacı, B.; Zografos, K. Enhancing the performance of one-way electric carsharing systems through the optimum deployment of fast chargers. Transportation Research Part B: Methodological. 2021, 152, 118–139. [Google Scholar] [CrossRef]
  145. Huo, X.; Wu, X.; Li, M.; Zheng, N.; Yu, G. The allocation problem of electric car-sharing system: A data-driven approach. Transportation Research Part D: Transport And Environment. 2020, 78, 102192. [Google Scholar] [CrossRef]
  146. Balac, M.; Becker, H.; Ciari, F.; Axhausen, K. Modeling competing free-floating carsharing operators – A case study for Zurich, Switzerland. Transportation Research Part C: Emerging Technologies. 2019, 98, 101–117. [Google Scholar] [CrossRef]
  147. Zhao, M.; Li, X.; Yin, J.; Cui, J.; Yang, L.; An, S. An integrated framework for electric vehicle rebalancing and staff relocation in one-way carsharing systems: Model formulation and Lagrangian relaxation-based solution approach. Transportation Research Part B: Methodological. 2018, 117, 542–572. [Google Scholar] [CrossRef]
  148. Bruglieri, M.; Pezzella, F.; Pisacane, O. An Adaptive Large Neighborhood Search for relocating vehicles in electric carsharing services. Discrete Applied Mathematics. 2019, 253, 185–200. [Google Scholar] [CrossRef]
  149. Angelopoulos, A.; Gavalas, D.; Konstantopoulos, C.; Kypriadis, D.; Pantziou, G. Incentivized vehicle relocation in vehicle sharing systems. Transportation Research Part C: Emerging Technologies 2018, 97, 175–193. [Google Scholar] [CrossRef]
  150. Bruglieri, M.; Pezzella, F.; Pisacane, O. Heuristic algorithms for the operator-based relocation problem in one-way electric carsharing systems. Discrete Optimization. 2017, 23, 56–80. [Google Scholar] [CrossRef]
  151. Molnar, G.; Almeida, Correia, G. Long-term vehicle reservations in one-way free-floating carsharing systems: A variable quality of service model. Transportation Research Part C: Emerging Technologies. 2019, 98, 298–322. [Google Scholar] [CrossRef]
  152. Weidinger, F.; Albiński, S.; Boysen, N. Matching supply and demand for free-floating car sharing: On the value of optimization. European Journal Of Operational Research. 2023, 308, 1380–1395. [Google Scholar] [CrossRef]
  153. Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. European Journal Of Operational Research. 2012, 223, 295–303. [Google Scholar] [CrossRef]
  154. Fielbaum, A.; Bai, X.; Alonso-Mora, J. On-demand ridesharing with optimized pick-up and drop-off walking locations. Transportation Research Part C: Emerging Technologies 2021, 126, 103061. [Google Scholar] [CrossRef]
  155. Soppert, M.; Steinhardt, C.; Müller, C.; Gönsch, J.; Bhogale, P. Matching functions for free-floating shared mobility system optimization to capture maximum walking distances. European Journal Of Operational Research. 2023, 305, 1194–1214. [Google Scholar] [CrossRef]
  156. Wu, J.; Hu, L.; Jiang, Y. Collaborative strategic and tactical planning for one-way station-based carsharing systems with trip selection and vehicle relocation. Transportation Letters. 2022. [Google Scholar] [CrossRef]
  157. Nourinejad, M.; Roorda, M. A dynamic carsharing decision support system. Transportation Research Part E: Logistics And Transportation Review. 2014, 66, 36–50. [Google Scholar] [CrossRef]
  158. Fayez, Eliyan, A. ; Kerbache, L.; Elomri, A. Shared clean mobility operations for first-mile and last-mile public transit connections: A case study of doha, Qatar. Journal Of Advanced Transportation. 2022, 2022, 1–14. [Google Scholar]
  159. Yan, X.; Zhao, X.; Broaddus, A.; Johnson, J.; Srinivasan, S. Evaluating shared e-scooters’ potential to enhance public transit and reduce driving. Transportation Research Part D: Transport And Environment. 2023, 117, 103640. [Google Scholar] [CrossRef]
  160. Tzouras, P.; Mitropoulos, L.; Koliou, K.; Stavropoulou, E.; Karolemeas, C.; Antoniou, E.; Karaloulis, A.; Mitropoulos, K.; Vlahogianni, E.; Kepaptsoglou, K. Describing Micro-Mobility First/Last-Mile Routing Behavior in Urban Road Networks through a Novel Modeling Approach. Sustainability. 2023, 15. [Google Scholar] [CrossRef]
  161. Beale, K.; Kapatsila, B.; Grisé, E. Integrating Public Transit and Shared Micromobility Payments to Improve Transportation Equity in Seattle, WA. Transportation Research Record. 2023, 2677, 968–980. [Google Scholar] [CrossRef]
  162. Oeschger, G.; Carroll, P.; Caulfield, B. Micromobility and public transport integration: The current state of knowledge. Transportation Research Part D: Transport And Environment. 2020, 89, 102628. [Google Scholar] [CrossRef]
  163. Romm, D.; Verma, P.; Karpinski, E.; S. ; ers, T.; McKenzie, G. Differences in first-mile and last-mile behaviour in candidate multi-modal Boston bike-share micromobility trips. Journal Of Transport Geography. 2022, 102, 103370. [Google Scholar] [CrossRef]
  164. Hua, Y.; Zhao, D.; Wang, X.; Li, X. Joint infrastructure planning and fleet management for one-way electric car sharing under time-varying uncertain demand. Transportation Research Part B: Methodological. 2019, 128, 185–206. [Google Scholar] [CrossRef]
  165. Deng, Y.; Cardin, M. Integrating operational decisions into the planning of one-way vehicle-sharing systems under uncertainty. Transportation Research Part C: Emerging Technologies. 2018, 86, 407–424. [Google Scholar] [CrossRef]
  166. Deng, Y.; Gupta, A.; Shroff, N. Fleet sizing and charger allocation in electric vehicle sharing systems. IFAC Journal Of Systems And Control. 2022, 22, 100210. [Google Scholar] [CrossRef]
  167. Laporte, G.; Meunier, F.; Wolfler, Calvo, R. Shared mobility systems: an updated survey. Annals Of Operations Research. 2018, 271, 105–126. [Google Scholar] [CrossRef]
  168. Nair, R.; Miller-Hooks, E. Fleet Management for Vehicle Sharing Operations. Transportation Science. 2011, 45, 524–540. [Google Scholar] [CrossRef]
  169. Daganzo, C.; Newell, G. Configuration of physical distribution networks. Networks. 1986, 16, 113–132. [Google Scholar] [CrossRef]
  170. Di Febbraro, A.; Sacco, N.; Saeednia, M. One-Way Car-Sharing Profit Maximization by Means of User-Based Vehicle Relocation. IEEE Transactions On Intelligent Transportation Systems. 2019, 20, 628–641. [Google Scholar] [CrossRef]
  171. Zou, Y.; Yang, C.; Yang, J. P-D pair based EV-sharing vehicle relocation problem with route familiarity. Computers & Industrial Engineering. 2021, 159, 107529. [Google Scholar] [CrossRef]
  172. Repoux, M.; Kaspi, M.; Boyacı, B.; Geroliminis, N. Dynamic prediction-based relocation policies in one-way station-based carsharing systems with complete journey reservations. Transportation Research Part B: Methodological. 2019, 130, 82–104. [Google Scholar] [CrossRef]
  173. Chen, Y.; Liu, Y. Integrated Optimization of Planning and Operations for Shared Autonomous Electric Vehicle Systems. Transportation Science. 2023, 57, 106–134. [Google Scholar] [CrossRef]
  174. Li, X.; Ma, J.; Cui, J.; Ghiasi, A.; Zhou, F. Design framework of large-scale one-way electric vehicle sharing systems: A continuum approximation model. Transportation Research Part B: Methodological. 2016, 88, 21–45. [Google Scholar] [CrossRef]
  175. Huang, W.; Huang, W.; Jian, S. One-way carsharing service design under demand uncertainty: A service reliability-based two-stage stochastic program approach. Transportation Research Part E: Logistics And Transportation Review. 2022, 159, 102624. [Google Scholar] [CrossRef]
  176. Bouza, Allende, G. ; Still, G. Solving bilevel programs with the KKT-approach. Mathematical Programming. 2012, 138. [Google Scholar] [CrossRef]
  177. Correia, G.; Jorge, D.; Antunes, D. The Added Value of Accounting For Users’ Flexibility and Information on the Potential of a Station-Based One-Way Car-Sharing System: An Application in Lisbon, Portugal. Journal Of Intelligent Transportation Systems. 2014, 18, 299–308. [Google Scholar] [CrossRef]
  178. Boyacı, B.; Zografos, K. Investigating the effect of temporal and spatial flexibility on the performance of one-way electric carsharing systems. Transportation Research Part B: Methodological. 2019, 129, 244–272. [Google Scholar] [CrossRef]
  179. Le Vine, S.; Polak, J. The impact of free-floating carsharing on car ownership: Early-stage findings from London. Transport Policy. 2019, 75, 119–127. [Google Scholar] [CrossRef]
  180. Tarnovetckaia, R.; Mostofi, H. Impact of Car-Sharing and Ridesourcing on Public Transport Use: Attitudes, Preferences, and Future Intentions Regarding Sustainable Urban Mobility in the Post-Soviet City. Urban Science. 2022, 6. [Google Scholar] [CrossRef]
  181. Liao, F.; Correia, G. Electric carsharing and micromobility: A literature review on their usage pattern, demand, and potential impacts. International Journal Of Sustainable Transportation. 2021, 16, 269–286. [Google Scholar] [CrossRef]
  182. Deza, A.; Huang, K.; Metel, M. Charging station optimization for balanced electric car sharing. Discrete Applied Mathematics. 2022, 308, 187–197. [Google Scholar] [CrossRef]
  183. Br, statter, G. ; Leitner, M.; Ljubić, I. Location of Charging Stations in Electric Car Sharing Systems. Transportation Science. 2020, 54, 1408–1438. [Google Scholar] [CrossRef]
  184. Biesinger, B.; Hu, B.; Stubenschrott, M.; Ritzinger, U. ; Pr, tstetter, M. Optimizing Charging Station Locations for Electric Car-Sharing Systems. Evolutionary Computation In Combinatorial Optimization.
  185. Sonneberg, M.; Kuehne, K.; Breitner, M. A Decision Support System for the Optimization of Electric Car Sharing Stations. International Conference On Interaction Sciences. 2015. [Google Scholar]
  186. Jorge, D.; Correia, G.; Barnhart, C. Testing the Validity of the MIP Approach for Locating Carsharing Stations in One-way Systems. Procedia - Social And Behavioral Sciences. 2012, 54, 138–148. [Google Scholar] [CrossRef]
Preprints 90129 g001
Figure 1. (a) two-way carsharing vs. (b) one-way carsharing.
Figure 1. (a) two-way carsharing vs. (b) one-way carsharing.
Preprints 90129 g001
Table 1. Tactical and operational decisions in modeling oneway carsharing.
Table 1. Tactical and operational decisions in modeling oneway carsharing.
Reference Tactical decisions Operational decisions Additional decisions
(1) (2) (3) (4) (5)
[145] - - ✓ - - Fleet allocation
[109] - - ✓ ✓ - Battery charge
[81] ✓ ✓ ✓ ✓ - Staff assignment to vehicles
Trip pricing
[100] - - ✓ ✓ - Dynamic trip pricing
[143] ✓ ✓ ✓ ✓ - Vehicle & staff initial allocation
[171] - - ✓ ✓ - -
[129] - - ✓ ✓ - Staff routs & schedules
[112] ✓ ✓ ✓ ✓ ✓ State of charge of
a vehicle at a specified time
Vehicle and staff inventory
at a specified time at a
certain station
Vehicle assignment to a trip
[172] ✓ ✓ ✓ ✓ ✓ Vehicle and staff initial allocation
[168] - - ✓ - - Parking space inventory
Vehicle inventory
[94] - - ✓ ✓ ✓ No. of rejected demand
No. of rejected vehicle return
[157] ✓ - ✓ - - Vehicle availability time
[140] ✓ ✓ ✓ ✓ - -
[147] ✓ ✓ ✓ ✓ - Fleet initial allocation
Staff initial allocation
Battery volume at time steps
[82] - - ✓ - ✓ Find a profitable trip chain
[142] ✓ ✓ ✓ ✓ ✓ No. of vehicles being charged
[178] ✓ - ✓ ✓ - -
[102] ✓ - ✓ - - Fleet initial allocation
Trip pricing
[110] - - ✓ ✓ - Staff routes & schedules for
vehicle relocation
Note: (1) Fleet size, (2) Staff size, (3) Vehicle relocation, (4) Staff balancing, (5) Trip selection.
Table 2. Tactical and strategic decisions while considering vehicle relocation
Table 2. Tactical and strategic decisions while considering vehicle relocation
Reference Strategic decisions Tactical decisions Objective function Additional decisions
(1) (2) (3) (4)
[186] ✓ ✓ ✓ ✗ Max profit No. of parking spaces
Vehicle inventory at each
station at each time step
[138] ✗ ✓ ✓ ✗ Max profit No. of parking spaces
Fleet allocation
[174] ✓ ✗ ✓ ✗ Min costs -
[69] ✓ ✓ ✓ ✗ Max profit Trip selection
[93] ✓ ✗ ✓ ✗ Max profit Trip selection
[182] ✓ ✓ ✗ ✗ Max No. of EV trips
Min No. of unserved
commuters.		 Charging station allocation
No. of parking spaces
[144] ✗ ✓ ✗ ✗ Max profits No. of chargers to be installed
Station upgrade with chargers
of a certain type.
No. of vehicles with a certain
battery level to be charged with
a charger of a certain type
[90] ✓ ✓ ✓ ✓ Multi-objective: max operator
profit and commuters’ benefit		 No. and location of shared stations
No. of served and unserved
orders
[175] ✗ ✓ ✓ ✓ Max profit No. of parking spaces
Vehicle movements
Vehicle and staff allocation
[92] ✗ ✓ ✓ ✗ Max profit No. of parking spaces in a zone
Fleet size in a zone
No. of satisfied travel demand
[70] ✓ ✓ ✓ ✗ Max profit Fleet allocation
Depot-size
Vehicle inventory
Trip selection
[72] ✓ ✓ ✓ ✗ Max profit No. of stations
No. of car parking spaces
Vehicle allocation
[183] ✓ ✓ ✓ ✗ Max profit Number of chargers
installed in a station
Trip selection
Trip assignment to vehicles
[184] ✓ ✓ ✓ ✗ Max profit First level:
No. of stations
Station capacity
Fleet size.
Second level:
Trip selection
[185] ✓ ✓ ✗ ✗ Max profit No. of vehicles being charged
with a regular charger
No. of vehicles being charged
with fast chargers
Trip assignment to a station
[165] ✗ ✓ ✓ ✗ Min costs Vehicle allocation
[156] ✓ ✓ ✓ ✗ Max profit No. of parking spaces
Vehicle allocation
Note: (1) Station/parking location, (2) Station capacity, (3) Fleet size, (4) Staff size.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated