Submitted:
09 November 2023
Posted:
10 November 2023
You are already at the latest version
Abstract
Keywords:
MSC: Primary 35Q30; 76T06; 76D05; 76D06; Secondary 35R35; 76D03
1. Introduction
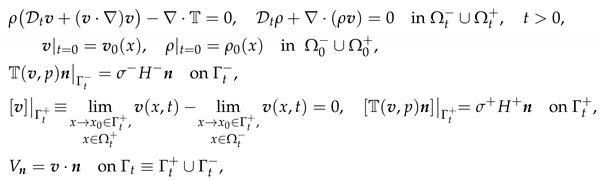
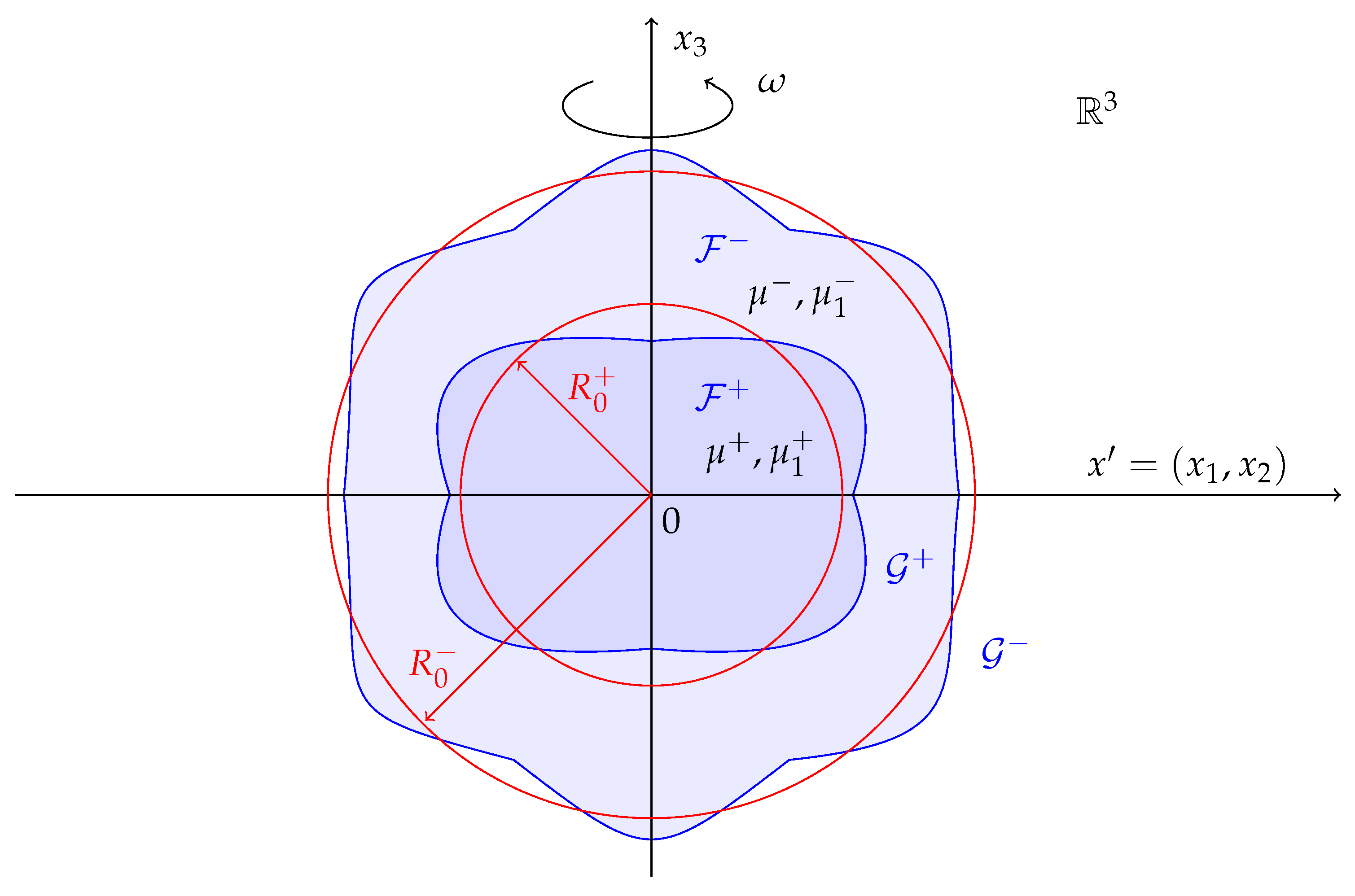
2. Proof of Theorem 1
3. General case
Conclusions
References
- Lyapunov, A. M.: On stability of ellipsoidal shapes of equilibrium of revolving liquid, Editiion of the Academy of Scien., 1884 (in Russian).
- Lyapunov, A. M.: Sur les questions qui appartiennent aux surfaces des figures d’equilibre dérivées des ellopsoïdes, News of the Academy of Scien., (1916) p. 139.
- Poincaré, H.: Figures d’équilibre d’une mass fluide, Paris, Gautier–Villars, 1902.
- Globa-Mikhailenko, B.: Figures ellipsoïdales d’équilibre d’une masse fluide en rotation quand on tient compte de la pression capillaire, Comptes rendus, 160, 233 (1915).
- Charrueau, A. Ètude d’une masse liquide de révolution homogène, sans pesanteur et à tension superficielle, animée d’une rotation uniforme. Ann. de Ècole Normale Supérieure 1926, 43, 129–176. [Google Scholar] [CrossRef]
- Charrueau, A. Sur les figures d’équilibre relatif d’une masse liquide en rotation à tension superficielle. C. R. 1927, 184, 1418. [Google Scholar]
- Appell, P. Figures d’Équilibre d’une Mass Liquide Homogène en Rotation—Traité de Mécanique Rationnelle, v. IV, Fasc. I, 2nd ed.; Gautier–Villars: Paris, France, 1932. [Google Scholar]
- Chandrasekhar, S. Ellipsoidal Figures of Equilibrium, Yale University Press: New Haven and London, 1969.
- Solonnikov, V. A.; Tani, A. Equilibrium figures of slowly rotating viscous compressible barotropic capillary liquid, Advances in Math. Sciences and Applications, 1993 2(1), 139–145.
- Denisova, I. V. Problem on the motion of two compressible fluids separated by a closed free interface, Zap. Nauch. Semin. POMI 1997, 243, 61–86; English transl. J. Math. Sci. 2000, 99, 837–853. [Google Scholar] [CrossRef]
- Denisova, I. V. Solvability in weighted Hölder spaces of a problem governing the evolution of two compressible fluids, Zap. Nauch. Semin. POMI 2003 295, 57–89; English transl. in J. Math. Sci. 2005 127(2), 1849–1868.
- Solonnikov, V. A.; Tani, A. Free boundary problem for a viscous compressible flow with surface tension, in: Constantin Carathéodory: An International Tribute, World Scientific (1991), 1270–1303.
- Denisova, I.V.; Solonnikov, V.A. Classical solvability of a model problem in the half-space related to the motion of an isolated mass of a compressible liquid. Zap. Nauchn. Semin. Petersburg. Otdel. Mat. Inst. Steklov. (POMI). 2000,271, 92–113 (Russian); English transl. J. Math. Sci. 2003, 115(6), 2753–2765.
- Blaschke, W. Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. I; Springer: Berlin, Germany, 1924. [Google Scholar]
- Solonnikov, V.A. On the problem of non-stationary motion of two viscous incompressible liquids. Probl. Mat. Analiz. 2006, 34, 103–121, Engl. transl. J. Math. Sci. 2007, 142, 1844–1866. [Google Scholar] [CrossRef]
- Solonnikov, V. A. Unsteady motions of a finite isolated mass of a self-gravitating fluid, Algebra i Analiz, 1989, 1(1), 207–249; English transl. in Leningrad Math. J. 1990, 1(1), 227–276.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




