Submitted:
10 November 2023
Posted:
13 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Band structure and electrical transport properties in high-mobility semimetals
2.1. Relation between topology and physics
2.2. Electrical transport properties: carrier mobility and electrical conductivity
3. High-mobility semimetals and magnetotransport properties
3.1. Magnetoresistance effect: theoretical framework and applications
3.2. Novel type of quantum Hall effect in 3D topological semimetals
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DFT | Density functional theory |
| MR | Magnetoresistance |
References
- Harrison, W.A.W.A. Electronic structure and the properties of solids: the physics of the chemical bond; Dover Publications, 1980.
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Thomson Learning, 2021.
- Kittel, C. 8th Edition. Introduction to Solid State Physics; JohnWiley & Sons Inc., 2004.
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nature Materials 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Das Sarma, S.; Hwang, E.H. Density-dependent electrical conductivity in suspended graphene: Approaching the Dirac point in transport. Physical Review B 2013, 87, 035415. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nature Nanotechnology 2008, 3, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.; Fuhrer, M.S. Charge transport and inhomogeneity near the minimum conductivity point in graphene. Physical Review B 2008, 77, 081402. [Google Scholar] [CrossRef]
- Hwang, E.H.; Adam, S.; Sarma, S.D. Carrier Transport in Two-Dimensional Graphene Layers. Physical Review Letters 2007, 98, 186806. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Akerman, N.; Ulbricht, G.; Lohmann, T.; Smet, J.H.; von Klitzing, K.; Yacoby, A. Observation of electron–hole puddles in graphene using a scanning single-electron transistor. Nature Physics 2008, 4, 144–148. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Communications 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Hone, J.; Stormer, H.L.; Kim, P. Temperature-Dependent Transport in Suspended Graphene. Physical Review Letters 2008, 101, 096802. [Google Scholar] [CrossRef]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y. Topological Insulator Materials. Journal of the Physical Society of Japan 2013, 82, 102001. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Moore, J.E. Three-Dimensional Topological Insulators. Annual Review of Condensed Matter Physics 2011, 2, 55–78. [Google Scholar] [CrossRef]
- Zhu, Z.; Winkler, G.W.; Wu, Q.; Li, J.; Soluyanov, A.A. Triple Point Topological Metals. Physical Review X 2016, 6, 031003. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Jiang, Y.; Song, Z.; Huang, H.; He, Y.; Fang, Z.; Weng, H.; Fang, C. Catalogue of topological electronic materials. Nature 2019, 566, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Jia, S. Crystal growth and electrical transport properties of niobium and tantalum monopnictide and dipnictide semimetals. Frontiers of Physics 2017, 12, 127211. [Google Scholar] [CrossRef]
- Niu, Q. Advances on topological materials. Frontiers of Physics 2020, 15, 43601. [Google Scholar] [CrossRef]
- Armitage, N.; Mele, E.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Reviews of Modern Physics 2018, 90, 015001. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef]
- Lv, B.; Qian, T.; Ding, H. Experimental perspective on three-dimensional topological semimetals. Reviews of Modern Physics 2021, 93, 025002. [Google Scholar] [CrossRef]
- Mori, R.; Wang, K.; Morimoto, T.; Ciocys, S.; Denlinger, J.D.; Paglione, J.; Lanzara, A. Observation of a Flat and Extended Surface State in a Topological Semimetal. Materials 2022, 15, 2744. [Google Scholar] [CrossRef] [PubMed]
- Hyart, T.; Heikkilä, T.T. Momentum-space structure of surface states in a topological semimetal with a nexus point of Dirac lines. Physical Review B 2016, 93, 235147. [Google Scholar] [CrossRef]
- Lv, B.; Weng, H.; Fu, B.; Wang, X.; Miao, H.; Ma, J.; Richard, P.; Huang, X.; Zhao, L.; Chen, G.; Fang, Z.; Dai, X.; Qian, T.; Ding, H. Experimental Discovery of Weyl Semimetal TaAs. Physical Review X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; Huang, S.M.; Zheng, H.; Ma, J.; Sanchez, D.S.; Wang, B.; Bansil, A.; Chou, F.; Shibayev, P.P.; Lin, H.; Jia, S.; Hasan, M.Z. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Yang, L.X.; Sun, Y.; Zhang, T.; Peng, H.; Yang, H.F.; Chen, C.; Zhang, Y.; Guo, Y.F.; Prabhakaran, D.; Schmidt, M.; Hussain, Z.; Mo, S.K.; Felser, C.; Yan, B.; Chen, Y.L. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nature Materials 2016, 15, 27–31. [Google Scholar] [CrossRef]
- Li, F.Y.; Luo, X.; Dai, X.; Yu, Y.; Zhang, F.; Chen, G. Hybrid Weyl semimetal. Physical Review B 2016, 94, 121105. [Google Scholar] [CrossRef]
- Xu, S.Y.; Alidoust, N.; Belopolski, I.; Yuan, Z.; Bian, G.; Chang, T.R.; Zheng, H.; Strocov, V.N.; Sanchez, D.S.; Chang, G.; Zhang, C.; Mou, D.; Wu, Y.; Huang, L.; Lee, C.C.; Huang, S.M.; Wang, B.; Bansil, A.; Jeng, H.T.; Neupert, T.; Kaminski, A.; Lin, H.; Jia, S.; Zahid Hasan, M. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nature Physics 2015, 11, 748–754. [Google Scholar] [CrossRef]
- Hein, P.; Jauernik, S.; Erk, H.; Yang, L.; Qi, Y.; Sun, Y.; Felser, C.; Bauer, M. Mode-resolved reciprocal space mapping of electron-phonon interaction in the Weyl semimetal candidate Td-WTe2. Nature Communications 2020, 11, 2613. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Y.; Zhang, Y.; Shi, W.J.; Parkin, S.S.P.; Yan, B. Topological Weyl semimetals in the chiral antiferromagnetic materials Mn3Ge and Mn3Sn. New Journal of Physics 2017, 19, 015008. [Google Scholar] [CrossRef]
- Lv, B.Q.; Feng, Z.L.; Xu, Q.N.; Gao, X.; Ma, J.Z.; Kong, L.Y.; Richard, P.; Huang, Y.B.; Strocov, V.N.; Fang, C.; Weng, H.M.; Shi, Y.G.; Qian, T.; Ding, H. Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature 2017, 546, 627–631. [Google Scholar] [CrossRef]
- Kanagaraj, M.; Ning, J.; He, L. Topological Co3Sn2S2 magnetic Weyl semimetal: From fundamental understanding to diverse fields of study. Reviews in Physics 2022, 8, 100072. [Google Scholar] [CrossRef]
- Carbotte, J.P. Dirac cone tilt on interband optical background of type-I and type-II Weyl semimetals. Physical Review B 2016, 94, 165111. [Google Scholar] [CrossRef]
- Koepernik, K.; Kasinathan, D.; Efremov, D.V.; Khim, S.; Borisenko, S.; Büchner, B.; van den Brink, J. TaIrTe4: A ternary type-II Weyl semimetal. Physical Review B 2016, 93, 201101. [Google Scholar] [CrossRef]
- Chang, T.R.; Xu, S.Y.; Chang, G.; Lee, C.C.; Huang, S.M.; Wang, B.; Bian, G.; Zheng, H.; Sanchez, D.S.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bansil, A.; Jeng, H.T.; Lin, H.; Zahid Hasan, M. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1-xTe2. Nature Communications 2016, 7, 10639. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; Jia, S.; Bansil, A.; Lin, H.; Hasan, M.Z. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nature Communications 2015, 6, 7373. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Wan, B.; Wang, D.; Sheng, L.; Duan, C.G.; Wan, X. Dirac and Weyl Semimetal in XYBi (X = Ba, Eu; Y = Cu, Ag and Au). Scientific Reports 2015, 5, 14423. [Google Scholar] [CrossRef] [PubMed]
- Udagawa, M.; Bergholtz, E. Field-Selective Anomaly and Chiral Mode Reversal in Type-II Weyl Materials. Physical Review Letters 2016, 117, 086401. [Google Scholar] [CrossRef]
- Swekis, P.; Sukhanov, A.S.; Chen, Y.C.; Gloskovskii, A.; Fecher, G.H.; Panagiotopoulos, I.; Sichelschmidt, J.; Ukleev, V.; Devishvili, A.; Vorobiev, A.; Inosov, D.S.; Goennenwein, S.T.B.; Felser, C.; Markou, A. Magnetic and Electronic Properties of Weyl Semimetal Co2MnGa Thin Films. Nanomaterials 2021, 11, 251. [Google Scholar] [CrossRef] [PubMed]
- Hirschberger, M.; Kushwaha, S.; Wang, Z.; Gibson, Q.; Liang, S.; Belvin, C.A.; Bernevig, B.A.; Cava, R.J.; Ong, N.P. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nature Materials 2016, 15, 1161–1165. [Google Scholar] [CrossRef]
- Li, H.; He, H.; Lu, H.Z.; Zhang, H.; Liu, H.; Ma, R.; Fan, Z.; Shen, S.Q.; Wang, J. Negative magnetoresistance in Dirac semimetal Cd3As2. Nature Communications 2016, 7, 10301. [Google Scholar] [CrossRef] [PubMed]
- Baidak, S.T.; Lukoyanov, A.V. Common Topological Features in Band Structure of RNiSb and RSb Compounds for R = Tb, Dy, Ho. Materials 2023, 16, 242. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Xu, S.Y.; Hasan, M.Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nature Materials 2016, 15, 1140–1144. [Google Scholar] [CrossRef]
- Balents, L. Weyl electrons kiss. Physics 2011, 4, 36. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Physical Review B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; Denlinger, J.; Fedorov, A.; Yang, H.; Duan, W.; Yao, H.; Wu, Y.; Fan, S.; Zhang, H.; Chen, X.; Zhou, S. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nature Physics 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Fang, C.; Gilbert, M.J.; Dai, X.; Bernevig, B.A. Multi-Weyl Topological Semimetals Stabilized by Point Group Symmetry. Physical Review Letters 2012, 108, 266802. [Google Scholar] [CrossRef]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Physical Review B 2013, 88, 125427. [Google Scholar] [CrossRef]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P.; Kim, T.; Hoesch, M.; Fang, Z.; Dai, X.; Shen, Z.X.; Feng, D.L.; Hussain, Z.; Chen, Y.L. A stable three-dimensional topological Dirac semimetal Cd3As2. Nature Materials 2014, 13, 677–681. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; Hussain, Z.; Chen, Y.L. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef]
- Mullen, K.; Uchoa, B.; Glatzhofer, D.T. Line of Dirac Nodes in Hyperhoneycomb Lattices. Physical Review Letters 2015, 115, 026403. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.S.; Schoop, L.M.; Seibel, E.M.; Gibson, Q.D.; Xie, W.; Cava, R.J. A new form of Ca3P2 with a ring of Dirac nodes. APL Materials 2015, 3, 083602. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, M.; Zhang, H.; Huang, H.; Arita, M.; Sun, Z.; Duan, W.; Wu, Y.; Zhou, S. Experimental evidence for type-II Dirac semimetal in PtSe2. Physical Review B 2017, 96, 125102. [Google Scholar] [CrossRef]
- Vafek, O.; Vishwanath, A. Dirac Fermions in Solids: From High-Tc Cuprates and Graphene to Topological Insulators and Weyl Semimetals. Annual Review of Condensed Matter Physics 2014, 5, 83–112. [Google Scholar] [CrossRef]
- Yan, M.; Huang, H.; Zhang, K.; Wang, E.; Yao, W.; Deng, K.; Wan, G.; Zhang, H.; Arita, M.; Yang, H.; Sun, Z.; Yao, H.; Wu, Y.; Fan, S.; Duan, W.; Zhou, S. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. Nature Communications 2017, 8, 257. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A=Na, K, Rb). Physical Review B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Physical Review Letters 2012, 108, 140405. [Google Scholar] [CrossRef]
- Gibson, Q.D.; Schoop, L.M.; Muechler, L.; Xie, L.S.; Hirschberger, M.; Ong, N.P.; Car, R.; Cava, R.J. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Physical Review B 2015, 91, 205128. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, R.; Fang, Z.; Dai, X.; Weng, H. Topological nodal line semimetals in the CaP3 family of materials. Physical Review B 2017, 95, 045136. [Google Scholar] [CrossRef]
- Yang, M.X.; Luo, W.; Chen, W. Quantum transport in topological nodal-line semimetals. Advances in Physics: X 2022, 7, 2065216. [Google Scholar] [CrossRef]
- Chang, T.R.; Pletikosic, I.; Kong, T.; Bian, G.; Huang, A.; Denlinger, J.; Kushwaha, S.K.; Sinkovic, B.; Jeng, H.T.; Valla, T.; Xie, W.; Cava, R.J. Realization of a Type-II Nodal-Line Semimetal in Mg3Bi2. Advanced Science 2019, 6, 1800897. [Google Scholar] [CrossRef]
- Du, Y.; Tang, F.; Wang, D.; Sheng, L.; Kan, E.j.; Duan, C.G.; Savrasov, S.Y.; Wan, X. CaTe: a new topological node-line and Dirac semimetal. npj Quantum Materials 2017, 2, 1–4. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.; Zhao, H.; Wu, M.; Pan, H. Magneto-Optical Transport Properties of Type-II Nodal Line Semimetals. Materials 2021, 14, 3035. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Saigusa, K.; Wada, T.; Yamakawa, Y.; Yamakage, A.; Sasagawa, T.; Katayama, N.; Takatsu, H.; Kageyama, H.; Takenaka, K. High-mobility carriers induced by chemical doping in the candidate nodal-line semimetal CaAgP. Physical Review B 2020, 102, 115101. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Dai, X.; Liu, G. Topological Type-II Nodal Line Semimetal and Dirac Semimetal State in Stable Kagome Compound Mg3Bi2. The Journal of Physical Chemistry Letters 2017, 8, 4814–4819. [Google Scholar] [CrossRef]
- Chang, G.; Xu, S.Y.; Sanchez, D.S.; Huang, S.M.; Lee, C.C.; Chang, T.R.; Bian, G.; Zheng, H.; Belopolski, I.; Alidoust, N.; Jeng, H.T.; Bansil, A.; Lin, H.; Hasan, M.Z. A strongly robust type II Weyl fermion semimetal state in Ta3S2. Science Advances 2016, 2, e1600295. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, T.; Fang, Z.; Fang, C. Quantitative mappings between symmetry and topology in solids. Nature Communications 2018, 9, 3530. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, T.; Fang, C. Diagnosis for Nonmagnetic Topological Semimetals in the Absence of Spin-Orbital Coupling. Physical Review X 2018, 8, 031069. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties; Graduate Texts in Physics, Springer: Berlin, Heidelberg, 2010. [Google Scholar] [CrossRef]
- Goringe, C.M.; Bowler, D.R.; Hernández, E. Tight-binding modelling of materials. Reports on Progress in Physics 1997, 60, 1447. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Physical Review 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Slater, J.C. Wave Functions in a Periodic Potential. Physical Review 1937, 51, 846–851. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Physical Review 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Parr, R.G.; Weitao, Y. Title Pages. In Density-Functional Theory of Atoms and Molecules; Parr, R.G.; Weitao, Y., Eds.; Oxford University Press, 1995; p. 0. doi:10.1093/oso/9780195092769.002.0001.
- Dreizler, R.M.; Gross, E.K.U. Density Functional Theory; Springer: Berlin, Heidelberg, 1990. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Physical Review B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Physical Review B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Singh, D.J.; Nordström, L. Planewaves, Pseudopotentials and the LAPW Method; Springer US, 2006. [CrossRef]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A.J. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Physical Review B 1981, 24, 864–875. [Google Scholar] [CrossRef]
- Burkov, A.A. Topological semimetals. Nature Materials 2016, 15, 1145–1148. [Google Scholar] [CrossRef]
- Tang, F.; Wan, X. Effective models for nearly ideal Dirac semimetals. Frontiers of Physics 2019, 14, 43603. [Google Scholar] [CrossRef]
- He, L.; Hong, X.; Dong, J.; Pan, J.; Zhang, Z.; Zhang, J.; Li, S. Quantum Transport Evidence for the Three-Dimensional Dirac Semimetal Phase in Cd3As2. Physical Review Letters 2014, 113, 246402. [Google Scholar] [CrossRef] [PubMed]
- Fei, F.; Bo, X.; Wang, R.; Wu, B.; Jiang, J.; Fu, D.; Gao, M.; Zheng, H.; Chen, Y.; Wang, X.; Bu, H.; Song, F.; Wan, X.; Wang, B.; Wang, G. Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2. Physical Review B 2017, 96, 041201. [Google Scholar] [CrossRef]
- Guo, P.J.; Yang, H.C.; Liu, K.; Lu, Z.Y. Type-II Dirac semimetals in the YPd2Sn. Physical Review B 2017, 95, 155112. [Google Scholar] [CrossRef]
- Shekhar, C.; Nayak, A.K.; Sun, Y.; Schmidt, M.; Nicklas, M.; Leermakers, I.; Zeitler, U.; Skourski, Y.; Wosnitza, J.; Liu, Z.; Chen, Y.; Schnelle, W.; Borrmann, H.; Grin, Y.; Felser, C.; Yan, B. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nature Physics 2015, 11, 645–649. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Physical Review X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Zhu, Z.; Yan, D.; Nie, X.A.; Xu, H.K.; Yang, X.; Guan, D.D.; Wang, S.; Li, Y.Y.; Liu, C.; Liu, J.W.; Luo, H.X.; Zheng, H.; Jia, J.F. Scanning tunneling microscopic investigation on morphology of magnetic Weyl semimetal YbMnBi2 *. Chinese Physics B 2019, 28, 077302. [Google Scholar] [CrossRef]
- Sie, E.J.; Nyby, C.M.; Pemmaraju, C.D.; Park, S.J.; Shen, X.; Yang, J.; Hoffmann, M.C.; Ofori-Okai, B.K.; Li, R.; Reid, A.H.; Weathersby, S.; Mannebach, E.; Finney, N.; Rhodes, D.; Chenet, D.; Antony, A.; Balicas, L.; Hone, J.; Devereaux, T.P.; Heinz, T.F.; Wang, X.; Lindenberg, A.M. An ultrafast symmetry switch in a Weyl semimetal. Nature 2019, 565, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Physical Review Letters 2011, 107, 127205. [Google Scholar] [CrossRef]
- Zhang, C.L.; Yuan, Z.; Jiang, Q.D.; Tong, B.; Zhang, C.; Xie, X.C.; Jia, S. Electron scattering in tantalum monoarsenide. Physical Review B 2017, 95, 085202. [Google Scholar] [CrossRef]
- Kumar, N.; Sun, Y.; Nicklas, M.; Watzman, S.J.; Young, O.; Leermakers, I.; Hornung, J.; Klotz, J.; Gooth, J.; Manna, K.; Süß, V.; Guin, S.N.; Förster, T.; Schmidt, M.; Muechler, L.; Yan, B.; Werner, P.; Schnelle, W.; Zeitler, U.; Wosnitza, J.; Parkin, S.S.P.; Felser, C.; Shekhar, C. Extremely high conductivity observed in the triple point topological metal MoP. Nature Communications 2019, 10, 2475. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhang, C.; Zou, Y.; Zhang, E.; Yang, L.; Hong, M.; Xiu, F.; Zou, J. Scalable Growth of High Mobility Dirac Semimetal Cd3As2 Microbelts. Nano Letters 2015, 15, 5830–5834. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, K.; Kawamuma, K.; Tsuzuku, T. Temperature Dependence of the Average Mobility in Graphite. Journal of the Physical Society of Japan 1979, 47, 1210–1215. [Google Scholar] [CrossRef]
- Pendrys, L.A.; Zeller, C.; Vogel, F.L. Electrical transport properties of natural and synthetic graphite. Journal of Materials Science 1980, 15, 2103–2112. [Google Scholar] [CrossRef]
- Ibach, H.; Lüth, H. Solid-State Physics: An Introduction to Principles of Materials Science; with 100 Problems; Springer, 1995.
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; Bansil, A.; Chou, F.; Hasan, M.Z. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nature Communications 2014, 5, 3786. [Google Scholar] [CrossRef] [PubMed]
- Hosur, P.; Qi, X. Recent developments in transport phenomena in Weyl semimetals. Comptes Rendus Physique 2013, 14, 857–870. [Google Scholar] [CrossRef]
- Khim, S.; Koepernik, K.; Efremov, D.V.; Klotz, J.; Förster, T.; Wosnitza, J.; Sturza, M.I.; Wurmehl, S.; Hess, C.; van den Brink, J.; Büchner, B. Magnetotransport and de Haas–van Alphen measurements in the type-II Weyl semimetal TaIrTe4. Physical Review B 2016, 94, 165145. [Google Scholar] [CrossRef]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.G.; Felser, C.; Cava, R.J.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353, aaf5037. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; Jia, S.; Bansil, A.; Lin, H.; Hasan, M.Z. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nature Communications 2015, 6, 7373. [Google Scholar] [CrossRef]
- Li, S.; Yu, Z.M.; Yao, Y.; Yang, S.A. Type-II topological metals. Frontiers of Physics 2020, 15, 43201. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; He, X.; Zhang, Q.; Xia, C.; Yu, Z.M.; Yang, S.A.; Zhu, Z.; Alshareef, H.N.; Zhang, X.X. Evidence for topological type-II Weyl semimetal WTe2. Nature Communications 2017, 8, 2150. [Google Scholar] [CrossRef]
- Autès, G.; Gresch, D.; Troyer, M.; Soluyanov, A.; Yazyev, O. Robust Type-II Weyl Semimetal Phase in Transition Metal Diphosphides XP2 (X=Mo, W). Physical Review Letters 2016, 117, 066402. [Google Scholar] [CrossRef]
- Tamai, A.; Wu, Q.; Cucchi, I.; Bruno, F.; Riccò, S.; Kim, T.; Hoesch, M.; Barreteau, C.; Giannini, E.; Besnard, C.; Soluyanov, A.; Baumberger, F. Fermi Arcs and Their Topological Character in the Candidate Type-II Weyl Semimetal MoTe2. Physical Review X 2016, 6, 031021. [Google Scholar] [CrossRef]
- Belopolski, I.; Sanchez, D.S.; Ishida, Y.; Pan, X.; Yu, P.; Xu, S.Y.; Chang, G.; Chang, T.R.; Zheng, H.; Alidoust, N.; Bian, G.; Neupane, M.; Huang, S.M.; Lee, C.C.; Song, Y.; Bu, H.; Wang, G.; Li, S.; Eda, G.; Jeng, H.T.; Kondo, T.; Lin, H.; Liu, Z.; Song, F.; Shin, S.; Hasan, M.Z. Discovery of a new type of topological Weyl fermion semimetal state in MoxW1-xTe2. Nature Communications 2016, 7, 13643. [Google Scholar] [CrossRef] [PubMed]
- Zyuzin, A.A.; Tiwari, R.P. Intrinsic anomalous Hall effect in type-II Weyl semimetals. JETP Letters 2016, 103, 717–722. [Google Scholar] [CrossRef]
- Haubold, E.; Koepernik, K.; Efremov, D.; Khim, S.; Fedorov, A.; Kushnirenko, Y.; van den Brink, J.; Wurmehl, S.; Büchner, B.; Kim, T.K.; Hoesch, M.; Sumida, K.; Taguchi, K.; Yoshikawa, T.; Kimura, A.; Okuda, T.; Borisenko, S.V. Experimental realization of type-II Weyl state in noncentrosymmetric TaIrTe4. Physical Review B 2017, 95, 241108. [Google Scholar] [CrossRef]
- Islam, M.R.; Mojumder, M.R.H.; Moghal, B.K.; Islam, A.S.M.J.; Miah, M.R.; Roy, S.; Kumar, A.; Shihavuddin, A.S.M.; Ashique, R.H. Impact of strain on the electronic, phonon, and optical properties of monolayer transition metal dichalcogenides XTe2 (X = Mo and W). Physica Scripta 2022, 97, 045806. [Google Scholar] [CrossRef]
- Borisenko, S.; Evtushinsky, D.; Gibson, Q.; Yaresko, A.; Koepernik, K.; Kim, T.; Ali, M.; van den Brink, J.; Hoesch, M.; Fedorov, A.; Haubold, E.; Kushnirenko, Y.; Soldatov, I.; Schäfer, R.; Cava, R.J. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nature Communications 2019, 10, 3424. [Google Scholar] [CrossRef] [PubMed]
- Tchoumakov, S.; Civelli, M.; Goerbig, M.O. Magnetic-Field-Induced Relativistic Properties in Type-I and Type-II Weyl Semimetals. Physical Review Letters 2016, 117, 086402. [Google Scholar] [CrossRef]
- Bedoya-Pinto, A.; Pandeya, A.K.; Liu, D.; Deniz, H.; Chang, K.; Tan, H.; Han, H.; Jena, J.; Kostanovskiy, I.; Parkin, S.S.P. Realization of Epitaxial NbP and TaP Weyl Semimetal Thin Films. ACS Nano 2020, 14, 4405–4413. [Google Scholar] [CrossRef]
- Lv, H.Y.; Lu, W.J.; Shao, D.F.; Liu, Y.; Tan, S.G.; Sun, Y.P. Perfect charge compensation in WTe2 for the extraordinary magnetoresistance: From bulk to monolayer. Europhysics Letters 2015, 110, 37004. [Google Scholar] [CrossRef]
- Tian, W.; Yu, W.; Liu, X.; Wang, Y.; Shi, J. A Review of the Characteristics, Synthesis, and Thermodynamics of Type-II Weyl Semimetal WTe2. Materials 2018, 11, 1185. [Google Scholar] [CrossRef] [PubMed]
- Rosmus, M.; Olszowska, N.; Bukowski, Z.; Starowicz, P.; Piekarz, P.; Ptok, A. Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2. Materials 2022, 15, 7168. [Google Scholar] [CrossRef]
- Wadge, A.S.; Grabecki, G.; Autieri, C.; Kowalski, B.J.; Iwanowski, P.; Cuono, G.; Islam, M.F.; Canali, C.M.; Dybko, K.; Hruban, A.; Łusakowski, A.; Wojciechowski, T.; Diduszko, R.; Lynnyk, A.; Olszowska, N.; Rosmus, M.; Kołodziej, J.; Wiśniewski, A. Electronic properties of TaAs2 topological semimetal investigated by transport and ARPES. Journal of Physics: Condensed Matter 2022, 34, 125601. [Google Scholar] [CrossRef] [PubMed]
- Mathur, P.C.; Kataria, N.D.; Jain, S.; Sharma, V. Electron mobility in n-InSb from 77 to 300K. Journal of Physics C: Solid State Physics 1975, 9, L89. [Google Scholar] [CrossRef]
- Pei, Q.L.; Luo, X.; Chen, F.C.; Lv, H.Y.; Sun, Y.; Lu, W.J.; Tong, P.; Sheng, Z.G.; Han, Y.Y.; Song, W.H.; Zhu, X.B.; Sun, Y.P. Mobility spectrum analytical approach for the type-II Weyl semimetal Td-MoTe2. Applied Physics Letters 2018, 112, 072401. [Google Scholar] [CrossRef]
- Ishiwata, S.; Shiomi, Y.; Lee, J.S.; Bahramy, M.S.; Suzuki, T.; Uchida, M.; Arita, R.; Taguchi, Y.; Tokura, Y. Extremely high electron mobility in a phonon-glass semimetal. Nature Materials 2013, 12, 512–517. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.M.; Sun, H.P.; Lu, H.Z.; Xie, X.C. 3D Quantum Hall Effect of Fermi Arcs in Topological Semimetals. Phys. Rev. Lett. 2017, 119, 136806. [Google Scholar] [CrossRef]
- Kumar, N.; Sun, Y.; Xu, N.; Manna, K.; Yao, M.; Süss, V.; Leermakers, I.; Young, O.; Förster, T.; Schmidt, M.; Borrmann, H.; Yan, B.; Zeitler, U.; Shi, M.; Felser, C.; Shekhar, C. Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2. Nature Communications 2017, 8, 1642. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Ali, M.N.; Liu, M.; Cava, R.J.; Ong, N.P. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nature Materials 2015, 14, 280–284. [Google Scholar] [CrossRef]
- Feng, J.; Pang, Y.; Wu, D.; Wang, Z.; Weng, H.; Li, J.; Dai, X.; Fang, Z.; Shi, Y.; Lu, L. Large linear magnetoresistance in Dirac semimetal Cd3As2 with Fermi surfaces close to the Dirac points. Physical Review B 2015, 92, 081306. [Google Scholar] [CrossRef]
- Pletikosić, I.; Ali, M.N.; Fedorov, A.V.; Cava, R.J.; Valla, T. Electronic structure basis for the extraordinary magnetoresistance in WTe2. Physical review letters 2014, 113, 216601. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.N.; Xiong, J.; Flynn, S.; Tao, J.; Gibson, Q.D.; Schoop, L.M.; Liang, T.; Haldolaarachchige, N.; Hirschberger, M.; Ong, N.P.; Cava, R.J. Large, non-saturating magnetoresistance in WTe2. Nature 2014, 514, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.M.; Yao, Y.; Yang, S.A. Predicted Unusual Magnetoresponse in Type-II Weyl Semimetals. Physical Review Letters 2016, 117, 077202. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, R.; Adhikari, S.; Faina, B.; Terschanski, M.; Bork, S.; Leimhofer, C.; Cinchetti, M.; Bonanni, A. Positive Magnetoresistance and Chiral Anomaly in Exfoliated Type-II Weyl Semimetal Td-WTe2. Nanomaterials 2021, 11, 2755. [Google Scholar] [CrossRef] [PubMed]
- Singha, R.; Pariari, A.K.; Satpati, B.; Mandal, P. Large nonsaturating magnetoresistance and signature of nondegenerate Dirac nodes in ZrSiS. Proceedings of the National Academy of Sciences 2017, 114, 2468–2473. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, C.; Ouardi, S.; Nayak, A.K.; Fecher, G.H.; Schnelle, W.; Felser, C. Ultrahigh mobility and nonsaturating magnetoresistance in Heusler topological insulators. Physical Review B 2012, 86, 155314. [Google Scholar] [CrossRef]
- Singleton, J.; Singleton, J. Band Theory and Electronic Properties of Solids; Oxford Master Series in Physics; Oxford University Press: Oxford, New York, 2001. [Google Scholar]
- Yang, J.; Song, Z.Y.; Guo, L.; Gao, H.; Dong, Z.; Yu, Q.; Zheng, R.K.; Kang, T.T.; Zhang, K. Nontrivial Giant Linear Magnetoresistance in Nodal-Line Semimetal ZrGeSe 2D Layers. Nano Letters 2021, 21, 10139–10145. [Google Scholar] [CrossRef]
- Arnold, F.; Shekhar, C.; Wu, S.C.; Sun, Y.; dos Reis, R.D.; Kumar, N.; Naumann, M.; Ajeesh, M.O.; Schmidt, M.; Grushin, A.G.; Bardarson, J.H.; Baenitz, M.; Sokolov, D.; Borrmann, H.; Nicklas, M.; Felser, C.; Hassinger, E.; Yan, B. Negative magnetoresistance without well-defined chirality in the Weyl semimetal TaP. Nature Communications 2016, 7, 11615. [Google Scholar] [CrossRef] [PubMed]
- Son, D.T.; Spivak, B.Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Physical Review B 2013, 88, 104412. [Google Scholar] [CrossRef]
- Wang, K.; Graf, D.; Li, L.; Wang, L.; Petrovic, C. Anisotropic giant magnetoresistance in NbSb2. Scientific Reports 2014, 4, 7328. [Google Scholar] [CrossRef]
- Li, P.; Qiu, P.; Xu, Q.; Luo, J.; Xiong, Y.; Xiao, J.; Aryal, N.; Li, Q.; Chen, L.; Shi, X. Colossal Nernst power factor in topological semimetal NbSb2. Nature Communications 2022, 13, 7612. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, N.J.; Luo, Y.; Neupane, M.; Williams, D.J.; Bauer, E.D.; Ronning, F. Magnetotransport of single crystalline NbAs. Journal of Physics: Condensed Matter 2015, 27, 152201. [Google Scholar] [CrossRef]
- Kumar, P.; Sudesh. ; Patnaik, S. Exceptional magnetoresistance in Weyl semimetal TaP. AIP Conference Proceedings 2019, 2115, 030409. [Google Scholar] [CrossRef]
- Shekhar, C.; Süss, V.; Schmidt, M. Mobility induced unsaturated high linear magnetoresistance in transition-metal monopnictides Weyl semimetals, 2016. arXiv:cond-mat.mtrl-sci/1606.06649.
- Wang, Y.; Wang, L.; Liu, X.; Wu, H.; Wang, P.; Yan, D.; Cheng, B.; Shi, Y.; Watanabe, K.; Taniguchi, T.; Liang, S.J.; Miao, F. Direct Evidence for Charge Compensation-Induced Large Magnetoresistance in Thin WTe2. Nano Letters 2019, 19, 3969–3975. [Google Scholar] [CrossRef]
- Mun, E.; Ko, H.; Miller, G.J.; Samolyuk, G.D.; Bud’ko, S.L.; Canfield, P.C. Magnetic field effects on transport properties of PtSn4. Physical Review B 2012, 85, 035135. [Google Scholar] [CrossRef]
- Fu, C.; Guin, S.N.; Scaffidi, T.; Sun, Y.; Saha, R.; Watzman, S.J.; Srivastava, A.K.; Li, G.; Schnelle, W.; Parkin, S.S.P.; Felser, C.; Gooth, J. Largely Suppressed Magneto-Thermal Conductivity and Enhanced Magneto-Thermoelectric Properties in PtSn4. Research 2020, 2020. [Google Scholar] [CrossRef]
- Gao, W.; Hao, N.; Zheng, F.W.; Ning, W.; Wu, M.; Zhu, X.; Zheng, G.; Zhang, J.; Lu, J.; Zhang, H.; Xi, C.; Yang, J.; Du, H.; Zhang, P.; Zhang, Y.; Tian, M. Extremely Large Magnetoresistance in a Topological Semimetal Candidate Pyrite PtBi2. Physical Review Letters 2017, 118, 256601. [Google Scholar] [CrossRef]
- Uchida, M.; Nakazawa, Y.; Nishihaya, S.; Akiba, K.; Kriener, M.; Kozuka, Y.; Miyake, A.; Taguchi, Y.; Tokunaga, M.; Nagaosa, N.; Tokura, Y.; Kawasaki, M. Quantum Hall states observed in thin films of Dirac semimetal Cd3As2. Nature Communications 2017, 8, 2274. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Yuan, X.; Lu, S.; Zhang, J.; Narayan, A.; Liu, Y.; Zhang, H.; Ni, Z.; Liu, R.; Choi, E.S.; Suslov, A.; Sanvito, S.; Pi, L.; Lu, H.Z.; Potter, A.C.; Xiu, F. Quantum Hall effect based on Weyl orbits in Cd3As2. Nature 2019, 565, 331–336. [Google Scholar] [CrossRef]
- Weis, J. Quantum Hall Effect. In Encyclopedia of Condensed Matter Physics; Bassani, F., Liedl, G.L., Wyder, P., Eds.; Elsevier: Oxford, 2005; pp. 22–29. [Google Scholar] [CrossRef]
- Klitzing, K.v.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Laughlin, R.B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 1981, 23, 5632–5633. [Google Scholar] [CrossRef]
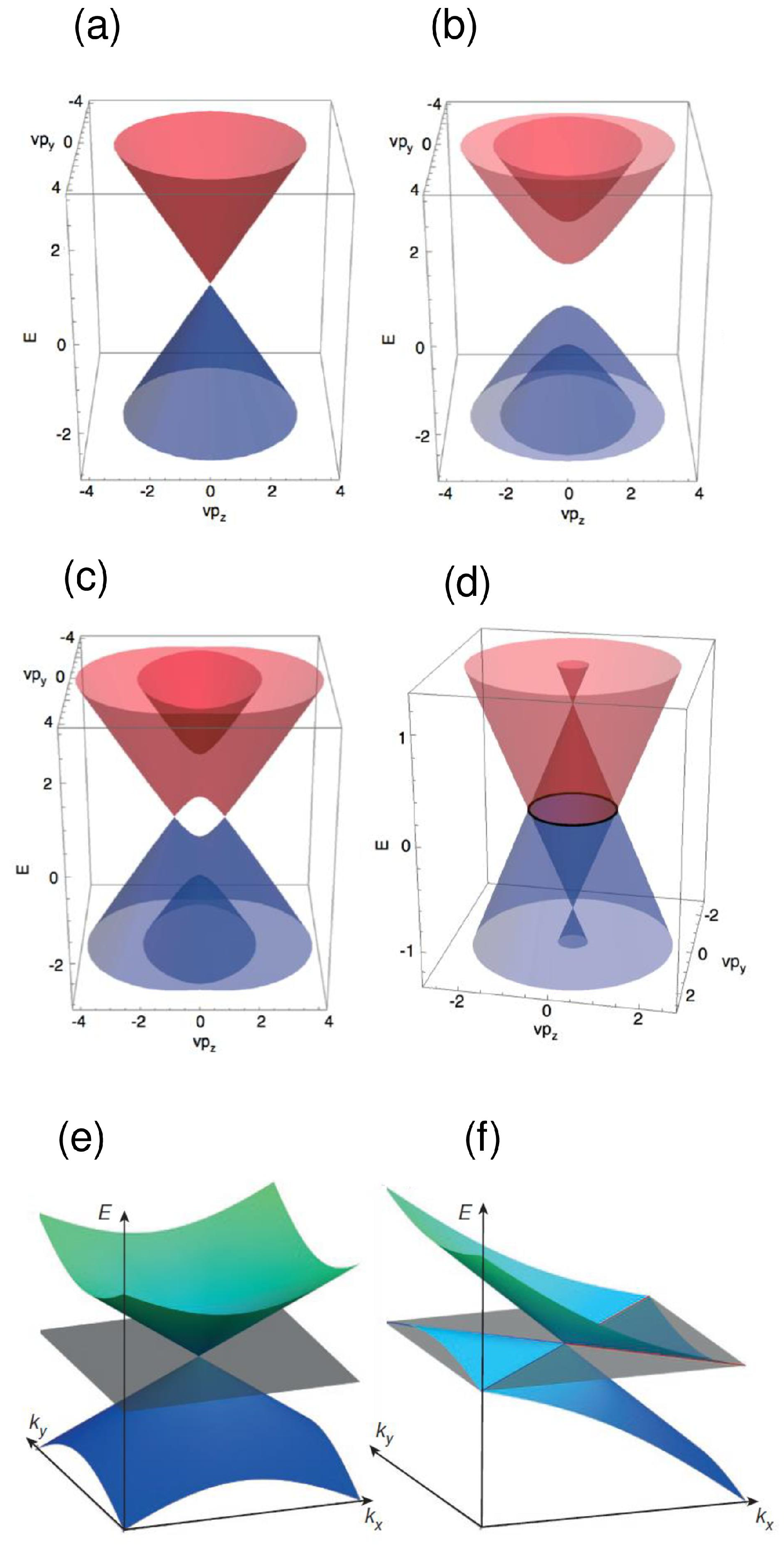
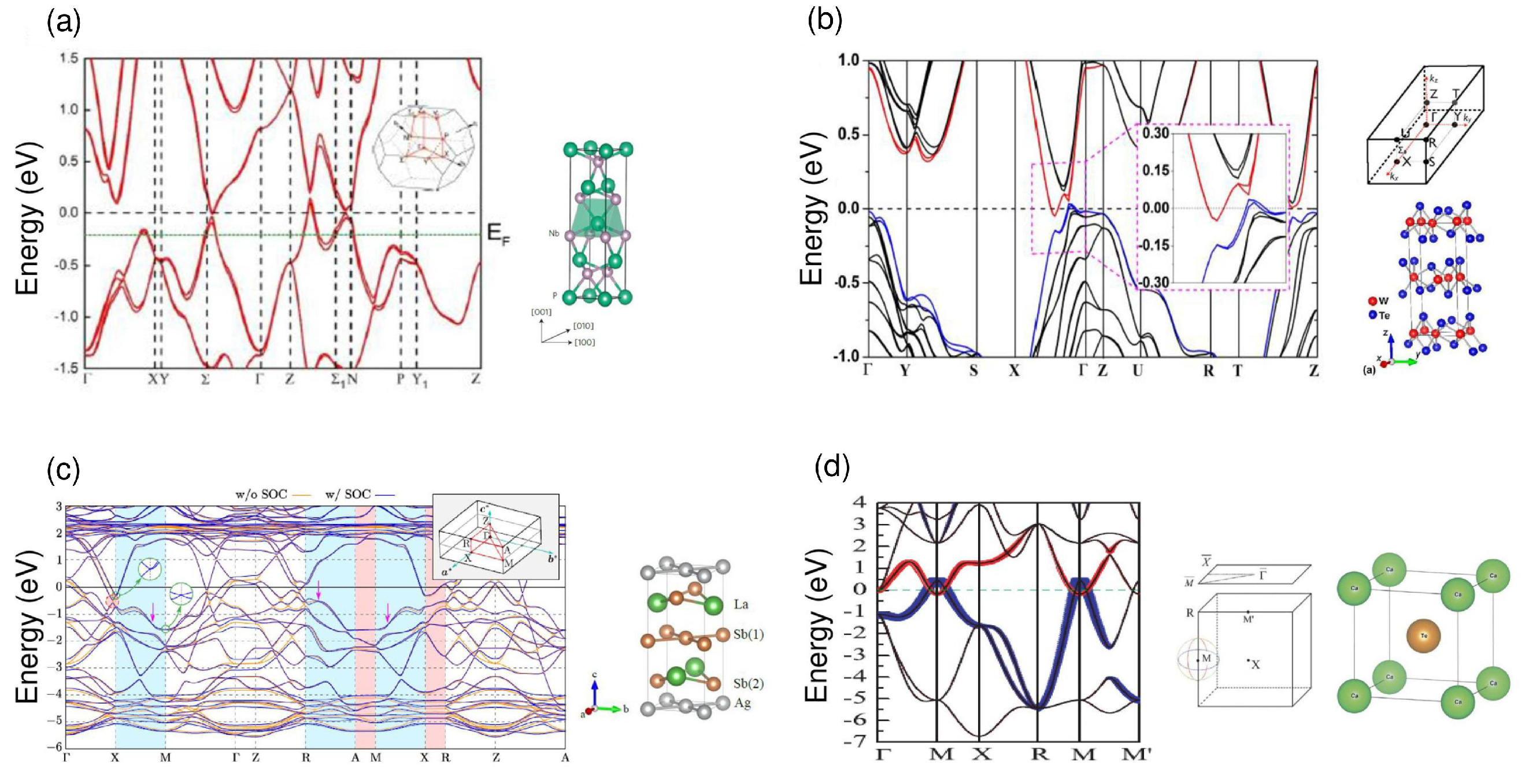
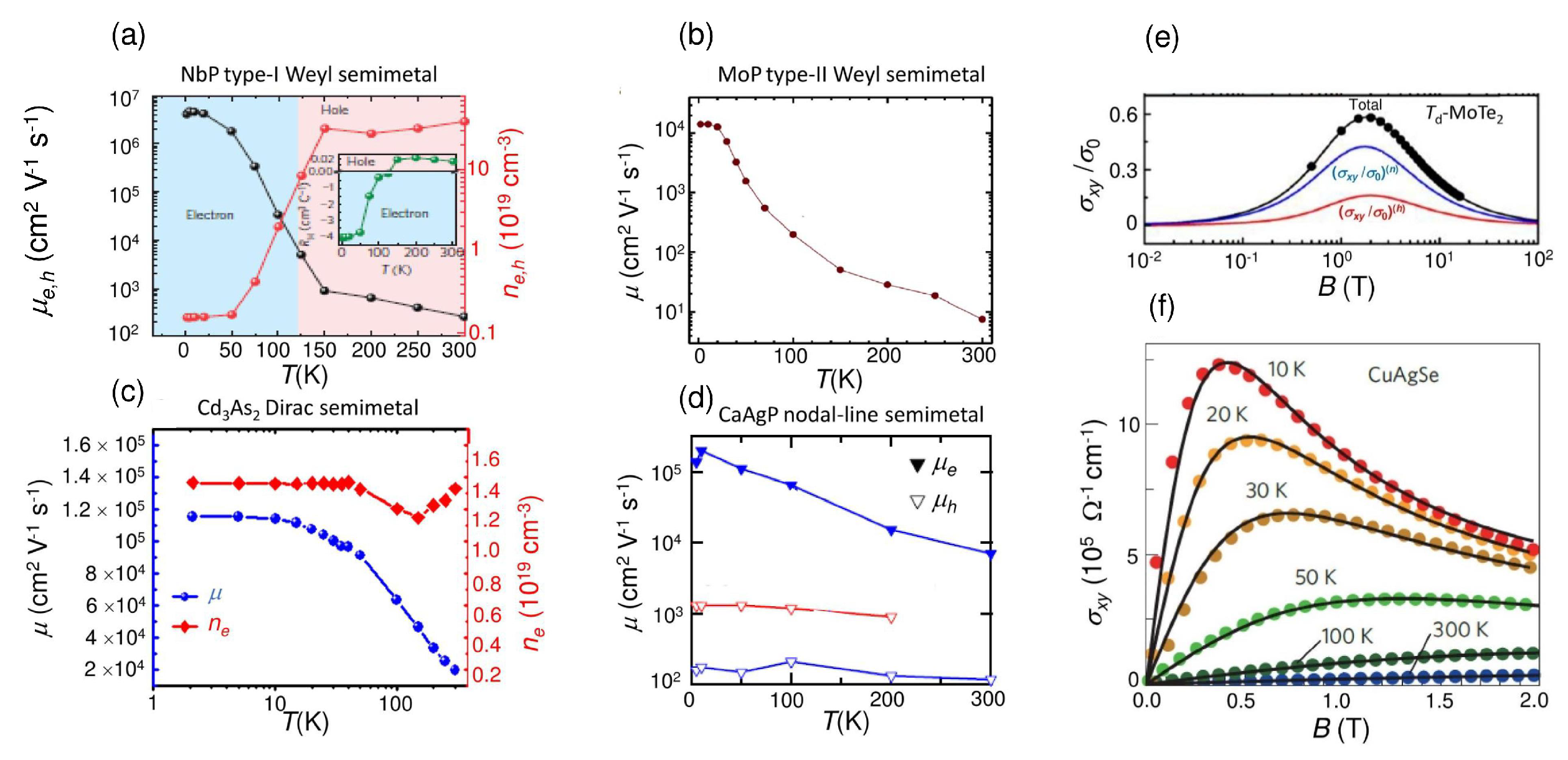
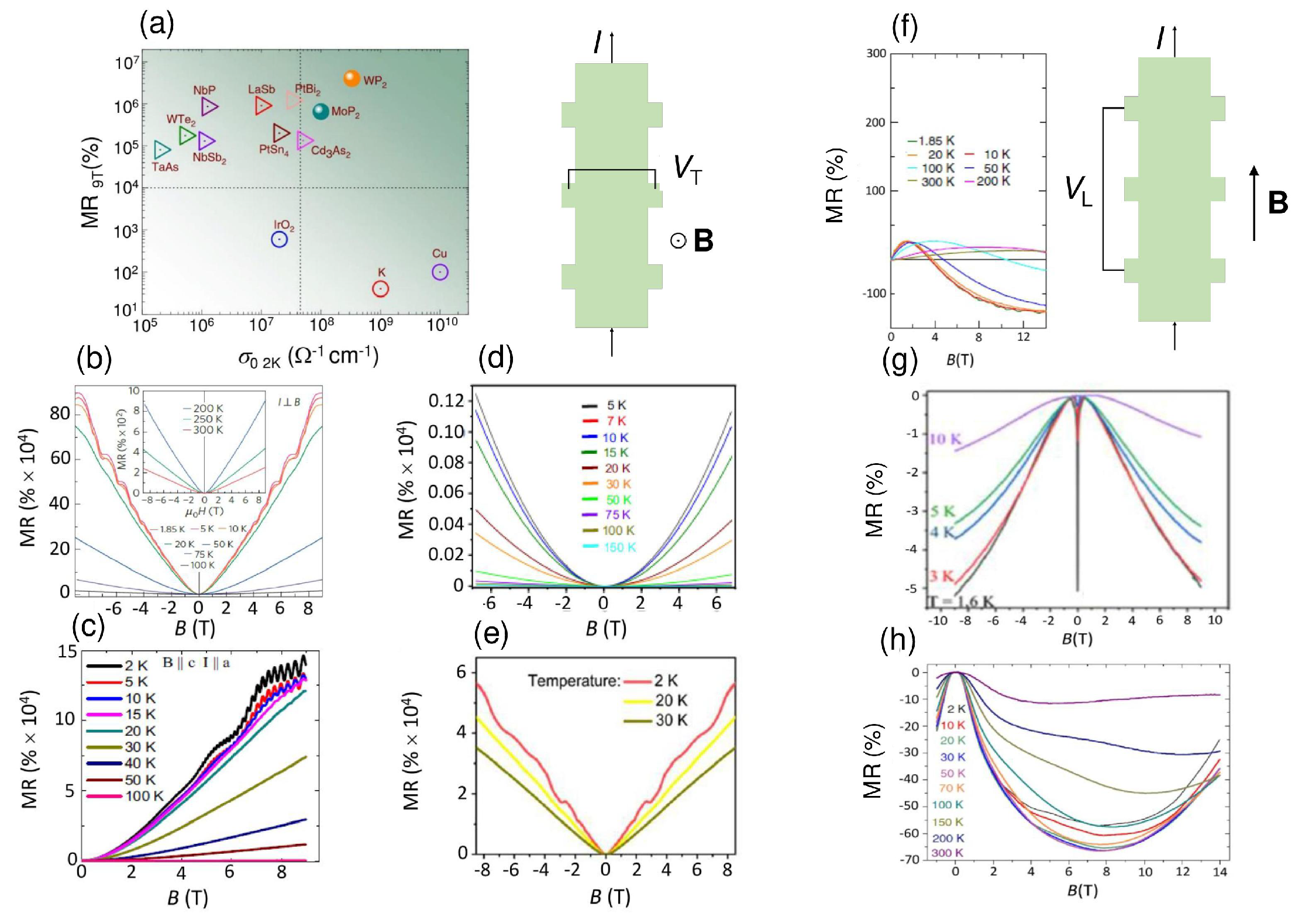

| Semimetal | Mobility (cm2·V−1·s−1) | Resistivity ( cm) | MR (%) |
|---|---|---|---|
| [91] | (1.85K) | (2 K) | (1.85K, 9T) |
| [139,140] | (5K) | (2K) | (2K, 9T) |
| [141] | (2K) | (2K) | (2K, 9T) |
| [117,142,143] | (2K) | (2.5 K) | (5K, 6T) |
| [96] | (2K) | (1K) | (10K, 9T) |
| [126] | (2K) | (2K) | (2K, 9T) |
| [130,144] | (1.6K) | (2K) | (4.5K, 14.7 T) |
| [145,146] | (2K) | (2K) | (1.8K, 14T) |
| [147] | (2K) | (2K) | (1.8K, 33T) |
| [128] | (5K) | (2K) | (2K, 9T) |
| [126] | (2K) | (2K) | (2K, 9T) |
| [97] | (2K) | (2K) | (2K, 14T) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





