Flutter of a Plate at High Supersonic Speeds

Preprint

Article

Flutter of a Plate at High Supersonic Speeds

This version is not peer-reviewed.

Altmetrics

Downloads

125

Views

Comments

Submitted:

14 November 2023

Posted:

14 November 2023

Read the latest preprint version here

A peer-reviewed article of this preprint also exists.

Abstract

Vibrations of plate structures placed in a supersonic flow is considered. The undisturbed fluid flow is parallel to the plate. Two specific problems are treated: in the first one the plate is in the form of an infinite strip and the flow is in the direction of its finite length. Rigid walls extend from the sides of the plate indefinitely. In the second problem, the plate is a finite rectangle and the flow is parallel to one of its sides. The first problem is a limiting case of the second problem. The flow is modeled by piston theory which assumes that the fluid pressure on the plate is proportional to local slope. This approximation is widely used at high speeds, and reduces the interaction between the fluid flow and the vibrations of the plate to an additional term in the vibration equation. The resulting problem can be solved by assumed mode methods. In this study, the solution is also carried out by using the collocation method. The main result is the flutter velocity of the free fluid flow under which the plate vibrations become unstable. Finally, simple expressions are proposed between the various non-dimensional parameters that allows quick estimation of flutter velocity.

Keywords:

Subject:

Engineering - Mechanical Engineering

1. Introduction

Fluid-elastic structure interactions are ubiquitous in many engineering disciplines. There are historically famous examples that demonstrate the interaction between fluid flow and the vibrations of the structure can cause catastrophic failure. It is observed that the character of vibrations typically depend on a characteristic flow velocity which, if exceeds a certain value (flutter velocity), will cause instability. Main thrust of fluid-elastic structure interaction research is the determination of flutter velocity.

The type of problem considered in this study is especially important in aerospace structures and is usually given the name panel flutter. Uzal et al. deal with incompressible and irrotational flow in a cylindrical channel to find the flutter velocity analytically [1]. Epureanu et al. investigated vibration-based damages with the chances in material and/or stiffness properties of structures. Kapkin et al. investigate the membrane vibrations located at the stagnation point of the flow and they give the flutter velocity for the system [2]. Vedeneev considers panel flutter at low supersonic speeds by using piston theory [3]. E. H. Dowell gives flutter velocity graphs for an infinite plate lays with the same direction of fluid motion by using the potential theory for different Mach Numbers [4]. Uzal et al. give an analytical solution for a plate placed in a rigid channel which fluid flows in [5]. Durak B. investigated the plate vibrations by using potential flow theory in his PhD thesis [6]. Also, some of the researchers are also try to avoid this flutter point by applying a force or moving one boundary to control the motion of the plate. Uzal and Korbahti control resonance frequencies of a rectangular plate vibrations by applying discrete force by measuring the displacement of the plate at a point [7]. Sezgin et al give a boundary backstepping control method to stabilize the flow-induced vibrations for a membrane [8]. Tubaldi et al. investigate a periodically supported flexible plate under flowing fluid axial flow which is in a bounded channel by a rigid wall [9]. The effects of the system parameters on the stability of the plate are discussed.

2. Infinite Strip Plate

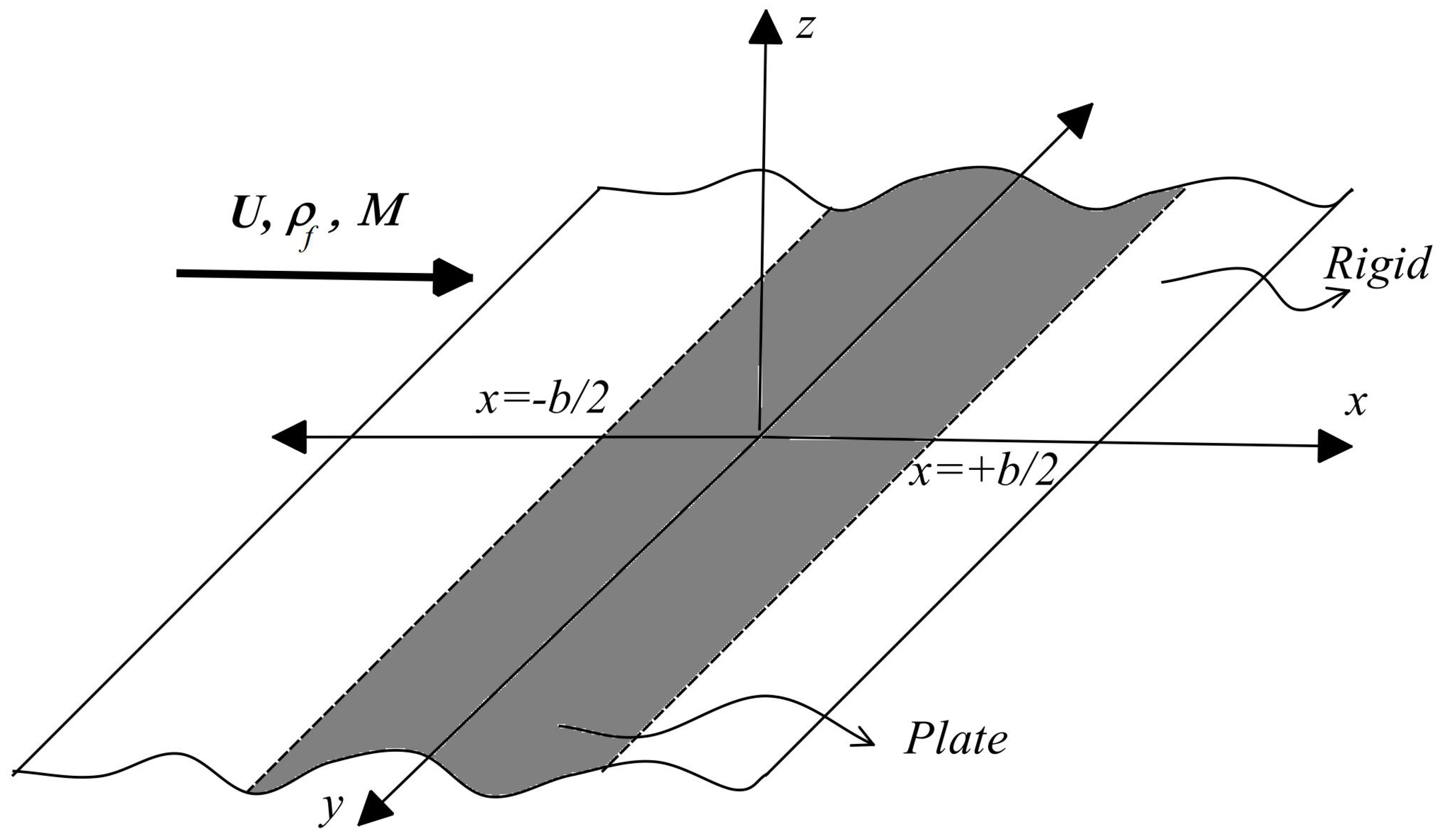
Figure 1 shows a schematic of the first problem. The flow occupies the region

z > 0

and is in

x -

direction with uniform velocity U. The region in

x y -

plane

- b / 2 < x < b / 2

- \infty < y < \infty

is an elastic plate (infinite strip) of width b; the rest of the

x y -

plane is rigid. The vibrations of the plate will cause small perturbations on flow velocity. The vibrations of the plate are governed by

D \frac{\partial^{4} w}{\partial x^{4}} + ρ_{p} h_{p} \frac{\partial^{2} w}{\partial t^{2}} {+ p |}_{z = 0} = 0

(1)

where

w = w (x, t)

is the displacement,

h_{p}

is the thickness and

ρ_{p}

is density of the plate, and

D = \frac{E h_{p}^{3}}{12 (1 - ν^{2})}

(2)

is flexural rigidity; E is young modulus and

ν

is the Poisson ratio. The last term in 1 denotes the fluid pressure on the plate. Although the plate is moving, fluid pressure can be assumed to have its value at

z = 0

within the linear theory. The fluid flow is assumed to be inviscid since viscous effects are negligible due to lack of flow separation. In general, the linearized form of compressible potential equation can be used, but here a simpler approximation called piston theory will be adopted. Piston theory is widely used and basically states that local pressure is proportional to local slope of the plate [10].

{p |}_{z = 0} = \frac{ρ_{f} U}{M} (\frac{\partial w}{\partial t} + U \frac{\partial w}{\partial x})

(3)

Thus the coupled fluid-plate vibrations obey

D \frac{\partial^{4} w}{\partial x^{4}} + ρ_{p} h_{p} \frac{\partial^{2} w}{\partial t^{2}} + \frac{ρ_{f} U}{M} (\frac{\partial w}{\partial t} + U \frac{\partial w}{\partial x}) = 0

(4)

where,

ρ_{f}

is the density of the fluid, U is the velocity of the fluid and M is the Mach number

M = \frac{U}{c}

. The boundary conditions on the plate will be taken as

\begin{matrix} w (- b / 2) = w (b / 2) = 0 \\ \frac{\partial^{2} w}{\partial x^{2}} (- b / 2) = \frac{\partial^{2} w}{\partial x^{2}} (b / 2) = 0 \end{matrix}

(5)

which state that the ends of the plate are simply-supported. The problem is non-dimensionalized as follows

\begin{matrix} x^{*} = \frac{x}{b}, w^{*} = \frac{w}{b}, z^{*} = \frac{z}{b}, t^{*} = \frac{t}{b^{2} \sqrt{\frac{ρ_{p} h_{p}}{D}}}, p^{*} = \frac{p}{\frac{D}{b^{3}}}, u = \frac{U}{\frac{1}{b} \sqrt{\frac{D}{ρ_{p} h_{p}}}}, c_{s}^{*} = \frac{u}{M} \end{matrix}

(6)

Starred quantities are non-dimensional. Substituting in (4,5) and simplifying, the result is, getting rid of the stars since dimensional quantities will not be needed

\frac{\partial^{4} w}{\partial x^{4}} + \frac{\partial^{2} w}{\partial t^{2}} + μ (\frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x}) = 0

(7)

and the boundary conditions

\begin{matrix} w (- 1 / 2) = w (1 / 2) = \frac{\partial^{2} w}{\partial x^{2}} (- 1 / 2) = \frac{\partial^{2} w}{\partial x^{2}} (1 / 2) = 0 \end{matrix}

(8)

here

\begin{matrix} μ = \frac{ρ_{f} b}{ρ_{p} h_{p}} c_{s} \end{matrix}

(9)

is a non-dimensional number, usually called the mass ratio, and

\begin{matrix} c_{s} = \frac{c}{\frac{1}{b} \sqrt{\frac{D}{ρ_{p} h_{p}}}} \end{matrix}

(10)

is the dimensionless sound velocity. To investigate stability, the plate displacement is assumed to be

\begin{matrix} w (x, t) = v (x) e^{i ω t} \end{matrix}

(11)

Then, (7,8) become

\frac{\partial^{4} v}{\partial x^{4}} + μ u \frac{\partial v}{\partial x} + K_{1} v = 0

(12)

\begin{matrix} v (- 1 / 2) = v (1 / 2) = \frac{\partial^{2} v}{\partial x^{2}} (- 1 / 2) = \frac{\partial^{2} v}{\partial x^{2}} (1 / 2) = 0 \end{matrix}

(13)

where

\begin{matrix} K_{1} = - ω^{2} + i ω μ \end{matrix}

(14)

\begin{matrix} u = \frac{U}{\frac{1}{b} \sqrt{\frac{D}{ρ_{p} h_{p}}}} \end{matrix}

(15)

(12,13) is an eigenvalue problem for

ω

. The vibrations of the plate will not grow as long as the imaginary part of

ω

is positive; the stability boundary is Im

(ω) = 0

. Since

ω

depends on u (as well as

μ

) , the condition Im

(ω) = 0

the non-dimensional flutter velocity. The problem defined by (12,13) will be solved using the collocation method. For this purpose, the approximate solution is expressed as

\begin{matrix} v (x) = \sum_{1}^{N} C_{n} ϕ_{n} (x) \end{matrix}

(16)

where

ϕ_{n}

suitably chosen base functions and

C_{n}

are constants to be determined. Base functions are to be chosen so as to satisfy the boundary conditions (12). Here, a family of polynomials will be chosen:

\begin{matrix} ϕ_{n} (x) = x^{n + 3} - \frac{2 n + 1}{4 n - 2} x^{n + 1} + \frac{2 n + 3}{16 (2 n - 1)} x^{n - 1} \end{matrix}

(17)

ϕ_{n} (x)

satisfies all the boundary conditions (13). Substituting the approximate solution (16) into the governing equation (12) will not satisfy it, but will result in a “residual”

\begin{matrix} R = R (C_{1}, C_{2}, . . ., C_{N}, x) = \sum_{n = 1}^{N} Q_{n} (x, ω, μ, u) C_{n} \end{matrix}

(18)

where, for brevity, we defined

\begin{matrix} Q_{n} (x, ω, μ, u) = & \sum_{n = 1}^{N} C_{n} (n + 3) (n + 2) (n + 1) n x^{n - 1} - \sum_{n = 1}^{N} C_{n} (n + 1) (n - 2) (n - 1) n A_{n} x^{n - 1} \\ + \sum_{n = 1}^{N} (n - 4) (n - 3) (n - 2) (n - 1) B_{n} x^{n - 5} + K_{1} \sum_{n = 1}^{N} C_{n} (x^{n + 3} - A_{n} x^{n + 1} + B_{n} x^{n - 1}) \\ + μ u \sum_{n = 1}^{N} C_{n} ((n + 3) x^{n + 2} - (n + 1) A_{n} x^{n} + (n - 1) + B_{n} x^{n - 2}) \end{matrix}

(19)

where

\begin{matrix} A_{n} = \frac{2 n + 1}{4 n - 2} \end{matrix}

(20)

\begin{matrix} B_{n} = \frac{2 n + 3}{16 (2 n - 1)} \end{matrix}

(21)

In the collocation method, the free parameters

C_{n}

are determined by equating the residual R to zero at N collocation points

x_{1}, x_{2}, x_{3}, . . . x_{N}

, which gives a linear homogeneous system of algebraic equations

\begin{matrix} \sum_{n = 1}^{N} Q_{n} (x, ω, μ, u) = 0 \end{matrix}

(22)

For non-trivial solution, the determinant of the coefficients should be zero

\begin{matrix} [\begin{matrix} Q_{1} (x_{1}, ω, μ, u) & Q_{1} (x_{2}, ω, μ, u) & \dots & Q_{N} (x_{N}, ω, μ, u) \\ Q_{2} (x_{1}, ω, μ, u) & Q_{2} (x_{2}, ω, μ, u) & \dots & Q_{N} (x_{N}, ω, μ, u) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ Q_{2} (x_{1}, ω, μ, u) & Q_{2} (x_{2}, ω, μ, u) & . . . & Q_{N} (x_{N}, ω, μ, u) \end{matrix}] = 0 \end{matrix}

(23)

The eigenvalue

ω

is determined from this equation in the form

\begin{matrix} ω = ω (μ, u) \end{matrix}

(24)

and the flutter velocity is found as a function of mass ratio

μ

from

\begin{matrix} I m [ω (μ, u)] = 0 . \end{matrix}

(25)

3. Rectangular Plate

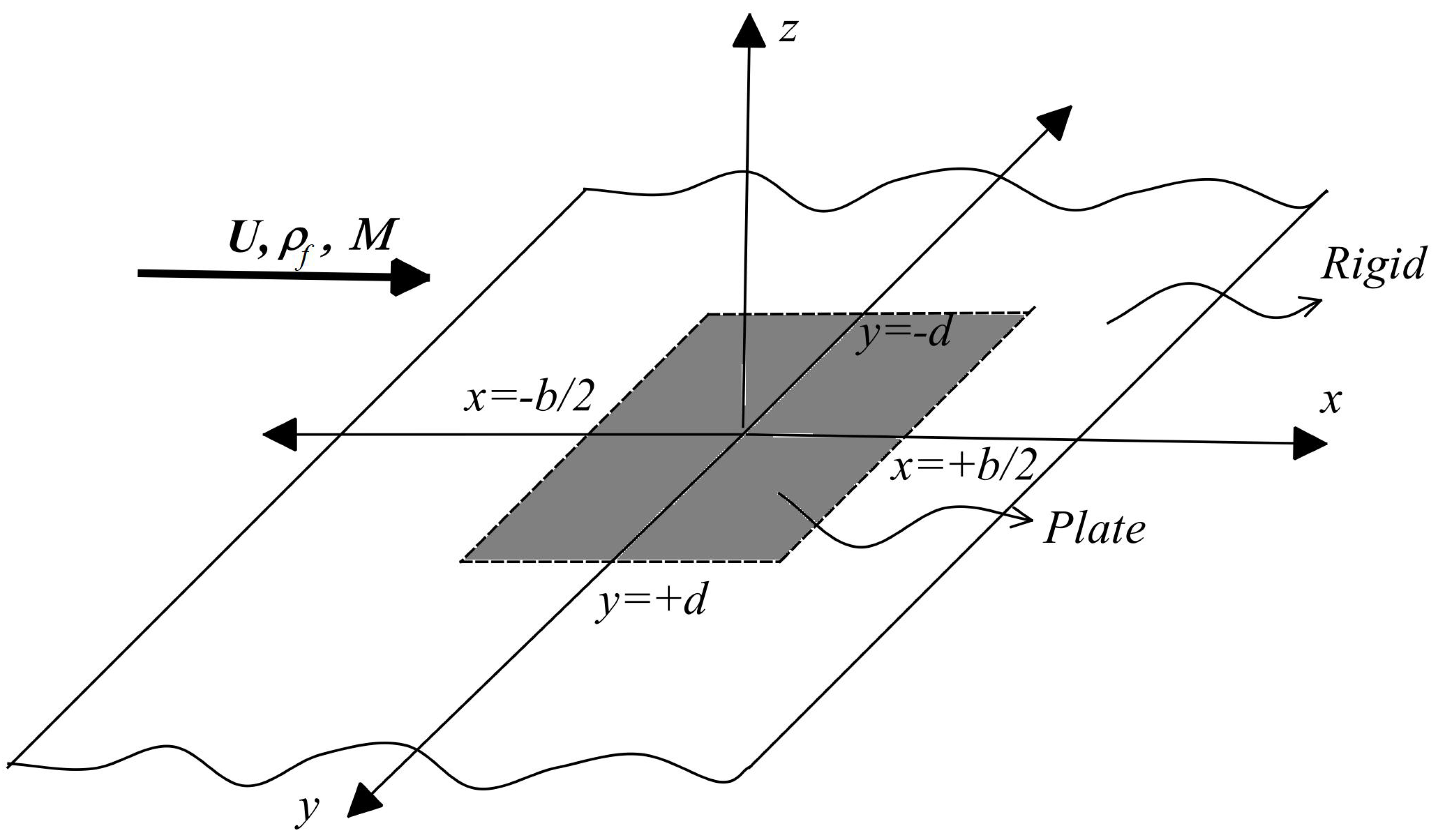
Figure 2 shows a schematic of the second problem considered. Now the plate also has a finite width 2d;

d = \infty

limit of this problem gives the first problem. Again using piston theory, the vibration equation takes the form

D (\frac{\partial^{4} w}{\partial x^{4}} + 2 \frac{\partial^{4} w}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w}{\partial y^{4}}) + ρ_{p} h_{p} \frac{\partial^{2} w}{\partial t^{2}} + \frac{ρ_{f} U}{M} (\frac{\partial w}{\partial t} + U \frac{\partial w}{\partial x}) = 0

(26)

The plate is assumed to be simply-supported at all sides, so the boundary conditions are

\begin{matrix} w (- b / 2, y, t) = w (b / 2, y, t) = w (x, - d, t) = w (x, d, t) = 0, \end{matrix}

(27)

\begin{matrix} \frac{\partial^{2} w}{\partial x^{2}} (- b / 2, y, t) = \frac{\partial^{2} w}{\partial x^{2}} (b / 2, y, t) = \frac{\partial^{2} w}{\partial x^{2}} (x, - d, t) = \frac{\partial^{2} w}{\partial x^{2}} (x, d, t) = 0 \end{matrix}

(28)

Non-dimensionalization is defined similarly

\begin{matrix} x^{*} = \frac{x}{b}, y^{*} = \frac{y}{b}, w^{*} = \frac{w}{b}, z^{*} = \frac{z}{b}, t^{*} = \frac{t}{b / U}, d^{*} = \frac{d}{b}, \end{matrix}

(29)

and again getting rid of stars, the non-dimensional problem is

\frac{\partial^{4} w}{\partial x^{4}} + 2 \frac{\partial^{4} w}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w}{\partial y^{4}} + \frac{\partial^{2} w}{\partial t^{2}} + μ (\frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x}) = 0,

(30)

\begin{matrix} w (- 1 / 2, y, t) = w (1 / 2, y, t) = w (x, - 1, t) = w (x, 1, t) = 0, \end{matrix}

(31)

\begin{matrix} \frac{\partial^{2} w}{\partial x^{2}} (- 1 / 2, y, t) = \frac{\partial^{2} w}{\partial x^{2}} (1 / 2, y, t) = \frac{\partial^{2} w}{\partial x^{2}} (x, - 1, t) = \frac{\partial^{2} w}{\partial x^{2}} (x, 1, t) = 0 \end{matrix}

(32)

with the same

μ

and u as before. In this case, the solution is assumed in the following form

\begin{matrix} w (x, y, t) = v (x) sin \frac{π y}{d} . e^{i ω t} \end{matrix}

(33)

This is the first term of a Fourier expansion in , but the common wisdom is that the higher terms do not affect the results [4,7]. (30-32) become

\frac{\partial^{4} v}{\partial x^{4}} - 2 {(\frac{π}{d})}^{2} \frac{d^{2} v}{d x^{2}} + μ u \frac{d v}{d x} + K_{2} v = 0,

(34)

\begin{matrix} v (- 1 / 2) = v (1 / 2) = \frac{d^{2} v}{d x^{2}} (- 1 / 2) = \frac{d^{2} v}{d x^{2}} (1 / 2) = 0, \end{matrix}

(35)

\begin{matrix} K_{2} = {(\frac{π}{d})}^{4} - ω^{2} + i ω μ \end{matrix}

(36)

The solution of (34,35) is carried out exactly as before, only the expression

Q_{n}

changes.

4. Analytical Solution

The solutions of both problems were performed by collocation method above. These problems can also be solved analytically; but the problem with analytical solution is that the solution procedure involves finding the roots of a quartic equation and the resulting determinant involves transcendent functions and searching for its zeroes is difficult. The collocation method is simpler to apply and is at similar to analytical solution in terms of performance. The solutions of both 12 and 34 are sought in the form

\begin{matrix} v = C e^{r x} . \end{matrix}

(37)

Substituting 37, 12 gives

\begin{matrix} r^{4} + μ u r + K_{1} = 0, \end{matrix}

(38)

and 34 gives

\begin{matrix} r^{4} - 2 {(\frac{π}{d})}^{2} r^{2} + μ u r + K_{2} = 0 . \end{matrix}

(39)

Denoting the roots of these equations

r_{1}, r_{2}, r_{3}, r_{4}

the solutions can be written as

\begin{matrix} v = C_{1} e^{r_{1} x} + C_{2} e^{r_{2} x} + C_{3} e^{r_{3} x} + C_{4} e^{r_{4} x} . \end{matrix}

(40)

Applying the boundary conditions 13 and 35 both give

\begin{matrix} [\begin{matrix} e^{\frac{1}{2} r_{1}} & e^{\frac{1}{2} r_{2}} & e^{\frac{1}{2} r_{3}} & e^{\frac{1}{2} r_{4}} \\ e^{- \frac{1}{2} r_{1}} & e^{- \frac{1}{2} r_{2}} & e^{- \frac{1}{2} r_{3}} & e^{- \frac{1}{2} r_{4}} \\ r_{1}^{2} e^{\frac{1}{2} r_{1}} & r_{2}^{2} e^{\frac{1}{2} r_{2}} & r_{3}^{2} e^{\frac{1}{2} r_{3}} & r_{4}^{2} e^{\frac{1}{2} r_{4}} \\ r_{1}^{2} e^{- \frac{1}{2} r_{1}} & r_{2}^{2} e^{- \frac{1}{2} r_{2}} & r_{3}^{2} e^{- \frac{1}{2} r_{3}} & r_{4}^{2} e^{- \frac{1}{2} r_{4}} \end{matrix}] [\begin{matrix} C_{1} \\ C_{2} \\ C_{3} \\ C_{4} \end{matrix}] = 0 \end{matrix}

(41)

The difference between the two solutions is due to the fourth-degree algebraic equations 38 and 39. For non-trivial solution, the determinant of the coefficients in 41 should be zero.

\begin{matrix} |\begin{matrix} e^{\frac{1}{2} r_{1}} & e^{\frac{1}{2} r_{2}} & e^{\frac{1}{2} r_{3}} & e^{\frac{1}{2} r_{4}} \\ e^{- \frac{1}{2} r_{1}} & e^{- \frac{1}{2} r_{2}} & e^{- \frac{1}{2} r_{3}} & e^{- \frac{1}{2} r_{4}} \\ r_{1}^{2} e^{\frac{1}{2} r_{1}} & r_{2}^{2} e^{\frac{1}{2} r_{2}} & r_{3}^{2} e^{\frac{1}{2} r_{3}} & r_{4}^{2} e^{\frac{1}{2} r_{4}} \\ r_{1}^{2} e^{- \frac{1}{2} r_{1}} & r_{2}^{2} e^{- \frac{1}{2} r_{2}} & r_{3}^{2} e^{- \frac{1}{2} r_{3}} & r_{4}^{2} e^{- \frac{1}{2} r_{4}} \end{matrix}| = 0 \end{matrix}

(42)

This gives omega as a function of the other parameters in the problem.

5. Results and Discussion

Collocation solutions were performed for

N = 10, 12

and 14 and sufficient convergence was observed for

N = 10

. Table 1 shows convergence of the results for flutter velocity

u_{f}

while increasing the number of collocation points. The collocation points were chosen to be equally spaced between

x = - 1 / 2, . . + 1 / 2

in all cases.

The solution of 38 (analytical solution) was carried out by an iterative shooting method [9]-[11]. Table 2 shows comparisons between collocation, and analytical solutions.

The collocation solution agrees with the analytical solution. As was mentioned, collocation method gives results quickly; analytical solution here is meant to check the correctness of the collocation solution. As another validation of the results presented here, comparison with Dowell 1966 shows similar results, bearing in mind that in the mentioned work, full potential theory was used, and the solution was carried out for a plate infinite in the direction of flow The results obtained in this study for small d agree with Dowell.

5.1. Infinite Strip

Figure 3 shows the non-dimensional flutter velocity as a function of mass ratio. As expected, flutter velocity decreases with increasing mass ratio. Since the curve in Figure 3 seems to have a simple structure, a mathematical expression between

u_{f}

and

μ

could be developed by using curve-fitting. This was done by using Matlab and the result is

\begin{matrix} u_{f} = \frac{333.7 + 3.249 μ + 0.1461 μ^{2}}{μ - 0.02} \end{matrix}

(43)

This equation gives the same points as in Figure 3 within an error of 1 percent.

5.2. Rectangular Plate

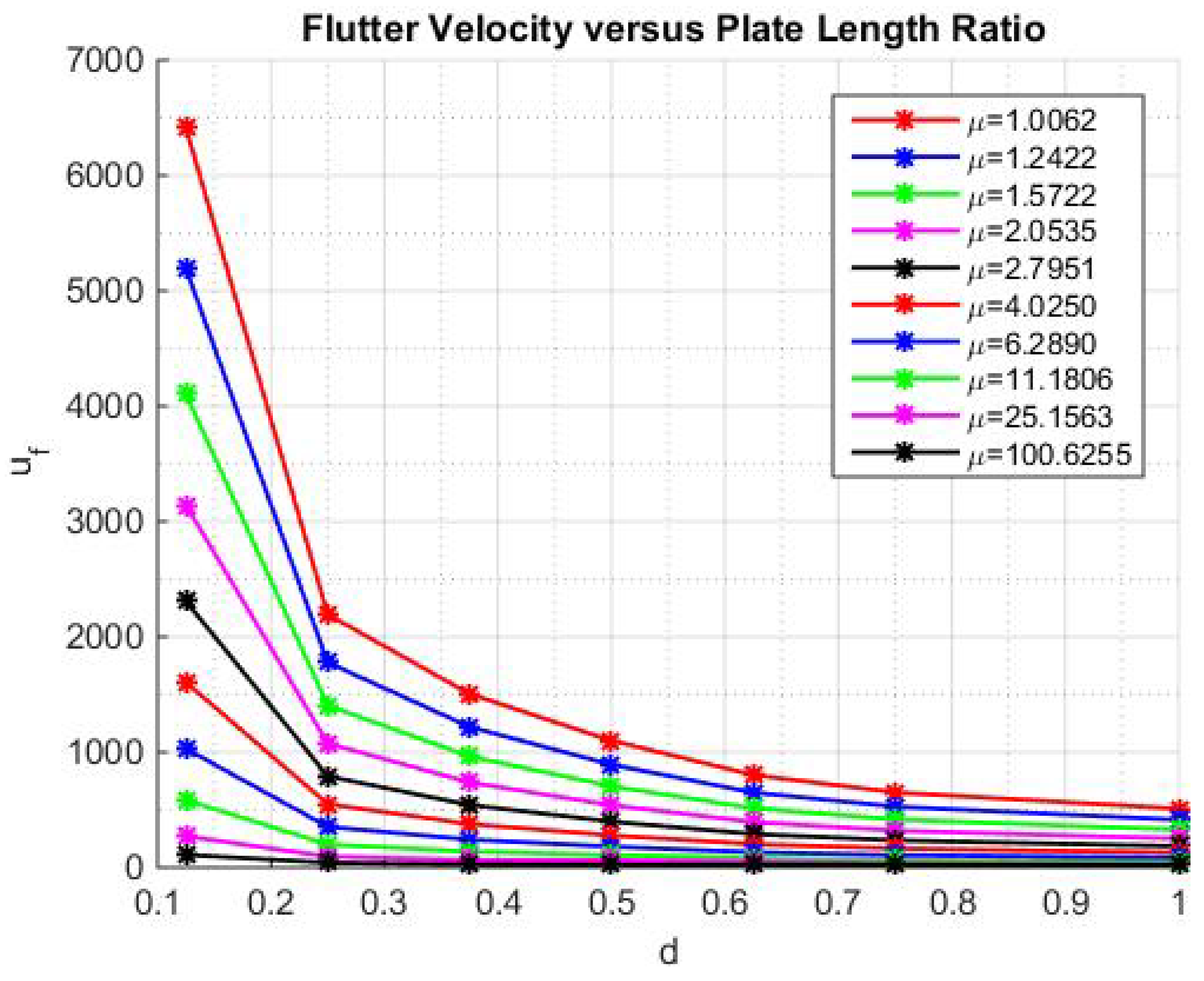
For rectangular plate, there are two parameters that the flutter velocity depends on; mass ratio and plate width ratio. Figure 4 shows the flutter velocity as a function of plate width ratio for various values of mass ratio, for

d > 1

. The results for

d < 1

are shown in a separate Figure 4. It is observed that the flutter velocity decreases and asymptotically converges to the value for the infinite strip as the plate width increases.

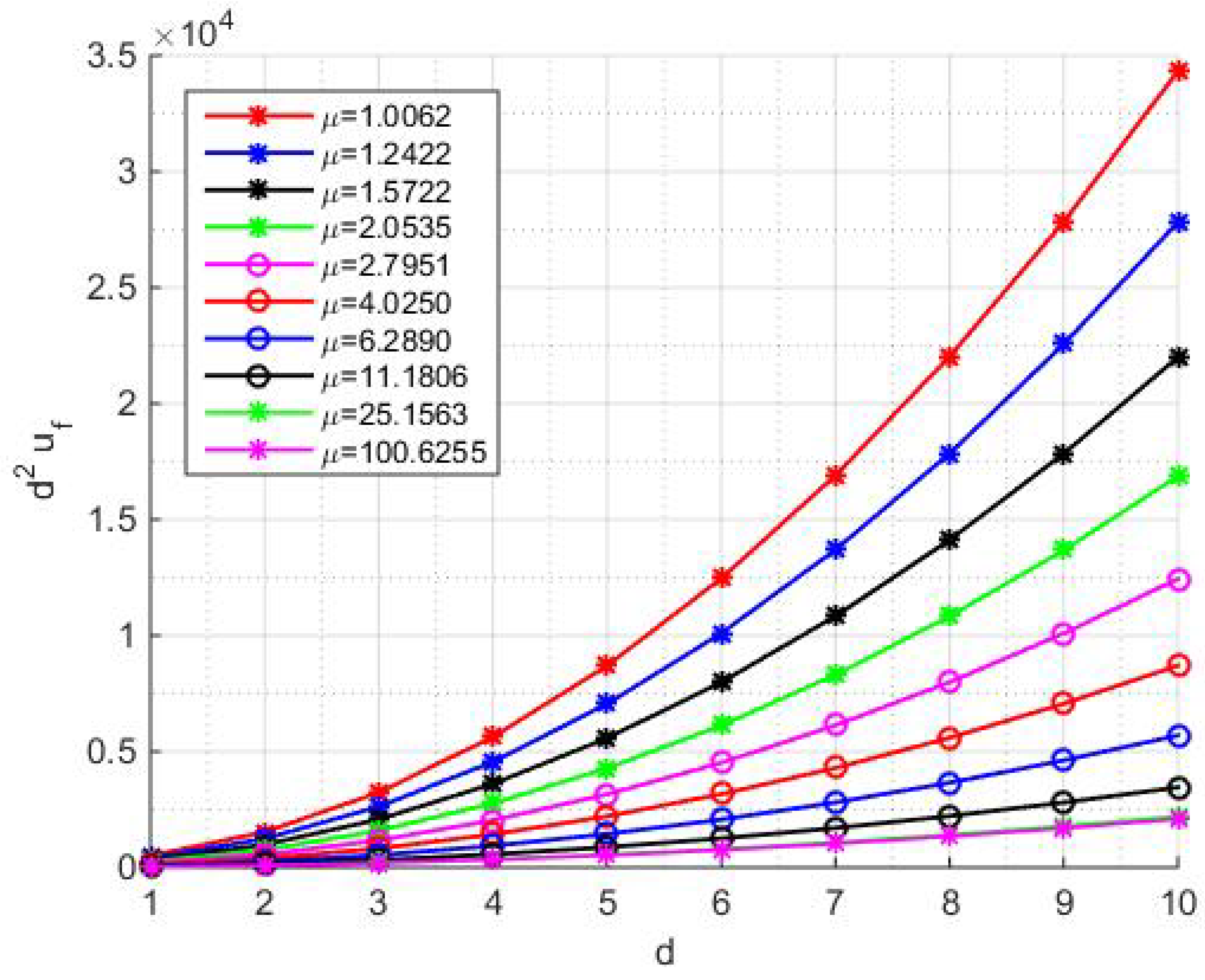
To generalize 43 to rectangular plate, it was found to be useful to look at the graph of

d^{2} u_{f}

(Figure 5). Assuming the relation between the flutter velocities for finite and infinite width plates to be

\begin{matrix} u_{f} = u_{\infty} + \frac{u}{d^{2}} . \end{matrix}

(44)

Here

u_{\infty}

is the expression 41, and, by curve-fitting

α

is found to be

\begin{matrix} α = 1.125 + \frac{159.4}{μ} + \frac{12.02}{μ^{2}} . \end{matrix}

(45)

44 gives the flutter velocity in Figure 5 within 1 percent for

d > 1

and

μ < 25

To give an example, for Aluminum (with density

ρ = 2720

k g / m^{3}

, Elasticity Modulus

E = 70

GPa and Poisson ratio

ν = 0.3

plate of thickness 5 mm for

b = 1 m

and

d = 3 m

equation 44 gives the non-dimensional flutter velocity as 91.7847 (91.166737 with collocation method) and the actual flutter velocity is 704.5209 m/s (699.7770 m/s with collocation method).

6. Conclusion

To summarize, the flutter velocity of a plate structure, under very varied geometric conditions can be estimated with simple algebraic expressions given in this study. These expressions were derived by curve fitting to data obtained by collocation method. To validate the collocation results, analytical solution was also carried out and seen to give the same results.

Author Contributions

Aziz Sezgin: Conceptualization of this study, Methodology. Birkan Durak: Methodology, Software. Alaattin Sayın: Software. Huseyin Yildiz: Software. Hasan Omur Ozer: Software. Lutfi Emir Sakman: Software. Erol Uzal: Software.

References

Erol, U.; Sule, K. Vibrations of an Infinite Plate Placed in a Circular Channel Containing Fluid Flow. Aircr. Eng. Aerosp. Technol. 2010, 81, 533–535. [Google Scholar]
Epureanu, B.I.; Yin, S.H. Identification of damage in an aeroelastic system based on attractor deformations. Computers and Structures 2004, 82, 2743–2751. [Google Scholar] [CrossRef]
Vedeneev, V.V. Panel flutter at low supersonic speeds. J. Fluids Struct. 2012, 29, 79–96. [Google Scholar] [CrossRef]
Dowell, E.H. Flutter of infinitely Long Plates and Shells. Part 1: Plate. AIAA Journal 1966, 4, 1370–1377. [Google Scholar] [CrossRef]
Erol, U.; Banu, K. Vibration control of an elastic strip by a singular force. Sadhana 2010, 35, 233–240. [Google Scholar]
Sezgin, A.; Krstic, M. Boundary Backstepping Control of Flow-Induced Vibrations of a Membrane at High Mach Numbers. Journal of Dynamic Systems, Measurement, and Control 2015, 137, 081003–1. [Google Scholar] [CrossRef]
Uzal, E.; Korbahti, B. Vibrations of an Anisotropic Plate Under Fluid Flow in a Channel. Journal of Vibration and Control 2007, 13, 1191–1204. [Google Scholar]
Tubaldi, E.; Alijani, F.; Amabili, M. Vibrations of an Anisotropic Plate Under Fluid Flow in a Channel. Journal of Vibration and Control 2007, 13, 1191–1204. [Google Scholar]
Morrison, D.D.; Riley, J.D.; Zancanaro, J.F. Multiple shooting method for two-point boundary value problems. Communications of the ACM 1962, 5, 613–614. [Google Scholar] [CrossRef]
Dowell, E.H.; Hall, K.C. Modeling of Fluid-Structure Iteration. Annual Rev. Fluid Mech. 2001, 33, 445–490. [Google Scholar] [CrossRef]
Fang, L.; Vandewalle, S.; Meyers, J. An SQP-based multiple shooting algorithm for large-scale PDE-constrained optimal control problems. Journal of Computational Physics 2023, 477, 111927. [Google Scholar] [CrossRef]

Figure 1. Fluid and strip plate coupled system

Figure 2. Fluid and rectangular coupled system

Figure 3. Relationship between the dimensionless state parameter

μ = \frac{ρ_{f} b}{ρ_{p} h_{p}} c_{s}

and the dimensionless flutter velocity for the strip plate given in Figure 1.

Figure 3. Relationship between the dimensionless state parameter

μ = \frac{ρ_{f} b}{ρ_{p} h_{p}} c_{s}

and the dimensionless flutter velocity for the strip plate given in Figure 1.

Figure 4. Relation between u and d in different situations for the case

d < 1

Figure 4. Relation between u and d in different situations for the case

d < 1

Figure 5. Relation between

d^{2} u_{f}

and d in different situations for the case

d > 1

Figure 5. Relation between

d^{2} u_{f}

and d in different situations for the case

d > 1

Table 1. The convergence of the results while increasing of the number of collocation points.

Number of collocation points	$u_{f}$
8	90.9697280425894
10	91.1667370035824
12	91.1563146276537
14	91.1564970192325

Table 2. Numerical results for a random chosen

d = 3

value of the two methods.

Table 2. Numerical results for a random chosen

d = 3

value of the two methods.

	Collocation Method		Analitical Results
$μ$	Before Flutter	After Flutter	Before Flutter	After Flutter
1.006255	358.920571	359.571969	359.467520	359.571969
1.242290	291.097486	291.372886	291.315280	291.372886
1.572273	230.265262	230.461233	230.377137	230.461233
2.053581	176.682416	176.762617	176.671744	176.762617
2.795152	130.248788	130.299136	130.23840	130.299136
4.025020	90.6746705	91.1957893	91.156960	91.195789
6.289093	59.2604927	59.6428185	59.604512	59.642818
11.18061	36.0023423	36.1616447	36.111424	36.161644

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Flutter of a Plate at High Supersonic Speeds

Abstract

Keywords:

Subject:

1. Introduction

2. Infinite Strip Plate

3. Rectangular Plate

4. Analytical Solution

5. Results and Discussion

5.1. Infinite Strip

5.2. Rectangular Plate

6. Conclusion

Author Contributions

References

MDPI Initiatives

Important Links

Subscribe