Obstacle Avoidance in Operational Configuration Space Kinematic Control of Redundant Serial Manipulators

Preprint

Article

Obstacle Avoidance in Operational Configuration Space Kinematic Control of Redundant Serial Manipulators

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.7z (16.65MB )

This version is not peer-reviewed

Submitted:

13 November 2023

Posted:

14 November 2023

You are already at the latest version

Alerts

Abstract

Kinematic control of redundant serial manipulators has been carried out for the past half century based primarily on a generalized inverse velocity formulation that is known to have mathematical deficiencies. A recently developed inverse kinematic position mapping is extended to an operational configuration space differentiable manifold formulation for kinematic control with obstacle avoidance is employed to resolve deficiencies in the generalized inverse velocity formulation. Output trajectory tracking with obstacle avoidance for four and twenty degree of redundancy manipulators is carried out to demonstrate the effectiveness of the differentiable manifold approach and that it resolves deficiencies of the conventional generalized inverse velocity formulation.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

1.1. Basics of Redundant Serial Manipulator Kinematics

A serial manipulator is comprised of a chain of bodies that are connected by single degree of freedom joints. Joint relative input coordinates

y_{i}

between bodies in the chain define the configuration of outboard bodies relative to their inboard counterparts. The terminal body in the chain is the end effector, whose output coordinates characterize manipulator working capability and are defined as twice continuously differentiable functions of input coordinates, in the form of the forward kinematic mapping

z = G (y)

(1)

Input coordinates

y \in R^{n}

are independent generalized coordinates [1] that define the configuration of the underlying mechanism and output coordinates

z \in R^{m}

of the end effector, with

m < n

, define functionality of the kinematically redundant manipulator. Here,

R^{k}

refers to k-dimensional Euclidean space with elements

x \in R^{k}

in the form of column vectors

x = {[\begin{matrix} x_{1} & \dots & x_{k} \end{matrix}]}^{T}

, where superscript ^T denotes matrix transpose. Bold characters denote vectors and matrices.

An input-output pair

(y, z)

that satisfies Eq. (1) defines a manipulator configuration, denoted

x = {[\begin{matrix} y^{T} & z^{T} \end{matrix}]}^{T} \in R^{n + m}

. The manipulator configuration space is defined as

X = {x \in R^{n + m} : G (y) - z = 0}

(2)

As observed in [2], X is the graph of the forward kinematic mapping of Eq. (1). As such, under moderate regularity conditions, it is a differentiable manifold with the single chart

(R^{n}, ϕ (x))

, where

ϕ (x) = y

[2]. This manifold, however, contains information only on forward kinematics and no information regarding inverse kinematics. It should be noted that configuration space in the manipulator literature is usually defined as the space of input (joint) coordinates. The manipulator configuration space defined herein is the product of input and output spaces. It thus embodies the topology of the manipulator, not just its input space.

The manipulator configuration space often contains singular configurations relative to inverse kinematics. If the rank of the

m \times n

Jacobian matrix of derivatives of

G (y)

with respect to

y

, defined as the

m \times n

matrix

G^{'} (y) \equiv [\partial G_{i} (y) / \partial y_{j}]

, is less than m at a configuration

\bar{x} = {[\begin{matrix} {\bar{y}}^{T} & {\bar{z}}^{T} \end{matrix}]}^{T} \in X

, then in a neighborhood of

\bar{x}

there exists no continuously differentiable set-valued inverse kinematic mapping with

n - m

arbitrary parameters [3,4]. To avoid difficulties associated with inverse kinematic singular configurations in X, the regular configuration space is defined as

\tilde{X} = {x \in X : rank (G^{'} (y)) = m}

(3)

\tilde{X}

, the manipulator degree of redundancy is

r = n - m

A Four Degree of Redundancy Manipulator

Most applications of redundant manipulators have just one degree of redundancy; i.e., r =

n - m = 1

. The serial manipulator of Figure 1 has

n = 6

inputs

y \in R^{6}

and two outputs

z \in R^{2}

Using the notation

y_{ij} = y_{i} + \dots + y_{j}

, the forward kinematic mapping of Eq. (1) is

z = G (y) = [\begin{matrix} y_{1} + {\cos y}_{3} + {\cos y}_{34} + {\cos y}_{35} + {\cos y}_{36} \\ y_{2} + {\sin y}_{3} + {\sin y}_{34} + {\sin y}_{35} + {\sin y}_{36} \end{matrix}]

(4)

with the full rank Jacobian, for all

x \in X = \tilde{X}

\begin{array}{l} G^{'} (y) = [\begin{matrix} 1 & 0 & a & b & - ({\sin y}_{35} + {\sin y}_{36}) & - {\sin y}_{36} \\ 0 & 1 & c & d & ({\cos y}_{35} + {\cos y}_{36}) & {\cos y}_{36} \end{matrix}] \\ a = - ({\sin y}_{3} + {\sin y}_{34} + {\sin y}_{35} + {\sin y}_{36}) \\ b = - ({\sin y}_{34} + {\sin y}_{35} + {\sin y}_{36}) \\ c = ({\cos y}_{3} + {\cos y}_{34} + {\cos y}_{35} + {\cos y}_{36}) \\ d = ({\cos y}_{3} + {\cos y}_{34} + {\cos y}_{35}) \end{array}

(5)

Thus, the manipulator has degree of redundancy r =

n - m = 4

1.2. Generalized Inverse Velocity-Based Redundancy Resolution

Differentiating Eq. (1) with respect to time yields the kinematic velocity equation

\dot{z} = G^{'} (y) \dot{y}

(6)

Since Eq. (6) is linear in velocity, for a given configuration, it may be thought that analysis in the linear velocity space is easier than in the nonlinear regular configuration space of Eq. (3). When

m = n

and the manipulator is nonredundant, this may in fact be the case. In

\tilde{X}

, if m = n the manipulator is nonredundant,

G^{'} (y)

is square and nonsingular, and there is a unique solution of Eq. (6) for

\dot{y}

\dot{y} = {G^{'}}^{(- 1)} (y) \dot{z}

(7)

In this special case, Eq. (7) is an ordinary differential equation (ODE). For specified continuous

\dot{z} (t)

and initial condition

y (0) = y^{0}

, the initial-value problem with Eq. (7) has a unique solution in a neighborhood of

t = 0

For redundant manipulators with

n > m

, attractive properties of ODE for Eq. (6)are no longer available. At a redundant manipulator configuration

x \in \tilde{X}

G^{'} (y)

has full rank,

G^{'} (y)

is not a square matrix, and Eq. (6) cannot be solved for a unique value of

\dot{y}

. In this case, Eq. (6) is not an ODE. It is a Pfaffian differential equation [5] that behaves more like a partial differential equation than an ODE. While the ODE of Eq. (7) with m = n has a general solution that depends on n arbitrary constants, a general solution of Eq. (6) with n > m depends on arbitrary vector functions

p (t)

[5]. As shown in [4], trading the nonlinear manipulator equations of Eqs. (2) and (3) for the Pfaffian differential equation of Eq. (6) is a questionable decision.

A generalized inverse velocity-based redundancy resolution formulation was introduced by Whitney [8] half a century ago in an attempt to create an ODE formulation for redundant manipulator kinematics. At a configuration

x \in \tilde{X}

with n > m,

G^{'} (y)

has full rank and the Moore-Penrose generalized inverse [6,7,8] is defined as

{G^{'}}^{†} (y) = {G^{'}}^{T} (y) {(G^{'} (y) {G^{'}}^{T} (y))}^{- 1}

(8)

Direct manipulation verifies that

G^{'} (y) {G^{'}}^{†} (y) = I

and

\dot{y} = {G^{'}}^{†} (y) \dot{z} + (I - {G^{'}}^{†} (y) G^{'} (y)) {\dot{y}}^{0} (t)

(9)

satisfies Eq. (6), where

{\dot{y}}^{0} (t) \in R^{n}

is arbitrary. While

\dot{y}

of Eq. (9) satisfies Eq. (6) with an arbitrary function

{\dot{y}}^{0} (t)

, it does not provide a solution

y (t)

of Eq. (1) and there is no reason to believe Eqs. (9) and (6) are equivalent.

1.3. Manipulator Trajectory Planning and Obstacle Avoidance

An extensive literature on kinematically redundant manipulator trajectory planning and kinematic control appeared in the last quarter of the 20^th century, based primarily on the manipulator velocity representation of Eq. (9); e.g., [6,7,8,9,10] and references cited therein. The most basic kinematic control formulation seeks to use manipulator redundancy to cause manipulator output z(t) to follow a desired output trajectory

z_{d} (t)

and to satisfy constraints such as avoidance of collision of manipulator links wirh obstacles. Objectives and constraints in these applications are most naturallly stated in terms of input and output coordinates, rather than manipulator velocities. The apparent simplicity of the velocity equations of Section 1.2, wih the redundancy related arbitrary velocity

{\dot{y}}^{0} (t)

of Eq. (9) , however, has led research and development engineers to adopt the generalized inverse velocity mapping of Eq. (9) to address the kinematic control objective; e.g., [6,7] and references cited therein.

Problems with inverse velocity kinematics that are summarized in Section 2.2 have required refinements in the generalized inverse velocity formulation, using feedback control methods to compensate for deficiencies; e.g., [11,12,13,14,15] and references cited therein. For purposes of this paper, the basic generalized inverse velocity kinematics formulation is employed for study of output trajectory tracking and obstacle avoidance with highly redundant serial manipulators that are not subject to Jacobian rank deficiency that require more refined feedback control methods.

Quite recently, a configuration-based inverse kinematic mapping for kinematically redundant serial manipulators has been presented that avoids deficiencies associated with the inverse velocity mapping approach [3,4]. This method is summarized in Section 3 and applied for manipulator path planning with obstacle avoidance. Another recent development that focuses on inverse position kinematics [16] holds potential to contribute to manipulator programming with obstacle avoidance.

2. Generalized Inverse Velocity-Based Kinematic Control and Obstacle Avoidance

2.1. Problems with Generalized Inverse Velocity Redundancy Resolution

In the redundant manipulator literature [6,7,8,9,10], Eq. (9) has been treated as a differential equation that relates output to input. It has been analytically and computationally shown, however, that use of Eq. (9) leads to irregularities in predicted manipulator performance [17,18,19,20], including numerical drift, nonholonomic behavior, and divergence of computation. Analysis has shown that use of the generalized inverse of Eq. (8) leads to nonholonomic equations of redundancy resolution that create systematic noncyclicity of the manipulator [19,20]; i.e., a periodic output trajectory maps into a nonperiodic input trajectory. While some effort has been devoted to creating generalized inverses that overcome these problems [14,15,21], no comprehensive result has been reported. A treatment based on concepts similar to those employed herein is shown to partially resolve the noncyclicity problem [22]. Theoretical and numerical results presented in [4,22] complement the literature cited and show that the generalized inverse velocity approach to manipulator redundancy resolution is fundamentally flawed.

While the foregoing analyses of deficiencies of the generalized inverse velocity approach do not focus specifically on obstacle avoidance, the inaccuracies implied cast doubt on use of the approach for obstacle avoidance. In particular, no self-motion coordinates at the configuration level are defined, which means that an indirect velocity approach to obstacle avoidance must be employed [11,12,13,15,21]. Since obstacle avoidance occurs in configuration space, not in velocity space, an adaptation of generalized inverse velocity differential equations must be created to treat what is a configuration-based application.

2.2. Generalized Inverse Velocity-Based Kinematic Control and Obstacle Avoidance

The conventional approach to obstacle avoidance using the generalized inverse velocity approach is to employ the second term of Eq. (9); i.e., the null space term, to minimize a cost function

f (y)

that penalizes manipulator link proximity to obstacles [23]. For example, by defining

{\dot{y}}^{0} (t) = - k \nabla_{y} f (y (t))

(10)

with

k > 0

, where

\nabla_{y} f (y) = {[\partial f (y) / \partial y_{1}, ..., \partial f (y) / \partial y_{n}]}^{T}

, and projecting it onto the null space of the Jacobian matrix by means of the projector

(I - {G^{'}}^{†} (y) G^{'} (y))

of Eq. (9). The manipulator will move y(t) in a direction that decreases f, without affecting the desired output trajectory z(t); i.e., self-motion. If f is defined as

f (y) = \sum_{i, j} 1 / d_{i j} (y)

(11)

where

d_{i j} (y)

is the minimum distance between link 𝑖 and obstacle 𝑗, the manipulator will tend to move its links away from the obstacles.

This is not a robust way to handle obstacle avoidance, because it is based on a velocity equation that needs to be numerically integrated in order to obtain the configuration of the manipulator. For example, if

f (y)

of Eq. (10) is inserted into Eq. (9), which is integrated numerically with a given time step Δt, the resulting trajectory of the manipulator may not be feasible. This is because, as time progresses, the equation is integrated, the manipulator moves forward, and the cost function

f (y)

may not be minimized at a sufficiently high rate to avoid obstacles. Indeed, if the minimization of

f (y)

is not performed sufficiently quickly as the manipulator approaches obstacles, penetration of an obstacle will occur that will produce a zero denominator in Eq. (11); i.e.,

d_{i j} (y) = 0

for some (i, j), and this will lead to failure of numerical integration. As will be demonstrated in Section 2.3 and 4.3, it is necessary to carefully select the values of Δt (time step) and k (gain appearing in Eq. (10)). In fact, as will be shown, it may be necessary to use extremely small values of Δt and k to obtain motion that is free of obstacle penetration. On the one hand, simulating the full trajectory using a small Δt means long computation times. On the other hand, when using Eq. (9) for real-time kinematic control of the manipulator, a small Δt imposes demanding requisites on the control hardware, which must be able to operate at such small sample times.

2.3. Four Degreee of Redundancy Generalized Inverse Velocity-Based Example

In this section, the approach described in Section 2.2 is applied to plan motion of the manipulator of Section 1.1.1 that has four degrees of redundancy. The manipulator starts with input

y_{0} = {[0 . 5688, 0 . 4694, 0 . 0119, 0 . 3371, 0 . 1622, 0 . 7943]}^{T}

and its end-effector is required to follow the periodic elliptic trajectory

z_{d} (t) = {[\cos (θ) \cdot a \cdot \cos (t) - \sin (θ) \cdot b \cdot \sin (t) + x_{0}, \sin (θ) \cdot a \cdot \cos (t) + \cos (θ) \cdot b \cdot \sin (t) + y_{0}]}^{T}

(12)

while its links must avoid a circular obstacle centered at (1.5, 2) with radius 0.5. Equation (12) is the parametric equation of an ellipse centered at (x₀ = 1.7, y₀ = 2.9) with semiaxes a = 2 and b = 0.25, whose longer semiaxis forms an angle of θ = -0.15 rad with the x axis. The end-effector is required to follow three cycles on this ellipse; i.e., t runs from t = 0 to t = 6π.

The method described in Section 2.2 is carried oujt by numerically integrating Eq. (9), using a fourth-order Runge-Kutta integrator [24] with a fixed time step

Δ t = 0.01

seconds. Note that, for a given time step

Δ t

, the main parameter that can be tuned in the method of Section 2.2 is the coefficient k > 0, which adjusts the intensity of the penalty function

f (y)

. A higher k will give greater weight to minimization of the cost function, which means that the manipulator links will tend to have larger distances to the obstacles.

Figure 2 presents a sequence of configurations adopted by the manipulator for three different values of k, when executing the first half of the first cycle of the periodic trajectory given by Eq. (12) (i.e., when integrating Eq. (9) from t = 0 to t = π seconds). According to Figure 2.c, for higher values of k the manipulator adopts configurations that are unnecessarily far from the obstacle. Thus, in the following, the value k = 0.01, which generates the result shown in Figure 2.a, will be used. Note, however, that if k is chosen too small, the rate of minimization of

f (y)

may be too slow for the motion of the robot and one or more links may penetrate the obstacle before the term

{\dot{y}}^{0} (t)

of Eq. (10) leads to a trajectory that avoids the obstacle.

When the manipulator is required to transit the elliptic trajectory three times by integrating Eq. (9) with k = 0.01 from t = 0 to t = 6π, the time evolution of inputs

y_{i} (t)

presented in Figure 3 is obtained. As this figure shows, the time history of

y_{i} (t)

is not cyclic, because the value of each

y_{i} (t)

at the end of each cycle of the output trajectory of Eq. (12) does not coincide with its value at the beginning. This is an example of noncyclicity of the generalized inverse velocity approach to redundancy resolution, as discussed in Section 2.2.

To better illustrate this noncyclic trajectory, Figure 4 presents a sequence of snapshots of the manipulator as its inputs

y_{i} (t)

traverse the trajectories graphed in Figure 3. Only the first two cycles are presented in Figure 4. Supplementary video S1 attached displays the animation of these two cycles, as well as a third cycle.

Figure 4.a-i shows execution of the first cycle. In Figure 4.a, the manipulator is approaching the obstacle. Between Figure 4.b and e, the gradient term of Eq. (10) acts to avoid the obstacle. Between Figure 4.f and i, the links of the manipulator are sufficiently far from the obstacle and the cost f of Eq. (11) is negligible (with negligible derivative), so the corrective term of Eq. (10) does not have significant effect. Figure 4.i shows the configuration of the manipulator at the end of the first cycle of the elliptic trajectory, which does not coincide with the initial configuration shown in Figure 4.a.

Figure 4.j-o show a sequence of snapshots of the configuration of the manipulator during execution of the second cycle, completing the second cycle in Figure 4.o. When comparing these snapshots to those of the first cycle, one observes the noncyclicity of the input trajectory, where the manipulator is further away from the obstacle than in Figure 4.i and 4.a. A third cycle can be observed in attached video S1, which ends with the manipulator even further away from the obstacle.

As this example shows, generalized inverse velocity-based kinematic control can be used for obstacle avoidance, but its performance is not easy to tune or predict. For this example, a time step of

Δ t = 0.01

seconds was sufficient to achieve obstacle avoidance for different values of k, and it was possible to avoid obstacles without excessively conservative distances between links and obstacles by choosing a small value of k = 0.01. However, this worked well only for the first cycle. After completing the first cycle, due to the nonholonomic nature of Eq. (9), the manipulator drifts and executes subsequent cycles far from the obstacle, where

{\dot{y}}^{0} (t)

of Eq. (10) becomes negligible, yielding postures similar to those that would have been adopted if the first cycle had been executed using a larger value of k, as demonstrated in Figure 2. This suggests that the choice of parameters k and

Δ t

(which have been kept constant throughout this example) may actually be rather arbitrary, because nonholonomy may end up wasting or undoing a careful choice of such parameters. This is even more important in difficult scenarios such as the one treated in Section 4.3, where a highly redundant manipulator must avoid several obstacles and choice of parameters k and

Δ t

is critical for performance of generalized inverse velocity-based kinematic control.

3. Operational Configuration Space Kinematic Control and Obstacle Avoidance

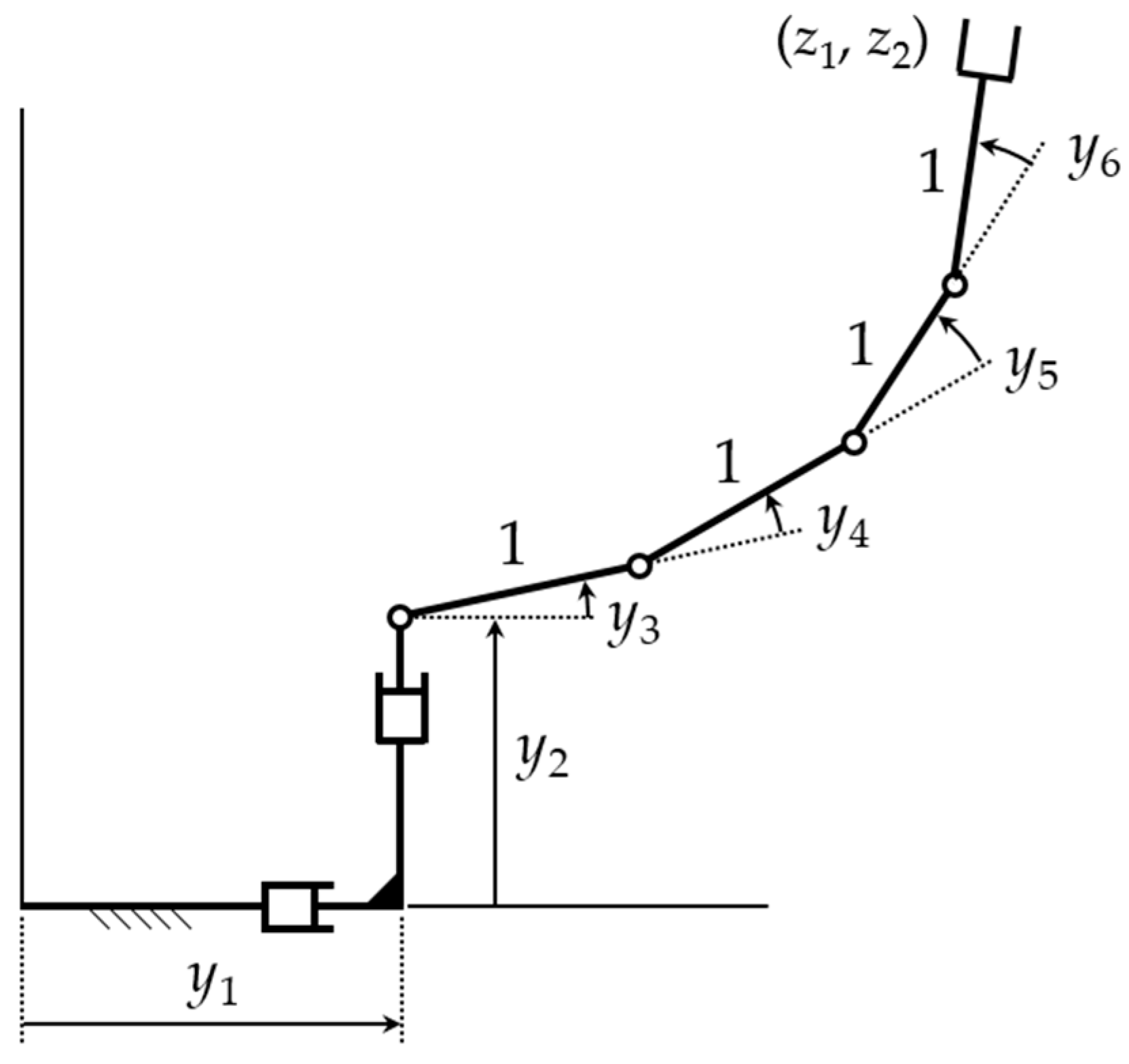
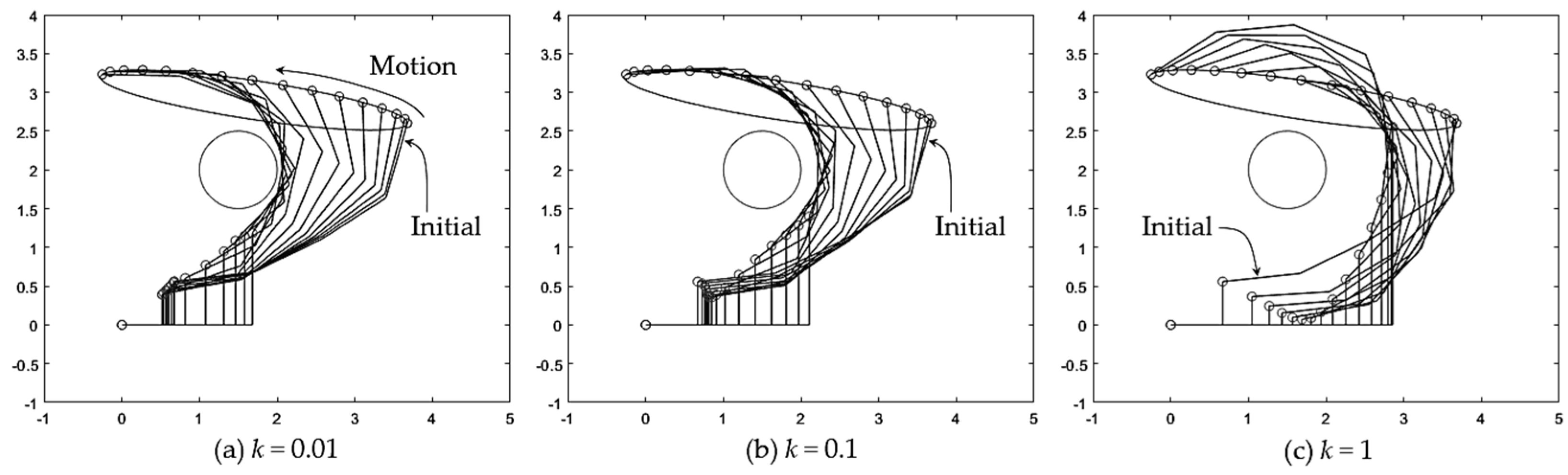
To replace the generalized inverse velocity formulation of Section 2 with a configuration space formulation, it is required that a set-valued inverse configuration kinematic mapping be constructed; i.e., a solution

y = g (z, v)

of Eq. (1) be found with an arbitrary vector of parameters

v \in R^{n - m}

. Such a mapping has been presented in [3] and extended in [4] on an operational space differentiable manifold, as summarized here.

3.1. Inverse Configuration Kinematics

The entire regular configuration space

\tilde{X}

cannot, in general, be characterized by a single continuously differentiable inverse kinematic mapping. The only practical global inverse kinematic representation is based on concepts of differential geometry [2] that employ local representations on open subsets

N^{j} \in \tilde{X}

, whose union is the entire regular configuration space; i.e.,

\cup_{j} N^{j} = \tilde{X}

. In each

N^{j}

, there is a base point

{\bar{x}}^{j}

about which the inverse kinematic mapping is constructed. The inverse kinematic mapping process that follows takes place on each

N^{j}

. For a given j and base point

{\bar{x}}^{j}

N^{j}

, define the

n \times m

matrix

U^{j}

and an

n \times (n - m)

matrix

V^{j}

such that

U^{j} = {G^{'}}^{T} ({\bar{y}}^{j}) G^{'} ({\bar{y}}^{j}) V^{j} = 0 V^{j T} V^{j} = I

(13)

where

V^{j}

is computed as a matrix whose columns form an orthonormal basis of the null space of

G^{'} ({\bar{y}}^{j})

in MATLAB, using singular value decomposition [24]. The matrices

U^{j} and V^{j}

are defined to be constant on

N^{j}

. Note from the second of Eqs. (13) that

U^{j T} V^{j} = 0

and

V^{j T} U^{j} = 0

. Since

G^{'} ({\bar{y}}^{j})

has full rank, so do

U^{j}

and

V^{j}

. Further, since

V^{j T} U^{j} = 0

, the columns of

V^{j}

are orthogonal to the columns of

U^{j}

and vice-versa. The n linearly independent columns of

U^{j}

(m columns) and

V^{j}

(

n - m

columns) therefore span

R^{n}

Using

V^{j}

and

U^{j}

of Eq. (13), any solution of Eq. (1) for y in a neighborhood of

{\bar{y}}^{j}

can be written in the form

y = {\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (u - {\bar{u}}^{j})

(14)

where

{\bar{v}}^{j} and {\bar{u}}^{j}

are values of v and u associated with

{\bar{x}}^{j}

on the trajectory that first enters

N^{j}

. They are introduced to assure continuity of y as a function of v and z. On

N^{1}

{\bar{v}}^{1} = 0

and

{\bar{u}}^{1} = 0

. Note that, at

y = {\bar{y}}^{j}

in Eq. (14),

v = {\bar{v}}^{j} and u = {\bar{u}}^{j}

. To see that there is a unique solution of Eq. (1) with y of Eq. (14); i.e., a unique solution of

G ({\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (u - {\bar{u}}^{j})) - z = 0

(15)

for u as a function of z and v in a neighborhood of

z = {\bar{z}}^{j}

and

v = {\bar{v}}^{j}

, the derivative of the left side of Eq. (15) with respect to u, evaluated at

{\bar{x}}^{j}

, is

- G^{'} ({\bar{y}}^{j}) U^{j} = - U^{j T} U^{j}

, which is nonsingular. Thus, the implicit function theorem [25] implies existence of a unique, twice continuously differentiable solution

u = h^{j} (z, v)

(16)

of Eq. (15) in a neighborhood of

{\bar{x}}^{j}

. From Eq. (14),

y (z, v) = {\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (h^{j} (z, v) - {\bar{u}}^{j})

(17)

This is the desired set-valued inverse position kinematic mapping on

N^{j}

z (t) and v (t)

are periodic of period

t_{p}

N^{j}

; i.e.,

z (t + t_{p}) = z (t)

and

v (t + t_{p}) = v (t)

, since Eq. (17) holds throughout

N^{j}

y (t + t_{p}) = {\bar{y}}^{j} + V^{j} v (t + t_{p}) + U^{j} (h (z (t + t_{p}), v (t + t_{p})) - {\bar{u}}^{j}) = y (t)

(18)

Thus,

y (t)

is periodic of period

t_{p}

and the manipulator is cyclic on

N^{j}

. This shows that, with the differentiable manifold formulation. the manipulator is locally cyclic. For more detail regarding cyclicity, see [22].

The role of the function

h^{j} (z, v)

is important in assuring satisfaction of Eq. (1). This is in contrast with the generalized inverse velocity approach presented in Section 2, in which Eq. (1) is ignored. A computationally efficient iterative method for evaluation of

h^{j} (z, v)

is presented in [3,4] and summarized in Section 3.2. In this computation, when the number of iterations required for convergence exceeds a specified tolerance, the associated configuration

x = {[\begin{matrix} y^{T} & z^{T} \end{matrix}]}^{T}

is designated

{\bar{x}}^{j + 1}

, the associated y, v, and u are designated

{\bar{y}}^{j + 1}

{\bar{v}}^{j + 1}

, and

{\bar{u}}^{j + 1}

, a new neighborhood

N^{j + 1}

is entered, and the parameterization is redefined. As shown in [26] for dynamic system simulation, less than 0.1% of CPU time and no user interaction is required for this reparameterization. For more detail on the process of selecting configurations

{\bar{x}}^{j}

and reparameterization calculations, see [3,4,26].

For a given output

z

, with

v \in R^{n - m}

arbitrary in a neighborhood of v =

{\bar{v}}^{j}

, Eq. (17) defines a set of input coordinates,

SMM (z) = {y = {\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (h^{j} (z, v) - {\bar{u}}^{j}) : v in a neighborhood of {\bar{v}}^{j}}

(19)

called the manipulator self-motion manifold in input space associated with output

z

. Since

h^{j} (z, v)

is the solution of Eq. (15),

G ({\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (h^{j} (z, v) - {\bar{u}}^{j})) - z

= 0, for all v in a neighborhood of v =

{\bar{v}}^{j}

y (z, v)

of Eq. (17) maps into

z

; i.e.,

z = G (y (z, v))

. Components of the vector

v \in R^{n - m}

are called self-motion coordinates. With arbitrary self-motion coordinates v in a neighborhood of

{\bar{v}}^{j}

, Eq. (17) defines

n - m

redundant degrees of freedom

v \in R^{n - m}

of the manipulator that enable it to meet requirements that could not be met with a nonredundant manipulator. The restriction of v to a neighborhood of

{\bar{v}}^{j}

in the foregoing is to meet hypotheses of the implicit function theorem. As will be shown in Section 3.5 and 4.2, Eqs. (17) and (19) may hold for large v in applications.

It is important to note that the self-motion manifold of Eq. (19) is defined at the configuration level. Since configuration information is not defined in the generalized inverse velocity formulation, the self-motion manifold and self-motion coordinates cannot be explicitly defined and are not available for obstacle avoidance and other performance optimization functions in the velocity-based formulation.

3.2. Numerical Evaluation of h(z,v)

Substituting y of Eq. (14) into Eq. (1) yields

K (v, u, z) \equiv G (\bar{y} + V (v - \bar{v}) - U (u - \bar{u})) - z = 0

(20)

Newton-Raphson iteration in numerical solution of Eq. (20) for u, with given values of z and v, is [24]

\begin{array}{l} K_{u} (v, u^{i}, z) Δ u^{i} = - G^{'} (y^{i}) U Δ u^{i} = - K (v, u^{i}, z) \\ u^{i + 1} = u^{i} + Δ u^{i} \end{array}

(21)

where

y^{i} = \bar{y} + V (v - \bar{v}) - U (u^{i} - \bar{u})

. Following convergence, u is the numerical evaluation of

u = h (z, v)

As analysis progresses along a trajectory in configuration space, if the matrix

G^{'} (y^{i}) U

in Eq. (21) becomes ill conditioned [24]; i.e., near singular, new values of

\bar{y}, \bar{z}, \bar{v}, and \bar{u}

must be defined in a new neighborhood

N^{j}

. This defines a reparameterization of the manipulator model and enables continuation of the trajectory in configuration space.

3.3. Operational Space Differentiable Manifold

Defining manipulator operational coordinates

w = {[\begin{matrix} z^{T} & v^{T} \end{matrix}]}^{T} \in R^{n}

and manipulator functional coordinates

s = {[\begin{matrix} y^{T} & w^{T} \end{matrix}]}^{T} \in R^{2 n}

, the manipulator regular configuration space is

\tilde{S} = \underset{N^{j}}{\cup} {s \in R^{2 n} : {\bar{x}}^{j} = {[\begin{matrix} {\bar{y}}^{j T} & {\bar{z}}^{j T} \end{matrix}]}^{T} \in \tilde{X}, y = {\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (h^{j} (z, v) - {\bar{u}}^{j})}

(22)

Similar to the definition of the manipulator configuration space of Eq. (2) as the product of input and output spaces, the serial manipulator regular configuration space is defined as the product of input and operational spaces. This is important in establishing

\tilde{S}

as a differentiable manifold.

From Eq. (17),

v = {\bar{v}}^{j} + V^{j T} (y - {\bar{y}}^{j})

, and the forward kinematic mapping of Eq. (1) defines a parameterization of

\tilde{S}

s = {\bar{ψ}}^{j} (y) = {[\begin{matrix} y^{T} & G^{T} (y) & {\bar{v}}^{j T} + {(y - {\bar{y}}^{j})}^{T} V^{j T} \end{matrix}]}^{T} \in \tilde{S}

, for arbitrary y in a neighborhood of

{\bar{y}}^{j}

, and its inverse is

{\bar{ϕ}}^{j} (s) = y

. Thus,

\tilde{S}

is a differentiable manifold [2] that is parameterized by input coordinates y. Conversely, the inverse kinematic mapping of Eq. (17) enables the parameterization,

s = ψ^{j} (w) = {[\begin{matrix} {({\bar{y}}^{j} + V^{j} (v - {\bar{v}}^{j}) - U^{j} (h^{j} (z, v) - {\bar{u}}^{j})}^{T} & z^{T} & v^{T} \end{matrix}]}^{T}

\tilde{S}

N^{j}

and its inverse is

ϕ^{j} (s) = w

. The set

N^{j}

and mapping

ψ^{j} (w)

comprise a chart [2], denoted (

N^{j}

ψ^{j} (w)

). Thus,

\tilde{S}

may also be parameterized by operational coordinates w. This duality of input and operational space coordinates provides the foundation for analytical and numerical representation of redundant serial manipulator kinematics and dynamics [4]. Because of its importance in manipulator operational space kinematics and dynamics [9,10],

\tilde{S}

is called the operational space differentiable manifold.

A family of charts (

N^{j}

ψ^{j} (w)

), called an atlas, is defined to cover

\tilde{S}

, such that the mappings

ψ^{j}

are compatible and

\tilde{S}

is a differentiable manifold that is parameterized by w [2]. The operational space differentiable manifold for a redundant manipulator can thus be parameterized by either y or w. It cannot, however, be parameterized by only output z. Kinematics on

\tilde{S}

must be carried out on individual charts

(N^{j}, ψ^{j} (w))

and transitioned to adjacent charts as manipulator configurations progress along a trajectory in

\tilde{S}

, as shown schematically in Figure 5. As explained in Section 3.2, piecewise analysis on charts is unavoidable since, in general, there is no globally valid operational coordinate parameterization

ψ (w)

\tilde{S}

. This attribute of differential geometry that transforms local to global properties of sets and mappings is one of its greatest contributions. The unavoidable reality, however, is that one must adopt local operational space parameterizations, since no global parameterization generally exists.

3.4. Differentiable Manifold-Based Output Trajectory Tracking and Obstacle Avoidance Algorithm

An output trajectory tracking and obstacle avoidance algorithm based on the inverse mapping of Eq. (17) is presented carry out kinematic control more rigorously and efficiently than the generalized inverse velocity-based method of Section 2.2. In [3], the inverse mapping was employed to avoid collisions in redundant manipulators using an algorithm that marched along 1-dimensional self-motion manifolds. The basic idea of that algorithm is explained, assuming that the degree of redundancy is 1. First, set a nominal trajectory

y_{n} (t)

for the inputs

y

that yields the desired output trajectory

z_{d} (t)

, without exploiting kinematic redundancy. When the manipulator starts to move, it follows this nominal trajectory until a collision is detected for some value

z *

of the desired output trajectory (i.e., until the intersection of two bodies is not empty). When a collision is detected, the algorithm presented in [3] performs self-motions defined by Eq. (19) that keeps

z = z *

; i.e., the self-motion coordinate

v

is varied on a grid with a given step

Δ v

along one direction (or the opposite) of the self-motion manifold until the interference disappears. Note that this algorithm is feasible only when the self-motion manifold is 1-dimensional, because one only needs to march along self-motion curves, exhaustively searching until a collision-free configuration is found.

In manipulators with higher degrees of redundancy, such as the manipulator of Section 1.1.1, the obstacle avoidance algorithm used in [3] is not feasible, because one would need to perform an exhaustive grid search in the higher-dimensional space of self-motion coordinates

v

, which would be computationally prohibitive (e.g., a 4-dimensional grid for the manipulator of Section 1.1.1). The new algorithm employed herein efficiently treats obstacle avoidance using the inverse mapping of Eq. (17) for higher degrees of redundancy, as the examples that follow demonstrate.

The new algorithm is based on the fact that, in the vicinity of a contact between two bodies, it is possible to define a gap function

g

[27,28] that is the signed distance between the closest points of the two bodies along their common normal. This works even when one of the bodies has a nonsmooth shape and does not have a unique normal at the point of contact [27,28]. Figure 6 illustrates this gap function

g

. Note that

g

is a signed distance, which is positive when the bodies do not intersect, zero when their boundaries touch, and negative when one body has penetrated the other. The gap function

g

depends on the relative pose of the contacting bodies, which is defined by input coordinates; i.e.,

g = g (y)

. Using the inverse mapping of Eq. (17), one can write the gap function in terms of the operational coordinates, i.e.,

g = g (y (z, v))

Taking the foregoing into account, the new algorithm is as follows:

Initialize $t = t_{0}$ and select a time step $Δ t$ . The desired output trajectory is $z_{d} (t)$ for $t_{0} < t < t_{1}$ . The initial configuration $y_{0}$ yields the initial desired $z$ ; i.e., $G (y_{0}) = z_{d} (t_{0})$ . Construct the inverse mapping of Eq. (17) in a neighborhood of $\bar{y} = y_{0}$ ; i.e., compute $U$ and V and initialize $v$ = 0 and u = 0. Throughout execution of the algorithm, the self-motion vector v is updated only when necessary to avoid obstacles. If other secondary goals are to be met, the self-motion vector v can be used to optimize these secondary goals. In the present algorithm, the focus is on use of redundancy only for obstacle avoidance.
Set $z = z_{d} (t)$ , solve for $u = h (z, v)$ as in Section 3.2, and evaluate $y = y (v, u)$ of Eq. (17). Whenever necessary, perform a reparameterization; i.e., a transition between charts illustrated in Figure 5, as outlined in Section 3.3.
For the computed configuration $y$ , check if interferences occur; i.e., if any link of the manipulator intersects an obstacle. If no intersections occur, continue with step 4. Otherwise, go to step 5.
Send the collision-free configuration $y$ to the controller of the manipulator and proceed to the next time step; i.e., update $t = t + Δ t$ . If $t \leq t_{1}$ , return to step 2. Otherwise, the desired trajectory has been completed and the algorithm ends.
If the algorithm has reached this step, there exists mechanical interference between the manipulator and at least one obstacle for the current value of $y = y *$ , which is obtained from $z = z *$ and $v = v *$ . Assume that $c > 0$ contacts have occurred between links of the manipulator and obstacles. In that case, contacts define gap functions $g_{i} (z, v)$ , $i = 1, ..., c$ , which will be negative because obstacles are penetrated. The objective is to find a value of v that renders the gap functions non-negative. This can be formulated as the following nonlinear system:

\begin{array}{l} g_{1} (z, v) = k_{1}^{2} \\ ... \\ g_{c} (z, v) = k_{c}^{2} \end{array}

(23)

where

k = {[k_{1}, ..., k_{c}]}^{T}

is a vector of auxiliary variables that are introduced to transform the desired inequalities

g_{i} (z, v) \geq 0

into equivalent equalities

g_{i} (z, v) = k_{i}^{2}

. Next, Eqs. (23) are solved for

r = {[v^{T}, k^{T}]}^{T}

, using the Newton-Raphson (N-R) method [24], where the starting values of v and k for N-R iteration are v = v* (i.e., the value that produced the interference that led to this step of the algorithm) and k = 0. Note that, since Eqs. (23) are c equations in (c + n - m) unknowns, they comprise an underdetermined system. Therefore, when inverting the Jacobian used in the N-R method, the minimum-norm Moore-Penrose pseudoinverse is used, which updates the unknowns r with the vector Δr of minimum norm. The N-R method used to solve Eq. (23) is as follows:

define

\tilde{g} (r) = {[g_{1} (z, v) - k_{1}^{2}, ..., g_{c} (z, v) - k_{c}^{2}]}^{T}

define

\tilde{g}' (r)

as the

c \times (c + n - m)

Jacobian of

\tilde{g} (r)

with respect to r.

set

r = {[{(v *)}^{T}, 0]}^{T}

set iterations = 0

\begin{array}{l} Δ r = - \tilde{g}'^{†} (r) \tilde{g} (r) \\ r = r + Δ r \\ iterations = iterations + 1 \end{array}

(24)

while

‖ \tilde{g} (r) ‖ > ε

AND iterations < max_iterations

Since the increment Δr with minimum norm is used in Eq. (24) to update the unknowns, this favors continuity of the configuration of the manipulator. In fact, as the following examples will demonstrate, the algorithm generates continuous trajectories for the manipulator, and execution of step 5 (whose objective is to find a new value of self-motion coordinates v that avoids collisions) takes only a few milliseconds on a modern computer. The N-R method stops when a solution

r = {[v^{T}, k^{T}]}^{T}

that satisfies Eq. (23) is found, or when a maximum of max_iterations is exceeded. In the first case, the algorithm yields a configuration y that is collision-free, and the algorithm jumps to step 4. In the second case, the desired trajectory

z_{d} (t)

can be considered as infeasible, because no configuration (sufficiently near to the configuration at the previous time step) can be found to continue executing the trajectory while avoiding obstacles, and the algorithm ends.

3.5. Four Degree of Redundancy Differentiable Manifold-Based Example

In this section, the algorithm of Section 3.4 is used to solve the problem treated in Section 2.3, where the manipulator with 4 degrees of redundancy must track the periodic trajectory given in Eq. (12). The manipulator starts at the same configuration

y_{0}

as in Section 2.3. The same time step

Δ t = 0.01

seconds is used but, unlike in the generalized inverse method, no numerical integration is required in the algorithm of Section 3.4, where the time step is used only to progress in time according to step 4 of the algorithm.

The algorithm described in Section 3.4 was run with the following parameters:

Iterations in (21) stop when $‖ Δ u ‖ < 0.0001$ .
Iterations in (24) stop when $‖ \tilde{g} (r) ‖ < 0.001$ or

when iterations > 10 = max_iterations

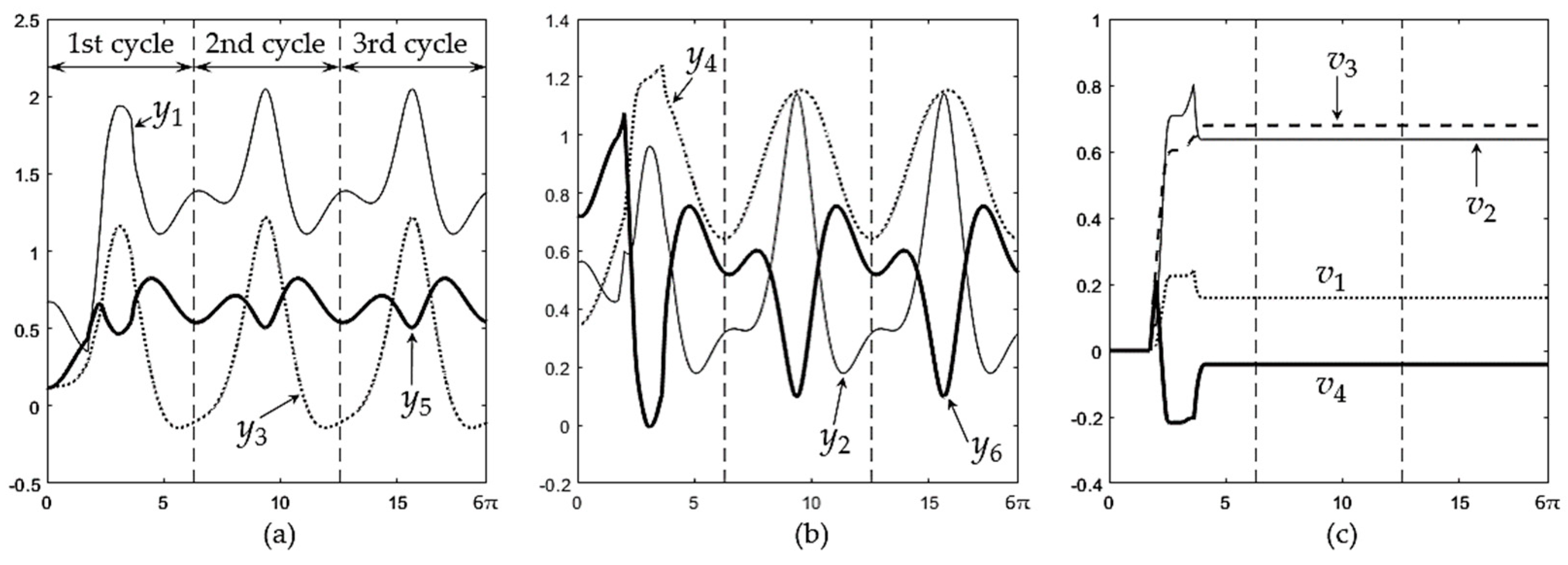
With these parameters, the algorithm generates the time histories of y(t) and v(t) shown in Figure 7. As this figure shows, the time history of these variables is periodic after the first cycle. In particular, v is constant after the first cycle. It can be seen in Figure 7 that the trajectory of y(t) becomes cyclic when v becomes constant, even before the output trajectory of Eq. (12) has completed its first cycle.

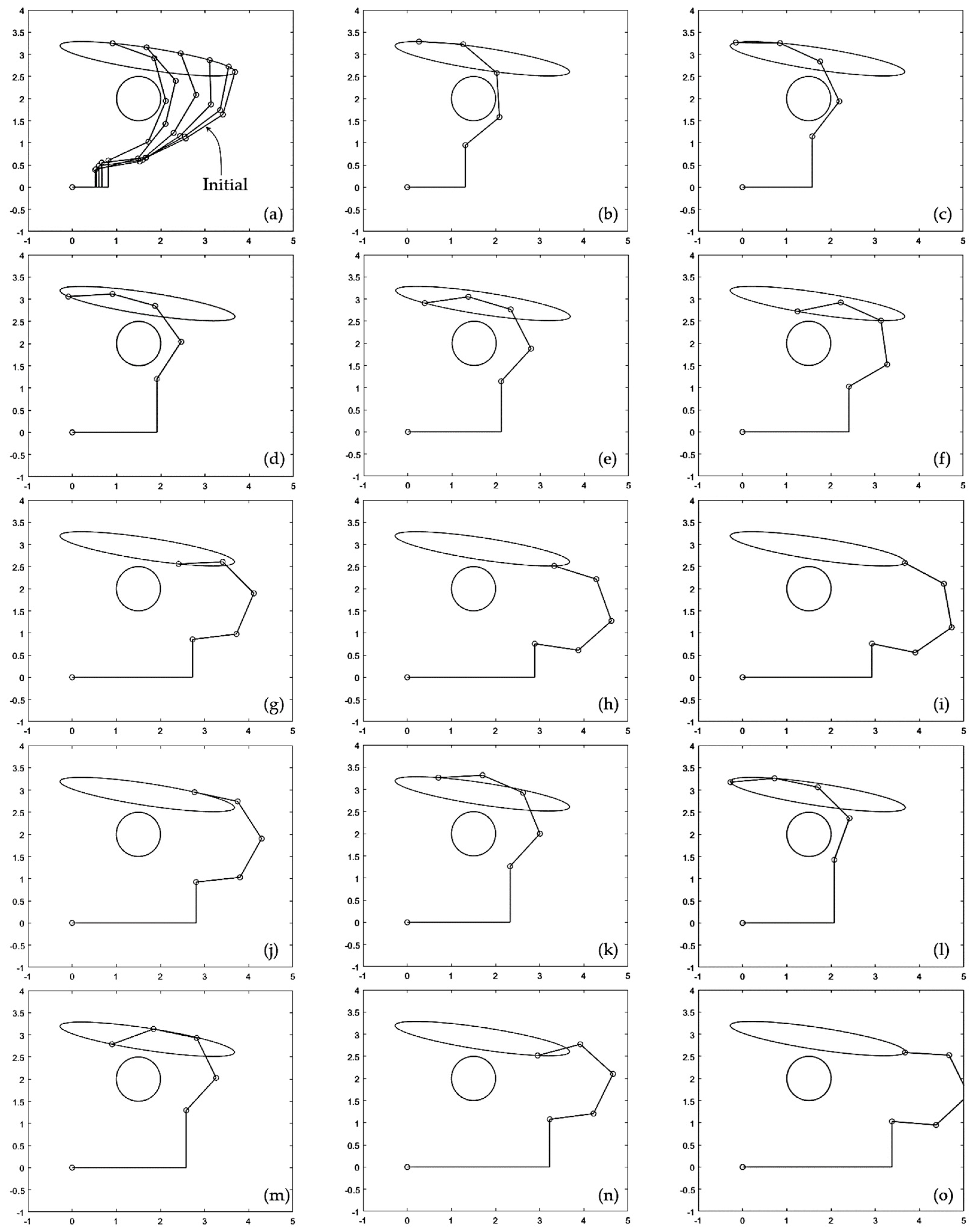
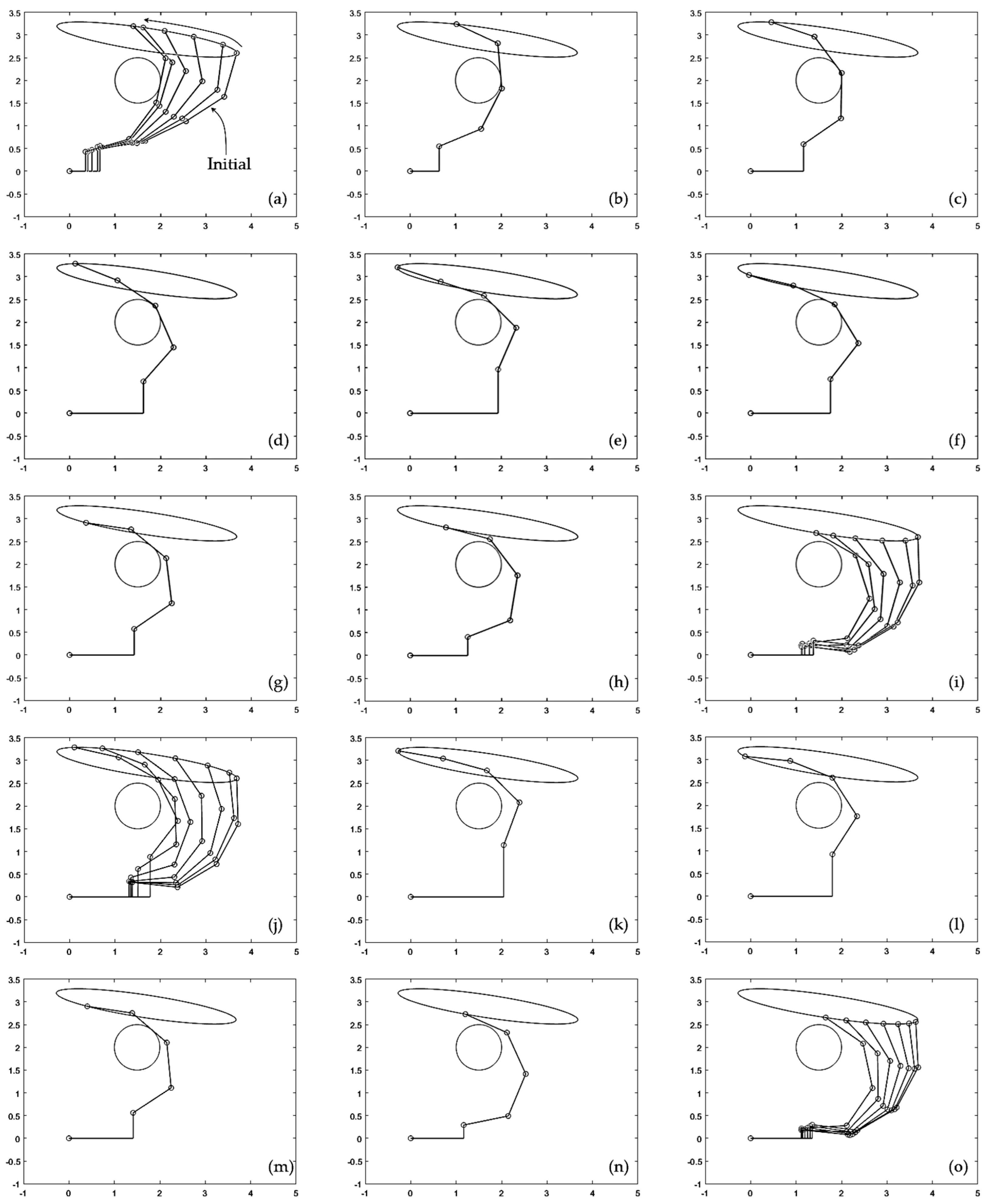
Snapshots of the manipulator executing this trajectory are shown in Figure 8 . Figure 8.a-i show execution of the first cycle. In Figure 8.a, the manipulator moves with v = 0 as it approaches the obstacle, until touching it. Then, the algorithm of Section 3.4 starts to actively update v(t) to avoid penetration of the obstacle. Figure 8.b-g show how the manipulator continues tracking the desired eliptical trajectory, while some of its links touch the obstacle, until contact is lost in Figure 8.h and v is no longer updated. After this, the manipulator continues executing the trajectory far from the obstacle until it completes the first cycle, as shown in Figure 8.i.

Execution of the second cycle begins with the manipulator approaching the obstacle, as illustrated in Figure 8.j. As shown in Figure 8.k-n, during the second cycle the manipulator is not in contact with the obstacle except during a very short period of time shown in Figure 8.m, in which one of the links becomes tangent to the obstacle. This contact period is very short, as can be better observed in the supplementary animation S2 attached to the paper. After this short contact is lost (Figure 8.n), the manipulator continues moving far from the obstacle until completing the second cycle (Figure 8.o). The third and subsequent cycles are identical to the second cycle described here, as shown in Figure 7.

As Figure 7 and Figure 8 show, during the first cycle of the desired trajectory given by Eq. (12), the algorithm described in Section 3.4 actively updates v(t) to prevent penetration of the obstacle during contact. After contact is lost, v(t) does not need to be further updated and the input trajectory becomes cyclic, by virtue of Eq. (18). Interestingly, the constant value that v(t) adopts after contact is lost in the first cycle allows the manipulator to continue repeating subsequent cycles during which contact without penetration occurs only during a very short fraction of the cycle, as illustrated in Figure 8.m.

The average time required to run step 5 of the algorithm is 1.2 miliseconds (time measured on the following CPU running Maltab R2022b: Intel Core i7-8750H at 2.20 GHz). This is the time required to find a new value of self-motion coordinates

v

that avoids penetration of obstacles every time that such penetration is detected, which demonstrates a rapid correction of the trajectory to avoid obstacles, compatible with real time requirements.

As shown in Figure 8, to prevent obstacle penetration, the algorithm of Section 3.4 keeps the links in contact with the obstacle and moving smoothly around it until contact is lost, as required by the trajectory of the end-effector. If it were necessary to avoid the obstacle without contacting it, leaving some safety distance

d_{s}

, then one would only need to change the gap functions in Eq. (23) to

g_{i} (z, v) - d_{s} = k_{i}^{2}

, making it easier to accurately regulate distance to obstacles than with the generalized inverse velocity-based approach illustrated in Section 2.3.

4. A Twenty Degree of Redundancy Output Trajectory Tracking and Obstacle Avoidance Example

4.1. A Twenty Degree of Redundancy Manipulator

Consider a highly redundant variant of the manipulator of Figure 1 that is shown in Figure 9. Instead of having four rotating links with relative angles

y_{3}

…

y_{6}

, it has 21 rotating links with relative angles

y_{3}

…

y_{23}

, where all links have unit length.

The initial configuration of the manipulator is shown in Figure 10.a, given by input angles

y_{0} = {[\begin{array}{l} 0 . 7727 0 . 1546 0 . 1040 0 . 4934 0 . 9715 0 . 3697 0 . 6284 ... \\ ... 0 . 2710 0 . 7981 0 . 2884 0 . 5227 0 . 6964 0 . 8729 0 . 9409 ... \\ ... 0 . 5358 0 . 1209 0 . 1221 0 . 2128 0 . 7854 0 . 2131 0 . 7936 0 . 2532 0 . 9685 \end{array}]}^{T}

(25)

This manipulator has n = 23 degrees of freedom. Outputs of the manipulator are the position coordinates of the outboard end of the last link and its orientation; i.e.,

z = G (y) = [\begin{matrix} y_{1} + \sum_{i = 3}^{23} \cos (\sum_{j = 3}^{i} y_{j}) \\ y_{2} + \sum_{i = 3}^{23} \sin (\sum_{j = 3}^{i} y_{j}) \\ \sum_{i = 3}^{23} y_{i} \end{matrix}]

(26)

Since there are m = 3 outputs, the degree of redundancy is r = n – m = 20, so this can be considered a hyper-redundant manipulator.

The task of this manipulator is to follow the output trajectory

z_{d} (t) = {[- 2.1164 + 2 . 5 (\cos (4 t) - 1), 4.0455 + \sin (3 t), - 1 . 6035 rad]}^{T}

(27)

which means that the outboad endpoint of the manipulator must describe the desired path given by the first two coordinates of Eq. (27) and the last link maintains a constant orientation given by the last coordinate of Eq. (27). The desired path is represented in each of the frames in Figure 10. The desired trajectory must be achieved from t = 0 to t = 1.2, while the manipulator avoids three circular obstacles that are represented in Figure 10. Two obstacles are stationary, labeled O1 and O2 in Figure 10.a, where O1 is a circle centered at (0, 2) with unit radius and O2 is another circle of unit radius centered at (-2, 7). Note that, initially, the manipulator wraps around obstacle O1. There is a third circular obstacle labeled Om in Figure 10.a with radius 0.75 that is mobile. Its center starts at (-4, 2) and translates with constant speed until reaching the point (-3, 5.5) at t = 1, remaining static at that point for t > 1.

4.2. Differentiable Manifold-Based Output Tracking and Obstacle Avoidance

The path planning obstacle avoidance problem is first treated using the differentiable manifold algorithm of Section 3.4 with a time step of

Δ t = 0.001 seconds

, which results in the sequence of postures shown in Figure 10 (a supplementary video S3 is attached that illustrates the continuous motion). As demonstrated by Figure 10, the algorithm is able to resolve redundancy and obtain a feasible motion that tracks the desired output trajectory of Eq. (27), while avoiding all obstacles at all times. First the manipulator contacts obstacle O1 (Figure 10.b), and then it contacts obstacle O2 (Figure 10.c-d), to lose contact later (Figure 10.e-h). In Figure 10.i the manipulator contacts the mobile obstacle Om and subsequently accomodates its configuration continuously to avoid penetrating this mobile obstacle as it approaches stationary obstacle O2 (Figure 10.i-l). Then a difficult situation occurs, as shown in Figure 10.m, when the mobile obstacle Om stops close to obstacle O2, after which Om and O2 create a narrow corridor in which the manipulator must maneuver (see the magnified view of the corridor in the inset of Figure 10.m). The differentiabe manifold algorithm of Section 3.4 is able to handle this situation seamlessly. It is able to complete the desired trajectory, as demonstrated in Figure 10.m-o.

4.3. Generalized Inverse Velocity-Based Output Tracking and Obstacle Avoidance

The same problem is attempted using the generalized inverse velocity method, numerically integrating Eq. (9) with the term of Eq. (10) to avoid obstacles. For this method, it is necessary to select two parameters, the time step

Δ t

used to numerically integrate Eq. (9) (using again the fourth-order Runge-Kutta method) and the coefficient k used in Eq. (10) to tune the rate of minimization of the cost function that penalizes proximity to obstacles. For a less complex example such as the one studied in Section 2.3, these two parameters were successfully set. However, for this more complex example with three obstacles (one of them mobile) and, more importantly, a narrow corridor such as the one shown in Figure 10.m, the choice of parameters becomes critical. A smaller time step

Δ t

allows accurate numerical integration and smooth motions, but the simulation takes more CPU time to complete the full trajectory (or, in case the method is used to update the configuration in a real-time controller, it requires a more demanding controller that is able to operate at smaller sample times

Δ t

). A smaller k performs the minimization of the cost function more slowly, which yields smoother motions that come closer to obstacles. However, a small value of k requires using a very small time step

Δ t

to enable the algorithm to avoid obstacles.

Table 2 shows 16 combinations of (k,

Δ t

) and the result of obstacle avoidance for each combination. The result of each combination is represented by a grade F, D, or C, with the following meaning:

Grade F means that the simulation fails when the first obstacles (O1 or O2) are contacted, long before the narrow corridor indicated in Figure 10.m is formed. The failure consists in the manipulator suffering a discontinuity in its configuration upon contact.
Grade D means that the simulation fails when the manipulator is trapped by the narrow corridor. The failure consists in the manipulator suffering a discontinuity in its configuration when the corridor is formed, without penetrating obstacles.
Grade C means that, when the narrow corridor is formed, the manipulator starts to penetrate obstacles but suffers discontinuous jumps in its configuration.

The lower-right case of Table 2 (k = 0.0001 and

Δ t = 0.00001

) is illustrated in Figure 11. This case has been chosen for illustration because, despite not being fully successful (in fact, no case of Table 2 is fully successful), it exhibits the most similar behavior to Figure 10. It should be noted that the result of Figure 11 required a very slow simulation, due to the small time step of 0.00001 seconds, in contrast to the simulation of Figure 10 that worked well with a time step of 0.001 seconds. As Figure 11 shows, the generalized inverse velocity-based method yields a solution that is not very different from the one shown in Figure 10 during the beginning of the trajectory. The links contact obstacles and wrap around them as the manipulator progresses, including the mobile obstacle Om. The problem occurs when the mobile obstacle forms the narrow corridor with static obstacle O2. In that case, as Figure 11.m shows, the manipulator starts to penetrate obstacles. It also suffers discontinuities in its configuration (such discontinuities occur between Figure 11.l and 11.m, but they can be better observed in supplementary video S4 attached). In any case, the trajectory becomes infeasible. In fact, according to Table 2, no valid combination of (k,

Δ t

) was found that accomplishes this trajectory while avoiding obstacles with the generalized inverse velocity method. In contrast, the differentiable manifold method of Section 3.4 was able to easily solve this problem, as demonstrated in Figure 10.

5. Discussion

Kinematic control of redundant manipulators has traditionally been conducted at the velocity level, where a pseudo-inverse is used with the velocity equation of Eq. (6) to obtain joint velocities

\dot{y}

of Eq. (9) in terms of the task (or output) velocities

\dot{z}

. Joint trajectories are then determined by numerical integration of

\dot{y}

. Obstacle avoidance is traditionally treated by considering it as a secondary task and performing self-motions that approximately minimize a cost function of Eq. (11) that penalizes proximity to obstacles. As shown in Section 2.3, this approach leads to difficult-to-predict behavior, due to nonholonomy, as the manipulator performs quite different postures between cycles of specified output trajectories for four degree of redundancy manipulators, despite fine tuning the parameters of the method (e.g., the rate of minimization of the cost function) to avoid obstacles during the first cycle. As shown in Section 4.3, regardless of the values of tunable parameters, such an approach encounters insurmountable difficulties for a twenty degree of redundancy manipulator in complicated situations such as narrow corridors between obstacles, leading to infeasible trajectories that exhibit discontinuities or penetration of obstacles. These examples show that theoretical deficiencies of the generalized inverse velocity-based redundancy resolution method identified in [4] lead to severe problems in applications.

An operational configuration space differentiable manifold formulation is presented for kinematic control of redundant manipulators during obstacle avoidance. In contrast with traditional velocity-based approaches, the differentiable manifold formulation resolves kinematic redundancy at the position level, constructing an inverse mapping that parameterizes input coordinates

y

as local functions of output coordinates

z

and self-motion coordinates

v

. This mapping is holonomic and cyclic and can be used to generate global obstacle-free motion plans, as described in Section 3.4. The algorithm presented defines a gap function

g

in the vicinity of every collision, which is a function of self-motion coordinates

v

. The algorithm actively adjusts self-motion coordinates

v

to avoid penetration of obstacles, keeping

g

nonnegative by solving an under constrained system of nonlinear equations. The example of Section 3.5 demonstrates the cyclicity and real-time capability of the algorithm. The example of Section 4.2 demonstrates its ability to treat very restrictive obstacle situations, negotiating a narrow corridor while completing the desired task for a highly redundant manipulator.

Although this paper has focused on redundant serial manipulators, the differentiable manifold formulation has been extended to nonserial redundant manipulators in [3], which makes it possible to extend the algorithm presented to nonserial manipulators. Future applications of the proposed formulation will not only consider control at kinematics level but also control at the dynamics level [4], where accurate holonomic control of obstacle avoidance can be exploited for controlling contact forces between links and obstacles.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Video S1: figure 4.mp4 (video of Figure 4); Video S2: figure 8.mp4 (video of Figure 8); Video S3: figure 10.mp4 (video of Figure 10); Video S4: figure 11.mp4 (video of Figure 11).

Author Contributions

Conceptualization, E. H.; methodology, E. H. and A. P.; software, A. P.; validation, E. H. and A. P.; data curation, A. P.; writing—original draft preparation, E. H.; writing, review and editing, E. H. and A. P.; visualization, A. P. Both authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

Pars, L. A., A Treatise on Analytical Dynamics, 1965, Reprint by Ox Bow Press (1979), Woodbridge, Conn.
Robbin, J. W., and Salamon, D. A., Introduction to Differential Geometry, 2022, Springer, Berlin.
Haug, E.J.; Peidro, A. Redundant Manipulator Kinematics and Dynamics on Differentiable Manifolds. J. Comput. Nonlinear Dyn. 2022, 17, 111008. [Google Scholar] [CrossRef]
Redundant Serial Manipulator Inverse Position Kinematics and Dynamics. J. Mech. Robot. 2023, 16, 1–11. [CrossRef]
Haack, W., and Wendland, W., Lectures on Partial and Pfaffian Differential Equations, 1972, Pergamon Press, Oxford.
Kinematic control of redundant robot manipulators: A tutorial. J. Intell. Robot. Syst. 1990, 3, 201–212. [CrossRef]
Chiaverini, S., Oriolo, G., and Maciejewski, A. A., Redundant Robots, Siciliano and Khatib eds, Springer Handbook of Robotics, 2nd ed, 2016, Springer-Verlag Berlin.
Whitney, D.E. Resolved Motion Rate Control of Manipulators and Human Prostheses. IEEE Transactions on Man-Machine Systems, 1969; 10, 47–53. [Google Scholar] [CrossRef]
Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE J. Robot. Autom. 1987, 3, 43–53. [Google Scholar] [CrossRef]
Khatib, O.,The Operational Space Framework, JSME International Journal, Series C. 1993, 36, 3, 277-287. [CrossRef]
Zergeroglu, E.; Dawson, D.; Walker, I.; Behal, A. Nonlinear tracking control of kinematically redundant robot manipulators. In Proceedings of the 2000 American Control Conference (ACC 2000), Chicago, IL, USA, 28-30 June 2000. [Google Scholar]
Cefalo, M.; Oriolo, G. A general framework for task-constrained motion planning with moving obstacles. Robotica 2018, 37, 575–598. [Google Scholar] [CrossRef]
Kazemipour, A.; Khatib, M.; Khudin, K. A.; Caz, C.; De Luca, A. Kinematic Control of Redundant Robots with Online Handling of Variable Generalized Hard Constraints. IEEE Robotics and Automation Letters 2022, 7, 9279–9286. [Google Scholar] [CrossRef]
Rocco, P., and Zanchettin, A. M., General Parametrization of Holonomic Inversion Algorithms for Redundant Manipulators, IEEE Int. Conf. on Robotics and Automation, May 3-8, 2010, Anchorage, Alaska, 3721-3726.
Simas, H.; Di Gregorio, R. A Technique Based on Adaptive Extended Jacobians for Improving the Robustness of the Inverse Numerical Kinematics of Redundant Robots. Journal of Mechanisms and Robotics 2010, 11, 020913. [Google Scholar] [CrossRef]
Albu-Scheffer, A.; Sachtler, A. Redundancy Resolution at Position Level. IEEE Transactions on Robotics 2023. Early Access. [Google Scholar] [CrossRef]
Klein, C.A.; Huang, C.-H. Review of pseudoinverse control for use with kinematically redundant manipulators. IEEE Trans. Syst. Man, Cybern. 1983, 13, 245–250. [Google Scholar] [CrossRef]
Zanchettin, A.M.; Rocco, P.; Ferretti, G. Numerical Issues in Integrating Holonomic Kinematic Inversion Algorithms for Redundant Manipulators. In Proceedings of the 8th IFAC Symposium on Nonlinear Control Systems, Bologna, Italy, 1–3 September 2010; pp. 999–1004. [Google Scholar]
De Luca, A.; Oriolo, G. Nonholonomic behavior in redundant robots under kinematic control. IEEE Trans. Robot. Autom. 1997, 13, 776–782. [Google Scholar] [CrossRef]
Shamir, T.; Yomdin, Y. Repeatability of redundant manipulators: mathematical solution of the problem. IEEE Trans. Autom. Control. 1988, 33, 1004–1009. [Google Scholar] [CrossRef]
Mussa-Ivaldi, F.A.; Hogan, N. Integrable Solutions of Kinematic Redundancy via Impedance Control. Int. J. Robot. Res. 1991, 10, 481–491. [Google Scholar] [CrossRef]
Haug, E.J. A Cyclic Differentiable Manifold Representation of Redundant Manipulator Kinematics. J. Mech. Robot. 2023, 16, 1–9. [Google Scholar] [CrossRef]
Yao, Y.; Zhao, J.; Huang, B. Motion planning algorithms of redundant manipulators based on self-motion manifolds. Chinese Journal of Mechanical Engineering 2010, 1, 80–87. [Google Scholar] [CrossRef]
Atkinson, K. E., An Introduction to Numerical Analysis, 1989, Second Ed., Wiley, New York.
Corwin, L. J. and Szczarba, R. H., Multivariable Calculus, 1982, Marcel Dekker, New York.
Haug, E. J., Computer-Aided Kinematics and Dynamics of Mechanical Systems, Volume II: Modern Methods, Third Ed., 2022, ResearchGate, www.researchgate.net.
Brogliato, B., Nonsmooth mechanics - Models, Dynamics and Control, 2016, Third Ed., Springer Cham, Springer International Publishing Switzerland.
Peidró, A.; Pérez-Navarro, P.D.; Puerto, R.; Payá, L.; Reinoso, O. Locking underactuated robots by shrinking their manifolds of free-swinging motion. Mech. Mach. Theory 2023, 188, 105403. [Google Scholar] [CrossRef]

Figure 1. Serial Manipulator with Degree of Redundancy 4.

Figure 2. Comparison of the postures adopted by the manipulator when integrating Eq. (9) using Eq. (10) for different values of k while describing half of the ellipse defined by Eq. (12).

Figure 3. Time evolution of

y_{i} (t)

when tracking the trajectory of Eq. (12) with k = 0.01.

Figure 3. Time evolution of

y_{i} (t)

when tracking the trajectory of Eq. (12) with k = 0.01.

Figure 4. (a-i) Execution of the first cycle of the desired output trajectory given by Eq. (12), for k = 0.01. (j-o) Execution of the second cycle. A supplementary video is attached, which shows this figure in motion, including a third cycle that is different from the previous two cycles.

Figure 5. Trajectory Along Charts in

\tilde{S}

Figure 5. Trajectory Along Charts in

\tilde{S}

Figure 6. Definition of Gap Function

g

Figure 6. Definition of Gap Function

g

Figure 7. Time history of y(t) and v(t) (which become cyclic after the first cycle) when the end-effector follows Eq. (12) while avoiding an obstacle using the obstacle avoidance algorithm of Section 3.4.

Figure 8. (a-i) Execution of the first cycle of the desired output trajectory given by Eq. (12). (j-o) Execution of the second cycle. A supplementary video is attached, which shows this figure in motion, including a third cycle that is identical to the second one.

Figure 9. A Manipulator with r = 20 Degrees of Redundancy.

Figure 10. Successful redundancy resolution in a highly redundant manipulator with obstacle avoidance, using the differentiable manifold algorithm of Section 3.4. A video of this sequence is attached as supplementary material.

Figure 11. Unsuccessful redundancy resolution in a highly redundant manipulator with obstacle avoidance, using the generalized inverse velocity method of Eq. (9). A video of this sequence is attached as supplementary material.

Table 2. Results of the generalized inverse velocity method for different pairs

(k, Δ t)

Table 2. Results of the generalized inverse velocity method for different pairs

(k, Δ t)

k \ $Δ t$ (seconds)	0.01	0.001	0.0001	0.00001 (very slow simulation)
0.1	F	D	D	D
0.01	F	D	D	D
0.001	F	C	D	C
0.0001	F	F	D	C

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Obstacle Avoidance in Operational Configuration Space Kinematic Control of Redundant Serial Manipulators

Abstract

1. Introduction

1.1. Basics of Redundant Serial Manipulator Kinematics

A Four Degree of Redundancy Manipulator

1.2. Generalized Inverse Velocity-Based Redundancy Resolution

1.3. Manipulator Trajectory Planning and Obstacle Avoidance

2. Generalized Inverse Velocity-Based Kinematic Control and Obstacle Avoidance

2.1. Problems with Generalized Inverse Velocity Redundancy Resolution

2.2. Generalized Inverse Velocity-Based Kinematic Control and Obstacle Avoidance

2.3. Four Degreee of Redundancy Generalized Inverse Velocity-Based Example

3. Operational Configuration Space Kinematic Control and Obstacle Avoidance

3.1. Inverse Configuration Kinematics

3.2. Numerical Evaluation of h(z,v)

3.3. Operational Space Differentiable Manifold

3.4. Differentiable Manifold-Based Output Trajectory Tracking and Obstacle Avoidance Algorithm

3.5. Four Degree of Redundancy Differentiable Manifold-Based Example

4. A Twenty Degree of Redundancy Output Trajectory Tracking and Obstacle Avoidance Example

4.1. A Twenty Degree of Redundancy Manipulator

4.2. Differentiable Manifold-Based Output Tracking and Obstacle Avoidance

4.3. Generalized Inverse Velocity-Based Output Tracking and Obstacle Avoidance

5. Discussion

Supplementary Materials

Author Contributions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe