Prerpints.org logo
Preprint
Article

Queueing-Inventory Systems with Catastrophes under Various Replenishment Policies

Altmetrics

Downloads

111

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 November 2023

Posted:

15 November 2023

You are already at the latest version

Alerts
Abstract
We discuss two queueing-inventory systems with catastrophes in the warehouse. Catastrophes occur according to Poisson process and upon arrival of a catastrophe all inventory in the system is instantly destroyed. But consumer customers in the system (in the server or in the buffer) continue still waiting for the replenishment of the stock. The arrivals of the consumer customers follow a Markovian Arrival Process (MAP) and they can be queued in an infinite buffer. Service time of a consumer customer follows a phase-type distribution. The system receives negative customers whose have Poisson flows to service facility and upon arrival of a negative customer one consumer customer is pushed out from the system, if any. One of two replenishment policies can be used in the system: either (s,S) or (s,Q). If upon arrival of the consumer customer, the inventory level is zero, then according to the Bernoulli scheme, this customer is either lost (lost sale scheme) or join the queue (backorder sale scheme). The system is formulated by a four-dimensional continuous-time Markov chain. Steady state distribution is obtained using the matrix-geometric method. A comprehensive numerical study is performed on the performance measures under various replenishment policies. Finally, an optimization study is presented.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

Until the early 90s of the last century, in the theory of operations research, models of queuing systems (QS) and models of inventory control systems (ICS) were studied separately. In other words, it was believed that in ICS there is no server for releasing items to consumers (i.e., a self-service rule is used), and in QS, only an idle server is required to service customers (i.e., no additional items are required). However, in real ICSs, the release of items to consumer customers (c-customers) requires the presence of a service station in which the incoming c-customer is processed, and the processing time is often a positive random variable. A classic example of such systems is the widespread systems of gas stations. These ICSs with positive service time can also be considered as QSs, in which in order to service c-customers, in addition to an idle server, a positive level of certain inventory is required.
Note that ICSs with positive service time are called queuing-inventory systems (QIS) in [1,2]. However, QIS models were first proposed earlier in [3,4] and have been intensively studied by various authors over the past three decades. For a detailed overview of known results on QIS models, see [5,6,7].
To classify QISs models, their various properties can be taken as a basis. Based on the type of QIS model being studied, the lifetime of the system’s inventory is taken as the basis for the classification. The vast majority of work on QIS assumes that the system’s inventory never deteriorates. However, in real situations, system inventories often lose their quality over time and after a certain time (deterministic or random) they become unsuitable for use. Such systems are called systems with perishable inventory and have been studied in detail in numerous works, see, for example, [8,9,10,11,12,13,14,15,16]. Note that inventory damage can occur instantly as a result of some accidents, like power outage, equipment failures, staff negligence, etc. A sequence of accidents can be considered as a flow of destructive customers (d-customers).
Note that QIS models with d-customers have been hardly studied, although, as indicated above, they are accurate models of systems in real life. In papers [17,18,19,20], it was assumed that upon arrival of d-customers, the inventory level was instantly reduced only by one. However, there are many realistic QISs in which upon arrival of d-customers all items damage together. Below this type of systems is called QISs with catastrophes in warehouse. It is necessary to distinguish between models of QIS with catastrophes in the warehouse and models of QIS with common lifetime (e.g., foods with the same expiry date, medicines manufactured with the same expiry date and so on), see [21,22,23,24]. In models of QISs with common lifetime, it is assumed that, at any given time, all items in the warehouse have the same age; in other words, it is considered that all items of inventory arrived as a result of execution of one batch of orders. However, in the model of QIS with catastrophes in the warehouse, this assumption is not required.
Note that similar models of QS (but not QIS) with catastrophes are widely investigated in available literature. In lieu of reviewing work related to models of QS with catastrophes, we highlight representative papers [25,26,27,28,29,30,31] and refer readers to their reference lists. In QS a disaster events immediately wipe out the system in that all customers waiting in the queue as well as the ones getting service are removed from the system.
To increase the adequacy of the QIS model under study to real situations, we also take into account the possibility of negative customers (n-customers) arriving to the service station. Negative customer can be interpreted as customer that agitate c-customers in the system so that they do not buy the inventory in that system. In other words, n-customers do not require the inventory, but upon arrival they force one c-customer out of the system, i.e. they can be considered as d-customers in the service station of QIS.
One of the main shortcomings of the known works devoted to QIS is that they analyze models with either backorders or lost sales, i.e. QIS models that simultaneously use both backorders and lost sales are practically not considered. However, in realistic QIS an arrived c-customer either join the queue (backorder) or lost the system without inventory (lost sale) if upon its arrival an inventory level is zero, i.e. hybrid sale rule is frequently used in realistic QISs. Regardless of popularity, models of QISs with hybrid sales are poorly understood due to their complexity.
The model of single-server perishable QIS (without d-customers) with finite waiting room for c-customers under ( s , Q ) , Q = S − s > s + 1 , replenishment policy for the first time was considered in [32]. It was assumed that both types of c-customers and n-customers arrive according to a Markovian arrival process ( M A P ) and the service time of c-customers, lead time and life time of each item have exponential distributions with finite means; a n-customer at an arrival epoch removes random number of waiting c-customers. The joint probability distribution of the number of c-customers in the system and the inventory level is obtained and key performance measures of the system are calculated. Similar double sources model of QIS was considered in a recent paper [33].
The motivation for this study is that models of QIS with warehouse catastrophes under realistic assumptions have been practically unstudied. To our best knowledge, only in recent paper [34] assuming the all kind of customers are arrived according to an independent Poisson processes and all other underlying random variables to be exponentially distributed (Poisson/exponential assumptions), authors study the such kind of models in steady-state under various replenishment policies. This paper is a continuation of the research begun in [34] under more realistic assumptions related to system operation, i.e. here we assume that c-customers arrive according to M A P , c-customers and n-customers arrives according to an independent Poisson processes, the service times to be of phase-type distribution ( P H -distribution), and lead times to be exponentially distributed. Under these assumptions we use matrix-analytic methods to study the QISs models with catastrophes in warehouse in steady-state under two replenishment policies: ( s , S ) and ( s , Q ) policies.
More specifically, the main differences between our model and the model considered in known works are as follows: (i) we consider model of QISs with catastrophes in warehouse; (ii) the model with infinite queue for c-customers is investigated; (iii) service time of c-customers have phase time ( P H ) distribution; (iv) only c-customers represents M A P flow; (v) hybrid sale rule is used, i.e. some customers may join the queue (backorder scheme) or be lost (lose sale scheme) according to the Bernoulli scheme if the inventory level is zero at the time of their arrival.
The paper is organized as follows. In Section 2 the proposed queueing-inventory system is thoroughly described. Section 3 demonstrates the construction of the generator matrices for the underlying processes and provides the steady-state analysis of the systems. That is, Section 3.1 includes matrices and analysis for the model-1 under ( s , S ) -policy, and Section 3.2 includes ones for the model-2 under ( s , Q ) -policy. Expressions for various essential performance measures to assess the both system’s efficiency are formulated in Section 4. Section 5 presents numerical analysis to highlight separately the qualitative behaviour of the queueing-inventory system under each inventory policy; the effect of the system parameters on the performance measures under various arrival process and service time distribution in Section 5.1 and optimization study for the each inventory policy in Section 5.2. Finally, concluding remarks are given in Section 6.
At this point, we define some notation for use in sequel. e is a unit column vector; e j is a unit column vector is of dimension j; e j ( i ) is a unit column vector with 1 in the i t h position and 0 elsewhere; and I k is an identity matrix of order k. The symbols ⊗ and ⊕ represent the Kronecker product and the Kronecker sum, respectively. If A is a matrix of order m × n and if B is a matrix of order p × q , then the Kronecker product of the two matrices is given by A ⊗ B , a matrix of order m p × n q ; the Kronecker sum of two square matrices, say, G of order g and H of h, is given by G ⊕ H = G ⊗ I h + I g ⊗ H , a square matrix of order g h . The transpose notation is denoted by ′.

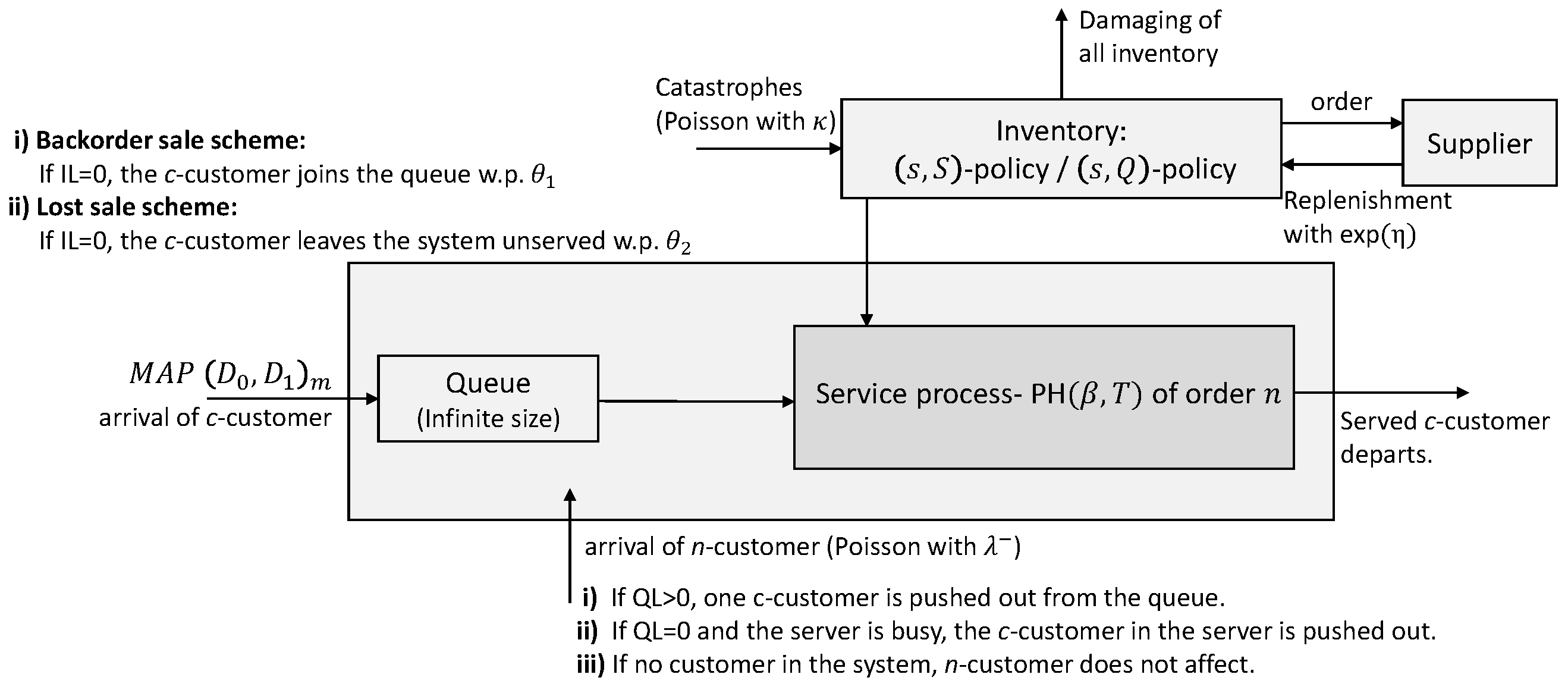
2. Model description

We analyze a queueing-inventory system with negative customers and catastrophes in the warehouse as demonstrated in Figure 1.
  • The c-customers (consumer customers) arrive in the system according to Markovian arrival process ( M A P ) with representation ( D 0 , D 1 ) m . The underlying Markov chain of the M A P is governed by the matrix D ( = D 0 + D 1 ) . Such that, the matrix D 0 denotes the transition rates without arrival while the matrix D 1 denotes the transition rates with arrival. So, the arrival rate of c-customers is given by λ + = δ D 1 e where δ is the stationary probability vector of the generator matrix D and it is satisfied
    δ D = 0 , δ e = 1 .
    For further details on M A P and their usefulness in QIS modelling, the reader may refer to [35,36,37,38,39,40].
  • The service times of the c-customers follow phase-type distribution with representation ( β , T ) n where β is the initial probability vector, β e = 1 , T is an infinitesimal generator matrix holding the transition rates among the n transient states, and T 0 is a column vector contains the absorption rates into state 0 from the transient states. It is clear that T e + T 0 = 0 . The phase-type distribution has the service rate μ = 1 / [ β ( − T ) − 1 e ] .
  • The system also receives n-customers (negative customers) that the arrivals occur according to Poisson process with rate λ − . When a n-customer arrives in the system, there are three possible cases; (i) if there is least one c-customer in the queue ( Q L > 0 ) at the time an n-customer arrives, then only the c-customer is pushed out from the queue (i.e., the servicing of the c-customer in the server continues), (ii) if the queue has no c-customer ( Q L = 0 ) and the server is busy with a c-customer, then the c-customer in the server is forced out of the system. However in this case, the inventory level does not change, since it is assumed that stocks are released after the completion of servicing a c-customer and (iii) the received n-customer does not affect the operation of the system if there are no c-customers in the system (in the queue and in the server).
  • Hybrid sales scheme is used in the system. When a c-customer arrives in the system, if the inventory level is zero ( I L = 0 ) , then the c-customer either joins the queue of infinite capacity with probability θ 1 (called backorder sale scheme), or leaves the system unserved with probability θ 2 (called lost sale scheme). Note that θ 1 + θ 2 = 1 . If th inventory level occurs to be zero with completion servicing of a c-customer, the c-customer in the queue (if any) waits for a replenishment.
  • In the warehouse part of the system, catastrophic events can occur according to Poisson process with parameter κ . At the moment of arrival of such an event, all the items in the system are instantly destroyed. As a result of the catastrophes, even the item, which is at the status of release to the c-customer, is destroyed. The c-customer whose service was interrupted due to a catastrophe is returned to the queue. We can say that the catastrophe only destroys the items of the system and does not force c-customers out of the system. If the inventory level is zero, then the disaster does not affect the operation of the system warehouse.
  • Two inventory replenishment policies are considered in this study. That is, as ( s , S ) -type policy for the Model-1 and an ( s , Q ) -type policy for the Model-2. The lead time of an order follows exponential distribution with parameter η for both replenishment policies. In a ( s , S ) -type policy (sometimes this policy is called "Up to S"), when the inventory level drops to the reorder point s, 0 ≤ s < S , an order is placed for replenishment and upon replenishment the inventory level becomes S. This policy states that the replenishment quantity varies in order to fill the maximum capacity of the inventory when the reorder is placed. In a ( s , Q ) -type policy, when the inventory level drops to the reorder point s, s < S 2 , an order quantity of a Q = S − s is placed for replenishment and upon replenishment the inventory level becomes sum of the current items in the inventory and order quantity. This policy states that the replenishment quantity is always fixed.

3. The steady-state analysis

In this section, the steady-state analysis of the queueing-inventory model described in Section 2 is performed. That is, we discuss Model-1 with ( s , S ) -type replenishmet policy in Section 3.1 and Model-2 with ( s , Q ) -type replenishmet policy in Section 3.2.
Let K ( t ) , I ( t ) , J 1 ( t ) and J 2 ( t ) denote, respectively, the number of c-customers in the system, the inventory level, the phase of the service and the phase of the arrival, at time t. The process { ( K ( t ) , I ( t ) , J 1 ( t ) , J 2 ( t ) ) , t ≥ 0 } is a continuous-time Markov chain (CTMC) and the state space in the lexicographical ordering is given by
Ω = { ( 0 , i , j 2 ) : 0 ≤ i ≤ S , j 2 = 1 , . . . , m } ⋃ { ( k , i , j 1 , j 2 ) : k > 0 , 0 ≤ i ≤ S , j 1 = 1 , . . . , n , j 2 = 1 , . . . , m } .
The level { ( 0 , i , j 2 ) : 0 ≤ i ≤ S , j 2 = 1 , . . . , m } of dimension m ( S + 1 ) corresponds to the case when there are no c-customers in the system and the inventory level is i. The arrival process is in one of m phases. The level { ( k , i , j 1 , j 2 ) : k > 0 , 0 ≤ i ≤ S , j 1 = 1 , . . . , n , j 2 = 1 , . . . , m } of dimension m n ( S + 1 ) corresponds to the case when there are kc-customers in the system and the inventory level is i. The service process and the arrival process are in one of n phases and in one of m phases, respectively.

3.1. Model-1 with ( s , S ) -type replenishment policy

The infinitesimal generator matrix of the Markov chain governing the queueing-inventory system under ( s , S ) -type policy has a block-tridiagonal matrix structure and is given by
G = B 0 A 0 C 0 B A C B A C B A ⋱ ⋱ ⋱ .
The matrices A 0 and A in the upper diagonal of the matrix G have dimensions m ( S + 1 ) × m n ( S + 1 ) and m n ( S + 1 ) × m n ( S + 1 ) , respectively.
A 0 = β ⊗ D 1 θ 1 β ⊗ D 1 ⋱ β ⊗ D 1 , A = I n ⊗ D 1 θ 1 I n ⊗ D 1 ⋱ I n ⊗ D 1 .
The matrices C 0 and C in the lower diagonal of the matrix G have dimensions m n ( S + 1 ) × m ( S + 1 ) and m n ( S + 1 ) × m n ( S + 1 ) , respectively.
C 0 = ( e n ⊗ I m ) λ − T 0 ⊗ I m ( e n ⊗ I m ) λ − ⋱ ⋱ T 0 ⊗ I m ( e n ⊗ I m ) λ − ,
C = I λ − T 0 β ⊗ I m I λ − T 0 β ⊗ I m I λ − ⋱ ⋱ T 0 β ⊗ I m I λ − .
The matrices B 0 and B in the main diagonal of the matrix G have dimensions m ( S + 1 ) × m ( S + 1 ) and m n ( S + 1 ) × m n ( S + 1 ) , respectively.
B 0 = D 0 θ 1 − η I η I κ I D 0 − ( η + κ ) I η I ⋮ ⋱ ⋮ κ I D 0 − ( η + κ ) I η I κ I D 0 − κ I ⋮ ⋱ κ I D 0 − κ I ,
B = b 0 η I κ I b 1 η I ⋮ ⋱ ⋮ κ I b 1 η I κ I b 2 ⋮ ⋱ κ I b 2
where b 0 = I n ⊗ D 0 θ 1 − ( η + λ − ) I , b 1 = ( T ⊕ D 0 ) − ( η + κ + λ − ) I and b 2 = ( T ⊕ D 0 ) − ( κ + λ − ) I

3.1.1. Stability condition

Let π = ( π 0 , π 1 , π 2 , ⋯ , π S ) be the steady-state probability vector of the finite generator F = A + B + C . The probability vector π i of dimension m n means that the inventory level is i, the service process and the arrival process are in one of n phases and in one of m phases, respectively. That is, π satisfies
π F = 0 and π e = 1 .
The steady-state equations in (3) can be rewritten as
π 0 [ ( I n ⊗ D 1 θ 1 ) + ( I n ⊗ D 0 θ 1 ) − η I ] + π 1 [ ( T 0 β ⊗ I m ) + κ I ] + [ π 2 + ⋯ + π S ] + κ I = 0 , π i [ ( I n ⊗ D 1 ) + ( T ⊕ D 0 ) − ( κ + η ) I ] + π i + 1 ( T 0 β ⊗ I m ) = 0 , 1 ≤ i ≤ s , π i [ ( I n ⊗ D 1 ) + ( T ⊕ D 0 ) − κ I ] + π i + 1 ( T 0 β ⊗ I m ) = 0 , s + 1 ≤ i ≤ S − 1 , [ π 0 + … + π s ] η I + π s [ ( I n ⊗ D 1 ) ] + ( T ⊗ D 0 ) − κ I ] = 0 ,
with the normalizing condition
∑ i = 0 S π i e = 1 .
Theorem 1.
The defined queuing-inventory system under an ( s , S ) -policy is stable if and only if the following condition is satisfied:
ρ = ( 1 − θ 2 π 0 e ) λ + μ ( 1 − π 0 e ) + λ − < 1 .
Proof of Theorem 1.
The defined queueing-inventory system is a Q B D process thus it will be stable if and only if  π A e < π C e (See in [35]). That is,
θ 1 π 0 + ∑ j = 1 S π j ( I n ⊗ D 1 ) e < λ − + ∑ j = 1 S π j ( T 0 β ⊗ I m ) e .
Adding the equations given in (4), the following equation is obtained
θ 1 π 0 ( I n ⊗ D ) + ∑ j = 1 S π j ( T + T 0 β ) ⊕ D = 0 .
Post-multiplying the equation in (7) by ( e n ⊗ I m ) and using the arrival rate of the c-customers λ + = δ D 1 e and the normalizing condition in (4), the left-side of the inequality in (6) is given
θ 1 π 0 + ∑ j = 1 S π j ( I n ⊗ D 1 ) e = θ 1 π 0 e + ∑ j = 1 S π j e λ + = ( 1 − θ 2 π 0 e ) λ + .
Post-multiplying the equation in (7) by ( I n ⊗ e m ) and using the service rate μ = 1 / [ β ( − T ) − 1 e ] and the normalizing condition in (4), we get
∑ j = 1 S π j ( T 0 β ⊗ I m ) e = μ ( 1 − π 0 e ) .
The right-side of the inequality in (6) is obtained. So, the proof of Theorem is completed. □
The probability vector π 0 in (5) can be calculated by solving the equations given in (4).
Not: In the paper [34], the authors studied the queueing-inventory system in which we have discussed in here by considering Poisson arrival and exponentially distributed service times. They obtained the closed-form solution of the probabilities for the special case. We suggest the paper in [34] to see the stability condition of the system under Poisson arrival and exponential service.

3.1.2. The steady-state probability vector of the matrix G

Let x = ( x ( 0 ) , x ( 1 ) , x ( 2 ) , ⋯ ) denote the steady-state probability vector of the generator matrix G in (2). That is, x satisfies
x G = 0 and x e = 1 .
m ( S + 1 ) dimensional row vector x ( 0 ) is further partitioned into vectors represented as x ( 0 ) = [ x ( 0 , 0 ) , x ( 0 , 1 ) , ⋯ , x ( 0 , S ) ] and the dimension of the each vector is m. The vector x ( 0 , i ) gives the steady-state probability that there are no c-customers in the system, the inventory level is i , 0 ≤ i ≤ S , and the arrival process is in one of m phases.
m n ( S + 1 ) dimensional row vector x ( k ) , k ≥ 1 , is further partitioned into vectors represented as x ( k ) = [ x ( k , 0 ) , x ( k , 1 ) , ⋯ , x ( k , S ) ] and the dimension of the each vector is m n . The vector x ( k , i ) gives the steady-state probability that there are kc-customers in the system, the inventory level is i , 0 ≤ i ≤ S , and the service process and the arrival process are in one of n phases and m phases, respectively.
Under the stability condition given in (5) the steady-state probability vector x is obtained (See [35]) as
x ( k ) = x ( 1 ) R k − 1 , k > 1 ,
where the matrix R is the minimal nonnegative solution to the following matrix quadratic equation
R 2 C + R B + A = 0 ,
and the vector x ( 0 ) and x ( 1 ) are obtained by solving
x ( 0 ) B 0 + x ( 1 ) C 0 = 0 , x ( 0 ) A 0 + x ( 1 ) [ B + R C ] = 0 ,
subject to the normalizing condition
x ( 0 ) e + x ( 1 ) ( I − R ) − 1 e = 1 .

3.2. Model-2 with ( s , Q ) -type replenishment policy

The infinitesimal generator matrix of the Markov chain governing the queueing-inventory system under ( s , Q ) -type policy has a block-tridiagonal matrix structure and is given by
G ˜ = B ˜ 0 A 0 C 0 B ˜ A C B ˜ A C B ˜ A ⋱ ⋱ ⋱ .
The matrices A 0 , A , C 0 and C are the same in the both generator matrices in (2) and (13). Considering a different replenishment policy only the modification occurs in the main diagonal. The matrices B ˜ 0 and B ˜ in the main diagonal of the matrix G ˜ are given by
B ˜ 0 = D 0 θ 1 − η I η I κ I D 0 − ( η + κ ) I η I ⋮ ⋱ ⋱ κ I D 0 − ( η + κ ) I η I κ I D 0 − κ I ⋮ ⋱ κ I D 0 − κ I ,
B ˜ = b 0 η I κ I b 1 η I ⋮ ⋱ ⋱ κ I b 1 η I κ I b 2 ⋮ ⋱ κ I b 2
where b 0 = I n ⊗ D 0 θ 1 − ( η + λ − ) I , b 1 = ( T ⊕ D 0 ) − ( η + κ + λ − ) I and b 2 = ( T ⊕ D 0 ) − ( κ + λ − ) I

3.2.1. Stability condition

Let π ˜ = ( π ˜ 0 , π ˜ 1 , π ˜ 2 , ⋯ , π ˜ S ) be the steady-state probability vector of the finite generator F ˜ = A + B ˜ + C . The probability vector π ˜ i of dimension m n means that the inventory level is i, the service process and the arrival process are in one of n phases and in one of m phases, respectively. That is, π satisfies
π ˜ F ˜ = 0 and π ˜ e = 1 .
The steady-state equations in (14) can be rewritten as
π ˜ 0 [ ( I n ⊗ D 1 θ 1 ) + ( I n ⊗ D 0 θ 1 ) − η I ] + π ˜ 1 [ ( T 0 β ⊗ I m ) + κ I ] + [ π ˜ 2 + ⋯ + π ˜ S ] + κ I = 0 , π ˜ i [ ( I n ⊗ D 1 ) + ( T ⊕ D 0 ) − ( κ + η ) I ] + π ˜ i + 1 ( T 0 β ⊗ I m ) = 0 , 1 ≤ i ≤ s , π ˜ i [ ( I n ⊗ D 1 ) + ( T ⊕ D 0 ) − κ I ] + π ˜ i + 1 ( T 0 β ⊗ I m ) = 0 , s + 1 ≤ i ≤ Q − 1 , π ˜ i − Q η I + π ˜ i [ ( I n ⊗ D 1 ) + ( T ⊕ D 0 ) − κ I ] + π ˜ i + 1 ( T 0 β ⊗ I m ) = 0 , Q ≤ i ≤ S − 1 , π ˜ s η I + π ˜ s [ ( I n ⊗ D 1 ) + ( T ⊗ D 0 ) − κ I ] = 0 ,
with the normalizing condition
∑ i = 0 S π ˜ i e = 1 .
The system is a Q B D process thus it will be stable if and only if π ˜ A e < π ˜ C e . The stability condition is given in the equation (16). The proof of Theorem 2 can be performed similar to Theorem 1 in the equation (5).
Theorem 2.
The defined queuing-inventory system under an ( s , Q ) -policy is stable if and only if the following condition is satisfied:
ρ ˜ = ( 1 − θ 2 π ˜ 0 e ) λ + μ ( 1 − π ˜ 0 e ) + λ − < 1 .
The probability vector π ˜ 0 can be calculated by solving the equations given in (15).

3.2.2. The steady-state probability vector of the matrix G ˜

Let x ˜ = ( x ˜ ( 0 ) , x ˜ ( 1 ) , x ˜ ( 2 ) , ⋯ ) denote the steady-state probability vector of the generator matrix G ˜ in (13). That is, x ˜ satisfies
x ˜ G ˜ = 0 and x ˜ e = 1 .
m ( S + 1 ) dimensional row vector x ˜ ( 0 ) is further partitioned into vectors represented as x ˜ ( 0 ) = [ x ˜ ( 0 , 0 ) , x ˜ ( 0 , 1 ) , ⋯ , x ˜ ( 0 , S ) ] and the dimension of the each vector is m. The vector x ˜ ( 0 , i ) gives the steady-state probability that there are no c-customers in the system, the inventory level is i , 0 ≤ i ≤ S , and the arrival process is in one of m phases.
m n ( S + 1 ) dimensional row vector x ˜ ( k ) , k ≥ 1 , is further partitioned into vectors represented as x ˜ ( k ) = [ x ˜ ( k , 0 ) , x ˜ ( k , 1 ) , ⋯ , x ˜ ( k , S ) ] and the dimension of the each vector is m n . The vector x ˜ ( k , i ) gives the steady-state probability that there are kc-customers in the system, the inventory level is i , 0 ≤ i ≤ S , and the service process and the arrival process are in one of n phases and m phases, respectively.
The steady-state probability vector x ˜ is obtained by using the matrix-geometric solution given in (9)-(12). Recall that the matrices B ˜ 0 and B ˜ are used for this solution.

4. Performance measures of Model-1 and Model-2

In this section, some performance measures of the queueing-inventory system under ( s , S ) -type and ( s , Q ) -type policies are listed. The following first seven items are valid for the both models. But, we recall that one should use the probabilities x and x ˜ for the ( s , S ) -type policy (Model-1) and for the ( s , Q ) -type policy (Model-2), respectively. On the other hand, the last item (item 8) includes different formula for each model.
  • The probability that there is no c-customer in the system
    P i d l e = x ( 0 ) e .
  • The mean number of c-customers in the system
    E ( N ) = ∑ k = 1 ∞ k x ( k ) e = x ( 1 ) ( I − R ) − 2 e .
  • The mean loss rate of c-customers because of no inventory
    E I ( L R ) = λ + θ 2 x ( 0 , 0 ) e m + ∑ k = 1 ∞ x ( k , 0 ) e m n .
  • The mean loss rate of c-customers because of n-customer
    E N ( L R ) = λ − 1 − x ( 0 ) e .
  • The mean loss rate of c-customers
    E ( L R ) = E I ( L R ) + E N ( L R ) .
  • The mean number of items in the inventory
    E ( I ) = ∑ i = 1 S i x ( 0 , i ) e m + ∑ k = 1 ∞ ∑ i = 1 S i x ( k , i ) e m n .
  • The mean reorder rate
    E ( R R ) = μ ∑ k = 1 ∞ i x ( k , s + 1 ) e m n + κ ∑ i = 1 S x ( 0 , i ) e m + ∑ k = 1 ∞ ∑ i = 1 S x ( k , i ) e m n .
  • The mean order size
    E 1 ( O S ) = ∑ i = S − s S i x ( 0 , S − i ) e m + ∑ k = 1 ∞ ∑ i = S − s S i x ( k , S − i ) e m n .
    E 2 ( O S ) = Q ∑ i = 0 s x ˜ ( 0 , i ) e m + ∑ k = 1 ∞ ∑ i = 0 s x ˜ ( k , i ) e m n .

5. Numerical study

For the arrival process, the following five sets of values for D 0 and D 1 are considered. The arrival processes have the same mean of 1 but each one of them is qualitatively different. The values of the standard deviation of the inter-arrival times of the arrival processes with respect to ERLA are, respectively, 1, 1.41421, 3.17451, 1.99336, and 1.99336. The M A P processes are normalized to have a specific arrival rate λ + as given in [41]. The arrival processes labeled MNCA and MPCA have negative and positive correlation for two successive inter-arrival times with values -0.4889 and 0.4889, respectively, whereas the first three arrival processes have zero correlation for two successive inter-arrival times.
Erlang distribution (ERLA):
D 0 = − 2 2 0 − 2 , D 1 = 0 0 2 0 .
Exponential distribution (EXPA):
D 0 = − 1 , D 1 = 1 .
Hyperexponential distribution (HEXA):
D 0 = − 1.9 0 0 − 0.19 , D 1 = 1.71 0.19 0.171 0.019 .
M A P with negative correlation (MNCA):
D 0 = − 1.00222 1.00222 0 0 − 1.00222 0 0 0 − 225.75 , D 1 = 0 0 0 0.01002 0 0.9922 223.4925 0 2.2575 .
M A P with positive correlation (MPCA):
D 0 = − 1.00222 1.00222 0 0 − 1.00222 0 0 0 − 225.75 , D 1 = 0 0 0 0.9922 0 0.01002 2.2575 0 223.4925 .
For the service times, we consider three phase-type distributions with parameter ( β , T ) . The phase-type distributions have the same mean of 1 but each one of them is qualitatively different. The values of the standard deviation of the distributions are, respectively, 0.70711, 1, and 2.24472. The distributions are normalized at a specific value for the service rate μ .
Erlang distribution (ERLS):
β = 1 , 0 , T = − 2 2 0 − 2 .
Exponential distribution (EXPS):
β = 1 , T = − 1 .
Hyperexponential distribution (HEXS):
β = 0.9 , 0.1 , T = − 1.9 0 0 − 0.19 .

5.1. The Effect of parameters on performance measures

We discuss the behavior of the performance measures under various the service time distributions and the arrival processes for the Model-1 with ( s , S ) -policy and Model-2 with ( s , Q ) -policy in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13. Towards this end, the reorder point is fixed by s = 3 and the maximum inventory level is fixed by S = 10 . The values of the other parameters can be seen in Table 1.
Firstly, we investigate the effects of the rates λ + , λ − , μ and κ on the mean number of c-customers in the system E ( N ) under the various scenarios in Table 2 for Model-1 with ( s , S ) -policy and in Table 3 for Model-2 with ( s , Q ) -policy.
As expected, the mean number of c-customers in the system increases with increasing values of λ + in Table 2. When looking only at ERLA arrivals, it is seen that the variability in P H -distribution is important. Especially in high traffic intensity situations. For example, at λ + = 5 (high intensity), the values of E ( N ) are 7.559, 8.458 and 16.444 for ERLS, EXPS, and HEXS, respectively, and at λ + = 4.2 (low intensity), the values occur 3.239, 3.490 and 5.611 for ERLS, EXPS, and HEXS, respectively. Similar comment can be made when HEXA arrivals occur. On the other hand, variability in M A P affects the values of E ( N ) more compared to the variability in PH-distribution. Let’s look ERLS services. The values of E ( N ) are 3.239 for ERLA and 7.730 for HEXA at λ + = 4.2 ; are 7.559 for ERLA and 20.759 for HEXA at λ + = 5 . Also, we can say that the values of E ( N ) dramatically increases in the case of HEXS (service with high variability) compared to the other P H -distributions.
As values of κ increase, the values of E ( N ) increase in Table 2. Comments similar to those above can be made regarding the effect of variability in M A P process and P H -distribution.
In Table 2, the mean number of c-customers in the system decreases with increasing the arrival rate of n-customers λ − or the service rate of c-customers μ as expected. The effect of variability in M A P process and P H -distribution on the values of E ( N ) is seen as μ (or λ − ) increases. Again, variability in the M A P process (variability in the inter-arrival times in other words) appears to be more significant compared to variability in P H -distribution, especially when the system has high traffic intensity (i.e., see the cases of μ = 7.6 or λ − = 1 ).
All comments made for Table 2 can also be made for Table 3. Compared to the values in Table 2, it can be seen that the values of E ( N ) in Table 3 are higher, especially at high traffic intensity. In addition, we can say that the variability in M A P process or P H -distribution is more effective when the inventory policy is ( s , Q ) . That is, as the system becomes denser, the increment or decrement becomes faster.
Secondly, we discuss the effects of the rates λ + , λ − , κ and the probability θ 1 on the mean number of items in the inventory E ( I ) under the various scenarios in Table 4 for Model-1 with ( s , S ) -policy and in Table 5 for Model-2 with ( s , Q ) -policy.
As the number of c-customers (by λ + or θ 1 ) or catastrophic events (by κ ) in the system increase, the mean inventory level in the system decreases. As expected, the values of E ( I ) increase with the increment of the n-customer in the system ( λ − ). On the other hand, the values of E ( I ) increase with increasing variability (from ERLS to HEXS for P H -distribution or from ERLA to HEXA for M A P process). Also, it is seen that when the system is dense, the effect of variation in arrival process is greater than the effect of variation in service times in Table 4 and Table 5. We note the values in Table 5 (at ( s , Q ) -policy) are slightly lower.
Thirdly, we examine the effects of the rates λ + , λ − , κ and the probability θ 1 on the mean reorder rate in Table 6Table 7 and the mean order size in Table 8Table 9 under the various scenarios.
As seen in Table 4Table 5, the decrease in the mean number of items in the inventory occurs with the increase in the number of customers in the system (by increasing the λ + and θ 1 rates) or with the increase of catastrophes events (by increasing the κ rate). The more customers there are, the more item in the inventory is needed. Therefore, it is seen that by increasing the values of λ + (by increasing the values of κ or θ 1 ), the values of the mean reorder rate increase in Table 6Table 7 and the values of the mean order size in Table 8Table 9. On the other hand, it is obvious that as n-customers come more frequently, the number of c-customers in the system will decrease (i.e., less item in the inventory will be needed). For the system under ( s , S ) -policy, it is seen that the values of E ( R R ) and E 1 ( O S ) decrease with increasing λ − in Table 6 and Table 8, respectively. Similarly, the values of E ( R R ) and E 2 ( O S ) decrease with increasing λ − in Table 7 and Table 9, respectively, for the system under ( s , Q ) -policy.
In all four parts (parts related to λ + , κ , θ 1 , λ − ) of Table 6 or Table 7, the values of the mean reorder rate decrease with increasing the variability in P H -distribution (ERLS and HEXS). On the other hand, with increasing the variability in M A P (ERLA and HEXA), the values of the mean reorder rate decrease in some parts (i.e., part κ in Table 6) and first increase and then decrease in some parts (i.e., part λ − in Table 6). Similarly, when looking at the four parts of Table 8 or Table 9, it is seen that with the increase in the variability of P H -distribution, the values of the mean order size increase in some parts (i.e., part θ 1 in Table 8), decrease in some parts (i.e., part κ in Table 9), and first increase and then decrease in some parts (i.e., part λ + in Table 9). That is, we cannot talk about a specific behavior regarding the effect of variation. Table 8Table 9 also shows an irregular behavior with increasing variation in M A P .
The results in Table 6, Table 7, Table 8 and Table 9 are for specific values of the parameters. The increases or decreases seen with increasing of variability depend on the values of the parameters. So, what we can clearly say is that the values of the mean order rate and the mean order size will definitely be affected by variability (instead of increase or decrease with variability).
When Table 6 and Table 7 are compared (when Table 8 and Table 9 are compared), it is seen that the results in the system under ( s , Q ) -policy are larger (smaller) than the results in the system under ( s , S ) -policy. Additionally, as the values of the performance measures faster increase (or decrease) with the increase of the values of the parameters in the system under ( s , Q ) -policy.
Finally, we examine the effects of system parameters on the mean lost rate of c-customers in the system. Let’s recall, c-customers can lost in the system studied in two cases; If there is no inventory at the time the c-customer comes to the system, he does not enter the system with probability θ 2 (he is said to be lost)- this case is indicated by E I ( L R ) in Table 10Table 11, and the arrival of n-customers to the system causes the loss of one c-customer- this case is denoted by E N ( L R ) in Table 12Table 13.
As the value of λ + or κ increases, the probability that the inventory is stock-out increases. This increases the rate at which c-customers are lost due to lack of item in the inventory. On the other hand, as λ − increases, the probability of the inventory falling to zero decreases (as it reduces the number of c-customers in the system), which causes the values of E I ( L R ) to decrease. As an interesting result, it is seen that as θ 1 probability increases, the values of E I ( L R ) decrease even though the number of c-customers in the system increases. All results can be seen in Table 10 for the system under ( s , S ) -policy and Table 11 for the system under ( s , Q ) -policy.
As expected, as long as there are c-customers in the system, c-customers will disappear as n-customers arrive. Therefore, it can be seen in Table 12 and Table 13 that E N ( L R ) values increase as the values of all parameters increase.

5.2. Optimization

For the described two models, the function of the expected total cost, E T C , is constructed and an optimization discussion about inventory policies is provided for some specific parameters. In the equation (18), we note that E i ( O R ) is the mean order size of the system with ( s , S ) -policy for i = 1 and of the system with ( s , Q ) -policy for i = 2 .
E T C = c k + c r E i ( O S ) E ( R R ) + c h E ( I ) + c p s κ E ( I ) + c l E ( L R ) + c w E ( N )
where
  • c k : the fixed cost of one order,
  • c r : the unit cost of the order size,
  • c h : the holding cost per item in the inventory per unit of time,
  • c p s : the damaging cost per item in the inventory,
  • c l : the cost incured due to the loss of a c-customer,
  • c w : the waiting cost of a c-customer in the system.
Towards finding the optimum values of the inventory level (that minimize E T C ) for the both model, we fix λ + = 4 , λ − = 1 , μ = 8 , η = 1 , κ = 1 and θ 1 = 0.6 and vary the reorder points s = 3 , 5 , 7 . Also, we fix the unit values of the defined above costs by c k = 10 , c r = 15 , c h = 10 , c p s = 15 , c l = 350 and c w = 300 . Under various distributions of the service times and arrival processes, we give the optimum values of E T C and S in Table 14 for the system under ( s , S ) -policy and in Table 15 for the system under ( s , Q ) -policy.
Let’s look at the cases of ERLA, EXPA and HEXA in Table 14. As the variability in arrival processes increases (respectively, ERLA, EXA and HEXA), the optimum value of S also increases. For both ERLS and EXPS services, the optimum S is generally the same, while the optimum cost varies slightly. In all cases, HEXS services with high variability require more inventory in the system. When the reorder point s is increased, the values of S generally do not change except for HEXA arrivals. However, in the case of HEXA, the optimum S is seen to decrease as s increases.
In Table 14 let’s look at the MNCA and MPCA cases where there is correlation. In negatively correlated arrivals (MNCA), the results in the HEXS service are significantly different from the others and the increase in the values of s is of no significance. On the other hand, in positively correlated arrivals (MPCA), the increase in the values of s and the increase in the variability in service times are separately very important. That is, as the variability in P H -distribution increases, the values of S increase, and as the reorder point increases, the values of S decrease.
First, it is noticeable that the optimum values of S in Table 15 are larger than the values in Table 14, while there is not much difference between the optimum cost values. In other words, in the ( s , Q ) -policy, there is a need to keep more inventory in the system. Although more inventory is carried, the total cost is almost the same as under the ( s , S ) -policy.
The comments made for Table 14 regarding the variability of service times or arrival process can also be said for Table 15. As variation increases, more inventory is needed. Also, positive correlation is important for the system under ( s , Q ) -policy similar to the system under ( s , S ) -policy.
Finally, the important difference between the two tables is the effect of the reorder point s. As the values of s increases, the values of S remain the same or decrease in Table 14 ( as we mentioned above). In Table 15, as the values of s increases, the values of S remain the same or increase.

6. Discussion

We study two queueing-inventory systems with catastrophes in the warehouse. Upon arrival of a catastrophe all inventory in the system is instantly destroyed. The arrivals of the c-customers follow a Markovian Arrival Process ( M A P ) and they can be queued in an infinite buffer. Service time of a c-customer follows a phase-type distribution. The system receives n-customers to service facility and upon arrival of a n-customer one c-customer is pushed out from the system, if any. One of two replenishment policies can be used in the system: either ( s , S ) or ( s , Q ) . If upon arrival of the c-customer, the inventory level is zero, then according to the Bernoulli scheme, this customer is either lost (lost sale scheme) or join the queue (backorder sale scheme).
The system is formulated by a four-dimensional continuous-time Markov chain. Steady state distribution is obtained using the matrix-geometric method. A comprehensive numerical study is performed on the performance measures and an optimization under various the service time distributions and the arrival processes. As a result of numerical studies, it is seen that the variability in service distribution, the variability in the arrival process and the arrivals with positive correlation have an impact on both the performance measures of the system and the optimum inventory policy. Also, it has been observed that the effect of variability is more specifically in the system with ( s , Q ) -policy than the system with ( s , S ) -policy.
For the future work, ones can improve the studied system by considering the batch service and/or batch arrival.

Author Contributions

Conceptualization, A.M. and S.O.; methodology, A.M. and S.O.; software, S.O.; investigation, A.M., S.O. and J.S.; writing—review and editing, A.M., S.O. and J.S.; supervision and project administration, A.M.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
QS Queueing System
QIS Queueing Inventory System
ICS Inventory Control System
MAP Markovian Arrival Process
PH Phase-type distribution
IL Inventory Level
QL Queue Length
CTMC Continuous Time Markov Chain
QBD Quasi-birth-and-death process
ETC Expected Total Cost

References

  1. Schwarz, M.; Daduna, H. Queuing Systems with Inventory Management with Random Lead Times and with Backordering. Math. Methods Oper. Res. 2006, 64, 383–414. [Google Scholar] [CrossRef]
  2. Schwarz, M.; Sauer, C.; Daduna, H.; Kulik, R.; Szekli, R. M/M/1 Queuing Systems with Inventory. Queuing Syst. Theory Appl. 2006, 54, 55–78. [Google Scholar] [CrossRef]
  3. Melikov, A.; Molchanov, A. Stock Optimization in Transport/Storage Systems. Cybernetics 1992, 28, 484–487. [Google Scholar]
  4. Sigman, K.; Simchi-Levi, D. Light Traffic Heuristic for an M/G/1 Queue with Limited Inventory. Ann. Oper. Res. 1992, 40, 371–380. [Google Scholar] [CrossRef]
  5. Krishnamoorthy, A.; Shajin, D.; Narayanan, W. Inventory with Positive Service Time: A Survey, Advanced Trends in Queueing Theory; Series of Books “Mathematics and Statistics” Sciences. V., 2, Anisimov, V., Limnios, N., Eds.; ISTE & Wiley: London, UK, 2021; pp. 201–238. [Google Scholar]
  6. Krishnamoorthy, A.; Lakshmy, B.; Manikandan, R. A survey on inventory models with positive service time. OPSEARCH 2011, 48, 153–169. [Google Scholar] [CrossRef]
  7. Karthikeyan, K.; Sudhesh, R. Recent review article on queueing inventory systems. Research J. Pharm. and Tech. 2016, 9, 1451–1461. [Google Scholar] [CrossRef]
  8. Ko, S.S. A Nonhomogeneous Quasi-Birth Process Approach for an (s,S) Policy for a Perishable Inventory System with Retrial Demands. J. Ind. Manag. Opt. 2020, 16, 1415–1433. [Google Scholar] [CrossRef]
  9. Melikov, A.; Krishnamoorthy, A.; Shahmaliyev, M.O. Numerical Analysis and Long Run Total Cost Optimization of Perishable Queuing Inventory Systems with Delayed Feedback. Queuing Model. Serv. Manag. 2019, 2, 83–111. [Google Scholar]
  10. Jenifer, J.S.A.; Sangeetha, N.; Sivakumar, B. Optimal Control of Service Parameter for a Perishable Inventory System with Service Facility, Postponed Demands and Finite Waiting Hall. Int. J. Inf. & Manag Sci. 2014, 25, 349–370. [Google Scholar]
  11. Reshmi, P.S.; Jose, K. A Perishable (s,S) Inventory System with an Infinite Orbit and Retrials. Math. Sci. Int. Res. J. 2022, 7, 121–126. [Google Scholar]
  12. Melikov, A.; Shahmaliyev, M.; Nair, S.S. Matrix-Geometric Method to Study Queuing System with Perishable Inventory. Autom. Remote Control 2021, 82, 2168–2181. [Google Scholar] [CrossRef]
  13. Goyal, S.; GiriB. Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 2001, 134, 1–16. [Google Scholar]
  14. Jeganathan, K.; Selvakumar, S.; Saravanan, S.; Anbazhagan, N.; Amutha, S.; Cho, W.; Joshi, G. P.; Ryoo, J. (2022). Performance of stochastic inventory system with a fresh item, returned item, refurbished item, and multi-class customers. Mathematics 2022, 10(7), 1137. [CrossRef]
  15. Karaesmen I., Scheller-Wolf A., Deniz B. Managing perishable and aging inventories: Review and future research directions- Planning production and inventories in the extended enterprise. A state-of-the-art handbook. (Eds. Kempf K., Keskinocak P, Uzsoy P.). Vol. 1. Springer, 2011, 393-438.
  16. Nahmias, S. Perishable inventory theory. Heidelberg: Springer. 2011.
  17. Melikov, A.; Aliyeva, S.; Nair, S.; Krishna Kumar, B. Retrial queuing-inventory systems with delayed feedback and instantaneous damaging of items. Axioms 2022, 11, 241. [Google Scholar] [CrossRef]
  18. Melikov, A.; Mirzayev, R.R.; Nair, S.S. Numerical investigation of double source queuing-inventory systems with destructive customers. J. Comput. Syst. Sci. Int. 2022, 61, 581–598. [Google Scholar] [CrossRef]
  19. Melikov, A.; Mirzayev, R.R.; Nair, S.S. Double Sources Queuing-Inventory System with Hybrid Replenishment Policy. Mathematics 2022, 10, 2423. [Google Scholar] [CrossRef]
  20. Melikov, A.; Mirzayev, R.R.; Sztrik, J. Double Sources QIS with finite waiting room and destructible stocks. Mathematics 2023, 11, 226. [Google Scholar] [CrossRef]
  21. Lian, Z.; Liu, L.; Neuts, F. A Discrete-Time Model for Common Lifetime Inventory Systems. Math. Oper. Res. 2005, 30, 718–732. [Google Scholar] [CrossRef]
  22. Chakravarthy, S.R. An inventory system with Markovian demands, and phase-type distributions for perishability and replenishment. OPSEARCH 2010, 47, 266–283. [Google Scholar] [CrossRef]
  23. Krishnamoorthy, A.; Shajin, D.; Lakshmy, B. On a queueing-inventory with reservation, cancellation, common life time and retrial. Ann. Oper. Res. 2016, 247, 365–389. [Google Scholar] [CrossRef]
  24. Shajin, D.; Krishnamoorthy, A.; Manikandan, R. On a Queueing-Inventory System with Common Life Time and Markovian Lead Time Process. Oper. Res. 2022, 22, 651–684. [Google Scholar] [CrossRef]
  25. Demircioglu, M.; Bruneel, H.; Wittevrongel, S. Analysis of a Discrete-Time Queueing Model with Disasters. Mathematics 2021, 9, 3283. [Google Scholar] [CrossRef]
  26. Krishna Kumar, B.; Arivudainambi, D. Transient Solution of an M/M/1 Queue with Catastrophes. Comput. Math. Appl. 2000, 40, 1233–1240. [Google Scholar] [CrossRef]
  27. Vinodhini, G.A.F.; Vidhya, V. Computational Analysis of Queues with Catastrophes in a Multiphase Random Environment. Math. Probl. Eng. 2016, 2917917. [Google Scholar] [CrossRef]
  28. Ye, J.; Liu, L.; Jiang, T. Analysis of a Single-Sever Queue with Disasters and Repairs under Bernoulli Vacation Schedule. J. Syst. Sci. Inf. 2016, 4, 547–559. [Google Scholar] [CrossRef]
  29. Chakravarthy, S. R. A catastrophic queueing model with delayed action. Appl. Math. Model. 2017, 46, 631–649. [Google Scholar] [CrossRef]
  30. Chakravarthy, S. R.; Dudin, A. N.; Klimenok, V. I. A retrial queueing model with MAP arrivals, catastrophic failures with repairs, and customer impatience. Asia-Pacific J. Oper. Res. 2010, 27, 727–752. [Google Scholar] [CrossRef]
  31. Raj, R.; Jain, V. (2023) Resource and traffic control optimization in MMAP[c]/PH[c]/S queueing system with PH retrial times and catastrophe phenomenon. Telecommun Syst. 2023, 84, 341–362. [Google Scholar] [CrossRef]
  32. Sivakumar, B.; Arivarignan, G. A Perishable Inventory System with Service Facilities and Negative Customers. Adv. Model. Optim. 2005, 7, 193–210. [Google Scholar]
  33. Soujanya, M.L.; Laxmi, P.V. Analysis on Dual Supply Inventory Model Having Negative Arrivals and Finite Lifetime Inventory. Reliab. Theory Appl. 2021, 16, 295–301. [Google Scholar]
  34. Melikov, A.; Poladova, L.; Edayapurath, S.; Sztrik, J. Single-server queuing-inventory systems with negative customers and catastrophes in the warehouse. Mathematics 2023, 11, 2380. [Google Scholar] [CrossRef]
  35. Neuts, M.F. (1981) Matrix-geometric solutions in stochastic models: An algorithmic approach; The Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
  36. Chakravarthy, S.R. Introduction to Matrix-Analytic Methods in Queues; John Wiley & Sons, Inc.: London, UK, 2022; Volume 1. [Google Scholar]
  37. Chakravarthy, S.R. Introduction to Matrix-Analytic Methods in Queues; John Wiley & Sons, Inc.: London, UK, 2022; Volume 2. [Google Scholar]
  38. Dudin, A.N.; Klimenok, V.I.; Vishnevsky, V.M. The Theory of Queueing Systems with Correlated Flows; Springer Nature Switzerland AG: Basel, Switzerland, 2020. [Google Scholar]
  39. He, Q.-M. Fundamentals of Matrix-Analytic Methods; Springer: New York, NY, USA, 2014. [Google Scholar]
  40. Latouche, G.; Ramaswami, V. Introduction to Matrix Analytic Methods in Stochastic Modeling; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
  41. Chakravarthy, S. R. Markovian arrival processes. Wiley Encyclopedia of Operations Research and Management Science 2010. [Google Scholar] [CrossRef]
Preprints 90492 g001
Figure 1. Block diagram of the QIS with negative customer and catastrophe in warehouse.
Figure 1. Block diagram of the QIS with negative customer and catastrophe in warehouse.
Preprints 90492 g001
Table 1. The values of the parameters in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13
Table 1. The values of the parameters in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13
As it is varied It is fixed
the arrival rate of c-customers: λ + λ − = 1 , μ = 8 , η = 1 , κ = 1 , θ 1 = 0.6
the arrival rate of n-customers: λ − λ + = 5 , μ = 8 , η = 1 , κ = 1 , θ 1 = 0.6
the service rate of c-customers: μ λ + = 5 , λ − = 1 , η = 1 , κ = 1 , θ 1 = 0.6
the rate of the catastrophic events: κ λ + = 5 , λ − = 1 , μ = 8 , η = 1 , θ 1 = 0.6
the probability that c-customer joins the queue when the inventory level is zero: θ 1 λ + = 5 , λ − = 1 , μ = 8 , η = 1 , κ = 1
Table 2. E ( N ) under ( s , S ) -policy
Table 2. E ( N ) under ( s , S ) -policy
ERLA HEXA
Values of the parameters ERLS EXPS HEXS ERLS EXPS HEXS
4.2 3.239 3.490 5.611 7.730 8.133 10.894
4.4 3.848 4.179 6.994 9.530 10.046 13.654
λ + 4.6 4.663 5.106 8.925 11.967 12.646 17.501
4.8 5.811 6.426 11.789 15.438 16.373 23.198
5 7.559 8.458 16.444 20.759 22.140 32.449
0.4 3.401 3.707 6.344 9.298 9.772 13.120
0.6 4.384 4.808 8.496 11.889 12.534 17.199
κ 0.8 5.686 6.291 11.589 15.463 16.380 23.117
1 7.559 8.458 16.444 20.759 22.140 32.449
1.2 10.577 12.023 25.194 29.468 31.767 49.303
7.6 9.620 10.940 22.927 27.554 29.633 45.447
8 7.559 8.458 16.444 20.759 22.140 32.449
μ 8.4 6.323 6.989 12.837 16.701 17.717 25.201
8.8 5.499 6.018 10.549 14.009 14.802 20.592
9.2 4.909 5.329 8.975 12.095 12.741 17.411
1 7.559 8.458 16.444 20.759 22.140 32.449
1.4 4.317 4.701 7.931 11.502 12.095 16.254
λ − 1.8 2.957 3.159 4.778 7.644 7.979 10.175
2.2 2.216 2.331 3.200 5.555 5.767 7.059
2.6 1.753 1.822 2.296 4.262 4.405 5.205
Table 3. E ( N ) under ( s , Q ) -policy
Table 3. E ( N ) under ( s , Q ) -policy
ERLA HEXA
Values of the parameters ERLS EXPS HEXS ERLS EXPS HEXS
4.2 3.701 4.001 6.579 9.563 10.081 13.596
4.4 4.560 4.976 8.584 12.213 12.924 17.831
λ + 4.6 5.811 6.412 11.701 16.100 17.133 24.402
4.8 7.803 8.737 17.165 22.329 23.979 35.903
5 11.486 13.156 29.116 33.888 37.021 61.022
0.4 4.462 4.861 8.427 13.026 13.702 18.572
0.6 5.900 6.499 11.895 17.145 18.173 25.651
κ 0.8 7.997 8.947 17.641 23.348 25.032 37.437
1 11.486 13.156 29.116 33.888 37.021 61.022
1.2 18.705 22.381 63.549 55.978 63.556 131.820
7.6 16.591 19.688 52.949 50.813 57.091 111.116
8 11.486 13.156 29.116 33.888 37.021 61.022
μ 8.4 8.971 10.066 20.110 25.573 27.542 42.060
8.8 7.472 8.265 15.396 20.636 22.028 32.114
9.2 6.477 7.086 12.507 17.370 18.426 26.003
1 11.486 13.156 29.116 33.888 37.021 61.022
1.4 5.187 5.675 9.862 14.842 15.683 21.456
λ − 1.8 3.270 3.498 5.346 9.048 9.451 12.058
2.2 2.354 2.476 3.412 6.281 6.516 7.939
2.6 1.822 1.892 2.386 4.682 4.833 5.677
Table 4. E ( I ) under ( s , S ) -policy
Table 4. E ( I ) under ( s , S ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 3.266 3.324 3.345 3.408 3.334 3.397
4.2 3.209 3.275 3.280 3.350 3.268 3.338
λ + 4.4 3.154 3.228 3.217 3.294 3.204 3.281
4.6 3.099 3.182 3.154 3.238 3.141 3.226
4.8 3.046 3.138 3.092 3.184 3.080 3.172
0.2 4.000 4.088 4.140 4.227 4.054 4.147
0.4 3.696 3.797 3.807 3.907 3.747 3.851
κ 0.6 3.431 3.537 3.513 3.616 3.475 3.582
0.8 3.199 3.303 3.255 3.358 3.234 3.339
1 2.994 3.094 3.030 3.130 3.020 3.120
0.1 3.655 3.665 3.774 3.795 3.767 3.796
0.3 3.500 3.526 3.606 3.643 3.598 3.639
θ 1 0.5 3.343 3.390 3.432 3.487 3.422 3.478
0.7 3.191 3.259 3.256 3.328 3.245 3.316
0.9 3.039 3.127 3.077 3.165 3.068 3.155
1 2.994 3.094 3.030 3.130 3.020 3.120
1.4 3.108 3.184 3.159 3.242 3.150 3.231
λ − 1.8 3.212 3.260 3.270 3.336 3.266 3.328
2.2 3.306 3.325 3.368 3.416 3.368 3.412
2.6 3.391 3.380 3.453 3.483 3.459 3.486
Table 5. E ( I ) under ( s , Q ) -policy
Table 5. E ( I ) under ( s , Q ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 2.266 2.289 2.275 2.303 2.250 2.277
4.2 2.214 2.240 2.221 2.252 2.200 2.231
λ + 4.4 2.162 2.192 2.167 2.201 2.150 2.184
4.6 2.109 2.143 2.113 2.150 2.101 2.138
4.8 2.057 2.095 2.060 2.100 2.051 2.091
0.2 2.949 2.984 2.976 3.015 2.960 3.000
0.4 2.634 2.671 2.648 2.689 2.633 2.675
κ 0.6 2.382 2.421 2.390 2.432 2.377 2.420
0.8 2.176 2.217 2.180 2.223 2.171 2.215
1 2.005 2.047 2.007 2.050 2.001 2.045
0.1 2.559 2.563 2.624 2.635 2.581 2.594
0.3 2.456 2.467 2.496 2.515 2.454 2.473
θ 1 0.5 2.335 2.354 2.351 2.377 2.320 2.345
0.7 2.193 2.219 2.195 2.225 2.177 2.207
0.9 2.030 2.059 2.027 2.059 2.020 2.053
1 2.005 2.047 2.007 2.050 2.001 2.045
1.4 2.121 2.152 2.124 2.161 2.112 2.148
λ − 1.8 2.218 2.236 2.222 2.252 2.205 2.233
2.2 2.301 2.303 2.306 2.327 2.285 2.303
2.6 2.371 2.355 2.378 2.389 2.353 2.362
Table 6. E ( R R ) under ( s , S ) -policy
Table 6. E ( R R ) under ( s , S ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.642 0.607 0.646 0.609 0.633 0.598
4.2 0.653 0.615 0.655 0.615 0.643 0.605
λ + 4.4 0.663 0.621 0.663 0.620 0.653 0.612
4.6 0.673 0.628 0.672 0.626 0.663 0.619
4.8 0.682 0.634 0.680 0.632 0.673 0.626
0.2 0.511 0.472 0.496 0.466 0.496 0.464
0.4 0.572 0.526 0.561 0.521 0.558 0.516
κ 0.6 0.620 0.570 0.613 0.566 0.607 0.561
0.8 0.659 0.608 0.655 0.605 0.649 0.600
1 0.691 0.639 0.689 0.637 0.683 0.633
0.1 0.587 0.566 0.594 0.571 0.581 0.559
0.3 0.604 0.580 0.613 0.585 0.599 0.573
θ 1 0.5 0.629 0.598 0.634 0.601 0.621 0.589
0.7 0.656 0.617 0.658 0.617 0.646 0.607
0.9 0.682 0.635 0.682 0.634 0.675 0.628
1 0.691 0.639 0.689 0.637 0.683 0.633
1.4 0.672 0.627 0.671 0.625 0.663 0.618
λ − 1.8 0.656 0.614 0.656 0.615 0.646 0.606
2.2 0.640 0.603 0.644 0.606 0.632 0.596
2.6 0.627 0.593 0.632 0.598 0.620 0.587
Table 7. E ( R R ) under ( s , Q ) -policy
Table 7. E ( R R ) under ( s , Q ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.777 0.699 0.762 0.687 0.752 0.678
4.2 0.788 0.705 0.774 0.694 0.766 0.687
λ + 4.4 0.798 0.711 0.785 0.701 0.779 0.695
4.6 0.807 0.716 0.796 0.708 0.792 0.704
4.8 0.816 0.721 0.807 0.714 0.804 0.711
0.2 0.623 0.576 0.608 0.569 0.610 0.568
0.4 0.692 0.627 0.679 0.619 0.679 0.618
κ 0.6 0.747 0.667 0.735 0.660 0.734 0.658
0.8 0.790 0.699 0.780 0.693 0.779 0.691
1 0.825 0.725 0.817 0.720 0.816 0.719
0.1 0.697 0.646 0.684 0.636 0.666 0.619
0.3 0.729 0.668 0.714 0.656 0.698 0.640
θ 1 0.5 0.762 0.690 0.746 0.677 0.733 0.665
0.7 0.792 0.708 0.779 0.698 0.771 0.691
0.9 0.820 0.723 0.814 0.719 0.811 0.717
1 0.825 0.725 0.817 0.720 0.816 0.719
1.4 0.806 0.715 0.794 0.706 0.789 0.701
λ − 1.8 0.789 0.704 0.774 0.693 0.766 0.686
2.2 0.773 0.693 0.757 0.682 0.746 0.672
2.6 0.758 0.682 0.742 0.672 0.728 0.659
Table 8. E 1 ( O S ) under ( s , S ) -policy
Table 8. E 1 ( O S ) under ( s , S ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 5.891 5.928 5.953 5.983 5.896 5.927
4.2 5.960 5.998 6.012 6.043 5.960 5.993
λ + 4.4 6.028 6.066 6.071 6.103 6.025 6.058
4.6 6.095 6.133 6.130 6.163 6.090 6.125
4.8 6.161 6.200 6.188 6.222 6.155 6.191
0.2 4.852 4.828 4.797 4.772 4.795 4.767
0.4 5.267 5.257 5.247 5.234 5.222 5.210
κ 0.6 5.629 5.636 5.632 5.635 5.599 5.604
0.8 5.947 5.970 5.962 5.982 5.930 5.952
1 6.227 6.265 6.247 6.281 6.220 6.257
0.1 5.545 5.567 5.607 5.625 5.547 5.562
0.3 5.654 5.682 5.732 5.754 5.671 5.691
θ 1 0.5 5.806 5.840 5.876 5.903 5.816 5.843
0.7 5.980 6.020 6.032 6.066 5.982 6.017
0.9 6.167 6.215 6.199 6.241 6.166 6.212
1 6.227 6.265 6.247 6.281 6.220 6.257
1.4 6.087 6.127 6.125 6.158 6.085 6.118
λ − 1.8 5.966 6.010 6.021 6.055 5.973 6.005
2.2 5.861 5.912 5.931 5.969 5.880 5.912
2.6 5.770 5.831 5.853 5.896 5.802 5.835
Table 9. E 2 ( O S ) under ( s , Q ) -policy
Table 9. E 2 ( O S ) under ( s , Q ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 4.605 4.611 4.613 4.614 4.573 4.574
4.2 4.666 4.669 4.671 4.670 4.637 4.637
λ + 4.4 4.725 4.726 4.728 4.724 4.700 4.698
4.6 4.784 4.781 4.784 4.778 4.763 4.759
4.8 4.841 4.835 4.840 4.832 4.825 4.818
0.2 4.036 4.006 3.993 3.959 3.994 3.959
0.4 4.319 4.293 4.294 4.265 4.288 4.259
κ 0.6 4.548 4.527 4.535 4.511 4.524 4.501
0.8 4.738 4.722 4.732 4.714 4.720 4.704
1 4.897 4.888 4.896 4.885 4.886 4.876
0.1 4.236 4.248 4.241 4.247 4.181 4.182
0.3 4.365 4.375 4.379 4.382 4.322 4.323
θ 1 0.5 4.521 4.529 4.532 4.534 4.485 4.486
0.7 4.691 4.696 4.698 4.698 4.665 4.668
0.9 4.872 4.875 4.875 4.876 4.861 4.865
1 4.897 4.888 4.896 4.885 4.886 4.876
1.4 4.771 4.770 4.773 4.766 4.750 4.745
λ − 1.8 4.659 4.671 4.668 4.668 4.634 4.634
2.2 4.562 4.589 4.579 4.586 4.536 4.542
2.6 4.476 4.519 4.501 4.518 4.452 4.464
Table 10. E I ( L R ) under ( s , S ) -policy
Table 10. E I ( L R ) under ( s , S ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.838 0.850 0.857 0.870 0.860 0.875
4.2 0.887 0.901 0.906 0.921 0.908 0.925
λ + 4.4 0.937 0.954 0.956 0.973 0.957 0.976
4.6 0.989 1.008 1.006 1.026 1.007 1.028
4.8 1.041 1.064 1.057 1.080 1.057 1.081
0.2 0.645 0.670 0.679 0.702 0.673 0.698
0.4 0.790 0.815 0.819 0.843 0.816 0.841
κ 0.6 0.910 0.936 0.934 0.959 0.932 0.958
0.8 1.010 1.037 1.029 1.054 1.028 1.055
1 1.095 1.122 1.109 1.134 1.108 1.135
0.1 1.838 1.845 1.867 1.878 1.877 1.894
0.3 1.437 1.447 1.468 1.480 1.476 1.493
θ 1 0.5 1.039 1.050 1.063 1.076 1.068 1.084
0.7 0.635 0.646 0.649 0.660 0.650 0.663
0.9 0.217 0.222 0.220 0.226 0.221 0.226
1 1.095 1.122 1.109 1.134 1.108 1.135
1.4 1.074 1.094 1.093 1.114 1.094 1.117
λ − 1.8 1.058 1.073 1.080 1.098 1.083 1.102
2.2 1.046 1.058 1.069 1.085 1.074 1.091
2.6 1.037 1.047 1.060 1.074 1.067 1.082
Table 11. E I ( L R ) under ( s , Q ) -policy
Table 11. E I ( L R ) under ( s , Q ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.883 0.902 0.907 0.926 0.905 0.926
4.2 0.939 0.961 0.961 0.984 0.958 0.982
λ + 4.4 0.996 1.022 1.017 1.042 1.013 1.040
4.6 1.055 1.085 1.073 1.102 1.070 1.100
4.8 1.115 1.149 1.130 1.163 1.127 1.161
0.2 0.772 0.808 0.809 0.843 0.799 0.836
0.4 0.906 0.943 0.936 0.971 0.928 0.965
κ 0.6 1.014 1.052 1.037 1.073 1.031 1.069
0.8 1.103 1.141 1.119 1.156 1.116 1.153
1 1.177 1.216 1.188 1.225 1.186 1.223
0.1 1.887 1.901 1.931 1.948 1.930 1.954
0.3 1.486 1.503 1.530 1.550 1.529 1.553
θ 1 0.5 1.087 1.106 1.119 1.139 1.117 1.139
0.7 0.674 0.691 0.690 0.707 0.688 0.706
0.9 0.234 0.242 0.237 0.245 0.236 0.244
1 1.177 1.216 1.188 1.225 1.186 1.223
1.4 1.144 1.174 1.164 1.194 1.161 1.192
λ − 1.8 1.117 1.141 1.144 1.170 1.141 1.168
2.2 1.097 1.117 1.127 1.150 1.125 1.149
2.6 1.081 1.098 1.113 1.134 1.113 1.134
Table 12. E N ( L R ) under ( s , S ) -policy
Table 12. E N ( L R ) under ( s , S ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.759 0.752 0.724 0.727 0.745 0.745
4.2 0.787 0.782 0.756 0.761 0.776 0.777
λ + 4.4 0.815 0.813 0.788 0.794 0.806 0.809
4.6 0.843 0.843 0.819 0.827 0.836 0.840
4.8 0.871 0.873 0.851 0.860 0.865 0.871
0.2 0.743 0.736 0.747 0.748 0.756 0.755
0.4 0.790 0.787 0.783 0.788 0.796 0.798
κ 0.6 0.830 0.830 0.818 0.825 0.831 0.835
0.8 0.866 0.869 0.851 0.860 0.864 0.870
1 0.898 0.903 0.882 0.893 0.894 0.902
0.1 0.438 0.417 0.446 0.434 0.459 0.446
0.3 0.601 0.583 0.572 0.567 0.586 0.578
θ 1 0.5 0.713 0.702 0.675 0.676 0.696 0.693
0.7 0.802 0.799 0.771 0.778 0.791 0.795
0.9 0.882 0.889 0.864 0.878 0.878 0.889
1 0.898 0.903 0.882 0.893 0.894 0.902
1.4 1.173 1.166 1.142 1.148 1.161 1.163
λ − 1.8 1.410 1.384 1.363 1.359 1.387 1.379
2.2 1.615 1.562 1.554 1.536 1.579 1.559
2.6 1.790 1.707 1.720 1.685 1.744 1.710
Table 13. E N ( L R ) under ( s , Q ) -policy
Table 13. E N ( L R ) under ( s , Q ) -policy
ERLA HEXA MPCA
Values of the parameters ERLS HEXS ERLS HEXS ERLS HEXS
4 0.778 0.776 0.755 0.762 0.772 0.777
4.2 0.809 0.810 0.788 0.798 0.805 0.812
λ + 4.4 0.840 0.844 0.822 0.834 0.836 0.845
4.6 0.870 0.877 0.856 0.870 0.868 0.879
4.8 0.900 0.910 0.889 0.905 0.899 0.912
0.2 0.783 0.783 0.794 0.800 0.800 0.805
0.4 0.828 0.832 0.829 0.839 0.837 0.846
κ 0.6 0.867 0.874 0.862 0.875 0.871 0.882
0.8 0.901 0.911 0.893 0.909 0.901 0.915
1 0.930 0.944 0.923 0.940 0.929 0.945
0.1 0.435 0.415 0.452 0.439 0.469 0.459
0.3 0.604 0.589 0.587 0.583 0.602 0.597
θ 1 0.5 0.726 0.719 0.700 0.704 0.719 0.720
0.7 0.828 0.831 0.808 0.821 0.824 0.833
0.9 0.924 0.942 0.915 0.938 0.923 0.943
1 0.930 0.944 0.923 0.940 0.929 0.945
1.4 1.206 1.208 1.187 1.200 1.201 1.212
λ − 1.8 1.441 1.424 1.410 1.414 1.430 1.431
2.2 1.642 1.597 1.600 1.590 1.624 1.612
2.6 1.813 1.738 1.764 1.738 1.789 1.764
Table 14. Optimum values of E T C * and S * for the system under ( s , S ) -policy
Table 14. Optimum values of E T C * and S * for the system under ( s , S ) -policy
s = 3 s = 5 s = 7
MAP PH S * ETC * S * ETC * S * ETC *
ERLA ERLS 12 1523.049 12 1526.263 12 1538.455
EXPS 12 1577.435 12 1579.782 12 1590.842
HEXS 14 2027.068 14 2025.895 14 2030.171
EXPA ERLS 13 1657.027 13 1657.273 13 1665.452
EXPS 13 1714.634 13 1714.218 13 1721.526
HEXS 15 2169.740 15 2167.181 14 2169.473
HEXA ERLS 18 2413.463 17 2402.938 16 2398.154
EXPS 18 2496.819 17 2486.839 17 2482.051
HEXS 19 3043.694 19 3034.463 18 3028.903
MNCA ERLS 13 1706.068 13 1706.237 13 1714.395
EXPS 13 1760.549 13 1760.072 13 1767.381
HEXS 15 2209.347 15 2206.767 15 2209.113
MPCA ERLS 39 28273.270 38 28245.217 36 28217.794
EXPS 40 28343.298 39 28316.825 37 28290.718
HEXS 45 28862.495 43 28840.115 42 28818.031
Table 15. Optimum values of E T C * and S * for the system under ( s , Q ) -policy
Table 15. Optimum values of E T C * and S * for the system under ( s , Q ) -policy
s = 3 s = 5 s = 7
MAP PH S * ETC * S * ETC * S * ETC *
ERLA ERLS 15 1522.919 17 1529.208 19 1547.543
EXPS 15 1577.272 17 1582.646 19 1599.781
HEXS 17 2026.762 19 2027.477 21 2035.853
EXPA ERLS 16 1656.737 18 1659.345 20 1672.515
EXPS 16 1714.313 18 1716.220 20 1728.459
HEXS 18 2169.372 20 2168.303 22 2173.935
HEXA ERLS 21 2412.971 22 2403.011 23 2399.884
EXPS 21 2496.307 22 2486.853 24 2483.935
HEXS 22 3043.138 24 3034.403 25 3029.949
MNCA ERLS 16 1705.783 18 1708.339 20 1721.544
EXPS 16 1760.236 18 1762.111 20 1774.414
HEXS 18 2208.991 20 2207.933 21 2213.632
MPCA ERLS 42 28273.128 43 28244.999 43 28217.403
EXPS 43 28343.163 44 28316.618 44 28290.344
HEXS 48 28862.372 48 28840.132 49 28817.682
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated