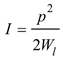Development and Analysis of Multistage Spraying of Liquids in Ultrasonic Field

Spraying various liquids (primarily aqueous solutions of various substances) is widely used in various technological processes. For most of them, high dispersibility and narrow droplet size distribution are essential. This facilitates ultrasonic spray technique. However, the higher the dispersity of droplets produced by ultrasonic spray, the lower the spray productivity. To solve this problem, we proposed a method of multistage spraying, consisting in generation of a large number of particles of large initial size (to ensure high productivity) and their subsequent destruction by propagation in a periodic ultrasonic field (to ensure small droplet sizes at high productivity). To experimentally determine the capabilities of this technique, a tubular emitter in the shape of a cylinder of stepped-variable cross-section was designed. Configuration of the ultrasonic field inside the emitter (22.2 kHz; 182 dB) implements three-stage spraying (the number of sputtering stages corresponds to the number of anti-nodes along the emitter axis). The effectiveness of proposed and developed technique suitable for generation of droplets sized less than 40 µm with performance exceeding the known ultrasonic spray techniques at least 10 times has been confirmed in the course of conducted research.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Spraying of liquids is the basic operation of many processes such as film coating, spray cooling, spray drying, humidification, fuel combustion, drug administration, inkjet printing, etc. [1,2,3]. In practice, the most common applications of spraying liquids are hydraulic spraying, pneumatic spraying, dual-liquid spraying [4], electrostatic spraying [5], pressurized spraying [6], and ultrasonic spraying [7,8,9]. Ultrasonic spraying offers a number of significant advantages among the used techniques, because it provides a minimum size variation of generated droplets relative to mean value, does not require additives, such as surfactants or emulsifiers and facilitates spraying highly viscous liquids with minimized consumption of energy [10].

Two main techniques of ultrasonic spraying are used in contemporary practice. Spraying in a fountain and spraying in a liquid layer. Spraying in fountain enables generation of aerosols with an average particle size of 2...5 µm at a frequency of up to 5 MHz. Yet, the productivity of this spraying technique is less than 1 ml/min, which is insufficient for practical applications in industry (for example, for application of coatings). Therefore, its most common application falls within inhalation therapy and humidifiers.

In turn, the concept of ultrasonic spraying of liquid in a layer is that the liquid in the form of a thin film disintegrates into small droplets when moving over a vibrating surface (frequency >20 kHz). Two main hypotheses, namely capillary wave hypothesis and cavitation hypothesis, have been proposed to explain the concept of liquid disintegration during ultrasonic spraying. The capillary wave hypothesis is based on Taylor’s instability criteria [11]. Lang [12] measured surface disturbances by photographing capillary wave peaks on a vibrating surface. The apparent correlation between the median droplet diameter and the wavelength of capillary waves is considered to confirm the capillary wave theory. Cavitation bubbles are assumed to be generated within liquid film when exposed to ultrasound, provided that the liquid film on the vibrating surface has certain minimum thickness. High intensity pressure surges are generated upon implosive collapse of these cavities, especially at implosion of cavities near the liquid surface. These pressure surges initiate disintegration of the liquid film and cause direct release of droplets. In this case, the size of shaped droplets is also proportional to the size of cavitation bubbles generated, i.e., the frequency of ultrasonic impact.

Buguslavsky and Eknadiosyants [13] combined these two theories and proposed the conjunctive theory. According to this theory, periodic pressure surges from cavitation disturbances generate and interact with capillary waves of finite amplitude, destroy and excite them with generation of droplets. It should also be noted that cavitation shock (which is essentially a statistically random phenomenon) results in non-uniform random disintegration, and observed non-uniformity of droplet distribution confirms this theory.

Since most droplets are formed through capillary wave generation, the droplet diameter can be estimated fairly accurately using Lang’s equation:

D_{1} = 0, 34 λ = 0, 34 \sqrt[3]{\frac{8 π σ}{ρ f^{2}}}

(1)

The use of this equation is justified by the fact that diameter of aerosol droplets is determined by frequency of ultrasonic oscillations applied to the liquid film. As the frequency increases, diameter of generated droplets decreases [14,15]. Obviously, the spraying productivity decreases proportionally, which is described by the well-known equation [16]:

P_{1} = 2 \frac{f}{λ^{2}} π \frac{D_{1}^{3}}{6}

(2)

It follows from presented expressions that the productivity is inversely proportional to the spraying frequency. In practice, dependence on frequency is not linear, which results in more significant decrease in spraying productivity. So a number of researchers have shown that with increase of vibration frequency from 22 kHz to 80 kHz, the median droplet diameter decreases from 93 µm to 30 µm (three times). But spraying productivity at practical implementation of the process decreases more than 12 times (from 3 ml/s to 0.25 ml/s) [17].

Thus, the key challenge of ultrasonic spraying technique in a liquid layer is the fundamental limitation of productivity with increasing dispersity of generated aerosol. Since all existing ultrasonic spraying techniques do not facilitate generation of finely dispersed aerosols with high productivity, this significantly limits the application scopes for solving many problems of contemporary high-tech industries.

In this connection a need arises to develop new ways of implementation of ultrasonic spraying, providing increase of productivity of generation of finely dispersed liquid phase.

2. Method of Multistage Ultrasonic Spraying

The ultrasonic spraying productivity in generation of highly dispersed aerosols is limited, primarily by the fact that the formation of droplets occurs in a single stage, consisting in detachment of a droplet from the surface of liquid layer.

Vibration frequencies up to 200 kHz are used at application of known implementations of ultrasonic spraying techniques of liquid in a layer for generation of highly dispersed liquid droplets [18,19,20,21]. However, generation of high-frequency vibrations with amplitude required for spraying limits the emitting surface area. Such vibrations are rapidly attenuated in the sprayed liquid and intensely absorbed in the ultrasonic emitter material. For these reasons, it is fundamentally impossible to achieve high dispersing performance at high dispersities by means of ultrasonic exposure in a single stage.

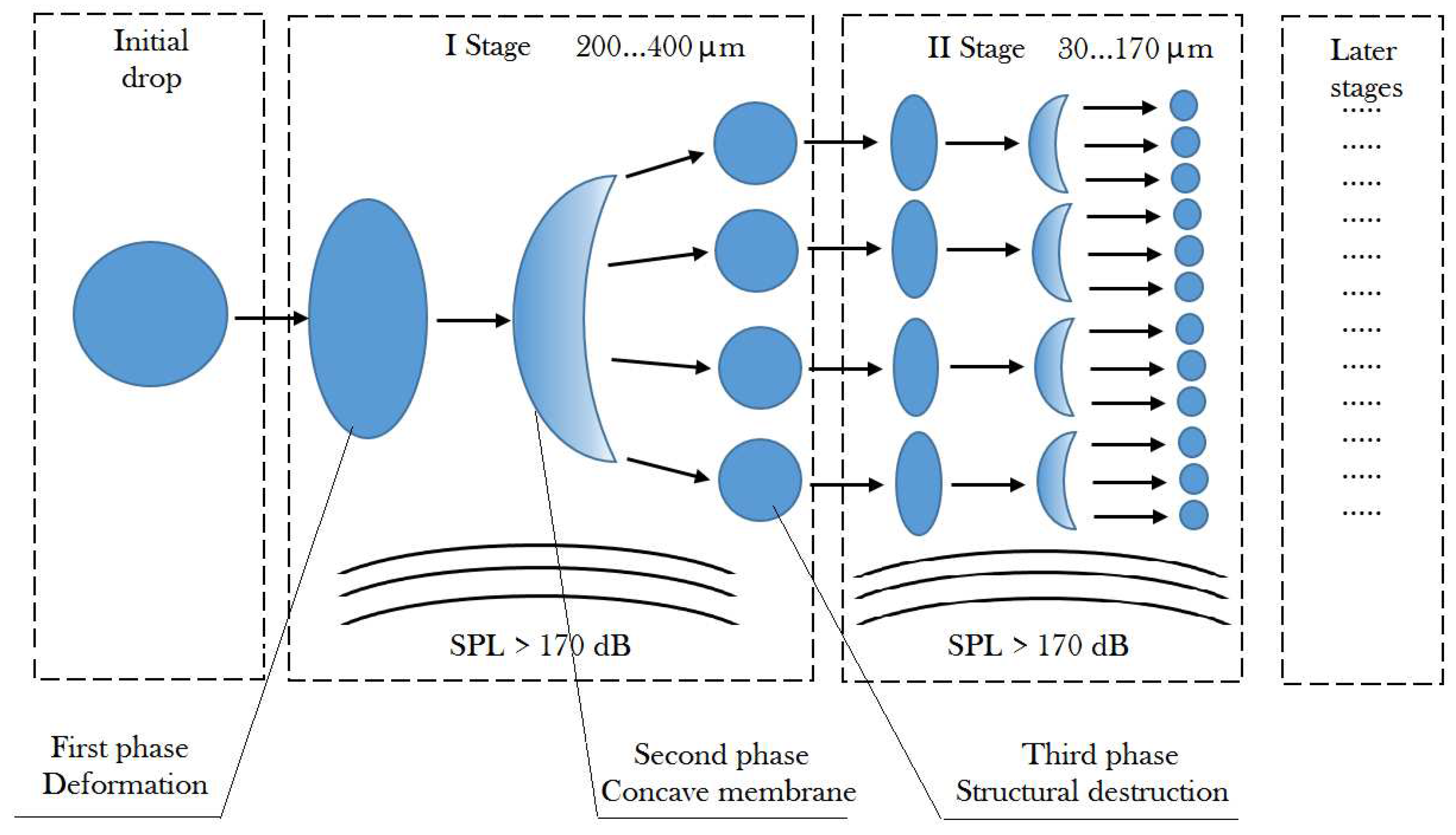
Therefore, in order to ensure the high-performance generation of highly dispersed aerosols under impact of ultrasonic vibrations, a method of multistage ultrasonic spraying with introduction of acoustic energy to the liquid through gas was proposed. The concept of implementation of the proposed technique of ultrasonic spraying is explained by diagram provided in Figure 1.

The proposed method is that sprayed liquid is subjected to dispersion into large droplets by any known method of spraying, ensuring sufficient productivity with large droplet diameters, up to several millimeters (e.g., by hydraulic, ultrasonic spray at low frequency of exposure, etc.) at the first stage. The productivity of initial large droplet formation will determine that of the overall multistage process. The initial droplets generated with high productivity, which are in the air and moving in the direction of gravity (or the gas flow transporting the droplets) are exposed to ultrasonic vibrations (standing ultrasonic wave) on the gas side.

Due to this, the droplets are deformed and destroyed, and the disperse composition of the droplets undergoes further evolution. The described process is repeated for each of the newly formed droplets many times, as many times as the droplet interacts with the velocity anti-node in the standing ultrasonic wave.

The process of droplet deformation and destruction while the droplet is in ultrasonic field continues until the surface tension forces do not equalize the effect of the acoustic field forces. Thus, the sound pressure level is the main quantity that determines the minimum size to which a droplet can collapse. Analyzing the forces effecting the particle, the value of the threshold intensity of particle destruction can be determined [14]:

(3)

where σ_stp is the strength of the particle, ω is the frequency of emission, ρ_l is the density of the fluid, W_l = ρ_l c is the wave resistance, c is the speed of sound.

It should be borne in mind that the strength of water σ_stp under pulse impact is several orders of magnitude less than the reference (theoretical) value [22]. An equation for the minimum droplet diameter to which the droplet can break down at a given level of exposure intensity I is obtained from Equation (3):

(4)

The intensity of exposure is related to the sound pressure level p by a known relationship:

(5)

Thus, there is a limiting size up to which a drop can be destroyed, depending on the intensity of ultrasonic vibrations. At low intensities of ultrasonic vibrations, this size will be larger than the initial size of the droplets, which means they will not be destroyed. In such a case, the primary droplets generated with high productivity, (e.g., 100 µm), will be exposed to ultrasonic vibrations (standing ultrasonic wave) on the gas side, for example, 3...5 times (stages) when moving in the direction of gravity (or the gas flow transporting the droplets), which will ensure generation of particles with an average size of less than 40 µm. The number of stages will be determined by the number of anti-nodes on the path of the drop.

3. Ultrasonic Emitter

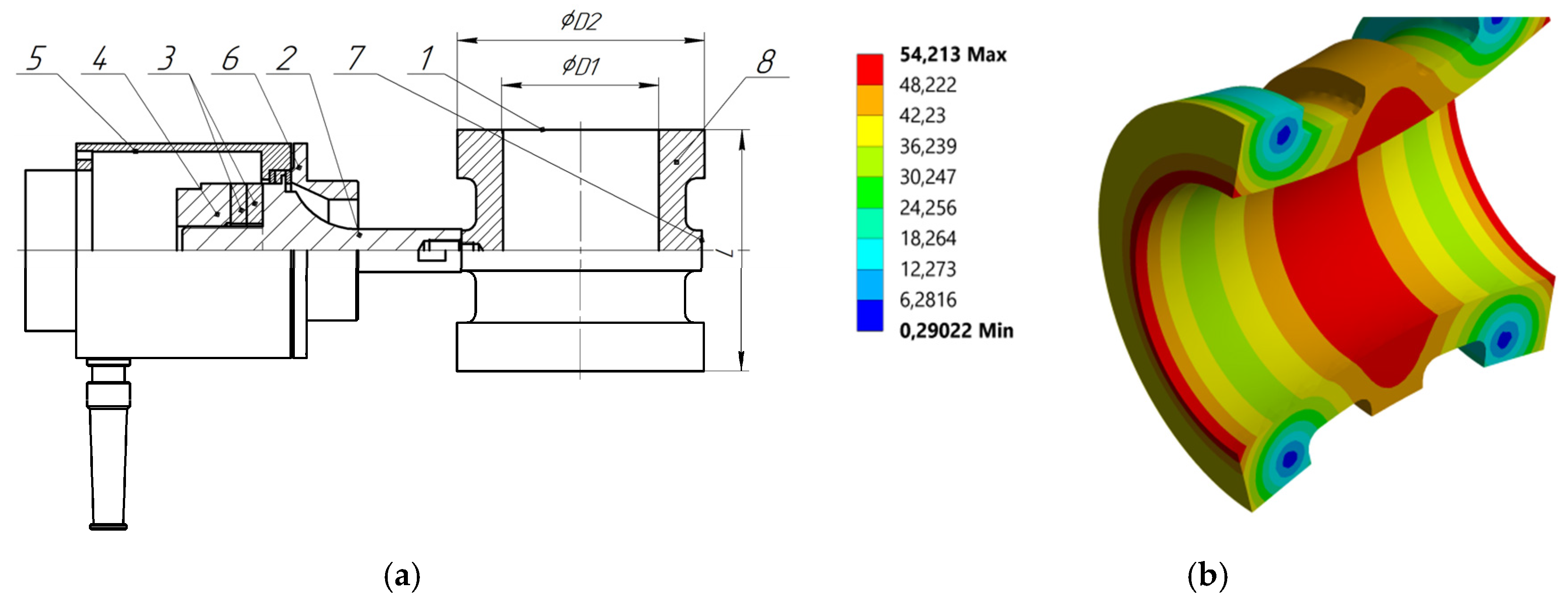
An ultrasonic emitter in the form of a hollow bending-oscillating cylinder (tubular emitter) was developed for practical implementation of the proposed multistage ultrasonic spraying technique. The emitter is a cylinder of stepped-variable cross-section, which generates bending-diametral vibrations at a frequency above 20 kHz. The shape of a hollow cylinder was chosen for this emitter in order to ensure self-focusing of ultrasonic vibrations in the internal cavity on the axis of the cylinder. Application of this type of emitter enables generation of a regular structure of vibrations of great length. Liquid droplets consistently passing the maximums of standing wave velocity inside the cylindrical emitter will deform and collapse until they reach the minimum possible particle size for the sound pressure level generated by the emitter.

To ensure sufficient ultrasonic vibration intensity at high ultrasonic frequencies, a multi-package transducer with radially spaced Langevin transducers can be used as the piezoelectric transducer [23,24]. Estimation of acoustic and geometric parameters and calculation of the emitter vibration waveform was performed using modal analysis in the finite element modeling system (ANSYS package).

The tetrahedral type of finite element was used for estimation and analysis of performance of an ultrasonic emitter exposed to volumetric stress state. When the modal analysis was performed, convergence of numerical results for different emitter designs was analyzed. A modeling result that corresponded to a finite element model with minimized number of finite elements, the increase of which results in change in the main values of design parameters (e.g., natural frequency of vibrations) by no more than 0.2 – 0.5 %, was considered satisfactory.

Figure 2 shows a drawing of tubular emitter and the waveform of its vibrations obtained from results of estimations.

The ultrasonic field generated by the tubular emitter was estimated by finite element analysis in ANSYS. The Harmonic Acoustics module of harmonic acoustic analysis was used. During modeling, the boundary conditions were set on the basis of the obtained design data specifying cylindrical emitter parameters (frequency of vibrations and distribution of vibration amplitudes of the emitting surface). The scope of calculation domain was limited by inner surface of the tubular emitter. Boundary conditions were set at the ends of the estimated area: radiation boundary. During the estimations of acoustic field, the iterative variation of tubular emitter dimensions was carried out to ensure the standing wave mode in the inner space of the emitter. Figure 3 shows the results of estimations of distribution of the sound pressure generated in the emitter and a picture of the manufactured emitter.

The results of estimations show that conditions and sufficient sound pressure level in the volume of the multistage spraying chamber (more than 190 dB) are available for implementation of multistage spraying. Three sound pressure maxima are formed along the emitter axis. Thus, a droplet moving inside the emitter will undergo up to three stages of disintegration. The sound pressure level was measured inside the fabricated emitter to confirm the estimations. The measurements were carried out by a noise meter/vibro-meter Ekofizika-110A with a microphone VMK-401. The measurements showed that the sound pressure level formed inside the tubular emitter is within 170...182 dB. The measurements were carried out at maximum power consumption.

Next, the acoustic power of the developed emitter was determined. It was determined as the difference between total electrical power consumed by the emitter and the emitter’s own loss power. The loss power was estimated by measuring the power consumed by the emitter when operating without a load. For this purpose, the emitter was placed in a vacuum chamber [25]. The air was evacuated from the vacuum chamber to residual pressure not exceeding 1000 Pa. The electric power consumed by the emitter was measured using the MT-1010 measuring instrument.

The performed calculations and measurements enabled estimation of the main technical parameters of the developed tubular emitter (Table 1).

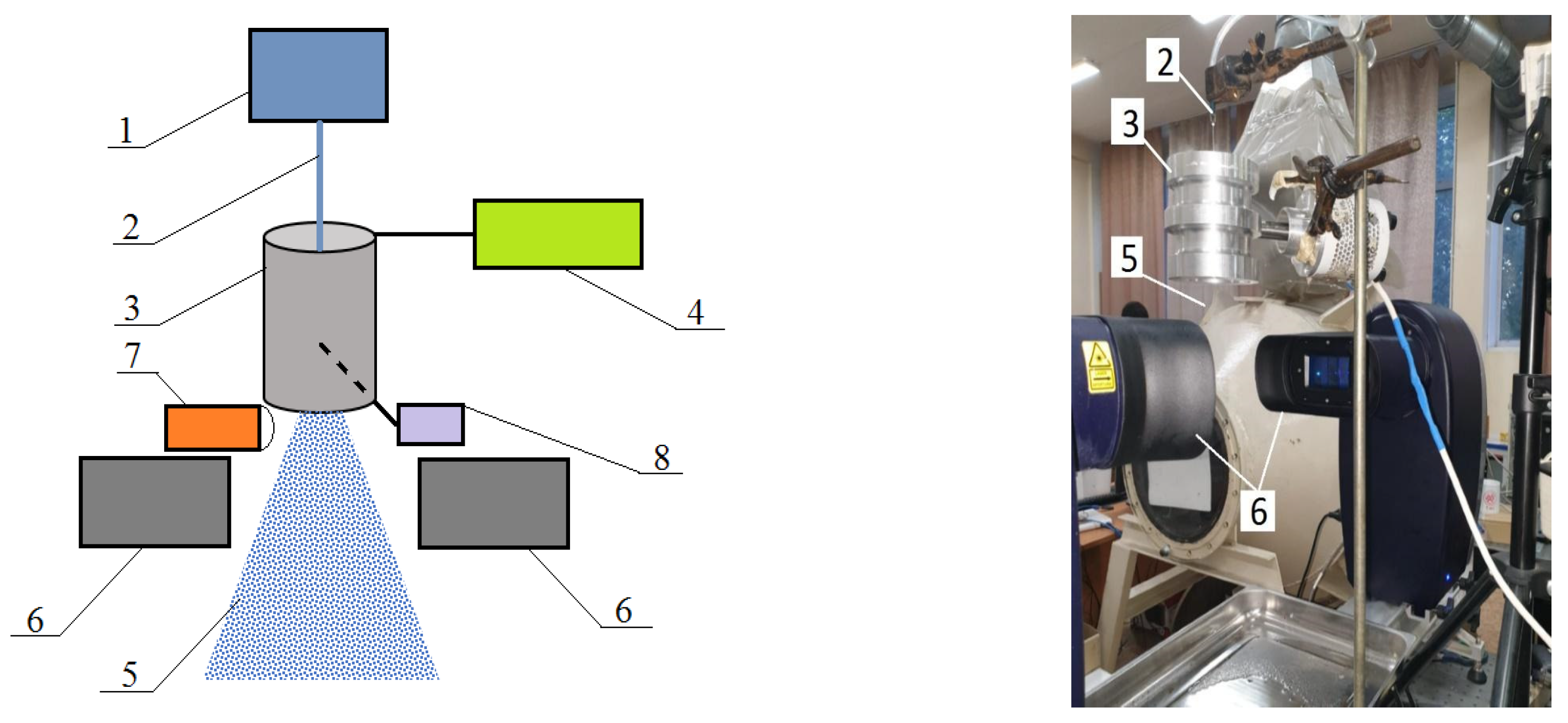
A test bench was developed in order to experimentally assess the feasibility and efficiency of the proposed method of multistage spraying of liquids. The design diagram of the test bench and its image are shown in Figure 4. The test bench allows to carry out high-speed video recording of the droplet breaking process and to estimate dispersion characteristics of generated aerosol depending on the sound pressure level and liquid properties.

The test bench consists of an ultrasonic tubular emitter (3) with a piezoelectric transducer powered by an electronic ultrasonic frequency generator (4), a dispenser (1) with mounted nozzle (2) and an optical aerosol analyzer 6 Malvern SprayTec. The principle of operation of the analyzer is based on laser diffraction. Spraytec analyzer enables measurement of particle dispersity with frequency up to 10 kHz in the range from 0.1 to 2000 μm. During the experiments, the sprayed liquid is fed by peristaltic pump (1) into the nozzle (2) installed at the end of the tubular emitter.

The nozzle generates liquid droplets of 1500...2000 µm in size (initial droplet size) with productivity up to 20 ml/s. The dispersion characteristics were measured at two points shown in Figure 4:

1): a distance of approximately 1/3 from the upper end of the tubular emitter, after the droplets passed the first standing wave vibrations anti-node inside the emitter. A vacuum aspirator was used to collect the aerosol droplets. The selected droplets corresponded to the aerosol after the first stage of spraying.
2): at a distance of 50 mm from the lower end of the tubular emitter, to determine the dispersion characteristics of the aerosol generated as a result of multistage spraying of liquids.

Since three ultrasonic vibration anti-nodes are formed along the axis of the developed emitter, it will provide three stages of droplet breakdown.

Visual observation and analysis of dynamics of deformation and destruction of liquid droplets in the sound field were performed using a high-speed video camera “VideoSprint”. The shooting rate was 5000 frames/s.

Water, aqueous solutions of glycerol (of different viscosity) and alcohol (of different surface tension) were used as sprayed liquids.

4. Results and Discussion

4.1. Droplet Disintegration Dynamics

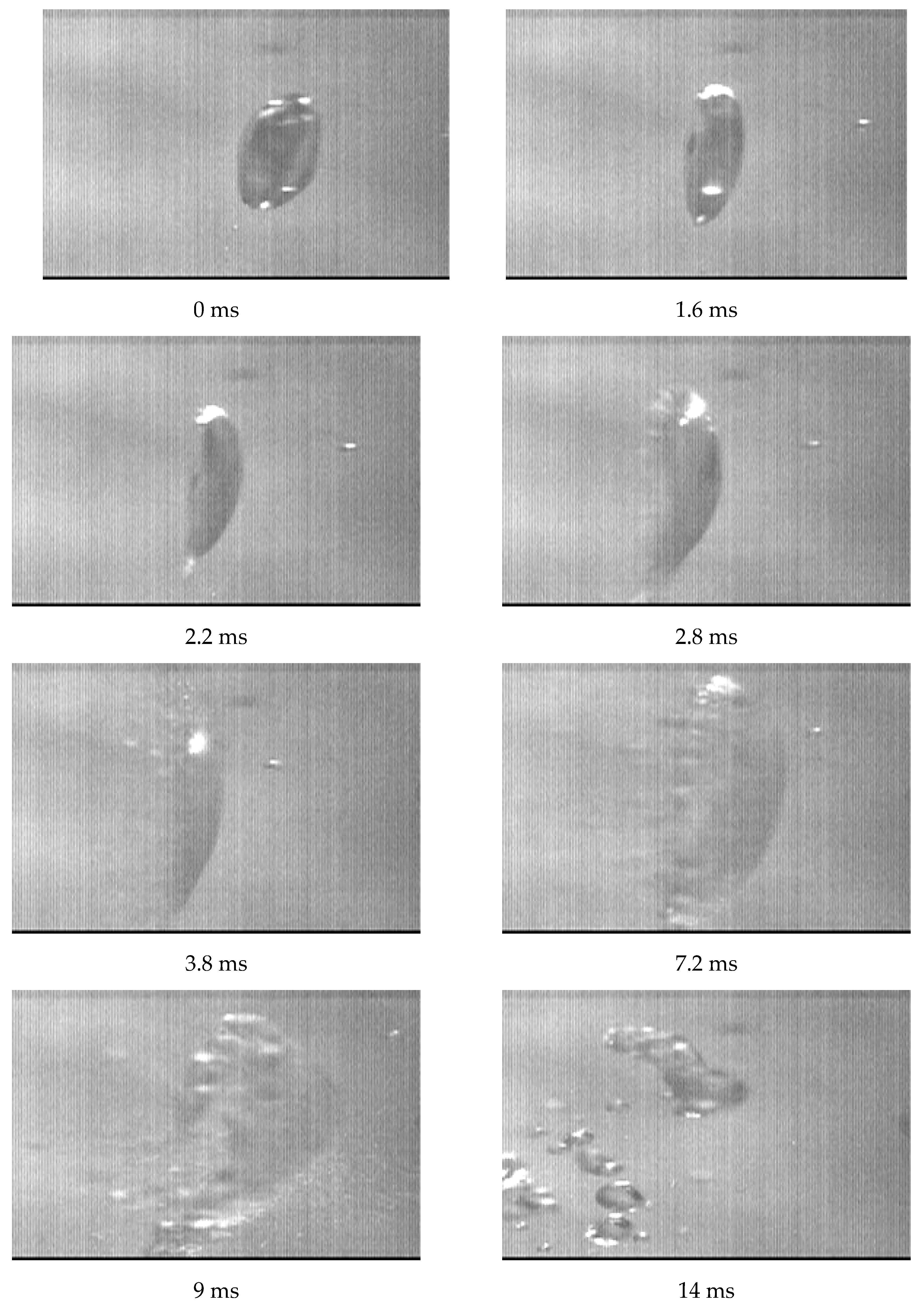
To study dynamics of the first stage of liquid droplet disintegration, the video camera was focused on the area on the tubular emitter axis located 20 mm below the upper end of the emitter (the first stage of droplet disintegration). The records of deformation and disintegration of the droplet with indicated time marks are shown in Figure 5. The sound pressure level inside the tubular emitter was 175 dB.

The presented sequence of high-speed video frames indicates that droplet undergoes a series of deformations while in ultrasonic field before breaking into smaller droplets. The following phases of deformation and disintegration of the droplet can be distinguished in the first stage:

First phase. The initial droplet possessing initial momentum (obtained by crushing the liquid jet at the nozzle outlet) deforms as it approaches the region of velocity anti-node in the standing wave. The droplet impacted by radiation pressure assumes the shape of a concave membrane (disk).
Second phase. As the diameter of the liquid membrane increases and its concavity degree increases, the liquid film thickness decreases. Faraday capillary waves [26] are generated on the surface of the liquid disk under the impact of ultrasonic vibrations. These waves reach the highest amplitude at the edges of the disk. When the Faraday waves reach their critical amplitude, disintegration of the liquid disk begins, starting from the outer edge. The smallest droplets are generated owing to implementation of this mechanism.
Third phase. Instability of the liquid film increases due to further increase of the disk size and decrease of its thickness. When the liquid membrane reaches certain limiting size, the liquid film thickness decreases below critical value. This results in structural destruction of the liquid disk with formation of large droplets.

This completes the first stage of droplet breakdown. The formed polydisperse droplets are subjected to structuring effect of secondary nonlinear effects arising in ultrasonic field. Large droplets (formed at the first stage), possessing, as a rule, lower emission rate (at liquid film destruction) move in the direction of the next vibration velocity anti-node in the standing wave. This motion is originated by the impact of the resultant radiation force, which is proportional to squared droplet radius.

Thus, sufficiently large (more than 100 µm) liquid droplets formed at the first stage of spraying, with a higher velocity (because the force effecting the droplet is proportional to squared droplet diameter) move into vibration velocity anti-node, where they undergo secondary and subsequent disintegration.

Accordingly, the smallest droplets move in the direction of the vibration velocity nodes, where the ultrasonic vibrations do not have a significant effect on them. Further such drops leave the ultrasonic exposure domain (in this case, from internal volume of the tubular emitter) by action of gravity or with the flow of transporting air. In this case, due to arrangement of small droplets in the nodes of vibrational velocity, their coagulation under impact of ultrasonic vibrations does not occur, in fact.

Thus, in the proposed technique of multistage spraying, ultrasonic vibrations have not only dispersing effect (breakdown of liquid droplets) but also a structuring effect (selective breakdown of the largest droplets) [27,28,29].

The recorded images of deformation and disintegration of the droplet at the second and subsequent stages are shown in Figure 6.

As can be seen from images presented on Figure 6, the secondary and subsequent breakdowns also deform the droplets into a flat disk. However, meniscus is not formed due to the smaller diameter of the droplet. Owing to this, Faraday waves are excited all over the surface of the disk. As a result, the disk collapses into small droplets whose diameters are proportional to wavelength of excited capillary waves. At the same time, since the capillary waves excited closer to edge of the disk have a shorter wavelength, the droplets formed from the edges of the disk will also have a smaller diameter. This explains the scatter of droplet diameters, relative to the median diameter.

4.2. Dispersion Characteristics of Formed Droplets

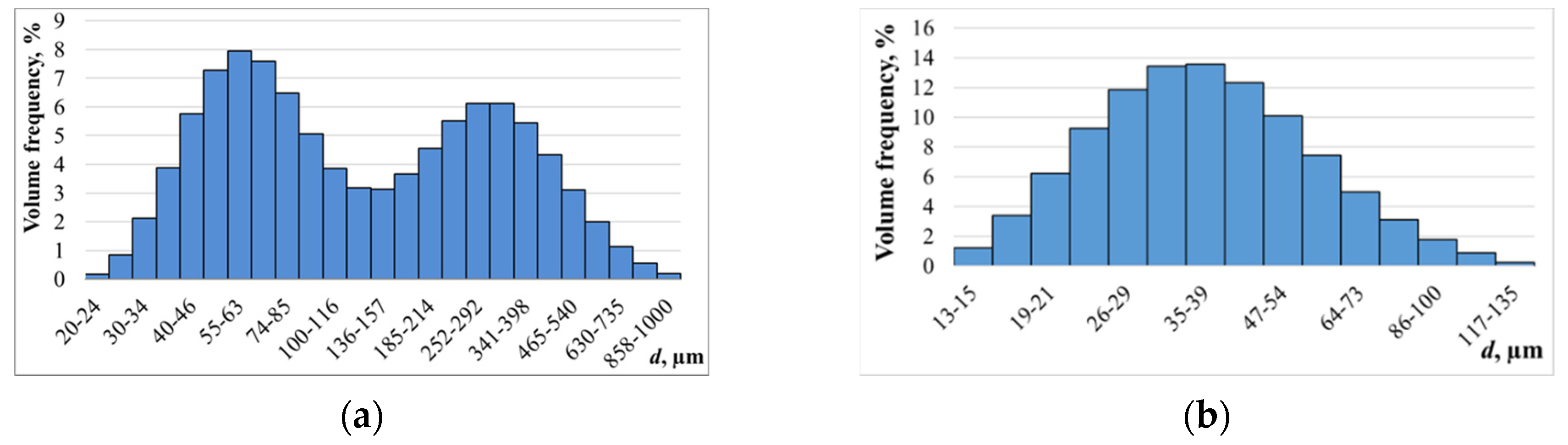
To confirm applicability of the proposed spraying technique, the disperse composition of droplets formed by spraying water (settled, tap water, temperature 23 °C) was previously analyzed. The sound pressure level was 182 dB. The water supply capacity was equal to 5 ml/s. The initial size of droplets injected into the tubular emitter was equal to 2000 µm. Histograms of droplet distribution, after the first stage of spraying and at the outlet of the tubular emitter are shown in Figure 7.

As can be seen from the histograms presented in Figure 7a, a bimodal aerosol consisting of small droplets (the first peak formed by capillary mechanism of liquid film breakdown) and large droplets (the second peak consisting of droplets formed after structural breakdown of liquid film) is generated at the first stage of dispersion of initial droplets. The median droplet diameter (hereinafter referred to as Sauter’s diameter) of the first peak is 89 μm.

The largest droplets formed at the first stage are subjected to subsequent stages of breakdown. As a result, the distribution of aerosol droplets at the tubular emitter outlet takes the shape shown in Figure 7b. The median (Sauter) diameter equals 34 µm. It can be concluded from comparison of obtained distributions that the median diameter of resulting droplets (Figure 7b) is smaller than the median diameter of small droplets after the first breakdown stage (the first peak, in Figure 6a). This indicates that coagulation processes have almost no effect on the disperse composition of the formed droplets. This is due to the fact that the ultrasonic frequency used (22.2 kHz) is significantly higher than that required for coagulation of the formed liquid droplets, and does not engage them with oscillatory motion [30,31,32]. This fact is the subject of future studies.

It was established that the droplets formed have a smaller diameter than the same obtained by known method of ultrasonic spraying of liquid in a layer at the same frequency of exposure. The proposed multistage spraying technique provides median (Sauter) diameter of 120 µm vs. 34 µm for ultrasonic spraying in a layer of liquid. This provides significantly higher (more than 10 times) spraying productivity than in the known ultrasonic spraying techniques [33,34].

4.3. Dependence of Droplet Diameter on Spraying Rate

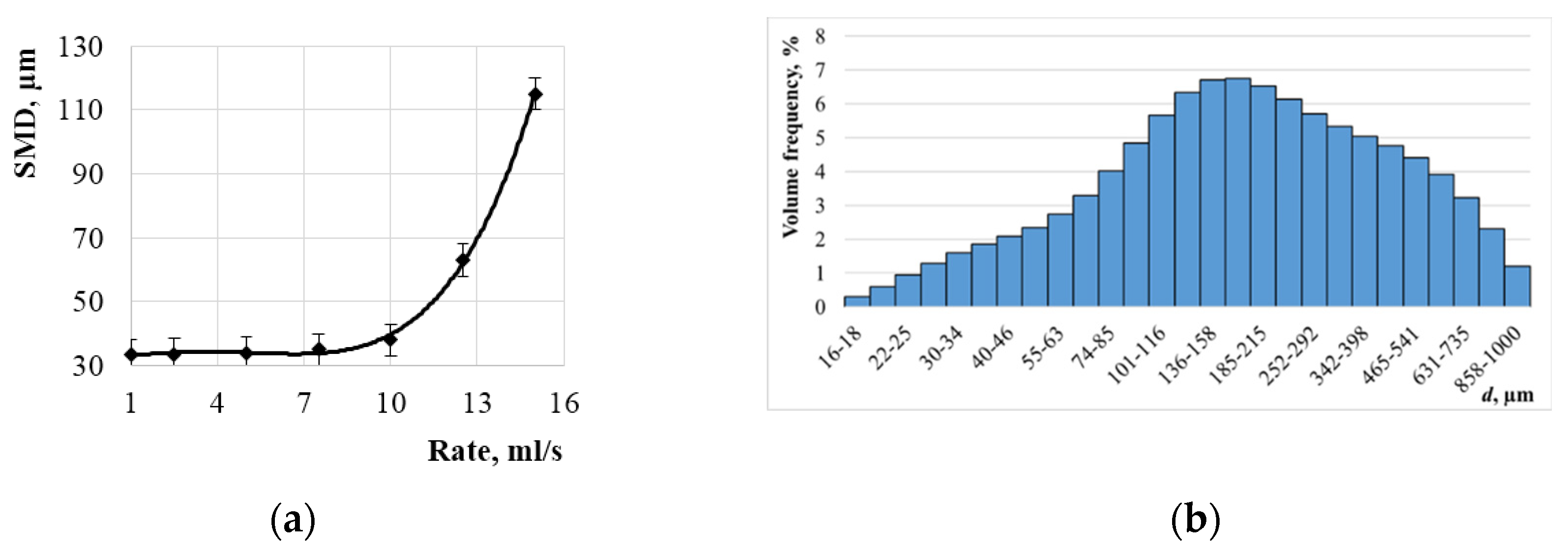
Figure 8, shows the histograms of droplet diameter distribution for increased liquid supply rate of 10 ml/s.

It follows from the presented histograms (Figure 8a) that at the increased liquid supply rate the proportion of coarse droplets increases at the first stage of spraying. Analysis of recorded images of droplet breakdown for increased liquid supply rate showed that due to increase in the rate of emission of primary droplets from the nozzle (supply rate is increased by increasing the pressure of liquid in the nozzle). Since the droplet travels into the anti-node region at a higher velocity, the time of its structural instability development is reduced. And the time of formation of small droplets due to capillary Faraday waves is reduced, on the contrary. In addition, an increased concentration of secondary droplets flying apart following breakdown of the primary droplet, resulting in their increased coagulation probability can result in generation of higher number of large droplets.

In turn, the disperse composition of the aerosol after passing all stages of spraying slightly shifts to the region of larger particles (Sauter’s diameter is 38 µm). The increase in the median diameter was not more than 5 µm. The fact that the droplets successively decelerate as they travel through anti-nodes of ultrasonic vibration velocity correlates with no significant increase in particle size with increasing spraying productivity. As a result, the time of droplet exposure to anti-nodes of ultrasonic vibration velocity is sufficient to generate Faraday capillary waves over the entire surface of the droplet (flattened into a disk). As a result, small droplets proportional to the length of excited capillary waves are formed.

The dependence of median diameter of the formed droplets on the sprayed liquid supply rate is shown in Figure 9a. Figure 9b shows the histogram of droplet diameter distribution for maximum output.

Thus, it was established that characteristics of droplets remain almost constant within a wide range of variations in the aerosol generation productivity. A slight increase in median diameter of formed droplets is associated with an increase in the probability of coagulation of droplets with increase in their concentration. However, when the productivity exceeds a certain limit value (depends on the emitter sizes; for the studied design - 10 ml/s), the median droplet diameter begins to increase significantly (Figure 9a). It continues increasing up to the values corresponding to median diameter of large droplets obtained at the first stage of droplet breakdown. In this case, the histogram of droplet diameter distribution takes the shape shown in Figure 9b.

4.4. Dependence on Sound Pressure Level

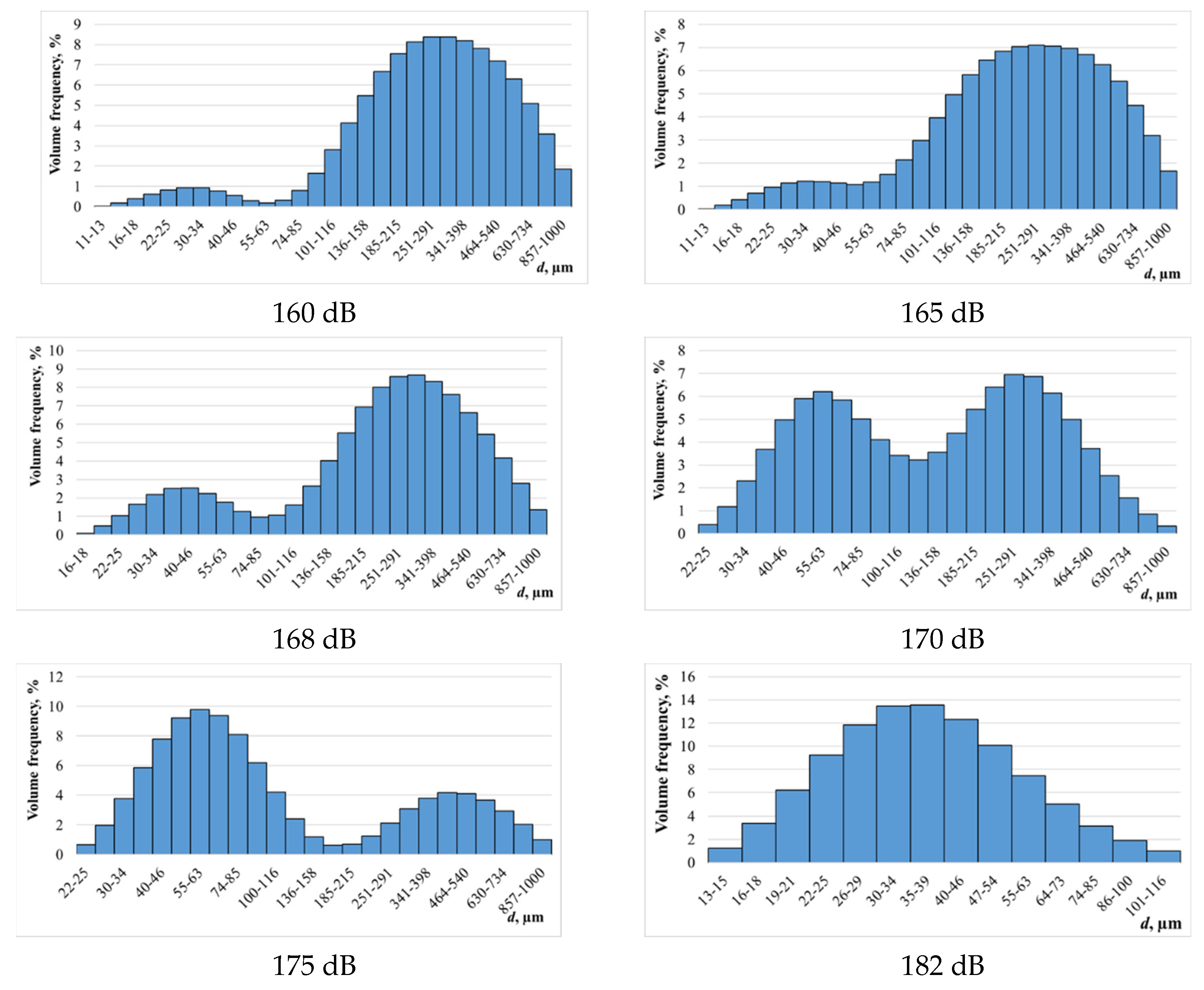
Figure 10 shows a sequence of histograms characterizing evolution of disperse composition of the formed droplets (at the outlet of the tubular emitter) depending on sound pressure level. Liquid supply rate of 5 ml/s.

It follows from the presented histograms that the sound pressure level is the main parameter of the process, which significantly affects the dispersion characteristics of generated aerosol. At the same time, hydrodynamic parameters (flow rate of the sprayed liquid) and physical properties of the liquid (will be shown below) have much less influence.

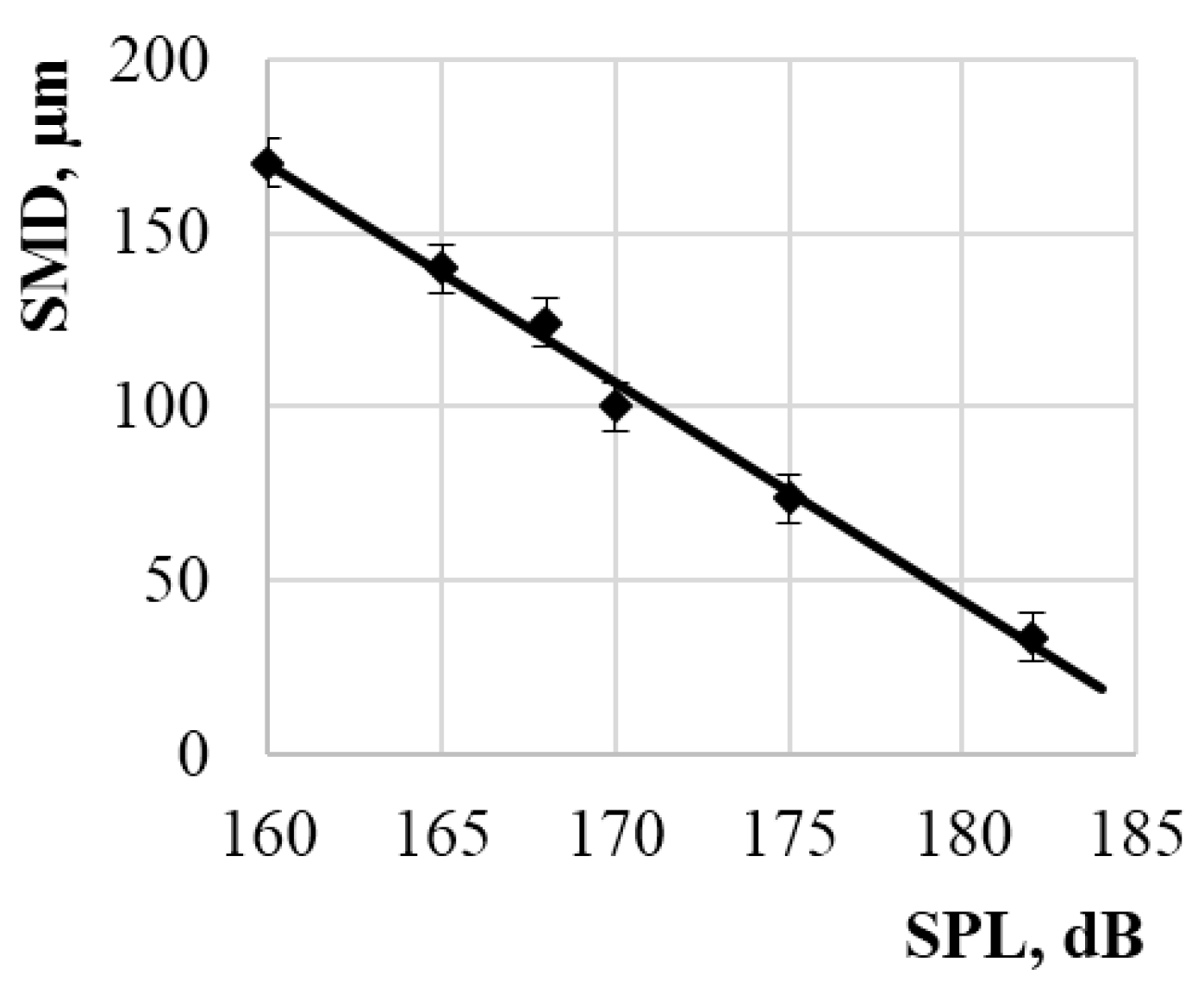
This makes the proposed technique invariant to conditions of the process (flow rate and physical properties of the liquid), but at the same time it can be configures through selection of ultrasonic exposure modes (sound pressure level). All this ensures adjustability of disperse characteristics of generated aerosol. Figure 11 shows the dependence of median diameter of formed droplets on the sound pressure level to identify the limits of controllability of disperse composition of formed droplets.

It can be seen that changing the sound pressure level in the range of 160-182 dB enables adjustment of the median diameter of the formed droplets in the range of 170-34 µm.

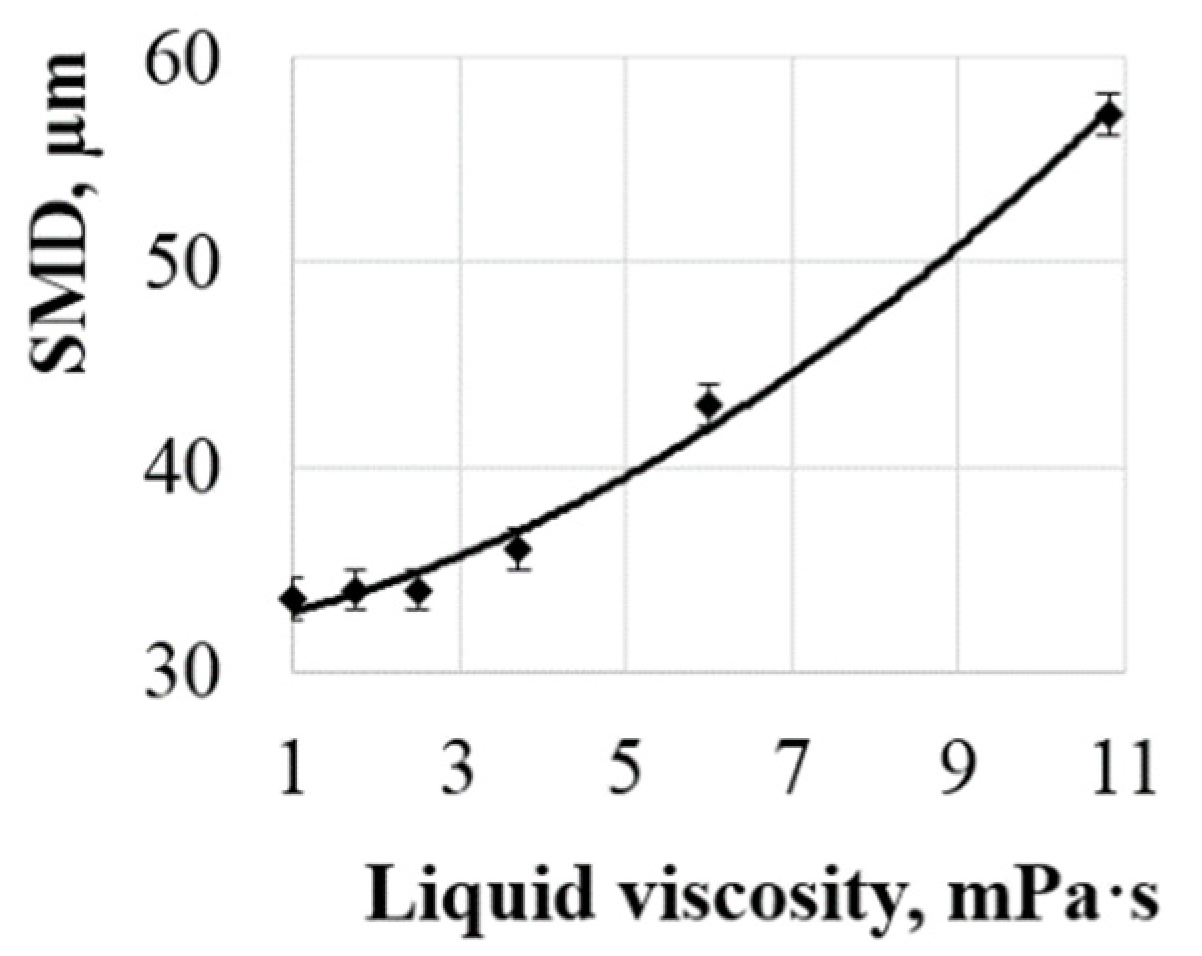
4.5. Dependence on Liquid Viscosity

As mentioned above, viscosity is one of the main physical properties of the liquid that influence disperse characteristics of the formed liquid droplets. To analyze the effect of liquid viscosity on disperse composition of the resulting aerosol, an aqueous solution with a volume content of glycerol of 20%; 30%; 40%; 50% and 60% was used. The viscosities of the liquid were respectively: 1.8; 2.5; 3.7; 6.0; 10.8 mPa·s. The sound pressure level was 182 dB and the liquid flow rate was 5 ml/s.

Histograms of droplet diameter distribution at spraying of liquids with different viscosity are presented in Figure 12.

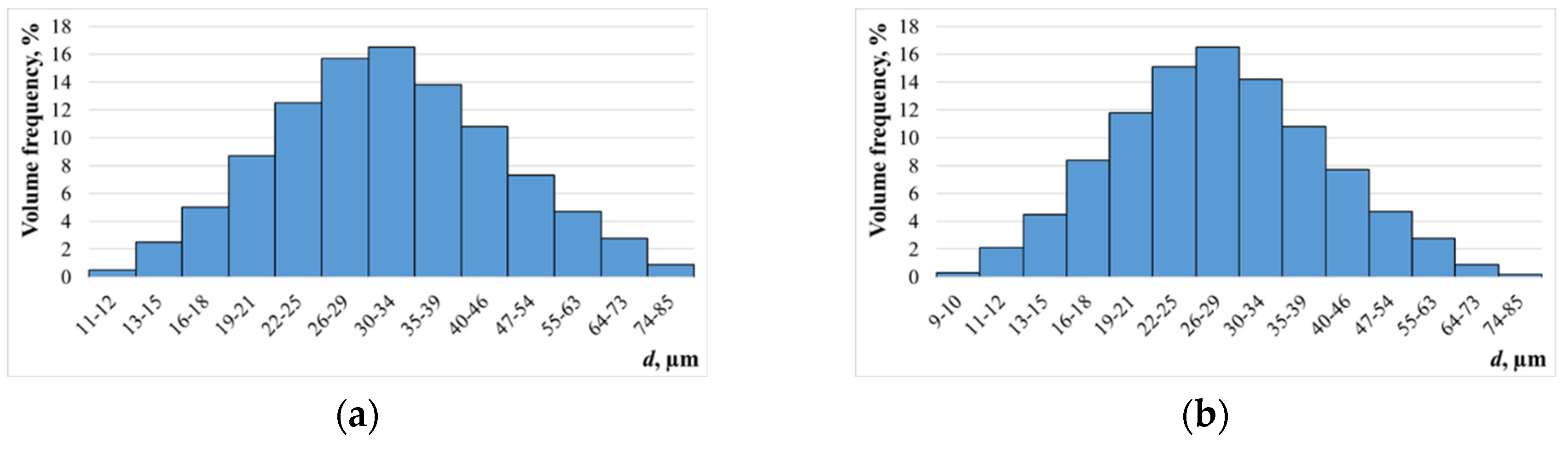
As can be seen from the histograms, with increasing viscosity of the liquid the droplet diameters tend to migrate to large diameters domain. The spread of drops relative to the median diameter increases likewise. For example, at liquid viscosity of 1.8 mPa·s – the median diameter of formed droplets is 34 μm, and with increasing viscosity up to 10.8 mPa·s the median diameter increases to 57 μm.

Dependence of median diameter of formed droplets on the viscosity of the liquid is presented in Figure 13.

The presented dependence shows that liquid viscosity has poor effect on diameter of formed droplets. In the range of viscosities from 1 mPa·s (water) to 3.7 mPa·s (40% aqueous glycerol solution), a weak increase in the median diameter of formed droplets (no more than 2 μm) is observed. Further increase in viscosity of the liquid results in increase in the median diameter of the resulting droplets, up to 57 µm. Apparently, this is explained by the fact that the forces of viscous friction prevent development of Faraday waves and generation of smaller droplets. At the same time, the majority of droplets are formed by mechanism of structural breakdown of a liquid droplet (large droplets larger than 100 µm are formed).

4.6. Dependence on Liquid Surface Tension

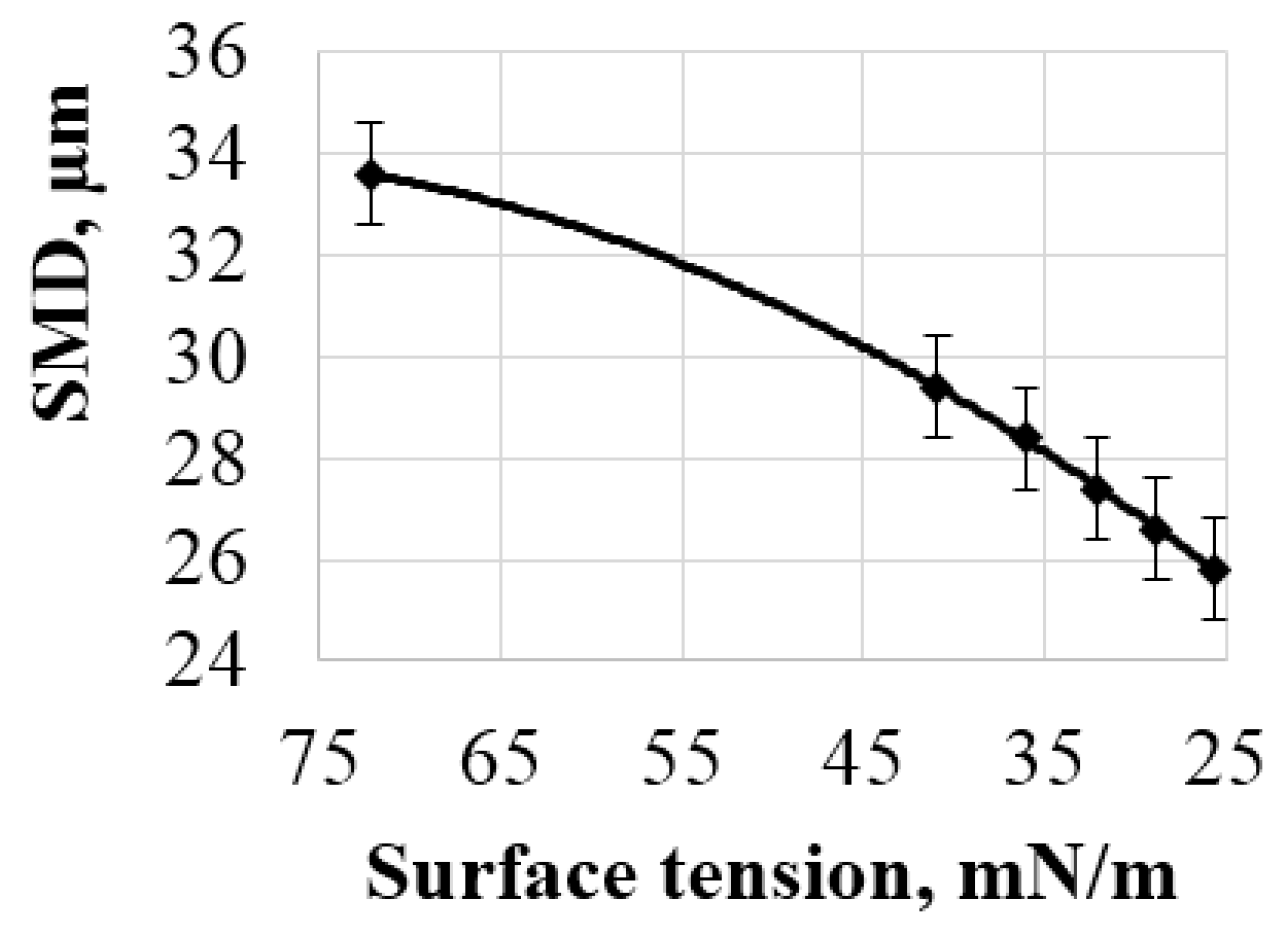
It is known that surface tension is the key factor effecting the wavelength of generated Faraday capillary waves and, consequently, diameter of generated liquid droplets. A solution of ethyl alcohol in water in proportions of 50%, 60%, 70%, 80%, and 90% was used as the spray liquid. The respective surface tensions of the solutions were equal: 40,9 mN/m, 36 mN/m, 32.1 mN/m, 28.8 mN/m, 25.6 mN/m. The sound pressure level was 182 dB and the liquid flow rate was 5 ml/s. Figure 14 shows comparative histograms of droplet distribution formed at minimum and maximum ethyl alcohol content in solution.

It follows from the presented histograms that a decrease in surface tension (higher alcohol content in the solution) contributes to decrease in diameter of the formed droplets. This is caused by decrease in the wavelength of generated Faraday capillary waves (see Equation (1)). In addition, the spread of the formed droplets diameters also decreases. The histogram in Figure 14b becomes narrower.

Figure 15 shows the dependence of median diameter of formed droplets on the surface tension of the liquid.

Figure 15 shows that the median diameter of formed droplets monotonically decreases with decreasing surface tension of the liquid. However, the dependence (decrease by 8 µm) of the median droplet size on the surface tension is not as significant as that on the sound pressure level.

Thus, a multistage spraying technique, consisting in generation of a large number of large initial diameter particles (to ensure high productivity) and their subsequent breakdown during propagation in ultrasonic field, was proposed. The disperse characteristics of the formed droplets, from the modes of ultrasonic exposure and the properties of liquid were studied. It is shown that the method of multistage spraying of liquid, enables generation of liquid droplets of smaller diameters and with higher productivity than other commonly used techniques of ultrasonic spraying (spraying in a layer and spraying in a fountain).

5. Conclusion

It has been established on the basis of analysis of numerous practical implementations of ultrasonic spraying why it wasn’t possible to provide high spraying productivity required by contemporary production (more than 50 ml/s) under the condition of formation of liquid particles with median diameter less than 20 µm.

In order to provide the required parameters of ultrasonic spraying required by modern high-tech industries, a method of multistage spraying was proposed and developed, consisting in generation of a large number of particles of large initial diameter (to ensure high productivity) and their subsequent destruction by propagation in a periodic ultrasonic field (to ensure small droplet sizes at high productivity).

To create the relevant conditions for multistage breakdown of preformed large droplets, an ultrasonic emitter, which is a cylinder of a stepped-variable cross-section, providing generation of bending-diameter oscillations, was developed and practically implemented. The shape of this emitter in the form of hollow cylinder was chosen to ensure self-focusing of ultrasonic vibrations in the internal cavity on the cylinder axis. The developed emitter provides generation of periodic ultrasonic field with frequency of 22.2 kHz and sound pressure level of up to 182 dB. Configuration of the ultrasonic field inside the emitter enables three-stage spraying.

To analyze the multistage spraying process and to assess its functionality, a test bench including tubular emitter, a nozzle for liquid supply and an aerosol analyzer SprayTec was manufactured. The test bench provides three-stage ultrasonic impact on liquid droplets with sound pressure level up to 182 dB. It is possible to visually observe the process of droplet breakdown using a high-speed video camera and control dispersion characteristics of the aerosol at different stages of formation. This allowed to identify the best conditions of ultrasonic exposure and spraying modes.

The effectiveness of proposed and developed technique suitable for generation of droplets of size less than 40 µm with performance exceeding the known ultrasonic spraying methods by 10 times at least has been confirmed in the course of analysis.

It is shown that disperse characteristics of the formed droplets mainly depend on the sound pressure level at which the droplets break down. So, the increase of sound pressure level from 160 dB to 182 dB change the average diameter of formed droplets in the range of 34-170 µm, while the spraying productivity is not changed. Physical properties of liquids have a much smaller effect on diameter of the formed droplets. This way, with increase in viscosity from 1 mPa·s (water) to 3.7 mPa·s (40% aqueous solution of glycerin) indicates weak increase in the median diameter of formed droplets (no more than 2 μm). Further increase in the viscosity of the liquid results in increase in the median diameter of resulting droplets, up to 57 µm. In turn, the result of decreasing the surface tension of the liquid from 72.8 mN/m to 25.6 mN/m is further decrease in the droplet size by 8 μm.

The obtained results confirmed applicability of the developed technique to intended functions of various processes (such as medicine, food industry, mechanical engineering, etc.).

Author Contributions

Conceptualization, A.S and V.K.; methodology, V.K. and A.S.; investigation, S.T., D.G. and V.N.; writing-original draft preparation, A.S. and S.T.; writing-review and editing, V.K. and D.G. All authors have read and agreed to the published version of the manuscript.

Funding

This study was carried out with a grant from the Russian Science Foundation № 23-19-00875, https://rscf.ru/project/23-19-00875/.

Data Availability Statement

The data that support the findings of this study are available upon request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ramisetty, K.A.; Pandit, A.B.; Gogate, P.R. Investigations into ultrasound induced atomization. Ultrason. Sonochem. 2013, 20, 254–264. [CrossRef]
Kustron, P., Korzeniowski, M., Sajbura, A., Piwowarczyk, T., Kaczynski, P., Sokolowski, P. Development of High-Power Ultrasonic System Dedicated to Metal Powder Atomization. Appl. Sci. 2023, 13, 8984. [CrossRef]
Yasuda, K.; Mochida, K.; Asakura, Y.; Koda, S. Separation characteristics of alcohol from aqueous solution by ultrasonic atomization. Ultrason. Sonochem. 2014, 21, 2026–2031. [CrossRef]
Gharsallaoui, A.; Roudaut, G.; Chambin, O. Applications of spray-drying in microencapsulation of food ingredients: An overview. Food Res. Int. 2007, 40, 1107–1121. [CrossRef]
Wang, J.-X.; Li, Y.-Z.; Li, J.-X.; Li, C.; Zhang, Y.i.; Ning, X.-W. A gas-atomized spray cooling system integrated with an ejector loop: Ejector modeling and thermal performance analysis. Energy Convers. Manage 2019, 180, 106–118. [CrossRef]
Guanglin, N.; Yiwang, B.; Detian, W.; Xiaogen, L. Effect of Atomization Gases on the Elastic Modulus of Thermal-sprayed NiCr Coatings. Rare Metal Materials and Engineering 2018, 47, 1025-1030. [CrossRef]
Yang, C.-C.; Chau, J.L.H.; Weng, C.-J.; Chen, C.-S.; Chou, Y.-H. Preparation of highentropy AlCoCrCuFeNiSi alloy powders by gas atomization process, Mater. Chem. Phys. 2017, 202, 151–158. [CrossRef]
Zhang, F., Chen, B., Gui, Z., zZhang, J., Huang, X., Liang, J., Zeng, Y., Tan, T., Xie, N., Wen, Y., Wang, J. Error Correction and Reanalysis of the Vibration Analysis of a Piezoelectric Ultrasonic Atomizer to Control Atomization Rate. Appl. Sci. 2023, 13(10), 6293. [CrossRef]
Guerra-Bravo, E., Lee, H-J., Baltazar, A., Loh K.J. Vibration Analysis of a Piezoelectric Ultrasonic Atomizer to Control Atomization Rate. Appl. Sci. 2021, 11, 8350. [CrossRef]
Yasuda, K.; Honma, H.; Asakura, Y.; Koda, S. Effect of frequency on ultrasonic atomization. Proc. of Symposium on Ultrasonic Electronics 2010, 31, 363.
Taylor, G.I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes, Proc. R. Soc. A CCI, 1950, p.192. [CrossRef]
Lang, R.J. Ultrasonic atomization of liquids. J. Acoust. Soc. Am. 1962, 34, 14. [CrossRef]
Bouguslavskii, Y.Y.; Eknadiosyants, O.K. Physical mechanism of the acoustic atomization of a liquid. Sov. Phys. Acoust. 1969, 15, 14.
Mora, J.; Maestre, S.; Hernandis, V.; Todolı, J.L. Liquid-sample introduction in plasma spectrometry. TrAC Trends in Analytical Chemistry 2003, 22, 123-132. [CrossRef]
Wood, R.W.; Loomis, A.L. The physical and biological effects of highfrequency sound-waves of great intensity. Journal of the Franklin Institute 1928, 205, 151–153. [CrossRef]
Rozenberg, L. (Ed.). Physical principles of ultrasonic technology. Springer Science & Business Media. 2013.
Galakhov, A.N.; Khmelev, V.N.; Golykh, R.N.; Shalunov, A.V.; Nesterov, V.A.; Shalunova, A.V. Study of the process of liquid atomization from the ultrasonic disk radiator. 14th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk 2013, 119.
Yasuda, K.; Honma, H.; Asakura, Y.; Koda, S. Effect of frequency on ultrasonic atomization. Proc. of Symposium on Ultrasonic Electronics 2010, 31, 363.
Dalmoro, A.; Angela Barba, A.; d’Amore, M. Analysis of size correlations for microdroplets produced by ultrasonic atomization. The Sci. World J. 2013, 7. [CrossRef]
Asami, T.; Yakou, R.; Ono, T.; Mlura, H. Ultrasonic atomization by difference between vibration displacements of two circular vibrating plates. J. Mech. Eng. Autom. 2016, 2, 30. [CrossRef]
Leea, M.W.; Parka, J.J.; Faridb, M.M.; Yoona, S.S. Comparison and correction of the drop breakup models for stochastic dilute spray flow. Applied Math. Modelling 2012, 36, 4512. [CrossRef]
Bogach, A. A.; Utkin, A. V. Strength of water under pulsed tension. Applied Mechanics and Engineering Physics, 2000, 41, 198-205. (In Russ.).
Khmelev, V.N.; Shalunov, A.V.; Nesterov, V.A. Summation of high-frequency Langevin transducers vibrations for increasing of ultrasonic radiator power. Ultrasonics 2021, 114, 1–12. DOI: 10.1016/j.ultras.2021.106413.
Khmelev, V.N.; Nesterov, V.A.; Shalunov, A.V. Ultrasonic Transducer with Increased Exposure Power and Frequency up to 100 kHz. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2021, 5, 1773-1782. [CrossRef]
Khmelev, V.N.; Shalunov, A.V.; Dorovskikh, R.S.; Golykh, R.N.; Nesterov, V.A. The measurements of acoustic power introduced into gas medium by the ultrasonic apparatuses with the disk-Type radiators. International Conference and Seminar on Micro/Nanotechnologies and Electron Devices EDM’2016: Conference Proceedings. – Novosibirsk: NSTU 2016, 251-256. [CrossRef]
Song, Y. L.; Cheng, C. H.; Reddy, M. K.; Islam, M. S. Simulation of onset of the capillary surface wave in the ultrasonic atomizer. Micromachines 2021, 12, 1146. [CrossRef]
Ramin, J.; Etienne, R. Acoustic separation of submicron solid particles in air Ultrasonics 2015, 63, 135–140. [CrossRef]
Townsend, R.J.; Hill, M.; Harri, N.R.; White, N.M. Modelling of particle paths passing through an ultrasonic standing wave. Ultrasonics 2004, 42, 319–324. [CrossRef]
Olivier, D.; Jean-Luc A. Varying the agglomeration position of particles in a micro-channel using Acoustic Radiation Force beyond the resonance condition Ultrasonics 2013, 53, 1280–1287. [CrossRef]
Knoop, C.; Fritsching, U. Dynamic forces on agglomerated particles caused by high-intensity ultrasound. Ultrasonics 2014, 54, 763–769. [CrossRef]
Hoda, Y.; Asami, T.; Miura, H. Aerosol agglomeration by aerial ultrasonic sources containing a cylindrical vibrating plate with the same diameter as a circular tube. Japanese Journal of Applied Physics 2022, 61, SG1073. [CrossRef]
Khmelev, V.N.; Shalunov, A.V.; Nesterov, V.A. Improving the separation efficient of particles smaller than 2.5 micrometer by combining ultrasonic agglomeration and swirling flow techniques. PLoS ONE 2020, 15, e0239593. [CrossRef]
Avvaru, B.; Patil, M.N.; Gogate, P.R.; Pandit, A.B. Ultrasonic atomization: effect of liquid phase properties. Ultrasonics 2006, 44, 146-158. [CrossRef]
Khmelev, V. N.; Shalunov, A. V.; Golykh, R. N.; Nesterov, V. A.; Dorovskikh, R. S.; Shalunova, A. V. Determination of the modes and the conditions of ultrasonic spraying providing specified productivity and dispersed characteristics of the aerosol. Journal of Applied Fluid Mechanics 2017, 10, 1409-1419. [CrossRef]

Figure 1. Multi-stage ultrasonic spraying.

Figure 2. Ultrasonic tubular emitter: (a) Tubular emitter drawing; (b) Vibration waveform; 1 - emitting element in the form of a bending and oscillating tube; 2 - concentrator of the piezoelectric transducer (emitting pad); 3 - piezoceramic elements; 4 - reflective pad; 5 - housing; 6 - flange; 7 - enforcement for the threaded hole; 8 - amplitude adjustment area of the emitter ends; L - emitter length; D1 - inner diameter; D2 - outer diameter.

Figure 3. Developed ultrasonic tubular emitter: (a) Distribution sound pressure inside the emitter; (b) Ultrasonic tubular emitter image.

Figure 4. Test Bench structure and photo: 1 - peristaltic pump; 2 - liquid supply tube; 3 - ultrasonic tubular emitter; 4 - ultrasonic generator; 5 - atomized liquid; 6 - droplet size analyzer; 7 - high-speed video camera; 8 - vacuum aspirator for collecting droplets after the first stage of spraying.

Figure 5. Images of primary droplet disintegration.

Figure 6. Images of secondary breakdown of the droplet (second stage).

Figure 7. Distribution of formed droplets: (a) after the first breakdown stage; (b) at the tubular emitter outlet.

Figure 8. Histograms of droplet diameter distribution at increased rate of 10 ml/s: (a) after the first breakdown stage; (b) at the tubular emitter outlet.

Figure 9. Dispersion characteristics of droplets at different rates: (a) dependence of median diameter on supply rate; (b) histogram of droplet diameter distribution at maximum rate (15 ml/s).

Figure 10. Evolution of disperse composition of droplets at different sound pressure levels.

Figure 11. Dependence of median diameters of formed droplets on sound pressure level.

Figure 12. Histograms of liquid droplet diameter distribution at different liquid viscosities: (a) 1.8 mPa·s; (b) 10.8 mPa·s.

Figure 13. Dependence of median droplet diameter on liquid viscosity.

Figure 14. Histograms of liquid droplet diameter distribution at different liquid surface tensions: (a) surface tensions 40.9 mN/m; (b) surface tensions 25.6 mN/m.

Figure 15. Dependence of median droplet diameter on liquid surface tension.

Table 1. Lists the main parameters of the developed tubular emitter.

Dimensions of tubular emitter, mm	D2=92 D1=52 L=96
Vibration frequency, kHz	22.2
Electric power consumption, W	50
Amplitude (sweep) of surface vibrations max-min	51-40
Acoustic power, W	35

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

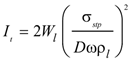Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer