Submitted:
13 December 2023
Posted:
14 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Working Principle and Design
3. Theoretical Modeling
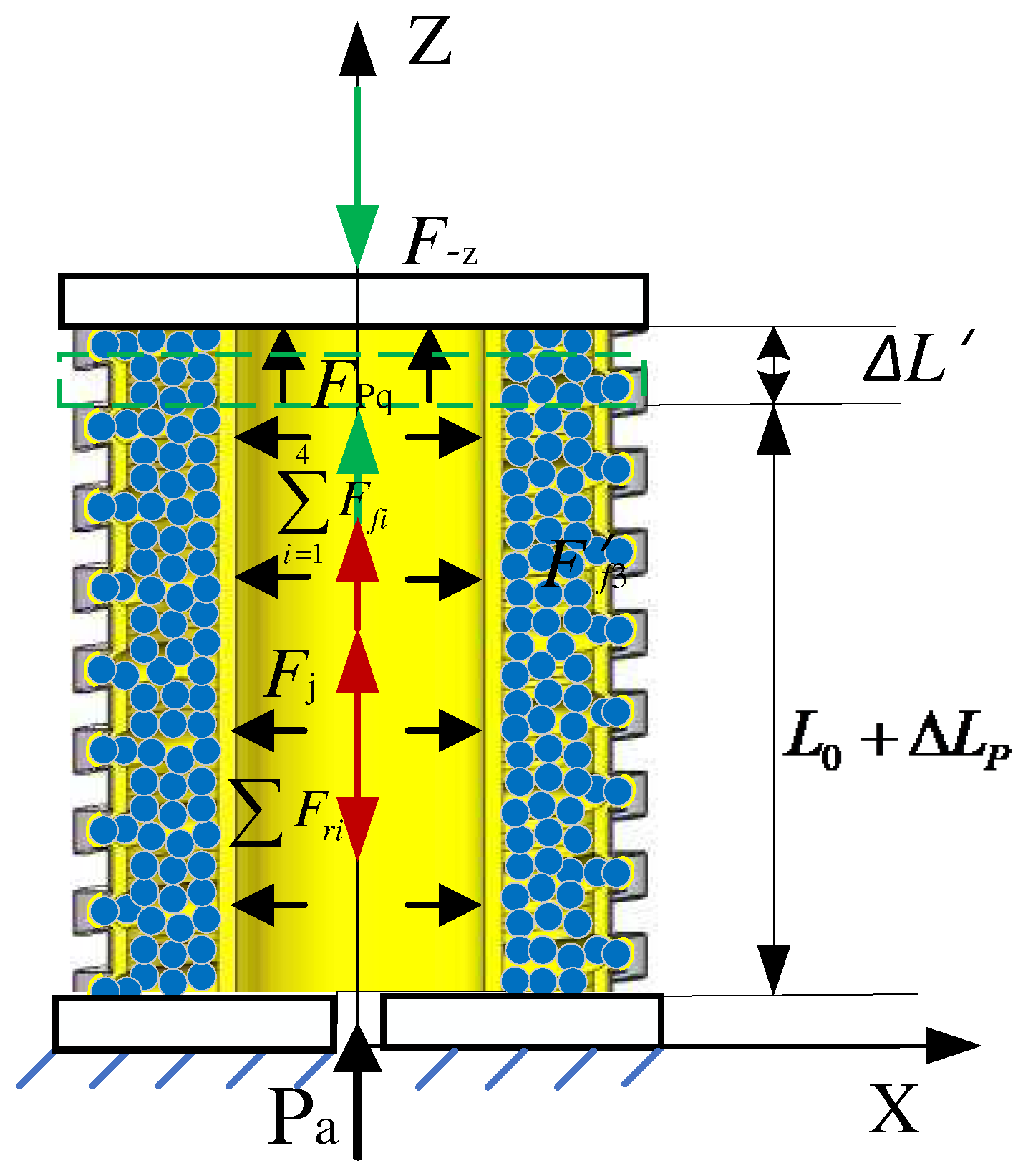
3.1. Anti-Tensile Stiffness at Any Position of the Variable-Stiffness Elastic Actuator
- Driving force
- 2.
- Friction resistance force
- 3.
- Deformation resistance force
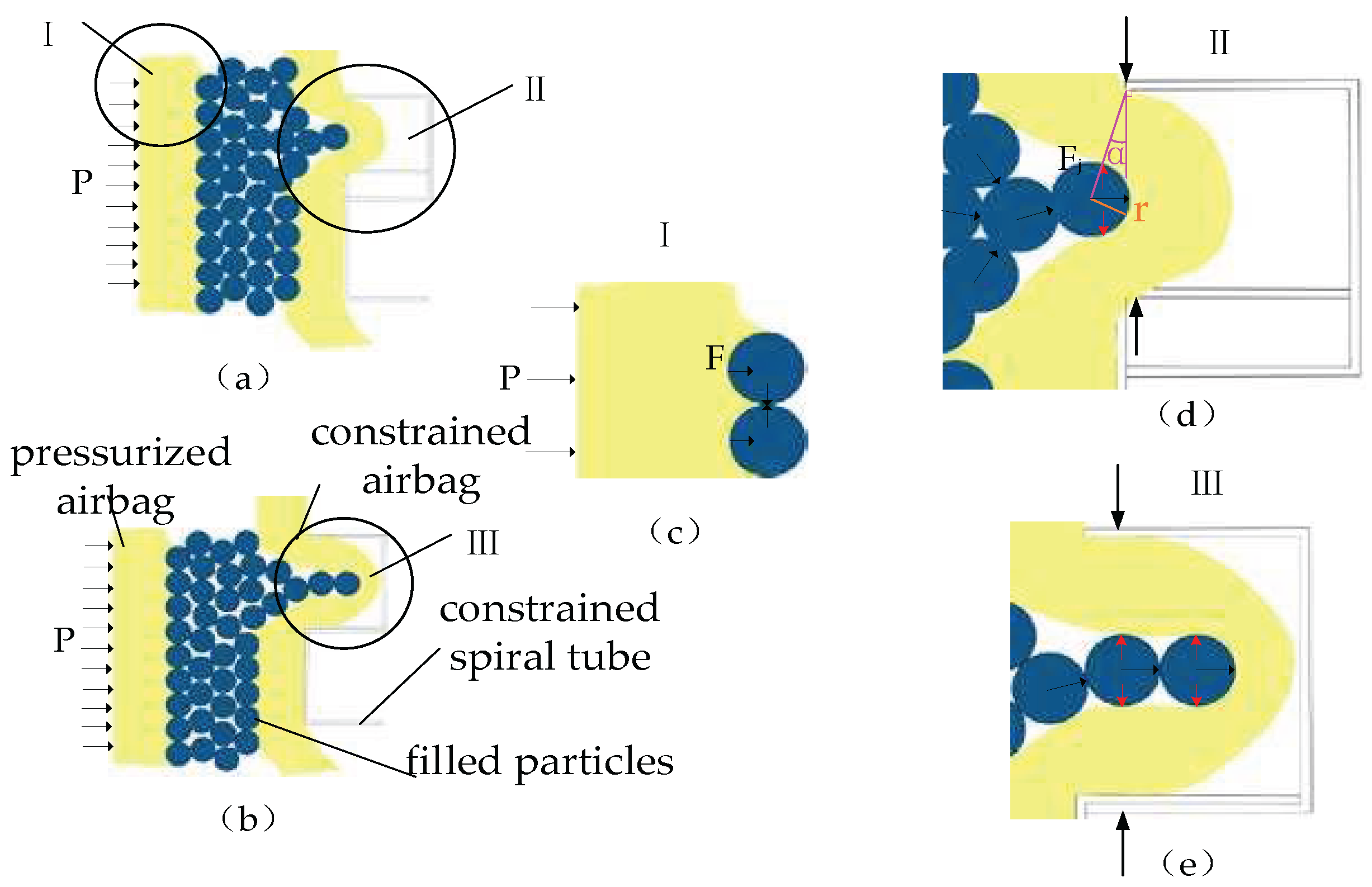
3.2. Anti-Compressive Stiffness at Any Position of the Variable-Stiffness Elastic Actuator
- 1.
- Driving force
- 2.
- Friction resistance force
- 3.
- Deformation resistance force
- 4.
- Wedge resistance moment
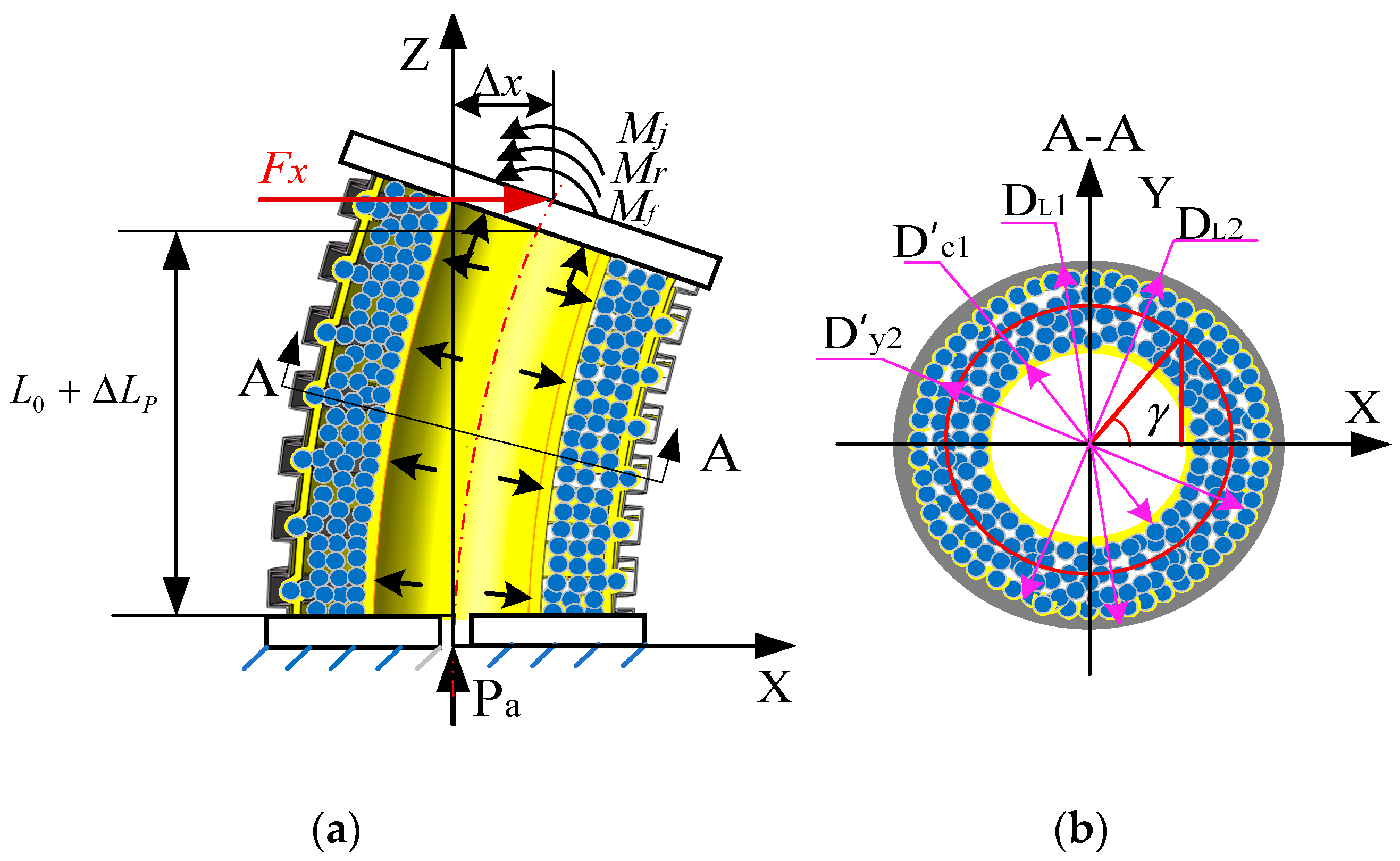
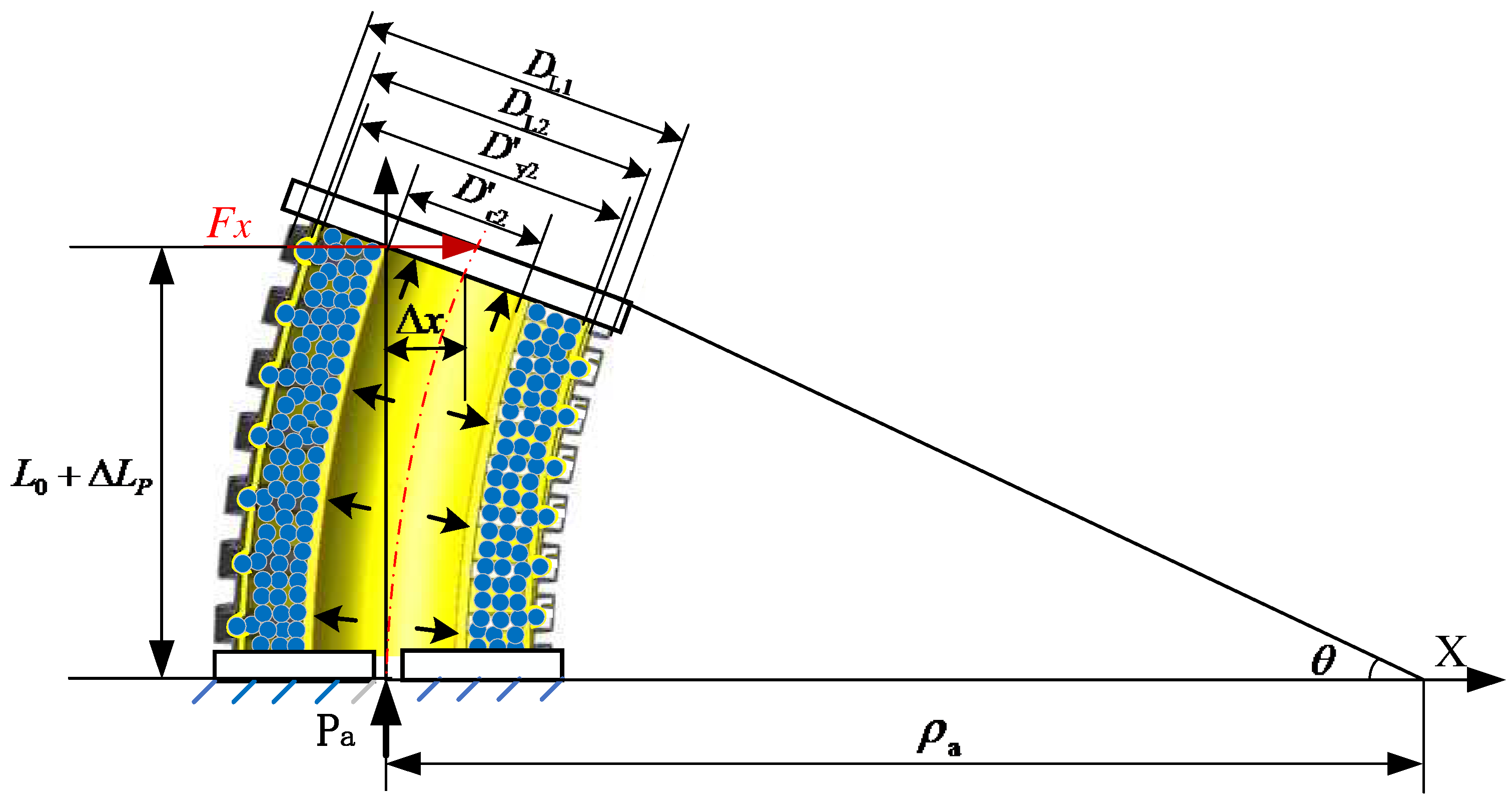
3.3. Lateral Stiffness at Any Position of the Variable-Stiffness Elastic Actuator
- 1.
- External moment
- 2.
- Friction resistance moment
- 3.
- Deformation resistance moment
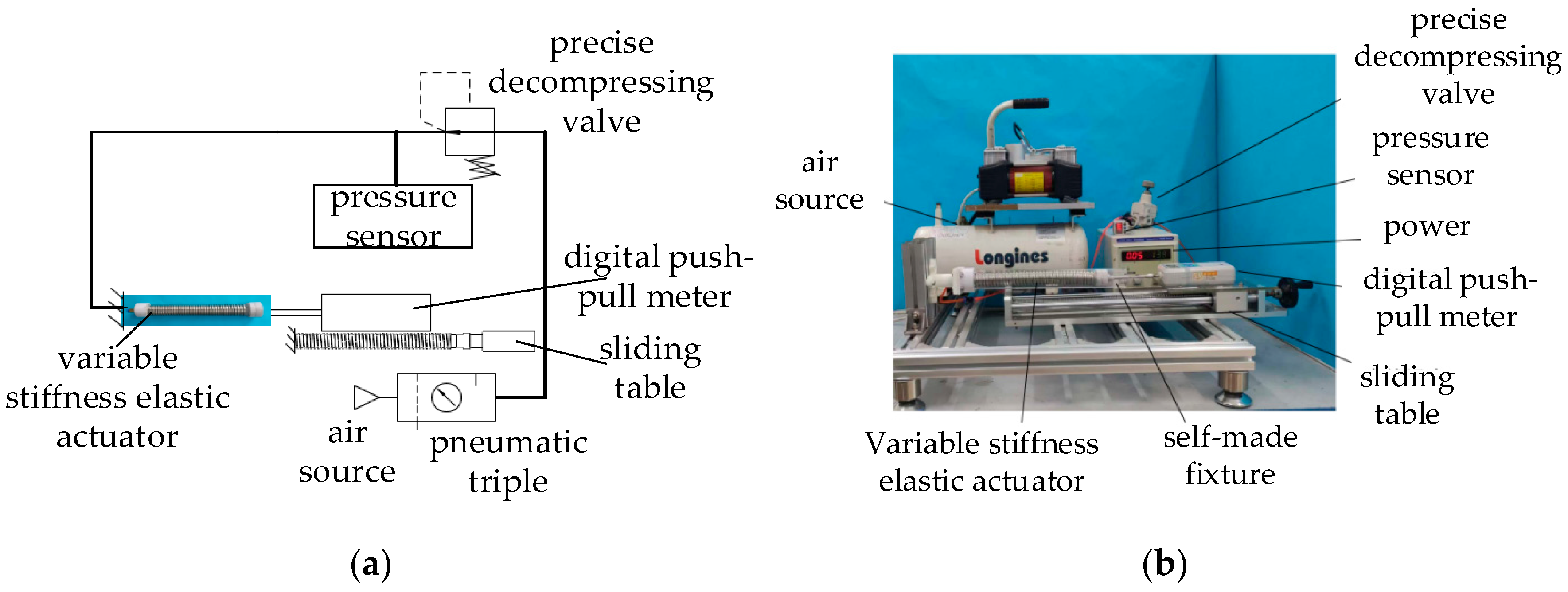
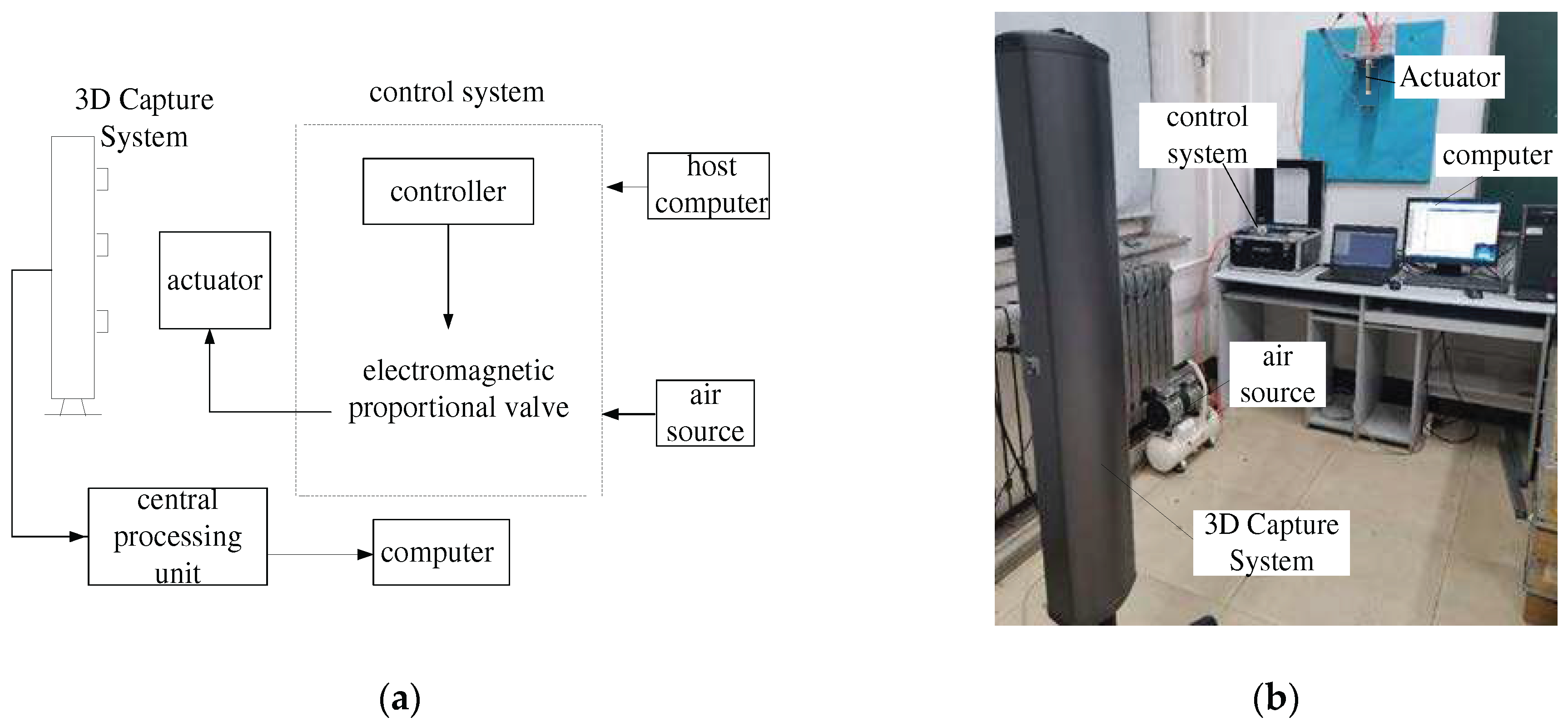
4. Experimental Analysis
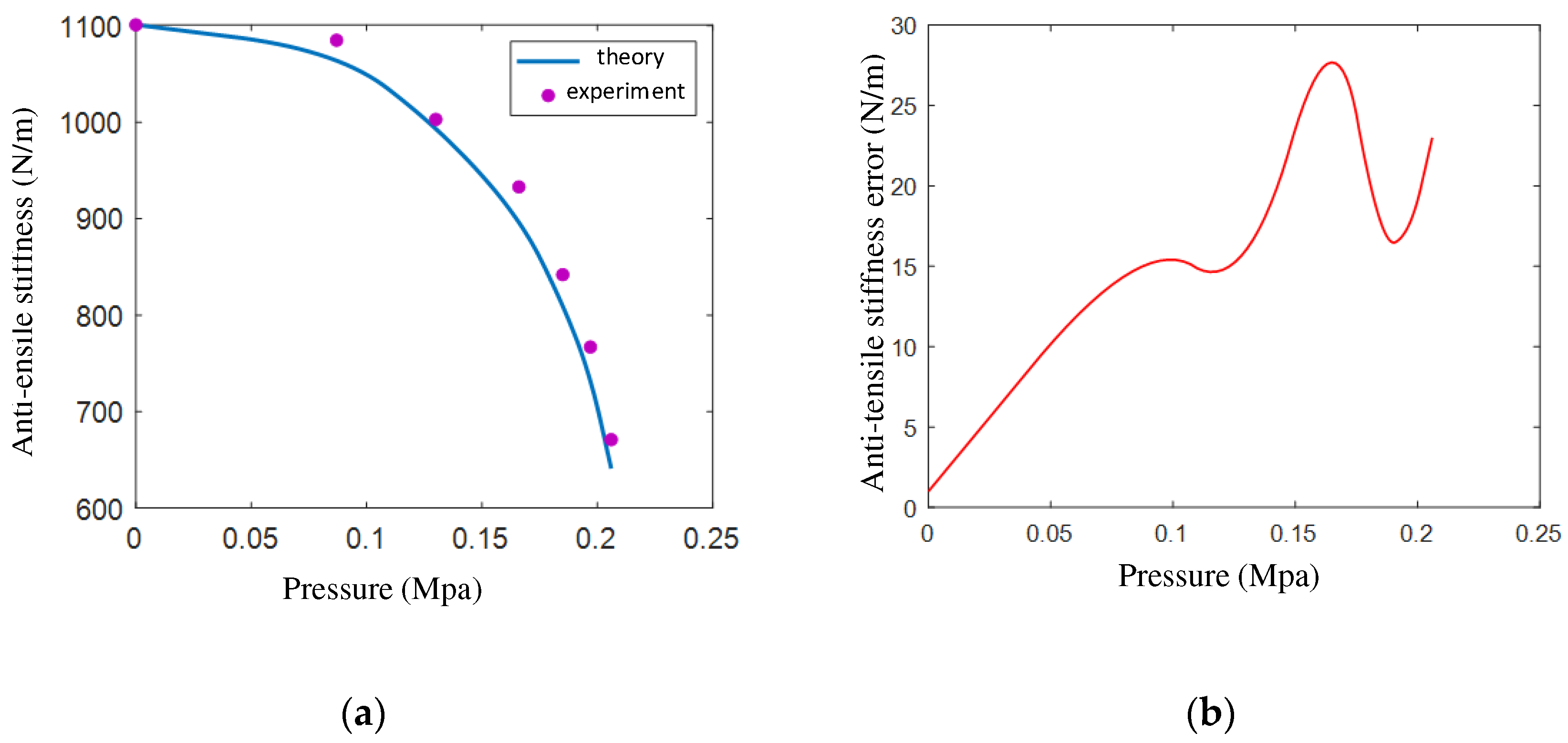
4.1. Anti-Tensile Stiffness Experiment
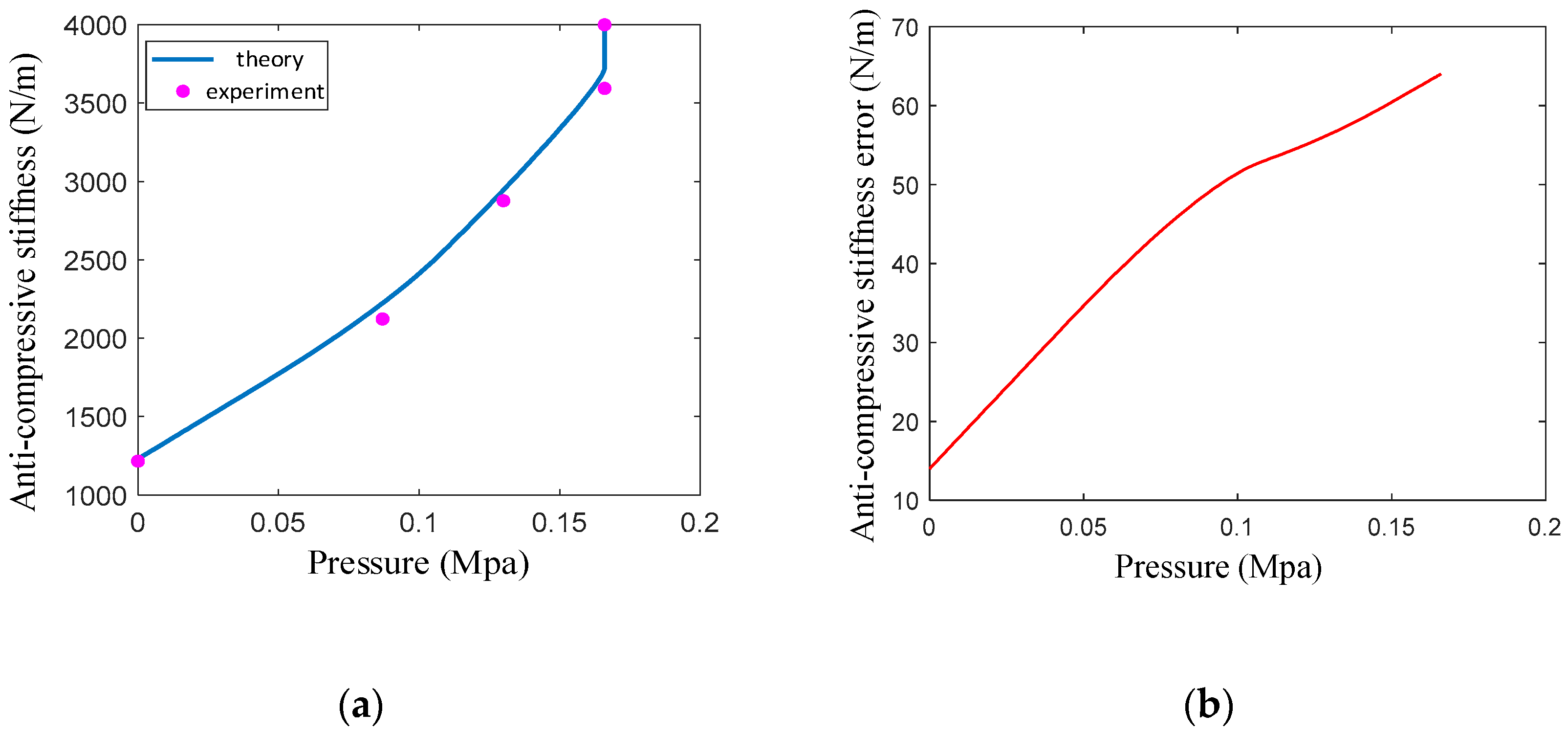
4.2. Anti-Compressive Stiffness Experiment
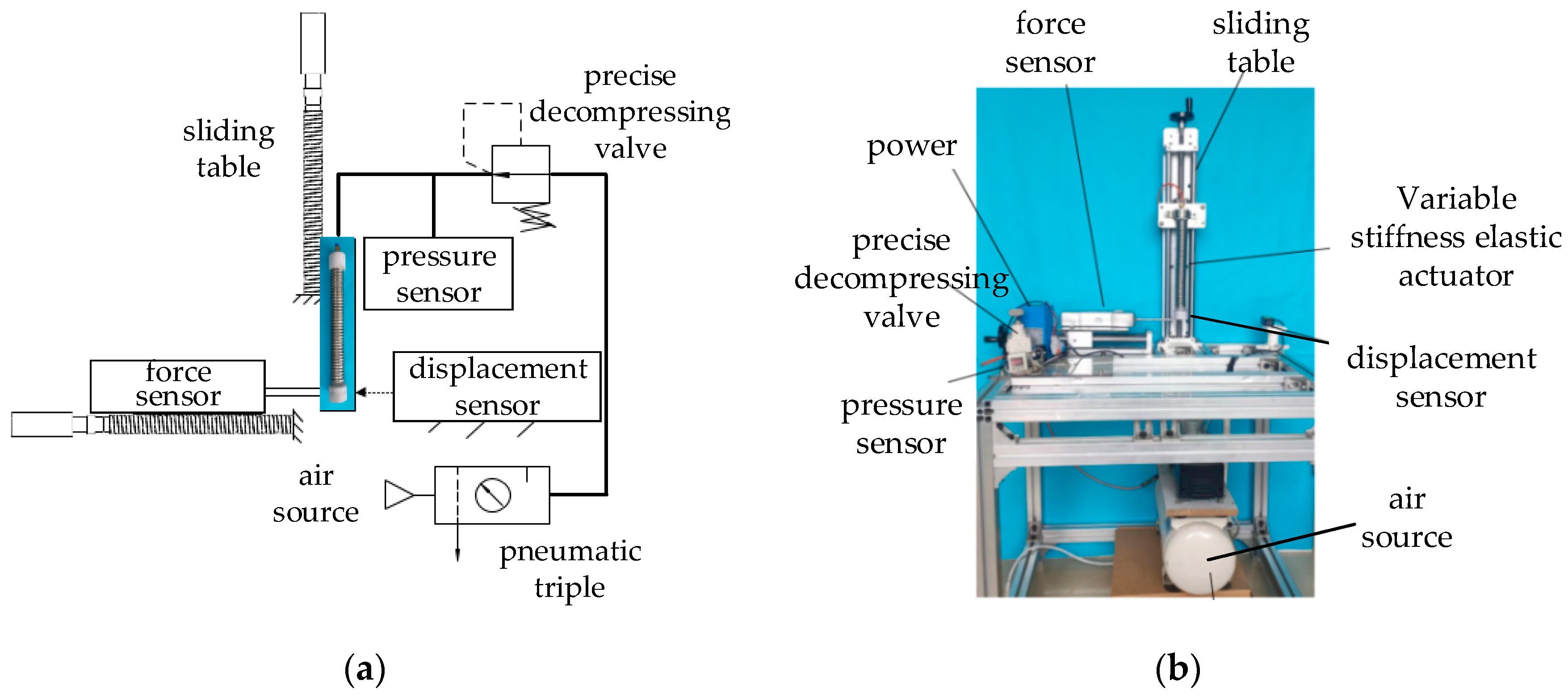
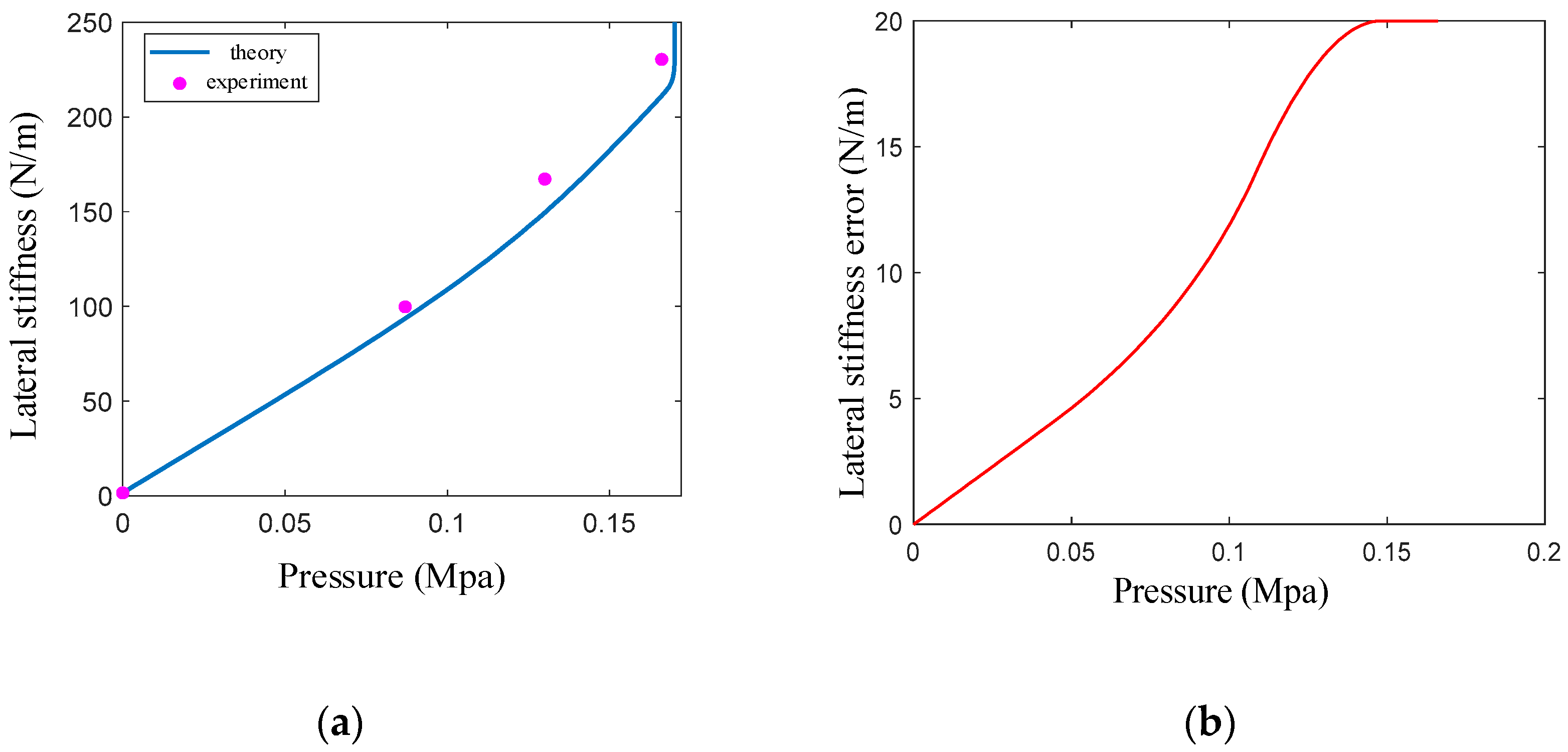
4.3. Lateral-Stiffness Experiment
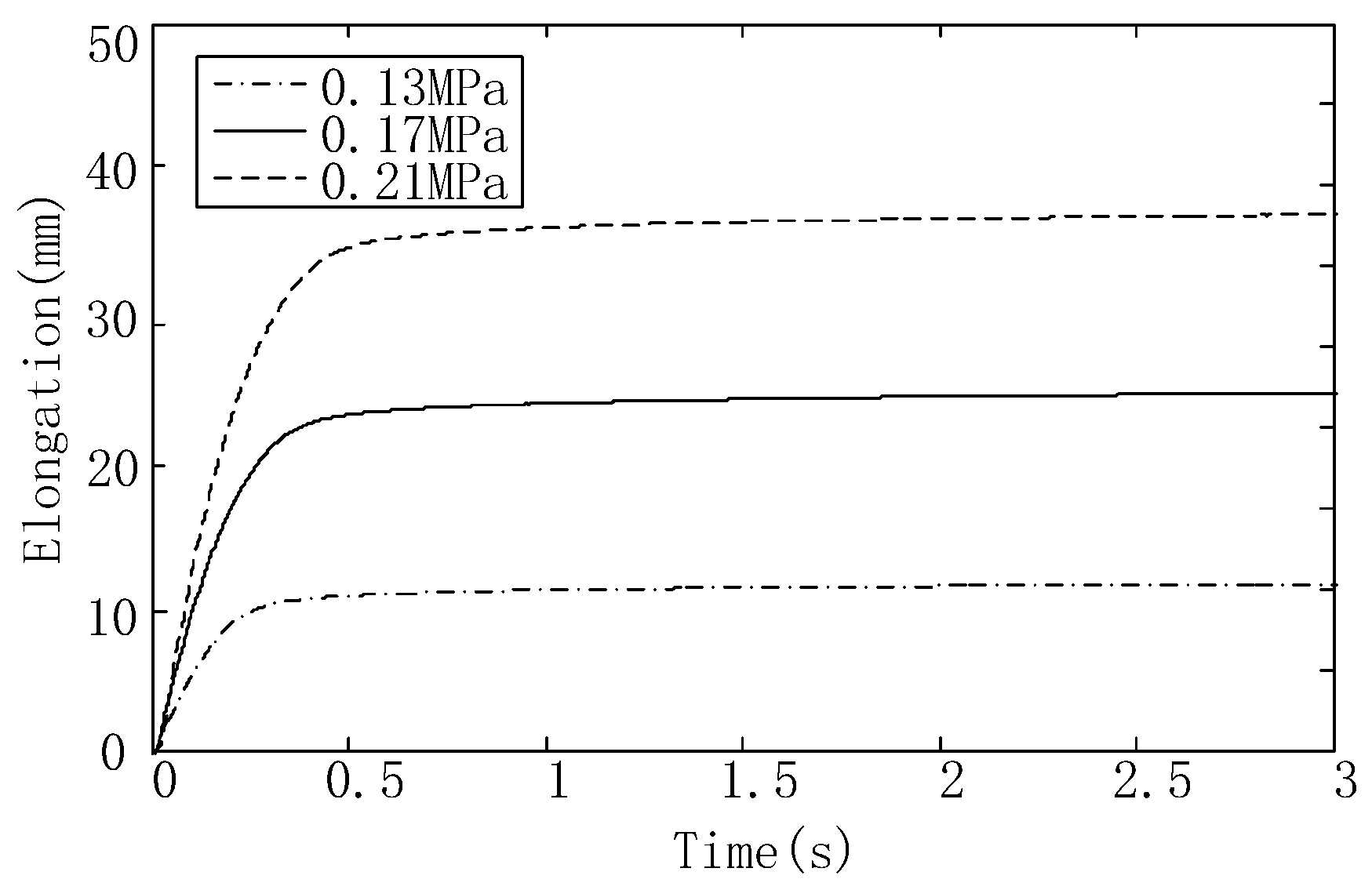
4.4. Dynamic Response Experiment
5. Conclusions
- (1)
- The anti-tensile stiffness of the actuator decreases with the increase in the air pressure when the air pressure is less than 0.21 MPa and the anti-tensile stiffness is very large, depending on the anti-tensile strength of the spiral tube when the air pressure is greater than 0.21 MPa.
- (2)
- The anti-compressive stiffness increases with the increase in air pressure. When the air pressure is 0.17 MPa, the stiffness is three times that when unpressurized, and the anti-compressive stiffness depends on the anti-compressive strength of the filling particles when the air pressure exceeds 0.17 MPa.
- (3)
- The lateral stiffness increases nonlinearly and is positively correlated with air pressure. When the air pressure is 0.17 MPa, the stiffness is 121 times higher than that when unpressurized, and this stepwise increase in stiffness continued beyond this pressure point.
- (4)
- The variable-stiffness elastic actuator can be applied to flexible robots, which can be used as a driving device and also as a variable-stiffness device to realize the integration of the structure and driving device, while improving the stiffness of the robot.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Filongna, S.; Paterno, L.; Vecchi, F.; Musco, L.; Iacovacci, V.; Menciassi, A. A bioinspired fluid- filled soft linear actuator. Soft Robot. 2023, 10, 454–466. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.; Choi, J.C.; Lee, H.; Cho, W.; Lee, K.; Kim, J.G.; Lee, J.W.; Joo, K.I.; Cho, M.; Kim, H.R.; et al. Continuous and Programmable Photo mechanical Jumping of Polymer Monoliths. Mater. Today 2021, 49, 97–106. [Google Scholar] [CrossRef]
- Ren, Z.; Kim, S.; Ji, X.; Zhu, W.; Niroui, F.; Kong, J.; Chen, Y. A high-lift micro-aerial-robot power by low-voltage and long-endurance dielectric elastomer actuator. Adv. Mater. 2022, 34, 2106757. [Google Scholar] [CrossRef] [PubMed]
- Bena, R.M.; Nguyen, X.T.; Calderón, A.A.; Rigo, A.; Pérez-Arancibia, N.O. SM ARTI: A 60-mg steerable robot driven by high-frequency shape-memory alloy actuation. IEEE Robot. Autom. Lett. 2021, 6, 8173–8180. [Google Scholar] [CrossRef]
- Pfeil, S.; Mieting, A.; Crun, R.; Katzer, K.; Mersch, J.; Breitkopf, C.; Zimmermann, M.; Gerlach, G. Underwater bending actuator based on integrated anisotropic textile materials and a conductive hydrogel electrode. Actuators 2021, 10, 270. [Google Scholar] [CrossRef]
- Dong, Y.; Li, B. The Opportunities and Challenges for the Rising Star of Soft Robots. Appl. Sci. 2023, 13, 9430. [Google Scholar] [CrossRef]
- Abeach, A.; Nefti-meziani, L.; Davis, S. Design of a Variable Stiffness Soft Dexterous Gripper. Soft Robot. 2017, 4, 274–284. [Google Scholar] [CrossRef] [PubMed]
- Li, X. Design and Control of Variable-Stiffness Flexible Drive Joint. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2022. [Google Scholar]
- Zhao, X.M. Design and Control of Variable-Stiffness Space Flexible Continuum Robot System. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2022. [Google Scholar]
- Zhao, X.D. Study on Flexible Gripper Driven by Controllable Variable-Stiffness Liquid Crystal Elastomer. Master’s Thesis, North University of China, Taiyuan, China, 2023. [Google Scholar]
- Amend, J.R. A Positive Pressure Universal Gripper Based on the Jamming of Granular Material. IEEE Trans. Robot. 2012, 28, 341–350. [Google Scholar] [CrossRef]
- Hua, C. Research on a Variable-Stiffness Soft Manipulator. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2021. [Google Scholar]
- Hauser, S.; Robertson, M.; Ijspeert, A.; Paik, J. Jammjoint: A variable stiffness device based on granular jamming for wearable joint support. IEEE Robot. Autom. Lett. 2017, 2, 849–855. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Yang, Y.; Li, Y. A soft robotic spine with tunable stiffness based on integrated ball joint and particle jamming. Mechatronics 2016, 33, 84–92. [Google Scholar] [CrossRef]
- Hiroya, I.; Kevin, K.; Minoru, T. A variable-stiffness dielectric elastomer actuator based on electrostatic chucking. Soft Matter 2017, 13, 3440–3448. [Google Scholar] [CrossRef]
- Giannaccini, M.E.; Xiang, C.; Atyabi, A.; Theodoridis, T.; Nefti-Meziani, S.; Davis, S.; Shen, Z.; Zhong, H.; Xu, E.; Zhang, R.; et al. Novel Design of a Soft Lightweight Pneumatic Continuum Robot Arm with Decoupled variable-stiffness and Positioning. Soft Robot. 2018, 5, 54–70. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ahn, S.H. Shape Memory Alloy-Based Soft Gripper with variable-stiffness for Compliant and Effective Grasping. Soft Robot. 2017, 4, 379–389. [Google Scholar] [CrossRef] [PubMed]
- Freckley, P.K.; Payne, A.R. Theory and Practice of Rubber Application in Engineering; Chemical Industry Press: Beijing, China, 1985. [Google Scholar]
- Geng, D.X. Bidirectional Active Bending Pneumatic Flexible Joint and Its Application in Mechanical Hand. Ph.D. Thesis, Jilin University, Changchun, China, 2011. [Google Scholar]
- Zhang, T.R.; Chao, X.J.; Guo, L.H. Mechanics of Materials; Chongqing University Press: Chongqing, China, 2018. [Google Scholar]
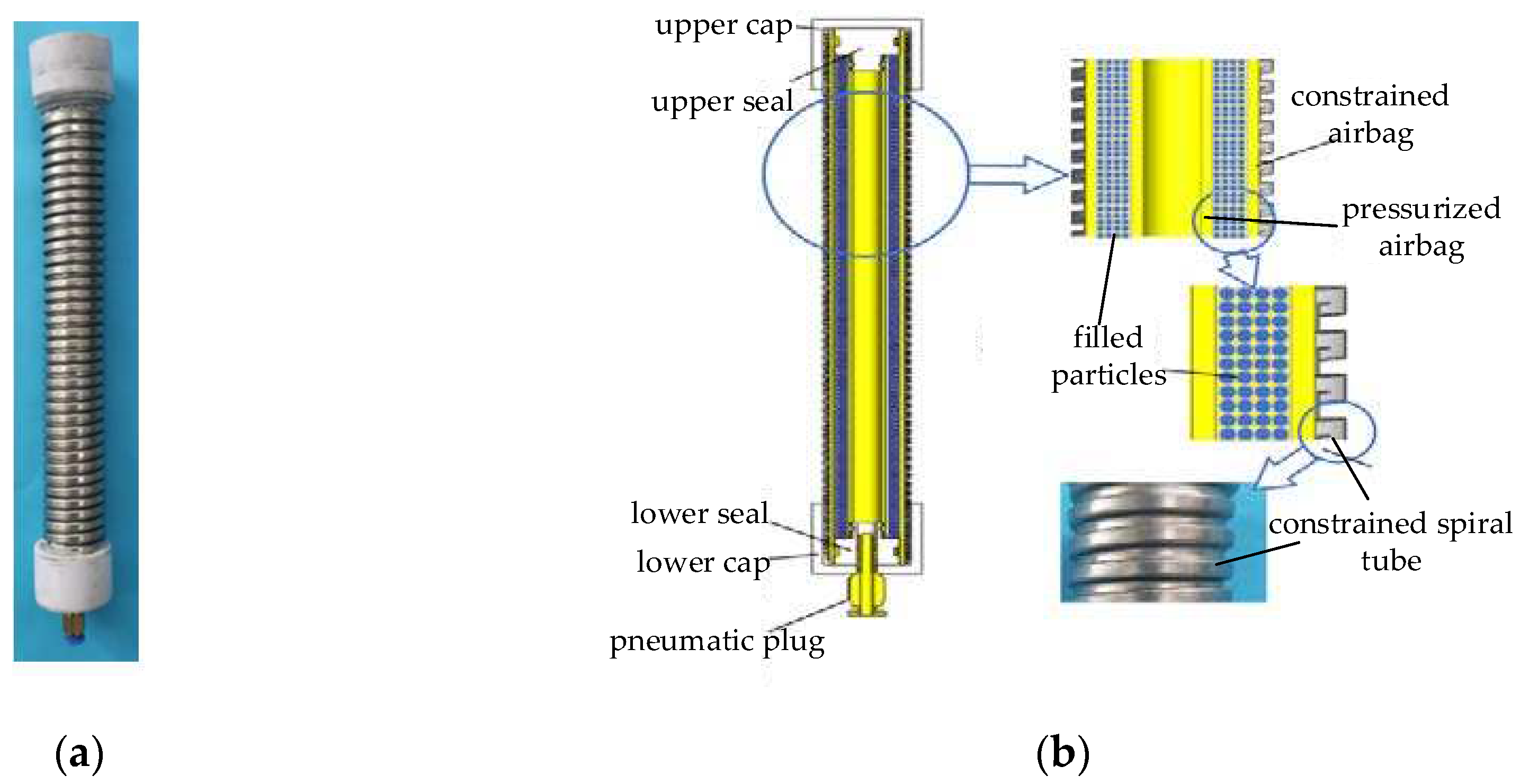
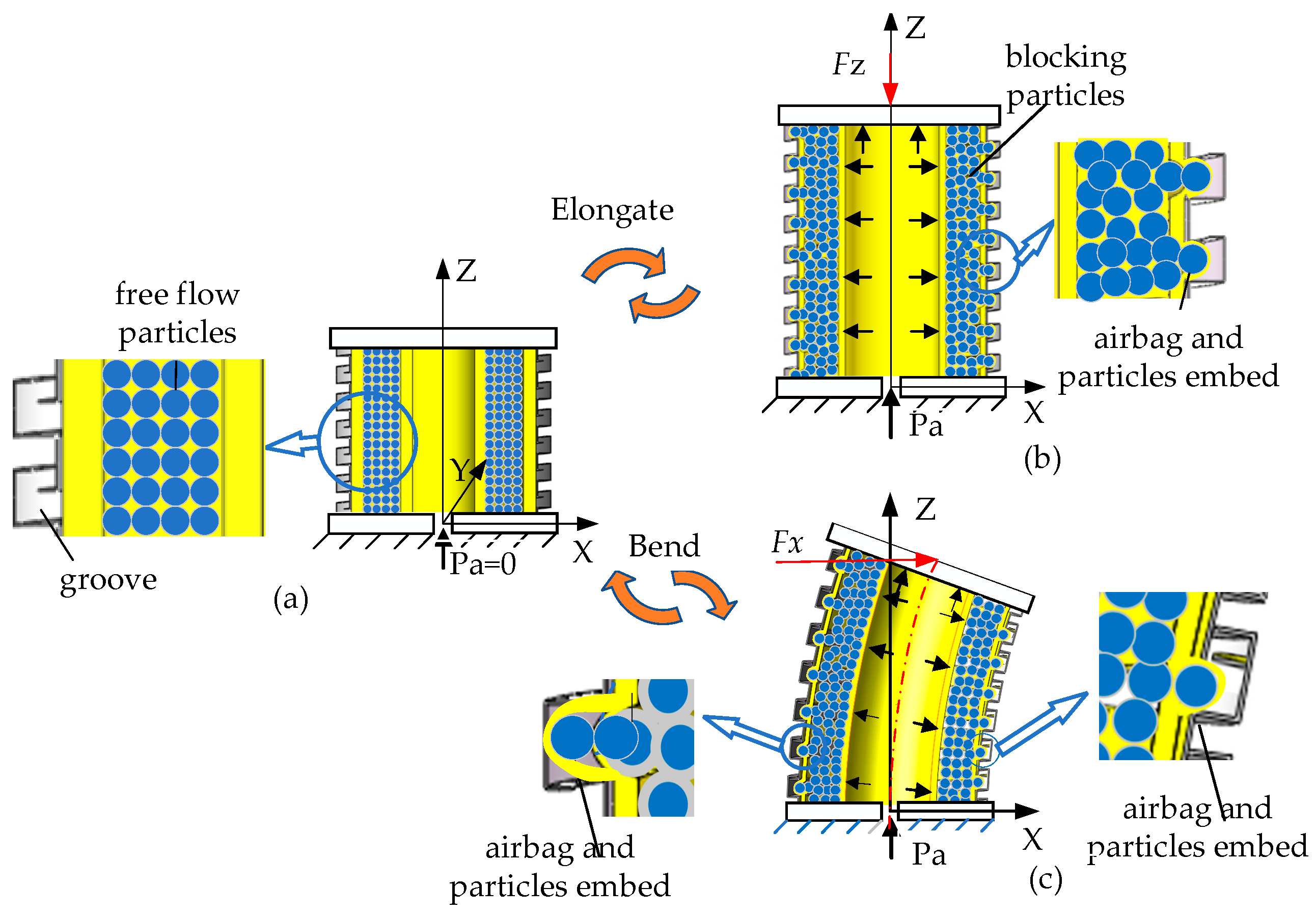
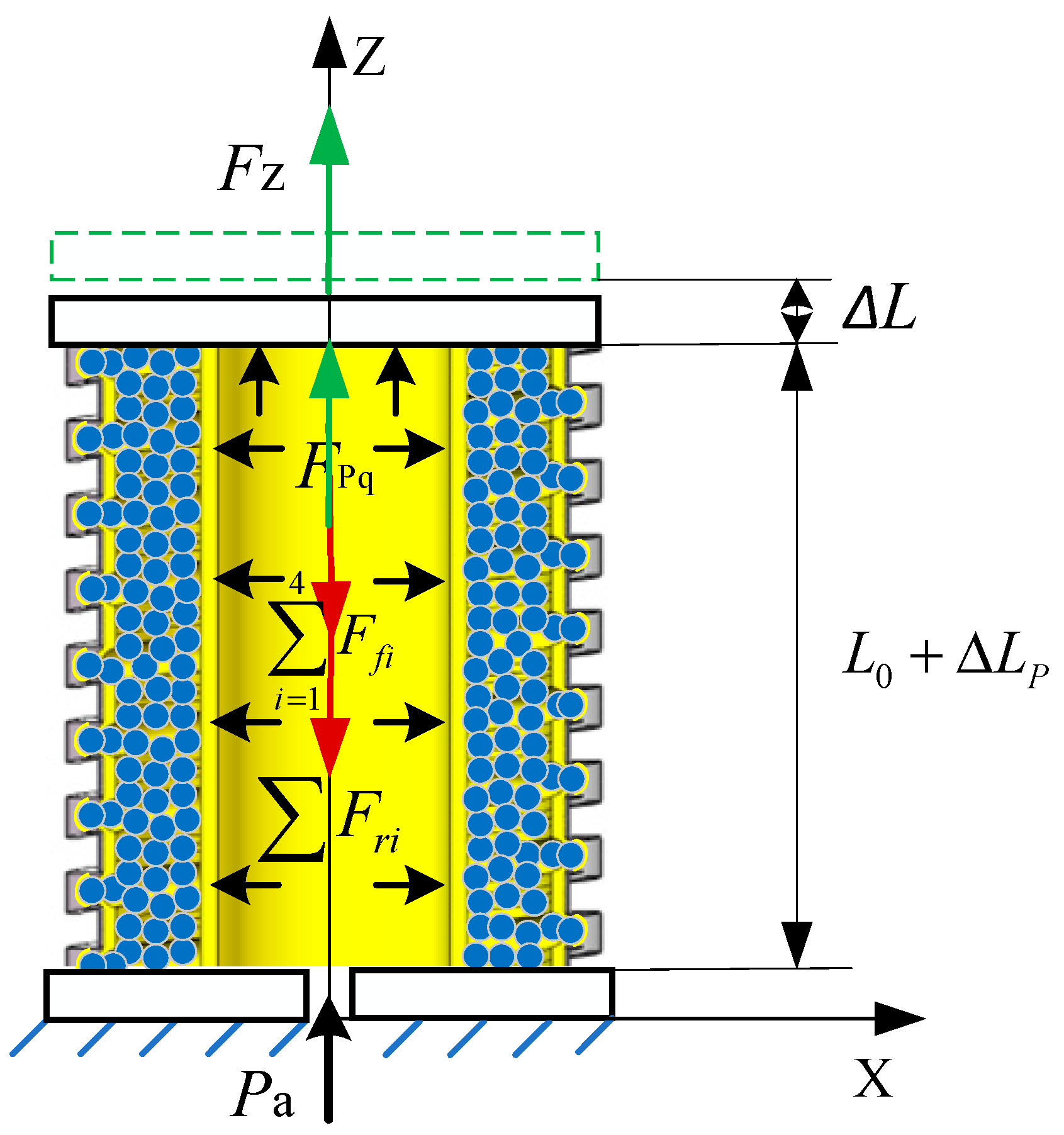
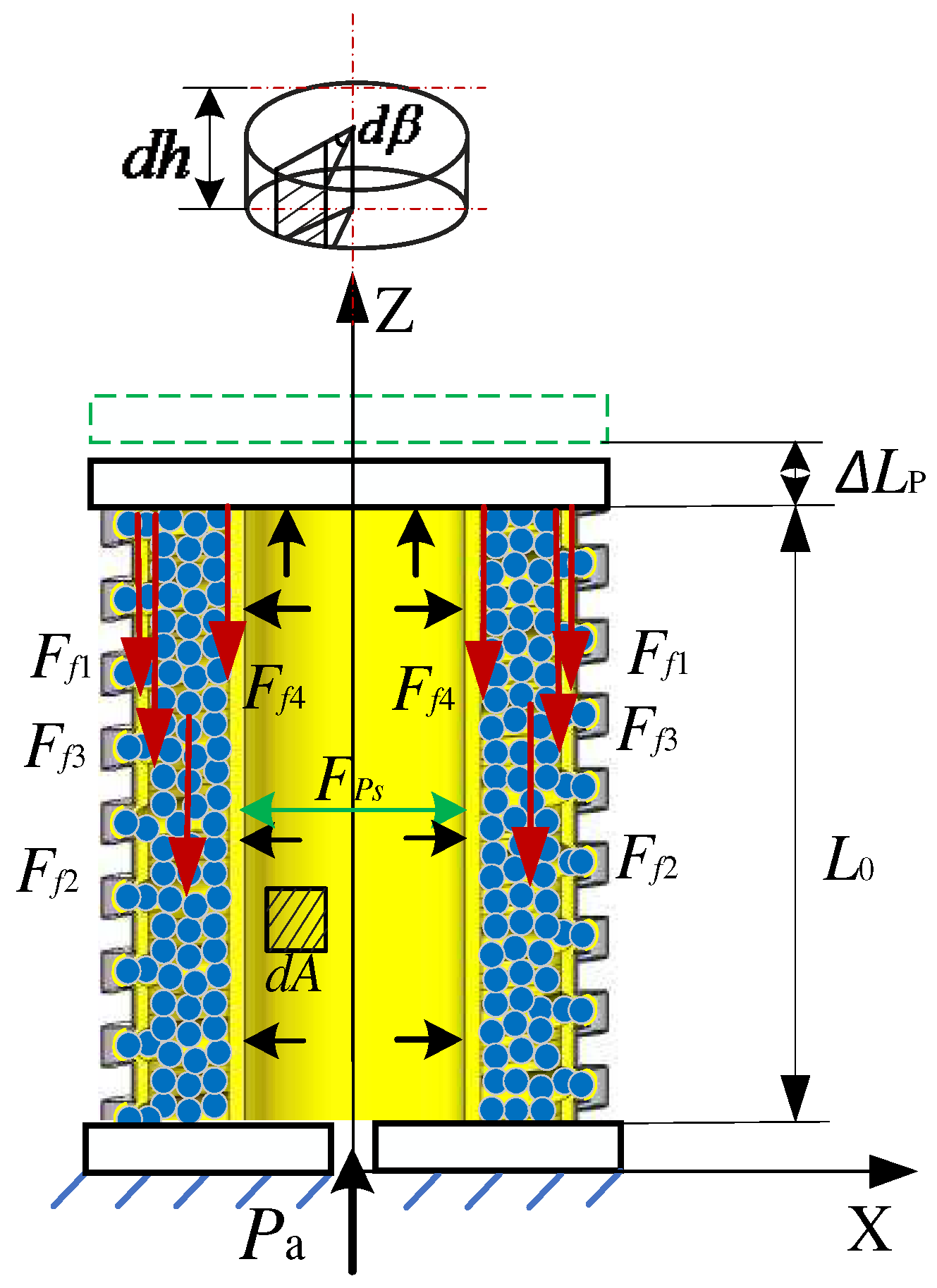
| Parameter Name | Value | Material | |
|---|---|---|---|
| Overall length | 230 mm | ||
| Effective length of airbag | 180 mm | ||
| Diameter of pressurized airbag | Inner diameter: 8 mm | Silicon–fluorine rubber | |
| Outer diameter: 12 mm | |||
| Diameter of constrained airbag | Inner diameter: 20 mm | Silicon–fluorine rubber | |
| Outer diameter: 24 mm | |||
| Diameter of constrained spiral tube | Inner diameter: 25 mm | 304 stainless steel | |
| Outer diameter: 29 mm | |||
| Maximum length: 216 mm | |||
| Minimum length: 180 mm | |||
| Maximum groove size | Length: 3.8 mm | ||
| Height: 4 mm | |||
| Filling particles | Diameter: 1 mm | Diamond sand | |
| Number: 36,170 | |||
| Parameter Name | Value |
|---|---|
| Elastic modulus of airbag E | 1.042 MPa |
| Friction coefficient | 0.12 |
| Friction coefficient | 0.13 |
| Friction coefficient | 0.1 |
| Friction coefficient | 0.13 |
| Component Name | Model | Precision |
|---|---|---|
| Pump | WX1.5HP | 0–0.9 MPa |
| Precise decompressing valve | IR2020-02 | 0.001 MPa |
| Laser displacement sensor | HG-C1030 | 0.01 mm |
| Digital push–pull meter | HF-100 | 0.001 N |
| Component Name | Model | Value |
|---|---|---|
| Electromagnetic proportional valve | SMC-ITV0030-2MN | 0–1.0 MPa |
| Air pressure sensor | SMC-ISG40A-W1-R-M | 0.001 MPa |
| Three-dimensional capture system | NDI Optotrak Certus | 0.1 mmRMS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





