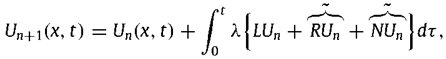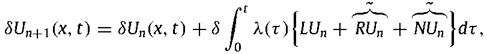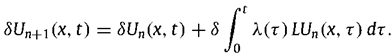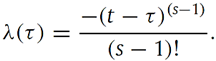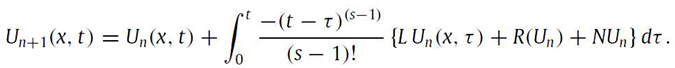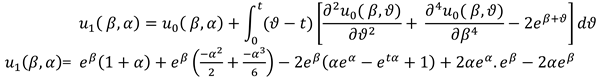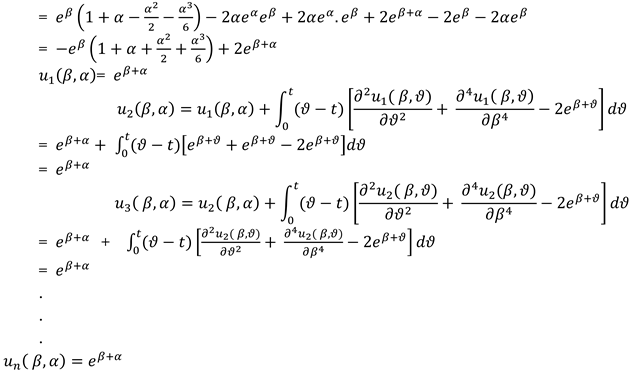Variational Iteration Method for Solving Nonlinear Partial Differential Equations in Fluid Dynamics

Preprint

Article

Variational Iteration Method for Solving Nonlinear Partial Differential Equations in Fluid Dynamics

Altmetrics

Downloads

106

Views

Comments

This version is not peer-reviewed

This preprints belongs to the Topic

Numerical Methods for Partial Differential Equations

Submitted:

04 November 2023

Posted:

23 November 2023

You are already at the latest version

Alerts

Abstract

In this work, the analytical treatment of Fourth order pd equations has been discussed with the variational iteration algorithm with an auxiliary parameter. The technique has the capability of reducing the size of computational work and easily overcomes the difficulty of the perturbation method or Adomian polynomials. Comparison with the classic variational iteration algorithm- is carried out, showing that the modification is more efficient and reliable.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Partial differential equations (PDEs) find use in a diverse range of academic areas, such as biology, chemistry, economics, engineering, and physics. In recent studies, researchers have identified the utilization of Partial Differential Equations (PDEs) in several domains such as nanotechnology, electronic communication platforms like blogs and Facebook, relativistic physics, condensed matter physics, fluid mechanics, non-linear optics, chemical kinetics, and wave phenomena, among others. (Ahmed et al., 2020; Inc et al., 2020; Shehata et al., 2019; Zayed 42 et al., 2020). Analytical solutions to many PDEs, particularly those that are non-linear and complex, may be extremely challenging. The utilization of ordinary differential equations (ODEs) or partial differential equations (PDEs) is employed to articulate intricate difficulties encountered in real-world systems. Due to the inherent difficulty in obtaining precise solutions for several partial differential equations (PDEs), it is often necessary to employ numerical methods to approximate the solutions of fractional partial differential equations (FPDEs) of varying orders. The utilization of commonly employed analytical methods for solving nonlinear equations is sometimes limited. Conversely, the discretization of variables through the application of numerical approaches introduces the possibility of encountering rounding errors.

In recent studies, the variational iteration technique (VIM) proposed by He [1,2] has been found to yield consecutive approximations of the exact solution that converge swiftly, provided that an exact solution exists. The successful derivation of analytical solutions for both linear and nonlinear differential equations has been demonstrated. The utilization of this technique is deemed more advantageous compared to numerical methods due to the absence of rounding mistakes. Additionally, this approach does not necessitate significant computational power or memory resources. He has used this technique to solve integro-differential equations, nonlinear partial differential equations with variable coefficients, and autonomous ordinary differential equations analytically. Several researchers have successfully employed the variational iteration method. The VIM (Variational Iteration Method) has been utilized in various applications, such as the nonlinear Boltzmann equation [3], Burger's and coupled Burger's equations [4], partial differential equation [5], parabolic integro-differential equations related to heat conduction in materials with memory [6], coupled Korteweg-de Vries (KdV) and Boussinesq-like B(m, n) equations [7], and Sawada-Kotera equations [8].

2. Variational Iteration Method by He

In order to demonstrate the technique of the proposed method, we initiate by examining a differential equation in a formal format, employing the variational iteration method.

By employing the variational iteration method [21,22,23,24,25,26,27,28], one may derive the subsequent variational iteration formula for solving the nonlinear partial differential equation.

The symbol λ is commonly referred to as a general Lagrange multiplier [20], which may be effectively determined by the application of variational theory.

Calculating variation with respect to Un,

The Lagrange multiplier, therefore, can be identified as [22,23,24,25,26,27,28].

Substituting the identified multiplier into Eq. results in the following iteration formula:

The term situated on the right side of the equation is commonly referred to as the correction term. The equation can be solved by an iterative process.

U₀(x, t) = f₀(x) + f₁(x)t +… … …+ f_s−1(x)t^s−1 as an initial approximation.

3. Diverse Implementations of the Analytical Expression Proposed:

Within this segment, the expression for the approximate solution or VIM solution of the fourth-order fluid dynamics equation is derived using a variety of functions g(x, t).

3.1. Example 1

Let us take into account the fourth order homogeneous partial differential equation,

\frac{\partial^{2} u}{\partial α^{2}} - \frac{\partial^{4} u}{\partial β^{4}} = 0

(1)

Initial conditions

u (β, 0) = \sin β - \cos β \frac{\partial u}{\partial \propto} (β, 0) = - (\sin β - \cos β)

Boundary conditions

u (0,

α

) =

-

1 +

α

u (1,

α

) = (sin 1

-

cos 1)

(

1 –

α

)

\frac{\partial^{2} u}{\partial α^{2}} (0, α) = 0 \frac{\partial^{2} u}{\partial α^{2}} (1, α) = (s i n 1 - c o s 1) e^{- α}

Applying VIM to equation (1)

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} λ (ϑ) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} - \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}}] d ϑ

Take

λ (ϑ) = ϑ - t

, then

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} - \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}}] d ϑ

Take u₀ (β,

α

) = (sin β

-

cos β) + (cos β -sin β)

α

u_{1} (β, α) = u_{0} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{0} (β, ϑ)}{\partial ϑ^{2}} - \frac{\partial^{4} u_{0} (β, ϑ)}{\partial β^{4}}] d ϑ

The exact solution is:

u (β, α) = (\sin β - \cos β) e^{- α}

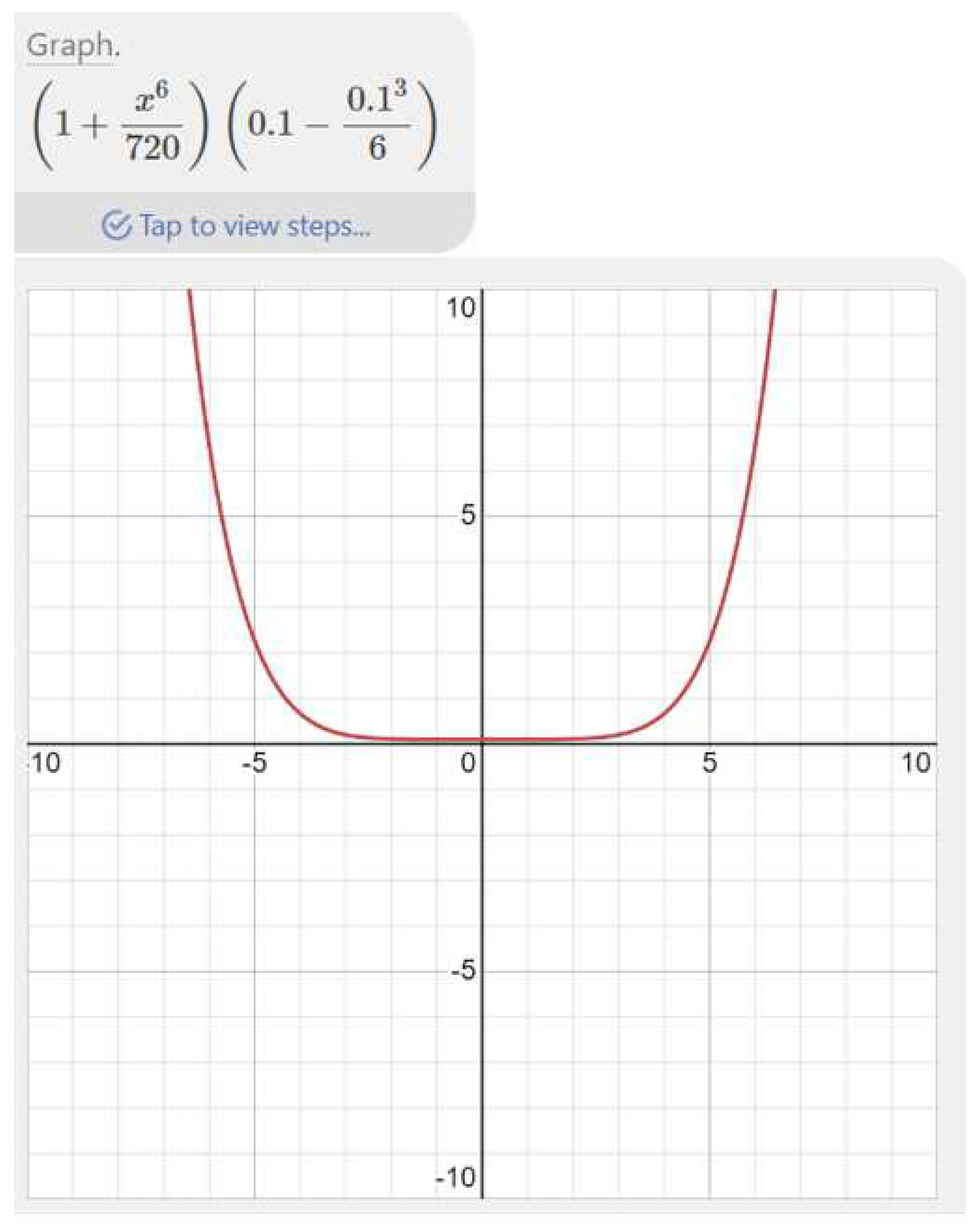
3.2. Example 2

Let us consider fourth order homogeneous partial differential equation,

\frac{\partial^{2} u}{\partial α^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u}{\partial β^{4}} = 0

(1)

With initial conditions

u (β, 0) = 0 \frac{\partial u}{\partial \propto} (β, 0) = 1 + \frac{β^{6}}{6!}

Boundary conditions

u (0, α) = s i n \propto, u (1, α) = (1 + \frac{1}{6!}) s i n t

\frac{\partial^{2} u}{\partial α^{2}} (0, α) = s i n \propto

Applying VIM to equation (1)

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} λ (ϑ) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}}] d ϑ

Take

λ (ϑ) = ϑ - t

, then

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}}] d ϑ

Take u₀ (β,

α

) = (1 +

\frac{β^{6}}{6!}

)

α

u_{1} (β, α) = u_{0} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{0} (β, ϑ)}{\partial ϑ^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u_{0} (β, ϑ)}{\partial β^{4}}] d ϑ

u_{1} (β, α)

= (1 +

\frac{β^{6}}{6!}

)

(α - \frac{\propto^{3}}{3!})

u_{2} (β, α) = u_{1} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{1} (β, ϑ)}{\partial ϑ^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u_{1} (β, ϑ)}{\partial β^{4}}] d ϑ

= (1 +

\frac{β^{6}}{6!}

)

(α - \frac{α^{3}}{3!} + \frac{α^{5}}{5!})

u_{3} (β, α) = u_{2} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{2} (β, ϑ)}{\partial ϑ^{2}} + 2 (\frac{1}{β^{2}} + \frac{β^{4}}{6!}) \frac{\partial^{4} u_{2} (β, ϑ)}{\partial β^{4}}] d ϑ

= (1 +

\frac{β^{6}}{6!}

)

(α - \frac{α^{3}}{3!} + \frac{α^{5}}{5!} - \frac{α^{7}}{7!})

u_{n} (β, α) = (1 + \frac{β^{6}}{6!}) (α - \frac{α^{3}}{3!} + \frac{α^{5}}{5!} - \frac{α^{7}}{7!} \dots \dots \dots \dots)

The exact solution is:

u(β,

α

) = (1 +

\frac{β^{6}}{6!}

) sinα

Table 1. The results of u₁ compared to the exact solution for

α

= 0.1and the VITM.

Table 1. The results of u₁ compared to the exact solution for

α

= 0.1and the VITM.

β	Exact	VIM	Error
0.1	0.09983341	0.09983333	0.00000008
0.2	0.09983342	0.09983334	0.00000008
0.3	0.09983351	0.09983343	0.00000008
0.4	0.09983398	0.0998339	0.00000008

Figure 1.

From the above Figrure ,we can see error is quite less and if we compare table with exact solutions its well suited.

3.3. Example 3

Consider fourth order nonhomogeneous partial differential equation,

\frac{\partial^{2} u}{\partial α^{2}} + \frac{\partial^{4} u}{\partial β^{4}} = 2 e^{β + α}

(1)

Initial conditions

u (β, 0) = e^{β} \frac{\partial u}{\partial α} u (β, 0) = e^{β}

Applying VIM to equation (1)

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} λ (ϑ) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} + \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}}] d ϑ

Take

λ (ϑ) = ϑ - t

then

u_{n + 1} (β, α) = u_{n} (β, α) + \int_{0}^{t} (ϑ - t) [\frac{\partial^{2} u_{n} (β, ϑ)}{\partial ϑ^{2}} + \frac{\partial^{4} u_{n} (β, ϑ)}{\partial β^{4}} - 2 e^{β + ϑ}] d ϑ

Take

u₀ (β,

α

) =

e^{β} (1 + α)

The exact solution is:

u (β,

α

) =

e^{β + α}

Figure 2.

Table 2. The results of u₁ compared to the exact solution for

α

=0.1and the VITM

Table 2. The results of u₁ compared to the exact solution for

α

=0.1and the VITM

.β	Exact	VIM
0.1	1.22140275	1.22140275
0.2	1.3496588	1.3496588
0.3	1.49182469	1.49182469
0.4	1.54872127	1.54872127

From the above table and curve we have found no error. Hence, VIM is most suited well for this type of problems.

4. Final Conclusion

The efficiency, robustness, and fast convergence of our suggested method for solving 4th order partial differential equations (PDEs) have been established. This article provides an analytical approximate solution for fourth-order partial differential equations. The suggested method is straightforward, and its approximation to PDE solutions can be easily evaluated. The proposed method has been used to calculate the solutions to a variety of cases. Additional data showing VIM's effectiveness can be found in the tables and figures provided. Finally, the analysis of VIM approximate solutions for different order equations with precise solutions confirms the efficiency and dependability of the proposed method. The proposed method's efficacy, resilience, and rapid convergence render it highly suitable for various domains within the realm of science and technology. However, the majority of the dynamic field of application encompasses communication signaling and nanoscience, particularly in the thermal evaluation of nanoparticles.

Acknowledgments

The authors express their gratitude to the anonymous reviewers for their insightful feedback.

References

Agutter, A.J. The linguistic significance of current British slang. PhD Thesis. 1995. Edinburgh University. J.H. He, A new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simulation 1997, 2, 230–235. [Google Scholar]
He, J.H. Variational iteration method a kind of non-linear analytical technique: some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
Fatima, N.; Daniel, S. Solution of Wave Equations and Heat Equations Using HPM. Applied Mathematics and Scientific Computing. Applied Mathematics and Scientific Computing. Trends in Mathematics 2019, 367–374. [Google Scholar]
J. H. He, Approximate analytical solution of Blasius’ equation. Commun. Nonlinear Sci. Numer. Simulation 1999, 4, 75–78. [Google Scholar] [CrossRef]
Fatima, N. © Solution of Gas Dynamic and Wave Equations with VIM; Springer Nature Singapore Pte Ltd. Advances in Fluid Dynamics, Lecture Notes in Mechanical Engineering, 2021, pp 81–91.
He, J.H. , Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
He, J.H.; Wu, X.H. Construction of solitary solution and compacton-like solution by variational iteration method. Chaos, Solitons & Fractals 2006, 29, 108–113. [Google Scholar]
Hopf, E. The partial differential equation ut + uux = μuxx. Comm. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
Soliman, A.A. A numerical simulation and explicit solutions of KdV-Burgers’ and Lax’s seventh-order KdV equations. Chaos, Solitons & Fractals 2006, 29, 294–302. [Google Scholar]
Fatima, N. The Study of Heat Conduction Equation by Homotopy Perturbation Method. SN COMPUT. SCI. 2022, 3, 65. [Google Scholar] [CrossRef]
Ghadle, K.; Khan, F.; Khan, A.A. Solution of FPDE in Fluid Mechanics by ADM, VIM and NIM. American Journal of Mathematical and Computer Modelling 2017, 2. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Variational Iteration Method for Solving Nonlinear Partial Differential Equations in Fluid Dynamics

Abstract

1. Introduction

2. Variational Iteration Method by He

3. Diverse Implementations of the Analytical Expression Proposed:

3.1. Example 1

3.2. Example 2

3.3. Example 3

4. Final Conclusion

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe