Prerpints.org logo
Preprint
Article

Experimental Research and Numerical Modelling of the Cold Forming Process of the Inconel 625 Alloy Sheets Using Flexible Punch

Altmetrics

Downloads

82

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 November 2023

Posted:

21 November 2023

You are already at the latest version

Alerts
Abstract
The paper presents the numerical and experimental results of research aimed at determining the influence of hardness in the range of 50-90 Shore A of layered tools made of elastomeric materials on the possibility of forming Inconel 625 nickel-based alloy sheets. A stamping die made of 90MnCrV8 steel (hardness 60HRC) was designed for forming embosses in drawpieces, ensuring various stress states on the cross-section of the formed element. The principle of operating the stamping die was based on the Guerin method. Finite element-based numerical modelling of the forming process for various configurations of polyurethane inserts was also carried out. The drawpieces obtained by sheet forming were subjected to geometry tests using optical 3D scanning. The results confirm that in the case of forming difficult-to-deform Inconel 625 Ni-based alloy sheets, the hardness of the polyurethane inserts significantly affects the geometric quality of the obtained drawpieces. The assumptions made in numerical simulations were verified in experimental studies. Based on the test results, it was concluded that the selection of polyurethane hardness should be determined by the shape of the formed element. Significant non-uniform sheet metal deformation was also found, which may pose a problem in the process of designing forming tools and technology of plastic forming of Inconel 625 Ni-based alloy sheets.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

For many years, sheets made of difficult-to-deform alloys has been widely used in the aviation industry [1,2]. In addition to conventional methods, electromagnetic forming methods [3] and those using flexible tools [4,5] are used. This is dictated by the need to produce many elements with different geometries in strictly limited quantities. Aircraft design involves the use of many components that must meet detailed standard requirements regarding dimensional accuracy and strength [6]. The most common types of sheet metal that are formed by processes using elastomeric materials are aluminium [7,8] and aluminium alloys [9]. However, difficult-to-deform materials such as high-strength steels [10], titanium alloys [11] or Ni-based superalloys [12,13] can be successfully formed. The use of this type of alloy to form processes with elastomeric materials causes many problems. The main limitation is the alloy’s inability to form at elevated temperatures owing to the limits of the elastomer's temperature resistance [14,15]. Moreover, obtaining drawpiece profiles with small edge rounding radii is also difficult owing to the springback phenomenon [16,17] and the limited formability of sheet metal [18].
The dies for sheet metal forming (SMF) using flexible punches can be made of various materials such as steel, aluminium, wood or plastics. The die material is selected based on the designer's experience, the properties it is required to meet and economic factors. Dies made of aluminium are used most often in industry as tools for processes using elastomeric materials for stamping [19]. This is due to a very good strength-to-weight ratio, which is very important because in most cases the dies are placed manually in the press working area. However, conventional steel dies are characterised by high wear resistance and mechanical strength. They are used to produce elements that are produced in mass production due to the high cost of making the tool [20].
Elastomeric materials belong to the group of cross-linked amorphous polymers, which can deform by up to 600%. They also show good shape memory properties [21,22]. The basic materials included in the group of elastomers include natural rubber, synthetic rubbers, silicones and polyurethanes [23,24,25]. The flexible material chosen most often for SMF tools is polyurethane. It is highly resistant to wear and is thermally stable. Furthermore, it is resistant to contact with chemicals. An important aspect is that polyurethane has viscoelastic properties [26]. This causes it to behave like an incompressible liquid during SMF, and when parts are formed in a closed container, the elastomeric material exerts uniform pressure on the sheet metal. Although elastomeric materials are widely used in the SMF process, their usefulness in this process remains insufficiently researched [27,28,29]. In many studies [24,30,31], the aim of which was to analyse SMF processes using flexible punches, a significant advantage of polyurethane over other materials was proven.
The literature also contains publications related directly to the simulation of plastic forming processes in which elastomeric materials are used [32,33,34,35,36,37]. The authors of these publications focused on numerical modelling of rubber forming [33,36], the flanging process [37] and stamping using a flexible punch [32,34,35]. The results presented in these publications confirm the possibility of obtaining results very close to those determined experimentally. Some authors, however, focused on determining the properties of the process or drawpiece. Ramezani et al. [23] presented results on the springback of sheet metal during forming with the use of flexible tools, while Ali et al. [38] referred to the friction conditions occurring during the forming process. Elastomeric tools have found wide application in the rubber-pad process for forming microchannels [39,40], embossing [41,42], and patterning of thin metallic plates [43].
In this work, the selection of Inconel-type nickel alloy sheets as materials intended for plastic forming tests using polyurethane punch was dictated by their high strength and slowness in cold forming with metallic tools, while Inconel alloys are used widely in the aviation industry to produce components mounted in aircraft engines. Giving the appropriate shape to products made of high-strength sheet metal means that the elastomeric material is operated on under high contact pressure, which is necessary to form components from these materials. Previous reports, in the form of both scientific publications and the written experiences of aviation company employees, conclude that there are no clearly defined guidelines regarding the type and properties of elastomeric materials used for SMF for difficult-to-form materials. This gap became the motivation to conduct the research presented in this article. The aim of the research was to determine the influence of the hardness and properties of polyurethane punch on the formability of Inconel 625 alloy sheets. Polyurethane inserts with a Shore A (ShA) hardness of 50, 60, 70, 80 and 90 were used for forming. A specially fabricated Cr123M steel die made it possible to assess the impact of the state of stress in the formed component on the quality of the drawpieces produced using the Guerin process [28].

2. Materials and Methods

2.1. Test Materials

2.1.1. Sheet metal

To test the forming of drawpieces using polyurethane punch, 1 mm thick sheets made of an Inconel 62 Ni-based alloy were used. The basic mechanical properties were determined in a uniaxial tensile test in accordance with EN ISO 6892-1:2020-05 standard [44]. The shape and dimensions of the samples for testing mechanical properties are shown in Figure 1.
A static uniaxial tensile test was performed using a Z100 (Zwick/Roell, Ulm, Germany) testing machine with a strain rate of 0.008 s-1. The basic mechanical parameters of the sheets were determined: ultimate tensile strength Rm, yield stress Rp0.2 and total elongation A. The analysis of the anisotropy of the sheets was also performed based on the uniaxial tensile test. Samples for testing were cut at angles of 0°, 90° and 45° relative to the sheet rolling direction. The base test length was set to 25% of the sample elongation, which was determined from the tensile test up to the failure of the sample.
Surface roughness parameters and surface topography of the Inconel 625 sheet metal and polyurethane inserts were analysed using the LEXT OLS4100 (Olympus, Tokio, Japan) laser scanning digital microscope for non-contact three-dimensional (3D) observations and measurements of surface features at 10 nm resolutions. The microscope was equipped with a 405 nm short-wavelength semiconductor laser. The average values of surface roughness parameters (average surface roughness Ra and ten-point height of irregularities Rz) were determined based on the three measurements of each sample. The average roughness Ra and ten-point height of irregularities Rz of the Inconel 625 sheet were equal of 0.105 μm and 0.646 μm, respectively. Figure 2 shows the surface topography and linear roughness profiles of the Inconel 625 nickel alloy samples.

2.1.2. Material of Punch

Commercial polyurethanes with a nominal hardness of 50, 60, 70, 80 and 90 ShA were used for the tests. The test samples and inserts for the forming tool were made from one batch of material so that there were no significant differences in their properties. Hardness tests and uniaxial compression tests were carried out.. The compression test of polyurethane samples was carried out in accordance with the ASTM D575-91 standard. Cylindrical samples with a diameter of D = 28.6 mm and a height of h = 13 mm were prepared. The samples were compressed at a speed of 12 mm/min to a height of 10 mm. Compression tests were carried out without the use of lubricant. The research was carried out taking into account three repetitions of each test. Table 1 shows the results of measuring basic roughness parameters of polyurethane inserts.

2.2. Wear Resistance of Elastomeric Materials

The abrasive wear resistance of polyurethane countersamples was tested on the T-05 roller-block tester (Institute of Precision Mechanics, Radom, Poland). The measurement was carried out at ambient temperature in a dry sliding contact. The operating principle of the tester is shown schematically in Figure 3a.
The self-adjusting mounting of the block, which consists of a sample holder and a hemispherical insert, ensures good adhesion of the block to the roller and even distribution of pressure in the contact surface. The tester enables tests to be carried out in accordance with the methods specified in the ASTM D2714, ASTM D3704, ASTM D2981 and ASTM G77 standards. The geometry and dimensions of the polyurethane countersample are shown in Figure 3b. The sample was made with Inconel 625 alloy.
All measurements were performed at a constant ring rotation speed of n = 136 rpm. During the test, a load of FN = 50 N was applied. The friction path was 150 m. During the tribological test, the friction force F was continuously recorded, which was used to determine the coefficient of friction (COF) µ according to the Eq. (1).
μ = F F N
COF was determined as the average value for the entire friction path. The measure of abrasion resistance is the mass loss of the tested material in relation to the friction path and the applied load. The percentage weight loss Δmcs of the polyurethane countersamples was determined according to Eq. (2):
∆ m c s = m p − m k m p × 100 %
where mp is initial mass of the countersample and mk is final mass of the countersample.
In a similar way, percentage weight loss Δms of the sample was determined for a sample made of Inconel 625.

2.3. Methodology of Numerical Simulations

Finite element-based numerical simulations of the forming process of Inconel 625 sheets were carried out using Impetus Afea (Impetusafea AB, Huddinge, Sweden) software. The determination of the material coefficients of polyurethane samples used in the simulations was based on a uniaxial compression test of a cylindrical sample as mentioned in section 2.1.2. The mechanical parameters of Inconel 625 alloy sheets were determined on the basis of a uniaxial tensile test using Z100 (Zwick/Roell, Ulm, Germany) uniaxial tensile testing machine. In the case of elastomeric materials, a two-parameter Mooney–Rivlin constitutive model was selected:
σ 1 = 2 C 1 3 2 λ 1 − λ 2 − λ 3 − 2 C 2 3 2 λ 1 − 1 λ 2 − 1 λ 3 − ρ
σ 2 = 2 C 1 3 2 λ 2 − λ 3 − λ 1 − 2 C 2 3 2 λ 2 − 1 λ 3 − 1 λ 1 − ρ
σ 3 = 2 C 1 3 2 λ 3 − λ 1 − λ 2 − 2 C 2 3 2 λ 3 − 1 λ 1 − 1 λ 2 − ρ
ρ = − K ε v
where σ 1 , σ 2 , σ 3 are principal stresses, λ 1 , λ 2 , λ 3 are eigenvalues of Cauchy-Green's right stretch tensor, the pressure ρ is a linear function of the volumetric strain ε v ,  C1, C2, K are material constants.
The Mooney–Rivlin material model was used due to its availability in the software used to perform the numerical simulations. For each material, a 3D model was developed reflecting the sample geometry and test conditions. Simulations were carried out to determine the material coefficients C1 and C2 in such a way that the experimental results were reflected in the simulations as much as possible. An example result of the simulation of the sample compression process and the fitting of the simulation results to the experimental curve is presented in Figure 4a and 4b, respectively.
Table 2 shows the material coefficients obtained from the simulation of compression tests.
The coefficient of friction (μ = 0.09) was assumed to be constant in the simulation model. The same value of the coefficient of friction was used for polyurethane inserts of different hardness due to the possibility of direct comparison of the results. The constitutive model has been designed as a temperature and strain rate dependant strength model in a simple isotopic form. The von Mises yield criterion, the elastic-plastic law of plastic flow and explicit time integration scheme were used in the calculations. A contact algorithm based on a penalty function was used. Shell elements were used to in the discretization of the forming tools (die, stamp and container). The forming tools were considered to be rigid. The workpiece and polyrurethane inserts were assumed as deformable. An optimum number of elements and element size were determined based on the mesh sensitivity analysis.
After determining all the necessary material parameters, a simplified 3D model of the stamping die was created to simulate the sheet metal forming process using polyurethane punches (Figure 5). The simplification of the stamping die model due to symmetry of the forming process was aimed at minimising the computational time of numerical simulations.
Several simulations were performed assuming different combinations of hardnesses of polyurethane inserts. Two variants were considered. In the first variant, a stack of five inserts with the same hardness was used. Simulations were also carried out assuming the use of hybrid variants of arrangement of polyurethane inserts, where the use of a stack of polyurethane inserts of different hardness in one tool was considered 2×50 ShA + 3×90 ShA and 3×50 ShA + 2×90 ShA (Figure 6).
The total thickness of the five layers of inserts was constant and amounts to 50 mm. The diameter of the polyurethane inserts was 160 mm. 90MnCrV8 steel dies with the shape shown in Figure 7 were used in the simulations and experiments.
The die was designed to allow the effect on the sheet formability of differences in the hardness of the polyurethane inserts to be determined. The forming process was intended to test the possibility of making three independent embosses on one element. The embosses have been designed so that the formed material is not significantly pressed to the bottom of the embosses. These embosses do not have technological slopes and are made at an angle of 90° to the die surface. This shape was intended to cause the sheet metal to lift in the areas between the embosses (Figure 7), due to the lack of slopes on the side wall of the embosses. The area of the lower part of the embosses has not been finished with a rounding radius, so it is impossible to reproduce accurately the shape of the die. In this way, it is possible to determine the differences between elements formed with polyurethane inserts with different hardness configurations.
In the outer area of the formed element, tensile stresses were assumed to occur towards the centre of the die with small compressive stresses caused by the rounded shape of the formed element. This stress varies depending on the area of the element, with the highest value of compressive stress occurring in the die axis, transverse to the length of emboss. There is a plane tensile stress state in the formed area (Figure 8). However, in the area between the embosses, there is a tensile stress in two axes parallel to the die surface.

2.4. Experimental Forming Procedure

To perform tests on the sheet forming of Inconel 625 alloy sheets, a stamping die was designed based on the Guerin process. The Guerin process was named after Henry Guerin, who in the late 1930s discovered the technique of using rubber as the half die instead of the metallic part. This process is commonly used to form short runs of complicated components such as aircraft panels and automobile panels [28]. Owing to the character of the forming process and the need for frequent replacement of polyurethane inserts, the device was developed in accordance with the author's concept of enabling the quick replacement of sets of components, such as the die, the workpiece and a set of polyurethane inserts. Experimental verification of the simulation results was carried out by performing forming tests using selected combinations of elastomeric materials on a hydraulic press Hydromega 150T (Hydromega, Gdynia, Poland) with a capacity of 1,500 kN. The set of tools which was installed on the hydraulic press is shown in Figure 9.
The top plate with the punch is attached to the upper part of the press. The bottom plate with installed accessories is attached to the work table of the press. The ejector is pulled out using an actuator located under the work table. The die, a workpiece and polyurethane inserts of a given hardness are placed on the base of the pushing system. Special chamfering in the upper part of the guide sleeve positions all elements relative to each other. Then, the upper cylinder of the press lowers the upper plate together with the punch, exerting force on the polyurethane punch, which causes the workpiece to be deformed. Figure 10 shows a photograph of the tool set mounted on the press.
Owing to the high friction occurring during forming, H-336 lubricant (Molydal, Saint-Maximin, France) was used. It is an oil intended for the plastic forming of sheet metals. It was used to reduce friction between the polyurethane sample and the sheet metal and between the sheet metal and the die surface.

2.5. 3D Optical Scanning Research Methodology

A three-dimensional optical scanning investigations of drawpiece geometry were performed using an Atos Core 200 3D scanner (Carl Zeiss GOM Metrology GmbH, Braunschweig, Germany). This device allows the creation of three-dimensional models of the analysed elements with a measurement accuracy of 0.017 mm. Thanks to the use of a scanner, 3D models of all constituent variants were created. An sample scanning result is shown in Figure 11.
The maximum forming depth was determined by point measurement of the distance between the area with the greatest depression and the reference plane formed on the face of the drawpiece. The measurement was performed to minimise the influence of differences in surface flatness on the measurement of forming depth. The scans of the drawpiece geometry were used to measure parameters such as surface flatness, thickness of the formed sheet, change in workpiece diameter and the uniformity of forming.
For surface flatness measurement, the best plane matching function was used. This function determines two parallel planes adjusted to the most protruding and the most concave part of the selected surface on the model. The flatness of the surface is determined by the distance between these planes. Figure 12 shows an example result of measuring surface flatness.
Generating the results of thickness changes (Figure 13a) is possible by determining the normal direction of the scanned surfaces.
It is obtained by analysing the distance between two surfaces of the model at each of the measured points. Distance measurement was used to measure the change in diameter (Figure 13b). Measurements were made in the direction parallel and perpendicular to the shaped emboss. The result is presented in numerical form as a reference value determined by the difference between the diameter of the workpiece before the forming process and the measured value.
The uniformity of forming was assessed by comparing the right side of the model with the left side. The best fit function was used to compare the results, which allows for the accurate matching of the two models. The result was presented using a colour map of deviations, with point markers placed in key places in the model (Figure 14a).
The difference in forming depth for selected polyurethane insert configurations was determined by superimposing 3D scans using the best fit function. To minimise the impact of the emboss depth on the degree of matching, the matching was performed for flat parts of the emboss (Figure 14b). Results for drawpieces produced under specific conditions will be presented in Section 3.

3. Results and Discussion

3.1. Mechanical Properties of Sheet Metals

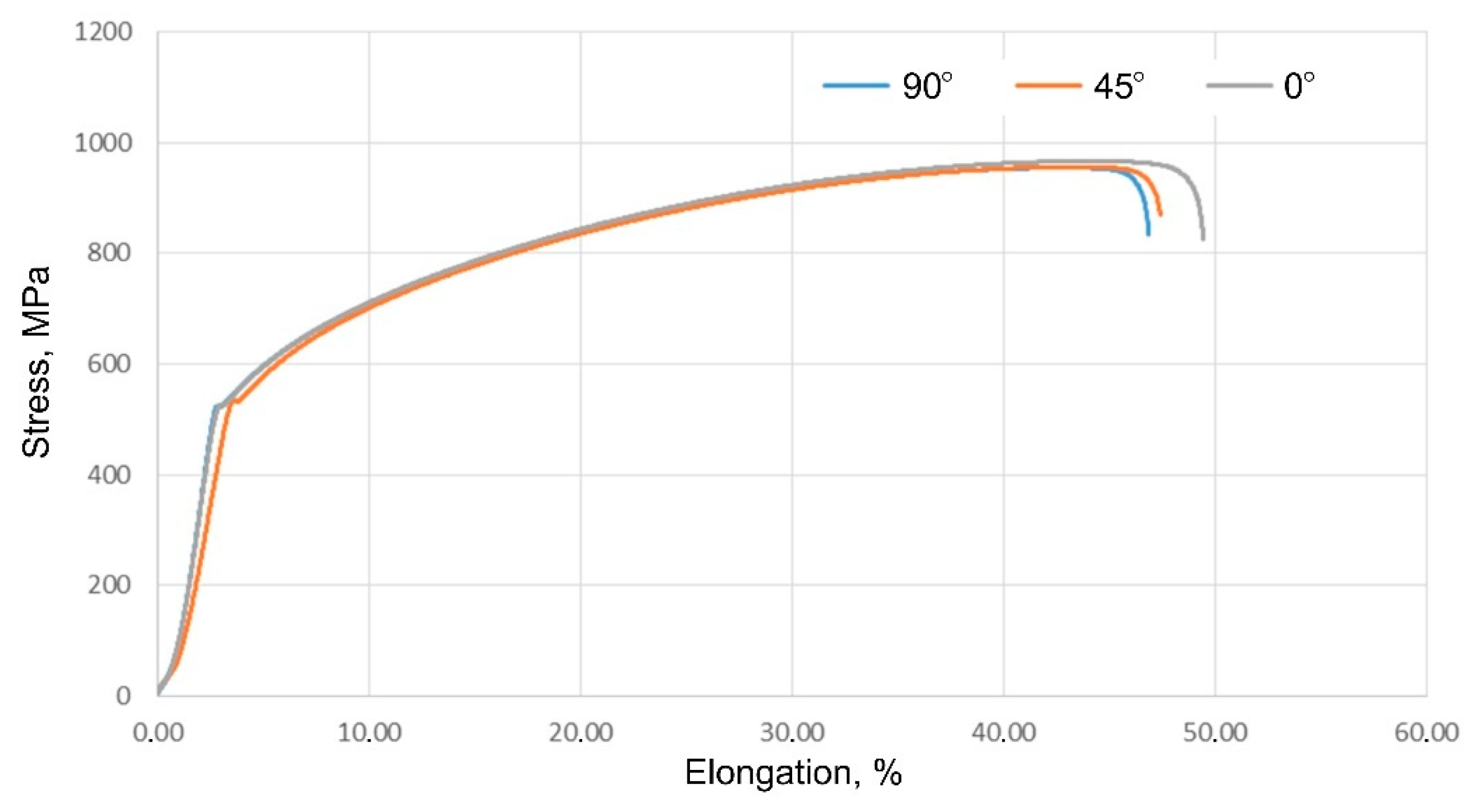
Figure 15 shows the tensile curves of Inconel 625 sheets.
The results include three data series, for samples cut at 0°, 45° and 90° angles to the rolling direction of the sheet. A summary of the results of the basic mechanical parameters and anisotropy coefficients is presented in Table 3 and Table 4, respectively.
The results were averaged from three replicates. Those obtained during the tensile test do not show significant differences depending on the orientation of the samples. The highest value of ultimate tensile strength (966.1 MPa) was obtained for a sample oriented parallel to the direction of sheet rolling. The difference in results depending on the direction of sampling is 11.7 MPa for tensile strength, 10.9 MPa for yield stress and 2.6% for elongation.

3.2. Mechanical Properties of Polyurethane Materials

The nominal hardness of the tested materials was verified by performing five measurements for each type of polyurethane used. The results of individual measurements and the average hardness are presented in Table 5.
In the case of materials with nominal hardness of 50, 80 and 90 ShA, the results indicate slight differences depending on the measurement location, not exceeding 2 ShA, which means that the hardness of the polyurethane materials is uniform. The average value differs significantly for materials with a nominal hardness of 70 ShA and is close to a hardness of 60 ShA.
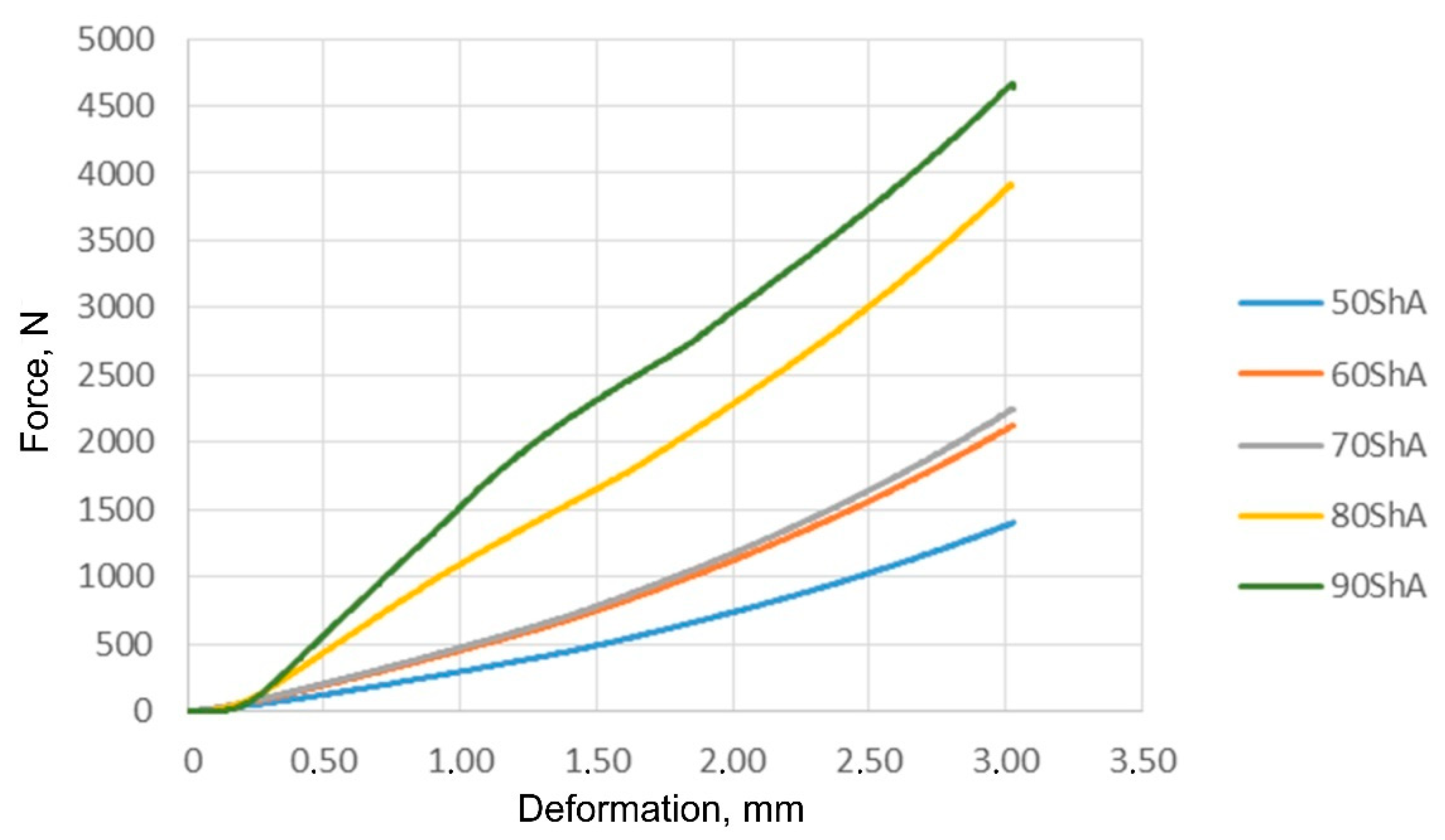
Figure 16 shows the results of compression measurements for all tested polyurethane materials.
These results were used to determine the material constants in the Mooney–Rivlin material model. The compression results show trends in increasing compressive strength with increasing hardness of the elastomeric material. For samples with a nominal hardness of 60 ShA and 70 ShA, there is a slight difference in the results obtained from the uniaxial compression test.

3.3. Wear Resistance

Forming sheets made of difficult-to-deform alloys using elastomeric materials of much lower hardness results in intensified wear [23,45]. Therefore, determining the quantitative wear of the friction pair is a key to establishing optimal conditions for the forming process. Table 6 shows the wear results of polyurethane and Inconel 625 nickel alloy samples.
A common feature of the tested polyurethanes was the deformation of their surface in contact with the sample, resulting from the applied force FN = 50 N. The value of this deformation influenced the size of the tribological contact surface in the friction node. Polyurethanes, constituting a countersample, were an element of the friction node in which mass losses were observed. However, some samples made of nickel alloy were characterised by an increase in mass resulting from the transfer of the countersample material. For the tested polyurethanes, the COF ranges between 0.263 and 0.622. The polyurethane with a hardness of 90 ShA is characterised by the lowest average value of the COF. The obtained result of 0.263 is a quite high COF in relation to other polymer materials.

3.4. Results of Numerical Simulations of the Forming Process

During the simulation, a forming force of 400 kN was applied to the surface of the polyurethane punch. Figure 17 shows the deformation of the drawpiece in subsequent stages of simulation.
Table 7 presents the simulation results of all variants of polyurethane insert systems.
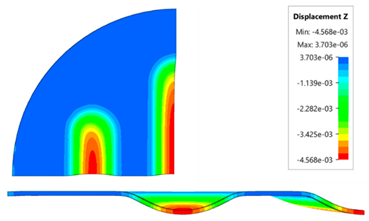
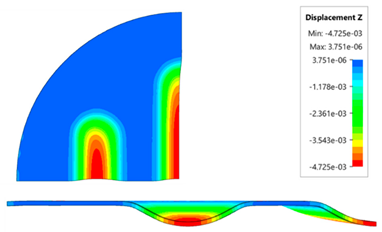
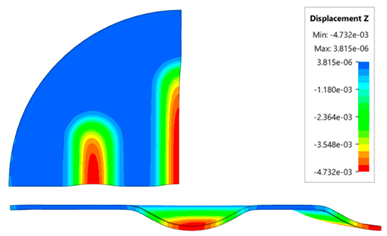
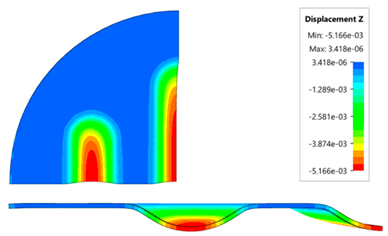
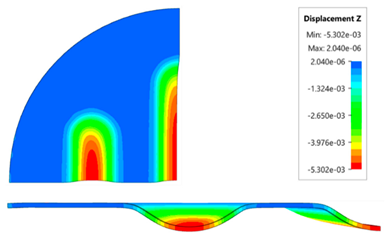
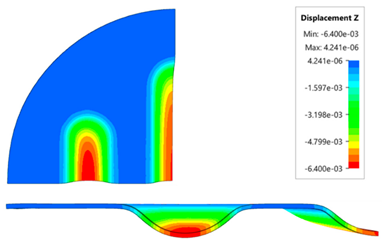
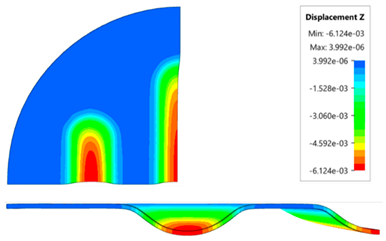
The results presented in this table are presented in the form of perpendicular and transverse views, which allows easier assessment of the obtained forming effects. A separate column contains the maximum measured depth of emboss, which was the main parameter analysed when comparing the tested configurations of polyurethane inserts. The forming depth was chosen as the most important result of numerical computations owing to the easily verified value obtained in numerical modelling, with the results determined during experimental tests. The highest values of sheet metal deformation in the emboss zone (6.124 and 6.4 mm) were obtained for hybrid configurations of the polyurethane inserts with varying hardness. It was found that polyurethane inserts of lower hardness in contact with the surface of the sheet being deformed provide greater degrees of sheet metal deformation in the embosses.
Figure 18 compares the maximum depth of emboss for individual polyurethane hardness variants.
The shape of the die was developed to compare the sheet metal forming process using a geometry in which the formed element has three separate areas, formed at the same time. The distance between the embosses was selected so that the deformation of the elastomeric material occurred at several independent areas, close to each other. This arrangement was intended to determine the influence of individual embosses on the overall deformation of the elastomeric material. In tests using 5-layer inserts with the same hardness, an increase in the hardness of a polyurethane insert ensures a greater degree of material deformation in the embosses (Figure 18). 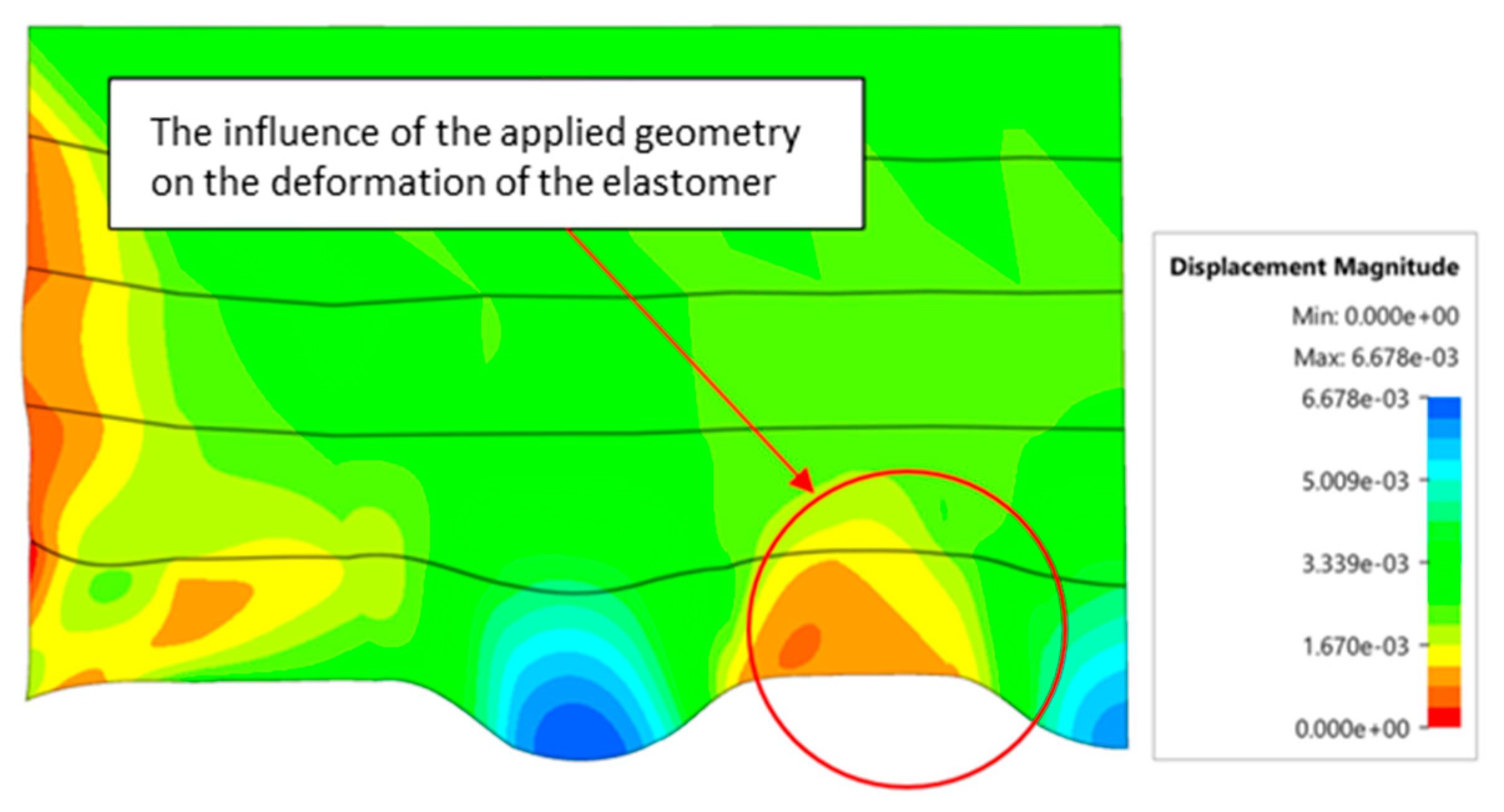The results presented in Figure 19 show the influence of the die geometry on the deformation of the elastomeric material.
The deepest embosses were achieved for configurations containing layered polyurethane inserts with a hardness of 2 × 50 ShA + 3 × 90 ShA. The values obtained using these configurations were 6.4 mm for the combination of two layers with a hardness of 50 ShA placed directly above the surface of the workpiece and three layers with a hardness of 90 ShA placed above inserts with a hardness of 50 ShA. For the variant with a changed arrangement of inserts, a value of 6.124 mm was obtained (Table 7). The least favourable result, which was 4.568 mm, was obtained for the polyurethane tool, which comprised five inserts with a hardness of 50 ShA. The difference between the result obtained for the best and worst combination is 1.832 mm. The use of a configuration of 2 × 50 ShA + 3 × 90 ShA allows for a 40.1% greater stamping depth than the combination containing five inserts with a hardness of 50 ShA.
Numerical simulations were also performed for the forming force, which had been increased to 1,000 kN. Despite such high force, no significant differences were observed to depend on the hardness of the polyurethane inserts. Figure 20 presents a summary of sheet metal deformations during forming with polyurethane inserts with a hardness of between 50 and 90 ShA at a pressure of 1,000 kN.
Owing to the lack of clear differences in the simulation results with a forming force of 1,000 kN, it was decided to use the results obtained with a forming force of 400 kN for experimental verification. For inserts of the same hardness, the smallest depth of emboss was obtained for inserts with a hardness of 50 ShA (Figure 18). However, for inserts comprising layers with varying hardness, the greatest depth of emboss was provided by inserts with the configuration 2 × 50 ShA + 3 × 90 ShA (Figure 18).

3.5. Results of Experimental Tests of the Forming Process

Table 8 presents a summary of the results obtained by forming drawpieces on a hydraulic press with a pressure of 1,000 kN, depending on the arrangement and hardness of the polyurethane inserts.
This table includes photos of the samples, a 3D scan view and the measured maximum forming depth for each variant. The difference in forming depth for the analysed configuration variants of polyurethane inserts was 0.14 mm. For the variant containing five inserts with a hardness of 50 ShA, the maximum forming depth was 5.81 mm, and for the configuration 2 × 50 ShA and 3 × 90 ShA, it was equal to 5.95 mm (Table 8).
Figure 21 and Figure 22 show the results of geometric analysis of drawpieces.
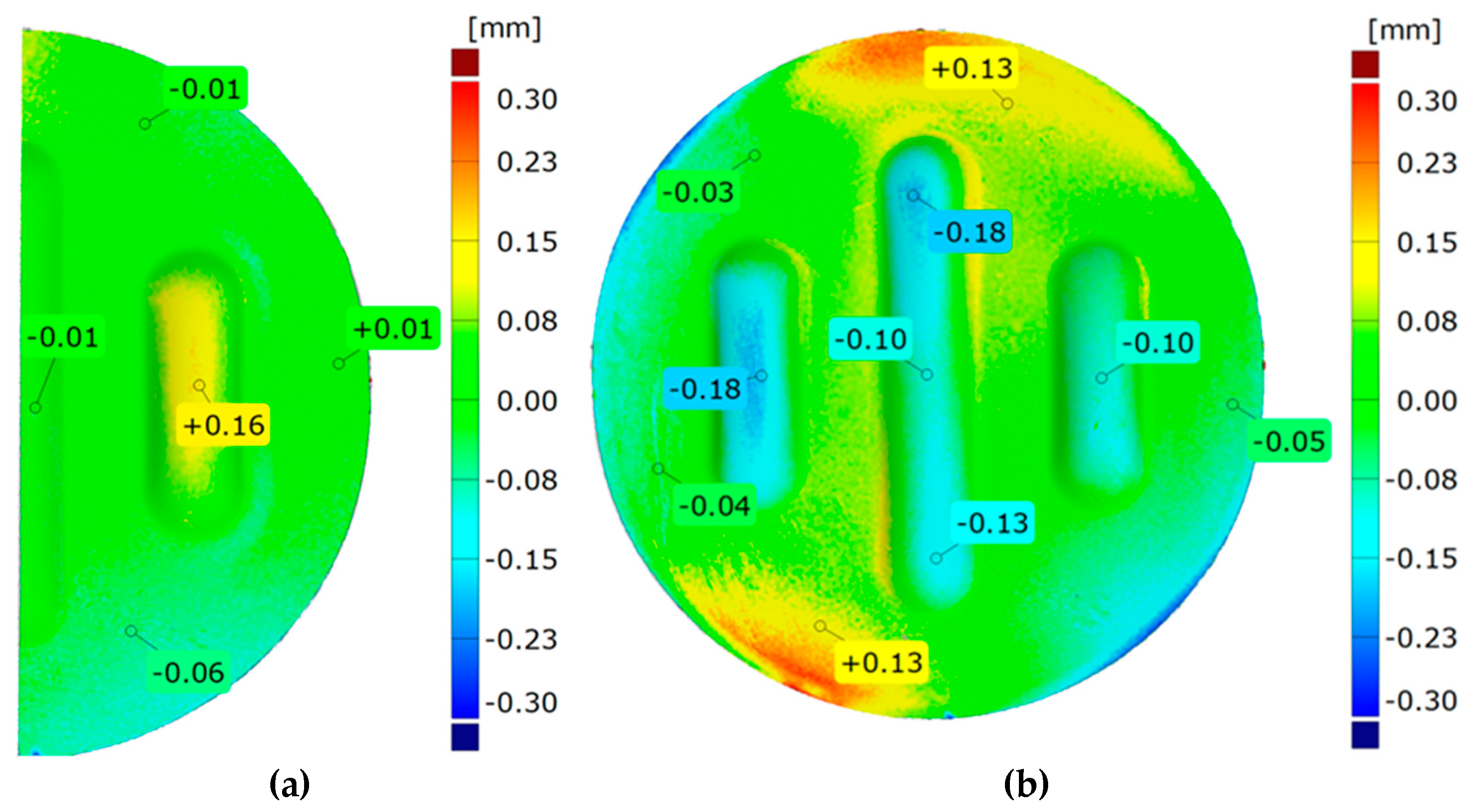
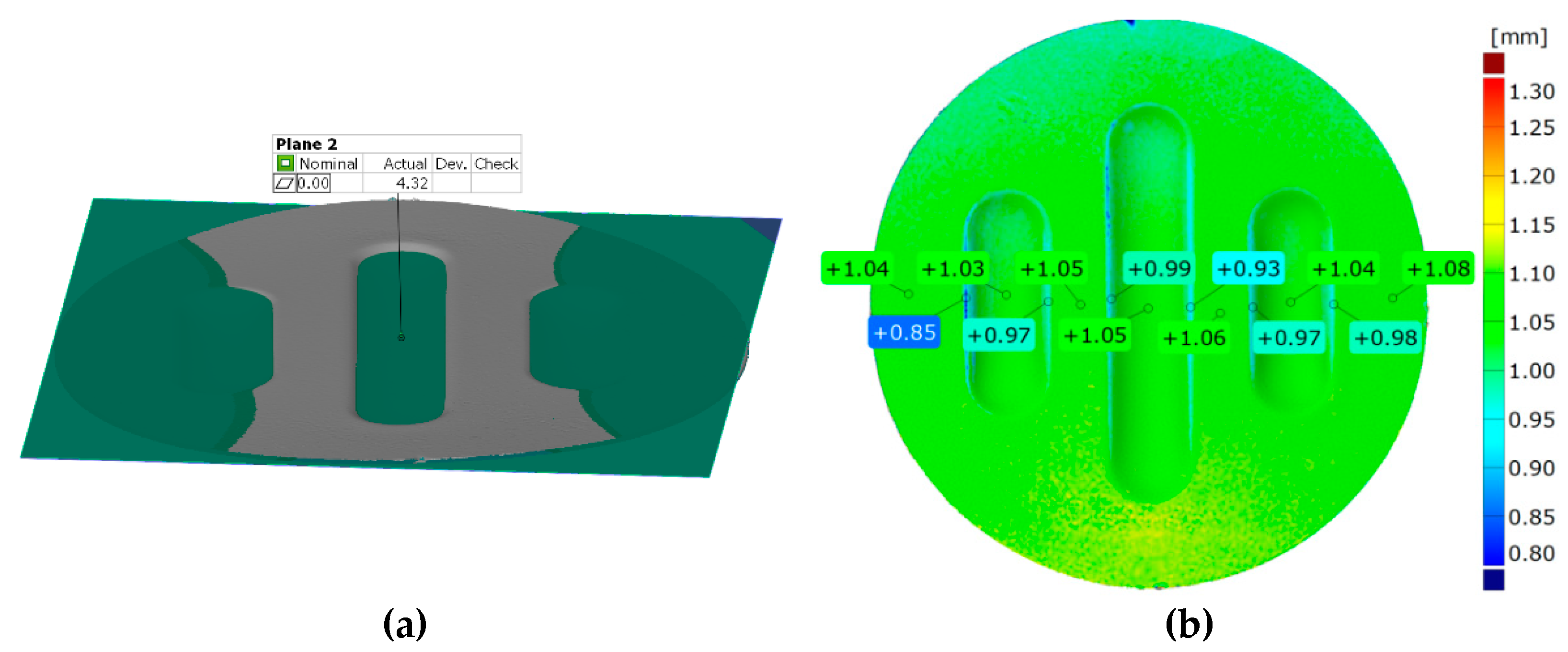
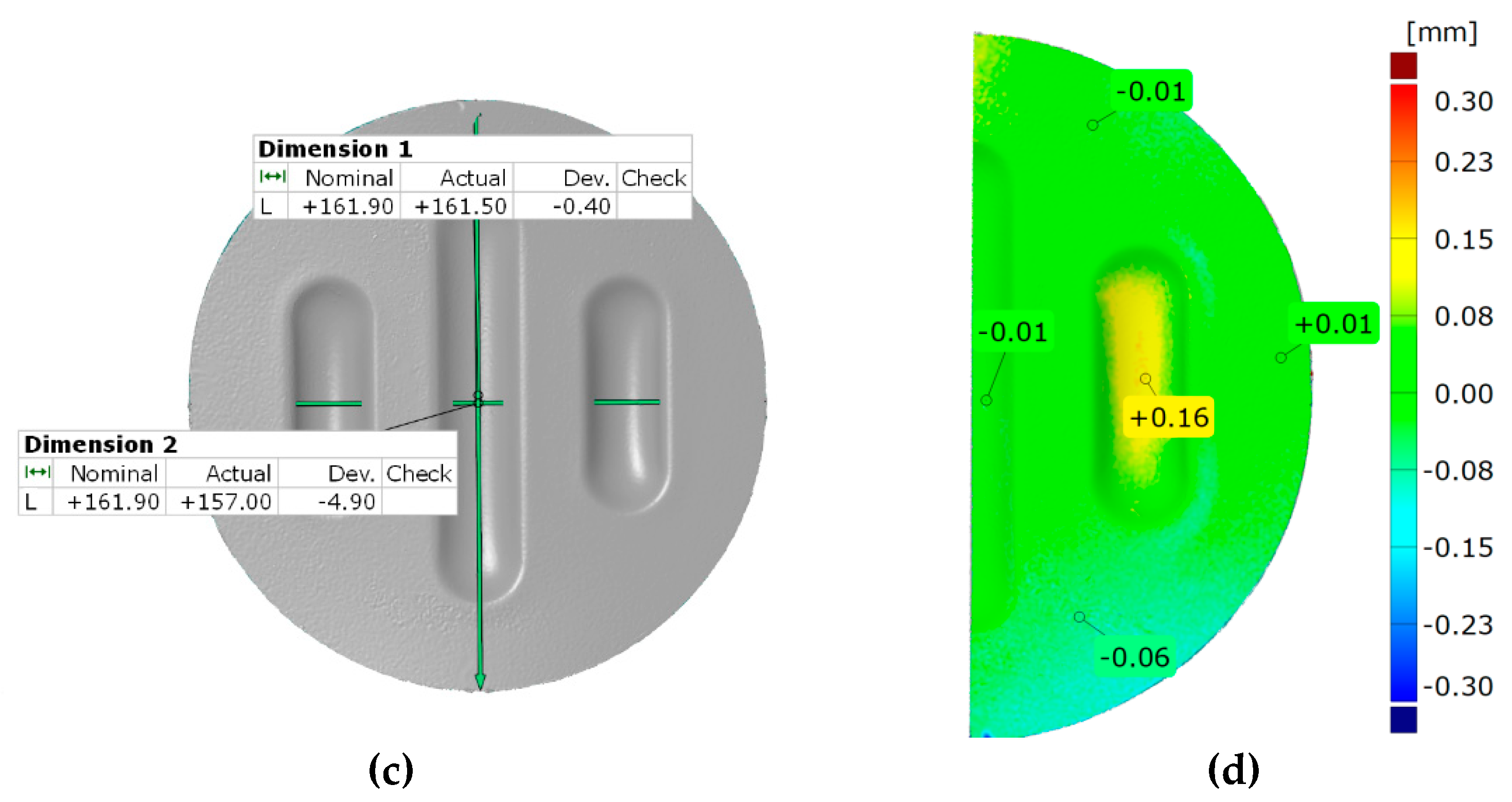
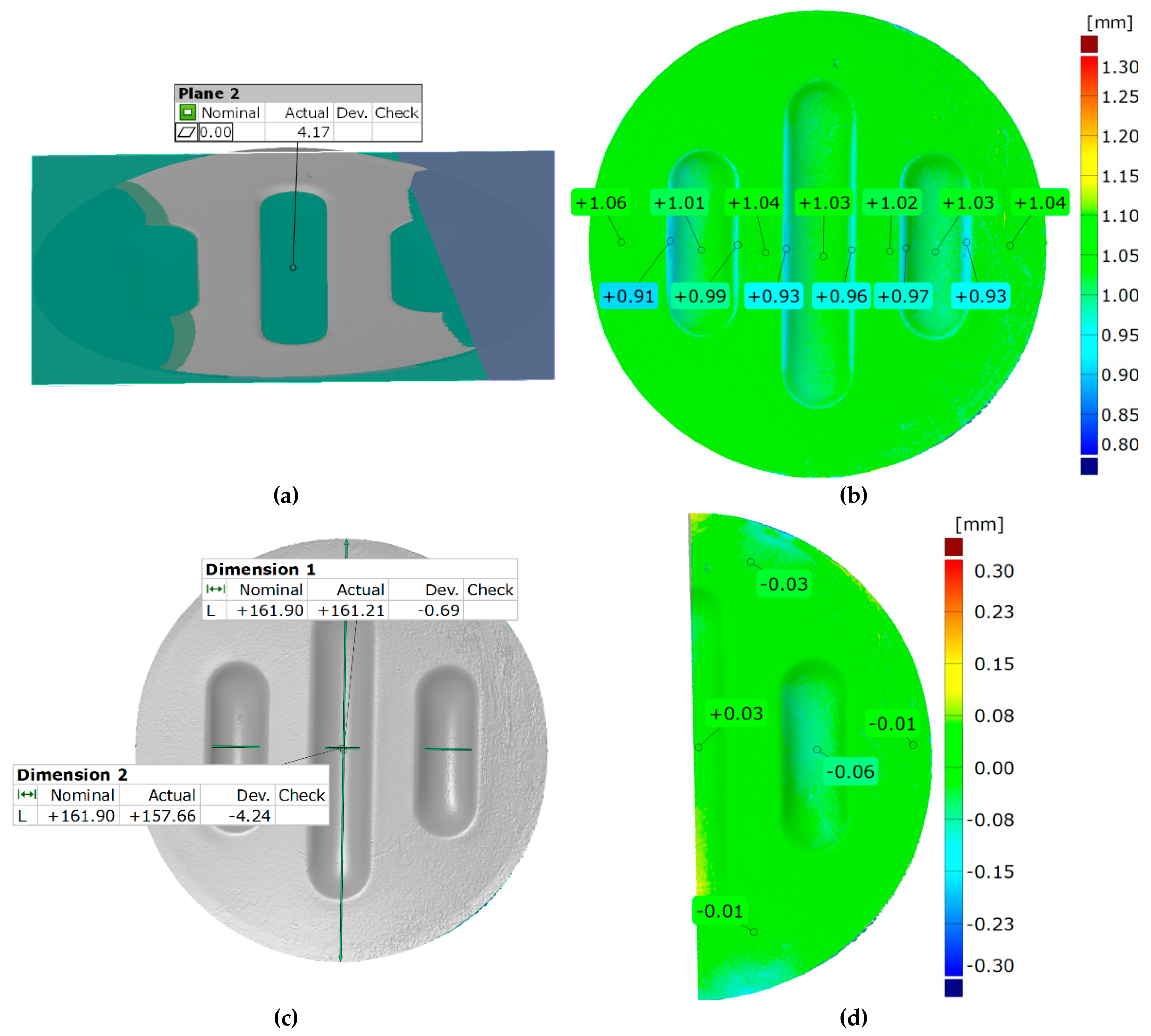
In the case of the results presented in Figure 21, a configuration containing five inserts with a hardness of 50 ShA was used, which in numerical analyses showed the worst ability to form an element made of the Inconel 625 alloy. Figure 22 shows the results for the same forming conditions, but using a configuration containing two inserts with a hardness of 50 ShA and three inserts with a hardness of 90 ShA. In numerical calculations this variant showed the best ability to form an element. In the case of surface flatness, there was a difference of 0.15 mm for both variants considered. For the 5 × 50 ShA variant, the surface flatness was 4.32 mm, and for the 2 × 50 ShA + 3 × 90 ShA configuration, it was 4.17 mm. In the case of the five inserts with hardness of 50 ShA, there is a uniform thickness distribution.
The difference between the maximum and minimum value is 0.2 mm, which gives a maximum wall thinning of 19%. In the case of the 2 × 50 ShA + 3 × 90 ShA configuration, the thinning is smaller. The minimum wall thickness value is 0.91 mm, which gives a wall thinning of 14%. The change in the diameter of the formed workpiece in the case of the 5 × 50 ShA system was –0.4 mm longitudinally in the direction of the formed embosses and –4.9 mm in the transverse direction. These values for the 2 × 50 ShA + 3 × 90 ShA configuration were –0.69 mm and –4.24 mm, respectively. For the 5 × 50 ShA system, clear differences in the uniformity of formation can be observed. There is a difference of 0.16 mm between the right and left sides of the formed drawpiece in the smaller emboss. For the 2 × 50 ShA + 3 × 90 ShA configuration, much greater uniformity of formation can be observed, with a maximum difference of 0.06 mm. Figure 23 shows a tabular summary of the measurement results of drawpieces.
Figure 24 shows a comparison of 3D scans of measured drawpieces obtained by using two different configurations of polyurethane inserts.
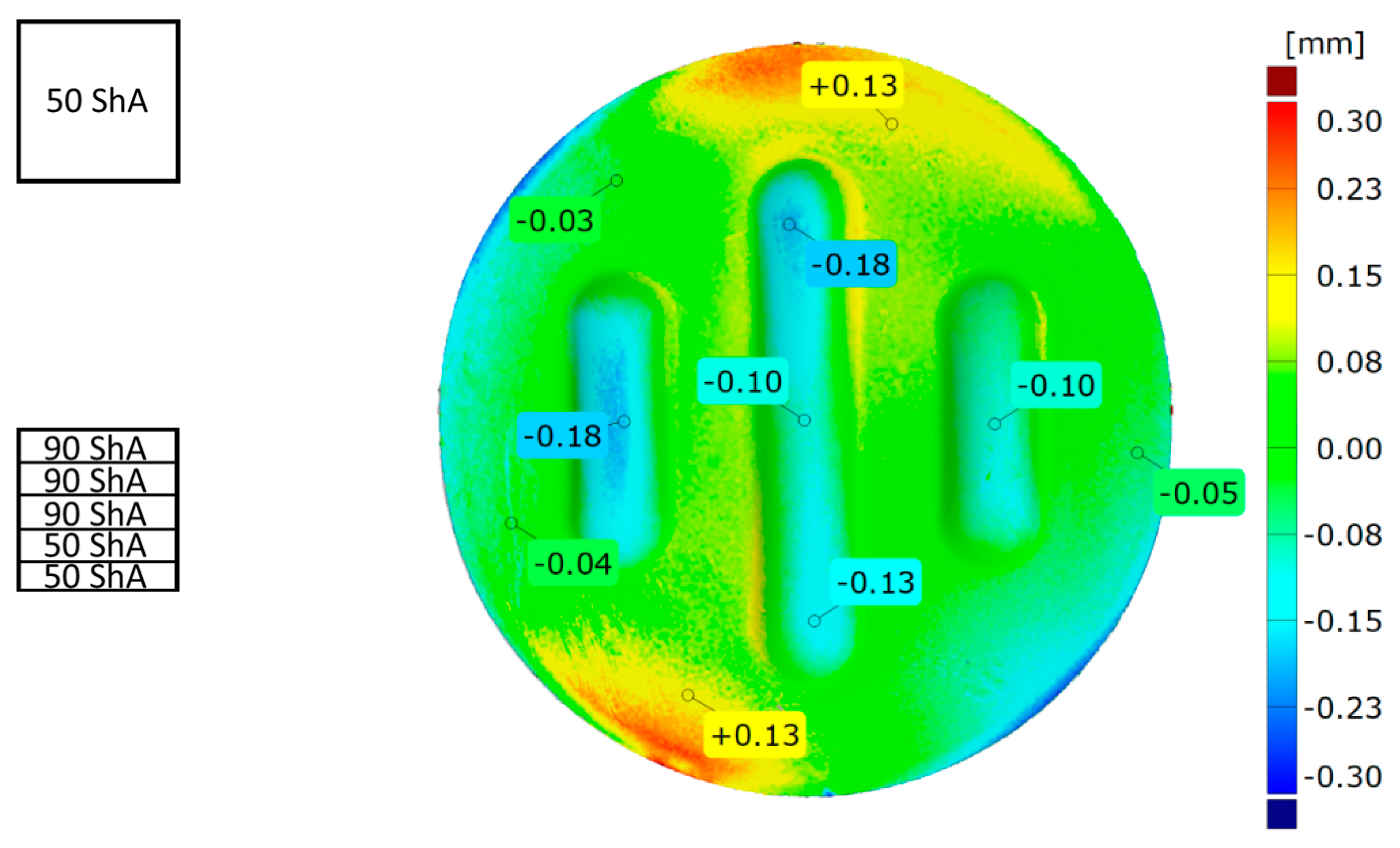
The results confirm deeper formation of embosses for the 2 × 50 ShA + 3 × 90 ShA configuration of polymeric inserts. The differences range from –0.18 mm to 0.13 mm on the surface of the embosses. Analysing the results of the combinations of inserts, it is possible to conclude that there is a significant difference in the quality of the obtained element depending on the hardness of the elastomeric material used. The results obtained during numerical simulations were also confirmed experimentally and for all measured values of geometric parameters the 2 × 50 ShA + 3 × 90 ShA configuration was more favourable.

4. Conclusions

This article presents the results of numerical and experimental research aimed at determining the influence of the hardness of layered tools made of polyurethane inserts on the possibility of forming drawpieces from Inconel 625 Ni-based alloy sheets. Based on the research performed, the following conclusions can be formulated:
  • The hardness of elastomeric materials and configuration of the hardness of layers in multilayer polyurethane punch have a significant impact on the geometric quality of the obtained drawpieces.
  • An analysis of the results of numerical simulations and experimental tests clearly indicates that the hardness of the punch material should be selected based on the shape of the formed element.
  • For most of the polyurethane inserts configurations, the depth of embosses in the Inconel 625 alloy sheet was similar, at approximately 5.95 mm. The value of the forming depth of emboss was 5.81 mm only for the system containing five inserts with a hardness of 50 ShA.
  • The characteristics of the forming process determine the greatest wear of polyurethane samples on the contact surface with the surface of the formed sheet. The use of multilayer systems of polyurethane inserts allows the cost of polyurethane tools to be reduced, owing to the possible replacement of only a single layer, which is in contact with the sheet metal surface, without the need to replace the entire polyurethane tool. It is also possible to rearrange the order of inserts after a certain, precisely defined number of formed drawpieces, to ensure uniform tool wear.
  • Determined and verified constitutive models as well as the obtained test results can be used in the design of forming processes in industrial conditions of the Inconel 625 nickel alloy sheets using polyurethane inserts of various hardness.
  • The results confirm that using the designed device, it is possible to form sheets of Inconel-type nickel alloys with a thickness of 1 mm, the forming of which in industrial cold forming conditions is a challenge. Owing to the nature of forming process, shaped components cannot be heated to high temperatures because of the contact of the polyurethane punch surface with the formed material.

Author Contributions

Conceptualization, K.Ż. and M.B.; methodology, K.Ż., M.B. and M.H.; software, M.B., M.H., S.P. and Ł.K.; validation, K.Ż., M.B. and M.H.; investigation, K.Ż., M.B., M.H., S.P., Ł.K., T.T., and V.N.; data curation, K.Ż., M.B., S.P., Ł.K., T.T. and V.N; writing—original draft preparation, K.Ż. and M.B.; writing—review and editing, K.Ż., M.B., T.T. and V.N.; visualization, K.Ż., M.B., S.P., Ł.K. and T.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Żaba, K.; Nowosielski, M.; Puchlerska, S.; Kwiatkowski, M.; Kita, P.; Głodzik, M.; Korfanty, K.; Pociecha, D.; Pieja, T. Investigation of the mechanical properties and microstructure of nickel superalloys processed in shear forming. Arch. Metall. Mater. 2015, 60, 2637–2644. [Google Scholar] [CrossRef]
  2. Frącz, W.; Stachowicz, F.; Trzepieciński, T.; Pieja, T. Forming limit diagram of the AMS 5599 sheet metal. Arch. Metall. Mater. 2013, 58, 1213–1217. [Google Scholar] [CrossRef]
  3. Li, J.; Li, J.; Wan, M.; Yu, H.; Liu, L. Innovation applications of electromagnetic forming and its fundamental problems. Procedia Manuf. 2018, 15, 14–30. [Google Scholar] [CrossRef]
  4. Rękas, A.; Luty, G.; Kuta, A.; Żaba, K. Zastosowanie narzędzi elastomerowych w procesie kształtowania wyrobów powłokowych. Rudy i Metale Nieżelazne 2011, 56, 212–216. [Google Scholar]
  5. Krakowski, M.; Bartnicki, J. Analiza procesu wytłaczania narzędziem elastycznym. Mechanik 2017, 11, 982–984. [Google Scholar] [CrossRef]
  6. Malinowski, T.; Pieja, T.; Bąk, A.; Hojny, M.; Trzepieciński, T. Formability analysis of rubber pad-based forming process of drawpieces. Proceedings of 25th Anniversary International Conference on Metallurgy and Materials METAL 2016, Tanger Ltd. (Ostrava), May 25th-27th, 2016, pp. 440-445.
  7. Quadrini, F.; Santo, L.; Squeo, E.A. Flexible forming of thin aluminum alloy sheets. Int. J. Modern Manuf. Technol. 2010, 2, 79–84. [Google Scholar]
  8. Belhassen, L.; Koubaa, S.; Wali, M.; Dammak, F. Numerical prediction of springback and ductile damage in rubber-pad forming process of aluminum sheet metal. Int. J. Mech. Sci. 2006, 117, 218–226. [Google Scholar] [CrossRef]
  9. Elghawail, A.; Essa, K.; Abousaf, M.; Tolipov, A.; Su, S.; Pham, D. Low-cost metal-forming process using an elastic punch and a reconfigurable multi-pin die. Int. J. Mater. Form. 2019, 12, 391–401. [Google Scholar] [CrossRef]
  10. Irthiea, I.; Green, G.; Hashim, S.; Kriama, A. Experimental and numerical investigation on micro deep drawing process of stainless steel 304 foil using flexible tools. Int. J. Mach. Tools Manuf. 2014, 76, 21–33. [Google Scholar] [CrossRef]
  11. Adamus, J.; Lacki, P. Investigation of sheet-titanium forming with flexible tool – experiment and simulation. Arch. Metall. Mater. 2012, 57, 1247–1252. [Google Scholar] [CrossRef]
  12. Kawoluk, P.; Jurek, D.; Schindler, I.; Kawoluk, R.; Opěla, P.; Němec, J.; Kawuloková, M.; Rusz, S.; Sauer, M. Formability of Invaw 36 alloy at high temperatures. Journal of Metallic Materials 2022, 74, 15–20. [Google Scholar] [CrossRef]
  13. Kawulok, P.; Kawulok, R.; Jurek, D.; Puzoň, D.; Schindler, I.; Opěla, P.; Rusz, S.; Kawuloková, M. The high-temperature strength and plastic properties of Incoloy 800HT and Invar 36 alloys. In Proceedings of the 30th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 26 - 28 May 2021, pp. 276–281. [Google Scholar]
  14. Benisa, M.; Babic, B.; Grbovic, A.; Stefanovic, Z. Computer-aided modeling of the rubber-pad forming process. Materiali in Technologije-Mater. Technol. 2012, 46, 503–510. [Google Scholar]
  15. Abbas, A.A.; Hussein, M.A.; Mohammad, M.M. Design Parameters Estimation and Design Sensitivity Analysis in Manufacturing Process of Rubber Pad by Using Finite Element Technique. Int. J. Mech. Mechatronics Eng. 2017, 18, 75–85. [Google Scholar]
  16. Pačák, T.; Tatíček, F.; Valeš, M. Compensation of springback in large sheet metal forming. Acta Polytechnica 2019, 59, 483–489. [Google Scholar] [CrossRef]
  17. Pačák, T.; Kubelka, M.; Tatíček, F.; Pilvousek, T. The methodology for determining the springback of large metal stampings. Key Engineering Materials 2014, 635, 151–156. [Google Scholar] [CrossRef]
  18. Kumar, J.P.; Kumar, R.U.; Ramakrishna, B.; Ramu, B.; Sehab, K.B. Formability of sheet metals – A review. IOP Conf. Series: Mater. Sci. Eng. 2018, 455, 012081. [Google Scholar] [CrossRef]
  19. Thiruvarudchelvan, The potential role of flexible tools in metal forming. J. Mater. Process. Technol. 2002, 122, 292–300. [CrossRef]
  20. Semiatin, S.L. Wear and Lubr4ication of sheet-metal forming dies. ASM Handbook. Metalworking: Sheet forming. ASM, vol. 14B, 2006.
  21. Suethao, S.; Prasopdee, T.; Buaksuntear, K.; Shah, D.U.; Smitthipong, W. Recent Developments in Shape Memory Elastomers for Biotechnology Applications. Polymers 2022, 14, 3276. [Google Scholar] [CrossRef]
  22. Reghunadhan, A.; Jibin, K.P.; Kaliyathan, A.V.; Velayudhan, P.; Strankowski, M.; Thomas, S. Shape Memory Materials from Rubbers. Materials 2021, 14, 7216. [Google Scholar] [CrossRef]
  23. Ramezani, M.; Ripin, Z.M.; Ahmad, R. Computer aided modeling of friction in rubber-pad forming process. J. Mater. Process. Technol. 2009, 209, 4925–4934. [Google Scholar] [CrossRef]
  24. Afteni, C.; Costin, G.; Iabob, I.; Păunoiu, V.; Virgil, T. A review on sheet metal rubber-pad forming. The Annals of „Dunărea De Jos” University of Galaţi Fascicle VI, Technologies In Machine Building 2018, 6, 1–6. [Google Scholar]
  25. Kumar, A.; Kumar, S.; Yadav, D.R. Review of rubber based sheet hydro-forming processes. In Proceedings of the 5th Int. & 26th All India manufacturing Technology, Design and Research Conference (AIMTDR 2014), Guwahati, India, 12-14 December 2014; pp. 100–106. [Google Scholar]
  26. Pelayo, F.; Blanco, D.; Fernández, P.; González, J.; Beltrán, N. Viscoelastic Behaviour of Flexible Thermoplastic Polyurethane Additively Manufactured Parts: Influence of Inner-Structure Design Factors. Polymers 2021, 13, 2365. [Google Scholar] [CrossRef]
  27. Sala, G. A numerical and experimental approach to optimise sheet stamping technologies - Part II aluminium alloys rubber-forming. Mater. Des. 2001, 22, 299–315. [Google Scholar] [CrossRef]
  28. Thiruvarudchelvan, S. Elastomers in metal forming - A review. J. Mater. Process. Technol. 1993, 39, 55–82. [Google Scholar] [CrossRef]
  29. Liu, Y.; Hua, L. Fabrication of metallic bipolar plate for proton exchange membrane fuel cells byrubber pad forming. J. Power Source 2010, 195, 3529–3535. [Google Scholar] [CrossRef]
  30. Ramezani, M.; Mohd, Z.; Ripin, Z.M.; Ahmad, R. Sheet metal forming with the aid of flexible punch, numerical approach and experimental validation. CIRP J. Manuf. Sci. Technol. 2010, 3, 196–203. [Google Scholar] [CrossRef]
  31. Woźniak, D.; Głowacki, M.; Hojny, M.; Pieja, T. Application of CAE systems in forming of drawpieces with use rubber-pad forming processes. Arch. Metall. Mater. 2014, 57, 1179–1187. [Google Scholar] [CrossRef]
  32. Dirikolu, M.; Akdemir, E. Computer aided modelling of flexible forming process. J. Mater. Process. Technol. 2004, 148, 376–381. [Google Scholar] [CrossRef]
  33. Benisa, M. Integrated process planning, die-design and simulation in sheet metal rubber forming. PhD Thesis, University of Belgrade, Belgrade, 2013. [Google Scholar]
  34. Ramezani, M.; Ripin, Z.M.; Ahmad, R. Numerical simulation of sheet stamping process using flexible punch. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 829–840. [Google Scholar] [CrossRef]
  35. Fu, M.W.; Li, H.; Lu, J.; Lu, S.Q. Numerical study on the deformation behaviors of the flexible dieforming by using viscoplastic pressure-carrying medium. Comput. Mat. Sci. 2009, 46, 1058–1068. [Google Scholar] [CrossRef]
  36. Sun, Y.; Wan, M.; Wu, X. Friction coefficient in rubber forming process of Ti-15-3 alloy. Trans. Nonferr. Met. Soc. China 2012, 22, 2952–2959. [Google Scholar] [CrossRef]
  37. Lei, C.; Huiqin, C.; Weigang, G.; Guojin, C.; Qiaoyi, W. Experimental and simulation studies of springback in rubber forming using aluminium sheet straight flanging process. Mater. Des. 2014, 54, 354–360. [Google Scholar] [CrossRef]
  38. Ali, A.; Hosseini, M.; Sahari, B.B. A review of constitutive models for rubber-like materials. Amer. J. Eng. Appl. Sci. 2010, 3, 232–239. [Google Scholar] [CrossRef]
  39. Hongyu, W.; Fei, T.; Zhen, W.; Pengchao, Z.; Juncai, S.; Shijun, J. Simulation research about rubber pad forming of corner channel with convex or concave mould. J. Manuf. Process. 2019, 40, 94–104. [Google Scholar] [CrossRef]
  40. Wang, C.; Wang, H.; Wang, Y.; Chen, G.; Zhu, Q. Investigation on forming methods in rubber pad forming process used for fabricating Cu/Ni clad foil microchannel. J. Manuf. Process. 2022, 76, 771–785. [Google Scholar] [CrossRef]
  41. Al-Qureshi, H.A. Analysis of simultaneous sheet metal forming operations using elastomer technique. J. Mater. Process. Technol. 2002, 125-126, 751–755. [Google Scholar] [CrossRef]
  42. Talebi-Ghadikolaee, H.; Elvasi, M.; Mirnia, M.J. Investigation of failure during rubber pad forming of metallic bipolar plates. Thin-Walled Struct. 2020, 150, 106671. [Google Scholar] [CrossRef]
  43. Jin, C.K.; Jeong, M.G.; Kang, C.G. Effect of rubber forming process parameters on micro-patterning of thin metallic plates. Procedia Eng. 2014, 81, 1439–1444. [Google Scholar] [CrossRef]
  44. EN ISO 6892-1:2020-05; Metallic materials. Tensile testing. Part 1: Method of test at room temperature. International Organization for Standardization: Geneva, Swirtzerland.
  45. Ramezani, M. Modeling of static and kinetic friction in rubber-pad forming process. PhD Thesis, University Science Malaysia, Peneng, 2009. [Google Scholar]
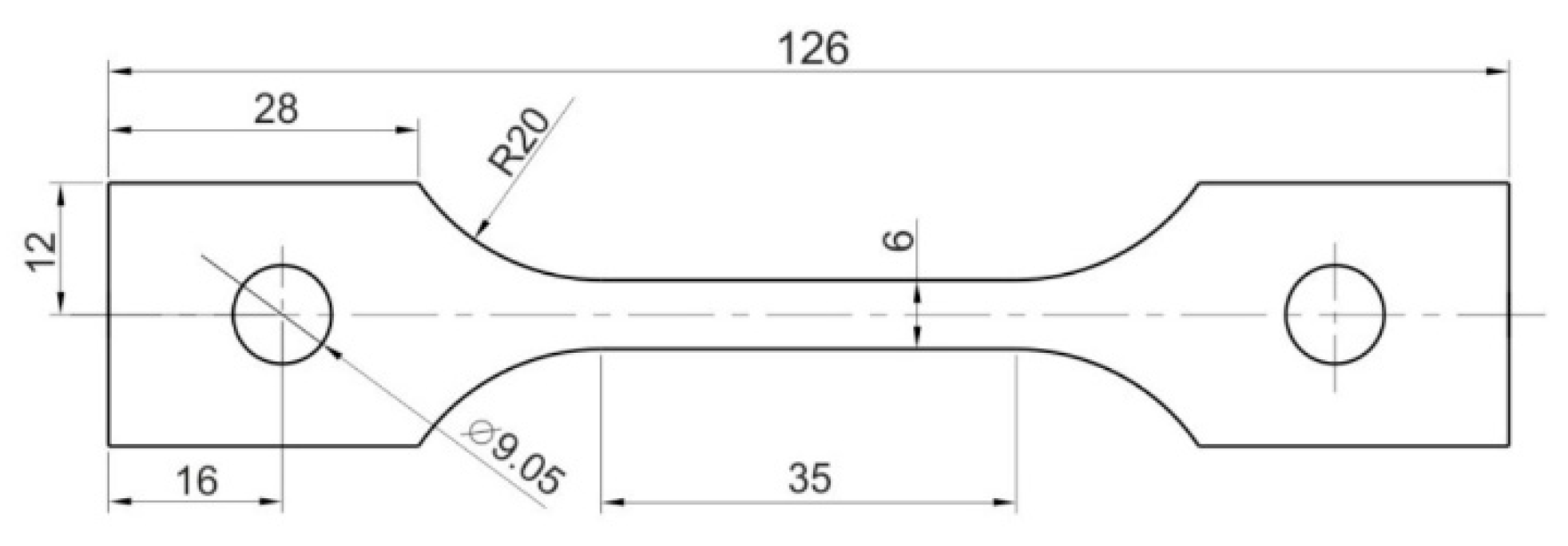
Preprints 90911 g001
Figure 1. Dimensions of uniaxial tensile test specimens.
Figure 1. Dimensions of uniaxial tensile test specimens.
Preprints 90911 g001
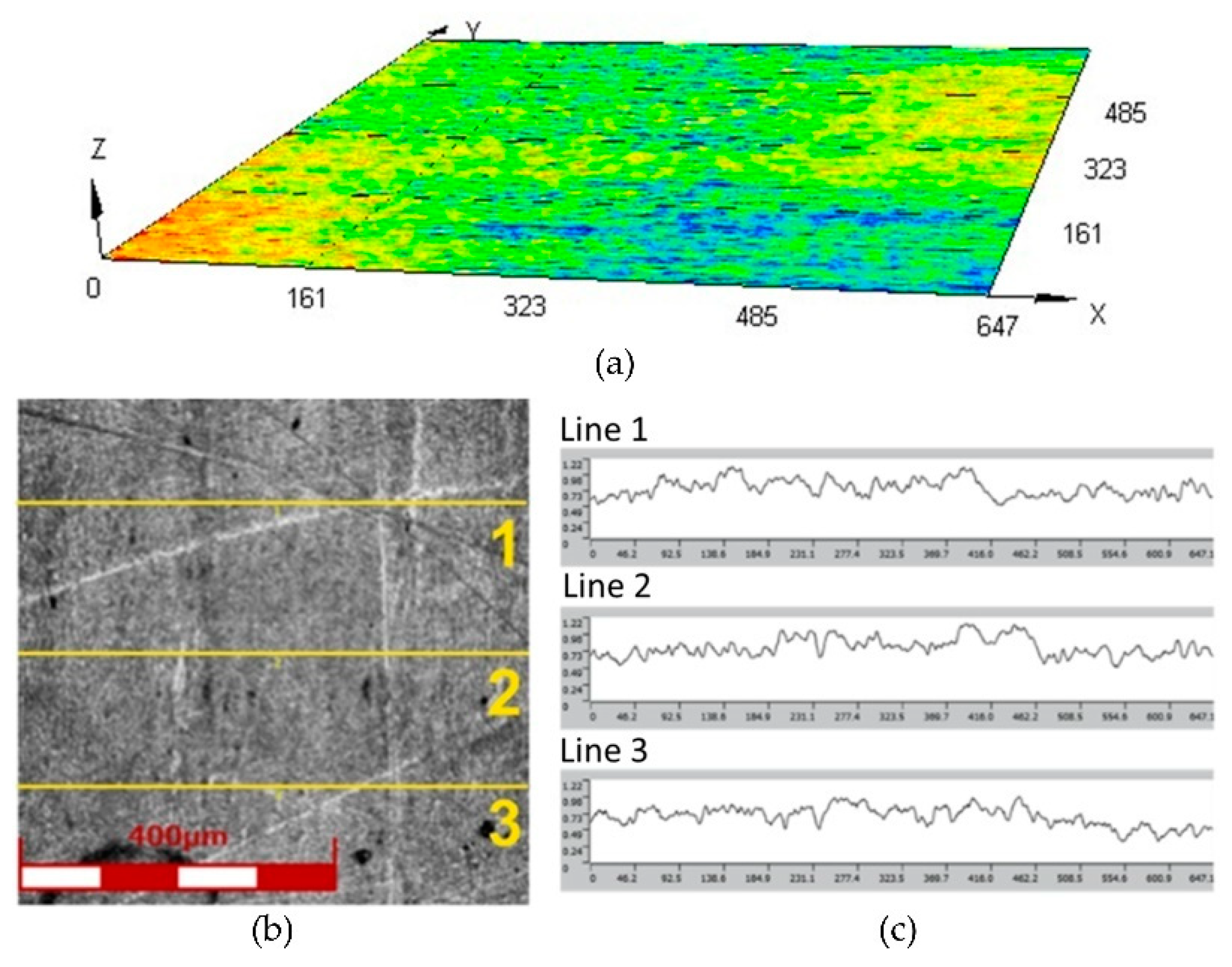
Preprints 90911 g002
Figure 2. (a) surface topography, (b) view of surface of the Inconel 625 sheet metal and (c) linear surface roughness profiles used to determine average value of surface roughness parameters.
Figure 2. (a) surface topography, (b) view of surface of the Inconel 625 sheet metal and (c) linear surface roughness profiles used to determine average value of surface roughness parameters.
Preprints 90911 g002
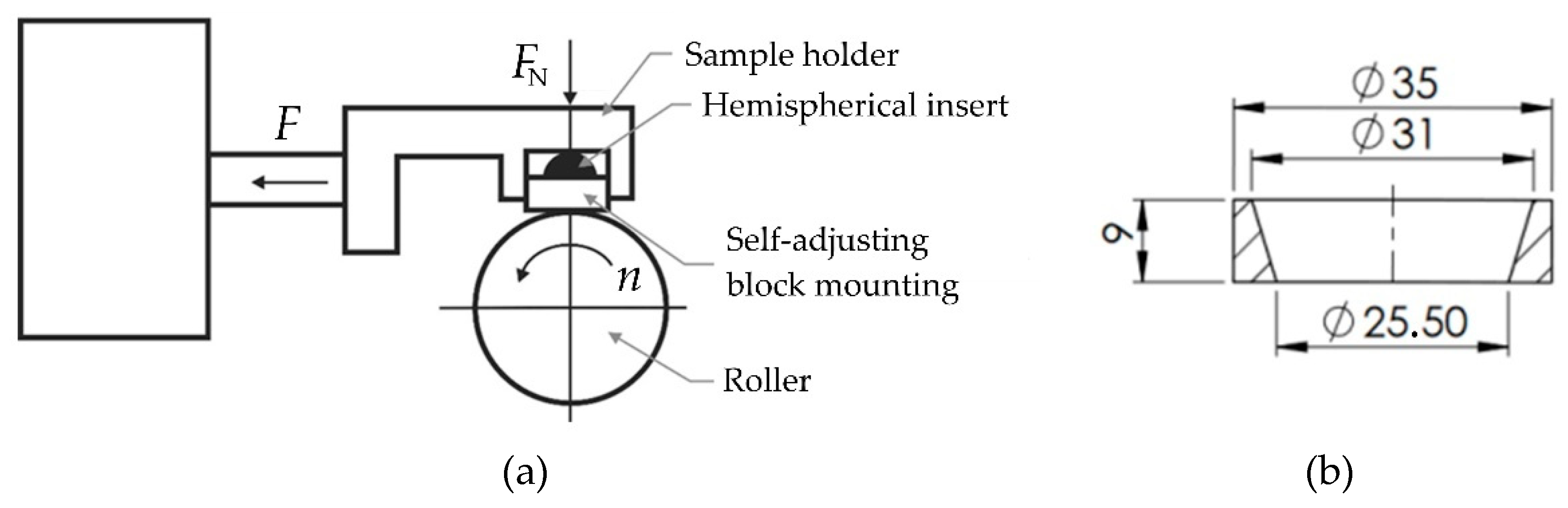
Preprints 90911 g003
Figure 3. (a) principle of operation of the T-05 tester and (b) geometry and dimensions of the polyurethane countersample.
Figure 3. (a) principle of operation of the T-05 tester and (b) geometry and dimensions of the polyurethane countersample.
Preprints 90911 g003
Preprints 90911 g004
Figure 4. (a) Simulated shape of the sample during the compression test, and (b) fit of the experimental compression curve with the simulation results.
Figure 4. (a) Simulated shape of the sample during the compression test, and (b) fit of the experimental compression curve with the simulation results.
Preprints 90911 g004
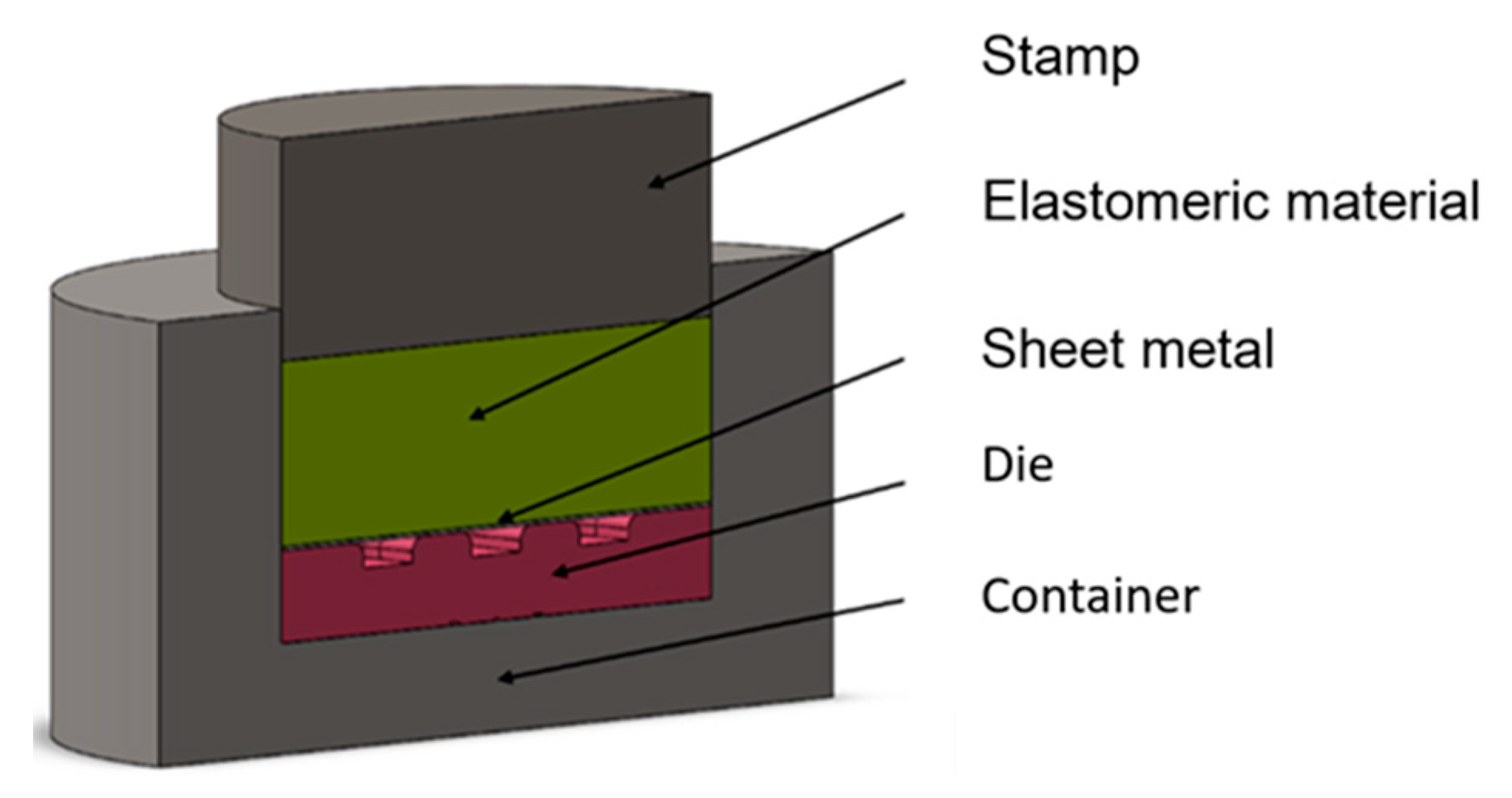
Preprints 90911 g005
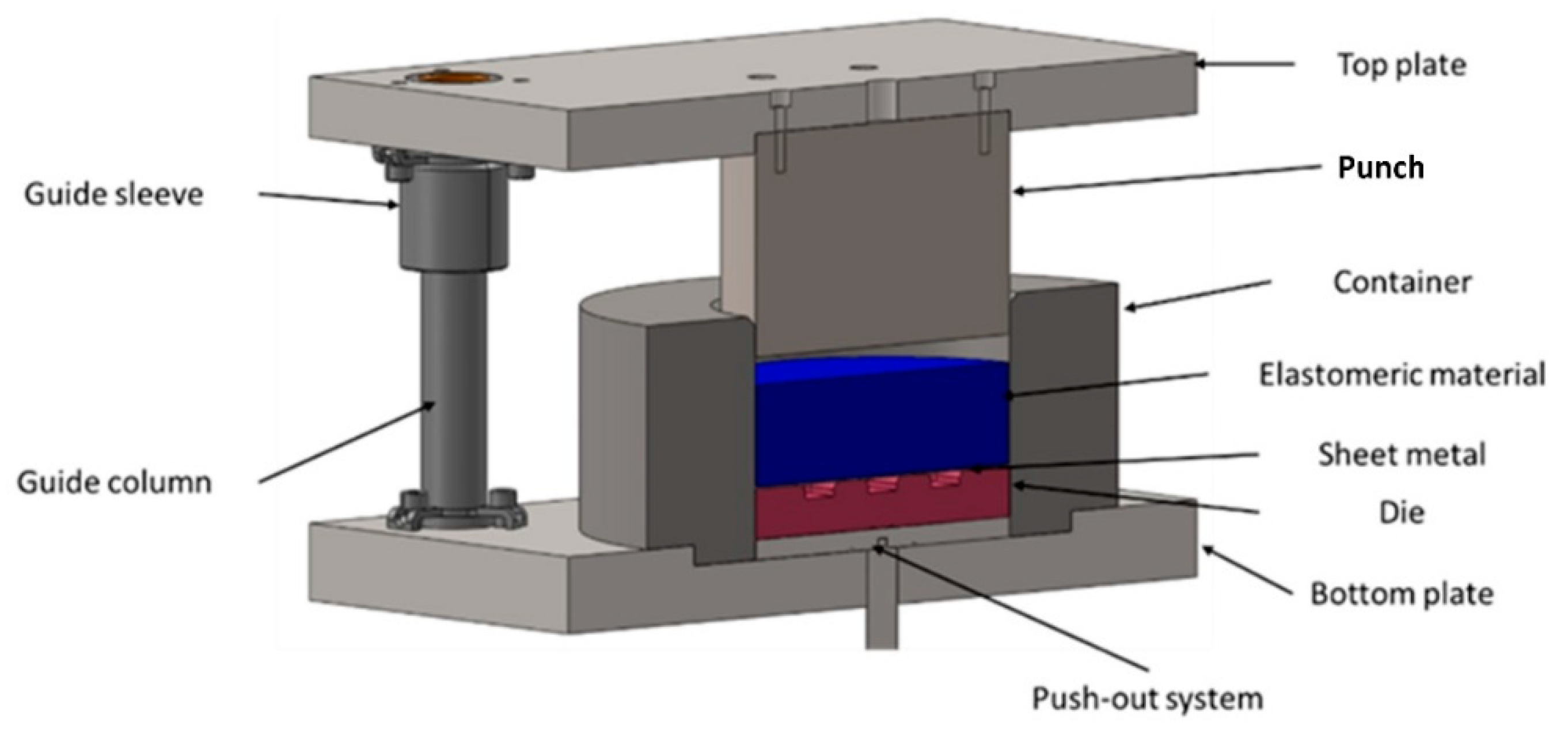
Figure 5. Cross-section of a 3D model of a stamping die used for numerical simulations.
Figure 5. Cross-section of a 3D model of a stamping die used for numerical simulations.
Preprints 90911 g005
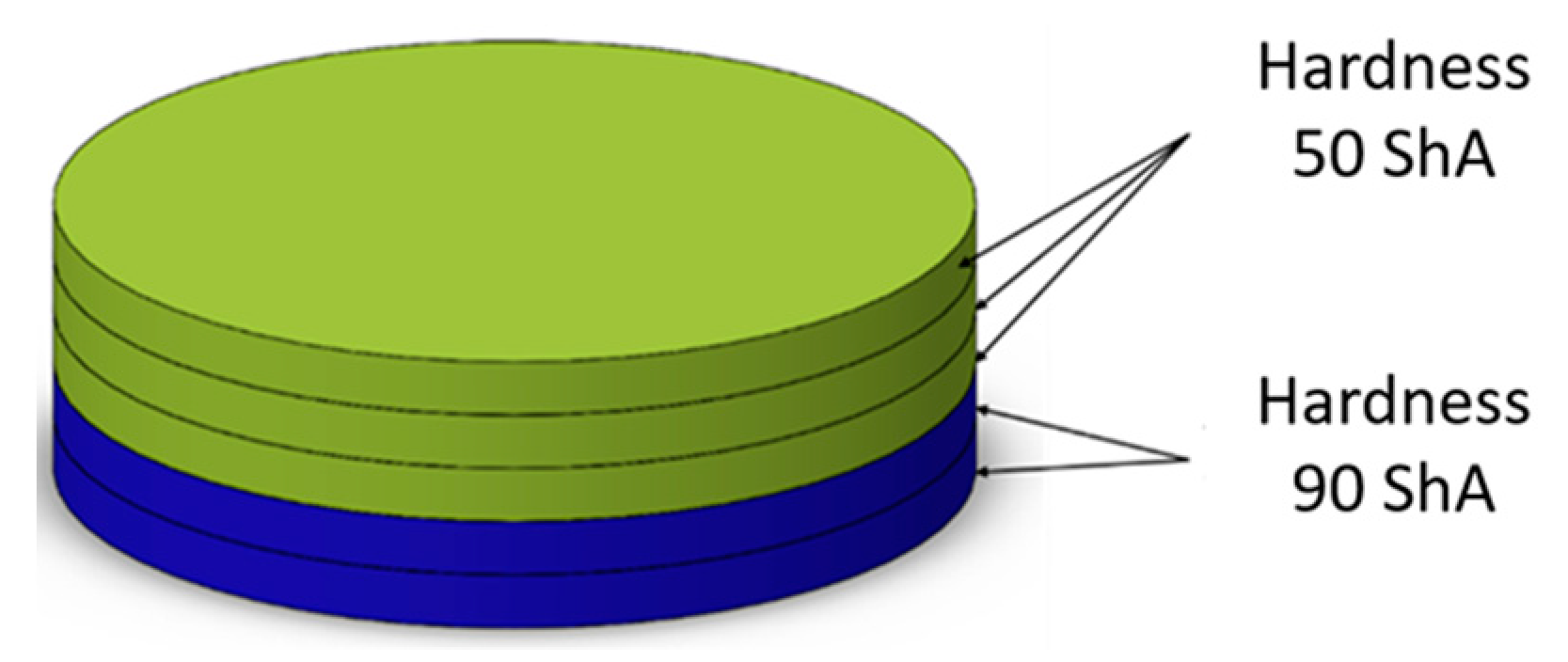
Preprints 90911 g006
Figure 6. Polyurethane punch configuration with five layers of inserts of different hardness (3×50 ShA + 2×90 ShA).
Figure 6. Polyurethane punch configuration with five layers of inserts of different hardness (3×50 ShA + 2×90 ShA).
Preprints 90911 g006
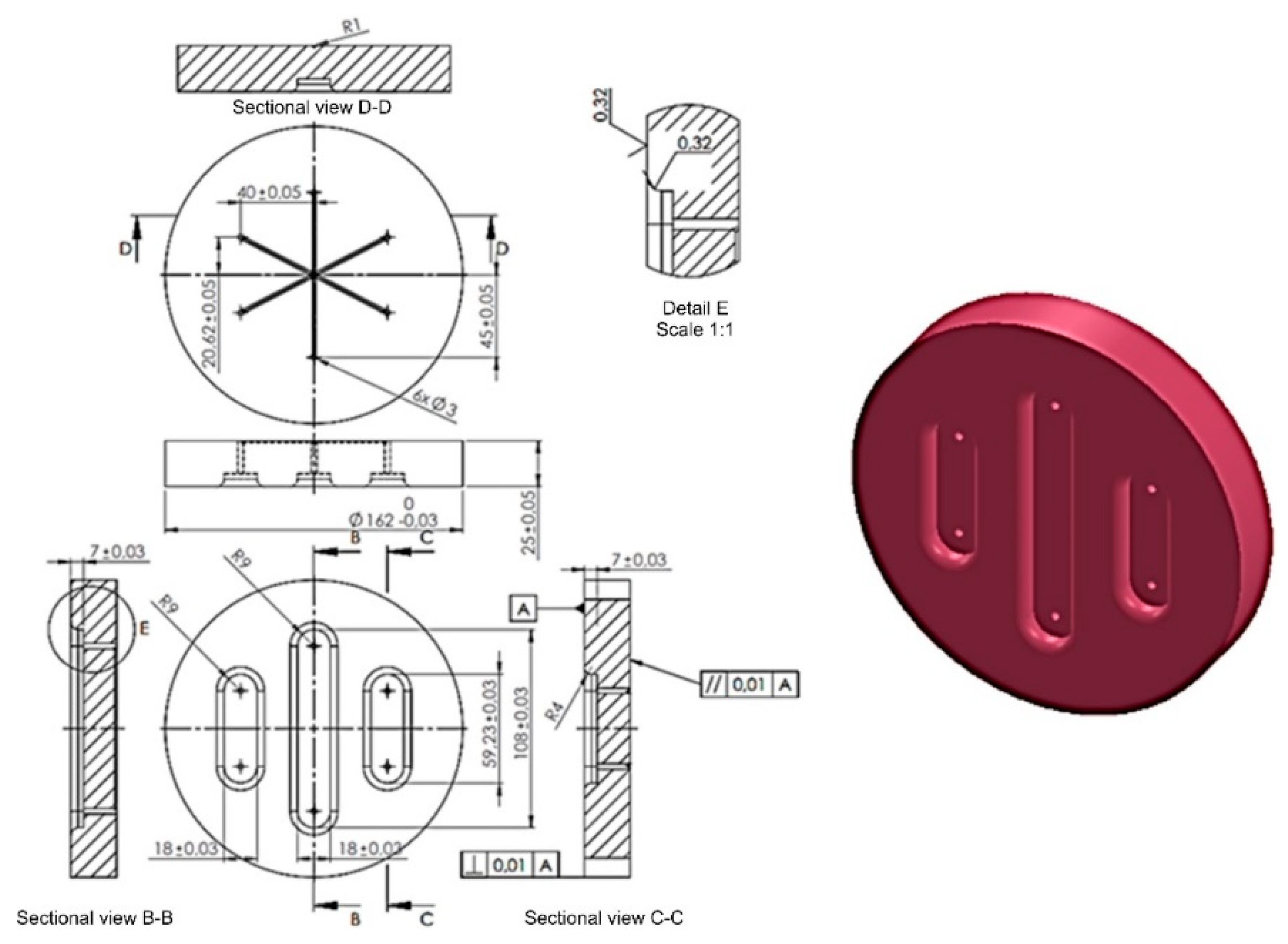
Preprints 90911 g007
Figure 7. Shape and dimensions of the die used to form Inconel 625 sheet metals.
Figure 7. Shape and dimensions of the die used to form Inconel 625 sheet metals.
Preprints 90911 g007
Preprints 90911 g008
Figure 8. Cross-section of a formed element with marked stress states in selected areas.
Figure 8. Cross-section of a formed element with marked stress states in selected areas.
Preprints 90911 g008
Preprints 90911 g009
Figure 9. 3D model of the stamping die.
Figure 9. 3D model of the stamping die.
Preprints 90911 g009
Preprints 90911 g010
Figure 10. Stamping die (a) mounted on a press and (b) during forming.
Figure 10. Stamping die (a) mounted on a press and (b) during forming.
Preprints 90911 g010
Preprints 90911 g011
Figure 11. The 3D scan of the drawpiece from different perspectives.
Figure 11. The 3D scan of the drawpiece from different perspectives.
Preprints 90911 g011
Preprints 90911 g012
Figure 12. Example result of the surface flatness measurement.
Figure 12. Example result of the surface flatness measurement.
Preprints 90911 g012
Preprints 90911 g013
Figure 13. Example result of measuring (a) the thickness of the drawpiece and (b) the change in drawpiece diameter after the forming process.
Figure 13. Example result of measuring (a) the thickness of the drawpiece and (b) the change in drawpiece diameter after the forming process.
Preprints 90911 g013
Preprints 90911 g014
Figure 14. Example results for (a) the strain uniformity and (b) the difference in forming depth.
Figure 14. Example results for (a) the strain uniformity and (b) the difference in forming depth.
Preprints 90911 g014
Preprints 90911 g015
Figure 15. Tensile curves of samples made of Inconel 625 sheet.
Figure 15. Tensile curves of samples made of Inconel 625 sheet.
Preprints 90911 g015
Preprints 90911 g016
Figure 16. Results of the uniaxial compression test of polyurethane samples.
Figure 16. Results of the uniaxial compression test of polyurethane samples.
Preprints 90911 g016
Preprints 90911 g017
Figure 17. Subsequent stages of forming the element for a) 20%, b) 40%, c) 60% and d) 90% of simulation time.
Figure 17. Subsequent stages of forming the element for a) 20%, b) 40%, c) 60% and d) 90% of simulation time.
Preprints 90911 g017
Preprints 90911 g018
Figure 18. The influence of the hardness of polyurethane inserts on forming depth.
Figure 18. The influence of the hardness of polyurethane inserts on forming depth.
Preprints 90911 g018
Preprints 90911 g019
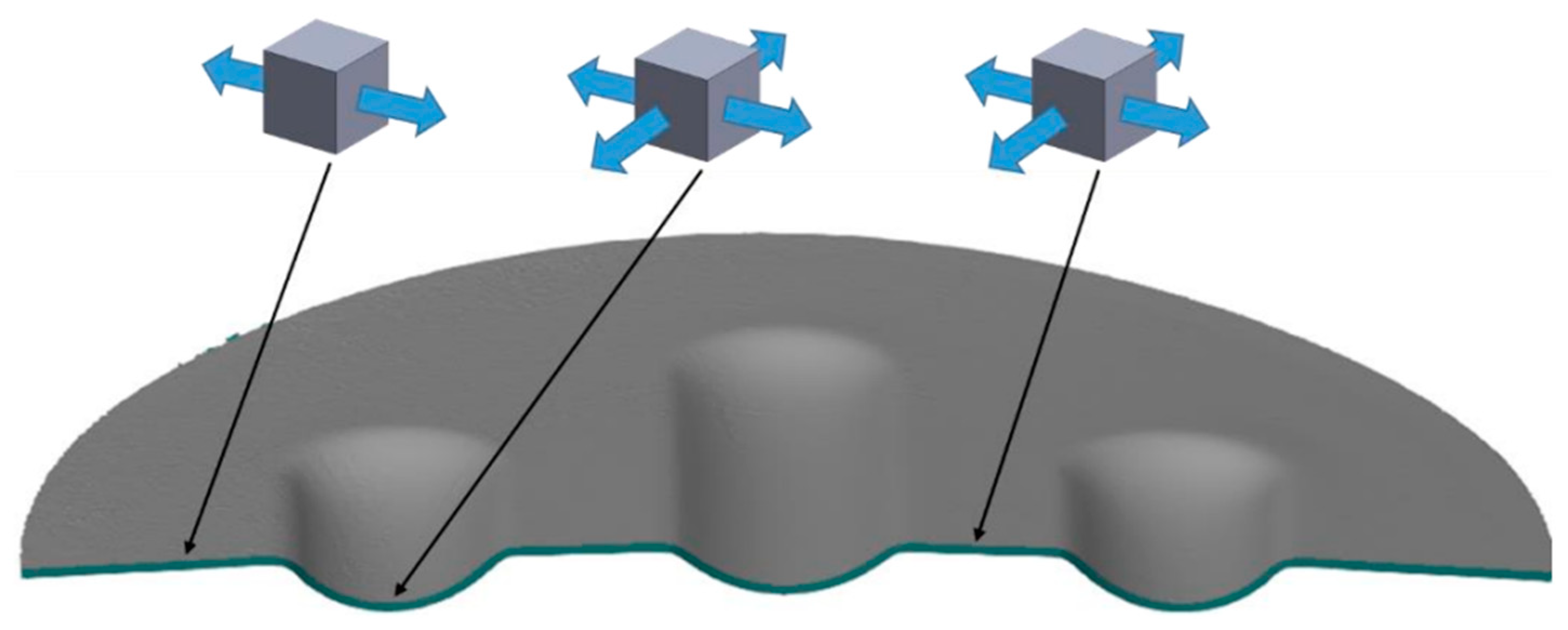
Figure 19. The influence of die geometry on the deformation of the polyurethane punch consisting of five layers of different hardness 2×50 ShA + 3×90 ShA.
Figure 19. The influence of die geometry on the deformation of the polyurethane punch consisting of five layers of different hardness 2×50 ShA + 3×90 ShA.
Preprints 90911 g019
Preprints 90911 g020
Figure 20. Comparison of the geometry of drawpieces obtained using polyurethane inserts with a hardness of 50 ShA and 90 ShA using a forming force of 1,000 kN.
Figure 20. Comparison of the geometry of drawpieces obtained using polyurethane inserts with a hardness of 50 ShA and 90 ShA using a forming force of 1,000 kN.
Preprints 90911 g020
Preprints 90911 g021aPreprints 90911 g021b
Figure 21. Results of measuring the geometry of the drawpieces formed using five inserts with a hardness of 50 ShA: (a) surface flatness, (b) thickness, (c) changes in the diameter of the workpiece, (d) uniformity of forming.
Figure 21. Results of measuring the geometry of the drawpieces formed using five inserts with a hardness of 50 ShA: (a) surface flatness, (b) thickness, (c) changes in the diameter of the workpiece, (d) uniformity of forming.
Preprints 90911 g021aPreprints 90911 g021b
Preprints 90911 g022
Figure 22. Results of measuring the geometry of the drawpieces formed using two inserts with a hardness of 50 ShA and three inserts with a hardness of 90 ShA: (a) surface flatness, (b) thickness, (c) changes in the diameter of the workpiece, (d) uniformity of forming.
Figure 22. Results of measuring the geometry of the drawpieces formed using two inserts with a hardness of 50 ShA and three inserts with a hardness of 90 ShA: (a) surface flatness, (b) thickness, (c) changes in the diameter of the workpiece, (d) uniformity of forming.
Preprints 90911 g022
Preprints 90911 g023
Figure 23. Summary of measurement results of the geometry of drawpieces made of Inconel 625 sheet metal.
Figure 23. Summary of measurement results of the geometry of drawpieces made of Inconel 625 sheet metal.
Preprints 90911 g023
Preprints 90911 g024
Figure 24. Comparison of the drawpieces formed using two different configurations of polyurethane inserts: 5×50 ShA and 2×50 ShA + 3×90 ShA.
Figure 24. Comparison of the drawpieces formed using two different configurations of polyurethane inserts: 5×50 ShA and 2×50 ShA + 3×90 ShA.
Preprints 90911 g024
Table 1. Surface roughness parameters of polyurethane inserts.
Table 1. Surface roughness parameters of polyurethane inserts.
Average value of the
surface roughness parameter		 Hardness of the polyurethane insert
50 ShA 60 ShA 70 ShA 80 ShA 90 ShA
Ra, μm 0.337 μm 0.191 μm 0.204 μm 1.228 μm 0.894 μm
Rz, μm 2.536 μm 1.244 μm 1.517 μm 7.918 μm 5.493 μm
Table 2. Material coefficients for polyurethane samples with varying hardness.
Table 2. Material coefficients for polyurethane samples with varying hardness.
Hardness of polyurethane sample Coefficient K, Pa Coefficient C1, Pa Coefficient C2, Pa
50 ShA 4.0 × 109 0.3 × 106 0.15 × 109
60 ShA 4.1 × 109 0.59 × 106 0.19 × 106
70 ShA 4.2 × 109 0.6 × 106 0.2 × 106
80 ShA 4.8 × 109 1.6 × 106 0.11 × 106
90 ShA 4.8 × 109 2.1 × 106 0.1 × 106
Table 3. Results of the basic mechanical parameters of Inconel 625 sheet.
Table 3. Results of the basic mechanical parameters of Inconel 625 sheet.
Sample orientation Ultimate tensile stress Rm, MPa Yield stress Rp0,2, MPa Elongation A, %
0° 966.1 526.5 49.4
45° 955.9 532.5 47.4
90° 954.4 521.6 46.8
Table 4. Anisotropy coefficients of Inconel 625 sheet.
Table 4. Anisotropy coefficients of Inconel 625 sheet.
Coefficient of normal anisotropy Coefficient of planar anisotropy
1.22 –0.64
Table 5. Results of the hardness measurements of polyurethane samples.
Table 5. Results of the hardness measurements of polyurethane samples.
Nominal hardness, ShA Number of measurement Measured average hardness, ShA
1 2 3 4 5
50 50 50 51 51 52 50.7
60 62 61 62 62 64 61.8
70 64 66 63 63 66 65.3
80 78 79 78 80 81 79.3
90 89 89 88 90 90 89.3
Table 6. Wear parameters and COF of polyurethane countersamples and Inconel 625 sample.
Table 6. Wear parameters and COF of polyurethane countersamples and Inconel 625 sample.
Parameter Hardness of polyurethane countersample
50 ShA 60 ShA 70 ShA 80 ShA 90 ShA
Weight loss of polyurethane countersample Δmcs, % 0.4031 0.1448 0.1956 0.0116 0.0762
Weight loss of Inconel 625 sample Δms, % 0.1958 –0.041 0.2483 –0.063 –0.0328
Average COF 0.465 0.526 0.622 0.545 0.263
Table 7. Results of the maximum depth of emboss in the Inconel 625 alloy sheet for individual variants of the polyurethane inserts.
Table 7. Results of the maximum depth of emboss in the Inconel 625 alloy sheet for individual variants of the polyurethane inserts.
Hardness of polyurethane inserts Results of displacement Maximum depth of emboss
Preprints 90911 i001 Preprints 90911 i002 4.568 mm
Preprints 90911 i003 Preprints 90911 i004 4.725 mm
Preprints 90911 i005 Preprints 90911 i006 4.732 mm
Preprints 90911 i007 Preprints 90911 i008 5.166 mm
Preprints 90911 i009 Preprints 90911 i010 5.302 mm
Preprints 90911 i011 Preprints 90911 i012 6.4 mm
Preprints 90911 i013 Preprints 90911 i014 6.124 mm
Table 8. Summary of the results of forming drawpieces with a pressure of 1000 kN.
Table 8. Summary of the results of forming drawpieces with a pressure of 1000 kN.
Measurement setup Image of the formed sheet 3D scan of the formed sheet Maximum forming depth
Preprints 90911 i015 Preprints 90911 i016
Preprints 90911 i017 		Preprints 90911 i018
Preprints 90911 i019 		5.81 mm
Preprints 90911 i020 Preprints 90911 i021
Preprints 90911 i022 		Preprints 90911 i023
Preprints 90911 i024 		5.95 mm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Experimental Research and Numerical Modelling of the Cold Forming Process of the Inconel 625 Alloy Sheets Using Flexible Punch

Maciej Balcerzak

et al.

,

2023

Sustainable Approach on the Metal Coin Cancelling Methods, Using 3D Modeling and FEM Analysis

Cornel Cătălin Gavrilă

et al.

,

2024

A Useful Manufacturing Guide for Rotary Piercing Seamless Pipe by ALE Method

Ameen Topa

et al.

,

2020

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated