Rethinking Energy Conservation and Generation for Sustainable Solutions-An Innovative Energy Circuitry Approach

1. Introduction

The ongoing pursuit of humanity to address the pressing energy crisis has been the driving force behind countless innovations and scientific endeavors [1,2,3,4,5,6,7]. The need for sustainable and abundant energy sources is more crucial than ever as we grapple with dwindling fossil fuels, environmental degradation, and a growing global population [8,9,10]. The successful disruption of the law of energy conservation to create more energy within classical settings could hold the key to resolving innumerable societal challenges, including mitigating the energy crisis, reducing noise pollution stemming from fossil fuel consumption, curbing greenhouse gas emissions, and unlocking new frontiers of knowledge in the fields of physics and engineering. This paper is born out of the recognition that these noble objectives have, in recent times, become entangled in a web of misconceptions. These misconceptions span a wide spectrum, ranging from unfounded claims of perpetual motion machines (PMMs) that can generate infinite energy [11,12,13,14,15,16,17], to the assertion that it is fundamentally impossible to create energy within a classical closed system [8,18,19,20,21,22]. These erroneous beliefs have often relied on conventional scientific beliefs, limiting the scope of exploration in the quest for innovative energy solutions. To this end, this paper seeks to provide a fresh perspective, first identifying and correcting the prevailing misconceptions surrounding the endeavor to breach the law of energy conservation [14,15,23,24]. Through examining these misconceptions from both scientific and philosophical standpoints, the aim is to illuminate the path forward. One prevalent misunderstanding lies in the notion that the creation of energy without dependence on external sources defies the fundamental philosophical principle that “something cannot come from nothing [25,26,27,28,29,30].” This paper underscores the necessity of reconciling the generation of energy within a closed system with this philosophical tenet. Additionally, it raises valid concerns about the commonly held belief that the absence of perpetual motion machines (PMMs) serves as irrefutable evidence that the law of energy conservation cannot be violated [19,21], implying that energy cannot be created. This paper questions this assumption by highlighting the inherent contradiction within the notion that energy can be derived from nothingness. Moreover, it challenges the idea of relying on PMMs as perfect models for demonstrating the impossibility of breaking the law of energy conservation. Such a perspective falls short of recognizing that a perfect PMM necessitates a machine with 100% efficiency, where energy is neither lost nor gained. This stance fails to substantiate the violation of the law and only underscores the practicality of a hypothetical system. The paper contends that treating experiments (such as energy creation or generation experiments) as inductive processes, particularly when examining systems modeled after PMMs, is a flawed approach to addressing the challenge of energy generation. Experiments, by nature, are not always inductive but rather rooted in specific empirical observations, making them unsuitable for refuting the notion of breaking the law of energy conservation. This paper offers a novel approach to breaking the law of energy conservation by presenting a unique circuit design that transitions from an anomalous state to the conventional circuits found in most electrical systems. This distinctive circuit capitalizes on leveraging Ohm’s law [31,32], beginning with an electrical short circuit [33], thereby challenging the limitations of traditional energy generation systems. While recognizing that concerns may arise regarding the suggested solution, as is common with any electric circuit, it is crucial to underscore the many benefits this solution offers compared to any arising safety maters. From ushering in a new era of electric vehicles to addressing a wide array of contemporary issues, the potential of this innovative circuit is as vast as the possibilities it presents. The journey towards breaking the law of energy conservation involves more than mere violation; it requires the exploration of energy destruction, creation, or a harmonious blend of both. Achieving such feats may necessitate the exploitation of scientific anomalies, such as the electrical short circuit presented in this paper. In the subsequent sections of the paper, a detailed exploration of these ideas will be delved into, encompassing scientific and philosophical dimensions, while presenting an innovative circuit as a practical demonstration of the approach.

2. Evaluating the Evolution of Efforts to Contest the Law of Energy Conservation

In the quest to challenge the law of energy conservation, a thorough examination of ongoing studies and objectives unveils a complex terrain filled with misconceptions and misguided approaches [8,11,13,14,19,21,34,35]. This analysis encompasses scientific, philosophical, historical, and contemporary viewpoints and highlights the changing nature of the challenge, which has transitioned over time from initial, well-intentioned investigations to increasingly audacious and unworkable innovations.

2.1. Scientific Perspective

From a scientific perspective, the pursuit of challenging the law of energy conservation often arises from a fundamental misconception about the nature of energy itself [36]. Many of these efforts disregard the concept of energy conservation as a fundamental principle, not just a convention [16,24]. Energy is inherently intertwined with the very essence of the universe, and any endeavor to generate energy from nothing contradicts the current understanding of the cosmos [25,27,28,29]. The scientific community has predominantly regarded such attempts as futile and fundamentally flawed. One prevalent misconception involves a misinterpretation of the perpetual motion machine (PMM) [11,13,14,24]. It is however, important to stress that the absence of a PMM does not provide evidence that the law of energy conservation cannot be violated. The criteria for a PMM not only require a violation of the law but also the creation of a machine with perpetual motion, which in itself presents a significant challenge. The inherent issues associated with PMMs have contributed to a misunderstanding of the broader concept of violating the law of energy conservation.

2.2. Philosophical Perspective

From a philosophical perspective, it is essential to tackle the fundamental question of whether it is possible for something to truly emerge from nothing. The fundamental philosophical concept that “something cannot arise from nothing [28,37,38]” significantly influences the concept of creating energy from nothing. Energy preservation is not exclusively governed by scientific laws; it is profoundly intertwined with philosophical principles regarding the essence of existence [28,30]. These philosophical considerations are frequently underestimated in present-day studies of defying the law of energy conservation.

Contextual Clarity: In the context of this paper, it is crucial to acknowledge the inherent philosophical quandaries surrounding the concept of energy. As Nobel Laureate Richard Feynman aptly articulated in his lectures, “It is important to realize that in physics today we have no knowledge of what energy is [39]”. This statement emphasizes the profound mystery that shrouds the nature of energy itself. While grappling with the philosophical intricacies of something arising from nothing, the paper consciously operates within the framework of established scientific principles, notably matter-energy equivalence [40,41]. The paper recognizes that our current understanding of energy is indirect, rooted in the detectable quantities of matter and their transformations. In the absence of a definitive definition of energy, this paper adopts a pragmatic approach, treating energy as a consequence of the observed phenomena associated with matter. The provided results in the paper, therefore, should be interpreted as models that elucidate the relationships and equivalences between matter and energy, as dictated by established scientific principles. The focus remains on deciphering and predicting energy-related phenomena without delving into the elusive nature of energy itself. This approach underscores the paper’s commitment to pragmatic and measurable outcomes while acknowledging the profound epistemological gaps in our understanding of the essence of energy.

2.3. Historical and Modern Shifts

Throughout history, initial efforts to challenge the law of energy conservation have arisen from sincere curiosity and a quest for exploring new scientific frontiers. Nevertheless, the lack of success in these endeavors has contributed to a shift in approaches. Present-day innovations sometimes display a concerning trend, where the practicality and scientific rigor of proposed solutions are increasingly overlooked. Instead, many recent endeavors rely on the idea of bypassing laws without substantial scientific or mathematical support [11,12,14,15,16,23,24]. It is vital to consider that these limitations and misconceptions can be attributed to the absence of a rigorous mathematical and scientifically valid proof concerning the validity of the law of energy conservation and its practical limitations as provided in [42]. The ambiguous nature of energy and the fundamental principles of conservation have allowed room for speculation, misunderstandings, and unverified theories.

2.4. The Need for a New Approach

Amid the previously addressed challenges and limitations, there is a clear need for a fresh approach to become evident. The fundamental premises of the law of energy conservation remain unchallenged, but this paper seeks to demonstrate that circumventing these principles is not only possible but can be practical. The paper introduces energy systems and studies, such as the utilization of the practical electrical short circuit, that extend beyond and even defy certain classical laws. Through these innovative methods, it aims to break the law of energy conservation while remaining firmly rooted within the confines of classical settings. With the presentation of a unique perspective, this paper endeavors to advance the dialogue surrounding the law of energy conservation and expand the horizons of what is achievable in energy generation. Throughout section (3.4) the exposed workflow underscores the pressing need to redefine the boundaries of energy conservation and expand our scientific and philosophical understanding of energy generation while simultaneously acknowledging the intricacies and nuances inherent in these endeavors.

3. Breaking the Law of Energy Conservation

The quest for creative solutions to address the world’s growing energy crisis has ignited a journey of exploration and transformation. In the domain of scientific investigation and technological advancement, an innovative circuit has emerged as a ray of hope. This circuit not only challenges the fundamental principles of energy conservation but also offers a potential solution to some of the most urgent issues of our time. This section presents a circuit design that goes beyond traditional approaches. It not only defies the long-established law of energy conservation but also pushes the boundaries of conventional settings. The implications of this innovative circuit design go well beyond its theoretical foundations; they extend to practical applications, fundamentally reshaping how we harness and generate energy in modern systems.

Remark 1 (On Contextual definition of the energy circuit):

For contextual clarity, the circuit as detailed in the subsequent sections is hereby referred to as the “energy circuit”. The circuit is further broken down into its primary functional components, identified by the nomenclature (“Circuit Block 1”, …, “Circuit Block 5”). This nomenclature encapsulates its unconventional design, which results in the creation of energy within the framework of classical physics.

3.1. The Energy Circuit-Unleashing the Power of Electrical Short Circuits

At its essence, this energy circuit challenges conventional scientific understanding by defying the principle of energy conservation through a unique use of electrical short circuits. Traditionally, electrical short circuits are typically seen as harmful and wasteful occurrences [43,44,45,46,47,48]. Nevertheless, this energy circuit takes a remarkable departure from this perspective, as it harnesses the latent energy and potential within the short circuit, transforming what has traditionally been viewed as an obstacle into a source of amplified energy production. The energy circuit design initiates an unconventional process, beginning in from Ohmic setting, shifting the circuit to a non-Ohmic, then, for illustrative and practical compatibility purposes, returning the circuit to Ohmic circuit setting so that its excess electrical power can be harnessed. As the energy circuit progresses through the mentioned various stages, energy undergoes an ongoing process of modification, capture, and amplification. This sequence ultimately leads to an overall circuit that not only challenges the principle of energy conservation but also consistently generates excess energy, all while maintaining essential safety precautions. What distinguishes this innovative approach from current energy research is its bold strategy in addressing long-standing concerns related to electrical short circuits. The circuit capitalizes on the untapped potential of electrical short circuit currents, transcending worries about their destructive nature and focusing on the advantages offered by surplus current. The strategies used to protect electrical systems from potential damage caused by electrical short circuits, such as the use of diodes to shield solar cells from electrical faults [49,50,51], highlight the practical benefits of tracking and utilizing electrical short circuit currents. This insight serves as the driving force behind innovations like the one presented in this paper’s energy circuit. The applications of such innovations span across various domains, including electric vehicles and industrial systems, fundamentally transforming how we approach energy generation and consumption.

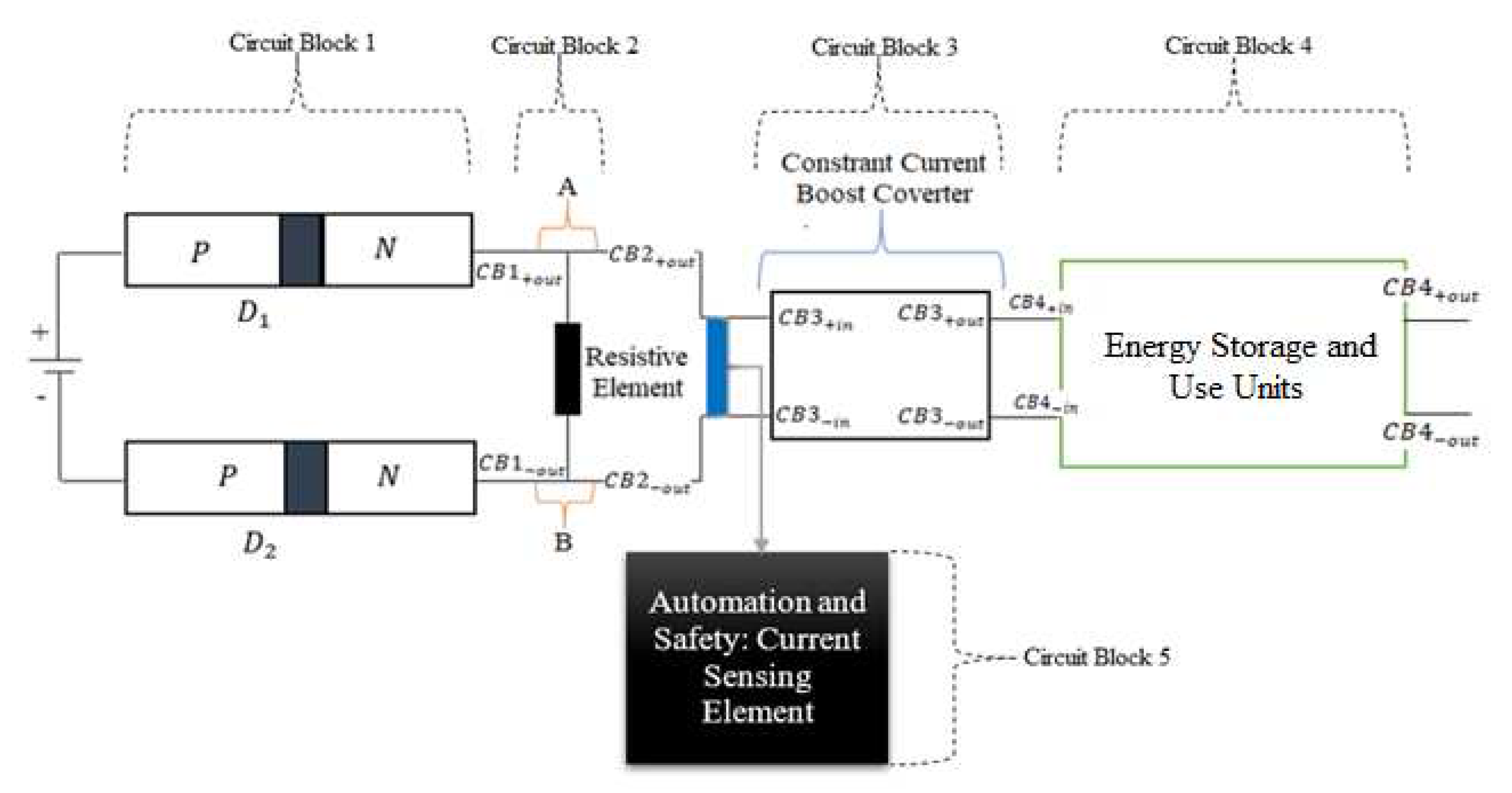
3.2. Design of the Proposed Energy Circuit (The Main Energy Circuit Operational Units)

This section describes the key components and design considerations of the energy circuit. It also offers the specific energy circuit units mathematical framework defining the necessary energy circuit ingredients, and their uses.

3.2.1. Circuit Component 1 (Power Source): The energy circuit begins with a power supply (for safety check, a direct voltage and direct current power source is selected). This power source (variable power supply or using different rating power sources may be considered, as applied in this paper) represents the starting point of the energy conservation challenge. Details on the starting current, the connecting codes (conductors) practical resistance (and conductors material types) will be of importance in working out the input power for the subsequent circuit blocks, modeling the real world scenarios.

Initial Exploration of Ohm’s Law (“Circuit Block 1”): This initial section of the energy circuit deviates from the traditional approach of demonstrating standard Ohm’s Law ($V=IR$) that characterizes traditional electrical circuits. Instead, “Circuit Block 1” primarily aims to use two identical one-directional current components in a parallel configuration (as shown in Figure 1), to prevent undesired electrical current from flowing back. First, let us set up the mathematical framework for “Circuit Block 1” using the diode equation, (equation 1) as applied in [52,53]. Thus, the current-voltage (IV) relationship for a diode is described by the diode equation as follows.

$$I_D=I_s\left(e^{\left(\raisebox{1ex}{$V_D$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)$$

(1)

where:

• $I_D$  is the diode current.
• $I_s$ ​ is the reverse saturation current.
• $V_D$  is the voltage across the diode.
• $n$ is the ideality factor (typically around $1$ for ideal diodes).
• $V_T$ is the thermal voltage, approximately $0.0259V$ at room temperature.

Since the diodes are in parallel, the total current through “Circuit Block 1” (denoted as $I_{CB1}$​) is the sum of the currents through each diode. Therefore, for two diodes ($D_1$ and $D_2$ as depicted in (figure 1)) in parallel we have;

$$I_{CB1}=I_{D_1}+I_{D_2}$$

(2)

Substituting the diode equation for this parallel diodes configuration;

$$I_{CB1}=I_s\left(e^{\left(\raisebox{1ex}{$V_{D_1}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)+I_s\left(e^{\left(\raisebox{1ex}{$V_{D_2}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)$$

(3)

Combining the like terms in equation (3) and factoring out $I_s$​ we get;

$$I_{CB1}=I_s\left[e^{\left(\raisebox{1ex}{$V_{D_1}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}+e^{\left(\raisebox{1ex}{$V_{D_2}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-2\right]$$

(4)

Equation (4) represents the total current flowing through the diodes in the parallel configuration. Further, the voltage across “Circuit Block 1” (denoted as $V_{CB1}$) can be expressed as;

$$V_{CB1}=V_{D_1}+V_{D_2}$$

(5)

To use equation (4); one is required to have the specific voltage values ($V_{D_1}$, and $V_{D_2}$), ideality factor ($n$), and reverse saturation current ($I_s$), for the different identical diodes to be applied in the circuit. In this context, the main role for “Circuit Block 1” is to inhibit current from returning to the power source, which is vital for ensuring the overall integrity of the following energy circuit stages. The subsequent stage, “Circuit Block 2”, introduces the concept of an electrical short circuit, a design that relies on the availability of a surplus of electrical current. Allowing the short circuit current to return to the power source could potentially harm the source. The effectiveness of “Circuit Block 1” in preventing backflow relies on the initial power supplied from the variable power supply component. Consequently, the selection of the specific one-directional current components used within “Circuit Block 1” may vary based on the circuit application’s power requirements. Further, it is important to stress that these one-directional current components are not fixed and can be adapted to the unique characteristics of each application, contributing to the energy circuit’s versatility.

3.2.2. Operation Principles of “Circuit Block 1” (Establishing Higher Resistive Circuit Element)

The crucial role of “Circuit Block 1” is to prevent the undesired backflow of short circuit current from “Circuit Block 2”. Its operation involves an uncommon configuration with parallel diodes, hindering the reverse flow of current. When the short circuit current tries to move backward, it forces the diodes into a reverse-biased mode, causing their depletion regions to widen. This widening of the depletion regions increases the resistance in “Circuit Block 1”, serving as a barrier and limiting the ability of the short circuit current (this current is quantifiable as worked out using equation (6)) to flow backward through the diodes.

Definition 1 (Diode Idle State or Mode):

This definition contextualizes a reverse-biased diode as active but not conducting (a diode set at $0V$from the source), and it only conducts in reverse bias mode when the anomalous event (the electrical short circuit) occurs within an electric circuit. In Figure 1, $D_2$is in the idle state or mode, becoming an infinite resistor (theoretically) when the short circuit happens.

Figure 1. Operational Principle of “Circuit Block 1”-Diode Configuration. (The diodes ($D_1$ and $D_2$) are configured in parallel with the specific arrangement to prevent undesired backflow of short circuit current from “Circuit Block 2”. As the short circuit current attempts to flow in reverse, the diodes transition to a reverse-biased mode, widening the depletion region and increasing resistance, acting as a barrier to the reverse flow. The block diagram illustrates the parallel connection of diodes).

Figure 1. Operational Principle of “Circuit Block 1”-Diode Configuration. (The diodes ($D_1$ and $D_2$) are configured in parallel with the specific arrangement to prevent undesired backflow of short circuit current from “Circuit Block 2”. As the short circuit current attempts to flow in reverse, the diodes transition to a reverse-biased mode, widening the depletion region and increasing resistance, acting as a barrier to the reverse flow. The block diagram illustrates the parallel connection of diodes).

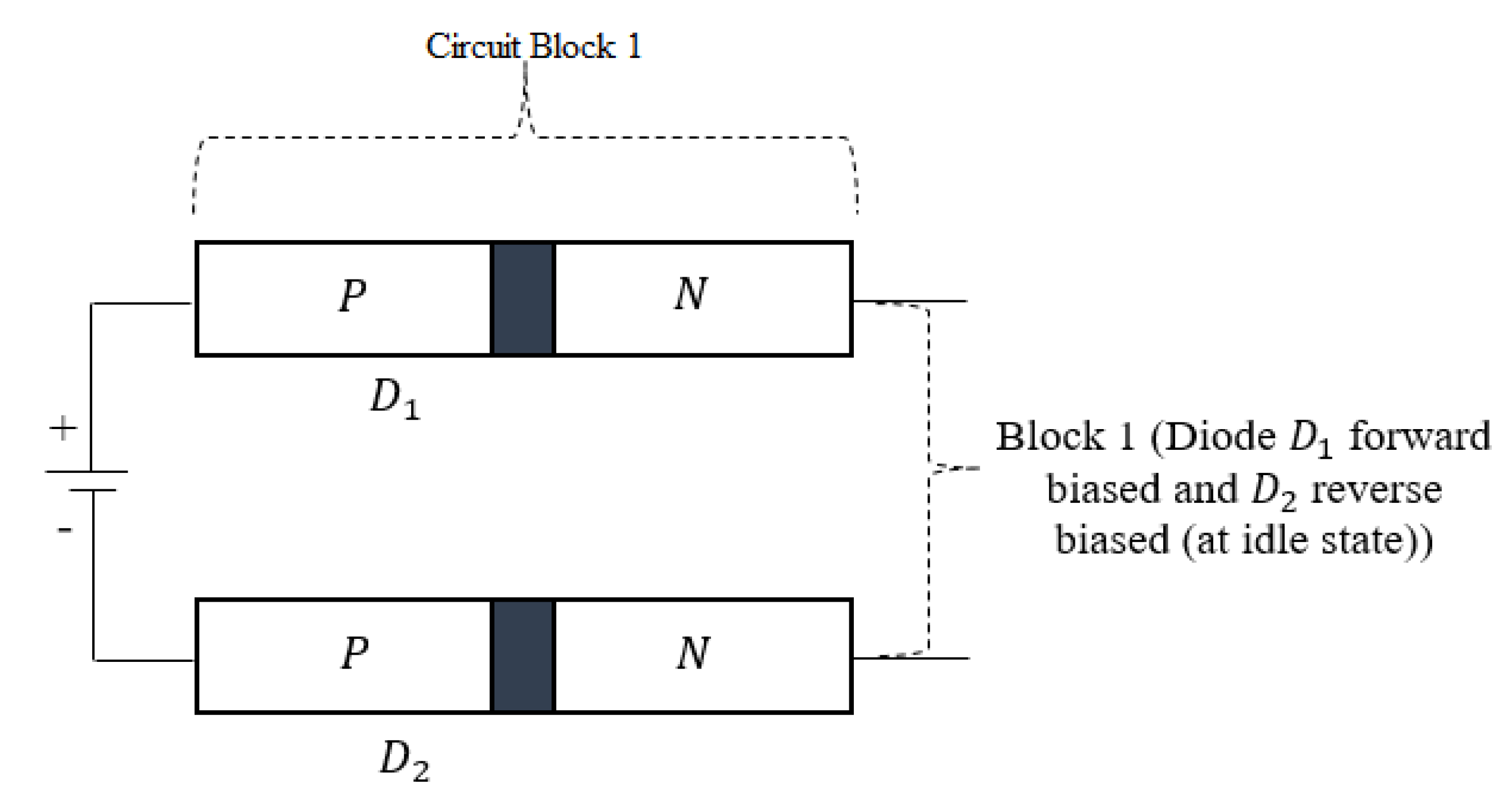
3.3. Harnessing the Short Circuit Power (“Circuit Block 2”)

The “Circuit Block 2” serves as an extension of the preceding stage, “Circuit Block 1”, directly receiving the current and voltage output from “Circuit Block 1”. As shown in Figure 2, a resistive element, which may be symbolized by a high-value resistor, is connected between the positive output terminal (labeled $A$) and the negative output terminal (labeled $B$) of “Circuit Block 1”. This connection introduces an electrical short circuit, fundamentally altering the energy dynamics within the circuit, facilitating exceptional energy conservation and utilization as demonstrated later.

3.3.1. Description of “Circuit Block 2” Components

Initial State (“Circuit Block 1”): Initially, Diode $D_1$ is forward-biased, being connected to the positive terminal of the voltage source. This allows current to flow through $D_1$ from its anode to cathode. Simultaneously, Diode $D_2$ is reverse-biased as it is connected to the negative terminal of the source, preventing significant current flow through it.

Short Circuit (“Circuit Block 2”)-Current Flow, Voltage Drop and After Short Circuit Event: Upon the creation of a short circuit by connecting points $A$ and $B$, a sudden surge of current traverses the short circuit, causing a momentary voltage drop across both diodes. The short circuit current and voltage has always been experimentally determined, with the short circuit events (current surge and voltage drop) reported in [54,55]). During this transient phase, $D_1$, initially forward-biased, experiences a reversal of voltage polarity. The voltage at point $A$ becomes lower than that at the cathode, prompting $D_1$ to enter a state of reverse bias. This causes the depletion layer to widen as electrons migrate away from the junction. Concurrently, $D_2$, which was in a state of reverse bias from the outset, continues to be reverse-biased even after the short circuit. The voltage at point $B$ remains higher than at the anode (since the anode is initially connected to the power source negative terminals, with $0V$ (the $0V$ voltage is theoretically assumed here)), sustaining the widened depletion layer in $D_2$. The widened depletion layers in both diodes play a pivotal role in controlling the flow of charge carriers, influencing the circuit’s behavior during transient events.

Remark 2 (Circuit Protection Mechanism)

: The protective nature of “Circuit Block 1” lies in the fact that, post short circuit, both diodes are in a state of reverse bias. This configuration impedes the flow of current in the reverse direction, safeguarding the source from potential damage. The depletion layers in $D_1$

and $D_2$act as barriers, restricting the movement of charge carriers and effectively isolating the circuit from any adverse effects caused by the short circuit.

The short circuit current here (named as $shortcircuiteffectcurrent$) is computed using the Ohm’s law modified formula that is designed for use in scenarios including low resistance applications provided by [56], and this current is expressed according to equation (6). Thus, equation (6) provides one of the important ingredients required to compute the electrical short circuit in the energy circuit, as the standard Ohm’s law will not be applicable is such settings.

$$I_{short\mathrm{}circuit\mathrm{}effect\mathrm{}current}=a\times e^{\frac{R_{short}}{R_0}}$$

(6)

Where:

$a=\frac{V}{{\mathrm{R}}_0}$, is current scaling factor.

$R_0$ is the reference resistance.

$V$ is the source or supply voltage.

$R_{short}$ is the change in resistance from its reference value $\left(R_0\right)$.

In this context, $R_{short}=R\left(x\right)-R_0$, and the details on parameter $x$ have been established at (Appendix I) by [56].

Using equations (5) and (6), the power input to “Circuit Block 2” can then be computed following equation (7).

$$P_{{input}_{CB2}}=V_{CB1}\times I_{short\mathrm{}circuit\mathrm{}effect\mathrm{}current}$$

(7)

The primary objectives of “Circuit Block 2” are two-fold. It focuses on generating excess short circuit current and effectively channeling this high current to the subsequent stages of the circuit. The high-value resistor (the resistive element shown in Figure 2), often termed the resistive element, plays a pivotal role in achieving these goals. It not only establishes the short circuit in tandem with “Circuit Block 1” but also ensures the high short circuit current flows forward in the circuit without causing damage. In the essence, this resistive element becomes the first path of low resistance after the electrical short circuit, preventing the excess current from finding its way back. This dual role is crucial, as the resistor, in collaboration with “Circuit Block 1”, prevents undesired backflow, while its high resistance directs the abundant short circuit current toward the next stages. The resistance of the resistive element can be varied by considering the overall resistance of the subsequent circuits to ensure that it is higher (for practical applications, this resistance can be determined based on the computed $I_{shortcircuiteffectcurrent}$), ensuring a forward flow of current and enhancing the overall efficiency and safety of the energy circuit. Importantly, “Circuit Block 1” current and voltage outputs transition to become the inputs for “Circuit Block 2”, maintaining the uninterrupted flow of power and energy throughout the circuit’s progression.

Further, it is imperative to take into account the effective resistance in the “Circuit Block 2”. This resistance will include the overall resistance in “Circuit Block 1”, and it can be computed following equation (8).

$$R_{shorteffective}=R_{{CB1}_{overall}}$$

(8)

It will then be considered that the combined resistance (named subsequently as $R_{forwardcurrent}$) between $R_{shorteffective}$ and the resistance due to the high resistive component facilitating the short circuit also contributes into ensuring the forward current flow, from “Circuit Block 2”. For practical purposes, we will express this resistance following equation (9).

$$R_{forward\mathrm{}current}=R_{short\mathrm{}effective}+R_{resistor}\left(this\mathrm{}could\mathrm{}be\mathrm{}some\mathrm{}value\right)$$

(9)

Here, $R_{resistor}$ is the resistive element resistance. Emphatically, understanding the value ($R_{forwardcurrent}$) is important, mainly because of the major role played by the resistive element in the energy circuit (ensuring that the resistive element is not easily damaged by the excess short circuit current, whenever this resistive element becomes the path of low resistance, from “Circuit Block 1”). There will be solely no other main reasons to compute the ($R_{forwardcurrent}$), besides this.

Then, consider that after the short circuit happens (this event should be time depended as described in “Circuit Block 5”) the input voltage into “Circuit Block 2” is expected to drop suddenly (as earlier established), to some value by some factor (let this factor be named $F_{shortcircuit}$ and for computational and simulation purposes here, it is set to the lowest say $F_{shortcircuit}=0.8$). The $F_{shortcircuit}$ means that the voltage drop after the short circuit is $80\%$ of the voltage before the short circuit.

So now the voltage across “Circuit Block 2” (referred as $V_{CB2}$) can be computed according to equation (10).

$$V_{CB2}=F_{shortcircuit}\times V_{CB1}$$

(10)

To this far, we have all the necessary ingredients to work out the power output form “Circuit Block 2”. The power output from “Circuit Block 2” is then computed as expressed in equation (11).

$$P_{{output}_{CB2}}=V_{CB2}\times I_{short\mathrm{}circuit\mathrm{}effect\mathrm{}current}$$

(11)

Figure 2. “Circuit Block 2”-Short Circuit Power Harnessing (“Circuit Block 2” illustrates the innovative approach to energy conservation and utilization).

Figure 2. “Circuit Block 2”-Short Circuit Power Harnessing (“Circuit Block 2” illustrates the innovative approach to energy conservation and utilization).

Remark 3:

The proposed circuit configuration (figure 2), while innovative in its application of diode characteristics to create a protective mechanism during short circuits, aligns seamlessly with established principles of semiconductor physics and diode behavior [57,58,59,60]. It adheres to the well-established properties of diodes in forward and reverse bias states, demonstrating a clear understanding of their depletion layer dynamics and the consequent influence on current flow.

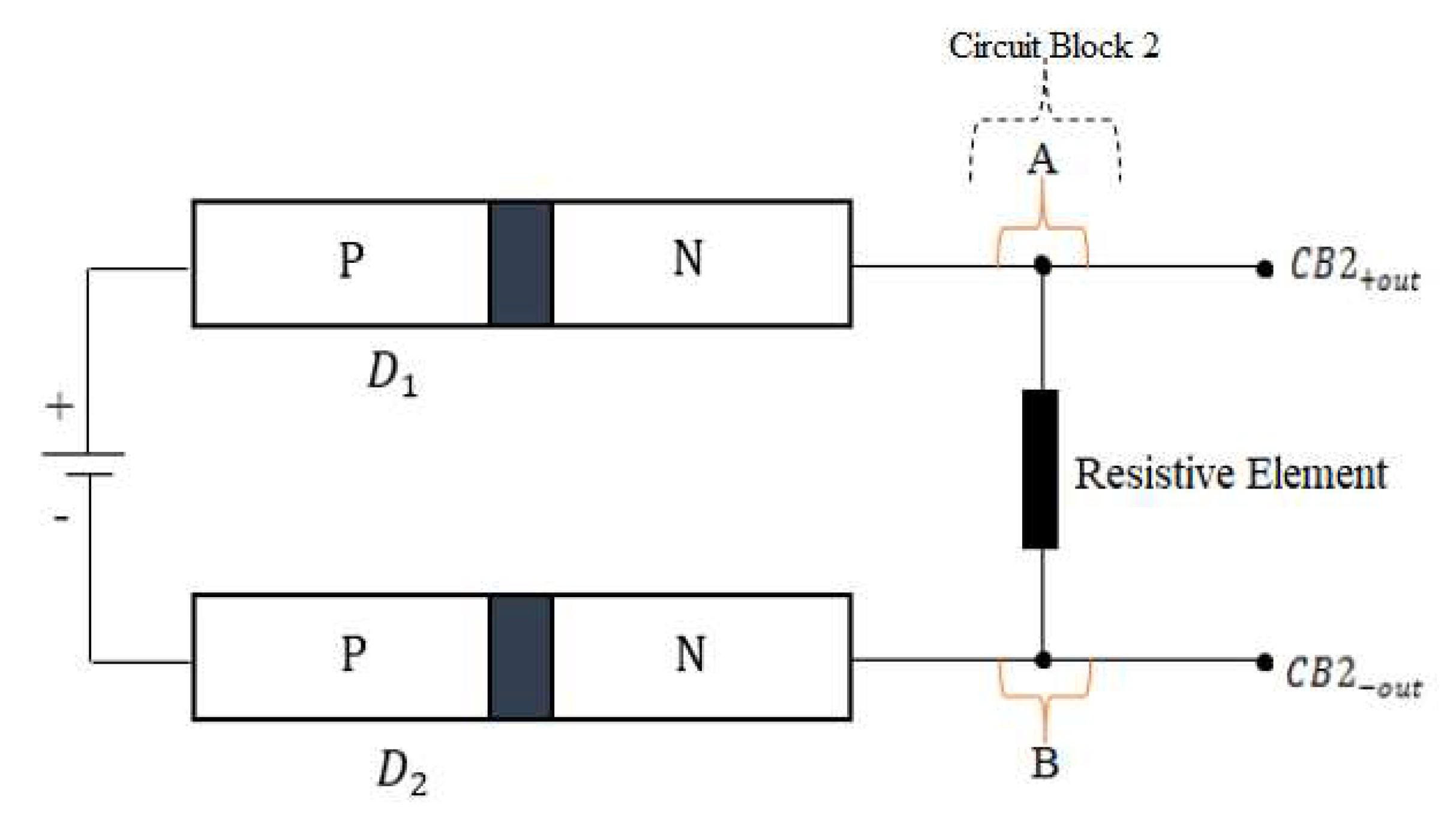
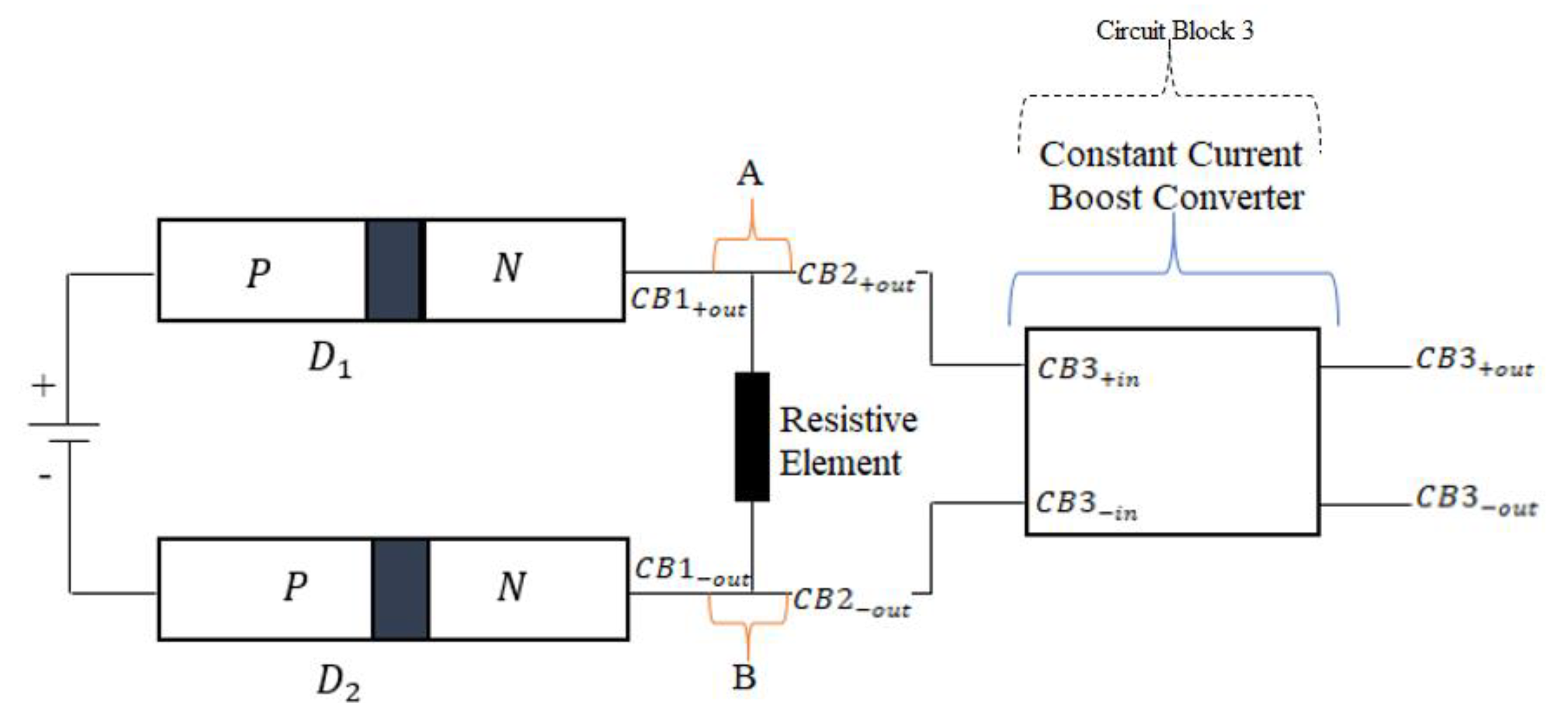
3.4. Advancing Energy Transformation (“Circuit Block 3”)

“Circuit Block 3” continue the process of energy transformation. This phase introduces the concept of “load component_CB3” also named “constant current boost converter”, a component that plays a pivotal role in reshaping the energy circuit, moving it from a non-Ohmic state (“Circuit Block 1” and “Circuit Block 2” are in the non-Ohmic states) to an Ohmic state while sustaining a high, constant current. In contrast to earlier stages, “Circuit Block 3” does not practically introduce additional resistance through additional resistive element besides its genetic resistance (this assumption is made for simulation purpose); instead, it concentrates on harnessing the preexisting circuit resistance from “Circuit Block 1”. The assumed effective resistance (computed earlier as $R_{shorteffective}$) from these prior stages is now incorporated into the analysis of energy conservation to investigate the outcomes.

3.4.1. Load Component_CB3

To achieve the transition from a non-Ohmic to an Ohmic state while ensuring the consistency of the short circuit current after the resistor junctions, we introduce a load component named as “load component_CB3”. The primary purpose of this component is to boost the voltage to the highest achievable level while maintaining a consistent short circuit current. So ideally, “load component_CB3” is a boost converter circuit or element. This section considers a simple design of the “load component_CB3”, based on the following mathematical formulation, that describe the dynamics of inductor current ($IL$) and capacitor voltage ($VC$) over time (with the inductor and capacitor considered the major components of the “load component_CB3”. These equations are later used in simulating the “load component_CB3” for the energy circuit).

3.4.2. Boost Converter (“Load Component_CB3”) Design Mathematical Description

The Inductor Current ($\mathit{I}\mathit{L}$): The basic formula for the voltage across an inductor is given by;

$$VL=L\frac{d{I}_L}{dt}$$

(12)

Here, $VL$ ​ is the voltage across the inductor, $L$ is the inductance, and $\frac{d{I}_L}{dt}$​​ is the rate of change of inductor current with respect to time (equation (12) has been applied in boost converter applications in modified forms [61,62]). In the boost converter circuit, during the on-time ($T_{on}$) of the switch, the voltage across the inductor is the difference between the input voltage ($V_{in}$) and the output voltage ($V_{out}$). This is because the inductor is effectively connected to the input during this time. Further, during the on-time ($T_{on}$) of the switching element, the inductor current ($I_L$) increases, and during the off-time ($T_{off}$), the inductor discharges through the load. In this case, we consider the scenarios; due to the on-time ($T_{on}$) and due to the off-time ($T_{off}$).

During ON time ($0\le \mathit{t}<{\mathit{T}}_{\mathit{o}\mathit{n}}$​): The voltage across the inductor ($VL$ ​) is equal to the difference between the input voltage ($V_{in}$​) and the output voltage ($V_{out}$) according to equation (13).

$$VL=V_{in}-V_{out}$$

(13)

Now, we can equate equation (13) to equation (12), so that we obtain equation (14), which is to be further reduced.

$$V_{in}-V_{out}=L\frac{d{I}_L}{dt}⟹\frac{d{I}_L}{dt}=\frac{V_{in}-V_{out}}{L}$$

Hence,

$$\frac{d{I}_L}{dt}=\frac{V_{in}-V_{out}}{L}$$

(14)

During OFF time (${\mathit{T}}_{\mathit{o}\mathit{f}\mathit{f}}\mathit{}\le \mathit{t}<\mathit{T}$): The voltage across the inductor ($VL$) is equal to the output voltage ($V_{out}$​), a situation expressible according to equation (15).

$$VL=-V_{out}$$

(15)

Applying equation (15) to equation (12) we obtain; $L\frac{d{I}_L}{dt}=-V_{out}$ which on rearranging becomes equation (16).

$$\frac{d{I}_L}{dt}=\frac{-V_{out}}{L}$$

(16)

Next, we need to express the duty cycle ($D$) in terms of time. The duty cycle is defined as the ratio of the on-time ($T_{on}$) of the switch to the total time period ($T$), as expressed in equation (17).

$$D=\frac{T_{on}}{T}$$

(17)

The total period is the sum of the ON and OFF times and can be expressible according to equation (18).

$$T=T_{on}+T_{off}$$

(18)

Using equation (17) in equation (18) we get;

$$T=T_{on}+\left(1-D\right)T$$

(19)

Solving for $T_{on}$ and $T_{off}$ we have;

$$T_{on}=D.T\mathrm{and}\mathrm{similarly},(T_{off}=(1-D).T)$$

(20)

Now, we can express the rate of change of inductor current $\left(\frac{d{I}_L}{dt}\right)$ during the entire period as;

$$\frac{d{I}_L}{dt}=D.\left(\frac{V_{in}-V_{out}}{L}\right)-\left(1-D\right).\frac{V_{out}}{L}$$

(21)

Simplifying equation (21) further, we obtain equation (22) as follows.

$$\frac{d{I}_L}{dt}=\frac{{D.V}_{in}-V_{out}}{L}$$

(22)

Equation (22) which is a first-order linear differential equation provides the final expression $\frac{d{I}_L}{dt}$ for the rate of change of inductor current with respect to​​ during the entire switching period within the “Circuit Block 3”. If we integrate this equation over time, we can obtain the actual expression for $i_L$ as worked out in the subsequent section.

Remark 4 (On Energy Circuit Simulation):

The on-time ($T_{on}$) event in “load component_CB3” can be related to the switching frequency ($f$) as $T_{on}=\frac{1}{f}$​. Substituting this into the duty cycle definition (equation (17)), we get $D=\frac{1}{fT}$. This duty cycle definition will later be used for simulating real-world scenarios of the proposed energy circuit.

Solution for the Constancy of${\mathit{I}}_{\mathit{L}}$: Proceeding from equation (22), the goal of this workflow is to find the actual expression for $I_L$​, by integrate both sides of the equation with respect to time $t$.

$$\int d{I}_L=\int \frac{1}{L}\left(V_{in}-V_{out}\right)dt$$

(23)

Solving equation (23) gives;

$$I_L\left(t\right)=\frac{1}{L}\int \left(V_{in}-V_{out}\right)dt$$

(24)

Integrating equation (24) gives;

$$I_L\left(t\right)=\frac{1}{L}\int V_{in}dt-\frac{1}{L}\int V_{out}dt$$

The integration of $V_{in}$ with respect to time results in $\left(V_{in}.t\right)$, and the integration of $V_{out}$ with respect to time results in $\left(V_{out}.t\right)$, and the operation can be expressed according to equation (25).

$$I_L\left(t\right)=\frac{1}{L}\left(V_{in}.t-V_{out}.t\right)+C$$

(25)

Here, $C$ is a constant of integration. To determine $C$, we need an initial condition. Let us assume that at $t=0$, the inductor current $I_L$ is equal to the short circuit effect current ($I_{shortcircuiteffect}$), which is the initial condition to be used in the energy circuit simulation.

$$I_L\left(0\right)=I_{shortcircuiteffect}$$

(26)

Substituting $t=0$ and equation (26) into equation (25), we then solve for $C$ as follows;

$I_{shortcircuiteffect}=\frac{1}{L}\left(0-0\right)+C$, which reduces to equation (27).

$$C=I_{shortcircuiteffect}$$

(27)

Now, substituting equation (27) back into equation (25) we obtain;

$$I_L\left(t\right)=\frac{1}{L}\left(V_{in}.t-V_{out}.t\right)+I_{short\mathrm{}circuit\mathrm{}effect}$$

(28)

Equation (28) provides the actual expression for the inductor current ($I_L$​) as a function of time $t$ in the boost converter circuit for “Circuit Block 3”.

Mathematical Structure for Capacitor Voltage ($\mathit{V}\mathit{C}$): To complete the mathematical representation of the capacitor voltage ($VC$) equation, this section uses the fundamental relationship in circuit analysis, which relates the current ($I$), capacitance ($C$), and voltage ($V$) for a capacitor according to equation (29).

$$I=C\frac{d{V}_c}{dt}$$

(29)

In this case, the current $I$ is the inductor current ($I_L$​), and the voltage $V$ is the capacitor voltage ($V_c$) [61]. Therefore, equation (29) becomes.

$$I_L=C\frac{d{V}_c}{dt}$$

(30)

Now, the next task is to solve the differential equation (30) for $V_c$​, since the inductor current ($I_L$) is known from the boost converter equations through equation (28).

Rearranging equation (30) we get;

$$\frac{I_L}{C}=\frac{d{V}_c}{dt}$$

(31)

We then integrate equation (31) with respect to time to obtain equation (32).

$$\int \frac{d{V}_c}{dt}dt=\int \frac{I_L}{C}dt⟹V_c=\frac{1}{C}\int I_{L}dt$$

(32)

Substituting for $I_L$ from equation 22 we obtain;

$$V_c=\frac{1}{C}\int \left(\frac{{D.V}_{in}-V_{out}}{L}\right)dt$$

(33)

Equation (33) gives the expression for the capacitor voltage ($V_c$​) in terms of the inductor current ($I_L$) and other circuit parameters constituting the “load component_CB3”. The mathematical formulations for “Circuit Block 3” will be highly relied on, through simulating the provided energy circuit. Overall, the described design approach reflects a sophisticated understanding of semiconductor physics and electrical engineering principles. As demonstrated through the energy circuit simulation results, the “load component_CB3” acts as a bridge between the unconventional energy circuit design and real-world applications, ensuring that the circuit aligns with established norms and can be seamlessly integrated into existing electrical systems.

3.4.3. Overview of “Load Component_CB3” (Constant Current Boost Converter) Major Elements

Inductor (L): The inductor value is critical for energy storage and transfer in the “load component_CB3”. This value is calculated based on the desired output voltage, input voltage, duty cycle, switching frequency, and the desired ripple current in the inductor [63]. The inductor should be capable of handling the desired current and suitable for the input voltage range. The inductor value ($L$) may be determined using the modified equation (34) (an extension of equation (22)), as applied in the later practical simulations.

$$L=\frac{\left(V_{out}-V_{in}\right).D}{f_s.∆I_L}$$

(34)

The equation considers:

• $L$ is the inductor value.
• $V_{out}$ is the desired output voltage.
• $V_{in}$​ is the input voltage.
• $D$ is the duty cycle of the converter.
• ​$f_s$ is the switching frequency.
• $∆I_L$​ is the peak-to-peak inductor ripple current.

Switching Element: The objective here is to choose a switching element (such as MOSFET) capable of handling the desired voltage and current while minimizing ON resistance ($R_{dson}$). The procedure involves considering the voltage rating, ensuring the switching element in this context can handle maximum current, and selecting a switching element with low ON resistance to reduce power losses.

Diode (D): In this step, a diode should be selected with a voltage rating higher than the output voltage. The diode is crucial for allowing current flow and maintaining the desired output voltage.

Output Capacitor (C): The “Load Component_CB3” output capacitor should be capable to handle the output current and maintain the required output voltage. This component assists in smoothing out voltage variations and ensuring stability in the output.

The selection of a suitable “load component_CB3” is crucial in this context. The choice for “load component_CB3” contributes to the overall efficiency of the energy circuit and its capacity to challenge the established laws of energy conservation by generating excess energy. In “Circuit Block 3”, the central objective is to investigate how the inputs derived from “Circuit Block 2”, can be effectively transformed into an Ohmic format suitable for standard circuit applications. This transformation is a pivotal step towards harnessing the innovative potential of the block and challenging the established laws of energy conservation. Figure 3 is a block diagram depicting the developed energy circuit, so far.

Remark 5 (Clarity on Energy Transformation in “Circuit Block 3”):

“Circuit Block 3” transforms the energy circuit from a non-Ohmic to an Ohmic state, not aiming for excess power generation. It acts as a bridge to align the circuit with conventional electrical systems, ensuring compatibility. With intentional higher power input than “Circuit Block 1”, as shown in Table (1), it facilitates smooth integration into existing infrastructure, utilizing excess power for voltage boost. This design emphasizes practicality and adaptability to contemporary electrical and electronic technologies.

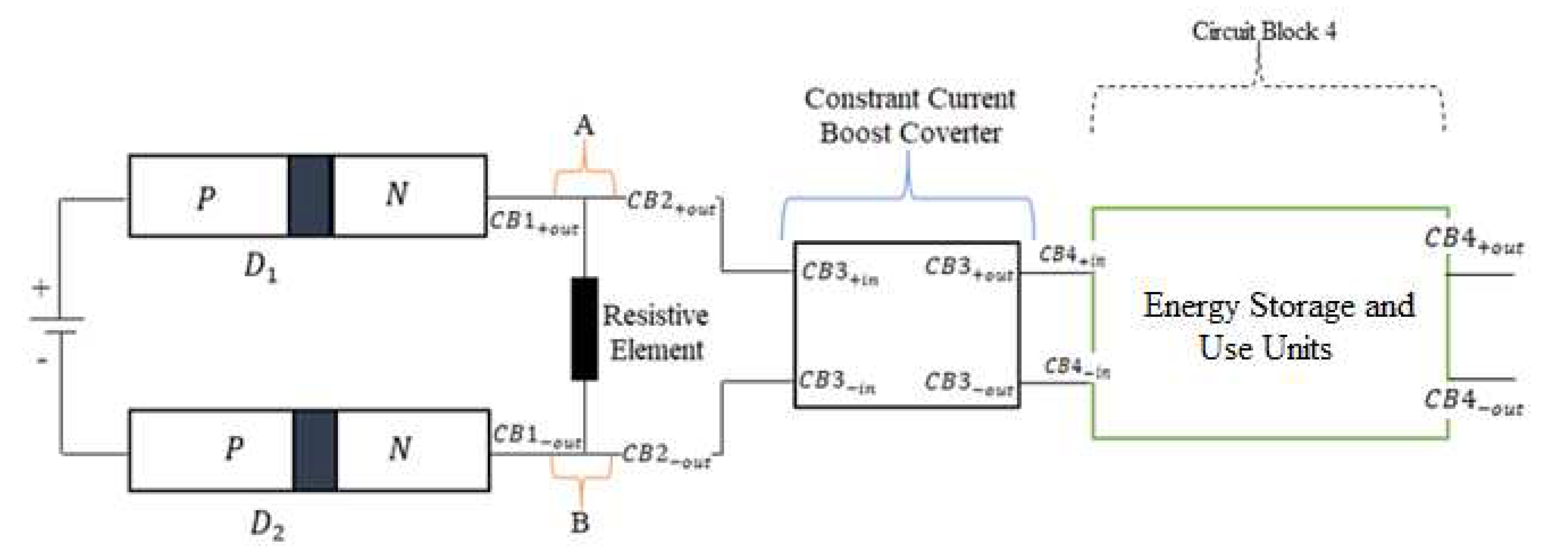
3.5. Energy Storage Component (“Circuit Block 4”)

“Circuit Block 3” has completed the most important section of the provided energy circuit with the intention of generating excess power starting with some input power, within an electrical circuitry. Without delving into the specific details, this section addresses the energy storage component, which is considered an integral ingredient is energy systems, for storing the harnessed power from the “Circuit Block 3”. Thus, “Circuit Block 4” plays a critical role in the energy conservation process by serving as an interface to both capture the output power from “Circuit Block 3” and efficiently oversee it for various applications. This part of the system may introduce a power control unit that reduces the output power from “Circuit Block 3”, optimizing it for different uses. Additionally, “Circuit Block 4” may be equipped with an energy storage mechanism designed to capture and store surplus energy for future purposes, including recharging the power supply source (making the energy circuit a self-recharging system) and powering other intended applications. The power control units within “Circuit Block 4” focuses on smoothly transitioning from the excess energy proceeding from “Circuit Block 3” output to a more manageable voltage level. By precisely adjusting the power, this unit facilitates an efficient distribution of energy throughout the entire system, reducing potential losses and ensuring power quality. The primary goal here is to align the voltage with the power supply voltage (or to some higher desired values), establishing a regenerative loop and enhancing the system’s ability to challenge the laws of energy conservation while providing a consistent power output. Figure 4 depicts a block diagram of “Circuit Block 4” configuration.

3.5.1. The Choice for “Circuit Block 4” Unit

Overall, in “Circuit Block 4”, the focus shifts to the implementation of an energy storage unit to effectively capture and manage the high power output generated by “Circuit Block 3”. Among the various energy storage options, this paper suggests a capacitor-based system, because of its unique advantages, and the following discussion elaborates on the circuit, offering alternative considerations as well.

Circuit for Capacitor-Based Storage Unit: The capacitor-based storage unit requires a well-designed circuit to ensure efficient charging and discharging. The charging circuit typically includes a diode to prevent reverse current, a current-limiting resistor, and a voltage regulator to maintain optimal charging levels. On the discharge side, a controlled switch and a load resistor may be employed to regulate the release of stored energy. The choice of a capacitor-based storage unit is grounded in several key advantages. Firstly, capacitors offer rapid charging and discharging capabilities, aligning with the high-power characteristics of “Circuit Block 3”. Secondly, capacitors boast a longer cycle life compared to batteries, ensuring durability and reliability for repeated charge-discharge cycles. Lastly, their inherent efficiency, owing to low internal resistance, makes capacitors well-suited for applications requiring quick energy transfer [64,65,66,67].

Alternative Storage Units: While the capacitor-based system is chosen for its specific merits, alternative energy storage units are worth considering based on application requirements. Traditional batteries [68,69], such as Li-ion or Li-poly, provide higher energy density but may not match capacitors in terms of rapid energy release. Super-capacitors ([67,70,71,72]) offer a middle ground, combining aspects of both capacitors and batteries. Another alternative, the flywheel energy storage system [73,74], relies on mechanical rotation for energy storage, providing high power but at the cost of space efficiency.

Remark 6 (Recommendation and Considerations):

The selection between capacitor-based storage and alternatives hinges on the specific needs of the application. For scenarios demanding quick response times and frequent charge-discharge cycles, the capacitor-based system stands out. Conversely, if higher energy density and longer storage durations are critical, alternatives like batteries or super-capacitors may be more appropriate. It is imperative to carefully evaluate the application's requirements and constraints to make an informed decision on the most suitable energy storage unit for “Circuit Block 4”.

3.6. Automation and Safety Control (“Circuit Block 5”)

“Circuit Block 5” plays a crucial role within the energy conservation system, aimed at automating and regulating the duration of short circuit events to ensure the safety of the energy circuit’s and the power supply source. To achieve this, a control mechanism, in the form of a sensor, is integrated into the block. The sensing element utilizes a current sensor and a microcontroller to detect variations in the short circuit current. This sensor continuously monitors the operational parameters of the system, specifically the short circuit current in “Circuit Block 2”. The primary objective of “Circuit Block 5” is to prevent extended and potentially harmful short circuit events that could endanger the system’s integrity and the safety of connected devices. By incorporating an automated control system, the block can adjust the duration of the short circuit to strike a balance between maintaining a high short circuit current, necessary for energy generation, and ensuring safety.

3.6.1. Design and Operation of the Sensing Element in “Circuit Block 5”

The sensing element in “Circuit Block 5” serves a critical role in monitoring the short circuit current and ensuring the safety and efficiency of the energy conservation system. The design of the sensing element involves using a current sensor and a microcontroller to detect variations in the short circuit current. Below are the details of the sensing element major components and its mechanism of operation:

Current Sensor: The choice of a suitable current sensor, such as a Hall-effect sensor or a current transformer, is determined by the specific system requirements. This sensor is positioned in the circuit to measure the short circuit current flowing through “Circuit Block 3”, specifically sensing the current between points $A$ and $B$, where the short circuit is introduced.

Microcontroller: An appropriate microcontroller, equipped with analog input capabilities, should be selected to process the output signal from the current sensor. The microcontroller serves as the core of the sensing element, interpreting current measurements and making real-time decisions based on predefined threshold settings.

3.6.2. The Sensing Element Operation Mechanism

The mechanism of operation involves continuous monitoring by the current sensor of the short circuit current in “Circuit Block 3”, detecting the current between points $A$ and $B$. The sensor generates an analog signal proportional to the short circuit current, which is then processed by the microcontroller. Predefined threshold settings are programmed into the microcontroller to establish acceptable limits for the short circuit current, ensuring a safe operating range. The microcontroller compares real-time current measurements with the predefined threshold values, making decisions regarding the duration of the short circuit event. If the short circuit current exceeds or falls below predetermined thresholds, the microcontroller triggers the automation mechanism within “Circuit Block 5”. The microcontroller control unit adjusts the duration of the short circuit event. If the current exceeds safe limits, the duration may be shortened to prevent damage. Conversely, if the current falls below optimal levels for energy generation, the duration may be extended to improve energy output. Further, “Circuit Block 5” establishes a closed feedback loop, facilitating continuous communication between the sensor, microcontroller, and the rest of the energy conservation system. This feedback loop ensures real-time adjustments to maintain both safety and energy efficiency.

Remark 7:

The Sensing Element in “Circuit Block 5” is designed and operated in a way that it initiates its functionality using an external power source. It is crucial to note that this external power source can be replaced with a recharging circuit, drawing power from the excess energy stored in “Circuit Block 4”. This deliberate design decision provides the sensing element with adaptability, enabling it to shift from relying on an external power source to a self-sustaining mode powered by the surplus energy generated within “Circuit Block 4”. This dual-mode functionality improves the overall efficiency and autonomy of the sensing element, aligning it with the innovative and self-recharging characteristics of the broader energy circuit.

3.7. Overall Energy Circuit Representation

The overall representation of the energy circuit, starting from the power supply and extending to the storage unit in “Circuit Block 4”, is outlined in the block diagram, Figure 5.The Automation block (“Circuit Block 5”) is connected before “Circuit Block 3”, forming a cohesive and integrated system. This block diagrammatic illustration encapsulates the innovative design and interconnected functionalities of each circuit block, emphasizing the progression from power input to storage, with the pivotal role of automation and safety control in optimizing energy generation.

3.8. Interpretation and Simulation of the Proposed Energy Circuit Blocks

This section discusses the code provided in Appendix A as an interpretation and numerical simulation of the described energy circuit, specifically from its inception at Circuit Component 1 (Power Source) to the culmination of “Circuit Block 3”. The simulation aims to offer a real-world perspective on the application of the proposed energy circuit, allowing for the exploration of a wide range of variable settings, from idealized scenarios to practical considerations.

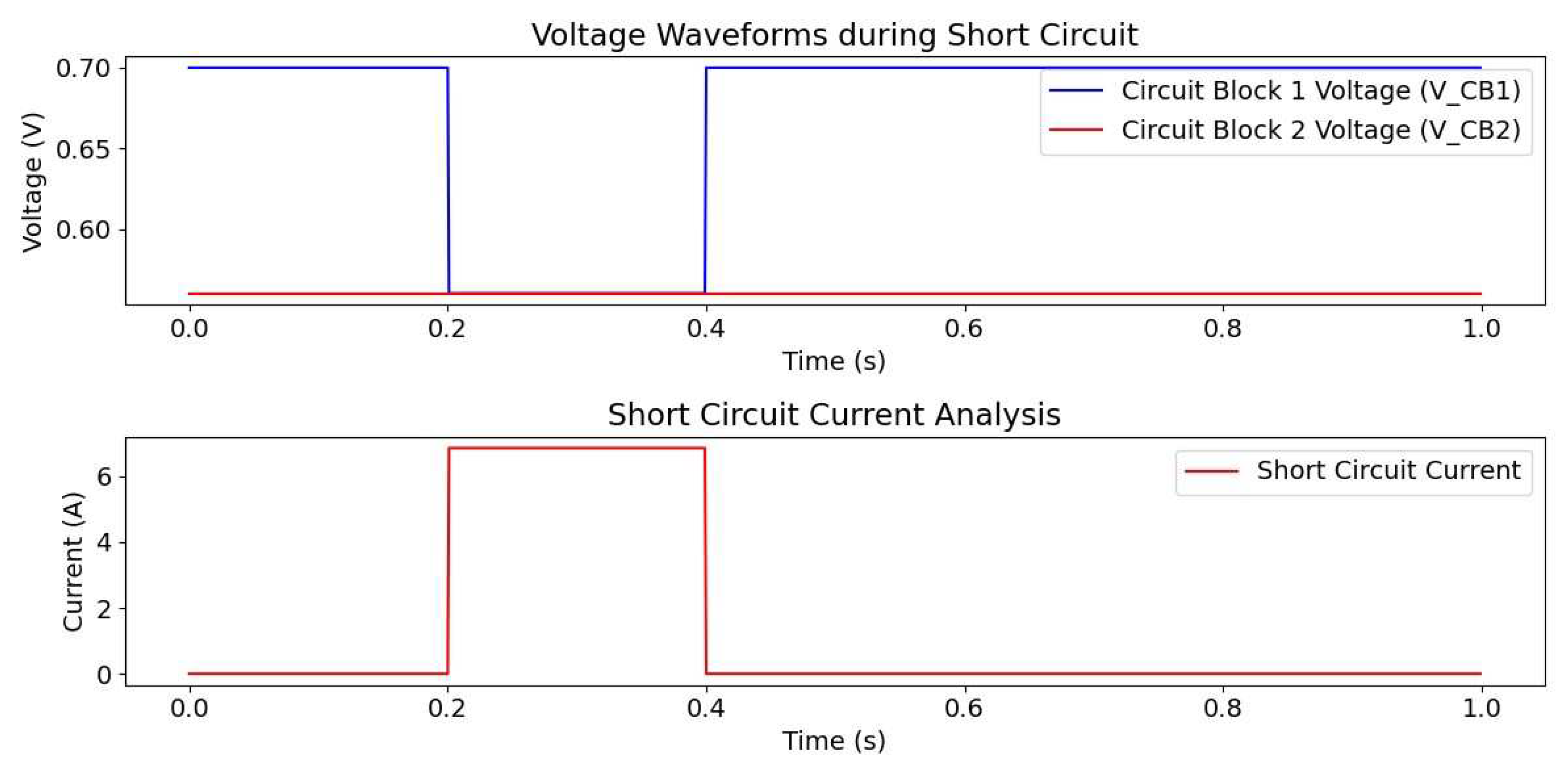
3.8.1. Simulated Results and Analysis

The simulation results presented in Table (1) provide insights into the behavior of the proposed energy circuit under various practical scenarios. The analysis focuses on understanding the circuit’s response to changing parameters and its ability to generate energy beyond the supplied energy. Table (1) outlines the results of 10 different supply voltages corresponding to 10 different specific circuit parameters. Since the circuit has applied two identical diodes (as established in figure 1), each diode parameters (the ideality factor ($n$), and reverse saturation current ($I_s$)) is considered for the respective corresponding 10 diodes.

3.8.2. Description of Main Sections of the Simulation

Variable Power Supply (Denoted$\mathit{V}\_\mathit{S}\mathit{o}\mathit{u}\mathit{r}\mathit{c}\mathit{e}$in the Simulation Code): The simulation commences with “Circuit Block 1”, representing the power source. Emphasizing real-world conditions, the inclusion of known resistances, including those from connecting wires and the internal resistance of the source, establishes a low-power supply scenario. This approach acknowledges the impracticality of a completely resistance-free circuit, aligning the simulation with practical considerations. Through the provided simulation and analysis, both $Case1$ and $Case2$ use Equation (6) for short circuit current computations, applying a single diode with characteristics: ideality factor ($n=1.7$) and Saturation Current ($I_s$) of $6^{-14}A$ for illustrative purposes. These cases provide insights into the circuit’s response to intentional disruptions and its ability to regulate and utilize excess power for continuous operation.

Case 1 (On the Evolution through “Circuit Block 1” and “Circuit Block 2”): The simulation of the energy circuit unfolds through distinct phases, with $Case1$ specifically focusing on the controlled short circuit initiation and the subsequent transient analysis. This case provides valuable insights into the circuit’s behavior during intentional disruptions, offering understanding of its protective mechanisms.

Initial State: The initial state of the simulated energy circuit is characterized by stable operating conditions and a nominal current flow. “Circuit Block 1” ($CB1$) is configured in a conventional manner starting with forward-biased and reverse-biased diodes, facilitating the normal and expected flow of current. In this steady state, the power supply voltage ($V_{CB1}$) is maintained at a constant level, providing the necessary energy for the circuit’s operation. The diodes within “Circuit Block 1” are actively conducting, allowing current to flow through from the anode to the cathode. This scenario establishes the baseline condition before any intentional disruption is introduced.

Short Circuit Initiation. The controlled short circuit event is initiated by deliberately manipulating the circuit parameters, such as resistance or triggering an external factor. This intentional disturbance is designed to mimic an anomalous electrical short circuit within “Circuit Block 1”. As the short circuit is introduced, there is a sudden surge of current through the affected part of the circuit. The manipulation leads to a temporary breakdown of the conventional operating conditions, causing a significant change in the current flow and voltage distribution. The introduction of the short circuit serves as a crucial element for demonstrating the protective mechanisms embedded in the circuit, and it triggers a cascade of responses in both “Circuit Block 1” and “Circuit Block 2”.

Transient Analysis. The transient analysis phase involves the recording and visualization of voltage and current waveforms at key points in both “Circuit Block 1” and “Circuit Block 2” during and after the short circuit event. This observation aims to capture the dynamic behavior of the circuit as it transitions from a stable state to a transient phase. The reversal of voltage polarity in the diodes becomes evident as the short circuit disrupts the established normal biasing conditions. As depicted in Figure 5(a), the voltage waveforms illustrate the changes in potential across the circuit components, highlighting the impact of the short circuit on the overall system. Simultaneously, the current flow undergoes significant alterations, with a surge occurring during the short circuit initiation. The widening of depletion layers in the diodes contributes to the observed changes in current flow, representing a crucial aspect of the circuit’s response to transient events. The transient analysis not only serves as a means to validate the protective mechanisms but also provides insights into the adaptability and resilience of the energy circuit in the face of sudden disruptions. Consider Figure 5(a), for the details.

Case 2 (Evolution through “Circuit Block 1” and “Circuit Block 2”, Considering Power Flow). In the simulated occurrence of the anomalous electrical short circuit, the circuit undergoes a transient response as described in the previous sections. Initially, “Circuit Block 1” provides a constant power input, and the short circuit event leads to a sudden surge of current. The power flow visualization reveals a dynamic interplay between “Circuit Block 2” and “Circuit Block 3” during and after the short circuit event. The momentary surge in power output from “Circuit Block 2” is efficiently harnessed by “Circuit Block 3”, maintaining a constant short circuit effect current. Figure 5b reveals the remarkable ability of “Circuit Block 3” to maintain a constant short circuit effect current, regulating the flow of excess power seamlessly. The synchronized power input and output in “Circuit Block 3” underscore the circuit’s efficiency in utilizing surplus energy for further stages. The power input to “Circuit Block 3” aligns with the power output from “Circuit Block 2”, showcasing a unified transition of excess power. This process illustrates the energy circuit’s capability to not only protect itself during transient events but also to effectively utilize the surplus power in subsequent stages, contributing to the overall efficiency and performance of the proposed energy circuitry.

Case 3 (Stability Testing of “Circuit Block 3”-Implications on Short Circuit Effect Current and Voltage Boosting). In the simulation of “Circuit Block 3”, the primary objective is to assess the stability of the energy circuit, particularly focusing on the constancy of the short circuit effect current and the voltage boosting mechanism. The results obtained from the simulation reveal noteworthy stability, crucial for understanding the behavior of the circuit during energy transformation. Examining the inductor current shown in Figure 5(c-(a)), it is evident that the current remains relatively stable over time. The consistency in inductor current is a crucial indicator of the stability of the energy circuit. The short circuit effect current, initiated in “Circuit Block 1” and efficiently harnessed through “Circuit Block 2”, maintains its constancy in “Circuit Block 3”. This stability is a key characteristic, signifying the robustness of the energy circuit as it progresses through various stages. Moving on to the capacitor voltage depicted in Figure 5(c-(b)), a notable observation is the steady increase in voltage over time. This voltage boost is a result of the energy transformation process facilitated by “Circuit Block 3”. This voltage boosting is a fundamental aspect of ““Circuit Block 3”’s” functionality. The steady rise in capacitor voltage is achieved through the carefully orchestrated energy transformation process. Notably, the simulation demonstrates that the boosting of voltage occurs without compromising the stability of the short circuit effect current. The capacitive element plays a pivotal role in maintaining this voltage increase, showcasing the circuit's ability to elevate voltage levels while ensuring stability. It is essential to emphasize that the focus of this voltage boost is not an attempt to generate excess energy but rather to return the circuit to an Ohmic state compatible with conventional electronic systems. Simultaneously, Figure 5(c-(c)) illustrates the voltage across the load resistor. The gradual rise in load resistor voltage aligns with the expectations of the energy circuit's behavior. The controlled increase in voltage across the load resistor ensures that the circuit operates within safe limits and adheres to established standards. This voltage adjustment is a deliberate design choice aimed at integrating the energy circuit seamlessly into existing electrical infrastructure. The absence of sudden spikes or irregularities in the load resistor voltage reinforces the reliability of the energy circuit in maintaining a stable output.

Implications and Adjustability in “Circuit Block 3”. The stability observed in the short circuit effect current and the controlled voltage boosting in “Circuit Block 3” imply a deliberate design choice focused on returning the circuit to an Ohmic state. The absence of hidden tricks or unpredictable variations in the short circuit effect current emphasizes the transparency of the energy generation process. This simulation reinforces the notion that the energy circuit operates with precision, directing its efforts toward achieving a stable and boosted voltage output. Adjusting the voltages in “Circuit Block 3” involves fine-tuning parameters such as inductor values, capacitor values, and load resistances. These adjustments can be made to align with specific application requirements or desired energy output levels. By manipulating these components, one can control the rate of voltage increase and ensure that the energy circuit adapts to real-world scenarios seamlessly.

Case 4 (Evolution Through “Circuit Block 1” and “Circuit Block 3”, Simulating Practical Settings). As the simulation progresses through “Circuit Block 1”, utilizing diode characteristics to prevent undesired backflow, and “Circuit Block 2”, tapping into short circuit power, the code dynamically computes and visualizes current, voltage, and power parameters. This dynamic evolution highlights the innovative aspects of the circuit, challenging traditional energy conservation principles.

Circuit Transformation to Ohmic State: The simulation reaches its culmination in “Circuit Block 3”, which is sufficient for showcasing the transformation of energy from a non-Ohmic (non-Ohmic here meaning not obeying the standard Ohms law) state to an Ohmic state (Ohmic here meaning obeying the standard Ohms law), and accomplishing the energy creation goal. Introducing the “load component_CB3” as a constant current boost converter, the code allows exploration of parameters such as inductor value, switching frequency, and duty cycle. This illustration emphasizes the circuit’s capability to achieve higher power output, surpassing the initially supplied power.

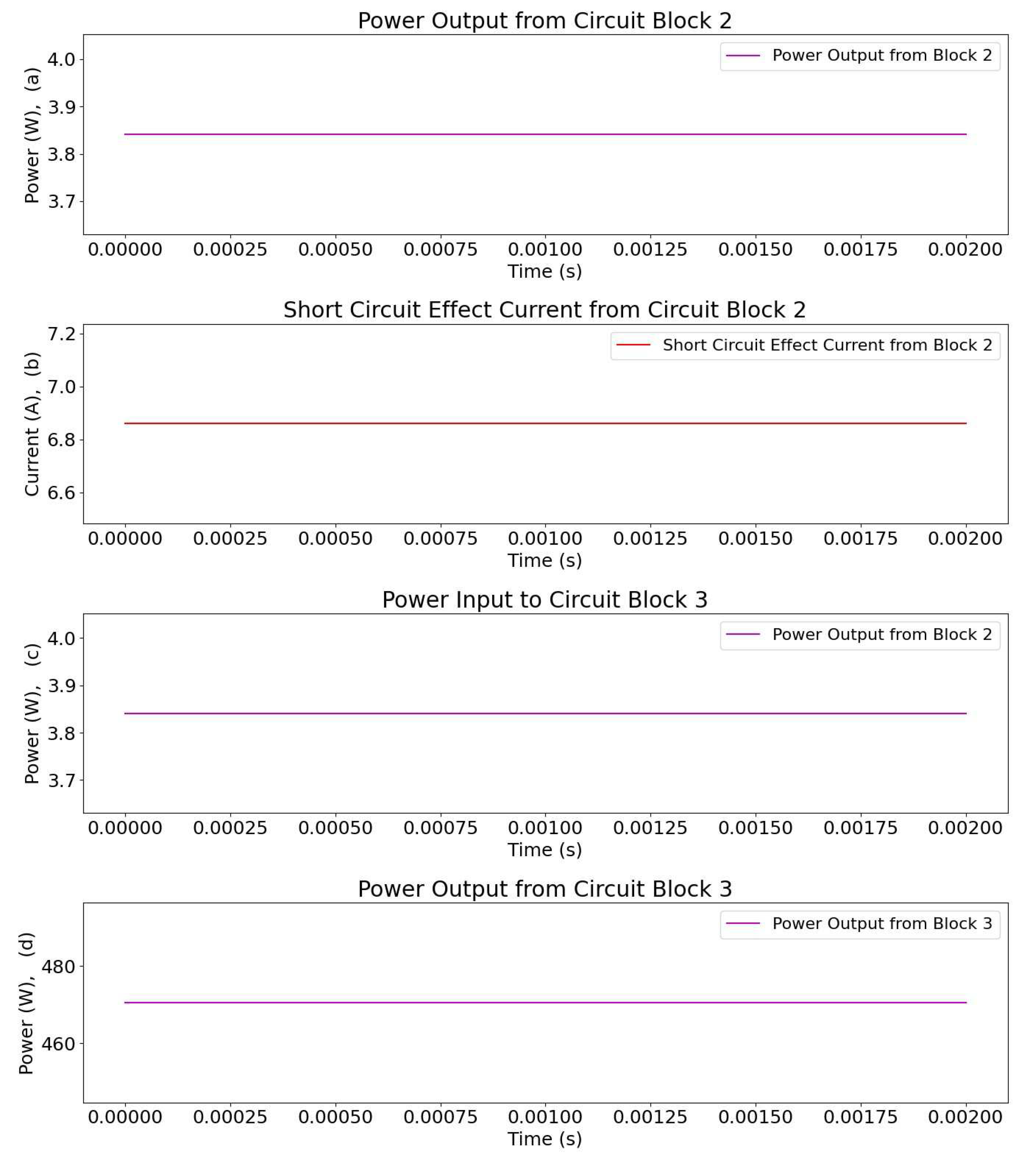
3.8.3. Analysis of Simulation Results

With the hypothetically chosen parameters, the tabulated results in Table (1) align with the overarching goal of illustrating the proposed energy circuit’s behavior under distinct real-world scenarios with varying power requirements. The “Supply Voltage (V)” directly corresponds to the variable “$V\_source$” in the provided simulation code, offering a practical perspective. The “Diode Forward Voltage (V)” is kept constant in the simulation table to isolate the effects of other variables on the performance of the proposed energy circuit blocks. By maintaining a consistent diode forward voltage, the study can systematically analyze the impact of changes in supply voltage, reference resistance (R0), ideality factor ($n$), and saturation current ($I_s$) on the behavior of the circuit. This approach allows for a focused investigation into how alterations in these parameters influence the overall power input to “Circuit Block 1” ($P_{{input}_{CB1}}$), the short circuit effect current ($I_{shortcircuiteffectcurrent}$), and the power input to “Circuit Block 3” ($P_{{input}_{CB3}}$) and its subsequent power output ($P_{{output}_{CB3}}$). In real-world application scenarios, the diode forward voltage might vary based on the type of diodes used or the specific characteristics of the semiconductor materials employed. However, by holding the diode forward voltage constant in the simulation, the study can provide a foundational understanding of the circuit’s response to variations in other key parameters. The table projects results across different real-world application scenarios by varying the supply voltage, reference resistance, ideality factor, and saturation current. Each row in the table represents a unique combination of these parameters, simulating diverse operational conditions. This systematic exploration allows researchers and engineers to observe how the proposed energy circuit performs under different settings, providing insights into its adaptability and efficiency across a range of practical applications.

Table 1 presents simulation results for different configurations of the proposed energy circuit blocks. The parameters include the supply voltage, diode forward voltage, reference resistance (R0), ideality factor ($n$), saturation current ($I_s$​), power input to “Circuit Block 1” ($P_{{input}_{CB1}}$) short circuit effect current ($I_{shortcircuiteffectcurrent}$​), power input to “Circuit Block 3” (​$P_{{input}_{CB3}}$), and power output from “Circuit Block 3” ($P_{{output}_{CB3}}$​). These results showcase the behavior and performance of the energy circuit under various conditions, providing valuable insights for further analysis and optimization.

3.8.4. Power Output from “Circuit Block 3”

From Table (1), the computed power into and from the “Circuit Block 3” ($P_{{input}_{CB3}}$) and ($P_{{output}_{CB3}}$) respectively, as demonstrated in the table, significantly exceeds the supplied power ($P_{{input}_{CB1}}$), validating the energy circuit’s ability to generate power beyond conceivable losses. This observation dismisses concerns about power losses, showcasing the circuit’s efficiency in converting and amplifying the supplied power.

3.9. How the Energy Circuit Breaks the Law of Energy Conservation

Analyzing the computed power inputs and outputs in Table (1) under different practical settings, the energy circuit seemingly defies the traditional law of energy conservation. The output power from “Circuit Block 3” ($P_{{output}_{CB3}}$) consistently exceeds the input power ($P_{{input}_{CB1}}$), challenging established principles. Further, this output power ($P_{{output}_{CB3}}$) has been transformed to Ohmic state, making the terminal of the energy circuit compatible with electrical and electronics systems within classical settings. The provided energy circuit offers departure from conventional energy generation methods, opening avenues for rethinking the boundaries of energy conservation.

3.10. Possible Applications of the Energy Circuit-Addressing Some Critical Challenges

The proposed energy circuit introduces innovative solutions to several challenges in modern energy systems. Its innovative design and operation challenge conventional scientific boundaries, offering a new perspective on energy conservation, creation, and practical applications. This section provides some detailed explanations of the applications of the energy circuit, its merits over existing systems, and an assessment of current systems it aims to address.

3.10.1. Energy Creation and Conservation

The proposed energy circuit explores new frontiers in the field of energy generation and conservation. It challenges conventional understanding and established principles of energy conservation by introducing an innovative approach that fundamentally redefines the boundaries of energy generation. The energy circuit’s journey from energy creation to conservation is marked by distinctive features, each contributing to its revolutionary nature.

Generating Energy from Anomalous State-Advantages of the Energy Circuit: The distinguishing feature of the energy circuit lies in its capacity to create energy from what has be described as an anomalous state (the energy circuit begins from a non-Ohmic state to a Ohmic state). This capability is harnessed through a well-defined formula (Appendix B provided detailed understanding of the formula), providing a systematic approach to computing the short circuit current. This formula serves as a foundational tool in addressing the aftermath of an electrical short circuit, aligning seamlessly with our intuitive understanding of the short circuit phenomena. This departure from conventional understanding challenges established principles of energy conservation. Through the utilization of the electrical short circuit model, the energy circuit accomplishes energy generation while upholding a consistent current flow. This innovative approach introduces a shift from traditional methods of energy generation. The circuit’s capacity to confront and redefine the confines of energy creation unveils fresh opportunities for addressing the growing demand for effective and sustainable energy sources [75].

A Possible Solution on the Principle Limitations of Current Systems in Energy Creation: The limitations of current conventional energy systems lie in their strict adherence to established principles of energy conservation, rooted in well-understood physical laws. These systems operate within the boundaries defined by the laws of thermodynamics, aiming for efficiency within those constraints. While this approach has merits in ensuring the predictability and stability of energy systems, it inherently restricts the potential for extracting additional advantages from the process of energy generation. Conventional energy systems operate under the premise that the total energy input must equal the total energy output [76], in line with the first law of thermodynamics. This adherence to the law, while essential for maintaining a reliable and consistent energy supply, limits the capacity for innovation within the existing framework. The proposed energy circuit, by contrast, challenges this conventional understanding and demonstrates that working within the confines of the law of energy conservation does not inherently yield extra advantages in energy creation. The examination of existing systems goes beyond the constraints imposed by principles of energy conservation. These systems often face challenges related to energy loss during transmission, reliance on finite resources, and environmental impact. The proposed energy circuit, operating within classical settings yet deviating from conventional norms, addresses some of these limitations. One significant limitation of current systems is their dependence on finite resources, such as fossil fuels [2,5,9], which not only contribute to environmental pollution but also face depletion over time. The proposed energy circuit, with its unconventional approach to energy generation, offers a potential avenue for reducing dependence on these finite resources, contributing to sustainability. Moreover, the conventional systems struggle with issues of energy loss during transmission through power lines. The proposed energy circuit, with its unique configuration and focus on short-circuit phenomena, introduces a novel perspective that may mitigate such transmission losses.

3.10.2. Applications in Electric Vehicles (EVs)

Electric vehicles (EVs) represent a crucial frontier in sustainable transportation [77,78], offering the potential to reduce environmental impact and dependence on traditional combustion engines. However, the widespread adoption of EVs faces challenges related to recharging infrastructure and operational limitations [79]. The proposed energy circuit intervenes in this domain, providing a novel solution to enhance the functionality and convenience of electric vehicles.

On Self-Recharging EVs-Application Merits: The merits of the energy circuit extend significantly to the realm of electric vehicles (EVs), providing an innovative solution to the challenges faced by these vehicles with the possibility of introducing the concept of self-recharging. Traditional electric vehicles rely heavily on external recharging infrastructure [79], limiting their operational range and posing challenges in areas with sparse charging stations. The proposed energy circuit revolutionizes the landscape by enabling EVs to become self-recharging entities. This transformative capability addresses a critical issue in the current domain of electric vehicles-the ability to generate power continuously while in operation. Unlike traditional EVs that require external recharging stations, vehicles integrated with the proposed energy circuit can harness excess power during operation. This self-recharging feature eliminates concerns about the availability and accessibility of recharging infrastructure, particularly in rural and less populated areas. The excess power generated during operation can be directed back into the energy circuit system, effectively recharging it without relying on external sources. This breakthrough not only enhances the autonomy of electric vehicles but also mitigates the challenges associated with limited recharging infrastructure. In practical terms, this means that electric vehicles equipped with the proposed energy circuit can continuously replenish their power reserves during operation. The excess harvested power serves a dual purpose-powering the vehicle and simultaneously recharging the energy circuit system. This self-sustaining capability offers a solution to one of the primary drawbacks of current EV systems, marking a significant advancement in the field of electric transportation.

Possible Solution for Limited Recharging Infrastructure: Current electric vehicles encounter significant challenges due to the limited availability of recharging infrastructure [80], particularly in rural and less populated areas. The scarcity of recharging stations poses a substantial barrier to the widespread adoption of EVs, leaving drivers anxious about finding a charging point. This limitation restricts the convenience of owning an EV and hampers long journeys, contributing to apprehensions among potential EV users. Additionally, the extended duration required for recharging an EV, even with fast-charging stations [79,80], remains a significant drawback. The energy circuit’s capacity to enable self-recharging in EVs addresses these limitations, offering a transformative solution to make EVs more practical and convenient for a broader range of users.

3.10.3. Microgrid Development

Microgrids represent a promising avenue for decentralized energy generation and distribution [81,82,83], offering a localized and often more resilient solution to energy needs. In the context of microgrid development, the proposed energy circuit assumes a pivotal role, providing a continuous power generation and storage solution that transforms the dynamics of microgrid resilience.

Enhanced Resilience-An Application Advantage: The energy circuit shows an application advantage in fostering the development of microgrids by providing a continuous power generation and storage solution. In the context of microgrid development, the proposed concept of introducing of self-recharging circuits offers a transformative enhancement in terms of resilience. Microgrids equipped with these circuits will gain the capability to operate autonomously and continuously generate and store their energy. This newfound resilience becomes particularly crucial in mitigating the vulnerabilities associated with power outages and disruptions. Unlike traditional microgrid systems that may face limitations in sustained power supply [83], those integrated with self-recharging circuits can provide uninterrupted energy even during grid failures or emergencies. The enhanced resilience offered by these circuits positions microgrids as more reliable and robust contributors to local energy solutions.

Possible Solution for Microgrid Systems-Grid Dependency: The existing energy infrastructure often leaves communities and industries reliant on centralized power grids [84], exposing them to vulnerabilities related to grid dependency. This dependence on external power sources makes these entities susceptible to power outages and disruptions, which can have cascading effects on various aspects of daily life and industrial operations. The introduction of self-recharging circuits addresses this limitation by empowering microgrids with the capability to generate and store their energy continuously. This shift towards energy independence enhances the resilience of microgrids, making them less susceptible to external disruptions and contributing to the development of a more robust and sustainable energy ecosystem.

3.10.4. Renewable Energy Integration

The integration of renewable energy sources into the existing power grid has been a longstanding goal in the pursuit of sustainable energy solutions [85]. The innovative design of the energy circuit plays a pivotal role in advancing this objective, offering a range of merits that significantly enhance the utilization of renewable energy.

Efficient Energy Storage-Application Merits: The innovative design of the energy circuit brings significant merits to the integration of renewable energy sources. One notable advantage lies in the energy circuit’s efficiency in capturing and storing excess energy generated by renewable sources such as solar and wind. The intermittent nature of renewable energy has been a longstanding challenge in the field. Solar panels produce energy when exposed to sunlight, and wind turbines generate power when the wind is blowing, creating periods of energy abundance and scarcity. The energy circuit addresses this issue by providing an efficient means of storing surplus energy during peak generation periods. This stored energy can then be utilized during periods of low or no renewable energy production, ensuring a more consistent and reliable energy supply.

Addressing Limitation of Intermittency of Renewable Sources: The unpredictable nature of weather conditions directly affects the generation capacity of these renewable sources, leading to fluctuations in energy production. This intermittency poses challenges to maintaining a stable and reliable energy supply to the grid. In periods of low renewable energy production, the reliance on traditional energy sources may increase, offsetting the environmental benefits of renewable energy. The energy circuit addresses this challenge by efficiently storing excess energy during peak generation, thereby mitigating the impact of intermittent renewable sources on the overall energy supply.

3.10.5. Addressing the Energy Crisis

As established earlier, the contemporary global energy landscape faces a complex crisis [2], marked by challenges arising from the depletion of finite resources, environmental degradation, and an escalating demand for energy. Traditional energy systems, primarily hinged on fossil fuels, have proven unsustainable, contributing significantly to these challenges. In response to this pressing issue, the innovative energy circuit emerges as a transformative solution, offering a departure from conventional approaches and presenting a pathway towards mitigating the global energy crisis.

Mitigating Global Energy Crisis-An Application Advantage: The energy circuit emerges as a transformative solution in mitigating the global energy crisis. One of its key merits lies in its ability to provide an alternative method of energy generation. Conventional energy systems, predominantly reliant on fossil fuels and finite resources, contribute significantly to the depletion of these resources, escalating the global energy crisis. The energy circuit challenges this norm by efficiently capturing excess energy and reducing the consumption of finite resources. By introducing a novel approach to energy creation, the circuit offers a pathway to sustainable energy generation, addressing the root causes of the ongoing energy crisis.

Addressing the Limitation of Dependency on Finite Resources: A major challenge of current energy systems centers around their heavy reliance on finite resources [86]. Traditional methods of energy generation, such as coal, oil, and natural gas, are not only environmentally detrimental but also contribute to the depletion of finite resources. The increasing demand for energy exacerbates this dependency, creating a looming crisis. The proposed energy circuit directly confronts this challenge by presenting an innovative model that minimizes reliance on finite resources. Through its capacity to efficiently capture and utilize excess energy, the circuit charts a course towards a more sustainable and environmentally conscious approach to energy generation, ultimately contributing to the alleviation of the global energy crisis.

4. Discussion and Implications

The development of the innovative energy circuit marks a significant departure from conventional approaches, ushering in a paradigm shift with far-reaching implications. This energy circuit breaks the established norms and introduces transformative solutions to address pressing global challenges.

4.1. Breaking Misconceptions and Limitations in Energy Conservation

One of the central aspects of this paradigm shift is the energy circuit’s bold confrontation of misconceptions entrenched in traditional solutions that seek to circumvent the law of energy conservation. Rather than accepting perpetual motion machines as indisputable proof, the energy circuit delves into sophisticated scientific and mathematical backgrounds. This analytical depth allows it to challenge not only the validity of perpetual motion machines but also to initiate a broader discourse on the limits of application for the first law of thermodynamics (or as applied in the paper, the law of energy conservation). This venture into the intricacies of energy conservation laws marks a pivotal moment that reshapes scientific understanding, pushing the boundaries of exploration into new frontiers.

4.2. Contributions to Addressing the Global Energy Crisis

A critical facet of the implications arising from this energy circuit revolves around its potential to address the relentless global energy crisis. Through efficiently capturing excess energy, the energy circuit challenges existing systems and provides a viable alternative to conventional energy generation. This goes beyond mere theoretical discussions and offers practical solutions to reduce dependency on finite resources. The energy circuit introduces a sustainable approach that has the potential to mitigate the strain on nations grappling with energy shortages. This shift towards sustainable energy solutions becomes imperative as the global demand for energy continues to escalate, presenting a promising avenue for long-term energy resilience.

4.3. Solutions to Noise Pollution and Innovations in Electric Vehicles

The introduction of the energy circuit brings forth a notable solution to the pervasive issue of noise pollution in urban environments. Noise pollution, often exacerbated by the operation of conventional vehicles, finds a mitigating solution through the transformation of electric vehicles (EVs) enabled by the energy circuit. In the domain of transportation, where noise is an inevitable byproduct of traditional combustion engines, the shift towards electric vehicles powered by the energy circuit becomes a pioneering solution. The energy circuit’s ability to continuously recharge EVs during operation not only enhances their sustainability but also substitutes the conventional vehicles internal combustion engines, significantly reduces noise emissions associated with frequent accelerations and decelerations. As cities strive for enhanced livability and reduced environmental impact, the incorporation of this energy circuit into electric vehicles aligns with the broader goals of creating eco-friendly urban spaces.

4.4. Greenhouse Gas Reduction and Addressing Current Clean Energy Systems

The energy circuit, with its emphasis on renewable energy integration, emerges as a pivotal player in the global initiative to reduce greenhouse gas emissions. This becomes particularly significant as it offers a constructive evaluation of current clean energy systems grappling with the intermittent nature of renewable sources. Traditional renewable energy systems often face challenges related to the inconsistent availability of energy from sources like solar and wind, leading to inefficiencies in energy capture and distribution. The transformative approach of the energy circuit lies in its ability to efficiently capture and store excess energy, thereby addressing the intermittency issues associated with renewable sources. In providing a more reliable and continuous energy supply, the circuit stands as a solution to the limitations of current clean energy systems. Its capacity to store and distribute energy aligns with the broader goals of mitigating climate change by reducing reliance on fossil fuels and decreasing overall greenhouse gas emissions.

4.5. Innovations in Electronic Materials and Semiconductor Development

The impact of the developed energy circuit resonates far beyond its immediate application in energy generation, reaching into the domain of materials science, particularly in the realm of electronic materials and semiconductor development. Traditionally, advancements in these fields have been incremental, building upon established principles. However, the proposed circuit introduces a paradigm shift by suggesting the modification of the current, or, creation of entirely new materials designed to operate within the energy circuit’s framework. One of the innovative aspects lies in the potential for materials capable of handling higher energy inputs while operating efficiently with lower voltage supplies. This envisaged characteristic marks a departure from the constraints imposed by current electronic materials. The circuit’s design prompts speculation on the development of semiconductors that can withstand and utilize higher energy thresholds, leading to electronic components with unprecedented efficiency and performance. While specific examples of such materials may not be prevalent in today’s technological landscape, the feasibility of their existence is grounded in the ongoing advancements in materials science and engineering, and semiconductor research. The circuit, by pushing the boundaries of traditional energy conservation laws, opens the door to a new era of electronic materials that could redefine the capabilities and applications of electronic devices.

4.6. Challenging Philosophical Assumptions and Scientific Thinking

Apart from its concrete applications, the developed energy circuit prompts a significant challenge to philosophical assumptions deeply ingrained in scientific thought. The review presented against perpetual motion machines, positioned as proofs for the law of energy conservation, marks a divergence from longstanding beliefs that have molded the underpinnings of classical physics. Challenging the validity of perpetual motion machines, the energy circuit sets in motion a reassessment of fundamental principles in science. This foray into unconventional scientific thinking acts as a driving force for fresh ideas and methodologies, potentially altering the terrain of scientific inquiry. The readiness to scrutinize established norms is inherent to scientific progress, and the circuit’s confrontation of philosophical assumptions serves as a spark for more extensive discussions regarding the essence of scientific laws and the potential for paradigm shifts in our comprehension of the physical world.

4.7. Merits over Current Systems-A Paradigm Shift in Energy Conservation

The provided energy circuit carries significant advantages, marking a genuine shift in the landscape of energy conservation. Unlike current systems bound by established scientific norms, this energy circuit breaks through conventional boundaries, presenting a distinctive approach that surpasses traditional limitations. Its notable feature lies in its capacity to question prevailing norms and provide practical resolutions to critical challenges confronted by modern energy systems. A key strength of the innovative circuit is its divergence from the established scientific confines that constrained previous energy conservation systems. Embracing an original approach, the energy circuit introduces a new perspective on energy generation and conservation. This departure is pivotal for fostering innovation, as it motivates researchers and engineers to explore unconventional methods previously considered implausible. The energy circuit’s uniqueness is apparent in its ability to offer practical solutions to urgent issues in energy conservation. Existing systems often struggle with problems like energy intermittency, dependence on finite resources, and environmental impact. The developed energy circuit, proficient in capturing excess energy and tackling these challenges, positions itself as a pragmatic and efficient alternative. Moreover, the circuit’s paradigm-shifting character is underscored by its role in paving the way for a more sustainable and innovative future. Traditional systems may encounter difficulties adapting to the evolving needs of a rapidly changing world. In contrast, the developed circuit opens up possibilities for progress in various fields, spanning from electric vehicles to microgrid development and the integration of renewable energy.

5. Conclusion

The innovative energy circuit introduced in this paper marks a revolutionary departure from conventional principles, questioning the long-established laws of energy conservation. The simulated results illustrate the energy circuit’s ability to generate power far exceeding the input energy, fundamentally challenging conventional expectations. The clear violation of energy conservation principles, exemplified through “Circuit Block 3”, carries profound consequences, prompting a reconsideration of accepted scientific norms. Beyond its impact on energy generation, the proposed energy circuit bends traditional knowledge, offering remedies to global energy challenges, diminishing environmental repercussions, and encouraging scientific exploration. It confronts misunderstandings rooted in limited scientific and mathematical backgrounds concerning the validity and constraints of the first law of thermodynamics (law of energy conservation). Moreover, it creates new possibilities for innovation, such as the advancement of electric vehicles, the reduction of noise pollution, and contributions to addressing environmental concerns like the greenhouse effect. Importantly, it questions prevailing clean energy systems, presenting a fresh outlook on energy conservation that goes beyond classical physics. It introduces an unconventional electrical short circuit as the instigator of atypical energy production, reshaping the boundaries of what is considered feasible in contemporary research. The energy circuit’s consistent ability to surpass traditional limitations and generate power output greater than the input signifies a paradigm shift in the realm of energy conservation. In essence, the paper challenges the very bedrock of our comprehension of energy conservation and generation. By unveiling an inventive energy circuit operating beyond established norms, it not only prompts inquiries about the philosophical implications of perpetual motion but also propels scientific thought into unexplored norms. The energy circuit’s advantages over current systems position it as a transformative influence, paving the way for a more sustainable and imaginative future.