Quantum Gravity: Parameters for Detection via Spin Entanglement and Theoretical Models

Preprint

Review

Quantum Gravity: Parameters for Detection via Spin Entanglement and Theoretical Models

Altmetrics

Downloads

166

Views

149

Comments

Anhad Kohli^*

This version is not peer-reviewed

Submitted:

25 August 2024

Posted:

27 August 2024

You are already at the latest version

Alerts

Abstract

Quantum gravity is crucial for unifying general relativity and quantum mechanics, which are two of the fundamental pillars of physics. Despite the significant advances in theoretical models of quantum gravity, experimental validation of these theories remains sparse. This review paper aims to address this gap by examining the experimental proposal by Bose et al., that aims to show the non classicality of gravity, alongside a discussion of semiclassical and quantum models and their shortcomings. We explore the Double Stern-Gerlach experiment to observe gravitational entanglement, detailing the procedure and the quantum states involved. The minimization of Casimir-Polder forces, which could interfere with the experiment, is highlighted as essential for optimizing conditions for maximal entanglement, calculated using von Neumann entropy, and measured using an Entanglement Witness. We discuss the inferences drawn from this experiment and introduce semiclassical gravitational models, outlining the assumptions made by Bose et al. Furthermore, we delve into perturbative Quantum Gravity (pQG) using the path integral approach, explaining its non renormalizability and the extent of its applicability. The conclusions indicate that observing entanglement would demonstrate the non-classicality of gravity. While semiclassical models are experimentally inaccurate, they serve as useful calculational tools for black hole physics. Although pQG has proved to be non-renormalizable so far, it functions as an effective field theory (EFT) at energies below 10¹⁹ GeV.

Keywords:

Subject: Physical Sciences - Particle and Field Physics

1. Introduction

In the realm of theoretical physics, quantum mechanics and quantum field theory have been able to describe three out of four fundamental known forces till now which are the electromagnetic interaction, the strong force, and the weak force. Gravity, however, still does not have a complete theoretical model. Our current model of gravity is based on Einstein’s General Theory of Relativity which has been remarkably accurate in describing many phenomena from the bending of light around mass to gravitational waves. However a fundamental problem we face is that space-time interacts with energy-momentum which are properties of fundamental particles that are currently best described by the quantum theory. General Relativity and Quantum Theory are incompatible models due to a variety of reasons [1], thus we must look for a way to introduce gravity to quantum physics.

In this paper we would look at an experimental proposal that aims to show that gravity can influence matter at quantum scales through the double Stern Gerlach Interferometer experiment devised by Bose et al in their paper [2]. This experiment might be able to show how gravitational field could cause entanglement between two particles. The first portion would look at the experimental parameters that would maximize spin entanglement in the experiment suggested by Bose et al under optimal conditions such as reduced decoherence due to Casimir Polder interaction.

Later we discuss what the implications of this experiment are and exploring semiclassical models can serve as a bridge between completely classical and quantum theories of gravity. The final section talks about the path integral formulation of gravity, analyzing the Einstein-Hilbert Action, and explains how perturbative quantum gravity is non-renormalizable by power counting. The cutoff energy for perturbative gravity is calculated to show the limit to which it works as an effective field theory.

2. Double Stern Gerlach Spin Entanglement

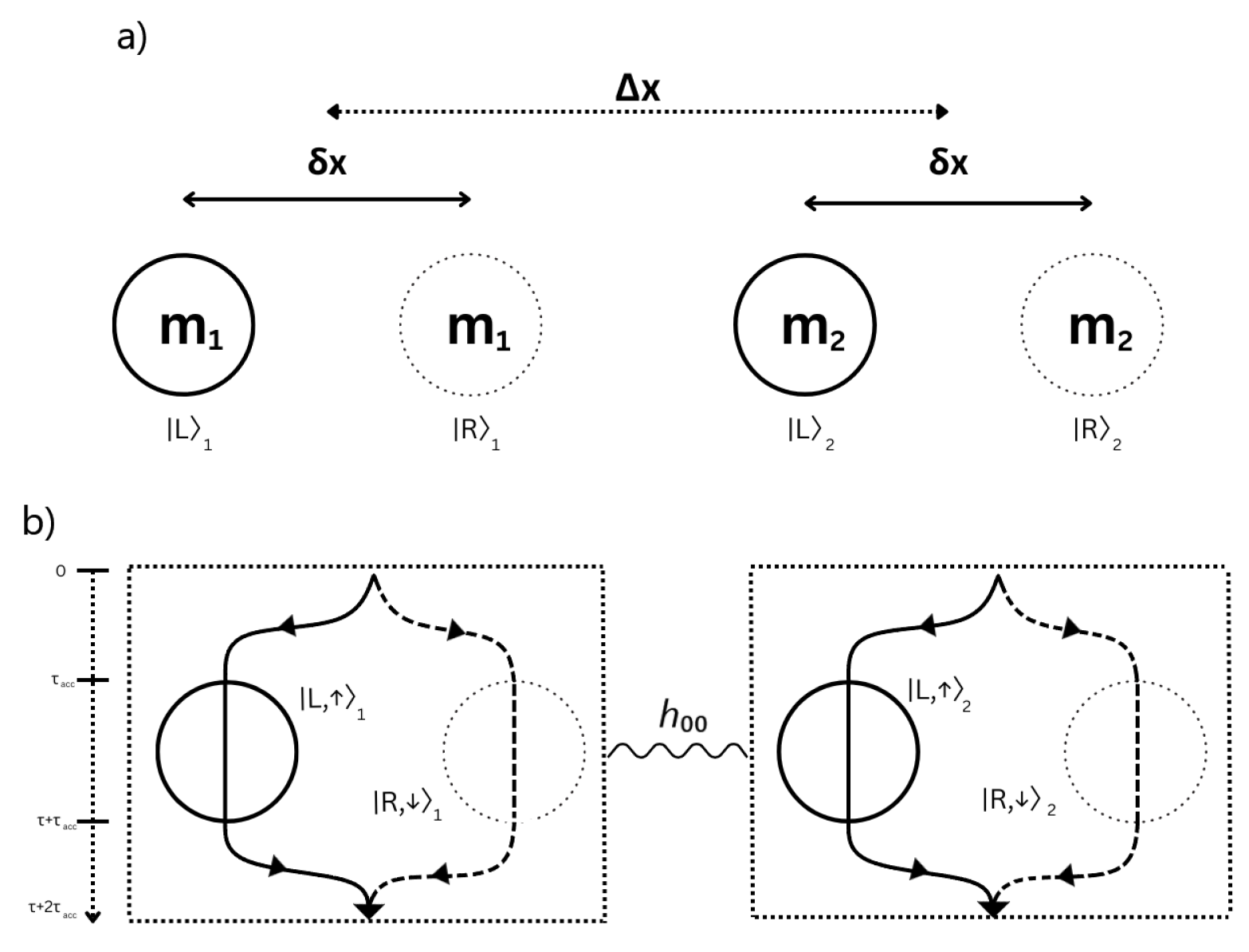
Figure 1. Schematic depiction of the double Stern-Gerlach experiment as proposed by Bose et al.

(a) Two mesoscopic particles of equal mass in this case in superposition of two spatially localized states

| L 〉 + | R 〉

(b) Evolution of states in SG interferometer into spin entangled states

{| L, ↑ 〉}_{j} + {| R, ↓ 〉}_{j} (j = 1, 2)

Only the

T_{00}

component of energy-momentum tensor is non-negligible due to speeds much slower than the speed of light c[2], hence only

h_{00}

component evolves (where

h_{μ ν}

is the small perturbation in linearized gravity

g_{μ ν} = η_{μ ν} + h_{μ ν}

η_{μ ν}

being the Minkowskian metric.)

Figure 1. Schematic depiction of the double Stern-Gerlach experiment as proposed by Bose et al.

(a) Two mesoscopic particles of equal mass in this case in superposition of two spatially localized states

| L 〉 + | R 〉

(b) Evolution of states in SG interferometer into spin entangled states

{| L, ↑ 〉}_{j} + {| R, ↓ 〉}_{j} (j = 1, 2)

Only the

T_{00}

component of energy-momentum tensor is non-negligible due to speeds much slower than the speed of light c[2], hence only

h_{00}

component evolves (where

h_{μ ν}

is the small perturbation in linearized gravity

g_{μ ν} = η_{μ ν} + h_{μ ν}

η_{μ ν}

being the Minkowskian metric.)

As suggested in Ref.[2], we keep two test masses in superposition of spatially localized states

| L 〉

and

| R 〉

. Their evolution happens under gravitational interaction and all other forces are minimized. These two states are localized Gaussian wavepackets and due to their relatively small diameters with respect to their distances

δ x

and

Δ x

, we can assume

〈 L | R 〉 = 0

In this setup, we take two masses

m_{1}

and

m_{2}

with the centers of the left and right states of both the particles separated by the distance

Δ x

as shown in the figure.

Closest distance between

{| R 〉}_{1}

and

{| L 〉}_{2}

(Δ x - δ x)

and farthest distance between

{| L 〉}_{1}

and

{| R 〉}_{2}

(Δ x + δ x)

The Classical gravitational potential energy is

E = - \frac{G m_{1} m_{2}}{d}

The initial state at

t = 0

is:

{| Ψ (t = 0) 〉}_{12} = \frac{1}{\sqrt{2}} {(| L 〉}_{1} + {| R 〉}_{1}) \otimes \frac{1}{\sqrt{2}} {(| L 〉}_{2} + {| R 〉}_{2})

(1)

= \frac{1}{2} {(| L 〉}_{1} \otimes {| L 〉}_{2} + {| L 〉}_{1} \otimes {| R 〉}_{2} + {| R 〉}_{1} \otimes {| L 〉}_{2} + {| R 〉}_{1} \otimes {| R 〉}_{2})

Using Schrödinger’s equation :

i ℏ t | Ψ 〉 = \hat{H} | Ψ 〉

(2)

The general solution is found to be

| Ψ (t) 〉 = e^{- i H t / ℏ} | Ψ (0) 〉

when the Hamiltonian is time-independent and

\hat{U} (t) = e^{- i H t / ℏ}

is the unitary time-evolution operator.

As E is an eigenvalue of the Hamiltonian, we can write the final state as

| Ψ (t) 〉 = e^{- i E t / ℏ} | Ψ (0) 〉

t = τ

, the state evolves to:

{| Ψ (t = τ) 〉}_{12} = \frac{e^{i ϕ}}{2} {(| L 〉}_{1} \otimes {| L 〉}_{2} + e^{i Δ ϕ_{L R}} {| L 〉}_{1} \otimes {| R 〉}_{2} + e^{i Δ ϕ_{R L}} {| R 〉}_{1} \otimes {| L 〉}_{2} + {| R 〉}_{1} \otimes {| R 〉}_{2})

(3)

Where

ϕ_{R L} \sim \frac{G m_{1} m_{2} τ}{ℏ (Δ x - δ x)}, ϕ_{L R} \sim \frac{G m_{1} m_{2} τ}{ℏ (Δ x + δ x)}, ϕ \sim \frac{G m_{1} m_{2} τ}{ℏ Δ x}

Δ ϕ_{L R} = ϕ_{L R} - ϕ

and

Δ ϕ_{R L} = ϕ_{R L} - ϕ

A state is said to be entangled if it cannot be factorized (non-separable) to be written as a product of states such as

| Ψ 〉 = {| ψ 〉}_{1} \otimes {| ψ 〉}_{2}

(a separable state). If we try to factorize Eq(3), we obtain:

\frac{e^{i ϕ}}{2} {(| L 〉}_{1} \otimes {(| L 〉}_{2} + e^{i Δ ϕ_{L R}} {| R 〉}_{2} {) + | R 〉}_{1} \otimes {(e^{i Δ ϕ_{R L}} | L 〉}_{2} + {| R 〉}_{2}))

The condition for this to be completely factorizable would be if

{(| L 〉}_{2} + e^{i Δ ϕ_{L R}} {| R 〉}_{2}) \sim {(e^{i Δ ϕ_{R L}} | L 〉}_{2} + {| R 〉}_{2})

e^{i Δ ϕ_{R L}} {| L 〉}_{2} + {| R 〉}_{2} = e^{i Δ ϕ_{R L}} {(| L 〉}_{2} + e^{- i Δ ϕ_{R L}} {| R 〉}_{2})

means

e^{- i Δ ϕ_{R L}} = e^{i (2 n π - Δ ϕ_{R L})}

where n is an arbitrary integer.

Therefore for the state to be entangled,

2 n π - Δ ϕ_{R L} \neq Δ ϕ_{L R}

This gives us the entanglement condition:

Δ ϕ_{L R} + Δ ϕ_{R L} \neq 2 n π

(4)

The SG interferometer accelerates the particles through a magnetic gradient for a time

τ_{acc}

and then the magnetic field is switched off for a greater amount of time

τ

enough to entangle both the superposition states.

In this process, the two joint states of the test masses evolve as shown in Eq.(1) and Eq.(3) the orbital states

{| L 〉}_{j}

and

{| R 〉}_{j}

get replaced by the spin-orbital qubit states

{| L, ↑ 〉}_{j}

and

{| R, ↑ 〉}_{j}

.(Ref.[2]).

Replacing the states in Eq.(3) with the spin-orbital states gives us:

| Ψ (t = τ + τ_{acc}) 〉_{12} = \frac{e^{i ϕ}}{2} {(| L, ↑ 〉}_{1} \otimes {| L, ↑ 〉}_{2} + e^{i Δ ϕ_{L R}} {| L, ↑ 〉}_{1} \otimes {| R, ↓ 〉}_{2} + e^{i Δ ϕ_{R L}} {| R, ↓ 〉}_{1} \otimes {| L, ↑ 〉}_{2} + {| R, ↓ 〉}_{1} \otimes {| R, ↓ 〉}_{2})

(5)

In the final step, the superposition is brought back through unitary transformations

{(| L, ↑ 〉}_{j} \to {| C, ↑ 〉}_{j} {, | R ↓ 〉}_{j} \to {| C, ↓ 〉}_{j}

| Ψ {(t = τ + 2 τ_{acc} 〉}_{12} = \frac{e^{i ϕ}}{2} {(| ↑ ↑ 〉}_{12} + e^{i Δ ϕ_{L R}} {| ↑ ↓ 〉}_{12} + e^{i Δ ϕ_{R L}} {| ↓ ↑ 〉}_{12} + {| ↓ ↓ 〉}_{12} {) | C 〉}_{1} {| C 〉}_{2}

(6)

This entanglement can be measured using an entanglement witness

W

which is discussed later in Appendix A. If

W

satisfies a certain condition for example exceeding unity in the one Bose et al. suggested, then the state is proven to be entangled.

3. Minimization of Casimir-Polder Interaction

While performing the experiment, it is important to reduce extra noise that may present itself due to other forces between the two particles we are using. One of them is the Casimir force which we will try to reduce.

We will be taking a linear setup for the experiment[3] and the particles as diamond nanoparticles of mass

\sim 10^{- 14} k g

The formula for the Casimir force between two neutral dielectric particles is

V_{C P} = - \frac{23 ℏ c}{4 π} \frac{R^{6}}{{(Δ x - δ x)}^{7}} {(\frac{ε - 1}{ε + 2})}^{2}

(7)

Where R is the radius of the particles,

Δ x - δ x

is the minimum distance between them, c is the speed of light in vacuum (

\sim 3 \times 10^{8}

m/s), ℏ is reduced Planck’s constant (

1.05 \times 10^{- 34}

Js)and

ε

is the dielectric constant (∼ 5.7 for diamonds).

For a minimum difference of one order of magnitude[3], we obtain

0.1 | V_{G} | \geq | V_{C P} |

\begin{matrix} \frac{G m^{2}}{Δ x - δ x} \geq \frac{230 ℏ c}{4 π} \frac{R^{6}}{{(Δ x - δ x)}^{7}} {(\frac{ε - 1}{ε + 2})}^{2} \\ \frac{G {(4 π ρ R^{3} / 3)}^{2}}{Δ x - δ x} \geq \frac{230 ℏ c}{4 π} \frac{R^{6}}{{(Δ x - δ x)}^{7}} {(\frac{ε - 1}{ε + 2})}^{2} \\ \frac{{(Δ x - δ x)}^{7}}{Δ x - δ x} \geq \frac{9}{G {(4 π ρ R^{3})}^{2}} \frac{23 ℏ c R^{6}}{40 π} {(\frac{ε - 1}{ε + 2})}^{2} \\ {(Δ x - δ x)}^{6} \geq \frac{230 ℏ c}{4 π G} {(\frac{3}{4 π ρ} \frac{ε - 1}{ε + 2})}^{2} \end{matrix}

Δ x - δ x \geq {[\frac{230 ℏ c}{4 π G} {(\frac{3}{4 π ρ} \frac{ε - 1}{ε + 2})}^{2}]}^{1 / 6} \equiv {(Δ x - δ x)}_{\min} \approx 157 μ m

(8)

Thus we need the minimum distance between the entangled particles to be

157 μ m

for the Casimir force to be negligible (one order of magnitude lower than gravitational force in this case).

4. Conditions for Maximal Entanglement

We will be converting the quantum state to a density operator (

\hat{ρ}

) in order to perform certain operations on it.

The state can be written as

| Ψ 〉 = \frac{e^{i ϕ}}{2} (| ↑ ↑ 〉 + e^{i Δ ϕ_{L R}} | ↑ ↓ 〉 + e^{i Δ ϕ_{R L}} | ↓ ↑ 〉 + | ↓ ↓ 〉)

Here

| ↑ 〉 = (\begin{matrix} 1 \\ 0 \end{matrix}), | ↓ 〉 = (\begin{matrix} 0 \\ 1 \end{matrix})

and

| α β 〉 = | α 〉 \otimes | β 〉

The density matrix is evaluated to be

\hat{ρ} = \frac{1}{4} (\begin{matrix} 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \\ e^{i Δ ϕ_{L R}} & 1 & e^{i (Δ ϕ_{L R} - Δ ϕ_{R L})} & e^{i Δ ϕ_{L R}} \\ e^{i Δ ϕ_{R L}} & e^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} & 1 & e^{i Δ ϕ_{R L}} \\ 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \end{matrix})

The bipartite von Neumann entropy can help us find the maximally entangled state of a quantum system and is represented by

S (ρ_{A}) = - [ρ_{A} log ρ_{A}] = - [ρ_{B} log ρ_{B}] = S (ρ_{B})

(9)

Where

ρ_{A} =_{B} (ρ)

and

ρ_{B} =_{A} (ρ)

are the reduced density matrices.

The reduced density matrix was calculated to be:

{\hat{ρ}}_{1} = \frac{1}{4} (\begin{matrix} 2 & e^{- i Δ ϕ_{R L}} + e^{i Δ ϕ_{L R}} \\ e^{i Δ ϕ_{R L}} + e^{- i Δ ϕ_{L R}} & 2 \end{matrix})

S (ρ_{1}) = - (ρ_{1} log (ρ_{1}))

The system is maximally entangled when

ρ_{1}

and

ρ_{2}

are maximally mixed[4] which is achieved when they are diagonal matrices with diagonal elements as

1 / d

where d is the dimension of the Hilbert space of the basis (which is 2 in our case).

To get these conditions, we set the non-diagonal entries to 0 first:

e^{- i Δ ϕ_{R L}} + e^{i Δ ϕ_{L R}} = 0

and

e^{i Δ ϕ_{R L}} + e^{- i Δ ϕ_{L R}} = 0

This gives us two equations

\{\begin{matrix} cos (- Δ ϕ_{R L}) + i sin (- Δ ϕ_{R L}) + cos (Δ ϕ_{L R}) + i sin (Δ ϕ_{L R}) = 0 \\ cos (Δ ϕ_{R L}) + i sin (Δ ϕ_{R L}) + cos (- Δ ϕ_{L R}) + i sin (- Δ ϕ_{L R}) = 0 \end{matrix}

They can be written as

\{\begin{matrix} (cos Δ ϕ_{R L} + cos Δ ϕ_{L R}) + i (sin Δ ϕ_{L R} - sin Δ ϕ_{R L}) = 0 \\ (cos Δ ϕ_{R L} + cos Δ ϕ_{L R}) + i (sin Δ ϕ_{R L} - sin Δ ϕ_{L R}) = 0 \end{matrix}

by collecting the real and imaginary parts of the expressions.

For

z \in C

to be 0,

ℜ (z) = 0

and

ℑ (z) = 0

(where ℜ and ℑ are the real an imaginary components of the complex number respectively)

Looking at the imaginary part,

sin Δ ϕ_{L R} - sin Δ ϕ_{R L} = sin Δ ϕ_{R L} - sin Δ ϕ_{L R} = 0

This implies that

sin Δ ϕ_{L R} = sin Δ ϕ_{R L}

Which means either

Δ ϕ_{L R} = Δ ϕ_{R L}

(10)

Δ ϕ_{L R} = (2 k + 1) π - Δ ϕ_{R L}

(11)

where k is an arbitrary integer.

Substituting Eq(10) in the real part,

cos Δ ϕ_{L R} + cos Δ ϕ_{R L} = cos Δ ϕ_{L R} + Δ ϕ_{L R} = 2 cos Δ ϕ_{L R}

This is not a satisfactory condition as

2 cos Δ ϕ_{L R} = 0

for only some values of

Δ ϕ_{L R}

Thus we can assume,

Δ ϕ_{L R} \neq Δ ϕ_{R L}

. This leads us to using Eq(11) as follows:

cos Δ ϕ_{L R} + cos Δ ϕ_{R L} = cos Δ ϕ_{L R} + cos ((2 k + 1) π - Δ ϕ_{L R}) = cos Δ ϕ_{L R} - cos Δ ϕ_{L R} = 0

This satisfies the given conditions, therefore

Δ ϕ_{L R} + Δ ϕ_{R L} = (2 k + 1) π

(12)

This is our condition for non-diagonal elements being 0. Now to verify for maximally mixed state, we can substitute these values in the reduced density matrix.

ρ_{1} = \frac{1}{4} (\begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix}) = (\begin{matrix} 2^{- 1} & 0 \\ 0 & 2^{- 1} \end{matrix})

S (ρ_{1}) = - (\frac{1}{2} (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) log (\begin{matrix} 2^{- 1} & 0 \\ 0 & 2^{- 1} \end{matrix})) = - (\frac{1}{2} (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) (\begin{matrix} log (2^{- 1}) & 0 \\ 0 & log (2^{- 1}) \end{matrix})) = - (\frac{1}{2} (\begin{matrix} - log 2 & 0 \\ 0 & - log 2 \end{matrix})) = - ((\begin{matrix} (- log 2) / 2 & 0 \\ 0 & (- log 2) / 2 \end{matrix})) = - (- \frac{l o g 2}{2} - \frac{log 2}{2}) = log 2 = log (dim (H_{1}))

By analogy with the classical entropy formula, the entanglement entropy has the following bounds:

0 \leq S (ρ_{1}) \leq log (d_{H_{1}})

As the system saturates the upper pound, the state is maximally entangled.

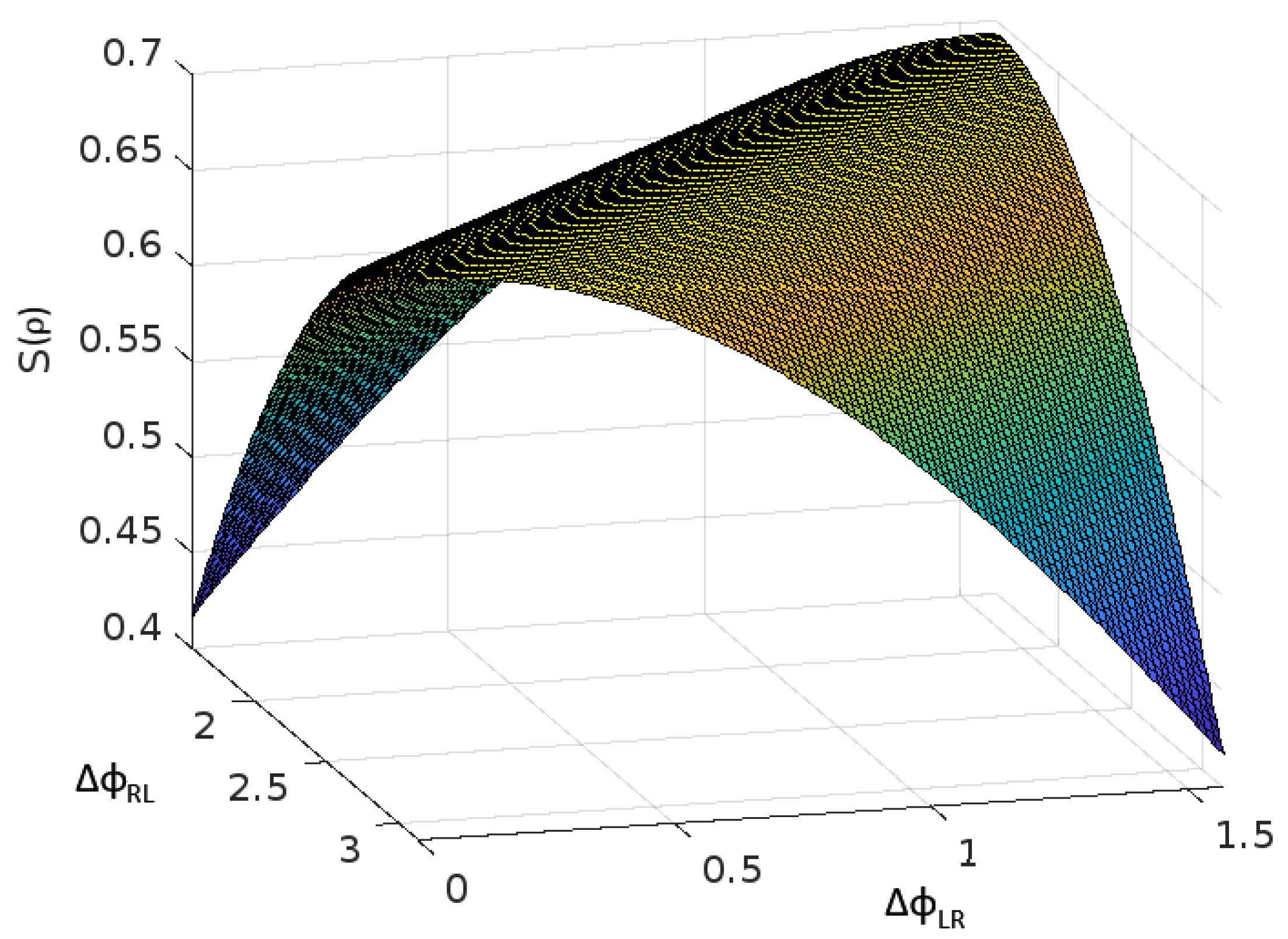
Figure 2. Plot of Entanglement Entropy as a function of

Δ ϕ_{L R}

(from 0 to

π / 2

) and

Δ ϕ_{R L}

(from

π / 2

π

It can be seen that the entropy achieves its maximum value of

log 2

when the sum of the phases approach

π

Figure 2. Plot of Entanglement Entropy as a function of

Δ ϕ_{L R}

(from 0 to

π / 2

) and

Δ ϕ_{R L}

(from

π / 2

π

It can be seen that the entropy achieves its maximum value of

log 2

when the sum of the phases approach

π

Now we can substitute the values of the phases to get an expression for the distances. For simplicity, we will take

k = 0

in Eq(12).

Δ ϕ_{L R} + Δ ϕ_{R L} = π \Rightarrow ϕ_{L R} - ϕ + ϕ_{R L} - ϕ = π \frac{G m^{2} τ}{ℏ (Δ x + δ x)} - \frac{G m^{2} τ}{ℏ Δ x} + \frac{G m^{2} τ}{ℏ (Δ x - δ x)} - \frac{G m^{2} τ}{ℏ Δ x} = π

gives

\frac{G m^{2} τ}{ℏ} (\frac{1}{Δ x + δ x} - \frac{2}{Δ x} + \frac{1}{Δ x - δ x}) = π

And finally,

\frac{2 {(δ x)}^{2}}{Δ x ({(Δ x)}^{2} - {(δ x)}^{2})} = \frac{π ℏ}{G m^{2} τ}

(13)

The expression for the distance between the left and right states is[2]:

δ x \sim \frac{1}{2} \frac{g μ_{B} \partial_{x} B}{m} τ_{acc}^{2}

(14)

Where

g \sim 2

is the electronic g-factor,

μ_{B} \approx 9.274 \cdot 10^{- 24} J T^{- 1}

is the Bohr magneton,

\partial_{x} B

is the magnetic field gradient in the x-direction. The mass of the particles we are taking is

10^{- 14}

kg, the magnetic field gradient is

10^{7} T m^{- 1}

τ_{acc}

is the time the masses are subjected to the magnetic field gradient and is a variable.

Substituting the distance for minimized CP-effect,

Δ x - δ x = 157 μ m \Rightarrow Δ x = δ x + 157 μ m

, we get:

\frac{2 {(\frac{g μ_{B} \partial_{x} B}{2 m} τ_{acc}^{2})}^{2}}{(\frac{g μ_{B} \partial_{x} B}{2 m} τ_{acc}^{2} + 157 \times 10^{- 6}) ({(\frac{g μ_{B} \partial_{x} B}{2 m} τ_{acc}^{2} + 157 \times 10^{- 6})}^{2} - {(\frac{g μ_{B} \partial_{x} B}{2 m} τ_{acc}^{2})}^{2})} = \frac{π ℏ}{G m^{2} τ}

(15)

As the experiment cannot be completely free from outside interaction, there would always be some sort of decoherence in the system. The collisional decoherence time is approximately of the same magnitude as the total fall time of the particle

τ_{decoherence} \sim τ_{total} = τ + 2 τ_{acc}

[2]. This will lead to a strong loss of coherence which will interfere with the gravitational entanglement. To minimize this, we can minimize the total time taken for the particle to fall (

τ_{total})

Minimizing

τ_{total}

by a simple python program mentioned in Appendix C gives

τ \approx 8.34349 s

and

τ_{acc} \approx 0.58829 s

Using these values, we can obtain the distances between the entangled states as

δ x = 3209.59 μ m and Δ x = 3366.59 μ m

Calculating the phase values:

ϕ_{L R} = \frac{G m^{2} τ}{ℏ (Δ x + δ x)} = 0.08059546

ϕ_{R L} = \frac{G m^{2} τ}{ℏ (Δ x - δ x)} 3.37586158

ϕ = \frac{G m^{2} τ}{ℏ Δ x} = 0.157432377

This gives

Δ ϕ_{R L} = 3.218429203, Δ ϕ_{L R} = - 0.076836917

These values can be substituted in Eq(12) to verify that the maximal entanglement conditions are met:

Δ ϕ_{R L} + Δ ϕ_{L R} = 3.141592286 \approx π

Some rounding error of

1.17 \cdot 10^{- 5}

% persists, however, it is almost negligible.

5. Inferences and Semiclassical Models

In order to make inferences from the proposed experiment, we will first need to know its assumptions and limitations.

The main theoretical assumptions of the Bose et al [2] paper is that the gravitational interaction between two masses is mediated by a gravitational field (not a direct action at a distance) and that entanglement between two systems cannot be created by Local Operations and Classical Communication (LOCC).

Another assumption made by them is using the Newtonian potential for mediating the gravitational entanglement which is not the true degree of freedom of the gravitational field and hence might have affected the implications of the experiment. (Discussed thoroughly in Ref.[5])

Based on the given assumptions, the entanglement generated by gravity would be non-classical. However, even if it eliminates the possibility of a completely classical model of gravity, it does not strictly imply that gravity is quantum and a semi-classical model of a gravity is still a valid possibility.

Due to the success of the general theory of relativity in explaining gravity, a good start to uncovering a valid theory would be to look at the semi-classical models of gravity. The classical Einstein’s Field Equations are

G_{μ ν} = 8 π G T_{μ ν}

(16)

Where

G_{μ ν}

is the Einstein Tensor and

T_{μ ν}

is the stress-energy tensor. However in a quantum scenario, the stress-energy tensor is promoted a quantum operator

{\hat{T}}_{μ ν}

which would be inconsistent with the left half of the equation which is why we take its expectation value according to Møller-Rosenfeld[5][6], giving us a classically measured value of the operator.

G_{μ ν} = 8 π G 〈 {\hat{T}}_{μ ν} 〉

(17)

Here

〈 {\hat{T}}_{μ ν} 〉 = 〈 ψ | {\hat{T}}_{μ ν} | ψ 〉

. We do run into mathematical and physical inconsistencies in this equation one of them being that the expectation value of the energy-momentum operator is not conserved while the Einstein tensor is conserved (

\nabla^{μ} 〈 {\hat{T}}_{μ ν} 〉 \neq 0, \nabla^{μ} G_{μ ν} = 0

). Thus we need to renormalize

T_{μ ν}

which would give us

\nabla^{μ} 〈 T_{μ ν} 〉 = 0

and other conditions discussed by Wald[7].

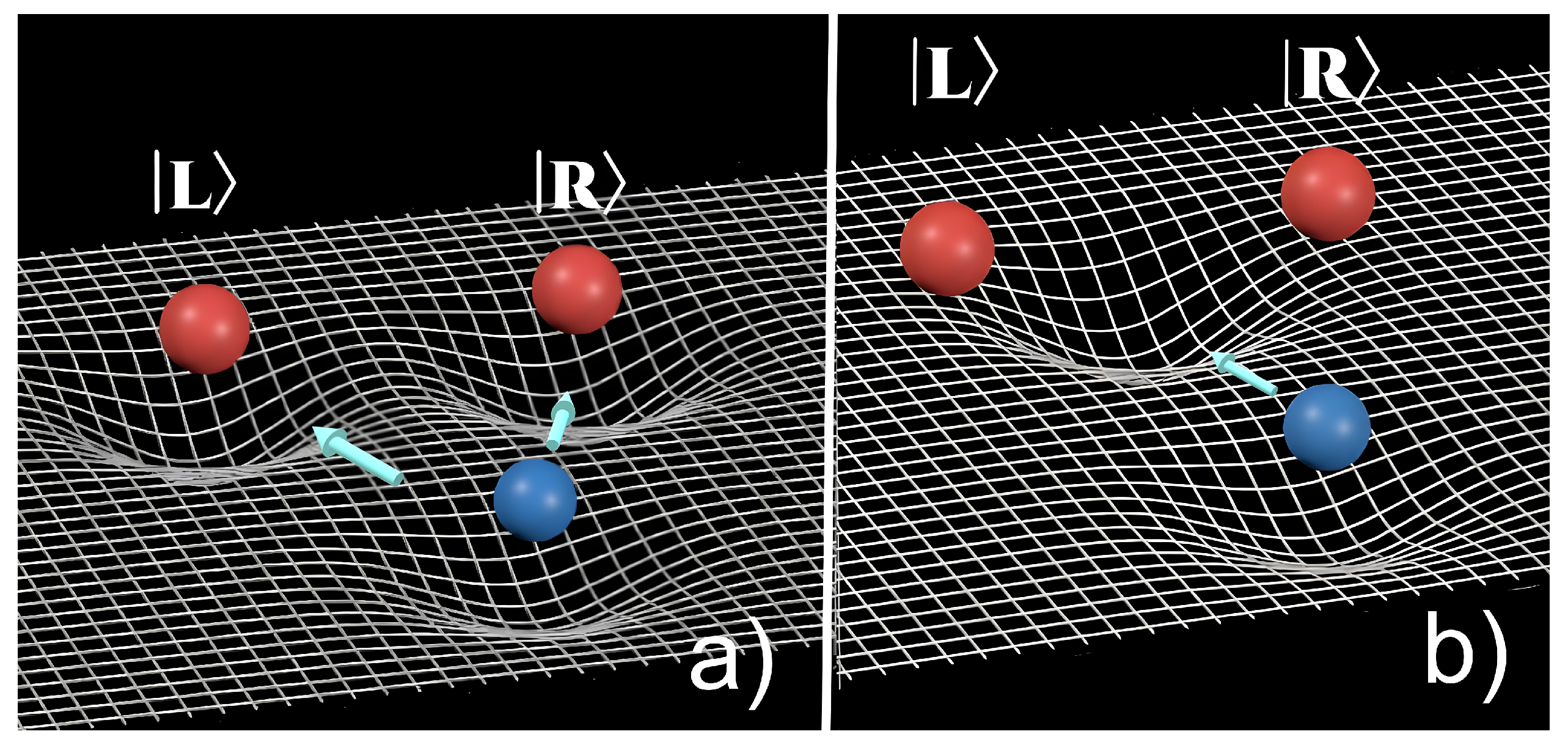
Another flaw with the field equations semi-classical gravity is that the expectation value in some cases implies that the net curvature of the superposition states would be averaged out in the center and we would expect a test particle to move towards that center. This is not what experiments have shown so it is a massive downside of this model. ([8][9]) This type of approximate semiclassical gravity where

〈 {\hat{T}}_{μ ν} 〉 \approx T_{μ ν}

does have some applications one of which includes the calculation for Hawking Radition of Black Holes[10].

Figure 3. a) Observed behaviour of particle in superposition

| L 〉 + | R 〉

vs b) Expected behaviour in Møller-Rosenfeld semi-classical gravity. (Credits: Designed using desmos.com/3d)

Figure 3. a) Observed behaviour of particle in superposition

| L 〉 + | R 〉

vs b) Expected behaviour in Møller-Rosenfeld semi-classical gravity. (Credits: Designed using desmos.com/3d)

Due to the limitations of this model, other semi-classical models have also been proposed, an important one being the stochastic model[11].

Two of the current leading models for quantum gravity are the Loop Quantum Gravity model[12] and the String Theory[13] which would not be discussed here being beyond the scope of this paper.

In conclusion, new experiments might help us eliminate more erroneous models and get closer to the right one.

Quantized Gravitational Field Theory

Gravitational Action

In flat spacetime QFT, we ordinarily set up a spacetime manifold

M

and integrate on quantum fields. However, in gravity spacetime is dynamic so we have to integrate over the geometries of spacetime itself. The propagator

〈 ψ_{f} | ψ_{i} 〉

is defined to be the probability transition amplitude between the wave-functions evaluated at two points. This can be defined in terms of the path integral:

〈 g_{f}, ϕ_{f}, S_{f} | g_{i}, ϕ_{i}, S_{i} 〉 = \int D [g, ϕ] exp (i I [g, ϕ])

(18)

Where g is a spin-2 tensor field,

ϕ

is a matter field,

S

is a surface, and I is the action. The subscripts i and f represent the initial and final states respectively [14].

The simplest choice for such an action would be the Einstein-Hilbert action.

S_{E H} = \int^{4} x (\frac{1}{2 κ} R + L_{M}) \sqrt{- g}

Here

κ = \frac{8 π G_{N}}{c^{4}}

, Ricci scalar

R = g^{μ ν} R_{μ ν}

g = det (g_{μ ν})

, and

L_{M}

is the matter field’s Lagrangian density.

To derive the equation of motion, by the stationary principle action we neet to set

δ S = 0

. For simplicity, we’ll consider the action without the matter interaction.

S = \frac{1}{2 κ} \int^{4} x R \sqrt{- g}

To vary S, we need to first find the variation of R and

\sqrt{- g}

. Starting with g:

Any diagonalizable matrix A obeys the identity

det (A) = exp (log A)

Applying this to g:

g = exp (log g_{μ ν})

Varying g:

δ g = g δ (log g_{μ ν})

Since

δ log g_{μ ν} \equiv {(g_{μ ν})}^{- 1} δ g_{μ ν}

, the inverse can be written as the metric with raised indices as

g_{μ ν} g^{ν α} = δ_{μ}^{α}

δ g = g g^{μ ν} δ g_{μ ν}

Using the derivative of inverse matrix formula,

δ g^{μ ν}

can be written as

- g^{μ α} (δ g_{α β}) g^{β ν}

and thus

δ g

can be rewritten as

δ g = - g g_{μ ν} δ g^{μ ν}

The variation of

\sqrt{- g}

would be

δ \sqrt{- g} = - \frac{1}{2 \sqrt{- g}} δ g = - \frac{1}{2 \sqrt{- g}} (- g g_{μ ν} δ g^{μ ν}) = - \frac{1}{2} \sqrt{- g} g_{μ ν} δ g^{μ ν}

Thus the variation with respect to

δ g^{μ ν}

\sqrt{- g} g^{μ ν} = - \frac{1}{2} \sqrt{- g} g_{μ ν}

Next, we vary the Ricci Scalar R. Since

R = g^{μ ν} R_{μ ν}

, using the product rule we get

δ R = (δ g^{μ ν}) R_{μ ν} + g^{μ ν} (δ R_{μ ν}) = (- g^{μ α} (δ g_{α β}) g^{β ν}) R_{μ ν} + g^{μ ν} \nabla_{α} A^{α}

Where

\nabla_{α} A^{α}

becomes a total derivative on being multiplied by

\sqrt{- g}

. Using Stokes’ Theorem

\int_{Ω} d ω = \int_{\partial Ω} ω

, the total derivative part of the action can be written as

\int_{M}^{4} x \sqrt{- g} \nabla_{α} A^{α} = \int_{\partial M} Σ_{α} A^{α}

Where

M

is the manifold we’re integrating on and

\partial M

is a closed hypersurface of the manifold.

This boundary term does not contribute to the variation of S (

δ S

) as it is dependent on the variation of the metric tensor (

δ g^{μ ν}

) which vanishes in a neighborhood of a boundary or when there is no boundary. When the manifold

M

has a boundary, the result is the Gibbons–Hawking–York boundary term.

Finally, the variation of S can be calculated

δ S = 0

= \frac{1}{2 κ} \int^{4} x (\sqrt{- g} R g^{μ ν}) g^{μ ν} = \frac{1}{2 κ} \int^{4} x (\sqrt{- g} g^{μ ν} R + \sqrt{- g} R g^{μ ν}) g^{μ ν}

So for

S g^{μ ν} = 0

, we have

\sqrt{- g} g^{μ ν} R + \sqrt{- g} R g^{μ ν} = 0

Substituting the terms calculated previously

(- \frac{1}{2} \sqrt{- g} g_{μ ν}) R + \sqrt{- g} R_{μ ν} = 0

This can be written in the form

R_{μ ν} - \frac{1}{2} R g_{μ ν} = 0

Thus we obtain the equation of motion as the Einstein Field equations in a vacuum.

By varying the EH-Action containing the matter Lagrangian, the complete field equations can be obtained with the stress-energy tensor.

Dimensional Analysis

For this paper, I will be using natural units and mass dimensions.

The natural units are

ℏ = c = 1

. On applying dimensional analysis, it can be concluded that

[c] = 1

{[L T]}^{- 1} = 1

[L] = [T]

Similarly for the reduced planck’s constant,

[ℏ] = 1

[M L^{2} T^{- 1}] = 1

[M L^{2} L^{- 1}] = 1

[M] = {[L]}^{- 1}

Using this, we can analyze the dimensions of other quantities.

Note that for some unknown quantity x,

[x] = {[M]}^{n}

can also be written as

[x] = n

as we’re only referring to mass dimensions. Since the action S appears in the path integral as

e^{i S}

, it must be dimensionless. Thus in 4 dimensions,

[\int^{4} x L] = 0

[^{4} x] + [L] = 0

4 [M^{- 1}] + [L] = 0

[L] = 4

Now to analyze the gravitational action, we first need the dimension of the coupling constant

G_{N}

. This can be calculated by referring to Newton’s inverse square law of gravity.

[F] = [\frac{G_{N} M_{1} M_{2}}{r^{2}}]

[M L T^{- 2}] = [G_{N}] + 2 [M] - 2 [r] = [G_{N}] + 2 + 2

2 = [G_{N}] + 4

[G_{N}] = - 2

Power Counting Renormalizability

Consider a pure scalar field theory in d-dimensions

L = \frac{1}{2} {(\partial_{μ} ϕ)}^{2} - \frac{1}{2} m^{2} ϕ^{2} - \frac{λ}{n!} ϕ^{n}

(19)

Where

ϕ

is the field,

λ

is the coupling constant, and

- \frac{λ}{n!} ϕ^{n}

is the interaction term[15]. In the Feynman diagrams, the contributing propagators are of the form

\sim \frac{i}{p^{2} + m^{2}}

and the loops are of the form

\sim \int d^{d} p

. Let the dimension of the propagators be P and L for the loops.

The degree of divergence is defined as

D = d L - 2 P

(20)

Let the Lagrangian density’s dimension be

[L] = d

. This means

[λ ϕ^{n}] = d

Analyzing the kinetic energy term,

[m^{2} ϕ^{2}] = d \Rightarrow 2 + 2 [ϕ] = d

. So the dimension of the field is

[ϕ] = \frac{d - 2}{2}

Coming back to the interaction term,

[λ ϕ^{n}] =] λ] + n [ϕ] = d

. Solving for

[λ]

[λ] = d - n [ϕ] = d - n (\frac{d - 2}{2})

For an arbitrary diagram with N external legs and V vertices, the interaction term is

η ϕ^{N}

. The dimension of

η

[η] = d - N (\frac{d - 2}{2})

Therefore any diagram with N external legs has dimension

d - N (d - 2) / 2

. The most divergent part is proportional to

λ^{V} Λ^{D}

and by dimensional analysis,

V [λ] + D = d - N (\frac{d - 2}{2})

D = d + V (n (\frac{d - 2}{2}) - d) - N (\frac{d - 2}{2})

Since

[n (d - 2) / 2 - d] = - [λ]

, we can classify this theory into three degrees of renormalizability:

Super-Renormalizable: $[λ] > 0$
Renormalizable: $[λ] = 0$
Non-Renormalizable: $[λ] < 0$

Since

[G_{N}] = - 2 < 0

, the gravitational perturbation theory is non-renormalizable by the power counting method.

This can be observed in QED where the coupling constant (fine structure constant)

α

is dimensionless and the theory is renormalizable.

Now to expand the scattering amplitude perturbative series in terms of E with the coupling constant G, in order for it to be dimensionless it should be in terms of

G E^{2}

since

[G] = - 2

and

[E] = 1

[16]. Thus we obtain

M \sim 1 + (G E^{2}) + {(G E^{2})}^{2} + \dots

(21)

Or more generally,

M \sim \sum_{n} {(G E^{2})}^{n}

Looking at the first loop corrections to the action,

S = \int^{4} x \sqrt{- g} (\frac{1}{16 π G} R + α R^{2} + β R_{μ ν} R^{μ ν})

By dimensional analysis,

[^{4} x] = - 4

[R] = 2

. Hence it can be observed that the E-H term is proportional to

{(G E)}^{- 1}

, and the one-loop corrections are proportional to

{(G E^{2})}^{0}

. Continuing this trend, the two-loop corrections would be proportional to

{(G E^{2})}^{1}

and thus are of the form

G R^{3}

where R is shorthand for either Riemann, Ricci curvature tensor or scalar.

More accurately, the one-loop corrections are

G = R^{2} - 4 R_{μ ν} R^{μ ν} + R_{μ ν ρ σ} R^{μ ν ρ σ}

also known as the Gauss-Bonnet Term.

The gravitational constant is also proportional to the inverse of the planck mass squared.

G \propto \frac{1}{m_{P l}^{2}}

Rewriting Eq(21) with the coupling as the Planck mass,

M \sim 1 + {(\frac{E}{m_{P l}})}^{2} + {(\frac{E}{m_{P l}})}^{4} + \dots

The sum

\sum_{n = 0}^{\infty} {(E / m_{P l})}^{2}

diverges when

{(\frac{E}{m_{P l}})}^{2} \geq 1 \Rightarrow E \leq m_{P l} \Rightarrow E \leq \frac{1}{\sqrt{G}}

. Thus, [Appendix D]

E \sim \frac{1}{\sqrt{G}} \approx 10^{19} G e V

(22)

This means new physics must emerge at higher energy level than this. Gravitational field theory acts as a low energy effective field theory for energies

E ≲ 10^{19} G e V

To cancel the UV divergences in perturbative quantum gravity, an infinite number of counterterms need to be added to the Lagrangian. This makes the theory non-predictive since an infinite number of experiments would be required to obtain the counterterms’ coefficients. To fix this UV divergence, a UV complete theory must be formulated. One such theory is the string theory[13].

Acknowledgments

I would like to express my deepest gratitude to Dr. Damián Pitalúa-García for his invaluable guidance and mentorship, which has been instrumental in helping me build a solid foundation in quantum physics. His expertise and insights into the key concepts explored in this paper have been indispensable in shaping my understanding and contributing to the quality of this work. I am also thankful to Mr. C.K. Campbell for helping me understand certain aspects of the experiment and for assisting me in locating essential research papers that served as crucial background reading for my paper and overall research.

Appendix A. Entanglement Witness

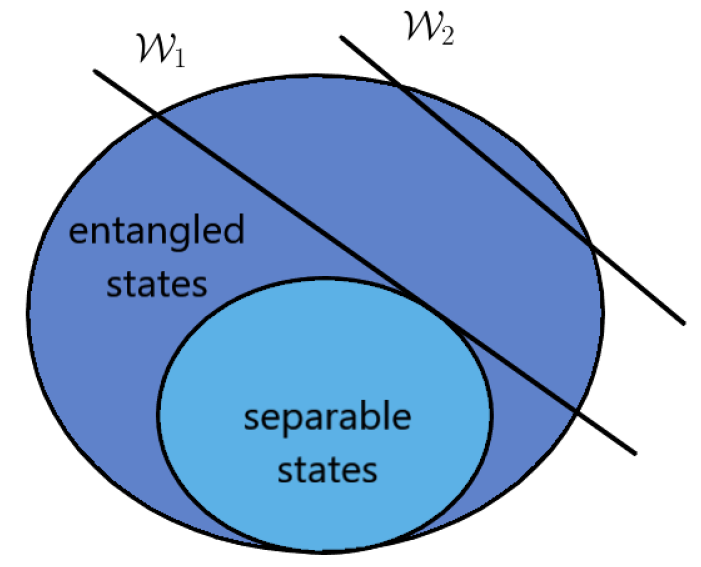
Entanglement witnesses are functions (often applied to the density matrix) to show that a state is entangled. These witnesses are useful as they do not give false positives and are helpful in confirming whether a given state is entangled. Of course a witness might not be able to detect all entangled states but they can be optimized to detect most of them.

Figure A1. Diagram depicting convex set of quantum states including separable and entangled states. The witness

W_{1}

detects more states than

W_{2}

and hence, is more efficient.

Figure A1. Diagram depicting convex set of quantum states including separable and entangled states. The witness

W_{1}

detects more states than

W_{2}

and hence, is more efficient.

Entanglement Witness suggested by Bose et al [2] is

W = | 〈 σ_{x}^{(1)} \otimes σ_{z}^{(2)} 〉 - 〈 σ_{y}^{(1)} \otimes σ_{z}^{(2)} 〉 |

Their condition is that if

W > 1

then the state is proven to be entangled. To verify this we will use the bell states as they are maximally entangled.

For

| Φ^{+} 〉 = \frac{| 00 〉 + | 11 〉}{\sqrt{2}}

W = | 〈 Φ^{+} | σ_{x}^{(1)} \otimes σ_{z}^{(2)} | Φ^{+} 〉 + 〈 Φ^{+} | σ_{y}^{(1)} \otimes σ_{z}^{(2)} | Φ^{+} 〉 |

= |(\frac{〈 00 | + 〈 11 |}{\sqrt{2}}) (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) \otimes (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) (\frac{| 00 〉 + | 11 〉}{\sqrt{2}}) - (\frac{〈 00 | + 〈 11 |}{\sqrt{2}}) (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}) \otimes (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) (\frac{| 00 〉 + | 11 〉}{\sqrt{2}})|

= |\frac{(\begin{matrix} 1 & 0 & 0 & 1 \end{matrix})}{2} (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \\ 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \end{matrix}) (\begin{matrix} 1 \\ 0 \\ 0 \\ 1 \end{matrix}) - \frac{(\begin{matrix} 1 & 0 & 0 & 1 \end{matrix})}{2} (\begin{matrix} 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ - 1 & 0 & 0 & 0 \end{matrix}) (\begin{matrix} 1 \\ 0 \\ 0 \\ 1 \end{matrix})|

= |\frac{(\begin{matrix} 1 & 0 & 0 & 1 \end{matrix})}{2} (\begin{matrix} 0 \\ - 1 \\ 1 \\ 0 \end{matrix}) - \frac{(\begin{matrix} 1 & 0 & 0 & 1 \end{matrix})}{2} (\begin{matrix} - 1 \\ 0 \\ 0 \\ - 1 \end{matrix})| = | 0 - \frac{(- 2)}{2} | = 1

Similarly,

W (| Φ^{-} 〉) = W (| Ψ^{+} 〉) = W (| Ψ^{-} 〉) = 1

As we can observe even the maximally entangled bell state does not exceed unity for this entanglement witness hence it might not be useful for the states calculated in this paper which is why the need to use a different witness arises.

Here we can use the common entanglement witness

W_{x y z} = 〈 σ_{x} \otimes σ_{x} 〉 + 〈 σ_{y} \otimes σ_{y} 〉 + 〈 σ_{z} \otimes σ_{z} 〉 < 0

for entangled states.

The state is

| Ψ 〉 = \frac{e^{i ϕ}}{2} (\begin{matrix} 1 \\ e^{i Δ ϕ_{L R}} \\ e^{i Δ ϕ_{R L}} \\ 1 \end{matrix}), 〈 Ψ | = \frac{e^{- i ϕ}}{2} (\begin{matrix} 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \end{matrix})

Evaluating the witness for this state:

W_{x y z} = 〈 Ψ | (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix}) | Ψ 〉 + 〈 Ψ | (\begin{matrix} 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ - 1 & 0 & 0 & 0 \end{matrix}) | Ψ 〉 + 〈 Ψ | (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) | Ψ 〉

= \frac{1}{4} (\begin{matrix} 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \end{matrix}) ((\begin{matrix} 1 \\ e^{i Δ ϕ_{R L}} \\ e^{i Δ ϕ_{L R}} \\ 1 \end{matrix}) + (\begin{matrix} - 1 \\ e^{i Δ ϕ_{R L}} \\ e^{i Δ ϕ_{L R}} \\ - 1 \end{matrix}) + (\begin{matrix} 1 \\ - e^{i Δ ϕ_{L R}} \\ - e^{i Δ ϕ_{R L}} \\ 1 \end{matrix}))

= \frac{1}{4} (\begin{matrix} 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \end{matrix}) (\begin{matrix} 1 \\ 2 e^{i Δ ϕ_{R L}} - e^{i Δ ϕ_{L R}} \\ 2 e^{i Δ ϕ_{L R}} - e^{i Δ ϕ_{R L}} \\ 1 \end{matrix}) = \frac{1}{4} (1 + 2 e^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} - 1 + 2 e^{i (Δ ϕ_{L R} - Δ ϕ_{R L})} - 1 + 1)

= \frac{1}{4} (2 e^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} + 2 e^{i (Δ ϕ_{L R} - Δ ϕ_{R L})}) = \frac{1}{2} (e^{3.2953 i} + e^{- 3.2953 i}) = - 1.97642 / 2 = - 0.98821

- 0.98 < 0

, we can say that the obtained state is definitely entangled.

Appendix B. Density Matrix Calculations

For notational convenience, we will be taking

| ↑ 〉 \equiv | 0 〉

and

| ↓ 〉 \equiv | 1 〉

In Section 4, the quantum state used is

| Ψ 〉 = \frac{e^{i ϕ}}{2} (| 00 〉 + e^{i Δ ϕ_{L R}} | 01 〉 + e^{i Δ ϕ_{R L}} | 10 〉 + | 11 〉)

The conjugate transpose of this ket is the corresponding bra:

〈 Ψ | = \frac{e^{- i ϕ}}{2} (〈 00 | + e^{- i Δ ϕ_{L R}} 〈 01 | + e^{- i Δ ϕ_{R L}} 〈 10 | + 〈 11 |)

The density operator

\hat{ρ} = | ψ 〉 〈 ψ |

\hat{ρ} = | Ψ 〉 〈 Ψ | = \frac{e^{i ϕ}}{2} (| 00 〉 + e^{i Δ ϕ_{L R}} | 01 〉 + e^{i Δ ϕ_{R L}} | 10 〉 + | 11 〉) \frac{e^{- i ϕ}}{2} (〈 00 | + e^{- i Δ ϕ_{L R}} 〈 01 | + e^{- i Δ ϕ_{R L}} 〈 10 | + 〈 11 |)

= \frac{1}{4} (| 00 〉 〈 00 | + e^{- i Δ ϕ_{L R}} | 00 〉 〈 01 | + e^{- i Δ ϕ_{R L}} | 00 〉 〈 10 | + | 00 〉 〈 11 | + e^{i Δ ϕ_{L R}} | 01 〉 〈 00 | + | 01 〉 〈 01 | + e^{i (Δ ϕ_{L R} - Δ ϕ_{R L})} | 01 〉 〈 10 | + e^{i Δ ϕ_{L R}} | 01 〉 〈 11 | + e^{i Δ ϕ_{R L}} | 10 〉 〈 00 | + e^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} | 10 〉 〈 01 | + | 10 〉 〈 10 | + e^{i Δ ϕ_{R L}} | 10 〉 〈 11 | + | 11 〉 〈 00 | + e^{- i Δ ϕ_{L R}} | 11 〉 〈 01 | + e^{- i Δ ϕ_{R L}} | 11 〉 〈 10 | + | 11 〉 〈 11 |)

This can be converted to matrix notation using the following:

| 00 〉 〈 00 | = ((\begin{matrix} 1 \\ 0 \end{matrix}) \otimes (\begin{matrix} 1 \\ 0 \end{matrix})) ((\begin{matrix} 1 & 0 \end{matrix}) \otimes (\begin{matrix} 1 & 0 \end{matrix})) = (\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}) (\begin{matrix} 1 & 0 & 0 & 0 \end{matrix}) = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})

Similarly,

| 00 〉 〈 01 | = (\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 00 〉 〈 10 | = (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 00 〉 〈 11 | = (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) | 01 〉 〈 00 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 01 〉 〈 01 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 01 〉 〈 10 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 01 〉 〈 11 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) | 10 〉 〈 00 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 10 〉 〈 01 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 10 〉 〈 10 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}), | 10 〉 〈 11 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{matrix}) | 11 〉 〈 00 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix}), | 11 〉 〈 01 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}), | 11 〉 〈 10 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}), | 11 〉 〈 11 | = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})

Adding the terms,

\hat{ρ} = \frac{1}{4} (\begin{matrix} 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \\ e^{i Δ ϕ_{L R}} & 1 & e^{i (Δ ϕ_{L R} - Δ ϕ_{R L})} & e^{i Δ ϕ_{L R}} \\ e^{i Δ ϕ_{R L}} & e^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} & 1 & e^{i Δ ϕ_{R L}} \\ 1 & e^{- i Δ ϕ_{L R}} & e^{- i Δ ϕ_{R L}} & 1 \end{matrix})

The reduced density matrix is defined as

ρ_{A} = \sum_{j}^{dim (H_{B})} (I_{A} \otimes 〈 j |_{B}) (| Ψ 〉 〈 Ψ |) {(I_{a} \otimes | j 〉}_{B}) = T r_{B} ρ_{A B}

Where

I_{A}

is the identity operator in

H_{A}

and

T r_{B}

is the partial trace of the density matrix.

_{2} (\hat{ρ}) = \frac{1}{4} (_{2} (| 0 〉 〈 0 |) | 0 〉 〈 0 | + e_{2}^{- i Δ ϕ_{L R}} (| 0 〉 〈 1 |) | 0 〉 〈 0 | + e_{2}^{- i Δ ϕ_{R L}} (| 0 〉 〈 0 |) | 0 〉 〈 1 | +_{2} (| 0 〉 〈 1 |) | 0 〉 〈 1 | + e_{2}^{i Δ ϕ_{L R}} (| 1 〉 〈 0 |) | 0 〉 〈 0 | +_{2} (| 1 〉 〈 1 |) | 0 〉 〈 0 | + e_{2}^{i (Δ ϕ_{L R} - Δ ϕ_{R L})} (| 1 〉 〈 0 |) | 0 〉 〈 1 | + e_{2}^{i Δ ϕ_{L R}} (| 1 〉 〈 1 |) | 0 〉 〈 1 | + e_{2}^{i Δ ϕ_{R L}} (| 0 〉 〈 0 |) | 1 〉 〈 0 | + e_{2}^{i (Δ ϕ_{R L} - Δ ϕ_{L R})} (| 0 〉 〈 1 |) | 1 〉 〈 0 | +_{2} (| 0 〉 〈 0 |) | 1 〉 〈 1 | + e_{2}^{i Δ ϕ_{R L}} (| 0 〉 〈 1 |) {| 1 〉 〈 1 |}_{2} (| 1 〉 〈 0 |) | 1 〉 〈 0 | + e_{2}^{- i Δ ϕ_{L R}} (| 1 〉 〈 1 |) | 1 〉 〈 0 | + e_{2}^{- i Δ ϕ_{R L}} (| 1 〉 〈 0 |) | 1 〉 〈 1 | +_{2} (| 1 〉 〈 1 |) | 1 〉 〈 1 |)

(| i 〉 〈 j |) = δ_{i j}

when

〈 i | j 〉 = δ_{i j}

, this leaves us with

\frac{1}{4} (| 0 〉 〈 0 | + e^{- i Δ ϕ_{R L}} | 0 〉 〈 1 | + | 0 〉 〈 0 | + e^{i Δ ϕ_{L R}} | 0 〉 〈 1 | + e^{i Δ ϕ_{R L}} | 1 〉 〈 0 | + | 1 〉 〈 1 | + e^{- i Δ ϕ_{L R}} | 1 〉 〈 0 | + | 1 〉 〈 1 |)

In matrix form:

ρ_{1} = \frac{1}{4} (\begin{matrix} 2 & e^{- i Δ ϕ_{R L}} + e^{i Δ ϕ_{L R}} \\ e^{i Δ ϕ_{R L}} + e^{- i Δ ϕ_{L R}} & 2 \end{matrix})

Appendix C. Minimization of Time Taken

Our minimization expression is

τ + 2 τ_{acc}

The minimization constraint is Eq(15) which we will be simplifying by assigning variables to the numerical constants

\{\begin{matrix} \frac{g μ_{B} \partial_{x} B}{2 m} = 9.274 \cdot 10^{- 3} = A \\ 157 \times 10^{- 6} = B \\ \frac{π ℏ}{G m^{2}} \approx 49455.3566 = C \end{matrix}

This reduces Eq(15) to:

\frac{2 A^{2} τ_{acc}^{4} τ}{(A τ_{acc}^{2} + B) ({(A τ_{acc}^{2} + B)}^{2} - {(A τ_{acc}^{2})}^{2})} = C

Now this can be rearranged to define

τ

as a function of

τ_{acc}

τ = \frac{C (A τ_{acc}^{2} + B) ({(A τ_{acc}^{2} + B)}^{2} - {(A τ_{acc}^{2})}^{2})}{2 A^{2} τ_{acc}^{4}}

(A1)

By substituting Eq(23) in our minimization expression, we obtain a function in one variable which can be minimized using a simple python code.

import numpy as np import scipy as sp

from scipy.optimize import minimize

Defining constants A = 9.274*10**(-3) B = 157*10**(-6) C = 49455.3566

Defining function def f(x): y = 2x + (C*(A*(x**2)+B)*(2*A*B*(x**2)+(B**2)))/(2*(A**2)*(x**4)) return y

Minimization res = minimize(f, 0.2)

res

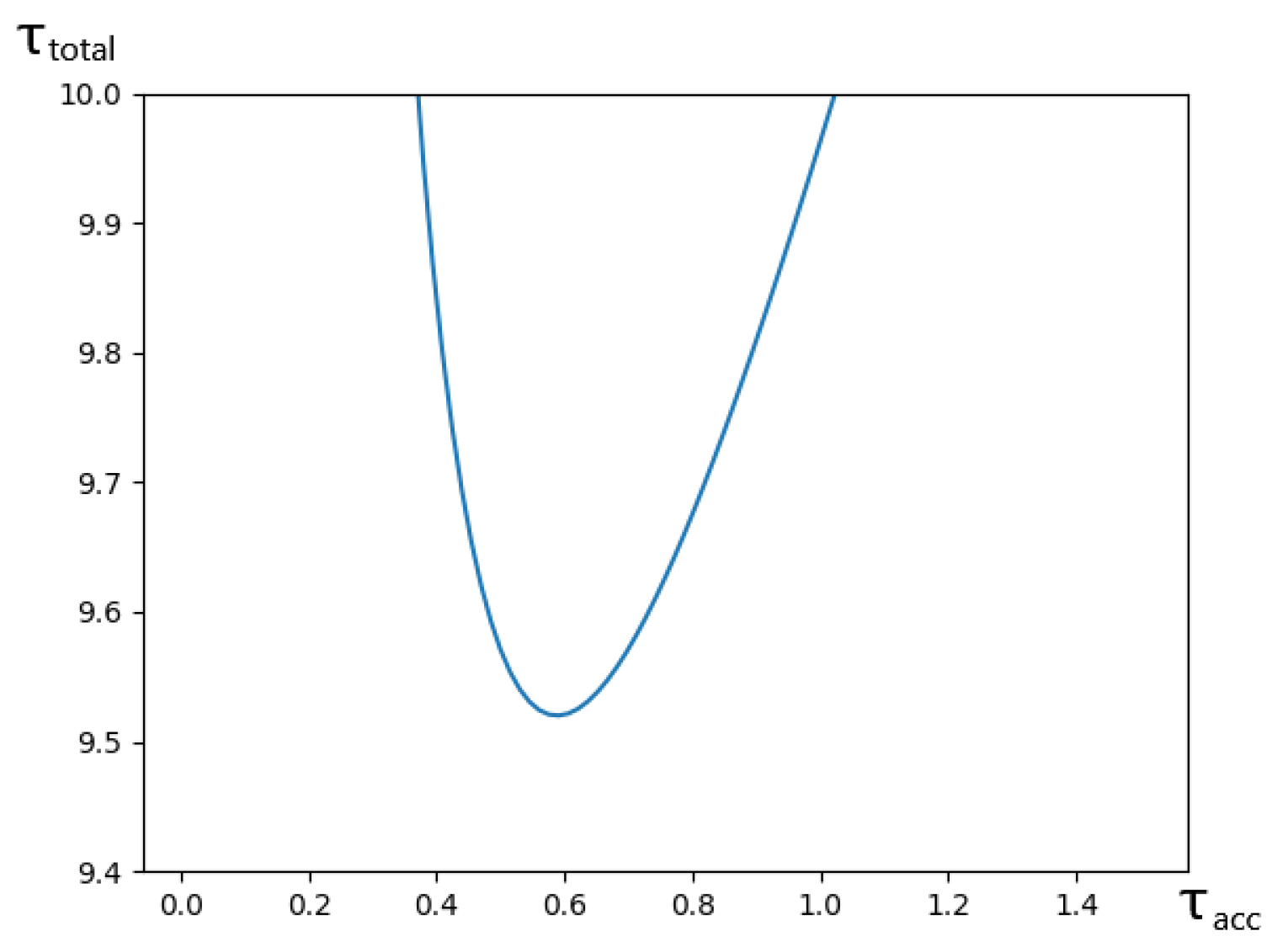
This gives

τ_{acc} \approx 0.58829 s

τ \approx 8.34349 s

and

τ + 2 τ_{acc} \approx 9.52007 s

Figure A2. Graph of

τ_{total}

as a function of

τ_{acc}

Figure A2. Graph of

τ_{total}

as a function of

τ_{acc}

Appendix D. Energy Cutoff for pQG

Eq. 22 shows that the energy cutoff of perturbative quantum gravity should be of the order

10^{19} G e V

. This can be calculated as follows:

\frac{1}{\sqrt{G}} = {(G)}^{- 1 / 2} = {(6.6743 \times 10^{- 11} \frac{N \cdot m^{2}}{k g^{2}})}^{- 1 / 2}

(A2)

The conversion from SI units to Natural units is shown in the table below:

Quantity	SI Units	Natural Units	Conversions
Force	$k g \cdot m / s^{2}$	$E^{2}$	1 Newton = $1.22 \times 10^{- 6} G e V^{2}$
Mass	$k g$	E	1 $k g$ = $5.56 \times 10^{26} G e V$
Length	m	$1 / E$	1 m = $5.076 \times 10^{15} G e V^{- 1}$

Substituting these values into Eq. 24 :

{(G)}^{- 1 / 2} = {(6.6743 \times 10^{- 11} \times \frac{1.22 \times 10^{- 6} \times {(5.076 \times 10^{15})}^{2}}{{(5.56 \times 10^{26})}^{2}} \times \frac{G e V^{2} \cdot G e V^{- 2}}{G e V^{2}})}^{- 1 / 2}

= {(8.143 \times 10^{- 17} \times \frac{25.766 \times 10^{30}}{30.91 \times 10^{52}} G e V^{- 2})}^{- 1 / 2}

= {(6.788 \times 10^{- 39} G e V^{- 2})}^{- 1 / 2} = 1.21 \cdot 10^{19} G e V

Therefore,

E \sim 10^{19} G e V

References

Macías, A. On the incompatibility between general relativity and quantum theory. 2008.
Bose, S.; Mazumdar, A.; Morley, G.W.; Ulbricht, H.; Toro, M.; Paternostro, M.; Geraci, A.A.; Barker, P.; Kim, M.S.; Milburn, G.J. Spin Entanglement Witness for Quantum Gravity. Physical review letters 2017, 119 24, 240401. [Google Scholar] [CrossRef]
Schut, M.; Grinin, A.; Dana, A.; Bose, S.; Geraci, A.A.; Mazumdar, A. Relaxation of experimental parameters in a Quantum-Gravity Induced Entanglement of Masses Protocol using electromagnetic screening. 2023.
Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press, 2000.
Lichnerowicz, M.A.; Tonnelat, M.A., Eds. Proceedings, Les théories relativistes de la gravitation : actes du colloque international (Relativistic Theories of Gravitation): Royaumont, France, June 21-27, 1959, Paris, 1962. CNRS.
Rosenfeld, L. On quantization of fields. Nucl. Phys. 1963, 40, 353–356. [Google Scholar] [CrossRef]
Wald, R.M. Trace anomaly of a conformally invariant quantum field in curved spacetime. Phys. Rev. D 1978, 17, 1477–1484. [Google Scholar] [CrossRef]
Eppley, K.R.; Hannah, E. The necessity of quantizing the gravitational field. Foundations of Physics 1977, 7, 51–68. [Google Scholar] [CrossRef]
Page, D.N.; Geilker, C.D. Indirect Evidence for Quantum Gravity. Physical Review Letters 1981, 47, 979–982. [Google Scholar] [CrossRef]
Lowe, D.A.; Thorlacius, L. Semiclassical dynamics of Hawking radiation. Classical and Quantum Gravity 2023, 40, 205006. [Google Scholar] [CrossRef]
Martí n, R.; Verdaguer, E. Stochastic semiclassical gravity. Physical Review D 1999, 60. [Google Scholar]
Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Reports on Progress in Physics 2021, 84. [Google Scholar] [CrossRef] [PubMed]
Seiberg, N.; Witten, E. String theory and noncommutative geometry. Journal of High Energy Physics 1999, 1999, 032–032. [Google Scholar] [CrossRef]
Hawking, S.; Israel, W. General Relativity: an Einstein Centenary Survey; 2010.
Peskin, M.E.; Schroeder, D.V. An Introduction to quantum field theory; Addison-Wesley: Reading, USA, 1995. [Google Scholar]
Zee, A. Quantum field theory in a nutshell; 2003.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Gravity: Parameters for Detection via Spin Entanglement and Theoretical Models

Abstract

1. Introduction

2. Double Stern Gerlach Spin Entanglement

3. Minimization of Casimir-Polder Interaction

4. Conditions for Maximal Entanglement

5. Inferences and Semiclassical Models

Quantized Gravitational Field Theory

Gravitational Action

Dimensional Analysis

Power Counting Renormalizability

Acknowledgments

Appendix A. Entanglement Witness

Appendix B. Density Matrix Calculations

Appendix C. Minimization of Time Taken

Appendix D. Energy Cutoff for pQG

References

MDPI Initiatives

Important Links

Subscribe