Prerpints.org logo
Preprint
Article

Influence of Perturbation’s Type and Location on Treadmill Gait Regularity

Altmetrics

Downloads

75

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 November 2023

Posted:

29 November 2023

You are already at the latest version

Alerts
Abstract
Background: This study aimed to investigate how external perturbations caused by the treadmill belt's acceleration (Acc) and deceleration (Dec) during the Initial Contact (Initial), Mid Stance (Mid) and Pre-Swing (ToeOff) phase affect gait regularity in young adults. Methods: Twenty-one healthy young females walked on a treadmill in a virtual environment (Grail, Motek), where four unexpected perturbations were applied to the left belt at Initial, Mid, and ToeOff. Sample Entropy (SampEn) was calculated for the center of mass (CoM) displacements, for six perturbation scenarios in three directions: anterior-posterior (AP), medial-lateral (ML), and vertical (vert), with SampEn vector lengths (m) ranging from 2 to 10. Results: The CoM displacement exhibited its highest regularity (low SampEn values) in the AP and vert-directions during Dec_ToeOff, across all m values. Similarly, this pattern was observed in the ML-direction, but exclusively for m = 2 and 4. The least regular CoM trajectories (high SampEn values) were for Dec_Mid in the AP-direction, across all m values. This trend persisted in the ML-direction, only for m = 2 and 4. However, the most irregular CoM displacements in the ML-direction occurred during Dec_ToeOff for the remaining m values. Vertical CoM displacements exhibited the highest irregularities during Dec_Initial for m ≥ 4. Conclusions: Evaluating the regularity of CoM displacements using SampEn can be a useful tool for assessing how gait perturbations are handled.
Keywords: 
Subject: Biology and Life Sciences  -   Other

1. Introduction

Gait perturbations refer to disruptions or irregularities in an individual's walking pattern or gait. These perturbations can occur due to various factors, including environmental obstacles [1], musculoskeletal conditions [2,3], neurological disorders [4], or external influences [5]. Environmental barriers include uneven terrain, path obstacles, or slippery surfaces. Musculoskeletal conditions will involve muscle weakness, joint pain, or injuries, while neurological disorders (Parkinson's disease, multiple sclerosis, or stroke) can cause changes in posture, balance and thus the walking pattern. External influences like carrying heavy objects, wearing different footwear, or experiencing fatigue can also lead to gait perturbations. All the above-mentioned factors can alter the way of walking and, most of all, the ability to maintain stability. According to Bruijn, et al. [6], stable gait can be defined as a gait pattern that does not lead to falls despite perturbations.
The literature provides several approaches for gait stability assessment, generally divided into clinical and quantitative methods [6,7,8]. Clinical tests that assess postural and gait stability are the initial source of knowledge about the patient's condition and can guide further diagnostic procedures. These tests evaluate functional characteristics, such as the time it takes to walk a distance safely and the ability to walk unassisted. These tests may include: the Timed 10-meter walk test, Heel-to-Toe test, Timed up and go test (TUG), and Babinski-Weil test [9]. Quantitative methods refer mainly to instrumented gait analysis, which involves using specialized equipment such as force plates, motion capture systems, and wearable sensors to collect data during walking. These tools provide detailed information on gait parameters, which are then analysed to assess gait stability. According to Hamacher, et al. [10], both linear and nonlinear measures can be used to assess gait stability. Among the linear methods used to assess gait stability, the authors listed the following: step and stride length variability, step and stride time variability, double support time, gait speed, cadence, and standard deviation of the analysed time series. However, in recent years, a method associated with the Margin of Stability (MoS) determination has gained popularity [11]. Among the nonlinear measures, Hamacher, et al. [10] listed wavelets and detrended fluctuation analysis, fractal scaling index, Lyapunov exponents, and Floquet multipliers. Similar methods were mentioned in the review by Bruijn, et al. [6]. It is worth noting that these two reviews [6,10] discussing the assessment of gait stability did not mention entropy despite its recent popularity among nonlinear measures. Entropy is a measure that assesses the regularity of the analyzed time series [12]. However, the papers mentioned focused on the possibility of predicting the probability of falling, and entropy does not have such predictive capabilities. Despite this, the use of entropy analysis in gait research has increased significantly over the past two decades [13]. Sample Entropy (SampEn) is one of the various types of entropy measures to quantify complexity/ regularity/ predictability/ probability of analysed motion [12,13]. SampEn algorithm need three inputs for analysis: tolerance window r (used to determine whether patterns within the time series are similar or not), vector length m (data length compared across the time series to determine conditional probabilities), and time series length N. For gait data analysis, m = 2, 4, 6, 8 or 10 is most often used, while r should be equal to 0.2xSD, where SD is the standard deviation of the analysed time series [14,15,16,17].
The primary aim of this study was to investigate how different perturbation possibilities, including their timing (Initial Contact, Mid Stance, and Pre-Swing) and direction (acceleration or deceleration of the one belt of the treadmill), impact the regularity of the center of the body mass movement. Since the regularity of time series is described using Sample Entropy, an additional purpose of this paper was closely related to the behaviour of this parameter. Accordingly, the next objective was to examine the values of SampEn in the anterior-posterior (AP), medial-lateral (ML) and vertical directions, depending on the length of the vector m for each type of perturbation possibilities.

2. Materials and Methods

2.1. Participants

Twenty-one young women (Y: age: 21.38 ± 1.32 y.o., body weight: 61.38 ± 6.48 kg, and body height: 165.9 ± 4.53 cm) participated in this study. Participants met the following inclusion criteria: no muscular or neural diseases, no lower limb injuries within the six months preceding testing, and at least two days of activity per week as part of a physical recreation routine. Exclusion criteria included poor physical condition (evaluated subjectively on the day of the study), lack of experience in treadmill walking, and the use of medications that could adversely affect the nervous system.
This research followed the ethical guidelines and principles of the Declaration of Helsinki and received approval from the university's institutional review board (no. SKE01-15/2023). Informed consent was obtained from all participants before the study.

2.2. Measurement protocol and perturbation characteristics

The kinematics and kinetics parameters of the perturbed gait were measured in a Gait Real-time Analysis Interactive Lab (GRAIL, Motek Medical B.V., Amsterdam, Netherlands). The GRAIL is equipped with a dual split-belt treadmill (1000 Hz), a motion capture system (Vicon Metrics Ltd., Oxford, UK) (100 Hz), three video cameras, and synchronised virtual reality environments. Participants' movements were captured using Human Body Model 2 (HBM2) with 26 reflective markers. Perturbation triggering and data acquisition were controlled using D-Flow software (Motek Medical B.V., Amsterdam, Netherlands).
In this study, participants walked on the treadmill wearing flat-soled sports shoes at a constant speed of 1.2 m/s. As a safety precaution, each participant wore a safety harness connected to the ceiling, even though the perturbations were not intended to cause falls. Two types of unexpected perturbations were applied to the left belt of the treadmill, involving acceleration and deceleration (Figure 1). Each perturbation occurred at three specific points during the support phase of the gait cycle: Initial Contact, Mid Stance, and Pre-Swing (Table 1). The magnitude of the perturbation was set at 5 on a scale of 1 – 5, involving a shift in treadmill belt speed of 0.5 meters per second [4].
Each participant performed one trial for all six perturbation possibilities (type x phase). In each attempt, perturbations occurred at 10-second intervals on the left treadmill belt. Consequently, these perturbations appeared at the 30th, 40th, 50th, and 60th seconds of treadmill walking. These perturbations were applied to the left lower limb, as it was the supporting (non-dominant) leg for all subjects [18]. Leg dominance was determined using the Kicking Test, where participants indicated their preferred lower limb for kicking a ball.

2.3. Time series identification

For each of the six perturbation possibilities (Table 1), CoM displacements in three directions: anterior-posterior (AP), medial-lateral (ML) and vertical (vert), which included four perturbations, were considered for analysis. To ensure homogeneity of the data, the CoM time series were identified based on the vertical components of the ground reaction forces (GRF). The starting point of each time series was defined as the moment when the gait cycle involving the perturbation began (i.e., the contact of the heel with the ground of the left lower limb), and the endpoint was determined as the final gait cycle containing the response to the perturbation (indicated by the renewed contact of the left heel with the ground) (Figure 2). This treatment ensured that the raw data had the same length (3189 points).

2.4. Sample Entropy calculation

SampEn is defined as the negative natural logarithm of the conditional probability that a sequence of data points, each separated by a specified distance m, will repeat within a distance of m+1, excluding self-matches:
SampEn m , r , N = − ln A m r B m r ,
where B represents the total number of matches of length m. A represents the subset of B that also matches for m+1. N is the total number of data points in the time series, m signifies the length of the vectors compared during data waveforms, and r denotes the sensitivity threshold in which comparable vectors are considered similar.
Sample Entropy was calculated for six perturbation possibilities (Table 1) on CoM_vert, CoM_AP, and CoM_ML signals using code obtained from the Physionet tool [19]. The values chosen for m were 2, 4, 6, 8, and 10, and r was set to 0.2 times the mean standard deviation of the time series (r = 0.2xSD) [15,16,17]. The selection of r = 0.2 for the time series was based on the method proposed by Lake, et al. [20].
In the case of human movement, a steady or periodic gait pattern has a low SampEn value, while a more complex gait pattern (a time series with large distances between data points) should have a higher SampEn value.

2.4. Statistical analysis

The normality of the distribution of SampEn values, calculated for all m values within six different perturbation possibilities, was assessed using the Shapiro-Wilk test. In most cases, the results indicated distributions different from normal. A Friedman ANOVA with Dunn-Bonferroni post-hoc tests was used to assess the influence of m levels on the SampEn calculated for each of the six perturbation possibilities. Subsequently, a similar analysis was performed to identify which of the six perturbation possibilities and which direction exhibited the lowest gait regularity. These last two analyses were conducted independently for each m level. Statistical analysis was performed using PQStat 2021 software version 1.8.2.238 (PQStat Software, Poznań, Poland). The level of significance was set at p ≤ 0.05.

3. Results

3.1. The impact of vector length (m) on Sample Entropy values across six perturbation possibilities

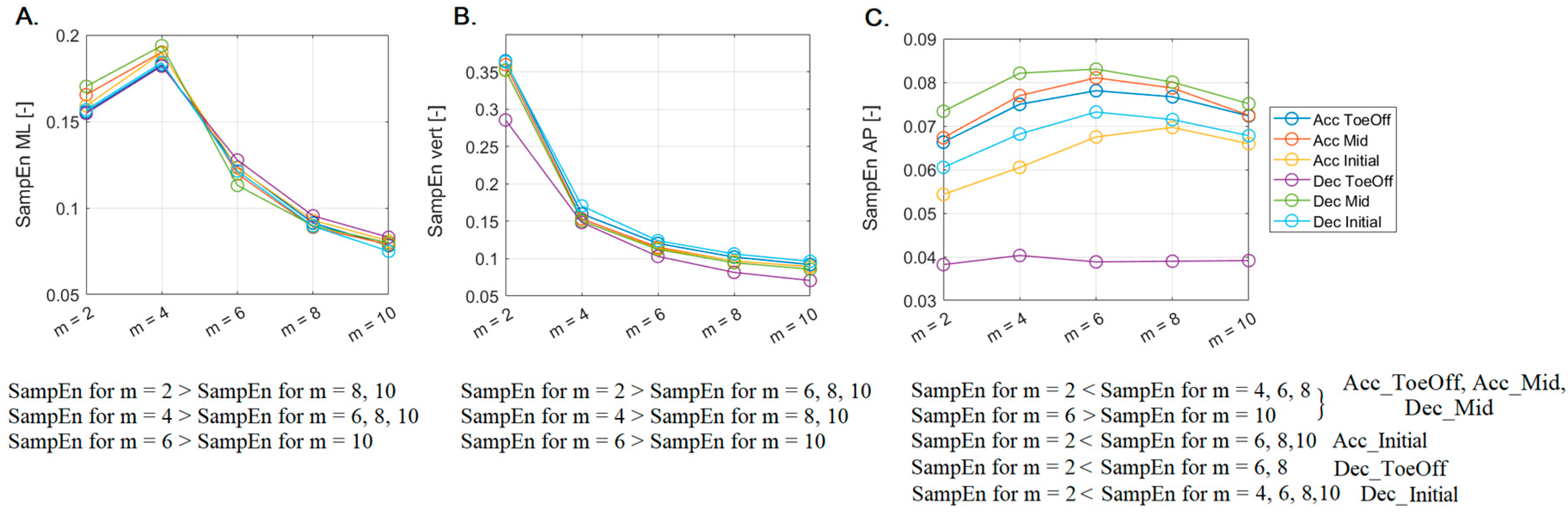
After conducting Friedman's ANOVA with Dunn-Bonferroni post hoc tests, it was shown that for the ML direction (Figure 3A), for each of the six perturbation possibilities, significantly higher (p < 0.0001) SampEn values were noted for m = 2 with respect to those recorded for m = 8, 10. Additionally, significantly higher (p < 0.0001) SampEn values were found for m = 4 in comparison to those calculated for m = 6, 8, and 10, as well as for m = 6 in comparison to those noted for m = 10.
In the vertical direction (Figure 3B), the trend of stacking SampEn values was consistent with that described for the ML direction, with two exceptions. For m = 2, SampEn values were significantly higher than those calculated for m = 6, a difference not observed in the ML direction. For m = 4, SampEn values were not significantly higher than those reported for m = 6, which was noted in the ML direction.
In the AP direction, the trend of SampEn values did not follow a pattern from the previous directions (Figure 3C), illustrating remarkable diversity. For m = 2, SampEn values were significantly lower than those recorded for m = 4, 6, and 8. Moreover, for m = 6, SampEn values were significantly higher than those associated with m = 10. These consistent trends extended across three perturbation possibilities (Acc_ToeOff, Acc_Mid, Dec_Mid). In the case of Acc_Initial, SampEn values at m = 2 were notably lower than those derived for m = 6, 8, and 10. The identical relationship existed for Dec_ToeOff, except for relations involving m = 10. In contrast, for Dec_Initial, SampEn values at m = 2 were significantly lower when compared to all other SampEn counting possibilities.

3.2. Impact of perturbation possibilities and m - values on gait regularity within directions

Friedman's ANOVA was performed within each combination of m values (m = 2, 4, 6, 8, 10) and movement directions (AP, ML, vert). The results of the Dunn-Bonferroni post-hoc test for each direction are described below.

3.2.1. Medio-lateral direction (ML)

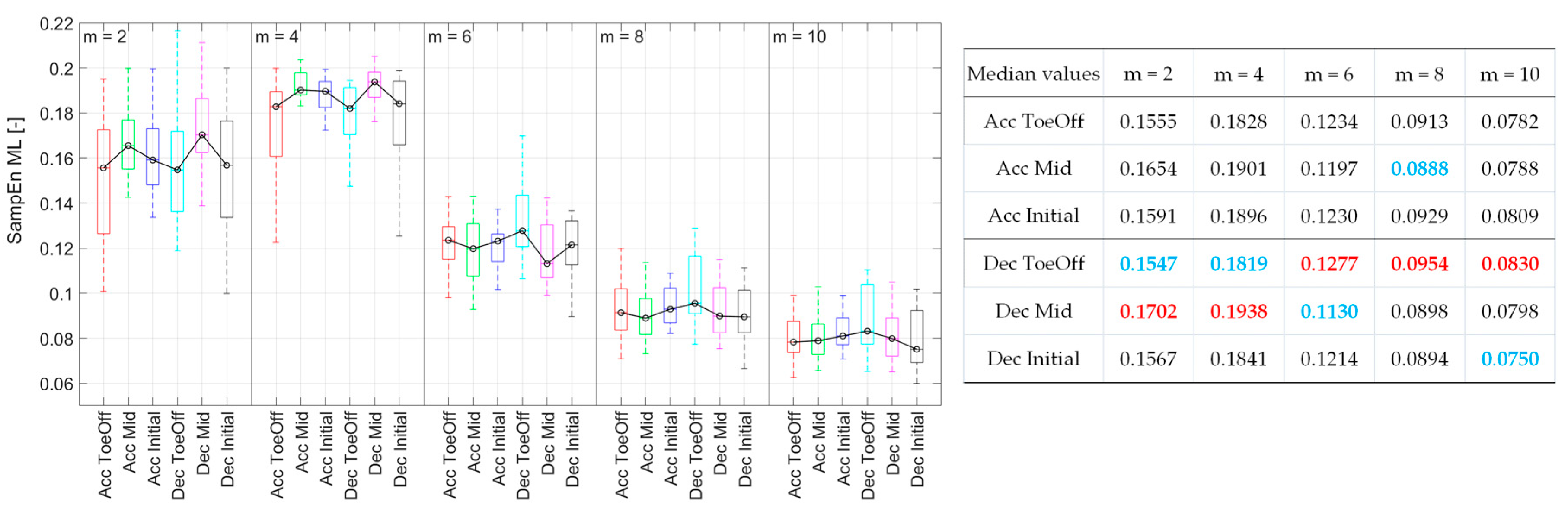
For m = 2 and 4, the SampEn values for Dec_Mid were the highest and significantly higher than that recorded for the Acc_ToeOff, Dec_ToeOff, and Dec_Initial (Figure 4).
For m = 6, the effect of treadmill deceleration in the Pre-Swing phase (Dec_ToeOff) caused the highest CoM irregularity. The SampEn value for this perturbation possibility was significantly higher than that recorded for the Acc_Mid and Dec_Mid. No significant differences in SampEn values were observed for m = 8 and 10.

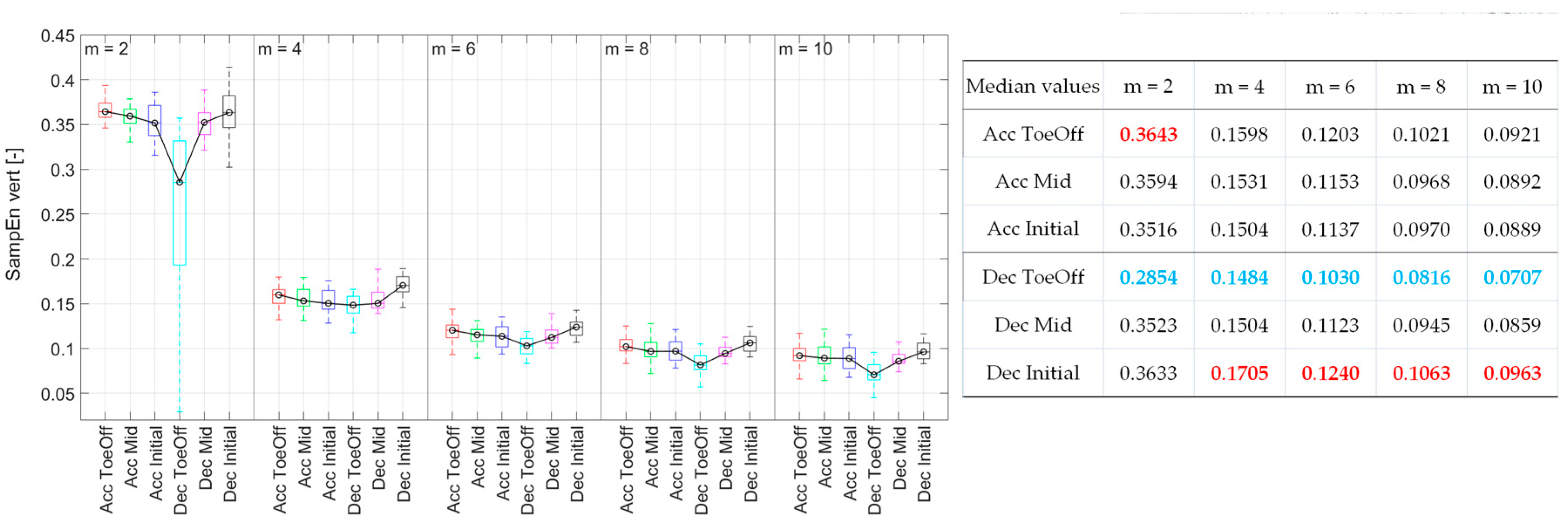
3.2.2. Vertical direction (vert)

For m = 2, the CoM signal exhibited the highest regularity during Dec_ToeOff. The SampEn value in this phase was significantly lower than that for the other five perturbations (Figure 5). This pattern persisted for m = 6, 8, and 10 but only for two perturbations. The CoM irregularity was significantly higher for Acc_ToeOff and Dec_Initial than those observed for Dec_ToeOff. Additionally, for m = 10, significantly higher SampEn values were recorded for Acc_Initial and Dec_Mid compared to Dec_ToeOff. In the case of m = 2, significantly higher SampEn values were for Acc_Mid than for Dec_ToeOff. For m = 4, SampEn values behaved differently, indicating the highest values for Dec_Initial. The values for this perturbation were significantly higher than those recorded for Acc_Initial, Dec_ToeOff, and Dec_Mid. In summary, the CoM displacement achieved its highest regularity, indicated by low SampEn values during Dec_ToeOff, across all m values. The lowest regularity was noted during Dec_Initial for m = 4, 6, 8, and 10.

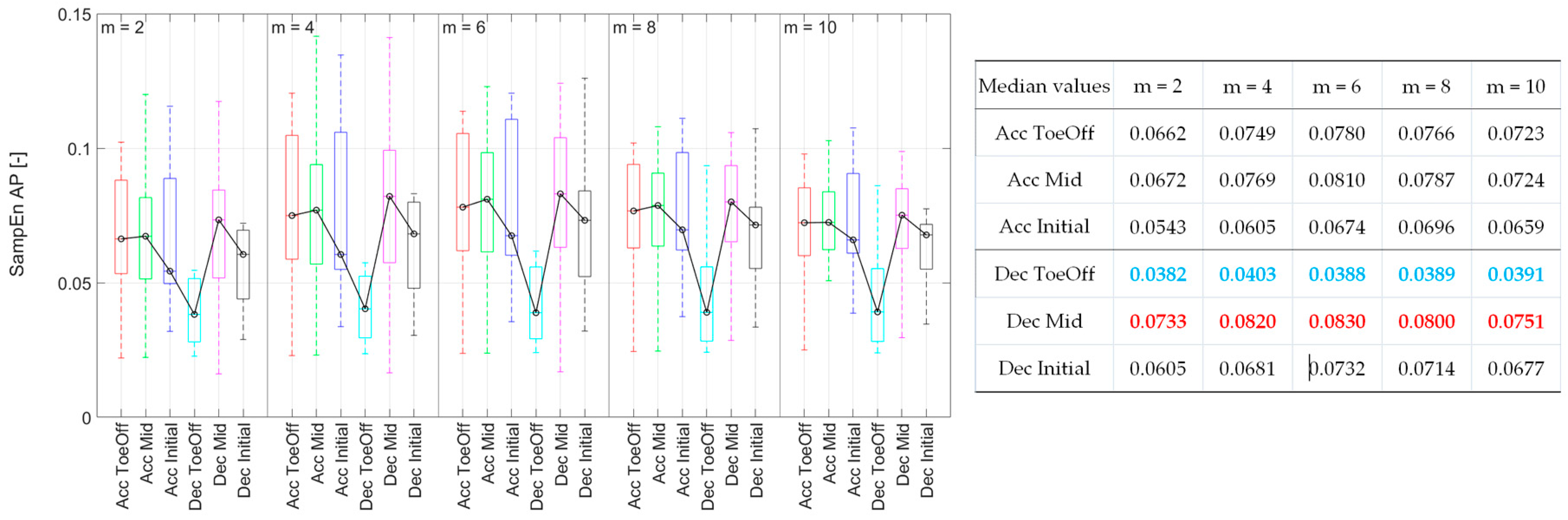
3.2.3. Anterior-posterior direction (AP)

Differently from the previous directions, for m = 2 and 4, it was shown that there are no statistically significant differences in the regularity of CoM displacement due to individual perturbations. For the remaining m values, it was demonstrated that treadmill accelerations during the Initial Contact, Mid Stance, and Pre-Swing phases led to a significant increase in the irregularity of CoM displacement compared to that observed for Dec_ToeOff. Additionally, for m = 8 and 10, a significant increase in SampEn value was observed for Dec_Mid perturbations compared to Dec_ToeOff perturbations (Figure 6). In summary, the CoM displacement exhibited its highest regularity, as indicated by low SampEn values during Dec_ToeOff, and the lowest regularity, as indicated by high SampEn values, during Dec_Mid, across all m values.

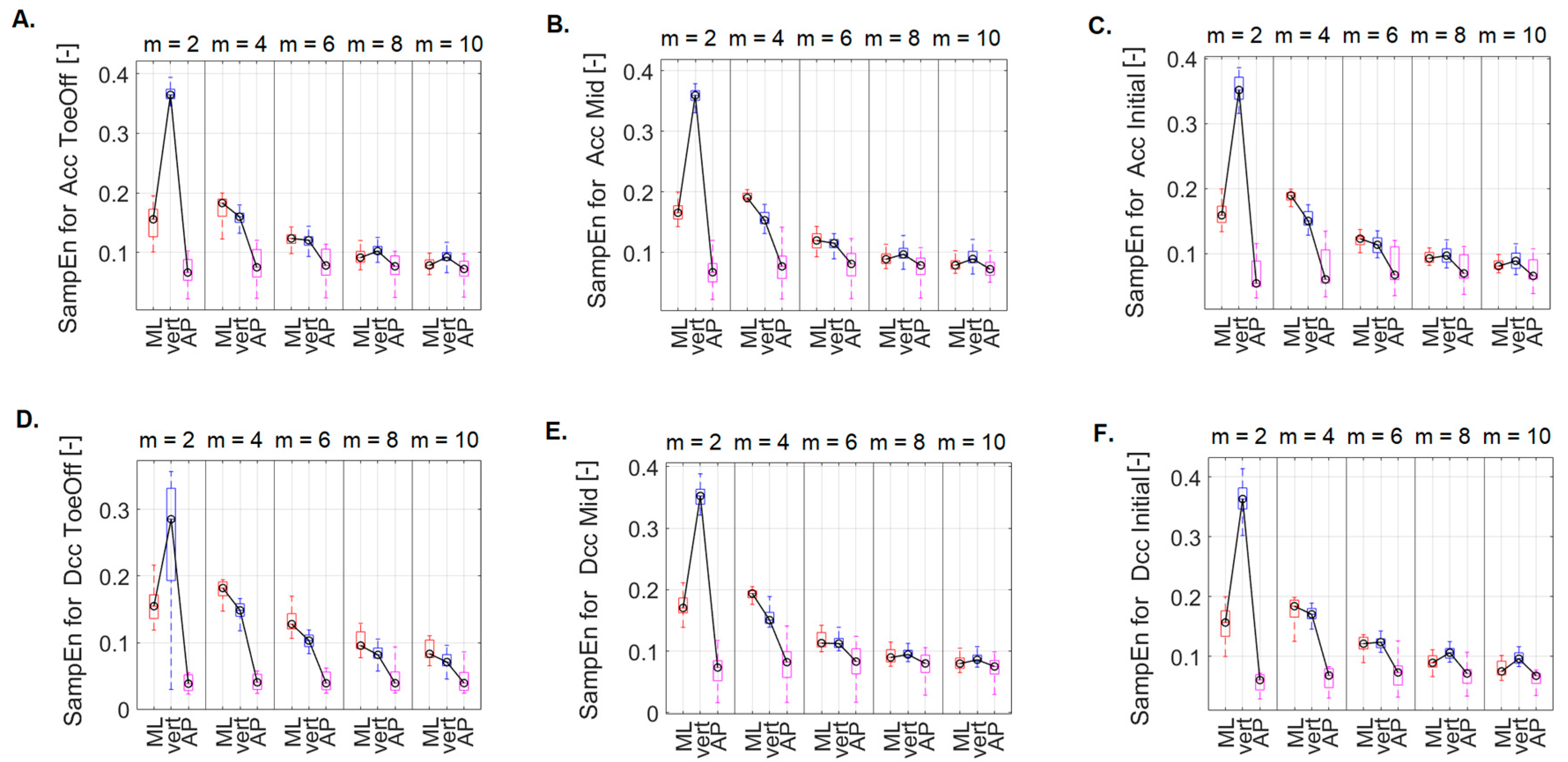
3.2. Effect of direction on gait regularity across different m-values

Examining the impact of direction (AP, ML, vert) on the regularity of the CoM signal within different m values, it was shown that for the perturbations related to treadmill acceleration in the Pre-Swing phase (Figure 7A), there was significantly higher irregularity of the CoM signal in the ML and vert directions compared to that noted for AP direction. This pattern held for m = 2, 4, and 6. Additionally, for m = 2, the SampEn value in the ML direction was significantly lower than that in the vertical direction. No statistically significant differences were found for the other m values.
For the perturbations related to treadmill acceleration in the Mid Stance phase (Figure 7B) and for m = 2, 4, and 6, notably higher SampEn values were in the ML and vert directions than those recorded in the AP direction. Furthermore, for m = 2, significantly higher SampEn values were recorded in the vert direction than those in the ML direction. For m = 4, this relationship was reversed. Additionally, for m = 10, significantly higher SampEn values were recorded in the vert direction than those in the AP direction.
For the perturbations related to treadmill acceleration in the Initial Contact phase (Figure 7C) and for m = 2, 4, significantly higher SampEn values were in the ML and vert directions than those noted for the AP direction. Furthermore, for m = 2, the SampEn value in the vert direction was significantly higher than that recorded in the ML direction. For m = 4, SampEn_ML was greater than SampEn_vert. For m = 6, SampEn_ML was greater than SampEn_AP, while for m = 10, SampEn_vert exceeded SampEn_AP. As with the previous perturbations, no statistically significant differences were for m = 8.
For treadmill deceleration in the Pre-Swing phase (Figure 7D), with m = 2, 4, 8, and 10, significantly higher SampEn values were in the ML and vert directions than those noted for the AP direction. For m = 6, significantly higher SampEn values were in the ML direction versus those in the vert and AP directions.
For a perturbation containing treadmill deceleration in the Mid Stance phase (Figure 7E), for m = 2, 4, 6, significantly higher SampEn values were in the ML and vert directions versus those recorded for the AP direction. Additionally, for m = 2, SampEn_vert was greater than SampEn_ML. On the other hand, for m = 4, this relationship was opposite. For m = 8, 10: SampEn_vert was greater than SampEn_AP.
For a perturbation containing treadmill lag in the initial contact phase (Figure 7F), for m = 2, 4, 6, 8, significantly higher SampEn values were in the ML and vert directions as compared to those recorded for the AP direction. In addition, for m = 2 and 8, SampEn_vert was greater than SampEn_ML. For m = 10, SampEn_vert was greater than SampEn_ML, and SampEn_AP.

4. Discussion

The primary aim of this study was to investigate the impact of different perturbation possibilities, including their timing (Initial Contact, Mid Stance, and Pre-Swing) and direction (acceleration or deceleration of the one treadmill belt), on the gait regularity. Gait regularity was assessed based on the displacement of the center of mass (CoM) in the anterior-posterior (AP), medial-lateral (ML), and vertical (vert) directions. As the regularity of the CoM time series was quantified using Sample Entropy (SampEn), an additional aim of this study was closely associated with understanding the behaviour of this parameter. Consequently, the subsequent aim was to analyse SampEn values in the above-mentioned directions, considering the comparison of the vector length (m).
This study implemented a perturbation protocol via the Grail system (Motek Medical BV, Amsterdam, the Netherlands), enabling precise timing and intensity control of perturbations. This accuracy facilitated the manipulation of the time series duration for analysis. Although the SampEn value is independent of the time series length, Richman and Moorman [21] recommend that the analysed data consist of at least 200 points. In this study, each dataset comprised 3189 points. However, the SampEn value depends on the choice of m and r parameters, and determining suitable parameters for gait analysis is not straightforward [22]. Studies focusing on postural control during quiet standing commonly use an m-value of 2, while r equals 0.2 times the standard deviation of the data (SD) [12]. However, when considering gait analysis, the selection of parameters becomes less clear, particularly due to the authors' focus on various parameters, such as joint angle and torque waveforms, as well as stride characteristics [23,24]. According to Tochigi, et al. [25], employing a longer m-template (higher m value) theoretically augments specificity in identifying matched templates but may lead to a potential decrease in discriminatory power. Many researchers [22,25] have opted for a minimum template length (m = 2) for gait-related data to maximize discriminatory power. Additionally, the authors [14,15,16] explored higher m values (m = 4, 6, 8, 10), resulting in consistently lower SampEn values, a trend also observed in this study, mainly for SampEn calculated in ML and vert direction. For the AP direction, the trend differed - SampEn values were the lowest for m = 2 across all perturbations, except for treadmill deceleration during the Pre-Swing phase. In this case, as m values increased, SampEn values decreased.
To date, no studies have been found that describe the regularity of the human body movement or its segments in reaction to gait perturbations using nonlinear measures, particularly sample entropy. This paper presented results regarding the SampEn values computed for the CoM time series separately in the anterior-posterior (AP), medial-lateral (ML), and vertical directions. This approach enabled the identification of perturbations causing the most irregular gait. It's important to note that the analysis was conducted for m equal to 2, 4, 6, 8, and 10. The study revealed clear patterns in the Center of Mass (CoM) displacement, particularly in the vertical and anterior-posterior directions. The most coherent CoM displacement, indicated by low SampEn values meaning regularity, occurred during treadmill deceleration in the Pre-Swing phase. This consistency was reproducible across all m in both AP and vertical directions. This coherence suggests that the body anticipated and skillfully adapted to this perturbation, recovering quickly to the baseline displacement of CoM, resulting in a regular gait. However, higher SampEn values, reflecting increased irregularity, were recorded at other times depending on the direction. In the AP direction, irregular CoM behavior was noticeable during treadmill deceleration in the Mid Stance phase, indicated by the highest SampEn values across all m-values. Conversely, in the vertical direction, the delay of the treadmill during the Initial Contact phase exhibited the highest SampEn values (for m = 4, 6, 8, 10), indicating irregularity. For m = 2, the highest irregularity occurred during treadmill acceleration in the Pre-Swing phase.
Regarding the medial-lateral direction, the highest irregularity in CoM displacement was observed due to treadmill belt deceleration during the Mid Stance phase, specifically for m = 2 and 4. However, other m-values increased CoM irregularity during treadmill deceleration in the Pre-Swing phase. It's important to note that when examining extreme values, the highest irregularity (maximum value of SampEn) was observed for the CoM time series involving acceleration-type perturbations during the Pre-Swing phase, calculated for m = 2 in the vertical direction. Conversely, the highest order (minimum value of SampEn) was for the CoM signal for the anterior-posterior direction during the deceleration perturbation in the Pre-Swing phase (also calculated for m = 2). According to a study by Sloot, et al. [4], the above results are adequately confirmed. Sloot, et al. [4] were among the few researchers who conducted experiments utilizing identical equipment and settings, operating under conditions similar to those presented in this paper (perturbation intensity and treadmill-based accelerations and decelerations). The authors demonstrated that the applied perturbations appeared to have a limited effect on the gait pattern. Even at the highest intensities, the observed impact resulted in less than a 4° knee flexion or extension. Furthermore, there was a decrease of less than 4% in stride length and less than a 3.5% change in both stride time and stance phase, some of which were inherent to the perturbation itself. Notably, during deceleration, there was a 6.1% increase in step width. This adjustment might indicate an attempt to improve the base of support in the medial-lateral direction, compensating for the decrease in the anterior-posterior direction resulting from the deceleration [26]. In contrast, during acceleration, step width remained unchanged, suggesting that the subjects were not affected by the perturbations.

5. Conclusions

Based on the observed patterns in the regularity of CoM displacements across gait perturbations, several conclusions can be drawn.
Firstly, during the treadmill deceleration in the Pre-Swing phase, the CoM displacement exhibited its most consistent pattern (indicated by low Sample Entropy values) in the AP and vertical directions across all m values. Conversely, the least regular CoM trajectories (with high SampEn values) were evident during treadmill deceleration in Mid Stance in the AP direction, consistent across all m values, and also observed in the ML direction, particularly for m = 2 and 4.
These findings highlight the significance of assessing the regularity of CoM movements using SampEn as a valuable tool in comprehending the management and response to gait perturbations. They shed light on how different perturbations influence the regularity of CoM movements in various directions, offering insight into the adaptability and stability of human gait under perturbed conditions.

Author Contributions

Conceptualization, M.B.; methodology, M.B.; software, M.B.; validation, M.B and A.H.; formal analysis, M.B.; investigation, M.B.; resources, M.B.; data curation, M.B.; writing—original draft preparation, M.B.; writing—review and editing, M.B. and A.H.; visualization, M.B. and A.H.; supervision, M.B.; project administration, M.B.; funding acquisition, M.B. and A.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Józef Piłsudski University of Physical Education in Warsaw, grant number UPB no. 2 (114/12/PRO/2023). Gait Real-time Analysis Interactive Lab (GRAIL, Motek Medical B.V., Amsterdam, Netherlands) was purchased under the project "Adaptation and equipment of innovative laboratories for diagnostic and therapeutic tests of the musculoskeletal system" co-financed by the European Union under the Operational Program Development of Eastern Poland 2007 – 2013. Apparatus maintained under a subjective subsidy from the Ministry of Education and Science under decision 41/529869/SPUB/SP/2022.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Józef Piłsudski University of Physical Education in Warsaw, Poland (protocol code SKE01-15/2023 and date of approval 24.03.2023).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study. Written informed consent has been obtained from the patient(s) to publish this paper.

Data Availability Statement

The measurement data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

We would like to thank Karol Kowieski, Katarzyna Kaczmarczyk, Martyna Jarocka and Agnieszka Zdrodowska for their help in data collection.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
  2. Błażkiewicz, M.; Wiszomirska, I.; Kaczmarczyk, K.; Brzuszkiewicz-Kuźmicka, G.; Wit, A. Mechanisms of compensation in the gait of patients with drop foot. Clin Biomech (Bristol, Avon) 2017, 42, 14–19. [Google Scholar] [CrossRef]
  3. Bartsch-Jimenez, A.; Błażkiewicz, M.; Azadjou, H.; Novotny, R.; Valero-Cuevas, F.J. "Fine synergies" describe motor adaptation in people with drop foot in a way that supplements traditional "coarse synergies". Frontiers in sports and active living 2023, 5, 1080170. [Google Scholar] [CrossRef] [PubMed]
  4. Sloot, L.H.; van den Noort, J.C.; van der Krogt, M.M.; Bruijn, S.M.; Harlaar, J. Can Treadmill Perturbations Evoke Stretch Reflexes in the Calf Muscles? PLOS ONE 2015, 10, e0144815. [Google Scholar] [CrossRef] [PubMed]
  5. Ali, Y.; Daniel, E.L. Effects of shoe heel height on ankle dynamics in running. bioRxiv 2023, 2023.2008.2008.552471. [Google Scholar] [CrossRef]
  6. Bruijn, S.M.; Meijer, O.G.; Beek, P.J.; van Dieën, J.H. Assessing the stability of human locomotion: a review of current measures. Journal of the Royal Society, Interface 2013, 10, 20120999. [Google Scholar] [CrossRef]
  7. Bisi, M.C.; Riva, F.; Stagni, R. Measures of gait stability: performance on adults and toddlers at the beginning of independent walking. Journal of NeuroEngineering and Rehabilitation 2014, 11, 131. [Google Scholar] [CrossRef]
  8. Hamacher, D.; Liebl, D.; Hödl, C.; Heßler, V.; Kniewasser, C.K.; Thönnessen, T.; Zech, A. Gait Stability and Its Influencing Factors in Older Adults. Front Physiol 2018, 9, 1955. [Google Scholar] [CrossRef]
  9. Józefowicz-Korczyńska, M.; Chmielecka-Rutkowska, J.; Mazerant, A. Clinical tests for balance stability and gait assessment–Bedside Tests. Polski Przegląd Otorynolaryngologiczny 2016, 5, 57–63. [Google Scholar]
  10. Hamacher, D.; Singh, N.B.; Van Dieën, J.H.; Heller, M.O.; Taylor, W.R. Kinematic measures for assessing gait stability in elderly individuals: a systematic review. Journal of the Royal Society, Interface 2011, 8, 1682–1698. [Google Scholar] [CrossRef]
  11. Watson, F.; Fino, P.C.; Thornton, M.; Heracleous, C.; Loureiro, R.; Leong, J.J.H. Use of the margin of stability to quantify stability in pathologic gait – a qualitative systematic review. BMC Musculoskeletal Disorders 2021, 22, 597. [Google Scholar] [CrossRef]
  12. Kędziorek, J.; Błażkiewicz, M. Nonlinear Measures to Evaluate Upright Postural Stability: A Systematic Review. Entropy (Basel) 2020, 22. [Google Scholar] [CrossRef]
  13. Yentes, J.M.; Raffalt, P.C. Entropy Analysis in Gait Research: Methodological Considerations and Recommendations. Annals of biomedical engineering 2021, 49, 979–990. [Google Scholar] [CrossRef]
  14. Brachman, A.; Sobota, G.; Bacik, B. The influence of walking speed and effects of signal processing methods on the level of human gait regularity during treadmill walking. BMC Sports Science, Medicine and Rehabilitation 2022, 14, 209. [Google Scholar] [CrossRef]
  15. Ahmadi, S.; Sepehri, N.; Wu, C.; Szturm, T. Sample Entropy of Human Gait Center of Pressure Displacement: A Systematic Methodological Analysis. Entropy 2018, 20, 579. [Google Scholar] [CrossRef]
  16. Ahmadi, S.; Wu, C.; Sepehri, N.; Kantikar, A.; Nankar, M.; Szturm, T. The Effects of Aging and Dual Tasking on Human Gait Complexity During Treadmill Walking: A Comparative Study Using Quantized Dynamical Entropy and Sample Entropy. Journal of biomechanical engineering 2018, 140. [Google Scholar] [CrossRef]
  17. Yentes, J.M.; Denton, W.; McCamley, J.; Raffalt, P.C.; Schmid, K.K. Effect of parameter selection on entropy calculation for long walking trials. Gait Posture 2018, 60, 128–134. [Google Scholar] [CrossRef] [PubMed]
  18. Promsri, A.; Longo, A.; Haid, T.; Doix, A.M.; Federolf, P. Leg Dominance as a Risk Factor for Lower-Limb Injuries in Downhill Skiers-A Pilot Study into Possible Mechanisms. International journal of environmental research and public health 2019, 16. [Google Scholar] [CrossRef] [PubMed]
  19. Goldberger, A.L.; Rigney, D.R.; West, B.J. Chaos and fractals in human physiology. Sci Am 1990, 262, 42–49. [Google Scholar] [CrossRef] [PubMed]
  20. Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. American journal of physiology. Regulatory, integrative and comparative physiology 2002, 283, R789–797. [Google Scholar] [CrossRef]
  21. Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. American journal of physiology. Heart and circulatory physiology 2000, 278, H2039–2049. [Google Scholar] [CrossRef] [PubMed]
  22. McCamley, J.D.; Denton, W.; Arnold, A.; Raffalt, P.C.; Yentes, J.M. On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data. Entropy 2018, 20, 764. [Google Scholar] [CrossRef] [PubMed]
  23. Stergiou, N.; Harbourne, R.; Cavanaugh, J. Optimal movement variability: a new theoretical perspective for neurologic physical therapy. Journal of neurologic physical therapy : JNPT 2006, 30, 120–129. [Google Scholar] [CrossRef] [PubMed]
  24. Khandoker, A.H.; Palaniswami, M.; Begg, R.K. A comparative study on approximate entropy measure and poincaré plot indexes of minimum foot clearance variability in the elderly during walking. J Neuroeng Rehabil 2008, 5, 4. [Google Scholar] [CrossRef]
  25. Tochigi, Y.; Segal, N.A.; Vaseenon, T.; Brown, T.D. Entropy analysis of tri-axial leg acceleration signal waveforms for measurement of decrease of physiological variability in human gait. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 2012, 30, 897–904. [Google Scholar] [CrossRef]
  26. Hak, L.; Houdijk, H.; Steenbrink, F.; Mert, A.; Wurff, P.; Beek, P.; Van Dieen, J. Stepping strategies for regulating gait adaptability and stability. Journal of biomechanics 2013, 46. [Google Scholar] [CrossRef]
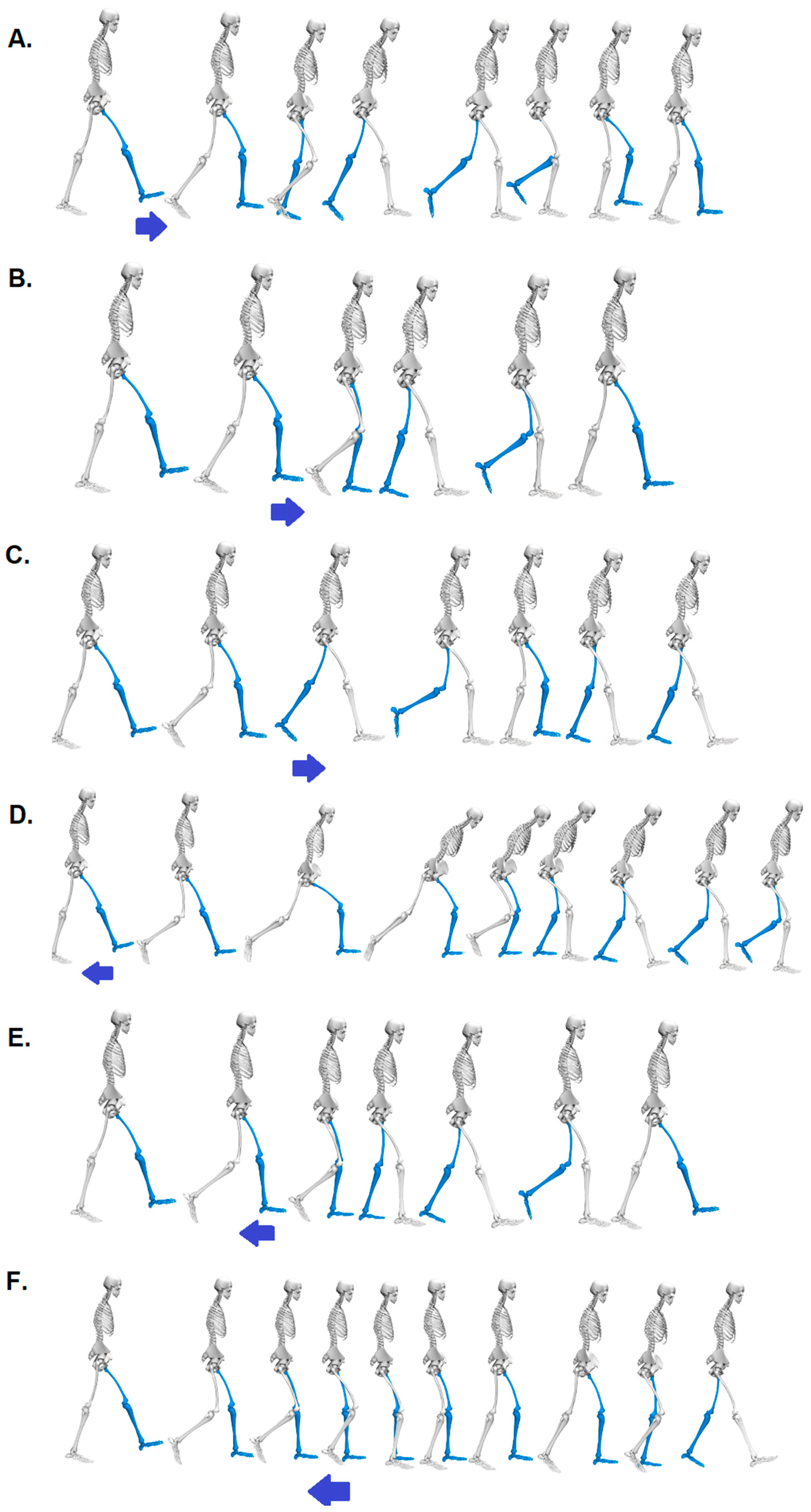
Preprints 91716 g001
Figure 1. Visualization of the response to the six perturbation possibilities, including the key behavioural elements for treadmill acceleration (arrow pointing to the right) in phases: A. Initial Contact, B. Mid Stance, C. Pre-Swing and for treadmill deceleration (arrow pointing to the left) in phases: D. Initial Contact, E. Mid Stance, F. Pre-Swing.
Figure 1. Visualization of the response to the six perturbation possibilities, including the key behavioural elements for treadmill acceleration (arrow pointing to the right) in phases: A. Initial Contact, B. Mid Stance, C. Pre-Swing and for treadmill deceleration (arrow pointing to the left) in phases: D. Initial Contact, E. Mid Stance, F. Pre-Swing.
Preprints 91716 g001
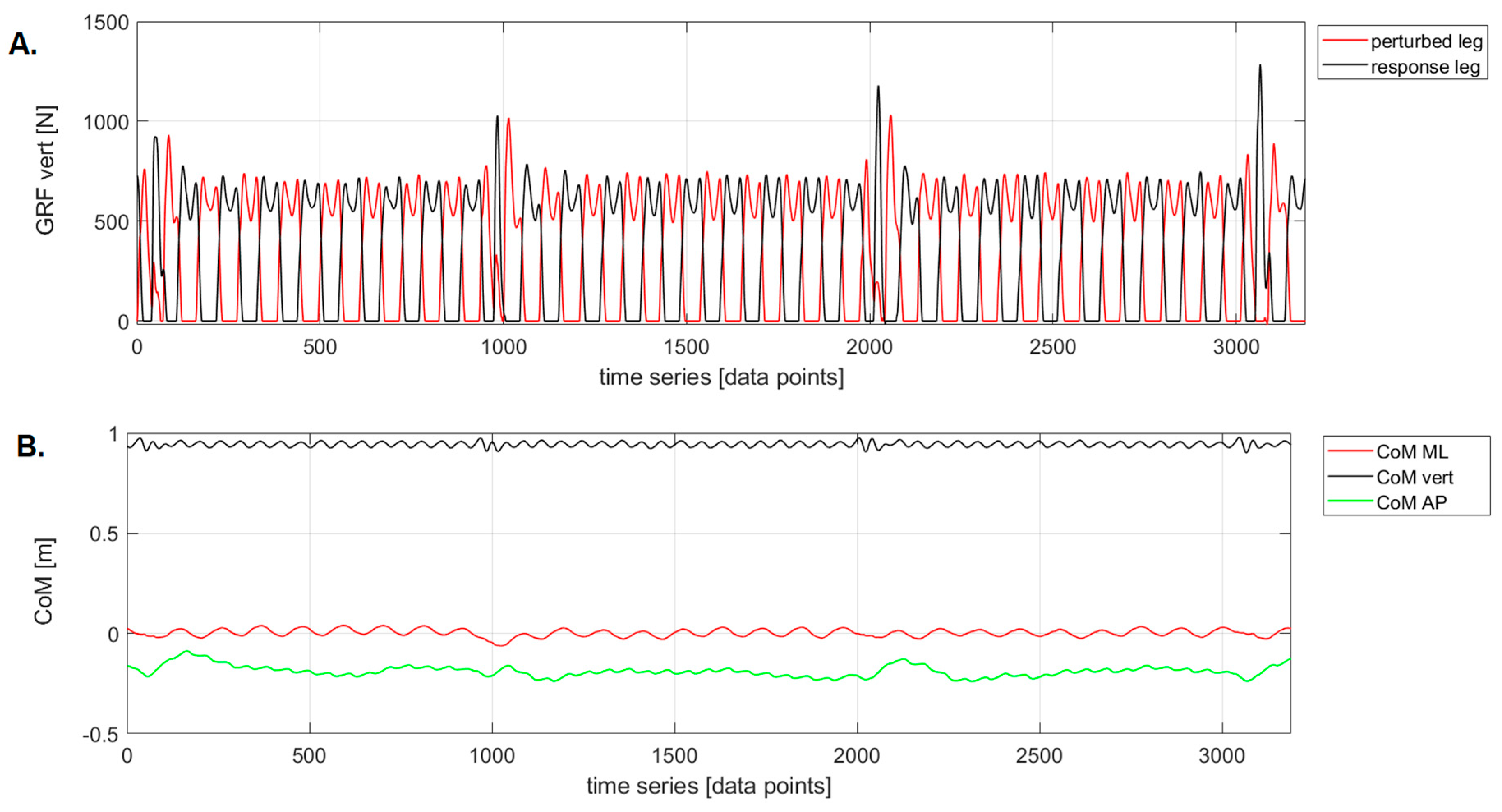
Preprints 91716 g002
Figure 2. An example of raw data for treadmill acceleration during the Pre-Swing phase: A. vertical ground reaction force trajectories (GRF_vert), B. Center of Mass (CoM) trajectories for medial-lateral (ML), vertical (vert), and anterior-posterior (AP) displacements.
Figure 2. An example of raw data for treadmill acceleration during the Pre-Swing phase: A. vertical ground reaction force trajectories (GRF_vert), B. Center of Mass (CoM) trajectories for medial-lateral (ML), vertical (vert), and anterior-posterior (AP) displacements.
Preprints 91716 g002
Preprints 91716 g003
Figure 3. The impact of varying vector length (m) on median Sample Entropy (SampEn) values calculated for the Center of Mass (CoM) across different perturbations possibilities in A. medio-lateral (ML), B. vertical (vert), and C. anterior-posterior (AP) directions. Statistical significance at the p < 0.001 level is shown at the bottom.
Figure 3. The impact of varying vector length (m) on median Sample Entropy (SampEn) values calculated for the Center of Mass (CoM) across different perturbations possibilities in A. medio-lateral (ML), B. vertical (vert), and C. anterior-posterior (AP) directions. Statistical significance at the p < 0.001 level is shown at the bottom.
Preprints 91716 g003
Preprints 91716 g004
Figure 4. Sample Entropy values for each perturbation possibility in the medio-lateral direction as a function of the value of m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Figure 4. Sample Entropy values for each perturbation possibility in the medio-lateral direction as a function of the value of m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Preprints 91716 g004
Preprints 91716 g005
Figure 5. Sample Entropy values for each perturbation possibility in the vertical direction for various m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Figure 5. Sample Entropy values for each perturbation possibility in the vertical direction for various m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Preprints 91716 g005
Preprints 91716 g006
Figure 6. Sample Entropy values for each perturbation possibility in the anterior-posterior direction as a function of the value of m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Figure 6. Sample Entropy values for each perturbation possibility in the anterior-posterior direction as a function of the value of m. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. In the table, blue values indicate the minimal Sample Entropy values, and red - the maximal ones.
Preprints 91716 g006
Preprints 91716 g007
Figure 7. Differences between SampEn values calculated for m = 2, 4, 6, 8, 10 for comparable directions (ML, vert, AP) for each of the six perturbation possibilities: A. Acc_ToeOff, B. Acc_Mid, C. Acc_Initial, D. Dec_ToeOff, E. Dec_Mid, F. Dec_Initial. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points.
Figure 7. Differences between SampEn values calculated for m = 2, 4, 6, 8, 10 for comparable directions (ML, vert, AP) for each of the six perturbation possibilities: A. Acc_ToeOff, B. Acc_Mid, C. Acc_Initial, D. Dec_ToeOff, E. Dec_Mid, F. Dec_Initial. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points.
Preprints 91716 g007
Table 1. Description of applied perturbations.
Table 1. Description of applied perturbations.
Perturbation type Phase of the gait cycle Labelling /
Perturbation possibilities
Acceleration Initial Contact Acc_Initial
Mid Stance Acc_Mid
Pre-Swing Acc_ToeOff
Deceleration Initial Contact Dec_Initial
Mid Stance Dec_Mid
Pre-Swing Dec_ToeOff
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated