Prerpints.org logo
Preprint
Article

Effects of Recurrent Selection on Population Structure and Allele Frequencies in the M3S Maize Population

Altmetrics

Downloads

61

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (109.30KB )

Submitted:

29 November 2023

Posted:

29 November 2023

You are already at the latest version

Alerts
Abstract
The effects of four cycles of recurrent selection on simple sequence repeat (SSR) marker allele frequencies and population structure were examined in the Maksimir 3 Synthetic (M3S) maize population (Zea mays L.). Genotyping of 32 plants from each cycle of selection at 38 SSR loci revealed that the mean number of alleles per locus and the mean expected heterozygosity were preserved over cycles of selection, indicating maintenance of sufficient genetic variability in the population needed for future genetic gain. Waples test of selective neutrality revealed that genetic drift was the main force in changing allele frequencies in the population. The proportion of selectively nonneutral loci in single cycles of selection varied between 16% and 37%. Some nonneutral loci shared the same genomic locations with previously published QTLs controlling important agronomic traits. Between 5% and 29% of loci were found to be in significant Hardy-Weinberg (HW) disequilibrium with the majority showing an excess of homozygosity. Excess of homozygosity at several loci was highly consistent across cycle populations suggesting positive assortative mating as the possible cause of the observed HW disequilibrium. Linkage disequilibrium (LD) tests revealed that the M3S population was essentially in linkage equilibrium. The proportion of pairs of loci in significant LD varied across cycles of selection between 0.1% and 1.8% probably due to the effects of genetic drift and epistatic selection.
Keywords: 
Subject: Biology and Life Sciences  -   Agricultural Science and Agronomy

1. Introduction

A broad class of selection methods referred to as recurrent selection (RS) use a cyclical approach to gradually increase the frequency of favorable alleles affecting quantitatively inherited traits in broad based plant populations while maintaining genetic variability for future selection [1]. The two primary forces affecting allele frequencies in RS programs are selection, which increases the frequencies of favorable alleles, and genetic drift, which is random change in allele frequencies due to small population sizes [2]. An expected effect of random genetic drift in a population is the dispersion of allele frequencies from intermediate values toward the extremes [3], the phenomenon, which has been observed in maize populations under RS [4,5,6,7]. Problems associated with finite population sizes, such as the fixation of undesirable alleles due to random genetic drift, affect response to selection [8], which implies a trade-off between short-term selection favoured by higher intensities and long-term selection favoured by higher effective population sizes [9]. A relevant question is the extent to which selection influences allele frequencies in a population subjected to recurrent selection. A number of studies have reported significant changes in allele frequencies at isozyme, RFLP, SSR and SNP marker loci due to selection [2,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Falke et al. [2], Coque and Gallais [12], and Wisser et al. [13] identified marker loci, whose allele frequencies were significantly changed by selection, to reside in genomic regions where QTLs affecting important maize agronomical traits had previously been identified. The observed correlation between allele frequency changes at markers linked to QTL and phenotypic performance indicated the possibility of using those markers in marker assisted breeding programs [2,12]. In addition to information on alleles subjected to selection, the extent of genetic diversity in improved selection cycles is also important information for breeders, because the future response of the population to selection depends on it. Significant decreases in genetic diversity as measured by the number of marker alleles per locus and expected heterozygosity (gene diversity) within populations that underwent RS have been reported in several studies [7,14,18,19,20,21,22]. On the other hand, Kolawole et al. [17] reported that the changes in the different measures of genetic diversity due to selection in two maize composites were either small or negligible.
RS methods were developed to gradually improve the mean performance of genetically broad-based populations and their incorporation in current breeding programs could facilitate the use of exotic germplasm [23] as well as locally adapted, but non-improved, germplasm [24] to increase the genetic base of maize breeding germplasm. Several researchers around the world, aware of the danger posed by the loss of genetic variability associated with the abandonment of landraces, made efforts to collect them before their total disappearance [25]. With the aim to exploit genetic variability existing in locally adapted maize germplasm from Southeast Europe, a synthetic maize population, named Maksimir 3 Synthetic (M3S), was developed at the Faculty of Agriculture, University of Zagreb (Croatia), by intercrossing 12 inbred lines originating from locally adapted open-pollinated varieties and landraces from different regions of the former Yugoslavia [26]. The 12 M3S progenitor lines showed equally good combining ability for grain yield with both the BSSS and the Lancaster testers [27], and the same level of isoenzymatic differences to both testers [28]. After its creation, M3S was subjected to four cycles of intrapopulation RS primarily for grain yield but the resistance to leaf and stalk diseases were also considered [26,29,30,31]. After two cycles of selection, grain yield increased slightly in the population per se, but selection was more effective in reducing inbreeding depression for grain yield [26]. After the third cycle of selection, Sabljo et al. [29] observed no further improvement in grain yield but stalk rot incidence significantly decreased. Bukan et al. [30] found a significant increase in grain yield after the fourth cycle of selection as well as evidence of the population’s increased specific adaptation to N deficient environments. Also, after application of RS methods, it appeared that the resistance to stalk rot diseases in the M3S population was maintained [31].
Šarčević et al. [6] examined changes in allele frequencies at nine SSR loci in the M3S maize population after two cycles of RS and found significant changes of allele frequencies at four loci. In some previous studies, including Šarčević et al. [6], genetic changes in populations under RS were assessed by comparing the starting (base) populations and the advanced populations developed through a certain number of selection cycles. However, according to Coque and Gallais [12], the primary question of interest when studying more than one cycle of selection is the test of whether allelic frequency changes are due to selection or genetic drift. To get a better insight into genetic changes of a population under RS, it would be useful to monitor the effects of selection on the molecular level from cycle to cycle. In the present study, we examined the M3S maize population at the molecular level after four cycles of RS by monitoring the selection response in each single cycle of selection using 38 SSR markers. Objectives of the study were to (1) investigate changes in allele frequencies in the population due to the effects of random genetic drift and selection and (2) investigate population structure with respect to Hardy–Weinberg (HW) disequilibrium at individual loci and linkage disequilibrium (LD) between pairs of loci within cycle populations.

2. Materials and Methods

2.1. Development of M3S cycle populations

The Maksimir 3 Synthetic (M3S) cycle 0 population (C0) was developed by intermating 12 maize inbred lines, whose origin traces back to several landraces and open-pollinated varieties from different regions of the former Yugoslavia [26]. Four cycles of intrapopulation recurrent selection (RS) primarily for grain yield were conducted in the M3S (Figure 1, Table S1).
In the first cycle, two-stage S1-S2 selection was performed with emphasis on disease resistance (Setosphaeria turcica and Colletotrichum graminicola (Ces) GW Wils) among S1 progenies and grain yield among S2 progenies resulting in the C1 population. In the second cycle, selection for higher grain yield was conducted among S1 progenies, resulting in the C2 population. In the third cycle, two selection methods, including evaluation of S1 and full-sib (FS) progenies, were conducted simultaneously to improve grain yield, resulting in two C3 populations, C3S1 and C3FS, respectively. The low response to selection observed in the C3S1 population [29] led to the fourth cycle of selection starting from the C3FS population, in which S1 progenies were evaluated simultaneously at low nitrogen fertilization (0 kg N ha-1) and high nitrogen fertilization (150 kg N ha-1), resulting in two C4 populations, C4N0 and C4N150, respectively. Details of the experimental procedures used in population synthesis and in the four cycles of selection have been described previously [26,29,30,31].

2.2. Simple sequence repeat (SSR) genotyping

Thirty-two plants randomly selected from each of the C0, C1, C2, C3S1, C3FS, C4N0 and C4N150 cycle populations of M3S were grown in a growth chamber. After about three weeks, DNA was extracted from each plant using a GenElute Plant Genomic DNA Miniprep Kit (Sigma-Aldrich, St. Louis, USA). Forty SSR primer pairs were chosen for analysis on the basis of previous polymorphism identification in M3S [6] and based upon genomic location in order to provide uniform coverage of all ten maize chromosomes. After an initial analysis, two markers were discarded because of poor amplification. Primer pairs were fluorescently labeled prior to polymerase chain reactions (PCRs). PCRs were performed in 15 μl final volumes containing 25 ng of template DNA, 1x PCR buffer with added 1.5 mM MgCl2, 0.2 μM of each of the forward and reverse primers, 0.2 mM of dNTPs, and 0.5 U of Taq polymerase (Sigma-Aldrich, St. Louis, USA). Reactions were carried out on a Veriti 96-Well Fast Thermal Cycler (Applied Biosystems, Foster City, USA). Reactions were denatured at 95 ºC for 2 min, followed by 30 cycles of 92 ºC for 1 min, 55 ºC for 1 min, and 72 ºC for 2 min. This was followed by a final extension step at 72 ºC for 10 minutes. Diluted PCR products (in ddH20) were mixed with 8.75 μlHiDi and 0.25 μlGenescan 500 LIZ size standard, centrifuged, denatured at 95 ºC for 5 min, and placed on ice. Fragment analysis was performed using an ABI 3130 Genetic Analyzer (Applied Biosystems, Foster City, USA). For detection of allele sizes, GeneMapper 4.0 software (Applied Biosystems, Foster City, USA) with sizing algorithm “2nd order least square” was used.

2.3. Statistical analysis of the SSR data

The total number of SSR alleles (At) amplified for each locus for each cycle population was determined. Allele frequencies were estimated using the software package Genealex 6 [32]. Waples test of temporal variation in allele frequency [33] was used to test selective neutrality of alleles at 38 SSR loci from cycle to cycle, as well as after four cycles of selection. The Waples method tests the hypothesis that observed differences in allele frequency can be explained entirely by sampling processes, both in choosing gametes to form the next generations (genetic drift) and in choosing the sample for genetic analysis (sampling error). Loci with one or more nonneutral alleles (rejecting the null hypothesis of the Waples test) were designated as nonneutral loci. The effective population size (Ne) for the particular cycle of selection was assumed to be equal to the number of intermated progenies (N) in that cycle. Because S2 progenies were intermated in the first cycle of selection, Ne for the first cycle of selection was corrected by multiplying N with the term 1/(1+Fp), where Fp=0.5 is the inbreeding coefficient of the parental generation (S1) from which the S2 progenies were produced [34]. The Ne after four cycles of selection was calculated as the harmonic mean of the Ne values from individual cycles of selection [3].
For each cycle population the mean number of alleles per locus (Am), the observed heterozygosity (Ho) and the expected heterozygosity (He) were calculated. Wright’s fixation index was estimated using the formula FIS = 1−(Ho/He) to quantify the lack or excess of heterozygosity. Significant deviations from Hardy-Weinberg (HW) equilibrium at individual loci were detected using the likelihood-ratio G test [35]. The significance of linkage disequilibrium (LD) between pairs of alleles from different loci was determined using the χ2 test outlined by Weir [36]. Calculations of Ho, He and FIS as well as HW equilibrium and LD tests were performed using the software package Popgene 1.31 [37].
To compare observed proportions of pairs of loci in significant LD involving linked vs. unlinked loci, as well as nonneutral vs. neutral loci (based on Waples neutrality test) in a particular cycle population, we derived two equations (1 and 2).
The probability that the two randomly selected loci are linked ( P l l ) was calculated as the number of possible pairs involving linked loci relative to the number of possible pairs involving all loci (Equation 1):
P l l = ∑ i = 1 10   n i ( n i − 1 ) N ( N − 1 )
where n i is the number of loci at the i-th chromosome and N is the total number of loci. The probability that the two randomly selected loci are nonneutral P n n l was calculated as the ratio of the number of possible pairs of nonneutral loci and the number of possible pairs of all loci (Equation 2):
P n n l = n n n l   ( n n n l − 1 ) N ( N − 1 )
where n n n l is the number of nonneutral loci and N is the total number of loci. The derivation of equations 1 and 2 is shown in Appendix A.
In order to detect differences in distribution of multilocus genotypes among and within the cycles of selection, we performed an analysis of molecular variance (AMOVA) [38] using Arlequin 3.5 [39]. The sources of variation included seven cycle populations (C0, C1, C2, C3S1, C3FS, C4N0 and C4N150) and 224 plants representing the entire sample. The pairwise fixation index, ΦST provides an indication of the genetic distance between cycle populations [12]. Significance of the average fixation index, as well as of each pairwise ΦST value, was obtained after 1023 permutations.

3. Results

3.1. Diversity statistics and allele frequency

The 38 SSR primer pairs generated a total of 133 different alleles (average of 3.5 alleles per locus) across seven M3S cycle populations. The number of alleles per locus varied from two to seven. The total number of alleles (At) for individual cycle populations varied from 123 (mean of 3.2 alleles per locus) found for C3FS to 130 (mean of 3.4 alleles per locus) found for C1 and C2, although the differences were not significant (Table 1). Mean expected heterozygosity (He) ranged from 0.49 in C4N150 to 0.53 in C1, but observed differences among cycle populations were not found to be significant. Six alleles found in advanced cycle populations were not found in the original base population (C0). Seventeen alleles from 13 loci which were present in C0 were absent from one or more improved cycle populations. Most of these alleles were found in low frequencies (less than 0.10) in the base population.
Mean allele frequencies remained unchanged (0.29 ± 0.02) after four cycles of selection, but the shape of the frequency distribution changed slightly (Table 2). Generally, slightly higher percentages of alleles with low (≤ 0.10) and high (> 0.80) frequencies were observed in improved cycle populations relative to the base population.
The number of nonneutral loci detected by the Waples test varied among single cycles of selection from six (as found between C2 and C3S1) to 14 (as found between C2 and C3FS), (Table 3). In the fourth cycle of selection more nonneutral loci were found for C4N150 than for C4N0 (nine vs. seven). However, cumulative changes in allele frequency over four selection cycles revealed a higher number of nonneutral loci for C4N0 (six) than for C4N150 (three). Considering single cycles of selection, nonneutral loci were found on all ten maize chromosomes, with the lowest incidence on chromosome 6 (four cases) and the highest incidence on chromosome 1 (nine cases). The occurrence of nonneutral loci was inconsistent across cycles of selection but discrepancies were also observed between neutrality status of loci after four cycles of selection and their neutrality status across individual cycles of selection. Out of 38 loci 28 were nonneutral in at least one single cycle, five were nonneutral across three cycles and none of them were nonneutral across all four cycles of selection. Even in cases where a particular marker locus was recognized as nonneutral over several cycles of selection, there was inconsistency in the neutrality status of different alleles at these loci (Table S2).

3.2. Analysis of molecular variance (AMOVA)

Analysis of molecular variance indicated 5.6% of genetic variation to be among and 94.4% to be within M3S cycle populations. The average fixation index, ΦST, commonly used to estimate the amount of differentiation in population subdivisions [19], was 0.0559. The pairwise ΦST values between cycle populations, here interpreted as genetic distance between them, were all significant (Table 4).
The highest ΦST was observed between C1 and C3FS (0.0872), followed by ΦST observed between C1 and C4N150 (0.0843). Lowest ΦST values were determined between C2 and C3S1 and between C4N0 and C4N150 (0.0143). The highest mean ΦST value of a cycle population to the remaining cycle populations was observed for C1.

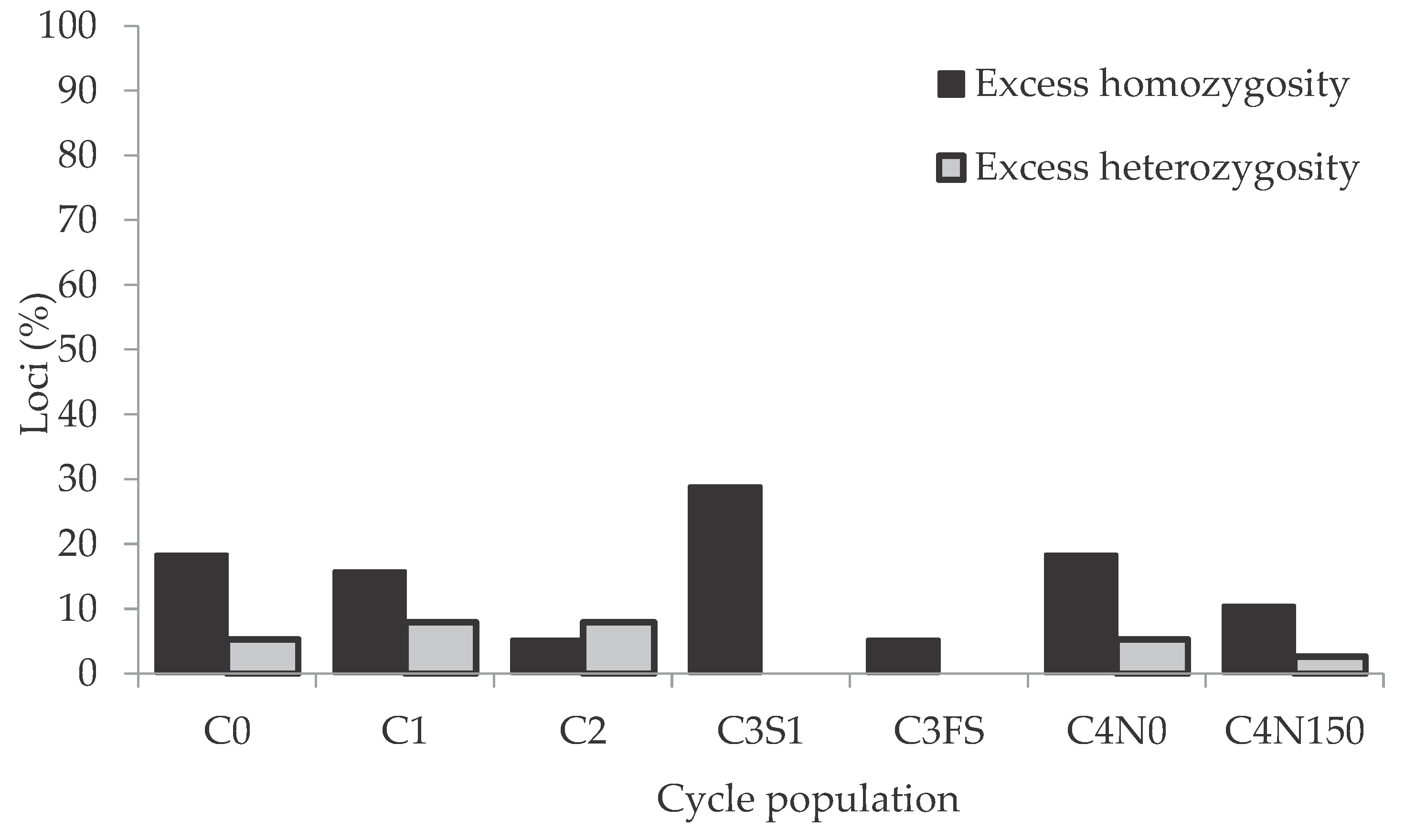
3.3. Hardy-Weinberg (HW) disequilibrium

The number of loci that were not in HW equilibrium varied across M3S cycle populations from two (5%), observed in C3FS, to 11 (29%), observed in C3S1 (Figure 2). Most of them showed an excess of homozygotes.
In total 26 SSR loci (68%) were identified to be in significant HW disequilibrium in at least one cycle population and such loci were found on all chromosomes except chromosome 3 (Table S3). Fixation indices (FIS) for six loci, which were not in HW equilibrium in three or more of the cycle populations, are shown in Table 5. Two of these loci (bnlg143 and phi050) showed significant excess of homozygosity (positive FIS value) in five and one locus (bnlg572) in six of seven cycle populations. All six loci had a positive FIS, averaged over populations, with the highest value observed for the locus bnlg572 (0.65).

3.4. Linkage disequilibrium (LD)

In the base population (C0), three (0.4%) out of 703 possible pairs of loci were in significant LD (Table 6). The number of significant LD tests in improved cycle populations varied between only one (0.1%) in C3S1 to 13 (1.8%) in C1. Out of three pairs of loci found to be in significant LD in C0, only one pair (which included two linked loci on chromosome 8), was found to be later in LD (in C3FS). Beside this pair, eight cases of newly generated LD between linked loci were found in improved cycle populations. However, the majority of the newly generated LD involved unlinked loci. The proportions of marker pairs in LD across cycle populations involving linked loci were 0.33 (C0), 0.23 (C1), 0.00 (C2), 1.00 (C3S1), 0.43 (C3FS), 0.40 (C4N0), and 0.25 (C4N150), which is in most cases more than three times higher than the probability that the two randomly selected loci were linked (0.08, according to Equation 1).
Some loci were found more frequently to be in significant LD, like bnlg197 and phi015 (in five and four out of seven cycle populations, respectively), but there were only three pairs of loci in significant LD, which were found at the same time in two or more improved cycle populations (dupssr12 and phi015 in C1 and C4N0; bnlg197 and dupssr12 in C1, C2 and C4N150; and bnlg128 and phi033 in C1 and C3FS). Most pairs of loci found to be in significant LD in improved cycle populations included one or both nonneutral loci (according to Waples neutrality test). The observed proportion of LD pairs including both nonneutral loci, was at least three times higher than expected (according to Equation 2) in four out of five improved cycle populations (C3S1 was not considered because only one test was significant), with observed to expected ratio being 0.31:0.11, 0.25:0.08, 0.43:0.13, 0.00:0.03 and 0.50:0.05 for C1, C2, C3FS, C4N0 and C4N150, respectively.

4. Discussion

4.1. Diversity statistics and allele frequency

In the present study, the effects of four cycles of recurrent selection on simple se-quence repeat (SSR) marker allele frequencies and population structure were examined in the Maksimir 3 Synthetic (M3S) maize population. The variability of the C0 population, in terms of mean number of alleles per locus and expected heterozygosity, was in the order of magnitude of starting population of other RS programs [5,7,9,14,19].
The mean number of alleles per locus and mean expected heterozygosity did not change significantly in the M3S population after four cycles of RS. Similarly, in the study of Wisser et al. [40], neither of the two diversity measures, revealed by SSR markers, changed significantly after four cycles of RS for quantitative disease resistance in a complex maize population from CIMMYT. Kolawole et al. [17] and Wisser et al. [40] reported that the changes in different measures of SNP diversity were either small or negligible in maize populations under recurrent selection. In the study by Daas et al. [41], the genetic diversity of the two maize populations also did not change significantly after two cycles of genomic selection. On the contrary, Labate et al. [18] and Hinze et al. [19] observed significant decreases in the mean number of alleles per locus and expected heterozygosity in the BSSS and BSCB1 populations after 12 and 15 cycles of reciprocal RS, respectively. A decrease in marker diversity (in terms of number of polymorphic loci, mean number of alleles per locus, expected heterozygosity, or observed heterozygosity) within maize populations, that underwent various numbers of RS cycles, has also been reported by several previous studies [7,14,20,21,22,42,43,44,45,46,47].
In the present study, some alleles found in the base population (C0) were absent from subsequent cycle populations, while some alleles absent from the base population were detected in one or more subsequent cycle populations. Most of the missing alleles were generally found at low frequencies (less than 0.10), similarly like in the study of McLean-Rodríguez et al. [48], where most of the lost or gained alleles over time in 13 Mexican landraces had rare or low frequency. Such rare alleles may not have been detected in the particular cycle population in the present study because of the relatively small sample size (32 plants per cycle population genotyped), which was also the case in the study by McLean-Rodriguez et al. [48], who sampled only 10 plants per population. Nevertheless, our sample size is similar to the sample size of 30 plants used for SSR analysis of the BSSS and BSCB1 populations studied by Hinze et al. [19]. In an earlier study, Labate et al. [18] genotyped 100 individuals of the same two maize populations using RFLP markers and reported higher estimates of the average number of alleles per locus, expected heterozygosity, heterozygous plants, and number of unique alleles, which reflects not only the differences between the two types of markers used in the two studies (RFLPs versus SSRs), but also the power of larger samples in detecting less frequent alleles [19]. Although the sample size of 32 genotyped plants per population in the present study was relatively small, it is comparable to sample sizes reported in some previous studies in maize using SSR markers [17,18] as well as SNP markers [19,20,48], which ranged from 10 to 36 individuals per population. The possible role of pollen or seed contamination during the development of the M3S cycle populations can also not be ruled out, however.
In improved M3S cycle populations as compared to C0, the mean allele frequency did not change, although slightly higher proportions of alleles with low and with high frequencies were found. Similar changes of allele distribution after various cycles of RS in maize have been earlier found by Labate et al. [4], Pinto et al. [5], and Šarčević et al. [6], whereas Kolawole et al. [17] reported the opposite, a decrease of proportion of alleles at both low and high frequencies and an increase of those at intermediate frequencies.
Changes in allele frequencies from cycle to cycle as well as after four cycles of selection in M3S as determined by Waples test were mainly attributable to the effects of random genetic drift. Similar results were reported in previous studies examining changes in allele frequencies in maize populations undergoing RS [2,4,5,43]. Assuming the value of Ne=N, the Waples test identified six (16%) and three (8%) nonneutral loci after four cycles of selection from C0 to C4N0 and C4N150, respectively (Table 3). The number of nonneutral loci in single cycles varied between six (16%) as found between C2 and C3S1, to 14 (37%) as found between C2 and C3FS. Labate et al. [4] observed 17% nonneutral loci in BSSS(R) and BSCB1(R) populations after 12 cycles of reciprocal RS. Pinto et al. [5] reported significant allele frequency changes due to selection at 13% and 7% of SSR loci in two tropical maize synthetics that underwent a single cycle of high intensity reciprocal RS. Falke et al. [2] detected 20.13% nonneutral loci in one and 12.87% in a second biparental maize population after four and seven cycles of intrapopulation RS, respectively. In these studies, loci with significant allele frequency changes due to selection were not confined to particular chromosomes or genomic regions but were dispersed over the whole genome. In our study, selectively nonneutral loci were found on all ten maize chromosomes, as well, but their number and chromosomal position varied among cycles of selection. The occurrence of nonneutral loci was inconsistent among the four cycles of selection but discrepancies were also observed between neutrality status of loci after four cycles of selection and their neutrality status across individual cycles of selection (Table S2). Even in cases where a particular marker locus was recognized as nonneutral over several cycles of selection in the M3S population, there was inconsistency in the neutrality status of different alleles at these loci. In addition to selfed progeny RS (used through all four cycles of selection), FS RS was implemented in the third cycle and, in addition to yield, other traits such as disease resistance in the first and N use efficiency in the fourth selection cycle were considered. These factors might have contributed to selection pressure on different QTLs during the four selection cycles in the M3S population. According to Wisser et al. [13] the most important drawback to selection mapping of an individual trait arises if selection is exerted for multiple traits, which is typically the case in breeding populations used for production. In such cases, selection mapping will not distinguish loci responding to a particular selection pressure.
It has also been shown that the effect of QTLs on trait values can vary among environments [49,50], thus causing significant QTL × environment interaction (QEI). Because selection of progenies for recombination in different cycles of RS in the M3S population were based on data collected in different sets of environments, QEI may have influenced the inconsistency in results of neutrality tests between individual cycles of selection. The reason for this, beside QEI, could be the fact that more than two alleles (up to seven) were found in the population at these marker loci. Thus, it can be assumed that more than one marker allele per locus was initially (in the base population) linked to favorable as well as unfavorable alleles at a particular QTL, leading to random changes of frequencies within the two groups of marker alleles as a result of selection pressure at that QTL.
The C1 cycle population of M3S was created by intermating the highest yielding S2 progenies after stringent selection for disease resistance among the preceding S1 progenies. The applied two-stage selection method resulted in a population with the highest mean ΦST value (Table 4) between a single cycle population and all other cycle populations (mean ΦST= 0.067). The selection for two generally negatively correlated traits might increase genetic distance of C1 to other cycle populations developed through selection for yield only. The observed differentiation of C1 based upon molecular data was also observed on the phenotypic level reported by Bukan et al. [30] (decreased yield of C1 at both N fertilization levels investigated). Yield decreases after primary selection for pest resistance was also reported by Devey and Russell [51] and Klenke et al. [52]. Butrón et al. [43] found a significant linear trend for departure from the random genetic drift model for some allelic versions of the two SSR markers, umc1329 and phi076, in their study of molecular changes in the maize composite during selection for resistance to pink stem borer. In the C1 population of M3S, a significant nonneutral SSR marker was also phi076. In the third cycle of selection, a high difference in the number of nonneutral markers was observed between the S1 and FS methods of selection (14 versus six from C2 to C3FS, and from C2 to C3S1, respectively). The higher number of nonneutral markers found for the FS method is in accordance with the higher yield and disease resistance observed for C3FS in comparison to C3S1 [29]. The pairwise ΦST values between C3S1 and C3FS (Table 4) showed divergence of the two populations from each other, confirming different effects of the two methods of selection applied in the third cycle. In the fourth cycle of selection, we observed higher number of nonneutral SSR loci in the C4N150 than in the C4N0 (nine vs. seven from C3FS to C4N150 and from C3FS to C4N0, respectively). Coque and Gallais [12] also found more SSR loci to be under selection in high N fertility environments. The same authors found that the two genomic regions responding to selection were common to both high N and low N conditions, which, according to them, corroborates the observation of Bertin and Gallais [53] that grain yield QTLs detected in low N conditions were very often a subset of QTLs detected in high N conditions, but probably differentially expressed. Three SSR markers used by Coque and Gallais [12] were located in genomic regions found to be associated with grain yield, N uptake, and kernel number under both high and low N conditions (bnlg1643); grain yield and kernel weight under low N conditions (umc1653); and N utilization efficiency under both high and low N conditions (bnlg1402). Those three SSR markers share the same bin location (1.08, 6.07 and 9.02, respectively) as the three selectively nonneutral SSR markers (dupssr12, phi123 and umc1033) in the fourth cycle of selection of the present study, which was conducted under contrasting N fertilization regimes. The C4N0 cycle population, besides exhibiting possible adaptation to low N conditions, also exhibited a significant reduction of anthesis-silking interval (ASI) in comparison to earlier cycle populations [30]. Two SSR loci which were selectively nonneutral in C4N0 (dupssr12 and phi438301) had the same bin location (1.08 and 4.05, respectively) as RFLP and SSR markers previously found to be associated with QTL affecting ASI in diverse sets of environments [54]. Recent studies [55,56] also reported that significant SNP bases and QTLs for ASI-delay due to drought or high-density stress were located on chromosomes 1 and 4.

4.2. Hardy-Weinberg (HW) disequilibrium

In the present study, loci which were in significant HW disequilibrium, in most cases, exhibited an excess of homozygosity, which is consistent with the results reported in previous studies [9,14,19,20,43,57]. Factors like sample size used during random mating and sample size used to estimate HW equilibrium [57], or genotyping errors [19] might affect departure from HW equilibrium in the M3S cycle populations in both directions, towards excess of homozygosity as well as heterozygosity. On the other hand, positive assortative mating within a population due to genotypic differences in flowering time is expected to increase homozygosity in the population [3]. The excess of homozygosity at several loci (bnlg143, bnlg572, and phi050) was highly consistent across M3S cycle populations, suggesting a possible role for positive assortative mating in the observed departure from HW equilibrium at these loci. One of these loci (bnlg572), which showed an excess of homozygosity (positive FIS value) in 7 out of 7 M3S cycle populations, shared the same bin location (7.03) as the SSR locus phi114, which had positive fixation index in nine out of nine maize populations studied by Ordas et al. [9]. Similarly, SSR loci bnlg572 and phi050, which showed the excess of homozygosity over cycles of selection in the M3S population, had the same bin locations (7.03 and 10.03, respectively) as SNP markers previously found to be associated with QTLs for flowering time-related traits [55].

4.3. Linkage disequilibrium (LD)

The LD test revealed that the M3S population, across cycles of selection, was essentially in linkage equilibrium with the number of significant LD tests varying between only one (0.14%) in C3S1 to 13 (1.85%) in C1. For the three pairs of loci found to be in LD in the base population (C0), we assumed to originate either from parental LD or that they were created during population maintenance by chain sib-mating. In all but one case of observed LD in improved cycle populations (from C1 to C4), the instances of LD were not found in the C0 population and must have been generated over the course of the RS program. The total number of pairs of markers in LD generally increased with selection, which is consistent with the results reported for other populations improved through RS [7,14,17,43]. Theoretically, LD in a population can arise from intermixture of populations with different allele frequencies, by chance in small populations (random genetic drift), from selection favoring one combination of alleles over another (epistatic selection), or assortative mating [3,58]. On the other hand, hitchhiking may lead to an increase but also a decrease of LD between two neutral loci linked to a locus experiencing positive directional selection, depending on the position of that locus relative to two neutral loci [59]. In several previous studies, the LD generated during the course of recurrent selection in maize synthetic populations was suggested to result mainly from genetic drift [60], from natural selection for epistatic effects [57], or from selection for epistatic effects [7,9,14,57]. All above mentioned evolutionary forces could be involved in creating LD between loci in M3S population as well. In a single cycle of selection, it is expected that genetic drift would generate new LD between different loci regardless of whether they are linked or unlinked. According to the Equation 1 (given in the chapter Materials and Methods), generation of drift-related LD for each single cycle of selection is in favor of unlinked loci with the probability of the two randomly selected loci being linked of only 0.08. However, due to positive correlations between the rate of decay of LD and the recombination rate between the two loci [3], we can assume that the rate of LD decay in the M3S population due to intercrossing of selected progenies and seed multiplication of cycle populations was lower for linked than for unlinked loci. This can possibly explain the observed surplus of LD pairs including linked loci in the present study. Selection for favorable epistatic interactions may have also be involved in generating LD in the M3S population because of observed overrepresentation of nonneutral pairs among pairs of loci detected to be in significant LD (based on Equation 2 given in the chapter Materials and Methods).

5. Conclusions

The present study was undertaken to investigate changes in allele frequencies and population structure in the M3S maize population that was subjected to four cycles of phenotypic recurrent selection for grain yield and disease resistance. Proportions of nonneutral SSR loci detected by Waples test of selective neutrality varied among single cycles of selection from 16% to 37%. Multiple trait selection and changing methods of selection applied in the M3S population may have caused some discrepancies in the neutrality status of loci among cycles of selection. In addition, competition among multiple ‘positive’ and multiple ‘negative’ alleles at loci under selection (random changes of allele frequencies within selectively nonneutral loci) may have also affected consistency of the results. In this sense, multiple allelomorphism of SSR markers can be a constraint, which decreases the power of neutrality test to detect genomic regions controlling quantitative traits in multiparental synthetic populations used in RS programs. Most previous studies reporting changes in maize populations under recurrent selection at the molecular level used SSR markers, whereas only some recent studies used SNP-based assays. Due to their biallelic nature, SNP markers can overcome the inadequacy of multiallelic SSR markers observed in the present study in terms of unambiguous detection of nonneutral loci/alleles. In addition, due to their high abundance in plant genomes, SNPs are the marker of choice for future studies on the molecular basis of population response to selection. On the other hand, multiallelic SSR markers are much more informative than biallelic SNP markers [61] and are convenient for studying genetic diversity within and among populations including synthetics, landraces and inbred lines. The results of the present study indicated that the mean number of alleles per locus and average gene diversity (expected heterozygosity) was preserved over cycles of selection, indicating maintenance of sufficient genetic variability in the population required for future genetic gain. Furthermore, several SSR loci declared as nonneutral in the present study have previously been reported to be under selection or share the same genomic locations with previously published QTLs controlling important agronomic traits and can be implemented in marker assisted breeding programs.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1: Selection protocols for the four selection cycles conducted in the M3S maize population; Table S2: Allele frequencies (P), changes of allele frequencies (ΔP) at 38 SSR loci in seven cycle populations and results of Waples test of selective neutrality in single cycles and across four cycles of selection in the Maksimir 3 Synthetic (M3S) population.; Table S3: Observed heterozygosity (Ho), expected heterozygosity (He), intrapopulation inbreeding coefficient (FIS), and the test of Hardy-Weinberg disequilibrium (H-W test) for 38 SSR loci in seven cycle populations (C0, C1, C2, C3S1, C3FS, C4N0 and C4N150).

Author Contributions

Conceptualization, V.K. and H.Š.; methodology, M.B., V.K. and H.Š.; software, M.B., A.M., and H.Š.; validation, V.K., R.L. and D.Š.; formal analysis, M.B., A.M. and H.Š.; investigation, M.B. and A.M.; resources, V.K. and H.Š.; data curation, M.B., R.L. and H.Š.; writing—original draft preparation, M.B.; writing—review and editing, A.M., V.K., R.L., D.Š. and H.Š.; visualization, M.B. and H.Š.; supervision, V.K., R.L. and H.Š.; project administration, M.B. and V.K.; funding acquisition, V.K. and H.Š. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by European agricultural fund for rural development (EAFRD), Rural Development Programme, sub-measure 10.2.: Support for conservation, sustainable use and development of genetic resources in agriculture, and by the Croatian Ministry of Science, Education, and Sports, research grant No. 178-1780691-0690

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The number of different combinations of k items from n items (Ck (n)), set without repetition (order not important), can be calculated as:
k n = n k = n ! k ! ( n − k ) !
Considering the two-locus disequilibrium, we are interested in number of combinations of two items (two loci) from n items (total number of loci) and the above expression can be rewritten as follows:
C 2 n = n 2 = n ! 2 ! ( n − 2 ) ! = n   n − 1 n − 2 ( n − 3 ) … 2   n − 2 n − 3 … = n   n − 1 2  
We used the above-derived equation, to express the number of possible combinations of two loci (pairs of loci) considering all loci, only linked loci, and only nonneutral loci. Therefore, the number of possible combinations of two loci from total number of loci is:
N ( N − 1 ) 2
where N is the total number of loci.
Similarly, the number of possible combinations of two loci, including only linked loci, can be calculated as the sum of the number of possible combinations of two loci for each individual chromosome. Having 10 linkage groups (10 chromosomes), the equation is:
∑ i = 1 10 n i ( n i − 1 ) 2
where n i is the number of loci at the i-th chromosome.
In the same way, the number of possible combinations of two loci involving nonneutral loci is:
n n n l ( n n n l − 1 ) 2
where n n n l is the number of nonneutral loci.
By combining the equations derived above, the probability that two randomly selected loci are linked ( P l l ) can be calculated as the ratio of the number of possible combinations (pairs) comprising linked loci and the number of possible pairs comprising all loci (Equation 1):
P l l = ∑ i = 1 10   n i ( n i − 1 ) N ( N − 1 )
Similarly, the probability that the two randomly selected loci are nonneutral can be calculated as the ratio of the number of possible combination of nonneutral loci and the number of possible combinations of all loci (Equation 2):
P n n l = n n n l   ( n n n l − 1 ) N ( N − 1 )

References

  1. Hallauer, A.R.; Darah, L.L. Compendium of recurrent selection methods and their application. Crit. Rev. of Plant. Sci. 1985, 3, 1–33. [Google Scholar] [CrossRef]
  2. Falke, K.C.; Flachenecker, C.; Melchinger, A.E.; Piepho, H.-P.; Maurer, H.P.; Frisch, M. Temporal changes in allele frequencies in two European F2 flint maize populations under modified recurrent full-sib selection. Theor. Appl. Genet. 2007, 114, 765–776. [Google Scholar] [CrossRef] [PubMed]
  3. Falconer, D.S.; Mackay, T.F.C. Introduction to quantitative genetics, 4th edn. Longman Sci and Tech, Harlow, 1996.
  4. Labate, J.A.; Lamkey, K.R.; Lee, M.; Woodman, W. Temporal changes in allele frequencies in two reciprocally selected maize populations. Theor. Appl. Genet. 1999, 99, 1166–1178. [Google Scholar] [CrossRef]
  5. Pinto, L.R.; Vieira, M.C.L.; de Souza Jr., C.L.; de Souza, A.P. Reciprocal recurrent selection effects on the genetic structure of tropical maize populations assessed at microsatellite loci. Genet. Mol. Biol. 2003, 26, 355–364.
  6. Šarčević, H.; Pejić, I.; Barić, M.; Kozumplik, V. Originality of M3S maize population and changes in allele frequencies revealed by SSR markers after two cycles of selfed progeny recurrent selection. Euphytica 2008, 161, 97–105. [Google Scholar] [CrossRef]
  7. Peña-Asin, J.; Álvarez, A.; Ordas, B. Molecular changes during intra and inter recurrent selection of two populations of maize: one adapted and one non adapted to the selection environment. Euphytica 2013, 193, 359–367. [Google Scholar] [CrossRef]
  8. Weyhrich, R.A.; Lamkey, K.A.; Hallauer, A.R. Hallauer Effective Population Size and Response to S1-Progeny Selection in the BS11 Maize Population. Crop Sci. 1998, 38, 1149–1158. [Google Scholar]
  9. Ordas, B.; Malvar, R. A.; Diaz, R.; Butron, A. Molecular changes in two maize (Zea mays L.) synthetics after reciprocal selection with two alternative methods. Mol. Breeding 2015, 35, 111. [Google Scholar] [CrossRef]
  10. Stuber, C.W.; Moll, R.H.; Goodman, M.M.; Schaffer, H.E.; Weir, B.S. Allozyme Frequency Changes Associated with Selection for Increased Grain Yield in Maize (Zea Mays L.). Genetics 1980, 95, 225–236. [Google Scholar] [CrossRef] [PubMed]
  11. Heredia-Diaz, O.; Alsirt, A.; Darrah, L.L.; Coe, E.H. Allelic frequency changes in the MoSCSSS maize synthetic in response to bi-directional recurrent selection for rind penetrometer resistance. Maydica 1996, 41, 65–76. [Google Scholar]
  12. Coque, M.; Gallais, A. Genomic regions involved in response to grain yield selection at high and low nitrogen fertilization from a maize recombinant inbred line population. Theor. Appl. Genet. 2006, 112, 1205–1220. [Google Scholar] [CrossRef]
  13. Wisser, R.J.; Murray, S.C.; Kolkman, J.M.; Ceballos, H.; Nelson, R. Selection mapping of loci for quantitative disease resistance in a diverse maize population. Genetics 2008, 180, 583–599. [Google Scholar] [CrossRef]
  14. Romay, M.C.; Butrón, A.; Ordás, A.; Revilla, P.; Ordás, B. Effect of Recurrent selection on the genetic structure of two broad-based Spanish maize populations. Crop Sci. 2012, 52, 1493–1502. [Google Scholar] [CrossRef]
  15. Beissinger, T.M.; Hirsch, C.N.; Vaillancourt, B.; Deshpande, S.; Barry, K.; Buell, C.R.; Kaeppler, S.M.; Gianola, D.; de Leon, N. A Genome-wide scan for evidence of selection in a maize population under long-term artificial selection for ear number. Genetics 2014, 196(3), 829–840. [Google Scholar] [CrossRef] [PubMed]
  16. Hirsch, C.N.; Flint-Garcia, S.A.; Beissinger, T.M.; Eichten, S.R.; Deshpande, S.; Barry, K.; McMullen, M.D.; Holland, J.B.; Buckler, E.S.; Springer, N.; Bue, C.R.; de Leon, N.; Kaeppler, S.M. Insights into the effects of long-term artificial selection on seed size in Maize. Genetics 2014, 198(1), 409–421. [Google Scholar] [CrossRef] [PubMed]
  17. Kolawole, A.O.; Menkir, A.; Gedil, M.; Blay, E.; Ofori, K.; Kling, J.G. Genetic divergence in two tropical maize composites after four cycles of reciprocal recurrent selection. Plant Breeding 2017, 134, 41–47. [Google Scholar] [CrossRef]
  18. Labate, J.A.; Lamkey, K.R.; Lee, M.; Woodman, W. Molecular genetic diversity after reciprocal recurrent selection in BSSS and BSCB1 maize populations. Crop Sci. 1997, 37, 416–423. [Google Scholar] [CrossRef]
  19. Hinze, L.L.; Kresovich, S.; Nason, J.D.; Lamkey, K.R. Population genetic diversity in a maize reciprocal recurrent selection program. Crop Sci. 2005, 45, 2435–2442. [Google Scholar] [CrossRef]
  20. Solomon, K.F.; Martin, I.; Zeppa, A. Temporal genetic structure patterns in tropical maize populations under reciprocal recurrent selection. Euphytica 2010, 176, 239–249. [Google Scholar] [CrossRef]
  21. Gerke, J.P.; Edwards, J.W.; Guill, K.E.; Ross-Ibarra, J.; McMullen, M.D. The genomic impacts of drift and selection for hybrid performance in maize. Genetics 2015, 201, 1201–1211. [Google Scholar] [CrossRef] [PubMed]
  22. Lamkey, C.; Lorenz, A. Relative effect of drift and selection in diverging populations within a reciprocal recurrent selection program. Crop Sci. 2014, 54, 576–585. [Google Scholar] [CrossRef]
  23. Hallauer, A. L.; Carena, M. J. Recurrent selection methods to improve germplasm in maize. Maydica 2012, 57, 266–283. [Google Scholar]
  24. Romay, M.C.; Ordás, B.; Revilla, P; Ordás, A. Three cycles of reciprocal recurrent selection in two Spanish maize synthetics. Crop Sci. 2011, 51,1016–1022.
  25. Ordás, B.; Malvar, R.A.; Revilla, P.; Ordás, A. Effect of three cycles of recurrent selection for yield in four Spanish landraces of maize. Euphytica 2023, 219, 77. [Google Scholar] [CrossRef]
  26. Sarcevic, H.; Pejic, I.; Baric, M.; Kozumplik, V. Performance and inbreeding depression of an exotic maize population under selfed progeny recurrent selection. Die Bodenkultur 2004, 55, 21–24. [Google Scholar]
  27. Pejic, I.; Kozumplik, V. Possibility of using local maize genotypes for development of breeding populations (in Croatian). Agriculturae Conspectus Scientificus, 1990, 55, 307–314. [Google Scholar]
  28. Pejic, I. Heterotic complementarity and genetic diversity of domestic maize germplasm (in Croatian). Agriculturae Conspectus Scientificus 1992, 57, 3–4. [Google Scholar]
  29. Sabljo, A.; Šarčević, H.; Palaveršić, B.; Buhiniček, I.; Kozumplik, V.; Bukan, M.; Gunjača, J.; Beljo, J.; Tomasović, S.; Ikić, I. Improvement of grain yield and Fusarium stalk rot resistance in the M3S maize population by recurrent selection. Cereal Res. Commun. 2008, 36, 159–160. [Google Scholar]
  30. Bukan, M.; Šarčević, H.; Gunjača, J.; Buhiniček, I.; Palaveršić, B.; Sabljo, A.; Jambrović, A.; Lewis, R.S.; Kozumplik, V. Evaluation of nitrogen use efficiency in the Maksimir 3 Synthetic maize population. Maydica 2011, 56, 67–75. [Google Scholar]
  31. Bukan, M.; Šarčević, H.; Buhiniček, I.; Palaveršić, B.; Lewis, R.S.; Kozumplik, V. Stalk rot resistance in Maksimir 3 Synthetic maize population after four cycles of recurrent selection. Genetika 2013, 45(3), 921–928. [Google Scholar] [CrossRef]
  32. Peakall, R.; Smouse, P.E. GenAlEx 6: genetic analysis in Excel. Population genetic software for teaching and research. Mol. Ecol. Notes. 2006, 6, 288–295. [Google Scholar] [CrossRef]
  33. Waples, R.S. Temporal variation in allele frequencies: testing the right hypothesis. Evolution 1989, 43, 1236–251. [Google Scholar] [CrossRef]
  34. Sprague, G.F.: Eberhart, S.A. Corn breeding. In: Corn and corn improvement, Sprague, G.F.; Dudley, J.W.; Agron. Monogr. ASA, CSSA and SSSA, Madison, WI. 1977, 18, 305–362. [CrossRef]
  35. Sokal, R.R.; Rohlf, F.J. Biometry: The principles and practice of statistics in biological research. 3rd edition. W.H. Freeman, New York, (USA), 1995.
  36. Weir, B.S. Inferences about linkage disequilibrium. Biometrics 1979, 35, 235–254. [Google Scholar] [CrossRef]
  37. Yeh, F.C.; Boyle, T.J.B. Population genetic analysis of co-dominant and dominant markers and quantitative traits. Belg. J. Bot. 1997, 129, 157. [Google Scholar]
  38. Excoffier, L.; Smouse, P.E.; Quattro, J.M. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 1992, 131, 479–491. [Google Scholar] [CrossRef] [PubMed]
  39. Excoffier, L.; Lischer, H.E.L. Arlequin suite ver 3.5: A new series of programs to perform population genetics analyses under Linux and Windows. Mol. Ecol. Resour. 2010, 10, 564–567. [Google Scholar] [CrossRef] [PubMed]
  40. Wisser, R.J.; Fang, Z.; Holland, J.B.; Teixeira, J.E.C.; Dougherty, J.; Weldekidan, T.; de Leon, N.; Flint-Garcia, S.; Lauter, N.; Murray, S.C. The genomic basis for short-term evolution of environmental adaptation in maize. Genetics 2019, 213(4), 1479–1494. [Google Scholar] [CrossRef] [PubMed]
  41. Daas, R.R.; Vinayan, M.T.; Patel, M.B.; Phagna, R.K.; Singh, S.B.; Shahi, J.P.; Sarma, A.; Barua, N.S.; Babu, R.; Seetharam, K.; Burgueño, J.A.; Zaidi, P.H. Genetic gains with rapid-cycle genomic selection for combined drought and waterlogging tolerance in tropical maize (Zea mays L.). Plant Genome 2020, 13, e20035. [Google Scholar] [CrossRef]
  42. Pinto, L.R.; Vieira, M.C.L.; de Souza Jr., C.L.; de Souza, A.P. Genetic diversity assessed by microsatellites in tropical maize populations submitted to a high-intensity reciprocal recurrent selection. Euphytica 2003, 134, 277–286.
  43. Butrón, A.; Tarrío, R.; Revilla, V.; Ordás, A.; Malvar R. A. Molecular changes in the maize composite EPS12 during selection for resistance to pink stem borer. Theor. Appl. Genet. 2005, 110, 1044–1051. [CrossRef]
  44. Franzoni, J.; Scapim, C.A.; Beviláqua, M.R.R.; De Fátima Pires da Silva Machado, M.; Pacheco, C.A.P.; Mangolin, C.A. Application of microsatellite markers to evaluate the heterozygosity from the popcorn composite CMS-43 (Zea mays L.) during eight cycles of selection. Plant Breeding. 2012, 131, 479–485. [Google Scholar] [CrossRef]
  45. Li, L.; Chen, W.; Xiang, K.; Reid, L.M.; Lan, H.; Yang, K.C.; Zhang, M.; Pan, G.T.; Rong, T. The effect of 5 cycles of biparental mass selection on a narrow base maize population based on phenotype, combining ability, and SSR analyses. Maydica 2013, 58(3–4), 238–242.
  46. Guimarães, A.G.; Amaral Júnior, A.T.; Almeida Filho, J.E.; Pena, G.F.; Vittorazzi, C.; Pereira, M.G. Population structure and impact of recurrent selection on popcorn using EST-SSR markers. Acta. Sci. Agron., 2018, 40, e35218. [Google Scholar] [CrossRef]
  47. Ledesma, A.; Ribeiro, F.A.S.; Uberti, A.; Edwards, J.; Hearne, S.; Frei, U., Lübberstedt, T. Molecular characterization of doubled haploid lines derived from different cycles of the Iowa Stiff Stalk Synthetic (BSSS) maize population. Front. Plant. Sci. 2023, 14, 1226072. [CrossRef]
  48. McLean-Rodríguez, F. D.; Elston Costich, D.; Carolina Camacho-Villa, T.; Enrico Pè, M.; Dell’Acqua, M. Genetic diversity and selection signatures in maize landraces compared across 50 years of in situ and ex situ conservation. Heredity 2021, 126, 913–928. [Google Scholar] [CrossRef]
  49. Crossa, J.; Vargas, M.; Van Eeuwijk, F.A.; Jiang, C.; Edmeades, G.O.; Hoisington, D. Interpreting genotype x environment interaction in tropical maize using linked molecular markers and environmental covariables. Theor. Appl. Genet. 1999, 99, 611–625. [Google Scholar] [CrossRef] [PubMed]
  50. Van Eeuwijk, F.A.; Crossa, J.; Vargas, M.; Ribaut, J-M. Analyzing QTL-environment interaction by factorial regression, with an application to the CIMMYT drought and low-nitrogen stress program in maize. In: Quantitative genetics, genomics and plant breeding, Kang, M.s., Ed., CABI International, New York, 2002.
  51. Devey, M.E.; Russell, W.A. Evaluation of recurrent selection for stalk quality in a maize cultivar and effects on other agronomic traits. Iowa State J. Res. 1983, 58, 207–219. [Google Scholar]
  52. Klenke, J.R.; Russell, W.A.; Guthrie, W.D. Recurrent selection for resistance to European corn borer in a corn synthetic and correlated effects on agronomic traits. Crop Sci. 1986, 26, 864–868. [Google Scholar] [CrossRef]
  53. Bertin, P.; Gallais, A. Physiological and genetic basis of nitrogen use efficiency. II. QTL detection and coincidences. Maydica 2001, 46, 53–68. [Google Scholar]
  54. Liu, X.; Zheng, Z.; Tan, Z.; Li, Z.; He, C.; Liu, D.; Zhang, G.; Luo, Y. QTL mapping for controlling anthesis-silking interval based on RIL population in maize. Afr. J. Biotechnol. 2000, 9, 950–955. [Google Scholar]
  55. Wang, L.; Zhou, Z.; Li, R.; Weng, J.; Zhang, Q.; Li, X.; Wang, B.; Zhang, W.; Song, W.; Li, X. Mapping QTL for flowering time-related traits under three plant densities in maize. Crop J. 2021, 9, 372–379. [Google Scholar] [CrossRef]
  56. Leng, P.; Khan, S.U.; Zhang, D.; Zhou, G.; Zhang, X.; Zheng, Y.; Wang, T.; Zhao, J. Linkage mapping reveals QTL for flowering time-related traits under multiple abiotics conditions in maize. Int. J. Mol. Sci. 2022, 23, 8410. [Google Scholar] [CrossRef] [PubMed]
  57. Labate, J.A.; Lamkey, K.R.; Lee, M.; Woodman, W. Hardy–Weinberg and linkage equilibrium estimates in the BSSS and BSCB1 random mated populations. Maydica 2000, 45, 243–255. [Google Scholar]
  58. Templeton, A. R. Population Genetics and Microevolutionary Theory, John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006.
  59. Pfaffelhuber, P.; Lehnert, A.; Stephan, W. Linkage disequilibrium under genetic hitchhiking in finite populations. Genetics 2008, 179, 527–537. [Google Scholar] [CrossRef]
  60. Brown, A.H.D.; Allard, R.W. Effect of reciprocal recurrent selection for yield on isozyme polymorphisms in maize (Zea mays L). Crop Sci. 1971, 11, 888–893. [Google Scholar] [CrossRef]
  61. Zhao, M; Shu, G; Hu, Y.; Cao, G; Wang, Y. Pattern and variation in simple sequence repeat (SSR) at different genomic regions and its implications to maize evolution and breeding. BMC Genomics 2023, 24,136. [CrossRef]
Preprints 91777 g001
Figure 1. Breeding scheme of the four cycles of recurrent selection in the M3S maize population. In each cycle of selection, the number and type of progenies intermated to form the next cycle population is shown.
Figure 1. Breeding scheme of the four cycles of recurrent selection in the M3S maize population. In each cycle of selection, the number and type of progenies intermated to form the next cycle population is shown.
Preprints 91777 g001
Preprints 91777 g002
Figure 2. Percentage of 38 SSR loci deviating from Hardy-Weinberg equilibrium for seven Maksimir 3 Synthetic (M3S) cycle populations.
Figure 2. Percentage of 38 SSR loci deviating from Hardy-Weinberg equilibrium for seven Maksimir 3 Synthetic (M3S) cycle populations.
Preprints 91777 g002
Table 1. Genetic diversity of the seven Maksimir 3 Synthetic (M3S) cycle populations: total number of alleles (At), mean number of alleles per locus (Am), and mean expected heterozygosity (He) with their standard errors.
Table 1. Genetic diversity of the seven Maksimir 3 Synthetic (M3S) cycle populations: total number of alleles (At), mean number of alleles per locus (Am), and mean expected heterozygosity (He) with their standard errors.
Cycle population At Am He
C0 127 3.34±0.242 0.5170±0.031
C1 130 3.42±0.231 0.5318±0.025
C2 130 3.42±0.234 0.5171±0.029
C3S1 126 3.32±0.207 0.5135±0.030
C3FS 123 3.24±0.218 0.5012±0.030
C4N0 129 3.39±0.240 0.5266±0.024
C4N150 125 3.29±0.237 0.4924±0.028
Table 2. Allele frequency distribution (%) in seven Maksimir 3 Synthetic (M3S) cycle populations.
Table 2. Allele frequency distribution (%) in seven Maksimir 3 Synthetic (M3S) cycle populations.
Allele
frequency
class		 Cycle population
C0 C1 C2 C3S1 C3FS C4N0 C4N150
%
0.00–0.10 23 28 28 26 29 27 29
0.11–0.20 25 12 21 22 20 15 20
0.21–0.30 13 21 15 14 9 17 12
0.31–0.40 11 11 8 10 13 14 12
0.41–0.50 8 10 8 11 10 8 4
0.51–0.60 8 6 8 6 6 4 7
0.61–0.70 5 2 4 3 6 5 7
0.71–0.80 4 8 5 3 2 8 4
0.81–1.00 3 2 3 5 5 2 5
Mean allele
frequency±SE		 0.29 ±0.021 0.29
±0.020		 0.29
±0.021		 0.29
±0.021		 0.29
±0.021		 0.29
±0.020		 0.29
±0.022
Table 3. Chromosomal position of nonneutral loci in single cycles and across four cycles of selection in the Maksimir 3 Synthetic (M3S) population.
Table 3. Chromosomal position of nonneutral loci in single cycles and across four cycles of selection in the Maksimir 3 Synthetic (M3S) population.
Bin Locus SCP1 C0 C1 C2 C2 C3FS C3FS C0 C0
RCP2 C1 C2 C3S1 C3FS C4N0 C4N150 C4N0 C4N150
1.01 phi056
1.03 phi339017
1.08 dupssr12
1.11 phi064
2.00 phi96100
2.02 phi098
2.04 phi083
3.02 phi036
3.05 phi053
3.07 bnlg197
4.01 phi213984
4.04 phi308090
4.05 phi438301
4.11 phi076
5.00 nc130
5.01 bnlg143
5.03 phi109188
5.07 phi128
6.00 phi126
6.03 phi389203
6.04 phi452693
6.07 phi123
7.02 phi034
7.03 bnlg572
7.05 phi082
7.06 phi116
8.00 umc1359
8.03 phi115
8.08 phi015
8.09 phi233376
9.01 phi033
9.02 umc1033
9.05 phi236654
9.07 bnlg128
10.02 phi96342
10.03 phi050
10.04 phi084
10.3 phi059
1SCP Starting cycle population.; 2RCP Resulting cycle population. Preprints 91777 i001 Significant Waples neutrality test at the 0.05 probability level.
Table 4. Pairwise ΦST values between Maksimir 3 Synthetic (M3S) cycle populations (bellow diago-nal) and their probability values after 1023 permutations (above diagonal).
Table 4. Pairwise ΦST values between Maksimir 3 Synthetic (M3S) cycle populations (bellow diago-nal) and their probability values after 1023 permutations (above diagonal).
Cycle
population		 C0 C1 C2 C3S1 C3FS C4N0 C4N150
C0 <0.0001 <0.0001 <0.0001 <0.0001 <0.0001 <0.0001
C1 0.0503 <0.0001 <0.0001 <0.0001 <0.0001 <0.0001
C2 0.0395 0.0535 <0.0001 <0.0001 <0.0001 <0.0001
C3S1 0.0437 0.0575 0.0143 <0.0001 <0.0001 <0.0001
C3FS 0.0702 0.0872 0.0542 0.0750 <0.0001 <0.0001
C4N0 0.0598 0.0664 0.0537 0.0728 0.0247 <0.0001
C4N150 0.0705 0.0843 0.0595 0.0739 0.0320 0.0143
Mean1 0.0560 0.0670 0.0460 0.0560 0.057 0.0490 0.0560
1Mean Φst value of a cycle population to the remaining cycle populations.
Table 5. Fixation index for six loci across seven Maksimir 3 Synthetic (M3S) cycle populations. Only those loci with significant departure from HW equilibrium in three or more cycle populations are shown.
Table 5. Fixation index for six loci across seven Maksimir 3 Synthetic (M3S) cycle populations. Only those loci with significant departure from HW equilibrium in three or more cycle populations are shown.
Locus Bin
 Cycle population
C0 C1 C2 C3S1 C3FS C4N0 C4N150 Mean
Fixation index (FIS)
phi098 2.02 -0.12 -0.38* ml1 1.00** -0.21 -0.27 0.53* 0.09
phi076 4.11 -0.07 0.43** 0.93** -0.07 -0.00 1.00** -0.02 0.31
bnlg143 5.01 0.09 0.49** 0.21 -0.03 0.19* 0.23* 0.26* 0.21
phi452693 6.04 0.34* 0.50** -0.21 -0.03 -0.19 0.30* 0.15 0.13
bnlg572 7.03 0.30** 0.86** 0.23 0.91** 0.59** 0.90** 0.77** 0.65
phi050 10.03 0.28** 0.20 0.57** 0.10** -0.02 0.19 1.00** 0.33
*, ** Significant at the 0.05 and 0.01 probability levels, respectively; 1ml monomorphic locus
Table 6. Pairs of loci in significant (P<0.05) linkage disequilibrium (LD) in seven Maksimir 3 Synthetic (M3S) cycle populations (C0, C1, C2, C3S1, C3FS, C4N0 and C4N150).
Table 6. Pairs of loci in significant (P<0.05) linkage disequilibrium (LD) in seven Maksimir 3 Synthetic (M3S) cycle populations (C0, C1, C2, C3S1, C3FS, C4N0 and C4N150).
Bin Locus Bin Locus Bin Locus Bin Locus
C0 C3S1
3.07 bnlg197 4.04 phi308090 9.01 phi033 9.02 umc1033
3.07 bnlg197 8.00 umc1359 C3FS
8.08 phi015 8.09 phi233376 9.07 bnlg128 9.01 phi033
C1 3.07 bnlg197 1.01 phi056
9.07 bnlg1281 9.01 phi033 3.07 bnlg197 6.00 phi126
9.07 bnlg128 5.03 phi109188 3.07 bnlg197 6.04 phi452693
3.07 bnlg197 1.08 dupssr12 8.08 phi015 8.09 phi233376
3.07 bnlg197 3.02 phi036 1.01 phi056 6.00 phi126
3.07 bnlg197 4.11 phi076 7.05 phi082 7.06 phi116
3.07 bnlg197 2.00 phi96100 C4N0
1.08 dupssr12 8.08 phi015 1.08 dupssr12 8.08 phi015
1.08 dupssr12 4.11 phi076 1.08 dupssr12 9.02 umc1033
1.08 dupssr12 4.05 phi438301 8.08 phi015 8.00 umc1359
1.08 dupssr12 2.00 phi96100 1.01 phi056 9.02 umc1033
8.08 phi015 4.05 phi438301 7.05 phi082 7.06 phi116
3.02 phi036 7.06 phi116 C4N150
10.03 phi050 10.04 phi084 3.07 bnlg197 1.08 dupssr12
C2 3.07 bnlg197 9.02 umc1033
3.07 bnlg197 1.08 dupssr12 9.01 phi033 8.03 phi115
3.07 bnlg197 10.03 phi050 4.04 phi308090 4.05 phi438301
3.07 bnlg197 6.03 phi389203
3.02 phi036 7.05 phi082
1Selectively nonneutral loci (according to Waples neutrality test at the 0.05 probability level) are indicated in bold.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated