Prerpints.org logo
Preprint
Article

Simple Non-linear Numerical Modelling for Unreinforced and Frp-Reinforced Masonry Domes

Altmetrics

Downloads

99

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
This paper presents a new method to model the nonlinear behaviour of masonry double curvature structures, possibly reinforced by composite materials, by means of conventional elasto-plastic analyses. It is meant to be used in professional design, especially for assessment and retrofitting purposes, therefore based on the exploitation of the simplest nonlinear Finite Elements available in a commercial software, namely trusses with elasto-fragile and elasto-ductile behaviour (Cutoff Bars). The numerical static nonlinear analyses are carried out by considering elastic hexahedral elements for bricks and lumping nonlinearities on joints. These have been assumed in turn elastic-brittle and elastic-plastic by using 1D elements, respectively Point Contacts, under No-Tension Material hypothesis, and Cutoff Bars, assigning small tensile resistance to the material. The reinforcement, realised with FRP hooping strips, has been successfully modelled in a similar fashion, i.e. by applying perfectly bonded elastic-plastic Cutoff Bars at the extrados of the dome, where the debonding is accounted for in a conventional way limiting the tensile strength according to Italian Standards indications. The procedure is validated against benchmark models with the same geometry, using experimental data and more refined structural model results for comparison.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Double curvature structures are a common type of roofing technology in historical buildings. They may be found all-round the world in different countries. They were used to cover large rooms in public buildings because of their resistance to vertical loads guaranteed by the acceptable mechanical properties of materials involved (i.e., in compression for masonry), friction, but especially by their shape. Drawbacks of these structures are lateral thrust, transversal shear for asymmetric loading, dynamic and horizontal loading.
Arches, vaults (and domes) are known to be “shape resistant” by virtue of their (double) curvature, as function of their loading condition [1]. In this paper, domes will be tackled in three dimensions. Indeed, they cannot be studied as arches or barrel vaults, because of stresses running horizontally. In Figure 1, the conical surfaces are those on which the mortar joints and bricks are laid. Because of this imposed shape and the slope toward the centre (O), on those surfaces only compression stresses act, as also demonstrated by means of membrane equations in [2]. Moreover, compression stress progressively increases, raising the height of the same cones (i.e., their slopes), up to the last crown. This can be an open oculus with a finite compression in the crown or a closed top, which – in large domes – may suffer from bending because of the verticality of the degenerate conical surface and insufficient compression.
Going from the springing to the top, on meridian section planes π i (see Figure 1), nonlinearities emerge and form cracks, which separate the dome in meridian sectors. This allows the formation of plastic annular hinges at a generic angle α h from the vertical axis (i.e., degenerate cone Cr0). In the case of closed top, one plastic hinge may open there ( α 0 = 0 ). In any case, an excessive – symmetric – loading opens plastic hinges at the springing ( α b = 90 ° ) and in an intermediate position α h . In [3] is demonstrated how the position of plastic hinge varies. When an oculus is present, it is more probable for the plastic hinge to occur lower on the base (at a major angle α h ). The presence of the oculus in facts visibly changes the equilibrium configuration in relation to the closed-top case.
Contrarily, the same authors [3] state that the position of the intermediate plastic hinge undergoes very small variations for a change in material tensile resistance. Anyway, it can be noted that increasing the tensile resistance, the angle of the intermediate plastic hinge increases because of a better distribution of stresses on meridian planes.
However, the higher the plastic hinge, the better it is because a larger portion of the lower part of the fuse expends more energy in uplifting the self-weight. Friction and interlocking of bricks – in stretcher bond above all – are advantageous for what stated. On the contrary, it is worth noting that going from the springing to the top, bricks geometry adapts worse to progressively smaller conical surfaces. Therefore, in building practice, they are cut, and head joints distribution becomes more irregular. This ends in giving straighter paths for fractures (minimum energy path [4]), lowering the fracture power, so the ultimate collapse load.
The present investigation deals with the nonlinear modelling of domes loaded at the crown by means of vertical point forces. Such configuration is typical for laboratory tests aimed at understanding the load carrying capacity of such structural elements. The newly proposed way of modelling is benchmarked against both experimental and advanced numerical techniques hereafter recalled. A hemispherical dome with an inner diameter of 2.2m, 0.12m thick (UNI Italian Bricks Size), with an oculus on the top of 0.2m in diameter was built in the Architectural University Institute of Venice and tested in its unreinforced and reinforced cases [5,6]. Further, a dome with the same geometry has been already studied numerically by Creazza et al. [7] through an isotropic Finite Element Damage Model, equipped with distinct damage parameters in tension and compression. The role played by orthotropy [8], which may have a certain importance in modifying the ultimate load carrying capacity, was left out and studied after in the framework of classic limit analysis [9]. The same problem has also been studied analytically by means of Lower Bound Limit Analysis approaches (LB-LA, Durand-Claye’s Method) and the Upper Bound Limit Analysis (UB-LA, kinematic method) [3,9,10,11], and by homogenised or macroscopic models [7,11,12,13,14].
Concentrated forces applied on the top in experiments and simulations roughly represent the load of lanterns or – in even more interesting cases – larger superimposed constructions as happens for instance in the Vipassana Pagoda (described in [15]), that will be studied in the sequel of the research, having in mind to compare the results obtained with already existing computations carried out with a novel method combining FEs and Thrust Line Analysis [16,17].
As noted in [14], all the methods stated so far, even though very accurate in giving results, are usually exploited in the academy only, because of the time necessary to set up the models and run the analyses and the advanced mechanical knowledge sometimes required. Moreover, some of the existing assessment methods regarding hemispherical domes introduce excessive simplifications, as in [18], where domes are considered as set of arches and the presence of small tensile strength and of finite compressive strength are neglected. Indeed, Masonry is often considered a “No-Tension Material” (NTM) [16,19,20,21] even though accounting for suitable tensile and compressive strengths leads to results which better fit reality.
The novel and simple method presented here for studying domes in a three-dimensional space avoids both the complexities (and limits) of homogenised or FE damage models and the excessive simplifications in the study of domes in Euclidean space or in 2D planes. It will consider clay bricks as always elastic, lumping material nonlinearities in mortar joints (as in [22]), which are modelled by simple unidimensional Finite Elements already available in commercial software (namely Point Contact and Cutoff Bars). In this way, masonry may be modelled both as a NTM and as a Tension Material (with small tensile resistance), according to the result to be pursued.
It is worth to remind that the modelling method proposed in this paper accounts for axisymmetric vertical loading only, which generates also a distribution of normal stresses on meridian planes. Moreover, the method is validated for a dome with an oculus on the top, against literature data about the same benchmark model. Further analyses will be carried out in future.
The paper is organised as follows: in the next section the reader will find information about the necessary instruments (i.e., the Finite Elements involved) to build a proper masonry model for pushover analysis, coherently with initial hypotheses. The motivation for the choice and the typology of 1D FE chosen will be exposed step by step. A section about the actual construction of the model and its validation follows. It will report the sensitivity analyses done to tune the mechanical parameters (e.g., joints fT) and to compare the results with literature data. In addition, the potential exploitability of the model for FRP reinforcement is proven.

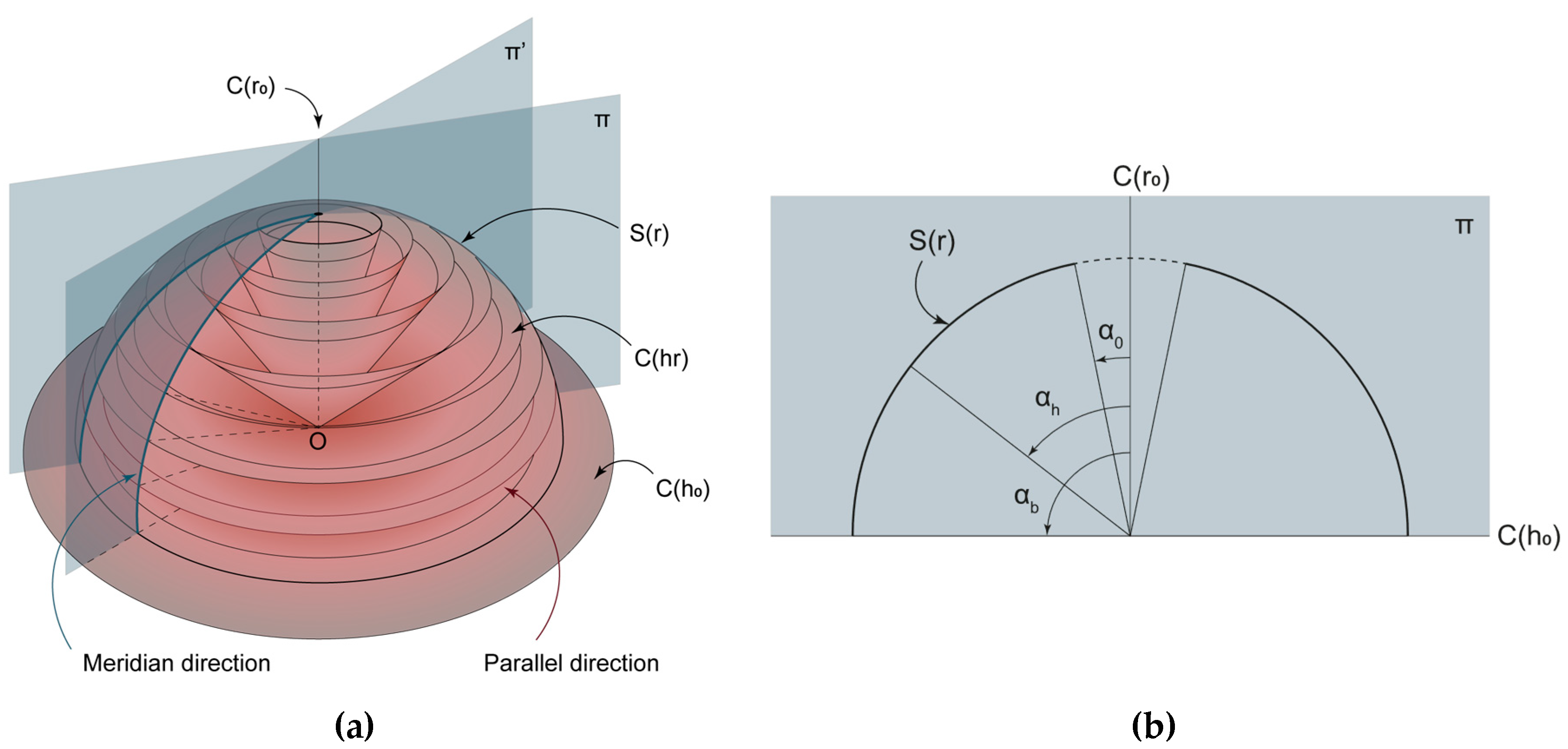
1. FE Modelling

1.1. Modelling for Nonlinear Analysis

In [18], domes have been modelled as arches on a vertical cross section, neglecting to some extent the actual axisymmetric geometry, especially as far as meridian boundary conditions are concerned. This makes a dome closer to a single curvature vault. However, differently from the latter case, domes should be better studied by properly considering their second curvature in the third dimension. Geometrically speaking they have infinite planes of symmetry intersecting in the vertical axis. Hence, to build a lighter model and speed up calculations, accounting for realistic boundary conditions, here only a meridian slice (or fuse, δθ/2π wide) of a dome has been considered [23] in the nonlinear analysis (NLA). Hence, the results for the slice are made commensurate with those of the whole dome. The width of the fuse shall not be too small in order to model separately all the materials involved (both bricks and mortar joints) in suitable proportions. Moreover, the fact that masonry is very rigid and typically made by interlocked units, allows to consider stresses as effectively exchanged between contiguous slices. Therefore, with reference to the single slice considered, the stresses are transferred on meridian planes imposing classic symmetry constraints on displacements (see Figure 2a).
In the modelling phase, the fuse has been generated by extruding an arch of an angle δθ (Figure 2a) in a cylindrical reference system. It is composed of 3D elements (8-node hexahedrons) with the mechanical characteristics of the blocks adapted from [11] and reported in the following Table 1, node-to-node connected by 1D truss elements lumping masonry nonlinearity. A rough scheme of how the material has been modelled is shown in Figure 2.
As a result of the extrusion in the cylindrical reference system, the model of the dome has bricks made by curved trapezoidal prisms, which let parallel joints have constant thickness through the dome cross section. In real scale domes it happens the contrary because mortar adapts the given geometry of the bricks (parallelepipeds with rectangular faces) to the double curvature. Vertical joints are tapered in any case. However, the assumption over the shape of the elements, already done by two of the authors in [22], does not significantly interfere with the results because of the relatively small size of the blocks.
Once obtained the meridian slice and set the boundary conditions as specified, the nonlinear analysis is run by the application of a progressively increasing displacement on the top of the fuse – i.e., on the crown surrounding the oculus – thus proceeding with a classic displacement control strategy. The solver will provide a node reaction for each step, in function of the displacement and for the given material properties. The final result, being the ultimate collapse load (λu) of the structure considered, is reached asymptotically because the nonlinear ‘beam’ elements are assumed either elastic-brittle or elastic-ductile. When elastic-brittle Cutoff Bars (null tensile strength) are used, the asymptotic value of λu is that of the classic NTM. In the following Figure 3 the reader finds a scheme summarizing the nonlinear analysis process.
In the next sections, two approaches in which nonlinearities can be modelled are detailed.

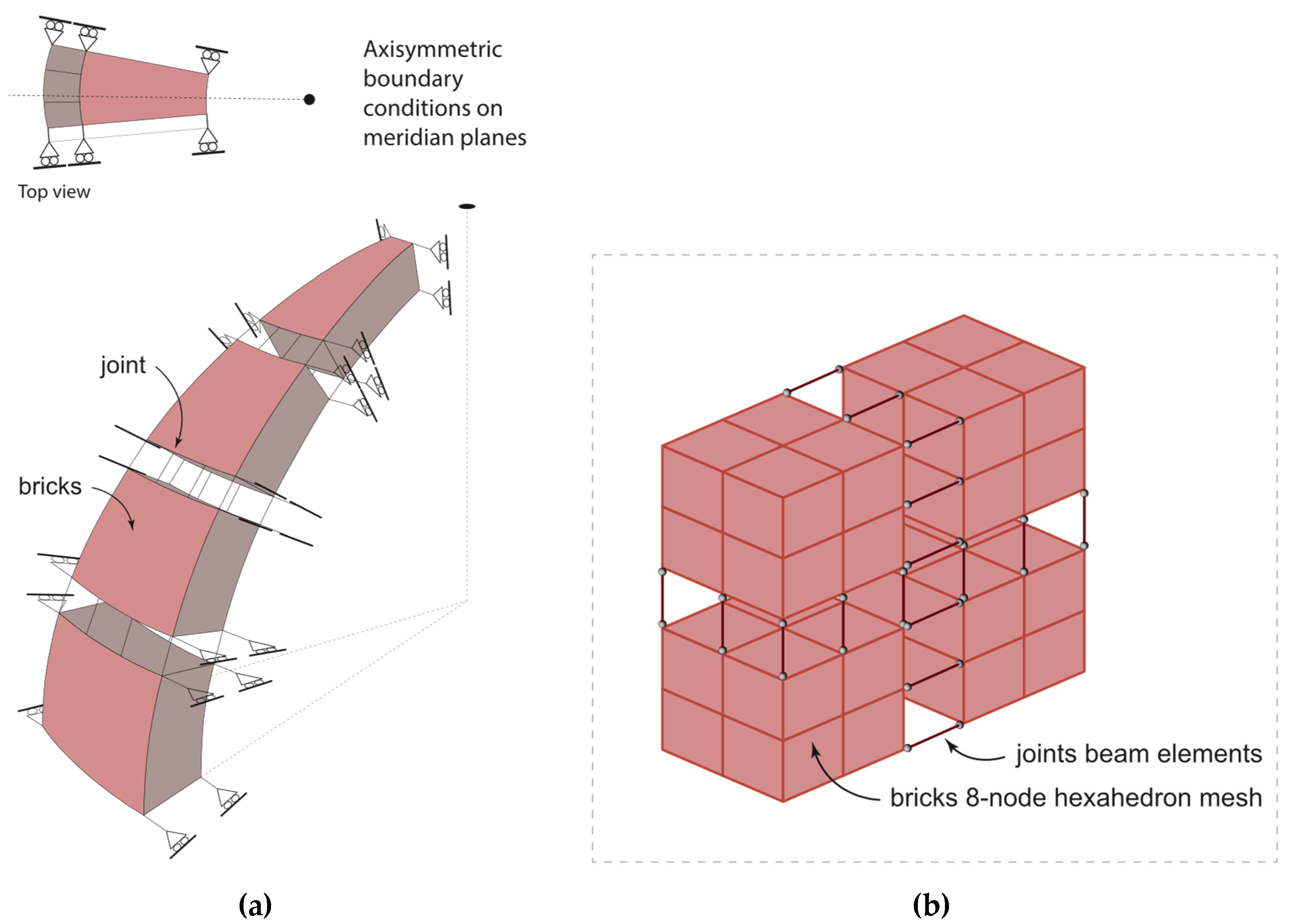
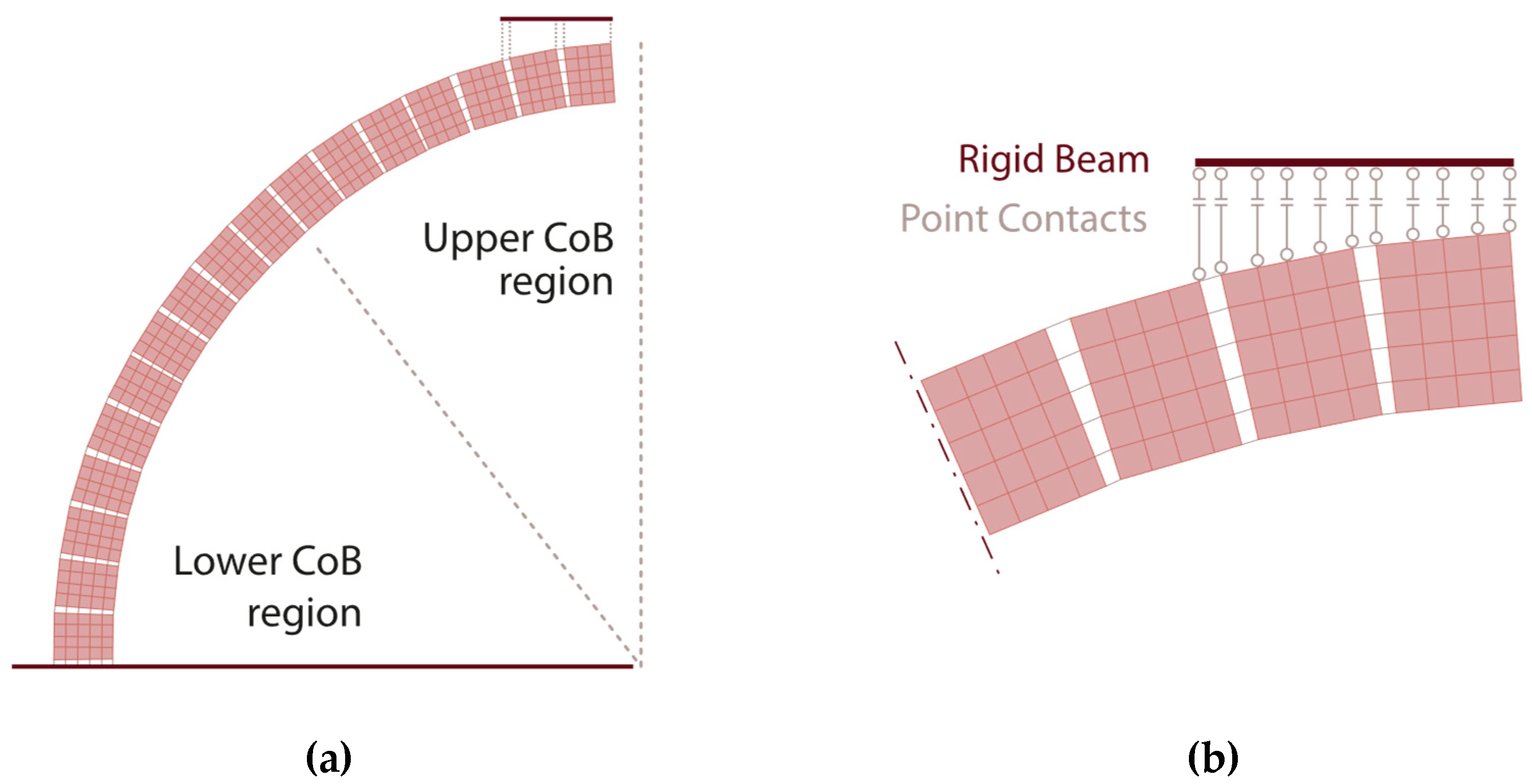
1.2. Modelling of Joints by Means of Point Contacts

Masonry is often modelled as a NTM. This comes from the studies of Heyman [2], who noted how in historical masonry constructions, compression acting in reality is far below the actual strength associated to crushing. On the contrary, any intense tensile contribution is impossible because of masonry incapacity to bear it. Hence, masonry was studied by Heyman [24] according to the following set of hypotheses:
f T ⟶ 0 f C ⟶ ∞ v b = 0
where f T is the tensile strength, f C is the compressive strength, v b is the sliding between blocks, valid for small displacements.
According to what stated so far, the best way to model nonlinearity of such a NTM is the use of unilateral frictional contacts, namely Point Contacts (PCs), working in compression. PCs are the implementation in FE software of the Signorini-Fichera contact problem, also known as “the problem with ambiguous boundary conditions”. It states the impossibility for an elastic non-homogeneous anisotropic body to penetrate a rigid frictionless surface. It has been already used in [25], which retraces the theoretical solution given by Fichera for one single body [26] then applied in [27] for multiple body interaction.
PC elements have been chosen specifically for the nonlinear analyses to constantly monitor the contact status. Indeed, between two nodes, there can be either the formation or the closure of a gap, but also sliding in function of the friction coefficients set. In the case presented in this paper, the friction coefficients assigned to the meridian joints (PCs set to work in compression) are equal to 1 (see Table 2), making the problem defined by a unilateral frictional contact (a little different from the theoretical frictionless problem of 1964 [26]).
Despite the PC models an impenetrability condition, a small value of penetration (“non-zero penetration”) is necessary for the solver to calculate the contact condition efficiently. So very high values of stiffness can be accounted for – until they do not generate numerical issues – to have the minor penetration possible. In this case the penetration was automatically controlled by the solver. An initial value of stiffness is set (k0 value in Table 2), which is then automatically adapted by the software through the steps of the NLA [28].

2.3. Load Distribution

The possibility to model a distributed load (a condition close to the experimental one) is checked. The imposed displacement for such NLA is distributed over a larger area thanks to a frame constituted by rigid beams (mechanical characteristics in Table 3) leaning on the extrados of the dome by PCs set to work only in compression (tension type with null tensile resistance). Indeed, doing like this, whenever a tensile stress reaches the contact surface, the boundaries are inactivated. The reader will find the mechanical characteristics of the PCs involved in Table 3 and a scheme of the FE model in Figure 4b.
By this expedient, it is possible to simulate historical domes surmounted by lanterns, and more realistically the actual loading conditions of a laboratory test (see Figure 3).

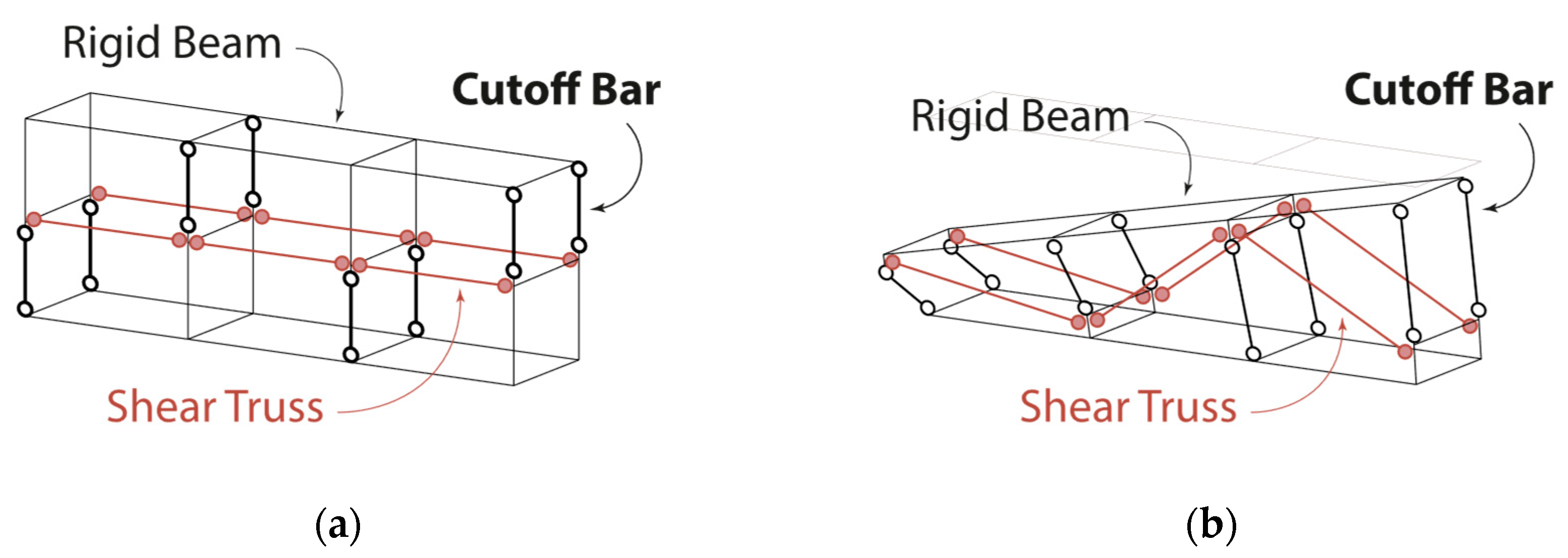
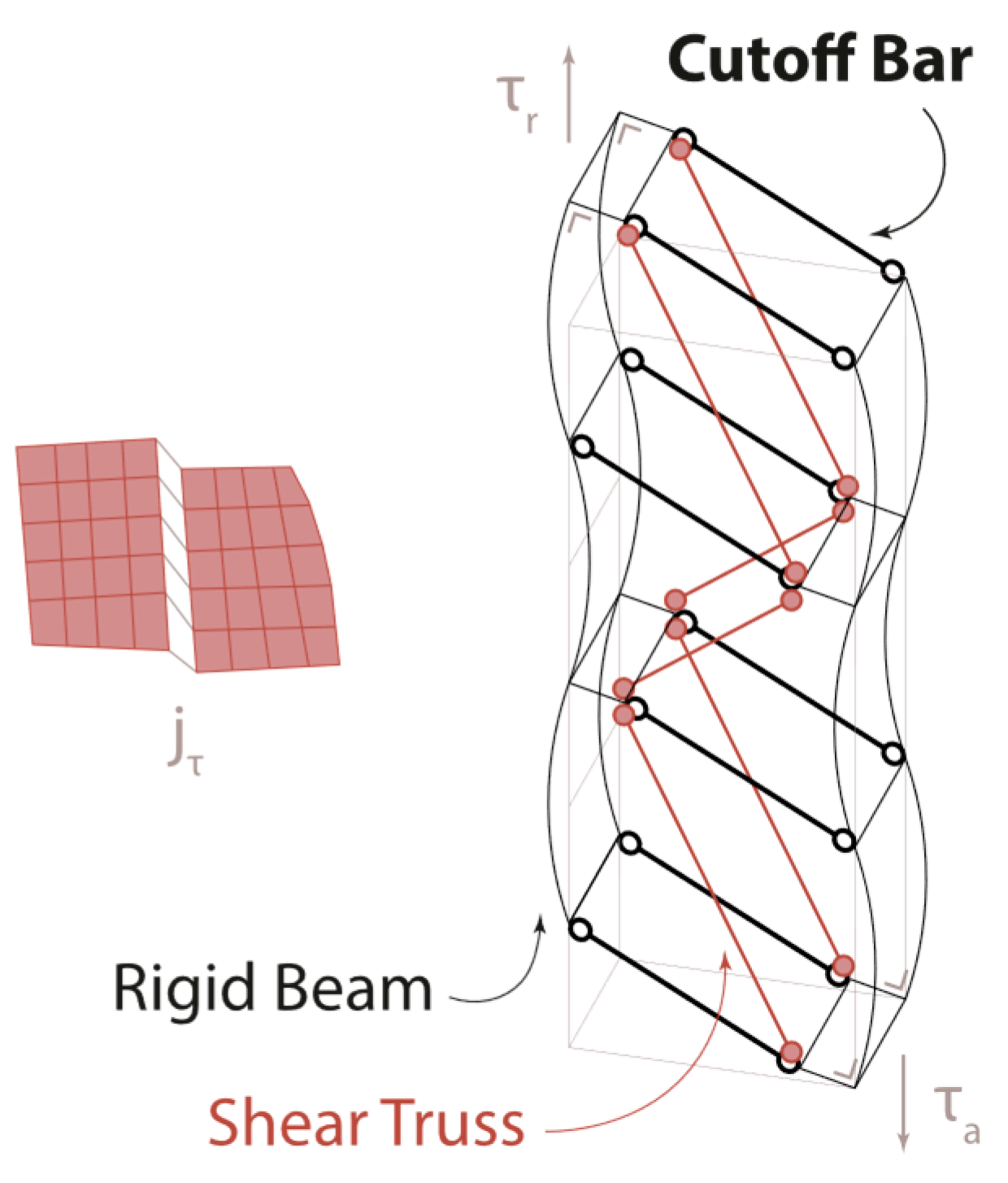
2.4. Modelling of Joints by Means of Cutoff Bars

The second approach to model masonry is by assuming small but non-zero tensile strength (fT) and orthotropy, which is given by material properties (taken as constant through the whole construction), can be modelled as well, by assigning different values for fT along both meridian and parallel directions. Typically, the fT is higher on meridians because of blocks staggering, whereas on parallels – if the cross section of the CoBs is assumed constant – it progressively decreases going from the bottom to the top to take into account the change of the influence area.
Elastic perfectly ductile Cutoff Bars (CoBs), which are truss elements with predefined tensile and compressive limits (i.e., cutoff values) represent the best option in this case. Cutoff values can be properly tuned to better model orthotropy by means of consolidated homogenisation techniques as illustrated in [9].
As already mentioned, in order to account for a change in fuse cross-section, the influence area of CoB should be changed going from the top to the bottom of the structure. In a very accurate model, the CoB properties of each horizontal joint should be changed smoothly. Anyway, being this method thought to be simple, the user can decide in how many regions divide the hemispherical dome to assign them an average value for CoBs influence area. In this case, the fuse is divided into two regions, which are considered to be enough to obtain sufficiently reliable results. The scheme in Figure 4a points them out.

2.4.1. Joint Modelling

Differently from the first model, for which the Heyman’s hypotheses [2,24] are valid and the dome vertically loaded until collapse sees its portions rotating around flexural plastic hinges, in the second model, the joints can fail also for shear. Therefore, a shear-resistant joint – i.e., a complex network of 1D elements involving the utilisation of rigid beams, CoBs and shear trusses – has been conceived.
It is the three-dimensional correspondent of the joint proposed in [22]. A scheme illustrating follows in Figure 5a, together with Table 4 reporting the mechanical parameters adopted for the 1D FEs involved.
The failure of such a joint allows the user to point out the actual presence and position of plastic and shear hinges. Representations of the way the failure occurs are provided in Figure 5b for flexural hinges and in Figure 6 for shear sliding. Because of the geometrical characteristics and mechanical properties assigned, in presence of shear inelastic sliding, blocks faces remain at the same angular distance (no mutual rotation) and failed shear trusses are removed (if CoBs are fragile) or substituted with nodal forces equal to the ultimate strength of the bars (if CoBs are ductile).
In order to avoid unnatural and excessive transversal displacements at the base, the nodes constraints have been set as fully fixed on the impost plane, as well as on the meridian section planes generating the fuse.

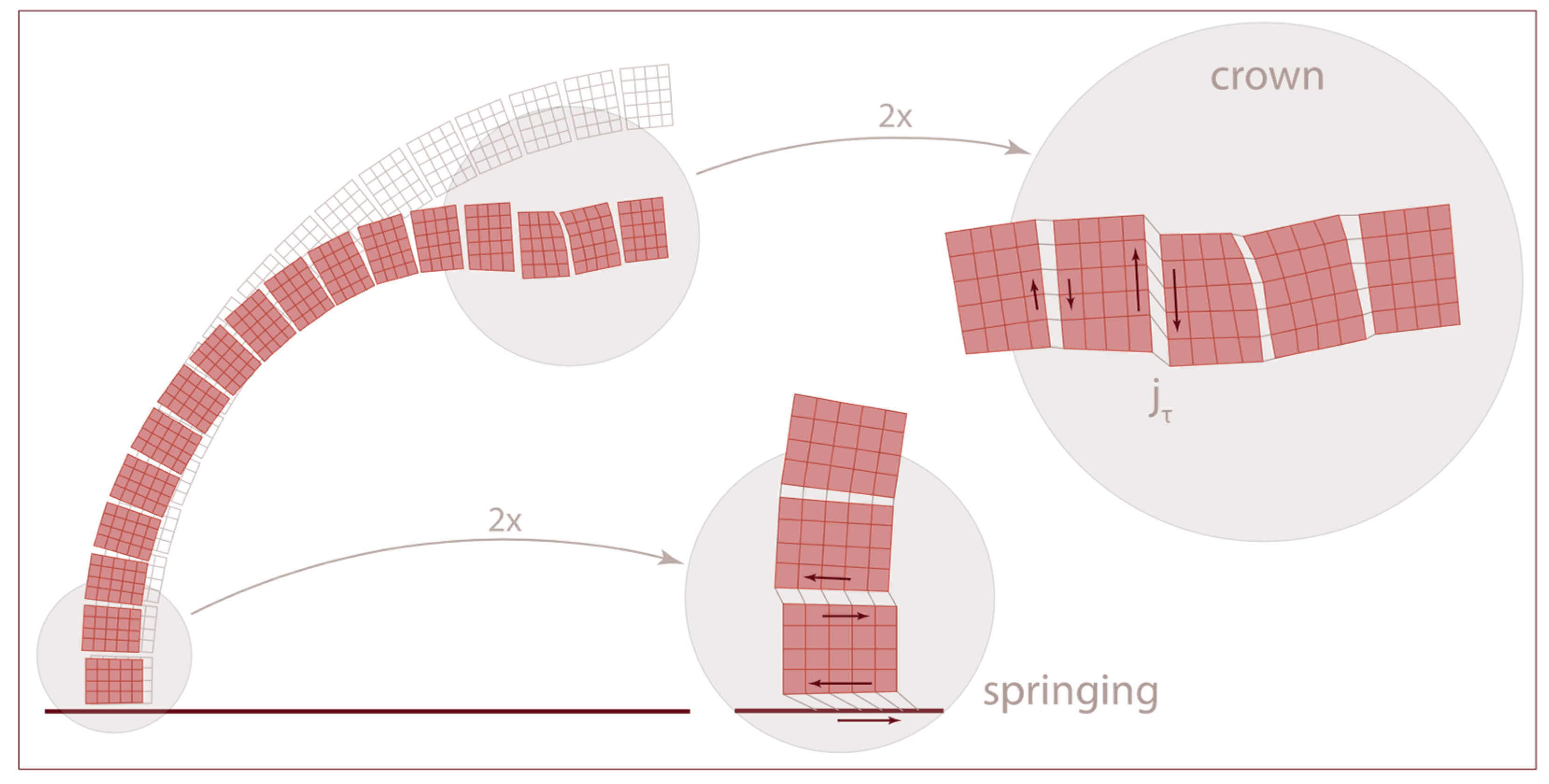
2.5. Modelling of FRP by Means of Cutoff Bars

This section deals with the modelling of a hooping reinforcement. As from common practice and experience, domes are mechanically stabilized on the extrados by addition of buttressing mass (e.g., Pantheon stepped rings up to half-height of the dome) or of drums (e.g., Middle Age crossing roofs). The act of reinforcing by hoops is the bi-dimensional correspondent of the one-dimensional tie for arches, usually put at springing level. The efficacy of applying a tensile-resistant material on the extrados of domes has been demonstrated by practical experience in history and in contemporary literature too [5,29].
Even though assigning a major tensile strength on meridian direction is very effective in rising the collapse load, the application of buttresses of any material on the extrados – when strongly linked to the structure – does not more than increasing the inertia of the section. For instance, the buttresses on St. Peter’s dome in Rome failed to contain the thrust of the dome. Therefore, it needed to be reinforced by iron rings according to the project proposed by Poleni. Reinforcing a dome with meridian strips of FRP would directly increase the tensile resistance of a fuse, while enforcing the formation of a failure mechanism associated to a higher collapse multiplier. Rings or hooping reinforcement indirectly contain the thrust and delay the opening of meridian cracks.
In order to model in a simple way the application of an FRP hooping reinforcement, elastic perfectly plastic (EPP) CoBs have been applied to the extrados of the fuse. In this model, the interface between FRP and masonry is in the nodes of the elements. ‘Perfect adhesion’ is assumed, so no relative displacement is contemplated and FRP CoBs are directly applied, node by node. The mechanical parameters adopted (see Table 5) correspond to those of the FRP and refer to those already used in a numerical model fund in the literature [30,31].
A conventional tensile strength (ffdd), which takes into account the possible failure due to debonding or delamination, is assigned by adopting the simplified procedure proposed by the Italian guidelines [30] and as elaborated in a specific case-study in [31]. The design bond strength ffdd is function of the fracture energy (ΓFK), which in case of debonding is spent in the damage of the support surface (i.e., of a foil with a certain thickness, depending on the actual mechanical properties of the masonry material, as specified in [31]).
Figure 7 illustrates the application of CoBs on the extrados at the same position as in [11], so that results will be comparable.
The application of FRP in a hooping reinforcement avoids the issue of the loss of exploitable strength in proximity of the strip margins (as highlighted in [31]), because of a virtually infinite bond length running within the hoop itself.

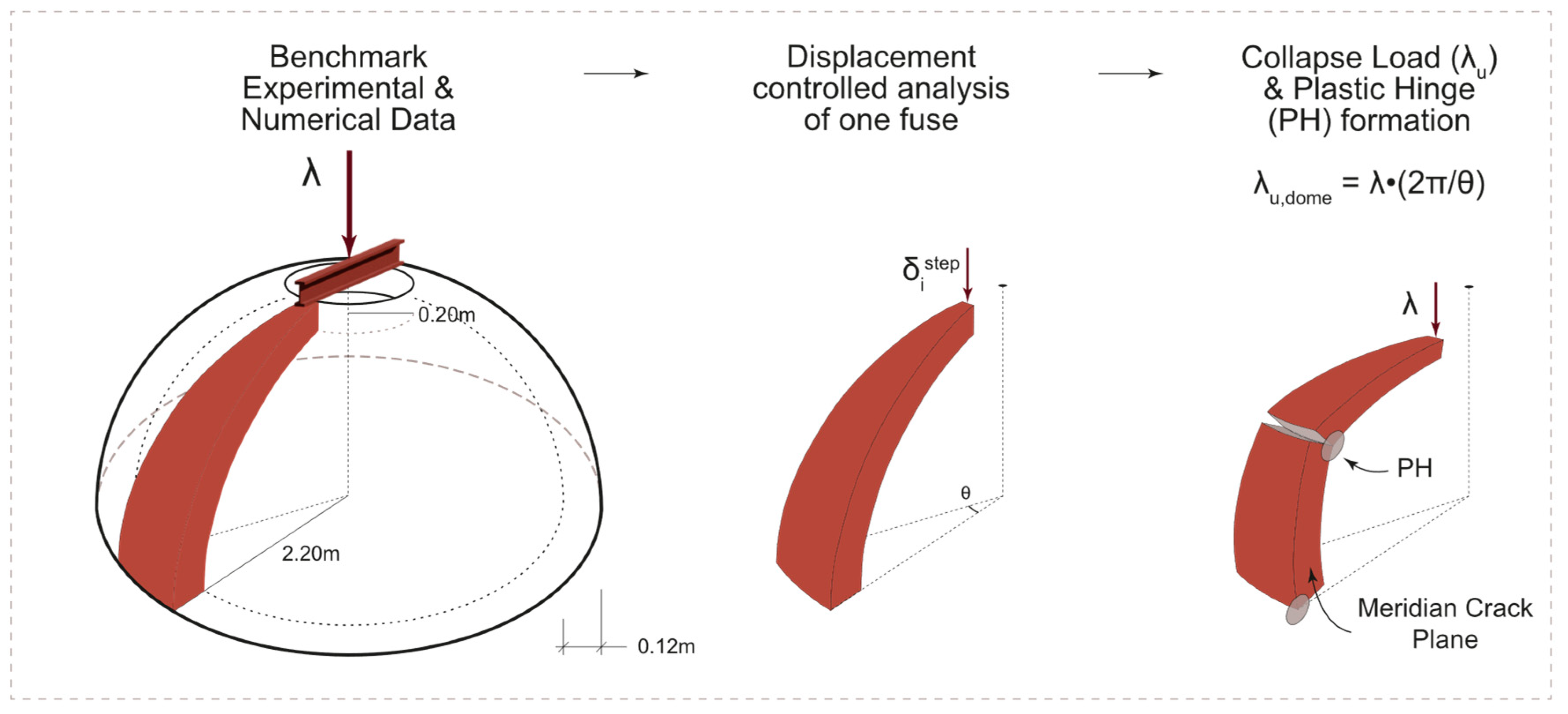
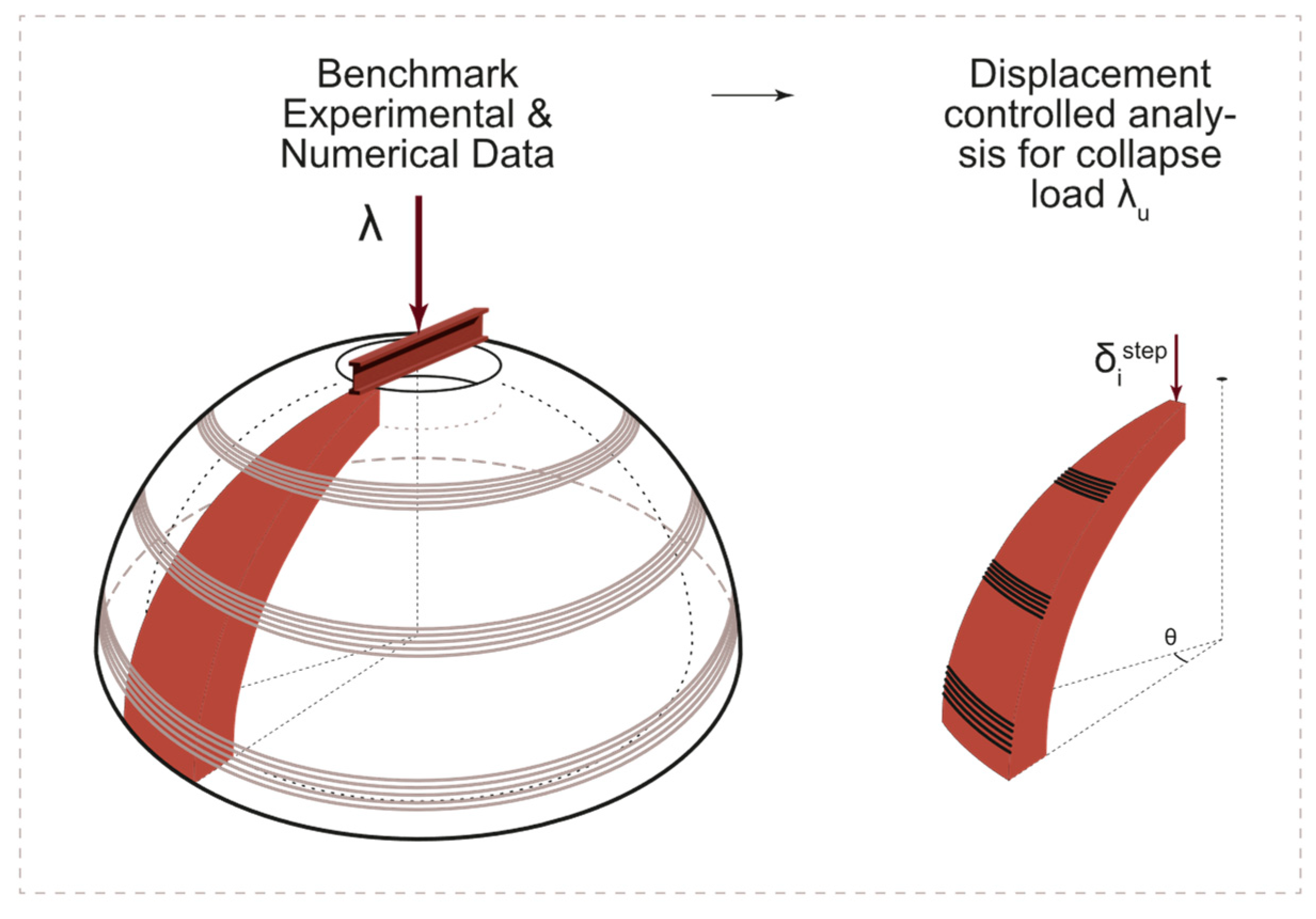
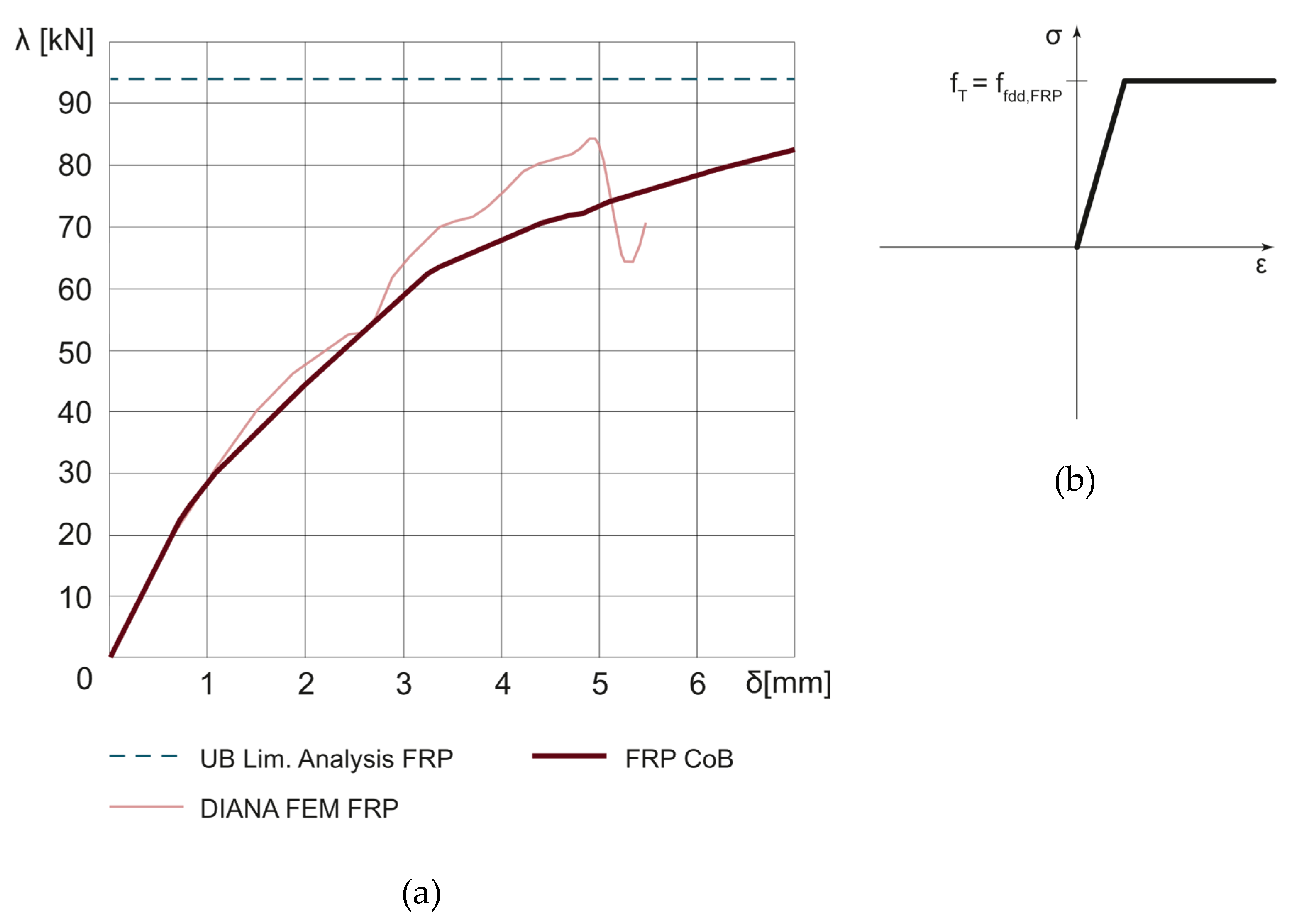
3. Non-Linear Static Analyses

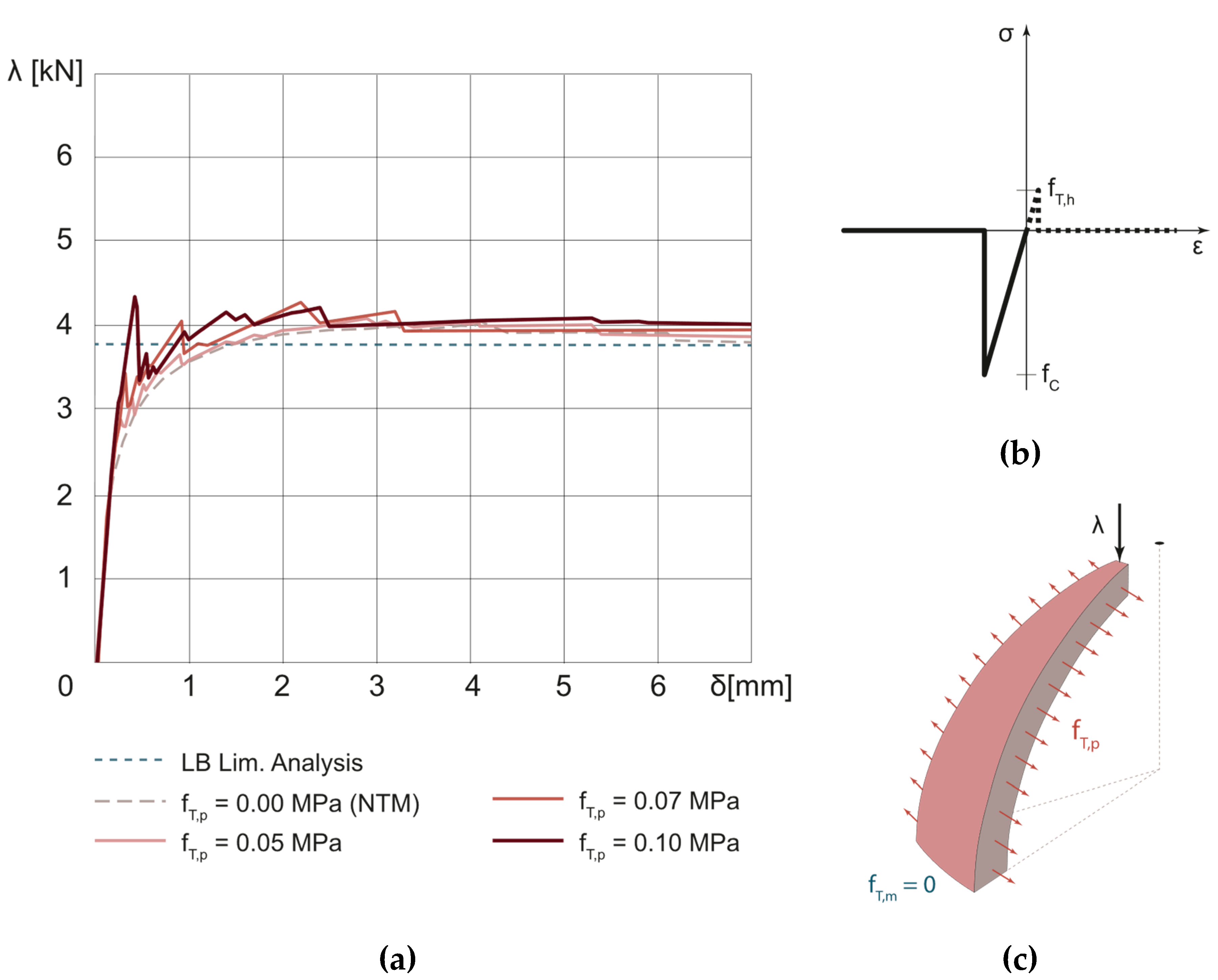
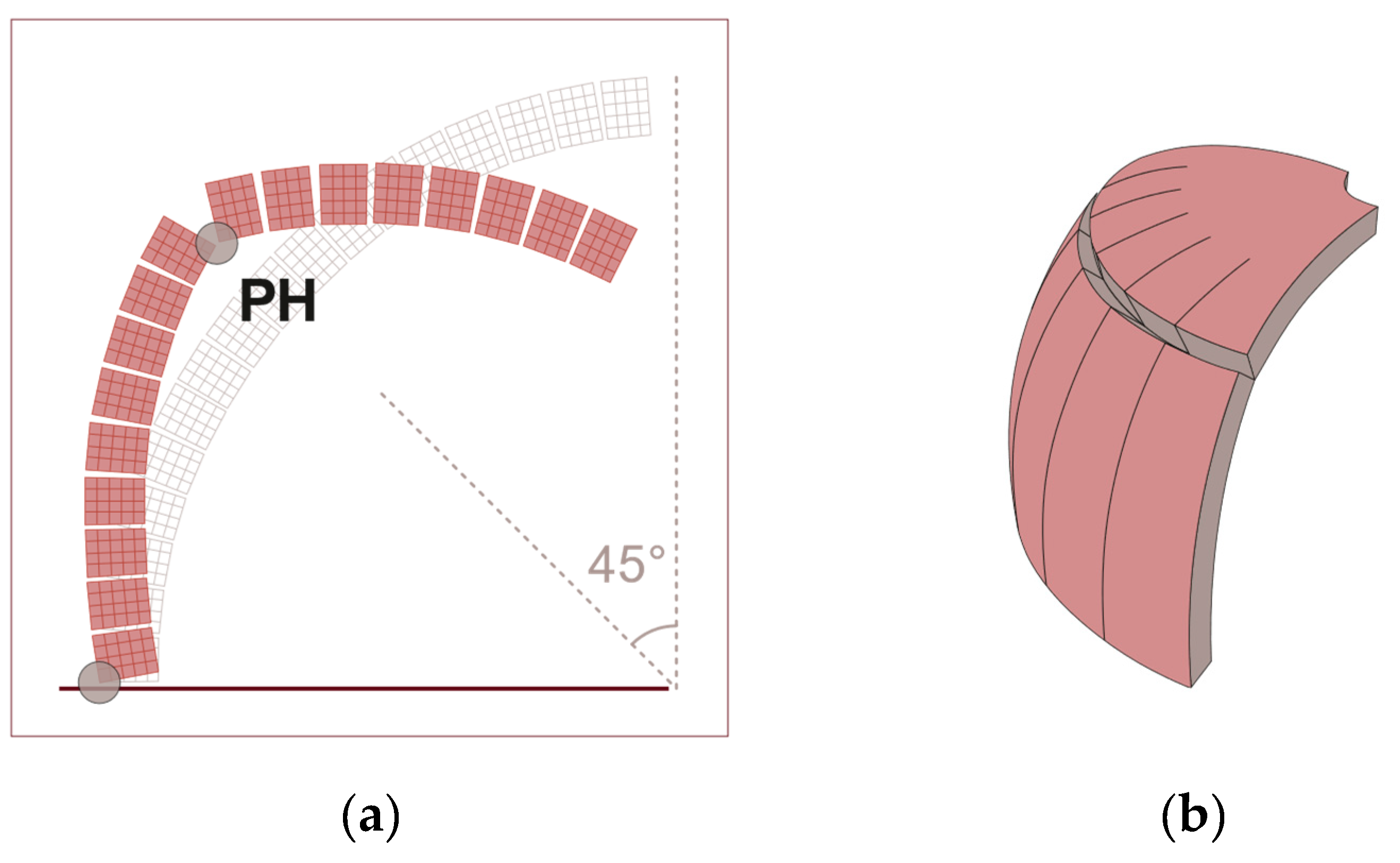
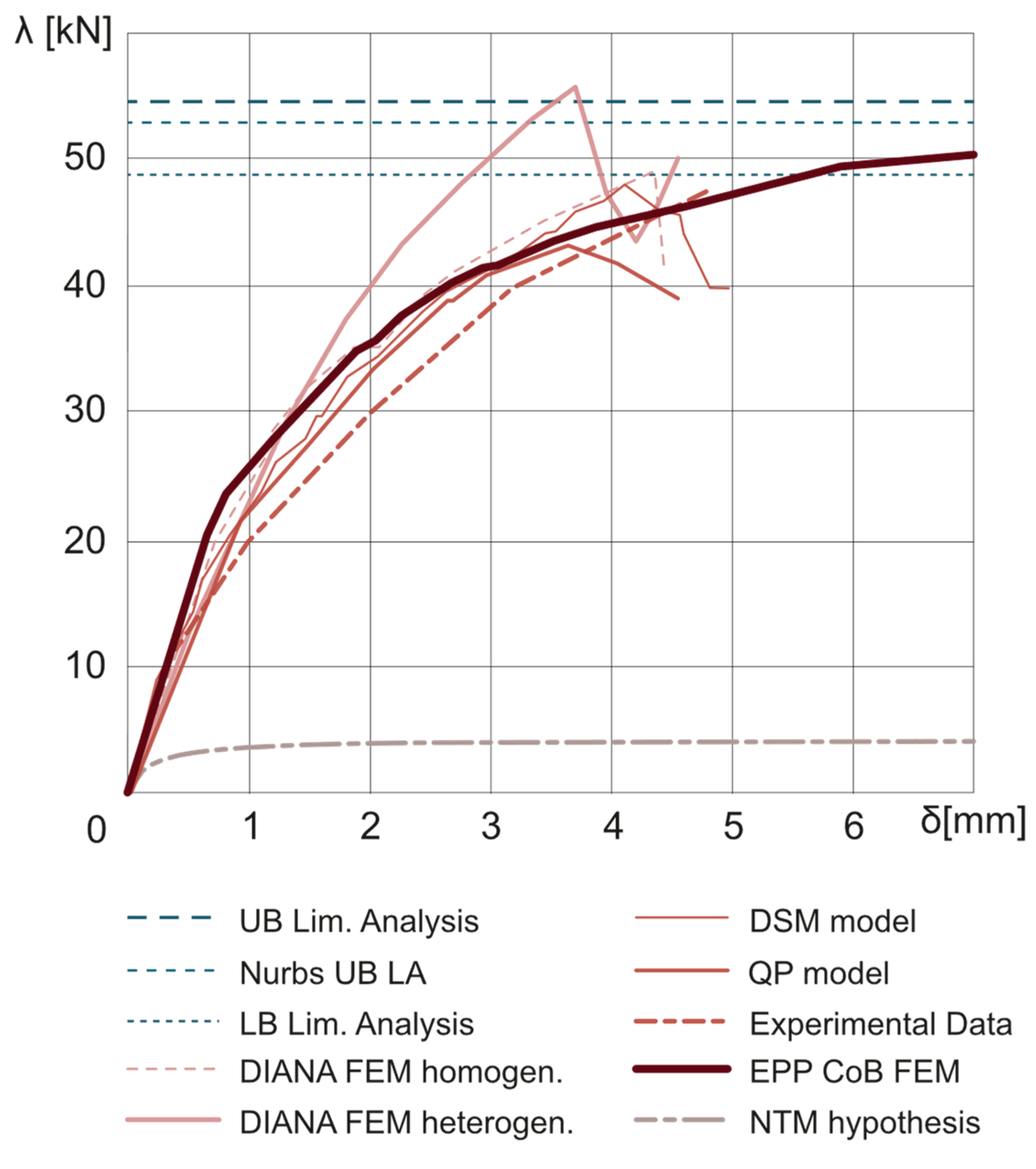
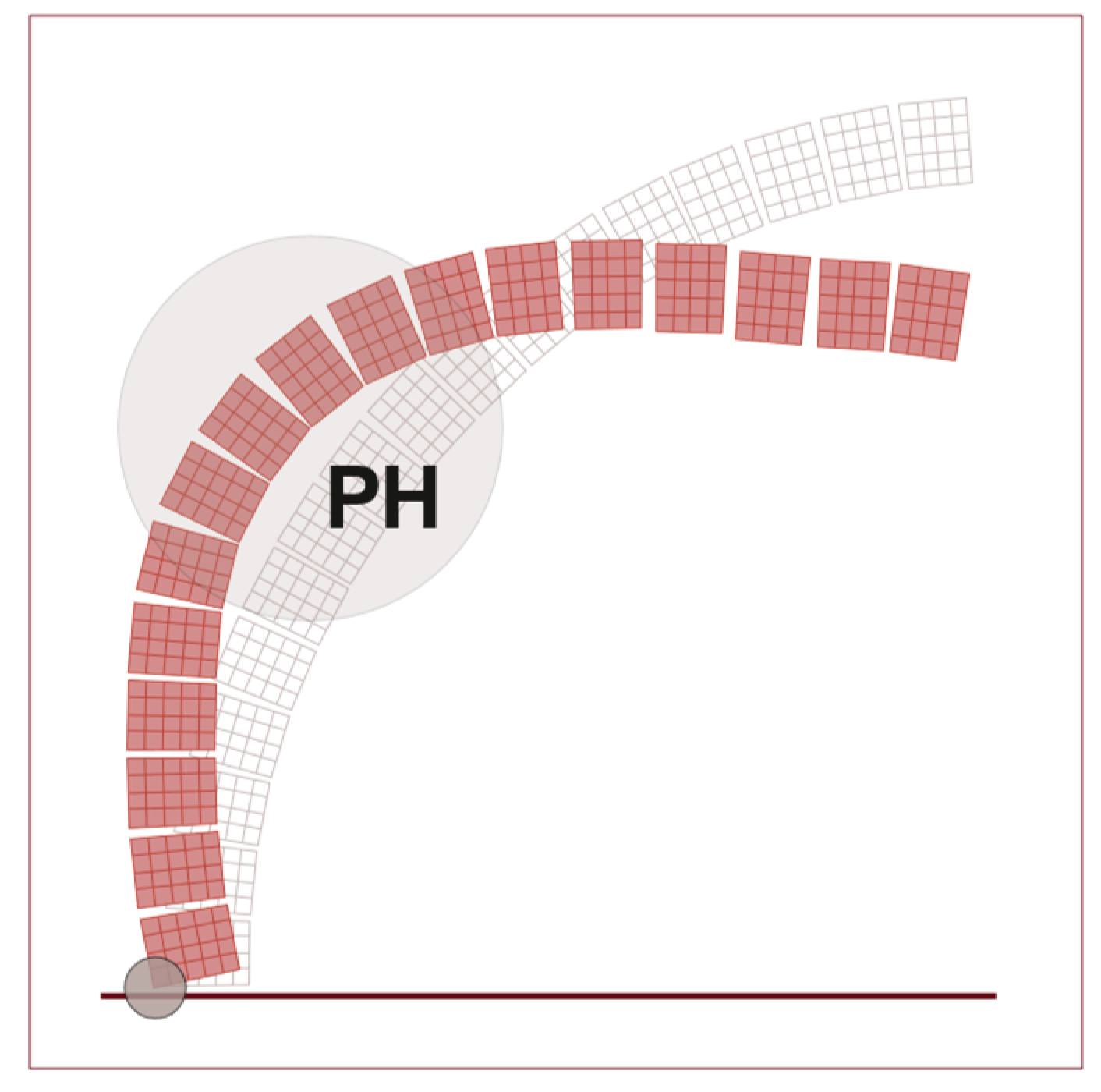
3.4. Unreinforced Dome

3.4.1. NTM hypothesis: Sensitivity Analysis

In Heyman’s demonstration [2], which however pertains to gravity loads and not to point forces, along the meridians of the dome, the stress is always compressive, progressively increasing going towards the oculus as already stated before (§1, & Figure 1). On the contrary, along the parallels, the stress distribution through the membrane section changes going from compression in the upper zone to tension in the lower part (from around 52° from the vertical axis to 90°, i.e., the base), where cracks start spreading and split the membrane in fuses. Annular tensile resistance of a real structure helps in preventing excessive deformation induced by parallel stresses and dome natural equilibrium configuration (catenary profile).
On the dome subjected to a point load at the crown and increased up to failure, a sensitivity analysis with the data reported in Table 2 has been carried out considering null tensile strengths down the meridian direction, so vertical joints fail every time tensile stress reaches them. Along parallel direction instead, small values of tensile strength ( f T , h ) are added and progressively increased to study the behaviour of the dome as function of them. Indeed, the tensile resistance along parallel directions helps the dome in bearing loads. The post-elastic behaviour is assumed perfectly brittle. A total number of 133 load steps under a displacement control analysis has been considered. The numerical model, for a 20° wide fuse, relies in 1700 elastic 8-node hexahedrons, 1128 PCs (516 meridians and 612 parallel), and 3612 nodes.
The results obtained are summarized in the load-displacement curves of Figure 8.
The higher f T , h , the more the load-displacement chart in Figure 8 has a jagged profile. Indeed, increasing the tensile resistance, the dome is made more capable of redistributing the stresses through its cross-section after the formation of plastic hinges. Plastic hinges occurrence is easily spotted on the chart wherever its profile suddenly drops. After each drop, some strength is recovered because of stress redistribution through the residual uncracked cross section. Going for major displacement (plastic hinge developing), the dome strength progressively decreases until the asymptote. The asymptote value roughly corresponds to the result given by a Lower Bound Limit Analysis (Durand-Claye approach) under NTM hypothesis [3], which has been used to validate the results. The collapse load obtained by means of such approach is in the range 3.8 k N < λ u < 4.0 k N , depending on the fT value considered.
The following Figure 9 shows the deformed shape resulting from the nonlinear analysis. As can be seen, because only a unilateral contact in compression has been accounted, intermediate plastic (annular) hinge forms roughly at 45° from the vertical axis of the dome and at the springing, in good accordance with the analytical results from the literature under the same hypothesis [3].

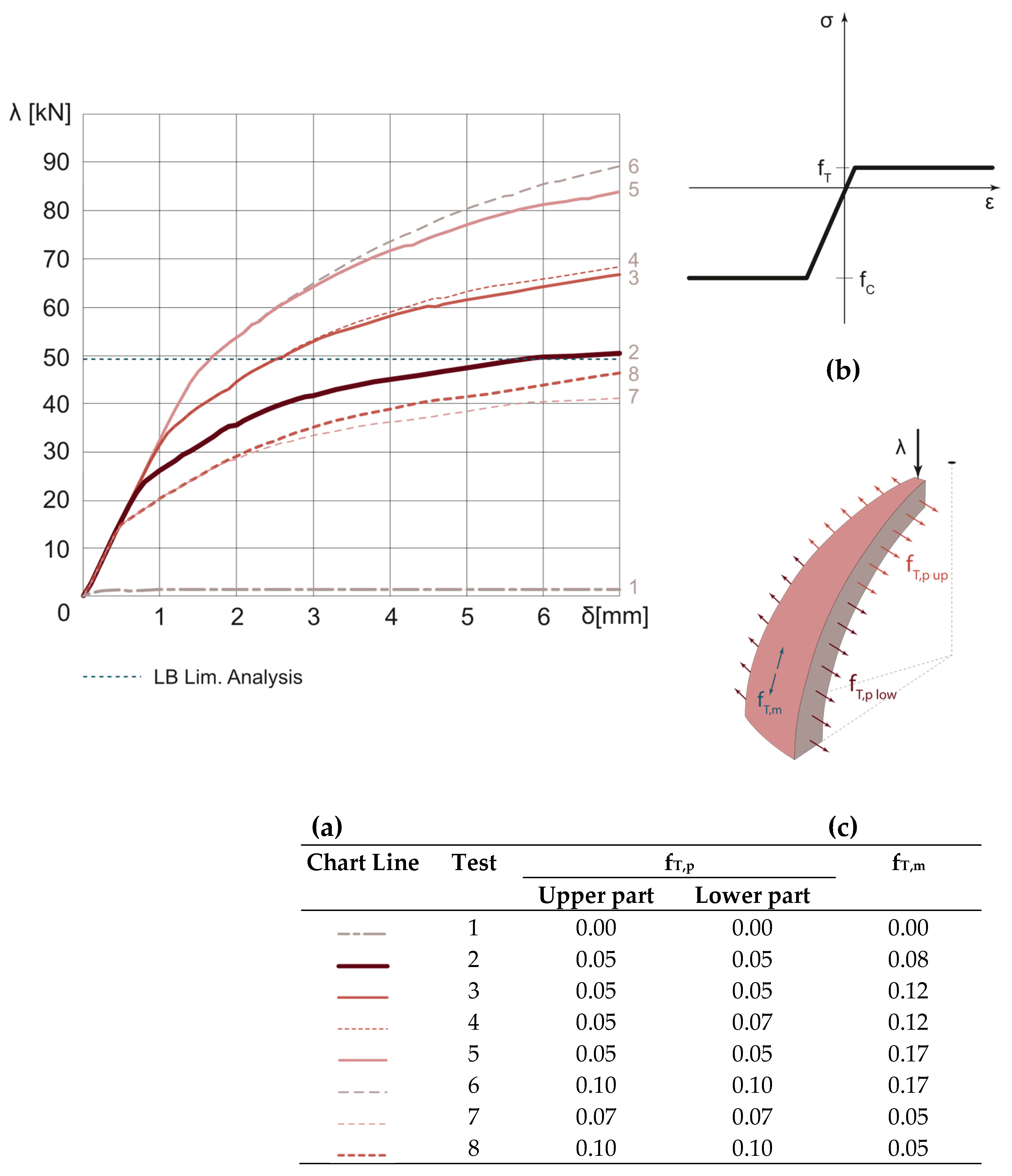
3.1.2. Orthotropic Material: Sensitivity Analysis

Considering masonry as an orthotropic material means considering the behaviour given by cohesion, friction, and interlocking of bricks. The last feature, combined with the first two is strongly related to masonry texture [4]. The consequences on the results will be explained soon in this section and are given assuming a perfect ductility of the joints.
A total number of 86 load steps under a displacement control analysis has been considered. The numerical model in this case, for a 10° wide fuse, relies in 340 elastic 8-node hexahedrons, 1551 unidimensional joints elements (20 Rigid Beams and 20 PCs for the top load, 622 Rigid Beams, 889 CoBs, 170 of which set as Shear Trusses) and 1773 nodes.
A sensitivity analysis has been carried out to properly tune the cutoff parameters and to reach the best configuration fitting the LA results. The different tensile resistances for the parallel fT,p and meridian directions fT,m (may the reader refer to the table in Figure 10) are multiplied by the influence area relative to the region considered. The Young’s Modulus of the elements is assumed equal to E = 1.7 103 MPa, while the maximum tension is in the order of 10-2 and the maximum compression in the order of 108. The chart in Figure 10 reports the results of the sensitivity analysis.
As can be noted from the previous chart and by comparing the input parameters reported in the table, a raise in fT,m is more effective in the improvement of the ultimate collapse load of the dome. Indeed, with a larger meridian tensile resistance, the energy expended in opening the meridians raises considerably [3,32].
In the following chart (Figure 11), the curve previously fitting the LA results of [11] is compared with the results of other studies on the same topic from the literature [6,7,9,10,11,33]. The closeness of the curves shows a general agreement among the results – yet with some differences due to the method exploited. The collapse load resulting from this approach is λ u = 50.6 k N .
In the following Figure 12, the deformed shape of one fuse is reported to show the position of the annular plastic hinges. While the plastic hinge at the base is still well defined, the one in the intermediate position is smeared. As demonstrated in the sections above (§2.4.1), due to the ductility of the joints, the energy is not fully dissipated in discrete loci (in single joints), but in a range of angles. Hence, in the area highlighted in the grey circle in Figure 12, the single joint-structures do not fully fail but they are subjected to a certain inelastic deformation.
However, in the first steps of the nonlinear analysis, the results in terms of deformed shape show to be different from those in the final configuration, as it usually occurs when the elastic part is still dominating. The deformation, concerning mutual sliding between blocks at the crown and at the springing, is illustrated in Figure 13.
As can be seen in the deformed shapes and as expected, the presence of the distributed load induces flexural and shear deformations on the top blocks of the dome. The joint construction, as detailed in §2.4.1, undergoes shear deformation as depicted in Figure 6. However, as already pointed out, this effect tends to subside further in the steps.

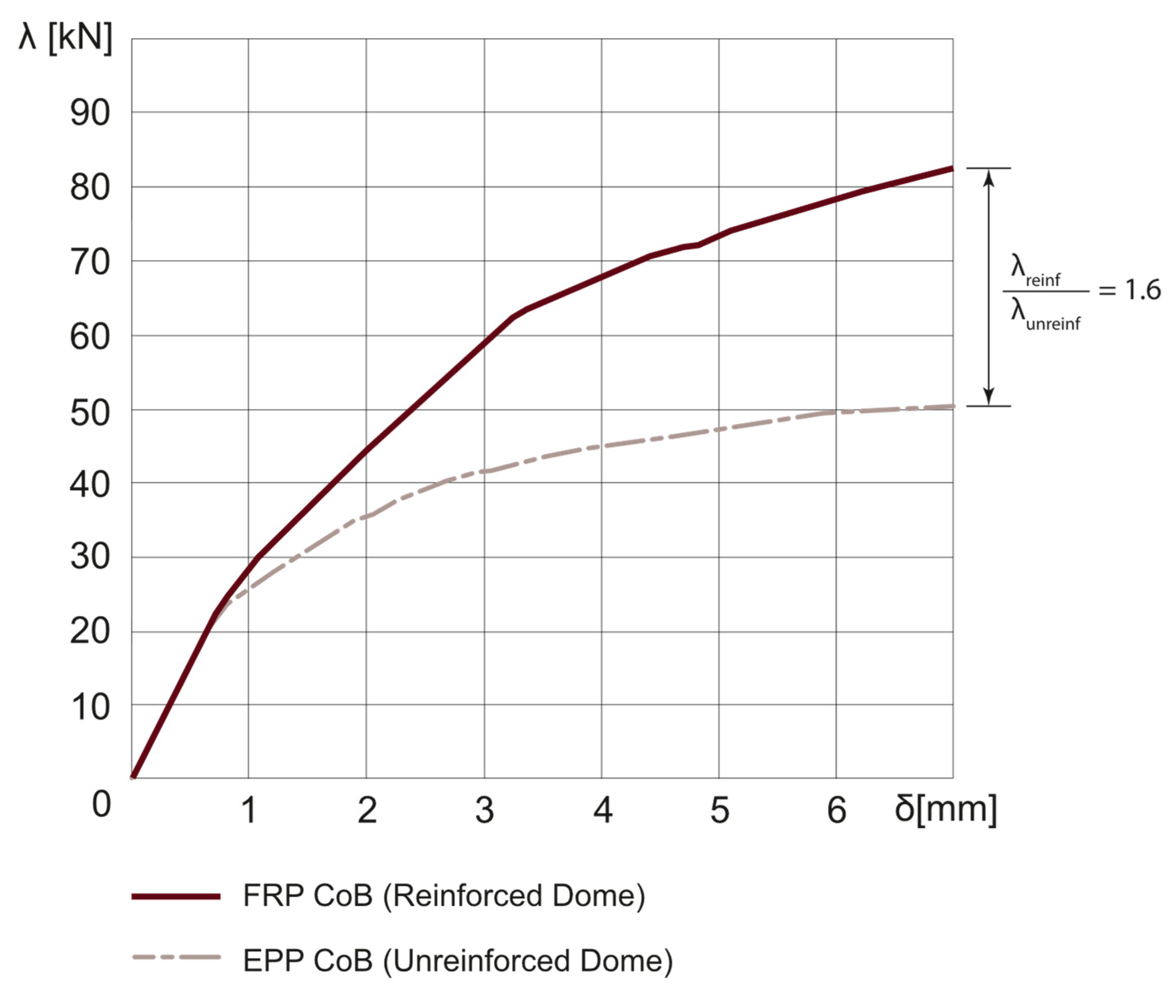
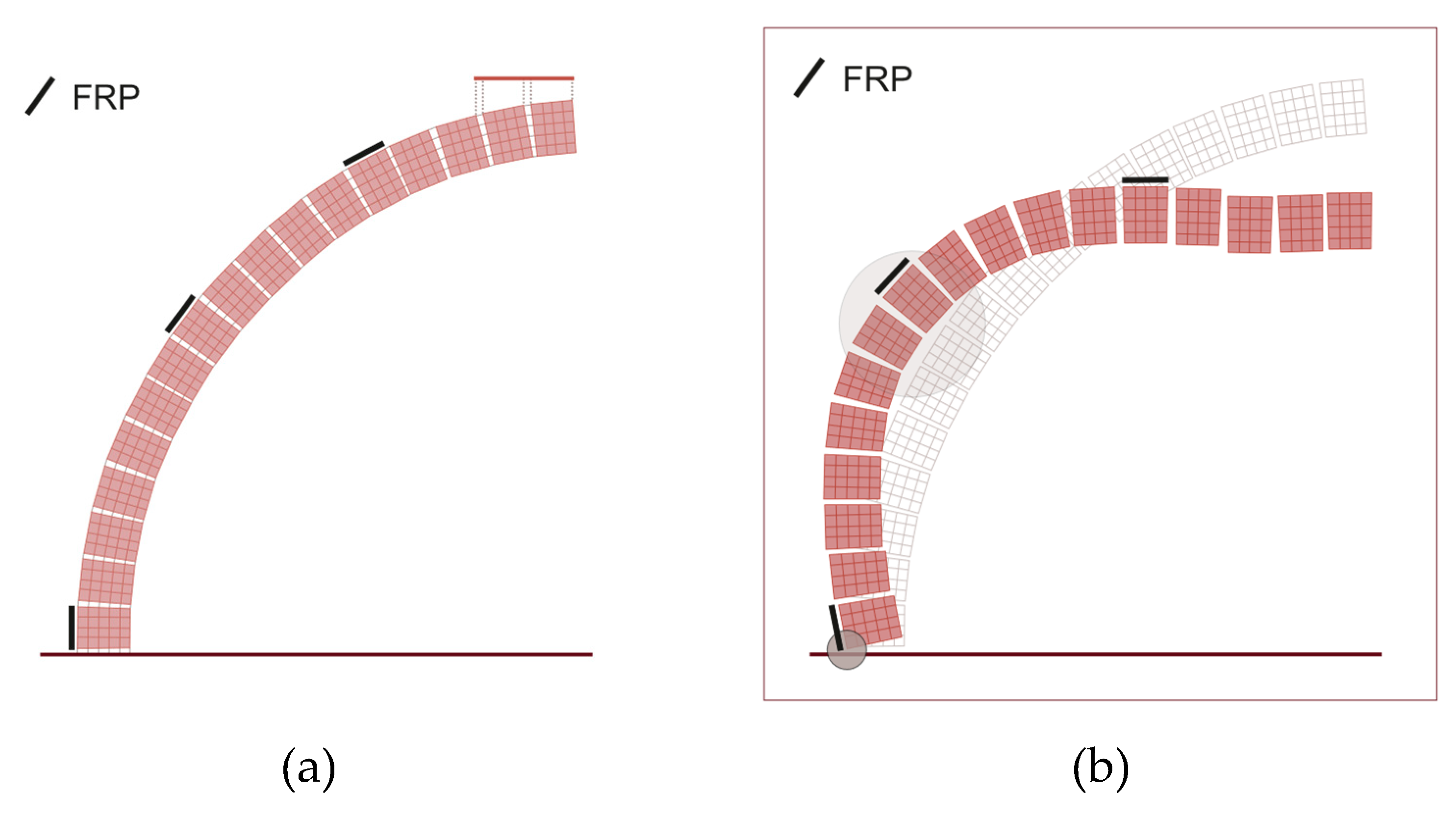
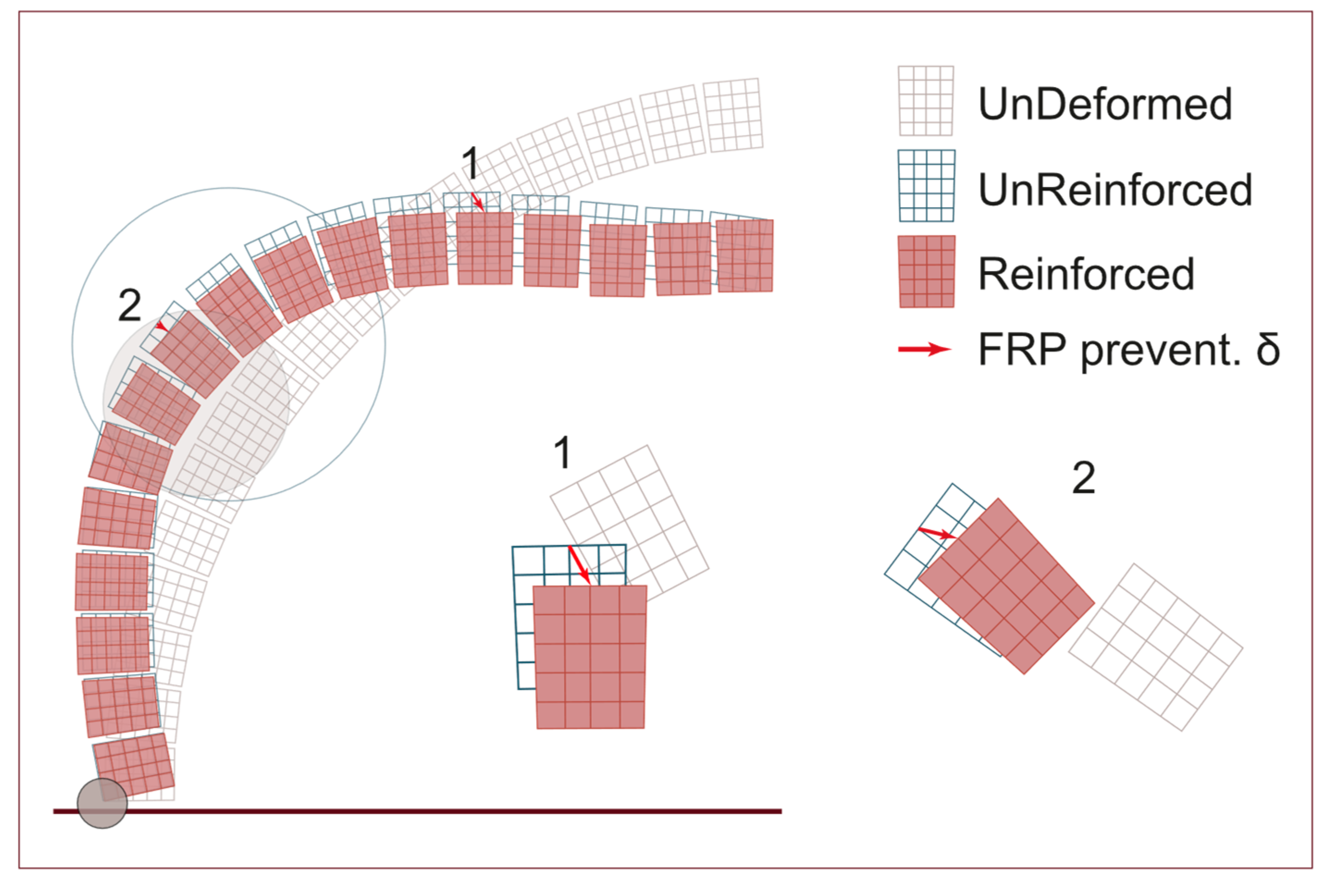
3.2. Reinforced Dome

In this section, some conclusions about the implementation of CFRP reinforcement in the model are reported. As from literature results, FRP annular reinforcement (see §2.5) for curved structures is more effective when applied at the extrados, where it can better work in tension, counteracting the tensile components in lower parallel planes. Figure 16a shows the position of the FRP annular reinforcement on a single fuse of the dome.
The use of nonlinear CoBs for simulating the behaviour of the reinforcement has some precedents in the literature, for both innovative [22,34,35] and simplified approaches [36]. Considering the applicability to real cases and the easiness in pre-processing, elastic perfectly plastic CoBs (see the constitutive behaviour reported in Figure 14b), assigned with the mechanical properties listed in Table 5, proved to be suitable for FRP reinforcement design.
In Figure 14, the results of such application (in terms of collapse load λ u = 82.5 k N ) are reported and compared with the few numerical results available in the literature [11]. No experimental data are available to the authors for the benchmark model considered.
In Figure 15, the ratio between the collapse loads of reinforced (λreinf.) and unreinforced (λunreinf.) dome is reported. The reinforced dome exhibited a load carrying capacity 1.6 times larger than that observed for the unreinforced one, because of the addition of a tensile-resistant material which delays the formation of meridian cracks, globally increasing their strength. In Figure 16, the deformation induced by the displacement-controlled analysis in presence of FRP reinforcement is shown. The FRP strips position is still indicated so that conclusions can be drawn on their influence on the global deformation. The position of intermediate plastic hinge field is highlighted in light grey and still indicated by the deformation of joints construction as shown in §2.4.1.
The following Figure 17 shows a comparison between the deformed shapes of unreinforced and reinforced cases. The red arrows in the image qualitatively represent the displacement prevented by the presence of FRP. While in correspondence of the lower reinforcement hooping the FRP tends to keep the dome from displacing outwards, the upper hooping increases compression and enhances the downward displacement. In the same image, the change in position of plastic hinge field is highlighted too. Indeed, it moved from the 8th – 9th – 10th joints from the vertical axis to the 10th – 11th joints in the FRP reinforced case, just under the hooping reinforcement – as already noted in [11].
Differently from arches, in which the FRP extrados reinforcement changes considerably the failure mechanism (triggering also shear sliding and reinforcement spalling) [22], in this case as modelled, the presence of hooping reinforcements does not significantly change the mode (at least as far as the typology of the mechanism is concerned).
Having assumed a perfect bonding as a hypothesis, a limitation of this study, is the interface relationship between the reinforcement and the substrate. Even though the anchoring length is here virtually infinite (as previously stated in §2.5), a brittle debonding from the substrate could happen letting the dome again unreinforced, which would be detrimental and dangerous in the case of a real case scenario. Further studies can be done to look for failure modes of the reinforcement that involve the interface with the substrate, according to more sophisticated modelling strategies [22,34].

5. Conclusions

The method proposed here for the non-linear static analysis of masonry domes proved to be enough accurate and robust to be used by practitioners. A detailed comparison with literature data proved the reliability of the model proposed. Masonry nonlinearities have been lumped in mortar joints by the use of elastic –brittle and –plastic in turn unidimensional finite elements. Evidently, the results obtained so far in terms of ultimate collapse load and plastic hinge position are strongly related to the initial hypothesis on joints.
Some considerations over a possible reinforcement layout have been done to generate a simple and fast modelling procedure including the possibility to use or adapt the method to cultural heritage conservation.

Author Contributions

Conceptualization, A. Gandolfi, N. Pingaro, and G. Milani; methodology, A. Gandolfi, N. Pingaro, and G. Milani; validation, A. Gandolfi, N. Pingaro; formal analysis, A. Gandolfi, N. Pingaro, and G. Milani; investigation, A. Gandolfi, N. Pingaro, and G. Milani; resources, G. Milani; data curation, A. Gandolfi, N. Pingaro, and G. Milani; writing—original draft preparation, A. Gandolfi, N. Pingaro, and G. Milani; writing—review and editing, A. Gandolfi, N. Pingaro, and G. Milani; visualization, A. Gandolfi, N. Pingaro; supervision, G. Milani. All authors have read and agreed to the published version of the manuscript. Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

This research received no external funding.

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. A. Tralli, C. Alessandri, and G. Milani, “Computational Methods for Masonry Vaults: A Review of Recent Results,” The Open Civil Engineering Journal, vol. 8, no. 1, pp. 272–287, 2014. [CrossRef]
  2. J. Heyman, The Stone Skeleton. 1996.
  3. D. Aita, G. Milani, and A. Taliercio, “Limit analysis of masonry domes with oculus and lantern: a comparison between different approaches,” Mathematics and Mechanics of Solids, 2023. In press.
  4. S. Szabó, M. F. Funari, and P. B. Lourenço, “Masonry patterns’ influence on the damage assessment of URM walls: Current and future trends,” Developments in the Built Environment, vol. 13, no. January, 2023. [CrossRef]
  5. P. Faccio, P. Foraboschi, and E. Siviero, “Masonry vaults reinforced with FPR strips,” L’Edilizia, vol. 7, pp. 44–50, 1999.
  6. P. Foraboschi, “Strengthening of Masonry Arches with Fiber-Reinforced Polymer Strips,” Journal of Composites for Construction, vol. 8, no. 3, pp. 191–202, 2004. [CrossRef]
  7. G. Creazza, A. V. Saetta, R. Matteazzi, and R. V. Vitaliani, “Analyses of masonry vaulted structures by using 3-D damage model,” European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2000, no. September, pp. 11–14, 2000.
  8. P. B. Lourenço, R. De Borst, and J. G. Rots, “A plane stress softening plasticity model for orthotropic materials,” Int J Numer Methods Eng, vol. 40, no. 21, pp. 4033–4057, 1997. [CrossRef]
  9. G. Milani, “Simple lower bound limit analysis model for masonry double curvature structures,” Comput Struct, vol. 269, p. 106831, 2022. [CrossRef]
  10. A. Chiozzi, G. Milani, and A. Tralli, “A Genetic Algorithm NURBS-based new approach for fast kinematic limit analysis of masonry vaults,” Comput Struct, vol. 182, pp. 187–204, 2017. [CrossRef]
  11. G. Milani, E. Milani, and A. Tralli, “Upper bound limit analysis model for FRP-reinforced masonry curved structures. Part II: Structural analyses,” Comput Struct, vol. 87, no. 23–24, pp. 1534–1558, 2009. [CrossRef]
  12. G. Milani, “Homogenized limit analysis of FRP-reinforced masonry walls out-of-plane loaded,” Comput Mech, vol. 43, no. 5, pp. 617–639, 2009. [CrossRef]
  13. E. Milani, G. Milani, and A. Tralli, “Limit analysis of masonry vaults by means of curved shell finite elements and homogenization,” Int J Solids Struct, vol. 45, no. 20, pp. 5258–5288, 2008. [CrossRef]
  14. G. Milani, “Closed form solutions in Limit Analysis for masonry cloister vaults and domes subjected to concentrated vertical loads applied at the top crown,” International Journal of Masonry Research and Innovation.
  15. N. R. Varma, “Global Vipassana Pagoda : Main features and history of construction,” 2023.
  16. M. N. Varma and S. Ghosh, “Finite element thrust line analysis of axisymmetric masonry domes,” International Journal of Masonry Research and Innovation, vol. 1, no. 1, pp. 59–73, 2016. [CrossRef]
  17. M. Varma et al., “Global Vipassana Pagoda : Finite Element Thrust Line FETLA analyses,” pp. 1–6, 2023.
  18. M. Pavlovic, E. Reccia, and A. Cecchi, “A Procedure to Investigate the Collapse Behavior of Masonry Domes: Some Meaningful Cases,” International Journal of Architectural Heritage, vol. 10, no. 1, pp. 67–83, 2016.
  19. M. Como, “Equilibrium and collapse analysis of masonry bodies,” Meccanica, vol. 27, no. 3, pp. 185–194, 1992.
  20. P. Block and J. Ochsendorf, “Thrust network analysis: A new methodology for three-dimensional equilibrium,” Journal of the International Association for Shell and Spatial Structures, vol. 48, no. 155, pp. 167–173, 2007.
  21. M. Varma, G. Milani, and S. Ghosh, “Finite element thrust line analysis of cracked axisymmetric masonry domes reinforced with tension rings,” International Journal of Masonry Research and Innovation 3(1), pp. 72–78, 2018. [CrossRef]
  22. N. Pingaro and G. Milani, “Simple non-linear numerical modelling of masonry arches reinforced with SRG using elasto-fragile and elasto-ductile truss finite elements,” Eng Struct, vol. 293, no. July, p. 116637, 2023. [CrossRef]
  23. J. Heyman, Arches, vaults and buttresses: masonry structures and their engineering. Variorum Ashgate Publishing, 1996.
  24. J. Heyman, “The safety of masonry arches,” Int J Mech Sci, vol. 11, no. 4, pp. 363–385, Apr. 1969. [CrossRef]
  25. A. Tralli, A. Chiozzi, N. Grillanda, and G. Milani, “Masonry structures in the presence of foundation settlements and unilateral contact problems,” Int J Solids Struct, vol. 191–192, pp. 187–201, 2020. [CrossRef]
  26. G. Fichera, “Elastostatic problems with unilateral constraints: the Signorini problem with ambigous boundary conditions (in Italian),” 1964.
  27. G. Fichera, “Boundary Value Problems of Elasticity with Unilateral Constraints,” in Linear Theories of Elasticity and Thermoelasticity, T. C., Ed., Springer, Berlin, Heidelberg, 1973.
  28. Strand7 Pty Ltd., Theoretical Manual. Theoretical backgrund to the Straus7 finite element analysis system. 2004.
  29. M. N. Varma, R. S. Jangid, and V. G. Achwal, “Tension Ring in Masonry Domes,” pp. 1–8, 2006.
  30. CNR-DT 200 R1/2013, “Istruzioni per la Progettazione, l’Esecuzione ed il Controllo di Interventi di Consolidamento Statico mediante l’utilizzo di Compositi Fibrorinforzati Materiali, strutture di c.a. e di c.a.p., strutture murarie,” 2013.
  31. E. Grande, G. Milani, and E. Sacco, “Modelling and analysis of FRP-strengthened masonry panels,” Eng Struct, vol. 30, no. 7, pp. 1842–1860, 2008. [CrossRef]
  32. D. Aita, R. Barsotti, and S. Bennati, “Collapse of masonry arches in Romanesque and Gothic constructions,” 2007. [Online]. Available: https://www.researchgate.net/publication/276205523.
  33. G. Milani and A. Tralli, “A simple meso-macro model based on SQP for the non-linear analysis of masonry double curvature structures,” Int J Solids Struct, vol. 49, no. 5, pp. 808–834, 2012. [CrossRef]
  34. N. Pingaro, A. S. Calabrese, G. Milani, and C. Poggi, “Debonding sawtooth analytical model and FE implementation with in-house experimental validation for SRG-strengthened joints subjected to direct shear,” Compos Struct, vol. 319, no. March, p. 117113, 2023. [CrossRef]
  35. G. Milani, “Simple model with in-parallel elasto-fragile trusses to characterize debonding on FRP-reinforced flat substrates,” Compos Struct, vol. 296, no. February, p. 115874, 2022. [CrossRef]
  36. E. Bertolesi, G. Milani, and R. Fedele, “Fast and reliable non-linear heterogeneous FE approach for the analysis of FRP-reinforced masonry arches,” Compos B Eng, vol. 88, pp. 189–200, 2016. [CrossRef]
Preprints 91836 g001
Figure 1. (a) Conical surfaces with vertexes in the centre of the hemisphere S(r) intersect the spherical surface in ‘parallel’ lines. Axisymmetric planes ( π ∩ π ' ∩ … = C ( r 0 ) ) intersect with S(r) in ‘meridian’ lines. The vertical axis of symmetry C(r0) is a degenerate cone of null radius, while the springing plane C(h0) is the same but with null height. (b) Definition of angles α 0 , α h , α b on a generic vertical cross section ( π plane).
Figure 1. (a) Conical surfaces with vertexes in the centre of the hemisphere S(r) intersect the spherical surface in ‘parallel’ lines. Axisymmetric planes ( π ∩ π ' ∩ … = C ( r 0 ) ) intersect with S(r) in ‘meridian’ lines. The vertical axis of symmetry C(r0) is a degenerate cone of null radius, while the springing plane C(h0) is the same but with null height. (b) Definition of angles α 0 , α h , α b on a generic vertical cross section ( π plane).
Preprints 91836 g001
Preprints 91836 g002
Figure 2. (a) Boundary conditions symmetry assigned to the fuse under analysis; (b) Small portion of a fuse showing 8-node elastic hexahedrons (for blocks) node-to-node connected by unidimensional nonlinear elements.
Figure 2. (a) Boundary conditions symmetry assigned to the fuse under analysis; (b) Small portion of a fuse showing 8-node elastic hexahedrons (for blocks) node-to-node connected by unidimensional nonlinear elements.
Preprints 91836 g002
Preprints 91836 g003
Figure 3. Nonlinear analysis procedure adopted for unreinforced dome.
Figure 3. Nonlinear analysis procedure adopted for unreinforced dome.
Preprints 91836 g003
Preprints 91836 g004
Figure 4. (a) Scheme of the second way of modelling, i.e. when a distributed load is applied on its crown. Example of regions of constant influence area for beam elements along the meridian are highlighted; (b) Scheme of the Distributed Load on the crown as implemented in the second model.
Figure 4. (a) Scheme of the second way of modelling, i.e. when a distributed load is applied on its crown. Example of regions of constant influence area for beam elements along the meridian are highlighted; (b) Scheme of the Distributed Load on the crown as implemented in the second model.
Preprints 91836 g004
Preprints 91836 g005
Figure 5. Figure 5. Scheme representing the ductile (or fragile) joint in its (a) undeformed & (b) deformed configurations. The latter one indicating the position of the plastic hinge.
Figure 5. Figure 5. Scheme representing the ductile (or fragile) joint in its (a) undeformed & (b) deformed configurations. The latter one indicating the position of the plastic hinge.
Preprints 91836 g005
Preprints 91836 g006
Figure 6. Scheme representing the ductile/fragile joint undergoing inelastic shear deformation, with the typical jagged deformed shape indicating the shear failure.
Figure 6. Scheme representing the ductile/fragile joint undergoing inelastic shear deformation, with the typical jagged deformed shape indicating the shear failure.
Preprints 91836 g006
Preprints 91836 g007
Figure 7. Nonlinear analysis process for reinforced dome. Application of FRP annular reinforcement on the extrados of the meridian slice at equal angular distance from the vertical axis.
Figure 7. Nonlinear analysis process for reinforced dome. Application of FRP annular reinforcement on the extrados of the meridian slice at equal angular distance from the vertical axis.
Preprints 91836 g007
Preprints 91836 g008
Figure 8. (a) Sensitivity analysis under NTM hypothesis on the unreinforced dome and validation by comparison with literature data; (b) Elastic perfectly brittle constitutional law for PCs; (c) Representation of the field of action of the tensions considered.
Figure 8. (a) Sensitivity analysis under NTM hypothesis on the unreinforced dome and validation by comparison with literature data; (b) Elastic perfectly brittle constitutional law for PCs; (c) Representation of the field of action of the tensions considered.
Preprints 91836 g008
Preprints 91836 g009
Figure 9. (a) Side view of the deformed shape at the 98th step of nonlinear analysis under NTM hypothesis. (b) Isometric scheme of annular plastic hinge formation on a fuse with brittle joints.
Figure 9. (a) Side view of the deformed shape at the 98th step of nonlinear analysis under NTM hypothesis. (b) Isometric scheme of annular plastic hinge formation on a fuse with brittle joints.
Preprints 91836 g009
Preprints 91836 g010
Figure 10. (a) Sensitivity Analysis with Orthotropy in tension; (b) Elastic perfectly plastic constitutional law for joints CoBs; (c) Representation of the field of action of the tensions considered.
Figure 10. (a) Sensitivity Analysis with Orthotropy in tension; (b) Elastic perfectly plastic constitutional law for joints CoBs; (c) Representation of the field of action of the tensions considered.
Preprints 91836 g010
Preprints 91836 g011
Figure 11. Validation of the present model by comparison with data found in the literature. Comparison between results from obtained with a NTM model and ductile-joints model.
Figure 11. Validation of the present model by comparison with data found in the literature. Comparison between results from obtained with a NTM model and ductile-joints model.
Preprints 91836 g011
Preprints 91836 g012
Figure 12. Deformed shape of the 82nd step of nonlinear analysis under orthotropy hypothesis.
Figure 12. Deformed shape of the 82nd step of nonlinear analysis under orthotropy hypothesis.
Preprints 91836 g012
Preprints 91836 g013
Figure 13. Deformed shape of the 12th step (out of 86), with, highlighted in light grey, the effect of sliding both at the base and as a result of the application of a distributed load on the crown.
Figure 13. Deformed shape of the 12th step (out of 86), with, highlighted in light grey, the effect of sliding both at the base and as a result of the application of a distributed load on the crown.
Preprints 91836 g013
Preprints 91836 g014
Figure 14. (a) Validation of the model with CFRP annular reinforcement by comparison with numerical analyses in the literature; (b) Elastic perfectly plastic constitutional law for CFRP CoBs.
Figure 14. (a) Validation of the model with CFRP annular reinforcement by comparison with numerical analyses in the literature; (b) Elastic perfectly plastic constitutional law for CFRP CoBs.
Preprints 91836 g014
Preprints 91836 g015
Figure 15. Figure 15. Efficiency of FRP reinforcement as designed.
Figure 15. Figure 15. Efficiency of FRP reinforcement as designed.
Preprints 91836 g015
Preprints 91836 g016
Figure 16. (a) Side view of the undeformed fuse with the position of FRP highlighted on the extrados; (b) Deformed shape of the 82nd step of nonlinear analysis for FRP reinforced dome.
Figure 16. (a) Side view of the undeformed fuse with the position of FRP highlighted on the extrados; (b) Deformed shape of the 82nd step of nonlinear analysis for FRP reinforced dome.
Preprints 91836 g016
Preprints 91836 g017
Figure 17. Effect of FRP application in displacement prevention, by comparison between UnReinforced and Reinforced cases (82nd step of NLA).
Figure 17. Effect of FRP application in displacement prevention, by comparison between UnReinforced and Reinforced cases (82nd step of NLA).
Preprints 91836 g017
Table 1. Mechanical properties of clay bricks assigned in the FE model [11].
Table 1. Mechanical properties of clay bricks assigned in the FE model [11].
Mechanical Properties u.m.
Young’s Modulus E 1.7 ∙ 103 MPa
Poisson Ratio ν 0 -
Density ρ 2.0 ∙ 10-6 Kg ∙ mm-3
Nonlinear Type Elastic Plastic
Yield Criterion Von Mieses
Table 2. Point Contact FE software settings.
Table 2. Point Contact FE software settings.
Joint Position Type Friction
Coefficients 		Stiffness
Values
C1 C2 Initial k0
[kN∙mm-1] 		Initial kiter
Parallel IN
OUT		 Tension
Tension		 -
-		 -
-		 61.2
30.6		 -
-
Meridian IN
OUT		 Normal
Normal		 1
1		 1
1		 93.84
46.92		 ✓
✓
Table 3. Mechanical characteristics of Load Distribution Plate and its restraints.
Table 3. Mechanical characteristics of Load Distribution Plate and its restraints.
Mechanical Properties u.m.
Rigid Beams (Load Plate)
Young’s Modulus E 1.7 ∙ 108 MPa
Section Area A 100 mm2
I11 = I22 I 8.33 ∙ 102 mm4
Point Contact
Type Tension
Initial Stiffness K0 1.0 ∙ 103 kN ∙ mm-1
Max Tension Tmax 0 kN
Table 4. Mechanical characteristics of Mortar Joint Elements: Parallel Joints.
Table 4. Mechanical characteristics of Mortar Joint Elements: Parallel Joints.
Mechanical Properties u.m.
Rigid Beams (Joints)
Young’s Modulus E 1.0 ∙ 103 MPa
Section Area A 100 mm2
I11 = I22 I 8.33 ∙ 102 mm4
Inertia J 1.41 ∙ 103 mm4
Shear Truss (CoB)
Young’s Modulus E 1.7 ∙ 104 MPa
Initial Stiffness K0 1.00 mm2
Max Compression Cmax 1.0 ∙ 1011 kN
Max Tension Tmax 1.0 ∙ 1011 kN
Table 5. Mechanical properties of FRP according to [31]
Table 5. Mechanical properties of FRP according to [31]
CFRP Properties u.m.
Thickness tfibre 0.2 mm
Young’s Modulus EFRP 1.6 ∙ 105 MPa
Factor c1 c1 0.015 -
Reducing code factor γfd 1.2 -
Masonry partial safety factor γM 1 -
Fracture Energy ΓFK 0.073 N ∙ mm-1
Design Bond Strength ffdd 164 MPa
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated