Prerpints.org logo
Preprint
Article

Spatiotemporal Variation and Long-Range Correlation of Groundwater Level in Odessa, Ukraine

Altmetrics

Downloads

88

Views

364

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
Increasing groundwater levels (GWL) may become one of the most serious issues for Odessa City, Ukraine. This study investigated the spatial distribution characteristics and multifractal scaling behaviour of groundwater level/depth fluctuation for a Quaternary aquifer in Odessa City using a geostatistical approach and a Multifractal Detrended Fluctuation Analysis (MF-DFA). These two methods were applied to monthly GWL fluctuation time series from 1970 to 2020 to monitor 72 hydrogeological wells situated in different parts of Odessa City. The spatial distribution of GWL revealed an overall trend of decline and recovery from 1970 to 2020 in the study area, except for most of the southern region, where a persistent recovery of groundwater depth was observed. The MF-DFA results suggest that the dynamics of GWL fluctuations have multifractal characteristics in the Odessa City area. In addition, both long-range correlation and fat-tail probability distribution contribute to multifractality. However, long-range correlations among fluctuations made a major contribution to the observed multifractality of the GWL fluctuations time series. The generalized Hurst exponent shows a wide range of change (0.20 < h(q) < 2.85), indicating the sensitivity of GWL fluctuations to changes in small scale factors and large-scale factors. Regarding the long range correlations of GWL depth, the Hurst exponents (q = 2) demonstrated the positive persistence of groundwater depth recovery in the southern region and the persistence of groundwater depth variation in the other regions of the study area. The dynamic changes in GWL depth in the Odessa City area may be affected by both natural structural and anthropogenic factors.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Groundwater, located in the steppe zone of southern Ukraine, is the main water source for agriculture in the Odessa district and domestic use in the city. The formation and distribution of groundwater in Quaternary deposits depend on climatic, hydrogeological, geomorphological, lithological, and facies conditions, as well as human economic activity [1,2].
This study focuses on the dynamics of the shallow groundwater level (GWL), that is, the depth of water in the first aquifer from the land surface. The study of GWL fluctuations is important to provide a better basis for assessing groundwater quality, quantity and management in general, as well as to understand the dynamics and quality of the hydrogeological system and, to predict processes associated with the rise and fluctuation of GWL, such as flooding, subsidence of loess and landslides. At present, we observe increased of GWL in most residential areas of Odessa. The rising groundwater affects the basement of buildings and, underground communications, and leads to the subsidence of soils under foundations, which may lead to subsidence of the building foundation, potentially sustaining structural damage.
In recent years, the natural regime of the Quaternary aquifers in the Odessa territory has changed radically. The water level shows a pronounced upward trend, and the area of its distribution in Odessa is also increasing. The maximum increase is confined to the central part of the city. The rise in the water level over the past 70-80 years was 12-15 m. In most parts of the city, the water table rose to a depth of 5 m below the land surface.
Many natural systems, the behaviours of which are outwardly perceived as chaotic, have one common property. This property is called self-affinity, also termed fractality, because nonstationary temporal fluctuations follow a power-law to some extent. Numerous studies have described self-affinity in nature. These include classic monographs of the creator of fractal geometry, Benoit Mandelbrot, and his successors [3,4,5], and reviews in scientific journals, books, and series [6,7,8]. Scientific papers devoted to the fractal properties of systems have appeared in completely different areas of natural science, including geophysics [9,10], topology [11], biology and medicine, economics and finance. The scientific journal “Fractals” is regularly published and completely devoted to this subject. Recently, the number of publications in hydrology and hydrogeology has increased.
Various researchers have explored the scaling characteristics of groundwater systems using the Detrended Fluctuation Analysis (DFA) method and other techniques to quantify groundwater fractal dynamics [12,13,14]. The DFA method was designed by Peng et al. [15] to investigate long-range fractal correlations in nonstationary time series. Although nonstationary fluctuations in GWL are often characterised and modelled as fractional Brownian motions [16], the nature of GWL fluctuations is mainly nonstationary, with significant trends in GWL changes that may not be entirely random [17,18,19]. By detrending the data using the DFA method via polynomial fittings, the impact of nostationarity in the data can be circumvented to reveal only the fluctuations and time-scaling of a process. GWL fluctuations have repeatedly demonstrated long-range dependence over time [13,20,21,22]. These are power-law relationships over a variety of time-scales that can be represented by fractals. Generally, the fractal structure of GWL fluctuations is determined by a power-law exponent based on the assumption that scaling is independent of space and time in the DFA.
The existence of crossover timescales with different scale exponents cannot be reliably and authentically characterised by a determined mathematical form. In this regard, DFA cannot describe the detailed behaviour of fractal scales. Multifractal DFA (MF-DFA) was introduced to overcome the limitations of DFA [23]. As an effective tool for fractal analysis, the MF-DFA method has been successfully applied to analyse complex phenomena in various areas of science, as well as to quantify the fractal dynamics of groundwater systems [12,13,18,22]. The local Hurst exponent [24] is a useful tool for characterising the multifractal behaviour of GWL fluctuations affected by variations in different factor in space and time. Moreover, it sheds light on the prediction of GWL fluctuation trends.
Understanding spatiotemporal changes in groundwater levels is of great importance for hydrogeological forecasting on the Odessa territory and for understanding the mechanisms of processes and phenomena associated with GWL fluctuations. In addition, variations in water level, as well as other parameters characterising the Quaternary aquifer, reflect the properties of groundwater to receive and transmit signals about changes in the stress-strain characteristics; the filtration characteristics of the aquifer rock are influenced by different factors.
This study aimed to analyse the spatial distribution characteristics of GWL depth and the multifractal features of a long-term monthly GWL time series of the Quaternary aquifer recorded in the Odessa City area, from 1970 to 2020, using the geostatistical approach and MF-DFA method. The main objective of this study was to predict GWL depth in the city of Odessa using a long-range fractal correlation approach.

2. Materials and Methods

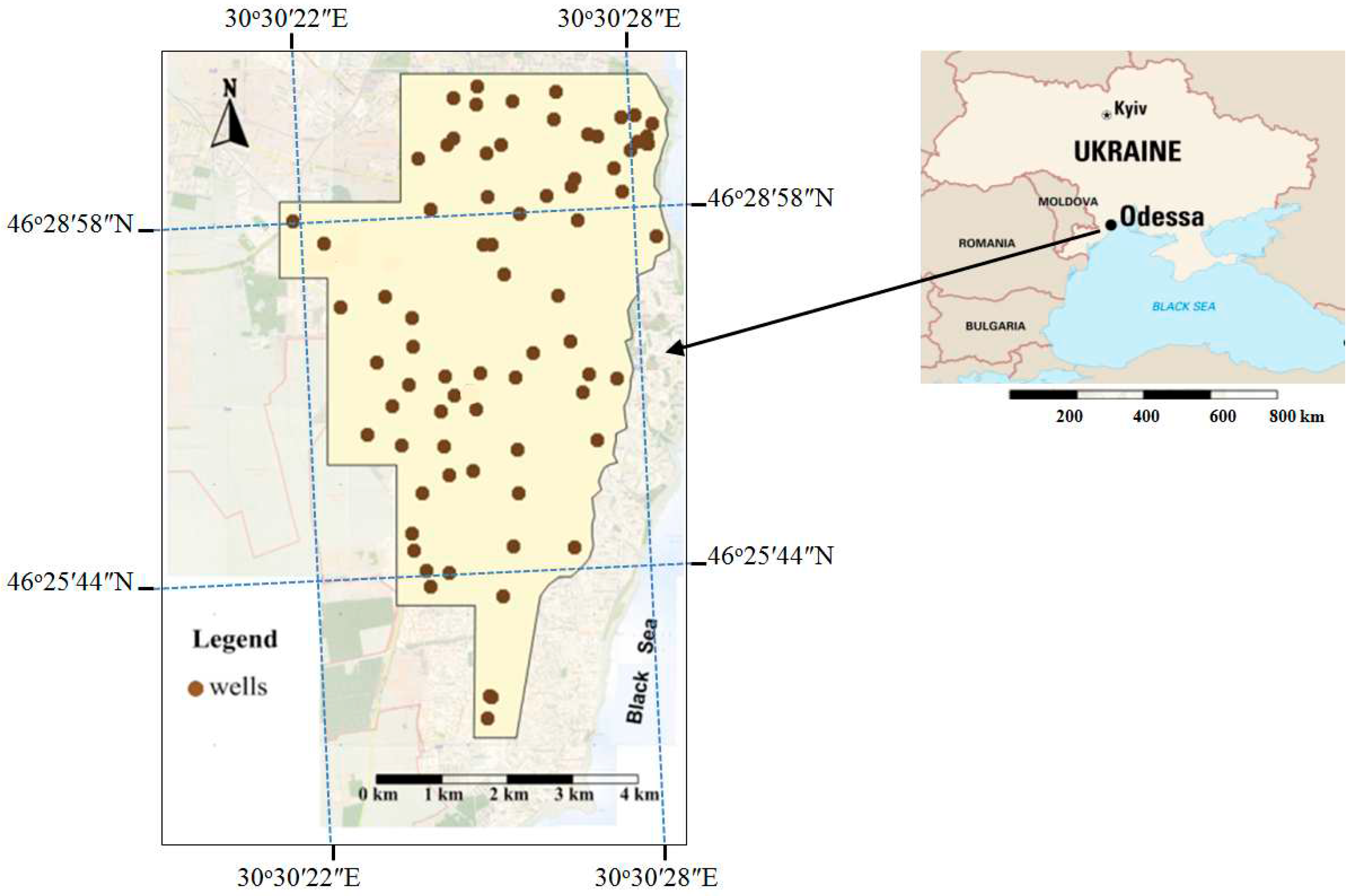
2.1. Site Description and Data Collection

The study area is located on the north-western shore of the Black Sea (Odessa, Ukraine; Figure 1), where Quaternary deposits are widespread. Groundwater in the Odessa territory is mainly concentrated in the Quaternary strata. Within these strata, two or three aquifers are typically observed. The aquifer sediments are composed mainly of loess and loessoid loams.
Groundwater can accelerate loess slope stability in Odessa City [25,26]. The intensity of sliding displacements on loess slopes in the Odessa territory increases with the appropriation of new territories, mainly because of the rising GWL in the Quaternary aquifer [1,2]. Loess rocks have poor filtration properties, with filtration coefficients typically between 0.1 and 1.0 m/day. The thickness of the water-bearing layer varies from 0.2 to 5.9 m. Groundwater table depth varies in the range of 3–10 m. Aquifer recharge is driven mainly by atmospheric precipitation and artificial recharge. Groundwater discharges on the slopes of ravines, gullies, estuaries and seashores.
Loessoid loams have pronounced filtration anisotropy, which is expressed by a significantly greater value of filtration coefficients in the vertical direction (2-8 times more) than in the horizontal [2,26]. Therefore, precipitation and wastewater move to the aquiclude quicker than they spread horizontally. Downward movement of groundwater into underlying aquifers mainly occurs in places where Pliocene reddish-brown clays underlying the loess layer are absent, in areas adjacent to gullies and ravines, and in areas of coastal cliffs through landslide bodies. Part of the Quaternary water is discharged into the Pontian sediments through the drainage system.
This research was conducted using data provided by the Department of Engineering Protection of the Territory of Odessa and the Department of Engineering geology and Hydrogeology of the Mechnikov Odessa National University.
Monthly GWL were measured over a 50-year period (starting in 1970) for 72 monitoring hydrogeological wells located on an area of 25.8 km2 in the Odessa city. The Newton interpolation method was used to interpolate the GWL time series for short-period missing data. The total area of the zones with a given range of groundwater depth is listed in Table 1 for the period 1970–2000. The table shows that during this time interval, the GWL occurred at a depth of 3-6 meters (4.5 m on average) for the largest area. The total area of these zones is 17.33 million m2, or 68.07 % of the total area occupied by hydrogeological well monitoring. The area of zones with a GWL depth of less than 3 m (average of 2.5 m) was 13.28 million m2 (13.28 %). In 18.65 % of the study area, the GWL did not reach depths of less than 6 m.

2.2. Method Description

In this study, the spatial variability and correlation of the GWL depth in Odessa City were studied using geostatistical methods in Golden Software Surfer 13. The MF-DFA method was used to examine the multifractal behaviour of GWL fluctuations and analyse the temporal variability of the GWL depth and long-range fractal correlations.

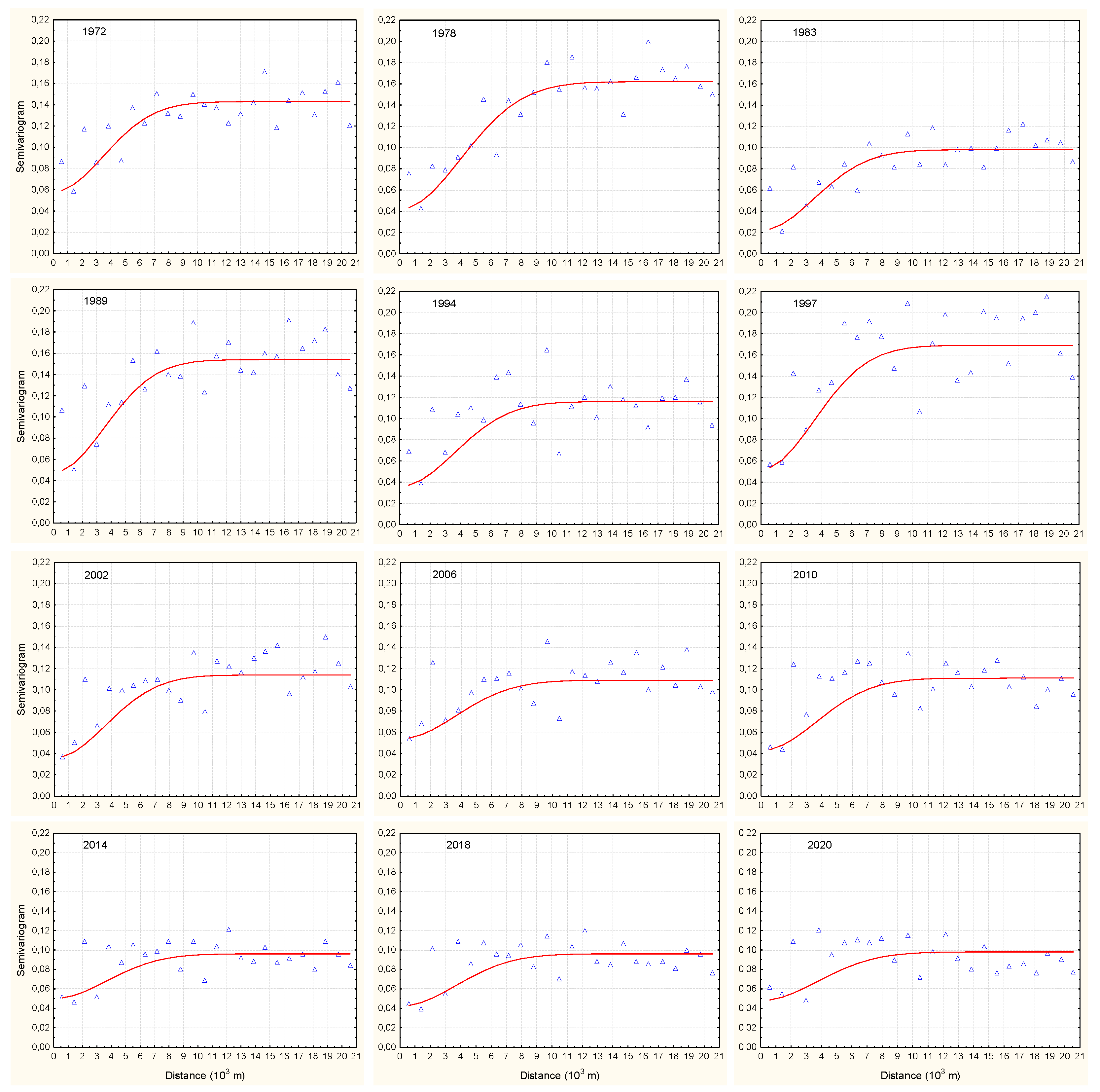
2.2.1. Geostatistical Methods

To consider the spatial correlation between the measured data we used geostatistical methods, including semivariogram functions and kriging interpolation. Many researchers have used these methods to reveal the spatial and temporal structures of GWL depth fluctuations [28,29,30]. In this study basic geostatistical methods were used to quantify the spatial variability of the GWL depth in the study area. Ordinary kriging (OK) was used as the interpolation method. For ordinary kriging, the data series should have a normal or lognormal distribution [31]. We tested the normality of the data using the Kolmogorov-Smirnov (K-S) test and Shapiro-Wilk (S-W) tests. As the GWL datasets followed a log-normal distribution, a log transformation was performed to normalise the data. Descriptive statistics were examined, including the median, mean, coefficient of variation, kurtosis, and skewness. A semivariogram was used to quantify the differences between the sampled data values as a function of separation distance.
A semivariogram plot was obtained by calculating the semivariograms at different lag distance. The generalised formula of the semivariogram function is [32,33]:
γ ( h ) = 1 2 N ( h ) ∑ i = 1 N ( h ) ( z ( x i ) − z ( x i + h ) 2
where γ(h) is the semivariogram value at the distance h; z(xi) is the sample value at the spatial point xi; N(h) is the total number of the variable pairs separated by distance h. For quantitative evaluation of the variation characteristics of the research area, determining the theoretical model of its semivariogram is necessary. Common semivariograms are generated using different models (exponential, spherical, and Gaussian) [34].
The semivariogram function of GWL in Odessa City can be fitted with a Gaussian function (Equation (2), parabolic shape):
γ ( h ) = 0                   h = 0 C 0 + C 1 − e − 3 h 2 a 2         h > 0
The three main parameters of the semivariogram are C0, C0+C, and a. Here C0 is the localised discontinuity or nugget, which refers to the value of the semivariogram function due to the measurement error and spatial variation when two sampling points are very close [30]; C0+C is the sill, a constant where the distance between sampling points increases by h when the semivariogram reaches a relatively stable value; a is the distance between the sampling points when the semivariogram reaches the sill from the nugget. This distance defines the range of the spatial correlation and C is the difference between the sill and nugget.
A fitting diagram of the semivariogram function of groundwater depth in Odessa City for the turning years is shown in Figure 2. Both the nugget and sill can be used to describe the degree of spatial variability in groundwater depths [30]. The nugget represents the variation caused by random factors on a small scale, including human factors such as local leaks from water-bearing utilities, local heavy precipitation, and local irrigation. The sill reflects large-scale variations caused by structural factors, including topography, geology, climate, and sea level and large-scale human factors, such as large-scale exploitation of groundwater. In general, the nugget/sill ratio (C0/(C0+C)) can be used to classify spatial dependence. The ratio of these two parameters (also called the nugget effect) may reflect the strength of the spatial correlation of GWL depths [30,35]. We denote this ratio as Cne, C n e = 1 + C C 0 − 1 . If Cne < 25 %, the variables are strongly influenced by natural structural factors and strongly correlated in space; if 25 % ≤ Cne ≤ 75 %, the variable is influenced by both natural structural and random factors, and moderately correlated in space; and when Cne >75 %, the variables are greatly affected by random factors and have a weak spatial correlation. When Cne is higher, and the spatial correlation is smaller, it is more apparent that spatial variability is caused by stochastic factors. A Cne close to one indicates that the variable exhibits constant variability on a small scale [30,36].
The universal kriging method with cross-validation was applied to determine whether the dataset followed any particular trend and to assess the accuracy of the chosen variograms in the estimation of GWL fluctuations for the spatial scale.
As noted by Lu et al. [30], rather than assuming that the mean groundwater depth is constant over the entire domain, we recognise that it may contain a spatial trend, that is appropriately interpolated by the OK procedure. Parameters for variogram models were derived following the step-by-step procedures outlined by Barnes [37], and an initial theoretical variogram was fitted to the experimental variogram using the Surfer computer program’s interactive interface. The high R2 values obtained from the kriging estimations proved that the variograms were chosen correctly.

2.2.2. Multifractal Detrended Fluctuation Analysis (MF-DFA)

There are two types of processes with fractal properties: monofractal (self-similar or self-affine) and multifractal. Multifractals are often found in nature, whereas, simple self-similar objects, such as monofractals, represent an idealisation of real phenomena. Monofractal processes are homogeneous, because their scaling characteristics remain unchanged over any scale range. Multifractal processes are characterized by different scaling behaviours (or by a spectrum of scaling exponents) of different moments over a full range of time scales.
MF-DFA is a generalisation of DFA, developed by Peng et al. [15], and is used to detect long-term correlations in nonstationary time series. Based on DFA, the MF-DFA was developed by Kantelhardt et al. [23] for the multifractal characterisation of nonstationary time series. The MF-DFA method has been applied to evaluate the characteristics of data, such as long-term weather records [38], geology time series [39], neuron spiking, and financial time-series. Although several studies on the fractal features of GWL fluctuations have been published in recent years [12,13,18,22], the MF-DFA method has not been sufficiently tested for the analysis of GWL fluctuations. Moreover, the application of this method to the study of temporal and spatial variations in GWL in Odessa is relatively rare.
The most important step in the execution of both DFA and MF-DFA is eliminating the local polynomial trend Y(j) in each segment of the cumulative series X(t) of length N.
Basic MF-DFA consists of the following steps [10,23,40,41,42].
1. The stochastic time series x(t), t = 1,.2…, N is shifted by the mean x and cumulatively summed:
X ( t ) = ∑ i = 1 t [ x i − x ] .
2. The integrated time series X(t) is segmented into N non-overlapping windows of equal size s (Ns = N/s). Because the length N of the time series is not always a multiple of the considered time scale s, a short part at the end of the series may remain. To avoid disregarding this part of the data, the same procedure is repeated starting from the opposite end. As a result, we get 2Ns segments altogether.
3. For calculation, the trend of each 2N segments a least square fit method is applied and the variance is determined by:
F 2 ( ν , s ) = 1 s ∑ j = 1 s Y [ ( ν − 1 ) s + j ] − Y ν ( j ) 2
for each segment ν, ν = 1,…, Ns, and
F 2 ( ν , s ) = 1 s ∑ j = 1 s Y [ N − ( ν − N s ) s + j ] − Y ν ( j ) 2
for ν = Ns + 1,…, 2Ns. In Equations (4) and (5), Yν (j) is a locally fitted polynomial of first order or higher. In this study, local trends were fitted using a first-order polynomial.
4. The fluctuation function of qth-order and 2Ns segments is determined as:
F q ( s ) = 1 2 N s ∑ ν = 1 2 N s [ F 2 ( ν , s ) ] q / 2 1 / q
where q ≠ 0 and s ≥ m + 2 (m is the order of Yν (j) to be fitted). In this study, m = 2, and s = N/4. To reveal how the function Fq(s) depends on s for different q, we need to repeat Equations (4)−(6) for s different time scales.
5. Finally, the scaling behaviour of the fluctuation functions was determined by analysing log-log plots of Fq(s) versus s for each value of q. If a long-range power-law correlation exists in the time series, Fq(s) for large values of s increases according to the power-law [23]:
F q ( s ) ~ s h ( q ) .
In Equation (7), h(q) is a generalized Hurst exponent and takes a variety of values for each value of q. For stationary time series, the exponent h(2) is identical to the classical Hurst exponent H and varies between 0 and 1 [3], and 𝐻 = ℎ(2) − 1 for nonstationary time series. For q > 0, h(q) depicts the scaling behaviour of the segments with large fluctuations and for q < 0, h(q) describes the scaling behaviour of the segments with small fluctuations [24]. Because Equation (6) contains uncertainty at q = 0, the following expression is preferred for F q ( s ) :
F 0 ( s ) = exp 1 2 N s ∑ ν = 1 2 N s ln [ F 2 ( ν , s ) ] ~ s h ( 0 )
The generalized Hurst exponent h(q) is independent of q for a time series of monofractal behaviour and strongly depends on q for a time series showing multifractal behaviour, which means that the scaling behaviour differs for fluctuations of different magnitudes. Hurst exponent h(q) is interpreted as follows [40]: h ∈ (0, 0.5) indicates antipersistency (or short-term persistence) of the time series. In this case, growth in the past means a decrease in the future, and a downward trend in the past makes an increase in the future likely; h = 0.5 indicates uncorrelated noise, indicating no correlation between past and future for all t, as it should be for a random process with independent increments indicating the absence of long-term correlations; h ∈ (0.5, 1) indicates persistency of the time series, meaning the time series is long-range positively correlated, that is, an increase is more likely to be followed by an increase and vice versa; h = 1.5 indicates Brownian motion (integrated white noise); h ≥ 2 indicates black noise.
The Hurst exponent h(q) relates to the classical multifractal scaling exponent τ(q) through the relation:
τ(q) = q h(q) − 1.
The transition from the Hurst exponent h(q) to the main characteristics of multifractals, such as the singularity index α that represents local Hurst exponents and spectral function f(α) of time series can be carried out by Legendre transform:
α(q) = d [τ(q)]/dq,
f(α) = α q(α) − τ(q(α)).
The singularity index α quantifies the singularity intensity and f(α) represents a multifractal spectrum of time series. This spectrum illustrates the deviation of segments with small and large fluctuations from the average fractal structure. The width of the spectrum is a direct measure of the degrees of multifractality, which reflects the strength of multifractality effects in the time series. This strength can be estimated by the width of (α), which is defined as the difference between the maximum and minimum values of (α): Δ𝛼 = 𝛼𝑚𝑎𝑥 − 𝛼𝑚𝑖𝑛. The wider the spectrum, the richer is the multifractality behaviour of the analysed time series. Usually, f(a) is a smooth upper convex curve. Each point on the f(a) ~ a(q) curve represents the fractal dimension of the subset with the same singular exponent a(q).
For MF-DFA, this study used a Python-based implementation of MF-DFA introduced by Gorjão et al. [43]. They have provided an open-source implementation at https://github.com/LRydin/MFDFA.

3. Results and Discussion

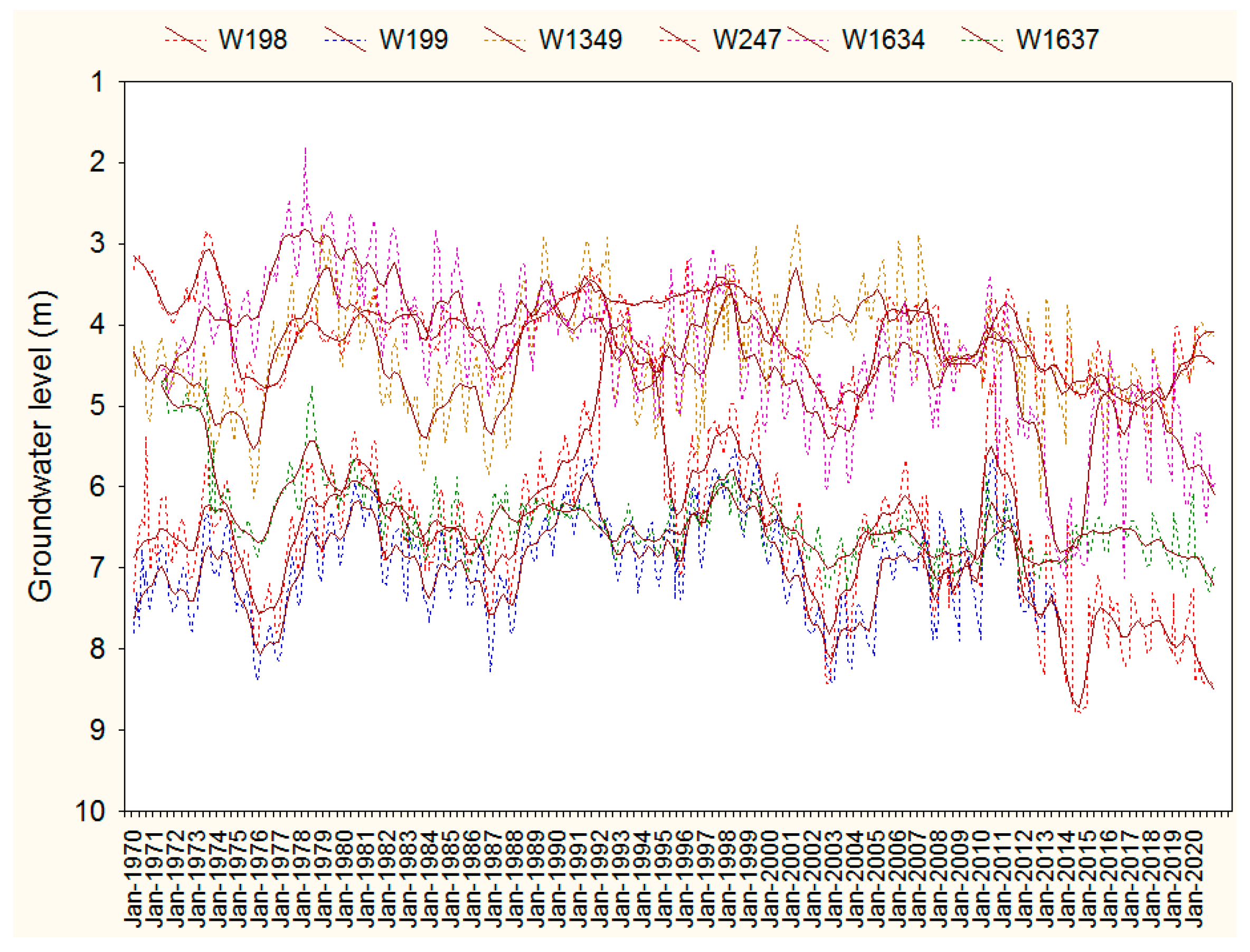
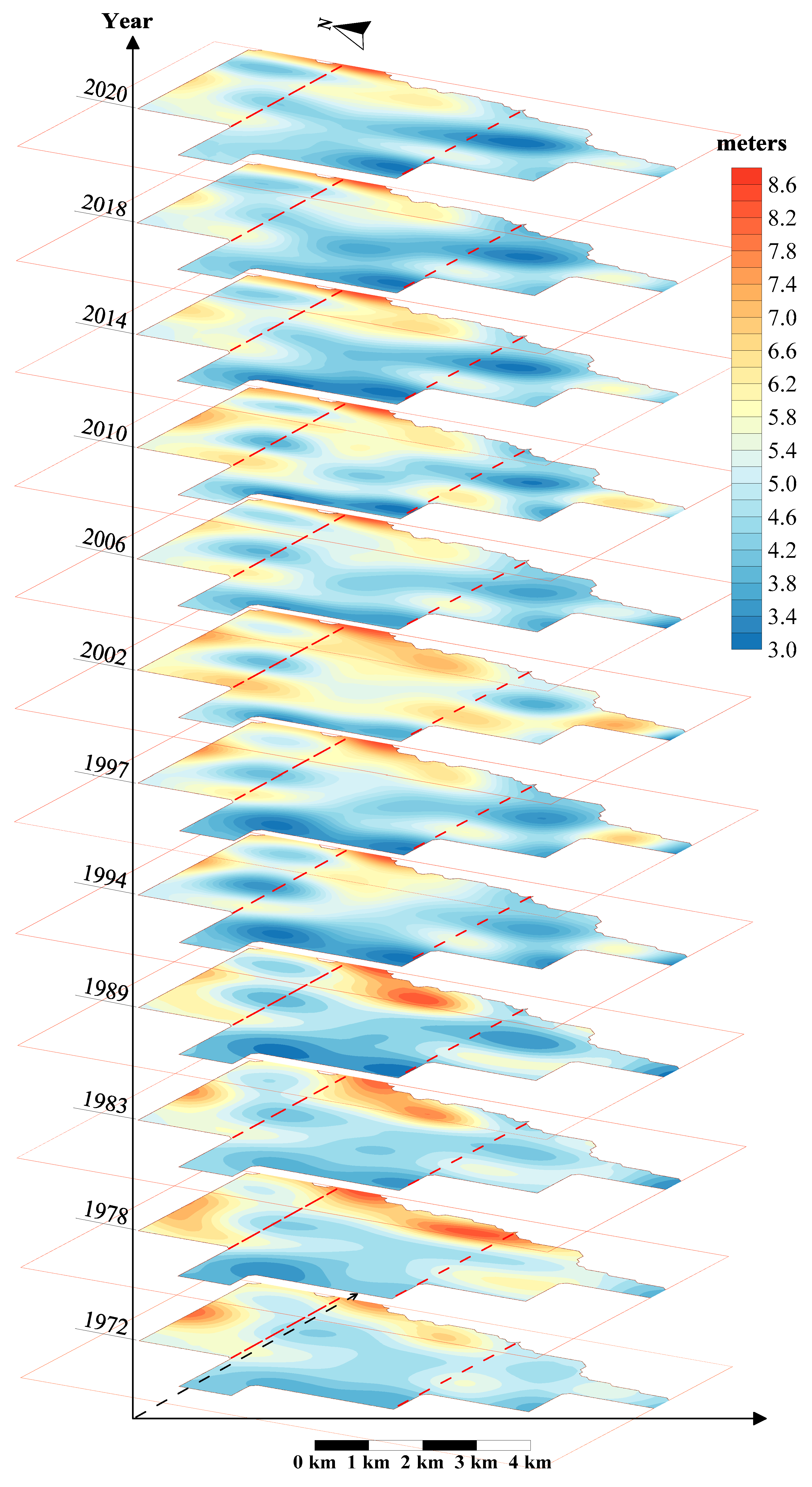
3.1. Groundwater Level Spatiotemporal Characteristics

As a preliminary investigation, graphs of the average monthly variation in GWL are shown in Figure 3 for selected wells: 198, 199, 1349, 247, 1634 and 1637. All 72 monitoring wells had at least 3198 water level records. The wells exhibited nonstationarity GWL changes. As shown in Figure 3, during the observation period of 1970-2020, the greatest rise in groundwater in the territory of Odessa took place several times: 1977-78, 1988-89, 1997-98, 2005-06, 2010-2011, and 2015-2016.
Figure 4 shows the average GWL depths with the corresponding seasonal distributions. The monthly boxplots show that in the average annual cycle, the water level peaks mainly in April and May and decreases in September and October. The rates of change vary from 0.9 to 0.2 m/year (mean = 0.19 m/year).
The K–S single-sample test showed that the logarithm of the GWL data was normally distributed. Table 2 summarises the statistics of the data from 1970 to 2020 for the turning years of GWL fluctuations: 1972, 1978, 1983, 1989, 1994, 1997, 2002, 2006, 2010, 2014, 2018, and 2020. The median and mean groundwater depths increased and then decreased with time. This pattern describes the overall trend of increasing and then decreasing groundwater depth in Odessa City from 1970 to 2020.
The characteristic depths of groundwater in the studied territory were not the same in different parts of the city. Therefore, maps to show the spatial distribution of the GWL depth in different years are necessary. We selected the turning years of GWL fluctuation. The maps for these years are presented in Figure 5 after ordinary kriging interpolation [44] and show the spatiotemporal evolution of the average GWL depth in the study area.
As shown in Figure 5, the study area was divided into three regions: northern, central and southern. The boundaries between the regions are indicated by red dotted lines. Overall, during the past decade, the GWL has been shallower in the central and southern regions. In these regions, the average groundwater depth was 5-6 m or less. In some cases, it reached up to 3 m, for example, in the western part of the central region and in the central part of the southern region. In the northern region, the GWL also becomes shallower than in the central and southern regions, although it is not as pronounced.
In this study we used the parameters of the semivariogram to analyse the spatiotemporal variation characteristics of groundwater depth autocorrelations. These parameters are shown in Figure 6, including the nugget (C0), sill (C0+C), and ratio of the nugget to the sill (Cne). It is noteworthy that C0 and C0+C reflect factors affecting groundwater depth. Parameter C0 captures the influence of small-scale factors, including small-scale human factors, such as local irrigation and leakage from water-bearing utilities, and climatic factors, such as local heavy precipitation. Parameter C0+C captures the influence of large-scale structural factors, including sea level, climate, topography, and geology, as well as large-scale human factors, such as large-scale mining and diversion.
The turning years of 1972, 1978, 1983, 1989, 1994, 1997, 2002, 2006, 2010, 2014, 2018, and 2020 were selected to analyse the dynamic changes in GWL depth in the Odessa City area.
As shown in Figure 6, the ratio of nugget to sill (Cne) was greater than 25 % (between 35 % and 43 %) and approached 25 % during 1972–1983, indicating a tendency to shift from moderate to strong spatial correlation of the GWL depth in the study area. Meanwhile, the C0+C value remained moderate, whereas the C0 value remained low, indicating that the groundwater in different parts of the study area showed an overall change. As shown in Figure 5, the spatial correlation of groundwater changes increased in 1972, 1978, and 1983. In these graphs, the cone of the depression continued to expand to the eastern area of the central region.
Groundwater rebounded in the western area of the central region and in the central and southern areas of the southern region. The overall variation indicated that the change in GWL depth during this period was mainly due to a combination of structural and local human factors.
During 1984-1990, the Cne value increased (35 %) and then decreased (26 %), indicating a strong correlation between GWL depths in different regions of the study area during this period.
This indicates that GWL depth showed an overall change during this period. As shown in Figure 5 (1989), the GWL depth in the eastern part of the central region increased, and rebounded in the western part of this region and in the central part of the northern and southern regions. Notably, during 1972–2004, the three parameters C0, C0+C, and Cne exhibited relatively synchronous fluctuations.
During 1991-2004, Cne value gradually increased and approached 35 %. As shown in the three graphs in Figure 5 (1994, 1997, and 2002), the groundwater cone of the depression continued to expand and the GWL depth continued to increase in all regions. In addition, C0 remained low. However, the C0+C value remained high, indicating that GWL depth variation is influenced by structural factors (i.e. climate, topography, and geology) and human factors (i.e. continuous leaks from water-bearing utilities, various waste filtration reservoirs, and large-scale mining).
During 2005-2020, Cne fluctuated between 35 % and 60 %, indicating a moderate spatial correlation with GWL depth in different areas of Odessa. The five GWL depth graphs for 2006, 2010, 2014, 2018, and 2020, plotted in Figure 5, show a slight decrease in the GWL depth in all regions of the study area. C0 and C0+C also reflect that since 2005, the GWL depth in Odessa may have been influenced by structural factors (i.e. climate, topography, and geology) and human factors (leaks from water-bearing utilities and various waste filtration reservoirs).

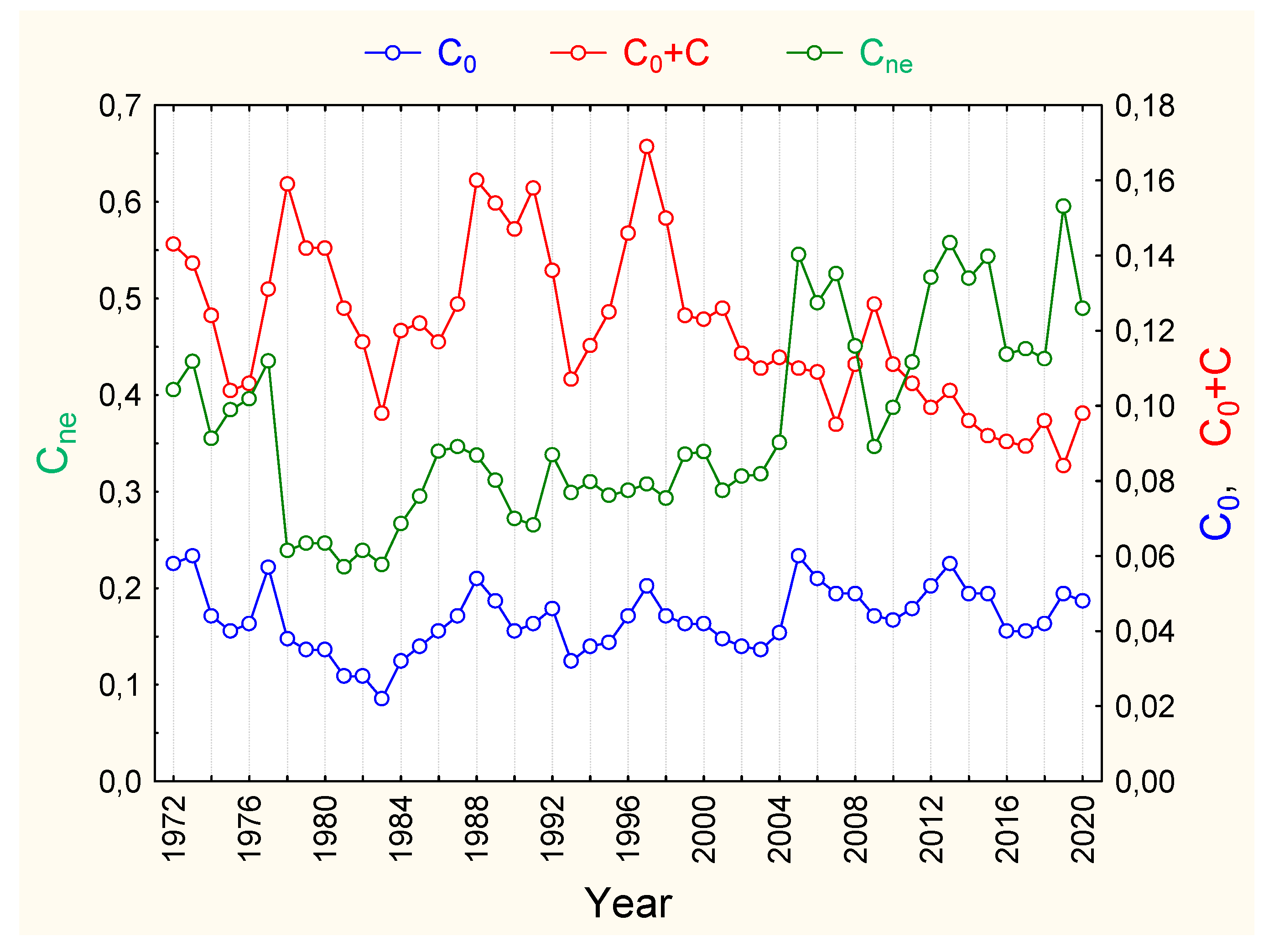
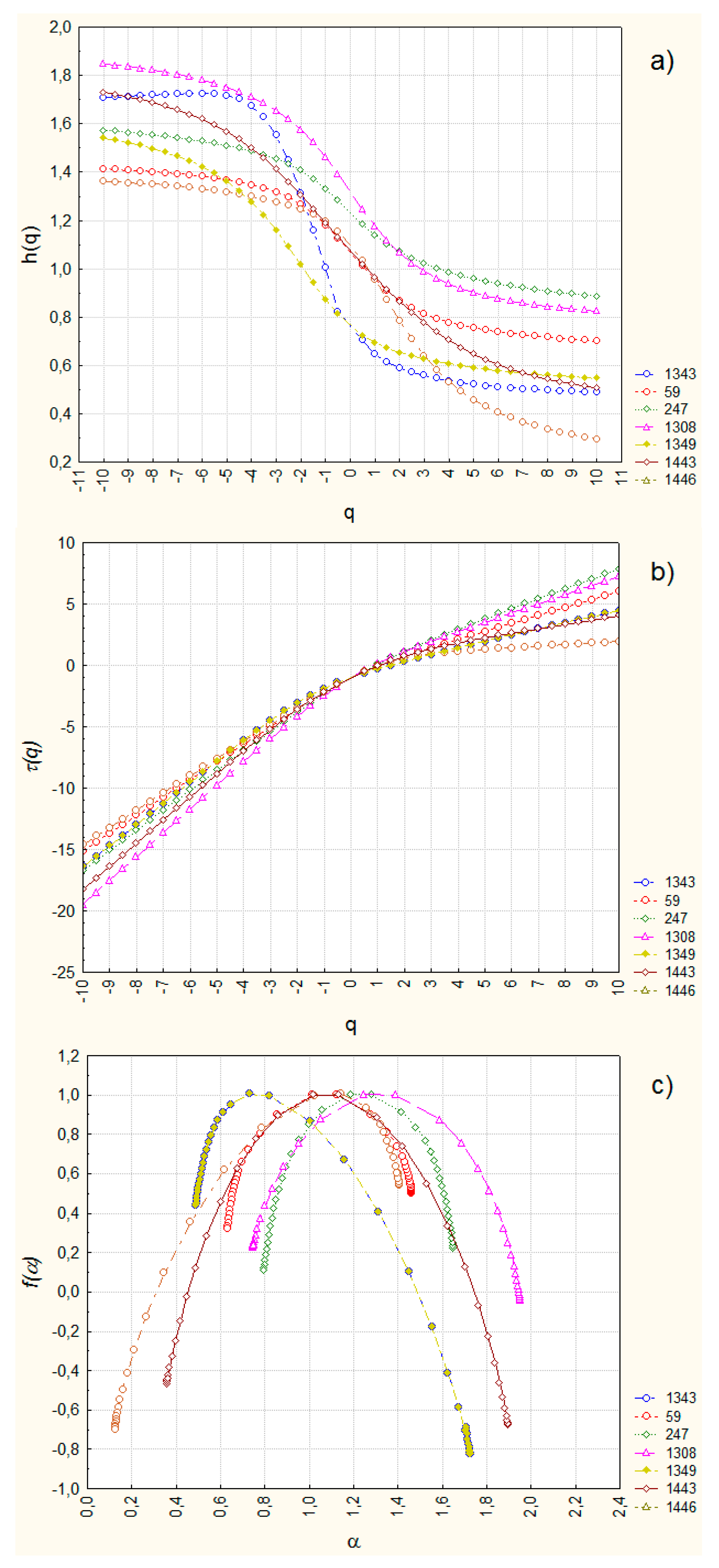
3.2. Groundwater Level Multifractal Characteristics

In this study, we analysed the monthly water level records for 72 monitoring wells using MF-DFA analysis for multifractal behaviour. The multifractal results include log-log plots of Fq(s) against time scale s, the generalized Hurst exponent h(q), the scaling exponent spectrum τ(q) and the singularity spectrum f(α) corresponding to a series of moments q (−10 ≤ q ≤ 10). In Figure 7, we present plots h(q) vs q, τ(q) vs q, and f(α) vs α for several wells. Our analysis shows that multifractal behaviour exists for GWL fluctuations in all wells since h(q) varies with q and the relationships between τ(q) and q are not linear, as demonstrated in Figure 7a,b for several wells.
The generalised Hurst exponent h(q) is a fluctuation parameter that describes the correlation structures of the time series at different magnitudes. Moreover, Figure 7a shows that h(q) continuously decreases as q increases, reflecting the fact that relatively small fluctuations occur more frequently in the time series than large ones [45]. The analysis of the GWL shows that for all considered wells, the generalized Hurst exponent h(q) has a wide range of change of 0.20 < h(q) < 2.85. Such a wide range of changes in h(q) indicates an increase in multifractal properties and the appearance of long-range correlations in the GWL time series. From a hydrogeological perspective, this is expressed by the strong sensitivity of GWL fluctuations to changes in small-scale factors, including human factors (local leaks from water-bearing utilities, local heavy precipitation, and local irrigation) and large-scale factors (topography, geology, climate, sea level, and large-scale human factors, such as large-scale mining and, irrigation).
The singularities of the processes at the GWL depths of the considered wells are shown in Figure 7c. The width of the singularity spectrum Δα (Δα = αmax – αmin) measures the degree of multifractality. The wider the singularity spectrum, the stronger the multifractal features. For all considering wells, Δα is found within 0.23 - 2.60, except for three wells, for which Δα was found 4.16, 4.26 and 4.47. This indicates a high degree of multifractality and suggests that the groundwater multifractal behaviour is quite specific.
Multifractal structures can be caused by the long-term correlations of different fluctuation processes and fat-tail probability distributions of the time series [23,45]. The random shuffling method was used to analyse the sources of multifractality. If multifractality is due to both types, the shuffled data presents weaker multifractality than the original data. For less than half of the wells, the shuffled data showed weaker multifractality, indicating that both types of multifractality were present in the time series.

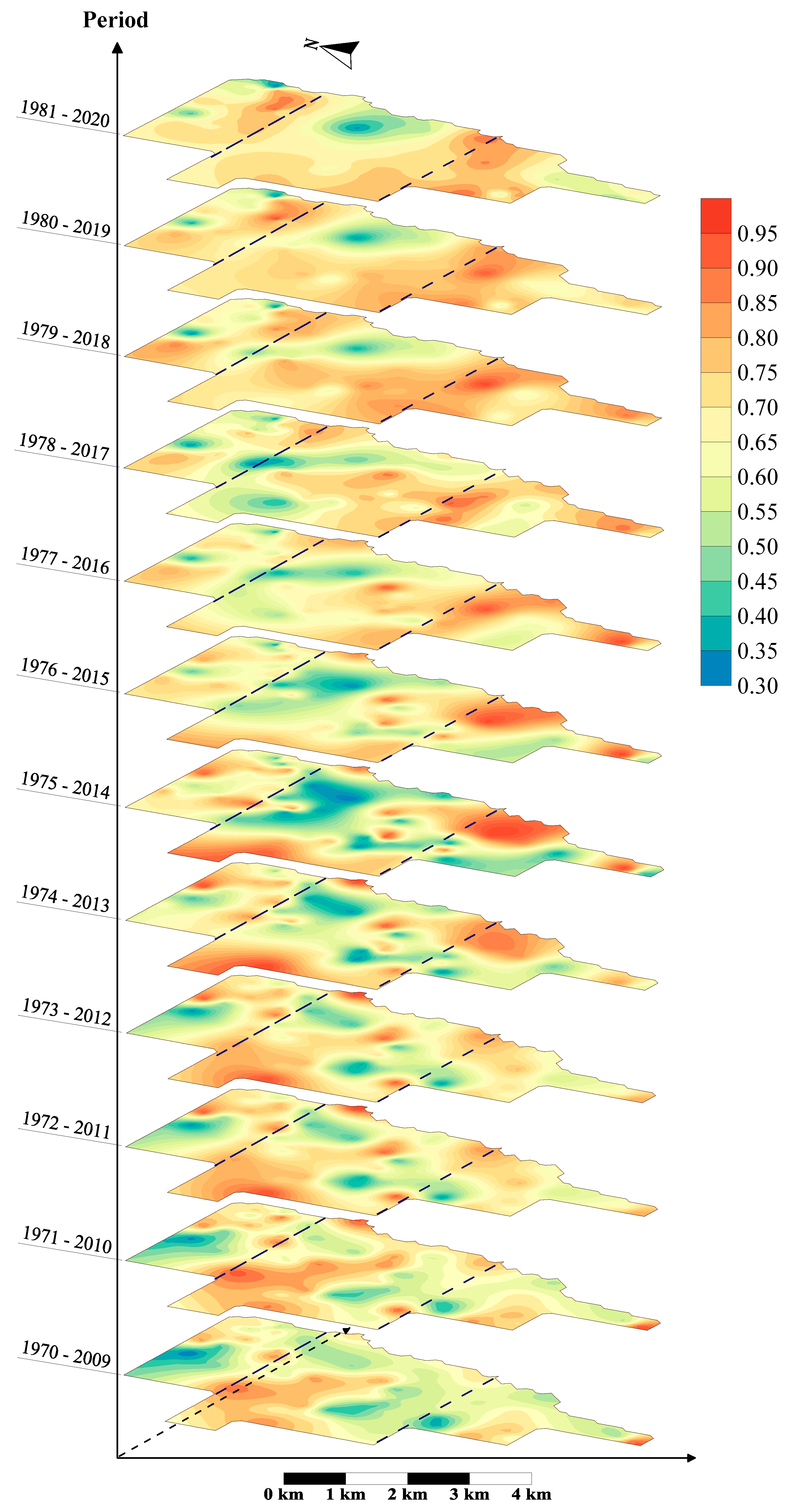
3.3. Hurst Exponent Spatial and Temporal Distribution and Groundwater Level Prediction

The Hurst exponents (h = 2) of the GWL fluctuation data quantified using the MF-DFA approach for the 72 monitoring wells were investigated. The Hurst exponent at q = 2 is identical to the classic Hurst exponent of a monofractal stochastic process. This study used a sliding time series to calculate the Hurst exponent by considering 480 monthly GWL depth data points as the length of the time series.
Sliding was performed in a sequence of 40 years and a step length of 1 year. The first Hurst exponent was calculated based on the GWL time series for the period 1970−2009, the second Hurst exponent was calculated for the period 1971−2010, and so on. The contour maps of the Hurst exponent for the studied GWL time series are shown in Figure 8.
The larger the Hurst exponent, the stronger the memory, the longer it will remember previous values, and the more consistent its ability to maintain the previous change trend [30,46]. Moreover, an increase in the sliding Hurst exponent indicates that the time series can remember the later GWL depth trends better. A decrease in the Hurst exponent indicates that the time series remembers earlier GWL depth trends better.
Figure 8 shows that the magnitude of the Hurst exponent changed between regions of the study area, showing varying degrees of long-range correlation. Thus, in most parts of the study area, the Hurst exponent exceeded 0.5, indicating that GWL fluctuations exhibit persistent behaviour and may exhibit a stable trend, and the long-range correlation of GWL depth is predicted to be significant. In addition, an increase in the Hurst exponent indicated that the overall GWL depth in most parts of the study area decreased. The accuracy of the Hurst exponent was confirmed by the spatiotemporal distribution of GWL depth in the study area (Figure 5).
Thus, by comparing the maps of the spatial distribution of GWL depth (Figure 5) and the Hurst exponent (Figure 8), we can roughly determine that for the eastern and north-western parts of the northern region, a slight recovery of groundwater may occur in the coming period. For other parts of the northern region, groundwater is expected to continue to increase in the coming years. In most parts of the central region, the groundwater may maintain a continuous rebound trend. In the eastern part of this region, groundwater may show a slight downward trend in the coming years. In most parts of the southern region, the GWL depth is expected to continue decreasing in the coming period. It should be noted that these trends in groundwater change may persist in the future if the conditions for GWL formation do not change (or change only slightly).

4. Conclusions

This study reports a 50-year time series (1970-2020) of GWL fluctuations in Odessa City, Ukraine. Geostatistical and MF-DFA analyses were performed to study the spatial distribution and multifractal behaviour of GWL fluctuations and predict trends in the coming period.
The geostatistical analysis provided the following results: Overall, GWL varied more significantly during the last decade. Groundwater was shallower in the western and southern parts of the central and southern regions, respectively. Groundwater was deeper in the eastern parts of the central and northern regions and in the north-western part of the northern region. Despite the decrease and increase in GWL depth in different parts of the study area, the GWL depth decreased monotonously in the western part of the central region and in the middle part of the southern region.
The MF-DFA results suggest that the dynamics of GWL fluctuations have multifractal characteristics in the city area. The generalized Hurst exponent has a wide range of change of 0.20 < h(q) < 2.85. From a hydrogeological perspective, this is expressed by the strong sensitivity of GWL fluctuations to changes in small-scale factors, including human factors (local leaks from water-bearing utilities, local heavy precipitation, etc.), and large-scale factors (topography, geology, sea level, climate, and large-scale human factors, such as large-scale mining). The singularity spectrum with Δα was found in the limits 0.23 - 2.60, except for three wells, for which Δα was found 4.16, 4.26 and 4.47, which indicates high degree of multifractality in GWL time series and suggests that the groundwater multifractal behavior is quite specific. For almost less than half of the wells, the time series demonstrate that both the long-range correlation and the fat-tail probability distribution contribute to multifractality. We can conclude that the long-range correlations among fluctuations have major contribution in the observed multifractality of the GWL fluctuations time series. Moreover, in most parts of the study area Hurst exponent (q = 2) is greater than 0.5, which indicates that GWL fluctuations have a persistent behavior and may exhibit a stable trend. The Hurst exponent shows that groundwater in most of northern region may show a slight upward trend in the coming period. In the eastern part of central region groundwater may show a downward trend in the coming period. In contrast, groundwater in the remaining parts of central region is likely to maintain a continuous rebounding trend. For the most part of southern region groundwater is expected to continue a rebounding trend in the coming period. It should be noted that these trends in groundwater changes may persist in the future if the conditions of GWL formation do not change (or change only slightly).
The GWL depth variation is influenced by both structural factors (i.e. climate, sea level, topography, and geology) and human factors (i.e. continuoues leaks from water-bearing utilities, various waste filtration reservoirs, and large-scale mining).

Author Contributions

All authors contributed to the conceptualization, and design of the study, and to reading and revising of the manuscript. Methodology, D.M.; softwarwe, S.S and D.M.; investigation, D.M.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, D.M. and S.S.; visualization, D.M. and S.S. ll authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors acknowledge support from the dScience – Centre for Computational and Data Science – at the University of Oslo (UiO).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cherkez, E.A.; Kozlova, T.V.; Shmouratko, V.I. Engineering geodynamics of landslide slopes of the Odessa seacoast after antilandslide measures. Visnyk Odeskoho Natsionalnoho Universytetu. Geographichni i geologichni nauky 2023, 18(1), 15–25. (In Russian) [Google Scholar]
  2. Zelinskiy, I.P.; Korzhenevskiy, B.A.; Cherkez, E.A.; Shatohina, L.N.; Ibragimzade, D.D.; Socalo, N.S. Landslides of the Black Sea North-Western Coast, their studying and forecasting; Naukova Dumka: Kyiv, Ukraine, 1993; pp. 36–40. (In Russian) [Google Scholar]
  3. Feder, J. Fractals; Plenum Press: New York and London, 1988. [Google Scholar]
  4. Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: Sun-Francisco, USA, 1982. [Google Scholar]
  5. Schroeder, M. Fractals, Chaos, Power-laws; W. H. Freeman: New York, USA, 1991. [Google Scholar]
  6. Fractals in the Natural and Applied Sciences; Novak, M.M. (Ed.) Elsevier Science B.V.: Amsterdam, 1994; Volume IFIP (A-41). [Google Scholar]
  7. Paladin, G.; Vulpiani, A. Anomalous scaling laws in multifractal objects. Phys. Rep. 1987, 156(4), 147–225. [Google Scholar]
  8. Smith, J.M. Fundamental of Fractals for Engineers and Scientists; John Wiley: New York, USA, 1991. [Google Scholar]
  9. Abarbanel, H.D.I. Analysis of Observed Chaotic Data; Springer: New York, USA, 1996; pp. 69–93. [Google Scholar]
  10. Bunde, A.; Bogachev, M.I.; Lennartz, S. Precipitation and river flow: Long-term memory and predictability of extreme events. Geophys. Monogr. Ser. 2012, 196, 139–152. [Google Scholar]
  11. Dæhlen, M.; Lyche, T.; Mørken, K.; Schneider, R.; Seidel, H.-P. Multiresolution analysis over triangles based on quadratic Hermite interpolation. Journal of Computational and Applied Mathematics 2000, 119, 97–114. [Google Scholar]
  12. Li, Z.; Zhang, Y.K. Quantifying fractal dynamics of groundwater systems with detrended fluctuation analysis. J. Hydrol. 2007, 336, 139–146. [Google Scholar]
  13. Tu, T.; Ercan, A.; Kavvas, M.L. Fractal scaling analysis of groundwater dynamics in confined aquifers. Earth Syst. Dynam. 2017, 8(4), 931–949. [Google Scholar]
  14. Zhu, J.; Young, M.H.; Osterberg, J. Impacts of riparian zone plant water use on temporal scaling of groundwater systems. Hydrol. Process, 2012; 26, 1352–1360. [Google Scholar]
  15. Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E. 1994, 49(2), 1685–1689. [Google Scholar]
  16. Hardstone, R.; Poil, S.; Schiavone, G.; Jansen, R.; Nikulin, W.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Detrended fluctuation analysis: a scale-free view on neuronal oscillations. Front. Physiol. 2012, 3, 450. [Google Scholar]
  17. Liang, X.; Zhang, Y.K. Temporal and spatial variation and scaling of groundwater levels in a bounded unconfined aquifer. J. Hydrol. 2013, 479, 139–145. [Google Scholar]
  18. Yu, X.; Ghasemizadeh, R.; Padilla, I.Y.; Kaeli, D.; Alshawabkeh, A. Patterns of temporal scaling of groundwater level fluctuation, J. Hydrol. 2016, 536, 485–495. [Google Scholar]
  19. Yu, H.; Wen, X.; Feng, Q.; Deo, R.C.; Si, J.; Wu, M. Comparative study of hybrid-wavelet artificial intelligence models for monthly groundwater depth forecasting in extreme arid regions, northwest China. Water Resour. Manag. 2018, 32, 301–323. [Google Scholar]
  20. Cai, H.J.; Shi, H.Y.; Liu, S.N.; Babovic, V. Impacts of regional characteristics on improving accuracy of groundwater level prediction using machine learning: the case of central eastern continental United States. J. Hydrol.: Reg. Stud 2021, 37, 100930. [Google Scholar]
  21. Schilling, K.E.; Zhang, Y.K. Temporal scaling of groundwater level fluctuations near a stream. Ground Water 2012, 50(1), 59–67. [Google Scholar]
  22. Sun, H.G.; Gu, X.; Zhu, J.; Yu, Z.; Zhang, Y. Fractal nature of groundwater level fluctuations affected by riparian zone vegetation water use and river stage variations. Scientific Reports 2019, 9, 15383. [Google Scholar]
  23. Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications 2002, 316, 87–114. [Google Scholar]
  24. Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar]
  25. Cherkez, E.A.; Melkonyan, D.V. The assessment of factors affecting the evolution of landslides in the Odessa coast. Herald of the Odessa National University, Series: Geographical and geological sciences 2009, 14(16), 268–279. (In Russian) [Google Scholar]
  26. Shmouratko V., I. The ground water regime and geoecological mapping of urban territories. Engineering geology and the environment. In Proceedings of the 8th international congress of the IAEG, Vancouver, Canada, 21–25 September 1998; Rotterdam: Balkema, 2000; pp. 4367–4373. [Google Scholar]
  27. Cherkez, E.A.; Shmouratko, V.I. Rotational dynamics and the level of the Quaternary aquifer in Odessa. Herald of the Odessa National University, Series: Geographical and geological sciences 2012, 17(2), 122–140. (In Russian) [Google Scholar]
  28. Ahmadi, S.H.; Sedghamiz, A. Geostatistical analysis of spatial and temporal variations of groundwater level. Environ. Monit. Assess, 2007; 129(1-3), 277–294. [Google Scholar]
  29. Delhomme, J.P. Spatial variability and uncertainty in groundwater flow parameters: a geostatistical approach. Water Resour. Res. 1979, 15(2), 269–280. [Google Scholar]
  30. Lu, C.; Song, Z.; Wang, W.; Zhang, Y.; Si, H.; Liu, B.; Shu, L. Spatiotemporal variation and long-range correlation of groundwater depth in the Northeast China Plain and North China Plain from 2000~2019. J. Hydrol.: Reg. Stud. 2021; 37, 100888. [Google Scholar]
  31. Gundogdu, K.S.; Guney, I. Spatial Analyses of Groundwater Levels Using Universal Kriging. J. Earth Syst. Sci. 2007, 116(1), 49–55. [Google Scholar]
  32. Journel, A.G.; Huijbregts, C.J. Mining geostatistics; Academic Press: London, 1978. [Google Scholar]
  33. Kitanidis, P.K. Introduction to Geostatistics: Applications in Hydrogeology; Cambridge university press: Cambridge, 1997. [Google Scholar]
  34. Isaaks, E.H.; Srivastava, R.M. An introduction to applied geostatistics; Oxford University Press: New York, 1989. [Google Scholar]
  35. Wallace, C.S.; Watts, J.M.; Yool, S.R. Characterizing the spatial structure of vegetation communities in the Mojave Desert using geostatistical techniques. Comput. Geosci. 2000, 26(4), 397–410. [Google Scholar]
  36. Delbari, M.; Amiri, M.; Motlagh, M.B. Assessing groundwater quality for irrigation using indicator kriging method. Appl. Water Sci. 2016, 6(4), 371–381. [Google Scholar]
  37. Barnes, R. Variogram tutorial. Golden, CO: Golden Software. 2003. Available online: http://www.goldensoftware.com/variogramTutorial.pdf.
  38. Philippopoulos, K.; Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Koutsogiannis, I. Multifractal Detrended fluctuation analysis of temperature reanalysis data over Greece. Atmosphere. 2019, 10, 336. [Google Scholar]
  39. Malamud, B.D.; Turcotte, D.L. Self-affine time series: I. Generation and analyses. Adv. Geophys. 1999, 40, 1–90. [Google Scholar]
  40. Kantelhardt, J.W. Fractal and multifractal time series. In Mathematics of Complexity and Dynamical Systems; Meyers, R.A., Ed.; Springer: New York, 2011; pp. 463–487. [Google Scholar]
  41. Livina, V.N.; Ashkenazy, Y.; Bunde, A.; Havlin, S. Seasonality effects on nonlinear properties of hydrometeorological records. In Extremis; Springer: Berlin, Germany, 2011; pp. 266–284. [Google Scholar]
  42. Li, E.; Mu, X.; Zhao, G.; Gao, P. Multifractal detrended fluctuation analysis of streamflow in Yellow river basin, China. Water 2015, 7, 1670–1686. [Google Scholar] [CrossRef]
  43. Gorjão, L.R.; Hassan, G.; Kurths, J.; Witthaut, D. MFDFA: Efficient multifractal detrended fluctuation analysis in python. Comput. Phys. Commun. 2022, 273, 108254. [Google Scholar]
  44. Kumar, V. Optimal contour mapping of groundwater levels using universal kriging - a case study. Hydrological Sciences J. 2007, 52(5), 1038–1050. [Google Scholar]
  45. Rakhshandehroo, G.R.; Amiri, S.M. Evaluating fractal behavior in groundwater level fluctuations time series. J. Hydrol. 2012, 464, 550–556. [Google Scholar]
  46. Habib, A. Exploring the physical interpretation of long-term memory in hydrology. Stoch. Environ. Res. Risk Assess. 2020, 34(12), 2083–2091. [Google Scholar]
Preprints 91482 g001
Figure 1. Black Sea and location of Odessa city. Location of groundwater monitoring wells in territory of Odessa.
Figure 1. Black Sea and location of Odessa city. Location of groundwater monitoring wells in territory of Odessa.
Preprints 91482 g001
Preprints 91482 g002
Figure 2. Semivariogram function of groundwater level depth in Odessa City (Gaussian model).
Figure 2. Semivariogram function of groundwater level depth in Odessa City (Gaussian model).
Preprints 91482 g002
Preprints 91482 g003
Figure 3. Inter-annual dynamic of groundwater levels in monitoring wells (198, 199, 1349, 247, 1634 and 1637) in the territory of Odessa City.
Figure 3. Inter-annual dynamic of groundwater levels in monitoring wells (198, 199, 1349, 247, 1634 and 1637) in the territory of Odessa City.
Preprints 91482 g003
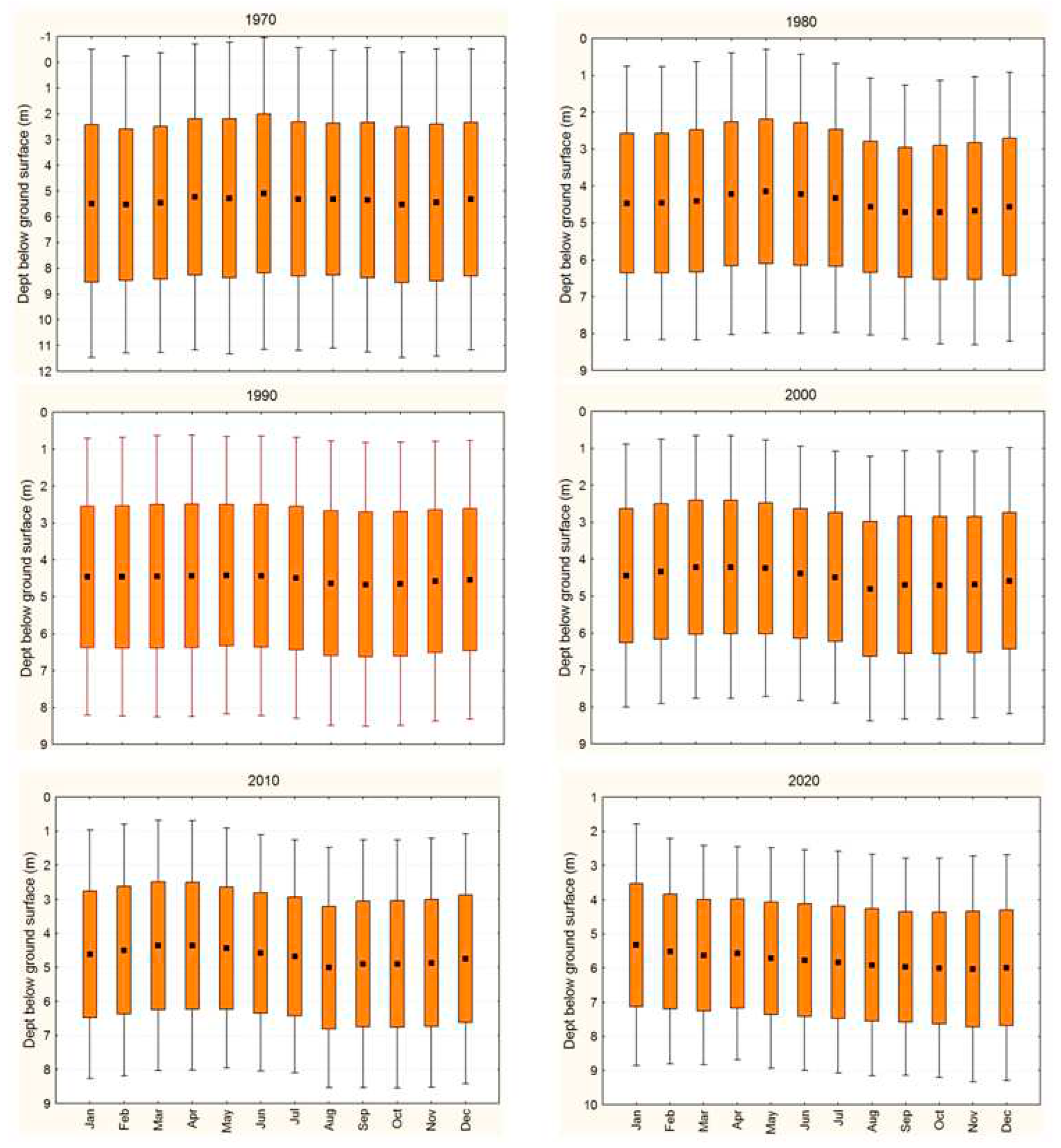
Preprints 91482 g004
Figure 4. Boxplots of monthly groundwater level distributions for 72 monitoring wells. (January to December of 1970, 1980, 1990, 2000, 2010, and 2020).
Figure 4. Boxplots of monthly groundwater level distributions for 72 monitoring wells. (January to December of 1970, 1980, 1990, 2000, 2010, and 2020).
Preprints 91482 g004
Preprints 91482 g005
Figure 5. Spatiotemporal distribution of groundwater level depth in the Odessa City area.
Figure 5. Spatiotemporal distribution of groundwater level depth in the Odessa City area.
Preprints 91482 g005
Preprints 91482 g006
Figure 6. Semivariogram function theoretical model and related parameters of groundwater level depth in the Odessa City area.
Figure 6. Semivariogram function theoretical model and related parameters of groundwater level depth in the Odessa City area.
Preprints 91482 g006
Preprints 91482 g007
Figure 7. Multifractal analysis for groundwater time series of wells 1343, 59, 247, 1308, 1349, 1443, 1446. a) generalized Hurst exponent h as a function of q for the groundwater level depths; (b) multifractal scaling exponent spectrum τ(q); (c) singularity spectrum f(α).
Figure 7. Multifractal analysis for groundwater time series of wells 1343, 59, 247, 1308, 1349, 1443, 1446. a) generalized Hurst exponent h as a function of q for the groundwater level depths; (b) multifractal scaling exponent spectrum τ(q); (c) singularity spectrum f(α).
Preprints 91482 g007
Preprints 91482 g008
Figure 8. Contour map of the Hurst exponent (h = 2) in the territory of Odessa City.
Figure 8. Contour map of the Hurst exponent (h = 2) in the territory of Odessa City.
Preprints 91482 g008
Table 1. Average depth of groundwater level in the Odessa territory in 1970–2000 [27].
Table 1. Average depth of groundwater level in the Odessa territory in 1970–2000 [27].
Depth interval, meters Average area, million m2 Average area, %
0 – 1 0.06 0.24 13.28
1 – 2 0.52 2.04
2 – 3 2.80 11.00
3 – 4 6.14 24.12 68.07
4 – 5 5.80 22.78
5 – 6 5.39 21.17
6 – 7 2.28 8.96 18.65
7 – 8 1.15 4.52
8 – 9 0.94 3.69
9 – 10 0.38 1.48
Table 2. Statistical characteristics of the groundwater level depth (in meters) in the study area.
Table 2. Statistical characteristics of the groundwater level depth (in meters) in the study area.
Year Mean Median Variation Kurtosis Skewness
1972 5,09 4,54 2,50 0,49 1,06
1978 4,25 3,77 1,94 0,46 2,10
1983 4,75 4,36 1,91 0,40 2,19
1989 4,49 3,91 2,04 0,46 3,03
1994 4,68 4,44 1,86 0,40 3,01
1997 4,04 3,73 1,89 0,47 2,35
2002 4,93 4,87 1,81 0,37 2,63
2006 4,51 4,15 1,77 0,39 2,94
2010 5,03 4,54 2,03 0,40 2,59
2014 5,80 5,49 2,02 0,35 3,91
2018 5,22 5,10 1,61 0,31 0,46
2020 5,77 5,74 1,63 0,28 0,78
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated