Application Of Peter Chew Theorem For Calculus (Second Order Linear Equations With Constant Coefficients)

Preprint

Article

Application Of Peter Chew Theorem For Calculus (Second Order Linear Equations With Constant Coefficients)

Altmetrics

Downloads

Views

Comments

Peter Chew^*

This version is not peer-reviewed

This preprints belongs to the Topic

Education for Sustainable Development and Science Teaching

Submitted:

28 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts

Abstract

Exercising surds to represent figures is a common practice in scientific and Engineering fields, especially in scripts where calculators are banned or unapproachable. Peter Chew Theorem make result becomes simple when dealing with converting Quadratic Surds. The substance of the Peter Chew Theorem lies in enabling the forthcoming generation to simple break problems related to Quadratic Surds more effectively, easing a direct comparison with contemporary results. By employing the Peter Chew Theorem, one can streamline the tutoring and literacy of math, particularly concerning second- order direct equations with constant portions. This theorem's objective aligns with Albert Einstein's famed quotation Everything should be made as simple as possible, but not simpler.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

1.1. Surd ¹

1.2. Surds Explained with Worked Examples by Shefiu S. Zakariyah(PhD) ¹

In a triangle ABC, AB = BC =

(\sqrt{3} - 1) c m

and

A C B = 30^{o}

, without using a calculator find the length of AC. Figure 5. (pg 30)

Figure 5.

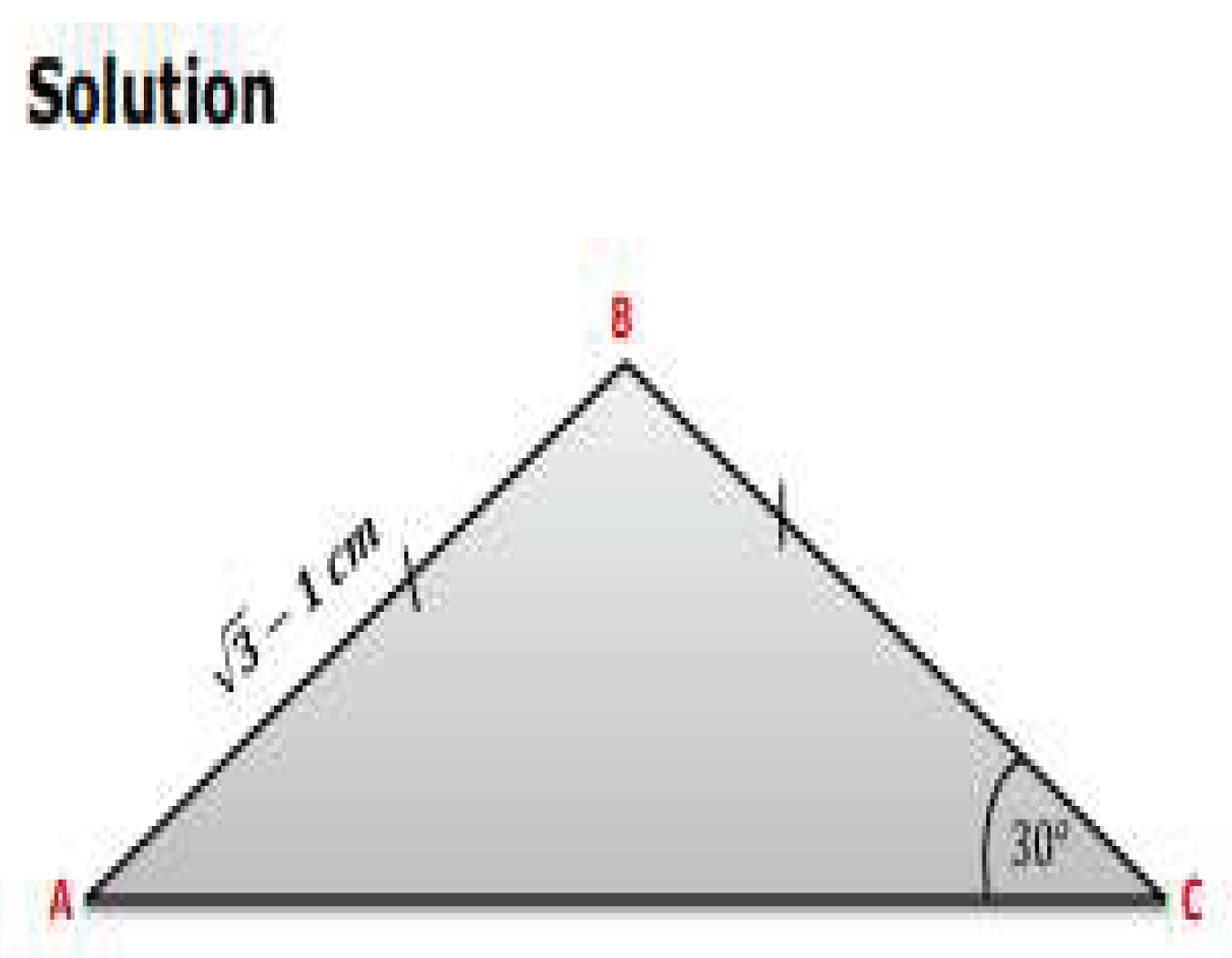
Where AB = c =

(\sqrt{3} - 1) c m

BC = a =

(\sqrt{3} - 1) c m

AC = b

Also, ∠ BAC = ∠ ACB =

30^{o}

AB= BC

∠ B =

180^{o}

- ( ∠ BAC + ∠ BAC )

120^{o}

b^{2}

{(\sqrt{3} - 1)}^{2} + {(\sqrt{3} - 1)}^{2} - 2 (\sqrt{3} - 1) (\sqrt{3} - 1) c o s 120^{o} .

= 2

{(\sqrt{3} - 1)}^{2} - 2 {(\sqrt{3} - 1)}^{2} (- c o s 60^{o})

= 2 [3 + 1 - 2 \sqrt{3}] - 2 [3 + 1 - 2 \sqrt{3}] (- \frac{1}{2})

= 2 [4 - 2 \sqrt{3}] + [4 - 2 \sqrt{3}]

= 3 [4 - 2 \sqrt{3}]

= 12 - 6 \sqrt{3}

b =

\sqrt{12 - 6 \sqrt{3}}

Current Method:

Let the square root of the

12 - 6 \sqrt{3}

\sqrt{x}

\sqrt{y}

for which x, y ∈R. Therefore

12 - 6 \sqrt{3} = (\sqrt{x} - \sqrt{y})^{2}

= x + y – 2

\sqrt{x y}

Comparing the both sides,

We’ve , x + y = 12

also - 2

\sqrt{x y} = - 6 \sqrt{3}

Divide 2sides by – 2,

\sqrt{x y} = 3 \sqrt{3}

Square 2 sides , xy = 27 ……………..…..(ii)

From (i), y = 12 – x …………………………(iii)

Substitute equation (iii) in equation (ii),

x ( 12 -x ) = 27

12 x -

x^{2}

= 27.

x^{2}

- 12 x + 27 = 0

( x – 9 ) ( x – 3 ) = 0

Therefore, either x – 9 = 0, x – 3 = 0

x = 9, 3

We now need to find the values for y, therefore

When x = 9, from (iii), y = 12 -9 = 3 .

And when x = 3 , from (iii) , y = 12 – 3 = 9

Hence , the square root of the 12 – 6

\sqrt{3}

are

\sqrt{x}

\sqrt{y}

\sqrt{9} - \sqrt{3}

3 - \sqrt{3}

and

\sqrt{a}

\sqrt{b}

\sqrt{3} - \sqrt{9}

\sqrt{3} - 3

∴

\sqrt{12 - 6 \sqrt{3}}

\pm

(

3 - \sqrt{3}

Since AC cannot be negative, thens AC = (

3 - \sqrt{3}

) cm . [

\sqrt{3} - 3

is negative ].

Peter Chew

{T h e o r e m}^{2}

\sqrt{12 - 6 \sqrt{3}}

\sqrt{12 - 2 \sqrt{27}}

Cause

x^{2}

- 12x + 27 = 0, then x = 9, 3

∴

\sqrt{12 + 2 \sqrt{27}}

\sqrt{9}

\sqrt{3}

3

\sqrt{3}

∴ Length AC =

3

\sqrt{3}

2. Current Method and Peter Chew Theorem

Example:

I f \sqrt{12 + 2 \sqrt{35}} = \sqrt{x} + \sqrt{y}, f i n d t h e v a l u e o f x a n d y . a n d

c o n v e r t \sqrt{12 + 2 \sqrt{35}} i n t o t h e

sum of 2 real number in surd form.

Current Method,

i) Solution 1:

\sqrt{12 + 2 \sqrt{35}}

\sqrt{7 + 5 + 2 \sqrt{(7) (5)}}

\sqrt{(\sqrt{7})^{2} + (\sqrt{5})^{2} + 2 \sqrt{(7) (5)}}

\sqrt{{(\sqrt{7} + \sqrt{5})}^{2}}

= \sqrt{7} + \sqrt{5}

ii) Solution 2: If

\sqrt{12 + 2 \sqrt{35}}

\sqrt{x}

\sqrt{y}

12 + 2 \sqrt{35}

= (

\sqrt{x}

\sqrt{y}

)^{2}

= x + y + 2

\sqrt{x y}

Comparing the both sides,

We’ve x + y = 12

y = 12- x ….. i)

also xy =35 ….….ii)

From i) and ii), x (12 - x) = 35

x^{2}

- 12x + 35 = 0

( x – 7 ) ( x – 5 ) = 0

Therefore, x = 7, 5

From i), If x = 7, y = 12- 7 = 5

If x = 5, y = 12- 5 = 7

∴

\sqrt{12 + 2 \sqrt{35}}

\sqrt{7}

\sqrt{5}

iii) Peter Chew Theorem,

Cause

x^{2}

- 12x + 35 = 0, then x = 7, 5

∴

\sqrt{12 + 2 \sqrt{35}}

\sqrt{7}

\sqrt{5}

3. Linear Second Order Differential Equation with Constant Coefficient

Solution to the Differential Equation.Diagram

Example 1: Find the solution to the differential equation:

\frac{d^{2} y}{{d x}^{2}}

- 3

\frac{d y}{d x}

- 10y =0.

Solution: The auxiliary equation is: m² - 3m - 10 = 0 .

m₁ = -2, m₂ = 5

∴ y = C₁ e ^-2x + C₂ e ^5x

Example 2: Find the general solution to the differential equation:

\frac{d^{2} y}{{d x}^{2}}

- 2

\frac{d y}{d x}

+ y =0.

Solution: The auxiliary equation is: m² - 2m + 1 = 0 .

m₁ = 1, m₂ = 1

∴ y = ( A + B x ) e^x

Example 3: Find the solution to the differential equation:

\frac{d^{2} y}{{d x}^{2}}

\frac{d y}{d x}

+13 =0.

Solution: The auxiliary equation is: m² +6m +13 = 0 .

m₁ = -3 + 2i , m₂ = -3 – 2 i , Therefore,α= -3,β= 2

∴ y =e ^-3x ( A cos 2 x + B sin 2 x )

4. Application of Peter Chew Theorem for Calculus (Second Order Linear Equations with Constant Coefficients)

Example 1 : Find the solution to the equation: .

y^{’ ’} + 3 y ’ + \sqrt{2} y = 0

Solution :

The auxiliary equation is: m ² + 3 m +

\sqrt{2}

= 0

m_{1,2} = \frac{- 3 \pm \sqrt{{(3)}^{2} - 4 (1) (\sqrt{2})}}{2 (1)}

= \frac{- 3 \pm \sqrt{9 - 2 (\sqrt{8})}}{2}

Current Method,

\sqrt{9 - 2 \sqrt{8}}

\sqrt{x}

\sqrt{y}

Then

9 - 2 \sqrt{8}

= (

\sqrt{x}

\sqrt{y}

)^{2}

∴

9 - 2 \sqrt{8}

= x + y - 2

\sqrt{x y}

Comparing the both sides ,

We’ve x + y = 9

y = 9 - x ….. i)

also x y = 8 ….….ii)

From i) and ii), x (9- x) = 8

x^{2}

- 9x +8 = 0

(x - 8)(x - 1) = 0

x = 8, 1

From i), If x = 8, y = 9- 8 = 1

If x = 1, y = 9- 1 = 8

∴

\sqrt{9 + 2 \sqrt{8}}

\sqrt{8}

\sqrt{1}

= 2 \sqrt{2} - 1

iii) Peter Chew Theorem,

Cause

x^{2}

- 9x + 8 = 0, then x = 8, 1

∴

\sqrt{9 + 2 \sqrt{8}}

\sqrt{8}

\sqrt{1}

= 2 \sqrt{2} - 1

Therefore

m_{1,2} = \frac{- 3 \pm \sqrt{9 - 2 (\sqrt{8})}}{2}

= \frac{- 3 \pm (2 \sqrt{2} - 1)}{2}

= \frac{2 \sqrt{2} - 4}{2}

\frac{- 2 \sqrt{2} - 2}{2}

= \sqrt{2} - 2

- \sqrt{2} - 1

For

m_{1} \neq m_{2}

, Solution To The Differential Equation is y = A

e^{m_{1} x}

+ B

e^{m_{2} x}

Therefore y(x)= A

e^{(\sqrt{2} - 1) x}

+ B

e^{(- \sqrt{2} - 2) x}

Example 2 : Find the solution to the equation: .

y^{’ ’} + 20 y ’ + 10 \sqrt{19} y = 0

Solution :

The auxiliary equation is: m ² + 20 m +

10 \sqrt{19}

= 0

m_{1,2} = \frac{- 20 \pm \sqrt{{(20)}^{2} - 4 (1) (10 \sqrt{19})}}{2 (1)}

= \frac{- 20 \pm \sqrt{400 - 40 (\sqrt{19})}}{2}

= - 10 \pm \sqrt{100 - 10 (\sqrt{19})}

= - 10 \pm \sqrt{100 - 2 \sqrt{475}}

Current Method,

\sqrt{100 - 2 \sqrt{475}}

\sqrt{x}

\sqrt{y}

T h e r e f o r e 100 - 2 \sqrt{475}

= (

\sqrt{x}

\sqrt{y}

)^{2}

= x + y - 2

\sqrt{x y}

Comparing the both sides,

We’ve x + y = 100

y = 100 - x ….. i)

also x y = 475 ….….ii)

From i) and ii), x (100 - x) = 475

x^{2}

- 100x +475 = 0

(x - 95) (x - 5) = 0

x = 95, 5

From i), If x = 95, y = 100 - 95 = 5

If x = 5, y = 100 - 5 = 95

∴

\sqrt{100 - 2 \sqrt{475}}

\sqrt{95}

\sqrt{5}

iii) Peter Chew Theorem,

Cause

x^{2}

- 100x + 475 = 0, then x = 95, 5

∴

\sqrt{100 - 2 \sqrt{475}}

\sqrt{95}

\sqrt{5}

From

m_{1,2} = - 10 \pm \sqrt{100 - 2 \sqrt{475}}

= - 10 \pm (\sqrt{95} - \sqrt{5})

= \sqrt{95}

\sqrt{5}

- 10 ,

- \sqrt{95}

\sqrt{5}

-10

For

m_{1} \neq m_{2}

, Solution To The Differential Equation is y = A

e^{m_{1} x}

+ B

e^{m_{2} x}

Therefore y(x) = A

e^{(\sqrt{95} - \sqrt{5} - 10) x}

+ B

e^{(- \sqrt{95} + \sqrt{5} - 10) x}

Example 3 : Find the solution to the equation: .

y^{’ ’} + 124 y ’ + 62 \sqrt{123} y = 0

Solution :

The auxiliary equation is: m ² + 20 m +

10 \sqrt{19}

= 0

m_{1,2} = \frac{- 124 \pm \sqrt{{(124)}^{2} - 4 (1) (62 \sqrt{123})}}{2 (1)}

= \frac{- 124 \pm \sqrt{15376 - 248 \sqrt{123}}}{2}

- 62 \pm \sqrt{3844 - 62 \sqrt{123}}

- 62 \pm \sqrt{3844 - 2 \sqrt{118203}}

Current Method,

\sqrt{3844 - 2 \sqrt{118203}}

\sqrt{x}

\sqrt{y}

3844 - 2 \sqrt{118 203}

= (

\sqrt{x}

\sqrt{y}

)^{2}

= x + y - 2

\sqrt{x y}

Comparing the both sides,

We’ve x + y = 3 844

y = 3 844 - x ….. i)

also x y = 118 203 ….….ii)

from i) and ii), x (3 844 - x) = 118 203

x^{2}

- 3 844 x + 118 203 = 0

(x – 3 813) (x - 31) = 0

x = 3 813, 31

From i), If x = 3 813, y = 3 844 - 3813 = 31

If x = 31 , y = 3 844 – 31 = 3 813

∴

\sqrt{3844 - 2 \sqrt{118 203}}

\sqrt{3 813}

\sqrt{31}

iii) Peter Chew Theorem,

Cause

x^{2}

- 100x + 475 = 0, then x = 95, 5

∴

x^{2}

- 3 844 x + 118 203 = 0 = =

\sqrt{3 813}

\sqrt{31}

From

m_{1,2} = - 62 \pm \sqrt{3844 - 2 \sqrt{118203}}

= - 62 \pm (\sqrt{3 813}

\sqrt{31})

= \sqrt{3 813}

\sqrt{31}

- 62 , -

\sqrt{3 813}

\sqrt{31}

- 62

For

m_{1} m_{2}

, Solution To The Differential Equation is y = A

e^{m_{1} x}

+ B

e^{m_{2} x}

Therefore y(x) = A

e^{(\sqrt{3 813} - \sqrt{31} - 62) x}

+ B

e^{(- \sqrt{3 813} + \sqrt{31} - 62) x}

Example 4 : Find the solution to the equation: .

2 y^{’ ’} + 2 \sqrt{2} y ’ + \sqrt{5} y = 0

Solution :

The auxiliary equation is: 2m ² +

2 \sqrt{2}

m +

\sqrt{5}

= 0

m_{1,2} = \frac{- 2 \sqrt{2} \pm \sqrt{{(2 \sqrt{2})}^{2} - 4 (2) (\sqrt{5})}}{2 (2)}

= \frac{- 2 \sqrt{2} \pm \sqrt{8 - 8 \sqrt{5}}}{4}

\frac{- \sqrt{2} \pm \sqrt{2 - 2 \sqrt{5}}}{2}

Current Method,

Let

\sqrt{2 - 2 \sqrt{5}}

\sqrt{x}

\sqrt{y}

2 - 2 \sqrt{5}

= (

\sqrt{x}

\sqrt{y}

)^{2}

= x + y - 2

\sqrt{x y}

Comparing the both sides,

We’ve x + y = 2

y = 2 - x ….. i)

also x y = 5 ….….ii)

From i) and ii), x (2 - x) = 5

x^{2}

- 2 x + 5 = 0

x = \frac{- (- 2) \pm \sqrt{{(- 2)}^{2} - 4 (1) (5)}}{2 (1)}

x = \frac{2 \pm \sqrt{- 16}}{2}

x = \frac{2 \pm 4 i}{2}

x = 1 \pm 2 i

From i), If x = 1+2i, y = 2 - (1+2i) = 1 - 2i

If x = 1-2i , y = 2 - (1-2i) = 1 + 2i

∴

\sqrt{2 - 2 \sqrt{5}}

\sqrt{1 + 2 i}

\sqrt{1 - 2 i}

iii) Peter Chew Theorem,

Cause

x^{2}

- 2 x + 5 = 0, then x =

1 + 2 i, 1 - 2 i

∴

\sqrt{2 - 2 \sqrt{5}}

\sqrt{1 + 2 i}

\sqrt{1 - 2 i}

From

m_{1,2}

\frac{- \sqrt{2} \pm \sqrt{2 - 2 \sqrt{5}}}{2}

\frac{- \sqrt{2} \pm (\sqrt{1 + 2 i} - \sqrt{1 - 2 i})}{2}

\frac{- \sqrt{2}}{2} + \frac{\sqrt{1 + 2 i} - \sqrt{1 - 2 i}}{2}, \frac{- \sqrt{2}}{2} - \frac{\sqrt{1 + 2 i} - \sqrt{1 - 2 i}}{2}

For m₁ = α + β i, m₂ = α - β i . let α=

\frac{- \sqrt{2}}{2}

, β =

\frac{\sqrt{1 + 2 i} - \sqrt{1 - 2 i}}{2}

Solution To The Differential Equation is y =

e^{x}

( A cos β x + B sin β x )

Therefore y(x) = y =

e^{\frac{- \sqrt{2}}{2} x}

[ A cos(

\frac{\sqrt{1 + 2 i} - \sqrt{1 - 2 i}}{2}

x) + B sin)

\frac{\sqrt{1 + 2 i} - \sqrt{1 - 2 i}}{2}

x ) ]

Example 5 : Find the solution to the equation: .

2 y^{’ ’} + 2 \sqrt{6} y ’ + \sqrt{13} y = 0

Solution :

The auxiliary equation is: 2m ² +

2 \sqrt{6}

m +

\sqrt{13}

= 0

m_{1,2} = \frac{- 2 \sqrt{6} \pm \sqrt{{(2 \sqrt{6})}^{2} - 4 (2) (\sqrt{13})}}{2 (2)}

= \frac{- 2 \sqrt{6} \pm \sqrt{24 - 8 \sqrt{13}}}{4}

\frac{- \sqrt{6} \pm \sqrt{6 - 2 \sqrt{13}}}{2}

Current Method,

Let

\sqrt{6 - 2 \sqrt{13}}

\sqrt{x}

\sqrt{y}

6 - 2 \sqrt{13}

= (

\sqrt{x}

\sqrt{y}

)^{2}

= x + y - 2

\sqrt{x y}

Comparing the both sides,

We’ve x + y = 6

y = 6 - x ….. i)

also x y = 13 ….….ii)

From i) and ii), x (6 - x) = 13

6 x -

x^{2}

= 13

x^{2}

- 6 x + 13 = 0

x = \frac{- (- 6) \pm \sqrt{{(- 6)}^{2} - 4 (1) (13)}}{2 (1)}

x = \frac{6 \pm \sqrt{- 16}}{2}

x = \frac{6 \pm 4 i}{2}

x = 3 \pm 2 i

From i), If x = 3+2i, y = 6 - (3+2i) = 3 - 2i

If x = 3-2i , y = 6 - (3-2i) = 3 + 2i

∴

\sqrt{6 - 2 \sqrt{13}}

\sqrt{3 + 2 i}

\sqrt{3 - 2 i}

iii) Peter Chew Theorem,

Cause

x^{2}

- 6 x + 13 = 0, then x =

1 + 2 i, 1 - 2 i

∴

\sqrt{6 - 2 \sqrt{13}}

\sqrt{3 + 2 i}

\sqrt{3 - 2 i}

From

m_{1,2}

\frac{- \sqrt{6} \pm \sqrt{6 - 2 \sqrt{13}}}{2}

\frac{- \sqrt{6} \pm (\sqrt{3 + 2 i} - \sqrt{3 - 2 i})}{2}

\frac{- \sqrt{6}}{2} + \frac{\sqrt{3 + 2 i} - \sqrt{3 - 2 i}}{2}, \frac{- \sqrt{6}}{2} - \frac{\sqrt{3 + 2 i} - \sqrt{3 - 2 i}}{2}

For m₁ = α + β i, m₂ = α - β i . let α=

\frac{- \sqrt{6}}{2}

, β =

\frac{\sqrt{3 + 2 i} - \sqrt{1 - 2 i}}{2}

Solution To The Differential Equation is y =

e^{x}

( A cos β x + B sin β x )

Therefore , y(x) = y =

e^{\frac{- \sqrt{6}}{2} x}

[ A cos(

\frac{\sqrt{3 + 2 i} - \sqrt{3 - 2 i}}{2}

x) + B sin)

\frac{\sqrt{3 + 2 i} - \sqrt{3 - 2 i}}{2}

x ) ]

5. Conclusion

In scientific and engineering domains, the use of surds as a representation for numbers holds substantial significance, especially in situations where the reliance on calculators is limited or non-existent. Surds become a crucial tool when dealing with complex computations involving irrational values. The application of the Peter Chew Theorem significantly simplifies solutions in the conversion of Quadratic Surds.

The Peter Chew Theorem stands as a transformative asset, aiming to facilitate a more simple and straightforward approach for the upcoming generation in handling and resolving problems associated with Quadratic Surds. Its primary objective revolves around empowering individuals to navigate and solve these intricate problems more efficiently, thereby enabling a direct comparison with the solutions derived through contemporary methodologies.

The integration of the Peter Chew Theorem into mathematical education serves to streamline the teaching and learning processes, particularly within the realm of calculus, specifically concerning second-order linear equations characterized by constant coefficients. This theorem acts as a pedagogical tool, enhancing the understanding and application of mathematical concepts related to Quadratic Surds, contributing to a more comprehensive grasp of calculus principles.

Aligned with the wisdom encapsulated in Albert Einstein’s renowned quote — " Everything should be made as simple as possible, but not simpler " — the Peter Chew Theorem embodies a philosophy centered on simplification without compromising accuracy or depth. Its pursuit of simplifying solutions to complex problems resonates with the fundamental principles driving mathematical innovation.

This theorem’s goal harmonizes with the perpetual quest within mathematics: to distill intricate problems into more manageable forms while preserving the precision required for comprehensive understanding and application.

References

Shefiu S. Zakariyah, PhD Surds Explained with Worked Examples. (26, 30) Feb.2014. https://www.academia.edu/6086823/Surds_Explained_with_Worked_Examples.
PETER CHEW . PETER CHEW THEOREM AND APPLICATION. CHEW, PETER, PETER CHEW THEOREM AND APPLICATION (MARCH 5, 2021). AVAILABLE AT SSRN: HTTPS://SSRN.COM/ABSTRACT=3798498 OR HTTP://DX.DOI.ORG/10.2139/SSRN.3798498.EUROPE PMC: PPR: PPR300039.
Agata Stefanowice, Joe Kyle, Michael Grove. Proofs and Mathematical Reasonung. University of Birmingham, September. 2014.
Dr. Yibiao Pan. Mathematical Proofs and Their Importance. December 5, 2017.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Application Of Peter Chew Theorem For Calculus (Second Order Linear Equations With Constant Coefficients)

Abstract

1. Introduction

1.1. Surd 1

1.2. Surds Explained with Worked Examples by Shefiu S. Zakariyah(PhD) 1

2. Current Method and Peter Chew Theorem

3. Linear Second Order Differential Equation with Constant Coefficient

4. Application of Peter Chew Theorem for Calculus (Second Order Linear Equations with Constant Coefficients)

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

1.1. Surd ¹

1.2. Surds Explained with Worked Examples by Shefiu S. Zakariyah(PhD) ¹