Prerpints.org logo
Preprint
Article

Redispatch Model for Real Time Operation with High Solar-Wind Penetration and its Adaptation to the Ancillary Services Market

Altmetrics

Downloads

89

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
Modern electrical power systems integrate renewable generation, with solar generation being one of the pioneers worldwide. In Latin America, the greatest potential and development of solar generation is found in Chile through the National Electric System. However, its energy matrix faces a crisis of drought and reduction of emissions that limits hydroelectric generation and involves the definitive withdrawal of coal generation. The dispatch of these plants is carried out by the system operator, who uses a simplified mechanism, called “economic merit list” and which does not reflect the real costs of the plants to the damage of the operating and marginal cost of the system. This inefficient dispatch scheme fails to optimize the availability of stored gas and its use over time. Therefore, a real-time redispatch model is proposed that minimizes the operation cost function of the power plants, integrating the variable generation cost as a polynomial function of the net specific fuel consumption, adding gas volume stock restrictions and water reservoirs. In addition, the redispatch model uses an innovative "maximum dispatch power" restriction, which depends on the demand associated with the automatic load disconnection scheme due to low frequency. Finally, by testing real simulation cases, the redispatch model manages to optimize the operation and dispatch costs of power plants, allowing the technical barriers of the market to be broken down with the aim of integrating ancillary services in the short term, using the power reserves in primary (PFC), secondary (SCF), and tertiary (TCF) frequency control.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction to Redispatch Models in Real-Time Operation with Solar-Wind Generation Integration

The expansion of solar and wind generation has been positioned for more than two decades in an energy market with high marginal costs and in recent times in the market of ancillary services that use bidding and auction mechanisms linked to conventional hydrothermal generation [1]. However, the higher the penetration of renewable energies, the greater the uncertainty causes eco-nomic mismatches in real-time operation, leading the system operator to quickly switch on/off plants by means of an economic merit list and, in the worst-case scenario, to execute a dispatch action randomly without mathematical support, based only on plant start/stop times.
The system operator uses unit commitment models prepared with information prior to the effective operating day. Unit commitment allows mitigating demand deviations, frequency variations due to the uncertainty of renewable generation and other externalities such as generation restrictions due to high emissions from fossil fuel power plants [2,3]. The problem for the system operator is the real-time operation where mismatch scenarios occur in the generation, transmission and demand system that are not foreseen in the unit commitment model, leaving the unit commitment model expired and unable to support the system operator's decisions. In several countries in South America, Europe and Asia, the economic merit list is used as a substitute for unit commitment to reduce the cost overrun gap between scheduled and real-time operation [4,5].
However, there are more sophisticated mathematical models such as real-time redispatch, which allow replacing the inefficient methods of random plant dispatches and the use of the economic merit list, given the uncertainty of renewable generation [6], the overload in the transmission system and generation failures [7]. The redispatch model is the main support for the system operator that helps to optimally execute economic decisions in accessible times for their timely elaboration, modeling, and execution [8]. The objective of this work is to propose a redispatch model for real-time operation adapted to any power system, capable of making profitable all the generation plants available to supply the demand (Figure 1), through the energy market, auctions, and the ancillary services market. This redispatch model is designed to withstand environmental, economic, and technical constraints. Such as the uncertainty of the high penetration of solar-wind renewable generation, restrictions on power reserves for frequency control, misjudged consumption of fossil fuel gas storage, consequences of water reservoirs depleted by droughts, and the limitations of conventional generation associated with the maximum dispatch power to avoid frequency instability.

1.1. Redispatch Reduces Coal-Fired Thermal Generation with No Chance of Economic Placement Toward Energy Transition

The energy transition is governed by a set of regulatory policies and economic perceptions that influence the development of renewable generation technologies to reduce emissions from coal-fired thermal generation through accelerated decarbonization [9]. Global warming implies that the energy transition should cover all levels of the system demand with a focus on residential consumption that allows the establishment of a regulatory policy that unifies the entire generation, transmission and especially the demand segment [10]. In this context, designing a redispatch model is essential to face the environmental security restrictions, because the economic consequences and the stability of the system can be detrimental due to the retirement of thermal power plants if it does not adapt an adequate renewable generation park in its replacement. The importance of renewable generation in terms of system dynamics and stability is fundamental [11]. Its current state of technological advancement and the mechanisms of renewable generation inertia performance markets have been increasing [12]. While in the ancillary services market solar-wind generation can perform voltage control with the appropriate use of reactive power reserves [13], frequency control with active power reserves [14], allowing to displace fossil fuel thermal power plants that provide high pollutant emissions.

1.2. Redispatch Stabilizes Marginal Costs due to Uncertainty of Renewable Generation and Improper Operation of Technical Minimums

The price of electric power depends on marginal costs, and in Chile they are mostly attributed to hydrothermal generation, despite the fact that renewable generation was installed more than two decades ago in South America, with Chile and Brazil being the pioneers in the development of renewable energies [15], causing marginal costs to decrease exponentially and even reaching marginal cost values of 0 USD/MWh in a period of one third of the daytime hours, as in the case of Chile's national electric power system [16]. While in the USA, decarbonization in the entire energy economy will require power systems to rely heavily on variable renewable energy, mainly solar-wind generation, very similar to the situation in South America since in the USA marginal costs are projected to be close to zero [17]. However, there are forecasting errors in the scheduled operation, deficit of tools or models to anticipate the uncertainty of renewable generation in real time [18]. These will lead to instability of marginal costs and inefficient control of demand curve tracking, generating a risk in real-time operation, because they require greater power reserve capacities to mitigate the resources associated with frequency control and dispatches of plants out of economic order [19]. Therefore, if current redispatch models do not integrate the uncertainty of renewable generation, the economic effects will be negative [20]. It is important that the redispatch development can resolve in advance the technical and economic consequences that could be caused in real time by the uncertainty of solar-wind generation due to forecast errors, and meteorological adversities such as cloudiness and extreme winds [21]. For the system operator, the redispatch model should have an anticipatory role and predominate over other scheduled operation models such as the unit commitment and the economic merit list.

1.3. The System Operator Supports its Technical and Economic Decisions with the use of Real-Time Redispatch

There are important contributions in unit commitment models that integrate frequency control with high penetration of renewable energies, considering the complexity involved in developing advanced mathematical modeling [22]. However, the elaboration of unit commitment models is performed with incomplete information, prior to real-time operation, leaving the unit commitment as a reference model for the system operator when unscheduled deviations in generation, transmission and demand occur. An advanced redispatch model allows modeling the market in real time to anticipate system deviations that misalign the unit commitment models. Redispatch delivers timely energy market information based on marginal costs to avoid market imbalance or monopolistic tendencies of generation companies [23]. It is complex to solve the challenges of redispatch because its literature is weakly strengthened and there is limited work on its modeling, elaboration, and execution. Therefore, implementing a redispatch is a novel proposal. A complete redispatch model must be able to dimension the technical and economic constraints and other characteristics of the market, such as the integration of renewable energies, ancillary services, and inertia modeling.
Among the main considerations in this redispatch model is to integrate a modeling of the gas stock storage for those combined cycle thermal power plants, through a correct optimization of the gas resource to avoid the monopolistic use by the generating companies. The redispatch model optimizes fuel consumption, which in many of the traditional models is equated to an economic merit list at the maximum value of the power generated as a linearized variable cost, which is why it does not faithfully reflect the variable cost of generation of thermal power plants. Therefore, the heat rate must be adapted to a correct modeling through polynomial equations linked to an operating cost function. In addition, the redispatch model integrates a dynamic constraint called maximum dispatch power and its objective is to avoid undesired low-frequency demand operation due to failures in generation plants. Finally, this redispatch model allows to adapt the power reserves of solar-wind renewable generation and to include them in the real-time ancillary services market to optimally exercise primary, secondary, and tertiary frequency control.

2. State of the Art Real-Time Operation Using Redispatch Models

Redispatch is optimal when its modeling and implementation allows supporting the system operator's decisions in real time, becoming a powerful operational and market tool. Redispatch is capable of projecting marginal costs and operating costs when there are deviations in the generation, transmission, and demand system. Its development allows covering various technical and economic restrictions of different types of renewable and conventional generation technologies, and it can even be coupled to the ancillary services market.

2.1. Power-to-Gas Technologies Take Advantage of Excess Renewable Generation

Most redispatch models limit renewable generation by causing zero-cost energy shedding, to respect n-1 security criteria [24]. However, in countries with higher energy development, such as the United States, they use renewable energy generation in power-to-gas (P2G) facilities as promising technologies for later use in combined cycle power plants and to make the electricity system more flexible with the gas networks for its supply [24]. There are also economic papers that model gas networks in detail with their pressure and flow capacities for power generation, considering safety and coupling constraints. The mathematical modeling of gas networks corresponds to an optimization with the Karush-Kuhn-Tucher (KKT) method that formulates a mixed integer linear programming (MILP) validated on a PJM-5 busbar test system and an IEEE 118 busbar system [25].
Given this situation, there are already unit commitment models that take advantage of gas grids with dynamic use of storage stock and even with the variability of solar and wind generation to avoid dispatches without merit order [26,27], but which is not evaluated in real time. It should be noted that the economic dispatch problem is the faithful reflection of the merit order list which then migrates to a mixed integer linear programming (MILP) unit commitment model using optimal direct current power flow (DC-OPF) [26,27]. Other works are devoted to planning redispatch models to mitigate the impact of fault events in gas networks [28]. That is, they develop a sequential Monte Carlo methodology, to simulate the real operation of the gas network and statistically deduce the fault events at the connection nodes of gas-fired power plants. Then, the fault events are introduced into a medium-term programming model in a daily electricity market clearing algorithm to quantify their impact on electricity prices and power plant dispatch [28].

2.2. Safety Criterion n-1 Favors Power Flow Control Through Demand Flexibility

Redispatch models have succeeded in integrating load flexibility, as is the case of the German electricity system that uses a zonal pricing mechanism [29]. This pricing mechanism incentivizes consumers in increasing and/or shedding load and allows exploiting the demand potential for a more efficient and sustainable redispatch model [29]. In Central and Western Europe, they use redispatch to manage transmission congestion within critical electricity zones using generation bids [30]. However, the model lacks a systemic dimension, and the aim is to quantify the results of zonal redispatch by testing the developed model in a power system with a larger number of power plants, lines and busbars. Currently, there are already works with redispatch methods with demand determination using stochastic simulation and the determination of zonal reserves with high penetration of wind generation by means of statistics with minimum confidence intervals [31]. Both methods are tested with numerical tests validated in an IEEE 39 busbar system and a real power system.
In situations of a total system blackout, there are works that propose two-stage schemes to predict the risk of a blackout in electric power systems [32]. In the first stage, they model the power islands using a mixed integer nonlinear integer programming model that minimizes the cost of redispatch and unsupplied energy. While, in the second stage, a data search technique is refined to predict the risk of separation electrical zones from the rest of the system [32]. In addition, there is the prediction of economic risk, as is the case in the Electric Reliability Council of Texas (ERCOT), which is caused by the uncertainty of the daily wholesale market (DAM), where real-time demand variability modifies the pricing and scheduled marginal costs. However, to fill this gap, a Bayesian statistical model is developed to track the real-time demand and price market trajectory with the aim of minimizing the amount of redispatch [33]. Methodologically, the developed Bayesian model is a suitable way to handle the economic relationship between ERCOT de-mand and DAM and RTM prices.

2.3. The Economic Merit List is a Basic and Inefficient Mechanism for Executing a Redispatch

In South America, the most usual method for redispatch models that help mitigate generation system and demand uncertainty is the merit order list power plant pricing model. The merit order is a ranking of plants ordered from lowest to highest based on variable generation costs. The merit order list redispatch model uses maximum power prices with demand responding to the price between the market equilibrium for both perfect competition and natural monopoly [34]. There are other advances called more specific redispatch submodels and targeting the market for ancillary services applied to automatic generation control (AGC) to maintain frequency and applied to a robust optimal power flow model to integrate renewable energy sources, where the non-affine redispatch constraints are designed so that the power outputs of the AGC units reach their lower or upper limit during redispatch [35]. All robust power dispatch methods based on fixed participation factors adopt the AGC redispatch scheme, due to its relatively easy computational property. However, in this scheme, each AGC unit needs to schedule enough reserve for energy redispatch, which results in a reduced feasible region of the base point and a more expensive dispatch solution [35].

2.4. The Increase of Losses in the Transmission System is a Fictitious Demand that Causes the Unnecessary Execution of a Redispatch

At present, transmission lines that do not undergo investments in maintenance, capacity increase or new expansions, cause congestion in power flow and increased losses. System losses is a fictitious demand that increases marginal costs and energy prices. This paper proposes a redispatch model that focuses on loss minimization using an objective function that includes the system loss model to minimize plant dispatches [36]. It is important to note that redispatch models should provide good performance of economic and operational solutions in real time. Therefore, it is key to deliver a robust solution for the unit commitment problem, as this uses an uncertainty set of data obtained in real time from the optimal power flows and power reserves [36]. The system parameters that generate uncertainty are calculated based on operational results in previous days and actual incoming data through knowledge delivered by the system operator, resulting in a real-time optimization with acceptable timing and solutions [37].

2.5. Real-Time Operation Needs a Sophisticated Redispatch Model to Embrace Other Markets and Massive Renewable Generation

The simulation of redispatch models has shortcomings in the tuning of technical and economic parameters, caused by the size of the system, high convergence times and global cost solution far from the optimum value. However, unsupplied energy is one of the most important. This happens when generation resources are exhausted or simply disconnecting demand is more economical than supplying it. Socially this action generates a negative impact. Load shedding is related to system stability, and this is where the redispatch model lacks robustness as it does not visualize this event. For this situation, there are works that focus on the stability before executing the redispatch, where they use a load shedding method using classical neural networks and shallow learning algorithms for a 39-bus system as is the case of New England and a 41-bus system in Nordic countries [38]. In addition, several redispatch models present a weak mathematical formulation of the variable cost equation associated with the heat rate of thermal power plants. In other words, not correctly formulating the variable cost function causes alterations in the operating costs and inadequate dispatches of the plants. Therefore, a variable cost function should be implemented with heat rate tests using international standard protocols [39,40,41]. These power measurements are effective for steam turbines at different power levels. In a very similar way, combined cycles take advantage of the combustion gases of gas turbines to define a series of variable cost functions by configuration (open cycle, half cycle and/or full cycle), by means of heat rate tests that also use protocols with international standards of the ASME type [42,43,44,45,46].
Finally, knowledge about redispatch is a problem that is not yet widely mastered. In the literature it is evident that there is a gap in such models, because redispatch integrates several constraints separately or partially combined (n-1 criteria, renewable integration, load shedding, merit order, gas integration, etc.) that have helped the new way of operating in real time modern power system markets. However, this work proposes a novel redispatch model, since it brings together most of what other models integrate separately and focuses on linking in real time the ancillary services market to establish the necessary reserves for frequency control. It also integrates unique economic and operational constraints such as maximum dispatch power to avoid underfrequency load shedding, polynomial modeling of thermal power plant heat rate, modeling of gas storage stock, and even the operational states of hydro power plants under dry, medium, and wet hydrology conditions. It is expected that this redispatch model can be a reference for other authors, since it specializes in real time operation matters with different types of generation technologies and exclusive demand conditions in a scientific field with a limited domain.

3. Methodology to Develop and Execute a Redispatch Model in Real-Time Operation

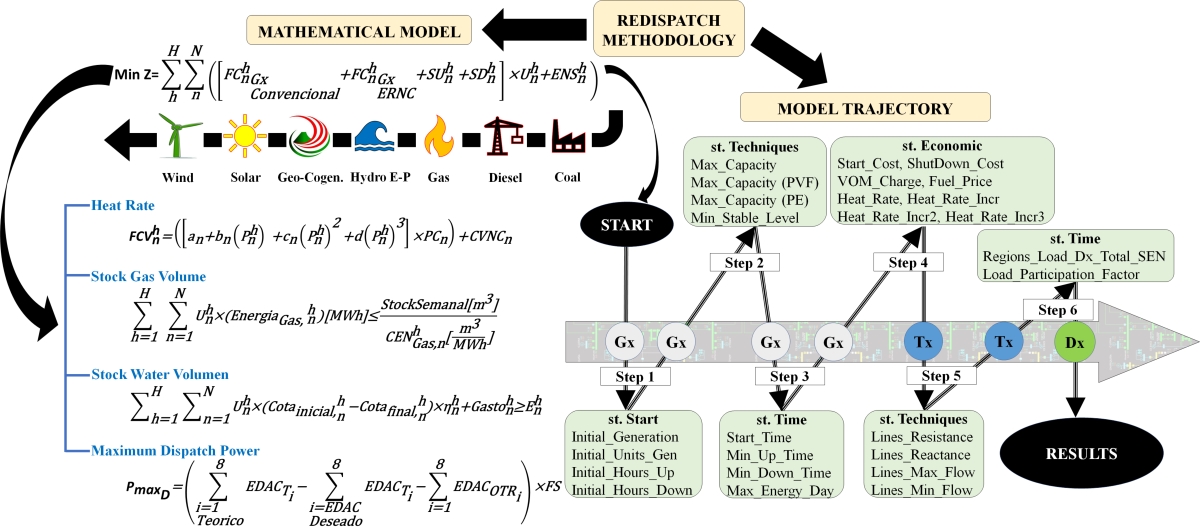
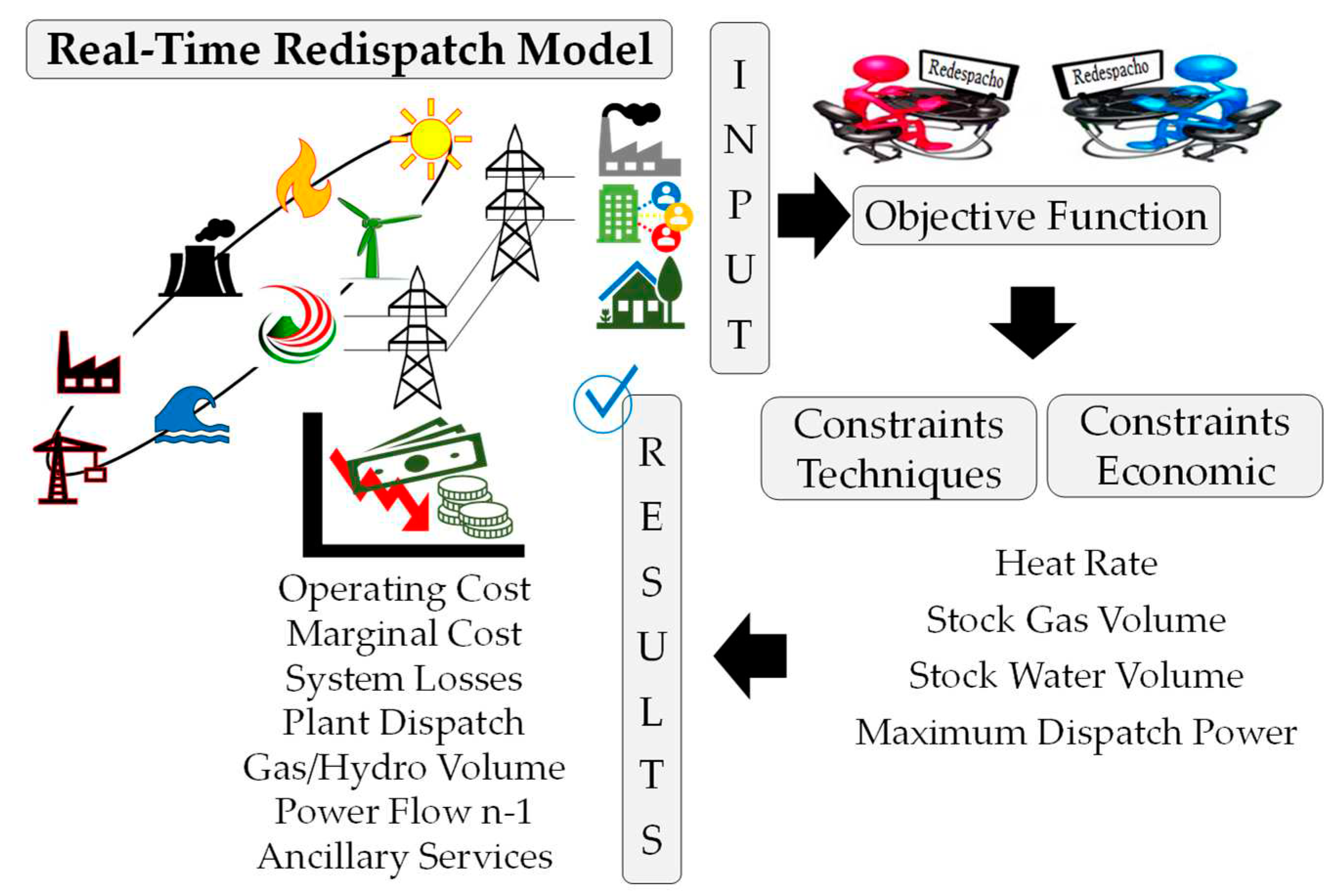
The methodology is executed in real time with a redispatch model that is designed to be tested and applied in any standard test power system and is even adaptable for a real power system of any country. This redispatch methodology is applied in real time operation, through the development of a sequence of theoretical foundations and implementation of mathematical equations, which optimally guide the system operator in the technical and economic actions, during the entire time horizon of higher generation uncertainty and that differentiate it from the rest of the traditional unit commitment and redispatch models.
Mathematically, the redispatch model methodology performs a multinodal optimization for any electrical system including busbars, lines, transformers, substations and generators, by means of an objective function that minimizes operating, start-up, outage and non-supplied energy costs. The redispatch results are obtained with fast convergence times and help the system operator to make timely decisions. Finally, the structure, modeling and implementation of the redispatch model is novel compared to the classical static economic dispatches and the economic merit list. The redispatch differs by integrating unique technical and economic constraints, such as the polynomial modeling of the heat rate for thermal power plants, modeling of gas volume stock and hydro reservoirs, uncertainty of solar-wind renewable energies and the maximum dispatch power that avoids underfrequency load shedding.

3.1. Theoretical Methodology Defining the Conceptual Structure of a Redispatch

This theoretical methodology is designed to support the system operator's decision in the optimal execution of a redispatch. However, it is important to emphasize that redispatches must be properly executed according to the system requirements, since their constant random execution without theoretical justification causes the system operator an operational stress that results in a sequence of unforced errors in the dispatches of the plants. Preliminarily, this methodology has a technical structure composed of four symptoms (a, b, c, d) of operating anomalies that must be detected by the system operator before executing a redispatch. Consequently, there are: (a) Deviations in generation (Gx) and demand (Dx); (b) Fault occurrences in the generation and transmission system (Tx); (c) Power limitation in generation plants due to technical causes; (d) Uncertainty of solar and wind renewable generation. After detecting at least one of the four technical anomalies that provide preliminary evidence of the need for a redispatch, a more specific analysis is performed, which consists of detecting seven critical system symptoms that determine the final decision to perform a real-time redispatch, as shown in Figure 2.
The first critical symptom of the system corresponds to the information received in real time by the dispatch and control center (CDC) outside the time limit established in the unit commitment modeling, which immediately causes a deviation in real time. In the second critical symptom, generation limitations of more than 8 hours are evidenced. The third critical symptom corresponds to the uncertainty of the availability of generation plants that allow a more economical operation. In the fourth critical symptom, there are deviations in generation higher than 5% of the total demand for a period longer than 8 hours. The fifth critical symptom is generation and transmission disconnections for a period of more than 8 hours. The sixth critical symptom is the availability of fossil fuels that allow a more economical dispatch. Finally, the seventh critical symptom corresponds to generation plants that are generating in a test state towards the system, considering whether this condition prevents or reduces the presence of unsupplied energy.

3.2. Mathematical Methodology to Implement the Modeling of a Redispatch

The numerical methodology proposed for the redispatch model corresponds to the implementation of nine mathematical formulations of a technical, economic and environmental nature, as shown in Figure 3.
First, there is the objective function that allows minimizing the global cost of redispatch, which depends on the cost of conventional generation, renewable generation, start-up cost, detention cost and energy not supplied, as shown in Equation (1). Second, we integrate the variable generation cost constraints by a polynomial function of the heat rate, as shown in Equations (2)-(3). Thirdly, three thermal states of the starting costs (hot, warm and cold) are defined as a function of the on and off times, according to Equations (4)-(8). In fourth place, there are the technical restrictions of the dispatch power between technical minimum and maximum generation, according to Equation (9). Finally, in fifth place is the power balance coupling constraint, according to Equations (10)-(11).
In addition, the main contribution of this work is highlighted and corresponds to the numerical equations of technical and economic constraints from point 3.1.6 to 3.1.9 of this section. Point 3.1.6 of this section describes Equations (12)-(14), which correspond to the primary power reserve, spinning reserve and cold reserve, intended for frequency control, and directly related to the ancillary services market. Section 3.1.7 describes a safety constraint called maximum dispatch power to avoid load shedding due to low frequency, as shown in Equation (15). Finally, points 3.1.8 and 3.1.9 of this section correspond to the mathematical modeling of gas volume stock control for thermal power plants and hydro generation storage through a level of control level for large reservoir hydro plants, as shown in Equations (16)-(18).

3.1.1. Real-Time Objective Function Defining the General Mathematical Structure of the Redispatch Model

Min   Z = ∑ h H ∑ n N FC n h G x C o n v e n c i o n a l + FC n h G x E R N C + SU n h + SD n h × U n h + ENS n h
Where the objective function Min   Z , represents the minimization of the operating costs of the n plants in hour h for conventional generation FC n h G x C o n v e n c i o n a l and renewable FC n h G x E R N C . In addition, it integrates start/stop costs SU n h / SD n h of the plants with the binary state [1,0] on/off status U n h and unsupplied energy ENS n h .

3.1.2. Polynomial Definition of Variable Generation Cost as a Function of Heat Rate

FCV n h = CEN n h × PC n + CVNC n
FCV n h = a n + b n P n h + c n P n h 2 + d n P n h 3 × PC n + CVNC n
Where FCV n h represents the variable cost of each plant n, which depends on the heat rate CEN n h , the polynomial coefficients a n , b n , c n , d n , the fuel price PC n . and the non-fuel variable cost CVNC n in the period h.

3.1.3. Three-State Thermal Economic Formulation of Start-Up and Detention Costs

S U n h = U n , h × ( 1 - U n , h - 1 ) × S ∧ n , h
S ∧ n , h = S ∧ n hot , s i T n , h Off ≤ T ∧ n hot S ∧ n warm , s i T ∧ n hot < T n , h Off < T ∧ n cold S ∧ n cold , s i T ∧ n cold ≤ T n , h Off
S D n h = U n , h - 1 × ( 1 - U n , h ) × S D n ∧
Ton n ≥ Tup n ,   n ∈ 1 ,   … . . , n
Toff n ≥ Tdn n ,   n ∈ 1 ,   … . . , n
Where SU n h is the starting cost and S D n h the stopping cost for the n plants, for the different temperature-temperature conditions (hot/warm/cold) S ∧ n hot , S ∧ n warm , S ∧ n cold , considering the on/off times h on/off switch Ton n / Toff n and the minimum on/off times Tup n / Tdn n .

3.1.4. Technical Constraint Defining the Minimum and Maximum Power Offset for a Power Plant

P min n h ≤ P n ≤ P max n h ,   n ∈ 1 , 2 , … . . . . . . . , n
Where P max n h and P min n h is to the maximum and minimum generation power in (MW) of the n plants in period h.

3.1.5. Coupling Constraint Defining the Balance of Power Generation to Supply Demand and Grid Losses

∑ h = 1 H ∑ n = 1 N [ U n h × P n h ] = PDx SEN h + P L h
∑ h = 1 H ∑ n = 1 N [ U n h × P min n h ] ≤ PDx SEN h
Where P n h is the power generated by plant n in hour h, to supply PDx SEN h which is the demand in hour h and the system losses P L h in hour h. In addition, it must be fulfilled that the minimum power P min n h of all the power plants is less than or equal to the power demand of the system PDx SEN h .

3.1.6. Determination of Power Reserves for Frequency Control and its Relationship to the Complementary Services Market

RG P h ≤ ∑ h = 1 H ∑ n = 1 N U n h × ( % Resp ± n - central h × P max n h )
RG U h ≤ ∑ h = 1 H ∑ n = 1 N U n h × ( P max n h - P n h )
RG B h ≤ ∑ h = 1 H ∑ n = 1 N U n h × ( P n h - P min n h )
Where power reserves are established by the RG P h as the primary reserve, RG U h is the spinning reserve and RG B h is the reserve for lowering the generation of the n plants in period h. hese primary and secondary power reserves are a function of the dynamic response factor % Resp ± n - central h , maximum power P m a x n h and the dispatch power P n h .

3.1.7. Mathematical Formulation Defining Maximum Dispatch Power for System Security

P max D = ∑ i = 1 T e o r i c o 8 EDAC T i - ∑ i = E D A C D e s e a d o 8 EDAC T i - ∑ i = 1 8 EDAC OTR i × FS
Where P max D is the maximum dispatch power in (MW) based on the theoretical automatic load disconnection scheme EDAC T i , real time automatic load shedding scheme EDAC OTR i and a safety factor FS with a value between (0,9) applied in the period h.
The maximum dispatch power is used as a safety parameter that limits any power plant to exploit its generation to the maximum when the safety of the system is put at risk. This work proposes to integrate the maximum dispatch power into the redispatch model to avoid automatic load shedding due to low frequency, as shown in Figure 4.

3.1.8. Mathematical Formulation for Gas Volume Stock Control for Thermal Power Plants in Combined Cycle and Open Cycle Configuration

∑ h = 1 H ∑ n = 1 N U n h × ( P Gas , n h ) [ MWh ] ≤ StockSemanal [ m 3 ] CE N Gas , n h [ m 3 MWh ]
∑ h = 1 H ∑ n = 1 N U n h × ( Energi a Gas , n h ) [ MWh ] ≤ StockSemanal [ m 3 ] CE N Gas , n h [ m 3 MWh ]
Where P Gas , n h is the power generated by the n gas-fired power plants, Energi a Gas , n h is the energy generated by n gas-fired power plants. While StockSemanal is the volume in m3 of gas per week in a period h and CE N Gas , n h . is the heat rate in m3/MWh.

3.1.9. Mathematical Model Defining Water Storage of Reservoir Power Plants by a Level of Height Control

∑ h = 1 H ∑ n = 1 N U n h × ( Cot a inicial , n h - Cot a final , n h ) × η n h + Gasto n h ≥ Ε n h
Where Cot a inicial , n h is the initial height level of the reservoir and the term Cot a final , n h is the final height level of the reservoir measured at (m.s.n.m). While η n h corresponds to the efficiency of the turbine in MWh/cm, the term Gasto n h is the tributary of the reservoir transformed to MWh and Ε n h is the daily accumulated energy in MWh-Day.

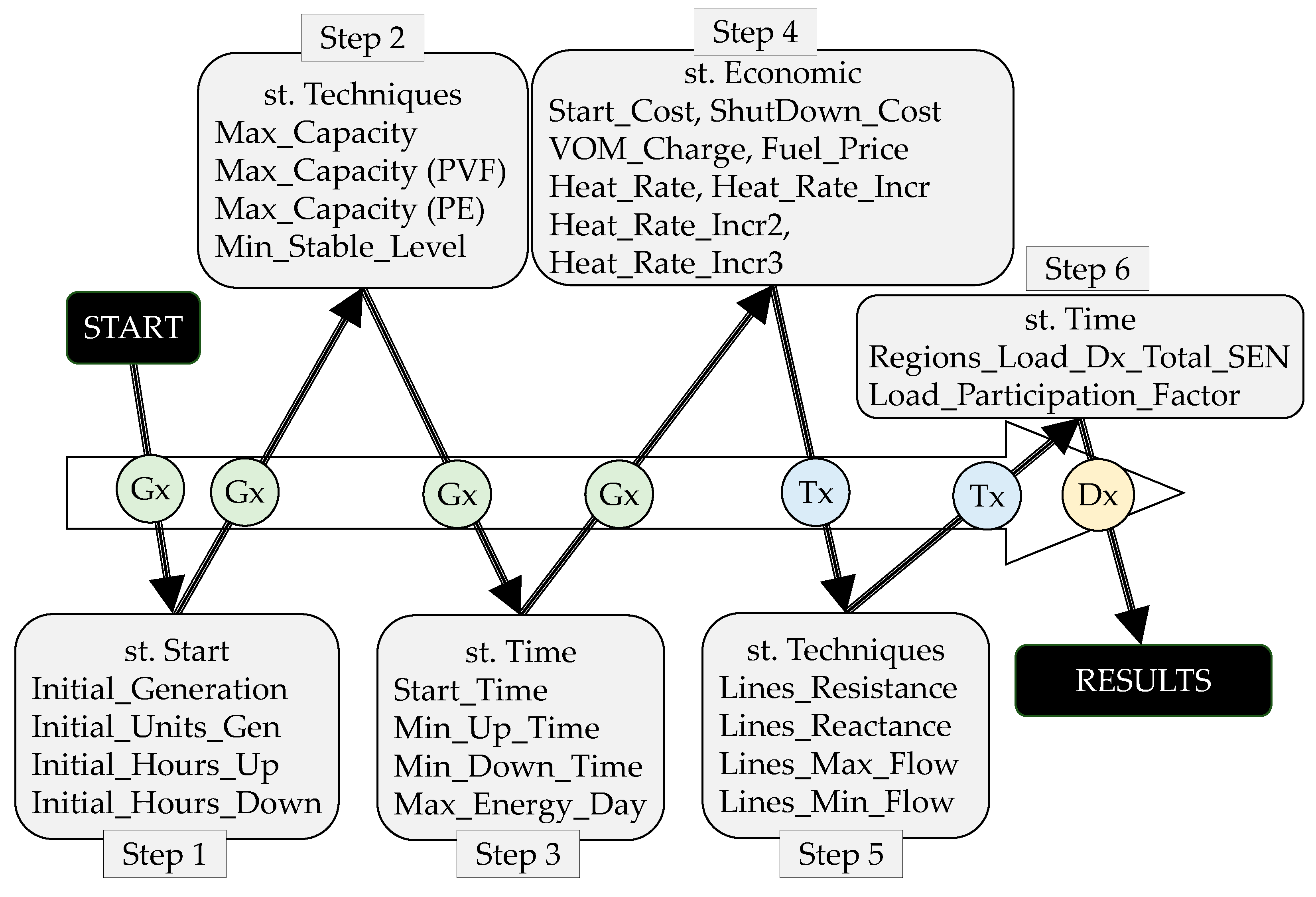
3.3. Methodology Defining the Process of Simulation and Validation of the Redispatch Model Using Optimization Software

The following methodology is developed to implement a sequence of simulation processes in any optimization software that integrates the theoretical foundations and mathematical expressions required by a redispatch. The modeling structure of a redispatch has a direct coupling axis between generation, transmission, and demand. Figure 5 shows a sequence of six stages of the simulation from the beginning of a redispatch to its final result. From stage one to stage four it is exclusively the generation segment that integrates initial system state constraints (plant on/off state, power level, on hours and off hours), plant technical constraints (maximum solar and wind generation capacity, maximum power and technical minimums), plant timing constraints (start-up times, minimum operation and shutdown times, maximum available hourly and daily energy) and economic constraints (start-up/shutdown costs, fuel price, operation/maintenance cost and heat rate). While stage five corresponds to the transmission segment, which includes the technical restrictions of line impedance, maximum and minimum limits of power flows. Finally, stage six is the demand segment which includes the time constraints due to the participation factors at each bus and the total demand curve evolution, as shown in Figure 5.
However, the modeling for this proposed redispatch model is run with PLEXOS software and the validation of results is tested in a real power system with high penetration of renewable energies, variability of fossil fuels and climatic consequences due to water deficit. This simulation tool uses an external optimizer to solve the mathematical optimization problem. The optimizer has a general purpose that employs the mixed integer programming method (Branch & Bound).

4. Modeling and Validation of Redispatch through Simulation of Realistic Scenarios of Technical-Economic Impact on Conventional and Renewable Generation

The redispatch model can capture in real time the deviations in generation, demand and faults in the network that are not included in the unit commitment models. This redispatch model is designed to be tested in any real system or test system and check its validity with the theoretical method and its mathematical formulation. However, it is important to present scientific advances with real electrical power systems, to increase the expectations of application in the industry. The validation of the redispatch model with real power systems is useful since its elaboration and later execution since it allows other researchers to find new advances in these matters to solve.

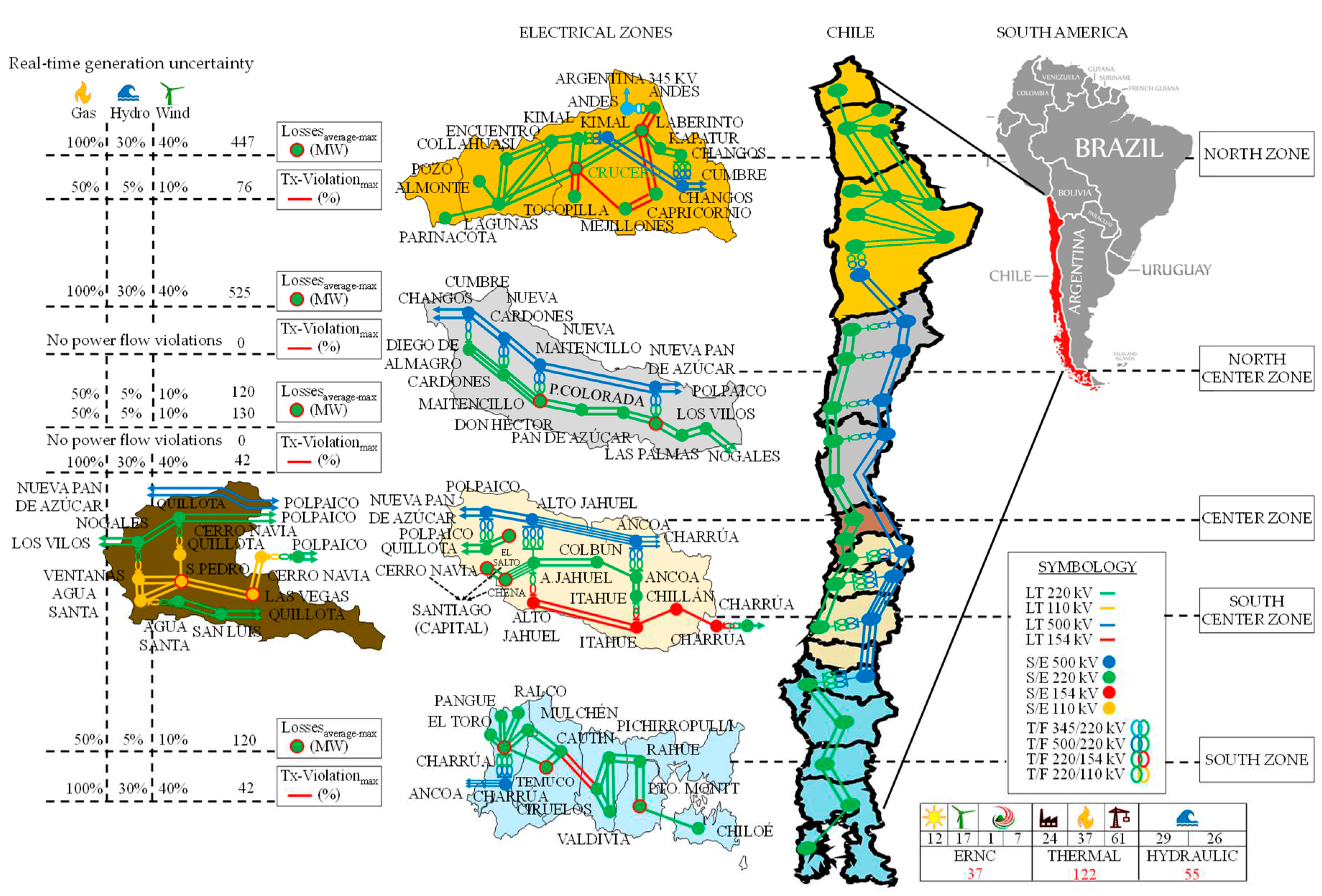
4.1. Structure and Design of a Multimodal Electric System that Adapts to the Modeling of a Segmented Redispatch in Generation, Transmission and Demand

The electrical network designed for the redispatch modeling includes the most relevant facilities of the National Electric System [47]. Mainly, the number and use of generators, transmission lines and critical bars of the system are highlighted to strategically guarantee the n-1 security criteria. In this electrical scheme, the generation, transmission, and demand segments are grouped and distributed by electrical zones, as shown in Figure 6.
The transmission segment is responsible for the exchange of power flow between generation and demand, preserving the n-1 security criterion. The transmission system is a set of elements such as busbars, transformers, voltage levels and transmission lines. Each of these transmission system elements is characterized by dynamic flexibility in their maximum/minimum power flow capacities and impedance levels. Table 1 indicates the number of transmission system elements that are integrated into the redispatch model and the impedance modeling flexibility for each component.
While solar, wind, geothermal, cogeneration, coal, gas, diesel, reservoir hydro and run-of-river hydro power plants are used for redispatch modeling with the ability to relax technical constraints, such as maximum power (PMAX), minimum power (PMIN), start time (TSTART), minimum operation time (TON), minimum shutdown time (TDOWN) and economic constraints, such as starting cost (CSTART), holding cost (CDOWN), non-fuel variable cost (CVNC), fuel price (PFUEL), heat rate (CEN), fuel variable cost (CVC), generation variable cost (CV), as shown in Table 2.
Thirdly, there is the modeling of demand, which is characterized by having regulated customers, which are divided into three segments: residential, commercial, and smaller scale industrial demand. There is also the demand of free customers, which is characterized by covering large consumers, such as mining. It is important to note that the methodology for integrating demand in the redispatch model is based on the participation factors as a percentage of the total demand distributed in each bus of the system, as shown in Table 3.

4.2. Execution of a Real-Time Redispatch through a Ranking of Technical-Economic Emergencies in Power System Generation

To test the redispatch model, six critical emergency cases of real-time operation are used. These case studies are called real-time extreme scenario (RTES) and subject the power system to complex market operation deviating from the normal values of operating cost and marginal cost. The extreme scenarios for each case study of the redispatch model cause severe disruptions in the volume of gas storage, indiscriminate use of water reservoirs and wind resource forecast errors, according to Table 4.

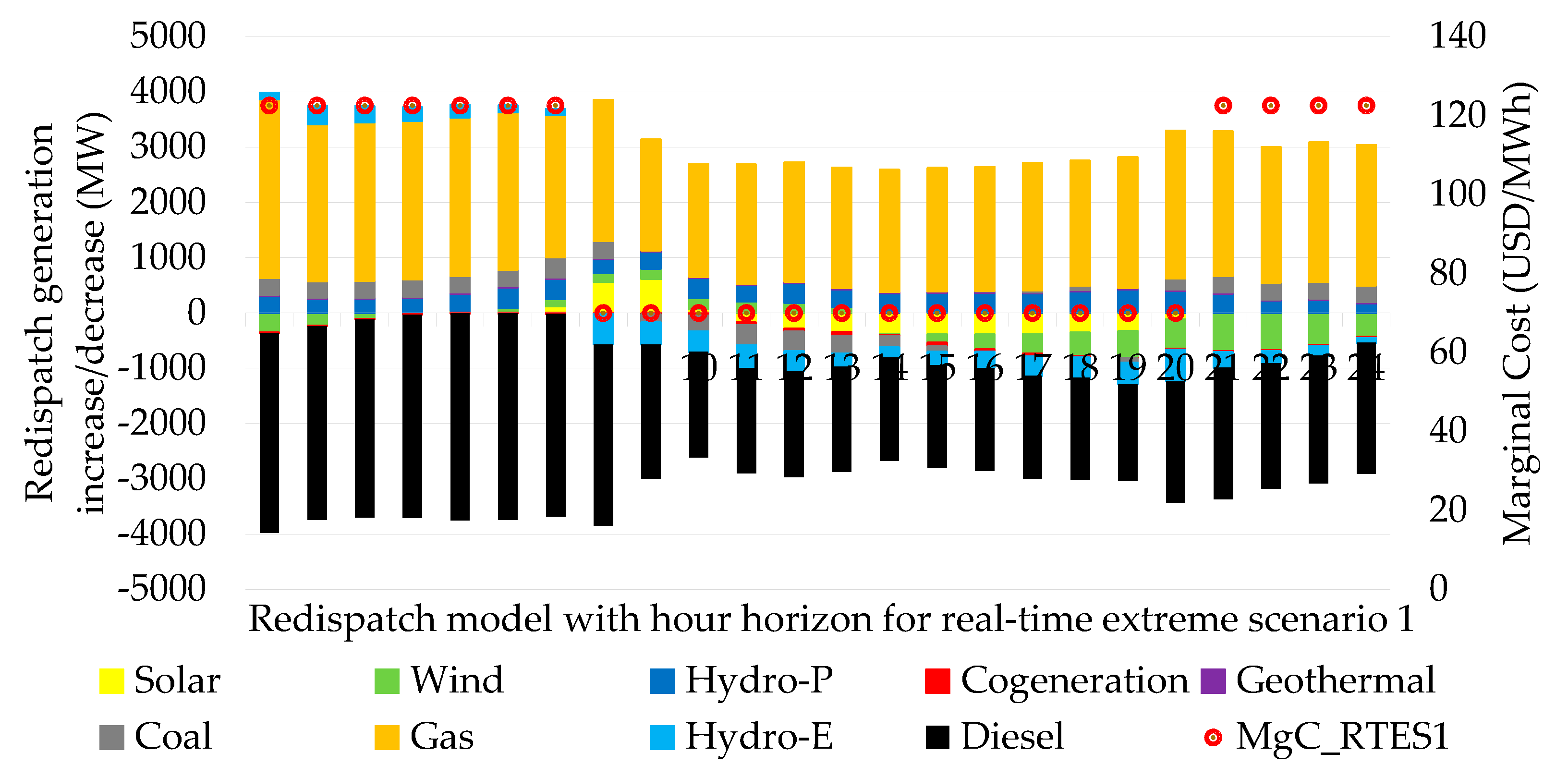
4.1.1. Real-Time Extreme Scenario 1: Partial Deviation of Water-Deficit Wind Generation in Reservoir Power Plants Compete with the Unlimited Resource of Coal-Fired Gas-Fired Thermal Power Plants with Higher Variable Generation Costs

This actual scenario considers the availability of gas-coal thermal generation with 100% gas volume and abundant coal stock. The variability of this real scenario is presented in wind generation with 40% of its programmed forecast, while hydroelectric generation from reservoirs and run-of-river is affected by a hydro reduction for generation of 30% of its programmed forecast, as shown in Figure 7.

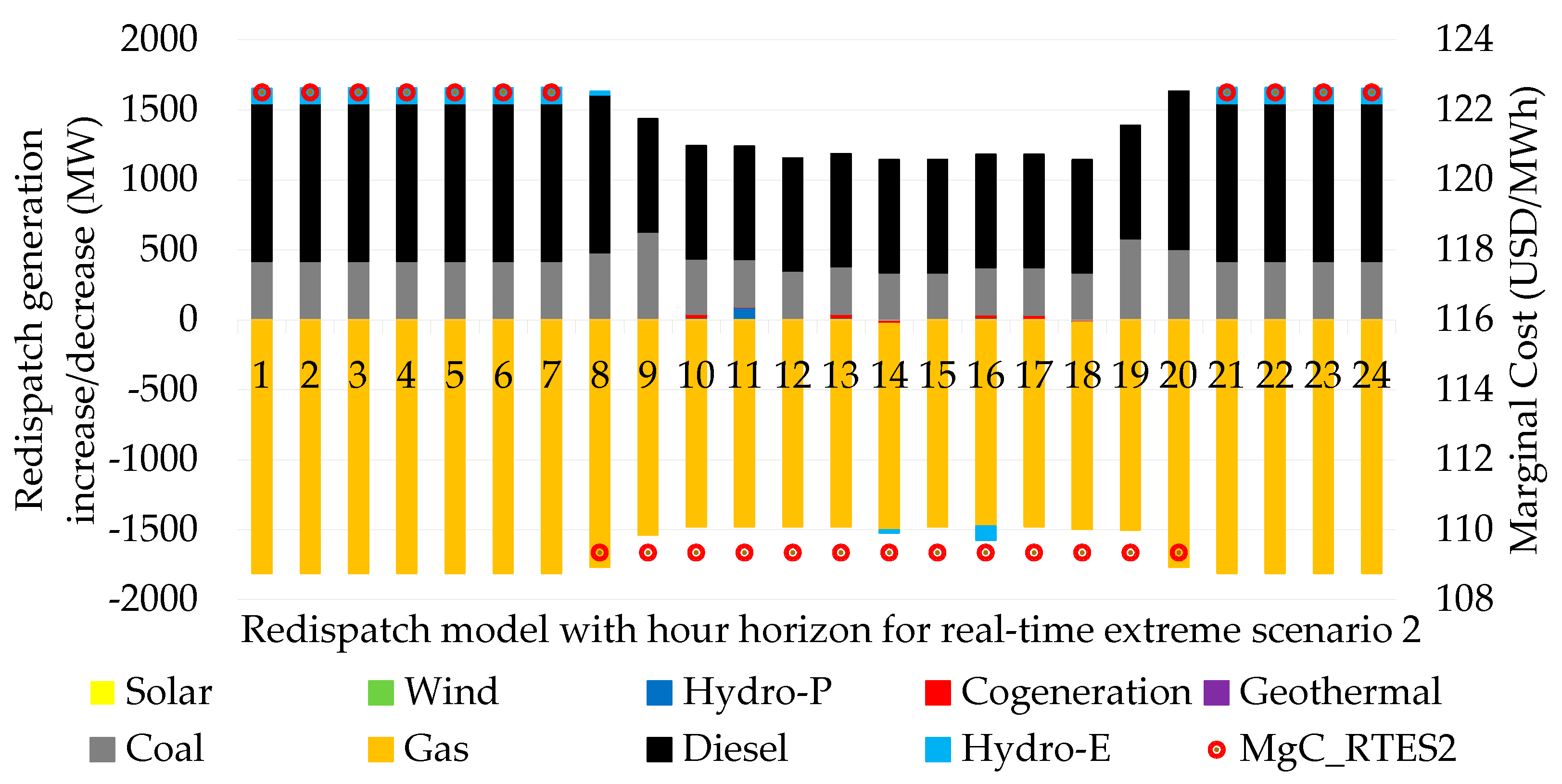
4.1.2. Real-Time Extreme Scenario 2: Lower Gas-Fired Thermal Generation with Partial Gas Volume Stock Causes Dispatch of Diesel Generation at High Marginal Costs

In this real scenario, variability and uncertainty conditions are maintained at 40% for wind generation, hydroelectric generation from reservoirs and run-of-river is at 30% deviation with respect to its programmed inflow, coal-fired generation with 100% fuel availability and hours of autonomy. However, gas-fired thermal generation presents variability in the storage volume stock by 50%. This consequence immediately causes the appearance of diesel generation to cover the demand, as shown in Figure 8.

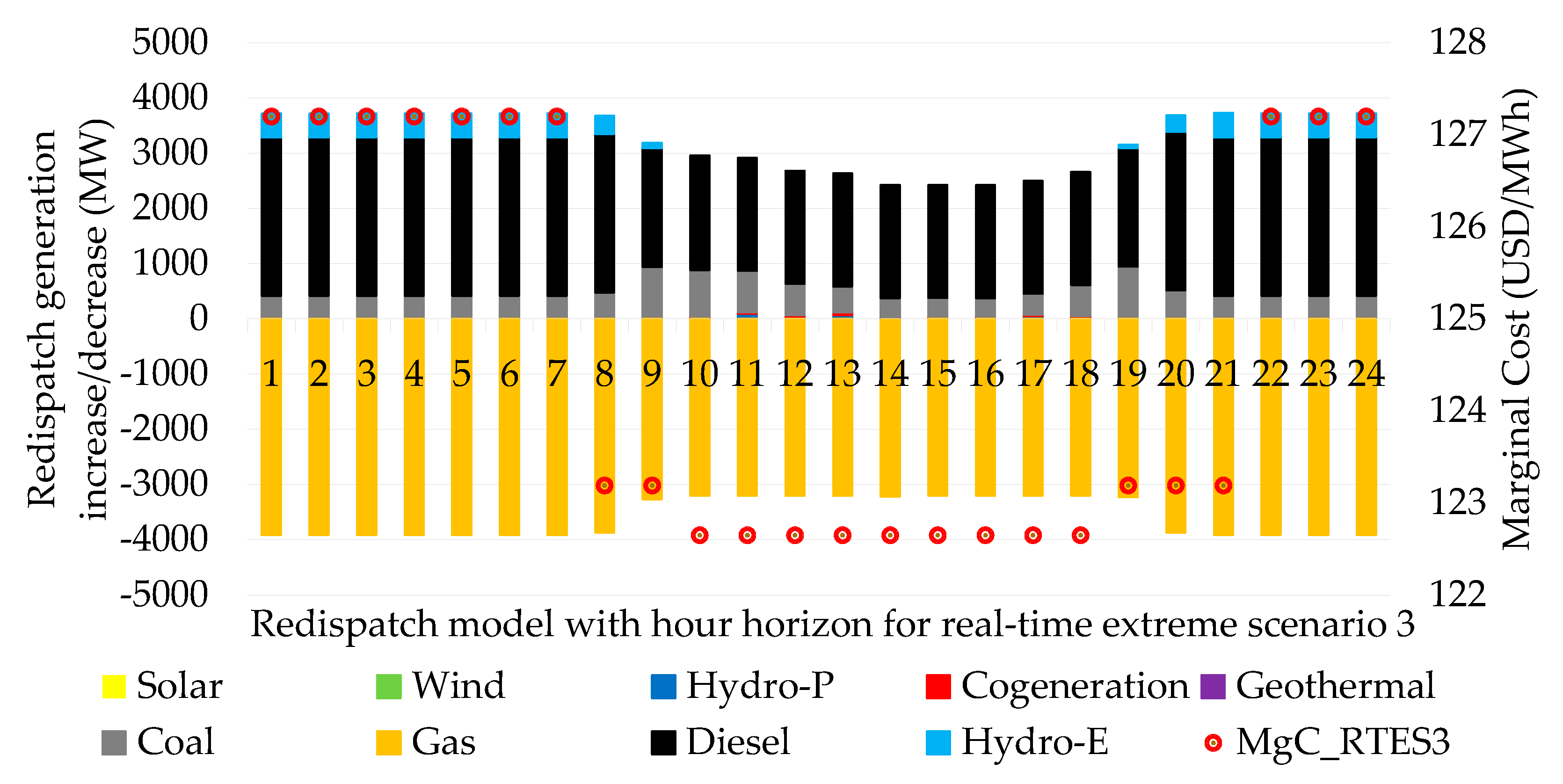
4.1.3. Real-Time Extreme Scenario 3: Non-supply of Gas Volumes in Stock Causes Forced Withdrawal of Gas-Fired Thermal Generation Complicating Frequency Regulation and Power Reserves

This is a critical real scenario, since it contemplates the null resource of gas volumes for thermal generation, a situation that induces gas-fired thermal generation to change fuel in combined cycles and open cycle gas turbines to generate with diesel. While wind variability remains at 40%, hydro variability remains at 30% and coal remains operating at 100%, as shown in Figure 9.

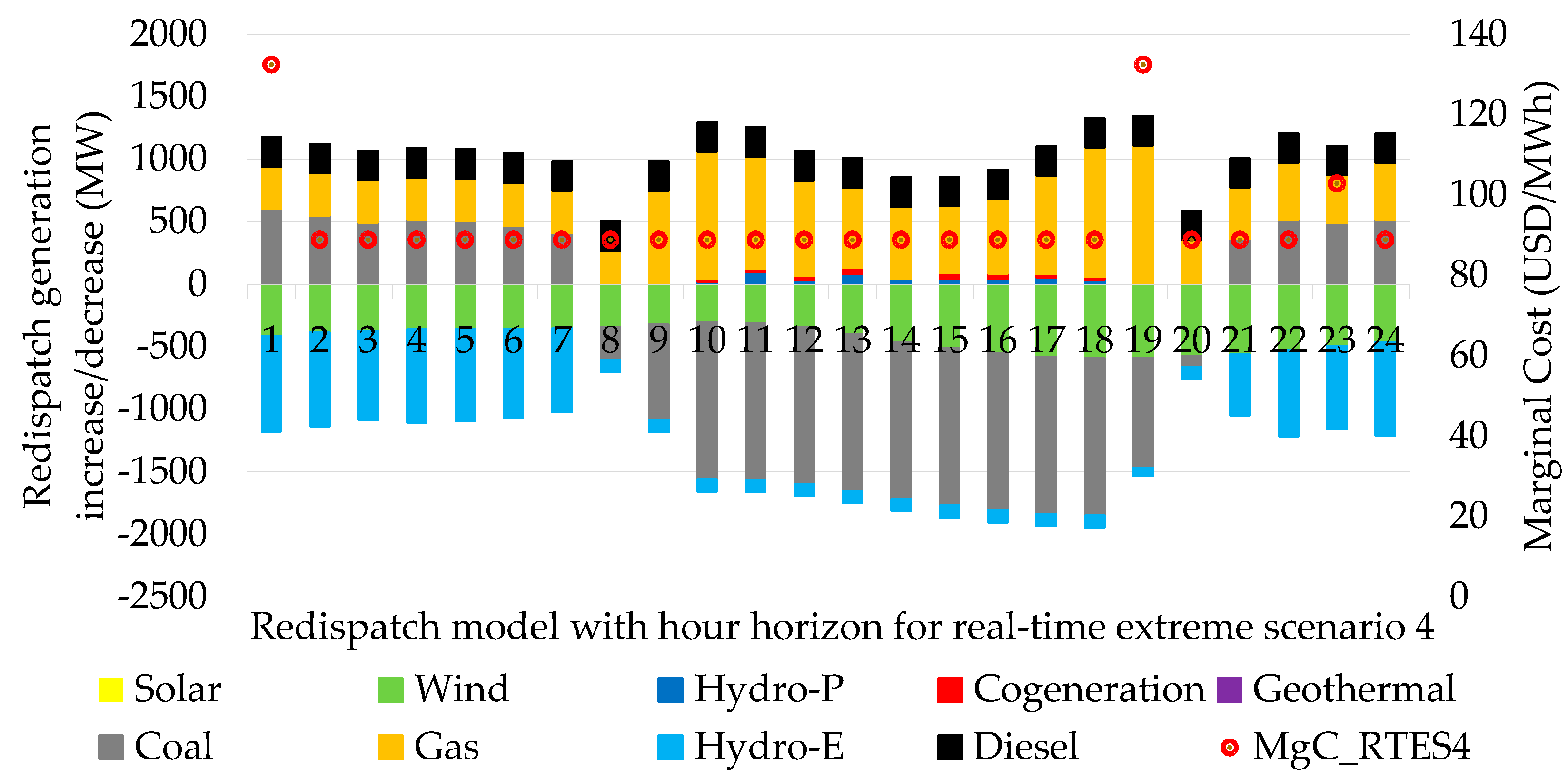
4.1.4. Real-Time Extreme Scenario 4: Depleted Hydroelectric Reservoirs and Scarce Wind Resource Transform a Thermal Generation Predominant Dispatch with High Emissions

This is a very severe real-world scenario that often occurs due to drought weather conditions and inaccurate wind forecasts. However, plant dispatches favor coal-gas thermal generation with 100% fuel availability and hours of autonomy without the need to resort to diesel fuel in large amounts of generation to meet demand, as shown in Figure 10.

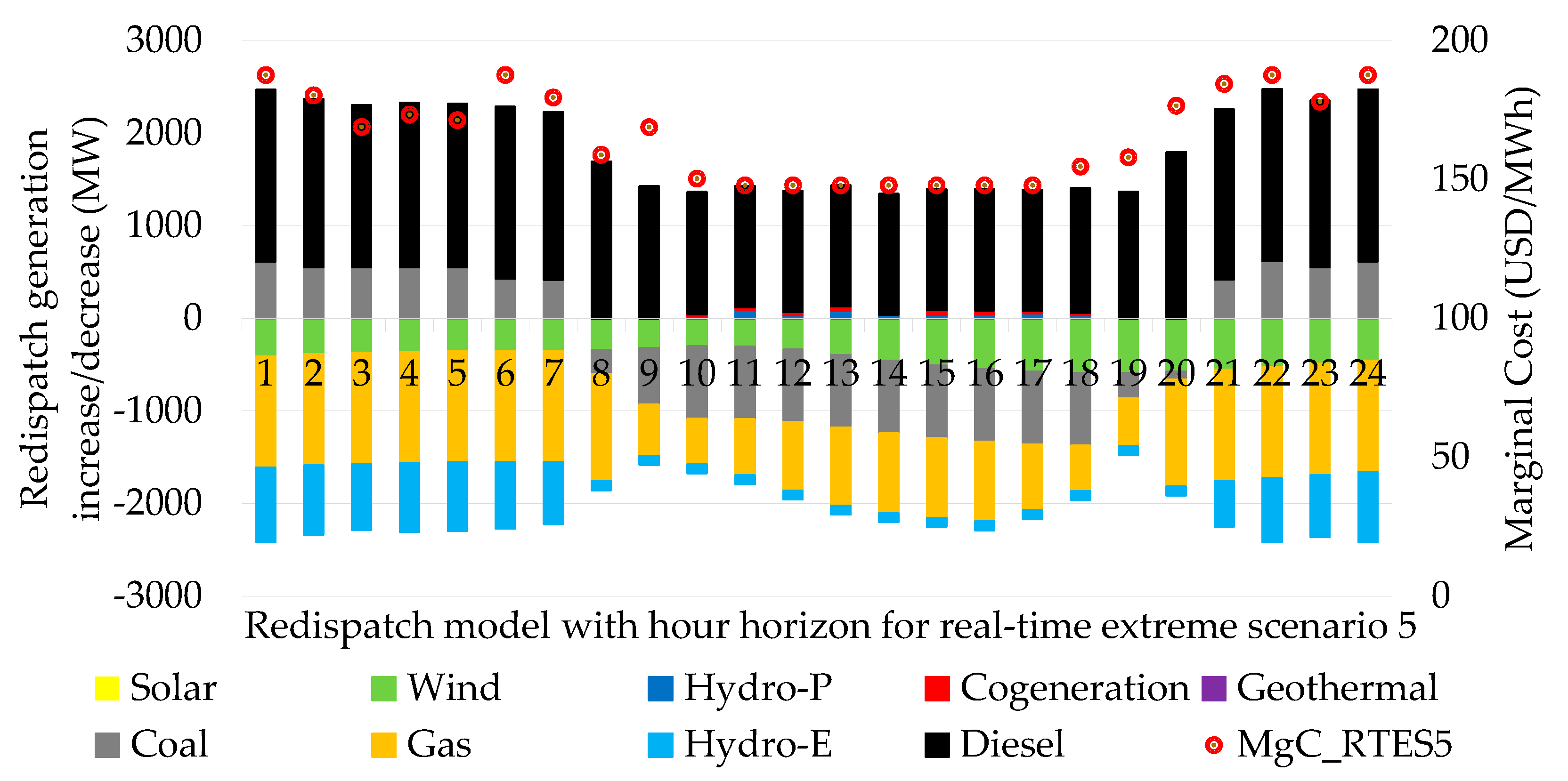
4.1.5. Real-Time Extreme Scenario 5: Regrettable Consolidation of Thermal Generation due to Extreme Energy Emergency that Leaves Hydro and Wind Generation without Dispatch Possibility

This real scenario considers low availability of wind power generation resources of around 10%, and hydroelectric generation from reservoirs is in a depleted state, i.e., with an availability of less than 5%. Gas-fired thermal generation is limited to 50%. However, this is one of the most complex scenarios due to the fact that 100% coal-fired thermal generation and more than 50% diesel generation must be used to supply demand, as shown in Figure 11.

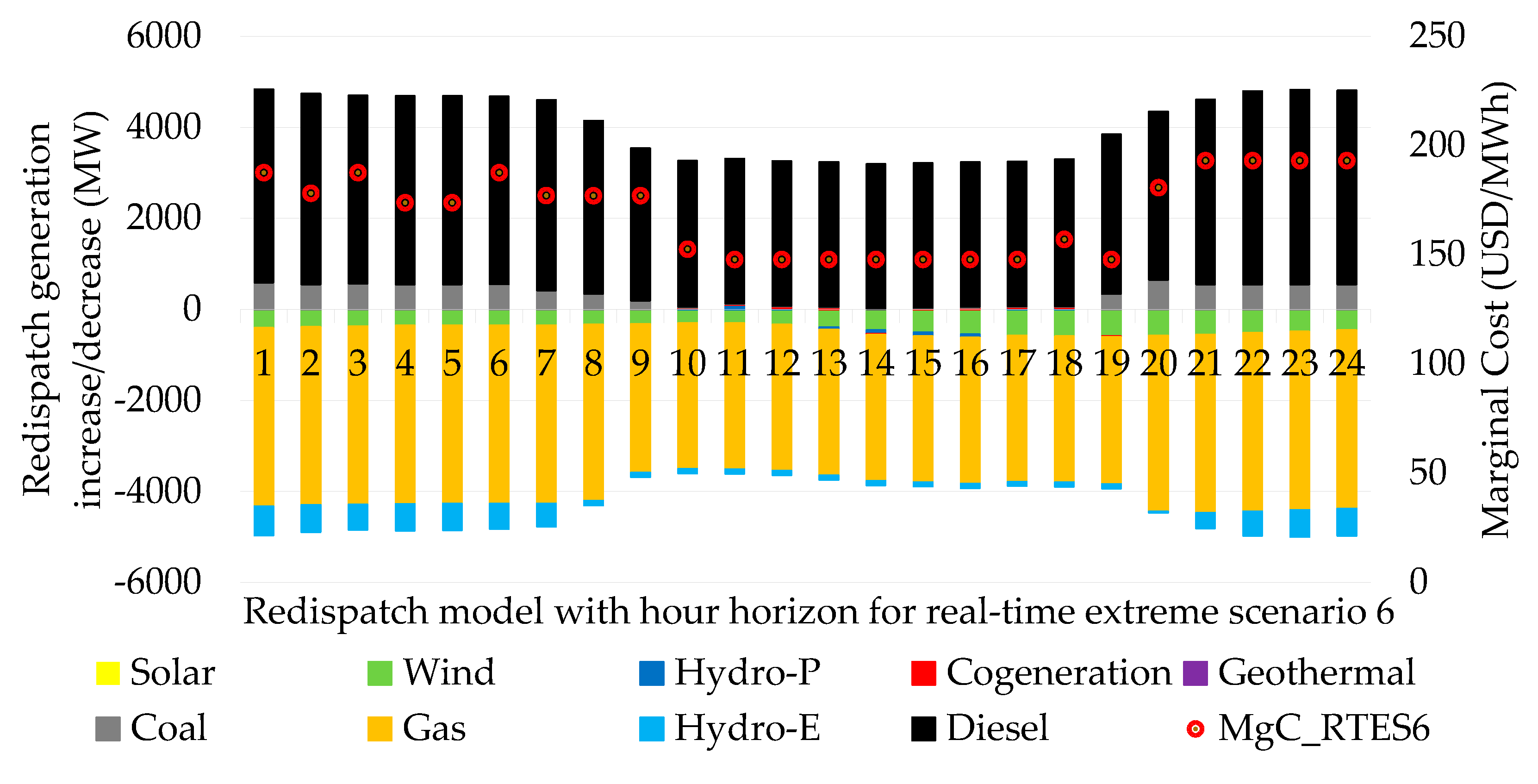
4.1.6. Real-Time Extreme Scenario 6: Decarbonization Stalls with the use of Coal-Fired Generation due to Crisis in Resources Destined for Hydro, Wind and Gas Generation

This is the most extreme real-time scenario, since demand supply is 100% dependent on coal-diesel thermal generation, emissions and the overall cost of operation increases in the face of zero water, gas and wind generation forecasts, as shown in Figure 12.
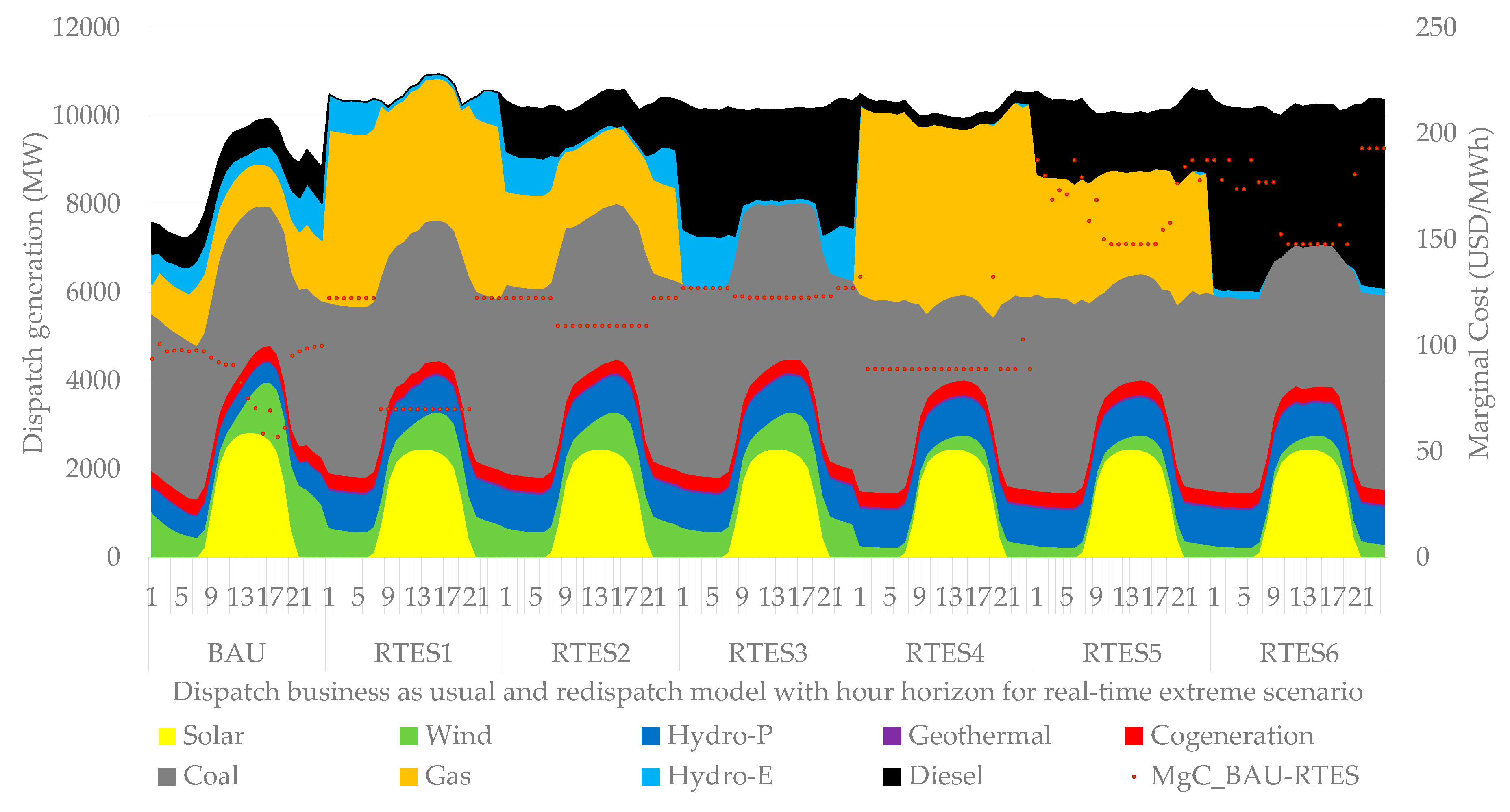
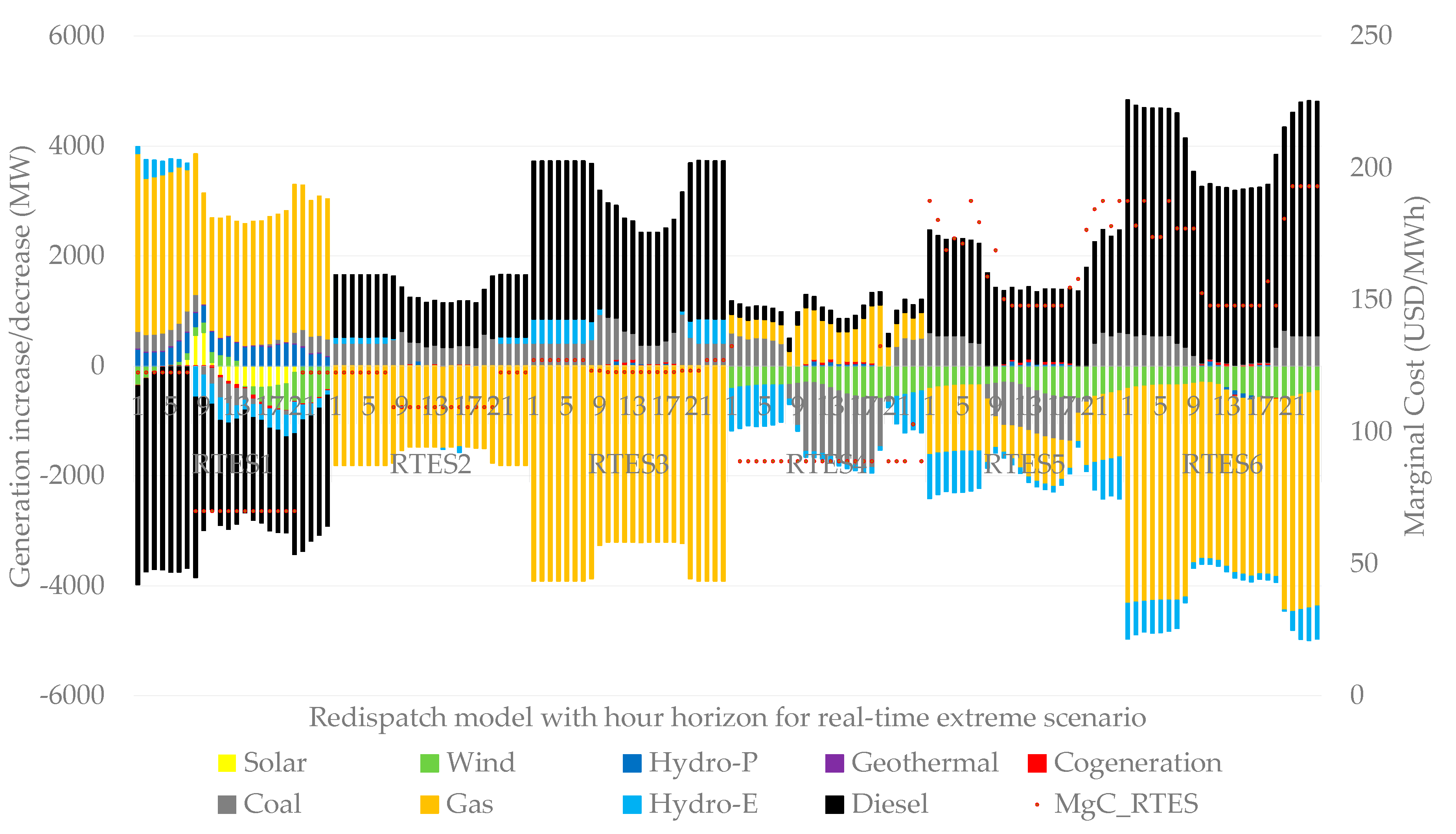
Finally, Figure 13 shows a summary of the dispatch of plants from a base scenario versus all the results of the redispatch model of the six extreme scenarios in real time that show an economic horizon with an hourly resolution. The results of each extreme scenario indicate the trajectory of marginal costs and total generation dispatch to supply demand due to variations in gas, wind and hydro generation.

5. Analysis and Discussion of the Results Obtained from the Redispatching Model in Real-Time Operation

The most relevant results of the redispatch model using the real-time extreme scenario are shown below. The advantages and shortcomings of the proposed model are compared with the unit commitment model and the operation of the system using the economic merit list.
The results in Table 5 and Figure 14 show a summary of the economic results of the redispatch model, such as operating costs (OpC), marginal cost (MgC) in different demand periods, with a three-day simulation horizon. However, the real scenarios with the best marginal cost are the RTES1, RTES2 and RTES4 scenarios (70 to 89 USD/MWh), which can compete with the unit commitment and economic merit list models. It is also evident from the redispatch model that the overall operating cost of the real-time extreme scenario ranges from 23,739,307 to 25,524,673 USD. Therefore, it is shown that for these scenarios the overall cost of operation is competitive, as opposed to the overall cost of operation of the actual scenarios using the economic merit list (40,898,179 USD).
However, the most critical real scenarios of RTES3, RTES5 and RTES6, represent a true reflection of the use of coal-diesel thermal generation, where the overall operating costs range from 33,341,278 to 40,592,628 USD, close to the operating cost of the economic merit list (40,898,179 USD) that is evaluated through a base scenario with no variation in the system. From these results we can deduce that, if we submit the redispatch using the economic merit list for RTES3, RTES5 and RTES6, the overall cost of operation could double.
On the other hand, the lower operating cost of the proposed model (23,739,307 USD) is higher than the unit commitment model, due to the fact that the network parameters are adapted to the reality of real-time operation. This shows that the operating cost of a unit commitment model is cheaper (15,804,718 USD). However, the unit commitment model has not been fitted with the actual variable cost functions of the plants, because its modeling is a linear cost function. Instead, the proposed work runs a redispatch model that integrates polynomial functions of the variable costs, which depend on the specific net consumption and the maximum dispatch power. In the real-time extreme scenario, a maximum dispatch power of 1050 MW is recorded without the need to limit generation. As for the convergence times of the redispatch model, it can be stated that they are acceptable (2-5 minutes) and meet the expectations for decision making in real-time operation, surpassing on a large scale the pre-dispatch model (1 hour) and the economic merit list (3 hours).
Regarding the dispatches of power plants that modify the initial generation of the unit commitment, for real-time extreme scenario 1, 3 and 4, gas-fired thermal generation has the largest share around 3000 MW with average marginal costs ranging from 94 to 128 USD/MWh. While in real-time extreme scenario 2, 5 and 6, diesel thermal generation registers the largest increase in power around 4000 MW with average marginal costs ranging from 113 to 193 USD/MWh, as shown in Figure 14.

6. Conclusion and Future Work on the Redispatch Model

The redispatch model developed in this work is successful because it contributes to the decisions made by the system operator over any other method related to the real-time electricity generation market. This redispatch model replaces the traditional and inefficient economic merit list used in several South American countries, allowing to mitigate the non-optimal results of operating costs due to unjustified dispatches of plants with the economic merit list methodology as the only resource in real time operation. Therefore, it is necessary to evolve to a more sophisticated redispatch model that adapts to the challenges of real-time operation and market, considering the massive solar-wind renewable generation that Chile and the world are facing, with thousands of megawatts added to conventional generation.
The proposed redispatch model is fast to execute in order to face the daily real time operation that deviates from the scheduled operation of the unit commitment. The convergence times for the different real case studies to which the redispatch model was subjected are acceptable and the economic results have absolute validity. The system operator can execute in real time the decisions of dispatch and retirement of plants optimally, leaving expired the use of the economic merit list that causes serious deviations in the real costs of operation of the system ranging from 20 to 50%, i.e., in the order of 8 to 20 MUSD with respect to the proposed redispatch model. As for the convergence times for the different real case studies that the redispatch model was subjected to, they are in the order of 2 to 5 minutes compared to the long convergence times of the unit commitment models and the merit list, which range from 1 to 3 hours in their execution.
Finally, this redispatch model does not fully resolve the dynamic trade-off between real-time operation and market. Unfortunately, it has economic shortcomings with the generation market allowing to encourage future researchers to link this work with the market of ancillary services, specifically in the economic mechanisms dedicated to frequency control integrating solar-wind generation. Large electric power systems are showing a decreasing capacity of inertia and power reserves for primary, secondary, and tertiary frequency control. Currently, this problem of stability control deficits is a short-term responsibility that solar-wind generation must assume in order to displace thermal generation and comply with the regulatory policies associated with the global energy transition.

Author Contributions

Conceptualization, K.B.; methodology, K.B.; validation, K.B.; formal analysis, K.B.; investigation, K.B.; writing—original draft preparation, K.B.; writing—review and editing, K.B. and D.W.; visualization, K.B.; supervision, D.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received external support and funding from Conicyt-Fondecyt 1221943 and Conicyt-FONDAP 1522A0006 (SERC Chile).

Data Availability Statement

The data and calculations obtained can be found in the following link. https://www.coordinador.cl/operacion/documentos/programas-de-operacion-2021/ (accessed on 20-21-22 February 2021).

Acknowledgments

The authors acknowledge the support and funding from Conicyt-Fondecyt 1221943 and Conicyt-FONDAP 1522A0006 (SERC Chile). Acknowledgments are extended to the Real-Time Dispatch and Control Center (CDC) of the National Electric Coordinator of Chile for the transparent in-formation provided to develop this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. G. Rancilio, A. Rossi, D. Falabretti, A. Galliani and M. Merlo, “Ancillary services markets in europe: Evolution and regulatory trade-offs,” Renewable and Sustainable Energy Reviews, vol. 154, Feb. 2022.
  2. Y. Zhang, Q. Guo, Y. Zhou and H. Sun, “Frequency-constrained unit commitment for power systems with high renewable energy penetration,” International Journal of Electrical Power & Energy Systems, Volume 153, 2023, 109274, ISSN 0142-0615. [CrossRef]
  3. C. Washburn and M. Pablo-Romero, “Measures to promote renewable energies for electricity generation in Latin American countries,” Energy Policy, Volume 128, 2019, Pages 212-222, ISSN 0301-4215. [CrossRef]
  4. K. Knuepfer, N. Rogalski, A. Knuepfer, M. Esteban and T. Shibayama, “A reliable energy system for Japan with merit order dispatch, high variable renewable share and no nuclear power,” Applied Energy, Volume 328, 2022, 119840, ISSN 0306-2619. [CrossRef]
  5. R. De Siano and A. Sapio, “Spatial merit order effects of renewables in the Italian power exchange,” Energy Economics, Volume 108, 2022, 105827, ISSN 0140-9883. [CrossRef]
  6. R. Liu, Z. Bao, J. Zheng, L. Lu, and M. Yu, “Two-Stage Robust and Economic Scheduling for Electricity-Heat Integrated Energy System under Wind Power Uncertainty,” Energies, vol. 14, no. 24, p. 8434, Dec. 2021. [CrossRef]
  7. Arenas-Crespo, J. Candelo-Becerra, and F. Hoyos Velasco, “Online Economic Re-dispatch to Mitigate Line Overloads after Line and Generation Contingencies,” Energies, vol. 12, no. 6, p. 966, Mar. 2019. [Google Scholar] [CrossRef]
  8. K. Wawrzyniak, E. Urresti Padrón, W. Jaworski, and R. Korab, “Risk-Based Active Power Redispatch Optimization,” Energies, vol. 13, no. 3, p. 716, Feb. 2020. [CrossRef]
  9. N. Mohammadi, H. Mostofi, and H.-L. Dienel, “Policy Chain of Energy Transition from Economic and Innovative Perspectives: Conceptual Framework and Consistency Analysis,” Sustainability, vol. 15, no. 17, p. 12693, Aug. 2023. [CrossRef]
  10. M. Al-Chalabi, “Targeted and Tangential Effects—A Novel Framework for Energy Research and Practitioners,” Sustainability, vol. 15, no. 17, p. 12864, Aug. 2023. [CrossRef]
  11. T. Wang, M. Jin, Y. Li, J. Wang, Z. Wang and S. Huang, "Adaptive Damping Control Scheme for Wind Grid-Connected Power Systems With Virtual Inertia Control," in IEEE Transactions on Power Systems, vol. 37, no. 5, pp. 3902-3912, Sept. 2022. [CrossRef]
  12. J. Hu, Z. Yan, X. Xu and S. Chen, "Inertia Market: Mechanism Design and Its Impact on Generation Mix," in Journal of Modern Power Systems and Clean Energy, vol. 11, no. 3, pp. 20 May; 23. [CrossRef]
  13. H. Karbouj and Z. H. Rather, "Voltage Control Ancillary Service From Wind Power Plant," in IEEE Transactions on Sustainable Energy, vol. 10, no. 2, pp. 20 April; 19. [CrossRef]
  14. Y. -K. Wu, W. -H. Yang, Y. -L. Hu and P. Q. Dzung, "Frequency Regulation at a Wind Farm Using Time-Varying Inertia and Droop Controls," in IEEE Transactions on Industry Applications, vol. 55, no. 1, pp. 213-224, Jan.-Feb. 2019. [CrossRef]
  15. Axel Bastián Poque González, José Eduardo Viglio, Yunesky Masip Macia, Lúcia da Costa Ferreira, Redistributing power? Comparing the electrical system experiences in Chile and Brazil from a historical institutional perspective, Energy Research & Social Science, Volume 101, 2023, 103129. ISSN 2214-6296. [CrossRef]
  16. Generadoras: “Costos marginales iguales a cero hace necesario complementar mercado con contratos de largo plazo”. (2022, 04 de noviembre). Electricidad. https://www.revistaei.cl/2022/11/04/generadoras-costos-marginales-iguales-a-cero-hace-necesario-complementar-mercado-con-contratos-de-largo-plazo/.
  17. Dharik S. Mallapragada, Cristian Junge, Cathy Wang, Hannes Pfeifenberger, Paul L. Joskow, Richard Schmalensee, Electricity pricing challenges in future renewables-dominant power systems, Energy Economics, 2023, 106981, ISSN 0140-9883,. [CrossRef]
  18. Wei Dai, Ceheng Luo, Jingshan Mo, Zining Liu, Zhongyao Jiang, Fangjun Wen, HuiHwang Goh, Flexibility enhanced strategies of generations to improve the integration of renewable energy considering uncertainties, Energy Reports, Volume 9, Supplement 7, 2023, Pages 1717-1725, ISSN 2352-4847. 9. [CrossRef]
  19. S. Bhavsar, R. Pitchumani, M.A. Ortega-Vazquez, A reforecasting-based dynamic reserve estimation for variable renewable generation and demand uncertainty, Electric Power Systems Research, Volume 211, 2022, 108157, ISSN 0378 7796. [CrossRef]
  20. José Almeida, Joao Soares, Bruno Canizes, Iván Razo-Zapata, Zita Vale, Day-ahead to intraday energy scheduling operation considering extreme events using risk-based approaches, Neurocomputing, Volume 543, 2023, 126229, ISSN 0925-2312. [CrossRef]
  21. Xiao Hu, Jūratė Jaraitė, Andrius Kažukauskas, The effects of wind power on electricity markets: A case study of the Swedish intraday market, Energy Economics, Volume 96, 2021, 105159, ISSN 0140-9883,. [CrossRef]
  22. Yuqian Zhang, Qinglai Guo, Yanzhen Zhou, Hongbin Sun, Frequency-constrained unit commitment for power systems with high renewable energy penetration, International Journal of Electrical Power & Energy Systems, Volume 153, 2023, 109274, ISSN 0142-0615. [CrossRef]
  23. Palovic Martin, Brandstätt Christine, Brunekreeft Gert, Buchmann Marius, Strategic behavior in market-based redispatch: International experience, The Electricity Journal, Volume 35, Issue 3, April 2022.
  24. B. Xiong, J. Predel, P. Crespo del Granado and R. Egging-Bratseth, “Spatial flexibility in redispatch: Supporting low carbon energy systems with Power-to-Gas,” Applied Energy, vol. 283, Feb. 2021.
  25. G. Li, R. Zhang, T. Jiang, H. Chen, L. Bai and X. Li, “Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process,” Applied Energy, vol. 194, pp. 696-704, May. 2017.
  26. O. Guerra, B. Sergi, M. Craig, K. Addo, C. Brancucci and B. Mathias Hodge, “Coordinated operation of electricity and natural gas systems from day-ahead to real-time markets,” Journal of Cleaner Production, vol. 281, Jan. 2021.
  27. H. Ameli, M. Qadrdan and G. Strbac, “Value of gas network infrastructure flexibility in supporting cost effective operation of power systems,” Applied Energy, vol. 202, pp. 571-580, Sep. 2017.
  28. T. Diagoupis, P. Andrianesis and E. Dialynas, “A planning approach for reducing the impact of natural gas network on electricity markets,” Applied Energy, vol. 175, pp. 189-198, Aug. 2016.
  29. S. Pearson, S. Wellnitz, P. Crespo del Granado and N. Hashemipour, “The value of TSO-DSO coordination in re-dispatch with flexible decentralized energy sources: Insights for Germany in 2030,” Applied Energy, vol. 326, Nov. 2022.
  30. K. Poplavskaya, G. Totschnig, F. Leimgruber, G. Doorman, G. Etienne and L. de Vries, “Integration of day-ahead market and redispatch to increase cross-border exchanges in the European electricity market,” Applied Energy, vol. 278, Nov. 2020.
  31. F. Liu, Z. Bie, S. Liu and T. Ding, “Day-ahead optimal dispatch for wind integrated power system considering zonal reserve requirements,” Applied Energy, vol. 188, pp. 399-408, Feb. 2017.
  32. S. Kamali and T. Amraee, “Blackout prediction in interconnected electric energy systems considering generation re-dispatch and energy curtailment,” Applied Energy, vol. 187, pp. 50-61, Feb. 2017.
  33. P. Damien, R. Fuentes-García, R. Mena and J. Zarnikau, “Impacts of day-ahead versus real-time market prices on wholesale electricity demand in Texas,” Energy Economics, vol. 81, pp. 259-272, Jun. 2019.
  34. W. Antweiler and F. Muesgens, “On the long-term merit order effect of renewable energies,” Energy Economics, vol. 99, Jul. 2021.
  35. L. Zeng, H. Dong and D. Liang, “Robust Optimal Power Flow under Renewable Uncertainty with Pairwise Convex Hull and Non-Affine AGC Redispatch Strategy,” Electric Power Systems Research, vol. 210, Sep. 2022.
  36. J, M. Bachtiar and A. Arief, “Network Losses-based Economic Redispatch for Optimal Energy Pricing in a Congested Power System,” Energy Procedia, vol. 100, pp. 311-314, Nov. 2016.
  37. D. Jiménez, A. Angulo, A. Street and Fernando Mancilla-David, “A closed-loop data-driven optimization framework for the unit commitment problem: A Q-learning approach under real-time operation,” Applied Energy, vol. 330, Part B, Jan. 2023.
  38. J. Liu, Y. Zhang, K. Meng, Z. Yang, Y. Xu and S. Han, “Real-time emergency load shedding for power system transient stability control: A risk-averse deep learning method,” Applied Energy, vol. 307, Feb. 2022.
  39. ASME PTC 46, “Performance Test Code on Overall Plant Performance,” The American Society of Mechanical Engineers, 1996.
  40. ASME PTC 4.0, “Fired Steam Generators,” The American Society of Mechanical Engineers, 2008.
  41. ASME PTC 19.1, “Test Uncertainty,” The American Society of Mechanical Engineers, 2005.
  42. ASME PTC 22, “Performance Test Code on Gas Turbines,” The American Society of Mechanical Engineers, 2005.
  43. ASME PTC 6, “Steam Turbines,” The American Society of Mechanical Engineers, 2004.
  44. ASME PTC 4.4, “Gas Turbine Heat Recovery Steam Generators,” The American Society of Mechanical Engineers, 2008.
  45. ASTM D 3588, “Standard Practice for Calculating Heat Value, Compressibility Factor, and Relative Density of Gaseous Fuels,” The American Society of Mechanical Engineers, 2008.
  46. Procedimiento DO, “Información de Pruebas de Consumo Específico Neto,” Coordinador Eléctrico Nacional, 2011. Available in: https://www.coordinador.cl/. (accessed on 20 March 2021).
  47. Operación, “Programas de Operación,” Coordinador Eléctrico Nacional, 2021. Available in: https://www.coordinador.cl/. (accessed on 20 March 2023).
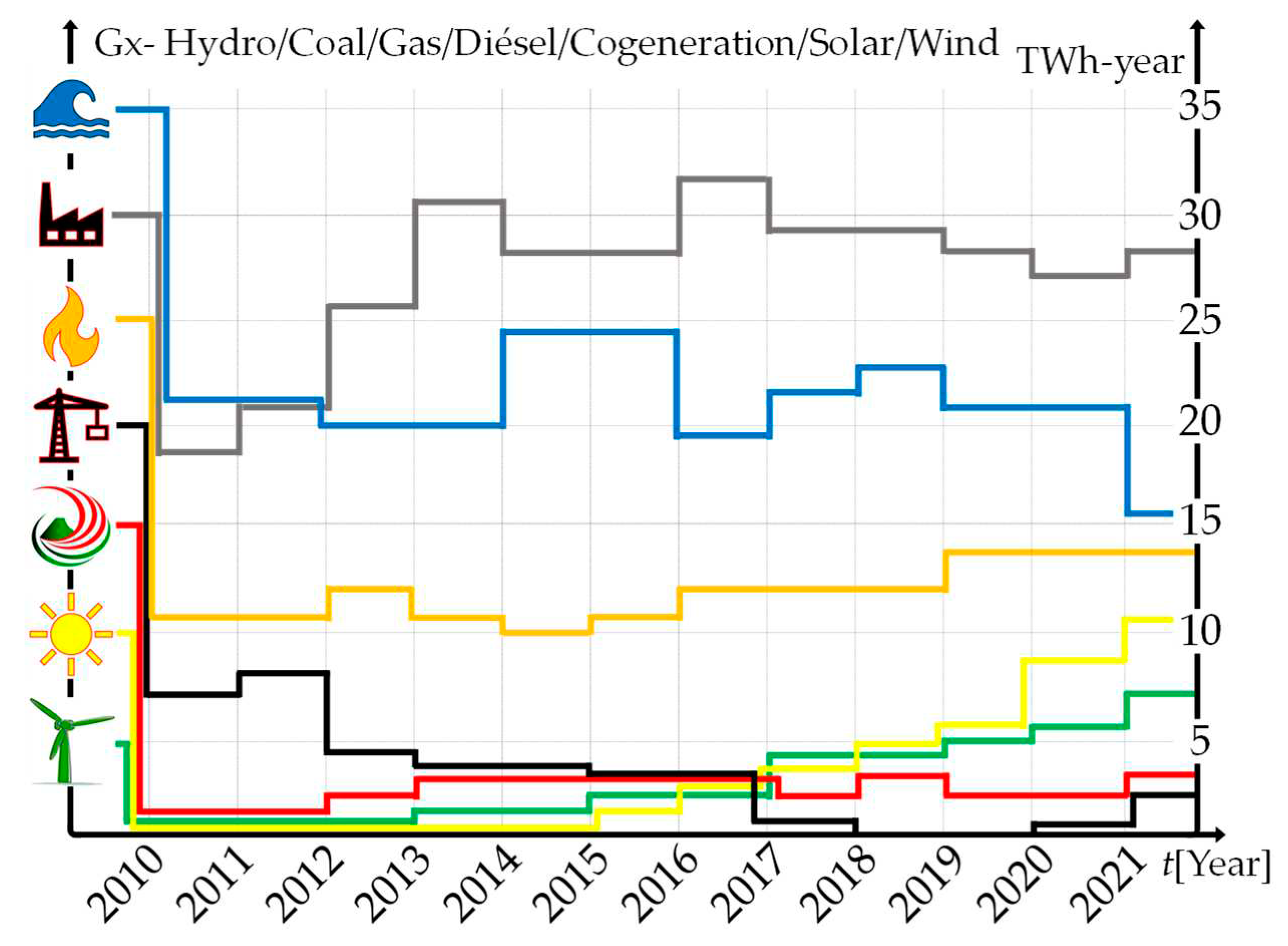
Preprints 91877 g001
Figure 1. Expansion in solar-wind generation and decrease in conventional generation.
Figure 1. Expansion in solar-wind generation and decrease in conventional generation.
Preprints 91877 g001
Preprints 91877 g002
Figure 2. Theoretical methodology and concepts for a redispatch.
Figure 2. Theoretical methodology and concepts for a redispatch.
Preprints 91877 g002
Preprints 91877 g003
Figure 3. General structure of the mathematical methodology for a redispatch.
Figure 3. General structure of the mathematical methodology for a redispatch.
Preprints 91877 g003
Preprints 91877 g004
Figure 4. The importance of integrating the maximum dispatch power due to the undesired action of frequency droop ramps.
Figure 4. The importance of integrating the maximum dispatch power due to the undesired action of frequency droop ramps.
Preprints 91877 g004
Preprints 91877 g005
Figure 5. Tuning of redispatch parameters in PLEXOS.
Figure 5. Tuning of redispatch parameters in PLEXOS.
Preprints 91877 g005
Preprints 91877 g006
Figure 6. Structure and design of an electrical power system segmented into electrical zones for a redispatch model.
Figure 6. Structure and design of an electrical power system segmented into electrical zones for a redispatch model.
Preprints 91877 g006
Preprints 91877 g007
Figure 7. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 1.
Figure 7. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 1.
Preprints 91877 g007
Preprints 91877 g008
Figure 8. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 2.
Figure 8. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 2.
Preprints 91877 g008
Preprints 91877 g009
Figure 9. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 3.
Figure 9. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 3.
Preprints 91877 g009
Preprints 91877 g010
Figure 10. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 4.
Figure 10. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 4.
Preprints 91877 g010
Preprints 91877 g011
Figure 11. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 5.
Figure 11. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 5.
Preprints 91877 g011
Preprints 91877 g012
Figure 12. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 6.
Figure 12. Redispatch of total hourly generation indicating marginal costs for real-time extreme scenario 6.
Preprints 91877 g012
Preprints 91877 g013
Figure 13. Economic dispatch of business as usual versus economic dispatch of generation redispatch for extreme scenarios in real time.
Figure 13. Economic dispatch of business as usual versus economic dispatch of generation redispatch for extreme scenarios in real time.
Preprints 91877 g013
Preprints 91877 g014
Figure 14. Generation redispatch indicating the increase and decrease of power by technology for the extreme scenarios in real time.
Figure 14. Generation redispatch indicating the increase and decrease of power by technology for the extreme scenarios in real time.
Preprints 91877 g014
Table 1. Elements of transmission system for the redispatch model.
Table 1. Elements of transmission system for the redispatch model.
Voltage (kV) Bus Line Transformer Simulation Z[pu]
500 10 21 - Yes
345 1 - - No
220 48 96 - Yes
154 3 4 - Yes
110 6 11 - Yes
500/220 - - 22 Yes
345/220 - - 1 Yes
220/154 - - 2 Yes
220/110 - - 4 Yes
Table 2. Central plant by technology and the technical-economic constraints of the redispatch model.
Table 2. Central plant by technology and the technical-economic constraints of the redispatch model.
Plants N° PMIN[MW] PMAX [MW] TSTART [h] TON[h] TDOWN[h] CSTART[$] CDOWN[$] CVNC[$/MWh] PFUEL[$/m3] CEN[m3/MWh] CVC[$/MWh] CV = CVC+CVNC[$/MWh]
Solar 12 No Yes No No No No No No No No No No
Wind 17 No Yes No No No No No No No No No No
Geothermal 1 No Yes No No No No No No No No No No
Cogeneration 7 No Yes No No No No No No No No No No
Coal 24 Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
Gas 37 Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
Oil 61 Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
Hydraulic-S 29 Yes Yes No No No No No Yes No Yes Yes Yes
Hydraulic-R 26 No Yes No No No No No No No Yes Yes No
Table 3. Demand participation factor by electrical zones.
Table 3. Demand participation factor by electrical zones.
Zone Electric Location in Chile Bus Demand Category Factor Demand
North Arica y Parinacota PARINACOTA_220 Residential 0.95
Tarapacá POZO ALMONTE_220 Residential 0.95
COLLAHUASI_220 Copper Mining 2.38
Antofagasta ENCUENTRO_220 Copper Mining 3.81
CRUCERO_220 Copper Mining 4.76
TOCOPILLA_220 Residential 0.95
MEJILLONES_220 Residential 1.43
CAPRICORNIO_220 Copper Mining 1.43
LABERINTO_220 Copper Mining 3.81
ANDES_220 Copper Mining 5.71
North Center Atacama DIEGO DE ALMAGRO_220 Copper Mining 1.90
CARDONES_220 Copper Mining 2.38
MAITENCILLO_220 Copper Mining 2.86
Coquimbo PAN DE AZUCAR_220 Commercial Tourism 3.81
Center Valparaíso VENTANAS_110 Residential 0.48
AGUA SANTA_110 Commercial Tourism 1.43
QUILLOTA_110 Residential 0.95
SAN PEDRO_110 Residential 1.90
LAS VEGAS_110 Residential 1.90
South Center Metropolitana EL SALTO_220 Residential 7.62
CERRO NAVIA_220 Residential 7.62
CHENA_220 Residential 7.62
O'Higgins ALTO JAHUEL_220 Farming Industry 5.71
ALTO JAHUEL_154 Farming Industry 2.86
Maule COLBUN_220 Farming Industry 0.95
ANCOA_220 Farming Industry 0.95
ITAHUE_154 Residential 1.90
Ñuble CHILLAN_154 Residential 1.43
South Bío-Bío CHARRUA_220 Residential 10.48
La Araucanía TEMUCO_220 Residential 2.38
Los Ríos VALDIVIA_220 Commercial Tourism 1.90
PICHIRROPULLI_220 Livestock Industry 1.43
Los Lagos PUERTO MONTT_220 Fishing Industry 2.38
CHILOE_220 Fishing Industry 0.95
Table 4. Critical scenario (%) of gas, hydro, and wind generation.
Table 4. Critical scenario (%) of gas, hydro, and wind generation.
Plants RTES1 RTES2 RTES3 RTES4 RTES5 RTES6
Solar 100% 100% 100% 100% 100% 100%
Wind 40% 40% 40% 10% 10% 10%
Geothermal 100% 100% 100% 100% 100% 100%
Cogeneration 100% 100% 100% 100% 100% 100%
Coal 100% 100% 100% 100% 100% 100%
Gas 100% 50% 0% 100% 50% 0%
Oil 100% 100% 100% 100% 100% 100%
Hydraulic-S 30% 30% 30% 5% 5% 5%
Hydraulic-R 30% 30% 30% 30% 30% 30%
Table 5. Summary of the economic information (MgC, OpC-total) the redispatch model (*)-hydro, (**)-gas, (***)-diesel, (****)-coal.
Table 5. Summary of the economic information (MgC, OpC-total) the redispatch model (*)-hydro, (**)-gas, (***)-diesel, (****)-coal.
Horizon Demand RTES1 RTES2 RTES3 RTES4 RTES5 RTES6 Unit commitment Merit list
Day 1MgC-Maximum [USD/MWh] Demand-Low
[03:00-04:00]		 127* 134* 134* 148*** 148*** 188*** 106*** 166***
Generation (Max)-Solar
[12:00-13:00]		 70** 83*** 123*** 89*** 123*** 148*** 63** 111***
Demand-High
[22:00-23:00]		 123* 123* 127* 103* 188*** 192*** 118*** 151***
Day 2MgC-Maximum [USD/MWh] Demand-Low
[03:00-04:00]		 123* 123* 127* 89*** 173*** 188*** 102** 45****
Generation (Max)-Solar
[12:00-13:00]		 70** 109*** 123*** 89*** 148*** 148*** 43**** 48****
Demand-High
[22:00-23:00]		 123*** 123* 127* 103* 188*** 174*** 107*** 58****
Day 3MgC-Maximum [USD/MWh] Demand-Low
[03:00-04:00]		 123*** 123* 127* 89*** 171*** 174*** 87*** 145***
Generation (Max)-Solar
[12:00-13:00]		 70** 109*** 123*** 89*** 148*** 148*** 74**** 70****
Demand-High
[22:00-23:00]		 123* 123* 127* 103* 188*** 193*** 89** 145**
Software OpC-Total [USD] 23,739,307 26,574,025 33,341,278 25,524,673 32,208,264 40,892,628 15,804,718 40,898,179
PLEXOS Time [Seg.] 120<seg. 120<seg. 120<seg. 300<seg. 300<seg. 300<seg. 3800<seg. 9200<seg.
Maximum Power Dispatch[MW] 1050[meets] 1050[meets] 1050[meets] 1050[meets] 1050[meets] 1050[meets] 1.050[meets] 1050[meets]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated