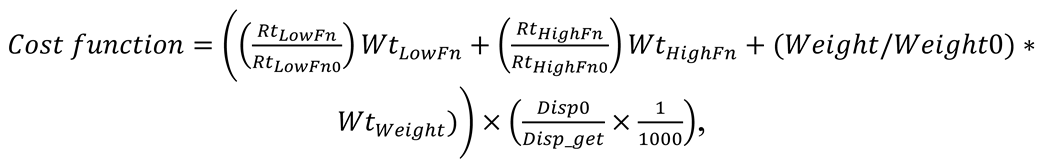Prerpints.org logo
Preprint
Article

A Systematic Series Development and Calm Water Resistance Prediction for a Fast Catamaran Ferry Utilizing Machine Learning Tools

Altmetrics

Downloads

112

Views

36

Comments

0

Submitted:

30 November 2023

Posted:

01 December 2023

You are already at the latest version

Alerts
Abstract
The aim of article is to design a calm water resistance predictor based on Machine Learning Tools and development of a systematic series for battery-driven catamaran hull forms. Regression Trees (RT), Support Vector Machines (SVM), and Artificial Neural Network (ANN) regression models are applied for dataset training on developed systematic series of catamarans. A hullform optimization was implemented for various catamarans including dimensional and hull coefficient parameters based on resistance and structural weight reduction and battery performance improvement. This paper provides a diverse database of catamaran hullform. Hence, an automated Matlab program was coded for geometry generation and cost function evaluation. Design distribution based on Lackenby transformation fulfills all design space and sequentially a novel self-blending method reconstructs new hullforms based on two parents blending. Finally, a machine learning approach was conducted on generated data of case study. This study shows that ANN algorithm correlates well with the measured resistance. Accordingly, a general and unique tool is proposed for optimized and desired design in first design stage.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

The EU funded project “TrAM-Transport: Advanced and Modular” develops battery-driven zero emission fast passenger vessels for coastal areas and inland waterways. Modular design and manufacturing methods are the focus of this project with the objectives to minimise environmental impact and life cycle cost [1,2]. The development of a systematic series of zero-emission catamaran hullform for different displacement tonnage and ship types can significantly help this process. Enormous catamaran hullforms will generate during the systematic series development and resistance calculation takes time for each design. An accurate and fast resistance predictor yields to convenient tool for a class of hullforms. Therefore, a new model for such diversity with an appropriate generalization to new predictions is desired in this field, this leads us the data mining approaches [3].

2. Background

Resistance calculations in past decades have been implemented by model tests or sea trial measurements. The classic regression models have limited to conventional vessels with specified general particulars. Besides, the accuracy and its cost were barriers to implement EFD and CFD measurements for new designs. During the past decades, some nonlinear dynamic approaches have been developed, which produces comparable results and more flexibility [4,5]
Ship resistance optimization plays an important role in the hullform development. Assessing the ship resistance in the first stage of ship design allows the designer to analyze the influence of different hull forms and parameters. Accordingly, different methods of geometry optimization and design study have been developed during past decades [6]. Papanikolaou et al. [7] implemented a global and local hullform optimization of the fast catamaran in two design study scenarios. In the first stage of optimization, 1000 hullforms were elaborated with surrogate-based design study using potential theory 3D panel code. After that, two most promising designs have been selected as initial hullform of local modification focusing on the stern region. However, a comprehensive design optimization might be proposed according to balance between accuracy and time, which is discussed in different previous papers [8,9,10]. An all-inclusive hullform optimization in the field of ship design defines various hullforms with different geometrical parameters. Accordingly, marine industry needs an optimization platform to minimize the required propulsion power according to various possibilities of hullform. Besides, a systematic series are developed on generated geometries to establish a resistance predictor.
Li et al. [11] by using Single-Parameter Lagrangian Support Vector Regression (SPL-SVR) developed a metamodel on seakeeping data. A multidisciplinary design optimization in concept design stage of ships has been proposed. Recently, Fahrnholz and Caprace [12] conducted a regression analysis on three sailboats' systematic series. Based on machine learning techniques, a resistance predictor was designed on resistance data. Nazemian and Ghadimi [13] by using a D-optimal DoE study investigated resistance performance of a trimaran hull series. A resistance analysis and its improvement was encompassed to extract optimum value of hull parameters and sidehull arrangement.
Machine learning techniques have commenced in the last decade in the field of ship design and hydrodynamics [14,15]. The resistance prediction has been developed and compared by traditional approaches by Radojic et al. [16,17]. An Artificial Neural Network regression method was designed for planing boats at different series types. The machine learning models can also implement on added resistance [18] and ice resistance [19]. Different aspects of ship design targets can be considered in dataset analysis. Liu and Papanikolaou [20] developed a semi-empirical formula, approximating the added resistance of ships in regular waves of arbitrary heading. Develop of a catamaran class alongside optimization process has been considered in the current study with an automatic design generation.
The present paper divides in two phases, focusing on systematic series development for a fast passenger and freight zero-emission catamaran and applying machine learning on generated data. Based on surveyed literature, it can be concluded that a hullform optimization process needs to be added to ship series. For each tonnage condition and ship type, a predictive machine learning model develops to calculate calm water resistance. Besides the final design would be the best design with respect to the lowest resistance at multi-design speeds. An automated optimization code is carried out in Matlab software to prepare data set of different hullform. In the frame of TrAM project, various optimized design options prepare based on ship dimension and coefficient and hullform alteration. Accordingly, design study starts with numerous ship types and tonnage and offer different possibility of catamaran hullform as flexibility for owner's selection. Owners can choose their optimized design based on their requirements.
Performing parametric transformations and self-blending method creates a series of hull forms with systematically varying parameters. Parametric transformation by moving ship sections and self-blending by moving Control Points implement parametric transformations to create new hulls. A regression formula calculates structural weight of catamarans for scantling and deck weights. The steel weight of shells computes based on wetted surface area when design draft is placed on main deck. Weight of installed battery automatically decreases by reduction of total resistance and consequently power requirement.

3. Methodology

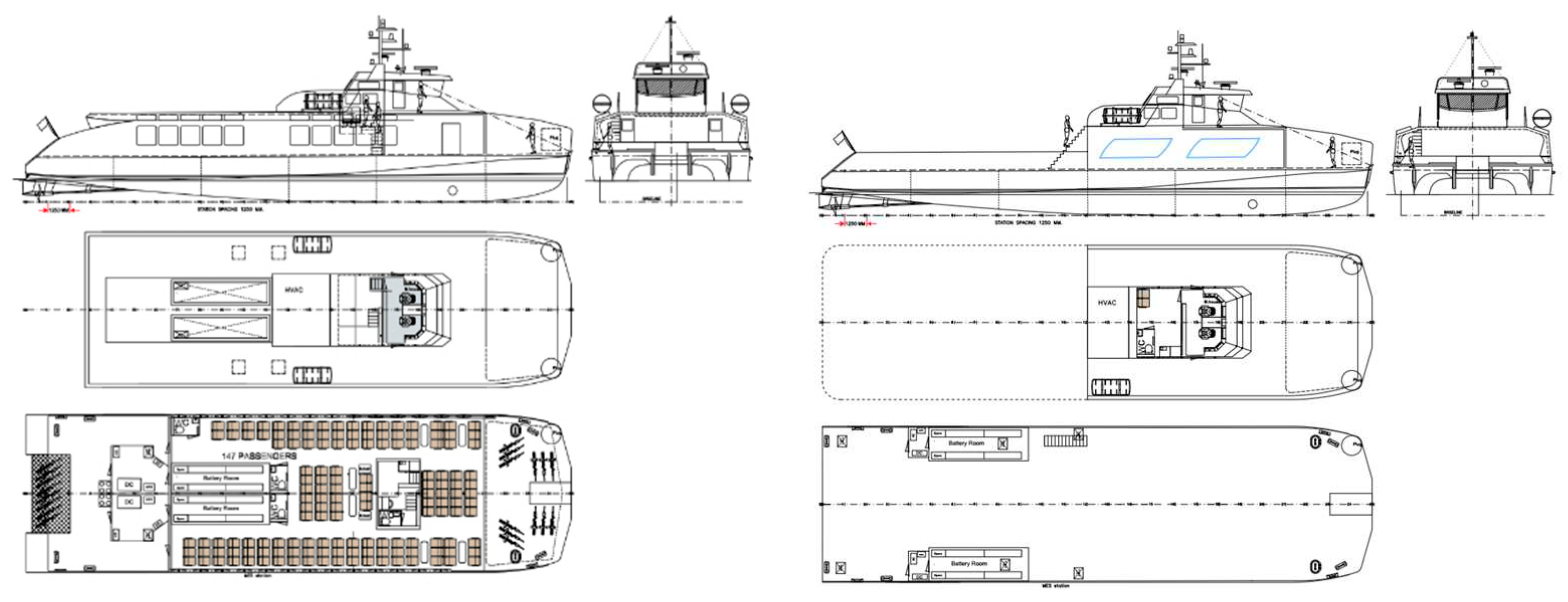
Present's optimization code capabilities, allowing any type of hullform to be modeled in case of different ship design targets, offer scope for the creation of a wide range of hull forms and provide an optional selection for owners. Combined with the built-in resistance, structure weight and battery-driven system performance calculations, you have the tools to experiment with shapes and explore design parameters. Accordingly, an extensive fast catamaran series has been developed and for each selection, an optimized hull obtains. The case study is a catamaran hull [1,2] as an initial design of database production. The database consists of three tonnages ( ∆ 1 = 75 , ∆ 2 = 80 , ∆ 3 = 85 ) tons. Two types of passenger and freight catamaran boats are defined as initial hullform. General arrangement of under-studied catamarans depicts in Figure 1.
Three design study processes apply to three hullforms (75 ton, 80 ton, 85 ton). After the model has been altered total resistance calculates via slender body method. Structural weight of each design is estimated by a regression formula and shell expansion of hull surface. Propulsion system of vessel works with electrically powered battery spares. Performance and battery weight computes based on resistance and consequently break power of the catamaran [21,22,23,24]. Output of optimization process is resistance at 12 knot and resistance at 22 knot, which represent by a weighting cost function:
Preprints 91928 i001
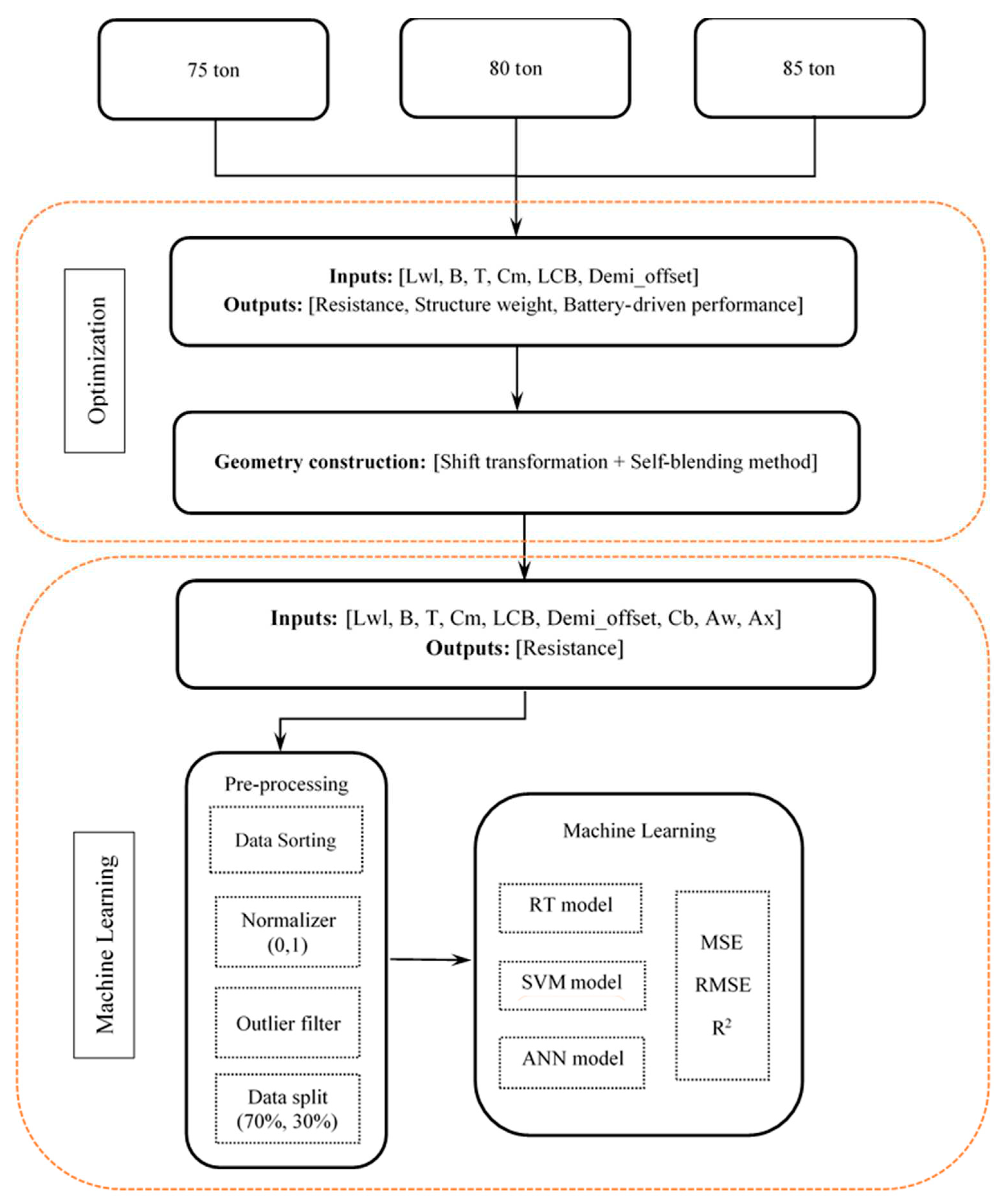
The framework of design study and machine learning illustrates in Figure 2. For each tonnage, ship geometry is designed and distributed on design space according to multi-level combination of design variables. Total resistance and weight estimation of structure and battery weight calculate for each design. Pre-processing progress is applied to obtained data to define different regression schemes. Herein, Regression Tree (RT), Support Vector Regression (SVR), and Artificial Neural Network (ANN) methods are used to predict other interesting designs and find a resistance predictive model.
The case study catamaran is the prototype hullform, which is designed and built in frame of Horizon 2020 European Research project TrAM [25]. The main purpose of this effort is to replicate this hullform based on small modifications. Optimization process conducts on 6 design variables and 2 constraints that are shown in Table 1. As a result, the displacement constraint is defined as follows:
∆ n e w − ∆ o r g ∆ o r g ≤ 0.01 ,
Another constraint of the present study is total beam of the catamaran to satisfy port requirements, therefore:
2 × D e m i h u l l   o f f s e t + d e m i h u l l   b e a m ≤ 9 ,
Demihull offset is the distance between centerline of each demihull.
9 design parameters of catamaran ship are selected as input data of regression learner. Total resistance value is output parameter of the study, which calculates through slender body method [26,27]. Attribute selection is depicted in Table 2. Regression models implements on each ship speed [12, 13.25, 14.5, 15.75, 17, 18.25, 19.5, 20.75, 22] knot. Finally, a comprehensive regression is applied to all generated hulls at different drafts and dimensions to generalize the systematic series.

4. Database generation of catamaran case study

Optimization process conducts for each design scenario to obtain the best design for each configuration. The developed geometry reconstruction model offers designer the possibility to control/specify the main particulars of the demihull along with the hull form details within a reasonable range of variation of the defined design variables, while at the same time, adequate quality of fairness and smoothness of the hull is ensured. The designer is enabled to explore the huge design space of automatically generated hull forms and decide on the most favorable ones based on rational, holistic criteria. Regression learners are applied on 5 design configurations every 1955 hullforms, which turns to 9775 designs. The pre-processing procedure reforms database to the application of machine learning techniques. Linear normalization is implemented on each parameter according to Eq.(4):
p a r a m e t e r n o r m a l i z e d = p a r a m e t e r o r i g i n a l − p a r a m e t e r m i n . v a l u e p a r a m e t e r m a x . v a l u e − p a r a m e t e r m i n . v a l u e ,
Another step of preprocessing is using a principal component analysis technique (PCA) and Outlier detection using the hotellings T2 test [28]. Selecting the outliers can be useful to remove them from the dataset or for deeper investigation. Dimensionality reduction is applied to the inputs to project data into a space of lower dimension while preserving a maximum of information. Number of data reduces from 9775 to 8745 records according to PCA and outlier detection with confidence interval of 0.05 [29,30]. Finally, the database is randomly split into a learning set and test set, which contains 70% and 30% of the records, respectively.
Regression trees (RT), support vector machines (SVM), and artificial neural network (ANN) regression models are applied for data set training based on 9 predictors and 1 response. The regression tree is a supervised learning algorithm with tree-structured classification. There is a decision-related algorithm for each node based on the attributes. Each step in a prediction involves checking the value of one predictor variable to determine whether an attribute is larger than or smaller or equal to a value of the following branch. The response value contains in the last node, which is known as leaf node. Second supervised regression tool is linear epsilon-insensitive SVM regression. This method disregards prediction errors that are less than some fixed hyperplane. Data points include in the support vectors that have errors larger than admissible error of the model. The function the SVM uses to predict new values depends only on the support vectors to minimize the error. Box constraint, Epsilon value, and Kernel scale parameter are set to automatic mode that the application uses a heuristic procedure to select appropriate value.
The artificial neural network is inter-connected neurons that organized in layers. An ANN algorithm works based on human neuron system, which consists of number of layers, the kind of neural synapses and the learning algorithm [12,31]. The artificial neural network is herein applied to dataset using multilayer feedforward networks. Ship hull parameters define at first fully connected layer, and each subsequent layer has a connection from the previous layer. Weight matrix multiplies to each fully connected layer. Weight intensity iteratively changes aiming to decrease the final error. The number of layers and their neurons is selected by the Bayesian optimizable algorithm [32].
Internal parameters of regression model can be chosen manually, however, the optimized regression methods can select optimized internal values by using hyperparameter optimization. Some of these options can strongly affect regression method's performance. Accordingly, Optimizable Regression Tree, Optimizable SVM, and Optimizable ANN methods are applied herein [33]. Model evaluation is implemented by statistical parameters and test datasets. Coefficient of model determination consists of R-squared (R2), mean squared error (MSE), mean absolute error (MAE), and root mean square error (RMSE):
R 2 = 1 − ∑ i y i − x i 2 ∑ i y i − y ¯ 2 ,
y ¯ = 1 n ∑ i = 1 n y i ,
M S E = 1 n ∑ i = 1 n y i − x i 2 ,
M A E = 1 n ∑ i = 1 n y i − x i ,
R M S E = 1 n ∑ i = 1 n y i − x i 2 ,
Where y i is predicted resistance of the record i, x i is the calculated resistance from dataset, and n is number of samples.

5. Results

Three regression models have been developed according to internal parameter selection to minimize MSE value. The PCA dimensionality reduction reduces number of features from 9 to 6 features. Table 3 presents evaluation results of model performance and internal obtained parameters of regression models.
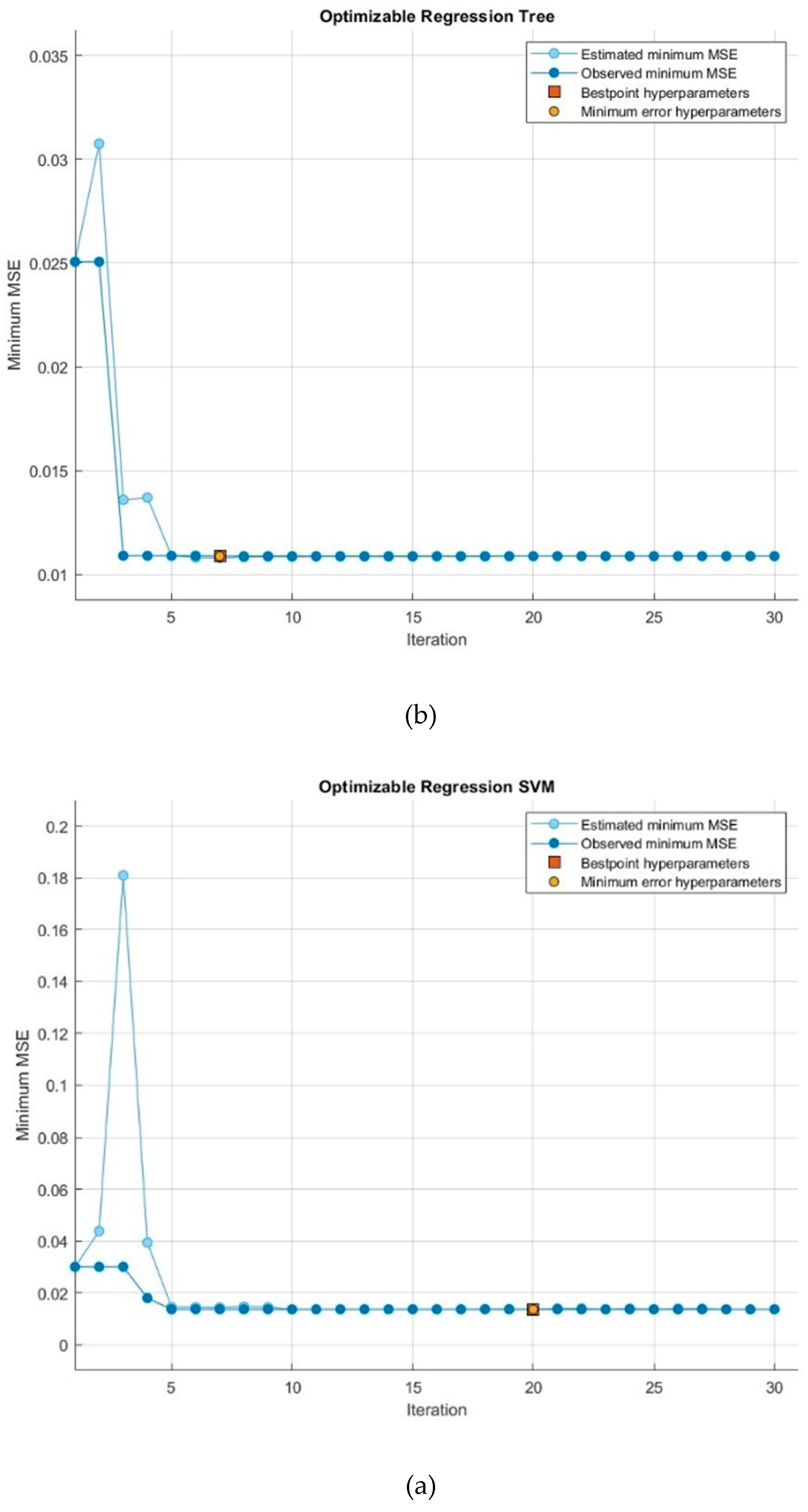
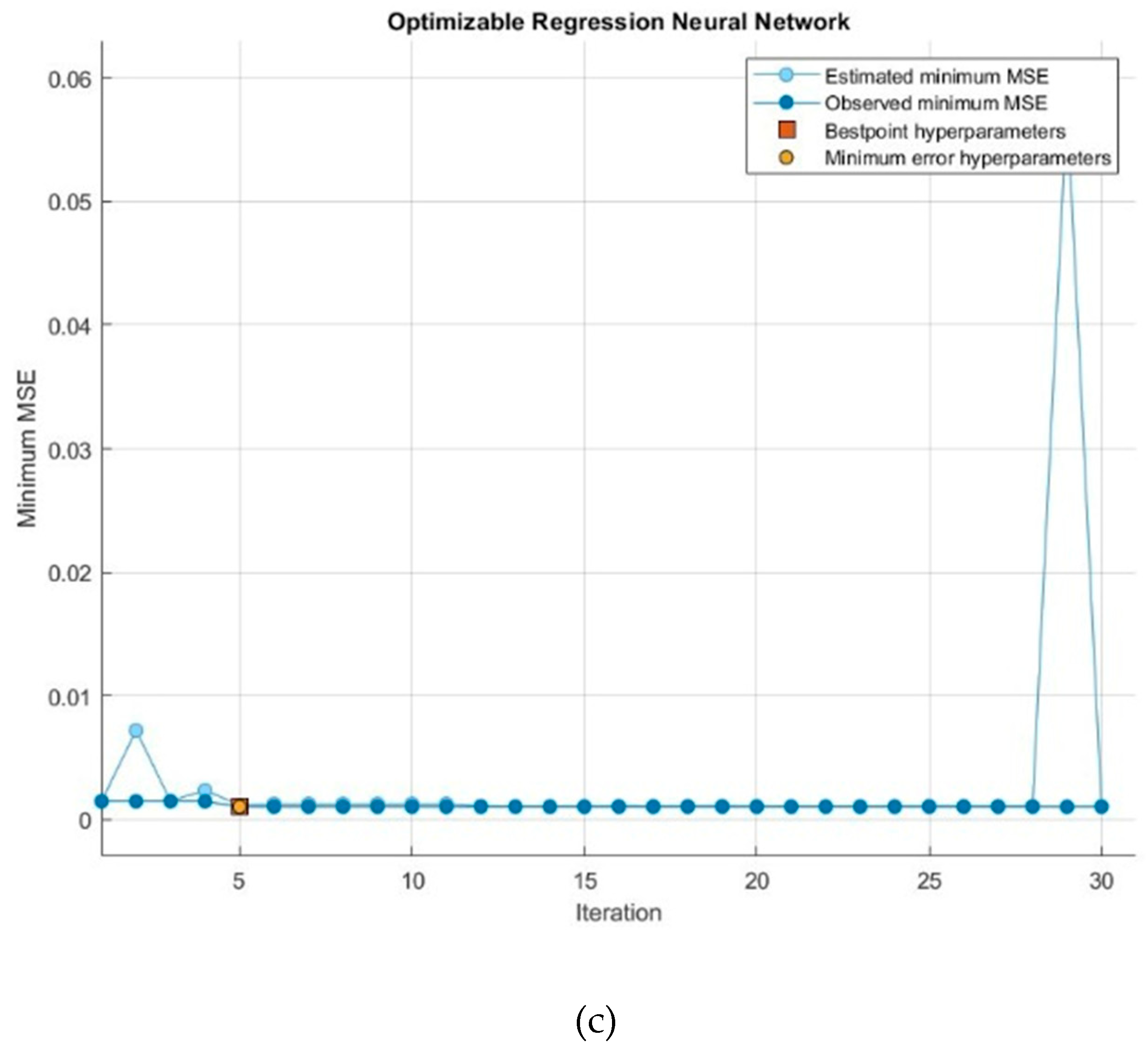
Regression evaluation results depict that the model developed using the artificial neural networks algorithm has been fitted more suitable than other implemented models. This model has R-squared determination equal to 1, while the errors and dispersion measurements are minimal. Figure 3 illustrates history of MSE parameter minimization for three applied methods. Dark blue point corresponds to observed minimum MSE and light blue one represents estimated minimum MSE. Number of iterations consider 30, which best point of MSE value is shown in red color.
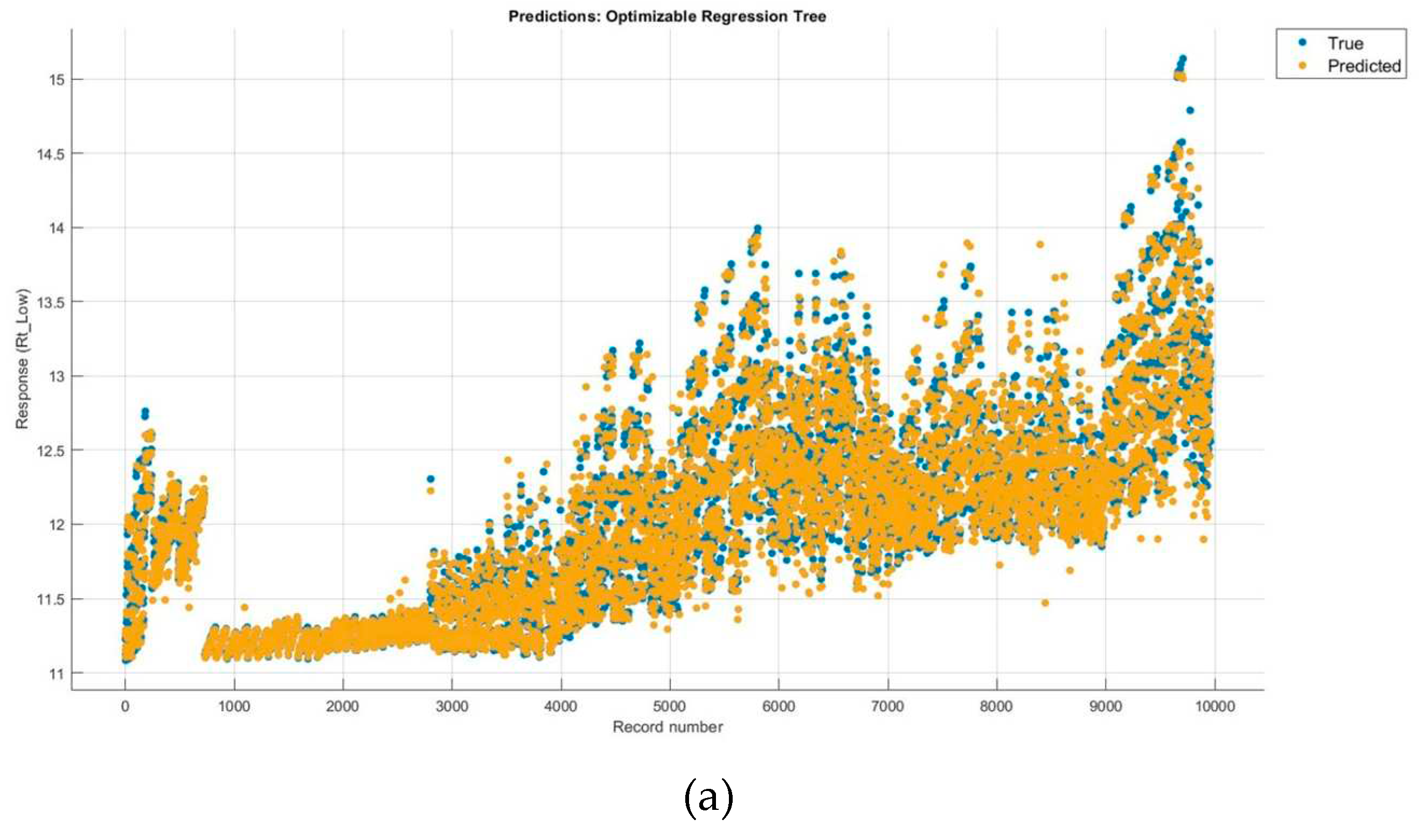
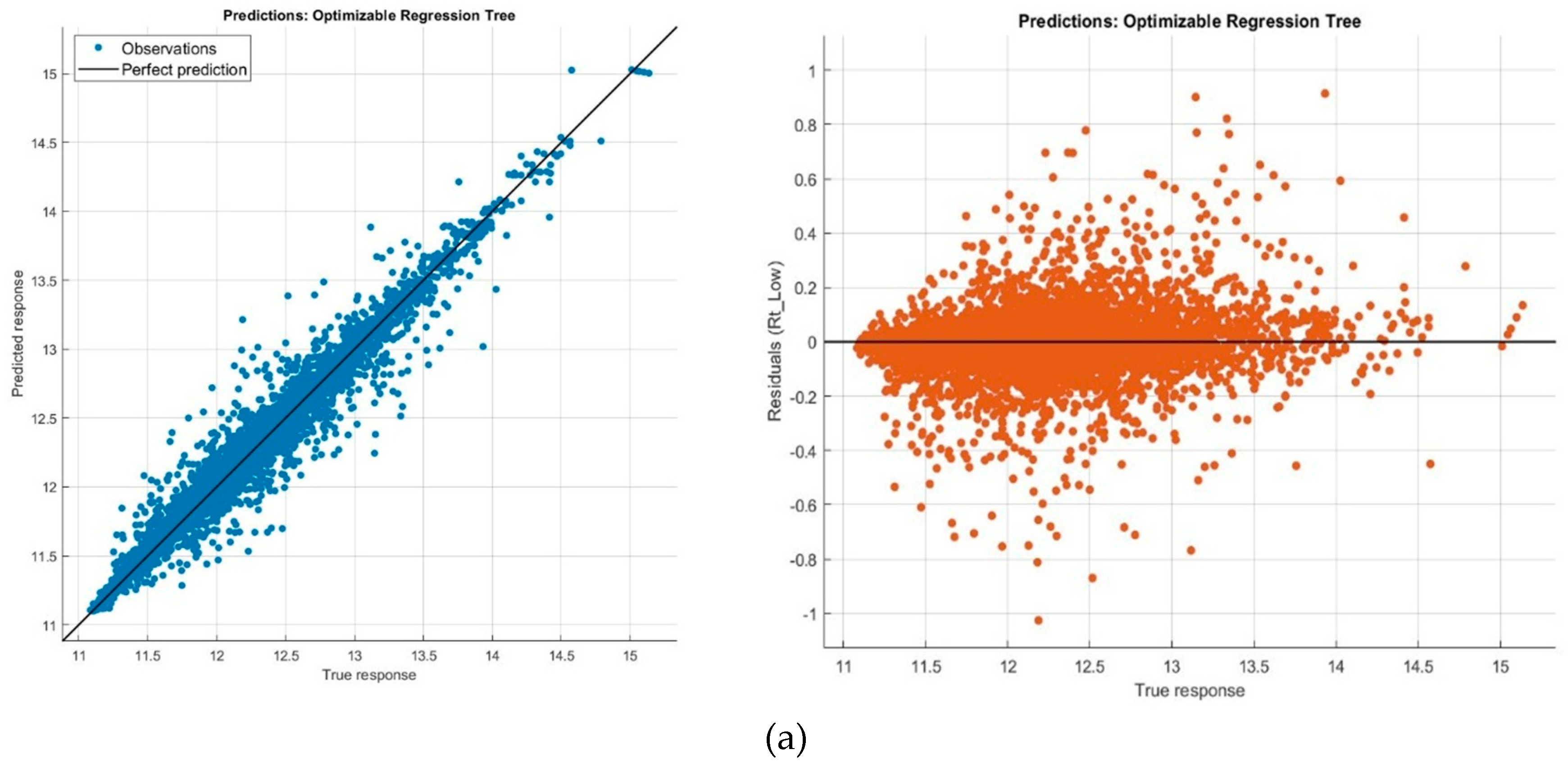
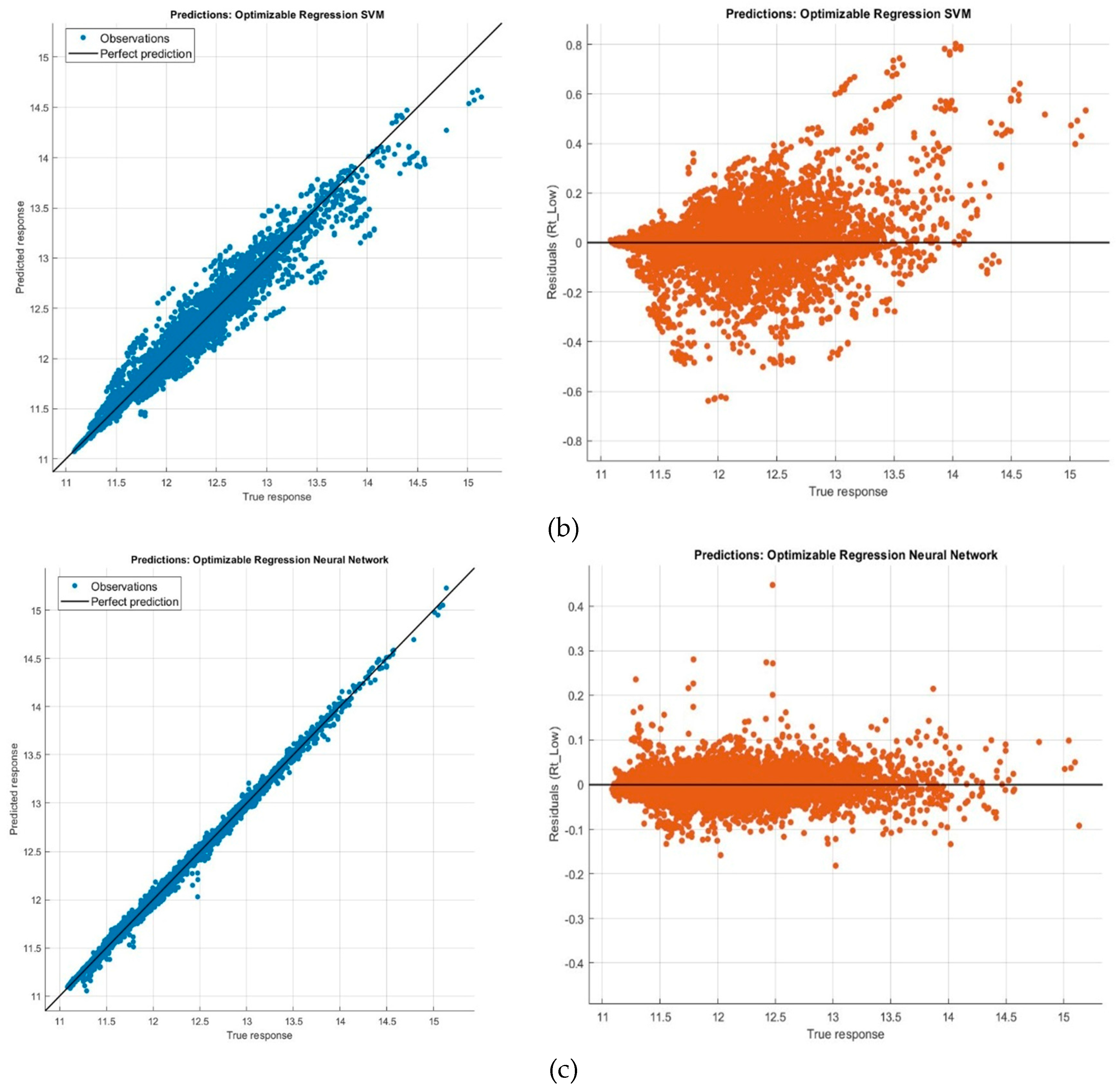
Response plot presents in Figure 4, shows the main and predicted response versus the record number. Besides, Predicted vs. Actual and Residual plots are shown in Figure 5 for each regression model. These plots help to understand how well the regression model makes predictions for different response values. It can be indicated that ANN method can predict responses close to actual ones due to well-scattered samples along the diagonal line. Additionally, residual plot depicts difference between the predicted and true responses, which can be interpreted as a clear distribution around zero for ANN regression method. Assessment of response plots represents the appropriate performance of ANN method against other implemented methods.

5.1. Regression model evaluation

5.1.1. Dataset test cases

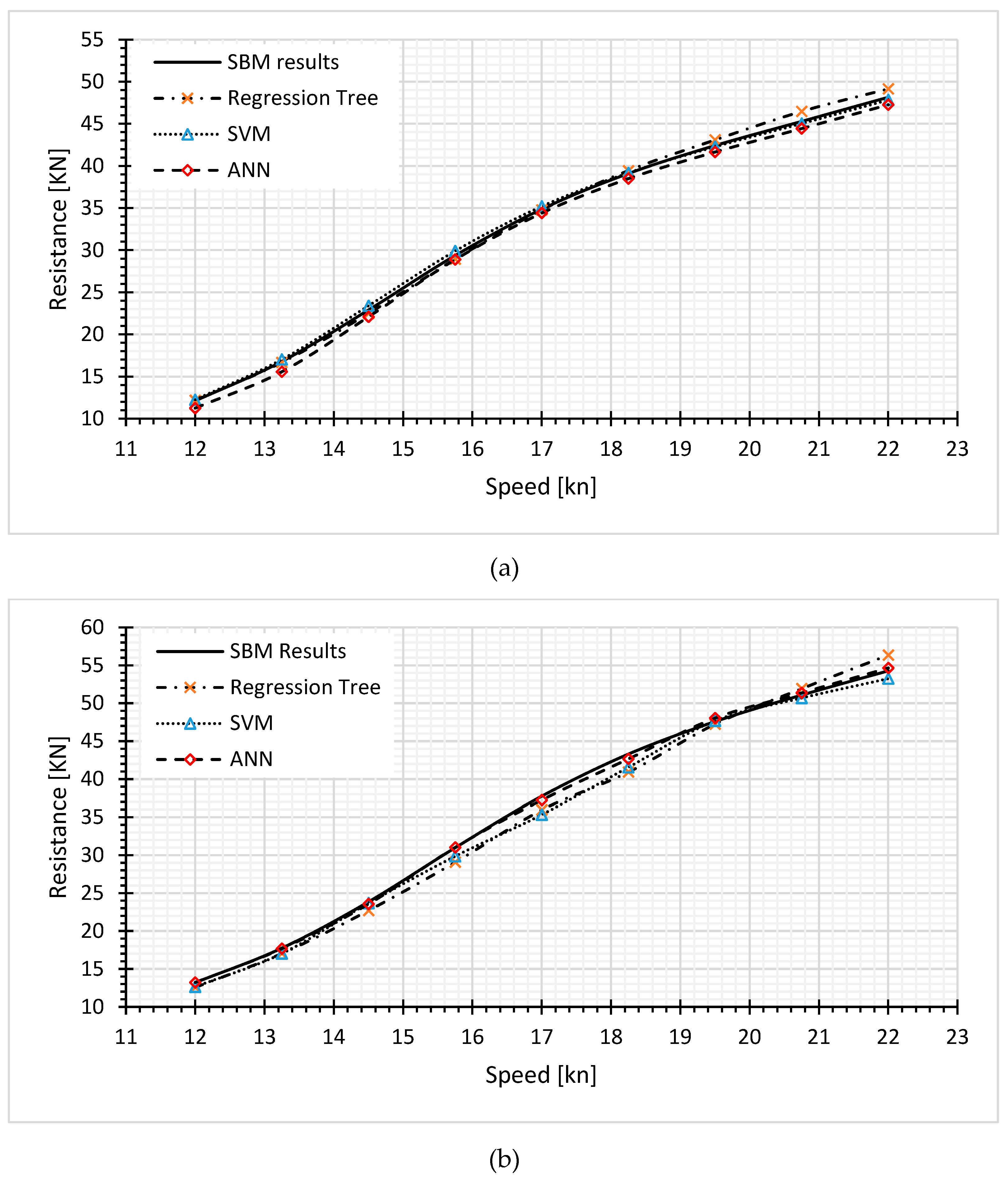
A comparison conducts between RT, SVM, and ANN methods for evaluating resistance predictors. Two designs of dataset have been selected randomly for evaluation in this subsection. Figure 6 (a) shows the results for a random hull in hullform series. In addition, Figure 6 (b) depicts the results for a random catamaran hullform for 85D series.
The proposed models fit well the observed data for test cases among dataset. However, it can be indicated a small underestimate values at speeds 15 to 18 knot. R-square and RMSE values for Figure 6 (random design test model 1&2) are presented in Table 4. The artificial neural networks algorithm fits observed data effectively according to lower values of prediction parameters.

5.1.2. Interpolation test cases

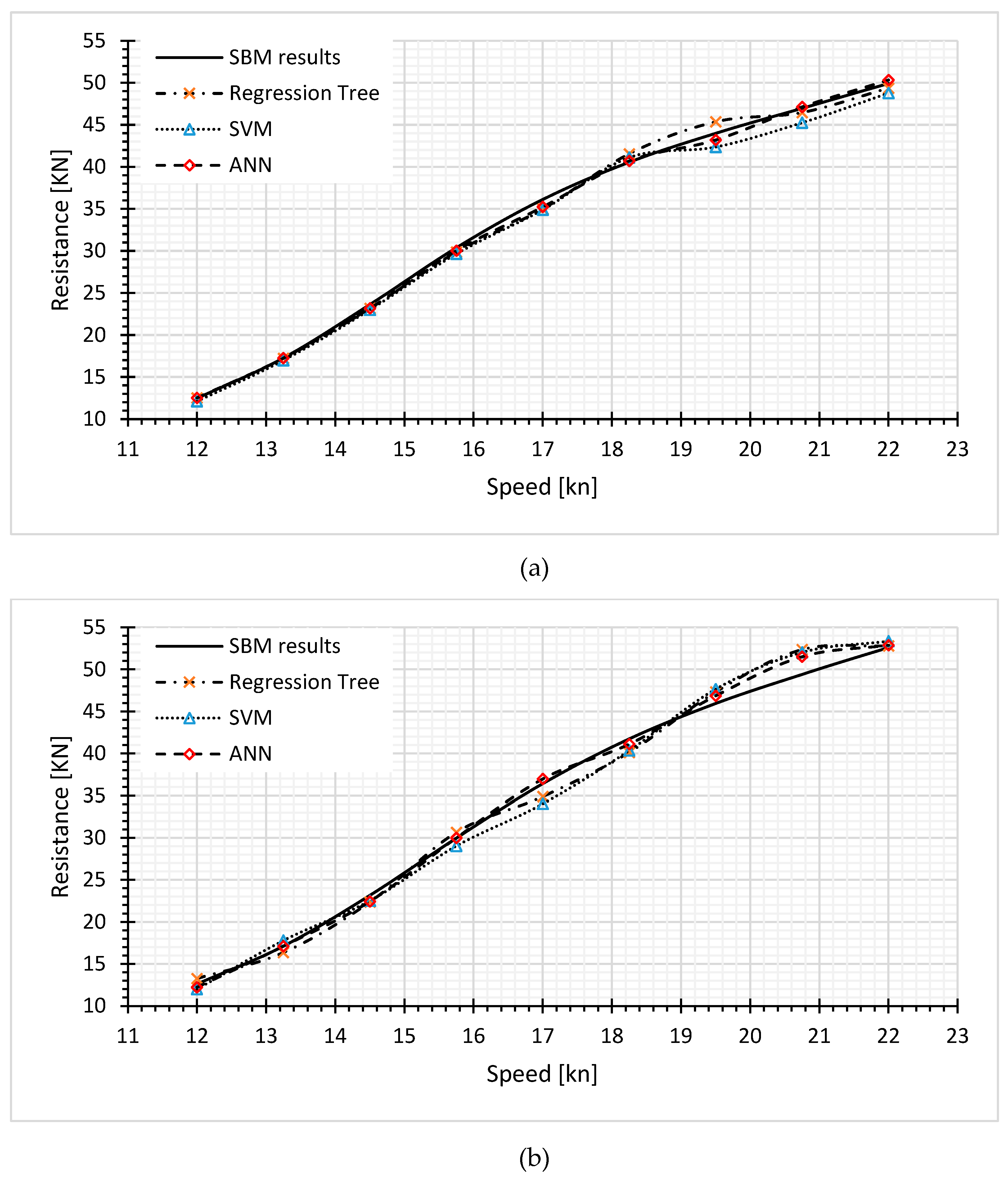
In this section, two interpolated designs based on ship tonnage have been imported to regression models. Catamaran hullforms of 77.5 ton and 82.5 ton are designed for regression model evaluation. Three implemented regression models are adjusted on 77.5 ton hullform (Figure 7 (a)) and 82.5 ton hullform (Figure 7 (b)). Regression data is well adjusted using ANN method for both designs according to predictor parameters presented in Table 5. However, a slight difference can be observed at higher speeds of case 82.5 ton, which is slightly superior.

5.1.3. Extrapolation test cases

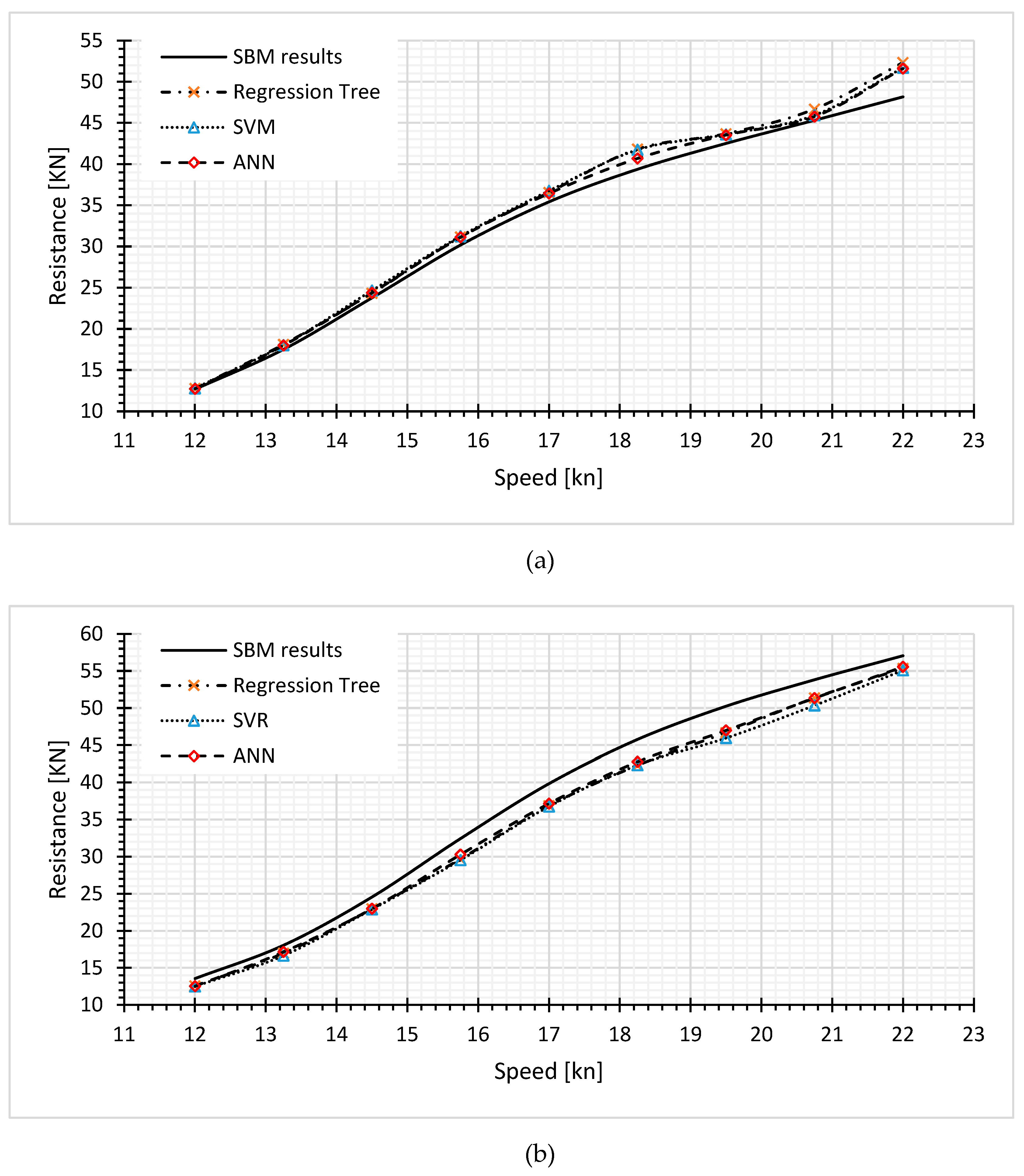
Extrapolation designs define hullforms out of displacement bound of dataset. Considering displacement of all designs from dataset are designed between 75 to 85 tones. Two Catamaran hullforms of 71.5 ton and 88.5 ton are considered for regression model evaluation. The purpose of extrapolation test is assessment of regression models for out-boundaries catamarans. Figure 8 (a) and Figure 8 (b) show resistance values against speed for Slender Body Method results and fitted regressions for 71.5 ton design and 88.5 ton design respectively. In Figure 8 (a), all regression models estimate resistance higher than actual values. On contrary, the proposed models are inferior to SBM results in Figure 8 (b). In the transition to high speeds, the models get less accurate. In addition, Table 6 presents prediction values of fitting quality, which depicts regressions are more precise in lower displacement design than in higher one.

6. Conclusions

A systematic series of novel catamaran ships has been developed for two types of passenger and freight boats. Three different ship tonnages 75, 80, and 85 tones are considered to produce new designs. A shift transformation and self-blending method are sequentially applied to generate different hullforms. Three different supervised machine learning methods have been applied to generated dataset of catamarans to predict resistance at different ship speeds. Generated hullforms have been sorted based on a cost function of resistance to obtain the optimum design for each displacement series. Accordingly, 9775 catamaran hullforms have been produced to make a vast optional condition for ship owners. Using machine learning algorithms, it is worth developing a continuous total resistance predictor well fitted to database of ship series. Three regression algorithms Regression Tree, Support Vector Machine, and Artificial Neural Network approaches are applied to dataset. Regression estimation has good compliance with results of SBM method at wide range of speeds. However, RT and SVM methods have some differences in higher speed. The ANN approach depicts well-adjusted regression on the data. The validation of fitting methods evaluates by case test of dataset, interpolation, and extrapolation catamarans. Accordingly, a general and unique tool is proposed to predict resistance of the series at different displacements and hullforms. The proposed model is a valuable tool to assess the resistance of catamaran hulls during the early design stages. Finally, a sophisticated ANN model is proposed by exploring different features and training/optimization algorithms. Resistance calculations by more precise methods including trim and sinkage effect can be carried out for future works.

Author Contributions

Conceptualization, A.N. and M.Z.A.; methodology, A.N.; software, A.N. and M.Z.A.; validation, A.N.; formal analysis, A.N.; investigation, A.N. and M.Z.A.; writing—original draft preparation, A.N. and M.Z.A. and E.B.; supervision, E.B. All authors have read and agreed to the published version of the manuscript.

Funding

The TrAM project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 769303. https://tramproject.eu/.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Maritime Safety Research Centre (MSRC) at Strathclyde University is an industry-University partnership involving Strathclyde's Department of Naval Architecture, Ocean & Marine Engineering, and sponsors of Royal Caribbean Group and DNV Classification Society. The opinions expressed herein are those of the authors and do not reflect the views of DNV and RCG.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Xing-Kaeding, Y.; Papanikolaou, A. Optimization of the Propulsive Efficiency of a Fast Catamaran. J Mar Sci Eng 2021, 9. [Google Scholar] [CrossRef]
  2. Wang, H.; Boulougouris, E.; Theotokatos, G.; Zhou, P.; Priftis, A.; Shi, G. Life Cycle Analysis and Cost Assessment of a Battery Powered Ferry. Ocean Engineering 2021, 241, 110029. [Google Scholar] [CrossRef]
  3. Sun, Q.; Zhang, M.; Zhou, L.; Garme, K.; Burman, M. A Machine Learning-Based Method for Prediction of Ship Performance in Ice: Part I. Ice Resistance. Marine Structures 2022, 83, 103181. [Google Scholar] [CrossRef]
  4. Grabowska, K.; Szczuko, P. Ship Resistance Prediction with Artificial Neural Networks. In Proceedings of the Signal Processing - Algorithms, Architectures, Arrangements, and Applications Conference Proceedings, SPA; IEEE, September 1 2015; Vol. 2015-Decem, pp. 168–173. [CrossRef]
  5. Cui, H.; Turan, O.; Sayer, P. Learning-Based Ship Design Optimization Approach. CAD Computer Aided Design 2012, 44, 186–195. [Google Scholar] [CrossRef]
  6. Nazemian, A.; Ghadimi, P. Simulation-Based Multi-Objective Optimization of Side-Hull Arrangement Applied to an Inverted-Bow Trimaran Ship at Cruise and Sprint Speeds. Engineering Optimization 2023, 55, 214–235. [Google Scholar] [CrossRef]
  7. Papanikolaou, A.; Xing-Kaeding, Y.; Strobel, J.; Kanellopoulou, A.; Zaraphonitis, G.; Tolo, E. Numerical and Experimental Optimization Study on a Fast, Zero Emission Catamaran. J Mar Sci Eng 2020, 8. [Google Scholar] [CrossRef]
  8. Nazemian, A.; Ghadimi, P. Shape Optimisation of Trimaran Ship Hull Using CFD-Based Simulation and Adjoint Solver. Ships and Offshore Structures 2022, 17, 359–373. [Google Scholar] [CrossRef]
  9. Nazemian, A.; Ghadimi, P. CFD-Based Optimization of a Displacement Trimaran Hull for Improving Its Calm Water and Wavy Condition Resistance. Applied Ocean Research 2021, 113, 102729. [Google Scholar] [CrossRef]
  10. Papanikolaou, A.; Zaraphonitis, G.; Boulougouris, E.; Langbecker, U.; Matho, S.; Sames, P. Multi-Objective Optimization of Oil Tanker Design. J Mar Sci Technol 2010, 15, 359–373. [Google Scholar] [CrossRef]
  11. Li, D.; Guan, Y.; Wang, Q.; Chen, Z. Support Vector Regression-Based Multidisciplinary Design Optimization for Ship Design. In Proceedings of the Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering - OMAE; American Society of Mechanical Engineers, July 1 2012; Vol. 1, pp. 77–84. [CrossRef]
  12. Fahrnholz, S.F.; Caprace, J.D. A Machine Learning Approach to Improve Sailboat Resistance Prediction. Ocean Engineering 2022, 257, 111642. [Google Scholar] [CrossRef]
  13. Nazemian, A.; Ghadimi, P. Global Optimization of Trimaran Hull Form to Get Minimum Resistance by Slender Body Method. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2021, 43, 67. [Google Scholar] [CrossRef]
  14. Margari, V.; Kanellopoulou, A.; Zaraphonitis, G. On the Use of Artificial Neural Networks for the Calm Water Resistance Prediction of MARAD Systematic Series’ Hullforms. Ocean Engineering 2018, 165, 528–537. [Google Scholar] [CrossRef]
  15. Yao, J.; Han, D. RBF Neural Network Evaluation Model for MDO Design of Ship.; 2012; Vol. 47, pp. 309–312.
  16. Radojcic, D. V.; Morabito, M.G.; Simic, A.P.; Zgradic, A.B. Modeling with Regression Analysis and Artificial Neural Networks the Resistance and Trim of Series 50 Experiments with V-Bottom Motor Boats. Journal of Ship Production and Design 2014, 30, 153–174. [Google Scholar] [CrossRef]
  17. Radojčić, D. V.; Kalajdžić, M.D.; Zgradić, A.B.; Simić, A.P. Resistance and Trim Modeling of a Systematic Planing Hull Series 62 (with 12.5°, 25°, and 30° Deadrise Angles) Using Artificial Neural Networks, Part 2: Mathematical Models. Journal of Ship Production and Design 2017, 33, 257–275. [Google Scholar] [CrossRef]
  18. Cepowski, T. The Prediction of Ship Added Resistance at the Preliminary Design Stage by the Use of an Artificial Neural Network. Ocean Engineering 2020, 195, 106657. [Google Scholar] [CrossRef]
  19. Kim, J.H.; Kim, Y.; Lu, W. Prediction of Ice Resistance for Ice-Going Ships in Level Ice Using Artificial Neural Network Technique. Ocean Engineering 2020, 217, 108031. [Google Scholar] [CrossRef]
  20. Liu, S.; Papanikolaou, A. Regression Analysis of Experimental Data for Added Resistance in Waves of Arbitrary Heading and Development of a Semi-Empirical Formula. Ocean Engineering 2020, 206, 107357. [Google Scholar] [CrossRef]
  21. Priftis, A.; Boulougouris, E.; Turan, O.; Atzampos, G. Multi-Objective Robust Early Stage Ship Design Optimisation under Uncertainty Utilising Surrogate Models. Ocean Engineering 2020, 197, 106850. [Google Scholar] [CrossRef]
  22. Shi, G.; Priftis, A.; Xing-Kaeding, Y.; Boulougouris, E.; Papanikolaou, A.D.; Wang, H.; Symonds, G. Numerical Investigation of the Resistance of a Zero-Emission Full-Scale Fast Catamaran in Shallow Water. J Mar Sci Eng 2021, 9, 563. [Google Scholar] [CrossRef]
  23. Nikolopoulos, L.; Boulougouris, E. Application of Holistic Ship Optimization in Bulkcarrier Design and Operation. In Computational Methods in Applied Sciences; 2019; Vol. 48, pp. 229–252. [CrossRef]
  24. Duman, S.; Boulougouris, E.; Aung, M.Z.; Xu, X.; Nazemian, A. Numerical Evaluation of the Wave-Making Resistance of a Zero-Emission Fast Passenger Ferry Operating in Shallow Water by Using the Double-Body Approach. J Mar Sci Eng 2023, 11. [Google Scholar] [CrossRef]
  25. Boulougouris, E.; Priftis, A.; Dahle, M.; Tolo, E.; Papanikolaou, A.; Xing-Kaeding, Y.; Jürgenhake, C.; Svendsen, T.; Bjelland, M.; Kanellopoulou, A.; et al. TrAM-Transport: Advanced and Modular. Proceedings of 8th Transport Research Arena TRA 2020 2020, 1–10. [Google Scholar]
  26. Couser, P.R.; Wellicome, J.F.; Molland, A.F. An Improved Method for the Theoretical Prediction of the Wave Resistance of Transom-Stern Hulls Using a Slender Body Approach. International Shipbuilding Progress 1999, 45, 331–349. [Google Scholar]
  27. Maxsurf Modeler, Maxsurf Resistance, and Automation, User Guide.
  28. Hotelling, H. Analysis of a Complex of Statistical Variables into Principal Components. J Educ Psychol 1933, 24, 417–441. [Google Scholar] [CrossRef]
  29. Tukey, J.W. (John W. Exploratory Data Analysis / John W. Tukey; Addison-Wesley series in behavioral science; Addison-Wesley Pub. Co.: Reading, Mass., 1977. ISBN 0201076160.
  30. Zaki, M.J.; Meira, Jr, W. Data Mining and Machine Learning; Cambridge University Press, 2020. ISBN 9781108564175.
  31. Aggarwal, C.C.; others Data Mining: The Textbook; Springer, 2015; Vol. 1. [CrossRef]
  32. Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks; IEEE, 1993; pp. 586–591. [Google Scholar]
  33. The Mathworks Inc. Statistics and Machine Learning Toolbox Documentation, 2022. Available online: https://www.mathworks.com/help/stats/index.html.
Preprints 91928 g001
Figure 1. General Arrangement plan of passenger and freight catamaran boat.
Figure 1. General Arrangement plan of passenger and freight catamaran boat.
Preprints 91928 g001
Preprints 91928 g002
Figure 2. Framework of design study and machine learning methodology.
Figure 2. Framework of design study and machine learning methodology.
Preprints 91928 g002
Preprints 91928 g003aPreprints 91928 g003b
Figure 3. MSE history reduction through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Figure 3. MSE history reduction through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Preprints 91928 g003aPreprints 91928 g003b
Preprints 91928 g004aPreprints 91928 g004b
Figure 4. Prediction vs True design comparison through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Figure 4. Prediction vs True design comparison through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Preprints 91928 g004aPreprints 91928 g004b
Preprints 91928 g005aPreprints 91928 g005b
Figure 5. Residual plot comparison through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Figure 5. Residual plot comparison through optimizable regression process (a) Regression Tree (b) Regression SVM (c) Regression ANN.
Preprints 91928 g005aPreprints 91928 g005b
Preprints 91928 g006
Figure 6. Model comparison between RT, SVM, and ANN methods for (a) random design Test model 1 and (b) random design Test model 2.
Figure 6. Model comparison between RT, SVM, and ANN methods for (a) random design Test model 1 and (b) random design Test model 2.
Preprints 91928 g006
Preprints 91928 g007
Figure 7. Model comparison between RT, SVM, and ANN methods for (a) interpolation design 77.5 ton and (b) interpolation design 82.5 ton.
Figure 7. Model comparison between RT, SVM, and ANN methods for (a) interpolation design 77.5 ton and (b) interpolation design 82.5 ton.
Preprints 91928 g007
Preprints 91928 g008
Figure 8. Model comparison between RT, SVM, and ANN methods for (a) extrapolation design 71.5 ton and (b) extrapolation design 88.5 ton.
Figure 8. Model comparison between RT, SVM, and ANN methods for (a) extrapolation design 71.5 ton and (b) extrapolation design 88.5 ton.
Preprints 91928 g008
Table 1. Design parameters of the catamaran case study.
Table 1. Design parameters of the catamaran case study.
Optimization parameter Symbol specifications
Design Variable Lwl Waterline length (m)
Design Variable B Demi hull Beam (m)
Design Variable T Draft (m)
Design Variable DT Demi hull transverse distance (m)
Free Variable Cb Block coefficient
Design Variable Cm Max section area coefficient
Design Variable LCB (% of Lwl) Longitudinal Center of Buoyancy
Constraint 𝞩 Displacement (Ton)
Constraint (DTx2)+B Total Beam (m)
Table 2. Selected attributes for data mining with their respective statistics values.
Table 2. Selected attributes for data mining with their respective statistics values.
specifications Symbol Min Max Mean Deviation
Ship speed [kn] V 12 22 17 3.4232
Waterline length (m) Lwl 28 33 30.2139 1.2354
Demi hull Beam (m) B 2.0985 2.2065 2.1407 0.0352
Draft (m) T 1.283 1.386 1.3152 0.0318
Demi hull transverse distance (m) DT 3.35 3.424 3.3889 0.0239
Block coefficient Cb 0.4349 0.5062 0.4663 0.0144
Max section area coefficient Cm 0.7091 0.7610 0.7293 0.0135
Longitudinal Center of Buoyancy (% of L) LCB 0.5346 0.5549 0.5463 0.0047
Waterplane area (m2) Aw 96.235 104.339 100.488 2.9536
Maximum section area (m2) Ax 3.923 4.153 4.094 0.0582
Table 3. Internal parameters of optimum regression models.
Table 3. Internal parameters of optimum regression models.
Optimizable Regression Tree Optimizable Neural Network Optimizable SVM
RMSE: 0.1043
R2: 0.98
MSE: 0.01088
MAE: 0.057334		 RMSE: 0.03037
R2: 1
MSE: 0.000922
MAE: 0.020429		 RMSE: 0.1168
R2: 0.97
MSE: 0.01365
MAE: 0.06614
Minimum leaf size: 3 Num. of layers: 2
Activation: Sigmoid
Lambda: 1.5276e-08
First Layer size: 26
Second Layer size: 77		 Box constraint: 17.0223
Kernel scale: 8.5763
Epsilon: 8.17e-4
Kernel function: Gaussian
Table 4. Prediction parameters of model test for dataset designs.
Table 4. Prediction parameters of model test for dataset designs.
Test model 1 Test model 2
RT RMSE: 0.6051
R2: 0.9991		 RMSE: 1.4895
R2: 0.9934
SVM RMSE: 0.3185
R2: 0.9996		 RMSE: 1.1625
R2: 0.9971
ANN RMSE: 0.8083
R2: 0.9997		 RMSE: 0.3606
R2: 0.9994
Table 5. Prediction parameters of model test for interpolation designs.
Table 5. Prediction parameters of model test for interpolation designs.
77.5 ton 82.5 ton
RT RMSE: 0.7597
R2: 0.9965		 RMSE: 1.4029
R2: 0.9911
SVM RMSE: 1.0426
R2: 0.9976		 RMSE: 1.4938
R2: 0.9906
ANN RMSE: 0.4677
R2: 0.9988		 RMSE: 0.8633
R2: 0.9977
Table 6. Prediction parameters of model test for extrapolation designs.
Table 6. Prediction parameters of model test for extrapolation designs.
71.5 ton 88.5 ton
RT RMSE: 1.8147
R2: 0.9964		 RMSE: 2.4631
R2: 0.9975
SVM RMSE: 1.6215
R2: 0.9965		 RMSE: 2.7815
R2: 0.9975
ANN RMSE: 1.3860
R2: 0.9968		 RMSE: 2.2180
R2: 0.9983
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated