1.0. Introduction
Achieving the goal of developing a product with all-embracing design features starts from brainstorming activities in the design phase of the product when several conceptual design concepts have been established. An important task at this stage is decision making on identification of the optimal conceptual design. Decision making in the preliminary design phase and extensive design concept selection from several conceptual designs can be accrued to the robust design of a product [
1,
2]. The number of design features that are embedded in the optimal design concept is also important because it depicts the multifarious function that the product can perform. A good way to develop a product with several design features is to examine the features in different conceptual designs during the concept selection phase. Selecting a design as an optimal design implies that the design has a satisfactory performance considering all the design features [
3,
4]. Also, an optimal design can be developed on the fact that, the design features from other conceptual designs can be added to the design. This makes the decision process to be important and the efforts put into it cannot be overemphasized. The design engineers provide several design solutions in the developmental stage before a detail analysis is carried out [
5,
6,
7]. Provision of several design solutions is necessary because the management of the manufacturing firm wants to reduce cost of fabrication and produce an extensive product that will have a high demand in the competitive market and extended useful life. Also, the firm may be interested in selecting a design that is realistic in terms of completion time and utilization of existing technologies of fabrication. In essence, selecting an optimal design concept from a set of alternative designs becomes inevitable considering the fact that all the design solutions have several benefits and shortcomings [
8,
9].
Research has shown that an excellent way to arrive at an optimal solution in the decision-making process in this scenario is to introduce the Multi-Criteria Decision Model (MCDM) [
10,
11]. In the preliminary phase of an equipment or a product, the design features and sub-features are identified alongside with the various design alternatives in order to allow the decision making on the optimal design concept to be modelled as a MCDM. Basically, MCDM models can be broadly divided into two categories; which are Multi-Attribute Decision Model (MADM) and Multi-Objective Decision Model (MODM) [
12,
13]. The MADM is applicable in cases that involves making a choice from a set of alternatives in a discrete or well-defined solution space. The MODM is applied to solve decision problems with several goals where there are no discrete sets of explicitly defined alternatives. Also, the MODM also applies to scenarios where the alternatives are to be ranked based on several criteria. In this case, the decision process is performed different times in order to satisfy the various objectives of decision criteria [
13,
14]. Several MADM models have been introduced to solve real-life decision-making problems but there is a need to investigate the suitability of these models in the design process. Among the MADM models used in decision making process is the Multi-Attribute Utility theories (MAUT). The MAUT includes the Analytic Hierarchy Process (AHP), Weighted Decision Matrix (WDM), Analytic Network Process (ANP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) and Elimination and Choice Translating Reality (ELECTRE) among others [
15,
16].
Several efforts have been made by researchers to apply these MADM models in the selection of optimal design from set of alternative conceptual designs. Considering the fact that the design features that are usually applied as criteria in the decision process are of different dimensions and units, researches have introduced the theory of fuzzy membership functions and rough numbers in the MADM models. The introduction of the fuzzy and rough number theories is to cater for the multifarious units and dimensions of the design features and ensure that the decision process is unprejudiced and there is no allocation of crips value to weights of the design features of different units and dimensions or performance of the design concepts in the decision matrix [
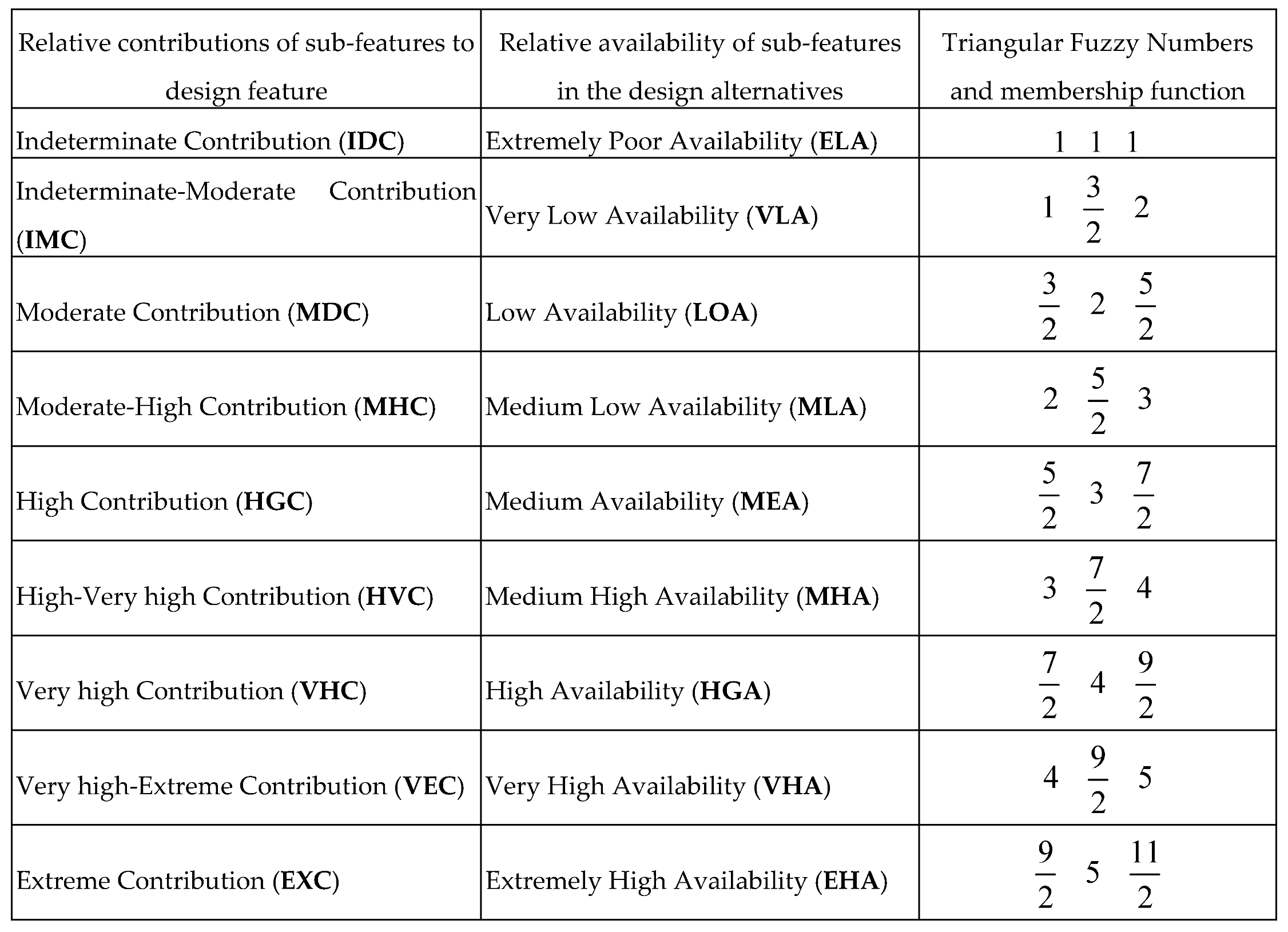
17]. Depending on the nature and objectives of the decision process and the complexity of the design features, Triangular Fuzzy Number (TFN) and Trapezoidal Fuzzy Number (TrFN) has been applied as membership functions in different MADM models in order to proffer solution in the decision process of selecting optimal conceptual design [
18].
Further, since the introduction of the Measurement Alternatives and Ranking according to COmpromise Solution (MARCOS) in the year 2020 [
19], it has gained attention by researchers and its application has been extended to several field of applications for decision making. Examples of the areas of applications include supplier selection [
20,
21,
22,
23,
24], logistics [
25,
26], infrastructure and Technology assessment [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36] and Management decisions [
37]. At inception, it was applied to assess the sustainable supplier selection in the medical industry which is a very important task in the medical firm that must be strategically addressed because of the quality expected from medical supplies. Considering eight suppliers and twenty-one deciosn criteria, the MARCOS method was able to define the relationship between the suppliers and the reference values in order to obtain the utility functions of the suppliers and rank them in relation to the reference values [
19]. Further, the MARCOS method was applied to determine the response of insurance companies in terms of healthcare services to the COVID-19 pandemic considering its ability to consider a large set of alternatives, decision criteria and sub-criteria without compromising on the stability and computational integrity of the decision process [
37]. In order to avoid a vague decision process, the intuitionistic fuzzy membership function was introduced to evaluate ten insurance companies considering five expert opinions and seven decision criteria. The decision process was able to identify payback period, premium price and network as the substantial criteria for evaluating healthcare insurance companies.
Also, considering the importance of effective supply chain management to the growth of industries and business and the fact that sustainable supply chain is essential in running the day-to-day activities of the company, several articles have provided explicit information on the application of the MARCOS method in supplier selection and its integration with other multi attribute models. An example of this application is the integration of extended VIKOR and MARCOS for sustainable supplier selection in organ transplantation Networks for healthcare Devices using interval-valued intuitionistic Fuzzy model [
38]. Ayşegül and Adali [
20], integrated the Fuzzy MARCOS model with Fuzzy SWARA (Stepwise Weight Assessment Ratio Analysis) in green supply chain management in order to identify the best supplier from alternative suppliers in a textile industry where green and environmentally friendly textile dyes are needed to be supplied in the industries. The implementation of this integrating Fuzzy MARCOS with Fuzzy SWARA for green supplier selection has also been verified by Tas
et. al, [
39]. The integration of SWARA and MARCOS also finds application in decision making in the logistic field where decision was made on inventory classification. The decision process involved evaluation of fifty products to be stored considering quantity of the products purchased, their unit price and annual value of purchase [
40]. Another important area of application of MARCOS model is the field of manufacturing. The MARCOS method was applied in the process for powder-mixed electrical discharge machining of cylindrical shaped parts using chromium silicon steel tool and the result obtained was compared with TOPSIS and MAIRCA (Multi-Attributive Ideal-Real Comparative Analysis). The results obtained showed that the three methods selected the same alternative as the optimal alternative from the eighteen alternatives considered in the decision process [
41]. Similarly, the MARCOS method was also compared with MAIRCA, TOPSIS and EAMR (Evaluation by an Area-based Method of Ranking) considering the turning process. The cutting speed, feed and depth of cut were the input parameters in the cutting process in order to determine the material removal rate and surface roughness of the workpiece. The results obtained from the application showed that the four models are in conformity as they identified the same alternative as the optimal process from the sixteen alternatives considered in the decision process [
42]. The result was similar to the application and comparison of MARCOS to EDAS (Evaluation based on Distance from Average Solution), TOPSIS, MOORA (Multi-Objective Optimization on the basis of Ratio Analysis) and PIV (Proximity Indexed Value) in the decision making in milling process [
43]. Further, the MARCOS method was applied in the grinding, turning and milling processes in order to determine the optimum material removal rate and effective surface finish considering nine trials with different machining parameters [
44].
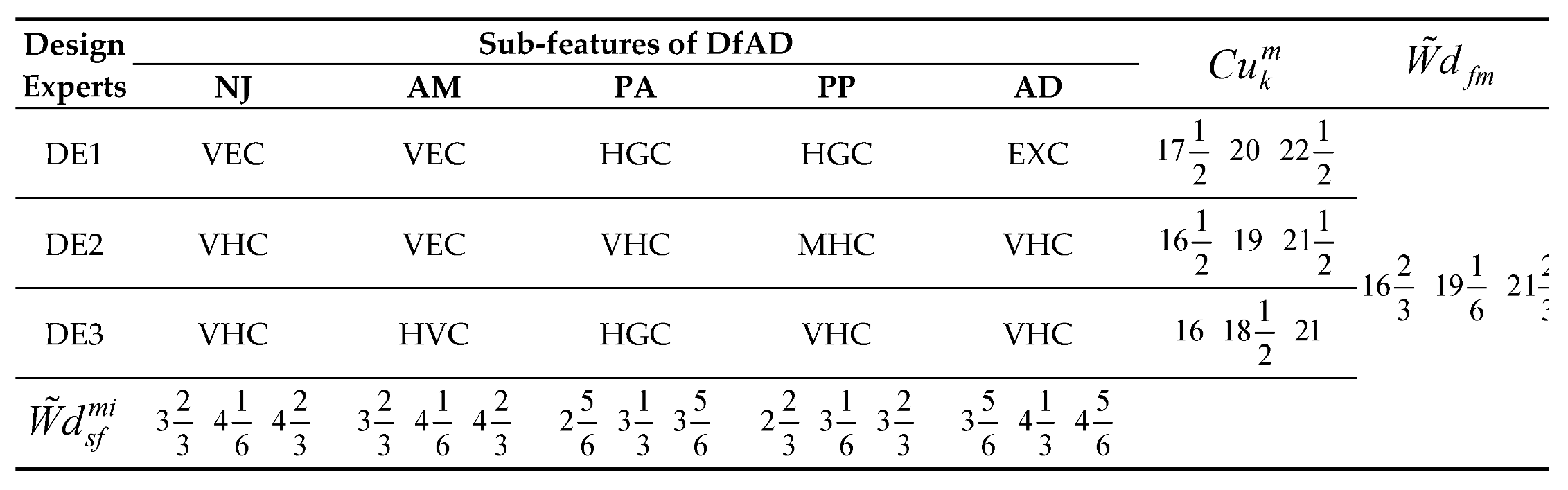
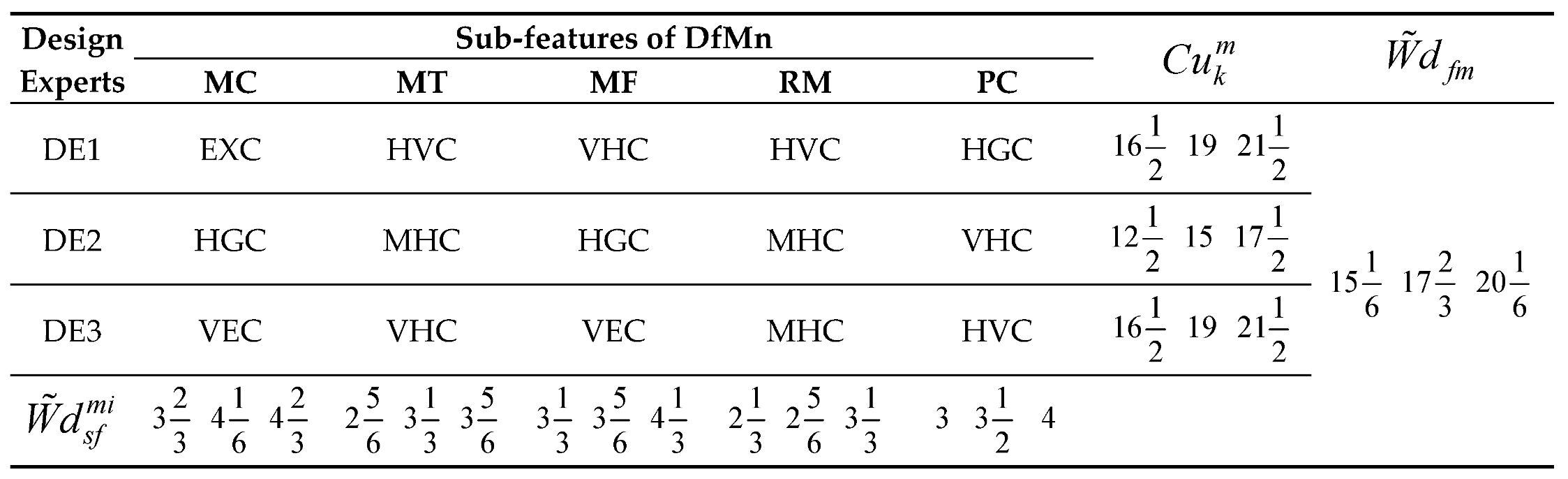
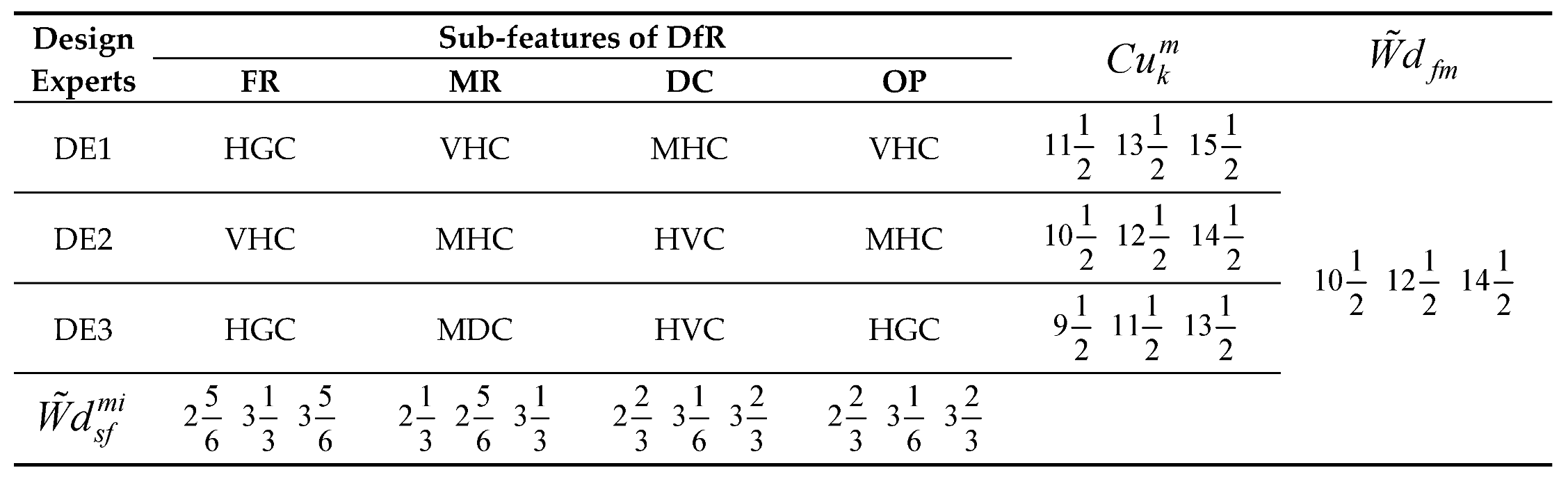
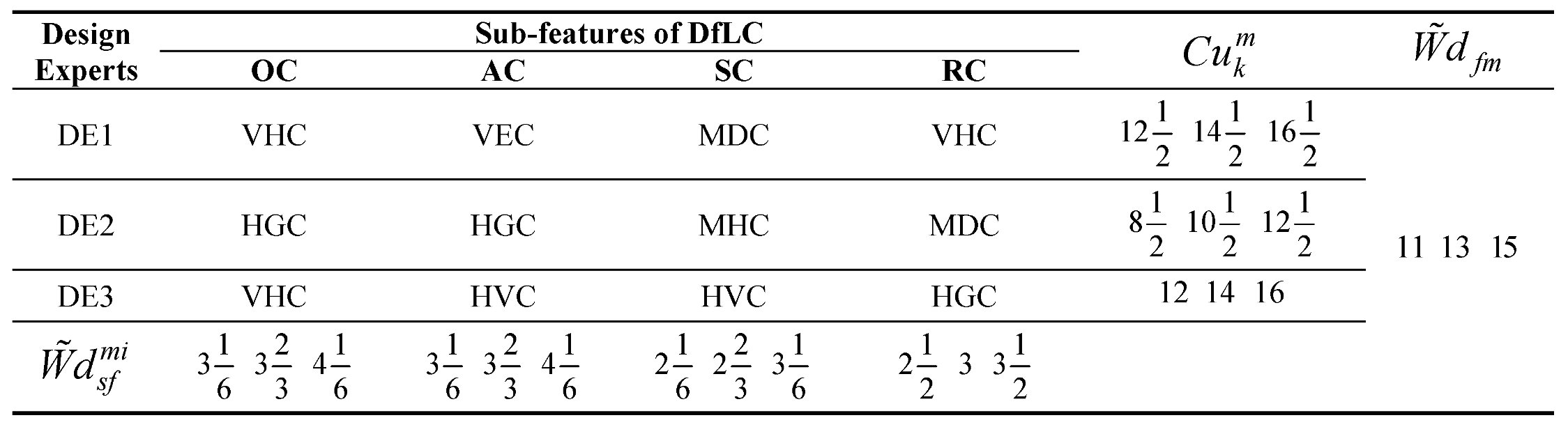
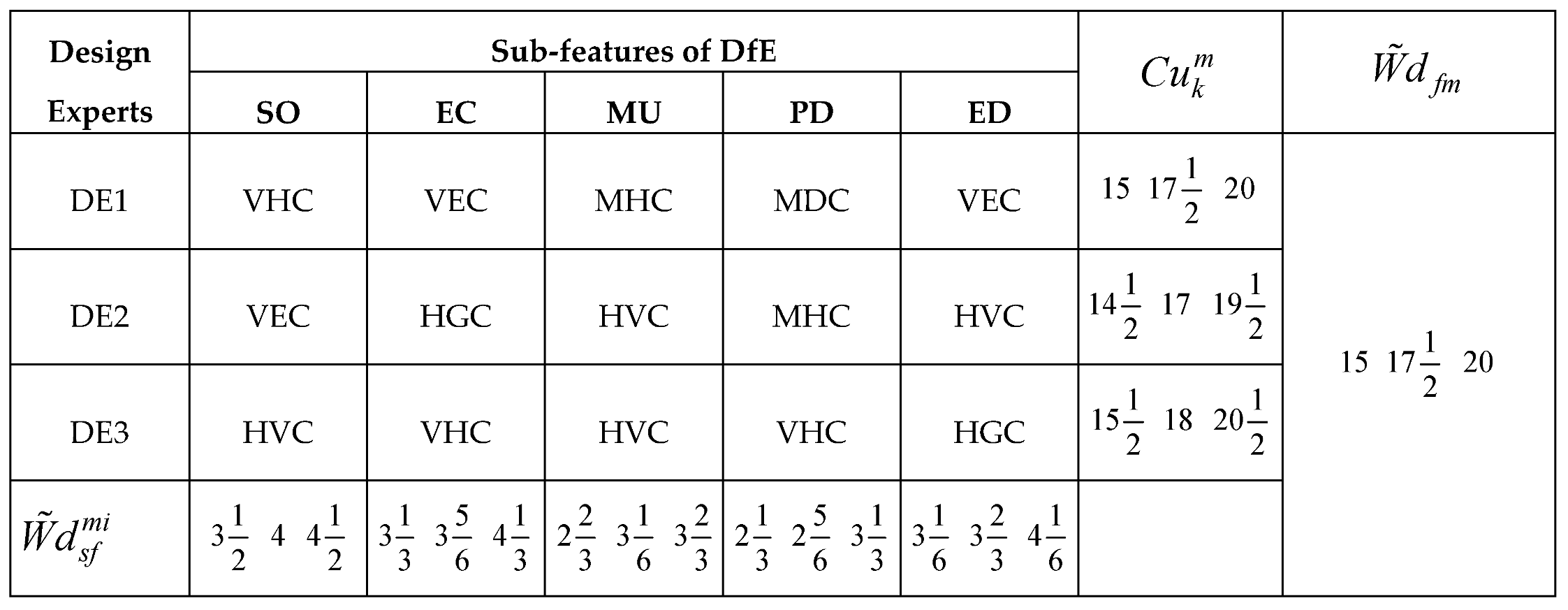
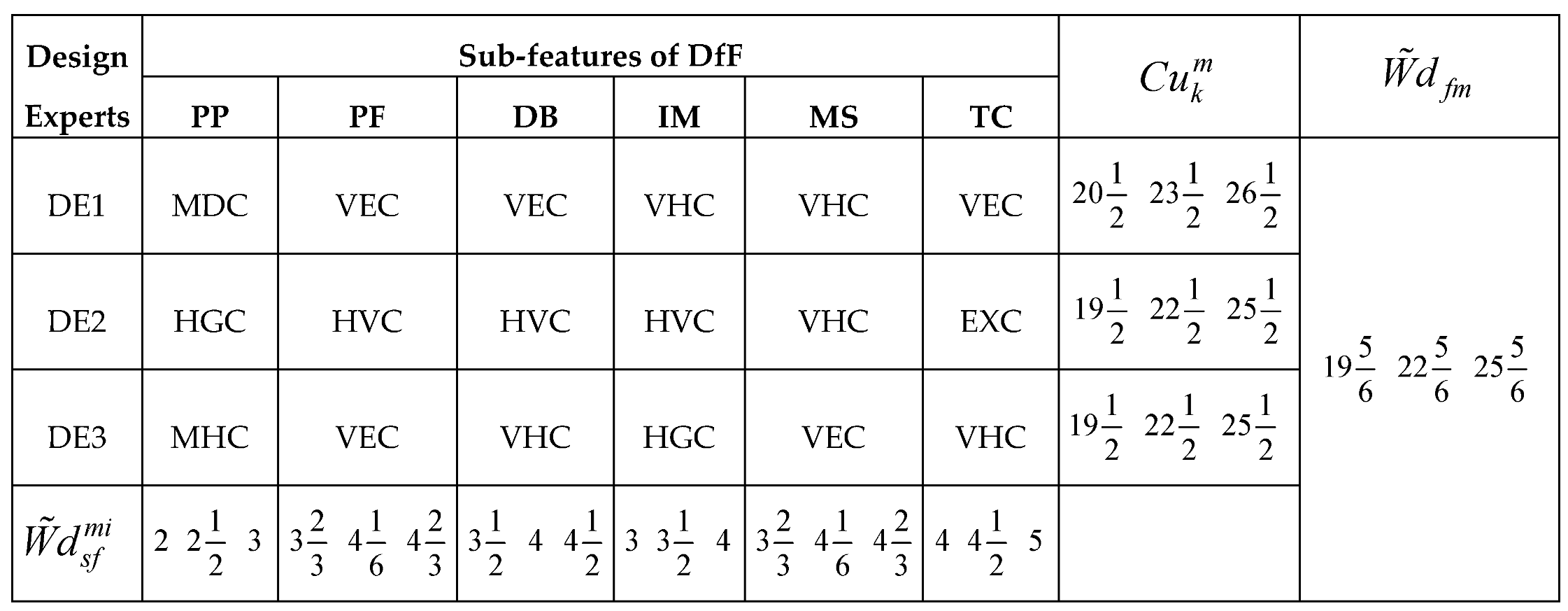
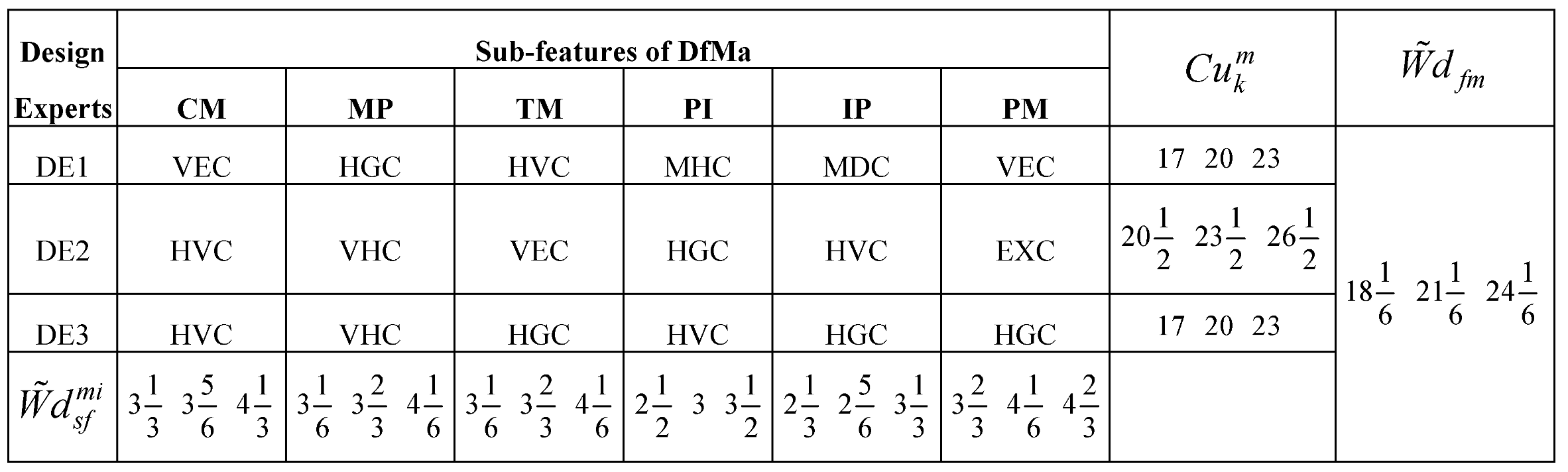
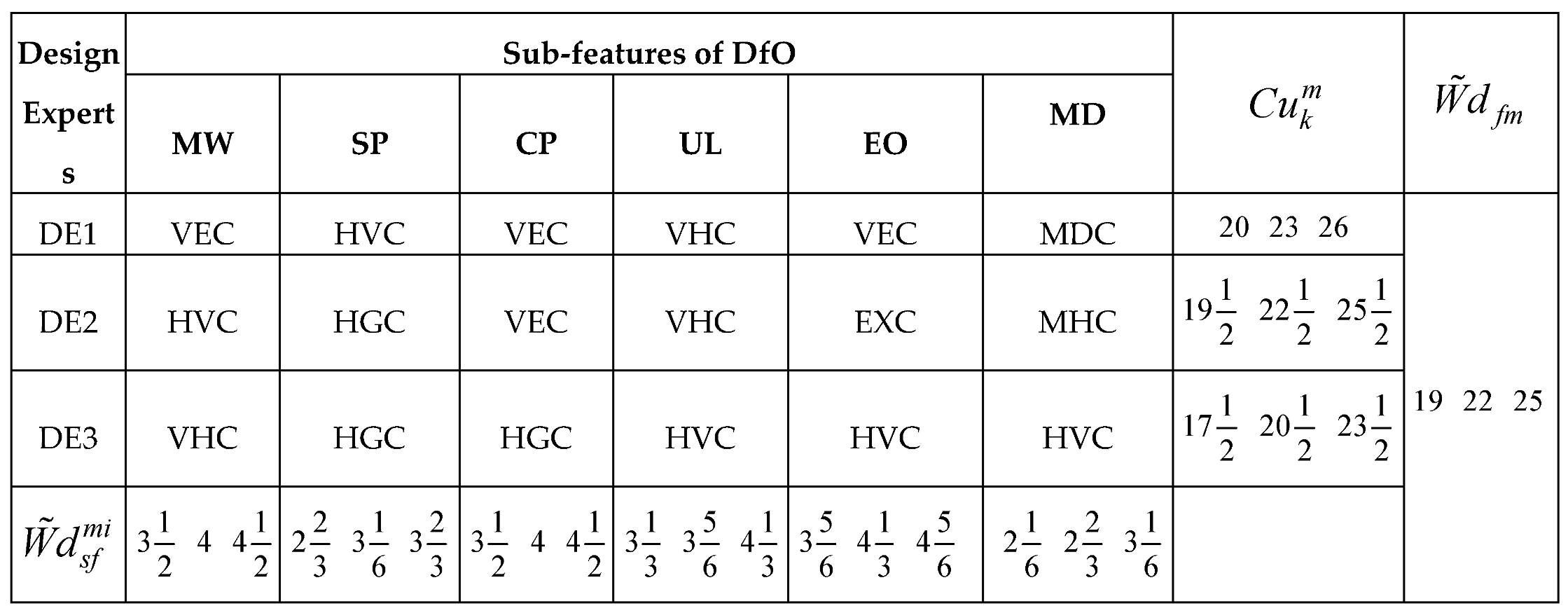
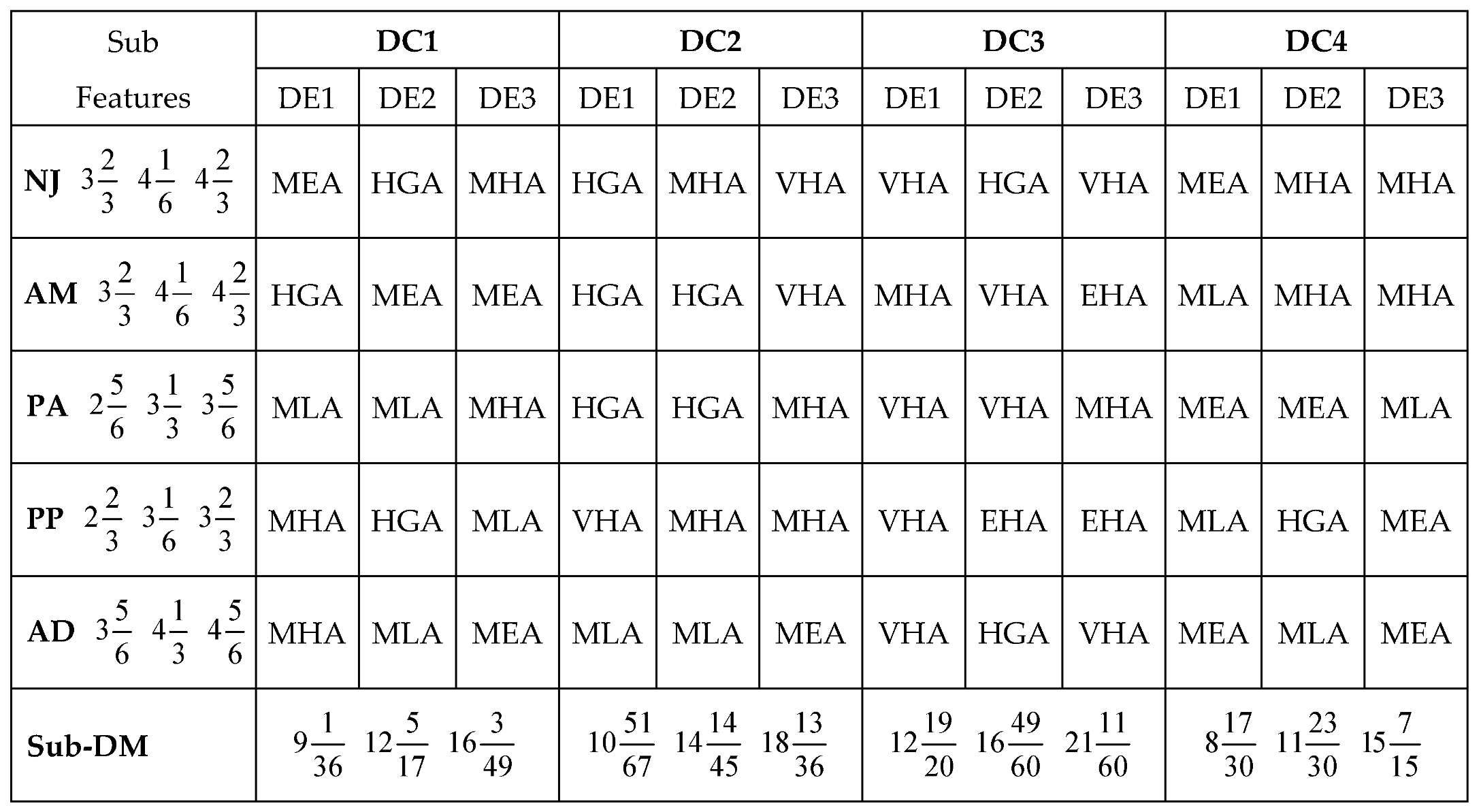
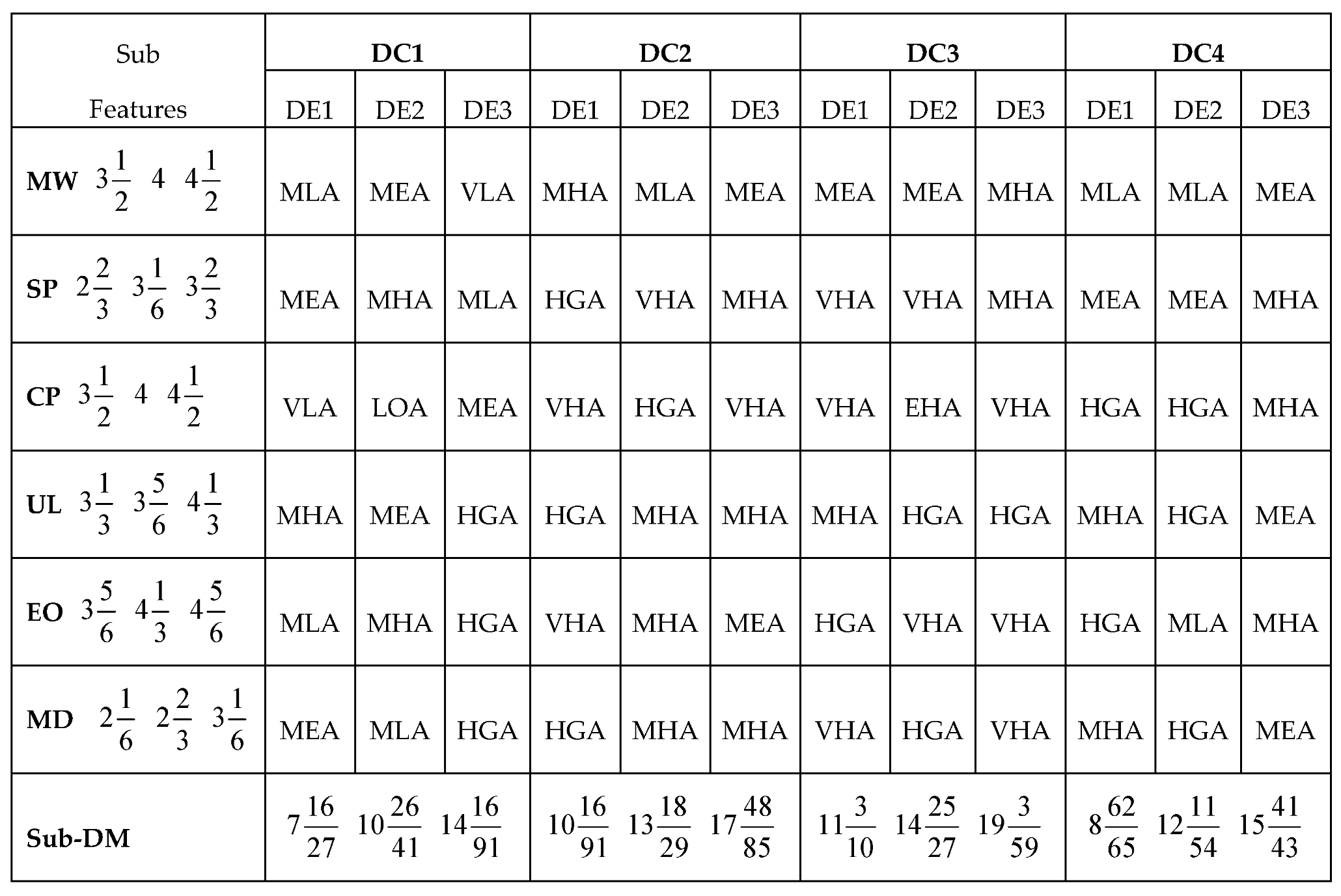
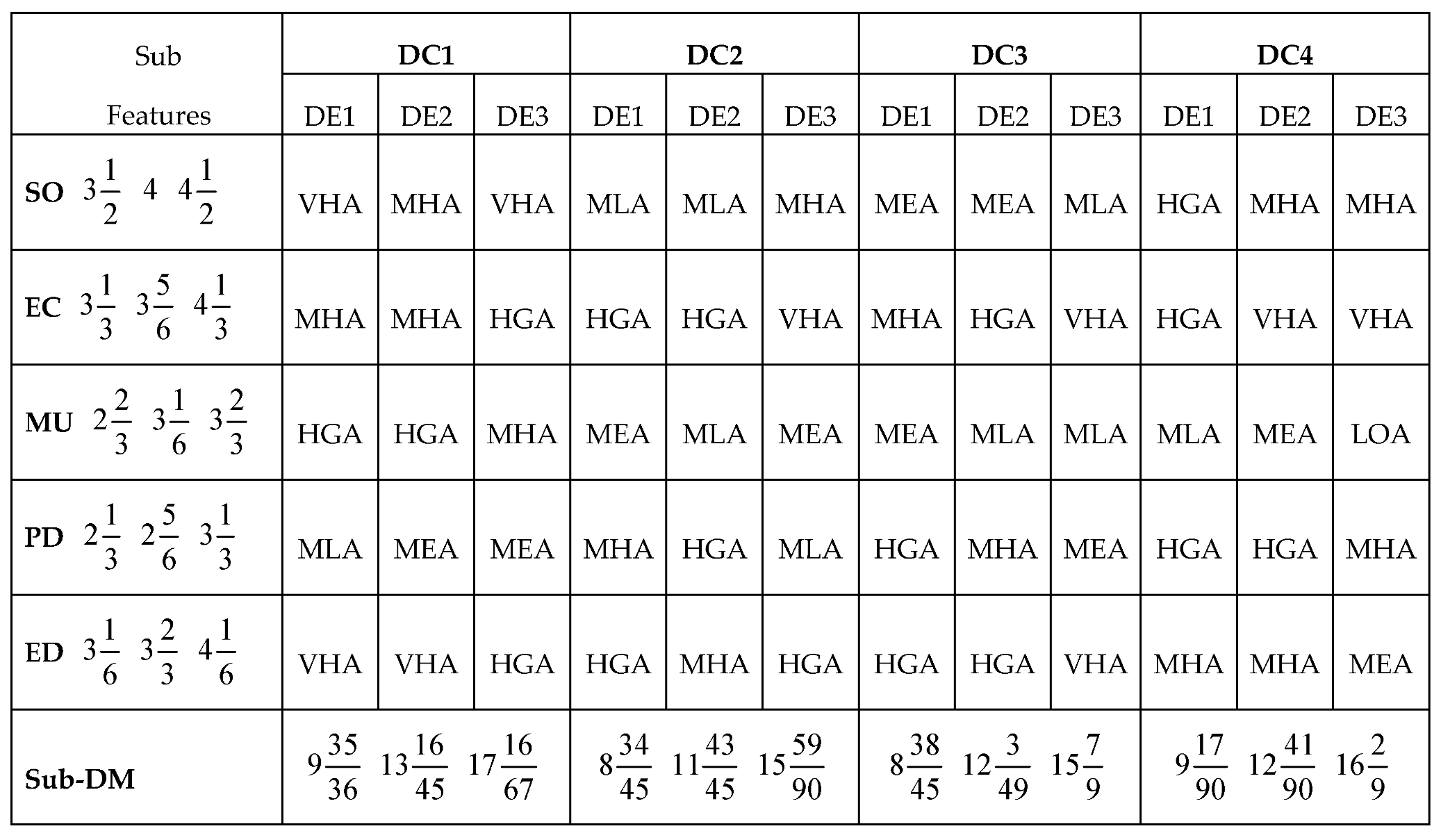
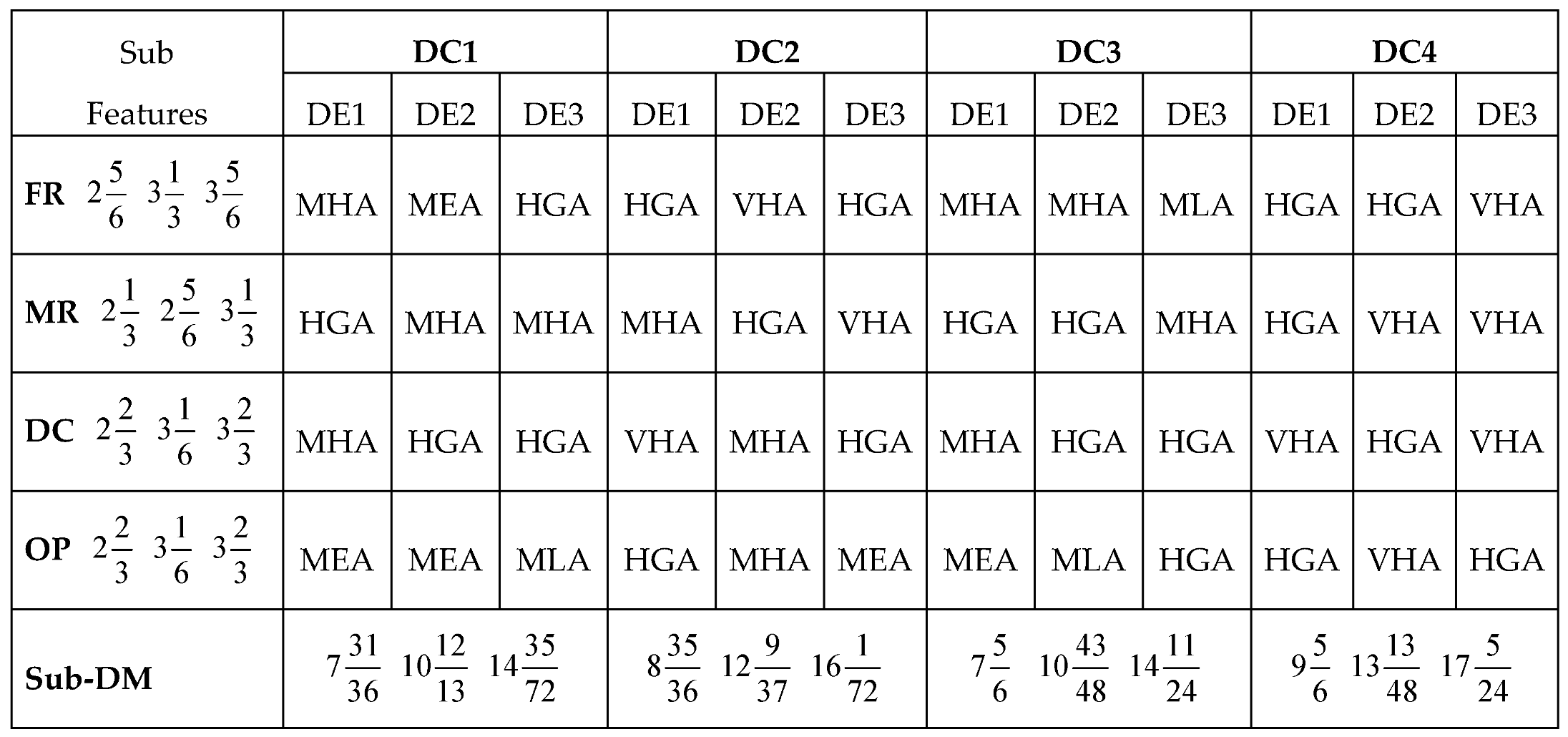
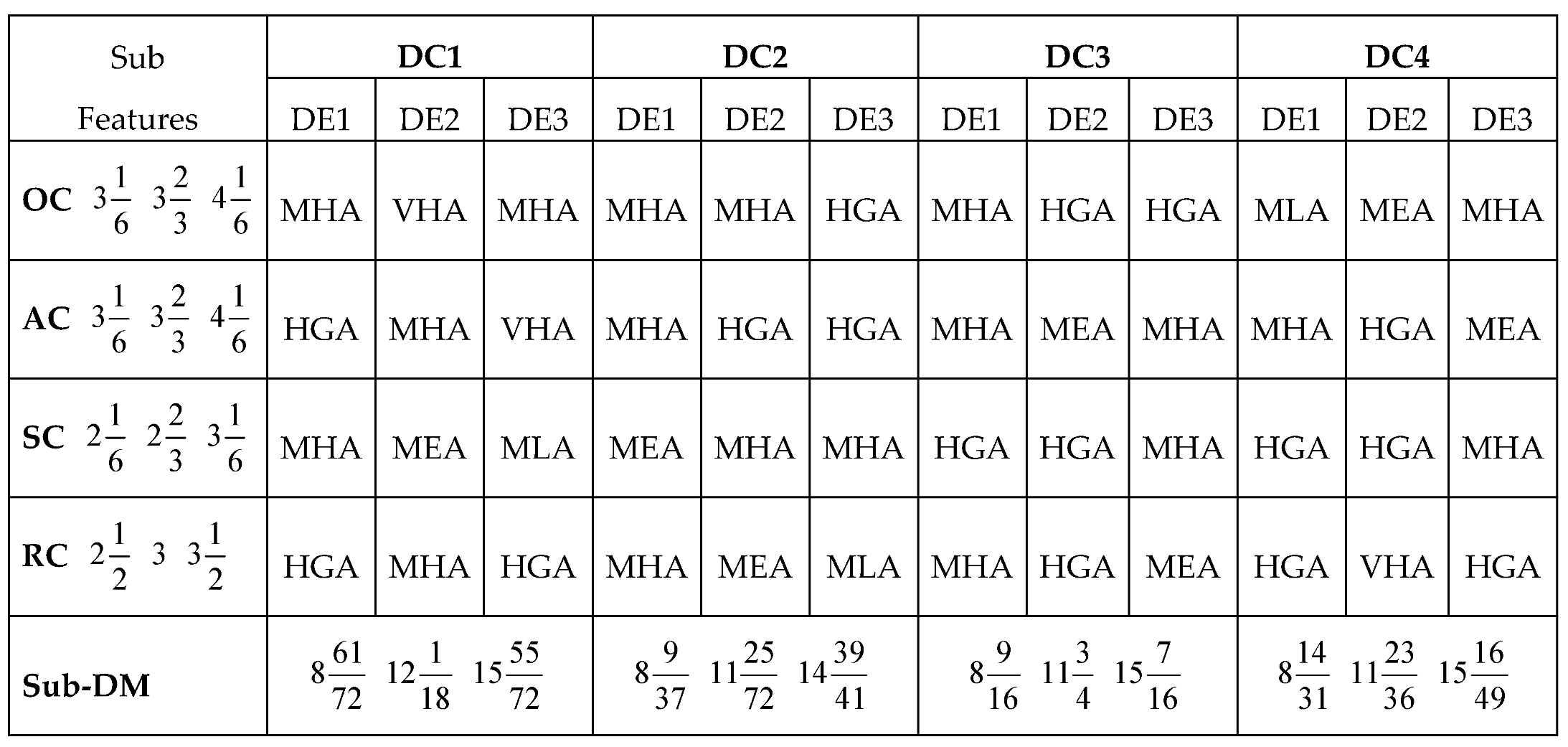
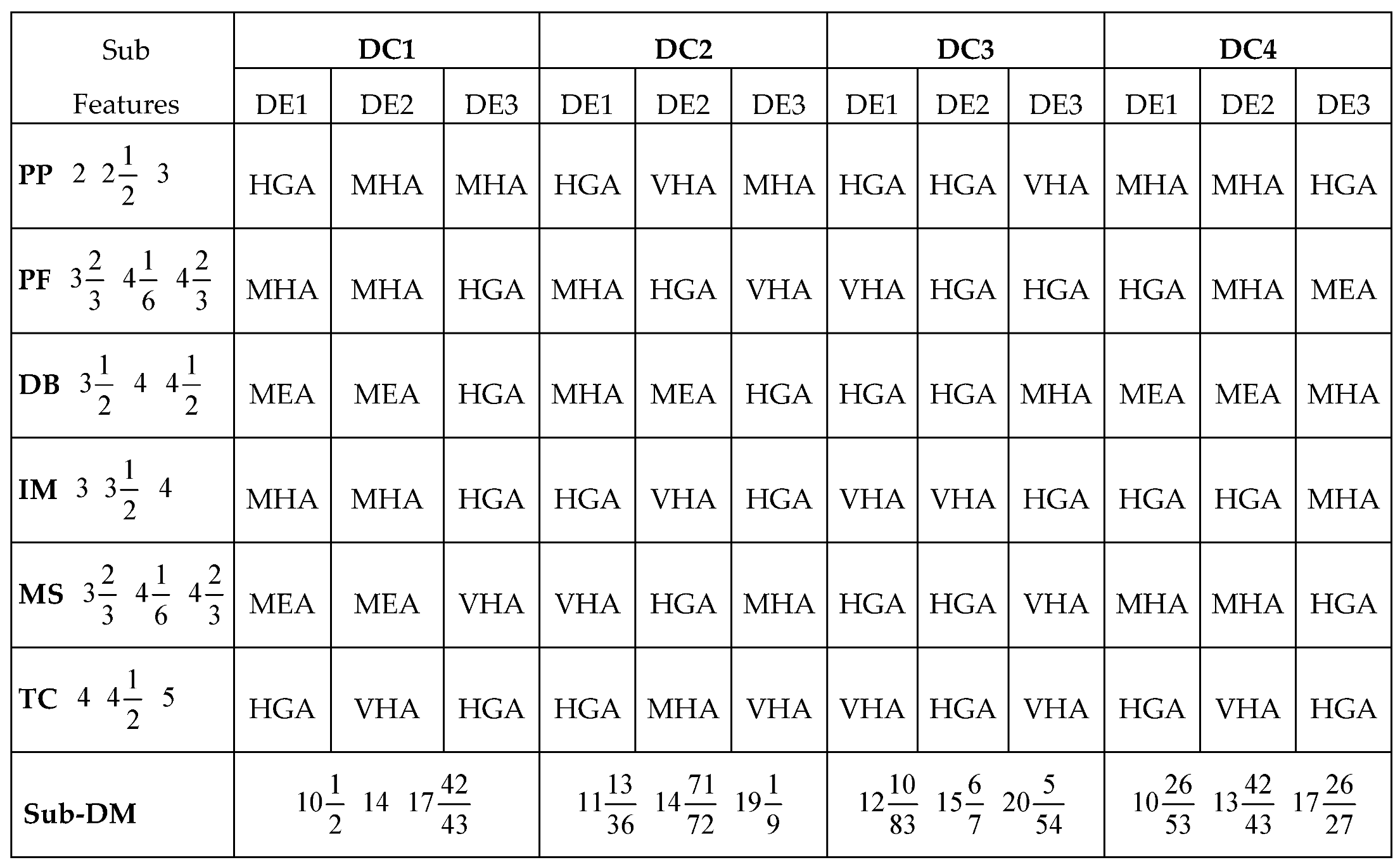
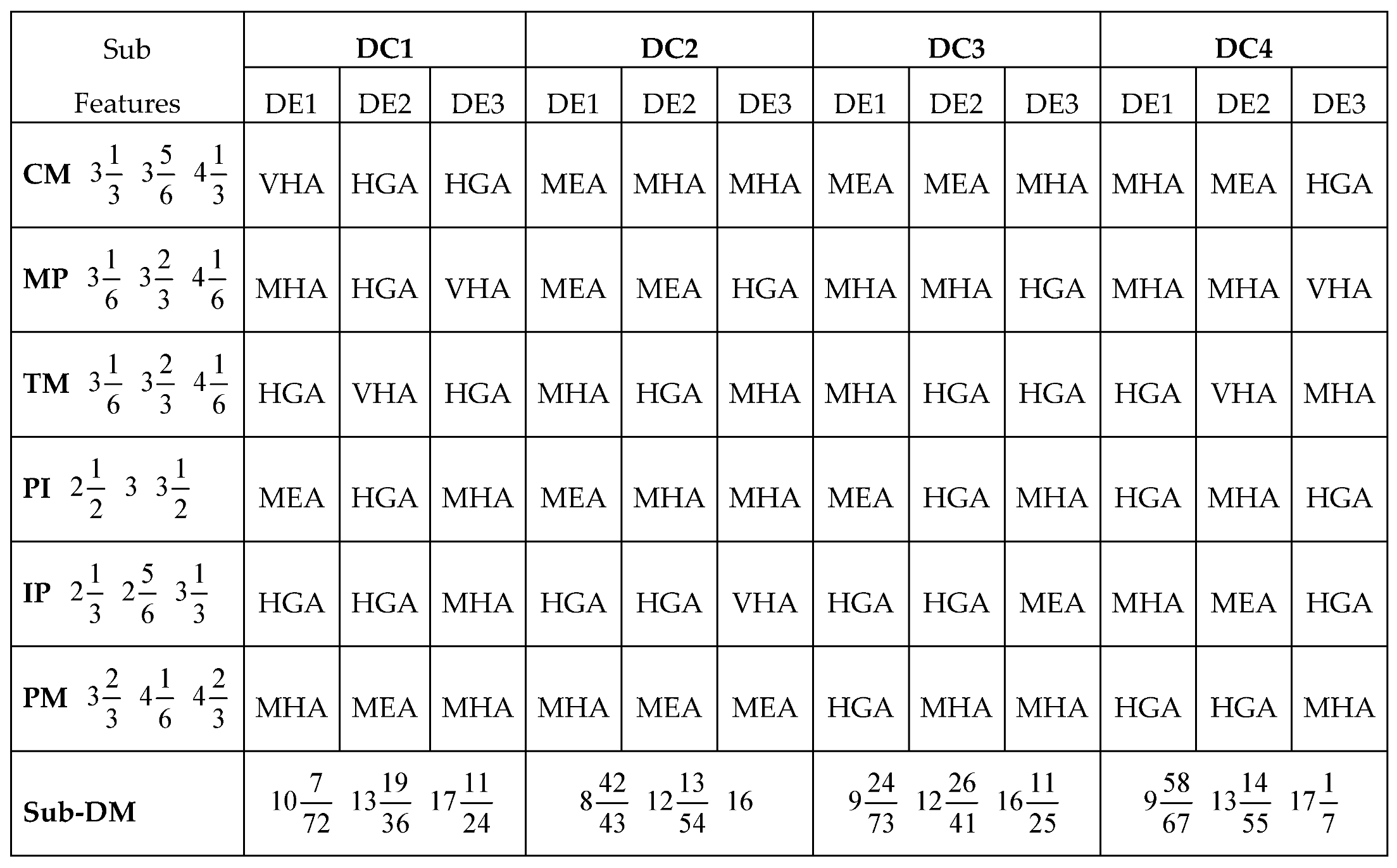
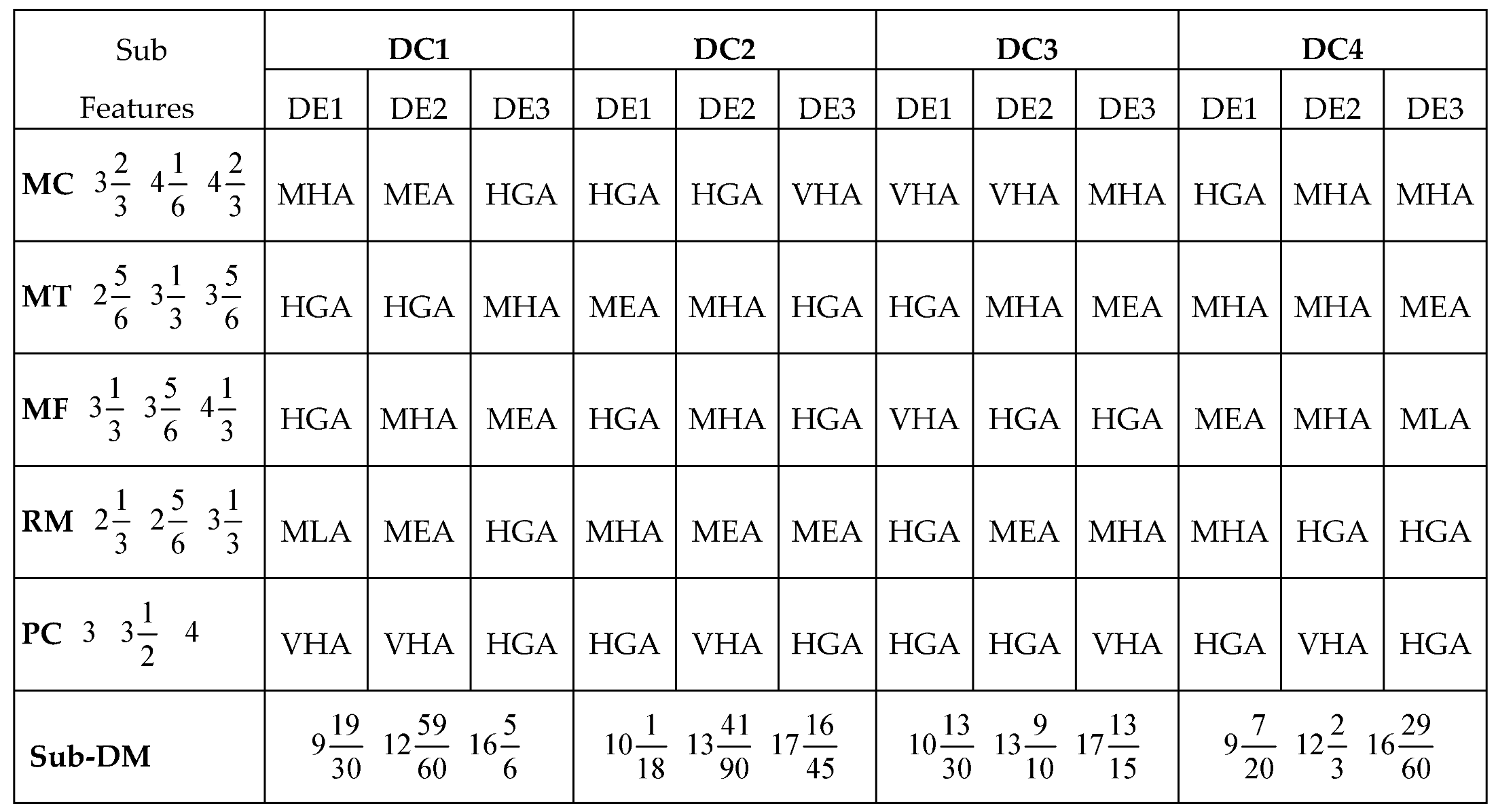
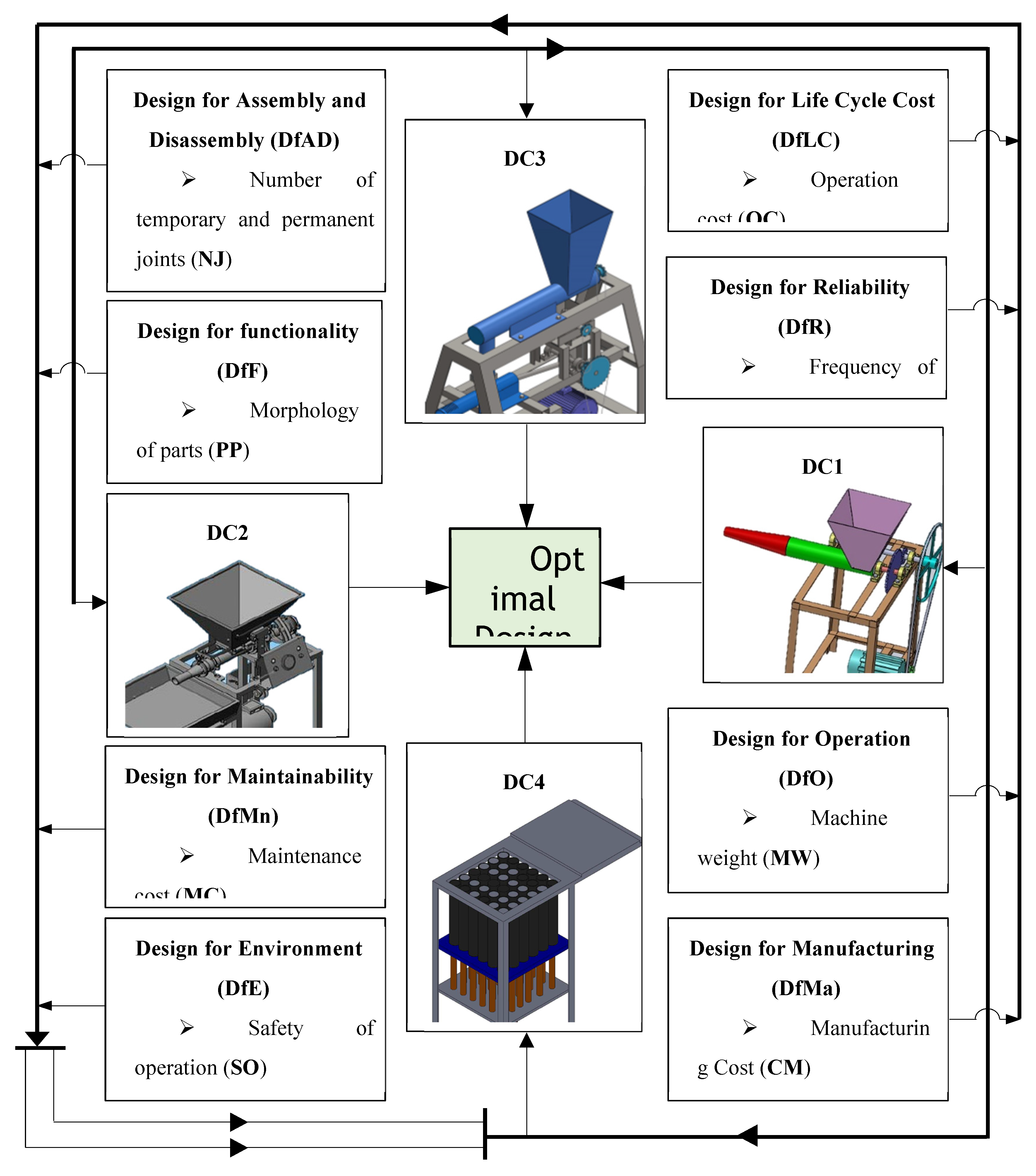
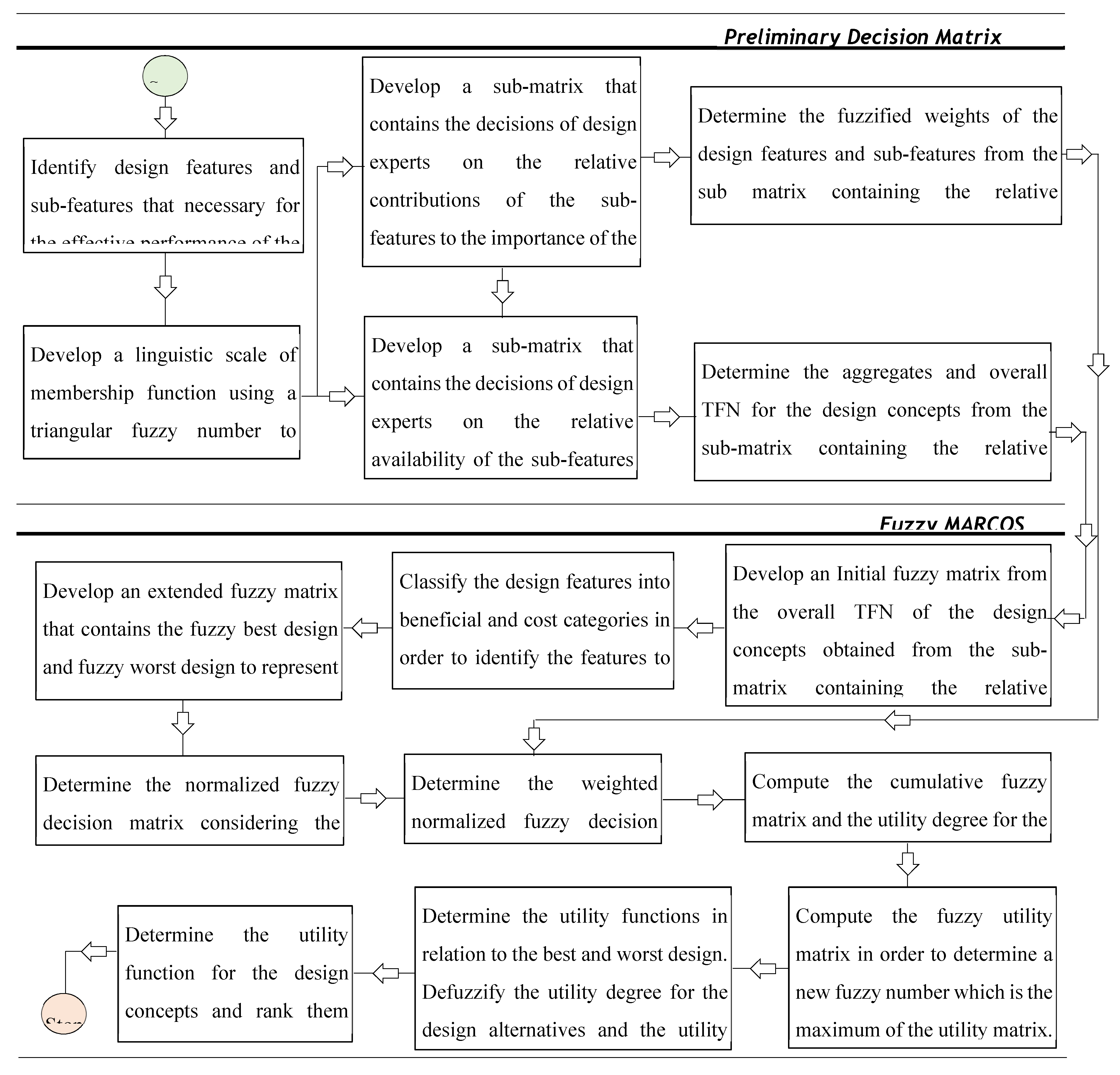
Considering the applications of the MARCOS model in different areas of application, it can be observed that the model is finds more application in infrastructure and technology assessment and it is suitable for handling several numbers of alternatives and it also has a consideration for the ideal and anti-ideal scenarios in the formation of the decision matrix. This makes it possible for the model to capture the variations of the alternatives from the ideal and anti-ideal solution considering the utility degree and functions of all the alternatives in order to affirm the optimal alternative. Also, considering the application areas of MARCOS model, it is necessary to investigate its suitability to decision making on the identification of optimal design concept considering several conceptual design alternatives. Hence, this article attempts to extend the application of the Fuzzy MARCOS model to identification of optimal design concept considering four conceptual designs of briquette making machine. The decision process considered eight design features with each of the design features having several sub-features. The importance of considering several design features is to ensure that the decision process is robust and all-encompassing in order to ascertain the computational integrity of the Fuzzy MARCOS model.
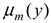 ’ is contained in [01] as defined in equation 1 [45].
’ is contained in [01] as defined in equation 1 [45].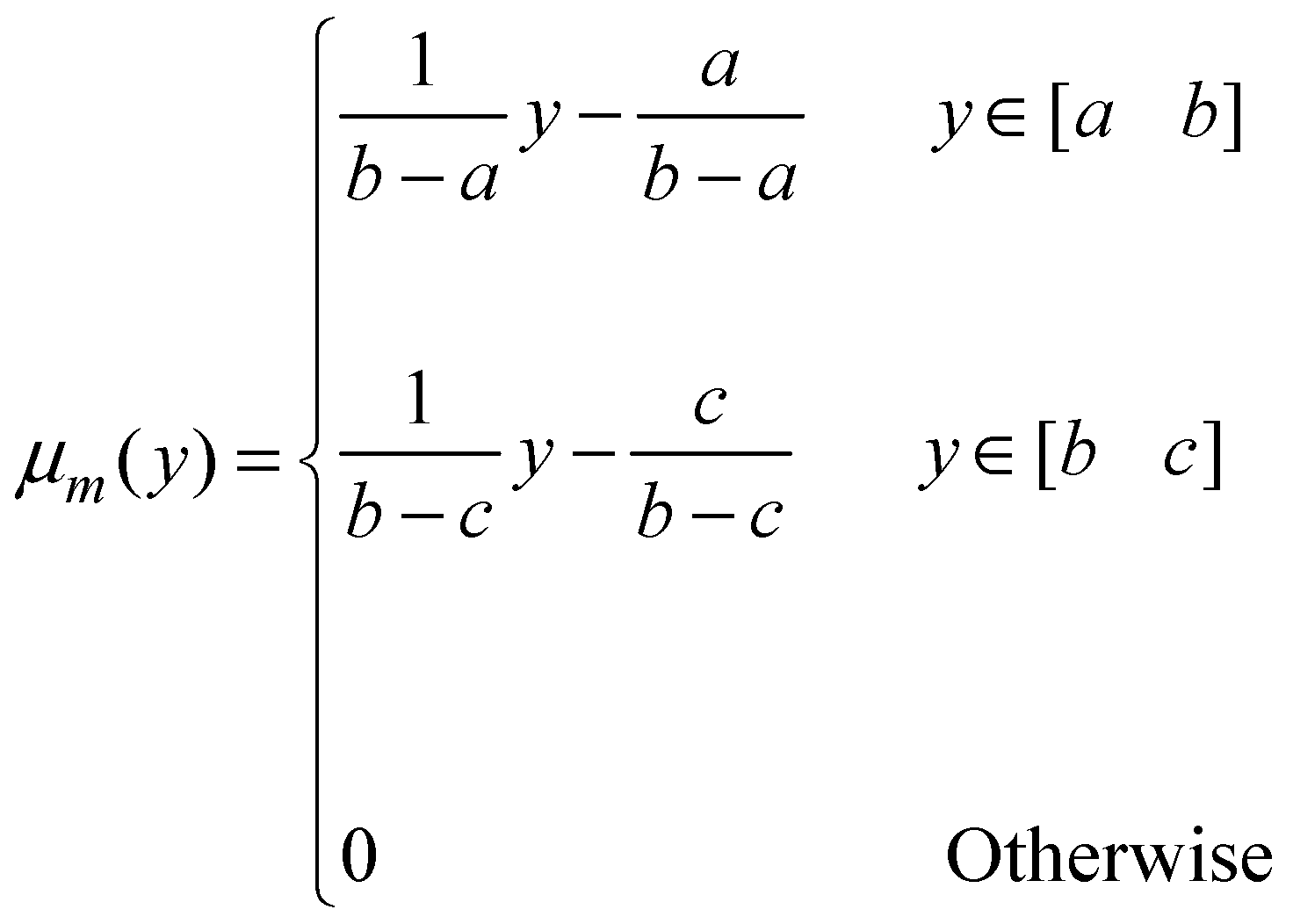
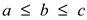 . The TFN (M)
described in equation 1 can be defuzzified to obtain a crisp value ‘
. The TFN (M)
described in equation 1 can be defuzzified to obtain a crisp value ‘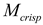 ’ which is the best
non-fuzzy performance value as presented in Equation (2) [46].
’ which is the best
non-fuzzy performance value as presented in Equation (2) [46]. 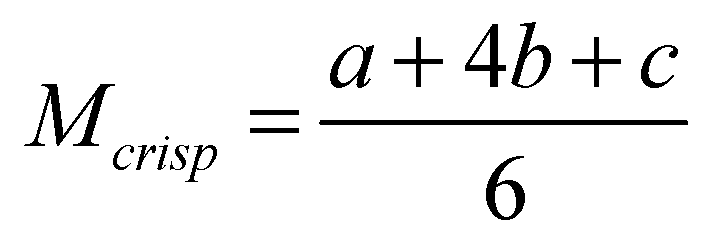
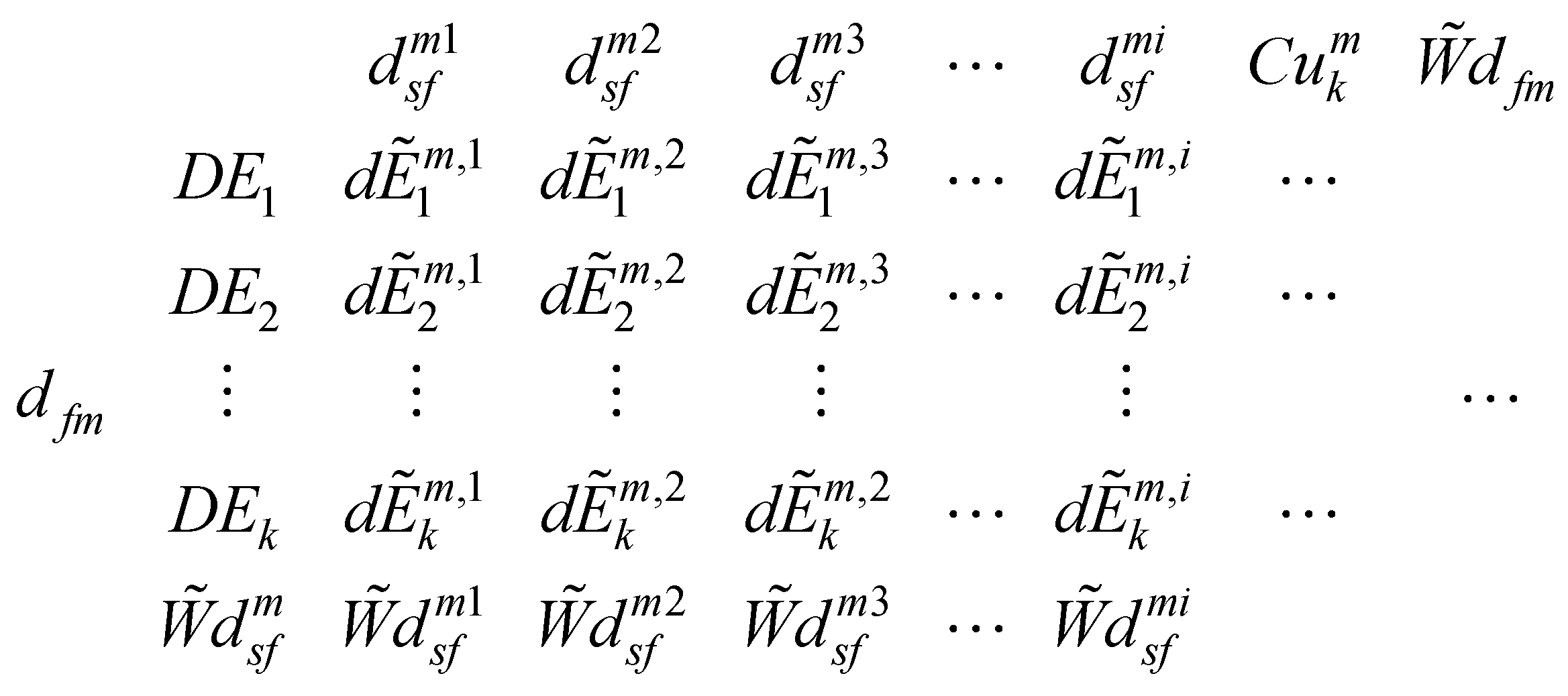
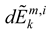 represents the decision of design expert ‘k’ for the relative contribution of ith sub-feature (
represents the decision of design expert ‘k’ for the relative contribution of ith sub-feature (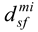 ) corresponding to design feature m (
) corresponding to design feature m (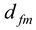 ).
). 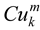 is the cumulative weight of the decisions of kth design expert which is obtainable in equation 5. Also,
is the cumulative weight of the decisions of kth design expert which is obtainable in equation 5. Also, 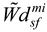 and
and 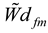 are the weights of the ith sub-feature and design feature m respectively.
are the weights of the ith sub-feature and design feature m respectively. 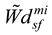 and
and 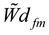 can also be obtained from equations 6 and 7 respectively.
can also be obtained from equations 6 and 7 respectively.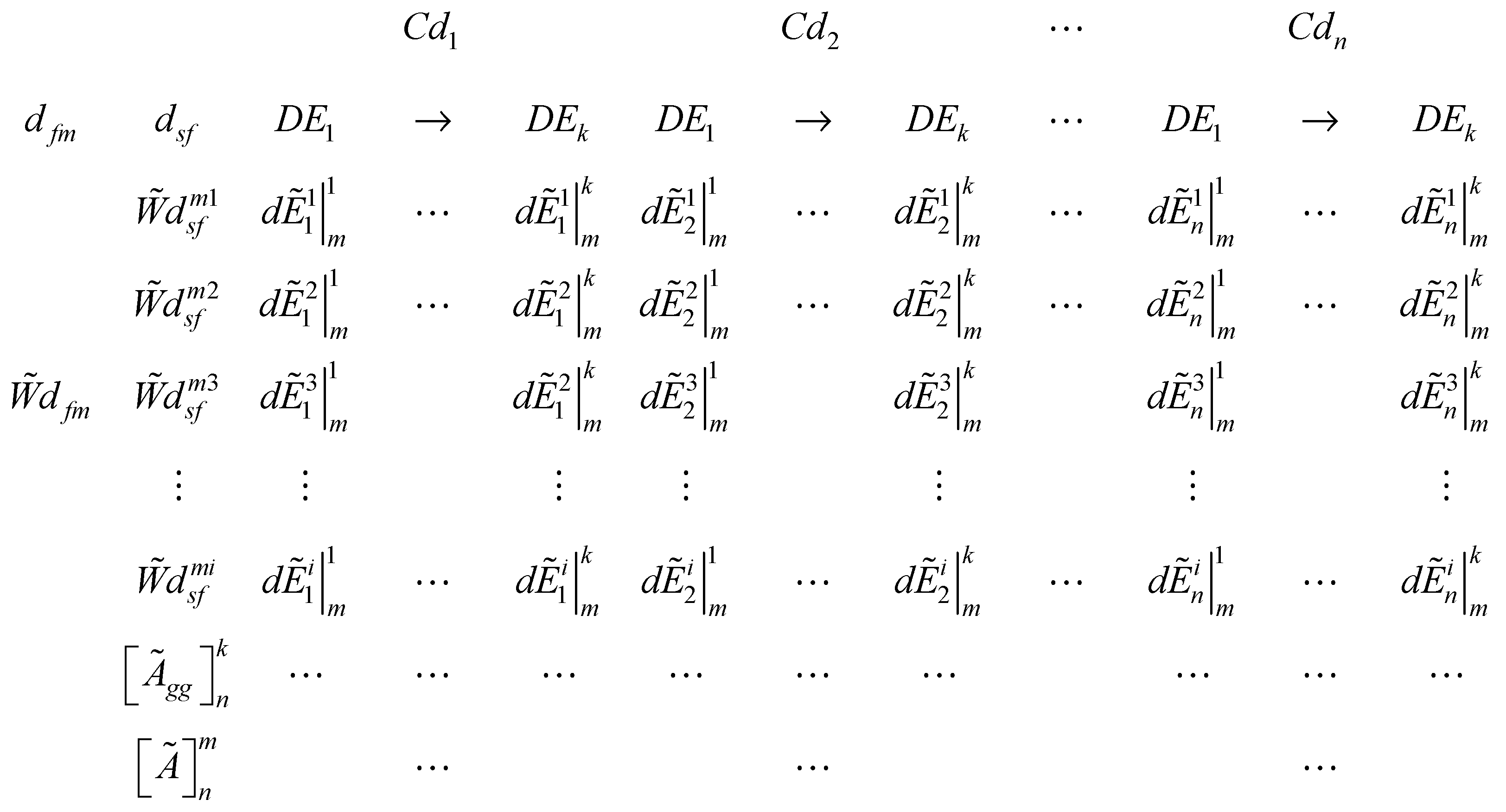
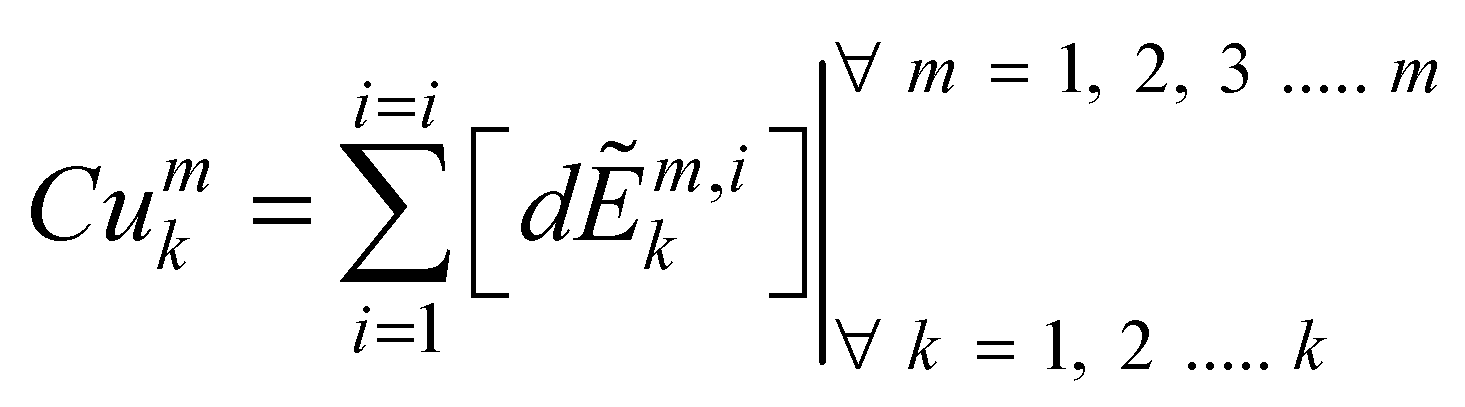


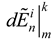 is the decision of design expert ‘k’ on the availability of sub-feature ‘i’ in design concept ‘n’ corresponding to design feature ‘m’. Also,
is the decision of design expert ‘k’ on the availability of sub-feature ‘i’ in design concept ‘n’ corresponding to design feature ‘m’. Also, 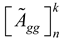 denotes the aggregate TFN for the nth design concept corresponding to the decision of kth design expert and
denotes the aggregate TFN for the nth design concept corresponding to the decision of kth design expert and 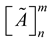 is the overall TFN for the nth design concept considering design feature ‘m’.
is the overall TFN for the nth design concept considering design feature ‘m’. 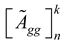 and
and 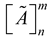 can be obtained from equations 8 and 9 respectively.
can be obtained from equations 8 and 9 respectively.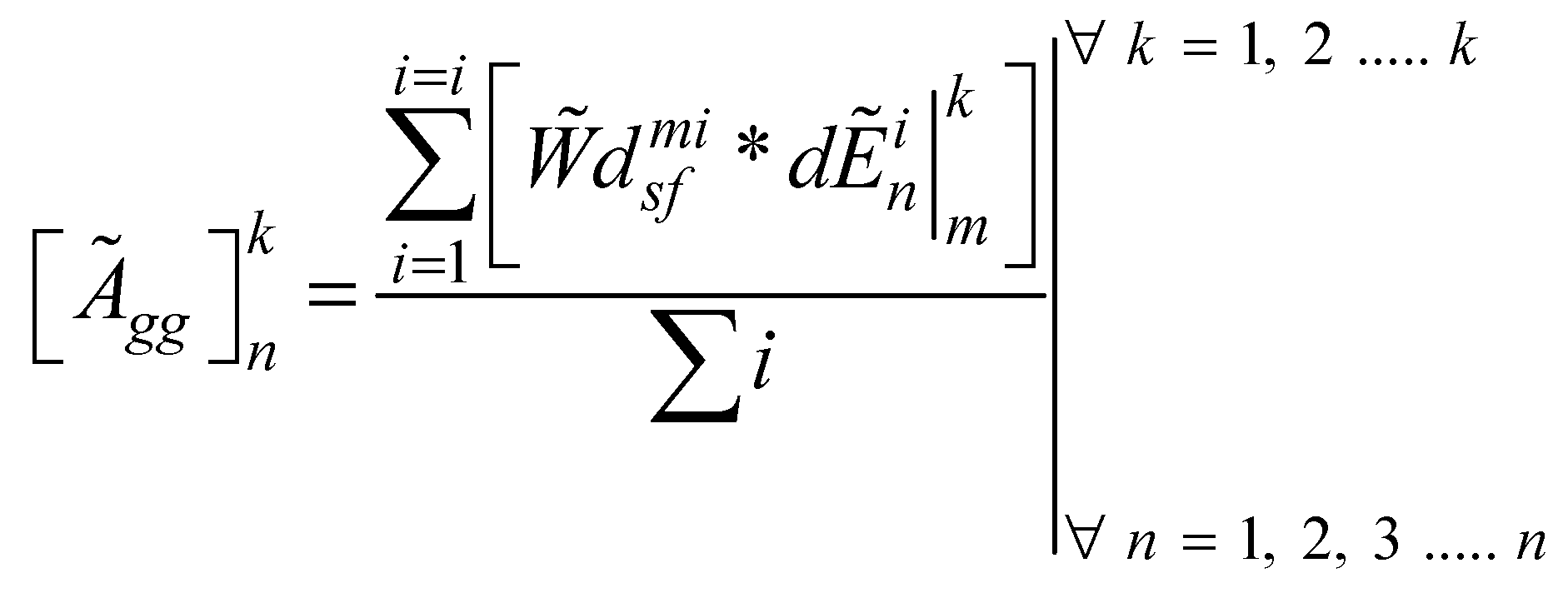
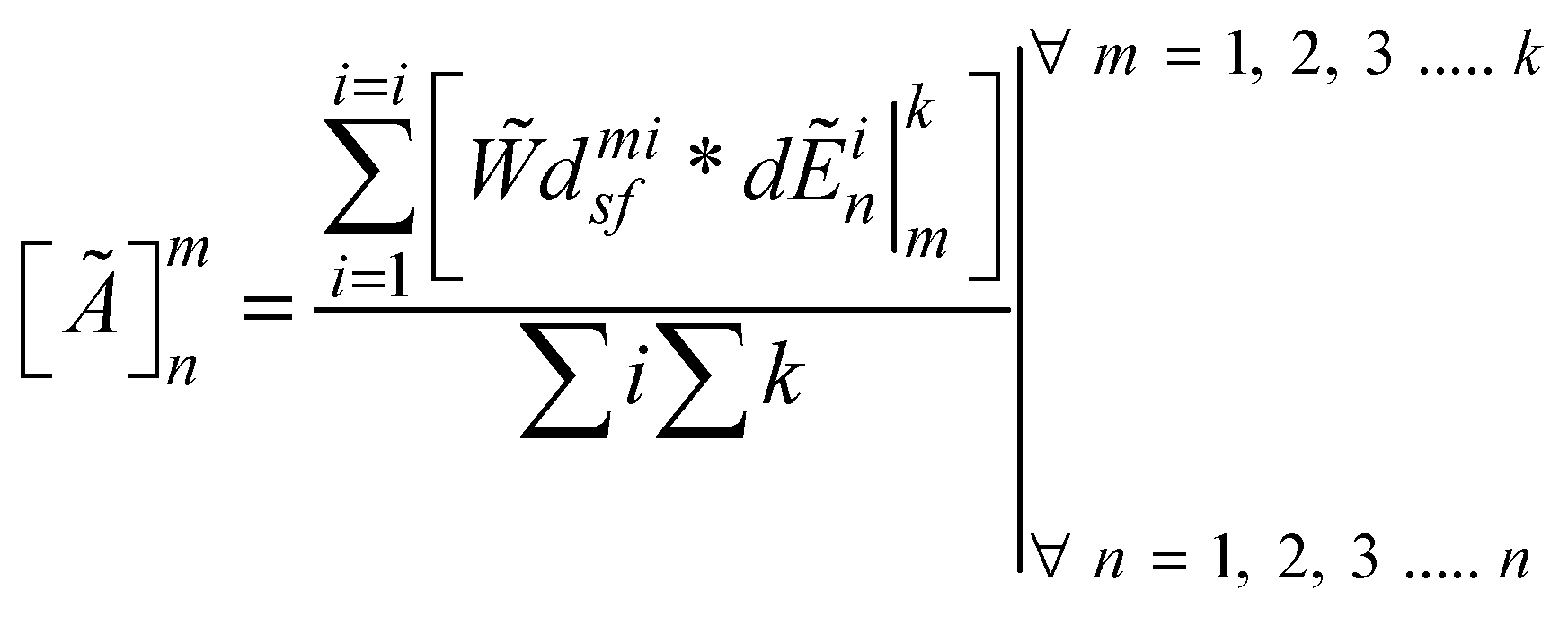
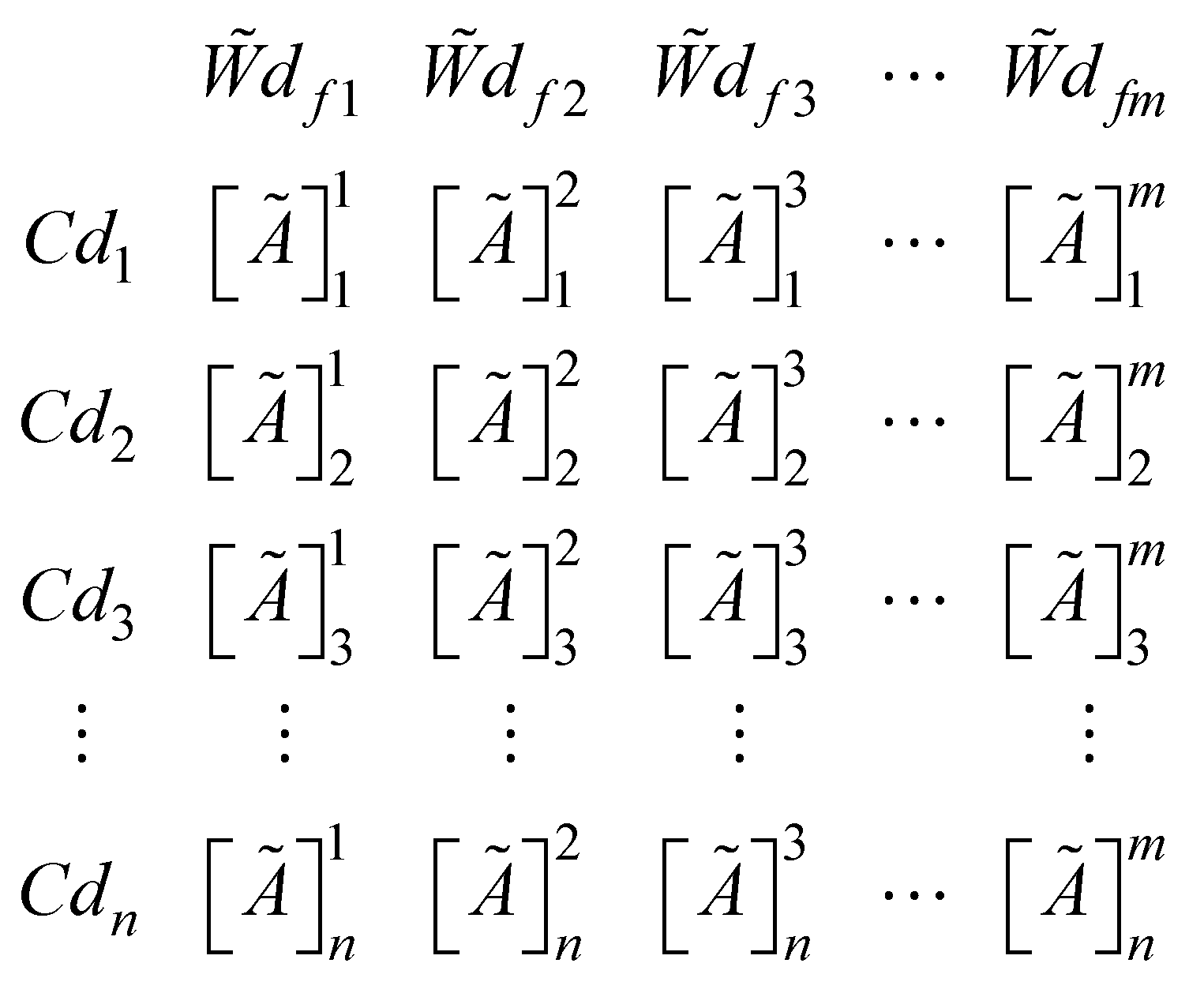
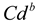 ) and worst (
) and worst (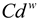 ) design concept based on the beneficial (
) design concept based on the beneficial (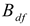 ) and cost (
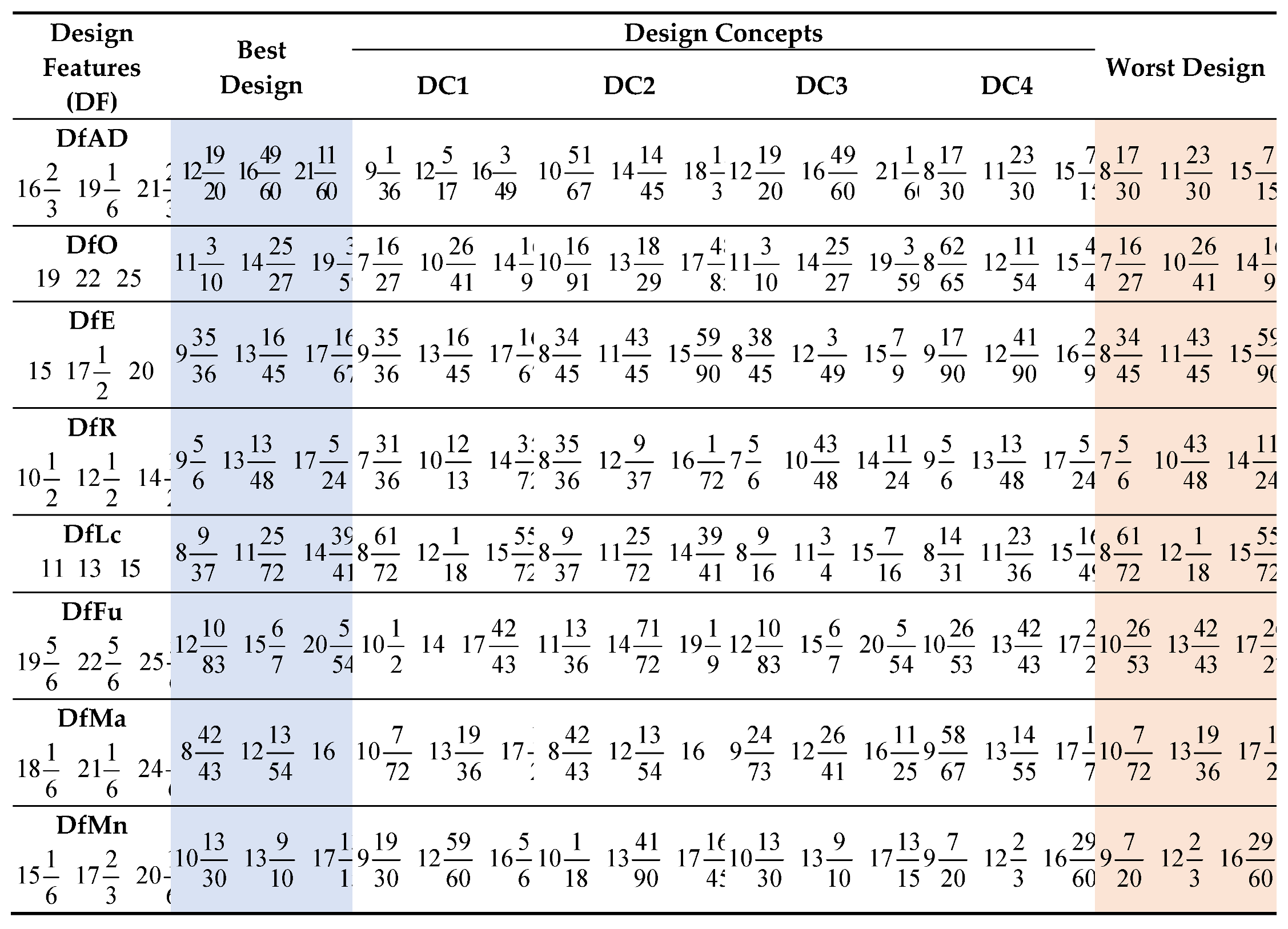
) and cost (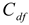 ) categories of design features. The best and worst design concept created in this case will represent the ideal and anti-ideal design concepts respectively. The best and worst design concepts can be obtained from equations 11 and 12 respectively. The matrix containing the best and worst design concept can be obtained by rewriting equation 10 as presented in equation 13.
) categories of design features. The best and worst design concept created in this case will represent the ideal and anti-ideal design concepts respectively. The best and worst design concepts can be obtained from equations 11 and 12 respectively. The matrix containing the best and worst design concept can be obtained by rewriting equation 10 as presented in equation 13. 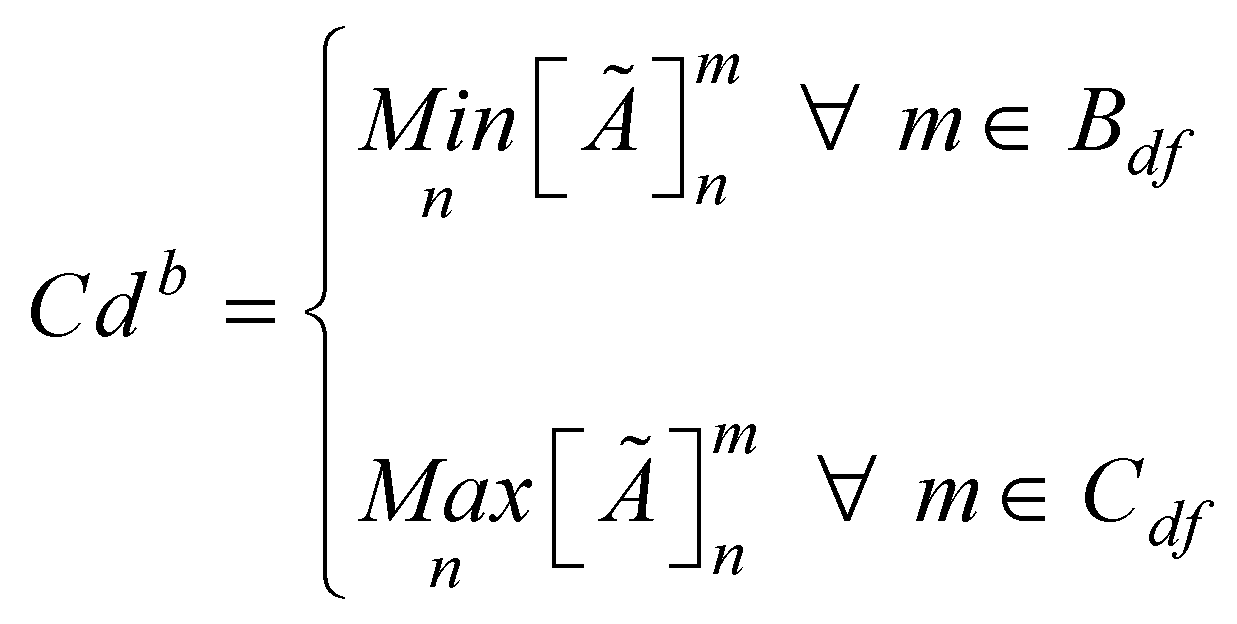
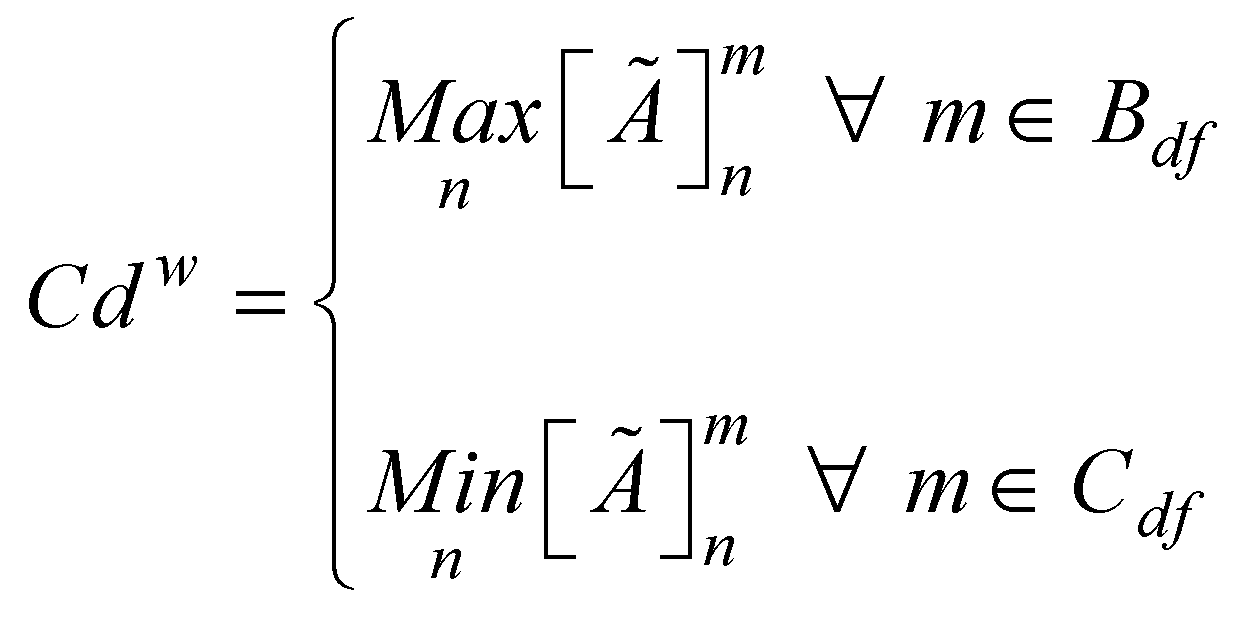

 ) and cost (
) and cost (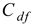 ) features considering the notations for the lower, modal and upper values of the TFN defined in Equation (1).
) features considering the notations for the lower, modal and upper values of the TFN defined in Equation (1).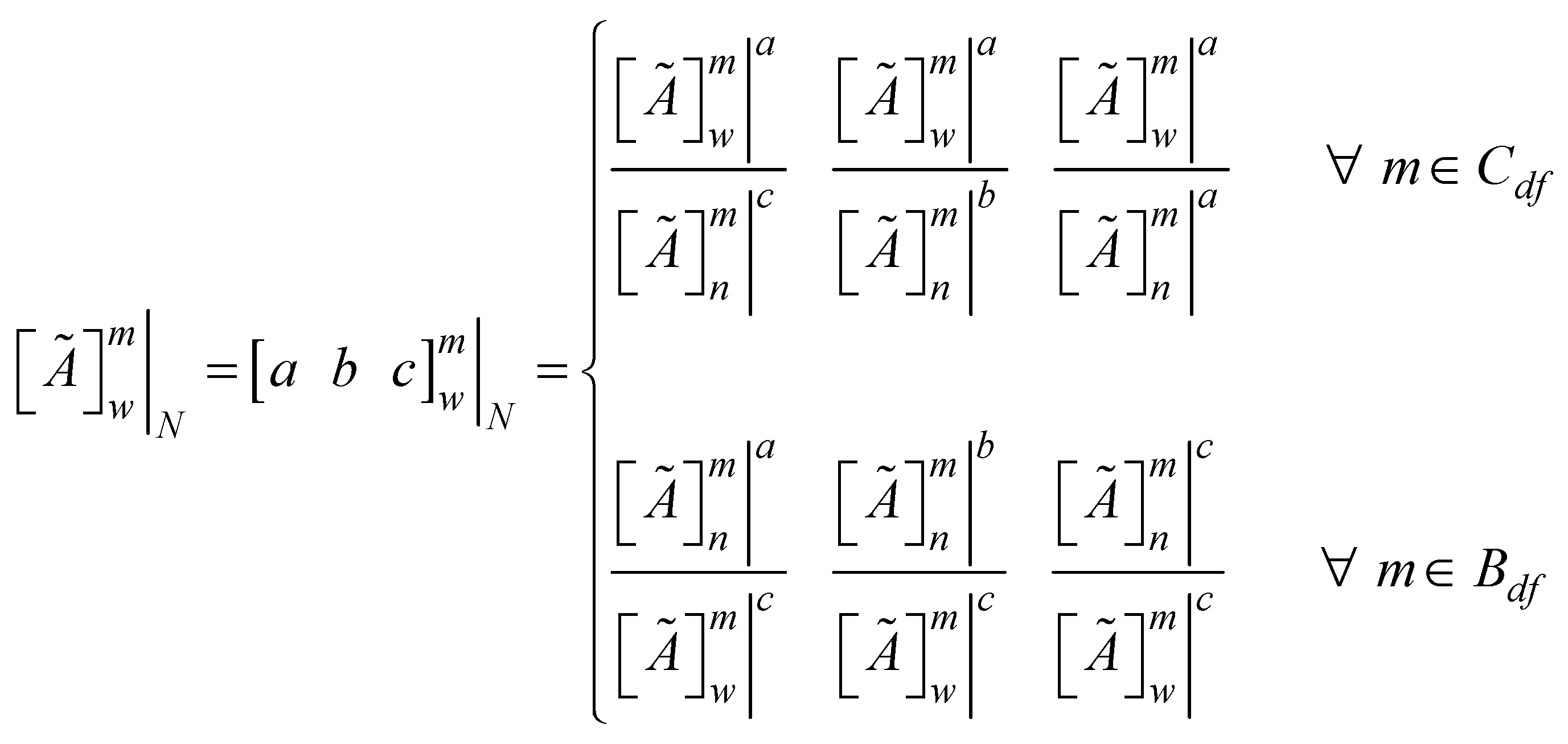
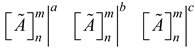 represents the lower, modal and upper values of the elements of the extended fuzzy decision matrix while
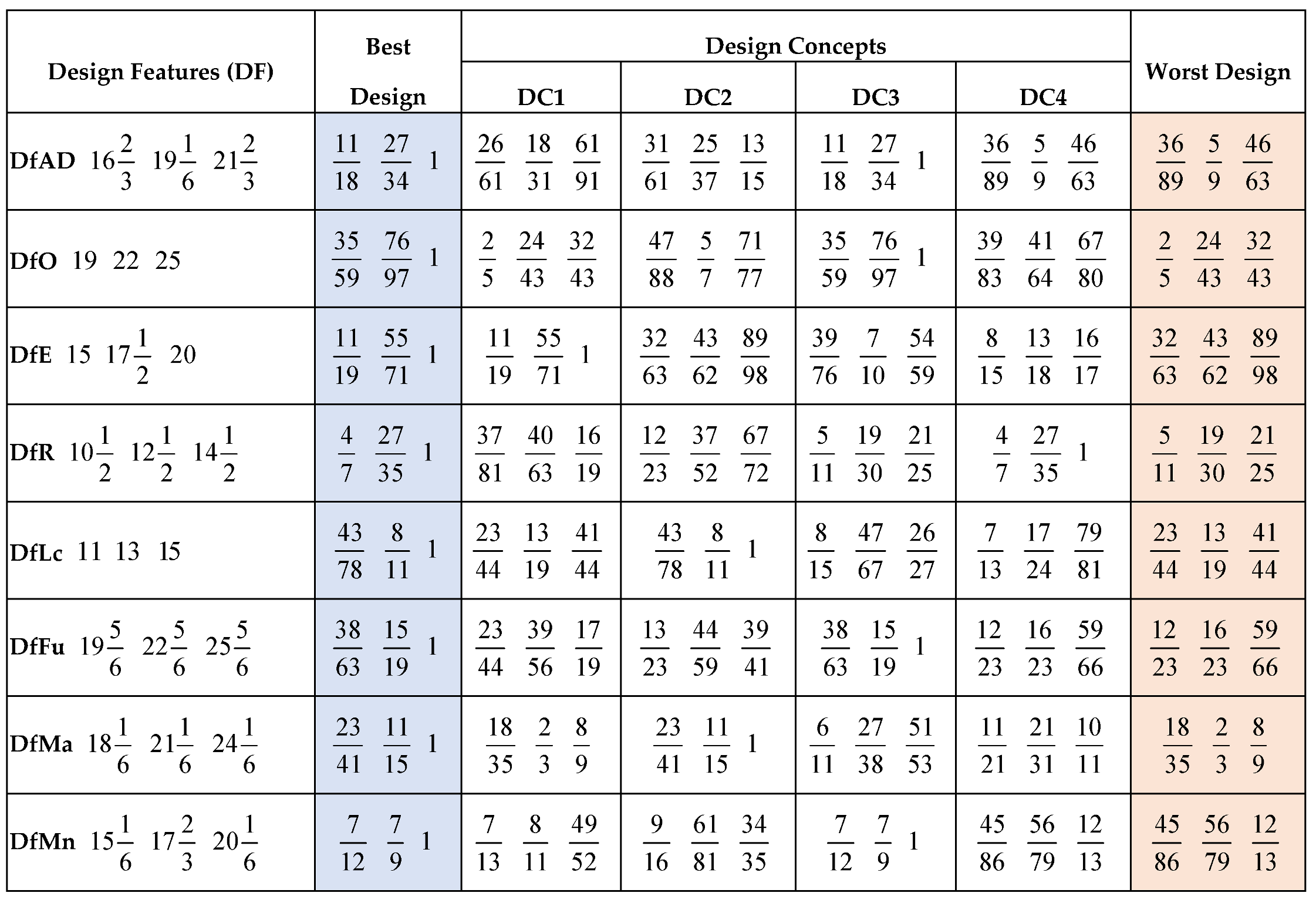
represents the lower, modal and upper values of the elements of the extended fuzzy decision matrix while 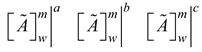 represents the lower, modal and upper values of the elements of the worst design. The next step is to compute the weighted normalized fuzzy decision matrix
represents the lower, modal and upper values of the elements of the worst design. The next step is to compute the weighted normalized fuzzy decision matrix 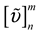 as presented in equation 15. This is obtainable by multiplying the weights of the design features with the normalized elements of the decision matrix. Hence, the weighted and normalized version of equation 13 can be expressed in equation 16.
as presented in equation 15. This is obtainable by multiplying the weights of the design features with the normalized elements of the decision matrix. Hence, the weighted and normalized version of equation 13 can be expressed in equation 16.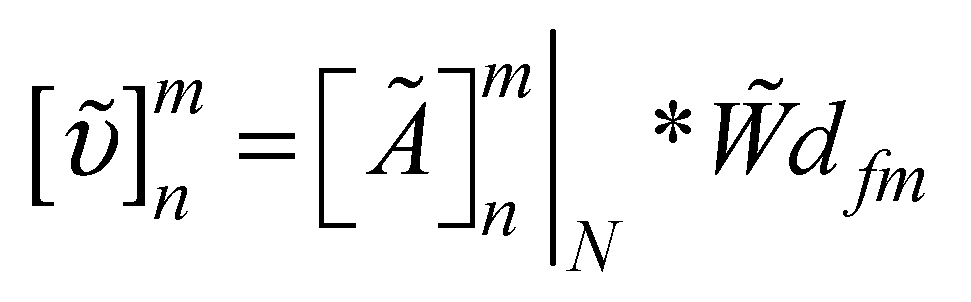
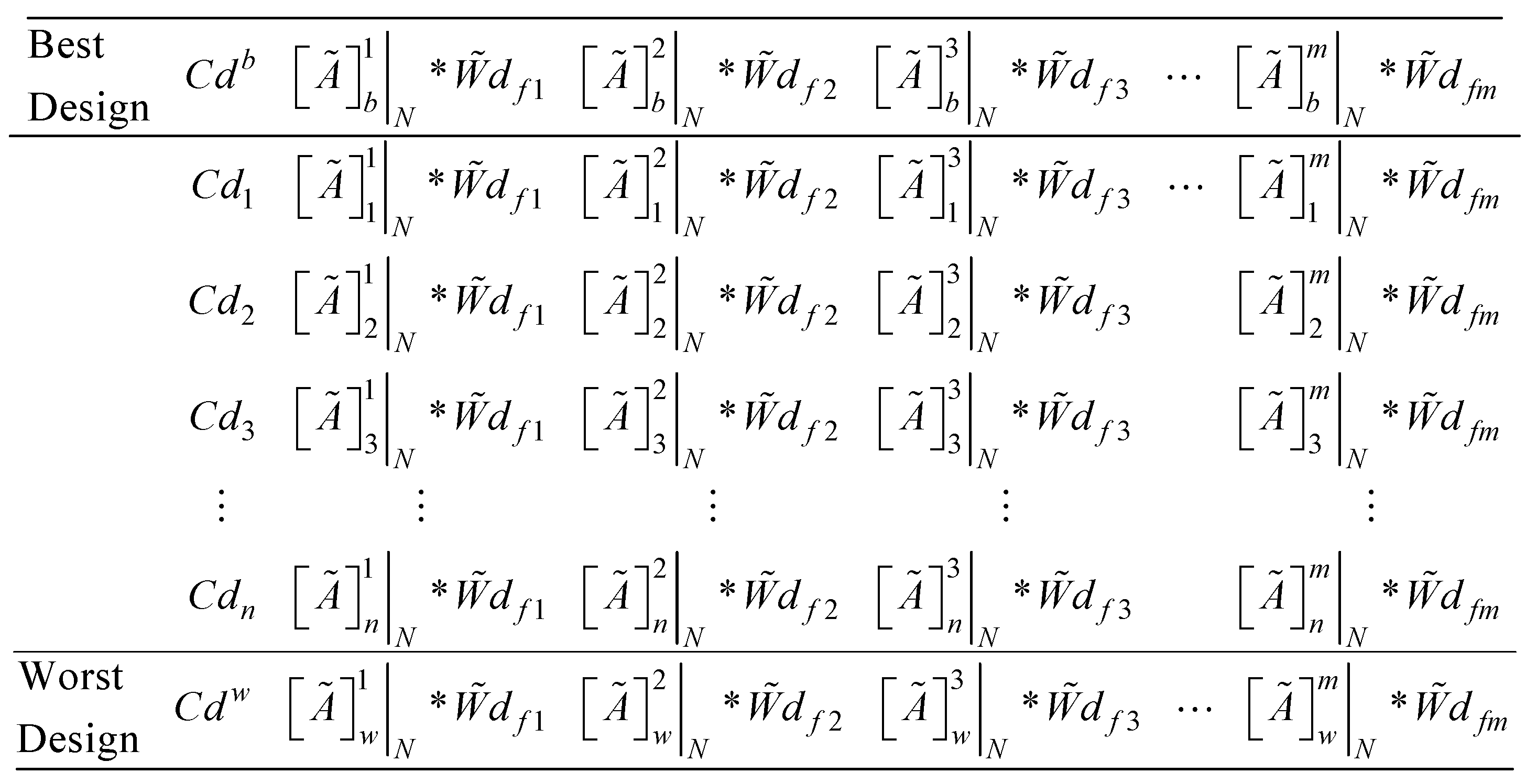
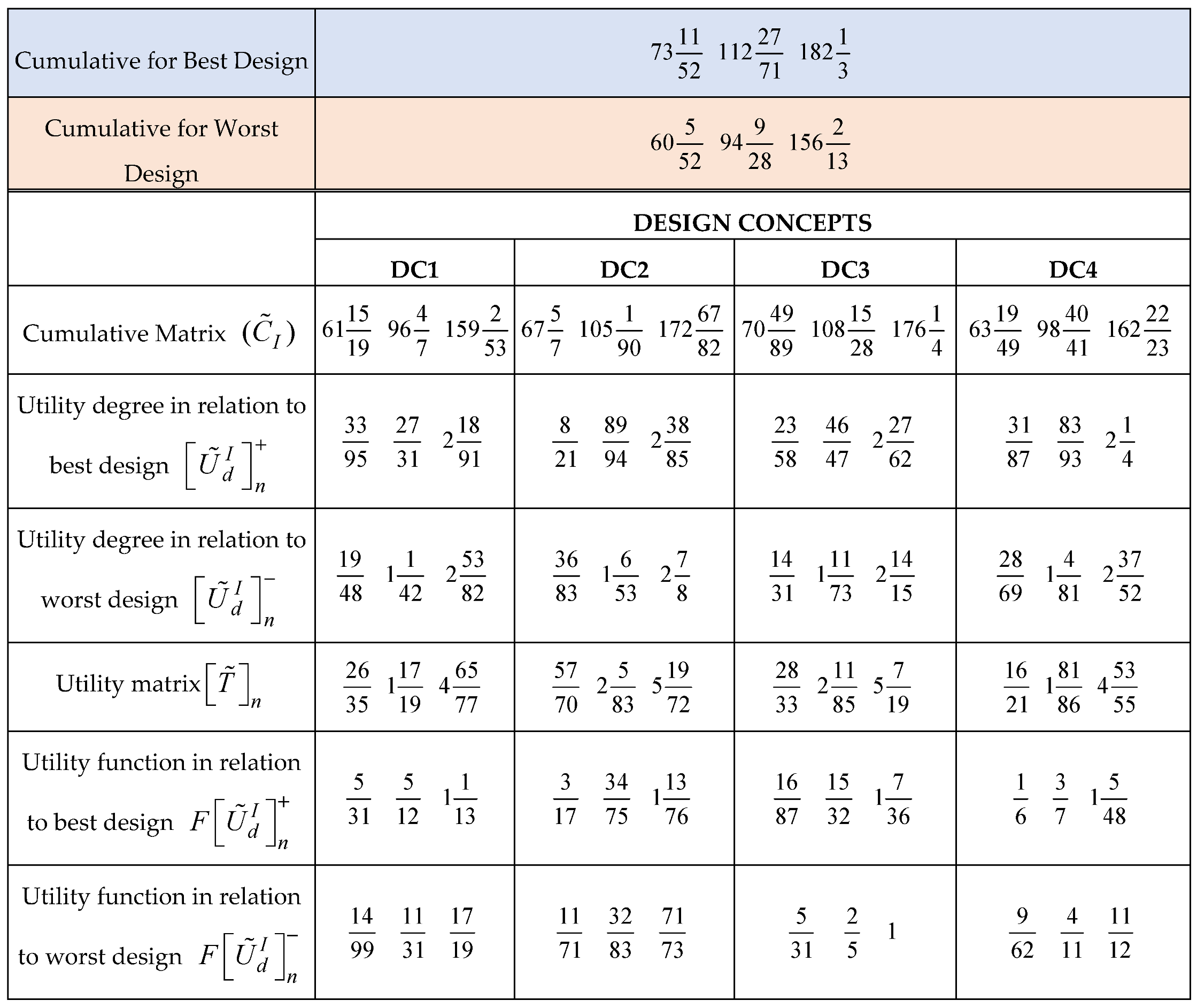
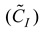 can be obtained by summing the elements of the weighted matrix. This is obtainable from equation 17. The cumulative fuzzy matrix is necessary for estimating the utility degree of the design alternatives
can be obtained by summing the elements of the weighted matrix. This is obtainable from equation 17. The cumulative fuzzy matrix is necessary for estimating the utility degree of the design alternatives 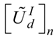 . The utility degree of the design alternatives is a function of the cumulative matrices of the best
. The utility degree of the design alternatives is a function of the cumulative matrices of the best 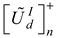 and worst
and worst 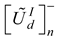 design. Hence, the utility degree can be expressed in terms of best and worst design scenarios as presented in equations 18 and 19 respectively. The next step is to compute the fuzzy utility matrix
design. Hence, the utility degree can be expressed in terms of best and worst design scenarios as presented in equations 18 and 19 respectively. The next step is to compute the fuzzy utility matrix 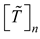 . The fuzzy utility matrix is a summation of the utility degrees for the best and worst scenario of the design concepts as presented in equation 20. Further, the fuzzy utility matrix is necessary for determining a new fuzzy number
. The fuzzy utility matrix is a summation of the utility degrees for the best and worst scenario of the design concepts as presented in equation 20. Further, the fuzzy utility matrix is necessary for determining a new fuzzy number 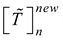 which is the maximum of the utility matrix as presented in equation 21. This new fuzzy number will be defuzzified using equation 2 in order to compute the utility functions in relation to the best
which is the maximum of the utility matrix as presented in equation 21. This new fuzzy number will be defuzzified using equation 2 in order to compute the utility functions in relation to the best 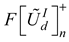 and worst
and worst 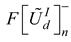 design alternatives as presented in equations 22 and 23 respectively. The next step is to defuzzify the TFNs for the best and worst utility degree scenarios and the best and worst utility functions. This is necessary in the determination of a crisp value for the overall utility function for the design concepts as presented in equation 24.
design alternatives as presented in equations 22 and 23 respectively. The next step is to defuzzify the TFNs for the best and worst utility degree scenarios and the best and worst utility functions. This is necessary in the determination of a crisp value for the overall utility function for the design concepts as presented in equation 24. 
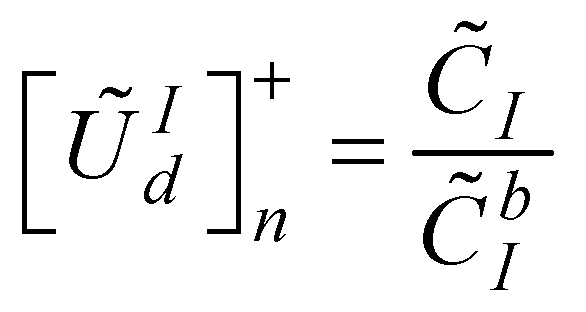
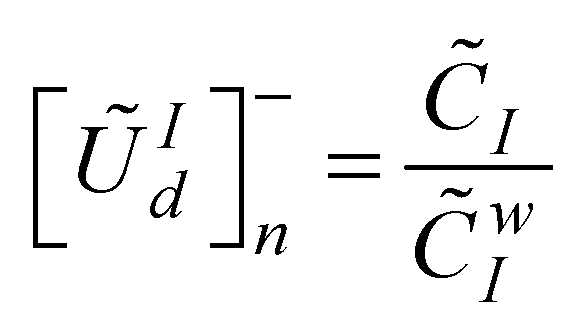
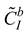 and
and 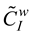 are the cumulative fuzzy matrix for the best and worst designs respectively.
are the cumulative fuzzy matrix for the best and worst designs respectively. 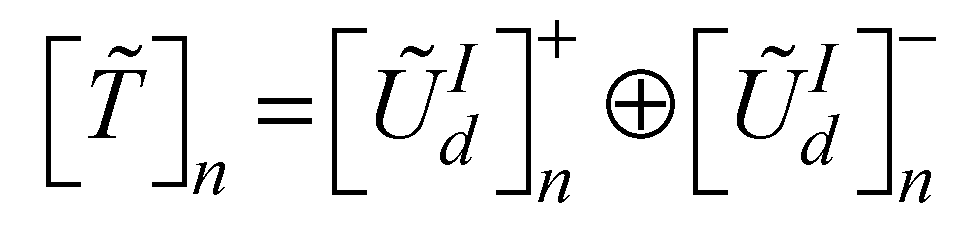
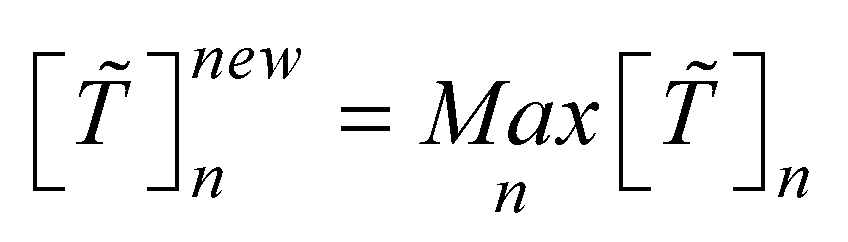
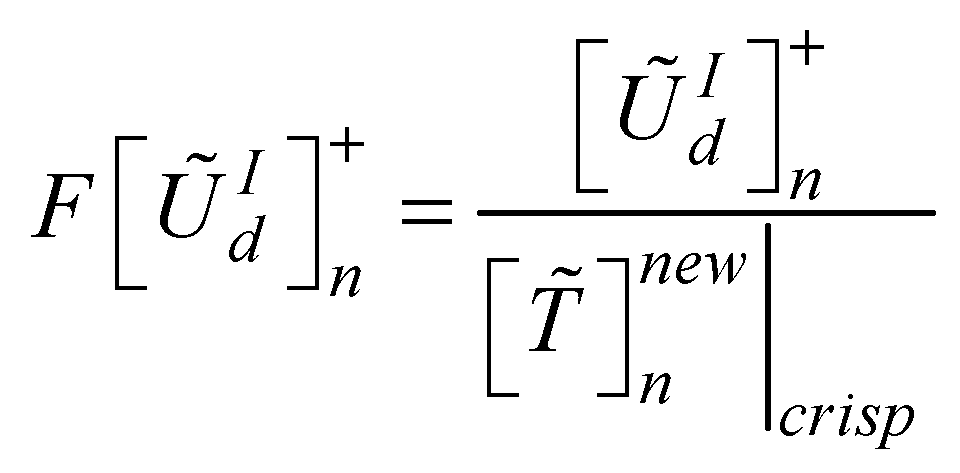
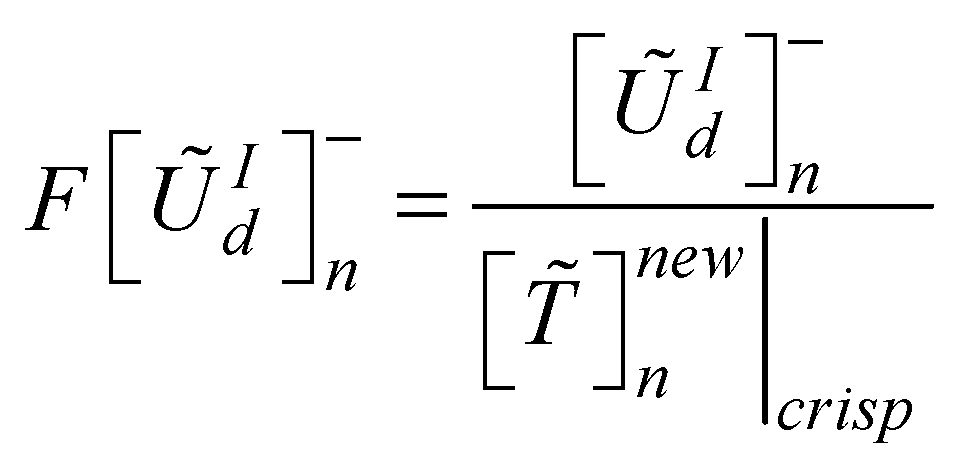
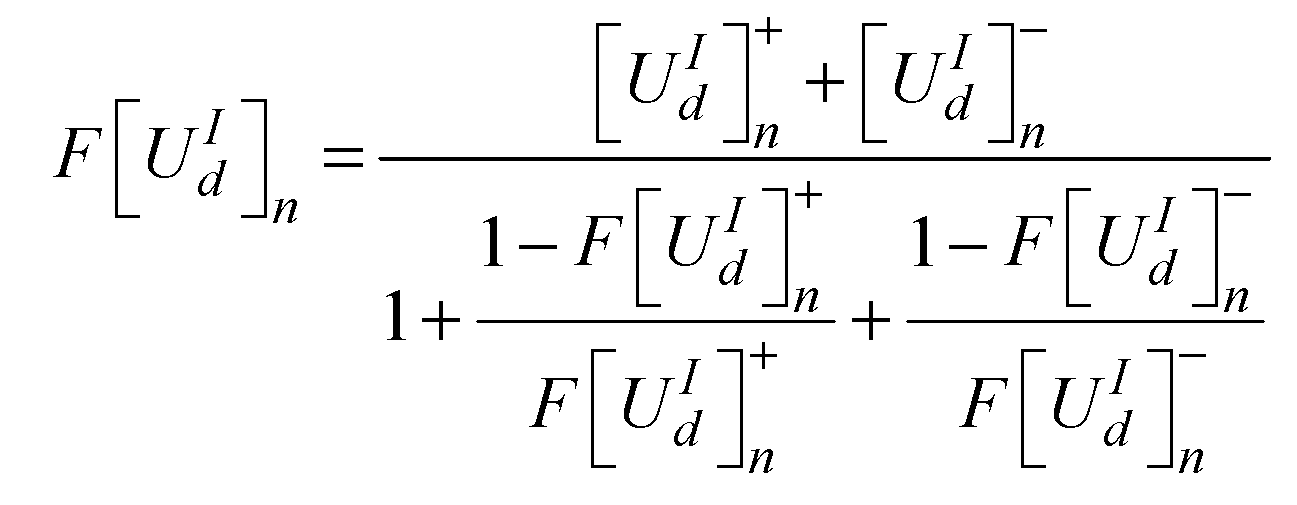
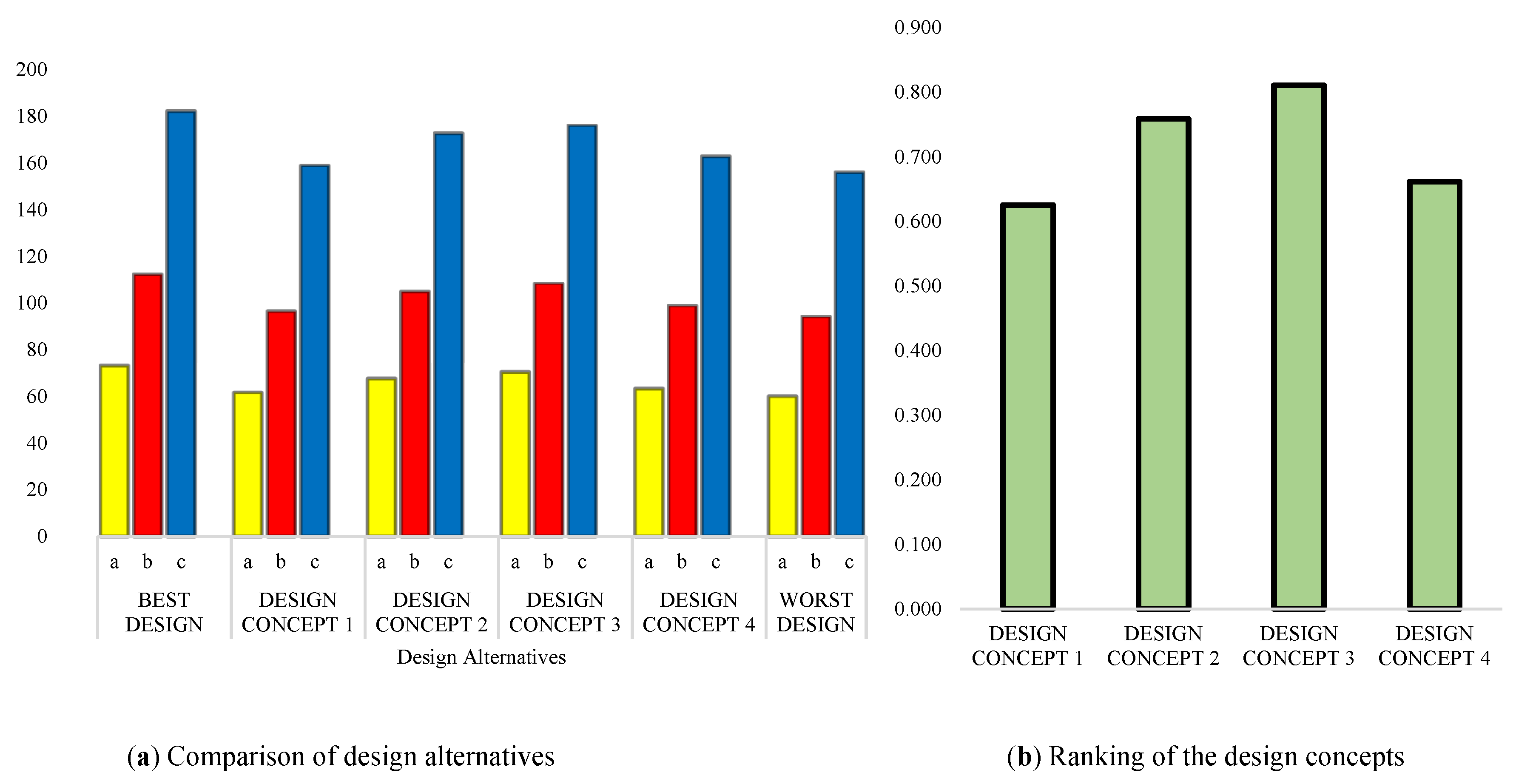
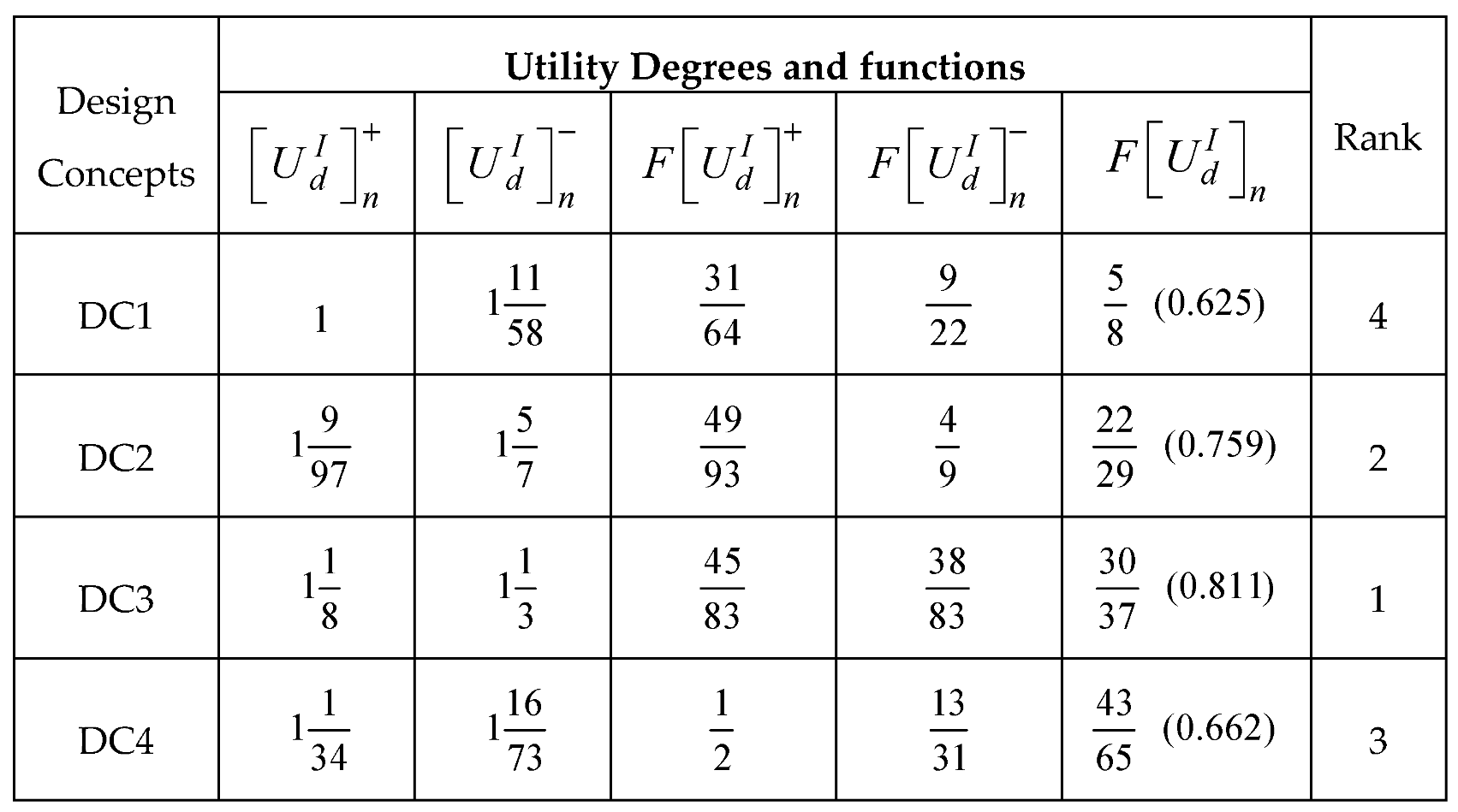
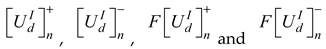 represents the crisp values for
represents the crisp values for 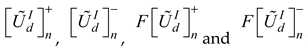 respectively. The design concepts are ranked according to the values of the overall utility functions such that the design with the highest value is the optimal design.
respectively. The design concepts are ranked according to the values of the overall utility functions such that the design with the highest value is the optimal design.