Prerpints.org logo
Preprint
Article

Calculation of the Three Partition Coefficients logPow, logKoa and logKaw of Organic Molecules at Standard Conditions at Once by Means of a Generally Applicable Group-Additivity Method

Altmetrics

Downloads

134

Views

111

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (3.34MB )

This version is not peer-reviewed

Submitted:

04 December 2023

Posted:

05 December 2023

You are already at the latest version

Alerts
Abstract
Assessment of the environmental impact of organic chemicals has become an important subject in chemical science. Efficient quantitative descriptors of their impact are their partition coefficients logPow, logKoa and logKaw. We present a group-additivity method that has proven its versatility for the reliable prediction of many other molecular descriptors for the calculation of the first two partition coefficients and indirectly of the third with high dependability. Based on the experimental logPow data of 3332 molecules and the experimental logKoa data of 1900 molecules at 298.15K the respective partition coefficients have been calculated with cross-validated standard deviations of only 0.42 and 0.48 log units and a goodness of fit Q^2 of 0.9599 and 0.9717, respectively, in a range of ca. 17 log units for both descriptors. The third partition coefficient logKaw has been derived from the calculated values of the former two descriptors and compared with the experimentally determined logKaw values of 1937 molecules, yielding a standard deviation of 0.67 log units and a correlation coefficient R^2 of 0.9467. This approach enabled the quick calculation of 29462 logPow, 27069 logKoa and 26220 logKaw values for the more than 37100 molecules of ChemBrain's database available to the public.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

Environmental considerations of organic molecules as potential contaminants have become an important subject in recent years. Several descriptors have been applied to quantify their impact on the natural environment, among them the octanol/water partition coefficient Pow, (more recently named Kow) a standard model for the description of the lipophilicity of drugs in the medicinal and agricultural chemistry, whereby octanol is the substitute for the natural organic matter, and the octanol/air partition coefficient Koa and the air/water partition coefficient Kaw which both indicate the role of the chemicals for air-breathing organisms [1,2,3]. In view of the time consumption and costs of their experimental determination, fast mathematical methods for the prediction of their value attributed to a molecule have been developed, all founded on the results of previous examinations on a relatively limited number of compounds. For the former coefficient Pow a number of authors [4,5,6,7,8,9,10,11] have successfully carried out calculations for a large variability of compounds based on various group-additivity methods. On the other hand, many publications [12,13,14,15,16,17,18,19,20,21,22,23] dealing with the prediction of the coefficient Koa, based on various QSPR methods, are limited to specific chemical families, thus lacking a general applicability. Li et al. [24] used a group-additivity method based on five fragment constants and one structural correction factor for the evaluation of Koa, limited to halogenated aromatic pollutants. Recently, Ebert et al. [25] suggested a general-purpose fragment model for the calculation of the air/water partition coefficient Kaw resembling the atom-group additivity method presented in one of our earlier papers [11] for the calculation of – among several further descriptors – the octanol/water partition coefficient Pow.
The goal of the present paper was to suggest the extension of a simple tool, which has already served well for the prediction of the octanol/water coefficient Pow (in its logarithmic value logPow) described in [11], to enable it to calculate all three mentioned partition coefficients at once by means of a uniform computer algorithm based on the atom-group additivity method detailed in [11]. Since under common standard conditions any third partition coefficient can be directly calculated from the other two if we neglect the effect of the contamination of water in octanol (and vice versa) influencing the determination of the Pow values which will be addressed later on, it made sense to select those two coefficients for which any group parameters could be founded on the most reliable as well as the largest number of experimental data. It turned out that the experimental data for the partition coefficients Pow and Koa provided excellent basis sets for the evaluation of their respective tables of atom- and special group parameters. Accordingly, from the subsequently calculated values of a molecule´s Pow and Koa its air/water partition coefficient Kaw should easily be evaluable following the equation Kaw ≈ Pow / Koa.

2. Method

The calculation method is based on a regularly updated object-oriented database of more than 37100 compounds stored in their geometry-optimized 3D structure encompassing pharmaceuticals, herbicides, pesticides, fungicides, textile and other dyes, ionic liquids, liquid crystals, metal-organics, lab intermediates and many more, collecting – among further molecular experimental and calculated descriptors – a large set of experimental Pow, Koa and Kaw data in their logarithmic form, outlined in the respective sections below. Accordingly, their terms will henceforth be named logPow, logKoa and logKaw. It should be stressed that for the calculation of the partition coefficients the 3D geometry-optimized form of the compounds is not required - except for the algorithm-based determination of intramolecular hydrogen bridges, the impact of which will be discussed further down. In order to avoid structural ambiguities in the presentation of the chemical structures to the computer algorithm defining the molecules´ atom groups, a special algorithm ensured at the time of the input of a new compound that any six-membered aromatic ring system is defined by six aromatic bonds instead of alternating single-double-bonds.

2.1. Definition of the Atom and Special Groups

The details of the atom-group additivity model applied in the present study have been outlined in [11]. Accordingly, the definition of the atom types and their immediate atomic neighbourhood and meaning are retained as described in Table 1 of [11] and are also valid for both the logPow and logKoa descriptors. However, since these atom groups are not able to cover certain additional structural effects such as intramolecular hydrogen-bridge bonds and the influence of saturated cyclic compared to saturated noncyclic systems, a number of additional special groups had to be introduced. In a paper applying a different group-additivity method for the calculation of logPow, Klopman et al. [6] discovered that the inclusion of a correction value per carbon atom in pure saturated and unsaturated hydrocarbons improved the compliance with experiment. This has indeed been confirmed in the present study.
In order to take account of these and further potential structure-related peculiarities, the list of atom groups has been extended by “special groups” for which the column-title terms “atom type” and “neighbours” in the subsequent tables should not be taken literally, but which the computer algorithm treats in the same way as ordinary atom groups. In Table 1, the respective special groups, their nomenclature and meaning are detailed. In order to enable a future comparison of the contributions of the special-group parameter sets within this study, the same special groups have been applied for the calculation of both descriptors logPow and logKoa.
At present, the list of elements is limited to H, B, C, N, O, P, S, Si, and halogen, but an extension is always possible, provided that corresponding molecules with experimental descriptor data are available.

2.2. Calculation of the Atom- and Special-Group Contributions

Since the algorithm for the evaluation of the parameter values of the atom groups has been outlined in detail in [11], its four steps may just be summarized as follows: the first step encompasses the selection from the database of at present more than 37100 compounds of all the compounds for which the experimental descriptor data in question are known and their storage in a temporary compounds list. In the second step, the molecules in the temporary list are broken down into their constituting atom groups, whereby their central atoms, called “backbone atoms”, are characterized in that they are bound to at least two covalently bound neighbour atoms. The atom groups´ atom types and neighbour terms are generated according to the rules described in [11] and their occurrence is registered. Any molecule carrying an atom group that is not found in the pre-defined group-parameters list is discarded from the temporary compounds list. The third step generates an M x (N + 1) matrix, wherein M is the number of molecules, N + 1 is the number of pre-defined atom groups plus the container for the molecule´s descriptor value, and wherein the matrix element (i,j) contains the the number of registered occurrences of the jth atom group in the ith molecule. Atom groups and their related jth column, which are not present in any molecule of the temporary molecules list, are removed from the M x (N + 1) matrix. In the final step, this adjusted matrix is normalized into an Ax = B matrix, followed by its balancing by means of a fast Gauss–Seidel calculus [26] to receive the atom- and special-group parameters x. These parameters are then added to their related atom and special group in the corresponding parameters table assigned to the specific descriptor.
The group-parameters calculation is then immediately followed by the computation of each molecule’s descriptor value in question on the basis of these group parameters according to equation (1) outlined in the next section and compared with its experimental value to receive the related statistics data which are finally added at the bottom of the parameters table. Following the above-mentioned procedure resulted in the two parameters sets in Table 2 and Table 3, designed for the calculation of the molecules’ logPow and logKoa values, respectively.

2.3. Calculation of Descriptors logPow and logKoa

Based on the aforementioned respective atom-group parameters tables, the descriptors logPow and logKoa of a molecule can now easily be calculated by simply summing up the contribution of each atom and special group occurring in the molecule, following the equation (1), wherein i and j is the number of atom groups Ai and special groups Bj respectively, ai is the contribution of atom group Ai, bj the contribution of special group Bj, and c the constant listed at the top of the respective parameters table.
Descriptor calc = ∑aiAi + ∑bjBj + c
In Table 4, a typical example is presented with endosulfan sulfate, demonstrating the ease of the calculation of logKoa for which the experimental value was 9.68 [25]. Note that the term "endocyclic bonds" only concerns C-C single bonds.
Preprints 92250 g001
Figure 1. Endosulfan Sulfate (graphics by ChemBrain IXL).
Figure 1. Endosulfan Sulfate (graphics by ChemBrain IXL).
Preprints 92250 g001
Evidently, the group-additivity method is limited to the calculation of a molecule‘s logPow or logKoa for which a parameter value in the Tables 2 or 3 respectively is known for each atom group that is found in the molecule. Beyond this, since the reliability of these parameter values increases with the number of independent molecules upon which their calculation is based, the lowest reliability limit for these parameters was set to three molecules which as a consequence excluded any atom group being based on less than three molecules from further calculations. Accordingly, only atom groups for which the number of molecules is three or more, shown in the rightmost column of Table 2 and Table 3, have been accepted as “valid” for descriptor calculations. This explains the lower number of molecules for which the logPow and logKoa have been calculated (lines B, C and D in Table 2 and Table 3) than the number upon which the evaluation of the complete set of parameters is based (line A).

2.4. Cross-Validation Calculations

Plausibility of the group-parameters calculations has immediately been checked applying a 10-fold cross-validation algorithm, which comprises 10 recalculations of the complete set of group parameters, whereby before each recalculation every other 10th compound of the total compounds‘ list has temporarily been removed from calculation and separated into a test list, thus ensuring that each molecule has played once the role of a test sample. The combined test data have then been statistically worked up and their results added to the Table 2 and Table 3 at the bottom in lines E, F, G and H. It may be noticed that the total number of test compounds shown in the right-most column of the statistics lines is lower than that in the training set in lines B, C and D; this is a consequence of the requirement that only “valid” atom groups are to be used for descriptor calculations, and due to the 10% lower number of training samples in each recalculation, the number of “valid” atom groups (as defined in the prior section) tends to decrease to an unpredictable degree. Atom groups, which are represented by less than three molecules as shown in the rightmost column and are thus not “valid” for descriptor calculations, are therefore remnants of the parameters calculation based on the complete compounds set (line A in the Table 2 and Table 3). Nevertheless, they have deliberately been left in the Table 2 and Table 3 for use in future calculations with additional molecules potentially carrying under-represented atom groups in this ongoing project.

3. Sources

3.1. Sources of logPow Values

The majority of the experimental logPow data originates from the comprehensive collection of Klopman et al. [6], supplemented by works of Sangster [27] and Lipinski et al. [28], already cited in [11]. Additional data have been provided for unsubstituted and substituted, saturated and unsaturated hydrocarbons, alcohols and esters in the works of Tewari et al. [29], for heterocycles, hetarenes and carboxylic acids by Ghose et al. [4,5], complemented for amines, amides and nitro derivatives by Leo [8]. Further data for the aforementioned compound classes have been found in papers of Abraham et al. [30], for certain drugs by Hou and Xu [10] and Wang et al. [9], for organophosphorus derivatives by Czerwinski et al. [31], for the specific energetic compound 2,4-dinitroanisole by Boddu et al. [32], for a number of fluorobenzenes, -anilines and -phenols by Li et al. [33] and finally for a number of pesticides and oil constituents in a paper of Saranjampour et al. [34].

3.2. Sources of logKoa Values

Recently, Ebert et al. [35] published a comprehensive collection of more than 2000 experimental logKoa values upon which the present study is essentially based. This set of data has been complemented with data for 75 chloronaphthalene derivatives by Puzyn et al. [36], for 14 PAHs by Odabasi et al. [37], for some methylsiloxanes and dimethylsilanol by Xu and Kropscott [38] and for ethyl nitrate by Easterbrook et al. [39].

3.3. Sources of logKaw Values

Ebert’s paper [25], cited in the introductory section, presented in their supplementary information a large collection of experimental logKaw data, which served as reference values for the calculated data. Sander [40] provided an extensive library of Henry’s law constants for more 2600 compounds which, after translation into logKaw values at 298.15K, complemented Ebert’s data set.

4. Results

4.1. Partition Coefficient logPow

As shown at the bottom of Table 2, the number of molecules upon which the present group-parameters set is based is with 3332 substantially larger than the 2780 samples in our earlier paper [11]. Beyond this, the significantly better statistical results in Table 2 (lines B to H) with e.g. a cross-validated standard deviation S of 0.42 (line H) vs. the earlier value of 0.51 is the result of the removal of molecules from the parameters computation for which the experimental value deviates by more that three times the value of S. The thus 122 removed molecules (3.5% of the total set) have been collected in an outliers list, available in the Supplementary Materials. The larger number of compounds for the group-parameters computation not only significantly improved the statistical results but also enlarged the list of "valid" atom groups from 195 to 214, enabling the calculation of the logPow value of at present 29462 molecules (79.4% of the total dataset). The correlation coefficients R2 of 0.9648 and (cross-validated) Q2 of 0.9599, based on 3246 and 3164 molecules respectively, are significantly better than in our earlier paper [11] and clearly outperform Klopman’s [6] results, which are based on less than half the number of molecules used in the present case and reveal an R2 and Q2 value of 0.93 and 0.926 respectively, applying a group-additivity method which is comparable to ours. As shown in the correlation diagram of Figure 2 and the histogram for Figure 3, the experimental logPow values range from -4.6 to +12.53 with a cross-validated standard error S of 0.42 with a fairly even Gaussian error distribution.
It is worth mentioning that the observation discussed in our earlier paper (see Table 9 in [11]) concerning the two forms of amino acids (nonionic or zwitterionic) is not only confirmed by the new and extended group-parameters set of Table 2, but that the logPow differences in nearly all cases even more clearly distinguish the two forms. On the other hand, the ambiguous results concerning the keto/enol forms of the compounds listed in Table 10 in [11] could not be lifted by the new parameters set, which is not surprising in view of the sometimes strong solvent dependence of the equilibrium, as exemplified with acetylacetone [41]. In view of the discussion of certain particularities concerning the subsequent calculation of the third partition coefficient logKaw in section 4.3., it should be stressed at this point that the calculated logPow values for the hydrocarbons do not show any abnormal or systematic deviations from experimental values.

4.2. Partition Coefficient logKoa

The calculation of the group-parameters set of Table 3 used for the prediction of the logKoa values essentially based on the curated data set provided in Ebert’s paper [35], whereby compounds with just one "backbone atom" such as the halomethanes or hydrocyanide had to be omitted as they are obviously not calculable by the present method. After the removal of another 129 compounds as outliers (6.36% of the total), following the same exclusion criterion as in the previous section, 1900 samples with their experimental data (line A in Table 3) remained for the computation of the group-parameter values. Again, the outliers have been collected in a separate list available in the Supplementary Materials for readers who might want to re-evaluate their logKoa values.
The subsequent calculation of the logKoa values of 1829 training and 1765 test molecules based on 167 "valid" atom and special groups (line A) revealed excellent statistical results with a correlation coefficient R2 of 0.9765, a standard deviation s of 0.44 (lines B and D), and a cross-validated Q2 of 0.9717 with a corresponding S of 0.48 (lines F and H), visualized in the correlation diagram on Figure 4 and the histogram on Figure 5. These statistics data even outperform those given in Ebert’s paper and thus also their competing methods mentioned therein such as COSMOtherm [42] and EPI-Suite KOAWIN [43], not only confirming the versatility but also the reliability of the present group-additivity approach, which allowed the calculation of the logKoa value for 27044 molecules (72.9% of the entire database). Again, it should be kept in mind that just like in section 4.1. there could not be observed any particularly large or systematic deviations between the experimental and calculated logKoa values for the hydrocarbons.

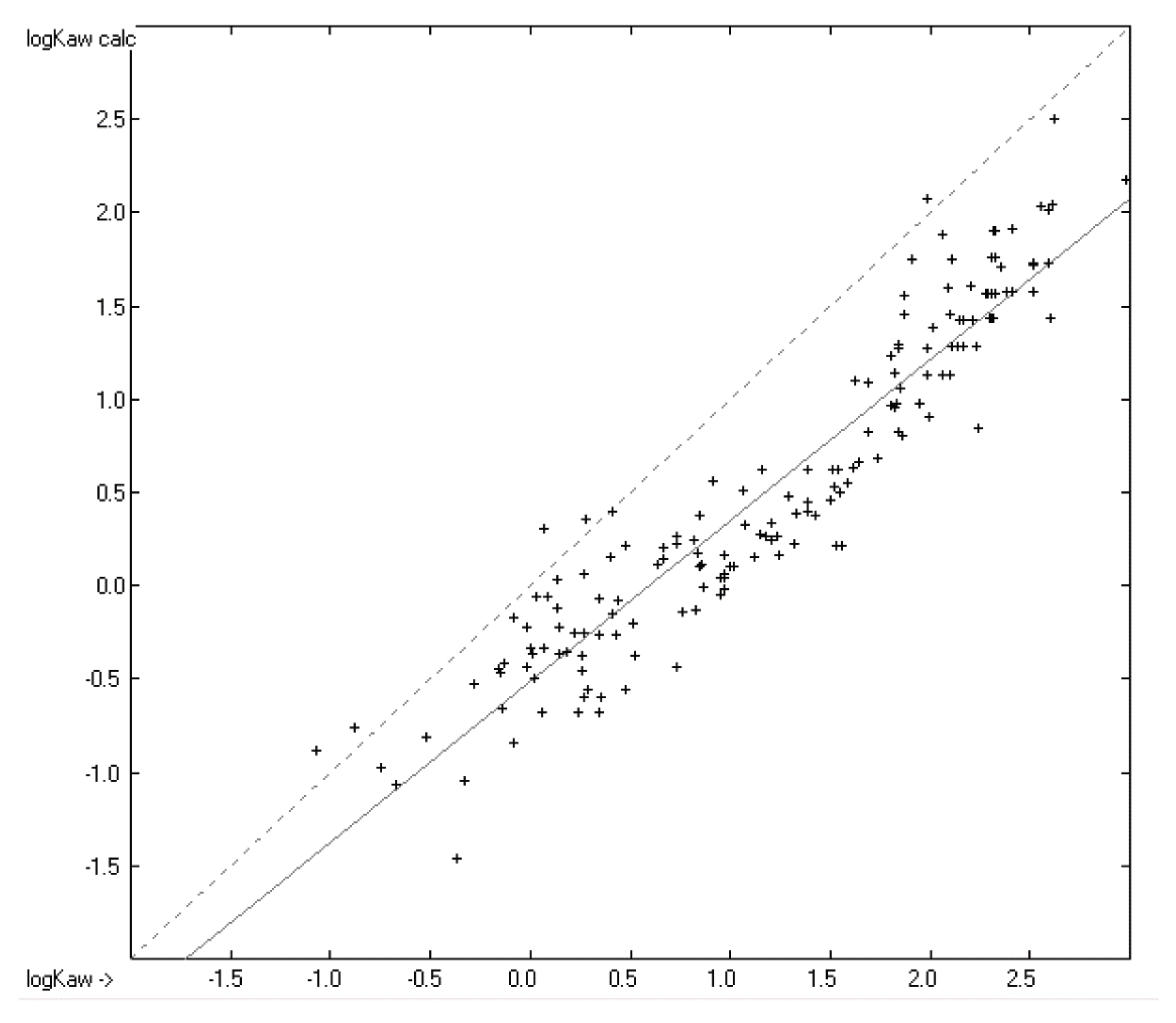
4.3. Partition Coefficient logKaw

Once the partition coefficients logPow and logKoa have been calculated by means of the group-additivity method based on Table 2 and Table 3 respectively, it was easy to determine the logKaw values, applying equation (2) on each molecule in the database for which both descriptors have been calculated, adding up to 26220 molecules. In order to assess the quality of the logKaw values, it is important to recognize the flaws of this approach: while the logPow values have been experimentally measured in a mixture of water-saturated octanol and octanol-saturated water, the logKoa measurements occurred in dry octanol, an aspect that has been discussed in detail by Ebert et al. [35]. Hence, equation (2) serves only as an aproximation. In addition, since both descriptors on the right side of the equation appear with their own standard error, the error-propagation rule stipulates a standard error of logKaw that is clearly larger than any of the two constituting descriptors. Entering the standard errors S for the test molecules of 0.42 (for logPow) and 0.48 (for logKoa) into an error-propagation calculation, the expected standard error S for logKaw is 0.638.
logKaw (calc) = logPow (calc) - logKoa (calc)
In order to test the reliability of the thus calculated logKaw values, a representative number of experimentally determined logKaw data, extracted from the comprehensive databases of Ebert et al. [25] and Sander [40], have been added to the database. In the latter case, the Henry’s law solubility constants Hscp have been translated into the corresponding logKaw values at 298.15K. The comparison of the calculated with the experimental logKaw values is visualized in the correlation diagram of Figure 6 and the histogram in Figure 7.
The complete set of experimental data has been separated from the outliers, applying the same exclusion conditions as for the logPow and logKoa values, and the outliers have been collected in a corresponding list, available in the Supplementary Material. Comparison of the remaining dataset with the calculated values yielded a standard error of 0.67, slightly higher than predicted by the error-propagation calculation. A detailed analysis of the experimental data revealed two potential explanations for the inordinate scatter: 1) Within a series of substitution isomers, e. g. the tetra- or hexachlorobiphenyls, the tri- or pentachlorodiphenyl ethers or the dichloroanisoles, the experimental logKaw values varied in a range of up to and over 1 unit, which is hard to assign to the specific positioning of the substituents. At any rate, the group-additivity-based calculation of the logPow and logKoa values is not able to distinguish between these substitution isomers. 2) Sander’s comprehensive database of Henry’s law constants [40], listing the experimental Hscp values for a compound originating from various authors, showed for many compounds large differences of their Hscp values, in some cases exceeding one unit after translation into logKaw, e. g. for undecane, acetylacetone or anthraquinone.
A thourough analysis of the correlation diagram in Figure 6 and the histogram in Figure 7 revealed an interesting peculiarity, visible as an indentation at the upper end of the correlation diagram and as a weak hump on the right side of the histogram: except for some siloxanes with experimental logKaw values above 1.6 and normal scatter about calculated values, the predicted logKaw for the remaining compounds having experimental logKaw values above -1.0 are nearly systematically too low by ca. 0.5 - 1 units. It turned out that they are all pure hydrocarbons, in particular alkanes, alkenes and alkynes. The correlation diagram of the logKaw data in Figure 8, focussing on these hydrocarbons, confirms this observation.
Since, as was mentioned in section 4.1. and 4.2., no particularly large or systematic deviations between the experimental and calculated logPow and logKoa data for the hydrocarbons could be detected, a potential explanation for this peculiarity might be based on the experimental conditions for the determination of the logPow values as mentioned by Ebert et al. [35]: since water-saturated octanol is a more polar solvent than pure octanol, whereas octanol-saturated water is less polar than pure water, the experimental logPow values, measured in an octanol/water mixture, tend to be shifted to smaller absolute values than theory would predict. While this is true for all measured solutes, it is possibly most effective for the least polar solutes such as the mentioned hydrocarbons, thus leading to experimental logPow values that are particularly low for the hydrocarbons. As a consequence, their calculation based on the group-additivity method predicts equally low logPow values, which again leads to low logKaw data when equation (2) is applied and then compared with experimental logKaw values that are determined under pure air/water conditions.

4.4. Interpretation of the Special-Groups Contributions for logPow and logKoa, and ultimately for logKaw

While the atom-group parameters are descriptor-specific and their comparison between descriptors does not make sense, special groups serve as differentiators of molecules that carry these groups from those that do not. Therefore, their meaning is descriptors-overlapping, their values however must be viewed in the context of the value range of the descriptors. In the present case, the value ranges of logPow and logKoa are similar (ca. 17 log units) and in the same area, a direct comparison of the special-group contributions in Table 2 and Table 3 is permissible and led to a few interesting observations: while the groups "(COH)n", "Alkane", "Unsaturated HC" and "Endocyclic bonds" in both tables only contributed to a minor degree (but nevertheless improved the statistical results) and consequently showed only minor differences between the two tables, a significant differentiation was found for the groups "H / H Acceptor" and "(COOH)n". The former special group, taking account of intramolecular hydrogen bridges, indicates a small but clear higher tendency of a compound carrying an intramolecular H-bridge towards the octanol side in an octanol/water mixture than without, thus raising the logPow value. In contrast, the same H-bridge-carrying molecule has its inclination significantly shifted more to the air side in an octanol/air environment than without H-bridge, expressed in a lower logKoa value. The reason may be found in the lower solvent-solute interaction caused by the H-bridge being bound intramolecularly, leading in both cases to a preference of the less polar of the respective two media. A typical example is the compounds couple 2- and 3-nitroaniline, sampled in Table 5, where the former molecule carries a H-bridge between an amino-H and an oxygen of the nitro group.
An inverse effect can be found with molecules carrying two or more carboxylic acid functions: while the additional contribution of a second or third COOH function shows little effect in an octanol/water environment with a slightly increased shift towards water, leading to a lower logPow value, in an octanol/air environment each additional COOH group drastically tilts the equlibrium towards the octanol side, thus strongly raising the logKoa value. This may be demonstrated by the couple of hexanoic/1,6-hexanedioic acid, where both have the same carbon-chain length but where the second molecule carries two carboxylic acid functions, which tilts the octanol/air equilibrium by a factor of more than 10000 towards the octanol side as shown in Table 6. Now, it is well known that monocarboxylic acids usually exist as dimeric associates in all three aggregate states. This association effect on the solubility is inherently taken account of in the atom-group parameters evaluation for the COOH function. On the other hand, dicarboxylic acids do not only form dimers but also cyclical and linear oligomeric associates, with drastic consequences on their solubility in the various solvents. It is these additional associations that are considered by the special group "(COOH)n".
As a consequence, solutes with a low tendency to interact with solvents, either inherent or induced by intramolecular hydrogen bridges, show a trend to higher logKaw values; the additional intermolecular association of di- and tricarboxylic acids, on the other hand, results in a significantly lower logKaw value, as is exemplified in Table 7, where the respective calculated data of the Table 5 and Table 6 have been applied in equation (2). The experimental logKaw values have been extracted from Ebert et al. [25].

5. Conclusions

The present study, which is part of an ongoing project, put to use a tool for the simple and reliable calculation of the two partition coefficients logPow and logKoa, that has proven its unmatched versatility in the equally reliable prediction of up to now 19 physical, thermodynamic, solubility-, optics-, charge-, and environment-related molecular descriptors [11,44,45,46,47,48,49,50], based on a common group-additivity method. The large database of more than 3300 and 1900 experimental data, respectively, upon which the group parameters for the logPow and logKoa calculations are founded enabled their prediction for nearly 29500 and more than 27000 molecules, respectively, of the presently more than 37100 compounds in ChemBrain’s database. In addition, these results also allowed the trustworthy calculation of the third partition coefficient logKaw for more than 26000 compounds. The big advantage of the present approach is its ease of use by simply adding by means of paper and pencil the parameters of the atoms and groups found in a particular molecule that are listed in the respective Table 2 and Table 3.
The mentioned project’s software is called ChemBrain IXL, available from Neuronix Software (www.neuronix.ch, Rudolf Naef, Lupsingen, Switzerland).

Supplementary Materials

The lists of compounds used in the present work, collected in their 3D structure together with their experimental data, are available as standard SDF files for use in external chemical software under the names of "S01. Compounds List for logPow-Parameters Calculations.sdf", "S02. Compounds List for logKoa-Parameters Calculations.sdf" and "S03. Compounds List with exp logKaw Data". The compounds used in the correlation diagrams and histograms are listed with their names and experimental and calculated data under the respective names of "S04. Compounds with Experimental vs. Calculated logPow Values.doc", "S05. Compounds with Experimental vs. Calculated logKoa Values.doc", S06. Compounds with Experimental vs. Calculated logKaw Values.doc" and "S07. Alkanes, Alkenes and Alkynes with Exp. vs. Calc. logKaw Values.doc". In addition, for each of the three partition coefficients a list of their outliers has been added under the names of "S08. Outliers of logPow.doc", "S09. Outliers of logKoa.doc" and "S10. Outliers of logKaw.doc". Beyond this, the supplementary material encompasses all the figures and tables cited in the text as .tif and .doc files, respectively.

Author Contributions

R. Naef developed project ChemBrain and its software upon which this paper is based, and also fed the database, calculated and analysed the results and wrote the paper. W. E. Acree suggested the extension of ChemBrain’s tool and contributed experimental data and the great majority of the literature references. Beyond this, R. Naef is indebted to W. E. Acree for the many valuable discussions.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in supplementary material.

Acknowledgments

R. Naef is indebted to the library of the University of Basel for allowing him full and free access to the electronic literature database.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Simonich, S. L.; Hites, R. A. Organic Pollutant Accumulation in Vegetation. Environ. Sci. Technol. 1995, 29, 2905−2914. [CrossRef]
  2. McLachlan, M. S. Bioaccumulation of Hydrophobic Chemicals in Agricultural Food Chains. Environ. Sci. Technol. 1996, 30, 252−259. [CrossRef]
  3. Doucette, W. J.; Shunthirsasingham, C.; Dettenmaier, E. M.; Zaleski, R. T.; Fantke, P.; Arnot, J. A. A Review of Measured Bioaccumulation Data on Terrestrial Plants for Organic Chemicals:Metrics, Variability, and the Need for Standardized Measurement Protocols. Environ. Toxicol. Chem. 2018, 37, 21−33. [CrossRef]
  4. Ghose, A.K.; Crippen, G.M. Atomic physicochemical parameters for three-dimensional structure-directed quantitative structure-activity relationships I. Partition coefficients as a measure of hydrophobicity. J. Computer. Chem. 1986, 7, 565–577. [CrossRef]
  5. Ghose, A.K.; Pritchett, A.; Crippen, G.M. Atomic physicochemical parameters for three dimensional structure directed quantitative structure-activity relationships III: Modeling hydrophobic interactions. J. Comput. Chem. 1988, 9, 80–90. [CrossRef]
  6. Klopman, G.; Li, J.-Y.; Wang, S.; Dimayuga, M. Computer automated log P calculations based on an extended group contribution approach. J. Chem. Inf. Comput. Sci. 1994, 34, 752–781. [CrossRef]
  7. Visvanadhan, V. N.; Ghose, A.K.; Revankar, G.R.; Robins, R.K. Atomic physicochemical parameters for three dimensional structure directed quantitative structure-activity relationships. 4. Additional parameters for hydrophobic and dispersive interactions and their application for an automated superposition of certain naturally occurring nucleoside antibiotics. J. Chem. Inf. Comput. Sci. 1989, 29, 163–172. [CrossRef]
  8. Leo, A.J. Calculating log Poct from structures. Chem. Rev. 1993, 93, 1281–1306. [CrossRef]
  9. Wang, R.; Fu, Y.; Lai, L. A new atom-additive method for calculating partition coefficients. J. Chem. Inf. Comput. Sci. 1997, 37, 615–621. [CrossRef]
  10. Hou, T.J.; Xu, X.J. ADME evaluation in drug discovery. 2. Prediction of partition coefficient by atom-additive approach based on atom-weighted solvent accessible surface areas. J. Chem. Inf. Comput. Sci. 2003, 43, 1058–1067. [CrossRef]
  11. Naef, R. A Generally Applicable Computer Algorithm Based on the Group Additivity Method for the Calculation of Seven Molecular Descriptors: Heat of Combustion, LogPO/W, LogS, Refractivity, Polarizability, Toxicity and LogBB of Organic Compounds; Scope and Limits of Applicability. Molecules 2015, 20, 18279-18351. [CrossRef]
  12. Chen, J.; Harner, T.; Schramm, K.W.; Quan, X.; Xue, X.; Wu, W.; Kettrup, A. Quantitative relationships between molecular structures, environmental temperatures and octanol/air partition coefficients of PCDD/Fs. Sci. Total Environ. 2002, 300, 155-166. [CrossRef]
  13. Chen, J.; Harner, T.; Yang, P.; Quan, X.; Chen, S.; Schramm, K.W.; Kettrup, A. Quantitative predictive models for octanol/air partition coefficients of polybrominated diphenyl ethers at different temperatures. Chemosphere 2003, 51, 577-584. [CrossRef]
  14. Chen, J.; Harner, T.; Schramm, K.W.; Quan, X.; Xue, X.; Kettrup, A. Quantitative relationships between molecular structures, environmental temperatures and octanol/air partition coefficients of polychlorinated biphenyls. Comput. Biol. Chem. 2003, 27, 405-421. [CrossRef]
  15. Hongxia, Z.; Jingwen, C.; Xie, Q.; Baocheng, Q.; Xinmiao, L. Octanol/air partition coefficients of polybrominated biphenyls. Chemosphere 2009, 74, 1490-1494. [CrossRef]
  16. Staikova, M.; Wania, F.; Donaldson, D. Molecular polarizability as a single parameter predictor of vapour pressures and octanoleair partitioning coefficients of non-polar compounds: a priori approach and results. Atmos. Environ. 2004, 38, 213-225. [CrossRef]
  17. Zhao, H.; Zhang, Q.; Chen, J.; Xue, X.; Liang, X. Prediction of octanol/air partition coefficients of semivolatile organic compounds based on molecular connectivity index. Chemosphere 2005, 59, 1421-1426. [CrossRef]
  18. Zeng, X.L.; Zhang, X.L.; Wang, Y. Qspr modeling of n-octanol/air partition coefficients and liquid vapor pressures of polychlorinated dibenzo-p-dioxins. Chemosphere 2013, 91, 229-232. [CrossRef]
  19. Liu, H.; Shi, J.; Liu, H.; Wang, Z. Improved 3D-QSPR analysis of the predictive octanol/air partition coefficients of hydroxylated and methoxylated polybrominated diphenyl ethers. Atmos. Environ. 2013, 77, 840-845. [CrossRef]
  20. Jiao, L.; Gao, M.; Wang, X.; Li, H. QSPR study on the octanol/air partition coefficient of polybrominated diphenyl ethers by using molecular distance-edge vector index. Chem. Cent. J. 2014, 8. [CrossRef]
  21. Chen, Y.; Cai, X.; Jiang, L.; Li, Y. Prediction of octanol-air partition coefficients for polychlorinated biphenyls (PCBs) using 3D-SQAR models. Ecotoxicol. Environ. Saf. 2016, 124, 202-212. [CrossRef]
  22. Fu, Z.; Chen, J.; Li, X.; Wang, Y.; Yu, H. Comparison of prediction methods for octanol-air partition coefficients of diverse organic compounds. Chemosphere 2016, 148, 118-125. [CrossRef]
  23. Jin, X.; Fu, Z.; Li, X.; Chen, J. Development of polyparameter linear free energy relationship models for octanol/air partition coefficients of diverse chemicals. Environ. Sci.: Process. Impact. 2017, 19, 300-306. [CrossRef]
  24. Li, X.; Chen, J.; Zhang, L.; Qiao, X.; Huang, L. The fragment constant method for predicting octanol/air partition coefficients of persistent organic pollutants at different temperatures. J. Phys. Chem. Ref. Data 2006, 35, 1365-1384. [CrossRef]
  25. Ebert, R.-U.; Kühne, R.; Schüürmann, G. Henry’s Law Constant ─ A General-Purpose Fragment Model to Predict Log Kaw from Molecular Structure. Environ. Sci. Technol. 2023, 57, 1, 160–167. [CrossRef]
  26. Hardtwig, E. Fehler- Und Ausgleichsrechnung; Bibliographisches Institut AG: Mannheim, Germany, 1968.
  27. Sangster, J. Octanol-water partition coefficients of simple organic compounds. J. Phys. Chem. Ref. Data 1989, 18, 1111–1229. [CrossRef]
  28. Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 1997, 23, 3–25. [CrossRef]
  29. Tewari, Y. B.; Miller, M. M.; Wasik, St. P.; Martire, D. E. Aqueous Solubility and Octanol/Water Partition Coefficient of Organic Compounds at 25.0 °C. J. Chem. Eng. Data 1982, 27, 451-454. [CrossRef]
  30. Abraham, M. H.; Chadha, H. S.; Whiting, G. S.; Mitchell, R. C. Hydrogen Bonding. 32. An Analysis of Water-Octanol and Water-Alkane Partitioning and the delta log P Parameter of Seiler. J. Pharm. Sci. 1994, 83(8) 1085 -1100. [CrossRef]
  31. Czerwinski, St. E.; Skvorak, J. P.; Maxwell, D. M.; Lenz, D. E.; Baskin, St. I. Organophosphorus Compounds on Biodistribution and Percutaneous Toxicity. J. Biochem. Mol. Tox. 2006, 20(5) 241-246. [CrossRef]
  32. Boddu, V. M.; Abburi, K.; Maloney, St. W.; Damavarapu, R. Thermophysical Properties of an Insensitive Munitions Compound, 2,4-Dinitroanisole. J. Chem. Eng. Data 2008, 53, 1120–1125. [CrossRef]
  33. Li, X.-J.; Shan, G.; Liu, H.; Wang, Z.-Y. Determination of lgKow and QSPR Study on Some Fluorobenzene Derivatives. Chin. J. Struct. Chem. 2009, 28(10) 1236-1241.
  34. Saranjampour, P.; Vebrosky, E. N.; Armbrust, K. L. Salinity Impacts on Water Solubility and n-Octanol/Water Partition Coefficients of Selected Pesticides and Oil Constituents. Environ Toxicol Chem 2017, 36, 2274–2280. [CrossRef]
  35. Ebert, R.-U.; Kühne, R.; Schüürmann, G. Octanol/Air Partition Coefficient. A General-Purpose Fragment Model to Predict Log Koa from Molecular Structure. Environ. Sci. Technol. 2023, 57, 976−984. [CrossRef]
  36. Puzyn, T.; Falandysz, J.; Rostkowski, P.; Piliszek, S.; Wilczynska, A. Computational estimation of logarithm of octanol/air partition coefficients and subcooled vapour pressures for each of 75 chloronaphtalene congeners. Phys.-Chem. Prop., Distr. Model. Organohal. Compds. 2004, 66, 2354- 2360. [CrossRef]
  37. Odabasi, M.; Cetin, E.; Sofuoglu, A. Determination of octanol–air partition coefficients and supercooled liquid vapor pressures of PAHs as a function of temperature: Application to gas–particle partitioning in an urban atmosphere. Atm. Environ. 2006, 40, 6615-6625. [CrossRef]
  38. Xu, Sh.; Kropscott, B.; Method for Simultaneous Determination of Partition Coefficients for Cyclic Volatile Methylsiloxanes and Dimethylsilanediol. Anal. Chem. 2012, 84, 1948−1955. [CrossRef]
  39. Easterbrook, K. D.; Vona, M. A,; Osthoff, H. D. Measurement of Henry’s law constants of ethyl nitrate in deionized water, synthetic sea salt solutions, and n-octanol. Chemosphere, 2024, 346, 140482. [CrossRef]
  40. Sander, R. Compilation of Henry’s law constants (version 5.0.0) for water as solvent. Atmos. Chem. Phys., 2023, 23, 10901–12440. [CrossRef]
  41. Allen, G.; Dwek, R.A. An n.m.r. study of keto-enol tautomerism in β-diketones. J. Chem. Soc. B 1966, 161–163. [CrossRef]
  42. COSMOlogic GmbH Co. KG. A Dassault Systèmes company, version 19.0.4, COSMOthermX, 2019. www.cosmologic.de.
  43. US EPA. Estimation Programs Interface Suite for Microsoft Windows, v. 4.11, module KOAWIN v. 1.11, United States Environmental Protection Agency: Washington, DC, USA, 2015.
  44. Naef, R.; Acree, W.E., Jr. Calculation of Five Thermodynamic Molecular Descriptors by Means of a General Computer Algorithm Based on the Group-Additivity Method: Standard Enthalpies of Vaporization, Sublimation and Solvation, and Entropy of Fusion of Ordinary Organic Molecules and Total Phase-Change Entropy of Liquid Crystals. Molecules 2017, 22, 1059. [CrossRef]
  45. Naef, R.; Acree, W.E. Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient inWater at Infinite Dilution. Molecules 2018, 23, 5. [CrossRef]
  46. Naef, R.; Acree, W.E., Jr. Calculation of the Surface Tension of Ordinary Organic and Ionic Liquids by Means of a Generally Applicable Computer Algorithm Based on the Group-Additivity Method. Molecules 2018, 23, 1224. [CrossRef]
  47. Naef, R. Calculation of the Isobaric Heat Capacities of the Liquid and Solid Phase of Organic Compounds at 298.15K by Means of the Group-Additivity Method. Molecules 2020, 25, 1147. [CrossRef]
  48. Naef, R.; Acree, W.E., Jr. Calculation of the Vapour Pressure of Organic Molecules by Means of a Group-Additivity Method and Their Resultant Gibbs Free Energy and Entropy of Vaporization at 298.15 K. Molecules 2021, 26, 1045. [CrossRef]
  49. Naef, R.; Acree,W.E., Jr. Revision and Extension of a Generally Applicable Group-Additivity Method for the Calculation of the Standard Heat of Combustion and Formation of Organic Molecules. Molecules 2021, 26, 6101. [CrossRef]
  50. Naef, R.; Acree, W.E., Jr. Revision and Extension of a Generally Applicable Group Additivity Method for the Calculation of the Refractivity and Polarizability of Organic Molecules at 298.15 K. Liquids, 2022, 2, 327–377. [CrossRef]
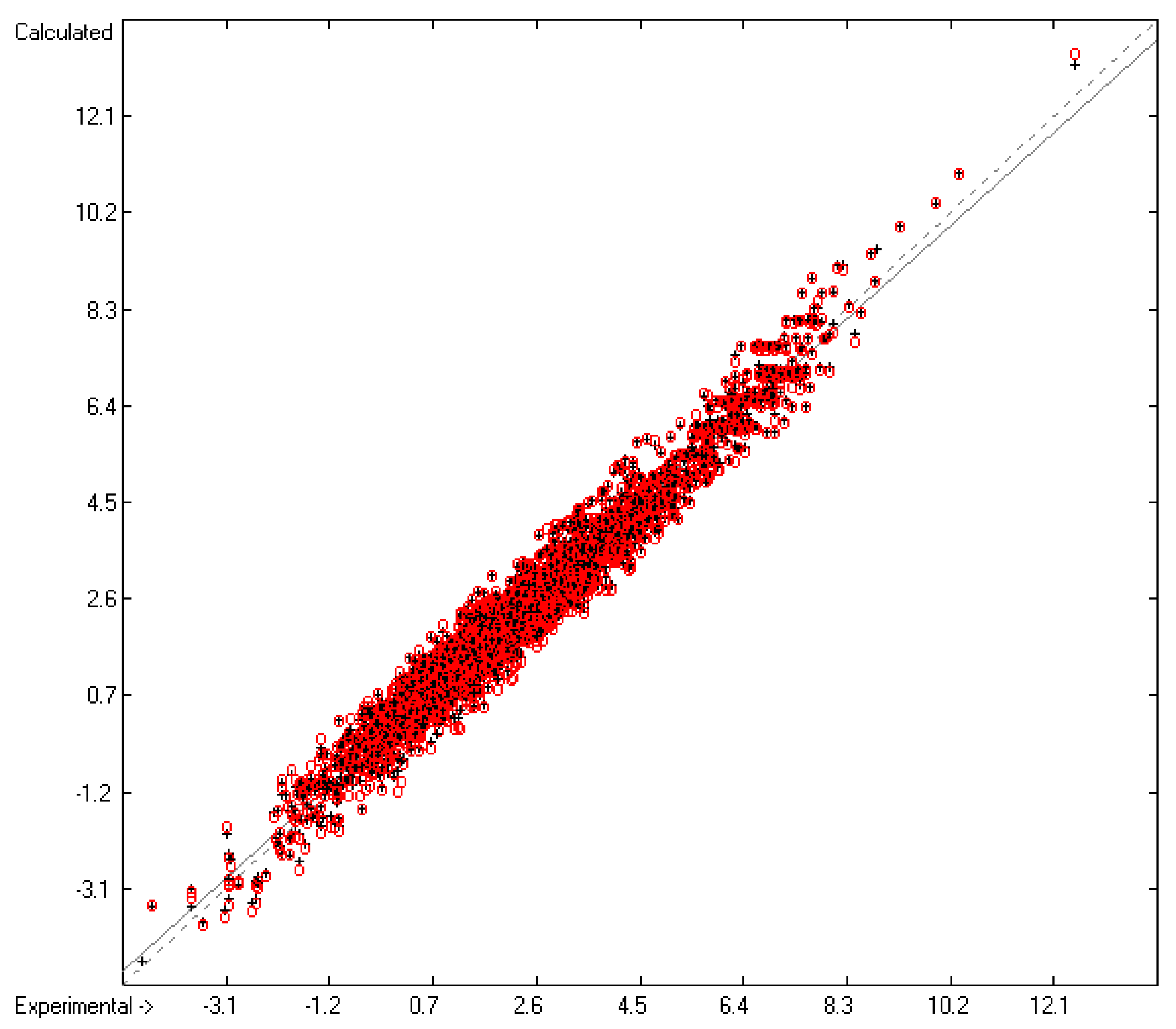
Preprints 92250 g002
Figure 2. Correlation diagram of the logPow data. Cross-validation data are superpositioned as red circles. (10-fold cross-valid.: N=3246, Q2=0.9599, regression line: intercept=0.1052; slope=0.9636).
Figure 2. Correlation diagram of the logPow data. Cross-validation data are superpositioned as red circles. (10-fold cross-valid.: N=3246, Q2=0.9599, regression line: intercept=0.1052; slope=0.9636).
Preprints 92250 g002
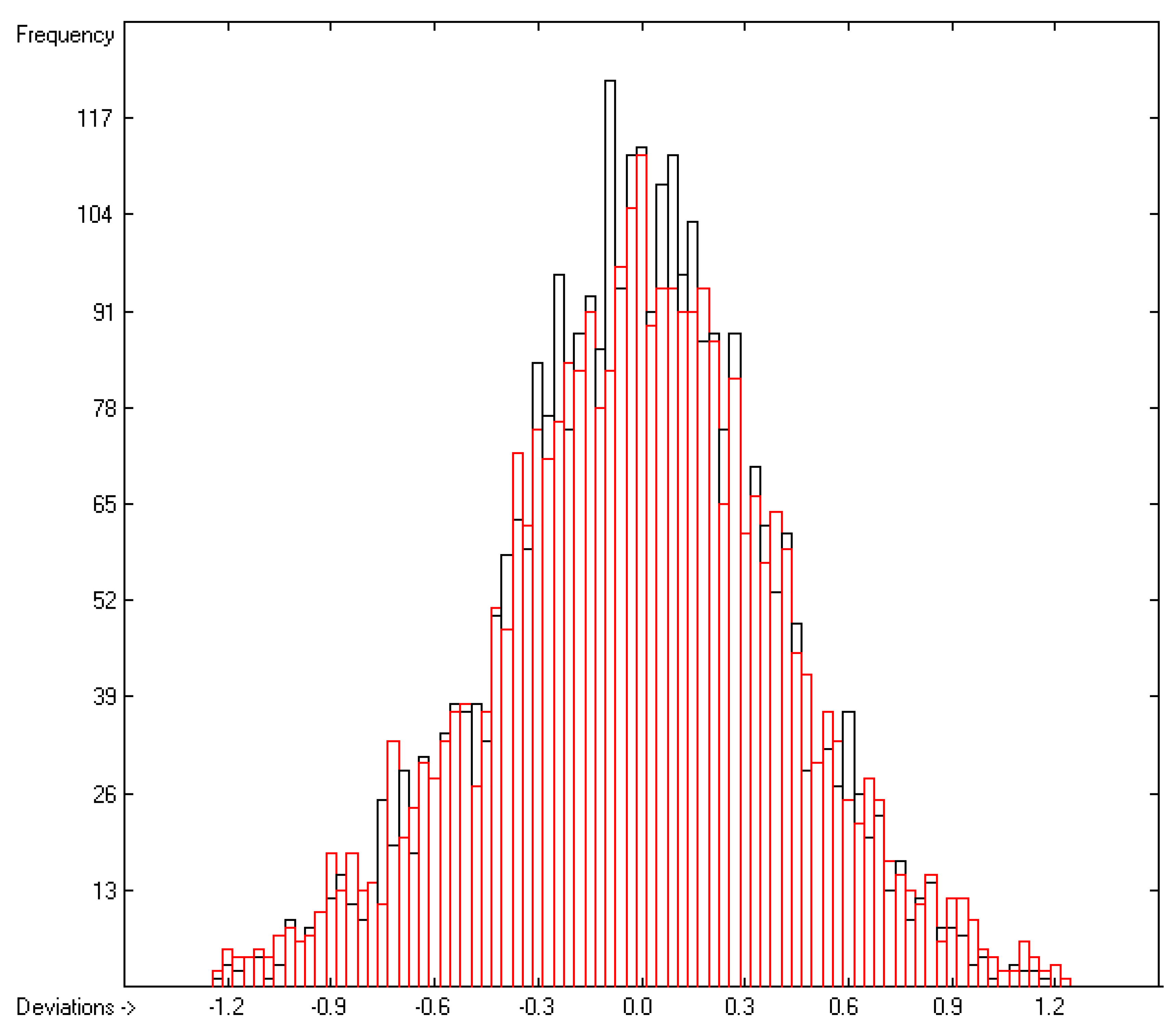
Preprints 92250 g003
Figure 3. Histogram of the logPow data. Cross-validation data are superpositioned as red bars. (Preprints 92250 i001 =0.39; S =0.42; experimental values range from -4.6 to +12.53).
Figure 3. Histogram of the logPow data. Cross-validation data are superpositioned as red bars. (Preprints 92250 i001 =0.39; S =0.42; experimental values range from -4.6 to +12.53).
Preprints 92250 g003
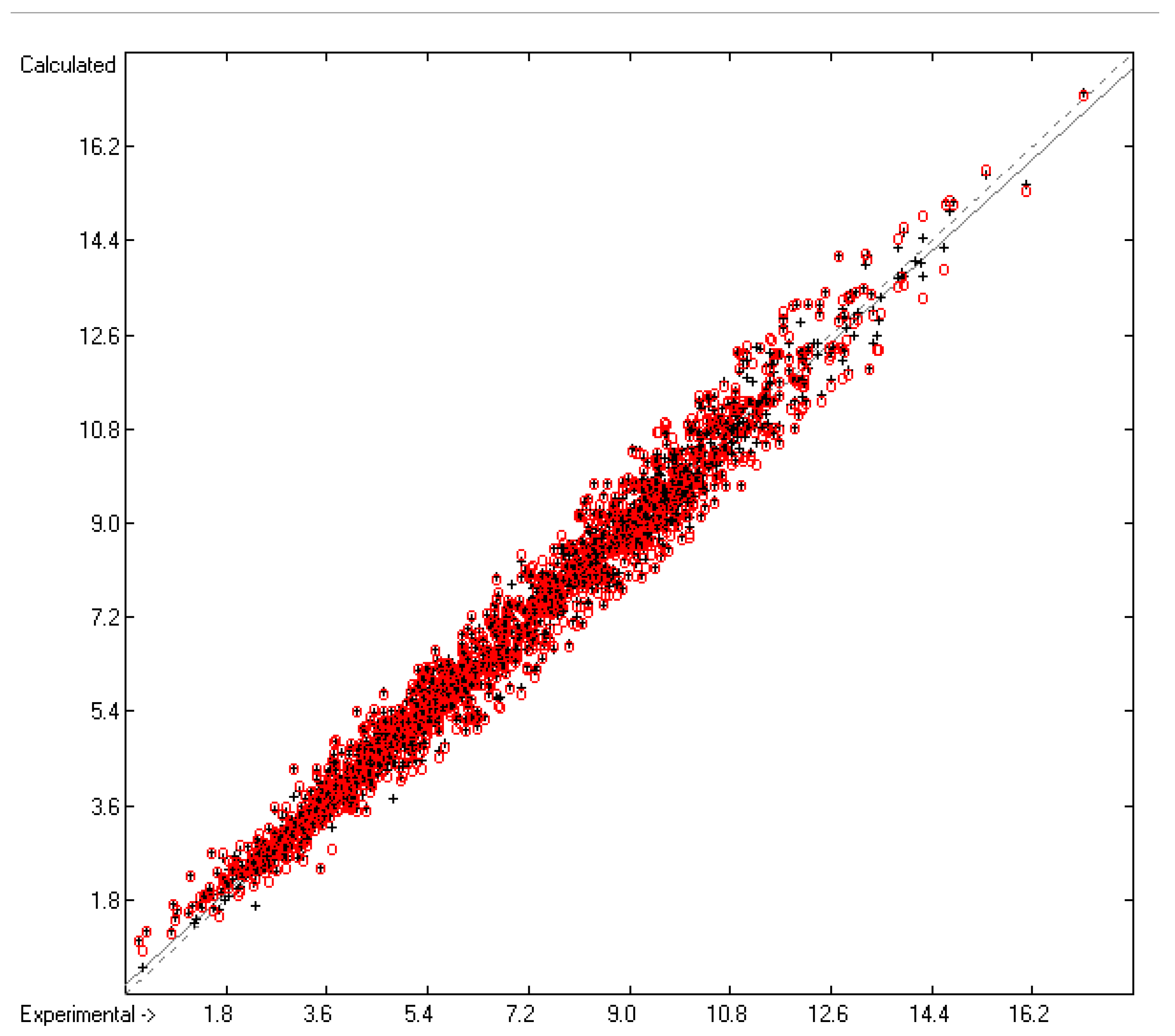
Preprints 92250 g004
Figure 4. Correlation diagram of the logKoa data. Cross-validation data are superpositioned as red circles. (10-fold cross-valid.: N=1829, Q2=0.9717, regression line: intercept=0.1997; slope=0.9729, MAPD= 6.39%).
Figure 4. Correlation diagram of the logKoa data. Cross-validation data are superpositioned as red circles. (10-fold cross-valid.: N=1829, Q2=0.9717, regression line: intercept=0.1997; slope=0.9729, MAPD= 6.39%).
Preprints 92250 g004
Preprints 92250 g005
Figure 5. Histogram of the logKoa data. Cross-validation data are superpositioned as red bars. (Preprints 92250 i001 =0.44; S =0.48; experimental values range from 0.28 to 17.15).
Figure 5. Histogram of the logKoa data. Cross-validation data are superpositioned as red bars. (Preprints 92250 i001 =0.44; S =0.48; experimental values range from 0.28 to 17.15).
Preprints 92250 g005
Preprints 92250 g006
Figure 6. Correlation diagram of the logKaw data. (N=1937, Q2=0.9467, regression line: intercept= -0.4196; slope=0.9044).
Figure 6. Correlation diagram of the logKaw data. (N=1937, Q2=0.9467, regression line: intercept= -0.4196; slope=0.9044).
Preprints 92250 g006
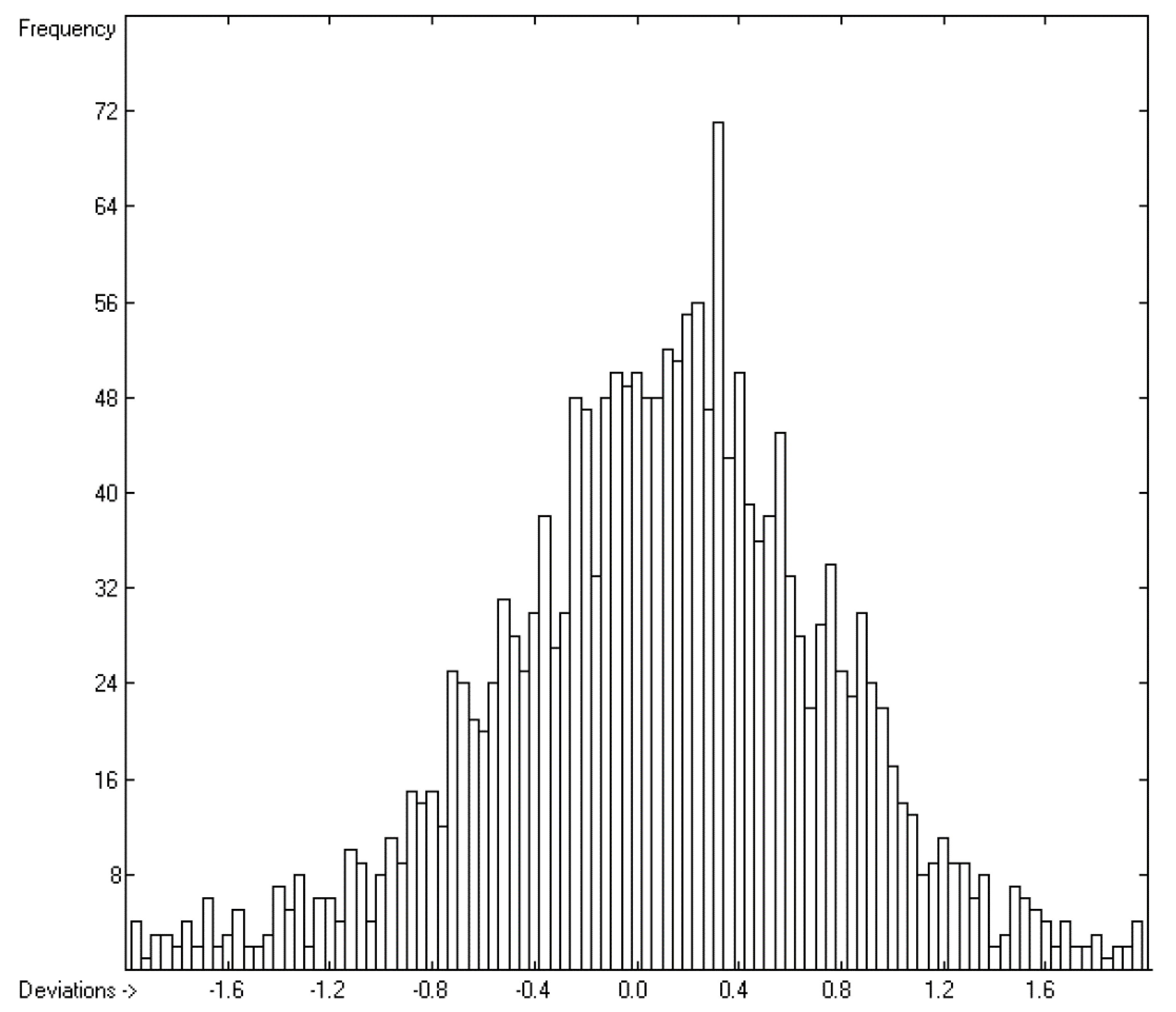
Preprints 92250 g007
Figure 7. Histogram of the logKaw data. S =0.67; experimental values range from -17.99 to +3.71).
Figure 7. Histogram of the logKaw data. S =0.67; experimental values range from -17.99 to +3.71).
Preprints 92250 g007
Preprints 92250 g008
Figure 8. Correlation diagram of the logKaw data for alkanes, alkenes and alkynes. (N=170).
Figure 8. Correlation diagram of the logKaw data for alkanes, alkenes and alkynes. (N=170).
Preprints 92250 g008
Table 1. Special Groups and their Meaning.
Table 1. Special Groups and their Meaning.
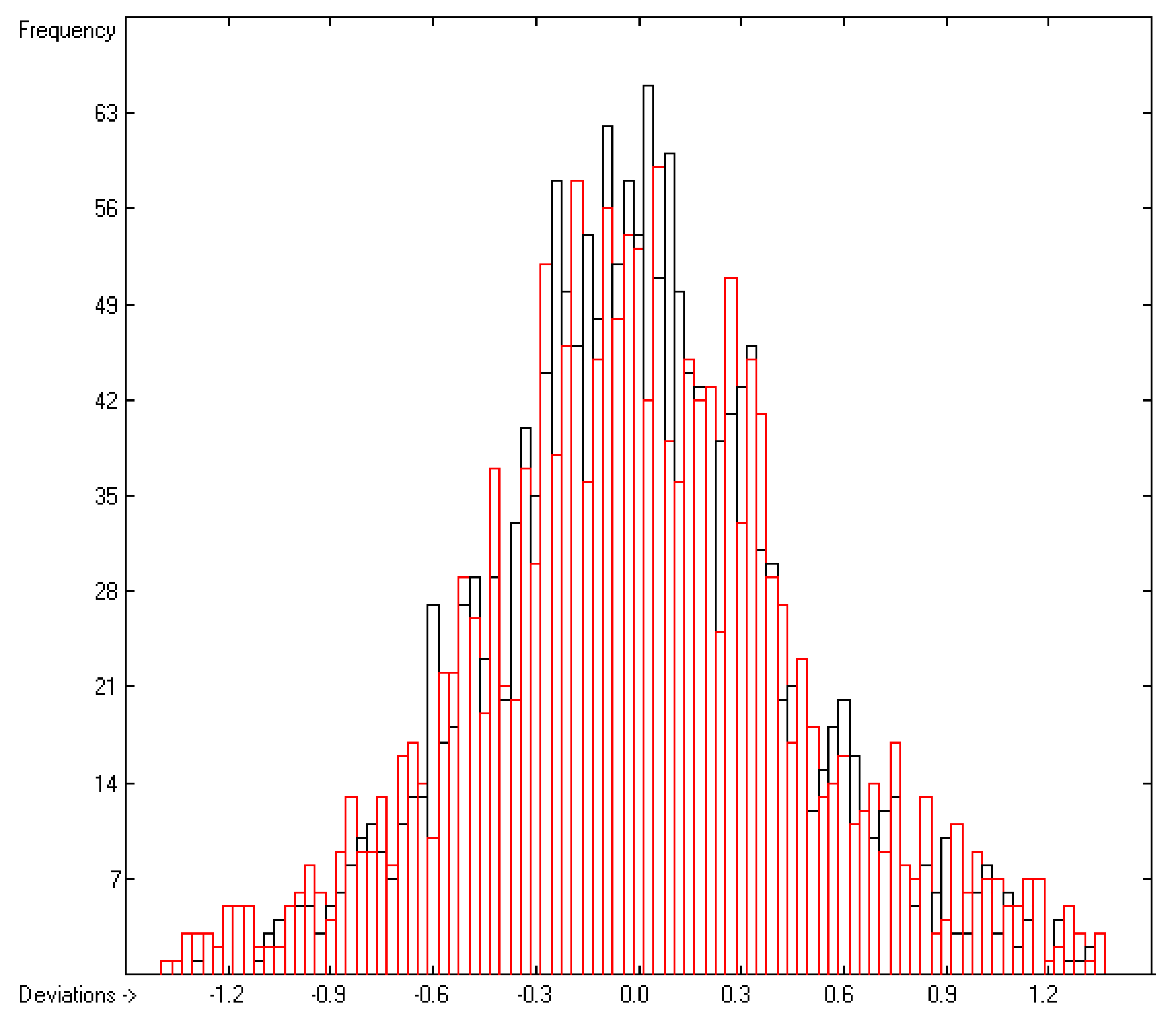
Atom type Neighbours Meaning
H H Acceptor Correction value for intramolecular H bridge between acidic H (on O, N or S) and basic acceptor (O, N or F)
(COH)n n>1 Correction value for each additional hydroxy group
(COOH)n n>1 Correction value for each additional carboxylic acid group
Alkane No of C atoms Correction value for each C atom in a pure alkane
Unsaturated HC No of C atoms Correction value for each C atom in an aromatic hydrocarbon
Endocyclic bonds No of single bonds Correction value for each single endocyclic bond
Table 2. Atom and Special Groups and their Contribution in logPow Calculations.
Table 2. Atom and Special Groups and their Contribution in logPow Calculations.
Entry Atom Type Neighbours Contribution Occurrences Molecules
1 Const 0.73 3332 3332
2 B(-) F4 2.71 10 10
3 C sp3 H3C 0.27 2614 1498
4 C sp3 H3N 0.14 457 320
5 C sp3 H3N(+) -1.35 2 2
6 C sp3 H3O -0.26 375 285
7 C sp3 H3P -0.3 4 4
8 C sp3 H3S -0.34 61 53
9 C sp3 H3Si 0.76 44 5
10 C sp3 H2C2 0.44 3262 1046
11 C sp3 H2CN 0.42 741 429
12 C sp3 H2CN(+) -0.86 32 25
13 C sp3 H2CO -0.1 799 604
14 C sp3 H2CS -0.33 97 69
15 C sp3 H2CF -0.29 5 5
16 C sp3 H2CCl 0.33 84 67
17 C sp3 H2CBr 0.41 54 48
18 C sp3 H2CJ 1.08 6 6
19 C sp3 H2CP 2.77 1 1
20 C sp3 H2N2 2.05 3 3
21 C sp3 H2NO 0.46 4 4
22 C sp3 H2NS 0.72 3 3
23 C sp3 H2O2 -0.17 6 6
24 C sp3 H2S2 -0.86 6 6
25 C sp3 HC3 0.45 417 269
26 C sp3 HC2N 0.58 200 157
27 C sp3 HC2N(+) -0.73 25 24
28 C sp3 HC2O 0.1 383 241
29 C sp3 HC2S -0.21 8 8
30 C sp3 HC2F -0.36 2 2
31 C sp3 HC2Cl 0.69 64 22
32 C sp3 HC2Br 0.81 26 22
33 C sp3 HCN2 1.2 6 5
34 C sp3 HCNO 1.15 17 17
35 C sp3 HCNS 0.9 25 25
36 C sp3 HCO2 -0.02 31 22
37 C sp3 HCOS 0.6 3 3
38 C sp3 HCOCl 0.19 3 1
39 C sp3 HCOBr 1.03 1 1
40 C sp3 HCOP 0.31 1 1
41 C sp3 HCF2 -0.02 2 2
42 C sp3 HCCl2 0.93 13 12
43 C sp3 HOF2 -0.04 1 1
44 C sp3 C4 0.54 144 111
45 C sp3 C3N 0.71 37 36
46 C sp3 C3N(+) -0.43 6 6
47 C sp3 C3O 0.04 54 52
48 C sp3 C3S -0.1 17 17
49 C sp3 C3F 0.94 4 4
50 C sp3 C3Cl 0.8 21 8
51 C sp3 C3Br 0.59 5 4
52 C sp3 C2N2 -1.17 1 1
53 C sp3 C2NO 0.52 5 5
54 C sp3 C2O2 1.65 5 5
55 C sp3 C2F2 0.67 2 2
56 C sp3 C2Cl2 0.84 9 9
57 C sp3 CNO2 1.46 1 1
58 C sp3 CF3 0.86 80 76
59 C sp3 CF2Cl 1.1 3 2
60 C sp3 CFCl2 1.1 3 2
61 C sp3 CCl3 1.6 23 21
62 C sp3 CCl2Br 0 1 1
63 C sp3 CBr3 2.44 1 1
64 C sp3 OF3 0.8 2 2
65 C sp3 SF3 1.04 8 8
66 C sp3 SFCl2 1.9 1 1
67 C sp3 SCl3 0.76 3 3
68 C sp2 H2=C 0.25 97 87
69 C sp2 H2=N -0.62 1 1
70 C sp2 HC=C 0.24 449 285
71 C sp2 HC=N -1.98 18 18
72 C sp2 HC=N(+) 0.94 10 10
73 C sp2 H=CN -0.08 146 109
74 C sp2 H=CN(+) -0.6 18 18
75 C sp2 HC=O -0.73 45 45
76 C sp2 H=CO 0.32 14 13
77 C sp2 H=CS 0.02 17 16
78 C sp2 H=CCl 0.51 8 6
79 C sp2 H=CBr 0.59 1 1
80 C sp2 HN=N -0.06 65 52
81 C sp2 HN=O -0.63 16 15
82 C sp2 HO=O -0.4 10 10
83 C sp2 H=NS -0.51 4 4
84 C sp2 C2=C 0.38 160 133
85 C sp2 C2=N -0.25 105 102
86 C sp2 C2=N(+) 2.45 1 1
87 C sp2 C2=O -0.86 242 194
88 C sp2 C=CN 0.76 76 64
89 C sp2 C=CN(+) -0.56 3 3
90 C sp2 C=CO 0.64 41 36
91 C sp2 C=CS -0.16 17 15
92 C sp2 C=CF -0.01 3 3
93 C sp2 C=CCl 0.81 31 21
94 C sp2 C=CBr 0.94 4 4
95 C sp2 C=CJ 0.89 1 1
96 C sp2 C=CP 0 1 1
97 C sp2 =CN2 1.36 19 19
98 C sp2 =CN2(+) 0.74 11 11
99 C sp2 CN=N 0.24 67 63
100 C sp2 CN=N(+) -0.67 1 1
101 C sp2 CN=O -0.69 449 364
102 C sp2 C=NO -0.76 1 1
103 C sp2 =CNO -0.01 4 4
104 C sp2 =CNO(+) -0.37 2 2
105 C sp2 CN=S -0.36 8 8
106 C sp2 C=NS 0.07 5 4
107 C sp2 =CNS 0.37 4 4
108 C sp2 =CNCl 1.94 1 1
109 C sp2 =CNBr 0.7 5 3
110 C sp2 C=NCl 1.75 1 1
111 C sp2 CO=O -0.13 700 613
112 C sp2 CO=O(-) -2.16 35 35
113 C sp2 C=OS -0.99 4 4
114 C sp2 C=OCl 0.28 4 4
115 C sp2 =COCl 1.27 1 1
116 C sp2 =CS2 0 3 3
117 C sp2 =CSBr -2.41 1 1
118 C sp2 =CF2 0.26 1 1
119 C sp2 =CCl2 1.21 12 10
120 C sp2 =CBr2 1.36 1 1
121 C sp2 N2=N 0.79 26 25
122 C sp2 N2=N(+) 0.74 1 1
123 C sp2 N2=O 0.07 135 134
124 C sp2 N=NO 0.11 1 1
125 C sp2 N2=S 0.11 9 8
126 C sp2 N=NS 0.24 25 24
127 C sp2 N=NCl 1.13 3 3
128 C sp2 N=NBr 0.24 3 2
129 C sp2 NO=O 0.2 117 114
130 C sp2 =NOS -0.19 1 1
131 C sp2 N=OS 0.05 7 7
132 C sp2 NO=S 0.97 1 1
133 C sp2 =NS2 -1.65 2 2
134 C sp2 NS=S -1.02 5 3
135 C sp2 =NSCl 1.17 1 1
136 C sp2 O2=O 0 3 3
137 C sp2 O=OCl -0.13 3 3
138 C aromatic H:C2 0.25 9963 2133
139 C aromatic H:C:N -0.49 283 193
140 C aromatic H:C:N(+) 0.22 33 27
141 C aromatic H:N2 -0.91 9 9
142 C aromatic :C3 0.25 389 170
143 C aromatic C:C2 0.32 2023 1351
144 C aromatic C:C:N -0.38 74 62
145 C aromatic C:C:N(+) -3.29 4 3
146 C aromatic :C2N 0.39 653 534
147 C aromatic :C2N(+) -0.15 194 161
148 C aromatic :C2:N -0.09 93 72
149 C aromatic :C2:N(+) -3.54 19 19
150 C aromatic :C2O 0.57 1076 742
151 C aromatic :C2S 0.08 208 170
152 C aromatic :C2F 0.27 126 86
153 C aromatic :C2Cl 0.78 1718 565
154 C aromatic :C2Br 0.9 248 111
155 C aromatic :C2J 1.26 50 34
156 C aromatic :C2P 1.08 1 1
157 C aromatic C:N2 -1.81 9 9
158 C aromatic :C:N2 -0.13 1 1
159 C aromatic :CN:N 0.49 38 34
160 C aromatic :CN:N(+) -0.83 1 1
161 C aromatic :C:NO 0.97 21 15
162 C aromatic :C:NS -0.16 5 5
163 C aromatic :C:NF -0.23 4 3
164 C aromatic :C:NCl 0.16 18 16
165 C aromatic :C:NBr 0.06 1 1
166 C aromatic N:N2 -0.05 51 41
167 C aromatic N:N2(+) 0 1 1
168 C aromatic :N2O 1.53 8 8
169 C aromatic :N2S 0.8 3 3
170 C aromatic :N2Cl 0.89 6 6
171 C(+) aromatic H:N2 0.21 25 25
172 C sp H#C -0.27 28 28
173 C sp C#C 0.2 86 57
174 C sp C#N -0.7 136 130
175 C sp N#N 0.04 3 3
176 C sp #NS -0.59 5 5
177 C sp =N=O 0.64 4 4
178 C sp =N=S 1.53 27 26
179 N sp3 H2C -1.57 86 84
180 N sp3 H2C(pi) -1.05 326 292
181 N sp3 H2N -0.85 20 20
182 N sp3 H2S -1.55 34 34
183 N sp3 HC2 -1.3 74 73
184 N sp3 HC2(pi) -0.93 225 203
185 N sp3 HC2(2pi) -0.47 311 272
186 N sp3 HCN -1.1 4 3
187 N sp3 HCN(pi) -0.49 14 13
188 N sp3 HCN(2pi) 1.65 42 42
189 N sp3 HCO(pi) -1.32 9 9
190 N sp3 HCS -1.69 4 4
191 N sp3 HCS(pi) -0.98 47 47
192 N sp3 HCP -1.78 3 3
193 N sp3 HCP(pi) -0.41 1 1
194 N sp3 C3 -1.03 122 108
195 N sp3 C3(pi) -0.73 153 138
196 N sp3 C3(2pi) -0.72 149 136
197 N sp3 C3(3pi) -0.75 23 23
198 N sp3 C2N -1.57 1 1
199 N sp3 C2N(pi) -1.41 31 28
200 N sp3 C2N(2pi) -0.67 51 47
201 N sp3 C2N(3pi) -0.44 10 10
202 N sp3 C2O(pi) -0.31 5 5
203 N sp3 C2S -1.42 5 5
204 N sp3 C2S(pi) 0.03 7 6
205 N sp3 C2S(2pi) 0.76 2 2
206 N sp3 C2P -0.33 5 3
207 N sp3 CN2(2pi) 1.36 1 1
208 N sp3 CS2 0.27 1 1
209 N sp3 CS2(pi) -0.29 1 1
210 N sp2 H=C -0.67 12 11
211 N sp2 C=C -0.72 200 180
212 N sp2 C=N 0.01 13 12
213 N sp2 =CN 0.49 96 78
214 N sp2 C=N(+) -6.61 1 1
215 N sp2 =CN(+) -1.02 2 2
216 N sp2 =CO -0.64 47 41
217 N sp2 C=O -1.05 2 2
218 N sp2 =CS -1.44 5 4
219 N sp2 N=N -0.78 25 18
220 N sp2 N=O 0.16 40 37
221 N aromatic C2:C(+) 0 50 25
222 N aromatic :C2 0.38 354 258
223 N aromatic :C:N -0.35 4 2
224 N(+) sp3 H3C -1.03 26 26
225 N(+) sp3 H2C2 1.2 5 5
226 N(+) sp3 HC3 2.68 1 1
227 N(+) sp3 C4 3.03 1 1
228 N(+) sp2 C=CO(-) -2.3 10 10
229 N(+) sp2 CO=O(-) 0.27 235 198
230 N(+) sp2 NO=O(-) -0.19 2 2
231 N(+) sp2 O2=O(-) 0.44 55 29
232 N(+) aromatic H:C2 2.5 3 3
233 N(+) aromatic C:C2 -0.48 7 6
234 N(+) aromatic :C2O(-) 1.73 19 19
235 N(+) sp =C=N(-) 1.8 1 1
236 N(+) sp =N2(-) 0 1 1
237 O HC -0.96 481 344
238 O HC(pi) -0.72 627 557
239 O HN -0.15 11 11
240 O HN(pi) -0.24 6 6
241 O C2 0.06 156 115
242 O C2(pi) -0.13 726 588
243 O C2(2pi) -0.51 301 280
244 O CN 0.4 3 3
245 O CN(pi) 0.82 4 4
246 O CN(+)(pi) 0.01 55 29
247 O CN(2pi) 0.53 13 12
248 O CS -0.13 13 8
249 O CS(pi) -0.1 3 3
250 O CP 0.23 132 68
251 O CP(pi) -0.49 36 26
252 O CSi -0.15 8 2
253 O N2(2pi) 1.91 5 5
254 O NP(pi) -1.95 14 14
255 O Si2 0.09 18 4
256 S2 HC 0.65 14 12
257 S2 HC(pi) 0.14 31 31
258 S2 C2 1.39 48 45
259 S2 C2(pi) 0.98 68 63
260 S2 C2(2pi) 0.98 55 54
261 S2 CN 0 3 3
262 S2 CN(2pi) 2.3 1 1
263 S2 CS 0.87 2 1
264 S2 CS(pi) 1.97 4 2
265 S2 CP 1.12 17 15
266 S2 CP(pi) 0.48 3 2
267 S2 N2 -2.2 2 2
268 S2 N2(2pi) 5.96 1 1
269 S4 C2=O -1.13 11 11
270 S4 C2=O2 -0.5 16 16
271 S4 CO=O2 -0.48 2 1
272 S4 CN=O2 -0.05 85 80
273 S4 C=O2F 0.24 2 2
274 S4 NO=O2 0 3 3
275 S4 N2=O2 0.77 5 5
276 S4 O2=O 0.83 2 2
277 S4 O2=O2 0.5 2 2
278 S4 O2=O2(-) -1.14 3 3
279 P4 CO2=O -1.11 2 2
280 P4 CO2=S 0.26 1 1
281 P4 CO=OS -2.58 1 1
282 P4 CO=OF -0.88 3 3
283 P4 COS=S -2.04 1 1
284 P4 O3=O -0.56 29 29
285 P4 O3=S 1.12 18 18
286 P4 O2S=S 0.7 12 11
287 P4 O=OS2 -0.54 2 2
288 P4 N3=O -0.31 1 1
289 P4 N2O=O 0.24 2 2
290 P4 NO=OS -1.5 2 2
291 Si C4 -0.51 1 1
292 Si C3O -1.7 2 1
293 Si C2O2 0.13 17 4
294 Si O4 0 2 2
295 Halide 1.1 20 19
296 H H Acceptor 0.51 164 154
297 (COH)n n>1 0.26 137 74
298 (COOH)n n>1 -0.15 26 25
299 Alkane No of C atoms 0.09 290 32
300 Unsaturated HC No of C atoms 0.02 1584 135
301 Endocyclic bonds No of single bds -0.14 2338 384
A Based on Valid groups 214 3332
B Goodness of fit R2 0.9648 3246
C Deviation Average 0.31 3246
D Deviation Standard 0.39 3246
E K-fold cv K 10 3164
F Goodness of fit Q2 0.9599 3164
G Deviation Average (cv) 0.33 3164
H Deviation Standard (cv) 0.42 3164
Table 3. Atom and Special Groups and their Contribution in logKoa Calculations.
Table 3. Atom and Special Groups and their Contribution in logKoa Calculations.
Entry Atom Type Neighbours Contribution Occurrences Molecules
1 Const 1.46 1900 1900
2 C sp3 H3C -0.07 1800 875
3 C sp3 H3N 3.42 131 87
4 C sp3 H3N(+) 1.42 1 1
5 C sp3 H3O 2.24 292 219
6 C sp3 H3S 1.51 30 26
7 C sp3 H3P -0.42 3 3
8 C sp3 H3Si 0.42 68 11
9 C sp3 H2C2 0.43 1732 538
10 C sp3 H2CN 3.91 191 129
11 C sp3 H2CN(+) 1.64 6 5
12 C sp3 H2CO 2.61 535 342
13 C sp3 H2CS 1.76 57 44
14 C sp3 H2CP 2.58 3 3
15 C sp3 H2CF -0.77 3 3
16 C sp3 H2CCl 0.71 75 56
17 C sp3 H2CBr 1.05 23 18
18 C sp3 H2CJ 1.13 5 5
19 C sp3 H2CSi 2.91 4 4
20 C sp3 H2N2 4.89 8 3
21 C sp3 H2NO 5.65 9 8
22 C sp3 H2NS 4.67 5 5
23 C sp3 H2O2 4.78 6 4
24 C sp3 H2S2 3.74 4 4
25 C sp3 HC3 0.64 268 180
26 C sp3 HC2N 4.08 64 53
27 C sp3 HC2N(+) 2.05 1 1
28 C sp3 HC2O 2.86 169 135
29 C sp3 HC2S 1.76 9 7
30 C sp3 HC2F -1.66 1 1
31 C sp3 HC2Cl 1.21 43 17
32 C sp3 HC2Br 1.31 14 9
33 C sp3 HC2J 1.95 1 1
34 C sp3 HCNO 8.18 3 3
35 C sp3 HCNS 2.08 1 1
36 C sp3 HCO2 5.73 6 6
37 C sp3 HCF2 -0.18 7 7
38 C sp3 HCFCl 0.02 2 2
39 C sp3 HCCl2 1.18 15 14
40 C sp3 HCClBr 0.77 1 1
41 C sp3 HOF2 1.79 3 3
42 C sp3 C4 0.73 98 84
43 C sp3 C3N 4.1 13 13
44 C sp3 C3O 3.11 40 37
45 C sp3 C3S 2.6 3 3
46 C sp3 C3Cl 0.87 37 15
47 C sp3 C2NO 5.94 1 1
48 C sp3 C2O2 5.94 6 6
49 C sp3 C2F2 0.23 58 10
50 C sp3 C2Cl2 1.24 18 17
51 C sp3 CNO2 9.56 1 1
52 C sp3 COF2 3.06 3 3
53 C sp3 CF3 -0.06 55 51
54 C sp3 CF2Cl -0.02 4 3
55 C sp3 CFCl2 0.37 3 2
56 C sp3 CCl3 1.62 17 16
57 C sp3 CBr3 0.57 1 1
58 C sp3 O2F2 6.85 1 1
59 C sp3 OF3 1.86 3 3
60 C sp2 H2=C -0.19 88 76
61 C sp2 HC=C 0.34 233 141
62 C sp2 HC=N 0.85 8 8
63 C sp2 HC=O 1 27 27
64 C sp2 H=CN 1.1 19 13
65 C sp2 H=CO 0.48 15 14
66 C sp2 H=CS -1.08 9 7
67 C sp2 H=CCl 0.44 12 10
68 C sp2 H=CBr 0.6 3 2
69 C sp2 H=CSi 2.17 1 1
70 C sp2 HN=N 1.73 53 30
71 C sp2 HN=O 2.27 3 3
72 C sp2 HO=O 0.92 4 4
73 C sp2 H=NS 2.88 1 1
74 C sp2 C2=C 0.8 103 79
75 C sp2 C2=N 1.62 34 30
76 C sp2 C=CN 1.6 19 16
77 C sp2 C2=O 1.08 87 75
78 C sp2 C=CO 1.22 27 26
79 C sp2 C=CP -0.09 1 1
80 C sp2 C=CS -0.41 14 10
81 C sp2 C=CCl 0.62 39 24
82 C sp2 C=CBr 1.01 12 5
83 C sp2 =CN2 2.98 2 2
84 C sp2 CN=N 2.75 7 7
85 C sp2 CN=O 2.64 93 88
86 C sp2 C=NO 1.26 5 5
87 C sp2 =CNO -1.24 3 3
88 C sp2 C=NS 0.46 6 6
89 C sp2 =CNCl 3.35 6 3
90 C sp2 CO=O 1.73 244 210
91 C sp2 C=OS -0.61 3 2
92 C sp2 =CS2 -0.66 1 1
93 C sp2 =CF2 -1.14 1 1
94 C sp2 =CCl2 1.14 16 14
95 C sp2 N2=N 3.36 9 9
96 C sp2 N2=O 3.65 43 40
97 C sp2 N=NO 2.64 4 4
98 C sp2 N=NS 0.71 7 7
99 C sp2 NO=O 2.81 38 36
100 C sp2 N=OS 0.93 17 17
101 C sp2 NO=S 4.26 1 1
102 C sp2 =NOS 0.68 3 3
103 C sp2 NS=S 6.03 3 2
104 C sp2 =NSCl -5.44 2 2
105 C sp2 O2=O 2.56 3 3
106 C aromatic H:C2 0.31 5436 1136
107 C aromatic H:C:N 0.53 81 49
108 C aromatic H:N2 0.17 6 6
109 C aromatic :C3 0.89 441 148
110 C aromatic C:C2 0.79 1163 657
111 C aromatic C:C:N 0.68 42 30
112 C aromatic :C2N 1.35 164 146
113 C aromatic :C2N(+) 2.09 96 69
114 C aromatic :C2:N 1.01 13 10
115 C aromatic :C2O 1.27 769 453
116 C aromatic :C2P 3.53 5 3
117 C aromatic :C2S -0.19 38 33
118 C aromatic :C2Si -0.25 1 1
119 C aromatic :C2F 0.13 99 41
120 C aromatic :C2Cl 0.91 1844 550
121 C aromatic :C2Br 1.24 391 143
122 C aromatic :C2J 2.14 10 9
123 C aromatic C:N2 0.77 11 10
124 C aromatic :CN:N 0.8 4 4
125 C aromatic :C:NO 1.2 28 24
126 C aromatic :C:NCl 0.9 14 12
127 C aromatic N:N2 1.18 60 36
128 C aromatic :N2O 1.15 11 11
129 C aromatic :N2S -0.6 8 8
130 C aromatic :N2Cl 0.43 9 8
131 C sp H#C -0.45 18 17
132 C sp C#C 0.67 18 17
133 C sp C#N 0.73 46 43
134 C sp N#N 5.32 1 1
135 C sp #NP -5.58 1 1
136 C sp =N=S -0.13 2 2
137 N sp3 H2C -2.18 17 16
138 N sp3 H2C(pi) 1.02 57 53
139 N sp3 H2N 3.57 5 5
140 N sp3 H2S 1.81 1 1
141 N sp3 HC2 -5.94 12 11
142 N sp3 HC2(pi) -2.38 93 70
143 N sp3 HC2(2pi) 0.08 65 56
144 N sp3 HCN(pi) 0.02 5 4
145 N sp3 HCN(2pi) 1.2 4 4
146 N sp3 HCO(pi) 1.13 1 1
147 N sp3 HCP -4.1 3 3
148 N sp3 HCP(pi) 1.51 1 1
149 N sp3 HCS(pi) -1.54 8 8
150 N sp3 C3 -9.44 17 17
151 N sp3 C3(pi) -6.39 58 55
152 N sp3 C3(2pi) -4.82 49 45
153 N sp3 C3(3pi) -3.61 9 9
154 N sp3 C2N -5.12 1 1
155 N sp3 C2N(pi) -2.54 15 14
156 N sp3 C2N(+)(pi) -1.93 7 2
157 N sp3 C2N(2pi) -3.84 36 36
158 N sp3 C2N(3pi) -0.65 13 12
159 N sp3 C2P 0 1 1
160 N sp3 C2P(pi) -2.97 1 1
161 N sp3 C2P(2pi) -4.07 1 1
162 N sp2 H=C 0.51 1 1
163 N sp2 C=C -0.97 54 48
164 N sp2 C=N 0.61 6 4
165 N sp2 =CN 0.03 54 49
166 N sp2 =CN(+) 9.74 2 2
167 N sp2 =CO -3.65 30 26
168 N sp2 N=N -1.3 4 3
169 N sp2 N=O -2.02 13 13
170 N aromatic :C2 0.54 194 109
171 N aromatic :C:N 0.47 4 1
172 N(+) sp2 CO=O(-) -0.36 104 76
173 N(+) sp2 NO=O(-) 0 9 4
174 N(+) sp2 O2=O(-) -1.09 63 35
175 O HC -0.66 143 121
176 O HC(pi) 1.39 175 159
177 O HN(pi) 4.18 2 2
178 O HP 2.11 4 2
179 O HSi 1.91 3 2
180 O C2 -4.17 139 105
181 O C2(pi) -2.68 392 317
182 O C2(2pi) -0.92 255 228
183 O CN(pi) 0.51 20 16
184 O CN(+)(pi) 0.1 63 35
185 O CN(2pi) 3.07 8 8
186 O CO(pi) -1.03 2 1
187 O CS -0.88 11 6
188 O CP -1.2 183 93
189 O CP(pi) -0.01 70 54
190 O CSi -2.38 9 3
191 O NP(pi) 4.65 1 1
192 O P2 1.7 1 1
193 O Si2 0 21 6
194 P4 C3=O -5.7 1 1
195 P4 CNO=O 1.2 1 1
196 P4 CO2=O 1.47 3 3
197 P4 CO2=S -1.5 3 3
198 P4 CO=OS 1.99 1 1
199 P4 CO=OF 1.94 1 1
200 P4 COS=S -0.86 1 1
201 P4 NO2=O 3.42 1 1
202 P4 NO2=S 1.88 3 3
203 P4 NO=OS 1.2 2 2
204 P4 O3=O 0.09 29 29
205 P4 O3=S -0.4 32 30
206 P4 O2=OS 0.43 5 5
207 P4 O2=OF -0.17 1 1
208 P4 O=OS2 1.58 3 3
209 P4 O2S=S -0.27 18 17
210 P4 =OS3 1.46 1 1
211 S2 HC -1.08 2 2
212 S2 HC(pi) 1.54 1 1
213 S2 C2 -1.5 14 14
214 S2 C2(pi) 0.4 41 39
215 S2 C2(2pi) 2.82 24 23
216 S2 CS -0.58 4 2
217 S2 CS(pi) -2.98 2 1
218 S2 CP -0.12 33 28
219 S2 CP(pi) 1.78 3 2
220 S4 C2=O 0.6 2 2
221 S4 C2=O2 2.13 3 3
222 S4 CN=O2 3.26 9 9
223 S4 CO=O2 -0.05 1 1
224 S4 O2=O -0.35 2 2
225 S4 O2=O2 0.24 3 3
226 S6 CF5 1.92 3 3
227 Si C4 -1.33 3 3
228 Si C3O -0.65 7 4
229 Si C2O2 0.1 19 6
230 Si CO3 0 3 3
231 H H Acceptor -1.51 47 45
232 (COH)n n>1 0.06 22 15
233 (COOH)n n>1 1.2 6 6
234 Alkane No of C atoms -0.05 268 34
235 Unsaturated HC No of C atoms -0.03 1512 140
236 Endocyclic bonds No of single bds -0.11 1109 210
A Based on Valid groups 167 1900
B Goodness of fit R2 0.9765 1829
C Deviation Average 0.34 1829
D Deviation Standard 0.44 1829
E K-fold cv K 10 1765
F Goodness of fit Q2 0.9717 1765
G Deviation Average (cv) 0.37 1765
H Deviation Standard (cv) 0.48 1765
Table 4. Example Calculation of the logKoa of Endosulfan Sulfate.
Table 4. Example Calculation of the logKoa of Endosulfan Sulfate.
Atom type C sp3 C sp3 C sp3 C sp3 C sp2 O S4 Endocycl. Bonds Const Sum
Neighbors H2CO HC3 C3Cl C2Cl2 C=CCl CS O2=O2 n C-C
Contribution 2.61 0.64 0.87 1.24 0.62 -0.88 0.24 -0.11 1.46
n Groups 2 2 2 1 2 2 1 9
n x Contribution 5.22 1.28 1.74 1.24 1.24 -1.76 0.24 -0.99 1.46 9.67
Table 5. Experimental (calculated) logPow and logKoa values of 2- and 3-Nitroaniline.
Table 5. Experimental (calculated) logPow and logKoa values of 2- and 3-Nitroaniline.
Descriptor 2-Nitroaniline 3-Nitroaniline
logPow 1.85 (1.70) 1.37 (1.19)
logKoa 6.46 (5.29) 7.62 (6.80)
Table 6. Experimental (calculated) logPow and logKoa of Hexanoic and 1,6-Hexanedioic Acid.
Table 6. Experimental (calculated) logPow and logKoa of Hexanoic and 1,6-Hexanedioic Acid.
Descriptor Hexanoic Acid 1,6-Hexanedioic Acid
logPow 1.92 (1.91) 0.08 (0.64)
logKoa 6.31 (6.23) 10.74 (10.62)
Table 7. Experimental and calculated logKaw of some Examples.
Table 7. Experimental and calculated logKaw of some Examples.
Compound logKaw exp logKaw calc
2-Nitroaniline -4.77 -3.59
3-Nitroaniline -6.49 -5.61
Hexanoic Acid -4.531 -4.32
1,6-Hexanedioic Acid -11.15 -9.98
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated