Preprint

Article

Correlation Between Surface Integrity and Low Cycle Fatigue Life of Machined Inconel 718

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 December 2023

Posted:

06 December 2023

You are already at the latest version

Alerts

Abstract

This work aims at improving surface integrity and LCF life of machined Inconel 718. The correlation between the LCF life of Inconel 718 and various states of machined surface integrity is explored. In this paper, the surface integrity of Inconel 718 specimens is enhanced by low plasticity burnishing (LPB). The LCF life with different surface integrity specimens is predicted by micro-macro finite element method (FEM). Firstly, the LCF specimens with different surface integrity are machined by turning (turned specimen), polishing (matrix specimen) and LPB process (LPBed specimen). Secondly, the LCF experiment is carried out to reveal the effect of surface integrity on LCF life. Finally, the LCF micro-macro FEM model is proposed to predict the LCF of machined Inconel 718 specimens. The representative volume element (RVE) model is established based on the measured surface integrity and microstructure of Inconel 718 specimens. The effect of surface integrity on LCF life is transformed to equivalent load. The micro-macro FEM model combined with Tanaka-Mura dislocation crack initiation theory and extended finite element method (XFEM) is applied to predict the LCF life the machined specimens. The study results show that the LCF life of LPBed specimens can be improved by 90.5% and 36.1% compared with that of turned specimens and polished matrix specimens, respectively. The errors between FEM prediction results and experimental results are 13.1%, 9.2% and 12.2%, respectively. The proposed micro-macro FEM model could be utilized to predict the LCF life of Inconel 718 with different surface integrity, and further to apply the LCF life prediction in industry.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Inconel 718 is widely used to manufacture aircraft engine turbine disks due to its excellent mechanical properties. The high mechanical load makes low cycle fatigue (LCF) failure as one of the main failure modes of Inconel 718 parts.

Fatigue cracks tend to initiate at the surface and subsurface of parts [1]. So, the fatigue life of machined parts is significantly affected by machined surface integrity, especially surface roughness and residual stress [2,3]. The lower surface roughness and compressive residual stress contribute to improving the fatigue properties of machined parts [4,5].

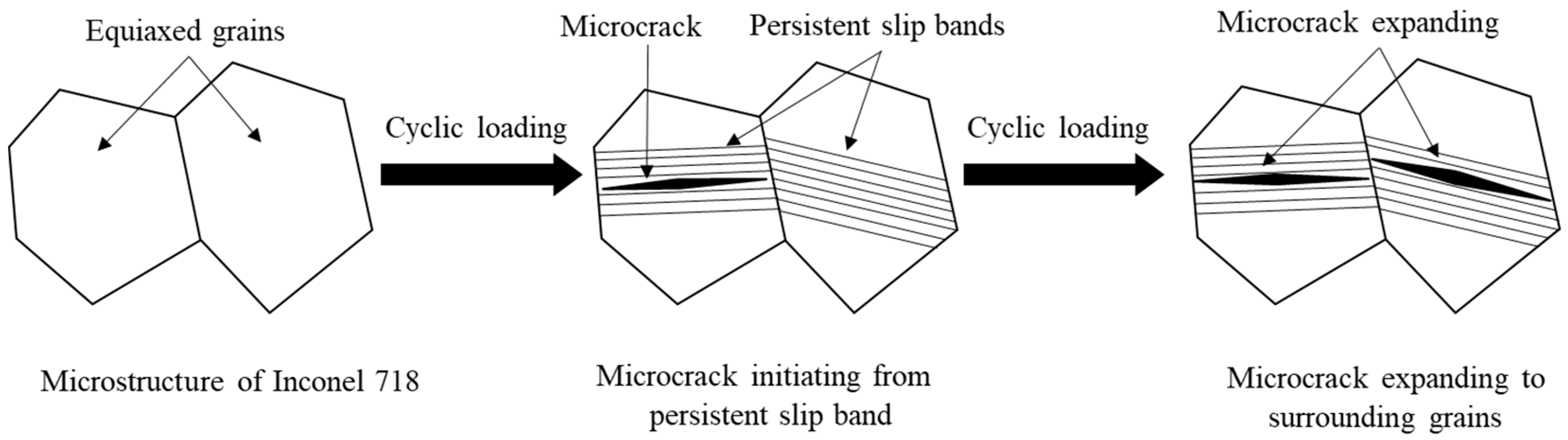
The fatigue crack initiation of polycrystalline metallic materials is caused by cyclic loading, as shown in Figure 1. Firstly, dislocations accumulate within grains under cyclic loading. Subsequently, the persistent slip bands are formed in the grains. The microcracks generated from persistent bands as cyclic loading proceeds. As cyclic load proceeds, the microcracks expand to surrounding grains due to the stress concentration at the crack tips. Finally, microcracks accumulate and transformed to a macrocrack [6,7]. The formation of persistent slip bands and microcracks within Inconel 718 was observed using replica method [8].

Tanaka and Mura proposed a theoretical cyclic slip dislocation pile-up model to describe crack nucleation in single-crystal [9], which is expressed as Eq. (1).

N_{i} = \frac{8 G W_{s}}{π (1 - υ) {(Δ τ - 2 k)}^{2} d}

(1)

where G is the shear modulus, W_s is the specific fracture energy per unit area of the material, ν is the Poisson’s ratio, Δτ is the average shear stress range on the slip band, k is the frictional stress of dislocations on the slip plane, d is the length of the slip band.

The Tanaka-Mura crack initiation cycle slip theory is suitable for single-crystal crack initiation life prediction. However, the model needs to be integrated with finite element methods (FEM) to predict crack initiation life of polycrystalline metallic materials. Bruckner et al. [10] analyzed the crack initiation process of martensitic stainless steel using Tanaka-Mura theory and FEM. Rahim et al. [11] predicted the crack initiation life of steel P91 at room temperature. Tanaka-Mura model has also been utilized in predicting the crack initiation life of welded structure [12]. However, Tanaka-Mura model has seldom been applied to investigate the effect of different surface integrity on crack initiation life.

Crack propagation life is related to the crack stress intensity factor. Crack propagation life can be estimated analytically by integrating Paris law for simple cracks. However, the analytical integrating method is rarely applicable to complicated cracks. The eXtended Finite Element Method (XFEM) was proposed to simulate crack propagation process [13,14]. The XFEM has already been utilized for simulating fatigue crack propagation [15,16] and predicting fatigue life [17,18].

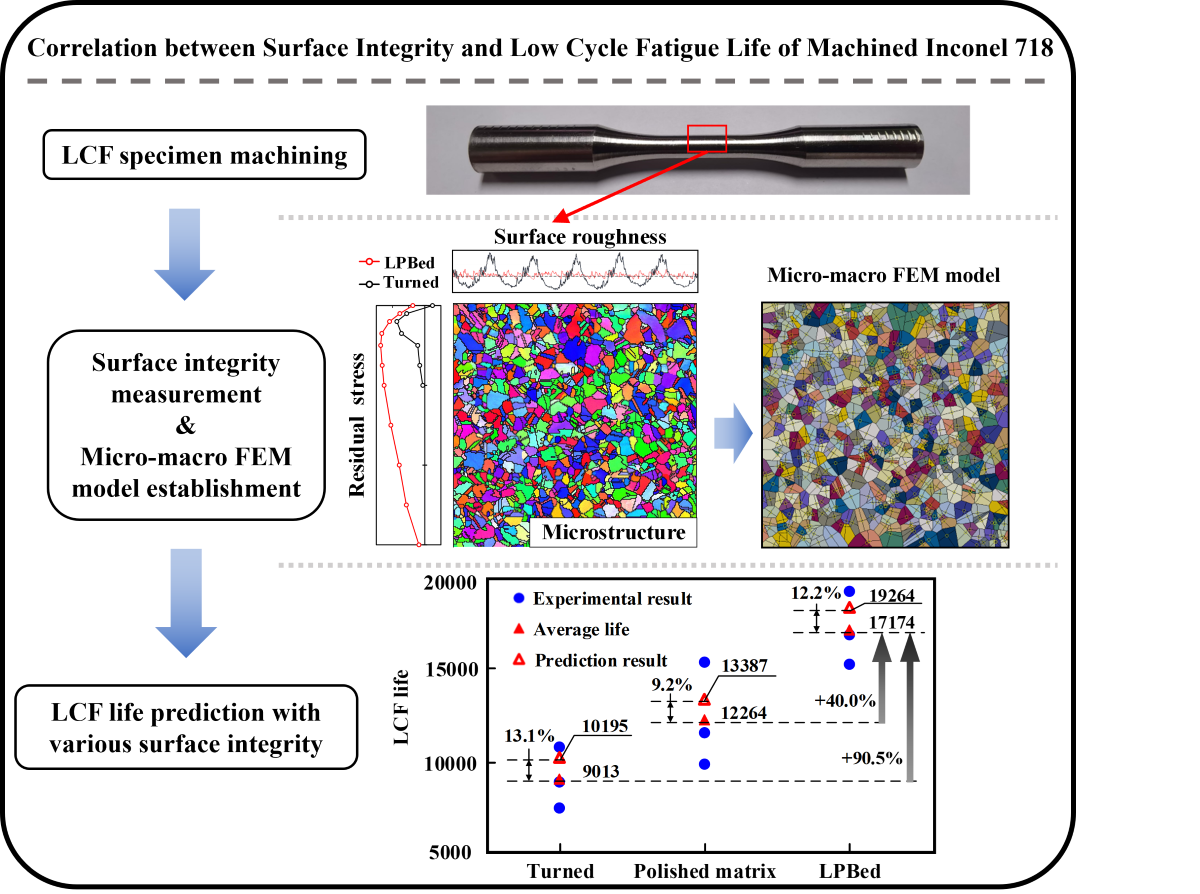
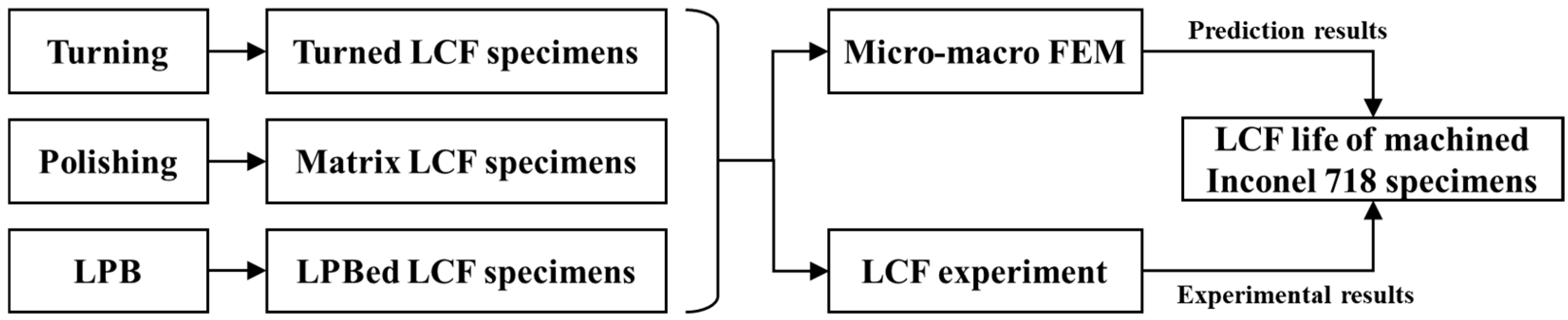
In this study, the micro-macro FEM model was established based on Tanaka-Mura model and XFEM. Firstly, three groups of LCF specimens with different surface integrity were machined using polishing (matrix LCF specimen), turning (turned LCF specimen) and LPB process (LPBed LCF specimen). The surface integrity of the specimens was measured and induced to the representative volume element (RVE) model. Subsequently, the effect of surface integrity on the Inconel 718 LCF life was investigated using the proposed model. The LCF life of the three groups specimens was predicted. Finally, LCF experiments were conduct to verified the proposed model. The flow diagram of this research is shown in Figure 2.

2. Experiments

2.1. Materials

The workpiece material of Inconel 718 was treated with the solution and aging treatment. In order to avoid the error caused by difference material batches, all specimens were manufactured from the same batch of material. The mechanical properties of Inconel 718 and are shown in Table 1.

2.1. Experimental method and process

The turning and LPB process is shown in Figure 3. The turning and LPB process were carried out on CNC turning center PUMA 200 MA (DAEWOO, Incheon, Korea). The coated carbide inserts VBMT160404-MF1105 (Sandvik, Sandviken, Sweden) were utilized for turning. The turning parameters are shown as follow: turning cutting speed v = 50m/min, feed rate f = 0.1mm/r, turning depth a_p = 0.1mm. The turned specimen was subjected to LPB process. The LPB parameters are shown as follow: LPB speed v = 50m/min, feed rate f = 0.1mm/r, LPB pressure P = 15MPa, LPB times N = 2.

The surface morphology and surface roughness of the turned-LPBed specimens were measured using laser confocal microscope VK-X250K (Keyence, Osaka, Japan), as shown in Figure 4. The surface roughness R_y was measured along feed direction. The surface roughness was measured three times, and the average values were taken as measurement result to reduce the measurement error.

Residual stress measuring process is shown in Figure 5. The residual stresses measuring specimens were machined using wire electrical discharge machining, as shown in Figure 5 (a). The residual stress was measured along feed direction since its significant effect on fatigue property [14]. The residual stresses were measured using the X-ray residual stress analyzer μ-X360n (Pulstec, Shizuoka, Japan). In order to measure residual stresses at different depths, the specimens were subjected to layer-by-layer stress-free electrolytic polishing using electrolytic polisher DPF-2 (Zhunquan, Shanghai, China). Saturated NaCl solution (mass fraction 26.5%) was used for electrolytic polishing. The removal depth was measured using micrometer screw. The residual stress measuring process is shown in Figure 5 (b).

Single-factor experiment was conducted to investigate the effect of different surface integrity on LCF life. The LCF experiment process is shown in Figure 6. The experimental specimens are shown in Figure 6 (a). Three groups of LCF specimens were machined using polishing (polished matrix LCF specimens), turning (turned LCF specimens) and LPB (LPBed LCF specimens). The LCF experiments were carried out on the electro-hydraulic servo fatigue testing machine LFV-250HH (Walter+bai, Löhningen, Switzerland), as shown in Figure 6 (b). The load formation was tensile-tensile sinusoidal loading with the loading parameters as follow: maximum load σ_max=1360MPa, stress ratio R=0.1. The LCF fatigue life of the test was recorded when the fatigue specimen fractured. In order to reduce error, three specimens were tested for each group, and the average value was taken as the LCF life of the tested group.

3. Micro-macro FEM LCF life prediction model for Inconel 718

The LCF life of Inconel 718 was subdivided into crack initiation life and crack propagation life. The crack initiation life was predicted utilizing the micro FEM model based on Tanaka-Mura theory. The crack propagation life was predicted using macro FEM model based on XFEM method.

The micro FEM model was established based on the Tanaka-Mura theoretical cyclic slip dislocation pile-up model shown in Eq. (1). The material parameters of Inconel 718 used in Tanaka-Mura model are shown in Table 2. The length of the slip band d and average shear stress range on the slip band Δτ are parameters to be determined. For polycrystalline material Inconel 718, the micro FEM analysis was performed cyclically to simulate crack initiation process and predict crack initiation life.

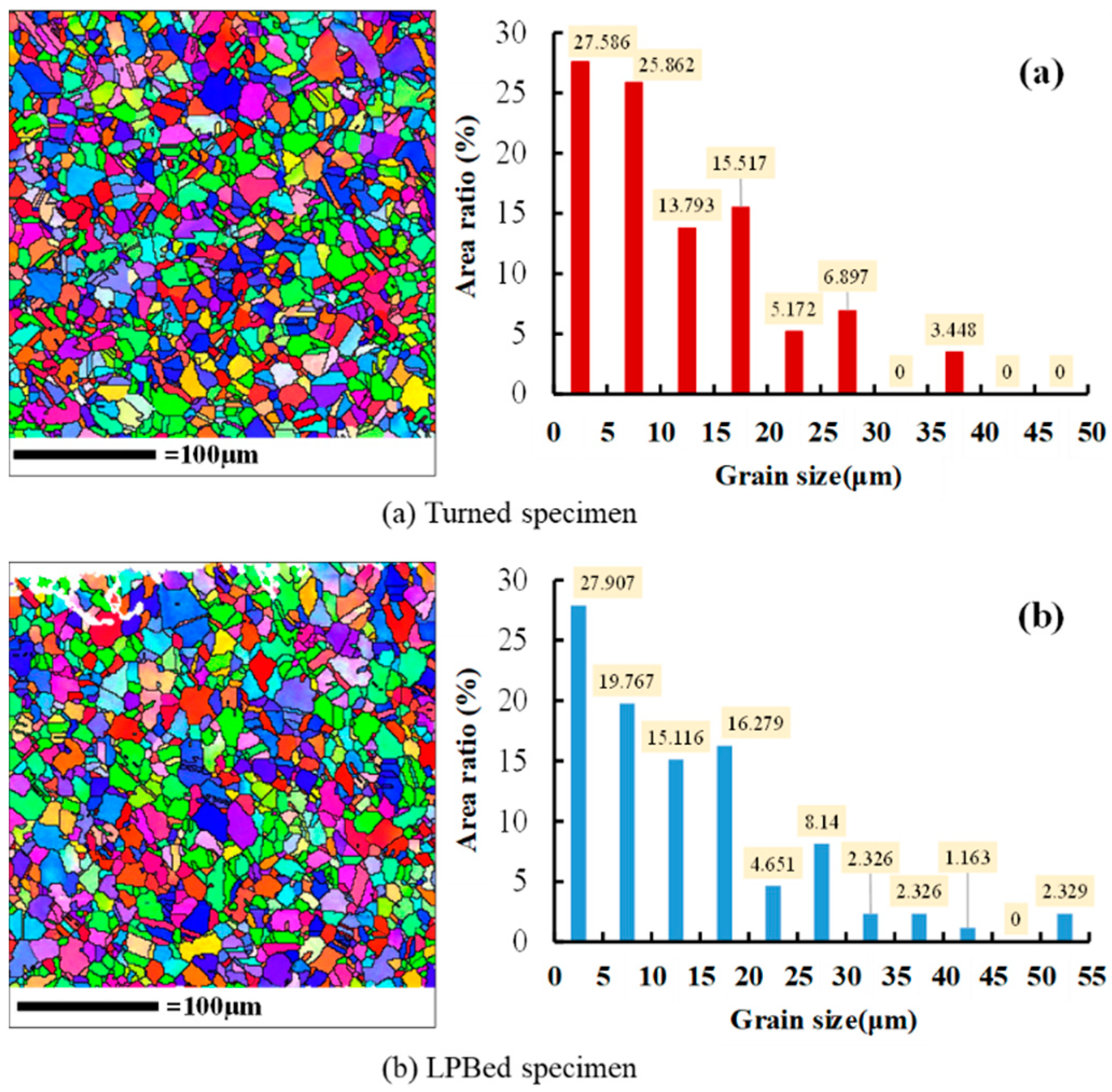
Firstly, the microstructure and grain size of the surface layer of specimens were measured using Electron Backscatter Diffraction (EBSD), as shown in Figure 7. The microstructure of Inconel 718 was composed of equiaxed grains and crystal twin. The grain average size of turned specimen was measured as 12.26μm and 13.42μm for LPBed specimen.

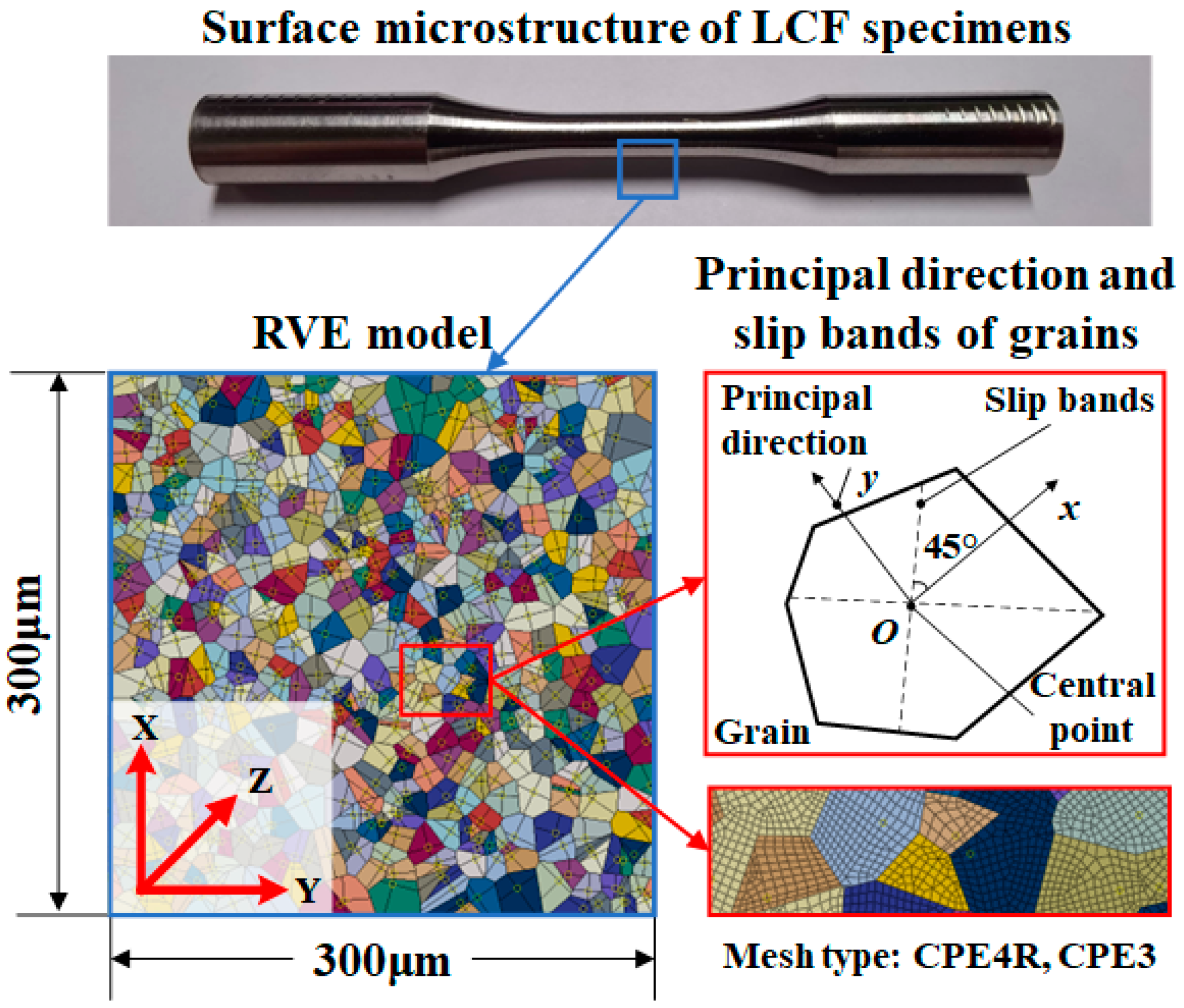
Subsequently, the representative volume element (RVE) model of Inconel 718 was established based on the observed Inconel 718 microstructure. The Voronoi diagram, a diagram consistent with the microstructure formation process of metal materials [22], was employed to simulate the microstructure of Inconel 718 specimens.

Finally, the shear stress internal the grains during LCF loading was calculated using FEM. The microcracks were set up in grains according to Tanaka-Mura model. According to the study of Kramberger et al. [23], the crack initiation stage concluded when the crack expanded to 300μm. Therefore, the RVE model with 600 grains was established within a 300μm*300μm square. The crack initiation simulation concluded when the microcrack penetrate the RVE model. The loading cycles corresponded to the crack initiation lifetime.

The mechanical properties of the Inconel 718 grains are anisotropic. The elastic orthotropic matrix parameters of Inconel 718 are shown in Table 3. Grain principal directions were assigned using random number method since the grain directions are randomly distributed in Inconel 718.

According to the Tanaka-Mura crack initiation cycle slip theory, cracks initiate at the persistent slip bands internal the grains. Therefore, the slip bands were drawn inside the grains at an angle of 45° to the main direction, as shown in Figure 8. The length of the slip bands and shear stress amplitude was substituted into the Tanaka-Mura model to calculate the crack initiation life of the grain. The RVE model was meshed using CPE4R and CPE3 with the size of 1μm. The established RVE model of Inconel 718 is shown in Figure 8.

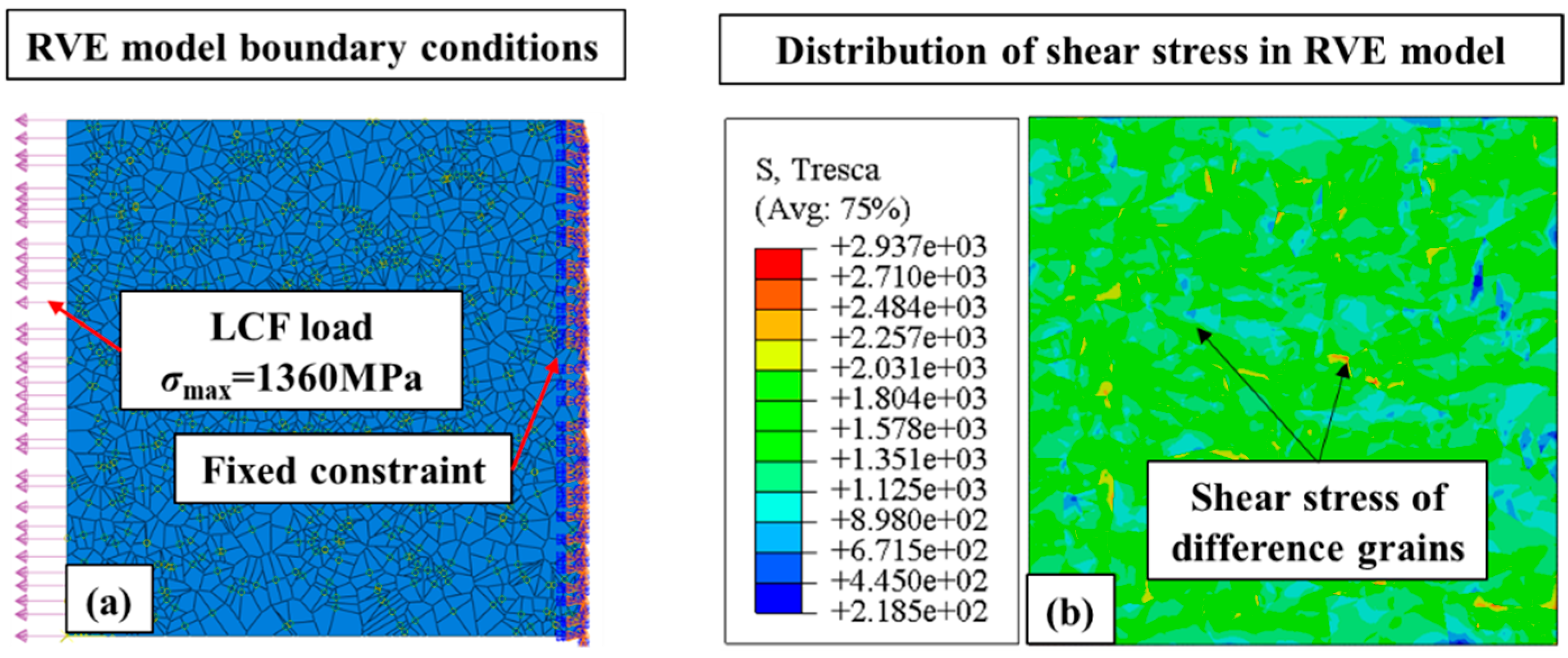
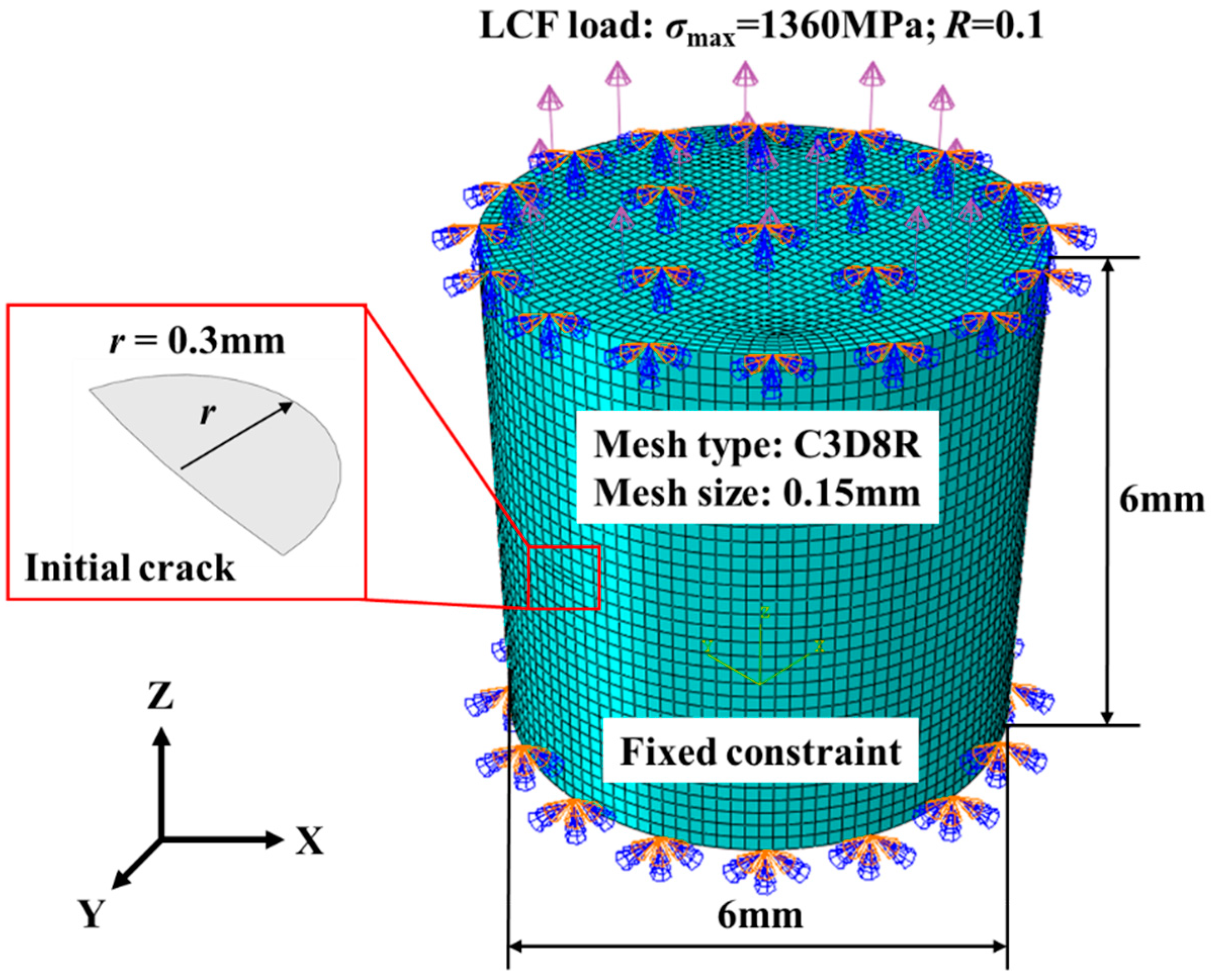
The boundary conditions were specified based on the surface integrity of the fatigue specimen and the LCF experiment. The maximum load was σ_max=1360 MPa and R=0.1 for stress ratio. The fixed constraint and load were applied on the RVE model as shown in Figure 9 (a). The distribution of shear stress in the RVE model is shown in Figure 9 (b). The shear stress was uniformly distributed within each grain while varied between different grains. It was due to the anisotropic mechanical properties of the grains.

The maximum load σ_max and minimum load σ_min were applied to the RVE model. The maximum shear stress τ_max and minimum shear stress τ_min of each grain were extracted using Python and Matlab. The average shear stress range Δτ and the length of the slip band d were substituted into Eq. (1) to calculate the crack initiation life of each grain. The grain with the lowest crack initiation life was marked as the critical grain. The critical grain was cracked at the end of a single simulation, and its crack initiation life was taken as the life of the simulation.

The shear stress distribution of the RVE model is shown in Figure 10. The shear stress within surrounding grains was changed by stress concentration at the crack tip. Cyclic FEM simulation was used to simulate the crack initiation process and predict the crack initiation life. The crack was assigned in the critical grain at the end of each single simulation, and then the FEM process proceeded to the subsequent simulation cycle. The simulation of the crack initiation cycle stopped when the crack length exceeded the criterion length (0.3mm), and the total crack initiation life was then outputted.

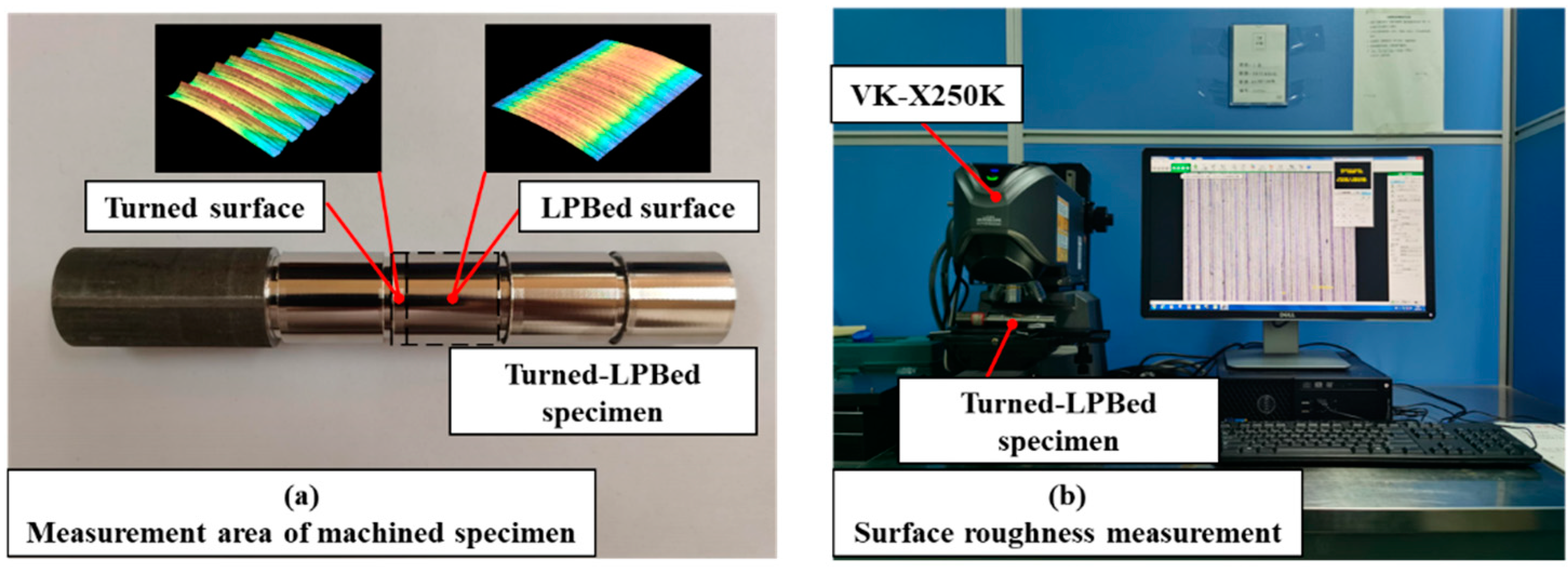
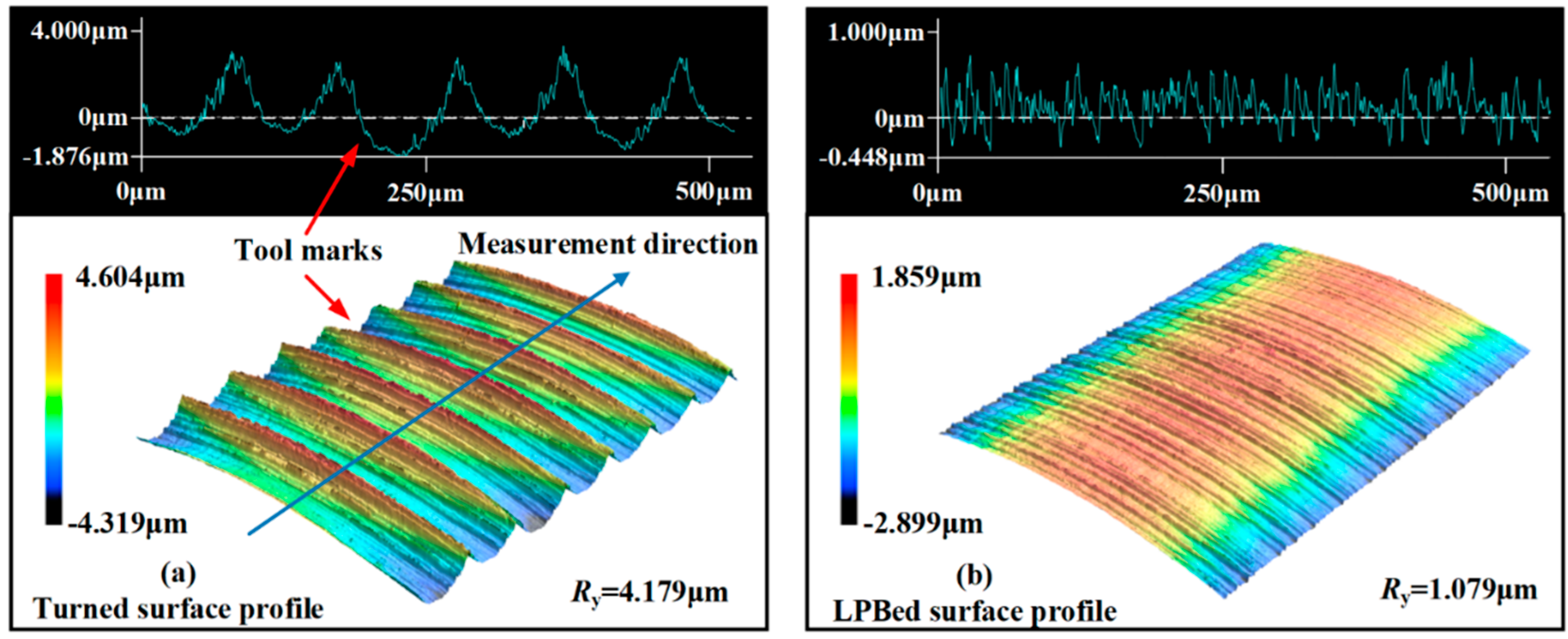
The surface integrity of the specimens was measured experimentally in Section 2.1. Surface morphology and surface roughness of the turned specimen and LPBed specimen are shown in Figure 11. As shown in Figure 11 (a), tool marks were observed on the turned surface. The surface roughness of the turned specimen was 4.179μm. Tool marks were smoothed after the LPB process as shown in Figure 11 (b), and the surface roughness was decreased to 1.079μm. The LPBed surface roughness was reduced by 77.6% compared to the turning results.

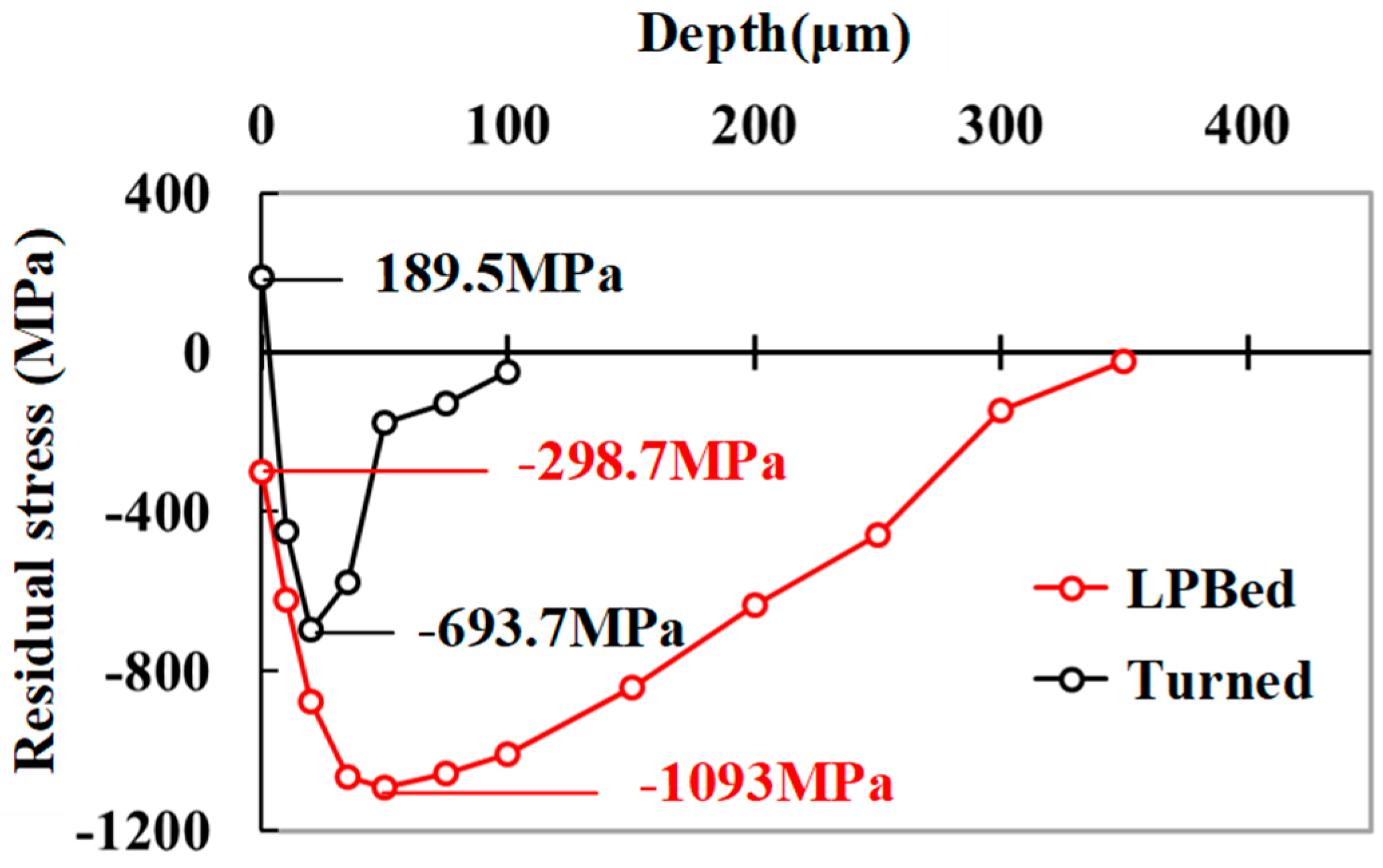
The residual stress field of the turned and LPBed specimens is depicted in Figure 12. Tensile residual stress with the value of 189.5MPa was induced on the turned surface. The maximum compressive residual stress of turned specimen was -693.7MPa. The depth of the turned residual stress field was 100μm. The surface compressive residual stress of the LPBed specimen was -298.7MPa. The maximum compressive residual stress of LPBed specimen was measured at 50μm from surface with the value of -1093MPa (57.6% increasing compared with turned specimen). The depth of the LPBed residual stress field of was 350μm.

Surface integrity affects the LCF life by altering actual stress applied on the LCF specimens [3,25]. Stress concentration, caused by surface roughness, increases the surface stress, which in turn reduces the LCF life of specimen [26]. The stress concentration field depth of the turned specimen was calculated using FEM, as shown in Figure 13. The multi-notch model was established according to the turning surface topography. Material mechanical parameters of Inconel 718 are shown in Table 1. The model was meshed using CPE4R. The size of fine meshes was 0.01mm. Fixed constraint was applied to the right side of the model, and load was applied to the left side. Microscopic morphology of the turned surface could not be replicated by FEM, so the surface roughness stress concentration coefficient was corrected using the Arola model [27], as shown in Eq. (2).

K_{t} = 1 + n (\frac{R_{a}}{ρ}) (\frac{R_{z}}{R_{y}})

(2)

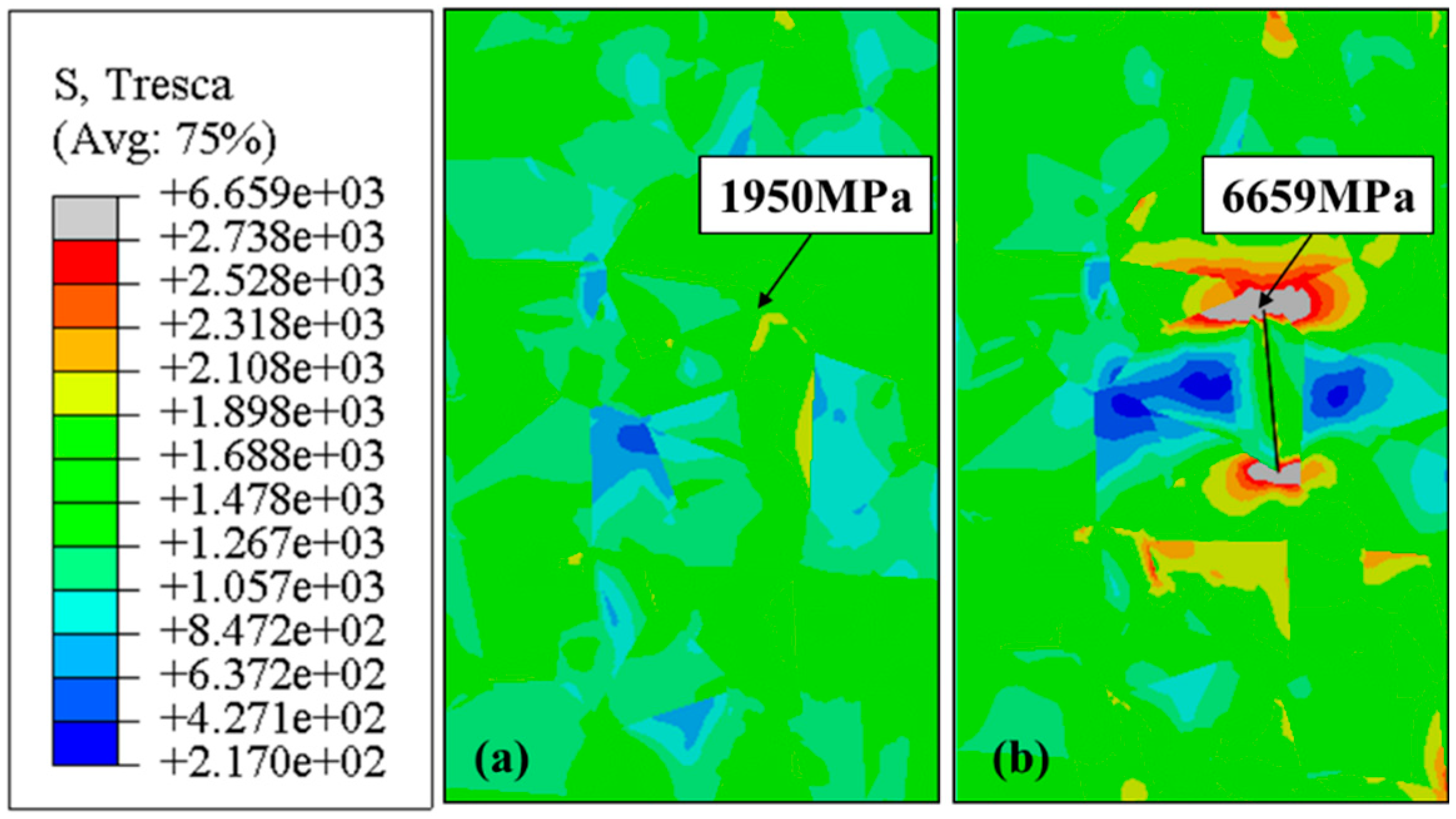
where R_a is the arithmetic mean deviation, ρ is the radius of the arc at notch bottom, and R_z is the maximum height. The surface roughness parameters of turning process are shown in Table 4. The stress concentration coefficient of the turned surface roughness was 1.72, and the depth of the stress concentration field was 40μm.

The actual stress of specimens considering surface integrity is expressed as Eq. (3).

σ_{real} = K_{t} σ_{applied} + σ_{res}

(3)

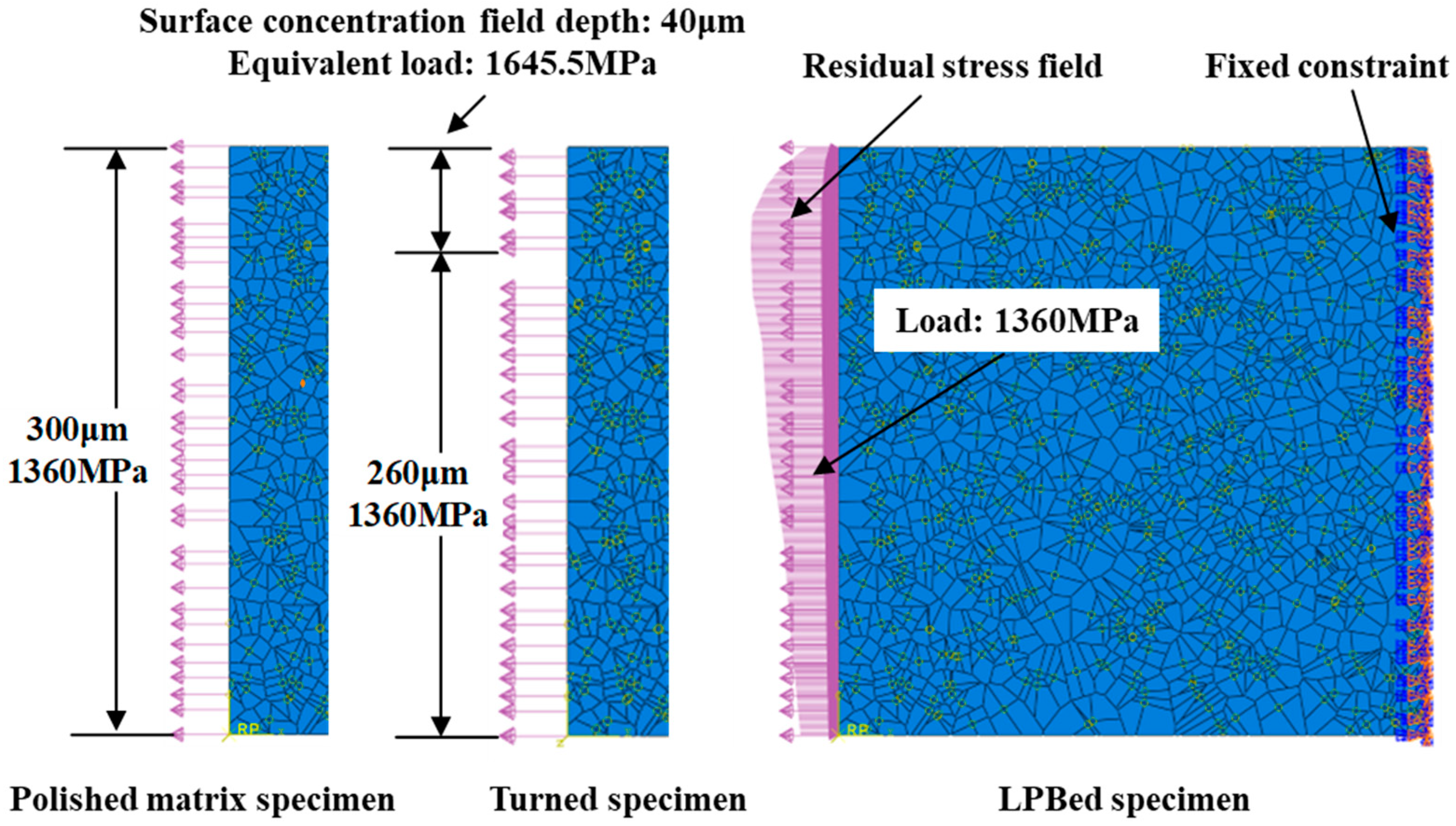
The actual stress on the turned specimen surface was 1645.5 MPa, and 1360 MPa internal the specimen. The compressive residual stress was applied to the LPBed specimen according to the measurement result shown in Figure 12. The boundary conditions of polished matrix, turned and LPBed RVE model are shown in Figure 14.

The crack propagation life of the specimens was predicted using the XFEM finite method. The 3D XFEM model was established based on the fatigue specimen structure, as shown in Figure 15. The initial crack with smooth curve front was formed after the crack initiation stage [28]. The semi-circular crack with the radius of 0.3mm was set up in middle of the model. Hexahedral meshes are the only suitable mesh for XFEM. The model was meshed using C3D8R with the size of 0.15mm to ensure convergence of XFEM simulation. The material parameters of Inconel 718 crack extension finite element analysis are shown in Table 5. The cyclic loading analysis step was used to simulate LCF cyclic loading process. Fixed constraint was set on the bottom of the model. The freedom of the upper surface was constrained except z-direction displacement. Sinusoidal load was applied to the model. 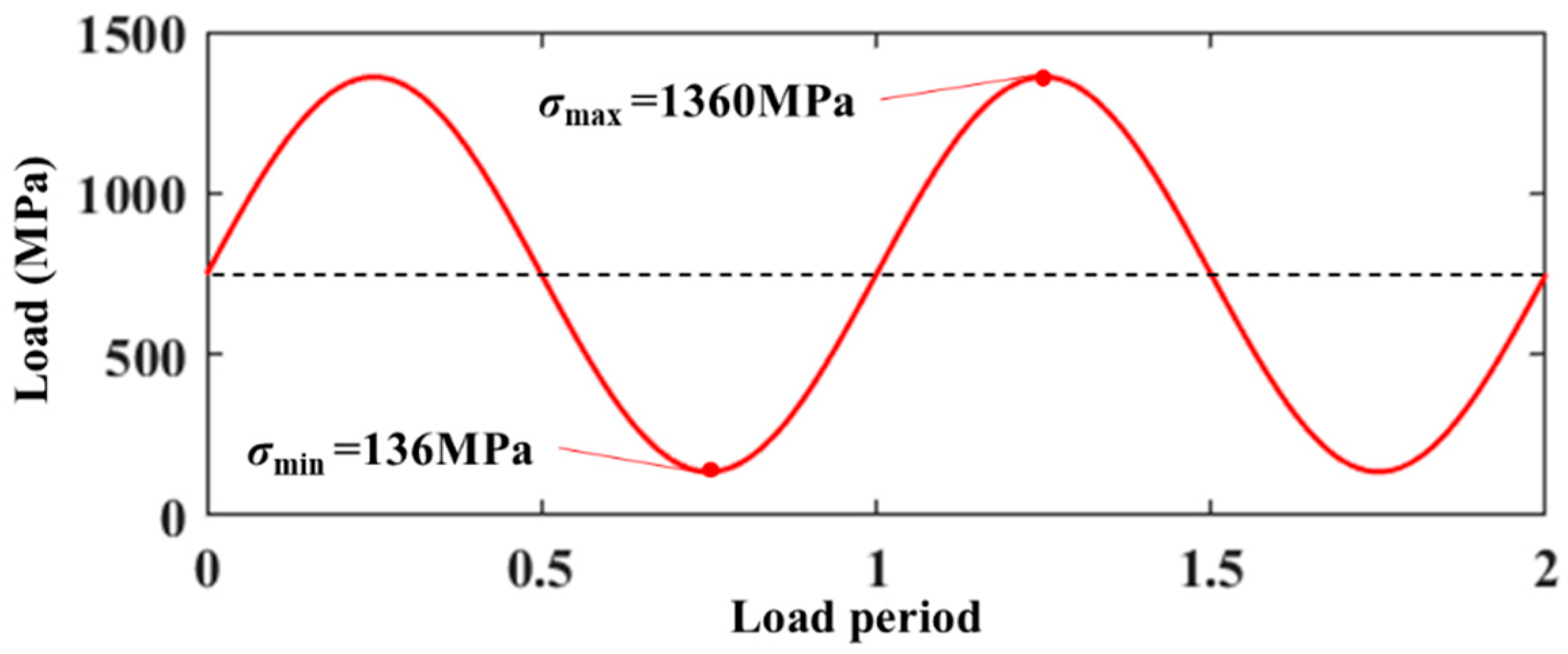The maximum load σ_max=1360 MPa, stress ratio R=0.1. The LCF load spectrum is shown in Figure 16.

4. Result and discussion

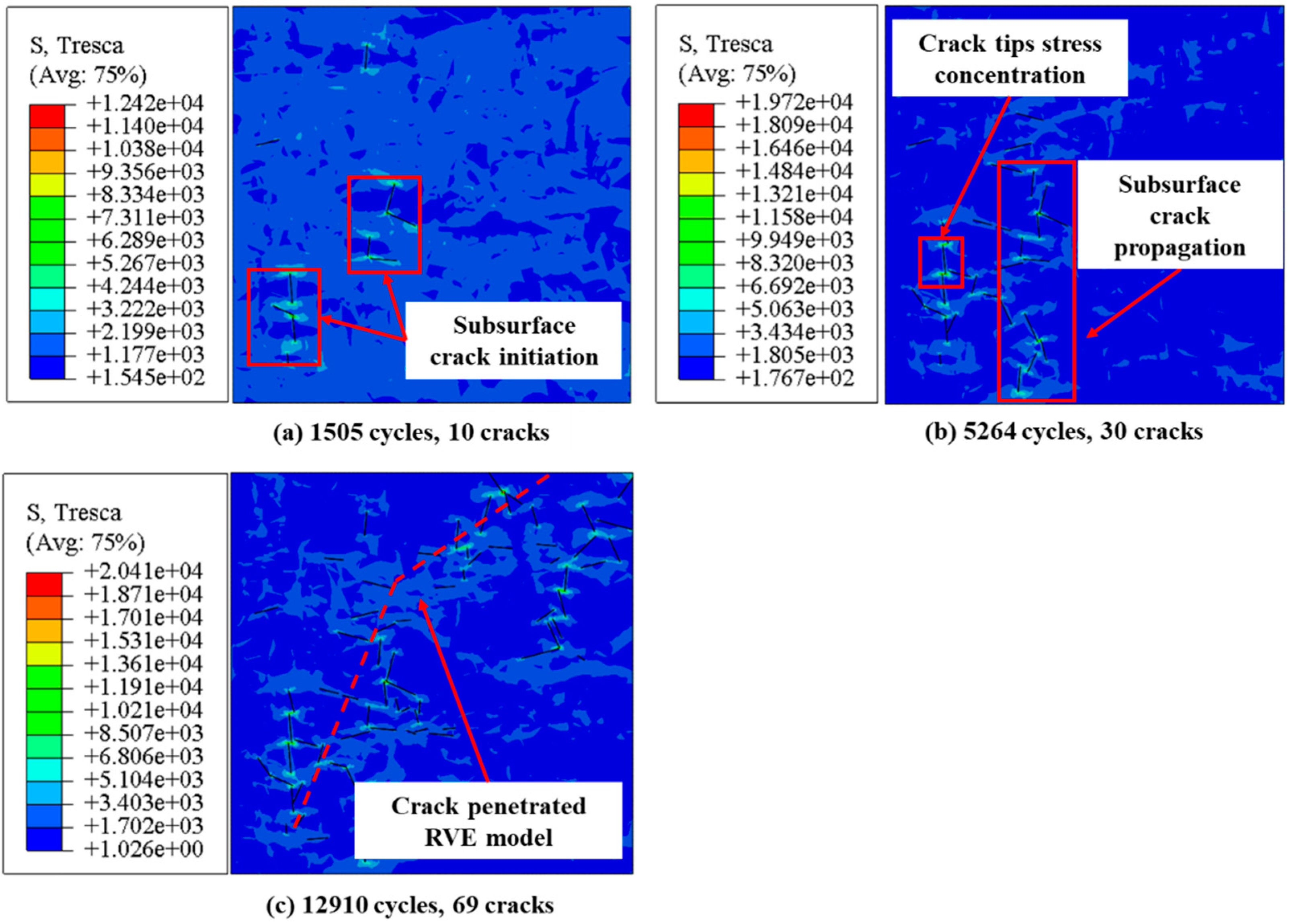
The crack initiation process of the polished matrix specimen simulated using FEM is shown in Figure 17. Microcracks initiated in subsurface grains when loaded after 1505 cycles as shown in Figure 17 (a). It is attributed to the absence of surface stress concentration on polished matrix specimen surface. The microcracks gathered and propagated to the surface with load proceeding as shown in Figure 17 (b). The microcracks penetrated the RVE model after 12910 cycles as shown in Figure 17 (c). The predicted crack initiation life for the polished matrix specimen was 9718 cycles.

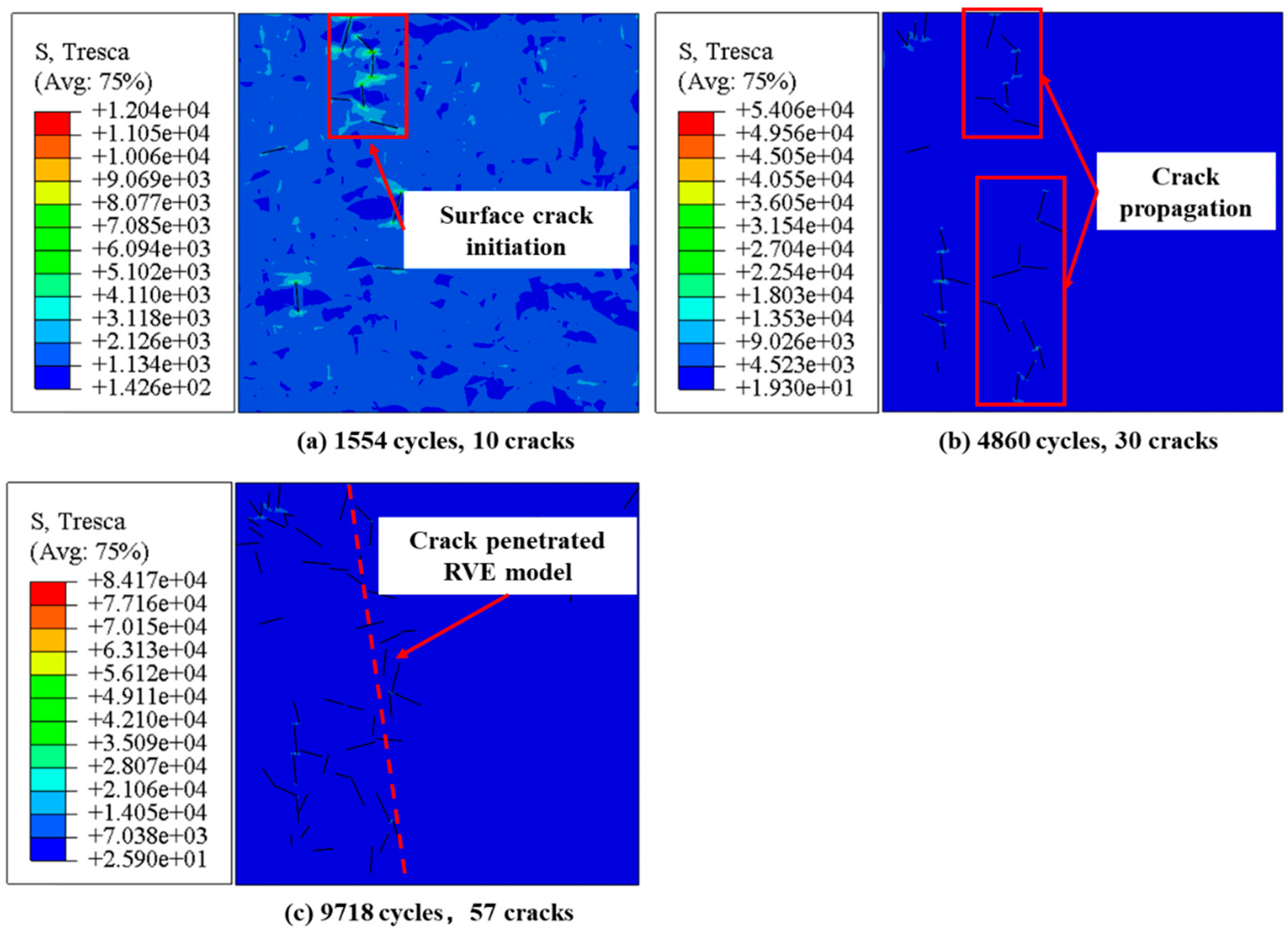
The crack initiation process of turned specimen simulated using FEM is shown in Figure 18. As shown in Figure 18 (a), microcracks initiated in the surface grains of turned specimen at 1554 cycles. The rapid crack initiation at the turned surface was attributed to the stress concentration induced by surface roughness. The actual stress on turned surface was much higher than the stress in substrate. As shown in Figure 18 (b), the microcracks initiated in both of the surface and subsurface, indicating that the compressive residual stress of the turned specimen was insufficient to inhibit crack initiation inside the specimen. The two microcracks merged and penetrated the RVE model at 9718 cycles as depicted in Figure 18 (c). The predicted crack initiation life of turned specimen was 9718 cycles.

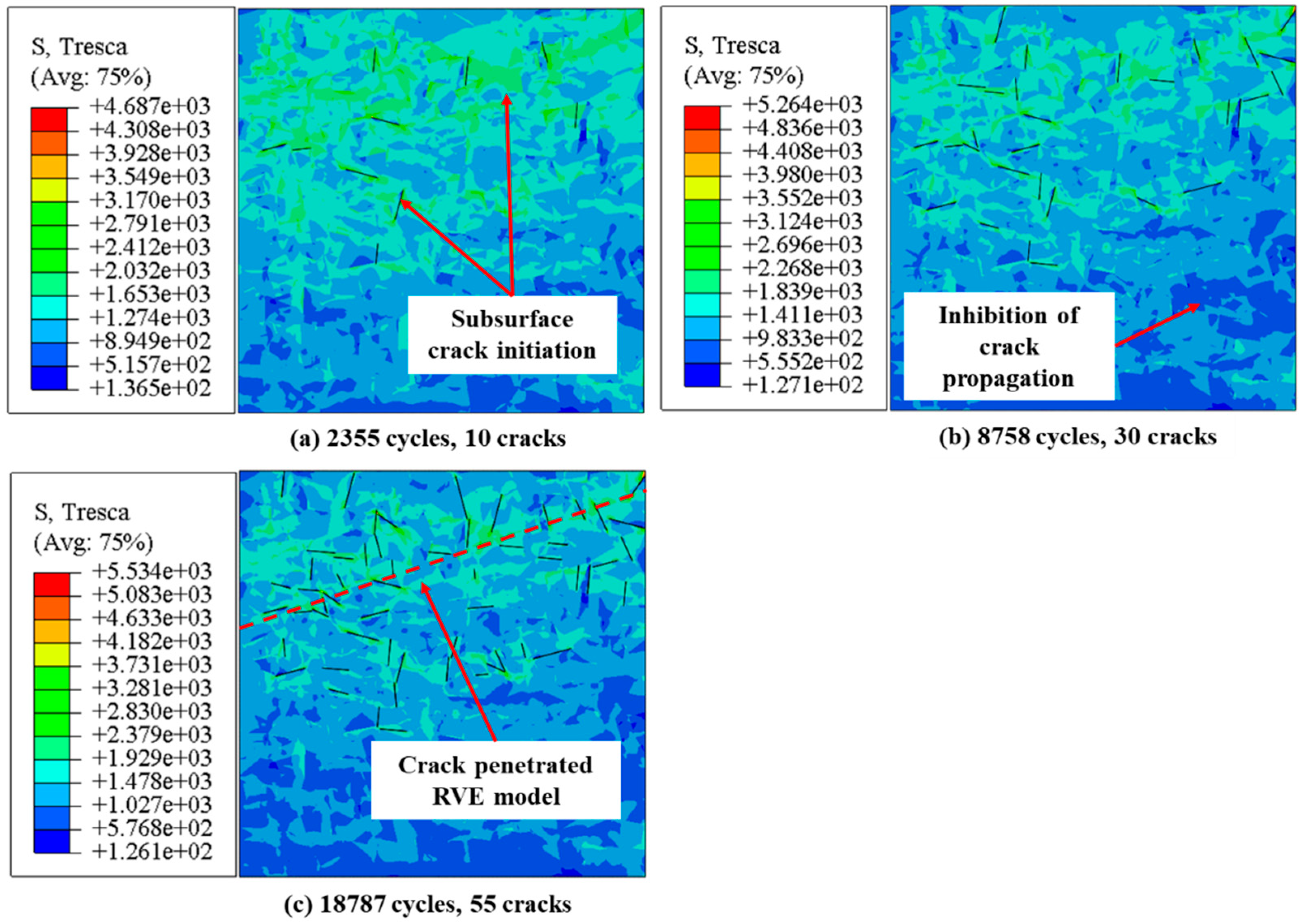
The crack initiation process of the LPBed specimen was simulated using FEM shown in Figure 19. Microcracks were initiated in the subsurface layer of the LPBed specimen at 2355 cycles as shown in Figure 19 (a). It is attributed to the low surface roughness and compressive residual stress field induced by the LPB process. The microcracks extended slowly within the LPBed specimen. The compressive residual stress delayed microcrack propagating to surrounding grains by mitigating the stress at the microcrack tips. The surface microcracks merged into the main crack penetrating the RVE model at 18787 cycles. The predicted crack initiation life of the LPBed specimen was 18787 cycles.

The XFEM model predicted crack propagation life is shown in Figure 20. The crack extended slowly perpendicular to the load at the beginning of the crack propagation stage. It was due to the lower intensity factor. As the crack length increased, the crack propagation accelerated with the stress intensity factor increasing. The shear lip formed at the end of the crack propagation was attributed to ductile fracture. The XFEM predicted crack propagation life N_p of Inconel 718 was 477.

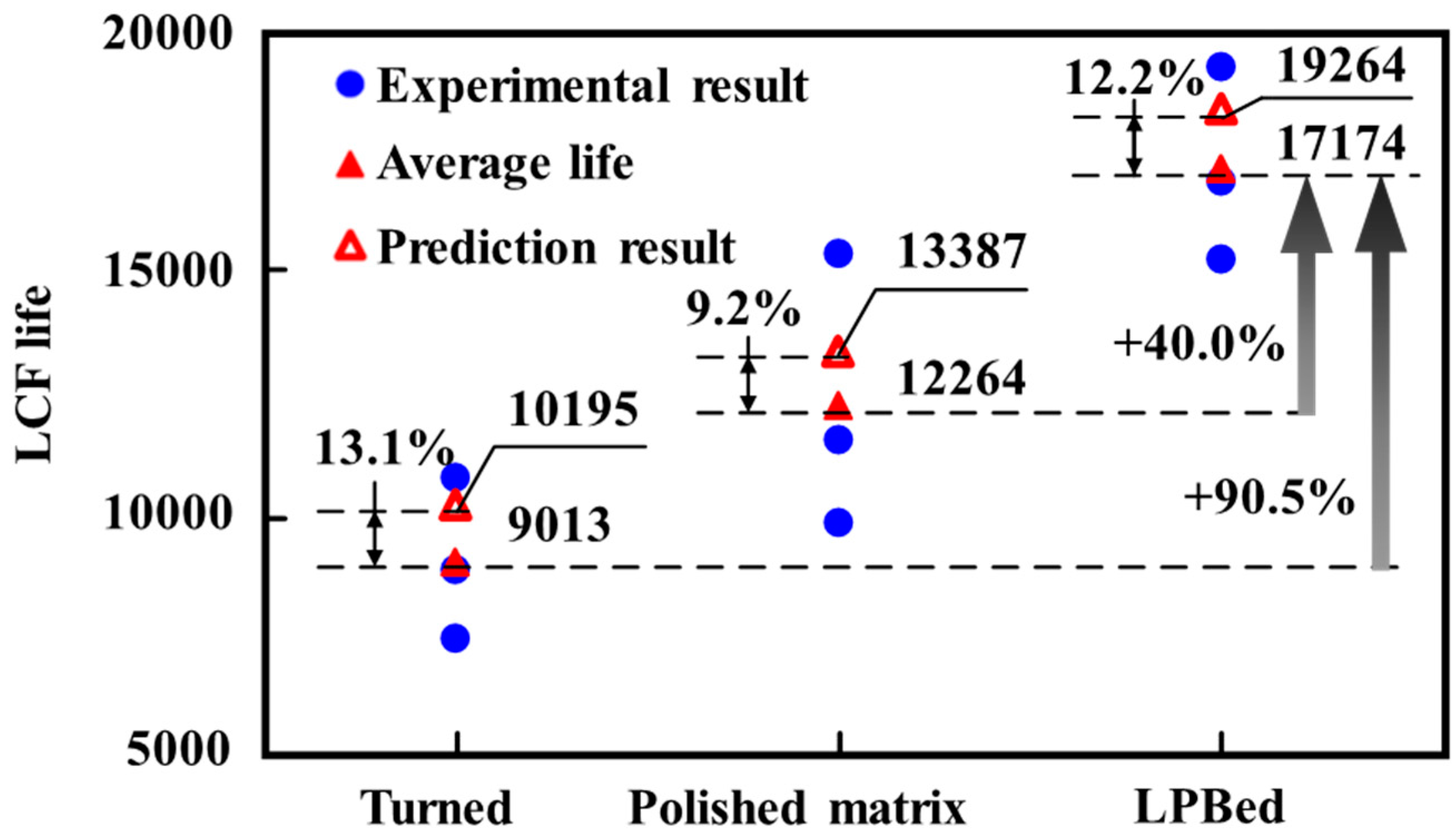
The experimental and FEM predicted results of Inconel 718 LCF life are shown in Figure 21. The average experimental LCF life of the polished matrix specimen was 12264 cycles. The turned specimen exhibited the lowest average experimental LCF life (9013 cycles), which decreased by 26.5% compared with the polished matrix specimen. It was due to the surface stress concentration induced by turned surface roughness. The average experimental LCF life of the LPBed specimen was the highest (17174 cycles), which increased by 40.0% and 90.5% compared with the polished matrix and turned specimen, respectively. It was attributed to the deep compressive residual stress field and low surface roughness induced by the LPB process, which reduced the stress on the specimen surface.

The Inconel 718 LCF life predicted by micro-macro FEM model was calculated as to equation (4).

N_{f} = N_{i} + N_{p}

(4)

where N_i, N_p and N_f are the crack initiation life, crack propagation life and LCF life predicted by micro-macro FEM method.

The predicted LCF life of Inconel 718 was all located within the experimental life range. The respective errors between the prediction and experimental results of the turned specimen, polished matrix specimen, and LPBed specimen were 13.1%, 9.2%, and 12.2%. It suggested that the micro-macro FEM method based on crack initiation and propagation mechanisms can be used to predict the LCF life of Inconel 718 with different surface integrity. The micro-macro FEM method predicted LCF life was slightly higher than the experimental results. The overestimation of the LCF life was due to the fact that the grain boundary crack was not considered in FEM model.

Fracture morphology of the polished matrix specimen, turned specimen and LPBed specimen is shown in Figure 22. The fracture morphology of the polished matrix specimen is shown in Figure 22 (a)-(c). The fatigue crack initiated on the surface of the polished matrix specimen as shown in Figure 22 (a). The transgranular fracture was observed at the crack initiation area. It is due to the lower surface stress concentration of the polished surface. The transgranular fracture and fatigue striation were observed at 150μm from surface as shown in Figure 22 (b). The crack propagation rate was calculated as 0.43μm per cycle by measuring fatigue striation per micron. The propagation rate increased to 0.80μm per cycle at 300μm from the surface as shown in Figure 22 (c). It is due to the increment of the stress intensity factor with the crack propagating.

The fracture morphology of the turned specimen is shown in Figure 22 (d)-(f). As shown in Figure 22 (d), the fatigue cracks initiated at the surface tool marks, which is consistent with micro FEM simulation results. It was attribute to the high surface stress induced by stress concentration. As shown in Figure 22 (e), fatigue streaks were observed at 150μm from turned surface. The crack propagation rate at 150μm of the turned specimen was measured at 0.57μm per cycle. The propagation rate increased to 0.67μm per cycle when the crack length grew to 300μm as shown in Figure 22 (f).

The fracture morphology of LPBed specimen is shown in Figure 22 (g)-(i). As shown in Figure 22 (g), the crack was initiated at the subsurface of the LPBed specimen. The transgranular fracture and fatigue striation was observed at 150μm from the surface as shown in Figure 22 (h). The LPBed specimens showed the densest fatigue striation compared with the other groups, and the crack propagation rate was calculated as 0.32μm per cycle. The surface crack initiation and propagation were delayed by the lower surface roughness and compressive residual stress field induced by LPB processing. The crack propagation rate at 300μm from surface was measured as 0.76μm per cycle as shown in Figure 22 (i), which was similar to the other groups. It was due to the fact that the crack propagation was seldom affected by the surface integrity because the crack propagated beyond the surface integrity influence field.

5. Conclusion

In this study, the LCF life of Inconel 718 with different surface integrity was researched using theoretical and experimental method. The micro-macro FEM model was established based on fatigue crack initiation and propagation mechanism. The LCF life of the turned specimen, polished matrix specimen and LPBed specimen was predicted using the proposed model. The LCF experiment was conduct to validate the proposed model. The conclusions are emphasized as follows:

1): Compared with the turned specimen, the surface roughness R_y of the LPBed specimen was reduced by 77.6%, and the maximum compressive residual stress was increased by 57.1%. The compressive residual stress field depth was increased by 2.5 times after LPB processing.
2): The LCF life of the LPBed specimens increased by 36.1% compared with the polished matrix specimen, and increased by 90.5% compared with the turned specimen. It was attribute to low surface roughness and compressive residual stress field induced by the LPB process.
3): The LCF life of Inconel 718 specimens with different surface integrity was predicted by the proposed model. The error between the prediction results and the experimental results was 13.1%.

Author Contributions

Conceptualization, P.C. and Z.L.; methodology, P.C. and Z.L.; validation, P.C., J.Z. and Z.L.; formal analysis, P.C. and Z.L.; investigation, P.C. and X.R.; data curation, P.C.; writing—original draft preparation, P.C., X.R. and Z.L.; project administration, Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the grants from National Natural Science Foundation of China (No.52275444), National Natural Science Foundation of China (No. 52205482), Natural Science Foundation of Shandong Province (ZR202111150191) and Shandong Province Key Research and Development Plan (2023JMRH0307).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Vayssette, B.; Saintier, N.; Brugger, C.; Mohamed, E. Surface roughness effect of SLM and EBM Ti-6Al-4V on multiaxial high cycle fatigue. Theor. Appl. Fract. Mec. 2020, 108, 102581. [Google Scholar] [CrossRef]
Javadi, H.; Jomaa, W.; Songmene, V.; Brochu, M.; Bocher, P. Inconel 718 superalloy controlled surface integrity for fatigue applications produced by precision turning. Int. J. Precis. Eng. Man. 2019, 20, 1297–1310. [Google Scholar] [CrossRef]
Javadi, H.; Jomaa, W.; Dalgaard, E.; Brochu, M.; Bocher, P. Influence of surface residual stresses on the fatigue life and crack propagation behavior of turned Inconel 718 super-alloy. MATEC Web of Conferences. EDP Sciences 2018, 165, 18004. [Google Scholar] [CrossRef]
Gao, Y.; Yang, W.; Huang, Z.; Lu, Z. Effects of residual stress and surface roughness on the fatigue life of nickel aluminium bronze alloy under laser shock peening. Eng. Fract. Mech. 2021, 244, 107524. [Google Scholar] [CrossRef]
Seemikeri, C.Y.; Brahmankar, P.K.; Mahagaonkar, S.B. Improvements in surface integrity and fatigue life of low plasticity burnished surfaces. Int. J. Microstruct. Mater. Prop. 2012, 7, 27–48. [Google Scholar] [CrossRef]
Jablonski, D.A. The effect of ceramic inclusions on the low cycle fatigue life of low carbon astroloy subjected to hot isostatic pressing. Mater. Sci. Eng. 1981, 48, 189–198. [Google Scholar] [CrossRef]
Alexandre, F.; Deyber, S.; Pineau, A. Modelling the optimum grain size on the low cycle fatigue life of a Ni based superalloy in the presence of two possible crack initiation sites. Scr. Mater. 2004, 50, 25–30. [Google Scholar] [CrossRef]
Guo, G.; Jiang, W.; Liu, X.; Chen, J.; Li, L.; Wang, J.; Zhang, Y.; Zhang, Z. In-situ SEM-EBSD investigation of the low-cycle fatigue deformation behavior of Inconel 718 at grain-scale. J. Mater. Res. Technol. 2023, 24, 5007–5023. [Google Scholar] [CrossRef]
Tanaka, K.; Mura, T. A dislocation model for fatigue crack initiation. J. Appl. Mech. 1981, 1, 97–103. [Google Scholar] [CrossRef]
Brucknerfoit, A.; Huang, X. Numerical simulation of micro-crack initiation of martensitic steel under fatigue loading. Int. J. Fatigue 2006, 28, 963–971. [Google Scholar] [CrossRef]
Rahim, M.R.A.; Schmauder, S.; Manurung, Y.H.P.; Binkele, P.; Ahmad, M.I.M.; Dogahe, K. Cycle number estimation method on fatigue crack initiation using Voronoi tessellation and the Tanaka Mura model. J. Fail anal. Prev. 2023, 23, 548–555. [Google Scholar] [CrossRef]
Zhou, J.; Barrett, R.A.; Leen, S.B. A physically-based method for predicting high temperature fatigue crack initiation in P91 welded steel. Int. J. Fatigue 2021, 153, 106480. [Google Scholar] [CrossRef]
Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
Nikishkov, G.P.; Park, J.H.; Atluri, S.N. SGBEM-FEM alternating method for analyzing 3D non-planar cracks and their growth in structural components. Cmes-comp. Model. Eng. 2001, 2, 401–422. [Google Scholar]
Chopp, D.L.; Sukumar, N. Fatigue crack propagation of multiple coplanar cracks with the coupled extended finite element/fast marching method. Int. J. Eng. Sci. 2003, 41, 845–869. [Google Scholar] [CrossRef]
Bergara, A.; Dorado, J.I.; Martín-Meizoso, A.; Martínez-Esnaola, J.M. Fatigue crack propagation in complex stress fields: experiments and numerical simulations using the extended finite element method (XFEM). Int. J. Fatigue 2017, 103, 112–121. [Google Scholar] [CrossRef]
Naderi, M.; Iyyer, N. Fatigue life prediction of cracked attachment lugs using XFEM. Int. J. Fatigue 2015, 77, 186–193. [Google Scholar] [CrossRef]
Chen, Z.; Bao, H.; Dai, Y.; Liu, Y. Numerical prediction based on XFEM for mixed-mode crack growth path and fatigue life under cyclic overload. Int. J. Fatigue 2022, 162, 106943. [Google Scholar] [CrossRef]
Hua, Y.; Liu, Z.; Wang, B.; Jiang, J. Residual stress regenerated on low plasticity burnished Inconel 718 surface after initial turning process. J. Manuf. Sci. Eng. 2019, 141, 121004. [Google Scholar] [CrossRef]
Deng, C.; Liu, G.; Gong, B.; Liu, Y. Fatigue crack initiation life prediction based on Tanaka-Mura dislocation model. Trans. China Weld. Inst. 2021, 42, 30–37. [Google Scholar]
Zhao, Y.Y.; Nieh, T.G. Correlation between lattice distortion and friction stress in Ni-based equiatomic alloys. Intermetallics 2017, 86, 45–50. [Google Scholar] [CrossRef]
Glodež, S.; Šori, M.; Kramberger, J. Prediction of micro-crack initiation in high strength steels using Weibull distribution. Eng. Fract. Mech. 2013, 108, 263–274. [Google Scholar] [CrossRef]
Kramberger, J.; Jezernik, N.; Göncz, P.; Glodež, S. Extension of the Tanaka–Mura model for fatigue crack initiation in thermally cut martensitic steels. Eng. Fract. Mech. 2010, 77, 2040–2050. [Google Scholar] [CrossRef]
Ou, C.; Voothaluru, R.; Liu, C.R. Fatigue crack initiation of metals fabricated by additive manufacturing—a crystal plasticity energy-based approach to IN718 life prediction. Crystals 2020, 10, 905. [Google Scholar] [CrossRef]
Wang, X.; Huang, C.; Zou, B.; Liu, G.; Zhu, H.; Wang, J. Experimental study of surface integrity and fatigue life in the face milling of Inconel 718. Front. Mech. Eng-prc. 2018, 13, 243–250. [Google Scholar] [CrossRef]
Itoga, H.; Tokaji, K.; Nakajima, M.; Ko, H.N. Effect of surface roughness on step-wise s–n characteristics in high strength steel. Int. J. Fatigue 2003, 25, 379–385. [Google Scholar] [CrossRef]
Arola, D.; Williams, C.L. Estimating the fatigue stress concentration factor of machined surfaces. Int. J. Fatigue 2002, 24, 923–930. [Google Scholar] [CrossRef]
Yadollahi, A.; Mahmoudi, M.; Elwany, A.; Doude, H.; Bian, L.; Newman, J.C., Jr. Fatigue-life prediction of additively manufactured material: effects of heat treatment and build orientation. Fatigue. Fract. Eng. M. 2020, 43, 831–844. [Google Scholar] [CrossRef]
Cai, W. Effect of long-term aging on microstructure evolvement and fatigue crack growth behavior of GH4169 alloy. MA thesis, Northeastern University, Liaoning Province, 2015. [Google Scholar]

Figure 1. Crack initiation dislocation mechanism of Inconel 718.

Figure 2. Research framework.

Figure 3. Turning and LPB process.

Figure 4. Surface roughness measurement of machined specimens.

Figure 5. Residual stress measurement of machined specimens.

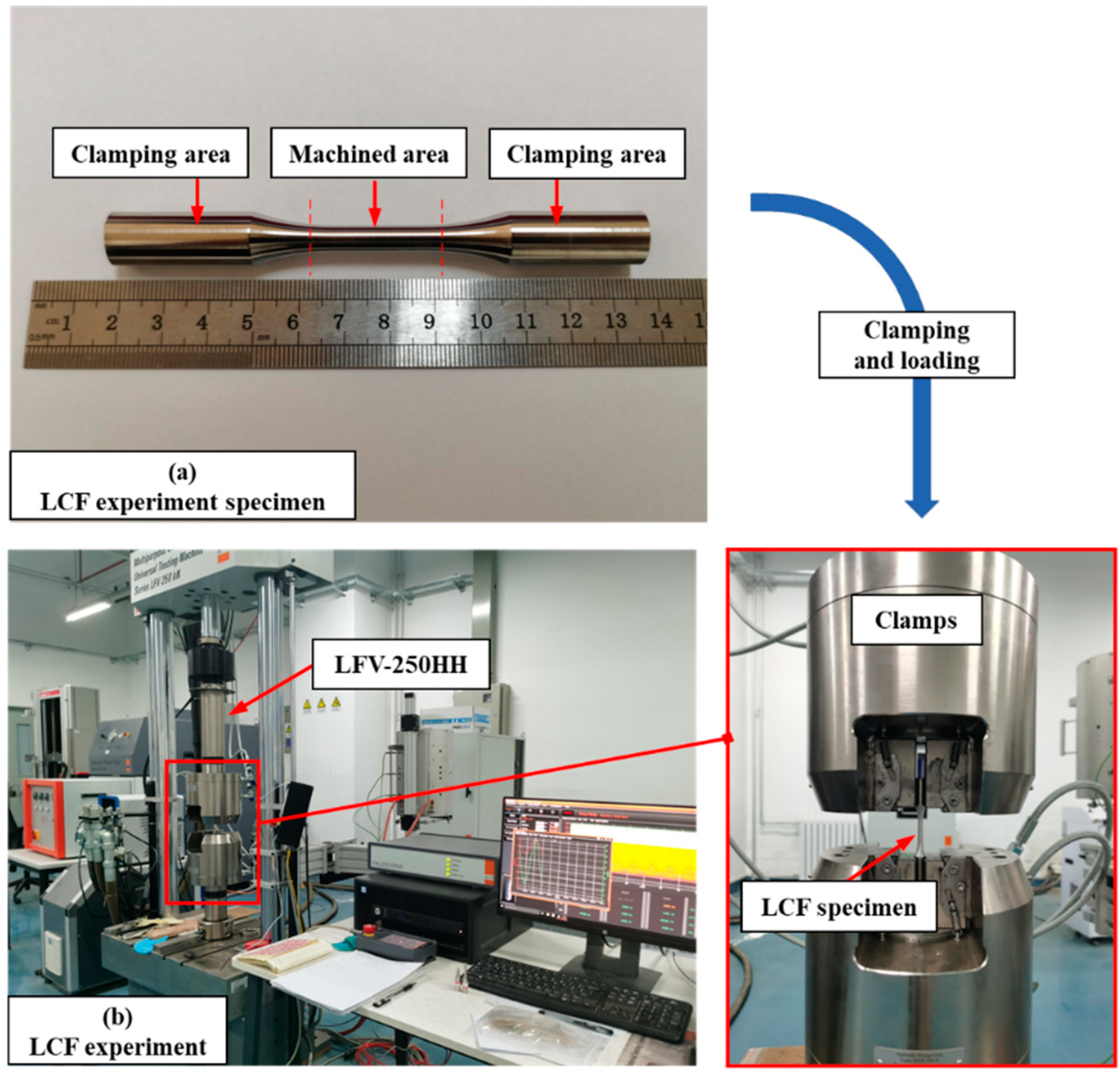
Figure 6. LCF experiment of machined LCF specimens with different surface integrity.

Figure 7. Surface microstructure and grain size statistic of turned and LPBed specimens.

Figure 8. RVE model of Inconel 718 LCF specimens.

Figure 9. Boundary conditions and shear stress of the RVE model.

Figure 10. Shear stress distribution of RVE model (a) without crack and (b) with crack.

Figure 11. Surface topography and surface roughness of turned and LPBed specimens.

Figure 12. Residual stress field of turning and LPB specimens.

Figure 13. Surface stress concentration field FEM model of turned Inconel 718 specimen.

Figure 14. Boundary conditions of polished matrix, turned and LPBed RVE model.

Figure 15. Crack propagation XFEM model.

Figure 16. LCF load spectrum of Inconel 718 specimens.

Figure 17. Crack initiation process of polished matrix RVE model.

Figure 18. Crack initiation process of turned RVE model.

Figure 19. Crack initiation process of LPBed RVE model.

Figure 20. Crack propagation XFEM analysis of Inconel 718 specimen.

Figure 21. Experimental and FEM prediction result of Inconel 718 specimens.

Figure 22. Fracture morphology of polished matrix specimen, turned specimen and LPBed specimens.

Table 1. Mechanical properties of superalloy Inconel 718 [19].

Elastic modulus	Yield strength	Tensile Strength	Elongation	Hardness
E(GPa)	σ_s(MPa)	σ_b(MPa)	(%)	(HBW)
210	1360.5	1502	19.3	439

Table 2. The Tanaka-Mura model parameters of Inconel 718 [20,21].

Material	G(MPa)	ν	k(MPa)	W_s(KJ·m^–2)
Inconel 718	78850	0.3	150	6.5

Table 3. The orthotropic elastic matrix constants of Inconel 718 [24].

C₁₁(GPa)	C₂₂(GPa)	C₃₃(GPa)	C₁₂(GPa)	C₁₃(GPa)	C₂₃(GPa)	C₄₄(GPa)	C₅₅(GPa)	C₆₆(GPa)
230	230	230	170	170	170	100	100	100

Table 4. Stress concentration factor of turned surface.

R_a(μm)	R_y(μm)	R_z(μm)	ρ(mm)	K_t	d_t(μm)
0.942	4.179	5.078	3.179	1.72	40

Table 5. Crack propagation XFEM model parameters of Inconel 718 [29].

Material	G(GPa)	ν	Paris model parameters
Material	G(GPa)	ν	C	m
Inconel 718	210	0.3	1.13×10^-11	2.74

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.