Preprint

Article

Mechanism and Experimental Investigation of Vibration Reduction for Container Crane Based on Particle Damping Technology

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Fangping Ye,Xinyi Xue,Weijie Jiang,

Xiyan Yin^*

Fangping Ye,Xinyi Xue,Weijie Jiang,

Xiyan Yin^*

This version is not peer-reviewed

Submitted:

30 November 2023

Posted:

07 December 2023

You are already at the latest version

Alerts

Abstract

Container crane has been widely used for port operation. However, the structure of port container crane is large, which always lead to crane damage under the vibration and strong wind. Therefore, a method for vibration reduction of container crane structure based on particle damping technology is proposed. In this investigation, the scale 1:80 crane model is built, the equivalent mechanical model is also established to preliminary verify the effect of vibration suppression. Furthermore, the dependence of vibration suppression effect on the key parameters of the damper, i.e., filling material, filling rate, particle size, and installation position of dampers are analyzed through experiments. The results indicate that the vibration peak of the crane structure displayed in Simulink oscilloscope is weakened and lags behind, the installation of the damper brings the effect of vibration suppression for the crane, the vibration suppression effect reaches 25%; the crane mode obtains the best vibration suppression effect under the condition that the material filled in the damper has a large density and elastic modulus, sufficient collision space and high collision frequency, and the dampers are installed far away from the crane center of gravity. The optimum parameters of the damper obtained from experiments, 12 mm lead beads, filling rate of 60%, installed in the distal ends within the strength range of the forearm of the crane. It is thus concluded that the particle damping technology has provided an effective way in wind and vibration reduction for container crane.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The container crane is the main equipment used to realize the loading and unloading of cargo in port transportation. The high and large size of the crane structure directly causes it to be more sensitive to wind load and more prone to vibration. Vibration poses a serious threat to the stability of cranes and causes excessive deflection or toppling of masts, thus threatening economic property and personal safety [1,2,3]. To achieve vibration suppression of the crane bridge with variable disturbances, Xing et.al [4] proposed a speed-estimator-based robust control (SERC). Al-Fadhli et.al [5] presented a smooth command (SC) input shaper which is used to suppress payload oscillations in rest-to-rest simultaneous radial and tangential motions of the tower crane. Zhao et.al [6] investigated a modified extra-insensitive (MEI) input shaper which is used to suppress the oscillations of the payload swing and pitch in the dual cranes. The MEI shaper has good robustness to large changes in frequency and has good performance in vibration suppression. Most researches on crane vibration suppression use algorithms to intervene the forces between crane modules to suppress crane vibration. Although the above methods play a key role in wind-proofing and vibration suppression of cranes, the above methods do not take into account that structural changes have a great impact on the stress distribution of crane parts, and the maintenance cost of the algorithm control system is high. Therefore, it is particularly important to formulate better vibration suppression technology for cranes based on their structural characteristics and response characteristics.

Particle damping technology is a promising damping technology, which is widely used in various fields, especially in many aerospace and industrial applications. It is used to control the vibration of the mechanical system, so as to increase the reliability of the mechanism [7,8,9]. Chockalingam et.al [10,11] used particle damping technology to suppress the vibration in the boring process. The research results and evaluation criteria show that the displacement amplitude of the boring bar is reduced to half of the original and the workpiece surface accuracy is improved. Meyer et.al [12] applied the particle damping technique to the horizontal transient vibration lightweight elastic manipulator to reduce the vibration response of the manipulator and improve its working stability. Wang et.al [13] used particle damper to reduce the vibration of pipeline system, through a reasonable selection of damper parameters, the pipeline system showed excellent anti-vibration ability under random excitation. The application of the above-mentioned particle damping technology is quite effective in vibration reduction. Therefore, the method of applying particle damping technology to crane vibration suppression is innovative proposed in this investigation. Moreover the feasibility of the proposed method is verified by Simulink. In addition, the effect of particle damper parameters on vibration suppression performance is investigated through vibration attenuation experiments.

2. Similar Model of Crane

The J248 crane is widely used in the cargo operation of various ports, so this investigation takes J248 crane as the research object, so as to provide some reference for the safety protection work of port crane. The length of the front end of J248 crane is 65 m, the distance between the front and rear rails is 30 m, and the vertical distance between the beam and the ground is 46 m.

Obviously, it is difficult to test as the large size of J248 crane. Therefore, the similar model of J248 crane is designed and experimented. According to the size of the available laboratory space, the length similarity constant of the design model is 1/80 [14]. Similarity relation of the scale model of actual structure of J248 crane is shown in Table 1.

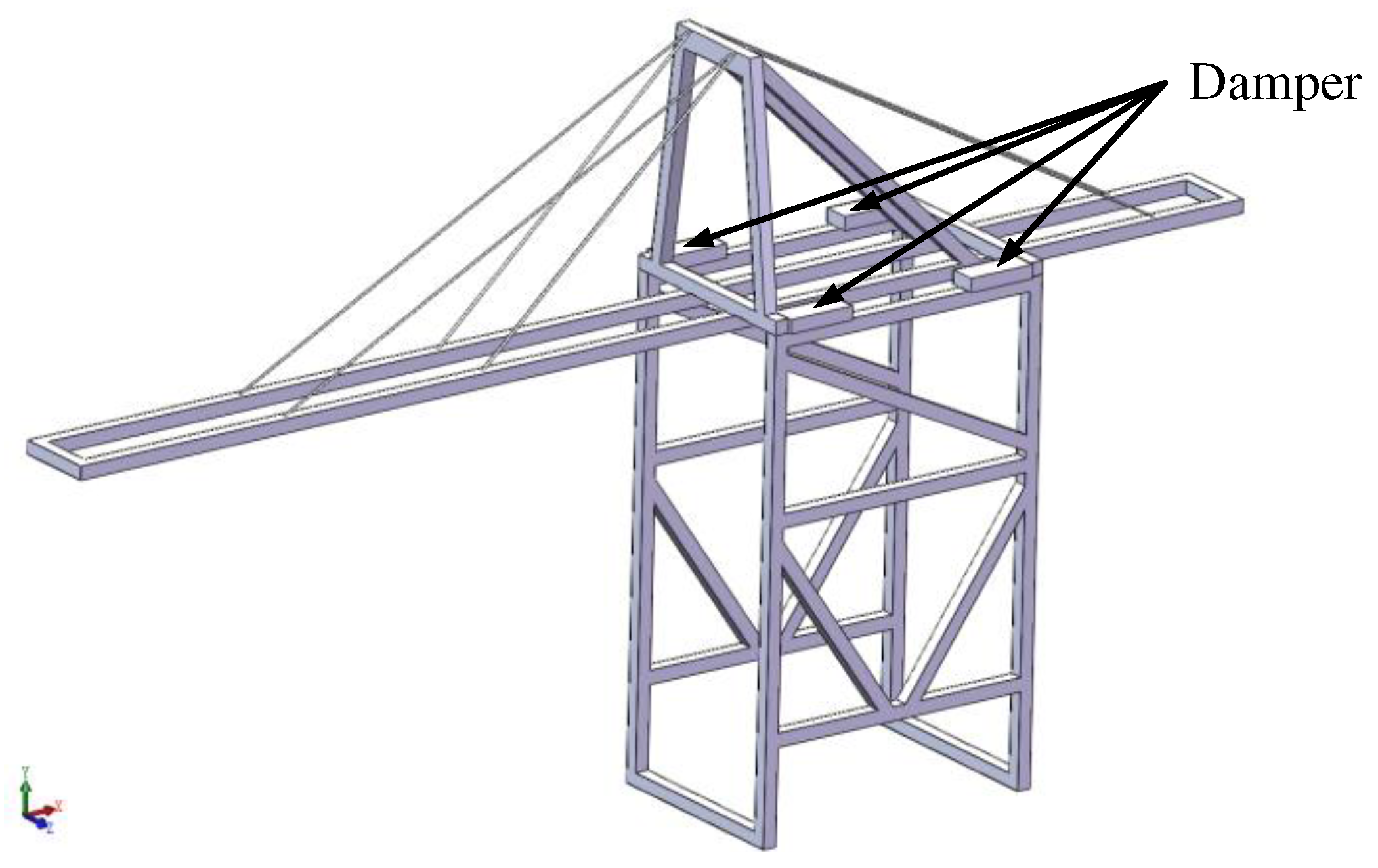
This study is only for the scenario when the transverse wind load acts on the crane, and the crane is under the anchoring state (rigid connection to the ground). Considering the mass distribution and the transportation space of crane, the four dampers are installed on the shoulder, as shown in Figure 1.

3. Theoretical Analysis

3.1. Design of Simplified Model and Calculation of Stiffness Equation

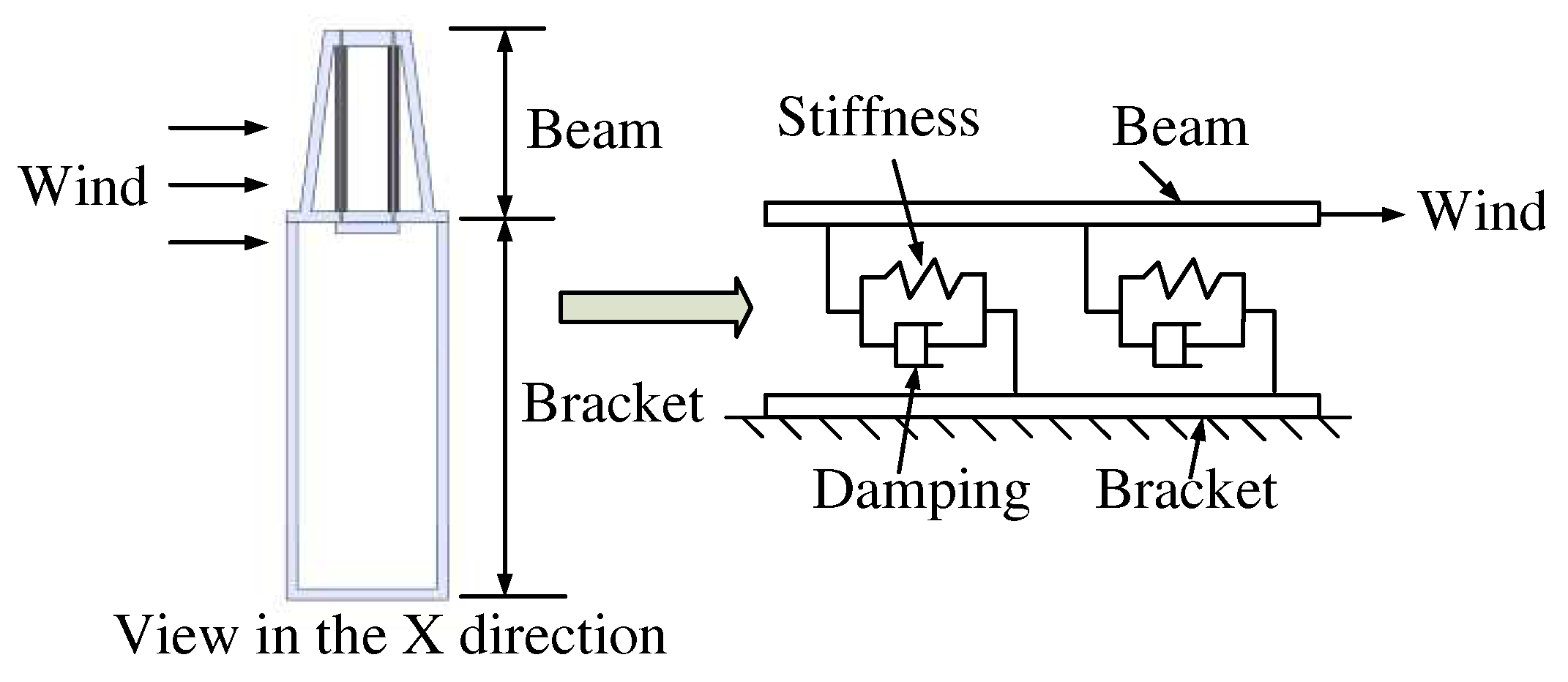
To investigate whether the installation of particle damper has vibration suppression effect on the crane in advance, it is necessary to establish the mathematical model of the installed with particle dampers and analyze it. Therefore, the actual crane system is simplified as 1-DOF system, the macro structure is divided into beam structure and bracket structure. The equivalent mechanical model is shown in Figure 2.

The results of large-scale shaking table tests conducted by some scholars show that multiple particles move in the form of "plug flow", that is, multiple particles move as a whole [15]. The multiple particles are established as a single particle in the damper based on the following assumption:

(1): The gap of the damper cavity before and after equivalent simplification is equal;
(2): The total mass of multiple particles before equivalent simplification is equal to the mass of individual particle after equivalent simplification;
(3): The particle damper before the equivalent simplification is a cuboid, the single particle damper after the equivalent simplification is a cylinder, and the diameter of the cylinder is equal to the diameter of the single particle after the equivalent simplification;
(4): The contact between the particle and the cavity wall is also expressed in terms of stiffness and damping.

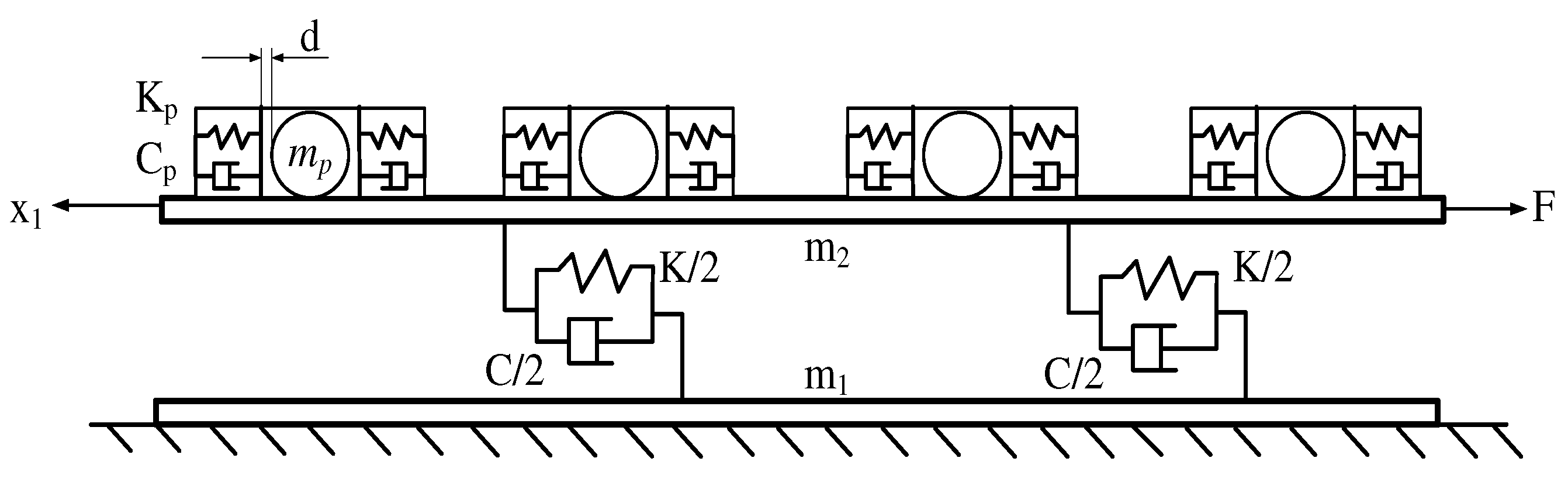
The 1-DOF equivalent mechanical model with dampers is established, as shown in Figure 3.

where K is equivalent stiffness of steel frame, C is equivalent damping of steel frame, m₁ is the mass of the bracket structure, m₂ is beam structural mass, m_p is the mass of sphere, K_p is the contact stiffness between sphere and cavity wall, C_p is contact damping between sphere and cavity wall, d is the initial distance between the sphere and the cavity wall, F is wind load, x₁ is the displacement of the beam structure.

Under the condition that the relative displacement between the sphere and the cavity is less than d, the collision behavior does not occur, and the elastic force and damping force are zero. Under the condition that the relative displacement between the sphere and the cavity is greater than d, collision behavior occurs, resulting in collision force. Therefore, the collision process between the sphere and the inner wall of cavity is represented by stage linearization to simulate the relative displacement and velocity of the inelastic collision between the rigid wall and the sphere. The functions G and H represents the stage linear stiffness and stage linear damping characteristic of the particle damper.

G (x_{p}) = \{\begin{cases} x_{p} - x_{1} + d, (x_{p} - x_{1} \leq - d) \\ 0, (- d < x_{p} - x_{1} < d) \\ x_{p} - x_{1} - d, (x_{p} - x_{1} \geq d) \end{cases}

(1)

H (x_{p}, {\dot{x}}_{p}) = \{\begin{cases} {\dot{x}}_{p} - {\dot{x}}_{1}, (x_{p} - x_{1} < d) \\ 0, (- d \leq x_{p} - x_{1} \leq d) \\ {\dot{x}}_{p} - {\dot{x}}_{1}, (x_{p} - x_{1} \geq d) \end{cases}

(2)

where x_p is the displacement of the sphere.

Under the action of wind load F, the beam structure represented by the mass block m is offset, that is, the displacement x₁ is generated. Therefore, the stiffness equation is obtained according to the model:

m_{2} {\ddot{x}}_{1} + C {\dot{x}}_{1} + K x_{1} + 4 w = 0

(3)

w = m_{p} {\ddot{x}}_{p} + C_{p} H (x_{p}, {\dot{x}}_{p}) + K_{p} G (x_{p})

(4)

F = K x_{1}

(5)

where w is the damping force generated by a single particle damper.

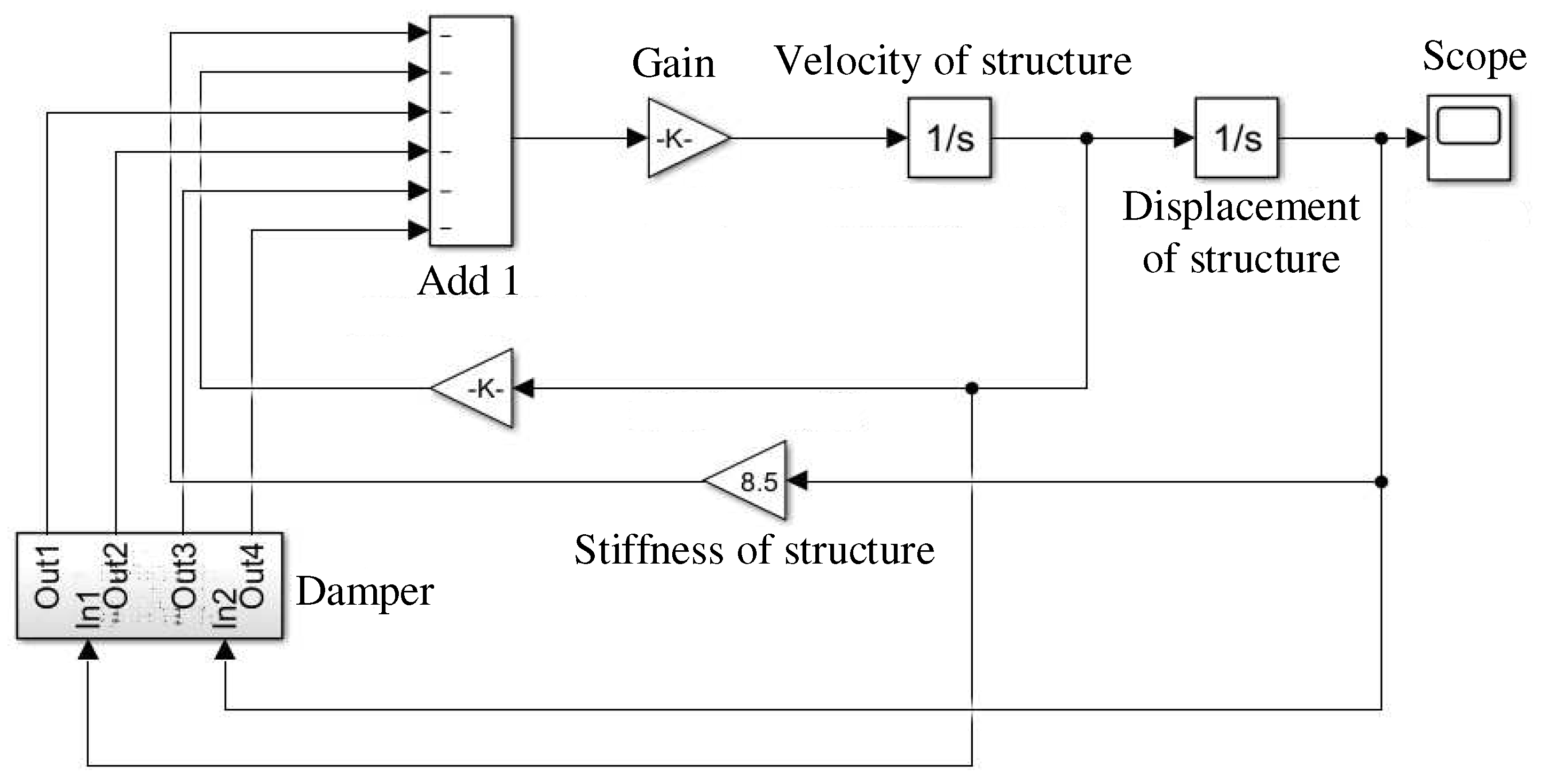
3.2. Simulink Modeling and Solution

To preliminary verify the effect of vibration suppression, the stiffness equation is expressed in the form of Simulink module and solved.

Calibrate the parameters in the stiffness equation:

(1): The weight of the crane model is obtained by weighing;
(1): A certain tension is applied to upper part of the model, and the upper part of the model is offset under action of the tension. The stiffness of bracket structure is calculated by the offset and the indicator of tension device.
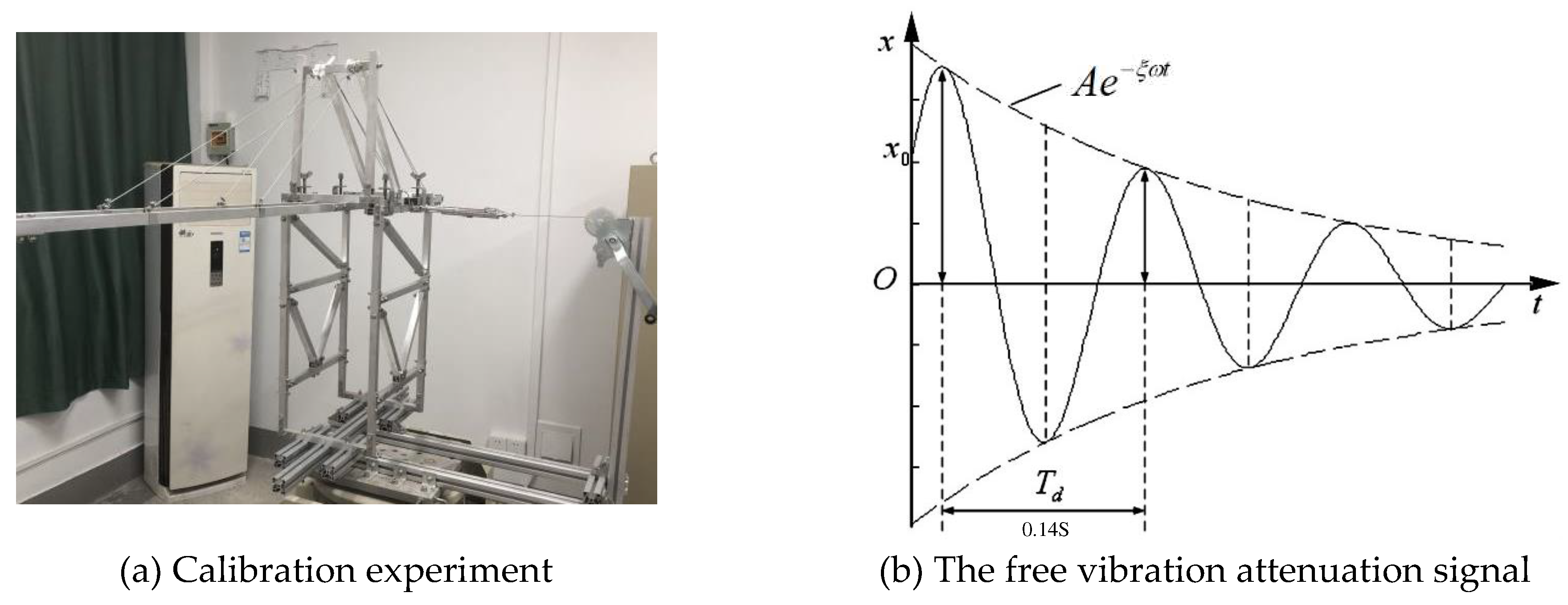
(2): The tension is released, the free vibration attenuation signal of model is detected by acceleration sensor, and the damping ratio of model is identified by the envelope of free vibration attenuation signal. Experiment layout is shown in Figure 4.

The acceleration attenuation response of the 1-DOF system with dampers can be expressed as:

\ddot{x} = A e^{- ξ ω t} \sin (\sqrt{1 - ξ^{2}} ω t + ϕ)

(6)

The corresponding envelope equation is:

\ddot{x} = A e^{- ξ ω t}

(7)

where A is the amplitude, ω is the natural frequency, Φ is the Phase Angle, ξ is the damping ratio.

The damping value is obtained from the following formula:

C = 2 ξ \sqrt{M K}

(8)

where M is the total mass of the model.

The equivalent spring stiffness and damping of the collision between the sphere and the cavity wall can be calculated by the angular frequency:

K_{p} = m_{p} {ω_{p}}^{2}

(9)

C_{p} = 2 m_{p} ξ_{p} ω_{p}

(10)

According to Masri's research, under the condition that the stiffness of the spring simulating collision is much larger than that of the main structure, the interaction between particles and the cavity wall can be more appropriately simulated. Therefore, 20 times the angular frequency of the main structure is taken as the angular frequency of the particle [16]. The particle material is steel, so the damping ratio is 0.375.

All of the parameters in stiffness equation are shown in Table 2:

The external load is gradually applied to 10 N and returns to zero at some point. At this time, the main structure presents free damping vibration. The specific solving model is shown in Figure 5.

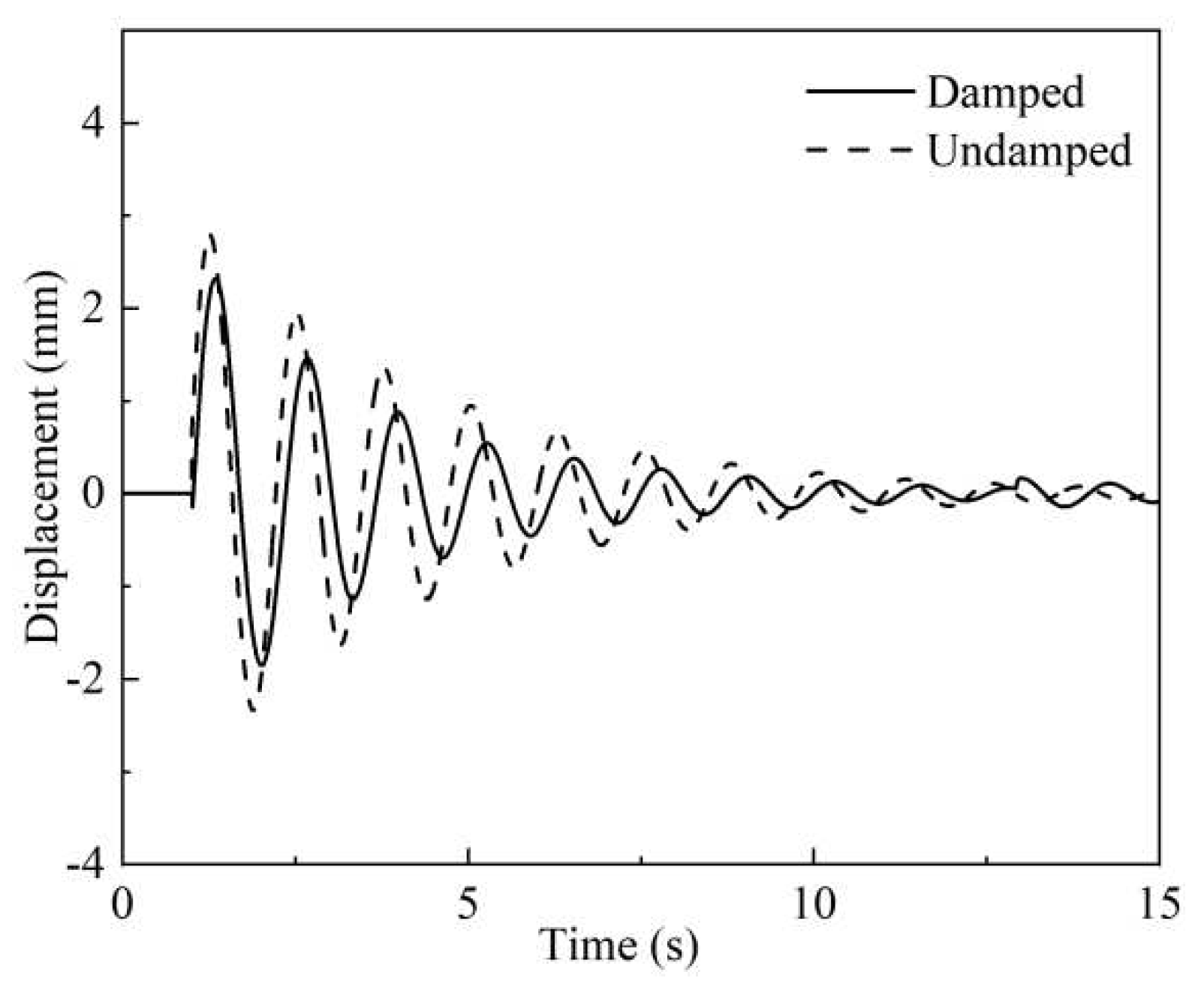
The solution results show that with the addition of particle dampers, the vibration amplitude of the beam structure decreases obviously, and the wave crest lags behind compared with that without particle dampers. In addition, the displacement attenuation amplitude of the main structure in the early stage of free attenuation vibration is large. But, the vibration suppression effect is gradually disappear with the vibration return to steady state, as shown in Figure 6.

Vibration suppression effect is measured by displacement response peak root mean square:

S = \frac{B - A}{A} \times 100 %

(11)

where S is the effect of vibration suppression, A is the root-mean-square displacement of the crane with the damper installed, B is the root-mean-square displacement of the crane without the damper installed.

It is calculated that the damping effect of the damper reaches 25%. The above numerical simulation method preliminary verifies the feasibility of particle damper applied in crane vibration reduction function. However, it is difficult to carry out parametric research on dampers based on the mathematical model. Thus, the following experiment is designed for further investigation.

4. Experimental

4.1. Experimental Platform

To further verify the vibration suppression effect and obtain optimal working parameters of the damper, the vibration attenuation experiments are done. The experimental model uses square tube as raw material, the model is fixed with screws and nuts, the rope on the boom is replaced by steel wire rope, the base of the crane model uses 40×40 European standard aluminium profiles, and the damper is made of aluminium alloy square pipe. In this investigation, steel, aluminium, lead and glass are used as the materials filled in the damper chamber. In order to facilitate the disassembly and installation of the particle damper, 304 stainless steel butterfly opening vice is used to fix the particle damper. The arrangement of experimental equipment is shown in Figure 7.

4.2. Description of Experiment Process

To simulate the residual vibration of the mechanism after experiencing wind load, a winch is used to pull the wire rope to offset the upper part of the experimental model, and the number shown by the indicator represents the initial wind load on the model. Then, after the model is stabilized and the number shown by the acceleration indicator is 0, the winch is released and the model generated residual vibration. Finally, the acceleration of the upper part of the experimental model is collected by BWT61CL acceleration sensor, and the differences between the model accelerations when particle dampers are installed under different working parameters are compared.

Particle material, filling quantity, particle size, and position of the damper are taken as change parameters to conduct experiment and explore the law of vibration suppression effect changing with parameters. Specific parameters of experimental objects and conditions are shown in Table 3 and Table 4.

4.3. Effect of Different Materials on Vibration Suppression Characteristics

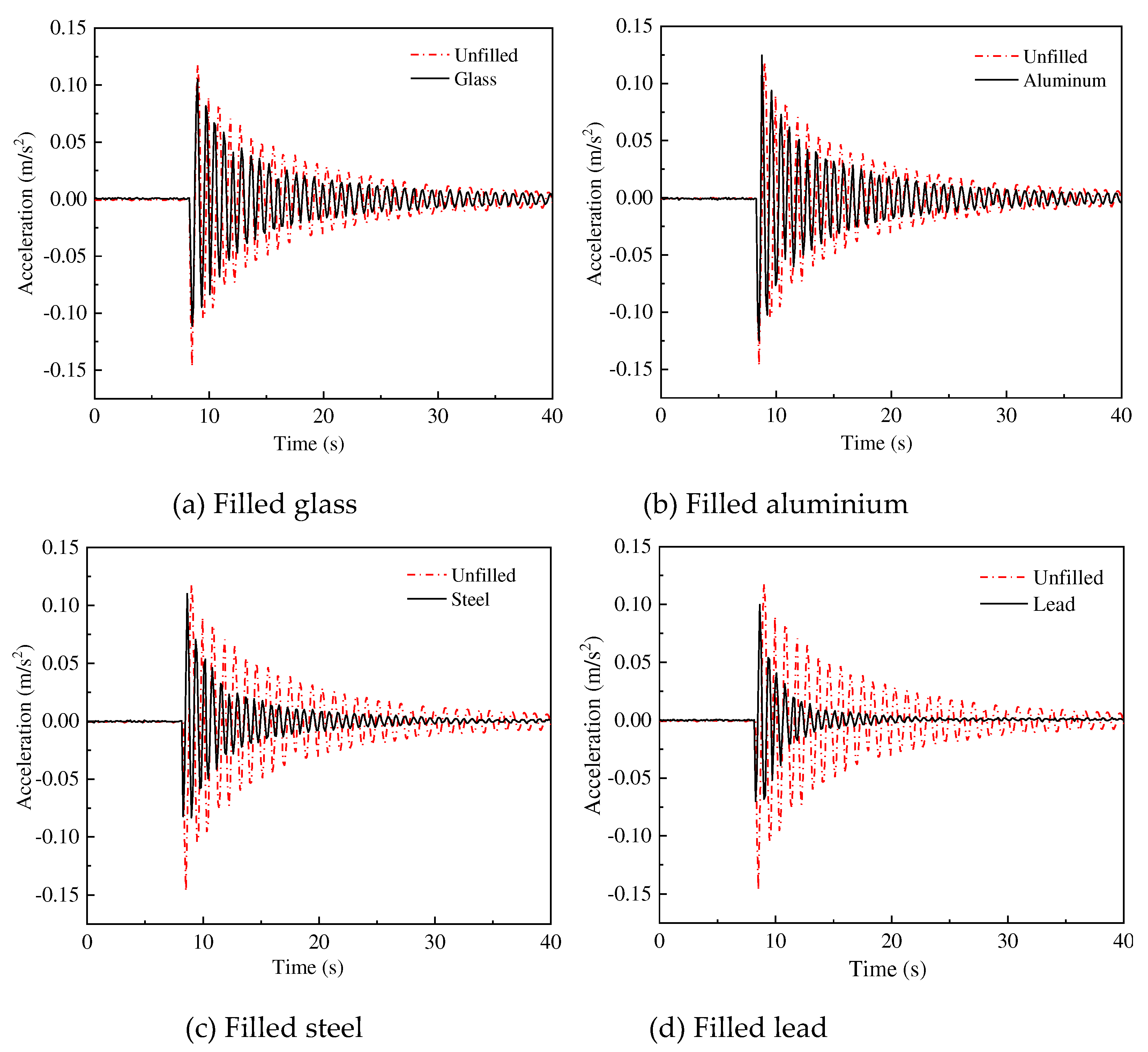
The energy dissipated by particle collision behavior in the damper determines the performance of the particle damper, and the difference in mechanical properties of different particle materials greatly affects their collision behavior. To investigate the effect of different materials on the performance of the damper, an experiment is conducted under the following conditions: the material of 10 mm particle groups is lead, steel, aluminium and glass, the quantity of each particle group is 25, external load is 10 N, and the installation position of the dampers is proximal end. The experimental results are shown in Figure 8 and Figure 9.

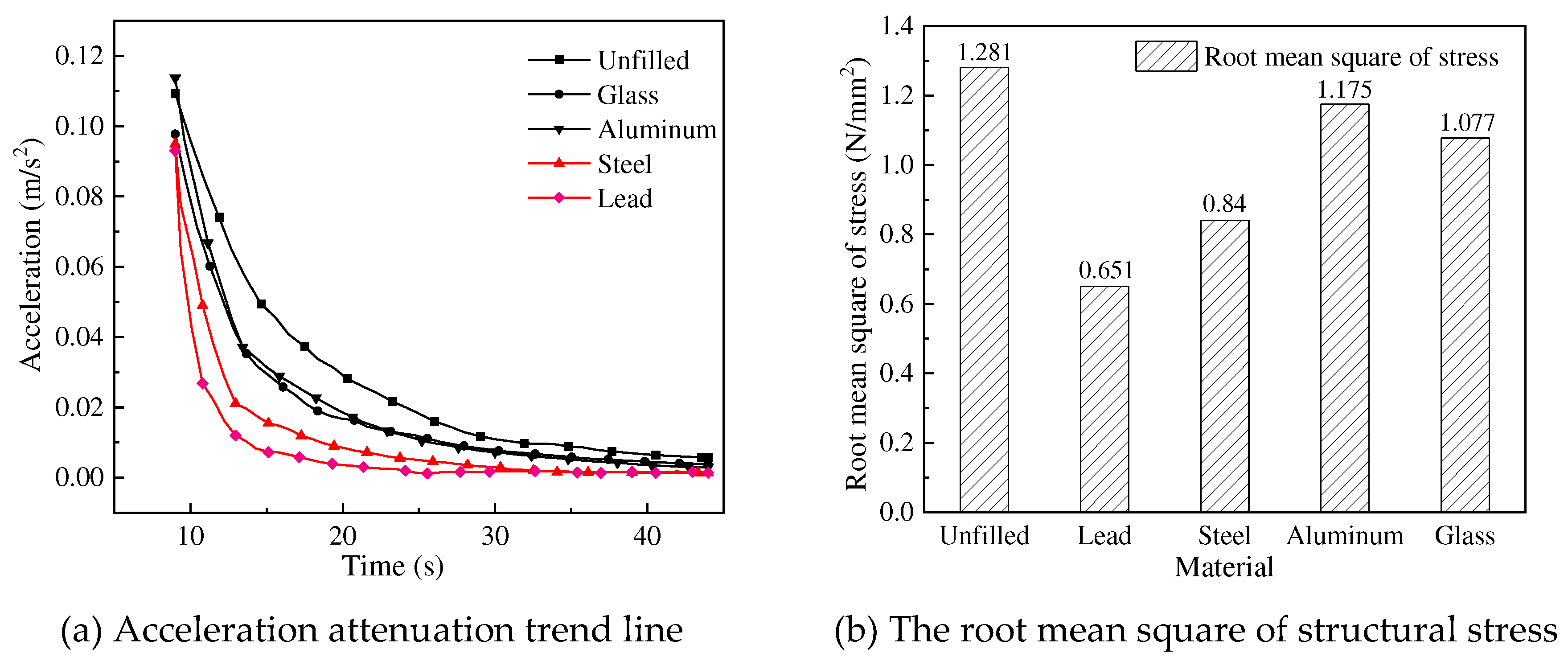
From Figure 8, whatever the filling material in damper, the installation of particle damper reduces the crest area of the acceleration and has an effect on the vibration suppression of the crane. Figure 9 shows that the acceleration of the model tends to steady state after the shortest time (18s) and the root mean square reaches 0.651 with the filling material of particle damper being lead beads. The time for the acceleration to reach the steady state becomes longer successively with the filling materials in the damper are steel, glass, and aluminium, which is 27s, 30s, and 32s respectively. In addition, the root mean square of stress increases successively, which is 0.84, 1.077, and 1.175 respectively. Therefore, the damping effect is the best with the material inside the damper being steel, this is due to the higher the density and elastic modulus of the material, the better the impact resistance performance.

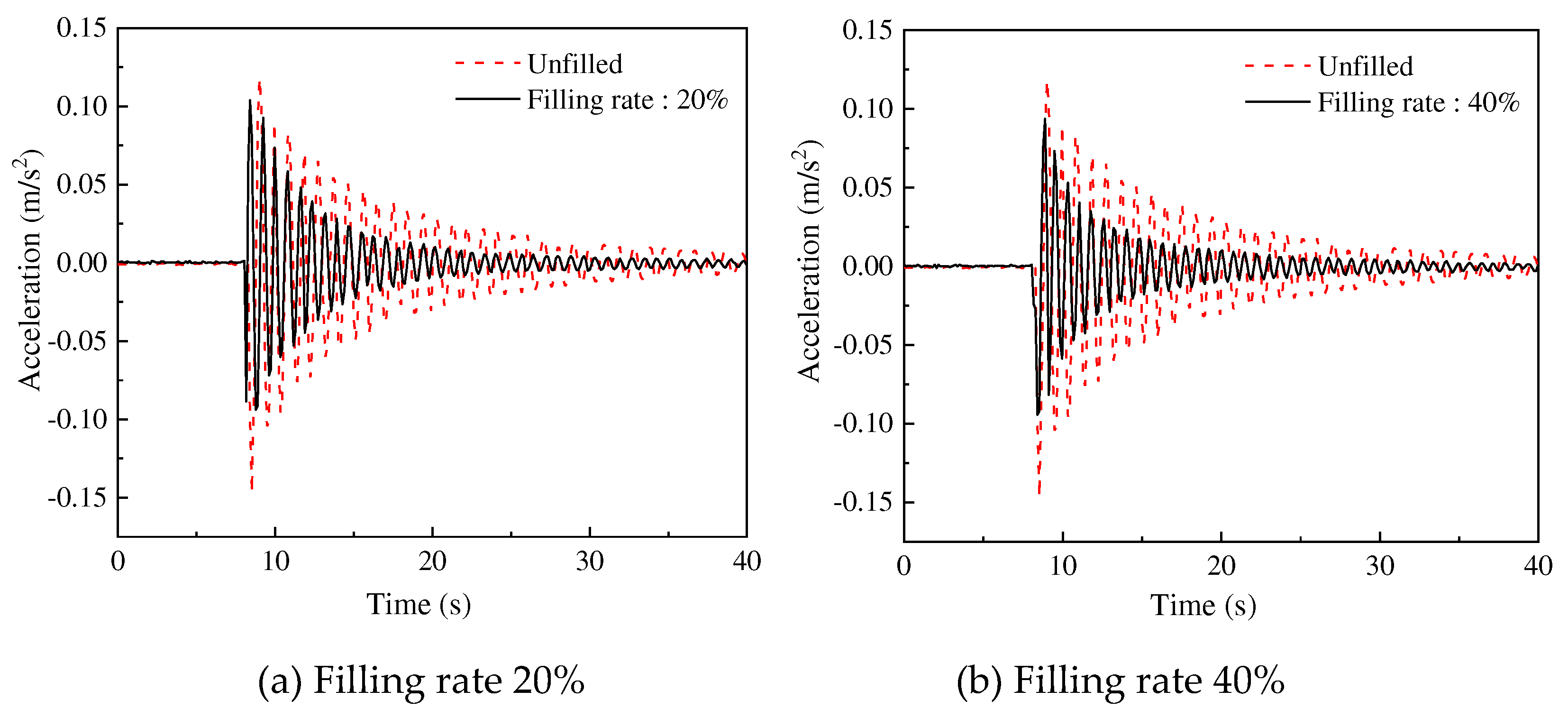
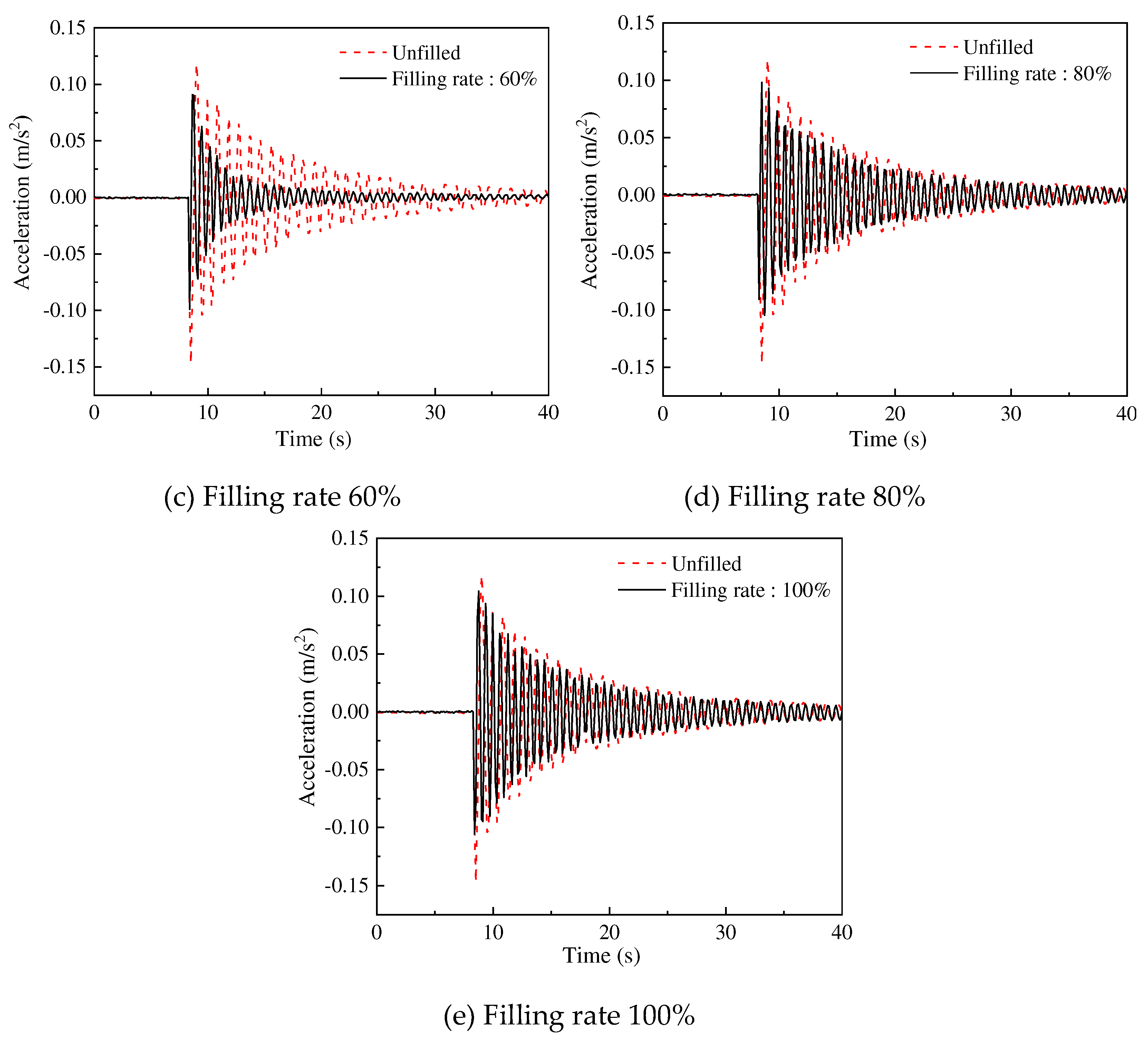
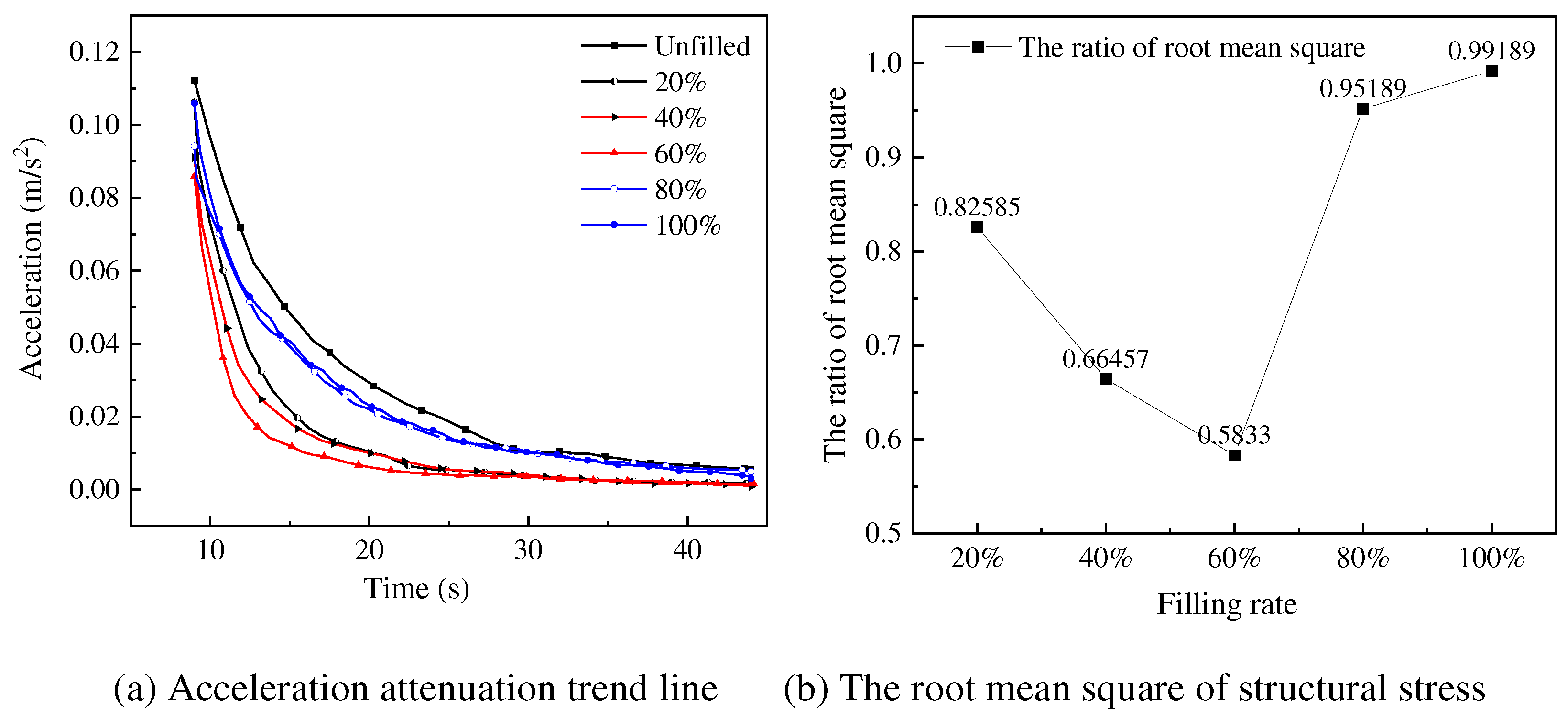
4.4. Effect of Different Filling Rate on Vibration Suppression Characteristics

With the increase of the quantity of the particles in the damper, the anti-impact ability of the damper increases correspondingly. However, the impact efficiency is also affected by the quantity of the particles. To investigate the optimal filling rate of the damper, the experiment is conducted under the following conditions: external load 10 N, the installation position of the dampers is proximal end, the quantity of 10 mm steel ball groups is 10 (filling rate 20%), 20 (filling rate 40%), 30 (filling rate 60%)), 40 (filling rate 80%), and 50 (filling rate 100%). The experimental results are shown in Figure 10 and Figure 11.

As shown in Figure 10, under the condition that without considering filling rate in damper (except for the filling rate of 0), the installation of particle dampers reduces the crest area of the acceleration and has an effect on the vibration suppression of the crane. From Figure 11, the increase in filling rate from around 20% to 60% reduces the time for the acceleration to reach a steady state and decreases the root mean square. However, as the filling rate continues to increase, it can be seen that the root mean square sharply increases and the decrease in vibration suppression effect. Therefore, the filling rate of the damper is 60% allowing for the best effect in the vibration suppression of the crane. This is due to under the premise that the number of particles in the damper brings enough impact strength, enough space for particles to have sufficient collision to make the damper obtain the best vibration suppression performance.

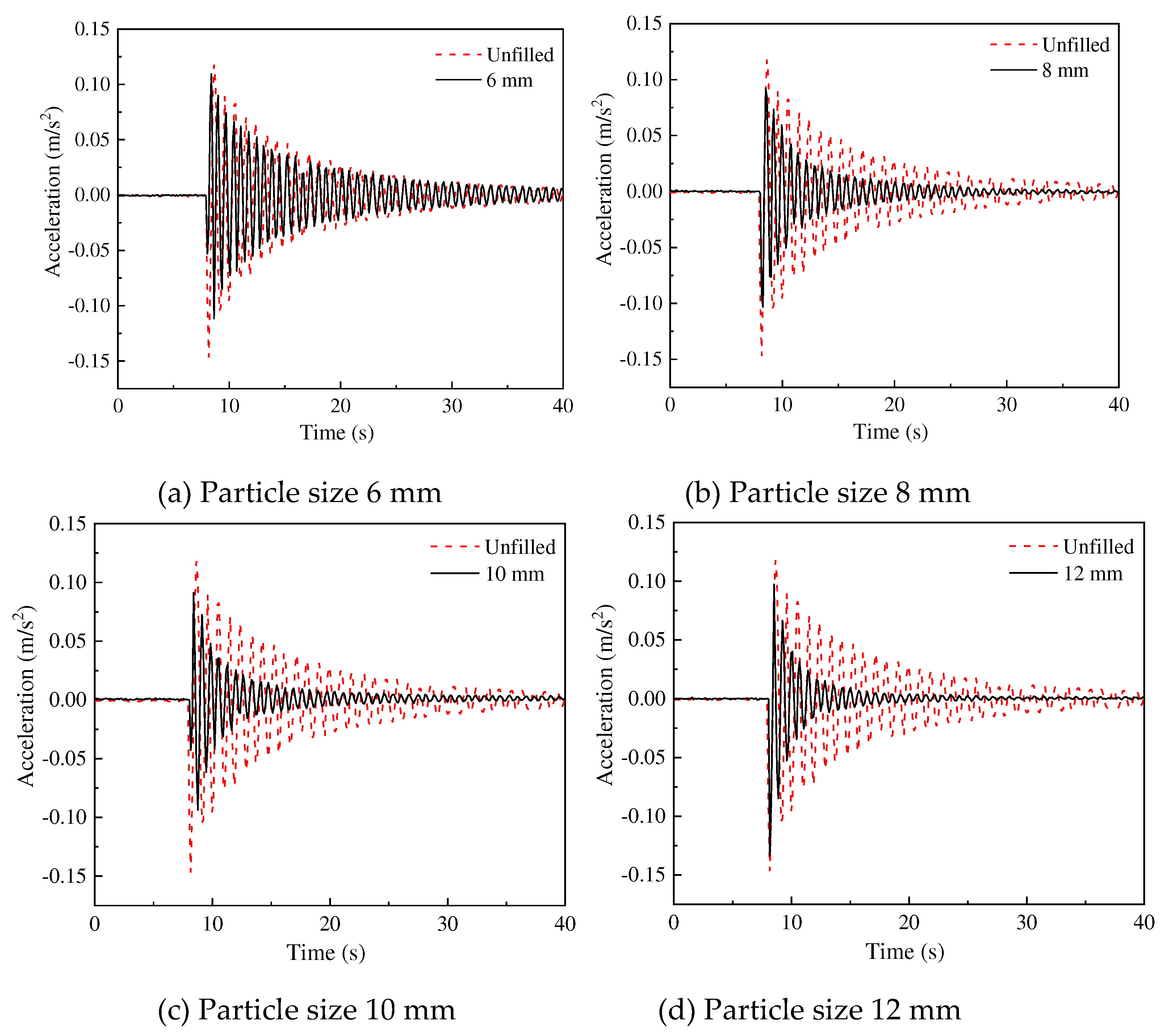
4.5. Effect of Different Particle Diameters on Vibration Suppression Characteristics

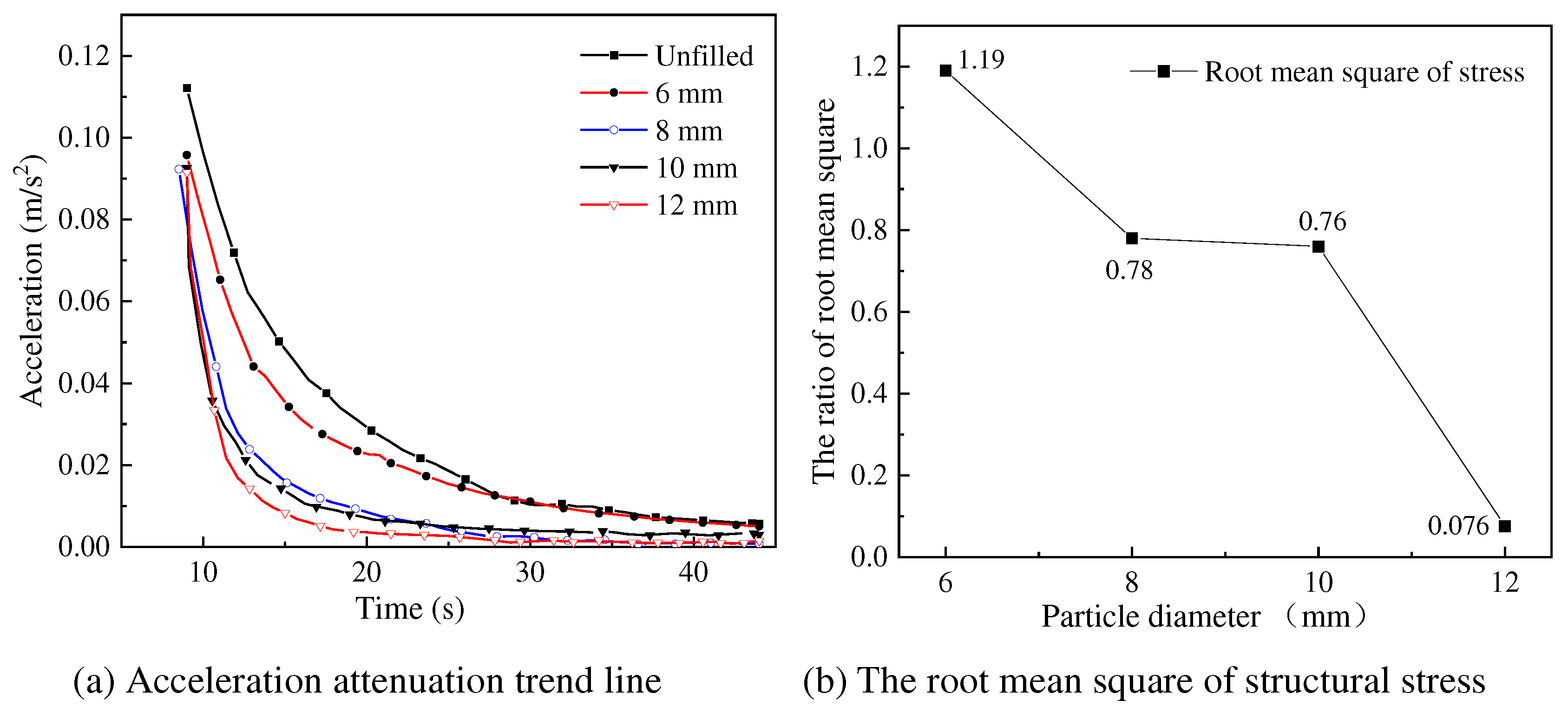
Particle size is a key factor that affects the movement of particles in a closed cavity. In case of the same filling mass, the increase of the contact efficiency between particles as the particle size is decreased. To investigate the effect of particle size on vibration suppression performance of particle damper, an experiment is conducted under the following conditions: particle group with diameter of 6 mm, 8 mm, 10 mm, and 12 mm, total weight of each particle group is 127 g, the external load is set at 10 N, and the installation position of the dampers is proximal end. The experimental results are shown in Figure 12 and Figure 13.

Figure 12 shows that regardless of the diameter of the particles packed in the damper, the installation of particle damper reduces the crest area of the acceleration and has an effect on the vibration suppression of the crane. From Figure 13, the increase in diameter of the particles from around 6 mm to 12 mm reduces the time for the acceleration to reach a steady state and decreases the root mean square. Obviously, compared to several other smaller diameters, the diameter of the particles packed in the damper is 12 mm allows for the best effect in the vibration suppression of crane. This is due to the fact that with the increase of particle diameter, the mobility presented by particle group motion decreases, and the dispersion of particle group increases, resulting in the increase of collision frequency, and the ability of the damper to convert external kinetic energy into heat energy and thus dissipate increases.

4.6. Effect of the Installation Position of Damper on Vibration Suppression Characteristics

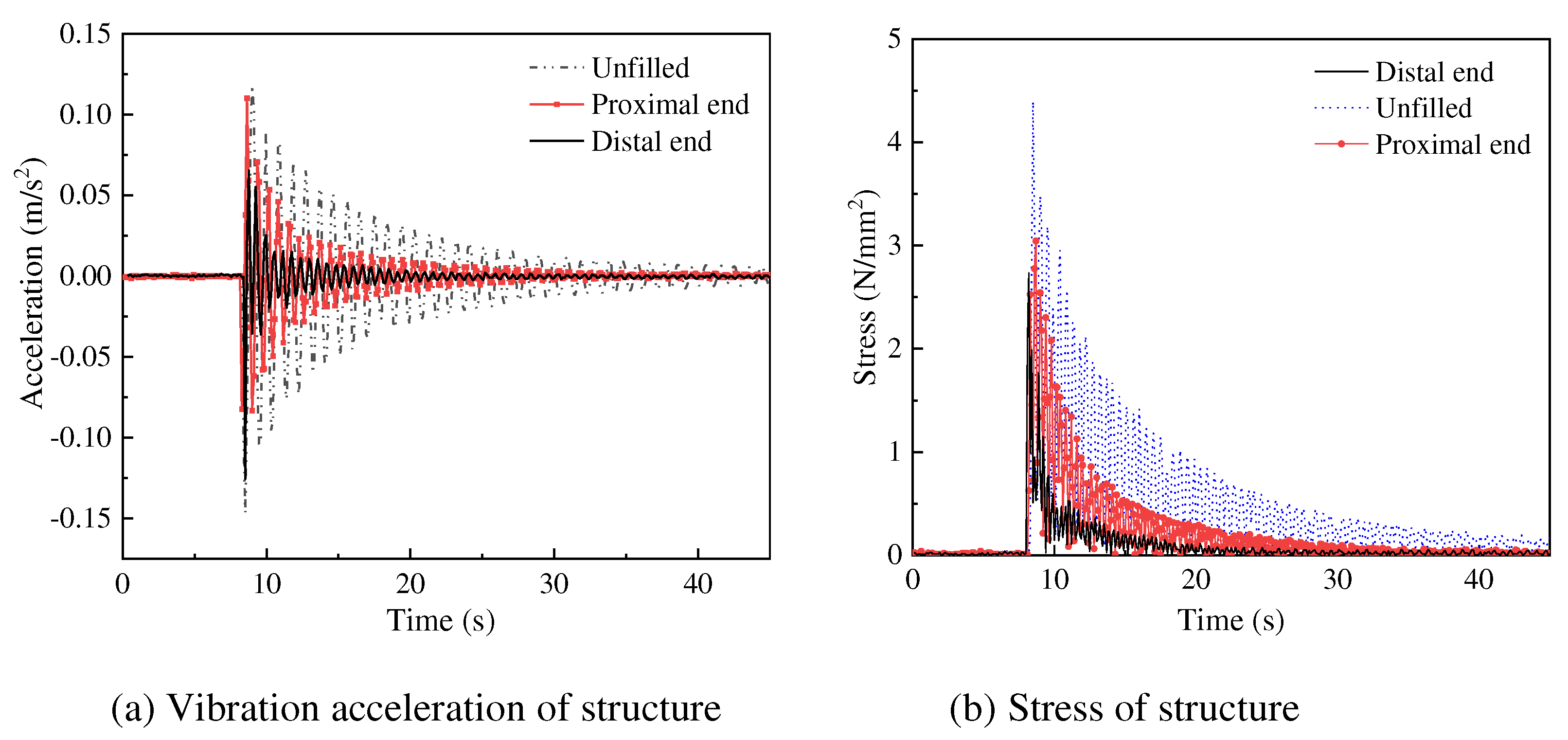
Most container cranes have a high center of gravity and a long extension distance, causing torsional torque to the bottom structure. To investigate the influence of the installation position of damper on the vibration suppression effect, the experiments are conducted under the following conditions: external load 10 N, the filling rate of 10 mm steel ball groups is 50%, installation position of the dampers is the proximal end and the distal end. Figure 14 shows the two installation methods, and the experimental results are shown in Figure 15.

It can be seen from the Figure 15 that the installation of damper at the proximal or distal end reduces the crest area of the structure acceleration and decreases the value of stress. Furthermore, the vibration suppression effect is better under the condition that the dampers are installed at the distal end. However, in practical engineering applications, to reduce the bending moment of the crane forearm and avoid overturning caused by the shift of the crane's center of gravity, the damper be avoided as far as possible on the crane forearm. Therefore, the damper is installed at the distal end as far as possible under the condition that the strength of the crane forearm allows.

5. Conclusions

It can be seen from the results and discussion above that:

(1): The vibration suppression effect of damper is preliminary verified by Simulink module, and it is concluded that the vibration amplitude of the beam structure decreases obviously, the wave crest of displacement lags with the dampers are installed, and the damping effect reaches 25% by calculation.
(2): The vibration suppression experiments are analysed with several groups of different conditions, it is concluded that the installation of particle damper decreases the acceleration crest area of the structure and reduces the time for the acceleration to reach a steady state.
(3): This vibration suppression method is firmed effective, with the filling parameter of the dampers is 12 mm lead bead, the filling rate is 60%, when the dampers are installed on the distal end of crane.

Author Contributions

Resources, F.Y.; Writing-original draft, X.X.; Investigation, W.J.; Funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the Major Science and Technology Project of Hubei Province Grants No.2021AAA007, Natural Science Foundation of Hubei Province Grants No.2023AFB400, and Hubei University of Technology Research Fund under Grants BSQD2020009.

Declarations

The authors declare that no conflicts of interest exist in this manuscript.

References

Hebiba, A.M.; Bouferguene, A.; Moon, S. Automated Stability Analysis for Selection of Tower Crane and Location. J CONSTR ENG M. 2022, 148, 04022127. [Google Scholar] [CrossRef]
Zhang, W.; Xue, N.N.; Zhang, J.R. Identification of Critical Causal Factors and Paths of Tower-Crane Accidents in China through System Thinking and Complex Networks. J CONSTR ENG M. 2021, 147, 04021174. [Google Scholar] [CrossRef]
Tran, Q.H.; Huh, J.; Doan, N.S. Fragility Assessment of a Container Crane under Seismic Excitation Considering Uplift and Derailment Behavior. APPL SCI-BASEL. 2019, 9, 4660. [Google Scholar] [CrossRef]
Xing, X.Y.; Liu, J.K. State-estimator-based robust vibration control of crane bridge system with trolley via PDE model. COMMUN NONLINEAR SCI. 2021, 99, 105799. [Google Scholar] [CrossRef]
Al-Fadhli, A.; Khorshid, E. Payload oscillation control of tower crane using smooth command input. J VIB CONTROL. 2021, 29, 902–915. [Google Scholar] [CrossRef]
Zhao, X.S.; Huang, J. Distributed-mass payload dynamics and control of dual cranes undergoing planar motions. MECH SYST SIGNAL PR. 2019, 126, 636–648. [Google Scholar] [CrossRef]
Meyer, N.; Seifried, R. Damping prediction of particle dampers for structures under forced vibration using effective fields. GRANUL MATTER. 2021, 23, 64. [Google Scholar] [CrossRef]
Rakhio, A.; Ido, Y.; Iwamoto, Y. Experimental and Numerical Analysis of Torque Properties of Rotary Elastomer Particle Damper considering the Effect of Gap and No Gap between Rotor and Body of the Damper. SHOCK VIB. 2022, 2021, 7724156. [Google Scholar] [CrossRef]
He, H.X.; Wang, B.S.; Yan, W.M. Mechanical Model and Optimization Analysis of Multiple Unidirectional Single-Particle Damper. J ENG MECH. 2021, 147, 04021040. [Google Scholar] [CrossRef]
Chockalingam, S.; Natarajan, U.; Cyril, A.G. Damping investigation in boring bar using hybrid copper-zinc particles. J VIB CONTROL. 2017, 23, 2128–2134. [Google Scholar] [CrossRef]
Hassui, A.; Suyama, D.I.; Magri, A. Reduction of internal turning surface roughness by using particle damping aided by airflow. INT J ADV MANUF TECH. 2019, 106, 125–131. [Google Scholar]
Meyer, N.; Schwartz, C.; Morlock, M. Systematic design of particle dampers for horizontal vibrations with application to a lightweight manipulator. J SOUND VIB. 2021, 510, 116319. [Google Scholar] [CrossRef]
Wang, J.; Juan, M.X.; Yang, S.G. Experimental Investigation of the Vibration Reduction of the Pipeline System with a Particle Impact Damper under Random Excitation. APPL SCI-BASEL. 2023, 13, 618. [Google Scholar] [CrossRef]
Li, Z.; Ye, F.P.; Wu, S.Y. Design and Experimental Verification of a 1/20 Scale Model of Quayside Container Crane Using Distortion Theory. SHOCK VIB. 2019, 2019, 5893948. [Google Scholar] [CrossRef]
Lu, Z.; Liao, Y.; Huang, Z.K. Stochastic response control of particle dampers under random seismic excitation. J SOUND VIB. 2020, 481, 115439. [Google Scholar] [CrossRef]
Masri, S.F.; Ibrahim, A.M. Response of the Impact Damper to Stationary Random Excitation. J ACOUST SOC AM. 1973, 53, 200–211. [Google Scholar] [CrossRef]

Figure 1. Crane model.

Figure 2. Process of mechanical modeling.

Figure 3. Equivalent mechanical model with dampers.

Figure 4. Experiment layout.

Figure 5. Motion equation modelling of main structure.

Figure 6. Numerical simulation displacement of main structure.

Figure 7. Experimental equipment.

Figure 8. Comparison of vibration acceleration of structure under different filling materials of damper.

Figure 9. Acceleration attenuation trend line and the root mean square of structural stress of structure.

Figure 10. Comparison of vibration acceleration of structure under different filling rate of damper.

Figure 11. Acceleration attenuation trend line and the ratio of root mean square of structural stress.

Figure 12. Comparison of vibration acceleration of structure under different filling particle sizes of dampers.

Figure 13. Acceleration attenuation trend line and the ratio of root mean square of structural stress.

Figure 14. Installation mode of the damper.

Figure 15. Vibration acceleration and stress of structure.

Table 1. Similarity relation of the scale model.

Similarity parameter	Similarity ratio	Similarity parameter	Similarity ratio
Geometric dimension	1/80	Frequency	$1 / \sqrt{80}$
Density	1	Time	$\sqrt{80}$
Mass	1/80³	Elastic modulus	1
Displacement	1/80	Section inertia radius	1/80

Table 2. Table of parameters in the stiffness equation.

Parameter	Symbol	Value
Mass of bracket structure	m₁	2.5 kg
Mass of beam mechanism	m₂	3.4 kg
Mass of sphere	m_p	0.135 kg
Structural stiffness of steel frame	K	8.5 N/mm
Damping ratio	ξ	0.178
Damping value of steel frame structure	C	1.94 N/(mm/s)
Displacement of traveling mechanism	x₁	0
External load	F	10 N
Equivalent spring stiffness	K_p	108570 N/mm
Equivalent spring damping value	C_p	4.54 N/(mm/s)
Equivalent displacement of sphere	x_p	-
Distance between sphere and cavity wall	d	3 mm

Table 3. Parameter table of experimental material.

Part name	Material	Density (kg/m³)	Young's modulus (GPa)	Poisson's ratio	Dimension (mm)
Crane structure	Al-Mg-Si	2880	72	0.25	h₂
Damper chamber	SS304	7930	11	0.29	40×100×20
Steel bead	45Cr	7850	209	0.3	r₆ / r₅ / r₄ / r₃
Aluminium bead	Al	2700	10.9	0.32	r₅
Lead bead	Pb	11343	70	0.42	r₅
Glass bead	SiO₂	2500	68	0.215	r₅

Table 4. Parameter table of experimental condition.

Experiment condition	Installation position	Material	Filling rate	Particle size
1	Proximal end	Lead	50%	10 mm
		Steel
		Aluminum
		Glass
2	Proximal end	Steel	20%~100%	10 mm
3	Proximal end	Steel	50%	6~12 mm
4	Proximal end	Steel	50%	10 mm
4	Distal end	Steel	50%	10 mm

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer