Prerpints.org logo
Preprint
Article

Electronic Properties of Graphene Nano-Parallelograms: A TAO-DFT Computational Study

Altmetrics

Downloads

122

Views

69

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 December 2023

Posted:

11 December 2023

You are already at the latest version

Alerts
Abstract
In this computational study, we investigate the electronic properties of zigzag graphene nano-parallelograms (GNPs), which are parallelogram-shaped graphene nanoribbons of various widths and lengths, using thermally-assisted-occupation density functional theory (TAO-DFT). Our calculations reveal a monotonic decrease in the singlet-triplet energy gap as the GNP length increases. The GNPs possess singlet ground states for all the cases examined. With the increase of GNP length, the vertical ionization potential and fundamental gap decrease monotonically, while the vertical electron affinity increases monotonically. Besides, as the GNP length increases, the symmetrized von Neumann entropy increases monotonically, denoting an increase in the degree of multi-reference character associated with ground-state GNPs. The occupation numbers and real-space representation of active orbitals indicate that there is a transition from the nonradical nature of the shorter GNPs to the increasing polyradical nature of the longer GNPs. In addition, the edge/corner localization of active orbitals is found for the wider and longer GNPs.
Keywords: 
Subject: Physical Sciences  -   Chemical Physics

1. Introduction

Carbon nanostructures are ubiquitous. This versatility comes from the ability of carbon to form bonds through sp, sp2, and sp3 hybridization. The different types of hybridization can lead to various allotropes and complexes. Carbon is also available in nature as diamond and graphite. It forms all organic matters and is the basis of life. It is also an essential element in many drugs [1,2]. The nanoforms of allotropes were first introduced by the discovery of C60 molecules [3,4], followed by the observation of carbon nanotubes [5], then followed by the isolation and many groundbreaking experiments in graphene [6,7]. All these nanostructures have various special properties that are interesting and can be advantageous for specific applications. The series of carbon nanoallotropes have created a fresh search for new 0D, 1D, and 2D nanomaterials [2]. Among carbon nanomaterials, graphene, which is a 2D nanomaterial, stands out, due to its fascinating properties and vast potential applications [7,8].
As graphene lacks a band gap, its finite nanostructures, such as graphene nanoribbons (GNRs), are also of great interest because of a wide range of possibilities to tune their properties for specific applications. GNRs can be thought of quasi-1D nanostructures carved from graphene. GNRs can exhibit intriguing electronic, optical, and magnetic characteristics [9,10,11,12,13,14,15,16], which can be useful for many applications [16,17,18,19]. In general, GNRs can be classified into two main categories: zigzag GNRs and armchair GNRs, based on their edge patterns [12,13,14]. Both zigzag and armchair GNRs of various widths have been successfully synthesized [12]. There are also other types of GNRs with different kinds of edge structures, such as the chevron, fjord, chiral, junction, cove, and gulf types of GNRs [20]. Although there is a rich literature on these electronic systems, ongoing theoretical and experimental studies aim to further explore the properties of GNRs.
Although zigzag and armchair GNRs have been extensively documented in the literature, reports on the parallelogram-shaped GNRs with zigzag edges (see Figure 1 for illustration), denoted as graphene nano-parallelograms (GNPs), are relatively scarce. In this study, the narrowest GNPs, which are n-acenes (i.e., acenes with n linearly fused benzene rings), are labeled as GNP[1,n]; the second narrowest GNPs are labeled as GNP[2,n], containing two parallelly fused n-acenes forming parallelograms; the third narrowest GNPs are labeled as GNP[3,n], containing three parallelly fused n-acenes forming parallelograms, and so on. For GNP[m,n], the m value specifies the GNP width, and the n value specifies the GNP length. Some GNPs, such as GNP[2,4] and GNP[2,5] (also called [n,2]peri-acenoacenes with n = 4 and 5, respectively) have been recently synthesized in molecular and crystalline forms [21,22]. Besides, for GNP[2,n] (with n = 3–5), their properties and lasing applications in the near-infrared (NIR) region have been recently reported [23]. In addition, a computational study has recently reported a few electronic properties of GNP[m,n] (with m = n = 2–4) [24]. However, several properties of GNP[m,n] with different widths and lengths remain unavailable. Investigating the finite-size effects of GNP[m,n] is essential to gain a comprehensive understanding of the width- and length-dependent electronic properties of GNP[m,n]. Therefore, this computational study aims at exploring the electronic properties of GNP[m,n] with various values of m and n. Our previous study has revealed the presence of strong static correlation effects and intriguing properties in the longer zigzag GNRs [25]. Accordingly, it can be anticipated that GNPs, which have similar shapes as zigzag GNRs, can also possess strong static correlation effects in their ground states (as will be shown later).
Among existing electronic structure methods, Kohn-Sham density functional theory (KS-DFT) [26,27] is popular and valuable for investigating the ground-state properties of electronic systems, especially for single-reference (SR) systems (i.e., electronic systems possessing SR character in their ground states). In fact, KS-DFT has served as the backbone of theoretical condensed matter physics, quantum chemistry, and computational materials science [28]. For the sake of computational efficiency, KS-DFT calculations are commonly carried out using the local density approximation (LDA) [29,30] and generalized gradient approximation (GGA) [31] exchange-correlation (xc) energy functionals. However, KS-DFT with the LDA and GGA xc energy functionals can encounter severe problems for issues related to the self-interaction error, non-covalent interaction error, and static correlation error [32,33,34,35]. Among these qualitative errors, the self-interaction error can be reduced by the use of hybrid xc energy functionals [36,37,38], incorporating a fraction of Hartree-Fock exchange into the parent LDA or GGA xc energy functionals. Besides, a number of computationally efficient dispersion correction schemes [39,40], which can be directly added to the parent LDA or GGA xc energy functionals, are readily available for improving the description of non-covalent interactions. Nevertheless, the presence of strong static correlation effects in multi-reference (MR) systems (i.e., electronic systems possessing MR character in their ground states) has posed a formidable challenge, particularly for KS-DFT with the conventional LDA, GGA, and hybrid xc energy functionals. Generally, SR electronic structure methods (e.g., KS-DFT with the conventional LDA, GGA, and hybrid xc energy functionals as well as the Hartree-Fock theory) are unreliable for studying the ground-state properties of MR systems.
Typically, to explore the ground-state properties of MR systems, ab initio MR electronic structure methods [41,42,43,44,45,46,47], such as the MR configuration interaction (MRCI) methods and density-matrix renormalization group (DMRG) algorithms, are essential [48,49]. However, these methods can become impractical for large electronic systems due to the prohibitively high cost of performing ab initio MR electronic structure calculations. Accordingly, the demand for a reliable and efficient electronic structure method for large MR systems is very high.
Recently, thermally-assisted-occupation density functional theory (TAO-DFT) [50] has emerged as an effective solution for addressing the challenges posed by large MR systems. Generally, TAO-DFT focuses on improving the representability of ground-state electron density by incorporating fractional orbital occupation numbers, which can be efficiently computed using the Fermi-Dirac (FD) distribution function with some fictitious temperature θ . The LDA [50], GGA [51], global hybrid [52], and range-separated [52,53] exchange-correlation- θ (xc θ ) energy functionals (i.e., the combined xc and θ -dependent energy functionals [54]) can be incorporated in TAO-DFT. Besides, simple models for defining the optimal system-independent [55] and system-dependent [56] fictitious temperatures of an energy functional in TAO-DFT have been recently proposed. Note also that the difference among KS-DFT [26,27], TAO-DFT [50], and finite-temperature density functional theory (FT-DFT) [27,57] (i.e., three generally different electronic structure methods) has been properly discussed in a recent work [54].
Very recently, various TAO-DFT-related extensions, such as TAO-DFT-based ab initio molecular dynamics (TAO-AIMD) [58], TAO-DFT with the polarizable continuum model (TAO-PCM) [59], and a real-time extension of TAO-DFT (RT-TAO-DFT) [54], have been developed, expanding the capabilities of TAO-DFT to handle a more diverse range of applications. Moreover, TAO-DFT has also been adopted to investigate the various properties (e.g., electronic properties [25,60,61,62,63,64,65,66,67,68], hydrogen storage properties [61,63], spectroscopic properties [58,69,70], and equilibrium thermodynamic properties [58]) of MR systems at the nanoscale.
Consequently, in this computational study, we utilize TAO-DFT to obtain the electronic properties of GNP[m,n] (with m = 1–4 and n = 2–30), including the singlet-triplet energy gaps, vertical electron affinities / ionization potentials, fundamental gaps, symmetrized von Neumann entropy, active orbital occupation numbers, and real-space representation of active orbitals.

2. Computational Details

We perform all calculations with Q-Chem 4.4 [71], using the 6-31G(d) basis set. The electronic properties of GNP[m,n] (with m = 1–4 and n = 2–30) are computed using TAO-LDA (i.e., TAO-DFT with the LDA xc θ energy functional) with the recommended fictitious temperature θ = 7 mhartree [50].

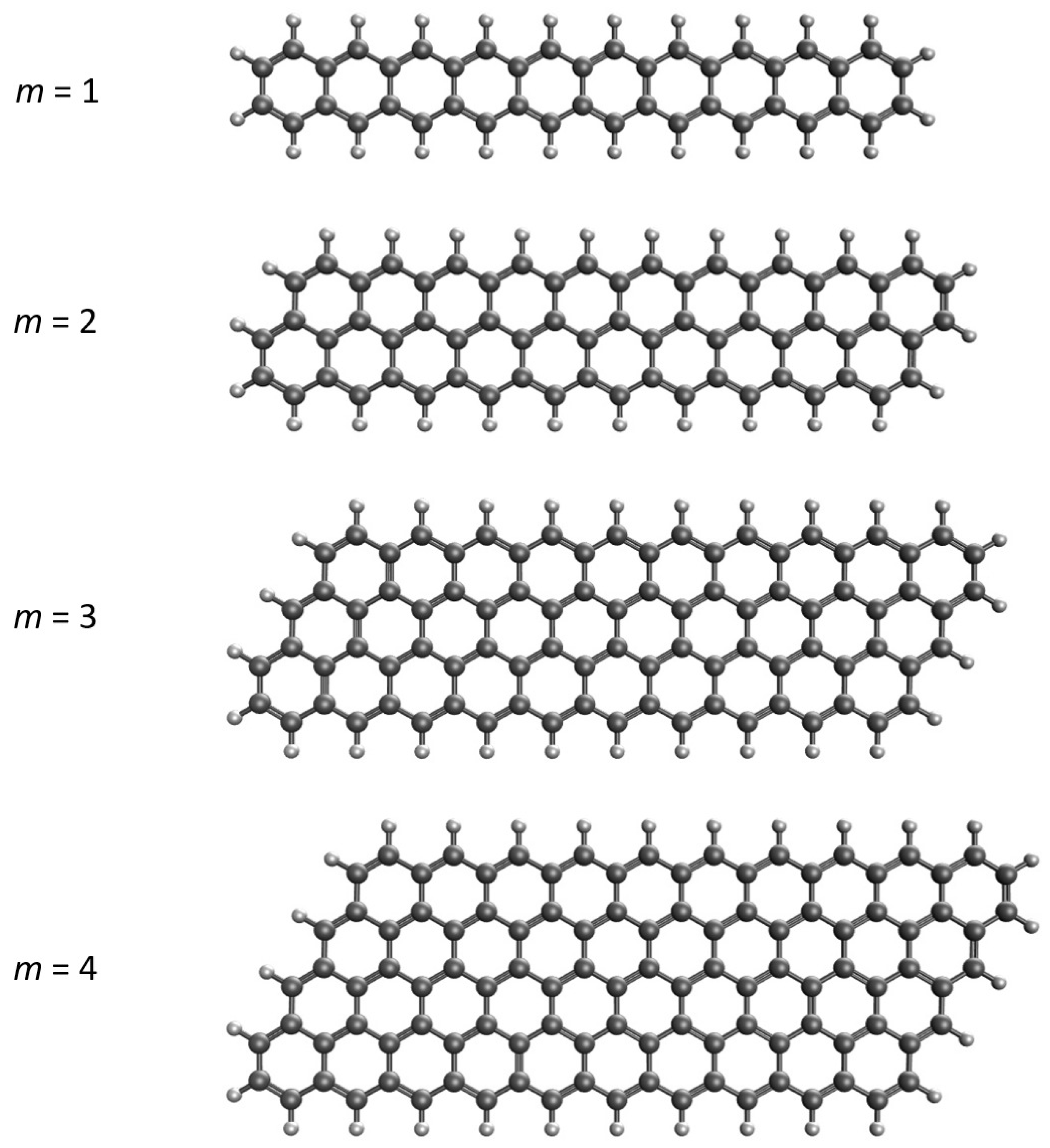
3. Results and Discussion

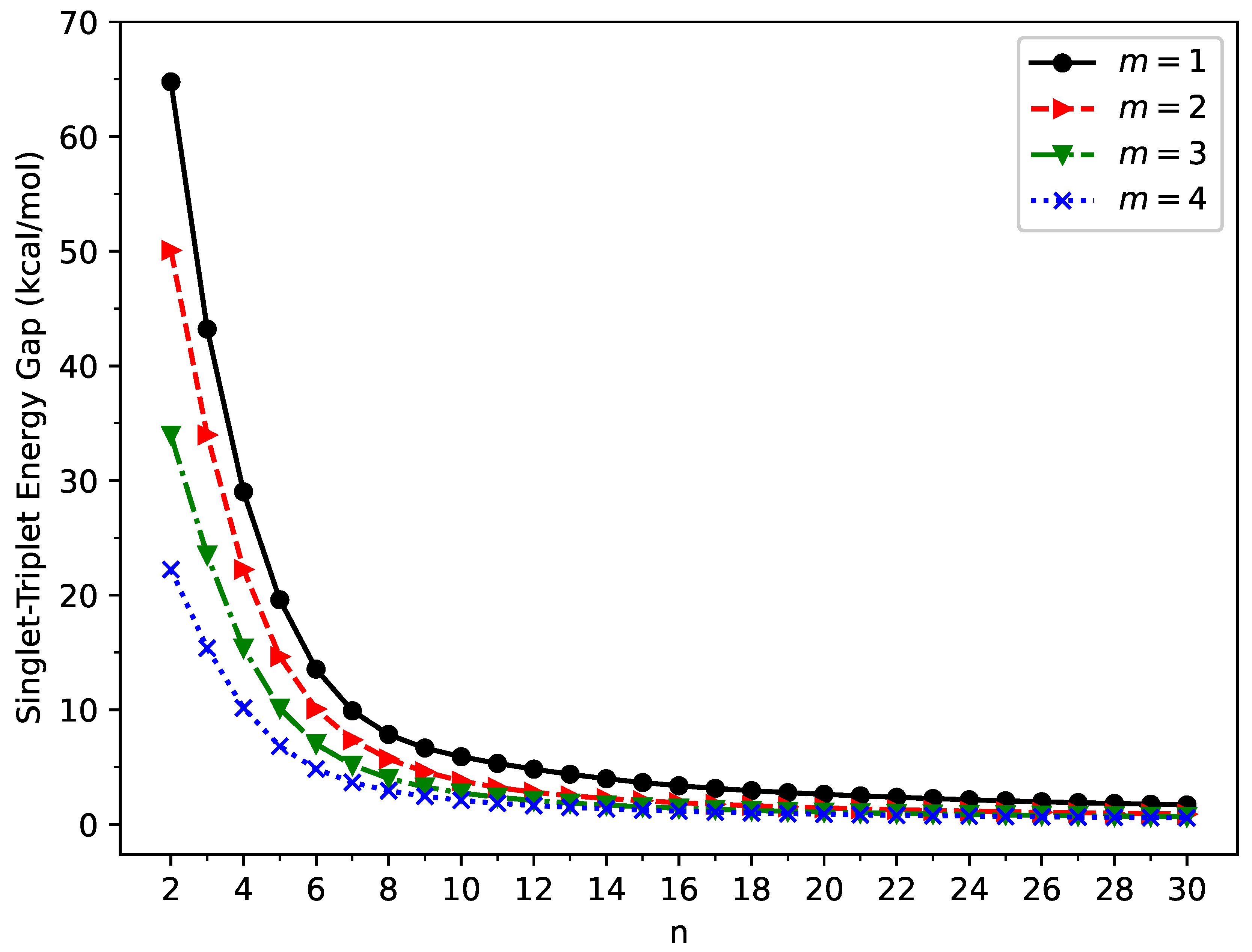
3.1. Singlet-Triplet Energy Gap

For a neutral molecule, the singlet-triplet energy gap (ST gap) provides an understanding on the ground-state nature and how far the lowest singlet and triplet states are separated in the energy landscape. The ST gap can also be useful for understanding the radical nature of molecules [72,73,74,75,76] as well as for providing valuable information for photovoltaic applications [77].
Here, the ST gap ( E ST ) of GNP[m,n] is calculated as the energy difference between the lowest singlet and triplet states of GNP[m,n] (evaluated on the respective optimized geometries):
E ST = E UT − E US ,
where E US / E UT is the energy of the lowest singlet / triplet state of GNP[m,n], obtained with spin-unrestricted TAO-LDA.
As presented in Figure 2, GNP[m,n] possess singlet ground states (also see Table S1 in Supplementary Information (SI)) for all the cases examined (i.e., m = 1–4 and n = 2–30). The ST gap decreases monotonically, as the GNP length increases. Since MR systems typically possess very small ST gaps, the longer GNPs can have MR character in their ground states.
It is well known that for the lowest singlet state of an MR system, the spin-symmetry constraint, which must be satisfied by an exact theory, can be violated by SR electronic structure methods (e.g., KS-DFT with the conventional LDA, GGA, and hybrid xc energy functionals as well as the Hartree-Fock theory) [25,33,50,51,52,54,58,59,78]. In other words, spin-unrestricted and spin-restricted SR electronic structure calculations can yield different energies for the lowest singlet state of an MR system, leading to unphysical spin-symmetry breaking effects. Here, to examine if this spin-symmetry constraint can be satisfied by TAO-LDA, spin-restricted TAO-LDA calculations are additionally carried out for the lowest singlet energies of GNP[m,n] (evaluated on the respective optimized geometries). Within the numerical accuracy considered in the present study, spin-unrestricted and spin-restricted TAO-LDA calculations essentially yield the same energies for the lowest singlet states of GNP[m,n] (with m = 1–4 and n = 2–30), indicating that essentially no unphysical spin-symmetry breaking effects occur in our spin-unrestricted TAO-LDA solutions for all the cases examined.

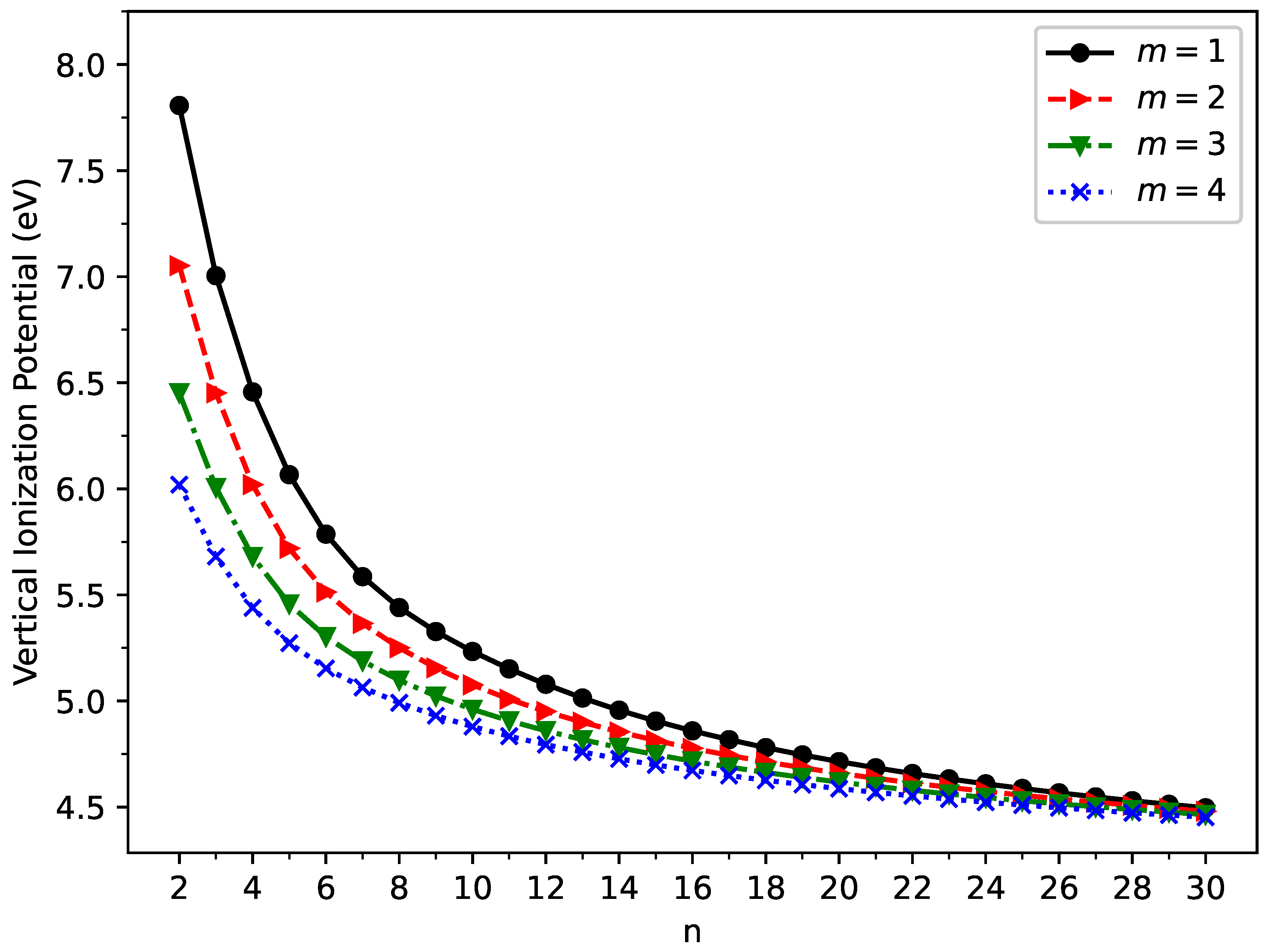
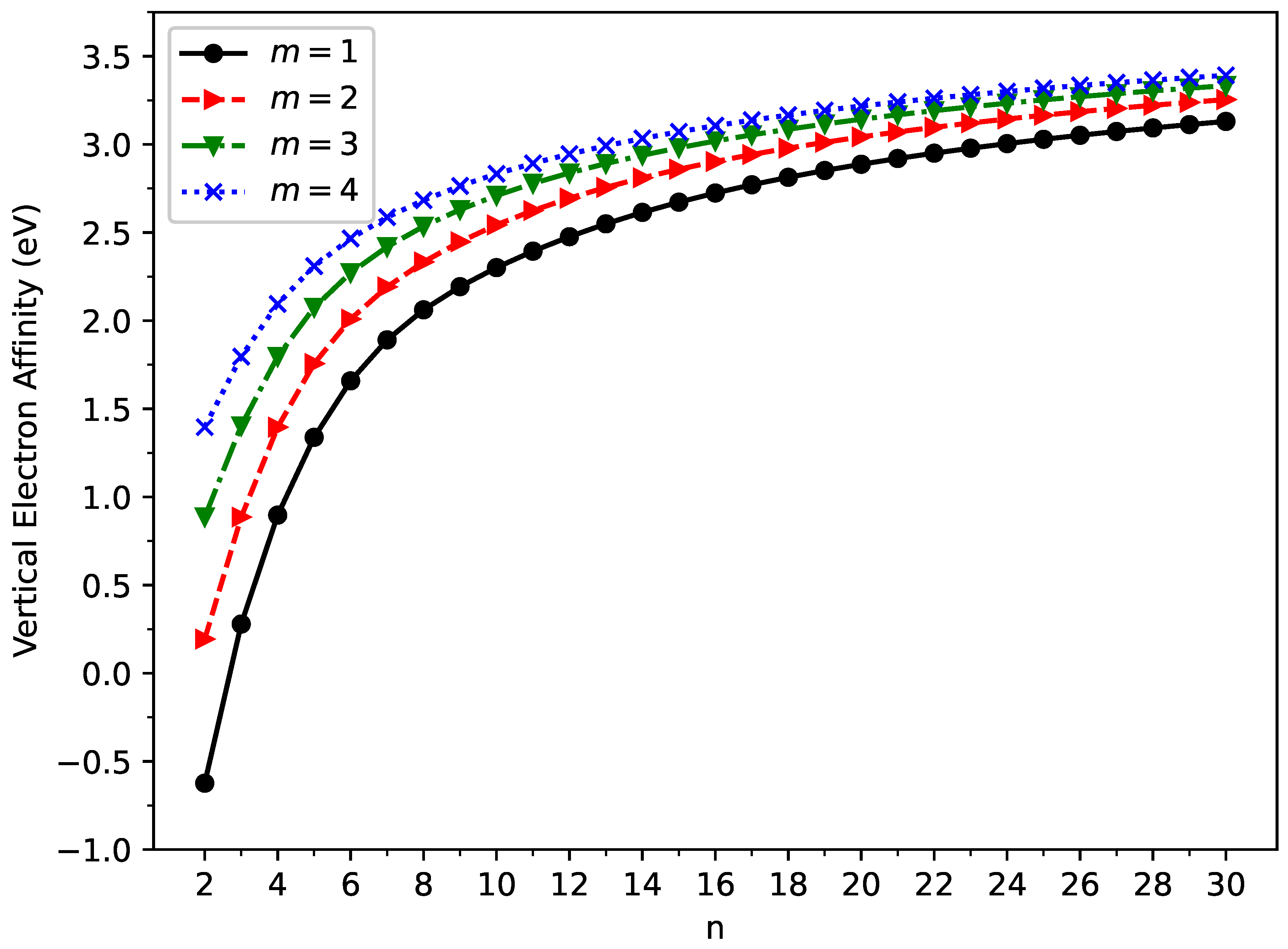
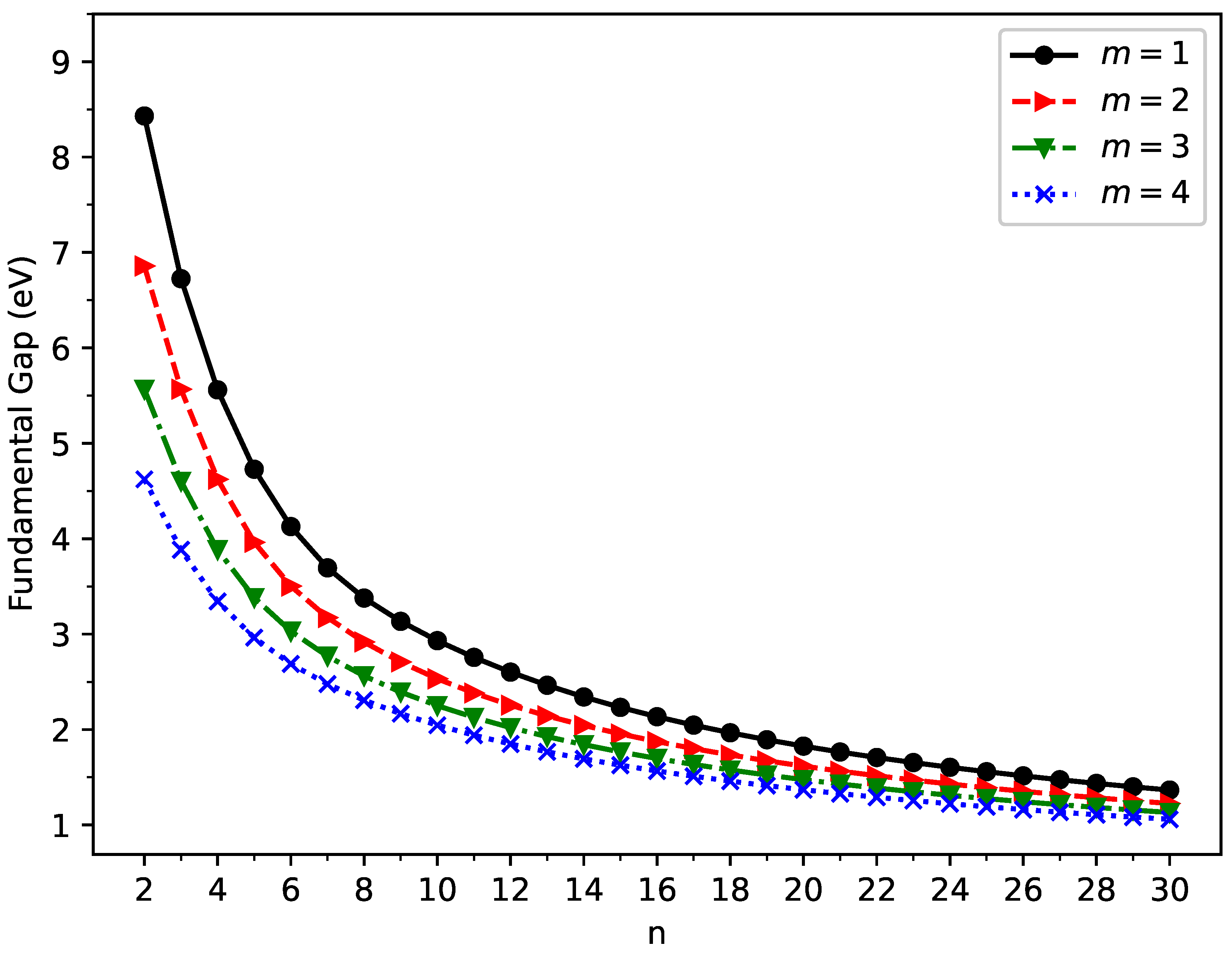
3.2. Vertical Ionization Potential, Vertical Electron Affinity, and Fundamental Gap

The vertical ionization potential, vertical electron affinity, and fundamental gap of a neutral molecule in the ground state are important electronic properties. The vertical ionization potential is the energy change when an electron is removed from the neutral molecule (without changing its geometry), and the vertical electron affinity is the energy change when an electron is added to the neutral molecule (without changing its geometry). The fundamental gap is the difference between the vertical ionization potential and vertical electron affinity.
According to their definitions, on the spin-unrestricted TAO-LDA optimized geometry of ground-state GNP[m,n], we compute the vertical ionization potential
IP v = E N − 1 − E N ,
vertical electron affinity
EA v = E N − E N + 1 ,
and fundamental gap
E g = IP v − EA v
of ground-state GNP[m,n], using multiple energy-difference calculations, with E N being the total energy of the N-electron molecule (i.e., GNP[m,n]) obtained with spin-unrestricted TAO-LDA.
The vertical ionization potential ( IP v ), vertical electron affinity ( EA v ), and fundamental gap ( E g ) of ground-state GNP[m,n] are shown in Figure 3, Figure 4, and Figure 5, respectively (also see Tables S2 to S5 in SI). With increasing GNP length, the IP v decreases monotonically, and the EA v increases monotonically, leading to a monotonically decreasing E g . These quantities are essential in materials science, spectroscopy, catalyst selection, etc., and are also important for the selection of candidate materials for electronic devices, solar cells, etc. Generally, electronic systems with the fundamental gaps in the range of 1–3 eV are desirable for photovoltaic applications. According to our TAO-LDA results, for all the cases studied in this work, GNP[1,n] (n = 10–30), GNP[2,n] (n = 8–30), GNP[3,n] (n = 7–30), and GNP[4,n] (n = 5–30) can be suitable candidates for photovoltaic applications.

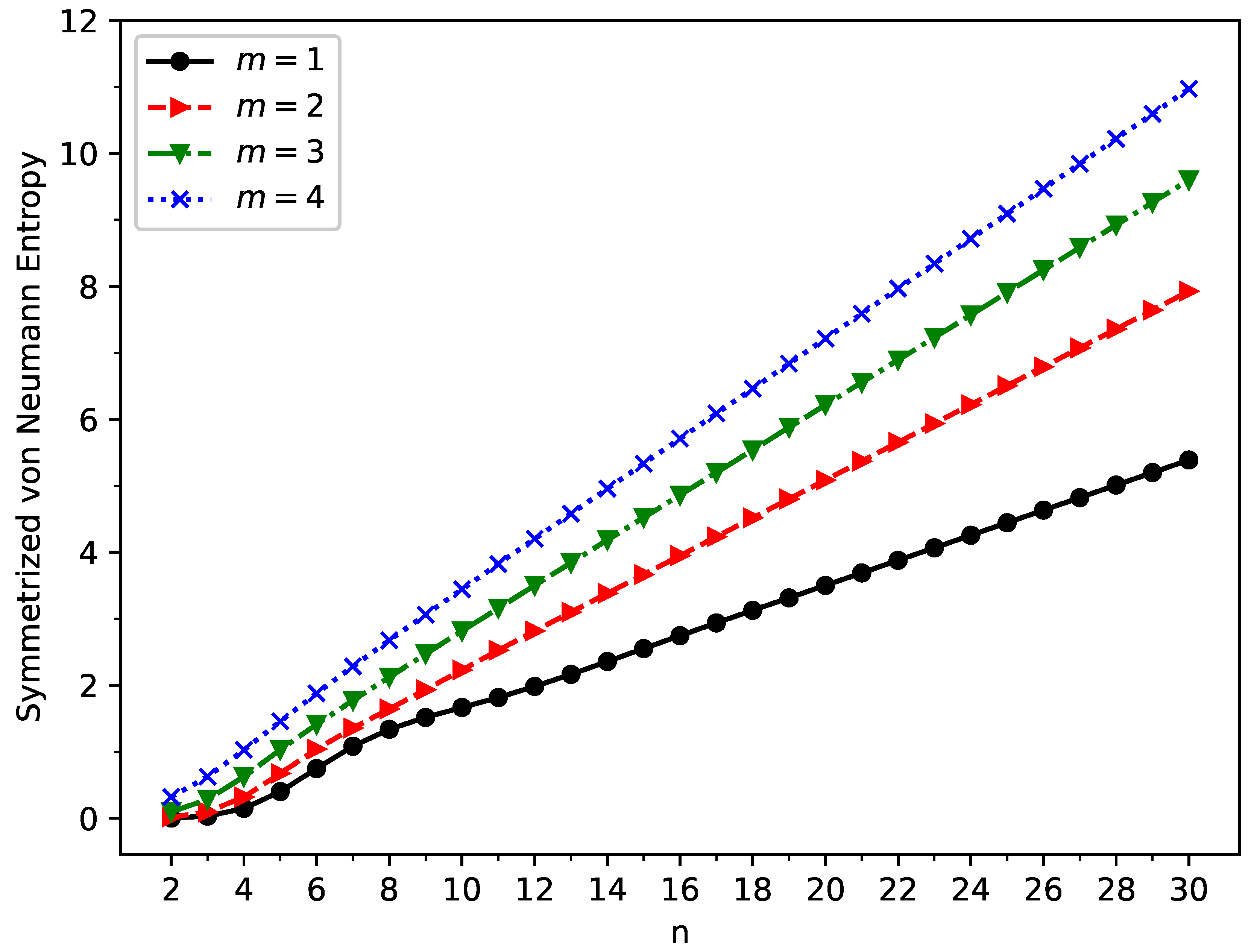
3.3. Symmetrized von Neumann Entropy

To estimate the degree of MR character associated with ground-state GNP[m,n], we compute the symmetrized von Neumann entropy [51,52,64,78]
S vN = − 1 2 ∑ σ = α , β ∑ i = 1 ∞ f i , σ ln ( f i , σ ) + ( 1 − f i , σ ) ln ( 1 − f i , σ ) ,
where f i , σ (a number between 0 and 1) is the occupation number of the i th σ -spin (i.e., α -spin or β -spin) orbital, calculated by spin-unrestricted TAO-LDA [50], approximately yielding the i th σ -spin natural orbital occupation number [60,79]. As can be seen in Eq. (5), a term with f i , σ = 0 or 1 has no contribution to the S vN , while a term with f i , σ significantly differing from 0 and 1 can cause a large increase in the S vN . As a result, for a SR system, all f i , σ values should be very close to 0 or 1, and hence, the S vN should be vanishingly small. By contrast, for an MR system, some f i , σ values can significantly differ from 0 and 1, and hence, the S vN can become very large.
As shown in Figure 6, the symmetrized von Neumann entropy ( S vN ) of ground-state GNP[m,n] increases monotonically with increasing GNP length (also see Tables S2 to S5 in SI). This indicates that the degree of MR character associated with ground-state GNP[m,n] should generally increase, as the GNP length increases.

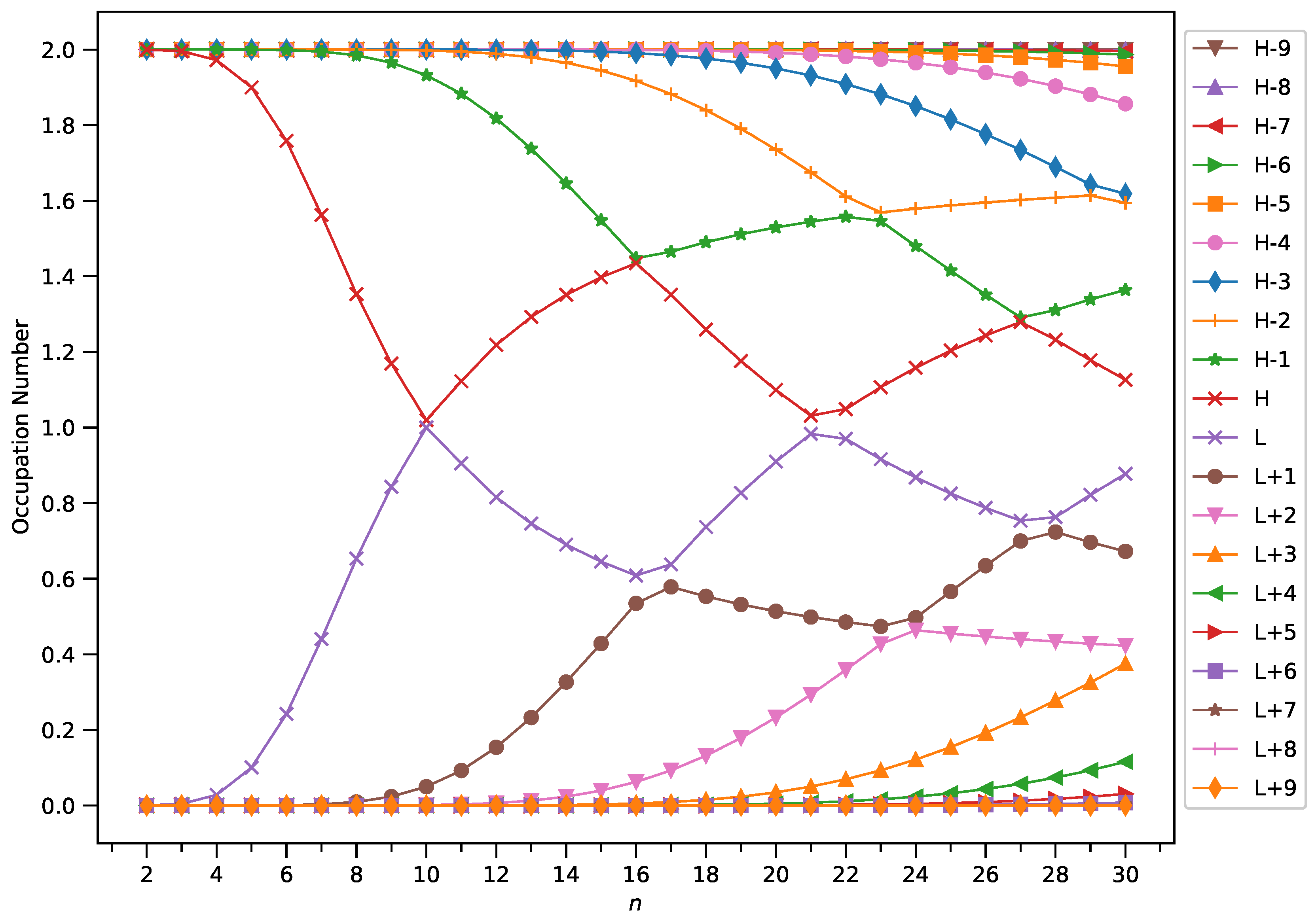
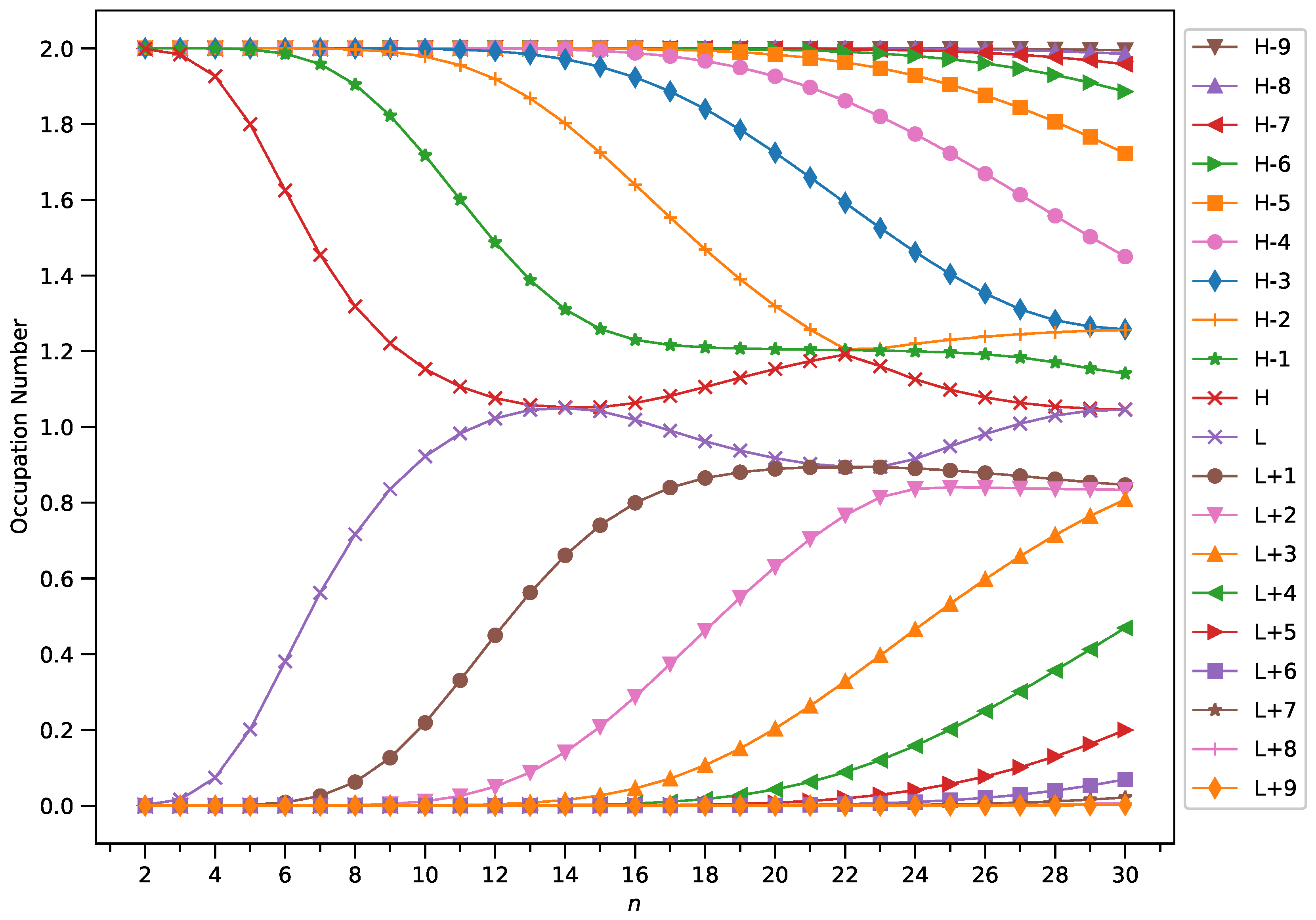
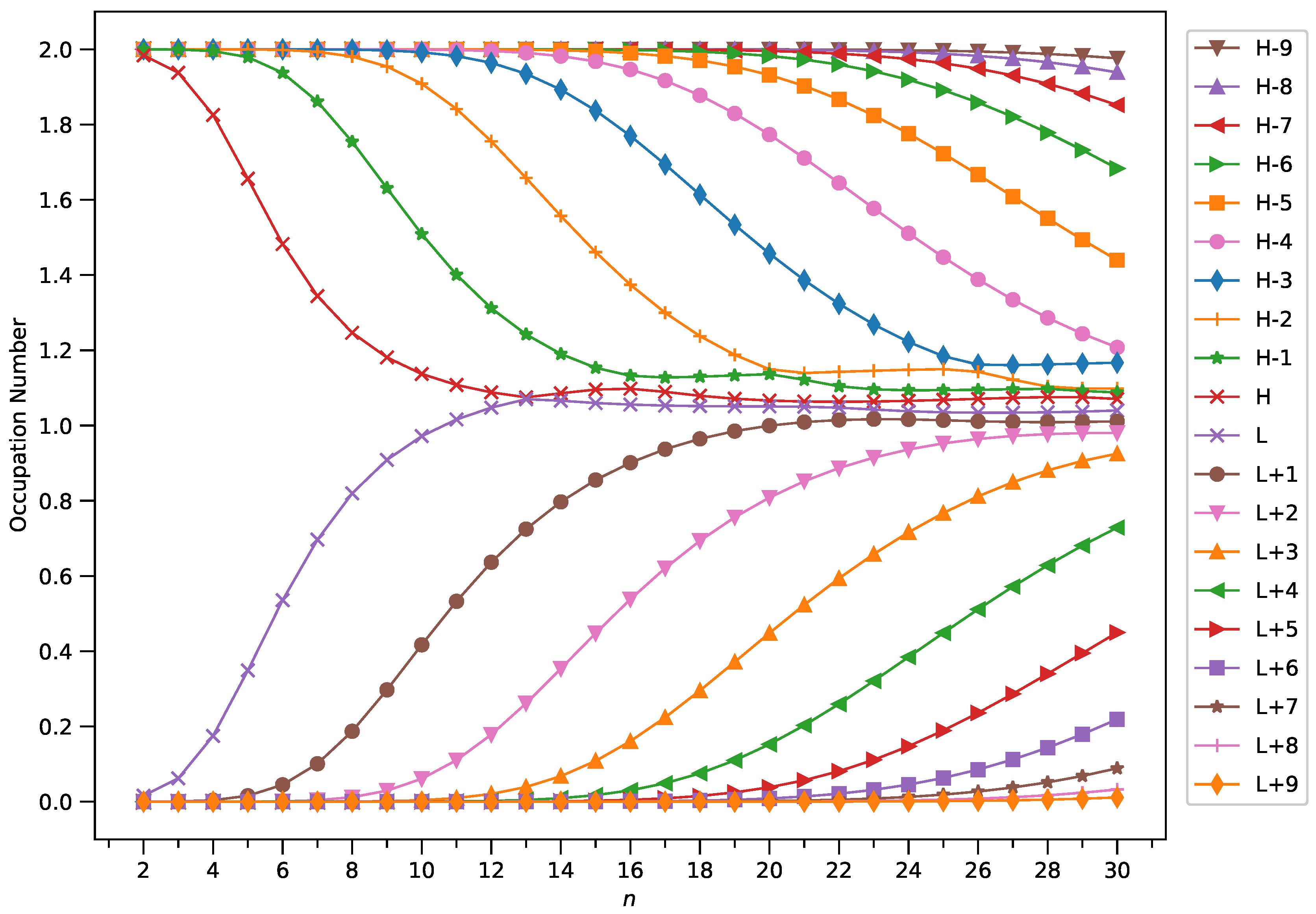
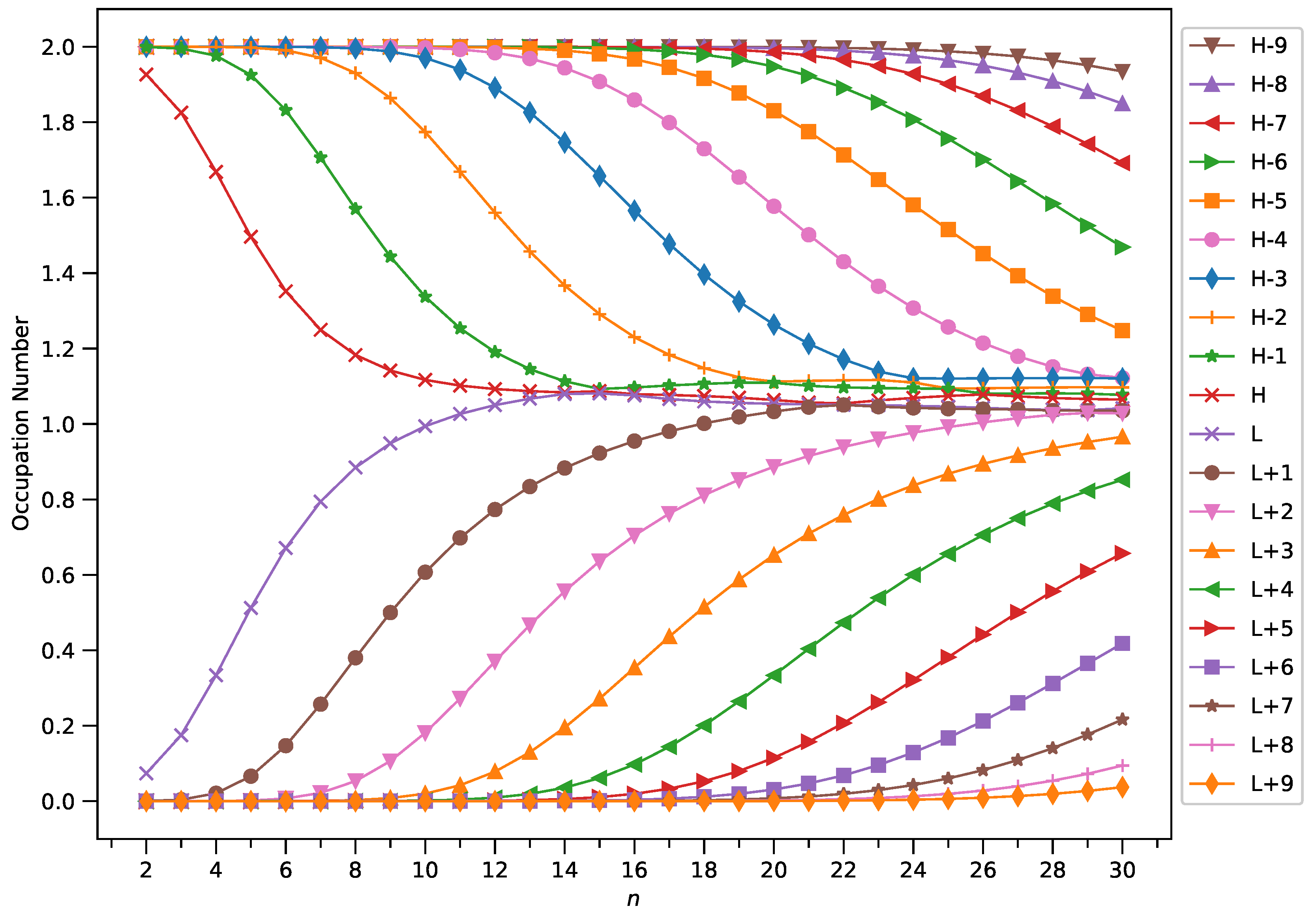
3.4. Active Orbital Occupation Numbers

With increasing GNP length, to justify the increasing trend of S vN of ground-state GNP[m,n], in spin-unrestricted TAO-DFT, there should be more active spin-orbitals [i.e., spin-orbitals with considerable fractional occupation numbers (e.g., in the range of 0.1–0.9)] and/or the occupation numbers of active spin-orbitals are closer to 0.5. In spin-restricted TAO-DFT, this indicates that there should be more active orbitals (i.e., orbitals with occupation numbers in the range of 0.2–1.8) and/or the occupation numbers of active orbitals are closer to 1.
To examine this, we plot the occupation numbers of active orbitals for the ground state of GNP[m,n], calculated using spin-restricted TAO-LDA [see Figure 7 (for m = 1), Figure 8 (for m = 2), Figure 9 (for m = 3), and Figure 10 (for m = 4)]. For the ground state of GNP[m,n] (containing N electrons), the HOMO (highest occupied molecular orbital) is the ( N / 2 ) th orbital, the LUMO (lowest unoccupied molecular orbital) is the ( N / 2 + 1 ) th orbital, and so on. In the present study, for brevity, HOMO and LUMO are denoted as H and L, respectively.
A common observation is that the shorter GNPs possess nonradical nature (i.e., all the orbital occupation numbers are very close to 0 or 2), and the longer GNPs possess increasing polyradical nature (i.e., as the GNP length increases, there are more active orbitals and/or the occupation numbers of active orbitals are closer to 1). Therefore, as the GNP length increases, the general feature of a transition from the nonradical nature of the shorter GNPs to the increasing polyradical nature of the longer GNPs is observed for each GNP width examined (i.e., m = 1–4). For the wider GNPs, the evolution of polyradical nature is faster.

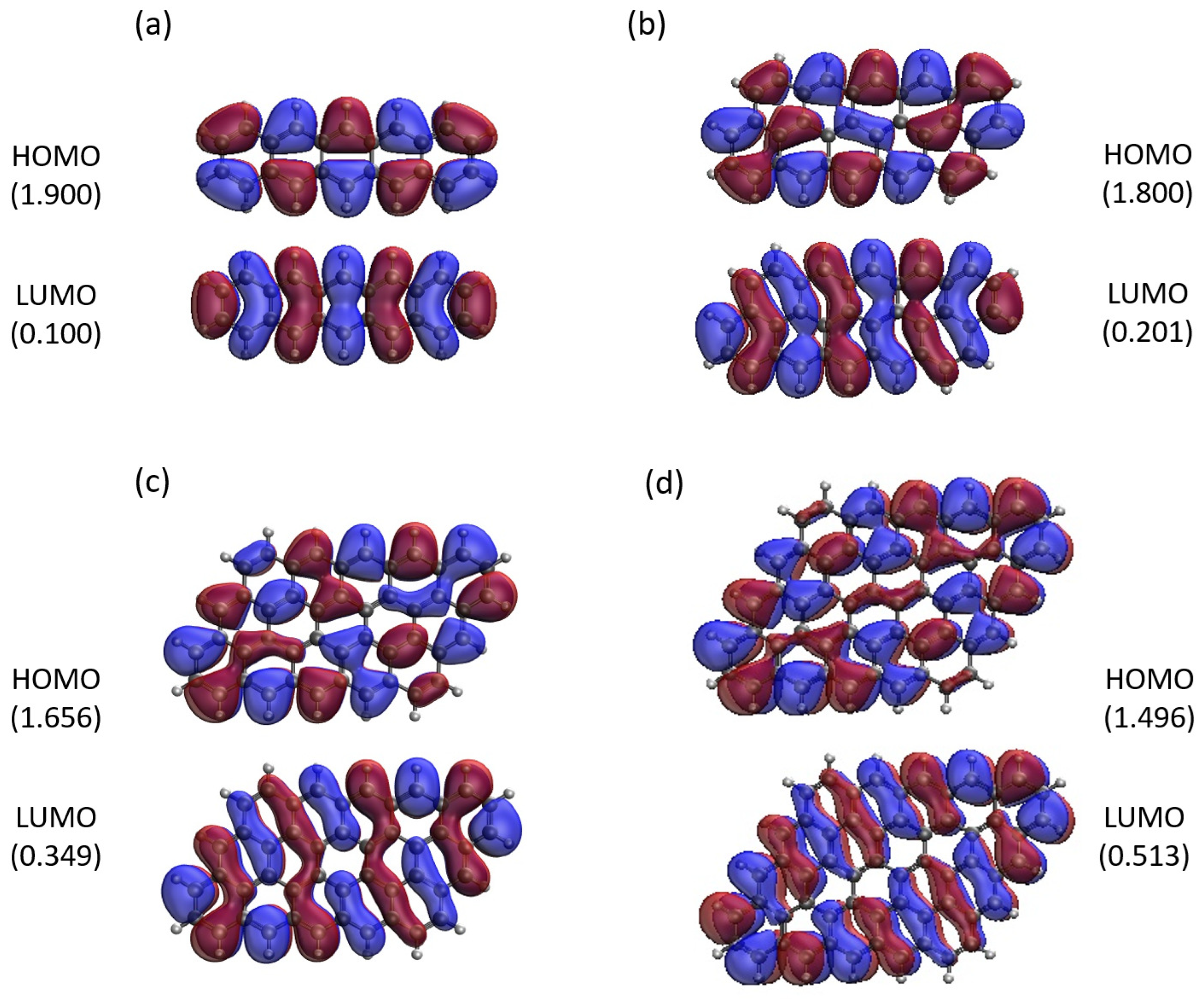
3.5. Real-Space Representation of Active Orbitals

Here, we report the real-space representation of active orbitals (HOMO and LUMO) for the ground state of some representative GNP[m,n], including GNP[m,5] with m = 1–4 (see Figure 11), GNP[m,10] with m = 1–4 (see Figure 12), GNP[m,15] with m = 1–4 (see Figure 13), and GNP[m,20] with m = 1–4 (see Figure 14), obtained with spin-restricted TAO-LDA.
As shown, for a very narrow and short GNP (e.g., GNP[1,n] with n = 2–5), the HOMO and LUMO are delocalized over the entire GNP. However, as the width and length of GNP (i.e., m and n) increase, the HOMO and LUMO of ground-state GNP[m,n] have an increasing tendency to localize at the longer edges as well as the corners of smaller interior angles. In contrast to the edge localization of active orbitals found for the wider and longer zigzag GNRs [25,78], the edge/corner localization of active orbitals for the wider and longer GNPs is observed in this study, possibly due to the parallelogram shapes of GNPs.

4. Conclusions

In summary, we have reported the electronic properties of GNP[m,n] (with m = 1–4 and n = 2–30) obtained with TAO-DFT. As the longer GNPs exhibit significant MR character (e.g., polyradical nature), KS-DFT with the conventional LDA, GGA, and hybrid xc energy functionals can lead to unreliable results. Besides, because of the large electronic systems considered, performing ab initio MR electronic structure calculations can be impractical due to the prohibitively high cost. Owing to its nice compromise between efficiency and accuracy, TAO-DFT appears to be an ideal electronic structure method for this computational study.
According to TAO-DFT, the ST gap decreases monotonically with increasing GNP length, and GNPs possess singlet ground states for all the cases examined. As the GNP length increases, the vertical ionization potential and fundamental gap decrease monotonically, whereas the vertical electron affinity and symmetrized von Neumann entropy increase monotonically. Similar to the findings of previous studies on zigzag GNRs [25,78], the shorter GNPs possess nonradical nature, and the longer GNPs possess increasing polyradical nature. Therefore, there is a transition from the nonradical nature of the shorter GNPs to the increasing polyradical nature of the longer GNPs. Besides, the evolution of polyradical nature is faster for the wider GNPs. However, in contrast to the edge localization of active orbitals found for the wider and longer zigzag GNRs [25,78], we observe the edge/corner localization of active orbitals for the wider and longer GNPs in this study, possibly due to the parallelogram shapes of GNPs.

Author Contributions

Conceptualization, S.S. and J.-D.C.; Formal analysis, S.S.; Data curation, S.S.; Funding acquisition, J.-D.C.; Investigation, S.S.; Methodology, S.S. and J.-D.C.; Project administration, J.-D.C.; Supervision, J.-D.C.; Software, J.-D.C.; Resources, J.-D.C.; Validation, S.S. and J.-D.C.; Visualization, S.S.; Writing–original draft, S.S.; Writing–review & editing, J.-D.C. Both authors have read and agreed to the published version of the manuscript.

Funding

This research work was previously funded by the Ministry of Science and Technology of Taiwan (Grant No. MOST110-2112-M-002-045-MY3).

Acknowledgments

This research work was previously supported by the Ministry of Science and Technology of Taiwan (Grant No. MOST110-2112-M-002-045-MY3), and was also supported by National Taiwan University as well as the National Center for Theoretical Sciences of Taiwan.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hirsch, A. The era of carbon allotropes. Nat. Mater. 2010, 9, 868–871. [Google Scholar] [CrossRef]
  2. Georgakilas, V.; Perman, J.A.; Tucek, J.; Zboril, R. Broad family of carbon nanoallotropes: classification, chemistry, and applications of fullerenes, carbon dots, nanotubes, graphene, nanodiamonds, and combined superstructures. Chem. Rev. 2015, 115, 4744–4822. [Google Scholar] [CrossRef]
  3. Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
  4. Meirzadeh, E. et al. A few-layer covalent network of fullerenes. Nature 2023, 613, 71–76. [Google Scholar] [CrossRef]
  5. Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
  6. Novoselov, K.S. et al. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
  7. Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
  8. Madurani, K.A.; Suprapto, S.; Machrita, N.I.; Bahar, S.L.; Illiya, W.; Kurniawan, F. Progress in graphene synthesis and its application: history, challenge and the future outlook for research and industry. ECS J. Solid State Sci. Technol. 2020, 9, 093013. [Google Scholar] [CrossRef]
  9. Houtsma, R.K.; de la Rie, J.; Stöhr, M. Atomically precise graphene nanoribbons: interplay of structural and electronic properties. Chem. Soc. Rev. 2021, 50, 6541–6568. [Google Scholar] [CrossRef]
  10. Gu, Y.; Qiu, Z.; Müllen, K. Nanographenes and graphene nanoribbons as multitalents of present and future materials science. J. Am. Chem. Soc. 2022, 144, 11499–11524. [Google Scholar] [CrossRef]
  11. Han, M.Y.; Özyilmaz, B.; Zhang, Y.; Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef]
  12. Friedrich, N. et al. Addressing electron spins embedded in metallic graphene nanoribbons. ACS Nano 2022, 16, 14819–14826. [Google Scholar] [CrossRef]
  13. Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef]
  14. Kimouche, A. et al. Ultra-narrow metallic armchair graphene nanoribbons. Nat. Commun. 2015, 6, 10177. [Google Scholar] [CrossRef]
  15. Jiang, S.; Neuman, T.; Boeglin, A.; Scheurer, F.; Schull, G. Topologically localized excitons in single graphene nanoribbons. Science 2023, 379, 1049–1054. [Google Scholar] [CrossRef]
  16. Kumar, S.; Pratap, S.; Kumar, V.; Mishra, R.K.; Gwag, J.S.; Chakraborty, B. Electronic, transport, magnetic, and optical properties of graphene nanoribbons and their optical sensing applications: a comprehensive review. Luminescence 2023, 38, 909–953. [Google Scholar] [CrossRef]
  17. Wang, H. et al. Graphene nanoribbons for quantum electronics. Nat. Rev. Phys. 2021, 3, 791–802. [Google Scholar] [CrossRef]
  18. Saraswat, V.; Jacobberger, R.M.; Arnold, M.S. Materials science challenges to graphene nanoribbon electronics. ACS Nano 2021, 15, 3674–3708. [Google Scholar] [CrossRef]
  19. Luo, H.; Yu, G. Preparation, bandgap engineering, and performance control of graphene nanoribbons. Chem. Mater. 2022, 34, 3588–3615. [Google Scholar] [CrossRef]
  20. Yano, Y.; Mitoma, N.; Ito, H.; Itami, K. A quest for structurally uniform graphene nanoribbons: synthesis, properties, and applications. J. Org. Chem. 2019, 85, 4–33. [Google Scholar] [CrossRef]
  21. Gu, Y.; Wu, X.; Gopalakrishna, T.Y.; Phan, H.; Wu, J. Graphene-like molecules with four zigzag edges. Ang. Chem. Int. Ed. 2018, 57, 6541–6545. [Google Scholar] [CrossRef]
  22. Gu, Y.; Tullimilli, Y.G.; Feng, J.; Phan, H.; Zeng, W.; Wu, J. peri-Acenoacenes. Chem. Comm. 2019, 55, 5567–5570. [Google Scholar] [CrossRef]
  23. Muñoz–Mármol, R. et al. Near-Infrared lasing in four-zigzag edged nanographenes by 1D versus 2D electronic π-conjugation. Adv. Funct. Mater. 2021, 31, 2105073. [Google Scholar] [CrossRef]
  24. Hauwali, N.U.J.; Syuhada, I.; Rosikhin, A.; Winata, T. Fundamental properties of parallelogram graphene nanoflakes: A first principle study. Mat. Today Proc. 2021, 44, 3305–3308. [Google Scholar] [CrossRef]
  25. Wu, C.-S.; Chai, J.-D. Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT. J. Chem. Theory Comput. 2015, 11, 2003–2011. [Google Scholar] [CrossRef]
  26. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  27. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  28. Teale, A.M. et al. DFT Exchange: sharing perspectives on the workhorse of quantum chemistry and materials science. Phys. Chem. Chem. Phys. 2022, 24, 28700–28781. [Google Scholar] [CrossRef]
  29. Dirac, P.A.M. Note on exchange phenomena in the Thomas atom. Proc. Cambridge Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
  30. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
  31. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  32. Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef]
  33. Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef]
  34. Engel, E.; Dreizler, R.M. Density Functional Theory: An Advanced Course, Springer, Heidelberg, 2011.
  35. Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef]
  36. Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
  37. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  38. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  39. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  40. Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
  41. Andersson, K.; Malmqvist, P.-Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218. [Google Scholar] [CrossRef]
  42. Hachmann, J.; Dorando, J.J.; Aviles, M.; Chan, G.K.L. The radical character of the acenes: a density matrix renormalization group study. J. Chem. Phys. 2007, 127, 134309. [Google Scholar] [CrossRef]
  43. Gidofalvi, G.; Mazziotti, D.A. Active-space two-electron reduced-density-matrix method: complete active-space calculations without diagonalization of the N-electron hamiltonian. J. Chem. Phys. 2008, 129, 134108. [Google Scholar] [CrossRef]
  44. Mizukami, W.; Kurashige, Y.; Yanai, T. More π electrons make a difference: emergence of many radicals on graphene nanoribbons studied by ab initio DMRG theory. J. Chem. Theory and Comput. 2013, 9, 401–407. [Google Scholar] [CrossRef]
  45. Gryn’ova, G.; Coote, M.L.; Corminboeuf, C. Theory and practice of uncommon molecular electronic configurations. WIREs Comput. Mol. Sci. 2015, 5, 440–459. [Google Scholar] [CrossRef]
  46. Fosso-Tande, J.; Nguyen, T.-S.; Gidofalvi, G.; DePrince III, A.E. Large-scale variational two-electron reduced-density-matrix-driven complete active space self-consistent field methods. J. Chem. Theory Comput. 2016, 12, 2260–2271. [Google Scholar] [CrossRef]
  47. Piris, M. Global method for electron correlation. Phys. Rev. Lett. 2017, 119, 063002. [Google Scholar] [CrossRef]
  48. Goli, V.D.P.; Prodhan, S.; Mazumdar, S.; Ramasesha, S. Correlated electronic properties of some graphene nanoribbons: a DMRG study. Phys. Rev. B 2016, 94, 035139. [Google Scholar] [CrossRef]
  49. Hagymási, I.; Legeza, Ö. Entanglement, excitations, and correlation effects in narrow zigzag graphene nanoribbons. Phys. Rev. B 2016, 94, 165147. [Google Scholar] [CrossRef]
  50. Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef]
  51. Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014, 140, 18A521. [Google Scholar] [CrossRef]
  52. Chai, J.-D. Role of exact exchange in thermally-assisted-occupation density functional theory: a proposal of new hybrid schemes. J. Chem. Phys. 2017, 146, 044102. [Google Scholar] [CrossRef]
  53. Xuan, F.; Chai, J.-D.; Su, H. Local density approximation for the short-range exchange free energy functional. ACS Omega 2019, 4, 7675–7683. [Google Scholar] [CrossRef]
  54. Tsai, H.-Y.; Chai, J.-D. Real-time extension of TAO-DFT. Molecules 2023, 28, 7247. [Google Scholar] [CrossRef]
  55. Chen, B.-J.; Chai, J.-D. TAO-DFT fictitious temperature made simple. RSC Adv. 2022, 12, 12193–12210. [Google Scholar] [CrossRef]
  56. Lin, C.-Y.; Hui, K.; Chung, J.-H.; Chai, J.-D. Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory. RSC Adv. 2017, 7, 50496–50507. [Google Scholar] [CrossRef]
  57. Mermin, N.D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
  58. Li, S.; Chai, J.-D. TAO-DFT-based ab initio molecular dynamics. Front. Chem. 2020, 8, 589432. [Google Scholar] [CrossRef]
  59. Seenithurai, S.; Chai, J.-D. TAO-DFT with the polarizable continuum model. Nanomaterials 2023, 13, 1593. [Google Scholar] [CrossRef]
  60. Yeh, C.-N.; Chai, J.-D. Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: a TAO-DFT study. Sci. Rep. 2016, 6, 30562. [Google Scholar] [CrossRef]
  61. Seenithurai, S.; Chai, J.-D. Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: a dispersion-corrected TAO-DFT study. Sci. Rep. 2016, 6, 33081. [Google Scholar] [CrossRef]
  62. Wu, C.-S.; Lee, P.-Y.; Chai, J.-D. Electronic properties of cyclacenes from TAO-DFT. Sci. Rep. 2016, 6, 37249. [Google Scholar] [CrossRef]
  63. Seenithurai, S.; Chai, J.-D. Effect of Li termination on the electronic and hydrogen storage properties of linear carbon chains: a TAO-DFT study. Sci. Rep. 2017, 7, 4966. [Google Scholar] [CrossRef]
  64. Seenithurai, S.; Chai, J.-D. TAO-DFT investigation of electronic properties of linear and cyclic carbon chains. Sci. Rep. 2020, 10, 13133. [Google Scholar] [CrossRef]
  65. Seenithurai, S.; Chai, J.-D. Electronic properties of carbon nanobelts predicted by thermally-assisted-occupation DFT. Nanomaterials 2021, 11, 2224. [Google Scholar] [CrossRef]
  66. Tönshoff, C.; Bettinger, H.F. Pushing the limits of acene chemistry: The recent surge of large acenes. Chem. Eur. J. 2021, 27, 3193–3212. [Google Scholar] [CrossRef]
  67. Gupta, D.; Omont, A.; Bettinger, H.F. Energetics of formation of cyclacenes from 2,3-didehydroacenes and implications for astrochemistry. Chem. Eur. J. 2021, 27, 4605–4616. [Google Scholar] [CrossRef]
  68. Nieman, R.; Carvalho, J.R.; Jayee, B.; Hansen, A.; Aquino, A.J.; Kertesz, M.; Lischka, H. Polyradical character assessment using multireference calculations and comparison with density-functional derived fractional occupation number weighted density analysis. Phys. Chem. Chem. Phys. 2023, 25, 27380–27393. [Google Scholar] [CrossRef]
  69. Hanson-Heine, M.W.D. Static correlation in vibrational frequencies studied using thermally-assisted-occupation density functional theory. Chem. Phys. Lett. 2020, 739, 137012. [Google Scholar] [CrossRef]
  70. Hanson-Heine, M.W.D. Static electron correlation in anharmonic molecular vibrations: a hybrid TAO-DFT study. J. Phys. Chem. A 2022, 126, 7273–7282. [Google Scholar] [CrossRef]
  71. Shao, Y. et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
  72. Su, Y. et al. Thermally controlling the singlet–triplet energy gap of a diradical in the solid state. Chem. Sci. 2016, 7, 6514–6518. [Google Scholar] [CrossRef] [PubMed]
  73. Yu, L.; Wu, Z.; Xie, G.; Zhong, C.; Zhu, Z.; Cong, H.; Ma, D.; Yang, C. Achieving a balance between small singlet-triplet energy splitting and high fluorescence radiative rate in a quinoxaline-based orange-red thermally activated delayed fluorescence emitter. Chem. Commun. 2016, 52, 11012–11015. [Google Scholar] [CrossRef] [PubMed]
  74. Smith, M.B.; Michl, J. Singlet fission. Chem. Rev. 2010, 110, 6891–6936. [Google Scholar] [CrossRef] [PubMed]
  75. Zhou, J.; Liu, Q.; Feng, W.; Sun, Y.; Li, F. Upconversion luminescent materials: advances and applications. Chem. Rev. 2015, 115, 395–465. [Google Scholar] [CrossRef] [PubMed]
  76. Romero, N.A.; Nicewicz, D.A. Organic photoredox catalysis. Chem. Rev. 2016, 116, 10075–10166. [Google Scholar] [CrossRef] [PubMed]
  77. Xia, J. et al. Singlet fission: progress and prospects in solar cells. Adv. Mater. 2017, 29, 1601652. [Google Scholar] [CrossRef] [PubMed]
  78. Rivero, P.; Jiménez-Hoyos, C.A.; Scuseria, G.E. Entanglement and polyradical nature of polycyclic aromatic hydrocarbons predicted by projected Hartree-Fock theory. J. Phys. Chem. B 2013, 117, 12750–12758. [Google Scholar] [CrossRef]
  79. Löwdin, P.-O.; Shull, H. Natural orbitals in the quantum theory of two-electron systems. Phys. Rev. 1956, 101, 1730–1739. [Google Scholar] [CrossRef]
Preprints 92802 g001
Figure 1. Structures of GNP[m,10] with m = 1 (i.e., 10-acene, containing 10 linearly fused benzene rings) and GNP[m,10] with m = 2–4 (containing m parallelly fused 10-acenes forming parallelograms).
Figure 1. Structures of GNP[m,10] with m = 1 (i.e., 10-acene, containing 10 linearly fused benzene rings) and GNP[m,10] with m = 2–4 (containing m parallelly fused 10-acenes forming parallelograms).
Preprints 92802 g001
Preprints 92802 g002
Figure 2. Singlet-triplet energy gap of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Figure 2. Singlet-triplet energy gap of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Preprints 92802 g002
Preprints 92802 g003
Figure 3. Vertical ionization potential for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Figure 3. Vertical ionization potential for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Preprints 92802 g003
Preprints 92802 g004
Figure 4. Vertical electron affinity for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Figure 4. Vertical electron affinity for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Preprints 92802 g004
Preprints 92802 g005
Figure 5. Fundamental gap for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Figure 5. Fundamental gap for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Preprints 92802 g005
Preprints 92802 g006
Figure 6. Symmetrized von Neumann entropy for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Figure 6. Symmetrized von Neumann entropy for the ground state of GNP[m,n], calculated using spin-unrestricted TAO-LDA.
Preprints 92802 g006
Preprints 92802 g007
Figure 7. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[1,n], calculated using spin-restricted TAO-LDA.
Figure 7. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[1,n], calculated using spin-restricted TAO-LDA.
Preprints 92802 g007
Preprints 92802 g008
Figure 8. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[2,n], calculated using spin-restricted TAO-LDA.
Figure 8. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[2,n], calculated using spin-restricted TAO-LDA.
Preprints 92802 g008
Preprints 92802 g009
Figure 9. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[3,n], calculated using spin-restricted TAO-LDA.
Figure 9. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[3,n], calculated using spin-restricted TAO-LDA.
Preprints 92802 g009
Preprints 92802 g010
Figure 10. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[4,n], calculated using spin-restricted TAO-LDA.
Figure 10. Occupation numbers of active orbitals (HOMO−9, HOMO−8, ..., HOMO, LUMO, ..., LUMO+8, and LUMO+9) for the ground state of GNP[4,n], calculated using spin-restricted TAO-LDA.
Preprints 92802 g010
Preprints 92802 g011
Figure 11. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,5] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Figure 11. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,5] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Preprints 92802 g011
Preprints 92802 g012
Figure 12. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,10] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Figure 12. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,10] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Preprints 92802 g012
Preprints 92802 g013
Figure 13. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,15] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Figure 13. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,15] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Preprints 92802 g013
Preprints 92802 g014
Figure 14. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,20] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Figure 14. Real-space representation of active orbitals (HOMO and LUMO) for the ground state of GNP[m,20] with (a) m = 1 , (b) m = 2 , (c) m = 3 , and (d) m = 4 , at an isovalue of 0.02 e/Å3, calculated using spin-restricted TAO-LDA, where the orbital occupation numbers are shown in parentheses.
Preprints 92802 g014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated