Rethinking the Use of Linear Forms of the Langmuir Isotherm in Adsorption Modeling to Calculate Langmuir Isotherm Parameters

Preprint

Article

Rethinking the Use of Linear Forms of the Langmuir Isotherm in Adsorption Modeling to Calculate Langmuir Isotherm Parameters

Altmetrics

Downloads

150

Views

161

Comments

Rohollah Ezzati^*

This version is not peer-reviewed

This preprints belongs to the Topic

New Advances in Adsorptive and Extractive Methods for Pollutant Removal

Submitted:

11 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts

Abstract

The Langmuir isotherm is a widely used model for analyzing adsorption equilibrium data. This study evaluated the efficiency and accuracy of all four linear forms of the Langmuir isotherm and its non-linear form using 67 experimental data sets selected from the literature. The results showed that only if all four linear forms simultaneously show high accuracy, then the non-linear form also shows high accuracy, and therefore it can be said that the process probably follows the Langmuir isotherm. On the contrary, when at least one of the four linear forms of the Langmuir isotherm has low accuracy, it means that the non-linear form also has low accuracy, and it can be concluded that this process does not follow the Langmuir isotherm. This research suggests that all four linear forms of the Langmuir isotherm should be evaluated simultaneously to conclude whether the studied system follows the Langmuir isotherm or not. In other words, relying on only one of the four linear forms of the Langmuir isotherm to model adsorption and calculate the Langmuir constant and maximum adsorption capacity is an incomplete approach, contrary to the conventional approach.

Keywords:

Subject: Chemistry and Materials Science - Surfaces, Coatings and Films

1. Introduction

Adsorption is a very important phenomenon in scientific research that plays a significant role in various applications such as drinking water purification [1], the development of advanced drug delivery systems [2], gas separation [3], gas storage [4], etc. Adsorption is the adhesion of atoms, ions, or molecules to a surface, and it is a key process in all these applications. The mathematical underpinning of adsorption science often leads scientists into the intriguing world of isotherms, particularly the Langmuir isotherm. Irving Langmuir proposed this mathematical model in 1918, and it serves as the cornerstone for understanding monolayer adsorption [5]. The Langmuir isotherm is a simple type of adsorption equilibrium model that is applicable at both high and low pressures. It relates the area covered by the adsorbate on the surface to the pressure of the gas or the concentration of the solute in solution. The Langmuir isotherm provides insights into the maximum adsorption capacity of a surface and the affinity between adsorbent and adsorbate. In the solution phase, the non-linear form of this isotherm is as follows [6,7]:

\frac{q_{e}}{q_{m}} = \frac{K_{L} C_{e}}{1 + K_{L} C_{e}}

(1)

Here,

q_{e}

represents the equilibrium amount of adsorbed molecules,

q_{m}

represents the maximum amount of adsorbed molecules,

K_{L}

signifies the equilibrium constant related to the adsorption process, and

C_{e}

is the concentration of the substance in the bulk phase.

The beauty of the Langmuir isotherm lies in its ability to define the monolayer adsorption capacity

q_{m}

the maximum amount of substance that a surface can adsorb. When the surface is saturated,

θ_{e} = \frac{q_{e}}{q_{m}}

equals unity, and this sets the stage for calculating

q_{m}

. Thus, the Langmuir isotherm provides essential information about the surface's adsorption capacity and the interaction strength between adsorbent and adsorbate [7].

The Langmuir isotherm is a non-linear model that presents both a challenge and an opportunity. While non-linear models like the Langmuir isotherm capture the complexities of real-world adsorption, they also complicate the analysis, often requiring sophisticated numerical methods to extract meaningful insights [8]. Analyzing non-linear models often involves solving equations that lack direct algebraic solutions, which can impede the estimation of model parameters, such as

q_{m}

and K [6]. When experimental data are noisy, the situation becomes even more complex, as noise can lead to parameter estimates that deviate significantly from the true values. The linearization of the Langmuir isotherm is motivated by the fact that fitting the original non-linear model to experimental data (

q_{e}

C_{e}

) to calculate the two model parameters, maximum adsorption capacity (

q_{m}

) and Langmuir constant (K), requires specialized mathematical software for non-linear regression. Due to the complications associated with the non-linear form of Langmuir isotherm, researchers often use the linear forms of this model to obtain its parameters, which is a powerful technique that simplifies the analysis [9,10]. These linear forms are given below [6,9,11,12]:

Form-1:

\frac{C_{e}}{q_{e}} = \frac{1}{q_{m} K} + \frac{C_{e}}{q_{m}}

(2)

Form-2:

\frac{1}{q_{e}} = \frac{1}{q_{m} K} \frac{1}{C_{e}} + \frac{1}{q_{m}}

(3)

Form-3:

q_{e} = q_{m} - \frac{1}{K} \frac{q_{e}}{C_{e}}

(4)

Form-4:

\frac{q_{e}}{C_{e}} = K q_{m} - K q_{e}

(5)

The Langmuir isotherm can be linearized by plotting

\frac{C_{e}}{q_{e}}

C_{e}

for Form-1,

\frac{1}{q_{e}}

\frac{1}{C_{e}}

for Form-2,

q_{e}

\frac{q_{e}}{C_{e}}

for Form-3 and

\frac{q_{e}}{C_{e}}

q_{e}

for Form-4. The linearization process involves converting initial data (

q_{e}

C_{e}

) to the required data for linearization (such as

\frac{q_{e}}{C_{e}}

\frac{C_{e}}{q_{e}}

, and

\frac{1}{q_{e}}

), which can inadvertently change the error structure and lead to differences in the values of the fitted parameters between linear and non-linear forms of the Langmuir model [13]. It has been shown that the accuracy of the non-linear form of the Langmuir model is higher than the linear forms in fitting the model parameters [14]. Therefore, the efficiency of the linear forms of the Langmuir isotherm is measured by comparing the results obtained from these forms with the results obtained from the non-linear form of the Langmuir isotherm [15].

Also, researchers often use the correlation coefficient, R², to compare the accuracy of different linear forms of the Langmuir isotherm and to determine the most suitable form for their experimental data. In other words, the R² value is the most commonly used parameter for estimating the accuracy of the fit of an isotherm model to experimental equilibrium data. In such a case, an isotherm giving an R² value closest to unity is accepted as the best fit isotherm in that particular case [10,15,16,17]. The linearization of the Langmuir isotherm can be done using spreadsheets such as Microsoft Excel, and the linear forms of the model are usually used to obtain its parameters [15].

When studying an adsorption process using the Langmuir isotherm, selecting the best and most accurate linear form among the four linear forms of the Langmuir isotherm is a fundamental challenge. Most research works only use Form-1 of the Langmuir isotherm to model the adsorption process without investigating the efficiency of the other linear forms. In other words, there is a belief among researchers that Form-1 is the most accurate linear form of the Langmuir isotherm [18,19,20,21].

This research work evaluates the efficiency and accuracy of all four linear forms of the Langmuir isotherm and its non-linear form using 67 selected experimental data sets from literature related to the adsorption of various substances on different adsorbents. The study discusses and concludes the relationship between the accuracy of the non-linear form of the Langmuir isotherm and the accuracy of its linear forms.

2. Experimental Data and Calculation Methods

In this study, 67 sets of experimental adsorption data from 42 papers were collected, regardless of the isotherm models followed by the studied processes. The adsorption data (

q_{e}

C_{e}

) were extracted from the

q_{e}

vs.

C_{e}

plots reported in these articles using Plot Digitizer Version 2.0 software. The obtained (

q_{e}

C_{e}

) data were used to evaluate the accuracy of linear and non-linear forms of Langmuir isotherm. Linear regression and analysis of linear Langmuir isotherm models were performed using Microsoft Excel 2010. Non-linear regression and analysis of non-linear Langmuir, Sips, Toth, and other isotherm models were performed using Polymath Version 6.1 software. The accuracy of linear forms of Langmuir isotherm was compared and evaluated using the coefficient of determination (R²). The accuracy of non-linear Langmuir, Sips, and other isotherms was compared and evaluated using the Coefficient of determination (R²) and Root Mean Square Deviation (Rmsd). Table 1 reports the sources of the collected experimental data along with information about the adsorbate, adsorbent, isotherm reported in the papers and the coefficients of determination obtained from linear and non-linear regression of Langmuir isotherm models. Also, the adsorption capacities and Langmuir constants obtained from linear and non-linear forms of the Langmuir isotherm for the adsorption systems are reported in Table 2.

3. Results and Discussion

In this research, to investigate the relationship between the accuracy of the linear and non-linear forms of the Langmuir isotherm, simple mathematical principles, hypothetical and experimental adsorption data will be used.

3.1. In what case can we say that an adsorption system follows the Langmuir isotherm?

To answer this question, two simple propositions regarding the relationship between the accuracy of linear and non-linear forms of Langmuir isotherm will be discussed and proved numerically.

Proposition 1: If a dataset (

q_{e}

C_{e}

) perfectly follows the Langmuir isotherm, indicated by

R^{2} = 1

for the non-linear Langmuir isotherm form, each of the four linear forms (Form-1, Form-2, Form-3, and Form-4) will also exhibit

R^{2} = 1

. Therefore, when all four linear forms accurately fit the data, they will produce identical values for the Langmuir constants (K) and maximum adsorption capacity (

q_{m}

Proof: To substantiate this proposition, a hypothetical dataset was utilized, as presented in Table 3 and Figure 1.

Table 3. A hypothetical adsorption system that follows the Langmuir isotherm.

$C_{e}$ (mg/L)	$q_{e}$ (mg/g)	Langmuir Parameters	Form-1	Form-2	Form-3	Form-4	Non-linear
0	0	$q_{m}$ (mg/g)	100	100	100	100	100
50	33.33333
100	50
150	60
200	66.66667
250	71.42857
300	75	$K$	0.01	0.01	0.01	0.01	0.01
350	77.77778
400	80
450	81.81818
500	83.33333
550	84.61538
600	85.71429
650	86.66667
700	87.5	$R^{2}$	1	1	1	1	1
750	88.23529
800	88.88889
850	89.47368
900	90
950	90.47619
1000	90.90909

Figure 1. Equilibrium adsorption capacity (qe) versus equilibrium concentration (Ce) for two hypothetical systems (Red circles for a system that completely follows the Langmuir isotherm and Blue circles for a system that does not follow the Langmuir isotherm).

The results from the analysis of this dataset demonstrate that the coefficient of determination of the non-linear Langmuir model is 1. Furthermore, the coefficients of determination for all four linear forms are also 1. These results indicate that all linear and non-linear forms yield consistent Langmuir constants of 0.01 and a maximum adsorption capacity of 100 mg/g. This illustrates that a dataset follows the Langmuir isotherm only if all four linear forms of the Langmuir isotherm simultaneously have a coefficient of determination equal to 1, yielding identical K and

q_{m}

values.

Proposition 2: The accuracy of each of the four linear forms of the Langmuir isotherm is crucial in determining the accuracy of the non-linear Langmuir isotherm form. If all four linear forms lack accuracy, it implies that the non-linear form isn’t similarly accurate. Therefore, the adsorption process is unlikely to adhere to the Langmuir model under such conditions.

Proof: To prove this proposition, a hypothetical data set, as presented in Table 4 and Figure 1, was used.

The results showed that the coefficient of determination (R²) for all four linear forms of the Langmuir isotherm, as well as the R² for its non-linear form, were less than 0.966 for this dataset, indicating that none of these forms were accurate. This suggests that if an adsorption system cannot be accurately described by any of the linear forms of the Langmuir isotherm; it means that the system does not follow the Langmuir isotherm. In other words, the inaccuracy of all four linear forms of the Langmuir isotherm in describing an adsorption system means the inaccuracy of the non-linear Langmuir form and consequently the nonconformity of the system with the Langmuir isotherm. For example, the analysis of adsorption data from systems 61, 63 and 64 shows that the data for Pb(II) and Cd(II) adsorption on amidoxime-functionalized chelating resin (PAO-g-PS) [19], and Cd(II) adsorption on modified lawny grass adsorbent (RG) containing H[BTMPP] (Cyanex272) surfaces [57] are poorly fitted by all four linear Langmuir isotherm forms (Form-1, Form-2, Form-3, and Form-4) with coefficients of determination between 0.4 and 0.985. Analysis of these data using the non-linear Langmuir isotherm also reveals that it lacks accuracy (0.94 < R² < 0.96). This suggests that when all four linear Langmuir forms are simultaneously inaccurate, the non-linear form is also inaccurate. Consequently, it can be concluded that the adsorption process does not follow the Langmuir isotherm. Further investigations indicate that these three systems likely adhere to the Toth isotherm. The results related to the assessment of these three systems using non-linear forms of Langmuir and Toth isotherms are reported in Table 5.

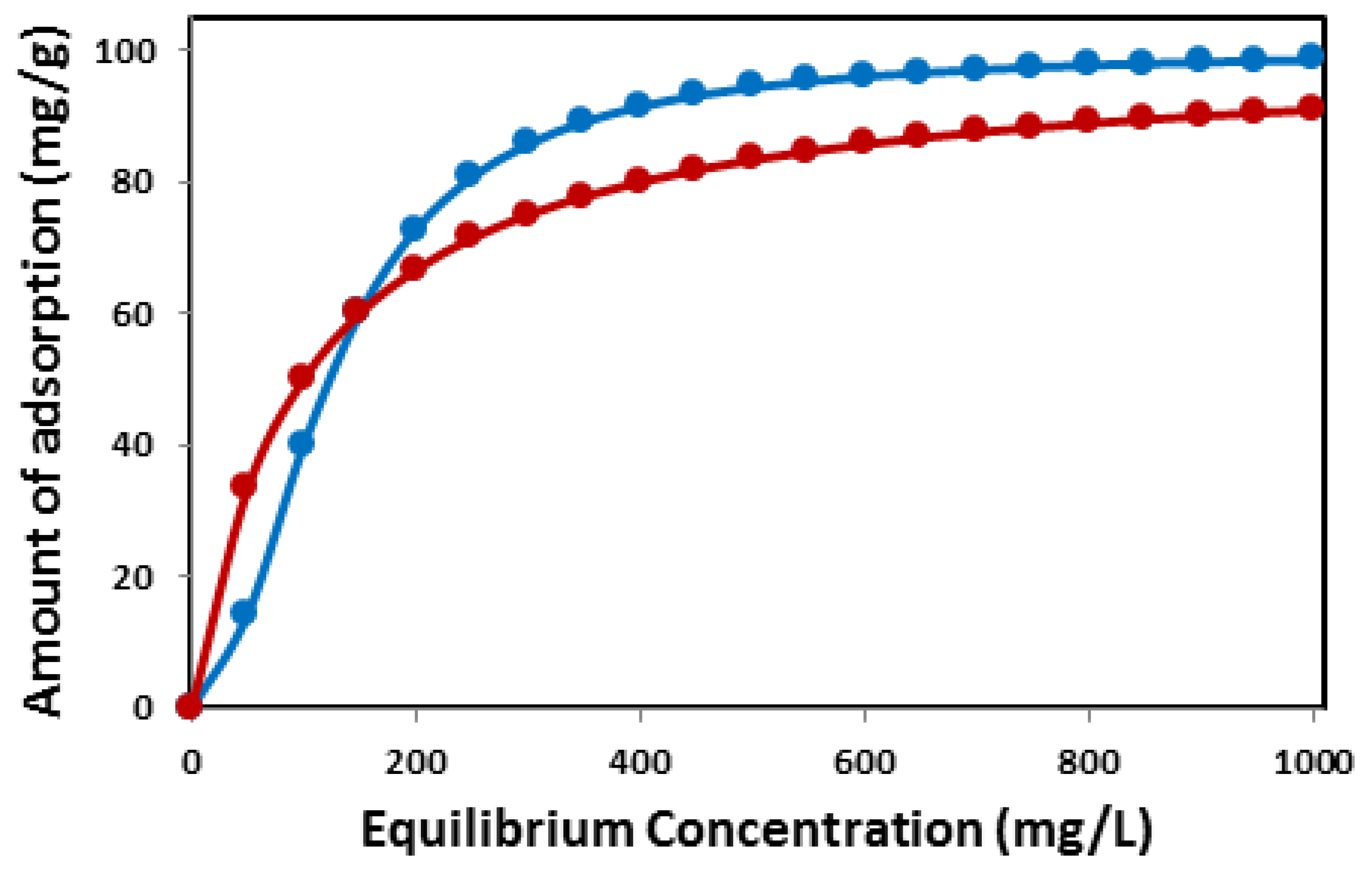
3.2. Can we say that an adsorption system follows the Langmuir isotherm if it is described only by one of the linear forms of the Langmuir isotherm?

One of the significant issues in adsorption research is the tendency to evaluate the adherence of experimental data to the Langmuir isotherm using only one of the linear forms of the Langmuir isotherm. However, this approach is flawed because according to the linear forms of the Langmuir isotherm (Eqs. 2, 3, 4, and 5), it can only be said that an adsorption system follows the Langmuir isotherm if the experimental data simultaneously have the following four characteristics:

1. The plot of

\frac{C_{e}}{q_{e}}

versus

C_{e}

is linear.

2. The plot of

\frac{1}{q_{e}}

versus

\frac{1}{C_{e}}

is linear.

3. The plot of

q_{e}

versus

\frac{q_{e}}{C_{e}}

is linear.

4. The plot of

\frac{q_{e}}{C_{e}}

versus

q_{e}

is linear.

Therefore, if any of these plots is not linear, it means that the adsorption system does not follow the Langmuir isotherm. In other words, merely having one of the linear forms fitting the data accurately doesn't necessarily indicate compliance with the Langmuir isotherm. For example, an analysis of adsorption data, presented in Table 1, from systems 23, 35 and 37, related to the adsorption of Methylene blue by adsorbent maleylated modified hydrochar at temperatures 303, 313, and 323 K [35], reveals that the data for these systems are perfectly fitted by the linear Form-1 of the Langmuir isotherm, with

R^{2} = 1

. However, analyzing the same data using non-linear forms of the Langmuir and Sips isotherms shows that the Sips isotherm is more accurate than the Langmuir isotherm. At temperatures 303, 313, and 323 K, the non-linear Sips isotherm has R² equal to 0.9962, 0.9940, and 0.9938, respectively, while the non-linear Langmuir isotherm has R² equal to 0.9961, 0.9927, and 0.9926, respectively. Similarly, the Rmsd values for the Sips isotherm at 303, 313, and 323 K are 6.7328, 8.6165, and 8.7886, respectively, while the Rmsd values for the Langmuir isotherm are 6.7421, 9.5168, and 9.531, respectively.

Also, based on the R² values for linear and non-linear forms of the Langmuir isotherm reported in Table 1, it can be concluded that systems 65, 66, and 67 do not follow the Langmuir isotherm. Specifically, Form-1 has R² greater than 0.99 for these systems, but R² for linear forms Form-2, Form-3, and Form-4 are less than 0.93, and R² for the non-linear form are 0.9334, 0.9156, and 0.9261, respectively. These results show that although Form-1 has R² close to 1 for these systems, the other linear forms of Langmuir isotherm and its non-linear form fail to describe the adsorption behavior of these systems. These examples prove that relying on only one of the linear forms to judge whether a system follows the Langmuir isotherm or not is not sufficient.

The efficiency of Form-1 was evaluated in comparison with the non-linear Langmuir isotherm for calculating the Langmuir constant and maximum adsorption capacity for systems 23, 35 and 37. The average absolute errors in calculating the Langmuir constant and maximum adsorption capacity by Form-1 at different temperatures were calculated, and the results are shown in Figure 2.

The error values for calculating the maximum adsorption capacity and Langmuir constant have been obtained from the following equations:

E_{q_{m}} (%) = \frac{q_{m}^{n o n - l i n e a r} - q_{m}^{l i n e a r}}{q_{m}^{n o n - l i n e a r}} \times 100

(6)

E_{K_{L}} (%) = \frac{K_{L}^{n o n - l i n e a r} - K_{L}^{l i n e a r}}{K_{L}^{n o n - l i n e a r}} \times 100

(7)

The average absolute error (AAE) values for calculating the maximum adsorption capacity and Langmuir constant can be obtained from the following equation:

{A A E}_{q_{m}} (%) = \frac{1}{n} \sum_{i = 1}^{n} |\frac{q_{m, i}^{n o n - l i n e a r} - q_{m, i}^{l i n e a r}}{q_{m, i}^{n o n - l i n e a r}} \times 100|

(8)

{A A E}_{K_{L}} (%) = \frac{1}{n} \sum_{i = 1}^{n} |\frac{K_{L, i}^{n o n - l i n e a r} - K_{L, i}^{l i n e a r}}{K_{L, i}^{n o n - l i n e a r}} \times 100|

(9)

Note that the error and average absolute error values have been calculated by comparing the

K_{L}

and

q_{m}

values obtained using linear forms of the Langmuir isotherm with the values obtained for these parameters using the non-linear Langmuir isotherm. This is because our goal is to compare the efficiency and accuracy of linear forms of the Langmuir isotherm with the non-linear form. Therefore, the larger the values of these errors, the more they indicate the inconsistency of the output of the linear forms with the output of the non-linear form of Langmuir isotherm. As shown in Figure 2, Form-1 creates significant average absolute error in calculating the Langmuir constant, while it works somewhat more accurately in calculating the maximum adsorption capacity. These large average absolute errors indicate the inefficiency of Form-1 in comparison with the non-linear Langmuir isotherm for calculating the Langmuir constant. In other words, a coefficient of determination equal to 1 for Form-1 does not indicate a perfect match between the output of this linear form and the output of the non-linear Langmuir isotherm. Therefore, having a coefficient of determination equal to 1 for Form-1 does not necessarily mean that the studied adsorption system follows the Langmuir isotherm, nor does it mean that the Langmuir constant and maximum adsorption capacity calculated using the desired linear form are accurate. In summary, even though the linear form, Form-1, boasts a coefficient of determination equal to 1 for systems 23, 35 and 37, it doesn't necessarily imply data adherence to the Langmuir isotherm. These results emphasize the importance of not relying solely on a single linear form when assessing adherence to the Langmuir isotherm.

An analysis of adsorption data from systems 54 and 46, which correspond to the adsorption of substances Reactive Red 120 and Congo red using adsorbents Hybrid crosslinked chitosan-epichlorohydrin/TiO₂ nanocomposite (CTS-ECH/TNC) [51] and hybrid alginate/natural bentonite [46], respectively, shows that the data for these systems are poorly fitted by linear Form-3 (with R² equal to 0.8485 and 0.7833 respectively) and Form-4 (with R² equal to 0.8485 and 0.7833, respectively). However, these data are accurately fitted by linear Form-1 (with R² equal to 0.9979 and 0.9938, respectively) and Form-2 (with R² equal to 0.9972 and 0.9916, respectively) of the Langmuir isotherm. Further analysis of these data using the non-linear Langmuir isotherm reveals that this equation lacks accuracy (with R² equal to 0.9795 and 0.9892, respectively). These results demonstrate that when at least one of the four linear forms exhibits inaccurate, the non-linear Langmuir isotherm is also inaccurate. In this scenario, it can be concluded that the adsorption process does not follow the Langmuir isotherm. Additional investigations suggest that these two systems (systems 54 and 46) likely adhere to the Sips isotherm (R²=0.9968) and Toth isotherm (R²=0.9981), respectively.

3.3. Statistical study

3.3.1. Accuracy relationship between linear and non-linear forms of the Langmuir isotherm

So far in this study, three rules have been briefly presented regarding the accuracy of the linear forms of the Langmuir isotherm. The summary of these rules is as follows:

Rule1: The higher the accuracy of all linear forms of the Langmuir isotherm in studying a system's adsorption, the more accurate the non-linear form will be. When all four linear forms of the Langmuir isotherm exhibit high accuracy, it indicates that the process likely follows the Langmuir isotherm.

Rule2: Conversely, if the accuracy of the linear forms of the Langmuir isotherm in studying a system's adsorption is lower, the non-linear form will also be less accurate. In other words, when all four linear forms are less accurate, it implies that the non-linear form is also less accurate, leading to the conclusion that the process definitely does not follow the Langmuir isotherm.

Rule3: If at least one of the four linear forms lacks accuracy, it indicates that the non-linear form is similarly inaccurate. Consequently, it can be concluded that the adsorption process does not follow the Langmuir isotherm.

To evaluate these rules, 67 sets of experimental data related to the adsorption of various substances using different adsorbents were selected. The accuracy of all four linear forms of the Langmuir isotherm (Form-1, Form-2, Form-3, and Form-4) as well as the non-linear form was assessed for these datasets. R² values were obtained for the linear and non-linear forms (see table 1) and the results for all the datasets were ranked based on the decrease in R² values of the non-linear form.

To establish a statistical relationship between the R² values of the non-linear form and the R² values of the linear forms, these values for all linear and non-linear forms were plotted against the dataset number. The results are shown in Figure 3.

Based on Figure 3, the closer the R² values of the non-linear Langmuir form is to 1, the closer the R² values of all four linear forms are to 1. These results demonstrate that the more accurate the non-linear Langmuir form, the more accurate the linear forms will be simultaneously. Also, if the R² values for Form-1 and non-linear form are plotted against the dataset number, an interesting result is obtained. As shown in Figure 4, in most datasets where the R² values for the non-linear form is less than 0.99 and therefore the non-linear form is inaccurate, the R² values for the Form-1 is close to 1. This indicates that an adsorption system may fit well with the Form-1 but not follow the Langmuir isotherm. In other words, the accuracy of Form-1 does not always indicate the adherence of the adsorption system to the Langmuir isotherm.

Therefore, the simultaneous accuracy of all linear forms of the Langmuir isotherm is what leads to a correct judgment about the adherence or non-adherence of an adsorption system to the Langmuir isotherm. In this case, according to Figure 3, the non-linear Langmuir form is also accurate.

Figure 5 and Figure 6 plot the error in calculating the maximum adsorption capacity (

q_{m}

) and the Langmuir constant (K) using linear forms of the Langmuir isotherm (Form-1, Form-2, Form-3, and Form-4) against the dataset number (The datasets are sorted from the most accurate non-linear form to the least accurate one).

The figures 5 and 6 show that as we move towards more accurate non-linear forms, the error in calculating

q_{m}

and K using linear forms decreases, and conversely, as we move towards less accurate non-linear forms, the error increases. By comparing Figure 3, Figure 4, Figure 5 and Figure 6, it can be concluded that the accuracy of the non-linear Langmuir isotherm is directly related to the simultaneous accuracy of the linear forms. The more accurately an adsorption system follows the non-linear Langmuir model, the more accurate the linear forms will be simultaneously, and the error of these forms in calculating the Langmuir constant and maximum adsorption value will be less. Therefore, this study suggests that for accurate modeling of an adsorption system using the Langmuir isotherm, either the non-linear Langmuir isotherm form should be used or if linear forms are used, all four linear Langmuir forms should be evaluated simultaneously. In other words, relying on only one of these linear forms to judge the conformity or non-conformity of the studied adsorption system with the Langmuir isotherm is not sufficient.

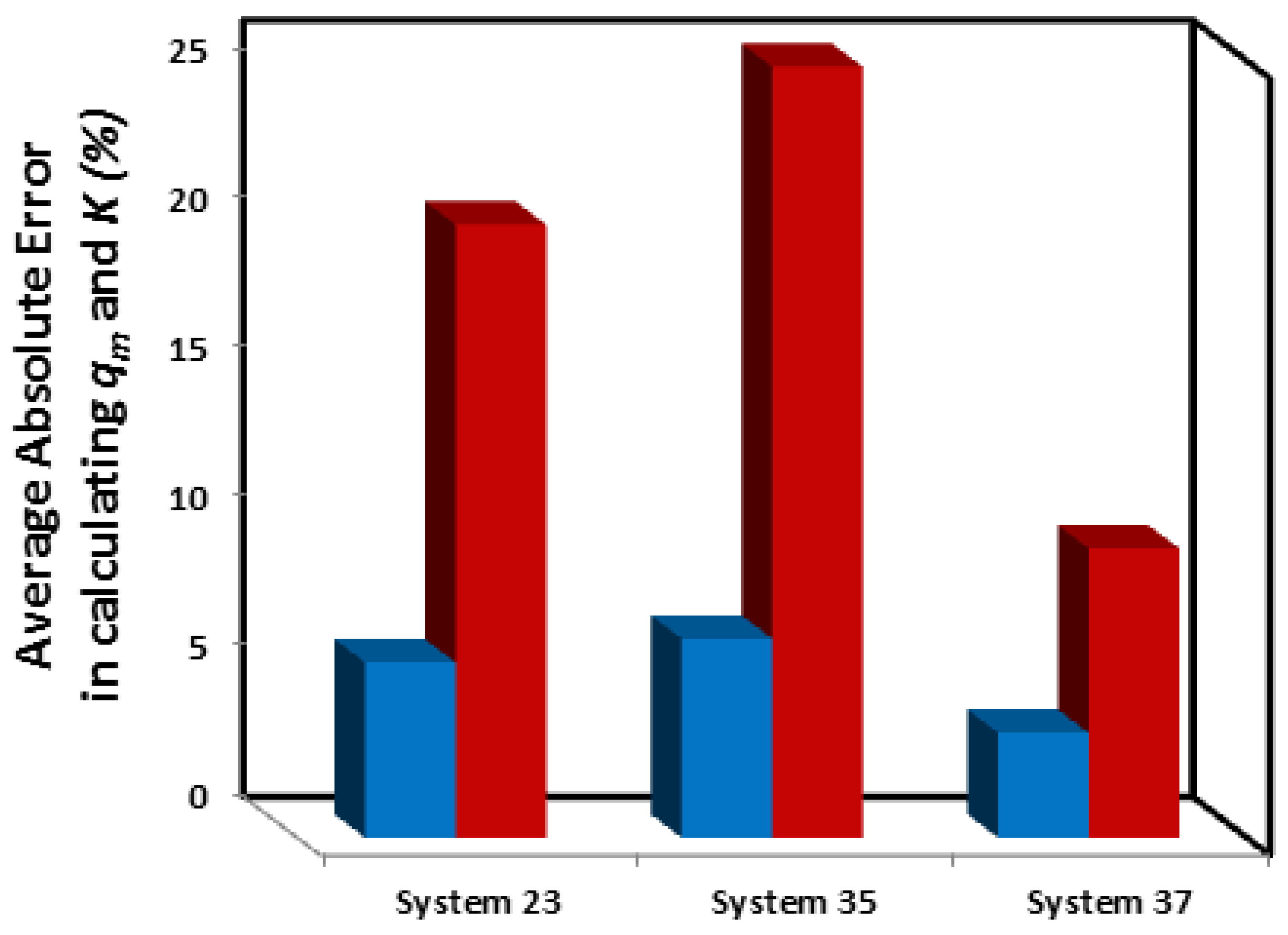
3.3.2. Which linear forms create the least error in calculating $q_{m}$ and K?

Figure 7 compares the Average Absolute Errors of the four linear forms of the Langmuir isotherm in calculating

q_{m}

and K.

These data related to six of the adsorption systems for which the coefficients of determination of all four linear forms and the non-linear form exceed 0.99 (systems 1, 2, 5, 6, 7 and 9). In other words, among the 67 studied adsorption systems, six systems had linear and non-linear Langmuir isotherm forms with R² > 0.99. Based on Figure 7, the accuracy of all four linear forms of the Langmuir isotherm in calculating

q_{m}

follows the order Form-1 > Form-3 > Form-4 > Form-2, while the accuracy of these forms in calculating K follows the order Form-4 > Form-3 > Form-2 > Form-1. In other words, the most accurate linear form for calculating

q_{m}

is Form-1, and the most accurate linear form for calculating K is Form-4.

4. Conclusion

In this study, the efficiency and accuracy of all four linear forms of the Langmuir isotherm and its non-linear form were evaluated using several experimental data sets selected from the literature. To accurately model an adsorption system using the Langmuir isotherm, this study suggests that either the non-linear Langmuir isotherm form should be used or all four linear forms should be evaluated simultaneously. Therefore, the results of this study showed that relying on only one of the four linear forms of the Langmuir isotherm to model adsorption is an incomplete approach.

Also, based on obtained results, the accuracy of all linear forms of the Langmuir isotherm in calculating

q_{m}

follows the order Form-1 (

\frac{C_{e}}{q_{e}}

C_{e}

) > Form-3 (

q_{e}

\frac{q_{e}}{C_{e}}

) > Form-4 (

\frac{q_{e}}{C_{e}}

q_{e}

) > Form-2 (

\frac{1}{q_{e}}

\frac{1}{C_{e}}

), while the accuracy of these forms in calculating K follows the order Form-4 > Form-3 > Form-2 > Form-1. The study provides a comprehensive evaluation of the Langmuir isotherm and its linear forms, which can help to improve the understanding of adsorption processes. The findings of this study can be useful for researchers who work with adsorption equilibrium data and need to determine whether the Langmuir isotherm is an appropriate model for their system. The results of this research can also help researchers to choose the most accurate linear form for calculating

q_{m}

and K.

References

Karthik, V.; Karuna, B.; Jeyanthi, J.; Periyasamy, S. Biochar production from Manilkara zapota seeds, activation and characterization for effective removal of Cu2+ ions in polluted drinking water. Biomass Convers. Biorefinery 2023, 13, 9381–9395. [Google Scholar] [CrossRef]
Chen, X.; Cheng, Y.; Pan, Q.; Wu, L.; Hao, X.; Bao, Z.; Li, X.; Yang, M.; Luo, Q.; Li, H. Chiral Nanosilica Drug Delivery Systems Stereoselectively Interacted with the Intestinal Mucosa to Improve the Oral Adsorption of Insoluble Drugs. ACS Nano 2023, 17, 3705–3722. [Google Scholar] [CrossRef]
Chen, G.; Liu, G.; Pan, Y.; Liu, G.; Gu, X.; Jin, W.; Xu, N. Zeolites and metal–organic frameworks for gas separation: the possibility of translating adsorbents into membranes. Chemical Society Reviews 2023. [Google Scholar] [CrossRef]
Wang, Y.; Othman, R. Natural gas storage by adsorption. In Surface Process, Transportation, and Storage, Elsevier: Amsterdam, The Netherlands, 2023; pp. 261–297.
Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
Bolster, C.H.; Hornberger, G.M. On the use of linearized Langmuir equations. Soil Sci. Soc. Am. J. 2007, 71, 1796–1806. [Google Scholar] [CrossRef]
Hu, Q.; Lan, R.; He, L.; Liu, H.; Pei, X. A critical review of adsorption isotherm models for aqueous contaminants: Curve characteristics, site energy distribution and common controversies. J. Environ. Manag. 2023, 329, 117104. [Google Scholar] [CrossRef]
Kumar, K.V.; Sivanesan, S. Comparison of linear and non-linear method in estimating the sorption isotherm parameters for safranin onto activated carbon. J. Hazard. Mater. 2005, 123, 288–292. [Google Scholar] [CrossRef]
Kumar, K.V.; Sivanesan, S. Prediction of optimum sorption isotherm: Comparison of linear and non-linear method. J. Hazard. Mater. 2005, 126, 198–201. [Google Scholar] [CrossRef]
Ncibi, M.C. Applicability of some statistical tools to predict optimum adsorption isotherm after linear and non-linear regression analysis. J. Hazard. Mater. 2008, 153, 207–212. [Google Scholar] [CrossRef]
Jasper, E.E.; Ajibola, V.O.; Onwuka, J.C. Nonlinear regression analysis of the sorption of crystal violet and methylene blue from aqueous solutions onto an agro-waste derived activated carbon. Appl. Water Sci. 2020, 10, 1–11. [Google Scholar] [CrossRef]
Schulthess, C.; Dey, D. Estimation of Langmuir constants using linear and nonlinear. Soil Sci. Soc. Am. J. 1996, 60, 433–442. [Google Scholar] [CrossRef]
Harter, R.D. Curve-fit errors in Langmuir adsorption maxima. Soil Sci. Soc. Am. J. 1984, 48, 749–752. [Google Scholar] [CrossRef]
Tsai, S.-C.; Juang, K.-W. Comparison of linear and nonlinear forms of isotherm models for strontium sorption on a sodium bentonite. J. Radioanal. Nucl. Chem. 2000, 243, 741–746. [Google Scholar] [CrossRef]
Parimal, S.; Prasad, M.; Bhaskar, U. Prediction of equillibrium sorption isotherm: comparison of linear and nonlinear methods. Ind. Eng. Chem. Res. 2010, 49, 2882–2888. [Google Scholar] [CrossRef]
López-Luna, J.; Ramírez-Montes, L.E.; Martinez-Vargas, S.; Martínez, A.I.; Mijangos-Ricardez, O.F.; González-Chávez, M.d.C.A.; Carrillo-González, R.; Solís-Domínguez, F.A.; Cuevas-Díaz, M.d.C.; Vázquez-Hipólito, V. Linear and nonlinear kinetic and isotherm adsorption models for arsenic removal by manganese ferrite nanoparticles. SN Appl. Sci. 2019, 1, 1–19. [Google Scholar] [CrossRef]
Chen, X. Modeling of experimental adsorption isotherm data. information 2015, 6, 14–22. [Google Scholar] [CrossRef]
Bai, C.; Wang, L.; Zhu, Z. Adsorption of Cr (III) and Pb (II) by graphene oxide/alginate hydrogel membrane: Characterization, adsorption kinetics, isotherm and thermodynamics studies. Int. J. Biol. Macromol. 2020, 147, 898–910. [Google Scholar] [CrossRef]
Chen, Y.; Zhao, H.; Li, Y.; Zhao, W.; Yang, X.; Meng, X.; Wang, H. Two-step preparation of an amidoxime-functionalized chelating resin for removal of heavy metal ions from aqueous solution. J. Chem. Eng. Data 2019, 64, 4037–4045. [Google Scholar] [CrossRef]
Darwish, A.; Rashad, M.; AL-Aoh, H.A. Methyl orange adsorption comparison on nanoparticles: Isotherm, kinetics, and thermodynamic studies. Dye. Pigment. 2019, 160, 563–571. [Google Scholar] [CrossRef]
Yao, X.; Ji, L.; Guo, J.; Ge, S.; Lu, W.; Cai, L.; Wang, Y.; Song, W.; Zhang, H. Magnetic activated biochar nanocomposites derived from wakame and its application in methylene blue adsorption. Bioresour. Technol. 2020, 302, 122842. [Google Scholar]
Tapan Kumar, S. Adsorption of methyl orange onto chitosan from aqueous solution. J. Water Resour. Prot. 2010, 2, 2969. [Google Scholar]
Ahmed, W.; Mehmood, S.; Núñez-Delgado, A.; Ali, S.; Qaswar, M.; Shakoor, A.; Mahmood, M.; Chen, D.-Y. Enhanced adsorption of aqueous Pb(II) by modified biochar produced through pyrolysis of watermelon seeds. Sci. Total. Environ. 2021, 784, 147136. [Google Scholar] [CrossRef]
Sajjadi, S.-A.; Meknati, A.; Lima, E.C.; Dotto, G.L.; Mendoza-Castillo, D.I.; Anastopoulos, I.; Alakhras, F.; Unuabonah, E.I.; Singh, P.; Hosseini-Bandegharaei, A. A novel route for preparation of chemically activated carbon from pistachio wood for highly efficient Pb(II) sorption. J. Environ. Manag. 2019, 236, 34–44. [Google Scholar] [CrossRef]
Liu, X.; Zhang, L. Removal of phosphate anions using the modified chitosan beads: Adsorption kinetic, isotherm and mechanism studies. Powder Technol. 2015, 277, 112–119. [Google Scholar] [CrossRef]
Imanipoor, J.; Mohammadi, M.; Dinari, M.; Ehsani, M.R. Adsorption and Desorption of Amoxicillin Antibiotic from Water Matrices Using an Effective and Recyclable MIL-53(Al) Metal–Organic Framework Adsorbent. J. Chem. Eng. Data 2020, 66, 389–403. [Google Scholar] [CrossRef]
Wang, W.; Maimaiti, A.; Shi, H.; Wu, R.; Wang, R.; Li, Z.; Qi, D.; Yu, G.; Deng, S. Adsorption behavior and mechanism of emerging perfluoro-2-propoxypropanoic acid (GenX) on activated carbons and resins. Chem. Eng. J. 2019, 364, 132–138. [Google Scholar] [CrossRef]
Wei, J.; Liu, Y.; Li, J.; Zhu, Y.; Yu, H.; Peng, Y. Adsorption and co-adsorption of tetracycline and doxycycline by one-step synthesized iron loaded sludge biochar. Chemosphere 2019, 236, 124254. [Google Scholar] [CrossRef]
Rashtbari, Y.; Hazrati, S.; Azari, A.; Afshin, S.; Fazlzadeh, M.; Vosoughi, M. A novel, eco-friendly and green synthesis of PPAC-ZnO and PPAC-nZVI nanocomposite using pomegranate peel: Cephalexin adsorption experiments, mechanisms, isotherms and kinetics. Adv. Powder Technol. 2020, 31, 1612–1623. [Google Scholar] [CrossRef]
Lv, S.-W.; Liu, J.-M.; Ma, H.; Wang, Z.-H.; Li, C.-Y.; Zhao, N.; Wang, S. Simultaneous adsorption of methyl orange and methylene blue from aqueous solution using amino functionalized Zr-based MOFs. Microporous Mesoporous Mater. 2019, 282, 179–187. [Google Scholar] [CrossRef]
Zheng, Y.; Cheng, B.; You, W.; Yu, J.; Ho, W. 3D hierarchical graphene oxide-NiFe LDH composite with enhanced adsorption affinity to Congo red, methyl orange and Cr (VI) ions. J. Hazard. Mater. 2019, 369, 214–225. [Google Scholar] [CrossRef]
Chang, Y.S.; Au, P.I.; Mubarak, N.M.; Khalid, M.; Jagadish, P.; Walvekar, R.; Abdullah, E.C. Adsorption of Cu(II) and Ni(II) ions from wastewater onto bentonite and bentonite/GO composite. Environ. Sci. Pollut. Res. 2020, 27, 33270–33296. [Google Scholar] [CrossRef]
Ahmed, M.; Okoye, P.; Hummadi, E.; Hameed, B. High-performance porous biochar from the pyrolysis of natural and renewable seaweed (Gelidiella acerosa) and its application for the adsorption of methylene blue. Bioresour. Technol. 2019, 278, 159–164. [Google Scholar] [CrossRef]
Asuquo, E.; Martin, A.; Nzerem, P.; Siperstein, F.; Fan, X. Adsorption of Cd (II) and Pb (II) ions from aqueous solutions using mesoporous activated carbon adsorbent: Equilibrium, kinetics and characterisation studies. J. Environ. Chem. Eng. 2017, 5, 679–698. [Google Scholar] [CrossRef]
Li, B.; Guo, J.; Lv, K.; Fan, J. Adsorption of methylene blue and Cd(II) onto maleylated modified hydrochar from water. Environ. Pollut. 2019, 254, 113014. [Google Scholar] [CrossRef]
Ahmed, M.; Islam, A.; Asif, M.; Hameed, B. Human hair-derived high surface area porous carbon material for the adsorption isotherm and kinetics of tetracycline antibiotics. Bioresour. Technol. 2017, 243, 778–784. [Google Scholar] [CrossRef]
Albadarin, A.B.; Collins, M.N.; Naushad, M.; Shirazian, S.; Walker, G.; Mangwandi, C. Activated lignin-chitosan extruded blends for efficient adsorption of methylene blue. Chem. Eng. J. 2017, 307, 264–272. [Google Scholar] [CrossRef]
Alizadeh, A.; Abdi, G.; Khodaei, M.M.; Ashokkumar, M.; Amirian, J. Graphene oxide/Fe₃O₄/SO₃H nanohybrid: A new adsorbent for adsorption and reduction of Cr (vi) from aqueous solutions. RSC Adv. 2017, 7, 14876–14887. [Google Scholar] [CrossRef]
Ghasemi, S.S.; Hadavifar, M.; Maleki, B.; Mohammadnia, E. Adsorption of mercury ions from synthetic aqueous solution using polydopamine decorated SWCNTs. J. Water Process. Eng. 2019, 32, 100965. [Google Scholar] [CrossRef]
Gao, Y.; Deng, S.-Q.; Jin, X.; Cai, S.-L.; Zheng, S.-R.; Zhang, W.-G. The construction of amorphous metal-organic cage-based solid for rapid dye adsorption and time-dependent dye separation from water. Chem. Eng. J. 2018, 357, 129–139. [Google Scholar] [CrossRef]
Pishnamazi, M.; Khan, A.; Kurniawan, T.A.; Sanaeepur, H.; Albadarin, A.B.; Soltani, R. Adsorption of dyes on multifunctionalized nano-silica KCC-1. J. Mol. Liq. 2021, 338, 116573. [Google Scholar] [CrossRef]
Jia, Y.; Zhang, Y.; Fu, J.; Yuan, L.; Li, Z.; Liu, C.; et al. A novel magnetic biochar/MgFe-layered double hydroxides composite removing Pb2+ from aqueous solution: Isotherms, kinetics and thermodynamics. Colloids Surf. A 2019, 567, 278–287. [Google Scholar] [CrossRef]
Li, X.; Wang, S.; Liu, Y.; Jiang, L.; Song, B.; Li, M.; et al. Adsorption of Cu (II), Pb (II), and Cd (II) ions from acidic aqueous solutions by diethylenetriaminepentaacetic acid-modified magnetic graphene oxide. J. Chem. Eng. Data 2017, 62, 407–416. [Google Scholar] [CrossRef]
Foroutan, R.; Peighambardoust, S.J.; Peighambardoust, S.H.; Pateiro, M.; Lorenzo, J.M. Adsorption of crystal violet dye using activated carbon of lemon wood and activated carbon/Fe3O4 magnetic nanocomposite from aqueous solutions: a kinetic, equilibrium and thermodynamic study. Molecules 2021, 26, 2241. [Google Scholar] [CrossRef]
Radi, S.; Tighadouini, S.; El Massaoudi, M.; Bacquet, M.; Degoutin, S.; Revel, B.; Mabkhot, Y.N. Thermodynamics and Kinetics of Heavy Metals Adsorption on Silica Particles Chemically Modified by Conjugated β-Ketoenol Furan. J. Chem. Eng. Data 2015, 60, 2915–2925. [Google Scholar] [CrossRef]
Oussalah, A.; Boukerroui, A.; Aichour, A.; Djellouli, B. Cationic and anionic dyes removal by low-cost hybrid alginate/natural bentonite composite beads: Adsorption and reusability studies. Int. J. Biol. Macromol. 2018, 124, 854–862. [Google Scholar] [CrossRef]
Vijayaraghavan, K.; Ashokkumar, T. Characterization and evaluation of reactive dye adsorption onto Biochar Derived from Turbinaria conoides Biomass. Environ. Prog. Sustain. Energy 2019, 38. [Google Scholar] [CrossRef]
Pei, Y.; Jiang, Z.; Yuan, L. Facile synthesis of MCM-41/MgO for highly efficient adsorption of organic dye. Colloids Surf. A 2019, 581, 123816. [Google Scholar] [CrossRef]
Tong, D.S.; Wu, C.W.; Adebajo, M.O.; Jin, G.C.; Yu, W.H.; Ji, S.F.; Zhou, C.H. Adsorption of methylene blue from aqueous solution onto porous cellulose-derived carbon/montmorillonite nanocomposites. Appl. Clay Sci. 2018, 161, 256–264. [Google Scholar] [CrossRef]
Nguyen, D.T.; Tran, H.N.; Juang, R.-S.; Dat, N.D.; Tomul, F.; Ivanets, A.; Woo, S.H.; Hosseini-Bandegharaei, A.; Nguyen, V.P.; Chao, H.-P. Adsorption process and mechanism of acetaminophen onto commercial activated carbon. J. Environ. Chem. Eng. 2020, 8, 104408. [Google Scholar] [CrossRef]
Jawad, A.H.; Mubarak, N.S.A.; Abdulhameed, A.S. Hybrid crosslinked chitosan-epichlorohydrin/TiO 2 nanocomposite for reactive red 120 dye adsorption: kinetic, isotherm, thermodynamic, and mechanism study. J. Polym. Environ. 2020, 28, 624–637. [Google Scholar] [CrossRef]
Guo, S.; Huang, L.; Li, W.; Wang, Q.; Wang, W.; Yang, Y. Willow tree-like functional groups modified magnetic nanoparticles for ultra-high capacity adsorption of dye. J. Taiwan Inst. Chem. Eng. 2019, 101, 99–104. [Google Scholar] [CrossRef]
Meili, L.; Lins, P.; Costa, M.; Almeida, R.; Abud, A.; Soletti, J.; Dotto, G.; Tanabe, E.; Sellaoui, L.; Carvalho, S.; et al. Adsorption of methylene blue on agroindustrial wastes: Experimental investigation and phenomenological modelling. Prog. Biophys. Mol. Biol. 2018, 141, 60–71. [Google Scholar] [CrossRef] [PubMed]
Wu, M.; Zhao, S.; Jing, R.; Shao, Y.; Liu, X.; Lv, F.; Hu, X.; Zhang, Q.; Meng, Z.; Liu, A. Competitive adsorption of antibiotic tetracycline and ciprofloxacin on montmorillonite. Appl. Clay Sci. 2019, 180, 105175. [Google Scholar] [CrossRef]
Wang, N.; Chen, J.; Wang, J.; Feng, J.; Yan, W. Removal of methylene blue by Polyaniline/TiO2 hydrate: Adsorption kinetic, isotherm and mechanism studies. Powder Technol. 2019, 347, 93–102. [Google Scholar] [CrossRef]
Marrakchi, F.; Khanday, W.; Asif, M.; Hameed, B. Cross-linked chitosan/sepiolite composite for the adsorption of methylene blue and reactive orange 16. Int. J. Biol. Macromol. 2016, 93, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
Chen, L.; Lü, L.; Shao, W.; Luo, F. Kinetics and Equilibria of Cd(II) Adsorption onto a Chemically Modified Lawny Grass with H[BTMPP]. J. Chem. Eng. Data 2011, 56, 1059–1068. [Google Scholar] [CrossRef]
Anirudhan, T.S.; Jalajamony, S.; Sreekumari, S.S. Adsorptive Removal of Cu(II) Ions from Aqueous Media onto 4-Ethyl Thiosemicarbazide Intercalated Organophilic Calcined Hydrotalcite. J. Chem. Eng. Data 2012, 58, 24–31. [Google Scholar] [CrossRef]
Yan, M.; Huang, W.; Li, Z. Chitosan cross-linked graphene oxide/lignosulfonate composite aerogel for enhanced adsorption of methylene blue in water. Int. J. Biol. Macromol. 2019, 136, 927–935. [Google Scholar] [CrossRef]
Boudechiche, N.; Fares, M.; Ouyahia, S.; Yazid, H.; Trari, M.; Sadaoui, Z. Comparative study on removal of two basic dyes in aqueous medium by adsorption using activated carbon from Ziziphus lotus stones. Microchem. J. 2019, 146, 1010–1018. [Google Scholar] [CrossRef]

Figure 2. The Average Absolute Error in calculating the maximum adsorption capacity (

q_{m}

) and Langmuir constant (

K

) using the Form-1 for systems 23, 35 and 37 (Blue column for Average Absolute Error in calculating qm and Red column for Average Absolute Error in calculating K).

Figure 2. The Average Absolute Error in calculating the maximum adsorption capacity (

q_{m}

) and Langmuir constant (

K

) using the Form-1 for systems 23, 35 and 37 (Blue column for Average Absolute Error in calculating qm and Red column for Average Absolute Error in calculating K).

Figure 3. The statistical relationship between the coefficients of determination of the non-linear form and the coefficients of determination of the linear forms of the Langmuir isotherm against the dataset number (Purple circle for non-linear form, Yellow circle for Form-1, Red circle for Form-2, Blue circle for Form-3, and Green circle for Form-4).

Figure 4. The coefficients of determination of the non-linear form and Form-1 against the dataset number (Purple circle for non-linear form, Yellow circle for Form-1).

Figure 5. The plot of the error in calculating the maximum adsorption capacity (

q_{m}

) using linear Langmuir forms (Yellow circle for Form-1, Red circle for Form-2, Blue circle for Form-3, and Green circle for Form-4) against the dataset number.

Figure 5. The plot of the error in calculating the maximum adsorption capacity (

q_{m}

) using linear Langmuir forms (Yellow circle for Form-1, Red circle for Form-2, Blue circle for Form-3, and Green circle for Form-4) against the dataset number.

Figure 6. The plot of the error in calculating the Langmuir constant (K) using linear Langmuir forms (Yellow circle for Form-1, Red circle for Form-2, Blue circle for Form-3, and Green circle for Form-4) against the dataset number.

Figure 7. Comparison of the accuracy of linear forms of the Langmuir isotherm, Form-1, Form-2, Form-3, and Form-4, in calculating Langmuir isotherm parameters,

K

and

q_{m}

, based on systems 1, 2, 5, 6, 7 and 9 (Blue column for Average Absolute Error in calculating q_m and Red column for Average Absolute Error in calculating K).

Figure 7. Comparison of the accuracy of linear forms of the Langmuir isotherm, Form-1, Form-2, Form-3, and Form-4, in calculating Langmuir isotherm parameters,

K

and

q_{m}

, based on systems 1, 2, 5, 6, 7 and 9 (Blue column for Average Absolute Error in calculating q_m and Red column for Average Absolute Error in calculating K).

Table 1. The characteristics of the adsorption systems used in this study, along with the coefficients of determination of the linear and non-linear forms of the Langmuir isotherm.

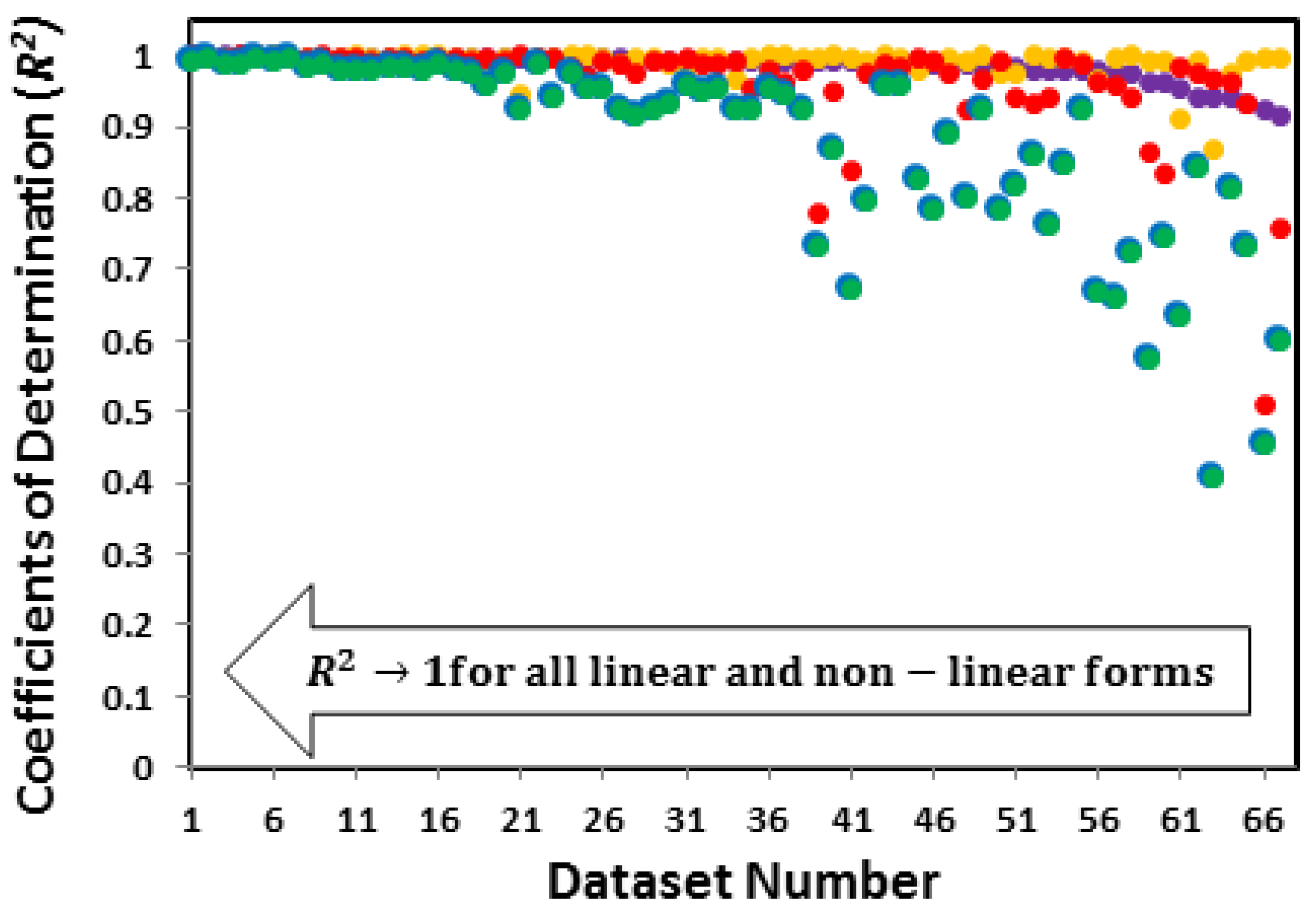
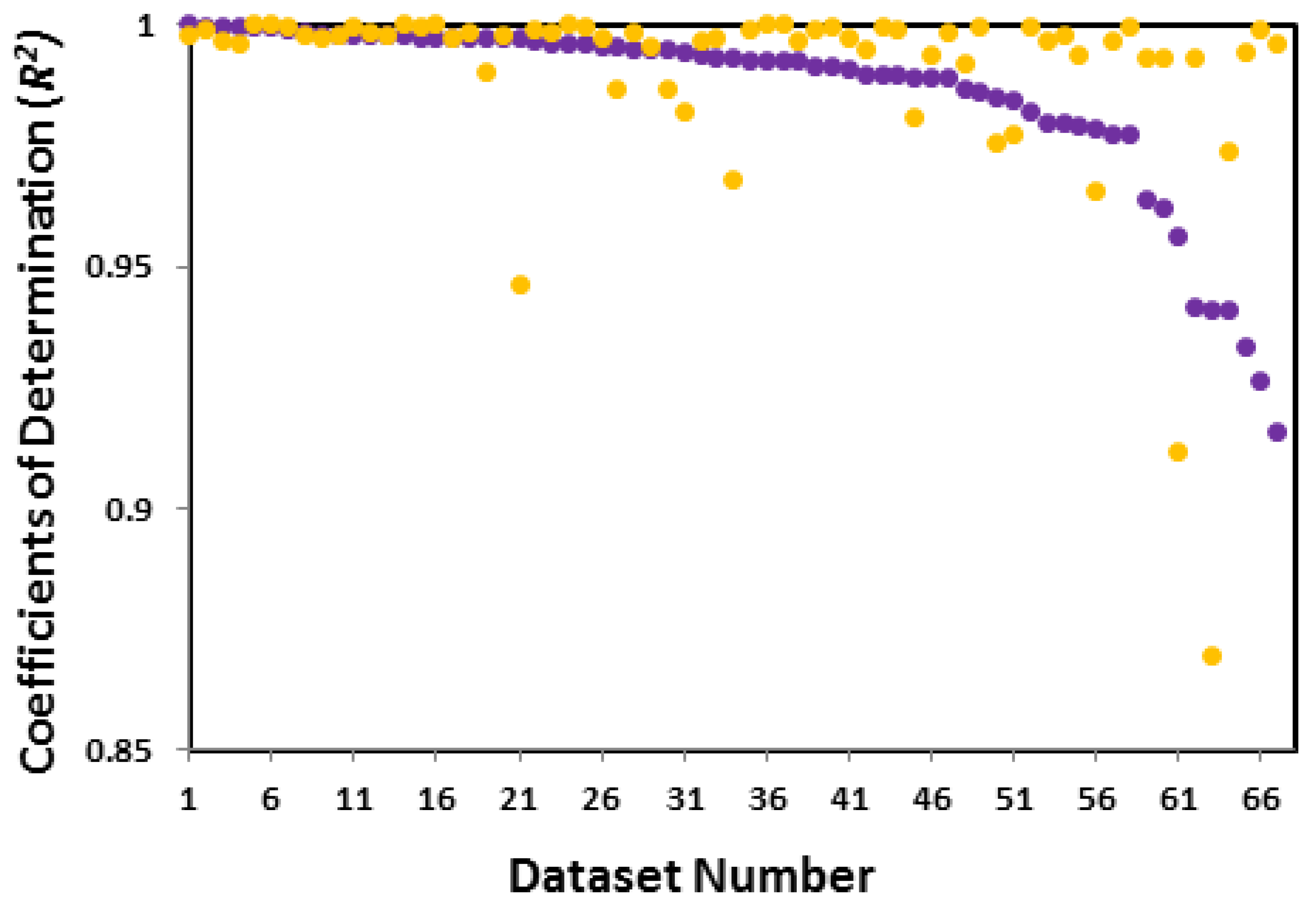
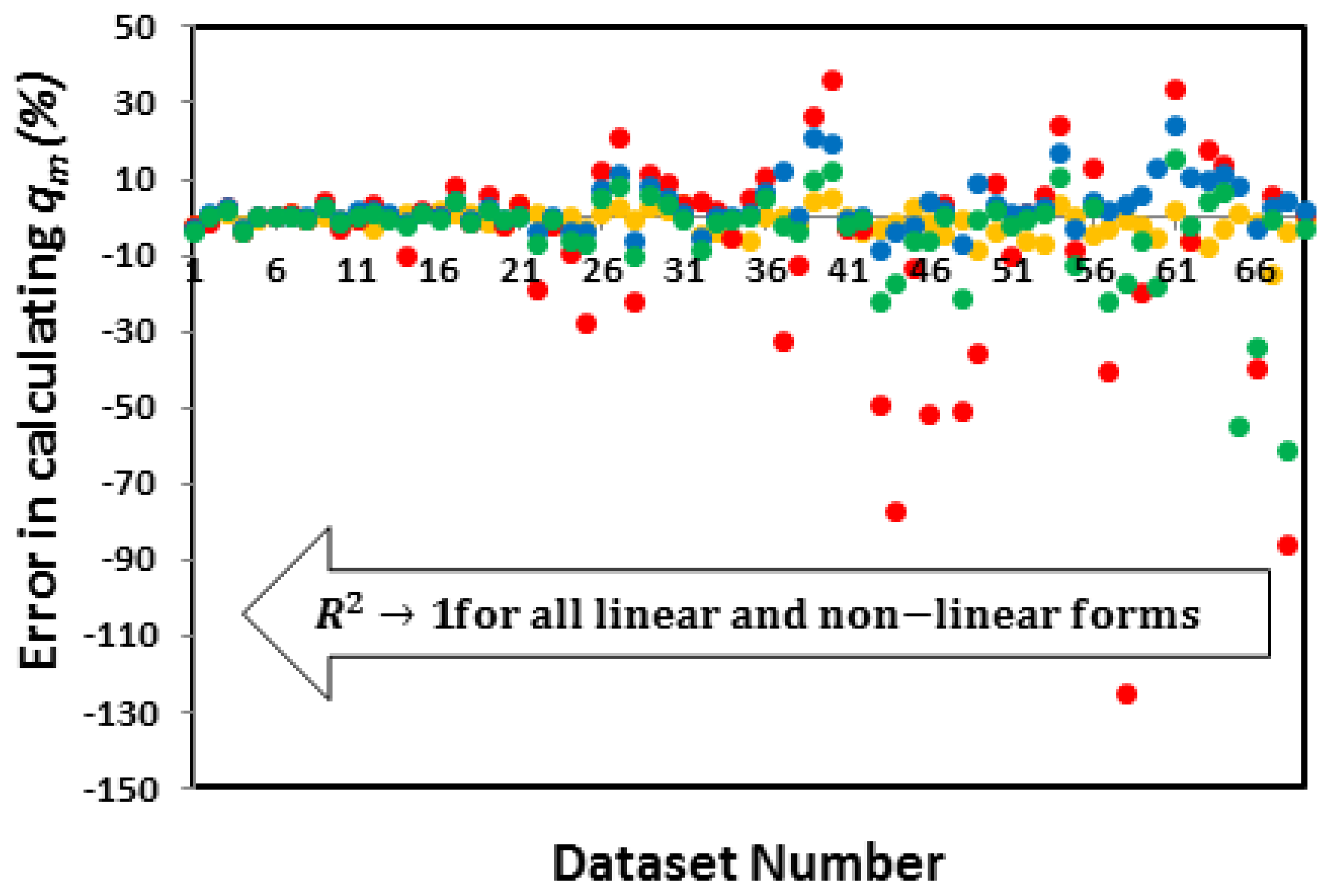
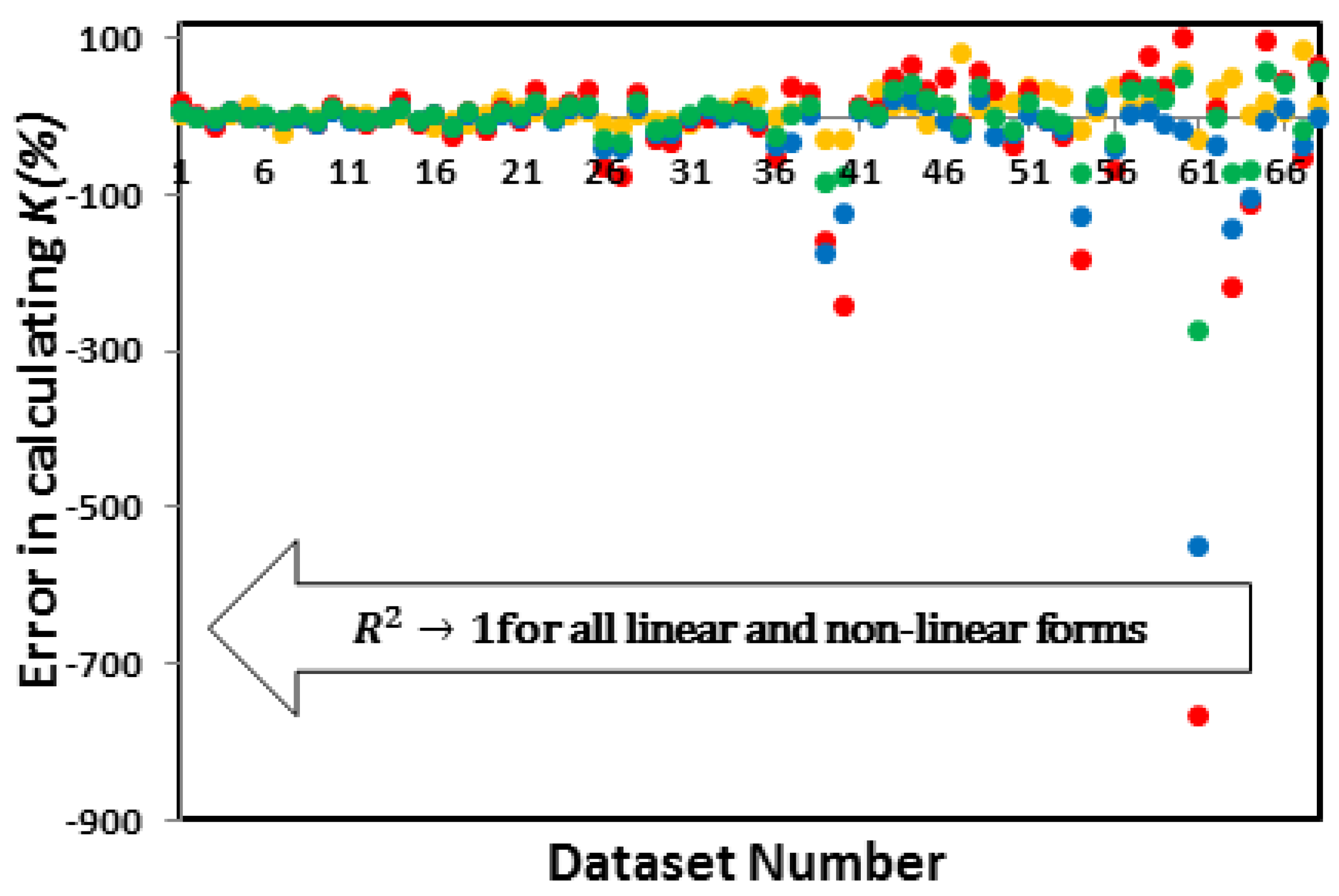
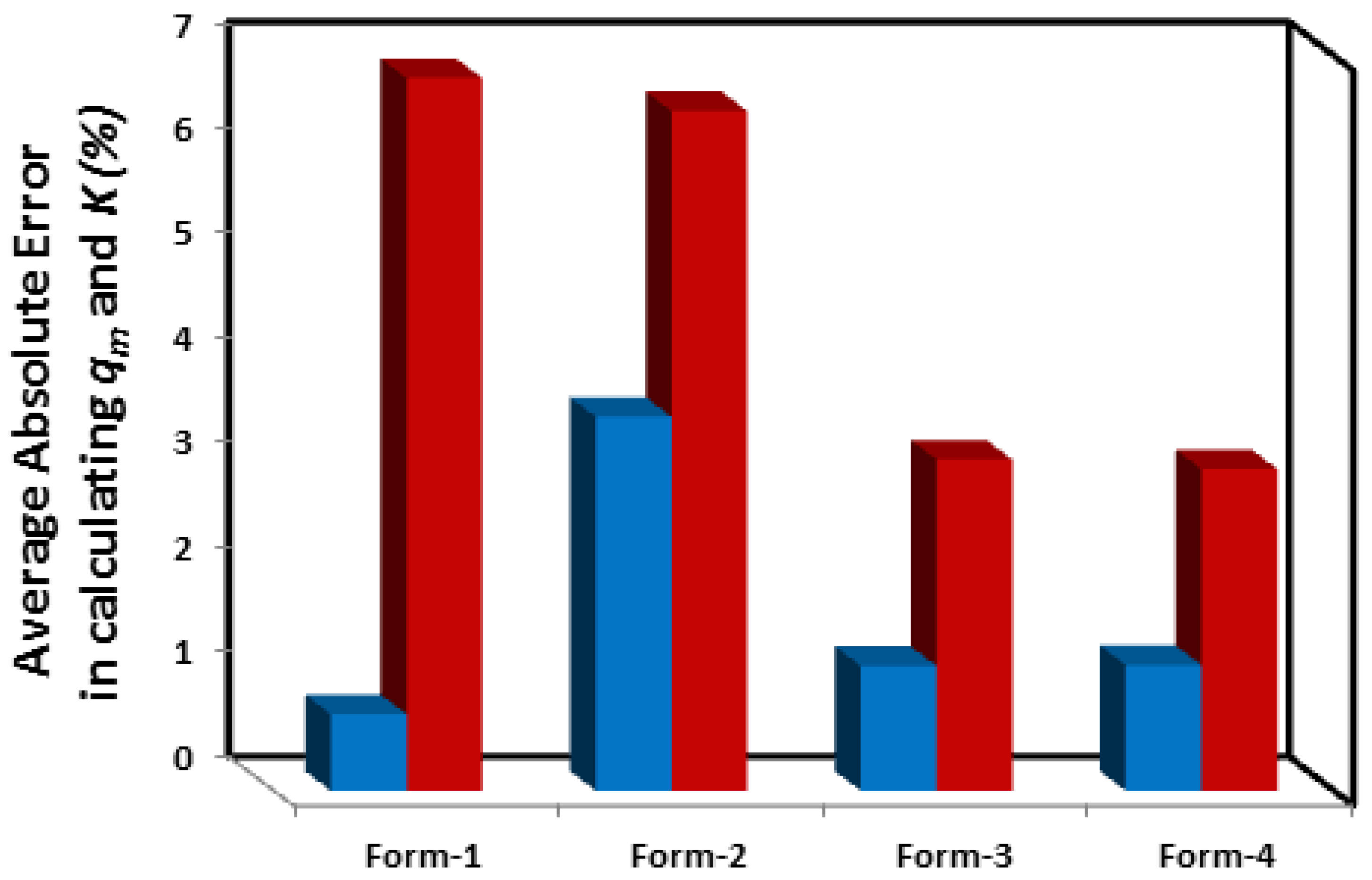
System	Adsorbate	Adsorbent	Reported Isotherm	Coefficients of determination (R2) of linear and Non-linear forms of the Langmuir Isotherm					Reference
System	Adsorbate	Adsorbent	Reported Isotherm	Non-linear	Form-4	Form-3	Form-2	Form-1	Reference
1	Methyl Orange	Chitosan	Langmuir	0.9999	0.9926	0.9926	0.9994	0.9979	[22]
1	-33	Chitosan	Langmuir	0.9999	0.9926	0.9926	0.9994	0.9979	[22]
2	Methyl Orange	Chitosan	Langmuir	0.9998	0.9978	0.9978	0.9998	0.9992	[22]
2	-27	Chitosan	Langmuir	0.9998	0.9978	0.9978	0.9998	0.9992	[22]
3	Methyl Orange	Chitosan	Langmuir	0.9998	0.9891	0.9891	0.9989	0.9967	[22]
3	-40	Chitosan	Langmuir	0.9998	0.9891	0.9891	0.9989	0.9967	[22]
4	Methyl Orange	Chitosan	Langmuir	0.9997	0.9891	0.9891	0.9996	0.9962	[22]
4	-45	Chitosan	Langmuir	0.9997	0.9891	0.9891	0.9996	0.9962	[22]
5	Pb(II)	Modified biochar by H₂O₂ (HP-BC)	Langmuir	0.9996	0.9991	0.9991	0.9999	1	[23]
6	Pb(II)	Pistachio wood-derived activated carbon	Toth	0.9993	0.994	0.994	0.9974	0.9999	[24]
7	Phosphate	Chitosan biosorbent modified with zirconium ions (ZCB)	Langmuir	0.9992	0.9955	0.9955	0.9987	0.9998	[25]
8	Amoxicillin	MIL-53(Al)	Langmuir	0.9981	0.9856	0.9856	0.9972	0.998	[26]
8	(at 303 K)	Metal−Organic Framework	Langmuir	0.9981	0.9856	0.9856	0.9972	0.998	[26]
9	Perfluoro-2-propoxypropanoic acid (GenX)	Powdered Activated Carbon (PAC)	Langmuir	0.998	0.9901	0.9901	0.9996	0.9971	[27]
10	Tetracycline	Iron loaded sludge biochar	Langmuir	0.9979	0.9809	0.9809	0.9968	0.9977	[28]
10	(at 313.15 K)	Iron loaded sludge biochar	Langmuir	0.9979	0.9809	0.9809	0.9968	0.9977	[28]
11	Pb(II)	Biochar (BC)	Langmuir	0.9979	0.9794	0.9794	0.9956	0.9998	[23]
12	Amoxicillin	MIL-53(Al)	Langmuir	0.9978	0.9832	0.9832	0.9963	0.9978	[26]
12	(at 323 K)	Metal−Organic Framework	Langmuir	0.9978	0.9832	0.9832	0.9963	0.9978	[26]
13	Amoxicillin	MIL-53(Al)	Langmuir	0.9978	0.9802	0.9802	0.9941	0.9983	[26]
13	(at 313 K)	Metal−Organic Framework	Langmuir	0.9978	0.9802	0.9802	0.9941	0.9983	[26]
14	Cephalexin	PPAC-nZVI	Langmuir	0.9976	0.9834	0.9834	0.9972	0.9999	[29]
15	Methyl Orange	UiO-66-NH2MOF	Langmuir	0.9973	0.9878	0.9878	0.9965	1	[30]
15	(at 35 ^oC)	UiO-66-NH2MOF	Langmuir	0.9973	0.9878	0.9878	0.9965	1	[30]
16	Cr(VI)	NiFe LDH microspheres	Liu	0.9973	0.9804	0.9804	0.9919	0.9996	[31]
17	Tetracycline	Iron loaded sludge biochar	Langmuir	0.9972	0.9815	0.9815	0.999	0.997	[28]
17	(at 303.15 K)	Iron loaded sludge biochar	Langmuir	0.9972	0.9815	0.9815	0.999	0.997	[28]
18	Cu(II)	Bentonite	Langmuir	0.9972	0.977	0.977	0.9942	0.9984	[32]
19	Amoxicillin	MIL-53(Al)	Langmuir	0.9971	0.9738	0.9738	0.9918	0.9979	[26]
19	(at 333 K)	Metal−Organic Framework	Langmuir	0.9971	0.9738	0.9738	0.9918	0.9979	[26]
20	Methylene Blue	Porous Biochar	Langmuir	0.9971	0.9594	0.9594	0.9991	0.9899	[33]
20	(at 30 ^oC)	Porous Biochar	Langmuir	0.9971	0.9594	0.9594	0.9991	0.9899	[33]
21	Methyl Orange	NiO	Langmuir	0.9969	0.9227	0.9227	0.9994	0.9462	[20]
21	(at 60 ^oC)	NiO	Langmuir	0.9969	0.9227	0.9227	0.9994	0.9462	[20]
22	Pb(II)	Commercial Activated Carbon (CGAC)	Langmuir	0.9966	0.987	0.987	0.9974	0.999	[34]
23	Methylene Blue	Maleylated modified	Langmuir	0.9961	0.974	0.974	0.9839	1	[35]
23	(at 303 K)	hydrochar	Langmuir	0.9961	0.974	0.974	0.9839	1	[35]
24	Tetracycline	Human hair-derived high surface area porous carbon material (HHC)	Langmuir	0.9961	0.9402	0.9402	0.9962	0.9984	[36]
24	(at 50 ^oC)		Langmuir	0.9961	0.9402	0.9402	0.9962	0.9984	[36]
25	Methylene Blue	Magnetic wakame biochar nanocomposites	Langmuir	0.9959	0.9562	0.9562	0.9695	0.9995	[21]
25	(at 20 ^oC)	Magnetic wakame biochar nanocomposites	Langmuir	0.9959	0.9562	0.9562	0.9695	0.9995	[21]
26	Tetracycline	Human hair-derived high surface area porous carbon material (HHC)	Langmuir	0.9956	0.9538	0.9538	0.9938	0.9973	[36]
26	(at 40 ^oC)		Langmuir	0.9956	0.9538	0.9538	0.9938	0.9973	[36]
27	Cd(II)	Commercial Activated Carbon (CGAC)	Langmuir	0.9955	0.9239	0.9239	0.9894	0.9869	[34]
28	Methyl Orange	Graphene oxide-NiFe LDH	Liu	0.9949	0.9142	0.9142	0.9741	0.9983	[31]
29	Methylene Blue	Activated lignin-chitosan extruded (ALiCE)	Langmuir	0.9947	0.9256	0.9256	0.9916	0.9956	[37]
30	Cr(VI)	Graphene oxide/Fe₃O₄/SO₃H nanohybrid	Langmuir	0.9946	0.9323	0.9323	0.9931	0.9866	[38]
31	Hg (II)	Polydopamine decorated SWCNTs	Freundlich	0.994	0.9583	0.9583	0.9972	0.9822	[39]
32	Methyl Orange	NiFe LDH microspheres	Liu	0.9939	0.9488	0.9488	0.9866	0.9968	[31]
33	Acid Fuchsin (AF)	Amorphous solid based on the Pd₁₂L₂₄ cage	Langmuir	0.9933	0.9547	0.9547	0.9884	0.9972	[40]
33	Acid Fuchsin (AF)	(αMOC-1)	Langmuir	0.9933	0.9547	0.9547	0.9884	0.9972	[40]
34	Methyl Orange	NiO	Langmuir	0.9928	0.9256	0.9256	0.9942	0.9676	[20]
34	(at 30 ^oC)	NiO	Langmuir	0.9928	0.9256	0.9256	0.9942	0.9676	[20]
35	Methylene Blue	Maleylated modified	Langmuir	0.9927	0.9554	0.9554	0.979	1	[35]
35	(at 313 K)	hydrochar	Langmuir	0.9927	0.9554	0.9554	0.979	1	[35]
36	Methylene Blue	Magnetic wakame biochar nanocomposites	Langmuir	0.9927	0.9261	0.9261	0.9531	0.9989	[21]
36	-30	Magnetic wakame biochar nanocomposites	Langmuir	0.9927	0.9261	0.9261	0.9531	0.9989	[21]
37	Methylene Blue	Maleylated modified	Langmuir	0.9926	0.9478	0.9478	0.9623	1	[35]
37	(at 323 K)	hydrochar	Langmuir	0.9926	0.9478	0.9478	0.9623	1	[35]
38	Tetracycline	Iron loaded sludge biochar	Langmuir	0.9922	0.9231	0.9231	0.979	0.9968	[28]
38	(at 293.15 K)	Iron loaded sludge biochar	Langmuir	0.9922	0.9231	0.9231	0.979	0.9968	[28]
39	Acid Fuchsin (AF)	Multifunctionalized micromesoporous	Langmuir	0.9915	0.7336	0.7336	0.781	0.999	[41]
		nano-silica KCC-1
		(MF-KCC-1)
40	Pb(II)	Magnetic biochar/MgFe-LDH	Langmuir	0.9912	0.8699	0.8699	0.952	0.9994	[42]
41	Pb(II)	Diethylenetriaminepentaacetic acid modified magnetic graphene oxide (DTPA/MGO)	Langmuir	0.9909	0.6721	0.6721	0.8392	0.9973	[43]
42	Cd (II)	Diethylenetriaminepentaacetic acid modified magnetic graphene oxide (DTPA/MGO)	Langmuir	0.9897	0.7975	0.7975	0.9736	0.9948	[43]
43	Crystal Violet	Activated Carbon of	Dubinin–Radushkevich	0.9894	0.9574	0.9574	0.9906	0.9997	[44]
43	Crystal Violet	Lemon Wood	Dubinin–Radushkevich	0.9894	0.9574	0.9574	0.9906	0.9997	[44]
44	Cd(II)	Silica	Langmuir	0.9893	0.9579	0.9579	0.9827	0.999	[45]
44	Cd(II)	Particles Chemically Modified by Conjugated β-Ketoenol Furan	Langmuir	0.9893	0.9579	0.9579	0.9827	0.999	[45]
45	Tetracycline	Human hair-derived high surface area porous carbon material (HHC)	Langmuir	0.9892	0.8244	0.8244	0.9961	0.9808	[36]
45	(at 30 ^oC)		Langmuir	0.9892	0.8244	0.8244	0.9961	0.9808	[36]
46	Congo Red	Hybrid alginate/	Langmuir	0.9892	0.7833	0.7833	0.9916	0.9938	[46]
46	Congo Red	natural bentonite	Langmuir	0.9892	0.7833	0.7833	0.9916	0.9938	[46]
47	Remazol Brilliant Blue	Biochar	Toth	0.989	0.892	0.892	0.9748	0.9984	[47]
48	Crystal Violet (CV)	MCM-41/MgO	Langmuir	0.9865	0.8014	0.8014	0.9258	0.992	[48]
48	Crystal Violet (CV)	A-20	Langmuir	0.9865	0.8014	0.8014	0.9258	0.992	[48]
49	Methylene Blue	Porous cellulosederived	Redlich-Peterson	0.986	0.9223	0.9223	0.9651	0.9994	[49]
49	Methylene Blue	carbon/montmorillonite nanocomposites	Redlich-Peterson	0.986	0.9223	0.9223	0.9651	0.9994	[49]
50	Methylene Blue	Amorphous solid based on the Pd12L24 cage	Langmuir	0.9846	0.7845	0.7845	0.9922	0.9755	[40]
50	Methylene Blue	(αMOC-1)	Langmuir	0.9846	0.7845	0.7845	0.9922	0.9755	[40]
51	Crystal Violet (CV)	MCM-41/MgO	Langmuir	0.9841	0.8156	0.8156	0.942	0.9771	[48]
51	Crystal Violet (CV)	B-20	Langmuir	0.9841	0.8156	0.8156	0.942	0.9771	[48]
52	Acetaminophen	Commercial	Redlich–Peterson	0.9821	0.8608	0.8608	0.9335	0.9995	[50]
52	Acetaminophen	Activated Carbon (CAC)	Redlich–Peterson	0.9821	0.8608	0.8608	0.9335	0.9995	[50]
53	Methyl Orange	Amorphous solid based on the Pd₁₂L₂₄ cage	Langmuir	0.9796	0.764	0.764	0.9411	0.9963	[40]
53	Methyl Orange	(αMOC-1)	Langmuir	0.9796	0.764	0.764	0.9411	0.9963	[40]
54	Reactive Red 120	Hybrid crosslinked chitosan-epichlorohydrin/TiO2 nanocomposite	Langmuir	0.9795	0.8485	0.8485	0.9972	0.9979	[51]
54	Reactive Red 120	(CTS-ECH/TNC)	Langmuir	0.9795	0.8485	0.8485	0.9972	0.9979	[51]
55	Congo Red (CR)	Fe₃O₄ -g-PGMA-g-PEI	Langmuir	0.9792	0.9265	0.9265	0.9889	0.9937	[52]
56	Methylene Blue	Agroindustrial wastes (Soursop residue)	Sips	0.9786	0.6666	0.6666	0.9631	0.9658	[53]
57	Ciprofloxacin (CIP)	Montmorillonite (Mt)	Langmuir	0.9774	0.725	0.725	0.9413	0.9995	[54]
58	Tetracycline	Montmorillonite (Mt)	Langmuir	0.9774	0.6595	0.6595	0.9593	0.9963	[54]
59	Cu(II)	Diethylenetriaminepentaacetic acid modified magnetic graphene oxide (DTPA/MGO)	Langmuir	0.9635	0.5736	0.5736	0.8655	0.9933	[43]
60	Methylene Blue	Polyaniline/TiO2 hydrate	Temkin	0.9621	0.7461	0.7461	0.8333	0.9932	[55]
61	Pb(II)	Amidoxime-functionalized chelating resin (PAO-g-PS)	Langmuir	0.9561	0.6339	0.6339	0.9835	0.9119	[19]
62	Methylene Blue	Cross-linked chitosan/sepiolite composite	Freundlich	0.9418	0.8442	0.8442	0.9745	0.9929	[56]
63	Cd (II)	Amidoxime-functionalized chelating resin (PAO-g-PS)	Langmuir	0.9411	0.4077	0.4077	0.9676	0.8693	[19]
64	Cd(II)	Modified lawny grass adsorbent (RG) containing H[BTMPP] (Cyanex272)	Sips	0.941	0.8148	0.8148	0.9632	0.9739	[57]
65	Cu(II)	4-ethyl thiosemicarbazide (ETSC) intercalated	Freundlich	0.9334	0.7326	0.7326	0.9338	0.9944	[58]
65	Cu(II)	organophilic calcined hydrotalcite (OHTC)	Freundlich	0.9334	0.7326	0.7326	0.9338	0.9944	[58]
66	Methylene Blue	Chitosan cross-linked graphene oxide/lignosulfonate composite	Langmuir	0.9261	0.4524	0.4524	0.509	0.9992	[59]
66	(at 323 K)		Langmuir	0.9261	0.4524	0.4524	0.509	0.9992	[59]
67	Basic Red 46 (BR46)	Activated carbon from Ziziphus lotus stones	Langmuir	0.9156	0.5982	0.5982	0.7574	0.9958	[60]

Table 2. The adsorption capacities and Langmuir constants obtained from linear and non-linear forms of the Langmuir isotherm for the adsorption systems used in this study.

System	$Adsorption capacity (q_{m}$ ) of linear and Non-linear forms of the Langmuir Isotherm					Langmuir constant (K) of linear and Non-linear forms of the Langmuir Isotherm
System	Non-linear	Form-4	Form-3	Form-2	Form-1	Non-linear	Form-4	Form-3	Form-2	Form-1
1	30.6	31.77	31.59	34.96	31.25	0.0684	0.0643	0.0648	0.0567	0.0658
2	29.04	28.91	28.85	29.58	28.98	0.0636	0.0642	0.0643	0.0622	0.0639
3	34.51	33.94	33.69	31.54	34.12	0.0653	0.0671	0.0678	0.0738	0.0665
4	36.18	37.6	37.29	37.73	37.03	0.0735	0.0692	0.0699	0.0687	0.0706
5	54.72	54.68	54.67	54.64	55.24	0.4464	0.4502	0.4505	0.4507	0.3859
6	192.2	192.6	192.2	192.3	192.3	1.822	1.806	1.816	1.857	1.8571
7	62.65	62.48	62.42	62.11	62.11	1.648	1.703	1.71	1.75	1.987
8	754.6	742.5	734.5	714.2	769.2	0.0195	0.021	0.0216	0.023	0.0187
9	0.7877	0.7693	0.7657	0.7547	0.789	4.055	4.319	4.363	4.4805	4.072
10	331.9	330.6	327.7	333.3	333.3	0.0465	0.0474	0.0483	0.0462	0.046
11	42.12	42.77	42.54	43.47	42.55	0.1312	0.119	0.1215	0.1126	0.1191
12	476.1	478.2	473.7	476.1	476.1	0.0129	0.0129	0.0131	0.0131	0.0129
13	644.4	636.9	634.2	625	666.6	0.0162	0.0169	0.0171	0.0178	0.0156
14	82.43	84.06	83.56	90.9	81.96	0.4699	0.4184	0.4254	0.3606	0.4436
15	211.2	204.5	201.3	192.3	208.3	0.0284	0.0324	0.0341	0.0382	0.0296
16	163.6	164.4	163.9	163.9	161.3	0.0887	0.0859	0.087	0.0877	0.1009
17	246.5	250.4	248.5	250	243.9	0.024	0.0225	0.023	0.0224	0.0263
18	198.4	191.1	189.6	181.8	196.1	0.0706	0.0798	0.0812	0.0878	0.0745
19	301.2	303	300.7	303	303	0.0119	0.0118	0.0119	0.0119	0.0117
20	513.2	454.5	442.9	384.6	500	0.0661	0.0881	0.0918	0.112	0.0754
21	776	934.8	859.6	833.3	909	0.0006	0.0005	0.0005	0.0005	0.0005
22	20.12	20.28	20.22	20.53	20.57	0.1177	0.1117	0.1132	0.1069	0.0933
23	209.4	224.2	217.2	250	208.3	0.0466	0.038	0.0404	0.0315	0.0443
24	1151	1154	1149	1111	1111	0.4745	0.4675	0.48	0.5	0.4285
25	489.4	491.8	488	500	500	0.8331	0.8327	0.8708	0.8333	0.7407
26	163.5	174	169.6	178.5	163.9	0.0246	0.0207	0.0217	0.0196	0.0236
27	27.34	29.34	28.31	34.96	28.16	0.0088	0.0075	0.008	0.0057	0.0081
28	35.7	35.53	35.41	35.21	35.46	0.3835	0.3981	0.406	0.4188	0.404
29	36.24	33.28	32.12	28.65	35.46	0.1206	0.1588	0.1715	0.211	0.134
30	220.6	243.9	233.8	270.2	222.2	0.0112	0.0092	0.0098	0.0077	0.0108
31	249.9	235	230	222.2	243.9	0.1119	0.1297	0.1353	0.1433	0.1188
32	404.5	384.9	375.3	357.1	400	0.0481	0.0612	0.0669	0.0784	0.0517
33	139.6	140.9	138.6	135.1	135.1	0.0308	0.0299	0.0312	0.0328	0.0339
34	273.2	296.3	288.1	263.1	285.7	0.0016	0.0014	0.0014	0.0016	0.0015
35	1180	1191	1183	1250	1250	0.5033	0.4698	0.4917	0.4444	0.4
36	536.4	544.1	534.5	526.3	555.5	0.8916	0.8379	0.9046	0.8636	0.7826
37	1171	1172	1163	1111	1250	0.5675	0.5756	0.6072	0.6428	0.421
38	103.2	98.49	96.24	92.59	103.1	0.1252	0.1572	0.1702	0.1888	0.1286
39	627.6	641.9	550.9	833.3	625	0.0711	0.0683	0.093	0.0439	0.0658
40	465.8	482.5	464.1	526.3	476.1	0.0694	0.059	0.0677	0.0481	0.0619
41	299.6	264.2	243	192.3	285.7	0.0446	0.0793	0.0994	0.1529	0.0578
42	134.2	113.5	101.7	89.28	131.5	0.0445	0.1656	0.2886	0.3862	0.0573
43	23.64	24.12	23.88	24.44	23.58	1.513	1.332	1.392	1.274	1.358
44	51.97	52.3	51.78	53.47	54.05	0.4185	0.4088	0.4267	0.3816	0.2724
45	351.9	414	367.2	625	357.1	0.0161	0.0096	0.0122	0.0053	0.0136
46	128.9	158.1	140.4	192.3	133.3	0.0158	0.0101	0.0122	0.0076	0.0135
47	92.99	98.63	95.05	105.2	90.9	0.0517	0.0396	0.0443	0.0336	0.056
48	1646	1754	1583	2500	1666	0.5895	0.4981	0.6215	0.2857	0.5
49	138.1	137.6	136	133.3	144.9	34.22	38.52	41.84	37.5	6.9
50	194.3	236.7	208.8	294.1	196.1	0.0162	0.0099	0.0126	0.0069	0.0145
51	1844	1860	1681	2500	2000	0.2046	0.2067	0.2534	0.1333	0.1785
52	226.6	232.5	225.4	250	232.8	0.1214	0.1013	0.1176	0.0778	0.0743
53	398	355.8	329.7	303	384.6	0.0531	0.0924	0.1209	0.1506	0.0631
54	208.6	235.5	215	227.2	208.3	0.8193	0.5924	0.6982	0.6197	0.7619
55	1909	1865	1827	1666	2000	0.0913	0.1204	0.1299	0.1538	0.0581
56	41.1	41.36	40.17	38.75	47.39	0.5751	0.6697	0.7933	0.8805	0.0913
57	1.065	1.254	1.032	2.398	1.072	5.812	3.53	5.353	1.401	4.8
58	0.9897	1.055	0.9372	1.183	1.011	50.31	39.25	54.05	30.4	32.19
59	2.063	3.338	1.978	3.837	2.147	0.3131	0.1315	0.3226	0.108	0.2689
60	585.7	601.6	524.5	625	625	0.0838	0.0849	0.1138	0.0765	0.054
61	118.7	88.38	63.8	35.84	112.3	0.0264	0.0836	0.2013	0.5017	0.0363
62	399.5	360.1	316.8	294.1	384.6	0.0527	0.0973	0.1447	0.1365	0.0678
63	1.405	1.89	1.445	1.966	1.43	0.2776	0.1606	0.2533	0.1511	0.2564
64	13.99	14.45	13.8	13.88	14.12	0.0163	0.0144	0.0176	0.0166	0.0145
65	57.85	56.39	53.74	50.25	64.1	0.2559	0.6073	0.829	0.99	0.0881
66	1015	1074	896.9	909.1	1111	1.134	1.134	2.508	1.5714	0.5625
67	259.5	271.6	257.8	250	312.5	1.064	0.7197	1.203	1.29	0.1088

Table 4. A hypothetical adsorption system that does not follow the Langmuir isotherm.

$C_{e}$ (mg/L)	$q_{e}$ (mg/g)	Langmuir Parameters	Form-1	Form-2	Form-3	Form-4	Non-linear
0	0	$q_{m}$ (mg/g)	119.05	227.27	118.81	152.03	118.25
50	14.28571
100	40
150	60
200	72.72727
250	80.64516
300	85.71429	$K$	0.0047	0.0015	0.0062	0.0032	0.0069
350	89.09091
400	91.42857
450	93.10345
500	94.33962
550	95.27559
600	96
650	96.57143
700	97.0297	$R^{2}$	0.9649	0.9214	0.5222	0.5222	0.9658
750	97.4026
800	97.70992
850	97.9661
900	98.18182
950	98.36512
1000	98.52217

Table 5. Parameters obtained using the non-linear forms of the Langmuir and Toth isotherms for systems 61, 63 and 64.

System	Langmuir Isotherm				Toth Isotherm
System	$q_{m}$ (mg/g)	$K$	$R^{2}$	$R m s d$	$q_{m}$ (mg/g)	$K$	$m$	$R^{2}$	$R m s d$
61	1.4055	0.2777	0.9561	0.0173	0.8862	0.2459	202.9	0.9950	0.0058
63	2.063	0.3131	0.9411	0.0309	1.338	0.2665	27.43	0.9990	0.0039
64	13.99	0.0164	0.9410	0.2921	14.96	0.0217	0.7773	0.9985	0.0288

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rethinking the Use of Linear Forms of the Langmuir Isotherm in Adsorption Modeling to Calculate Langmuir Isotherm Parameters

Abstract

1. Introduction

2. Experimental Data and Calculation Methods

3. Results and Discussion

3.1. In what case can we say that an adsorption system follows the Langmuir isotherm?

3.2. Can we say that an adsorption system follows the Langmuir isotherm if it is described only by one of the linear forms of the Langmuir isotherm?

3.3. Statistical study

3.3.1. Accuracy relationship between linear and non-linear forms of the Langmuir isotherm

3.3.2. Which linear forms create the least error in calculating q m and K?

4. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

3.3.2. Which linear forms create the least error in calculating $q_{m}$ and K?