Multi-Mode Vector Light Fields Generation Using Modified Off-Axis Interferometric Holography and Liquid Crystal Spatial Light Modulators

The increasing enhancement in the modulation accuracy of spatial light modulators has garnered significant attention towards real-time control technology for light fields based on these modulators. It has been empirically demonstrated that this technology possesses a remarkable capability to generate vector beams with arbitrary complex amplitude distributions. Nevertheless, past studies indicate that the generation of only one vector beam at a time has been observed. The simultaneous generation of numerous vector light fields can give rise to several challenges, including compromised picture quality, limited single mode operation, and intricate optical path configurations. In pursuit of this objective, we present a novel methodology that integrates the coding methodology of modified off-axis interferometric holography with the idea of optical superposition. This technique facilitates the concurrent generation of several vector beams. In this study, we present a demonstration of the simultaneous creation of twelve vector beams using a single spatial light modulator (SLM) as a proof of concept. Significantly, this technology has the ability to generate an unlimited quantity of vector light fields concurrently, under the assumption that the resolution of the SLM does not impose any limitations. The findings indicate that the imaging quality achieved by this technology is of a high standard. Furthermore, it is possible to separately control the beam waist radius, topological charge, polarization order, and extra phase of each beam.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

Presently, nearly all applications involving light rely on the dimensional resources of photons. It is common knowledge that electrons possess extremely restricted dimensions, such as electron spin. Photons, on the other hand, are distinguished by their multiple dimensions. Photons' fundamental dimensions consist of wavelength/frequency, time, complex amplitude, polarization, and spatial domain. By modifying the photons' spatial domain, one can generate a vector light field. The polarization characteristics of the vector field make it have broad application prospects in the fields of transverse or longitudinal super-resolution [1,2], optical needle [3,4], optical information transmission [5], optical chain [6], optical channel [7], particle capture, and manipulation [8,9].

Obviously, the generation of a vector light field is the premise of studying its novel characteristics and developing its new applications. In previous reports, the known generation techniques were mainly divided into the intracavity method and the extra-cavity method. The intracavity method not only requires a specific design of the resonant cavity but also only generates a vector light field with a specific polarization distribution. In contrast, the extra-cavity method is very flexible. Different vector light fields can be obtained by adjusting the optical path or element, which makes the generation of vector light fields diverse. The main devices involved are the optical metasurface [10,11,12], q plate [13], cylindrical lens [14,15], bifurcated grating [16], spiral phase plate [17,18] and SLM [19]. Among them, the polarization state and complex amplitude distribution of the vector light field can be adjusted in real time by means of SLM, which highlights the flexibility of the extra-cavity method. Therefore, the vector light field generation method based on SLM is widely used. For example, Ding 's research group [20] divided the incident beam into two beams from the computer-generated hologram (CGH) written to the SLM. Each beam is encoded using the specified complex field, and then effectively combined into a single vector beam through the Wollaston prism. In the triangular co-pass interferometer system proposed by Zhao Jianlin 's research group [21], a beam of light passes through the beam splitting system first, and then two orthogonal polarization components are reflected by a right-angle prism to the left and right regions on the screen of the SLM, respectively. And then coupled through the combined beam system to form a single vector beam. Carmelo et al. [22] can simultaneously generate multiple vector beams with different spatial shapes and polarization distributions by using the interference method and the optical superposition principle. Compared with the former two, this greatly improves the generation efficiency of vector beams and increases the types of generation. However, it is limited to the generation of vector beams with cylindrical symmetry. In the path, it is necessary to use wave plates to adjust, and the requirements for optical path construction are strict, which will increase the difficulty of actual operation.

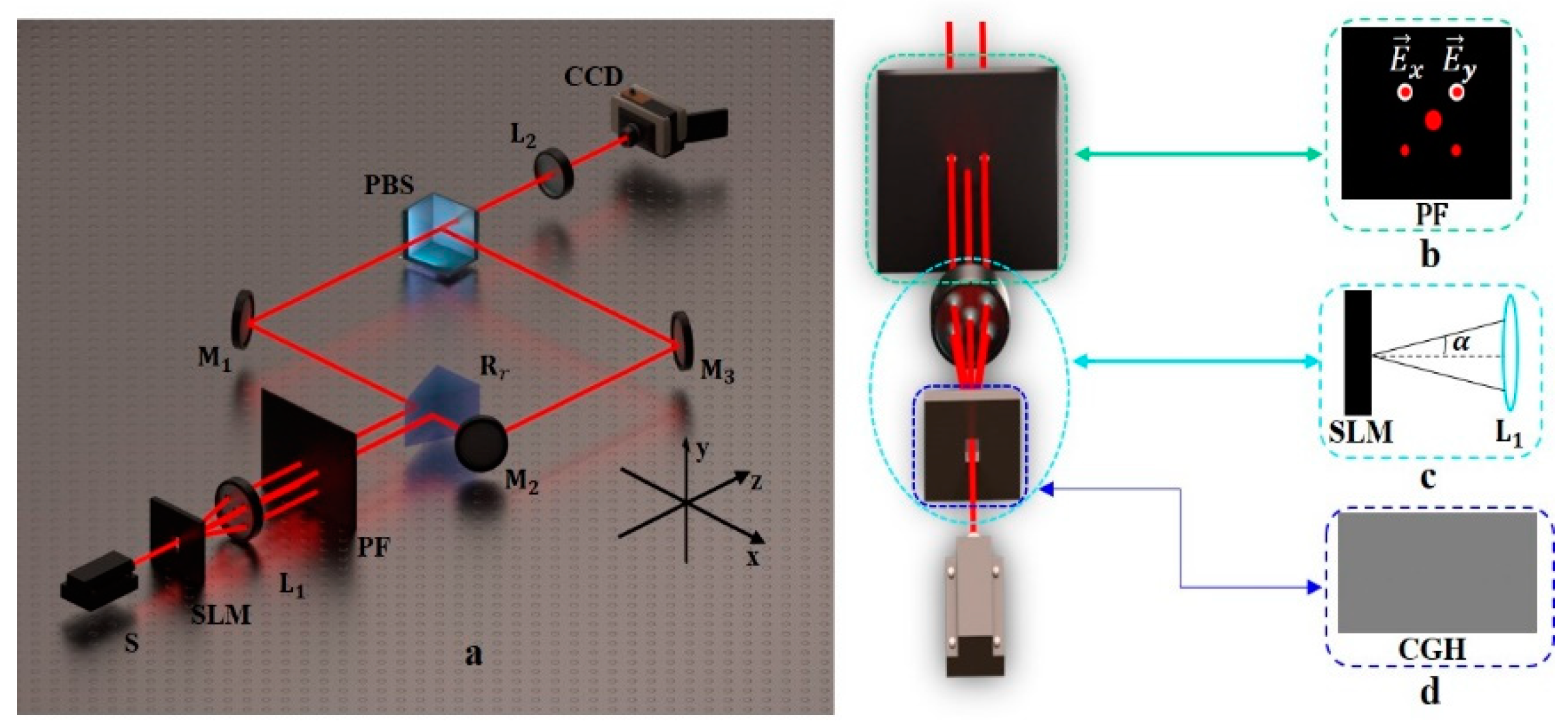
In this paper, a modulation method based on liquid crystal SLM is proposed. By using the coding method based on the modified off-axis interference hologram, combined with the transmission liquid crystal SLM and a shunt coupling system, the multimode vector light field with an arbitrary complex amplitude distribution is finally generated. Complex optical components are not involved in the whole experiment. The optical system is small in size, which reduces the complexity of the experimental optical path, and the vector beam quality is high. As a proof of principle, the experimental results show that this method can not only generate multiple types of vector beams at the same time, but also that the beam waist radius, topological charge number, polarization order, and additional phase of each beam are independently controllable. In addition, although we only show 12 cylindrically symmetric vector beams, the actual number is much larger than this, which is mainly limited by the resolution of SLM. If the resolution region of SLM is idealized, infinite vector beams can be generated. Section 2 introduces the experimental methods and theoretical analysis of this work. Section 3 shows the experimental results and discussion.

2. Materials and Methods

2.1. Experimental device and method

Figure 1a is the schematic diagram of the experimental system proposed by this method. The required CGH is displayed on the SLM, where the SLM is equivalent to a two-dimensional diffraction grating, which is used to assign a specific carrier frequency to the diffracted beams at all levels. A collimated beam of light with a wavelength of 632.8 nm is modulated by a SLM and divided into multi-level diffraction beams, which are then spatially transformed by a Fourier lens L₁. The corresponding spectral points will appear on the back focal plane of L₁. In order to prevent unnecessary noise from occurring at other diffraction levels, a double-channel pinhole filter (PF, as shown in Figure 1b) is placed here, allowing only the required level 1 diffraction through which the other levels of diffraction are blocked; the diffraction angle diagram between the first-order diffraction order and the zero-order diffraction order is shown in Figure 1c, and the angle is

α

. Subsequently, the two beams of diffraction light are separated by the triangular reflective prism R_r, through which one beam of diffusion light reaches the polarization beam splitter (PBS) through the reflective M₁, and its polarization is modulated to the horizontal state, during which time two reflections (R_r and M₁) are experienced. The other beam of diffraction light passes through the reflector M₂, M₃ to the PBS, and its polarization state is adjusted to a vertical, during which time 4 reflections have been experienced (R_r, M₂, M₃, PBS), because both beams have experienced even-numbered reflections, so that the original light field in the PBS can be combined. In this method, the carrier frequency in the z direction is increased to accurately control the optical path difference when encoding and calculating the hologram, so that the optical path of the two diffracted beams is the same. Finally, the two beams are coupled at PBS to generate the required vector light field, which is imaged on the charge-coupled device (CCD) by the Fourier lens L₂ and recorded. The experimental results can be used to analyze the polarization state by placing a polarizer in front of the CCD.

2.2. Principle analysis

As an electromagnetic wave, any electric field vector perpendicular to the propagation direction z can be decomposed into two orthogonal vectors in the x and y directions. Therefore, the polarization state of light or the electric field vector can be expressed by the vector sum of these two orthogonal components:

\vec{E} = [\begin{matrix} U_{x} (x, y) \\ U_{y} (x, y) \end{matrix}] = [\begin{matrix} E_{x} \exp (j φ_{x}) \\ E_{y} \exp (j φ_{y}) \end{matrix}]

(1)

Among them, (

U x

U y

) is the complex amplitude of the two polarization components, (

E_{x}

E_{y}

) and (

φ_{x}

φ_{y}

) are the amplitude and phase distribution of the two polarization components, and

j

is the imaginary symbol.

On the input plane, it is assumed that the complex amplitude transmittance function

T (x, y)

loaded on the SLM can be expressed as the following matrix form:

T (x, y) = [\begin{matrix} \begin{matrix} t_{11} t_{12} t_{13} \dots t_{1 b} \\ t_{21} t_{22} t_{23} \dots t_{2 b} \\ ⋮ ⋱ ⋱ ⋱ ⋮ \\ t_{a 1} \dots \dots \dots t_{a b} \end{matrix} \end{matrix}]

(2)

Where

a

represents the number of rows of the matrix, and

b

represents the number of columns of the matrix.

In order to make full use of the gray level and pixel resolution of SLM, taking the commonly used modified off-axis interferometric CGH as an example, the CGH in this method can be encoded according to the following formula:

t (x, y) = β {|1 + U_{x} (x, y) e x p [j k_{α} (x + y + z_{x})]|}^{2} + β {|1 + U_{y} (x, y) e x p [j k_{α} (- x + y + z_{x})]|}^{2}

(3)

Among them, the constant

β

represents the loss coefficient of the beam after passing through the liquid crystal spatial light modulator, with a value range of [0, 1], which can be ignored in coding;

α

is the diffraction angle between the first-order diffracted light and the zero-order diffracted light;

k_{α} = 2 π \sin α / λ

is the spatial carrier frequency, and

λ

is the wavelength of the input light;

e x p [j k_{α} (x + y + z_{x})]

and

e x p [j k_{α} (- x + y + z_{y})]

are the carrier frequency components of

U_{x}

and

U_{y}

on the x, y and z axes, respectively, where z is the constant introduced by adjusting the optical path of two diffracted beams, and can be ignored after adjusting the optical path of the two diffracted beams to be equal in the later period. The negative sign only indicates that

U_{x}

and

U_{y}

are encoded in the diffraction directions of +45° and -45° respectively with the x axis, which is convenient for spatial filtering in the later period.

Assuming that the incident plane light field is

{\vec{E}}_{i n}

, the output light field after the action of the CGH can be expressed as:

{\vec{E}}_{o u t} (x, y) = {\vec{E}}_{i n} T (x, y)

(4)

Where

{\vec{E}}_{i n}

is the complex amplitude of the input light field, and

{\vec{E}}_{o u t}

is the complex amplitude of the output light field.

For ease of explanation, select only when

a = b = 1

to proceed with the inference, in which case calculate the transmission function of the hologram

T_{11} (x, y) = t (x, y)

, and replace it with the following formula:

{\vec{E}}_{o u t} (x, y) = {\vec{E}}_{i n} T_{11} (x, y) = β {\vec{E}}_{i n} \{\begin{matrix} E_{0} + U_{x} (x, y) e x p [j k_{α} (x + y + z_{x})] \\ + U_{x}^{*} (x, y) e x p [- j k_{α} (x + y + z_{x})] \\ + U_{y} (x, y) e x p [j k_{α} (- x + y + z_{y})] \\ + U_{y}^{*} (x, y) e x p [- j k_{α} (- x + y + z_{y})] \end{matrix}\}

(5)

Among them,

E_{0}

represents the amplitude of the incident light, and "

*

" represents the complex conjugate operation. It is clear that the second and fourth elements of the

{}

are necessary for the vector light field, through the dual-channel pinhole filter for space filtration, only the required part can pass, and using the triangular reflective prism splitting, components can be obtained for the final generation of the two beam light field components, whose complex amplitude distribution is as follows:

{\vec{E}}_{x}^{11} (x, y) = β {\vec{E}}_{i n} U_{x} (x, y) \exp [j k_{α} (x + y + z_{x})]

(6)

{\vec{E}}_{y}^{11} (x, y) = β {\vec{E}}_{i n} U_{y} (x, y) \exp [j k_{α} (- x + y + z_{y})]

The above formula shows that there is a surplus of phase factors after the required

U_{x}

and

U_{y}

due to the impact of the time load frequency of the encoding hologram. In order to eliminate this influence, it is possible to adjust the light path so that the two beams of diffuse light spread along the z axis, at this time

x = y = 0

; at the same time when the beams are equal in the diffused light range,

\exp (j k_{α} z_{x}) = \exp (j k_{α} z_{y})

. Therefore, the above formula can be simplified as follows:

{\vec{E}}_{x}^{11} (x, y) = β {\vec{E}}_{i n} U_{x} (x, y), {\vec{E}}_{y}^{11} (x, y) = β {\vec{E}}_{i n} U_{y} (x, y)

(7)

The Jones matrix of the two incident surfaces at the PBS can be expressed in the following form:

J_{P B S_{0}} = [\begin{matrix} 1 \\ 0 \end{matrix}], J_{P B S_{e}} = [\begin{matrix} 0 \\ 1 \end{matrix}]

(8)

Since the two polarization components need to be coupled by a polarization splitting prism, the final output vector light field can be expressed as:

{\vec{E}}_{o u t}^{11} = {\vec{E}}_{x}^{11} (x, y) J_{P B S_{0}} + {\vec{E}}_{y}^{11} (x, y) J_{P B S_{e}} = β {\vec{E}}_{i n} [\begin{matrix} U_{x} (x, y) \\ U_{y} (x, y) \end{matrix}] = β {\vec{E}}_{i n} {\vec{E}}_{11}

(9)

Similarly, if

a

and

b

take any values:

{\vec{E}}_{o u t}^{a b} = β {\vec{E}}_{i n} [\begin{matrix} \begin{matrix} E_{11} E_{12} E_{13} \dots E_{1 b} \\ E_{21} E_{22} E_{23} \dots E_{2 b} \\ ⋮ ⋱ ⋱ ⋱ ⋮ \\ E_{a 1} \dots \dots \dots E_{a b} \end{matrix} \end{matrix}]

(10)

Therefore, through the coding method and optical path construction of the above design, the required multi-mode vector light field can be obtained in the recording plane.

3. Results and discussion

In order to ensure that the two orthogonal polarization components have independent imaging capabilities and determine the system parameters, two binary grayscale images with black and white in Figures 2a,b are substituted into Equation (2) as the

U_{x}

component and the

U_{y}

component, respectively, to control the additional phase of the vector light field. The period and distribution of the moiré fringes (as shown in Figure 2c) generated during the control process can explain the periodic difference between the two orthogonal polarization components and the direction of relative tilt. The system parameters can be defined by eliminating the moiré fringes (as shown in Figure 2d), which is known by the formula (1) that controlling a vector beam requires the modulation of its four degrees of freedom, respectively; that is, the two vertical partitions of a vector beam will have their respective spatial frequency parameters

k_{α}

in the x and y directions, and by modulating the four spatially-frequency partition parameters separately, the

U_{x}

component and

U_{y}

component are finally common and coplanar. The background gray values in Figure 2a,b are 1 and 0, respectively, and the gray values of ' O ', ' P ', ' T ', ' I ', ' C ' and ' S ' are 0 and 1, respectively. The additional phases corresponding to the image gray values of 0 and 1 are 0 and

π / 2

, respectively.

Figure 2d shows that the intensity of the light field is evenly distributed without the polarizer, because the amplitude of the light field is not additionally regulated. When the polarization direction of the polarizer is horizontal, the light intensity of the background light is the smallest, and the light intensity of the four characters of ' O ', ' P ', ' T ', ' I ', ' C ' and ' S ' of horizontal linear polarization is the largest. The experimental results are shown in Figure 2e. When the polarization direction of the polarizer is 45°, the light intensity of characters' O ', ' P ', ' T ', ' I ', ' C ' and ' S ' is the same as that of the background light. The experimental results are shown in Figure 2f. When the polarization direction of the polarizer is vertical, the light intensity of the background light is the largest, and the light intensity of the four characters of ' O ', ' P ', ' T ', ' I ', ' C ' and ' S ' is the smallest. The experimental results are shown in Figure 2g. When the polarization direction of the polarizer is 135°, the intensity of the four characters of ' O ', ' P ', ' T ', ' I ', ' C ' and ' S ' is the same as that of the background light. The experimental results are shown in Figure 2h. Through the above experimental results, it can be seen that in the case of a polarizer, due to the background and the different polarization directions of different words, different light intensity distribution effects will be presented. It is verified that the two orthogonal polarization components of the vector beam in this method have good imaging ability, and the additional phase is controllable.

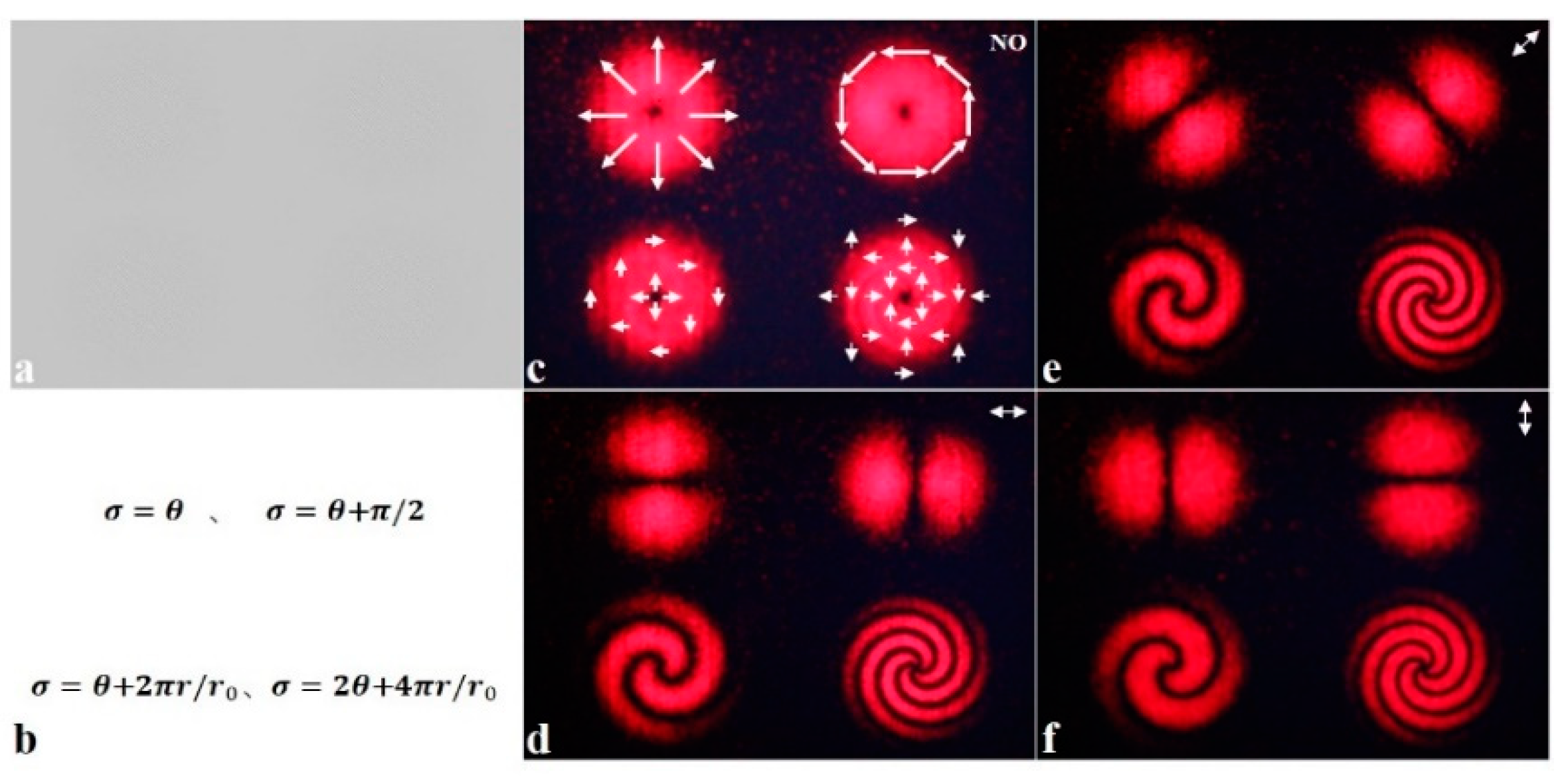
In order to verify that this method can produce multiple vector light fields simultaneously, a special calculated holography is produced. The first row of the figure, from left to right, is the diameter of the vector beam, the rotating vectorial beam of light, and the second row is the vibrant beam, as shown in Figure 3a.

The additional phase of the column-symmetric vector light field can be synthesized with the rotating variable and the diameter variable in both cases, so that its additional phase can be expressed as:

σ = m θ + 2 n π \frac{r}{r_{0}} + φ_{0}

(11)

Among them, (

r

θ

) is the polar coordinate of the input plane, satisfying:

r = \sqrt{x^{2} + y^{2}}

θ = \tan^{- 1} (y / x)

r

is the radius on the cross section of the light wave,

r_{0}

is the spot radius of the Hermitian Gaussian beam,

φ_{0}

is the initial phase, integer

m

is the topological charge of the required vector beam, and

n

is the radial index of the required vector beam.

Figure 3c is the light field intensity distribution map without the polarizer, and the polarization direction of each point is marked in the map. Figure 3d-f shows the intensity distribution of the light field when the polarizer is at 0°, 45° and 90° respectively. It can be seen from these three figures that when the angle of the polarizer changes, the radial vector beam and the azimuth vector beam will change accordingly. In this process, the extinction direction of the radial vector beam is always perpendicular to the polarizer, while the azimuth vector beam rotates counterclockwise at the same angle. In summary, this method can produce multiple vector light fields at the same time and improve image quality.

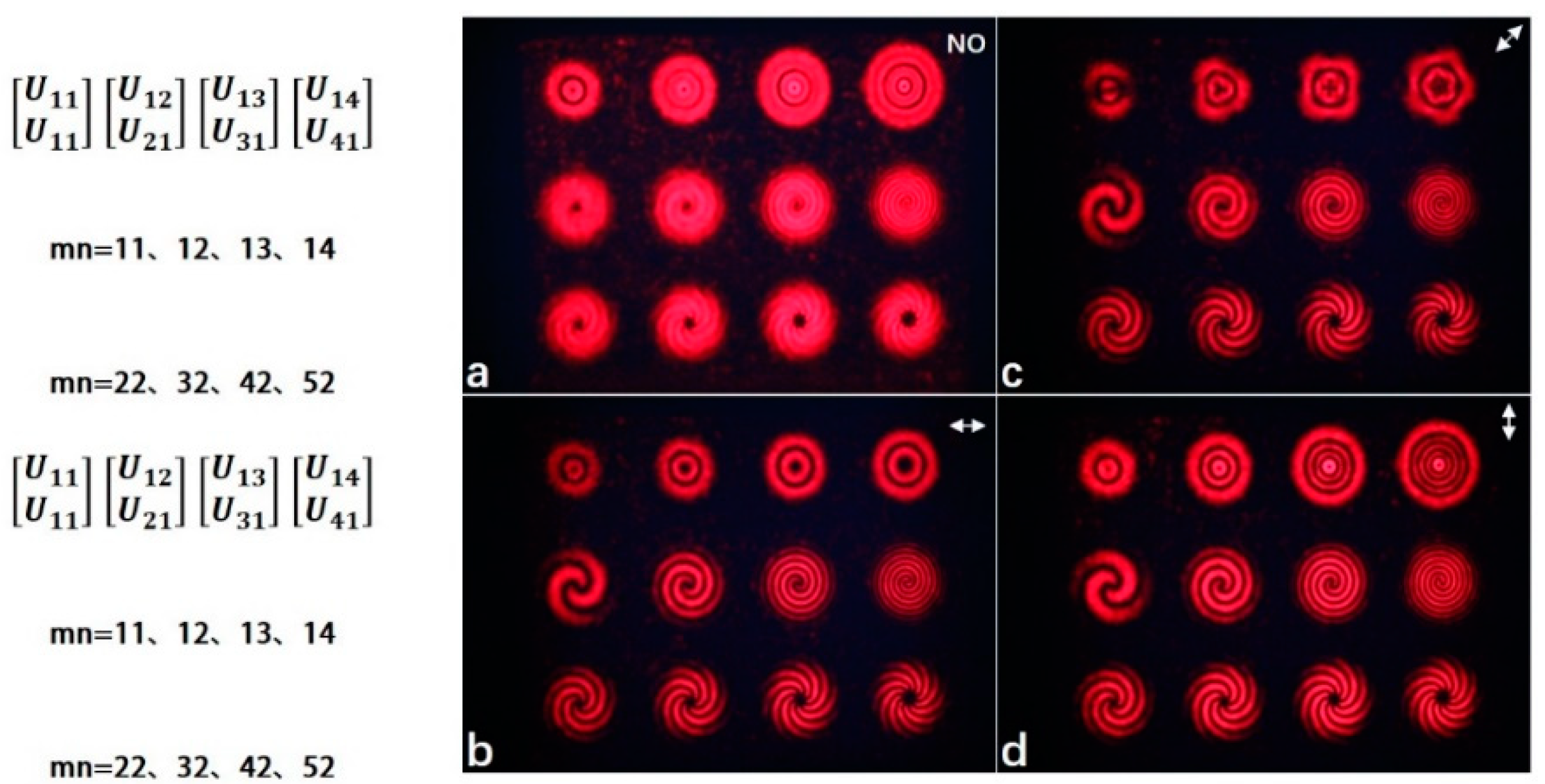
In order to ultimately determine that this method can produce several different types of vector beams simultaneously and that each beam can be independently controlled by its waist radius, topological charge number, polarization order, and additional phase, a special design of a multi-vector light field holography shows a total of 12 different patterns (take

a

=3,

b

=4): the first row is four kinds of Laguerre-Gaussian vector light beams, and vector beams with different radial exponents and topological charges in the second and third rows, as shown in Figure 4a.

Among them, the Laguerre-Gaussian beam, a typical spiral phase distribution of uneven turbulent vector beams, can be rewritten (1) as:

\vec{E} = [\begin{matrix} U_{x} (x, y) \\ U_{y} (x, y) \end{matrix}] = [\begin{matrix} U_{n_{1} m_{1}} (x, y) \\ U_{n_{2} m_{2}} (x, y) \end{matrix}]

(12)

Among them,

U_{m n} (x, y) = C_{m n} {(\frac{\sqrt{2}}{ω_{0}})}^{|m|} L_{n}^{m} (\frac{2 r^{2}}{{ω_{0}}^{2}}) \exp (i m φ - \frac{r^{2}}{{ω_{0}}^{2}})

(13)

Where

C_{m n}

is the normalized constant,

ω_{0}

is the beam width, and

L_{n}^{m}

is the Laguerre polynomial. A scalar Laguerre-Gaussian beam is a typical optical vortex whose topological charge is equal to an integer

m

. For Laguerre-Gaussian vector beams, due to the existence of the orthogonal polarization state, the topological charge has different vectors.

The results shown in Figure 4a–d are the experimental results of a multimode vector light field without polarizer, 0°, 45° and 90° respectively.

Figure 4a shows the sampling of the total intensity distribution of the output multi-mode vector beam by CCD when the polarizer is not placed. Due to the lack of additional regulation of the complex amplitude of the light field, the light intensity of each spot is evenly distributed in this state. There are central dark spots in the 12 patterns in the figure. The central dark spot in the first row is caused by the fact that the center of the Laguerre-Gaussian beam is a dark core, that is, the central light intensity here is zero. In the second row, when the topological charge

m

is constant, the area of the central dark spot will decrease with the increase of the radial index

n

. In the third row, when the radial index

n

is constant, the area of the central dark point will increase with the increase in the topological load

m

. The central dark point in the second row and the third row is collectively referred to as the phase singularity. The reason for the phase singularity is that the phase of the light wave field becomes uncertain and the amplitude of the field is zero. Another reason is that the polarization distribution of the polarized light at the center point is the same, but the phase is opposite, so the interference condition is satisfied and the destructive interference dark spot is formed. Figure 4b shows the intensity distribution of the multimode vector beam when the polarizer is 0°. It can be seen from the diagram that when the first row,

n

is constant, the radius of the extinction ring increases gradually with the increase of the topological charge

m

. The second row, with the increase of the radial index

n

, the radius of the spiral extinction gradually decreases; The third row says, “with the increase of topological charge

m

, the spiral extinction of the vector beam increases gradually, and the number is 2|

m

|. The intensity distribution rotates counterclockwise with the polarizer, and the extinction is a left-handed spiral.” Figure 4c is the intensity distribution of a multimode vector beam when the polarizer is 45°. By observing the first row of the diagram, it can be seen that the shape of the Laguerre-Gaussian spot is changed into linear, triangular, quadrilateral and pentagon, respectively. Figure 4d shows the intensity distribution of the multimode vector beam when the polarizer is 90°. It can be seen from the first row of the figure that when the topological charge

m

is constant, the number of extinction rings increases with the increase of

n

and the number is |

n

|. In the second and third rows in Figure 4c, and 4d, the same phenomenon occurs as in the second and third rows in Figure 4b, the only difference is that they are equivalent to rotating 45° and 90°, respectively, on the basis of Figure 4b. Based on the above experimental results, it can be seen that the beam waist radius, topological charge number, polarization order, and additional phase of each beam can be independently controlled using this method. The first and second columns of the second row in Figure 3 d-f correspond to the second and third rows of the first column of Figure 4 b-d, respectively, and the image quality in Figure 4 is inferior to that of Figure 3. In other words, the light spots are more uniform and the noise is less in Figure 3. The fundamental reason is that the pixel size of SLM is constant, and there are many types of vector beams generated in Figure 4, so the number of samples in Figure 4 is relatively small, which eventually leads to the fact that the more types of vector light fields, the worse the imaging quality.

4. Conclusions

A In this paper, we propose an optical system that leverages the modified off-axis interference hologram coding method and the superposition principle in optics. This system is based on a transmission liquid crystal SLM combined with optical elements, including optical lenses. It has the capability to generate multi-mode vector light fields with complex amplitude distributions. As a proof of concept, we demonstrate the simultaneous generation of 12 vector beams with varying polarization distributions and spatial shapes on a single SLM. Importantly, this method is not limited to generating only 12 beams; it can generate an unlimited number of vector beams, primarily restricted by the resolution of the SLM. This innovative approach allows for independent control of parameters such as waist radius, topological charge number, polarization order, and additional phase for each beam. Compared to existing methods, our system boasts a compact optical design, avoiding the need for complex optical components, while offering excellent programmability and flexible control. The potential applications are vast, from enhancing optical communication and optical interconnection to expanding the bandwidth of optical field channels. Furthermore, it holds promise in optical manufacturing and optical capture, making it a versatile and impactful technology in the realm of optics.

Author Contributions

Writing—original draft preparation, W.Z.; writing—review and editing, F.G., Q.F., X.Z, Y.X., B.Z, and S.K.; project administration, funding acquisition—Y.X. and F.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by National Natural Science Foundation of China (61905103, 61905136); Natural Science Foundation of Shandong Province (ZR2021QF025).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

S. Kumar acknowledge to Double-Hundred Talent Plan of Shandong Province, China

Conflicts of Interest

The authors declare no conflict of interest.

References

H. Zhang, K. Gao, L. Han, S. Liu, T. Mei, F. Xiao and J. Zhao, "Nanometric displacement sensor with a switchable measuring range using a cylindrical vector beam excited silicon nanoantenna,". Opt. Express 2021, 29, 25109–25117. [CrossRef] [PubMed]
K.B. Rajesh and P.M. Anbarasan, "Generation of sub-wavelength and super-resolution longitudinally polarized non-diffraction beam using lens axicon,". Chin. Opt. Lett. 2008, 6, 785–787. [CrossRef]
X.-Z. Gao, P.-C. Zhao, X.-F. Sun, F. Yang, Y. Pan, Y. Li, C. Tu and H.-T. Wang, "Highly purified transversely polarized optical needle generated by the hybridly polarized vector optical field with hyperbolic symmetry,". J. Opt. 2020, 22, 105604. [CrossRef]
C.M. Sundaram, K. Prabakaran, P.M. Anbarasan, K.B. Rajesh and A.M. Musthafa, "Creation of Super Long Transversely Polarized Optical Needle Using Azimuthally Polarized Multi Gaussian Beam,". Chin. Phys. Lett. 2016, 33, 064203. [CrossRef]
W. Zhang, L. Zhang, C. Meng and F. Gao, "Generation of nanosecond cylindrical vector beams in two-mode fiber and its applications of stimulated Raman scattering,". Chin. Opt. Lett. 2021, 19, 010603. [CrossRef]
G.-B. Zhang, X.-Z. Gao, X.-F. Sun, R. Ma, Y. Wang and Y. Pan, "Airy-Gaussian vector beam and its application in generating flexible optical chains,". Opt. Express. 2023, 31, 30319–30331. [CrossRef] [PubMed]
L. Zhu, M. Deng, B. Lu, X. Guo and A. Wang, "Turbulence-resistant high-capacity free-space optical communications using OAM mode group multiplexing,". Opt. Express. 2023, 31, 14454–14463. [CrossRef] [PubMed]
B. Yang, Y. Chen, F. Wang and Y. Cai, "Trapping two types of Rayleigh particles simultaneously by a focused rotational elliptical Laguerre–Gaussian correlated Schell-model beam,". J. Quant. Spectrosc. Radiat. Transfer. 2021, 262, 107518. [CrossRef]
K. Chen, Z. Li, X. Sun, X. Kang, G. Wang and X. Gao, "Free-space generation of three-dimensional tunable vector optical cages,". J. Opt. Soc. Am. A. 2023, 40, 1809–1816. [CrossRef]
H. Yang, Z. Xie, G. Li, K. Ou, F. Yu, H. He, H. Wang and X. Yuan, "All-dielectric metasurface for fully resolving arbitrary beams on a higher-order Poincaré sphere,". Photonics Res. 2021, 9, 331–343. [CrossRef]
D. Wang, F. Liu, T. Liu, S. Sun, Q. He and L. Zhou, "Efficient generation of complex vectorial optical fields with metasurfaces,". Light: Sci. Appl. 2021, 10, 67. [CrossRef] [PubMed]
Y. Liang, Y. Dong, Y. Jin, L. Ke, C. Li and X. Jing, "Terahertz vortex beams generated by the ring-arranged multilayer transmissive metasurfaces,". Infrared Phys. Technol. 2022, 127, 104441. [CrossRef]
Y. Hu, Z. Ma, W. Zhao, J. Zhao, J. Liu, Q. Jing, J. Dou and B. Li, "Controlled generation of mode-switchable nanosecond pulsed vector vortex beams from a Q-switched fiber laser,". Opt. Express. 2022, 30, 33195–33207. [CrossRef] [PubMed]
J. Courtial and M.J. Padgett, "Performance of a cylindrical lens mode converter for producing Laguerre–Gaussian laser modes,". Opt. Commun. 1999, 159, 13–18. [CrossRef]
X. Zhao, J. Liu, M. Liu, R. Li, L. Zhang, G. Jin and X. Chen, "Off-axis pumped Tm: YLF vortex laser with continuously tunable wavelength,". Infrared Phys. Technol. 2022, 122, 104064. [CrossRef]
Y. Vasylkiv, I. Martynyuk-Lototska, I. Skab and R. Vlokh, "Generation of an optical vortex array in the course of acousto-optic diffraction,". Appl. Opt. 2018, 57, 10284–10289. [CrossRef]
Y. Zhang, S. Wen, S. Wang, J. Zhang, C. Tang, H. Zuo, F. Gao, F. Fan, Q. Zhang and Q. Xu, "Fully continuous spiral phase plate for ultraintense optical vortices,". Opt. Lett. 2023, 48, 2760–2763. [CrossRef] [PubMed]
H. Liu, S. Zheng, H. Wang, H. Gao, S. Wu, C. Li, C. Chang and G. Fang, "Time-domain characteristics of twisted pulses based on spiral phase plate at terahertz frequencies,". Infrared Phys. Technol. 2020, 106, 103265. [CrossRef]
Y. Zhu, W. Zhao, C. Zhang, K. Wang and J. Bai, "Non-iterative multifold strip segmentation phase method for six-dimensional optical field modulation,". Opt. Lett. 2022, 47, 1335–1338. [CrossRef]
B. Qian, T. Zeng, Z. Chen and J. Ding, "Generation of vector beams using a Wollaston prism and a spatial light modulator,". Optik. 2017, 148, 312–318. [CrossRef]
S. Liu, S. Qi, Y. Zhang, P. Li, D. Wu, L. Han and J. Zhao, "Highly efficient generation of arbitrary vector beams with tunable polarization, phase, and amplitude,". Photonics Res. 2018, 6, 228–233. [CrossRef]
C. Rosales-Guzmán, N. Bhebhe and A. Forbes, "Simultaneous generation of multiple vector beams on a single SLM,". Opt. Express. 2017, 25, 25697–25706. [CrossRef] [PubMed]

Figure 1. The schematic diagram and local section structure diagram of the experimental device. (a) S: He-Ne light source; SLM: transmission liquid crystal spatial light modulator; L₁-L₂: lens; PF: dual-channel pinhole filter; R_r: triangular reflection prism; M₁, M₂, M₃: mirrors; PBS: polarization beam splitter; CCD: charge-coupled device. (b) the schematic diagram of the dual-channel pinhole filter and the spatial spectrum diagram of the L₁ back focal plane of the lens. (c) diffraction angle chart between first-order and zero-order diffraction levels. (d) CGH loaded on the SLM.

Figure 2. Schematic diagram of the system-related parameter adjustment results.

Figure 3. Distribution of the light field intensity in different directions of the detector when

σ = θ

σ = θ + π / 2

σ = θ + 2 π r / r_{0}

σ = 2 θ + 4 π r / r_{0}

Figure 3. Distribution of the light field intensity in different directions of the detector when

σ = θ

σ = θ + π / 2

σ = θ + 2 π r / r_{0}

σ = 2 θ + 4 π r / r_{0}

Figure 4. Experimental results of multimode vector light field.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multi-Mode Vector Light Fields Generation Using Modified Off-Axis Interferometric Holography and Liquid Crystal Spatial Light Modulators

Abstract

1. Introduction

2. Materials and Methods

2.1. Experimental device and method

2.2. Principle analysis

3. Results and discussion

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe