C.1. Preamble file
function [rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, DBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal)
%=========================================================================
% Preamble for Missile Launched from Geostationary Orbit to Specific Target min time
%=========================================================================
%Scaled Values
rBar = primal.states(1,:); %States
thetaBar = primal.states(2,:);
phiBar = primal.states(3,:);
vBar = primal.states(4,:);
gammaBar = primal.states(5,:);
psiBar = primal.states(6,:);
LgammaBar = primal.controls(1,:); %Controls
LpsiBar = primal.controls(2,:);
tBar = primal.time; %Time
r0Bar = primal.initial.states(1); %Initial States
theta0Bar = primal.initial.states(2);
phi0Bar = primal.initial.states(3);
v0Bar = primal.initial.states(4);
gamma0Bar = primal.initial.states(5);
psi0Bar = primal.initial.states(6);
t0Bar = primal.initial.time; %Initial Time
rfBar = primal.final.states(1); %Final States
thetafBar = primal.final.states(2);
phifBar = primal.final.states(3);
vfBar = primal.final.states(4);
gammafBar = primal.final.states(5);
psifBar = primal.final.states(6);
tfBar = primal.final.time; %Final Time
uBar = primal.constants.uBar; %Constants
TBar = primal.constants.TBar;
mBar = primal.constants.mBar;
DBar = primal.constants.DBar;
g = primal.constants.g;
Cd = primal.constants.Cd;
S = primal.constants.S;
FU = primal.constants.FU;
R = primal.constants.R;
V = primal.constants.V;
TU = primal.constants.TU;
kq = primal.constants.kq;
DU = primal.constants.DU;
KU = primal.constants.KU;
%eof
C.1. Pz %Search Space for rBar
-pi, pi; %Search Space for thetaBar (Longitude)
-pi/2, pi/2; %Search Space for phiBar (Latitude)
0, 5; %Search Space for vBar
-pi, pi; %Search Space for gammaBar
-pi, pi]; %Search Space for psiBar
search.controls = [-11, 11; %Search Space for Lgamma
-11, 11]; %Search Space for Lpsi
%=========================================================================
%Defining Problem Specific Constants
%Unscaled Constants
mu = 3.986004418e5; %Earth Gravitational Parameter km/sec2
Thrust = 17.799; %4000lbf converted to kgkm/s^2
mass = 5000; %Initial Mass
MS4.constants.g = 0.00981; %Gravitational Constant of Earth in km/s^2
MS4.constants.Cd = 0.8; %Drag Coefficient
MS4.constants.S = 3.44e-6; %Drag Reference Area (km^2)
MS4.constants.kq = sqrt(1000)*9e-5; %kg^.5/km^.5
%Scaling Factors
MS4.constants.R = 6378; %Distance Scaling
MS4.constants.TU = sqrt(MS4.constants.R/MS4.constants.g);%Time Scaling
MS4.constants.AU = 1; %Angle Scaling => Radians remain unscaled
MS4.constants.V = MS4.constants.R/MS4.constants.TU; %Velocity Scaling
MS4.constants.M = 10; %Mass Scaling
MS4.constants.A = MS4.constants.R/(MS4.constants.TU^2);%Acceleration Scaling
MS4.constants.FU = MS4.constants.M*MS4.constants.A; %Force Scaling
MS4.constants.DU = MS4.constants.M/(MS4.constants.R^3); %Density Scaling
MS4.constants.KU = (MS4.constants.M^.5)/(MS4.constants.R^.5);
%Scaled Constants
MS4.constants.uBar = (MS4.constants.TU^2/(MS4.constants.R^3))*mu; %Scaled Earth Gravitational Parameter
%MS4.constants.TBar = Thrust/MS4.constants.FU; %Scaled Thrust
MS4.constants.TBar = Thrust;
MS4.constants.mBar = mass/MS4.constants.M; %Scaled Mass in kg
MS4.constants.DBar = 1.2344;
%=========================================================================
%Boundary Conditions
rInitial = 43378; %kilometers - Does not change
rFinal = 6378; %kilometers - Changes with tgt location
r0Bar = rInitial/MS4.constants.R; %Scale initial condition
rfBar = rFinal/MS4.constants.R; %Scale final condition
phi0Bar = deg2rad(0); %Latitude is unscaled in radians
theta0Bar = deg2rad(-90); %Longitude is unscaled in radians
v0Bar = 1/MS4.constants.V; %Initial velocity is near zero
gamma0Bar = deg2rad(-89); %Flight Path angle is unscaled in radians
psi0Bar = deg2rad(0); %Flight Path Azimuth is unscaled in radians
phifBar = deg2rad(36.6002); %Latitude of target to radians
thetafBar = deg2rad(-121.8947); %Longitude of target to radians
bounds.events = [r0Bar, r0Bar; %Radius of geosynchronous orbit
theta0Bar, theta0Bar;%Set initial latitude of orbit
phi0Bar, phi0Bar; %Set initial longitude of orbit
v0Bar, v0Bar; %v0 is 0
gamma0Bar, gamma0Bar;%Set initial flightpath angle
psi0Bar, psi0Bar; %Set initial flightpath azimuth
rfBar, rfBar; %Target radius
thetafBar, thetafBar;%Target latitude
phifBar, phifBar]; %Target longitude
%=========================================================================
%Initial and Final Time Constraints
bounds.initial.time = [0, 0]; %Clock starts at beginning
bounds.final.time = [0, 15]; %Guess on upper bound
%=========================================================================
%Path Constraints
bounds.path = [-10, 10; %Control Constraint, -10<=LBar<=10
-10, 10; %Control Constraint, -10<=LBar<=10
0, 4.9]; %Heating Rate Constraint
%=========================================================================
%Problem Definition
MS4.cost = 'MS4Cost';
MS4.dynamics = 'MS4Dynamics';
MS4.events = 'MS4Events';
MS4.path = 'MS4Path';
MS4.search = search;
MS4.bounds = bounds;
%=========================================================================
%DIDO Formulation check
check(MS4);
%=========================================================================
%Node selection
algorithm.nodes = 55;
%=========================================================================
%Run DIDO and time the program
tic
[cost, primal, dual] = dido(MS4, algorithm);
toc
%=========================================================================
%Output Analysis
[rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, DBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal);
MinTime = cost*MS4.constants.TU
lam_rBar = dual.dynamics(1,:);
lam_thetaBar = dual.dynamics(2,:);
lam_phiBar = dual.dynamics(3,:);
lam_vBar = dual.dynamics(4,:);
lam_gammaBar = dual.dynamics(5,:);
lam_psiBar = dual.dynamics(6,:);
eps1 = dual.path(1,:);
eps2 = dual.path(2,:);
eps3 = dual.path(3,:);
stat1 = lam_gammaBar./(mBar.*vBar);
stat2 = lam_psiBar./(mBar.*vBar.*cos(gammaBar));
%=========================================================================
%PLOTS
figure;
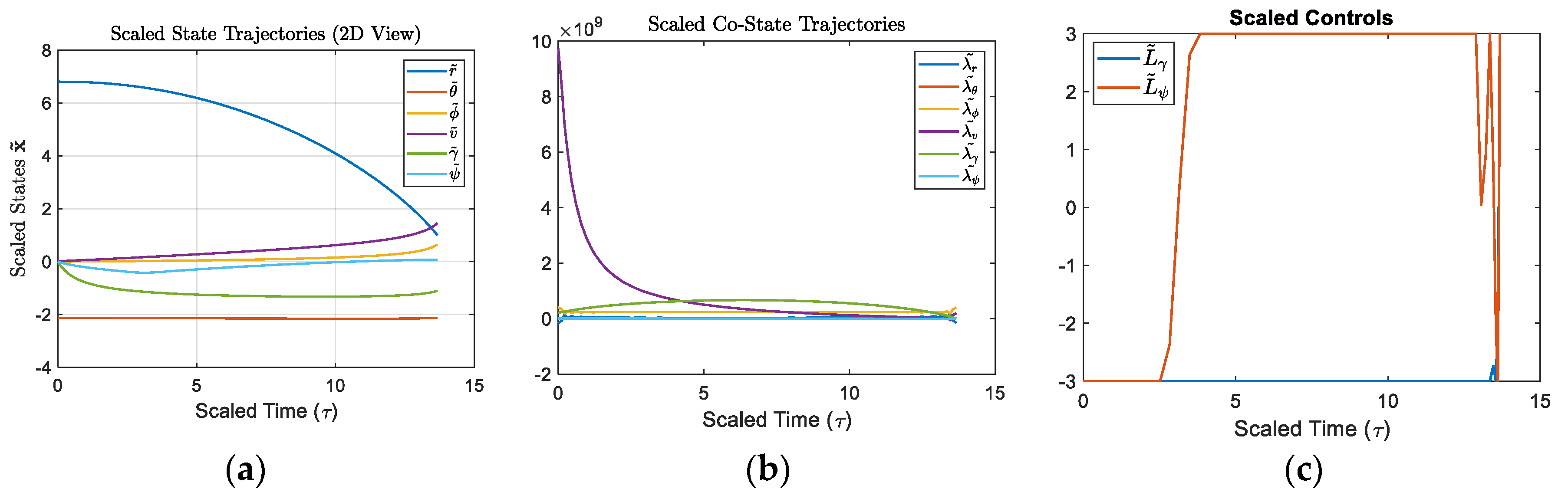
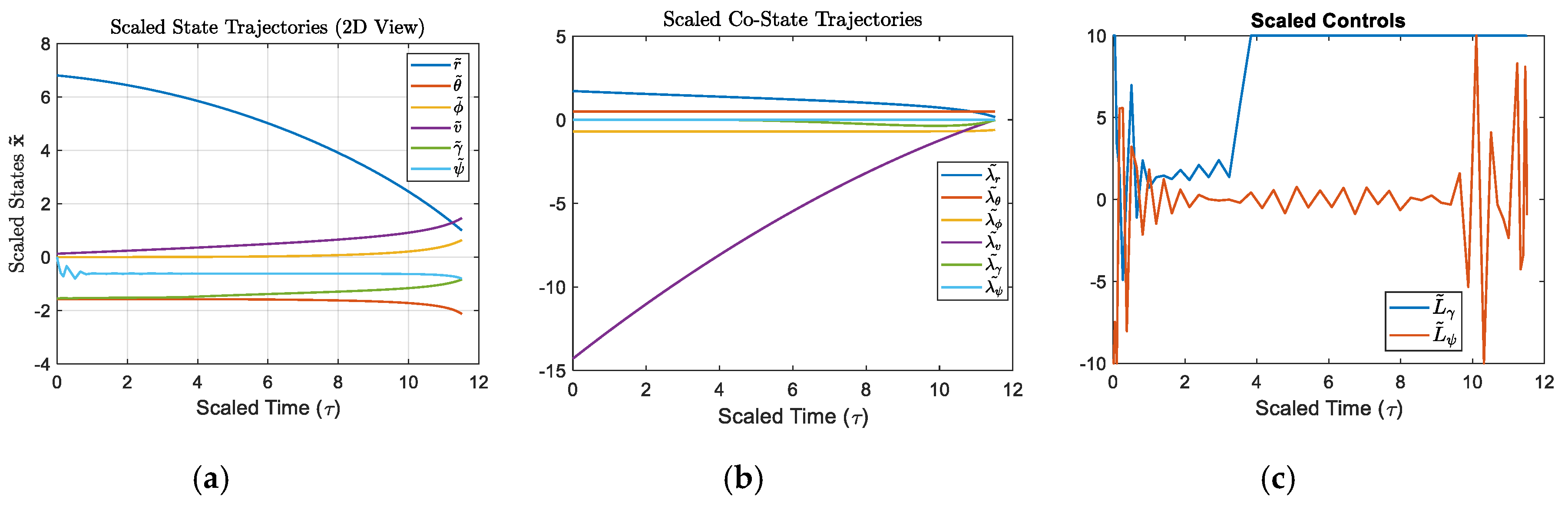
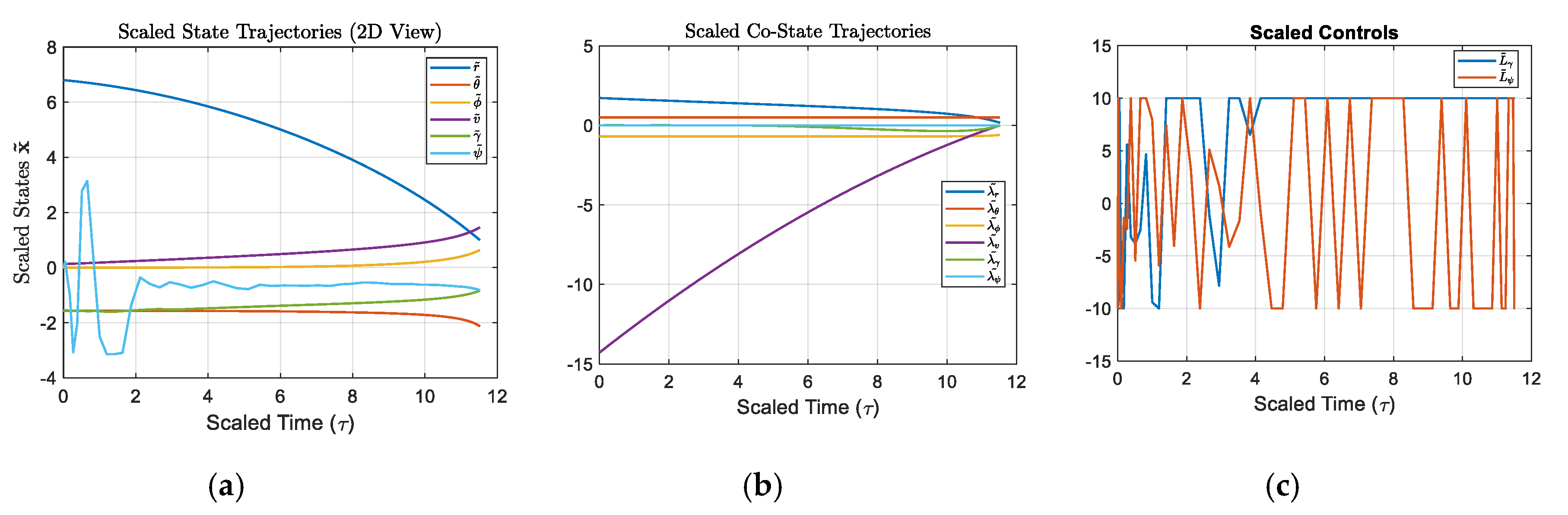
plot(tBar, [rBar; thetaBar; phiBar; vBar; gammaBar; psiBar]); grid on;
title('Scaled State Trajectories (2D View)','Interpreter','latex');
xlabel('Scaled Time (\tau)','FontSize',16);
ylabel('Scaled States $\mathbf{\tilde{x}}$','Interpreter','latex','FontSize',16);
legend('$\tilde{r}$','$\tilde{\theta}$','$\tilde{\phi}$','$\tilde{v}$','$\tilde{\gamma}$','$\tilde{\psi}$','Interpreter','latex','FontSize', 10);
figure;
plot(tBar, [LgammaBar; LpsiBar]); grid on;
title('Scaled Controls')
legend('$\tilde{L}_\gamma$','$\tilde{L}_\psi$','Interpreter','latex','FontSize',10)
xlabel('Scaled Time (\tau)','FontSize',16)
figure;
plot(tBar, [lam_rBar; lam_thetaBar; lam_phiBar; lam_vBar; lam_gammaBar; lam_psiBar]); grid on;
title('Scaled Co-State Trajectories','Interpreter','latex');
legend('$\tilde{\lambda_r}$','$\tilde{\lambda_\theta}$','$\tilde{\lambda_\phi}$','$\tilde{\lambda_v}$','$\tilde{\lambda_\gamma}$','$\tilde{\lambda_\psi}$','Interpreter','latex','FontSize', 10);
xlabel('Scaled Time (\tau)','FontSize',16);
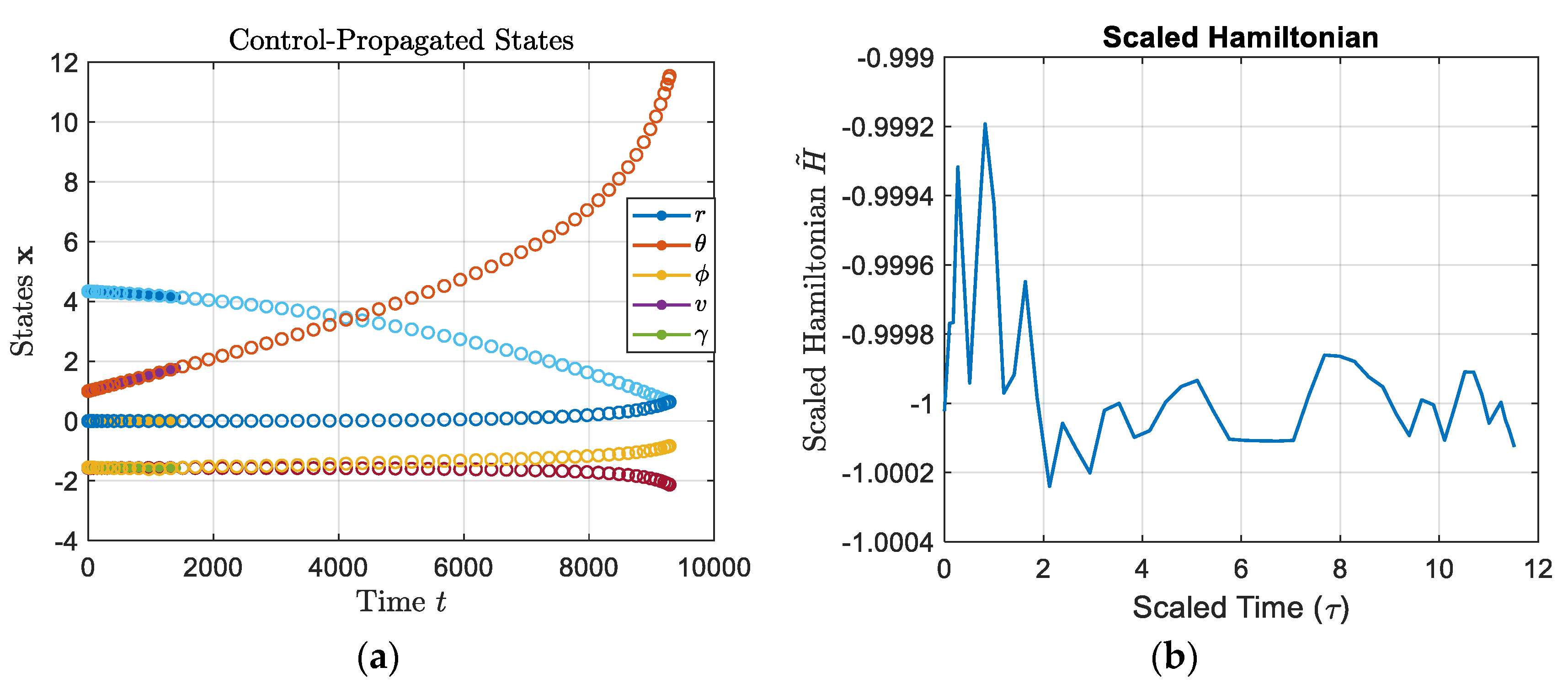
figure;
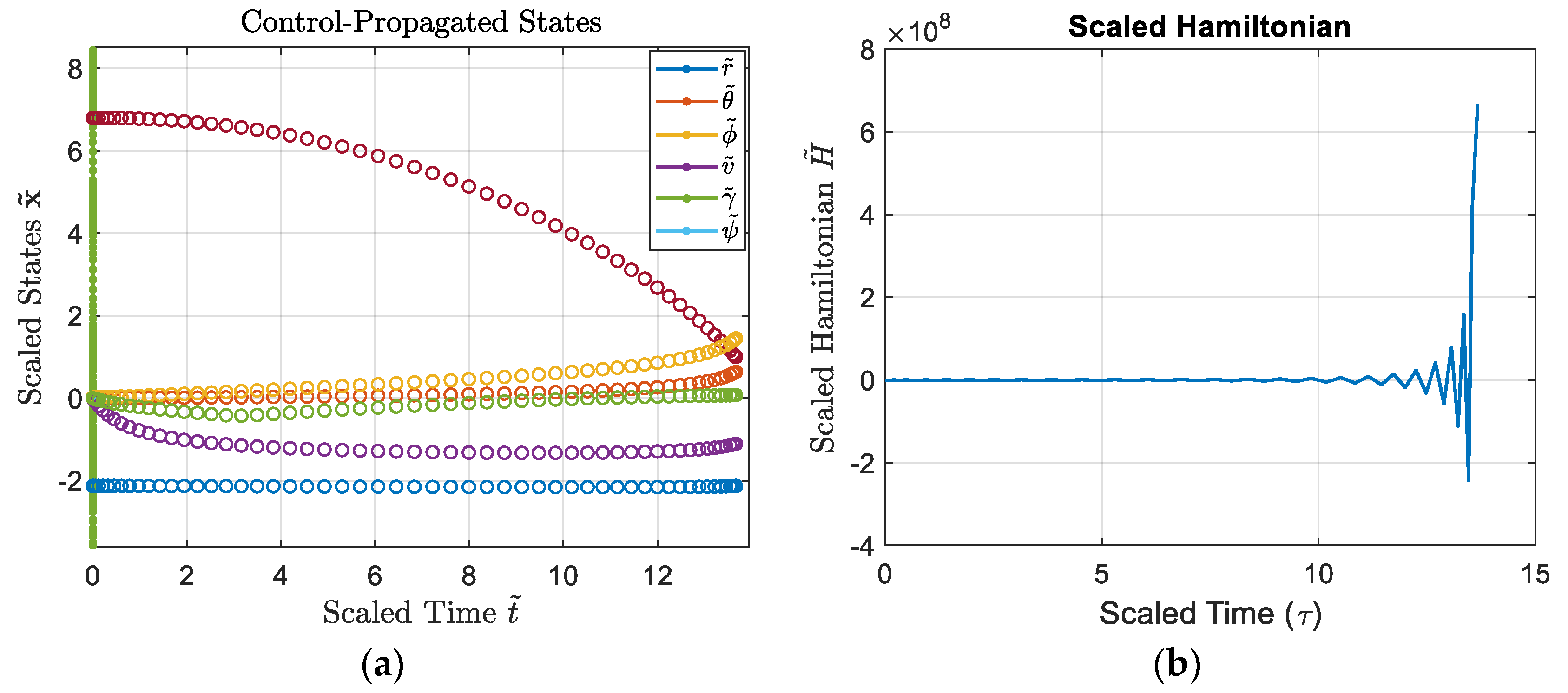
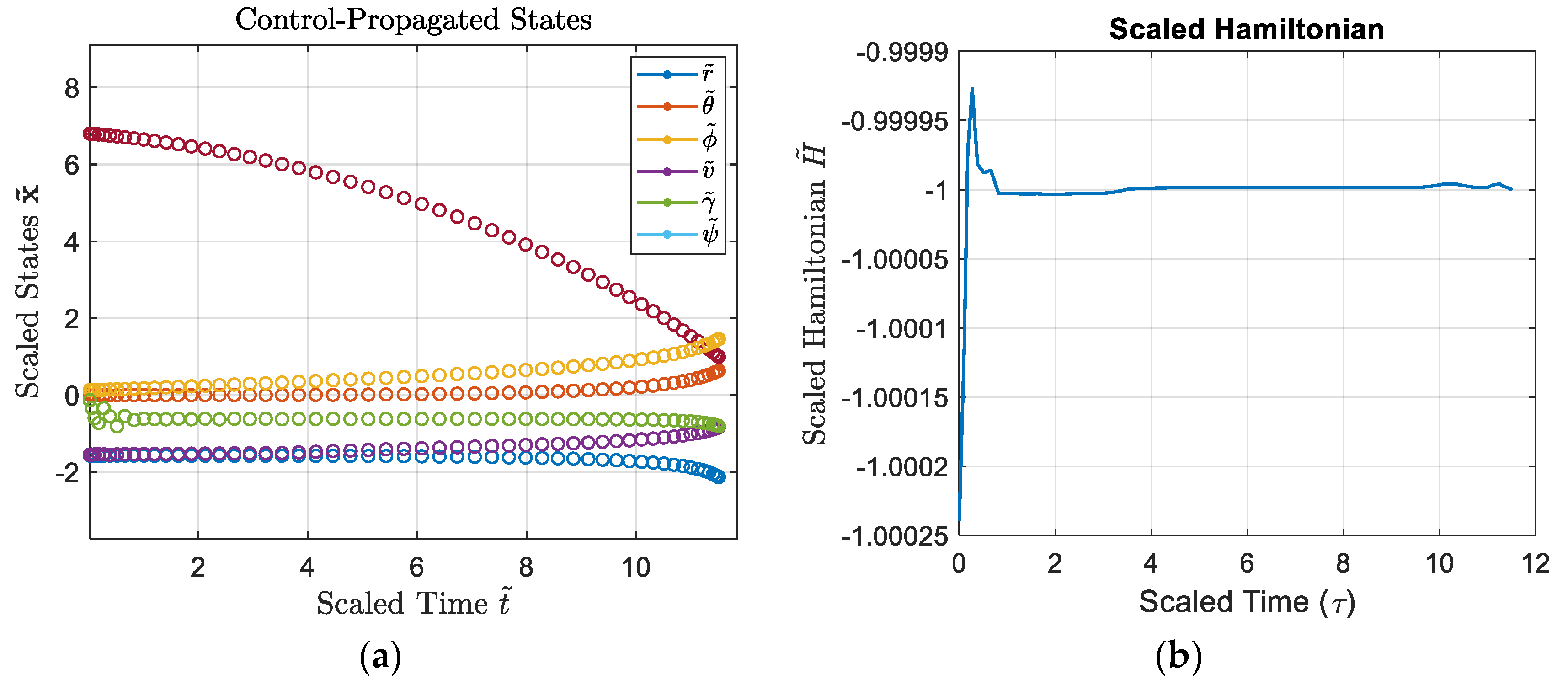
plot(tBar, dual.Hamiltonian); grid on;
title('Scaled Hamiltonian');
xlabel('Scaled Time (\tau)','FontSize',16);
ylabel('Scaled Hamiltonian $\tilde{H}$','Interpreter','latex','FontSize',16);
figure;
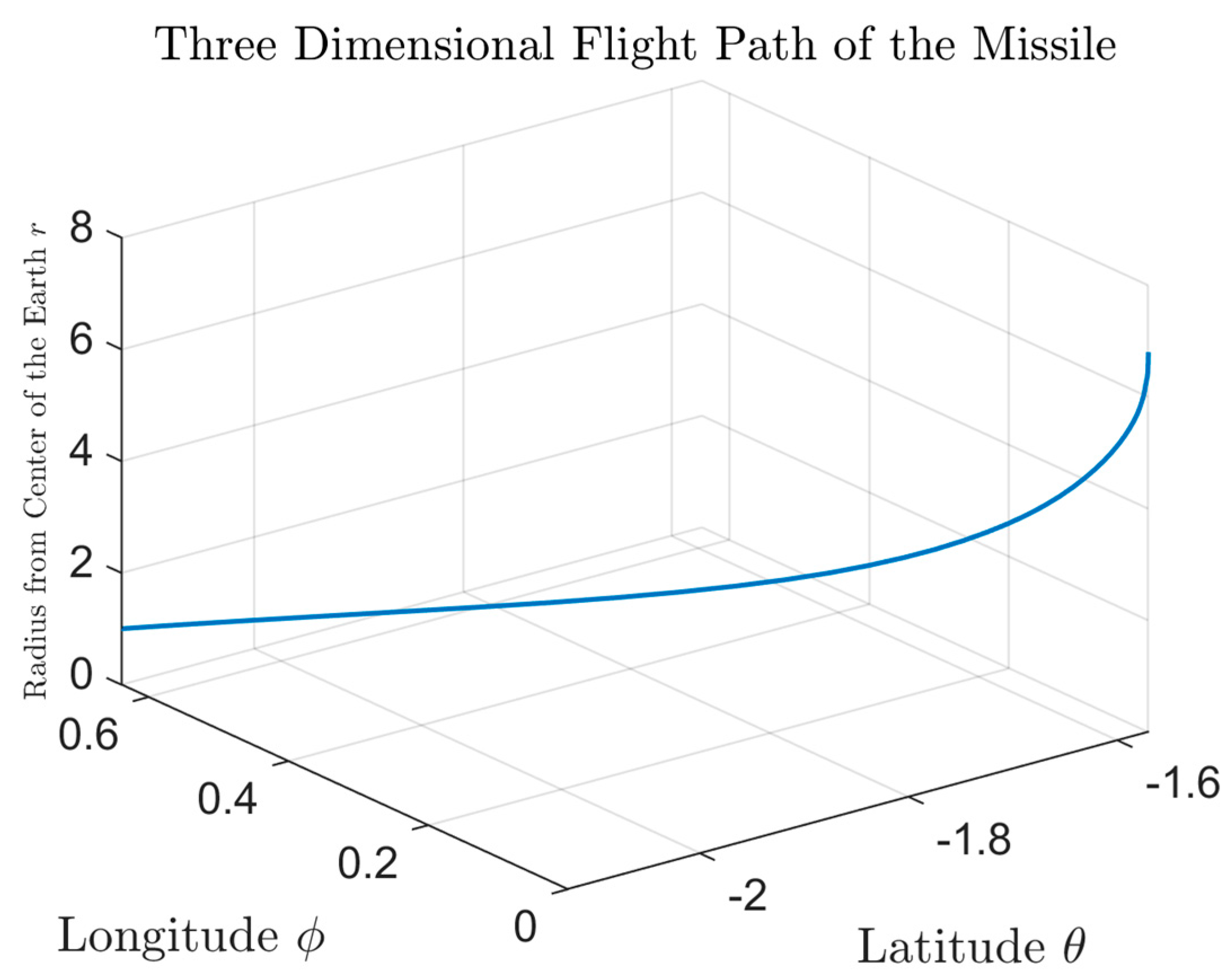
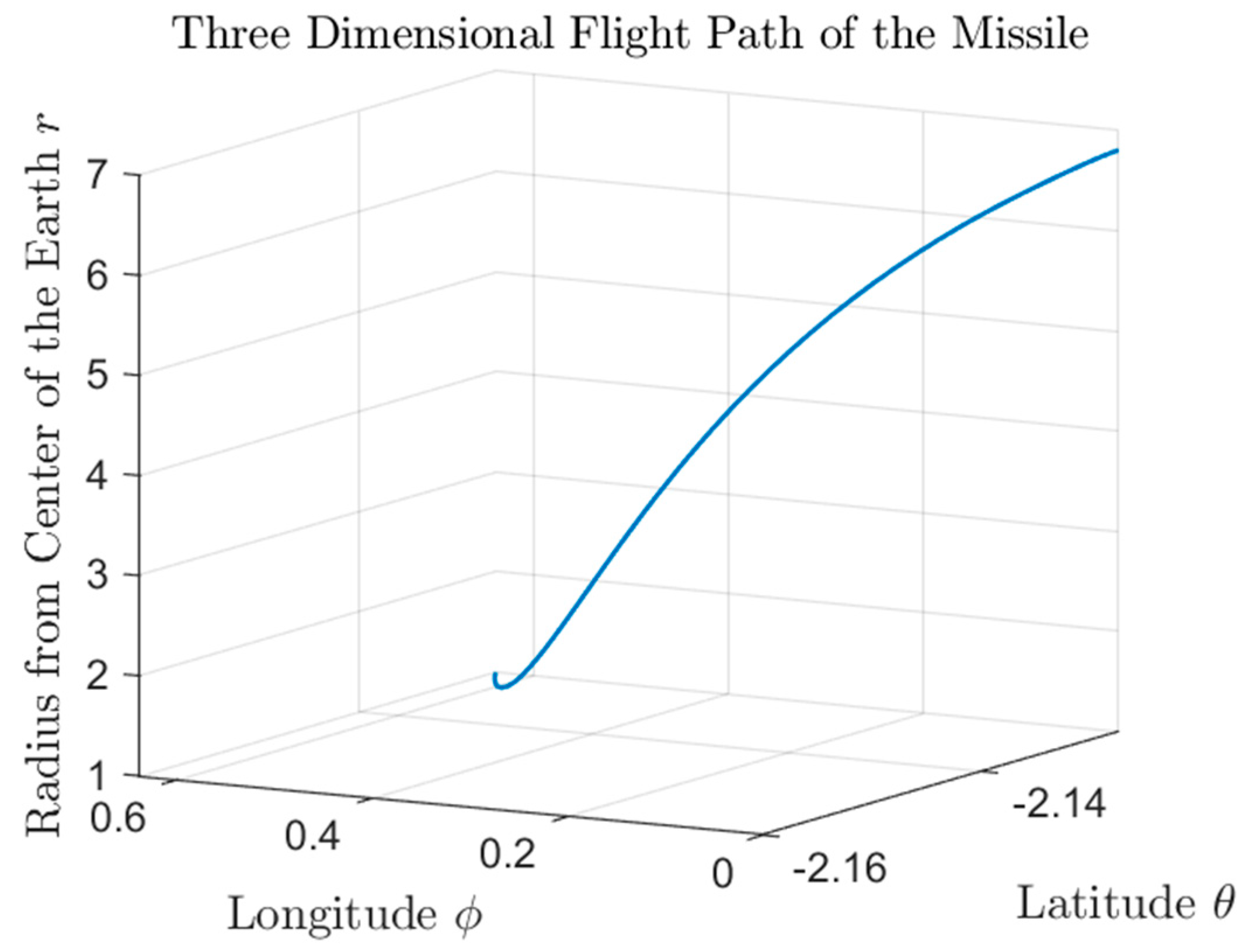
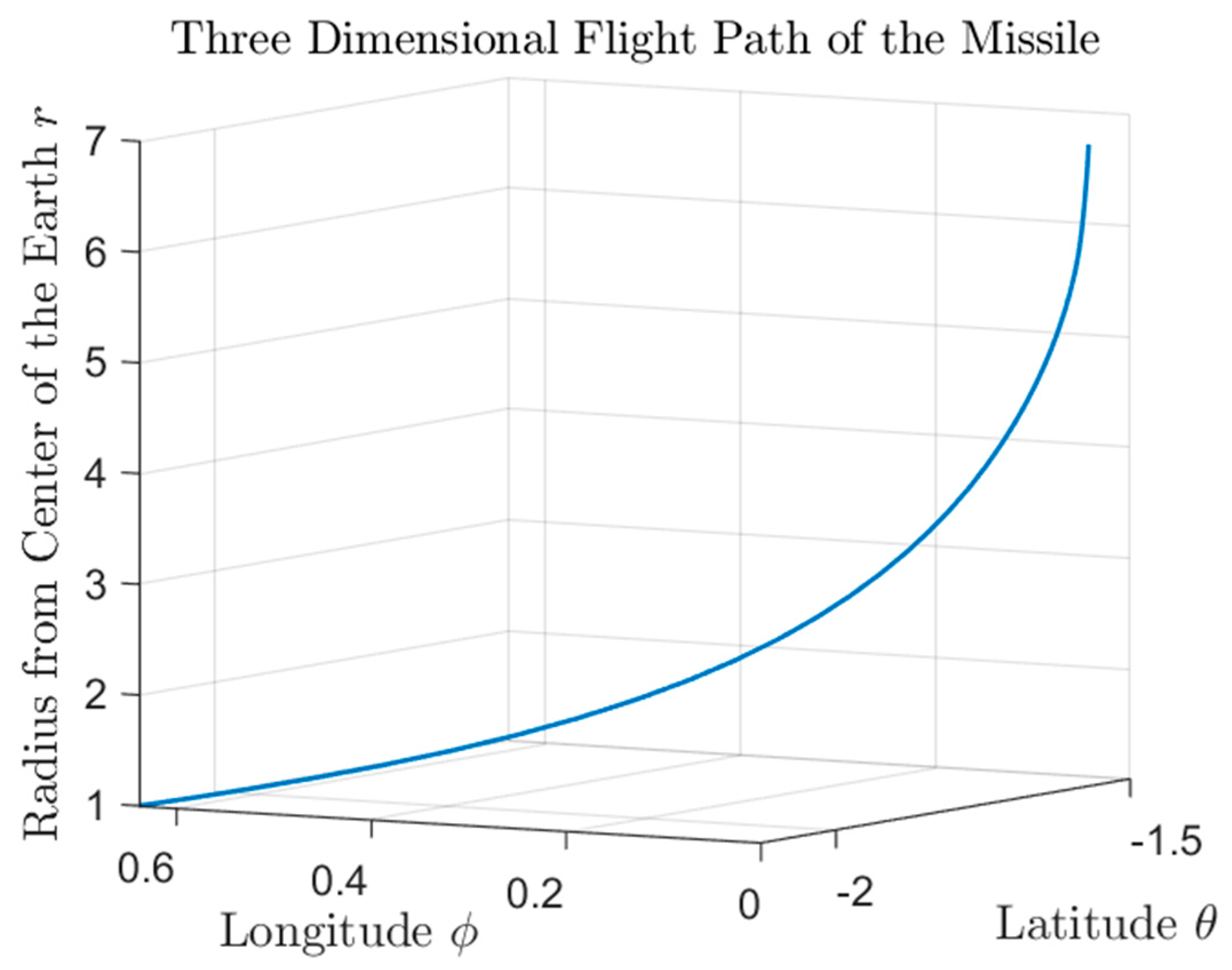
plot3(thetaBar,phiBar,rBar); grid on;
title('Three Dimensional Flight Path of the Missile','Interpreter','latex');
xlabel('Latitude ${\theta}$','Interpreter','latex','FontSize',16);
ylabel('Longitude ${\phi}$','Interpreter','latex','FontSize',16);
zlabel('Radius from Center of the Earth ${r}$','Interpreter','latex','FontSize',10);
figure;
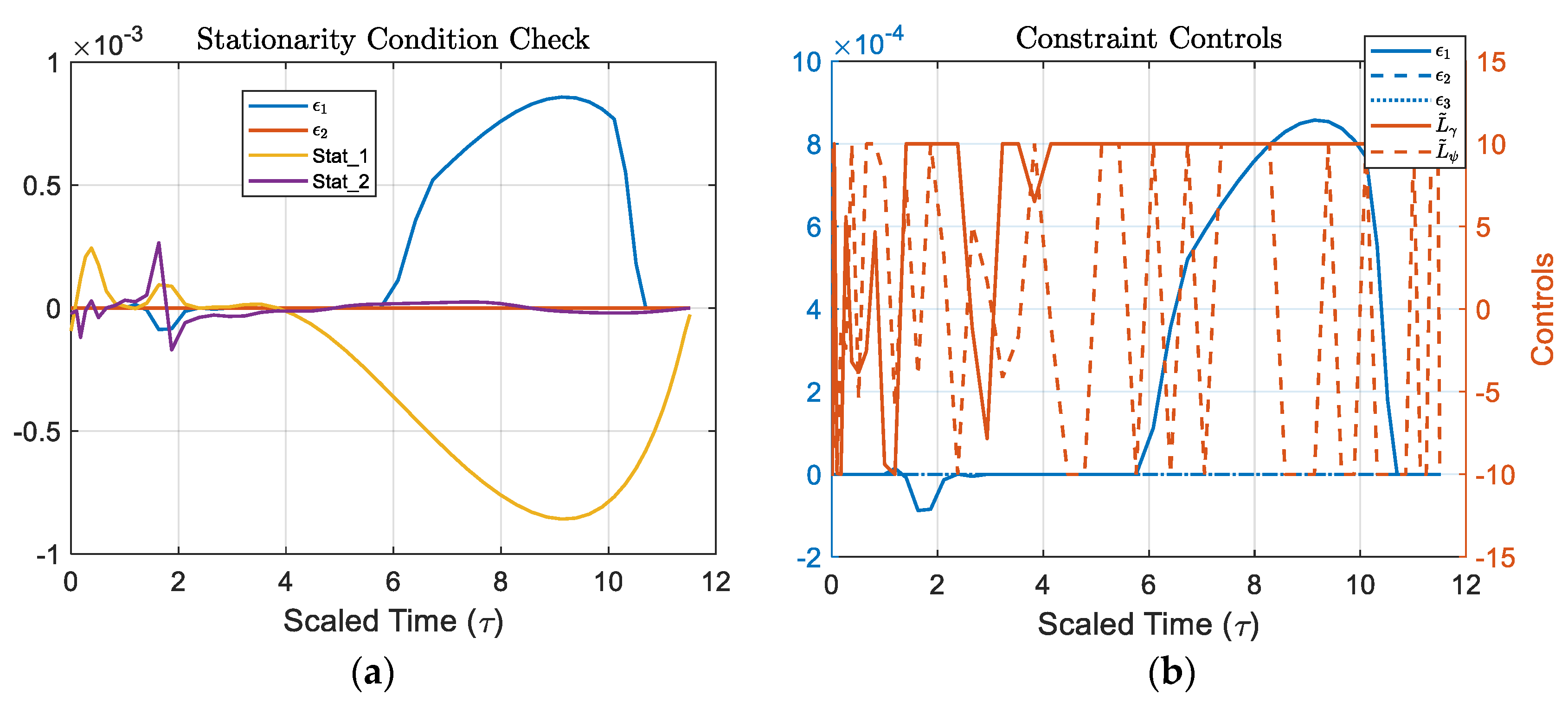
yyaxis left
plot(tBar, [eps1; eps2; eps3]); grid on;
title('Constraint Controls','Interpreter','latex');
xlabel('Scaled Time (\tau)','FontSize',16);
ylabel('${\epsilon}$','Interpreter','latex','FontSize',16);
yyaxis right
plot(tBar, [LgammaBar; LpsiBar]);
legend('${\epsilon_1}$','${\epsilon_2}$','${\epsilon_3}$','$\tilde{L}_\gamma$','$\tilde{L}_\psi$','Interpreter','latex','FontSize', 10);
ylabel('Controls');
figure;
plot(tBar, [eps1; eps2; stat1; stat2]); grid on;
title('Stationarity Condition Check','Interpreter','latex');
xlabel('Scaled Time (\tau)','FontSize',16);
legend('${\epsilon_1}$','${\epsilon_2}$','Stat_1','Stat_2','Interpreter','latex','FontSize',10);
%==========================================================================
%Unscale States, Co-States, Controls
r = rBar.*MS4.constants.R;
theta = thetaBar;
phi = phiBar;
v = MS4.constants.V.*vBar;
gamma = gammaBar;
psi = psiBar;
T = tBar.*MS4.constants.TU;
lam_r = (MS4.constants.TU/MS4.constants.R) .* lam_rBar;
lam_theta = (MS4.constants.TU/MS4.constants.AU) .* lam_thetaBar;
lam_phi = (MS4.constants.TU/MS4.constants.AU) .* lam_phiBar;
lam_v = (MS4.constants.TU/MS4.constants.V) .* lam_vBar;
lam_gamma = (MS4.constants.TU/MS4.constants.AU) .* lam_gammaBar;
lam_psi = (MS4.constants.TU/MS4.constants.AU) .* lam_psiBar;
Lgamma = LgammaBar./(MS4.constants.TU^2/(MS4.constants.R*MS4.constants.M));
Lpsi = LpsiBar./(MS4.constants.TU^2/(MS4.constants.R*MS4.constants.M));
% figure;
% plot(T, [(r.*.0003); v]); grid on;
% title('State Trajectories','Interpreter','latex');
% xlabel('Time ${t}$','Interpreter','latex','FontSize',16);
% ylabel('States $\mathbf{{x}}$','Interpreter','latex','Fontsize',16);
% legend('${r}$','${v}$','Interpreter','latex','FontSize',16);
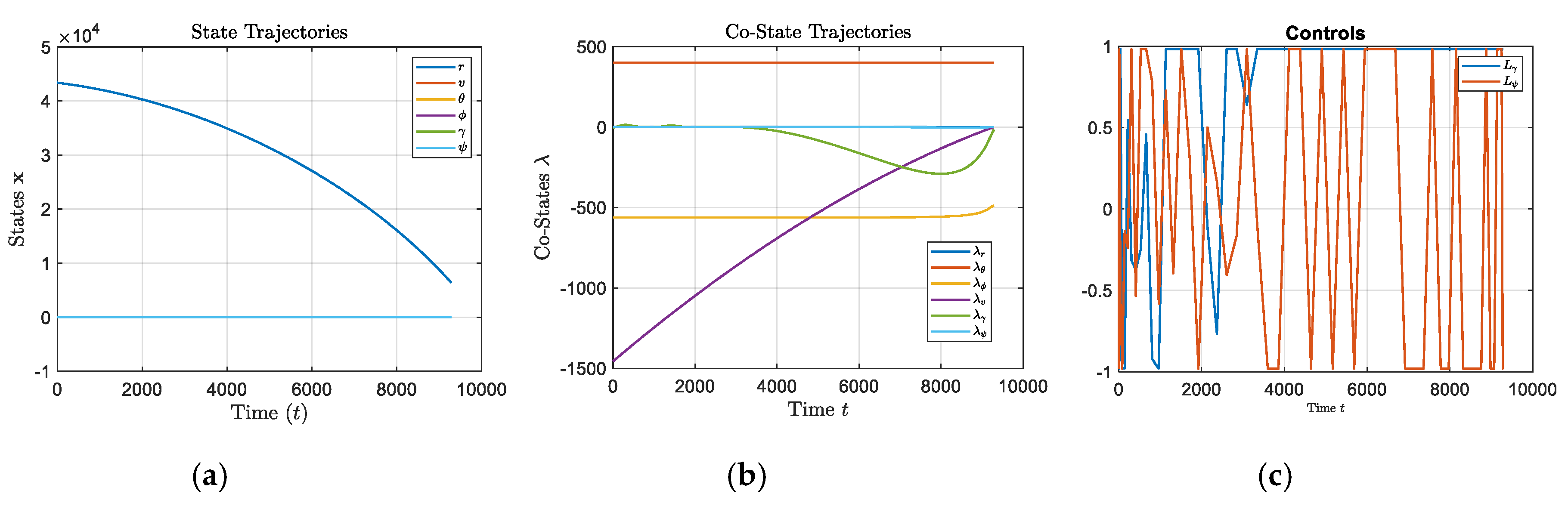
figure;
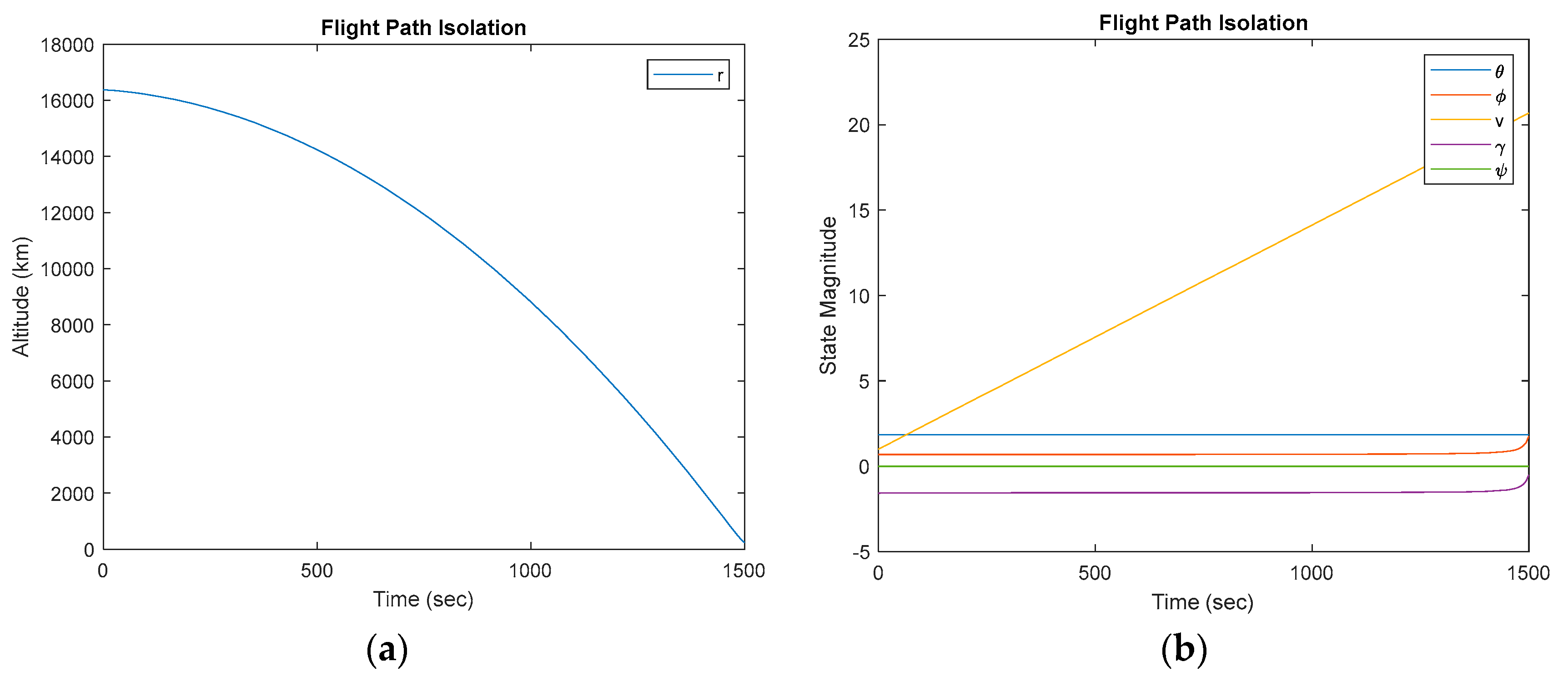
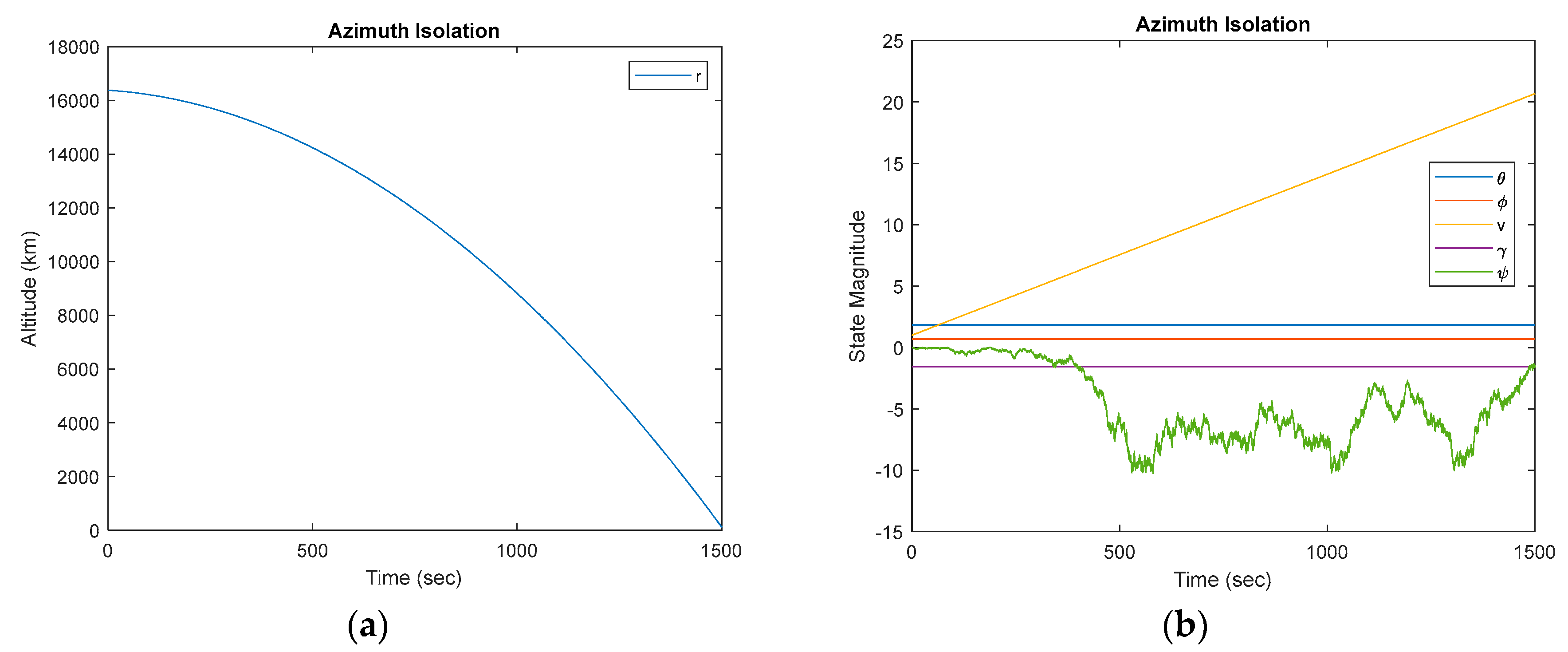
plot(T, [r; v; theta; phi; gamma; psi]); grid on;
title('State Trajectories','Interpreter','latex');
xlabel('Time $(t)$','Interpreter','latex','FontSize',16);
ylabel('States $\mathbf{{x}}$','Interpreter','latex','FontSize',16);
legend('${r}$','${v}$','${\theta}$','${\phi}$','${\gamma}$','${\psi}$','Interpreter','latex','FontSize',10);
figure;
plot(T, [lam_r; lam_theta; lam_phi; lam_v; lam_gamma; lam_psi]); grid on;
title('Co-State Trajectories','Interpreter','latex');
xlabel('Time ${t}$','Interpreter','latex','FontSize',16);
ylabel('Co-States $\mathbf{{\lambda}}$','Interpreter','latex','FontSize',16);
legend('${\lambda_r}$','${\lambda_\theta}$','${\lambda_\phi}$','${\lambda_v}$','${\lambda_\gamma}$','${\lambda_\psi}$','Interpreter','latex','FontSize',10);
figure;
plot(T, [Lgamma; Lpsi]); grid on;
title('Controls');
legend('${L_\gamma}$','${L_\psi}$','Interpreter','latex','FontSize',10);
xlabel('Time ${t}$','Interpreter','latex','FontSize',10);
%==========================================================================
%Individual State Comparisons
figure;
yyaxis left
plot(T,r);
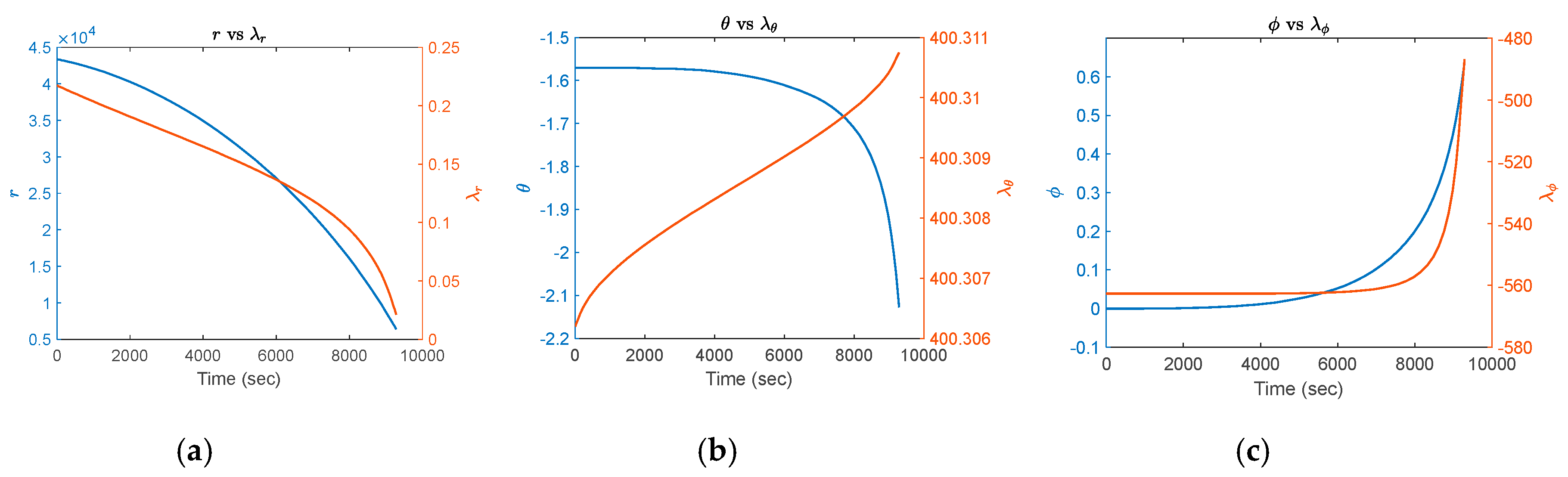
xlabel('Time (sec)'),ylabel('${r}$','Interpreter','latex');
yyaxis right
plot(T,lam_r);
ylabel('${\lambda_r}$','Interpreter','latex')
title('${r}$ vs ${\lambda_r}$','Interpreter','latex')
figure;
yyaxis left
plot(T,theta);
xlabel('Time (sec)'),ylabel('${\theta}$','Interpreter','latex');
yyaxis right
plot(T,lam_theta);
ylabel('${\lambda_\theta}$','Interpreter','latex')
title('${\theta}$ vs ${\lambda_\theta}$','Interpreter','latex')
figure;
yyaxis left
plot(T,phi);
xlabel('Time (sec)'),ylabel('${\phi}$','Interpreter','latex');
yyaxis right
plot(T,lam_phi);
ylabel('${\lambda_\phi}$','Interpreter','latex')
title('${\phi}$ vs ${\lambda_\phi}$','Interpreter','latex')
figure;
yyaxis left
plot(T,v);
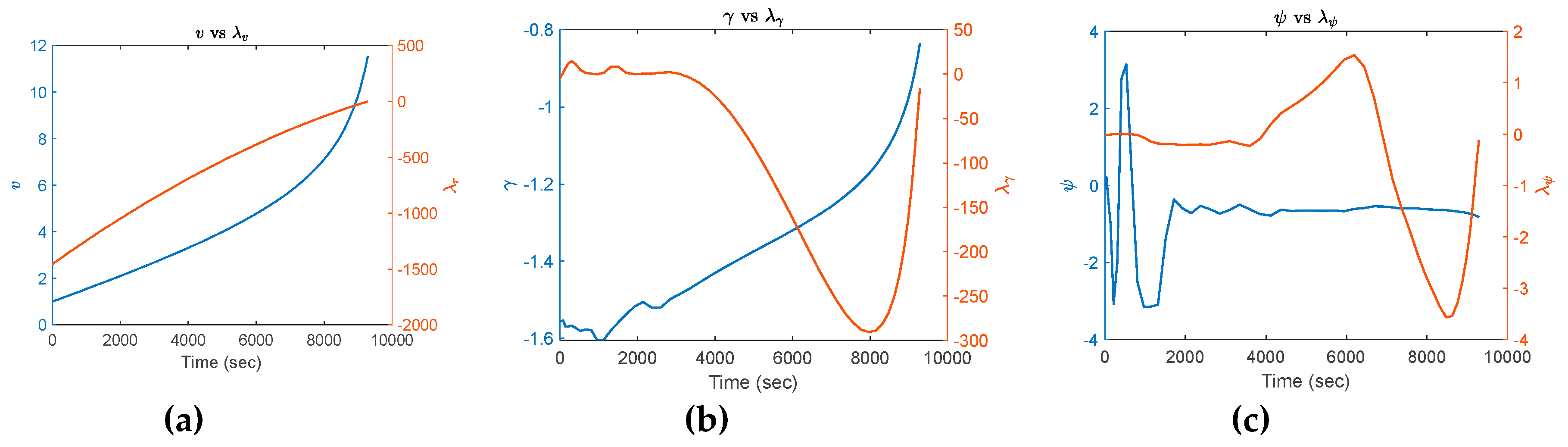
xlabel('Time (sec)'),ylabel('${v}$','Interpreter','latex');
yyaxis right
plot(T,lam_v);
ylabel('${\lambda_r}$','Interpreter','latex')
title('${v}$ vs ${\lambda_v}$','Interpreter','latex')
figure;
yyaxis left
plot(T,gamma);
xlabel('Time (sec)'),ylabel('${\gamma}$','Interpreter','latex');
yyaxis right
plot(T,lam_gamma);
ylabel('${\lambda_\gamma}$','Interpreter','latex')
title('${\gamma}$ vs ${\lambda_\gamma}$','Interpreter','latex')
figure;
yyaxis left
plot(T,psi);
xlabel('Time (sec)'),ylabel('${\psi}$','Interpreter','latex');
yyaxis right
plot(T,lam_psi);
ylabel('${\lambda_\psi}$','Interpreter','latex')
title('${\psi}$ vs ${\lambda_\psi}$','Interpreter','latex')
% %==========================================================================
% Feasibility Check
t_vec = T(:);
[T_feas, X_feas] = ode45(@(t,y)stateDynamics(t,y,t_vec,[Lgamma; Lpsi]),[t_vec(1) t_vec(end)],[r(1);theta(1);phi(1);v(1);gamma(1);psi(1)]);
r_feas = X_feas(:,1);
theta_feas = X_feas(:,2);
phi_feas = X_feas(:,3);
v_feas = X_feas(:,4);
gam_feas = X_feas(:,5);
psi_feas = X_feas(:,6);
figure;
hLines = plot(T_feas,(r_feas./1e4),'.-',T_feas,theta_feas,'.-',T_feas,phi_feas,'.-',T_feas,v_feas,'.-',T_feas,gam_feas,'.-',T_feas,psi_feas,'.-'); hold on; grid on;
hMarkers4 = plot(t_vec,[r./1e4; theta; phi; v; gamma; psi],'o');
set(hLines,'MarkerSize',12);
set(hMarkers4,'LineWidth',1);
title('Control-Propagated States','Interpreter','latex');
xlabel('Time ${t}$','Interpreter','latex','FontSize',16);
ylabel('States $\mathbf{{x}}$','Interpreter','latex','FontSize',16);
legend('${r}$','${\theta}$','${\phi}$','${v}$','${\gamma}$','Interpreter','latex');
%==========================================================================
%% FEASIBILITY CHECK FUNCTION
function dXdt = stateDynamics(t,X,tData,uData,MS4)
Lg_t = interp1(tData,uData(1,:),t,'pchip');
Lp_t = interp1(tData,uData(2,:),t,'pchip');
r = X(1);
theta = X(2);
phi = X(3);
v = X(4);
gamma = X(5);
psi = X(6);
drdt = v .* sin(gamma);
dtdt = (v.*cos(gamma).*sin(psi))./(r.*cos(phi));
dpdt = (v.*cos(gamma).*cos(psi))./r;
dvdt = -(.1211/5000)-((3.986004418e5.*sin(gamma))./(r.^2))+(1.7461/5000);
dgdt = (Lg_t./(5000.*v))-((3.9860044815e5.*cos(gamma))./((r.^2).*v))+((v./r).*cos(gamma));
didt = (Lp_t./(5000.*v.*cos(gamma)))+((v./r).*cos(gamma).*sin(psi).*tan(phi));
dXdt = [drdt; dtdt; dpdt; dvdt; dgdt; didt];
end
C.1. Dynamics file
All appendix sections must be cited in the main text. In the appendices, Figures, Tables, etc. should be labeled starting with “A”—e.g., Figure A1, Figure A2, etc.
function dxdtBar = MS4Dynamics(primal)
%Missile from Geosynchronous Orbit to target on Earth in minimum time
%=========================================================================
[rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, DBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal);
%Equations of Motion
rdotBar = vBar.*sin(gammaBar);
thetadotBar = (vBar.*cos(gammaBar).*sin(psiBar))./(rBar.*cos(phiBar));
phidotBar = (vBar.*cos(gammaBar).*cos(psiBar))./rBar;
[T, a, P, rho] = atmosisa((rBar.*R.*1000)-(R*1000));%Unscale altitude and change to meters
rhoBar = rho./DU; %Scale Density by Density Unit Scale Factor
SBar = S/(R^2); %Scale ReferenceArea
Dscale = .5.*rhoBar.*vBar.^2*Cd*SBar; %Scaled Drag
vdotBar = -(DBar/mBar)-((uBar.*sin(gammaBar))./(rBar.^2))+(TBar./mBar);
gammadotBar = (LgammaBar./(mBar.*vBar))-((uBar*cos(gammaBar))./(rBar.^2.*vBar))+((vBar./rBar).*cos(gammaBar));
psidotBar = (LpsiBar./(mBar.*vBar.*cos(gammaBar)))+((vBar./rBar).*cos(gammaBar).*sin(psiBar).*tan(phiBar));
dxdtBar = [rdotBar;
thetadotBar;
phidotBar;
vdotBar;
gammadotBar;
psidotBar];
%eof
C.1. Cost file
function [EndpointCost, RunningCost] = MS4Cost(primal)
%Missile from Geosynchronous Orbit to target on Earth in minimum time
%=========================================================================
[rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, DBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal);
EndpointCost = tfBar;
RunningCost = 0;
%eof
C.1. Events file
function endpointFunction = MS4Events(primal)
%Missile from Geosynchronous Orbit to target on Earth in minimum time
%Endpoint File
%=========================================================================
[rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal);
endpointFunction = zeros(9,1);
%Beginnning Enpoints
endpointFunction(1) = r0Bar;
endpointFunction(2) = theta0Bar;
endpointFunction(3) = phi0Bar;
endpointFunction(4) = v0Bar;
endpointFunction(5) = gamma0Bar;
endpointFunction(6) = psi0Bar;
%Final Endpoints
endpointFunction(7) = rfBar;
endpointFunction(8) = thetafBar;
endpointFunction(9) = phifBar;
C.1. Path file
function H = MS4Path(primal)
%Missile from Geosynchronous Orbit to target on Earth in minimum time
%-----------------------------------------
% Call preamble and load primal variables:
%-----------------------------------------
[rBar, thetaBar, phiBar, vBar, gammaBar, psiBar, LgammaBar, LpsiBar, tBar, ...
r0Bar, theta0Bar, phi0Bar, v0Bar, gamma0Bar, psi0Bar, t0Bar, ...
rfBar, thetafBar, phifBar, vfBar, gammafBar, psifBar, tfBar, ...
uBar, TBar, mBar, DBar, Cd, S, R, V, kq, FU, DU, KU] ...
= MS4Preamble(primal);
%=======================================================
% path constraint function:
H(1,:) = LgammaBar;
H(2,:) = LpsiBar;
h = (rBar.*R.*1000);
rho0 = 1.225; %Sea level density in kg/m^3
Hs = 7500; %Height scale
rp = R*1000;
rho = rho0*exp(-(h-rp)/Hs);
vd = vBar.*V.*1000;
qdot = kq.*sqrt(rho).*(vd.^3);
H(3,:) = qdot/1e9; %Scale in Engineering Units