Prerpints.org logo
Preprint
Article

Simulation Study of The Dump Trucks' Speed Profile Impact on Open Pit Efficiency

Altmetrics

Downloads

201

Views

29

Comments

0

This version is not peer-reviewed

Submitted:

13 December 2023

Posted:

14 December 2023

You are already at the latest version

Alerts
Abstract
An algorithm is presented for a micro-model of a mining dump truck movement, which allows determining the optimal speed and acceleration of a vehicle, considering the change of the road grade. The structure of the simulation macro-model of an excavator-and-dump truck complex has been developed. The procedure for integrating a micro-model of a dump truck movement into a simulation model is shown. As a result of a series of experiments with a macro-model, the influence of open pit roads grade on the performance and efficiency of excavator-and-dump truck complexes was established. The necessity of considering in simulation excavator-and-dump truck complexes the speed regulation of dump trucks depending on the change in road grade is shown.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

The efficiency and productivity of the open pits and excavator-and-dump truck complexes has a significant impact on the performance of mining enterprises. Most open pits in the world use dump trucks to transport rock mass from excavators to unloading points. The share of transport costs in energy consumption of the process of mining reaches 55-60% when mining from a depth of 100-150 m, and with an increase in depth to 200-250 m – 65-70%. More than 50% of them are accounted for by road transport [1]. The decrease in the productivity of dump trucks is 25-39%, with an increase in the depth of open pits for every 100 meters [2]. Mining enterprises operate in conditions of a decrease in the percentage of minerals in the rock mass, an increase in prices for fuels and lubricants, and a tightening of environmental requirements. In such conditions, the importance of the scientific task of increasing the productivity of excavator-and-dump truck complexes increases.
Automation of all processes, including transport work, is a modern solution to improve the efficiency of mining enterprises [3]. Robotic transport complexes [4,5], Wheeled Mobile Robots (WMR) [6], Autonomous Haulage Systems (AHS) [7], as well as Automated guided vehicles (AGVs) [8,9,10] are now becoming more widespread.
Such vehicles can potentially consider many factors affecting speed performance and determine the optimal current speed, depending on the tasks and constraints. For example, in studies [11,12,13], the effect on the dynamics of a car of its mass and longitudinal road grade, as well as speed, is shown [14]. This, in turn, reduces the driving time [15] or travel time along the route [16], increases the number of trips during the operation of the mining dump truck.
The efficiency of using an Autonomous Driving Vehicle, ADV [14] or AHS makes it possible to increase the efficiency of vehicle operation also because of reducing emissions of harmful and polluting substances, reducing tire wear and fuel consumption [17]. Thus, the study [18] shows the influence of the value of the longitudinal profile of the road on the volume of PM2.5 particulate matter emissions for various types of vehicles. Moreover, vehicle emissions also depend on experience, and the gender of the driver [19], as well as his response to changes in the longitudinal road grade and the intensity of traffic [20]. The results of these studies show the effectiveness of using ADV or AHS to reduce or eliminate the influence of subjective factors on the speed of the car.
Research in the field of intellectualization of vehicles and improvement of autonomous driving systems, at present, is aimed at considering various factors that affect the speed of both an individual car and the efficiency of vehicle fleet operation. The main factors include: the value of the longitudinal slope of both individual sections of the road [21,22,23] and several sections along the entire length of the highway route [15,16], inertia forces [24], the interaction of vehicles in the traffic flow [25].
Regression models, Bayesian approach [20], nonlinear mathematical models [26], dynamic programming methods [16], Markov chains [15] are most widely used as research methods and models of vehicle speed characteristics.
We propose to divide the existing studies of the speed characteristics of mining dump trucks into three groups. In the first group, we included studies that allow us to justify various design solutions. Such decisions include: the rationale for the choice of a model of dump trucks depending on the parameters of the open pit [27], as well as the calculation of the critical length of the inclined section of the route uphill [22,28]. The second group combines the development and research of various models of dump trucks’ speed profiles [21,23]. The studies of this group are focused on establishing the dependencies of the vehicle speed on various factors and are designed to build generalized speed profiles or speed diagrams. These patterns are used to create ADV or AHS control algorithms. Finally, in the third group, the authors included studies that systematically consider the effect of the longitudinal profile of open pit roads [26] and the speed of dump trucks [29] on the performance of excavator-and-dump truck complexes [1], the cost of transportation [30], and the productivity of the open pit.
Analysis of the studies of the third group shows that the speed of the mining dump trucks has a significant impact on the performance of the open pit. The need to optimize the speed of dump trucks is due to the presence of two conflicting requirements. On the one hand, when driving at low speed, the overhaul mileage of dump trucks is lengthened, fuel consumption and tire wear are reduced. On the other hand, the productivity of the excavator-and-dump truck complex decreases and there is a need to increase the number of the working fleet of dump trucks.
Thus, the authors concluded that it is necessary to take a systematic account of many factors that affect the performance of excavator-and-dump truck complexes of open pits. To implement this approach, the authors propose to combine the micro-model of the dump trucks’ speed profile with the macro-model of the operation of the dump truck fleet in an open pit. The novelty of the developed micromodel of the dump truck speed profile lies in the complex consideration of the influence of several factors on the speed. We propose to consider the influence of the following factors: the value of the longitudinal road grade in individual sections of the route, the presence of protracted descents and ascents, changes in the road grade of the route sections, changes in the gear ratio. The macro-model of the dump truck fleet operation presented in the article allows determining the optimal number of the working fleet of dump trucks, considering the dynamics of the speed of individual vehicles, calculated using the micro-model. In addition, the macro-model considers the technical characteristics of excavators and the geometrical parameters of the open pit.
The rest of the paper is organized as follows. Section 2 describes the algorithm of the micro-model of dump truck motion. The algorithm illustrates the procedure for calculating the dump truck speed at specified time intervals, considering the change in the longitudinal profile of the highway route and the technical characteristics of the dump truck model. Section 3 presents the composition and structure of a simulation model that implements the micro-model algorithm for a dump truck within the open pit macro-model. The description of the initial data for the experimental verification of the developed model and the plan of experiments is presented in Section 4, and the experimental results – in Section 5. Finally, section 6 contains conclusions, limitations, and future research.

2. Micro-Model of Dump Truck Movement

The main idea of the developed micro-model is to calculate the speed and acceleration of a dump truck at each moment of the model time, depending on the longitudinal road grade of the highway route. The speed of the dump truck in the model changes dynamically, using the equation for calculating the speed through uniformly accelerated or uniformly slowed motion. We use the current speed as the zero speed, and we determine the acceleration considering the current longitudinal road grade of the highway route. The developed algorithm is based on the techniques presented in [31,32].
The initial data set of the micro-model of dump truck motion includes the following variables:
  • The durations of the model time step t ¯ and the simulation period T,
  • Route specified by the set of coordinates of points in three-dimensional space M = {{x1, x2, …, xn}, {y1, y2, …, yn}, {z1, z2, …, zn}},
  • Gear ratios of the main gear, wheel gear, transfer case (if any), the number of gears,
  • Transmission efficiency,
  • Maximum engine power,
  • The engine speed corresponding to the maximum engine power,
  • Wheel rolling radius,
  • engine displacement,
  • Dump truck weight without and with fuels and lubricants, carrying capacity,
  • Resistance force of the road surface,
  • Average pressure in the engine, gas constant of air, temperature of gases in the cylinder, filling ratio of the engine, excess fuel ratio, weight amount of air.
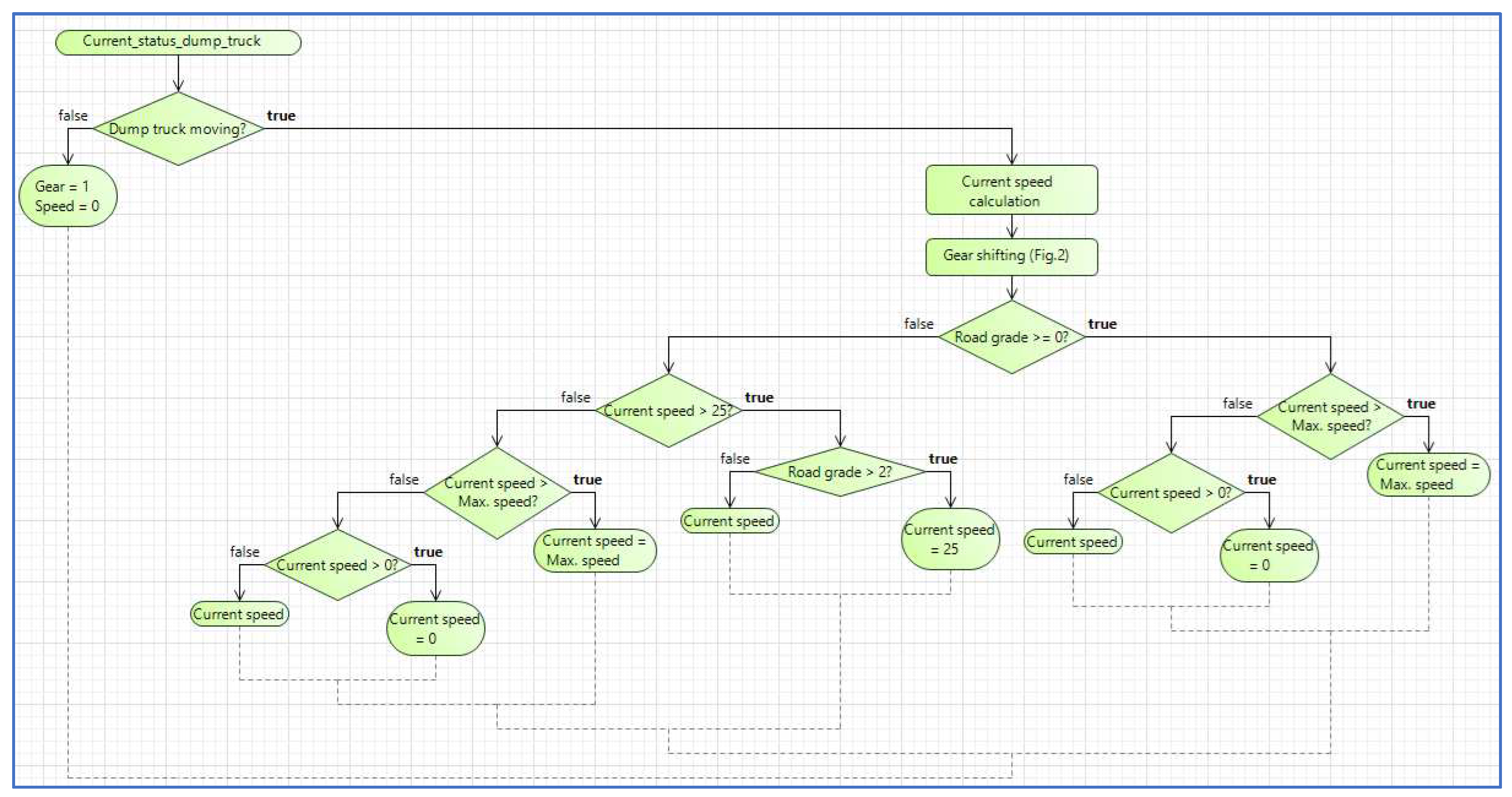
We propose to perform the calculation according to the micro-model algorithm presented below, sequentially for each moment of the model time t.
Step 1. Determination of the coordinates of the dump truck in three-dimensional space Mt = {xt, yt, zt} at the moment of model time t.
Step 2. Calculation of the distance Lt covered by the dump truck during the model time step t ¯ with the current speed Vt.
Step 3. Calculation of the value of the longitudinal road grade as follows
It = tg((zt-1 – zt)/Lt).
Step 4. Calculation of the current motor power, the number of revolutions of the motor shaft and the torque on the motor shaft in accordance with the methodology [31]. The number of revolutions of the motor shaft is calculated as the product of the crankshaft speed at maximum engine power by the ratio of the current number of revolutions of the motor shaft to the shaft speed corresponding to the maximum engine power.
Step 5. Calculation of the traction force on the driving wheels of a dump truck by multiplying the torque on the engine shaft by the gear ratios of the current gear, main gear, wheel gear, transfer case and transmission efficiency. The resulting value is divided by the rolling radius of the wheel.
Step 6. Calculation of the current acceleration of the dump truck using the formula (3.11) from [31]. When calculating the acceleration, the following values are used: the traction force on the driving wheels of the car, calculated at the previous step of the algorithm, the resistance force of the road surface, the mass of the dump truck, and the road grade.
Step 7. Calculation of the current speed of the dump truck using the uniform acceleration formula based on the known speed of the dump truck at time t-1 and the acceleration calculated in the previous step of the algorithm.
Step 8. Calculation of the maximum possible speed (Max. Speed) for the current gear ratio in accordance with the methodology [31]. This value is used in the algorithm (Figure 1) as a speed limiter for a dump truck in a micro-model.
Step 9. Calculation the gear shifting speed – the speed at which the gear ratio changes or gear changes. It is calculated in the same way as the maximum possible speed in the previous step of the algorithm. The exception is that the ratio of the current engine speed to the speed corresponding to the maximum engine power is taken to be 0.55. The gear shifting speed value is used in the gear ratio changes algorithm shown in Figure 2.
Step 10. Calculation of the gear shifting acceleration of the dump truck. It is calculated in the same way as the acceleration of a dump truck for the moment t. However, when calculating the torque on the engine shaft, it uses the gear ratio of the gearbox for the corresponding gear. The gear shifting acceleration calculation is used in the gear shifting algorithm (Figure 2). In contrast to step 6, acceleration for the higher gear is calculated here. Step 10 of the algorithm eliminates irrational gear changes.
Step 11. Checking the condition of the dump truck and determining the maximum possible speed for each condition (Figure 1). A dump truck can be in the following states, for each of which the maximum speed is set moving to loading, moving to unloading, moving to a parking, waiting for the end of loading, waiting for the end of unloading, parking.
Step 12. Checking the need to change the current gear and changing the gear ratio, if necessary, in accordance with the algorithm (Figure 2). The recalculation of the traction force on the driving wheels of the dump truck (Step 5), acceleration (Step 6) and the design speed (Step 7) is performed if a change in the gear ratio.
Step 13. Simulation of the dump truck’s movement at the calculated speed along the M route, that is, changing the current coordinates of the dump truck in three-dimensional space. This change corresponds to the increment in the distance traveled by the dump truck during one simulation step.
Step 14. Calculation of fuel consumption during one step of modeling according to the method [33]. The calculation uses the calculated value of the engine speed (Step 4), as well as the specified parameters of the engine displacement, average pressure in the engine, gas constant of air, temperature of gases in the cylinder, filling ratio of the engine, excess fuel ratio, and weight amount of air.
Step 15. Increasing the estimated time by the size of the simulation step t = t+ t ¯ . Algorithm repetition, starting from the first step until the end of the specified simulation period T.
The presented algorithm makes it possible to build the speed profile of a dump truck depending on the value of the longitudinal road grade. We propose to use the developed micro-model of dump truck motion in simulation models of road traffic. At present, in such models, the speed of movement is constant and changes with a given acceleration at the moments of starting or stopping, as well as to prevent a collision of cars. The developed algorithm makes it possible to simulate the movement of vehicles more realistically, which improves the accuracy of calculations and the adequacy of simulation models.

3. Macro-Model of Excavator-and-Dump Truck Complex Operation

The algorithm presented in the previous section is universal. However, the developed micro-model currently has the greatest practical value for modeling the movement of vehicles along fixed routes known in advance. These routes are used by mining dump trucks as part of excavator-and-dump truck complexes. The developed macro-model of such an excavator-and-dump truck complex allows solving the following tasks:
  • Calculation of the optimal number of dump trucks, according to the criterion of ensuring a given open pit performance,
  • Substantiation of the optimal, according to the criterion of minimum operating costs, models of dump trucks and excavators,
  • Justification of the width of the transport berm and open pit slopes.
The authors used the AnyLogic software platform [34] as a tool for macro-modeling the operation of an excavator-and-dump truck complexes. The choice of this platform is due to the support in it of the agent-based paradigm of simulation modeling, which makes it possible to simulate the behavior of individual dump trucks, in this case. In addition, modern versions of AnyLogic include a Material Handling Library, which allows to simulate the movement of vehicles along specified routes. Finally, this platform provides visual creation and editing of the road alignment in three-dimensional space.
The initial data of the developed macro-model are:
  • A set of paths (path) of movement of dump trucks. Each path is specified in the model by the coordinates of the start and end points in three-dimensional space,
  • A set of point and rectangular nodes (node), defining, respectively, the points of loading (excavators) or unloading (dumps), as well as parking of dump trucks. Each point node is specified in the model by a coordinate in three-dimensional space and size (area, capacity),
  • Duration of loading and unloading dump trucks,
  • Overall dimensions of dump trucks,
  • Number of dump trucks fleet.
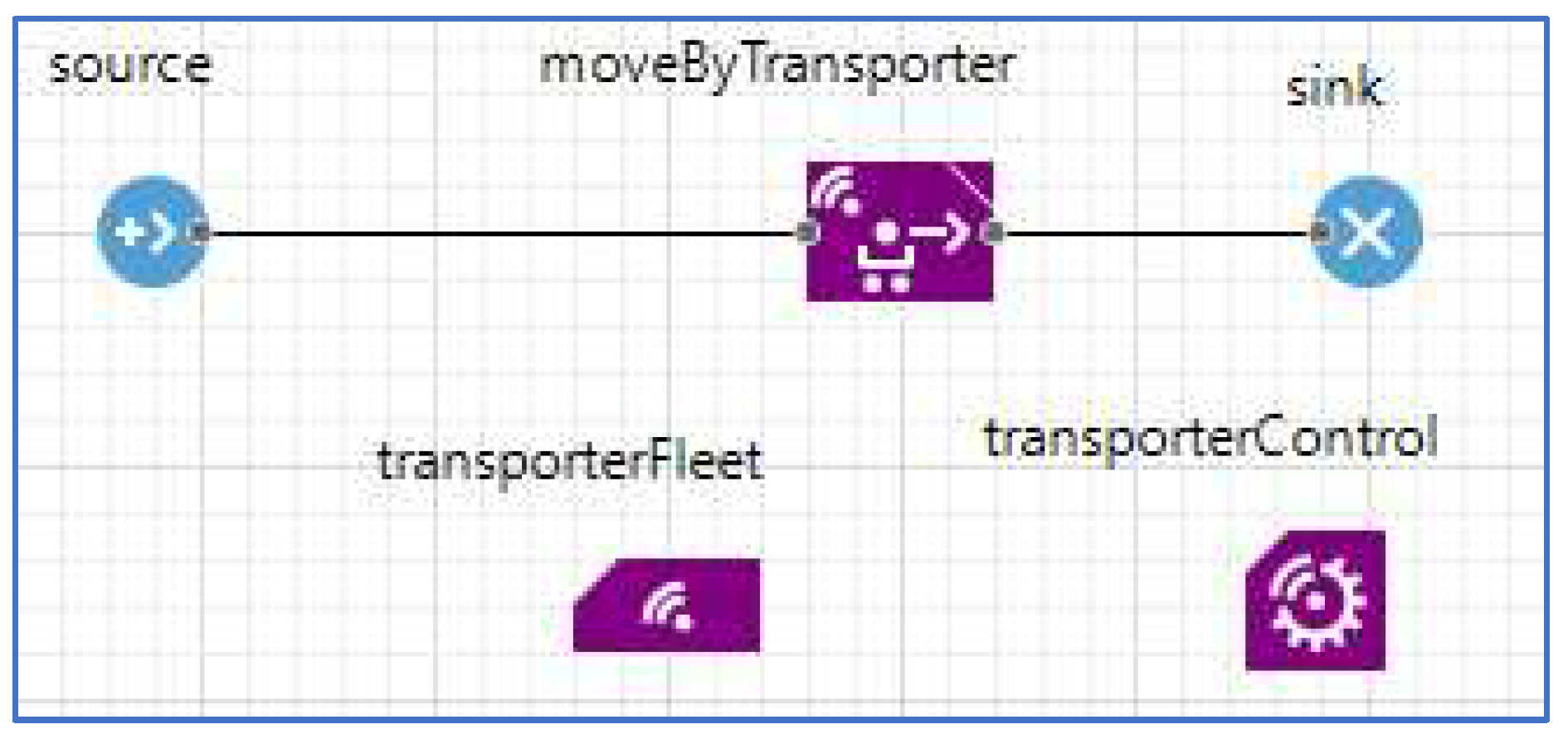
The basic logic of the functioning of the macro-model of the excavator-and-dump truck complex is presented by the flowchart (Figure 3).
The main functional blocks of this chart are:
  • The “source” block generates material flow, rock,
  • The “moveByTransporter” block simulates of loading, movement, and unloading of the dump trucks,
  • The “transporterFleet” block sets the number of dump trucks and their overall dimensions,
  • The “transporterControl” block determines the rules for the movement of dump trucks along the route and prevents collisions.
The flow diagram of the simulation model for the case of one excavator and loading point generating one material flow is shown in Figure 3. Concerning several excavators in an open pit, for each of them it is necessary to create a separate “source” block.
The algorithm for calculating the speed and acceleration of a dump truck (Section 2) is implemented as a function of the “Transporter” agent. The simulation model calls this function at the specified simulation time intervals. The “transporterFleet” block creates a population of "Transporter” agents in the specified number at the time of the simulation model initialization.

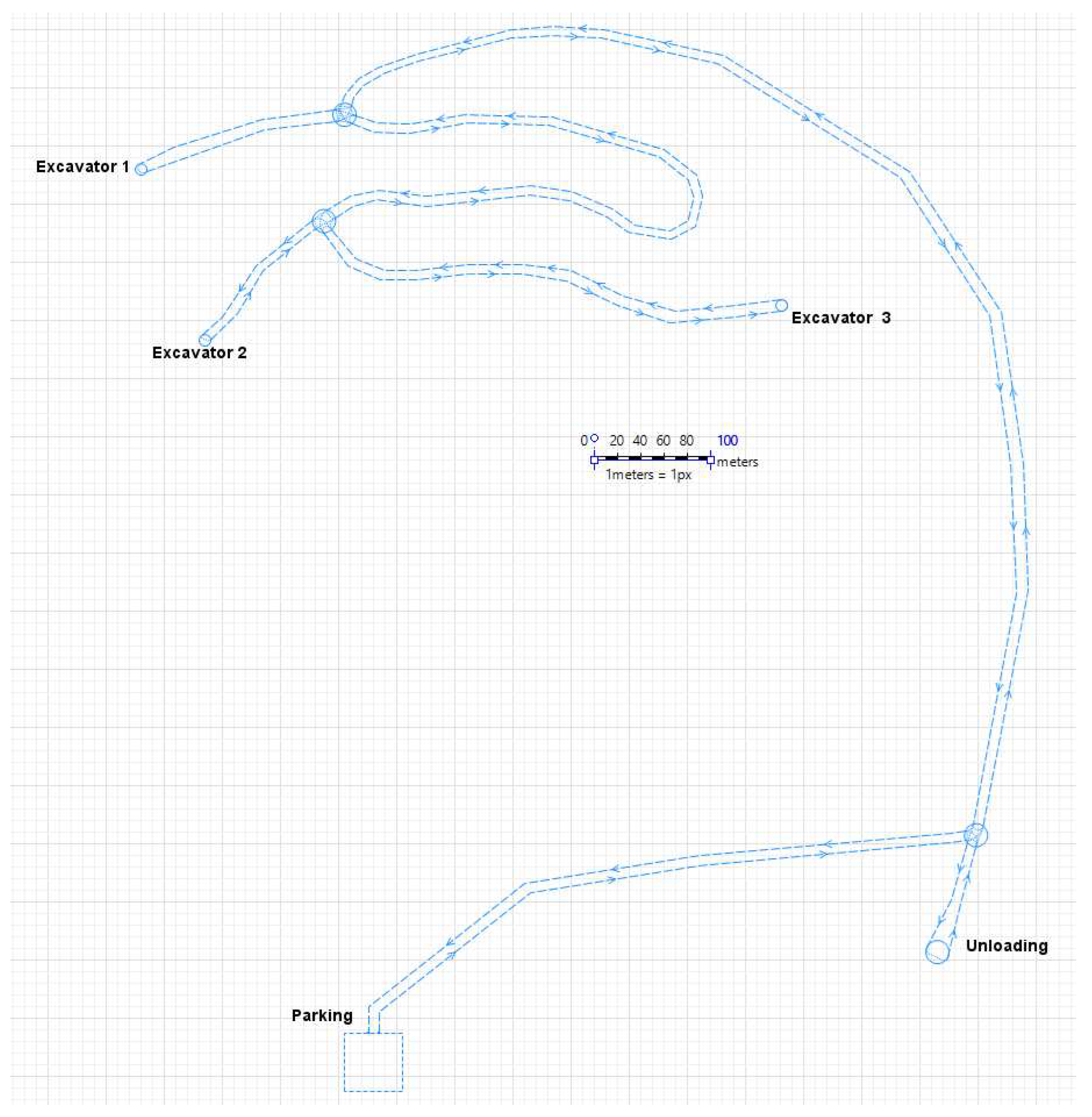
4. Initial Data and Experiment Plan

The authors used as a model example an excavator-and-dump truck complex, which includes three excavators. Unloading of rock is carried out at one point. The layout of the route, the placement of excavators, the point of unloading and parking of dump trucks is shown in Figure 4.
The authors chose BelAZ 7540 as a mining dump truck [35]. The average duration of loading a dump truck is taken equal to 4 minutes, unloading – 0.5 minutes. The technical characteristics of a dump truck (Figure 5a) are the parameters of the “transporterFleet” simulation model block, and the time spent on loading and unloading operations is the “moveByTransporter” block (Figure 5b).
The duration of the model time step t ¯ = 1 s, the simulation period T = 86400 s (24 h).
The authors experimented with the model to assess the effect of the speed profile of a dump truck on the performance of an excavator-and-dump track complex. For this, the authors made the following experimental plan (Table 1).

5. Results

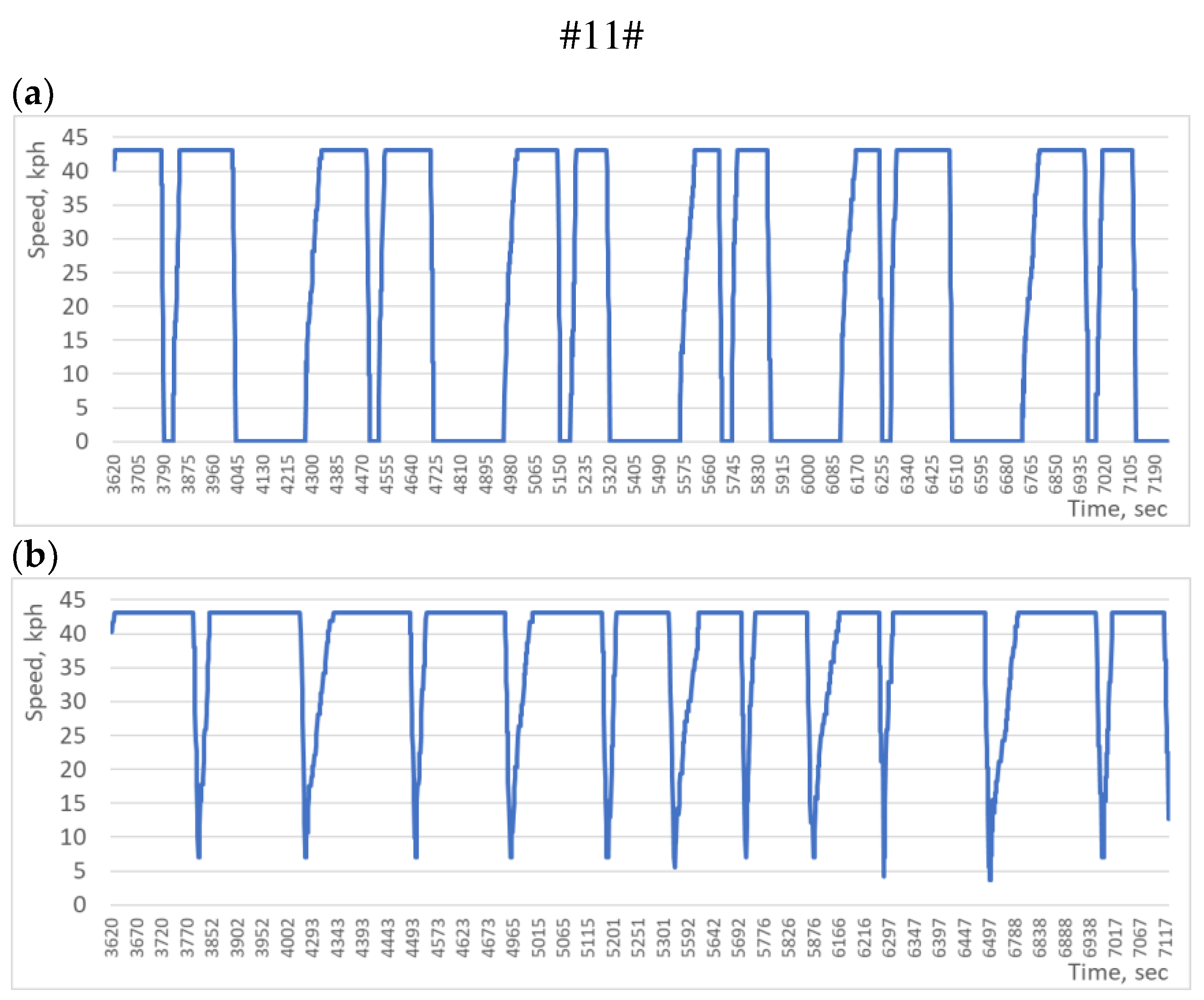
We obtained the results of the first experiment (Table 1), characterizing the speed profile of a dump truck during one hour of operation of an excavator-and-dump truck complex (Figure 6). Figure 6a shows the change in the speed of a dump truck considering the downtime for cargo operations, and Figure 6b – without considering the downtime, but considering the deceleration and acceleration of the dump truck. The presented graphs prove the adequacy of the model of the excavator-and-dump truck complex under the condition of movement on the road with a zero slope of the longitudinal profile.
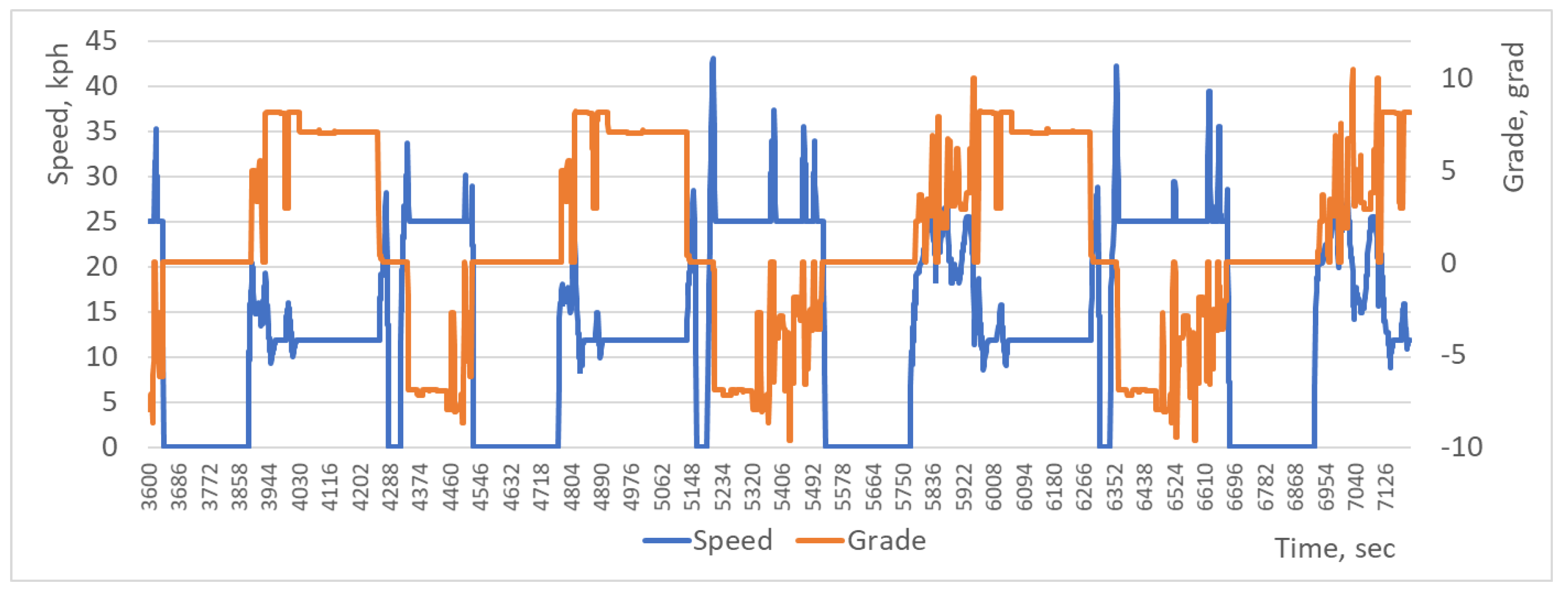
The dynamics of the speed of a dump truck with a change in the road grade is shown in Figure 7. When moving uphill, the speed of the dump truck in the model, as a rule, decreases, and when it goes downhill, it increases.
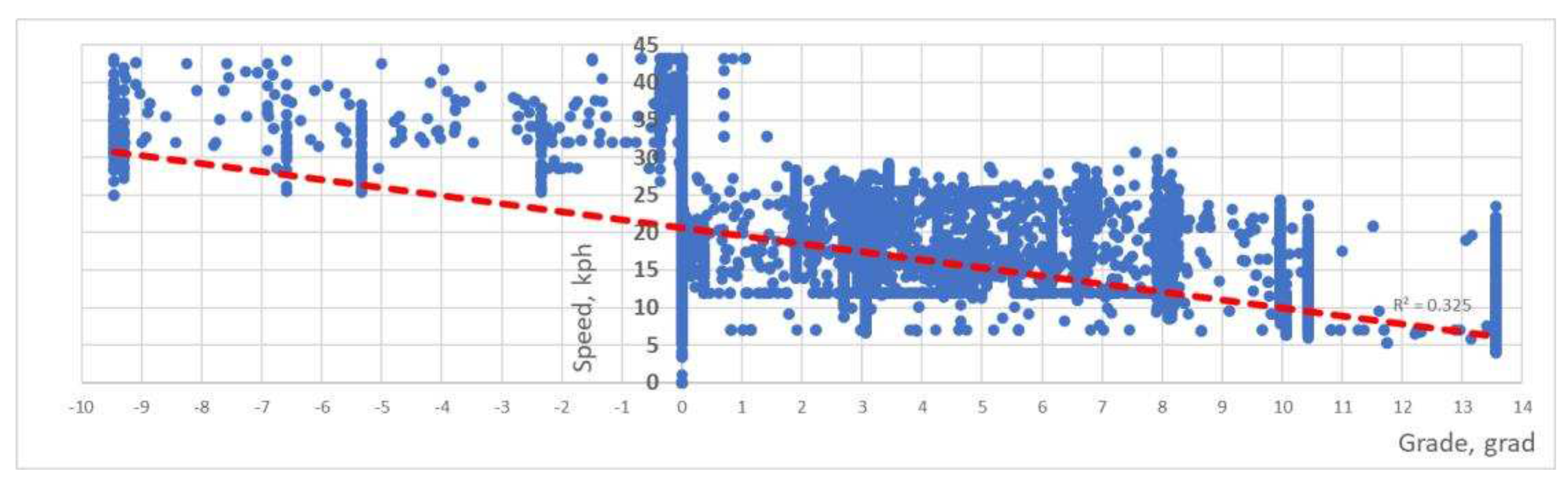
We built a trend of speed variation depending on the magnitude and sign of the slope (Figure 8) to evaluate the effect of the slope on the speed of the dump truck in the model. Each point on the graph corresponds to the speed of the dump truck, measured at one-second intervals.
We excluded zero values of the speed of dump trucks during parking from the resulting data set as independent of the value of the longitudinal slope of the road. We made this decision to improve the accuracy of the assessment.
The trend line shows (Figure 8) that when driving downhill, the speed varies within the range from 25 to 45 km/h, while when driving uphill – in the range from 5 to 35 km/h. The relatively large value of the approximation error (R2 = 0.325) is explained by the influence of other factors on the speed of the dump truck accelerations and deceleration, including at the moments of gear shifting.
The presented results show the adequacy of the developed micro-model of the dump truck movement, considering the change in the road grade.
We evaluated the influence of the road grade on the efficiency of the excavator-and-dump truck complex by gradually increasing the number of dump trucks in the macro-model. We compared the results obtained with the control data obtained on the macro-model of the movement of dump trucks on the road with a zero slope. Our hypothesis was that considering the longitudinal profile of the road in the macro-model of the excavator-and-dump truck complex increases the accuracy of modeling. This, in turn, leads to an increase in the adequacy of the model and the possibility of a more accurate solution of macro-modeling problems (Section 3) and the calculation of the optimal number of dump trucks fleet.
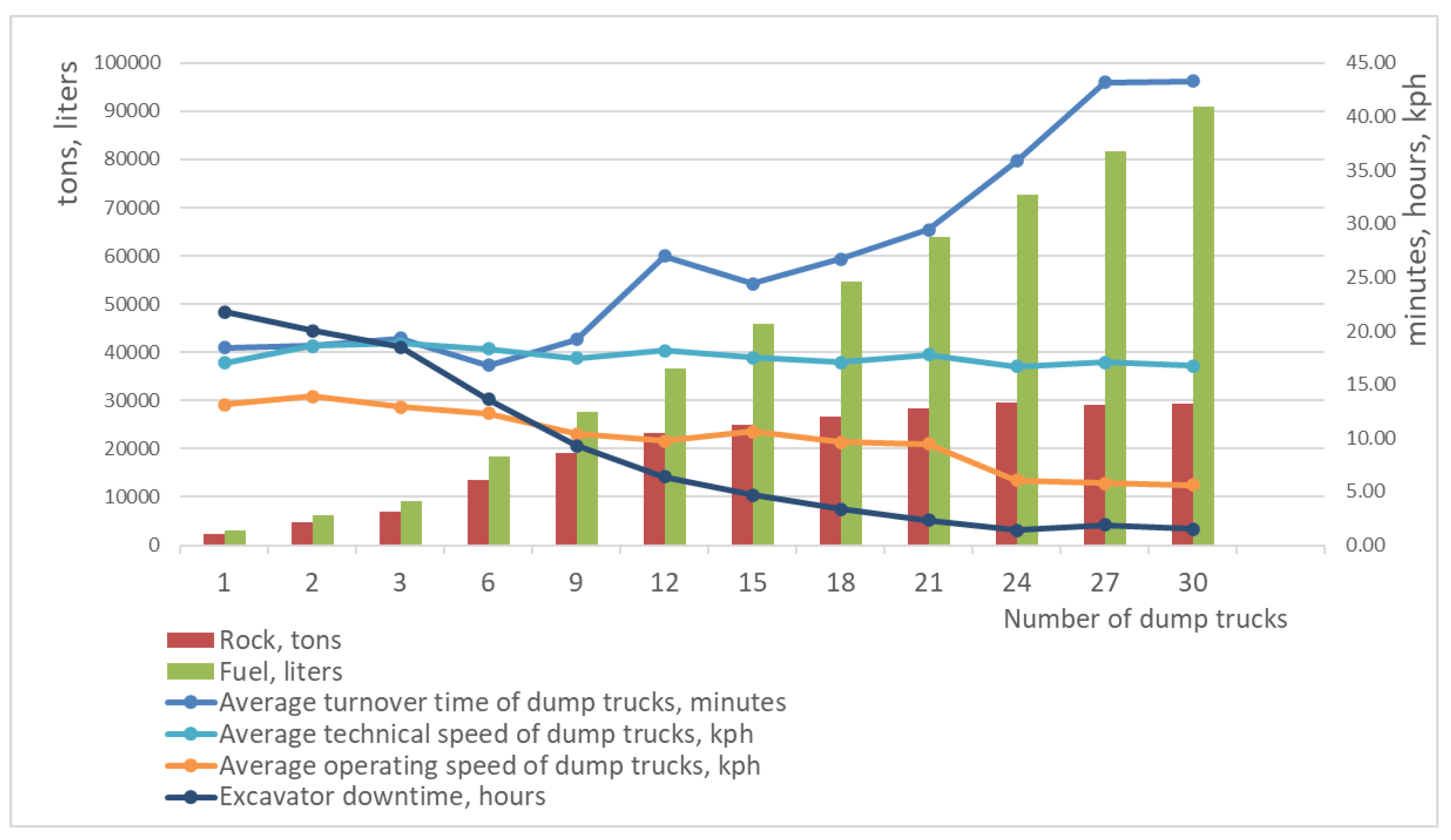
The dynamics of the indicators of the excavator-dumping complex, calculated on the model example (Section 4), is shown in Figure 9. It can be seen from the graph that with an increase in the number of dump trucks over 24 units, the growth of rock mass production stops. This is because dump trucks are starting to stand idle while waiting for loading. As a result, there is an increase in the average turnover time, a decrease in their average operating speed. At the same time, maximum utilization of excavator productivity is observed as a result of reduced excavator downtime. Excavator performance does not increase as the number of dump trucks in the simulation model grows.
The increase in fuel consumption in experiments is because this consumption mainly depends on the number of dump trucks that consume fuel not only in motion, but also when idle while waiting for loading.
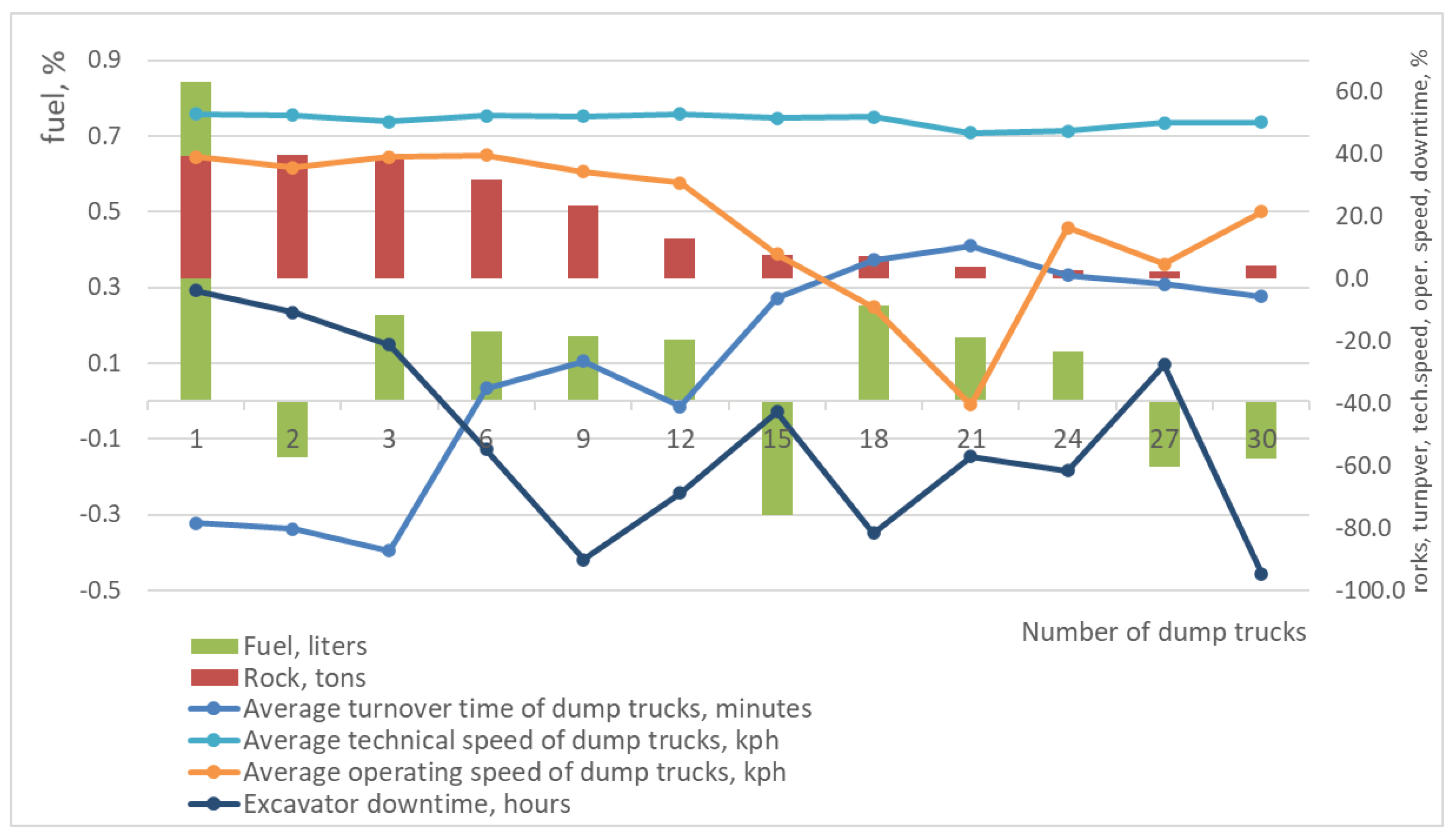
We assessed the influence of considering of the road grade on the results of the excavator-and-dumping track complex’ simulation modeling by comparing the results of experiments No. 3–33 and No. 34-64 (Table 1). Deviations of the results obtained in percent for each experiment depending on the number of dump trucks are shown in Figure 10.
The analysis of the results obtained showed that the largest deviations (+ 45%), regardless of the number of dump trucks, are observed for the “average technical speed” indicator. This result also proves the need to consider of the road grade in the simulation modeling. The difference in the turnover time of dump trucks tends to 0% as the number of dump trucks increases. This indicates a gradual decrease in the impact of the road grade on the performance of the excavator-and-dump truck complex due to an increase in the idle time of dump trucks while waiting for loading.
The simulation results showed insignificant deviations in fuel consumption in the model considering the slopes in comparison with the control model of the movement of dump trucks on roads with zero longitudinal slope (from -0.3% to + 0.85%). This indicates a stronger influence on this indicator of the number of dump trucks, compared to the road grade. On the other hand, the developed micro-model does not consider the driver’s regulation of the fuel rate depending on the change in the slope of the road. This conclusion motivates the authors to improve the micro-model of vehicle movement in future studies by modeling different driving styles.

6. Conclusion

Analysis of the research results proves the need to consider the road grade when modeling the operation of excavator-and-dump truck complexes and open pits in general. Furthermore, it is necessary when creating algorithms for automated control of the movement of mining dump trucks. The use of such algorithms will help reduce investment and operating costs for dump trucks.
The authors presented a micro-model of car movement on a road with a changing longitudinal slope and applied it to calculate the speed and acceleration of mining dump trucks in a macro-model of an excavator-and-dump truck complex. We have experimentally proved the hypothesis that considering the road grade in the simulation macro-model of the excavator-and-dump truck complex increases the accuracy of modeling. This, in turn, leads to an increase in the adequacy of the model and the possibility of a more accurate solution of macro-modeling problems and the calculation of the optimal number of dump trucks fleet.
The main limitation of the developed micro-model is insufficient accounting for the intensity of fuel supply, that is, regulation of the speed of movement considering the road grade. This intensity is constant in the presented algorithm.
We propose to improve the developed simulation model by including an algorithm for scheduling the work of dump trucks into its composition. We plan to obtain the optimal distribution of dump trucks between excavators to reduce the total downtime of the elements of the excavator-and-dump truck complex. Thus, the influence of the optimal speed control of a dump truck on the efficiency of the excavator-and-dump truck complex will increase as a result of a reduction in the idle time of dump trucks while waiting for loading.
Finally, the authors consider a promising direction in the development of the study to conduct a series of experiments with a micro-model of the movement of dump trucks under the control of drivers with different driving styles. Such experiments will make it possible to evaluate the efficiency of application of algorithms for auto-driving of mining dump trucks.

Funding

The study was supported by the Russian Science Foundation (RSF) Grant No. 23-11-00164: https://rscf.ru/en/project/23-11-00164/.

References

  1. Horeshok, A.A. & Furman, A.S. The effect of longitudinal slope of the road on the performance of the excavator-motorcar complexes. Bulletin of the Kuzbass State Technical University.
  2. Bakhturin, Y. The current state of the open pit transport. Catalog-reference book “Mining Technics - 2005”.
  3. Corke, P. & Roberts, J. & Cunningham, J. & et al. Mining Robotics. In: Springer Handbook of Robotics, B. Siciliano and O. Khatib, eds. Berlin, Heidelberg: Springer Berlin Heidelberg. 2008. P.1127–1150. [CrossRef]
  4. Voronov, A.Y. & Voronov, Y.E. Current state and development prospects of the autonomous haulage at open-pit mines. MEE (Mining Equipment and Electromechanics). [CrossRef]
  5. Temkin, I.O. & Deryabin, S.A. & Konov, I.S. & Klebanov, D.A. Haul road condition determination under controlled interaction of robotic elements in open pit mining and transport system. Gornyi Zhurnal. [CrossRef]
  6. Morin, P. & Samson, C. Motion Control of Wheeled Mobile Robots. In: Springer Handbook of Robotics. Siciliano, B. & Khatib, O. (eds). Berlin, Heidelberg: Springer Berlin Heidelberg. 2008. P. 799-826. [CrossRef]
  7. Parreira, J. & Meech, J. Autonomous Haulage Systems – Justification and Opportunity. In: Autonomous and Intelligent Systems. In: Kamel, M. & Karray, F. & Gueaieb, W. & Khamis, A. (eds). Berlin, Heidelberg: Springer Berlin Heidelberg. 2011. P. 63-72. [CrossRef]
  8. Chi, H. & Zhan, K. & Shi, B. Automatic guidance of underground mining vehicles using laser sensors. Tunnelling and Underground Space Technology. 2011. Vol. 36. No. 3. P. 103-103. [CrossRef]
  9. Stojčić, M. & Stević, Ž. & Nikolić, A. & et al. A multi-criteria model for evaluation and selection of AGV’s in a warehouse. Modern Problems of Russian Transport Complex. 2019. Vol. 9. No. 1. P. 4-20. [CrossRef]
  10. Oyekanlu, E.A. & Smith, A.C. & Thomas, W.P. & et al. A Review of Recent Advances in Automated Guided Vehicle Technologies: Integration Challenges and Research Areas for 5G-Based Smart Manufacturing Applications. IEEE Access. 2020. Vol. 8. P. 202312–202353. [CrossRef]
  11. Karoshi, P. & Ager, M. & Schabauer, M. & et al. Robust and Numerically Efficient Estimation of Vehicle Mass and Road Grade. In: Advanced Microsystems for Automotive Applications. 2017. In: Zachäus, C. & Müller, B. & Meyer, G. (eds). Cham: Springer International Publishing. 2018. P. 87-100. [CrossRef]
  12. Kidambi, N. & Harne, R.L. & Fujii, Y. & et al. Methods in Vehicle Mass and Road Grade Estimation. SAE International Journal of Passenger Cars - Mechanical Systems. 2014. Vol. 7. No. 3. P. 981–991. [CrossRef]
  13. Li, X. & Ma, J. & Zhao, X. & et al. Intelligent Two-Step Estimation Approach for Vehicle Mass and Road Grade. IEEE Access. 2020. Vol. 8. P. 218853-218862. [CrossRef]
  14. Ma, B. & Guo, H. & Zhang, H. & et al. Estimation of road grade and vehicle velocity for autonomous driving vehicle. In: IECON 2017 - 43rd Annual Conference of the IEEE Industrial Electronics Society. Beijing: IEEE. 29.10.2017 - 01.11.2017. P. 4621-4626. [CrossRef]
  15. Zhang, M. & Shi, S. & Cheng, W. & et al. Using the AMCE Algorithm to High-Efficiently Develop Vehicle Driving Cycles with Road Grade. IEEE Access. 2019. Vol. 7. P. 160449-160458. [CrossRef]
  16. Sahlholm, P. & Gattami, A. & Johansson, K.H. Piecewise Linear Road Grade Estimation. In: SAE Technical Paper Series: SAE International400 Commonwealth Drive, Warrendale, PA, United States. 2011. [CrossRef]
  17. Meech, J. & Parreira, J. An interactive simulation model of human drivers to study autonomous haulage trucks. Procedia Computer Science. 2011. Vol. 6. No. 2. P. 118-123. [CrossRef]
  18. Liu, H. & Rodgers, M.O. & Guensler, R. The impact of road grade on vehicle accelerations behavior, PM2.5 emissions, and dispersion modeling. Transportation Research Part D: Transport and Environment. 2019. Vol. 75. No. 9. P. 297-319. [CrossRef]
  19. Khader, A.I. & Martin, R.S. On-the-road testing of the effects of driver’s experience, gender, speed, and road grade on car emissions. Journal of the Air & Waste Management Association. 2019. Vol. 69. No. 10. P. 1182-1194. [CrossRef]
  20. Liu, H. & Rodgers, M.O. & Liu, F. & et al. Bayesian approach in estimating the road grade impact on vehicle speed and acceleration on freeways. Transportmetrica A: Transport Science. 2020. Vol. 16. No. 3. P. 602-625. [CrossRef]
  21. Arellano, D. & Echaveguren, T. & Vargas-Tejeda, S. A model of truck speed profiles on short upward slopes. Proceedings of the ICE - Transport. 2015. Vol. 168. No. 5. P. 475-483. [CrossRef]
  22. Lan, C.-J. & Menendez, M. Truck Speed Profile Models for Critical Length of Grade. Journal of Transportation Engineering. 2003. Vol. 129. No. 4. P. 408-419. [CrossRef]
  23. Žikić, M. & Kukolj, I. & Stojadinović, S. & et al. Automatic control of haul truck travel speed on open pits. Tehnika. 2018. Vol. 73. No. 5. P. 497-502. [CrossRef]
  24. Sładkowski, A. & Utegenova, A. & Kolga, A.D. & et al. Improving the efficiency of using dump trucks under conditions of career at open mining works. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu. 2019. No. 2. P. 36-42. [CrossRef]
  25. Parker, L.E. Multiple Mobile Robot Systems. In: Springer Handbook of Robotics. In: Siciliano, B. & Khatib, O. (eds). Berlin, Heidelberg: Springer Berlin Heidelberg. 2008. P. 921-941. [CrossRef]
  26. Navarro Torres, V.F. & Ayres, J. & Carmo, P.L.A. & et al. Haul Productivity Optimization: An Assessment of the Optimal Road Grade. In: Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection - MPES 2018. In: Widzyk-Capehart, E. & Hekmat, A. & Singhal, R. (eds). Cham: Springer International Publishing. 2019. P. 345-353. [CrossRef]
  27. Burmistrov, K.V. & Osintsev, N.A. & Shakshakpaev, A.N. Selection of Open-Pit Dump Trucks during Quarry Reconstruction. Procedia Engineering. 2017. Vol. 206. No. 5. P. 1696-1702. [CrossRef]
  28. Bester, C.J. Truck Speed Profiles. In Transportation Research Record: Journal of the Transportation Research Board. 2000. Vol. 1701. No. 1. P. 111-115. [CrossRef]
  29. Ashikhmin, V. & Furman, A.S. & Shadrin, V.N. High-speed and operational modes of mining dump trucks. Bulletin of the Kuzbass State Technical University.
  30. Furman, A. & Tyunina, N. & Furman, N.V. Patterns of changes in the cost of transporting rock mass depending on the road grade.
  31. Grishkevich, A.I. Vehicle Transmission Design: A Handbook. Moscow: Mashinostroenie.
  32. Verevochkin, Y. Mechanics (brief theory and examples of a problem-solving). Moscow: Moscow State University of Geodesy and Cartography.
  33. Lukin, P. & Gaspariantc, G. & Rodionov, V. Vehicle designing. Moscow: Mashinostroenie.
  34. AnyLogic simulation software. Available at: https://www.anylogic.com/.
  35. BelAZ-7540 series. Available at: https://belaz.by/en/products/products-belaz/dumpers/dump-trucks-with-hydromechanical-transmission/dump-truck-series-7540/?redirectcustom=Y.
Preprints 93202 g001
Figure 1. Flowchart for calculation and limitation of a dump truck speed in the micro-model.
Figure 1. Flowchart for calculation and limitation of a dump truck speed in the micro-model.
Preprints 93202 g001
Preprints 93202 g002
Figure 2. Flowchart for gear shifting algorithm in the micro-model.
Figure 2. Flowchart for gear shifting algorithm in the micro-model.
Preprints 93202 g002
Preprints 93202 g003
Figure 3. Flowchart of the basic logic of the excavator-and-dump truck complex macro-model.
Figure 3. Flowchart of the basic logic of the excavator-and-dump truck complex macro-model.
Preprints 93202 g003
Preprints 93202 g004
Figure 4. The scheme of the road route and the placement of the excavator-and-dump truck complex’ elements.
Figure 4. The scheme of the road route and the placement of the excavator-and-dump truck complex’ elements.
Preprints 93202 g004
Preprints 93202 g005
Figure 5. a) Dump truck fleet parameters, and b) Loading and unloading parameters in the simulation model.
Figure 5. a) Dump truck fleet parameters, and b) Loading and unloading parameters in the simulation model.
Preprints 93202 g005
Preprints 93202 g006
Figure 6. Changing the dump truck speed on a road without slope a) considering stops and b) not considering stops.
Figure 6. Changing the dump truck speed on a road without slope a) considering stops and b) not considering stops.
Preprints 93202 g006
Preprints 93202 g007
Figure 7. Changing the speed of a dump truck with variable road grade.
Figure 7. Changing the speed of a dump truck with variable road grade.
Preprints 93202 g007
Preprints 93202 g008
Figure 8. The dependence of the dump truck speed on the road grade.
Figure 8. The dependence of the dump truck speed on the road grade.
Preprints 93202 g008
Preprints 93202 g009
Figure 9. Simulation results of the excavator-and-dump truck complex.
Figure 9. Simulation results of the excavator-and-dump truck complex.
Preprints 93202 g009
Preprints 93202 g010
Figure 10. The gap of simulation results of the excavator-and-dump truck complex, %.
Figure 10. The gap of simulation results of the excavator-and-dump truck complex, %.
Preprints 93202 g010
Table 1. Experiment plan.
Table 1. Experiment plan.
Experiment No. Number of dump trucks Road grade Experiment task
1 1 Constant, slope = 0 Obtaining control data for assessment of the impact of the road grade, model verification
2 1 Variable, from -11° to + 20°36′ Assessment of the impact of the road grade on the dump truck’ speed profile
3 – 33 2-30 Constant, slope = 0 Obtaining control data for assessing the influence of the road grade on the excavator-and-dump track complex performance
34 – 64 2-30 Variable, from -11° to + 20°36′ Assessment of the influence of the road grade on the excavator-and-dump track complex performance
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated