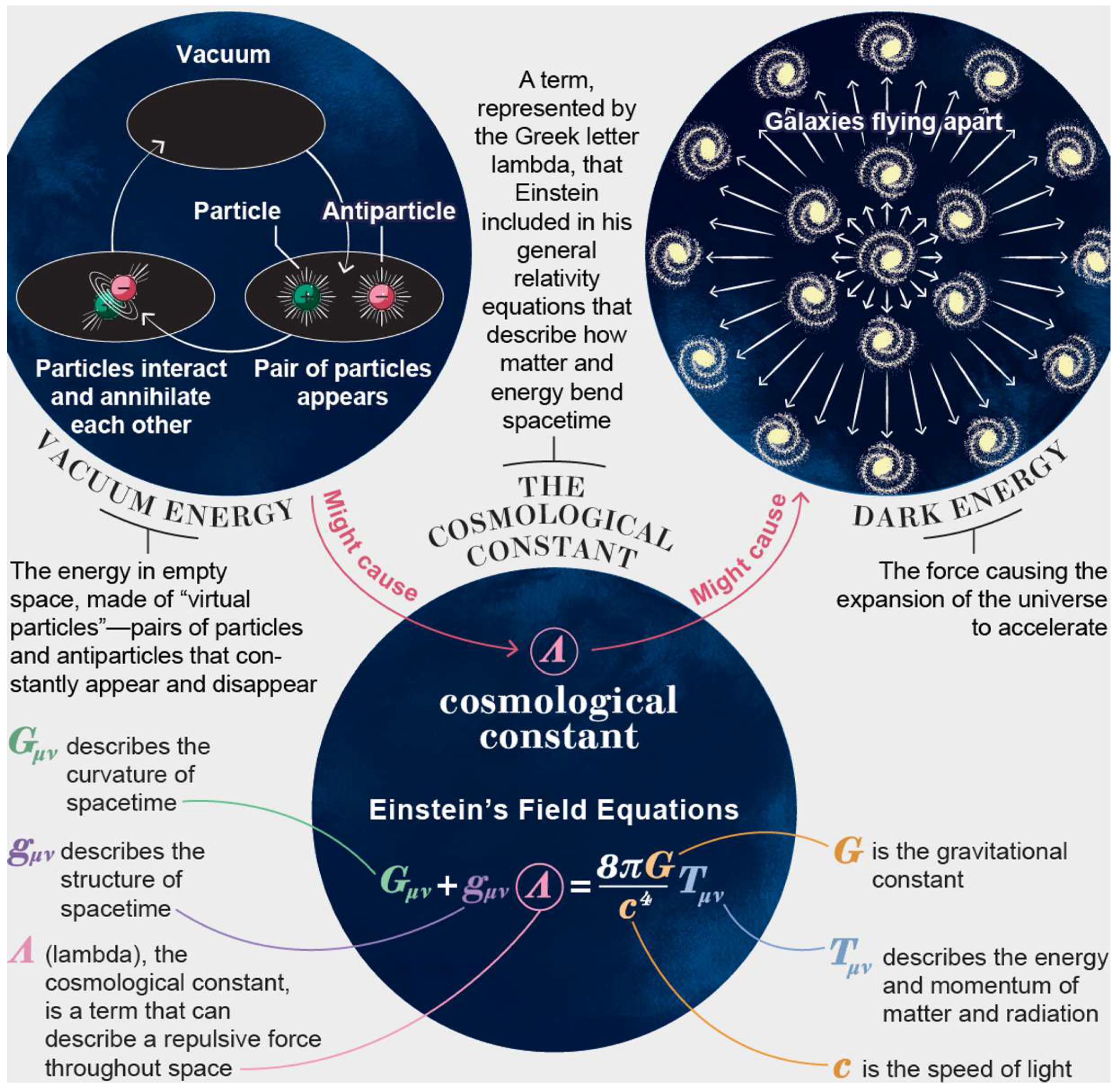
In cosmology, the cosmological constant problem or vacuum catastrophe is the disagreement between the observed small value of dark energy density and the theoretical large value of zero-point energy suggested by quantum field theory (See
Figure 1) [
17,
18,
19,
20]. In quantum mechanics, the vacuum itself should experience quantum fluctuations known as Casimir effects [
21]. In gravity, those quantum fluctuations constitute energy that would add to the cosmological constant. However, this calculated vacuum energy density is many orders of magnitude bigger than the observed cosmological constant. Original estimates of the degree of mismatch were as high as 120 orders of magnitude [
11]. To find a solution, some physicists resort to the anthropic principle and argue that we live in one region of a vast multiverse that has different regions with different vacuum energies [
22]. Others modify gravity and diverge from the theory of general relativity. There are also proposals that the cosmological constant problem is trivial [
23], is canceled [
24], does not gravitate [
25,
26], or does not arise [
27]. Many physicists argue that, due to a lack of better alternatives, proposals to modify gravity should be considered as one of the most promising routes to tackling the problem [
28].
In our dark energy paradigm, there is no need to modify gravity or any other proven theories in physics. The essence of the cosmological constant problem is not in the disagreement between theoretical prediction and observed data but in the lack of a proper vacuum energy model that is supported by observable evidence.
Dark Energy Paradigm for Vacuum Energy
The dark energy paradigm is a a unified dark sector [
13,
14,
15] that is based on Planck’s dimensional analysis [
29,
30,
31,
32,
33],
[
34], energy conservation and force equilibrium to explain the nature of dark energy and dark matter. In this paradigm, dark energy is similar to a photon in that its propagation speed is equal to the speed of light
c, and its energy
E is proportional to its frequency
where
ℏ is the reduced Planck constant,
m is the mass equivalent to dark energy,
l is the wavelength of dark energy (divided by
) and
t is the time to travel distance
l. However, dark energy is fundamentally different from a photon in that it oscillates
in space, while a photon travels
through space. Furthermore, a collection of dark energy particles forms a vacuum energy field or a background, which takes up about
of the energy in the universe and follows Planck’s dimensional analysis.
Planck’s dimensional analysis
Planck studied vacuum energy and suggested that there exist some fundamental natural units for length, mass, time and energy. He used only the Newton gravitational constant
G, the speed of light
c and the Planck constant
h to derive them [
29,
30,
31,
32,
33]. The natural units became known as Planck length
, Planck mass
, Planck time
, and Planck energy
which satisfy the following equations
where
is the Planck momentum, and
is the Planck frequency.
Dark energy modeled as a particle
Planck’s dimensional analysis can be generalized to model dark energy as a particle with mass
m, energy
E, momentum
p, time
t, frequency
, and wavelength
l
and their zero-point values are denoted with the subscript
o, which satisfy
where zero-point energy
is the lowest possible energy in a system, and vacuum energy fluctuation [
35] can cause dark energy
E to vary from
to Planck scale
.
In the dark energy paradigm, dark energy particles are governed by the rules of Planck’s dimensional analysis on energy density, pressure, matter waves, and attractive and repulsive forces [
29,
30,
31,
32,
33] (See
Table 1). Here, a scalar field
can be defined as a dimensionless parameter (See Equation (
3))
and
can be defined as a dimensionless constant (See Equation (4))
which corresponds to the cosmological constant
of the
model.
Dark Energy Modeled with
The dark energy can be modeled to be consistent with
whose pressure
is
where
is the dark energy density of
. In Planck’s dimensional analysis, the repulsive force
is (See
Table 1)
where
is the dark energy density of the dark energy paradigm,
is the force per unit area and
is the spherical Planck area. Thus,
is
where
from Planck’s dimensional analysis [
29,
30,
31,
32,
33]. Assuming
is equal to the
pressure
,
is (See Equation (
7))
After rearranging the terms,
in terms of
is
where
accounts for the difference between Planck’s dimensional analysis and
in modeling surface under pressure (spherical surface
vs. flat surface). Here, the dark energy density
of
is [
34]
where
is the Hubble constant, and
is the dark energy fraction estimated to be about 0.68 from Planck 2018 results [
34]. Thus,
is
where inserting
from Planck’s dimensional analysis [
29,
30,
31,
32,
33] yields
and
in terms of
is (See
Table 1)
where
is inserted (See Equation (
6)). On the other hand,
which minimizes the difference between the predicted and observed electron masses is (See Equation (
32))
which is within the converged value of observed data using calibrated distance ladder techniques of the Hubble tension (
) [
34,
36,
37,
38,
39]. Thus,
is
and
is
where all lepton masses can be predicted based on the Hubble constant (See
Table 2 and
Table 3), which will be described in the following section.
Table 1.
Planck’s dimensional analysis
Table 1.
Planck’s dimensional analysis
| |
Planck units |
dark energy (zero-point) |
| matter wave |
|
|
| energy density |
|
|
| attractive force |
|
|
| repulsive force |
|
|
| spherical Planck area |
|
|
| pressure (force per area) |
|
|
Table 2.
Equations of three generations to predict and lepton masses
Table 2.
Equations of three generations to predict and lepton masses
| |
particle |
neutrino
|
|
electron e
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Prediction of Lepton Masses as Evidence
Leptons and quarks come in three sets of nearly-identical copies except mass. It has been one of the mysteries of modern physics why there are three generations of particles, rather than fewer or more [
40].
Origin of three generations
In the dark energy paradigm, three generations are caused by 3-dimensional interaction among a particle, an antiparticle and dark energy particles where energy density can be represented as
where
m is mass, and
and
are dark energy wavelength in
and
directions respectively. As shown in
Figure 2, the 1
st generation is simply described by 1-dimensional interaction of a particle at the origin
o with its antiparticle at
r. On the other hand, the 2
nd generation involves 2-dimensional interaction of a particle with its relativistic dark energy particle at
. Finally, the 3
rd generation requires 3-dimensional interaction of a particle with dark energy particles at
and
, where the dotted line represents the vector sum of
and
directional interactions.
Energy conservation and force equilibrium
The conservation of energy states that the total energy of an isolated system remains constant. In the dark energy paradigm, the equal amount of dark energy is needed for a particle to be created in the vacuum. Dark energy can have only a certain energy value in force equilibrium which corresponds to a particle’s mass. The process for predicting a mass consists of three steps. First, the velocity v and the Lorentz factor are obtained and inserted into the matter wave equation . Second, the equation is rearranged so that mass m and wavelength l can be derived from v and . Third, the dark energy density is evaluated in force equilibrium to predict the particle’s mass m. Sometimes mass m can be directly obtained and the steps can be further simplified.
Table 3.
Predicted vs. observed lepton masses
Table 3.
Predicted vs. observed lepton masses
| mass |
particle |
predicted |
observed |
difference |
|
|
|
|
◯ |
|
|
|
|
◯ |
|
|
|
|
◯ |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
The 1st generation lepton masses
For the 1
st generation, the matter wave equation is
where
at the creation of a lepton is the same as the velocity of an electron in the Bohr model (See Methods)
where
is the fine structure constant, and the Lorentz factor
is
Since a neutrino at creation is expected to have the same wavelength of dark energy in force equilibrium (See Methods),
is
and
is
Thus, the electron neutrino’s mass is (See Equation
18)
where
is within the observed range of a neutrino (See
Table 3), and the energy density is
which is generated by the 1-dimensional interaction between a neutrino and its antineutrino as shown in
Figure 2(a). According to the particle data group, a neutrino consists of three eigenstates whose masses are unknown [
41]. If each eigenstate is assumed to have the same mass at particle creation, the mass of a neutrino’s eigenstate is
of an electron neutrino’s mass, and the energy density is
which is
of the neutrino’s density.
As a next step, if a neutrino gets excited where
is close to the speed of light, the matter wave equation becomes
where
,
and the wavelength changes to
and the density of one excited eigenstate is (See Equation (
27) and Equation (
29))
where
is excited dark energy to create an electron, and
is the wavelength of dark energy in force equilibrium (See Methods). Thus, the electron mass is
which agrees with the observed data (See
Table 3). On the other hand,
in terms of
is (See Equation (
14))
and
in terms of
is (See Equation (
31))
which shows the relation between the Hubble constant
and the electron mass
.
The 2nd generation lepton masses
For the 2
nd generation, the matter wave equation is
where the Lorentz factor
is
If
gets excited where
, the matter wave equation is rearranged as
where
and
have changed to
where
is for the length contraction, which causes
to change accordingly. Here, the density in the particle’s moving direction
is
where
is an excited dark energy mass with
as the wavelength in force equilibrium (See Methods). Assuming that an excited
could become
while momentum is conserved,
yields
After rearranging the terms,
is
where
is a function of
. Likewise, when
is replaced by
(for the 3
rd generation),
is
where
is also a function of
.
For an excited neutrino, if the 2
nd generation of a neutrino is created instead of the 1
st generation of an electron, the mass of a muon neutrino can be derived from Equation (
31). If the energy of
is equally divided among three eigenstates of a muon neutrino [
41],
is
where
is within the observed range of a muon neutrino (See
Table 3), and
is (See Equation
40)
from which
and
can be calculated (See Methods).
For an excited electron, the matter wave equation of the excited dark energy is
where
and
have changed to
where
is for the length contraction, which causes the mass to change accordingly. and the density in the
-direction is
where
represents the length contraction concentrated in the particle’s moving direction. On the other hand, the density in the
r-direction is
where
is the wavelength contraction due to the charge interaction of a particle and an antiparticle. In order for the repulsive forces to be in force equilibrium,
(See
Table 1)
where
yields (See Equation (
46) and Equation (
47))
and
is (See Equation (
28) and Equation (
31))
and
for muon is (See Equation (
40))
which agrees with the observed data within 1% (See
Table 3). It is interesting to note that the theoretical
at muon creation is close to the experimental
at the CERN muon storage ring experiment [
45]. We anticipate that the dark energy paradigm could be applied in future lepton storage ring experiments. See Methods for derivation of the 3
rd generation of lepton masses as shown in
Table 2 and
Table 3.
Conclusion
A dark energy paradigm has been presented, where predicted values of lepton masses agree with the observed values to
(or within error ranges). In the dark energy paradigm, a particle has the same amount of
dark energy before particle creation (or after particle annihilation) due to energy conservation in the vacuum (See
Figure 1). Hence, both predicted and observed lepton masses can be interpreted as the predicted and observed dark energy values. Therefore, we can argue that the predicted dark energy is equal to the observed dark energy, and the cosmological constant problem is solved for leptons (See
Table 2 and
Table 3). Interestingly enough, the cosmological constant problem could be solved for proton, quarks and fundamental bosons as well, which will be described in the following papers (See Methods).
Methods
Particle and antiparticle interaction
Let’s assume that each fermion particle has a fractional charge
which generates the Coulomb force between a particle and its antiparticle. Here, all fermions share the same matter wave equation
where
is momentum,
is the Lorentz factor,
m is mass,
v is velocity, and
l is wavelength (divided by
. Assuming a particle with
charge and its antiparticle with
charge form a circular orbit, the centripetal force is equal to the Coulomb force between
and
fractional charges (See
Table 4)
where
k is the Coulomb constant and
. After rearranging the terms,
v is
where
is the fine structure constant and
. Here, fractional charge parameters for leptons are
, where
v is
which is the velocity of the 1
st generation of leptons. Thus,
at the creation of a lepton particle has the same value as the velocity of an electron in the Bohr model. It is important to note that neutrino charge is unique in that it only interacts with neutrino charge, while electron and quark charges interact with each other.
Now the fractional charge parameters for down quarks are
, where
v is
and fractional charge parameters for up quarks are
and
, where
v is
Thus, fractional charges in force equilibrium play an important role in determining velocity
v at the creation of a particle and antiparticle pair.
Table 4.
Fractional charge parameters for fermions
Table 4.
Fractional charge parameters for fermions
| |
neutrino |
electron |
down quark |
up quark |
|
|
(particle) |
1 |
1 |
3 |
|
|
|
(antiparticle) |
1 |
1 |
3 |
3 |
|
|
1 |
1 |
9 |
|
|
Particle and dark energy in force equilibrium
Let’s imagine a particle and a dark energy particle at distance
l with masses
m and
, respectively. Here the attractive force is (See
Table 1)
and the repulsive force is
In force equilibrium, setting
produces
after rearranging the terms,
l is
where inserting the matter wave equation
yields
where the wavelength of a particle
l is equal to the wavelength of dark energy
.
The 3rd generation lepton masses
For the 3
rd generation, the matter wave equation is
where the Lorentz factor
is
If
gets excited where
,
is (See Equation (
41))
and replacing
by
yields (See Equation (
40))
where
is a function of
.
While the 2
nd generation is generated by the 2-dimensional interaction
the 3
rd generation is caused by the 3-dimensional interaction (See
Figure 2 and
Table 5)
where vector
corresponds to force vector
(See
Table 1)
where
is dark energy density in a particle’s moving direction which is under
length contraction. Thus,
changes to (See Equation (
46))
where
is for the additional length contraction in the
direction. Assuming
in force equilibrium,
is
and the magnitude of the vector sum is (See Equation
68)
where
is due to the orthogonal vector sum in
and
directions (See
Figure 2). Here, the matter wave equation is
where
represents the length contraction, and
in terms of
is
Thus, the relation between
and
is
After rearranging the terms,
is
where
(See Equation (
43)), and
for tau neutrino is (See Equation (
66))
where
is within the observed range of a tau neutrino (See
Table 3).
On the other hand,
for tau is
where
(See Equation (
50)), and
for tau is (See Equation (
51) and Equation (
66))
which agrees with the observed data within 1% (See
Table 3).
Table 5.
Matter wave & energy density equations for three generations
Table 5.
Matter wave & energy density equations for three generations
| generation |
mass |
neutrino |
electron |
matter wave |
energy density |
|
|
|
|
=ℏ
|
|
|
|
|
|
=ℏ
|
=
|
|
|
|
|
=ℏ
|
=+
|
Author Contributions
W. Koh and Y. J. Moon wrote the main manuscript. All authors reviewed the manuscript.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Acknowledgments
We thank the anonymous referees for improving this manuscript.
Conflicts of Interest
The authors declare no competing interests.
References
- Dirac, P.A. The cosmological constants. Nature 1937, 139, 323–323. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living reviews in relativity 2001, 4, 1–56. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: a review. Classical and Quantum Gravity 2013, 30, 214003. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Physical Review D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Martin, J. Quintessence: a mini-review. Modern Physics Letters A 2008, 23, 1252–1265. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Physics Letters B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Physical Review D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature quintessence. International Journal of Modern Physics D 2002, 11, 483–491. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Reviews of modern physics 1989, 61, 1. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—the weight of the vacuum. Physics Reports 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological Constant. Annual Review of Astronomy and Astrophysics 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Caldwell, R.; Linder, E.V. Limits of quintessence. Physical review letters 2005, 95, 141301. [Google Scholar] [CrossRef] [PubMed]
- Arbey, A.; Mahmoudi, F. One-loop quantum corrections to cosmological scalar field potentials. Physical Review D 2007, 75, 063513. [Google Scholar] [CrossRef]
- Ferreira, E.G.; Franzmann, G.; Khoury, J.; Brandenberger, R. Unified superfluid dark sector. Journal of Cosmology and Astroparticle Physics 2019, 2019, 027–027. [Google Scholar] [CrossRef]
- Arbey, A.; Coupechoux, J.F. Unifying dark matter, dark energy and inflation with a fuzzy dark fluid. Journal of Cosmology and Astroparticle Physics 2021, 2021, 033. [Google Scholar] [CrossRef]
- Koh, W.; Moon, Y.J. A Dark Energy Paradigm: II. Cold Dark Matter Model and Observed Properties in Galactic Dynamics as Evidence. Submitted to Scientific Reports 2023. [Google Scholar]
- Moskowitz, C. The Cosmological Constant Is Physics’ Most Embarrassing Problem. Scientific American 2021. [Google Scholar]
- Weinberg, S. The cosmological constant problem. Reviews of Modern Physics 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Peebles, P.J.; Ratra, B. The cosmological constant and dark energy. Reviews of Modern Physics 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—the weight of the vacuum. Physics Reports 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Casmir, H.B.; Polder, D. Influence of Retardation on the London–van der Waals Forces. Nature 1946, 158, 787–788. [Google Scholar] [CrossRef]
- Linde, A. A brief history of the multiverse. Reports on Progress in Physics 2017, 80, 022001. [Google Scholar] [CrossRef] [PubMed]
- Brodsky, S.J.; Roberts, C.D.; Shrock, R.; Tandy, P.C. Confinement contains condensates. Physical Review C 2012, 85. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Speeding up the Universe using dust with pressure. Physical Review D 2018, 98. [Google Scholar] [CrossRef]
- Ellis, G.F. The trace-free Einstein equations and inflation. General Relativity and Gravitation 2013, 46. [Google Scholar] [CrossRef]
- Percacci, R. Unimodular quantum gravity and the cosmological constant. Foundations of Physics 2018, 48, 1364–1379. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Physical Review D 2017, 95. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Beltrán Jiménez, J.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Physics of the Dark Universe 2016, 12, 56–99. [Google Scholar] [CrossRef]
- Gaarder Haug, E. The gravitational constant and the Planck units. A simplification of the quantum realm. Physics Essays 2016, 29, 558–561. [Google Scholar] [CrossRef]
- Planck, M. Ueber das Gesetz der Energieverteilung im Normalspectrum. Annalen der Physik 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Wadlinger, R.L.; Hunter, G. Max Planck’s natural units. The Physics Teacher 1988, 26, 528–529. [Google Scholar] [CrossRef]
- Planck, M. The theory of heat radiation; New York, N.Y., 1991.
- Planck Units.
- Aghanim, N.e.a. Planck 2018 results. vi. cosmological parameters. Astronomy & Astrophysics 2022, 652, 67. [Google Scholar] [CrossRef]
- Carroll, B.W.; Ostlie, D.A. An introduction to modern astrophysics; Addison-Wesley, 2001.
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; others. A comprehensive measurement of the local value of the Hubble constant with 1 km s- 1 mpc- 1 uncertainty from the Hubble space telescope and the sh0es team. The Astrophysical Journal Letters 2022, 934, L7. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Classical and Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astronomy Reviews.
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; others. The pantheon+ analysis: cosmological constraints. The Astrophysical Journal 2022, 938, 110. [Google Scholar] [CrossRef]
- Greene, B. The elegant universe: superstrings, hidden dimensions, and the quest for the ultimate theory; W. W. Norton, 2010.
- Particle-Data-Group. Review of particle physics. Progress of Theoretical and Experimental Physics 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- KATRIN-Collaboration. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nature Physics 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Assamagan, K.; Bronnimann, C.; Daum, M.; Forrer, H.; Frosch, R.; Gheno, P.; Horisberger, R.; Janousch, M.; Kettle, P.R.; Spirig, T.; others. Upper limit of the muon-neutrino mass and charged-pion mass from momentum analysis of a surface muon beam. Physical Review D 1996, 53, 6065. [Google Scholar] [CrossRef] [PubMed]
- Aleph-Collaboration. An upper limit on the neutrino mass from three-and five-prong tau decays. The European Physical Journal C-Particles and Fields 1998, 2, 395–406. [Google Scholar]
- Bailey, J.; Borer, K.; Combley, F.; Drumm, H.; Eck, C.; Farley, F.; Field, J.; Flegel, W.; Hattersley, P.; Krienen, F.; others. Final report on the CERN muon storage ring including the anomalous magnetic moment and the electric dipole moment of the muon, and a direct test of relativistic time dilation. Nuclear Physics B 1979, 150, 1–75. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).