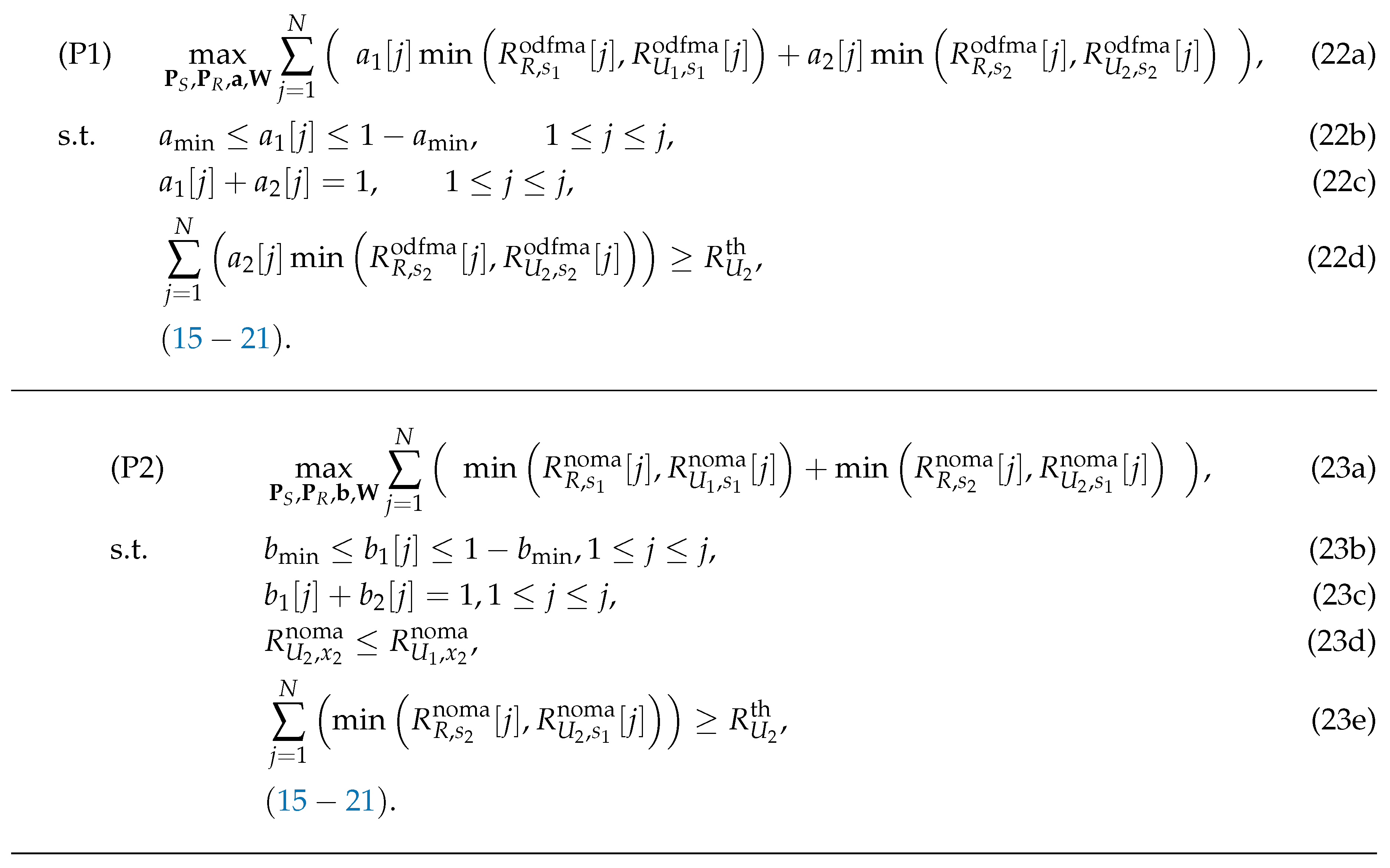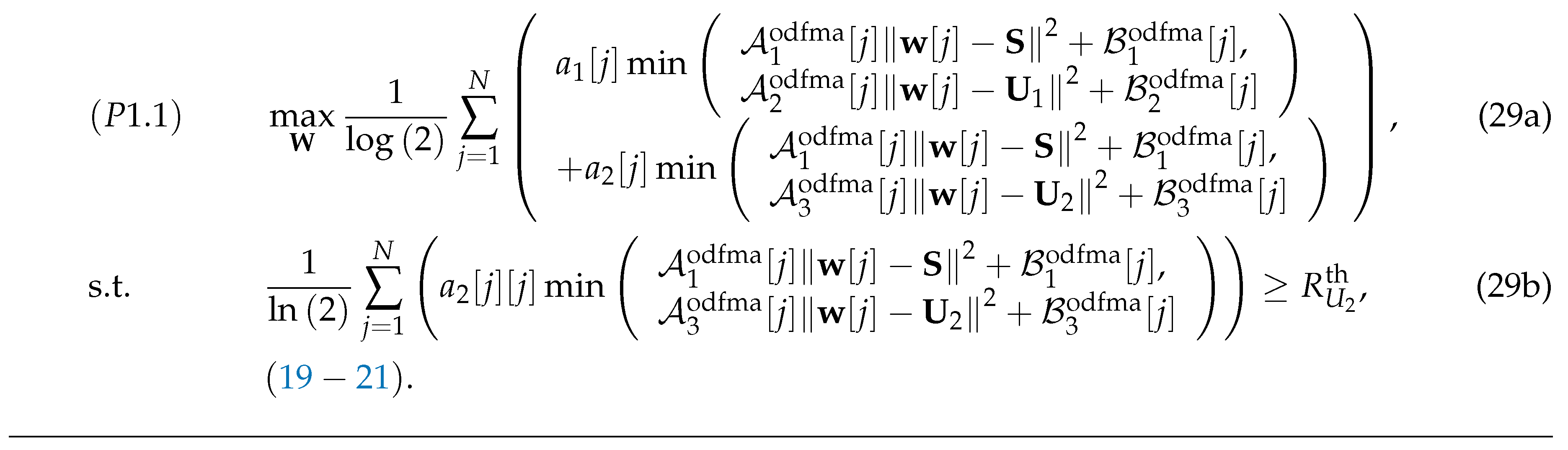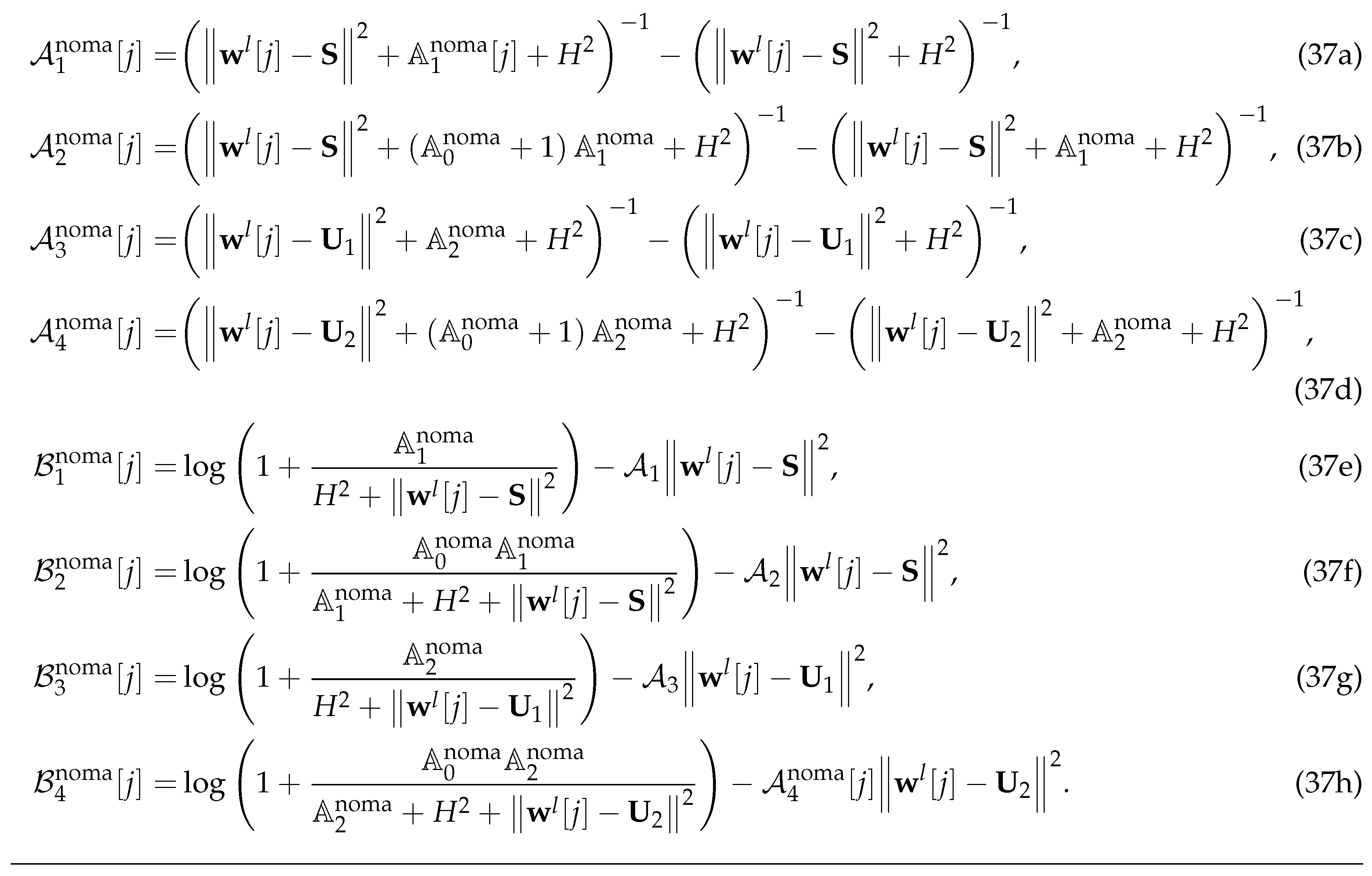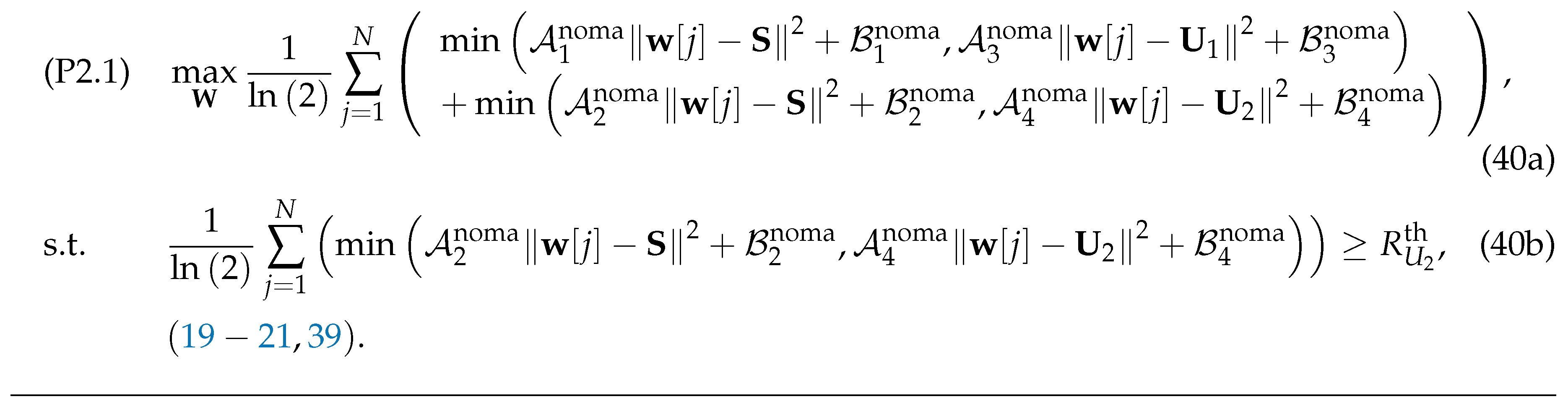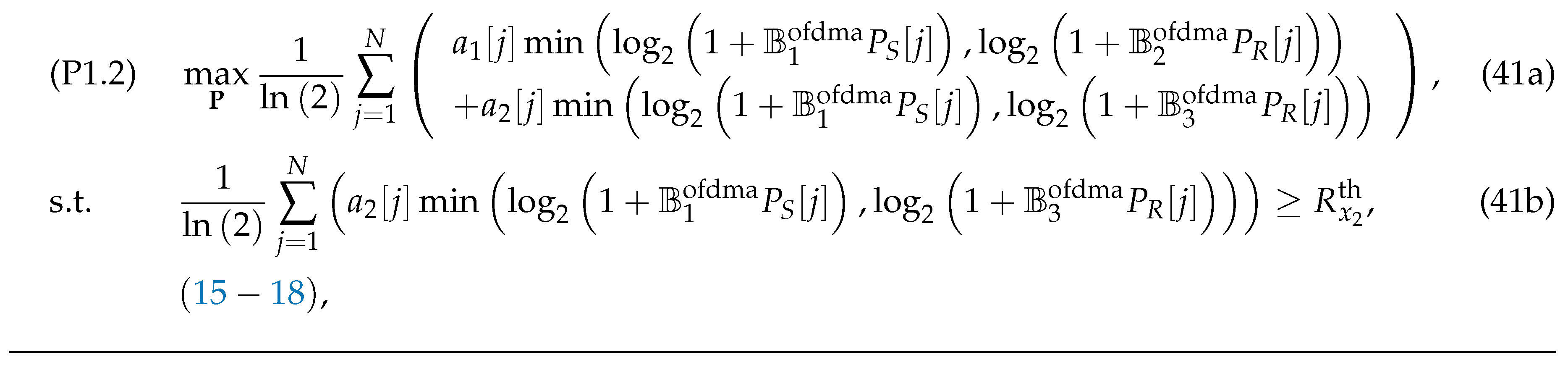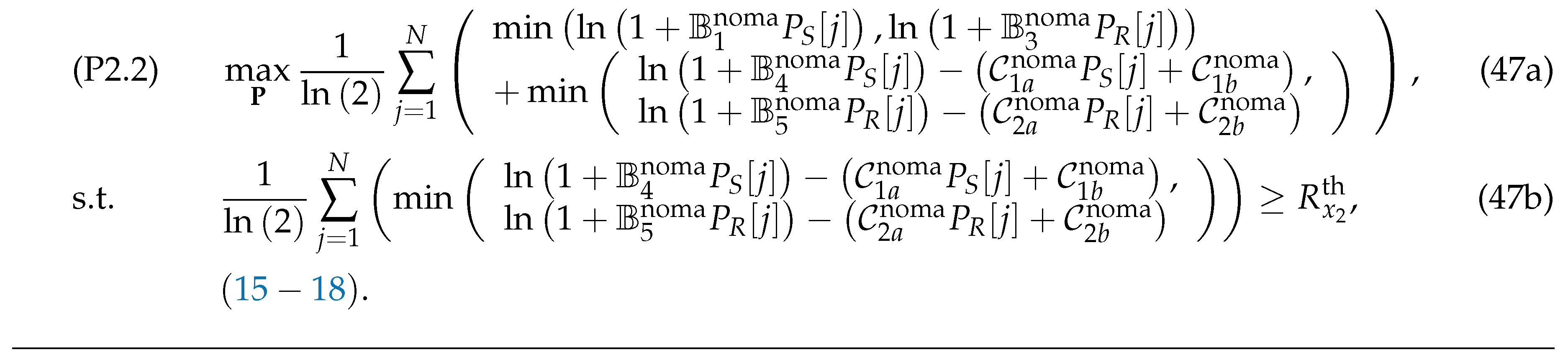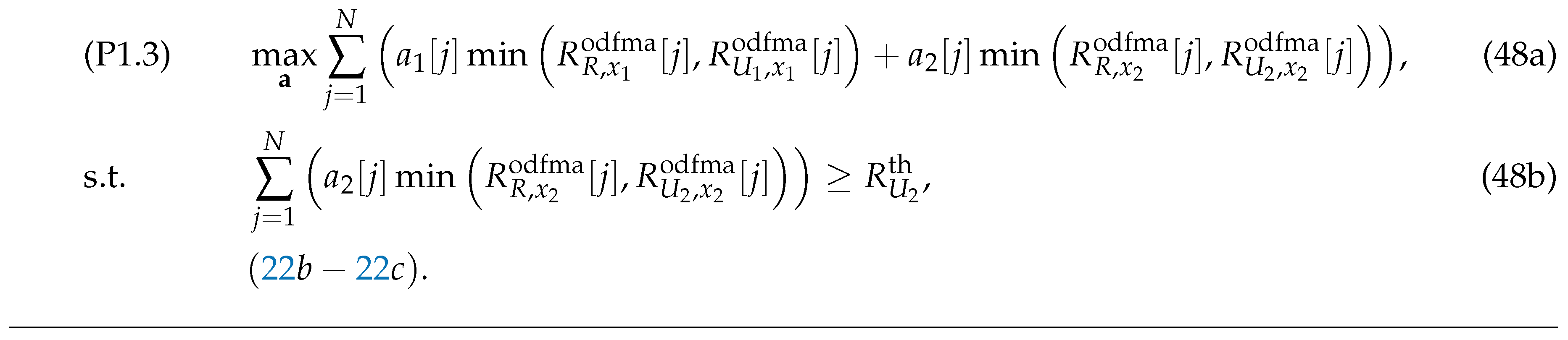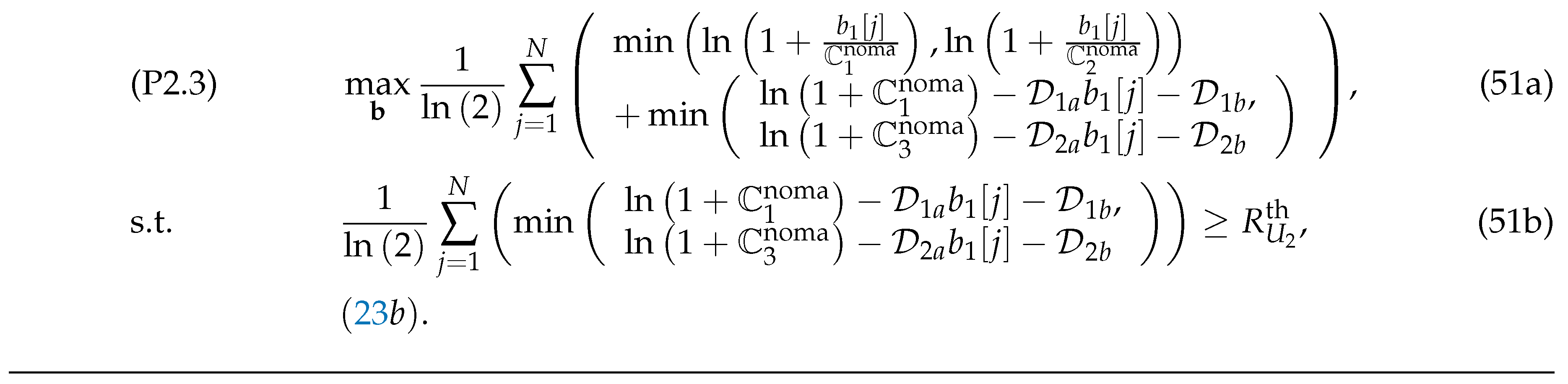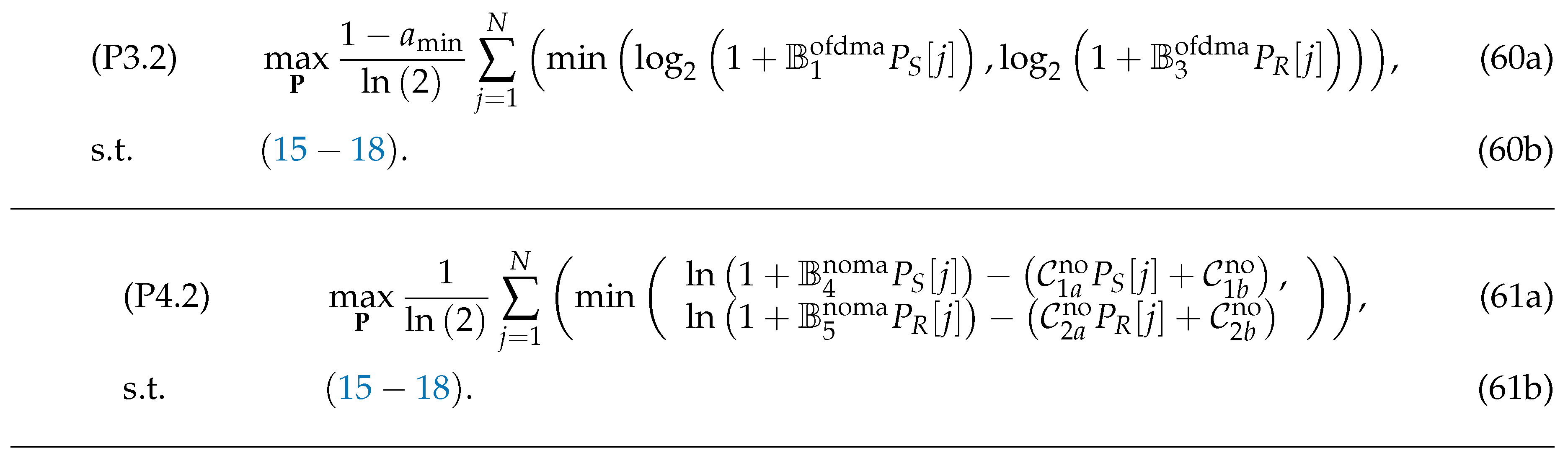1. Introduction
Over the past decade, unmanned aerial vehicles (UAVs), with their advantages of high mobility, low cost, and rapid deployment, have been used in diverse applications, including surveillance, rescue, cargo transport, and data collection in wireless sensor networks [
1,
2]. The research community is highly interested in the new emerging application of UAVs, that is, UAV-assisted wireless communication (UAVWC). Communication with the support of UAVs is an effective wireless network deployment solution for future communication models, specifically for 6G network systems [
3]. Unlike terrestrial wireless networks where the wireless channel undergoes multi-path fading, UAVWC can provide line-of-sight connections to wireless devices by using aerial base stations; hence, UAVWC is expected to have a higher performance than existing terrestrial wireless systems. Moreover, the mobility and flexibility of UAVs allow UAVWCs to operate with broader coverage or in dangerous areas that require high deployment and maintenance costs of the base stations. To exploit the great benefits of UAVWC, many recent studies on wireless communication have done a lot of work to solve technical challenges and optimize the performance of UAVWC [
4,
5,
6].
Furthermore, UAVs have gained extensive utilization within wireless sensor networks. Functioning as mobile access points or base stations, UAVs present a promising resolution to address the substantial storage demands prevalent in wireless sensor networks [
2,
7]. By facilitating UAV-assisted data aggregation from numerous sensor nodes equipped with wireless capabilities, the singular-antenna UAV empowers all sensor nodes within its coverage scope to transmit data. Consequently, these sensor nodes relay their collected information back to the UAV. Given the significant implications identified, there exists an imperative necessity to delve into research regarding the NOMA-UAV model. Thus, the model communication of the UAV-NOMA combination can significantly enhance the performance of wireless networks in a broader context and specifically contribute to advancing wireless sensor networks. Consequently, greater attention and scrutiny are warranted to explore the NOMA-UAV model’s capabilities and implications comprehensively.
1.1. Related Work
To optimize the performance of UAVWCs and exploit their benefits, recent studies on wireless communication have worked on overcoming various technical challenges. In [
8], the authors examined and provided statistical models for an air-to-ground radio frequency (RF) channel in a dense urban environment, then air-to-ground RF statistical models for different conditions were investigated in [
9]. These results allow network designers to make planning and performance easier evaluations for WN-aNWs. The studies of UAVWCs can be classified into two groups, one using UAVs as static aerial transceivers and another exploiting the mobility of UAVs, known as static and mobile UAVWCs, respectively. Moreover, in [
10], the authors proposed a UAV deployment algorithm to minimize the number of UAVs needed to provide wireless coverage for a given area. In [
11], the authors solved the up-link sum-rate maximization problem of a static wireless-powered UAVWC. Authors in [
12] optimized the UAV’s location and user association for UAV-assisted mobile networks with the goal of making the traffic loads of UAVs almost equal so that the networks can be stable. In [
13], the authors considered a low-altitude aerial platform (LAP) for the urban environment and provided a mathematical model of the altitude and wireless coverage, allowing network designers to predict the optimum altitude of the static UAVWC.
NOMA has been evaluated as a potential solution for future networks, such as beyond fifth-generation (B5G) and sixth-generation (6G) networks, because its benefits can meet the new 6G performance requirement, especially for huge connectivity [
14,
15,
16,
17]. Thus, many publications have investigated the application of NOMA for UAV networks. Notably, authors in [
18] outlined new opportunities and challenges with NOMA with the assistance of UAV in more significant rate regions, balanced performance between system throughput and fairness, and reduced delay. In [
19], the authors evaluated the outage probability of UAV-aided non-orthogonal multiple access (NOMA) networks and uplink and downlink transmissions. In [
20], the authors analyzed a UAV-aided device-to-device network’s sum rate and average coverage probability for both static and mobile UAV scenarios. Moreover, authors in [
21] investigated the delay-constrained performance analysis of a multi-antenna assisted multiuser NOMA-based spectrum sharing system and examined the sum effective rate for the downlink NOMA system. The work of [
22] solved the problem of improving the secrecy performance in a UAV-assisted NOMA communication by jointly optimizing the UAV’s trajectory and the transmit powers of legitimate users. A UAV-enabled space-air-ground integrated relay system applying the NOMA technique is presented in [
23]. In this publication, authors summarized the UAV-ground NOMA communication into a max-min problem regarding UAV’s energy efficiency. The use of artificial intelligence-driven UAV-NOMA to improve the quality of experiences of terrestrial multi-users is studied in the works [
24,
25]. Moreover, authors in [
26] investigated the UAV in PD-NOMA with concurrent uplink transmission of the aerial user (AU) and terrestrial user (TU). To enhance the achievable data rate of both AU and TU, these authors developed an analytical framework to calculate the probability of rate coverage; the results showed that the min height of the AUE is contingent upon its distance from the BS as it follows a designated trajectory. This underscores the significance of accurately modeling the AUE trajectory within cellular-connected UAV systems. In [
27], a heuristic algorithm and logarithmic approximation are applied to solve the problem of the total energy efficiency for UAV communication in a downlink NOMA network. In summary, these related works exploring UAV facilitating NOMA communication are delineated in
Table 1 and presented below.
1.2. Main Contributions
As the analysis has shown above, specifically in
Table 1, we see that the studies of the UAV flight trajectory, its influence, and transmitted power allocation to the NOMA-UAV network using mathematical methods are limited. Therefore, in this paper, we investigated a UAV relaying system including two users, a near user and a far user. The UAV’s flight path is from a beginning position to an ending position, and it will assist in communication between a ground base station (GBS) and two destination users (DUs). Two multiple access techniques, orthogonal frequency division multiple access (OFDMA), in which the frequency resource is split for each user, and non-orthogonal multiple access (NOMA), in which the user’s signals are transmitted on the same frequency resource with different power levels, are examined. The contributions of our work are encapsulated as follows:
We consider non-convex problems of maximizing the system sum rate of the proposed UAVWC system under constrained conditions of the total bandwidth, total transmitted power at GBS and the UAV, and required sum rate of the far user for the NOMA and OFDMA scenarios;
We propose algorithms using the SCO and BCGD techniques to identify excellent solutions for the proposed non-convex optimization problem of sum rate based on the UAV’s trajectory and transmitted power. We show that our algorithms are guaranteed to coverage;
Achievable simulated results Achieve simulated results reveal that the system sum data rate is remarkably ameliorated by applying our proposed algorithms and pointing out the optimal trends of critical system parameters with both NOMA and OFDM.
The remainder of this article is arranged as follows. The system model and preliminary results for OFDMA/NOMA-based UAV relaying (OFDMA/NOMA-UAVR) protocols are described in
Section 2. The problem formulation and solution for the sum-rate maximization for OFDMA/NOMA-UAVR protocol are presented in
Section 3. The overall algorithm and convergence analysis are presented in
Section 4. The simulation results and discussions are presented in
Section 5. Finally, the conclusions are presented in
Section 6.
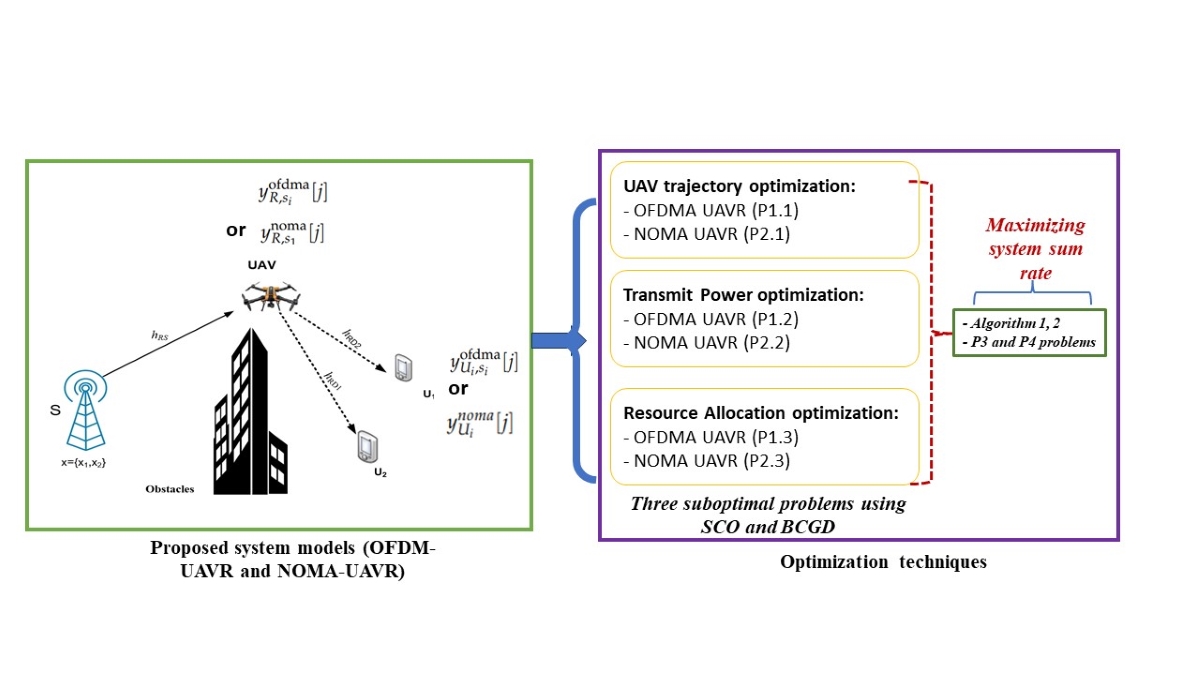
2. System Model
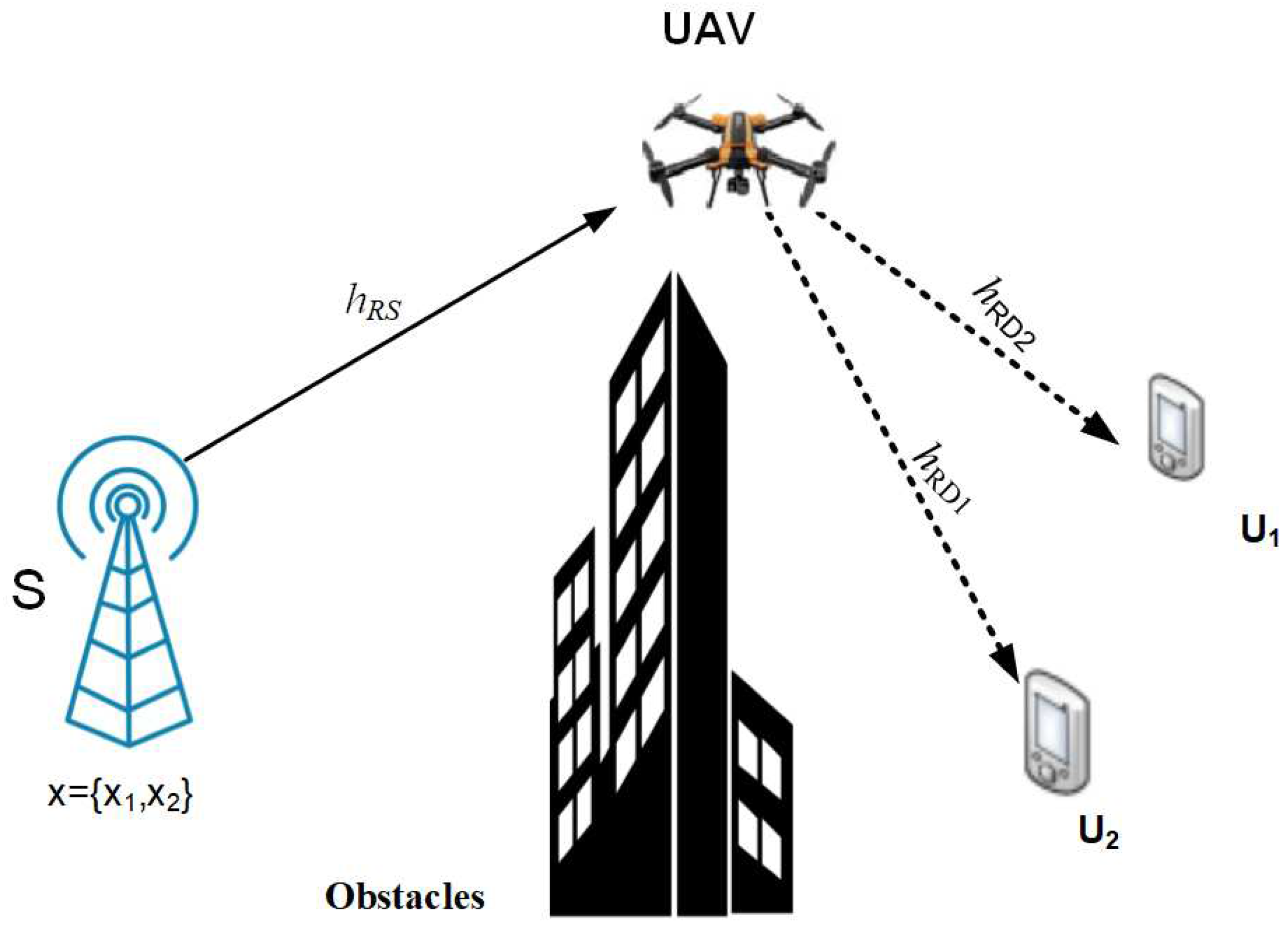
We consider a UAV relaying system, as illustrated in
Figure 1, in which a UAV,
R, flies at a fixed altitude
H from an initial location
to a final location
, and helps a source
S communicate with a closer user
and a further user
.
S,
, and
are terrestrial single-antenna nodes.
R uses the decode-and-forward (DF) protocol to assist the communication. We assume that: (i) there is no direct link between
S and users because of obstacles; (ii) the Relay’s operation is in a length of time
T; (iii) the UAV taking off and landing are not considered, and we concentrate on the UAV operation period and altitude
H; and (iv)
T is split into
N equal time slots
, where
is adequately small such that the position of UAV can be determined as a constant during
. Finally, in this paper, system variables for this system model are summarized in
Table 2.
The horizontal positions of
S,
,
, and
R during
are represented by
,
,
, and
, respectively. The channel gain from
R to a ground source node
X,
, during
is given by:
here,
is the channel gain at a
(m).
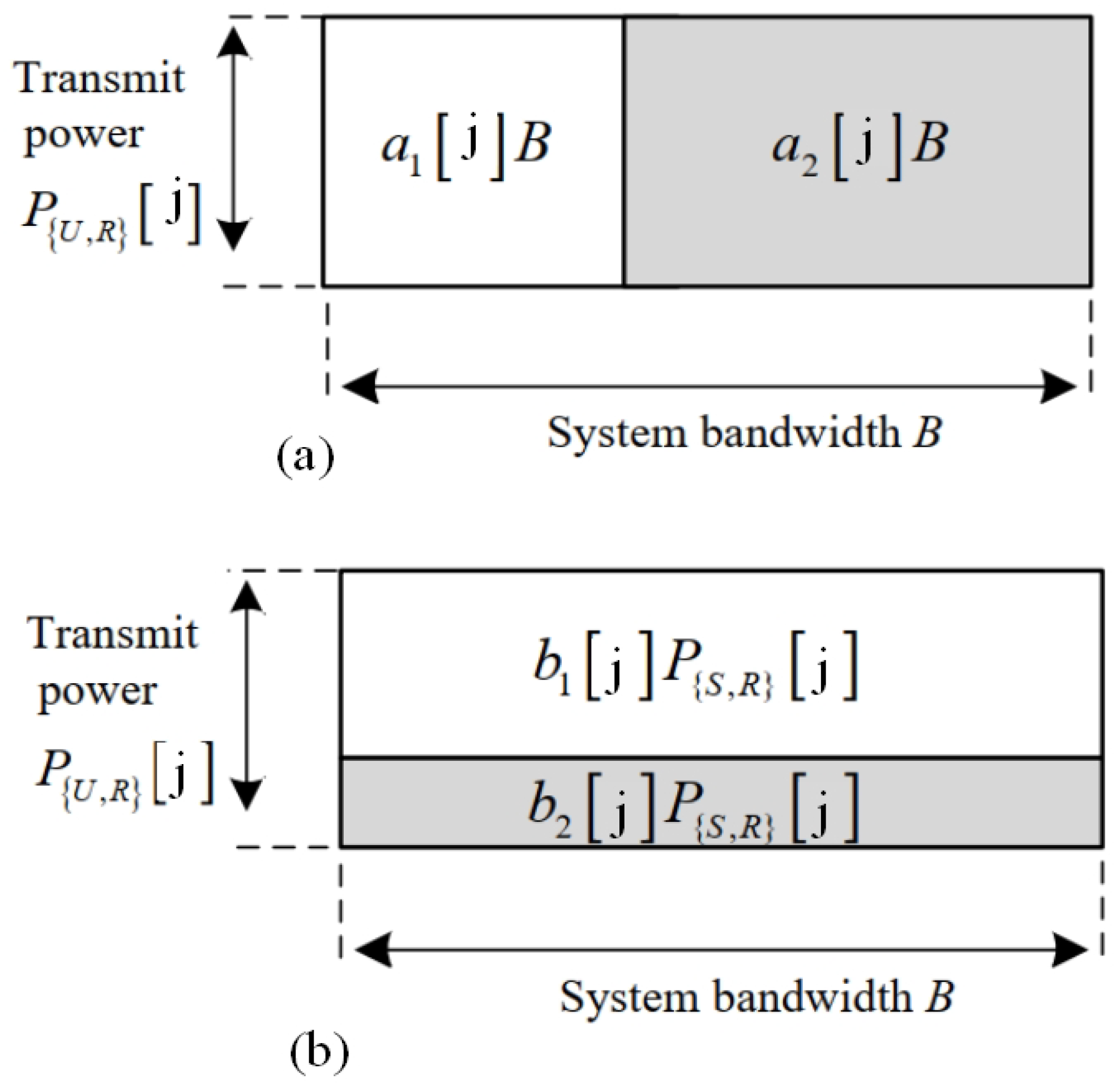
In the following, we present the transmission in each time slot for the OFDMA-based UAV relaying (OFDMA-UAVR) and NOMA-based UAV relaying (NOMA-UAVR) protocols in the half-duplex mode. Thus, the communication for each time slot is split into two sub-time slots, as shown in
Figure 2.
2.1. OFDMA-Based UAV Relaying Protocol
S transmits the signals in the initial sub-time slot within
that are
and
, with the power
on the bandwidths
and
, respectively, where
B is the system bandwidth,
is the bandwidth allocation factor of OFDMA and satisfies both
and
with
is the smallest values of
. The received signal and instantaneous rate at
R are given by
here
is the additive white Gaussian noise (AWGN) at
R.
During the following sub-time slot within
, Relay node will forward
and
to
and
, respectively, on their corresponding bandwidths. The received signal and instantaneous rate at
are given by
here,
is the transmitted power of
R node and
is AWGN at
.
Due to
R node acts as the DF relay, the end-to-end instantaneous rate of
for guaranteeing successful decoding at
is given by
2.2. NOMA-Based UAV Relaying Protocol
In the initial sub-time slot within
,
S broadcasts the superimposed signals,
and
, with the powers
and
, respectively, on bandwidth
B where
is the power allocation factor of NOMA and satisfies both
and
with
is the smallest values of
. The received signal at
R node can be expressed as
Using SIC (successive interference cancellation),
R decodes
first and then eliminates
from the received signal before decoding
. The instantaneous rates of
and
for guaranteeing successful decoding at
R are given by
In the second sub-interval slot within
,
R node will forward
and
with the powers
and
, respectively, on bandwidth
B. The received signal at
is given by
At
, SIC is employed to decode
before decoding
. The instantaneous rates of
and
for guaranteeing successful decoding at
are given by
The instantaneous rate of
at
is given by
Since
R is the DF relay, the end-to-end instantaneous rate of
for guaranteeing successful decoding at
is given by
3. Analysis of Sum-Rate Optimization Problem
Within this section, we define the problem of maximizing the sum rate of the proposed system under the constraint of the required sum rate at
,
, for both OFDMA-UAVR and OFDMA-UAVR protocols. Letting
and
denote the power budget and maximum transmit power during
of node
, we have the following inequalities
With above assumptions in
Section 2, the constraints of the UAV trajectory or of
R are expressed as
Next, letting , , , and , the issues related to maximizing the sum-rate of our proposed system for both the OFDMA-UAVR and NOMA-UAVR protocols are respectively formulated as in (22) and (23) shown at the top of the next page.
For the NOMA-UAVR protocol, the SIC of must decode before trying to detect the signal ; hence, constraint in Equation (23d) is the condition for successful decoding at that allows the SIC at to operate correctly.
Since the objective functions in (22a) and (23a) are neither convex nor concave, (P1) and (P2) is not convex optimizing problems. Subsequently, we propose alternative solutions for these problems using the BCGD and SCO approaches. In particular, we apply the BCGD approach to optimize individual variable blocks of (P1) and (P2) while maintaining the other variable blocks unchanged. For a given resource allocation factor (or ) and transmit powers , we optimize the trajectory of R, , (defined as (P1.1) and (P2.1) for the OFDMA-UAVR and NOMA-UAVR protocols, respectively). For a given UAV’s trajectory and (or ), we optimize the transmit powers (defined as (P1.2) and (P2.2) for the OFDMA-UAVR and NOMA-UAVR protocols, respectively). Finally, for a given and , we optimize for the OFDMA-UAVR protocol (defined as (P1.3)) and for the NOMA-UAVR protocol (defined as (P2.3)). The non-convex objective functions are addressed by applying the SCO method. Ultimately, we introduce the comprehensive algorithms and prove the convergence behaviour of these proposed methods.
3.1. UAV Trajectory Optimization
In this subsection, we use the SCO method to optimize the trajectory of R for the OFDMA-UAVR and NOMA-UAVR protocols.
3.1.1. OFDMA-Based UAV Relaying Protocol
Substituting (
1) into (3) and (5) yields
where
and
.
It is seen that although (24) and (25) lack convexity concerning
, they exhibit convexity in relation to
and
, respectively. This attribute allows us to derive lower bounds for
and
that are convex with respect to
. Specifically, at a given point
(we assume that
is the optimal UAV’s flight trajectory obtained after the
-th iteration), the following lower bounds can be obtained using the first-order Taylor expansion [
17].
where
and
are given by
Using (26) and (27), at any given , and , (P1) is approximated by (P1.1) (or (29)) shown at the top of the next page.
It is seen that (P1.1) is a convex optimization problem that can be efficiently solved by standard convex optimization solvers (such as CVX implemented in Matlab).
3.1.2. NOMA-Based UAV Relaying Protocol
Substituting (
1) into (
8), (9), (
11), () and (
13) and after some manipulations, we have
where
and
.
Following the similar approach as in
Section 3.1.1, we can obtain the following inequalities using the first-order Taylor expansion.
where
and
are given in (37) shown at the top of the next page.
Next, using (33) and (34), Constraint (23d) can be rewritten as
It is seen that (
38) is not a convex constraint. Since the right-hand side of (
38) is convex with respect to
, (
38) can be rewritten applying the first-order Taylor expansion as follows.
Using (35), (36) and (39), for any given , and , (P2) is approximated by (P2.1) (or (40)) shown at the top of the next page.
It is seen that (P2.1) is a convex optimization problem, and we can apply standard convex optimization techniques to address this efficiently.
3.2. Transmit Power Optimization
In this subsection, we optimize the transmit powers of S and R for the OFDMA-UAVR and NOMA-UAVR protocols.
3.2.1. OFDMA-Based UAV Relaying Protocol
Substituting (
6) into (22), at a given
and
, (P1) can be expressed as (P1.2) (or (41)) shown at the top of the next page
where and .
It is seen that (P1.2) represents a convex optimization problem amenable to efficient resolution using standard convex optimization solvers.
3.2.2. NOMA-based UAV relaying protocol
For any given
and
, (9) and (
13) can be rewritten as
where
and
.
Let
, where
and
are the optimal transmit powers of
S and
R, respectively, obtained after the
l-th iteration. The application of the first-order Taylor expansion allows us to derive the following inequalities.
where
and
are given by
Substituting (
8), (
11), (44) and (45) into (23), (P2) can be approximated by (P2.2) (or (47)) shown at the top of the next page
where . It is seen that (P2.2) is a convex problem that can be efficiently addressed by using conventional convex optimization solvers.
3.3. Optimizing the Resource Allocation
In this subsection, we optimize the bandwidth allocation factor and power allocation factor for the OFDMA-UAVR and NOMA-UAVR protocols.
3.3.1. OFDMA-based UAV relaying protocol
For any given and , (P1) can be rewritten as (P1.3) (or (48)) shown at the top of the next page.
It is seen that (P1.3) is a convex optimization problem that can be efficiently addressed by using conventional convex optimization solvers.
3.3.2. NOMA-based UAV relaying protocol
For any given
and
, (9) and (
13) are rewritten as
where
and
.
Substituting (
8), (
11), (
49) and (50) into (23), (P2) can be approximated by (P2.3) (or (51)) shown at the top of the next page.
We can see that (P2.3) is also a convex optimization problem that can be ably addressed by standard convex optimization methods.
4. Proposed Comprehensive Algorithm
4.1. Proposed Algorithm
In this part, we introduce the comprehensive algorithms for obtaining efficient approximate solutions for (P1) and (P2) through the utilization of BCGD method. We also present the outcomes of suboptimal problems, namely (P1.1), (P1.2), (P1.3), (P2.1), (P2.2) and (P2.3). More precisely, the optimization variables consist of three blocks where is the resource allocation factor, i.e., for the OFDMA-UAVR protocol and for the NOMA-UAVR protocol. Each block of is optimized via addressing (P1.1), (P1.2) and (P1.3) (or (P2.1), (P2.2) and (P2.3)) correspondingly while fixing the values of the rest blocks. The obtained solution after optimizing each block is updated to correspondingly. This process is repeated until a certain condition is met. The details of this algorithm are summarized in Algorithm 1.
Table 3.
Algorithm 1: The Sum-Rate Maximization Algorithm for OFDMA/NOMA-UAVR Protocols.
Table 3.
Algorithm 1: The Sum-Rate Maximization Algorithm for OFDMA/NOMA-UAVR Protocols.
| 1. |
Initialize . Let . |
| 2. |
Repeat |
| 3. |
With given , solve (P1.1) or P(2.1) to find and then update |
| |
the optimal UAV’s trajectory to . |
| 4. |
With given , solve (P1.2) or P(2.2) to find and then |
| |
update the optimal transmit powers to . |
| 5. |
With given , solve (P1.3) or P(2.3) to find and then |
| |
update the optimal PS ratio to . |
| 6. |
Update . |
| 7. |
Until The fractional increase of the objective value is below a small |
| |
threshold . |
In the following, we show the convergence of Algorithm 1. Let
,
,
and
be respectively the objective functions of either (P1), (P1.1), (P1.2) and (P1.3) for the OFDMA-UAVR protocol or of (P2), (P2.1), (P2.2) and (P2.3) for the NOMA-UAVR protocol. First, at any provided point
, the subsequent inequalities are derived through the execution of Step (3) in Algorithm 1:
where (a) holds, since the first-order Taylor expansions at (
26), (27), (
35), (36) are performed at the point
; (b) holds, since
is the optimal solution of (P1.1) (or P(2.1)); and (c) holds, since the objective functions of (P1.1) and (P2.1) are the lower bounds of those of (P1) and (P2), respectively.
Using similar explanations for (P1.2), (P1.3), (P2.2), and (P2.3), the inequalities in (53) and (54) can be proven as follows. Then, at any provided point
, we can get the following inequalities via Step (4) of Algorithm 1:
Next, at any provided point
, we also get the following inequalities via Step (5) of Algorithm 1:
This observation reveals that the objective values of (P1) and (P2) are non-decreasing trend throughout iterations. Furthermore, the optimized values of (P1) and (P2) are finite, ensuring the guaranteed convergence of Algorithm 1.
4.2. Initialization Scheme
In this part, we introduce the Algorithm 2 which aims to discover an attainable initial variable block for Algorithm 1. Due to the constraint of the sum data rate of , the key concept behind Algorithm 2 that is maximizing the sum-rate of for the OFDMA-UAVR and NOMA-UAVR protocols, respectively defined as (P3) and (P4). Note that the values of and are set at their highest values; hence, for the OFDMA-UAVR protocol and for the NOMA-UAVR protocol. If the maximum achievable sum rate with Algorithm 2 surpasses that of , the current optimal flight trajectory and transmit powers are and , respectively; otherwise, (P1) and (P2) are infeasible optimization problems. By modifying (P1) and (P2), we can obtain (P3) and (P4) as

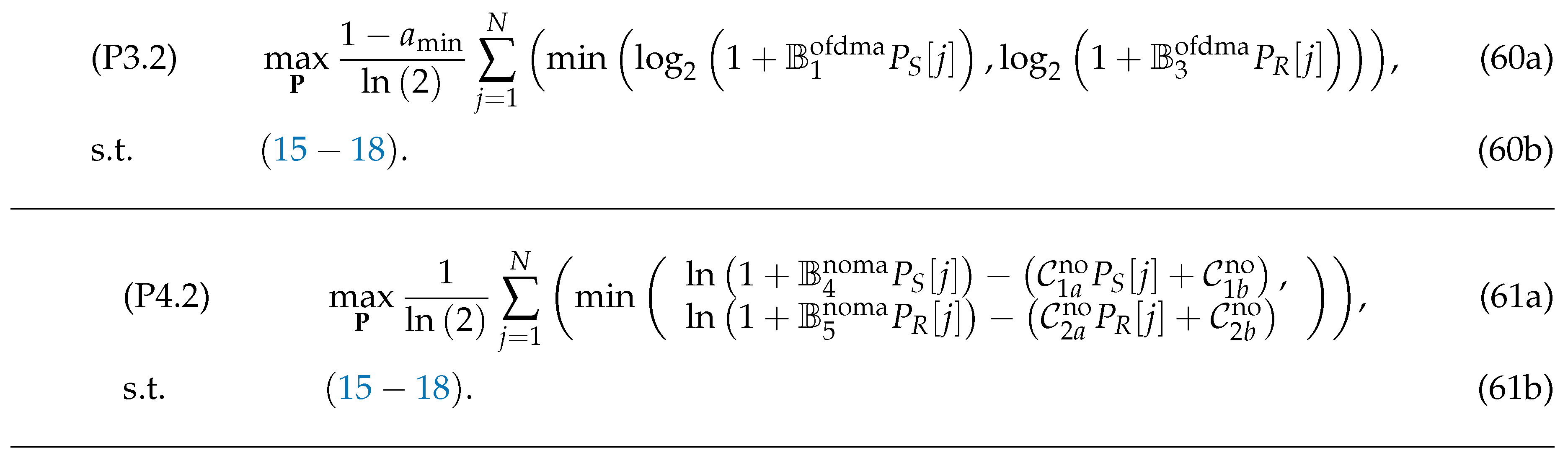
Similarly, the problems of (P3) and (P4) are not convex optimization. Therefore, we have introduced alternative solutions for (P3) and (P4)employing the BCGD and SCO approaches. Concretely, the optimization variables consist of two blocks . Subsequently, the BCGD technique is employed to perform optimization for each of these variable blocks within the context of (P3) (or (P4)), while holding the other variable blocks constant. With transmit powers , we optimize (defined as (P3.1) and (P4.1) for the OFDMA-UAVR and NOMA-UAVR protocols, respectively); and for a given UAV’s trajectory , we optimize (defined as (P3.2) and (P4.2) for the OFDMA-UAVR and NOMA-UAVR protocols, respectively). The result achieved through the optimization of each block is then adjusted in accordance with . This iteration continues until a specific criterion is satisfied. Furthermore, the objective functions with non-convex characteristics are addressed by applying the SCO technique.
Table 4.
Algorithm 2: The Initialization Scheme for Algorithm 1.
Table 4.
Algorithm 2: The Initialization Scheme for Algorithm 1.
| 1. |
Initialize . Let . |
| 2. |
Repeat |
| 3. |
With given , solve (P3.1) or P(4.1) to find and then |
| |
update the optimal UAV’s trajectory to . |
| 4. |
With given , solve (P3.2) or P(4.2) to find and then |
| |
update the optimal transmit powers to . |
| 5. |
Update . |
| 6. |
Until The objective value is higher than or . |
| 7. |
If
|
| 8. |
|
| 9. |
Else |
| 10. |
(P1) and (P2) are infeasible optimization problems. |
| 11. |
End if |
By applying (29) and (40), the optimization problems of (P3.1) and (P4.1) at any given and are respectively given by (58) and (59), shown in the top of the next page.
Using (41), (47), the optimization problems of (P3.2) and (P4.2) at any given and are respectively given by (60) and (61), shown in the top of the next page.
Ultimately, a summary of Algorithm 2 can be located in
Table 2, where
is the utmost limit of iterations.
Algorithm 2 begins with an initial flight path of the UAV , which consists of a straight line connecting points and and maintains a constant velocity of , where . Additionally, the initial transmission power settings are established and .
5. Simulation Results
This section presents numerical findings to validate the effectiveness of our proposed optimization algorithms. The system parameters are set-up in our simulations as: T= 300 (s), N = 60, , (dB), , , , , (m/s), (meters) and . The measured coordinates in meters for , , , and are respectively set as and .
5.1. UAV’s Fight Trajectory and Velocity Analysis
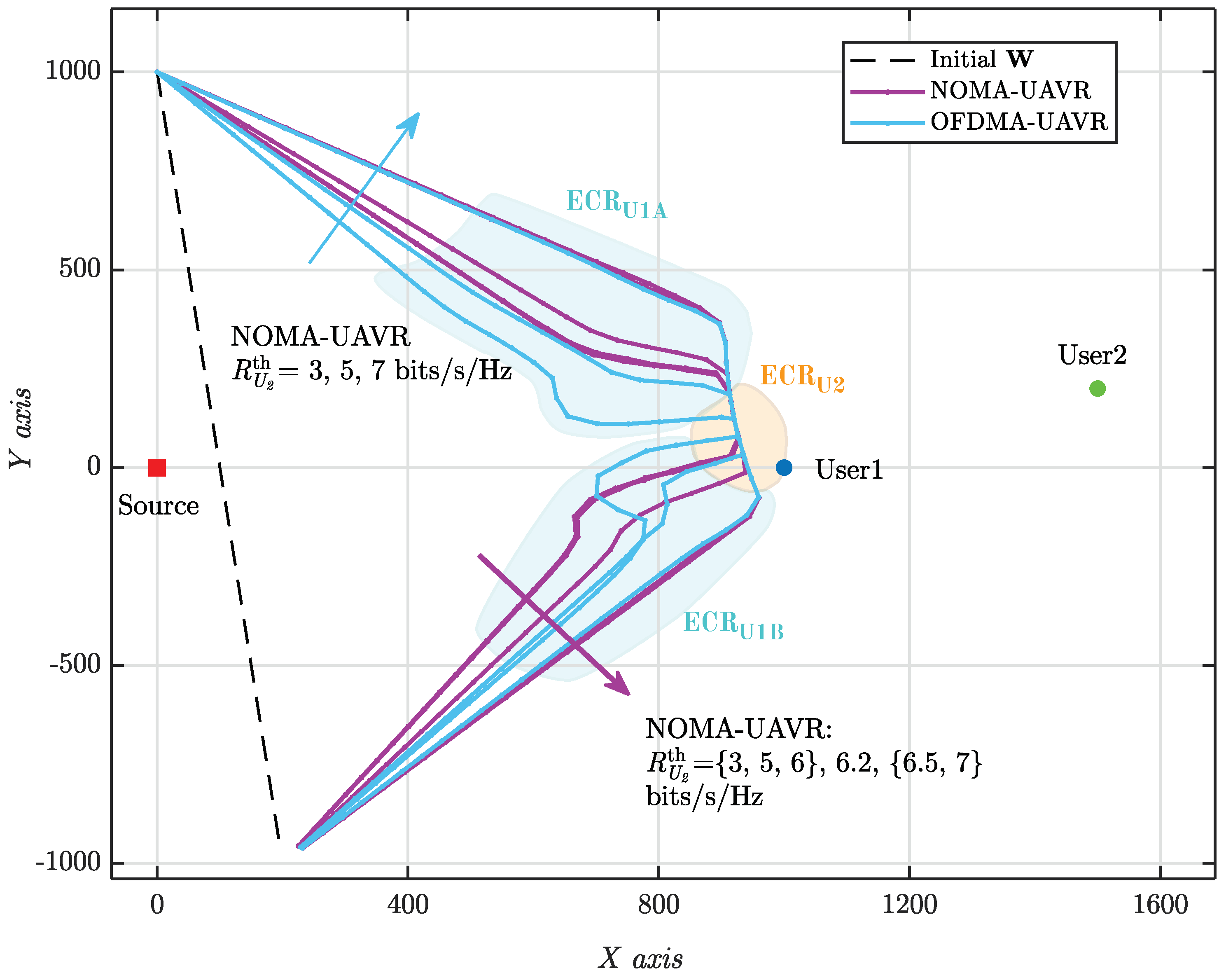
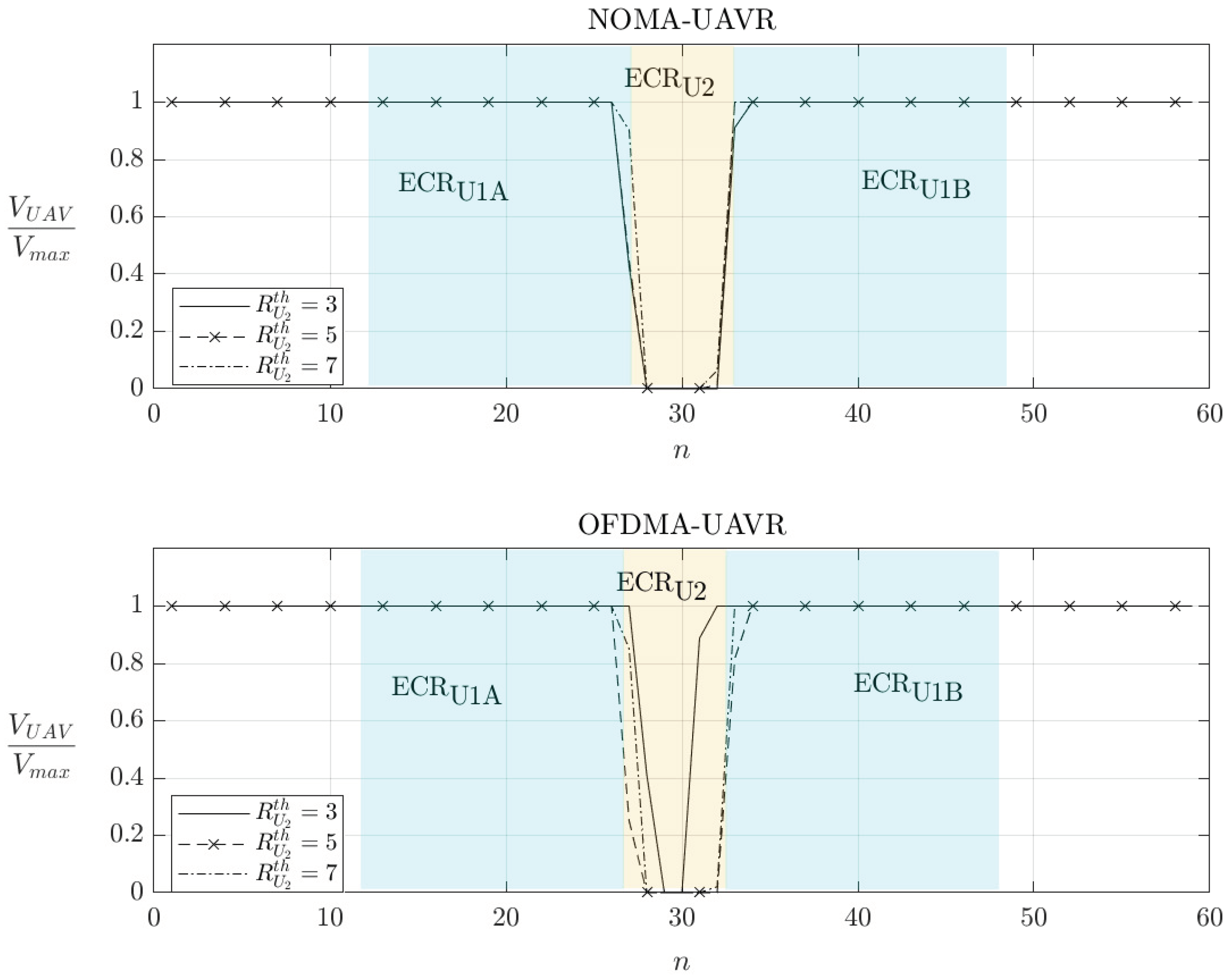
In
Figure 3 and
Figure 4, we investigate the optimum flight path and velocity of
R obtained using the proposed algorithms. The trajectory of
R is separated into three phases. At the initial phase (
), the positions of
R are far from the source and users; this leads to low efficient communication. For this reason, during the initial phase,
R almost does not forward any information to users and it flies quickly to efficient communication regions (ECRs) where it can assist the commutation at higher data rates. At the second phase, the efficient-communication phase (ECP),
,
R operates over the two specific ECRs, the
,
, for providing the good
communication and
for providing the good
communication.
and
are illustrated as in
Figure 3. Depending on the configuration of the system, the size of ECRs can be larger or smaller. It is seen that the ECRs are between the source and users that agree with the assessment for the optimum location of the static relay in the conventional relaying systems. As shown in
Figure 4,
R spends a duration (around
) to stay at
to guarantee the required sum-rate of
,
, and also to maximize the system sum-rate. When
requires more data, i.e.,
increases,
R tends to spend more time at
. This can be confirmed using the results for velocity for the case of
(bits/s/Hz). For the NOMA-UAVR protocol, the trajectory significantly changes as
increases from 6 to 6.5 (bits/s/Hz), otherwise it almost does not change. For the OFDMA-UAVR protocol, the trajectory substantially changes with the increase of
. For high values for
,
R flies with a similar trajectory in both NOMA-UAVR and ODFMA-UAVR protocols. At the final phase
,
R stops forwarding the information to users and quickly flies from
and/or
to the final location.
5.2. Transmission Powers and Resource Allocation Analysis
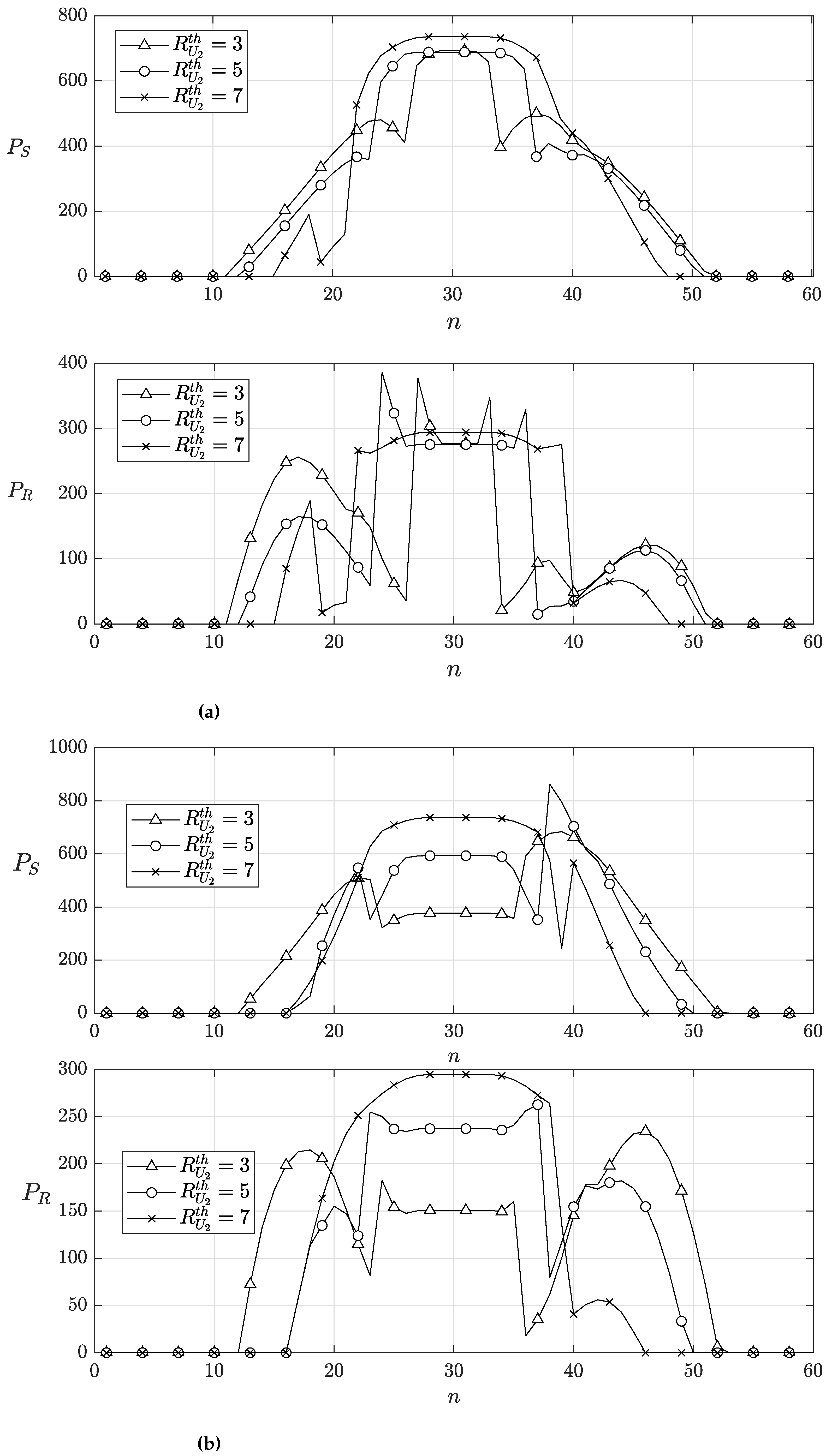
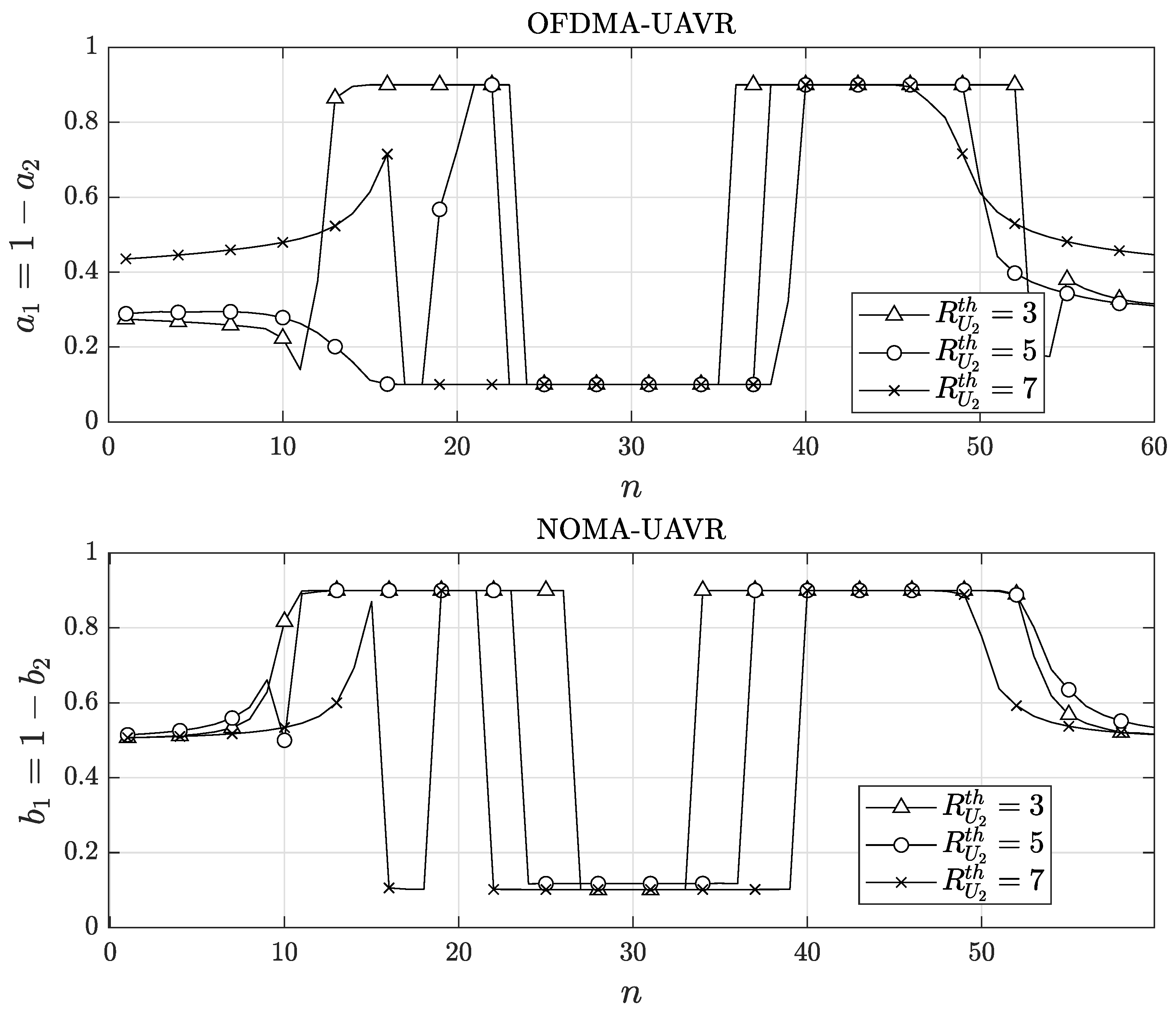
In
Figure 5 and
Figure 6, we present the optimal transmitted powers and resource allocation elements (i.e.,
and
) obtained using the proposed algorithms. In these figures, we focus on the patterns in the transmission power levels,
and
) during the ECP
. Particularly, these trends are separated into three sub-phases. During the first sub-phase of the ECP, the transmit powers increase as
R flies closer to
, then reach a peak and decrease as
R flies far away from
to transit to
. Next, during the second sub-phase of the ECP, the transmits powers increase again as
R flies toward to
, then they slightly vary as
R flies in
, and finally, they decrease as
R flies far away from
and transits to
The trends of the transmit powers in the last sub-phase of the ECP are the opposite trends for that during the first sub-phase of ECP. Moreover, the trends observed at low values of
(e.g.,
) are more obvious than those observed at high values of (e.g.,
(bits/s/Hz)). As shown in
Figure 6, the general trend of
(or
) is receiving high values as
R flies near
and low values as
R flies near
. Similarly, we can also explain the trend of
(or
) using the effects of the trajectory of
R,
and
on the instantaneous rates at
and
.
5.3. Analysis of Instantaneous Rate and Sum Data Rate of Each User
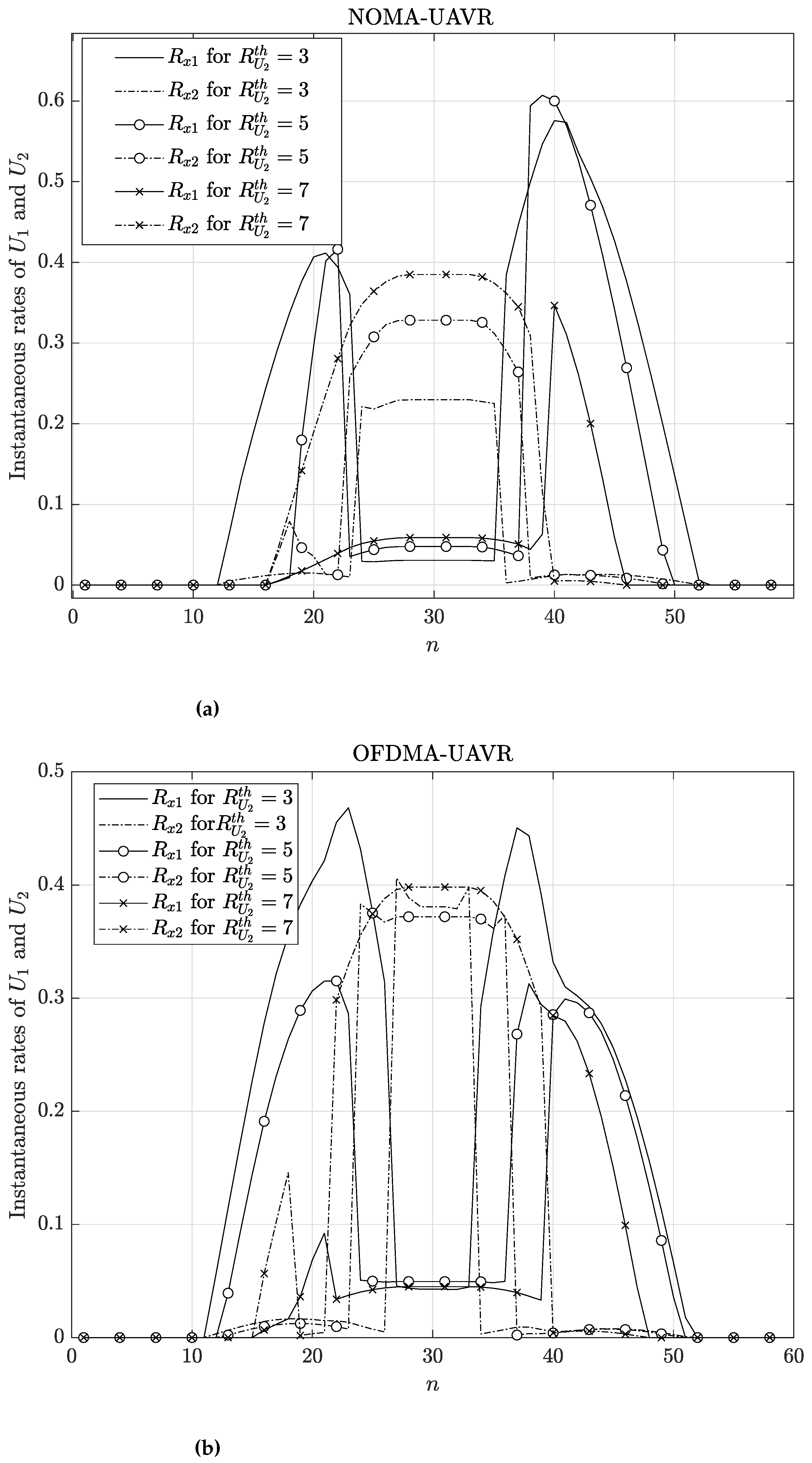
Figure 7 examines each user’s optimal patterns in the instantaneous rate. The instantaneous rate is positive during the ECP and equal to zero during the rest phases. The instantaneous rate of
receives high values at the beginning and end of the ECP, while the instantaneous rate of
receives elevated values in the middle of the ECP. These patterns can be elucidated by referring to the outcomes regarding the flight trajectory of
R, transmission power levels, and and
(or
). When
increases, the instantaneous rate of
for each time slot becomes higher; moreover, the high-rate region of
expands on both sides of the
n axis, while the high-rate region of
follows the inverse trend.
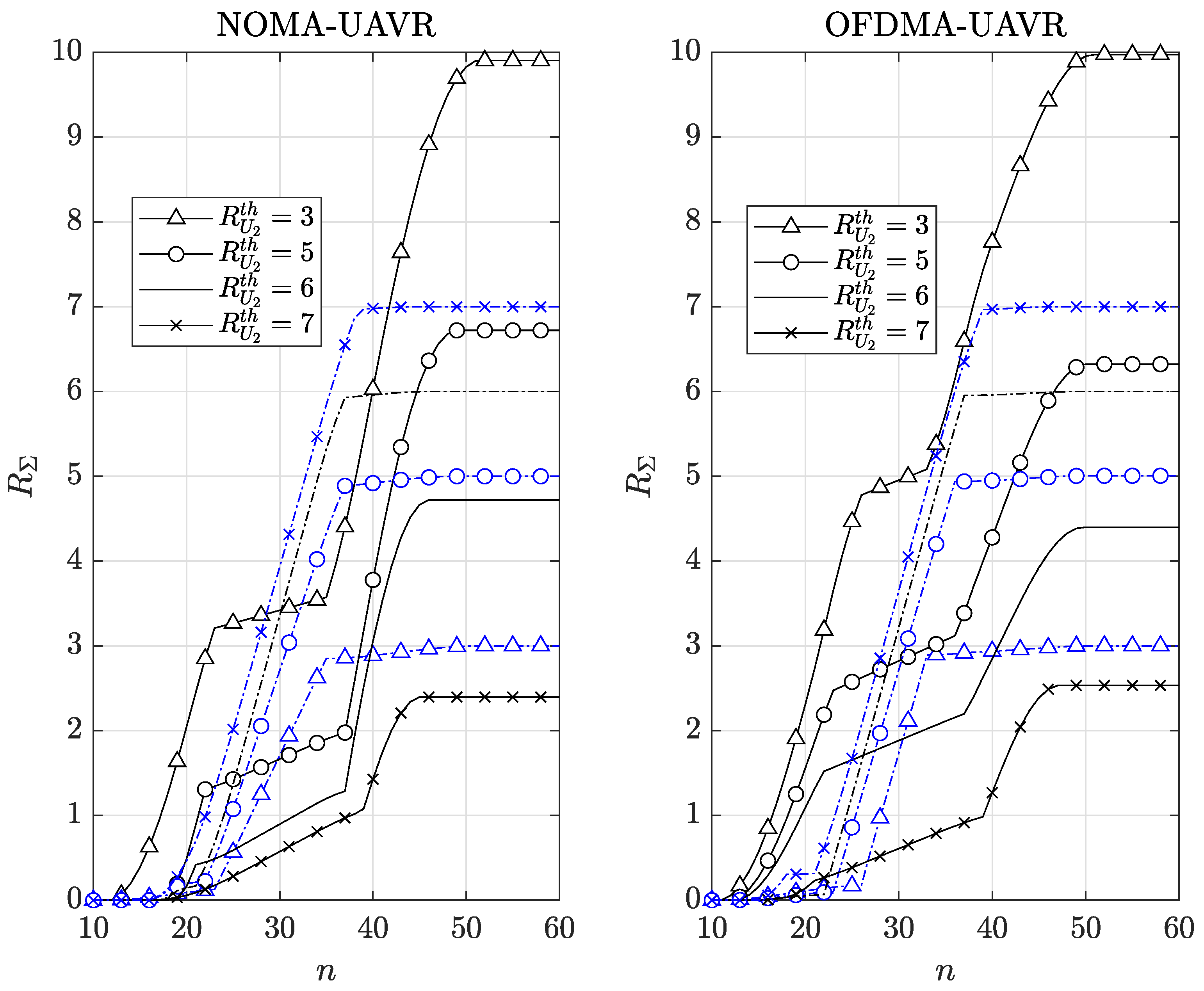
Figure 7 presents the trend of the optimal sum data rate for
of
and the optimal sum data rate for
of
. The purpose of our proposed algorithms is to maximize the system total data rate; however,
Figure 8 shows that the obtained efficient solution using the proposed algorithm aims to maximize the sum data rate of
while guaranteeing the required sum data rate of
. This is a reasonable result due to the disadvantageous position of
. Comparing ODFMA-UAVR and NOMA-UAVR protocols, we realize that the OFDMA-UAVR protocol outperforms the NOMA-UAVR protocol at very low or very high values for
whereas the NOMA-UAVR protocol outperforms the OFDMA-UAVR protocol at medium values for
is medium (such as
or
). These results emphasize the benefits of the NOMA-UAVR protocol in providing fair communication service for the multi-user system.
6. Conclusions
In this paper, we proposed algorithms to solve the system sum data rate maximization problem of a UAV-based relaying two-user system for two multiple access techniques, OFDMA and NOMA. Our proposed algorithms aim to guarantee service for the far user while maximizing the sum data rate for both users. By applying the SCO and BCGD techniques, the proposed algorithms optimized the UAV’s flight trajectory, factors of resource allocation, and transmission powers. The numerical results confirmed that the system sum data rate significantly improved coverage. Furthermore, the optimal patterns in critical parameters, such as transmitted powers from GBS, the flight path and velocity of the UAV, and the resource allocation ratio, were revealed. Notably, the UAV tends to fly near or stay in specific areas, allowing efficient communication between the source and each user. The proposed algorithms tend to guarantee the minimum required sum data rate at the further destination user and maximize the sum data rate at the closer destination user. Finally, the obtained results demonstrate that the NOMA-UAVR protocol outperforms the OFDMA-UAVR protocol for the fair user-service scenario, whereas the OFDMA-UAVR protocol outperforms the NOMA-UAVR protocol in maximizing the system sum-rate for very low or very high required sum-rate rate for the far user.
Author Contributions
Building model, analysis, and writing—original draft preparation Thuc Kieu-Xuan; Building algorithms, performing experiments, and validation-Supervision Anh Le-Thi; All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This study is supported by the Research Fund of Hanoi University of Industry and thanks to Dr.Tuan Van-Phu, who supported us during the process.
Conflicts of Interest
We wish to confirm that there are no known conflicts of interest associated with this paper. We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the order of authors listed in the manuscript has been approved by all of us.
Abbreviations
The following abbreviations are used in this manuscript:
| BCGD |
Block-coordinate gradient descent |
| DU |
Destination user |
| GBS |
Round base station |
| NOMA |
Non-Orthogonal Multiple Access |
| OMA |
Orthogonal Multiple Access |
| OFDMA |
Orthogonal frequency
division multiple access |
| SCO |
Successive Convex Optimization |
| SIC |
Successive Interference Cancellation |
| SINR |
Signal-to-Interference and Noise Ratio |
| UAV |
Unmanned aerial vehicles |
| UAVR |
UAV relaying |
| UAVWC |
UAV-assisted wireless communication |
References
- Vinogradov, E.; Sallouha, H.; De Bast, S.; Azari, M.M.; Pollin, S. Tutorial on UAV: A blue sky view on wireless communication. arXiv preprint arXiv:1901.02306 2019.
- Shen, T.; Ochiai, H. A UAV-Enabled Wireless Powered Sensor Network Based on NOMA and Cooperative Relaying With Altitude Optimization. IEEE Open Journal of the Communications Society 2021, 2, 21–34. [Google Scholar] [CrossRef]
- Michailidis, E.T.; Maliatsos, K.; Skoutas, D.N.; Vouyioukas, D.; Skianis, C. Secure UAV-aided mobile edge computing for IoT: A review. IEEE Access 2022, 10, 86353–86383. [Google Scholar] [CrossRef]
- Duong, T.Q.; Kim, K.J.; Kaleem, Z.; Bui, M.P.; Vo, N.S. UAV caching in 6G networks: A Survey on models, techniques, and applications. Physical Communication 2022, 51, 101532. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wang, J.; Chen, J.; Yao, K.; Wu, Q.; Anpalagan, A. Opportunistic UAV utilization in wireless networks: Motivations, applications, and challenges. IEEE Communications Magazine 2020, 58, 62–68. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, P. The Effectiveness of Unmanned Aerial Vehicle (UAV) on Farmlands with Artificial Intelligence (AI) System. 2022 7th International Conference on Financial Innovation and Economic Development (ICFIED 2022). Atlantis Press, 2022, pp. 1664–1669.
- Thi Tam, D.; Cao Nguyen, B.; Manh Hoang, T.; The Dung, L.; Vinh, N.V.; Kim, T.; Lee, W. Combining FD-UAV and NOMA technologies in IoT sensor network with millimeter-wave communications. International Journal of Communication Systems 2023, p. e5492.
- Greenberg, E.; Bar, A.; Klodzh, E. Los classification of UAV-to-ground links in built-up areas. 2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS). IEEE, 2019, pp. 1–5.
- Cui, Z.; Briso-Rodríguez, C.; Guan, K.; Güvenç, I.; Zhong, Z. Wideband air-to-ground channel characterization for multiple propagation environments. IEEE Antennas and Wireless Propagation Letters 2020, 19, 1634–1638. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, L. Fast deployment of UAV networks for optimal wireless coverage. IEEE Transactions on Mobile Computing 2018, 18, 588–601. [Google Scholar] [CrossRef]
- Shahzadi, R.; Ali, M.; Khan, H.Z.; Naeem, M. UAV assisted 5G and beyond wireless networks: A survey. Journal of Network and Computer Applications 2021, 189, 103114. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, T.; Wang, S. Location optimization and user association for unmanned aerial vehicles assisted mobile networks. IEEE Transactions on Vehicular Technology 2019, 68, 10056–10065. [Google Scholar] [CrossRef]
- Khan, S.K.; Naseem, U.; Sattar, A.; Waheed, N.; Mir, A.; Qazi, A.; Ismail, M. UAV-aided 5G network in suburban, urban, dense urban, and high-rise urban environments. 2020 IEEE 19th International Symposium on Network Computing and Applications (NCA). IEEE, 2020, pp. 1–4.
- Liu, Y.; Yi, W.; Ding, Z.; Liu, X.; Dobre, O.; Al-Dhahir, N. Application of NOMA in 6G networks: Future vision and research opportunities for next generation multiple access. arXiv preprint arXiv:2103.02334 2021.
- Khan, W.U.; Jameel, F.; Jamshed, M.A.; Pervaiz, H.; Khan, S.; Liu, J. Efficient power allocation for NOMA-enabled IoT networks in 6G era. Physical Communication 2020, 39, 101043. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, W.; Ding, Z.; Liu, X.; Dobre, O.A.; Al-Dhahir, N. Developing NOMA to Next Generation Multiple Access: Future Vision and Research Opportunities. IEEE Wireless Communications 2022. [Google Scholar] [CrossRef]
- Le, T.A.; Kong, H.Y. Evaluating the performance of cooperative NOMA with energy harvesting under physical layer security. Wireless Personal Communications 2019, 108, 1037–1054. [Google Scholar] [CrossRef]
- New, W.K.; Leow, C.Y.; Navaie, K.; Sun, Y.; Ding, Z. Application of NOMA for cellular-connected UAVs: Opportunities and challenges. Science China Information Sciences 2021, 64, 1–14. [Google Scholar] [CrossRef]
- Do, D.T.; Nguyen, T.T.T.; Nguyen, T.N.; Li, X.; Voznak, M. Uplink and downlink NOMA transmission using full-duplex UAV. IEEE Access 2020, 8, 164347–164364. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, Z. The full-duplex device-to-device security communication under the coverage of unmanned aerial vehicle. KSII Transactions on Internet and Information Systems (TIIS) 2019, 13, 1941–1960. [Google Scholar]
- Kumar, V.; Ding, Z.; Flanagan, M.F. On the Effective Rate of NOMA in Underlay Spectrum Sharing. IEEE Transactions on Vehicular Technology 2021, 70, 12220–12225. [Google Scholar] [CrossRef]
- Van Phu, T.; Kong, H.Y. Secrecy sum rate maximization for UAV-aided NOMA communication systems. Annals of Telecommunications 2022, 77, 127–138. [Google Scholar] [CrossRef]
- Wang, N.; Li, F.; Chen, D.; Liu, L.; Bao, Z. NOMA-based Energy-Efficiency optimization for UAV enabled space-air-ground integrated relay networks. IEEE Transactions on Vehicular Technology 2022, 71, 4129–4141. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Liu, X.; Liu, Y.; Chen, Y.; Cui, S.; Poor, H.V. AI-driven UAV-NOMA-MEC in next generation wireless networks. IEEE Wireless Communications 2021, 28, 66–73. [Google Scholar] [CrossRef]
- Hariz, H.M.; Sheikhzadeh, S.; Mokari, N.; Javan, M.R.; Abbasi-Arand, B.; Jorswieck, E.A. Ai-based radio resource management and trajectory design for pd-noma communication in irs-uav assisted networks. arXiv preprint arXiv:2111.03869 2021.
- Senadhira, N.; Durrani, S.; Zhou, X.; Yang, N.; Ding, M. Uplink NOMA for Cellular-Connected UAV: Impact of UAV Trajectories and Altitude. IEEE Transactions on Communications 2020, 68, 5242–5258. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K.; Jiang, C.; Guizani, M. Joint Resource Allocation and Trajectory Optimization With QoS in UAV-Based NOMA Wireless Networks. IEEE Transactions on Wireless Communications 2021, 20, 6343–6355. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).