Modelling the Distribution of Cognitive Outcomes for Early Stage Neurocognitive Disorders: A Model Comparison Approach

Background: Cognitive for patients with neurocognitive disorders are mostly measured by Montreal Cognitive Assessment (MoCA) and Visual Cognitive Assessment Test (VCAT) as screening tools. These cognitive scores are usually left skewed and the results of association analysis might not be robust. This study aims to study the distribution of the cognitive outcomes and to discuss potential solutions. Materials and Methods: The inverse transformed cognitive outcomes are modelled using different statistical distributions. Robustness of the proposed models are checked under different scenarios: with intercept only, models with covariate, with and without bootstrapping. Results: Main results were based on VCAT score, and validated via MoCA score. Findings suggested that the inverse transformation method improves modelling the cognitive scores compared to the conventional methods using the original cognitive scores. Association of baseline characteristics (age, gender and years of education) and the cognitive outcomes were reported as estimates and 95% confidence intervals. Bootstrap methods improved the estimate precision and the bootstrapped standard errors of the estimates are more robust. Cognitive outcomes are widely analyzed using linear regression models with default normal distribution as a conventional method. We compared the results of our suggested models with the normal distribution under various scenarios. Goodness-of-fit measurements were compared between proposed models and conventional methods. Conclusions: The findings support the use of the inverse transformation method to model the cognitive outcomes instead of the original cognitive scores for early stage neurocognitive disorders where the cognitive outcomes are left skewed.

Keywords:

Subject: Biology and Life Sciences - Neuroscience and Neurology

1. Introduction

The recognition of cognitive impairment in neurocognitive disorders is important due to its association with shorter life expectancy, caregiver anxiety and potential side effects of cognitive enhancers. Furthermore, early diagnosis and timely intervention can result in delayed or slowed progression from mild cognitive impairment (MCI) to dementia. Hence, it is paramount to detect early cognitive deficits to provide appropriate treatment decisions to reduce complications and morbidities. For these reasons, routine cognitive screening is important for the optimal management of patients with neurocognitive disorder [1,2,3,4,5,6,7,8]. Though the gold standard of such cognitive evaluation should be based on neuropsychological testing, these are time consuming and hence a more practical screening approach is usually performed by clinicians. Cognitive tests are usually performed to assess patients in clinical conditions with cognitive impairment. Such cognitive tests should be short, simple to perform, sensitive to subtle changes in cognition, not confounded by motor and visual problems, and able to assess a full range of cognitive domains. Some global cognitive screening tools that have been developed for patients with neurocognitive disorders are the Montreal Cognitive Assessment (MoCA) and Visual Cognitive Assessment Test (VCAT) among others [4,7,9,10,11,12,13].

Among the screening tools, the MoCA is a screening instrument that can be administered within 10-15 minutes and is developed to identify patients with MCI and dementia [13,14]. The VCAT is a visual-based cognitive screening tool that is comparable to the MoCA for the time of administration, and is designed to detect early cognitive impairment and takes 15.7±7.3 minutes to complete [11,12,15]. The MOCA and VCAT have been demonstrated to be particularly useful for the detection of early stage neurocognitive disorders such as MCI and mild dementia. The outcome for each of these screening tools total up to 30-points and ranges in integers between 0 and 30, where a lower score indicates worse cognition. In cross-sectional and association studies, these outcomes are usually treated as continuous variables. Therefore, in terms of statistical analysis, linear regression models are likely performed to study outcomes of MoCA and VCAT [11,16,17].

There are some limitations while using linear regression models to examine the outcomes of such screening tools. One such limitation is that the underlying statistical distribution of the residuals is assumed to be normally distributed. While this assumption can be checked using normal quantile (Q-Q) plot, histogram or goodness-of-fit test (e.g., the Kolmogorov-Smirnov test), it should be noted that such goodness-of-fit tests lack sensitivity in small studies, whereas on the other hand, the violation of normality assumption becomes less important with increasing sample sizes. In addition, a major limitation of the normal distribution for the cognitive outcomes is that the predicted values are symmetric around the mean value. This is usually not the case for left-skewed outcome variables such as MoCA and VCAT, when used to detect early stages of neurocognitive disorders where a high proportion of individuals are on the right side of the distribution and minorities at the left side. Outcome transformation is one solution to overcome the skewness. Such transformation should be straightforward and generates interpretable results. Hence, the results of a complex transformation may not be transparent and needs back-calculations [18,19].

To counter the limitations of the normal distribution in linear regression model, some alternative statistical distributions may be worth considering overcome this problem; and eventually improve the model performance and predictions. However, the domain of some statistical distributions is for non-negative values, and as mentioned above, the cognitive outcomes are non-negative integers (ranged between 0 and 30). In addition, count distributions belong to this category and they have the advantages of dealing with integers. Given that the two cognitive outcomes are right-skewed, an alternative option is to look at the inverse outcomes (which is left-skewed) and fit statistical distributions where allows for left-skewness. This paper aims to investigate the distribution of the cognitive outcomes under various scenarios. First, both VCAT outcome and inverse-VCAT outcome will be modeled using different statistical distributions in the presence and absence of predictor variables. Next, bootstrap method will be applied to investigate whether such resampling techniques could improve the modelling. Lastly, goodness-of-fit measurements will be compared among candidate models. The results various scenarios mentioned above will be validated using the MoCA cognitive outcome and its inverse version.

2. Materials and Methods

2.1. Study Setting

In this retrospective cohort study, 883 participants at risk of dementia having a diagnosis of subjective cognitive decline (SCD) or MCI were recruited from the community as well as from a tertiary neurology centre between January 2015 and December 2020. These participants were recruited from the community through posters and they reported subjective cognitive complains and were not diagnosed with dementia at the time of recruitment. This study was approved by the SingHealth Centralized Institutional Review Board and written informed consent was obtained according to the Declaration of Helsinki from all participants. SCD and MCI were diagnosed based on the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-5) criteria [20] or the National Institute on Aging-Alzheimer's Association (NIA-AA) criteria [21]. Participants were excluded if they had a prior diagnosis of major psychiatric diseases or dementia.

2.2. Outcome Assessments

Data on demographics (including age, gender and years of education) and cognitive outcomes (VCAT and MoCA) were obtained through clinical interview and assessment. The two cognitive outcomes in this paper are VCAT and MoCA.

MoCA is a widely used cognitive screening test, and its items include attention, concentration, executive functions, memory, language, visuospatial skills, abstraction, calculation and orientation [10,22]. The MoCA adds one point for those whose educational level is ≤12 years or <10 years in local population [23]. More recently, the VCAT was developed as a language-neutral cognitive screening tool to detect early cognitive impairment. The main advantage of the VCAT is that there is no necessity to translate the test as long as the rater and the participant speak the same language, thus more applicable to the multilingual populations throughout the world. This visual-based test includes 11 items, which contains five specific cognitive domains: episodic memory, attention/working memory (WM), executive function, visuospatial ability, and language [12,15].

2.3. Outcome Distribution

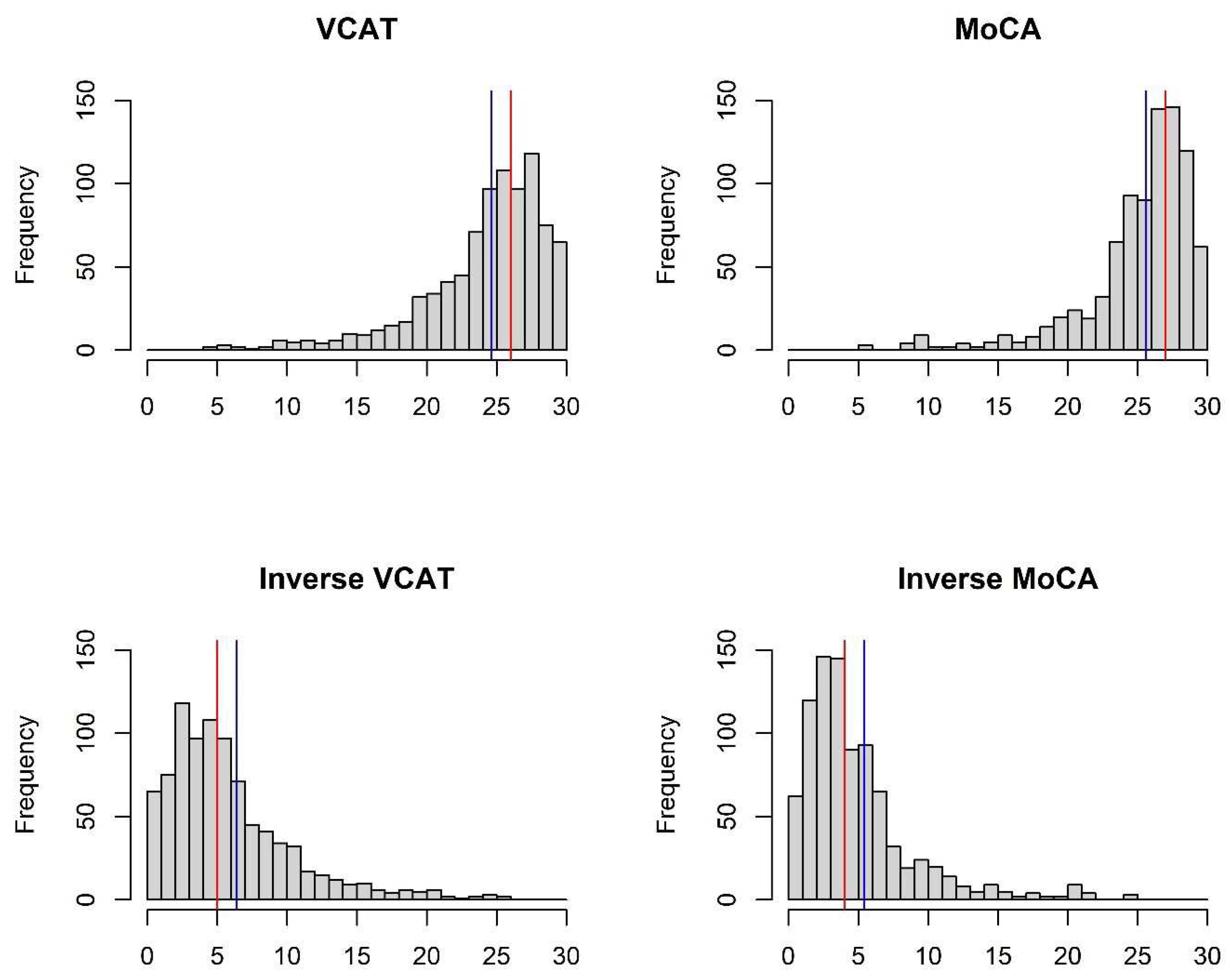
The two cognitive outcomes (VCAT and MoCA) scored from 0 to 30, whereby a higher score denotes higher cognitive functioning. As it can be seen in Figure 1a, they are left skewed. The distribution of the inverse outcomes (indicating the number of errors in the questionnaire), where a lower score indicates higher cognitive functioning, is shown in Figure 1b. The inverse outcomes are also scored between 0 and 30, and defined as follows:

\begin{matrix} I n v e r s e (M o C A) & = & 30 - M o C A \\ I n v e r s e (V C A T) & = & 30 - V C A \end{matrix}

(1)

2.4. Statistical Analysis Plan

The distribution of cognitive outcomes is modelled using the normal distribution as baseline model. Although normal distribution is considered mostly as default model, the distribution of cognitive outcomes is not symmetric and some skewness is usually observed. To address this issue, log-Normal, Gamma and Weibull distributions are used as potential candidate models. As the cognitive outcome variables (including VCAT and MoCA) can only be non-negative integers, count distributions are also considered as alternative models. Count models considered in this paper include Poisson, Negative binomial (NB), Conway-Maxwell-Poisson (CMP) and Generalized Poisson (GP).

The two cognitive outcomes (original scores) are left-skewed; hence their inverse score would be right-skewed, as seen in Figure 1. As most of the above distributions could handle right skewed data, the same models are used for the inverse outcomes (right skewed) as well. The proposed alternative distributions have shape and scale parameters, which makes them flexible towards skewness.

Normal distribution along with the proposed distributions are modelled to the cognitive outcomes and their inverse versions. For each model, two scenarios are explored: intercept-only model (without predictor variables) and models with predictors (age, gender and education). Intercept-only models are explored to purely investigate the distribution of the cognitive outcomes, whereas models with predictors are studied to improve the fitted distributions and explore the associations of baseline characteristics and cognitive outcomes.

The bootstrap resampling method is applied to investigate whether bootstrapping could improve the model performance under the above two scenarios (intercept-only and models with predictors) and for both VCAT and inverse (VCAT) outcomes. The unrestricted random method is used as resampling technique, which selects patients with equal probability and with replacement, and therefore patients could be selected for the bootstrapped sample more than once. The sampling rate of 100% is used, where results in bootstrapped sample sizes of 883 (which equals to the cohort sample size), and 10,000 replications are used. The bootstrap percentile method is used to calculate the confidence interval (CI). A 95% percentile bootstrap CI with 10,000 bootstrap samples is determined using the interval between the 2.5th percentile and the 97.5th percentile value of the 10,000 bootstrap parameter estimates, i.e., minimum and maximum value of the 10,000 bootstrap estimates after excluding the 2.5% in each tail of the distribution.

Models performances are compared using goodness-of-fit statistics, including -2log-likelihood (

- 2 L L

), Akaike's Information Criterion (AIC) and Bayesian Information Criterion (BIC) measurements. Predicted VCAT outcomes are compared to the observed VCAT for all the above settings. To validate the findings on model performances of VCAT outcome, similar methodology is applied on MoCA outcome. Goodness-of-fit statistics and models’ fits are compared across the two cognitive outcomes. Statistical analysis is performed using PROC NLMIXED in SAS software version 9.4 for Windows (Cary, NC: SAS Institute Inc.).

3. Results

3.1. Patient Characteristics

Descriptive statistics of demographic variables are reported in Table 1. In this cross-sectional study, 883 patients are enrolled. Mean age is 63.5 ± 7.8 years with 302 (34.2%) being male. Median of education is 11 years (first- and third-quartile of 10-14 years). Mean/median of VCAT and MoCA are as follows: 24.6/26 and 25.6/27. The distribution of the cognitive outcomes is shown in Figure 1. Left skewness with long tail on the left side of the distribution is observed in VCAT and MoCA scores. The inverse outcomes, on the other hand, shows a long tail on the right side of the distribution. Mean and median values of the outcome and inverse outcome scores shown in Figure 1 indicate that a normal distribution may not be a good model to fit the data.

3.2. Model Comparisons-VCAT

Goodness-of-fit measurements are reported in Table 2. A lower

- 2 L L

(as well as

A I C a n d B I C

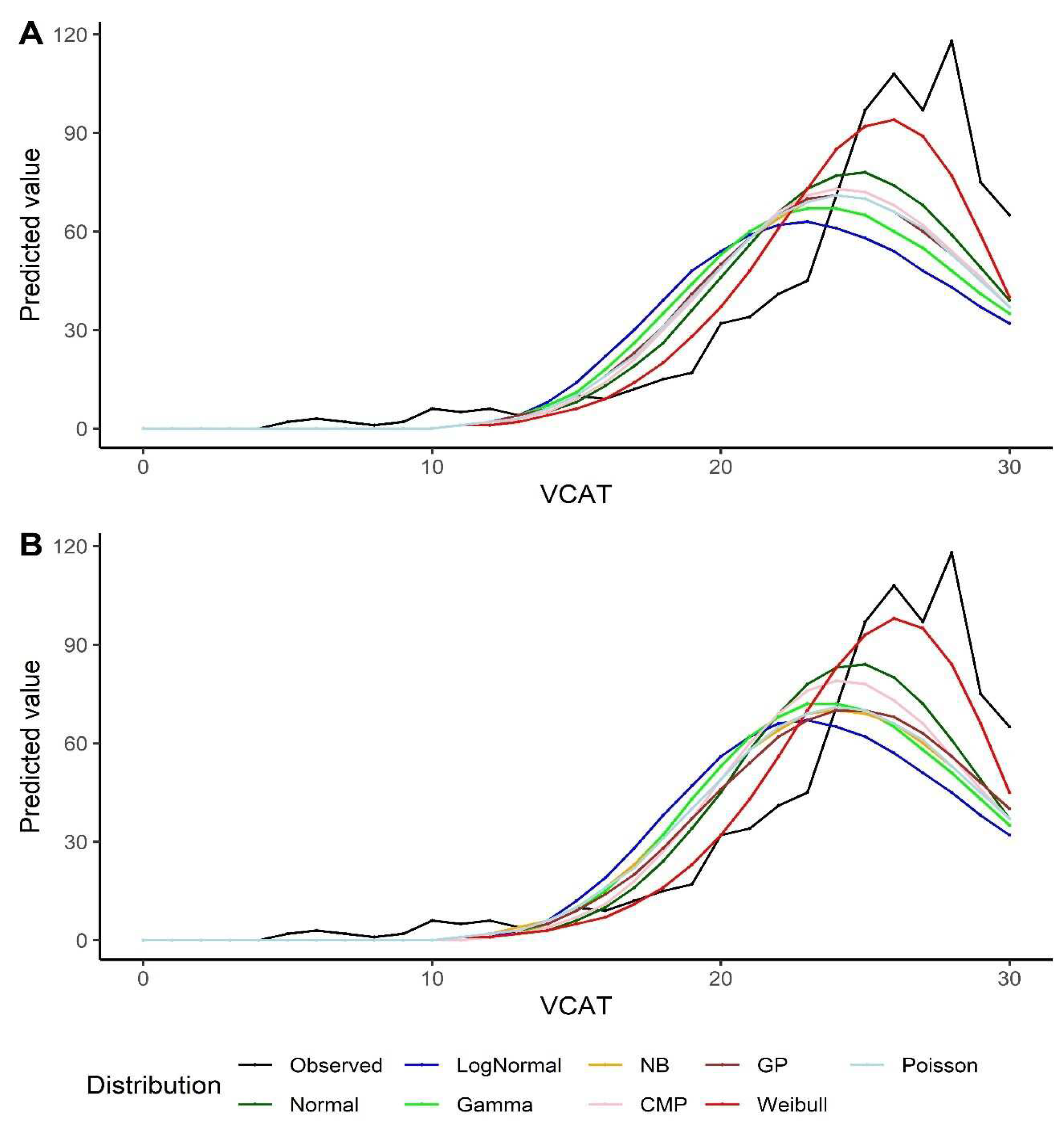
) value indicates a better fit. Normal distribution outperforms all other alternative models except Weibull distribution in both intercept-only model and model with covariates. The predicted model-based values for VCAT using Weibull model also results in a better fit compared to all other distributions (Figure 2). It should also be noted that the Poisson model shows similar fit compared to CMP and GP under intercept-only models and models with covariates.

3.3. Model Comparisons-Inverse VCAT

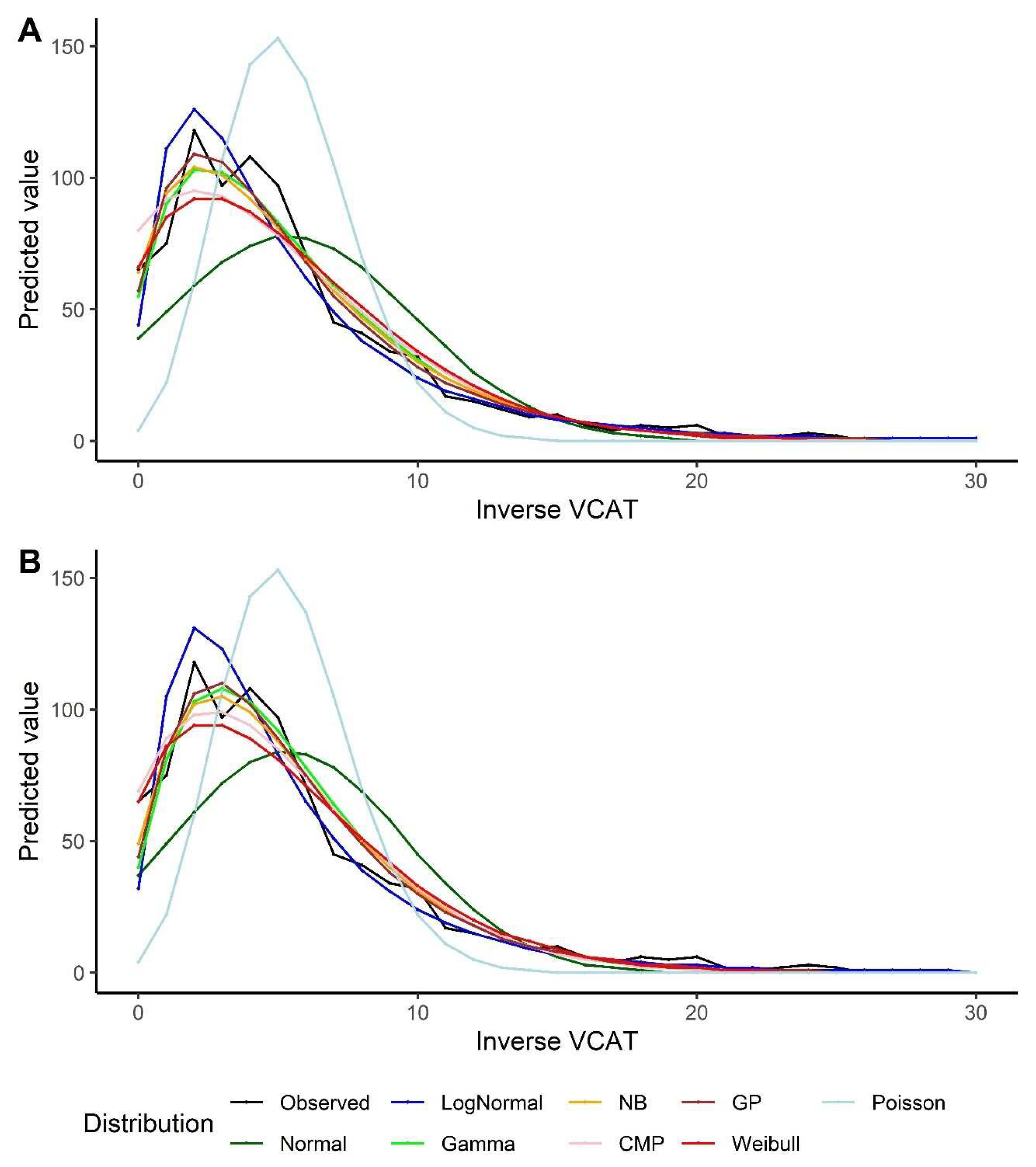
For the inverse VCAT, GP and NB models followed by Gamma model shows better performance in terms of goodness-of-fit measurements under intercept-only scenario. In models with covariates, GP and gamma distributions followed by NB model outperform other models (Table 3). The same results could be extracted from the predicted VCAT values, looking at Figure 3. It should be also noted that lognormal model over-estimate the predicted inverse VCAT values at the left side of the distribution (when the original VCAT values are high); and the fitted values out of the normal distribution are far off from the observed values and other models’ predictions. The model goodness-of-fits also indicate that Poisson model results in the highest statistics, i.e., poorest model.

3.4. Bootstrapping Method

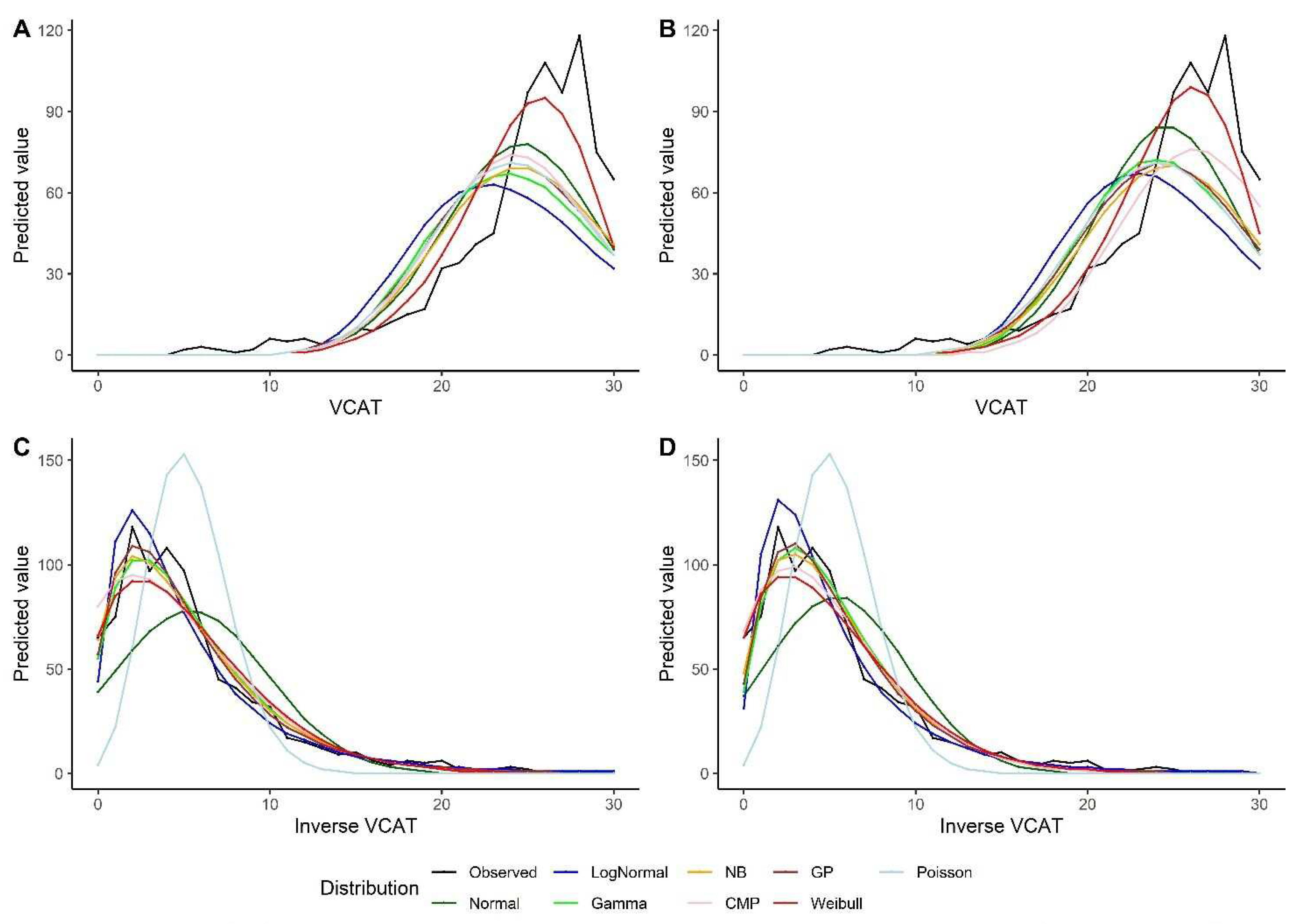
The models show similar results using the bootstrap method. Weibull model outperforms other models under intercept-only model and models with predictors when looking at VCAT outcome (Table 4). For the inverse VCAT outcome, GP, NB and gamma models indicate better performance compared to other distributions (Table 5). Similar conclusions could be made based on the predicted values for VCAT and inverse VCAT scores in Figure 4.

3.5. Association Analysis

Using the model with best-fit performances, the association analyses of baseline characteristics and VCAT outcome were reported as beta coefficients and 95% confidence interval using the Weibull model. Male gender and lower education were found to be significantly associated with worse VCAT scores with and without bootstrapping. For the inverse VCAT outcome, the association results using the GP model (as the best model) are reported. Older age and lower education were found to be significantly associated with worse VCAT score. The results of VCAT and inverse VCAT models are not consistent for age (being significant in the inverse VCAT model, but not in VCAT model) and gender (being significant in VCAT model, but not in inverse VCAT). Except for gender variables under VCAT model, the confidence intervals are very similar to the bootstrapped confidence intervals (Table 6).

3.6. Validation of the Findings

The findings of the model performances on VCAT scores are validated using MoCA outcome scores. Weibull model (followed by Normal distribution) consistently shows the lowest goodness-of-fit measurements under intercept-only models and models with covariates in MoCA outcome. In the inverse outcome scenarios (for MoCA), log-normal followed by GP and NB (and then gamma) models indicates the best performances based on goodness-of-fit statistics (supplement Table S1). Predicted scores of MoCA and their inverse scores also result in similar findings (supplement Figure S1).

4. Discussion

This study investigated the distribution of cognitive scores in the early stages of neurocognitive disorders different statistical models. Different models were conducted on the VCAT outcome as primary endpoint variable. Intercept-only models and models with covariates were considered and the model fits were compared using goodness-of-fit measurements. Bootstrapping methods were conducted to calculate robust confidence intervals for the point estimates. The inverse VCAT outcome was modelled using the same distributions and under the above scenarios (intercept-only model and model with covariates, with and without bootstrapping) to present the precision of the estimates via confidence intervals. To validate the findings, similar methods were applied to MoCA outcome variable.

Our findings showed that Weibull distribution is a better fit in both intercept-only models and models with covariates on VCAT compared to other models. This is because other models are not flexible towards left-skewed data, while Weibull distribution could deal with such data. An alternative model to consider is Normal distribution which shows a better fit compared to other models. This may be because other distributions are slightly right-skewed models and away from being symmetric. Hence, the normal distribution (symmetric model) will be preferred over right-skewed models with left skewed VCAT outcome.

Under inverse VCAT outcome scenario, the GP model indicates a better fit compared to other distributions for both intercept-only models and models with covariates. In addition, NB and Gamma models also indicate close fit to GP model. This is an expected finding given that GP, NB and Gamma models can handle right skewed distributions. However, at the left side of the distribution (within cognitively normal range), all the above three models show a reasonably close fit to the observed scores, Weibull and Normal distributions under-predict and log-normal model over-predict the outcome. It is also noted that all the above models perform better under inverse VCAT compared to the original VCAT results, unlike Normal distribution which shows similar fit under both scenarios which is expected as such outcome transformation does not reduce data skewness, i.e., only switches the left-skewness to right-skewness where both are far away from symmetric distribution.

Among the methods with bootstrap method, similar findings are found under both VCAT (Weibull model outperforms other models) and inverse VCAT (GP followed by NB and Gamma models showing the best fit) scenarios. Comparing the goodness-of-fit statistics between with and without bootstrapping is not recommended, because such statistics are used as model selection criteria among the various distributions under the same settings. Bootstrap methods improved the estimate precision and the bootstrapped standard errors of the estimates are more robust. Hence, it is recommended to use bootstrapping methods to present robust estimates along with 95% CI for both VCAT and inverse VCAT models for all models.

The results of the VCAT and inverse VCAT modelling were validated on the MoCA outcome variable. As the distribution of MoCA scores is right skewed, Weibull model, as expected, showed a better fit compared to other models. Hence, the findings are consistent across the two cognitive outcomes under the original scores. However, when using the inverse score method, the results of model fits for MoCA are different compared to VCAT outcome. Log-normal distribution indicated the lowest goodness-of-fit statistics compared to other models for inverse MoCA outcome (supplement Table S1). This is an inconsistent finding compared to the results of the inverse VCAT outcome where three other distributions (GP, NB and Gamma) showed a better performance compared to Log-normal model. Looking at the distribution of the cognitive outcomes (Figure 1), MoCA is a unimodal distribution, unlike VCAT with a bimodal distribution. Hence, it seems that GP, NB and Gamma models are not flexible enough to handle bimodal distributions, and log-normal model could fit bimodal data better than alternative distributions. Another point which should not be ignored is the good fit performance of log-normal distribution under inverse MoCA models at a normal range of cognition, where GP, NB and Gamma under-estimated the scores. Normal distribution, under the inverse scenario, shows the poorest fit for the two cognitive inverse outcomes (supplement Figure S1).

The results of the association analysis indicated that male gender and lower education, but not age, are significantly associated with worse VCAT using Weibull distribution. Same findings are seen when testing MoCA as the cognitive outcome. On the other hand, we found inconsistent findings when testing the two cognitive outcomes using the inverse score scenarios. When using the GP model, we found that higher age and lower education are significantly associated with worse VCAT outcomes, while male gender was marginally associated with worse VCAT outcome. However, male gender and lower education are significantly associated with worse MoCA outcome under GP model and inverse transformation scenario (supplement Table S2). Although the association directions (positive/negative association) are consistent across all models and scenarios (except Weibull model under inverse transformed outcomes) and make clinical sense, it should be noted that the effect sizes might be different. Hence, a wrong assumed distribution for cognitive outcomes may under- or over-estimate the effect size of the predictors.

As the original cognitive scores are left skewed, there might be some computational issues with models without distributional flexibility towards left skewness. For example, the final Hessian matrix may be full rank but has at least one negative eigenvalue, or the second-order optimality condition may be violated. Not Estimable confidence interval reported in Supplement Table S2 are few examples of such computational issues, where Moore-Penrose inverse is used in covariance matrix and the estimates are reported based on the finite difference approximation used for the derivative of the probability density function. However, there are potential solutions to this issue (such as changing the optimization technique or integration method), it should be noted that a reasonable model is selected to apply. On the other hand, under the inverse transformation scenario, no computational and convergence problem is found.

The results of this study support the use of analysis of inverse cognitive scores over the original scores. From a clinical point of view, the inverse score actually measures the number of errors corresponding to the specific cognitive outcome of interest. That means higher cognitive functioning (greater value in the original cognitive outcome) equals to lower number of errors (smaller value of the inverse cognitive outcome). Hence, the results of the suggested inverse transformation are easy to interpret and transparent compared to other potential transformations. An example of a challenging transformation, where a back-calculation is required to interpret the results, is the square root of the number of errors, which was suggested to reduce the bias (to justify the normality assumption of normal distribution) [18,19]. Compared to such alternative transformation, our suggested solution is simple, robust and easy to interpret.

Limitations of this study include the limited number of models performed. More complex distributions can be applied on cognitive outcomes and the results could be compared to the results of this study. Although this study tried to validate the results via an additional cognitive outcome with similar distributional pattern, validation on independent cohorts will be needed to verify the findings.

The findings of this study suggest that the inverse transformation method improves modelling the cognitive scores for all proposed models, except normal distribution. Therefore, the recommendation is to use the inverse cognitive outcomes instead of the original cognitive scores, no matter how the outcome distribution looks like (unimodal/bimodal) at the early stage of the disease where the cognitive outcomes are left skewed. The proposed inverse method and the suggested statistical distributions could be also applied to other behavioral outcomes where the original scores are left skewed (such as Mini–Mental State Examination, MMSE), however one should be careful with the outcome distribution. Although normal distribution is commonly used for cognitive outcomes, the results of this study show that the model performance of normal distribution is the poorest among the proposed inverse models. Under the unimodal scenario, it is recommended to model the inverse cognitive outcomes via log-normal distribution and GP distribution (as alternative model). However, GP and NB distributions (and Gamma as alternative model) are recommended in the presence of bimodal inverse cognitive variables. When applying the above proposed models on inverse cognitive outcomes, it is suggested that the model performances should be assessed via predicted scores versus observed cognitive scores as well as goodness-of-fit statistics to make sure the findings are valid and robust. In conclusion, future studies can consider using inverse models to analyze the outcomes of cognitive screening tools such as the MoCA and VCAT.

Supplementary Materials

Supplement Table S1. Model's performance, MoCA and inverse MoCA outcome scores. Supplement Table S2: Association analysis of the baseline characteristics with MoCA and inverse (MoCA) outcomes. Supplement Figure S1: Predicted values among the fitted models, MoCA and Inverse MoCA outcomes

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, X.X. and Y.Y.; methodology, X.X.; software, X.X.; validation, X.X., Y.Y. and Z.Z.; formal analysis, X.X.; investigation, X.X.; resources, X.X.; data curation, X.X.; writing—original draft preparation, X.X.; writing—review and editing, X.X.; visualization, X.X.; supervision, X.X.; project administration, X.X.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.” Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

No funding was received for the conduct of this research.

Informed Consent Statement

Patient consent to the publication of de-identified information.

Data Availability Statement

All data and materials are available from the corresponding author upon reasonable request.

Acknowledgments

This research is supported by the Ministry of Education, Singapore, under its MOE AcRF Tier 3 Award MOE2017-T3-1-002, National Medical Research Council (NMRC), Singapore, under its Clinician Scientist Award (MOH-CSAINV18nov-0007) and National Neuroscience Institute-Health Research Endowment Fund, Singapore (NNI-HREF 991016).

Conflicts of Interest

The authors declare that they have no competing interests.

References

De Vugt, M. E.; Verhey, F. R. , The impact of early dementia diagnosis and intervention on informal caregivers. Prog. Neurobiol. 2013, 110, 54–62. [Google Scholar] [CrossRef] [PubMed]
Hoops, S.; Nazem, S.; Siderowf, A.; Duda, J.; Xie, S.; Stern, M.; Weintraub, D. , Validity of the MoCA and MMSE in the detection of MCI and dementia in Parkinson disease. Neurology 2009, 73, 1738–1745. [Google Scholar] [CrossRef]
Hugo, J.; Ganguli, M. , Dementia and cognitive impairment: epidemiology, diagnosis, and treatment. Clin. Geriatr. Med. 2014, 30, 421–442. [Google Scholar] [CrossRef] [PubMed]
Kulisevsky, J.; Pagonabarraga, J. , Cognitive impairment in Parkinson's disease: tools for diagnosis and assessment. Mov. Disord. 2009, 24, 1103–1110. [Google Scholar] [CrossRef] [PubMed]
Liss, J.; Seleri Assunção, S.; Cummings, J.; Atri, A.; Geldmacher, D.; Candela, S.; Devanand, D.; Fillit, H.; Susman, J.; Mintzer, J. , Practical recommendations for timely, accurate diagnosis of symptomatic Alzheimer’s disease (MCI and dementia) in primary care: a review and synthesis. J. Intern. Med. 2021, 290, 310–334. [Google Scholar] [CrossRef] [PubMed]
McDonald, W. M. , Overview of neurocognitive disorders. Focus 2017, 15, 4–12. [Google Scholar] [CrossRef]
van Steenoven, I.; Aarsland, D.; Hurtig, H.; Chen-Plotkin, A.; Duda, J. E.; Rick, J.; Chahine, L. M.; Dahodwala, N.; Trojanowski, J. Q.; Roalf, D. R. , Conversion between mini-mental state examination, montreal cognitive assessment, and dementia rating scale-2 scores in Parkinson's disease. Mov. Disord. 2014, 29, 1809–1815. [Google Scholar] [CrossRef] [PubMed]
Wolf, R. C.; Vasic, N.; Schönfeldt-Lecuona, C.; Ecker, D.; Landwehrmeyer, G. B. , Cortical dysfunction in patients with Huntington's disease during working memory performance. Hum. Brain Mapp. 2009, 30, 327–339. [Google Scholar] [CrossRef] [PubMed]
Dubois, B.; Burn, D.; Goetz, C.; Aarsland, D.; Brown, R. G.; Broe, G. A.; Dickson, D.; Duyckaerts, C.; Cummings, J.; Gauthier, S. , Diagnostic procedures for Parkinson's disease dementia: recommendations from the movement disorder society task force. Mov. Disord. 2007, 22, 2314–2324. [Google Scholar] [CrossRef]
Galvin, J. E.; Sadowsky, C. H. , Practical guidelines for the recognition and diagnosis of dementia. J. Am. Board Fam. Med. 2012, 25, 367–382. [Google Scholar] [CrossRef]
Kandiah, N.; Zhang, A.; Bautista, D. C.; Silva, E.; Ting, S. K. S.; Ng, A.; Assam, P. , Early detection of dementia in multilingual populations: Visual Cognitive Assessment Test (VCAT). J. Neurol. Neurosurg. Psychiatry 2016, 87, 156–160. [Google Scholar] [CrossRef] [PubMed]
Low, A.; Lim, L.; Lim, L.; Wong, B.; Silva, E.; Ng, K. P.; Kandiah, N. , Construct validity of the Visual Cognitive Assessment Test (VCAT)—a cross-cultural language-neutral cognitive screening tool. Int. Psychogeriatr. 2020, 32, 141–149. [Google Scholar] [CrossRef] [PubMed]
Nasreddine, Z. S.; Phillips, N. A.; Bédirian, V.; Charbonneau, S.; Whitehead, V.; Collin, I.; Cummings, J. L.; Chertkow, H. , The Montreal Cognitive Assessment, MoCA: a brief screening tool for mild cognitive impairment. J. Am. Geriatr. Soc. 2005, 53, 695–699. [Google Scholar] [CrossRef] [PubMed]
Zadikoff, C.; Fox, S. H.; Tang-Wai, D. F.; Thomsen, T.; De Bie, R. M.; Wadia, P.; Miyasaki, J.; Duff-Canning, S.; Lang, A. E.; Marras, C. , A comparison of the mini mental state exam to the Montreal cognitive assessment in identifying cognitive deficits in Parkinson's disease. Mov. Disord. 2008, 23, 297–299. [Google Scholar] [CrossRef] [PubMed]
Lim, L.; Ng, T. P.; Ong, A. P.; Tan, M. P.; Cenina, A. R.; Gao, Q.; Ng, A.; Kandiah, N. , A novel language-neutral Visual Cognitive Assessment Test (VCAT): validation in four Southeast Asian countries. Alzheimer's Res. Ther. 2018, 10, 1–9. [Google Scholar] [CrossRef]
Lucza, T.; Karádi, K.; Kállai, J.; Weintraut, R.; Janszky, J.; Makkos, A.; Komoly, S.; Kovács, N. , Screening mild and major neurocognitive disorders in Parkinson’s disease. Behav. Neurol. 2015, 2015, 983606. [Google Scholar] [CrossRef]
Santangelo, G.; Siciliano, M.; Pedone, R.; Vitale, C.; Falco, F.; Bisogno, R.; Siano, P.; Barone, P.; Grossi, D.; Santangelo, F. , Normative data for the Montreal Cognitive Assessment in an Italian population sample. Neurol. Sci. 2015, 36, 585–591. [Google Scholar] [CrossRef]
Jacqmin-Gadda, H.; Fabrigoule, C.; Commenges, D.; Dartigues, J.-F. , A 5-year longitudinal study of the Mini-Mental State Examination in normal aging. Am. J. Epidemiol. 1997, 145, 498–506. [Google Scholar] [CrossRef]
Pradier, C.; Sakarovitch, C.; Le Duff, F.; Layese, R.; Metelkina, A.; Anthony, S.; Tifratene, K.; Robert, P. , The mini mental state examination at the time of Alzheimer's disease and related disorders diagnosis, according to age, education, gender and place of residence: a cross-sectional study among the French National Alzheimer database. PloS One 2014, 9, e103630. [Google Scholar] [CrossRef]
20. American Psychiatric Association. Diagnostic and statistical manual of mental disorders: DSM-5, 2: association Washington, DC, 2013.
Albert, M. S.; DeKosky, S. T.; Dickson, D.; Dubois, B.; Feldman, H. H.; Fox, N. C.; Gamst, A.; Holtzman, D. M.; Jagust, W. J.; Petersen, R. C. , The diagnosis of mild cognitive impairment due to Alzheimer's disease: recommendations from the National Institute on Aging-Alzheimer's Association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimer's Dement. 2011, 7, 270–279. [Google Scholar] [CrossRef]
Trzepacz, P. T.; Hochstetler, H.; Wang, S.; Walker, B.; Saykin, A. J.; Initiative, A. s. D. N. , Relationship between the Montreal Cognitive Assessment and Mini-mental State Examination for assessment of mild cognitive impairment in older adults. BMC Geriatr. 2015, 15, 1–9. [Google Scholar] [CrossRef] [PubMed]
Ng, A.; Chew, I.; Narasimhalu, K.; Kandiah, N. , Effectiveness of Montreal Cognitive Assessment for the diagnosis of mild cognitive impairment and mild Alzheimer’s disease in Singapore. Singap. Med J 2013, 54, 616–619. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Distribution of the two outcomes and their inverse version (VCAT, MoCA).

Figure 2. Predicted values by various distributions under different scenarios, VCAT outcome: (a) Without covariates (intercept-only); (b) With covariates (age, gender, and education variables as predictors).

Figure 3. Predicted values by various distributions under different scenarios, VCAT inverse outcome: (a) Without covariates (intercept-only); (b) With covariates (age, gender, and education variables as predictors).

Figure 4. Predicted values by various distributions under different scenarios, VCAT and Inverse VCAT outcomes, with bootstrap: (a) Without covariates (intercept-only), original score; (b) With covariates (age, gender, and education variables as predictors), original score; (c) Without covariates (intercept-only), inverse score; (d) With covariates (age, gender, and education variables as predictors), inverse score.

Table 1. Patients’ characteristics and outcome distributions, n=883.

Variable	Frequency (%)	Mean ± SD	Median (Q1 - Q3)
Age (year)		63.5 ± 7.8	63 (58 - 69)
Male Gender	302 (34.2%)
Education (year)		11.6 ± 4	11 (10 - 14)
MoCA		25.6 ± 4.1	27 (24 - 28)
VCAT		24.6 ± 4.5	26 (23 - 28)

Abbreviations: MoCA = Montreal Cognitive Assessment; VCAT = Visual Cognitive Assessment Test; SD = standard deviation; Q1 and Q3 = first and third quartile.

Table 2. Model's performance, VCAT outcome.

Distribution	Intercept-only Model			Model with covariates
Distribution	-2LL	AIC	BIC	-2LL	AIC	BIC
Normal	5170.6	5174.6	5184.2	5028.6	5038.6	5062.5
Log-Normal	5603.5	5607.5	5617.0	5490.4	5500.4	5524.3
Gamma	5432.7	5436.7	5446.3	5304.3	5314.3	5338.2
Poisson	5279.9	5281.9	5286.7	5165.4	5173.4	5192.6
NB	5415.4	5419.4	5429.0	5452.8	5462.8	5486.7
CMP	5278.1	5282.1	5291.6	5146.8	5156.8	5180.7
GP	5280.2	5284.2	5293.8	5171.7	5181.7	5205.6
Weibull	4992.9	4996.9	5006.5	4916.8	4926.8	4950.7

Abbreviations: LL = log-likelihood; AIC = Akaike's Information Criterion; BIC = Bayesian Information Criterion; NB = Negative Binomial; CMP = Conway-Maxwell-Poisson; GP = Generalized Poisson.

Table 3. Model's performance, VCAT inverse outcome.

Distribution	Intercept-only Model			Model with covariates
Distribution	-2LL	AIC	BIC	-2LL	AIC	BIC
Normal	5170.6	5174.6	5184.2	5028.6	5038.6	5062.5
Log-Normal	4791.9	4795.9	4805.4	4654.2	4664.2	4688.1
Gamma	4780.9	4784.9	4794.5	4634.5	4644.5	4668.4
Poisson	5878.0	5880.0	5884.8	5459.4	5467.4	5486.5
NB	4770.1	4774.1	4783.6	4646.6	4656.6	4680.6
CMP	4786.9	4790.9	4800.5	4668.2	4678.2	4702.2
GP	4766.7	4770.7	4780.3	4626.2	4636.2	4660.1
Weibull	4817.1	4821.1	4830.7	4801.0	4811.0	4834.9

Abbreviations: LL = log-likelihood; AIC = Akaike's Information Criterion; BIC = Bayesian Information Criterion; NB = Negative Binomial; CMP = Conway-Maxwell-Poisson; GP = Generalized Poisson.

Table 4. Model's performance, VCAT outcome, with bootstrap.

Distribution	Intercept-only Model			Model with covariates
Distribution	-2LL	AIC	BIC	-2LL	AIC	BIC
Normal	5167.33 ^* (5169.01)	5171.33 (5173.01)	5180.89 (5182.58)	5020.69 (5022.41)	5030.69 (5032.41)	5054.6 (5056.33)
Log-Normal	5596.42 (5599.39)	5600.42 (5603.39)	5609.98 (5612.96)	5477.49 (5480.48)	5487.49 (5490.48)	5511.41 (5514.39)
Gamma	5427.36 (5429.73)	5431.36 (5433.73)	5440.93 (5443.3)	5292.85 (5294.5)	5302.85 (5304.5)	5326.76 (5328.42)
Poisson	5279.28 (5277.90)	5281.28 (5279.90)	5286.06 (5284.69)	5161.84 (5160.15)	5169.84 (5168.15)	5188.97 (5187.29)
NB	5285.56 (5284.23)	5289.56 (5288.23)	5299.12 (5297.80)	5875.61 (5182.70)	5885.61 (5192.70)	5909.52 (5216.62)
CMP	5274.06 (5275.76)	5278.06 (5279.76)	5287.62 (5289.32)	5138.46 (5140.29)	5148.46 (5150.29)	5172.37 (5174.2)
GP	5279.88 (5278.5)	5283.88 (5282.5)	5293.45 (5292.07)	5174.34 (5171.94)	5184.34 (5181.94)	5208.25 (5205.85)
Weibull	4990.21 (4991.17)	4994.21 (4995.17)	5003.78 (5004.74)	4909.14 (4909.17)	4919.14 (4919.17)	4943.06 (4943.08)

^* Reported numbers are mean (median), Abbreviations: LL = log-likelihood; AIC = Akaike's Information Criterion; BIC = Bayesian Information Criterion; NB = Negative Binomial; CMP = Conway-Maxwell-Poisson; GP = Generalized Poisson.

Table 5. Model's performance, VCAT inverse outcome, with bootstrap.

Distribution	Intercept-only Model			Model with covariates
Distribution	-2LL	AIC	BIC	-2LL	AIC	BIC
Normal	5167.33 ^* (5169.01)	5171.33 (5173.01)	5180.89 (5182.58)	5020.69 (5022.41)	5030.69 (5032.41)	5054.6 (5056.33)
Log-Normal	4789.75 (4790.15)	4793.75 (4794.15)	4803.32 (4803.72)	4648.85 (4649.1)	4658.85 (4659.1)	4682.77 (4683.02)
Gamma	4778.83 (4779.02)	4782.83 (4783.02)	4792.4 (4792.59)	4629.23 (4629.44)	4639.23 (4639.44)	4663.15 (4663.35)
Poisson	5874.34 (5873.37)	5876.34 (5875.37)	5881.12 (5880.16)	5444.91 (5444.17)	5452.91 (5452.17)	5472.04 (5471.31)
NB	4767.86 (4767.99)	4771.86 (4771.99)	4781.43 (4781.55)	4626.65 (4627.04)	4636.65 (4637.04)	4660.56 (4660.96)
CMP	4784.53 (4784.92)	4788.53 (4788.92)	4798.1 (4798.48)	4661.92 (4662.69)	4671.92 (4672.69)	4695.83 (4696.61)
GP	4764.55 (4764.88)	4768.55 (4768.88)	4778.12 (4778.45)	4620.38 (4620.63)	4630.38 (4630.63)	4654.29 (4654.55)
Weibull	4814.9 (4815.09)	4818.9 (4819.09)	4828.47 (4828.66)	4795.86 (4796.39)	4805.86 (4806.39)	4829.77 (4830.31)

^* Reported numbers are mean (median).

Table 6. Association analysis of the baseline characteristics with VCAT and inverse (VCAT) outcomes.

Variable	Whole cohort (n=883)		Whole cohort (n=883)+ bootstrap method
Variable	Beta (95% CI)	P value	Beta (95% CI)	P value
VCAT
Age (year)	-0.31 (-0.75, 0.13)	0.162	-0.33 (-1.07, 0.35)	0.261
Female Gender	1.47 (0.67, 2.26)	<0.001	1.46 (0.36, 2.53)	0.037
Education (year)	1.05 (0.87, 1.24)	<0.001	1.05 (0.85, 1.26)	<0.001

Inverse (VCAT)
Age (year)	0.15 (0.10, 0.20)	<0.001	0.15 (0.09, 0.21)	<0.001
Female Gender	-0.10 (-0.20, 0.01)	0.062	-0.10 (-0.20, 0.01)	0.174
Education (year)	-0.19 (-0.22, -0.15)	<0.001	-0.19 (-0.23, -0.15)	<0.001

Abbreviations: VCAT = Visual Cognitive Assessment Test; CI = Confidence Interval.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer