Prerpints.org logo
Preprint
Article

Optimal Planning of PV Sources and D-STATCOM Devices with Network Reconfiguration Employing Modified Ant Lion Optimizer

Altmetrics

Downloads

121

Views

42

Comments

0

This version is not peer-reviewed

Submitted:

15 December 2023

Posted:

18 December 2023

You are already at the latest version

Alerts
Abstract
This research emphasizes a meta-heuristic Modified Ant Lion Optimizer (MALO) optimization approach for simultaneous utilization of DSTATCOM devices and distributed Photovoltaic (PV) sources with network reconfiguration in a radial power distribution scheme. In a radial power distribution network with network reconfiguration majority of the research is based on Constant Power model analysis. However, it is noticed that load models have a substantial impact on the distributed PV sources and the D-STATCOM device's optimal size and position. The effect of the Constant Power (CP) and Polynomial (ZIP) with load growth load models for the simultaneous insertion of distributed PV sources and DSTATCOM devices with network reconfiguration examined in this research work for power system planning. The penetration levels of distributed PV sources considered for the investigation are 25%, 50%, 75%, and 100%. The principal objective of this research is to reduce network total power losses, enhance the voltage magnitude profile at all buses, and reduce the overall operating cost while adhering to equality and inequality constraints. The proposed algorithm verified on 118-node test systems. The investigation is carried out for planning network upgradation to a High Voltage Distribution System(HVDS) on 317 nodes in the rural Bangalore Electricity Supply Company Limited(BESCOM) radial distribution scheme. Simulated results obtained by this method are validated with the BAT algorithm and available techniques in the literature.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The distribution network is a complex network incorporating many devices and different consumer categories. Distribution companies should redesign networks to optimize their operation procedure, voltage magnitude profile, energy loss, and voltage stability. Utility companies are implementing recent technologies to mitigate these issues by equilibrating reactive power in the distribution scheme. Reactive power compensator schemes like Capacitor positioning, incorporation of DG, and allotment of customer power devices reduce total power loss and betterment of voltage magnitude profile and stability index [1].
Capacitor allocation:
Several methods like Mixed Integer Linear Programming(MILP), Linear Programming(LP), Non-Linear Programming (NLP), Genetic Algorithm (GA), Ant colony, Artificial Neural Network (ANN), Tabu search, Particle Swarm Optimization (PSO), and Simulated Annealing are suggested for solving the issues of capacitor positioning to achieve power flow control, administration of voltage profile, rectification of pf, reduction of total power loss. The challenges involved here are designing of appropriate capacity and number of capacitor units with placement. The optimal capacitor placement using various Metaheuristic techniques does not providing reactive power compensation for dynamically changing loads and suffers from resonance with an inductive component in the network [2,3].
DG allocation:
DG allocation in the network enhances the network reliability, reduces the cost of delivery, reduction of losses, and reduces emission levels. Factors considered while choosing DG locations depend on economic, technical, and energy factors. Optimal allotment of multiple DG sources for diminution of total power loss and administration of voltage issues to enhance the performance of the network to achieve financial benefit. The author demonstrated a Composite Grey Wolf optimizing approach for effective DG-type allotment to minimize power loss [4]. The author investigates a Meta-heuristic BAT technique for the optimum location of DG sources for total power loss minimization [5]. Optimal allocation of DG units considering the uncertainties in active power load results in significant energy saving [6]. The connection of DG sources to the distribution scheme will lead to a rise in local voltage. As there is a restriction on permittable voltage rise, this will restrict the maximum permissible penetration limit of DG sources [7]. An increase in DG penetration level reduces power loss and betterment of voltage magnitude profile. However, it will have a consequence on the voltage stability margin and total power loss of network [8]. A higher penetration level of solar power generation into a power distribution system facilitates a stable microgrid [9]. The New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm and Student Psychology Optimization (SPBO) algorithm rule has been suggested by authors [10,11] as a solution to the optimum allotment of the DG problem.
Therefore, a problem associated with the allocation of DG is sizing, type of the DG, location, and penetration level. The optimal allotment of DG is a complicated optimization formulation problem because due to continuous and discrete choice variants, non-linear objective problem formulation, and several operational restrictions. Analytical, meta-heuristic, heuristic, and hybrid strategies are suggested to address this problem. The solution to the optimum allocation of DG in a multi-objective problem formulation is developed by [12] using a hybrid GA and Stain Bowerbird Optimization.
DSTATCOM allocation:
FACTS devices such as SVC, DFACTS, and DSTATCOM are utilized by the utilities for reactive power compensation. Among all the devices DSTATCOM has several benefits like real and reactive power exchange, compact size, low cost, less harmonic production, provides instantaneous reactive power, and better-regulating capability [13]. DSTATCOM device is a voltage source converter capable of mitigating current-related power quality issues like poor voltage regulation, poor pf, resonance reduction, low noise, load balancing, and compensation for neutral current. The problem with the allocation of DSTATCOM is the location, sizing, and number of DSTATCOM units and their control strategies. Many researchers have addressed the problems of DSTATCOM allocation using metaheuristic techniques like Bacterial Foraging, Differential Evolutionary algorithm, Immune Algorithm approach [14], PSO, Fuzzy GA approach, BAT algorithm, Harmony search algorithm [15], Firefly algorithm [16]. To enhance technical performance, this paper optimized the grid configuration and location of a distributed STATCOM in a State Board's actual power distribution topology by applying the Ant Colony Algorithm [17].
Improper allotment and capacity computation of compensating devices may lead to adverse consequences on network total power loss reduction. Allocation of DSTATCOM devices optimally provides greater stability, and power quality, minimizing total power loss and maximizing loading capability [18,19]. It observed that the allocation of DG will bring down network total power loss more than the allocation of Capacitors or DSTATCOM devices [20]. The author investigated the impact of several load models on distributed STATCOM device allotment in a radial power distributed scheme [21]. The simultaneous arrangement and capacity optimization of several distributed STATCOM devices to decrease total power loss and voltage magnitude divergence proposed by implementing the modified Sine Cosine Algorithm (mSCA)[22]. Optimal distribution of DG sources and DSTATCOM devices reduces total power loss and improves voltage magnitude profile compared to multiple DSTATCOM allocation approaches. Several studies of DSTATCOM allocation optimization carried out by various researcher lacks comparison between them. Utilization of DG sources and DSTATCOM devices concurrently results in a much larger reduction.
Network reconfiguration:
The operation procedure in network reconfiguration is the synchronous changing of sectionalizing switches and tie switches in distribution line feeders to modify the topological arrangement. The primary motive of reconfiguration is 1. Service re-establishment 2. System maintenance through outage planning 3. Load balancing 4. Bus voltage magnitude enhancement, and 5. Total real power Loss reduction. The DNR constraints to be implemented are bus voltage magnitude and line current magnitudes within the limits. The fundamental control action implicated in system reconfiguration is the switching operation procedure. 1. Step-by-step method and 2. simultaneous switching. However, due to various switching sequences and distinct switching nature, system reconfiguration is a complicated problem [23]. Classical Techniques forbid solving this complicated problem of system reconfiguration due to the radial network and distinct switch nature. Hence, the majority of the techniques in the literature for the resolution of this problem are supported by heuristic techniques. The conception of network reconfiguration for total power loss minimization was initially suggested by Merlin and Back. Several researchers implemented diverse algorithms like the Plant Growth Simulation algorithm, Firework Algorithm, Particle Swarm Optimization, BAT algorithm, Bacterial Foraging Optimization Algorithm, Cuckoo Search Algorithm, and Harmony Search Techniques. Various researchers reported on reconfiguration of the power distribution scheme to reduce overall power loss and increase reliability [24].
Simultaneous techniques:
All these individual techniques discussed above are capable of total power loss diminution. However, their synchronous grouping, operation, and execution will enhance the system's performance enormously. The idea of concurrent system reconfiguration, DG sources, capacitor, and Distributed STATCOM devices allotment has returned superior output comparison with the solo conceptualization. Also, the simultaneous techniques will intensify the search speed and prevent the local optima [25]. To bring down total real power losses, enhance the voltage stability indicator, and better voltage profile, the BAT method is projected in this study for the ideal position and rating of DG sources in radial power distribution systems. In this work various DG (single/multiple) unit types are considered for optimization [26]. The author of this paper [27] examines the most current publications, several authors' methodologies, and conceptualization of the problem particularly objective formulation and constraints.
Studies on simultaneous reconfiguration, DG sources, and capacitor placement in the distribution scheme demonstrated their capacity to reduce total power loss, which can increase system performance and efficiency [28]. A Binary Genetic Algorithm is applied by [29] to position multi DG units and capacitors simultaneously in an intelligent driven automatic reconfigured radial network to reduce power loss. In [30], an improved equilibrium optimization formulation is exploited to examine the issues of DG sources allocation in a reconfigured scheme. This study proposes a Max-Min-supported multi-subjective formulation optimization strategy for the best arrangement of dispersed generators with the best power distribution reconfigured scheme [31].
To maximize the techno-economic potential of the system, it is now usual practice to deploy both DG sources and DSTATCOM devices concurrently in distribution networks. PSO approach was employed to minimize loss by assigning DG source and distributed STATCOM device in the power distribution topology. It has the drawback of having convergence properties [32]. This paper reports the simultaneous network reconfiguration and location of distributed STATCOM devices and solar arrays in a power distribution scheme utilizing the Fuzzy-Ant colony optimization method [33]. Loss sensitivity analysis was employed to assign DG and Bacterial Foraging Optimizing Algorithm in the distribution network to size DG source and DSTATCOM device for various load levels. This research intends to bring down overall total power losses and enhance voltage magnitude profiles [34]. The cuckoo search method, presented by the authors demonstrates the best allocation and rating of DG sources and DSTATCOM devices in the power distribution scheme at the same instant [35]. Water cycle algorithm to allocate DG source and distributed STATCOM device in the power distribution scheme, the author obtained environmental, technical, and economic benefits [36]. The author presented a Meta-heuristic approach for network reconfiguration using DG (photovoltaic) and distributed STATCOM for total power loss mitigation and voltage magnitude profile enhancement [37]. A grasshopper optimization method is employed in this document due to the existence of distributed STATCOM devices and PV arrangement in the power distribution network under reconfiguration. The essential goal of this effort is to decrease total power losses and betterment of voltage magnitude profiles under varied loading scenarios [1]. Authors [38] utilized a composite Firefly Algorithm and Particle Swarm Optimization techniques, considering various technical, financial, and environmental indicators in a multi-objective problem formation for the best distribution of PV-DG sources and D-STATCOM devices. The best DG and D-STATCOM rating and placement are computed by implementing Hybrid Lightning Search, simplex method, and Loss Sensitivity Factor to reduce total power losses [39]. A Modified Ant Lion Optimizer is employed for PV-DGs and D-STATCOMs allocation. They are simultaneously optimized for their sizes and locations while considering system load and solar irradiance uncertainty into account [40]. To improve the accuracy of the photovoltaic power prediction PSO-GWO-BP prediction model was proposed [41]. With due respect to reducing total power loss, simultaneous assignment of DG sources and several Shunt Compensators, considering Static Var Compensator, and distributed STATCOM devices are proposed in [42].
A unique approach based on the Coyote algorithm for simultaneous network reconfiguration and Distributed Generation unit allocation to minimize power loss. The investigation has shown that a network with DG is more effective for loss reduction than network configuration [43]. The proposed Modified Marine Predators Optimizer (MMPO) is employed to solve simultaneous network reconfiguration (SNR) and DG allotment. The performance of the distribution system is improved by minimizing overall real power loss and enhancing voltage stability [44]. For synchronized network reconfiguration and distributed generation allocation to minimize real power loss, a new chaotic search group algorithm (CSGA) was put forth by [45]. Considering three different load levels, the CSGA was verified on IEEE busses 33, 69, 84, and 118. With this SNR-DG technique, the actual power loss and voltage profile of the system greatly improved. To reduce grid dependence and greenhouse gas emissions from conventional power plants, the Archimedes Optimization algorithm presented the best planning of solar photovoltaic systems under deterministic conditions [46].
The majority of the researchers reported low precision, sluggish assembly, and high CPU improvement needs. The basic BAT algorithm combines a population-based algorithm and local search strategy to produce a better-performing metaheuristic algorithm that can be employed for both local and global exploration [47]. BAT has shown effectiveness in resolving a variety of optimization issues in various contexts, including the power and energy system, economic load dispatch, engineering designs, image processing, and medical applications. The problem confined to the actual world, and the first solution that fulfills all the constraints is unknown. The ease of hybridization with other optimization methods, simplicity, and search speed are some of its advantages over other optimization techniques [48].
Goldberg demonstrated when compared to PSO and GA, several benchmark unimodal and multimodal functions performed well for BAT.This algorithm is employed to tackle extremely difficult problems from the real world that are difficult to solve using more traditional calculus-based techniques. The emphasis turned to Bat variations, such as Chaotic BAT, Directional BAT, BAT with mutation, BAT with Differential Evolution (DE) mutation and crossover, BAT with DE mutation, and Levy flight trajectories, which further improved and used to solve real-world optimization problems for better outcomes. The majority of Bat variants involve tiny adjustments to the loop's basic system of evolution [49]. The nonconvex, nonlinear, Multiobjective, multivariant, and constrained optimization issue was successfully handled using the conventional form of the Bat algorithm [50].
An effective method Ant Lion Optimizer (ALO) built around the hunting habits of ant lions. The ALO algorithm combines the two essential techniques, namely population-based search strategy and local-based search strategy, to create an intelligent technique that can search efficiently by the two primary search strategies (global exploration and local exploitation). ALO algorithm is less complicated, easier to use, and more customizable than other meta-heuristic techniques. As a result, numerous optimization issues have resolved using ALO [51,52,53]. But despite sometimes experiencing a standstill, ALO capable of resolving several optimization issues. The ALO has since undergone several modifications and improvements to increase its search capabilities.
A modified ALO that uses Lévy flying to optimize feature selection presented in [54]. A modified form of the ALO based on opposition learning with Lévy Flight was introduced [55].The Levy Flight Distribution (LFD) application has already been offered. The LFD is commonly used, nevertheless, to improve the exploration of optimization algorithms since it allows people to move to new locations and prevent optimization algorithms from becoming stagnant. A useful method for improving the search and exploitation phases of several optimization algorithms is the spiral movement of populations around the optimal solution [56,57,58].
Thus, a modified Ant Lion Optimizer (MALO) is suggested in this article to increase the basic ALO's exploration and exploitation by improving the basic ALO's seeking capabilities using Levy Flight Distribution (LFD) and spiral population direction.
The previous research concentrated on optimizing the positioning and size of a DG source or a D-STATCOM device in a network. Few researchers have focused on simultaneous techniques with prime objective problem formulation functions such as total power loss minimization, voltage magnitude profile enhancement, sizing, location, total operating cost reduction, and enhancement of stability index. The best location for DSTATCOM devices and PV DG sources is continuous,while the solution to the network reconfiguration problem is discrete. As a result, this is a complicated, multi-objective, nonlinear optimization problem.
Only a few studies in literature focused on network reconfiguration with D-STATCOM devices and DG sources by considering the Constant Power load model. In the mentioned literature survey on the simultaneous installation of DG sources and DSTATCOM devices, authors have not considered the DG penetration level. Hence, the author of the current research work investigates the influence of the CP and ZIP load models, including load increase on a radial distribution system with a reconfigured network by simultaneously installing distributed PV sources and DSTATCOM devices considering PV penetration level using BAT and MALO algorithm. Load models found to have a substantial impact on the sizing and positioning of distributed PV sources and D-STATCOM devices. The novelty of the research work presented in this paper is as follows:
(i) The three objectives considered are (a) Minimization of total power loss (b) Voltage magnitude profile enhancement (c) Overall operating cost reduction during network reconfiguration by simultaneously installing distributed PV sources and DSTATCOM devices.
(ii) Three operational scenarios considered are (a) Network without reconfiguration and additional distributed PV sources/DSTATCOM devices (b) Network reconfiguration without additional distributed PV sources/DSTATCOM devices (c) Combined assignment of DSTATCOM devices and distributed PV sources allocation with network reconfiguration considering penetration level 0.25, 0.5, 0.75, and 1.0 in radial distribution topology using BAT and MALO method.
(iii) To evaluate the positioning and capacity of the distributed PV sources, D-STATCOM devices, and network reconfiguration, considering the influence of load models and PV penetration levels.
(iv) The recommended BAT and MALO method is well-tried on standard IEEE 118-node test systems.
(v) The real-time data State Utility 317 nodes in the rural BESCOM radial distribution scheme is also considered for testing by utilizing BAT and MALO.
The Investigations were carried to assess the total power losses, voltage profile, capacity, and positioning of PV sources and DSTATCOM devices along with network reconfiguration in rural feeder BESCOM for high voltage distribution system (22kV) under Deendayal Upadhyaya Gram Jyoti Yojana(DDUGJY) launched by Government of India for planning network.
This scheme intends to provide 24-hour continuous power to rural areas for agricultural needs through a High Voltage Distribution System(HVDS) by upgrading infrastructure to handle 22 kV including feeder segregation. HVDS is a practice where the HV line extends up to the load point. This planning reduces the length of the LT line to just sufficient for the service cable. Also, the HV line can manage extra peak hour load demand, reducing tripping due to overloading.
The structure of the present research is as follows: The objective function problem formulation for minimizing power loss is explained in Section 2. Load models are discussed in Section 3. The MALO approach is presented in Section 4. The results and analysis of the IEEE 118 node test systems and State Utility 317 nodes in the rural BESCOM radial distribution scheme are explained in Section 5, and the resulting outcomes are compared with various methodologies published in the available literature. The findings of the present BAT and MALO approach are summarized in Section 6.

2. Problem Formulation

The suggested MALO algorithm's objective is to determine the best design for the radial power distribution network topology, D-STATCOM devices, and distributed PV sources allotment simultaneously during reconfiguration. The intention is to reduce total power loss and the overall operating cost and improve the voltage magnitude profile under limitations stated by equation (4) for load models and DG penetration levels considered.

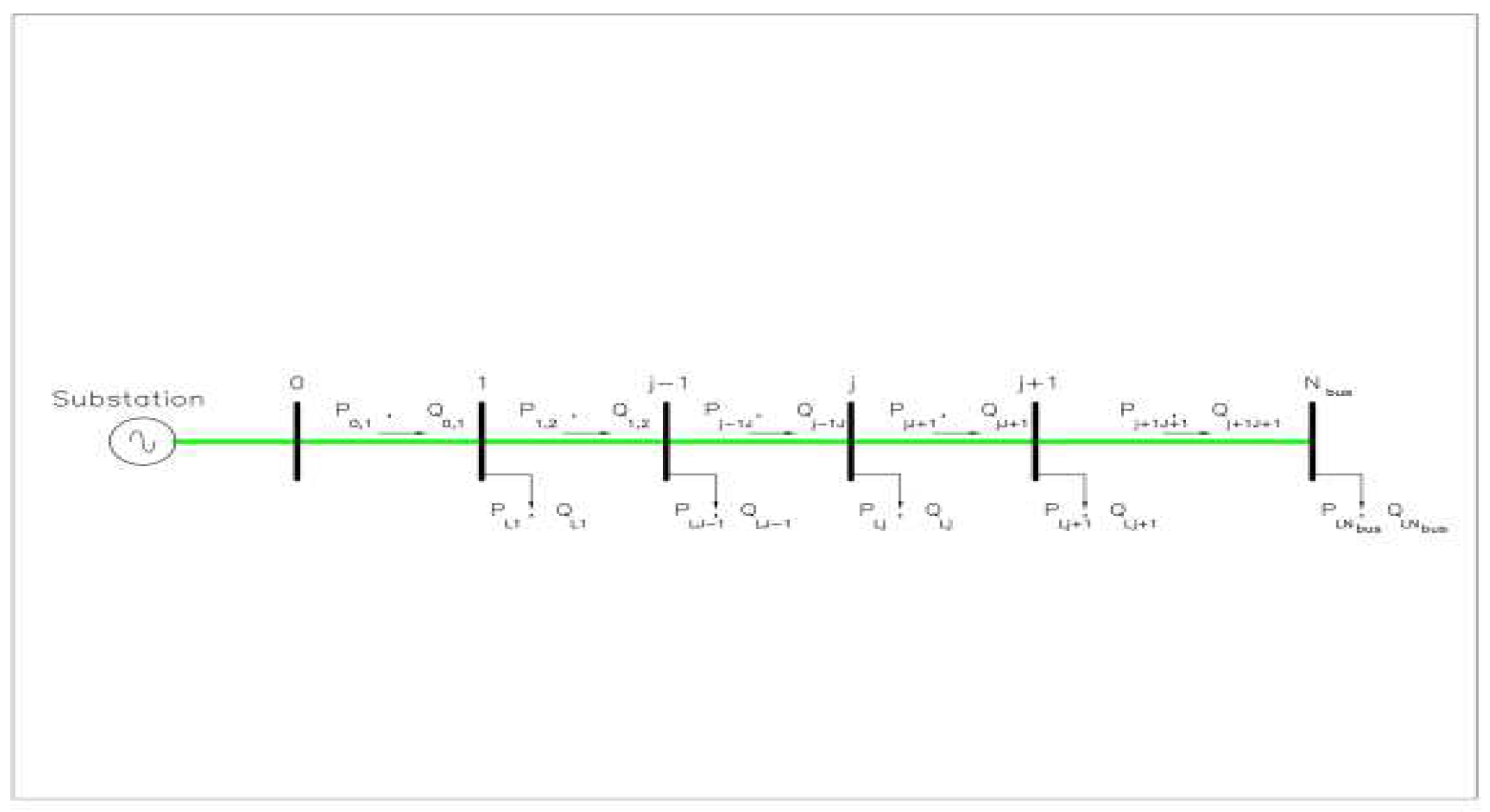
2.1. Power Flow Study for Distribution Network

A direct method to the distribution scheme for load flow solution has been applied in this research to achieve a superior outcome [59]. Figure 1 shows the schematic representation of a simple distribution strategy. Equation (1) utilized to calculate the equivalent injected current at node 't'
I t = P t + j Q t V t ∗
Kirchhoff’s current law adapted to compute the branch current in the feeder section connected between buses ‘t’ and ‘t+1’, mentioned in equation (2)
J t , t + 1 = I t + 1 + I t + 2
Using the Bus Injected to Branch Current matrix (BIBC) shown in equation (3)
J = B I B C I
Kirchhoff’s voltage law is implemented to compute the voltage at bus ‘t+1’, indicated by equation (4)
V t + 1 = V t − J t , t + 1 ( R t , t + 1 + j X t , t + 1 )
The power loss in the distribution line segment connected between buses ‘t’ and ‘t+1’ is computed in equation (5)
P L o s s ( t , t + 1 ) = [ P t , t + 1 2 + Q t , t + 1 2 ] R t , t + 1 V t , t + 1 2
The overall power loss (PTLoss) of the power distribution scheme is estimated by the summation of losses in all distribution line segments [3], specified by equation (6),
P T L o s s = ∑ t = 1 m P L o s s ( t , t + 1 )

2.2. Network Reconfiguration

Changing the status of normally open tie switches and normally closed sectionalizing switches, the distribution system's topology is altered. While opening sectionalizing switches lowers active power losses, closing tie switches will transfer voltage between feeders. The radiality of the network is considered to resolve the reconfiguration issue.
In a radial power distribution scheme, the network reconfiguration issue is resolved by satisfying the enforced system operating constraints like voltage magnitude profile, feeder current carrying capability, and radial power distribution topology. This ideal network structure delivers the lowest power loss. Equation (7) utilized to calculate the power loss in the feeder line segment connected between "t" and "t+1" following reconfiguration
P Loss ( t , t + 1 ) ′ = I t ′ 2 * R t = ( P t ′ 2 + Q t ′ 2 ) V t ′ 2 * R t
The reconfigured scheme overall power loss computed by summing up line losses in all line segments shown in equation (8)
P T L o s s ′ = ∑ t = 1 m P L o s s ( t , t + 1 ) ′
The structure net power loss ΔPRTLoss obtained by difference in power loss before and after network reconfiguration [37] stated in the equation (9),
Δ P T L o s s R = P T L o s s ' − P T L o s s

2.3. D-STATCOM Modelling

D-STATCOM is a voltage source converter, a shunt connected to the utility network through an injection transformer. D-STATCOM can mitigate current related power quality issues. The magnitude of the generated voltage of D-STATCOM is controlled to modify the amount of reactive power [33]. The real power adjusted to zero and the reactive power of the network after D-STATCOM devices distribution can computed by equation (10),
Q D S T A T C O M = ( V t 2 X L ) − ( V t V s X L ) Cos α
where, Vt = utility bus voltage; Vs = D-STATCOM bus voltage; XL = reactance of the power distribution line; α = Phase angle displacement between Vt and VS.

2.4. PV modelling

Distributed PV sources considered here based on solar irradiance model stated in equations (11) (12) (13).
P P V = P − P V r a t e d × ( G s 2 G S T D × X c ) , f o r 0 ≤ G s ≤ X c
P P V = P − P V r a t e d × G s G S T D f o r 0 ≤ G s ≤ G S T D
P P V = P − P V r a t e d   for   G S T D ≤ G s
where P-PV = PV output power (MW), GSTD = Solar irradiance in the standard conditions typically fixed to 1000 W/m2, XC = certain radiation point, generally fixed to 150 W/m2, Gs = Solar irradiance at selected location and P−PV rated =PV rated power (MW) [40].

2.5. Total Power Loss Reduction with Simultaneous Installation of Distributed PV Sources/DSTATCOM Devices along with Network Reconfiguration

The total power losses are reduced by the optimum positioning of distributed PV sources and DSTATCOM devices during network reconfiguration in the radial power distribution structure obtained in equation (14).
F 1 ( x ) = P T L ( Re c o n f i g + P V D G + D S T A T C O M )

2.6. Total Operating Cost Minimization

The Total Operating Cost(TOC) of real/reactive power generated by the connected distributed PV sources/D-STATCOM devices and the cost of real power losses after reconfiguration [15] is computed using equation (15)
T O C = A P ∗ P T L o s s ' ∗ H + A d ∗ ∑ j = 1 m P c j + A c ∗ ∑ k = 1 n Q c k
Where,
Pcj = PV DG source real power size (kW); Qck = D-STATCOM device size (kVAr); Ap = Energy cost ($/kWh);
Ac = DSTATCOM device cost ($/kVAr); Ad= PV DG source real power supplied cost ($/ kW); H = Total number of hours per annum.

2.7. Voltage Profile Improvement by Installing Distributed PV Sources and DSTATCOM Device along with Network Reconfiguration

Optimal installation of distributed PV sources and DSTATCOM devices enhances voltage profile in reconfigured networks. Here distributed PV sources and Distributed STATCOM devices supply the requisite quantity of real power and reactive power into the network to diminish power losses and enhance the voltage magnitude at the buses. To validate the improvement of the voltage magnitude profile, voltage variation at each node is considered mentioned in equation (16) and this value is maintained at a minimum value [33].
F 3 ( x ) = Δ T V D = M i n ( V r e f − V i V r e f ) 0.95 ≤ V r e f ≤ 1.05
The voltage magnitude with PV DG sources and DSTATCOM devices installation in a reconfigured network can be enhanced by minimizing the overall voltage magnitude deviation shown in equation (16).

2.8. Objective Function

The focal objective of the recommended technique is to minimize the total power losses, total operating cost, and to maximize the voltage magnitude profile by simultaneously installing distributed PV sources and DSTATCOM devices along with network reconfiguration stated by equation (17),
M i n F ( x ) = M i n [ F 1 ( x ) + F 2 ( x ) + F 3 ( x ) ]
Where,
F 1 ( x ) = M i n P T L ( Re c o n f i g + P V D G + D S T A T C O M ) F 2 ( x ) = M i n ( T O C ) F 3 ( x ) = M i n ( Δ T V D )

2.8.1. Equality Constraints

The equality restrictions pertain to the distribution system's actual and reactive power flow balance shown in equations (18) and (19).
P d e m a n d + P T L o s s = ∑ P P V D G , j + P G , G r i d j = 1.......... N b
Q d e m a n d + Q T L o s s = ∑ Q D S T A T C O M , j + Q G , G r i d j = 1.......... N b

2.8.2. Inequality Constraints

1. Node voltage limit
Equation (20) refers to the magnitude of node voltages that must be between the V min = 0.95 p.u. and V max =1.05 p.u. at all buses to maintain power quality.
V j min ≤ V j ≤ V j max j = 1.......... N b
2. Feeder capacity limit
The size of the branch current Ii should not exceed Imax flowing in the branch to prevent insulation failure mentioned [37] in equation (21).
I i ≤ I max i = 1......... N b r
3. DG constraints
The minimum and maximum real power generation from distributed PV sources are restricted shown in equation (22).
P P V D G , j min ≤ P P V D G , j ≤ P PVDG max , j j = 1 ......... N D G
4. D-STATCOM constraints
The minimum and maximum reactive power generation from distributed static Compensator devices are stated by equation (23).
Q D S T A T C O M , j min ≤ Q D S T A T C O M , j ≤ Q D S T A T C O M , j max j = 1.......... N D S T A T
5. Rule to maintain the radial topology
A radial layout is preferred to have a simple, inexpensive cost of operation and distribution grid protection. All loops should include a tie line switch and a sectionalizing switch, according to the specification. As a result, a single switch should be allowed to open in a loop when a tie switch is closed [15]. The following rule should be followed to keep the radial topology:
Closing all the tie lines yielded the total number of main loops using equation (24),
N m a i n l o o p s = ( N b r − N b ) + 1
Where, Nbr = Overall number of branches ; Nb = Overall number of nodes
An overall number of sectionalizing switches is computed using equation (25).
N b r = N b − 1
The overall count of tie switches and main loops should be identical.

3. Load Model

In an exponential form stated in equation (26) and (27), the real and reactive powers of the static load models are
P = P 0 ( V V 0 ) n p
Q = Q 0 ( V V 0 ) n q
The actual and reactive powers at node nominal voltage V0 are P0 and Q0, respectively. The bus load voltage is denoted by V, and the load exponents are denoted by np and nq [21] [60]. Both np and nq have the following values:
n _ p and   n _ q = ‘0’ value for the ”Constant Power load model” (CP).
n _ p and   n _ q = ’1’ value for the “Constant Current load model”(CI).
n _ p and   n _ q = ‘2’ value for the “Constant Impedance load model” (CZ).

3.1. Polynomial (ZIP) Load Model

The entire ZIP load constants for both real and reactive loads denoted by equation (28) is 1. As a result, aq + bq + cq = 1 and ap + bp + cp = 1. The simulation parameters considered are ap = aq = 0.1, bp = bq = 0.1, and cp = cq = 0.8. At nominal voltage V0, P0 and Q0 represent actual and reactive power.
P = P 0 [ a p ( V V 0 ) 2 + b p ( V V 0 ) + c p ]
Q = Q 0 [ a q ( V V 0 ) 2 + b q ( V V 0 ) + c q ]

3.2. Load Growth Model

“Load growth” is reflected in the equation (29) for the planning of the power distribution scheme [64].
L o a d   d e m a n d = L o a d   d e m a n d ∗ ( 1 + R ) ^ T  
R= annual load growth rate (7%)
T= period (5 years)

4. MALO Algorithm

Table 1 lists the parameters utilized for the BAT and MALO technique, and Table 2 cost factors that were chosen. MALO focused on improving the exploration and exploitation process to increase the fundamental ALO's searching capability. Applying Levy Flight Distribution (LFD) improves the exploration phase by allowing the algorithm to jump to different regions to abstain from the primitive ALO's stagnation [40].
X _ i ^ n e w = X i + ∝ × L e v y ( β )
where ∝ signifies a random step parameter; × respresents the entry-wise multiplication. β symbolizes a parameter related to the LFD. The step size stated as follows:
α × L e v y ( β ) ∼ 0.01 u v 1 / β ( X t i − A n t l i o n i t )
where u and v indicate variables achieved by normal distribution ,
u ∼ N ( 0 , ϕ u 2 ) , v ∼ N ( 0 , ϕ v 2 )
ϕ u = [ τ ( 1 + β ) × Sin ( π × β 2 ) τ [ 1 + β 2 ] × β ] 1 / β , ϕ v = 1
where, τ = standard gamma function; 0 ≤ β ≤ 2
The exploitation phase of the algorithm is improved by moving the ants in a spiral manner around the elite (best) solution as follows:
X i n e w = A n t l i o n i t − X i t e b t Cos ( 2 π t ) + A n t l i o n i t
The shape of the logarithmic spiral is defined by the constant ’ b’. An adaptive operator employed for this purpose in order to strike a balance between exploitation and exploration, as seen in the following:
A ( t ) = A min + ( A max − A min τ ) × t
where A max and A min are the highest and lowest allowed values for A. A max to Amin represents a significant change in this number. When the value of A is close to A min, the position of the populations will be updated in equation(32) to enhance the exploration of this technique, whereas the value of A is close to A max, the position of the populations will be updated in equation (36), which enhances the exploitation of this technique [40].

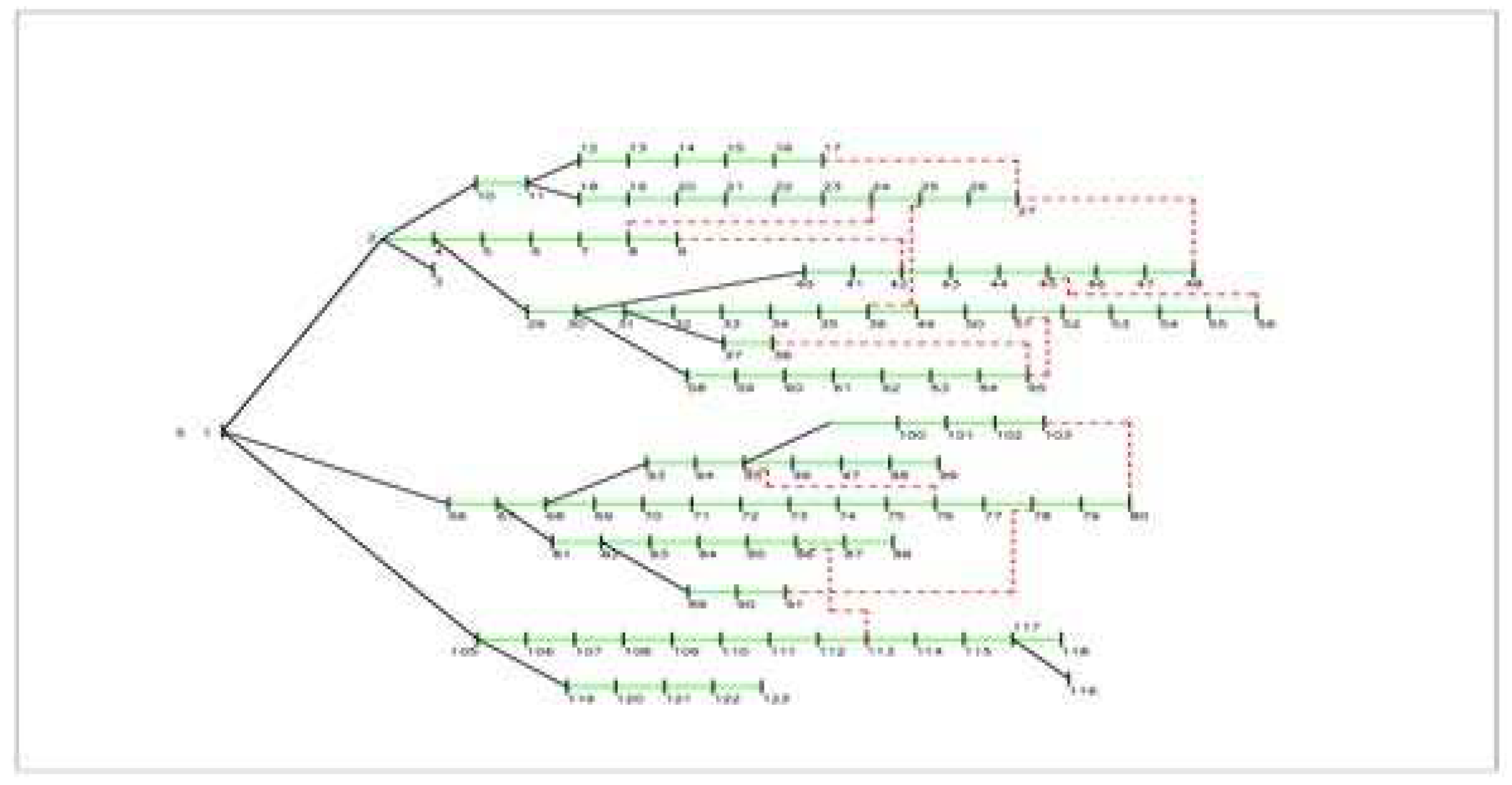
5. Results

The impact of various load models is evaluated for the concurrent deployment of multiple PV sources and Distributed STATCOM devices with network reconfiguration for power distribution networks in this suggested research work. BAT and MALO technique is applied to solve network reconfiguration issues using MATLAB software. The direct load flow algorithm calculates base case power flows, power losses, voltage values in the power distribution scheme, and the ideal location, and size of distributed PV sources /D-STATCOM devices considering PV penetration levels 0.25,0.5, 0.75, and 1.0. The recommended technique is proved on IEEE 118 node test scheme, and State Utility 317 nodes in rural BESCOM radial distribution scheme to validate algorithm performance. Three contrasting situations were investigated to evaluate the effectiveness of the proposed strategy.
For the standard arrangement in Scenario 1, total power losses, total voltage variation, and total running costs were assessed for the load models considered. In Scenario 2, the best network reconfiguration design is performed. Additionally, estimates are made for total power losses, total voltage variation, and total operating costs. The optimal design for network reconfiguration in Scenario 3 is assessed for load models, considering factors like size, location of PV DG sources, DSTATCOM devices, total power losses, total voltage deviation, and total operating costs. In this instance, the PV DG penetration level is evaluated at 0.25, 0.5, 0.75, and 1.0.
On a rural feeder real-time network, the BAT and MALO method is applied for high voltage distribution network planning. Investigations are conducted on 11 kV and 22 kV feeders to determine the size, position, and PV penetration level at 0.25, 0.5, 0.75, and 1.0 as well as to estimate total power losses, total voltage deviation, total operating costs, and DSTATCOM device sizing and location.
Scenario-1- System with uncompensated condition and standard configuration.
Scenario-2 - System with network reconfiguration and without compensation.
Scenario-3- Simultaneous positioning of multiple distributed PV sources and DSTATCOM devices with network reconfiguration.
Load increase is considered while planning the power distribution scheme. For the future next five years, a 7% increment in load is anticipated. Network load models in the distribution system are sensitive to voltage levels. The load modeled using a distinct model to examine the real condition.
Case 1: Network under Constant Power model (CP)
Case 2: Network under ZIP model with load growth
Test system 1: IEEE 118 node radial power distribution scheme
The second test scheme is a radial power distribution scheme with 118 buses, 15 tie switches, and 117 sectionalizing switches as depicted in Figure 2. The overall actual and reactive power needs of the scheme are 22.7 MW and 17 MVAr, respectively. The network power flow study is executed utilizing S base = 100 MVA along with V base = 11 kV. A reference paper [1] is cited for the power distribution scheme feeder line data and load data. The total number of distributed PV sources evaluated for simulation is three, with sizes ranging from 10 to 2000 kW considering a penetration level of 0.25. Two DSTATCOMs are being examined, with sizes ranging from 10 to 1900 kVAr. Table 3. shows the outcomes of 10 iterations of solving all situations of a 118-bus system. Load growth is assumed to be 7% span over five years for planning purposes.
The total actual power loss estimated for scenarios 1 to 3 is 1298.14, 935.48, and 871.34 for the constant power model. Similarly, for situations 1 to 3, the total reactive power loss estimated is 978.70, 1054.14, and 887.01, respectively. Figure 3 shows that the voltage profile improved from scenarios 1 to 3 and V min 0.86 (77), 0.95(40), and 0.95(40) p.u respectively. The percentage loss reduction computed for scenarios 2 to 3 is 27.93 and 32.87 utilizing the BAT algorithm. The optimal system configuration for the constant power model is found in scenario 3 using the BAT method by modifying the tie lines 130,122,128,101,131,21,47,126,125,132,123,119,124,118,127 as an alternative for 118 TO 132. Three PV sources are sized and located at 871(81), 1014(72) , 1193(3) considering PV penetratin level as 0.25. Two DSTATCOM devices are sized and located at 274(26), 1864 (84).
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 2631.08, 1611.99, and 1447.85 utilizing the BAT method. The total reactive power loss estimated for situations 1 through 3 is 1979.25, 1385.87, and 1393.75. As indicated in Figure 4, the voltage profile improved from scenario 1 to scenario 3 and V min 0.81 (77), 0.95(22), and 0.95(22) (p.u.). The percentage loss estimated for scenarios 2 to 3 is 38.73 and 37.36. Similarly, for the ZIP model with load growth in scenario 3 with the assistance of the BAT algorithm, the optimal system structure is established by modifying the tie lines 129, 130, 128, 125, 119, 132, 120, 126, 124, 21, 103, 40, 122, 127 as a substitute of 118 to 132. Three PV sources are sized and located at 1336(90), 984(41), and 1418(76) considering the PV penetration level as 0.25. Two DSTATCOM devices are sized and located at 1367(101), and 1463(27).
The total actual power loss estimated for scenarios 1 to 3 is 1298.14, 800.62, and 759.75 using the constant power model. Similarly, for situations 1 to 3, the total reactive power loss estimated is 978.90, 925.50, and 856.01 respectively Figure 3 shows that the voltage profile improved from scenarios 1 to 3 and V min 0.86 (77), 0.95(33), and 0.95(48) p. u. The percentage loss estimated for scenarios 2 to 3 are 38.32 and 41.47 utilizing the MALO algorithm. The optimal system configuration for the constant power model is found in scenario 3 using the MALO method by modifying the tie lines 132, 120, 128, 124, 121, 102, 126, 51, 118, 55, 125, 127, 129, 119 as an alternative for 118 to 132. Three PV sources are sized and located at 1993 (65), 604(84), 621(102) considering PV penetratin level as 0.25. Two DSTATCOM devices are sized and located at 382(106), 1317(47).
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 2631.08, 1603.08, and 1500.13 utilizing the MALO method. Similarly, the total reactive power loss estimated for situations 1 through 3 is 1979.25, 1162.50, and 1145.64. As indicated in Figure 4, the voltage profile improved from scenario-1 to scenario-3, and V min 0.81 (77), 0.95(42), and 0.95(42) (p.u.). The percentage loss estimated for scenarios 2 to 3 are 39.07 and 42.98. Similarly, for the ZIP model with load growth in scenario- 3 with the assistance of the MALO algorithm, the optimal system structure is established by modifying timelines 129, 121, 132, 120, 130, 118, 124, 72, 128, 123, 106, 125, 126, 49, 119 as a substitute of 118 to 132. Three PV sources are sized and located at 2000(11), 2000(118), and 1858(118) considering the PV penetration level as 0.25. Two DSTATCOM devices are sized and located at 1900(118), and 1900(118).
The results presented in Figure 5 and Figure 7 demonstrate that IEEE 118 bus system for the constant power model, the MALO method minimizes power loss at penetration levels of 25% greater than the BAT approach. For penetration levels of 50% and 75%, the BAT algorithm predicts a higher power loss reduction than the MALO method.
Similar findings were observed for the IEEE 118 bus system ZIP with load growth model (Figure 6 and Figure 8). When estimating power loss reduction at the 25% penetration levels, the MALO algorithm performed better than the BAT approach. Nevertheless the BAT algorithm yields a better-predicted power loss reduction for penetration levels of 50% and 75% than the MALO algorithm.
Table 4. shows the performance of the suggested BAT and MALO algorithm for the IEEE 118 node test scheme compared to the results of other approaches for the constant power load model available in the literature. According to the observed results, considerable reduction in overall actual power loss, reactive power loss, and betterment in voltage magnitude profile for scenario -3 when placed concurrently in a reconfigured network considering PV penetration level.
Test system 2: 317 Node rural BANGALORE ELECTRCITY COMPANY LIMITED radial distribution scheme
The real-time rural (BESCOM) radial distribution scheme consists of 317 buses, Three tie switches initially open [317,318,319], and 316 sectional switches initially closed. The overall actual and reactive power needs of the scheme are 660.69 MW and 773.73 MVAr, respectively. The network power flow study was executed using S base = 100 MVA along with V base = 11 kV (For the present system) and 22kV (planned HVDS). The system uses a Rabbit conductor type, and its specifications are as follows: C/S area = 50 mm2 (Aluminium), DC resistance = 0.5524 ohm per kilometer, current rating = 185 A, diameter of wire = 6/3.35 mm, and diameter of steel = 1/3.35 mm. The total number of distributed PV sources evaluated for simulation is three, with sizes ranging from 10 to 5000 kW considering a penetration level of 0.25. Two DSTATCOMs are being examined, with sizes ranging from 10 to 10,000 kVAr. Table 5 shows the outcomes of 5 iterations of solving all situations of a 317-bus for the present system at 11kV. For planning purposes, load growth is assumed to be 7% over five years.
The overall real power loss for the 11kV system from scenarios 1 to 3 is 3.5 E +5, 3.1 E+5, and 2.57 E+5 according to the results of the 317 node utility scheme for the constant power load model utilizing BAT algorithm. The overall reactive power loss from situations 1 through 3 is 2.0E+5, 1.77E+5, and 1.40E+5. The minimum voltage from scenarios 1 to 3 is 0.95(12), 0.95(15), 0.95(10) (p.u.), and the voltage profile is illustrated in Fig.9. The percentage loss reduction estimated for scenarios 2 and 3 are 9.65 and 26.56. In the Constant power model for scenario 3, the optimal system configuration is determined using the BAT method by modifying the tie lines 50, 318, and 44 instead of 317, 318, 319 and placing three distributed PV source sizes at bus 2013(117), 2113(76) and 1021(23). Two D-STATCOM devices are sized and located on buses 6765(122), and 2000(192).
The overall real power loss from scenarios 1 to 3 is 3.05 E+5, 2.83 E+5, and 1.10 E+5 according to the results of the 317 node utility scheme for the ZIP load with a load growth model utilizing the BAT algorithm. The overall reactive power loss from scenarios 1–3 is 1.78 E+5, 1.60 E+5, and 0.54E+5. The improved voltage profile from scenarios 1 to 3 illustrated in Fig.10 and V min is 0.95(12), 0.95(12), 0.95(11) (p.u.). The percentage loss reduction computed for scenarios 2 and 3 are 7.36 and 63.78. In the ZIP model with load increase, the optimal system configuration is produced in scenario 3 using the BAT method by modifying the tie lines 75, 45, and 63 instead of 317, 318, 319 and placing three distributed PV sources sized and placed are 3033(294),3432(6) and 378(229). Two D-STATCOM devices sized and placed are 9173(136) and 7979(85).
The total actual power loss estimated for scenarios 1 to 3 is 3.5E+5, 3.25E+5, and 1.75E+5 considering the constant power model employing the MALO algorithm. Similarly, for situations 1 to 3, the total reactive power loss estimated is 2.0E+5, 1.83E+5, and 0.95E+5, respectively. Figure 9 shows that the voltage profile improved from scenarios 1 to 3 and V min 0.95 (12), 0.95(14), and 0.95(10) p. u respectively. The percentage loss estimated for scenarios 2 to 3 is 7.11 and 49.77 utilizing the MALO algorithm. The optimal system configuration for the constant power model is found in scenario 3 using the MALO method by modifying the tie lines 45,59,76 instead of 317, 318, and 319. Three PV sources are sized and located at 2142 (258), 3022(27), and 2568(317) considering the PV penetration level as 0.25. Two DSTATCOM devices are sized and located at 5355(190), and 8878(101).
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 3.05E+5, 2.68E+5, and 1.24E+5 respectively utilizing the MALO method. Similarly, the total reactive power loss estimated for situations 1 through 3 is 1.78E+5, 1.51E+5, and 1.77E+5. As indicated in Figure 10 the voltage profile improved from scenario 1 to scenario 3, and V min 0.95 (12), 0.95(12), and 0.95(12) (p.u.). The percentage loss estimated for scenarios 2 to 3 are 12.30 and 59.34. Similarly, for the ZIP model with load growth in scenario 3 with the assistance of the MALO algorithm, the optimal system structure is established by modifying the tie lines 45, 73, and 56 as a substitute for 317, 318, and 319. Three PV sources are sized and located at 5000(294), 5000(317), and 5000(317) considering PV penetration level as 0.25. Two DSTATCOM devices are sized and located at 10000(97), and 10000(317).
Table 6 shows the outcomes of the investigation carried out on the planned High Voltage Distribution System(22kV) to assess the feeder line losses and voltage magnitude profile(Figure 11 and Figure 12) in the rural BESCOM feeder. This investigation is carried out to analyze the simultaneous placement of distributed PV sources and D- STATCOM devices along with network reconfiguration considering PV penetration levels at 0.25, 0.5, 0.75, and 1.0. The Figure 13 and Figure 14 shows fitness function for 317 bus utility system (ZIP model) at 11kV and 22kV.
It observed that from Table 6. upgrading the present system from 11kV to HVDS 22kV system for Constant power model considering penetration level as 0.25, 0.5, 0.75, and 1.0, the real power loss reduction achieved is 55.21%, 60.29%, 24.74%, and 36.25% respectively. Similarly, from Table 6 for the ZIP load model with load growth, considering penetration levels as 0.25, 0.5, 0.75, and 1.0, the real power loss reduction is 38.42%, 51.45%,16.60%, and 43.84% achieved by utilizing BAT algorithm. Also, it observed that the minimum bus voltage magnitude remains the same for all situations considered. From Table 6 by employing the MALO algorithm, upgrading the present system from 11kV to HVDS 22kV system for the Constant power model considering penetration levels as 0.25, 0.5, 0.75, and 1.0, the real power loss reduction achieved is 51.69%, 21.76%, 59.67%, and 44.30% respectively. Similarly, for the ZIP load model with load growth considering penetration levels as 0.25, 0.5, 0.75, and 1.0, the real power loss reduction of 55.75%, 55.29%, 35.87%, and 56.35% was achieved. Also, it observed that the minimum bus voltage magnitude remains the same for all situations considered. The total technical losses reduced observed from the results, and upgrading to an HVDS (22kV) system will prevent pilferage, tampering, and hooking on the feeder (Non-technical losses). The primary objective of Ujjawal DISCOM Assurance Yojana(UDAY) is to reduce AT & C losses by less than 12 to 15% could be achieved.

6. Conclusion

The BAT and MALO optimization method is applied in this research work to optimize the simultaneous allotment and sizing of distributed PV sources and DSTATCOM devices in the redesigned power distribution scheme. The main intention is to minimize overall power losses, enhance the voltage magnitude profile, and reduce overall operating costs. The influence of load models, sizing and positioning of distributed PV sources, and DSTATCOM devices analysis applied to the IEEE 118 node test schemes, and State Utility 317 bus Bangalore Rural Distribution system. The suggested technique considered three scenarios: the base case, network reconfiguration, and simultaneous integration of distributed PV sources and Distributed STATCOM devices in a radial power distribution scheme for the redesigned network with PV penetration levels 0.25, 0.5, 0.75, and 1.0. The suggested method results obtained for standard IEEE 118 power distribution systems validated against the results available in the literature for the constant power model. Also, this technique proved to be effective in solving real-time State Utility 317 nodes in rural Bangalore distribution power system problems for planning purposes. Investigation carried out on planned HVDS (22kV) demonstrates that total line losses are reduced substantially. In addition, computational findings demonstrated that the BAT and MALO algorithm outperformed other approaches in scenario -2 and promising results in scenario- 3. The suggested technique produces better outcomes concerning total actual power reduction, voltage magnitude profile enhancement, and overall operating cost reduction. It observed that the size and positioning of DG sources/DSTATCOM devices change with the load models considered. Further research work can be extended on planning PV-DG systems with energy storage systems and DSTATCOM devices to maximize efficiency.

Author Contributions

The first author contributed to the study conception and design, material preparation, data collection and analysis were performed by SUJATHA B. C. The first draft of the manuscript was written bySUJATHA B. C. and all authors commented on previous version of the manuscript. All authors read and approved the manuscript.

Funding

The Authors declare that no funds, grants, or other support were received during preparation of the manuscript.

Competing Interest

The Authors have no relevant financial or non –financial interests to disclose.

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author SUJATHA B. C.

Acknowledgments

The authors wish to thank the Authorities of BESCOM, KPTCL, Bangalore, Karnataka, India for furnishing the relevant distribution network data for the current investigation activity.

Conflicts of Interest

The authors affirm no conflicts of interest in respect of the publication of this research work.

References

  1. Kola Sampangi Sambaiah, Jayabharathi, T., Optimal reconfiguration of Distribution Network in presence of D-STATCOM and Photovoltaic array using Metaheuristic algorithm, European Journal of Electrical Engineering and Computer Science,vol.4(2020). [CrossRef]
  2. Cholapandian, V., Yuvaraj, T., Devabalaji, K.R., Optimal Allocation of Photo-Voltaic Units in Radial Distribution Networks Using a New Student Psychology Based Optimization Algorithm, Int. J. Electr. Eng. Inf., vol.13, pp 318–335 (2021). [CrossRef]
  3. Yuvaraj, Thangaraj, et al., Optimal integration of Capacitor and Distributed Generation in distribution system considering load variation using BAT optimization algorithm, Energies vol.14, no.12, pp 3548(2021). [CrossRef]
  4. Sanjay, R., Jayabarathi, T., Raghunathan, T., Ramesh, V., Mithulananthan, N., Optimal allocation of distributed generation using hybrid grey wolf optimizer, IEEE Access, vol.5, pp.14807-18 (2017). [CrossRef]
  5. Yuvaraj, T., Devabalaji, K.R., Ravi, K., Optimal allocation of DG in the radial distribution network using bat optimization algorithm, Advances in Power Systems and Energy Management, Springer, Singapore, pp. 563–569 (2018). [CrossRef]
  6. Likhith Kumar , M.V, et al., Optimal allocation of DG units in distribution system considering variation in active power load, Archives of Electrical Engineering, Vol.68,no.2, pp 265-277(2019). [CrossRef]
  7. Morrn ,J., Haan,S.D., Maximum penetration level of distribution generation without violating voltage limits, Engineering, Material Science(2008). [CrossRef]
  8. Rawat , Shelly, A Comprehensive Review on Impact of Wind and Solar Photovoltaic Energy Sources on Voltage Stability of Power Grid, Journal of Engineering Research, vol.7, no.4, pp.178-202 (2020).
  9. Sampath Ediriweera, W.E.P, et al., Robust microgrid for distribution systems with high solar photovoltaic penetration, Archives of Electrical Engineering, vol.72, no 3, pp.785-809 (2023). Doi: 10.24425/aee.2023.146050. [CrossRef]
  10. Dash, S.K, Mishra, S, Abdelaziz, A.Y, Alghaythi, M Lallehyani, A., Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm, Energies, vol. 15, pp.2267 (2022). [CrossRef]
  11. Balu K., Mukherjee, V., Optimal siting and sizing of distributed generation in radial distribution system using a novel student psychology-based optimization algorithm. Neural Comput. Appl., vol.33, pp.15639–15667 (2021). [CrossRef]
  12. Hemeida, A.M, Bakry, O.M., Mohamed, A.A., Mahmoud, E.A., Genetic Algorithms and Satin Bowerbird Optimization for optimal allocation of distributed generators in radial system, Appl. Soft Comput., vol. 111, pp.107727 (2021). [CrossRef]
  13. Montoya, O.D, Gil-González, W, Hernández, J.C., Efficient Operative Cost Reduction in Distribution Grids Considering the Optimal Placement and Sizing of D-STATCOMs Using a Discrete-Continuous VSA. Appl. sci., vol.11, pp.2175(2021). [CrossRef]
  14. Taher, S. A., Afsari, S. A., Optimal location and sizing of DSTATCOM in distribution systems by immune algorithm, International Journal of Electrical Power & Energy Systems, vol. 60, pp 34-44 (2014). [CrossRef]
  15. Yuvaraj, T., Devabalaji, K. R., Ravi, K., Optimal placement and sizing of STATCOM using harmony search algorithm, Energy Procedia, vol.79, pp.759-65 (2015). [CrossRef]
  16. Farhoodnea, M., Mohamed, A., Shareef, H., Zayandehroodi, H., Optimum D-STATCOM placement using firefly algorithm for power quality enhancement, IEEE 7th international power engineering and optimization conference (PEOCO),vol. 3, pp. 98- 102, Langkawi (2013). [CrossRef]
  17. Arouna Oloulade, Adolphe Moukengue Im ano, Xavier Fifatin, Antoine Vianou, Herman Tamadaho, Ramanou Badarou., Multi-Objective Optimization of the Safe Operation of the Electrical Distribution System by Placing D-FACTS and Network Reconfiguration, Journal of Power and Energy Engineering, vol.7, pp.94-113 (2019). [CrossRef]
  18. Balamurugan, P., Yuvaraj, T., Muthukannan, P (2018).,Optimal allocation of DSTATCOM in distribution network using Whale optimization algorithm, Eng. Technol. Appl. Sci Res, vol.8, no.5, pp.3445-3449 (2018). [CrossRef]
  19. Ghatak, Sriparna Roy, Sannigrahi, Surajit, Acharjee, Parimal., Optimised planning of distribution network with photovoltaic system, battery storage, and DSTATCOM, IET Renew. Power. Gener, vol.12, no.15, pp.1823-1832 (2018). [CrossRef]
  20. Yuvaraj, Devabalaji, K.R., et al., Comparative analysis of various compensating devices in energy trading radial distribution system for voltage regulation and loss mitigation using Blockchain technology and Bat algorithm, Energy reports, ELSEVIER (2022). [CrossRef]
  21. Gupta, A. R, Kumar, A., Impact of various load models on D-STATCOM allocation in DNO operated distribution network, Proc Comput Sci , vol.125, pp.862–870 (2018). [CrossRef]
  22. Dash, S.K., Mishra, S., Simultaneous Optimal Placement and Sizing of D-STATCOMs Using a Modified Sine Cosine Algorithm, Advances in Intelligent Computing and Communication, Springer, Singapore, pp.423–436 (2021). [CrossRef]
  23. Sambaiah, K.S, Jayabarathi, T., Optimal reconfiguration and renewable distributed generation allocation in electric distribution systems, International Journal of Ambient Energy, pp.1-29 (2019). [CrossRef]
  24. Sultana, B., Mustafa, M.W., Sultana, U., Rauf, A., Review on reliability improvement and power loss reduction in distribution system via network reconfiguration, Renew Sustain Energy Rev., vol.66, pp.297-310(2016). [CrossRef]
  25. Kola Sampangi Sambaiah, A review on optimal allocation and sizing techniques of DG in distribution systems, International Journal of Renewable Energy Research, vol.8, no.3, pp.1236-1256( 2018). [CrossRef]
  26. Ramprakash, sujatha B. C., Optimal placement and sizing of DG for power loss minimization and VSI improvement using BAT algorithm, IEEE conference NPSC 2016, IIT Bhubaneshwar, INDIA. [CrossRef]
  27. Ana Moura, Juliana Salvadorinho, Barbara Soares and Joana Cordeiro., Comparative study of Distribution Networks reconfiguration problem approaches, RAIRO Operations Research, vol. 55, pp. 2083-2124 (2021). [CrossRef]
  28. Hamida, I.B., Salah, S. B., Msahli, F., Mimouni, M.F., Optimal network reconfiguration and renewable DG integration considering time sequence variation in load and DGs, Renewable Energy,vol.121, pp.66-80 (2018). [CrossRef]
  29. Hassan, S. et al., Optimization techniques applied for optimal planning and integration of renewable energy sources based on distributed generation: Recent trends, Cogent engineering, Taylor & Francis Group, vol.3, pp. 1–25(2020). [CrossRef]
  30. Shaheen, A.M., Elsayed, A.M., El-Sehiemy, R.A., Abdelaziz, A.Y., Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems, Appl. Soft Comput., vol.98, pp.106867 (2021). [CrossRef]
  31. Vinod Kumar Thunuguntla and Satish Kumar Injeti., Butterfly optimizer assisted Max–Min based multi-objective approach for optimal connection of DGs and optimal network reconfiguration of distribution networks, Journal of Electrical Systems and Information Technology, SPRINGER (2022). [CrossRef]
  32. Devi, S., Geethanjali, M., Optimal location and sizing determination of Distributed Generation and DSTATCOM using Particle Swarm Optimization algorithm, International Journal of Electrical Power & Energy Systems, vol.62, pp.562-70 (2014). [CrossRef]
  33. Tolabi, H.B., Ali, M.H., Rizwan, M., Simultaneousreconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach, IEEE Transactions on sustainable Energy,vol. 6, pp. 210-8 (2015). [CrossRef]
  34. Devabalaji, K.R., Ravi, K., Optimal size and siting of multiple DG and DSTATCOM in radial distribution system using Bacterial Foraging Optimization Algorithm, Ain Shams Engineering Journal, vol.7, pp.959-71 (2016). [CrossRef]
  35. El-Ela, A.A., El-Sehiemy, R.A., Abbas, A.S., Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using water cycle algorithm, IEEE Systems Journal, vol.12, pp.3629-36 (2018). [CrossRef]
  36. Ganesh, S., Kanimozhi, R., Meta-heuristic technique for network reconfiguration in distribution system with photovoltaic and DSTATCOM, IET Generation, Transmission & Distribution,vol.12, pp.4524-35 (2018). [CrossRef]
  37. Zellagui, M., Lasmari, A., Settoul, S., El-Sehiemy, R.A., El-Bayeh, C.Z. Chenni, R., Simultaneous allocation of photovoltaic DG and DSTATCOM for echno-economic and environmental benefits in electrical distribution systems at different loading conditions using novel hybrid optimization algorithms. Int. Trans. Electr. Energy Syst., vol.31, pp.12992(2021). [CrossRef]
  38. Chinnaraj, S.G.R., Kuppan, R., Optimal sizing and placement of multiple renewable distribution generation and DSTATCOM in radial distribution systems using hybrid lightning search algorithm-simplex method optimization algorithm, Comput. Intell., vol.37, pp.1673–1690 (2021). [CrossRef]
  39. Oda, E.S., Abd El Hamed, A.M., Ali, A., Elbaset, A. A., Abd El Sattar, M., Ebeed, M., Stochastic optimal planning of distribution system considering integrated photovoltaic-based DG and DSTATCOM under uncertainties of loads and solar irradiance, IEEE Access, vol.9, pp.6541–26555 (2021). [CrossRef]
  40. Ping He, et al., Photovoltaic power prediction based on improved grey wolf algorithm optimized back propagation, Archives of Electrical Engineering, vol.72, no. 3, pp. 613-628(2023). [CrossRef]
  41. Eid A., Kamel S., Zawbaa H.M., Dardeer M., Improvement of active distribution systems with high penetration capacities of shunt reactive compensators and distributed generators using Bald Eagle Search, Ain Shams Eng. J., vol.13, pp.101792 (2022). [CrossRef]
  42. Thuan Thanh Nguyen, Thang Trung Nguyen, Ngoc Au Nguyen, Thanh Long Duong , A Novel method based on Coyote algorithm for simultaneous network reconfiguration and distribution generation placement, Ain Shams Engineering Journal, vol.12, Issue 1, pp.665-676(2021), doi.org/10.1016/j.asej.2020.06.005. [CrossRef]
  43. Abdullah M. Shaheen, Abdallah M. Elsayed, Ragab A., EI-Sehiemy, Salah Kamel, Sherif S.M., Ghoneim, A modified marine predators optimization algorithms for simultaneous network reconfiguration and distributed generator allocation in distribution systems under different loading conditions, Engineering Optimization, Issue 4(2020), doi/org/10.1080/0305215X.2021.1897799. [CrossRef]
  44. Truong Hoang Bao Huy, Thanh Van Tran, Dieu Ngoc Vo, Ho Thi Thao Nguyen, An improved metaheuristic method for simultaneous network reconfiguration and distributed generation allocation, Alexandria Engineering Journal, vol. 61, Issue 10, pp.8069-8088(2022). [CrossRef]
  45. Varaprasad Janamala, Radha Rani, K, Optimal allocation of solar photovoltaic distributed generation in electrical distribution networks using Archimeds optimization algorithm, Clean Energy, vol. 6, pp.271-287(2022). [CrossRef]
  46. Yang, X.S., He, X., Bat algorithm: literature review and applications, International Journal of Bio-Inspired Computation, vol.5, pp.141–149 (2013). [CrossRef]
  47. Mohammad Shehab et al., A Comprehensive Review of Bat Inspired Algorithm: Variants, Applications, and Hybridization, Computational methods in Engineering, vol.30, pp.765-797(2023). [CrossRef]
  48. T. Jayabarathi et al., The Bat Algorithm, Variants and Some Practical Engineering Applications: A Review, Nature-Inspired Algorithms and Applied Optimization, Studies in Computational Intelligence ,pp.744 (2017). [CrossRef]
  49. Zaid Abdi Alkareem Alyasseri et al., Recent advances of bat-inspired algorithm, its versions and applications, Neural Computing and Applications vol.34,16387 –16422 (2022). [CrossRef]
  50. Mirjalili, S., The ant lion optimizer, Adv. Eng. Softw., vol.83, pp.80-98 (2015). [CrossRef]
  51. Heidari, A. A., Faris, H., Mirjalili, S., Aljarah, I., and Mafarja,M., Ant lion optimizer: Theory, literature review, and application in multi-layer perceptron neural networks, in Nature-Inspired Optimizers. Springer, pp.23-46 (2020). [CrossRef]
  52. Assiri, A. S., Hussien, A. G., and Amin, M., Ant lion optimization:Variants, hybrids, and applications, IEEE Access, vol.8, pp.77746-77764 (2020). [CrossRef]
  53. Wang, M., Wu, C., Wang,L., Xiang, D., and Huang, X., A feature selection approach for hyperspectral image based on modified ant lion optimizer, Knowl.-Based Syst., vol.168, pp.39-48 (2019). [CrossRef]
  54. Dinkar,S.K., and Deepa, K. An efficient opposition based Lévy flight antlion optimizer for optimization problems, J. Comput. Sci., vol.29, pp.119-141(2018). [CrossRef]
  55. Barshandeh, S. and Haghzadeh, M., A new hybrid chaotic atom search optimization based on tree-seed algorithm and Levy flight for solving optimization problems, Eng. Comput.,pp. 1-44 (2020). [CrossRef]
  56. Zhao, R., Wang, Y., Liu, C., Hu, P., Li, Y., Li, H., and Yuan, C., Selfish herd optimizer with Levy flight distribution strategy for global optimization problem, Phys. A, Stat. Mech. Appl., vol.538, pp.122687 (2020). [CrossRef]
  57. Liu, Y. and Cao, B., A novel ant colony optimization algorithm with Levy flight, IEEE Access,vol. 8, pp.67205-67213( 2020). [CrossRef]
  58. Jen-Hao, Teng., A direct approach for distribution system load flow solutions,IEEE Trans. Power Deliv. Vol.18, no.3, pp. 882–887 (2003). [CrossRef]
  59. Atma Ram Gupta, Ashwani Kumar., Energy saving using D-STATCOM placement in radial distribution system under reconfigured network, Energy Procedia (2015). [CrossRef]
Preprints 93482 g001
Figure 1. Schematic diagram of distribution scheme.
Figure 1. Schematic diagram of distribution scheme.
Preprints 93482 g001
Preprints 93482 g002
Figure 2. IEEE 118 Node radial power distribution scheme.
Figure 2. IEEE 118 Node radial power distribution scheme.
Preprints 93482 g002
Preprints 93482 g003
Figure 3. Bus Voltage magnitude profile (p. u) of IEEE118 nodes for CP model.
Figure 3. Bus Voltage magnitude profile (p. u) of IEEE118 nodes for CP model.
Preprints 93482 g003
Preprints 93482 g004
Figure 4. Bus Voltage magnitude profile (p. u) of IEEE118 node for ZIP model with load growth.
Figure 4. Bus Voltage magnitude profile (p. u) of IEEE118 node for ZIP model with load growth.
Preprints 93482 g004
Preprints 93482 g005
Figure 5. IEEE 118 bus power loss reduction considering 3 PV DG=2000 kW and 3 DSTATCOM =1900 kVAr (Constant Power model).
Figure 5. IEEE 118 bus power loss reduction considering 3 PV DG=2000 kW and 3 DSTATCOM =1900 kVAr (Constant Power model).
Preprints 93482 g005
Preprints 93482 g006
Figure 6. IEEE 118 bus power loss reduction considering 3 PV DG=2000kW and 3 DSTATCOM =1900kVAr(ZIP power model with load growth).
Figure 6. IEEE 118 bus power loss reduction considering 3 PV DG=2000kW and 3 DSTATCOM =1900kVAr(ZIP power model with load growth).
Preprints 93482 g006
Preprints 93482 g007
Figure 7. IEEE 118 bus power Loss reduction considering Single PV DG=2000kW and single DSTATCOM =1900 kVAr( Constant Power model).
Figure 7. IEEE 118 bus power Loss reduction considering Single PV DG=2000kW and single DSTATCOM =1900 kVAr( Constant Power model).
Preprints 93482 g007
Preprints 93482 g008
Figure 8. IEEE 118 bus power Loss reduction considering single PV DG=2000kW and single DSTATCOM=1900 kVAr(ZIP power model with load growth.
Figure 8. IEEE 118 bus power Loss reduction considering single PV DG=2000kW and single DSTATCOM=1900 kVAr(ZIP power model with load growth.
Preprints 93482 g008
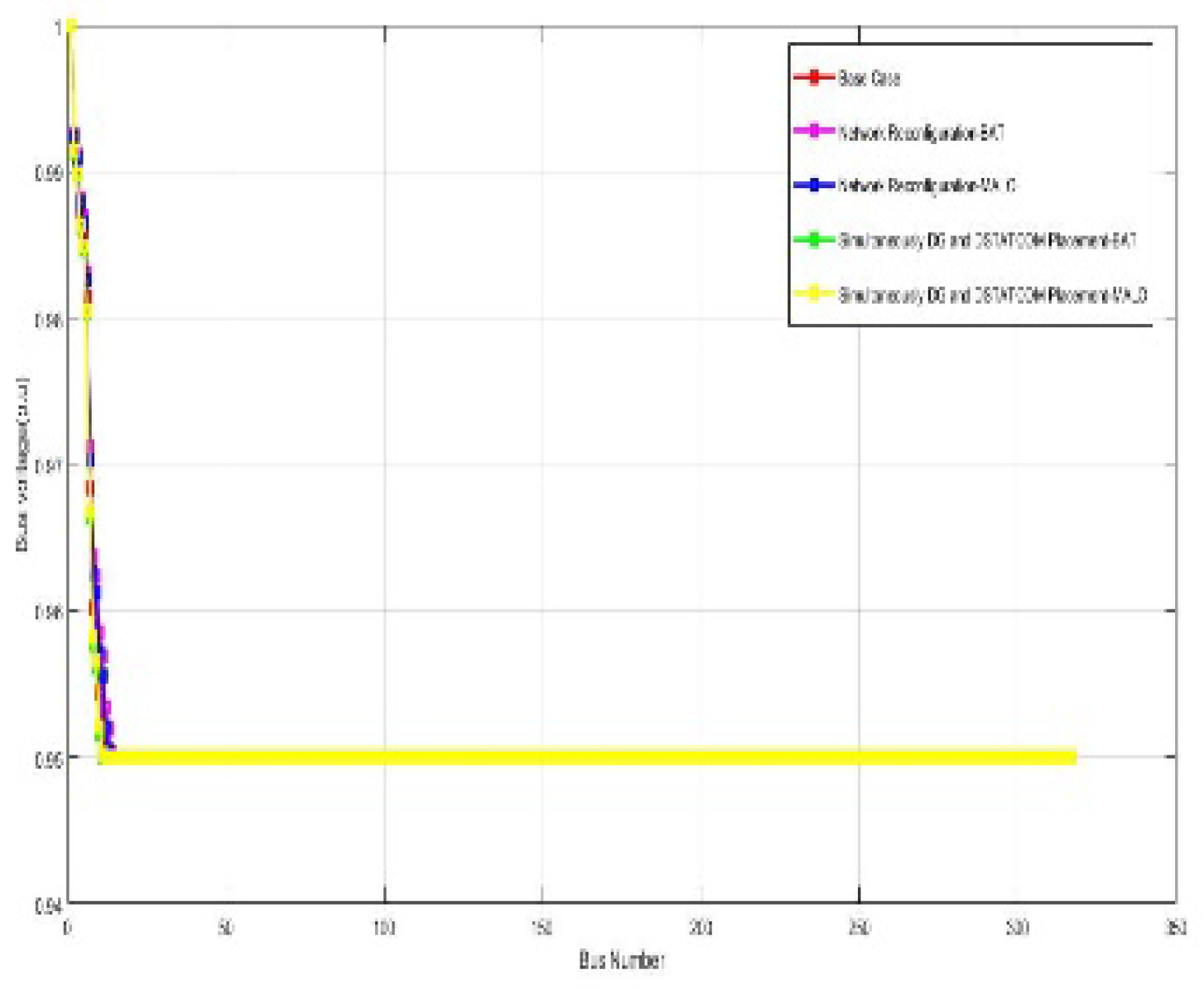
Preprints 93482 g009
Figure 9. Bus voltage magnitude profile of 317 bus at 11kV (Constant power model).
Figure 9. Bus voltage magnitude profile of 317 bus at 11kV (Constant power model).
Preprints 93482 g009
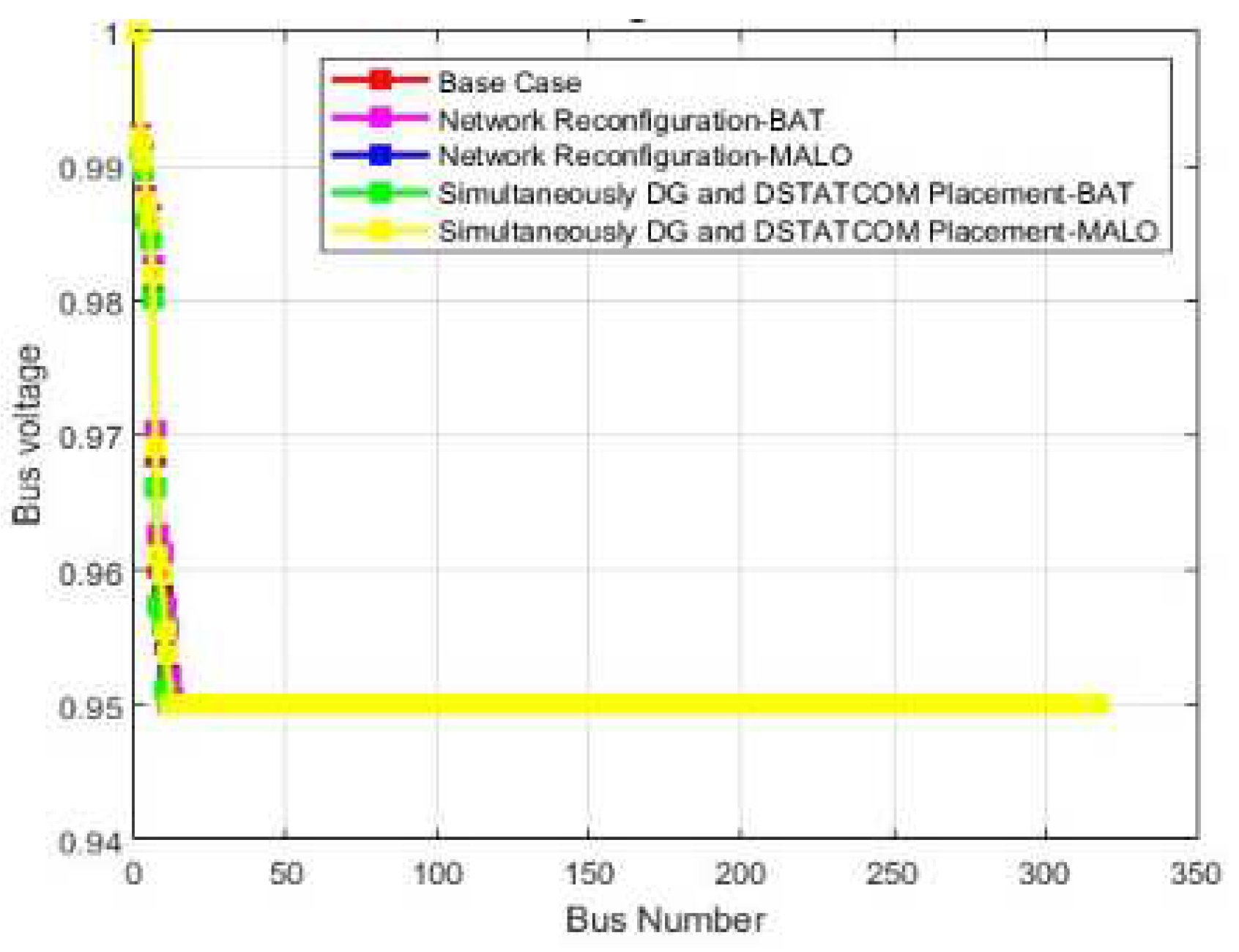
Preprints 93482 g010
Figure 10. Bus voltage magnitude of 317 bus at 11 kV (ZIP power model with load growth).
Figure 10. Bus voltage magnitude of 317 bus at 11 kV (ZIP power model with load growth).
Preprints 93482 g010
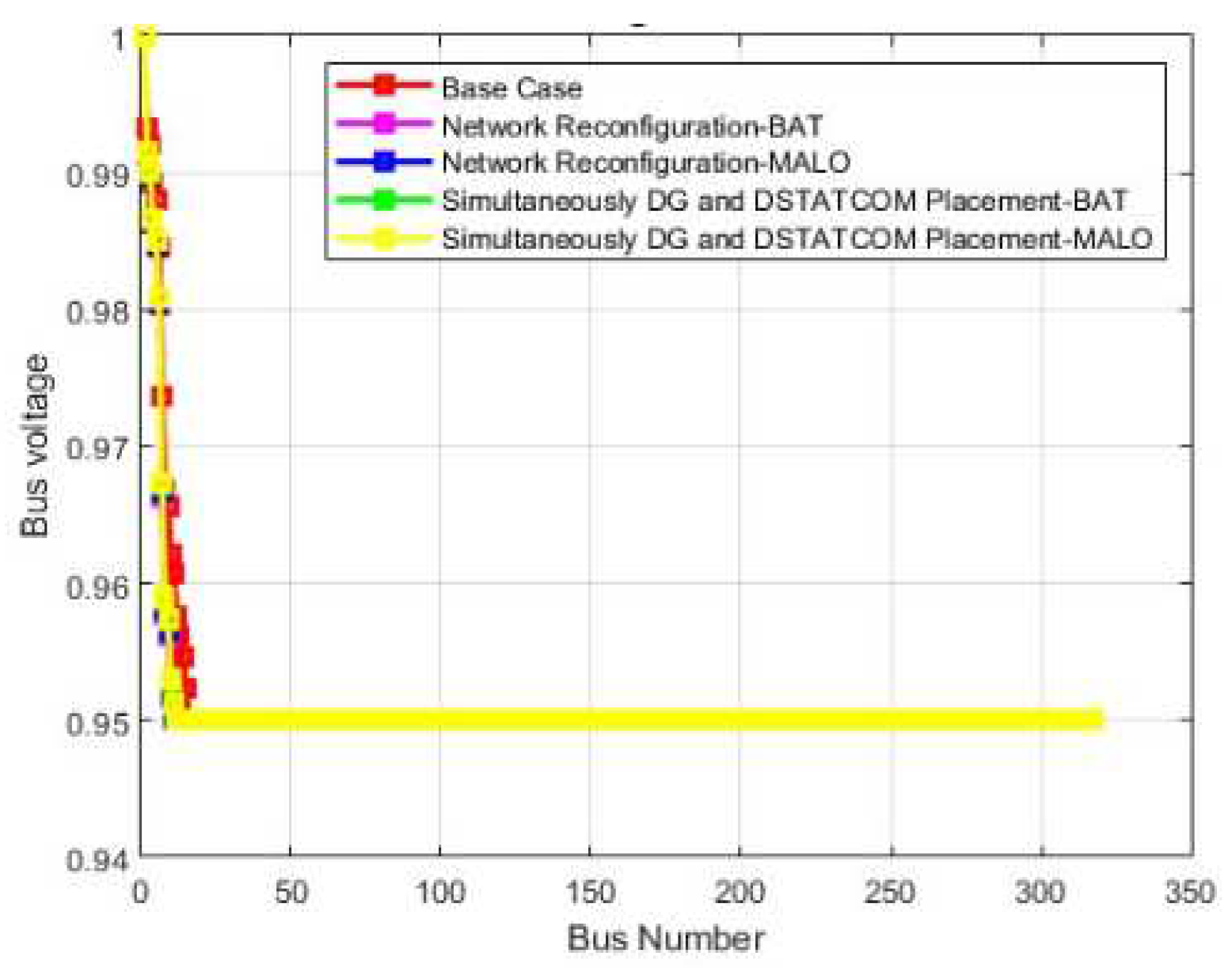
Preprints 93482 g011
Figure 11. Bus voltage magnitude profile of 317 bus at 22kV(Constant power model).
Figure 11. Bus voltage magnitude profile of 317 bus at 22kV(Constant power model).
Preprints 93482 g011
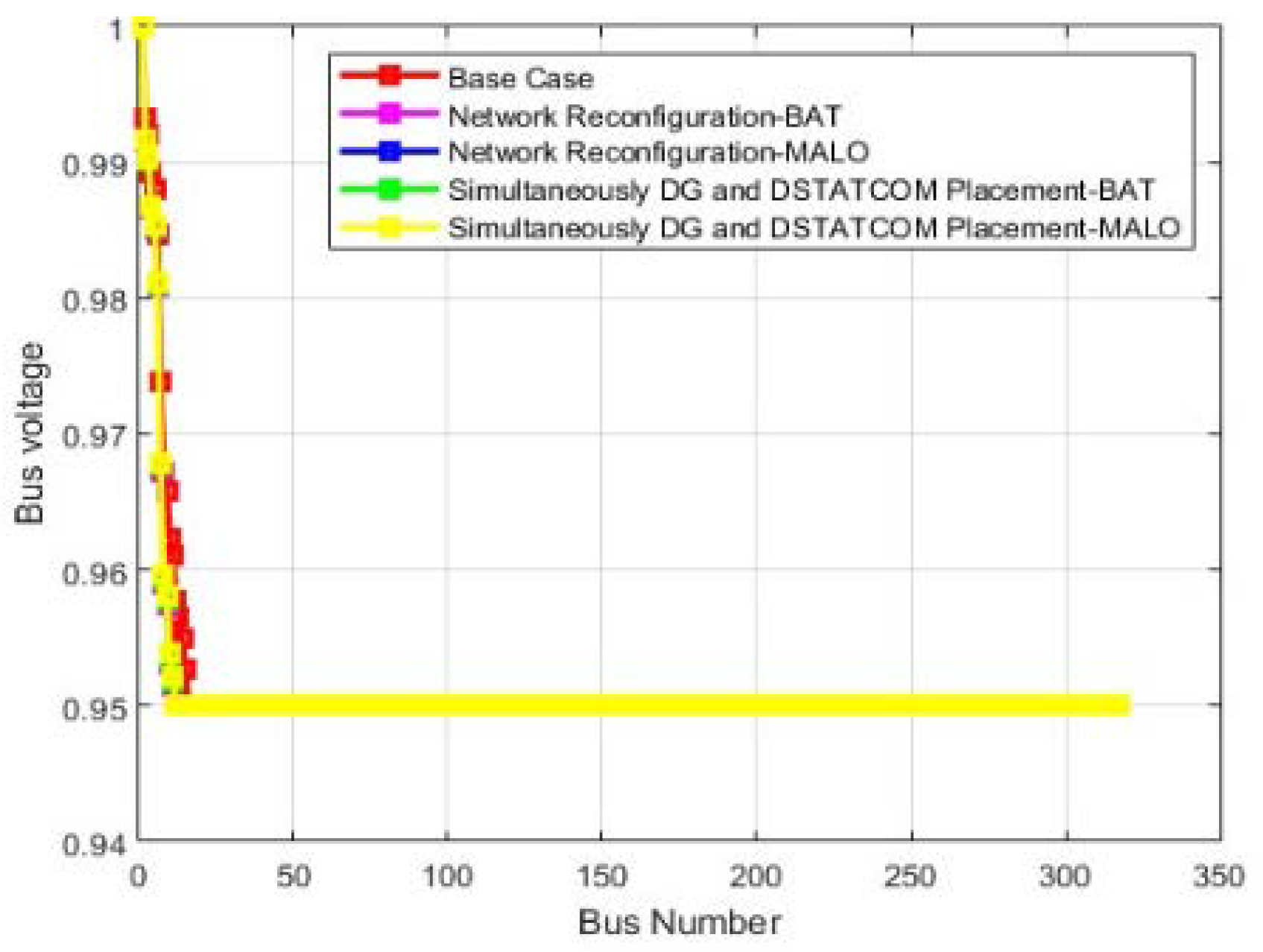
Preprints 93482 g012
Figure 12. Bus voltage magnitude of 317 bus 22kV(ZIPpower model with load growth).
Figure 12. Bus voltage magnitude of 317 bus 22kV(ZIPpower model with load growth).
Preprints 93482 g012
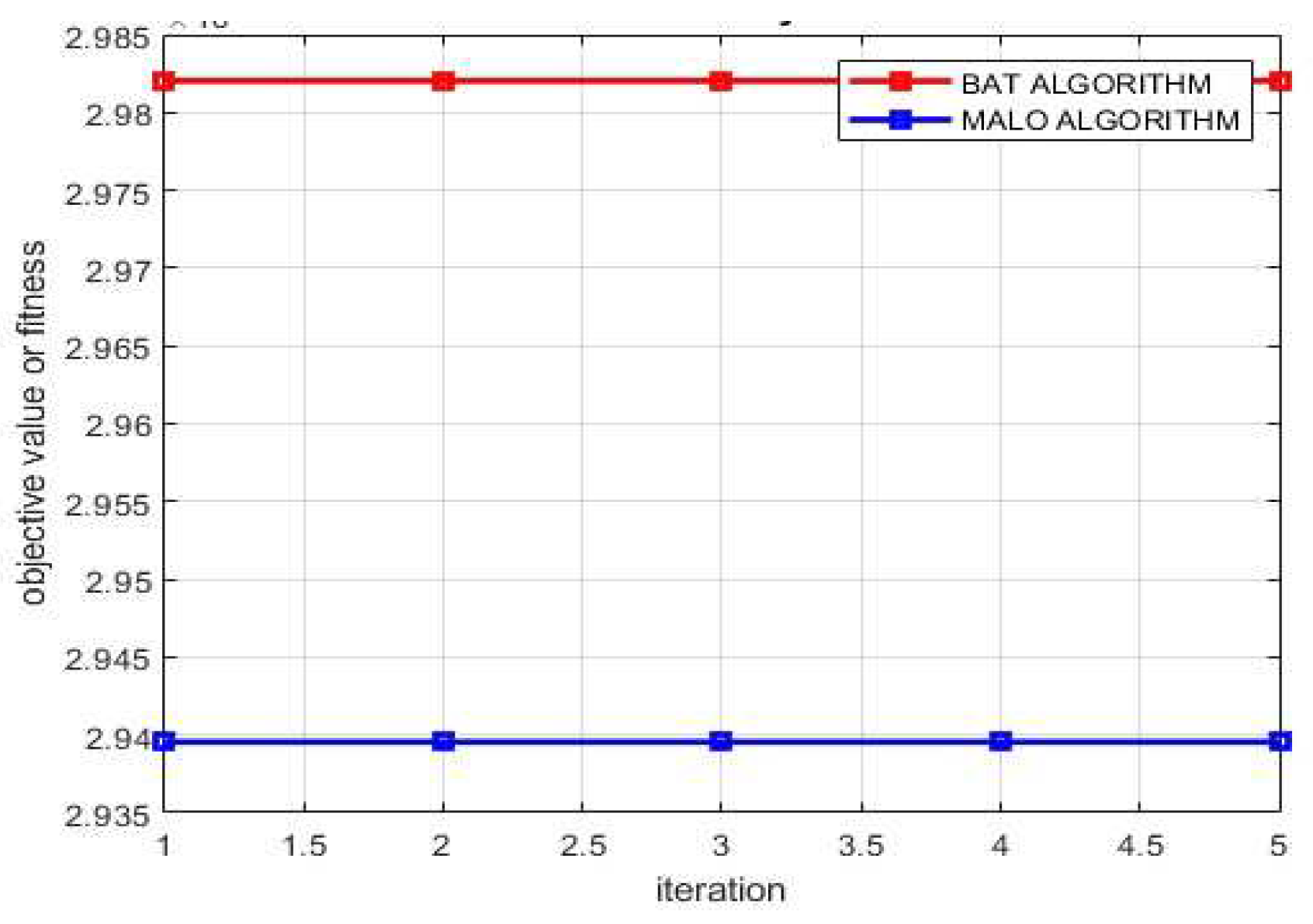
Preprints 93482 g013
Figure 13. Fitness function of 317 bus utility power distribution ZIP model with load growth(11kV).
Figure 13. Fitness function of 317 bus utility power distribution ZIP model with load growth(11kV).
Preprints 93482 g013
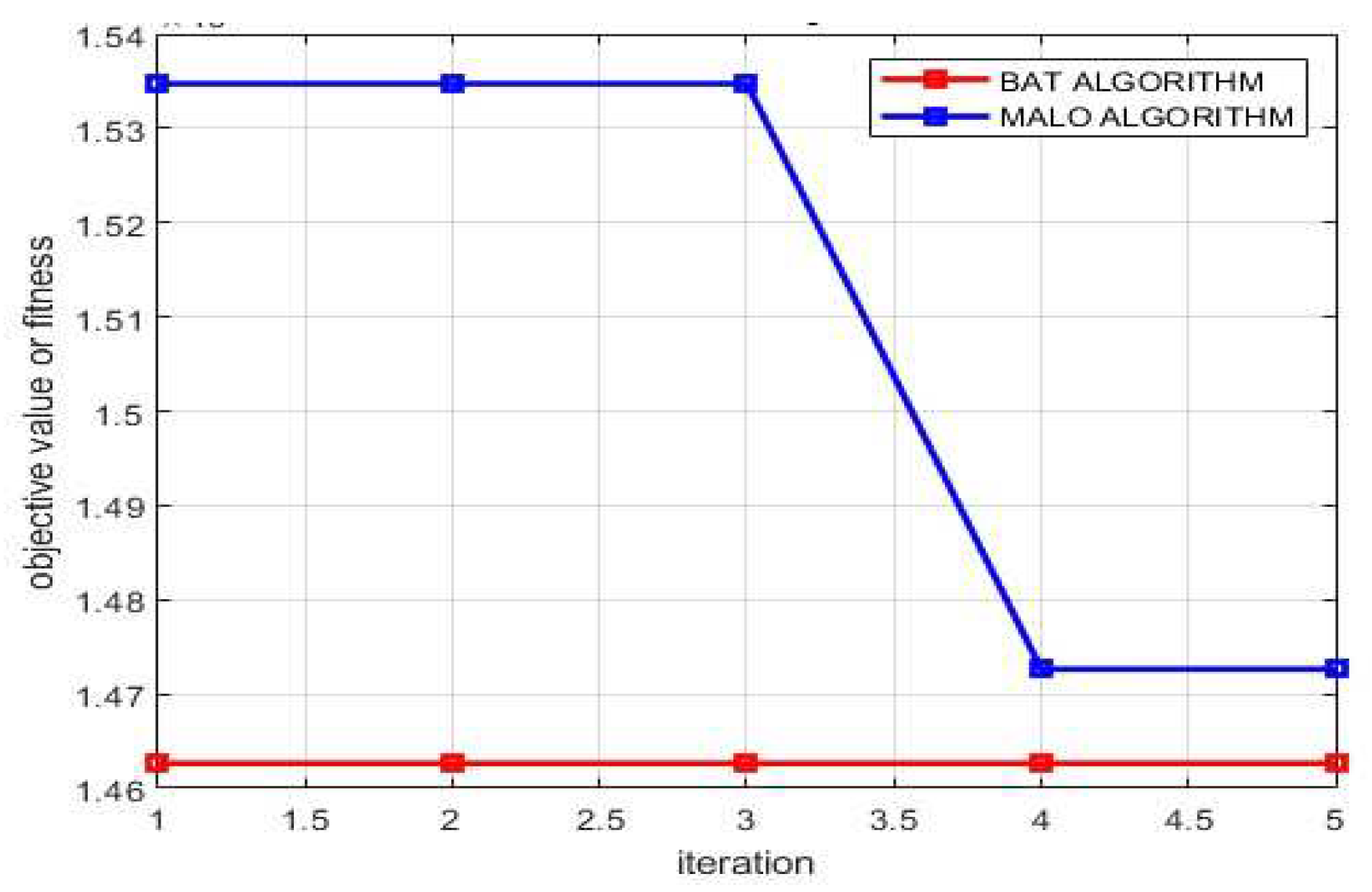
Preprints 93482 g014
Figure 14. Fitness function of 317 bus utility power distribution with load growth(22kV).
Figure 14. Fitness function of 317 bus utility power distribution with load growth(22kV).
Preprints 93482 g014
Table 1. Parameters for BAT and MALO algorithm.
Table 1. Parameters for BAT and MALO algorithm.
Algorithm MALO
Number of population 10
Number of Iterations 10
A min 0.4
A max 0.85
Spiral shape=b 0.3
Algorithm BAT
Number of population 10
Number of Iteration 10
Loudness 0.5
Emission rate 0.5
Frequency 0-2
Table 2. Cost Factors.
Table 2. Cost Factors.
Cost of Energy 0.05$/kWh
Cost of DSTATCOM 50$/kVAr
Cost of PV DG 1$/kW
Table 3. Assessment of IEEE 118 test scheme for load models considered with network reconfiguration considering PV penetration level=0.25.
Table 3. Assessment of IEEE 118 test scheme for load models considered with network reconfiguration considering PV penetration level=0.25.
MODEL Constant Power Model ZIP load Model
Cases Base Case Recon BAT Reconfig
MALO		 DG+DSTAT+ Reconfig BAT DG+DSTAT+Reconfig MALO Base Case Reconfig BAT Reconfig MALO DG+DSTAT+Reconfig BAT DG+DSTAT+Reconfig MALO
Real power losses kW 1298.14 935.48 800.62 871.34 759.75 2631.08 1611.99 1603.08 1447.85 1500.13
Reactive power loss kVAr 978.70 1054.14 925.50 887.01 856.01 1979.25 1385.87 1162.50 1393.75 1145.64
PV size and location - - - 871(81),
1014 (72)
1193 (3)		 1993(65), 604(84), 621 (102) - - - 1336(90) ,984 (41) ,1418 (76) 2000(111) ,2000 (118) ,1858 (118)
DSTATCOM size and location - - - 274 (26), 1864(84) 382 (106) ,1317 (47) - - - 1367(101), 1463(27) 1900(118),1900 (118)
Total operating cost ($) - - - 334383.5 312047.98 - - - 422452.3 617555
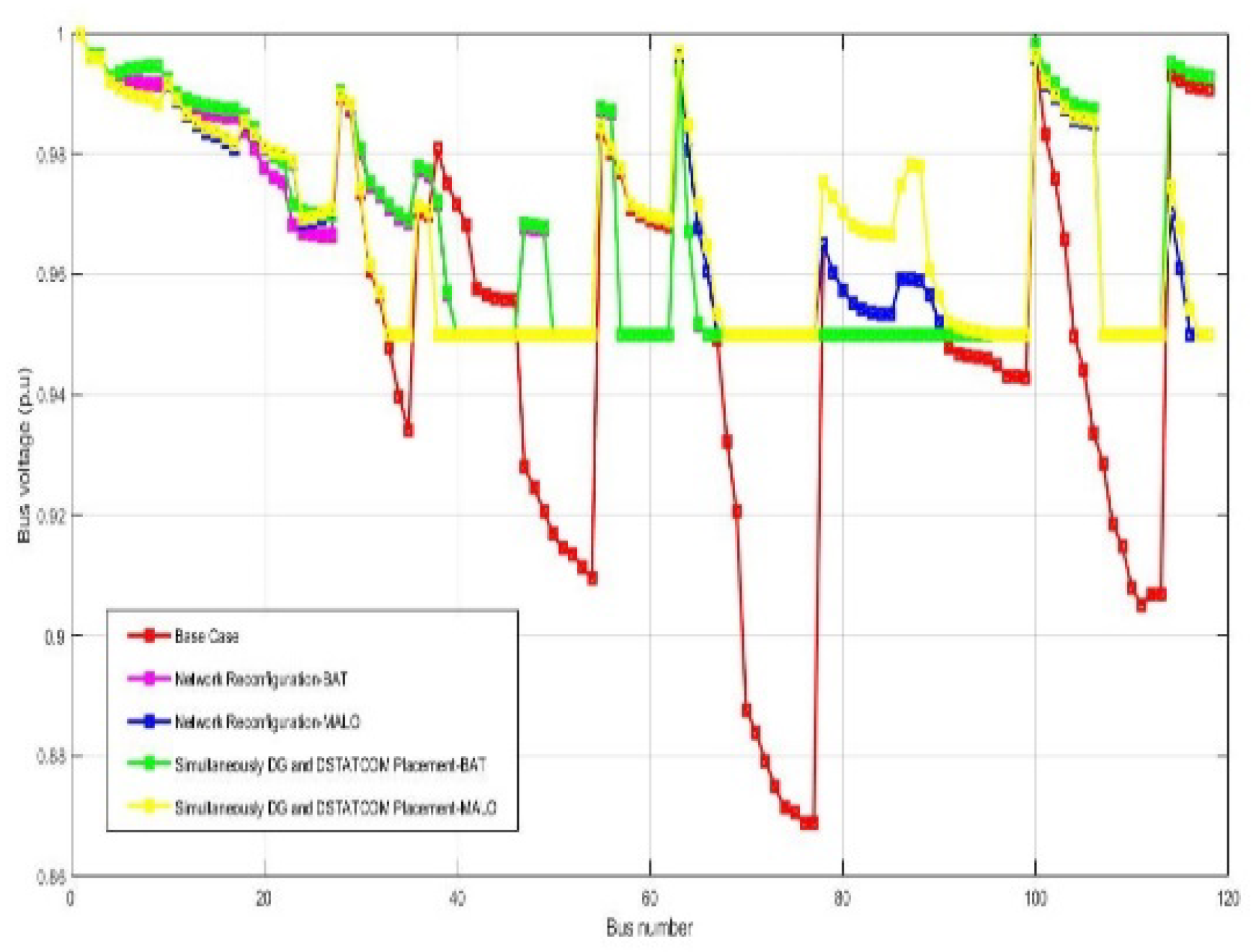
Vmin @bus 0.86 (77) 0.95(40) 0.95(33) 0.95(40) 0.95(48) 0.811 (77) 0.95(22) 0.95(42) 0.95(22) 0.95(42)
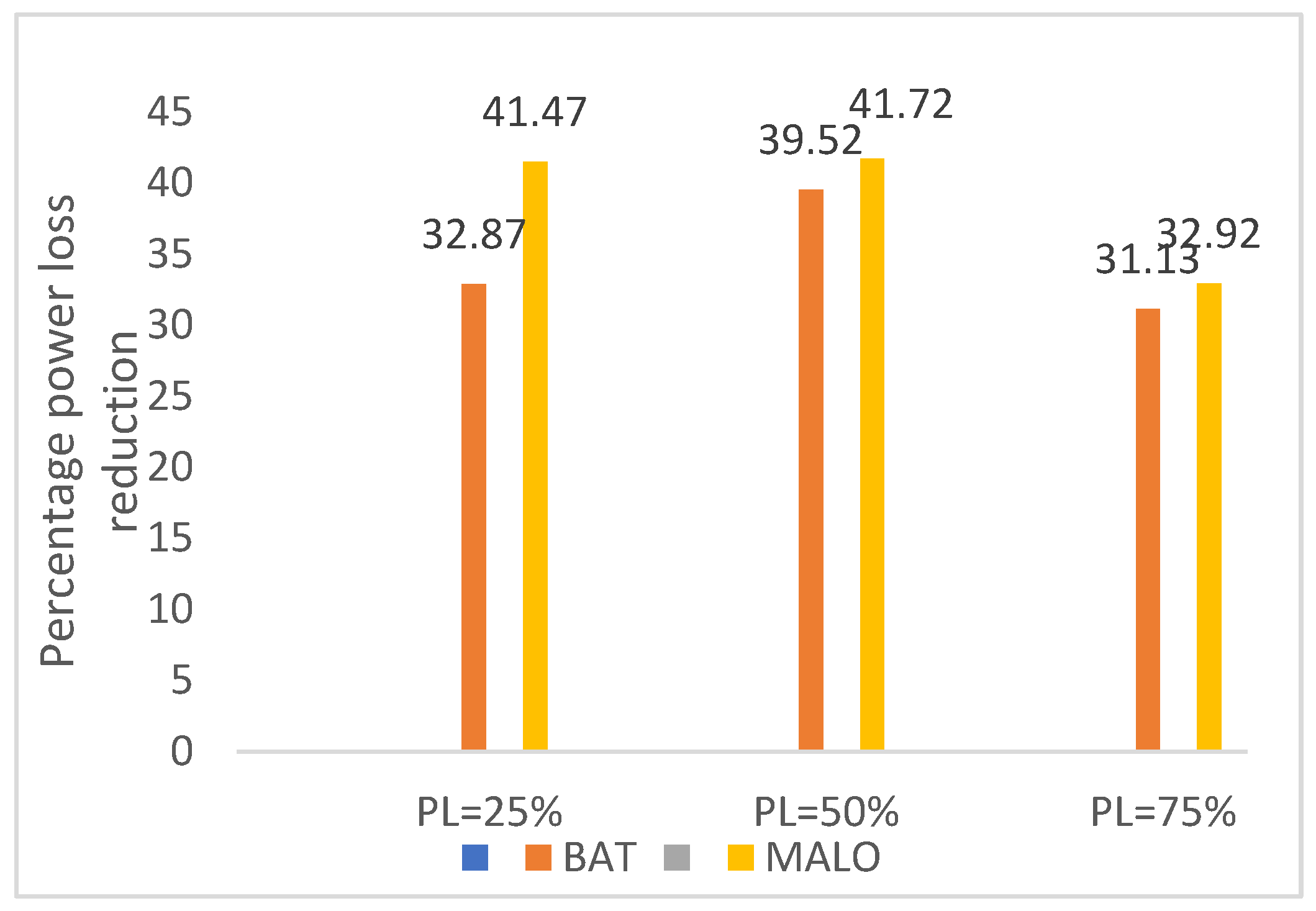
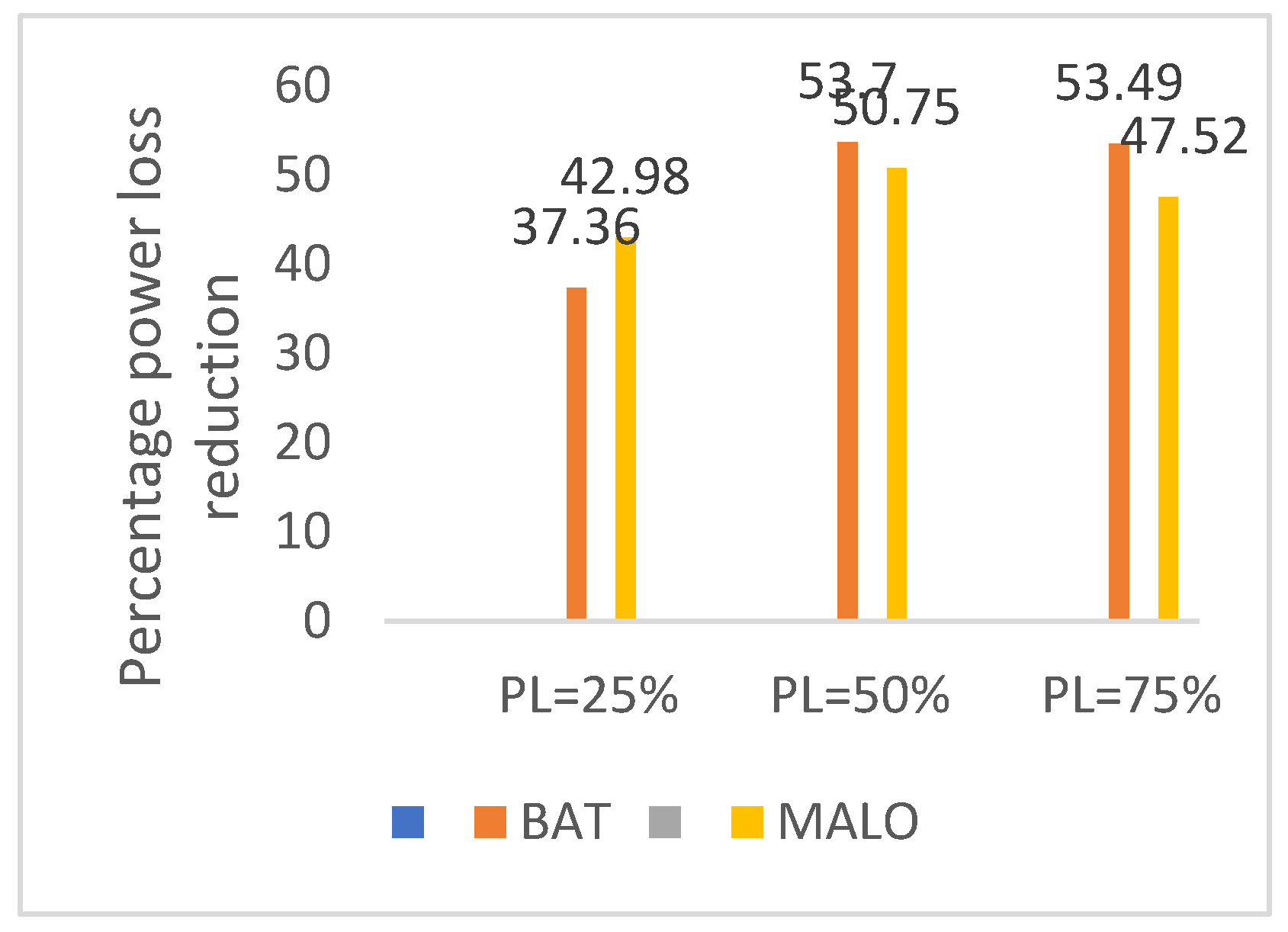
%Loss reduction - 27.93 38.32 32.87 41.47 - 38.73 39.07 37.36 42.98
Execution time in seconds 0.0471 1.19 1.38 0.78 0.70 0.027 0.71 0.72 0.62 0.457
Table 4. Comparative analysis of the BAT and MALO for the IEEE 118 nodes test scheme.
Table 4. Comparative analysis of the BAT and MALO for the IEEE 118 nodes test scheme.
Model CP Model CP Model CP Model CP Model
Scenario-1 Parameter quantity MO-MFPA (Ganesh and (Kanimozhi 2018)
 Grass Optimising Algorithm (Sambaiah and Jayabharathi 2020)
 Proposed BAT (Three distributed PV sources with 25% penetration and two DSTATCOMs) Proposed MALO(Three distributed PV sources with 25% penetration and two DSTATCOMs)
Scenario-2
Open switches		 42,25,22,121,50,58,39,95,71,74,97,129,130,109,34 25,23,39,43,34,58,124,95,71,97,74,129,130,109,5 130,122,128,101,131,21,47,126,125,132,123,119,124,118,127 132,120,128,124,121,102,126,51,118,55,125,127,129,119
P Loss(kW) 854 878.57 935.48 800.62
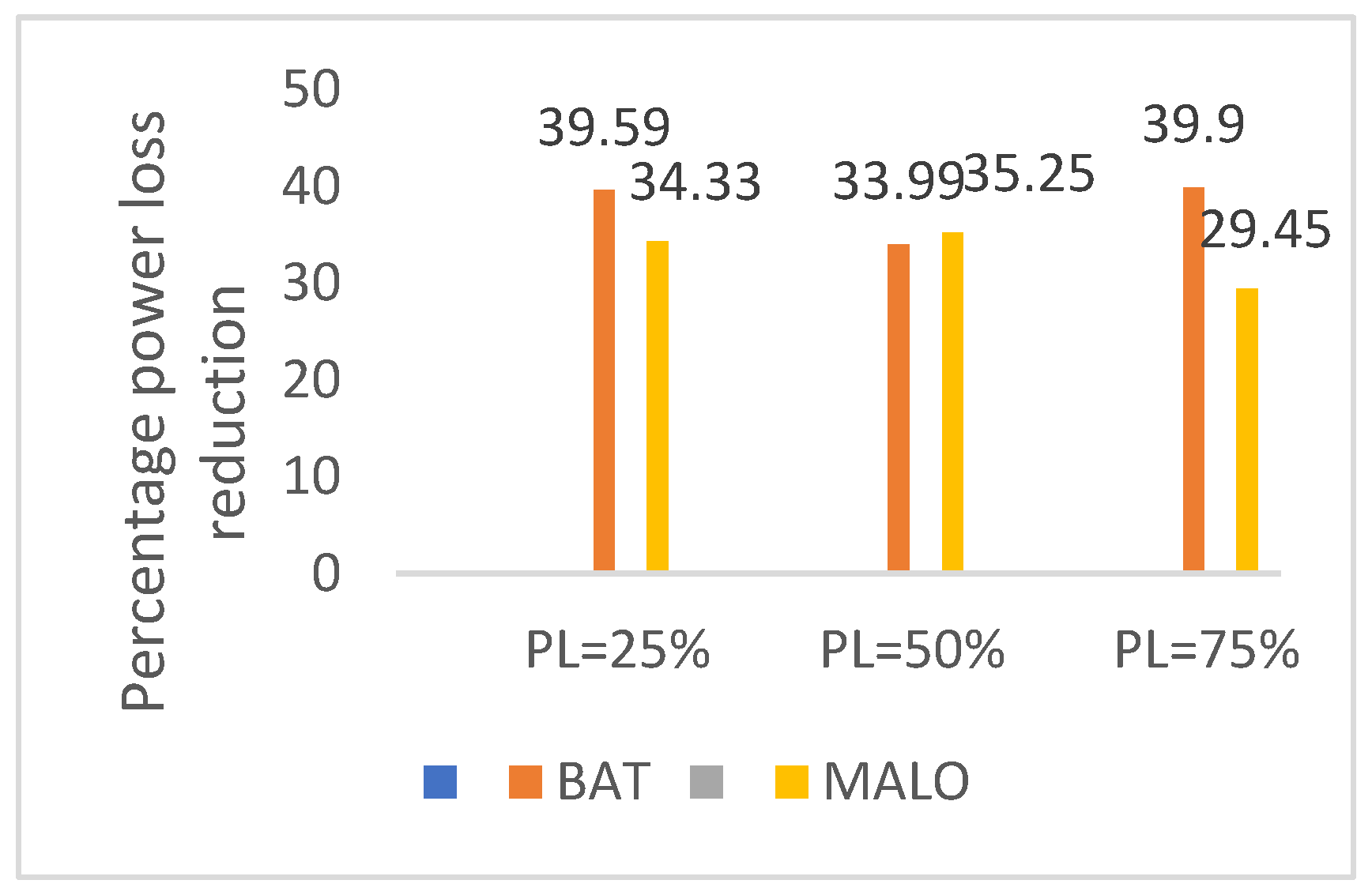
% Loss reduction 32.90 31.94 27.93 38.32
Vmin(p.u) 0.9310 0.9394(74) 0.95(40) 0.95(33)
Scenario-3
Open switches		 42, 25, 21, 121, 48, 60, 39, 125, 126, 68, 76, 129, 130, 109, 33 16, 21, 39, 43, 32, 58, 124, 125, 71, 97, 128, 85, 130, 108, 132 130,122,128,101,131,21,47,126,125,132,123,119,124,118,127 132,120,128,124,121,102,126,51,118,55,125,127,129,119
P Loss(kW) 544 435.39 871.34 759.75
% Loss reduction 57.2 66.27 32.87 41.47
Vmin (p.u) 0.9654 0.9459(71) 0.95(40) 0.95(48)
D-STATCOM size and location (kVAr) 1568(97)
 1868.7(50),1269.47(75),1104.7(111) 274 (26), 1864(84) 382 (106), 1317 (47)
PV DG size and location(kW) 1656(109) 1743.96(51),1989.9(92),1919.6(109) 871(81), 1014 (72), 1193 (3) 1993(65), 604 (84), 621 (102)
Table 5. Assessment of 317 node rural BANGALORE ELECTRCITY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering PV penetration level=0.25 at 11 kV power distribution network.
Table 5. Assessment of 317 node rural BANGALORE ELECTRCITY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering PV penetration level=0.25 at 11 kV power distribution network.
MODEL Constant Power Model ZIP load Model
Cases Base Case BAT Reconfig MALO Reconfig BAT DG+DSTAT+Reconfig MALO DG+DSTAT+Reconfig Base Case BAT Reconfig MALO Reconfig BAT DG+DSTAT+Reconfig MALO DG+DSTAT+Reconfig
Real power losses kW 3.5 E+5 3.1 E+5 3.25 E+5 2.57E+5 1.75E+5 3.05 E+5 2.83E+5 2.68E+5 1.10E+5 1.24E+5
Reactive power loss kVAr 2.0 E+5 1.77 E+5 1.83 E+5 1.40 E+5 0.95 E+5 1.78E+5 1.60 E+5 1.51 E+5 0.54E+5 1.770.67E+5
PV size and location - - - 2013(117), 2113(76), 1021(23) 2142(258), 3022(27), 2568(317) - - - 3033(294), 3432(6) 378(229) 5000(294) , 5000(317), 5000(317)
DSTATCOM size and location - - - 6765(122)
2000(192)		 5355(190)
8878(101)		 - - - 9173(136)
7979(85)		 10000(97)
10000(317)
Total Operating Cost ($) - - - 935220 1468980 - - - 1616720 2306200
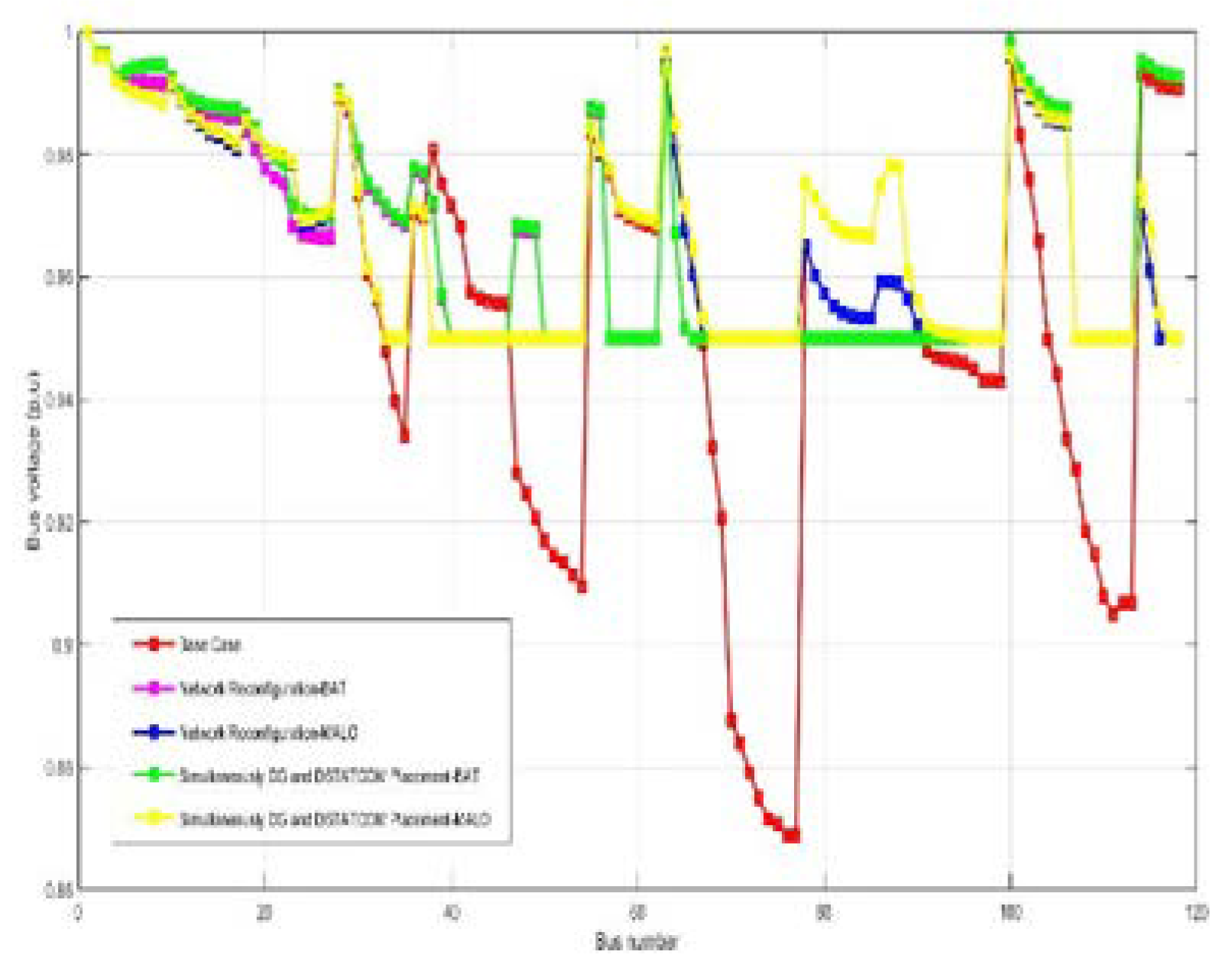
Vmin @bus 0.95 (12) 0.95(15) 0.95(14) 0.95(10) 0.95(10) 0.95 (12) 0.95(12) 0.95(12) 0.95(11) 0.95(12)
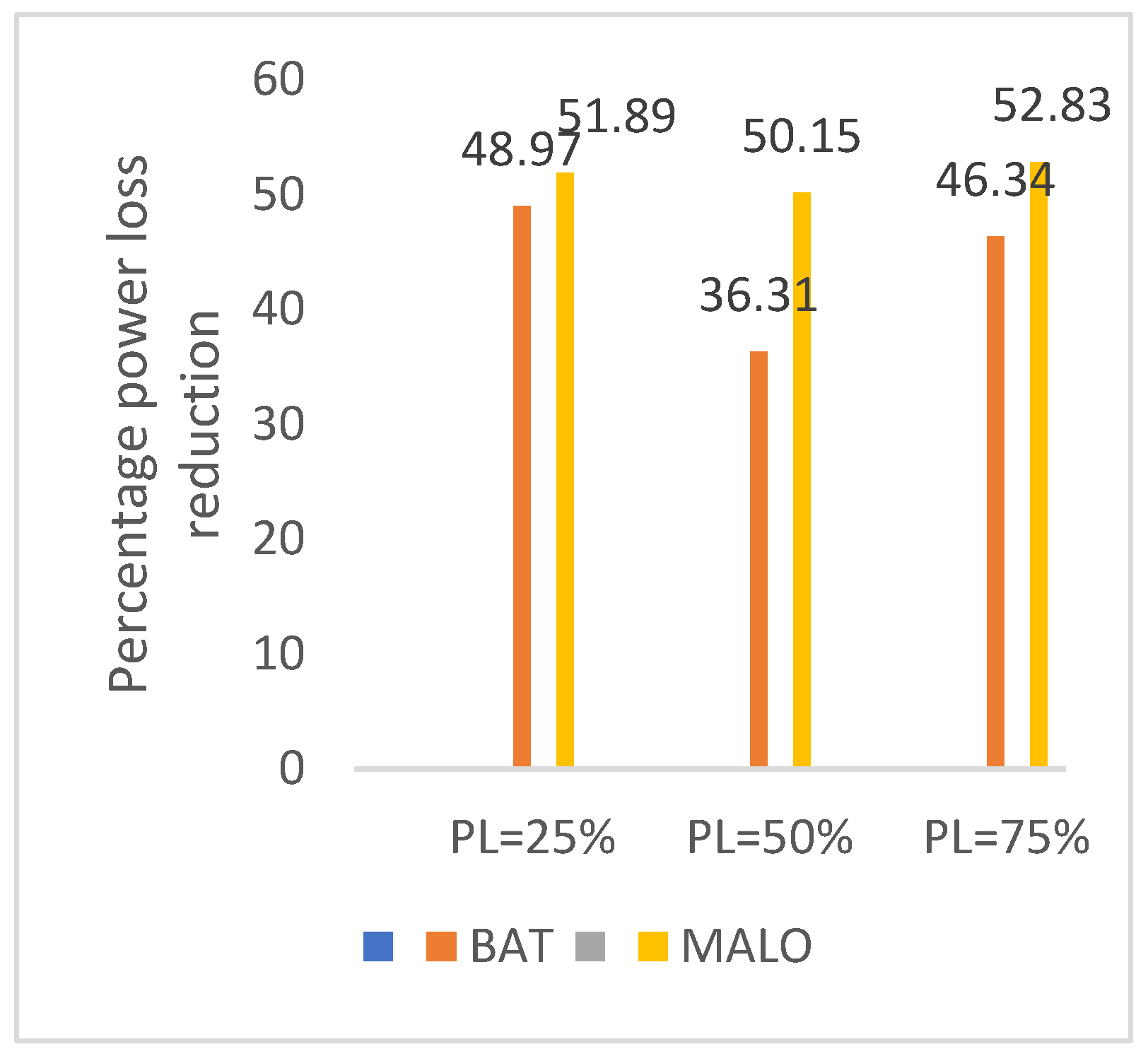
%Loss reduction - 9.65 7.11 26.56 49.77 - 7.36 12.30 63.78 59.34
Execution time in seconds 0.23 20.53 20.73 7.06 6.42 0.19 6.65 29.52 6.27 6.51
Table 6. Assessment of 317 node rural BANGALORE ELECTRCITY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering PV penetration level=0.25 at 22 kV power distribution netw.
Table 6. Assessment of 317 node rural BANGALORE ELECTRCITY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering PV penetration level=0.25 at 22 kV power distribution netw.
MODEL Constant Power Model ZIP load Model
Cases Base Case BAT Reconfig MALO Reconfig BAT DG + DSTAT+ Reconfig MALO DG +DSTAT +Reconfig Base Case BAT Reconfig MALO Reconfig BAT DG + DSTAT +Reconfig MALO DG +DSTAT +Reconfig
Real power losses kW 2.21E+5 2.38E+5 2.08 E+5 0.99E+5 1.067 E+5 1.65E+5 1.75E+5 1.46E+5 1.02+5 0.73E+5
Reactive power loss kVAr 1.29E+5 1.29 E+5 1.22 E+5 0.51E+5 0.61 E+5 0.97 E+5 0.98 E+5 0.85E+5 0.57 E+5 0.40E+5
PV size and location - - - 1654(305), 4775(207) ,1967 (219) 4647 (35) ,2888 (166) ,1212(212) - - - 253(115), 923(170), 4847 (133) 5000 (317),5000 (249), 5000 (228)
DSTATCOM size and location - - - 9752 (149)
8864(604)		 6922 (42)
8166 (216)		 - - - 3534(19)
6231 (242)		 10000 (202)
4719 (317)
Total operating Cost ($) - - - 1905880 1586315 - - - 1110030 1933980
Vmin @bus 0.95 (16) 0.95(11) 0.95(16) 0.95(12) 0.95(16) 0.95 (16) 0.95(12) 0.95(12) 0.95(12) 0.95(12)
%Loss reduction - -8.08 5.58 55.21 51.69 - -5.64 11.50 38.42 55.75
Execution time in seconds 0.222 30.11 29.80 6.24 2.52 0.1946 3.28 28.0 2.31 4.76
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated