1. Introduction
Ocean microwave remote sensing provides an important technology for global sea surface observation. Many scatterometers and radar missions have observed the ocean in space, such as Microwave Imaging Radiometer with Aperture Synthesis (MIRAS) on the ESA SMOS satellite, L-band microwave radiometer on NASA's Aquarius satellite, phased array L-band synthetic aperture radar (PALSAR) on Japan's ALOS satellite, Deutsche Aerospace's TerraSAR-X radar satellite and the microwave scatterometers on China's HaiYang-2 (HY-2) satellites. Based on certain inversion models, some marine environmental parameters, such as ocean wind vector, sea surface salinity/temperature, sea surface height, and so on, can be obtained from the observation data [
1,
2,
3,
4]. General, the inversion accuracy strictly relies on the electromagnetic (EM) scattering models of rough sea surfaces, which mainly include the empirical models and the physical models. The empirical models, generally called as geophysical model functions (GMF), are often obtained by fitting the observation data with the non-physical models, so they are limited by measurement geometry and physical mechanisms [
5,
6]. Therefore, it’s necessary to establish a physical model in line with real marine environments according to EM scattering mechanism.
Among the existing rough sea surface scattering models, the two-scale method (TSM) is widely used due to its ability to simultaneously consider the scattering contributions of both large-scale and small-scale roughness [
4,
6,
7,
8]. However, it’s well known that the simulation accuracy of TSM mainly depends on the input models, such as seawater permittivity, roughness spectrum of sea surface and cutoff wavenumber.
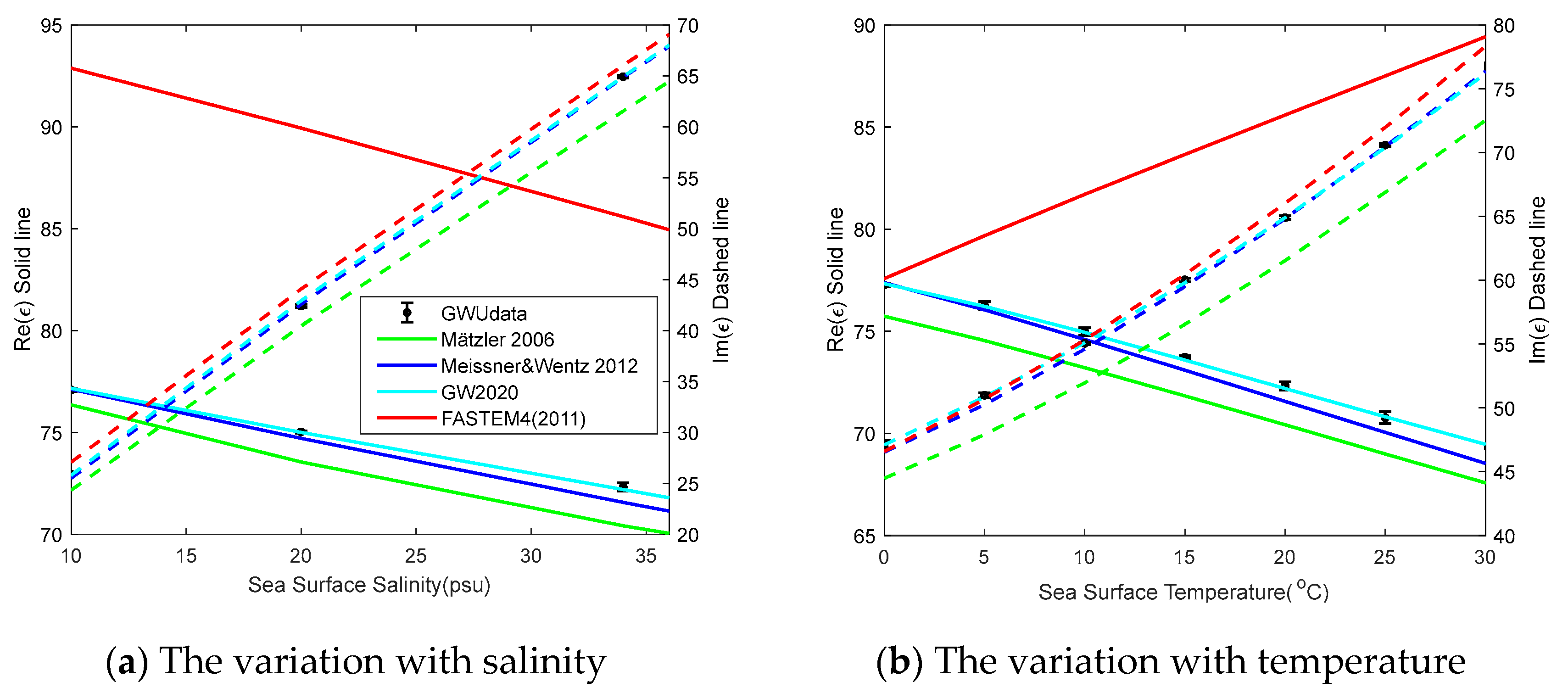
Most classical permittivity models were developed based on Debye model and measured data. Meissner and Wentz (2004) combined their measurements and the observation data of Special Sensor Microwave/Imager (SSM/I) to fit the Debye relaxation parameter of the seawater permittivity by minimizing the total error between the observations and the model calculations [
9]. Furthermore, Meissner et al. improved the fitting model in 2012 by combining WindSat measurements at C-band and X-band [
10]. Zhou et al. (2021) developed the GW2020 model based on the measurement with the resonance method [
11]. Since these models are fitted based on specific observation data, they all have their own applicable ranges. So, we will sift a suitable one from the existing models [
4,
9,
10,
11,
12] for TSM computation.
The sea spectrum is another important input for TSM computation. Researchers have developed many roughness spectrums based on experimental data, wave formation mechanism and scattering/radiation data. For example, Pierson and Moskowitz developed the first reliable PM wave spectrum according to the data of the North Atlantic experiment. The PM spectrum describes a fully developed sea surface, that is, it describes stable and uniform wind-driven waves on infinite sea surface, and there is a balance between input and dissipation of each wavelength [
13]. As the fully developed wind wave is an ideal concept, researchers further developed JONSWAP spectrum, Phillips spectrum and so on based on PM spectrum and experimental data [
6]. However, these spectrums only describe the gravity wave accurately and are only suitable for EM scattering simulation of sea surface in some frequency bands. In 1979, Bjerkaas and Riedel put forward the first full wavenumber BR spectrum by connecting four independent wavenumber ranges including gravity wave, short gravity wave, gravity capillary wave and capillary wave [
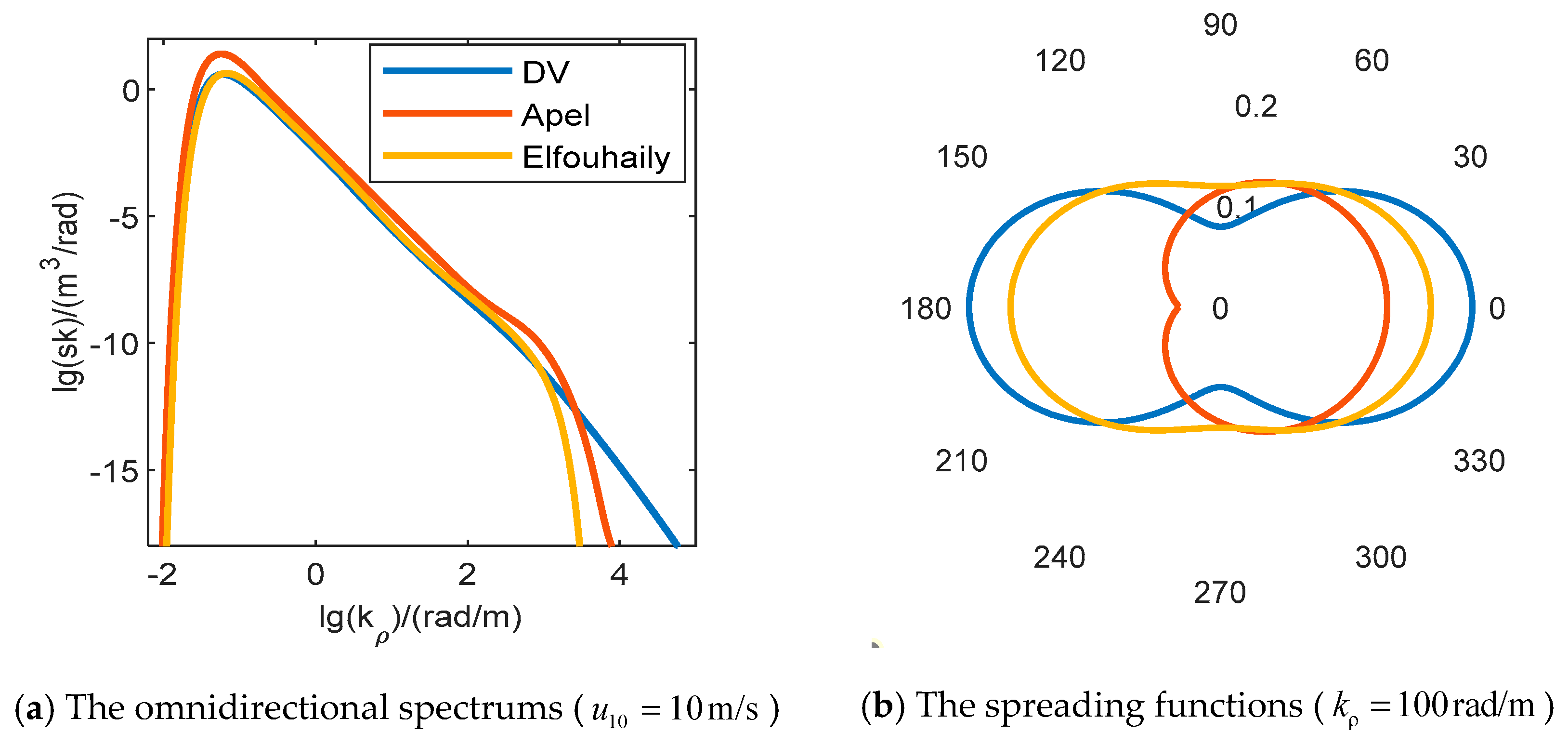
14]. Since the arbitrary constants used to connect independent bands in BR spectrum have no physical significance, researchers later proposed Durden-Vesecky spectrum, Apel spectrum, Elfouhaily spectrum, KHCC03 spectrum [
15], etc. Elfouhaily et al. also developed a unified angular spread function as they thought that the Fourier transform of the real even spreading function in the sea spectrum should have the characteristics of central symmetry [
16]. Moreover, Hwang et al. proposed a series of H spectrum models by inverting the polarized echo data (scattering cross-section and emissivity data) to obtain the short-scale properties of the ocean surface [
17]. Until now, numerous spectrum models have been proposed to describe the sea surface geometry, but none of these spectra has been proven suitable for EM scattering simulation in full frequency band, full polarization and full sea state [
6]. In this paper, three commonly used spectrums, including DV spectrum [
18], Apel spectrum [
19] and Elfouhaily spectrum, are analyzed for backscattering computation.
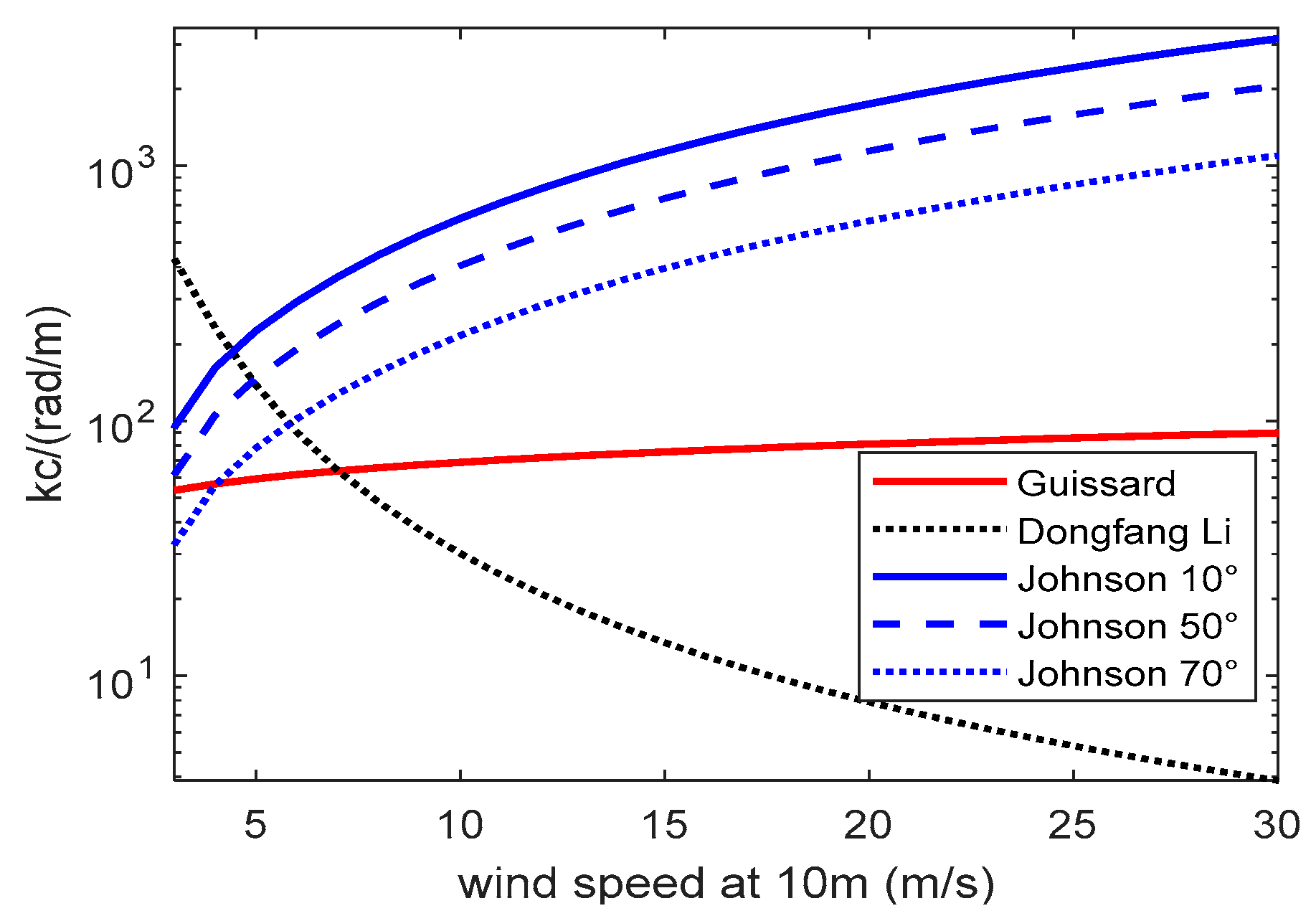
The TSM algorithm divides the sea surface spectrum into large- and small- scales, with Kirchhoff approximation (KA) for large-scale scattering contribution and small perturbation method (SPM) for small-scale part. Therefore, the value of cutoff wavenumber for division of large-scale and small-scale spectrum is crucial for the scattering results. Some researchers empirically selected the cutoff wavenumber according to the scattering characteristics in different situations [
18,
20,
21], but these empirical cutoff wavenumbers are always limited to specific conditions. As early as 1987, Guissard and Sobieski proposed a cutoff wavenumber criterion that varies with frequency and roughness spectrum by simplifying the applicability conditions for large-scale and small-scale surfaces [
22]. Then, this criterion was used by Liu et al. in FASTEM-4 [
4]. Furthermore, Li et al. (2020) proposed an adaptive cutoff wavenumber by making the measured sea surface roughness equal to the root mean square height of the small-scale sea surface spectrum [
23]. Based on the assumption that the physical optical integral is asymptotically "α-stable distribution" under high frequency limit conditions, Johnson et al. (2022) proposed a cutoff wavenumber model that depends on frequency, spectrum, and incident angle. They have proved that this method can improve the consistency between geometric optical prediction and small slope approximation under some incident conditions [
24]. But there is still no comprehensive evaluation of these methods.
In this paper, seawater permittivity, sea spectrum and cutoff wavenumber are studied for exact EM scattering computation with TSM. The paper is organized as follows.
Section 2 describes the principle of TSM.
Section 3 discusses the selection of the input models in TSM. The model of seawater permittivity is determined by comparing four different models. With the corresponding GMFs as reference (CMOD7 in C-band [
25], XMOD2 in X-band [
1] and NSCAT-4 in Ku-band [
26]), the optimal cutoff wavenumbers and the most suitable spectrum are obtained. Then the fitting functions of the optimal cutoff wavenumber with respect to radar parameters and wind speed are obtained by multiple regression analysis. In
Section 4, the simulation results using Apel spectrum and different cutoff wavenumber models are compared with GMFs and Haiyang-2 satellite data to evaluate the fitting functions.
Section 5 gives some conclusions.
2. The Theory of Two-Scale Method
TSM was first proposed by Wentz et al. to expand the application scope by combining KA and SPM [
20]. It treats the sea surface as a composite model, with a small-scale fluctuation superimposed on a large-scale fluctuation (
Figure 1). The Kirchhoff approximation and geometric optical (KA-GO) method is used to solve EM scattering of the large-scale rough surface, and the backscattering coefficient is expressed as [
27]
Here stands for the Fresnel reflection coefficient at normal incidence, , respectively represent the root mean square slope in upwind and crosswind directions.
Figure 1.
The two-scale model of electromagnetic scattering from rough sea surface.
Figure 1.
The two-scale model of electromagnetic scattering from rough sea surface.
The SPM is used to solve EM scattering of the small-scale rough surface. Because of the variance of local incident angle caused by the large-scale surface slope, the horizontal and vertical polarization backscattering coefficients in local coordinate system are expressed as
Here
is local incident angle caused by the large-scale surface slope,
represents the small-scale roughness spectrum,
is the cutoff wavenumber,
is the spatial wave number of ocean waves,
is the incident wave number,
represents the relative permittivity of seawater. Since the above SPM formulas are expressed in the local coordinate system, the following polarization transformation is needed.
where
,
are horizontal and vertical polarization. The subscript
represents the local coordinate system,
and
represent the incident and scattering directions, respectively.
,
represent the scattering amplitude in the local coordinate system and the globe coordinate system. The relationship between
and
is
here
stands for set averaging. The amplitude of
can be obtained by (2) and (6). A random phase, uniformly distributed in
, is often added to represent the phase of
[
28]. Once the
is obtained, we can use (5) and (6) to get the scattering coefficients in the globe coordinate system
. Finally, according to the tilt modulation of large-scale surface, the backscattering coefficient of TSM is written as
Here is the distribution function of large-scale slope. , are the slopes along and axes in the principle system, and , are the slopes in the observation system of radiometer.
4. Comparison and Discussion
To further illustrate that the TSM backscattering simulation of Apel spectrum can be improved with the appropriate cutoff wavenumber, the simulation results in C-, X- and Ku-bands with different cutoff wavenumber models are compared. The results are also compared with the corresponding GMFs in these bands. Moreover, the HY-2 satellite data (backscattering cross section products of orbit-17453 on 2022, Apr.17, 18:53~20:38) provided by the China Ocean Satellite Service System is used for comparison in Ku-band.
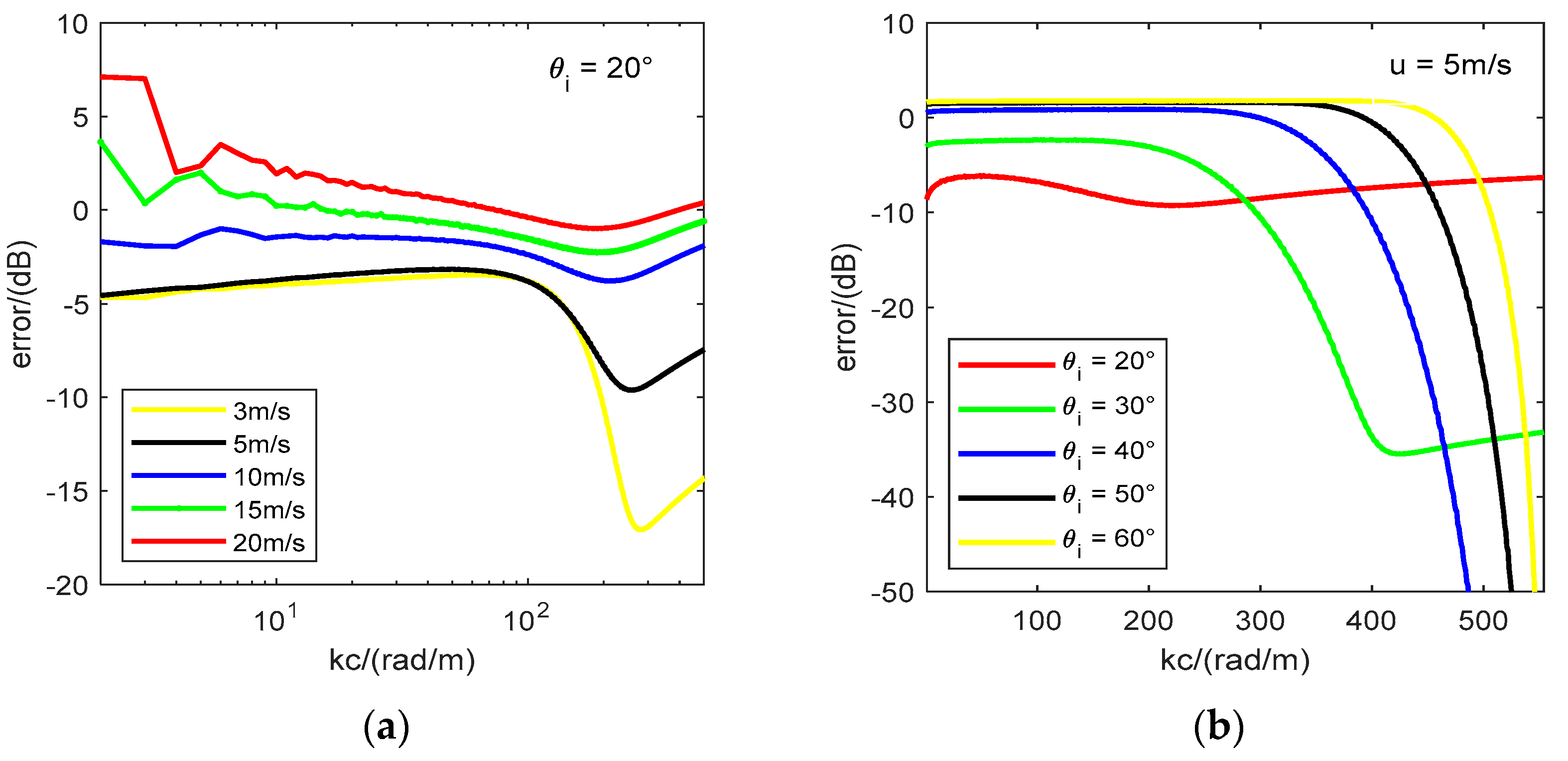
Figure 12, 13 and 14 show the comparison results of backscattering coefficients as a function of scattering azimuth in C-, X- and Ku-bands respectively. The black solid line represents the simulation results of GMFs model, the red solid line represents the TSM simulation results using the cutoff wavenumber given by our empirical function, and the green dotted line represents the TSM simulation results with the optimal cutoff wavenumber data. The dashed lines show the results of other cutoff wavenumber models. In comparison with the dashed lines, the simulation results with our cutoff wavenumber model are more consistent with the GMFs. The slight difference between the green dotted line and red solid line is due to the error of the fitting function, but the maximum difference is less than 0.5dB for C-band and less than 1dB for both X- and Ku-band. Considering this difference, additional research is required to establish a more simplified empirical function of cutoff wavenumber by exploring alternative function forms for regression analysis.
Figure 12.
Comparison of simulation results using different cutoff wavenumber with CMOD7 (C-band, , m/s).
Figure 12.
Comparison of simulation results using different cutoff wavenumber with CMOD7 (C-band, , m/s).
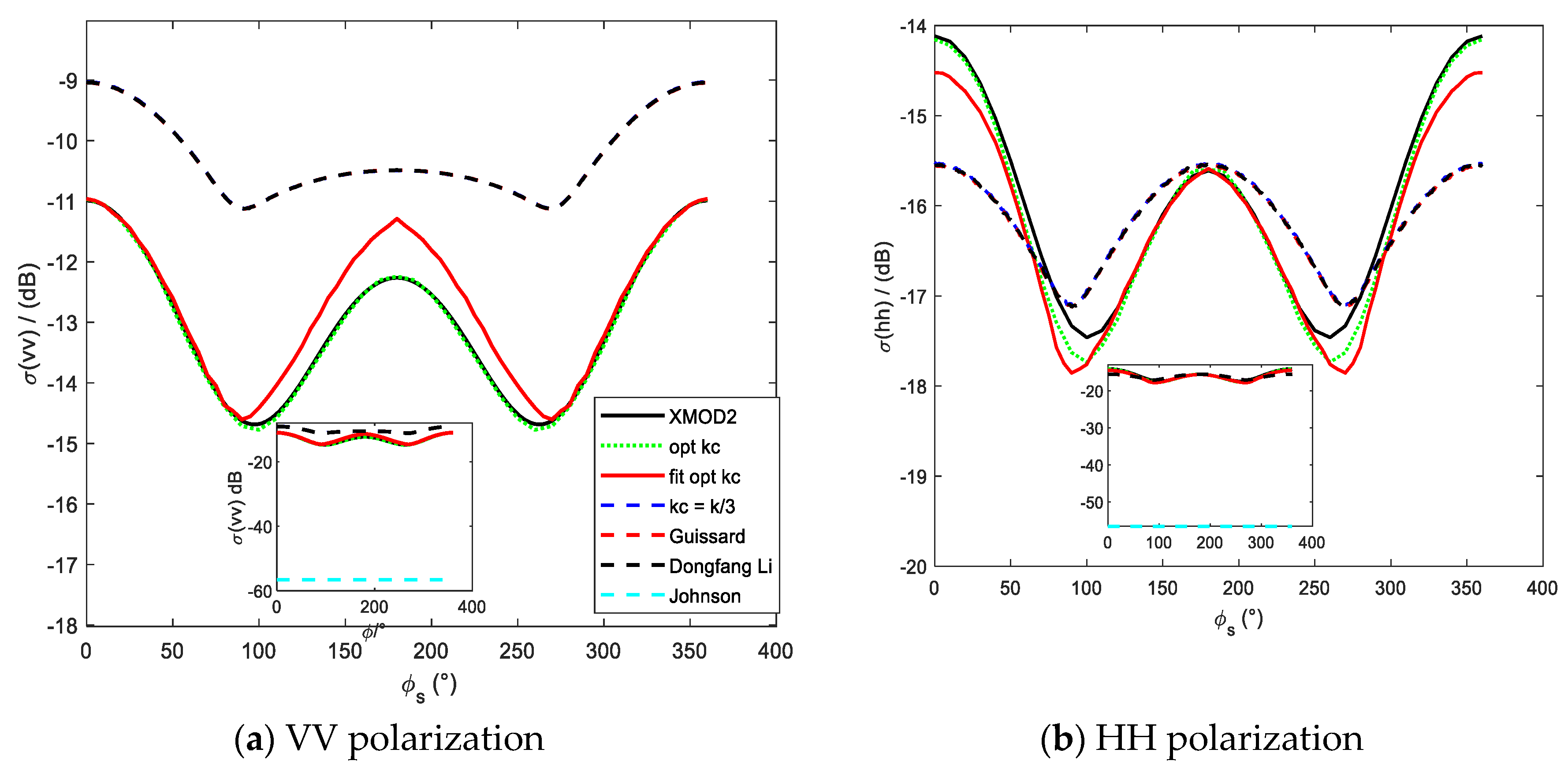
Figure 13.
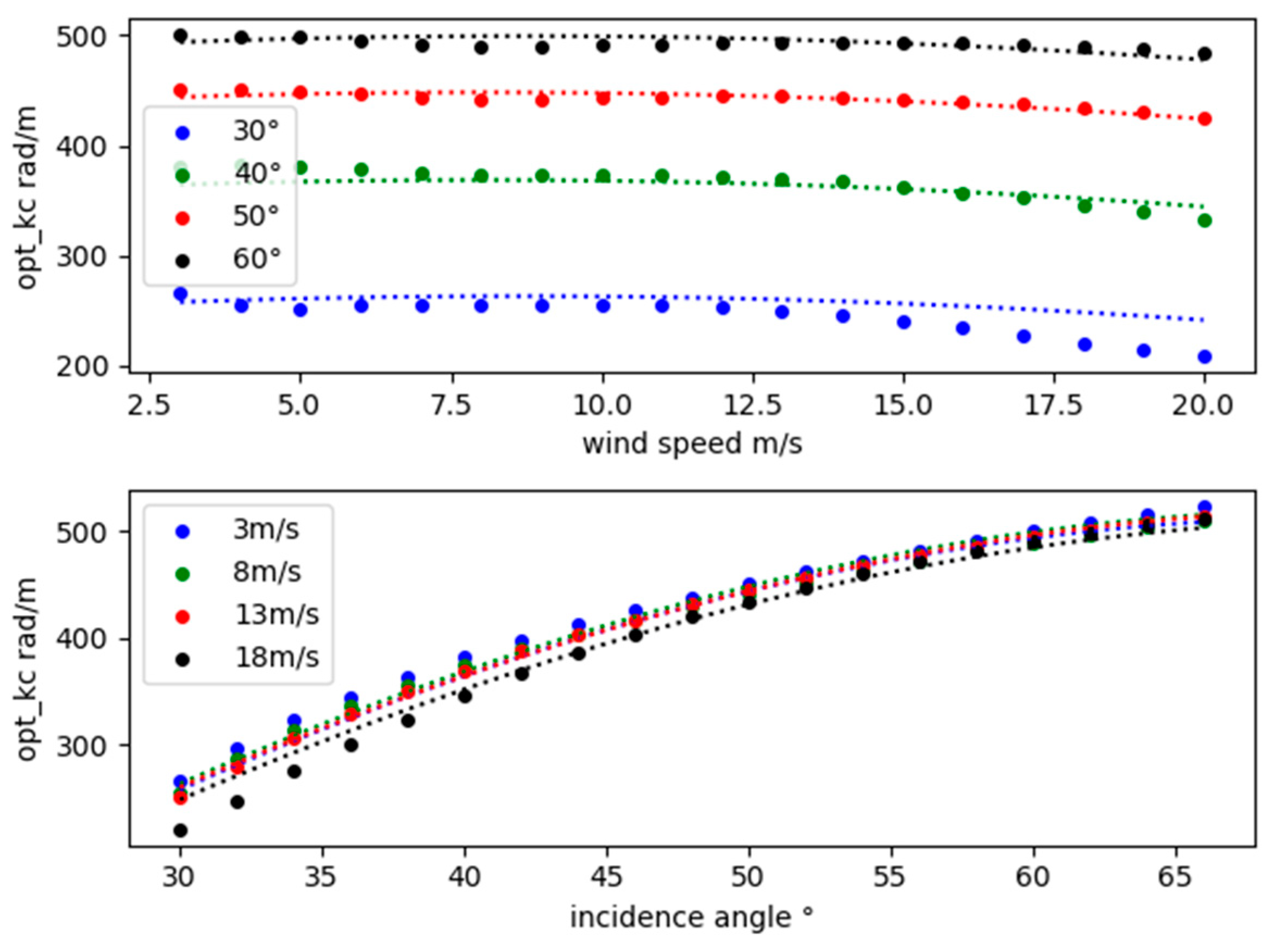
Comparison of simulation results using different cutoff wavenumber with XMOD2(X-band, , m/s).
Figure 13.
Comparison of simulation results using different cutoff wavenumber with XMOD2(X-band, , m/s).
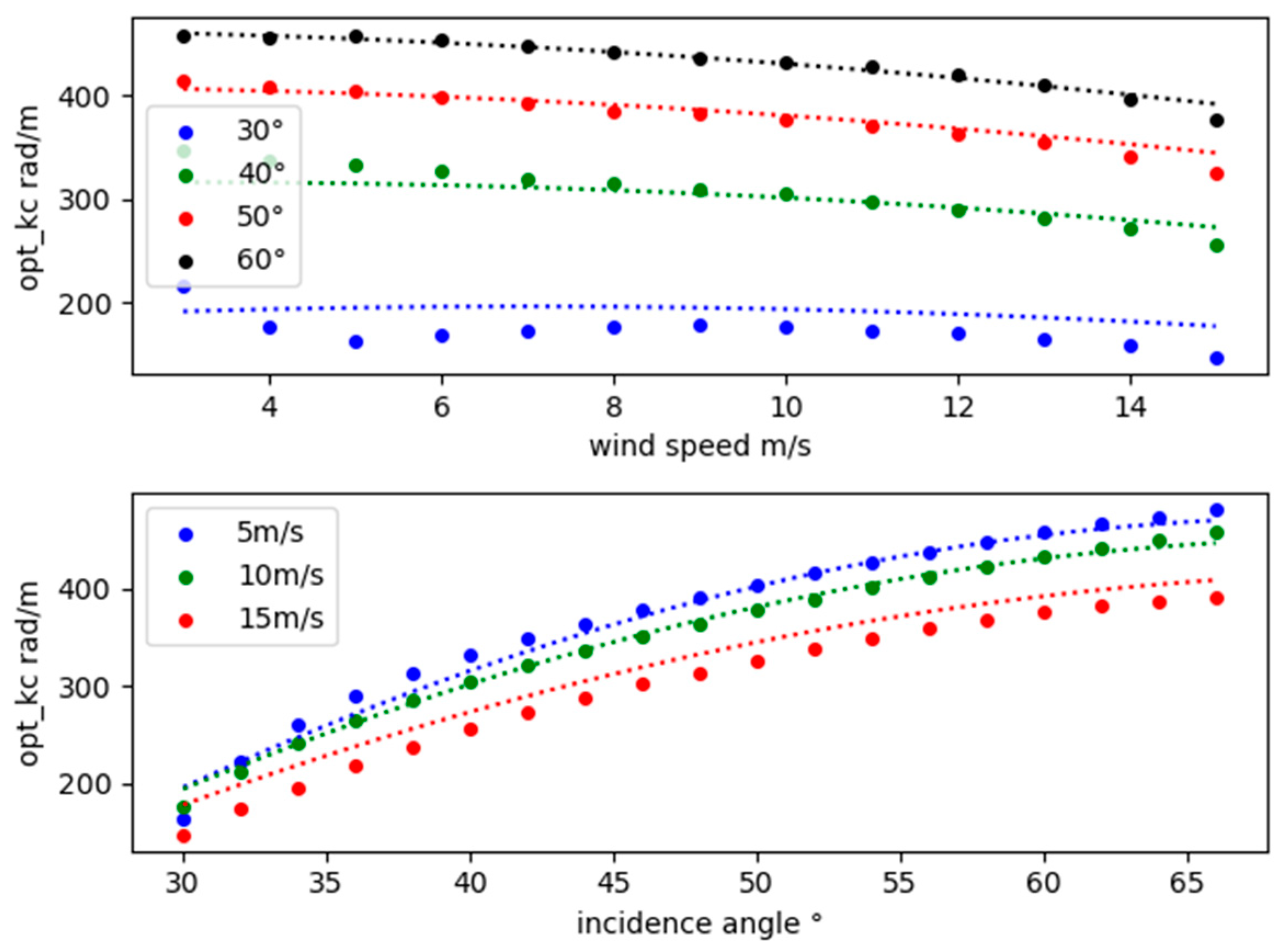
Figure 14.
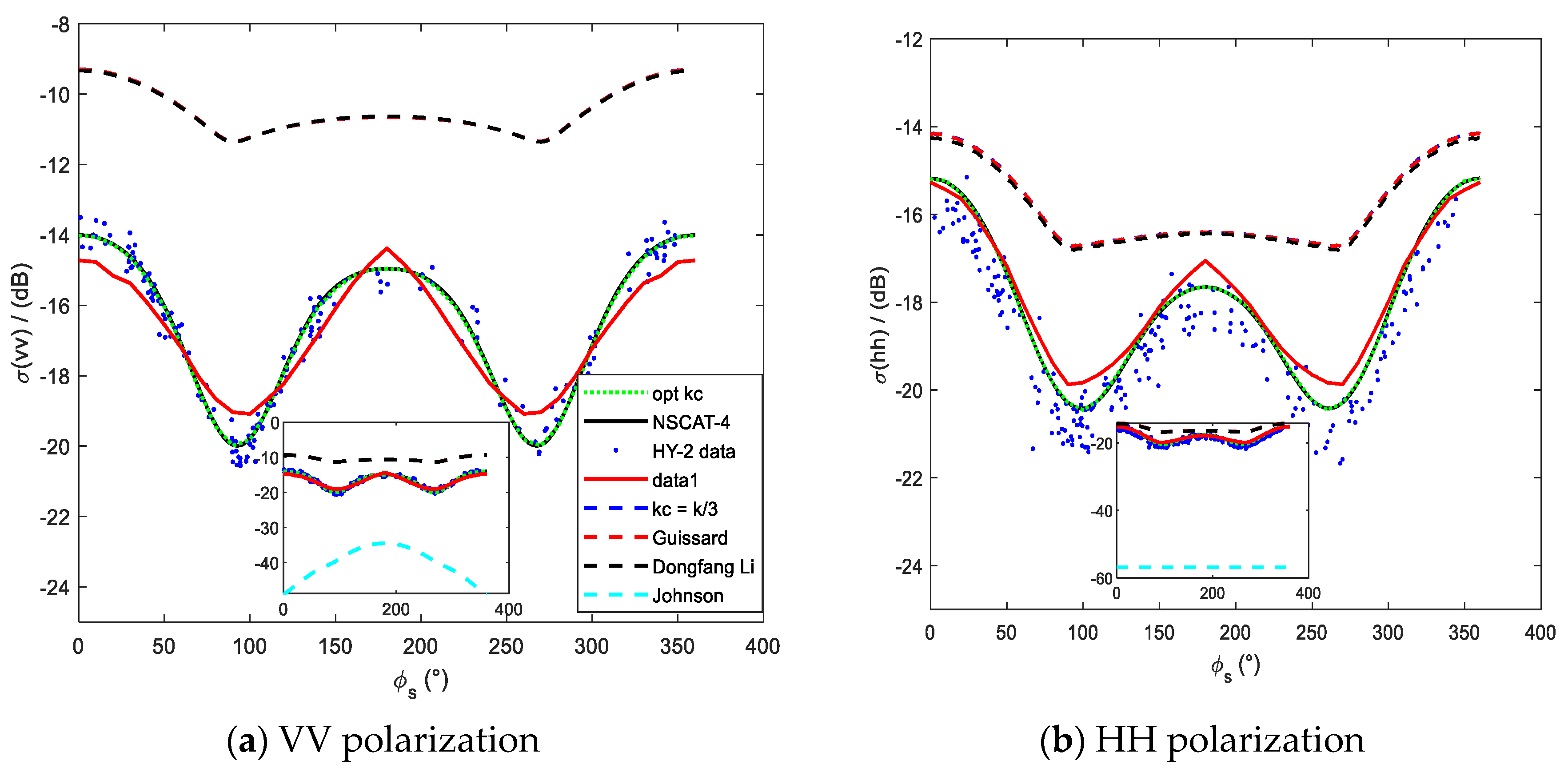
Comparison of simulation results with HY-2 satellite data and NSCAT-4 (Ku-band, m/s). (a) ; (b) .
Figure 14.
Comparison of simulation results with HY-2 satellite data and NSCAT-4 (Ku-band, m/s). (a) ; (b) .
From these figures, we can also see that the simulation results of other models (dashed lines) are basically coincident, except for Johnson's model. To explain this phenomenon,
Table 4 lists cutoff wavenumber values of different models and it shows that the cutoff wavenumbers of these models are different at the same incident conditions. To illustrate the reason why the TSM simulation results of different cutoff wavenumbers changes greatly, we select the large-scale surface slopes satisfying
and calculate the local incident angles
used in the integral term of Equation (7). Here, we assumed that the slope distributions of large-scale surface at different cutoff wavenumbers are basically the same due to slow changes of
,
with cutoff wavenumbers [
24]. Then
is used to get the wavenumber range involved in SPM calculation when the wave spectrum is not truncated.
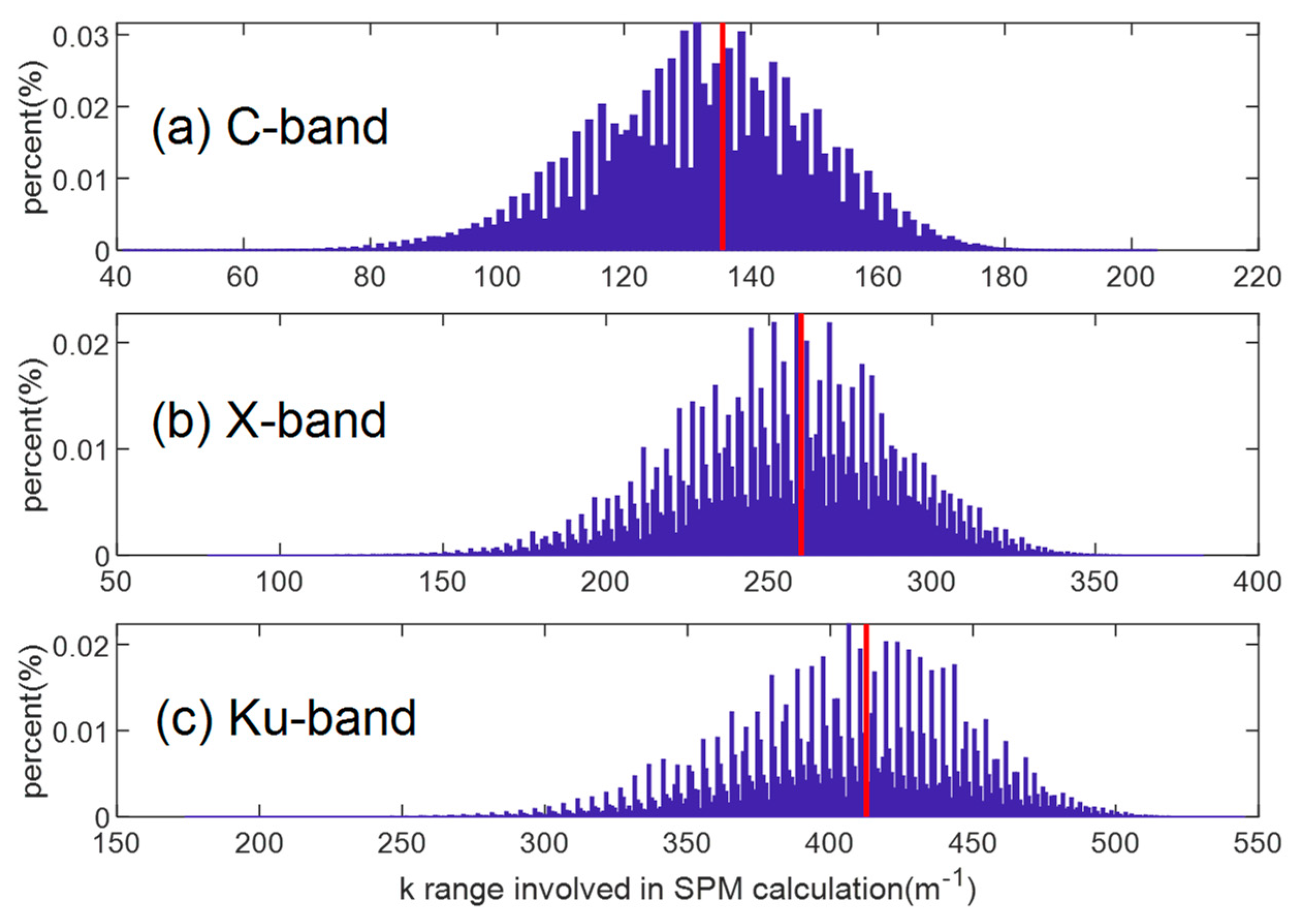
Figure 15 shows the range and distribution of wavenumbers used in SPM before sea spectrum is divided, and the red line is the Bragg wavenumbers at the corresponding global incident conditions. In the final TSM simulation, only the components larger than the cutoff wavenumber are retained. The cutoff wavenumbers of other models in
Table 4 seem ineffective for dividing the sea spectrum components in
Figure 15. For example, the cutoff wavenumbers of Johnson's model are too large in these bands, so that the spectral components involved in SPM simulation are not included and the results are dominated by KA-GO. While the cutoff wavenumbers of other models are too small, and all spectrum components in
Figure 15 are used for small-scale SPM. So, the simulated backscattering coefficients are all too large, as shown by the blue, red and black dashed lines in the
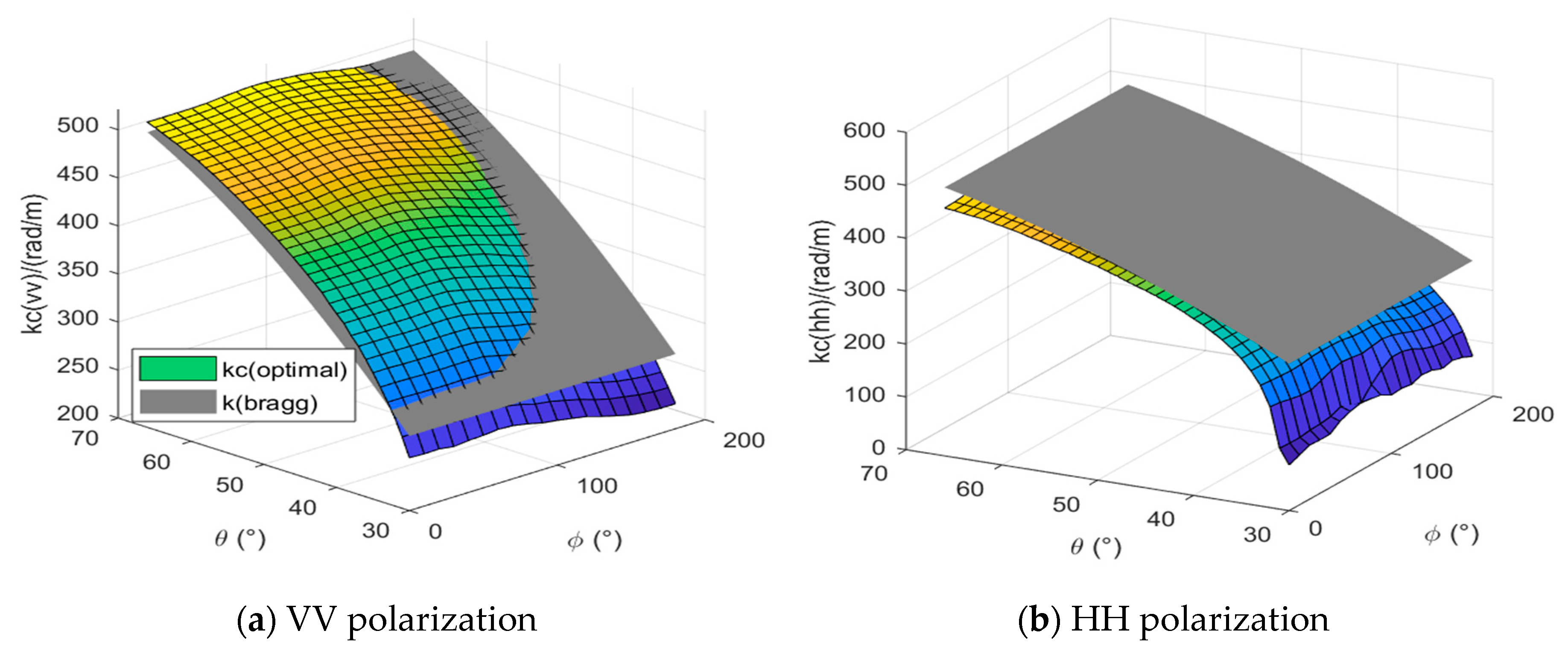
Figure 12(a), 13(a), 14(a) and 14 (b). And it is also the reason that the simulation results of the fixed cutoff wavenumber, Guissard criterion and Li’s model are always basically the same in these three bands. In these cases, the division of sea spectrum becomes meaningless. The cutoff wavenumber of our model can effectively divide the sea spectrum into large and small scales, and the Bragg wavenumbers can contribute to the SPM computation.
Table 4 also illustrates that other four models generally give a constant value for a given frequency as these models do not vary with the azimuth angle of satellite observation, while our model gives a value range. The comparison between the results of other cutoff wavenumber models and our empirical model in
Figure 12(b) and
Figure 13(b) suggests that different cutoff wavenumber should be valued for different incident azimuth angle.
| |
Cutoff wavenumber
(C-band) |
Cutoff wavenumber
(X-band) |
Cutoff wavenumber
(Ku-band) |
| Fixed value |
|
|
|
| Guissard et al. |
32.55 |
62.42 |
89.58 |
| Dongfang Li et al. |
64.15 |
64.15 |
64.15 |
| Johnson et al. |
240.93 |
430.10 |
573.16 |
| Optimal kc |
105~136(vv)
67~115(hh) |
214~253(vv)
151~196(hh) |
405~448(vv)
275~341(hh) |
5. Conclusions
The selection of the sea surface roughness spectrum and cutoff wavenumber is always important in the simulation analysis of sea surface EM scattering by TSM. By comparing the results of DV spectrum, Apel spectrum and Elfouhaily spectrum with their respective optimal cutoff wavenumbers, we concluded that Apel spectrum is more suitable for C-, X- and Ku-bands backscattering simulation of TSM. The optimal cutoff wavenumbers for different incident condition were numerically obtained by comparison the simulation results with the GMFs. Then, a four-variable polynomial containing twenty-six terms was obtained by regression analysis to represent these optimal cutoff wavenumbers. When the wind speed is 10m/s, the error between the simulation results using Apel spectrum and empirical function of cutoff wavenumber and the results of GMFs is less than 1dB. Compared with the simulation results of other cutoff wavenumber models, our cutoff wavenumber empirical function is obviously better. Besides, we also compared the performance of five classical seawater dielectric constant models based on the seawater dielectric constant data measured by Zhou et al. (2021), and finally chose GW2020 model proposed by Zhou et al. as the permittivity input of the two-scale model.
The conclusions obtained in this paper are applicable to the backscattering simulation of TSM with wind speed of 3~20m/s and incident angle of 30° ~ 66°. The lower limit was chosen based on the observation that when the incident angle is less than 30°, the minimum error between the simulation results of Apel spectrum and GMF mostly falls between 2~3dB. We analyzed the reason may be that KA-GO plays a dominant role in TSM when the incident angle is less than 30° as the KA-GO simulation results depend weakly on the selected cutoff wavenumber [
24]. Hence, for small incident angle scattering, we plan to conduct an in-depth investigation into the Kirchhoff approximation and physical optics method (KA-PO) as a potential replacement for KA-GO in the future. What’s more, further research will be made on the EM scattering model of sea surface at wind speed above 20m/s and other frequency bands combining the satellite observation data and other more accurate sea surface geometric models.