Prerpints.org logo
Preprint
Article

A New Dynamic Game-Based Pricing Model for Cloud Environment

Altmetrics

Downloads

162

Views

47

Comments

1

A peer-reviewed article of this preprint also exists.

Submitted:

24 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts
Abstract
Resource pricing in cloud computing has become one of the main challenges for cloud providers. The challenge is determining a fair and appropriate price to satisfy users and resource providers. To determine a fair price, it is necessary to consider the conditions and needs of both parties: provider and user. This research tries to provide a pricing mechanism for cloud computing based on game theory. The proposed mechanism takes into account three factors including fault possibility, interaction between virtual machines, and energy consumption to reach a fair price. In the proposed game, the provider decides on the price of the virtual machine which can be offered to the user on each physical machine and the user decides between the virtual machines offered to run its application. The whole game is implemented as a function of the resource broker component. The proposed mechanism is simulated and evaluated using the CloudSim simulator. Its performance is compared with several previous recent mechanisms. According to the results, the proposed mechanism has been able to determine a more reasonable price for the user and the provider which increases the overall profitability of the cloud system.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

Over the past few decades, cloud computing has emerged as a new technology in the information technology industry [1]. This technology provides users with many resources and services based on user demand [2]. Cloud computing services are offered in three categories: infrastructure as a service, platform as a service, and software as a service. Google Docs, Google App Engine, and Amazon Elastic Compute Cloud (Amazon Ec2) are examples of the most popular cloud computing services [3]. Cloud computing is becoming increasingly popular among users due to features such as high computing power, low costs, and flexibility. Users can use cloud computing resources without having to pay for expensive hardware and software only by paying for rental services according to the Service Level Agreement (SLA), from the cloud service providers [4]. The SLA is formulated as a formal commitment between the user and the provider to compensate the users if the provider fails to provide the expected level of service [5].
With decades of emerging cloud computing technology, there are still many challenges that need to be addressed. The services provided by the cloud providers are not free and customers have to pay a fee based on the amount of resources and the length of time they are used. Cloud pricing plan has a significant impact on the system's economic benefits. Pricing policies in the cloud are in two fixed and dynamic types. Fixed pricing is a strategy in which a price is established and maintained for services during a specific period. This price can be determined based on hours of resource usage, gigabytes of data storage, etc. Usage-based and subscription-based are examples of fixed pricing strategies [2]. In dynamic pricing, users pay for services based on service features, user characteristics, and the interaction of supply and demand in the market. Although a dynamic pricing strategy imposes more computational overhead, it also has more economic benefits [6].
Due to the complex, large-scale, and competitive environment of the cloud, resource allocation and pricing have always been important challenges for researchers. Cloud providers want to optimize their resource utilization and also keep the customers satisfied and loyal to maximize their revenue. The purpose of this study is to present a fair pricing method based on game theory. The proposed method determines the price based on both users’ resource consumption and providers’ expenses such as Purchase and maintenance costs. Furthermore, the proposed pricing method takes some new factors that play an important role in cloud operational costs into account. These factors are the amount of power consumed for the user’s request, the probability of successful job execution as well as the interactions between virtual machines when allocated on the same resource. The game-based pricing method also considers the market supply and demand to provide a more precise and fairer price.
The rest of the paper is organized as follows: in section 2, a review of the recent literature on pricing methods is presented. Section 3 provides a detailed description of the proposed game-based pricing method and the preliminaries required. The experimental results and performance evaluation of the proposed method are discussed in Section 4. The performance of the proposed method is evaluated in comparison with other recent pricing methods based on the simulation study. Finally, section 5 concludes the paper with a summary.

2. Related work

In this section, a review of related works about Pricing Models in cloud computing environments is presented. Some previous research such as [7] and [4] introduced and compared different types of pricing methods in cloud computing. Auction-based pricing which is sometimes referred to as dynamic pricing, is a common pricing mechanism for clouds [8,9,10,38].
In [11], the authors proposed the online extended consensus revenue estimate mechanism for conducting a recurrent, multiunit, and single-price auction in the Infrastructure as a Service (IaaS) cloud resource setting. This mechanism is both envy-free and truthful, and it is capable of generating profits that are close to optimal. It incorporates a system for dynamically determining reserve prices based on the Power Usage Effectiveness (PUE) of the data center and the costs of electricity. Through simulation-based evaluation, its effectiveness has been demonstrated in various market conditions, surpassing the traditional uniform price auction. The authors also investigated the importance of prior knowledge in maximizing profit by considering the execution time of virtual machines. A small-scale experimental study involving 10 users has confirmed the truthfulness of this mechanism in a real-world testing environment.
In [8], a double-auction pricing model named Combinatorial Double Auction Resource Allocation (CDARA) is proposed to balance profit between user and provider. In [11], the CDARA model has been improved. To achieve more fairness, this model not only considers the price but also other quality of service parameters in the resource allocation process. If the provider does not meet the required service quality, it imposes penalties on providers and diminishes their reputation. In [10], the resource allocation problem is formulated as a linear programming model to maximize the total profit of users and providers using a combinatorial double auction-based pricing mechanism. In [38], a QoS-based auction method is proposed which attempts to dynamically determine the price based on the quality of service parameters (such as availability) to increase the provider’s profit.
Performance-based pricing is another approach in which cloud providers are paid based on the actual consumption of their resources. For example, Lucani et al. proposed a pricing model according to the CPU capacity consumed by the user application [12]. They considered the number of CPU cores and even the selected CPU frequency in the pricing model. Similarly, in another study, Aldossary et al. proposed an energy-aware pricing policy that considers the amount of energy consumption in addition to the actual resource usage per unit such as memory, network, and disk. For this purpose, a mathematical approach has been used to calculate energy consumption and resource usage [13].
The distinction between customers and the use of incentive mechanisms has always been the focus of pricing methods. For example, Chi et al. proposed a fairness-aware pricing model to increase the profitability of cloud infrastructure providers [14]. They offered lower prices to the customers whose requested resources can be allocated easily to encourage them to use cloud services more. Using algorithms from financial option theory, Sharma et al. proposed a pricing architecture for cloud services. A general formula, called compound-Moores law, was proposed for computing the price based on parameters such as resources’ characteristics, inflation rate, and depreciation. They also used a genetic algorithm and fuzzy logic-based approach to measure the amount of potential loss of cloud providers [15].
The law of supply and demand in marketing is another basis for determining cloud service prices. Cong et al. proposed a dynamic model that determines the price for cloud services according to the real supply and demand relationship. They used a closed loop control mechanisms to dynamically adjust the price for cloud services. They also considered penalties for service level agreement violation by the provider and rewards for users who are not sensitive to delay [5]. In similar research presented in [16], authors also proposed a value-based pricing solution that uses a hedonic regression model to estimate how much a customer is willing to pay for the cloud service.
The amount of energy consumed is another important factor that has been considered recently in pricing methods for both achieving a more fair price and making computation more green [13,17]. For example, Qui et al. [17] have presented a greedy-based pricing solution to reducing cloud energy consumption and moving towards Green cloud computing. They showed that the price of resources should be proportional to their energy consumption.
Several dynamic pricing models have been conducted based on game theory [18,19,20,21,22,37]. In [18], authors suggest a framework for the cloud computing market to make the market uniform and competitive, whereby users can purchase resources from different companies and flexibly exchange their idle resources. Then, a static Game-based pricing method is proposed to mathematically model the pricing problem and develop an optimal strategy for the user and cloud provider.
In a study of price competition in a diverse cloud market, the authors examined the rivalry between cloud service providers (CSPs) and cloud users [19]. They devised a two-stage non-cooperative game, where CSPs established prices to maximize their revenue in the first stage. By utilizing an iterative algorithm, they obtained Nash equilibrium prices and analyzed the convergence properties. In the second stage, cloud users opted for services based on both performance and price, employing an evolutionary game approach. The result demonstrated that the rate of arrival or resource capacity had a more substantial impact on the CSP side, influencing equilibrium prices and utilities, as opposed to the cloud user side, which affected user cost and arrival rates.
In [23], a framework was introduced that acts as an intermediary between multiple cloud platforms to facilitate the processing of large-scale data streams. This framework offers cloud services for streaming big data processing to users. The process includes renting computer resources from various cloud services and providing users with different service interfaces. To enhance revenue and mitigate risk, a Pricing-Repurchasing strategy is developed, which entails entering into long-term rental contracts with users. The Pricing-Repurchasing problem was mathematically formulated as a two-stage leader-follower game (Stackelberg), and the equilibrium was thoroughly analyzed. The simulations were conducted to evaluate the effectiveness of the pricing strategy, demonstrating that it generates more revenue for the intermediary compared to other approaches.
Authors in [20], formulated the problem of setting prices for cloud web services with a collaborative game theory approach. They concluded that cloud platforms can co-exist if they adopt the same type of pricing strategy.
In [24], the authors explored the issue of maximizing revenue in the context of Software as a Service (SaaS) and IaaS providers. They depicted this issue by viewing it as a Stackelberg game and examining the presence and uniqueness of the game equilibrium. Furthermore, the examination of the influence of resource prices on the users' desire to utilize the service was conducted, and a dynamic pricing strategy was proposed to maximize the revenue for both SaaS and IaaS providers. By conducting simulations, the results demonstrate that the proposed strategy surpasses fixed pricing and auction-based pricing mechanisms in terms of revenue maximization and resource utilization.
Yeet al. put forward a pricing strategy that is equitable for cloudlet resources to strike a balance between the interests of Cloudlet Infrastructure Providers (CIPs) and enhance overall profits [25]. They introduced a model based on game theory that takes into account the initial quotes, idle resource rates of CIPs, and the overall profit of the Cloudlet Federation (CLF). The strategy for adjusting prices takes into consideration demand-side psychology and the rate at which the game process converges. The research demonstrates the existence of a solution that achieves Nash equilibrium and introduces an algorithm, known as the game pricing approach based on selection times, to solve the model. The results indicate significant improvements in total profit (more than 20%) and resource utilization (over 50%) when compared to existing methods.
A study in cloud manufacturing examined three resource-sharing strategies: independence, alliance, and cooperation with a cloud platform operator [26]. The study analyzed the impact of these strategies on meeting client requirements. The results, modeled as a two-stage Stackelberg game, demonstrated that an alliance among suppliers resulted in lower system profit compared to independent sharing. This was in contrast to the preferences of the platform operator. The analysis also highlighted the complexities involved in task and profit allocation when multiple suppliers were involved. Suppliers with lower prices had the advantage in tasks and profits, based on varying marginal prices. These findings guide suppliers in choosing appropriate resource-sharing strategies in cloud manufacturing.
In [27], a hybrid approach is used to optimize fair prices of resources through stock market-based technical analysis and maximize resource utilization using Stackelberg output volume in a cloud service provider pool. The experiment incorporates three price rebalancing methods: exponential moving average, pivot point analysis, and relative strength index. The proposed approach ensures higher revenues and improved utilization rates for service providers, while subscribers benefit from fair prices and enhanced resource availability. Overall, this solution benefits both service providers and subscribers by optimizing revenue, and resource utilization, and ensuring fair pricing and resource availability.
As mentioned above, cloud pricing policies can be categorized as fixed and dynamic ones. In fixed methods, the price cannot be well adapted based on the supply and demand of the cloud market. Therefore, lower economic profit and customer satisfaction are expected for fixed pricing strategies in compared to dynamic ones. In this paper, a dynamic game-based pricing method is proposed to make the estimated price fairer and increase the provider’s profit and customer satisfaction. The proposed method is modeled using a dynamic game framework. The game is defined between the provider and the user. The effect of other cloud providers and market conditions is seen as the relation of supply and demand in the proposed method. To achieve a near to fair price, the proposed method considers a comprehensive set of factors influencing price such as energy consumption, the amount and duration of resource usage, depreciation, and maintenance costs. Furthermore, virtual machines' performance interference effects and failure probability of cloud resources are incorporated into the proposed pricing method as two new influencing factors.

3. System model

The system model adopted in this study is introduced in this section. This study aims to propose a game-based pricing model; by using it, a cloud provider can set a fair price for their services and increase its economic profits while attracting customers. The cloud environment consists of m physical machines ( P M 1 , P M 2 , … , P M m ) that each one can execute multiple virtual machines. The system model also includes a resource broker for the cloud environment. This component is responsible for managing resources and acts as an intermediary between the cloud user and the cloud provider. The cloud broker component receives the user request which includes the amount of resources required, the volume of the task (expressed in million instructions), the deadline of the task, and also the amount of total budget the user can spend. Therefore, a user request can be described by the following Quadruple.
U s e r _ R e q u e s t = N u m _ o f _ C o m p u t i n g _ E l e m e n t s ,   T a s k _ v o l u m e , D e a d l i n e , B u d g e t
The cloud broker finds the equilibrium of the game between players and allocates the proper virtual machine with a fair price to the user’s request. The general model of the system is shown in Figure 1.

4. The proposed game-based pricing method

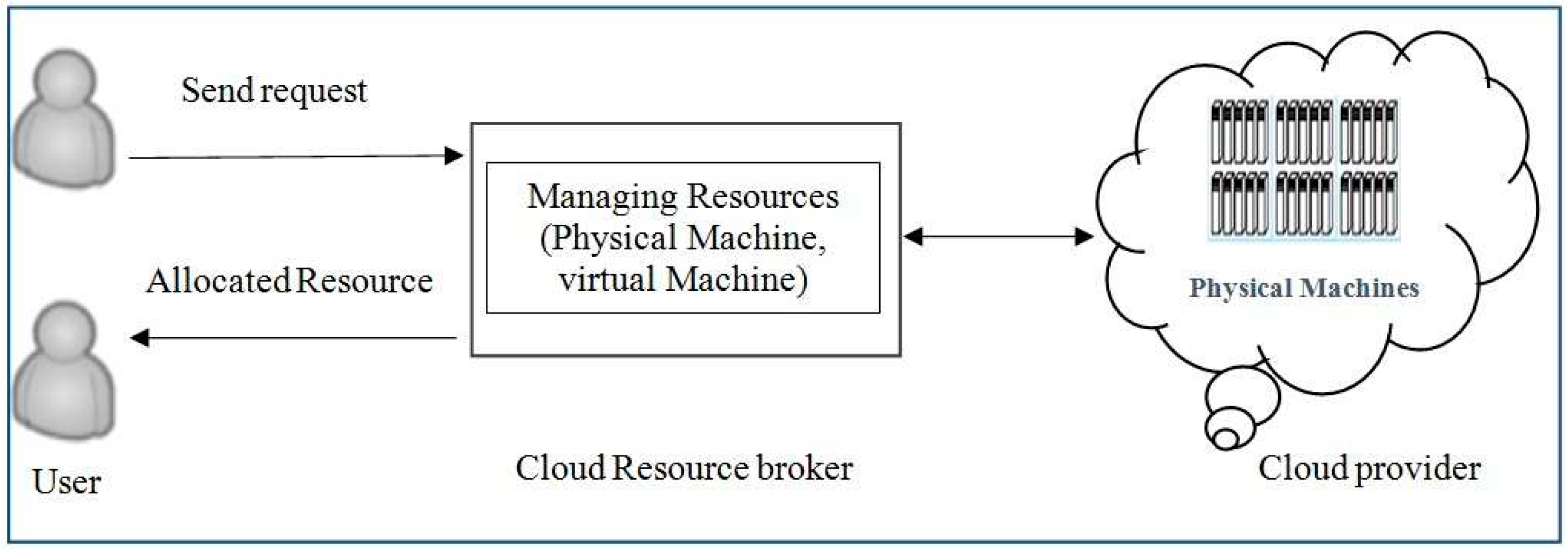
As mentioned before, the proposed pricing method is formulated using a dynamic game. The details of the proposed pricing method are described in this section by introducing the game model, the game’s player and their action space, and the game’s payoff functions. It describes how the game tree (extensive form) is constructed by the cloud broker and how a proper virtual machine with a fair price is allocated to the user by finding the Nash equilibrium of the game.

4.1. The game’s components

The game consists of two players. The first player is the user and the second player is the cloud service provider. The possible actions (action set) for each player are defined as follows: The first player can select between different n virtual machines that are offered by the provider ( V M 1 , V M 2 , … , V M n ). Each virtual machine offered will have its price, the action set of the second player is the interval 0 , P 0 where P 0 is the maximum price that the user is willing to pay for the service. The user decides such that he/she can get the required quality of service at the lowest cost. However, the cloud provider chooses the proper price such that it can maximize its profit. Therefore, the utility (payoff) functions of the players can be defined as follows:
Definition 1: The utility of the Cloud Provider (CP) corresponding to action P i of the cloud provider and action V M j of the user is computed based on the equation 1:
π c p V M j   ,   P i = P − F P × P
Where parameter F P indicates the probability that the user’s task faces a failure during its execution and doesn’t complete successfully; parameter P is calculated based on the following equations:
P = r q + Q i Q 0 × P i T W
Q i = α   P i + β
W = w 1 R e q u e s t e d _ P r o c e s s i n g _ p o w e r D e f a u l t _ P r o c e s s i n g _ P o w e r + w 2 R e q u e s t e d _ M e m o r y _ s i z e D e f a u l t _ M e m o r y _ s i z e
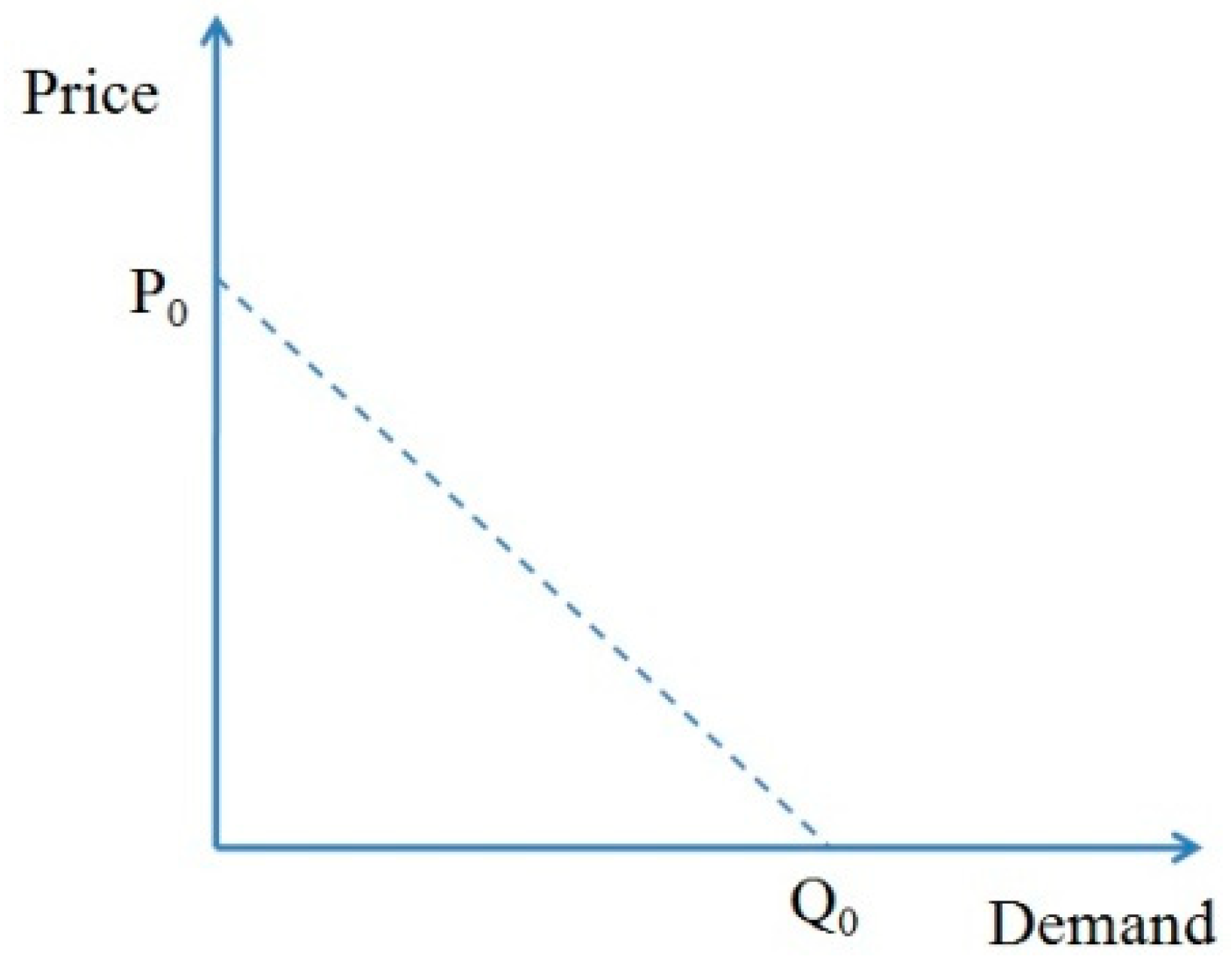
Where parameter Q i in equation 3 indicates the number of users requesting the service at the price P i and Q 0 represents the maximum market demand (in terms of customer number) for the cloud services at the price of zero (Figure 2 shows the relationship between demand and price). When the number of users applying for cloud resources is high, the cloud provider can also raise the bid price. Conversely, when the number of applicants decreases, the price should also be lowered to attract more customers [15]. The Q i parameter is considered for this purpose and is calculated using equation 3. The value of α , β , and Q 0 parameters can be determined by studying the demand and supply relationship for the cloud services in the market. It should be noted that the value of α parameter is less than zero ( α < 0 ). The r q parameter is a coefficient to make a difference in the cost of using expensive hardware over the low-cost one. Parameter T indicates the duration of the resource usage. The longer the resource usage duration is, the higher the cost of using the resource would be. The P i parameter specifies the price for a virtual machine with default processing power and memory amount. If the user requests a virtual machine with different processing power or memory amounts, the price of the virtual machine should be adjusted according to the amount of resources consumed. This adjustment is done by the use of parameter   W . The value of the W parameter is calculated based on the equation 4. This parameter helps to set the price based on the amount of resources consumed. The more requested resources will cost more. The w 1 and w 2 parameters represent the weight of two memory and the processing element resources in the final price of the virtual machine and can be set by the cloud provider.
Definition 2: The utility of the user (customer) corresponding to action P i of the cloud provider and action V M j of the user himself/herself is computed based on equation 5:
π u V M j   ,   P i = B u d g e t − C
Where the B u d g e t parameter indicates the money that is available to the user and parameter C represents all costs required to provide the service (the user’s final payment amount). The C parameter is computed based on the following equation:
C = π c p V M j   ,   P i + E j
Parameter E j indicates the expenses corresponding to the energy consumed by virtual machine j ( V M j ) for performing the user’s job. This parameter is calculated based on the equation 7:
E j = P o w e r j × T × E l e c t r i c i t y _ C o s t
Where P o w e r j shows the power consumption rate of the machine j .

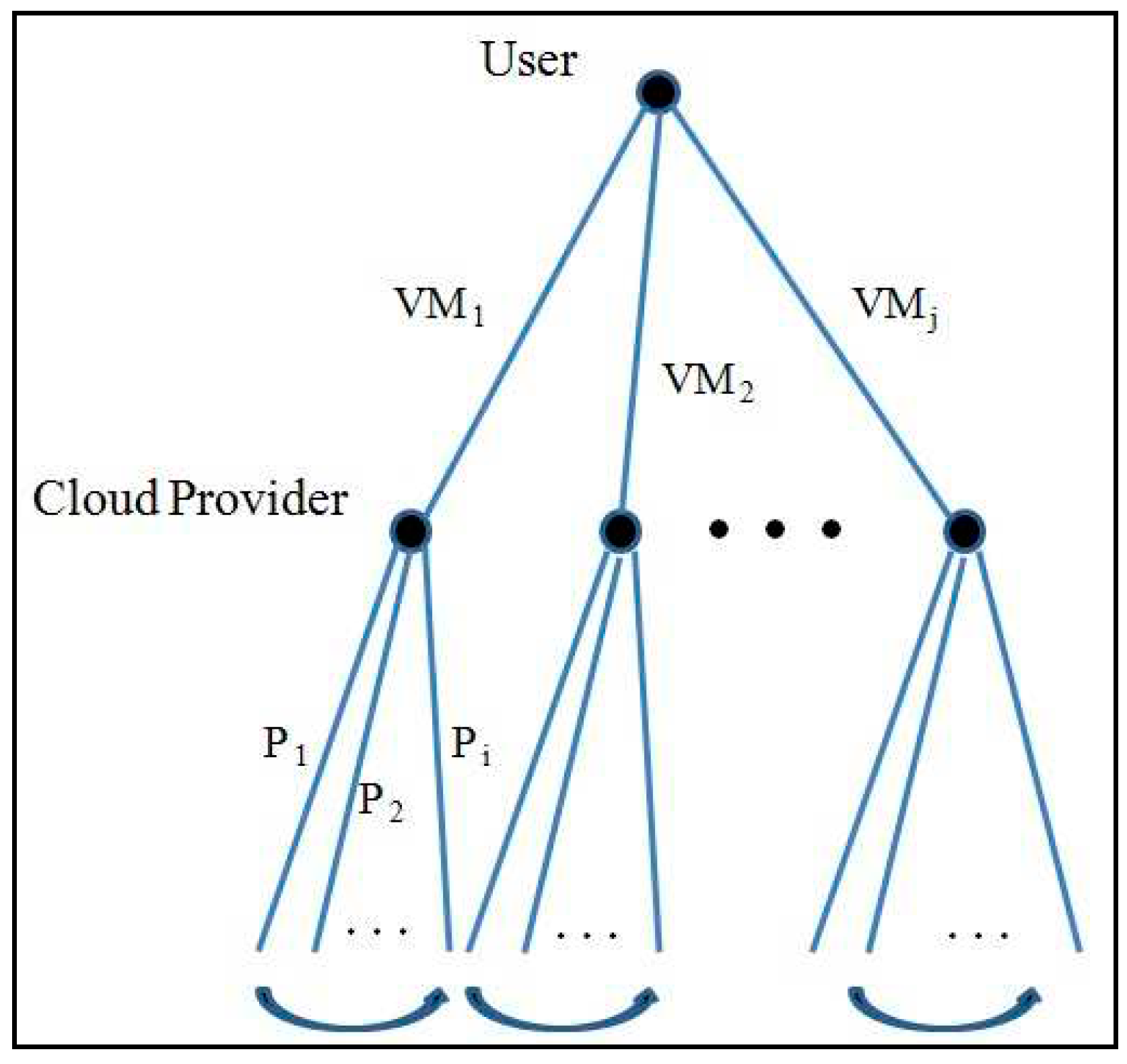
4.2. Constructing the game tree

As mentioned before, the proposed game involves one decision step for each player. Therefore, the game has a tree of depth 2. The root is a decision node for the user that each branch leading away from it, represents a possible action that could be taken by the user. At this decision node, the user should select a virtual machine among different candidate virtual machines offered by the cloud provider. It is assumed that the cloud would offer one virtual machine on each physical machine if it is possible (for example, if enough resources are available on that physical machine to create the requested virtual machine). The nodes placed at depth one are the decision nodes for the cloud provider. Each node corresponds to a situation in which the provider should decide on the price ( P i ) of the offered virtual machine. The structure of the game tree is shown in Figure 3. Constructing the extensive form (tree) of the proposed game would consist of two main steps. The first step is to form the action set of the first player (user) by finding the candidate virtual machines. The second step is to determine the possible actions of the provider and finally the expected payoffs for the two players.

4.2.1. Step one: finding the candidate virtual machines

In the process of constructing the game tree, the proposed method checks each physical machine whether it is possible to create the requested virtual machine of the user on it. This checking is necessary to constitute the action set of the first player (user). Creation of the requested virtual machine might not be possible on all physical machines due to the lack of available resources or the adverse effect of other virtual machines on the performance. Different virtual machines running simultaneously on the same physical machine can adversely affect the performance of each other due to the shared use of resources [36]. To have a good resource allocation, increase system efficiency, and also offer a fairer price considering such effects would be beneficial. In cases where multiple virtual machines placed on the same physical machine are responsible for executing programs with high consumption of a particular resource, such as CPU and memory, these effects would be more serious [28]. In such cases, the over-utilized resource could become a bottleneck or a breakpoint for the system and eventually lead to service degradation. As studied and reported in [29], the completion time of a processor- or memory-intensive task can be double or even worse if another processor- or memory-intensive task use simultaneously the same physical resource. Using the findings of [29], the proposed method considers these conflicts and leaves the physical machines that cannot execute the user’s task promptly out of the tree construction process. Furthermore, physical machines that don’t have enough available resources would be also excluded from the tree construction process.

4.2.2. Step two: Constructing the cloud provider’s sub-games

At this step, the proposed method constructs the second depth of the game tree. The resource broker (which is responsible for constructing and solving the game) computes the provider’s payoff for choosing different prices in each decision point based on equation 1. As an increase in the price leads to a lower demand for the resource, choosing higher prices doesn't necessarily mean more profit for the cloud provider.
According to equation 1, for computing the benefit of each action for the provider, the penalty corresponding to each action must also be calculated. The proposed approach considers this penalty for cloud providers due to the probability of unsuccessful execution of the user’s task and SLA violation. Considering this probability leads to better resource allocation since the provider tends to improve its profit. Execution of users’ tasks may fail due to various reasons, such as resource breakdown and system overload [32]. In the event of an error or a malfunction, the provider should be obliged to compensate the user for violating the service level agreement. To reduce the amount of penalty paid by the provider, the proposed method uses a failure probability model presented in [33]. This model helps to predict the failure probability of a task execution on a physical machine with a high accuracy (up to 90%).
In addition, the cost of energy amount needed to be consumed for executing the user’s task on each virtual machine is estimated at this step (according to the model in equation 7). Because large-scale computing systems such as clouds have high energy consumption rates, a significant portion of their operating costs are related to paying electricity bills [30,31]. Given that high energy consumption imposes high expenses on the cloud providers, the proposed model considers energy consumption as an effective factor in resource allocation and pricing mechanisms.

4.3. Finding the sub-game perfect Nash equilibrium of the game

To solve the game and find the sub-game perfect Nash equilibrium, the backward induction method is used. First, the lower level (provider level) sub-games are solved. It should be determined which actions the provider (final mover) should take in each possible circumstance to maximize its profit. Second, the upper level (user level) sub-game should be solved. By solving this sub-game the Nash equilibrium actions for both players would be determined.
Lower-level sub-games: in each of these sub-games, the optimal price for the corresponding candidate virtual machine should be determined so that the cloud provider’s profit is maximized. Therefore, the derivative of the provider’s payoff function concerning variable P i should be found. This derivative is set equal to zero and the equation is solved for P i . First, the extended form of the provider’s payoff function is written as follows:
π c p V M j , P i = r q   P i T W + α P i 2 T W + β P i T W Q 0
− F P r q P i T W + F P α P i 2 T W + F P β P i T W Q 0
Now:
∂ π c p V M j   ,   P i ∂ P i = 0 ⇒  
r q   T W + 2   α   P i T W + β T W Q 0 − F P r q T W + 2   F P α P i T W + F P β T W Q 0 = 0
Therefore, the optimal price in each possible circumstance can be finally calculated as follows:
P * = Q 0 r q + β − 2   α
Upper-level sub-game: after determining the best response of the second player ( P * ) to the user’s actions in the lower-level sub-games, now, the upper-level sub-game can be solved. At this step, the best response of the user to the cloud provider’s action would be also determined. Knowing the price selected by the provider for each candidate virtual machine, the resource broker can calculate the amount of the user’s profit for each action and choose the most proper virtual machine for the user. For calculating the user’s profit, equations 5, 6, and 7 are employed by the resource broker. Therefore, the best response of the user to action P * of the provider can be determined as follows:
V M * = Argmax VM j ⁡ π u V M j   ,   P *
The action pair ( V M * ,   P * ) is a Nash equilibrium because both players’ action is the best response to each other.

5. Results

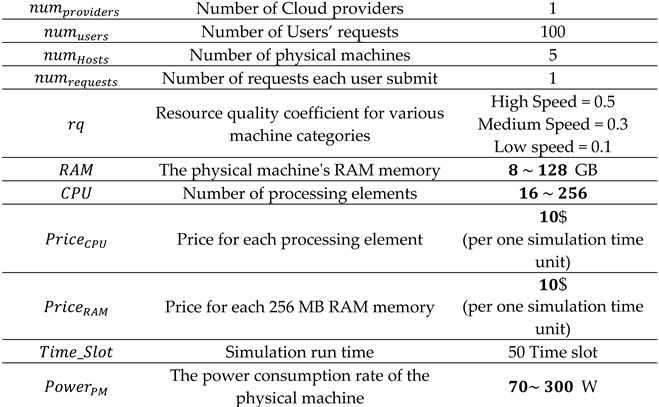
In order to evaluate the performance of the proposed pricing model, it has been compared with the methods offered by Chi et al [14] and Dabbagh et al [34]. The proposed model was implemented by using the NetBeans integrated development environment and the CloudSim 4.0 [35] simulator. In the simulation, the cloud provider has several physical machines with various hardware characteristics. One hundred user requests have been considered to be submitted to the system through the simulation period. The implementation parameters are considered the same as shown in Table 1.
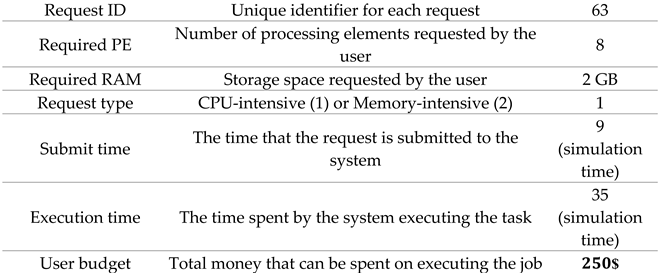
Each physical machine is a powerful server that consists of several computing elements. Therefore, multiple virtual machines can be assigned to one physical machine simultaneously. Physical machines are considered to be heterogeneous and thus have different resource characteristics as can be seen from Table 1. The resource broker that is responsible for building the game tree and solving it, has full information about the physical machines and their characteristics. The broker has also a list of the available resources on each physical machine which is updated continually. Having such information helps the broker determine all the candidate virtual machines. An example of a user’s request is shown in Table 2. It should be noted that all the considered 100 user requests are not necessary to be submitted to the system through the simulation period. In fact, a number of the requests that are submitted to the system follow a simple linear supply and demand model.

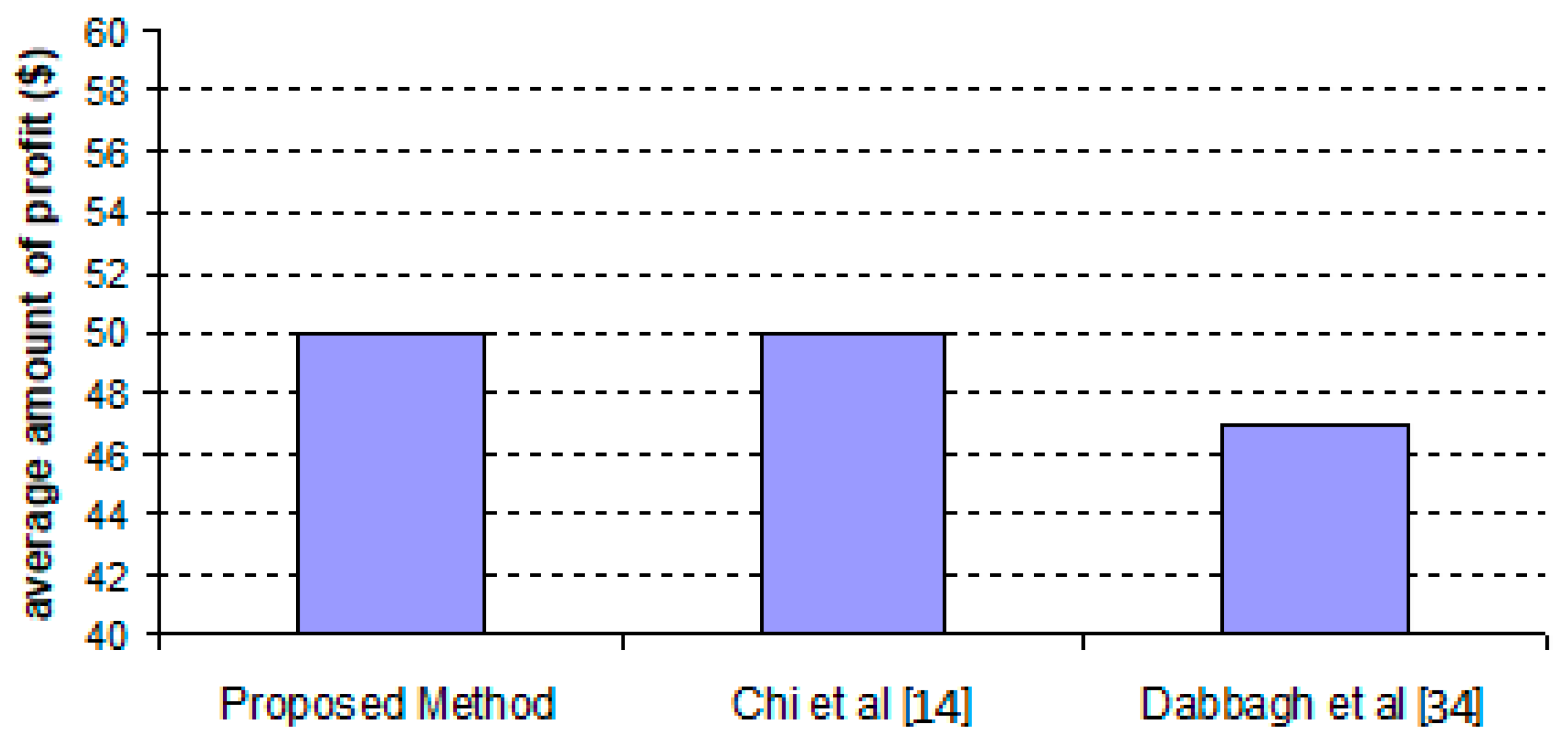
5.1. Evaluation of the proposed method in terms of users’ profit

Users' profits are defined as the amount of money left over from their budget after their request is met by the system. To have a fairer evaluation, the average amount is reported in Figure 4. Since the number of users who submit their requests to the system can be different based on the supply and demand model as well as the pricing method applied, the average amount of profit per user would be a better comparison criterion. It is calculated based on the following equation:
P r o f i t u s e r s = 1 n ∑ i = 1 n B u d g e t i − ( π c p V M i *   , P i *   + E V M i * )
Where n indicates the total number of requests submitted to the system and fulfilled during the simulation time. The other parameters are described in the previous sections.
As can be seen, the average amount of profits users gain by the proposed approach and the method proposed by Chi et al are the same. However, with this difference based on the demand and supply model employed, the total number of requests submitted to the system during the simulation period is 94, 98, and 85 for the proposed method, the approaches proposed by Chi et al. and Dabbagh et al. respectively. It should also be noted that 93, 86, and 85 requests from the submitted ones have been fulfilled during the simulation period respectively.
Since most of the focus in the method proposed by Chi et al. has been on increasing the profitability of the users, they have made significant strides in this direction as can be seen in Figure 4. Their method usually offers the lowest price per time unit for the virtual machines; however, considering the conflicts between virtual machines and heterogeneity in resources by the proposed method, results in better mapping of the jobs and thus usually lower execution time. This is why the final cost for users is reduced in the proposed method and the users experience almost the same profit in the proposed method and the one proposed by Chi et al.

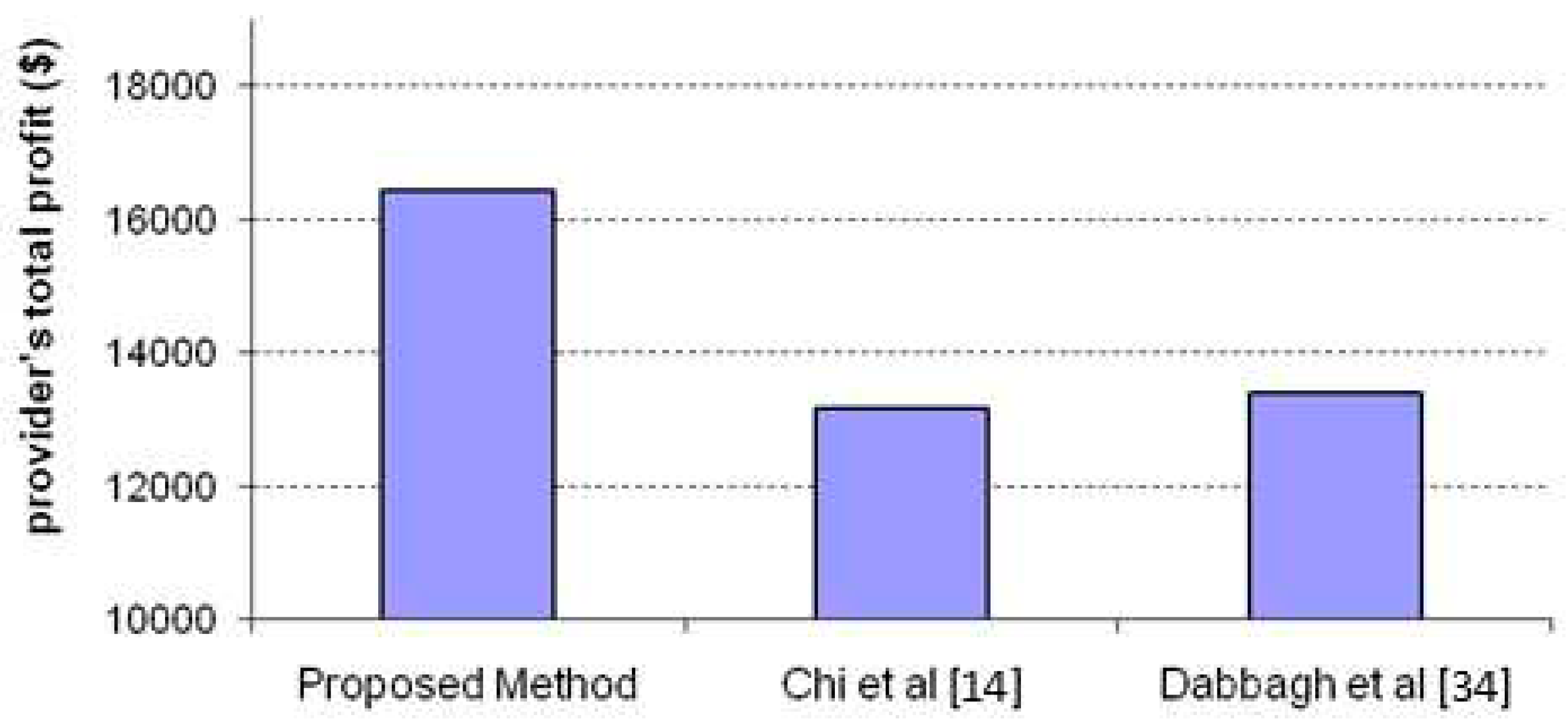
5.2. Evaluation of the proposed method in terms of provider’s profit

Considering conflicts between virtual machines, heterogeneity in resources, and energy consumption costs, helps the broker reduce the operational costs of the cloud provider and increase the success rate in performing users’ requests. As stated in the previous section, the broker takes these parameters into account when constructing the game tree and calculating the players’ utility for each possible action. Paying attention to various aspects when assigning users’ requests to virtual machines and offering a price for that virtual machine not only can increase the cloud provider’s revenue but also its profit. The total revenue of the provider is calculated by the following formula:
R e v e n u e c p = ∑ i = 1 n ( π c p V M i *   , P i *   − P e n a l t y i )
Where n indicates the total number of requests submitted to the system and fulfilled during the simulation time. The cloud provider’s utility ( π c p ) is calculated based on equation 1 and P e n a l t y i represents the financial penalty paid by the cloud for the i t h request if it fails to perform successfully. It is assumed that in case of violating SLA, the provider must refund the total funds received to the user. Since the operating costs of the system can be changed with different policies for mapping and executing requests, the profit of the provider is also calculated by reducing the expenses from revenue (equation 10).
P r o f i t c p = ∑ i = 1 n ( π c p V M i *   , P i *   − P e n a l t y i − E i )
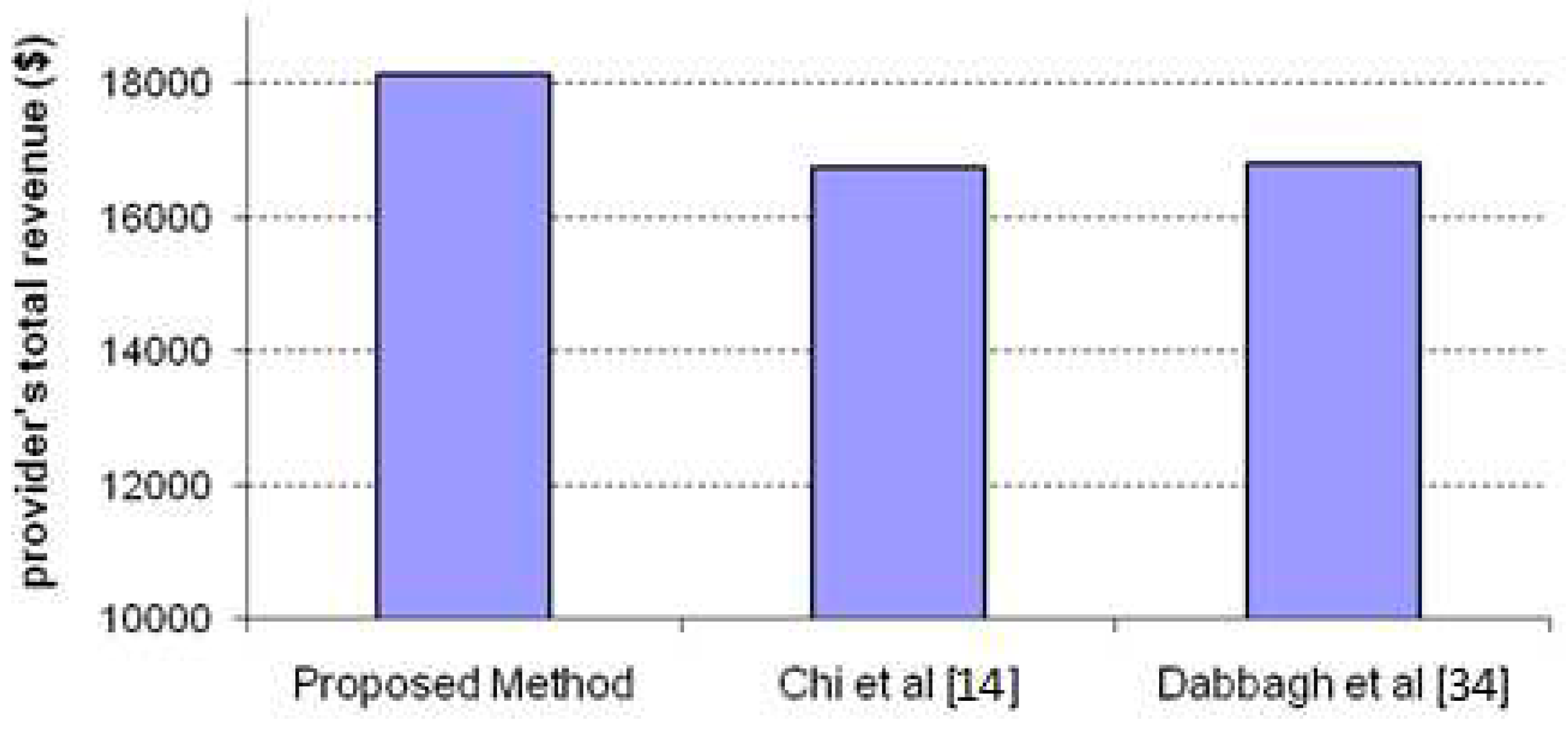
Where parameter E i indicates the expenses corresponding to the energy consumed for performing the i t h request and calculated based on equation 7. Figure 5 and Figure 6 shows the performance of the proposed approach in comparison to the other methods from the viewpoints of the provider’s total revenue and profit.
As can be seen in Figure 6, the proposed method is more successful in performing users’ requests with lower energy consumption. The mapping obtained from the Nash equilibrium point results in reduced energy consumption and sometimes reduced response time to user requests. This leads to more profit for the cloud provider.

5.3. Comparing the number of submitted and unanswered requests

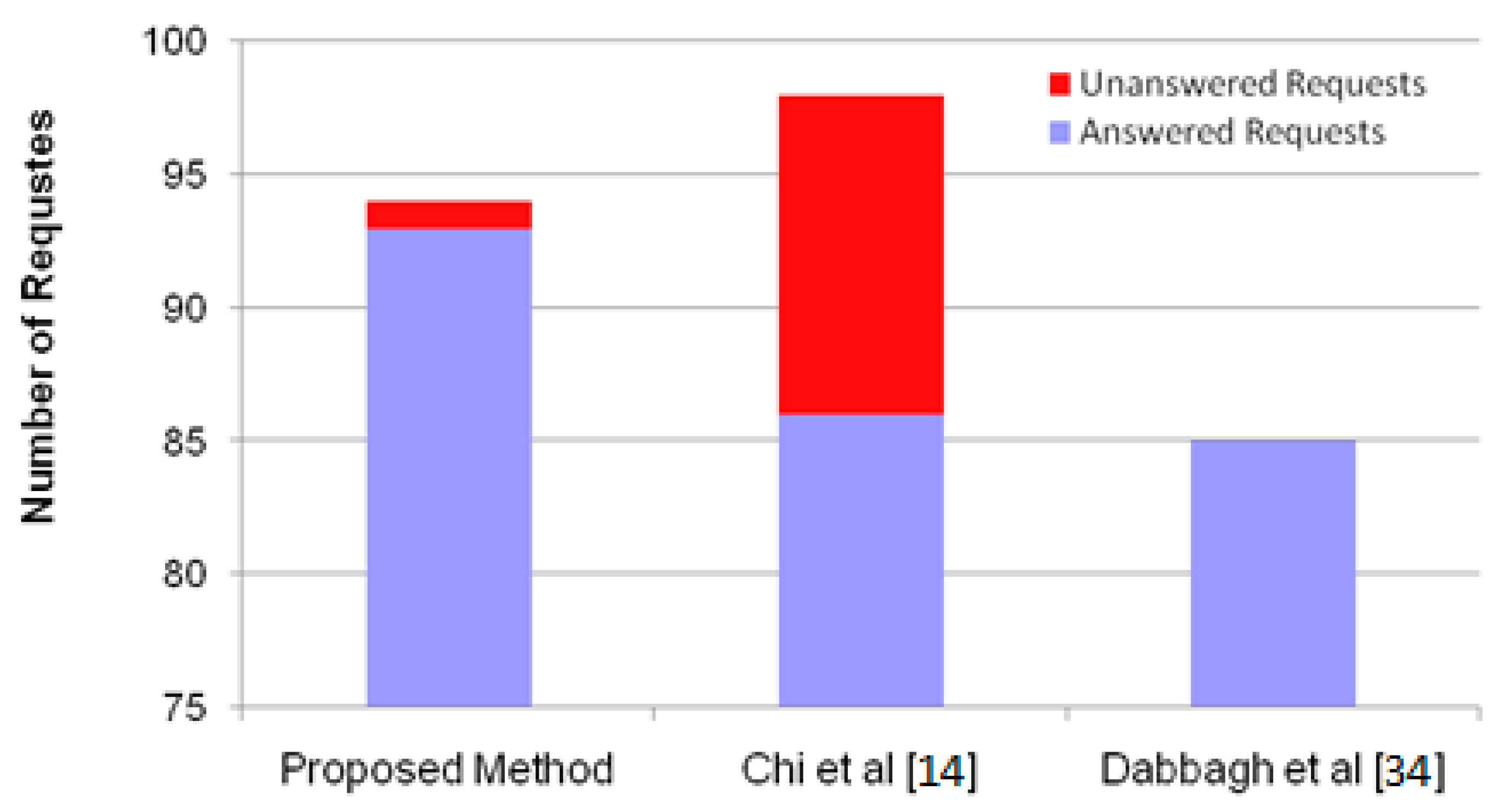
The proposed method has offered a higher price to the users than the method presented in [14] and a lower price than the method presented in [34]. As a result, the number of requests submitted to the system during the simulation period must be a number between the input loads for the other two methods. Considering operational costs in utility functions of the players could be the reason behind this higher price. On the other hand, considering the heterogeneity of hardware resources and conflicts between virtual machines in constructing the game tree, lead to better job mappings and thus resource utilization. Nash equilibrium strategy helps the cloud provider to make the optimal decision in choosing the right virtual machine for the user request and provide it to the user at a reasonable price. Assigning efficient virtual machines to user requests has resulted in more requests being submitted to the system being answered within the simulation interval. Figure 7 shows the total number of submitted and the total number of answered requests during the simulation interval. As it can be seen, the proposed method has the highest number of answered requests in compared to the other competitive methods.

5.4. Comparison under different system loads

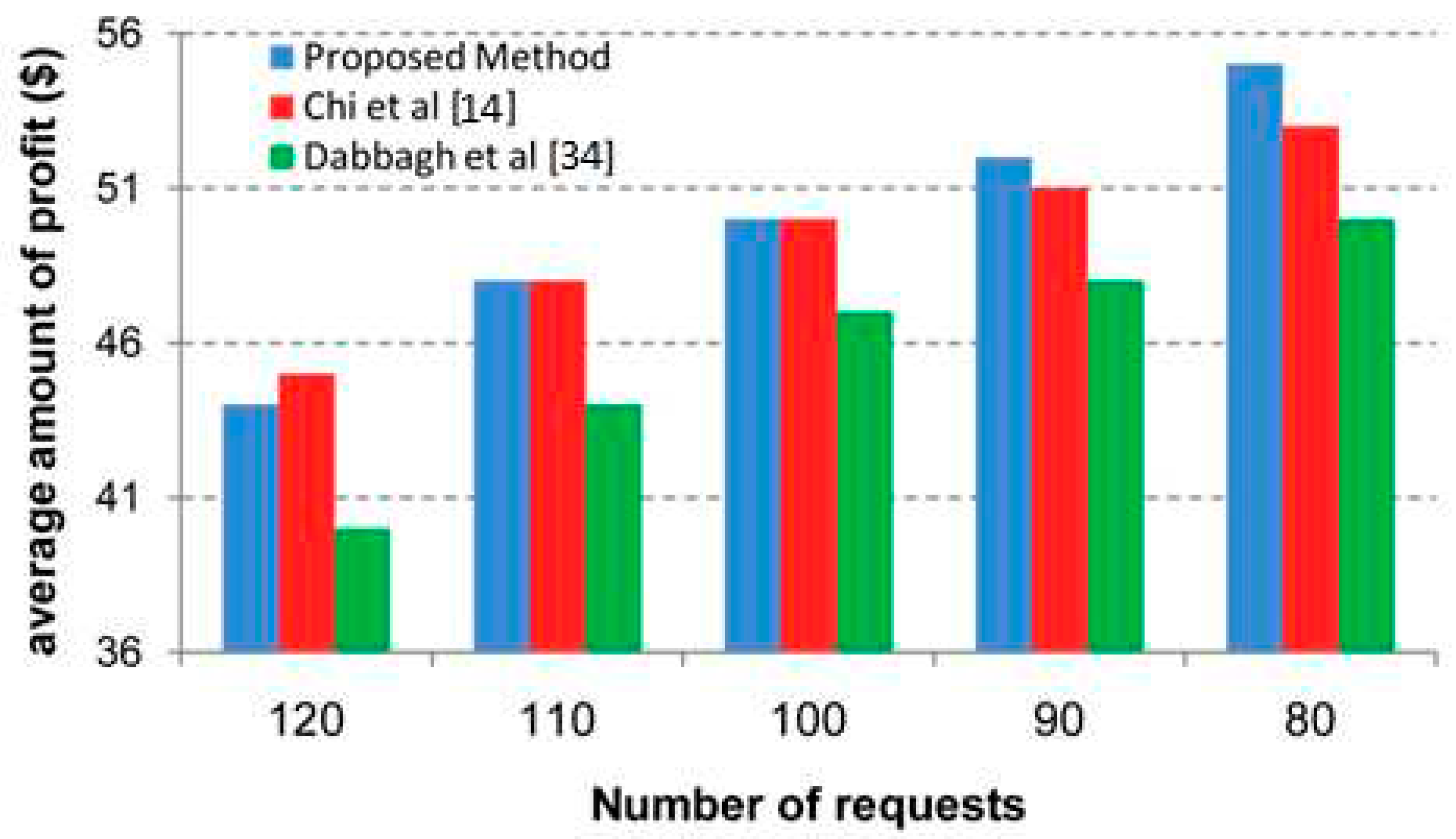
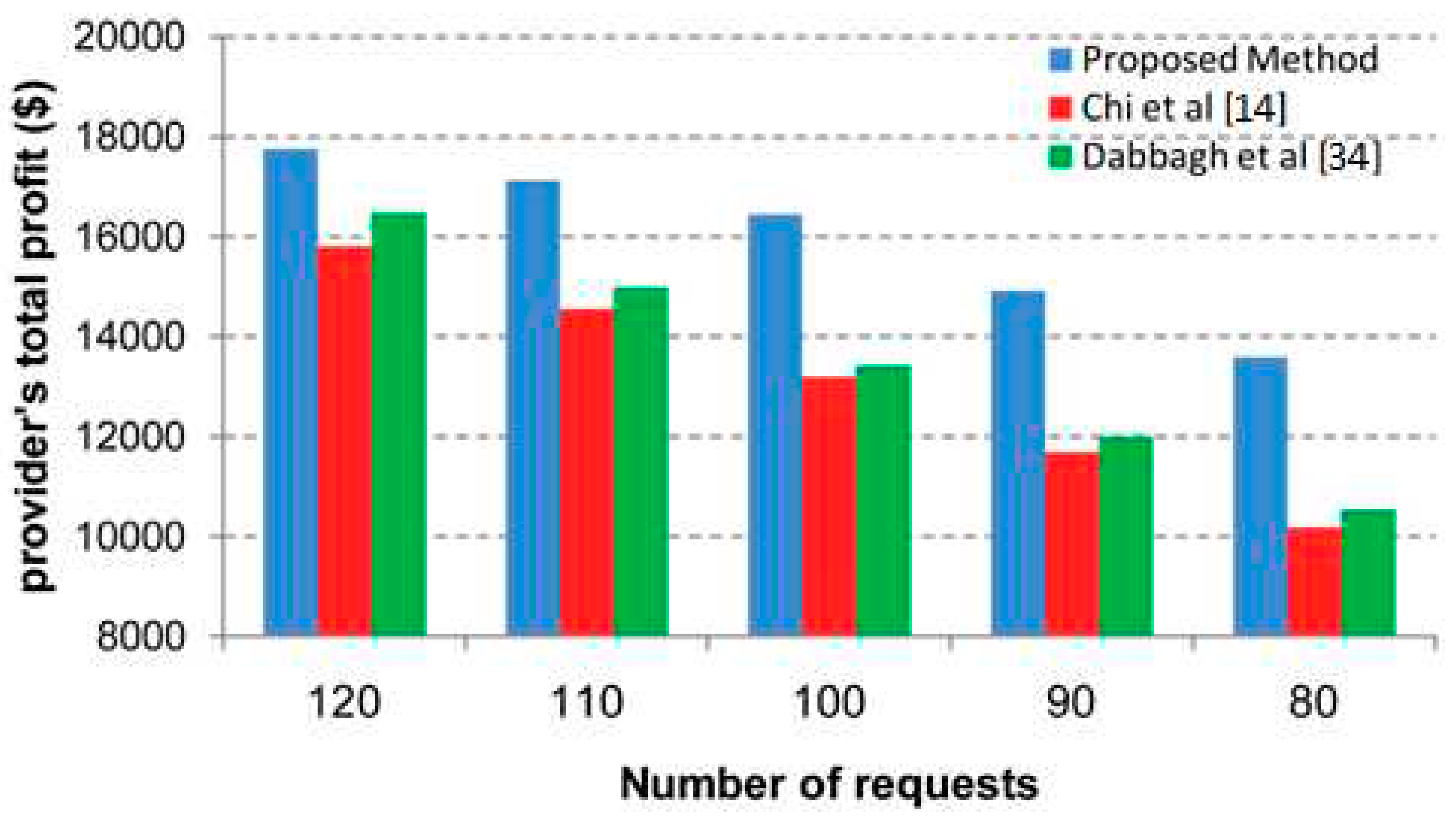
A good pricing algorithm should perform well in different system loads. The algorithm must respond appropriately to the decreases and increases in demand. To simulate various system loads, the number of requests that should be submitted during the simulation period is considered different in different simulation runs. Figure 8 and Figure 9 show the average user profit and total profit of the cloud provider under different system loads, respectively.
As can be seen, the performance of the proposed method is better than the two other methods in terms of both average user profit and total provider profit for different loads. The superiority of the proposed method in lighter loads compared to other competitors is also more evident. The reason for this behavior is that in a light workload, the options ahead to allocate the appropriate resource to a request are more and the maneuverability of the proposed method is higher. Since the proposed method has a more comprehensive view of the factors influencing the finding of a good resource and its appropriate price, compared to the other two methods, increasing the number of options ahead will naturally lead to better performance as expected.

6. Conclusions

Since the advent of clouds, choosing the right price for the services offered by this large-scale computing system has been a challenge. Considering all the various factors such as supply and demand, operating costs such as electricity bills, the possibility of a resource failure and the resulting financial and operational losses, and heterogeneity of resources in terms of the ability to execute different programs in a comprehensive pricing model is an issue that is less common in the past related work.
In this paper, a game theory-based approach is proposed that provides a formal framework for considering different effective factors in solving resource allocation and pricing problems. The proposed approach models these problems in the form of a dynamic game between cloud user and provider. Since it is ultimately the user who decides whether or not to rent a resource from the cloud, we consider the user as the leader of the game and the player who has priority in the decision. Various factors have been tried to be considered in the players' profit functions to help bring the model closer to the real situation. The game tree is constructed and solved by the resource broker who is responsible for the resource allocation and management processes. The simulation results show the superiority of the proposed method in reducing the operating costs for the cloud provider despite providing a reasonable price for renting resources by users compared to previous related methods.

Author Contributions

Conceptualization, H.S. and J.H.j.; methodology, H.S. and J.H.J; software, H.S.; validation, H.S., J.H.J and H.G.; formal analysis, H.S.; investigation, J.H.J; resources, H.G.; data curation, H.S.; writing—original draft preparation, H.S., J.H.J. and H.G; writing—review and editing, H.S. and J.H.J; visualization, H.S.; supervision, H.S.; project administration, J.H.J; funding acquisition, J.H.J. All authors have read and agreed to the published version of the manuscript.

Funding

Mr. Javad Hassannataj Joloudari is grateful for the financial support of MDPI Publisher, which was provided for refereeing in MDPI journals by receiving 20 vouchers.

Data Availability Statement

Data are simulated and generated during the experiment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Teng, F.; Magoulès, F. A new game theoretical resource allocation algorithm for cloud computing. In Advances in Grid and Pervasive Computing: 5th International Conference, GPC 2010, Hualien, Taiwan, 10-13, May 2010; pp. 321-330.
  2. Mazrekaj, A.; Shabani, I.; Sejdiu, B. Pricing schemes in cloud computing: an overview. International Journal of Advanced Computer Science and Applications, 2016, 7, 80-86.
  3. Tang, L.; Chen, H. Joint pricing and capacity planning in the IaaS cloud market. IEEE Transactions on Cloud Computing, 2014 5, 57-70.
  4. Luong, N. C.; Wang, P.; Niyato, D.; Wen, Y.; Han, Z. Resource management in cloud networking using economic analysis and pricing models: A survey. IEEE Communications Surveys & Tutorials, 2017,19, 954-1001.
  5. Cong, P.; Li, L.; Zhou, J.; Cao, K.; Wei, T.; Chen, M.; Hu, S. Developing user perceived value-based pricing models for cloud markets. IEEE Transactions on Parallel and Distributed Systems, 2018, 29, 2742-2756.
  6. Zhao, Y.; Huang, Z.; Liu, W.; Peng, J. ; Zhang, Q. A combinatorial double auction-based resource allocation mechanism with multiple rounds for geo-distributed data centers. In 2016 IEEE International Conference on Communications (ICC) Kuala Lumpur, Malaysia 22-27 may 2016 pp. 1938-1883.
  7. Kumar, D.; Baranwal, G.; Raza, Z.; Vidyarthi, D. P.A survey on spot pricing in cloud computing. Journal of Network and Systems Management, 2018, 26, 809-856.
  8. Parnia Samimi, Youness Teimouri, Muriati Mukhtar,A combinatorial double auction resource allocation model in cloud computing,Information Sciences, 2016, 357 , 201-216.
  9. Baranwal, G.; Vidyarthi, D. P. A fair multi-attribute combinatorial double auction model for resource allocation in cloud computing. Journal of systems and software, 2015, 108, 60-76.
  10. S. A. Tafsiri and S. Yousefi, Combinatorial double auction-based resource allocation mechanism in cloud computing market‏, Journal of Systems and Software, 2018, 137, 322-334.
  11. N. Toosi, K. N. Toosi, K. Vanmechelen, F. Khodadadi, and R. Buyya, "An auction mechanism for cloud spot markets," ACM Transactions on Autonomous and Adaptive Systems (TAAS), 2016, 11, pp. 1-33.
  12. Lučanin, D.; Pietri, I.; Holmbacka, S.; Brandic, I.; Lilius, J. ; Sakellariou, R. Performance-based pricing in multi-core geo-distributed cloud computing. IEEE Transactions on Cloud Computing, 2016, 8, 1079-1092.
  13. Aldossary, M.; Djemame, K. Energy consumption-based pricing model for cloud computing. In 32nd UK Performance Engineering Workshop. September, 2016. pp. 16-27.
  14. Chi, Y.; Li, X.; Wang, X.; Leung, V. C.; Shami, A. A fairness-aware pricing methodology for revenue enhancement in service cloud infrastructure. IEEE Systems Journal, 2015, 11, 1006-1017.
  15. Sharma, B.; Thulasiram, R. K. ; Thulasiraman, P, & Buyya, R. Clabacus: A risk-adjusted cloud resources pricing model using financial option theory. IEEE Transactions on Cloud Computing, 2014, 3, 332-344.
  16. Wu, C.; Toosi, A. N.; Buyya, R.; Ramamohanarao, K. Hedonic pricing of cloud computing services. IEEE Transactions on Cloud Computing, 2018, 9, 182-196.
  17. Qiu, C.; Shen, H.; Chen, L. Towards green cloud computing: Demand allocation and pricing policies for cloud service brokerage. IEEE Transactions on Big Data, 2018, 5, 238-251.
  18. Shang, S.; Jiang, J.; Wu, Y.; Huang, Z.; Yang, G.; Zheng, W. DABGPM: A double auction Bayesian game-based pricing model in cloud market. In Network and Parallel Computing: IFIP International Conference, NPC 2010, Zhengzhou, China, 13-15 September 2010. pp. 155-164.
  19. Do, C. T.; Tran, N. H.; Huh, E. N.; Hong, C. S.; Niyato, D.; Han, Z. Dynamics of service selection and provider pricing game in heterogeneous cloud market. Journal of Network and Computer Applications, 2016; 69, 152–165. [Google Scholar]
  20. Shi, B.; Huang, Y.; Wang, J.; Xiong, S. A game-theoretic analysis of pricing strategies for competing cloud platforms. In 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), 13-16 December 2016, pp. 653-660.
  21. Niu, D.; Feng, C.; Li, B. A theory of cloud bandwidth pricing for video-on-demand providers. In 2012 Proceedings IEEE INFOCOM,25-30 march 2012, pp. 711-719.
  22. Xiao, P.; Tang, Z. Game theory–based resource pricing model in cloud platforms. International Journal of Communication Networks and Distributed Systems, 2015, 14, 256-271.
  23. H. Li, M. H. Li, M. Dong, K. Ota, and M. Guo, "Pricing and repurchasing for big data processing in multi-clouds," IEEE Transactions on Emerging Topics in Computing, 2016, 4, pp. 266-277.
  24. Z. Zhu, J. Z. Zhu, J. Peng, K. Liu, and X. Zhang, "A game-based resource pricing and allocation mechanism for profit maximization in cloud computing," Soft Computing, 2020, 24, 4191-4203.
  25. H. Ye, B. H. Ye, B. Feng, and X. Li, "A game-based approach for cloudlet resource pricing for cloudlet federation," The Journal of Supercomputing, 2023, 79, 1-21.
  26. X. Cao, H. X. Cao, H. Bo, Y. Liu, and X. Liu, "Effects of different resource-sharing strategies in cloud manufacturing: A Stackelberg game-based approach," International Journal of Production Research, 2023, 61, 520-540.
  27. H. Godhrawala and R. Sridaran, "A dynamic Stackelberg game based multi-objective approach for effective resource allocation in cloud computing," International Journal of Information Technology, 2023, 15, 803-818.
  28. Su, K.; Xu, L.; Chen, C.; Chen, W.; Wang, Z. (2015, March). Affinity and conflict-aware placement of virtual machines in heterogeneous data centers. In 2015 IEEE Twelfth International Symposium on Autonomous Decentralized Systems. 25-27 March 2015, pp. 289-294.
  29. Shim, Y. C. (2015). Inter-VM performance interference aware static VM consolidation algorithms for cloud-based data centers. Recent Adv. Electr. Eng, 2015, 18.
  30. Kenga, M. D.; Omwenga O, V. O.; Ogao, P. J. (2017). Energy consumption in cloud computing environments. 2017. [Google Scholar]
  31. Aldossary, M.; Djemame, K.; Alzamil, I.; Kostopoulos, A.; Dimakis, A. ; Agiatzidou, E.Energy-aware cost prediction and pricing of virtual machines in cloud computing environments. Future Generation Computer Systems, 2019, 93, 442-459.
  32. Sutaria, V.; Prasad, V. K.; Bhavsar, M. Fault Prediction and Mitigation in Cloud Computing. International Journal of Advanced Research in Computer Science, 2017, 8 , 1042-1050.
  33. Saadatfar, H.; Fadishei, H.; Deldari, H. Predicting job failures in AuverGrid based on workload log analysis. New Generation Computing, 2012, 30, 73-94.
  34. Dabbagh, M.; Hamdaoui, B.; Guizani, M.; Rayes, A. Exploiting task elasticity and price heterogeneity for maximizing cloud computing profits. IEEE Transactions on Emerging Topics in Computing, 2015, 6, 85-96.
  35. Calheiros, R. N.; Ranjan, R.; Beloglazov, A.; De Rose, C. A.; Buyya, R. CloudSim: a toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Software: Practice and experience, 2011, 4, 23-50.
  36. Koh, Y.; Knauerhase, R.; Brett, P.; Bowman, M.; Wen, Z.; Pu, C. (2007, April). An analysis of performance interference effects in virtual environments. In 2007 IEEE International Symposium on Performance Analysis of Systems & Software 25-27 April 2007, pp. 200-209.
  37. Lee, I. Pricing and profit management models for SaaS providers and IaaS providers. Journal of Theoretical and Applied Electronic Commerce Research, 2021, 16, 859-873.
  38. Lu, Y.; Zheng, X.; Li, L.; Xu, L. D. Pricing the cloud: a QoS-based auction approach. Enterprise Information Systems, 2020, 14, 334-351.
Preprints 94352 g001
Figure 1. The architecture of cloud computing system.
Figure 1. The architecture of cloud computing system.
Preprints 94352 g001
Preprints 94352 g002
Figure 2. The relationship between price and demand.
Figure 2. The relationship between price and demand.
Preprints 94352 g002
Preprints 94352 g003
Figure 3. The tree of the proposed game.
Figure 3. The tree of the proposed game.
Preprints 94352 g003
Preprints 94352 g004
Figure 4. Comparison of the proposed method with related ones from the viewpoint of average profit per user.
Figure 4. Comparison of the proposed method with related ones from the viewpoint of average profit per user.
Preprints 94352 g004
Preprints 94352 g005
Figure 5. Comparison of the proposed method with related methods from the viewpoint of the provider’s total revenue.
Figure 5. Comparison of the proposed method with related methods from the viewpoint of the provider’s total revenue.
Preprints 94352 g005
Preprints 94352 g006
Figure 6. Comparison of the proposed method with related methods from the viewpoint of the provider’s total profit.
Figure 6. Comparison of the proposed method with related methods from the viewpoint of the provider’s total profit.
Preprints 94352 g006
Preprints 94352 g007
Figure 7. Comparison of the proposed method with related methods from the viewpoint of the number of users’ requests that can be met.
Figure 7. Comparison of the proposed method with related methods from the viewpoint of the number of users’ requests that can be met.
Preprints 94352 g007
Preprints 94352 g008
Figure 8. Comparison of the proposed method with related methods under different system loads from the viewpoint of average user’s profit.
Figure 8. Comparison of the proposed method with related methods under different system loads from the viewpoint of average user’s profit.
Preprints 94352 g008
Preprints 94352 g009
Figure 9. Comparison of the proposed method with related methods under different system loads from the viewpoint of the provider’s total profit.
Figure 9. Comparison of the proposed method with related methods under different system loads from the viewpoint of the provider’s total profit.
Preprints 94352 g009
Table 1. Implementation Parameters.
Table 1. Implementation Parameters.
Parameter (Symbol) Definition Value
Preprints 94352 i001
Table 2. A user request example.
Table 2. A user request example.
Request fields Definition Value
Preprints 94352 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated