Prerpints.org logo
Preprint
Article

Fabrication and Characterization of 2D Nonlinear Structures Based on DAST Nanocrystals and SU-8 Photoresist for Terahertz Application

Altmetrics

Downloads

83

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 December 2023

Posted:

19 December 2023

You are already at the latest version

Alerts
Abstract
We demonstrate a method for realization of highly nonlinear optical 4-(4-dimethylaminostyryl)-1-methylpyridinium tosylate (DAST) two-dimensional structures by a double step technique. The desired polymeric structures have been first fabricated by using the multiple-exposure of two-beam interference technique, and the DAST nanoscrystals were then prepared inside the air-voids of these photoresist templates, resulting in nonlinear periodic structures. The nonlinear properties were characterized by optical and scanning microscopies, as well as by second-harmonic generation technique. This nonlinear modulation is very promising for the enhancement nonlinear conversion rates, such as terahertz generation, by using the quasi-phase matching technique.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Within the last ten years, the field of terahertz (THz) science and technology has developed greatly. Many new and promising advances in the technology for the generation, manipulation, and detection of THz radiation have been made. The most important task is the development of the new materials and technology for THz generation and detection [1]. Optical rectification in electro-optical crystals has been demonstrated as the best technique for generating subpicosecond, THz bandwidth radiation [2]. For THz application, the three most important requirements for nonlinear optical crystals are i) high nonlinear coefficient, ii) low absorption of THz irradiation by the crystal, and iii) phase matching between pump and THz waves propagations.
Several groups in the world have examined different nonlinear materials for THz emission by optical rectification. These materials include organic salts such as dimethyl amino 4-N-methylstilbazolium tosylate (DAST) [3], dielectric inorganic electro-optical materials like LiTaO3, and semiconductors such as GaAs and GaP. Among them, DAST is the most efficient THz rectification material [5], due to its large electro-optics (EO) coefficient and its low dielectric constant ( ϵ = 5.2 ), giving rise to a high modulator figure of merit [5]. Indeed, according to data in [6], DAST exhibits a huge second-order nonlinear optical susceptibility χ ( 2 ) = 2020 ± 220 pm/V at λ = 1318 nm and its corresponding electro-optical figure of merit being n 1 3 r 11 = ( 530 ± 60 ) pm/V at λ = 1313 nm. However, phase matching between optical wave and THz radiation propagation, a major factor determining the efficiency and the bandwidth of THz emission from nonlinear crystal, is still a challenge. Actually, only few electro-optical crystals possessing a long coherence length is suitable for THz generation. Most nonlinear materials possess a coherence length in a range of few micrometers to dozens of micrometers, thus limiting the THz generation efficiency. It is necessary to find out a way to solve the problem of phase mismatch in DAST crystals.
Quasi-phase matching (QPM) is a technique which compensates the phase mismatch of nonlinear processes by creating a grating of spatially modulated nonlinear properties with a period corresponding to twice of coherence length. Typically, the QPM structures have periods in the range of few micrometers to dozens micrometers, which is quite easy to be realized today. In a quasi-phase matched structure, the interaction length between THz and pump pulses can be dramatically extended to centimeters range. For example, QPM structures were used for the generation of THz wave packets with tunable central frequency [7] or for the generation of multicycle narrow-bandwidth THz radiation based on phase synchronous optical rectification [8]. It is clear that nonlinear gratings or QPM structures may provide an efficient control of THz generation.
Conventionally, the QPM effect is obtained in a nonlinear material in which the nonlinear property is modulated between negative and positive signs (+/- QPM). However, this is not easy to realize in practice, in particular for three-dimensional (3D) QPM structures. An alternative way to achieve the same effect is to combine the nonlinear material with a linear material, corresponding to a periodical modulation of χ ( 2 ) between zero and non-null value (+/0 QPM). The theoretical model of this particular QPM structure was presented in our recent work [9] for a general nonlinear optical effect. Very few works have been demonstrated to realize these +/0 QPM structures. For example, one of our old works [10] demonstrated a layer-by-layer direct laser writing technique to obtain a polymeric 3D QPM structure. This technique has been applied for copolymer nonlinear material requiring an additional poling technique, since the copolymer is centrosymmetric. It could be applied for patterning DAST nanocrystals as well. However, this technique requires spin-coating of different materials layer by layer and thus very time consuming, and imprecise in term of periodicity. Recently, two other groups experimentally demonstrated a direct fabrication by employing a femto-second laser based bleaching technique [11,12] in LiNbO3 material. We also applied this technique to patterning DAST nanoscrystals structures, as shown in reference [15]. This direct technique allows to solve the problem of imprecision, but again, it does not produce a large QPM structure in a short time.
There are different methods to realize QPM structures based on DAST nonlinear material. However, DAST requires a customized approach, because DAST material is usually fabricated in the form of micro- and nanoparticles. By using the assembling of multiple layer technique, DAST/SiO2 multilayers has been proposed for THz generation [13]. We can see that QPM elements based on DAST and SiO2 micrometer-size layers can be effective for THz generation, but their fabrication is still a great challenge. In our recent work, we have demonstrated a way to obtain desired DAST structures by mixing DAST nanocrystals with a passive polymer matrix. Indeed, we have successfully obtained a nonlinear nanocomposite based on DAST nanocrystals embedded in a PMMA polymer matrix and showed that the nonlinear conversion efficiency doesn’t depend on the DAST crystals size [14]. We have also fabricated 2D grating structures by photobleaching DAST nanocrystals using a technique called one-photon absorption based direct laser writing [15]. The last one is very efficient but rather slow and therefore time consuming. Very recently, we proposed an alternative method by combining a mask lithography and thermal annealing to produce + / 0 QPM DAST structure [16]. Highly efficient THz generation by this DAST nanocomposite is demonstrated upon excitation by femtosecond pulses and generation by the method of optical rectification. However, since the mask technique was used, it is not suitable to adjust the structures configurations and periodicity, and also it is not possible to produce small periods and 3D structures.
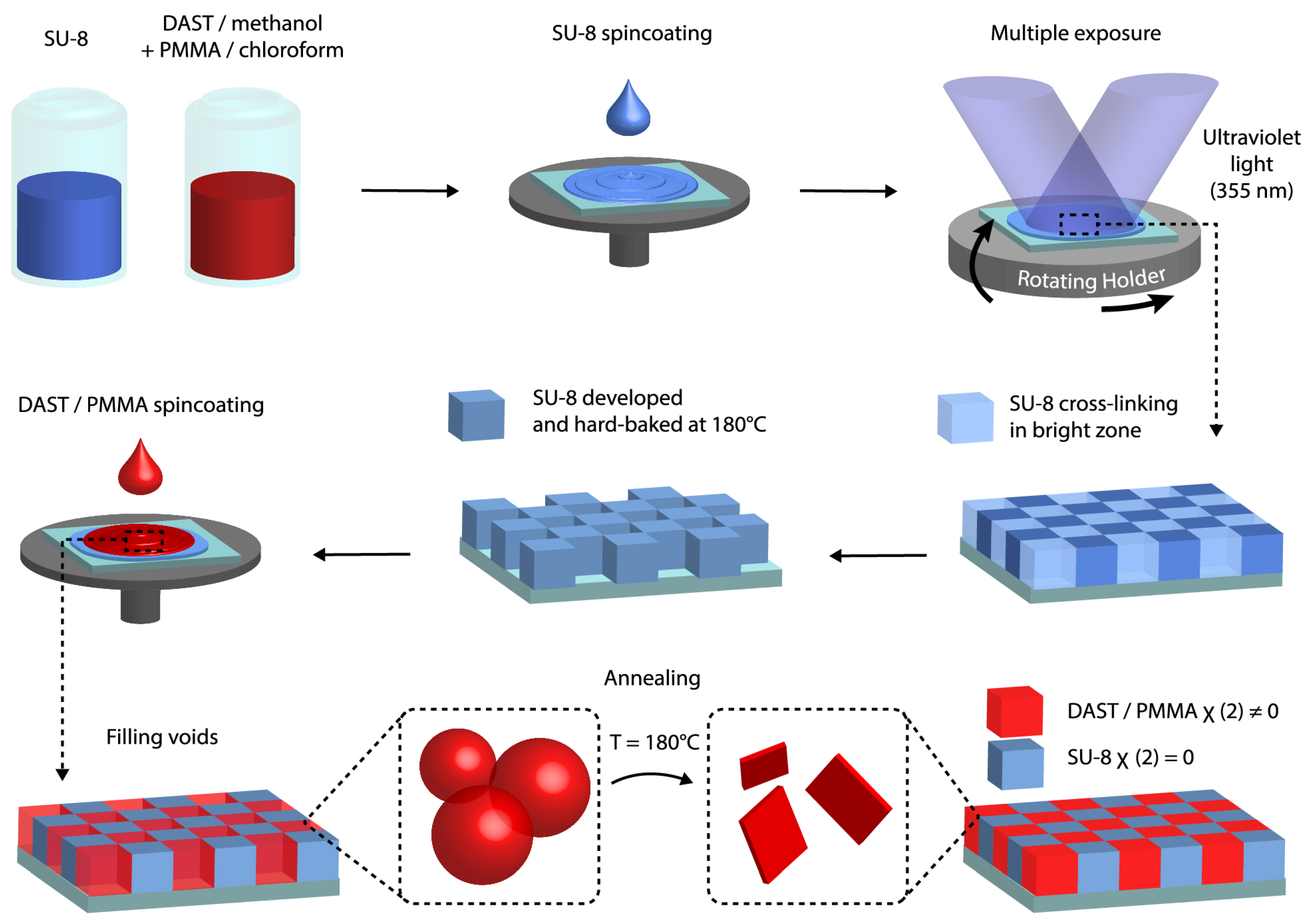
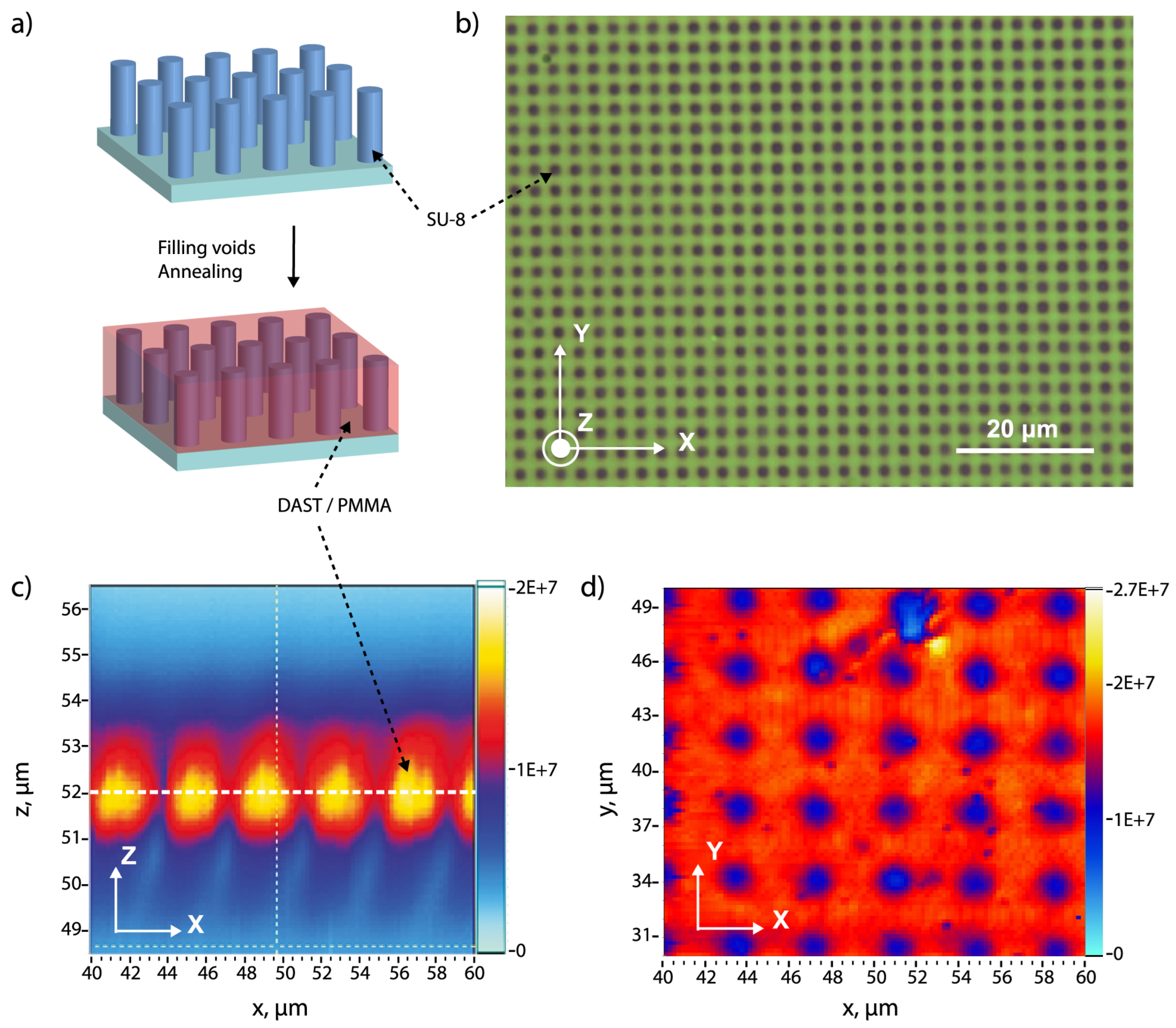
In this work, we demonstrated an alternative way to fabricate DAST/polymer large structures in a short time, which is based on filling a holographically fabricated SU-8 template by a DAST-PMMA composite. Figure 1 shows the fabrication process of desired DAST/polymer structures. First, this method consists in the preparation of the SU-8 template by an interference technique [17], which has many advantages such as rapidity, simplicity, large and uniform structures. Second, the DAST-PMMA composite is spin-coated into SU-8 template and thermally annealed to remove the solvent and to induce DAST crystallization. The final result is a linear/nonlinear structure having a controllable period and desirable configurations, which is equivalent to a + / 0 QPM structure, and which could be useful for THz generation. We demonstrated the nonlinear properties of these fabricated structures by measuring the second-harmonic generation (SHG) signals.

2. Theory and numerical calculations of two-beam interference technique

2.1. Theory of two-beam interference

Fabrication of one-, two- and three-dimensional (1D, 2D, and 3D) micro and nano-structures is of great interest nowadays. Multi-beam interference technique allows getting different photoresist-based structures depending on the number of laser beams and their arrangement. The common advantage for all holographic techniques is a parallel fabrication process, which results in uniform structures over large area and in a short fabrication time. However since multiple laser beams should be used, the fabrication setup becomes quite complicated [18,19]. Two-beam interference technique processes many advantages because of its simplicity [17]. In particular, this technique provides high contrast between the minimal and maximal intensities of interference pattern because of identical polarization of two laser beams in interference area. Furthermore, multi-exposure of two-beam interference pattern allows to realize various structures with different configurations in multi-dimensions. In this work, we employed this two-beam interference technique to realize DAST nonlinear photonic structures.
Figure 2a illustrates the schematic setup of the two-beam interference technique. A lenses system was used to enlarge the initial laser beam and to get large and uniform working area. The extended beam is divided by a prism into two beams of the same profiles and intensities, which are then deviated by two reflecting mirrors towards the photoresist where they interfere, resulting in an intensity modulation. The electric fields of two laser beams can be written as:
E 1 ( r , t ) = Re [ E 01 e i ( k 1 . r − ω t ) ] ,
E 2 ( r , t ) = Re [ E 02 e i ( k 2 . r − ω t ) ] ,
where k1 and k2 are the wave vectors of two laser beams, r is the position vector in the overlapping space, and E01 and E02 are the amplitudes of electric fields. Sum of the electric field of individual plane waves is modulated (interference) at overlapping area:
E T ( r , t ) = E 1 ( r , t ) + E 2 ( r , t ) .
The interference intensity distribution of the resultant wave is given by
I T ( r , t ) = 〈 E T * ( r , t ) . E T ( r , t ) 〉 t ,
where 〈 . . . 〉 t represents the time average of the resultant electric field. The interference of two laser beams is a 1D pattern, whose period ( Λ ) is calculated by
Λ = λ 2 sin θ ,
where θ is a half-angle between two laser beams and λ is the wavelength of the laser beams. In our case, we assume that the polarizations of two beams are the same (vertical direction) for all values of θ -angle allowing to obtain 1D structure with maximal and same contrast for any periodicity. According to the equation 5, the structure period can be adjusted from as small as λ / 2 , i . e . few hundreds of nanometers, to as large as we want. It means that this is fully adaptable to realize the QPM structures with desired period, which is twice of the coherence length of the nonlinear crystal and usually in the range of micrometers.
As it is shown in the Figure 2a and Figure 3, the photoresist sample is fixed on a rotating holder. Both rotation angles, α and β , influence resultant 1D structure. Therefore, we realize a rotation of the 1D interference pattern around two axes, z by an angle α , and y by an angle β , as seen in Figure 3b,c. The corresponding rotation matrices are:
R z ( α ) = cos α − sin α 0 sin α cos α 0 0 0 1 ,
R y ( β ) = cos β 0 sin β 0 1 0 − sin β 0 cos β .
In this case, the resultant intensity distribution becomes:
I α , β = 2 E 0 2 cos 2 [ k z sin θ sin β + k cos θ cos β ( x cos α + y sin α ) ] ,
where |E01|=|E02|= E 0 .
If a multiple-exposure of the two-beam interference pattern is applied, the total intensity from all exposures is calculated by:
I multiple = ∑ i I α i , β i ,
where i = 1 , 2 , 3 , . . represent the number of exposures realized at corresponding α i and β i angles.

2.2. Numerical calculations

By using personal MATLAB codes, we simulated the resultant structures for different exposures with different parameters. If α and β are equal to zero and only one expose is applied, it is possible to get a simple 1D structure as shown in Figure 3d. Additional exposes with β = 0 and α ≠ 0 provides 2D structure as shown in Figure 3e. The configuration of 2D structures depends on the number of exposures and the rotation α –angle. For example, with only two exposures, a 2D square structure is obtained with α = 0 ∘ and α = 90 ∘ and a 2D hexagonal structure is obtained with α = 0 ∘ and α = 60 ∘ . 2D quasi-periodic structures can be also created by this way with more than three exposures. One more rotation by a β –angle leads to fabrication of 3D structures, as shown in Figure 3f. Here again, the two-beam interference technique with multiple-exposure allows to obtain any 3D structure on demand [20], depending on the number of exposures and the rotation α and β angles.
One of the advantages of the interference technique is that it allows to control the filling factor of fabricated structures. Indeed, manipulations with exposure time or power of the laser beam give a precise doses control. It leads to possibility to fabricate variety of structures from so-called “cylinders” (Figure 4a) to “air holes” (Figure 4b). The longer exposure time the more photoresist become cross-linked (in case of negative SU-8 photoresist), resulting in “air holes” structure. In contrast, short exposure time or less power results in separate cylinders. Controlling the filling factor is thus to get better efficiency for different QPM orders [9].
In this work, we will demonstrate the idea by simply fabricating the 2D periodic structures and characterization of their SHG effect.

3. Experimental section

3.1. Preparation of polymeric template

SU-8 2002 (Micro. Chem. Corp.) was spin-coated onto glass substrates with a thickness of 2 μ m. The sample was soft baked at 65 ∘ C for 1 min and then at 95 ∘ C for 2 min to remove the residual solvent. For the preparation of multi-dimensional (1D, 2D and 3D) periodic structures, we have used a multiple-exposure two-beam interference method. For that, a continuous-wave (CW) UV laser (Cobalt) with λ = 355 nm was used, as shown in Figure 2a. After light exposure, the sample was post baked on a hot plate at 95 ∘ C for 5 min. The sample was then developed by a SU-8 developer for 4 min, and rinsed by isopropanol and DI water. Finally, the sample was hard baked for 40 min at 180 ∘ C. This annealing of SU-8 matrix at high temperature is needed to remove residual solvents for proper environment for further DAST crystallization.

3.2. Preparation of DAST/PMMA solution

PMMA (Plexiglas® V045) was dissolved in chloroform (CL0218 Scharlau) and DAST (CAS:80969-52-4 Genolite biotek) was dissolved in methanol (322415 Aldrich). The DAST mass is equal to 2% of the PMMA mass, and DAST + PMMA is 15% of mass in chloroform. The amount of methanol was calculated from the solubility limit of DAST in methanol at room temperature [21]. Dissolved DAST was added into PMMA solution and was stirred together to achieve a DAST/PMMA solution with high homogeneity.

3.3. Mechanism of crystallization

The formation of nanocrystals in PMMA is based on DAST aggregation, upon which the size of particles is limited by the diffusion of material through the viscous polymer solution. Both solvents used for PMMA and DAST have close boiling temperatures and relatively close vapor pressures. At the beginning of the process, PMMA and DAST are dissolved in the mixture of two solvents. The formation of the PMMA matrix and DAST nanocrystals in the mixture starts with centrifugation and terminates after complete evaporation of the solvent during annealing. First, the DAST/PMMA composite was dropped on the SU-8 template and spin-coated at a low speed rate to remove extra solution from the top. It forms amorphous DAST particles distributed in PMMA. Second, during annealing at elevated temperature of 180 ∘ C for 30 min amorphous particles transform into noncentrosymmetric crystalline structure. The mechanism of the formation of DAST crystals in the PMMA matrix and the effect of the synthesis parameters on the crystallite size were considered in detail in our previous works [14,16,22].

3.4. Sample characterization

The linear and nonlinear properties of fabricated samples were characterized by different optical instruments, such as optical microscope, electron scanning microscope, as well as confocal laser scanning microscope. Figure 2b shows a laser system used to characterize both linear and nonlinear properties of DAST periodic structures. Indeed, DAST crystals can absorb and emit the light as a fluorescence emitter. For that the sample was excited by a CW 532-nm Oxxius frequency-doubled Nd-YAG laser (maximum power: 300 mW, coherence length: 300 m; pointing stability: 0.005 mrad/C). DAST crystal also possesses a strong nonlinear response. In our case, the second-harmonic generation (SHG) signal of DAST nanocrystal was demonstrated by exciting the sample by a pulsed 1064 nm laser (maximum averaged power: 80 mW; pulse duration: 1 ns, repetition rate: 24.5 kHz). These two lasers, 532 nm and 1064 nm, are perfectly aligned in front of the objective lens (OL), and were used alternatively, depending on the desired measurement. The laser beam is focused into the sample by a high numerical aperture OL. The fluorescent or SH signals were detected by the OL and sent back to the avalanche photodiode (APD), after filtering out the excitation light beam. By scanning the focusing beam (movement of the piezoelectric translator (PTZ)), we can obtain a color map of fluorescent or SH signals, which confirm the creation of periodic linear/nonlinear patterns. The emission spectra, fluorescence or SHG, were also analyzed by using a spectrometer.

4. Results and discussion

To demonstrate the idea of our proposal, we fabricated different 2D SU-8 templates by using the multiple-exposure two-beam interference technique with a period of 3 μ m. The fabrication of 2D structure depends on the number of exposures and on sample orientation with respect to each exposure [17]. For example, two mutually perpendicular positions of the sample allowed us to fabricate 2D square structures, as shown in Figure 5b. By using a modest exposure dose (2,1 mW/cm2 per interference beam and 2 seconds for each exposure), this fabricated structure is made of SU-8 pillars, as modelling by the simulation, which is shown in Figure 5a.
Figure 5c–d shows the fluorescence mapping image of the final sample, after filling the air-areas of the SU-8 template by the DAST nanocrystals. It is well seen that SU-8 pillars with a weak fluorescence signal are surrounded by DAST/PMMA composite, where DAST crystals show a fluorescence quantum yield of 14 − 20 % [23] and provide a strong fluorescence signal. By scanning the sample along transverse and longitudinal directions, we obtain complete information, i . e . 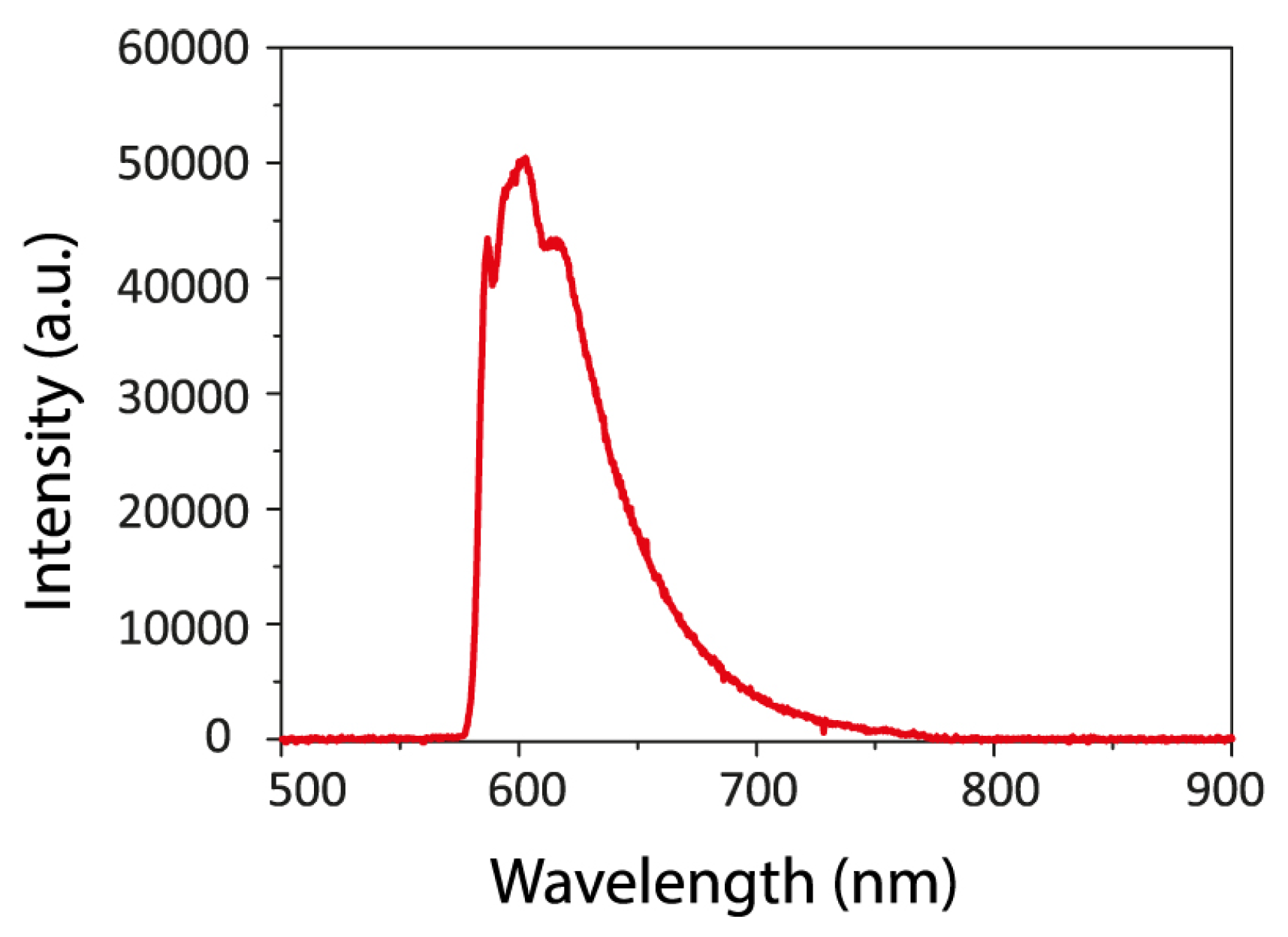the structure thickness and periodicity. The sample thickness agrees well with the value measured by a profilometer, and the structure period is also very consistent with the designed structure. The fluorescence spectrum of DAST/PMMA area (Figure 6) shows typical fingerprint of DAST crystals with noncentrosymmetric “red-green” form [24].
Similar to the fluorescence experiment, when using a 1064 nm pulsed laser, we obtained the SHG mapping image of corresponding sample. Figure 7 shows the SHG wavelength and mapping image. A clear peak at 532 nm was obtained as a proof of the nonlinear property (SHG) of the DAST nanocrystals. Figure 7b shows that the SH signal is very high from DAST nanocrystals, as compared to the weak signal from SU-8 pillars. Thus, a periodic linear/nonlinear microstructure has been demonstrated by this scanning method. The advantage of this structure as compared to those fabricated by other methods [15] is that there exists a clear border between linear (SU-8 photoresist) and nonlinear (DAST nanocrystal) responses, and the structure is also very large, since it was realized by the interference method, for which the structure area depends on the diameter of the interference laser beam. Unfortunately, we cannot realize QPM measurements with these samples since the film thickness is only 2 μ m. However, this work demonstrates that the combination of interference template and thermal annealing method is an excellent way to obtain rapidly large QPM structures. We expect to investigate this method for 3D QPM, and apply it for efficient THz generation.

5. Conclusions

In this work, we demonstrated a novel method to realize large nonlinear QPM structures for efficient nonlinear conversion. The proposed method is based first on SU-8 template preparation by a conventional interference method. Then a PMMA-DAST solution was deposited by spin coating and DAST nanocrystals were formed in the air voids of SU-8 template via the thermal annealing method. The nonlinear structure was characterized by SHG and fluorescence 3D microscopy. Mapping results evidences the formation of red crystalline form of DAST nanocrystals grown in holes of SU-8 matrix, forming well delimited periodic nonlinear domains which open interesting perspective for QPM-based nonlinear applications of these structures, such as THz emission by optical rectification.

Author Contributions

Funding from Russian Foundation for Basic Research project N∘18-52-16014.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. S.S. Dhillon, M.S. Vitiello, E.H. Linfield, A. G. Davies, M.C. Hoffmann, J. Booske, C. Paoloni, M. Gensch, P. Weightman, G.P. Williams, E. Castro-Camus, D. R. S. Cumming, F. Simoens, I. Escorcia-Carranza, J. Grant, S. Lucyszyn, M. Kuwata-Gonokami, K. Konishi, M. Koch, C. A. Schmuttenmaer, T. L. Cocker, R. Huber, A. G. Markelz, Z. D. Taylor, V. P. Wallace, J. A. Zeitler, J. Sibik, T. M. Korter, B. Ellison, S. Rea, P. Goldsmith, K. B. Cooper, R. Appleby, D. Pardo, P. G. Huggard, V. Krozer, H. Shams, M. Fice, C. Renaud, A. Seeds, A. Stöhr, M. Naftaly, N. Ridler, R. Clarke, J. E. Cunningham, and M. B. Johnston. The 2017 terahertz science and technology roadmap. J. Phys. D: Appl. Phys. 2017, 50, 043001. [CrossRef]
  2. L. Xu, X.-C. Zhang, and D. H. Auston. Terahertz beam generation by femtosecond optical pulses in electro-optic materials. Appl. Phys. Lett. 1992, 61, 1784 –1992. [CrossRef]
  3. C. P. Yakymyshyn, K. R. Stewart, E. P. Boden, S. R. Marder, J. W. Perry, and W. P. Schaefer. Second-order non-linear optical properties of 4n-methylstilhazolium tosylate salts. Appl. Phys. Lett. 1992, 61, 1784 –1992. In Organic Materials for Non-linear Optics II; R. A. Hann, D. Bloor, Eds.; Royal Society of Chemistry, London, UK, 1991; pp. 108–114.
  4. A. Schneider and P. Gunter. Spectrum of Terahertz Pulses from Organic DAST Crystals. Ferroelectrics 2005, 318, 83–88. [CrossRef]
  5. F. Pan, G. Knopfle, Ch. Bosshard, S. Follonier, R. Spreiter, M. Wong, and P. Gunter. Electro-optic properties of the organic salt 4-N,N-dimethylamino-4’-N’-methylstilbazolium tosylate. Appl. Phys. Lett. 1996, 69, 13–15.
  6. B. Ruiz, M. Jazbinsek, and P. Gunter. Crystal Growth of DAST. J. Crystal Growth Design 2008, 8, 4173–4184.
  7. K. L. Vodopyanov, M. M. Fejer, X. Yu, J. S. Harris, Y.-S. Lee, W. C. Hurlbut, V. G. Kozlov and D. Bliss, and C. Lynch. Terahertz-wave generation in quasi-phase-matched GaAs. Appl. Phys. Lett. 2006, 89, 141119. [CrossRef]
  8. Y.-S. Lee, W. C. Hurlbut, K. L. Vodopyanov, M. M. Fejer, and V. G. Kozlov. Generation of multicycle terahertz pulses via optical rectification in periodically inverted GaAs structures. Appl. Phys. Lett. 2006, 89, 181104. [CrossRef]
  9. T. N. Pogosian and N. D. Lai. Theoretical investigation of three-dimensional quasi-phase-matching photonic structures. Phys. Rev. A 2016, 94, 063821. [CrossRef]
  10. D. B. Do, J. H. Lin, N. D. Lai, H. C. Kan, and C. C. Hsu. Fabrication of three-dimensional polymer quadratic nonlinear grating structures by layer-by-layer direct laser writing technique. Appl. Opt. 2011, 50, 4664–4670. [CrossRef]
  11. T. Xu, K. Switkowski, X. Chen, S. Liu, K. Koynov, H. Yu, H. Zhang, J. Wang, Y. Sheng, and W. Krolikowski, Three-dimensional nonlinear photonic crystal in ferroelectric barium calcium titanate. Nature Photonics 2018, 12, 591–595. [CrossRef]
  12. D. Wei, C. Wang, H. Wang, X. Hu, D. Wei, X. Fang, Y. Zhang, D. Wu, Y. Hu, J. Li, S. Zhu, and M. Xiao, Experimental demonstration of a three- dimensional lithium niobate nonlinear photonic crystal, Nature Photonics 2018, 12, 596–600. [CrossRef]
  13. A. G. Stepanov, L. Bonacina, and J. P. Wolf. DAST/SiO2 multilayer structure for efficient generation of 6 THz quasi-single-cycle pulses via cascaded optical rectification. Opt. Lett. 2012, 37, 2439–2441.
  14. T. N. Pogosian, I. Y Denisyuk, and N. D. Lai. The Influence of Dimensional Parameters of DAST Nanocrystals on Their Linear and Nonlinear Optical Parameters. Optics and Spectroscopy 2019, 126, 262–264. [CrossRef]
  15. T. N. Pogosian, I. Y. Denisyuk, N. D. Lai, and I. Ledoux-Rak. Photobleaching of Submicron DAST Crystals in a PMMA Film by Direct Laser Writing. Optics and Spectroscopy 2019, 127, 735–737. [CrossRef]
  16. I. Denisyuk, I. Ozheredov, M. Fokina, I. Ignateva, and A. Sinko. Terahertz Properties of Polymers for 2D Nonlinear Grating Formation. J. Infrared, Millimeter, and Terahertz Waves 2022, 43, 972–982. [CrossRef]
  17. N. D. Lai, W. P. Liang, J. H. Lin, and C. C. Hsu. Rapid fabrication of large-area periodic structures containing well-defined defects by combining holography and mask techniques. Opt. Express 2005, 13, 9605–9611. [CrossRef]
  18. T. Kondo, S. Matsuo, S. Juodkazis, V. Mizeikis, and H. Misawa. Multiphoton fabrication of periodic structures by multibeam interference of femtosecond pulses. Appl. Phys. Lett. 2003, 82, 2758–2760. [CrossRef]
  19. Y. C. Zhong, S. A. Zhu, H. M. Su, H. Z. Wang, J. M. Chen, Z. H. Zeng, and Y. L. Chen. Photonic crystal with diamondlike structure fabricated by holographic lithography. Appl. Phys. Lett. 2005, 87, 061103. [CrossRef]
  20. N. D. Lai, J. H. Lin, D. B. Do, W. P. Liang, Y. D. Huang, T. S. Zheng, Y. Y. Huang, and C. C. Hsu. Fabrication of two- and three-dimensional photonic crystals and photonic quasi-crystals by interference technique. Chapitre 12 of the book “Holography, Research and Technologies”, INTECH, 253–278 (2011).
  21. T. Thomas, J. V. Ramaclus, F. P. Mena, E. Mosquera, P. Sagayaraj, and E. A. Michael. Influence of oleic acid on the nucleation and growth of 4-N,N-dimethylamino-934-N-methyl-stilbazoliumtosylate (DAST) crystals. CrystEngComm 2015, 17, 1989–1996.
  22. T. Pogosian, T. N. A. Mai, I. Denisyuk, N. D. Lai. Synthesis and nonlinear optics characterization of DAST submicron crystals in polymerized thin films.Proc. SPIE 10681, Micro-Structured and Specialty Optical Fibres V, 106811A (2018).
  23. A. K. Bhowmik, J. Xu, and M. Thakur. Polarized optical absorption and photoluminescence measurements in single-crystal thin films of 4’-dimethylamino-N-methyl-4-stilbazolium tosylate. Appl. Phys. Lett. 1999, 75, 3291. [CrossRef]
  24. R. Macchi, E. Cariati, D. Marinotto, D. Roberto, E. Tordin, R. Ugo, R. Bozio, M. Cozzuol, D. Pedron, and G Mattei. Stable SHG from in situ grown oriented nanocrystals of ((E)-N,N-dimethylamino-N’-methylstilbazolium)(p-toluenesulfonate) in a PMMA film . J. Mater. Chem. 2010, 20, 1885–1890.
Preprints 93719 g001
Figure 1. Fabrication process of +/0 QPM structure by filling voids of a photoresist template with DAST nonlinear material. The template is fabricated by the multiple-exposure two-beam interference technique. The DAST nanocrystals are obtained by the thermal annealing method.
Figure 1. Fabrication process of +/0 QPM structure by filling voids of a photoresist template with DAST nonlinear material. The template is fabricated by the multiple-exposure two-beam interference technique. The DAST nanocrystals are obtained by the thermal annealing method.
Preprints 93719 g001
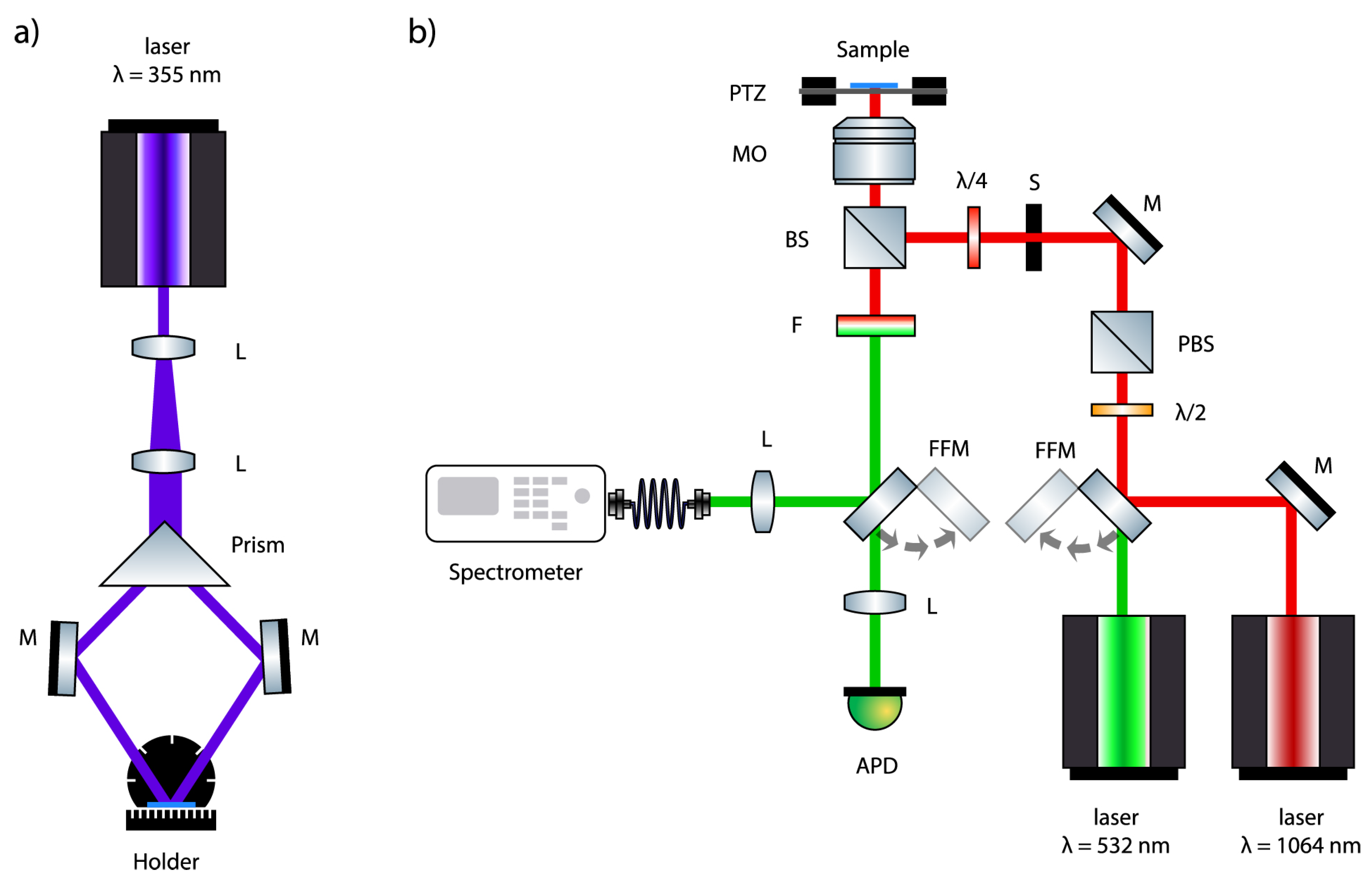
Preprints 93719 g002
Figure 2. (a) Two-beam interference setup used for the fabrication of multidimensional polymeric templates. L: lenses, M: mirrors. Sample is placed in a holder which can rotate in two dimensions for multiple exposures; (b) Confocal laser scanning setup used for the characterization of QPM structures. PZT: piezoelectric translator, MO: microscope objective, λ / 4 : quarter-wave plate, λ / 2 : half-wave plate, BS: beam splitter, PBS: polarizing beam splitter, M: mirror, FFM: flip-flop mirror, S: electronic shutter, L: lens, F: infrared filter, APD: avalanche photodiode.
Figure 2. (a) Two-beam interference setup used for the fabrication of multidimensional polymeric templates. L: lenses, M: mirrors. Sample is placed in a holder which can rotate in two dimensions for multiple exposures; (b) Confocal laser scanning setup used for the characterization of QPM structures. PZT: piezoelectric translator, MO: microscope objective, λ / 4 : quarter-wave plate, λ / 2 : half-wave plate, BS: beam splitter, PBS: polarizing beam splitter, M: mirror, FFM: flip-flop mirror, S: electronic shutter, L: lens, F: infrared filter, APD: avalanche photodiode.
Preprints 93719 g002
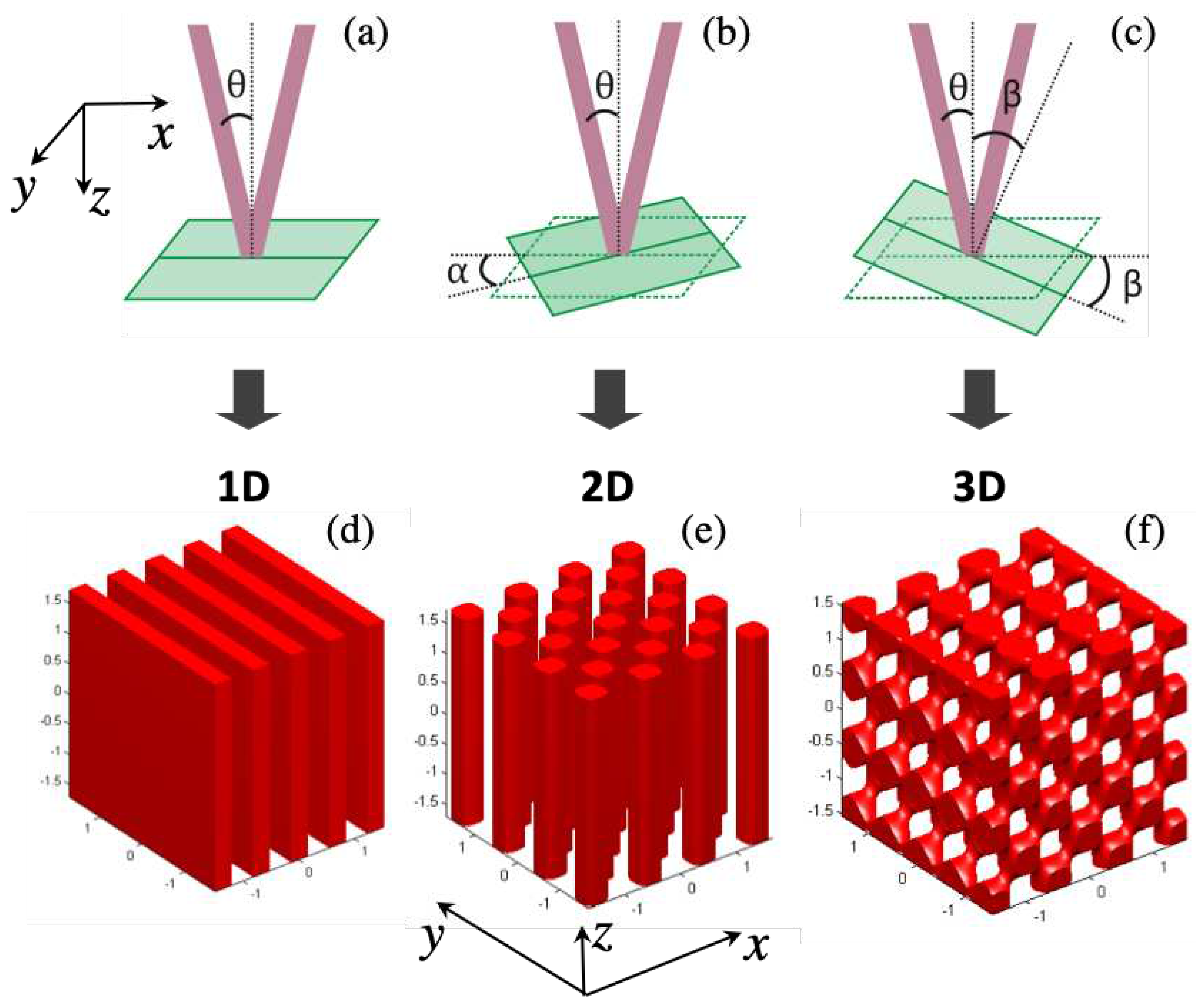
Preprints 93719 g003
Figure 3. Illustration of θ –angle (a), which is half of angle between two beams, and rotation angles α (b) and β (c). Matlab simulations of iso-intensity distribution ( I i s o = 0 . 6 I m a x ) of two-beam interference with λ = 355 nm, θ = 15 ∘ : (d) one exposure with ( α , β )=( 0 ∘ , 0 ∘ ); (e) two exposures with ( α , β )=( − 45 ∘ , 0 ∘ ) and ( 45 ∘ , 0 ∘ ); (f) three exposures with ( α , β )=( 90 ∘ , 0 ∘ ), ( 0 ∘ , 45 ∘ ) and ( 180 ∘ , 45 ∘ ), respectively.
Figure 3. Illustration of θ –angle (a), which is half of angle between two beams, and rotation angles α (b) and β (c). Matlab simulations of iso-intensity distribution ( I i s o = 0 . 6 I m a x ) of two-beam interference with λ = 355 nm, θ = 15 ∘ : (d) one exposure with ( α , β )=( 0 ∘ , 0 ∘ ); (e) two exposures with ( α , β )=( − 45 ∘ , 0 ∘ ) and ( 45 ∘ , 0 ∘ ); (f) three exposures with ( α , β )=( 90 ∘ , 0 ∘ ), ( 0 ∘ , 45 ∘ ) and ( 180 ∘ , 45 ∘ ), respectively.
Preprints 93719 g003
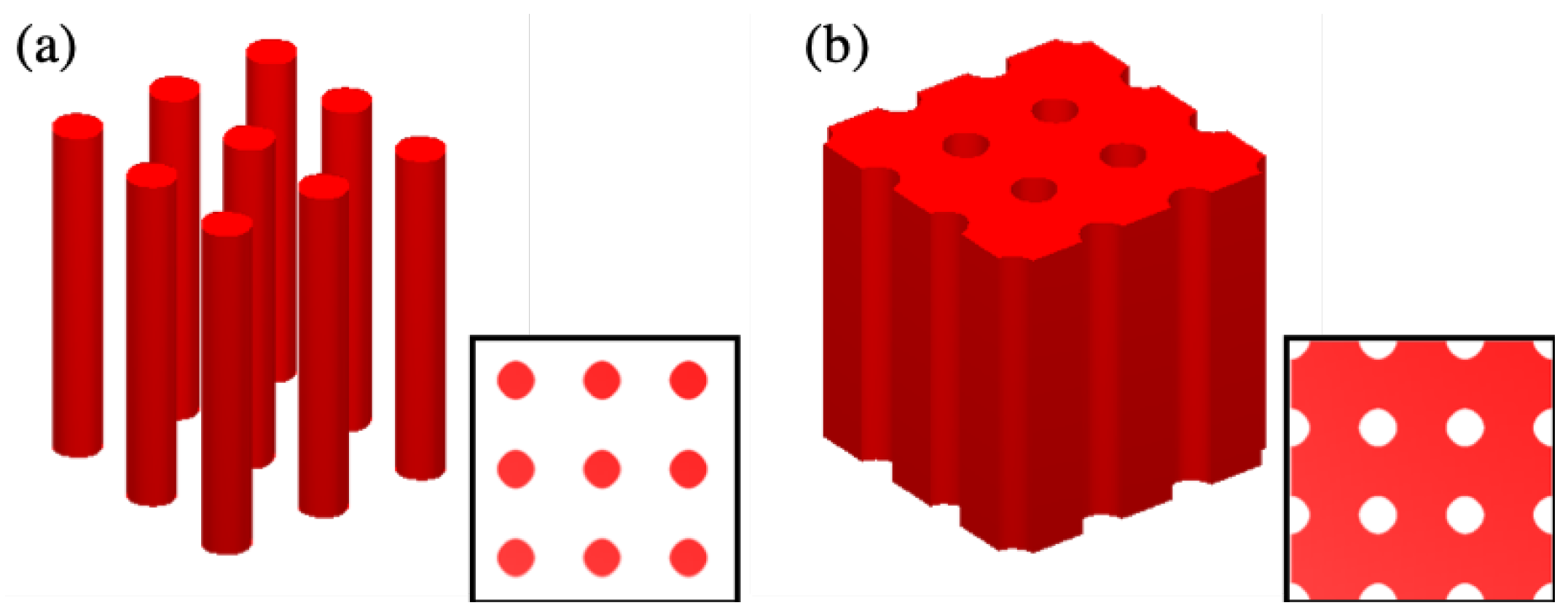
Preprints 93719 g004
Figure 4. Matlab simulations of iso-intensity distribution of two-beam interference with λ = 355 nm, θ = 15 ∘ and with two exposures with ( α , β )=( 0 ∘ , 0 ∘ ) and ( 90 ∘ , 0 ∘ ), respectively. (a) “Cylinders” structure obtained with an I i s o = 0 . 8 I m a x . (b) “Air-holes” structure obtained with an I i s o = 0 . 2 I m a x .
Figure 4. Matlab simulations of iso-intensity distribution of two-beam interference with λ = 355 nm, θ = 15 ∘ and with two exposures with ( α , β )=( 0 ∘ , 0 ∘ ) and ( 90 ∘ , 0 ∘ ), respectively. (a) “Cylinders” structure obtained with an I i s o = 0 . 8 I m a x . (b) “Air-holes” structure obtained with an I i s o = 0 . 2 I m a x .
Preprints 93719 g004
Preprints 93719 g005
Figure 5. (a) Simulation of the photoresist structure; (b) optical microscope image of SU-8 2D square structure fabricated by two-beam interference method. The black/grey color represents the SU-8 pillars; (c) and (d) Fluorescence mapping images of fabricated sample by using a cw 532 nm laser beam. (c) Scanning along z x -plane; (d) Scanning along x y -plane at a z-position as marked by the white dashed line of the image shown in (c).
Figure 5. (a) Simulation of the photoresist structure; (b) optical microscope image of SU-8 2D square structure fabricated by two-beam interference method. The black/grey color represents the SU-8 pillars; (c) and (d) Fluorescence mapping images of fabricated sample by using a cw 532 nm laser beam. (c) Scanning along z x -plane; (d) Scanning along x y -plane at a z-position as marked by the white dashed line of the image shown in (c).
Preprints 93719 g005
Preprints 93719 g006
Figure 6. Fluorescence spectra of DAST nanocrystals in 2D structure, obtained by exciting at 532 nm wavelength. In this experiment, a filter having a cut-off wavelength of 580 nm was used.
Figure 6. Fluorescence spectra of DAST nanocrystals in 2D structure, obtained by exciting at 532 nm wavelength. In this experiment, a filter having a cut-off wavelength of 580 nm was used.
Preprints 93719 g006
Preprints 93719 g007
Figure 7. SHG of DAST nanoparticles embedded in a 2D periodic structure, obtained by using a fundamental laser beam at 1064 nm. (a) SHG spectrum. (b) SH mapping image obtained by scanning the sample in x y -plane.
Figure 7. SHG of DAST nanoparticles embedded in a 2D periodic structure, obtained by using a fundamental laser beam at 1064 nm. (a) SHG spectrum. (b) SH mapping image obtained by scanning the sample in x y -plane.
Preprints 93719 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated