Monitoring and maintenance of cracked structures are generally done using structural integrity assessments. The plastic zone (PZ) crack path (CP) criteria state that a crack grows in the direction when the radius of the plastic zone ahead of the crack tip reaches a minimum value. The PZ can be evaluated using Stress intensity factors (SIF). The SIFs under mixed-mode loading were extracted from literature from three samples: two SENT samples made from polycarbonate and one modified C(T) sample made from low-carbon steel. In addition, the CP angle was evaluated for the W and R-criteria. It was found that both can predict the CP for lateral cracks in both tested materials and monotonic and cyclic load when the mode-mixity does not change considerably from one crack length to the next one or goes beyond 0.2. Moreover, the R-criterion exhibited an error as high as 1.7%, whereas the W-criterion showed a 6% error on the last crack length for the low carbon steel sample under cyclic load, which had a 100% increase in mode-mixity. Finally, the applicability of LEFM is checked, while the CP is sought by finding the size of the PZ.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

In the maintenance of cracked components and structures, the rate at which the crack front advances needs to be established and monitored [1,2,3] as well as the crack path (CP) in case there is mixed-mode loading. However, CP prediction is not entirely understood [1,2,4,5,6]. Nevertheless, for crack kinking and equivalent SIF, there are already several postulated criteria [1,7], mainly based on linear elastic fracture mechanics (LEFM), being the maximum tangential stress criteria the most used for mixed-mode loading [6]. However, the applicability of LEFM must be checked before a suitable model can be applied. Using a model that checks the applicability and predicts CP simplifies those two tasks.

Overall, it can be said that all CP prediction models state a hypothesis for a crack to change direction by a small Δθ from its original path. Such increment is generally created when an equivalent SIF (Keq) exceeds material toughness (K_Ic) [6] in the LEFM approach. Wasiluk and Golos [4] proposed a model based on a dimensionless plastic zone radius, P_zr. Ren et al. [8] proposed a model based on the plastic zone radius and evaluated it for plane stress and plane strain conditions. Both models were devised for a central crack. Comprehensive reviews of CP models can be found in [1,7].

Although the CP models described here use SIF (monotonic load), in literature [7,9,10], a swap between monotonic SIF (K) and fatigue SIF range (ΔK) for proportional load is found acceptable. Consequently, such exchange implies that if a monotonic criterion assumes a crack increment when the equivalent SIF (K_eq) exceeds fracture toughness (K_c), then a crack under fatigue loading grows when ΔK_eq exceeds the fatigue threshold (ΔK_th), as it has been postulated before [9].

Although both evaluated models were proposed for central cracks in infinite plates, this paper evaluates them on lateral cracks. The first set of experimental data is for proportional fatigue load [11], whereas the second is for proportional monotonic load [12], both under different mode-mixity ratios (K_II/K_I). The first data set was obtained with the Digital Image Correlation (DIC) technique, whereas the second set was obtained through finite element modeling (FEM) and validated with photoelasticity. The performance of both CP models is shown along the crack length.

2. Criteria for crack path

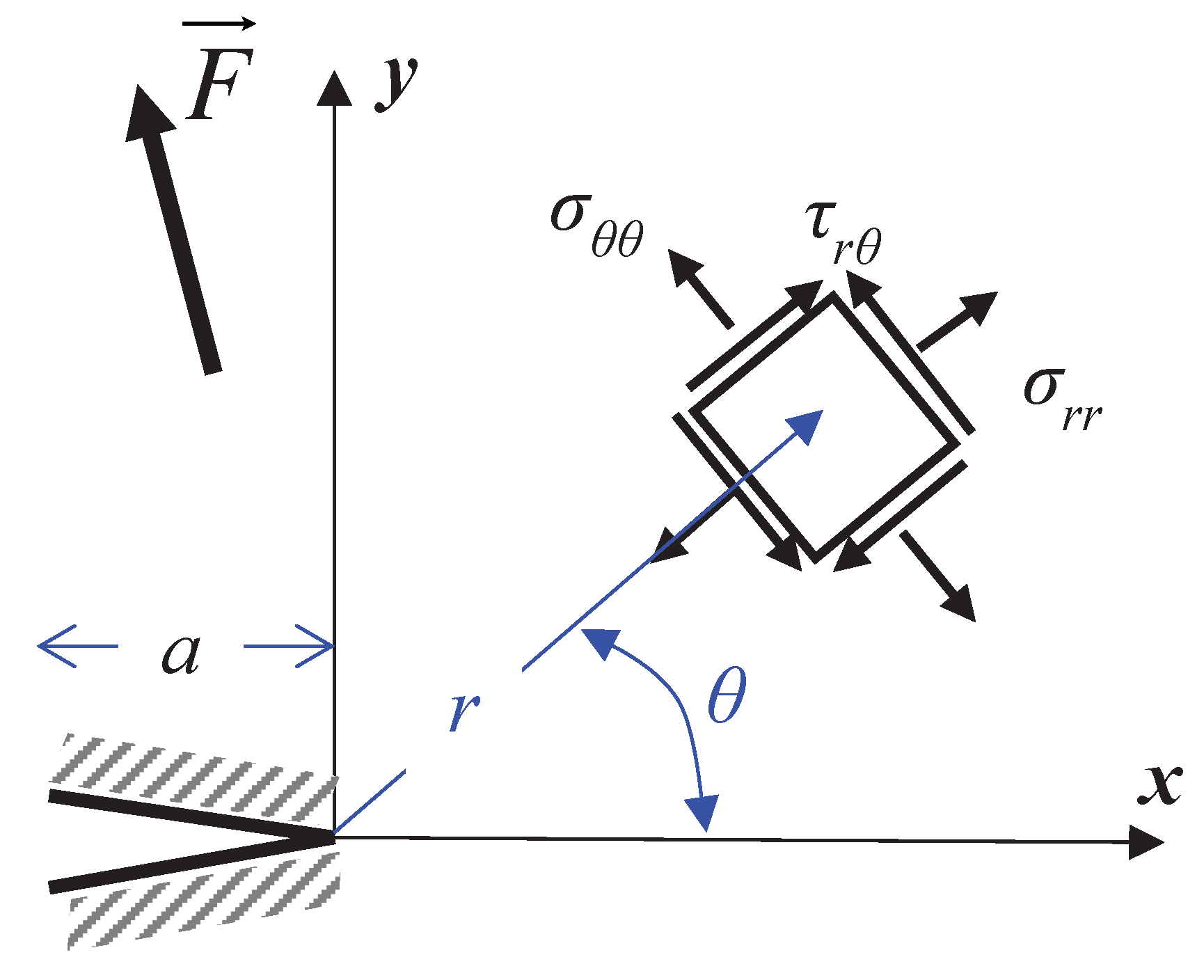
The stress field in a cracked body under an applied force F is schematically represented in Figure 1, where σ and τ are the normal and shear stress respectively, r and θ are radial and tangential directions respectively, and a is crack length.

In 2000, Wasiluk and Golos proposed the W-criterion [4]. It states that a central crack under mixed-mode loading grows in the direction where the radius from the crack tip to the boundary of the plastic zone is the shortest [4]. They started from the radius of the plastic zone, r_pz, proposed by Pook [13] for mode I and II loading and compared the stress field with the Von Misses yield criteria for a plate with a centrally inclined crack, as shown in Equation (1).

r_{p z} = \frac{1}{2 π {σ_{y}}^{2}} [{K_{I}}^{2} \cos^{2} (\frac{θ}{2}) (1 + 3 \sin^{2} (\frac{θ}{2})) + K_{I} K_{I I} \sin θ (3 \cos θ - 1) + {K_{I I}}^{2} (3 + \sin^{2} (\frac{θ}{2}) (1 - 9 \sin^{2} (\frac{θ}{2})))]

(1)

where σ_y is yield stress, K_I and K_II are SIF in modes I and II, respectively. Then, naming W the factor of dividing r_pz over half the crack length and using K_I=σsin2θ√πa and K_II=σsinθcosθ√πa, they obtained Equation (2).

W = \frac{σ^{2}}{2 {σ_{y}}^{2}} [\begin{array}{l} \sin^{4} (θ_{W}) \cos^{2} (\frac{θ}{2}) (1 + 3 \sin^{2} (\frac{θ}{2})) + \\ + \sin^{4} (θ_{W}) \sin (θ) (3 \cos θ - 1) + \sin^{2} (θ_{W}) \cos^{2} (θ_{W}) (3 + \sin^{2} (\frac{θ}{2}) (1 - 9 \sin^{2} (\frac{θ}{2}))) \end{array}]

(2)

Thus, taking the first and second derivative of W, Equation (2) with respect to θ, as seen in Equation (3), it gives a W_min at which the direction of crack growth, θ_W, will happen.

{\frac{\partial W_{(θ, θ *, σ)}}{\partial θ} |}_{θ = θ *} = 0 and {\frac{\partial^{2} W_{(θ, θ *, σ)}}{\partial θ^{2}} |}_{θ = θ *} > 0

(3)

Then, if the applied load is cyclic, SIF, K, becomes SIF range, ΔK, and the fracture toughness, Kc, becomes fatigue threshold, ΔK_th, as proposed and tested in [10], so Equation (1) can be rewritten as Equation (4).

r_{p z - W} = \frac{1}{2 π {σ_{y}}^{2}} [\begin{array}{l} Δ {K_{I}}^{2} \cos^{2} (\frac{θ}{2}) (1 + 3 \sin^{2} (\frac{θ}{2})) + Δ K_{I} Δ K_{I I} \sin θ (3 \cos θ - 1) + \\ + Δ {K_{I I}}^{2} (3 + \sin^{2} (\frac{θ}{2}) (1 - 9 \sin^{2} (\frac{θ}{2}))) \end{array}]

(4)

On the other hand, in 2014, Ren [8] proposed a model based on the PZ radius and evaluated it for plane stress and plane strain conditions for a centrally inclined crack. The radius of the plastic zone is shown in Equation (5).

r_{p z} = \frac{1}{2 π {σ_{y}}^{2}} [\begin{array}{l} {K_{I}}^{2} \frac{2 {(1 - 2 ν)}^{2}}{3} [(1 + \cos θ) + \sin^{2} θ] + 2 K_{I} K_{I I} (\sin 2 θ - \frac{2 {(1 - 2 ν)}^{2}}{3}) + \\ + {K_{I I}}^{2} (1 + \frac{2 {(1 - 2 ν)}^{2}}{3}) (1 - \cos θ) (3 + \cos^{2} θ) \end{array}]

(5)

where ν is Poisson’s modulus. Moreover, assuming the interchangeability of K, and ΔK and Kc with ΔK_th Equation (5) for monotonic loading can be rewritten as Equation (6) for fatigue loading.

r_{p z} = \frac{1}{2 π {σ_{y}}^{2}} [\begin{array}{l} Δ {K_{I}}^{2} \frac{2 {(1 - 2 ν)}^{2}}{3} [(1 + \cos θ) + \sin^{2} θ] + 2 Δ K_{I} Δ K_{I I} (\sin 2 θ - \frac{2 {(1 - 2 ν)}^{2}}{3}) + \\ + Δ {K_{I I}}^{2} (1 + \frac{2 {(1 - 2 ν)}^{2}}{3}) (1 - \cos θ) (3 + \cos^{2} θ) \end{array}]

(6)

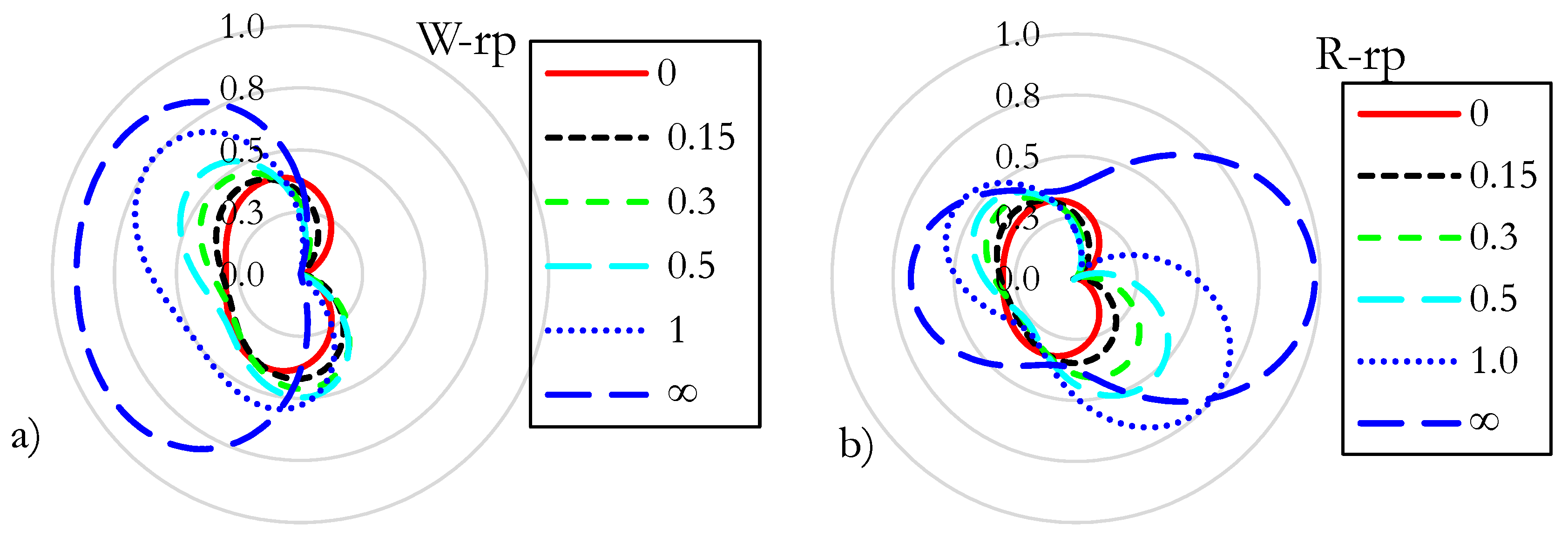
where ΔK is the FIT range, and ΔK_th is the fatigue threshold. It is noted how the PZ can give an insight or crack initiation at the shortest radius. Furthermore, an analysis of Equation (4) and Equation (6) gives the angles at which the minimum radius occurs. That is 0º for mode I and 82.5º for pure mode II in the R-R-criterion and 77º in the W-criterion. Furthermore, Figure 2 shows how the PZ changes for different mode-mixity (K_II/K_I) ratios for both the W and R criteria, the latest plotted for plain stress. The PZ is plotted for different mode-mixity ratios, from pure mode I, K_II/K_I=0 until pure mode II, K_II/K_I = ∞, but keeping Keq constant, √(K_I²+K_II²) = 1. Both K_I and K_II were always kept positive. A negative K_I does not make physical sense as it requires the crack lips to overlap, whereas a negative K_II implies the relative displacements of two opposite-to-crack points. It is seen how the PZ changes the applied load’s direction.

One can see in Figure 2 that the crack orientation of the PZ changes from perpendicular-to-the-tensile stress, mode I to parallel-to-shear stress, mode II. Therefore, a parameter M [5,14], is used to tell whether the crack growth is dominated by tensile or shear mode, as shown in Equation (7).

M = \frac{2}{π} \tan^{- 1} (\frac{K_{I I}}{K_{I}})

(7)

3. Materials and methods

Data used to evaluate the two CP models was obtained from two samples subjected to proportional loading tests. The first was an 8.7 mm thick modified compact test C(T) specimen made out of low carbon steel with a drilled hole in front of the CP to modify the stress field [11], as seen in Figure 3a, where the testing set up shown in Figure 3b. Miranda tested a similar sample [15], whose results were computationally verified later on [16]. The experimentally observed CP for this sample and the six measured points are shown in Figure 3a. The hole modified the stress field, which curved the crack and induced opening mode II over the applied mode I load. Moreover, because the load inversion ratio was 0.1, the SIF range (ΔK) was calculated as Kmax-Kmin from DIC displacement measurements and verified through FEM. A general reference for DIC, capabilities, limitations, and implementation can be found in [17,18]. Table 1 shows this sample’s retrieved crack length, CP angle, SIF ranges, and mode-mixity for the six measured points.

Because the applied load on this sample was cyclic, Equation (4) and Equation (6) were used to establish the sample’s PZ radius and shape. Extensive details about this test and specifics on how the SIFs were calculated are found in [11].

The second type of samples was two 3 mm thick polycarbonate SENT samples [12], see schematics in Figure 3c, subjected to simple remote tension with a 22.5º and another with 45º inclined preexisting crack produced mixed-mode (I and II) loading conditions. The retrieved data included SIF modes I and II, obtained through numerical simulation and validated with photoelasticity, shown in Table 2. Because the applied loading on these samples was monotonic, Equation (1) and Equation (5) were used to establish the PZ radius and shape.

Finally, the performance of the CP models was evaluated with the expression proposed in Equation (8), as recently proposed [19].

e r r = \frac{θ_{\exp} - θ *}{π}

(8)

where θ_exp is the experimental CP angle and θ* is the angle predicted by either model.

4. Results and Discussion

4.1. CP prediction for modified C(T)

Figure 4 compares the experimentally observed CP for the W and R criteria predicted angle for the six measured points in the modified C(T) sample. One can see the prediction is very close for short cracks as the mode mixity-ratio, ΔK_II/ΔK_I, is low. However, at the last measurement before unstable crack growth, the ΔK_II/ΔK_I rises to 0.13, and the predicted angle gives a 6% error for the W-criterion. In contrast, the R-criterion shows a 1.7% error.

The W-criteria makes a close prediction for most of the crack lengths. Figure 5 shows the comparative size and shape of the PZ, Equation (4) W-criterion, and Equation (5) R-criterion, for six different crack lengths in this specimen. It is seen how the PZ orientation turns as the crack length increases and the mode-mixity changes. This turning is attributed to the increase of ΔK_II_, which makes the crack deviate from the applied more I load. Moreover, it is observed that the size of the largest PZ, about 2.54 mm for the W-criterion and about 2.9 mm for the R-criterion, in their largest axis, is below the thickness of the specimen 8.7mm. Thus, LEFM adequately describes the stress field. For this sample, the W criterion showed larger PZ for the first five crack sizes, whereas the R criterion retrieved a more extensive zone for the last one, where K_II reaches a 3.55 MPa√m and the mode-mixity, K_II/K_I, is 0.13.

4.2. CP prediction for SENT samples

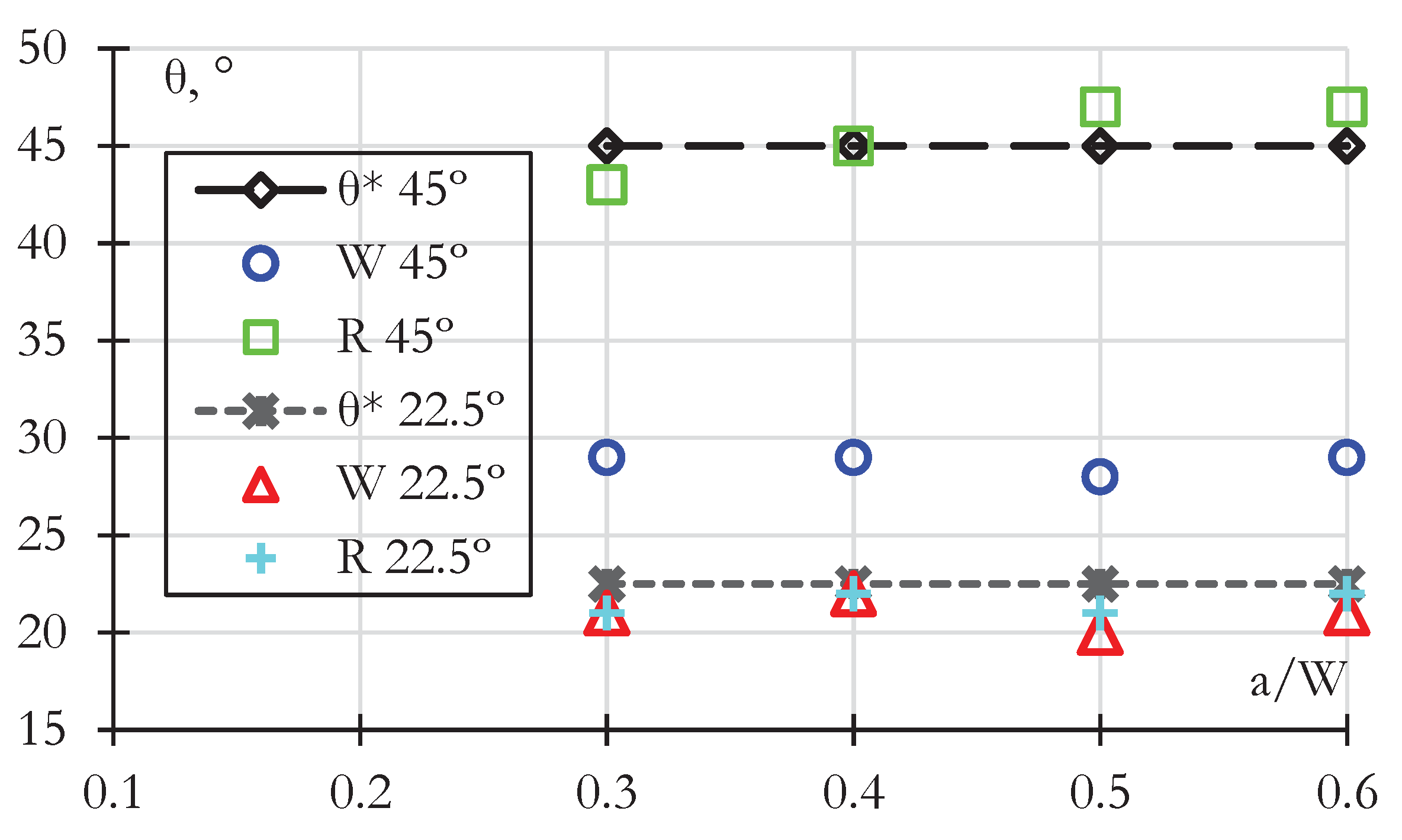
On the other hand, the performance of the CP models for both SENT specimens for dimensionless crack length is shown in Figure 6. The models were evaluated with the retrieved K_I and K_II. Unlike the C(T) sample, the applied load is monotonic, so there is no need to assume that K is ΔK and K_c is ΔK_th. The SENT with a 45º crack showed a K_II/K_I ratio from 0.46 at the longest to 0.58 for the shortest a/W. Polycarbonate is a material prone to shear-dominated failure and the 45º crack induces a high K_II/K_I ratio. Therefore, the W criterion is not expected to perform well under these conditions, so it predicts a quasi-constant 29º, whereas the R criterion predicts a closer CP between 43 and 47º.

Conversely, the SENT with a 22.5º crack showed a quasi-constant K_II/K_I ratio of 0.23. Because of this constant K_II/K_I ratio, the predicted CP angle is also quasi-constant, about 21º degrees for the W criterion, very close to the experimentally observed angle of 22.5º. Conversely, the R criterion predicts a quasi-constant angle of 17º.

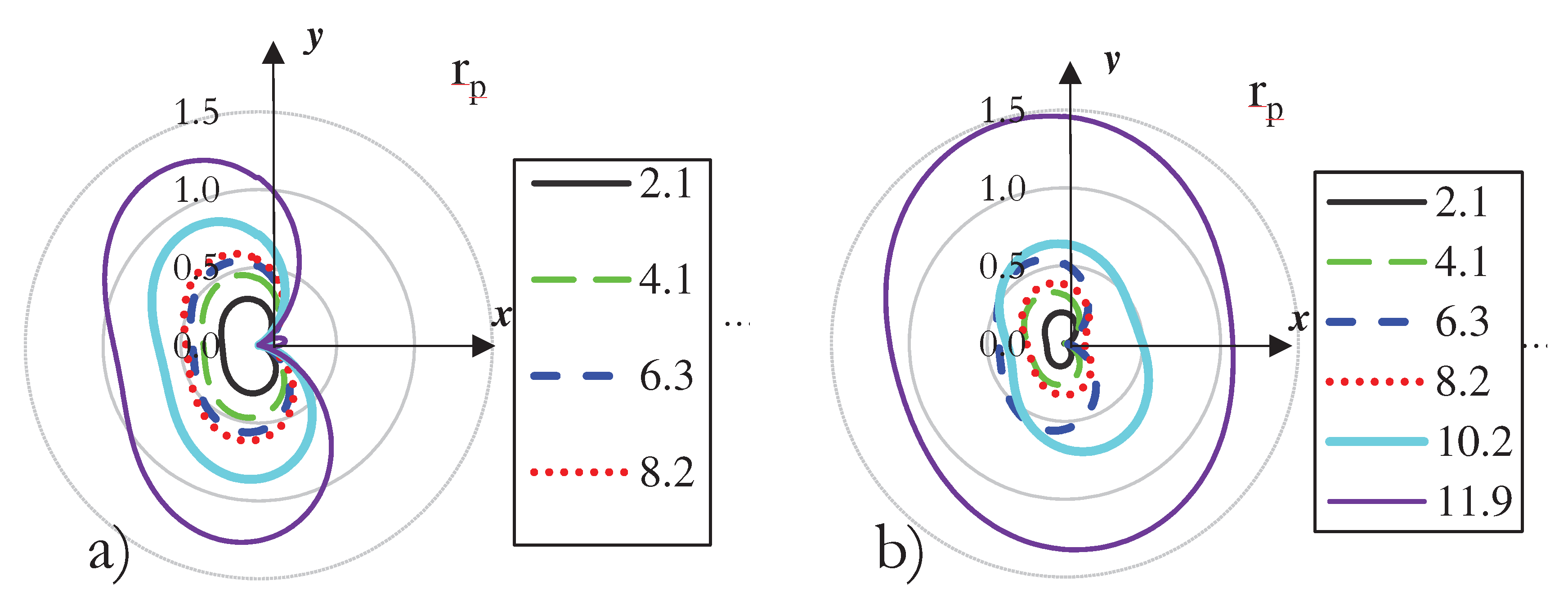
The shape and size of the plastic zone are shown in Figure 7 for the SENT with an initial crack of 45º for the four different reported crack lengths. It is seen how the orientation of the plastic zone stays pretty much constant as the crack length increases for the W and R criteria. This situation is attributed to the steady K_II/K_I ratio, as seen in Table 2, making the crack grow straight from its original path, even though only the mode I applied. Moreover, it is observed that the size of the largest plastic zone on its largest axis is about 0.7 mm for the W criterion and 0.58 mm for the R criterion. In both cases, this size is below the thickness of the specimen, 3.0 mm, so LEFM can be used to describe the stress field satisfactorily. Finally, it is noted that the W criterion predicts a slightly larger PZ than the R criterion.

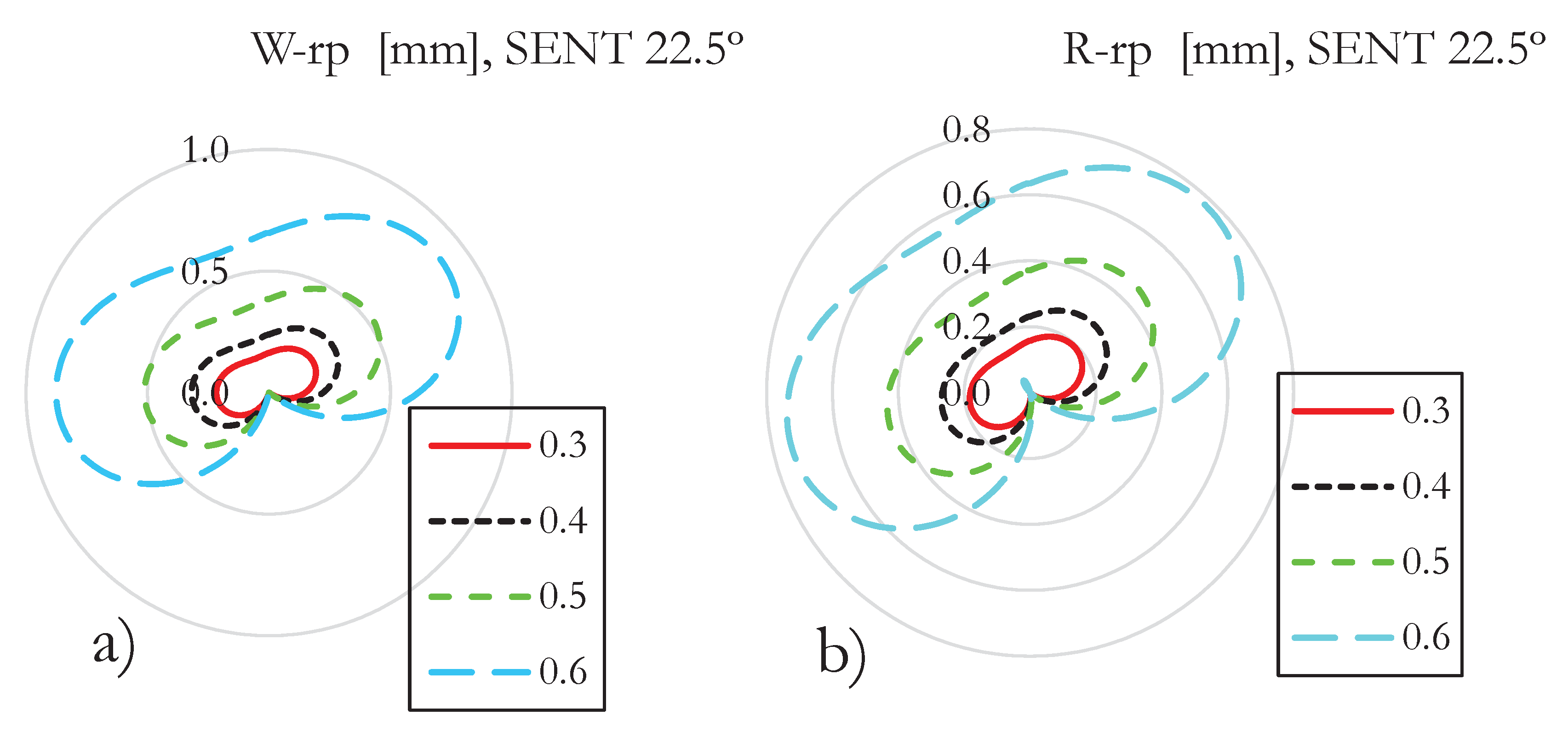
Figure 8 shows the PZ size for the SENT with an initial crack of 22.5º for the four different reported crack lengths. It is seen how the orientation of the plastic zone stays pretty much constant as the crack length increases. This situation is attributed to the steady K_II/K_I ratio, making the crack grow straight from its original inclined path, even though there is an applied load in mode I. Moreover, it is observed that the size of the largest PZ, about 1.8 mm for the W criterion and about 1.54 mm for the R criterion in its largest axis, is below the thickness of the specimen, 3.0 mm, so LEFM can be used to describe properly the stress field. In this sample, it is also observed that the W criterion predicts a slightly larger PZ than the R criterion.

4.3. Discussion

Highsmith [6] stated that a crack under mixed-mode will grow when the equivalent SIF exceeds the material toughness, Kc, or the equivalent SIF range exceeds the material fatigue threshold, K_th. In both cases, the crack grew under either monotonic or fatigue loading. So, the Keq was larger than the Kc for the monotonic load, and the ΔKeq was larger than the K_th for the cycling load. However, because more than one loading mode was present, the CP must be established to describe crack growth completely [19].

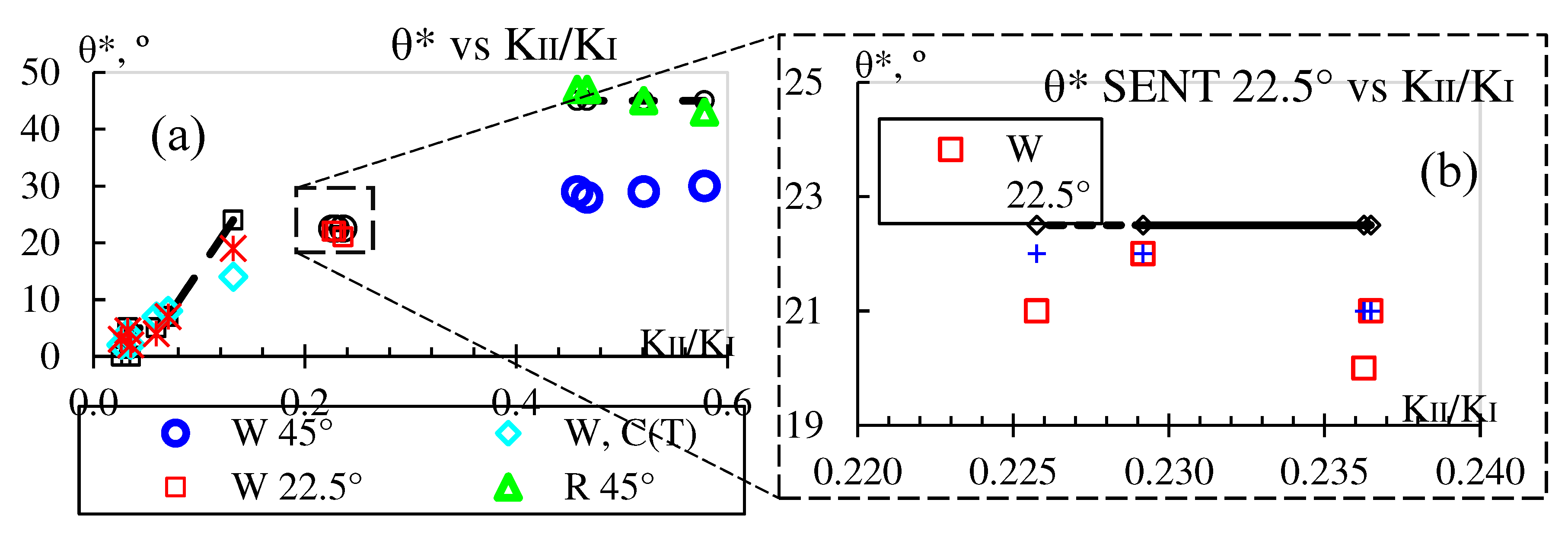
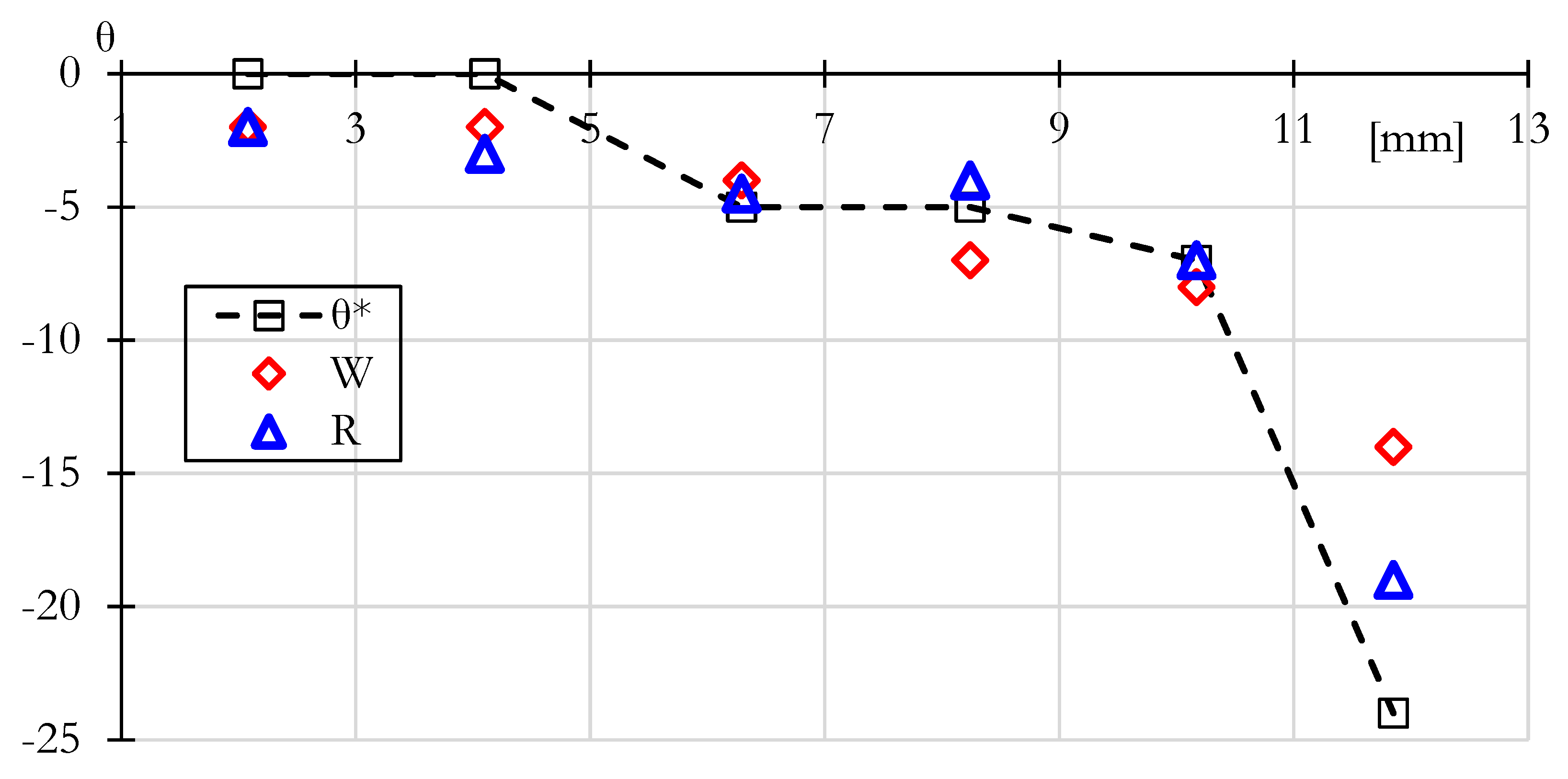
On the other hand, Vormwald et al. [5] argued that the mode-mixity ratio [14] might be the parameter that could tell when a crack growth scenario can change from tensile to shear-dominating load. It could make a crack turn when it reaches 0.5. Figure 9 shows the variation of CP angle with mode-mixity for both samples. For the SENT samples, neither the load nor the mode-mixity changed much with crack length. For the 22.5º SENT, the K_II/K_I ratio kept a 0.24 constant value, whereas, for the 45º sample, the K_II/K_I ratio went from 0.56 to 0.46, as seen in Figure 6. Vormwald et al. [5] argued that when transitioning from tensile to entirely dominated shear crack growth, such mode-mixity parameter might not be able to tell the CP. Therefore, the CP for the SENT samples was not expected to deviate from its initial angle. This is seen in Figure 9a for the three samples and Figure 9b for a close-up of the SENT 22.5°.

On the other hand, for the modified C(T) sample, the mode-mixity changes constantly, starting at 0.04 and reaching 0.13. As a result, the CP for the modified C(T) sample changes as well, as seen in Figure 9 in the black. Thus, the mode-mixity indeed influences the CP angle. This analysis shows that a change in the K_II/K_I ratio involves a change in the CP angle.

Furthermore, in Figure 8, one can see the size of the largest plastic zone is about 1.5 mm, so it does not exceed the holed C(T) sample thickness, 8.7 mm. On the other hand, the largest plastic zone size for the SENT sample is seen in Figure 7 for the 22.5º and Figure 8 for the 45º sample, where the plastic zone does not exceed the 3 mm sample thickness. Therefore, the applicability of LEFM is checked at once.

On the other hand, the CP prediction error is shown in Table 3. Both criteria are close in prediction with errors as low as 0.28% and as high as 1.67% for the modified C(T). For the largest mode-mixity on the modified C(T), the W criterion shows a 5.56, whereas the R criterion shows a 2.78% error. The same case for the SENT 45° sample is 8.33 versus 1.11% error, respectively. In both cases, the mode-mixity (ΔK_II/ΔK_I) had a wide range of about 0.1, in both cases. For the SENT 22.5 sample, both are really close to each other; the largest difference being 0.56%. In this case, it could be explained by the quasi-constant ΔK_II/ΔK_I.

On a final note, it has to be said that the computational cost of these two criteria is high compared to other criteria, as recently evaluated [19]. For that reason, the computational cost, in terms of floating-point operations (FLOPS), is compared in Table 4. The R criterion is slightly less costly than the W criterion.

5. Conclusion

The crack path was calculated for specimens under fatigue and monotonic load using the LEFM-based plastic zone radius criteria. The LEFM parameters for the fatigued sample were characterized experimentally with DIC, whereas the monotonic samples were characterized numerically with FEM and validated with photoelasticity, both obtained from the literature. An advantage of plastic zone-based criteria is that the applicability of LEFM is checked in the same Equation. Furthermore, using prediction models rather than FEM modeling makes a faster prediction by avoiding time-consuming modeling and simulation. Finally, the selected models worked for numerical and experimentally obtained SIF. The literature has discussed how the experimentally acquired SIFs include nonlinear effects such as rugosity, plasticity-induced closure, and crack flank interlocking.

The W and R criteria were devised for monotonic load, and here, they were tested for monotonic and fatigue load. The swap of K with ΔK was checked, which was found applicable in these cases. The error analysis showed that the W and R criteria predicted angles very close for short cracks as the mode mixity-ratio, ΔK_II/ΔK_I, is below 0.25, with the R criterion exhibiting lower error values. However, at the last measurement for the modified C(T) low carbon steel sample before unstable crack growth, the ΔK_II/ΔK_I doubles its value and makes an unstable W-criterion prediction. The R criterion has about 88% of the W’s computational cost, which could impact performance for recurrent calculations. Furthermore, the models were devised for central cracks, and here, they were tested in lateral cracks. The predicted versus experimental CP comparison showed that the models could be used for fatigue and monotonic loads.

Acknowledgments

The authors acknowledge the financial support from Pontifícia Universidade Católica do Rio de Janeiro—PUC-RJ.

References

Mróz, K.P.; Mróz, Z. On Crack Path Evolution Rules. Eng Fract Mech 2010, 77, 1781–1807. [Google Scholar] [CrossRef]
Yu, X.; Li, L.; Proust, G. Fatigue Crack Growth of Aluminium Alloy 7075-T651 under Proportional and Non-Proportional Mixed Mode I and II Loads. Eng Fract Mech 2017, 174, 155–167. [Google Scholar] [CrossRef]
Kujawski, D. Discussion and Comments on KOP and ∆Keff. Materials 2020, 13, 4959. [Google Scholar] [CrossRef] [PubMed]
Wasiluk, B.; Golos, K. Prediction of Crack Growth Direction under Plane Stress for Mixed-Mode I and II Loading. Fatigue Fract Eng Mater Struct 2000, 23, 381–386. [Google Scholar] [CrossRef]
Vormwald, M.; Hertel, O.; Zerres, P. Fatigue of Engineering Structures under Combined Nonproportional Loads: An Overview. Fatigue Fract Eng Mater Struct 2018, 41, 1449–1468. [Google Scholar] [CrossRef]
Highsmith, S. Crack Path Determination for Non-Proportional Mixed-Mode Fatigue, Georgia University of Technology, 2009.
Rozumek, D.; Macha, E. A Survey of Failure Criteria and Parameters in Mixed-Mode Fatigue Crack Growth. Materials Science 2009, 45, 190–210. [Google Scholar] [CrossRef]
Ren, L.; Zhu, Z.; Wang, M.; Zheng, T.; Ai, T. Mixed-Mode Elastic-Plastic Fractures: Improved R-Criterion. J Eng Mech 2014, 140, 04014033. [Google Scholar] [CrossRef]
Richard, H.A.; Fulland, M.; Sander, M. Theoretical Crack Path Prediction. Fatigue Fract Eng Mater Struct 2005, 28, 3–12. [Google Scholar] [CrossRef]
Vormwald, M.; Hos, Y.; Freire, J.L.F.; Gonzáles, G.L.G.; Díaz, J.G. Variable Mode-Mixity during Fatigue Cycles—Crack Tip Parameters Determined from Displacement Fields Measured by Digital Image Correlation. Frattura ed Integrità Strutturale 2017, 11, 314–322. [Google Scholar] [CrossRef]
Díaz Rodríguez, J.G.; Gonzales, G.; Ortiz Gonzalez, J.A.; Freire, J. Analysis of Mixed-Mode Stress Intensity Factors Using Digital Image Correlation Displacement Fields. In Proceedings of the 24th ABCM International Congress of Mechanical Engineering; ABCM, Ed.; ABCM: Curitiba, 2017. [Google Scholar]
Merah, N.; Albinmousa, J. Experimental and Numerical Determination of Mixed Mode Crack Extension Angle. J Test Eval 2009, 37, 95–107. [Google Scholar] [CrossRef]
Pook, LP. The Effect of Crack Angle on Fracture Toughness. Eng Fract Mech 1971, 3, 205–218. [Google Scholar] [CrossRef]
Aliha, M.R.M.; Berto, F.; Mousavi, A.; Razavi, S.M.J. On the Applicability of ASED Criterion for Predicting Mixed Mode I+II Fracture Toughness Results of a Rock Material. Theoretical and Applied Fracture Mechanics 2017, 92, 198–204. [Google Scholar] [CrossRef]
Miranda, A.C.O.; Meggiolaro, M.A.; De Castro, J.T.P.; Martha, L.F. Fatigue Life Prediction of Complex 2D Components under Mixed-Mode Variable Amplitude Loading. Int J Fatigue 2003, 25, 1157–1167. [Google Scholar] [CrossRef]
Chatzigeorgiou, A.; Theotokoglou, E.; Tsamasphyros, G.I. Code Development for the Computational Analysis of Crack Propagation in Structures. Frattura ed Integrità Strutturale 2020, 14, 306–324. [Google Scholar] [CrossRef]
Castillo, I.M.; Peñaranda, A.E.; Diaz, J.G. Implementación de La Técnica de Correlación de Imágenes Digitales Con Software Libre. Aibi 2020, 8, 25–32. [Google Scholar] [CrossRef]
Díaz-Rodríguez, J.G. Comparison of Stress Separation Procedures. Experiments versus Theoretical Formulation. Engineering Solid Mechanics 2022, 10, 153–164. [Google Scholar] [CrossRef]
Díaz, J.G.; Freire, J.L. de F. LEFM Crack Path Models Evaluation under Proportional and Non-Proportional Load in Low Carbon Steels Using Digital Image Correlation Data. Int J Fatigue 2022, 156, 106687. [Google Scholar] [CrossRef]

Figure 1. Schematics and notation of acting stress in a cracked body.

Figure 2. Dimmensionless PZ for different mode-mixity ratios (K_II/K_I). a) W-criterion; a) R-criterion.

Figure 3. Schematics of tests. (a) Measured points for the holed CT specimen; (b) Testing set up for holed CT sample; c). SENT with inclined crack. a) and b) From [11].

Figure 4. Evaluation of crack kinking models for modified C(T) sample.

Figure 5. Size and shape or plastic zone for modified C(T) specimen; a) from W-criterion, b) from R-criterion.

Figure 6. Evaluation of crack kinking models for SENT samples.

Figure 7. Size and shape of the plastic zone for SENT sample 45º, a) from W-criterion, b) from R-criterion.

Figure 8. Size and shape of the plastic zone for SENT sample 22.5º, a) from W-criterion, b) from R-criterion.

Figure 9. CP angle variation with mode-mixity; a) modified C(T), SENT samples; b) close up of SENT 22.5°.

Table 1. Experimental parameters for the modified C(T); from [11].

point	a [mm]	θ*	ΔK_I	ΔK_II	ΔK_II/ΔK_I
0	2.1	0	13.12	0.46	0.04
a	4.1	0	17.78	0.47	0.03
b	6.3	-5	18.14	0.59	0.03
c	8.2	-5	19.67	1.17	0.06
d	10.2	-7	22.00	1.55	0.07
e	11.9	-24	26.85	3.55	0.13

Table 2. Experimental parameters for the thin strips; from [12].

a/W	K_I /(σ√πa)	K_II /(σ√πa)	K_II/K_I
45º
0.3	0.83	0.48	0.58
0.4	0.96	0.50	0.52
0.5	1.22	0.57	0.47
0.6	1.42	0.65	0.46
22.5º
0.3	1.48	0.35	0.24
0.4	1.80	0.41	0.23
0.5	2.28	0.54	0.24
0.6	2.99	0.68	0.23

Table 3. Error percentage in crack kinking angle prediction.

C(T)			SENT 45°			SENT 22.5°
ΔK_II/ΔK_I	W, C(T)	R, C(T)	ΔK_II/ΔK_I	W 45°	R 45°	ΔK_II/ΔK_I	R 22.5°	R 22.5°
0.04	-1.11	-1.11	0.58	8.33	1.11	0.24	0.83	0.83
0.03	-1.11	-1.67	0.52	8.89	0.00	0.23	0.28	0.28
0.03	0.56	0.28	0.47	9.44	-1.11	0.24	1.39	0.83
0.06	-1.11	0.56	0.46	8.89	-1.11	0.23	0.83	0.28
0.07	-0.56	0.00
0.13	5.56	2.78

Table 4. Computational cost for the evaluated criteria.

Operator	+, -, *, /	√	Sin, Cos, Atan	Acos	Tan	ABS, SGN	^	Total cost
Operator cost	2	2	5	4	6	2	8	Total cost
Cost in W model	23	0	10	0	0	0	10	176
Cost in R model	33	0	5	0	0	0	8	155

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.