zk-DASTARK: A quantum-resistant, data authentication and zero-knowledge proof scheme for protecting data feed to smart contracts

With the emergence of blockchain and smart contracts, traditional digital applications 1 such as identity management, supply chain management, banking and finance etc. are expected 2 to be transformed into Decentralized Applications (DApps). Blockchain interoperability is a new 3 and exciting aspect of blockchain technology that is quickly gaining popularity in many industries. 4 However, the widespread use of blockchains has not yet been achieved because DApps running on the 5 blockchain using smart contracts require access to authentic off-chain data. Users are more conscious 6 of their personal data privacy and consequently are more reluctant to share their data, posing a 7 challenge in the adoption of DApps. To solve this challenge, we present a novel quantum-resistant, 8 data authentication and zero-knowledge proof scheme named zk-DASTARK. Based on our proposed 9 scheme, we present a novel framework which can be used to feed authenticated off-chain data to 10 DApps without compromising user data privacy. Our proposed framework is quite efficient against 11 well-known off-chain data authentication frameworks. The proposed framework is implemented on 12 state-of-the-art quantum-resistant IOTA Blockchain and is highly efficient as it takes approximately 13 60 ms to generate a proof and approximately 10 ms to verify a proof.

Keywords:

Subject: Computer Science and Mathematics - Information Systems

1. Introduction

Blockchain is a decentralized immutable digital ledger used for recording transactions permanently across a peer-to-peer(P2P) network of computers. Blockchain offers a number of distinct features such as immutability, transparency, robust security and fault tolerance. The security of blockchain depends on a decentralized network of validators which follows a consensus algorithm to validate any transactions. The decentralization feature of blockchain enables transparency, integrity and trust among participants. Since its inception, from simply being implemented as a peer-to-peer cryptocurrency such as Bitcoin [1] with limited features and capabilities, blockchain has evolved rapidly over the years. New protocols, consensus algorithms and use cases such as smart contracts, and Decentralized Finance (DeFi) have been proposed in literature. [2] [3].

Nick Szabo [4] proposed the idea of smart contracts, to automate and digitize manual contracts. In blockchain scenario, a smart contract can be taken as a digital contract executing on the blockchain and its execution is validated via consensus mechanism. Ethereum [5] being turing complete enables smart contracts to execute any complex logic. The coupling of smart contracts with blockchain offers attractive features, which has enabled rapid adoption and application of blockchain in various application areas such as, smart grids, health care, supply chain, finance, IoT etc.

When real-world applications such as supply chain management, identity management, banking and finance etc. are built utilizing smart contracts and blockchain, real-world data from external sources such as input from users or an API etc. are needed to be fed into the smart contract as input values. There are two issues related to input data. The first one is related to the authentication of the data and the second one is related to the privacy of the data because in some use cases such as medical records input data cannot be public to everyone. In such scenarios to execute smart contract the authenticity of data being fed into smart contract needs to be verified by the blockchain validators. This gives rise to a challenging problem, i.e., the blockchain validators should not only be able to verify the authenticity of the available plain text input data but also maintain the privacy of that input data.

The traditional data feed schemes for smart contracts do not ensure privacy and authentication of data moreover these schemes require an initial trusted setup and are vulnerable to quantum threats, risking both the privacy and integrity of data. Our solution leverages the strengths of quantum secure zk-STARK, CRYSTALS Dilithium, and the IOTA blockchain. zk-STARK provides a framework for zero-knowledge proofs, preserving data privacy without a trusted setup. CRYSTALS Dilithium offer a quantum-resistant mechanism for digital signatures, ensuring data integrity. The IOTA blockchain, with its unique Tangle technology, provides a scalable platform for implementing these technologies in smart contracts. This combination presents a quantum-safe data feed scheme that not only maintains privacy but also verifies data authenticity. It’s a significant stride towards securing digital transactions against quantum threats, fostering trust in the system.

The main contribution of our work is as follows:

We propose a quantum-resistant Zero-Knowledge Data Authentication Scalable Transparent Argument of Knowledge (zk-DASTARK) scheme, which is designed to solve the challenging problem of preserving privacy and providing authentication of private data.
Our proposed scheme is the extension of quantum secure zk-STARK [6] with a post-quantum digital signature scheme named the CRYSTALS Dilithium [7].
Our proposed scheme is an extension of zk-STARK with a hash circuit. It will be used to generate a hash of the generated zero-knowledge proof, which is then used to generate a digital signature by a trusted data authenticator. Our proposed approach will assure the integrity and confidentiality of our data, without revealing any specifics about the input values.
We propose a novel framework based on our proposed zk-DASTARK scheme. The proposed framework ensures the complete protection and confidentiality of user’s private data when interacting with DApps.
We implemented our proposed framework on state-of-the-art quantum secure IOTA Blockchain [8]. To evaluate its feasibility and performance, we tested it on a smart contract running on the IOTA blockchain.

2. Background and Related work

In this section, we discuss preliminaries related to zero-knowledge proof, smart contracts, CRYSTALS Dilithium, IOTA Blockchain and zk-STARK.

2.1. Zero Knowledge Proof (ZKP)

Zero-knowledge proof is a cutting-edge cryptographic technique in which an entity acting as a prover can prove to an entity acting as a verifier that a given statement is true without revealing any extra information about the data. The fundamental idea behind zero-knowledge proof is that one can prove that he knows a certain piece of information without the need to be exposed to the actual/complete information. Three essential properties must be present in a Zero-Knowledge Proof protocol are listed below

Completeness: The principle of completeness in a ZKP dictates that if both the prover and verifier adhere to the protocol’s guidelines there is a high probability that the verifier will accept the proof.
Zero Knowledge: This property ensures that the verifying entity gains no additional information about the proving entity’s secret when executing the protocol.
Soundness: The principle of soundness in a ZKP protocol ensures that the proving entity cannot deceive the verifying entity into accepting a false statement as true.

2.2. Blockchain

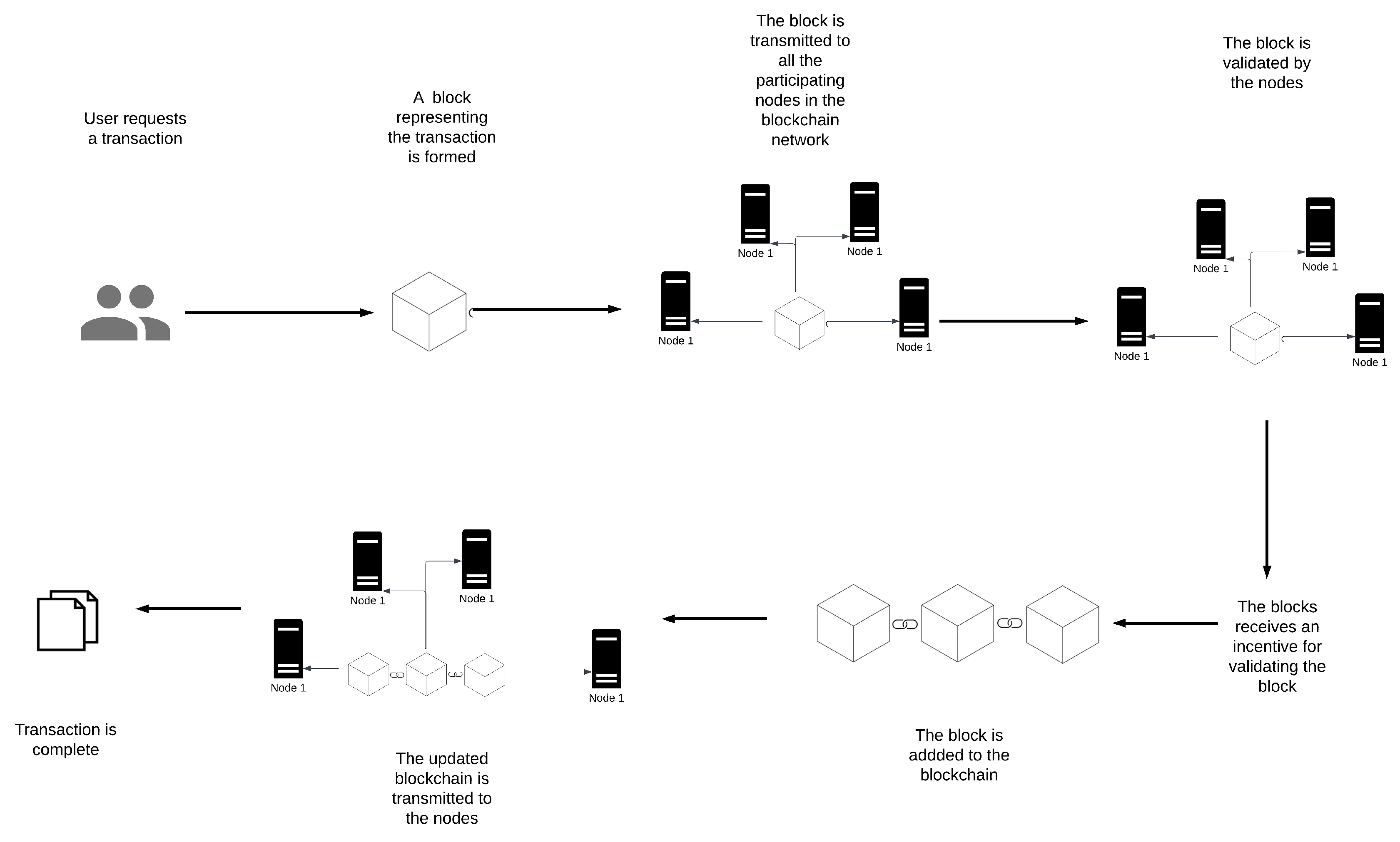
A blockchain is a digital distributed ledger that records transactions between users. A blockchain network is made up of interlinked decentralized nodes and the uniformity of data across participating nodes is maintained based on a set of pre-established rules known as consensus. Blockchain is formed up of a series of blocks that connect using hash values. The block body stores the transaction information, while the block header records digest information and other identifiers. In simpler terms, a blockchain is like a digital notebook that keeps track of transactions between people. Figure 1 shows the working flow of blockchain.

2.3. Smart Contract

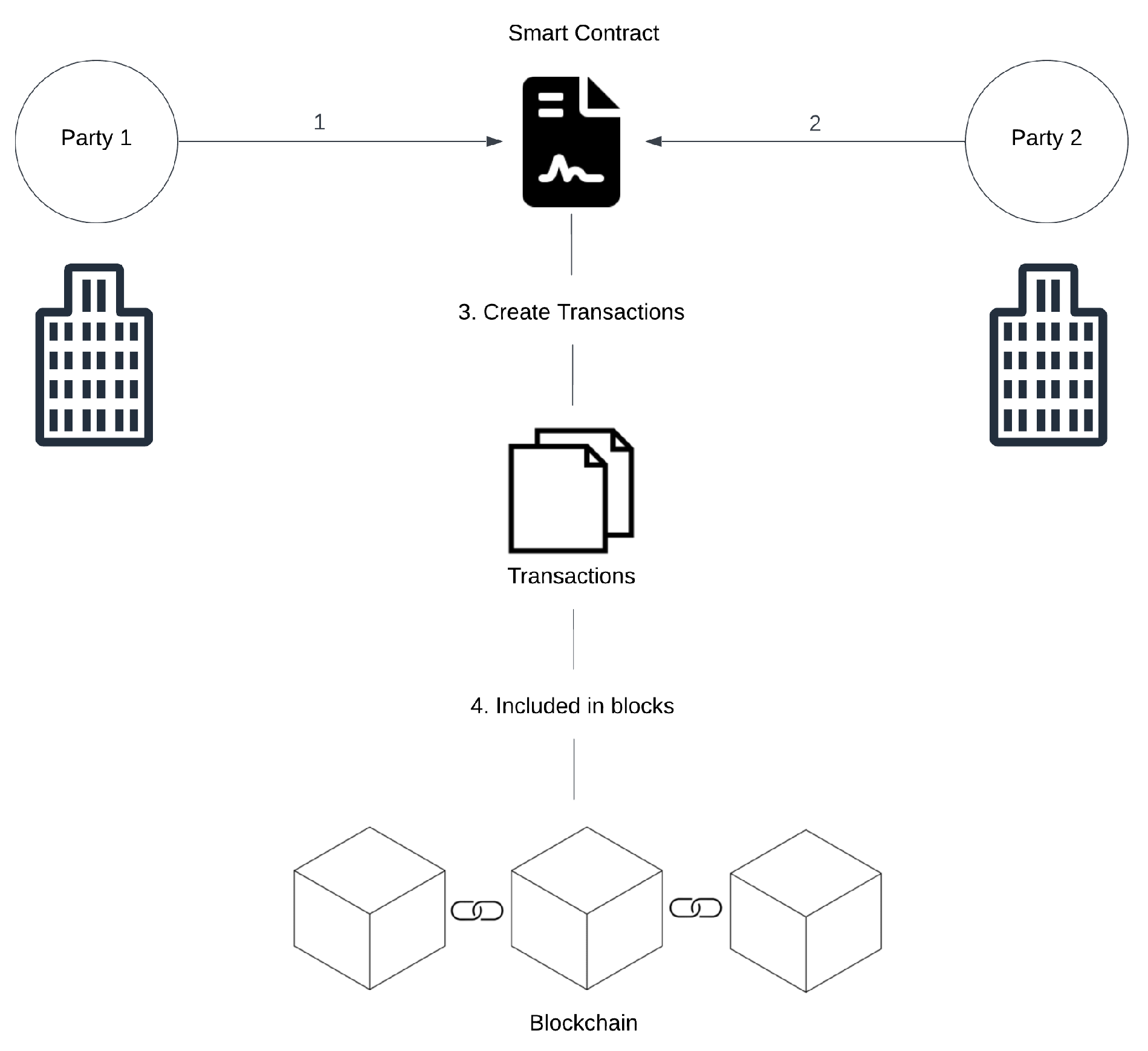
Smart contracts are programs that enforce and execute the terms of a contract without the need for participating parties. Smart contracts are built and stored on the blockchain. Smart contracts offer a safe and transparent method for carrying out transactions or transferring assets. Smart contracts can be used for a wide range of applications, such as financial and banking services, supply chain management, e-voting systems etc. Smart contracts eliminate the need for intermediaries and thus offer greater efficiency, security, transparency and cost savings. Figure 2 shows the working of a smart contract.

2.4. CRYSTALS Dilithium

Post-quantum cryptography, also known as quantum-safe, or quantum-resistant cryptography, is a type of cryptography that uses algorithms which are believed to be secure against attacks by quantum computers [9]. The goal of post-quantum cryptography is to develop cryptographic systems that are secure against both quantum and classical computer attacks and can work with existing communication protocols and networks. CRYSTALS-Dilithium is a post quantum digital signature scheme that was selected for standardisation due to its strong security and excellent performance by the National Institute of Standards and Technology (NIST) in the US [7]. It is based on the hard problem of lattices and is a member of the Cryptographic Suite for Algebraic Lattices (CRYSTALS) family of algorithms. The detailed description of CRYSTALS Dilithium is listed in [7].

2.5. Decentralized Ledger

Blockchain is a decentralized ledger that works similarly to a public ledger, but it’s not under the control of a single authority. It’s a system for recording information, such as the details of transactions, in a manner that’s difficult to alter or forge. For example, imagine a transaction as a shift of value from one account to another, similar to transferring money from one wallet to another. However, in this case, wallets are replaced by accounts, and money is replaced by value. A network of computers, known as nodes, ensures the validity of each transaction. Once they confirm the transaction’s authenticity, it’s added to the ledger as a new block. This process updates the balances of all accounts involved. As a result, the ledger always displays the most recent account balances. The key advantage of blockchain is its transparency and security. All transactions are visible to everyone, but they cannot be tampered with. Moreover, it eliminates the need for a central authority, providing a more straightforward way to manage and track assets.

2.6. IOTA Blockchain

IOTA is a cutting-edge distributed ledger blockchain technology that’s primarily tailored for the Internet of Things (IoT), although it can also operate like other blockchain systems. It employs a directed acyclic graph (DAG) to achieve scalability and low latency, which allows for simultaneous transaction processing. The consensus algorithm of IOTA facilitates rapid confirmation times, making it perfectly suited for applications that require real-time responses. One of the distinguishing features of the IOTA network is that it doesn’t charge gas fees for transactions. This sets IOTA apart from many other blockchain technologies. However, when it comes to smart contracts on the IOTA network, there is a gas fee to execute smart contracts [10]. In the context of IOTA’s smart contracts, there exists a committee of validators [11]. that are responsible for executing the smart contracts and calculating the state of the contract. All validators execute the same code and reach a consensus on the updated state. The IOTA Smart Contracts Protocol (ISC) allows for flexibility in the selection and reward system for these validators, which can be rotated, added, or replaced depending on the governance model. This flexibility paves the way for a customizable and efficient approach to smart contract execution on the IOTA network.

2.7. Zero-Knowledge Scalable Transparent Arguments of Knowledge (zk-STARK)

zk-STARK is a quantum secure proof system that allows efficient verification of large computations without disclosing any private information about the computation itself. [6] It is based on the concept of polynomial evaluation, where a polynomial is used to encode the computation and a set of public evaluations of the polynomial serve as the proof. Unlike other proof systems like zk-SNARK [12] which requires a trusted third party setup phase, zk-STARK does not require an initial trusted setup phase, which makes it more transparent and eliminates the need for a trusted setup. Moreover, zk-STARK is quantum secure in its construction, i,e., resistant to attacks by quantum computers. zk-STARK is composed of two polynomial time algorithms, named, Prove and Verify.

Prove $(\vec{x}, \vec{y}) \to π$ : This algorithm takes a private input $\vec{x}$ , computes output $\vec{y}$ and generates a proof $π$ encoding the polynomial computation.
Verify $(\vec{y}, π) \to \{0, 1\}$ : This algorithm takes the output $\vec{y}$ and the proof $π$ as inputs and verifies them. If the verification is successful, it returns 1 otherwise 0.

It also satisfies properties like scalability, zero knowledge, transparency, perfect completeness and knowledge extractability.

Scalability: zk-STARK is scalable due to its exponentially small proof verification time and nearly linear proof generation time.
Zero Knowledge: zk-STARK constructs proof $π$ using a set of polynomials which hides the information about the statement being proven. The proof $π$ is then verified by the verifier, who can check for the correctness of the proof without needing any of the details of the statement itself.
Transparency: zk-STARK does not require an initial trusted setup between the prover and verifier. Thus, unlike other proof systems, it is more transparent.
Perfect Completeness: An honest prover having a valid proof $π$ generated through zk-STARK will always be able to persuade an honest verifier with a probability 1.

$\begin{matrix} P [V e r i f y (\vec{y}, π) = 1 | π \leftarrow P r o v e (\vec{x}, \vec{y})] = 1 \end{matrix}$
Knowledge Extractability: In zk-STARKs, the knowledge extractor is a probabilistic polynomial-time algorithm. that, given a valid proof and public input. It extracts the witness used to generate the proof. The security of zk-STARK relies on the hardness of finding a valid proof without the witness. Consequently the ability to extract the witness from a valid proof is an important property. The proof of knowledge extraction can be expressed formally defined as:

Let P be a probabilistic polynomial-time (PPT) prover that generates a valid proof $π$ for an instance y with witness x. $n e g l (n)$ is a negligible function in n. Let V be a PPT verifier that takes input, the instance y and proof $π$ and outputs 1 if the proof is valid and 0 otherwise.

Let E be a PPT knowledge extractor that takes as input the instance y and proof $π$ , and outputs x with probability p. Then for any adversary A that runs in time $T (n)$ , there exists a simulator S that runs in time $O (T (n))$ and outputs a pair $(y, π)$ that is indistinguishable from a pair $(y, π)$ generated by the prover P, such that

$\begin{matrix} P r [A (y, π) = 1] - P r [E (y, π) = x] \leq n e g l (n) \end{matrix}$

2.8. Related Work

To address the issue of authentication of external data being fed into smart contracts, several noticeable work has been proposed in the literature. In 2016, Ahmed et al. [13] proposed a blockchain-based smart contract architecture, named Hawk, that protects user privacy, resolving the issue of transactions privacy and security for smart contracts. A smart contract program can be constructed using the compiler tool that Hawk also offers. However, Hawk’s application has limited functionality because it does not take data authenticity into account, unlike our proposed scheme. Later in 2016, Town Crier [14] proposed a Software Guard Extension (SGX) based solution. In this scheme, the external data are fed into a smart contract that was first processed and then fed into smart contract inside the secure SGX enclave. However, this solution is prone to attacks like meltdown [15] and spectre [16]. Furthermore, Town Crier does not offer any data privacy capabilities. In 2018, Yuan et al. [17] proposed a decentralized solution to crowdsource data for blockchain smart contracts. The proposed solution leveraged Zero-Knowledge Succinct Non-interactive Argument of Knowledge (zk-SNARKS) [12] to preserve the privacy of data and provided data authentication by binding the identities of participants with the data. The downside of this solution is it requires an initial trusted setup to work. Later in 2018, Jacob et al. [18], proposed ZoKrates, a solution to offload on-chain computation. ZoKrates also offers a toolkit to equip smart contracts with zero-knowledge proofs. The toolkit helps smart contracts to generate zero-knowledge proof and verify them. However, ZoKrates does not offer data authenticity. In late 2018, Astraea [19], a solution based on a voting game approach to solve data authentication was proposed. In the proposed solution, the participants play a voting game to verify and certify that the data being fed into the smart contract is authentic. However, Astraea did not address the data privacy issue.

In 2019, Bjorn et al. [20], proposed a solution named MUSCLE to bring external data to the Ethereum blockchain. The proposed solution leverages ECDSA [21] and BGLS [22] signature schemes to provide data authentication; however, the solution fails to address the problem of user data privacy. In 2020, Rishi et al. [23], proposed a smart contract protocol for business-to-business (B2B) blockchain. The proposed protocol allowed participants to execute subroutines in smart contracts with authenticity and anonymity, while our work is mainly focused on achieving data privacy and data authenticity. In late 2020, Junhoo et al. [24] proposed a framework based on zk-SNARKS for preserving the privacy of smart contract data feed. However, the proposed framework does not address the issue of data authentication and requires an initial trusted setup to work. In 2021, Chen et al [25] proposed a solution named Tora to ensure data authenticity. The proposed solution utilizes a Trusted Execution Environment (TEE) based on intel software guard extension. The proposed solution also provides high data availability via a decentralized hybrid layer-2 consensus mechanism. However, the proposed solution cannot preserve data privacy. Moreover, TEE is known to be prone to attacks like meltdown [15] and spectre [16]. In late 2021, Zhipeng et al. [26], proposed a solution named select-storage to feed external data to smart contracts. The proposed solution offers an efficient storage of data being fed into the smart contract but, no mechanism for data authentication and privacy has been offered.

In 2022, ZK-Authfeed [27], proposed a solution to solve the problem of data authentication and privacy while feeding data to smart contracts. The proposed solution uses zk-SNARKS and a digital signature scheme to provide privacy and data authentication. However, the drawback of this solution is that it requires a trusted setup to be established before its application. In 2023, Yijing et al [28], suggested a framework that uses blockchain technology and zero-knowledge proof to aid semantic communication between edge devices and virtual transportation networks. The proposed framework helps detection between malicious and authentic semantic data. However, the proposed solution does not offer a data privacy feature and requires an initial trusted setup to work.

In 2023, Emami et al [29], proposed a blockchain and zero-knowledge proof-based solution to auction big data to ensure transparency, authenticity and data privacy. The proposed solution leveraged the Ethereum blockchain and zk-SNARK zero-knowledge proof system. However, the drawback of this solution is, that it requires a trusted setup to be established before its application. Tianyu et al [30] in 2023 proposed Health-zkIDM, a decentralized identity verification system, leveraging zero-knowledge proof and blockchain technology to address the limitations of centralized healthcare identity management systems. It enhances patient identity sharing across healthcare institutions, mitigating data isolation and privacy risks. Despite its unique ID-based user identification and automatic post-registration identity verification, it lacks mechanisms for authenticating and protecting user input data privacy in DApps. Qiu et al [31] in 2023 proposed a blockchain and zero-knowledge proof-based solution to address the challenges in insurance claims of cars, such as inefficient and complex insurance claiming processes, unreliable data, and data leakage. The proposed scheme leverages these technologies to enhance privacy and efficiency in the car insurance claim process. However, the proposed scheme does not offer data authentication and also requires an initial trusted setup to work.

3. Our Construction of zk-DASTARK

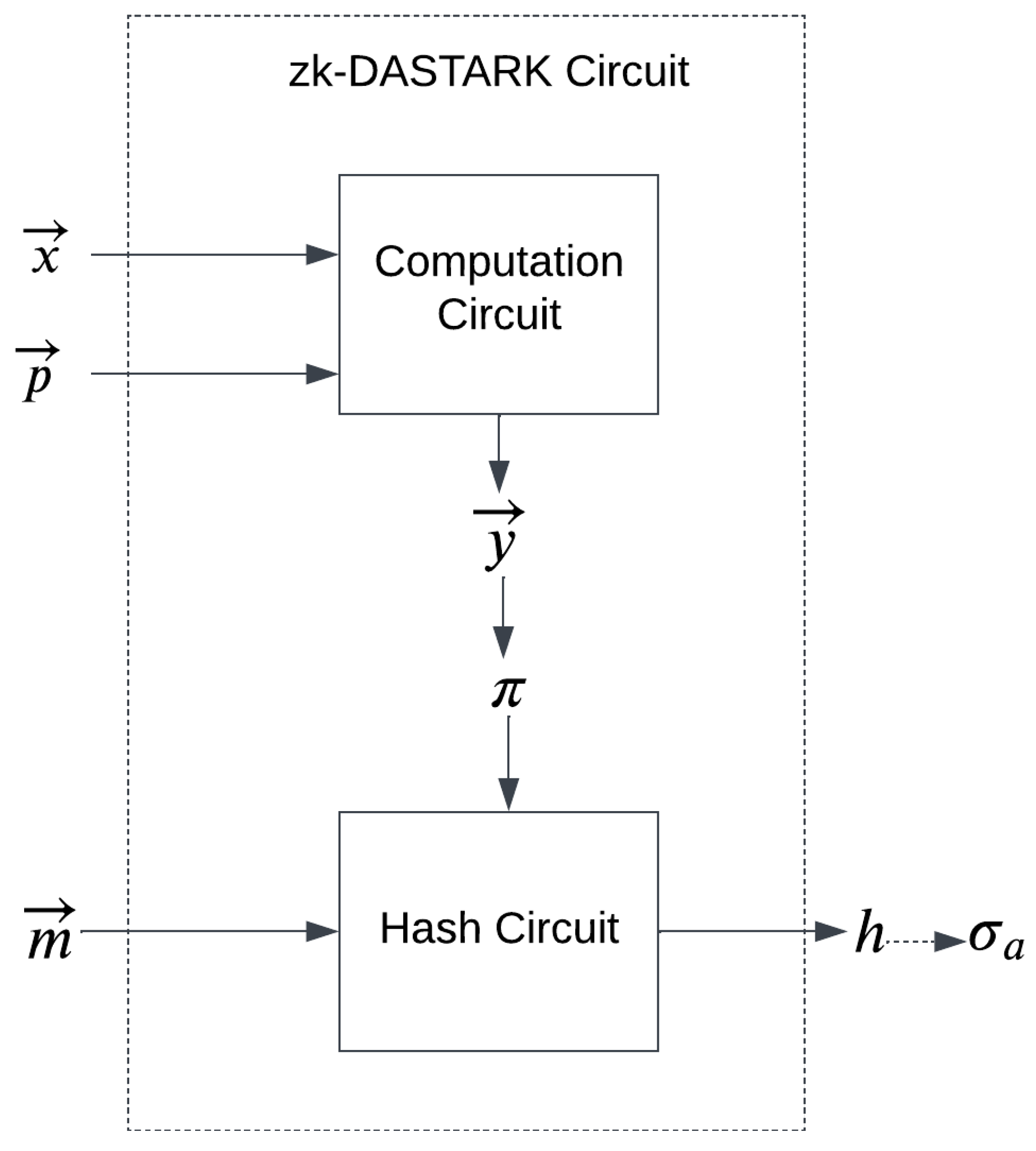
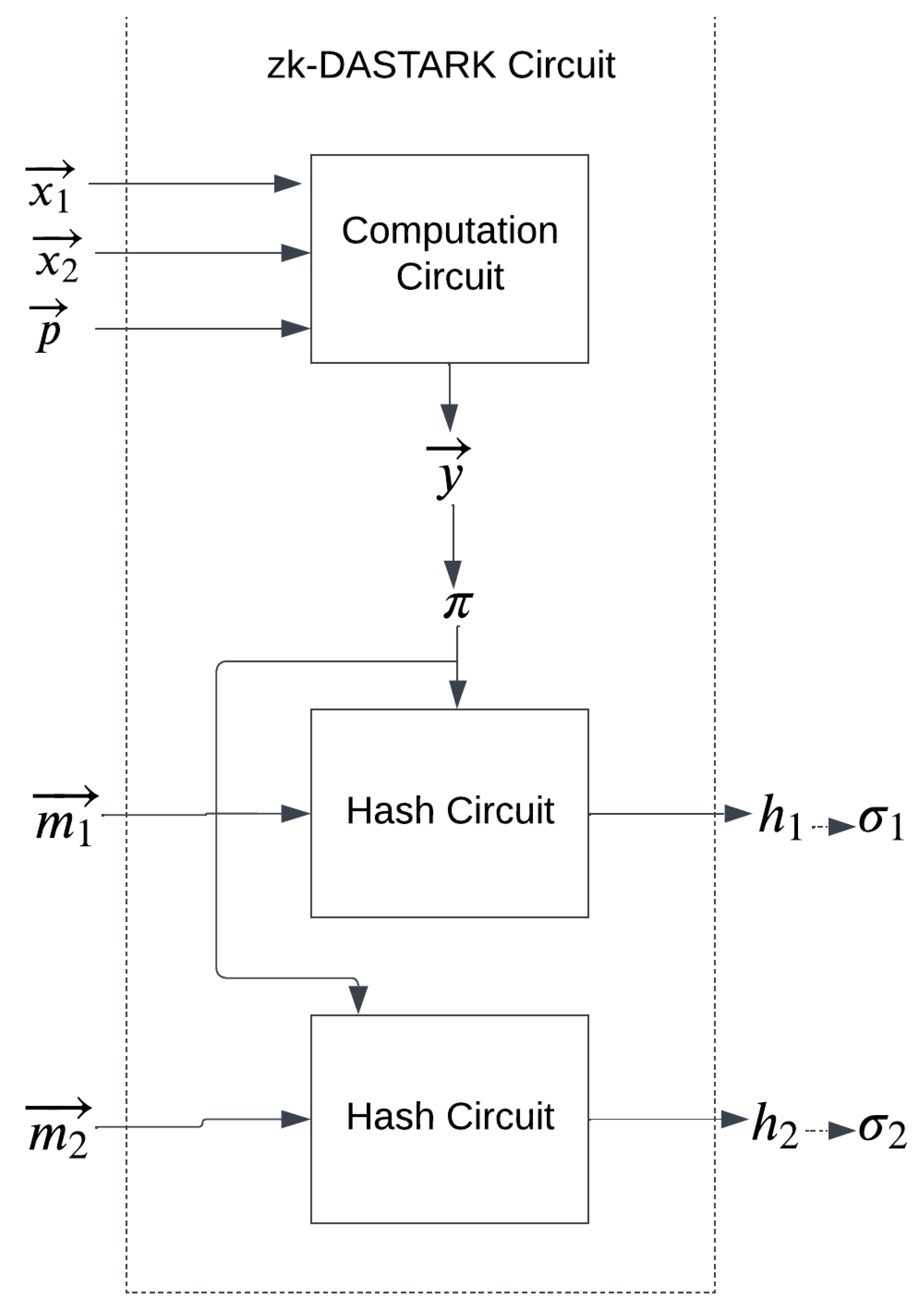
In this section, we discuss the construction of our proposed system zk-DASTARK. Our proposed construction is designed to solve the challenging problem of privacy preservation and private data authentication. Our proposed system comprises a circuit called the zk-DASTARK circuit which consists of a computation circuit and a hash circuit as shown in Figure 3

The computation circuit takes private input

\vec{x}

and public input

\vec{p}

to compute

\vec{y}

. The hash circuit takes the generated zero-knowledge proof

π

and metadata

\vec{m}

that is associated with private input to generate a hash which will be signed by a data authenticator for authentication.

In addition, zk-DASTARK has four polynomial time algorithms that include Setup, DataAuth, Prove and Verify. The functionality of each algorithm is described as follows:

Setup $\to (s k_{a}, p k_{a})$ : This algorithm generates a public/private key pair $(s k_{a}, p k_{a})$ using a post-quantum cryptographic algorithm named CRYSTALS Dilithium [7]. The generated keys will be later used by the DataAuth algorithm.
DataAuth $(π, \vec{m}, s k_{a}) \to σ_{a}$ : To authenticate the proof, this algorithm takes the proof $π$ , and the metadata vector $\vec{m}$ associated with input vector $\vec{x}$ which was used to generate the proof $π$ , hashes them together using SHA-256 [32] and then using the private key $s k_{a}$ generates a signature $σ_{a}$ over the hash by using CRYSTALS Dilithium digital signature algorithm.
Prove $(\vec{x}, \vec{y}) \to π$ : This algorithm takes the vector $\vec{y}$ obtained by performing the computation using zk-DASTARK circuit on private input vector $\vec{x}$ . Performs the computation on it and generates a proof $π$ over it using zk-STARK and outputs a proof $π$
Verify $(\vec{y}, π, p k_{a}, σ_{a}) \to \{0, 1\}$ : This algorithm takes the output vector $\vec{y}$ , the proof $π$ , public key $p k_{a}$ , hash h and signature $σ_{a}$ . The algorithm first, verifies the signature. If the signature is valid, then it proceeds to verify the proof. If both the values are valid it outputs 1, otherwise, in case of invalid proof or signature, the output is 0.

In zk-DASTARK, there are three entities which are Prover, Data Authenticator and Verifier, that interact with the proposed system. The prover, Data Authenticator and verifier are described as follows:

Prover: A prover is someone who wants to prove a statement to the verifier. The data authenticator generates a proof for the prover using the prove algorithm along with the private input vector $\vec{x}$ provided by the prover, and tries to persuade the verifier that the proof $π$ and output $\vec{y}$ is indeed generated from the input vector $\vec{x}$ , by getting a digital signature of the data authenticator over the hash of the proof $π$ and the output $\vec{y}$ .
Data Authenticator: A data authenticator is a reliable trusted entity, responsible for authenticating the input vector $\vec{x}$ by verifying the metadata associated with the input vector. After verification, the data authenticator uses the prove algorithm to generate proof $π$ by performing the computation using zk-DASTARK circuit on the input vector $\vec{x}$ that is provided by the prover and then signs the proof $π$ with his secret key $σ_{a}$
Verifier: A verifier is someone who wants to verify the claim being made by the prover. The verifier takes the proof $π$ , output $\vec{y}$ , and signature $σ_{a}$ and uses the verify algorithm to verify the claim. If the output obtained by the verify algorithm is 1 the claim is valid otherwise in case the output value is 0 the claim is invalid.

Example: To demonstrate how zk-DASTARK can be utilized to feed authenticated inputs to DApps without compromising privacy, we can take a simple example of a medical insurance DApp. The DApp takes values of blood pressure, sugar level, age and pulse rate that are stored in the variables

x_{1}, x_{2}, x_{3}, x_{4}

respectively. The insurance company has defined a simple polynomial function

\begin{matrix} y = f (x_{1}, x_{2}, x_{3}, x_{4}) = 3 x_{1} + 7 x_{2} + 11 x_{3} + 13 x_{4} \end{matrix}

The insurance amount is determined based on output. Variables

x_{1}, x_{2}, x_{3}, x_{4}

are sensitive values of the user which he wants to protect from being exposed whereas the coefficients are known public parameters. zk-STARK can be utilized to encode the polynomial computation in a proof

π

to show that output y was calculated from

x_{1}, x_{2}, x_{3}, x_{4}

without disclosing them. However, zk-STARK does not offer data authenticity to the user, hence the data may comprise fake/forged values. To prevent this scenario, a hash circuit is used additionally with zk-STARK. This hash circuit takes the proof

π

hashes it and generates a hash value. The hash value generated is then signed by a reliable trusted data authenticator to ensure the authenticity of the input data. This ensures that before the proof verification, one can verify whether the signature is valid or not. If it is valid, then one can proceed to verify the proof

π

, which guarantees that y was indeed computed from the correct inputs.

4. ZK-STARK in zk-DASTARK

In this section, we describe how zk-DASTARK integrates zk-STARK to feed authenticated inputs to DApps without compromising privacy. With an interactive zero-knowledge proof system, the correctness of complex statements can be proven interactively. This was formally introduced in [33] as Interactive Oracle Proof (IOP). In IOP, instead of verifying the entire proof, the verifier queries on some part of the proof selected uniformly at random.

The proof system zk-SNARK [6] belongs to this IOP family. In zk-STARK, the proof system works on an algebraic representation of computation, where there is a chain of internal states

A_{1}, A_{2}, \dots, A_{m}

and several polynomial relations (

p_{i}

’s) among those:

p_{i} (A_{i_{1}}, A_{i_{2}}, \dots, A_{i_{m}}) = 0

. It is then asserted that the computation is correct if and only if it satisfies the relations.

As explained in Example 1, a medical insurance DApp takes values of blood pressure, sugar level, age and pulse rate represented as

x_{i}

’s. The insurance company has defined a simple polynomial function

\begin{matrix} y = f (x_{1}, x_{2}, \dots, x_{n}) = \sum a_{i} x_{i} . \end{matrix}

The insurance company wants to convince the party that y has been computed on correct

x_{i}

’s as input. In the context of zk-STARK as a verifiable computation, we can define the language

L

as a set of pairs

(X, X^{'})

such that

C (X) = X^{'}

for deterministic computation C. Then one can assert that

X^{'}

is the result of C applied to X by proving that

(X, X^{'}) \in L

. In the context of medical insurance DApp, the party wants to compute

C (X) = 〈 A . X 〉

which outputs y where

X = (x_{1}, x_{2}, \dots, x_{n})

and

A = (a_{1}, a_{2}, \dots, a_{n})

. The insurance company returns y and the proof

π

as the output of

P r o v e (X, y)

. Here we describe this algorithm. Before that, we provide some tools which are essential for this algorithm.

Let

F (x, N)

be a function which on input x and N, computes

x_{N}

as follows:

x_{0} = x

and

x_{i} = x_{i - 1}^{2}

for

i = 1 \dots N

. Consider the function

f (i) = x_{i}

for

i = 0, 1, \dots, p

. This function can be constructed by interpolation. Let us consider the constraint

c (A, B) = B^{2} - A

. Thus

C (f (i + 1), f (i)) = 0

for all

i \in {1, \dots, N}

. It can be noted that the polynomial

C (f (x + 1), f (x))

is of degree

2 N

and has roots

0, 1, 2, \dots, N

. So the polynomial

D (x) = x (x - 1) \dots (x - p)

divides C. Define

g (x) = \frac{C (f (x + 1), f (x))}{D (x)}

. It may be noted that if the prover computes all the steps correctly then for all

s \in_{R} Z_{N}

g (s)

\frac{C (f (s + 1), f (s))}{D (s)}

. Using these steps, we first describe zk-STARK-Prover() and zk-STARK-Verifier() which are basic building blocks for zk-DASTARK-Prover() and zk-DASTARK-Verifier().

Algorithm 1 zk-STARK-Prover()

Input:: N, s, x
Output:: $x_{N}$ , $π_{x}$
1:: set i = 1; and S = ϕ;
2:: while i ≤ n do
3:: set $i = 1;$ and $S = ϕ$ ;
4:: while $i \leq n$ do
5:: compute $x_{i} = x_{i - 1}^{2}$ ;
6:: set $f (i) = x_{i}$ ;
7:: $S = S ⋃ {(i, f (i)}$ ;
8:: end while
9:: interpolate to construct $f ()$ from datapoints in $S$ ;
10:: construct $D (x) = \prod_{j = 0}^{N} (x - j)$ ;
11:: Construct $g (x) = \frac{C (f (x + 1), f (x))}{D (x)}$ ;
12:: compute $f (s)$ , $f (s + 1)$ , $g (s)$ ;
13:: $π = (f (s), f (s + 1), g (s))$ ;
14:: output $x_{N} | | π_{x}$ ;

Algorithm 2 zk-STARK-Verifier()

Input:: $π_{x}$
Output:: $b_r e t_v a l$
1:: set $b_r e t_v a l = false$ ;
2:: parse
3:: set $b_r e t_v a l = f a l s e$ ;
4:: parse $π = (f (s), f (s + 1), g (s))$ ;
5:: if $(g (s) = = \frac{C (f (s + 1), f (s))}{D (s)})$ then
6:: set $b_r e t_v a l = t r u e$ ;
7:: end if
8:: return $b_r e t_v a l$ ;

In the interactive proof system, the verifier inputs a number N and a random number

s \in_{R} Z_{N}^{*}

. In the following lemma we study an important property which is crucial for the final proof of zk-DASTARK-Prover() (see Remark ). Let

y = \sum_{i = 1}^{n} a_{i} x_{i}

. Also let

Y_{j + 1} = Y_{j}^{2}

, where

Y_{0} = y

. Similarly let

V_{i, 0} = a_{i} x_{i}

and

V_{i, j + 1} = V_{i, j}^{2}

for all

i \in {1, \dots, n}

. Then, in

Z_{2^{N}}

Y_{N} = \sum V_{i, N}

Proof.

It may be noted that,

Y_{N} = y^{2^{N}}

and

V_{j, N} = V_{j, 0}^{2^{N}}

for all

i \in {0, \dots, n}

. Also in

Z_{2^{N}}

y^{2^{N}} = {(\sum_{j = 1}^{n} a_{j} x_{j})}^{2^{N}} = \sum_{j = 1}^{n} {(a_{j} x_{j})}^{2^{N}} = \sum_{j = 1}^{n} V_{j, 0}^{2^{N}} = \sum_{j = 1}^{n} V_{j, N}

□

Algorithm 3 zk-DASTARK-Prover()

Input:: p, s, $X = (x_{1}, \dots, x_{n})$ , $A = (a_{1}, \dots, a_{n})$
Output:: y, $π$
1:: compute
2:: compute $y = 〈 A . X 〉$ mod p;
3:: compute $(Y_{N}, π_{y}) =$ zk-STARK-Prover( $N, s, y$ );
4:: while $i \leq n$ do
5:: compute $(V_{i, N}, π_{x_{i}}) =$ zk-STARK-Prover( $N, s, x_{i}$ );
6:: end while
7:: compute $π = π_{y} | | π_{x_{1}} | | \dots | | π_{x_{n}}$ ;
8:: output $(y | | Y_{N} | | V_{1, N} | | \dots | | V_{n, N} | | π)$ ;

Algorithm 4 zk-DASTARK-Verifier()

Input:: $π$
Output:: $b_r e t_v a l$
1:: set $b_r e t_v a l_{0} = f a l s e$ ;
2:: parse $π$ as $(y | | Y_{N} | | V_{1, N} | | \dots | | V_{n, N} | | π_{y} | | π_{x_{1}} | | \dots | | π_{x_{n}})$ ;
3:: if $(Y_{N} m o d 2^{N} = = (\sum_{j = 1}^{n} V_{j, N}) m o d 2^{N})$ then
4:: set $b_r e t_v a l_{0} = t r u e$ ;
5:: end if
6:: while $i \leq n$ do
7:: $b_r e t_v a l_{i} =$ zk-STARK-Verifier( $π_{x_{i}}$ );
8:: end while
9:: $b_r e t_v a l = ⋀_{i = 0}^{n} b_r e t_v a l_{i}$ ;
10:: return $b_r e t_v a l$ ;

It may be noted that Lemma 4 forms the ground of the proof of correctness of zk-DASTARK-Verifier() algorithm. The left hand side of line 3 of zk-DASTARK-Verifier() is

Y_{N}

and the right hand side is

\sum_{j = 1}^{n} V_{j, N}

Z_{2^{N}}

. Thus, clearly from Lemma 4, the correctness of zk-DASTARK-Verifier() is asserted.

From line 4 of zk-DASTARK-Prover(), the number of calls to the zk-STARK-Prover() is only as much as the number of variables n in the polynomial defined by the insurance company in Example 1 which is linear in the complexity of zk-STARK-Prover() algorithm. Similarly, from line 7 of zk-DASTARK-Verifier(), the complexity is liner in n.

5. STARKFeed: A Framework for authenticated data feed to DApp smart contract

In this section, we propose a novel framework based on zk-DASTARK, which can be used for authenticated data feed to DApps without compromising data privacy. Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 describes the architecture and working of the zk-DASTARK framework.

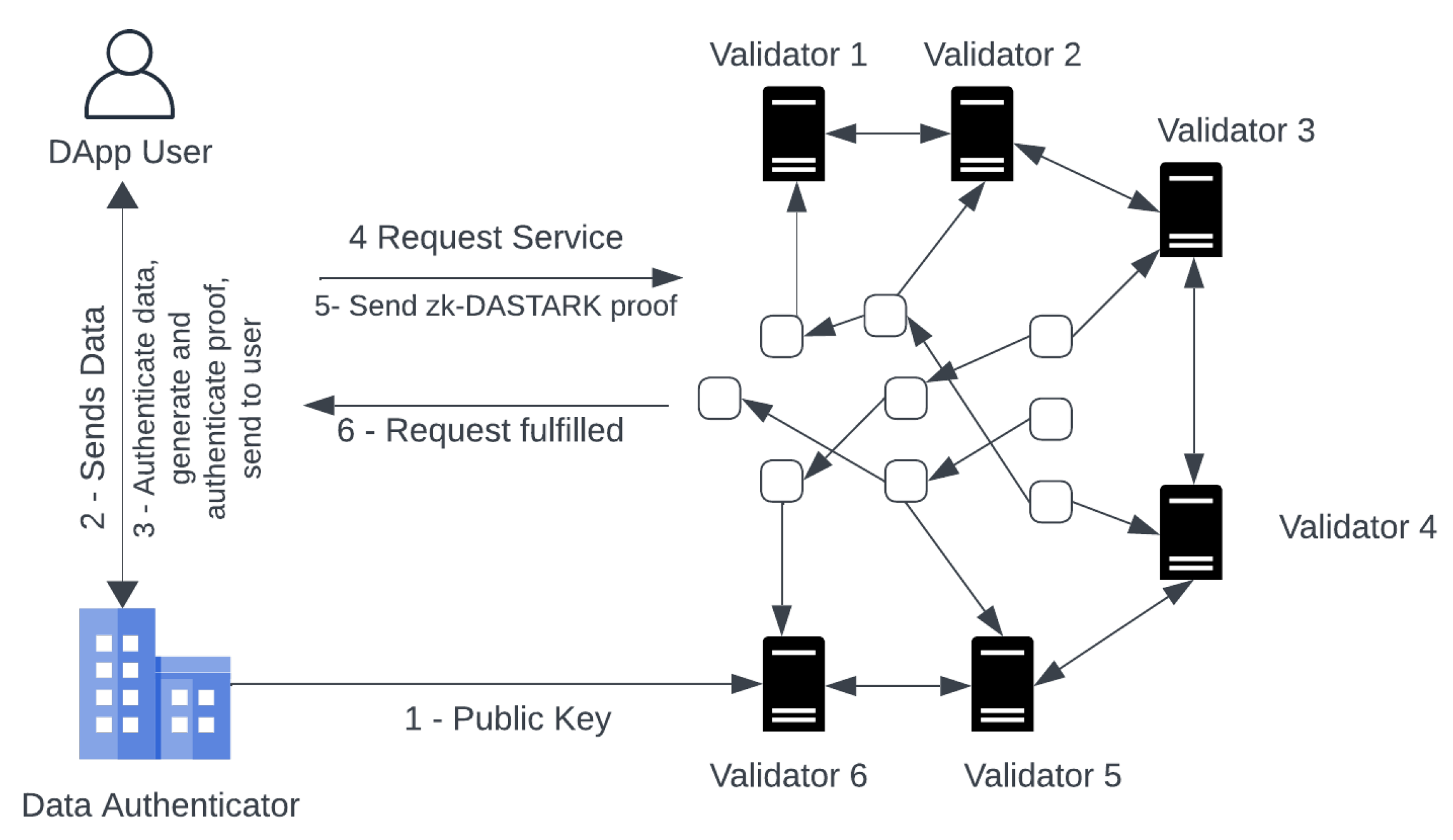
The framework consists of four participants: Decentralized Application (DApp), DApp-User, Data Authenticator and Blockchain validators.

DApp: DApp are autonomous applications that operate on a blockchain. The most common examples of DApps are OpenSea, MakerDAO, Uniswap etc. DApps services are offered through a smart contract. Due to the decentralized nature of smart contracts, DApps are authority-free and cannot be controlled by a single entity.
DApp-User: A DApp-user is a user who wishes to use the services being offered by the DApp. The user does not want to share his private information which is required to use the services being offered by the DApp due to data privacy concerns.
Data Authenticator: A data authenticator is a trusted entity which is used to perform the computation, generate the proof $π$ and then authenticate it. The data authenticator is an external entity to the blockchain ecosystem. The data authenticator authenticates the proof $π$ by signing it with his private key $s k_{a}$ . Anyone having the public key $p k_{a}$ of the data authenticator can verify the signed proof $π$ .
Blockchain Validators: All the transactions submitted, to be included in the blockchain need to be verified first. This task of verification of transactions is delegated to blockchain validators (miners). Validators execute complex consensus algorithms to verify and include transactions into blocks.

We take two scenarios to describe how our proposed framework works and how it leverages zk-DASTARK. In Scenario A, privacy and authentication of private input data are required. In Scenario B, only the privacy of private input data is required without the need for input authentication.

Scenario A: (Privacy Protected Authenticated Data Feed)

In this scenario, both privacy and authentication of private input data are required. The working mechanism of the proposed framework is explained in the following steps:

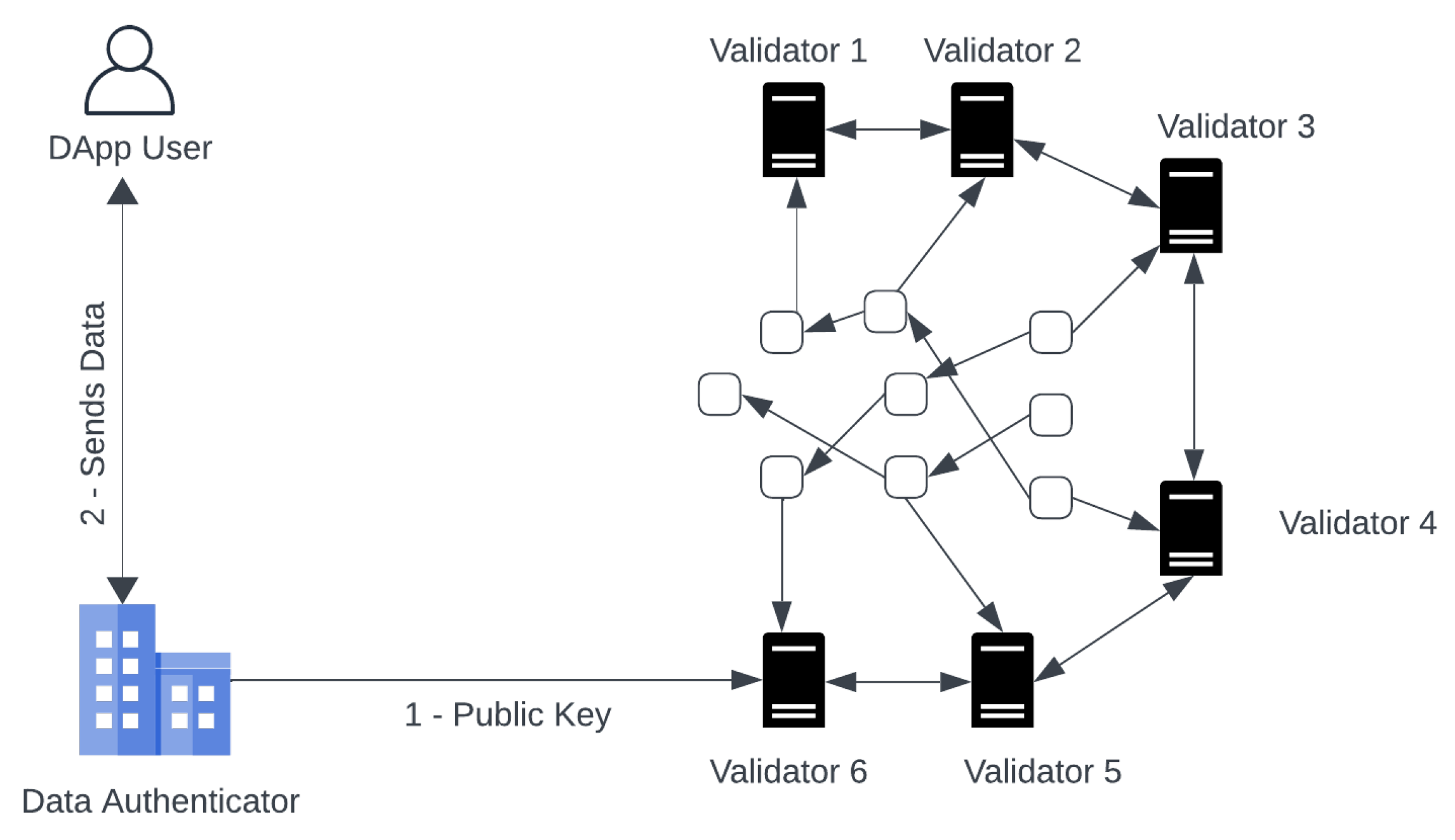
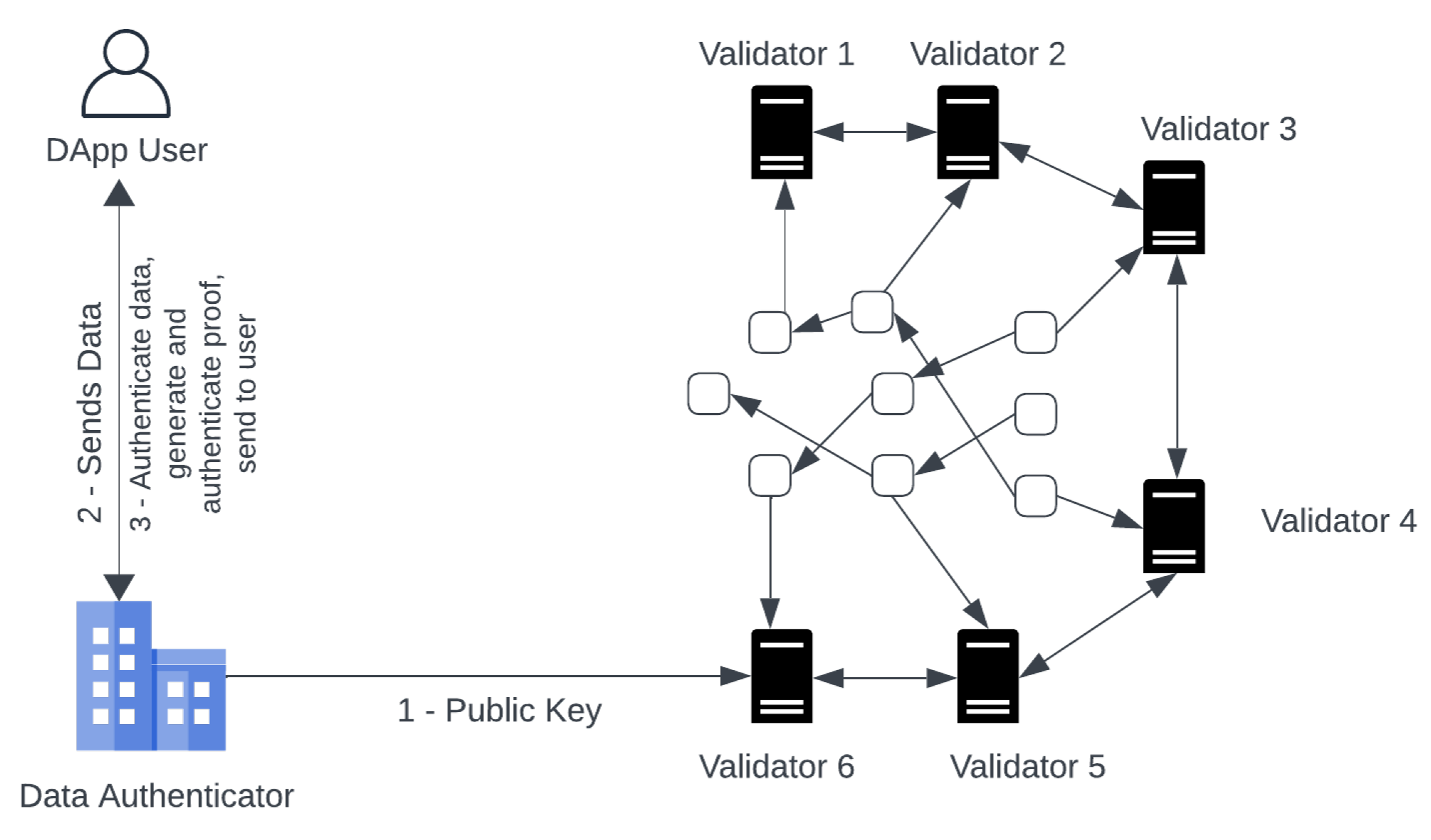
Initialization: First of all, the data authenticator will execute the setup function. This is a one-time setup that is used, to generate his public/private key pair $(s k_{a}, p k_{a})$ . The public/private key pair is used to authenticate the proof $π$ generated against DApp user’s private data.
DataAuth: As per requirement to use the service offered by the DApp. The DApp user takes the private input $\vec{x}$ , and metadata $\vec{m}$ to Data Authenticator. First, it will use the zk-DASTARK circuit to compute output $\vec{y}$ and hash h. Then, it executes zk-DASTARK.Prove $(\vec{x}, \vec{y})$ to generate proof $π$ and in the end, it execute zk-DASTARK.DataAuth $(π, \vec{m}, s k_{a})$ to produce a signature $σ_{a}$ .
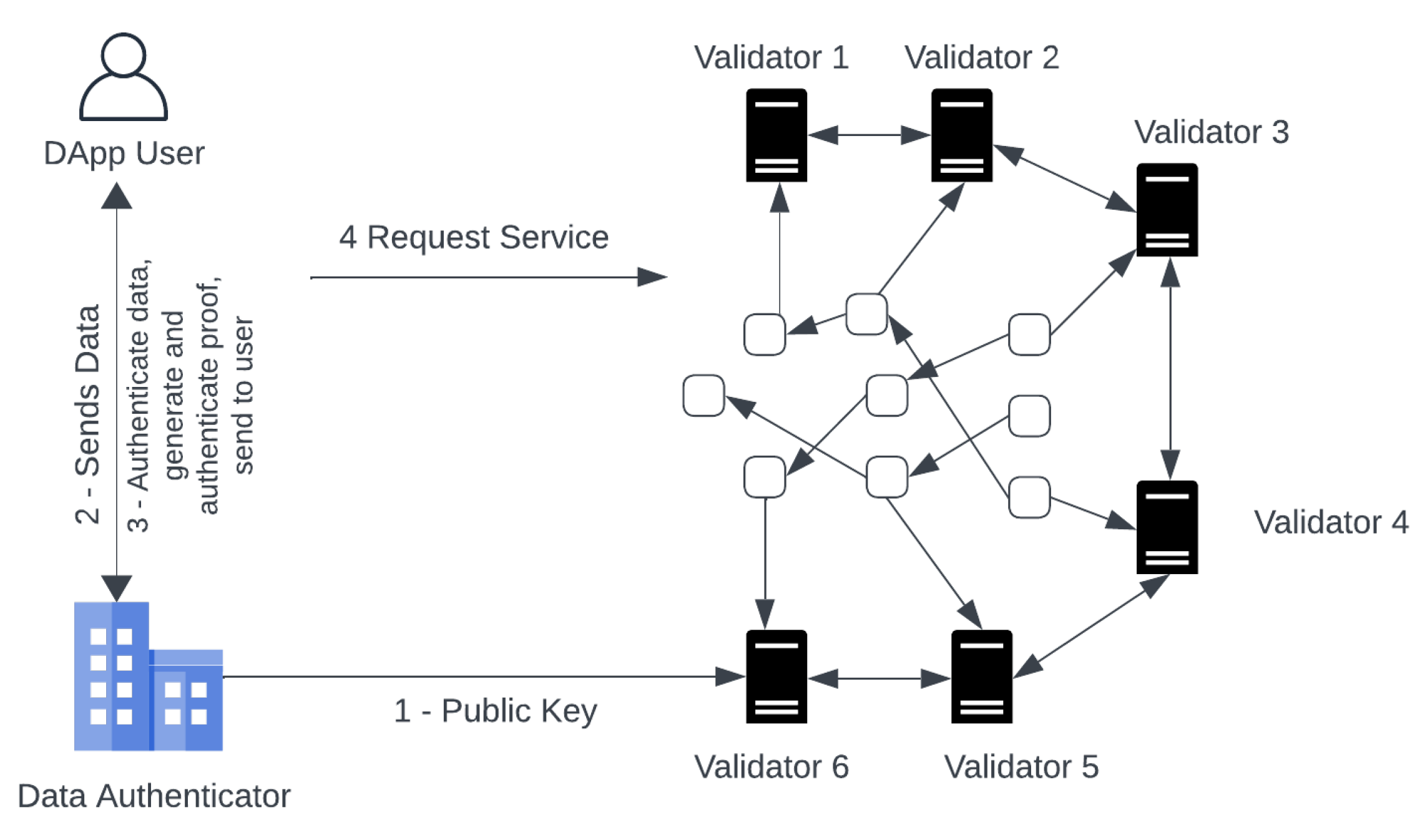
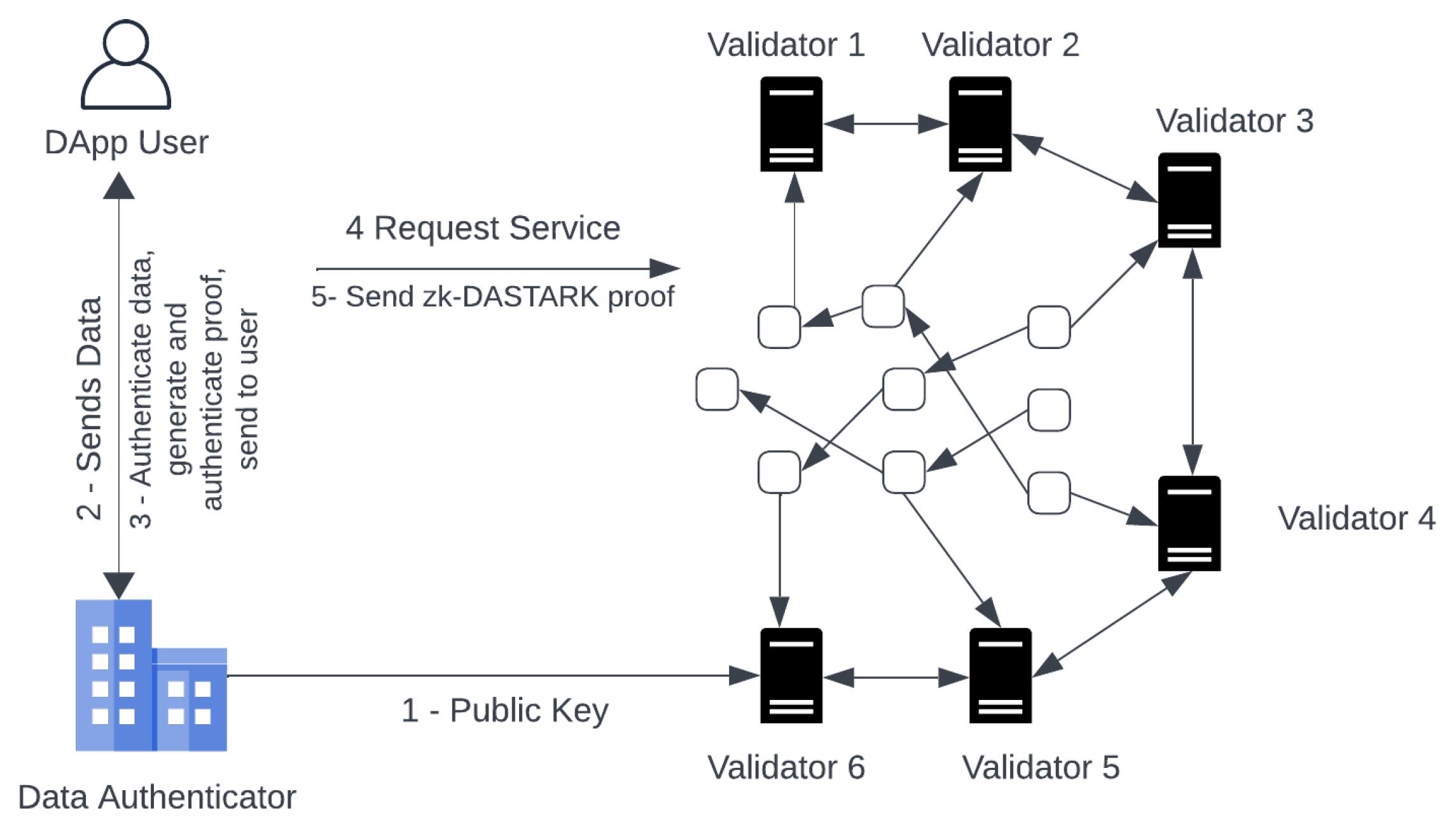
Service Request: The DApp user after obtaining the signature $σ_{a}$ , output $\vec{y}$ and the proof $π$ , will send the DApp a request for service containing the proof $π$ , signature $σ_{a}$ , output $\vec{y}$ .
Service Request Fulfillment: On receiving the service request, the blockchain validators execute the DApp to fulfill the request made by the DApp user. The validators first verify the request made, by executing zk-DASTARK.Verify $(\vec{y}, π, p k_{a}, σ_{a})$ if the verification is successful, then the DApp service logic will be executed with the output $\vec{y}$ and the request will be fulfilled.

The proposed framework execution protocol along with smart contract is given in Figure 10

Scenario B (Privacy Protected Data Feed)

In this scenario, the privacy of private input data is required without the need for input authentication. The detailed working of the proposed framework is explained in the following steps:

Service Request: To avail of the service offered by the DApp. The DApp user will use the zk-DASTARK circuit to compute output $\vec{y}$ . In this case, we do not need input data authentication. The DApp user can proceed directly to generate a zero-knowledge proof $π$ by executing zk-DASTARK.Prove $(\vec{x}, \vec{y})$ , without authenticating input data by Data Authenticator. After obtaining the proof $π$ , the DApp user sends the Dapp a request for service containing the proof $π$ output $\vec{y}$ .
Service Request Fulfillment: On receiving the service request, the blockchain validators execute the DApp to fulfil the request made by the DApp user. Firstly, the validators will verify the request, by executing zk-DASTARK.Verify $(\vec{y}, π, n u l l, n u l l)$ . If the verification is successful, then the DApp service logic will be executed with the output $\vec{y}$ and the request will be fulfilled. An example of such a smart contract algorithm is mentioned in Figure 11

6. Discussion and Analysis

In this section, we discuss the design considerations for our zk-DASTARK scheme and then compare it with existing well-known schemes.

6.1. Security Analysis

The authenticity of data in our proposed framework is ensured through a specially designed circuit in the zk-DASTARK scheme. The Data authenticator endorses the authenticity of the DApp user’s private input data, by first computing the output

\vec{y}

. It then generates proof

π

and then computes a hash value

h = H (π, \vec{m})

using SHA-256 as the hash function and signs the computed hash value with its private key

s k_{a}

using a quantum-resistant digital signature scheme CRYSTALS Dilithium2 [7]. The security of CRYSTALS Dilithium2 is based on the hardness of Fiat Shamir with Aborts, Ring Short Integer Solution (SIS) and Learning with Errors (LWE) modules. Due to the collision resistance property offered by the hash function, it is impossible to find another user’s private input and metadata such that

h = H (π^{'}, \vec{m^{'}})

. Additionally, zk-DASTARK guarantees computational zero-knowledge property, which ensures that

\vec{y}

is computed from

\vec{x}

and

\vec{p}

without disclosing

\vec{x}

, also zk-STARK offers resistance against quantum attacks.

To prove the knowledge extractability of our scheme zk-DASTARK, let’s assume there is a probabilistic polynomial-time adversary A and knowledge extractor E which can break the knowledge extraction of zk-DASTARK. There also exist

\hat{S e t u p}

and

\hat{P r o v e}

simulator algorithms for the adversary. The probability for extracting witness

\vec{x}

is non-negligible, the formal proof is given below:

\begin{matrix} 1 . \hat{S e t u p} \to s k_{a}, p k_{a} \\ 2 . A^{\hat{P r o v e} (.), \hat{D a t a A u t h (s k_{a}, .)}} \to (π, \vec{p}, \vec{y}, σ_{a}) \\ 3 . P r [E (O u t p u t L i s t_{A}) \to \vec{x}] \leq n e g l (n) \end{matrix}

where

O u t p u t L i s t_{A}

is the list of inputs and outputs generated by adversary A,

n e g l (n)

is a negligible function in n.

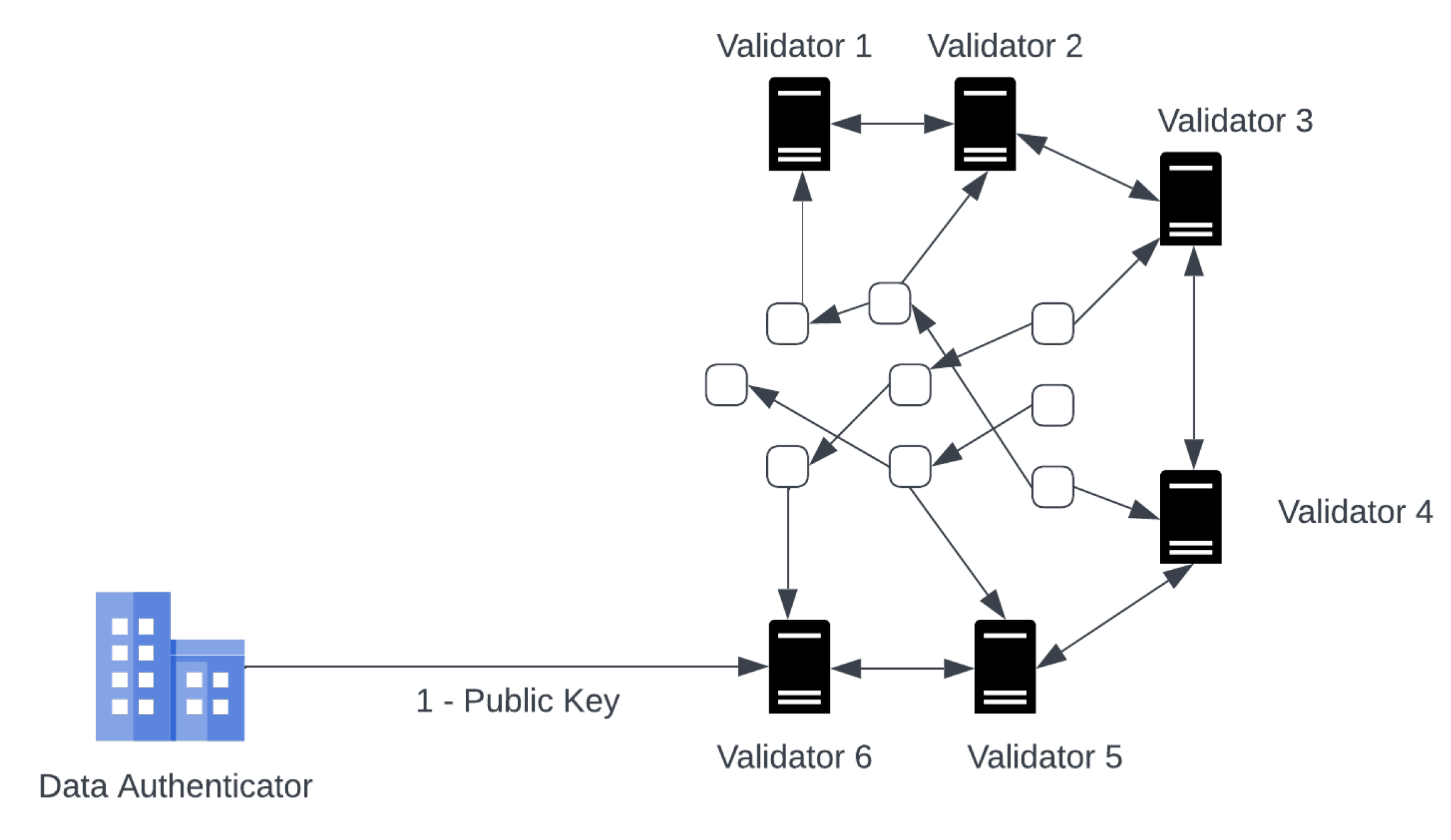
6.2. Multiple Data Authenticators Support

Our proposed framework currently supports one data authenticator but it can be extended to use cases where input data need to be authenticated from multiple data authenticators or different sets of inputs require authentication from different data authenticators. Our proposed framework has the flexibility to be extended to multiple data authenticators as shown in Figure 12.

6.3. Computation Cost Analysis

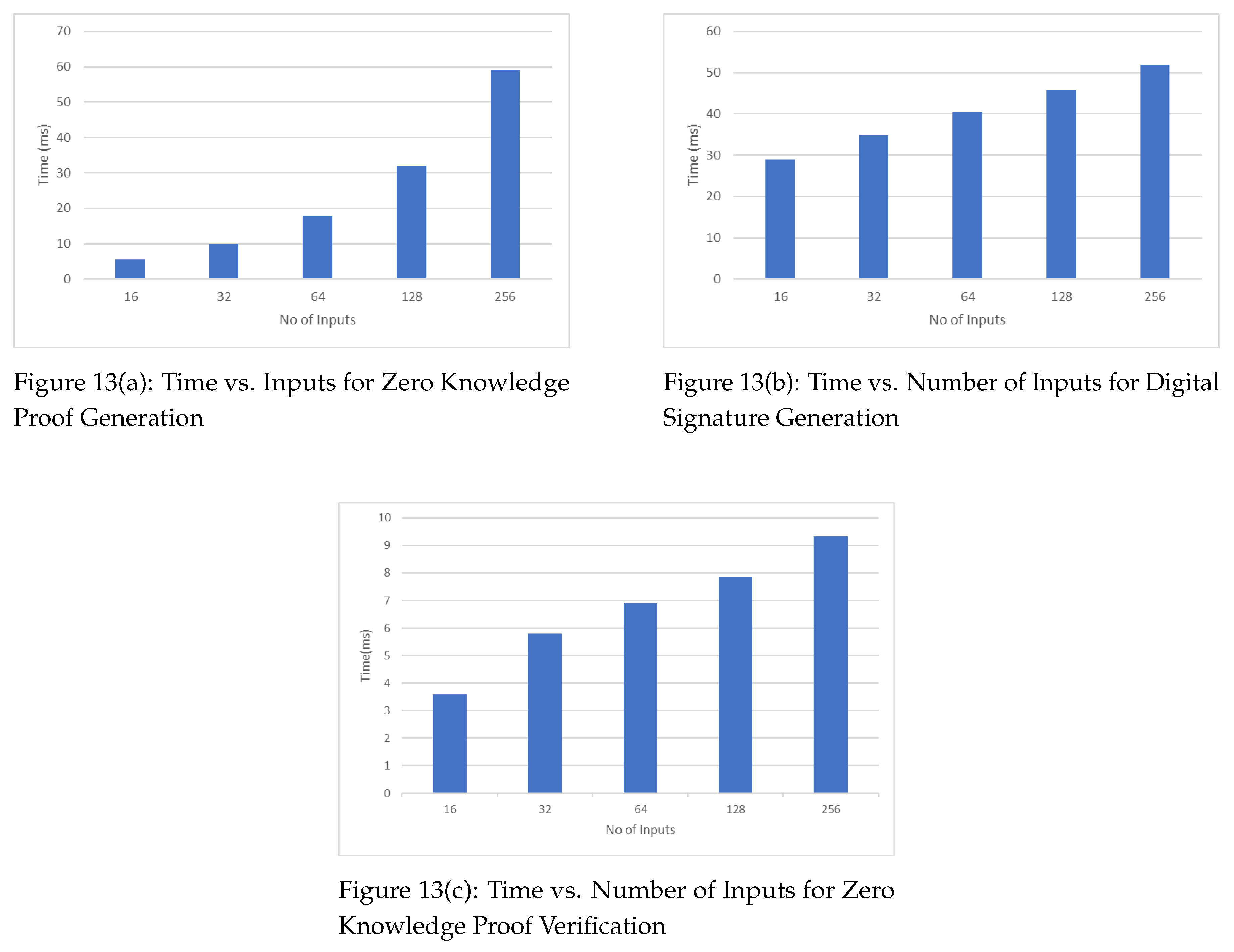
The computation cost of zk-DASTARK depends on several factors that include the complexity of the arithmetic circuit being verified, the degree of the polynomial used to generate the zk-STARK zero knowledge proof, and the desired level of security. The computation time and storage space required in our proposed scheme depends upon the provided number of inputs. The increase in the number of inputs increases the time and storage space required to generate zero knowledge proof The same phenomenon goes for the digital signature generation. But on the other hand, if we compare proof generation time and proof verification time, the proof verification time is significantly less than the proof generation time. It proves that the zk-STARK verifier works in much faster way in verifying zero knowledge proofs.

6.4. Comparison of our proposed framework with Well-known frameworks

A comparison of our proposed zk-DASTARK framework against well-known frameworks in terms of data privacy, data authentications, trusted third party setup and quantum attack resistance given in Table 1. It shows that our proposed framework offers better data privacy and authentication and it does not require any trusted third party setup. A salient feature of our proposed framework quantum attacks resistance [34].

7. Implementation and Performance Evaluation

The implementation and performance evaluation of our proposed framework was conducted on a Personal Computer (PC) with following specifications: Processor Intel Core i5-8250U@1.60GHz*8 and 24GB RAM, running 64bit Ubuntu 22.04. Our implementation consists of the following three components:

zk-DASTARK Module: The zk-DASTARK implements the four functions that include Setup, Prove, Verify, and DataAuth. The functionality of each of these functions has already been discussed in Section 3. This module also implements the zk-DASTARK computation calculation circuit.
IOTA Blockchain: IOTA is a distributed ledger technology mainly designed for the Internet of Things (IoT) ecosystem but can also be used just like any other blockchain ecosystem [5]. It uses a directed acyclic graph (DAG) instead of a traditional blockchain to achieve scalability and low latency. IOTA’s DAG architecture allows parallel transaction processing to make it highly scalable. IOTA’s network consensus algorithm allows for fast confirmation times, making it suitable for real-time applications. IOTA blockchain offers many distinct features such as allowing users to do micro-transactions with a very minimal transaction fee, the data transfer feature provided by IOTA blockchain can be used to transfer data securely, masked messaging feature provided by IOTA blockchain can be used to broadcast encrypted and authenticated messages to subscribers.
The DApp Smart Contract We implemented an example medical insurance DApp as an IOTA Smart Contract (ISC) running on webassembly (WASM) virtual machine (VM) in rust language [35]. The DApp user must be registered with DApp. To claim the insurance premium, the DApp user can use the proposed framework to prove his claim and the authenticity of his input data. The insurance premium is calculated from the output of following equation $y = f (x) = c_{1} x_{1} + c_{2} x_{2} + c_{3} x_{3} + . . . . + c_{n} x_{n}$ where $c_{1}, c_{2} . . . c_{n}$ are public parameters.

The blockchain network was constructed of five IOTA Wasp nodes and five Hornet nodes running inside docker containers [36]. Figure 13 shows the time taken in milliseconds (ms) to generate zero-knowledge proof against the given number of inputs. As the number of inputs increases, the time taken to generate the zero-knowledge proof also increases. It shows that number of inputs is linearly proportional to zero-knowledge proof generation time. Figure 13 shows a similar increasing trend in computational time (milliseconds or ms) taken to generate the digital signature by the Data Authenticator against the given number of inputs. Similarly, Figure 13 depicts the time taken in ms to verify zero-knowledge proof against the given number of inputs. As the number of inputs increases, the time taken to verify the zero-knowledge proof also increases.

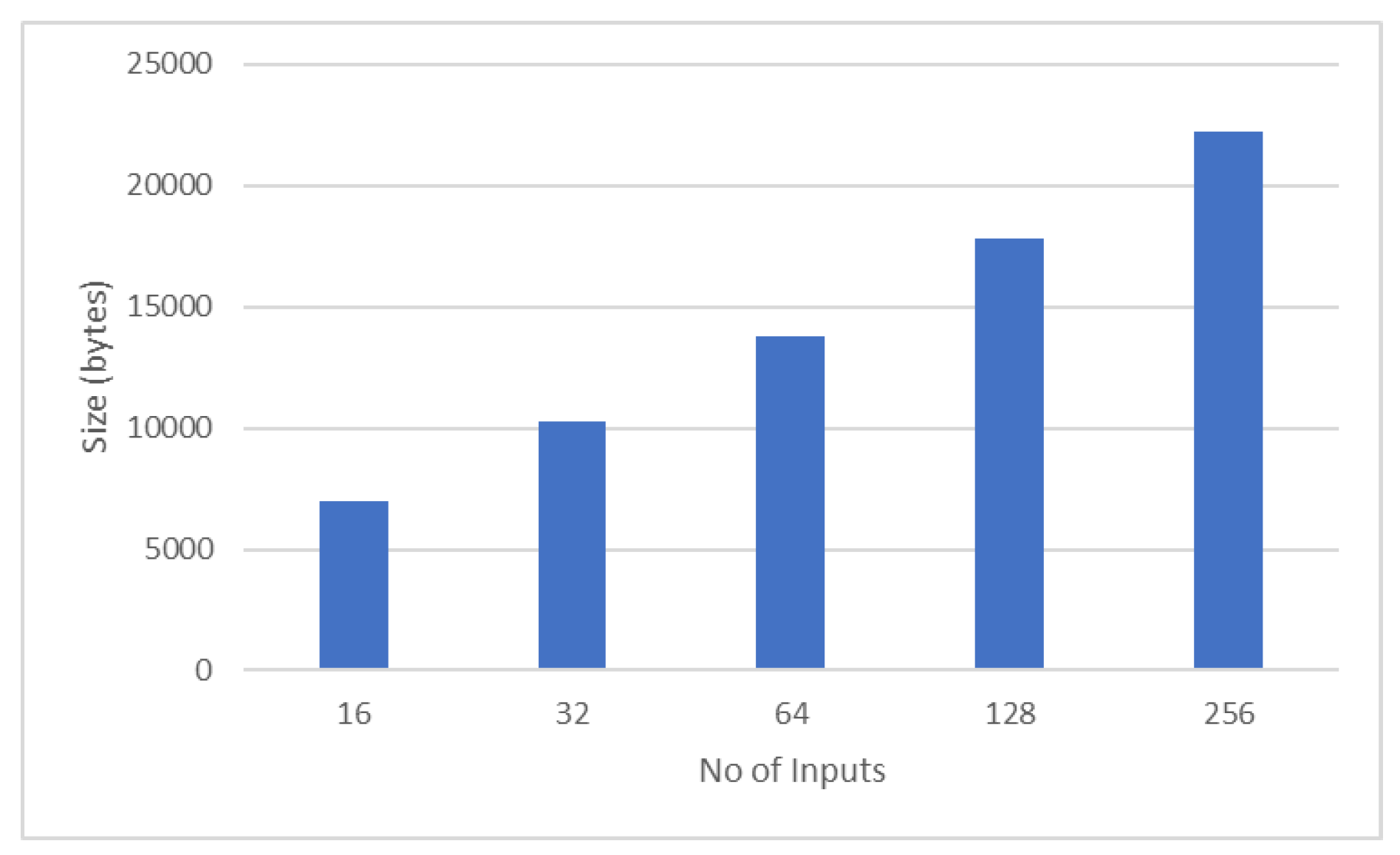
Figure 14 depicts the increasing relationship trend between the number of inputs and zero-knowledge proof size (computed in bytes). Figure shows the relationship between the number of inputs and gas units consumed by DApp during zero-knowledge proof verification. An increase in gas consumption can be seen as the number of inputs increases.

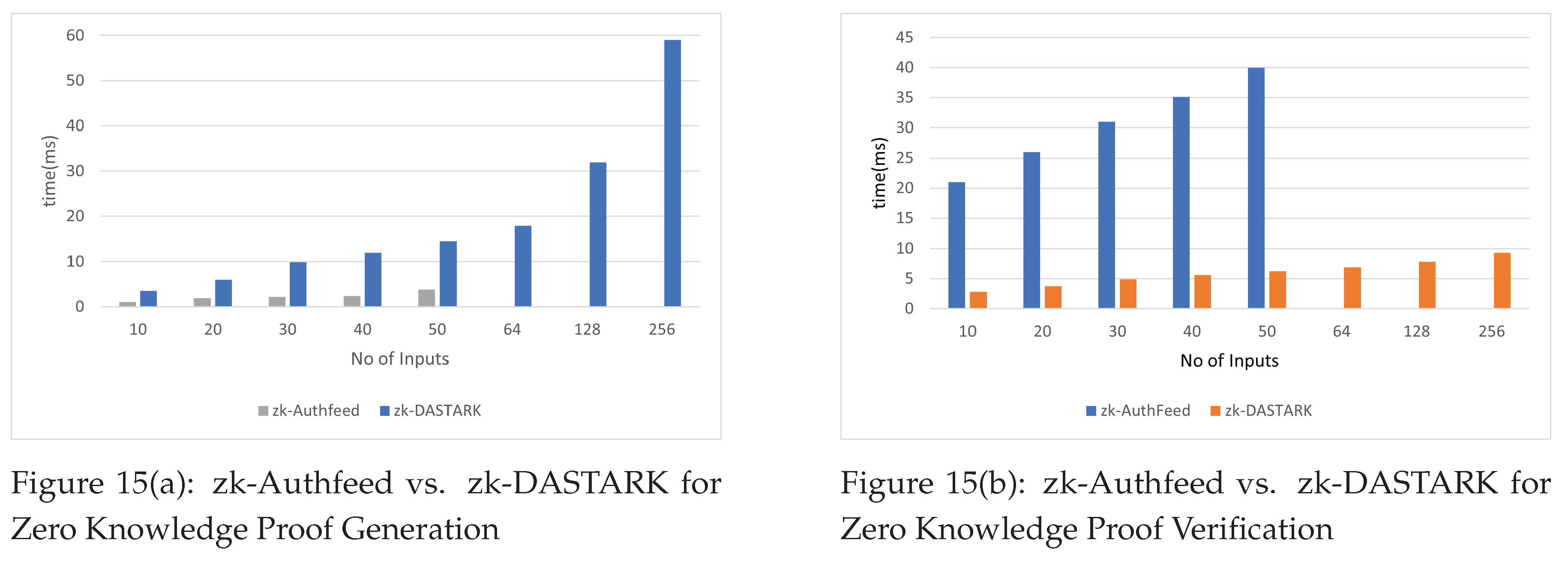
Figure 15, Figure 15 depicts a comparison between zk-DASTARK and zk-AuthFeed [27]. Figure 15 shows that zk-Authfeed is much faster than zk-DASTARK in Zero Knowledge Proof generation whereas Figure 15 shows that zk-DASTARK is much faster in verifying Zero Knowledge Proof than zk-Authfeed.

8. Conclusion

The emergence of blockchain and smart contracts evolves traditional digital applications such as identity management, supply chain management, banking and finance etc. into DApps. The DApps running on the blockchain using smart contracts require access to authentic off-chain data but the users are more conscious of the privacy of their data and consequently are more reluctant to share their data. This poses a significant challenge in the adoption of DApps worldwide. In this work, we introduce the zk-DASTARK, a quantum attack-resistant framework that provides both privacy and authenticity for off-chain private data input to smart contracts on the blockchain. Our framework is built upon an extended zk-STARK with a hash circuit and a post-quantum digital signature scheme. Our proposed framework eliminates the need for the establishment of a trusted setup, as required by other well-known zero-knowledge schemes. Our proposed framework is quite efficient in performance as compared with well-known off-chain data authentication frameworks.

References

Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized business review 2008, 21260. [Google Scholar]
Daley, S. Blockchain Applications and Real-World Use Cases, 2023.
coinbase. What is DeFi? https://www.coinbase.com/learn/crypto-basics/what-is-defi.
Szabo, N. Smart contracts: building blocks for digital markets. EXTROPY: The Journal of Transhumanist Thought,(16) 1996, 18, 28. [Google Scholar]
Buterin, V.; others. A next-generation smart contract and decentralized application platform. white paper 2014, 3, 2–1. [Google Scholar]
Ben-Sasson, E.; Bentov, I.; Horesh, Y.; Riabzev, M. Scalable, transparent, and post-quantum secure computational integrity. Cryptology ePrint Archive 2018. [Google Scholar]
Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Dilithium: A lattice-based digital signature scheme. IACR Transactions on Cryptographic Hardware and Embedded Systems.
Popov, S.; Lu, Q. IOTA: Feeless and free. IEEE Blockchain Technical Briefs 2019. [Google Scholar]
Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
Invocation - IOTA Learn, 2023.
Validators - IOTA Learn, 2023.
Parno, B.; Howell, J.; Gentry, C.; Raykova, M. Pinocchio: Nearly practical verifiable computation. Communications of the ACM 2016, 59, 103–112. [Google Scholar] [CrossRef]
Kosba, A.; Miller, A.; Shi, E.; Wen, Z.; Papamanthou, C. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. 2016 IEEE symposium on security and privacy (SP). IEEE, 2016, pp. 839–858.
Zhang, F.; Cecchetti, E.; Croman, K.; Juels, A.; Shi, E. Town crier: An authenticated data feed for smart contracts. Proceedings of the 2016 aCM sIGSAC conference on computer and communications security, 2016, pp. 270–282.
Lipp, M.; Schwarz, M.; Gruss, D.; Prescher, T.; Haas, W.; Mangard, S.; Kocher, P.; Genkin, D.; Yarom, Y.; Hamburg, M. Meltdown. arXiv preprint arXiv:1801.01207, arXiv:1801.01207 2018.
Kocher, P.; Horn, J.; Fogh, A.; Genkin, D.; Gruss, D.; Haas, W.; Hamburg, M.; Lipp, M.; Mangard, S.; Prescher, T.; others. Spectre attacks: Exploiting speculative execution. Communications of the ACM 2020, 63, 93–101. [Google Scholar] [CrossRef]
Lu, Y.; Tang, Q.; Wang, G. Zebralancer: Private and anonymous crowdsourcing system atop open blockchain. 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS). IEEE, 2018, pp. 853–865.
Eberhardt, J.; Tai, S. Zokrates-scalable privacy-preserving off-chain computations. 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). IEEE, 2018, pp. 1084–1091.
Adler, J.; Berryhill, R.; Veneris, A.; Poulos, Z.; Veira, N.; Kastania, A. Astraea: A Decentralized Blockchain Oracle. 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), 2018, pp. 1145–1152. [CrossRef]
van der Laan, B.; Ersoy, O.; Erkin, Z. Muscle: Authenticated external data retrieval from multiple sources for smart contracts. Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, 2019, pp. 382–391.
Johnson, D.; Menezes, A.; Vanstone, S. The elliptic curve digital signature algorithm (ECDSA). International journal of information security 2001, 1, 36–63. [Google Scholar] [CrossRef]
Boneh, D.; Gentry, C.; Lynn, B.; Shacham, H. Aggregate and verifiably encrypted signatures from bilinear maps. Advances in Cryptology—EUROCRYPT 2003: International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, –8, 2003 Proceedings 22. Springer, 2003, pp. 416–432. 4 May.
Saket, R.; Singh, N.; Dayama, P.; Pandit, V. Smart contract protocol for authenticity and compliance with anonymity on hyperledger fabric. 2020 IEEE International Conference on Blockchain and Cryptocurrency (ICBC). IEEE, 2020, pp. 1–9.
Park, J.; Kim, H.; Kim, G.; Ryou, J. Smart contract data feed framework for privacy-preserving oracle system on blockchain. Computers 2020, 10, 7. [Google Scholar] [CrossRef]
Chen, L.; Yuan, R.; Xia, Y. Tora: A trusted blockchain oracle based on a decentralized tee network. 2021 IEEE International Conference on Joint Cloud Computing (JCC). IEEE, 2021, pp. 28–33.
Gao, Z.; Zhuang, Z.; Lin, Y.; Rui, L.; Yang, Y.; Zhao, C.; Mo, Z. Select-Storage: A New Oracle Design Pattern on Blockchain. 2021 IEEE 20th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom). IEEE, 2021, pp. 1177–1184.
Wan, Z.; Zhou, Y.; Ren, K. zk-AuthFeed: Protecting data feed to smart contracts with authenticated zero knowledge proof. IEEE Transactions on Dependable and Secure Computing 2022. [Google Scholar] [CrossRef]
Lin, Y.; Du, H.; Niyato, D.; Nie, J.; Zhang, J.; Cheng, Y.; Yang, Z. Blockchain-Aided Secure Semantic Communication for AI-Generated Content in Metaverse. IEEE Open Journal of the Computer Society 2023, 4, 72–83. [Google Scholar] [CrossRef]
Emami, A.; Keshavarz Kalhori, G.; Mirzakhani, S.; Akhaee, M.A. A blockchain-based privacy-preserving anti-collusion data auction mechanism with an off-chain approach. The Journal of Supercomputing.
Bai, T.; Hu, Y.; He, J.; Fan, H.; An, Z. Health-zkIDM: A Healthcare Identity System Based on Fabric Blockchain and Zero-Knowledge Proof. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
Qiu, Z.; Xie, Z.; Jiang, X.; Ran, C.; Chen, K. Novel Blockchain and Zero-Knowledge Proof Technology-Driven Car Insurance. Electronics 2023, 12, 3869. [Google Scholar] [CrossRef]
of Standards, N.I. ; Technology. Secure hash standard (SHS), 2015.
Ben-Sasson, E.; Chiesa, A.; Spooner, N. Interactive oracle proofs. Theory of Cryptography: 14th International Conference, TCC 2016-B, Beijing, China, -November 3, 2016, Proceedings, Part II 14. Springer, 2016, pp. 31–60. 31 October.
Arshad, R.; Riaz, Q. Quantum and Post-Quantum Cybersecurity Challenges and Finance Organizations Readiness. In Handbook of Research on Cybersecurity Issues and Challenges for Business and FinTech Applications; IGI Global, 2023; pp. 314–337.
The Rust Programming Language. Accessed: 2023-09-12.
Docker. What is a container? https://www.docker.com/resources/what-container/.

Figure 1. Blockchain flow diagram

Figure 2. Smart contract flow diagram

Figure 3. An extended computation circuit for zk-DASTARK with an additional hash circuit.

Figure 4. STARKFeed - Setup

Figure 5. STARKFeed - Sharing data with data authenticator

Figure 6. STARKFeed - Getting proof and authenticated data back

Figure 7. STARKFeed - Requesting service

Figure 8. STARKFeed - Sending the proof to DApp

Figure 9. STARKFeed - Request fulfilled

Figure 10. Framework execution protocol and smart contract with data authentication

Figure 11. Framework execution protocol and smart contract without data authentication

Figure 12. zk-DASTARK with multiple data authenticators

Figure 13. Computational latency (in ms) as the number of inputs increase to the Zero Knowledge Proof Generation (a), Digital Signature Generation (b) and the Zero Knowledge Proof Verification (c)

Figure 14. Size vs. Number of Inputs for Zero Knowledge Proof Generation

Figure 15. Computational latency (in ms) comparison for Zero Knowledge Proof generation between zk-Authfeed and zk-DASTARK (a), Computational latency (in ms) comparison for Zero Knowledge Proof verification between zk-Authfeed and zk-DASTARK (b)

Table 1. Comparison of zk-DASTARK framework with well-known frameworks

Frameworks	Data Privacy	Data Authentication	Trusted third party setup	Quantum attack resistance
Kosba et al [13]	Yes	No	Yes	No
Zhang et al [14]	No	Yes	No	No
Lu et al [17]	Yes	Yes	Yes	No
Eberhardt et al [18]	Yes	No	Yes	No
Adler et al [19]	No	Yes	No	No
Bjorn et al [20]	No	Yes	No	No
Saket et al [23]	No	Yes	No	No
Junhoo et al [24]	Yes	No	Yes	No
Chen et al [25]	No	Yes	No	No
Zhipeng et al [26]	No	No	No	No
Zhiguo et al [27]	Yes	Yes	Yes	No
Yijing et al [28]	No	Yes	Yes	No
Emami et al [29]	Yes	Yes	Yes	No
Tianyu et al [30]	No	No	Yes	No
Qiu et al [31]	Yes	No	Yes	No
zk-DASTARK	Yes	Yes	Yes	Yes

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

zk-DASTARK: A quantum-resistant, data authentication and zero-knowledge proof scheme for protecting data feed to smart contracts

Abstract

1. Introduction

2. Background and Related work

2.1. Zero Knowledge Proof (ZKP)

2.2. Blockchain

2.3. Smart Contract

2.4. CRYSTALS Dilithium

2.5. Decentralized Ledger

2.6. IOTA Blockchain

2.7. Zero-Knowledge Scalable Transparent Arguments of Knowledge (zk-STARK)

2.8. Related Work

3. Our Construction of zk-DASTARK

4. ZK-STARK in zk-DASTARK

5. STARKFeed: A Framework for authenticated data feed to DApp smart contract

Scenario A: (Privacy Protected Authenticated Data Feed)

Scenario B (Privacy Protected Data Feed)

6. Discussion and Analysis

6.1. Security Analysis

6.2. Multiple Data Authenticators Support

6.3. Computation Cost Analysis

6.4. Comparison of our proposed framework with Well-known frameworks

7. Implementation and Performance Evaluation

8. Conclusion

References

MDPI Initiatives

Important Links

Subscribe