Elastic Wave Propagation Control in Porous and Finitely Deformed Locally Resonant Nacre-Like Metamaterials

Preprint

Article

Elastic Wave Propagation Control in Porous and Finitely Deformed Locally Resonant Nacre-Like Metamaterials

Altmetrics

Downloads

106

Views

Comments

A peer-reviewed article of this preprint also exists.

,Girolamo Sgambitterra

,Girolamo Sgambitterra

This version is not peer-reviewed

Submitted:

19 December 2023

Posted:

20 December 2023

You are already at the latest version

Alerts

Abstract

Recent studies have shown that the mechanical properties of bioinspired periodic composite materials can be strongly influenced by finite deformation effects, leading to highly nonlinear static and dynamic behaviors at multiple length scales. For instance, in porous periodic nacre-like microstructures, microscopic and macroscopic instabilities may occur for a given uniaxial loading process and, as a consequence, wave attenuation properties may evolve as a function of the microstructural evolution, giving it the designation of metamaterials. The numerical outcomes provide new opportunities to design bioinspired soft composite metamaterials characterized by high deformability and enhanced elastic wave attenuation capabilities given by the insertion of voids and lead cores.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Over the last twenty years, as a result of the high mechanical, thermal, and electrical performance requirements [1], advanced composite materials have been preferred over traditional ones in many extreme engineering applications [2,3,4]. For example, structural members or engine parts of space shuttles or aircraft have been designed thanks to advanced composite materials. In addition, recently, bioinspired microstructures were used by researchers to develop innovative materials with exceptional properties. For instance, it has been found that nacre-like materials possess unique mechanical properties resulting from the alternating layering of soft protein and hard aragonite platelets [5,6,7] and, thanks to the recent development in additive manufacturing [8,9,10], many researchers started to investigate the mechanical properties of 3D printed microstructured bioinspired materials [11,12,13,14]. Due to their complex microstructures, such bioinspired composite materials are generally regarded as highly heterogeneous media liable to several nonlinear phenomena such as microscopic and macroscopic instabilities caused by large deformations [15] or, also, microscopic damage processes could occur as a result of platelets debonding from the matrix [16]. Several studies have demonstrated that such microscopic damage phenomena are closely related to fracture phenomena occurring at the macroscopic scale, such as delamination and crack propagation, and that they strongly influence the dynamic response of the structure in terms of natural frequency vibrations [17,18,19], thus representing the most frequent failure precursor for advanced materials employed in extreme engineering applications. Hyperelastic constitutive laws are commonly employed to predict with accuracy the mechanical behavior of such advanced composite materials in a large deformation framework. To prevent numerical modeling from becoming too expensive from the computational point of view, several advanced numerical modeling strategies have been proposed, for example, nonlinear homogenization [20] and multiscale methods [21]. In recent works, it has been demonstrated that bioinspired nacre-like composite materials may be optimized to improve their mechanical performance under static loadings [22,23], and, due to their periodic microstructures, they are also intrinsically capable of influencing elastic wave propagation. For this reason, their vibrational response is attracting extraordinary attention [24,25,26] leading to the design of new advanced bioinspired nacre-like metamaterials, which are composite materials characterized by periodic microstructures inspired by nature. They are commonly distinguished from traditional bioinspired materials by properties that are not found in nature [27]. While metamaterial research has made remarkable progress over the past decade, there are still several drawbacks. For example, frequently, their material characteristics fail to fulfill the energy dissipation criteria essential for managing the transmission of waves and reducing noise in mechanically challenging procedures. In recent years, the study of elastic wave propagation in nacre-like composite metamaterials has focused on finding the optimal combination of material and geometric parameters. It is therefore the objective of this study to improve the scientific knowledge about nacre-like composite metamaterials, exhibiting microscopic instability under extreme loading conditions, by proposing a lightened nacre-like composite metamaterial with hollow reinforcing platelets and lead cores to investigate the influence of the main microscopic material and geometrical parameters together with the addition of lead cores on the evolution of its wave attenuation properties. A brief recap of the theoretical concepts related to the nonlinear static and dynamic response of periodic composite materials has been reported in Section 2, while the numerical results obtained by superimposing an elastic wave motion through the Bloch-wave technique [28,29,30] on a finitely deformed configuration of the proposed lightened composite metamaterials have been reported in Section 3. As a result of this work, we highlighted that there are great design potentials for porous advanced bioinspired locally resonant metamaterials characterized by excellent wave absorption properties given by the addition of lead cores and by the onset of microscopic instabilities.

2. Theoretical background

In this section, the theoretical background related to the evaluation of the homogenized properties (Section 2.1) is reported together with the problem statement of the Bloch-wave analysis employed to investigate the micro- and macroscopic instability conditions and the elastic wave propagation in prestressed periodic materials (Section 2.2).

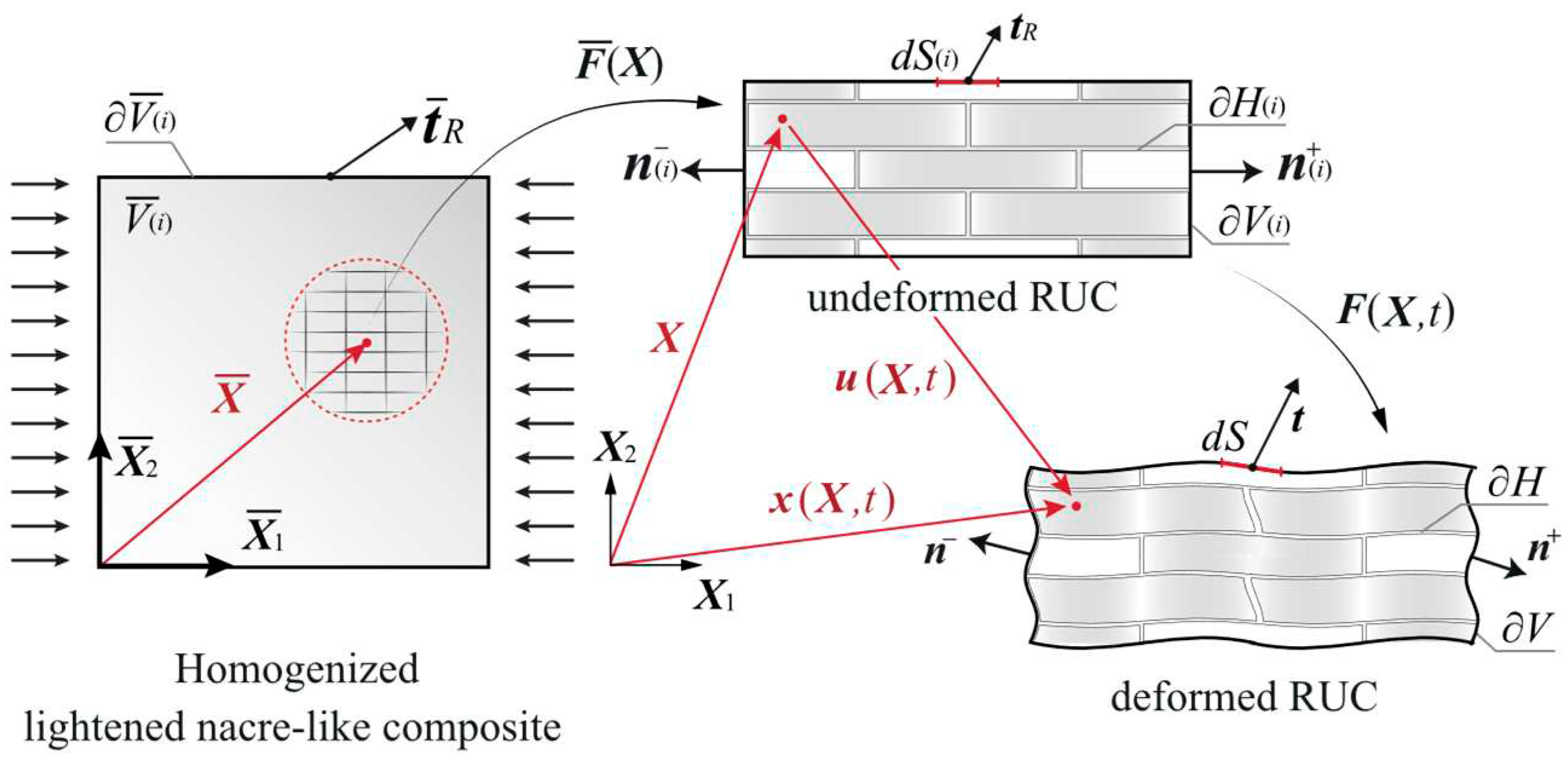
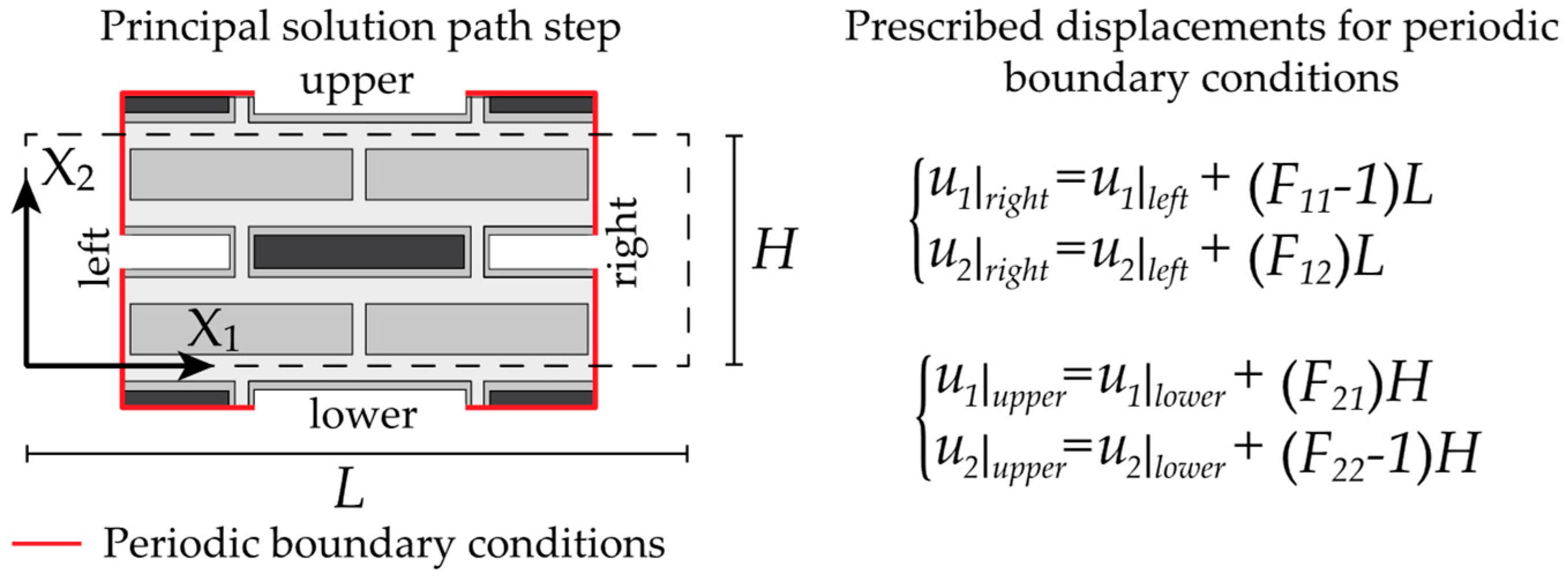
2.1. Homogenized properties in periodic media

Consider a representative volume element (RVE) of the nonlinear composite microstructure made by an assembly of the repetitive unit cell (RUC), as reported in Figure 1, representing a lightened nacre-like microstructure consisting of alternating stiff platelets, matrix, and voids.

The volume of the homogenized nacre-like composite material is denoted by

{\bar{V}}_{(i)}

and is enclosed by the surface

\partial {\bar{V}}_{(i)}

on which the first Piola-Kirchhoff traction vector acts

{\bar{t}}_{R}

. All the quantities reported in Figure 1 with the subscript (i) are referred to the undeformed configuration. The volume of the primitive unit cell (RUC) is identified as

U_{(i)}

The undeformed and deformed RVE configurations are associated with an infinitesimal neighborhood of a generic point

\bar{X}

which is related to the homogenized lightened nacre-like composite material subjected to a macroscopic gradient deformation

\bar{F}

. The position vectors are defined as

X

and

x

, with reference to the undeformed and the deformed RVE configuration, respectively. The microscopic gradient deformation tensor is defined as

F = \partial x / \partial X

, while its determinant

J \equiv \det F

represents the Jacobean of the transformation giving the volume change measure. For an easier imposition of the essential boundary condition on the RVE, the microscopic equilibrium problem is formulated in terms of the deformation gradient tensor

F

and the first-Piola Kirchhoff stress tensor

T_{R}

. By assuming a sufficiently small value of the time-like parameter t governing the monotonically increasing loading, the quantities in the incremental form can be considered as rate quantities. Therefore, the microconstituents are characterized by the following incrementally linear relation:

{\dot{T}}_{R} = C^{R} [\dot{F}],

(1)

where

{\dot{T}}_{R}

C^{R}

and

\dot{F}

denote the rate of the first Piola-Kirchhoff stress tensor, the fourth-order tangent moduli tensor, and the rate of the deformation gradient tensor, respectively. Here, we consider a finitely deformed composite material composed by nearly-incompressible hyperelastic constituents characterized by a strain energy density

W (F)

. The first and the second derivatives of

W (F)

represent the stress tensor

T_{R}

and the tangent moduli tensor

C^{R}

, respectively:

T_{R} = \frac{\partial W}{\partial F}, C^{R} = \frac{\partial^{2} W}{\partial F^{2}} .

(2)

By considering a quasi-static loading process and the absence of volume forces, the equation of motion in the undeformed configuration can be written in the following form:

Div T_{R} = 0 .

(3)

The averaging relationships define the macroscopic gradient deformation tensor

\bar{F}

and the macroscopic first Piola-Kirchhoff stress tensor

{\bar{T}}_{R}

in terms of the boundary values of the microscopic deformation field and the nominal traction vector (in turn functions of the volume average of

F

and

T_{R}

), as follows:

\bar{F} = \frac{1}{| V_{(i)} |} \int_{\partial V_{(i)}} x \otimes n_{(i)} d S_{(i)} = \frac{1}{| V_{(i)} |} \int_{B_{(i)}} F (X) d V_{(i)} - \frac{1}{| V_{(i)} |} \int_{\partial H_{(i)}} x \otimes n_{(i)} d S_{(i)},

(4)

{\bar{T}}_{R} = \frac{1}{| V_{(i)} |} \int_{\partial V_{(i)}} t_{R} \otimes X d S_{(i)} = \frac{1}{| V_{(i)} |} \int_{B_{(i)}} T_{R} (X) d V_{(i)},

(5)

where

t_{R} = T_{R} n_{(i)}

denotes the traction vector with

n_{(i)}

the outward normal at

X \in \partial V_{(i)}

and

\otimes

denotes the tensor product. Moreover,

B_{(i)}

and

H_{(i)}

denote the solid and void portions of the volume

V_{(i)}

occupied by the RVE. The microscopic deformation field

x

can be expressed as a sum of two contributes, the homogeneous deformations representing the linear part

\bar{F} X

and the fluctuation field representing the correction part

w

x = \bar{F} X + w .

(6)

By substituting the expression (6) into the expression (4), we obtain that the following integral constraint must be satisfied to make the fluctuation field

w

kinematically admissible:

\int_{\partial V_{(i)}} w \otimes n_{(i)} d S_{(i)} = 0 .

(7)

Coherently with the periodic distribution of the reinforcing platelets and void inclusions, the above-mentioned integral constraint could be satisfied by imposing a periodic distribution of the stress and strain fields, corresponding, from the viewpoint of the deformation field, to impose periodic deformations on

\partial V_{(i)}

x^{+} - x^{-} = \bar{F} (X^{+} - X^{-}),

(8)

while, from the viewpoint of the stress field, it corresponds to imposing antiperiodic traction on

\partial V_{(i)}

{(T_{R} n_{(i)})}^{+} = {(- T_{R} n_{(i)})}^{-},

(9)

where the superscripts

+

and

-

denote pairs of points located on the opposite sides of the RVE boundaries. The variational form of the associated boundary value problem is defined in terms of the fluctuation field

w

at a given macroscopic gradient deformation tensor

\bar{F}

\int_{B_{(i)}} T_{R} \cdot \nabla δ w d V_{(i)} = 0 \forall δ w \in H_{#}^{1} (V_{(i)}),

(10)

where

H_{#}^{1} (V_{(i)})

represents the first-order Hilbert space of the vector-valued functions periodic over

V_{(i)} =^{N} U_{(i)}

, that is over all possible assembly of

k^{N} = {[0, k]}^{N}

unit cells, with N = 2 for bidimensional problems and N = 3 for tridimensional ones, with k denoting a strictly positive integer and # denoting the field periodicity. The variational equation (10) is consistent with a microstructural equilibrium state characterized by antiperiodic traction on the external boundaries (9) and zero tractions on the hole boundaries

\partial H_{(i)}

T_{R} n_{(i)} = 0 .

(11)

By imposing an incremental change in the macroscopic gradient deformation tensor

\dot{\bar{F}}

the following incremental boundary value problem is obtained:

\int_{B_{(i)}} C^{R} [\dot{\bar{F}} + \nabla \dot{w}] \cdot \nabla δ \dot{w} d V_{(i)} = 0 \forall δ \dot{w} \in H {}_{#}^{1}{(V_{(i)})},

(12)

where

\dot{w}

represents the incremental fluctuation field. By considering the following relations:

{\dot{\bar{T}}}_{R} = {\bar{C}}^{R} [\dot{\bar{F}}], with {\dot{\bar{T}}}_{R} = {\bar{\dot{T}}}_{R},

(13)

the constitutive macroscopic response is then determined in terms of homogenized tangent moduli tensor

{\bar{C}}^{R}

{\bar{C}}_{i j h k}^{R} (\bar{F}) = \frac{1}{| V_{(i)} |} \int_{B_{(i)}} C_{i j m n}^{R} (X, \bar{F}) [I_{m n}^{h k} + \nabla {\dot{w}}_{m n}^{h k}] d V_{(i)},

(14)

where

{\dot{w}}^{h k}

denotes the incremental fluctuation field induced by

\dot{\bar{F}} = I^{h k}

with

I_{m n}^{h k} = δ_{m h} δ_{n k}

2.2. Nonlinear static and dynamic response of periodic media

The nonlinear static and dynamic responses of a porous periodic bioinspired microstructure subjected to uniaxial macroscopic compressive loading processes are analyzed (see also [31] for additional information). In the former case, the microstructure static equilibrium solution path, together with the accompanying instability analysis, is determined, while in the latter one, the incremental wave motion problem superimposed on a finitely deformed configuration of the microstructure equilibrium path is considered. Interrelations between the microscopic instabilities occurring at a given uniaxial compression and wave propagation phenomena are also analyzed.

Firstly, the static response was investigated by solving the nonlinear boundary value problem formulated on an adequately chosen RVE, adopting the homogenization theory assumptions together with periodic boundary conditions, as reported in Figure 2. The finite deformed configuration was obtained by imposing the following macroscopic gradient deformation tensor:

\bar{F} (β) = (1 - β) e_{1} \otimes e_{1} + {(1 - β)}^{- 1} e_{2} \otimes e_{2} = [\begin{matrix} (1 - β) & 0 \\ 0 & {(1 - β)}^{- 1} \end{matrix}],

(15)

with

e_{1}

e_{2}

denoting the unit basis vectors along the direction X₁ and X₂, respectively and β denoting the load parameter. By imposing that

{\bar{F}}_{22} = {\bar{F}}_{11}^{- 1}

, an acceptable approximation of the incompressibility constraint may be established for low percentages of void volume fractions. Subsequently, the onset of primary instabilities with short (microscopic instability) or long (macroscopic instability) wavelength was detected by solving the following frequency domain wave equation through the Floquet-Bloch theorem:

D i v {C^{R} [\nabla \dot{κ} (X)]} + ρ_{(i)} ω^{2} \dot{κ} (X) = 0,

(16)

where

ρ_{(i)}

is the mass density in the undeformed configuration

V_{(i)}

ω^{2}

are the roots of the characteristic equation,

C^{R}

denotes the nominal tangent moduli tensor determined with reference to a unit cell, and

\dot{κ} (X)

denotes the wave function in a periodic solid based on the Floquet-Bloch theorem which is equal to:

\dot{κ} (X) = \hat{κ} (X) e^{i K^{0} \cdot X},

(17)

where

\hat{κ} (X)

denotes a wave function which is periodic on the unit cell and

K^{0}

denotes the Bloch wave vector defining the direction of the wave propagation and the wavelength. Primary instabilities are detected when the lowest eigenvalue of the equation (16) first vanishes. Secondly, the dynamic response was investigated through a Bloch-Wave analysis by evaluating the dispersion relations associated with the proposed periodic microstructure. Specifically, the dispersion relations evolution for increasing levels of deformation was performed by superimposing the following Bloch-Floquet boundary conditions on the external boundaries of the unit cell on a finitely deformed configuration:

{\begin{cases} {\dot{u}}_{1} |_{r i g h t} = {\dot{u}}_{1} |_{l e f t} e^{i (K_{1}^{0} L + K_{2}^{0} H)} \\ {\dot{u}}_{2} |_{r i g h t} = {\dot{u}}_{2} |_{l e f t} e^{i (K_{1}^{0} L + K_{2}^{0} H)} \end{cases}, {\begin{cases} {\dot{u}}_{1} |_{u p p e r} = {\dot{u}}_{1} |_{l o w e r} e^{i (K_{1}^{0} L + K_{2}^{0} H)} \\ {\dot{u}}_{2} |_{u p p e r} = {\dot{u}}_{2} |_{l o w e r} e^{i (K_{1}^{0} L + K_{2}^{0} H)} \end{cases},

(18)

where

K_{1}^{0}

and

K_{2}^{0}

denote the components of the Bloch wave vector

K^{0}

which are defined as a function of a scalar parameter k ranging from 0 to 4 following the relations reported below:

K_{1}^{0} = {\begin{cases} k (π / L) \\ (π / L) \\ (3 - k) (π / L) \\ 0 \end{cases} \begin{matrix} 0 \leq k < 1 \\ 1 \leq k < 2 \\ 2 \leq k < 3 \\ 3 \leq k \leq 4 \end{matrix}, K_{2}^{0} = {\begin{cases} 0 \\ (k - 1) (π / H) \\ (π / H) \\ (4 - k) (π / L) \end{cases} \begin{matrix} 0 \leq k < 1 \\ 1 \leq k < 2 \\ 2 \leq k < 3 \\ 3 \leq k \leq 4 \end{matrix} .

(19)

Ranging the parameter k from 0 to 4, the Bloch-Wave vector is swapped on the external boundaries of the first Brillouin zone allowing to determine the so-called bandgap structure of the periodic unit cell in terms of dispersion graph. The dispersion curves, relating the wavelength of the propagating waves to their frequency, were analyzed to determine the evolution of the complete bandgaps as a function of the applied strains. The numerical investigations were carried out through a finite element discretization performed on the simulation software COMSOL Multiphysics v6.1.

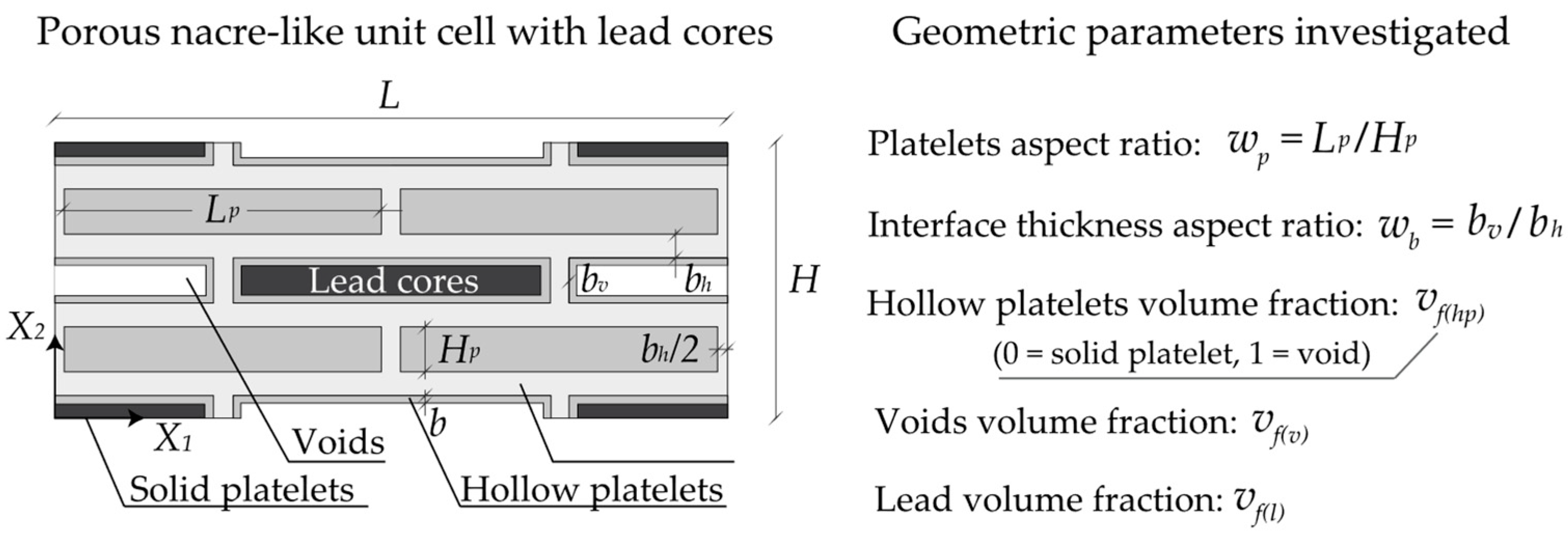
3. Numerical simulations for different geometrical and material parameters

We investigated the propagation of elastic waves firstly at the undeformed configuration (Case 1) and secondly at the bifurcated state for increasing loading levels on a standard porous nacre-like microstructure containing periodically arranged solid and hollow platelets (Case 2) and a lead-enhanced nacre-like microstructure containing also periodically arranged lead cores (Case 3).

The geometry of the numerical model is reported in Figure 3, the unit cell length is equal to L and its height is equal to H, in addition, two different thicknesses for the horizontal b_h and vertical b_v matrix interphases were considered. The platelet's length and height are equal to L_p and H_p, respectively. The parametric analyses were performed by varying the geometrical parameters in terms of volume fraction v_f, the hollow platelets volume fraction v_f(hp), platelets aspect ratio w_p= L_p /H_p, with L_p=10μm, and interface thickness aspect ratio w_b= b_v / b_h with b_h equal to:

b_{h} = \frac{(- v_{f} w_{b} - v_{f} w_{p} + \sqrt{v_{f}^{2} w_{b}^{2} - 2 v_{f}^{2} w_{b} w_{p} + v_{f}^{2} w_{p}^{2} + 4 v_{f} w_{b} w_{p}}) L_{p}}{2 v_{f} w_{b} w_{p}} .

(20)

The thickness of the hollow platelets is defined by the following relation:

b = \frac{H_{p}}{4} + \frac{L_{p}}{4} - \frac{\sqrt{4 H_{p} L_{p} v_{f (h p)} + H_{p}^{2} - 2 H_{p} L_{p} + L_{p}^{2}}}{4} .

(21)

The volume fraction

v_{f} = 8 L_{p} H_{p} / [(2 L_{p} + 2 b_{v}) (4 H_{p} + 4 b_{h})]

is evaluated by considering both the volume occupied by the platelets and voids. The hollow platelets volume fraction v_f(hp) defines the percentage of the voids with reference to the hollow platelets (v_f(hp)=1 denotes full void inclusions while v_f(hp) = 0 represents full platelets), while v_f(v), v_f(p) and v_f(l) define the volume fraction of the voids, platelets and the lead, respectively.

In the following, the relations between the above-reported geometrical quantities are reported:

[\begin{array}{l} v_{f (h p)} = \frac{(L_{p} - 2 b) (H_{p} - 2 b)}{L_{p} H_{p}} with b \leq \min (\frac{L_{p}}{2}, \frac{H_{p}}{2}) \\ v_{f (v)} = v_{f (l)} = \frac{1}{4} v_{f} v_{f}^{h p} \\ v_{f (p)} = \frac{1}{2} v_{f} + (\frac{1}{2} v_{f}) (1 - v_{f}^{h p}) \end{array} .

(22)

The mechanical behavior of the matrix, the platelets and the lead was modeled employing a neo-Hookean hyperelastic constitutive law based on the following strain energy density function:

W = \frac{1}{2} μ (tr (C) - 3) - μ \ln (J) + \frac{1}{2} λ \ln {(J)}^{2} .

(23)

Where μ is the initial shear modulus, C is the right elastic Cauchy-Green tensor,

J

is the Jacobian while λ defines the material compressibility which is taken equal to 1000μ to model the incompressible behavior of material phases. The initial shear modulus of the matrix phase is set equal to μ_m = 0.16 MPa corresponding to Young's modulus equal to 0.5 MPa (typical of a Tango Plus 3D printed material) and the initial shear modulus of the platelets is μ_m = kμ_m, while their material density and Poisson's ratio are set equal to each other as

ρ_{(p)} = ρ_{(m)} = 1.145 kg / m^{3}

and

ν_{(p)} = ν_{(m)} = 0.49

, respectively. The lead cores are characterized by the following material parameters:

μ_{(l)} = 4929 MPa

ν_{(l)} = 0.42

, and

ρ_{(l)} = 11340 kg / m^{3}

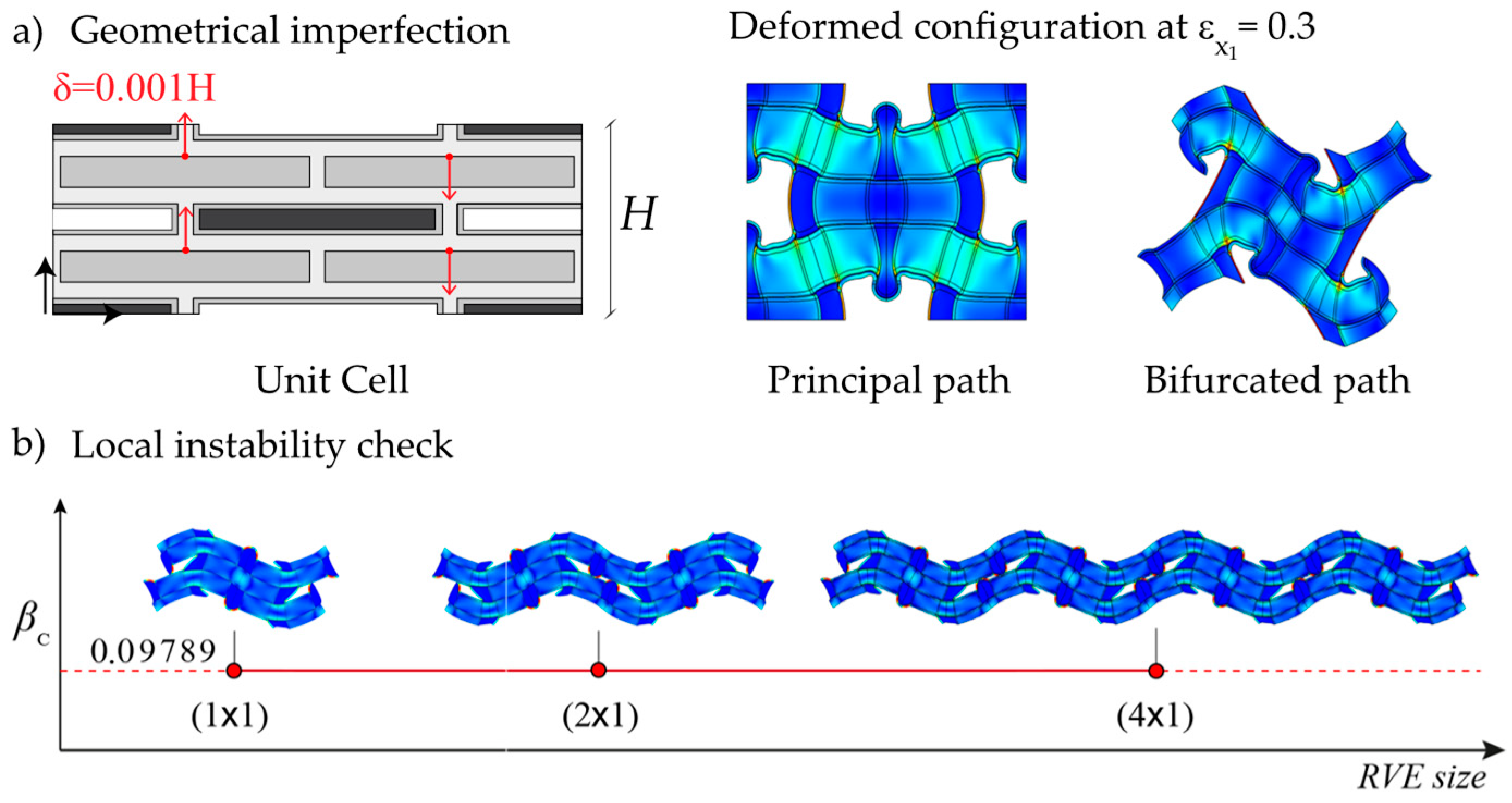
3.1. Case 1: Lightened nacre-like metamaterials without hollow platelets and lead cores at the undeformed configuration

Firstly, the bandgap structure was investigated for the limit case with v_f(hp) = 1 ( corresponding to the case without hollow platelets and lead cores) at the undeformed configuration for increasing values of volume fraction v_f (i.e. from 91% to 99%) and by varying the main geometrical and material parameters, as reported in Table 1. The highlighted areas represent the frequency ranges corresponding to complete bandgaps for which the wave propagation is forbidden in any direction of wave propagation. This first set of parametric investigations was conducted focusing on high values of stiffness ratio for a frequency range equal to 0 - 150 kHz, while lower values of the stiffness ratio will be investigated subsequently.

The numerical outcomes in Figure 4 show that joint aspect ratio w_b = 1 (i.e. with equal thickness between vertical and horizontal matrix joints) leads to better performance in terms of wave propagation attenuation compared with the other values investigated.

Generally speaking, the numerical outcomes highlighted that the complete bandgaps become wider for increasing values of volume fraction v_f from 91% to 99%, while for v_f <91%, no bandgaps were found for all the investigated parameters. In addition, we highlighted that the ranges of frequency of the complete bandgaps become higher for increasing values of platelets aspect ratio w_p and also wider for increasing values of stiffness ratio k; in fact, the lowest investigated stiffness ratio k=1,000 gives the worst performance in terms of wave propagation giving few and narrow bandgaps and thus the results were not reported. Thus, the bandgap range can be tuned by varying the geometrical parameters v_f and w_p considering that the wider bandgap ranges were obtained with w_b = 1_, w_p = 4 and the highest investigate value of k =100,000.

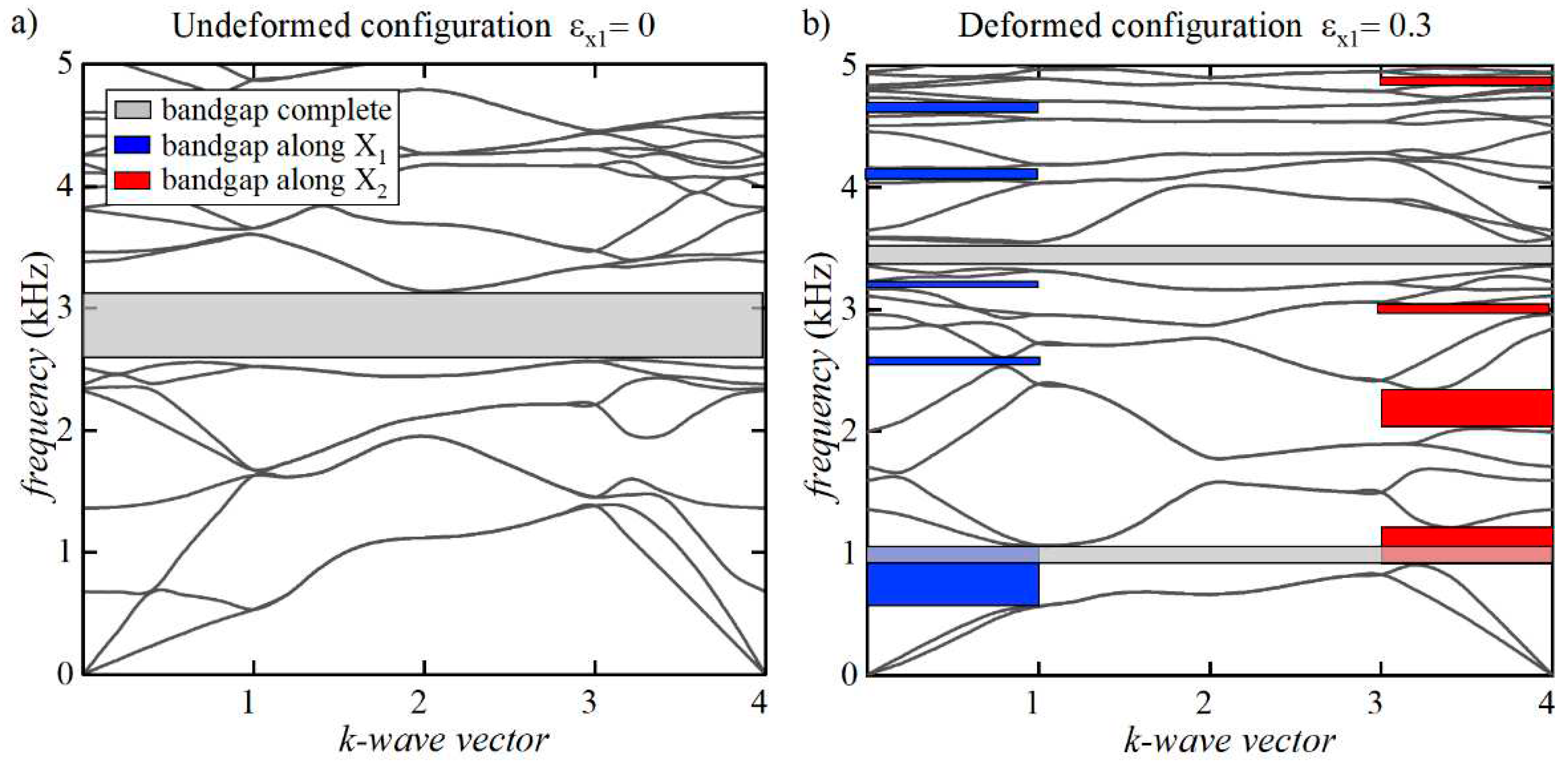
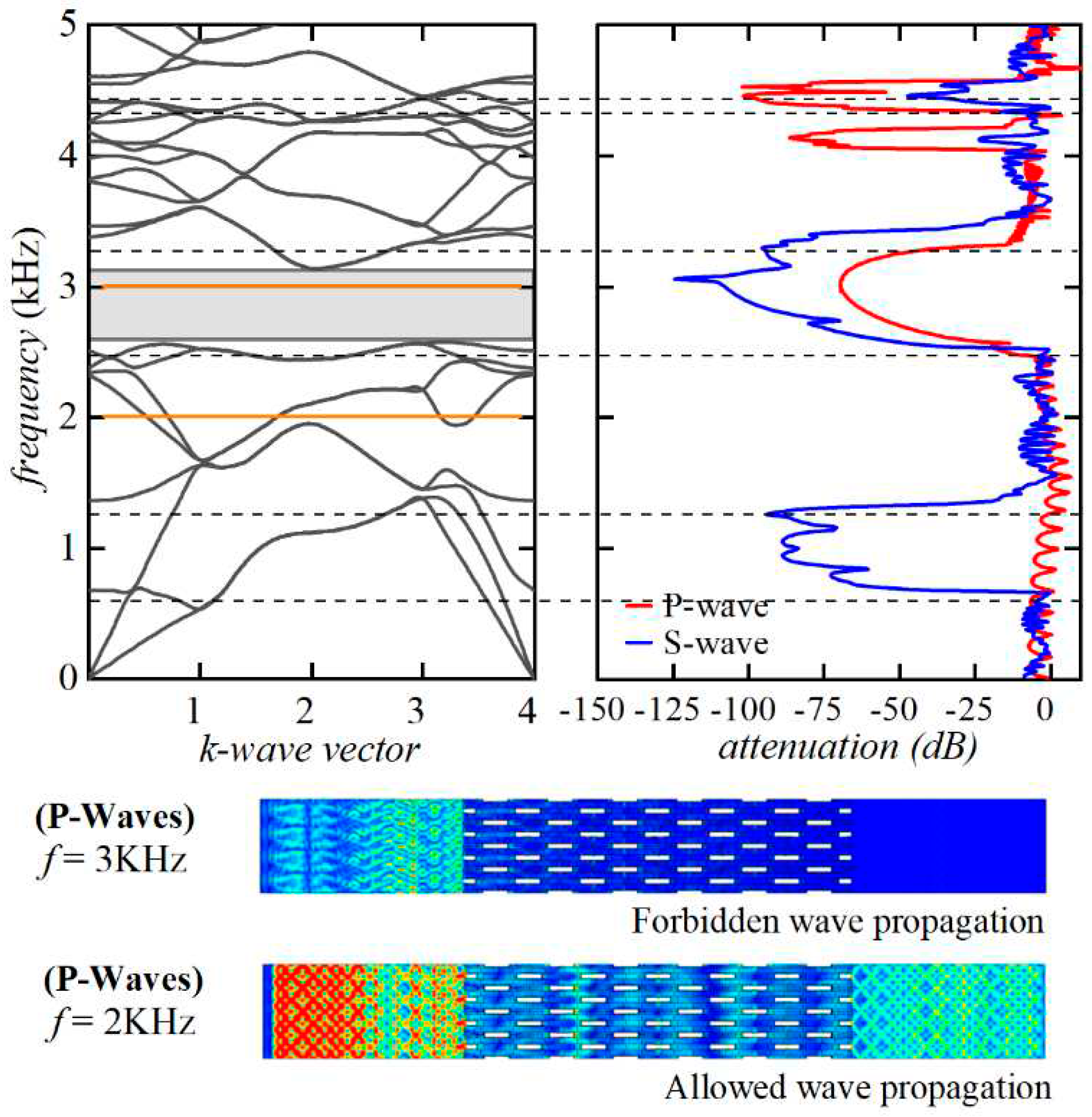
3.2. Case 2: Lightened nacre-like metamaterials with hollow platelets and without lead cores for increasing levels of deformation (standard microstructure)

The previous set of preliminary investigations reported in Section 3.1 was conducted focusing on high values of stiffness ratio, which leads to the appearance of bandgaps in a high range of frequency (often outside the acoustic range of frequencies), making such composite metamaterials unsuitable for acoustic applications.

In addition, in previous work by some of the authors [15], it was obtained that with increasing values of stiffness ratio and platelets aspect ratio, the critical load factors associated with the macroscopic instability notably decrease, leading to a higher risk of catastrophic failures due to the onset of macroscopic instability phenomena. Subsequently, in the light of the obtained bandgap structures reported in Figure 4, the investigation was focused on lower values of stiffness ratio k (leading to ranges of frequency belonging to the acoustic range 20 Hz – 20 kHz), also investigating the influence of the applied deformations together with the onset of instabilities at the microscopic scale. A consistent set of parametric investigations was performed concerning the following geometrical and material parameters to identify the best combination giving the widest bandgaps:

Table 2. Geometrical and material parameters investigated for the standard metamaterial for increasing levels of deformation.

k	1	5	10	20	30	40	50	100
w_b	1	5	10	20	30	40	50	100
w_p	4	5	6	7	-	-	-	-
v_f	0.5	0.55	0.6	0.65	0.7	0.75	0.8	-
v_f(hp)	1	0.95	0.9	0.85	0.8	0.75	0.7	-

After some preliminary investigation, the best combination of geometrical and material parameters, giving a wide bandgap in the undeformed configuration, was found: L_p = 10 mm, k = 20, w_b = 50, w_p = 4, v_f = 0.8, v_f(hp) = 0.8. First of all, the microscopic and the macroscopic instability analyses were performed, and we found that the microscopic instability occurs before the macroscopic one at a load parametric value equal to 0.09789, representing a percentage of deformation along the compression direction (X₁ direction with reference Figure 3) equal to about 10%. Subsequently, as can be seen in Figure 5a, by adding a geometrical imperfection in the form of the identified critical mode shape, the bifurcated solution was determined, and the bandgap analysis was performed at each loading step to determine the evolution of the dispersion graphs. The proof that the primary instability is characterized by a local instability (wavelength of the critical mode shape comparable with the unit cell size) was given by the local instability check reported in Figure 5b.

In Figure 6, the evolution of the bandgap structure at the undeformed configuration and for increasing levels of deformation after the onset of the microscopic instability is reported. We observed that at the undeformed configuration, a complete wide bandgap is found in the range from 2.6 kHz to 3.2 kHz, while, as the level of deformation increases, the dispersion graph evolves considerably, showing a thinning of the bandgaps up to the complete extinction of the one identified at the undeformed configuration. However, new and wider complete bandgaps also appear in lower ranges of frequencies, and numerous partial bandgaps along the X and Y directions of wave propagation appear due to the prestress state inducing the onset of microscopic instability.

The results obtained through the Bloch-wave analyses were also validated by the attenuation test and the transient analyses reported in Figure 7. In this figure, it is highlighted that the elastic pressure waves propagating with a frequency equal to 2 kHz (outside the bandgap range) can propagate through the proposed microstructured metamaterials while with a frequency equal to 3 kHz (inside the complete bandgap range) the elastic wave propagation is completely forbidden.

Further numerical validations by the transmittance spectra determination were performed on every investigated microstructure reported, both at the deformed and undeformed configuration, but for the sake of brevity, only the first validation was reported in the text.

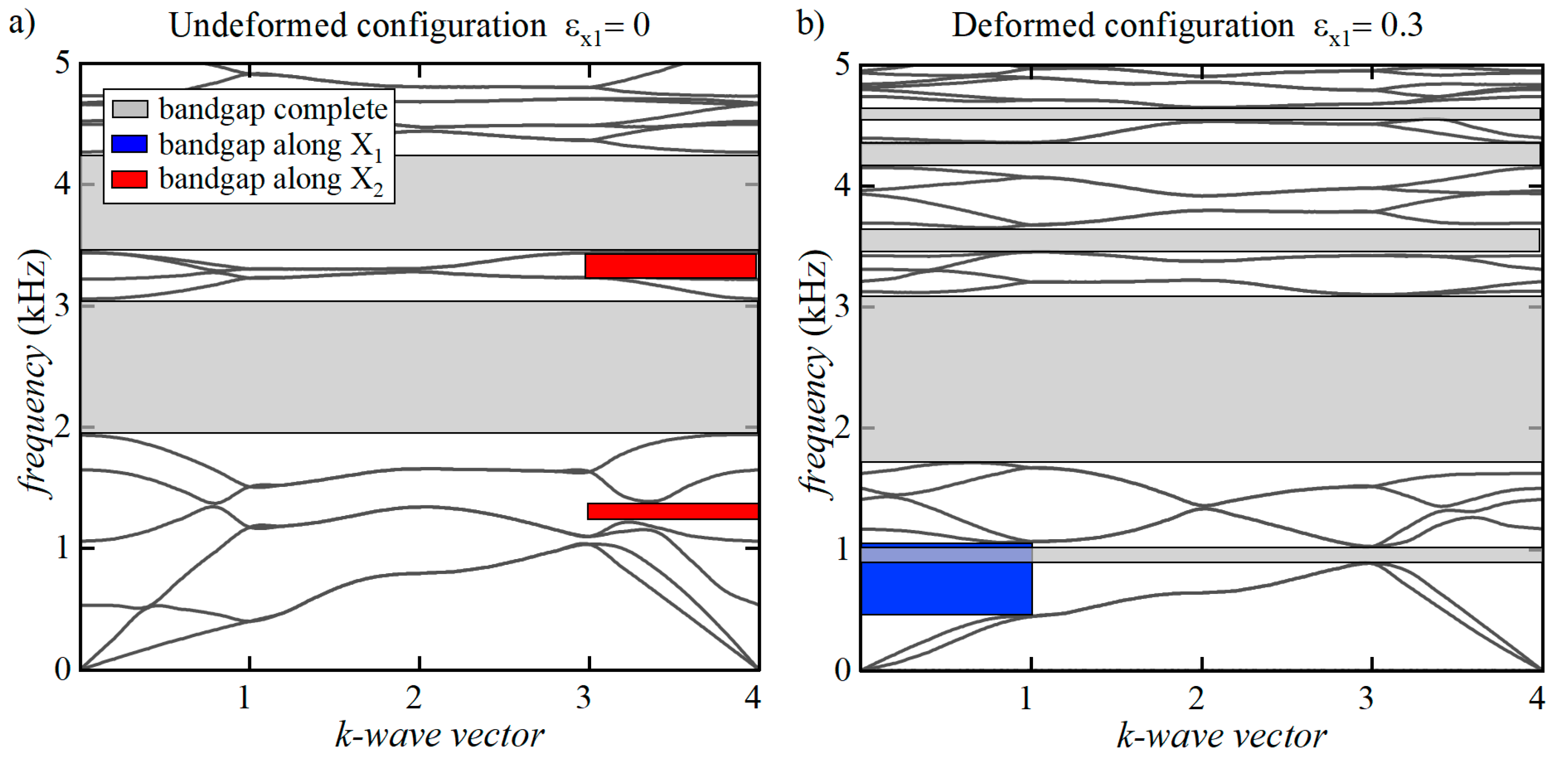
3.3 Case 3: Lightened nacre-like metamaterials with hollow platelets and lead cores for increasing levels of deformation (lead-enhanced microstructure)

In this section, the numerical results related to the evolution of the bandgap structure in a locally resonant metamaterial were reported. The previously investigated nacre-like microstructure with hollow platelets and voids was modified with the addition of lead cores. In Figure 8, the dispersion relations at the undeformed and deformed configurations were reported to investigate the intricate interplay between structural modifications and the resulting acoustic properties.

At the undeformed configuration, Figure 8a illustrates the presence of wide and complete bandgaps spanning the frequency ranges from 2 to 3 kHz and from 3.4 kHz to 4.2 kHz, together with two thinner bandgaps along the X₂ direction of elastic wave propagation. The bandgaps found results to be incredibly wider compared with those obtained for a microstructure without the insertion of lead cores (Figure 7a).

The introduction of lead cores surrounded by a soft matrix plays a fundamental role in shaping these acoustic properties. The lead cores, acting as local resonators, are influential in enhancing the material's ability to absorb energy. This is especially noteworthy at lower vibration frequencies, where the lead-modified microstructure demonstrates superior performance compared to its non-modified microstructure. This highlights the potential of the locally resonant metamaterial to attenuate vibrations within this specific frequency band effectively.

However, as deformation levels intensify, the dispersion graph undergoes significant transformations. Notably, in Figure 7b, there is a discernible widening of the first complete bandgap, with a complete extinction of the second complete bandgap, which is followed by the appearance of a thinner complete bandgap in low and high-frequency ranges. In addition, the results highlight the emergence of a new wider bandgap along the X₁ direction in an incredibly low-frequency range (0.5 kHz to 1 kHz). These phenomena are directly attributed to the prestress state induced by the structural modifications, leading to the onset of microscopic instability. With its lead-enhanced configuration, the proposed locally resonant metamaterial offers a valuable design alternative to control and tune the elastic wave propagation in bioinspired nacre-like metamaterials.

4. Conclusions

In this work, the main goal was to design soft metamaterials inspired by nacre, capable of bearing significant deformations before the onset of microscopic instabilities, together with the capability to attenuate the elastic wave propagation in specified frequency ranges beneficial for advanced engineering applications. To achieve this goal, a comprehensive set of parametric analyses was conducted, systematically varying the main geometrical and material parameters of a novel microstructure inspired by nacre-like and modified by the addition of reinforcing hollow platelets and lead cores. The aim was to identify the optimal combination that would yield superior wave attenuation capabilities.

The numerical findings highlighted that an elevated shear stiffness ratio between the reinforcing platelets and the soft matrix contributes to the appearance of wide and complete bandgaps. Interestingly, we found that the promising attenuation properties are not exclusive to scenarios with high contrast between the platelets and the matrix. Instead, they can also be achieved at lower contrast levels by tuning the percentage values of platelet, lead cores, and void inclusions volume fraction.

Additionally, it has been observed that the initiation of microscopic instability results in a transformation of the microstructural pattern. This transformation, in conjunction with applied deformations, significantly influences the investigated microstructure's wave propagation properties, giving rise to the formation of both new complete and partial bandgaps.

Definitively, this study presents novel opportunities for the design of bioinspired soft composite metamaterials. Incorporating lead cores, acting as local resonators, we found a strong increase in the wave attenuation properties, contributing to the overall versatility and performance of the engineered locally resonant metamaterials. Consequently, this research provides valuable insights for developing innovative, bioinspired metamaterials tailored for applications requiring high deformability and effective wave attenuation capabilities.

Author Contributions

Conceptualization: A.P.; methodology: F.G. and A.P.; software: U.D.M., G.S. and A.P.; validation: U.D.M., G.S. and A.P.; formal analysis: U.D.M., G.S. and A.P.; investigation: U. D. M. and A.P.; resources: U.D.M. and A.P.; data curation: U.D.M. and A.P.; writing—original draft preparation: U.D.M., G.S. and A.P.; writing—review and editing: F.G. and P.N.B.; visualization, U.D.M. and A.P.; supervision: F.G. and P.N.B.; project administration: F.G. and P.N.B.; funding acquisition: F.G. and P.N.B. All authors have read and agreed to the published version of the manuscript.

Funding

Fabrizio Greco, Umberto De Maio, Paolo Nevone Blasi, Girolamo Sgambitterra gratefully acknowledges financial support by the Next Generation EU - Italian NRRP, Mission 4, Component 2, Investment 1.5, call for the creation and strengthening of 'Innovation Ecosystems', building 'Territorial R&D Leaders' (Directorial Decree n. 2021/3277) - project Tech4You - Technologies for climate change adaptation and quality of life improvement, n. ECS0000009; Andrea Pranno gratefully acknowledges financial support from the POR Calabria FESR-FSE 2014-2020, Rep. N. 1006 of 30/03/2018, Line B, Action 10.5.12. This work reflects only the authors’ views and opinions, neither the Ministry for University and Research nor the European Commission can be considered responsible for them.

Conflicts of Interest

The authors declare no conflict of interest.

References

Zhang, Q.; Cherkasov, A. V.; Xie, C.; Arora, N.; Rudykh, S. Nonlinear Elastic Vector Solitons in Hard-Magnetic Soft Mechanical Metamaterials. International Journal of Solids and Structures 2023, 280, 112396. [Google Scholar] [CrossRef]
Amarante dos Santos, F.; Fraternali, F. Novel Magnetic Levitation Systems for the Vibration Control of Lightweight Structures and Artworks. Structural Contr & Hlth 2022, 29. [Google Scholar] [CrossRef]
Santos, F. A.; Caroço, C.; Amendola, A.; Miniaci, M.; Fraternali, F. 3D TENSEGRITY BRACES WITH SUPERELASTIC RESPONSE FOR SEISMIC CONTROL. Int J Mult Comp Eng 2022, 20, 53–64. [Google Scholar] [CrossRef]
Ammendolea, D.; Greco, F.; Leonetti, L.; Lonetti, P.; Pascuzzo, A. A Numerical Failure Analysis of Nano-Filled Ultra-High-Performance Fiber-Reinforced Concrete Structures via a Moving Mesh Approach. Theoretical and Applied Fracture Mechanics 2023, 103877. [Google Scholar] [CrossRef]
Zhao, N.; Wang, Z.; Cai, C.; Shen, H.; Liang, F.; Wang, D.; Wang, C.; Zhu, T.; Guo, J.; Wang, Y.; Liu, X.; Duan, C.; Wang, H.; Mao, Y.; Jia, X.; Dong, H.; Zhang, X.; Xu, J. Bioinspired Materials: From Low to High Dimensional Structure. Adv. Mater. 2014, 26, 6994–7017. [Google Scholar] [CrossRef]
Zhang, C.; Mcadams, D. A.; Grunlan, J. C. Nano/Micro-Manufacturing of Bioinspired Materials: A Review of Methods to Mimic Natural Structures. Adv. Mater. 2016, 28, 6292–6321. [Google Scholar] [CrossRef] [PubMed]
Bosia, F.; Dal Poggetto, V. F.; Gliozzi, A. S.; Greco, G.; Lott, M.; Miniaci, M.; Ongaro, F.; Onorato, M.; Seyyedizadeh, S. F.; Tortello, M.; Pugno, N. M. Optimized Structures for Vibration Attenuation and Sound Control in Nature: A Review. Matter 2022, 5, 3311–3340. [Google Scholar] [CrossRef]
Huang, Y.; Li, J.; Chen, W.; Bao, R. Tunable Bandgaps in Soft Phononic Plates with Spring-Mass-like Resonators. International Journal of Mechanical Sciences 2019, 151, 300–313. [Google Scholar] [CrossRef]
Liu, F.; Li, T.; Jia, Z.; Wang, L. Combination of Stiffness, Strength, and Toughness in 3D Printed Interlocking Nacre-like Composites. Extreme Mechanics Letters 2020, 35, 100621. [Google Scholar] [CrossRef]
Slesarenko, V.; Kazarinov, N.; Rudykh, S. Distinct Failure Modes in Bio-Inspired 3D-Printed Staggered Composites under Non-Aligned Loadings. Smart Mater. Struct. 2017, 26, 035053. [Google Scholar] [CrossRef]
Wang, B.; Hu, X.; Lu, P. Modelling and Testing of Large-Scale Masonry Elements under Three-Point Bending – Tough and Strong Nacre-like Structure Enlarged by a Factor of 20,000. Engineering Fracture Mechanics 2020, 229, 106961. [Google Scholar] [CrossRef]
Wei, Z.; Xu, X. Gradient Design of Bio-Inspired Nacre-like Composites for Improved Impact Resistance. Composites Part B: Engineering 2021, 215, 108830. [Google Scholar] [CrossRef]
Wan, H.; Leung, N.; Algharaibeh, S.; Sui, T.; Liu, Q.; Peng, H.-X.; Su, B. Cost-Effective Fabrication of Bio-Inspired Nacre-like Composite Materials with High Strength and Toughness. Composites Part B: Engineering 2020, 202, 108414. [Google Scholar] [CrossRef]
Bouville, F. Strong and Tough Nacre-like Aluminas: Process–Structure–Performance Relationships and Position within the Nacre-Inspired Composite Landscape. J. Mater. Res. 2020, 35, 1076–1094. [Google Scholar] [CrossRef]
Greco, F.; Leonetti, L.; De Maio, U.; Rudykh, S.; Pranno, A. Macro- and Micro-Instabilities in Incompressible Bioinspired Composite Materials with Nacre-like Microstructure. Composite Structures 2021, 269, 114004. [Google Scholar] [CrossRef]
Greco, F.; Leonetti, L.; Lonetti, P. A Novel Approach Based on ALE and Delamination Fracture Mechanics for Multilayered Composite Beams. Composites Part B: Engineering 2015, 78, 447–458. [Google Scholar] [CrossRef]
Pranno, A.; Greco, F.; Lonetti, P.; Luciano, R.; De Maio, U. An Improved Fracture Approach to Investigate the Degradation of Vibration Characteristics for Reinforced Concrete Beams under Progressive Damage. International Journal of Fatigue 2022, 163, 107032. [Google Scholar] [CrossRef]
De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Nevone Blasi, P.; Pranno, A. The Reinforcing Effect of Nano-Modified Epoxy Resin on the Failure Behavior of FRP-Plated RC Structures. Buildings 2023, 13, 1139. [Google Scholar] [CrossRef]
De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. The Damage Effect on the Dynamic Characteristics of FRP-Strengthened Reinforced Concrete Structures. Composite Structures 2023, 309, 116731. [Google Scholar] [CrossRef]
Bertoldi, K.; Bigoni, D.; Drugan, W. J. Nacre: An Orthotropic and Bimodular Elastic Material. Composites Science and Technology 2008, 68, 1363–1375. [Google Scholar] [CrossRef]
Greco, F.; Leonetti, L.; Lonetti, P.; Luciano, R.; Pranno, A. A Multiscale Analysis of Instability-Induced Failure Mechanisms in Fiber-Reinforced Composite Structures via Alternative Modeling Approaches. Composite Structures 2020, 251, 112529. [Google Scholar] [CrossRef]
Grossman, M.; Pivovarov, D.; Bouville, F.; Dransfeld, C.; Masania, K.; Studart, A. R. Hierarchical Toughening of Nacre-Like Composites. Adv Funct Materials 2019, 29, 1806800. [Google Scholar] [CrossRef]
Flores-Johnson, E. A.; Shen, L.; Guiamatsia, I.; Nguyen, G. D. Numerical Investigation of the Impact Behaviour of Bioinspired Nacre-like Aluminium Composite Plates. Composites Science and Technology 2014, 96, 13–22. [Google Scholar] [CrossRef]
Chen, Y.; Wang, L. Multiband Wave Filtering and Waveguiding in Bio-Inspired Hierarchical Composites. Extreme Mechanics Letters 2015, 5, 18–24. [Google Scholar] [CrossRef]
Lu, Y.; Huang, G.-Y.; Wang, Y.-F.; Wang, Y.-S. A Mechanical Model for Elastic Wave Propagation in Nacre-Like Materials With Brick-and-Mortar Microstructures. Journal of Applied Mechanics 2022, 89, 091002. [Google Scholar] [CrossRef]
Pranno, A.; Greco, F.; Leonetti, L.; Lonetti, P.; Luciano, R.; De Maio, U. Band Gap Tuning through Microscopic Instabilities of Compressively Loaded Lightened Nacre-like Composite Metamaterials. Composite Structures 2022, 282, 115032. [Google Scholar] [CrossRef]
Mazzotti, M.; Foehr, A.; Bilal, O. R.; Bergamini, A.; Bosia, F.; Daraio, C.; Pugno, N. M.; Miniaci, M. Bio-Inspired Non Self-Similar Hierarchical Elastic Metamaterials. International Journal of Mechanical Sciences 2022, 107915. [Google Scholar] [CrossRef]
Li, J.; Slesarenko, V.; Rudykh, S. Auxetic Multiphase Soft Composite Material Design through Instabilities with Application for Acoustic Metamaterials. Soft Matter 2018, 14, 6171–6180. [Google Scholar] [CrossRef]
Shim, J.; Wang, P.; Bertoldi, K. Harnessing Instability-Induced Pattern Transformation to Design Tunable Phononic Crystals. International Journal of Solids and Structures 2015, 58, 52–61. [Google Scholar] [CrossRef]
Dalklint, A.; Wallin, M.; Bertoldi, K.; Tortorelli, D. Tunable Phononic Bandgap Materials Designed via Topology Optimization. Journal of the Mechanics and Physics of Solids 2022, 163, 104849. [Google Scholar] [CrossRef]
De Maio, U.; Greco, F.; Luciano, R.; Sgambitterra, G.; Pranno, A. Microstructural Design for Elastic Wave Attenuation in 3D Printed Nacre-like Bioinspired Metamaterials Lightened with Hollow Platelets. Mechanics Research Communications 2023, 128, 104045. [Google Scholar] [CrossRef]

Figure 1. Homogenized lightened nacre-like composite metamaterial and the corresponding undeformed and deformed unit cell configurations.

Figure 2. Geometrical representation of the RVE adopted for the nonlinear static analysis together with the imposed prescribed displacement under the assumption of periodic fluctuations.

Figure 3. Investigated lightened nacre-like unit cell and associated RVE assembly with the main geometrical parameters.

Figure 4. Bandgap structure at the undeformed configuration versus the volume fraction for different values of stiffness ratio k, platelets aspect ratio w_p and joints aspect ratio w_b.

Figure 5. Deformed configuration of the metamaterial RVE for the principal solution path step together with the bifurcated one a) and the results of the local instability check b).

Figure 6. Dispersion relations for the standard microstructure at the undeformed configuration a) and at the bifurcated one b) with a uniaxial stretch ratio along the X direction equal to 0.3.

Figure 7. Transmittance spectra at the undeformed configuration and transient simulation results for propagating waves inside and outside the bandgap range.

Figure 8. Dispersion relations for the lead-enhanced microstructure at the undeformed configuration a) and at the bifurcated one b) with a uniaxial stretch ratio along the X direction equal to 0.3.

Table 1. Geometrical and material parameters investigated for the composite metamaterial at the undeformed configuration.

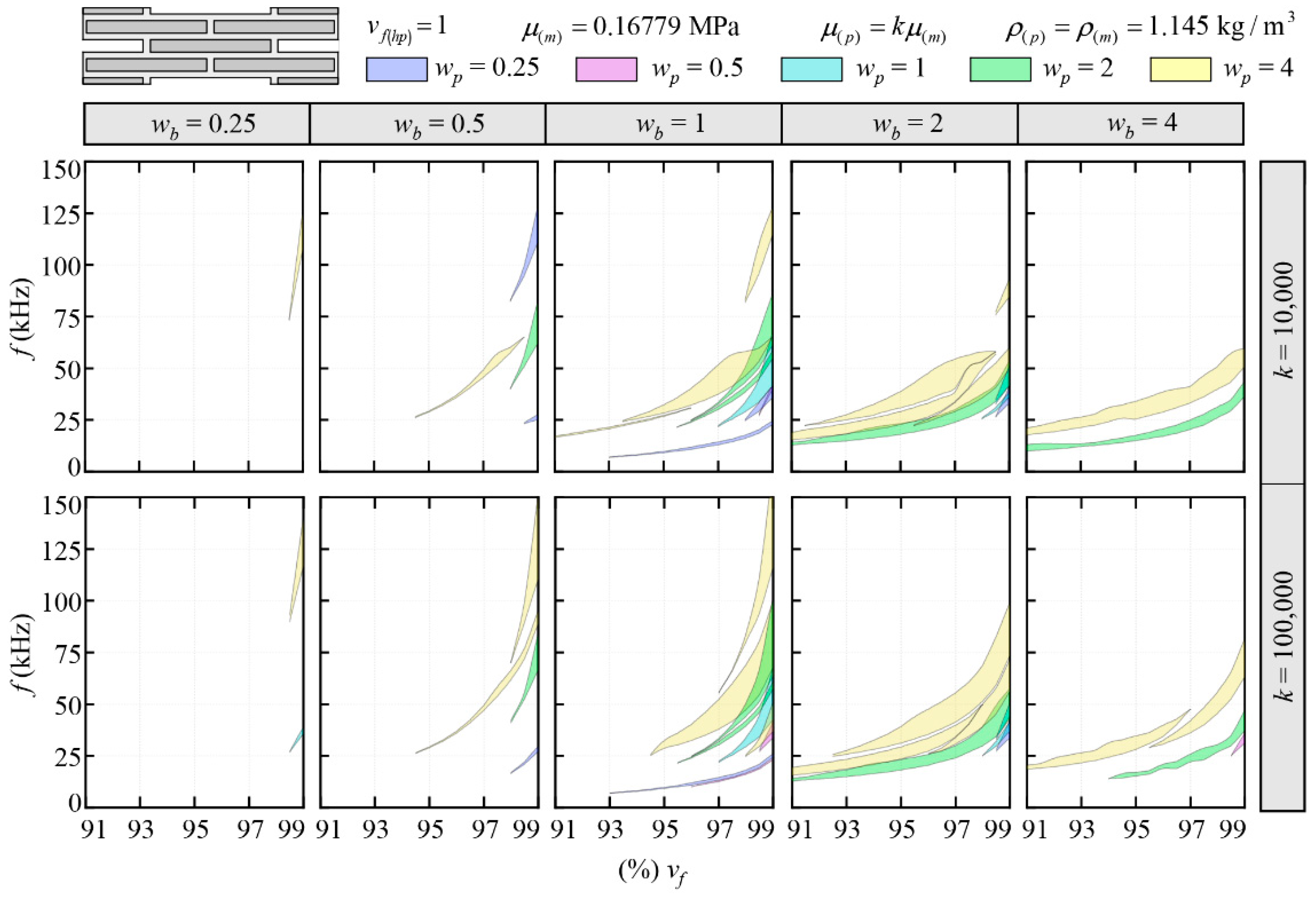
w_p	0.25	0.5	1	2	4
w_b	0.25	0.5	1	2	4
k	1,000	10,000	100,000	-	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Elastic Wave Propagation Control in Porous and Finitely Deformed Locally Resonant Nacre-Like Metamaterials

Abstract

1. Introduction

2. Theoretical background

2.1. Homogenized properties in periodic media

2.2. Nonlinear static and dynamic response of periodic media

3. Numerical simulations for different geometrical and material parameters

3.1. Case 1: Lightened nacre-like metamaterials without hollow platelets and lead cores at the undeformed configuration

3.2. Case 2: Lightened nacre-like metamaterials with hollow platelets and without lead cores for increasing levels of deformation (standard microstructure)

3.3 Case 3: Lightened nacre-like metamaterials with hollow platelets and lead cores for increasing levels of deformation (lead-enhanced microstructure)

4. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe