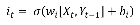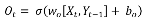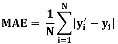Enhancing Day-Ahead Cooling Load Prediction in Tropical Commercial Buildings Using Advanced Deep Learning Models: A Case Study in Singapore

1. Introduction

Tropical climate is characterized by its all-year-round elevated temperature and humidity. Air conditioning systems play a pivotal role in maintaining occupant comfort in the built environment in tropical regions. As the rise in atmospheric temperature becomes a major concern about global warming, the energy demand of the buildings is expected to drastically increase. Successively, global warming and energy demand fuel each other’s growth. At the same time, CO₂ emission by buildings is increasing at an alarming rate and likely to contribute to one third of the overall CO₂ emissions soon [2]. Reducing the energy demand of buildings is particularly important in these circumstances.

Heating, Ventilation and Air Conditioning (HVAC) systems account for 60% of the energy usage of buildings in tropical climates [1,2]. Central chilled water plants produce chilled water for the air-conditioning needs of the large commercial or public buildings in tropical climates. Predictive control can enhance the energy efficiency of the central cooling system. Accurate prediction of cooling load is a crucial part of this predictive control. Predictions at various time horizons cater to different purposes. While short-term load predictions on an hourly basis or at a more reduced time granularity help to dynamically control the chilled water flow rates of the chiller, long-term load predictions, such as day-ahead forecast help to plan the next day’s energy demands. Using day-ahead cooling load predictions, additional demands can be satisfied easily, resources can be managed efficiently, or a proper demand-response system can be activated [3].

Cooling load predictions can be done in two ways – either by physical models or by data-driven models. Physical models are governed by first principle approaches and hence require detailed information about building, its internal environment, and various external factors. These systems can be complex and less tolerant of errors. Data-driven models, on the other hand, utilize historical data to derive the relationship between input variables and the cooling load. They are easy to develop and might unravel the hidden patterns in data. The upsurge in sensor technologies makes data availability no longer an issue in built environments. Advanced Building Automation Systems (BAS) are available in many buildings nowadays. And big data techniques foster the storage and analysis of substantial amounts of data. These facts have fueled the growth of more data-driven techniques for cooling load prediction of buildings. If enough quantity of data is available, reliable data-driven models can be developed.

Statistical, machine learning and deep learning methods are the three important categories of data-driven techniques utilized in cooling load prediction. Compared to statistical and machine learning methods, deep learning techniques often provide improved prediction accuracies. This success is attributed to the architectural trait of deep learning algorithms. Deep learning techniques are vigorous in learning the hidden non-linear characteristics of the data. The term ‘deep’ indicates that the data undergoes transformation in multiple layers before reaching the output layer. They are derived from the Neural Network architecture, but the layered deep architecture sequentially extracts higher level features from the input data. A few drawbacks associated with data-driven models can be listed as follows. 1) Data is needed of good quantity and quality to develop reliable data-driven models, and 2) Often data-driven models are less interpretable compared to physical models.

This paper is an endeavor to harness the potential of deep learning techniques to predict the hourly cooling load of the next day. External weather parameters, internal parameters like room humidity and temperature, calendar information, and historical cooling load were available as input parameters. Although occupancy data has been reported to have a pivotal role in cooling load predictions, this paper could not explore its potential as the information is not collected by the case buildings [29]. Calendar features are added to substitute the occupancy data to the extent possible. Next day’s hourly cooling load is predicted 12 hours ahead. Deep learning algorithms, including Deep Neural Network (DNN), Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), and Long Short-Term Memory networks (LSTM) are used as standalone models first. Then, their coactive strength is experimented by combining them into hybrid models. CNN-LSTM and Sequence-to-sequence models are assayed in this sort.

2. Literature Survey

Conventional cooling load prediction methods used statistical time series regression techniques. These algorithms include Multiple Linear Regression (MLR), Auto-Regression (AR), Auto-Regressive Integrated Moving Average (ARIMA), Auto-Regression with Exogenous Inputs (ARX) etc. [5,6,7]. They are simpler methods, but often less accurate compared to machine learning and deep learning counterparts in load prediction [4].

Day ahead load prediction can be done in two ways – either predict a single value that is the anticipated peak load for the next day [4] or predict multiple values, which are the anticipated load for each hour of the next day. The second problem is called multi-step prediction task, which is more challenging compared to the first one. Compared to statistical methods, machine learning and deep learning approaches are prevalent for multi-step prediction. In literature, multi-step prediction is done in two ways. In the first approach the multi-output problem will be transformed into multiple independent single-output problems [8]. The second approach deploys an inherently multi-target capable algorithm to produce the output. Support Vector Regression (SVR) is an example of the first category, as it is inherently a single target algorithm, but many times used in multi-step load prediction tasks [3,4,9,10].

Decision Tree (DT) based methods encompassing Random Forest (RF) and XGBoost are also prevailing techniques in day-ahead load prediction. Dudek in [12] discusses day ahead load curve prediction using Random Forest. Rule-based feature selection for improvising the prediction results of Random Forest is proposed by Lahouar et.al [11]. An online learning method is followed to predict the next 24-hour load. XGBoost is an ensemble of decision trees which uses boosting techniques to enhance performance. XGBoost is inherently designed as a single output model but can be transformed to multi-output case as well. This ensemble method used for day-ahead load prediction can be found in [3] and [13]. Another ensemble decision tree method named bagged regression trees are employed for day ahead load prediction in [14].

The skill of Artificial Neural Networks (ANN) in unveiling the non-linear relationships in the data makes them specifically suitable for load forecasting problems. Performance can be further upgraded by combining other Machine Learning techniques with ANN. For example, k-means clustering applied to cluster the patterns and then ANN sub-models for each cluster can be found in [15]. A similar sort of performance improvement is materialized in [16] by integrating Self-organizing maps (SOM) with ANN. SOM functions as a preprocessing technique for daily electric load forecasting. A two-step approach where Wavelet Transform (WT) is blended with ANN is discussed in [17]. WT is used for decomposing the input signal before applying ANN for the next day’s load prediction. Then the results are refined by a fuzzy inference system in the second step.

Many recent ventures can be seen where deep learning techniques are exerted for the load forecast in buildings. But they are prevalently used for short-term load forecasts like hour ahead or half an hour ahead predictions where a single step is predicted. Cai et al. [18] experimented with the effectiveness of Convolutional Neural Networks (CNN) and Recurrent Neural Network (RNN) for multi-step prediction. Electricity load for the next 24 hours is predicted in this work with improved performance compared to seasonal autoregressive integrated moving average with exogenous inputs (SARIMAX). 24-hour ahead electricity load forecasting is discussed in [19] as well. This work compares the power of different shallow machine learning techniques against the deep learning technique – CNN. This paper reports that MLR, SVR and Multivariate Adaptive Regression Splines (MARS) performed better than CNN for day-ahead electricity load forecasting.

Sequence-to-sequence architecture has been tried in electricity load forecasting and building energy consumption forecasting. [21] discusses electricity load forecasting of variable refrigerant flow systems. Building energy consumption forecasting is another time series regression problem where sequence-to-sequence model is reported to be providing satisfactory results [22]. Multiple time horizons have been attempted in this work. In the context of 24-hour cooling load prediction, a deep neural network (DNN) architecture tried both as a feature selector and predictor can be found in [9]. But the DNN architecture is just a deep artificial neural network. This paper reports that the DNN was found to enhance the performance while used as a feature selector. Li et.al., [20] reports the merit of sequence-to-sequence architecture in short-term one-step ahead cooling load prediction. But multi-step prediction is not considered in this work.

Applicability of attention based RNN for 24-hour ahead cooling load prediction has been discussed in [23]. Attention mechanism is utilized to improve the interpretability of the model. Multi-step ahead cooling load prediction by using RNN model is discussed in [24] as well. Three distinct aspects of RNN based forecasting have been considered here - direct approach, recursive approach, and multi-input multi-output approach.

This paper explores various deep learning architectures for day-ahead cooling load profile prediction. DNN, CNN, RNN and LSTM models are used as standalone models and then they are combined to form hybrid architectures as well. The importance of input parameters has been assessed and parameters are chosen based on their influence on target variable. In addition to this, the contribution of each category of input variables to the prediction performance has been assessed. The best performing model is chosen based on the comparison studies done as part of the experiments.

3. Materials and Methods

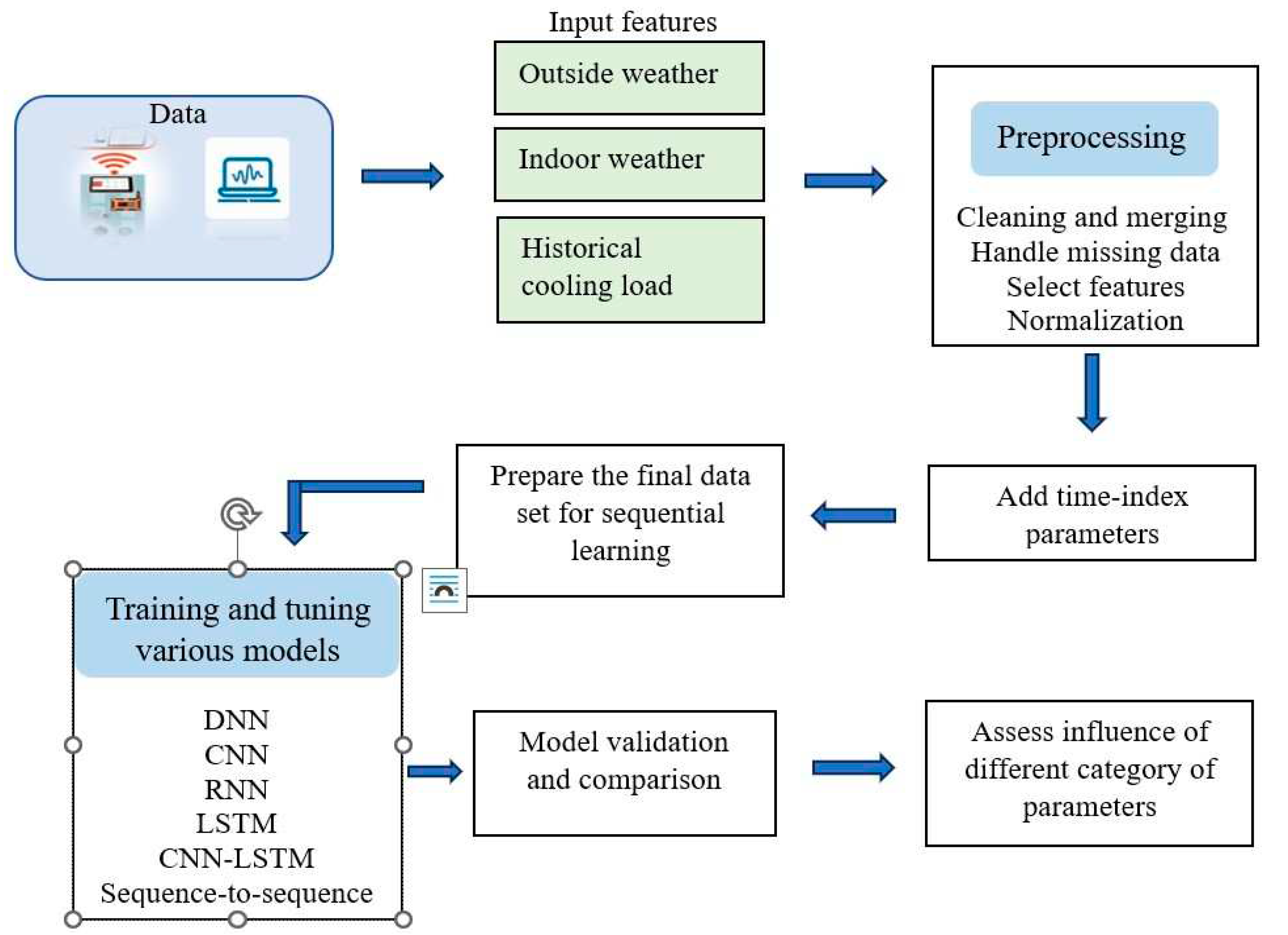
The overall research methodology is depicted in Figure 1. The first step comprises data collection from various sources like Building Management Systems, simulations, and external weather sources. External weather parameters including temperature, relative humidity, wind speed, and solar radiation are collected from Solcast website [28]. As data from diverse sources had different time scales, cleaning and merging them to make an hourly dataset constitutes the first step in data preprocessing. In the ensuing step, the missing data was identified, and the corresponding days were removed from the final dataset. Indoor weather parameters and historical cooling load data were collected through the help of the Building Management System. Historical cooling load is calculated by extracting the flow rates, chilled water supply and return temperatures from the building management system.

3.1. Feature selection

After cleaning, merging, and handling missing data, an exhaustive analysis was performed to select the features required for prediction. Instead of performing a correlation analysis, importance of parameters was assessed with the help of a deep learning model itself. The LSTM model with a single layer of hidden neurons is selected as the base model to do this assessment. Total parameters available for analysis are listed in Table 1.

Different combinations of these parameters were tried for feature selection. It was found that historical cooling load and hour of the day are the most key features when day-ahead cooling load prediction is considered. From the outdoor weather parameters group, temperature, wind speed, humidity and solar radiation are found to be important, whereas precipitable water does not affect the results much. Similarly indoor variables like temperature, humidity and CO₂ levels were not found important in prediction. A culmination was drawn that the indoor weather parameters do not considerably influence the next day’s hourly cooling load prediction. The analysis was wound up with the list of parameters enclosed in Table 2 chosen for prediction. The subsequent experiments and comparisons are performed by using this selected feature set.

3.2. Normalization and data preparation

As can be observed from Table 2, a total of seven input features were selected for the prediction task. This refined dataset is passed through a normalization process. Normalization brings all the features to a standard scale of 0 to 1, facilitating the convergence of prediction models easy and fast. This process is done as per equation 1.

$$x_i^{\text{'}}=\frac{x_i-x_{min}}{x_{max}-x_{min}}$$

(1)

where $x_i$ is the ith sample, $x_{min}$ and $x_{max}$ are the minimum and maximum values for that feature and $x_i^{\text{'}}$ is the normalized value.

The next step entails preparing the dataset for different learning tasks, as each might need a slightly different treatment of the input data. For example, Deep Neural Networks requisite input data in a 2-dimensional shape. Data can be fed in format (x,y) where x is the input feature vector of shape Nxd and y is the output vector of shape Nxh. Here N denotes the number of samples in the dataset, d is the dimension of the input, and h is the number of hours of the next day being predicted. To cater deep learning models, data is converted to three-dimensional input samples and complementary target samples. The input dataset has shape NxTxd and the target dataset has the shape Nxhx1, where T denotes the number of historical hours given as input to the model. For example, if 12 hour’s data of the daytime of the previous two days is given as input to the model, then $T=24$.

3.3. Prediction models

To perform an extensive comparison of the ascendancy of various deep learning models in day-ahead cooling load prediction, four standalone models and two hybrid models are implemented in this work. DNN, CNN, RNN and LSTM are the standalone models while CNN-LSTM and sequence-to-sequence are the hybrid models. A brief description about each of these learning algorithms is given in the sub-sections below.

3.3.1. Deep neural network

Deep neural networks have a layered architecture. It is like Artificial Neural Networks in terms of its functioning and architecture, but the difference mainly comes from the number of layers added to make the network ‘deep’. Each layer will help the network to extract more higher-level features. Unlike conventional neural networks, DNN can add more densely connected layers, each of which can use different activation functions if required. Its deftness in adding dropout layers also makes them superior to the ANN architecture [9]. This feature makes it capable of dropping a percentage of neurons randomly from any layer, and consequently avoids overfitting. The input layer will accept the input, hidden layers process the input to extract higher level features and finally output layer provides the output. This network can be used as a multi-output model. Depending on the number of neurons present in the output layer, multi-output feature can be easily tailored to this architecture.

3.3.2. Convolutional neural network

A convolutional Neural Network is a kind of Deep learning network with feed forward structure. They use kernels or filters to process the input, which slide over the input and compute the cross correlation between the kernel and each part of the input. In this way highly correlated part of the input will get more weightage. This method was originally built for image processing tasks, but nowadays found successful in time series regression problems like load prediction [18,25,26] as well. In addition to the input layer, convolution layers and pooling layers, CNN can have dense layer also at the end of the network. This architecture makes it suitable for prediction tasks. With a suitably designed dense layer at the end, multi-output prediction is also possible with this network. Upon removal of the eventual dense layer, the same architecture serves the purpose of a feature extractor. Depending on the size of the kernels used in filtering, higher-level features can be extracted from the input.

When used as a standalone model, CNN follows its conventional architecture with a dense layer at the end. Convolution layers can be one dimensional or two-dimensional, the selection commensurate with the shape of the filter. One dimensional convolution layer requires only the length of the filter to be mentioned, whereas the width is automatically set equal to the width of the input data set. Width in this case refers to the number of features in the dataset. Conversely, two-dimensional convolution layer works with a two-dimensional kernel which will be usually mentioned like 2x2, 3x3 or 5x5. Convolution layers extract higher level features from the input data, which helps it to predict better.

3.3.3. Recurrent neural network

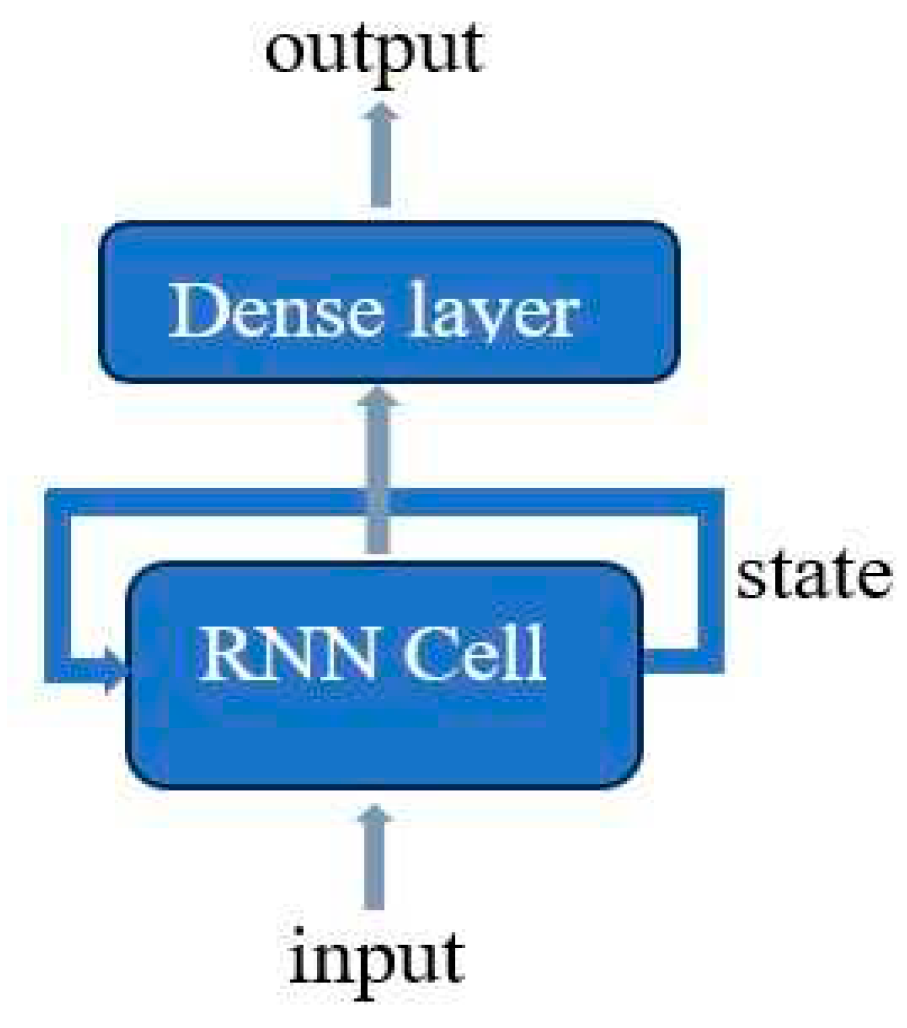
Recurrent neural networks have a structure different from the feed forward neural networks. In feed forward networks, input flows in the forward direction only, whereas in recurrent neural networks, recurrent connections are possible, which means that output from an internal node can impact the subsequent input to the same node. These recurrent connections make this network specifically suitable for learning from sequential data like time series. The basic architecture of an RNN is depicted in Figure 2.

Recurrent neural network cell has multiple fixed numbers of hidden units one for each time step the network processes. Each unit can maintain an internal hidden state which represents the memory that unit holds regarding the sequential data. This hidden state will be updated at each timestep to reflect the changes in the sequential data. Hidden state update is done as per equation 2.

$$h_t=f\left(W_h{h}_{t-1}+W_x{X}_t+b_h\right)$$

(2)

where $h_t$ is the vector representing hidden state at time t, $W_x$ denotes the weights associated with inputs, $W_h$ are the weights associated with hidden neurons, $X_t$ is the input vector and $b_h$is the bias vector at the hidden layer. $f$ denotes the activation function used at the hidden layer. Based on the number of inputs and outputs, RNN can be configured as one-to-one, one-to-many, many-to-one, or many-to-many. In this work, the RNN takes multiple time steps as input and produces multiple time steps as output. Hence it is used as a many-to-many network.

3.3.4. Long short-term memory

Long short-term memory (LSTM) is an advanced sort of recurrent neural network, specially designed to contend with the problem of vanishing gradients. With the help of a cell and three gates as the basic building blocks, it enhances the memorizing capability of recurrent neural networks. These three gates are termed as input, output and forget gates. LSTM network can memorize thousands of time steps, and this makes it particularly suitable for handling time series problems. The gates are used to regulate the flow in and out of cell state. The input gate regulates the flow of input to the memory cell and hence decides what latest information is to be added to the current state. The output gate determines what information from the memory cell is to be passed to the output. Conversely, forget gate helps to decide what information is to be discarded or forgot from the current state. With forget gate, LSTM network efficiently forgets the old or irrelevant information. In short, LSTM can discriminatively maintain or discard information as the data flows through the network, which makes it suitable for learning long sequences. LSTM performs its work with the following four steps.

Step 1: Output of the forget gate, $f_t$ is calculated in the first step.

$$\begin{array}{c}{f}_t=\sigma \left(w_f\left[X_t,Y_{t-1}\right]+b_f\right)\end{array}$$

(3)

where $w_f$ and $b_f$ denote the weight vector and the bias vector at forget gate, respectively. $X_t$is the input at current iteration, $Y_{t-1}$ is the output from the previous iteration, and σ is the activation function.

Step 2: The cell state output $C_t^{\text{'}}$and the output of the input gate $i_t$ are calculated.

$$\begin{array}{c}{C}_t^{\text{'}}=a_i\left(w_c\left[X_t,Y_{t-1}\right]+b_c\right)\end{array}$$

(4)

(5)

Here, $a_i$ is the input activation function, $w_c$ and $b_c$ are the weight and bias vectors of the cell state, $w_i$ and $b_i$ are the weight and bias vectors at input gate.

Step 3: The cell state value $C_t$ is updated in this step.

$$\begin{array}{c}{C}_t=i_t . C_t^{\text{'}}+f_t . C_{t-1}\end{array}$$

(6)

Step 4: Output of the output gate, $O_t$ is calculated in this step. This gate combines previous iterations output $Y_{t-1}$ and the current input $X_t$, using $b_o$as the bias and $w_o$ as the weight vector. Finally, the output $Y_t$is computed.

(7)

$$\begin{array}{c}{Y}_t=O_t . a_o\left(C_t\right)\end{array}$$

(8)

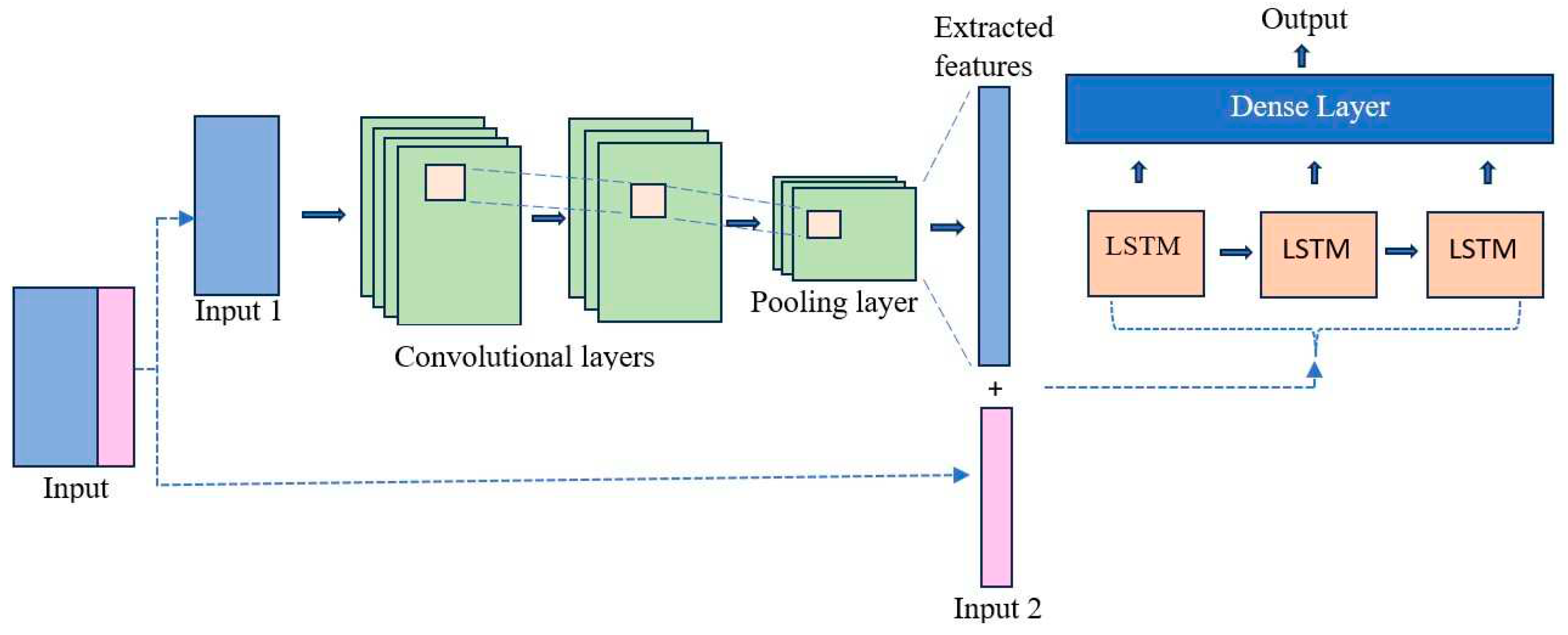
3.3.5. CNN-LSTM

Convolutional neural network and long short-term memory are connected sequentially to make a hybrid structure [27]. The structure of this hybrid model is shown in Figure 3. CNN is used as a feature extractor here. During the feature selection process done in the beginning, it was identified that the historical cooling load is the most influential parameter in prediction. Hence extensive experiments are conducted to analyze what combination of inputs to CNN and LSTM will enhance the results. Through experiments, it is concluded that the hybrid model provides maximum performance when the inputs excluding cooling load are given as input to the CNN. More informative features are extracted from these input parameters using CNN. Then the extracted features are combined with the original cooling load features before providing as input to the LSTM model. This process is shown in Figure 3.

Outputs of LSTM network is processed by a dense layer to finally obtain the desired multi-step prediction. One dimensional as well as two-dimensional convolution layers are tried in CNN. The LSTM can consider the sequential behavior of historical cooling load as the cooling load is given in raw form to the LSTM network, without passing through the CNN. The configuration of the CNN-LSTM model used for processing SIT@Dover dataset in this work is shown in Table 3. The number of features and the kernel size at each convolution layer are set in an ascending order as depicted in the table. One-dimensional convolution gave better performance compared to the two-dimensional one.

3.3.6. Sequence-to-sequence

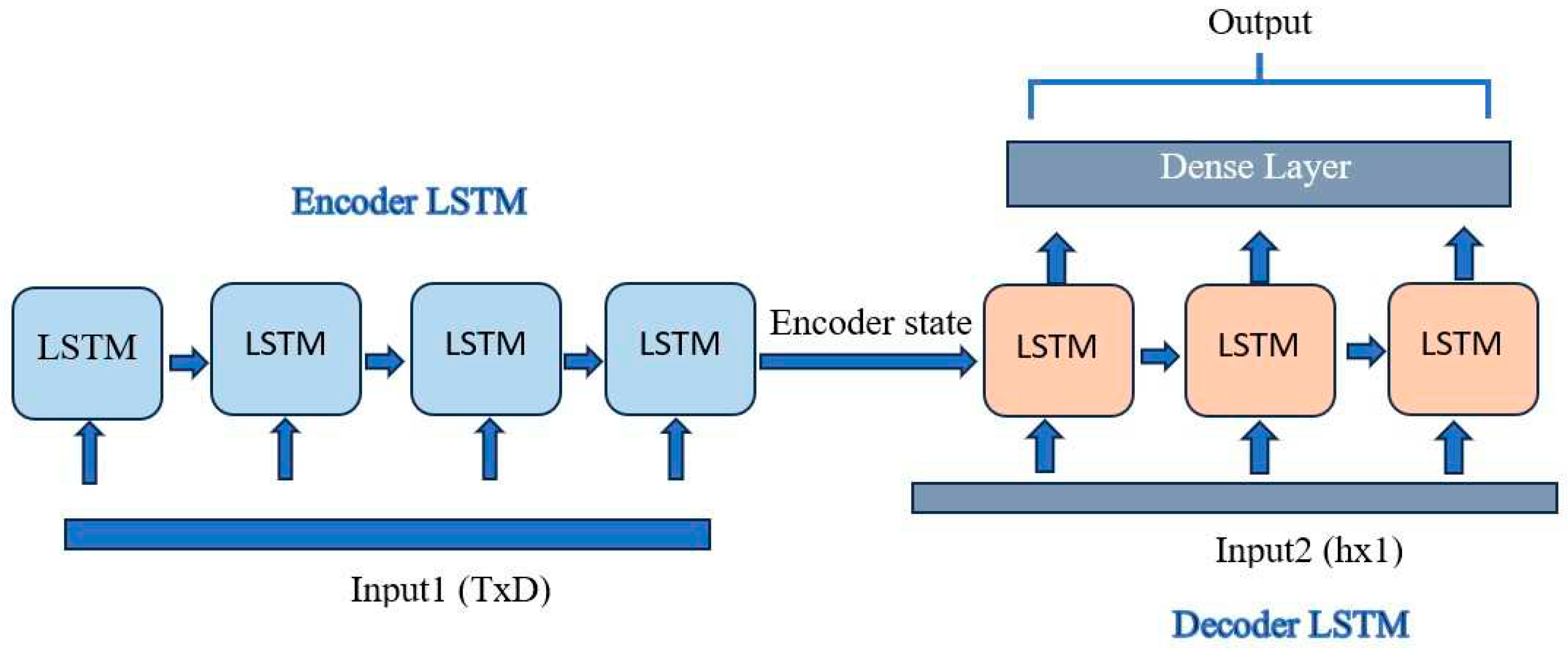
The sequence-to-sequence model, also known as encoder-decoder model is a combination of two LSTM networks, the first one being used for encoding the information contained in the input sequence and the second one being used for generating the output sequence. A dense layer will be connected at the end of LSTM network to take multi-step prediction as output. Encoder LSTM passes its hidden states and cell states to the decoder; hence this state is the encoded information. Encoder and decoder can have diverse configurations including the number of hidden units, activation functions and other parameters. In this work, both LSTM networks use 64 hidden neurons and ‘tanh’ as the activation function. Final dense layer has ‘h’ neurons and ‘linear’ activation being used. The encoder’s return state is set to true to retrieve the hidden state information from the encoder.

In addition to the state information retrieved from the encoder, decoder LSTM can take separate input from outside, mentioned as input2 in Figure 4. Generally, on decoder side, previous LSTM units’ output can be given as input to the consequent LSTM unit. Another alternative option is to provide ground truth information as input to the decoder. This method is known as teacher forcing and is usually popular in language processing models. Teacher forcing ensures fast and effective training of the model. A problem associated with this method is that it might cause errors while using a model trained this way in real scenarios for prediction. The model might confront unforeseen sequences in real prediction scenarios. In this work also, it is not found realistic to provide the ground truth as input to the decoder, and hence an alternate option is adopted here. From the historical cooling load series, the most similar day’s load sequence is given as input to the decoder. During correlation analysis it is observed that the time lags that have more resemblance to the target load sequence are the previous day’s load sequence and the previous week’s same day’s load sequence. Experiments revealed that instead of previous day’s load sequence, previous week’s, same day’s load sequence is giving better results. Hence this load sequence is given as input to the decoder model.

3.3.7. Performance metrics

The performance evaluation metrics are carefully chosen to epitomize an extensive validation and comparison of the developed models. To ensure the reliability of results, 10 trial runs are conducted for each experiment and the performance measures are averaged over these trials. Root Mean Squared Error (RMSE), Coefficient of variation of Root Mean Squared Error (CV-RMSE), Mean Absolute Percentage Error (MAPE), and Mean Absolute Error (MAE) are the performance metrics selected in this work. Computation of these metrics can be found in equations 9 to 12.

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(y_i^{\text{'}}-y_i\right)}^2}$$

(9)

$$CV-RMSE=\frac{\sqrt{\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{\left(y_i^{\text{'}}-y_i\right)}^2}}{\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{y}_i^{\text{'}}}$$

(10)

$$\begin{array}{c}MAPE=\frac{1}{N}{\displaystyle {\displaystyle \sum }_{i=1}^N}\frac{\left|y_i^{\text{'}}-y_i\right|}{y_i}*100\% \end{array}$$

(11)

(12)

where N is the number of samples in test set, $y_i^{\text{'}}$is the predicted value and $y_i$ is the original value of the i^th sample in the test set.

4. Results and discussion

Experiments are conducted on a Windows 11 machine with an Intel(R) Core (TM) i7-12650H Processor and 64 GB physical memory. PyCharm Integrated Development Environment is used for implementing prediction models, whereas Keras deep learning library on the TensorFlow platform functioned as the supporting software platform.

4.1. Data

Three datasets are used in the experiments; two of them are authentic building datasets and the third one is a simulated dataset. The buildings are educational institution buildings in Singapore. The first dataset appertains to a single office floor in the SIT@Dover building, referred to as the SIT@Dover dataset in this paper. Attributable to the fact that this dataset is limited to a single office floor, the range of cooling load values is comparatively narrower. The maximum recorded cooling load value is 43 kW in this dataset. This building has 75F building management system implemented in it, making attainment of data easier. Data spans the timeframe from 1st January 2023 to 7th July 2023, recorded at 1-hour intervals. Holidays are not considered while preparing the dataset. Since this office works only during daytime, data between 7 AM and 6 PM is considered here, making a total of 1524 samples to this dataset.

The second real dataset, referred as the 'SIT@NYP dataset,' is collected from another institutional building in Singapore which is the SIT@NYP building. This dataset has a wider range of cooling load values as it spans an entire building with seven floors. The highest cooling load recorded within this dataset is 1525 kW. Considering the working hours of the building, holidays are excluded and only the data from 8 AM to 6PM is selected for experiments. Minute wise dataset is transformed to an hourly one. The period of the dataset spans from May 1st, 2022, to September 30th, 2022, encompassing a total of 1144 individual samples.

The third dataset is simulated by the Integrated Environmental Solution Virtual Environment (IESVE) software. The simulated space corresponds to the Co-Innovation and Translation Workshop Room, situated on the 16th floor of the innovative Super Low-Energy Building, overseen by the Building Construction Authority in Singapore. The simulation model incorporates input variables encompassing outdoor and indoor design conditions, including location, space data, and weather data. Temperature, relative humidity, internal heat gain and the factors attributed to occupants, lighting, and computers are the input attributes considered. This dataset comprises one year of data collected at 1-hour intervals, but only day hours from 9 AM to 6PM are considered, and hence totals to 3650 samples.

Train and test sets are derived from the datasets by keeping the sequential order unperturbed. For the SIT@Dover dataset, data from 1st January to 15th June 2023 is considered as the training set and the rest used to create the test set. Similarly, for SIT@NYP dataset, training set corresponds to the period 1st May to 9th September 2023 and for simulated dataset, training set corresponds to 1st January to 30th November 2022.

4.2. Tuning hyper parameters of models

For all the models, ‘Adamax’ performed the function of optimizer. This conclusion was drawn after comparing it with the other optimizers like Adam, SGD and RMSprop. Learning rate of 0.001 was chosen from the set [0.1, 0.01, 0.001]. Compared to mean squared error, mean absolute error is found providing better results when used as loss function in learning, and hence the models were implemented with this loss function. Consistently among all the models, the number of hidden units used in the final dense layer was determined based on the number of hours of the next day to be predicted.

For the Deep Neural Network, experiments were conducted to compare the effect of increasing the number of hidden layers. It was found that a single hidden layer with 1024 hidden neurons is providing better results. Increasing the number of neurons or number of hidden layers further did not improve the results. This may be attributed to the fact that when the number layers or neurons increases much, the total number of hyper parameters to be learned also increases which consequently leads to overfitting.

For convolutional neural networks, the number of convolution layers and the size of the filter were tuned based on the dimension of the input data. For SIT@NYP and simulation datasets, six convolution layers were used whereas for SIT@Dover dataset, seven convolution layers were used. RNN and LSTM networks used single hidden layers with 64 neurons, a decision taken after comparing the performance rendered with a greater number of hidden layers and hidden units.

The CNN-LSTM hybrid model structure used in this paper necessitates tuning the number of layers and the filter size based on the dimension of the input data. It is done in the same way as discussed earlier for the standalone CNN model. The LSTM network in this hybrid model used 64 hidden neurons. For sequence-to-sequence model, both the encoder and decoder LSTM models had 64 hidden nodes.

4.3. Decision on time horizons to be given as input

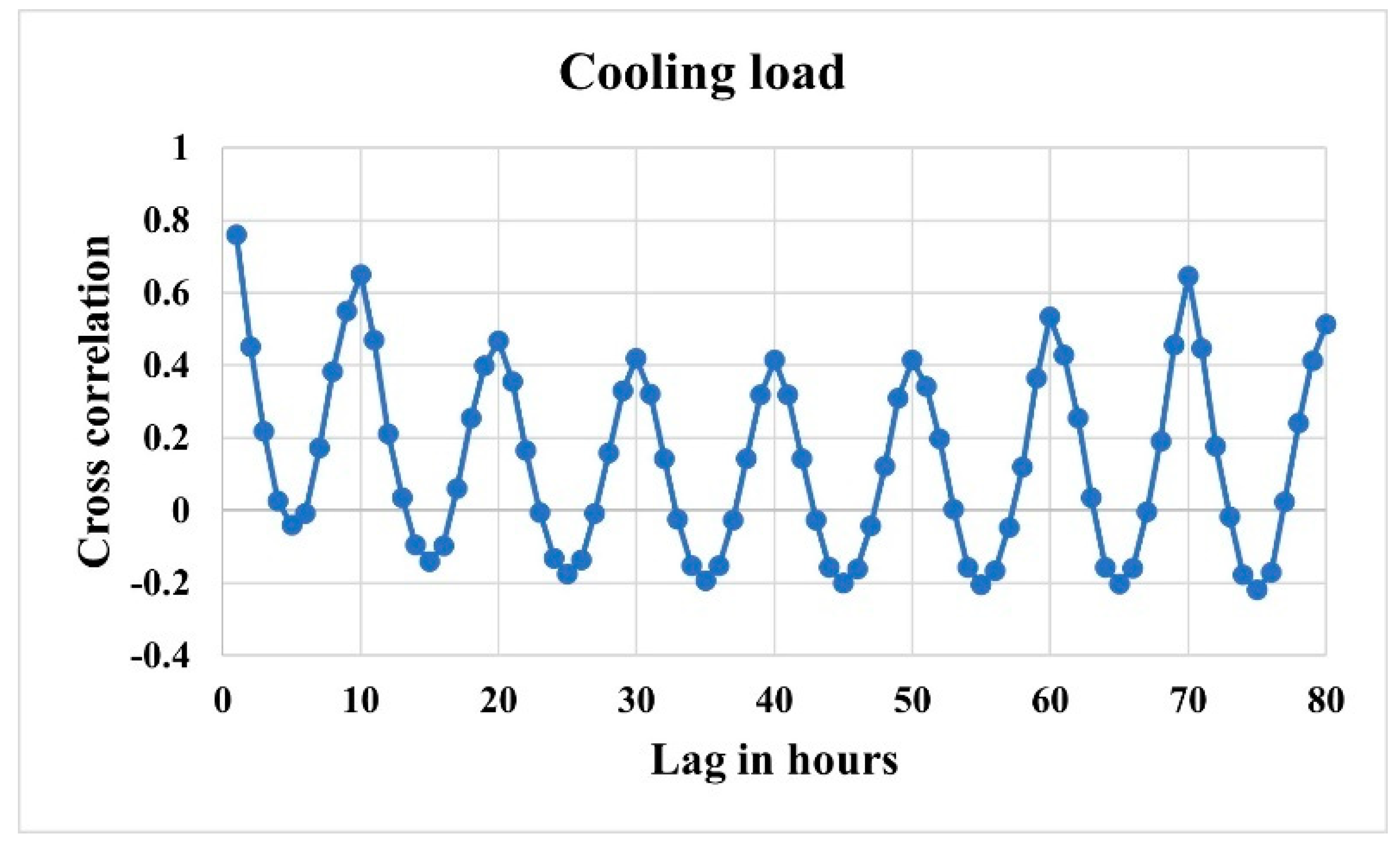
Depending on the time horizons selected as input from the historical data, the prediction accuracy of different models can vary. Identifying the most informative time horizons is found crucial. A cross correlation analysis is performed for this purpose. Cross correlation coefficient is a statistical method to analyze the correlation between the target variable and the time lags of the independent variables. It helps to decide the time lags which are more correlated to the target variable, the selection of which as input enhances the prediction accuracies. Figure 5 shows the cross-correlation analysis done for the cooling load variable of the simulated dataset.

Cross correlation of cooling load to itself is computed to identify the lag points which are more correlated each other. Notably, the simulated dataset has ten hours on each day, and seven days considered in a week. As we can see from Figure 5, 10th and 70th time lags are more correlated to the cooling load at any hour. The time lag of 10 hours refers to the same hour on the previous day whereas the time lag of 70 hours denotes the same hour, on same day of the previous week. The next highest correlation can be seen at time lags 60 and 80 followed by the time lag 20. Based on this analysis, the previous one or two days and the similar two days in the previous week look important in prediction. Two sets of experiments were done to choose the most relevant inputs from these time horizons.

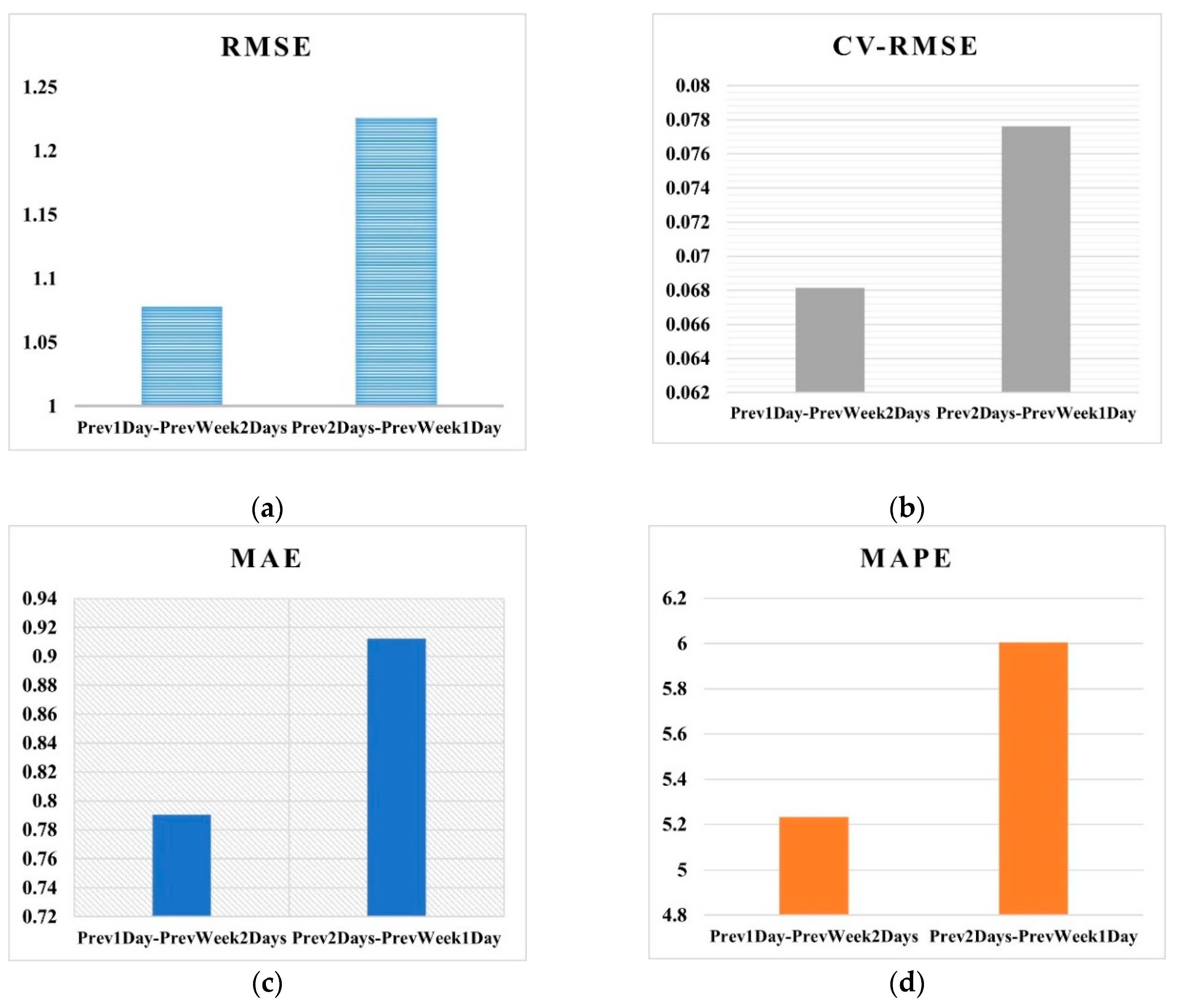
In the first set of experiments, data of the previous day, same day of previous week and the day before that are taken. This set is denoted as ‘Prev1Day-PrevWeek2Days’ in Figure 6. The second set of experiments considers the previous two days and same day of the previous week, which is denoted as ‘Prev2Days-PrevWeek1Day’ in the figure. Performance comparison between these two sets of experiments is depicted in Figure 6. As can be observed from this Figure, all the performance measures agree on the fact that the set ‘Prev1Day-PrevWeek2Days’ outperforms the other version. Hence the paper follows this time horizon selection as input to the model.

4.4. Results

The comparative performance of all the six models is assessed through experiments. The datasets are transformed to samples having shapes suitable for different models. The input samples are formed by joining historical data samples as discussed in the above section. Data of previous one day and previous week’s two days makes a total of 3xh rows in each sample. Thus, the number of historical hours given as input to the model is T=3xh. This value comes out to be 36 for SIT@Dover dataset, 33 for SIT@NYP dataset and 30 for the simulated dataset. DNN requires a flattened data structure as input to the model. Hence, T hours, each with 7 features makes a total of 252 features for SIT@Dover dataset, 231 features for SIT@NYP dataset, and 210 features for the simulated dataset. In cases involving deep learning models, the input samples must have a three-dimensional structure of shape NxTxD, where N is the number of samples, T is the number of hours and D equals the number of input features. A comparison among the performance offered by various models on different datasets under consideration can be seen in Table 4.

As the performance metrics quoted in Table 4 depicts, sequence-to-sequence model offered the best performance for all the three datasets. When a second LSTM network is added to make a sequence-to-sequence architecture, and the most matching load sequence from the history given as external input to the decoder LSTM, the performance got boosted. An extensive examination was conducted to check the performance variations when providing various combinations of inputs at encoder and decoder sides. The above-mentioned input selection is found the most reliable. DNN, CNN and RNN offered the least relative performance on all the datasets. While comparing the performance of the base deep learning architectures – DNN, RNN, CNN and LSTM – LSTM offered consistently better performance on all the datasets under consideration. This superior performance of LSTM is attributed to its competence in handling the vanishing gradients problem and memorizing long sequences.

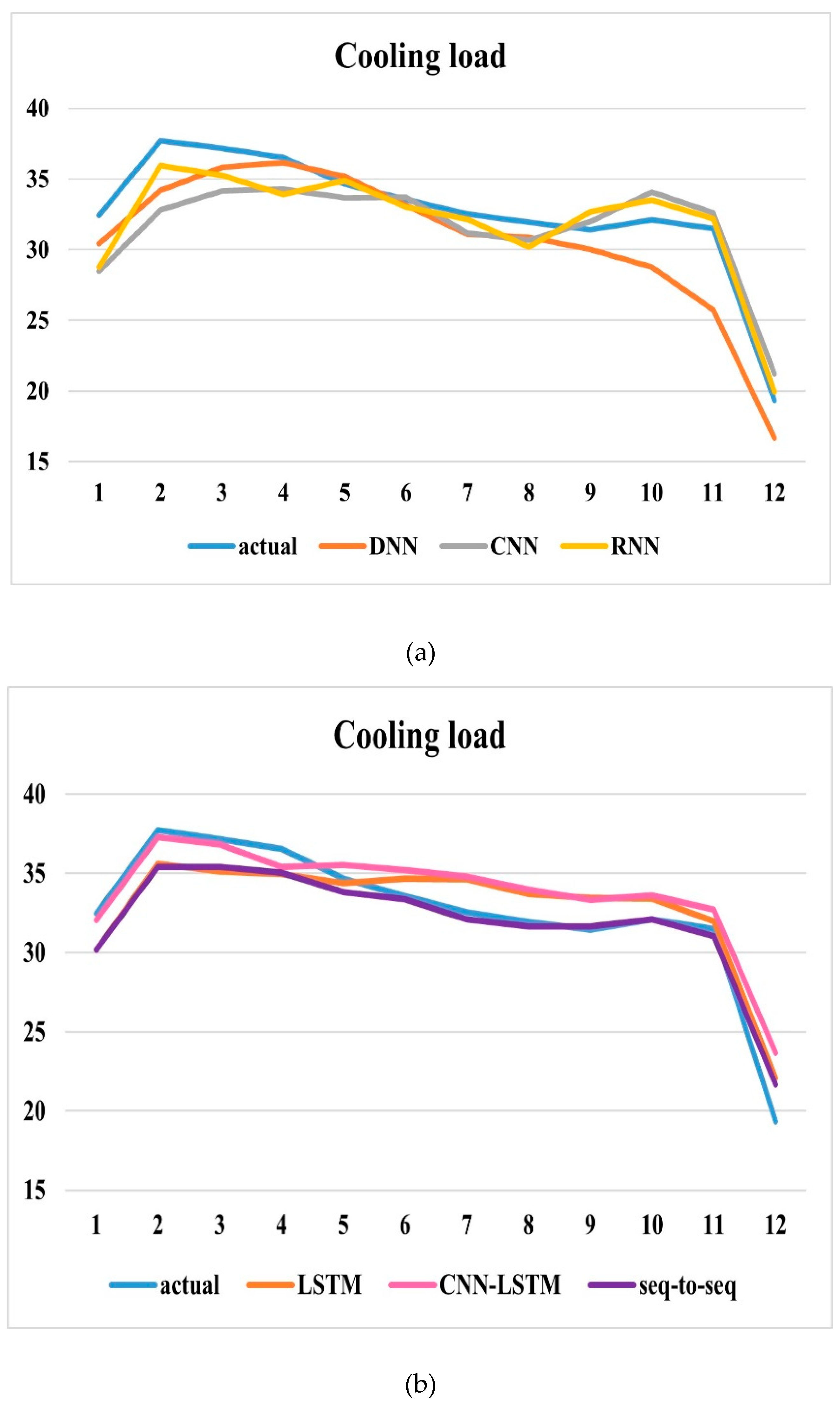
An example of 12-hour cooling load predictions done by various models for SIT@Dover dataset has been shown in Figure 7. The example day corresponds to Wednesday, 5th July 2023. A normal working day is chosen as the example day to show the predictions done by various deep learning models. Figure 7a depicts the predictions of DNN, CNN and RNN, while Figure 7b shows predictions of LSTM, CNN-LSTM and Sequence-to-sequence models. Overall, the second set of models, LSTM and the two hybrid models derived from LSTM showed better performance compared to DNN, CNN and RNN. And, while comparing among the LSTM derived models, the Sequence-to-sequence model prediction showed a better match to the actual load.

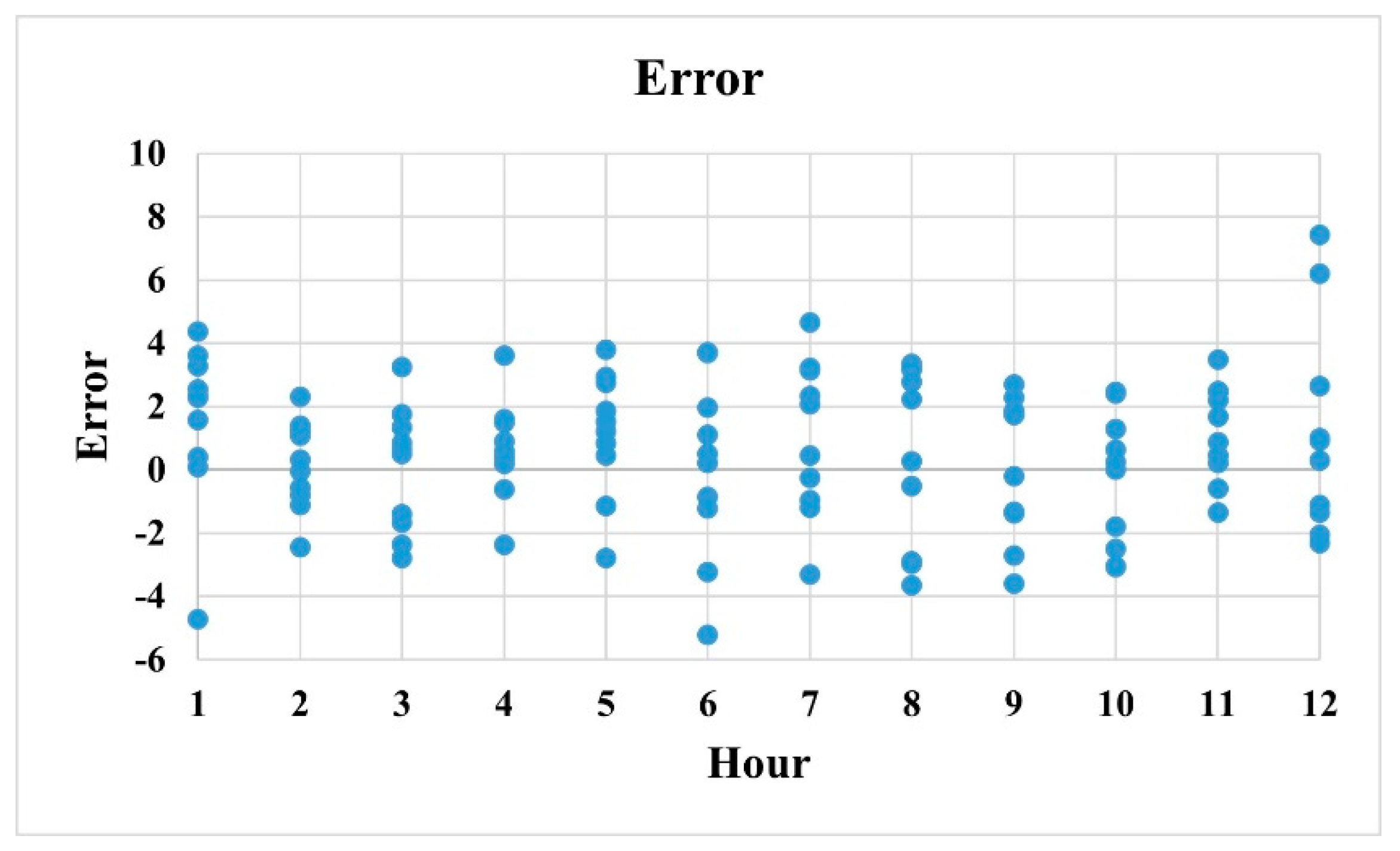
Figure 8 shows the error computed between the actual load and the predicted cooling load for sequence-to-sequence model. As can be observed in this Figure, the first, last and lunch hours have the highest errors. While analyzing the general trend in error distribution, it is observed that the highest error values occur during the hours where the load values are lower. And, while comparing the first half of the day with the second half, the error is more on afternoon hours, and the same trend follows generally on all days. This error is mainly attributed to the fact that explicit occupancy information is missing in the dataset, and the general trend of people leaving the office in the afternoon hours can be captured only if the actual occupancy information is available. This emphasizes the fact that occupancy data has an equivalent role on prediction accuracy as external weather parameters and the absence of this information can be crucial in performance of the prediction model. Even though calendar features can give hint on occupancy patterns, this information has limitations in real predictions.

4.5. Validating the importance of various categories of parameters

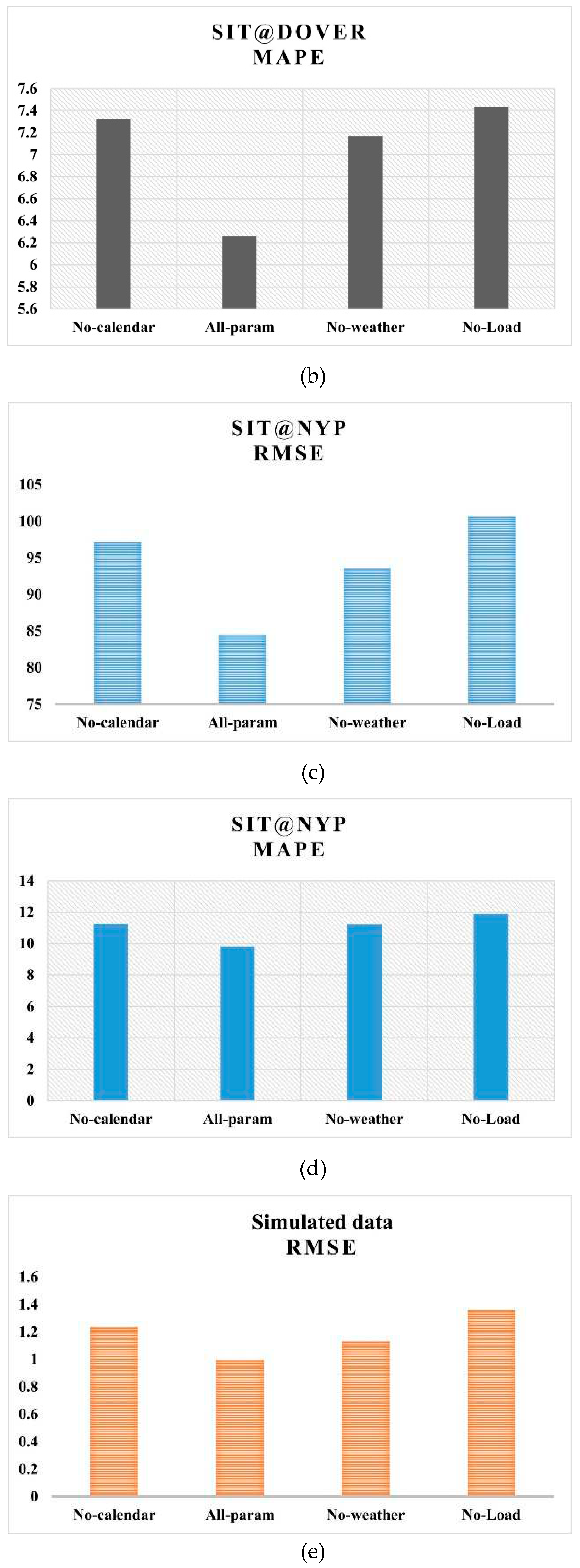
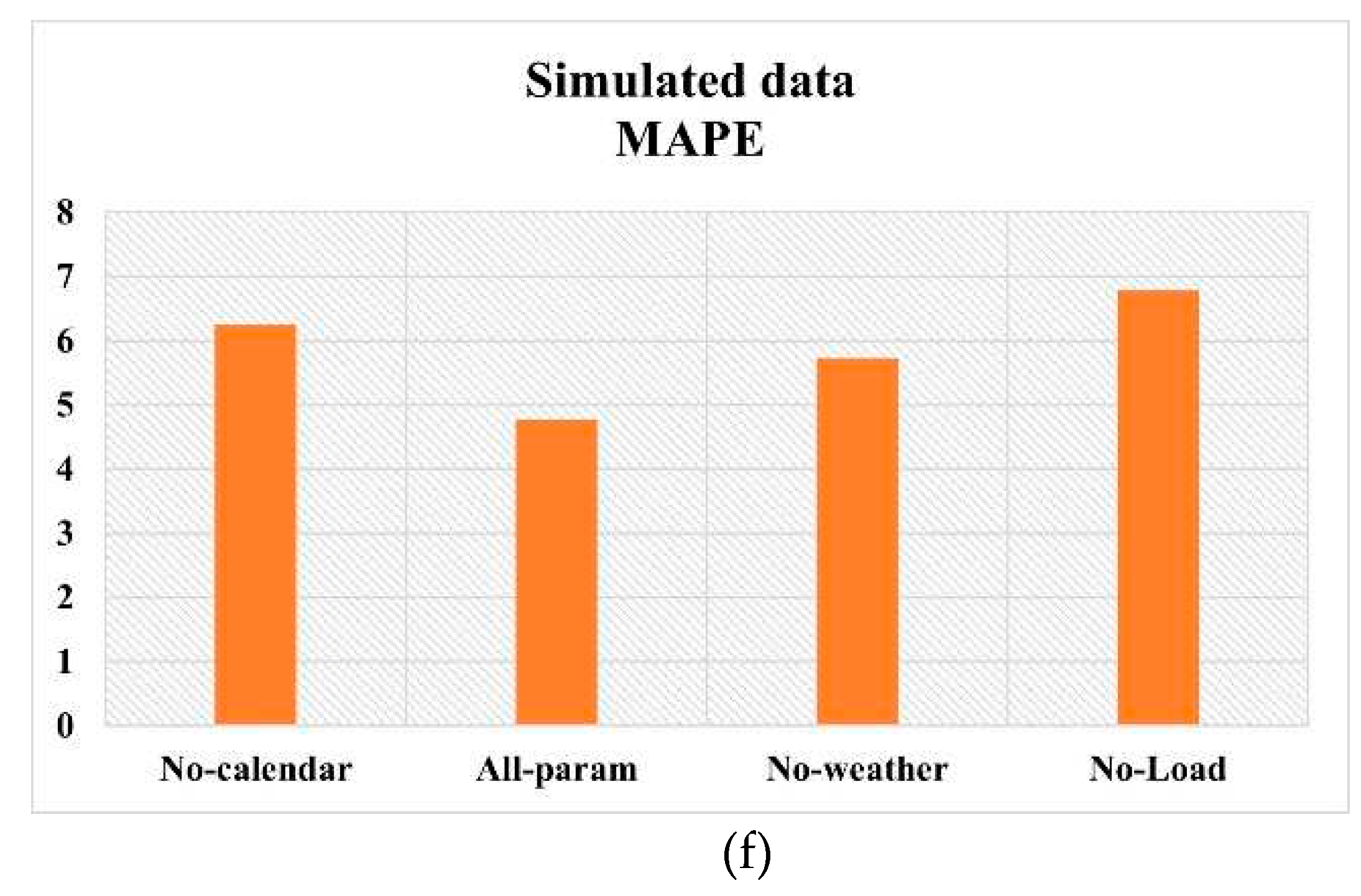
Experiments are conducted to assess the influence of various groups of parameters on prediction performance. Only those categories included in the final dataset are considered in this experiment. ‘Outdoor weather parameters’ is one such category which contains outdoor temperature, solar radiation, wind speed and relative humidity. ‘Calendar features’ included day-of-the-week and hour-of-the-day. Historical cooling load is the third category of parameters. The prediction performance reported in Table 4 corresponds to the input combining all these parameter categories. In the present set of experiments, each category is excluded one by one, and the performance is validated. 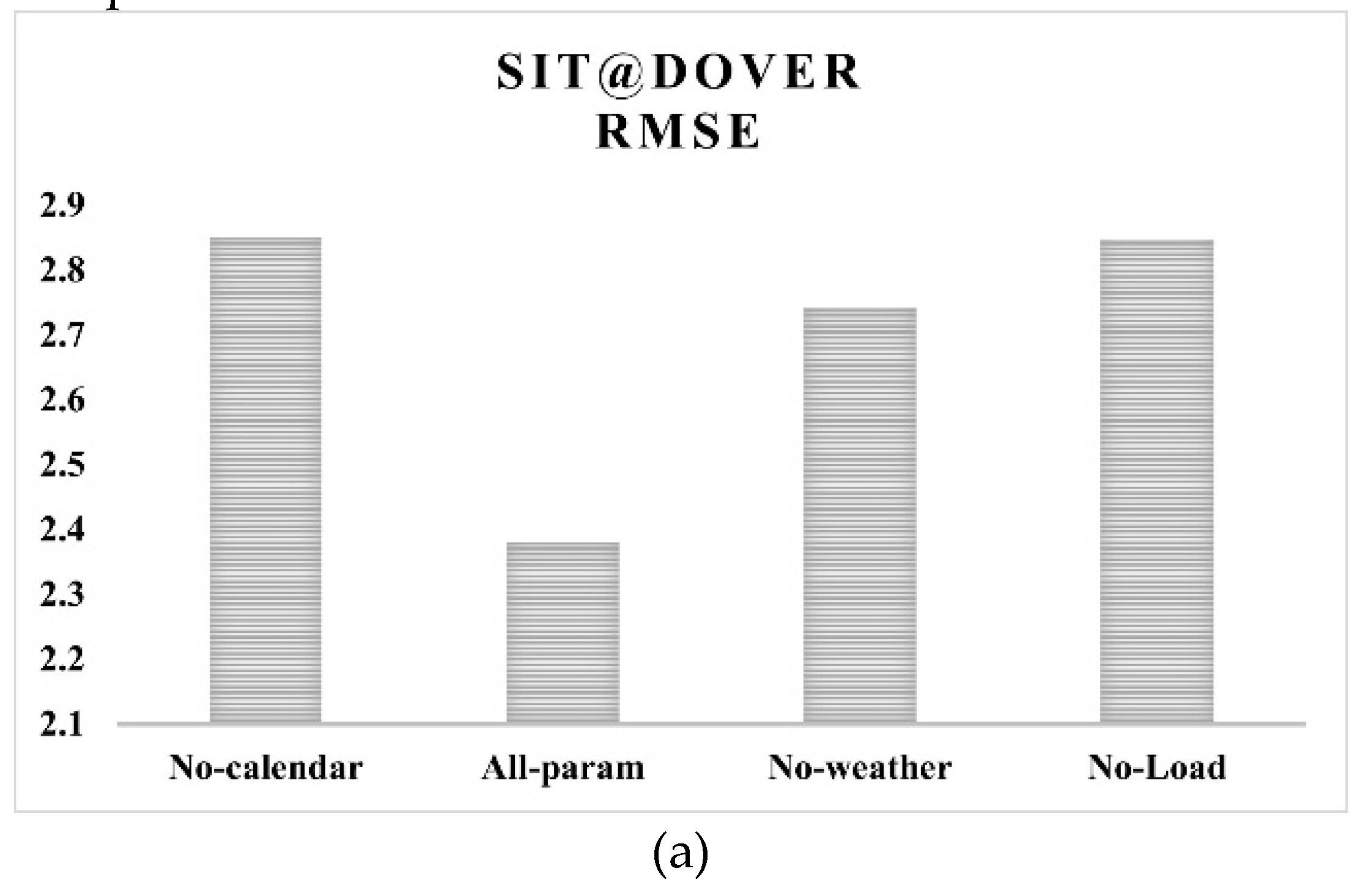Figure 9 shows the RMSE and MAPE values computed by Sequence-to-sequence model for the three datasets excluding each category of parameters. ‘All-param’ denotes the normal case in which all three categories of parameters are included. The names ‘No-calendar,’ ‘No-weather’ and ‘No-Load’ correspond to the cases when calendar features, outdoor weather features and historical cooling load are excluded from the input list.

As can be observed from the plots in Figure 9, the best performance is obtained from sequence-to-sequence model when all three categories of input parameters are combined in the input parameter list. Historical cooling load among the input features has the most influential effect on prediction performance and hence the removal of which degrades the performance more. Calendar features have the next highest influence followed by outdoor weather features.

5. Conclusion

Compared to short term cooling load predictions like hour-ahead load prediction, deep learning techniques are less attempted in day-ahead cooling load predictions. Day-ahead cooling load prediction falls into the category of multi-step prediction which is more challenging compared to short-term single step prediction. This paper endeavors the application of advanced deep learning techniques for the next day’s cooling load prediction. Six different deep learning architectures including four single standalone models and two hybrid architectures are attempted for long-term cooling load prediction. The selected algorithms represent distinct categories of deep learning architectures, like deep neural network, recurrent neural network, convolutional neural network, and long short-term memory. Hybrid architectures are formed by combining CNN with LSTM and LSTM with LSTM, the latter being called sequence-to-sequence model.

Experiments and results concluded that relative to the other single standalone models, long-short term memory provided better results. Input, output and forget gates present in LSTM architecture help to decide what information to forget and how much information to be carried forwarded to the next steps. LSTM can remember long sequences due to the presence of these gates, which is especially useful in day-ahead hourly load predictions. LSTM combined with another LSTM as an encoder-decoder architecture is found to enhance the prediction accuracy further. The results supported the fact that sequence-to-sequence model is the best performing model among all the deep learning models tried in this paper. Future work includes extension of the present sequence-to-sequence model with an attention mechanism.